2 Reglerentwurf und Simulation
|
|
|
- Kai Färber
- vor 6 Jahren
- Abrufe
Transkript
1 2 Reglerentwurf und Simulation Ziel dieser Übung ist der Entwurf einer geeigneten Regelung für dynamische Systeme sowie der Verifikation dieser Regelung mittels Simulation. Dies wird an einer Operationsverstärkerschaltung und an einer Gleichstrommaschine mit Propeller durchgeführt. Der Reglerentwurf soll mittels Frequenzkennlinienverfahren (FKL) sowohl im s-bereich als auch im q-bereich erfolgen. Die für die Zeitdiskretisierung und den Reglerentwurf nach dem Frequenzkennlinienverfahren benötigten Grundlagen wurden in der VU Automatisierung vorgestellt. Studieren Sie daher zur Vorbereitung dieser Übung das folgende Skriptum: Skriptum zur VU Automatisierung (WS 2015/16) [2.1] Kapitel 1 bis Kapitel 6 Bei Fragen oder Anregungen zu dieser Übung wenden Sie sich bitte an Andreas Deutschmann <deutschmann@acin.tuwien.ac.at> oder Patrik Zips <zips@acin.tuwien.ac.at>. Für organisatorische Fragen wenden Sie sich bitte an Georg Stadler <stadler@acin.tuwien.ac.at>. 2.1 Elektrisches System In der folgenden Aufgabe soll das elektrische System aus der ersten Übung (Abbildung 2.1) untersucht werden. Das betrachtete Netzwerk besteht aus einem Operationsverstärker, den Kapazitäten C 1 und C 2 sowie den Widerständen R 1, R 2 und R 3. Weiterhin bezeichnet U s eine auftretende Störung. Die Führungsübertragungsfunktion des Netzwerks ist durch G(s) = V 1 + 2ξ(sT ) + (st ) 2 mit V = 1.377, ξ = und T = ms gegeben. Aufgabe 2.1 (Reglerentwurf). In dieser Aufgabe soll ein zeitkontinuierlicher Regler für das elektrische System nach dem Frequenzkennlinienverfahren entworfen werden. Der geschlossene Kreis soll dabei folgende Spezifikationen erfüllen: bleibende Regelabweichung e r(t)=σ(t) = 0 Überschwingen ü 5 % Anstiegszeit t r = 3 ms
2 2.1 Elektrisches System Seite 20 C 1 (U C1 ) U s R2 U C1 U e R 1 R 2 U C2 C 2 i ein,p u d OP V V + (K 1)R 3 U a i ein,n R 3 Abbildung 2.1: Elektrisches System. 1. Ist das Frequenzkennlinienverfahren ein exaktes Entwurfsverfahren, wenn wie im vorliegenden Fall die Strecke ein Verzögerungsglied 2-ter Ordnung ist? 2. Entwerfen Sie in Matlab einen Regler nach dem Frequenzkennlinienverfahren, der obige Anforderungen erfüllt. 3. Im Weiteren soll zusätzlich zu den oben angeführten Anforderungen die bleibende Regelabweichung e r(t)=t = gelten. Entwerfen Sie hierfür einen PID-Regler, wobei die Zeitkonstante des Integralterms T I = 1 ms betragen soll. 4. Stellen Sie den geschlossenen Kreis mit dem linearisierten System in Form eines Blockschaltbildes dar. Berechnen Sie die Führungsübertragungsfunktion T r,y (s) und die Störübertragungsfunktion T d,y (s) des geschlossenen Kreises und die zugehörigen Sprungantworten in Matlab. 5. Implementieren Sie beide Regler im Simulink-Modell E_Netzwerk.slx, welches in der Datei uebung2.zip von der Homepage der Lehrveranstaltung zur Verfügung gestellt wird, und testen Sie diese am linearisierten sowie am vollständigen nichtlinearen Modell. Ist der geschlossene Regelkreis stabil? Begründen Sie Ihre Antwort. Simulieren Sie das Verhalten des geschlossenen Kreises für eine sprungförmige Eingangsgröße mit und ohne Störung. Werden die Anforderungen erfüllt? 6. Bisher wurde davon ausgegangen, dass dem Regler ein idealer Messwert der Ausgangsgröße y zur Verfügung steht. Da dies in der Realität nicht der Fall ist, ist es
3 2.2 Gleichstrommaschine mit Propeller Seite 21 sinnvoll in einer Simulation den Einfluss von Messrauschen zu untersuchen. Dazu kann in der Simulation mit einem Schalter zusätzliches Messrauschen auf den Systemausgang aufgeschalten werden. Testen Sie Ihren Regler in der Simulation mit und ohne Messrauschen. Wie verhält sich das System mit Messrauschen im Vergleich zum idealen System? In dieser Simulation steht ein weiterer Schalter zur Verfügung, der die zeitliche Änderungsrate des Sollwertes begrenzt. Welche Auswirkung hat die Steigungsbeschränkung auf die Stellgröße und den Ausgang? Welcher Vorteil kann sich aus der Begrenzung der Änderungsrate ergeben? 2.2 Gleichstrommaschine mit Propeller Propeller M rgsm L GSM R GSM igsm M P J P c GSMP J GSM M GSM M GSM u indgsm u GSM ϕ P, ω P d GSMP ϕ GSM, ω GSM ϕ GSM, ω GSM (a) (b) Abbildung 2.2: Gleichstrommaschine mit Propeller, (a) mechanisches Teilsystem, (b) elektrisches Teilsystem. Abbildung 2.2 zeigt schematisch eine permanenterregte Gleichstrommaschine (Index GSM), die über eine linear elastische und dämpfende Welle (konstante Steifigkeit c GSMP, viskose Dämpfung d GSMP ) einen Propeller (Index ] P) antreibt. Die Freiheitsgrade q des Systems sind die Drehwinkel q T = [ϕ GSM ϕ P. Die zugehörigen Winkelgeschwindigkeiten werden ] mit q T = [ω GSM ω P benannt. Im Folgenden wird stets von ω GSM > 0 und ω P > 0 ausgegangen, so dass Haftreibungseffekte beim Nulldurchgang der Geschwindigkeit hier unberücksichtigt bleiben können. Auf den Propeller (Massenträgheitsmoment J P ) wirkt ein Lastmoment der Form M P = d cp + d vp ω P + d qp ω 2 P + M ext, (2.1) wobei d cp die Coulombsche Reibkonstante, d vp die viskose Dämpfungskonstante, d qp der Koeffizient des zum Geschwindigkeitsquadrat proportionalen Dämpfungsanteils und M ext ein zusätzliches externes Moment ist. Die Lagerung des Ankers verursacht ein Reibmoment der Form M rgsm = d cgsm + d vgsm ω GSM (2.2) mit der Coulombschen Reibkonstante d cgsm und der viskosen Dämpfungskonstante d vgsm. Das Kopplungsmoment M kopp zwischen Motor und Propeller, also das über die Feder
4 2.2 Gleichstrommaschine mit Propeller Seite 22 c GSMP und den Dämpfer d GSMP übertragene Moment, berechnet sich zu M kopp = (ω GSM ω P )d GSMP + (ϕ GSM ϕ P )c GSMP. Das von der (idealen) Gleichstrommaschine erzeugte elektrische Moment ist M GSM = k GSM i GSM, wobei k GSM die Ankerkreiskonstante bezeichnet, die aus der Maschinenkonstante c A und dem verketteten Fluss der Erregerwicklung Ψ EGSM in der Form k GSM = c A Ψ EGSM berechnet wird. Aufgrund der Impulserhaltung ergeben sich die Bewegungsgleichungen zu J GSM ω GSM = M GSM M rgsm M kopp J P ω P = M kopp M P. (2.3a) (2.3b) Dabei bezeichnet J GSM das Massenträgheitsmoment der Gleichstrommaschine und J P das Massenträgheitsmoment des Propellers. Die Differentialgleichung für das elektrische Subsystem wird mithilfe der Maschenregel bestimmt. Für die induzierte Spannung gilt u indgsm = k GSM ω GSM. Die Ankerkreisinduktivität wird mit L GSM, der Ankerkreiswiderstand mit R GSM und die Eingangsspannung mit u GSM bezeichnet. Damit erhält man d dt i GSM = 1 (u GSM R GSM i GSM k GSM ω GSM ). (2.4) L GSM Somit kann das vollständige, nichtlineare mathematische Modell der Gleichstrommaschine in der Form ẋ m = f m (x m, u m, d m ) (2.5) ] mit den Zustandsgrößen xm T = [i GSM ϕ GSM ω GSM ϕ P ω P, dem Eingang u m = u GSM und der Störung d m = M ext dargestellt werden. Als Ausgang des Systems wird y = ω P verwendet. Aufgabe 2.2 (Vollständiges Modell). 1. Im System (2.5) treten die Größen ϕ GSM und ϕ P stets in Form der Differenz (ϕ GSM ϕ P ) = ϕ GSMP auf. Mithilfe der nichtregulären Zustandstransformation x M = i GSM ϕ GSMP ω GSM ω P = x (2.6) m kann daher eine Differentialgleichung eingespart werden. Führen Sie diese Transformation durch, d. h. bestimmen Sie wobei u M = u m und d M = d m gelten soll. ẋ M = f M (x M, u M, d M ), (2.7)
5 2.2 Gleichstrommaschine mit Propeller Seite Bestimmen Sie für stationäre Eingangswerte die Ruhelage des Systems (2.7), linearisieren Sie es bezüglich derselben und stellen Sie es in der Form ẋ = A x + b u u + b d d y = c T x (2.8a) (2.8b) dar. Berechnen Sie weiterhin numerisch die Eigenwerte der Dynamikmatrix des linearisierten Systems in Matlab, wobei die Parameterwerte aus Tabelle 2.1 und für die stationären Eingangsgrößen u GSM,R = 5.6 V und M ext,r = 0 N m zu verwenden sind. Parameter Wert L GSM 1.4 mh R GSM 0.46 Ω k GSM 0.1 N m A 1 J GSM kg m 2 d cgsm N m d vgsm N m s rad 1 J P kg m 2 d cp N m d vp N m s rad 1 d qp N m s 2 rad 2 c GSMP N m rad 1 d GSMP N m s rad 1 Tabelle 2.1: Parameter des Systems Gleichstrommaschine mit Propeller. Bestimmt man die Eigenwerte λ i mit i = 1,..., 4 der Dynamikmatrix A des um die Ruhelage linearisierten Systems (2.8), so ergeben sich diese in aufsteigend sortierter Reihenfolge zu λ 1 = s 1, λ 2,3 = s 1 ± I s 1 und λ 4 = s 1. Offensichtlich ist das System (lokal) asymptotisch stabil. Auffällig ist jedoch, dass λ 1 λ i i {2, 3, 4}, (2.9) d. h. der Eigenwert λ 1 liegt in der komplexen Ebene sehr viel weiter links als die übrigen Eigenwerte, was eine relativ schnelle Dynamik im zugehörigen Unterraum der Lösung nach sich zieht. Es lässt sich nun mithilfe der singulären Störungstheorie [2.2] zeigen, dass dieser Eigenwert zumindest näherungsweise der Stromdynamik zugewiesen werden darf. Somit kann in weiterer Folge die Dynamik des elektrischen Teilsystems als quasistationär betrachtet
6 2.2 Gleichstrommaschine mit Propeller Seite 24 werden, womit sich die zugehörige Differentialgleichung zu einer algebraischen Gleichung der Form reduziert. Aufgabe 2.3 (Reduziertes System). i GSM = 1 R GSM u GSM k GSM R GSM ω GSM (2.10) 1. Verwenden Sie die Näherung (2.10), um im System (2.7) die zugehörige Differentialgleichung der Stromdynamik zu eliminieren. Damit erhalten Sie ein reduziertes System ẋ red = f red (x red, u, d) y = h red (x red ) (2.11a) (2.11b) [ mit dem neuen Zustandsvektor xred T = ϕ GSMP ω GSM ω P ], wobei Eingang u, Störung d und Ausgang y unverändert bleiben. 2. Bestimmen Sie für stationäre Eingangswerte die Ruhelage des reduzierten Systems (2.11) und linearisieren Sie es bezüglich derselben. 3. Ist die Ruhelage des reduzierten Systems (2.11) gleich jener des vollständigen Systems (2.7)? Begründen Sie Ihre Antwort. Aufgabe 2.4 (Implementierung in Matlab/Simulink). Erstellen Sie für das System Gleichstrommaschine mit Propeller ein Simulationsmodell. Es soll das vollständige nichtlineare Modell (2.7) (inklusive Stromdynamik) in Form einer Level 2 M-Code s-function enthalten. ] Wählen Sie hierzu als Eingang [ der s-function den Vektor] u T = [u GSM M ext und als Ausgangsvektoren y1 T = i GSM ϕ GSMP ω GSM ω P bzw. [ y2 T = M GSM M Kopp ]. Verwenden Sie als Anfangszustand die Ruhelage für u GSM = 5.6 V und M ext = 0 N m. Implementieren Sie außerdem das vollständige linearisierte Modell und das reduzierte linearisierte Modell in Form von State-Space-Blöcken. Simulieren Sie alle Systeme für eine Eingangsgröße der Form M ext = 0.25σ(t 11) und u GSM = 5.6 σ(t 2) + σ(t 5) 2σ(t 8) + 2σ(t 13) (M ext in N m und u GSM in V). Vergleichen Sie die Ausgangsgrößen der Systeme und dokumentieren Sie Ihre Ergebnisse.
7 2.2 Gleichstrommaschine mit Propeller Seite 25 Hinweis: Beachten Sie bei der Implementierung nachfolgende Punkte: Alle Systemparameter und Anfangszustände sollen als Parameter von außen an die s-function übergeben werden. Definieren Sie diese Größen in einem M-file, das Sie jeweils vor dem Start der Simulation ausführen. Übernehmen Sie dabei die analytischen Ausdrücke der Ruhelagen und des linearisierten Modells aus Aufgabe 2.2, Teilaufgabe 2 in besagtes M-file und berechnen Sie erst dort die numerischen Werte. Damit ist es später einfach möglich beliebige Ruhelagen zu untersuchen. Weiterhin steht Ihnen zum Test und Abgleich ihres Modells im zip-archiv uebung2.zip auf der Homepage der Lehrveranstaltung die Datei GSM_Student_- S_m.p zum Download zur Verfügung. Es handelt sich um eine chiffrierte s-function der Gleichstrommaschine. Die Einbindung erfolgt analog zur Level 2 M-file s- function und ist im Simulationsmodell Simulation_GSM_out.mdl gezeigt. Das Modell enthält bereits die oben genannten Verläufe der Eingangsgrößen. Lediglich die berechnete Ruhelage x 0 aus der Aufgabe 2.2 Punkt 2 ist in der Maske der s-function des vollständigen Modells (2.7) zu ergänzen. Um Namenskonflikte zu vermeiden, darf die von Ihnen erstellte s-function nicht den Namen GSM_- Student_S_m.m tragen. Aufgabe 2.5 (Reglerentwurf). Entwerfen Sie mithilfe des Frequenzkennlinienverfahrens im q-bereich einen zeitdiskreten Kompensationsregler für das reduzierte linearisierte Modell der Gleichstrommaschine mit Propeller mit der Winkelgeschwindigkeit ω P als Ausgang. Als Arbeitspunkt für den Betrieb des Reglers wählen Sie die von Ihnen berechnete Ruhelage aus Aufgabe 2.3 Punkt 2 für u GSM,R = 5.6 V und M ext,r = 0 N m. Der geschlossene Kreis soll folgende Spezifikationen für einen Sollsprung r = 20 rad s 1 erfüllen: bleibende Regelabweichung e (rk )=(1 k ) = 0 Anstiegszeit t r = 1 s Überschwingen ü 0 % Stellgrößenbeschränkung 0 V u GSM 12 V Beurteilen Sie die Stabilität des geschlossenen Regelkreises. Begründen Sie Ihre Antwort. Als Reglerstruktur wird R # (q) = V I(1 + qt I ) q 1 + 2ξ(qT ) + (qt ) 2 2j=1 (q q r,j ) (2.12) gewählt, wobei 1 + 2ξ(qT ) + (qt ) 2 das konjugiert komplexe Polpaar der Streckenübertragungsfunktion als Nullstellen besitzt und q r,j die gewünschten Realisierungspole
8 2.2 Gleichstrommaschine mit Propeller Seite 26 bezeichnen. Überlegen Sie, warum die obige Reglerstruktur gewählt wird. Sie können dazu zusätzlich einen PI-Regler ohne Kompensationsterm entwerfen und das Verhalten der beiden Regelkreise miteinander vergleichen! Um den Regler später am Laborversuch testen zu können, muss der zeitdiskrete Regler R(z) in Proportional-, Integral- sowie Kompensationsteil aufgespalten werden, R(z) = Sie können dazu den Matlab-Befehl residue verwenden. ( P + I ) R komp (z). (2.13) z 1 Hinweis: Verwenden Sie als Abtastzeit T a = 50 ms. Weiterhin sei erwähnt, dass in Matlab folgende Prozeduren für die Transformationen zwischen s-, z- und q-bereich zur Verfügung stehen: G(s) Ta G(z) Matlab-Befehl: Gz=c2d(Gs,Ta, zoh ) G(z) G # (q) Matlab-Befehl: Gq=d2c(Gz, tustin ) G # (q) Ta G(z) Matlab-Befehl: Gz=c2d(Gq,Ta, tustin ) Aufgabe 2.6 (Verifikation). Testen Sie durch Simulation in Simulink, ob der so entworfene Regelkreis die Spezifikationen auch tatsächlich erfüllt. Vergleichen Sie wieder die Ergebnisse für die drei betrachteten Systeme. Aufgabe 2.7 (Einfluss des Messrauschens). Testen Sie Ihren Regler in der Simulation mit Messrauschen a. Wie verhält sich das System mit Messrauschen im Vergleich zum idealen System? Welchen Einfluss hat die Wahl der Anstiegszeit t r auf Rauschanteile im Ausgang und der Stellgröße? Analysieren Sie dies formal und dokumentieren Sie aussagekräftige Ergebnisse für verschiedene Parameter. a Üblicherweise wird Messrauschen als bandbeschränktes, weißes Rauschen modelliert.
9 2.3 Literatur Seite Literatur [2.1] A. Kugi, Skriptum zur VU Automatisierung (WS 2015/2016), < Institut für Automatisierungs- und Regelungstechnik, TU Wien, [2.2] P. Kokotovic, H. K. Khalil und J. O Reilly, Singular Pertubation Methods in Control: Analysis and Design. USA, Philadelphia: Society for Industrial Mathematics, 1999.
Regelung einer Luft-Temperatur-Regelstrecke
 Technische Universität Berlin Fakultät IV Elektrotechnik und Informatik Fachgebiet Regelungssysteme Leitung: Prof. Dr.-Ing. Jörg Raisch Praktikum Grundlagen der Regelungstechnik Regelung einer Luft-Temperatur-Regelstrecke
Technische Universität Berlin Fakultät IV Elektrotechnik und Informatik Fachgebiet Regelungssysteme Leitung: Prof. Dr.-Ing. Jörg Raisch Praktikum Grundlagen der Regelungstechnik Regelung einer Luft-Temperatur-Regelstrecke
PRAKTIKUM REGELUNGSTECHNIK 2
 FACHHOCHSCHULE LANDSHUT Fachbereich Elektrotechnik Prof. Dr. G. Dorn PRAKTIKUM REGELUNGSTECHNIK 2 1 Versuch 4: Lageregelung eines Satelitten 1.1 Einleitung Betrachtet werde ein Satellit, dessen Lage im
FACHHOCHSCHULE LANDSHUT Fachbereich Elektrotechnik Prof. Dr. G. Dorn PRAKTIKUM REGELUNGSTECHNIK 2 1 Versuch 4: Lageregelung eines Satelitten 1.1 Einleitung Betrachtet werde ein Satellit, dessen Lage im
Reglerentwurf mit dem Frequenzkennlinienverfahren
 Kapitel 5 Reglerentwurf mit dem Frequenzkennlinienverfahren 5. Synthese von Regelkreisen Für viele Anwendungen genügt es, Standard Regler einzusetzen und deren Parameter nach Einstellregeln zu bestimmen.
Kapitel 5 Reglerentwurf mit dem Frequenzkennlinienverfahren 5. Synthese von Regelkreisen Für viele Anwendungen genügt es, Standard Regler einzusetzen und deren Parameter nach Einstellregeln zu bestimmen.
Ersatzschaltbild eines Operationsverstärkers für den Betrieb bei niederen Frequenzen
 Institut für Leistungselektronik und Elektrische Antriebe Prof. Dr.-Ing. J. Roth-Stielow Ersatzschaltbild eines Operationsverstärkers für den Betrieb bei niederen Frequenzen Unterlagen zur Vorlesung Regelungstechnik
Institut für Leistungselektronik und Elektrische Antriebe Prof. Dr.-Ing. J. Roth-Stielow Ersatzschaltbild eines Operationsverstärkers für den Betrieb bei niederen Frequenzen Unterlagen zur Vorlesung Regelungstechnik
Versuchsanleitung MV_5_1
 Modellbildung und Simulation Versuchsanleitung MV_5_1 FB 2 Stand August 2011 Prof. Dr.-Ing. Hartenstein Seite 1 von 11 1. Versuchsgegenstand Versuchsziel Ziel des Versuches ist es, die im Lehrfach Mechatronische
Modellbildung und Simulation Versuchsanleitung MV_5_1 FB 2 Stand August 2011 Prof. Dr.-Ing. Hartenstein Seite 1 von 11 1. Versuchsgegenstand Versuchsziel Ziel des Versuches ist es, die im Lehrfach Mechatronische
AUTOMATISIERUNGS- & REGELUNGSTECHNIK
 - FACHVERTIEFUNG AUTOMATISIERUNGS- & REGELUNGSTECHNIK Übung SS 2015 Univ.-Prof. Dr. techn. Andreas Kugi Fachvertiefung Automatisierungs- und Regelungstechnik Übung SS 2015 Univ.-Prof. Dr. techn. Andreas
- FACHVERTIEFUNG AUTOMATISIERUNGS- & REGELUNGSTECHNIK Übung SS 2015 Univ.-Prof. Dr. techn. Andreas Kugi Fachvertiefung Automatisierungs- und Regelungstechnik Übung SS 2015 Univ.-Prof. Dr. techn. Andreas
1. Laborpraktikum. Abbildung 1: Gleichstrommotor Quanser QET
 Prof. Dr.-Ing. Jörg Raisch Dipl.-Ing. Stephanie Geist Fachgebiet Regelungssysteme Fakultät IV Elektrotechnik und Informatik Technische Universität Berlin Integrierte Lehrveranstaltung Grundlagen der Regelungstechnik
Prof. Dr.-Ing. Jörg Raisch Dipl.-Ing. Stephanie Geist Fachgebiet Regelungssysteme Fakultät IV Elektrotechnik und Informatik Technische Universität Berlin Integrierte Lehrveranstaltung Grundlagen der Regelungstechnik
Übung 4.1: Dynamische Systeme
 Übung 4.1: Dynamische Systeme c M. Schlup, 18. Mai 16 Aufgabe 1 RC-Schaltung Zur Zeitpunkt t = wird der Schalter in der Schaltung nach Abb. 1 geschlossen. Vor dem Schliessen des Schalters, betrage die
Übung 4.1: Dynamische Systeme c M. Schlup, 18. Mai 16 Aufgabe 1 RC-Schaltung Zur Zeitpunkt t = wird der Schalter in der Schaltung nach Abb. 1 geschlossen. Vor dem Schliessen des Schalters, betrage die
PRAKTIKUM REGELUNGSTECHNIK 2
 FACHHOCHSCHULE LANDSHUT Fachbereich Elektrotechnik Prof. Dr. G. Dorn PRAKTIKUM REGELUNGSTECHNIK 2 1 Versuch 2: Übertragungsfunktion und Polvorgabe 1.1 Einleitung Die Laplace Transformation ist ein äußerst
FACHHOCHSCHULE LANDSHUT Fachbereich Elektrotechnik Prof. Dr. G. Dorn PRAKTIKUM REGELUNGSTECHNIK 2 1 Versuch 2: Übertragungsfunktion und Polvorgabe 1.1 Einleitung Die Laplace Transformation ist ein äußerst
Klausur. Grundlagen der Mechatronik und Systemtechnik
 23.08.2012 Klausur Grundlagen der Mechatronik und Systemtechnik Name: Matrikel-Nr.: Hinweise zur Bearbeitung: Die Klausur besteht aus 4 Aufgaben. Es sind alle Aufgaben zu bearbeiten. Die Bearbeitungszeit
23.08.2012 Klausur Grundlagen der Mechatronik und Systemtechnik Name: Matrikel-Nr.: Hinweise zur Bearbeitung: Die Klausur besteht aus 4 Aufgaben. Es sind alle Aufgaben zu bearbeiten. Die Bearbeitungszeit
Theory Swiss German (Liechtenstein) Lies die Anweisungen in dem separaten Umschlag, bevor Du mit dieser Aufgabe beginnst.
 Q2-1 Nichtlineare Dynamik in Stromkreisen (10 Punkte) Lies die Anweisungen in dem separaten Umschlag, bevor Du mit dieser Aufgabe beginnst. Einleitung Bistabile nichtlineare halbleitende Komponenten (z.b.
Q2-1 Nichtlineare Dynamik in Stromkreisen (10 Punkte) Lies die Anweisungen in dem separaten Umschlag, bevor Du mit dieser Aufgabe beginnst. Einleitung Bistabile nichtlineare halbleitende Komponenten (z.b.
RT-E: Entwurf der Drehzahlregelung eines Gebläsemotors
 RT-E: Entwurf der Drehzahlregelung eines Gebläsemotors Quelle: http://de.wikipedia.org/w/index.php?title=datei:radialventilator- Wellringrad.jpg&filetimestamp=20061128101719 (Stand: 26.09.2012) Martin
RT-E: Entwurf der Drehzahlregelung eines Gebläsemotors Quelle: http://de.wikipedia.org/w/index.php?title=datei:radialventilator- Wellringrad.jpg&filetimestamp=20061128101719 (Stand: 26.09.2012) Martin
Die regelungstechnischen Grundfunktionen P, I, D, Totzeit und PT1. 1. Methoden zur Untersuchung von Regelstrecken
 FELJC P_I_D_Tt.odt 1 Die regelungstechnischen Grundfunktionen P, I, D, Totzeit und PT1 (Zum Teil Wiederholung, siehe Kurs T2EE) 1. Methoden zur Untersuchung von Regelstrecken Bei der Untersuchung einer
FELJC P_I_D_Tt.odt 1 Die regelungstechnischen Grundfunktionen P, I, D, Totzeit und PT1 (Zum Teil Wiederholung, siehe Kurs T2EE) 1. Methoden zur Untersuchung von Regelstrecken Bei der Untersuchung einer
Kritik der Regler-Dimensionierung nach Ziegler und Nichols
 Axel Rossmann Thema: Regelungstechnik Kritik der Regler-Dimensionierung nach Ziegler und Nichols http://strukturbildung-simulation.de/ Kritik an Ziegler/Nichols - 1 - Apr 2013 Seite 1 Zum Thema Regelungstechnik:
Axel Rossmann Thema: Regelungstechnik Kritik der Regler-Dimensionierung nach Ziegler und Nichols http://strukturbildung-simulation.de/ Kritik an Ziegler/Nichols - 1 - Apr 2013 Seite 1 Zum Thema Regelungstechnik:
14 Übungen zu Regelung im Zustandsraum Teil 2
 Zoltán Zomotor Versionsstand: 9. März 25, :32 This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 3. Germany License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3./de/
Zoltán Zomotor Versionsstand: 9. März 25, :32 This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 3. Germany License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3./de/
Übung 2 Einschwingvorgänge 2 Diode Linearisierung
 Universität Stuttgart Übung 2 Einschwingvorgänge 2 Diode Linearisierung Institut für Leistungselektronik und Elektrische Antriebe Abt. Elektrische Energiewandlung Prof. Dr.-Ing. N. Parspour Aufgabe 2.1
Universität Stuttgart Übung 2 Einschwingvorgänge 2 Diode Linearisierung Institut für Leistungselektronik und Elektrische Antriebe Abt. Elektrische Energiewandlung Prof. Dr.-Ing. N. Parspour Aufgabe 2.1
Prozessautomatisierung 2. Praktikum
 Johannes Kepler Universität Linz Institut für Regelungstechnik und Prozessautomatisierung Prozessautomatisierung 2 Praktikum ẋ = Ax+Bu v u y y = Cx+Du ẇ = Âw+ ˆB u u+ ˆB y y ˆx = Ĉw+ ˆD u u+ ˆD y y K ˆx
Johannes Kepler Universität Linz Institut für Regelungstechnik und Prozessautomatisierung Prozessautomatisierung 2 Praktikum ẋ = Ax+Bu v u y y = Cx+Du ẇ = Âw+ ˆB u u+ ˆB y y ˆx = Ĉw+ ˆD u u+ ˆD y y K ˆx
Automatisierungstechnik Praktikum Tutorium zum Laboraufbau Elektrisches Netzwerk
 J O H A N N E S K E P L E R U N I V E R S I T Ä T L I N Z I n s t i t u t f ü r R e g e l u n g s t e c h n i k u n d P r o z e s s a u t o m a t i s i e r u n g Automatisierungstechnik Praktikum Tutorium
J O H A N N E S K E P L E R U N I V E R S I T Ä T L I N Z I n s t i t u t f ü r R e g e l u n g s t e c h n i k u n d P r o z e s s a u t o m a t i s i e r u n g Automatisierungstechnik Praktikum Tutorium
Aufgabensammlung. eines Filters: c) Wie stark steigen bzw. fallen die beiden Flanken des Filters?
 Aufgabensammlung Analoge Grundschaltungen 1. Aufgabe AG: Gegeben sei der Amplitudengang H(p) = a e eines Filters: a) m welchen Filtertyp handelt es sich? b) Bestimmen Sie die Mittenkreisfrequenz des Filters
Aufgabensammlung Analoge Grundschaltungen 1. Aufgabe AG: Gegeben sei der Amplitudengang H(p) = a e eines Filters: a) m welchen Filtertyp handelt es sich? b) Bestimmen Sie die Mittenkreisfrequenz des Filters
Ausarbeitung Regelungstechnik
 Ausarbeitung Regelungstechnik by Poth & Fiechtner 2005 by Poth & Fiechtner Seite 1/14 Inhalt Grundsätzliches zur Regelungstechnik Untersuchung des als Regelstrecke verwendeten Heizlüfters Regelkreis als
Ausarbeitung Regelungstechnik by Poth & Fiechtner 2005 by Poth & Fiechtner Seite 1/14 Inhalt Grundsätzliches zur Regelungstechnik Untersuchung des als Regelstrecke verwendeten Heizlüfters Regelkreis als
4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung. 4. Dämpfungsmodelle. Elastodynamik 1 3.
 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 4. Dämpfungsmodelle 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische
4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 4. Dämpfungsmodelle 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische
Vordiplomprüfung Grundlagen der Elektrotechnik III
 Vordiplomprüfung Grundlagen der Elektrotechnik III 16. Februar 2007 Name:... Vorname:... Mat.Nr.:... Studienfach:... Abgegebene Arbeitsblätter:... Bitte unterschreiben Sie, wenn Sie mit der Veröffentlichung
Vordiplomprüfung Grundlagen der Elektrotechnik III 16. Februar 2007 Name:... Vorname:... Mat.Nr.:... Studienfach:... Abgegebene Arbeitsblätter:... Bitte unterschreiben Sie, wenn Sie mit der Veröffentlichung
Umdruck RT: Grundlagen der Regelungstechnik. 1 Grundbegriffe der Steuerungs- und Regelungstechnik. 1.2 Regelung
 Universität Stuttgart Institut für Leistungselektronik und lektrische Antriebe Prof. Dr.-Ing. J. Roth-Stielow.2 Regelung ÜBUG ZU LKRISCH RGICHIK II Umdruck R: Grundlagen der Regelungstechnik Grundbegriffe
Universität Stuttgart Institut für Leistungselektronik und lektrische Antriebe Prof. Dr.-Ing. J. Roth-Stielow.2 Regelung ÜBUG ZU LKRISCH RGICHIK II Umdruck R: Grundlagen der Regelungstechnik Grundbegriffe
Musterlösung zur Klausur. Grundlagen der Mechatronik
 26.3.212 Musterlösung zur Klausur Grundlagen der Mechatronik Name: Matrikel-Nr.: Hinweise zur Bearbeitung: Die Klausur besteht aus 4 Aufgaben. Es sind alle Aufgaben zu bearbeiten. Die Bearbeitungszeit
26.3.212 Musterlösung zur Klausur Grundlagen der Mechatronik Name: Matrikel-Nr.: Hinweise zur Bearbeitung: Die Klausur besteht aus 4 Aufgaben. Es sind alle Aufgaben zu bearbeiten. Die Bearbeitungszeit
Regelungstechnik I (WS 15/16) Übung 2
 Regelungstechnik I (WS 5/6) Übung Prof. Dr. Ing. habil. Thomas Meurer Lehrstuhl für Regelungstechnik Aufgabe. (Linearität, Zeitinvarianz). Überprüfen Sie die folgenden dynamischen Systeme auf Linearität
Regelungstechnik I (WS 5/6) Übung Prof. Dr. Ing. habil. Thomas Meurer Lehrstuhl für Regelungstechnik Aufgabe. (Linearität, Zeitinvarianz). Überprüfen Sie die folgenden dynamischen Systeme auf Linearität
Praktikum Grundlagen Regelungstechnik
 Praktikum Grundlagen Regelungstechnik Versuch P-GRT 05 Versuchsziel Versuch 5 - Reglerentwurf im Frequenzbereich COM3LAB Veränderung des Streckenfrequenzganges durch einen vorgeschalteten Regler Datum
Praktikum Grundlagen Regelungstechnik Versuch P-GRT 05 Versuchsziel Versuch 5 - Reglerentwurf im Frequenzbereich COM3LAB Veränderung des Streckenfrequenzganges durch einen vorgeschalteten Regler Datum
Dämpfung. . Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung. Elastodynamik 2 SS
 Dämpfung. Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung 5. Dämpfung 5-1 1. Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische Energie
Dämpfung. Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung 5. Dämpfung 5-1 1. Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische Energie
Schriftliche Prüfung aus Control Systems 1 am
 TU Graz, Institt für Regelngs- nd Atomatisierngstechnik A Schriftliche Prüfng as Control Systems am 5 0 006 Name / Vorname(n): Kenn-MatrNr: Gebrtsdatm: BONUSPUNKTE as Compterrechenübng: 3 erreichbare Pnkte
TU Graz, Institt für Regelngs- nd Atomatisierngstechnik A Schriftliche Prüfng as Control Systems am 5 0 006 Name / Vorname(n): Kenn-MatrNr: Gebrtsdatm: BONUSPUNKTE as Compterrechenübng: 3 erreichbare Pnkte
M1 Maxwellsches Rad. 1. Grundlagen
 M1 Maxwellsches Rad Stoffgebiet: Translations- und Rotationsbewegung, Massenträgheitsmoment, physikalisches Pendel. Versuchsziel: Es ist das Massenträgheitsmoment eines Maxwellschen Rades auf zwei Arten
M1 Maxwellsches Rad Stoffgebiet: Translations- und Rotationsbewegung, Massenträgheitsmoment, physikalisches Pendel. Versuchsziel: Es ist das Massenträgheitsmoment eines Maxwellschen Rades auf zwei Arten
2. Lagrange-Gleichungen
 2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
Theory Austrian German (Austria) Lies, bitte, bevor du mit der Aufgabe beginnst die allgemeinen Anweisungen im separaten Briefumschlag.
 Q2-1 Nichtlineare Dynamik in Stromkreisen (10 points) Lies, bitte, bevor du mit der Aufgabe beginnst die allgemeinen Anweisungen im separaten Briefumschlag. Einleitung Bistabile nichtlineare halbleitende
Q2-1 Nichtlineare Dynamik in Stromkreisen (10 points) Lies, bitte, bevor du mit der Aufgabe beginnst die allgemeinen Anweisungen im separaten Briefumschlag. Einleitung Bistabile nichtlineare halbleitende
Analysis und Lineare Algebra mit MuPAD
 Analysis und Lineare Algebra mit MuPAD Dehling/Kubach Mögliche Themen für Abschlussprojekte 1 Fourier-Reihen Zu einer integrierbaren Funktion f : [0,2π] R definieren wir die Fourier-Reihe wobei a 0 = 1
Analysis und Lineare Algebra mit MuPAD Dehling/Kubach Mögliche Themen für Abschlussprojekte 1 Fourier-Reihen Zu einer integrierbaren Funktion f : [0,2π] R definieren wir die Fourier-Reihe wobei a 0 = 1
Flüsse, Fixpunkte, Stabilität
 1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
Fall 1: Diode D1 sperrt (u D1 < 0), Diode D2 leitet (i D2 > 0) Fall 2: Diode D1 leitet (i D1 > 0), Diode D2 sperrt (u D2 < 0)
 2 Aufgabe 1 Operationsverstärker (31 Punkte) Zuerst soll folgende Schaltung mit einem Operationsverstärker, linearen Widerständen und idealen Dioden untersucht werden. R 1 i z =0 R 1 u D2 D2 i D2 u e u
2 Aufgabe 1 Operationsverstärker (31 Punkte) Zuerst soll folgende Schaltung mit einem Operationsverstärker, linearen Widerständen und idealen Dioden untersucht werden. R 1 i z =0 R 1 u D2 D2 i D2 u e u
Frequenzgang und Übergangsfunktion
 Labor Regelungstechnik Frequenzgang und Übergangsfunktion. Einführung In diesem Versuch geht es um: Theoretische und experimentelle Ermittlung der Frequenzgänge verschiedener Übertragungsglieder (Regelstrecke,
Labor Regelungstechnik Frequenzgang und Übergangsfunktion. Einführung In diesem Versuch geht es um: Theoretische und experimentelle Ermittlung der Frequenzgänge verschiedener Übertragungsglieder (Regelstrecke,
Lageregelung eines Magnetschwebekörpers
 Technische Universität Berlin Fakultät IV Elektrotechnik und Informatik Fachgebiet Regelungssysteme Leitung: Prof. Dr.-Ing. Jörg Raisch Praktikum Digitale Signalverabeitung Praktikum Regelungstechnik 1
Technische Universität Berlin Fakultät IV Elektrotechnik und Informatik Fachgebiet Regelungssysteme Leitung: Prof. Dr.-Ing. Jörg Raisch Praktikum Digitale Signalverabeitung Praktikum Regelungstechnik 1
Drehzahlregelung eines Gleichstrommotors
 Technische Universität Berlin Fakultät IV Elektrotechnik und Informatik Fachgebiet Regelungsssteme Leitung: Prof. Dr.-Ing. Jörg Raisch Praktikum Grundlagen der Regelungstechnik 1 Einführung Versuch 1b
Technische Universität Berlin Fakultät IV Elektrotechnik und Informatik Fachgebiet Regelungsssteme Leitung: Prof. Dr.-Ing. Jörg Raisch Praktikum Grundlagen der Regelungstechnik 1 Einführung Versuch 1b
Fachpraktikum Hochdynamische Antriebssysteme. Theoretische Grundlagen Gleichstrommaschine
 Fachpraktikum Hochdynamische ntriebssysteme Gleichstrommaschine Christof Zwyssig Franz Zürcher Philipp Karutz HS 2008 Gleichstrommaschine Die hier aufgeführten theoretischen Betrachtungen dienen dem Grundverständnis
Fachpraktikum Hochdynamische ntriebssysteme Gleichstrommaschine Christof Zwyssig Franz Zürcher Philipp Karutz HS 2008 Gleichstrommaschine Die hier aufgeführten theoretischen Betrachtungen dienen dem Grundverständnis
Zulassungsprüfung für den Master-Studiengang in Elektrotechnik und Informationstechnik an der Leibniz Universität Hannover
 Zulassungsprüfung für den Master-Studiengang in Elektrotechnik und Informationstechnik an der Leibniz Universität Hannover Zulassungsjahr: 04 (Sommersemester) Allgemeine Informationen: Der deutschsprachige
Zulassungsprüfung für den Master-Studiengang in Elektrotechnik und Informationstechnik an der Leibniz Universität Hannover Zulassungsjahr: 04 (Sommersemester) Allgemeine Informationen: Der deutschsprachige
Institut für Leistungselektronik und Elektrische Antriebe. Übungen Regelungstechnik 2
 Institut für Leistungselektronik und Elektrische Antriebe Prof. Dr.-Ing. J. Roth-Stielow Übungen Regelungstechnik 2 Inhalt der Übungen: 1. Grundlagen (Wiederholung RT1) 2. Störgrößenaufschaltung 3. Störgrößennachbildung
Institut für Leistungselektronik und Elektrische Antriebe Prof. Dr.-Ing. J. Roth-Stielow Übungen Regelungstechnik 2 Inhalt der Übungen: 1. Grundlagen (Wiederholung RT1) 2. Störgrößenaufschaltung 3. Störgrößennachbildung
Stromregelung eines Gleichstrommotors
 Technische Universität Berlin Fakultät IV Elektrotechnik und Informatik Fachgebiet Regelungssysteme Leitung: Prof. Dr.-Ing. Jörg Raisch Praktikum Grundlagen der Regelungstechnik 1 Einführung Versuch 1a
Technische Universität Berlin Fakultät IV Elektrotechnik und Informatik Fachgebiet Regelungssysteme Leitung: Prof. Dr.-Ing. Jörg Raisch Praktikum Grundlagen der Regelungstechnik 1 Einführung Versuch 1a
Zusammenfassung der 9. Vorlesung
 Zusammenfassung der 9. Vorlesung Analyse des Regelkreises Stationäres Verhalten des des Regelkreises Bleibende Regelabweichung für ffür r FFührungs- und und Störverhalten Bleibende Regelabweichung für
Zusammenfassung der 9. Vorlesung Analyse des Regelkreises Stationäres Verhalten des des Regelkreises Bleibende Regelabweichung für ffür r FFührungs- und und Störverhalten Bleibende Regelabweichung für
Einführung in die Robotik Regelung. Mohamed Oubbati Institut für Neuroinformatik. Tel.: (+49) 731 / 50 24153 mohamed.oubbati@uni-ulm.de 04. 12.
 Einführung in die Robotik Regelung Mohamed Oubbati Institut für Neuroinformatik Tel.: (+49) 731 / 50 24153 mohamed.oubbati@uni-ulm.de 04. 12. 2012 The human is perhaps the most intelligent control system
Einführung in die Robotik Regelung Mohamed Oubbati Institut für Neuroinformatik Tel.: (+49) 731 / 50 24153 mohamed.oubbati@uni-ulm.de 04. 12. 2012 The human is perhaps the most intelligent control system
PP Physikalisches Pendel
 PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
Übungsaufgaben zu Mathematik III (ohne Lösungen)
 Übungsaufgaben zu Mathematik III (ohne Lösungen) 1. Lösen Sie intuitiv (d.h. ohne spezielle Verfahren) die folgenden DGLn (allgemeine Lösung): = b) =! c) = d)!! = e at. Prüfen Sie, ob die gegebenen Funktionen
Übungsaufgaben zu Mathematik III (ohne Lösungen) 1. Lösen Sie intuitiv (d.h. ohne spezielle Verfahren) die folgenden DGLn (allgemeine Lösung): = b) =! c) = d)!! = e at. Prüfen Sie, ob die gegebenen Funktionen
1.) Aufrufen des Programms WinFACT 7 (BORIS)
 Dampftemperaturregelung mit WAGO und WinFACT 7 (BORIS) 1.) Aufrufen des Programms WinFACT 7 (BORIS) Über die Start Menüleiste gelangen Sie über Programme, WinFACT 7 und Blockorientierte Simulation BORIS
Dampftemperaturregelung mit WAGO und WinFACT 7 (BORIS) 1.) Aufrufen des Programms WinFACT 7 (BORIS) Über die Start Menüleiste gelangen Sie über Programme, WinFACT 7 und Blockorientierte Simulation BORIS
Einleitung Einführung in die Aufgabenstellung der Regelungstechnik Beispiel einer Wasserstandsregelung 5
 INHALTSVERZEICHNIS Einleitung 1 1. Einführung in die Aufgabenstellung der Regelungstechnik 5 1.1 Beispiel einer Wasserstandsregelung 5 1.1.1 Verbale Systembeschreibung 5 1.1.2 Anforderungen an die Regelung
INHALTSVERZEICHNIS Einleitung 1 1. Einführung in die Aufgabenstellung der Regelungstechnik 5 1.1 Beispiel einer Wasserstandsregelung 5 1.1.1 Verbale Systembeschreibung 5 1.1.2 Anforderungen an die Regelung
Schaltungstechnik 1 (Wdh.)
 Grundlagenorientierungsprüfung für Elektro- und Informationstechnik Schaltungstechnik 1 (Wdh.) Univ.-Prof. Dr. techn. Josef A. Nossek Freitag, den 13.4.27 9. 1.3 Uhr Name: Vorname: Matrikel-Nr.: Hörsaal:
Grundlagenorientierungsprüfung für Elektro- und Informationstechnik Schaltungstechnik 1 (Wdh.) Univ.-Prof. Dr. techn. Josef A. Nossek Freitag, den 13.4.27 9. 1.3 Uhr Name: Vorname: Matrikel-Nr.: Hörsaal:
Maschinenlabor Versuch V12
 Universität Siegen Institut für Mess- und Regelungstechnik - Mechatronik Prof. Dr.-Ing. Oliver Nelles Maschinenlabor Versuch V12 Reglerentwurf mit MATLAB/SIMULINK Betreuer: Dipl.-Ing. Julian Belz M. Sc.
Universität Siegen Institut für Mess- und Regelungstechnik - Mechatronik Prof. Dr.-Ing. Oliver Nelles Maschinenlabor Versuch V12 Reglerentwurf mit MATLAB/SIMULINK Betreuer: Dipl.-Ing. Julian Belz M. Sc.
PRAKTIKUMSVERSUCH M/S 2
 Fakultät Informatik, Institut für Angewandte Informatik, Professur Technische Informationssysteme PRAKTIKUMSVERSUCH M/S 2 Betreuer: Dipl.-Ing. Burkhard Hensel Dr.-Ing. Alexander Dementjev ALLGEMEINE BEMERKUNGEN
Fakultät Informatik, Institut für Angewandte Informatik, Professur Technische Informationssysteme PRAKTIKUMSVERSUCH M/S 2 Betreuer: Dipl.-Ing. Burkhard Hensel Dr.-Ing. Alexander Dementjev ALLGEMEINE BEMERKUNGEN
Entwurf robuster Regelungen
 Entwurf robuster Regelungen Kai Müller Hochschule Bremerhaven Institut für Automatisierungs- und Elektrotechnik z P v K Juni 25 76 5 OPTIMALE ZUSTANDSREGELUNG 5 Optimale Zustandsregelung Ein optimaler
Entwurf robuster Regelungen Kai Müller Hochschule Bremerhaven Institut für Automatisierungs- und Elektrotechnik z P v K Juni 25 76 5 OPTIMALE ZUSTANDSREGELUNG 5 Optimale Zustandsregelung Ein optimaler
Martin Horn Nicolaos Dourdoumas. Regelungstechnik. Rechnerunterstützter Entwurf zeitkontinuierlicher und zeitdiskreter Regelkreise
 Martin Horn Nicolaos Dourdoumas Regelungstechnik Rechnerunterstützter Entwurf zeitkontinuierlicher und zeitdiskreter Regelkreise ein Imprint der Pearson Education München Boston San Francisco Harlow, England
Martin Horn Nicolaos Dourdoumas Regelungstechnik Rechnerunterstützter Entwurf zeitkontinuierlicher und zeitdiskreter Regelkreise ein Imprint der Pearson Education München Boston San Francisco Harlow, England
Überlegungen zur Leistung und zum Wirkungsgrad von Solarkochern
 Überlegungen zur Leistung und zum Wirkungsgrad von Solarkochern (Dr. Hartmut Ehmler) Einführung Die folgenden Überlegungen gelten ganz allgemein für Solarkocher, unabhängig ob es sich um einen Parabolkocher,
Überlegungen zur Leistung und zum Wirkungsgrad von Solarkochern (Dr. Hartmut Ehmler) Einführung Die folgenden Überlegungen gelten ganz allgemein für Solarkocher, unabhängig ob es sich um einen Parabolkocher,
70 Jahre Reglereinstellung nach Ziegler und Nichols
 Fakultät Informatik, Institut für angewandte Informatik, Professur für technische Informationssysteme Proseminar Technische Informationssysteme Johannes Postel Dresden, 14. November 2011 Überblick 1. Systembegriff
Fakultät Informatik, Institut für angewandte Informatik, Professur für technische Informationssysteme Proseminar Technische Informationssysteme Johannes Postel Dresden, 14. November 2011 Überblick 1. Systembegriff
2 Elektrischer Stromkreis
 2 Elektrischer Stromkreis 2.1 Aufbau des technischen Stromkreises Nach der Durcharbeitung dieses Kapitels haben Sie die Kompetenz... Stromkreise in äußere und innere Abschnitte einzuteilen und die Bedeutung
2 Elektrischer Stromkreis 2.1 Aufbau des technischen Stromkreises Nach der Durcharbeitung dieses Kapitels haben Sie die Kompetenz... Stromkreise in äußere und innere Abschnitte einzuteilen und die Bedeutung
So viel wie möglich Extremwertaufgaben aus Geometrie
 So viel wie möglich Extremwertaufgaben aus Geometrie Andreas Ulovec 1 Einführung Die meisten Leute sind mit Extremwertaufgaben vertraut: Was ist das flächengrößte Dreieck, das man in einen Kreis einschreiben
So viel wie möglich Extremwertaufgaben aus Geometrie Andreas Ulovec 1 Einführung Die meisten Leute sind mit Extremwertaufgaben vertraut: Was ist das flächengrößte Dreieck, das man in einen Kreis einschreiben
5. Fourier-Transformation
 Fragestellungen: 5. Fourier-Transformation Bei Anregung mit einer harmonischen Last kann quasistatitisch gerechnet werden, wenn die Erregerfrequenz kleiner als etwa 30% der Resonanzfrequenz ist. Wann darf
Fragestellungen: 5. Fourier-Transformation Bei Anregung mit einer harmonischen Last kann quasistatitisch gerechnet werden, wenn die Erregerfrequenz kleiner als etwa 30% der Resonanzfrequenz ist. Wann darf
Strukturbildung und Simulation technischer Systeme. Strukturbildung und Simulation technischer Systeme. strukturbildung-simulation.
 Leseprobe zu Kapitel 9 Regelungstechnik des Buchs Strukturbildung und Simulation technischer Systeme Weitere Informationen zum Buch finden Sie unter strukturbildung-simulation.de Im Gegensatz zu Steuerungen
Leseprobe zu Kapitel 9 Regelungstechnik des Buchs Strukturbildung und Simulation technischer Systeme Weitere Informationen zum Buch finden Sie unter strukturbildung-simulation.de Im Gegensatz zu Steuerungen
Differentialgleichungen
 Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
TECHNISCHE MECHANIK III (DYNAMIK)
 Klausur im Fach TECHNISCHE MECHANIK III (DYNAMIK) WS 2014 / 2015 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 2 3 4 Summe Punkte: 15 7 23 15 60 Davon erreicht Bearbeitungszeit: Hilfsmittel:
Klausur im Fach TECHNISCHE MECHANIK III (DYNAMIK) WS 2014 / 2015 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 2 3 4 Summe Punkte: 15 7 23 15 60 Davon erreicht Bearbeitungszeit: Hilfsmittel:
6 Elektromagnetische Schwingungen und Wellen
 6 Elektromagnetische Schwingungen und Wellen Gegen Ende des 19.Jahrhunterts gelang dem berühmten deutschen Physiker Heinrich Rudolph Hertz (1857-1894) zum ersten Mal in der Geschichte der Menschheit der
6 Elektromagnetische Schwingungen und Wellen Gegen Ende des 19.Jahrhunterts gelang dem berühmten deutschen Physiker Heinrich Rudolph Hertz (1857-1894) zum ersten Mal in der Geschichte der Menschheit der
Musterlösung zur Klausur. Grundlagen der Mechatronik und Systemtechnik
 23.08.2012 Musterlösung zur Klausur Grundlagen der Mechatronik und Systemtechnik Name: Matrikel-Nr.: Hinweise zur Bearbeitung: Die Klausur besteht aus 4 Aufgaben. Es sind alle Aufgaben zu bearbeiten. Die
23.08.2012 Musterlösung zur Klausur Grundlagen der Mechatronik und Systemtechnik Name: Matrikel-Nr.: Hinweise zur Bearbeitung: Die Klausur besteht aus 4 Aufgaben. Es sind alle Aufgaben zu bearbeiten. Die
2 Systemanalyse mit Matlab/Simulink
 2 Systemanalyse mit Matlab/Simulink Ziel dieser Übung ist es, das Computerprogramm Matlab/Simulink für die Systemanalyse einzusetzen. Alle Aufgabenstellungen dieser Übungseinheit sind mit diesem Softwarepaket
2 Systemanalyse mit Matlab/Simulink Ziel dieser Übung ist es, das Computerprogramm Matlab/Simulink für die Systemanalyse einzusetzen. Alle Aufgabenstellungen dieser Übungseinheit sind mit diesem Softwarepaket
Regelsysteme Tutorial: Stabilitätskriterien. George X. Zhang HS Institut für Automatik ETH Zürich
 Regelsysteme 1 5. Tutorial: Stabilitätskriterien George X. Zhang Institut für Automatik ETH Zürich HS 2015 George X. Zhang Regelsysteme 1 HS 2015 5. Tutorial: Stabilitätskriterien Gliederung 5.1. Stabilität
Regelsysteme 1 5. Tutorial: Stabilitätskriterien George X. Zhang Institut für Automatik ETH Zürich HS 2015 George X. Zhang Regelsysteme 1 HS 2015 5. Tutorial: Stabilitätskriterien Gliederung 5.1. Stabilität
Zulassungsprüfung für den Master-Studiengang in Elektrotechnik und Informationstechnik an der Leibniz Universität Hannover
 Zulassungsprüfung für den Master-Studiengang in Elektrotechnik und Informationstechnik an der Leibniz Universität Hannover Zulassungsjahr: 202 (Sommersemester) Allgemeine Informationen: Der deutschsprachige
Zulassungsprüfung für den Master-Studiengang in Elektrotechnik und Informationstechnik an der Leibniz Universität Hannover Zulassungsjahr: 202 (Sommersemester) Allgemeine Informationen: Der deutschsprachige
Regelungstechnik 1 Praktikum Versuch 1.1. 1 Unterschied zwischen Steuerung und Regelung Reglereinstellung mittels Schwingversuch
 Regelungstechnik 1 Praktikum Versuch 1.1 1 nterschied zwischen Steuerung und Regelung Reglereinstellung mittels Schwingversuch Die Aufgabe der Regelungstechnik besteht im weitesten Sinne darin, einen bestimmten
Regelungstechnik 1 Praktikum Versuch 1.1 1 nterschied zwischen Steuerung und Regelung Reglereinstellung mittels Schwingversuch Die Aufgabe der Regelungstechnik besteht im weitesten Sinne darin, einen bestimmten
Digitale Regelungssysteme - Versuchsanleitung 2. Digitale Regelung eines inversen Pendels
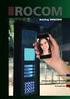 4 6 Fachgebiet Regelungstechnik Leiter: Prof. Dr.-Ing. Johann Reger Digitale Regelungssysteme - Versuchsanleitung 2 Digitale Regelung eines inversen Pendels Voraussetzungen Voraussetzungen für die Vorbereitung
4 6 Fachgebiet Regelungstechnik Leiter: Prof. Dr.-Ing. Johann Reger Digitale Regelungssysteme - Versuchsanleitung 2 Digitale Regelung eines inversen Pendels Voraussetzungen Voraussetzungen für die Vorbereitung
Transistor- und Operationsverstärkerschaltungen
 Name, Vorname Testat Besprechung: 23.05.08 Abgabe: 30.05.08 Transistor- und Operationsverstärkerschaltungen Aufgabe 1: Transistorverstärker Fig.1(a): Verstärkerschaltung Fig.1(b): Linearisiertes Grossignalersatzschaltbild
Name, Vorname Testat Besprechung: 23.05.08 Abgabe: 30.05.08 Transistor- und Operationsverstärkerschaltungen Aufgabe 1: Transistorverstärker Fig.1(a): Verstärkerschaltung Fig.1(b): Linearisiertes Grossignalersatzschaltbild
Einführung in die Numerik strukturerhaltender Zeitintegratoren. Leonard Schlag 6. Dezember 2010
 Einführung in die Numerik strukturerhaltender Zeitintegratoren Leonard Schlag 6. Dezember 2010 1 Inhaltsverzeichnis 1 Einführung in die Numerik strukturerhaltender Zeitintegratoren 3 1.1 Häuge Problemstellung:
Einführung in die Numerik strukturerhaltender Zeitintegratoren Leonard Schlag 6. Dezember 2010 1 Inhaltsverzeichnis 1 Einführung in die Numerik strukturerhaltender Zeitintegratoren 3 1.1 Häuge Problemstellung:
Physik-Department. Ferienkurs zur Experimentalphysik 2 - Musterlösung
 Physik-Department Ferienkurs zur Experimentalphysik 2 - Musterlösung Daniel Jost 27/08/13 Technische Universität München Aufgaben zur Magnetostatik Aufgabe 1 Bestimmen Sie das Magnetfeld eines unendlichen
Physik-Department Ferienkurs zur Experimentalphysik 2 - Musterlösung Daniel Jost 27/08/13 Technische Universität München Aufgaben zur Magnetostatik Aufgabe 1 Bestimmen Sie das Magnetfeld eines unendlichen
Automatisierungstechnik 1
 Johannes epler Universität Linz Institut für Regelungstechnik und Prozessautomatisierung Übung Automatisierungstechnik 1 l x x soll 0 2r J A m J B U +U J G x soll R P +U U L A U F = konst. u A R A i A
Johannes epler Universität Linz Institut für Regelungstechnik und Prozessautomatisierung Übung Automatisierungstechnik 1 l x x soll 0 2r J A m J B U +U J G x soll R P +U U L A U F = konst. u A R A i A
Robotik. Prüfung. Prüfer Note
 Prüfung Robotik Anmerkungen: Nur Blätter mit Namen und Matr.Nr. werden korrigiert. Keine rote Farbe verwenden. Zu jeder Lösung Aufgabennummer angeben. Aufgabe max. Punkte 1 a) 3 b) 2 c) 6 d) 3 e) 3 2 a)
Prüfung Robotik Anmerkungen: Nur Blätter mit Namen und Matr.Nr. werden korrigiert. Keine rote Farbe verwenden. Zu jeder Lösung Aufgabennummer angeben. Aufgabe max. Punkte 1 a) 3 b) 2 c) 6 d) 3 e) 3 2 a)
Tutorium Mathematik II, M Lösungen
 Tutorium Mathematik II, M Lösungen März 03 *Aufgabe Bestimmen Sie durch Hauptachsentransformation Lage und Typ der Kegelschnitte (a) 3x + 4x x + 3x 4x = 0, (b) 3x + 4x x + 3x 4x 6 = 0, (c) 3x + 4x x +
Tutorium Mathematik II, M Lösungen März 03 *Aufgabe Bestimmen Sie durch Hauptachsentransformation Lage und Typ der Kegelschnitte (a) 3x + 4x x + 3x 4x = 0, (b) 3x + 4x x + 3x 4x 6 = 0, (c) 3x + 4x x +
OPV-Schaltungen. Aufgaben
 OPVSchaltungen Aufgaben 2 1. Skizzieren Sie die vier für die Meßtechnik wichtigsten Grundschaltungen gegengekoppelter Meßverstärker und charakterisieren Sie diese kurz bezüglich des Eingangs und Ausgangssignals!
OPVSchaltungen Aufgaben 2 1. Skizzieren Sie die vier für die Meßtechnik wichtigsten Grundschaltungen gegengekoppelter Meßverstärker und charakterisieren Sie diese kurz bezüglich des Eingangs und Ausgangssignals!
Prozessautomatisierung 1 Praktikum
 Johannes Kepler Universität Linz Institut für Regelungstechnik und Prozessautomatisierung Prozessautomatisierung 1 Praktikum u P d y M c e Identifikation Stand: WS 2016/17 Sven-Olaf Lindert Organisation
Johannes Kepler Universität Linz Institut für Regelungstechnik und Prozessautomatisierung Prozessautomatisierung 1 Praktikum u P d y M c e Identifikation Stand: WS 2016/17 Sven-Olaf Lindert Organisation
Gewöhnliche Differentialgleichungen am Beispiel des harmonischen Oszillators
 Gewöhnliche Differentialgleichungen am Beispiel des harmonischen Oszillators Horst Laschinsky 12. Oktober 1999 Inhaltsverzeichnis 1 Gewöhnliche lineare homogene Differentialgleichungen 2. Ordnung mit konstanten
Gewöhnliche Differentialgleichungen am Beispiel des harmonischen Oszillators Horst Laschinsky 12. Oktober 1999 Inhaltsverzeichnis 1 Gewöhnliche lineare homogene Differentialgleichungen 2. Ordnung mit konstanten
Temperaturregelung PID-Regler beim 3D-Druck
 Temperaturregelung PID-Regler beim 3D-Druck 15. Juni 2016 1/25 Gliederung Temperaturregelung beim 3D-Drucker Einleitung PID-Regler PID Berechnung Schaltung Tuning Simulation Aussichten Quellen 2/25 Einsatz
Temperaturregelung PID-Regler beim 3D-Druck 15. Juni 2016 1/25 Gliederung Temperaturregelung beim 3D-Drucker Einleitung PID-Regler PID Berechnung Schaltung Tuning Simulation Aussichten Quellen 2/25 Einsatz
Leistungselektronik Grundlagen und Standardanwendungen. Praktikumsunterlagen (Vorläufig bis einschließlich Kap. 3 vom 25.04.2016)
 Lehrstuhl für Elektrische Antriebssysteme und Leistungselektronik Technische Universität München Arcisstraße 21 D 80333 München Email: eal@ei.tum.de Internet: http://www.eal.ei.tum.de Prof. Dr.-Ing. Ralph
Lehrstuhl für Elektrische Antriebssysteme und Leistungselektronik Technische Universität München Arcisstraße 21 D 80333 München Email: eal@ei.tum.de Internet: http://www.eal.ei.tum.de Prof. Dr.-Ing. Ralph
FACHHOCHSCHULE KÖLN FAKULTÄT IME NT BEREICH REGELUNGSTECHNIK PROF. DR. H.M. SCHAEDEL / PROF. DR. R. BARTZ. RT - Praktikum. Thema des Versuchs :
 FACHHOCHSCHULE KÖLN FAKULTÄT IME NT BEREICH REGELUNGSTECHNIK PROF. DR. H.M. SCHAEDEL / PROF. DR. R. BARTZ Gruppe: RT - Praktikum Thema des Versuchs : Analyse von Ausgleichsstrecken höherer Ordnung im Zeit-
FACHHOCHSCHULE KÖLN FAKULTÄT IME NT BEREICH REGELUNGSTECHNIK PROF. DR. H.M. SCHAEDEL / PROF. DR. R. BARTZ Gruppe: RT - Praktikum Thema des Versuchs : Analyse von Ausgleichsstrecken höherer Ordnung im Zeit-
Zustandsraum: Historische Einordnung
 Zustandsraum: Historische Einordnung Die Grundlagen der Zustandsraummethoden wurden im Zeitraum 1955 1965 von Kalman und seinen Kollegen in dem Research Institute for Advanced Studies in Baltimore entwickelt.
Zustandsraum: Historische Einordnung Die Grundlagen der Zustandsraummethoden wurden im Zeitraum 1955 1965 von Kalman und seinen Kollegen in dem Research Institute for Advanced Studies in Baltimore entwickelt.
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik - Schwingungen und Wellen - Prof. Dr. Ulrich Hahn SS 28 Mechanik elastische Wellen Schwingung von Bauteilen Wasserwellen Akustik Elektrodynamik Schwingkreise elektromagnetische
Physik III im Studiengang Elektrotechnik - Schwingungen und Wellen - Prof. Dr. Ulrich Hahn SS 28 Mechanik elastische Wellen Schwingung von Bauteilen Wasserwellen Akustik Elektrodynamik Schwingkreise elektromagnetische
LTAM FELJC jean-claude.feltes@education.lu 1 T2EE. Regelungstechnik ASSERVISSEMENTS
 LTAM FELJC jean-claude.feltes@education.lu 1 T2EE Regelungstechnik ASSERVISSEMENTS Z W E R Y S X LTAM FELJC jean-claude.feltes@education.lu 2 1. Grundlagen 1.1. Steuerung Beispiel 1: Drehzahlsteuerung
LTAM FELJC jean-claude.feltes@education.lu 1 T2EE Regelungstechnik ASSERVISSEMENTS Z W E R Y S X LTAM FELJC jean-claude.feltes@education.lu 2 1. Grundlagen 1.1. Steuerung Beispiel 1: Drehzahlsteuerung
Regelungs- und Systemtechnik 3
 Regelung Mechatronischer Systeme, Regelungs- und Systemtechnik 3 Kapitel 1: Einführung Prof. Dr.-Ing. Pu Li Fachgebiet Simulation und Optimale Prozesse (SOP) Luft- und Raumfahrtindustrie 2 Zu regelnde
Regelung Mechatronischer Systeme, Regelungs- und Systemtechnik 3 Kapitel 1: Einführung Prof. Dr.-Ing. Pu Li Fachgebiet Simulation und Optimale Prozesse (SOP) Luft- und Raumfahrtindustrie 2 Zu regelnde
5 Schwingungen und Wellen
 5 Schwingungen und Wellen Schwingung: Regelmäßige Bewegung, die zwischen zwei Grenzen hin- & zurückführt Zeitlich periodische Zustandsänderung mit Periode T ψ ψ(t) [ ψ(t-τ)] Wellen: Periodische Zustandsänderung
5 Schwingungen und Wellen Schwingung: Regelmäßige Bewegung, die zwischen zwei Grenzen hin- & zurückführt Zeitlich periodische Zustandsänderung mit Periode T ψ ψ(t) [ ψ(t-τ)] Wellen: Periodische Zustandsänderung
Vorlesung 13. Die Frequenzkennlinien / Frequenzgang
 Vorlesung 3 Die Frequenzkennlinien / Frequenzgang Frequenzkennlinien geben das Antwortverhalten eines linearen Systems auf eine harmonische (sinusförmige) Anregung in Verstärkung (Amplitude) und Phasenverschiebung
Vorlesung 3 Die Frequenzkennlinien / Frequenzgang Frequenzkennlinien geben das Antwortverhalten eines linearen Systems auf eine harmonische (sinusförmige) Anregung in Verstärkung (Amplitude) und Phasenverschiebung
Materialien WS 2014/15 Dozent: Dr. Andreas Will.
 Master Umweltingenieur, 1. Semester, Modul 42439, Strömungsmechanik, 420607, VL, Do. 11:30-13:00, R. 3.21 420608, UE, Do. 13:45-15:15, R. 3.17 Materialien WS 2014/15 Dozent: Dr. Andreas Will will@tu-cottbus.de
Master Umweltingenieur, 1. Semester, Modul 42439, Strömungsmechanik, 420607, VL, Do. 11:30-13:00, R. 3.21 420608, UE, Do. 13:45-15:15, R. 3.17 Materialien WS 2014/15 Dozent: Dr. Andreas Will will@tu-cottbus.de
2.4 Stoßprozesse. entweder nicht interessiert o- der keine Möglichkeit hat, sie zu untersuchen oder zu beeinflussen.
 - 52-2.4 Stoßprozesse 2.4.1 Definition und Motivation Unter einem Stoß versteht man eine zeitlich begrenzte Wechselwirkung zwischen zwei oder mehr Systemen, wobei man sich für die Einzelheiten der Wechselwirkung
- 52-2.4 Stoßprozesse 2.4.1 Definition und Motivation Unter einem Stoß versteht man eine zeitlich begrenzte Wechselwirkung zwischen zwei oder mehr Systemen, wobei man sich für die Einzelheiten der Wechselwirkung
Verbindung Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 1
 Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 1 Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 2 Arbeitsauftrag für Gruppenarbeit
Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 1 Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 2 Arbeitsauftrag für Gruppenarbeit
Zusammenfassung der 8. Vorlesung
 Zusammenfassung der 8. Vorlesung Beschreibung und und Analyse dynamischer Systeme im im Zustandsraum Steuerbarkeit eines dynamischen Systems Unterscheidung: Zustandssteuerbarkeit, Zustandserreichbarkeit
Zusammenfassung der 8. Vorlesung Beschreibung und und Analyse dynamischer Systeme im im Zustandsraum Steuerbarkeit eines dynamischen Systems Unterscheidung: Zustandssteuerbarkeit, Zustandserreichbarkeit
1. Bewegungsgleichung
 1. Bewegungsgleichung 1.1 Das Newtonsche Grundgesetz 1.2 Dynamisches Gleichgewicht 1.3 Geführte Bewegung 1.4 Massenpunktsysteme 1.5 Schwerpunktsatz Prof. Dr. Wandinger 2. Kinetik des Massenpunkts Dynamik
1. Bewegungsgleichung 1.1 Das Newtonsche Grundgesetz 1.2 Dynamisches Gleichgewicht 1.3 Geführte Bewegung 1.4 Massenpunktsysteme 1.5 Schwerpunktsatz Prof. Dr. Wandinger 2. Kinetik des Massenpunkts Dynamik
14. Mechanische Schwingungen und Wellen
 14. Mechanische Schwingungen und Wellen Schwingungen treten in der Technik in vielen Vorgängen auf mit positiven und negativen Effekten (z. B. Haarrisse, Achsbrüche etc.). Deshalb ist es eine wichtige
14. Mechanische Schwingungen und Wellen Schwingungen treten in der Technik in vielen Vorgängen auf mit positiven und negativen Effekten (z. B. Haarrisse, Achsbrüche etc.). Deshalb ist es eine wichtige
Ein Stromfluss ist immer mit einem Magnetfeld verbunden und umgekehrt: Abb Verknüpfung von elektrischem Strom und Magnetfeld
 37 3 Transformatoren 3. Magnetfeldgleichungen 3.. Das Durchflutungsgesetz Ein Stromfluss ist immer mit einem Magnetfeld verbunden und umgekehrt: H I Abb. 3..- Verknüpfung von elektrischem Strom und Magnetfeld
37 3 Transformatoren 3. Magnetfeldgleichungen 3.. Das Durchflutungsgesetz Ein Stromfluss ist immer mit einem Magnetfeld verbunden und umgekehrt: H I Abb. 3..- Verknüpfung von elektrischem Strom und Magnetfeld
Aufgabe Max.Pkt. Punkte Visum 1 Visum Total 60
 D-MATH/D-PHYS Prof. W. Fetscher Studienjahr HS07 - FS08 ETH Zürich Testklausur, Frühjahr 2008, Physik I+II Füllen Sie als erstes den untenstehenden Kopf mit Name und Legi-Nummer aus. Beachten Sie: Nicht
D-MATH/D-PHYS Prof. W. Fetscher Studienjahr HS07 - FS08 ETH Zürich Testklausur, Frühjahr 2008, Physik I+II Füllen Sie als erstes den untenstehenden Kopf mit Name und Legi-Nummer aus. Beachten Sie: Nicht
Kursprüfung Methoden der VWL Klausurteil Dynamische Methoden der VWL (Prof. Dr. Lutz Arnold) Wintersemester 2009/
 Kursprüfung Methoden der VWL Klausurteil Dynamische Methoden der VWL (Prof. Dr. Lutz Arnold) Wintersemester 2009/10 2.3.2010 Bitte gut leserlich ausfüllen: Name: Vorname: Matr.-nr.: Wird vom Prüfer ausgefüllt:
Kursprüfung Methoden der VWL Klausurteil Dynamische Methoden der VWL (Prof. Dr. Lutz Arnold) Wintersemester 2009/10 2.3.2010 Bitte gut leserlich ausfüllen: Name: Vorname: Matr.-nr.: Wird vom Prüfer ausgefüllt:
Grundlagen der Automatisierungstechnik Klausur Februar 2011
 Grundlagen der Automatisierungstechnik Klausur Februar 2011 Aufgabe 1 Boolsche Algebra (10 Punkte) Die Normalform für eine XOR Verknüpfung lautet F=. a) Geben sie die Wahrheitstabelle für die XOR-Verknüpfung
Grundlagen der Automatisierungstechnik Klausur Februar 2011 Aufgabe 1 Boolsche Algebra (10 Punkte) Die Normalform für eine XOR Verknüpfung lautet F=. a) Geben sie die Wahrheitstabelle für die XOR-Verknüpfung
Labor elektrische Antriebe und Leistungselektronik
 . Messungen am stillstehenden Motor a) Induktivität L U-V 4,7mH RU V + RV W + RW V,55Ω +,6Ω +,6Ω b) Widerstand R,5833Ω 3 3.2 Erwärmungsversuch Bei diesem Versuch wird der Motor bei n2000min - über 36 Minuten
. Messungen am stillstehenden Motor a) Induktivität L U-V 4,7mH RU V + RV W + RW V,55Ω +,6Ω +,6Ω b) Widerstand R,5833Ω 3 3.2 Erwärmungsversuch Bei diesem Versuch wird der Motor bei n2000min - über 36 Minuten
