- Entscheidungsmöglichkeit / Alternativen. + (idealerweise) Methode der Entscheidung / Verfahren
|
|
|
- Klaudia Linden
- vor 6 Jahren
- Abrufe
Transkript
1 be/ji/3(2) "Entscheidung" setzt voraus - Entscheidungsmöglichkeit / Alternativen - Prinzip der Entscheidung / Ziel + (idealerweise) Methode der Entscheidung / Verfahren Bisher trivial OR-Optimierungsmodelle - "enthalten bereits" Alternativen: Abgrenzung über Nebenbedingungen - "nennen bereits" Ziel: zu optimierende Zielfunktion + (idealerweise) erlauben Angabe Entscheidungsverfahren: (zb bei linearer Optimierung:) Simplex-Verfahren "im allgemeinen" schwieriger: Alternativen / Ziele / Verfahren "zu erarbeiten" wobei man ahnen kann (möchte), daß es dafür "allgemeinen Rahmen" gibt (geben sollte)
2 be/ji/ breites Gebiet - mit unterschiedlichen Schwerpunkten Untersuchung des Entscheidungs-Prozesses und / oder des Wahlaktes *) Untersuchung der logischen Grundlagen von Entscheidungen normative, auch: präskriptive *) als Formalwissenschaft: - trifft logische Entscheidungen auf Basis von Axiomen - beabsichtigt nicht Aussagen über Realität ( höchstens indirekt, bei "vernünftiger" Wahl von Axiomen + Ableitungsregeln ) von Vorgängen der realen Entscheidungsfindung deskriptive, auch: empirische als Realwissenschaft - erklärt Entscheidungsverhalten, Entscheidungsprozesse von Individuen und Gruppen - beabsichtigt Prognosen realer Entscheidungen in konkreten Situationen + statistische als Gebiet der Statistik unser Interesse wird bei " *) " liegen
3 be/ji/ Grundmodell der Grund-"Schemata" der Entscheidungsfindung ( "Modell"-Begriff variierend! ) Entscheidung betrifft - Auswahl aus möglichen Alternativen - im Hinblick auf Resultat der Entscheidung - wo Resultat zusätzlich von (unbeeinflußbarer) Umgebung bestimmt Grundmodell ist geschlossen: "alle Informationen bekannt" endliche Menge A von Alternativen Aktionen (actions) a i genau eine gewählt einzelne Alternative realiter ia bestimmt durch mehrere / viele Einzelaktionen mehrere / viele Entscheidungsvariable durch Tupel von Werten charakterisiert endliche Menge S von Umgebungssituationen Zuständen (states) s j genau eine eintretend einzelne Situation realiter uu bestimmt durch mehrere Aspekte / beschreibende Variable durch Tupel von Werten charakterisiert
4 be/ji/3 4-4 Menge E von Resultaten Ergebnissen (effects) e ij E Ergebnis durch Aktion a i und Zustand s j eindeutig bestimmt einzelnes Ergebnis beinhaltet realiter ia mehrere / viele Konsequenzen einer Entscheidung Beschänkung auf maßgebende Zielgrößen, Grad "Zufriedenheit" ausdrück'd durch Tupel von Werten (z 1,,z.) charakterisiert Hinsichtlich Umgebungssituation 3 Fälle ausgezeichnet - Umweltzustand eindeutig bekannt: Sicherheit - verschiedene Umweltzustände möglich, vorliegender / eintretender aber unbekannt: Ungewißheit - verschiedene Umweltzustände möglich, vorliegender / eintretender unbekannt aber Erwartungen durch rel. Häufigkeiten Wahrscheinlichkeiten abschätzbar : Risiko Entscheidungen?? Grundlage ist (zu erstellen:) Zielfunktion / Entscheidungskriterium bestehend aus - Präferenzfunktion, welche den Alternativen Präferenzwerte ( R? ) zuordnet - Optimierungskriterium (max, min, =, >, <, ) bzgl Wert hier durchgängig: max
5 be/ji/ dabei Präferenzfunktion pr "sinnvoll" festzulegen, so daß "max" gewünschte Entscheidung "trifft" auf Ergebnisse + deren Bewertung abzustützen dazu: Nutzenfunktion, welche Ergebnissen Nutzenwerte ( R? ) zuordnet dabei Nutzenfunktion u "sinnvoll" festzulegen, so daß "max" gewünschte Entscheidungsbasis "trifft" + auf "sinnvolle" Berücksichtigung der Nutzenwerte in Präferenzfunktion zu achten Zusammenhang in einfachen Fällen trivial: zb eine Zielgröße, ihrem "Sinn" gemäß zu maximieren Nutzenwert Ergebnis = Zielgrößenwert + Sicherheit bzgl Zustand Präferenzwert Alternative = Nutzenwert Zusammenhang in komplizierten Fällen nicht trivial, auf "Metaentscheidungen" basierend: zb mehrere Zielgrößen, Ungewißheit + Risiko
6 be/ji/3(2) 4-6 Präferenzwerte + Nutzenwerte sollten "vernünftig" / rational sein: Basis: Rationalitätsaxiome bzgl Ergebnissen + Präferenzen Ergebnisse e,f,g E (bzw e,f,g A) Präferenzoperatoren «,», mit den Bedeutungen - e» f, f «e e wird f vorgezogen - e f e und f werden als gleichwertig betrachtet (a) Vollständigkeit(saxiom) für jedes Paar e,f E gilt entweder e» f oder e «f oder e f (b) Transitivität e» f und f» g e» g e» f und f g e» g e f und f» g e» g e f und f g e g (c) Asymmetrie und Reflexivität e» f f «e e e schwache Ordnung über E bzw A, Ordinalskala "Rationale" Präferenz- / Nutzen-Funktionen pr: A R? bzw u: E R? erhalten diese Ordnung: e» f pr(f) > pr(e) e f pr(f) = pr(e) u(f) > u(e) u(f) = u(e)
7 be/ji/3(2) 4-7 uu weitere Forderungen an u: (d) Stetigkeit für den Fall der Charakterisierung von e als n-tupel des R n (e) explizite Berücksichtigung der Nutzendifferenzen(" R?" ) schwache Ordnung Konsistenz zur Ergebnisordnung Transitivität Schematische Erfassung des Entscheidungsmodells Ergebnismatrix Zustand s 1 s j s. Aktion a 1 e 11 e 1j a i e i1 e ij a. bzw, mit u ij := u(e ij ), Nutzenmatrix Zustand s 1 s j s. Aktion a 1 u 11 u 1j a i u i1 u ij a.
8 be/ji/3 4-8 bzw, im Risiko-Fall ( diskrete Verteilung für Eintreten der Zustände, p j := P[s j ] ) Zustand s 1 s j s. Wahrscheinlichkeit p 1 p j p. Aktion a 1 u 11 u 1j a i u i1 u ij a. bzw, noch komplexer ( zusätzliche diskrete Verteilung für Nutzenwert je Aktions-/Zustands-Konstellation ) Zustand s j Wahrscheinlichkeit p j Aktion a i q ij1 :u ij1,,q ij. :u ij. weitere Verallgemeinerungen durchaus denkbar, aber ia nicht verfolgt Entscheidungskriterium in zwei Formen: - Entscheidungsregel legt Präferenzen fest - Entscheidungsprinzip legt Rahmen für Präferenzen fest
9 be/ji/3(2) Entscheidungen bei Sicherheit Umweltzustand s eindeutig bekannt für Einzelentscheidung genau eine Spalte der Entscheidungs- / Nutzentafel relevant Trivialfall, falls - Nutzen deterministisch - nur eine Zielgröße Nutzen als Zufallsvariable beschrieben spezielles Feld erster Ausweg: mit Erwartungswerten Nutzen arbeiten (nicht immer sinnvoll!) mehrere Zielgrößen vorliegend Zielgrößen z 1,,z. Erfassung in Ergebnismatrix Zustand fest (relevant) Aktion a i e i := (z i1,,z i. ) ("aufgeblähte" Spalten, jeweils nur eine relevant) z ij := z j bei Aktion a i
10 be/ji/ oder (direkt) als Zielgrößenmatrix Zielgröße z 1 z j z. Aktion a 1 z 11 z 1j a i z i1 z ij a. Zielgrößen können im Konflikt stehen, Rationalitätsaxiome bzgl der a i nicht o. weiteres erfüllt, ia nicht "offensichtlich" erfüllbar empirisch / heuristisch könnten Erfüllungsmöglichkeiten vorliegen - eindeutige vollständige "Vorzugs"-Ordnung der Zielgrößen + "ähnliche" allgemein kann Dominanzkriterium - Konflikte mildern: Ausscheiden von Alternativen a i, die von anderer Alternative a j dominiert: k: k: z jk z ik z jk > z ik - Konflikte beseitigen: genau eine dominante Alternative
11 be/ji/ im Falle von genau 2 Zielgrößen relativ breit ausgebaut - Graphik-basierte Methoden, ua auf (Nutzen-)Indifferenzkurven arbeitend z 2 Linien gleichen Nutzens z 1 (Zeichnung setzt Stetigkeit über (z 1,z 2 ) voraus) Paare (z 1,z 2 ) axiomengerecht vergleichbar (zb Linien-Indizes als u-werte) + Methoden der Festlegung der Indifferenzkurven zb über Befragungen + konsistente Erweiterung Im Falle mehrerer ( 2) Zielgrößen auch behandelt - Maximierung (genau) einer Zielgröße bei gegebenen "Anspruchsniveaus" der anderen 1 x : Maximierung, sonst : "Satisfizierung" - sowie (immer erfolgreich, wenn möglich / sinnvoll) Zielgewichtung über Nutzenfunktion, welche Zielgrößen (absolut / relativ) gewichtet u i := Σ k a k z ik - spezielle Ansätze, zb Bereich lineare Optimierung: Vektoroptimierung, Goal Programming (n. behandelt)
12 be/ji/ Entscheidungen bei Ungewißheit Fassung über Nutzenmatrix Zustand s 1 s j s. Aktion a 1 u 11 u 1j a i u i1 u ij a. u's genügen (zumindest) Rationalitätsaxiomen über Eintreten des Umweltzustands (genau einer) "praktisch nichts bekannt" Einige Entscheidungs-Kriterien (-Regeln / -Prinzipien) Anwendung Dominanzkriterium (erneut) führt zu - Ausscheiden dominierter Aktionen - uu Auswahl genau einer Aktion ia kein eindeutiges Kriterium
13 be/ji/ Maximin-Regel - bestimmt je Aktion "schlechtesten" Nutzen pr i := min j - bestimmt daraus "besten" Nutzen pr opt := pr i (beides wg Rationalitätsaxiomen, paarweiser Vergleichbarkeit - wählt zugehöriges a opt "bestmöglicher Minimalnutzen" möglich) sehr pessimistische Regel, wäre "gerechtfertigt" bei Annahme "boshafter Umgebung" (vgl Abschn. 5, "Spieltheorie") Maximax-Regel - bestimmt je Aktion "besten" Nutzen pr i := max j u ij max i u ij - bestimmt daraus "besten" Nutzen pr opt := pr i max i (beides wg Rationalitätsaxiomen, paarweiser Vergleichbarkeit - wählt zugehöriges a opt "bestmöglicher Maximalnutzen" möglich) sehr optimistische Regel, wäre "gerechtfertigt" bei Annahme "gutwilliger Umgebung"
14 be/ji/ Hurwicz-Prinzip - Kompromiß Minimax / Maximax, Berücksichtigung besten + schlechtesten Nutzens je Aktion in pr i := α max j ( Ordinalskala für u's nicht hinreichend, Intervallskala nötig, hier idr u. R ) α subjektiv festgelegt - bestimmt daraus "besten Kompromiß" pr opt := pr i max i u ij + (1 α) min u j ij 0 α 1 - wählt zugehöriges a opt "bestmöglicher Kompromißnutzen" je α eine "Regel": "Prinzip" Minimax und Maximax als Grenzfälle sicher "anpaßbarer" als diese (Niveau des Optimismus / Pessimismus), aber auch hier nur Auswahl möglicher u-werte je Aktion berücksichtigt
15 be/ji/ Savage-Niehans-Regel - bestimmt je Aktion "größte Enttäuschung" pr i := - bestimmt daraus Minimalwert pr opt := max j min i max j pr i u ij u ij - wählt zugehöriges a opt "kleinstes Bedauern" Regel (+ ähnliche) erlaubt gewisse Berücksichtigung psychologischer Faktoren "Vermeidung von Ärger" Laplace-Regel (auch Sonderfall der Entscheidungen bei Risiko, s. 4.4) - wenn über Eintreten des Umweltzustands "praktisch nichts bekannt", Erwartungshaltung "identisch", erscheint Transformation nach "gleichwahrscheinlich" gerechtfertigt (auch: Erinnerung an "maximum entropy"-verfahren) Festlegung mittleren Nutzens je Aktion als S pr i := S 1 Σ u ij j=1 wo S: = Zustände
16 be/ji/ und daraus beste Alternative pr opt := pr i max i - Wahl zugehörigen a opt "bestmöglicher mittlerer Nutzen" Diskussion s. 4.4 Insgesamt - schwache Entscheidungsgrundlagen bei Ungewißheit - in der Praxis meist Richtung "Risiko" transformiert - Einsatzmöglichkeit für Ergebnisse aus Gebiet "unscharfe (fuzzy) Mengen / unscharfe Entscheidungen" (hier nicht diskutiert)
17 be/ji/ Entscheidungen bei Risiko Fassung über Nutzenmatrix Zustand s 1 s j s S Wahrscheinlichkeit p 1 p j p S Aktion a 1 u 11 u 1j a i u i1 u ij a. einzelne Zielgröße diskrete Verteilung für Eintreten der Zustände, p j := P[s j ] Nutzen numerisch: u. R zunächst: = (numerischer) Zielgröße z. Einige Entscheidungs-Kriterien (-Regeln / -Prinzipien) Anwendung Dominanzkriterium (erneut) führt zu - Ausscheiden dominierter Aktionen - uu Auswahl genau einer Aktion ia kein eindeutiges Kriterium
18 be/ji/3(2) Regel - gebräuchliche Bezeichnung für Entscheidung nach bestem Erwartungswert (auch: Bayes-Regel) - Erwartungswert Nutzen je Aktion pr i := S Σ j=1 p j u ij (Laplace-Regel, p j 1/ S, Sonderfall Gleichverteilung) - bestimmt daraus besten Wert pr opt := pr i max i wo S: = Zustände wählt zugehöriges a opt "bester mittlerer Nutzen" einfache, häufigst (kritiklos) angewandte Regel bei Risiko fallabhängige Beurteilung erforderlich - Wiederholungsfall / Einzelfall (von Entscheidungen) - Durchschnittserfolg / Gesamterfolg (als Entscheidungsbasis im Wiederholungsfall) Wiederholungsfall "immer wieder diese Entscheidung nach dieser Regel" Erfolg Aktion a i gemessen durch Zufallsvariable U i (ZVs groß notiert) charakterisiert durch diskrete Verteilung { (p 1 :u i1 ),,(p S :u is ) } mit ("Kennwerte":) Erwartungswert E, Varianz V, Streuung V, Variationskoeffizient VK µ i := E[U i ] σ i := V[U i ] = E[(U i -µ i ) 2 ] VK[U i ] := σ i /µ i
19 be/ji/3(2) 4-19 n Entscheidungen {1,,k,,n} für Aktion a i - liefern Gesamterfolg Ug i Ug i := n Σ k=1 U i E Ug i = n µ i V Ug i = n V U i = n σ i 2 VK Ug i = 1 σ i n µ i (bzgl VAR Unabhängigkeit der Entscheidungsfälle vorausgesetzt) - liefern Durchschnittserfolg Ud i Ud i := 1 n Ug i E Ud i = 1 n E Ug i = µ i V Ud i = 1 n 2V Ug i = 1 n σ i 2 VK Ud i = 1 n σ i µ i liefern (gleichermaßen, abweichend von "Behauptungen") Berechtigung, Entscheidungen a i» a j bei µ i > µ j zu fällen aber (generell) "Mittelwertproblem": "subjektive Entscheidungen oft unvernünfig"
20 be/ji/3(2) 4-20 Einzelfall "eine / wenige Entscheidung(en) nach dieser Regel" - Berechtigung entfällt (eigentlich) + (verstärkt): "subjektive Entscheidungen oft unvernünfig" eher Ungewißheitsentscheidung? (, )-Prinzip - Versuch, "mehr" Eigenschaften der Verteilung zu berücksichtigen durch Präferenzfunktionen der Art pr(µ,σ) Entscheidungsregeln nach Form der pr-funktion - bei selbem µ "risikoscheue" Entscheidung, wenn σ kleiner "risikofreudige" Entscheidung, wenn σ größer kann im Widerspruch zu Dominanz-Prinzip stehen! maximum likelihood - Regel - wählt wahrscheinlichsten Zustand maximiert Nutzen für diesen pr i := u ik p k = max p j j pr opt := max pr i i (wieder:) nur "ganz wenig" von der Verteilung berücksichtigt
21 be/ji/ Vorgestellte Entscheidungs-Regeln / -Prinzipien bei Unsicherheit berücksichtigen lediglich Teile der Information, die in Nutzen-Verteilung vorliegt Auf dieser Basis Übergang Nutzenwerte u. Präferenzwerte pr. nicht überzeugend zb fällt Entscheidung im Falle Zustand s 1 s 2 Wahrscheinlichkeit Aktion a DM 2000 DM a 2 0DM 1Mio DM wirklich (höherer Erwartungswert) zugunsten a 2? oder lassen sich alle (mittl. Verlust) von Lotterie abhalten? Bernoulli-Prinzip - setzt Erwartungswert- (µ-)regel pr i := S Σ j=1 p j u ij als Zusammenhang Nutzenwerte / Präferenzwerte ein - allerdings nicht: über "irgendwie" ermittelten Nutzenwerten (wie etwa Resultaten einer num. Zielfkt. z) sondern: über Nutzenwerten, welche den Ergebnissen - subjektiv - aber unter Beachtung rationaler Kriterien zugeordnet werden teilweise spezielle Bezeichnung: "Bernoulli-Nutzen" uä
22 be/ji/ Ausgangspunkt: Ergebnis-Matrix Zustand s 1 s j s S W'keit p 1 p j p S Aktion a 1 e 11 e 1j a i e i1 e ij a A Ziel: Nutzen-/Präferenz-Matrix Zustand s 1 s j s S W'keit p 1 p j p S Aktion/Präferenz a 1 /pr 1 u 11 u 1j a i /pr i u i1 u ij a A /pr A derart daß - pr-werte / u-werte "konsistent" is Erwartungswert (pr-regel E[ ] gegeben u zu finden) "Wertschätzungen" u ij (e ij ) der Einzelergebnisse konsistent (is Erwartungswert) mit "Wertschätzungen" pr i ( {p 1 :u(e i1 ),,p S :u(e is )} ) der Nutzenverteilungen
23 be/ji/3(2) 4-23 Als Grundlage der Wertschätzung (und damit des Nutzens) Wiederaufnahme Rationalitätsaxiome bzgl Präferenz von Ergebnissen e,f,g, E mittels Präferenzoperatoren», ("etwas anders", identisch) mit den Bedeutungen - e» f e wird f vorgezogen - e f e und f werden als gleichwertig betrachtet (1) für jedes Paar e,f gilt genau eine der Beziehungen e» f f» e e f (2) e e (3) e f f e (4) e f und f g e g (5) e» f und f» g e» g (6) e» f und f g e» g (7) e f und f» g e» g sowie Forderungen an rationale Nutzenfunktionen e» f u(e) > u(f) e f u(e) = u(f) Grundlegende Idee Weiterführung ist vergleichende Einschätzung von elementaren Ergebnissen mit Risikosituationen seien Elementarereignisse e,f,g E mit e» f» g und Risikosituation h={ (r:e),(1-r:g } 0 r 1 dann sollte es Wahrscheinlichkeit r geben, bei der (subjektiv) f und h als gleichwertig eingeschätzt, d.h. f h
24 be/ji/3(2) 4-24 Risikosituation { (r:e),(1-r:g) } - als Lotterie bezeichnet - unterschiedlich notiert, hier r e + (1-r) g für rationale Nutzenfunktionen sollte weiter gelten u(f) = u(h) sowie mit Identifizierung u(lotterie) und pr(nutzenverteilung) unter Anwendung Erwartungswertregel u(f) = u(h) = pr(h) = r u(e) + (1-r) u(g) erhoffter konsistenter Zusammenhang zwischen Wertschätzungen Elementarereignis / Nutzenverteilung Mit Vergleichbarkeit von Lotterien und Elementarergebnissen: {Elementarergebnisse} {Lotterien} = {Ergebnisse}=E (unter Einschluß Rationalit.axiome + Rationalität N'fktionen) Vergleichende Einschätzungen gern eingeführt unter Fixierung: t = bestes, b = schlechtestes Ergebnis und Setzung: u(t)=1, u(b)=0 (wird sich als unerheblich herausstellen) "sollte gelten", "sollte es geben" gerechtfertigt durch - Aufstellung "plausiblen" Axiomensystems + Ableitung "sollte"-eigenschaften aus diesem Verschiedene solche (einander ähnliche) Axiomensysteme entwickelt im Folgenden eines davon (NB: + "ähnliche" auch für Fall der Ungewißheit)
25 be/ji/ Zusatzaxiome zur "Rationalität des Bernoulli-Prinzips" zentral (und "diskutierbar") ist sog. Stetigkeitsaxiom (13) e» f» g r (0,1): [r e + (1-r) g] f ferner (8) r e + (1-r) g = (1-r) g + r e ("harmlos") (10) r e + (1-r) e = e ("harmlos") (9) r e + (1-r) [s f + (1-s) g] = r e + (1-r)s f + (1-r)(1-s) g ("einleuchtend") (11) e f, r [0,1] [r e + (1-r) g] [r f + (1-r) g] ("diskutierbar") (12) e» f, r>0 [r e + (1-r) g]» [r f + (1-r) g] ("diskutierbar") Erwünschte Eigenschaften aus Axiomen ableitbar? Satz : Eindeutigkeit vergleichender Einschätzung Der Wert von r im Stetigkeitsaxiom (13) ist eindeutig. Widerspruchsüberlegung (H) r nicht eindeutig: e» f» g [r e + (1-r) g] f [s e + (1-s) g] f 0 < r,s < 1, r s, obda s < r (10): r s 1 s g + 1 r 1 s g = g (H), (12): r s 1 s e + 1 r 1 s g» g
26 be/ji/ (9): (10): (**) s e + (1 s) r s 1 s e s r g = s e + (r s) e + (1 r) g = r e + (1 r) g (H): (**): (*),(12): (H): f r e + (1 r) g = s e + (1 s) r s 1 s e + 1 r 1 s g» [s e + (1 s) g] f Widerspruch Satz : Existenz rationaler Nutzenfunktion Es existiert eine Funktion u: E R für welche e» f u(e) > u(f) gilt und welche u( r e + (1-r) f ) = r u(e) + (1-r) u(f) erfüllt u ist bis auf lineare Transformationen eindeutig: gelten die Beziehungen für u und u', dann α>0, β R derart daß u'(e) = α u(e) + β
27 be/ji/3(2) 4-27 Zum Beweis wird - eine konkrete Funktion u vorgelegt - nachgewiesen, daß Behauptungen für u zutreffen Nutzenfunktion (eine der Möglichkeiten, vgl. "lin. Transf.", zuvor bereits angedeutet) Falls nicht alle Elementarergebnisse gleichwertig (uninteressanter Sonderfall) existieren (Ordinal-Ordnung Rationalitätsaxiome) - "beste" Ergebnisse (kein anderes im Vergl. vorgezogen) eines daraus: t - "schlechteste" Ergebnisse (alle andere i.v. vorgezogen) eines daraus: b Setzung: u(t) = 1 u(b) = 0 g t : u(g) = u(t) = 1 g b : u(g) = u(b) = 0 alle anderen Ergebnisse e,f: t» e» b t» f» b (13): e s e t + (1-s e ) b Setzung: u(e) = s e f s f t + (1-s f ) b Setzung: u(f) = s f zu Behauptung 1: für s e =s f (4): e f u(e) = s e = s f = u(f)
28 be/ji/3(2) 4-28 für s e >s f aus Beweis S : und analog e [s e t + (1 s e ) b]» [s f t + (1 s f ) b] f s e > s f e» f s f > s e f» e zu Behauptung 2: r e + (1 r) f r [s e t + (1 s e ) b] + (1 r) [s f t + (1 s f ) b] = [rs e + (1 r)s f ] t + [r(1 s e ) + (1 r)(1 s f )] b u(r e + (1 r) f) = rs e + (1 r)s f = ru(e) + (1 r)u(f) zu Behauptung 3: Nutzenfunktion u' mit u'(b) = β u'(t) = β+α e mit u(e)=s d.h. e s t + (1-s) b u'(e) = u'(s t + (1-s) b) = s u'(t) + (1-s) u'(b) = s (β+α) + (1-s) β = sα + β = α u(e) + β
29 be/ji/3(2) 4-29 Insgesamt: (wenn Axiome akzeptiert:) - subjektive Nutzeneinschätzungen Ergebnisse möglich über Nutzeneinschätzung Lotterien - konsistent mit Bernoulli-Präferenzfunktion (Erwartungswert Nutzenverteilung) wegen formaler Gleichheit Bernoulli-Präferenz / Risiko-Nutzen (tatsächliche Festlegung Nutzenwerte nicht trivial!) "Abbruch": füllt Bücher z.b. Laux H.; ; Springer 1995
30 be/ji/ LEER
31 be/ji/ LEER
32 be/ji/ LEER
2.2 Entscheidung bei Sicherheit
 2.2 Entscheidung bei Sicherheit Umweltzustand ist bekannt oder irrelevant, so dass die Ergebnisse der Handlungsalternativen sicher sind Bei mehreren Zielgrößen besteht die Herausforderung darin, den Entscheider
2.2 Entscheidung bei Sicherheit Umweltzustand ist bekannt oder irrelevant, so dass die Ergebnisse der Handlungsalternativen sicher sind Bei mehreren Zielgrößen besteht die Herausforderung darin, den Entscheider
3. Entscheidungen bei mehreren Szenarien. Entscheidungen. bei Unsicherheit A i, S j und x ij sowie die Zielfunktion
 3. Entscheidungen bei mehreren Szenarien Entscheidungen bei Sicherheit A i und x i sowie die Zielfunktion determinieren das Entscheidungsproblem bei Unsicherheit A i, S j und x ij sowie die Zielfunktion
3. Entscheidungen bei mehreren Szenarien Entscheidungen bei Sicherheit A i und x i sowie die Zielfunktion determinieren das Entscheidungsproblem bei Unsicherheit A i, S j und x ij sowie die Zielfunktion
2. Entscheidungsregeln. Handhabung von Unsicherheit
 II Agenda 1. Sensitivitätsanalyse 2. Entscheidungsregeln 3. Dialektische Planung 2 1. Sensitivitätsanalyse 3 Definition: Sensitivitätsanalyse = Sensibilitätsanalyse Empfindlichkeitsanalyse Verfahren zur
II Agenda 1. Sensitivitätsanalyse 2. Entscheidungsregeln 3. Dialektische Planung 2 1. Sensitivitätsanalyse 3 Definition: Sensitivitätsanalyse = Sensibilitätsanalyse Empfindlichkeitsanalyse Verfahren zur
2.4 Entscheidung bei Risiko
 2.4 Entscheidung bei Risiko Entscheidung bei Risiko nimmt an, dass für jeden Zustand S j seine Eintrittswahrscheinlichkeit P(S j ) bekannt ist Eintrittswahrscheinlichkeiten bestimmbar als statistische
2.4 Entscheidung bei Risiko Entscheidung bei Risiko nimmt an, dass für jeden Zustand S j seine Eintrittswahrscheinlichkeit P(S j ) bekannt ist Eintrittswahrscheinlichkeiten bestimmbar als statistische
Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }.
 1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }. Annahmen: Der Entscheidungsträger ist gezwungen, eine der betrachteten
1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }. Annahmen: Der Entscheidungsträger ist gezwungen, eine der betrachteten
3. Betriebswirtschaftliche Entscheidungslehre 3.6 Entscheidung unter Risiko
 Dominanzprinzipien : Absolute Dominanz: Eine Alternative A i dominiert eine Alternative A j absolut, wenn das geringstmögliche Ergebnis von A i nicht kleiner ist als das grösstmögliche Ergebnis von A j,
Dominanzprinzipien : Absolute Dominanz: Eine Alternative A i dominiert eine Alternative A j absolut, wenn das geringstmögliche Ergebnis von A i nicht kleiner ist als das grösstmögliche Ergebnis von A j,
1. Aufgabe: Entscheidungen bei Ungewissheit
 ( WS 2012/13) 1. Aufgabe: Entscheidungen bei Ungewissheit Ein Entscheider steht vor dem Problem aus einer Menge von Investitionsalternativen (a 1, a 2,..., a 5 ) die beste Alternative auszuwählen. Zu welchem
( WS 2012/13) 1. Aufgabe: Entscheidungen bei Ungewissheit Ein Entscheider steht vor dem Problem aus einer Menge von Investitionsalternativen (a 1, a 2,..., a 5 ) die beste Alternative auszuwählen. Zu welchem
Präferenzen zu Zahlwerten I
 II-1 Präferenzen zu Zahlwerten I Erster Versuch: Durchzählen a > b > c > d > e Zuordnung von Zahlenwerten durch eine Funktion V e 1, d 2, c 3, b 4, a 5 Es gilt: Wenn x > y, dann V(x) > V(y) Aber: Differenzen
II-1 Präferenzen zu Zahlwerten I Erster Versuch: Durchzählen a > b > c > d > e Zuordnung von Zahlenwerten durch eine Funktion V e 1, d 2, c 3, b 4, a 5 Es gilt: Wenn x > y, dann V(x) > V(y) Aber: Differenzen
Entscheidungstheorie Teil 4
 Entscheidungstheorie Teil 4 Sommersemester 2011 Prof. Dr. Antje Mahayni Mercator School of Management Department of Accounting & Finance Prof. Dr. Antje Mahayni Entscheidungstheorie Teil 4 1/74 Gliederung
Entscheidungstheorie Teil 4 Sommersemester 2011 Prof. Dr. Antje Mahayni Mercator School of Management Department of Accounting & Finance Prof. Dr. Antje Mahayni Entscheidungstheorie Teil 4 1/74 Gliederung
3. Betriebswirtschaftliche Entscheidungslehre 3.1 Einleitung
 3.1 Einleitung Auf Basis von Zielvorstellungen sollen die Konsequenzen von Handlungsalternativen ermittelt werden deskriptive Entscheidungstheorie: beschreibt, wie in der Realität Entscheidungen in konkreten
3.1 Einleitung Auf Basis von Zielvorstellungen sollen die Konsequenzen von Handlungsalternativen ermittelt werden deskriptive Entscheidungstheorie: beschreibt, wie in der Realität Entscheidungen in konkreten
Mikroökonomik. Unsicherheit. Harald Wiese. Universität Leipzig. Harald Wiese (Universität Leipzig) Unsicherheit 1 / 46
 Mikroökonomik Unsicherheit Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Unsicherheit 1 / 46 Gliederung Einführung Haushaltstheorie Das Budget Präferenzen, Indi erenzkurven und Nutzenfunktionen
Mikroökonomik Unsicherheit Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Unsicherheit 1 / 46 Gliederung Einführung Haushaltstheorie Das Budget Präferenzen, Indi erenzkurven und Nutzenfunktionen
Betriebswirtschaftliche Entscheidungstheorie und Anwendung
 Betriebswirtschaftliche Entscheidungstheorie und Anwendung Kapitel 4: Entscheidungen unter Unsicherheit Prof. Dr. Thorsten Poddig Lehrstuhl für Allgemeine Betriebswirtschaftslehre, insbes. Finanzwirtschaft
Betriebswirtschaftliche Entscheidungstheorie und Anwendung Kapitel 4: Entscheidungen unter Unsicherheit Prof. Dr. Thorsten Poddig Lehrstuhl für Allgemeine Betriebswirtschaftslehre, insbes. Finanzwirtschaft
Lösungen der Aufgaben zu Entscheidungen bei Ungewissheit
 Lösungen der Aufgaben zu Entscheidungen bei Ungewissheit Lösungen der Aufgaben zu Entscheidungen bei Ungewissheit Aufgabe.3- Gegeben sei ein Entscheidungsproblem unter Ungewissheit mit der Ergebnismatrix
Lösungen der Aufgaben zu Entscheidungen bei Ungewissheit Lösungen der Aufgaben zu Entscheidungen bei Ungewissheit Aufgabe.3- Gegeben sei ein Entscheidungsproblem unter Ungewissheit mit der Ergebnismatrix
Übung zu Risiko und Versicherung Entscheidungstheoretische Grundlagen
 Übung zu Risiko Entscheidungstheoretische Grundlagen Stefan Neuß Sebastian Soika http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_203/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Übung zu Risiko Entscheidungstheoretische Grundlagen Stefan Neuß Sebastian Soika http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_203/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 3 38
 Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 3 38 Offene Fragen Warum ist ein ET bereit, für eine Feuerversicherung mit einer Versicherungshöhe von 1 Million und einer Jahreseintrittswahrscheinlichkeit
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 3 38 Offene Fragen Warum ist ein ET bereit, für eine Feuerversicherung mit einer Versicherungshöhe von 1 Million und einer Jahreseintrittswahrscheinlichkeit
Kapitel I - Das klassische Entscheidungsmodell
 Institut für Volkswirtschaftslehre (ECON) Lehrstuhl für Ökonometrie und Statistik Kapitel I - Das klassische Entscheidungsmodell Induktive Statistik Prof. Dr. W.-D. Heller Hartwig Senska Carlo Siebenschuh
Institut für Volkswirtschaftslehre (ECON) Lehrstuhl für Ökonometrie und Statistik Kapitel I - Das klassische Entscheidungsmodell Induktive Statistik Prof. Dr. W.-D. Heller Hartwig Senska Carlo Siebenschuh
Vorlesung 2: Erwartungsnutzen
 Vorlesung 2: Erwartungsnutzen Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 2 (FS 11) Erwartungsnutzen 1 / 28 1. Modellrahmen 1.1 Die Alternativen Wir betrachten
Vorlesung 2: Erwartungsnutzen Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 2 (FS 11) Erwartungsnutzen 1 / 28 1. Modellrahmen 1.1 Die Alternativen Wir betrachten
Operations Research kompakt
 Operations Research kompakt von Michael Sauer Oldenbourg Verlag München Inhalt s Verzeichnis 1 Einführung 1 1.1 Vorwort 1 1.2 Anwendungsbeispiel 2 1.3 Inhaltsüberblick 3 1.4 Einige Grundlagen 4 1.4.1 Grundbegriffe
Operations Research kompakt von Michael Sauer Oldenbourg Verlag München Inhalt s Verzeichnis 1 Einführung 1 1.1 Vorwort 1 1.2 Anwendungsbeispiel 2 1.3 Inhaltsüberblick 3 1.4 Einige Grundlagen 4 1.4.1 Grundbegriffe
Übung zu Risiko und Versicherung Entscheidungstheoretische Grundlagen
 Übung zu Risiko Entscheidungstheoretische Grundlagen Christoph Lex Dominik Lohmaier http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_04/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Übung zu Risiko Entscheidungstheoretische Grundlagen Christoph Lex Dominik Lohmaier http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_04/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Vorlesung 2: Präferenzen über Lotterien
 Vorlesung 2: Präferenzen über Lotterien Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 2, FS 12 Präferenzen über Lotterien 1/24 2.1 Modellrahmen Wir betrachten im
Vorlesung 2: Präferenzen über Lotterien Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 2, FS 12 Präferenzen über Lotterien 1/24 2.1 Modellrahmen Wir betrachten im
Einführung in die Betriebswirtschaftslehre
 Einführung in die Betriebswirtschaftslehre Entscheidungstheorie Wintersemester 2006/2007 Prof. Dr. M. Ponader Literatur Bartscher, Susanne, Bomke, Paul, Unternehmensführung, Stuttgart 1995; Kapitel 3:
Einführung in die Betriebswirtschaftslehre Entscheidungstheorie Wintersemester 2006/2007 Prof. Dr. M. Ponader Literatur Bartscher, Susanne, Bomke, Paul, Unternehmensführung, Stuttgart 1995; Kapitel 3:
2.3 Kriterien der Entscheidungsfindung: Präferenzen
 .3 Kriterien der Entscheidungsfindung: Präferenzen Der Einfachheit halber beschränken wir uns auf n = ( zwei Güter). Annahme: Konsumenten können für sich herausfinden, ob sie x = ( x, ) dem Güterbündel
.3 Kriterien der Entscheidungsfindung: Präferenzen Der Einfachheit halber beschränken wir uns auf n = ( zwei Güter). Annahme: Konsumenten können für sich herausfinden, ob sie x = ( x, ) dem Güterbündel
Vorlesung 2: Präferenzen über Lotterien
 Vorlesung 2: Präferenzen über Lotterien Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 2, FS 13 Präferenzen über Lotterien 1/26 2.1 Modellrahmen Wir betrachten im
Vorlesung 2: Präferenzen über Lotterien Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 2, FS 13 Präferenzen über Lotterien 1/26 2.1 Modellrahmen Wir betrachten im
Statistisches Testen
 Statistisches Testen Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Differenzen Anteilswert Chi-Quadrat Tests Gleichheit von Varianzen Prinzip des Statistischen Tests Konfidenzintervall
Statistisches Testen Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Differenzen Anteilswert Chi-Quadrat Tests Gleichheit von Varianzen Prinzip des Statistischen Tests Konfidenzintervall
Probleme bei reinen Strategien. Nash Gleichgewichte in gemischten Strategien Kopf 1, 1 1, 1 Zahl 1, 1 1, 1. Gemischte Strategien
 Probleme bei reinen Strategien Bisher hatten wir angenommen, daß sich jeder Spieler b auf genau eine Strategie S b S b festlegt. Das ist nicht immer plausibel. Nash Gleichgewichte in gemischten Strategien
Probleme bei reinen Strategien Bisher hatten wir angenommen, daß sich jeder Spieler b auf genau eine Strategie S b S b festlegt. Das ist nicht immer plausibel. Nash Gleichgewichte in gemischten Strategien
Grundlagen der Versicherungs- und Sozialversicherungsökonomik. Risiko: objektive oder subjektive Wahrscheinlichkeiten
 Grundlagen der Versicherungs- und Sozialversicherungsökonomik Entscheidungstheorie bei Sicherheit (z. B. trad. Mikroökonomik, lineare Programmierung etc. bei Risiko (Unsicherheit und Ungewissheit Risiko:
Grundlagen der Versicherungs- und Sozialversicherungsökonomik Entscheidungstheorie bei Sicherheit (z. B. trad. Mikroökonomik, lineare Programmierung etc. bei Risiko (Unsicherheit und Ungewissheit Risiko:
Statistische Tests (Signifikanztests)
 Statistische Tests (Signifikanztests) [testing statistical hypothesis] Prüfen und Bewerten von Hypothesen (Annahmen, Vermutungen) über die Verteilungen von Merkmalen in einer Grundgesamtheit (Population)
Statistische Tests (Signifikanztests) [testing statistical hypothesis] Prüfen und Bewerten von Hypothesen (Annahmen, Vermutungen) über die Verteilungen von Merkmalen in einer Grundgesamtheit (Population)
Kapitel ML:IV. IV. Statistische Lernverfahren. Wahrscheinlichkeitsrechnung Bayes-Klassifikation Maximum-a-Posteriori-Hypothesen
 Kapitel ML:IV IV. Statistische Lernverfahren Wahrscheinlichkeitsrechnung Bayes-Klassifikation Maximum-a-Posteriori-Hypothesen ML:IV-1 Statistical Learning c STEIN 2005-2011 Definition 1 (Zufallsexperiment,
Kapitel ML:IV IV. Statistische Lernverfahren Wahrscheinlichkeitsrechnung Bayes-Klassifikation Maximum-a-Posteriori-Hypothesen ML:IV-1 Statistical Learning c STEIN 2005-2011 Definition 1 (Zufallsexperiment,
Beispiel 6 (Einige Aufgaben zur Gleichverteilung)
 Beispiel 6 (Einige Aufgaben zur Gleichverteilung) Aufgabe (Anwendung der Chebyshev-Ungleichung) Sei X eine Zufallsvariable mit E(X) = µ und var(x) = σ a) Schätzen Sie die Wahrscheinlichkeit dafür, daß
Beispiel 6 (Einige Aufgaben zur Gleichverteilung) Aufgabe (Anwendung der Chebyshev-Ungleichung) Sei X eine Zufallsvariable mit E(X) = µ und var(x) = σ a) Schätzen Sie die Wahrscheinlichkeit dafür, daß
Einführung in die (induktive) Statistik
 Einführung in die (induktive) Statistik Typische Fragestellung der Statistik: Auf Grund einer Problemmodellierung sind wir interessiert an: Zufallsexperiment beschrieben durch ZV X. Problem: Verteilung
Einführung in die (induktive) Statistik Typische Fragestellung der Statistik: Auf Grund einer Problemmodellierung sind wir interessiert an: Zufallsexperiment beschrieben durch ZV X. Problem: Verteilung
Wichtige Definitionen und Aussagen
 Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Theorie Parameterschätzung Ausblick. Schätzung. Raimar Sandner. Studentenseminar "Statistische Methoden in der Physik"
 Studentenseminar "Statistische Methoden in der Physik" Gliederung 1 2 3 Worum geht es hier? Gliederung 1 2 3 Stichproben Gegeben eine Beobachtungsreihe x = (x 1, x 2,..., x n ): Realisierung der n-dimensionalen
Studentenseminar "Statistische Methoden in der Physik" Gliederung 1 2 3 Worum geht es hier? Gliederung 1 2 3 Stichproben Gegeben eine Beobachtungsreihe x = (x 1, x 2,..., x n ): Realisierung der n-dimensionalen
Einführung in die Statistik
 Einführung in die Statistik 1. Deskriptive Statistik 2. Induktive Statistik 1. Deskriptive Statistik 1.0 Grundbegriffe 1.1 Skalenniveaus 1.2 Empirische Verteilungen 1.3 Mittelwerte 1.4 Streuungsmaße 1.0
Einführung in die Statistik 1. Deskriptive Statistik 2. Induktive Statistik 1. Deskriptive Statistik 1.0 Grundbegriffe 1.1 Skalenniveaus 1.2 Empirische Verteilungen 1.3 Mittelwerte 1.4 Streuungsmaße 1.0
6. Schätzverfahren für Parameter
 6. Schätzverfahren für Parameter Ausgangssituation: Ein interessierender Zufallsvorgang werde durch die ZV X repräsentiert X habe eine unbekannte Verteilungsfunktion F X (x) Wir interessieren uns für einen
6. Schätzverfahren für Parameter Ausgangssituation: Ein interessierender Zufallsvorgang werde durch die ZV X repräsentiert X habe eine unbekannte Verteilungsfunktion F X (x) Wir interessieren uns für einen
Entscheidungs theorie
 Helmut Laux Entscheidungs theorie Sechste, durchgesehene Auflage Mit 95 Abbildungen 4y Springer Inhalts verzeichni s Vorwort Überblick V IX XXI TEILA: EINFÜHRUNG 1 I. Probleme und Lösungskonzepte der Entscheidungstheorie
Helmut Laux Entscheidungs theorie Sechste, durchgesehene Auflage Mit 95 Abbildungen 4y Springer Inhalts verzeichni s Vorwort Überblick V IX XXI TEILA: EINFÜHRUNG 1 I. Probleme und Lösungskonzepte der Entscheidungstheorie
Seminararbeit zur Spieltheorie. Thema: Rationalisierbarkeit und Wissen
 Seminararbeit zur Spieltheorie Thema: Rationalisierbarkeit und Wissen Westfälische-Wilhelms-Universität Münster Mathematisches Institut Dozent: Prof. Dr. Löwe Verfasst von: Maximilian Mümken Sommersemester
Seminararbeit zur Spieltheorie Thema: Rationalisierbarkeit und Wissen Westfälische-Wilhelms-Universität Münster Mathematisches Institut Dozent: Prof. Dr. Löwe Verfasst von: Maximilian Mümken Sommersemester
Grundlagen der Wahrscheinlichkeitstheorie
 Priv.-Doz. Dr. H. Steinacker Wintersemester 2013/2014 Grundlagen der Wahrscheinlichkeitstheorie betrachte Wiederholungen eines Experimentes, gleicher Vorbereitung (z.b. Würfeln, Dart werfen, Doppelspaltexperiment,...)
Priv.-Doz. Dr. H. Steinacker Wintersemester 2013/2014 Grundlagen der Wahrscheinlichkeitstheorie betrachte Wiederholungen eines Experimentes, gleicher Vorbereitung (z.b. Würfeln, Dart werfen, Doppelspaltexperiment,...)
Grundzüge der. Kapitel 5 Mikroökonomie (Mikro I) Entscheidungen unter Unsicherheit
 Grundzüge der Kapitel 5 Mikroökonomie (Mikro I) Entscheidungen unter Unsicherheit 1 BESCHREIBUNG VON RISIKO 2 Entscheidung unter Risiko Annahme: Wir kennen alle möglichen (sich gegenseitig ausschliessenden)
Grundzüge der Kapitel 5 Mikroökonomie (Mikro I) Entscheidungen unter Unsicherheit 1 BESCHREIBUNG VON RISIKO 2 Entscheidung unter Risiko Annahme: Wir kennen alle möglichen (sich gegenseitig ausschliessenden)
Vergleich von Entscheidungsträgern bzgl. ihrer Risikoaversion:
 Ist das Arrow-Pratt-Maß der absoluten Risikoaversion bekannt, so lässt sich daraus die Nutzenfunktion bestimmen: Mithilfe der Substitution y := U (w) dy = U (w)dw gilt: und daher U (w) U (w) dw = A a (w)dw
Ist das Arrow-Pratt-Maß der absoluten Risikoaversion bekannt, so lässt sich daraus die Nutzenfunktion bestimmen: Mithilfe der Substitution y := U (w) dy = U (w)dw gilt: und daher U (w) U (w) dw = A a (w)dw
2 Die Dimension eines Vektorraums
 2 Die Dimension eines Vektorraums Sei V ein K Vektorraum und v 1,..., v r V. Definition: v V heißt Linearkombination der Vektoren v 1,..., v r falls es Elemente λ 1,..., λ r K gibt, so dass v = λ 1 v 1
2 Die Dimension eines Vektorraums Sei V ein K Vektorraum und v 1,..., v r V. Definition: v V heißt Linearkombination der Vektoren v 1,..., v r falls es Elemente λ 1,..., λ r K gibt, so dass v = λ 1 v 1
4 ZU V5"4. Er wart ungsnut zenhyp ot hese. Dogmenhistorische Ausgangslage, analytische Voraussetzungen und moderne Entwicklungen
 4 ZU V5"4 Er wart ungsnut zenhyp ot hese Dogmenhistorische Ausgangslage, analytische Voraussetzungen und moderne Entwicklungen Vorwort 15 1.1 Zufall und die Erwartungsnutzentheorie 16 1.2 Inhalt und Fortgang
4 ZU V5"4 Er wart ungsnut zenhyp ot hese Dogmenhistorische Ausgangslage, analytische Voraussetzungen und moderne Entwicklungen Vorwort 15 1.1 Zufall und die Erwartungsnutzentheorie 16 1.2 Inhalt und Fortgang
7.5 Erwartungswert, Varianz
 7.5 Erwartungswert, Varianz Def. 7.5.: a) X sei eine diskrete ZV, die bei unendl. vielen Werten x k folgende Zusatzbedingung erfüllt: x k p k
7.5 Erwartungswert, Varianz Def. 7.5.: a) X sei eine diskrete ZV, die bei unendl. vielen Werten x k folgende Zusatzbedingung erfüllt: x k p k
Donnerstag, 11. Dezember 03 Satz 2.2 Der Name Unterraum ist gerechtfertigt, denn jeder Unterraum U von V ist bzgl.
 Unterräume und Lineare Hülle 59 3. Unterräume und Lineare Hülle Definition.1 Eine Teilmenge U eines R-Vektorraums V heißt von V, wenn gilt: Unterraum (U 1) 0 U. (U ) U + U U, d.h. x, y U x + y U. (U )
Unterräume und Lineare Hülle 59 3. Unterräume und Lineare Hülle Definition.1 Eine Teilmenge U eines R-Vektorraums V heißt von V, wenn gilt: Unterraum (U 1) 0 U. (U ) U + U U, d.h. x, y U x + y U. (U )
Dieses Vielfach hängt ab von der Form der Nutzenfunktion. Man bezeichnet dies auch als Arrow-Pratt Koeffizient.
 Die Riskoprämie ergibt sich also als ein Vielfaches der Varianz der zugrundeliegenden Unsicherheit Dieses Vielfach hängt ab von der Form der Nutzenfunktion. Man bezeichnet dies auch als Arrow-Pratt Koeffizient.
Die Riskoprämie ergibt sich also als ein Vielfaches der Varianz der zugrundeliegenden Unsicherheit Dieses Vielfach hängt ab von der Form der Nutzenfunktion. Man bezeichnet dies auch als Arrow-Pratt Koeffizient.
Bildverarbeitung: Filterung. D. Schlesinger () Bildverarbeitung: Filterung 1 / 17
 Bildverarbeitung: Filterung D. Schlesinger () Bildverarbeitung: Filterung 1 / 17 Allgemeines Klassische Anwendung: Entrauschung (Fast) jeder Filter basiert auf einem Modell (Annahme): Signal + Rauschen
Bildverarbeitung: Filterung D. Schlesinger () Bildverarbeitung: Filterung 1 / 17 Allgemeines Klassische Anwendung: Entrauschung (Fast) jeder Filter basiert auf einem Modell (Annahme): Signal + Rauschen
Grundzüge der Spieltheorie
 Grundzüge der Spieltheorie Prof. Dr. Stefan Winter Ruhr-Universität Bochum Begleitmaterialien zur Vorlesung sind abrufbar unter: http://www.rub.de/spieltheorie 1 Die folgende Vorlesungsaufzeichnung und
Grundzüge der Spieltheorie Prof. Dr. Stefan Winter Ruhr-Universität Bochum Begleitmaterialien zur Vorlesung sind abrufbar unter: http://www.rub.de/spieltheorie 1 Die folgende Vorlesungsaufzeichnung und
Allgemeines zu Tests. Statistische Hypothesentests
 Statistische Hypothesentests Allgemeines zu Tests Allgemeines Tests in normalverteilten Grundgesamtheiten Asymptotische Tests Statistischer Test: Verfahren Entscheidungsregel), mit dem auf Basis einer
Statistische Hypothesentests Allgemeines zu Tests Allgemeines Tests in normalverteilten Grundgesamtheiten Asymptotische Tests Statistischer Test: Verfahren Entscheidungsregel), mit dem auf Basis einer
Tutorium in Investition und Finanzierung Entscheidungstheorie
 Tutorium in Investition und Finanzierung Entscheidungstheorie Kathrin Holtze, Simon Funken, Sascha Schworm finance-tutorien@wiwi.uni-wuppertal.de Lehrstuhl für Finanzwirtschaft und Corporate Governance
Tutorium in Investition und Finanzierung Entscheidungstheorie Kathrin Holtze, Simon Funken, Sascha Schworm finance-tutorien@wiwi.uni-wuppertal.de Lehrstuhl für Finanzwirtschaft und Corporate Governance
Mathematische Statistik Aufgaben zum Üben. Schätzer
 Prof. Dr. Z. Kabluchko Wintersemester 2016/17 Philipp Godland 14. November 2016 Mathematische Statistik Aufgaben zum Üben Keine Abgabe Aufgabe 1 Schätzer Es seien X 1,..., X n unabhängige und identisch
Prof. Dr. Z. Kabluchko Wintersemester 2016/17 Philipp Godland 14. November 2016 Mathematische Statistik Aufgaben zum Üben Keine Abgabe Aufgabe 1 Schätzer Es seien X 1,..., X n unabhängige und identisch
Grundbegriffe der Wahrscheinlichkeitsrechnung
 Algorithmen und Datenstrukturen 349 A Grundbegriffe der Wahrscheinlichkeitsrechnung Für Entwurf und Analyse randomisierter Algorithmen sind Hilfsmittel aus der Wahrscheinlichkeitsrechnung erforderlich.
Algorithmen und Datenstrukturen 349 A Grundbegriffe der Wahrscheinlichkeitsrechnung Für Entwurf und Analyse randomisierter Algorithmen sind Hilfsmittel aus der Wahrscheinlichkeitsrechnung erforderlich.
Rational Choice Theory
 Rational Choice Theory Rational Choice and Rationale Entscheidung ist eine Sammelbezeichnung für verschiedene Ansätze in den Wirtschafts- und Sozialwissenschaften. Generell schreiben diese Ansätze handelnden
Rational Choice Theory Rational Choice and Rationale Entscheidung ist eine Sammelbezeichnung für verschiedene Ansätze in den Wirtschafts- und Sozialwissenschaften. Generell schreiben diese Ansätze handelnden
Kapitel 2: Entscheidungstheorie
 Kapitel 2: Entscheidungstheorie 2.1 Einleitung Wie schon im Modulararbeitsbuch angegeben, wollen wir im zweiten Kapitel die Problemgebiete behandeln, die sich auf folgende Situationen beziehen: 2.2 Entscheidungen
Kapitel 2: Entscheidungstheorie 2.1 Einleitung Wie schon im Modulararbeitsbuch angegeben, wollen wir im zweiten Kapitel die Problemgebiete behandeln, die sich auf folgende Situationen beziehen: 2.2 Entscheidungen
3.2.5 Dualität der linearen Optimierung I
 3..5 Dualität der linearen Optimierung I Jedem linearen Programm in Standardform kann ein sogenanntes duales Programm zugeordnet werden. Es entsteht dadurch, daß man von einem Minimierungsproblem zu einem
3..5 Dualität der linearen Optimierung I Jedem linearen Programm in Standardform kann ein sogenanntes duales Programm zugeordnet werden. Es entsteht dadurch, daß man von einem Minimierungsproblem zu einem
Dualitätssätze der linearen Optimierung
 Kapitel 9 Dualitätssätze der linearen Optimierung Sei z = c T x min! Ax = b 9.1 x 0 mit c, x R n, b R m, A R m n ein lineares Programm. Definition 9.1 Duales lineares Programm. Das lineare Programm z =
Kapitel 9 Dualitätssätze der linearen Optimierung Sei z = c T x min! Ax = b 9.1 x 0 mit c, x R n, b R m, A R m n ein lineares Programm. Definition 9.1 Duales lineares Programm. Das lineare Programm z =
Historische Renditen, Experteninterviews, Analyse von Marktpreisen
 1 Portfoliotheorie 1.1 Grundlagen der Portfoliotheorie 1.1.1 Welche vier grundsätzlichen Anlageziele werden von Investoren verfolgt? Minimales Risiko Liquidation wenn nötig Hohe Rendite Gewinnmaximierung
1 Portfoliotheorie 1.1 Grundlagen der Portfoliotheorie 1.1.1 Welche vier grundsätzlichen Anlageziele werden von Investoren verfolgt? Minimales Risiko Liquidation wenn nötig Hohe Rendite Gewinnmaximierung
Risikomessung mit dem Conditional Value-at-Risk
 Jendrik Hanisch Risikomessung mit dem Conditional Value-at-Risk Implikationen für das Entscheidungsverhalten. Bibliothek j k Mit einem Geleitwort von \* \, -^ Prof. Dr. Wolfgang Kürsten A; Verlag Dr. Kovac
Jendrik Hanisch Risikomessung mit dem Conditional Value-at-Risk Implikationen für das Entscheidungsverhalten. Bibliothek j k Mit einem Geleitwort von \* \, -^ Prof. Dr. Wolfgang Kürsten A; Verlag Dr. Kovac
Universität Potsdam Institut für Informatik Lehrstuhl Maschinelles Lernen. Bayes sches Lernen. Niels Landwehr
 Universität Potsdam Institut für Informatik Lehrstuhl Maschinelles Lernen Bayes sches Lernen Niels Landwehr Überblick Grundkonzepte des Bayes schen Lernens Wahrscheinlichstes Modell gegeben Daten Münzwürfe
Universität Potsdam Institut für Informatik Lehrstuhl Maschinelles Lernen Bayes sches Lernen Niels Landwehr Überblick Grundkonzepte des Bayes schen Lernens Wahrscheinlichstes Modell gegeben Daten Münzwürfe
und Investition Finanzierung R. Verlag München Wien an der Freien Universität Von Dr. Lutz Kruschwitz Professor für Betriebswirtschaftslehre
 Finanzierung und Investition Von Dr. Lutz Kruschwitz Professor für Betriebswirtschaftslehre an der Freien Universität 4., überarbeitete und erweiterte Auflage R. Verlag München Wien 1 Einmalige sichere
Finanzierung und Investition Von Dr. Lutz Kruschwitz Professor für Betriebswirtschaftslehre an der Freien Universität 4., überarbeitete und erweiterte Auflage R. Verlag München Wien 1 Einmalige sichere
Kapitel III. Aufbau des Zahlensystems
 Kapitel III. Aufbau des Zahlensystems 1 Addition und Multiplikation natürlicher Zahlen Wir wollen erklären, wie man natürliche Zahlen addiert und multipliziert und dabei nur den Begriff das Zählens verwenden.
Kapitel III. Aufbau des Zahlensystems 1 Addition und Multiplikation natürlicher Zahlen Wir wollen erklären, wie man natürliche Zahlen addiert und multipliziert und dabei nur den Begriff das Zählens verwenden.
Implizite Funktionen, der Umkehrsatz und Extrema unter Nebenbedingungen
 Kapitel XII Implizite Funktionen, der Umkehrsatz und Extrema unter Nebenbedingungen 53 Implizite Funktionen und allgemeine partielle Differenzierbarkeit 54 Der Umkehrsatz 55 Lokale Extrema unter Nebenbedingungen,
Kapitel XII Implizite Funktionen, der Umkehrsatz und Extrema unter Nebenbedingungen 53 Implizite Funktionen und allgemeine partielle Differenzierbarkeit 54 Der Umkehrsatz 55 Lokale Extrema unter Nebenbedingungen,
1 Axiomatische Charakterisierung der reellen. 3 Die natürlichen, die ganzen und die rationalen. 4 Das Vollständigkeitsaxiom und irrationale
 Kapitel I Reelle Zahlen 1 Axiomatische Charakterisierung der reellen Zahlen R 2 Angeordnete Körper 3 Die natürlichen, die ganzen und die rationalen Zahlen 4 Das Vollständigkeitsaxiom und irrationale Zahlen
Kapitel I Reelle Zahlen 1 Axiomatische Charakterisierung der reellen Zahlen R 2 Angeordnete Körper 3 Die natürlichen, die ganzen und die rationalen Zahlen 4 Das Vollständigkeitsaxiom und irrationale Zahlen
Wahrscheinlichkeitsrechnung
 Statistik und Wahrscheinlichkeitsrechnung Prof. Dr. Michael Havbro Faber 28.05.2009 1 Korrektur zur letzten Vorlesung Bsp. Fehlerfortpflanzung in einer Messung c B a 2 2 E c Var c a b A b 2 2 2 n h( x)
Statistik und Wahrscheinlichkeitsrechnung Prof. Dr. Michael Havbro Faber 28.05.2009 1 Korrektur zur letzten Vorlesung Bsp. Fehlerfortpflanzung in einer Messung c B a 2 2 E c Var c a b A b 2 2 2 n h( x)
I Grundbegriffe 1 1 Wahrscheinlichkeitsräume Bedingte Wahrscheinlichkeiten und Unabhängigkeit Reellwertige Zufallsvariablen...
 Inhaltsverzeichnis I Grundbegriffe 1 1 Wahrscheinlichkeitsräume......................... 1 2 Bedingte Wahrscheinlichkeiten und Unabhängigkeit........... 7 3 Reellwertige Zufallsvariablen........................
Inhaltsverzeichnis I Grundbegriffe 1 1 Wahrscheinlichkeitsräume......................... 1 2 Bedingte Wahrscheinlichkeiten und Unabhängigkeit........... 7 3 Reellwertige Zufallsvariablen........................
2 Wiederholung statistischer Grundlagen Schließende Statistik empirischen Information aus Stichprobenrealisation x von X
 Hypothesentests Bisher betrachtet: Punkt- bzw. Intervallschätzung des unbekannten Mittelwerts Hierzu: Verwendung der 1 theoretischen Information über Verteilung von X empirischen Information aus Stichprobenrealisation
Hypothesentests Bisher betrachtet: Punkt- bzw. Intervallschätzung des unbekannten Mittelwerts Hierzu: Verwendung der 1 theoretischen Information über Verteilung von X empirischen Information aus Stichprobenrealisation
Fachbuchreihe für Studium Fortbildung Praxis. Rehkugler/Schindel. Entscheidungstheorie. Erklärung und Gestaltung betrieblicher Entscheidungen
 Fachbuchreihe für Studium Fortbildung Praxis Rehkugler/Schindel Erklärung und Gestaltung betrieblicher Entscheidungen 3. Auflage, München 1986 53 INHALT Seite EINFÜHRUNG 11 1. Was ist? 11 2. Wege entscheidungstheoretischer
Fachbuchreihe für Studium Fortbildung Praxis Rehkugler/Schindel Erklärung und Gestaltung betrieblicher Entscheidungen 3. Auflage, München 1986 53 INHALT Seite EINFÜHRUNG 11 1. Was ist? 11 2. Wege entscheidungstheoretischer
13 Mehrdimensionale Zufallsvariablen Zufallsvektoren
 3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
13 Auswahlaxiom und Zornsches Lemma
 13 Auswahlaxiom und Zornsches Lemma Handout zur Funktionalanalysis I von H. Glöckner, 25.11.2008 Wichtige Teile der modernen Mathematik beruhen auf dem sogenannten Auswahlaxiom der Mengenlehre. Dieses
13 Auswahlaxiom und Zornsches Lemma Handout zur Funktionalanalysis I von H. Glöckner, 25.11.2008 Wichtige Teile der modernen Mathematik beruhen auf dem sogenannten Auswahlaxiom der Mengenlehre. Dieses
4. Verteilungen von Funktionen von Zufallsvariablen
 4. Verteilungen von Funktionen von Zufallsvariablen Allgemeine Problemstellung: Gegeben sei die gemeinsame Verteilung der ZV en X 1,..., X n (d.h. bekannt seien f X1,...,X n bzw. F X1,...,X n ) Wir betrachten
4. Verteilungen von Funktionen von Zufallsvariablen Allgemeine Problemstellung: Gegeben sei die gemeinsame Verteilung der ZV en X 1,..., X n (d.h. bekannt seien f X1,...,X n bzw. F X1,...,X n ) Wir betrachten
3.4 Asymptotische Evaluierung von Sch atzer Konsistenz Konsistenz Definition 3.4.1: konsistente Folge von Sch atzer
 3.4 Asymptotische Evaluierung von Schätzer 3.4.1 Konsistenz Bis jetzt haben wir Kriterien basierend auf endlichen Stichproben betrachtet. Konsistenz ist ein asymptotisches Kriterium (n ) und bezieht sich
3.4 Asymptotische Evaluierung von Schätzer 3.4.1 Konsistenz Bis jetzt haben wir Kriterien basierend auf endlichen Stichproben betrachtet. Konsistenz ist ein asymptotisches Kriterium (n ) und bezieht sich
1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, Annahmen:
 1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }. Annahmen: Der Entscheidungsträger ist gezwungen, eine der betrachteten
1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }. Annahmen: Der Entscheidungsträger ist gezwungen, eine der betrachteten
Klassifikation von Signifikanztests
 Klassifikation von Signifikanztests nach Verteilungsannahmen: verteilungsabhängige = parametrische Tests verteilungsunabhängige = nichtparametrische Tests Bei parametrischen Tests werden im Modell Voraussetzungen
Klassifikation von Signifikanztests nach Verteilungsannahmen: verteilungsabhängige = parametrische Tests verteilungsunabhängige = nichtparametrische Tests Bei parametrischen Tests werden im Modell Voraussetzungen
Einfaktorielle Varianzanalyse
 Kapitel 16 Einfaktorielle Varianzanalyse Im Zweistichprobenproblem vergleichen wir zwei Verfahren miteinander. Nun wollen wir mehr als zwei Verfahren betrachten, wobei wir unverbunden vorgehen. Beispiel
Kapitel 16 Einfaktorielle Varianzanalyse Im Zweistichprobenproblem vergleichen wir zwei Verfahren miteinander. Nun wollen wir mehr als zwei Verfahren betrachten, wobei wir unverbunden vorgehen. Beispiel
Kapitel 1.5 und 1.6. Ein adäquater Kalkül der Aussagenlogik
 Kapitel 1.5 und 1.6 Ein adäquater Kalkül der Aussagenlogik Teil 1: Kalküle und Beweisbarkeit und die Korrektheit des Shoenfield-Kalküls Mathematische Logik (WS 2010/11) Kapitel 1.5 und 1.6: Kalküle 1 /
Kapitel 1.5 und 1.6 Ein adäquater Kalkül der Aussagenlogik Teil 1: Kalküle und Beweisbarkeit und die Korrektheit des Shoenfield-Kalküls Mathematische Logik (WS 2010/11) Kapitel 1.5 und 1.6: Kalküle 1 /
DWT 2.3 Ankunftswahrscheinlichkeiten und Übergangszeiten 400/467 Ernst W. Mayr
 2. Ankunftswahrscheinlichkeiten und Übergangszeiten Bei der Analyse von Markov-Ketten treten oftmals Fragestellungen auf, die sich auf zwei bestimmte Zustände i und j beziehen: Wie wahrscheinlich ist es,
2. Ankunftswahrscheinlichkeiten und Übergangszeiten Bei der Analyse von Markov-Ketten treten oftmals Fragestellungen auf, die sich auf zwei bestimmte Zustände i und j beziehen: Wie wahrscheinlich ist es,
Erwartungswert, Umgebungswahrscheinlichkeiten und die Normalverteilung
 R. Brinkmann http://brinkmann-du.de Seite 5.05.0 Erwartungswert, Umgebungswahrscheinlichkeiten und die Normalverteilung Erwartungswert binomialverteilter Zufallsgrößen Wird ein Bernoulli- Versuch, bei
R. Brinkmann http://brinkmann-du.de Seite 5.05.0 Erwartungswert, Umgebungswahrscheinlichkeiten und die Normalverteilung Erwartungswert binomialverteilter Zufallsgrößen Wird ein Bernoulli- Versuch, bei
Statistische Tests. Kapitel Grundbegriffe. Wir betrachten wieder ein parametrisches Modell {P θ : θ Θ} und eine zugehörige Zufallsstichprobe
 Kapitel 4 Statistische Tests 4.1 Grundbegriffe Wir betrachten wieder ein parametrisches Modell {P θ : θ Θ} und eine zugehörige Zufallsstichprobe X 1,..., X n. Wir wollen nun die Beobachtung der X 1,...,
Kapitel 4 Statistische Tests 4.1 Grundbegriffe Wir betrachten wieder ein parametrisches Modell {P θ : θ Θ} und eine zugehörige Zufallsstichprobe X 1,..., X n. Wir wollen nun die Beobachtung der X 1,...,
Kapitel 5: Entscheidung unter Unsicherheit
 Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert
 Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert Beispiel für Konfidenzintervall Im Prinzip haben wir
Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert Beispiel für Konfidenzintervall Im Prinzip haben wir
Kapitel 8. Erwarteter Nutzen. Intertemporaler Nutzen für Mehrperioden-Entscheidungen
 Kapitel 8 Erwarteter Nutzen Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen / 27 Lernziele Nutzenfunktion zur Risikobewertung Erwarteter Nutzen Maße für Risikoaversion Indifferenzkurven
Kapitel 8 Erwarteter Nutzen Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen / 27 Lernziele Nutzenfunktion zur Risikobewertung Erwarteter Nutzen Maße für Risikoaversion Indifferenzkurven
Vorlesung 2: Risikopräferenzen im Zustandsraum
 Vorlesung 2: Risikopräferenzen im Zustandsraum Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie VL 2, FS 12 Risikopräferenzen im Zustandsraum 1/29 2.1 Motivation
Vorlesung 2: Risikopräferenzen im Zustandsraum Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie VL 2, FS 12 Risikopräferenzen im Zustandsraum 1/29 2.1 Motivation
Überblick: Entscheidungstheoretische Konzepte Seminar Online-Optimierung Diana Balbus
 Überblick: Entscheidungstheoretische Konzepte Seminar Online-Optimierung Diana Balbus Einleitung Ein Online-Algorithmus muss Ausgaben berechnen, ohne zukünftige Eingaben zu kennen. Für die Bewertung von
Überblick: Entscheidungstheoretische Konzepte Seminar Online-Optimierung Diana Balbus Einleitung Ein Online-Algorithmus muss Ausgaben berechnen, ohne zukünftige Eingaben zu kennen. Für die Bewertung von
Biomathematik für Mediziner, Klausur WS 1999/2000 Seite 1
 Biomathematik für Mediziner, Klausur WS 1999/2000 Seite 1 Aufgabe 1: Wieviele der folgenden Variablen sind quantitativ stetig? Schulnoten, Familienstand, Religion, Steuerklasse, Alter, Reaktionszeit, Fahrzeit,
Biomathematik für Mediziner, Klausur WS 1999/2000 Seite 1 Aufgabe 1: Wieviele der folgenden Variablen sind quantitativ stetig? Schulnoten, Familienstand, Religion, Steuerklasse, Alter, Reaktionszeit, Fahrzeit,
I. Grundlagen. I. Grundlagen 1. Entscheidungen unter Unsicherheit. 1. Entscheidungen unter Unsicherheit
 . Entscheidungen unter Unsicherheit I. Grundlagen. Entscheidungen unter Unsicherheit Elemente des Entscheidungsproblems eines Wirtschaftssubekts: Der Entscheidungsträger kann zwischen verschiedenen Aktionen
. Entscheidungen unter Unsicherheit I. Grundlagen. Entscheidungen unter Unsicherheit Elemente des Entscheidungsproblems eines Wirtschaftssubekts: Der Entscheidungsträger kann zwischen verschiedenen Aktionen
Einführung in die Maximum Likelihood Methodik
 in die Maximum Likelihood Methodik Thushyanthan Baskaran thushyanthan.baskaran@awi.uni-heidelberg.de Alfred Weber Institut Ruprecht Karls Universität Heidelberg Gliederung 1 2 3 4 2 / 31 Maximum Likelihood
in die Maximum Likelihood Methodik Thushyanthan Baskaran thushyanthan.baskaran@awi.uni-heidelberg.de Alfred Weber Institut Ruprecht Karls Universität Heidelberg Gliederung 1 2 3 4 2 / 31 Maximum Likelihood
LINEARE ALGEBRA II. FÜR PHYSIKER
 LINEARE ALGEBRA II FÜR PHYSIKER BÁLINT FARKAS 4 Rechnen mit Matrizen In diesem Kapitel werden wir zunächst die so genannten elementaren Umformungen studieren, die es ermöglichen eine Matrix auf besonders
LINEARE ALGEBRA II FÜR PHYSIKER BÁLINT FARKAS 4 Rechnen mit Matrizen In diesem Kapitel werden wir zunächst die so genannten elementaren Umformungen studieren, die es ermöglichen eine Matrix auf besonders
7.7 Spezielle diskrete Wahrscheinlichkeitsverteilungen
 7.7 Spezielle diskrete Wahrscheinlichkeitsverteilungen 7.7.1 Die Laplace-Verteilung Sei X eine gleich verteilte Zufallsvariable mit den Werten in der Menge Ω X = {x i R : i = 1,...,n}, d.h. f (x i = 1
7.7 Spezielle diskrete Wahrscheinlichkeitsverteilungen 7.7.1 Die Laplace-Verteilung Sei X eine gleich verteilte Zufallsvariable mit den Werten in der Menge Ω X = {x i R : i = 1,...,n}, d.h. f (x i = 1
Statistik I. 1. Klausur Wintersemester 2010/2011 Hamburg, Art der Anmeldung: STiNE FlexNow Zulassung unter Vorbehalt
 Statistik I 1. Klausur Wintersemester 2010/2011 Hamburg, 11.02.2011 BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN! Nachname:............................................................................ Vorname:.............................................................................
Statistik I 1. Klausur Wintersemester 2010/2011 Hamburg, 11.02.2011 BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN! Nachname:............................................................................ Vorname:.............................................................................
Verfeinerungen des Bayesianischen Nash Gleichgewichts
 Spieltheorie Sommersemester 007 Verfeinerungen des Bayesianischen Nash Gleichgewichts Das Bayesianische Nash Gleichgewicht für Spiele mit unvollständiger Information ist das Analogon zum Nash Gleichgewicht
Spieltheorie Sommersemester 007 Verfeinerungen des Bayesianischen Nash Gleichgewichts Das Bayesianische Nash Gleichgewicht für Spiele mit unvollständiger Information ist das Analogon zum Nash Gleichgewicht
Kapitel 6. Verteilungsparameter. 6.1 Der Erwartungswert Diskrete Zufallsvariablen
 Kapitel 6 Verteilungsparameter Wie bei einem Merkmal wollen wir nun die Lage und die Streuung der Verteilung einer diskreten Zufallsvariablen durch geeignete Maßzahlen beschreiben. Beginnen wir mit Maßzahlen
Kapitel 6 Verteilungsparameter Wie bei einem Merkmal wollen wir nun die Lage und die Streuung der Verteilung einer diskreten Zufallsvariablen durch geeignete Maßzahlen beschreiben. Beginnen wir mit Maßzahlen
Reelle Zufallsvariablen
 Kapitel 3 eelle Zufallsvariablen 3. Verteilungsfunktionen esultat aus der Maßtheorie: Zwischen der Menge aller W-Maße auf B, nennen wir sie W B ), und der Menge aller Verteilungsfunktionen auf, nennen
Kapitel 3 eelle Zufallsvariablen 3. Verteilungsfunktionen esultat aus der Maßtheorie: Zwischen der Menge aller W-Maße auf B, nennen wir sie W B ), und der Menge aller Verteilungsfunktionen auf, nennen
Pr[X t+1 = k] = Pr[X t+1 = k X t = i] Pr[X t = i], also. (q t+1 ) k = p ik (q t ) i, bzw. in Matrixschreibweise. q t+1 = q t P.
![Pr[X t+1 = k] = Pr[X t+1 = k X t = i] Pr[X t = i], also. (q t+1 ) k = p ik (q t ) i, bzw. in Matrixschreibweise. q t+1 = q t P. Pr[X t+1 = k] = Pr[X t+1 = k X t = i] Pr[X t = i], also. (q t+1 ) k = p ik (q t ) i, bzw. in Matrixschreibweise. q t+1 = q t P.](/thumbs/64/51976840.jpg) 2.2 Berechnung von Übergangswahrscheinlichkeiten Wir beschreiben die Situation zum Zeitpunkt t durch einen Zustandsvektor q t (den wir als Zeilenvektor schreiben). Die i-te Komponente (q t ) i bezeichnet
2.2 Berechnung von Übergangswahrscheinlichkeiten Wir beschreiben die Situation zum Zeitpunkt t durch einen Zustandsvektor q t (den wir als Zeilenvektor schreiben). Die i-te Komponente (q t ) i bezeichnet
Finanzierung und Investition
 Finanzierung und Investition 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Von Dr. Lutz Kruschwitz Professor für
Finanzierung und Investition 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Von Dr. Lutz Kruschwitz Professor für
Inhaltsverzeichnis. Inhalt Teil I: Beschreibende (Deskriptive) Statistik Seite. 1.0 Erste Begriffsbildungen Merkmale und Skalen 5
 Inhaltsverzeichnis Inhalt Teil I: Beschreibende (Deskriptive) Statistik Seite 1.0 Erste Begriffsbildungen 1 1.1 Merkmale und Skalen 5 1.2 Von der Urliste zu Häufigkeitsverteilungen 9 1.2.0 Erste Ordnung
Inhaltsverzeichnis Inhalt Teil I: Beschreibende (Deskriptive) Statistik Seite 1.0 Erste Begriffsbildungen 1 1.1 Merkmale und Skalen 5 1.2 Von der Urliste zu Häufigkeitsverteilungen 9 1.2.0 Erste Ordnung
Kardinalzahlen. Bemerkung. Eine unendliche Kardinalzahl α muss eine Limesordinalzahl sein. (Beweis zur Übung)
 Kardinalzahlen Kardinalzahlen sollen die Größe von Mengen messen, daher suchen wir eine Aussage der Form, dass jede Menge bijektiv auf eine Kardinalzahl abgebildet werden kann. Um eine brauchbare Theorie
Kardinalzahlen Kardinalzahlen sollen die Größe von Mengen messen, daher suchen wir eine Aussage der Form, dass jede Menge bijektiv auf eine Kardinalzahl abgebildet werden kann. Um eine brauchbare Theorie
Nochmal: Indifferenzwahrscheinlichkeiten und Nutzenfunktion Reihung: Selbständigkeit Erfolg Geschäftsführer Vorstandsassistent Insolvenz
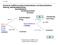 Nochmal: Indifferenzwahrscheinlichkeiten und Nutzenfunktion Reihung: Selbständigkeit Erfolg Geschäftsführer Vorstandsassistent Insolvenz Ref.-L.1: Selbst. Erfolg Sicher (300000) π = 1 1-π = 0 Selbständigkeit
Nochmal: Indifferenzwahrscheinlichkeiten und Nutzenfunktion Reihung: Selbständigkeit Erfolg Geschäftsführer Vorstandsassistent Insolvenz Ref.-L.1: Selbst. Erfolg Sicher (300000) π = 1 1-π = 0 Selbständigkeit
Kapitel 9. Schätzverfahren und Konfidenzintervalle. 9.1 Grundlagen zu Schätzverfahren
 Kapitel 9 Schätzverfahren und Konfidenzintervalle 9.1 Grundlagen zu Schätzverfahren Für eine Messreihe x 1,...,x n wird im Folgenden angenommen, dass sie durch n gleiche Zufallsexperimente unabhängig voneinander
Kapitel 9 Schätzverfahren und Konfidenzintervalle 9.1 Grundlagen zu Schätzverfahren Für eine Messreihe x 1,...,x n wird im Folgenden angenommen, dass sie durch n gleiche Zufallsexperimente unabhängig voneinander
Informatik II Grundbegriffe der Wahrscheinlichkeitsrechnung
 lausthal Begriffe Informatik II rundbegriffe der Wahrscheinlichkeitsrechnung. Zachmann lausthal University, ermany zach@in.tu-clausthal.de Definition: Unter einem Zufallsexperiment versteht man einen,
lausthal Begriffe Informatik II rundbegriffe der Wahrscheinlichkeitsrechnung. Zachmann lausthal University, ermany zach@in.tu-clausthal.de Definition: Unter einem Zufallsexperiment versteht man einen,
Carlheinrich Heiland WS 00/01 ABWL- Übungsaufgaben zum Abschnitt I Grundlagen und zum Abschnitt II Entscheidungstheorie Seite 1 von 14
 Seite 1 von 14 I./2. [1] Rationalprinzip a) Welche Handlungsweisen gibt das allgemeine Rationalprinzip vor übertragen auf wirtschaftliche Entscheidungen für die Fälle (1) der output ist fest vorgegeben;
Seite 1 von 14 I./2. [1] Rationalprinzip a) Welche Handlungsweisen gibt das allgemeine Rationalprinzip vor übertragen auf wirtschaftliche Entscheidungen für die Fälle (1) der output ist fest vorgegeben;
Die Funktion f X;Y (x; y) := Pr[X = x; Y = y] heit gemeinsame Dichte der Zufallsvariablen X und Y. Aus der gemeinsamen Dichte f X;Y kann man ableiten
![Die Funktion f X;Y (x; y) := Pr[X = x; Y = y] heit gemeinsame Dichte der Zufallsvariablen X und Y. Aus der gemeinsamen Dichte f X;Y kann man ableiten Die Funktion f X;Y (x; y) := Pr[X = x; Y = y] heit gemeinsame Dichte der Zufallsvariablen X und Y. Aus der gemeinsamen Dichte f X;Y kann man ableiten](/thumbs/71/64227736.jpg) Die Funktion f ;Y (x; y) := Pr[ = x; Y = y] heit gemeinsame Dichte der Zufallsvariablen und Y. Aus der gemeinsamen Dichte f ;Y kann man ableiten f (x) = y2w Y f ;Y (x; y) bzw. f Y (y) = Die Funktionen
Die Funktion f ;Y (x; y) := Pr[ = x; Y = y] heit gemeinsame Dichte der Zufallsvariablen und Y. Aus der gemeinsamen Dichte f ;Y kann man ableiten f (x) = y2w Y f ;Y (x; y) bzw. f Y (y) = Die Funktionen
Wird ein Bernoulli- Versuch, bei dem die Trefferwahrscheinlichkeit p = 0,2 ist, n = 40 mal durchgeführt, dann erwarten wir im Mittel 8 Treffer.
 R. Brinkmann http://brinkmann-du.de Seite 1 06.1008 Erwartungswert binomialverteilter Zufallsgrößen. Wird ein Bernoulli- Versuch, bei dem die Trefferwahrscheinlichkeit p = 0,2 ist, n = 40 mal durchgeführt,
R. Brinkmann http://brinkmann-du.de Seite 1 06.1008 Erwartungswert binomialverteilter Zufallsgrößen. Wird ein Bernoulli- Versuch, bei dem die Trefferwahrscheinlichkeit p = 0,2 ist, n = 40 mal durchgeführt,
