Kapitel 8. Erwarteter Nutzen. Intertemporaler Nutzen für Mehrperioden-Entscheidungen
|
|
|
- Klemens Feld
- vor 6 Jahren
- Abrufe
Transkript
1 Kapitel 8 Erwarteter Nutzen Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen / 27 Lernziele Nutzenfunktion zur Risikobewertung Erwarteter Nutzen Maße für Risikoaversion Indifferenzkurven in der σ 2 π e Ebene Intertemporaler Nutzen für Mehrperioden-Entscheidungen Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 2 / 27 Überblick Die Nutzentheorie wird hier auf Entscheidungen unter Unsicherheit angewandt. Sie dient auch zur Charakterisierung von Investoren. Der abnehmende Grenznutzen einer zusätzlichen Weinflasche (konkave Nutzenfunktion) wird hier einem risikoaversen Investor zugeschrieben. Ist der Beitrag der zweiten Weinflasche zum Nutzen größer als die erste (konvexe Nutzenfunktion), so werden wir sagen, der Investor ist risikofreudig. Dazwischen (die erste Flasche ist genauso gut wie die zweite) liegt Risikoneutralität. Konsumströme, die über mehrere Perioden verteilt sind, werden über einen diskontierten Nutzen bewertet. Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 3 / 27
2 Erwarteter Nutzen Wir bezeichnen mit U(W) den Nutzen des Vermögens W (wealth). Im Gegensatz zum deterministischen Fall ist W hier stochastisch, eine Zufallsvariable. Das bedeutet, W ist keine feste Zahl, sondern kann verschiedene Werte annehmen, die wir im Voraus nicht kennen. In einem Zeitpunkt ist W klein (Pech), manchmal ist W groß (Glück). Unsere Entscheidung wird nicht bezüglich des erwarteten (durchschnittlichen) Vermögens getroffen, sondern bezüglich des erwarteten (durchschnittlichen) Nutzens unseres Vermögens. E[U(W)] = U(w) P(w) w Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 4 / 27 Steigende Nutzenfunktion Wir wollen annehmen, dass eine Nutzenfunktion stets differenzierbar und streng monoton steigend ist. U (W) > 0 Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 5 / 27 Risikoneutralität und Risikoaversion Beispiel: Wir werfen eine perfekte Münze. Die Auszahlungen sind 2 c bei Kopf bzw. 0 c bei Zahl bei einem Spieleinsatz von c. Der erwartete monetäre Wert des (riskanten) Spiels ist c, also der Einsatz: = Der Wert, dieses Spiel nicht zu spielen, ist ebenfalls c (der Einsatz). Der risikoaverse Investor wird an diesem Spiel nicht teilnehmen. Es stehen den sicheren c, unsichere c (2 c bzw. 0 c je mit Wahrscheinlichkeit 2 ) gegenüber. Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 6 / 27
3 Risikoneutralität und Risikoaversion / (2) Unter Risikoaversion gilt U() > U(2) /2 + U(0) /2 d.h. U() U(0) > U(2) U() Die erste Ableitung nimmt ab. Risikoaversion impliziert daher U (W) < 0 Bei Risikoneutralität gilt das Gleichheitszeichen, U (W) = 0 Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 7 / 27 Nutzenfunktion: Unsicherheit und Risiko Übersicht: U (W) < 0 U (W) = 0 U (W) > 0 risikoavers risikoneutral Die Nutzenfunktion ist linear. risikofreudig Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 8 / 27 Risikoavers, Riskoneutral, Risikofreudig U(W) risikoavers U(2) U() risikoneutral risikofreudig U(0) 0 2 W Risikoavers: U() U(0) > U(2) U() Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 9 / 27
4 Maßzahlen für die Risikoaversion Das Arrow-Pratt Maß für die absolute Risikoaversion ist R A (W) = U (W)/U (W) Das Maß für die relative Risikoaversion ist R R (W) = R A (W) W Bei Risikoaversion sind R A (W) und R R (W) > 0. Je größer R A bzw. R R desto größer ist die Risikoaversion. Sie sind ein Maß dafür, wie sich die Risikopräferenzen mit steigendem W verändern. Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 0 / 27 Abnehmende Risikoaversion Abnehmende absolute Risikoaversion: Angenommen ein (risikoaverser) Investor mit c Vermögen hält c in riskanten Anlagen. Falls sein Vermögen um weitere c ansteigt und er dann davon mehr als c riskant zu veranlagen bereit ist, spricht man von abnehmender Risikoaversion. Abnehmende relative Risikoaversion: Angenommen ein (risikoaverser) Investor hält 50% von c in riskanten Anlagen. Falls sein Vermögen sich verdoppelt und er bereit ist den Anteil der riskanten Anlagen auf mehr als 50% zu erhöhen, spricht man von abnehmender relativer Risikoaversion. Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen / 27 U(W) = ln(w) Die Nutzenfunktion U(W) = ln(w) beschreibt Risikoaversion, U (W) < 0. U (W) = [ln(w)] = [/W] = /W 2 < 0 hat eine abnehmende absolute Risikoaversion. R A (W) = U (W)/U (W) = ( /W 2 )/(/W) = /W > 0 R A (W) = /W fällt mit W. hat eine konstante relative Risikoaversion. R W (W) = R A (W) W = (/W) W =. Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 2 / 27
5 U(W) = a b exp( cw) Die Nutzenfunktion U(W) = a b exp( cw), a, b, c > 0 beschreibt Risikoaversion. U (W) = [a b exp( cw)] = [ b exp( cw) ( c)] = = b c 2 exp( cw) Da b positiv, b > 0, ist U (W) < 0: Risikoaversion. hat eine konstante absolute Risikoaversion. R A (W) = U (W)/U (W) = (b c2 exp( cw) ( c)) ( b c exp( cw) ( c)) = c Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 3 / 27 Stochastisches Modell Das Vermögen W morgen (Zeitpunkt ) sei W = ( + π) W 0 Wobei W 0 das Vermögen im Zeitpunkt 0 bezeichnet, und π die ungewisse Rendite (stochastisch) von Zeitpunkt 0 bis : π = W/W 0. Die Rendite sei normalverteilt mit der Erwartung E(π) = π e und der Varianz V(π) = σπ 2. Schreibweise π N (π e, σπ 2 ). Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 4 / 27 Stochastisches Modell / Erwarteter Nutzen Die Maximierung des erwarteten Nutzens max W E[U(W)] = max E[a b exp( cw)] W ist in diesem Model äquivalent zur Maximierung von U(π e, σ 2 π) = π e c 2 σ2 π Bemerkung: Die Herleitung verwendet, dass exp( cw) (bedingt) lognormal-verteilt ist. Für π e wird später die Bezeichnung µ verwendet werden, für σ 2 π nur σ2. Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 5 / 27
6 Nutzenfunktion in π e und σ 2 π Wir beschränken uns auf Nutzenfunktionen, die sich als Funktion der erwarteten Rendite, π e, und der Varianz der Rendite, σ 2 π, darstellen lassen: U = U(π e, σ 2 π) mit U > 0, U 2 < 0, U, U 22 < 0 U ist die partielle Ableitung nach π e, U 2 die partielle Ableitung nach σπ 2. U steht für [ 2 U/( π e ) 2 ], U 22 steht für [ 2 U/( σπ) 2 2 ]. Bemerkung: Die Funktion U(π e, σπ) 2 = π e c 2 σ2 π erfüllt für c > 0 nur die Bedingungen U > 0, U 2 < 0. (U, U 22 = 0) Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 6 / 27 Nutzenfunktion in π e und σ 2 π / (2) Der Nutzen steigt mit der erwarteten Rendite, fällt aber mit der Varianz (Risiko) in der Rendite. Für beide Argumente, π e und σπ 2, gelten abnehmende Grenznutzen. Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 7 / 27 Indifferenzkurven für U = U(π e, σ 2 π ) Eine Indifferenzkurve ist definiert als die Menge aller Punkte für die die Nutzenfunktion den gleichen Wert c aufweist. U(π e, σ 2 π ) = c Alle Kombinationen (π e, σ 2 π) auf einer Indifferenzkurve mit Niveau c, liefern denselben Nutzen mit dem Wert c. Der Investor ist indifferent zwischen diesen Kombinationen. Jede dieser Kombinationen ist für ihn gleich gut/schlecht. Die Nutzenfunktion wird in der Portfoliooptimierung verwendet werden. Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 8 / 27
7 Darstellung der Indifferenzkurve Wir stellen die Indifferenzkurven in der σ 2 π πe Ebene dar. σ 2 π wird hier auf der x Achse aufgetragen, πe auf der y Achse! Da der Wert der (Nutzen-)Funktion konstant ist, beschreibt U(π e, σ 2 π) = c eine (implizite) Funktion in 2 Variablen, π e und σ 2 π. Da wir die σ 2 π πe Ebene zugrunde legen, sehen wir π e als Funktion von σ 2 π an: πe = π e (σ 2 π ). Lage: Ein höheres π e bei konstantem σπ 2 erzeugt einen höheren Nutzen, da U > 0 ist. Daher verschieben sich die Indifferenzkurven bei steigendem Nutzen nach links oben. Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 9 / 27 Steigung und Krümmung der Indifferenzkurve Steigung: Für die Steigung dieser Kurve erhalten wir: dπ e dσ 2 π = U σ 2 π U π e = U 2 U = ( ) (+) = (+) Unsere Indifferenzkurven steigen für jede Wahl von c. Steigt σ 2 π, das Risiko, so muss das ein höheres πe ausgleichen. 2. Ableitung: Die zweite Ableitung der Indifferenzkurven ist durch die Angaben der Vorzeichen von U, U 2, U, U 22 noch nicht bestimmt. Unter Risikoaversion folgt, dass sie konvex bez. der Risiko- σ 2 Achse sein müssen. Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 20 / 27 Indifferenzkurve bei Risikoaversion π e I 2 U(I ) < U(I 2 ) I π e 2 B π e A σ 2 π σ 2 0 Investor verlangt in B eine größere Rendite für den gleichen Zuwachs an Risiko als in A. Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 2 / 27
8 Intertemporaler Nutzen Einige ökonomische Modelle gehen davon aus, dass ein Investor seinen Nutzen nur aus seinem Konsum, C, gewinnt. U = U(C t ), U (C t ) > 0, U (C t ) < 0 t ist ein Zeitindex: t = 0,, 2, 3,.... Die Nutzenfunktion ist ähnlich der risikoaversen. Die allgemeine intertemporale Lebensnutzenfunktion ist N ist das (fixe) Lebensalter. U N = U(C t, C t+,..., C t+n ) Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 22 / 27 Separable Nutzenfunktion Mathematisch einfacher ist die additiv separable Funktion mit einer konstanten, subjektiven Diskontrate 0 < δ < : U N = U(C t ) + δ U(C t+ ) δ n U(C t+n ) δ = + r r ist die subjektive Zeitpräferenzrate. (Meist ähnlich dem Marktzinssatz.) Der Nutzen in verschiedenen Perioden ist geeignet diskontiert direkt vergleichbar. Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 23 / 27 U(C) = a C d Eine einfache Form (vom Cobb-Douglas-Typ) mit a > 0 und 0 < d < ist: U(C t ) = a C d t U (C t ) = a ( d) C d t U (C t ) = a ( d) d C d t U(C t ) > 0, U (C t ) > 0, U (C t ) < 0 Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 24 / 27
9 U = C α 0 Cα 2 Eine andere einfache Form (vom Cobb-Douglas-Typ) mit 0 < α, α 2 < (meist α 2 < α ) ist: U = C α 0 Cα 2 Sie wird durch Logarithmierung separabel: ln(u) = α ln(c 0 ) + α 2 ln(c ) Die Indifferenzkurven können hier explizit angegeben werden; z.b. in der C 0 C Ebene. Sei Ū das fixierte Nutzenniveau, Ū = C α 0 Cα 2, dann kann nach C aufgelöst werden: C = Ū α 2 C α α 2 0 = (+) C α /α 2 0 Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 25 / 27 Intertemporale Indifferenzkurven / Beispiel C I I 0 C 0 Anwendungen: Mehrperioden-Investitionsentscheidungen, Mehrperioden-Konsumentscheidungen, Portfoliowahl. Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 26 / 27 Grenzrate der Substitution Die Grenzrate der Substitution des zukünftigen für den laufenden Konsum ist dc dc 0 U=Ū Der aktuelle Konsum ist C 0, der zukünftige C. Die Grenzrate gibt den Wert einer zusätzlichen Einheit vom heutigen Konsum in Einheiten des zukünftigen an. Sie ist die Steigung der Indifferenzkurve mit dem Niveau Ū. Beispiel: U = C α 0 Cα 2 dc dc 0 U=Ū = ( α α 2 ) Ū /α 2 C α /α Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen 27 / 27
Vorlesung 2: Risikopräferenzen im Zustandsraum
 Vorlesung 2: Risikopräferenzen im Zustandsraum Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie VL 2, FS 12 Risikopräferenzen im Zustandsraum 1/29 2.1 Motivation
Vorlesung 2: Risikopräferenzen im Zustandsraum Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie VL 2, FS 12 Risikopräferenzen im Zustandsraum 1/29 2.1 Motivation
Vergleich von Entscheidungsträgern bzgl. ihrer Risikoaversion:
 Ist das Arrow-Pratt-Maß der absoluten Risikoaversion bekannt, so lässt sich daraus die Nutzenfunktion bestimmen: Mithilfe der Substitution y := U (w) dy = U (w)dw gilt: und daher U (w) U (w) dw = A a (w)dw
Ist das Arrow-Pratt-Maß der absoluten Risikoaversion bekannt, so lässt sich daraus die Nutzenfunktion bestimmen: Mithilfe der Substitution y := U (w) dy = U (w)dw gilt: und daher U (w) U (w) dw = A a (w)dw
2.3 Kriterien der Entscheidungsfindung: Präferenzen
 .3 Kriterien der Entscheidungsfindung: Präferenzen Der Einfachheit halber beschränken wir uns auf n = ( zwei Güter). Annahme: Konsumenten können für sich herausfinden, ob sie x = ( x, ) dem Güterbündel
.3 Kriterien der Entscheidungsfindung: Präferenzen Der Einfachheit halber beschränken wir uns auf n = ( zwei Güter). Annahme: Konsumenten können für sich herausfinden, ob sie x = ( x, ) dem Güterbündel
Präferenzen und Nutzen. Kapitel 3. Präferenzrelationen. Präferenzrelationen. Präferenzen und Nutzen. Darstellung individueller Präferenzen
 Präferenzen und Nutzen Kapitel 3 Präferenzen und Nutzen Darstellung individueller Präferenzen Ordinale Ordnung vom Besten zum Schlechtesten Charakterisierung von Nutzenfunktionen Kardinale Ordnung, Alternativen
Präferenzen und Nutzen Kapitel 3 Präferenzen und Nutzen Darstellung individueller Präferenzen Ordinale Ordnung vom Besten zum Schlechtesten Charakterisierung von Nutzenfunktionen Kardinale Ordnung, Alternativen
2.4 Entscheidung bei Risiko
 2.4 Entscheidung bei Risiko Entscheidung bei Risiko nimmt an, dass für jeden Zustand S j seine Eintrittswahrscheinlichkeit P(S j ) bekannt ist Eintrittswahrscheinlichkeiten bestimmbar als statistische
2.4 Entscheidung bei Risiko Entscheidung bei Risiko nimmt an, dass für jeden Zustand S j seine Eintrittswahrscheinlichkeit P(S j ) bekannt ist Eintrittswahrscheinlichkeiten bestimmbar als statistische
Vorlesung 3: Risikoaversion
 Vorlesung 3: Risikoaversion Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 3 (FS 11) Risikoaversion 1 / 21 1. Modellrahmen In diesem Kapitel betrachten wir nur monetäre
Vorlesung 3: Risikoaversion Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 3 (FS 11) Risikoaversion 1 / 21 1. Modellrahmen In diesem Kapitel betrachten wir nur monetäre
Versicherungsökonomie Lösungshinweise zu dem Aufgabenblatt zu Vorlesung 4
 Georg Nöldeke Frühjahr 2012 Versicherungsökonomie Lösungshinweise zu dem Aufgabenblatt zu Vorlesung 4 1. Ist Individuum 1 risikoneutral, so ist u konstant. Insbesondere gilt also für beliebieg Allokationen
Georg Nöldeke Frühjahr 2012 Versicherungsökonomie Lösungshinweise zu dem Aufgabenblatt zu Vorlesung 4 1. Ist Individuum 1 risikoneutral, so ist u konstant. Insbesondere gilt also für beliebieg Allokationen
Nochmal: Indifferenzwahrscheinlichkeiten und Nutzenfunktion Reihung: Selbständigkeit Erfolg Geschäftsführer Vorstandsassistent Insolvenz
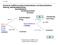 Nochmal: Indifferenzwahrscheinlichkeiten und Nutzenfunktion Reihung: Selbständigkeit Erfolg Geschäftsführer Vorstandsassistent Insolvenz Ref.-L.1: Selbst. Erfolg Sicher (300000) π = 1 1-π = 0 Selbständigkeit
Nochmal: Indifferenzwahrscheinlichkeiten und Nutzenfunktion Reihung: Selbständigkeit Erfolg Geschäftsführer Vorstandsassistent Insolvenz Ref.-L.1: Selbst. Erfolg Sicher (300000) π = 1 1-π = 0 Selbständigkeit
Kapitel 19: Technologie. moodle.tu-dortmund.de. Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 52
 Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 52 Kapitel 19: Technologie moodle.tu-dortmund.de Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 2 / 52 Outline Technologie mit
Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 52 Kapitel 19: Technologie moodle.tu-dortmund.de Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 2 / 52 Outline Technologie mit
IK Ökonomische Entscheidungen und Märkte
 IK Ökonomische Entscheidungen und Märkte LVA-Leiterin: Ana-Maria Vasilache Einheit 2: Haushaltstheorie (Kapitel 3) Verbraucherverhalten KonsumentInnen erwerben jene Güter,. die bei gegebenem Einkommen
IK Ökonomische Entscheidungen und Märkte LVA-Leiterin: Ana-Maria Vasilache Einheit 2: Haushaltstheorie (Kapitel 3) Verbraucherverhalten KonsumentInnen erwerben jene Güter,. die bei gegebenem Einkommen
Kapitel 5: Entscheidung unter Unsicherheit
 Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Wann ist diese Vorgehensweise berechtigt? Hierzu:
 IV. Risiko und Unsicherheit Risiko: Eine Entscheidung treffen, ohne den wahren Zustand der Welt zu kennen. Aber man kennt die Wahrscheinlichkeitsverteilung für die relevanten Zustände der Welt. z. B. {
IV. Risiko und Unsicherheit Risiko: Eine Entscheidung treffen, ohne den wahren Zustand der Welt zu kennen. Aber man kennt die Wahrscheinlichkeitsverteilung für die relevanten Zustände der Welt. z. B. {
IK Ökonomische Entscheidungen & Märkte
 LVA-Leiter: Martin Halla Einheit 4: Das Verbraucherverhalten (Kapitel 3) Einheit 4-1 - Verbraucherverhalten Budgetbeschränkung: Man kann nicht alles haben, was man sich wünscht! Konsumentenpräferenzen:
LVA-Leiter: Martin Halla Einheit 4: Das Verbraucherverhalten (Kapitel 3) Einheit 4-1 - Verbraucherverhalten Budgetbeschränkung: Man kann nicht alles haben, was man sich wünscht! Konsumentenpräferenzen:
I. Grundlagen. I. Grundlagen 1. Entscheidungen unter Unsicherheit. 1. Entscheidungen unter Unsicherheit
 . Entscheidungen unter Unsicherheit I. Grundlagen. Entscheidungen unter Unsicherheit Elemente des Entscheidungsproblems eines Wirtschaftssubekts: Der Entscheidungsträger kann zwischen verschiedenen Aktionen
. Entscheidungen unter Unsicherheit I. Grundlagen. Entscheidungen unter Unsicherheit Elemente des Entscheidungsproblems eines Wirtschaftssubekts: Der Entscheidungsträger kann zwischen verschiedenen Aktionen
Rationale Wahl aus Sicht des Wählenden optimal Abbildung/Modellierung von Präferenzen durch paarweisen Vergleich Präferenzrelation: math.
 Whd. Präferenzen Rationale Wahl aus Sicht des Wählenden optimal Abbildung/Modellierung von Präferenzen durch paarweisen Vergleich Präferenzrelation: math. Gebilde zur Darstellung des paarweisen Vergleiches
Whd. Präferenzen Rationale Wahl aus Sicht des Wählenden optimal Abbildung/Modellierung von Präferenzen durch paarweisen Vergleich Präferenzrelation: math. Gebilde zur Darstellung des paarweisen Vergleiches
16 Risiko und Versicherungsmärkte
 16 Risiko und Versicherungsmärkte Entscheidungen bei Unsicherheit sind Entscheidungen, die mehrere mögliche Auswirkungen haben. Kauf eines Lotterieloses Kauf einer Aktie Mitnahme eines Regenschirms Abschluss
16 Risiko und Versicherungsmärkte Entscheidungen bei Unsicherheit sind Entscheidungen, die mehrere mögliche Auswirkungen haben. Kauf eines Lotterieloses Kauf einer Aktie Mitnahme eines Regenschirms Abschluss
Aufgabe 1.3. Teil a) Teil b)
 Informationsökonomik: Anreize, Verträge, Institutionen L ösung Blatt 1 FT 2012 Aufgabe 1.3 Faire Prämie Versicherungen können nicht beobachten, welchen Typen sie vor sich haben, daher werden sie den Erwartungswert
Informationsökonomik: Anreize, Verträge, Institutionen L ösung Blatt 1 FT 2012 Aufgabe 1.3 Faire Prämie Versicherungen können nicht beobachten, welchen Typen sie vor sich haben, daher werden sie den Erwartungswert
IK Ökonomische Entscheidungen & Märkte
 M. Lackner (JKU Linz) IK ÖE&M E4, WS 2015/16 1 / 44 IK Ökonomische Entscheidungen & Märkte Mario Lackner JKU Linz Einheit 4, WS 2015/16 Das Verbraucherverhalten (Kap. 3) Verbraucherverhalten Bugetbeschränkung:
M. Lackner (JKU Linz) IK ÖE&M E4, WS 2015/16 1 / 44 IK Ökonomische Entscheidungen & Märkte Mario Lackner JKU Linz Einheit 4, WS 2015/16 Das Verbraucherverhalten (Kap. 3) Verbraucherverhalten Bugetbeschränkung:
Mikroökonomik für Wirtschaftsingenieure
 Mikroökonomik für Wirtschaftsingenieure Organisatorisches: Folien: Lehrstuhl für Politische Ökonomik & Empirische Wirtschaftsforschung: http://www.hsu-hh.de/berlemann/index_rmzpwqkjagkmopaq.html Agenda
Mikroökonomik für Wirtschaftsingenieure Organisatorisches: Folien: Lehrstuhl für Politische Ökonomik & Empirische Wirtschaftsforschung: http://www.hsu-hh.de/berlemann/index_rmzpwqkjagkmopaq.html Agenda
Monotonie, Konkavität und Extrema
 Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
Grundzüge der. Kapitel 5 Mikroökonomie (Mikro I) Entscheidungen unter Unsicherheit
 Grundzüge der Kapitel 5 Mikroökonomie (Mikro I) Entscheidungen unter Unsicherheit 1 BESCHREIBUNG VON RISIKO 2 Entscheidung unter Risiko Annahme: Wir kennen alle möglichen (sich gegenseitig ausschliessenden)
Grundzüge der Kapitel 5 Mikroökonomie (Mikro I) Entscheidungen unter Unsicherheit 1 BESCHREIBUNG VON RISIKO 2 Entscheidung unter Risiko Annahme: Wir kennen alle möglichen (sich gegenseitig ausschliessenden)
EV = (0, 2)(125) + (0, 3)(100) + (0, 5)(50) = 80.
 Mikroökonomie I Übungsaufgaben Erwartungsnutzen 1. Warum ist die Varianz ein besseres Maß der Variabilität als die Spannweite? Die Spannweite ist der Unterschied zwischen dem höchsten möglichen Ergebnis
Mikroökonomie I Übungsaufgaben Erwartungsnutzen 1. Warum ist die Varianz ein besseres Maß der Variabilität als die Spannweite? Die Spannweite ist der Unterschied zwischen dem höchsten möglichen Ergebnis
Taylorreihen. Kapitel 9. Lernziele. Taylorreihe. (x x 0 ) + f (x 0 ) 2! (x x 0 ) f (n) (x 0 ) (x x 0 ) n. Taylorreihe und MacLaurinreihe
 Kapitel 9 Taylorreihen Josef Leydold c 2006 Mathematische Methoden IX Taylorreihen 1 / 25 Lernziele Taylorreihe und MacLaurinreihe Beispiele Alternative Schreibweisen Approimation der Veränderung einer
Kapitel 9 Taylorreihen Josef Leydold c 2006 Mathematische Methoden IX Taylorreihen 1 / 25 Lernziele Taylorreihe und MacLaurinreihe Beispiele Alternative Schreibweisen Approimation der Veränderung einer
Übung zu Risiko und Versicherung Entscheidungstheoretische Grundlagen
 Übung zu Risiko Entscheidungstheoretische Grundlagen Stefan Neuß Sebastian Soika http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_203/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Übung zu Risiko Entscheidungstheoretische Grundlagen Stefan Neuß Sebastian Soika http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_203/bachelorveranstaltungen/risiko_und_versicherungen/index.html
5.2DasKriteriumdeserwartetenNutzens
 5.2DasKriteriumdeserwartetenNutzens BisherhabenwirunsichereSituationen beschrieben, jedoch noch nicht gesagt, wie die HaltunggegenüberRisikodasVerhaltenbeeinflußt.DieswerdenwirindiesemAbschnitt untersuchen.
5.2DasKriteriumdeserwartetenNutzens BisherhabenwirunsichereSituationen beschrieben, jedoch noch nicht gesagt, wie die HaltunggegenüberRisikodasVerhaltenbeeinflußt.DieswerdenwirindiesemAbschnitt untersuchen.
Übung zu Risiko und Versicherung Entscheidungstheoretische Grundlagen
 Übung zu Risiko Entscheidungstheoretische Grundlagen Christoph Lex Dominik Lohmaier http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_04/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Übung zu Risiko Entscheidungstheoretische Grundlagen Christoph Lex Dominik Lohmaier http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_04/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Lösungshinweise zu Übungsblatt 2
 Lösungshinweise zu Übungsblatt 2 Aufgabe 1: Unsicherheit Gegeben sei ein Individuum mit streng monoton steigender und konkaver von Neumann- Morgenstern Nutzenfunktion. a) Erklären Sie anhand einer geeigneten
Lösungshinweise zu Übungsblatt 2 Aufgabe 1: Unsicherheit Gegeben sei ein Individuum mit streng monoton steigender und konkaver von Neumann- Morgenstern Nutzenfunktion. a) Erklären Sie anhand einer geeigneten
Globalübung Mikroökonomie. Globalübung Mikroökonomie SoSe 2017, Linda Hirt-Schierbaum, Till Wagner 1 / 34
 Globalübung Mikroökonomie Globalübung Mikroökonomie SoSe 2017, Linda Hirt-Schierbaum, Till Wagner 1 / 34 Globalübung Mikroökonomie SoSe 2017, Linda Hirt-Schierbaum, Till Wagner 2 / 34 Kapitel 4: Nutzen
Globalübung Mikroökonomie Globalübung Mikroökonomie SoSe 2017, Linda Hirt-Schierbaum, Till Wagner 1 / 34 Globalübung Mikroökonomie SoSe 2017, Linda Hirt-Schierbaum, Till Wagner 2 / 34 Kapitel 4: Nutzen
Allgemeine Betriebswirtschaftslehre: Kapitalmarkt, Finanzierung und Investition SS 2009
 Allgemeine Betriebswirtschaftslehre: Kapitalmarkt, Finanzierung und Investition SS 2009 Vorlesung: Freitag 10-12, PD Dr. Dorothea Schäfer, Deutsches Institut für Wirtschaftsforschung (DIW) Übung 12-14
Allgemeine Betriebswirtschaftslehre: Kapitalmarkt, Finanzierung und Investition SS 2009 Vorlesung: Freitag 10-12, PD Dr. Dorothea Schäfer, Deutsches Institut für Wirtschaftsforschung (DIW) Übung 12-14
Kapitel 4 Nutzenmaximierung
 Kapitel 4 Nutzenmaximierung Vor- und Nachbereitung: Varian, Chapters 4 und 5 (mit Appendix) Frank, Chapter 3 (mit Appendix) Übungsblatt 4 Klaus M. Schmidt, 008 4.1 Die Nutzenfunktion Indifferenzkurven
Kapitel 4 Nutzenmaximierung Vor- und Nachbereitung: Varian, Chapters 4 und 5 (mit Appendix) Frank, Chapter 3 (mit Appendix) Übungsblatt 4 Klaus M. Schmidt, 008 4.1 Die Nutzenfunktion Indifferenzkurven
Konvexe Menge. Eine Menge D R n heißt konvex, wenn für zwei beliebige Punkte x, y D auch die Verbindungsstrecke dieser Punkte in D liegt, d.h.
 Konvexe Menge Eine Menge D R n heißt konvex, wenn für zwei beliebige Punkte x, y D auch die Verbindungsstrecke dieser Punkte in D liegt, dh Kapitel Extrema konvex: h x + h y D für alle h [0, ], und x,
Konvexe Menge Eine Menge D R n heißt konvex, wenn für zwei beliebige Punkte x, y D auch die Verbindungsstrecke dieser Punkte in D liegt, dh Kapitel Extrema konvex: h x + h y D für alle h [0, ], und x,
Kapitel 6: Die Nachfrage. moodle.tu-dortmund.de. Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 52
 Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 52 Kapitel 6: Die Nachfrage moodle.tu-dortmund.de Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 2 / 52 Outline normale und
Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 52 Kapitel 6: Die Nachfrage moodle.tu-dortmund.de Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 2 / 52 Outline normale und
Vorlesung 3: Versicherungsnachfrage
 Vorlesung 3: Versicherungsnachfrage Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie, FS 12 Versicherungsnachfrage 1/20 2 / 20 3. 1 Das Versicherungsnachfrageproblem
Vorlesung 3: Versicherungsnachfrage Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie, FS 12 Versicherungsnachfrage 1/20 2 / 20 3. 1 Das Versicherungsnachfrageproblem
Intermediate Microeconomics Lösungshinweise zu Aufgabenblatt 2
 Georg Nöldeke Herbstsemester 2011 Intermediate Microeconomics Lösungshinweise zu Aufgabenblatt 2 1. (a) Indifferenzkurven verlaufen streng fallend und streng konvex; Pfeile zeigen nach rechts-oben. Siehe
Georg Nöldeke Herbstsemester 2011 Intermediate Microeconomics Lösungshinweise zu Aufgabenblatt 2 1. (a) Indifferenzkurven verlaufen streng fallend und streng konvex; Pfeile zeigen nach rechts-oben. Siehe
2.6 Theorie des Haushalts
 .6 Theorie des Haushalts WS 007/08 Nutzenfunktionen und Indifferenzkurven Nutzenfunktion: Hilfsmittel, um Präferenzen zu beschreiben Eine Präferenzordnung lässt sich unter den obigen Annahmen über eine
.6 Theorie des Haushalts WS 007/08 Nutzenfunktionen und Indifferenzkurven Nutzenfunktion: Hilfsmittel, um Präferenzen zu beschreiben Eine Präferenzordnung lässt sich unter den obigen Annahmen über eine
Grundlagen der Versicherungs- und Sozialversicherungsökonomik. Risiko: objektive oder subjektive Wahrscheinlichkeiten
 Grundlagen der Versicherungs- und Sozialversicherungsökonomik Entscheidungstheorie bei Sicherheit (z. B. trad. Mikroökonomik, lineare Programmierung etc. bei Risiko (Unsicherheit und Ungewissheit Risiko:
Grundlagen der Versicherungs- und Sozialversicherungsökonomik Entscheidungstheorie bei Sicherheit (z. B. trad. Mikroökonomik, lineare Programmierung etc. bei Risiko (Unsicherheit und Ungewissheit Risiko:
Vertiefungsbox Nachfragekurve: Nutzen und Budget
 Vertiefungsbox Nachfragekurve: Nutzen und Budget Motivation In dieser Vertiefung wollen wir untersuchen, wie die individuelle Nachfrage kurve hergeleitet wird. Im Gegensatz zur Analyse der aggregierten
Vertiefungsbox Nachfragekurve: Nutzen und Budget Motivation In dieser Vertiefung wollen wir untersuchen, wie die individuelle Nachfrage kurve hergeleitet wird. Im Gegensatz zur Analyse der aggregierten
VWL 3: Mikroökonomie Lösungshinweise zu Aufgabenblatt 1
 Georg Nöldeke Frühjahrssemester 2009 VWL 3: Mikroökonomie Lösungshinweise zu Aufgabenblatt Siehe Abbildung x 2 m p = 25 2 Budgetgerade: { xpx + px 2 2 = m} Budgetmenge: { xpx + px 2 2 m} 0 0 m p = 20 x
Georg Nöldeke Frühjahrssemester 2009 VWL 3: Mikroökonomie Lösungshinweise zu Aufgabenblatt Siehe Abbildung x 2 m p = 25 2 Budgetgerade: { xpx + px 2 2 = m} Budgetmenge: { xpx + px 2 2 m} 0 0 m p = 20 x
IK Ökonomische Entscheidungen und Märkte LVA
 IK Ökonomische Entscheidungen und Märkte LVA LVA-Leiter: Michael Noldi Einheit 4: Das Verbraucherverhalten (Kap. 3) Verbraucherverhalten IK WS 2014/15 1 Verbraucherverhalten Bugetbeschränkung: Einkommen,
IK Ökonomische Entscheidungen und Märkte LVA LVA-Leiter: Michael Noldi Einheit 4: Das Verbraucherverhalten (Kap. 3) Verbraucherverhalten IK WS 2014/15 1 Verbraucherverhalten Bugetbeschränkung: Einkommen,
Makro II, Prof. Dr. T. Wollmershäuser. Kapitel 1-4 (Ausblick) Endogenes Wachstum und endogene Sparquote
 Makro II, Prof. Dr. T. Wollmershäuser Kapitel 1-4 (Ausblick) Endogenes Wachstum und endogene Sparquote Version: 22.11.2011 Endogene Wachstumstheorie Literatur N. Gregory Mankiw, Makroökonomik, 6. Auflage,
Makro II, Prof. Dr. T. Wollmershäuser Kapitel 1-4 (Ausblick) Endogenes Wachstum und endogene Sparquote Version: 22.11.2011 Endogene Wachstumstheorie Literatur N. Gregory Mankiw, Makroökonomik, 6. Auflage,
Einführung in die Volkswirtschaftslehre
 Einführung in die Volkswirtschaftslehre Übung zu Kapitel 2: Theorie des Haushalts Dipl.-Volksw. J.-E.Wesselhöft/ Dipl.-Volksw. J.Freese Bachelor WS-11-V-01.1 HT 2009 Dipl.-Volksw. J.-E.Wesselhöft/ Dipl.-Volksw.
Einführung in die Volkswirtschaftslehre Übung zu Kapitel 2: Theorie des Haushalts Dipl.-Volksw. J.-E.Wesselhöft/ Dipl.-Volksw. J.Freese Bachelor WS-11-V-01.1 HT 2009 Dipl.-Volksw. J.-E.Wesselhöft/ Dipl.-Volksw.
Vorlesung. Informationsökonomik und die Theorie der Firma
 Vorlesung Informationsökonomik und die Theorie der Firma Ulrich Schwalbe Universität Hohenheim 3. Vorlesung 14.11.2007 Ulrich Schwalbe (Universität Hohenheim) Informationsökonomik 3. Vorlesung 14.11.2007
Vorlesung Informationsökonomik und die Theorie der Firma Ulrich Schwalbe Universität Hohenheim 3. Vorlesung 14.11.2007 Ulrich Schwalbe (Universität Hohenheim) Informationsökonomik 3. Vorlesung 14.11.2007
Intermediate Microeconomics Lösungshinweise zu Aufgabenblatt 2
 Georg Nöldeke Herbstsemester 2010 Intermediate Microeconomics Lösungshinweise zu Aufgabenblatt 2 1. (a) Indifferenzkurven verlaufen streng fallend und streng konvex; Pfeile zeigen nach rechts-oben. Siehe
Georg Nöldeke Herbstsemester 2010 Intermediate Microeconomics Lösungshinweise zu Aufgabenblatt 2 1. (a) Indifferenzkurven verlaufen streng fallend und streng konvex; Pfeile zeigen nach rechts-oben. Siehe
Vorlesung 4: Risikoallokation
 Vorlesung 4: Risikoallokation Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie, FS 12 Risikoallokation 1/23 2 / 23 4.1 Einleitung Bisher haben wir uns ausschliesslich
Vorlesung 4: Risikoallokation Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie, FS 12 Risikoallokation 1/23 2 / 23 4.1 Einleitung Bisher haben wir uns ausschliesslich
Finanzwirtschaft. Foliensatz Vertiefungskurs aus ABWL: im Sommersemester Teil / 2 und 7 Univ. Ass. Dr. Matthias G.
 Universität Wien Institut für Betriebswirtschaftslehre ABWL IV: Finanzwirtschaft 400 026/2+7 Univ. Ass. Dr. M.G. Schuster Foliensatz Vertiefungskurs aus ABWL: Finanzwirtschaft im Sommersemester 2004 2.
Universität Wien Institut für Betriebswirtschaftslehre ABWL IV: Finanzwirtschaft 400 026/2+7 Univ. Ass. Dr. M.G. Schuster Foliensatz Vertiefungskurs aus ABWL: Finanzwirtschaft im Sommersemester 2004 2.
2. Theorie des Haushalts
 . Theorie des Haushalts. Konsumentenpräferenzen. Theorie des Haushalts Theorie des Verbraucherverhaltens Theorie des Faktorangebots Vorgehensweise in drei Schritten: ) Konsumentenpräferenzen ) Budgetrestriktion
. Theorie des Haushalts. Konsumentenpräferenzen. Theorie des Haushalts Theorie des Verbraucherverhaltens Theorie des Faktorangebots Vorgehensweise in drei Schritten: ) Konsumentenpräferenzen ) Budgetrestriktion
Kapitel 3: Präferenzen. moodle.tu-dortmund.de. Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 29
 Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 29 Kapitel 3: Präferenzen moodle.tu-dortmund.de Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 2 / 29 Präferenzordnung Die Konsumentscheidung
Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 29 Kapitel 3: Präferenzen moodle.tu-dortmund.de Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 2 / 29 Präferenzordnung Die Konsumentscheidung
IK Ökonomische Entscheidungen & Märkte ( )
 IK Ökonomische Entscheidungen & Märkte (239.255) SS 2008 LVA-Leiter: Andrea Kollmann Einheit 5: Kapitel 4.3-4.4, 6 Administratives Fragen zum IK??? Fragen zum Kurs??? Die Marktnachfrage Die Marktnachfragekurve
IK Ökonomische Entscheidungen & Märkte (239.255) SS 2008 LVA-Leiter: Andrea Kollmann Einheit 5: Kapitel 4.3-4.4, 6 Administratives Fragen zum IK??? Fragen zum Kurs??? Die Marktnachfrage Die Marktnachfragekurve
Allgemeine Volkswirtschaftslehre I für WiMA und andere (AVWL I)
 I WiMA und andere WS 007/08 Institut Wirtschaftswissenschaften www.mathematik.uni-ulm.de/wiwi/ . Grundzüge der Mikroökonomik WS 007/08.6 Theorie des Haushalts .6 Theorie des Haushalts WS 007/08 Haushaltstheorie
I WiMA und andere WS 007/08 Institut Wirtschaftswissenschaften www.mathematik.uni-ulm.de/wiwi/ . Grundzüge der Mikroökonomik WS 007/08.6 Theorie des Haushalts .6 Theorie des Haushalts WS 007/08 Haushaltstheorie
Übungsblatt 5. Aufgabe 36 (Budgetrestriktion)
 Friedrich-Schiller-Universität Jena Postfach D-7743 Jena BM Mikroökonomik Aufgabensammlung Übung/Tutorien WS 6/7 Prof. Dr. Uwe Cantner Wirtschaftswissenschaftliche Fakultät Lehrstuhl für Volkswirtschaftslehre/Mikroökonomik
Friedrich-Schiller-Universität Jena Postfach D-7743 Jena BM Mikroökonomik Aufgabensammlung Übung/Tutorien WS 6/7 Prof. Dr. Uwe Cantner Wirtschaftswissenschaftliche Fakultät Lehrstuhl für Volkswirtschaftslehre/Mikroökonomik
Mietinteressent A B C D E F G H Vorbehaltspreis a) Im Wettbewerbsgleichgewicht beträgt der Preis 250.
 Aufgabe 1 Auf einem Wohnungsmarkt werden 5 Wohnungen angeboten. Die folgende Tabelle gibt die Vorbehaltspreise der Mietinteressenten wieder: Mietinteressent A B C D E F G H Vorbehaltspreis 250 320 190
Aufgabe 1 Auf einem Wohnungsmarkt werden 5 Wohnungen angeboten. Die folgende Tabelle gibt die Vorbehaltspreise der Mietinteressenten wieder: Mietinteressent A B C D E F G H Vorbehaltspreis 250 320 190
Teil I: Konsumententheorie
 Teil I: Konsumententheorie 1 Kapitel 1: Präferenzen Hauptidee: Eine Konsumentscheidung kann als Wahl zwischen Güterbündeln modelliert werden, gemäß der Präferenzen des Konsumenten. Die Konzepte Indifferenzkurve,
Teil I: Konsumententheorie 1 Kapitel 1: Präferenzen Hauptidee: Eine Konsumentscheidung kann als Wahl zwischen Güterbündeln modelliert werden, gemäß der Präferenzen des Konsumenten. Die Konzepte Indifferenzkurve,
Einführung in die Finanzwirtschaft
 Platzhalter für Bild, Bild auf Titelfolie hinter das Logo einsetzen Einführung in die Finanzwirtschaft Prof. Dr. Marc Gürtler Gegenstand: Maßnahmen der Beschaffung und Verwendung monetärer Mittel im Rahmen
Platzhalter für Bild, Bild auf Titelfolie hinter das Logo einsetzen Einführung in die Finanzwirtschaft Prof. Dr. Marc Gürtler Gegenstand: Maßnahmen der Beschaffung und Verwendung monetärer Mittel im Rahmen
Vorkurs Mikroökonomik
 Vorkurs Mikroökonomik Das Haushaltsoptimum Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Das Haushaltsoptimum 1 / 27 Gliederung Einführung Haushaltstheorie Das Budget Präferenzen,
Vorkurs Mikroökonomik Das Haushaltsoptimum Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Das Haushaltsoptimum 1 / 27 Gliederung Einführung Haushaltstheorie Das Budget Präferenzen,
Kapitel 4: Nutzen. moodle.tu-dortmund.de. Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 46
 Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 46 Kapitel 4: Nutzen moodle.tu-dortmund.de Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 2 / 46 Outline Rangnummern und ordinale
Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 46 Kapitel 4: Nutzen moodle.tu-dortmund.de Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 2 / 46 Outline Rangnummern und ordinale
Übung 2: Konsumententheorie
 Übung 2: Konsumententheorie Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Intermediate Microeconomics HS 11 Übung 2 1 / 44 2 / 44 Präferenzen Aufgabe 1 Worum geht es? Annahmen
Übung 2: Konsumententheorie Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Intermediate Microeconomics HS 11 Übung 2 1 / 44 2 / 44 Präferenzen Aufgabe 1 Worum geht es? Annahmen
Einführung in die Finanzwirtschafti Einführung in die Finanzwirtschaft. Institut für Finanzwirtschaft Prof. Dr. Marc Gürtler 0
 Einführung in die Finanzwirtschafti Einführung in die Finanzwirtschaft Institut für Finanzwirtschaft Prof. Dr. Marc Gürtler Einführung in die Finanzwirtschafti Gegenstand: Maßnahmen der Beschaffung und
Einführung in die Finanzwirtschafti Einführung in die Finanzwirtschaft Institut für Finanzwirtschaft Prof. Dr. Marc Gürtler Einführung in die Finanzwirtschafti Gegenstand: Maßnahmen der Beschaffung und
VWL 3: Mikroökonomie Lösungshinweise zu Aufgabenblatt 2
 Georg Nöldeke Frühjahrssemester 2009 VWL 3: Mikroökonomie Lösungshinweise zu Aufgabenblatt 2 1. (a) Die Grenzprodukte der Produktionsfaktoren sind: MP 1 (x 1, x 2 ) = f(x 1, x 2 ) x 1 MP 2 (x 1, x 2 )
Georg Nöldeke Frühjahrssemester 2009 VWL 3: Mikroökonomie Lösungshinweise zu Aufgabenblatt 2 1. (a) Die Grenzprodukte der Produktionsfaktoren sind: MP 1 (x 1, x 2 ) = f(x 1, x 2 ) x 1 MP 2 (x 1, x 2 )
Einführung in die Finanzwirtschaft
 Platzhalter für Bild, Bild auf Titelfolie hinter das Logo einsetzen Einführung in die Finanzwirtschaft Prof. Dr. Marc Gürtler Einführung Gegenstand betrieblicher Finanzwirtschaft: Maßnahmen der Beschaffung
Platzhalter für Bild, Bild auf Titelfolie hinter das Logo einsetzen Einführung in die Finanzwirtschaft Prof. Dr. Marc Gürtler Einführung Gegenstand betrieblicher Finanzwirtschaft: Maßnahmen der Beschaffung
Mikroökonomik 2. Vorlesungswoche
 Mikroökonomik 2. Vorlesungswoche Tone Arnold Universität des Saarlandes 30. Oktober 2007 Tone Arnold (Universität des Saarlandes) 2. Vorlesungswoche 30. Oktober 2007 1 / 108 Präferenzen Wie treffen Konsumenten/Individuen
Mikroökonomik 2. Vorlesungswoche Tone Arnold Universität des Saarlandes 30. Oktober 2007 Tone Arnold (Universität des Saarlandes) 2. Vorlesungswoche 30. Oktober 2007 1 / 108 Präferenzen Wie treffen Konsumenten/Individuen
Einführung in die Mikroökonomie Das Verbraucherverhalten
 Einführung in die Mikroökonomie as Verbraucherverhalten Universität Erfurt Wintersemester 07/08 rof. ittrich (Universität Erfurt) as Verbraucherverhalten Winter 1 / 30 Übersicht Offenbarte räferenzen und
Einführung in die Mikroökonomie as Verbraucherverhalten Universität Erfurt Wintersemester 07/08 rof. ittrich (Universität Erfurt) as Verbraucherverhalten Winter 1 / 30 Übersicht Offenbarte räferenzen und
Investition und Finanzierung
 - Zusatzfolien zur Portfoliotheorie und CAPM- Portfoliotheorie Die Portfoliotheorie geht auf Harry Markowitz zurück. Sie gibt Anlegern Empfehlungen, wie sie ihr Vermögen auf verschiedenen Anlagemöglichkeiten
- Zusatzfolien zur Portfoliotheorie und CAPM- Portfoliotheorie Die Portfoliotheorie geht auf Harry Markowitz zurück. Sie gibt Anlegern Empfehlungen, wie sie ihr Vermögen auf verschiedenen Anlagemöglichkeiten
Vorkurs Mikroökonomik
 Vorkurs Mikroökonomik Präferenzen Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Präferenzen 1 / 29 Gliederung Einführung Haushaltstheorie Das Budget Präferenzen, Indi erenzkurven
Vorkurs Mikroökonomik Präferenzen Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Präferenzen 1 / 29 Gliederung Einführung Haushaltstheorie Das Budget Präferenzen, Indi erenzkurven
Kapitel 5: Die Entscheidung. moodle.tu-dortmund.de. Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 46
 Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 46 Kapitel 5: Die Entscheidung moodle.tu-dortmund.de Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 2 / 46 Outline Optimale
Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 46 Kapitel 5: Die Entscheidung moodle.tu-dortmund.de Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 2 / 46 Outline Optimale
Mikroökonomie 1. Präferenzen
 Mikroökonomie 1 Präferenzen 18.03.2010 1 Wiederholung: ökonomische Theorie des Konsumenten was man sich leisten kann (Budgetrestriktion) die besten Dinge wählen (Präferenzen) In der letzten Veranstaltung
Mikroökonomie 1 Präferenzen 18.03.2010 1 Wiederholung: ökonomische Theorie des Konsumenten was man sich leisten kann (Budgetrestriktion) die besten Dinge wählen (Präferenzen) In der letzten Veranstaltung
IK Ökonomische Entscheidungen und Märkte LVA
 IK Ökonomische Entscheidungen und Märkte LVA LVA-Leiter: Michael Noldi Einheit 6: Die Produktion (Kap. 6) Produktionstheorie IK WS 2014/15 1 Haushaltstheorie vs. Produktionstheorie Die Haushaltstheorie
IK Ökonomische Entscheidungen und Märkte LVA LVA-Leiter: Michael Noldi Einheit 6: Die Produktion (Kap. 6) Produktionstheorie IK WS 2014/15 1 Haushaltstheorie vs. Produktionstheorie Die Haushaltstheorie
Übung zur Vorlesung Multiagentensysteme
 Ludwig-Maximilians-Universität München SS 2007 Institut für Informatik Aufgabenblatt 1 Dr. Brandt / Fischer & Harrenstein 23. April 2007 Übung zur Vorlesung Multiagentensysteme Tutorübung: 25. April 2007
Ludwig-Maximilians-Universität München SS 2007 Institut für Informatik Aufgabenblatt 1 Dr. Brandt / Fischer & Harrenstein 23. April 2007 Übung zur Vorlesung Multiagentensysteme Tutorübung: 25. April 2007
Mikroökonomik für Wirtschaftsingenieure. Dr. Christian Hott
 Mikroökonomik für Wirtschaftsingenieure Agenda 1. Einführung 2. Analyse der 2.1 Budgetrestriktion und Nutzen 2.2 funktion und Intertemporale Entscheidung 2.3 Vermögenswerte und Unsicherheit 2.4 Konsumentenrente
Mikroökonomik für Wirtschaftsingenieure Agenda 1. Einführung 2. Analyse der 2.1 Budgetrestriktion und Nutzen 2.2 funktion und Intertemporale Entscheidung 2.3 Vermögenswerte und Unsicherheit 2.4 Konsumentenrente
IK Ökonomische Entscheidungen & Märkte
 M. Lackner (JKU Linz) IK ÖE&M E6, WS 2014/15 1 / 25 IK Ökonomische Entscheidungen & Märkte Mario Lackner JKU Linz Einheit 6, WS 2014/15 Die Produktion (Kap. 6) M. Lackner (JKU Linz) IK ÖE&M E6, WS 2014/15
M. Lackner (JKU Linz) IK ÖE&M E6, WS 2014/15 1 / 25 IK Ökonomische Entscheidungen & Märkte Mario Lackner JKU Linz Einheit 6, WS 2014/15 Die Produktion (Kap. 6) M. Lackner (JKU Linz) IK ÖE&M E6, WS 2014/15
Neue Institutionenökonomik, Aufgabe 18 Seite 1
 Neue Institutionenökonomik, Aufgabe 18 Seite 1 Allgemeine Informationen zum Principal-Agent-Modell Es geht hier nun um die Vertragsausgestaltung zwischen dem Eigentümer (Prinzipal) einer Firma und dem
Neue Institutionenökonomik, Aufgabe 18 Seite 1 Allgemeine Informationen zum Principal-Agent-Modell Es geht hier nun um die Vertragsausgestaltung zwischen dem Eigentümer (Prinzipal) einer Firma und dem
Mikroökonomik. Das Haushaltsoptimum. Harald Wiese. Universität Leipzig. Harald Wiese (Universität Leipzig) Das Haushaltsoptimum 1 / 37
 Mikroökonomik Das Haushaltsoptimum Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Das Haushaltsoptimum 1 / 37 Gliederung Einführung Haushaltstheorie Das Budget Präferenzen, Indi erenzkurven
Mikroökonomik Das Haushaltsoptimum Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Das Haushaltsoptimum 1 / 37 Gliederung Einführung Haushaltstheorie Das Budget Präferenzen, Indi erenzkurven
Kapitel 20: Gewinnmaximierung. moodle.tu-dortmund.de. Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 27
 Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 27 Kapitel 20: Gewinnmaximierung moodle.tu-dortmund.de Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 2 / 27 Kompetitive Märkte
Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 1 / 27 Kapitel 20: Gewinnmaximierung moodle.tu-dortmund.de Wirtschaftstheorie I: Mikroökonomie SoSe 2017, Lars Metzger 2 / 27 Kompetitive Märkte
Haushalts- und Konsumökonomie
 Haushalts- und Konsumökonomie Vorlesung 2: Konsum und Ersparnisse Vorlesungsübersicht (prov.) Termin 20.10 27.10 3.11 Thema Einführung Haushaltsgleichgewicht und Konsumentennachfrage Übung 1 Literatur
Haushalts- und Konsumökonomie Vorlesung 2: Konsum und Ersparnisse Vorlesungsübersicht (prov.) Termin 20.10 27.10 3.11 Thema Einführung Haushaltsgleichgewicht und Konsumentennachfrage Übung 1 Literatur
Differenzialrechnung. Mathematik-Repetitorium
 Differenzialrechnung 5.1 Die Ableitung 5.2 Differentiation elementarer Funktionen 5.3 Differentiationsregeln 5.4 Höhere Ableitungen 5.5 Partielle Differentiation 5.6 Anwendungen Differenzialrechnung 1
Differenzialrechnung 5.1 Die Ableitung 5.2 Differentiation elementarer Funktionen 5.3 Differentiationsregeln 5.4 Höhere Ableitungen 5.5 Partielle Differentiation 5.6 Anwendungen Differenzialrechnung 1
Gesundheitsökonomik. Thema 6 Das Individuum als Produzent seiner Gesundheit I. Prof. Dr. Alfonso Sousa-Poza, Universität Hohenheim 1
 Gesundheitsökonomik Thema 6 Das Individuum als Produzent seiner Gesundheit I Prof. Dr. Alfonso Sousa-Poza, Universität Hohenheim 1 Rückblick Die Nachfragefunktion: Q = f(preis, Einkommen, Preise von Komplementen
Gesundheitsökonomik Thema 6 Das Individuum als Produzent seiner Gesundheit I Prof. Dr. Alfonso Sousa-Poza, Universität Hohenheim 1 Rückblick Die Nachfragefunktion: Q = f(preis, Einkommen, Preise von Komplementen
Kapitel 6: Produktion und Technologie
 Kapitel 6: Produktion und Technologie Hauptidee: Die Firma verwandelt Inputs in Outputs. Dieser Transformationsprozess wird beschrieben durch die Produktionsfunktion. 6.1 Die Firma und ihre Technologie
Kapitel 6: Produktion und Technologie Hauptidee: Die Firma verwandelt Inputs in Outputs. Dieser Transformationsprozess wird beschrieben durch die Produktionsfunktion. 6.1 Die Firma und ihre Technologie
Historische Renditen, Experteninterviews, Analyse von Marktpreisen
 1 Portfoliotheorie 1.1 Grundlagen der Portfoliotheorie 1.1.1 Welche vier grundsätzlichen Anlageziele werden von Investoren verfolgt? Minimales Risiko Liquidation wenn nötig Hohe Rendite Gewinnmaximierung
1 Portfoliotheorie 1.1 Grundlagen der Portfoliotheorie 1.1.1 Welche vier grundsätzlichen Anlageziele werden von Investoren verfolgt? Minimales Risiko Liquidation wenn nötig Hohe Rendite Gewinnmaximierung
Was versteht man unter Konsumenten- und Produzentenrente? Zeigen Sie diese Größen in einem Preis-Mengen-Diagramm.
 Klausuraufgaben für das Mikro 1 Tutorium Sitzung 1 WS 03/04 Aufgabe 1 Was versteht man unter Konsumenten- und Produzentenrente? Zeigen Sie diese Größen in einem Preis-Mengen-Diagramm. WS 04/05 Aufgabe
Klausuraufgaben für das Mikro 1 Tutorium Sitzung 1 WS 03/04 Aufgabe 1 Was versteht man unter Konsumenten- und Produzentenrente? Zeigen Sie diese Größen in einem Preis-Mengen-Diagramm. WS 04/05 Aufgabe
Vorlesung 5: Probleme der Erwartungsnutzentheorie
 Vorlesung 5: Probleme der Erwartungsnutzentheorie Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 5 (FS 11) Probleme der Erwartungsnutzentheorie 1 / 24 1. Einleitung
Vorlesung 5: Probleme der Erwartungsnutzentheorie Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 5 (FS 11) Probleme der Erwartungsnutzentheorie 1 / 24 1. Einleitung
IK Ökonomische Entscheidungen & Märkte
 LVA-Leiter: Martin Halla Einheit 6: Die Produktion (Kapitel 6) Einheit 6-1 - Theorie der Firma - I In den letzten beiden Kapiteln: Genaue Betrachtung der Konsumenten (Nachfrageseite). Nun: Genaue Betrachtung
LVA-Leiter: Martin Halla Einheit 6: Die Produktion (Kapitel 6) Einheit 6-1 - Theorie der Firma - I In den letzten beiden Kapiteln: Genaue Betrachtung der Konsumenten (Nachfrageseite). Nun: Genaue Betrachtung
Mathematik für Wirtschaftswissenschaftler Kapitel 4-6. Universität Trier Wintersemester 2013 / 2014
 Mathematik für Kapitel 4-6 Universität Trier Wintersemester 2013 / 2014 Kapitel 4 1. Extremwerte 2. Lokale Optimalpunkte 3. Wendepunkte 2 Kapitel 4.1 EXTREMWERTE 3 Extrempunkte und Extremwerte 4 Strikte
Mathematik für Kapitel 4-6 Universität Trier Wintersemester 2013 / 2014 Kapitel 4 1. Extremwerte 2. Lokale Optimalpunkte 3. Wendepunkte 2 Kapitel 4.1 EXTREMWERTE 3 Extrempunkte und Extremwerte 4 Strikte
Dynamische Systeme und Zeitreihenanalyse // Multivariate Normalverteilung und ML Schätzung 11 p.2/38
 Dynamische Systeme und Zeitreihenanalyse Multivariate Normalverteilung und ML Schätzung Kapitel 11 Statistik und Mathematik WU Wien Michael Hauser Dynamische Systeme und Zeitreihenanalyse // Multivariate
Dynamische Systeme und Zeitreihenanalyse Multivariate Normalverteilung und ML Schätzung Kapitel 11 Statistik und Mathematik WU Wien Michael Hauser Dynamische Systeme und Zeitreihenanalyse // Multivariate
1. EINFÜHRUNG INS STATE-PRICING 1
 1. EINFÜHRUNG INS STATE-PRICING 1 1. Einführung ins State-Pricing In diesem Kapitel betrachten wir eine Periode. Das heisst, wir können nur zu den Zeitpunkten 0 und 1 handeln. Im weiteren arbeiten wir
1. EINFÜHRUNG INS STATE-PRICING 1 1. Einführung ins State-Pricing In diesem Kapitel betrachten wir eine Periode. Das heisst, wir können nur zu den Zeitpunkten 0 und 1 handeln. Im weiteren arbeiten wir
Übungsaufgaben zu Kapitel 6: Finanzmärkte und Erwartungen
 Kapitel 6 Übungsaufgaben zu Kapitel 6: Finanzmärkte und Erwartungen Übungsaufgabe 6-1a 6-1a) Welche Typen von Zinsstrukturkurven kennen Sie? Stellen Sie die Typen graphisch dar und erläutern Sie diese.
Kapitel 6 Übungsaufgaben zu Kapitel 6: Finanzmärkte und Erwartungen Übungsaufgabe 6-1a 6-1a) Welche Typen von Zinsstrukturkurven kennen Sie? Stellen Sie die Typen graphisch dar und erläutern Sie diese.
Kapitel 3 Die Konsumententheorie
 Kapitel 3 Die Konsumententheorie Lekt. Dr. Irina-Marilena Ban Pearson Studium 2014 2014 Literatur Pindyck, Robert S; Rubinfeld, Daniel L., Mikroökonomie, 7. Auflage, Pearson Studium, 2009, S. 104-132;
Kapitel 3 Die Konsumententheorie Lekt. Dr. Irina-Marilena Ban Pearson Studium 2014 2014 Literatur Pindyck, Robert S; Rubinfeld, Daniel L., Mikroökonomie, 7. Auflage, Pearson Studium, 2009, S. 104-132;
Teil II: Produzententheorie
 Teil II: Produzententheorie 1 Kapitel 6: Produktion und Technologie Hauptidee: Eine Firma verwandelt Inputs in Outputs. Dieser Transformationsprozess wird beschrieben durch die Produktionsfunktion. 6.1
Teil II: Produzententheorie 1 Kapitel 6: Produktion und Technologie Hauptidee: Eine Firma verwandelt Inputs in Outputs. Dieser Transformationsprozess wird beschrieben durch die Produktionsfunktion. 6.1
Name: Matr.-Nr.: Sitzplatz-Nr.: Modulklausur im Grundstudium (Dipl.) und ersten Studienabschnitt (B.Sc.) (PO 2005, PO 2008) Mikroökonomik I
 Name: Matr.-Nr.: Sitzplatz-Nr.: Modulklausur im Grundstudium (Dipl.) und ersten Studienabschnitt (B.Sc.) (PO 2005, PO 2008) Mikroökonomik I Prof. Dr. P. Michaelis 30. Juli 2014 Dauer: 90 Minuten 5 Leistungspunkte
Name: Matr.-Nr.: Sitzplatz-Nr.: Modulklausur im Grundstudium (Dipl.) und ersten Studienabschnitt (B.Sc.) (PO 2005, PO 2008) Mikroökonomik I Prof. Dr. P. Michaelis 30. Juli 2014 Dauer: 90 Minuten 5 Leistungspunkte
und Investition Finanzierung R. Verlag München Wien an der Freien Universität Von Dr. Lutz Kruschwitz Professor für Betriebswirtschaftslehre
 Finanzierung und Investition Von Dr. Lutz Kruschwitz Professor für Betriebswirtschaftslehre an der Freien Universität 4., überarbeitete und erweiterte Auflage R. Verlag München Wien 1 Einmalige sichere
Finanzierung und Investition Von Dr. Lutz Kruschwitz Professor für Betriebswirtschaftslehre an der Freien Universität 4., überarbeitete und erweiterte Auflage R. Verlag München Wien 1 Einmalige sichere
Was versteht man unter Konsumenten- und Produzentenrente? Zeigen Sie diese Größen in einem Preis-Mengen-Diagramm.
 Klausuraufgaben für das Mikro 1 Tutorium Sitzung 1 WS 03/04 Aufgabe 1 Was versteht man unter Konsumenten- und Produzentenrente? Zeigen Sie diese Größen in einem Preis-Mengen-Diagramm. WS 04/05 Aufgabe
Klausuraufgaben für das Mikro 1 Tutorium Sitzung 1 WS 03/04 Aufgabe 1 Was versteht man unter Konsumenten- und Produzentenrente? Zeigen Sie diese Größen in einem Preis-Mengen-Diagramm. WS 04/05 Aufgabe
Probeklausur zur Mikroökonomik I
 Prof. Dr. Robert Schwager Sommersemester 2005 Probeklausur zur Mikroökonomik I 08. Juni 2005 Name: Matrikelnr.: Bei Multiple-Choice-Fragen sind die zutreffenden Aussagen (wahr bzw. falsch) anzukreuzen.
Prof. Dr. Robert Schwager Sommersemester 2005 Probeklausur zur Mikroökonomik I 08. Juni 2005 Name: Matrikelnr.: Bei Multiple-Choice-Fragen sind die zutreffenden Aussagen (wahr bzw. falsch) anzukreuzen.
Mikroökonomik 4. Vorlesungswoche Fortsetzung
 Mikroökonomik 4. Vorlesungswoche Fortsetzung Tone Arnold Universität des Saarlandes 14. November 2007 Tone Arnold (Universität des Saarlandes) 4. Vorlesungswoche Fortsetzung 14. November 2007 1 / 41 Slutzky
Mikroökonomik 4. Vorlesungswoche Fortsetzung Tone Arnold Universität des Saarlandes 14. November 2007 Tone Arnold (Universität des Saarlandes) 4. Vorlesungswoche Fortsetzung 14. November 2007 1 / 41 Slutzky
2. Entscheidungsregeln. Handhabung von Unsicherheit
 II Agenda 1. Sensitivitätsanalyse 2. Entscheidungsregeln 3. Dialektische Planung 2 1. Sensitivitätsanalyse 3 Definition: Sensitivitätsanalyse = Sensibilitätsanalyse Empfindlichkeitsanalyse Verfahren zur
II Agenda 1. Sensitivitätsanalyse 2. Entscheidungsregeln 3. Dialektische Planung 2 1. Sensitivitätsanalyse 3 Definition: Sensitivitätsanalyse = Sensibilitätsanalyse Empfindlichkeitsanalyse Verfahren zur
Musterlösungen Mikroökonomie II
 Musterlösungen Mikroökonomie II Kardinaler Nutzen Aufgabe 1 Man hält den Nutzen, der aus dem Konsum von Gütern entsteht für meßbar. Konkret wird angenommen, daß man den Nutzenabstand zwischen zwei Güterbündeln
Musterlösungen Mikroökonomie II Kardinaler Nutzen Aufgabe 1 Man hält den Nutzen, der aus dem Konsum von Gütern entsteht für meßbar. Konkret wird angenommen, daß man den Nutzenabstand zwischen zwei Güterbündeln
Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban
 Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban Lösungsvorschlag studienbegleitende Klausur Finanzmathematik I Aufgabe (7 Punkte) Vorgelegt sei ein Wahrscheinlichkeitsraum (Ω, F, P) und
Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban Lösungsvorschlag studienbegleitende Klausur Finanzmathematik I Aufgabe (7 Punkte) Vorgelegt sei ein Wahrscheinlichkeitsraum (Ω, F, P) und
Mikroökonomik. Präferenzen, Indi erenzkurven und Nutzenfunktionen. Harald Wiese. Universität Leipzig
 Mikroökonomik Präferenzen, Indi erenzkurven und Nutzenfunktionen Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Präferenzen, Indi erenzkurven und Nutzenfunktionen 1 / 33 Gliederung
Mikroökonomik Präferenzen, Indi erenzkurven und Nutzenfunktionen Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Präferenzen, Indi erenzkurven und Nutzenfunktionen 1 / 33 Gliederung
Präferenzen und Nutzenfunktionen. 10.März 2017
 Präferenzen und Nutzenfunktionen 10.März 2017 Präferenzen und Nutzenfunktionen Darstellung der Präferenzen mittels Nutzenfunktion (utility function) Eine Nutzenfunktion u(x) ordnet jedem Element x aus
Präferenzen und Nutzenfunktionen 10.März 2017 Präferenzen und Nutzenfunktionen Darstellung der Präferenzen mittels Nutzenfunktion (utility function) Eine Nutzenfunktion u(x) ordnet jedem Element x aus
Mikroökonomie I Kapitel 3 Das Käuferverhalten WS 2004/2005
 Mikroökonomie I Kapitel 3 Das Käuferverhalten WS 2004/2005 Die Themen in diesem Kapitel Konsumentenpräferenzen Budgetbeschränkungen Verbraucherentscheidung Die Grenznutzen und die Verbraucherentscheidung
Mikroökonomie I Kapitel 3 Das Käuferverhalten WS 2004/2005 Die Themen in diesem Kapitel Konsumentenpräferenzen Budgetbeschränkungen Verbraucherentscheidung Die Grenznutzen und die Verbraucherentscheidung
Übung 3: Unternehmenstheorie
 Übung 3: Unternehmenstheorie Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Intermediate Microeconomics HS 11 Unternehmenstheorie 1 / 42 Produktion Zur Erinnerung: Grenzprodukt
Übung 3: Unternehmenstheorie Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Intermediate Microeconomics HS 11 Unternehmenstheorie 1 / 42 Produktion Zur Erinnerung: Grenzprodukt
Zusammenfassung der Vorlesung und Globalübung Mikroökonomie 2017
 Zusammenfassung der Vorlesung und Globalübung Mikroökonomie 2017 Die Durchnummerierung der Kapitel und Unterkapitel bezieht sich auf das Textbuch Grundzüge der Mikroökonomik von Hal R. Varian, 9. Auflage.
Zusammenfassung der Vorlesung und Globalübung Mikroökonomie 2017 Die Durchnummerierung der Kapitel und Unterkapitel bezieht sich auf das Textbuch Grundzüge der Mikroökonomik von Hal R. Varian, 9. Auflage.
Kapitel 3 Rationales Konsumentenverhalten
 Kapitel 3 Rationales Konsumentenverhalten Vor- und Nachbereitung: Varian, Chapter 2, 3 und 5 Frank, Chapter 3 (mit Appendix) Übungsblatt 3 Achtung: Es wird anspruchsvoller! Klaus M. Schmidt, 2008 3.1 Die
Kapitel 3 Rationales Konsumentenverhalten Vor- und Nachbereitung: Varian, Chapter 2, 3 und 5 Frank, Chapter 3 (mit Appendix) Übungsblatt 3 Achtung: Es wird anspruchsvoller! Klaus M. Schmidt, 2008 3.1 Die
