Was sagt dieses sog. van`t Hoffsche Gesetz aus? Welche Randbedingungen gelten für die Gesetzmäßigkeiten der Osmose?
|
|
|
- Leonard Fleischer
- vor 8 Jahren
- Abrufe
Transkript
1 Osmose C.Stick Eine spezielle Form der Diffusion ist die Osmose. Dieser Prozess spielt eine zentrale Rolle in der Volumen- und Wasserregulation der Zellen und Organismen. Als Osmose bezeichnet man die Diffusion des Lösungsmittels über semipermeable Membranen von einer weniger konzentrierten in eine konzentriertere Lösung. Dabei kommt es tendenziell zum Ausgleich der Konzentrationen.
2 Abb. 1: Schematische Darstellung der Vorgänge bei Diffusion und Osmose. Die Ausgandszustände sind in beiden Fällen gleich: Es befinden sich in dem Lösungsmittel Wasser auf beiden Seiten einer Membran gelöste Moleküle, die sich in ihren eigenschaften nicht weiter unterscheiden mögen. Nur zur Verdeutlichung der wanderungen sind die Moleküle links rot, rechts blau markiert. Die Anfangskonzentration ist in beiden Fällen links doppelt so groß wie rechts: c1= 2 c2. Der einzige Unterschied zwischen Diffusion und Osmose besteht darin, dass bei der Diffusion sowohl das Wasser als auch die gelösten Moleküle sich durch die Membran bewegen können. Es kommt im Übergangszustand zu unterschiedlich großen Flüssen sowohl des Lösungsmittels als auch der gelösten Teilchen mit dem Ergebnis, dass sich schließlich ein Gleichgewicht bei völliger Durchmischung einstellt, so dass kein Nettotransport mehr erfolgt. Bei der Osmose besteht der einzige Unterschied darin, dass die gelösten Moleküle nicht durch diemembran diffundieren können, sondern nur das Lösungsmittel. Im Übergangszustand besteht ein Nettotransport von Lösungsmittel in die Lösung mit höherer Konzentration. Dies führt zur Verdünnung und zum Aufbau eines osmotischen Druckes, bis ein Gleichgewicht erreicht ist. Die Abbildung ist in diesem letzten Teil nicht ganz exakt: Tatsächlich werden gleiche Konzentrationen nur dann erreicht, wenn gleichzeitig kein osmotischer Druck aufgebaut wird. Umgekehrt wird der volle osmotische Druck nur dann erreicht, wenn kein Nettotransport des Lösungsmittels erfolgt (siehe Abbildung 2 am Schluss). Osmose führt überall dort, wo Teilchen (Moleküle oder Ionen) an semipermeablen Membranen in unterschiedlichen Konzentrationen vorliegen, zu einem Nettovolumentransport. Wird der Volumenänderung, welche die Lösungsmitteldiffusion bewirkt, beispielsweise durch starre Wände ein mechanischer Widerstand entgegengesetzt, so baut sich in der Lösung mit der höheren Konzentration ein Druck, der sog. osmotische Druck, auf. Semipermeabel bedeutet, dass eine Membran für eine Komponente einer Lösung permeabel, d. h. durchlässig ist, für eine andere Komponente jedoch impermeabel, d. h. undurchlässig ist. Typischerweise sind Membranen für das Lösungsmittel permeabel, aber impermeabel für gelöste Stoffe. Theoretisch kommt es lediglich auf die Unterscheidung zwischen permeablen Molekülen und impermeablen Molekülen an. Die Unterscheidung zwischen Lösungsmittel und gelöster Substanz ist hingegen prinzipiell unwichtig. Trotz dieser theoretischen Gleichberechtigung ist es für die folgende Betrachtung sinnvoll, zwischen Lösungsmittel und gelöster Substanz zu unterscheiden. Dies gilt zumal für biologische Objekte, Zellen, Organellen und Organe, wo Wasser als Lösungsmittel für die verschiedenen biologischen Intra- und Extrazellulärflüssigkeiten fungiert. Im Allgemeinen sind die biologischen Membranen für Wasser permeabel, für einzelne oder mehrere in den verdünnten Lösungen enthaltenen Stoffe jedoch nicht oder nur wenig permeabel. In Fällen, in denen nur Makromoleküle wie beispielsweise die Plasmaproteine in ihrer Diffusion durch Membranen behindert und damit osmotisch wirksam werden, spricht man von Kolloidosmose, bzw. kolloidosmotischem Druck. Viele Gesetze und Aussagen über die Osmose sind zunächst empirisch experimentell gefunden worden. So hat der Botaniker Wilhelm Pfeffer (1845 Grebenstein Leipzig) umfangreiche Untersuchungen angestellt, um die Mechanismen, die Pflanzen zu gerichteten Bewegungen befähigen, herauszufinden (Pfeffer 1877). Ohne den
3 osmotischen Druck lassen welke Blumen beispielsweise die Blüten hängen. Pfeffer erzeugte durch den Niederschlag von Kupfercyanoferrat(III) in den Wänden von Tongefäßen künstliche semipermeable Membranen und stellte mit Hilfe dieser nach ihm benannten Zelle systematische Versuche an. Die daraus gewonnenen Messreihen ermöglichten es van`t Hoff (Jacobus Henricus, 1852 Rotterdam Berlin; erster Nobelpreisträger für Chemie 1901), 1896 eine Gleichung über die Osmose zu formulieren: π = cosm R T Was sagt dieses sog. van`t Hoffsche Gesetz aus? Welche Randbedingungen gelten für die Gesetzmäßigkeiten der Osmose? Der osmotische Druck einer ideal verdünnten Lösung lässt sich durch eine Gleichung beschreiben, die eine formale Analogie zum allgemeinen Gasgesetz darstellt. So ist der osmotische Druck ist wie der Druck eines idealen Gases proportional zur absoluten Temperatur. Der osmotische Druck π einer ideal verdünnten Lösung ist proportional der molaren Konzentration c osm. des gelösten Stoffes. Die Gleichung gilt für ideal verdünnte Lösungen, d. h. für Lösungen, die so stark verdünnt sind, dass die gelösten Moleküle ohne Wechselwirkungen untereinander sich völlig unabhängig voneinander im Lösungsmittel bewegen können. Das van`t Hoffsche Gesetz ist insofern ein Grenzgesetz. Für reale Lösungen ist die osmolare Aktivität maßgebend. Der osmotische Druck ist völlig unabhängig von der Natur der gelösten Teilchen, von deren physikalischen und chemischen Eigenschaften oder deren Größe. Der osmotische Druck wird allein von der Anzahl der impermeablen Teilchen bestimmt. Dieser Umstand wird durch die osmolare Konzentration c osm in der van`t Hoffschen Gleichung berücksichtigt: c osm = osmol V. Dabei bedeutet osmol analog zur Definition des mol die Anzahl aller osmotisch wirksamen Teilchen bezogen auf die Avogadro- Konstante. Weiter ist für die osmotischen Erscheinungen allein die Semipermeabilität der Membran entscheidend, d. h. die Frage, welches Molekül kann durch die Membran diffundieren und welches kann nicht diffundieren. Alle nicht diffusiblen Moleküle gehen ihrer Anzahl nach in die osmolare Konzentration ein. Wie oben erwähnt sind Lösungsmittel und gelöste Stoffe ansonsten völlig gleichberechtigt. Die Membran ist im Hinblick auf die diffusiblen Moleküle völlig symmetrisch. Die Membran entscheidet nur, ob ein Molekül diffusibel ist oder nicht. Sie entscheidet nicht über die Richtung der Diffusion. Hin- und Her-Diffusion werden entweder beide verhindert oder nicht.
4 Die Behinderung erfolgt auch nicht durch die gelösten Teilchen, etwa in der Weise, dass diese beispielsweise aufgrund ihrer Größe den Weg versperren oder die Membran einseitig verstopfen oder ähnliches. Die Osmose ist eben völlig unabhängig von Größe oder Natur der gelösten Teilchen und nur abhängig von deren Zahl. Der Fall, dass die Membran für gelöste Moleküle nicht vollständig impermeabel ist, kann in der van`t Hoffsche Gleichung durch einen sog. Reflexionsfaktor σ berücksichtigt werden. σ kann Werte zwischen 0 und 1 annehmen. σ =1 bedeutet ideale Impermeabilität, σ = 0 dagegen völlige Durchlässigkeit. Diffusion ist völlig regellos und zufällig durch die thermische Bewegung der Moleküle. Eine Richtung erhält der Stofftransport allein durch die Wahrscheinlichkeit, wenn Konzentrationsunterschiede vorhanden sind. Wegen der zufälligen Bewegung der Moleküle ist die Wahrscheinlichkeit, dass mehr Moleküle zufällig vom Ort höherer Anzahldichte in einen Raum mit geringerer Anzahldichte diffundieren, größer als umgekehrt. Wegen der enormen Größe der Avogadro-Zahl ist die Wahrscheinlichkeit äußerst mächtig. Diese Prinzipien gelten uneingeschränkt auch für die Osmose. Für Lösungen unterschiedlicher Konzentrationen ist nun nicht allein die Zahl der gelösten Teilchen unterschiedlich, sondern auch die des Lösungsmittels, so dass sich über die Membranen Konzentrationsdifferenzen ergeben. Dies wird aus den Molenbrüchen klar. x g sei der Molenbruch für den gelösten Stoff, x L der für das Lösungsmittel. n g und n L seien die Stoffmengen für den gelösten Stoff respektive das Lösungsmittel jeweils in mol. x g = n g n L + n g x L = n L n L + n g Die Stoffmengen für den gelösten Stoff und für das Lösungsmittel addieren sich zu 1, so dass die Stoffmenge für das Lösungsmittel umso kleiner ist, je höher die Konzentration der Lösung ist. Für das reine Lösungsmittel ist der Molenbruch 1. Es besteht also für das Lösungsmittel ein Konzentrationsgefälle von der verdünnteren Lösung, bzw. vom reinen Lösungsmittel hin zur konzentrierteren Lösung. Entsprechend diesem Konzentrationsgefälle diffundiert das Lösungsmittel von der verdünnteren in die konzentriertere Lösung, bzw. vom reinen Lösungsmittel in die Lösung. Diese Diffusion gehorcht dem ersten Fickschen Diffusionsgesetz. Nach ihm lässt sich die Diffusionsstromstärke, die Geschwindigkeit der Lösungsmitteldiffusion berechnen. Für die Physiologie des Menschen, der Tiere und der Pflanzen ist von elementarer Wichtigkeit, dass durch die Osmose immer dort, wo unterschiedliche Konzentrationen nicht diffusibler Moleküle auftreten, gerichtete Flüsse von Wasser auftreten, die zu
5 Volumenänderungen von Zellen, Zellorganellen oder Geweben führen. Hierauf beruht die osmotische Hämolyse, die Funktion von Osmorezeptoren oder der ADHabhängige Konzentrationsmechanismus in den Sammelrohren der Niere. In Kompartimenten mit geringer Dehnbarkeit führt die Diffusion von Lösungsmittel in die konzentriertere Lösung zum Aufbau eines osmotischen Drucks. Dieser Druck wirkt der Diffusion entgegen, so dass die Diffusion mit steigendem Druck immer langsamer erfolgt und schließlich ein dynamisches Gleichgewicht erreicht wird. Dabei ist die Diffusion keineswegs unterbunden. Nur sind im Gleichgewicht Hin- und Rückdiffusion gleich groß, so dass kein Nettotransport von Lösungsmittel mehr erfolgt. Der volle osmotische Druck, wie er durch das van`t Hoffsche Gesetz beschrieben wird, ist ein potentieller Druck, der dann in voller Höhe gemessen werden kann, wenn die Nettodiffusion von Lösungsmittel in die Lösung durch einen äußeren Druck auf die Lösung gerade vollständig kompensiert wird. Das heißt der äußere Druck auf die Lösung muss den Strom von Lösungsmittelmolekülen aus der Lösung so erhöhen, dass der osmotische Diffusionsstrom von Lösungsmittelmolekülen in die Lösung gerade ausgeglichen wird. Während die osmotischen Flüssigkeitsverschiebungen über semipermeable Membranen auf molekularer Ebene bereits plausibel mit der Diffusion von Lösungsmittelmolekülen entlang eines Konzentrationsgradienten für das Lösungsmittel erklärt werden kann, erfordert die Beschreibung des osmotischen Druckes die Betrachtung des chemischen Potentials. Aus thermodynamischen Gründen setzen die gelösten Moleküle in einer Lösung das chemische Potential des Lösungsmittels herab. Die Ursache hierfür liegt darin, dass die gelösten Moleküle die Ordnung, die in einem reinen Lösungsmittel herrscht, herabsetzen. Da die gelösten Moleküle sich im Lösungsmittel ähnlich unabhängig voneinander bewegen wie Moleküle in Gasen, erhöhen sie die Entropie der Lösung. Dies führt gewissermaßen im Gegenzug zu einer Herabsetzung des chemischen Potentials des Lösungsmittels in der Lösung. Die Senkung des chemischen Potentials des Lösungsmittels in einer Lösung ist die gemeinsame Grundlage für die sog. kolligativen Eigenschaften von Lösungen: die Dampfdruckerniedrigung, die Siedepunktserhöhung, die Gefrierpunktserniedrigung und
6 die Osmose. Alle diese Effekte hängen für ideal verdünnte Lösungen bei konstanter Temperatur nur von der Zahl der gelösten Teilchen ab, nicht jedoch von deren Größe oder deren chemischen oder physikalischen Eigenschaften. Das chemische Potential ist die auf die Stoffmenge bezogene freie Enthalpie: µ = G mol. Das chemische Potential µ L einer Lösung ist eine Funktion des Molenbruchs x L für das Lösungsmittel: µ L = µ Lo + RT ln x L µ Lo bedeutet das chemische Potential des reinen Lösungsmittels mit dem Molenbruch n L x L =1. Da der Molenbruch x L = n L + n g für das Lösungsmittel in einer Lösung < 1 ist, ist auch das chemische Potential des Lösungsmittels in der Lösung kleiner als das des reinen Lösungsmittels. Daraus folgt, dass das Lösungsmittel spontan in die Lösung diffundiert. Obwohl die Unterschiede in der Osmolarität biologischer Flüssigkeiten typischerweise gering sind, wird der Einfachheit halber in der folgenden Betrachtung eine Lösung dem reinen Lösungsmittel gegenübergestellt. Lösung und reines Lösungsmittel seien durch eine ideal semipermeable Membran getrennt. Die Erhöhung des Druckes, der auf die Lösung ausgeübt werden muss, um die Nettodiffusion zu kompensieren, erhöht das chemische Potential des Lösungsmittels in der Lösung auf den Wert, den das reine Lösungsmittel auf der anderen Seite der Membran hat. Das chemische Potential des Lösungsmittels ist also eine Funktion des Druckes µ Lo (P): µ L = µ Lo ( P) + RT ln x L. Bezeichnet man die Größen in den Kompartimenten diesseits und jenseits der semipermeablen Membran mit den Indizes 1 und 2 und sei im Kompartiment 1 ein reines Lösungsmittel (Molenbruch x L1 =1,ln x L1 = 0), in Kompartiment 2 die Lösung mit dem Molenbruch für das Lösungsmittel x L2, so ergibt sich für die Gleichgewichtsbedingung folgender Ansatz: µ o L1 (P 1 ) = µ o L 2 (P 2 ) + RT ln x L 2
7 µ o (P L 2 2 ) µ o L1 (P 1 ) = RT ln x L2 Die Differenz der vom Druck abhängigen chemischen Potentiale für das reine Lösungsmittel dµ Lo entspricht in infinitesimaler Schreibweise der auf die Stoffmenge in mol bezogenen freien Enthalpie dg n : dµ Lo = dg n = 1 ( SdT +VdP) n Für konstante Temperatur (dt = 0)vereinfacht sich der Ausdruck auf: dµ Lo = V n dp. Hierin bedeutet V n das Molvolumen des Lösungsmittels, das wegen der äußerst geringen Kompressibilität von Flüssigkeiten bei der Integration als unabhängig vom Druck P angesehen werden darf. Die Integration in den Grenzen P 1 bis P 2 führt auf: µ o L (P 2 ) o dµ L µ L o (P 1 ) = V n P 2 P 1 dp µ Lo (P 2 ) µ Lo (P 1 ) = V n (P 2 P 1 ) Die Druckdifferenz P 2 P 1 ist die gesuchte Druckerhöhung, die notwendig ist, um die Nettodiffusion des Lösungsmittels zu unterbinden, das heißt sie entspricht dem osmotischen Druck π. Einsetzen in obige Gleichung ergibt die Abhängigkeit des osmotischen Drucks vom Molenbruch x L2 des Lösungsmittels in der Lösung in Kompartiment 2: π = RT V nl ln x L2 V nl ist das Molvolumen des Lösungsmittels V ; für Wasser bei üblichen Temperaturen n ist V n 18ml. Aus dieser Gleichung für den osmotischen Druck lässt sich das van`t Hoffsche Gesetz durch einige Vereinfachungen gewinnen: Zunächst wird nach x L2 =1 x g der Molenbruch für das Lösungsmittel x L2 durch den
8 Molenbruch für den gelösten Stoff x g ersetzt. Da für sehr verdünnte Lösungen der n g Molenbruch x g = n g + n L eine kleine Zahl ist, lässt sich ln(1 x g ) x g weiter vereinfachen. Schließlich ist für sehr verdünnte Lösungen das Produkt V nl n L annähernd gleich dem Gesamtvolumen V, so dass der Bruch n g V nl n L n g V Konzentration c des gelösten Stoffes angibt. Mit diesen Vereinfachungen für sehr verdünnte Lösungen ergibt sich aus der allgemeinen Gleichung für den osmotischen Druck das van`t Hoffsche Gesetz: π = RT c In dieser Form stellt das empirisch gefundene van`t Hoffsche Gesetz eine formale Analogie zum allgemeinen Gasgesetz dar. Wie die vorgenommenen Vereinfachungen zeigen, ist es ein Grenzgesetz für sehr verdünnte ideale Lösungen. Aus diesem Grunde erlaubt es die Analogie zum Gasgesetz nicht, eine anschauliche molekulare Deutung des osmotischen Druckes vorzunehmen, wie sie für den Gasdruck in der kinetischen Gastheorie einen realen physikalischen Inhalt hat. Die oben vorgenommene thermodynamische Herleitung zeigt vielmehr, dass sowohl die gerichtete Diffusion des Lösungsmittels, als auch der osmotische Druck auf die Senkung des chemischen Potentials des Lösungsmittels in der Lösung zurückzuführen sind. Diese wiederum ist, wie oben erwähnt, thermodynamisch dadurch zu erklären, dass die gelösten Moleküle, die sich in der Lösung unabhängig voneinander regellos bewegen können, die Entropie gegenüber dem vergleichsweise geordneten Zustand des reinen Lösungsmittels erhöhen. Zusammengefasst können bei der Osmose, also bei der Diffusion an semipermeablen Membranen zwei extreme Fälle (siehe Abb. 2) unterschieden werden: Entweder lässt man einen gerichteten Lösungsmittelfluss zu, dann wird es so lange zu einer Nettodiffusion kommen, bis die Konzentrationen ausgeglichen sind, d.h. bis die Wahrscheinlichkeiten für die Diffusion von Lösungsmittelmolekülen in beide Richtungen über die Membran gleich groß sind. Oder man übt auf die Lösung einen Druck aus, der einen Strom von Lösungsmittel aus der Lösung erzeugt, also dem Diffusionsstrom entgegengesetzt ist. Dabei wird der volle osmotische Druck dann erreicht, wenn der Diffusionsstrom genau so kompensiert wird, dass der Nettostrom Null ist. Zwischen den Extremen gibt es alle Übergänge. Die Extreme existieren aber nicht gleichzeitig. die
9
10 Abb. 2: Schematische Darstellung der beiden Extremsituationen der Osmose. Darstellung und Ausgangssituation wie in Abb. 1. Auf der linken Seite ist die Membran beweglich gedacht, so dass eine osmotische Volumenverschiebung ohne Erzeugung eines osmotischen Druckes erfolgen kann. Auf der rechten Seite verhindert die Anwendung eines äußeren Druckes jeglichen Nettotransport von Lösungsmittel. Der äußere Druck entspricht unter dieser Bedingung dem osmotischen Druck. Wird der Druck auf die Lösung über den osmotischen Druck hinaus erhöht, so kommt es zur Antiosmose. Das bedeutet, es wird Lösungsmittel aus der Lösung über die semipermeable Membran abgepresst. Dieses Verfahren wird beispielsweise zur Seewasserentsalzung eingesetzt. Pfeffer, W.: Osmotische Untersuchungen zur Zellmechanik.Engelmann,Leipzig (1877) Carsten Stick, März 2004, geändert/erweitert Juni 2005/Oktober 2006 Anschrift des Verfassers: Prof. Dr. Carsten Stick Institut für Medizinische Klimatologie Universität Kiel Olshausenstr. 40 D Kiel
Die innere Energie eines geschlossenen Systems ist konstant
 Rückblick auf vorherige Vorlesung Grundsätzlich sind alle möglichen Formen von Arbeit denkbar hier diskutiert: Mechanische Arbeit: Arbeit, die nötig ist um einen Massepunkt von A nach B zu bewegen Konservative
Rückblick auf vorherige Vorlesung Grundsätzlich sind alle möglichen Formen von Arbeit denkbar hier diskutiert: Mechanische Arbeit: Arbeit, die nötig ist um einen Massepunkt von A nach B zu bewegen Konservative
Thermodynamik. Basics. Dietmar Pflumm: KSR/MSE. April 2008
 Thermodynamik Basics Dietmar Pflumm: KSR/MSE Thermodynamik Definition Die Thermodynamik... ist eine allgemeine Energielehre als Teilgebiet der Chemie befasst sie sich mit den Gesetzmässigkeiten der Umwandlungsvorgänge
Thermodynamik Basics Dietmar Pflumm: KSR/MSE Thermodynamik Definition Die Thermodynamik... ist eine allgemeine Energielehre als Teilgebiet der Chemie befasst sie sich mit den Gesetzmässigkeiten der Umwandlungsvorgänge
8.2 Thermodynamische Gleichgewichte, insbesondere Gleichgewichte in Mehrkomponentensystemen Mechanisches und thermisches Gleichgewicht
 8.2 Thermodynamische Gleichgewichte, insbesondere Gleichgewichte in Mehrkomponentensystemen Mechanisches und thermisches Gleichgewicht 8.2-1 Stoffliches Gleichgewicht Beispiel Stickstoff Sauerstoff: Desweiteren
8.2 Thermodynamische Gleichgewichte, insbesondere Gleichgewichte in Mehrkomponentensystemen Mechanisches und thermisches Gleichgewicht 8.2-1 Stoffliches Gleichgewicht Beispiel Stickstoff Sauerstoff: Desweiteren
8.2 Thermodynamische Gleichgewichte, insbesondere Gleichgewichte in Mehrkomponentensystemen Mechanisches und thermisches Gleichgewicht
 8.2 Thermodynamische Gleichgewichte, insbesondere Gleichgewichte in Mehrkomponentensystemen Mechanisches und thermisches Gleichgewicht 8.2-1 Stoffliches Gleichgewicht Beispiel Stickstoff Sauerstoff: Desweiteren
8.2 Thermodynamische Gleichgewichte, insbesondere Gleichgewichte in Mehrkomponentensystemen Mechanisches und thermisches Gleichgewicht 8.2-1 Stoffliches Gleichgewicht Beispiel Stickstoff Sauerstoff: Desweiteren
Ideale und Reale Gase. Was ist ein ideales Gas? einatomige Moleküle mit keinerlei gegenseitiger WW keinem Eigenvolumen (punktförmig)
 Ideale und Reale Gase Was ist ein ideales Gas? einatomige Moleküle mit keinerlei gegenseitiger WW keinem Eigenvolumen (punktförmig) Wann sind reale Gase ideal? Reale Gase verhalten sich wie ideale Gase
Ideale und Reale Gase Was ist ein ideales Gas? einatomige Moleküle mit keinerlei gegenseitiger WW keinem Eigenvolumen (punktförmig) Wann sind reale Gase ideal? Reale Gase verhalten sich wie ideale Gase
Chemie Zusammenfassung KA 2
 Chemie Zusammenfassung KA 2 Wärmemenge Q bei einer Reaktion Chemische Reaktionen haben eine Gemeinsamkeit: Bei der Reaktion wird entweder Energie/Wärme frei (exotherm). Oder es wird Wärme/Energie aufgenommen
Chemie Zusammenfassung KA 2 Wärmemenge Q bei einer Reaktion Chemische Reaktionen haben eine Gemeinsamkeit: Bei der Reaktion wird entweder Energie/Wärme frei (exotherm). Oder es wird Wärme/Energie aufgenommen
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Gase, Flüssigkeiten, Feststoffe
 Gase, Flüssigkeiten, Feststoffe Charakteristische Eigenschaften der Aggregatzustände Gas: Flüssigkeit: Feststoff: Nimmt das Volumen und die Form seines Behälters an. Ist komprimierbar. Fliesst leicht.
Gase, Flüssigkeiten, Feststoffe Charakteristische Eigenschaften der Aggregatzustände Gas: Flüssigkeit: Feststoff: Nimmt das Volumen und die Form seines Behälters an. Ist komprimierbar. Fliesst leicht.
Für die Abhängigkeit der Freiheitsgrade von der Zahl der Komponenten und der Phasen eines Systems existiert die Gibbs sche Phasenregel: F = K P + 2
 hasengleichgewichte Definitionen: hase: Homogener Raumbereich, innerhalb dessen sich keine physikalische Größe (z.b. Dichte, Zusammensetzung, emperatur...) sprunghaft ändert. Das Berührungsgebiet zweier
hasengleichgewichte Definitionen: hase: Homogener Raumbereich, innerhalb dessen sich keine physikalische Größe (z.b. Dichte, Zusammensetzung, emperatur...) sprunghaft ändert. Das Berührungsgebiet zweier
2.8 Grenzflächeneffekte
 - 86-2.8 Grenzflächeneffekte 2.8.1 Oberflächenspannung An Grenzflächen treten besondere Effekte auf, welche im Volumen nicht beobachtbar sind. Die molekulare Grundlage dafür sind Kohäsionskräfte, d.h.
- 86-2.8 Grenzflächeneffekte 2.8.1 Oberflächenspannung An Grenzflächen treten besondere Effekte auf, welche im Volumen nicht beobachtbar sind. Die molekulare Grundlage dafür sind Kohäsionskräfte, d.h.
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
5.1. Kinetische Gastheorie. Ziel: Der Gasdruck: Kolben ohne Reibung, Gasatome im Volumen V Wie groß ist F auf den Kolben?
 5.1. Kinetische Gastheorie z.b: He-Gas : 3 10 Atome/cm diese wechselwirken über die elektrische Kraft: Materie besteht aus sehr vielen Atomen: gehorchen den Gesetzen der Mechanik Ziel: Verständnis der
5.1. Kinetische Gastheorie z.b: He-Gas : 3 10 Atome/cm diese wechselwirken über die elektrische Kraft: Materie besteht aus sehr vielen Atomen: gehorchen den Gesetzen der Mechanik Ziel: Verständnis der
Multiple-Choice Test. Alle Fragen können mit Hilfe der Versuchsanleitung richtig gelöst werden.
 PCG-Grundpraktikum Versuch 8- Reale Gas Multiple-Choice Test Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Reale Gas wird dieses Vorgespräch durch einen Multiple-Choice Test
PCG-Grundpraktikum Versuch 8- Reale Gas Multiple-Choice Test Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Reale Gas wird dieses Vorgespräch durch einen Multiple-Choice Test
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand
 Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand Vorüberlegung In einem seriellen Stromkreis addieren sich die Teilspannungen zur Gesamtspannung Bei einer Gesamtspannung U ges, der
Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand Vorüberlegung In einem seriellen Stromkreis addieren sich die Teilspannungen zur Gesamtspannung Bei einer Gesamtspannung U ges, der
6. Tag: Chemisches Gleichgewicht und Reaktionskinetik
 6. Tag: Chemisches Gleichgewicht und Reaktionskinetik 1 6. Tag: Chemisches Gleichgewicht und Reaktionskinetik 1. Das chemische Gleichgewicht Eine chemische Reaktion läuft in beiden Richtungen ab. Wenn
6. Tag: Chemisches Gleichgewicht und Reaktionskinetik 1 6. Tag: Chemisches Gleichgewicht und Reaktionskinetik 1. Das chemische Gleichgewicht Eine chemische Reaktion läuft in beiden Richtungen ab. Wenn
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
6. Reaktionsgleichungen 6.1 Chemisches Reaktionsschema Wortschema Reaktionsschema Beispiel 1: Kupfer und Schwefel Vorzahlen
 6. Reaktionsgleichungen 6.1 Chemisches Reaktionsschema Das Wortschema benennt die Ausgangsstoffe und die Reaktionsprodukte einer chemischen Reaktion. Das Reaktionsschema sagt zusätzlich etwas über das
6. Reaktionsgleichungen 6.1 Chemisches Reaktionsschema Das Wortschema benennt die Ausgangsstoffe und die Reaktionsprodukte einer chemischen Reaktion. Das Reaktionsschema sagt zusätzlich etwas über das
Einführung in. Logische Schaltungen
 Einführung in Logische Schaltungen 1/7 Inhaltsverzeichnis 1. Einführung 1. Was sind logische Schaltungen 2. Grundlegende Elemente 3. Weitere Elemente 4. Beispiel einer logischen Schaltung 2. Notation von
Einführung in Logische Schaltungen 1/7 Inhaltsverzeichnis 1. Einführung 1. Was sind logische Schaltungen 2. Grundlegende Elemente 3. Weitere Elemente 4. Beispiel einer logischen Schaltung 2. Notation von
18. Magnetismus in Materie
 18. Magnetismus in Materie Wir haben den elektrischen Strom als Quelle für Magnetfelder kennen gelernt. Auch das magnetische Verhalten von Materie wird durch elektrische Ströme bestimmt. Die Bewegung der
18. Magnetismus in Materie Wir haben den elektrischen Strom als Quelle für Magnetfelder kennen gelernt. Auch das magnetische Verhalten von Materie wird durch elektrische Ströme bestimmt. Die Bewegung der
Das große ElterngeldPlus 1x1. Alles über das ElterngeldPlus. Wer kann ElterngeldPlus beantragen? ElterngeldPlus verstehen ein paar einleitende Fakten
 Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
Innere Reibung von Gasen
 Blatt: 1 Aufgabe Bestimmen Sie die Viskosität η von Gasen aus der Messung der Strömung durch Kapillaren. Berechnen Sie aus den Messergebnissen für jedes Gas die Sutherland-Konstante C, die effektiven Moleküldurchmesser
Blatt: 1 Aufgabe Bestimmen Sie die Viskosität η von Gasen aus der Messung der Strömung durch Kapillaren. Berechnen Sie aus den Messergebnissen für jedes Gas die Sutherland-Konstante C, die effektiven Moleküldurchmesser
Thermodynamik. Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur
 Thermodynamik Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur kann voraussagen, ob eine chemische Reaktion abläuft oder nicht kann nichts über den zeitlichen
Thermodynamik Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur kann voraussagen, ob eine chemische Reaktion abläuft oder nicht kann nichts über den zeitlichen
Protokoll des Versuches 5: Messungen der Thermospannung nach der Kompensationsmethode
 Name: Matrikelnummer: Bachelor Biowissenschaften E-Mail: Physikalisches Anfängerpraktikum II Dozenten: Assistenten: Protokoll des Versuches 5: Messungen der Thermospannung nach der Kompensationsmethode
Name: Matrikelnummer: Bachelor Biowissenschaften E-Mail: Physikalisches Anfängerpraktikum II Dozenten: Assistenten: Protokoll des Versuches 5: Messungen der Thermospannung nach der Kompensationsmethode
Druckgleichung nach Daniel Bernoulli (Bernoulligleichung)
 HTW Dresden V-SL1 Lehrgebiet Strömungslehre 1. Vorbetrachtung Druckgleichung nach Daniel Bernoulli (Bernoulligleichung) In ruhenden und bewegten Flüssigkeiten gilt, wie in der Physik allgemein, das Gesetz
HTW Dresden V-SL1 Lehrgebiet Strömungslehre 1. Vorbetrachtung Druckgleichung nach Daniel Bernoulli (Bernoulligleichung) In ruhenden und bewegten Flüssigkeiten gilt, wie in der Physik allgemein, das Gesetz
Statistische Thermodynamik I Lösungen zur Serie 1
 Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
3.2 Spiegelungen an zwei Spiegeln
 3 Die Theorie des Spiegelbuches 45 sehen, wenn die Person uns direkt gegenüber steht. Denn dann hat sie eine Drehung um die senkrechte Achse gemacht und dabei links und rechts vertauscht. 3.2 Spiegelungen
3 Die Theorie des Spiegelbuches 45 sehen, wenn die Person uns direkt gegenüber steht. Denn dann hat sie eine Drehung um die senkrechte Achse gemacht und dabei links und rechts vertauscht. 3.2 Spiegelungen
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
 Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Warum benutzt man verdrillte Leitungspaare in LANs und nicht Paare mit parallel geführten Leitungen?
 Warum benutzt man verdrillte Leitungspaare in LANs und nicht Paare mit parallel geführten Leitungen? Das kann man nur verstehen, wenn man weiß, was ein magnetisches Feld ist und was das Induktionsgesetz
Warum benutzt man verdrillte Leitungspaare in LANs und nicht Paare mit parallel geführten Leitungen? Das kann man nur verstehen, wenn man weiß, was ein magnetisches Feld ist und was das Induktionsgesetz
Übungen zur VL Chemie für Biologen und Humanbiologen 05.12.2011 Lösung Übung 6
 Übungen zur VL Chemie für Biologen und Humanbiologen 05.12.2011 Lösung Übung 6 Thermodynamik und Gleichgewichte 1. a) Was sagt die Enthalpie aus? Die Enthalpie H beschreibt den Energiegehalt von Materie
Übungen zur VL Chemie für Biologen und Humanbiologen 05.12.2011 Lösung Übung 6 Thermodynamik und Gleichgewichte 1. a) Was sagt die Enthalpie aus? Die Enthalpie H beschreibt den Energiegehalt von Materie
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
V 2 B, C, D Drinks. Möglicher Lösungsweg a) Gleichungssystem: 300x + 400 y = 520 300x + 500y = 597,5 2x3 Matrix: Energydrink 0,7 Mineralwasser 0,775,
 Aufgabenpool für angewandte Mathematik / 1. Jahrgang V B, C, D Drinks Ein gastronomischer Betrieb kauft 300 Dosen Energydrinks (0,3 l) und 400 Liter Flaschen Mineralwasser und zahlt dafür 50, Euro. Einen
Aufgabenpool für angewandte Mathematik / 1. Jahrgang V B, C, D Drinks Ein gastronomischer Betrieb kauft 300 Dosen Energydrinks (0,3 l) und 400 Liter Flaschen Mineralwasser und zahlt dafür 50, Euro. Einen
Theoretische Grundlagen der Informatik WS 09/10
 Theoretische Grundlagen der Informatik WS 09/10 - Tutorium 6 - Michael Kirsten und Kai Wallisch Sitzung 13 02.02.2010 Inhaltsverzeichnis 1 Formeln zur Berechnung Aufgabe 1 2 Hamming-Distanz Aufgabe 2 3
Theoretische Grundlagen der Informatik WS 09/10 - Tutorium 6 - Michael Kirsten und Kai Wallisch Sitzung 13 02.02.2010 Inhaltsverzeichnis 1 Formeln zur Berechnung Aufgabe 1 2 Hamming-Distanz Aufgabe 2 3
erster Hauptsatz der Thermodynamik,
 1.2 Erster Hautsatz der hermodynamik Wir betrachten ein thermodynamisches System, dem wir eine beliebige Wärmemenge δq zuführen, und an dem wir eine Arbeit da leisten wollen. Werden umgekehrt dem System
1.2 Erster Hautsatz der hermodynamik Wir betrachten ein thermodynamisches System, dem wir eine beliebige Wärmemenge δq zuführen, und an dem wir eine Arbeit da leisten wollen. Werden umgekehrt dem System
2. Chemische Reaktionen und chemisches Gleichgewicht
 2. Chemische Reaktionen und chemisches Gleichgewicht 2.1 Enthalpie (ΔH) Bei chemischen Reaktionen reagieren die Edukte zu Produkten. Diese unterscheiden sich in der inneren Energie. Es gibt dabei zwei
2. Chemische Reaktionen und chemisches Gleichgewicht 2.1 Enthalpie (ΔH) Bei chemischen Reaktionen reagieren die Edukte zu Produkten. Diese unterscheiden sich in der inneren Energie. Es gibt dabei zwei
14. Minimale Schichtdicken von PEEK und PPS im Schlauchreckprozeß und im Rheotensversuch
 14. Minimale Schichtdicken von PEEK und PPS im Schlauchreckprozeß und im Rheotensversuch Analog zu den Untersuchungen an LDPE in Kap. 6 war zu untersuchen, ob auch für die Hochtemperatur-Thermoplaste aus
14. Minimale Schichtdicken von PEEK und PPS im Schlauchreckprozeß und im Rheotensversuch Analog zu den Untersuchungen an LDPE in Kap. 6 war zu untersuchen, ob auch für die Hochtemperatur-Thermoplaste aus
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Fachdidaktik der Informatik 18.12.08 Jörg Depner, Kathrin Gaißer
 Fachdidaktik der Informatik 18.12.08 Jörg Depner, Kathrin Gaißer Klassendiagramme Ein Klassendiagramm dient in der objektorientierten Softwareentwicklung zur Darstellung von Klassen und den Beziehungen,
Fachdidaktik der Informatik 18.12.08 Jörg Depner, Kathrin Gaißer Klassendiagramme Ein Klassendiagramm dient in der objektorientierten Softwareentwicklung zur Darstellung von Klassen und den Beziehungen,
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR)
 Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Thermodynamik Wärmeempfindung
 Folie 1/17 Warum fühlt sich 4 warmes wesentlich heißer an als warme? Und weshalb empfinden wir kühles wiederum kälter als kühle? 7 6 5 4 2 - -2 32 32 Folie 2/17 Wir Menschen besitzen kein Sinnesorgan für
Folie 1/17 Warum fühlt sich 4 warmes wesentlich heißer an als warme? Und weshalb empfinden wir kühles wiederum kälter als kühle? 7 6 5 4 2 - -2 32 32 Folie 2/17 Wir Menschen besitzen kein Sinnesorgan für
Bewertung des Blattes
 Bewertung des Blattes Es besteht immer die Schwierigkeit, sein Blatt richtig einzuschätzen. Im folgenden werden einige Anhaltspunkte gegeben. Man unterscheidet: Figurenpunkte Verteilungspunkte Längenpunkte
Bewertung des Blattes Es besteht immer die Schwierigkeit, sein Blatt richtig einzuschätzen. Im folgenden werden einige Anhaltspunkte gegeben. Man unterscheidet: Figurenpunkte Verteilungspunkte Längenpunkte
4. AUSSAGENLOGIK: SYNTAX. Der Unterschied zwischen Objektsprache und Metasprache lässt sich folgendermaßen charakterisieren:
 4. AUSSAGENLOGIK: SYNTAX 4.1 Objektsprache und Metasprache 4.2 Gebrauch und Erwähnung 4.3 Metavariablen: Verallgemeinerndes Sprechen über Ausdrücke von AL 4.4 Die Sprache der Aussagenlogik 4.5 Terminologie
4. AUSSAGENLOGIK: SYNTAX 4.1 Objektsprache und Metasprache 4.2 Gebrauch und Erwähnung 4.3 Metavariablen: Verallgemeinerndes Sprechen über Ausdrücke von AL 4.4 Die Sprache der Aussagenlogik 4.5 Terminologie
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Repetitionsaufgaben Wurzelgleichungen
 Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Erstellen von x-y-diagrammen in OpenOffice.calc
 Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Kapitalerhöhung - Verbuchung
 Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Verflüssigung von Gasen / Joule-Thomson-Effekt
 Sieden und Kondensation: T p T p S S 0 1 RTSp0 1 ln p p0 Dampfdrucktopf, Autoklave zur Sterilisation absolute Luftfeuchtigkeit relative Luftfeuchtigkeit a ( g/m 3 ) a pw rel S ps rel 1 Taupunkt erflüssigung
Sieden und Kondensation: T p T p S S 0 1 RTSp0 1 ln p p0 Dampfdrucktopf, Autoklave zur Sterilisation absolute Luftfeuchtigkeit relative Luftfeuchtigkeit a ( g/m 3 ) a pw rel S ps rel 1 Taupunkt erflüssigung
Achim Rosch, Institut für Theoretische Physik, Köln. Belegt das Gutachten wesentliche fachliche Fehler im KPK?
 Impulsstrom Achim Rosch, Institut für Theoretische Physik, Köln zwei Fragen: Belegt das Gutachten wesentliche fachliche Fehler im KPK? Gibt es im Gutachten selbst wesentliche fachliche Fehler? andere wichtige
Impulsstrom Achim Rosch, Institut für Theoretische Physik, Köln zwei Fragen: Belegt das Gutachten wesentliche fachliche Fehler im KPK? Gibt es im Gutachten selbst wesentliche fachliche Fehler? andere wichtige
Skript und Aufgabensammlung Terme und Gleichungen Mathefritz Verlag Jörg Christmann Nur zum Privaten Gebrauch! Alle Rechte vorbehalten!
 Mathefritz 5 Terme und Gleichungen Meine Mathe-Seite im Internet kostenlose Matheaufgaben, Skripte, Mathebücher Lernspiele, Lerntipps, Quiz und noch viel mehr http:// www.mathefritz.de Seite 1 Copyright
Mathefritz 5 Terme und Gleichungen Meine Mathe-Seite im Internet kostenlose Matheaufgaben, Skripte, Mathebücher Lernspiele, Lerntipps, Quiz und noch viel mehr http:// www.mathefritz.de Seite 1 Copyright
Ruinwahrscheinlichkeiten im Glücksspiel
 Ruinwahrscheinlichkeiten im Glücksspiel Wilhelm Stannat Fachbereich Mathematik TU Darmstadt February 24, 2007 Stochastik = Wahrscheinlichkeitstheorie + Statistik Wahrscheinlichkeitstheorie = Mathematische
Ruinwahrscheinlichkeiten im Glücksspiel Wilhelm Stannat Fachbereich Mathematik TU Darmstadt February 24, 2007 Stochastik = Wahrscheinlichkeitstheorie + Statistik Wahrscheinlichkeitstheorie = Mathematische
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
AGROPLUS Buchhaltung. Daten-Server und Sicherheitskopie. Version vom 21.10.2013b
 AGROPLUS Buchhaltung Daten-Server und Sicherheitskopie Version vom 21.10.2013b 3a) Der Daten-Server Modus und der Tresor Der Daten-Server ist eine Betriebsart welche dem Nutzer eine grosse Flexibilität
AGROPLUS Buchhaltung Daten-Server und Sicherheitskopie Version vom 21.10.2013b 3a) Der Daten-Server Modus und der Tresor Der Daten-Server ist eine Betriebsart welche dem Nutzer eine grosse Flexibilität
1 Arbeit und Energie. ~ F d~r: (1) W 1!2 = ~ F ~s = Beispiel für die Berechnung eines Wegintegrals:
 1 Arbeit und Energie Von Arbeit sprechen wir, wenn eine Kraft ~ F auf einen Körper entlang eines Weges ~s einwirkt und dadurch der "Energieinhalt" des Körpers verändert wird. Die Arbeit ist de niert als
1 Arbeit und Energie Von Arbeit sprechen wir, wenn eine Kraft ~ F auf einen Körper entlang eines Weges ~s einwirkt und dadurch der "Energieinhalt" des Körpers verändert wird. Die Arbeit ist de niert als
Zwischenablage (Bilder, Texte,...)
 Zwischenablage was ist das? Informationen über. die Bedeutung der Windows-Zwischenablage Kopieren und Einfügen mit der Zwischenablage Vermeiden von Fehlern beim Arbeiten mit der Zwischenablage Bei diesen
Zwischenablage was ist das? Informationen über. die Bedeutung der Windows-Zwischenablage Kopieren und Einfügen mit der Zwischenablage Vermeiden von Fehlern beim Arbeiten mit der Zwischenablage Bei diesen
Grundlagen der Elektronik
 Grundlagen der Elektronik Wiederholung: Elektrische Größen Die elektrische Stromstärke I in A gibt an,... wie viele Elektronen sich pro Sekunde durch den Querschnitt eines Leiters bewegen. Die elektrische
Grundlagen der Elektronik Wiederholung: Elektrische Größen Die elektrische Stromstärke I in A gibt an,... wie viele Elektronen sich pro Sekunde durch den Querschnitt eines Leiters bewegen. Die elektrische
Austausch- bzw. Übergangsprozesse und Gleichgewichtsverteilungen
 Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
4.12 Elektromotor und Generator
 4.12 Elektromotor und Generator Elektromotoren und Generatoren gehören neben der Erfindung der Dampfmaschine zu den wohl größten Erfindungen der Menschheitsgeschichte. Die heutige elektrifizierte Welt
4.12 Elektromotor und Generator Elektromotoren und Generatoren gehören neben der Erfindung der Dampfmaschine zu den wohl größten Erfindungen der Menschheitsgeschichte. Die heutige elektrifizierte Welt
3. Halbleiter und Elektronik
 3. Halbleiter und Elektronik Halbleiter sind Stoe, welche die Eigenschaften von Leitern sowie Nichtleitern miteinander vereinen. Prinzipiell sind die Elektronen in einem Kristallgitter fest eingebunden
3. Halbleiter und Elektronik Halbleiter sind Stoe, welche die Eigenschaften von Leitern sowie Nichtleitern miteinander vereinen. Prinzipiell sind die Elektronen in einem Kristallgitter fest eingebunden
Anleitung über den Umgang mit Schildern
 Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
R ist freie Software und kann von der Website. www.r-project.org
 R R ist freie Software und kann von der Website heruntergeladen werden. www.r-project.org Nach dem Herunterladen und der Installation von R kann man R durch Doppelklicken auf das R-Symbol starten. R wird
R R ist freie Software und kann von der Website heruntergeladen werden. www.r-project.org Nach dem Herunterladen und der Installation von R kann man R durch Doppelklicken auf das R-Symbol starten. R wird
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Modellbildungssysteme: Pädagogische und didaktische Ziele
 Modellbildungssysteme: Pädagogische und didaktische Ziele Was hat Modellbildung mit der Schule zu tun? Der Bildungsplan 1994 formuliert: "Die schnelle Zunahme des Wissens, die hohe Differenzierung und
Modellbildungssysteme: Pädagogische und didaktische Ziele Was hat Modellbildung mit der Schule zu tun? Der Bildungsplan 1994 formuliert: "Die schnelle Zunahme des Wissens, die hohe Differenzierung und
Kugel-Fächer-Modell. 1fach. 3fach. Für die Einzelkugel gibt es 3 Möglichkeiten. 6fach. 3! Möglichkeiten
 Kugel-Fächer-Modell n Kugeln (Rosinen) sollen auf m Fächer (Brötchen) verteilt werden, zunächst 3 Kugeln auf 3 Fächer. 1fach 3fach Für die Einzelkugel gibt es 3 Möglichkeiten } 6fach 3! Möglichkeiten Es
Kugel-Fächer-Modell n Kugeln (Rosinen) sollen auf m Fächer (Brötchen) verteilt werden, zunächst 3 Kugeln auf 3 Fächer. 1fach 3fach Für die Einzelkugel gibt es 3 Möglichkeiten } 6fach 3! Möglichkeiten Es
Administratives BSL PB
 Administratives Die folgenden Seiten sind ausschliesslich als Ergänzung zum Unterricht für die Schüler der BSL gedacht (intern) und dürfen weder teilweise noch vollständig kopiert oder verbreitet werden.
Administratives Die folgenden Seiten sind ausschliesslich als Ergänzung zum Unterricht für die Schüler der BSL gedacht (intern) und dürfen weder teilweise noch vollständig kopiert oder verbreitet werden.
Programm 4: Arbeiten mit thematischen Karten
 : Arbeiten mit thematischen Karten A) Anteil der ausländischen Wohnbevölkerung an der Wohnbevölkerung insgesamt 2001 in Prozent 1. Inhaltliche und kartographische Beschreibung - Originalkarte Bei dieser
: Arbeiten mit thematischen Karten A) Anteil der ausländischen Wohnbevölkerung an der Wohnbevölkerung insgesamt 2001 in Prozent 1. Inhaltliche und kartographische Beschreibung - Originalkarte Bei dieser
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Physik 4, Übung 8, Prof. Förster
 Physik 4, Übung 8, Prof. Förster Christoph Hansen Emailkontakt Dieser Text ist unter dieser Creative Commons Lizenz veröffentlicht. Ich erhebe keinen Anspruch auf Vollständigkeit oder Richtigkeit. Falls
Physik 4, Übung 8, Prof. Förster Christoph Hansen Emailkontakt Dieser Text ist unter dieser Creative Commons Lizenz veröffentlicht. Ich erhebe keinen Anspruch auf Vollständigkeit oder Richtigkeit. Falls
1. Theorie: Kondensator:
 1. Theorie: Aufgabe des heutigen Versuchstages war es, die charakteristische Größe eines Kondensators (Kapazität C) und einer Spule (Induktivität L) zu bestimmen, indem man per Oszilloskop Spannung und
1. Theorie: Aufgabe des heutigen Versuchstages war es, die charakteristische Größe eines Kondensators (Kapazität C) und einer Spule (Induktivität L) zu bestimmen, indem man per Oszilloskop Spannung und
Statuten in leichter Sprache
 Statuten in leichter Sprache Zweck vom Verein Artikel 1: Zivil-Gesetz-Buch Es gibt einen Verein der selbstbestimmung.ch heisst. Der Verein ist so aufgebaut, wie es im Zivil-Gesetz-Buch steht. Im Zivil-Gesetz-Buch
Statuten in leichter Sprache Zweck vom Verein Artikel 1: Zivil-Gesetz-Buch Es gibt einen Verein der selbstbestimmung.ch heisst. Der Verein ist so aufgebaut, wie es im Zivil-Gesetz-Buch steht. Im Zivil-Gesetz-Buch
Mathematik. UND/ODER Verknüpfung. Ungleichungen. Betrag. Intervall. Umgebung
 Mathematik UND/ODER Verknüpfung Ungleichungen Betrag Intervall Umgebung Stefan Gärtner 004 Gr Mathematik UND/ODER Seite UND Verknüpfung Kommentar Aussage Symbolform Die Aussagen Hans kann schwimmen p und
Mathematik UND/ODER Verknüpfung Ungleichungen Betrag Intervall Umgebung Stefan Gärtner 004 Gr Mathematik UND/ODER Seite UND Verknüpfung Kommentar Aussage Symbolform Die Aussagen Hans kann schwimmen p und
A1.7: Entropie natürlicher Texte
 A1.7: Entropie natürlicher Texte Anfang der 1950er Jahre hat Claude E. Shannon die Entropie H der englischen Sprache mit einem bit pro Zeichen abgeschätzt. Kurz darauf kam Karl Küpfmüller bei einer empirischen
A1.7: Entropie natürlicher Texte Anfang der 1950er Jahre hat Claude E. Shannon die Entropie H der englischen Sprache mit einem bit pro Zeichen abgeschätzt. Kurz darauf kam Karl Küpfmüller bei einer empirischen
Arbeit Leistung Energie
 Arbeit Leistung Energie manuell geistig Was ist Arbeit Wie misst man Arbeit? Ist geistige Arbeit messbar? Wann wird physikalische Arbeit verrichtet? Es wird physikalische Arbeit verrichtet, wenn eine Kraft
Arbeit Leistung Energie manuell geistig Was ist Arbeit Wie misst man Arbeit? Ist geistige Arbeit messbar? Wann wird physikalische Arbeit verrichtet? Es wird physikalische Arbeit verrichtet, wenn eine Kraft
Güte von Tests. die Wahrscheinlichkeit für den Fehler 2. Art bei der Testentscheidung, nämlich. falsch ist. Darauf haben wir bereits im Kapitel über
 Güte von s Grundlegendes zum Konzept der Güte Ableitung der Gütefunktion des Gauss im Einstichprobenproblem Grafische Darstellung der Gütefunktionen des Gauss im Einstichprobenproblem Ableitung der Gütefunktion
Güte von s Grundlegendes zum Konzept der Güte Ableitung der Gütefunktion des Gauss im Einstichprobenproblem Grafische Darstellung der Gütefunktionen des Gauss im Einstichprobenproblem Ableitung der Gütefunktion
Aufbau der Materie: Oberflächenspannung von Flüssigkeiten EÖTVÖSsche Regel
 Hochschule Physikalische Chemie Vers.Nr. 11 Emden / Leer Praktikum Sept. 2005 Aufbau der Materie: Oberflächenspannung von Flüssigkeiten EÖTVÖSsche Regel In diesem Versuch soll die Oberflächenspannung einer
Hochschule Physikalische Chemie Vers.Nr. 11 Emden / Leer Praktikum Sept. 2005 Aufbau der Materie: Oberflächenspannung von Flüssigkeiten EÖTVÖSsche Regel In diesem Versuch soll die Oberflächenspannung einer
Musterprüfung Chemie Klassen: MPL 09 Datum: 14. 16. April 2010
 1 Musterprüfung Chemie Klassen: MPL 09 Datum: 14. 16. April 2010 Themen: Metallische Bindungen (Skript S. 51 53, inkl. Arbeitsblatt) Reaktionsverlauf (Skript S. 54 59, inkl. Arbeitsblatt, Merke, Fig. 7.2.1
1 Musterprüfung Chemie Klassen: MPL 09 Datum: 14. 16. April 2010 Themen: Metallische Bindungen (Skript S. 51 53, inkl. Arbeitsblatt) Reaktionsverlauf (Skript S. 54 59, inkl. Arbeitsblatt, Merke, Fig. 7.2.1
FlowFact Alle Versionen
 Training FlowFact Alle Versionen Stand: 29.09.2005 Rechnung schreiben Einführung Wie Sie inzwischen wissen, können die unterschiedlichsten Daten über verknüpfte Fenster miteinander verbunden werden. Für
Training FlowFact Alle Versionen Stand: 29.09.2005 Rechnung schreiben Einführung Wie Sie inzwischen wissen, können die unterschiedlichsten Daten über verknüpfte Fenster miteinander verbunden werden. Für
40-Tage-Wunder- Kurs. Umarme, was Du nicht ändern kannst.
 40-Tage-Wunder- Kurs Umarme, was Du nicht ändern kannst. Das sagt Wikipedia: Als Wunder (griechisch thauma) gilt umgangssprachlich ein Ereignis, dessen Zustandekommen man sich nicht erklären kann, so dass
40-Tage-Wunder- Kurs Umarme, was Du nicht ändern kannst. Das sagt Wikipedia: Als Wunder (griechisch thauma) gilt umgangssprachlich ein Ereignis, dessen Zustandekommen man sich nicht erklären kann, so dass
Comenius Schulprojekt The sun and the Danube. Versuch 1: Spannung U und Stom I in Abhängigkeit der Beleuchtungsstärke E U 0, I k = f ( E )
 Blatt 2 von 12 Versuch 1: Spannung U und Stom I in Abhängigkeit der Beleuchtungsstärke E U 0, I k = f ( E ) Solar-Zellen bestehen prinzipiell aus zwei Schichten mit unterschiedlichem elektrischen Verhalten.
Blatt 2 von 12 Versuch 1: Spannung U und Stom I in Abhängigkeit der Beleuchtungsstärke E U 0, I k = f ( E ) Solar-Zellen bestehen prinzipiell aus zwei Schichten mit unterschiedlichem elektrischen Verhalten.
Studieren- Erklärungen und Tipps
 Studieren- Erklärungen und Tipps Es gibt Berufe, die man nicht lernen kann, sondern für die man ein Studium machen muss. Das ist zum Beispiel so wenn man Arzt oder Lehrer werden möchte. Hat ihr Kind das
Studieren- Erklärungen und Tipps Es gibt Berufe, die man nicht lernen kann, sondern für die man ein Studium machen muss. Das ist zum Beispiel so wenn man Arzt oder Lehrer werden möchte. Hat ihr Kind das
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Membran- und Donnanpotentiale. (Zusammenfassung)
 Membranund Donnanpotentiale (Zusammenfassung) Inhaltsverzeichnis 1. Elektrochemische Membranen...Seite 2 2. Diffusionspotentiale...Seite 2 3. Donnanpotentiale...Seite 3 4. Zusammenhang der dargestellten
Membranund Donnanpotentiale (Zusammenfassung) Inhaltsverzeichnis 1. Elektrochemische Membranen...Seite 2 2. Diffusionspotentiale...Seite 2 3. Donnanpotentiale...Seite 3 4. Zusammenhang der dargestellten
Profil A 49,3 48,2 50,7 50,9 49,8 48,7 49,6 50,1 Profil B 51,8 49,6 53,2 51,1 51,1 53,4 50,7 50 51,5 51,7 48,8
 1. Aufgabe: Eine Reifenfirma hat für Winterreifen unterschiedliche Profile entwickelt. Bei jeweils gleicher Geschwindigkeit und auch sonst gleichen Bedingungen wurden die Bremswirkungen gemessen. Die gemessenen
1. Aufgabe: Eine Reifenfirma hat für Winterreifen unterschiedliche Profile entwickelt. Bei jeweils gleicher Geschwindigkeit und auch sonst gleichen Bedingungen wurden die Bremswirkungen gemessen. Die gemessenen
Dr. Kraus & Partner Ihr Angebot zu Konfliktmanagement
 Dr. Kraus & Partner Ihr Angebot zu Konfliktmanagement Sämtliche Zeichnungen und Karikaturen dieser Präsentation sind urheberrechtlich geschützt und dürfen nur mit schriftlicher Genehmigung seitens Dr.
Dr. Kraus & Partner Ihr Angebot zu Konfliktmanagement Sämtliche Zeichnungen und Karikaturen dieser Präsentation sind urheberrechtlich geschützt und dürfen nur mit schriftlicher Genehmigung seitens Dr.
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
Wenn der Druck aus der reibungsfreien Außenströmung aufgeprägt wird, dann gilt wegen der Bernoulli-Gleichung
 Wenn der Druck aus der reibungsfreien Außenströmung aufgeprägt wird, dann gilt wegen der Bernoulli-Gleichung ρ p ( x) + Uδ ( x) = const Damit kann die Druckänderung in Strömungsrichtung auch durch die
Wenn der Druck aus der reibungsfreien Außenströmung aufgeprägt wird, dann gilt wegen der Bernoulli-Gleichung ρ p ( x) + Uδ ( x) = const Damit kann die Druckänderung in Strömungsrichtung auch durch die
DIFFERENTIALGLEICHUNGEN
 DIFFERENTIALGLEICHUNGEN GRUNDBEGRIFFE Differentialgleichung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten Ordnung auftreten, heisst gewöhnliche Differentialgleichung
DIFFERENTIALGLEICHUNGEN GRUNDBEGRIFFE Differentialgleichung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten Ordnung auftreten, heisst gewöhnliche Differentialgleichung
Was ist das Budget für Arbeit?
 1 Was ist das Budget für Arbeit? Das Budget für Arbeit ist ein Persönliches Geld für Arbeit wenn Sie arbeiten möchten aber nicht mehr in einer Werkstatt. Das gibt es bisher nur in Nieder-Sachsen. Und in
1 Was ist das Budget für Arbeit? Das Budget für Arbeit ist ein Persönliches Geld für Arbeit wenn Sie arbeiten möchten aber nicht mehr in einer Werkstatt. Das gibt es bisher nur in Nieder-Sachsen. Und in
Arbeitsheft Quantitative Aspekte Jakob 1
 Arbeitsheft Quantitative Aspekte Jakob 1 Inhaltsverzeichnis: 1 Rechnen in der Chemie - wozu? 1.1 Aussagen einer Reaktionsgleichung - wieviel? 2 1.2, Wert und Einheit - gefährliche Schlamperei! 3 1.3 n
Arbeitsheft Quantitative Aspekte Jakob 1 Inhaltsverzeichnis: 1 Rechnen in der Chemie - wozu? 1.1 Aussagen einer Reaktionsgleichung - wieviel? 2 1.2, Wert und Einheit - gefährliche Schlamperei! 3 1.3 n
Animationen erstellen
 Animationen erstellen Unter Animation wird hier das Erscheinen oder Bewegen von Objekten Texten und Bildern verstanden Dazu wird zunächst eine neue Folie erstellt : Einfügen/ Neue Folie... Das Layout Aufzählung
Animationen erstellen Unter Animation wird hier das Erscheinen oder Bewegen von Objekten Texten und Bildern verstanden Dazu wird zunächst eine neue Folie erstellt : Einfügen/ Neue Folie... Das Layout Aufzählung
Was ist Sozial-Raum-Orientierung?
 Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Scheper Ziekenhuis Emmen. Tel.: + 31 (0) 591-691 320 Fax: + 31 (0) 591-691 321 Web: www.plastici.nl
 Scheper Ziekenhuis Emmen Tel.: + 31 (0) 591-691 320 Fax: + 31 (0) 591-691 321 Web: www.plastici.nl PREISE Wir bieten Ihnen Brustvergrößerungen von 3000,- bis 5.500,- Euro an. ALLGEMEINE INFORMATIONEN Die
Scheper Ziekenhuis Emmen Tel.: + 31 (0) 591-691 320 Fax: + 31 (0) 591-691 321 Web: www.plastici.nl PREISE Wir bieten Ihnen Brustvergrößerungen von 3000,- bis 5.500,- Euro an. ALLGEMEINE INFORMATIONEN Die
Berechnung der Erhöhung der Durchschnittsprämien
 Wolfram Fischer Berechnung der Erhöhung der Durchschnittsprämien Oktober 2004 1 Zusammenfassung Zur Berechnung der Durchschnittsprämien wird das gesamte gemeldete Prämienvolumen Zusammenfassung durch die
Wolfram Fischer Berechnung der Erhöhung der Durchschnittsprämien Oktober 2004 1 Zusammenfassung Zur Berechnung der Durchschnittsprämien wird das gesamte gemeldete Prämienvolumen Zusammenfassung durch die
APP-GFP/Fluoreszenzmikroskop. Aufnahmen neuronaler Zellen, mit freund. Genehmigung von Prof. Stefan Kins, TU Kaiserslautern
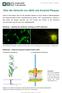 Über die Herkunft von Aβ42 und Amyloid-Plaques Heute ist sicher belegt, dass sich die amyloiden Plaques aus einer Vielzahl an Abbaufragmenten des Amyloid-Vorläufer-Proteins (amyloid-precursor-protein,
Über die Herkunft von Aβ42 und Amyloid-Plaques Heute ist sicher belegt, dass sich die amyloiden Plaques aus einer Vielzahl an Abbaufragmenten des Amyloid-Vorläufer-Proteins (amyloid-precursor-protein,
Funktion Erläuterung Beispiel
 WESTFÄLISCHE WILHELMS-UNIVERSITÄT WIRTSCHAFTSWISSENSCHAFTLICHE FAKULTÄT BETRIEBLICHE DATENVERARBEITUNG Folgende Befehle werden typischerweise im Excel-Testat benötigt. Die Beispiele in diesem Dokument
WESTFÄLISCHE WILHELMS-UNIVERSITÄT WIRTSCHAFTSWISSENSCHAFTLICHE FAKULTÄT BETRIEBLICHE DATENVERARBEITUNG Folgende Befehle werden typischerweise im Excel-Testat benötigt. Die Beispiele in diesem Dokument
