Warten auf einen Run und was kommt dann?

Transkript

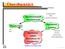
1 Warten auf einen Run und was kommt dann? GERD RIEHL, BARSINGHAUSEN Zusammenfassung: Das Problem, die Wahrsheinlihkeit für einen Run der Länge 4 (also 4 gleihe Zahlen hintereinander) beim n-maligen Würfeln zu berehnen, lässt sih mit Markow-Ketten wesentlih leihter als mit der von Motzer (200) angegebenen Rekursion lösen. Neben der Möglihkeit zur Visualisierung der stohastishen Situation hat diese Methode den Vorzug, mühelos auf die verallgemeinerte Fragestellung nah der Verteilung der Zufallsgröße Anzahl Runs der Länge λ beim n-maligen Würfeln übertragbar zu sein. Die Problemstellung Serien von gleihen Würfelzahlen so der Titel von Motzers Aufsatz ersheinen stohastishen Laien oft unwahrsheinliher als sie tatsählih sind. Viele Menshen halten einen häufigen Wehsel zwishen zwei aufeinander folgenden Ausfällen beim wiederholten Würfeln, in Serien von Münzwürfen, Folgen von Zufallsziffern usw. für ein tyishes Merkmal des Zufalls. Wäre dies so, würden in einer solhen Serie mehr, dafür aber kürzere Runs (Folgen gleiher Ergebnisse) auftreten, als theoretish zu erwarten und in Versuhen auh zu beobahten sind. Wir greifen hier ein Beisiel aus Motzer (200) auf. Aufgabe : Bei einer Würfelserie der Länge n = 00 fragt man nah der Wahrsheinlihkeit für einen (genauer: mindestens einen) Run von 4 oder mehr gleihen Augenzahlen. Diese Aufgabe werden wir in Abshnitt 2 mithilfe einer Markow-Kette lösen. Deren Grahen brauht man dann nur geringfügig abzuändern, um auh die Wahrsheinlihkeit für mindestens einen Run der genauen Länge 4 berehnen zu können. In Abshnitt 3 zeigen wir, dass man mit demselben Verfahren auh berehnen kann, wie wahrsheinlih es ist, genau einen Run und allgemein genau k Runs in der Serie zu erzielen. Auf einige Varianten des Problems und eine ähnlih zu bearbeitende Verallgemeinerung gehen wir in den Abshnitten 4 und 5 ein. 2 Ein neue Lösungsmethode durh Visualisierung Wir veranshaulihen zunähst die stohastishe Situation mithilfe des folgenden Übergangsgrahen: Abb. : Übergangsgrah zu Aufgabe Nah dem ersten Wurf hat man eine Zahl als Anfang eines im Aufbau begriffenen Runs, man befindet sih im Zustand. Beim zweiten Mal wirft man mit der Wahrsheinlihkeit = /6 dieselbe Zahl, in diesem Fall wähst der Run auf die Länge 2, d. h. man gelangt in den Zustand 2. Andernfalls hat der erste Run die Länge, während die Augenzahl des zweiten Wurfs zum Anfang eines neuen Runs wird und man somit im Zustand bleibt dies geshieht mit der Wahrsheinlihkeit = 5/6. Genauso fällt man aus den Zuständen 2 und 3 nah zurük, wenn die geworfene Zahl wehselt damit endet ein Run der Länge 2 bzw. 3. Bei gleiher Augenzahl wähst dagegen die Runlänge um, und man gelangt in den Zustand 3 bzw. 4. Im Zustand 4 ist das Ziel mindestens ein Run der Länge λ 4 erreiht, alle weiteren Würfe sind niht mehr von Interesse, wir befinden uns in einem absorbierenden Zustand, den man niht mehr verlassen kann (dies wird sih in Abshnitt 3 ändern). Wir bezeihnen mit a jz die Wahrsheinlihkeit, nah j Würfen im Zustand z zu sein, und bilden aus den a jz für jedes j einen vierdimensionalen Zeilenvektor a j = (a a a a ), j j2 j3 j4 den so genannten Zustandsvektor. Offenbar gilt a = ( 0 0 0). Abbildung und die obigen Überlegungen führen dann auf folgende Rekursionsformeln für die Koordinaten von a j+ : a j+ = ( ) a j + ( ) a j2 + ( ) a j3 a j+ 2 = a j a j+ 3 = a j2 a j+ 4 = a j3 + a j4. Tabelle zeigt die Umsetzung dieser Formeln mit EXCEL in einem Ausshnitt (tehnishe Einzelheiten werden im folgenden Abshnitt angesrohen). 6 Stohastik in der Shule 3 (20) 3, S. 6 2

2 Tabelle liefert also den auh von Motzer (200) angegebenen Wert a ,36. Dieses Ergebnis ist allerdings unbefriedigend, da es alle Würfe nah dem Auftreten von vier gleihen Zahlen ignoriert und damit offen bleibt, ob noh weitere Vierer-Runs in der Gesamtserie auftreten (diese Frage behandeln wir im folgenden Abshnitt 3) und ob tatsählih ein Vierer-Run vorliegt und niht einer der Länge 5. 6 oder mehr. j a j a j 2 a j 3 a j ,8333 0, ,8333 0,389 0, ,8333 0,389 0,023 0, ,8295 0,389 0,023 0, ,8263 0,382 0,023 0, ,767 0,283 0,025 0, ,6956 0,64 0,095 0, ,6308 0,056 0,077 0, ,572 0,0957 0,060 0,362 Tab. : Ausgewählte Zustandsvektoren zu Aufgabe Zur Klärung dieser Frage formulieren wir folgende Aufgabe. Aufgabe 2: Wie wahrsheinlih ist es, in 00 Würfen mindestens einen Run mit genau der Länge 4 zu erzielen? Jetzt fragen wir nah einem ehten Run der Länge 4. Der Run darf niht länger als 4 werden. In Aufgabe war dies möglih, es wurde nah Runs von mindestens 4 gefragt. Dazu ändern wir den Grahen zu Aufgabe leiht ab (Abb. 2). 2 3 Abb. 2: Übergangsgrah zu Aufgabe 2 4 Der Zustand 4 ist jetzt ein Durhgangszustand, den man auf zwei vershiedenen Wegen verlassen kann. Nah vier gleihen Zahlen bleibt es nur dann bei einem Run der Länge 4, wenn die Augenzahl wehselt. womit der absorbierende Zustand A erreiht wird fällt dagegen dieselbe Zahl noh einmal, dann entsteht zunähst ein längerer Run (Zustand ), ehe mit dem Wehsel zu einer neuen Augenzahl der Aufbau eines neuen Runs im Zustand beginnt. Entsrehend ändern sih die Rekursionsformeln für die Koordinaten b j+ z des Zustandsvektors: A b j+ = ( ) (b j + b j2 + b j3 + b j ) b j+ 2 = b j b j+ 3 = b j2 b j+ 4 = b j3 b j+ = (b j4 + b j ) b j+ A = ( ) b j4 + b j A. Tabelle 2 zeigt ausgewählte Zustandsvektoren b j für Aufgabe 2. Am Ende einer Serie von 00 Würfen befindet man sih mit der Wahrsheinlihkeit 0,003 im Zustand 4 und mit 0,268 im Zustand A. In beiden Fällen ist das Ziel, mindestens ein Run der genauen Länge 4, erreiht, insgesamt mit der Wahrsheinlihkeit 0,27. Die Differenz von 0,045 gegenüber der Lösung von Aufgabe entfällt auf solhe Serien, die keine ehten Vierer-Runs, dafür aber mindestens einen längeren Run enthalten. j b j b j 2 b j 3 b j 4 b j b j A, ,833 0, ,833 0,39 0, ,777 0,30 0,022 0,004 0,00 0, ,77 0,20 0,020 0,003 0,00 0, ,66 0,0 0,08 0,003 0,00 0, ,609 0,02 0,07 0,003 0,00 0,268 Tab. 2: Ausgewählte Zustandsvektoren zu Aufgabe 2 3 Verteilung der Zufallsgröße X n λ Wir verallgemeinern die Fragen aus Abshnitt 2 zu folgender Aufgabe. Aufgabe 3: Wie wahrsheinlih ist es, dass beim n-maligen Würfeln 0,, 2, Runs auftreten, die genau die Länge λ = 4 haben? Gesuht ist also die Verteilung einer Zufallsgröße, nämlih X n λ := Anzahl der λ-runs beim n-maligen Würfeln (bezogen auf die Aufgaben und 2 ist das X 00 4 ). Der Übergangsgrah von Abbildung 3 veranshauliht die neue Situation. Die Bezeihnung ka der Zustände besagt, dass bis dahin k Vierer-Runs aufgetreten sind und der aktuell begonnene Run die Länge a hat (oder > 4). Im Untershied zu Aufgabe 2 gibt es keinen absorbierenden Zustand mehr die Rolle von 4 in Abbildung 2 übernimmt 0, von wo man wie oben nah 0 und statt nah A nun in den neuen Durhgangszustand gelangen kann. Damit ist ein erster Vierer-Run abgeshlossen. Analog ist die Situation in den Zuständen 20, 30 usw. 7

3 Abb. 3: Übergangsgrah zu Aufgabe Wir ordnen die Koordinaten des Zustandsvektors j, der nun die Dimension n hat, nah Abbildung 3 an: 0, 02, 03, 0, 0, usw. der Startvektor nah dem ersten Wurf ist dann = ( ). Die Koordinaten von j+ lassen sih aus denen von j wieder mithilfe von Rekursionsformeln berehnen, die man Abbildung 3 entnimmt. Wir shreiben diese Formeln so, dass man sie direkt in EXCEL übernehmen kann (Abb. 4): und stehen in den Zellen C5 bzw. F5 und der Startvektor in Zeile 8 in den Salten F, L, R und X steht jeweils die Wahrsheinlihkeit, nah j Würfen k Vierer-Runs zu haben (k {0,, 2, 3}). Für den Übergang von j = nah j = 2 (also von Zeile 8 nah Zeile 9) entnimmt man Abbildung 3: Für 0 : B9=$F$5*SUMME(B8:E8), für 02 : C9=$C$5*B8, für 03 : D9=$C$5*C8, für 0 : E9=$C$5*(E8+G8), k = 0: F9=SUMME(B9:E9), für 0 : G9=$C$5*D8. Koiert man nun die Zellen B9 bis G9 nah rehts (H9 bis M9), so stehen in den Salten I, J, K und M bereits die korrekten Formeln für 2, 3, und 20 (man beahte die absolute Adressierung der Zellen C5 und F5, in denen die gleih bleibenden Werte von und stehen). Die Formeln für und k = erfordern folgende Korrekturen: Für : H9=$F$5*SUMME(G8:K8) anstatt H9=$F$5*SUMME(H8:K8) (aktuell markierte Zelle in Abb. 4), k = : L9=SUMME(G9:K9) anstatt L9=SUMME(H9:K9). Nun kann man H9 bis M9 ohne weitere Korrekturen nah N9 bis S9 und T9 bis Y9 (oder noh weiter) koieren. Die sehr kleinen Wahrsheinlihkeiten für k 4 fassen wir in Salte Z zusammen: k 4: Z9= (F9+L9+R9+X9). Abshließend koiert man Zeile 9 für j = 3 bis 00 in die 98 folgenden Zeilen nah unten. Auh hier ergibt sih P(k = 0) 0,729 wie am Ende von Abshnitt 2 (Zelle F07), doh sind jetzt differenziertere Aussagen zum Gegenereignis k > 0 möglih. Auh den Erwartungswert μ kann man nun berehnen für unser Beisiel ist μ = E(X 00 4 ) 0,33. 4 Varianten des Problems In diesem Abshnitt betrahten wir einige Varianten und Verallgemeinerungen unserer Aufgaben. Länge der Serie Eine Änderung der Serienlänge brauht man niht eigens zu untersuhen, denn beim rekursiven Berehnen einer Verteilung X n λ durhläuft man ja auh alle Verteilungen mit j < n, die man dann aus einer Tabelle wie in Abbildung 4 entnehmen kann. Trefferwahrsheinlihkeit Unsere Abbildungen bis 3 sind bereits auf eine Variation der Trefferwahrsheinlihkeit hin angelegt, Abb. 4: EXCEL-Tabelle für die Verteilung von X 00 4 (Salten O bis U und Zeilen bis 05 ausgeblendet) 8

4 indem dort als Übergangswahrsheinlihkeiten und statt der konkreten Werte /6 und 5/6 eingetragen sind. Die Grahen gelten daher auh für Folgen von Zufallsziffern ( = /0) oder Münzwürfen ( = /2). Die Verteilungen von X 00 4 für diese Fälle zeigt Tabelle 3. k = 0 k = k = 2 k = 3 k = 4 k 5 /0 0,924 0,073 0, /6 0,729 0,233 0,035 0, /2 0,035 0,27 0,22 0,243 0,89 0,86 Tab. 3: Verteilungen von X 00 4 für vershiedene Erwartete Zahl der Runs Auh die Erwartungswerte für die neuen Werte von kann man nun berehnen für = 0, ist μ 0,08 und für = 0,5 errehnet man (mit mehr Werten als in Tabelle 3 wiedergegeben) μ 3,. Runlänge Als Nähstes variieren wir die Runlänge λ. Für λ = 5 ist beisielsweise Zustand 4 in Abbildung ein innerer und erst 5 der absorbierende Zustand, und in Abbildung 3 ist entsrehend für jedes k ein neuer Zustand k4 hinter k3 einzufügen. Mit den entsrehend geänderten EXCEL-Formeln findet man für die Variante von Aufgabe den der letzten Zeile aus Tabelle entsrehenden Zustandsvektor a 00 : j a j a j 2 a j 3 a j 4 a j ,7837 0,307 0,028 0,0036 0,060 Tab. 4: Zustandsvektor nah 00 Shritten für Runs der Länge 5 Für einen Run der Mindestlänge 5 erhalten wir also wie shon Motzer (200) den Wert P(z = 5) 0,06. Für die Variante von Aufgabe 3 mit λ = 5 ergeben sih die Verteilungen von Tabelle 5. k = 0 k = k = 2 k = 3 k = 4 k 5 /0 0,992 0, /6 0,950 0,049 0, /2 0,98 0,340 0,27 0,33 0,045 0,03 Tab. 5: Verteilungen von X 00 5 für vershiedene Wie bei μ = 4 ist beim Würfeln ein ehter Fünfer- Run mit P(X 00 5 ) 0,05 weniger wahrsheinlih als ein Run der Mindestlänge 5 mit a ,06. 5 Verallgemeinerung des Problems Die bisherigen Beisiele betrafen Lalae-Exerimente Runs waren dabei Folgen irgendeines der gleihwahrsheinlihen Ergebnisse. Aufgabe 4: Als Run wird jetzt nur eine unmittelbare Folge eines bestimmten Ergebnisses gewertet (entsriht einer Folge von Treffern bei einem Bernoulli-Exeriment). Die Zufallsgröße Anzahl der Vierer- Runs nennen wir nun Y und fragen, wie P(Y 00 4 = k) allgemein von abhängt. Wir könnten beim Würfeln etwa nur die Sehsen betrahten und ihre Runs zählen. Im Untershied zu den bisherigen Aufgaben ist nun rinziiell jeder Wert von möglih. Wie hängt die Wahrsheinlihkeit für k Runs von ab? Der Übergangsgrah zeigt gegenüber Abbildung 3 einige Änderungen (Abb. 5). Wieder bedeutet ka, dass bis dahin k Vierer-Runs aufgetreten sind und der aktuell begonnene Run die Länge a hat (oder > 4). Die aus dem Grahen abzulesenden Rekursionsformeln überträgt man wieder analog zu Abbildung 4 in eine EXCEL-Tabelle Abb. 5: Übergangsgrah für Runs eines Einzelausfalls Um in EXCEL bequem den Parameter variieren zu können, ist ein Shieberegler zwekmäßig. Man ändert bei festem λ = 4 shrittweise und koiert jeweils die für P(Y 00 4 = k) gewonnenen Werte in eine neue Tabelle, die wir als Wertetabelle einer Shar von Funktionen f k : f k () = P(Y 00 4 = k) 9

5 auffassen können. Die EXCEL-Otion Diagramm liefert dann die zugehörigen Grahen Abbildung 6 zeigt diese für k {0 2}. f k ( ) k = 0 Überlegungen zur erwarteten Zahl von λ-runs In ähnliher Weise kann man untersuhen, wie die Anzahl der λ-runs in einer 00er-Serie, also der Erwartungswert E(Y 00 λ ), von abhängt. Abbildung 7 zeigt für ausgewählte Werte von λ die Grahen der Funktionen g λ mit g λ () = E(Y 00 λ ). g ( ) 5 = = /6 k = k = = /6 = 2 = Abb. 6: Wahrsheinlihkeit für k Runs der Länge 4 abhängig von Diese Grahen sind zwar niht erfekt symmetrish, zeigen aber für nahe ein ähnlihes Verhalten wie nahe 0. Für kleine sind vier Treffer naheinander sehr unwahrsheinlih, und für nahe werden längere Runs immer wahrsheinliher. In beiden Fällen ist also kaum ein Vierer-Run zu erwarten, in Abbildung 6 erkennbar an f 0 (). Für k > 0 muss in diesen Bereihen daher f k () 0 sein. Bei mittleren Werten von dagegen ist f 0 () relativ klein während f () und f 2 () in diesem Bereih ihre größten Werte annehmen, d. h., sehr wahrsheinlih tritt mindestens ein Vierer-Run ein. Ist die Trefferwahrsheinlihkeit ein Stammbruh, so besteht ein Zusammenhang mit unseren früheren Ergebnissen (Tab. 3), wie wir nun an einem Beisiel zeigen: Es sind f 0 (/6) 0,949 und f (/6) 0,050 die Wahrsheinlihkeiten dafür, keinen bzw. genau einen Vierer-Run einer bestimmten Augenzahl zu erreihen (vgl. Abb. 6). Die Wahrsheinlihkeit, genau einen Vierer-Run irgendeiner Augenzahl zu haben, kann man nun folgendermaßen shätzen: Eine der 6 Zahlen liefert den Run, aber keine der 5 anderen darf ebenfalls einen Vierer-Run bilden daher ist P(X 00 4 = ) 6 0,05 0, ,23. Dieser Wert stimmt gut mit dem entsrehenden aus Tabelle 3 überein die Abweihung rührt daher, dass der Faktor 0,949 die totale Wahrsheinlihkeit für k = 0 ist, während man eigentlih mit der durh den shon vorhandenen Vierer-Run bedingten Wahrsheinlihkeit rehnen müsste, die etwas größer ist. = Abb. 7: Erwartete Zahl von Runs der Länge λ abhängig von Auh hier besteht ein enger Zusammenhang zu den Ergebnissen aus Abshnitt 4. Wir vergleihen die Erwartungswerte von X 00 λ und Y 00 λ beim Werfen eines Lalae-Würfels ( = /6, Tab. 6). λ E(X λ ) 69,70,50,90 0,3 5, ,5 0 3 E(Y λ ),59,92 0,32 0,05 8,6 0 3,4 0 3 Tab. 6: Erwartungswerte von X 00 λ und Y 00 λ für = /6 Die Werte für X λ sind jeweils 6-mal so groß wie die von Y λ, da ja jede der 6 Augenzahlen Treffer sein kann. Entsrehendes gilt in den Fällen = 0, und = 0,5, wo E(X λ ) 0-mal bzw. doelt so groß ist wie E(Y λ ). Eine ähnlihe Beobahtung maht man, wenn man E(Y λ ) mit E(Y λ+ ) in Tabelle 5 bzw. in Abbildung 7 vergleiht: Nimmt λ um zu, so ist μ λ+ ungefähr /6 von μ λ. Auh dies ist leiht zu verstehen, denn die Wahrsheinlihkeit für einen λ-run nah einem Fehlwurf ist λ ( ), bei einem (λ + )-Run kommt noh ein Faktor hinzu. Die letzte Überlegung führt auf eine neue Möglihkeit, einen Näherungswert für E(Y λ ) zu bestimmen. Es sei r := E(Y ), dann ist E(Y λ ) = r λ. Man kann also in einer Serie von n Würfen bei großem n etwa t = r λ λ = r ( ) λ= Treffer erwarten. Andererseits gilt aber auh t n. Wie man durh Multilikation mit ( ) bestätigt, hat die Summe in der Klammer den Wert, so dass man die Beziehung ( ) 2 20

6 r n ( ) 2 und damit für r den Näherungswert n ( ) 2 erhält. Für das Beisiel n = 00 und = /6 ergibt sih so r,574, der exakte Wert ist, Shlussbemerkungen Als im Zuge der Oberstufenreform der 70er-Jahre die Stohastik einen höheren Stellenwert im Mathematikunterriht erhielt, waren auh Markow-Ketten groß in Mode und im Sinne von Anwendungsorientierung der Stohastik Thema vershiedener Lehrbüher und Kursvorshläge (Lehmann 973, Kittler 975, Engel 976). Die Bedeutung des Themas, zumindest die ihm zuerkannt wurde, kann man auh an Sheid (986) ablesen, der ein ganzes Kaitel der Stohastik auf der Kollegstufe dazu ausarbeitet. Der Autor selbst hat sih wiederholt mit Markow-Ketten im Shulunterriht beshäftigt, wie etwa shon in Riehl (982). Bemerkenswert ist, dass sih das Wissen um Markow-Ketten niht nur im deutshsrahigen Raum doh niht so weit verbreitet hat. So geriet Holmes (99) bei der Analyse von Runs in methodishe Shwierigkeiten, was darauf zurükzuführen war, dass er das Problem eben niht mit Markow-Ketten beshrieb (siehe Riehl 994). Ein Grund für die mangelnde Akzetanz war wohl, dass damals leistungsfähige Hilfsmittel für die notwendigen umfangreihen Rehnungen noh niht allgemein zur Verfügung standen. Auh sah man die Anforderungen aus der Linearen Algebra als zu umfassend an, sodass man sih entweder wieder vom Thema abgewendet oder mit durh Simulation gewonnenen näherungsweisen Lösungen begnügt hat, die jedoh immer unbefriedigend bleiben. Mit den neuen Rehenhilfen wie einer Tabellenkalkulation kann man nun fast unter Umgehung von Linearer Algebra Berehnungen leiht durhführen und wesentlihe Erkenntnisse gewinnen, wie der vorliegende Beitrag auh demonstrieren soll. Der wesentlihe Vorzug des hier dargestellten Lösungsweges besteht in der Veranshaulihung der stohastishen Situation durh Übergangsgrahen, die niht nur begabten Shülerinnen und Shülern zugänglih sind, wie es Motzer (200) für das von ihr dargestellte Vorgehen einshätzt. Da sih die Rekursionsformeln für die rehnerishe Lösung unmittelbar aus den Grahen ablesen und dann in eine EXCEL-Tabelle umsetzen lassen, ist es niht notwendig, eine Theorie der Markow-Ketten aufzubauen insbesondere kann man auf Matrizen völlig verzihten. Wie man tyishe Fragestellungen aus der Theorie der Markow-Ketten (Absor tionswahr sheinlihkeiten, mittlere Wartezeiten) im Unterriht mit Matrizen behandeln kann, habe ih an anderer Stelle ausgeführt (Riehl 200). Literatur Engel, A. (976): Wahrsheinlihkeitsrehnung und Statistik, Bd. 2. Stuttgart: Klett. Holmes, P. (99): Comuter-erzeugtes Denken. In: Stohastik in der Shule (3), S Kittler, H. (975): Grundkurs: Einführung in die Wahrsheinlihkeitsrehnung unter besonderer Berüksihtigung Markoffsher Ketten. In: Niedersähsishes Kultusministerium (Hrsg.): Handreihungen für Lernziele, Kurse und Projekte im Sekundarbereih II für das mathematish-naturwissenshaftlihe Aufgabenfeld, 3. Folge, S Lehmann, E. (973): Endlihe homogene Markoffshe Ketten eine Anwendung von Wahrsheinlihkeits- und Matrizenrehnung. Münhen: Bayerisher Shulbuh- Verlag. Motzer, R. (200): Serien von gleihen Würfelzahlen. In: Stohastik in der Shule 30 (3), S Riehl, G. (982): Elementare Behandlung genetisher Probleme im Stohastikunterriht mit Hilfe von Grahen. In: Didaktik der Mathematik 0 (), S Riehl, G. (994): Noh einmal: Comuter-erzeugtes Denken. In: Stohastik in der Shule 4 (3), S Riehl, G. (200): Markow-Ketten, eine alternative Methode zur Lösung stohastisher Probleme. In: MNU 63 (7), S Sheid, H. (986): Stohastik auf der Kollegstufe. Mannheim: Bibliograhishes Institut. Anmerkungen Mein Dank gilt den beiden Gutahtern und Herrn Borovnik als Heftherausgeber für hilfreihe Hinweise und Anregungen. Interessenten finden die Zusammenstellung einer EXCEL- Mae mit Tabellenblättern für die hier behandelten Aufgaben sowie für deren Simulation unter wwwg.uni-klu. a.at/stohastik.shule/boro/index_inhalt.htm. Anshrift des Verfassers Gerd Riehl Obere Mark Barsinghausen Elfriede.Riehl@t-online.de 2