Technische Universität München
|
|
|
- Wilhelmine Kalb
- vor 8 Jahren
- Abrufe
Transkript
1 Technische Universität München Zentrum Mathematik Risikobewertung von modernen Lebensversicherungsprodukten am Beispiel von dynamischen Drei-Topf-Hybriden Risk Estimation of modern Life Insurance Products using the example of dynamic three-pot-hybrids Diplomarbeit von Johannes Rusche Themensteller: Prof. Dr. T. Klein Betreuer: B. Thiel, F. Geislinger Abgabetermin: 15. Februar 2012
2 Hiermit erkläre ich, dass ich die Diplomarbeit selbstständig angefertigt und nur die angegebenen Quellen verwendet habe. Garching, den 15. Februar 2012
3 i Danksagung Zu allererst möchte ich mich bei Herrn Prof. Klein bedanken. Zum einen für die Bereitschaft das von meiner Seite aus vorgeschlagene Thema anzunehmen. Diese war nicht selbstverständlich, zumal das Diplomarbeitsthema nicht direkt in seinem Forschungsgebiet anzusiedeln ist. Was Thema betrifft, habe ich am meisten von den Hinweisen von Herrn Thiel profitiert. Mit seiner Expertise im Bereich des Risikomanagements konnte er mir schon anfangs eine Richtung zeigen. Auch wenn aufgrund der großen örtlichen Distanz die Anzahl der Treffen nicht hoch war, so waren sie doch sehr hilfreich. Vielen Dank dafür! Gar nicht zustande gekommen wäre die Arbeit ohne Herrn Geislinger, der mit seinem ökonomischen Sachverstand die Problematik des dynamischen Drei-Topf-Hybrid-Produkts erkannte und daraus die Idee entwickelte, ein Diplomarbeitsthema zu formen. Darüber hinaus war er jederzeit ein hilfsbereiter Ansprechpartner und ein wertvoller Verbündeter bei auftauchenden Problemen unterschiedlichster Art. Merci! Außerdem bin ich meinen Eltern zu Dank verpflichtet, die mich nicht nur während der Diplomarbeit, sondern über die gesamte Studiumsdauer gefördert und unterstützt haben. Zu guter Letzt will ich auch meiner Freundin Romea danken. Nicht nur für die seelische Unterstützung, sondern auch für die entgegen gebrachte Toleranz für die anstrengende Zeit.
4 Inhaltsverzeichnis 1 Einleitung Motivation Ziel der Diplomarbeit Aufbau der Arbeit Literaturüberblick Lebensversicherungsmathematik Stochastisches Modell Leibrenten Nettoprämien Nettodeckungskapital Bruttoprämien Funktionsweise der dynamischen Drei-Topf-Hybride Eigenschaften des Produkts Erklärung des Umschichtungsalgorithmus Optimalität des Umschichtungsalgorithmus Ein graphisches Beispiel zur Umschichtung Solvency II Solvency II - die Grundstruktur Stand der Diskussion und SCR-Modellierungsansätze Risikoidentifikation beim dynamischen Hybridprodukt im Rahmen von Solvency II Versicherungstechnische Risiken Ausfallrisiko der Bank Marktrisiko im Allgemeinen Aktienrisiko Umschichtungsrisiko Liquiditätsrisiko Zinsgarantierisiko Zinsänderungsrisiko Fazit der Risikoidentifikation und Folgen daraus ii
5 INHALTSVERZEICHNIS iii 5 Risikomodellierung Kapitalmarktmodell Modellierung von Aktienkursen Modellierung der sicheren Anlage Grundlagen der Finanzmathematik Arbitragefreiheit des Binomialmodells Mehrperiodisches Binomialmodell Einbettung des Produkts in den Kapitalmarkt Cashflow-Modellierung Cashflow-Erläuterung Cashflow-Modellannahmen Ausgleich des Sterblichkeitsrisikos im Kollektiv Mathematische Formulierung des Cashflows Cashflow-Simulation Motivation der Startwerte Ein deterministisches Beispiel zum Einstieg Stochastische Simulationen Cashflow-Hedging Theorie Konstruktion einer Hedgingstrategie Optimierung der Variablen dieser Hedgingstrategie Ergebnisse des Hedgings Fazit 84
6 Abbildungsverzeichnis 2.1 Verteilung der gestutzten Restlebensdauer eines 30-jährigen (eigene Darstellung) Entwicklung des Nettodeckungskapitals, der Prämienbarwerte und der Leistungsbarwerte in der Aufschubzeit (eigene Darstellung) Beispielhafter 18-monatiger Verlauf der Verteilung eines Kundenguthabens (eigene Darstellung) Solvency II - Bilanz (vgl. EIOPA [9]) SCR-Modulstruktur (vgl. EIOPA [9, S. 90]) Zweiperiodischer Binomialbaum (eigene Darstellung) Beispielhafte 30-monatige Aktienkursentwicklung mit 30 % Volatilität p. a. (eigene Darstellung) Beispielhafter deterministischer 30-monatiger Verlauf der Topfverteilungen - Rohentwicklung (eigene Darstellung) Beispielhafter deterministischer 30-monatiger Verlauf der Topfverteilungen - mit Ausscheidevektor (eigene Darstellung) Beispielhafter deterministischer 30-monatiger Verlauf des Cashflows (eigene Darstellung) Beispielhafte monatliche Aktienrenditen mit 30 % Volatilität p. a. (eigene Darstellung) Cashflowquantile bei 30 % Aktienvolatilität p. a. (eigene Darstellung) Quantile des relativen Cashflows bei 30 % Aktienvolatilität p. a. (eigene Darstellung) Vergleich der Quantile des Cashflows mit denen der gehedgten Cashflows bei 20 % Aktienvolatilität p. a. (eigene Darstellung) Vergleich der Quantile des Cashflows mit denen der gehedgten Cashflows bei 30 % Aktienvolatilität p. a. (eigene Darstellung) Vergleich der Quantile des Cashflows mit denen der gehedgten Cashflows bei 40 % Aktienvolatilität p. a. (eigene Darstellung) iv
7 Abkürzungsverzeichnis Abkürzung Beschreibung ALM Asset Liability Management ASM Available Solvency Margin (anrechenbare Eigenmittel) CPPI Constant Proportion Portfolio Insurance Def. Definition DK Deckungskapital EIOPA European Insurance and Occupational Pensions Authority EU Europäische Union FF Freie Fonds f. s. fast sicher GF Garantiefonds GDV Gesamtverband der Deutschen Versicherungswirtschaft max maximiere MCR Minimumkapitalanforderungen min minimiere Mio. Millionen Euro NEP Nettoeinmalprämie QIS Quantitative Impact Studies p. a. per annum PIIGS Portugal, Italien, Irland, Griechenland, Spanien RBC Risk Based Capital Modell SCR Solvenzkapitalanforderungen T. Tausend Euro u. d. N. unter der Nebenbedingung Vor. Voraussetzung v
8 Symbolverzeichnis Symbol Beschreibung Seite 1 Indikatorfunktion 18 A x Erwartungswert von W 8 Ax:n 1 Nettoeinmalprämie 10 ä x:n vorschüssige temporäre Leibrente der Dauer n 9 vorschüssige lebenslängliche Leibrente, ä x ä (12) x ä (12) x:n Erwartungswert von Y 8 Nettoeinmalprämie einer lebenslänglichen Rente bei monatlicher Zahlung 9 vorschüssige temporäre Leibrente der Dauer n bei monatlicher Zahlung 11 α α-kosten 13 β β-kosten 13 B(t + ) gezahlter Beitrag zum Zeitpunkt t + 16 B j (t) vom j-ten Kunden gezahlter Beitrag zum Zeitpunkt t 58 B sum (t) Summe aller bis zum Zeitpunkt t gezahlten Beiträge 16 B j sum(t) Summe aller vom j-ten Kunden bis zum Zeitpunkt t gezahlten Beiträge 59 γ γ-kosten 13 C Contingent Claim 43 C diskontierter Claim 44 CF (t) Wert des Cashflows zum Zeitpunkt t 35; 56 CF rel (t) Wert des relativen Cashflows zum Zeitpunkt t 71 CF H (t) Wert des gehedgten Cashflows zum Zeitpunkt t 77 D mac = D(r) Macauley-Duration 35 D mod modifizierte Duration 35 d down-faktor 39 Barwert der Differenz zwischen zukünftigen Leistungen und zukünftigen Prämien 12 δ Substitution: v := e 2δ 8 t Diskretisierung der Zeit 48 IE Erwartungswert 5 e Eulersche Zahl 8 ė x Lebenserwartung eines x-jährigen 5 e x gestutzte Lebenserwartung eines x-jährigen 6 vi
9 Symbol Beschreibung Seite η Anzahl der betrachteten versicherten Personen 55 η t Anzahl der versicherten Personen im Bestand im Zeitraum (t 1; t] 57 f Bewertungsfunktion eines Contingent Claims 48 F t Filtration 39 G x (t) Verteilungsfunktion der zukünftigen Lebensdauer 4 g x Dichte der Verteilungsfunktion G M 4 G x (z) unterjährige Verteilungsfunktion der Sterblichkeit 7 γ Gamma-Kosten 13 Γ Wert eines ψ-quantils 78 H Hedging-Strategie allgemein 75 h Handelsstrategie 42 h X t Anzahl an Aktien im Portfolio 43 h S t Anteil der sicheren Anlage am Gesamtportfolio 43 I(t + 1) das zur Absicherung der Erlebensfallgarantie mindestens erforderliche Vermögen 16 I DK Deckungskapital-Sicherungslinie 27 I GF Garantiefonds-Sicherungslinie 27 i Mindestgarantieverzinsung 7 K = K x ganzzahlig gestutzte zukünftige Lebensdauer 5 k Laufparameter von K oder X 5; 40 L η Verluste des Versicherers, bei η Verträgen im Bestand 55 l Zählparameter des Zählprozesses N 46 λ Konstante, die das Hedgingvolumen angibt 75 λ opt das optimale λ 78 ln natürlicher Logarithmus 5 M = M x zukünftige Lebensdauer eines x-jährigen 4 m sto (t) Anteil des Bestands, der im Zeitraum (t 1; t] storniert wurde 58 m tod (t) Anteil des Bestands, der im Zeitraum (t 1; t] verstorben ist 58 µ Sterblichkeitsintensität 5 N t Binomialzählprozess 47 N η T Anzahl der Überlebenden zum Zeitpunkt T 56 n Versicherungsdauer in Jahren (bis zum Tod oder zum Garantiezeitpunkt) 9 O Auszahlung einer Erlebensfallversicherung 10 Ω Zustandsraum 39 ω Ereignis in Ω 7 Opt H Optimierungsproblem, das die optimale Strategie H sucht 77
10 Symbol Beschreibung Seite P Wahrscheinlichkeit unter P 43 P Realworld-Wahrscheinlichkeitsmaß 39 Px:n 1 jährliche Nettoprämie 10 Px:n 12 monatliche Nettoprämie 11 Px:n a jährliche ausreichende Prämie 13 p Realworld-Wahrscheinlichkeit von up 39 p k x Wahrscheinlichkeit einer x-jährigen Person noch k Jahre zu überleben 4 Φ H (t) durch das Hedging H induzierter Portfolioprozess 76 π C Preis eines Contingent Claims 44 πρ X Call t (t) Preis einer europäischen Call-Option zum Zeitpunkt t bei einem Strikepreis von ρ X t mit einmonatiger Laufzeit 75 π H Preis des Hedgings H 79 Π stochastischer Prozess für arbitragefreien Preis von C 44 Pr Wahrscheinlichkeit 4 ψ Quantilwahrscheinlichkeit 77 P V (B sum (t)) Erlebensfallbarwert von B sum (t) (bis zum Garantiezeitpunkt - insb. nicht stochastisch) 16 q risikoneutrale Wahrscheinlichkeit des Ereignisses up 45 kq x Wahrscheinlichkeit einer x-jährigen Person innerhalb von k Jahren zu sterben 4 Q risikoneutrale Wahrscheinlichkeit im Allgemeinen 44 Q risikoneutrales Wahrscheinlichkeitsmaß 43 R Wachstumsprozess der Aktienanlage 40 r jährlicher Zins einer risikolosen Anlage 35 r CRR Zins der risikolosen Anlage S pro Zeiteinheit 40 ρ Verhältnis von Strikepreis zu Aktienkurs 74 S t Wert der risikolose Anlage zum Zeitpunkt t 31 S Preisprozess der diskontierten Anlage S 44 s Laufparameter der Funktion G oder des Zuwachsprozesses R 5; 39 σ X Kapitalmarktvolatilität bzw. Standardabweichung von X 47 σ(x) Sigma-Algebra von X 39 t Handelszeitpunkt oder allgemeine Zeitangabe 16; 50 t + Beginn eines Monats (t; t + 1) 16 t Ende des Monats (t 1; t) 16 T Fälligkeit, Endzeitpunkt 48; 51 τ j GF (t) Anzahl der Aktien, die den Garantiefondstopf des Kunden j im Zeitraum (t 1; t] abbilden 60 τ j F F (t) Anzahl der Aktien, die den Freien Fondstopf des Kunden j im Zeitraum (t 1; t] abbilden 60 Θ H Durchschnittkosten eines Hedgings H 80
11 Symbol Beschreibung Seite U Call Strike-Preis einer Call-Option 49 U P ut Strike-Preis einer Put-Option 49 u up -Faktor 39 V ar Varianz 7 v Diskontierungsfaktor 8 kv x:n Nettodeckungskapital 12 V j GF (t ) Garantiefondsvermögen des j-ten Kunden zum Zeitpunkt t (vor einer Umschichtung) 60 V j F F (t ) Freies Fondsvermögen des j-ten Kunden zum Zeitpunkt t (vor einer Umschichtung) 60 V j DK (t ) Deckungskapitalvermögen des j-ten Kunden zum Zeitpunkt t (vor einer Umschichtung) 61 V ηt GF (t ) kumuliertes Garantiefondsvermögen aller Kunden zum Zeitpunkt t (vor einer Umschichtung) 60 V ηt F F (t ) kumuliertes Vermögen der Freien Fonds aller Kunden zum Zeitpunkt t (vor einer Umschichtung) 60 V ηt DK (t ) kumuliertes Deckungskapitalvermögen aller Kunden zum Zeitpunkt t (vor einer Umschichtung) 60 V opt GF (t+ ) optimales Vermögen im GF nach einer Umschichtung 18 V opt F F (t+ ) optimales Vermögen im FF nach einer Umschichtung 18 V opt DK (t+ ) optimales Vermögen im DK nach einer Umschichtung 18 V j GF (t+ ) Vermögen des j-ten Kunden im GF nach einer Umschichtung 59 V j F F (t+ ) Vermögen des j-ten Kunden im FF nach einer Umschichtung 59 V j DK (t+ ) Vermögen des j-ten Kunden im DK nach einer Umschichtung 59 V (t ) Vermögen zum Ende des Monats (t 1, t) 16 V (t + ) Vermögen zum Beginn des Monats (t, t + 1) 16 V ηt GF (t+ ) Vermögen in den Garantiefonds aller Kunden nach einer Umschichtung 59 V ηt F F (t+ ) Vermögen in den Freien Fonds aller Kunden nach einer Umschichtung 59 V ηt DK (t+ ) Vermögen im Deckungskapital aller Kunden nach einer Umschichtung 59 V ηt (t) gesamtes Vertragsvermögen aller Kunden zum Zeitpunkt t 59 V j (t) Vertragsvermögen des j-ten Kunden zum Zeitpunkt t 59 Vt h Wertprozess 42 VH Call (t) Payoff der Hedgingstrategie H zum Zeitpunkt t 77 Ṽt h diskontierter Wertprozess 42 V C Wert eines Contingent Claims 45
12 Symbol Beschreibung Seite W Zufallsvariable des durch die Sterblichkeit bedingten Diskontfaktors 8 w Restlaufzeit bis zum Garantiezeitpunkt, vom Zeitpunkt t (in Monaten) 16 w j (t) Restvertragslaufzeit des j-ten Kunden bis zum Garantiezeitpunkt, ausgehend vom Zeitpunkt t (in Monaten) 59 X stochastischer Prozess, Binomialprozess 39; 40 X t Wert der Aktienanlage zum Zeitpunkt t 39; 40 X t diskontierter Preisprozess 42 x Alter allgemein oder Eintrittsalter 4; 16 ξ Schwellenwert der Hedging-Strategie 76 ξ opt das optimale ξ 81 Y Barwert einer lebenslänglichen vorschüssigen lebenslänglichen Leibrente 8 y diskontierter Zinswert 8 Z x Restlebensdauer eines x-jährigen im Sterbejahr 6 z unterjähriger Anteil eines Jahres 7
13 Kapitel 1 Einleitung 1.1 Motivation Die Versicherungsbranche sieht sich seit einigen Jahren vielfältigen Veränderungen sowohl der wirtschaftlichen Realitäten als auch der rechtlichen bzw. institutionellen Konditionen ausgesetzt. Einerseits sind z. B. beim Kapitalanlagegeschäft der Versicherer nach wie vor die Folgen der weltweiten Finanzkrise 2008 erkennbar. Auf der anderen Seite ergeben sich neue Herausforderungen aus der Änderung wichtiger Rahmenbedingungen. Hier ist neben zahlreichen Überarbeitungen des Versicherungsaufsichtsgesetzes, die im Jahr 2008 erfolgte Novellierung des Versicherungsvertragsgesetzes zu nennen. Auf EU-Ebene sind die Diskussionen zu Solvency II weit fortgeschritten und die Grundprinzipien eines neuen Konzepts der Versicherungsaufsicht und der Kapitalausstattung stehen weitgehend fest. Solvency II ist eine europäische Aufsichtsrichtlinie, die nach dem Vorbild des Pendants der Bankenbrache - Basel II (inzwischen Basel III) - aus folgenden drei Säulen besteht: (i) Die Erfüllung von Solvenzkapitalanforderungen (ii) Die Gewährleistung eines qualitativen Risikomanagements (iii) Die Berichterstattungspflichten jedes einzelnen Versicherungsunternehmens Im Jahr 2013 wird Solvency II als Richtlinie bereits gelten, gesetzlich in Kraft tritt sie vermutlich aber erst in Die Finanzkrise und ihre Auswirkungen (Stichwort PIIGS) erhöhen die Relevanz eines quantitativen Risikomanagements weiter. Diese Entwicklungen bleiben nicht ohne Auswirkungen auf das Produktangebot der Lebensversicherungsbranche. Nicht zuletzt als Folge der Marktliberalisierung Mitte der 90er Jahre entstanden bei der Suche nach einer optimalen Verknüpfung von Sicherheit und hoher Rendite für den Kunden, bei finanzierbarer Risikobelastung des Versicherers, zunehmend komplexere Produkte. Dies gipfelte im Jahr 2006, als erstmals ein sogenanntes dynamisches Drei-Topf-Hybrid-Produkt auf den Markt kam. Bei dieser Kombination von klassischer Lebensversicherung und fondsgebundenem Produkt wird das Kundenguthaben auf drei Töpfe aufgeteilt: Das konventionelle Vermögen (auch Deckungskapital genannt), den Garantiefonds und die freie Fondsanlage ohne Garantien. Dabei wird monatlich zwischen den drei Töpfen umgeschichtet. Die dynamische Umschichtung des untersuchten Produkts hat 1
14 KAPITEL 1. EINLEITUNG 2 für den Versicherer die Folge, dass die hier möglicherweise auftretenden Risiken zu erkennen, zu bewerten und danach angemessen handzuhaben sind. 1.2 Ziel der Diplomarbeit Das Ziel dieser Diplomarbeit ist es, die Risiken, die mit diesem Produkt aus Versicherungsunternehmenssicht entstehen können, zu identifizieren, zu messen und zu bepreisen. Nachdem die Risiken identifiziert worden sind, soll hierzu ein Kapitalmarktmodell entwickelt werden, womit diese gemessen werden können. Im Rahmen dieses Kapitalmarktmodells können dann die versicherungstechnischen Cashflows, die durch das Produkt entstehen, stochastisch simuliert werden. Für die Bepreisung der enthaltenen Garantien und Optionen sollen diese Cashflows gehedgt werden. Die Kosten dieses Hedgings können als Pricing herangezogen werden. 1.3 Aufbau der Arbeit Die Arbeit ist wie folgt aufgebaut: Kapitel 2 erklärt die lebensversicherungsmathematischen Grundlagen. Kapitel 3 erläutert Funktionsweise des Umschichtungsalgorithmus des untersuchten Produkts und liefert einen Beweis von dessen Optimalität. Kapitel 4 behandelt die zukünftig geltenden aufsichtsrechtlichen Rahmenbedingungen und die Ausprägung der Risikoarten bei den dynamischen Drei-Topf-Hybriden. Kapitel 5 beschreibt das verwandte mathematische Modell und erklärt wie der Cashflow definiert wird. Kapitel 6 zeigt auf wie realitätsnahe Bestandsdaten eines Versicherungsunternehmens in das Modell integriert wurden und wie daraus Cashflows simuliert wurden. Kapitel 7 handelt von der Optimierung und anschließenden Anwendung einer Cashflow- Hedging-Strategie. Kapitel 8 liefert eine ökonomische Interpretation der in Kapitel 7 erzielten Ergebnisse und würdigt sie im Hinblick auf die ursprüngliche Problemstellung.
15 KAPITEL 1. EINLEITUNG Literaturüberblick In der Wissenschaft wurde die Risikoquantifizierung von dynamischen Drei-Topf-Hybridprodukten bisher lediglich aus einzelvertraglicher Kundensicht durchgeführt. Hier ist MM 2 Volatium zu erwähnen - ein Modell zur stochastischen Simulation von Altersvorsorgeprodukten. Die Morgen & Morgen GmbH wollte damit eine Vergleichbarkeit von Lebensversicherungsprodukten aus Kundensicht schaffen. Als problematisch erweist sich hierbei aber die darin getroffene Annahme, dass für alle zu vergleichenden Tarife dieselben Fondskosten unterstellt werden. Da dieses Modell nicht die Unternehmenssicht fokussiert, ist es bei der hier betrachteten Fragestellung nur indirekt hilfreich. Die Bewertung von Lebensversicherungen in Form von fondsgebundenen oder klassischen Produkten wurde hingegen schon sehr ausführlich diskutiert. Während bei der Modellierung von fondsgebundenen Versicherungen, wie z. B. bei Brennan und Schwartz [3] die Kapitalmarktmodellierung und insbesondere die Aktienkursmodellierung im Vordergrund stand, konzentrierten sich Modellierungen von klassischen Lebensversicherungen wie z. B. bei Kling [22] auf Unsicherheiten bzgl. Storno, Überschussbeteiligung, Zinsentwicklung und dem daraus folgenden Wert von Garantien und Optionen. Ein komplettes Modell, das alle wichtigen Risiken des dynamischen Drei-Topf-Hybridprodukts aus Unternehmenssicht beinhaltet, existiert von Seiten der EIOPA [9] noch nicht. Gegenstand aktueller Diskussionen sind allerdings die Wechselwirkungen eines dynamischen Drei-Topf-Hybriden mit dem restlichen Bestand, die Berechnung des Solvenzkapitalbedarfs aus Solvency II - Sicht und erste Ansätze zur Modellierung des Umschichtungsrisikos (vgl. Ruß und Reuß [30] und Kochanski und Karnarski [23]).
16 Kapitel 2 Lebensversicherungsmathematik Dieses Kapitel soll dem Leser die wahrscheinlichkeitstheoretische Fundierung der Lebensversicherungsmathematik nahe bringen. Darin wird insbesondere der Begriff Deckungskapital definiert, der wiederum für das Verständnis des Deckungskapitaltopfes des dynamischen Drei-Topf-Hybrid-Produkts essentiell ist. Auf die in diesem Kapitel enthaltenen Notationen wird danach nicht mehr Bezug genommen, um dem der Lebensversicherungsmathematik vertrauten Leser die Möglichkeit zu geben, dieses Kapitel überspringen zu können. Sämtliche Definitionen und Bemerkungen dieses Kapitels sind an Gerber [17] angelehnt. Das zugrundegelegte stochastische Modell beruht darauf, dass die zukünftige Lebensdauer einer neugeborenen Person durch eine Zufallsvariable modelliert wird. Um damit auch rechnen zu können, werden einige Annahmen bzgl. dieser Zufallsvariable gemacht, die im Folgenden ausgeführt werden. Darauf aufbauend werden außerdem die für das Risikomodell essentiellen Begriffe Nettoprämie und Deckungsrückstellung eingeführt. 2.1 Stochastisches Modell Definition 2.1 (Die Lebensdauer eines x-jährigen). Sei x das Alter einer bestimmten Person. Die zukünftige Lebensdauer wird mit M oder genauer M x bezeichnet. M x ist eine Zufallsvariable mit Verteilungsfunktion G x (t). Für ein festes t ist also G x (t) die Wahrscheinlichkeit, dass der x-jährige innerhalb von t Jahren sterben wird: G x (t) = t q x := Pr(M x t), t 0. (2.1) Im Folgenden wird die Verteilung von M als bekannt vorausgesetzt. Außerdem wird angenommen, dass sie stetig ist und eine Wahrscheinlichkeitsdichte g x (t) = G (t) besitzt. Für die Dichte gilt dann g x (t) dt = Pr(t < M x < t + dt). (2.2) Analog dazu ist t p x = 1 t q x die t-jährige Überlebenswahrscheinlichkeit eines x-jährigen. 4
17 KAPITEL 2. LEBENSVERSICHERUNGSMATHEMATIK 5 Die bedingte Wahrscheinlichkeit dafür, dass der x-jährige nach Erreichen des Alters x + s weitere t Jahre leben wird, gegeben, dass er dieses Alter erreicht, wird mit t p x+s bezeichnet: Analog dazu ist Daraus folgen unmittelbar und tp x+s = Pr(M x > s + t M x > s) = 1 G x(s + t) 1 G x (s) tq x+s = Pr(M x s + t M x > s) = G x(s + t) G x (s) 1 G x (s) s+tp x = 1 G x (s + t) = [1 G x (s)] 1 G x(s + t) 1 G x (s) s+tq x = G x (s + t) G x (s) = [1 G x (s)] G x(s + t) G x (s) 1 G x (s) Aufgrund von Gleichung (1.5) gilt dann. (2.3). (2.4) = s p x t p x+s (2.5) = s p x t q x+s. (2.6) kp x = p x p x+1 p x+2... p x+k 1, k = 1, 2, (2.7) Definition 2.2 (Die Lebenserwartung eines x-jährigen). Die Lebenserwartung eines x- jährigen ist ė x = IE[M x ] = t g x (t) dt = [1 G x (t)] dt = tp x dt. (2.8) Definition 2.3 (Die Sterblichkeitsintensität). Die Sterblichkeitsintensität des x-jährigen im Alter x+t ist definiert als µ x+t = g x(t) 1 G x (t) = d dt ln[1 G x(t)] = d dt ln tp x. (2.9) Ein für die Auswertung einfacherer Ansatz zur Approximation der Lebenserwartung lässt sich wie folgt definieren: Definition 2.4 (Die gestutzte Restlebensdauer eines x-jährigen). Sei K = M die ganzzahlig gestutzte zukünftige Lebensdauer. Die Verteilung von K folgt aus der Verteilung von M wie folgt: Pr(K x = k) = Pr(k < M x k + 1) = Pr(M x k + 1 M x > k) Pr(M x > k) = k p x q x+k (2.10) für k = 0, 1,..., d. h. die Verteilung der diskreten Zufallsvariable K ist bestimmt durch Wahrscheinlichkeiten q x+k und k p x.
18 KAPITEL 2. LEBENSVERSICHERUNGSMATHEMATIK 6 Der Erwartungswert von K heißt gestutzte Lebenserwartung des x-jährigen und wird mit e x bezeichnet. Es ist also e x := E[K] = k Pr(K x = k) = k=1 k k p x q x+k (2.11) k=1 oder e x = Pr(K x k) = k=1 kp x. (2.12) Der Vorteil dieses Ansatzes besteht auch darin, dass lediglich Annahmen über die Verteilung von K gemacht werden müssen. k=1 Definition 2.5 (Sterbetafeln). Eine Sterbetafel ist im Wesentlichen eine Tabelle von einjährigen Sterbewahrscheinlichkeiten, durch die dann die Verteilung von K definiert ist. Dadurch ließe sich auch in weiterer Folge eine Verteilung für M konstruieren. Sterbetafeln werden für bestimmte Gruppen konstruiert, welche gemäß Merkmalen wie Geschlecht, Rasse, Generation, Art der Versicherung definiert sind. Innerhalb einer solchen Gruppe kann das anfängliche Alter x eine bedeutende Rolle spielen. Beispiel 1. Es soll nun eine konkrete Verteilung von K ausgerechnet werden. Wir setzen die Gleichung (2.7) in die Gleichung (2.10) ein, und erhalten: Pr(K x = k) = p x p x+1 p x+2... p x+k 1 q x+k, k = 1, 2, Wir betrachten nun einen 30-jährigen Mann, d. h. wir suchen Pr(K 30 = k) = p 30 p 31 p p 30+k 1 q 30+k für k = 1, 2, 3,.... Das Ergebnis ist in der Abbildung 2.1 auf den folgenden Seite dargestellt. Definition 2.6 (Die Restlebensdauer einer Person im Sterbejahr). Um die Zufallsvariablen M und K zu verknüpfen, wird die unterjährige Restlebensdauer einer Person eingeführt als Z x = M x K x. (2.13) Die Zufallsvariable Z hat eine stetige Verteilung, die zwischen 0 und 1 konzentriert ist. Wenn wir ihren Erwartungswert mit 1 approximieren und in obiger Gleichung den 2 Erwartungswert bilden, so erhalten wir die Näherung 1 2 ė x e x. (2.14)
19 KAPITEL 2. LEBENSVERSICHERUNGSMATHEMATIK 7 Abbildung 2.1: Verteilung der gestutzten Restlebensdauer eines 30-jährigen (eigene Darstellung) Die einjährigen Sterbe- und Überlebenswahrscheinlichkeiten q x und p x wurden der Sterbetafel der deutschen Aktuarvereingung [8] entnommen. Nicht betrachtet wurde der rechte Rand der Verteilung, d. h. das Erreichen des 102. Lebensjahres. Das Schlussalter der Sterbetafel ist ω = 100, woraus die Wahrscheinlichkeit des Erreichens des 102. Lebensjahres mit unter 0,5 % beziffert werden kann und daher vernachlässigbar klein ist. Interessant ist der Fall, in dem die bedingte Verteilung Z (gegeben K) unabhängig von K ist. Dann ist nämlich Pr(Z z K = k) = z q x+k q x+k (2.15) eine von k unabhängige Verteilungsfunktion G x (z), 0 z 1, d. h. zq x+k = G x (z) q x+k k = 0, 1,.... (2.16) Wird insbesondere G x (z) = z vorausgesetzt (Gleichverteilung zwischen 0 und 1), so ist obige Approximation exakt. Überdies erhalten wir dann aus Z x = M x K x sofort einen Zusammenhang zwischen den Varianzen von M und K: V ar(m) = V ar(k) (2.17) An den Annahmen K und Z unabhängig und Z gleichverteilt zwischen 0 und 1 wird von nun an festgehalten. Definition 2.7 (Die unterjährige Sterbewahrscheinlichkeit). Eine Sterbetafel gestattet es, die Verteilung von K auszurechnen. Um daraus die Verteilung von M erhalten zu können, werden die Annahmen aus vorangegangener Definition genutzt. Durch Interpolation zwischen z=0 und z=1 sehen wir dann, dass zq x = z q x. (2.18)
20 KAPITEL 2. LEBENSVERSICHERUNGSMATHEMATIK 8 Folglich ist und aus der Definition der Sterblichkeitsintensität folgt zp x = 1 z q x (2.19) µ x+z = q x 1 z q x. (2.20) 2.2 Leibrenten Um Nettoprämien berechnen zu können, sind einige Vorüberlegungen von Nöten: i bezeichne den Zins, v = 1 den Diskontierungsfaktor und y = i der diskontierte Wert 1+i 1+i des am Jahresende bezahlten Zinses i. Zunächst wird die Zufallsvariable W mit W = v K+1, K = 0, 1,... (2.21) definiert. Die möglichen Werte von W sind also v, v 2, v 3,..., und die Verteilung von W folgt aus Gleichung (2.21) und der Verteilung aus K: Pr(W = v k+1 ) = Pr(K = k) = k p x q x+k. (2.22) Der Erwartungswert von W ist IE[W ] = IE[v K+1 ] = A x = Die Varianz von W berechnet sich durch v k+1 kp x q x+k. (2.23) k=0 V ar(w ) = IE[Z 2 ] A 2 x = IE[e 2δ(K+1) ], (2.24) wobei v durch e 2δ substituiert wurde und Z die unterjährige Restlebensdauer einer Person ist. Definition 2.8 (Die vorschüssige lebenslängliche Leibrente). Wir betrachten nun eine vorschüssige, lebenslängliche Leibrente, die aus Zahlungen von je 1 besteht. Die Zahlungen finden also zu den Zeitpunkten 0, 1,..., K statt. Der Barwert dieser Rente ist Y = 1 + v + v v K = ä K+1. (2.25) Die Verteilung der Zufallsvariable Y ist gegeben durch Pr(Y = ä k+1 ) = Pr(K = k) = k p x q x+k. (2.26) Die lebenslängliche vorschüssige Leibrente ä x ist gegeben durch ä x := IE[Y ] = ä k+1 k p x q x+k = k=0 v k kp x. (2.27) k=0
21 KAPITEL 2. LEBENSVERSICHERUNGSMATHEMATIK 9 Für die Berechnung der Varianz von Y wird die Gleichung ä K+1 = ä v K+1 ä = 1 y vn 1 y = 1 vn y (2.28) genutzt. Dabei ist Daraus folgt ä = 1 + v + v = 1 1 v = 1 y. (2.29) V ar(y ) = V ar(z)) y 2 = IE[e 2δ(K+1) ] y 2. (2.30) Definition 2.9 (Die vorschüssige temporäre Leibrente der Dauer n). Analog zu Gleichung (2.27) ist die vorschüssige temporäre Leibrente der Dauer n ist definiert als n 1 ä x:n := v k kp x. (2.31) k=0 Definition 2.10 (Die unterjährige Bezahlung). Für die unterjährige Zahlung, bei der uns später insbesondere die Monatliche interessieren wird, betrachten wir nun den Fall, in dem Zahlungen von je 1 1 zu den Zeitpunkten 0,, 2,... gemacht werden, solange der anfänglich x-jährige noch lebt. Die Nettoeinmalprämie dieser (lebenslänglichen) Rente wird mit dem Symbol ä (12) x bezeichnet. Unter der Annahme der Gleichverteilung von u und Unabhängigkeit von K und Z (siehe Def. der Restlebensdauer im Sterbejahr) gilt: ä (12) x = yi y (12) i (12) äx i i(12), (2.32) y (12) i (12) wobei i (12) = 12 [(1 + i) 1/12 1] den nominellen Zins und y (12) = Vorauszinsrate bezeichnet. i(12) 1+i (12) /12 die nominelle Die Nettoeinmalprämie einer temporären Rente mit monatlicher Zahlung kann wie folgt berechnet werden: ä (12) x:n = ä(12) x n p x v n ä (12) x+n. (2.33)
22 KAPITEL 2. LEBENSVERSICHERUNGSMATHEMATIK Nettoprämien Zur Herleitung der Nettoprämien muss zu Beginn der Vertragslaufzeit folgendes versicherungstechnische Äquivalenzprinzip erfüllt sein: IE[Verluste] = Summe aller erbrachten Leistungen Summe aller gezahlter Beiträge = 0. (2.34) Zu beachten ist, dass die Nettoprämien durch diese Gleichung noch nicht eindeutig bestimmt sind. Dazu brauchen wir eine weitere Bedingung an den Zahlungsmodus, z. B. durch Forderung konstanter Prämienzahlungsweise oder einer Einmalprämie. Definition 2.11 (Die Nettoeinmalprämie). Die einfachste Form der Nettoprämie ist die Nettoeinmalprämie (NEP). Der Rest des Kapitels wird auf den Fall einer reinen Erlebensfallversicherung beschränkt. Bei einer Dauer von n Jahren werde das Kapital in der Höhe von 1 im Erlebensfall (und nichts bei vorzeitigem Ableben) ausbezahlt: { 0 für K = 0, 1,..., n 1, O = v n für K n. (2.35) Die NEP wird mit A 1 x:n bezeichnet und beträgt IE[O] = A 1 x:n = v n np x. (2.36) Aus der Formel für die Varianz einer Bernoulli-Verteilung erhalten wir direkt V ar(o) = v 2n np x n q x. (2.37) Beispiel 2. Für einen 30-jährigen Mann mit Vertragslaufzeit n = 37 Jahre und einem unterstellten Rechnungszins von 2,25 % ist A 1 30:37 = 1 (1, 0225) p 30 = 1 (1, 0225) 37 p 30 p 31 p p 66 0, 3612 und V ar(o) = 1 (1, 0225) p q 30 0, Definition 2.12 (Die jährliche Nettoprämie). Wir interessieren uns nun für jährliche Nettoprämien Px:n 1. Der Verlust des Versicherers ist in diesem Fall { P 1 L = x:n äk+1 für K = 0, 1,..., n 1 v n Px:n 1 für K n, (2.38)
23 KAPITEL 2. LEBENSVERSICHERUNGSMATHEMATIK 11 wobei K wieder die gestutzte zukünftige Lebensdauer bezeichnet. Die Verteilung von L ist diskret auf n+1 Punkten konzentriert: Pr(L = Px:n 1 = K p x q x+k für K = 0, 1,..., n 1 und Pr(L = v n Px:n 1 = n p x für K = n. (2.39) Aus dem Äquivalenzprinzip folgt n 1 Px:n 1 ä k+1 kp x q x+k = (v n Px:n 1 ä n ) np x. (2.40) k=0 Nach einigen Umformungen erhalten wir x:n = A x:n 1 = ä x:n P 1 v n np x n 1 k=0 vk kp x. (2.41) Beispiel 3. Um auf das vorangegangene Beispiel wieder zurück zu kommen, betrachten wir wieder x = 30, n = 37 und v = 1. Die jährliche Nettoprämie beläuft sich demnach 1,0225 auf P 1 30:37 = v37 37p k=0 vk kp 30 0, Definition 2.13 (Die monatliche Nettoprämie). Wenn wir die konstante monatliche Nettoprämie P (12) x:n berechnen wollen, dann ist aus der Formel (2.39) lediglich ä x:n durch 12 ä(12) x:n zu ersetzen. Die monatliche Nettoprämie beläuft sich demnach auf x:n = A x:n 1 12 ä (12) P (12) = = = x:n 1 12 vn np x ä (12) x n p x v n ä (12) x+n yi 1 12 vn np x ( ä y (12) i (12) x i i(12) ) y (12) i (12) n p x v n ( ä y (12) i (12) x+n i i(12) ( yi y (12) i (12) yi 1 12 vn np x k=0 vk kp x i i(12) ) y (12) i (12) n p x v n ( yi y (12) i (12) y (12) i (12) ) k=0 vk kp x+n i i(12) y (12) i (12) ). (2.42) Beispiel 4. Wir bleiben bei dem Beispiel x = 30, n = 37 und v = 1 Nettoprämie beläuft sich demnach auf P (12) 30:37 = 0, ,0225. Die monatliche
24 KAPITEL 2. LEBENSVERSICHERUNGSMATHEMATIK Nettodeckungskapital Es wurde festgestellt, dass zum Zeitpunkt des Vertragsabschlusses Äquivalenz zwischen Prämien und Leistungen gefordert wird. Zu einem späteren Zeitpunkt besteht im Allgemeinen aber keine Äquivalenz mehr. Zu einem Zeitpunkt t wird die Zufallsvariable t als die Differenz zwischen dem Barwert der zukünftigen Leistungen und dem Barwert der zukünftigen Prämien definiert. Das Nettodeckungskapital (auch Deckungsrückstellung genannt) zum Zeitpunkt t wird mit t V bezeichnet und ist definiert als der bedingte Erwartungswert von t gegeben M > t. In den in der Praxis auftretenden Versicherungsformen ist in der Regel der Erwartungswert von t positiv oder allenfalls null, da der Versicherte ein Interesse an der Fortsetzung der Versicherung haben soll. Im Erwartungswert übertrifft also der Barwert der zukünftigen Leistungen den Barwert der zukünftigen Prämien. Zur Kompensation sollte daher der Versicherer das Deckungskapital t V bereitstellen oder reservieren. Definition 2.14 (Das Nettodeckungskapital). Es seien k die bereits zurückgelegte Vertragslaufzeit, Px:n 1 die jährliche (konstante) Nettoprämie, A 1 x+k:n k der Barwert der künftigen Versicherungsleistungen, ä x+k:n k die vorschüssige temporäre Leibrente der Dauer n k und k Vx:n 1 die Deckungsrückstellung (d. h. der Wert der Versicherung zum Zeitpunkt t) im Alter x + k. Dann muss gemäß der verallgemeinerten Äquivalenzgleichung gelten: kvx:n 1 + Px:n 1 1 ä x+k:n k = Ax+k:n k,, k = 0, 1,..., n 1. (2.43) Das durch das verallgemeinerte Äquivalenzprinzip bestimmte Deckungskapital k V x heißt prospektives Deckungskapital. Beispiel 5. Wir wollen in dem bekannten Beispiel (x = 30, n = 37, v = 1 1 P30:37 = 0, 01469) den Verlauf des Nettodeckungskapital in der Aufschubzeit bei jährlicher Prämienzahlung berechnen. Gesucht ist also: ,0225 und kv30:37 = A30+k:37 k P30:37 ä 30+k:37 k, für jedes k = 0, 1,..., 37.
25 KAPITEL 2. LEBENSVERSICHERUNGSMATHEMATIK 13 Abbildung 2.2: Entwicklung des Nettodeckungskapitals, der Prämienbarwerte und der Leistungsbarwerte in der Aufschubzeit (eigene Darstellung) Hier ist die Entwicklung der Deckungsrückstellung zu erkennen, die sich aus der Differenz zwischen Leistungsbarwerten und Prämienbarwerten ergibt. Betrachtet wurde nur die Aufschubzeit, also die Zeitpunkte von Vertragsbeginn bis Renteneintrittsalter. 2.5 Bruttoprämien Es wurden bisher ausschließlich Nettoprämien betrachtet. Um eine ausreichende Prämie zu erhalten, müssen auch die Kosten des Versicherungsunternehmens, die durch den Vertragsabschluss entstehen, mit einbezogen werden: (i) Abschlusskosten, α-kosten (ii) Inkassokosten, β-kosten (iii) Verwaltungskosten, γ-kosten. Definition 2.15 (Die ausreichende Prämie). Die jährliche ausreichende Prämie P ergibt sich aus der Bedingung, dass a Px:n ä x:n = A x:n + α + β Px:n ä x:n + γ ä x:n. (2.44) Daraus folgt, dass a x:n a Px:n a = A x:n + α + γ ä x:n. (2.45) (1 β) ä x:n
26 KAPITEL 2. LEBENSVERSICHERUNGSMATHEMATIK 14 Beispiel 6. Ein letztes Mal wird unser bekanntes Beispiel herangezogen, um die ausreichende Prämie zu veranschaulichen. Es werden Abschlusskosten von α = 5%, Verwaltungskosten von β = 1, 6% und Inkassokosten von γ = 1, 5% unterstellt. Die ausreichende Prämie beläuft sich somit auf a P30:37 = A 30:37 + 0, , 015 ä 30:37 = 0, (1 0, 016) ä 30:37 Bemerkung. Die von Kunden zu zahlende Tarif- oder Bruttoprämie wird außer von den Faktoren, die bei der Berechnung der ausreichenden Prämie eine Rolle spielen, noch von folgenden weiteren Einflussgrößen bestimmt: (i) Stückkostenzuschlag (ii) Risikozuschlag (iii) Rundungsvorschriften.
27 Kapitel 3 Funktionsweise der dynamischen Drei-Topf-Hybride 3.1 Eigenschaften des Produkts Bei dynamischen Drei-Topf-Hybrid-Produkten handelt es sich um eine fondsgebundene Rentenversicherung auf ein Leben mit aufgeschobener Rentenzahlung, garantierter Erlebensfallleistung mit garantiertem Verrentungsfaktor und flexiblem Rentenbeginn. Bei Tod in der Aufschubzeit wird das aktuelle Kundenguthaben, also mindestens die derzeitige Garantie ausbezahlt. Für die garantierte Erlebensfallleistung kann ein (auch anteiliger) Beitragserhalt der für den Vertrag gezahlten Beiträge vereinbart werden. Der Rest der Arbeit ist jedoch der Einfachheit halber auf den vollen Beitragserhalt beschränkt. Es erfolgt monatlich eine automatisierte Aufteilung des Vertragsvermögens auf die Vermögenstöpfe Klassisches Deckungskapital (DK), Garantiefonds (GF) und Freie Fonds (FF). Dabei wird ein spezieller Garantiefonds zugrunde gelegt, der jeweils zum Monatsende einen festgelegten Anteil (üblicherweise 80 %) des zum Ende des Vormonats gültigen Kurswertes des Garantiefonds garantiert. Mit Hilfe der Unterschranke und der Option, das Vermögen durch Umschichtung ins Deckungskapital zu sichern, kann eine Garantie zum Vertragsende abgebildet werden. Der Garantiefonds wird in der Realität durch den sogenannten Constant-Proportion- Portfolio-Insurance (CPPI) - Algorithmus gemanaged. Dieser Mechanismus trägt durch tägliche Portfolioanpassungen dafür Sorge, dass die Nichtunterschreitung der 80 % -Hürde eingehalten wird. Für dieses Extra werden Fondskosten vom Kunden verlangt. Wie der CPPI genau funktioniert, ist hier nicht weiter von Interesse, da der Garantiefonds später alternativ modelliert wird. Für Details sei aber auf Albrecht und Maurer [1, S. 616] verwiesen. In diesem Kapitel wird zunächst davon ausgegangen, dass der Garantiefonds tatsächlich maximal 20 % an Wert pro Monat verlieren kann, ohne dass dem Kunden dabei Kosten entstehen. Die Idee des dritten Topfes besteht darin, dass neben der Gewährleistung der Garantie - durch Investieren in das klassisches Deckungskapital und den Garantiefonds - das dafür nicht benötigte Vermögen renditeträchtiger angelegt werden kann. Dabei hat der Kunde je nach Risikoaversion die Wahl zwischen verschiedenen Fondsgruppen, wie z. B. Aktien, Immobilien- oder Rentenfonds. Aufgrund der Volatilität der Fondskurse und der sich 15
28 KAPITEL 3. FUNKTIONSWEISE DER DYNAMISCHEN DREI-TOPF-HYBRIDE 16 daraus ergebenden Änderungen im Kundenportfolio ist eine monatliche Neuausrichtung nötig, um die Garantie sicherstellen zu können. Diese periodische Umschichtung folgt immer demselben Algorithmus. Wir betrachten nun den Monatsübergang vom t-ten zum t + 1-ten Monat: Um den Ablauf transparenter zu machen, werden die Bezeichnungen t für das Ende des Monats (t 1, t) und t + für den Beginn des Monats (t, t + 1) eingeführt. Zum Ende eines Monats werden dem Kundenvermögen Kosten entnommen und etwaige fällige Leistungen ausbezahlt. Dem Monatsübergang t wird kein Ereignis zugeordnet. Zu Beginn des neuen Monats werden dann die Umschichtungen durchgeführt und danach die Beiträge eingezogen. Der Einfachheit halber werden im Folgenden die versicherungstechnischen Kosten und die Fondsmanagementkosten vernachlässigt. Während eines Monats beeinflusst das Versicherungsunternehmen die Zusammensetzung eines Kundenportfolios nicht. Der Wert eines einzelnen Topfes kann sich im Falle des DK durch Verzinsung und im Falle von GF oder FF durch Entwicklungen der Fondskurse jedoch während eines Monats sehr wohl ändern. 3.2 Erklärung des Umschichtungsalgorithmus Für die Darstellung des Umschichtungsmechanismus werden nun folgende Bezeichnungen eingeführt: Bezeichnung Beschreibung x Eintrittsalter n Versicherungsdauer (in Jahren) bis zum Garantiezeitpunkt w(t) Restlaufzeit bis zum Garantiezeitpunkt, ausgehend vom Zeitpunkt t (in Monaten) B(t + ) gezahlter Beitrag zum Zeitpunkt t + B sum (t) Summe aller bis zum Zeitpunkt t gezahlten Beiträge I(t + 1) das zur Garantiegewährleistung nötige Vermögen i Garantieverzinsung P V Barwert V DK (t ) klassisches Deckungskapital zum Ende des Monats (t 1, t) V GF (t ) Garantiefondsvermögen zum Ende des Monats (t 1, t) V F F (t ) Vermögen im Freien Fonds zum Ende des Monats (t 1, t) V (t ) Vermögen zum Ende des Monats (t 1, t) V (t + ) Vermögen zum Beginn des Monats (t, t + 1) V DK (t + ) Vermögen im klassischen Deckungskapitaltopf zum Beginn des Monats (t, t + 1) V GF (t + ) Vermögen im Garantiefonds zum Beginn des Monats (t, t + 1) V F F (t + ) Vermögen im Freien Fonds zum Beginn des Monats (t, t + 1) Bemerkung. Alle Variablen aus dieser Tabelle haben Werte 0.
29 KAPITEL 3. FUNKTIONSWEISE DER DYNAMISCHEN DREI-TOPF-HYBRIDE 17 Zu jedem beliebigen Zeitpunkt t = 1,..., T 1 gelten folgende Gleichungen: V DK (t ) + V GF (t ) + V F F (t ) + B((t 1) + ) = V (t ) = V (t + ) = V DK (t + ) + V GF (t + ) + V F F (t + ). (3.1) Aus letzterer Gleichung und obiger Bemerkung folgen direkt die oberen Schranken V DK (t + ) V (t + ), V GF (t + ) V (t + ) und V F F (t + ) V (t + ), t = 0,..., T 1. (3.2) Die Gleichungen (3.1) sind folgendermaßen zu interpretieren: Zum Ende eines Monats wird geprüft, wieviel die Teilvermögen der einzelnen Töpfen wert sind. Die Summe dieser drei Positionen plus dem vorschüssig gezahlten Monatsbeitrag ergeben die zur Verfügung stehende Geldmenge V (t ). Da während des Monatsübergangs nichts passiert, kann zum Zeitpunkt t + die gleiche Geldmenge verwendet werden, um gemäß dem Umschichtungsalgorithmus die drei Topfgrößen neu zu bestimmen. Dafür muss zunächst berechnet werden wieviel Vermögen für die Garantiegewährleistung notwendig ist. Dieser Betrag, der mit I(t + 1) bezeichnet wird, ist so hoch, dass er in einem Monat gerade ausreicht, um die Summe der bisher gezahlten Beiträge zum Ende der Laufzeit garantieren zu können. Das klassische Deckungskapital wird mit dem garantierten Zinssatz von i = 2, 25 % pro Jahr verzinst. Dies entspricht der bis gesetzlich vorgeschriebenen Mindestgarantieverzinsung für das Neugeschäft. Zum wurde i vom Gesetzgeber um 0,5 Prozentpunkte verringert. Der Rest der Arbeit ist jedoch auf den für den Bestand noch gültigen alten Zinssatz beschränkt. Die Wertentwicklung des Deckungskapitaltopfes während eines Monats ist somit durch V DK((t+1) ) V DK = (1 + i) (1/12) gegeben. (t + ) Wir betrachten nun den Fall, dass das Kundenvermögen ausschließlich in den Deckungskapitaltopf umgeschichtet wird und diese Verteilung bis zum Ende der Vertragslaufzeit fixiert wird. Dann ist bereits zum Zeitpunkt t bekannt wieviel Vermögen zum Endzeitpunkt T vorhanden sein wird. Umgekehrt kann also auch ausgehend von den bekannten Parametern B sum (t), i und t berechnet werden, wie groß I(t+1) sein muss. Dieser Wert ist somit der finanzmathematische Barwert (PV) der bisher gezahlten Beiträge multipliziert mit dem monatlichen Garantiezins: I(t + 1) = 1, 0225 (1/12) P V (B sum (t)) = 1, , 0225 ( w(t) 12 ) B sum (t) = 1, w(t) 12 B sum (t). (3.3) Der deterministische finanzmathematische Barwert ist zu unterscheiden vom lebensversicherungsmathematischen Barwert, bei dem die Biometrie und somit stochastische Größen
30 KAPITEL 3. FUNKTIONSWEISE DER DYNAMISCHEN DREI-TOPF-HYBRIDE 18 mit einfließen. Mathematisch ausgedrückt handelt es sich bei der Entwicklung eines Kundenguthabens um einen Markovprozess. Definition 3.1 (Umschichtungsalgorithmus). Der Umschichtungsalgorithmus ist für alle t = 0,..., T 1 folgendermaßen definiert: (i) V opt F F (t+ ) := 1 { 0,8 V (t + ) I(t+1)} [V (t + ) I(t+1) 0,8 ] (ii) V opt GF (t+ ) := 1 { 0,8 V (t + ) I(t+1)} I(t+1) 0,8 + 1 { 0,8 V (t + ) < I(t+1)} I(t+1) 1,0225(1/12) V (t + ) 0,8 1,0225 (1/12) (iii) V opt DK (t+ ) := 1 { 0,8 V (t + ) < I(t+1)} I(t+1) 0,8 V (t+ ) 1,0225 (1/12) 0, Optimalität des Umschichtungsalgorithmus Die Grundidee des dynamischen Drei-Topf-Hybrid-Produkts kann durch ein Optimierungsproblem beschrieben werden: Zu einem Zeitpunkt t soll das Kundenvermögen in (t + 1) und somit die monatliche Rendite des Kundenportfolios im Monat (t, t + 1) unter der Nebenbedingung der Garantiegewährleistung maximiert werden. Als Zielfunktion dient dabei [V F F (t + ) V DK (t + )], wobei einerseits unterstellt wird, dass die Fondstöpfe innerhalb eines Monats eine höhere zu erwartende Rendite haben als die des Deckungskapitaltopfes. Und andererseits wird angenommen, dass die zu erwartende Rendite des Freien Fonds größer als die des Garantiefonds ist. Statt mit Erwartungswerten zu arbeiten, wird einfach der Anteil des Freien Fonds am Kundenvermögen maximiert und der des Deckungskapitaltopfes minimiert. Satz 3.2 (Optimalität des Umschichtungsalgorithmus). Sei t {0,..., T 1}. Es seien die Größen I(t + 1) und V (t + ) gegeben. Unter der Voraussetzung, dass die Wertentwicklung des Deckungskapitaltopfes innerhalb eines Monats (t, t + 1) definiert ist durch V DK ((t + 1) ) V DK (t + ) = 1, 0225 (1/12), (3.4) und der maximale Verlust des Garantiefondsvermögens im Monat (t, t + 1) begrenzt ist durch V GF (t + ) V GF ((t + 1) ) 0, 2, (3.5) V GF (t + ) ist der Umschichtungsalgorithmus für jedes t = 0,..., T 1 die Lösung des folgenden Optimierungsproblems: max [V F F (t + ) V DK (t + )] (Rendite des Kundenportfolios) (3.6) u. d. N. V ((t + 1) ) I(t + 1) (Garantiegewährleistung) (3.7)
31 KAPITEL 3. FUNKTIONSWEISE DER DYNAMISCHEN DREI-TOPF-HYBRIDE 19 0 V DK (t + ) V (t + ) (Zulässigkeit des DK-Volumens) (3.8) 0 V F F (t + ) V (t + ) (Zulässigkeit des FF-Volumens) (3.9) 0 V GF (t + ) V (t + ) (Zulässigkeit des GF-Volumens). (3.10) Beweis 3.3 (des Satzes). Aus der Voraussetzung folgt zunächst min{v ((t + 1) ) = 0, 8 V opt GF (t+ ) + 1, 0225 (1/12) V opt DK (t+ ). (3.11) Motiviert durch die Def. 3.1 unterscheiden wir für den Beweis die Fälle 0, 8 V (t + ) I(t + 1) und 0, 8 V (t + ) < I(t + 1). (3.12) 1. Fall: 0, 8 V (t + ) I(t + 1) Es folgt unmittelbar, dass V opt DK (t+ ) = 0 gilt. (i) Wir zeigen, dass die Def. 3.1 die Bedingung (3.7) erfüllt: V ((t + 1) ) min{v ((t + 1) )} (3.11) {}}{ = 0, 8 V opt GF (t+ ) + 1, 0225 (1/12) V opt DK (t+ ) Def.3.1 {}}{ = 0, 8 1 { 0,8 V (t + ) I(t+1)} = 0, 8 I(t + 1) 0, 8 + 0, 8 1 { 0,8 V (t + ) < I(t+1)} I(t + 1) 1, 0225(1/12) V (t + ) 0, 8 1, 0225 (1/12) + 1, 0225 (1/12) 0 I(t + 1) 0, = I(t + 1). Def. 3.1 erfüllt (3.7), womit die Garantie gewährleistet ist.
32 KAPITEL 3. FUNKTIONSWEISE DER DYNAMISCHEN DREI-TOPF-HYBRIDE 20 (ii) Wir zeigen, dass V opt F F (t+ ) die Ungleichungen (3.9) erfüllt: V opt F F (t+ ) Def.3.1 {}}{ = 1 { 0,8 V (t + ) I(t+1)} [V (t + ) = V (t + I(t + 1) ) 0, 8 I(t + 1) I(t + 1) 0, 8 0, 8 = 0 I(t + 1) ] 0, 8 V opt F F (t+ ) = V (t + I(t + 1) ) 0, 8 V (t + ). (iii) Wir zeigen, dass V opt GF (t+ ) die Ungleichungen (3.10) erfüllt: V opt GF (t+ ) Def.3.1 {}}{ = 1 { 0,8 V (t + ) I(t+1)} = I(t + 1) 0, { 0,8 V (t + ) < I(t+1)} I(t + 1) 1, 0225(1/12) V (t + ) 0, 8 1, 0225 (1/12) I(t + 1) + 0 > I(t + 1) > 0 0, 8 V opt GF (t+ ) = I(t + 1) 0, 8 V (t + ). (iv) Für den Beweis der Optimalität betrachten wir die Zielfunktion V F F (t + ) und zeigen, dass V opt F F (t+ ) = V (t + ) I(t+1) der maximale Zielfunktionswert ist. Dies weisen wir 0,8 nach, indem wir via Widerspruchsbeweis zeigen, dass die Ungleichung (3.7) eine aktive Nebenbedingung ist. Wir addieren ein beliebiges ɛ > 0 zu V opt F F (t+ ) und erhalten ein alternatives V F F (t+ ): VF F (t + ) = V opt F F (t+ ) + ɛ = V (t + I(t + 1) ) + ɛ. 0, 8 Daraus und aus V opt F F (t+ ) + V opt GF (t+ ) = V (t + ) resultiert V GF (t + ) = = V opt GF (t+ ) ɛ I(t + 1) ɛ. 0, 8
33 KAPITEL 3. FUNKTIONSWEISE DER DYNAMISCHEN DREI-TOPF-HYBRIDE 21 Wir zeigen nun unter Verwendung von (3.11), dass V GF (t+ ) die Garantienebenbedingung verletzt: V ((t + 1) ) min{v ((t + 1) )} (3.11) {}}{ = 0, 8 V GF (t + ) + 1, 0225 (1/12) V opt I(t + 1) = 0, 8 [ ɛ] + 0 0, 8 = I(t + 1) 0, 8 ɛ ɛ>0 {}}{ < I(t + 1). Es handelt sich also bei (3.7) um eine aktive Nebenbedingung. V opt F F (t+ ) ist bereits maximal. q.e.d. DK (t+ ) 2. Fall: 0, 8 V (t + ) < I(t + 1) Es folgt unmittelbar, dass V opt F F (t+ ) = 0 gilt. (i) Wir zeigen, dass die Def. 3.1 die Bedingung (3.7) erfüllt: V ((t + 1) ) min{v ((t + 1) )} (3.11) {}}{ = 0, 8 V opt GF (t+ ) + 1, 0225 (1/12) V opt DK (t+ ) Def.3.1 {}}{ = 0 + 0, 8 I(t + 1) 1, 0225(1/12) V (t + ) 0, 8 1, 0225 (1/12) + 1, 0225 (1/12) I(t + 1) 0, 8 V (t+ ) 1, 0225 (1/12) 0, 8 = 0, 8 I(t + 1) 0, 8 1, 0225 (1/12) V (t + ) 0, 8 1, 0225 (1/12) 1, 0225(1/12) I(t + 1) 1, 0225 (1/12) 0, 8 V (t + ) 0, 8 1, 0225 (1/12) = 0, 8 I(t + 1) 1, 0225 (1/12) I(t + 1) 0, 8 1, 0225 (1/12) = I(t + 1). Def. 3.1 erfüllt (3.7), womit die Garantie gewährleistet ist.
34 KAPITEL 3. FUNKTIONSWEISE DER DYNAMISCHEN DREI-TOPF-HYBRIDE 22 (ii) Wir zeigen, dass V opt DK (t+ ) die linke Ungleichung in (3.8) erfüllt: V opt DK (t+ ) Def.3.1 {}}{ = 1 { 0,8 V (t + ) < I(t+1)} I(t + 1) 0, 8 V (t+ ) 1, 0225 (1/12) 0, 8 = I(t + 1) 0, 8 V (t + ) 1, 0225 (1/12) 0, 8 > I(t + 1) I(t + 1) 1, 0225 (1/12) 0, 8 = 0. (iii) Wir zeigen, dass V opt GF (t+ ) die rechte Ungleichung in (3.10) erfüllt: Dafür zeigen wir zunächst, dass die Summe aus den in Def. 3.1 definierten Größen das Gesamtvermögen V (t + ) ist. V opt (t + ) = V opt GF (t+ ) + V opt DK (t+ ) = I(t + 1) 1, 0225 (1/12) V (t + ) + I(t + 1) 0, 8 V (t+ ) 0, 8 1, 0225 (1/12) 1, 0225 (1/12) 0, 8 (3.13) 1, 0225 (1/12) V (t + ) 0, 8 V (t + ) = 1, 0225 (1/12) 0, 8 = V (t + ). Zusammen mit V opt DK (t+ ) > 0 aus ii) folgt unmittelbar V opt GF (t+ ) < V (t + ). (iv) Wir zeigen nun simultan, dass V opt DK (t+ ) die rechte Ungleichung in (3.8) und V opt GF (t+ ) die linke Ungleichung in (3.10) erfüllt: Dafür schätzen wir zunächst min(v ((t + 1) + )) mit Hilfe der Voraussetzung nach oben ab: min(v ((t + 1) + )) = 1, 0225 (1/12) V DK (t + ) + 0, 8 V GF (t + ) (3.1) {}}{ = 1, 0225 (1/12) V DK (t + ) + 0, 8 (V (t + ) V DK (t + ) V F F (t + )) 1, 0225 (1/12) V DK (t + ) + 0, 8 (V (t + ) V DK (t + )) = V (t + ) [1, 0225 (1/12) VDK(t + ) V (t + ) 1, 0225 (1/12) V (t + ). + 0, 8 (1 V DK(t + ) V (t + ) )] Zusammen mit der in i) bewiesenen Aussage, das Def. 3.1 die Nebenbedingung (3.7) erfüllt, gilt folglich I(t + 1) = min(v ((t + 1) + )) 1, 0225 (1/12) V (t + ).
35 KAPITEL 3. FUNKTIONSWEISE DER DYNAMISCHEN DREI-TOPF-HYBRIDE 23 Damit können wir V opt DK (t+ ) wie folgt abschätzen: V opt DK (t+ ) = I(t + 1) 0, 8 V (t + ) 1, 0225 (1/12) 0, 8 1, 0225(1/12) V (t + ) 0, 8 V (t + ) 1, 0225 (1/12) 0, 8 = V (t + ). Analog können wir V opt GF (t+ ) abschätzen: V opt GF (t+ ) = I(t + 1) 1, 0225 (1/12) V (t + ) 0, 8 1, 0225 (1/12) 1, 0225(1/12) V (t + ) 1, 0225 (1/12) V (t + ) 0, 8 1, 0225 (1/12) = 0. (v) Für den Beweis der Optimalität betrachten wir die Zielfunktion V DK (t + ) und zeigen, dass V opt DK (t+ ) = I(t+1) 0,8 V (t+ ) der maximale Zielfunktionswert ist. Dies weisen 1,0225 (1/12) 0,8 wir nach, indem wir via Widerspruchsbeweis zeigen, dass die Ungleichung (3.7) eine aktive Nebenbedingung ist. Wir subtrahieren ein beliebiges ɛ > 0 von V opt DK (t+ ) und erhalten ein alternatives V DK (t+ ) : Daraus und aus (3.13) resultiert V DK(t + ) = V opt DK (t+ ) ɛ V GF (t + ) = V opt GF (t+ ) + ɛ = I(t + 1) 0, 8 V (t+ ) 1, 0225 (1/12) 0, 8 ɛ. = I(t + 1) 1, 0225(1/12) V (t + ) 0, 8 1, 0225 (1/12) + ɛ. Wir zeigen nun unter Verwendung von (3.11), dass V GF (t+ ) die Garantienebenbedingung verletzt: V ((t + 1) ) min{v ((t + 1) )} (3.11) {}}{ = 0, 8 V GF (t + ) + 1, 0225 (1/12) V DK(t + ) = 0, 8 [ I(t + 1) 1, 0225(1/12) V (t + ) 0, 8 1, 0225 (1/12) + ɛ] + 1, 0225 (1/12) [ I(t + 1) 0, 8 V (t+ ) 1, 0225 (1/12) 0, 8 ɛ] =
36 KAPITEL 3. FUNKTIONSWEISE DER DYNAMISCHEN DREI-TOPF-HYBRIDE 24 = 0, 8 1, 0225(1/12) V (t + ) 0, 8 I(t + 1) 1, 0225 (1/12) 0, 8 + 1, 0225(1/12) I(t + 1) 0, 8 1, 0225 (1/12) V (t + ) 1, 0225 (1/12) 0, 8 + (0, 8 1, 0225 (1/12) ) ɛ = 0, 8 1, 0225(1/12) V (t + ) 0, 8 I(t + 1) 1, 0225 (1/12) 0, 8 + 1, 0225(1/12) I(t + 1) 0, 8 1, 0225 (1/12) V (t + ) 1, 0225 (1/12) 0, 8 + (0, 8 1, 0225 (1/12) ) ɛ = 1, 0225(1/12) I(t + 1) 0, 8 I(t + 1) 1, 0225 (1/12) 0, 8 + (0, 8 1, 0225 (1/12) ) ɛ = I(t + 1) + (0, 8 1, 0225 (1/12) ) ɛ ɛ>0 {}}{ < I(t + 1). q.e.d. Es handelt sich also bei (3.7) um eine aktive Nebenbedingung. V opt DK (t+ ) ist bereits minimal. q.e.d. Bemerkung. Da es sich also tatsächlich um die optimalen Aufteilungen in Def. 3.1 handelt, können die hochgestellten opt weggelassen werden. Die Bezeichnungen V F F (t + ), V GF (t + ) und V DK (t + ) werden von nun an gleichbedeutend mit den in Def. 3.1 erklärten Aufteilungen verwendet.
37 KAPITEL 3. FUNKTIONSWEISE DER DYNAMISCHEN DREI-TOPF-HYBRIDE Ein graphisches Beispiel zur Umschichtung Folgende Grafik zeigt einen beispielhaften Verlauf eines Kundenguthabens unter den Annahmen: (i) Vertragsdauer n = 30 Jahre (ii) Eintrittsalter x = 37 Jahre (iii) Restlaufzeit w(156) = 204 Monate = 17 Jahre (iv) konstanter monatlicher Beitrag B(t) = 100 Euro (v) Vernachlässigung der Kosten (vi) Mindestgarantiezins von 2, 25 % p. a. (vii) sehr volatile Fondskurse (um Umschichtungen hervor zu heben) (viii) nur Umschichtungen in den kommenden 18 Monaten, d. h. t = 157,..., 174, werden betrachtet. Abbildung 3.1: Beispielhafter 18-monatiger Verlauf der Verteilung eines Kundenguthabens (eigene Darstellung) Neben dem Kundenguthaben V in Abhängigkeit vom Zeitpunkt t + sind dessen Aufteilungen auf die drei Töpfe FF, GF und DK abgebildet. Zu jedem Zeitpunkt t + = 157 +,..., 174 +, also direkt nach einer Umschichtung, ergeben die kumulierten Säulen der drei Töpfe gerade wieder V (t + ).
38 KAPITEL 3. FUNKTIONSWEISE DER DYNAMISCHEN DREI-TOPF-HYBRIDE 26 Außerdem ist die DK-Sicherungslinie dargestellt. Sie folgt der Funktion I DK (t) = I(t). (3.14) Das garantierte monatliche Verlustminimum von 20 % des Garantiefonds und der Umschichtungsalgorithmus stellen stets sicher, dass sich das Vermögen V(t) oberhalb dieser Sicherungslinie befindet. Die GF-Sicherungslinie wird hingegen durch die Funktion I GF (t) = I(t + 1) 0, 8 (3.15) beschrieben. Diese Linie gibt das momentan maximal benötige Garantiefonds-Volumen an. Hinzu kommt, dass sie in Kombination mit V (t + ) ein Indikator dafür ist, ob sich Guthaben im Deckungskapital oder in den Freien Fonds befindet. Damit kann also die Indikatorfunktion aus dem Umschichtungsalgorithmus (Def. 3.1) bzw. die zentrale Fallunterscheidung (3.12) im Beweis auch geometrisch interpretiert werden.
39 Kapitel 4 Solvency II Nachdem im vorigen Kapitel die Funktionsweise der dynamischen Drei-Topf-Hybrid-Produkte erläutert wurde, können wir nun den Fokus auf die daraus resultierenden Risiken richten. Zunächst wird der rechtliche Rahmen (Solvency II) etwas umfänglicher als in der Einleitung beleuchtet. Im Anschluss daran können die entstehenden Risikoarten identifiziert werden. 4.1 Solvency II - die Grundstruktur Solvency II als ein auf drei Säulen beruhendes Gesamtkonzept für die Sicherheitskapitalausstattung und die Aufsicht umfasst u. a. folgende Punkte (Säule I): ˆ Im Hinblick auf ihre intern und extern begründete Risikolage sollen Versicherungsunternehmen mit einer möglichst geringen Ruinwahrscheinlichkeit tätig sein. Solvency II erfasst daher Einzelrisiken und aggregiert sie zu einem Gesamtrisiko (vgl. Farny [11, S. 842]). Soweit es um die Betrachtung der Eigenkapitalausstattung geht, ist die Idee mit dem sogenannten Risk Based Capital Modell (RBC) vergleichbar. ˆ Solvency II hat (auch) das Ziel, Versicherungsunternehmen anzuregen, eigene Risikomanagementsysteme (sogenannte interne Modelle) zu entwickeln. Zur Ermittlung der erforderlichen Eigenkapitalausstattung ist ein Verfahren mit zwei Stufen vorgesehen. (i) Stufe 1: Ein Mindestkapital (Minimum Capital Requirement - MCR) ähnlich der Solvabilitätsspanne nach dem Vorbild des Vorgängers Solvency I (ii) Stufe 2: Das höhere Zielkapital bzw. Solvenzkapital (Solvency Capital Requirement - SCR). Diesen Kapitalanforderungen werden die sogenannten anrechnungsfähigen Eigenmittel (Available Solvency Margin - ASM) gegenübergestellt. Die Anforderungen an Solvency II sind erfüllt, wenn ASM das geforderte bzw. nötige Solvenzkapital SCR übersteigt. Liegt ASM über MCR aber unter SCR werden Maßnahmen 27
40 KAPITEL 4. SOLVENCY II 28 der Aufsichtsbehörde ausgelöst. Unterschreitet ASM (auch) MCR, muss ein Restrukturierungsplan vorgelegt werden, in dem die Wiederherstellung der (Mindest-) Kapitalanforderung beschrieben wird. Wird die MCR-Schwelle nachhaltig unterschritten, kommt es zum Entzug der Erlaubnis des Geschäftsbetriebes durch die Aufsichtsbehörde (vgl. Farny [11, S.844 f]. Abbildung 4.1: Solvency II - Bilanz (vgl. EIOPA [9]) Diese Graphik verschafft einen Überblick über die Solvency II - Bilanz. Dabei ist der Soll-Fall abgebildet, d. h. das ökonomische Eigenkapital (ASM) ist größer als MCR und auch größer als SCR. Die Sollgröße SCR kann entweder im Rahmen eines sogenannten Standardmodells oder unter Verwendung eines internen Modells berechnet werden. Der Solvenzkapitalbedarf (SCR) als Ausdruck der Soll-Solvabilität soll in beiden Varianten die individuelle Gesamtrisikolage des einzelnen Versicherungsunternehmens berücksichtigen. Zu diesem Zweck werden zunächst einzelne Risikoarten und deren Solvenzkapitalbedarf ermittelt, wobei die Erfassungsmodelle, die Gliederung der Einzelrisiken, das verwendete Risikomaß und ein Konfidenzniveau festgelegt werden; letzteres gibt an, mit welcher Wahrscheinlichkeit (z. B. 99, 5 % ) die Solvabilitätsmittel nach einem Jahr noch positiv sind, ihr Komplementärwert (z. B. 0, 5 % ) ist somit Ausdruck einer einjährigen Verlustwahrscheinlichkeit. Im nächsten Schritt werden die Einzelrisiken bzw. deren Solvenzbedarf unter Beachtung von Korrelationen zur Berücksichtigung interner Risikoausgleichseffekte zum Gesamtrisiko des Versicherungsunternehmens bzw. zum Gesamtsolvenzkapitalbedarf aggregiert (vgl. Farny [11, S. 840 f]).
41 KAPITEL 4. SOLVENCY II 29 Abbildung 4.2: SCR-Modulstruktur (vgl. EIOPA [9, S. 90]) Die angesprochenen Risikoarten werden im Standardmodell durch Module abgegrenzt, deren Aufteilung hier ersichtlich ist. Die Solvenzkapitalanforderungen können auch nach einem internen Modell berechnet werden. Dieses muss der Aufsicht zur Überprüfung und Zertifizierung vorgelegt werden. Die Zertifizierung hat zur Voraussetzung, dass das interne Modell das Risikoprofil des Unternehmens besser als das Standardmodell abbildet. Zudem sind die Standards betreffend der Kalibrierung, Validierung und Dokumentation der statistischen Methoden einzuhalten. Motivation zur Verwendung eines internen Modells ist auch, dass durch die passgenauere Risikoabbildung der Eigenkapitalbedarf geringer ist als bei einem Standardmodell mit seiner One-size-fits-all-Philosophie. Der errechnete Solvenzkapitalbedarf wird dann fortlaufend mit den verfügbaren Eigenmitteln (ASM) abgeglichen. In der zweiten Säule werden Governance-Prozesse definiert. Diese Säule umfasst insbesondere die aufsichtsbehördliche Prüfung interner Risikomodelle und schließt die Qualitätsprüfung des Risikomanagementsystems mit ein. Die dritte Säule sieht Offenlegungsanforderungen zur Schaffung von Markttransparenz und Marktdisziplin sowohl gegenüber der Aufsicht als auch gegenüber der Öffentlichkeit vor. Der (Teil-) Prozess aus der ersten Säule umfasst auch Risiken, die aus Garantien und Optionsrechten entstehen. Als Beispiel kann hier die Umschichtungsoption des Versicherungsnehmers im hier untersuchten Produkt dienen. Diese Option hängt, nicht wie im eigentlichen Sinne, von der Entscheidung des Kunden, sondern viel mehr von der
Zinseszins- und Rentenrechnung
 Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor
 Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor Ihre private Gesamtrente setzt sich zusammen aus der garantierten Rente und der Rente, die sich aus den über die Garantieverzinsung
Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor Ihre private Gesamtrente setzt sich zusammen aus der garantierten Rente und der Rente, die sich aus den über die Garantieverzinsung
Kapitalversicherungen
 Kapitalversicherungen Birgit Scharwitzl 10. Dezember 2008 Inhaltsverzeichnis 1 Begriffe und wichtige Definitionen 2 1.1 Prämie................................................... 2 1.2 Gewinnbeteiligung............................................
Kapitalversicherungen Birgit Scharwitzl 10. Dezember 2008 Inhaltsverzeichnis 1 Begriffe und wichtige Definitionen 2 1.1 Prämie................................................... 2 1.2 Gewinnbeteiligung............................................
Kapitalversicherungen
 Kapitalversicherungen Sanela Omerovic Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 Inhaltsverzeichnis 1 Einführung 1 2 Einfache Versicherungsformen 3 2.1 Todesfallversicherungen (Life Insurance)....................
Kapitalversicherungen Sanela Omerovic Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 Inhaltsverzeichnis 1 Einführung 1 2 Einfache Versicherungsformen 3 2.1 Todesfallversicherungen (Life Insurance)....................
vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist.
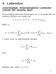 4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
Deckungskapital. Proseminar Versicherungsmathematik. TU Graz. 11. Dezember 2007
 Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
Swiss Life Vorsorge-Know-how
 Swiss Life Vorsorge-Know-how Thema des Monats: Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und
Swiss Life Vorsorge-Know-how Thema des Monats: Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung (Grundwissen)
 Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung Grundwissen) Jürgen Strobel Köln) und Hans-Jochen Bartels Mannheim) Am 04.10.2003 wurde in Köln die zehnte Prüfung über Mathematik
Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung Grundwissen) Jürgen Strobel Köln) und Hans-Jochen Bartels Mannheim) Am 04.10.2003 wurde in Köln die zehnte Prüfung über Mathematik
4. Versicherungsangebot
 4. Versicherungsangebot Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie (FS 11) Versicherungsangebot 1 / 13 1. Einleitung 1.1 Hintergrund In einem grossen Teil
4. Versicherungsangebot Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie (FS 11) Versicherungsangebot 1 / 13 1. Einleitung 1.1 Hintergrund In einem grossen Teil
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
Beispiel 48. 4.3.2 Zusammengesetzte Zufallsvariablen
 4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
Lebensversicherung. http://www.konsument.at/cs/satellite?pagename=konsument/magazinartikel/printma... OBJEKTIV UNBESTECHLICH KEINE WERBUNG
 Seite 1 von 6 OBJEKTIV UNBESTECHLICH KEINE WERBUNG Lebensversicherung Verschenken Sie kein Geld! veröffentlicht am 11.03.2011, aktualisiert am 14.03.2011 "Verschenken Sie kein Geld" ist der aktuelle Rat
Seite 1 von 6 OBJEKTIV UNBESTECHLICH KEINE WERBUNG Lebensversicherung Verschenken Sie kein Geld! veröffentlicht am 11.03.2011, aktualisiert am 14.03.2011 "Verschenken Sie kein Geld" ist der aktuelle Rat
Statistische Thermodynamik I Lösungen zur Serie 1
 Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
Finanzmathematik. Wirtschaftswissenschaftliches Zentrum Universität Basel. Mathematik für Ökonomen 1 Dr. Thomas Zehrt
 Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Finanzmathematik Literatur Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen, Band 1, 17. Auflage,
Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Finanzmathematik Literatur Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen, Band 1, 17. Auflage,
Sofort-Rente. Mit Sicherheit ein Leben lang
 Sofort-Rente Mit Sicherheit ein Leben lang Warum ist die lebenslange Absicherung so wichtig? Wir werden immer älter. Das heißt aber auch, der Ruhestand wird immer teuerer. Wer das Ziel kennt kann entscheiden,
Sofort-Rente Mit Sicherheit ein Leben lang Warum ist die lebenslange Absicherung so wichtig? Wir werden immer älter. Das heißt aber auch, der Ruhestand wird immer teuerer. Wer das Ziel kennt kann entscheiden,
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Das Black-Scholes Marktmodell
 Das Black-Scholes Marktmodell Andreas Eichler Institut für Finanzmathematik Johannes Kepler Universität Linz 8. April 2011 1 / 14 Gliederung 1 Einleitung Fortgeschrittene Finanzmathematik einfach erklärt
Das Black-Scholes Marktmodell Andreas Eichler Institut für Finanzmathematik Johannes Kepler Universität Linz 8. April 2011 1 / 14 Gliederung 1 Einleitung Fortgeschrittene Finanzmathematik einfach erklärt
Senkung des technischen Zinssatzes und des Umwandlungssatzes
 Senkung des technischen Zinssatzes und des Umwandlungssatzes Was ist ein Umwandlungssatz? Die PKE führt für jede versicherte Person ein individuelles Konto. Diesem werden die Beiträge, allfällige Einlagen
Senkung des technischen Zinssatzes und des Umwandlungssatzes Was ist ein Umwandlungssatz? Die PKE führt für jede versicherte Person ein individuelles Konto. Diesem werden die Beiträge, allfällige Einlagen
Im weiteren werden die folgenden Bezeichnungen benutzt: Zinsrechnung
 4.2 Grundbegriffe der Finanzmathematik Im weiteren werden die folgenden Bezeichnungen benutzt: K 0 Anfangskapital p Zinsfuß pro Zeiteinheit (in %) d = p Zinssatz pro Zeiteinheit 100 q = 1+d Aufzinsungsfaktor
4.2 Grundbegriffe der Finanzmathematik Im weiteren werden die folgenden Bezeichnungen benutzt: K 0 Anfangskapital p Zinsfuß pro Zeiteinheit (in %) d = p Zinssatz pro Zeiteinheit 100 q = 1+d Aufzinsungsfaktor
Güte von Tests. die Wahrscheinlichkeit für den Fehler 2. Art bei der Testentscheidung, nämlich. falsch ist. Darauf haben wir bereits im Kapitel über
 Güte von s Grundlegendes zum Konzept der Güte Ableitung der Gütefunktion des Gauss im Einstichprobenproblem Grafische Darstellung der Gütefunktionen des Gauss im Einstichprobenproblem Ableitung der Gütefunktion
Güte von s Grundlegendes zum Konzept der Güte Ableitung der Gütefunktion des Gauss im Einstichprobenproblem Grafische Darstellung der Gütefunktionen des Gauss im Einstichprobenproblem Ableitung der Gütefunktion
III. Grundlagen der Lebensversicherungsmathematik III.5. Deckungskapital für Lebensversicherungsprodukte
 III. Grundlagen der Lebensversicherungsmathematik III.5. Deckungskapital für Lebensversicherungsprodukte Universität Basel Herbstsemester 2015 Dr. Ruprecht Witzel ruprecht.witzel@aktuariat-witzel.ch www.aktuariat-witzel.ch
III. Grundlagen der Lebensversicherungsmathematik III.5. Deckungskapital für Lebensversicherungsprodukte Universität Basel Herbstsemester 2015 Dr. Ruprecht Witzel ruprecht.witzel@aktuariat-witzel.ch www.aktuariat-witzel.ch
Korrigenda Handbuch der Bewertung
 Korrigenda Handbuch der Bewertung Kapitel 3 Abschnitt 3.5 Seite(n) 104-109 Titel Der Terminvertrag: Ein Beispiel für den Einsatz von Future Values Änderungen In den Beispielen 21 und 22 ist der Halbjahressatz
Korrigenda Handbuch der Bewertung Kapitel 3 Abschnitt 3.5 Seite(n) 104-109 Titel Der Terminvertrag: Ein Beispiel für den Einsatz von Future Values Änderungen In den Beispielen 21 und 22 ist der Halbjahressatz
Tarifarten im Rahmen der Tarifoptimierung
 Tarifarten im Rahmen der Tarifoptimierung BA510_201601 txt 2 3 Wir unterscheiden im Rahmen der Tarifoptimierung folgende Tarifarten Konventionell Konzeptversicherungen Dax-Rente Fondsgebunden OptimumGarant
Tarifarten im Rahmen der Tarifoptimierung BA510_201601 txt 2 3 Wir unterscheiden im Rahmen der Tarifoptimierung folgende Tarifarten Konventionell Konzeptversicherungen Dax-Rente Fondsgebunden OptimumGarant
Tutorium zur Mathematik (WS 2004/2005) - Finanzmathematik Seite 1
 Tutorium zur Mathematik WS 2004/2005) - Finanzmathematik Seite 1 Finanzmathematik 1.1 Prozentrechnung K Grundwert Basis, Bezugsgröße) p Prozentfuß i Prozentsatz i = p 100 ) Z Prozentwert Z = K i bzw. Z
Tutorium zur Mathematik WS 2004/2005) - Finanzmathematik Seite 1 Finanzmathematik 1.1 Prozentrechnung K Grundwert Basis, Bezugsgröße) p Prozentfuß i Prozentsatz i = p 100 ) Z Prozentwert Z = K i bzw. Z
Lebensdauer eines x-jährigen
 Lebensdauer eines x-jährigen Sabrina Scheriau 20. November 2007, Graz 1 INHALTSVERZEICHNIS 2 Inhaltsverzeichnis 1 Einleitung 3 2 Sterbewahrscheinlichkeiten 4 2.1 Definition und Ermittlung....................
Lebensdauer eines x-jährigen Sabrina Scheriau 20. November 2007, Graz 1 INHALTSVERZEICHNIS 2 Inhaltsverzeichnis 1 Einleitung 3 2 Sterbewahrscheinlichkeiten 4 2.1 Definition und Ermittlung....................
Derivate und Bewertung
 . Dr. Daniel Sommer Marie-Curie-Str. 0 6049 Frankfurt am Main Klausur Derivate und Bewertung.......... Wintersemester 006/07 Klausur Derivate und Bewertung Wintersemester 006/07 Aufgabe 1: Statische Optionsstrategien
. Dr. Daniel Sommer Marie-Curie-Str. 0 6049 Frankfurt am Main Klausur Derivate und Bewertung.......... Wintersemester 006/07 Klausur Derivate und Bewertung Wintersemester 006/07 Aufgabe 1: Statische Optionsstrategien
Anhand des bereits hergeleiteten Models erstellen wir nun mit der Formel
 Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
GEGENÜBERSTELLUNG PRODUKTINFORMATIONSBLATT
 GEGENÜBERSTELLUNG PRODUKTINFORMATIONSBLATT Gesamtverband der Deutschen Versicherungswirtschaft (GDV) / Prof. Hans-Peter SCHWINTOWSKI, Humboldt-Universität (beide Berlin) Produktinformationsblatt GDV Formulierungsvorschlag
GEGENÜBERSTELLUNG PRODUKTINFORMATIONSBLATT Gesamtverband der Deutschen Versicherungswirtschaft (GDV) / Prof. Hans-Peter SCHWINTOWSKI, Humboldt-Universität (beide Berlin) Produktinformationsblatt GDV Formulierungsvorschlag
Finanzwirtschaft. Teil II: Bewertung
 Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
Themenschwerpunkt Sofortrente
 Themenschwerpunkt Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und Steuern Über die Besteuerung
Themenschwerpunkt Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und Steuern Über die Besteuerung
Aufgabenset 1 (abzugeben 16.03.2012 an LK@wacc.de)
 Aufgabenset 1 (abzugeben 16.03.2012 an LK@wacc.de) Aufgabe 1 Betrachten Sie die Cashflows der Abbildung 1 (Auf- und Abwärtsbewegungen finden mit gleicher Wahrscheinlichkeit statt). 1 Nehmen Sie an, dass
Aufgabenset 1 (abzugeben 16.03.2012 an LK@wacc.de) Aufgabe 1 Betrachten Sie die Cashflows der Abbildung 1 (Auf- und Abwärtsbewegungen finden mit gleicher Wahrscheinlichkeit statt). 1 Nehmen Sie an, dass
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
Kommutationszahlen und Versicherungsbarwerte für Leibrenten 2001/2003
 Kommutationszahlen und Versicherungsbarwerte für Leibrenten 2001/2003 Tabellen zur jährlich und monatlich vorschüssigen Zahlungsweise Statistisches Bundesamt Impressum Herausgeber: Statistisches Bundesamt
Kommutationszahlen und Versicherungsbarwerte für Leibrenten 2001/2003 Tabellen zur jährlich und monatlich vorschüssigen Zahlungsweise Statistisches Bundesamt Impressum Herausgeber: Statistisches Bundesamt
Verteilungsmodelle. Verteilungsfunktion und Dichte von T
 Verteilungsmodelle Verteilungsfunktion und Dichte von T Survivalfunktion von T Hazardrate von T Beziehungen zwischen F(t), S(t), f(t) und h(t) Vorüberlegung zu Lebensdauerverteilungen Die Exponentialverteilung
Verteilungsmodelle Verteilungsfunktion und Dichte von T Survivalfunktion von T Hazardrate von T Beziehungen zwischen F(t), S(t), f(t) und h(t) Vorüberlegung zu Lebensdauerverteilungen Die Exponentialverteilung
AUTOMATISIERTE HANDELSSYSTEME
 UweGresser Stefan Listing AUTOMATISIERTE HANDELSSYSTEME Erfolgreich investieren mit Gresser K9 FinanzBuch Verlag 1 Einsatz des automatisierten Handelssystems Gresser K9 im Portfoliomanagement Portfoliotheorie
UweGresser Stefan Listing AUTOMATISIERTE HANDELSSYSTEME Erfolgreich investieren mit Gresser K9 FinanzBuch Verlag 1 Einsatz des automatisierten Handelssystems Gresser K9 im Portfoliomanagement Portfoliotheorie
Aufgaben Brealey/Myers [2003], Kapitel 21
![Aufgaben Brealey/Myers [2003], Kapitel 21 Aufgaben Brealey/Myers [2003], Kapitel 21](/thumbs/25/5752225.jpg) Quiz: 1, 2, 4, 6, 7, 10 Practice Questions: 1, 3, 5, 6, 7, 10, 12, 13 Folie 0 Lösung Quiz 7: a. Das Optionsdelta ergibt sich wie folgt: Spanne der möglichen Optionspreise Spanne der möglichen Aktienkurs
Quiz: 1, 2, 4, 6, 7, 10 Practice Questions: 1, 3, 5, 6, 7, 10, 12, 13 Folie 0 Lösung Quiz 7: a. Das Optionsdelta ergibt sich wie folgt: Spanne der möglichen Optionspreise Spanne der möglichen Aktienkurs
+ Sicherheit + Flexibilität + Preisvorteil. Berufsunfähigkeitsversicherung. neue leben. start plan GO
 + Sicherheit + Flexibilität + Preisvorteil Berufsunfähigkeitsversicherung neue leben start plan GO Jetzt durchstarten und dreimal Pluspunkte sammeln Sichern Sie Ihr Einkommen ab. Vom ersten Arbeitstag
+ Sicherheit + Flexibilität + Preisvorteil Berufsunfähigkeitsversicherung neue leben start plan GO Jetzt durchstarten und dreimal Pluspunkte sammeln Sichern Sie Ihr Einkommen ab. Vom ersten Arbeitstag
Was kosten Garantien?
 Alternative Zinsgarantien in der Lebensversicherung, Köln, 1. Juni 2012 Was kosten Garantien? Prof. Dr. Ralf Korn Technische Universität Kaiserslautern, Fachbereich Mathematik EI-QFM und Fraunhofer ITWM
Alternative Zinsgarantien in der Lebensversicherung, Köln, 1. Juni 2012 Was kosten Garantien? Prof. Dr. Ralf Korn Technische Universität Kaiserslautern, Fachbereich Mathematik EI-QFM und Fraunhofer ITWM
 Name:... Matrikel-Nr.:... 3 Aufgabe Handyklingeln in der Vorlesung (9 Punkte) Angenommen, ein Student führt ein Handy mit sich, das mit einer Wahrscheinlichkeit von p während einer Vorlesung zumindest
Name:... Matrikel-Nr.:... 3 Aufgabe Handyklingeln in der Vorlesung (9 Punkte) Angenommen, ein Student führt ein Handy mit sich, das mit einer Wahrscheinlichkeit von p während einer Vorlesung zumindest
LV-Umschichtung. Kurzgutachtliche Stellungnahme zu Ihrer Lebensversicherung (LV)
 LV-Umschichtung Kurzgutachtliche Stellungnahme zu Ihrer Lebensversicherung (LV) 1 Inhalt Seite 1. Einleitung 3 2. Freizeichnung 5 3. Legende 6 4. Anmerkungen 7 15.02.2010 Hartmann + Hübner 2 1. Einleitung
LV-Umschichtung Kurzgutachtliche Stellungnahme zu Ihrer Lebensversicherung (LV) 1 Inhalt Seite 1. Einleitung 3 2. Freizeichnung 5 3. Legende 6 4. Anmerkungen 7 15.02.2010 Hartmann + Hübner 2 1. Einleitung
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 3 1. Semester ARBEITSBLATT 3 RECHNEN MIT GANZEN ZAHLEN
 ARBEITSBLATT 3 RECHNEN MIT GANZEN ZAHLEN Wir wollen nun die Rechengesetze der natürlichen Zahlen auf die Zahlenmenge der ganzen Zahlen erweitern und zwar so, dass sie zu keinem Widerspruch mit bisher geltenden
ARBEITSBLATT 3 RECHNEN MIT GANZEN ZAHLEN Wir wollen nun die Rechengesetze der natürlichen Zahlen auf die Zahlenmenge der ganzen Zahlen erweitern und zwar so, dass sie zu keinem Widerspruch mit bisher geltenden
Vertical-Spreads Iron Condor Erfolgsaussichten
 www.mumorex.ch 08.03.2015 1 Eigenschaften Erwartung Preis Long Calls Long Puts Kombination mit Aktien Vertical-Spreads Iron Condor Erfolgsaussichten www.mumorex.ch 08.03.2015 2 www.mumorex.ch 08.03.2015
www.mumorex.ch 08.03.2015 1 Eigenschaften Erwartung Preis Long Calls Long Puts Kombination mit Aktien Vertical-Spreads Iron Condor Erfolgsaussichten www.mumorex.ch 08.03.2015 2 www.mumorex.ch 08.03.2015
Rekursionen. Georg Anegg 25. November 2009. Methoden und Techniken an Beispielen erklärt
 Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
Das Persönliche Budget in verständlicher Sprache
 Das Persönliche Budget in verständlicher Sprache Das Persönliche Budget mehr Selbstbestimmung, mehr Selbstständigkeit, mehr Selbstbewusstsein! Dieser Text soll den behinderten Menschen in Westfalen-Lippe,
Das Persönliche Budget in verständlicher Sprache Das Persönliche Budget mehr Selbstbestimmung, mehr Selbstständigkeit, mehr Selbstbewusstsein! Dieser Text soll den behinderten Menschen in Westfalen-Lippe,
Reformpaket zur Absicherung stabiler und fairer Leistungen für Lebensversicherte. Fragen und Antworten
 Reformpaket zur Absicherung stabiler und fairer Leistungen für Lebensversicherte Fragen und Antworten Reformpaket zur Absicherung stabiler und fairer Leistungen für Lebensversicherte Fragen und Antworten
Reformpaket zur Absicherung stabiler und fairer Leistungen für Lebensversicherte Fragen und Antworten Reformpaket zur Absicherung stabiler und fairer Leistungen für Lebensversicherte Fragen und Antworten
einfache Rendite 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110
 Übungsbeispiele 1/6 1) Vervollständigen Sie folgende Tabelle: Nr. Aktie A Aktie B Schlusskurs in Schlusskurs in 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110 Arithmetisches Mittel Standardabweichung
Übungsbeispiele 1/6 1) Vervollständigen Sie folgende Tabelle: Nr. Aktie A Aktie B Schlusskurs in Schlusskurs in 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110 Arithmetisches Mittel Standardabweichung
Wirtschaftsmathematik für International Management (BA)
 Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 193 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei einer Abschreibung werden eines Gutes während der Nutzungsdauer festgehalten. Diese Beträge stellen dar und dadurch
SS 2014 Torsten Schreiber 193 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei einer Abschreibung werden eines Gutes während der Nutzungsdauer festgehalten. Diese Beträge stellen dar und dadurch
n... Laufzeit der Kapitalanlage = Zeit, während der Zinsen zu zahlen sind (oder gezahlt werden) in Zinsperioden (z.b. Jahre)
 3. Finanzmathematik 3.1. Zinsrechnung 3.1.1. Grundbegriffe K... Kapital (caput - das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen
3. Finanzmathematik 3.1. Zinsrechnung 3.1.1. Grundbegriffe K... Kapital (caput - das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen
16 Risiko und Versicherungsmärkte
 16 Risiko und Versicherungsmärkte Entscheidungen bei Unsicherheit sind Entscheidungen, die mehrere mögliche Auswirkungen haben. Kauf eines Lotterieloses Kauf einer Aktie Mitnahme eines Regenschirms Abschluss
16 Risiko und Versicherungsmärkte Entscheidungen bei Unsicherheit sind Entscheidungen, die mehrere mögliche Auswirkungen haben. Kauf eines Lotterieloses Kauf einer Aktie Mitnahme eines Regenschirms Abschluss
Ausarbeitung des Seminarvortrags zum Thema
 Ausarbeitung des Seminarvortrags zum Thema Anlagepreisbewegung zum Seminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn von Imke Meyer im W9/10 Anlagepreisbewegung
Ausarbeitung des Seminarvortrags zum Thema Anlagepreisbewegung zum Seminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn von Imke Meyer im W9/10 Anlagepreisbewegung
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 221 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird im Bereich der Rentenrechnung die zugehörige zu Beginn eines Jahres / einer Zeitperiode eingezahlt, so spricht
SS 2014 Torsten Schreiber 221 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird im Bereich der Rentenrechnung die zugehörige zu Beginn eines Jahres / einer Zeitperiode eingezahlt, so spricht
Auftrag zum Fondswechsel
 Lebensversicherung von 1871 a.g. München Postfach 80326 München Auftrag zum Fondswechsel Versicherungsnummer Versicherungsnehmer Änderung zum: Bei fehlender Eintragung, findet die Änderung für den Switch
Lebensversicherung von 1871 a.g. München Postfach 80326 München Auftrag zum Fondswechsel Versicherungsnummer Versicherungsnehmer Änderung zum: Bei fehlender Eintragung, findet die Änderung für den Switch
Aufgaben zur Vorlesung Finanzmanagement
 Aufgaben zur Vorlesung Finanzmanagement B. rke FH Gelsenkirchen, Abteilung Bocholt February 4, 006 Aufgabenblatt: "Bewertung von Optionen" 1 Lösungshinweise 1 uropean Put Option Zeichnen Sie den einer
Aufgaben zur Vorlesung Finanzmanagement B. rke FH Gelsenkirchen, Abteilung Bocholt February 4, 006 Aufgabenblatt: "Bewertung von Optionen" 1 Lösungshinweise 1 uropean Put Option Zeichnen Sie den einer
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
allensbacher berichte
 allensbacher berichte Institut für Demoskopie Allensbach 2006 / Nr. 8 ALTERSVORSORGE THEMA NUMMER 1 Allensbach am Bodensee, Mitte Mai 2006. - Das Thema Altersvorsorge beschäftigt die Bevölkerung immer
allensbacher berichte Institut für Demoskopie Allensbach 2006 / Nr. 8 ALTERSVORSORGE THEMA NUMMER 1 Allensbach am Bodensee, Mitte Mai 2006. - Das Thema Altersvorsorge beschäftigt die Bevölkerung immer
Beweisbar sichere Verschlüsselung
 Beweisbar sichere Verschlüsselung ITS-Wahlpflichtvorlesung Dr. Bodo Möller Ruhr-Universität Bochum Horst-Görtz-Institut für IT-Sicherheit Lehrstuhl für Kommunikationssicherheit bmoeller@crypto.rub.de 6
Beweisbar sichere Verschlüsselung ITS-Wahlpflichtvorlesung Dr. Bodo Möller Ruhr-Universität Bochum Horst-Görtz-Institut für IT-Sicherheit Lehrstuhl für Kommunikationssicherheit bmoeller@crypto.rub.de 6
Auf der Bilanzpressekonferenz am 4. Juni hat Leben-Vorstand Guido. Schaefers Stellung bezogen zum geplanten Gesetzespaket der
 Lebensversicherung Auf der Bilanzpressekonferenz am 4. Juni hat Leben-Vorstand Guido Schaefers Stellung bezogen zum geplanten Gesetzespaket der Bundesregierung in Sachen Lebensversicherung. Sein Statement
Lebensversicherung Auf der Bilanzpressekonferenz am 4. Juni hat Leben-Vorstand Guido Schaefers Stellung bezogen zum geplanten Gesetzespaket der Bundesregierung in Sachen Lebensversicherung. Sein Statement
Finanzwirtschaft. Teil II: Bewertung. Zinssätze und Renten
 Zinssätze und Renten 1 Finanzwirtschaft Teil II: Bewertung Zinssätze und Renten Agenda Zinssätze und Renten 2 Effektivzinsen Spot-Zinsen Forward-Zinsen Bewertung Kennziffern Zusammenfassung Zinssätze und
Zinssätze und Renten 1 Finanzwirtschaft Teil II: Bewertung Zinssätze und Renten Agenda Zinssätze und Renten 2 Effektivzinsen Spot-Zinsen Forward-Zinsen Bewertung Kennziffern Zusammenfassung Zinssätze und
mylife Lebensversicherung AG
 mylife Lebensversicherung AG Lassen Sie uns über MEHR GELD sprechen. www.mylife-leben.de 2 mylife heißt: MEHR GELD für Sie. 3 Die besten finanziellen Entscheidungen treffen wir nicht aus einem Bauchgefühl
mylife Lebensversicherung AG Lassen Sie uns über MEHR GELD sprechen. www.mylife-leben.de 2 mylife heißt: MEHR GELD für Sie. 3 Die besten finanziellen Entscheidungen treffen wir nicht aus einem Bauchgefühl
Wachstum 2. Michael Dröttboom 1 LernWerkstatt-Selm.de
 1. Herr Meier bekommt nach 3 Jahren Geldanlage 25.000. Er hatte 22.500 angelegt. Wie hoch war der Zinssatz? 2. Herr Meiers Vorfahren haben bei der Gründung Roms (753. V. Chr.) 1 Sesterze auf die Bank gebracht
1. Herr Meier bekommt nach 3 Jahren Geldanlage 25.000. Er hatte 22.500 angelegt. Wie hoch war der Zinssatz? 2. Herr Meiers Vorfahren haben bei der Gründung Roms (753. V. Chr.) 1 Sesterze auf die Bank gebracht
Ihre Joker für eine entspannte Vorsorge
 Ihre oker für eine entspannte Vorsorge GarantiePlus Pflegeption GarantiePlus Ihr Vorsorge-oker in oker ist immer etwas Besonderes, denn damit haben Sie einen Trumpf in der Hand. So wie unsere neue Leistung
Ihre oker für eine entspannte Vorsorge GarantiePlus Pflegeption GarantiePlus Ihr Vorsorge-oker in oker ist immer etwas Besonderes, denn damit haben Sie einen Trumpf in der Hand. So wie unsere neue Leistung
Data Mining: Einige Grundlagen aus der Stochastik
 Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
Quantilsschätzung als Werkzeug zur VaR-Berechnung
 Quantilsschätzung als Werkzeug zur VaR-Berechnung Ralf Lister, Aktuar, lister@actuarial-files.com Zusammenfassung: Zwei Fälle werden betrachtet und die jeweiligen VaR-Werte errechnet. Im ersten Fall wird
Quantilsschätzung als Werkzeug zur VaR-Berechnung Ralf Lister, Aktuar, lister@actuarial-files.com Zusammenfassung: Zwei Fälle werden betrachtet und die jeweiligen VaR-Werte errechnet. Im ersten Fall wird
Finanzwirtschaft. Teil II: Bewertung
 Zeitwert des Geldes 1 Finanzwirtschaft Teil II: Bewertung Zeitwert des Geldes Zeitwert des Geldes 2 Bewertung & Zeitwert des Geldes Finanzwirtschaft behandelt die Bewertung von Real- und Finanzwerten.
Zeitwert des Geldes 1 Finanzwirtschaft Teil II: Bewertung Zeitwert des Geldes Zeitwert des Geldes 2 Bewertung & Zeitwert des Geldes Finanzwirtschaft behandelt die Bewertung von Real- und Finanzwerten.
Derivate und Bewertung
 . Dr. Daniel Sommer Marie-Curie-Str. 30 60439 Franfurt am Main Klausur Derivate und Bewertung.......... Wintersemester 2008/09 Klausur Derivate und Bewertung Wintersemester 2008/09 Aufgabe 1: Zinsurven,
. Dr. Daniel Sommer Marie-Curie-Str. 30 60439 Franfurt am Main Klausur Derivate und Bewertung.......... Wintersemester 2008/09 Klausur Derivate und Bewertung Wintersemester 2008/09 Aufgabe 1: Zinsurven,
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Krankenversicherungsmathematik
 Krankenversicherungsmathematik Florian Peycha 8. Januar 2008 Inhaltsverzeichnis 1 Kopfschaden 1 1.1 Die Methode von Rusam..................... 2 1.2 Altersgruppenbildung....................... 3 1.3 Die
Krankenversicherungsmathematik Florian Peycha 8. Januar 2008 Inhaltsverzeichnis 1 Kopfschaden 1 1.1 Die Methode von Rusam..................... 2 1.2 Altersgruppenbildung....................... 3 1.3 Die
Änderung des IFRS 2 Anteilsbasierte Vergütung
 Änderung IFRS 2 Änderung des IFRS 2 Anteilsbasierte Vergütung Anwendungsbereich Paragraph 2 wird geändert, Paragraph 3 gestrichen und Paragraph 3A angefügt. 2 Dieser IFRS ist bei der Bilanzierung aller
Änderung IFRS 2 Änderung des IFRS 2 Anteilsbasierte Vergütung Anwendungsbereich Paragraph 2 wird geändert, Paragraph 3 gestrichen und Paragraph 3A angefügt. 2 Dieser IFRS ist bei der Bilanzierung aller
Charakteristikum des Gutachtenstils: Es wird mit einer Frage begonnen, sodann werden die Voraussetzungen Schritt für Schritt aufgezeigt und erörtert.
 Der Gutachtenstil: Charakteristikum des Gutachtenstils: Es wird mit einer Frage begonnen, sodann werden die Voraussetzungen Schritt für Schritt aufgezeigt und erörtert. Das Ergebnis steht am Schluß. Charakteristikum
Der Gutachtenstil: Charakteristikum des Gutachtenstils: Es wird mit einer Frage begonnen, sodann werden die Voraussetzungen Schritt für Schritt aufgezeigt und erörtert. Das Ergebnis steht am Schluß. Charakteristikum
Nein. Einmalbeitragsprodukte können grundsätzlich nicht zurück datiert werden. Im normalen Rahmen (üblicherweise nicht mehr als 1 Jahr).
 Fragen Antworten Standardfragen / Allgemeine Fragen zum Produkt Was ist Rente Chance Plus für ein Tarif? Rente Chance Plus ist eine klassische Rentenversicherung der 3. Schicht, die gegen einen Einmalbeitrag
Fragen Antworten Standardfragen / Allgemeine Fragen zum Produkt Was ist Rente Chance Plus für ein Tarif? Rente Chance Plus ist eine klassische Rentenversicherung der 3. Schicht, die gegen einen Einmalbeitrag
Beitragsfreiheit bei der Kalkulation von Pflegetagegeldtarifen in der KV
 Beitragsfreiheit bei der Kalkulation von Pflegetagegeldtarifen in der KV 1 Beitragsfreiheit bei der Kalkulation von Pflegetagegeldtarifen in der KV Gliederung: 1. Grundlagen der Beitragskalkulation in
Beitragsfreiheit bei der Kalkulation von Pflegetagegeldtarifen in der KV 1 Beitragsfreiheit bei der Kalkulation von Pflegetagegeldtarifen in der KV Gliederung: 1. Grundlagen der Beitragskalkulation in
Merkblatt Fondsgebundene Lebens- oder Rentenversicherung abgeschlossen Was nun?
 Merkblatt Fondsgebundene Lebens- oder Rentenversicherung abgeschlossen Was nun? Sie überlegen sich, ob Sie Ihre fondsgebundene Lebens- oder Rentenversicherung fortführen möchten. Diese Entscheidung können
Merkblatt Fondsgebundene Lebens- oder Rentenversicherung abgeschlossen Was nun? Sie überlegen sich, ob Sie Ihre fondsgebundene Lebens- oder Rentenversicherung fortführen möchten. Diese Entscheidung können
Risikoeinstellungen empirisch
 Risikoeinstellungen empirisch Risk attitude and Investment Decisions across European Countries Are women more conservative investors than men? Oleg Badunenko, Nataliya Barasinska, Dorothea Schäfer http://www.diw.de/deutsch/soep/uebersicht_ueber_das_soep/27180.html#79569
Risikoeinstellungen empirisch Risk attitude and Investment Decisions across European Countries Are women more conservative investors than men? Oleg Badunenko, Nataliya Barasinska, Dorothea Schäfer http://www.diw.de/deutsch/soep/uebersicht_ueber_das_soep/27180.html#79569
KBC-Life Capital 1 ist eine Sparte 21 Lebensversicherung mit einer vom Versicherungsunternehmen garantierten Mindestertrag.
 KBC-Life Capital Art der Lebens- Versicherung KBC-Life Capital 1 ist eine Sparte 21 Lebensversicherung mit einer vom Versicherungsunternehmen garantierten Mindestertrag. Hauptdeckung: Auszahlung der Reserve
KBC-Life Capital Art der Lebens- Versicherung KBC-Life Capital 1 ist eine Sparte 21 Lebensversicherung mit einer vom Versicherungsunternehmen garantierten Mindestertrag. Hauptdeckung: Auszahlung der Reserve
Prof. Dr. Arnd Wiedemann Methodische Grundlagen des Controlling und Risikomanagements
 Prof. Dr. Arnd Wiedemann Methodische Grundlagen des Controlling und Risikomanagements Prof. Dr. Arnd Wiedemann Methoden CRM / WS 12-13 1 Agenda Teil A: Teil B: Teil C: Finanzmathematisches Basiswissen
Prof. Dr. Arnd Wiedemann Methodische Grundlagen des Controlling und Risikomanagements Prof. Dr. Arnd Wiedemann Methoden CRM / WS 12-13 1 Agenda Teil A: Teil B: Teil C: Finanzmathematisches Basiswissen
Ist Fernsehen schädlich für die eigene Meinung oder fördert es unabhängig zu denken?
 UErörterung zu dem Thema Ist Fernsehen schädlich für die eigene Meinung oder fördert es unabhängig zu denken? 2000 by christoph hoffmann Seite I Gliederung 1. In zu großen Mengen ist alles schädlich. 2.
UErörterung zu dem Thema Ist Fernsehen schädlich für die eigene Meinung oder fördert es unabhängig zu denken? 2000 by christoph hoffmann Seite I Gliederung 1. In zu großen Mengen ist alles schädlich. 2.
Einleitung. Das Ein-Perioden-Modell ist das einfachste. von derivaten Finanzinstrumenten (hier: Optionen) zu erklären.
 Einleitung Das Ein-Perioden-Modell ist das einfachste Modell, um die Idee der Preisgebung von derivaten Finanzinstrumenten (hier: Optionen) zu erklären. naive Idee der Optionspreisbestimmung: Erwartungswertprinzip
Einleitung Das Ein-Perioden-Modell ist das einfachste Modell, um die Idee der Preisgebung von derivaten Finanzinstrumenten (hier: Optionen) zu erklären. naive Idee der Optionspreisbestimmung: Erwartungswertprinzip
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN
 ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
Beschreibung der einzelnen Berechnungsarten
 Beschreibung der einzelnen Berechnungsarten 1.0 Historische Wertentwicklungen 1.1 Berechnung einer Einzelanlage in Prozent Die Berechnung der Wertentwicklung erfolgt nach den Vorgaben des BVI: Die Berechnung
Beschreibung der einzelnen Berechnungsarten 1.0 Historische Wertentwicklungen 1.1 Berechnung einer Einzelanlage in Prozent Die Berechnung der Wertentwicklung erfolgt nach den Vorgaben des BVI: Die Berechnung
Übungsklausur. Bitte wählen Sie fünf Aufgaben aus! Aufgabe 1. Übungsklausur zu Mathematik I für BWL und VWL (WS 2008/09) PD Dr.
 Übungsklausur zu Mathematik I für BWL und VWL (WS 2008/09) PD Dr. Gert Zöller Übungsklausur Hilfsmittel: Taschenrechner, Formblatt mit Formeln. Lösungswege sind stets anzugeben. Die alleinige Angabe eines
Übungsklausur zu Mathematik I für BWL und VWL (WS 2008/09) PD Dr. Gert Zöller Übungsklausur Hilfsmittel: Taschenrechner, Formblatt mit Formeln. Lösungswege sind stets anzugeben. Die alleinige Angabe eines
Die Lösung des Altenproblems der PKV. Nie wieder Angst vor explodierenden PKV-Beiträgen im Alter!
 Die Lösung des Altenproblems der PKV Nie wieder Angst vor explodierenden PKV-Beiträgen im Alter! Inhalt 1. 2. 3. 4. 5. 6. 7. 8. 9. Management Summary Das Altenproblem Die Vision Annahmen Die Ist-Situation
Die Lösung des Altenproblems der PKV Nie wieder Angst vor explodierenden PKV-Beiträgen im Alter! Inhalt 1. 2. 3. 4. 5. 6. 7. 8. 9. Management Summary Das Altenproblem Die Vision Annahmen Die Ist-Situation
8. Berechnung der kalkulatorischen Zinsen
 8. Berechnung der kalkulatorischen Zinsen 8.1. Allgemeines In der laufenden Rechnung werden im Konto 322.00 Zinsen nur die ermittelten Fremdkapitalzinsen erfasst. Sobald aber eine Betriebsabrechnung erstellt
8. Berechnung der kalkulatorischen Zinsen 8.1. Allgemeines In der laufenden Rechnung werden im Konto 322.00 Zinsen nur die ermittelten Fremdkapitalzinsen erfasst. Sobald aber eine Betriebsabrechnung erstellt
Rürup-Rente Informationen
 Rürup-Rente Informationen Die zunehmende Altersarmut hat die Regierung dazu veranlasst neben der Riester-Rente, die in erster Linie für Arbeitnehmer interessant ist, auch den Selbstständigen die Möglichkeit
Rürup-Rente Informationen Die zunehmende Altersarmut hat die Regierung dazu veranlasst neben der Riester-Rente, die in erster Linie für Arbeitnehmer interessant ist, auch den Selbstständigen die Möglichkeit
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Ruinwahrscheinlichkeiten im Glücksspiel
 Ruinwahrscheinlichkeiten im Glücksspiel Wilhelm Stannat Fachbereich Mathematik TU Darmstadt February 24, 2007 Stochastik = Wahrscheinlichkeitstheorie + Statistik Wahrscheinlichkeitstheorie = Mathematische
Ruinwahrscheinlichkeiten im Glücksspiel Wilhelm Stannat Fachbereich Mathematik TU Darmstadt February 24, 2007 Stochastik = Wahrscheinlichkeitstheorie + Statistik Wahrscheinlichkeitstheorie = Mathematische
Langlebigkeitschance oder Risiko? Keine Alternativen zur Rentenversicherung?
 Langlebigkeitschance oder Risiko? Keine Alternativen zur Rentenversicherung? Folie 1 Langlebigkeit: Chance oder Risiko? Folie 2 Langlebigkeit: Chance oder Risiko? Folie 3 Langlebigkeit: Chance oder Risiko?
Langlebigkeitschance oder Risiko? Keine Alternativen zur Rentenversicherung? Folie 1 Langlebigkeit: Chance oder Risiko? Folie 2 Langlebigkeit: Chance oder Risiko? Folie 3 Langlebigkeit: Chance oder Risiko?
Rendite vs. Risiko Garantiekonzepte im Vergleich
 Rendite vs. Risiko Garantiekonzepte im Vergleich Klicken Sie, um das Titelformat zu bearbeiten, Allianz Lebensversicherungs-AG Klicken Sie, um das Format des Untertitel-Masters zu bearbeiten. GDV-Pressekolloquium,
Rendite vs. Risiko Garantiekonzepte im Vergleich Klicken Sie, um das Titelformat zu bearbeiten, Allianz Lebensversicherungs-AG Klicken Sie, um das Format des Untertitel-Masters zu bearbeiten. GDV-Pressekolloquium,
Sie möchten beruhigt in die Zukunft blicken Wir bieten flexiblen und günstigen Schutz.
 Persönliche Risikoabsicherung Sie möchten beruhigt in die Zukunft blicken Wir bieten flexiblen und günstigen Schutz. Absicherung nach schweren Krankheiten oder Unfällen Existenzschutzversicherung Wichtige
Persönliche Risikoabsicherung Sie möchten beruhigt in die Zukunft blicken Wir bieten flexiblen und günstigen Schutz. Absicherung nach schweren Krankheiten oder Unfällen Existenzschutzversicherung Wichtige
Ermittlung kalkulatorischer Zinsen nach der finanzmathematischen Durchschnittswertmethode
 Ermittlung r finanzmathematischen (von D. Ulbig, Verfahrensprüfer der SAKD) 1. Einleitung Die n Zinsen können gemäß 12 SächsKAG nach der oder der ermittelt werden. Bei Anwendung der sind die n Zinsen nach
Ermittlung r finanzmathematischen (von D. Ulbig, Verfahrensprüfer der SAKD) 1. Einleitung Die n Zinsen können gemäß 12 SächsKAG nach der oder der ermittelt werden. Bei Anwendung der sind die n Zinsen nach
Ein Cap ist eine vertragliche Vereinbarung, bei der der kaufenden Partei gegen Zahlung einer Prämie eine Zinsobergrenze garantiert wird.
 Zinsoptionen Eine Option ist eine Vereinbarung zwischen zwei Vertragsparteien, bei der die kaufende Partei das Recht hat, ein bestimmtes Produkt während eines definierten Zeitraums zu einem vorher bestimmten
Zinsoptionen Eine Option ist eine Vereinbarung zwischen zwei Vertragsparteien, bei der die kaufende Partei das Recht hat, ein bestimmtes Produkt während eines definierten Zeitraums zu einem vorher bestimmten
1 Einleitung. 1.1 Motivation und Zielsetzung der Untersuchung
 1 Einleitung 1.1 Motivation und Zielsetzung der Untersuchung Obgleich Tourenplanungsprobleme zu den am häufigsten untersuchten Problemstellungen des Operations Research zählen, konzentriert sich der Großteil
1 Einleitung 1.1 Motivation und Zielsetzung der Untersuchung Obgleich Tourenplanungsprobleme zu den am häufigsten untersuchten Problemstellungen des Operations Research zählen, konzentriert sich der Großteil
