Appendix A: Grundlagen der Populationsbiologie
|
|
|
- Ernst Scholz
- vor 8 Jahren
- Abrufe
Transkript
1 L Pop - & Evol biol - A.1 - App. A: Grundlagen der Populationsbiologie Appendix A: Grundlagen der Populationsbiologie Einige grundlegende Prinzipien der Populationsbiologie sind wichtig zum Verständnis des Evolutionsprozesses. Der Grund ist einfach: Evolution geschieht innerhalb von Populaionen, indem sich Genfrequenzen verschieben (s. Kap. 4, 5). Dieser Appendix ist gedacht für Studierende, die bis zu dieser Vorlesung die Grundlagen der Populationsbiologie noch nicht gehört haben 1. A.1 Populationsdynamik Die Populationsdynamik ist die zeitliche und räumliche Veränderung von Populationen. Die einfachsten Modelle der Populationsdynamik ignorieren die Altersstruktur, das Geschlechtsverhältnis und weitere Komplikationen. a) Populationsgrösse Eine wichtige Variable ist die Populationsgrösse, N, d.h. die Anzahl der Individuen in einer Population. Zu jedem Zeitpunkt t bestimmt und verändert sich die Populationsgrösse N(t) durch vier Prozesse: Geburtsrate (Natalität), Sterberate (Mortalität), Rate der Abwanderung (Emigration) und Rate der Zuwanderung (Immigration) (Fig. A.1). Zuwanderungsrate Immigration Geburtsrate Natalität Populationsgrösse N zur Zeit t Sterberate Mortalität Abwanderungsrate Emigration Fig A.1 Die Populationsgrösse N zur Zeit t ist das Ergebnis verschiedener Prozesse. Das resultierende Wachstum (bzw, Veränderung von N) aufgrund dieser vier Prozesse kann auf verschiedene Weise modelliert werden. Hier werden die einfachsten Modelle vorgestellt. 1 Empfohlene Lehrbücher zum Thema: Begon, M., Harper, J. L. & Townsend, C. R Ecology: from individuals to ecosystems.: Blackwell. (Als Tachenbuchausgabe erhältlich.) Neal, D Introduction to Population Biology. Cambridge University Press. (behandelt auch weitere Themen der vorliegenden Vorlesung).
2 L Pop - & Evol biol - A.2 - App. A: Grundlagen der Populationsbiologie b) Exponentielles Wachstum (Dichte-unabhängig) Falls das Wachstum nicht von der Dichte der Population abhängt, lässt sich ein einfaches Modell formulieren, mit r = momentane Wachstumsrate (pro Kopf) (r = MALTHUS' Parameter, instantaneous rate of natural increase): dn dt = rn N(t) = N 0 e rt, eq.(a.1) wobei r = b - µ (b = Natalitäts-, µ = Mortalitätsrate, N 0 = Populationsgrösse für t = 0) (Beachte: in solchen Modellen wird N oft synonym für Grösse oder Dichte der Population gebraucht). c) Logistisches Wachstum (Dichte-abhängig) Hängt die Wachstumsrate von der Dichte der Population (N) ab, so gilt im einfachsten Modell mit K = Kapazität (carrying capacity), und a = eine Konstante: dn = rn K N dt K K N(t) = 1+e a rt ( ) eq.(a.2) Begrenzungen (K) können eintreten durch Erschöpfen der Ressourcen (Nahrung, Deckung etc.: intraspezifische Konkurrenz), Reduktion der Fertilität (Stress), Epidemien etc. Die Kapazität K ist eine hypothetische Grösse und kaum messbar im Freiland. Entscheidend ist jedoch das Konzept der Dichteabhängigkeit, welches durch K operationalisiert wird. c) Diskretes Wachstum In vielen Fällen sind die Generationen diskret, dh. überlappen sich nicht. Im allgemeinen Fall: Nt+1 = F(Nt) eq.(a.3) wobei F() eine Abbildungsfunktion für N von der gegenwärtigen (t) in die nächste (t+1) Generation darstellt (Fig. A.2). Dichte-unabhängig: mit F() = R = konstant (R = Netto-Reproduktionsrate; s. unten) : Nt+1 = Nt R, dh. Nt = N0 R t (Diskretes, geometrisches Wachstum) eq.(a.3a)
3 L Pop - & Evol biol - A.3 - App. A: Grundlagen der Populationsbiologie Aus dem Vergleich von eq. (A.1) mit eq. (A.3) folgt (nach einigen Umformungen): r = ln R eq.(a.4) Wachstum N(t+1) = F(Nt) 1:1 -Linie N(t+1) = F(Nt) 1:1 -Linie Schrumpfung N(t) N(t) Fig A.2 Diskretes Populationswachstum kann dargestellt werden als eine Abbildung der Populationsgrösse N zum Zeitpunkt t auf die Grösse N zum Zeitpunkt t+1 (links). Die Abbildungsfunktion, bzw, Zuwachs-Funktion, F(t), kann eine Linie sein (mit Steigung = 1 würde keine Veränderung resultieren) oder auch eine beliebige Kurve F(t) (rechts). Dichte-abhängig: mit F() = F(N,R,a,b) dh. die Abbildungsfunktion hängt von N und Parametern a,b ab: Nt+1=R Nt 1+ ant ( [ ] b ) eq.(a.5) Diese einfache Formel dieses diskreten Wachstums erzeugt ein weites Spektrum dynamischen Verhaltens (Fig. A.3). Fig A.3 Die Populationsdynamik diskreten Wachstums. R = Netto-Reproduktionsrate, b = Parameter der Konkurrenz (b<1: Unter-Kompensation; b=1: exakte Kompensation; b >1: Ueber-Kompensation). Bei Ueber- Kompensation leiden alle Individuen unter der intra-spezifischen Konkurrenz und im Extremfall (b-> ) gibt es keine Gewinner, bei exakter Kompensation gibt es eine konstante Anzahl Gewinner, bei Unter- Kompensation gibt es eine variable Anzahl Gewinner und nicht alle leiden. Beachte, dass hohes R und b deterministisches Chaos erzeugt. Links: Parameter-Raum (R,b). Rechts: Beispiel des dynamischenverhaltens in verschiedenen Regionen.
4 L Pop - & Evol biol - A.4 - App. A: Grundlagen der Populationsbiologie A.2 Populationen mit Altersstruktur (Demographie) Die Dyanmik Alters-strukturierter Population ist besonders interessant für das Studium der Mikroevolution (speziell für die sog. Life-history Theorie, s. Kap.8). Populationen mit Altersstruktur können mit Lebenstafeln charakterisiert werden (Tab. A.1). Daraus lassen sich charakteristische Werte errechnen, wie die Netto-Reproduktionsrate, momentane Wachstumsrate, Generationszeit, usw. Lebenstafeln machen vor allem. Sinn bei Populationen mit überlappenden Generationen. Es gibt Kohorten-Tafeln (= Horizontale Tafel). Eine Kohorte umfasst alle Individuen mit gleichem Geburtsdatum. Alternative gibt es Statische Tafeln (= Vertikale Tafel). Statische Tafeln benutzen die Populationsdaten zu einem bestimmten Zeitpunkt, um daraus die Kohorten zu rekonstruieren. Tab A.1 Kohorten-Lebenstafel für die Seepocke Balanus glandula an der NW-Küste Amerikas 1 Alter Lebende Ueberlebenswahrscheinlichkeit Fekundität Hilfsgrössen (Jahre) (Individuen) (Neugeborene) x ax lx mx lxmx xlxmx Für diese Tafel: R0 = 1.282, Tc = 3.1, r Die Werte der Lebenstafel sind das Resultat ökologischer Bedingungen (z.b. Nahrungsangebot) und evolutiver Anpassungen (z.b. frühe Reproduktion). Aus der Lebenstafel rechnen sich folgende nützliche Grössen: Ro = lx mx Netto-Reproduktionsrate eq.(a.6) Tc ( x lx mx ) / Ro Generationszeit eq.(a.7) Die Netto-Reproduktionsrate, R 0, ist die erwartete, durchschnittliche Anzahl Nachkommen pro Kopf und Generation. Die Generationszeit, T c, ist der zeitlichen Abstand zwischen Geburt des Elter und der Geburt des durchschnittlichen Nachkommen. Mit diesen Angaben berechnet sich die momentane Wachstumsrate, r, der Population (Beachte: r bezieht sich auf die Zeiteinheit, R 0 auf die Generation) als: r ln (Ro) / Tc Momentane Wachstumsrate eq.(a.8) Bleiben die Parameter lx und mx über längere Zeit konstant, konvergiert jede Population zu einer stabilen Altersverteilung, dh. zu konstanten Anteilen der Altersklassen an der Gesamtpopulation. Populationen mit stabiler Altersverteilung wachsen exponentiell und erfüllen die folgende Gleichung:
5 L Pop - & Evol biol - A.5 - App. A: Grundlagen der Populationsbiologie e -rx lx mx = 1 Gleichung von EULER-LOTKA eq.(a.9) (Diese Gleichung lässt sich meist nur iterativ lösen) Bleibt eine Population gleich gross (d.h. N = konstant) und hat sie eine stabile Altersverteilung, so spricht man von einer stationären Altersverteilung (alle Anteile und absoluten Zahlen bleiben gleich). Die Dynamik altersstrukturierter Populationen lässt sich aus den Daten (wie ax, lx oder mx) am besten mit Hilfe von Matrizen-Modellen berechnen (Leslie-Matrix). Reproduktionswert Der Reproduktionswert beschreibt den Anteil an der gesamten Nachkommenschaft der Population, welcher auf die Eltern einer Altersklasse entfällt. Für eine stationäre Population (d.h. r = 0): v = x erx lx a=z e ra lama Reproduktionswert nach FISHER 2 eq.(a.10) a=x ( ) mit a = Altersklassen von x bis zur letzten Altersklasse (z). Der Wert v x charakterisiert den Anteil an der zukünftigen Population, den die Altersklasse noch beitragen wird (von heute = x bis zum Überleben in die letzte Altersklasse, l x ). Der Wert von vx ist typischerweise klein für junge und alte Individuen. Die Demographie einer Population bestimmt damit die evolutive Wirkung der Selektion. Im Beispiel der Tafel A.1 hätte ein Selektionsereignis im Alter 7 weit weniger Effekt als im Alter 3, da ein kleinerer Anteil der Population davon betroffen ist, bzw. der Reproduktionswert dieser Altersklasse kleiner ist. A.3 Gleichgewicht und Stabilität Populationen können einen Zustand erreichen, der als Gleichgewicht beschrieben wird. Zum Beispiel veärndert sich die Population nicht mehr in ihrer Grösse oder Zusammensetzung. Nach Störungen kehrt die Population unter Umständen wieder zum Gleichgewichts-Punkt zurück. Ein entsprechende negative Rückkopplung wäre z.b. durch Dichte-abhängiges Wachstum möglich. Es ist auch denkbar, dass die Population nach Störung zu einem neuen Zustand konvergiert. Die beiden Möglichkeiten entsprechen dem Konzept eines stabilen bwz. instabilen Gleichgewichts. Eine wichtige Frage in der Evolutions- und Populationsbiologie ist, ob eine Invasion einer neuen Variante in eine existierende Population möglich sei? Die Population reagiert auf eine solche Störung je nachdem, ob sie sich an einem stabilen bzw. instabilen Gleichgewichtspunkt befindet. Die Möglichkeit einer Invasion durch eine neue Variante ist eine wesentliche Voraussetzung für die Evolution einer Population. Beachte, dass in Kap. 4 und 5, diese Möglichkeit durch den Wert des Selektionskoeffizienten, s, in die Rechnung eingebaut wurde. 2 Das Symbol v x für den Reproduktionswert (x = Altersklasse) sollte nicht mit dem Symbol V x für die Varianz der Variablen x verwechselt werden.
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
6.2 Scan-Konvertierung (Scan Conversion)
 6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
Berechnung der Erhöhung der Durchschnittsprämien
 Wolfram Fischer Berechnung der Erhöhung der Durchschnittsprämien Oktober 2004 1 Zusammenfassung Zur Berechnung der Durchschnittsprämien wird das gesamte gemeldete Prämienvolumen Zusammenfassung durch die
Wolfram Fischer Berechnung der Erhöhung der Durchschnittsprämien Oktober 2004 1 Zusammenfassung Zur Berechnung der Durchschnittsprämien wird das gesamte gemeldete Prämienvolumen Zusammenfassung durch die
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN
 HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand
 Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand Vorüberlegung In einem seriellen Stromkreis addieren sich die Teilspannungen zur Gesamtspannung Bei einer Gesamtspannung U ges, der
Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand Vorüberlegung In einem seriellen Stromkreis addieren sich die Teilspannungen zur Gesamtspannung Bei einer Gesamtspannung U ges, der
Tangentengleichung. Wie lautet die Geradengleichung für die Tangente, y T =? Antwort:
 Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen
 Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Statistische Thermodynamik I Lösungen zur Serie 1
 Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
Leichte-Sprache-Bilder
 Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
Repetitionsaufgaben Wurzelgleichungen
 Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Formelsammlung zur Kreisgleichung
 zur Kreisgleichung Julia Wolters 6. Oktober 2008 Inhaltsverzeichnis 1 Allgemeine Kreisgleichung 2 1.1 Berechnung des Mittelpunktes und Radius am Beispiel..... 3 2 Kreis und Gerade 4 2.1 Sekanten, Tangenten,
zur Kreisgleichung Julia Wolters 6. Oktober 2008 Inhaltsverzeichnis 1 Allgemeine Kreisgleichung 2 1.1 Berechnung des Mittelpunktes und Radius am Beispiel..... 3 2 Kreis und Gerade 4 2.1 Sekanten, Tangenten,
Ein Einfaches AIDS Modell
 Ein Einfaches AIDS Modell Martin Bauer: 990395 Guntram Rümmele: 99008 Das SIR - Modell Die Modellierung von epidemischen Modellen hat schon lange Tradition. Man hat schon immer versucht Erklärungen für
Ein Einfaches AIDS Modell Martin Bauer: 990395 Guntram Rümmele: 99008 Das SIR - Modell Die Modellierung von epidemischen Modellen hat schon lange Tradition. Man hat schon immer versucht Erklärungen für
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen?
 Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Die Invaliden-Versicherung ändert sich
 Die Invaliden-Versicherung ändert sich 1 Erklärung Die Invaliden-Versicherung ist für invalide Personen. Invalid bedeutet: Eine Person kann einige Sachen nicht machen. Wegen einer Krankheit. Wegen einem
Die Invaliden-Versicherung ändert sich 1 Erklärung Die Invaliden-Versicherung ist für invalide Personen. Invalid bedeutet: Eine Person kann einige Sachen nicht machen. Wegen einer Krankheit. Wegen einem
9.2. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83
 9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
15.3 Bedingte Wahrscheinlichkeit und Unabhängigkeit
 5.3 Bedingte Wahrscheinlichkeit und Unabhängigkeit Einführendes Beispiel ( Erhöhung der Sicherheit bei Flugreisen ) Die statistische Wahrscheinlichkeit, dass während eines Fluges ein Sprengsatz an Bord
5.3 Bedingte Wahrscheinlichkeit und Unabhängigkeit Einführendes Beispiel ( Erhöhung der Sicherheit bei Flugreisen ) Die statistische Wahrscheinlichkeit, dass während eines Fluges ein Sprengsatz an Bord
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Funktion Erläuterung Beispiel
 WESTFÄLISCHE WILHELMS-UNIVERSITÄT WIRTSCHAFTSWISSENSCHAFTLICHE FAKULTÄT BETRIEBLICHE DATENVERARBEITUNG Folgende Befehle werden typischerweise im Excel-Testat benötigt. Die Beispiele in diesem Dokument
WESTFÄLISCHE WILHELMS-UNIVERSITÄT WIRTSCHAFTSWISSENSCHAFTLICHE FAKULTÄT BETRIEBLICHE DATENVERARBEITUNG Folgende Befehle werden typischerweise im Excel-Testat benötigt. Die Beispiele in diesem Dokument
Stellen Sie bitte den Cursor in die Spalte B2 und rufen die Funktion Sverweis auf. Es öffnet sich folgendes Dialogfenster
 Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Übungsaufgaben Tilgungsrechnung
 1 Zusatzmaterialien zu Finanz- und Wirtschaftsmathematik im Unterricht, Band 1 Übungsaufgaben Tilgungsrechnung Überarbeitungsstand: 1.März 2016 Die grundlegenden Ideen der folgenden Aufgaben beruhen auf
1 Zusatzmaterialien zu Finanz- und Wirtschaftsmathematik im Unterricht, Band 1 Übungsaufgaben Tilgungsrechnung Überarbeitungsstand: 1.März 2016 Die grundlegenden Ideen der folgenden Aufgaben beruhen auf
Forschen - Schreiben - Lehren
 Forschen - Schreiben - Lehren Kontakt: Mareike Gronich mgronich@uni-bielefeld.de Fach/Fachgebiet: Germanistik Art der Lehrveranstaltung: Seminar Ausgangspunkt Geschütztes konstruktives Peer-Feedback in
Forschen - Schreiben - Lehren Kontakt: Mareike Gronich mgronich@uni-bielefeld.de Fach/Fachgebiet: Germanistik Art der Lehrveranstaltung: Seminar Ausgangspunkt Geschütztes konstruktives Peer-Feedback in
Entwicklung nach der Geburt
 Entwicklung nach der Geburt Entwicklung des Babys nach der Geburt. Wie sich ein Baby in den ersten Monaten entwickelt,verändert und was sich in ihren ersten 12 Monaten so alles tut. Entwicklungsphasen
Entwicklung nach der Geburt Entwicklung des Babys nach der Geburt. Wie sich ein Baby in den ersten Monaten entwickelt,verändert und was sich in ihren ersten 12 Monaten so alles tut. Entwicklungsphasen
Rekursionen (Teschl/Teschl 8.1-8.2)
 Rekursionen (Teschl/Teschl 8.1-8.2) Eine Rekursion kter Ordnung für k N ist eine Folge x 1, x 2, x 3,... deniert durch eine Rekursionsvorschrift x n = f n (x n 1,..., x n k ) für n > k, d. h. jedes Folgenglied
Rekursionen (Teschl/Teschl 8.1-8.2) Eine Rekursion kter Ordnung für k N ist eine Folge x 1, x 2, x 3,... deniert durch eine Rekursionsvorschrift x n = f n (x n 1,..., x n k ) für n > k, d. h. jedes Folgenglied
Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. z(t) = at + b
 Aufgabe 1: Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. (a) Nehmen Sie lineares Wachstum gemäß z(t) = at + b an, wobei z die Einwohnerzahl ist und
Aufgabe 1: Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. (a) Nehmen Sie lineares Wachstum gemäß z(t) = at + b an, wobei z die Einwohnerzahl ist und
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Musterlösung Arbeitsblatt 2 - Wachstum und Easy ModelWorks
 ETH Zürich, FS 2009 Musterlösung Arbeitsblatt 2 - Wachstum und Easy ModelWorks Dieses Arbeitsblatt dient dem näheren Kennenlernen des Modellierungs- und Simulationswerkzeugs Easy ModelWorks. Hierzu dient
ETH Zürich, FS 2009 Musterlösung Arbeitsblatt 2 - Wachstum und Easy ModelWorks Dieses Arbeitsblatt dient dem näheren Kennenlernen des Modellierungs- und Simulationswerkzeugs Easy ModelWorks. Hierzu dient
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
In diesem Tutorial lernen Sie, wie Sie einen Termin erfassen und verschiedene Einstellungen zu einem Termin vornehmen können.
 Tutorial: Wie erfasse ich einen Termin? In diesem Tutorial lernen Sie, wie Sie einen Termin erfassen und verschiedene Einstellungen zu einem Termin vornehmen können. Neben den allgemeinen Angaben zu einem
Tutorial: Wie erfasse ich einen Termin? In diesem Tutorial lernen Sie, wie Sie einen Termin erfassen und verschiedene Einstellungen zu einem Termin vornehmen können. Neben den allgemeinen Angaben zu einem
Hinweise zur Kalibrierung von Kameras mit einer AICON Kalibriertafel
 Hinweise zur Kalibrierung von Kameras mit einer AICON Kalibriertafel AICON 3D Systems GmbH Celler Straße 32 D-38114 Braunschweig Telefon: +49 (0) 5 31 58 000 58 Fax: +49 (0) 5 31 58 000 60 Email: info@aicon.de
Hinweise zur Kalibrierung von Kameras mit einer AICON Kalibriertafel AICON 3D Systems GmbH Celler Straße 32 D-38114 Braunschweig Telefon: +49 (0) 5 31 58 000 58 Fax: +49 (0) 5 31 58 000 60 Email: info@aicon.de
Binäre Bäume. 1. Allgemeines. 2. Funktionsweise. 2.1 Eintragen
 Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Erstellen von x-y-diagrammen in OpenOffice.calc
 Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Anleitung über den Umgang mit Schildern
 Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Vorgehensweise bei Lastschriftverfahren
 Vorgehensweise bei Lastschriftverfahren Voraussetzung hierfür sind nötige Einstellungen im ControlCenter. Sie finden dort unter Punkt 29 die Möglichkeit bis zu drei Banken für das Lastschriftverfahren
Vorgehensweise bei Lastschriftverfahren Voraussetzung hierfür sind nötige Einstellungen im ControlCenter. Sie finden dort unter Punkt 29 die Möglichkeit bis zu drei Banken für das Lastschriftverfahren
Linearen Gleichungssysteme Anwendungsaufgaben
 Linearen Gleichungssysteme Anwendungsaufgaben Lb S. 166 Nr.9 Im Jugendherbergsverzeichnis ist angegeben, dass in der Jugendherberge in Eulenburg 145 Jugendliche in 35 Zimmern übernachten können. Es gibt
Linearen Gleichungssysteme Anwendungsaufgaben Lb S. 166 Nr.9 Im Jugendherbergsverzeichnis ist angegeben, dass in der Jugendherberge in Eulenburg 145 Jugendliche in 35 Zimmern übernachten können. Es gibt
Physik & Musik. Stimmgabeln. 1 Auftrag
 Physik & Musik 5 Stimmgabeln 1 Auftrag Physik & Musik Stimmgabeln Seite 1 Stimmgabeln Bearbeitungszeit: 30 Minuten Sozialform: Einzel- oder Partnerarbeit Voraussetzung: Posten 1: "Wie funktioniert ein
Physik & Musik 5 Stimmgabeln 1 Auftrag Physik & Musik Stimmgabeln Seite 1 Stimmgabeln Bearbeitungszeit: 30 Minuten Sozialform: Einzel- oder Partnerarbeit Voraussetzung: Posten 1: "Wie funktioniert ein
5. Bildauflösung ICT-Komp 10
 5. Bildauflösung ICT-Komp 10 Was sind dpi? Das Maß für die Bildauflösung eines Bildes sind dpi. Jeder spricht davon, aber oft weiß man gar nicht genau was das ist. Die Bezeichnung "dpi" ist ein Maß, mit
5. Bildauflösung ICT-Komp 10 Was sind dpi? Das Maß für die Bildauflösung eines Bildes sind dpi. Jeder spricht davon, aber oft weiß man gar nicht genau was das ist. Die Bezeichnung "dpi" ist ein Maß, mit
Wachstum 2. Michael Dröttboom 1 LernWerkstatt-Selm.de
 1. Herr Meier bekommt nach 3 Jahren Geldanlage 25.000. Er hatte 22.500 angelegt. Wie hoch war der Zinssatz? 2. Herr Meiers Vorfahren haben bei der Gründung Roms (753. V. Chr.) 1 Sesterze auf die Bank gebracht
1. Herr Meier bekommt nach 3 Jahren Geldanlage 25.000. Er hatte 22.500 angelegt. Wie hoch war der Zinssatz? 2. Herr Meiers Vorfahren haben bei der Gründung Roms (753. V. Chr.) 1 Sesterze auf die Bank gebracht
GEVITAS Farben-Reaktionstest
 GEVITAS Farben-Reaktionstest GEVITAS Farben-Reaktionstest Inhalt 1. Allgemeines... 1 2. Funktionsweise der Tests... 2 3. Die Ruhetaste und die Auslösetaste... 2 4. Starten der App Hauptmenü... 3 5. Auswahl
GEVITAS Farben-Reaktionstest GEVITAS Farben-Reaktionstest Inhalt 1. Allgemeines... 1 2. Funktionsweise der Tests... 2 3. Die Ruhetaste und die Auslösetaste... 2 4. Starten der App Hauptmenü... 3 5. Auswahl
Technische Analyse der Zukunft
 Technische Analyse der Zukunft Hier werden die beiden kurzen Beispiele des Absatzes auf der Homepage mit Chart und Performance dargestellt. Einfache Einstiege reichen meist nicht aus. Der ALL-IN-ONE Ultimate
Technische Analyse der Zukunft Hier werden die beiden kurzen Beispiele des Absatzes auf der Homepage mit Chart und Performance dargestellt. Einfache Einstiege reichen meist nicht aus. Der ALL-IN-ONE Ultimate
Grundlagen der Theoretischen Informatik, SoSe 2008
 1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung: Lösungsvorschlag
 Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 13 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 13 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Studieren- Erklärungen und Tipps
 Studieren- Erklärungen und Tipps Es gibt Berufe, die man nicht lernen kann, sondern für die man ein Studium machen muss. Das ist zum Beispiel so wenn man Arzt oder Lehrer werden möchte. Hat ihr Kind das
Studieren- Erklärungen und Tipps Es gibt Berufe, die man nicht lernen kann, sondern für die man ein Studium machen muss. Das ist zum Beispiel so wenn man Arzt oder Lehrer werden möchte. Hat ihr Kind das
Lösungsmethoden gewöhnlicher Differentialgleichungen (Dgl.)
 Lösungsmethoden gewöhnlicher Dierentialgleichungen Dgl) Allgemeine und partikuläre Lösung einer gewöhnlichen Dierentialgleichung Eine Dierentialgleichung ist eine Gleichung! Zum Unterschied von den gewöhnlichen
Lösungsmethoden gewöhnlicher Dierentialgleichungen Dgl) Allgemeine und partikuläre Lösung einer gewöhnlichen Dierentialgleichung Eine Dierentialgleichung ist eine Gleichung! Zum Unterschied von den gewöhnlichen
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
Angebote der Landesregierung zur großzügigen Bewilligung von Teilzeitbeschäftigung und Beurlaubung ohne Bezüge für die Landesbediensteten 3.
 Angebote der Landesregierung zur großzügigen Bewilligung von Teilzeitbeschäftigung und Beurlaubung ohne Bezüge für die Landesbediensteten 3. Teil Werner-Seelenbinder-Str. 14 D-99096 Erfurt Telefon 03 61-602
Angebote der Landesregierung zur großzügigen Bewilligung von Teilzeitbeschäftigung und Beurlaubung ohne Bezüge für die Landesbediensteten 3. Teil Werner-Seelenbinder-Str. 14 D-99096 Erfurt Telefon 03 61-602
Urlaubsregel in David
 Urlaubsregel in David Inhaltsverzeichnis KlickDown Beitrag von Tobit...3 Präambel...3 Benachrichtigung externer Absender...3 Erstellen oder Anpassen des Anworttextes...3 Erstellen oder Anpassen der Auto-Reply-Regel...5
Urlaubsregel in David Inhaltsverzeichnis KlickDown Beitrag von Tobit...3 Präambel...3 Benachrichtigung externer Absender...3 Erstellen oder Anpassen des Anworttextes...3 Erstellen oder Anpassen der Auto-Reply-Regel...5
Der monatliche Tarif für ein Handy wurde als lineare Funktion der Form f(x) = k x + d modelliert (siehe Grafik).
 1) Handytarif Der monatliche Tarif für ein Handy wurde als lineare Funktion der Form f(x) = k x + d modelliert (siehe Grafik). Euro Gesprächsminuten Tragen Sie in der folgenden Tabelle ein, welche Bedeutung
1) Handytarif Der monatliche Tarif für ein Handy wurde als lineare Funktion der Form f(x) = k x + d modelliert (siehe Grafik). Euro Gesprächsminuten Tragen Sie in der folgenden Tabelle ein, welche Bedeutung
Eine Logikschaltung zur Addition zweier Zahlen
 Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
4.3 Bevölkerungsprozessstatistik: Raten und Tafeln
 Dynamik der Bevölkerungsstruktur ergibt sich aus Zugängen (Geburt, Zuwanderung) Abgängen (Tod, Abwanderung) Bewegungen zwischen Sektoren (ledig verheiratet, erwerbstätig nicht erwerbstätig, verschiedene
Dynamik der Bevölkerungsstruktur ergibt sich aus Zugängen (Geburt, Zuwanderung) Abgängen (Tod, Abwanderung) Bewegungen zwischen Sektoren (ledig verheiratet, erwerbstätig nicht erwerbstätig, verschiedene
1 C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R
 C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R L Ö S U N G E N Seite 7 n Wenn vier Menschen auf einem Quadratmeter stehen, dann hat jeder eine Fläche von 50 mal 50 Zentimeter
C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R L Ö S U N G E N Seite 7 n Wenn vier Menschen auf einem Quadratmeter stehen, dann hat jeder eine Fläche von 50 mal 50 Zentimeter
Rekursionen. Georg Anegg 25. November 2009. Methoden und Techniken an Beispielen erklärt
 Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
PTV VISWALK TIPPS UND TRICKS PTV VISWALK TIPPS UND TRICKS: VERWENDUNG DICHTEBASIERTER TEILROUTEN
 PTV VISWALK TIPPS UND TRICKS PTV VISWALK TIPPS UND TRICKS: VERWENDUNG DICHTEBASIERTER TEILROUTEN Karlsruhe, April 2015 Verwendung dichte-basierter Teilrouten Stellen Sie sich vor, in einem belebten Gebäude,
PTV VISWALK TIPPS UND TRICKS PTV VISWALK TIPPS UND TRICKS: VERWENDUNG DICHTEBASIERTER TEILROUTEN Karlsruhe, April 2015 Verwendung dichte-basierter Teilrouten Stellen Sie sich vor, in einem belebten Gebäude,
WinWerk. Prozess 4 Akonto. KMU Ratgeber AG. Inhaltsverzeichnis. Im Ifang 16 8307 Effretikon
 Prozess 4 Akonto WinWerk 8307 Effretikon Telefon: 052-740 11 11 Telefax: 052 740 11 71 E-Mail info@kmuratgeber.ch Internet: www.winwerk.ch Inhaltsverzeichnis 1 Akonto... 2 1.1 Allgemein... 2 2 Akontobeträge
Prozess 4 Akonto WinWerk 8307 Effretikon Telefon: 052-740 11 11 Telefax: 052 740 11 71 E-Mail info@kmuratgeber.ch Internet: www.winwerk.ch Inhaltsverzeichnis 1 Akonto... 2 1.1 Allgemein... 2 2 Akontobeträge
Handbuch. NAFI Online-Spezial. Kunden- / Datenverwaltung. 1. Auflage. (Stand: 24.09.2014)
 Handbuch NAFI Online-Spezial 1. Auflage (Stand: 24.09.2014) Copyright 2016 by NAFI GmbH Unerlaubte Vervielfältigungen sind untersagt! Inhaltsangabe Einleitung... 3 Kundenauswahl... 3 Kunde hinzufügen...
Handbuch NAFI Online-Spezial 1. Auflage (Stand: 24.09.2014) Copyright 2016 by NAFI GmbH Unerlaubte Vervielfältigungen sind untersagt! Inhaltsangabe Einleitung... 3 Kundenauswahl... 3 Kunde hinzufügen...
Finanzwirtschaft. Teil II: Bewertung
 Zeitwert des Geldes 1 Finanzwirtschaft Teil II: Bewertung Zeitwert des Geldes Zeitwert des Geldes 2 Bewertung & Zeitwert des Geldes Finanzwirtschaft behandelt die Bewertung von Real- und Finanzwerten.
Zeitwert des Geldes 1 Finanzwirtschaft Teil II: Bewertung Zeitwert des Geldes Zeitwert des Geldes 2 Bewertung & Zeitwert des Geldes Finanzwirtschaft behandelt die Bewertung von Real- und Finanzwerten.
Lösung. Prüfungsteil 1: Aufgabe 1
 Zentrale Prüfung 01 Lösung Diese Lösung wurde erstellt von Cornelia Sanzenbacher. Sie ist keine offizielle Lösung des Ministeriums für Schule und Weiterbildung des Landes. Prüfungsteil 1: Aufgabe 1 a)
Zentrale Prüfung 01 Lösung Diese Lösung wurde erstellt von Cornelia Sanzenbacher. Sie ist keine offizielle Lösung des Ministeriums für Schule und Weiterbildung des Landes. Prüfungsteil 1: Aufgabe 1 a)
Die Online-Meetings bei den Anonymen Alkoholikern. zum Thema. Online - Meetings. Eine neue Form der Selbsthilfe?
 Die Online-Meetings bei den Anonymen Alkoholikern zum Thema Online - Meetings Eine neue Form der Selbsthilfe? Informationsverhalten von jungen Menschen (Quelle: FAZ.NET vom 2.7.2010). Erfahrungen können
Die Online-Meetings bei den Anonymen Alkoholikern zum Thema Online - Meetings Eine neue Form der Selbsthilfe? Informationsverhalten von jungen Menschen (Quelle: FAZ.NET vom 2.7.2010). Erfahrungen können
Analysis I für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg WiSe 2015/16 Prof. Dr. M. Hinze Dr. P. Kiani Analysis I für Studierende der Ingenieurwissenschaften Lösungshinweise zu Blatt 2 Aufgabe 1: (12 Punkte) a) Beweisen
Fachbereich Mathematik der Universität Hamburg WiSe 2015/16 Prof. Dr. M. Hinze Dr. P. Kiani Analysis I für Studierende der Ingenieurwissenschaften Lösungshinweise zu Blatt 2 Aufgabe 1: (12 Punkte) a) Beweisen
Anhand des bereits hergeleiteten Models erstellen wir nun mit der Formel
 Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
Bedienungsanleitung für den Online-Shop
 Hier sind die Produktgruppen zu finden. Zur Produktgruppe gibt es eine Besonderheit: - Seite 1 von 18 - Zuerst wählen Sie einen Drucker-Hersteller aus. Dann wählen Sie das entsprechende Drucker- Modell
Hier sind die Produktgruppen zu finden. Zur Produktgruppe gibt es eine Besonderheit: - Seite 1 von 18 - Zuerst wählen Sie einen Drucker-Hersteller aus. Dann wählen Sie das entsprechende Drucker- Modell
Aufgaben Wechselstromwiderstände
 Aufgaben Wechselstromwiderstände 69. Eine aus Übersee mitgebrachte Glühlampe (0 V/ 50 ma) soll mithilfe einer geeignet zu wählenden Spule mit vernachlässigbarem ohmschen Widerstand an der Netzsteckdose
Aufgaben Wechselstromwiderstände 69. Eine aus Übersee mitgebrachte Glühlampe (0 V/ 50 ma) soll mithilfe einer geeignet zu wählenden Spule mit vernachlässigbarem ohmschen Widerstand an der Netzsteckdose
Mean Time Between Failures (MTBF)
 Mean Time Between Failures (MTBF) Hintergrundinformation zur MTBF Was steht hier? Die Mean Time Between Failure (MTBF) ist ein statistischer Mittelwert für den störungsfreien Betrieb eines elektronischen
Mean Time Between Failures (MTBF) Hintergrundinformation zur MTBF Was steht hier? Die Mean Time Between Failure (MTBF) ist ein statistischer Mittelwert für den störungsfreien Betrieb eines elektronischen
Die Post hat eine Umfrage gemacht
 Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer
 Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
Prozentrechnung. Wir können nun eine Formel für die Berechnung des Prozentwertes aufstellen:
 Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Deutliche Mehrheit der Bevölkerung für aktive Sterbehilfe
 Allensbacher Kurzbericht 6. Oktober 2014 Deutliche Mehrheit der Bevölkerung für aktive Sterbehilfe Zwei Drittel sind für die Erlaubnis aktiver Sterbehilfe, 60 Prozent für die Zulassung privater Sterbehilfe-Organsationen.
Allensbacher Kurzbericht 6. Oktober 2014 Deutliche Mehrheit der Bevölkerung für aktive Sterbehilfe Zwei Drittel sind für die Erlaubnis aktiver Sterbehilfe, 60 Prozent für die Zulassung privater Sterbehilfe-Organsationen.
WEGE IN DEN RUHESTAND
 WEGE IN DEN RUHESTAND Regelaltersgrenze für Lehrkräfte Ende des Schulhalbjahres, in dem die gesetzliche Altersgrenze erreicht wird das bedeutet: Ende des Monats, in dem das 65. Lebensjahr vollendet wird
WEGE IN DEN RUHESTAND Regelaltersgrenze für Lehrkräfte Ende des Schulhalbjahres, in dem die gesetzliche Altersgrenze erreicht wird das bedeutet: Ende des Monats, in dem das 65. Lebensjahr vollendet wird
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
 Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
APP-GFP/Fluoreszenzmikroskop. Aufnahmen neuronaler Zellen, mit freund. Genehmigung von Prof. Stefan Kins, TU Kaiserslautern
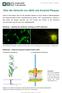 Über die Herkunft von Aβ42 und Amyloid-Plaques Heute ist sicher belegt, dass sich die amyloiden Plaques aus einer Vielzahl an Abbaufragmenten des Amyloid-Vorläufer-Proteins (amyloid-precursor-protein,
Über die Herkunft von Aβ42 und Amyloid-Plaques Heute ist sicher belegt, dass sich die amyloiden Plaques aus einer Vielzahl an Abbaufragmenten des Amyloid-Vorläufer-Proteins (amyloid-precursor-protein,
Virtueller Seminarordner Anleitung für die Dozentinnen und Dozenten
 Virtueller Seminarordner Anleitung für die Dozentinnen und Dozenten In dem Virtuellen Seminarordner werden für die Teilnehmerinnen und Teilnehmer des Seminars alle für das Seminar wichtigen Informationen,
Virtueller Seminarordner Anleitung für die Dozentinnen und Dozenten In dem Virtuellen Seminarordner werden für die Teilnehmerinnen und Teilnehmer des Seminars alle für das Seminar wichtigen Informationen,
LU-Zerlegung. Zusätze zum Gelben Rechenbuch. Peter Furlan. Verlag Martina Furlan. Inhaltsverzeichnis. 1 Definitionen.
 Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
Outlook. sysplus.ch outlook - mail-grundlagen Seite 1/8. Mail-Grundlagen. Posteingang
 sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Vergleichsklausur 12.1 Mathematik vom 20.12.2005
 Vergleichsklausur 12.1 Mathematik vom 20.12.2005 Mit CAS S./5 Aufgabe Alternative: Ganzrationale Funktionen Berliner Bogen Das Gebäude in den Abbildungen heißt Berliner Bogen und steht in Hamburg. Ein
Vergleichsklausur 12.1 Mathematik vom 20.12.2005 Mit CAS S./5 Aufgabe Alternative: Ganzrationale Funktionen Berliner Bogen Das Gebäude in den Abbildungen heißt Berliner Bogen und steht in Hamburg. Ein
Beispiel 48. 4.3.2 Zusammengesetzte Zufallsvariablen
 4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
Lineare Funktionen. 1 Proportionale Funktionen 3 1.1 Definition... 3 1.2 Eigenschaften... 3. 2 Steigungsdreieck 3
 Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Kernfach Mathematik Thema: Analysis
 Kernfach Mathemati Bahnlinie Bei A-Stadt endet eine Bahnlinie. In nebenstehender Zeichnung ist ein Koordinatenreuz so gelegt worden, dass A mit dem Ursprung zusammenfällt. Die Bahnlinie verläuft entlang
Kernfach Mathemati Bahnlinie Bei A-Stadt endet eine Bahnlinie. In nebenstehender Zeichnung ist ein Koordinatenreuz so gelegt worden, dass A mit dem Ursprung zusammenfällt. Die Bahnlinie verläuft entlang
W-Rechnung und Statistik für Ingenieure Übung 11
 W-Rechnung und Statistik für Ingenieure Übung 11 Christoph Kustosz (kustosz@statistik.tu-dortmund.de) Mathematikgebäude Raum 715 Christoph Kustosz (kustosz@statistik.tu-dortmund.de) W-Rechnung und Statistik
W-Rechnung und Statistik für Ingenieure Übung 11 Christoph Kustosz (kustosz@statistik.tu-dortmund.de) Mathematikgebäude Raum 715 Christoph Kustosz (kustosz@statistik.tu-dortmund.de) W-Rechnung und Statistik
Das große ElterngeldPlus 1x1. Alles über das ElterngeldPlus. Wer kann ElterngeldPlus beantragen? ElterngeldPlus verstehen ein paar einleitende Fakten
 Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Informatik Kurs Simulation. Hilfe für den Consideo Modeler
 Hilfe für den Consideo Modeler Consideo stellt Schulen den Modeler kostenlos zur Verfügung. Wenden Sie sich an: http://consideo-modeler.de/ Der Modeler ist ein Werkzeug, das nicht für schulische Zwecke
Hilfe für den Consideo Modeler Consideo stellt Schulen den Modeler kostenlos zur Verfügung. Wenden Sie sich an: http://consideo-modeler.de/ Der Modeler ist ein Werkzeug, das nicht für schulische Zwecke
Chemie Zusammenfassung KA 2
 Chemie Zusammenfassung KA 2 Wärmemenge Q bei einer Reaktion Chemische Reaktionen haben eine Gemeinsamkeit: Bei der Reaktion wird entweder Energie/Wärme frei (exotherm). Oder es wird Wärme/Energie aufgenommen
Chemie Zusammenfassung KA 2 Wärmemenge Q bei einer Reaktion Chemische Reaktionen haben eine Gemeinsamkeit: Bei der Reaktion wird entweder Energie/Wärme frei (exotherm). Oder es wird Wärme/Energie aufgenommen
Kapitalerhöhung - Verbuchung
 Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Du hast hier die Möglichkeit Adressen zu erfassen, Lieferscheine & Rechnungen zu drucken und Deine Artikel zu verwalten.
 Bedienungsanleitung Professionell aussehende Rechnungen machen einen guten Eindruck vor allem wenn du gerade am Beginn deiner Unternehmung bist. Diese Vorlage ist für den Beginn und für wenige Rechnungen
Bedienungsanleitung Professionell aussehende Rechnungen machen einen guten Eindruck vor allem wenn du gerade am Beginn deiner Unternehmung bist. Diese Vorlage ist für den Beginn und für wenige Rechnungen
Korrelation (II) Korrelation und Kausalität
 Korrelation (II) Korrelation und Kausalität Situation: Seien X, Y zwei metrisch skalierte Merkmale mit Ausprägungen (x 1, x 2,..., x n ) bzw. (y 1, y 2,..., y n ). D.h. für jede i = 1, 2,..., n bezeichnen
Korrelation (II) Korrelation und Kausalität Situation: Seien X, Y zwei metrisch skalierte Merkmale mit Ausprägungen (x 1, x 2,..., x n ) bzw. (y 1, y 2,..., y n ). D.h. für jede i = 1, 2,..., n bezeichnen
AGROPLUS Buchhaltung. Daten-Server und Sicherheitskopie. Version vom 21.10.2013b
 AGROPLUS Buchhaltung Daten-Server und Sicherheitskopie Version vom 21.10.2013b 3a) Der Daten-Server Modus und der Tresor Der Daten-Server ist eine Betriebsart welche dem Nutzer eine grosse Flexibilität
AGROPLUS Buchhaltung Daten-Server und Sicherheitskopie Version vom 21.10.2013b 3a) Der Daten-Server Modus und der Tresor Der Daten-Server ist eine Betriebsart welche dem Nutzer eine grosse Flexibilität
Rechnung wählen Lernstandserfassung
 Rechnungen verstehen Richtige F1 Rechnung wählen Lernstandserfassung 1. Wie rechnen Sie? Höhe eines Personenwagens Schätzen Sie die Höhe des Gebäudes. Schätzen Sie die Grundfläche des Gebäudes. Schätzen
Rechnungen verstehen Richtige F1 Rechnung wählen Lernstandserfassung 1. Wie rechnen Sie? Höhe eines Personenwagens Schätzen Sie die Höhe des Gebäudes. Schätzen Sie die Grundfläche des Gebäudes. Schätzen
V 2 B, C, D Drinks. Möglicher Lösungsweg a) Gleichungssystem: 300x + 400 y = 520 300x + 500y = 597,5 2x3 Matrix: Energydrink 0,7 Mineralwasser 0,775,
 Aufgabenpool für angewandte Mathematik / 1. Jahrgang V B, C, D Drinks Ein gastronomischer Betrieb kauft 300 Dosen Energydrinks (0,3 l) und 400 Liter Flaschen Mineralwasser und zahlt dafür 50, Euro. Einen
Aufgabenpool für angewandte Mathematik / 1. Jahrgang V B, C, D Drinks Ein gastronomischer Betrieb kauft 300 Dosen Energydrinks (0,3 l) und 400 Liter Flaschen Mineralwasser und zahlt dafür 50, Euro. Einen
Simulation LIF5000. Abbildung 1
 Simulation LIF5000 Abbildung 1 Zur Simulation von analogen Schaltungen verwende ich Ltspice/SwitcherCAD III. Dieses Programm ist sehr leistungsfähig und wenn man weis wie, dann kann man damit fast alles
Simulation LIF5000 Abbildung 1 Zur Simulation von analogen Schaltungen verwende ich Ltspice/SwitcherCAD III. Dieses Programm ist sehr leistungsfähig und wenn man weis wie, dann kann man damit fast alles
Klausur zur Vorlesung Stochastische Modelle in Produktion und Logistik im SS 09
 Leibniz Universität Hannover Wirtschaftswissenschaftliche Fakultät Institut für Produktionswirtschaft Prof. Dr. Stefan Helber Klausur zur Vorlesung Stochastische Modelle in Produktion und Logistik im SS
Leibniz Universität Hannover Wirtschaftswissenschaftliche Fakultät Institut für Produktionswirtschaft Prof. Dr. Stefan Helber Klausur zur Vorlesung Stochastische Modelle in Produktion und Logistik im SS
Anleitung BFV-Widget-Generator
 Anleitung BFV-Widget-Generator Seite 1 von 6 Seit dem 1. Oktober 2014 hat der Bayerische Fußball-Verband e.v. neue Widgets und einen neuen Baukasten zur Erstellung dieser Widgets veröffentlicht. Im Folgenden
Anleitung BFV-Widget-Generator Seite 1 von 6 Seit dem 1. Oktober 2014 hat der Bayerische Fußball-Verband e.v. neue Widgets und einen neuen Baukasten zur Erstellung dieser Widgets veröffentlicht. Im Folgenden
Aufgaben zur Flächenberechnung mit der Integralrechung
 ufgaben zur Flächenberechnung mit der Integralrechung ) Geben ist die Funktion f(x) = -x + x. a) Wie groß ist die Fläche, die die Kurve von f mit der x-chse einschließt? b) Welche Fläche schließt der Graph
ufgaben zur Flächenberechnung mit der Integralrechung ) Geben ist die Funktion f(x) = -x + x. a) Wie groß ist die Fläche, die die Kurve von f mit der x-chse einschließt? b) Welche Fläche schließt der Graph
Die Bundes-Zentrale für politische Bildung stellt sich vor
 Die Bundes-Zentrale für politische Bildung stellt sich vor Die Bundes-Zentrale für politische Bildung stellt sich vor Deutschland ist ein demokratisches Land. Das heißt: Die Menschen in Deutschland können
Die Bundes-Zentrale für politische Bildung stellt sich vor Die Bundes-Zentrale für politische Bildung stellt sich vor Deutschland ist ein demokratisches Land. Das heißt: Die Menschen in Deutschland können
