Lösungen zu den Übungen zur Newtonschen Mechanik
|
|
|
- Robert Arnold
- vor 6 Jahren
- Abrufe
Transkript
1 Lösungen zu den Übungen zur Newtonschen Mechanik Jonas Probst Bahnkurve eines Massenpunktes Aufgabe: Ein Massenpunkt bewegt sich auf folgender Trajektorie: 1. Skizzieren Sie die Bahnkurve. r(t) (a cos(ωt), b sin(ωt), ct). Bestien Sie das Potential U, unter dessen Einfluss sich das Teilchen der Masse bewegt. 3. Bestien Sie die Gesatenergie E des Teilchens. 4. Bestien Sie Drehipuls und Drehoent des Teilchens (bezogen auf den Ursprung) für c. Lösung: 1. Das Teilchen bewegt sich auf einer Spiralbahn u die z-achse. In der xy- Ebene vollführt es eine ellipsenförige Bewegung it den Halbachsen a und b, während es sich zugleich it konstanter Geschwindigkeit c in positive z-richtung bewegt.. Erinnerung: Definition des Potentials U als skalare Funktion, für die gilt: U( r) F ( r) r Also: Bestiung der Beschleunigung r, darüber Erittlung der wirkenden Kraft F, u daraus U zu gewinnen. r(t) ( aω sin(ωt), bω cos(ωt), c) r(t) ( aω cos(ωt), bω sin(ωt), ) ω r(t) 1
2 F ( r) r ω x y Kontrolle: U( r) x U y U z U U( r) ω (x + y ) ω x ω y F ( r) 3. Gesatenergie des Teilchens: E T + U r + U ( x + y + z ) + U (a ω sin (ωt) + b ω cos (ωt) + c ) + U (a ω (1 cos (ωt)) + b ω (1 sin (ωt)) + c ) + U (a ω ω x + b ω ω y + c ) + ω (x + y ) (a ω + b ω + c ) 4. Drehipuls: L r p c a cos(ωt) b sin(ωt) ct abω cos (ωt) + baω sin (ωt) aω sin(ωt) bω cos(ωt) c abωˆe z Drehoent: D L Anerkung: Dass es sich bei Drehipuls u eine Erhaltungsgröße handelt, hätte an auch ohne Rechnung erkennen können, da das betrachtete Potential U( r) U(x + y ) nur vo Abstand x + y zur z-achse abhängt und
3 dait rotationssyetrisch bezüglich der z-achse ist. Aus de Noether- Theore (wird in einer der folgenden Vorlesungen wiederholt) folgt daraus die Erhaltung der Projektion des Drehipulses auf die z-achse. Und da für c die Bewegung in der xy-ebene stattfindet, hat der Drehipuls wegen L r(t) nur eine Koponente in z-richtung, woit der gesate Drehipuls eine Erhaltungsgröße ist. Energieerhaltung Aufgabe: Ein beliebiges Potential U( r, t) ist invariant gegenüber zeitlichen Verschiebungen, d.h.: U( r, t) U( r, t + a), a R Zeigen Sie, dass die Gesatenergie E eines Massenpunktes in diese Potential eine Erhaltungsgröße ist. Lösung: Als erstes betrachten wir die zeitliche Änderung des Potentials: d dt U( r, t) U( r, t) r + U( r, t) t U( r, t) r U( r, t + h) U( r, t) + li h h U( r, t) r Daraus ergibt sich für die Zeitableitung der Energie: d dt E d dt ( r + U( r, t)) r r + U( r, t) r r ( r + U( r, t)) 3 Bewegung in eine allgeeinen radialsyetrischen Potential Aufgabe: Ein Teilchen der Masse bewege sich unter Einfluss des allgeeinen Zentralpotentials U(r) c r λ, 3
4 wobei λc >, λ und zugleich λ <. 1. Wie lautet das zugehörige effektive Potential U eff (r)?. Finden Sie die Beziehung zwischen Radius und Drehipuls, für die sich das Teilchen auf einer stabilen Kreisbahn it Radius r bewegt. Sie können ohne Beweis vorraussetzen, dass U eff (r) bei geeigneten Energien gebundene Bewegungen erlaubt. 3. Zeigen Sie explizit, dass an für die Kreisfrequenz ω eines Ulaufs auf dieser Kreisbahn folgenden Ausdruck erhält: cλ ω r λ+ 4. Betrachten Sie nun zusätzlich zur Kreisbewegung kleine Schwingungen u die Kreisbahn in radialer Richtung. Wie lautet das effektive Potential für diese radiale Bewegung i Fall kleiner Schwingungen? Führen Sie dazu eine Taylorentwicklung von U eff (r) bis zu ersten kineatisch relevanten Ter durch. 5. Leiten Sie den Zusaenhang zwischen der Kreisfrequenz der radialen Schwingung ω R und ω her. 6. Welche Beziehung uss λ erfüllen, dait sich trotz kleiner radialer Schwingung periodische, geschlossene Orbits ergeben? 7. Diskutieren Sie das Verhältnis ωr ω für den Fall des Coulob-Potentials und für den Fall das haronischen Oszillators. Lösung: 1. Zur Erinnerung: Das effektive Potential wurde folgenderaßen definiert: E Lr φ In unsere Fall ergibt sich: r + r φ + U(r) r + L r + U(r) r + U eff (r) U eff (r) L r + U(r) L r c r λ 4
5 . stabile Kreisbahn it Radius r U eff hat Miniu bei r d dr U eff(r) L r 3 + λc! r λ+1 L r λ+1 + λcr 3 r λ L λc r ( L λc ) 1 λ L r λ λc U eff erlaubt gebundene Zustände U eff besitzt ein lokales Miniu U eff besitzt nur ein lokales Extreu bei r U eff hat Miniu bei r 3. Die Kreisfrequenz ω erhält an über den Drehipuls L r φ der Kreisbewegung: ω φ L r 4 r λ λc r 4 λc r λ+ o.e ω ω > λc r λ+ 4. Für betrachten kleine Abweichungen vo Kreisbahnradius r r und führen dafür eine Taylorentwicklung des effektiven Potentials U eff bis zu ersten kineatisch relevanten Ter, also bis zur zweiten Ordnung durch: d U eff (r) U eff (r ) + (r r ) dr U eff(r ) + (r r ) d dr U eff(r ) U eff (r ) + (r r ) d dr U eff(r ) Für die zweite Ableitung von U eff an der Stelle r erhält an: d dr U eff(r ) 3L (λ + 1)λc r 4 r λ+ 3r λ λc r 4 5 (λ + 1)λc r λ+
6 3λc r λ+ ( λ)λc r λ+ (λ + 1)λc r λ+ Für die Taylorentwicklung von U eff ergibt sich dait: U eff (r) U eff (r ) + (r r ) ( λ)λc r λ+ 5. U einen Zusaenhang zwischen der Winkelgeschwindigkeit der Kreisbewegung ω und der Winkelgeschwindigkeit der radialen Schwingung ω R herstellen zu können, üssen wir uns erst einal überlegen, was wir unter ω R zu verstehen haben. In der vorhergehenden Teilaufgabe haben wir das effektive Potential u ein Miniu bis zur zweiten Ordnung entwickelt. Dadurch erhält an allgeein wie auch in unsere speziellen Fall ein haronisches Potential, das zu einer haronischen Schwingung des Massenpunktes u das Potentialiniu führt, denn: Substitution: ξ r r r + d dr U eff(r) d r + (r r ) dr U eff(r ) r + (r r ) ξ + ξ ( λ)λc r λ+ ( λ)λc r λ+ Nach Vorraussetzung gilt λc > und λ <, wir können also setzen: ωr 1 ( λ)λc. Dait erigbt sich für die kleine Auslenkung ξ aus de r λ+ Kreisbahnradius r die Differentialgleichung für den haronischen Oszillator: ξ + ω Rξ ξ(t) A cos(ω R t) + B sin(ω R t) Dait können wir nun den gesuchten Zusaenhang zwischen ω R und ω angeben: ( λ)λc ω R ω r λ+ λc r λ+ λ 6
7 6. Dait sich geschlossene, periodische Orbits ergeben, uss sich das Teilchen nach regeläßigen Abständen wieder a selben Ort befinden. Dazu uss es eine Zeitspanne geben, nach der sowohl die Kreisbewegung it ω als auch die radiale Schwingung it ω R synchron an ihren Ausganspunkt gelangt sind, denn dann befindet sich das Teilchen insgesat wieder an seine Ausgangsort. Die Kreisbewegung befindet sich nach der Zeit n T n π ω, n N wieder in ihre Ausganszustand, für die radiale Schwingung ist das nach der Zeit k T R k π ω R, k N der Fall. Wir suchen nun eine Zeit, nach der beide Bedingungen erfüllt sind, für die also gilt: nt kt R ω R n ω k λ Q 7. Für den haronischen Oszillator (λ ) erhält an ωr ω + Die radiale Schwingung oszilliert doppelt so schnell wie die Kreisbewegung, nach zwei Perioden der Kreisbewegung befindet sich der Massenpunkt wieder an seine Ausgangsort. Für das Coulob-Potential (λ 1) erhält an ωr ω 1 1 Radiale Schwingung und Kreisbewegung finden it derselben Winkelgeschwindigkeit statt, die Periode der Bewegung entspricht derjenigen der ungestörten Kreisbewegung. 4 Bewegung in eine speziellen radialsyetrischen Potential Aufgabe: Ein Massenpunkt der Masse bewege sich in folgende Zentralpotential: U(r) α r, α > 1. Wie lautet die Energie E des Teilchens?. Unter welchen Bedingungen kann der Massenpunkt das Zentru des Potentials (r ) erreichen, wenn sein Drehipuls L ist? Welche Besonderheit ergibt sich für den Fall L α? 3. Wir betrachten nun den Fall ins Zentru eines Körpers, der sich zu Zeitpunkt t i Abstand r(t ) r befindet und keine Radialbewegung 7
8 besitzt ( r(t ) ). Sein Drehipuls L erlaubt ih, das Zentru zu erreichen. Die Abkürzung λ L α kann hilfreich sein. (a) Berechnen Sie die dafür benötigte Zeit und weisen Sie dait nach, dass diese endlich ist. (b) Zeigen Sie, dass allerdings die Winkelgeschwindigkeit und auch die Geschwindigkeit des Teilchens für r gegen Unendlich gehen. Lösung: 1. Für die Energie des Teilchens erhält an: E r + L r + U(r) r + L r α r r + U eff (r). U die Frage, unter welchen Bedingungen der Massenpunkt das Zentru erreichen kann, zu beantworten, betrachten wir das effektive Potential U eff (r) L α r it L (Skizze!): Für L α > ergibt sich U eff (r) für r, ein Sturz ins Zentru ist in diese Fall wegen E U eff (r) nicht öglich. Für L α < dagegen erhält an U eff (r) < r und U eff (r) für r. In diese Fall führt stürzt der Massenpunkt also ins Zentru, da er für jeden Abstand r in Richtung des Zentrus beschleunigt wird (an jeder Stelle d gilt: dr U eff(r) > r d dr U eff(r) < ). Für den speziellen Fall L α verschwindet das effektive Potential. Dait ist der radiale Ipuls des Teilchens r konstant, das Teilchen stürzt entweder it konstanter Radialgeschindigkeit r ins Zentru oder entfernt sich it konstante r vo Zentru. 3. Fall ins Zentru L α λ L α (a) Für die (konstante) Energie des Teilchens erhält an über Betrachtung des Zeitpunktes t : E r (t ) + U eff (r ) L α r λ r < 8
9 Über die Energie zu eine beliebigen Zeitpunkt lässt sich nun die Forel zur Berechnung der Zeitdauer herleiten: E r + U eff (r) r ± (E U eff(r)) dr dt dr dt ± (E U eff(r)) Für die Dauer Δt des Sturzes ins Zentru vo Ausgangspunkt r(t ) r aus berechnet an (das Vorzeichen von r ist hierbei negativ, da das Teilchen seinen Abstand zu Ursprung verringert): Δt ˆ r ˆ r ˆ r dx (E U eff(x)) dx λ ( + λ r x ) r xdx λ r x ˆ r ˆ r dx (E U eff(x)) dx λ(r x ) r x Substitution: u x du xdx dx du x Δt r λ ˆ r r [ λ r ( + λ r λ du r u ] r r u r ) (b) Drehipulserhaltung: Energieerhaltung: L r φ const L φ für r r E r + U eff (r) const 9
10 r (E U eff(r)) (E ( )) für r 5 Gravitationsfeld der Erde Aufgabe: Ein Körper der Masse bewegt sich ausschließlich radial i Gravitationsfeld der Erde (Radius R, Masse M).. 1. Wie lauten die Gravitationskraft und das Gravitationspotential, die auf den Körper i Abstand r vo Erdittelpunkt wirken.. Geben Sie die Gesatenergie des Körpers i Gravitationsfeld an. Die Anfangsgeschwindigkeit des Körpers in seine Startpunkt auf der Erdoberfläche sei v. Wie groß ist seine Geschwindigkeit v in Abhängigkeit des Abstandes r vo Erdittelpunkt? 3. Wie groß uss die Anfangsgeschwindigkeit v indestens sein, dait der Körper das Gravitationspotential der Erde überwinden kann? 4. Wie lautet der Zusaenhang zwischen Gravitationskonstante G und der lokalen Gravitationsbeschleunigung g an der Erdoberfläche? 5. Die International Space Station kreist in einer Ulaufbahn ca. d 35 k über der Erdoberfläche (R 64 k). Wie groß ist dort in etwa die lokale Gravitationsbeschleunigung g ISS i Vergleich zu g auf der Erdoberfläche? Weshalb spricht an trotzde von Schwerelosigkeit? Lösung: 1. Wenn an den Ursprung des Koordinatensystes in den Erdittelpunkt legt, ergibt sich für die Gravitationskraft auf den Körper a Ort r: F ( r) G M r r r F (r) r r Das radialsyetrische Gravitationspotential lautet denach: Kontrolle: U(r) G M r U(r) d dr U(r) r r GM r r r F ( r) 1
11 . Da er nach Vorraussetzung nur radiale Bewegungen ausführen soll, lautet die Gesatenergie E des Körpers: E T + U(r) r G M r Die Geschwindigkeit v(r) in Abhängigkeit des Abstandes zu Erdittelpunkt erhält an über die Energieerhaltung: E v G M R const v (r) G M r v (r) v + GM( 1 r 1 R ) v(r) v + GM( 1 r 1 R ) (Das Vorzeichen von v(r) r(r) ist positiv, weil wir davon ausgehen, dass sich das Teilchen nicht in die Erdoberfläche hineinbewegt...) 3. Außerhalb des Gravitationspotentials der Erde, also für r beträgt die potentielle Energie des Teilchens U(r ). Dait sich das Teilchen dort aufhalten kann, uss es also wegen E U eff eine positive Energie besitzen. Nach Energieerhaltung uss also auch a Startpunkt auf der Erdoberfläche gelten: E v G M R v G M R GM v R 4. Auf der Erdoberfläche gilt: F (R) g G M R g G M R 11
12 5. Auf der ISS gilt: F (R + d) g Iss G M (R + d) g ISS g g ISS g R (R + d) R (R + d).9 Die Raustation nutzt bei ihrer Ukreisung der Erde die Gravitationskraft als Zentripetalkraft. I Bezugssyste eines Besatzungsitgliedes auf der ISS wirkt daher noch die Zentrifugalkraft, die stets radial vo Mittelpunkt der Kreisbahn, de Gravitationszentru, wegweist und die Schwerkraft dait genau kopensiert. Deswegen ist es berechtigt trotz einer noch sehr hohen Gravitationsbeschleunigung g ISS von Schwerelosigkeit zu sprechen. 1
Übungen zu Lagrange-Formalismus und kleinen Schwingungen
 Übungen zu Lagrange-Foralisus und kleinen Schwingungen Jonas Probst.9.9 Teilchen auf der Stange Aufgabe: Ein Teilchen der Masse wird durch eine Zwangskraft auf einer asselosen Stange gehalten, auf der
Übungen zu Lagrange-Foralisus und kleinen Schwingungen Jonas Probst.9.9 Teilchen auf der Stange Aufgabe: Ein Teilchen der Masse wird durch eine Zwangskraft auf einer asselosen Stange gehalten, auf der
Fallender Stein auf rotierender Erde
 Übungen zu Theoretische Physik I - Mechanik im Sommersemester 2013 Blatt 4 vom 13.05.13 Abgabe: 27. Mai Aufgabe 16 4 Punkte allender Stein auf rotierender Erde Wir lassen einen Stein der Masse m in einen
Übungen zu Theoretische Physik I - Mechanik im Sommersemester 2013 Blatt 4 vom 13.05.13 Abgabe: 27. Mai Aufgabe 16 4 Punkte allender Stein auf rotierender Erde Wir lassen einen Stein der Masse m in einen
(2 π f C ) I eff Z = 25 V
 Physik Induktion, Selbstinduktion, Wechselstrom, mechanische Schwingung ösungen 1. Eine Spule mit der Induktivität = 0,20 mh und ein Kondensator der Kapazität C = 30 µf werden in Reihe an eine Wechselspannung
Physik Induktion, Selbstinduktion, Wechselstrom, mechanische Schwingung ösungen 1. Eine Spule mit der Induktivität = 0,20 mh und ein Kondensator der Kapazität C = 30 µf werden in Reihe an eine Wechselspannung
Formelsammlung: Physik I für Naturwissenschaftler
 Formelsammlung: Physik I für Naturwissenschaftler 1 Was ist Physik? Stand: 13. Dezember 212 Physikalische Größe X = Zahl [X] Einheit SI-Basiseinheiten Mechanik Zeit [t] = 1 s Länge [x] = 1 m Masse [m]
Formelsammlung: Physik I für Naturwissenschaftler 1 Was ist Physik? Stand: 13. Dezember 212 Physikalische Größe X = Zahl [X] Einheit SI-Basiseinheiten Mechanik Zeit [t] = 1 s Länge [x] = 1 m Masse [m]
Übungen zu Lagrange-Formalismus und kleinen Schwingungen
 Übungen zu Lagrange-Formalismus und kleinen Schwingungen Jonas Probst 22.09.2009 1 Teilchen auf der Stange Ein Teilchen der Masse m wird durch eine Zwangskraft auf einer masselosen Stange gehalten, auf
Übungen zu Lagrange-Formalismus und kleinen Schwingungen Jonas Probst 22.09.2009 1 Teilchen auf der Stange Ein Teilchen der Masse m wird durch eine Zwangskraft auf einer masselosen Stange gehalten, auf
Blatt 03.1: Scheinkräfte
 Fakultät für Physik T1: Klassische Mechanik, SoSe 2016 Dozent: Jan von Delft Übungen: Benedikt Bruognolo, Sebastian Huber, Katharina Stadler, Lukas Weidinger http://www.physik.uni-muenchen.de/lehre/vorlesungen/sose_16/t1_theor_mechanik/
Fakultät für Physik T1: Klassische Mechanik, SoSe 2016 Dozent: Jan von Delft Übungen: Benedikt Bruognolo, Sebastian Huber, Katharina Stadler, Lukas Weidinger http://www.physik.uni-muenchen.de/lehre/vorlesungen/sose_16/t1_theor_mechanik/
Symmetrie von Naturgesetzen - Galilei-Transformationen und die Invarianz der Newton schen Gesetze
 Symmetrie von Naturgesetzen - Galilei-Transformationen und die Invarianz der Newton schen Gesetze Symmetrie (Physik) (aus Wikipedia, der freien Enzyklopädie) Symmetrie ist ein grundlegendes Konzept der
Symmetrie von Naturgesetzen - Galilei-Transformationen und die Invarianz der Newton schen Gesetze Symmetrie (Physik) (aus Wikipedia, der freien Enzyklopädie) Symmetrie ist ein grundlegendes Konzept der
Modell der Punktmasse
 Kinematik Die Kinematik (kinema, griech., Bewegung) ist die Lehre von der Bewegung von Punkten und Körpern im Raum, beschrieben durch die Größen Weg (Änderung der Ortskoordinate) s, Geschwindigkeit v und
Kinematik Die Kinematik (kinema, griech., Bewegung) ist die Lehre von der Bewegung von Punkten und Körpern im Raum, beschrieben durch die Größen Weg (Änderung der Ortskoordinate) s, Geschwindigkeit v und
Probeklausur zur Theoretischen Physik I: Mechanik
 Prof. Dr. H. Friedrich Physik-Department T3a Technische Universität München Probeklausur zur Theoretischen Physik I: Mechanik Montag, 2.7.29 Hörsaal 1 1:15-11:5 Aufgabe 1 (8 Punkte) Geben Sie möglichst
Prof. Dr. H. Friedrich Physik-Department T3a Technische Universität München Probeklausur zur Theoretischen Physik I: Mechanik Montag, 2.7.29 Hörsaal 1 1:15-11:5 Aufgabe 1 (8 Punkte) Geben Sie möglichst
Blatt 1. Kinematik- Lösungsvorschlag
 Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 011 Blatt 1. Kinematik- Lösungsvorschlag Aufgabe 1.1. Schraubenlinie Die
Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 011 Blatt 1. Kinematik- Lösungsvorschlag Aufgabe 1.1. Schraubenlinie Die
Übungen zu: Theoretische Physik I klassische Mechanik W 2213 Tobias Spranger - Prof. Tom Kirchner WS 2005/06
 Übungen zu: Theoretische Physik I klassische Mechanik W 2213 Tobias Spranger - Prof. Tom Kirchner WS 25/6 http://www.pt.tu-clausthal.de/qd/teaching.html 16. November 25 Übungsblatt Lösungsvorschlag 3 Aufgaben,
Übungen zu: Theoretische Physik I klassische Mechanik W 2213 Tobias Spranger - Prof. Tom Kirchner WS 25/6 http://www.pt.tu-clausthal.de/qd/teaching.html 16. November 25 Übungsblatt Lösungsvorschlag 3 Aufgaben,
Name: Gruppe: Matrikel-Nummer:
 Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 1/13/14) Dozent: J. von Delft Übungen: B. Kubala Klausur zur Vorlesung T1: Theoretische Mechanik, SoSe 008 (3. Juli 007) Bearbeitungszeit:
Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 1/13/14) Dozent: J. von Delft Übungen: B. Kubala Klausur zur Vorlesung T1: Theoretische Mechanik, SoSe 008 (3. Juli 007) Bearbeitungszeit:
Allgemeine Mechanik Musterlösung 1.
 Allgemeine Mechanik Musterlösung. HS 24 Prof. Thomas Gehrmann Übung. Kraftfelder und Linienintegrale. a) Gegeben sei das Kraftfeld F, 2 ). Berechnen Sie das Linienintegral von r, ) nach r 2 2, ) entlang
Allgemeine Mechanik Musterlösung. HS 24 Prof. Thomas Gehrmann Übung. Kraftfelder und Linienintegrale. a) Gegeben sei das Kraftfeld F, 2 ). Berechnen Sie das Linienintegral von r, ) nach r 2 2, ) entlang
Name: Gruppe: Matrikel-Nummer:
 Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 12/13/14) Dozent: J. von Delft Übungen: B. Kubala Nachklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 2008 (1. Oktober
Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 12/13/14) Dozent: J. von Delft Übungen: B. Kubala Nachklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 2008 (1. Oktober
Praktikumssemesterarbeit für Numerik Aufgabe 1 HU-Berlin, Sommersemester 2005
 Praktikumssemesterarbeit für Numerik Aufgabe HU-Berlin, Sommersemester 2005 Mario Krell Volker Grabsch 24. Juli 2005 Inhaltsverzeichnis Herleitung aus der Physik. Voraussetzungen und Annahmen Allgemein
Praktikumssemesterarbeit für Numerik Aufgabe HU-Berlin, Sommersemester 2005 Mario Krell Volker Grabsch 24. Juli 2005 Inhaltsverzeichnis Herleitung aus der Physik. Voraussetzungen und Annahmen Allgemein
Federpendel. Einführung. Das Federpendel. Basiswissen > Mechanische Schwingungen > Federpendel. Skript PLUS
 www.schullv.de Basiswissen > Mechanische Schwingungen > Federpendel Federpendel Skript PLUS Einführung Wärst du utig genug für einen Bungee-Sprung? Oder hast du gar schon einen geacht? Wenn ja, hast du
www.schullv.de Basiswissen > Mechanische Schwingungen > Federpendel Federpendel Skript PLUS Einführung Wärst du utig genug für einen Bungee-Sprung? Oder hast du gar schon einen geacht? Wenn ja, hast du
Übungen zu Theoretische Physik I - Mechanik im Sommersemester 2013 Blatt 7 vom Abgabe:
 Übungen zu Theoretische Physik I - Mechanik im Sommersemester 03 Blatt 7 vom 0.06.3 Abgabe: 7.06.3 Aufgabe 9 3 Punkte Keplers 3. Gesetz Das 3. Keplersche Gesetz für die Planetenbewegung besagt, dass das
Übungen zu Theoretische Physik I - Mechanik im Sommersemester 03 Blatt 7 vom 0.06.3 Abgabe: 7.06.3 Aufgabe 9 3 Punkte Keplers 3. Gesetz Das 3. Keplersche Gesetz für die Planetenbewegung besagt, dass das
11. Vorlesung Wintersemester
 11. Vorlesung Wintersemester 1 Ableitungen vektorieller Felder Mit Resultat Skalar: die Divergenz diva = A = A + A y y + A z z (1) Mit Resultat Vektor: die Rotation (engl. curl): ( rota = A Az = y A y
11. Vorlesung Wintersemester 1 Ableitungen vektorieller Felder Mit Resultat Skalar: die Divergenz diva = A = A + A y y + A z z (1) Mit Resultat Vektor: die Rotation (engl. curl): ( rota = A Az = y A y
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 3: Dynamik und Kräfte Dr. Daniel Bick 09. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 09. November 2016 1 / 25 Übersicht 1 Wiederholung
Physik für Biologen und Zahnmediziner Kapitel 3: Dynamik und Kräfte Dr. Daniel Bick 09. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 09. November 2016 1 / 25 Übersicht 1 Wiederholung
8.1 Gleichförmige Kreisbewegung 8.2 Drehung ausgedehnter Körper 8.3 Beziehung: Translation - Drehung 8.4 Vektornatur des Drehwinkels
 8. Drehbewegungen 8.1 Gleichförmige Kreisbewegung 8.2 Drehung ausgedehnter Körper 8.3 Beziehung: Translation - Drehung 8.4 Vektornatur des Drehwinkels 85 8.5 Kinetische Energie der Rotation ti 8.6 Berechnung
8. Drehbewegungen 8.1 Gleichförmige Kreisbewegung 8.2 Drehung ausgedehnter Körper 8.3 Beziehung: Translation - Drehung 8.4 Vektornatur des Drehwinkels 85 8.5 Kinetische Energie der Rotation ti 8.6 Berechnung
Name: Gruppe: Matrikel-Nummer: Aufgabe Punkte
 T1: Klassische Mechanik, SoSe007 Prof. Dr. Jan von Delft Theresienstr. 37, Zi. 40 Dr. Vitaly N. Golovach vitaly.golovach@physik.lmu.de Nachholklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 007 (8.
T1: Klassische Mechanik, SoSe007 Prof. Dr. Jan von Delft Theresienstr. 37, Zi. 40 Dr. Vitaly N. Golovach vitaly.golovach@physik.lmu.de Nachholklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 007 (8.
Übungen Theoretische Physik I (Mechanik) Blatt 8 (Austeilung am: , Abgabe am )
 Übungen Theoretische Physik I (Mechanik) Blatt 8 (Austeilung am: 14.09.11, Abgabe am 1.09.11) Hinweis: Kommentare zu den Aufgaben sollen die Lösungen illustrieren und ein besseres Verständnis ermöglichen.
Übungen Theoretische Physik I (Mechanik) Blatt 8 (Austeilung am: 14.09.11, Abgabe am 1.09.11) Hinweis: Kommentare zu den Aufgaben sollen die Lösungen illustrieren und ein besseres Verständnis ermöglichen.
Probestudium der Physik 2011/12
 Probestudium der Physik 2011/12 1 Schwingungen und Wellen: Einführung in die mathematischen Grundlagen 1.1 Die Sinus- und die Kosinusfunktion Die Sinusfunktion lässt sich genauso wie die Kosinusfunktion
Probestudium der Physik 2011/12 1 Schwingungen und Wellen: Einführung in die mathematischen Grundlagen 1.1 Die Sinus- und die Kosinusfunktion Die Sinusfunktion lässt sich genauso wie die Kosinusfunktion
Reibungskräfte. Haftreibung. (µ H hängt von Material und Oberflächenbeschaffenheit ab, aber nicht von der Größe der reibenden Oberflächen)
 Reibungskräfte F =g=g N F zug Reibung ist eine der Bewegung entgegenwirkende Kraft, die entsteht, wenn zwei sich berührende Körper sich gegeneinander bewegen. Haftreibung F zug = F H ist die Kraft, die
Reibungskräfte F =g=g N F zug Reibung ist eine der Bewegung entgegenwirkende Kraft, die entsteht, wenn zwei sich berührende Körper sich gegeneinander bewegen. Haftreibung F zug = F H ist die Kraft, die
Theoretische Physik I Mechanik Probeklausur - Lösungshinweise
 Prof. H. Monien St. Kräer R. Sanchez SS2014 Theoretische Physik I Mechanik Probeklausur - Lösungshinweise Hinweise: Diese Lösung/Lösungshinweise erhebt keinen Anspruch auf Richtigkeit oder Vollständigkeit,
Prof. H. Monien St. Kräer R. Sanchez SS2014 Theoretische Physik I Mechanik Probeklausur - Lösungshinweise Hinweise: Diese Lösung/Lösungshinweise erhebt keinen Anspruch auf Richtigkeit oder Vollständigkeit,
2. Vorlesung Wintersemester
 2. Vorlesung Wintersemester 1 Mechanik von Punktteilchen Ein Punktteilchen ist eine Abstraktion. In der Natur gibt es zwar Elementarteilchen (Elektronen, Neutrinos, usw.), von denen bisher keine Ausdehnung
2. Vorlesung Wintersemester 1 Mechanik von Punktteilchen Ein Punktteilchen ist eine Abstraktion. In der Natur gibt es zwar Elementarteilchen (Elektronen, Neutrinos, usw.), von denen bisher keine Ausdehnung
9. Übungsblatt zur VL Einführung in die Klassische Mechanik und Wärmelehre Modul P1a, 1. FS BPh 8. Dezember 2009
 9. Übungsblatt zur VL Einführung in die Klassische Mechanik und Wärmelehre Modul P1a, 1. FS BPh 8. Dezember 009 Aufgabe 9.1: Doppelfeder Eine Kugel wird im Schwerefeld der Erde zwischen zwei Federn mit
9. Übungsblatt zur VL Einführung in die Klassische Mechanik und Wärmelehre Modul P1a, 1. FS BPh 8. Dezember 009 Aufgabe 9.1: Doppelfeder Eine Kugel wird im Schwerefeld der Erde zwischen zwei Federn mit
M1 Maxwellsches Rad. 1. Grundlagen
 M1 Maxwellsches Rad Stoffgebiet: Translations- und Rotationsbewegung, Massenträgheitsmoment, physikalisches Pendel. Versuchsziel: Es ist das Massenträgheitsmoment eines Maxwellschen Rades auf zwei Arten
M1 Maxwellsches Rad Stoffgebiet: Translations- und Rotationsbewegung, Massenträgheitsmoment, physikalisches Pendel. Versuchsziel: Es ist das Massenträgheitsmoment eines Maxwellschen Rades auf zwei Arten
1. Kinematik. Untersucht wird die Bewegung eines Punktes P in Bezug auf zwei Bezugssysteme: Bezugssystem Oxyz ist ruhend:
 Untersucht wird die ewegung eines Punktes P in ezug auf zwei ezugssysteme: ezugssystem Oxyz ist ruhend: Ursprung O Einheitsvektoren e x, e y, e z Koordinaten x, y, z ezugssystem ξηζ bewegt sich: Ursprung
Untersucht wird die ewegung eines Punktes P in ezug auf zwei ezugssysteme: ezugssystem Oxyz ist ruhend: Ursprung O Einheitsvektoren e x, e y, e z Koordinaten x, y, z ezugssystem ξηζ bewegt sich: Ursprung
2. Klausur zur Theoretischen Physik I (Mechanik)
 2. Klausur zur Theoretischen Physik I (echanik) 09.07.2004 Aufgabe 1 Physikalisches Pendel 4 Punkte Eine homogene, kreisförmige, dünne Platte mit Radius R und asse ist am Punkt P so aufgehängt, daß sie
2. Klausur zur Theoretischen Physik I (echanik) 09.07.2004 Aufgabe 1 Physikalisches Pendel 4 Punkte Eine homogene, kreisförmige, dünne Platte mit Radius R und asse ist am Punkt P so aufgehängt, daß sie
TECHNISCHE MECHANIK III (DYNAMIK)
 Klausur im Fach TECHNISCHE MECHANIK III (DYNAMIK) WS 2014 / 2015 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 2 3 4 Summe Punkte: 15 7 23 15 60 Davon erreicht Bearbeitungszeit: Hilfsmittel:
Klausur im Fach TECHNISCHE MECHANIK III (DYNAMIK) WS 2014 / 2015 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 2 3 4 Summe Punkte: 15 7 23 15 60 Davon erreicht Bearbeitungszeit: Hilfsmittel:
Ergänzende Materialien zum Seminar Theoretische Mechanik WS 2005/06
 Ergänzende Materialien zum Seminar Theoretische Mechanik WS 2005/06 Dörte Hansen 4. Dezember 2005 1 Lagrangepunkte oder: Das restringierte 3-Körper-Problem der Himmelsmechanik 1.1 Motivation Die Trojaner
Ergänzende Materialien zum Seminar Theoretische Mechanik WS 2005/06 Dörte Hansen 4. Dezember 2005 1 Lagrangepunkte oder: Das restringierte 3-Körper-Problem der Himmelsmechanik 1.1 Motivation Die Trojaner
Gruppenarbeit Federn, Kräfte und Vektoren
 1 Gruppenarbeit Federn, Kräfte und Vektoren Abzugeben bis Woche 10. Oktober Der geschätzte Zeitaufwand wird bei jeder Teilaufgabe mit Sternen angegeben. Je mehr Sterne eine Aufgabe besitzt, desto grösser
1 Gruppenarbeit Federn, Kräfte und Vektoren Abzugeben bis Woche 10. Oktober Der geschätzte Zeitaufwand wird bei jeder Teilaufgabe mit Sternen angegeben. Je mehr Sterne eine Aufgabe besitzt, desto grösser
Experimentalphysik E1
 Experientalphysik E1 Drehbewegung, Drehipuls Keplersche Gesetze Alle Inforationen zur Vorlesung unter : http://www.physik.lu.de/lehre/vorlesungen/index.htl 11. Nov. 2016 Ipuls p = v Definition des Ipulses
Experientalphysik E1 Drehbewegung, Drehipuls Keplersche Gesetze Alle Inforationen zur Vorlesung unter : http://www.physik.lu.de/lehre/vorlesungen/index.htl 11. Nov. 2016 Ipuls p = v Definition des Ipulses
0.1 Versuch 4C: Bestimmung der Gravitationskonstante mit dem physikalischen Pendel
 0.1 Versuch 4C: Bestimmung der Gravitationskonstante mit dem physikalischen Pendel 0.1.1 Aufgabenstellung Man bestimme die Fallbeschleunigung mittels eines physikalischen Pendels und berechne hieraus die
0.1 Versuch 4C: Bestimmung der Gravitationskonstante mit dem physikalischen Pendel 0.1.1 Aufgabenstellung Man bestimme die Fallbeschleunigung mittels eines physikalischen Pendels und berechne hieraus die
Klassische Mechanik - Ferienkurs; Lösungem. Sommersemester 2011, Prof. Metzler
 Klassische Mechanik - Ferienkurs; Lösunge Soerseester 2011, Prof. Metzler 1 Inhaltsverzeichnis 1 Quickies 3 2 Lagrange Gleichung 1. Art 3 2.1 Perle auf Schraubenlinie..................................
Klassische Mechanik - Ferienkurs; Lösunge Soerseester 2011, Prof. Metzler 1 Inhaltsverzeichnis 1 Quickies 3 2 Lagrange Gleichung 1. Art 3 2.1 Perle auf Schraubenlinie..................................
Bewegung in Systemen mit mehreren Massenpunkten
 Bewegung in Systemen mit mehreren Massenpunkten Wir betrachten ein System mit mehreren Massenpunkten. Für jeden Massenpunkt i einzeln gilt nach Newton 2: F i = d p i dt. Für n Massenpunkte muss also ein
Bewegung in Systemen mit mehreren Massenpunkten Wir betrachten ein System mit mehreren Massenpunkten. Für jeden Massenpunkt i einzeln gilt nach Newton 2: F i = d p i dt. Für n Massenpunkte muss also ein
Betrachtet man einen starren Körper so stellt man insgesamt sechs Freiheitsgrade der Bewegung
 Die Mechanik besteht aus drei Teilgebieten: Kinetik: Bewegungsvorgänge (Translation, Rotation) Statik: Zusammensetzung und Gleichgewicht von Kräften Dynamik: Kräfte als Ursache von Bewegungen Die Mechanik
Die Mechanik besteht aus drei Teilgebieten: Kinetik: Bewegungsvorgänge (Translation, Rotation) Statik: Zusammensetzung und Gleichgewicht von Kräften Dynamik: Kräfte als Ursache von Bewegungen Die Mechanik
Theoretische Mechanik
 Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 2008 Theoretische Mechanik 9. Übung 9.1 d alembertsches Prinzip: Flaschenzug Wir betrachten
Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 2008 Theoretische Mechanik 9. Übung 9.1 d alembertsches Prinzip: Flaschenzug Wir betrachten
3. Kreisbewegung. Punkte auf einem Rad Zahnräder, Getriebe Drehkran Turbinen, Hubschrauberrotor
 3. Kreisbewegung Ein wichtiger technischer Sonderfall ist die Bewegung auf einer Kreisbahn. Dabei hat der Massenpunkt zu jedem Zeitpunkt den gleichen Abstand vom Kreismittelpunkt. Beispiele: Punkte auf
3. Kreisbewegung Ein wichtiger technischer Sonderfall ist die Bewegung auf einer Kreisbahn. Dabei hat der Massenpunkt zu jedem Zeitpunkt den gleichen Abstand vom Kreismittelpunkt. Beispiele: Punkte auf
1. Eindimensionale Bewegung
 1. Eindimensionale Bewegung Die Gesamtheit aller Orte, die ein Punkt während seiner Bewegung einnimmt, wird als Bahnkurve oder Bahn bezeichnet. Bei einer eindimensionalen Bewegung bewegt sich der Punkt
1. Eindimensionale Bewegung Die Gesamtheit aller Orte, die ein Punkt während seiner Bewegung einnimmt, wird als Bahnkurve oder Bahn bezeichnet. Bei einer eindimensionalen Bewegung bewegt sich der Punkt
Harmonische Schwingung die einfachste Schwingung ist die harmonische Schwingung
 1. Schwingungen Fast alles schwingt, d.h. der Zustand ändert sich periodisch it der Zeit wie in Kreisbewegung. Bsp. Uhr, Kolben i Autootor, wippende Boote auf de Wasser. Haronische Schwingung die einfachste
1. Schwingungen Fast alles schwingt, d.h. der Zustand ändert sich periodisch it der Zeit wie in Kreisbewegung. Bsp. Uhr, Kolben i Autootor, wippende Boote auf de Wasser. Haronische Schwingung die einfachste
6. Orbits und die Runge-Lenz Vektor
 Übungen zur T: Theoretische Mechani, SoSe3 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray James.Gray@physi.uni-muenchen.de 6. Orbits und die Runge-Lenz Vetor Übung 6.: Die Rücehr der Kanonenugel
Übungen zur T: Theoretische Mechani, SoSe3 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray James.Gray@physi.uni-muenchen.de 6. Orbits und die Runge-Lenz Vetor Übung 6.: Die Rücehr der Kanonenugel
Übungen zu Physik 1 für Maschinenwesen
 Physikdepartent E13 WS 011/1 Übungen zu Physik 1 für Maschinenwesen Prof. Dr. Peter Müller-Buschbau, Dr. Eva M. Herzig, Dr. Volker Körstgens, David Magerl, Markus Schindler, Moritz v. Sivers Vorlesung
Physikdepartent E13 WS 011/1 Übungen zu Physik 1 für Maschinenwesen Prof. Dr. Peter Müller-Buschbau, Dr. Eva M. Herzig, Dr. Volker Körstgens, David Magerl, Markus Schindler, Moritz v. Sivers Vorlesung
Aufgabe 1: Senkrechtkomponente [8] GegebensinddieVektoren a = (1,2,3) und b = (3,1,2). BerechnenSiedieKomponente a von a,die auf b senkrecht steht.
![Aufgabe 1: Senkrechtkomponente [8] GegebensinddieVektoren a = (1,2,3) und b = (3,1,2). BerechnenSiedieKomponente a von a,die auf b senkrecht steht. Aufgabe 1: Senkrechtkomponente [8] GegebensinddieVektoren a = (1,2,3) und b = (3,1,2). BerechnenSiedieKomponente a von a,die auf b senkrecht steht.](/thumbs/59/43512421.jpg) Aufgabe 1: Senkrechtkomponente [8] GegebensinddieVektoren a = (1,2,3) und b = (3,1,2). BerechnenSiedieKomponente a von a,die auf b senkrecht steht. Aufgabe 2: ǫ Tensor [6] Gegeben sind die Vektoren a =
Aufgabe 1: Senkrechtkomponente [8] GegebensinddieVektoren a = (1,2,3) und b = (3,1,2). BerechnenSiedieKomponente a von a,die auf b senkrecht steht. Aufgabe 2: ǫ Tensor [6] Gegeben sind die Vektoren a =
Blatt 4. Stoß und Streuung - Lösungsvorschlag
 Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 211 Blatt 4. Stoß und Streuung - Lösungsvorschlag Aufgabe 4.1. Stoß Zwei
Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 211 Blatt 4. Stoß und Streuung - Lösungsvorschlag Aufgabe 4.1. Stoß Zwei
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik - Schwingungen und Wellen - Prof. Dr. Ulrich Hahn SS 28 Mechanik elastische Wellen Schwingung von Bauteilen Wasserwellen Akustik Elektrodynamik Schwingkreise elektromagnetische
Physik III im Studiengang Elektrotechnik - Schwingungen und Wellen - Prof. Dr. Ulrich Hahn SS 28 Mechanik elastische Wellen Schwingung von Bauteilen Wasserwellen Akustik Elektrodynamik Schwingkreise elektromagnetische
Massenträgheitsmomente homogener Körper
 http://www.youtube.com/watch?v=naocmb7jsxe&feature=playlist&p=d30d6966531d5daf&playnext=1&playnext_from=pl&index=8 Massenträgheitsmomente homogener Körper 1 Ma 1 Lubov Vassilevskaya Drehbewegung um c eine
http://www.youtube.com/watch?v=naocmb7jsxe&feature=playlist&p=d30d6966531d5daf&playnext=1&playnext_from=pl&index=8 Massenträgheitsmomente homogener Körper 1 Ma 1 Lubov Vassilevskaya Drehbewegung um c eine
Gleichförmige Kreisbewegung, Bezugssystem, Scheinkräfte
 Aufgaben 4 Translations-Mechanik Gleichförmige Kreisbewegung, Bezugssystem, Scheinkräfte Lernziele - die Grössen zur Beschreibung einer Kreisbewegung und deren Zusammenhänge kennen. - die Frequenz, Winkelgeschwindigkeit,
Aufgaben 4 Translations-Mechanik Gleichförmige Kreisbewegung, Bezugssystem, Scheinkräfte Lernziele - die Grössen zur Beschreibung einer Kreisbewegung und deren Zusammenhänge kennen. - die Frequenz, Winkelgeschwindigkeit,
Das mathematische Pendel
 1 Das mathematische Pendel A. Krumbholz, S. Effendi 25. Juni 2013 2 Inhaltsverzeichnis Inhaltsverzeichnis Inhaltsverzeichnis 1 Einführung 3 1.1 Das mathematische Pendel........................... 3 1.2
1 Das mathematische Pendel A. Krumbholz, S. Effendi 25. Juni 2013 2 Inhaltsverzeichnis Inhaltsverzeichnis Inhaltsverzeichnis 1 Einführung 3 1.1 Das mathematische Pendel........................... 3 1.2
Theoretische Physik: Mechanik
 Ferienkurs Theoretische Physik: Mechanik Blatt 2 - Lösung Technische Universität München 1 Fakultät für Physik 1 Perle Eine Perle der Masse m gleite reibungsfrei auf einem vertikal stehenden Ring vom Radius
Ferienkurs Theoretische Physik: Mechanik Blatt 2 - Lösung Technische Universität München 1 Fakultät für Physik 1 Perle Eine Perle der Masse m gleite reibungsfrei auf einem vertikal stehenden Ring vom Radius
Theoretische Physik: Mechanik
 Ferienkurs Theoretische Physik: Mechanik Blatt 4 - Lösung Technische Universität München 1 Fakultät für Physik 1 Zwei Kugeln und der Satz von Steiner Nehmen Sie zwei Kugeln mit identischem Radius R und
Ferienkurs Theoretische Physik: Mechanik Blatt 4 - Lösung Technische Universität München 1 Fakultät für Physik 1 Zwei Kugeln und der Satz von Steiner Nehmen Sie zwei Kugeln mit identischem Radius R und
Differentialgleichungen sind überall!
 Differentialgleichungen sind überall! Helmut Abels Fakultät für Mathematik Universität Regensburg Folien und Co.: http://www.uni-r.de/fakultaeten/nat Fak I/abels/Aktuelles.html Tag der Mathematik am Albrecht-Altdorfer-Gymnasium
Differentialgleichungen sind überall! Helmut Abels Fakultät für Mathematik Universität Regensburg Folien und Co.: http://www.uni-r.de/fakultaeten/nat Fak I/abels/Aktuelles.html Tag der Mathematik am Albrecht-Altdorfer-Gymnasium
Lösung 12 Klassische Theoretische Physik I WS 15/16
 Karlsruher Institut für Technologie Institut für theoretische Festkörperphysik www.tfp.kit.edu ösung 1 Klassische Theoretische Physik I WS 1/16 Prof. Dr. G. Schön + Punkte Sebastian Zanker, Daniel Mendler
Karlsruher Institut für Technologie Institut für theoretische Festkörperphysik www.tfp.kit.edu ösung 1 Klassische Theoretische Physik I WS 1/16 Prof. Dr. G. Schön + Punkte Sebastian Zanker, Daniel Mendler
15. Vorlesung Sommersemester
 15. Vorlesung Soerseester 1 Kontinuusgrenzfall der Bewegungsgleichungen Was wird aus den Bewegungsgleichungen i Kontinuusgrenzwert? I diskreten Fall sind diese η j = kη j+1 η j + η j 1 1 und an führt wieder
15. Vorlesung Soerseester 1 Kontinuusgrenzfall der Bewegungsgleichungen Was wird aus den Bewegungsgleichungen i Kontinuusgrenzwert? I diskreten Fall sind diese η j = kη j+1 η j + η j 1 1 und an führt wieder
Formelsammlung: Physik I für Naturwissenschaftler
 Formelsammlung: Physik I für Naturwissenschaftler 1 Was ist Physik? Stand: 24. Januar 213 Physikalische Größe X = Zahl [X] Einheit SI-Basiseinheiten Mechanik Zeit [t] = 1 s Länge [x] = 1 m Masse [m] =
Formelsammlung: Physik I für Naturwissenschaftler 1 Was ist Physik? Stand: 24. Januar 213 Physikalische Größe X = Zahl [X] Einheit SI-Basiseinheiten Mechanik Zeit [t] = 1 s Länge [x] = 1 m Masse [m] =
5. Vorlesung Wintersemester
 5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
F r = m v2 r. Bewegt sich der Körper mit der konstanten Winkelgeschwindigkeit ω = 2π, T
 Kreisbewegung ================================================================== Damit sich ein Körper der Masse m auf einer Kreisbahn vom Radius r, dannmuss die Summe aller an diesem Körper angreifenden
Kreisbewegung ================================================================== Damit sich ein Körper der Masse m auf einer Kreisbahn vom Radius r, dannmuss die Summe aller an diesem Körper angreifenden
Gander Daniel, WS 2004 Mayrhofer Reinhard; GEOPHYSICS & GEODYNAMICS TU GRAZ
 Gander Daniel, WS 004 TECHNISCHE BEICHT st lab: Gravity and Pressure in the Earth s Interior POBLEMSTELLUNG... LÖSUNG UND EGEBNISSE.... Berechnung der Massen.... Berechnung der Schwerebeschleunigung...4.
Gander Daniel, WS 004 TECHNISCHE BEICHT st lab: Gravity and Pressure in the Earth s Interior POBLEMSTELLUNG... LÖSUNG UND EGEBNISSE.... Berechnung der Massen.... Berechnung der Schwerebeschleunigung...4.
Beispiel 1:Der Runge-Lenz Vektor [2 Punkte]
![Beispiel 1:Der Runge-Lenz Vektor [2 Punkte] Beispiel 1:Der Runge-Lenz Vektor [2 Punkte]](/thumbs/59/43248755.jpg) Übungen Theoretische Physik I (Mechanik) Blatt 9 (Austeilung am: 1.9.11, Abgabe am 8.9.11) Hinweis: Kommentare zu den Aufgaben sollen die Lösungen illustrieren und ein besseres Verständnis ermöglichen.
Übungen Theoretische Physik I (Mechanik) Blatt 9 (Austeilung am: 1.9.11, Abgabe am 8.9.11) Hinweis: Kommentare zu den Aufgaben sollen die Lösungen illustrieren und ein besseres Verständnis ermöglichen.
PP Physikalisches Pendel
 PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
Theoretische Physik I Mechanik Blatt 1
 PD Dr. S. Mertens S. Falkner, S. Mingramm Theoretische Physik I Mechanik Blatt 1 WS 27/28 8. 1. 27 1. Parabelbahn. Ein Punkt bewege sich auf der Kurve, die durch die Gleichung y 2 = 4ax + 4a 2 a > beschrieben
PD Dr. S. Mertens S. Falkner, S. Mingramm Theoretische Physik I Mechanik Blatt 1 WS 27/28 8. 1. 27 1. Parabelbahn. Ein Punkt bewege sich auf der Kurve, die durch die Gleichung y 2 = 4ax + 4a 2 a > beschrieben
5 Schwingungen und Wellen
 5 Schwingungen und Wellen Schwingung: Regelmäßige Bewegung, die zwischen zwei Grenzen hin- & zurückführt Zeitlich periodische Zustandsänderung mit Periode T ψ ψ(t) [ ψ(t-τ)] Wellen: Periodische Zustandsänderung
5 Schwingungen und Wellen Schwingung: Regelmäßige Bewegung, die zwischen zwei Grenzen hin- & zurückführt Zeitlich periodische Zustandsänderung mit Periode T ψ ψ(t) [ ψ(t-τ)] Wellen: Periodische Zustandsänderung
Theoretische Physik I: Lösungen Blatt Michael Czopnik
 Theoretische Physik I: Lösungen Blatt 2 15.10.2012 Michael Czopnik Aufgabe 1: Scheinkräfte Nutze Zylinderkoordinaten: x = r cos ϕ y = r sin ϕ z = z Zweimaliges differenzieren ergibt: ẍ = r cos ϕ 2ṙ ϕ sin
Theoretische Physik I: Lösungen Blatt 2 15.10.2012 Michael Czopnik Aufgabe 1: Scheinkräfte Nutze Zylinderkoordinaten: x = r cos ϕ y = r sin ϕ z = z Zweimaliges differenzieren ergibt: ẍ = r cos ϕ 2ṙ ϕ sin
9. Vorlesung Wintersemester
 9. Vorlesung Wintersemester 1 Die Phase der angeregten Schwingung Wertebereich: bei der oben abgeleiteten Formel tan φ = β ω ω ω0. (1) ist noch zu sehen, in welchem Bereich der Winkel liegt. Aus der ursprünglichen
9. Vorlesung Wintersemester 1 Die Phase der angeregten Schwingung Wertebereich: bei der oben abgeleiteten Formel tan φ = β ω ω ω0. (1) ist noch zu sehen, in welchem Bereich der Winkel liegt. Aus der ursprünglichen
Technische Mechanik 3
 Technische Mechanik 3 2. Kinematik eines Massenpunktes 2.1. Grundbegriffe, kartesische Koordinaten 2.2. Geradlinige Bewegung 2.3. Ebene Bewegung, Polarkoordinaten 2.4. räumliche Bewegung, natürliche Koordinaten
Technische Mechanik 3 2. Kinematik eines Massenpunktes 2.1. Grundbegriffe, kartesische Koordinaten 2.2. Geradlinige Bewegung 2.3. Ebene Bewegung, Polarkoordinaten 2.4. räumliche Bewegung, natürliche Koordinaten
2.2 Arbeit und Energie. Aufgaben
 2.2 Arbeit und Energie Aufgaben Aufgabe 1: Auf eine Katapult befindet sich eine Kugel der Masse, die durch eine Feder beschleunigt wird. Die Feder ist a Anfang u die Strecke s 0 zusaengedrückt. Für die
2.2 Arbeit und Energie Aufgaben Aufgabe 1: Auf eine Katapult befindet sich eine Kugel der Masse, die durch eine Feder beschleunigt wird. Die Feder ist a Anfang u die Strecke s 0 zusaengedrückt. Für die
2.2 Arbeit und Energie. Aufgaben
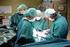 Technische Mechanik 3 2.2-1 Prof. Dr. Wandinger Aufgabe 1 Auf eine Katapult befindet sich eine Kugel der Masse, die durch eine Feder beschleunigt wird. Die Feder ist a Anfang u die Strecke s 0 zusaengedrückt.
Technische Mechanik 3 2.2-1 Prof. Dr. Wandinger Aufgabe 1 Auf eine Katapult befindet sich eine Kugel der Masse, die durch eine Feder beschleunigt wird. Die Feder ist a Anfang u die Strecke s 0 zusaengedrückt.
Flüsse, Fixpunkte, Stabilität
 1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
Übungen zur Vorlesung PN1 Lösung zu Blatt 5
 Aufgabe 1: Geostationärer Satellit Übungen zur Vorlesung PN1 Lösung zu Blatt 5 Ein geostationärer Satellit zeichnet sich dadurch aus, dass er eine Umlaufdauer von einem Tag besitzt und sich folglich seine
Aufgabe 1: Geostationärer Satellit Übungen zur Vorlesung PN1 Lösung zu Blatt 5 Ein geostationärer Satellit zeichnet sich dadurch aus, dass er eine Umlaufdauer von einem Tag besitzt und sich folglich seine
Musterlösung 2. Klausur Physik für Maschinenbauer
 Universität Siegen Sommersemester 2010 Fachbereich Physik Musterlösung 2. Klausur Physik für Maschinenbauer Prof. Dr. I. Fleck Aufgabe 1: Freier Fall im ICE Ein ICE bewege sich mit der konstanten Geschwindigkeit
Universität Siegen Sommersemester 2010 Fachbereich Physik Musterlösung 2. Klausur Physik für Maschinenbauer Prof. Dr. I. Fleck Aufgabe 1: Freier Fall im ICE Ein ICE bewege sich mit der konstanten Geschwindigkeit
5. Kritische Drehzahl
 Aufgabenstellung: 5. Kritische Drehzahl y y Ω c/4 c/4 m c/4 e z O O S c/4 x Prof. Dr. Wandinger 6. Schwingungen Dynamik 2 6.5-1 Der starre Körper mit der Masse m dreht sich mit der konstanten Winkelgeschwindigkeit
Aufgabenstellung: 5. Kritische Drehzahl y y Ω c/4 c/4 m c/4 e z O O S c/4 x Prof. Dr. Wandinger 6. Schwingungen Dynamik 2 6.5-1 Der starre Körper mit der Masse m dreht sich mit der konstanten Winkelgeschwindigkeit
Wie fällt ein Körper, wenn die Wirkung der Corioliskraft berücksichtigt wird?
 Wie fällt ein Körper, wenn die Wirkung der Corioliskraft berücksichtigt wird? Beim freien Fall eines Körpers auf die Erde, muss man bedenken, dass unsere Erde ein rotierendes System ist. Um die Kräfte,
Wie fällt ein Körper, wenn die Wirkung der Corioliskraft berücksichtigt wird? Beim freien Fall eines Körpers auf die Erde, muss man bedenken, dass unsere Erde ein rotierendes System ist. Um die Kräfte,
1. Klausur in K2 am
 Name: Punkte: Note: Ø: Kernfach Physik Abzüge für Darstellung: Rundung:. Klausur in K am 0.0. Achte auf die Darstellung und vergiss nicht Geg., Ges., Formeln, Einheiten, Rundung...! Angaben: Schallgeschwindigkeit
Name: Punkte: Note: Ø: Kernfach Physik Abzüge für Darstellung: Rundung:. Klausur in K am 0.0. Achte auf die Darstellung und vergiss nicht Geg., Ges., Formeln, Einheiten, Rundung...! Angaben: Schallgeschwindigkeit
5. Übungsblatt zur VL Einführung in die Klassische Mechanik und Wärmelehre Modul P1a, 1. FS BPh 10. November 2009
 5. Übungsblatt zur VL Einführung in die Klassische Mechanik und Wärmelehre Modul P1a, 1. FS BPh 10. November 009 Aufgabe 5.1: Trägheitskräfte Auf eine in einem Aufzug stehende Person (Masse 70 kg) wirken
5. Übungsblatt zur VL Einführung in die Klassische Mechanik und Wärmelehre Modul P1a, 1. FS BPh 10. November 009 Aufgabe 5.1: Trägheitskräfte Auf eine in einem Aufzug stehende Person (Masse 70 kg) wirken
Grundlagen Arbeit & Energie Translation & Rotation Erhaltungssätze Gravitation Reibung Hydrodynamik. Physik: Mechanik. Daniel Kraft. 2.
 Physik: Mechanik Daniel Kraft 2. März 2013 CC BY-SA 3.0, Grafiken teilweise CC BY-SA Wikimedia Grundlagen Zeit & Raum Zeit t R Länge x R als Koordinate Zeit & Raum Zeit t R Länge x R als Koordinate Raum
Physik: Mechanik Daniel Kraft 2. März 2013 CC BY-SA 3.0, Grafiken teilweise CC BY-SA Wikimedia Grundlagen Zeit & Raum Zeit t R Länge x R als Koordinate Zeit & Raum Zeit t R Länge x R als Koordinate Raum
Theoretische Physik I: Weihnachtszettel Michael Czopnik
 Theoretische Physik I: Weihnachtszettel 21.12.2012 Michael Czopnik Aufgabe 1: Rudolph und der Weihnachtsmann Der Weihnachtsmann (Masse M) und sein Rentier Rudolph (Masse m) sind durch ein Seil mit konstanter
Theoretische Physik I: Weihnachtszettel 21.12.2012 Michael Czopnik Aufgabe 1: Rudolph und der Weihnachtsmann Der Weihnachtsmann (Masse M) und sein Rentier Rudolph (Masse m) sind durch ein Seil mit konstanter
Kapitel 2. Kinematik des Massenpunktes. 2.1 Einleitung. 2.2 Massenpunkt. 2.3 Ortsvektor
 Kapitel 2 Kinematik des Massenpunktes 2.1 Einleitung In diesem Kapitel behandeln wir die Bewegung von einem oder mehreren Körpern im Raum. Wir unterscheiden dabei zwischen Kinematik und Dynamik. Die Kinematik
Kapitel 2 Kinematik des Massenpunktes 2.1 Einleitung In diesem Kapitel behandeln wir die Bewegung von einem oder mehreren Körpern im Raum. Wir unterscheiden dabei zwischen Kinematik und Dynamik. Die Kinematik
Differentialgleichungen 2. Ordnung
 Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
2. Klausur zur Vorlesung Theoretische Physik A Universität Karlsruhe WS 2004/05
 . Klausur zur Vorlesung Theoretische Physik A Universität Karlsruhe WS 004/05 Prof. Dr. Gerd Schön Dr. Matthias Eschrig Dauer: Stunden Gesamtpunktzahl: 30 Punkte + 5 Zusatzpunkte Hinweise: Beginnen Sie
. Klausur zur Vorlesung Theoretische Physik A Universität Karlsruhe WS 004/05 Prof. Dr. Gerd Schön Dr. Matthias Eschrig Dauer: Stunden Gesamtpunktzahl: 30 Punkte + 5 Zusatzpunkte Hinweise: Beginnen Sie
Mathematischer Vorkurs für Physiker WS 2011/12 Vorlesung 3
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2011/12 Vorlesung 3 Differenziation und Integration von Vektorfunktionen Der Ortsvektor: Man kann einen Punkt P im Raum eindeutig durch die
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2011/12 Vorlesung 3 Differenziation und Integration von Vektorfunktionen Der Ortsvektor: Man kann einen Punkt P im Raum eindeutig durch die
Vordiplomsklausur in Physik Mittwoch, 23. Februar 2005, :00 Uhr für den Studiengang: Mb, Inft, Geol, Ciw
 Institut für Physik und Physikalische Technologien 23.02.2005 der TU Clausthal Prof. Dr. W. Daum Vordiplomsklausur in Physik Mittwoch, 23. Februar 2005, 09.00-11:00 Uhr für den Studiengang: Mb, Inft, Geol,
Institut für Physik und Physikalische Technologien 23.02.2005 der TU Clausthal Prof. Dr. W. Daum Vordiplomsklausur in Physik Mittwoch, 23. Februar 2005, 09.00-11:00 Uhr für den Studiengang: Mb, Inft, Geol,
Hochschule Düsseldorf University of Applied Sciences. 22. Dezember 2016 HSD. Physik. Schwingungen
 Physik Schwingungen Zusammenfassung Mechanik Physik Mathe Einheiten Bewegung Bewegung 3d Newtons Gesetze Energie Gravitation Rotation Impuls Ableitung, Integration Vektoren Skalarprodukt Gradient Kreuzprodukt
Physik Schwingungen Zusammenfassung Mechanik Physik Mathe Einheiten Bewegung Bewegung 3d Newtons Gesetze Energie Gravitation Rotation Impuls Ableitung, Integration Vektoren Skalarprodukt Gradient Kreuzprodukt
I. Mechanik. Die Lehre von den Bewegungen und den Kräften. I.1 Kinematik Die Lehre von den Bewegungen. Physik für Mediziner 1
 I. Mechanik Die Lehre von den Bewegungen und den Kräften I.1 Kinematik Die Lehre von den Bewegungen Physik für Mediziner 1 Mechanik I: Bewegung in einer Dimension Idealisierung: Massenpunkt ( Punktmasse)
I. Mechanik Die Lehre von den Bewegungen und den Kräften I.1 Kinematik Die Lehre von den Bewegungen Physik für Mediziner 1 Mechanik I: Bewegung in einer Dimension Idealisierung: Massenpunkt ( Punktmasse)
Harmonische Schwingungen
 Kapitel 6 Harmonische Schwingungen Von periodisch spricht man, wenn eine feste Dauer zwischen wiederkehrenden ähnlichen oder gleichen Ereignissen besteht. Von harmonisch spricht man, wenn die Zeitentwicklung
Kapitel 6 Harmonische Schwingungen Von periodisch spricht man, wenn eine feste Dauer zwischen wiederkehrenden ähnlichen oder gleichen Ereignissen besteht. Von harmonisch spricht man, wenn die Zeitentwicklung
2. Lagrange-Gleichungen
 2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
Die Zylinderfunktionen
 Die Zylinderfunktionen Betrachten Schwingungen einer Pauke. Auslenkung v = v(t, x, y) des Trommelfells ist Lösung der Wellengleichung 2 v t = v := 2 v 2 x + 2 v 2 y 2 als Produkt aus zeitabhängiger und
Die Zylinderfunktionen Betrachten Schwingungen einer Pauke. Auslenkung v = v(t, x, y) des Trommelfells ist Lösung der Wellengleichung 2 v t = v := 2 v 2 x + 2 v 2 y 2 als Produkt aus zeitabhängiger und
Aufgabensammlung. Experimentalphysik für ET. 2. Erhaltungsgrößen
 Experimentalphysik für ET Aufgabensammlung 1. Erhaltungsgrößen An einem massenlosen Faden der Länge L = 1 m hängt ein Holzklotz mit der Masse m 2 = 1 kg. Eine Kugel der Masse m 1 = 15 g wird mit der Geschwindigkeit
Experimentalphysik für ET Aufgabensammlung 1. Erhaltungsgrößen An einem massenlosen Faden der Länge L = 1 m hängt ein Holzklotz mit der Masse m 2 = 1 kg. Eine Kugel der Masse m 1 = 15 g wird mit der Geschwindigkeit
Kinematik des starren Körpers
 Technische Mechanik II Kinematik des starren Körpers Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/2010 Übersicht 1. Kinematik des Massenpunktes
Technische Mechanik II Kinematik des starren Körpers Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/2010 Übersicht 1. Kinematik des Massenpunktes
Formelsammlung. Lagrange-Gleichungen: q k. Zur Koordinate q k konjugierter Impuls: p k = L. Hamilton-Funktion: p k. Hamiltonsche Gleichungen: q k = H
 Formelsammlung Lagrange-Gleichungen: ( ) d L dt q k L q k = 0 mit k = 1,..., n. (1) Zur Koordinate q k konjugierter Impuls: p k = L q k. (2) Hamilton-Funktion: n H(q 1,..., q n, p 1,..., p n, t) = p k
Formelsammlung Lagrange-Gleichungen: ( ) d L dt q k L q k = 0 mit k = 1,..., n. (1) Zur Koordinate q k konjugierter Impuls: p k = L q k. (2) Hamilton-Funktion: n H(q 1,..., q n, p 1,..., p n, t) = p k
10. und 11. Vorlesung Sommersemester
 10. und 11. Vorlesung Sommersemester 1 Die Legendre-Transformation 1.1 Noch einmal mit mehr Details Diese Ableitung wirkt einfach, ist aber in dieser Form sicher nicht so leicht verständlich. Deswegen
10. und 11. Vorlesung Sommersemester 1 Die Legendre-Transformation 1.1 Noch einmal mit mehr Details Diese Ableitung wirkt einfach, ist aber in dieser Form sicher nicht so leicht verständlich. Deswegen
Harmonische Schwingung
 Harmonische Schwingung Eine harmonische Schwingung mit Amplitude c 0, Phasenverschiebung δ und Frequenz ω bzw. Periode T = 2π/ω hat die Form x x(t) = c cos(ωt δ). δ/ω c t T=2π/ω Harmonische Schwingung
Harmonische Schwingung Eine harmonische Schwingung mit Amplitude c 0, Phasenverschiebung δ und Frequenz ω bzw. Periode T = 2π/ω hat die Form x x(t) = c cos(ωt δ). δ/ω c t T=2π/ω Harmonische Schwingung
Geozentrisches und heliozentrisches Weltbild. Das 1. Gesetz von Kepler. Das 2. Gesetz von Kepler. Das 3. Gesetz von Kepler.
 Geozentrisches und heliozentrisches Weltbild Geozentrisches Weltbild: Vertreter Aristoteles, Ptolemäus, Kirche (im Mittelalter) Heliozentrisches Weltbild: Vertreter Aristarch von Samos, Kopernikus, Galilei
Geozentrisches und heliozentrisches Weltbild Geozentrisches Weltbild: Vertreter Aristoteles, Ptolemäus, Kirche (im Mittelalter) Heliozentrisches Weltbild: Vertreter Aristarch von Samos, Kopernikus, Galilei
Applets: Um diese anzusehen, downloaden sie das Programm Ruler and Compass CaR aus dem Internet (kostenlosen Download)
 Unterrichtsmaterial (Links: auf der ersten Seite der Internet-Version) Folien: Trigonometrische Funktion (power-point) Applets: Um diese anzusehen, downloaden sie das Programm Ruler and Compass CaR aus
Unterrichtsmaterial (Links: auf der ersten Seite der Internet-Version) Folien: Trigonometrische Funktion (power-point) Applets: Um diese anzusehen, downloaden sie das Programm Ruler and Compass CaR aus
Einführung in die Physik
 Einführung in die Physik für Pharmazeuten und Biologen (PPh) Mechanik, Elektrizitätslehre, Optik Übung : Vorlesung: Tutorials: Montags 13:15 bis 14 Uhr, Liebig-HS Montags 14:15 bis 15:45, Liebig HS Montags
Einführung in die Physik für Pharmazeuten und Biologen (PPh) Mechanik, Elektrizitätslehre, Optik Übung : Vorlesung: Tutorials: Montags 13:15 bis 14 Uhr, Liebig-HS Montags 14:15 bis 15:45, Liebig HS Montags
Physik I Übung 5 - Lösungshinweise
 Physik I Übung 5 - Lösungshinweise Stefan Reutter WS 2011/12 Moritz Kütt Stand: 22.12.2011 Franz Fujara Aufgabe 1 May the Force be with you Jedi possess the remarkable ability to ignore non-linear friction
Physik I Übung 5 - Lösungshinweise Stefan Reutter WS 2011/12 Moritz Kütt Stand: 22.12.2011 Franz Fujara Aufgabe 1 May the Force be with you Jedi possess the remarkable ability to ignore non-linear friction
Physik für Biologen und Geowissenschaftler 15. Juni Grundlagen 2 SI - Einheiten... 2 Fehlerberechnung... 2
 Formelsammlung Physik für Biologen und Geowissenschaftler 15. Juni 2005 Inhaltsverzeichnis 1 Grundlagen 2 SI - Einheiten............................................... 2 Fehlerberechnung.............................................
Formelsammlung Physik für Biologen und Geowissenschaftler 15. Juni 2005 Inhaltsverzeichnis 1 Grundlagen 2 SI - Einheiten............................................... 2 Fehlerberechnung.............................................
Theoretische Mechanik
 Theoretische Mechanik Übungen R. Kirschner, ITP, Univ. Leipzig 1-1 1. Betrachten Sie ein System aus 4 Massenpunkten, ( r i,m i ),i = 1,2,3,4, das sich in trivialer geradlinig-gleichförmiger Bewegung befindet.
Theoretische Mechanik Übungen R. Kirschner, ITP, Univ. Leipzig 1-1 1. Betrachten Sie ein System aus 4 Massenpunkten, ( r i,m i ),i = 1,2,3,4, das sich in trivialer geradlinig-gleichförmiger Bewegung befindet.
