PFLICHTTEIL FRANZ LEMMERMEYER
|
|
|
- Eike Breiner
- vor 9 Jahren
- Abrufe
Transkript
1 PFLICHTTEIL FRANZ LEMMERMEYER ( Bestimmen Sie die erste Ableitung der Funktion f(x mit f(x = (3x x + und Vereinfachen Sie so weit wie möglich. ( Bestimmen Sie diejenige Stammfunktion F (x von ( π f(x = sin x + π, welche F (0 = genügt. (3 Lösen Sie die Gleichung für 0 x π. (sin(x + sin(x = 3 (4 Gegeben sind die beiden Funktionen f(x = x und g(x = c x. Bestimmen Sie c so, dass sich die Schaubilder von v und g senkrecht schneiden. (5 Die folgenden Abbildungen zeigen die Schaubilder einer Funktion f, ihrer Ableitung f, und zweier Stammfunktionen F und F. a Ordnen Sie die Schaubilder diesen Funktionen zu. b Die Funktion f hat die Form f(x = axe x. Bestimmen Sie den Wert von a.
2 FRANZ LEMMERMEYER (6 Eine Ebene E geht durch den Ursprung und schneidet das durch die Ebenen E : x = 0, E : x = 0, E 3 : x + x = bestimmte Prisma in einem gleichseitigen Dreieck. Bestimme die Koordinatengleichungen der beiden möglichen Ebenen E. (7 Zeigen Sie, dass die Gerade g und die Ebene E, die durch ( 3 g : x = 3 + t( und E : x = r( + s( parallel sind, und bestimmen Sie ihren Abstand. Geben Sie die Gleichung einer weiteren Geraden h g an, die von E denselben Abstand hat wie g. (8 In einer Urne befinden sich 7 blaue und rote Kugeln. Es werden zwei Kugeln ohne Zurücklegen gezogen. Bestimmen Sie den Erwartungswert für die Anzahl der gezogenen blauen Kugeln. (9 Gegeben ist ein Punkt P und zwei nicht parallele Ebenen E und E in Parameterform. Beschreiben Sie ein Verfahren zur Bestimmung einer Koordinatengleichung derjenigen Ebene E, welche P enthält und senkrecht auf E und E steht.
3 PFLICHTTEIL 3 Lösungen ( Bestimmen Sie die erste Ableitung der Funktion f(x mit f(x = (3x x + und Vereinfachen Sie so weit wie möglich. f (x = (6x (3x x + = 36x 3 36x + 0x + 4. ( Bestimmen Sie diejenige Stammfunktion F (x von ( π f(x = sin x + π, welche F (0 = genügt. Daran denken, dass die Klammer hinter sin stehen bleibt! Damit wird F (x = 4 ( π π cos x + π + c; Einsetzen von F (0 = gibt = 4 cos π + c = c, also c =. π (3 Lösen Sie die Gleichung für 0 x π. (sin(x + sin(x = 3 Wir setzen sin x = z und erhalten z + z 3 = 0, also z = und z = 3. Die Gleichung sin x = 3 hat keine Lösung, da sin x Amplitude hat. Es ist also sin x = zu lösen. Wegen sin(u = für u = π und u = π + π = 9π muss also x = π oder x = 9π sein, was auf x = π und x 4 = 5π führt. Die nächste Lösung (x 4 3 = 9π 4 liegt schon außerhalb des Intervalls [0; π]. (4 Gegeben sind die beiden Funktionen f(x = x und g(x = c x. Bestimmen Sie c so, dass sich die Schaubilder von v und g senkrecht schneiden. Senkrecht schneiden bedeutet, dass für die Steigungen m und m der Tangenten in den Schnittpunkten m m = gelten muss.
4 4 FRANZ LEMMERMEYER Wegen f (x = x und g (x = x muss also x ( x =, d.h. 4x = und x, = ± sein. In diesen beiden Punkten müssen sich die Schaubilder von f und g schneiden, d.h. es muss f( = g( sein (für x = erhält man nichts Neues. Dies ergibt 4 = c 4, also c =. (5 Die folgenden Abbildungen zeigen die Schaubilder einer Funktion f, ihrer Ableitung f, und zweier Stammfunktionen F und F. a Ordnen Sie die Schaubilder diesen Funktionen zu. b Die Funktion f hat die Form f(x = axe x. Bestimmen Sie den Wert von a. a Die beiden Stammfunktionen unterscheiden sich nur durch Verschiebung in Richtung y-achse: also sind die beiden rechten Schaubilder Stammfunktionen von f. Da F nur einen Extrempunkt (in x = 0 hat, muss f genau eine Nullstelle mit Vorzeichenwechsel haben, d.h. das Schaubild von f ist links unten. Damit bleibt das erste Schaubild für f übrig. b Einsetzen von x = 0 in f bringt nichts, da f(0 = 0 wird. Also setzen wir x = 0 in die Ableitung f (x = ae x ax e x ein und finden f (0 = a. Aus dem ersten Schaubild liest man f (0 = ab, und es folgt a =. (6 Eine Ebene E geht durch den Ursprung und schneidet das durch die Ebenen E : x = 0, E : x = 0, E 3 : x + x = bestimmte Prisma in einem gleichseitigen Dreieck. Bestimme die Koordinatengleichungen der beiden möglichen Ebenen E. Es empfiehlt sich, die Ebenen zu skizzieren (x x 3 -Ebene, x x 3 - Ebene, die dritte hat Spurpunkte S ( 0 0, S (0 0, und ist parallel zur x 3 -Achse. Man sieht dann, dass das gleichseitige Dreieck aus O(0 0 0 und den Punkten P ( 0 z und Q(0 z über (bzw. unter den beiden Spurpunkten bestehen muss. Gleichsetzen der Abstände P Q = und OP = + z liefert z =, also z, = ±.
5 PFLICHTTEIL 5 Die erste Ebene geht also durch O(0 0 0, P ( 0 und Q(0, und hat die Gleichung x +x x 3 = 0 (ausrechnen wie üblich; die zweite Ebene durch O(0 0 0, P ( 0 und Q(0 ist E : x + x + x 3 = 0. (7 Zeigen Sie, dass die Gerade g und die Ebene E, die durch ( 3 g : x = 3 + t( und E : x = r( + s( parallel sind, und bestimmen Sie ihren Abstand. Geben Sie die Gleichung einer weiteren Geraden h g an, die von E denselben Abstand hat wie g. g und E sind parallel, wenn der Richtungsvektor von g senkrecht auf den Normalenvektor ( ( ( 4 n E = = 3 steht, was wegen ( ( = = 0 der Fall ist. Da alle Punkte von g gleichen Abstand von E haben, brauchen wir nur den Abstand eines Punktes auf g, z.b. P ( 3, zu E bestimmen. Dazu verwandeln wir die Ebenengleichung in Koordinatenform: E : 4x 3x + x 3 = d; Einsetzen von (0 0 0 liefert d = 0, also E : 4x 3x + x 3 = 0. Damit ist die HNF E : 4x 3x + x 3 = 0, 6 und wir finden d = = 8 6. Wir erhalten eine zweite Gerade h mit demselben Abstand, wenn h parallel zu E ist und ebenfalls durch P geht, z.b. ( 0 h : x = 3 + t( 3 ( ( 0 4 wegen 3 = 0. 3
6 6 FRANZ LEMMERMEYER (8 In einer Urne befinden sich 7 blaue und rote Kugeln. Es werden zwei Kugeln ohne Zurücklegen gezogen. Bestimmen Sie den Erwartungswert für die Anzahl der gezogenen blauen Kugeln. Man kann entweder 0, oder blaue Kugeln ziehen. Wir finden p(rr = = 0 306, p(bb = = 4 306, also ist 0 4 = 54. Damit haben wir Anz. blaue 0 p und wir finden E = = (9 Gegeben ist ein Punkt P und zwei nicht parallele Ebenen E und E in Parameterform. Beschreiben Sie ein Verfahren zur Bestimmung einer Koordinatengleichung derjenigen Ebene E, welche P enthält und senkrecht auf E und E steht. (a Berechne die Normalenvektoren n von E und n von E. (b Der Normelenvektor vecn einer Ebene E, welche senkrecht auf E steht, genügt n n = 0. Daher muss n n = n n = 0 sein, also können wir n = n n nehmen. (c Die Normalenform der Ebene E lautet ( x OP n = 0. Ausmultiplizieren liefert die Koordinatenform.
K2 KLAUSUR 2. Aufgabe Punkte (max) Punkte. (1) Bestimmen Sie die Ableitung von f(x) = 2 x
 K2 KLAUSUR 2 PFLICHTTEIL 202 Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () Bestimmen Sie die Ableitung von f(x) = 2 x 2 + 4. (2) Berechnen Sie das Integral 4 ( ) x 2 dx. (3) Lösen Sie die
K2 KLAUSUR 2 PFLICHTTEIL 202 Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () Bestimmen Sie die Ableitung von f(x) = 2 x 2 + 4. (2) Berechnen Sie das Integral 4 ( ) x 2 dx. (3) Lösen Sie die
www.mathe-aufgaben.com
 Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = x sin( x + ) Aufgabe : ( VP) Berechnen Sie das Integral
Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = x sin( x + ) Aufgabe : ( VP) Berechnen Sie das Integral
www.mathe-aufgaben.com
 Abiturprüfung Mathematik 00 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit Aufgabe : ( VP) f() e =. Bestimmen Sie eine Stammfunktion
Abiturprüfung Mathematik 00 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit Aufgabe : ( VP) f() e =. Bestimmen Sie eine Stammfunktion
G13 KLAUSUR 1. (1) (2 VP) Bilden Sie die erste Ableitung der Funktion f mit. f(x) = e 2x+1 x
 G3 KLAUSUR PFLICHTTEIL Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () (2 VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = e 2x+. x (2) (2 VP) Gegeben ist die Funktion f mit f(x)
G3 KLAUSUR PFLICHTTEIL Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () (2 VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = e 2x+. x (2) (2 VP) Gegeben ist die Funktion f mit f(x)
Abiturprüfung Mathematik 2012 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen
 Abiturprüfung Mathematik 202 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen [email protected] www.elearning-freiburg.de Pflichtteil 202 2 Aufgabe : Bilden Sie die erste Ableitung
Abiturprüfung Mathematik 202 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen [email protected] www.elearning-freiburg.de Pflichtteil 202 2 Aufgabe : Bilden Sie die erste Ableitung
 Abiturprüfung Mathematik 006 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f(x) sin(4x ). Aufgabe : ( VP) Geben Sie eine Stammfunktion
Abiturprüfung Mathematik 006 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f(x) sin(4x ). Aufgabe : ( VP) Geben Sie eine Stammfunktion
Abitur - Übung 1 Glege 9/11
 Abitur - Übung 1 Glege 9/11 Aufgabe 1.1) ganz-rationale Funktion 1.1.a) Bestimmen Sie eine ganz-rationale Funktion 3.Grades, deren Graph bei =4 die -Achse berührt und an deren Punkt (2/f(2)) die Tangente
Abitur - Übung 1 Glege 9/11 Aufgabe 1.1) ganz-rationale Funktion 1.1.a) Bestimmen Sie eine ganz-rationale Funktion 3.Grades, deren Graph bei =4 die -Achse berührt und an deren Punkt (2/f(2)) die Tangente
Aufgaben mit Ebenen. Parameterform Normalenform Koordinatenform. Darstellung = + r + s =0 ax 1 + bx 2 + cx 3 = d. Beispiel
 Aufgaben mit Ebenen Parameterform Normalenform Koordinatenform Spurpunkte Zur grafischen Darstellung der Ebene die Spurpunkt berechnen. Zwei Koordinaten gleich 0 setzen und jeweils die dritte ausrechnen.
Aufgaben mit Ebenen Parameterform Normalenform Koordinatenform Spurpunkte Zur grafischen Darstellung der Ebene die Spurpunkt berechnen. Zwei Koordinaten gleich 0 setzen und jeweils die dritte ausrechnen.
Abiturprüfung Mathematik 2014 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen
 Abiturprüfung Mathematik Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen [email protected] www.elearning-freiburg.de Pflichtteil Aufgabe : Bilden Sie die Ableitung der Funktion f
Abiturprüfung Mathematik Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen [email protected] www.elearning-freiburg.de Pflichtteil Aufgabe : Bilden Sie die Ableitung der Funktion f
K2 MATHEMATIK KLAUSUR 4. Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K MATHEMATIK KLAUSUR 4 17.03.017 Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max 0 0 10 10 60 Punkte Notenpunkte PT 1 3 4 5 6 7 * Summe P. (max 3 3 4 4 0 Punkte WT Ana A.1a b c A 1. Summe P. (max 6
K MATHEMATIK KLAUSUR 4 17.03.017 Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max 0 0 10 10 60 Punkte Notenpunkte PT 1 3 4 5 6 7 * Summe P. (max 3 3 4 4 0 Punkte WT Ana A.1a b c A 1. Summe P. (max 6
Lösungen zur Prüfung 2014: Pflichtteil
 Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte Kenntnisse: Analysis: Ableiten mit Produktregel, Integral mit Stammfunktion berechnen, Gleichung lösen, Kosinusfunktion, Nullstellen, Funktionswerte
Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte Kenntnisse: Analysis: Ableiten mit Produktregel, Integral mit Stammfunktion berechnen, Gleichung lösen, Kosinusfunktion, Nullstellen, Funktionswerte
Zusammenfassung Vektorrechnung und Komplexe Zahlen
 Zusammenfassung Vektorrechnung und Komplexe Zahlen Michael Goerz 8. April 006 Inhalt Vektoren, Geraden und Ebenen. Länge eines Vektors.......................... Skalarprodukt..............................
Zusammenfassung Vektorrechnung und Komplexe Zahlen Michael Goerz 8. April 006 Inhalt Vektoren, Geraden und Ebenen. Länge eines Vektors.......................... Skalarprodukt..............................
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
 Abiturprüfung Mathematik 0 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f() = ( sin() + 7) 5. Aufgabe : ( VP) Berechnen Sie eine Stammfunktion
Abiturprüfung Mathematik 0 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f() = ( sin() + 7) 5. Aufgabe : ( VP) Berechnen Sie eine Stammfunktion
Pflichtteil - Exponentialfunktion
 Pflichtteil - Eponentialfunktion Aufgabe (Ableiten) Bestimme die. und. Ableitung der folgenden Funktionen: a) f() = ln() + b) g() = e Aufgabe (Integrieren) Berechnen Sie die Integrale: a) e d b) c) h()
Pflichtteil - Eponentialfunktion Aufgabe (Ableiten) Bestimme die. und. Ableitung der folgenden Funktionen: a) f() = ln() + b) g() = e Aufgabe (Integrieren) Berechnen Sie die Integrale: a) e d b) c) h()
K2 MATHEMATIK KLAUSUR 1. Gesamtpunktzahl /30 Notenpunkte. (1) Bilden Sie die erste Ableitung der Funktion f mit f(x) = 1 + x ln(2x + 1).
 K MATHEMATIK KLAUSUR NACHTERMIN..6 Aufgabe 3 4 6 7 8 9 Punkte (max 3 3 4 4 Punkte Gesamtpunktzahl /3 Notenpunkte ( Bilden Sie die erste Ableitung der Funktion f mit f(x = + x ln(x +. ( Bestimmen Sie das
K MATHEMATIK KLAUSUR NACHTERMIN..6 Aufgabe 3 4 6 7 8 9 Punkte (max 3 3 4 4 Punkte Gesamtpunktzahl /3 Notenpunkte ( Bilden Sie die erste Ableitung der Funktion f mit f(x = + x ln(x +. ( Bestimmen Sie das
Hauptprüfung Abiturprüfung 2017 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 07 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com Mai 07 Aufgabe : (,5 VP) Bilden Sie die Ableitung
Hauptprüfung Abiturprüfung 07 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com Mai 07 Aufgabe : (,5 VP) Bilden Sie die Ableitung
Mathematik. Abiturprüfung 2014. Prüfungsteil A. Arbeitszeit: 90 Minuten. Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden.
 Mathematik Abiturprüfung 2014 Prüfungsteil A Arbeitszeit: 90 Minuten Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden. Zu den Themengebieten Analysis, Stochastik und Geometrie
Mathematik Abiturprüfung 2014 Prüfungsteil A Arbeitszeit: 90 Minuten Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden. Zu den Themengebieten Analysis, Stochastik und Geometrie
(Quelle Landungsbildungsserver BW) (Quelle Landungsbildungsserver BW)
 Aufgabe M01 Lösen Sie das lineare Gleichungssystem 7 2 2 3 5 4 4 7 Aufgabe M02 14 Stellen Sie den Vektor 5 als Linearkombination der drei Vektoren 7 0 1 5 1, 3 und 2 dar. 3 7 2 Aufgabe M03 0 2 Gegeben
Aufgabe M01 Lösen Sie das lineare Gleichungssystem 7 2 2 3 5 4 4 7 Aufgabe M02 14 Stellen Sie den Vektor 5 als Linearkombination der drei Vektoren 7 0 1 5 1, 3 und 2 dar. 3 7 2 Aufgabe M03 0 2 Gegeben
Pflichtteil... 2. Wahlteil Analysis 1... 6. Wahlteil Analysis 2... 9. Wahlteil Analysis 3... 13. Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analsis 1... 6 Wahlteil Analsis... 9 Wahlteil Analsis 3... 13 Wahlteil Analtische Geometrie 1... 16 Wahlteil Analtische Geometrie... 3 Lösungen: 006 Pflichtteil Lösungen zur Prüfung
Pflichtteil... Wahlteil Analsis 1... 6 Wahlteil Analsis... 9 Wahlteil Analsis 3... 13 Wahlteil Analtische Geometrie 1... 16 Wahlteil Analtische Geometrie... 3 Lösungen: 006 Pflichtteil Lösungen zur Prüfung
Hauptprüfung 2007 Aufgabe 3
 Hauptprüfung 7 Aufgabe. Gegeben sind die Funktionen f, g und h mit f (x) = sin x g (x) = sin(x) +, x h(x) = sin x Ihre Schaubilder sind Beschreiben Sie, wie hervorgehen.. Skizzieren Sie K g. K f, K f,
Hauptprüfung 7 Aufgabe. Gegeben sind die Funktionen f, g und h mit f (x) = sin x g (x) = sin(x) +, x h(x) = sin x Ihre Schaubilder sind Beschreiben Sie, wie hervorgehen.. Skizzieren Sie K g. K f, K f,
Aufgaben zur Vektorrechnung
 ) Liegt der Punkt P(; -; 2) auf der Geraden 4 g: x = 5+t 2? 6 2 Aufgaben zur Vektorrechnung 2) a) Wie groß ist der Abstand der Punkte A(4; 2; -4) und B(;-2;-4) zueinander? b) Gesucht wir der Mittelpunkt
) Liegt der Punkt P(; -; 2) auf der Geraden 4 g: x = 5+t 2? 6 2 Aufgaben zur Vektorrechnung 2) a) Wie groß ist der Abstand der Punkte A(4; 2; -4) und B(;-2;-4) zueinander? b) Gesucht wir der Mittelpunkt
Analytische Geometrie Aufgaben und Lösungen
 Analytische Geometrie Aufgaben und Lösungen http://www.fersch.de Klemens Fersch. Januar Inhaltsverzeichnis Punkte:Vektor - Abstand - Steigung - Mittelpunkt. Aufgaben....................................................
Analytische Geometrie Aufgaben und Lösungen http://www.fersch.de Klemens Fersch. Januar Inhaltsverzeichnis Punkte:Vektor - Abstand - Steigung - Mittelpunkt. Aufgaben....................................................
Pflichtteil Pflichtteil Pflichtteil Abiturprüfung Mathematik 2013 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen
 Abiturprüfung Mathematik Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen Pflichtteil Aufgabe : Bilden Sie die erste Ableitung der Funktion mit +5 ( VP) Verwende Produkt- und Kettenregel
Abiturprüfung Mathematik Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen Pflichtteil Aufgabe : Bilden Sie die erste Ableitung der Funktion mit +5 ( VP) Verwende Produkt- und Kettenregel
Abitur Mathematik Baden-Württemberg 2012
 Abitur Mathematik: Baden-Württemberg 2012 Im sind keine Hilfsmittel zugelassen. Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist die Verkettung der Potenzfunktion g(x)
Abitur Mathematik: Baden-Württemberg 2012 Im sind keine Hilfsmittel zugelassen. Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist die Verkettung der Potenzfunktion g(x)
Aufgabe A1. Aufgabe A2. Aufgabe A3 Die Funktion mit 3 3 hat die Nullstelle 1. Bestimmen Sie die weiteren Nullstellen.
 Aufgabe A1 Bilden Sie die Ableitung der Funktion mit 4. Aufgabe A2 Geben Sie eine Stammfunktion der Funktion mit an. Aufgabe A3 Die Funktion mit 3 3 hat die Nullstelle 1. Bestimmen Sie die weiteren Nullstellen.
Aufgabe A1 Bilden Sie die Ableitung der Funktion mit 4. Aufgabe A2 Geben Sie eine Stammfunktion der Funktion mit an. Aufgabe A3 Die Funktion mit 3 3 hat die Nullstelle 1. Bestimmen Sie die weiteren Nullstellen.
 Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit x f(x) = (x + 5) e. Aufgabe : ( VP) Gegeben ist die Funktion
Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit x f(x) = (x + 5) e. Aufgabe : ( VP) Gegeben ist die Funktion
Demo: Mathe-CD. Prüfungsaufgaben Mündliches Abitur. Analysis. Teilbereich 1: Ganzrationale Funktionen 1. März 2002
 Prüfungsaufgaben Mündliches Abitur Analysis Teilbereich : Ganzrationale Funktionen Hier nur Aufgaben als Demo Datei Nr. 9 März 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Vorwort Die in dieser Reihe von
Prüfungsaufgaben Mündliches Abitur Analysis Teilbereich : Ganzrationale Funktionen Hier nur Aufgaben als Demo Datei Nr. 9 März 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Vorwort Die in dieser Reihe von
K2 KLAUSUR Pflichtteil
 K2 KLAUSUR 10.02.2012 MATHEMATIK Pflichtteil: Aufgabe 1 2 3 4 5 6 7 8 Punkte (max) 2 2 3 4 5 3 4 3 Punkte Wahlteil Analysis Aufgabe a b c Punkte (max) 9 5 4 Punkte Wahlteil Geometrie Aufgabe a b c Punkte
K2 KLAUSUR 10.02.2012 MATHEMATIK Pflichtteil: Aufgabe 1 2 3 4 5 6 7 8 Punkte (max) 2 2 3 4 5 3 4 3 Punkte Wahlteil Analysis Aufgabe a b c Punkte (max) 9 5 4 Punkte Wahlteil Geometrie Aufgabe a b c Punkte
 Abiturprüfung Mathematik 004 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f() = + 3 Aufgabe : ( VP) Geben Sie eine Stammfunktion
Abiturprüfung Mathematik 004 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f() = + 3 Aufgabe : ( VP) Geben Sie eine Stammfunktion
Formelsammlung Analytische Geometrie
 Formelsammlung Analytische Geometrie http://www.fersch.de Klemens Fersch 6. August 6 Inhaltsverzeichnis 6 Analytische Geometrie 6. Vektorrechung in der Ebene......................................... 6..
Formelsammlung Analytische Geometrie http://www.fersch.de Klemens Fersch 6. August 6 Inhaltsverzeichnis 6 Analytische Geometrie 6. Vektorrechung in der Ebene......................................... 6..
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Abiturprüfung Mathematik 2005 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A
 Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
Inhalt der Lösungen zur Prüfung 2015:
 Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
Formelsammlung Analytische Geometrie
 Formelsammlung http://www.fersch.de Klemens Fersch. September 8 Inhaltsverzeichnis 6 6. Vektorrechung in der Ebene.............................................. 6.. Vektor - Abstand - Steigung - Mittelpunkt.................................
Formelsammlung http://www.fersch.de Klemens Fersch. September 8 Inhaltsverzeichnis 6 6. Vektorrechung in der Ebene.............................................. 6.. Vektor - Abstand - Steigung - Mittelpunkt.................................
6.6. Abstandsbestimmungen
 6.6. Abstandsbestimmungen 6. Geraden und Ebenen im Raum In diesem Kapitel werden folgende Fälle vorgestellt:. Abstand zweier Punkte. Abstand zweier paralleler Geraden 3. Abstand einer Ebene zu einer zur
6.6. Abstandsbestimmungen 6. Geraden und Ebenen im Raum In diesem Kapitel werden folgende Fälle vorgestellt:. Abstand zweier Punkte. Abstand zweier paralleler Geraden 3. Abstand einer Ebene zu einer zur
Aufgaben zu den Ableitungsregeln
 Aufgaben zu den Ableitungsregeln 1.0 Bestimmen Sie die Gleichung der Tangente im Punkt P(2;?) an den Graphen der folgenden Funktionen. 1.1 f(x) = x 2 2x 1.2 f(x) = (x + 1 2 )2 1.3 f(x) = 1 2 x2 3x 1 2.
Aufgaben zu den Ableitungsregeln 1.0 Bestimmen Sie die Gleichung der Tangente im Punkt P(2;?) an den Graphen der folgenden Funktionen. 1.1 f(x) = x 2 2x 1.2 f(x) = (x + 1 2 )2 1.3 f(x) = 1 2 x2 3x 1 2.
MATHEMATIK K1 EINSTIEGSARBEIT (OHNE GTR)
 MATHEMATIK K EINSTIEGSARBEIT (OHNE GTR Einige Stichworte: Bruchrechnen: bei Addition und Subtraktion beide Brüche auf den Hauptnenner bringen Man teilt durch einen Bruch, indem man mit dessen Kehrwert
MATHEMATIK K EINSTIEGSARBEIT (OHNE GTR Einige Stichworte: Bruchrechnen: bei Addition und Subtraktion beide Brüche auf den Hauptnenner bringen Man teilt durch einen Bruch, indem man mit dessen Kehrwert
Übungen 4 Gerade, Ebene - Kurze Aufgaben Ebene: Spurpunkte, Spurgerade, Achsenabschnittsform Gerade, Ebene U04 Übungen 4 - Seite 1 (von 5)
 Übungen Gerade, Ebene - Kurze Aufgaben ) Gesucht ist Normalenform einer Ebene, die den Punkt P( ) enthält und auf der x- Achse senkrecht steht. ) Gegeben ist die Ebene E: x ( Gesucht ist der Winkel zwischen
Übungen Gerade, Ebene - Kurze Aufgaben ) Gesucht ist Normalenform einer Ebene, die den Punkt P( ) enthält und auf der x- Achse senkrecht steht. ) Gegeben ist die Ebene E: x ( Gesucht ist der Winkel zwischen
1.3 Berechnen Sie die Koordinaten der Wendepunkte des Schaubildes der Funktion f mit f( x) x 6x 13
 Pflichtteil Aufgabe BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit 4 f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ()) an das Schaubild der Funktion
Pflichtteil Aufgabe BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit 4 f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ()) an das Schaubild der Funktion
K2 ÜBUNGSBLATT 2 F. LEMMERMEYER
 K2 ÜBUNGSBLATT 2 F. LEMMERMEYER Aufgabe 1. Hier ein knappes Beispiel, wie man einen Punkt P an einer Geraden g spiegelt (Wer sich gerne was merkt: Lotfußpunkte auf Ebene mit Lotgerade, Lotfußpunkte auf
K2 ÜBUNGSBLATT 2 F. LEMMERMEYER Aufgabe 1. Hier ein knappes Beispiel, wie man einen Punkt P an einer Geraden g spiegelt (Wer sich gerne was merkt: Lotfußpunkte auf Ebene mit Lotgerade, Lotfußpunkte auf
1 aus allen 3 Zeilen folgt t = 1, also liegt A auf g. Orsvektor und Richtungsvektor der Geraden werden übernommen, den zweiten Spannvektor bekommt
 Lösungsskizzen Klassische Aufgaben Lösung zu Abi - PTV Punktprobe: = + t aus allen Zeilen folgt t =, also liegt A auf g. Richtungsvektor von g: u = ; Normalenvektor von E: n = Da die n und u Vielfache
Lösungsskizzen Klassische Aufgaben Lösung zu Abi - PTV Punktprobe: = + t aus allen Zeilen folgt t =, also liegt A auf g. Richtungsvektor von g: u = ; Normalenvektor von E: n = Da die n und u Vielfache
3 Differenzialrechnung
 Differenzialrechnung 3 Differenzialrechnung 3.1 Ableitungsregeln Übersicht Beispiel Vorgehen Potenzfunktionen f(x) = x 4 f (x) = 4 x 3 f(x) = x f (x) = 1 x 0 = 1 f(x) = x Hochzahl f (x) = Hochzahl x Hochzahl
Differenzialrechnung 3 Differenzialrechnung 3.1 Ableitungsregeln Übersicht Beispiel Vorgehen Potenzfunktionen f(x) = x 4 f (x) = 4 x 3 f(x) = x f (x) = 1 x 0 = 1 f(x) = x Hochzahl f (x) = Hochzahl x Hochzahl
Pflichtteil. Baden-Württemberg Aufgabe 1. Aufgabe 2. Musterlösung. Abitur Mathematik Baden-Württemberg Abitur Mathematik: Musterlösung
 Abitur Mathematik: Baden-Württemberg 2013 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer ganzrationalen Funktion u(x) = 2x 2 + 5x und einer Verkettung
Abitur Mathematik: Baden-Württemberg 2013 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer ganzrationalen Funktion u(x) = 2x 2 + 5x und einer Verkettung
Kursstufe K
 Kursstufe K 6..6 Schreiben Sie die Ergebnisse bitte kurz unter die jeweiligen Aufgaben, lösen Sie die Aufgaben auf einem separaten Blatt. Aufgabe : Berechnen Sie das Integral Lösungsvorschlag : exp(3x
Kursstufe K 6..6 Schreiben Sie die Ergebnisse bitte kurz unter die jeweiligen Aufgaben, lösen Sie die Aufgaben auf einem separaten Blatt. Aufgabe : Berechnen Sie das Integral Lösungsvorschlag : exp(3x
Viele Aufgaben sind ähnlich, beim Bearbeiten ist genaues Hinsehen
 Die Lerndominos sind ein idealer Weg, um Gelerntes zu vertiefen. Das Domino wird mit der Start-Karte begonnen, dann werden die passenden Antwort-Karten angelegt bis die Ziel-Karte erreicht ist. Bewährt
Die Lerndominos sind ein idealer Weg, um Gelerntes zu vertiefen. Das Domino wird mit der Start-Karte begonnen, dann werden die passenden Antwort-Karten angelegt bis die Ziel-Karte erreicht ist. Bewährt
PFLICHTTEIL NT = e x (x+2) = x+2 Oder Umschreiben: f(x) = 1. = (x 2 e x ) 1, und dann Kettenregel
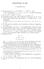 PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
Abiturprüfung Mathematik 2007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Mathematik Name: Nr.5 K2 Punkte: /30 Note: Schnitt:
 Pflichtteil (etwa min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden dürfen.) Aufgabe 1: [P] Bestimmen
Pflichtteil (etwa min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden dürfen.) Aufgabe 1: [P] Bestimmen
Aus folgt: 1; 3 Eingesetzt in : $$$$$ #! * 1 + ; # $$$$$$$ # $$$$$ 2 $$$$$! * 3 Der Bildpunkt hat die Koordinaten
 Abituraufgaben Analytische Geometrie (Pflichtteil) ab Lösung A6/ Wir stellen die gegebene Normalengleichung von in die Koordinatengleichung um und bilden. Im Gleichungssystem mit drei Unbekannten und zwei
Abituraufgaben Analytische Geometrie (Pflichtteil) ab Lösung A6/ Wir stellen die gegebene Normalengleichung von in die Koordinatengleichung um und bilden. Im Gleichungssystem mit drei Unbekannten und zwei
Mathematik Name: Klausur Nr.6 K1 Punkte: /30 Note: Schnitt:
 K1 Punkte: /30 Note: Schnitt: 0.1.18 Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet
K1 Punkte: /30 Note: Schnitt: 0.1.18 Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet
Lernkarten. Analytische Geometrie. 6 Seiten
 Lernkarten Analytische Geometrie 6 Seiten Zum Ausdrucken muss man jeweils eine Vorderseite drucken, dann das Blatt wenden, nochmals einlegen und die Rückseite drucken. Am besten druckt man die Karten auf
Lernkarten Analytische Geometrie 6 Seiten Zum Ausdrucken muss man jeweils eine Vorderseite drucken, dann das Blatt wenden, nochmals einlegen und die Rückseite drucken. Am besten druckt man die Karten auf
MATHEMATIK KLAUSUR V. Gesamtpunktzahl /30 Notenpunkte. (1) Bestimmen Sie die erste Ableitung der folgenden Funktionen: f(x) = 3x sin(x) + x ln(2x)
 MATHEMATIK KLAUSUR V 296216 Aufgabe 1 2 3 4 5 6 7 8 9 Punkte (max 4 2 3 3 3 3 5 6 1 Punkte Gesamtpunktzahl /3 Notenpunkte (1 Bestimmen Sie die erste Ableitung der folgenden Funktionen: (2 Berechnen Sie
MATHEMATIK KLAUSUR V 296216 Aufgabe 1 2 3 4 5 6 7 8 9 Punkte (max 4 2 3 3 3 3 5 6 1 Punkte Gesamtpunktzahl /3 Notenpunkte (1 Bestimmen Sie die erste Ableitung der folgenden Funktionen: (2 Berechnen Sie
d 2 b 2 c 2 d 3 b 3 c 3 , D a 1 d 1 c 1 v 3 Definiton (Verbindungsvektor): Zwei Punkte A(a 1 a 2 a 3 ) und B(b 1 b 2 b 3 ) legen den Vektor b 1 a 1
 2008/2009 Das Wichtigste in Kürze Klasse 3 Lineare Gleichungssysteme und Determinanten Definiton (Lineare Gleichungssysteme: Lineare Gleichungssysteme löst man entweder mit dem Gauß-Algorithmus oder nach
2008/2009 Das Wichtigste in Kürze Klasse 3 Lineare Gleichungssysteme und Determinanten Definiton (Lineare Gleichungssysteme: Lineare Gleichungssysteme löst man entweder mit dem Gauß-Algorithmus oder nach
Aufgabe A6/13. Aufgabe A7/13. Aufgabe A6/14
 Aufgabe A6/ Gegeben sind die Ebene 4 : Abituraufgaben Analytische Geometrie (Pflichtteil) ab und : 8. Bestimmen Sie eine Gleichung der Schnittgeraden. (Quelle Abitur BW Aufgabe 6) Aufgabe A7/ Gegeben sind
Aufgabe A6/ Gegeben sind die Ebene 4 : Abituraufgaben Analytische Geometrie (Pflichtteil) ab und : 8. Bestimmen Sie eine Gleichung der Schnittgeraden. (Quelle Abitur BW Aufgabe 6) Aufgabe A7/ Gegeben sind
www.mathe-aufgaben.com
 Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit sin() f() =. Aufgabe : ( VP) Berechnen Sie das Integral ( )
Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit sin() f() =. Aufgabe : ( VP) Berechnen Sie das Integral ( )
Bayern Musterlösung zu Klausur Analysis, Aufgabengruppe I
 Diese Lösung wurde erstellt von Tanja Reimbold. Sie ist keine offizielle Lösung des Bayerischen Staatsministeriums für Unterricht und Kultus. Teil 1 Aufgabe 1 Definitionsbereich: Bestimmung der Nullstelle
Diese Lösung wurde erstellt von Tanja Reimbold. Sie ist keine offizielle Lösung des Bayerischen Staatsministeriums für Unterricht und Kultus. Teil 1 Aufgabe 1 Definitionsbereich: Bestimmung der Nullstelle
DAS ABI-PFLICHTTEIL Büchlein
 DAS ABI-PFLICHTTEIL Büchlein für Baden-Württemberg Alle Originalaufgaben Haupttermine 004 0 Ausführlich gerechnete und kommentierte Lösungswege Mit vielen Zusatzhilfen X π Von: Jochen Koppenhöfer und Pascal
DAS ABI-PFLICHTTEIL Büchlein für Baden-Württemberg Alle Originalaufgaben Haupttermine 004 0 Ausführlich gerechnete und kommentierte Lösungswege Mit vielen Zusatzhilfen X π Von: Jochen Koppenhöfer und Pascal
MATHEMATIK K1. Aufgabe F Punkte (max) Punkte. Gesamtpunktzahl /30 Notenpunkte
 MATHEMATIK K1.06.015 Aufgabe 1 5 6 7 8 9 10 F Punkte (max 11 1 1 Punkte Gesamtpunktzahl /0 Notenpunkte Für vorbildliche Darstellung wird ein Extrapunkt vergeben. (1 Bestimmen sie die ersten beiden Ableitungen
MATHEMATIK K1.06.015 Aufgabe 1 5 6 7 8 9 10 F Punkte (max 11 1 1 Punkte Gesamtpunktzahl /0 Notenpunkte Für vorbildliche Darstellung wird ein Extrapunkt vergeben. (1 Bestimmen sie die ersten beiden Ableitungen
www.mathe-aufgaben.com
 Abiturprüfung Mathematik 008 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe 1: ( VP) x Gegeben ist die Funktion f mit f(x). x Bilden Sie die Ableitung von f und fassen Sie diese so weit wie
Abiturprüfung Mathematik 008 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe 1: ( VP) x Gegeben ist die Funktion f mit f(x). x Bilden Sie die Ableitung von f und fassen Sie diese so weit wie
b) [2P] 7x Lösungsvorschlag 1: f '(x) = cos 3x 6x = 6x cos 3x
![b) [2P] 7x Lösungsvorschlag 1: f '(x) = cos 3x 6x = 6x cos 3x b) [2P] 7x Lösungsvorschlag 1: f '(x) = cos 3x 6x = 6x cos 3x](/thumbs/58/42387852.jpg) K1 Punkte: / Note: Schnitt:.10.1 Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden
K1 Punkte: / Note: Schnitt:.10.1 Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden
Inhalt der Lösungen zur Prüfung 2012:
 Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analsis... 8 Wahlteil Analsis... Wahlteil Analsis... 4 Wahlteil Analtische Geometrie... 8 Wahlteil Analtische Geometrie... Pflichtteil Lösungen
Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analsis... 8 Wahlteil Analsis... Wahlteil Analsis... 4 Wahlteil Analtische Geometrie... 8 Wahlteil Analtische Geometrie... Pflichtteil Lösungen
K2 MATHEMATIK KLAUSUR 2. Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K2 MATHEMATIK KLAUSUR 2 06.12.2013 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 27 15 15 3 60 Punkte Notenpunkte PT 1 2 3 4 5 6 7 8 P. (max 2 3 2 4 5 3 4 4 Punkte WT Ana a b Summe P. (max 8 7
K2 MATHEMATIK KLAUSUR 2 06.12.2013 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 27 15 15 3 60 Punkte Notenpunkte PT 1 2 3 4 5 6 7 8 P. (max 2 3 2 4 5 3 4 4 Punkte WT Ana a b Summe P. (max 8 7
1.3 Berechnen Sie die Koordinaten der Wendepunkte des Schaubildes der Funktion f mit f( x) x 6x 13
 Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
Inhalt der Lösungen zur Prüfung 2011:
 Inhalt der Lösungen zur Prüfung : Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 6 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 6 Pflichtteil Lösungen zur Prüfung
Inhalt der Lösungen zur Prüfung : Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 6 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 6 Pflichtteil Lösungen zur Prüfung
13. Klasse TOP 10 Grundwissen 13 Geradengleichungen 01
 . Klasse TOP 0 Grundwissen Geradengleichungen 0 Punkt-Richtungs-Form Geraden sind gegeben durch einen Aufpunkt A (mit Ortsvektor a) auf der Geraden und einen Richtungsvektor u: x = a + λ u, λ IR. (Interpretation:
. Klasse TOP 0 Grundwissen Geradengleichungen 0 Punkt-Richtungs-Form Geraden sind gegeben durch einen Aufpunkt A (mit Ortsvektor a) auf der Geraden und einen Richtungsvektor u: x = a + λ u, λ IR. (Interpretation:
A Vektorrechnung. B Geraden und Ebenen
 A Vektorrechnung Seite 1 Lineare Gleichungssysteme... 4 2 Gauß-Algorithmus... 6 3 Vektoren... 10 4 Vektorberechnungen und Vektorlängen... 12 5 Linearkombination und Einheitsvektor... 16 6 Lineare Abhängigkeit
A Vektorrechnung Seite 1 Lineare Gleichungssysteme... 4 2 Gauß-Algorithmus... 6 3 Vektoren... 10 4 Vektorberechnungen und Vektorlängen... 12 5 Linearkombination und Einheitsvektor... 16 6 Lineare Abhängigkeit
5. Geraden und Ebenen im Raum 5.1. Lineare Abhängigkeit und Unabhängigkeit von Vektoren
 5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
Abiturprüfung Mathematik 2008 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe Für jedes t f t () + t R ist die Funktion f t gegeben durch = mit R. Das Schaubild von f t heißt K t.. (6 Punkte)
Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe Für jedes t f t () + t R ist die Funktion f t gegeben durch = mit R. Das Schaubild von f t heißt K t.. (6 Punkte)
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... 7 Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analytische Geometrie... 9 Wahlteil Analytische Geometrie... 008 Pflichtteil Lösungen zur Prüfung 008: Pflichtteil
Pflichtteil... Wahlteil Analysis... 7 Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analytische Geometrie... 9 Wahlteil Analytische Geometrie... 008 Pflichtteil Lösungen zur Prüfung 008: Pflichtteil
e-funktionen f(x) = e x2
 e-funktionen f(x) = e x. Smmetrie: Der Graph ist achsensmmetrisch, da f( x) = f(x).. Nullstellen: Bed.: f(x) = 0 Es sind keine Nullstellen vorhanden, da e x stets positiv ist. 3. Extrema: notw. Bed.: f
e-funktionen f(x) = e x. Smmetrie: Der Graph ist achsensmmetrisch, da f( x) = f(x).. Nullstellen: Bed.: f(x) = 0 Es sind keine Nullstellen vorhanden, da e x stets positiv ist. 3. Extrema: notw. Bed.: f
Impressum. Torsten Möller Augustastraße Flensburg. 1. Auflage. Idee und Ausführung in L A TEX: Torsten Möller
 Impressum Torsten Möller Augustastraße 6 4937 Flensburg. Auflage 8 Idee und Ausführung in L A TEX: Torsten Möller Umschlaggestaltung: Torsten Möller Illustrationen: Torsten Möller Das Werk, einschließlich
Impressum Torsten Möller Augustastraße 6 4937 Flensburg. Auflage 8 Idee und Ausführung in L A TEX: Torsten Möller Umschlaggestaltung: Torsten Möller Illustrationen: Torsten Möller Das Werk, einschließlich
K2 KLAUSUR MATHEMATIK
 K2 KLAUSUR MATHEMATIK NACHTERMIN 16.02.2012 Pflichtteil: Aufgabe 1 2 3 4 5 6 7 8 (max) 2 2 3 4 5 3 4 3 Wahlteil Analysis Aufgabe a b c (max) 10 3 5 Wahlteil Geometrie Aufgabe a b c (max) 7 4 5 Gesamtpunktzahl
K2 KLAUSUR MATHEMATIK NACHTERMIN 16.02.2012 Pflichtteil: Aufgabe 1 2 3 4 5 6 7 8 (max) 2 2 3 4 5 3 4 3 Wahlteil Analysis Aufgabe a b c (max) 10 3 5 Wahlteil Geometrie Aufgabe a b c (max) 7 4 5 Gesamtpunktzahl
Geometrie / Lineare Algebra
 6 Geometrie / Lineare Algebra Vektoren und Rechenregeln Länge, Winkel, Abstand Darstellung von Geraden und Ebenen Umformungen Abstandsbestimmungen Lage, Schnitte, Schnittwinkel Spiegelungen E-Mail: [email protected],
6 Geometrie / Lineare Algebra Vektoren und Rechenregeln Länge, Winkel, Abstand Darstellung von Geraden und Ebenen Umformungen Abstandsbestimmungen Lage, Schnitte, Schnittwinkel Spiegelungen E-Mail: [email protected],
M I N I S T E R I U M F Ü R K U L T U S, J U G E N D U N D S P O R T. Berufsoberschule (BOS) SO/TO/WO. 2 2x
 Mathematik (43) Musteraufgabe Gruppe I: Analysis ohne Hilfsmittel ab 07 Seite /3 Gegeben ist die Funktion f mit 4 3 f(x) x x 3x 4x ; xir. 6 Bestimmen Sie den Bereich, in dem das Schaubild von f rechtsgekrümmt
Mathematik (43) Musteraufgabe Gruppe I: Analysis ohne Hilfsmittel ab 07 Seite /3 Gegeben ist die Funktion f mit 4 3 f(x) x x 3x 4x ; xir. 6 Bestimmen Sie den Bereich, in dem das Schaubild von f rechtsgekrümmt
Crashkurs sin 2 x + 5 cos 2 x = sin 2 x 2 sin x = 3
 Crashkurs. Funktion mit Parameter/Ortskurve - Wahlteil Analysis.. Gegeben sei für t > die Funktion f t durch f t (x) = 4 x 4t x 2 ; x R\{}. a) Welche Scharkurve geht durch den Punkt Q( 4)? b) Bestimme
Crashkurs. Funktion mit Parameter/Ortskurve - Wahlteil Analysis.. Gegeben sei für t > die Funktion f t durch f t (x) = 4 x 4t x 2 ; x R\{}. a) Welche Scharkurve geht durch den Punkt Q( 4)? b) Bestimme
MATHEMATIK K1. Gesamtpunktzahl /30 Notenpunkte
 MATHEMATIK K1 21.11.2013 Aufgabe 1 2 3 4 5 6 7 Punkte (max) 6 3 4 4 2 10 1 Punkte Gesamtpunktzahl /30 Notenpunkte Der GTR ist nur für die Lösung der Textaufgabe (und zur Kontrolle der andern) zugelassen.
MATHEMATIK K1 21.11.2013 Aufgabe 1 2 3 4 5 6 7 Punkte (max) 6 3 4 4 2 10 1 Punkte Gesamtpunktzahl /30 Notenpunkte Der GTR ist nur für die Lösung der Textaufgabe (und zur Kontrolle der andern) zugelassen.
Abituraufgaben allg. bildendes Gymnasium Pflichtteil 2007 BW Aufgabe A1
 Aufgabe A1 Bilden Sie die Ableitung der Funktion mit 1. Aufgabe A2 Berechnen Sie das Integral. Aufgabe A3 Lösen Sie die Gleichung 2 0. Aufgabe A4 Gegeben ist die Funktion mit. a) Bestimmen Sie die Punkte
Aufgabe A1 Bilden Sie die Ableitung der Funktion mit 1. Aufgabe A2 Berechnen Sie das Integral. Aufgabe A3 Lösen Sie die Gleichung 2 0. Aufgabe A4 Gegeben ist die Funktion mit. a) Bestimmen Sie die Punkte
8. Übungsblatt zur Mathematik I für Maschinenbau
 Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 8. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS / 6..-.. Aufgabe G (Matrixinversion mit Gauß-Algorithmus
Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 8. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS / 6..-.. Aufgabe G (Matrixinversion mit Gauß-Algorithmus
1.2 Berechne den Inhalt der Fläche, die das Schaubild von mit 5P der -Achse einschließt.
 Diese Aufgaben sind zu bearbeiten. Sie können nicht abgewählt werden. Aufgabe A1 1. Gegeben ist die Funktion mit 2 3; 1.1 Eine der folgenden Abbildung zeigt das Schaubild. 6P Untersuche für jede der Abbildungen,
Diese Aufgaben sind zu bearbeiten. Sie können nicht abgewählt werden. Aufgabe A1 1. Gegeben ist die Funktion mit 2 3; 1.1 Eine der folgenden Abbildung zeigt das Schaubild. 6P Untersuche für jede der Abbildungen,
Hauptprüfung Abiturprüfung 2014 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 04 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 04 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 04 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 04 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Hauptprüfung Abiturprüfung 2016 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 06 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 06 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 06 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 06 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com
Passerellen-Prüfungen 2007 Mathematik: 4 Stunden (3 Seiten)
 Punkte: Note: BME ISME MfB MSE Berner Maturitätsschule für Erwachsene Interstaatliche Maturitätsschule für Erwachsene St. Gallen/Sargans Maturitätsschule für Berufstätige, Basel Maturitätsschule für Erwachsene,
Punkte: Note: BME ISME MfB MSE Berner Maturitätsschule für Erwachsene Interstaatliche Maturitätsschule für Erwachsene St. Gallen/Sargans Maturitätsschule für Berufstätige, Basel Maturitätsschule für Erwachsene,
3. Übungsblatt Aufgaben mit Lösungen
 . Übungsblatt Aufgaben mit Lösungen Aufgabe 6: Gegeben seien die Ebene E : 4x + x + 8 =, der Punkt P = ( und die Gerade H : x(λ = (4,, + λ(,,, λ R. (a Bestimmen Sie eine Gerade durch den Punkt P, die senkrecht
. Übungsblatt Aufgaben mit Lösungen Aufgabe 6: Gegeben seien die Ebene E : 4x + x + 8 =, der Punkt P = ( und die Gerade H : x(λ = (4,, + λ(,,, λ R. (a Bestimmen Sie eine Gerade durch den Punkt P, die senkrecht
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
E : y=0. g : x= ) +s ( 1 1. d = 17. Partnerquiz Punkte, Geraden und Ebenen im Raum Ausschneidebogen
 Partnerquiz Aufgabe A Partnerquiz Aufgabe B Gib eine Ebenengleichung in Parameterform für die xz-ebene an. Gib eine Ebenengleichung in Koordinatenform für die xz-ebene an. E : y= E : x=r +s Partnerquiz
Partnerquiz Aufgabe A Partnerquiz Aufgabe B Gib eine Ebenengleichung in Parameterform für die xz-ebene an. Gib eine Ebenengleichung in Koordinatenform für die xz-ebene an. E : y= E : x=r +s Partnerquiz
K2 MATHEMATIK KLAUSUR 3
 K2 MATHEMATIK KLAUSUR 3 NACHTERMIN 2..23 Aufgabe PT WTA WTGS Gesamtpunktzahl Punkte (max 3 5 5 6 Punkte Notenpunkte PT 2 3 4 5 6 7 8 9 P. (max 2 2 3 4 5 3 4 4 3 Punkte WT Ana a b c Summe P. (max 8 4 3
K2 MATHEMATIK KLAUSUR 3 NACHTERMIN 2..23 Aufgabe PT WTA WTGS Gesamtpunktzahl Punkte (max 3 5 5 6 Punkte Notenpunkte PT 2 3 4 5 6 7 8 9 P. (max 2 2 3 4 5 3 4 4 3 Punkte WT Ana a b c Summe P. (max 8 4 3
Bayern Aufgabe 1. Abitur Mathematik: Musterlösung. V = 1 G h, wobei G die Fläche des quadratischen Bodens und h die Höhe V = = 384 [VE]
![Bayern Aufgabe 1. Abitur Mathematik: Musterlösung. V = 1 G h, wobei G die Fläche des quadratischen Bodens und h die Höhe V = = 384 [VE] Bayern Aufgabe 1. Abitur Mathematik: Musterlösung. V = 1 G h, wobei G die Fläche des quadratischen Bodens und h die Höhe V = = 384 [VE]](/thumbs/80/80887276.jpg) Abitur Mathematik: Bayern 2 Aufgabe a). SCHRITT: KOORDINATEN DES PUNKTS B ANGEBEN 2 2 OB = OA + AB = OA + DC = ( ) + ( 2) = ( 2) B(2 2 ) 2. SCHRITT: VOLUMEN BERECHNEN V = G h, wobei G die Fläche des quadratischen
Abitur Mathematik: Bayern 2 Aufgabe a). SCHRITT: KOORDINATEN DES PUNKTS B ANGEBEN 2 2 OB = OA + AB = OA + DC = ( ) + ( 2) = ( 2) B(2 2 ) 2. SCHRITT: VOLUMEN BERECHNEN V = G h, wobei G die Fläche des quadratischen
Geometrie / Lineare Algebra. Rechenregeln. Geometrische Deutung. Vektoren
 Vektoren Geometrie / Lineare Algebra Vektoren und Rechenregeln Länge, Winkel, Abstand Darstellung von Geraden und Ebenen Umformungen Abstandsbestimmungen Lage, Schnitte, Schnittwinkel Spiegelungen E-Mail:
Vektoren Geometrie / Lineare Algebra Vektoren und Rechenregeln Länge, Winkel, Abstand Darstellung von Geraden und Ebenen Umformungen Abstandsbestimmungen Lage, Schnitte, Schnittwinkel Spiegelungen E-Mail:
Mathematik-Aufgabenpool > Grundaufgaben zur Vektorrechnung I
 Michael Buhlmann Mathematik-Aufgabenpool > Grundaufgaben zur Vektorrechnung I Einleitung: Elemente der Vektorrechnung im dreidimensionalen reellen kartesischen x -x -x 3-Koordinatensystem sind Punkte P(p
Michael Buhlmann Mathematik-Aufgabenpool > Grundaufgaben zur Vektorrechnung I Einleitung: Elemente der Vektorrechnung im dreidimensionalen reellen kartesischen x -x -x 3-Koordinatensystem sind Punkte P(p
Abitur 2011 G8 Musterabitur Mathematik Geometrie VI
 Seite http://www.abiturloesung.de/ Seite Abitur G8 Musterabitur Mathematik Geometrie VI In einem kartesischen Koordinatensystem ist ein Würfel W der Kantenlänge gegeben. Die Eckpunkte G ( ) und D ( ) legen
Seite http://www.abiturloesung.de/ Seite Abitur G8 Musterabitur Mathematik Geometrie VI In einem kartesischen Koordinatensystem ist ein Würfel W der Kantenlänge gegeben. Die Eckpunkte G ( ) und D ( ) legen
Pflichtteil. Baden-Württemberg Aufgabe 1. Aufgabe 2. Musterlösung. Abitur Mathematik Baden-Württemberg Abitur Mathematik: Musterlösung
 Abitur Mathematik: Baden-Württemberg 14 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer einfachen Funktion u(x) = x und einer Verkettung v(x) = e x
Abitur Mathematik: Baden-Württemberg 14 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer einfachen Funktion u(x) = x und einer Verkettung v(x) = e x
Pflichtteilaufgaben zu Gegenseitige Lage, Abstand, Baden-Württemberg
 Pflichtteilaufgaben zu Gegenseitige Lage, Abstand, Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz wwwmathe-aufgabencom September 6 Abituraufgaben (Haupttermin) Aufgabe
Pflichtteilaufgaben zu Gegenseitige Lage, Abstand, Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz wwwmathe-aufgabencom September 6 Abituraufgaben (Haupttermin) Aufgabe
K2 MATHEMATIK KLAUSUR. Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K2 MATHEMATIK KLAUSUR 4.02.204 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 28 5 5 2 60 Punkte Notenpunkte PT 2 3 4 5 6 7 8 9 P. (max 2 2 2 4 5 3 3 4 3 Punkte WT Ana A.a b A2.a b Summe P. (max
K2 MATHEMATIK KLAUSUR 4.02.204 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 28 5 5 2 60 Punkte Notenpunkte PT 2 3 4 5 6 7 8 9 P. (max 2 2 2 4 5 3 3 4 3 Punkte WT Ana A.a b A2.a b Summe P. (max
