Eigenschaften trigonometrischer Reihen. Trigonometrische Reihen. Reihenentwicklung. Reihenentwicklung. Fourierreihenentwicklung

3. Spezielle diskrete Wahrscheinlichkeitsmodelle

Lhrsuhl ür Emrsch Wrschasorschug ud Ökoomr Dr. Rolad Füss Sask II: Schlßd Sask SS 007 3. Szll dskr Wahrschlchksmodll 3. Glchvrlug Glchvrlug: B dr Glchvrlug ha jds Ergs d glch Erswahrschlchk: Wahrschlchksuko:

Mikrofon. Vorverstärker. Digitales Signal (zeit- und wertediskret) Analoges Signal (zeit- und wertekontinuierlich) Digitalisierung

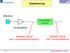Dglrug Mroo Alog/Dgl- Umzr Vorvrärr Alog Sgl z- ud wrourlch Dgl Sgl z- ud wrdr Sld Sglvrrbug, G. Hrch Abug Vorvrärr p Abug P P b H =/ / Frquz Zur Abug d log Mroogl rolg zuäch log plrug, dm d Abhorm > mx

Einschub: Fourier-Transformation

Ermlhys III TU Dormud WS/4 Shu Kh @ TU - Dormud. d Kl Eschub: Fourr-Trsormo Prodsch Vorgäg Nur ud Tch Erdroo, Hrzschlg, Schll, Lch, Schwgrs... movr d Zrlgug s Vorggs d blg Frquz. Bm Lch gschh ds m Prsm

Wir betrachten hier nur den Fall m,n N, also m>0 und n>0. Die anderen Fälle, bei denen m=0 oder n=0 ist, können leicht selbst gelöst werden.

Übugsaufgab Fourirrih Mahmaik III M Prof. Dr. B. Grabowski Bla 6 grabowski@hw-saarlad.d Lösug zu Übugs-Bla 6 Zu Aufgab Wir brach hir ur d Fall m, N, also m> ud >. Di adr Fäll, bi d m odr is, kö lich slbs

dt ist stabil, wenn es für gegebene Werte ε > 0 und t 0 einen Wert η = η( ε,t 0 ) gibt, so daß jede

. Sbl ud sbl soär Zusäd M urschd sbl ud sbl soär Zusäd, j chdm, ob ds Sysm ch Auslkug dr Näh dsr Zusäd vrblb odr ch. Khr ds Sysm ür d ursprüglch Zusd zurück, s s symposch sbl. Echs mchschs Alogo: sbl sbl

Inhalt: Modellbildung technischer Systeme Zustandsraum

Modllbldug hhr Sym Zuadraum hw aar Ihal:. Dagoalform. Jorda-Normalform 3. Blokdagoalform 4. Zuammfaug zu d Dagoalform 5. Traformaorgl dr Zuadglhug auf Normalform 6. Awdug kaohr Traformao Qull: Ubhau Barbara

L Hospital - Lösungen der Aufgaben B1

L Hospital - Lösug dr Aufgab B Gsucht: = Übrprüf ob di Rgl vo L'Hospital agwdt wrd darf Für ght dr Zählr gg L'Hospital darf agwdt wrd, Für ght dr Nr gg = da Zählr ud Nr gg gh Zählr ud Nr diffrzir: ' =

Lösungen zu Übungsblatt 5 Fourier-Integral

Zu Aufgab : Si f() für - < und f() sons. Zu a) Es gil: F( d d jω j j j [ ] D.h., di Spkralfunkion F ( zu inr sückwis konsann Funkion f() is in grad Funkion. Si is in gdämpf Schwingung, drn Asympon für

zur Freiwilligenarbeit im Alter

12 0 2 r o A s r v r k G ü f hr d J s h ch zwsc s pä rä o r Eu d o S d u r A h k m S c F b F & r g D rw F r zu D & Fk zur Frwgrb m Ar V är ud Msch s wchg Bräg für d Gsschf. Ds rch vo dr Arb urschdchs Vr

= G. 2.1 Beschreibung linearer Systeme im Zeitbereich. 24 Beschreibung linearer Systeme im Zeitbereich. Parallelschaltung mit gemeinsamem Eingang G 1

4 Bschrbng lnrr ysm m Zbrch Prlllschlng m gmnsmm ngng x + x ± x ± x x ± x gnrlllschlng ücführschlng x x m rlgn ns rzwgngsns vor nn Bloc / rlgn ns rzwgngsns hnr nn Bloc + - + - rlgn nr Mschsll hnr nn Bloc.

1.3.9 Ko- und kontravariante Darstellung vektoriell betrachtet

4..9 Ko- und ontravarant Darstun vtor btrachtt Mt H dr Bass aus Gchun.. schrbn wr ür nn bbn Vtor :... ndrsts t auch:... so schßt an Vrch au:..4 d.h. n dr Darstun snd d tatsächch as d ontravarantn Koponntn

Das Max-Flow Min-Cut Theorem

Das Max-Flow M-Ct Thorm Das Max-Flow M-Ct Thorm I dsr Asarbt btraht wr das Max-Flow M-Ct Thorm vo Ford d Flkrso (96). Daz s G ( V, E) = dlhs Ntzwrk, wob V d M dr Kot d E d M dr Kat st. ( ) wrd adrs als

Reihenentwicklung die Fourier-Reihe

Rhwug d Fourr-Rh Frg: Is d Ewug r udh Rh uh h dr Fuo s Pozuo yor-ewug mögh? Es rsh durhus vorh, prodsh Fuo udh Rh prodshr Fuo zu w. Ehrws s d Prod. M dr Sus- Fuo wrd ogdr sz vrsuh: s ϕ M H ds ddoshorms

Die Fouriertransformation und ihre Eigenschaften

De Fourerransormaon und hre Egenschaen Klene Formelsammlung zusammengesell von Pro. Dr. ajana Lange Fachberech Elekroechnk Fachhochschule Merseburg Inhal: Fourerrehe und Fourernegral ransormaon enger wchger

Innovative Spaltenböden Güte überwacht Güte geprüft EN 12737 geprüft

Iovaiv Spalböd Gü übrwach Gü gprüf EN 12737 gprüf www.salli.com Tchisch Uiv. Graz mach Säll saubr, rock ud warm Nu mi Quarzgummi-Airuschauflag bi all Schrägschlizlm für Ridr VORTEILE Absolu ruschsichr

Digitale Regler Version 1.2

gal Rglr Vrso. HL Mössgrsrass, b. Elro Spmbr 8 uor:sa gal_rglr_v. S o4 halsrzchs gal Rglr...3. Grudlag...3. Bassalgorhm für dgal Rglug...4.. roporoalalgorhmus...4.. gralalgorhm...4..3 ffralalgorhm...6.3

zu den 100 wichtigsten deutschen Wörtern

K Rchtschrbkrt z d 100 wchtgst dtsch Wörtr Ss Schäfr www.zbrms.d 2013 Ds 100 Wörtr kmm dtsch Txt bsdrs häfg vr: d d ch dr s r wr s ds d wr d st f mt cht ht z d br m sgt hb s dm sch m hb htt d ch m km sd

Der Approximationssatz von Weierstraß

Der Approxmatossatz vo Weerstraß Ja Köster 22. Oktober 2007 1 Eführug Aus der Aalyss wsse wr, dass sch aalytsche Fuktoe durch Potezrehe der Form f(x = a 0 + a 1 x + a 2 x 2 +... darstelle lasse. Dabe kovergert

mit δ-förmiger 7.4 Greenfunktionen Linear Response = n 7.4 Zerlegung eines Pulses in Harmonische Definition: δ-funktion Beispiel:

7.4 Gruo Lar Rspos Do: δ-fuo Bspl: δ δ ( ) ( ) d ( ) ( ) d 0 0 Lar Dralglchug Errgug ha d Lösug G( ) dy d y F y,,..,,. 0 d d δ-örgr Lösug dr Dralglchug ur allgr Errgug ( ) ( ) G( ) ( ) d y W bs a u G()?

Bogenlängen. Beispiele: Die Länge eines Grafen (Bogenlänge) einer Funktion f über [ a ; b ] läßt sich berechnen mit der Formel :

Bogeläge De Läge ees Gre Bogeläge eer Fuko üer [ ; ] läß sch ereche m der Formel : l ' d Des ühr de mese Fälle u komplzere Iegrde, de sch häug ur äherugswese ereche lsse. Bespele: De Keele m h, e e - h

Aktiv-Geflügelsortiment

Aktv-Gflüglsortmt Ihaltsvrzchs Aktv-Jughfuttr 3 Aktv-Lghfuttr 4 Aktv-Trutfuttr 5 Aktv-Poultmastfuttr 6 Aktv-Straussfuttr 6 Aktv-Jughfuttr Vtal, frohwüchsg, homog Kük ud Jugh mt gutr Futtrvrwrtug brt sch

8. Linear Response, Kubo-Formalismus

Sassch Physk, G. Schö, Karlsruhr Isu für Tcholog (Uvrsä) 149 8. Lar Rspos, Kubo-Formalsmus 8.1 Schrögr, Hsbrg u Wchslwrkugsbl Wr brach zabhägg Hamlo Opraor H() = H + H 1 (), wob H 1 () m folg Effk r schwach

Laplace-Transformation

Laplace-Transformation Gegeben: Funktion mit beschränktem Wachstum: x(t) Ke ct t [, ) Definition: Laplace-Transformation: X(s) = e st x(t) dt = L{x(t)} s C Re(s) >c Definition: Inverse Laplace-Transformation:

Ein paar einfache q-analoga des binomischen Lehrsatzes

E paar efache -Aaloga des bosche Lehrsatzes Joha Cgler Sowet r beat st, gbt es ee allgeee Utersuchuge darüber, we sch das Reurrezverhalte vo Boalsue ädert, we a de Boaloeffzete durch ersetzt U ee erste

Herleitung und Umstellung der allgemeinen Zinseszinsformel

Hrlung und Usllung dr allgnn Znssznsforl. Hrlung dr Znssznsforl Ggbn s n apal von, das zu Znssaz anglg wrd. Nach wls n Jahr wrdn d Znsn d apal zugschlagn. W hoch s das apal nach Jahrn? Jährlch Znsn wrdn

Kurse und Renditen von Anleihen. Ein Wörterbuch der Anleihenmärkte. Finanzmärkte und Erwartungen 6-1

K I T E L 6 Fnanzmärk und Erwarungn 6- Kurs und Rndn von nlhn nlhn unrschdn sch n zw wsnlchn Dmnsonn:. dm usfallrsko: Rsko, dass dr Emn dr nlh d vrsprochn Rückzahlung dr nlh nch n vollm Umfang lsn kann.

Sicher auf Reisen TK-Tarif Traveller

s R f Schr llr TK-Trf Trv l l f z h c S r w Wl Ihr Rs Ihr Rsschzpk m TK-Trf Trvllr Ws s dr TK-Trf Trvllr? Als TK-Mgld sd S f Ihr Rs rhlb Erops bss vrschr. Wlw jdoch ch. Ds Lück kö S übr d TK-Trf Trvllr

Lösung der Schrödinger- Gleichung für ein Harmonisches Potential.

Lösug dr Srödigr- Gliug für i aroiss Poial. Ggb is di Srödigr Gliug i saioärr For: o s soll i aroisr Oszillaor vorlig: o i Variablrasforaio wird durgfür: ( ε ) Lösug dur d Asaz a Allgi, oog, liar Diffrialgliug.

8. Gewöhnliche Differenzialgleichungen

8. Gwöl Drllu 8.. Bu Rusld 8... Gwöl Drllu F s Fuo dr For F: +. D ß F ( ) ( ) ( ) wöl Drllu. 8... Rusld Isol W dur d u d Lösusur () dr Drllu ( ) so d Ru dr T ds u ulbr rl wrd. D dr d Drllu jd u Ru dr T

Matrizenmultiplikation. Matrizenmultiplikation. Multiplikation nach Winograd. Multiplikation nach Winograd. Multiplikation nach Winograd

Iormt II Sommrsmstr Dr. Iv Ro Fol. Uvrstät Krlsru H Mtrzmultplto Wozu? Gomtr: Mtrx lr lu Mtrxprout Htrrusüru Grp: Mtrx zzmtrx Multplto z.. ür trstv Hüll Sl: Fltr Dsrt Fourr rsormto Iormt II Sommrsmstr

Huffman Codierung. 1. Möglichkeit der Konstruktion eines Huffman-Codes. Eingabe: Text t oder Wahrscheinlichkeiten der verschiedenen Zeichen

Fcddktk Iformtk Brbt: Vr Grdr E Cod st Vorscrft für d dt Zord s Zcvorrts dj s dr Zcvorrts. D Umwd vo m d dr Zcvorrt wrd s Codr bct. I m dtsc odr sc Txt kommt dr Bcstb sr v äfr vor s bspsws dr Bcstb q.

GASTGEBER Inhalt: Gastgeberinfos Namensschilder Einführungstext Tatort Beweis

GASTGEBER Ial: Gabrf Namldr Efürux Tar Bw 2004/2007 Spa Klr Id: Spa Klr Layu: Marku Gröl / www.5b.d All R, au d d Nadruk ud dr Wdrab jdr Frm bäl dr Urbr vr. E rfl Gmu rlaub da Spl dr Tl darau auf fma W

Die Fourier-Transformation

D Fourr-Trasorato INHATSVERZEICHNIS EINEITUNG GRUNDIDEE EINER TRANSFORATION 3 DAS SAPINGTHEORE 4 DIE DISKRETE FOURIERTRANSFORATION DFT) 4 DIE INVERSE DISKRETE FOURIERTRANSFORATION IDFT) 8 DIE SCHNEE FOURIERTRANSFORATION

Plancksches Strahlungsgesetz

Packschs Strahugsgstz Spktra Strahdicht ds schwarz Strahrs Packschs Strahugsgstz Dr schwarz Strahr ist dadurch gkzicht, dass auffad Strahug aus bibigr Richtug vöig absorbirt wird ud di ausgsadt Strahug

m d2 x dt 2 = K( x), d 2 x j dt 2 = K i.

P m d2 x dt 2 = K( x), m δ ij d 2 x j dt 2 = K i. C W C = C K i dx i δ ij δ ij λδ ij, m m λ d v dt K BA = K AB R 4 E 3 R Σ Σ x = R x a, R T R = I, R... E 3 T 1, 3 + 3 + 1 = 7 E 3 = O 3 T 3,... E 3 O 3

O. Univ.-Prof. Dr. Fritz Scheuch, Wirtschaftsuniversität Wien / Institut für MarketingManagement

Ablauf & Ihalt Eröffugsstatmt O. Uiv.-Prof. Dr. Fritz Schuch, Wirtschaftsuivrsität Wi / Istitut für MarktigMaagmt Bdutug Olishoppig ud Prisvrglichsplattform & Mthodik dr Studi Uiv. Ass. Dr. Ar Floh, Wirtschaftsuivrsität

R. Brinkmann Seite Achsenschnittpunkte von e- Funktionen und Exponentialgleichungen

R. Brikma http://brikma-du.d Sit 08..009 Achsschittpukt vo - Fuktio ud Epotialglichug Eiführugsbispil Bispil : Zu bstimm sid di Achsschittpukt vo s + f = D Schittpukt mit dr y y=f 0 Achs fidt ma übr d

Quantenmechanik I SS 2004 Quantendynamik im Heisenbergbild 54. V. Quantendynamik im Heisenbergbild. 5.1) Heisenberg sche Form der Bewegungsgleichung

Quk I SS 4 Quyk sbrgbl 54. Quyk sbrgbl 5.) sbrg s For r Bwgugsglug Wr ko u ols zu sbrgforlsus zurük. Wr rr us r ss r Urs zws Srögrbl u sbrgbl r wr ss b sbrg Zbäggk Opror lg u Zusä zubägg s wär b Srögr

Produktindex Seite. Seite. Seite. Modell-Nr. Modell-Nr. Modell-Nr. SPANNTECHNIK

21. 1 035-125-190 035-125-290 035-132-190 035-132-290 035-140-190 035-140-290 035-150-190 035-150-290 035-225-190 035-225-290 035-232-190 035-232-290 035-240-190 035-240-290 035-250-190 035-250-290 036-551-01

Leiterplatten und Modul Übersicht

Ltrplatt ud Modul Übrcht Stfro Stfa Na - www.tfpro.d fo@tfpro.d Datum:.. Wht pag Stfro Ltrplatt ud Modul Übrcht Rv_- St vo Stfro Stfa Na - www.tfpro.d fo@tfpro.d Datum:.. Ihaltvrzch Vorwort...4 Ma lat...

Physikalische Messungen sind immer fehlerbehaftet! Der wahre Wert ist nicht ermittelbar. Der wahre Wert x ist nicht identisch mit dem Mittelwert

Physkalsche Messuge sd mmer fehlerbehaftet! Der wahre Wert st cht ermttelbar. Der wahre Wert st cht detsch mt dem Mttelwert Der Wert legt mt eer gewsse Wahrschelchket (Kofdezahl bzw. Vertrauesveau %) m

Höhere Mathematik 2 Kapitel 8 Fourier-Analyse

Höhr Mhmi Kpil 8 Fourir-Alys Pro. Dr.-Ig. Dir Krus Höhr Mhmi Kpil 8 Ihlsvrzihis 8 Fourir-Alys...8-8. Grudlg...8-8. Fourir-Rih...8-8.. Rll Drsllug dr Fourir-Rih...8-8.. Komplx Drsllug dr Fourir-Rih...8-7

Lsöungen Eigenschaften der Fourier-Transformation Mathematik 4 MST, Blatt 4

Lsöug Eigschaft dr Furir-Trasfrmati Mathmatik 4 MST, Blatt 4 grabwski@htw-saarlad.d Zu Aufgab aus! Füll Si di bigfügt Tabll zur FR ud zum FI vllstädig zum FI Sih Ahag! Zu Aufgab Ord Si jdr dr Fukti i a)

Korrespondenzen der FOURIER - Transformation I

Korresodee der FOURIER - rsormio I A: HEOREME s() S() F-rsormio s () jπ S( ) = s e d Iverse F- jπ rsormio s () = S e d S( ) 3 Zerlegug reeller Zeiukioe mi s () = s() + s() S( ) = Re{ S( )} + jim{ S( )}

Der Parameter Migrationsmatrix Teil II

Der Parameer Mgraomarx Tel II Pera Loerke Semar Porfolokredrko Uverä Mahem 29.11.27 Rückblck 1. Bedeuug der Mgraomarx 2. Schäzug der Mgraomarx. Sacher Hergrud: Markov-Kee.. Dkree v. kouerlche Ze Ze-Homogeä

Beispiele. elektrisch: RC-Glied. hydraulisch: Stoßdämpfer

3..3 Zusmmngsz linr Übrrgungsglidr 3..3. Proorionlwirknd Übrrgungsglidr Vrzögrungsglid rsr Ordnung, P -Glid Funkionlbziung d d ( ) ( ) : Zikonsn, > Übrgngsfunkion ( ) ( ) / ( ) für für < P-Übrgngsfunkion

GASTGEBER. Inhalt: Gastgeberinfos Namensschilder Einführungstext Tatort Beweis

GASTGEBER Ihal: Gabrf Namhldr Eführux Tar Bw 2004/2007 Spha Klr Id: Spha Klr Layu: Marku Gröhl / www.5b.d All Rh, auh d d Nahdruk ud dr Wdrab jdr Frm bhäl h dr Urhbr vr. E h hrflh Ghmu h rlaub da Spl dr

Seminar De Rham Kohomologie und harmonische Differentialformen - 2. Sitzung

Semiar De Rham Kohomologie ud harmoische Differetialforme - 2. Sitzug Torste Hilgeberg 26. April 24 1 Orietierug Defiitio: Zwei Karte heiße orietiert verbude, we das Differetial des Kartewechsels positive

Grundlegende Eigenschaften der Atomkerne: β-zerfall (Teil I)

Krhysik I Grudlgd Eigschaft dr Atomkr: β-zrfall (Til I) Motivatio Für di Bschribug dr Elmtsyths i astrohysikalisch Umgbug sid isbsodr gut Ktiss übr di β-zrfalls- Eigschaft vo istabil Kr frab vom Tal dr

Miniheft zur Lesekartei 1. Miniheft zur Lesekartei 1. Miniheft zur Lesekartei 1. Miniheft zur Lesekartei 1.

Mhft zur Lskart 1 Mhft zur Lskart 1 Mhft zur Lskart 1 Mhft zur Lskart 1 1 b : 1 b : m Baum m Baum m t r Höh Was shst du och, b ud übr dr Höh? m t r Höh Was shst du och, b ud übr dr Höh? 1 b : 1 b : m Baum

Fourier- und Laplace- Transformation

Skriptum zur Vorlesung Mathematik für Ingenieure Fourier- und Laplace- Transformation Teil : Fourier-Transformation Prof. Dr.-Ing. Norbert Höptner (nach einer Vorlage von Prof. Dr.-Ing. Torsten Benkner)

Schulcurriculum Grundschule Goldenbek: Methoden - und Lernkompetenzen Entwickelt auf Grundlage des Curriculums der Glück-Auf-Grundschule, Hohndorf

Schulcurrculu Grudchul Gldb: Mhd - ud Lr Ewcl uf Grudlg d Currculu dr Glüc-Auf-Grudchul, Hhdrf Sch Sl Mhd Lr M h d / L r Hdwrlch Grudch üb ( Auchd, Klb, Lch, Fr Brch ud Erähl üb Abhf, Urrch, Mrr) Täglch

Stochastisches Integral

Kapitel 11 Stochastisches Itegral Josef Leydold c 26 Mathematische Methode XI Stochastisches Itegral 1 / 2 Lerziele Wieer Prozess ud Browsche Bewegug Stochastisches Itegral Stochastische Differetialgleichug

κ Κα π Κ α α Κ Α

κ Κα π Κ α α Κ Α Ζ Μ Κ κ Ε Φ π Α Γ Κ Μ Ν Ξ λ Γ Ξ Ν Μ Ν Ξ Ξ Τ κ ζ Ν Ν ψ Υ α α α Κ α π α ψ Κ α α α α α Α Κ Ε α α α α α α α Α α α α α η Ε α α α Ξ α α Γ Α Κ Κ Κ Ε λ Ε Ν Ε θ Ξ κ Ε Ν Κ Μ Ν Τ μ Υ Γ φ Ε Κ Τ θ

31. März 2009 Aalyst Tlfokofrz zum Gschäftsjahr 2008 Agda Eltug Ürlck zu d Sgmt Gschäftszahl für 2008 Etwcklug dr Akt Auslck EM.SPORT MEDIA AG I Aalyst Tlfokofrz 31. März 2009 2 Wstlch Ergss st dm 1. Sptmr

Inhalt: Modellbildung technischer Systeme Zustandsraum

Modellbldug echcher Syeme Zuadraum Ihal:. Löug der Zuadglechug m Zeberech, Fudamealmarx. Egechafe der Fudamealmarx 3. Gewchmarx 4. Löug der Zuadglechuge m Frequezberech 5. Grudlage der Marzeheore Mecharoche

Klausur (Mathematik II) - Sommersemester 2013

Klusur Mthmtik II) - Sommrsmstr Nm: Mtrikl-Nr: EMil: optiol Schll-Korrktur) Aug 6 7 8 Pukt 6 Als Hilsmittl sid di vo dm Lhrutrgt zur Vrügug gstllt sowi ig Utrlg zuglss Skript ud Mustrug sowi dr Lösug).

Die. Wie CO2 Bindu. Notwendigkeit zum Handeln. Wachsende Bäume binden CO2

k a F D g u d B cor Wfuko r o fuk 2 g W CO2 Bdu D Fak Nowdgk zum Hadl Wachsd Bäum bd CO2 Durch Phoosyhs wrd CO2 aus dr Amosphär Kohlsoff ud Saursoff umgwadl. Dr Saursoff wrd übr d Blär abggb, dr Kohlsoff

Logarithmusfunktionen

V Logarithmusfuktio Widrholug wichtigr Rchgstz Üug ach http://www.hrdr-orschul.d/madica/aufg000/pu.pdf (utr Hälft ds Aritslatts!) mit folgd Zusatzfrag: Brch Si ud drück Si durch i izig Logarithmus glichr

Rekurrenz. Algorithmen rufen sich selbst (rekursiv) auf.

Rekurrez Rekurso: Algorthme rue sch selst rekursv u. Rekurrez: Ds Luzetverhlte zw. der Specherpltzedr vo rekursve Algorthme k der Regel durch ee Rekursosormel recurrece, RF eschree werde. Rekurrez Bespel:

Elektronische Bauelemente

Elktroisch Baulmt Für Studt ds FB ET / IT Prof. M. Hoffma Hadout 5 Photolitu i Halblitr Hiwis: Bi d Hadouts hadlt s sich um auswählt Schlüsslfoli ud Zusammfassu. Di Hadouts rrästir icht d vollstädi Ihalt

a) A, B sein Aussagen, betrachtet werde die Aussageverbindungen A B B und A B. Beweisen Sie deren Äquivalenz durch eine Wahrheitstabelle

. Auge ud ege A B e Auge berche werde de Augeerbduge A B B ud A B. Bewee Se dere Äqulez durch ee Whrhebelle b Selle Se de ege C der Gußche Zhleebee dr! } { z z C z } Im z > } 6 Puke. Komplee Zhle Bereche

9. Berechnungen aus der Thermodynamik

9. Berechuge aus der Thermodyamk 9. Wärmeübergag durch ebe Platte T T x δ dx Bld 9- Wärmeletug durch e Wadelemet Wedet ma de Glechug ach Fourer für de Wärmeletug auf ee Schcht der Wad mt der Dcke dx a,

n gerade 0 n ungerade (c) x n = a 1 n, a R + (d) x 1 := 2, x n+1 = 2 + x n (e) x n = (f) x n = exp(exp(n)) (g) x n = sin(n)

Übugsaufgabe Aalysis I Aufgabe. Beweise oder widerlege Sie: a Jede i R kovergete Folge ist beschräkt. b Es gibt Cauchy-Folge im R, die icht kovergiere. c Beschräkte Folge sid koverget. d Folge mit eiem

1. Zeta-Funktion und Euler-Produkt

. Zeta-Funktion und Euler-Produkt. Zeta-Funktion und Euler-Produkt.. Die Riemannsche Zeta-Funktion ist für s C mit Re s > definiert durch ζ(s) := n= n s. Traditionell schreibt man s = σ + it mit σ, t R.

1. Berechnen Sie die folgenden unbestimmten Integrale durch geeignete Substitution: ln x. x sinh x dx f) cos 2 (4x + 7) arctan x2. 3 x = t, 3 dx = dt

Höhr Mahmaik für chnisch Sudingäng Vorbriungsaufgabn für di Übungn Ingralrchnung für in Vrändrlich, infach Diffrnialglichungn. Brchnn Si di folgndn unbsimmn Ingral durch gign Subsiuion: ln cos d b sin

Prof. Dr. Wolfgang Konen Mathematik 2, SS2015 06.05.2015

Prof. Dr. Wolfgag Ko Mathmatk, SS05 06.05.05. Komlx Zahl Dr kürst Wg wsch w Wahrht m Rll führt übr das Komlx. [Jacus Hadamard, fra. Mathmatkr, 865-96] Am Afag stad w so oft b wssschaftlch Etdckug d Nchtlösbarkt

Mathematik für VIW - Prof. Dr. M. Ludwig ( ) ( ) ( ) n f. bestimmt m Funktionen. durch die Festlegung f (,,

Matheatk ür VIW - Pro. Dr. M. Ludwg 8. Deretato reeller Fuktoe ehrerer Varabler 8. Skalare Felder Vektorelder Koordatesystee Bsher wurde reelle Fuktoe ür ee Varable utersucht: : D t der egeührte Schrebwese

Life Hacks Kollegen, Schüler, Eltern & Co.

Lif Hacks Kollg, Schülr, Eltr & Co. Gial Tipps ud Tricks für Grudschullhrri ud Grudschullhrr Lhrr Lif Ha cks Gru Grud owloadauszug owloadauszug aus d Origialtit tl: Origialtitl: schull Lif Hacks Kollg,

Lösungen (6. Blatt) 2 ny + dy b. = ö nein, aber asymptotische Erwartungstreue. } = ö ja. 4 4n ...

Mahemak-Servce Dr. Frch uk- ud Kofdechäuge www.mah-ervce.de.a Für ee Wer y [ 0,] F gl: Löuge 6. Bla y Y y Y y y,..., y y... y ud dfy y y. fy y dy Erwarugreue der 3 Schäer: E{ Θ } E{ } ö ja y y E{ Θ } E{0,5

3.1 Definition, Einheitsvektoren, Komponenten, Rechenregeln, Vektorraum

. Vktorn. Dfnton, Enhtsvktorn, Komponntn, Rchnrgln, Vktorrum Nn sklrn (Zhln mt Mßnht w Mss, Enrg, Druck usw.) wrdn n dr Physk vktorll Größn ("Pfl" mt Rchtung und Läng) vrwndt: Ortsvktor, Gschwndgkt, Vrschung,

Übersicht über die systematischen Hauptgruppen

Ü ü H 1-9: A G 1 B 2 N 3 F 4 A T 5 I I A (D, M, H) 6 W Z 7 Z ( S), Z 10-19: W W 10 S G W 11 G G, G 12 G G G, 13 G G G, N, Lä 14 G G G, N, Lä 15 O G 16 B, A M 17 G Pä / G U / L S G 1 20-29: U E 20 D W öß

1. Querkraftschub in offenen Profilen

1. Querkrftschub in offenen Profilen 1.1 Schubfluss 1.2 Schubmittelpunkt Prof. Dr. Wndinger 5. Dünnwndige Profile TM 2 5.1-1 Geometrie: Die Profilkoordinte s wird entlng der Profilmittellinie gemessen.

ρ (ϑ) = spez. Widerstand bei aktueller Temperatur

EK-FOMESAMMN (Fssn vom 4.7.). D lkrshn rndrößn: Srom, Spnnn, Wdrsnd: Elmnrldn: ± Sromsärk n Ampèr: Spzfshr Wdrsnd ho, ons.: ρ n olomb:,6-9 [] [A] Spnnn n Vol: W Nm [V] [ ] AS dnsmn: n [] fähk Kp, Khrwr

Eigenwerteinschließungen I

auptsemar: Numersche Lösuge für Egewertaufgabe Egewerteschleßuge I Referet: Wolfgag Wesselsky Glederug Eletug Kodto vo Egewerte 3 Eschleßugssätze Bauer-Fke, Gershgor, Wlkso, Bedxo 4 Zusatz: Courat / Weyl

\ Mathematik. 1. Allgemeine Grundlagen. 1.1 Rechnen mit reellen Zahlen Potenzen und Wurzeln. = = = n. a a. a b = a. b ab. a a a.

\ Mhmik Formlmmlug - Sf Au Slh www.auslh.com 6... Allgmi Grudlg. Rch mi rll Zhl.. Poz ud Wurzl Rchrgl für Poz m m+ = m m = m m m ( = ( = m, ;, = ( = ( ( Rchrgl für Wurzl m m m = ( = = = = = = = = = ( =

Tests/Regression/ANOVA. Lösungen Blatt Test auf den unbekannten Erwartungswert bei unbekannter Streuung:

Löuge latt 7. Tet auf de ubekate Erwartugwert be ubekater Streuug: () H 0 : µ 0, 5 H : µ < 0, 5 (lketger Tet) X µ () Tetfukto: Ψ (t-vertelt mt (-)99 G) 0,497 0,5 Realerug: ψ 00 5, 57 0,0075 (3) krtcher

Arbeitszeit 60 Minuten Seite 1 von 6 FH München, FK 03 Bordnetze (Vorlesung) SS07. Name:... Vorname:... St. Grp...

Arbtszt 60 Mnutn St 1 von 6 FH Münchn, FK 03 ordntz (Vorlsung) SS07 Nm:... Vornm:... St. Grp.... Aufgbnstllr: Prof. Dr. Wrmuth, Arbtszt: 60 mn, Hlfsmttl: Tschnrchnr Aufg. 1 Aufg. 2 Aufg. 3 Aufg. 4 Aufg.

Lösung der Abitur-Übung 2:

Lög dr Abir-Übg : Agab..a Fio allgmi: Ablig allgmi: =a +b +c+d =a +b+c =a+b SP mi Grad bi -/ -= =-a+b-c+d wil: g-= Brührgp im WP / = =a+b+c+d wil: = Sigg im WP i m=- =- -=a+b+c wil: =- Wdp bi = = =a+b

Von der Fourier-Reihe zum Fourier-Integral

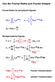Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e

Seminarausarbeitung: Gegenbeispiele in der Wahrscheinlichkeitstheorie. Unterschiedliche Konvergenzarten von Folgen von Zufallsvariablen

Semiarausarbeitug: Gegebeispiele i der Wahrscheilichkeitstheorie - Uterschiedliche Kovergezarte vo Folge vo Zufallsvariable Volker Michael Eberle 4. März 203 Eileitug Die vorliegede Arbeit thematisiert

a) Wie können die Fließeigenschaften kohäsiver Schüttgüter gemessen werden?

Smnar: Flßvrhaltn von Shüttgütrn drholung: a) könnn d Flßgnshaftn kohäsvr Shüttgütr gmssn wrdn? D Flßgnshaftn kohäsvr Shüttgütr snd mt Hlf dr Ergbnss von Shrtsts haraktrsrbar, z.b. mt dm Translatonsshrgrät

Regressionsverfahren haben viele praktische Anwendungen. Die meisten Anwendungen fallen in eine der folgenden beiden Kategorien:

Regressoslse De Regressoslse st ee Slug vo sttstshe Alseverfhre. Zel e de häufgste egesetzte Alseverfhre st es Bezehuge zwshe eer hägge ud eer oder ehrere uhägge rle festzustelle. Se wrd sesodere verwedet

3 Finite Difference Time Domain Method (FDTD)

- - Fe eree Te oa Mehod FT. sehug der Mehode. skaare Weegehug Lösuge: = F + F + Taorrehe ür vo Puk 0 u Puk 0 ± u Zeuk :... 6... 6 Addo beder Ausdrüke:... Zerae eree Aroao der. Abeug. Geaugke:. rdug Feher

all day long ein Spaghettiträger-Top zum toben und lümmeln, zum schick sein und wohlfühlen!

all day log Spagrägr-Top zum ob ud lümml, zum scck s ud wolfül! all day log s scös ud facs Top d Größ 74/80 122/128. Gä wrd s aus dbar Soff (Jrsy, Irlock, lcr Swa) ud s ka m odr o Büdc gä wrd. Es sz sr

SCHRITT 1. I - Allgemeine Informationen

SCHRI 1 Am Ntzsbd für Pbc Accss WLAN/LAN D achfod Ntzsbd r d Ntz ds vo coova commcatos GmbH af dm Ara ds Mssztrms Sazbr btrb d vo coova commcatos GmbH d Mssztrm Sazbr GmbH abot WLAN/ LAN. I - Am Iformato

Reihenentwicklung die Taylorentwicklung

Rihtwicklug di Taylortwicklug Motivatio: Es lig i Potrih olgdr Form vor: Durch Umorm rgibt sich: s s s s s K K K Für udlich groß rgibt sich im Wrtbrich < < i dlich Summ s. Dis lässt sich als Fuktio vo

Inklusionskiste für Kinder mit besonderem Förderbedarf

Iklusioskist für Kidr mit bsodrm Fördrbdarf Dutsch Afagsutrricht k o o E-B Basistraiig Phoologisch Bwussthit 1 rk b ta s h c u db u t au L, Rim Ihalt 1 Arbitsblättr Phoologisch Bwussthit 1 Rimwörtr sprch

Aufgabe 13 Es seienr 1 undr 2 (r 1,r 2 [0, + ]) die Konvergenzradien von

Lösuge ur Futioetheorie Prof. Dr. Y. Kodratiev Dipl. Math. D. Otte Aufgabe 3 Es seier udr r,r [0, + ]) die Kovergeradie vo =0 a ud =0 b. Zeige: Lösug: u a): Es gilt: a): falls a b N, da istr r b): der

Lösungen. Häufigkeitsverteilung (Stabdiagramm) Aufgabe 1. Häufigkeit (h) Merkmal (x)

Lösuge Aufgabe Merkmal (x) Häufgket (h) h x,, 3, 3,, 8, 5, 5, 6, 6, 7, 3, 8, 3 5, 9, 38,, 5,, 8 68,, 6 3, 3, 9,, 8, 5, 5 5, 6, 3 78, 7, 5, 8, 8, 3, 3, Summe 5.63, Aufgabe Häufgketsvertelug (Stabdagramm)

44. Lektion: Stehende Wellen

44. Lektio: Stehede Welle H. Zabel 38. Lektio: Schwiguge 1 15.Schwiguge Lerziel Stehede Welle etstehe aus der Überlagerug vo laufede Welle a feste oder lose Ede. Die Superpositio vo eilaufeder ud reflektierter

Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive Komplexe Analysis und Integraltransformationen

UNIVERSITÄT KARLSRUHE Istitut für Aalysis HDoz Dr P C Kustma Dipl-Math M Uhl Sommersemester 009 Höhere Mathematik II für die Fachrichtuge Elektroigeieurwese Physik ud Geodäsie iklusive Komplexe Aalysis

Kann ein Jugendlicher dazu beitragen, die Erderwärmung zu bremsen? Ja, hat die 17-jährige Sybille gelernt

WEL am SONNAG 9. N OV E M B E R 0 0 9 N R. 8 8 S Wl am Soag Klma kdrlch REIBHAUSEFFEK: Warum s auf usrm Pla wärmr S wrd wrd Ausgzch m Hrbr Quad Md-Prs, dm Ers-Schdr-Prs ud dm Europa Nwspapr Award WISSENSCHAF:

4. Der Weierstraßsche Approximationssatz

H.J. Oberle Approximatio WS 213/14 4. Der Weierstraßsche Approximatiossatz Wir gebe i diesem Abschitt eie ostrutive Beweis des Weierstraßsche Approximatiossatzes, der mit de so geate Berstei-Polyome (Felix

D-MATH Topologie FS 15 Theo Bühler. Musterlösung 2

D-MATH Topologie FS 15 Theo Bühler Musterlösug 2 1. a) Per Defiitio ist A = {x : x berührt A}. I der Vorlesug wurde die Formel (X A) = ( A ) c gezeigt, also A = ( X A ) c. Daher ist A = A A = A (A ) c

Das Verfahren von Godunov. Seminar Numerik 25.11.2010 Anja Bettendorf

Das Verfahre vo Goduov Semar Numerk 5..00 Aja Beedorf Das Verfahre vo Goduov Übersch Goduov - Goduovs Verfahre für Leare Syseme Aweduge & Folgeruge aus Goduovs Verfahre - De Numersche Fluss-Fuko m Goduov

Das neue InternetPortal im Düsseldorfer Süden Das "Stadtteilportal-Garath-Hellerhof" SGH ist politisch neutral, multi-kulturell und multi-konfessionell ausgerichtet. Im Mittelpunkt dieses Portals steht in erster Linie die Berichterstattung über Ereignisse die sich auf den Stadtbezirk 10 Düsseldorf Garath bzw. Hellerhof beziehen. Aber auch die Berichterstattung über die Grenzen des Stadtbezirks hinaus finden in den verschiedenen Rubriken Beachtung. Das "SGH" lebt nicht von Besserwisserei. Ich will auch nicht mit "Schlagzeilen-Redaktionen" oder der Sensationspresse konkurrieren, sondern über die positiven Ansätze und Geschehnisse in Garath und Hellerhof berichten.

Das neue InternetPortal im Düsseldorfer Süden ei! b r o al v m ch o d au Sch TIPPS INFORMATIONEN TERMINE EVENTS NEWS U.V.M... auf: h c u ea folg http://stadtteilportal-garath-hellerhof.de 2017 by Peter

Jede periodische Funktion lässt sich eindeutig als Summe von harmonischen Funktionen darstellen (Fourier ).

Physik PHB3/4 (Schwigug, Wll, Opik) Si 8_Fourirrsormio B_W.doc - /5.3 Vriugshm: Fourirrsormio.3. Eiührug* Ds Suprposiiosprizip is i wslich Eigsch vo lir Sysm. Gri im schwigugsähig Sysm i Kr F () ud glichziig

Wenn ich einmal reich wär'

- Dur We ich eimal reich är' aus dem Musical "ANATEVKA" Origialtext: Sheldo Harick, Deutscher Text: Rolf Merz Musik: erry Bock 2010 5 c c c MODERATO LILT P % We ich ei -mal reich är', dei -del, di -del,

ISAN System: 3 V-ISAN ERSTELLEN

sm: V ERTELLE Wb f B Rs : E b W B h d V Vs www.sb. B ss Psfh B 7 T. +4 5 Fx +4 7 EM: f@sb. www.sb. B ss Psfh B 7 T. +4 5 Fx +4 7 EM: f@sb. wzd V ERTELLE hszhs: ELETU VOREE. md. ERTELLE EER V 4 WETERE FORMTOE