Zusammenfassung der ersten Vorlesung
|
|
|
- Lioba Lang
- vor 5 Jahren
- Abrufe
Transkript
1 Zusammenfassung der ersten Vorlesung 1. Es geht um de Mechank.. Jedes mechansche System kann mttels ener Lagrangefunkton charaktersert werden. De Lagrangefunkton hängt von den verallgemenerten Koordnaten, den Geschwndgketen und der Zet ab. L({q }, { },t) 3. De Lagrangefunkton st durch de Dfferenz von knetscher und potenteller Energe des Systems gegeben. NX m ~ r L = T U L = U(~r 1, ~r,..,~r N ) 4. Integrert man de Lagrangefunkton über de Zet, bekommt man de Wrkung. =1 S[{q (t)}] = Z t dtl({q }, { },t),t), q (t 1 )=q,1, q (t )=q, t 1 5. De Bahn de de Wrkung mnmert ensprcht der Bewegung enes mechanschen Systems n der Natur. Dese Bahn st de Lösung der Euler-Lagrange Glechungen. @q
2 1. Prnzp der klensten Wrkung De unabhänggen Grössen, welche man braucht um en mechansches System vollständg zu beschreben nennt man Frehetsgrade. De Zahl der Frehetsgrade st durch Zwangsbednungen beschränkt. f(q 1,q,...q N,t)=0 z.b. x + y + z R =0 Es gbt zwe Möglchketen mt Zwangsbednungen umzugehen. Entweder elmnert man abhängge Koordnaten aus der Lagrangefunkton oder man benutzt Lagrangefaktoren und ändert damt de Lagrangefunkton. L! L 0 = L + f(q 1,...,q N,t) d 0 = ) 0=f(q 1,...q N,t)
3 1. Prnzp der klensten Wrkung En Bespel: We bewegt sch en Telchen auf ener Stange m Gravtatonsfeld? Wr nehmen an, dass das Telchen sch be t=0 mt null Geschwndgket m Punkt befndet. Es gbt ken Rebung. x =0, y = L cos Wr begnnen mt der Lagrangefunkton n kartesschen Koordnaten. L = mẋ + mẏ mgy 0 <x<lsn, 0 <y<lcos. De Koordnaten x und y snd ncht unabhängg! x = s sn, y = L cos s cos y sn + x cos L sn cos =0 Wr können dese Abhänggket entweder los werden oder de Lagrangefaktoren benutzen.
4 1. Prnzp der klensten Wrkung a) Zwangsbednungen explzt elmneren. Wr wählen de Länge s entlang der Stange als de neue Koordnate. L = mẋ + mẏ mgy 0 <s<l x = s sn, y = L cos s cos ẋ =ṡ sn, ẏ = ṡ cos L = mṡ mg(l cos s cos ) m s = mg cos ) s(t) = g cos t x = g cos sn t, y = L cos g cos t
5 b). Lagrangefaktoren 1. Prnzp der klensten Wrkung L = mẋ + mẏ mgy L = mẋ + mẏ mgy + (y sn + x cos L sn cos )) y sn + x cos L sn =0 y sn + x cos L sn cos =0 mẍ = cos mÿ = mg + sn ÿ sn +ẍ cos =0 mÿ = mg sn cos mÿ ÿ = g cos ẍ = g cos sn x = g cos sn t y = L cos g cos t
6 1. Prnzp der klensten Wrkung c) Das zwete newtonsche Gesetz. Zwe Kräfte: De Gravtatonskraft und de Zwangskraft. De Zwangsskraft wrkt orthogonal zur Stange, d.h. se hat kene Komponente entlang der Stange. De Komponente der Gravtatonskraft entlang der Stange bestmmt de Bewegung des Telchens. F = mg cos m s = mg cos s = g cos t
7 1. Prnzp der klensten Wrkung Zwe allgemene Bemerkungen. 1) Snd de Zwangsbednungen von Geschwndgketen abhängg, muss man de abhangge Grösse aus der Lagrangefunkton elmneren; Lagrangefaktoren kann man n desem Fall ncht benutzen. ) De Lagrangefunkton enes mechanschen Systems st nur bs auf de totale Zetabletung ener belebgen Funkton von verallgemenerten Koordnaten defnert. S = Z t t 1 dtl(q, q, t), q(t 1 )=q 1, q(t )=q L(q, q, t)! L(q, q, t)+ d Kene f(q, t) dt Abhanggket von der Geschwndgket! S new = Z t dt L(q, q, t)+ ddt f(q, t) = S + f(q,t ) f(q 1,t 1 ) t 1 S new = S Identsche Bewegungsglechungen!
8 Wo kommt der Prnzp den klensten Wrkung her? VO1.UME 0, NUMBER Aran., 1948 Space-.. me A~~~roac. 1:o.5 on-. le..a1:vstc 4 uantuns.v. :ec.zanes R. P. I EvNMAN Cornell Unversty, Ithaca, Veto York Non-relatvstc quantum mechancs s formulated here n a dfferent way. It s, however, mathematcally equvalent to the famlar formulaton. In quantum mechancs the probablty of an event whch can happen n several dfferent ways s the absolute square of a sum of complex contrbutons, one from each alternatve way. The probablty that a partcle wll be found to have a path x(t) lyng somewhere wthn a regon of space tme s the square of a sum of contrbutons, one from each path n the regon. The contrbuton from a sngle path s postulated to be an exponental whose (magnary) phase s the classcal acton (n unts of h) for the path n queston. The total contrbuton from all paths reachng x, t from the past s the wave functon P(x, t). Ths s shown to satsfy Schroednger's equaton. The relaton to matrx and operator algebra s dscussed. Applcatons are ndcated, n partcular to elmnate the coordnates of the feld oscllators from the equatons of quantum electrodynamcs. Quanten Mechank: alle Bahnen snd erlaubt und kann auch n der Natur passeren. De Wahrschenlchketen das en Bahn verfolgt wrd unterscheden sch aber gewaltg. P[q(t)] e S[q(t)]/~ ~ = m kg/s
9 . Erhältungssätze Zetunabhängge Funktonen von Koordnaten und Geschwndgketen des Systems und auch von der Zet, hessen Bewegungsntegrale. I I({q }, { },t), di dt =0 q(t) + q(t) = I 1, q(t) q(t) = I r I1 ± I (q(t), q(t)) = En Bespel: Zetunabhängge Lagrangefunkton dl dt = X d dt dl dt = + @ + q = X dt L = L({q }, = q ) d L =0. Dese Grösse nennt man de Energe des Systems: E L L = T U({q }), T = 1 X m ({q }) q q ) E = T + U Falls en mechansches System durch ene zetunabhängge Lagrangefunkton beschreben wrd, st für deses System de Energe ene erhaltende Grösse.
Zusammenfassung. 1) Falls Zwangsbedinungen die Freiheitsgrade einschränken, kann man die abhängige Koordinaten aus der Lagrangfunktion elimieren;
 Zusammenfassung 1) Falls Zwangsbednungen de Frehetsgrade enschränken, kann man de abhängge Koordnaten aus der Lagrangfunkton elmeren; 2) Es st auch möglch de Zwangsbednungen mt Hlfe der Lagrangefaktoren
Zusammenfassung 1) Falls Zwangsbednungen de Frehetsgrade enschränken, kann man de abhängge Koordnaten aus der Lagrangfunkton elmeren; 2) Es st auch möglch de Zwangsbednungen mt Hlfe der Lagrangefaktoren
Theoretische Physik 2 (Theoretische Mechanik)
 Theoretsche Physk 2 (Theoretsche Mechank Prof. Dr. Th. Feldmann 28. Oktober 2013 Kurzzusammenfassung Vorlesung 4 vom 25.10.2013 1.6 Dynamk mehrerer Massenpunkte Dynamk für = 1... N Massenpunkte mt.a. komplzerter
Theoretsche Physk 2 (Theoretsche Mechank Prof. Dr. Th. Feldmann 28. Oktober 2013 Kurzzusammenfassung Vorlesung 4 vom 25.10.2013 1.6 Dynamk mehrerer Massenpunkte Dynamk für = 1... N Massenpunkte mt.a. komplzerter
Theoretische Physik: Mechanik
 Ferenkurs Theoretsche Physk: Mechank Sommer 2017 Vorlesung 2 (mt freundlcher Genehmgung von Merln Mtscheck und Verena Walbrecht) Technsche Unverstät München 1 Fakultät für Physk Inhaltsverzechns 1 Systeme
Ferenkurs Theoretsche Physk: Mechank Sommer 2017 Vorlesung 2 (mt freundlcher Genehmgung von Merln Mtscheck und Verena Walbrecht) Technsche Unverstät München 1 Fakultät für Physk Inhaltsverzechns 1 Systeme
Theoretische Physik: Mechanik
 Ferenkurs Theoretsche Physk: Mechank Sommer 2013 Vorlesung 2 Technsche Unverstät München 1 Fakultät für Physk Inhaltsverzechns 1 Systeme von Massenpunkten 3 1.1 Schwerpunktsmpuls..............................
Ferenkurs Theoretsche Physk: Mechank Sommer 2013 Vorlesung 2 Technsche Unverstät München 1 Fakultät für Physk Inhaltsverzechns 1 Systeme von Massenpunkten 3 1.1 Schwerpunktsmpuls..............................
Zusammenfassung. 1. Die Bewegungsintegrale sind eng mit den Symmetrien der Wirkung verbunden. Was das genau bedeutet, zeigt das Noether-Theorem.
 Zusaenfassung 1. De Bewegungsntegrale snd eng t den Syetren der Wrkung verbunden. Was das genau bedeutet, zegt das Noether-Theore. Noether-Theore: Falls de Wrkung enes echansches Systes unter der folgenden
Zusaenfassung 1. De Bewegungsntegrale snd eng t den Syetren der Wrkung verbunden. Was das genau bedeutet, zegt das Noether-Theore. Noether-Theore: Falls de Wrkung enes echansches Systes unter der folgenden
Theoretische Physik: Mechanik
 Ferenkurs Theoretsche Physk: Mechank Sommer 018 Vorlesung 4 (mt freundlcher Genehmgung von Gramos Qerm, Jakob Unfred und Verena Walbrecht) Technsche Unverstät München 1 Fakultät für Physk Inhaltsverzechns
Ferenkurs Theoretsche Physk: Mechank Sommer 018 Vorlesung 4 (mt freundlcher Genehmgung von Gramos Qerm, Jakob Unfred und Verena Walbrecht) Technsche Unverstät München 1 Fakultät für Physk Inhaltsverzechns
18. Vorlesung Sommersemester
 8. Vorlesung Sommersemester Der Drehmpuls des starren Körpers Der Drehmpuls des starren Körpers st etwas komplzerter. Wenn weder de Wnkelgeschwndgket um de feste Rotatonsachse st, so wrd mt Hlfe des doppelten
8. Vorlesung Sommersemester Der Drehmpuls des starren Körpers Der Drehmpuls des starren Körpers st etwas komplzerter. Wenn weder de Wnkelgeschwndgket um de feste Rotatonsachse st, so wrd mt Hlfe des doppelten
Lagrangesche Mechanik
 Kaptel Lagrangesche Mechank De Newtonsche Mechank hat enge Nachtele. 1) De Bewegungsglechungen snd ncht kovarant, d.h. se haben n verschedenen Koordnatensystemen verschedene Form. Z.B., zwedmensonale Bewegungsglechungen
Kaptel Lagrangesche Mechank De Newtonsche Mechank hat enge Nachtele. 1) De Bewegungsglechungen snd ncht kovarant, d.h. se haben n verschedenen Koordnatensystemen verschedene Form. Z.B., zwedmensonale Bewegungsglechungen
Die Hamilton-Jacobi-Theorie
 Kaptel 7 De Hamlton-Jacob-Theore Ausgearbetet von Rolf Horn und Bernhard Schmtz 7.1 Enletung Um de Hamlton schen Bewegungsglechungen H(q, p q k = p k H(p, q ṗ k = q k zu verenfachen, führten wr de kanonschen
Kaptel 7 De Hamlton-Jacob-Theore Ausgearbetet von Rolf Horn und Bernhard Schmtz 7.1 Enletung Um de Hamlton schen Bewegungsglechungen H(q, p q k = p k H(p, q ṗ k = q k zu verenfachen, führten wr de kanonschen
MOD-01 LAGRANGE FORMALISMUS -- TEIL 1
 MOD- LAGRAGE FORMALISMUS -- EIL. Zustandsfunktonen Defnton -: Zustandsfunkton Ene Zustandsfunkton W( () t, t) = W(, t) bzw. W ( ) st jede belebge skalare Funkton der Zustandsgrößen () t und der Zet t,
MOD- LAGRAGE FORMALISMUS -- EIL. Zustandsfunktonen Defnton -: Zustandsfunkton Ene Zustandsfunkton W( () t, t) = W(, t) bzw. W ( ) st jede belebge skalare Funkton der Zustandsgrößen () t und der Zet t,
Hamiltonsche Mechanik
 Kaptel 3 Hamltonsche Mechank Das Lagrange-Formalsmus lefert uns de Bewegungsglechungen n der Form von enem System von Dfferentalglechungen zweter Ordnung für verallgemenerte Koordnaten. Solches System
Kaptel 3 Hamltonsche Mechank Das Lagrange-Formalsmus lefert uns de Bewegungsglechungen n der Form von enem System von Dfferentalglechungen zweter Ordnung für verallgemenerte Koordnaten. Solches System
Noethertheorem. 30. Januar 2012
 Noethertheorem 30. Januar 2012 1 Inhaltsverzechns 1 Symmetre 3 1.1 Symmetre n der Geometre................... 3 1.2 Symmetre n der Mathematk.................. 3 1.3 Symmetre n der Physk.....................
Noethertheorem 30. Januar 2012 1 Inhaltsverzechns 1 Symmetre 3 1.1 Symmetre n der Geometre................... 3 1.2 Symmetre n der Mathematk.................. 3 1.3 Symmetre n der Physk.....................
3. Vorlesung Sommersemester
 3. Vorlesung Sommersemester 1 Bespele (Fortsetzung) 1. Der starre Körper: Formulerung der Zwangsbedngungen später. Anschaulch snd schon de Frehetsgrade: dre der Translaton (z. B. Schwerpuntsoordnaten)
3. Vorlesung Sommersemester 1 Bespele (Fortsetzung) 1. Der starre Körper: Formulerung der Zwangsbedngungen später. Anschaulch snd schon de Frehetsgrade: dre der Translaton (z. B. Schwerpuntsoordnaten)
3 Vorlesung: Lagrange Mechanik I. 3.1 Zwangsbedingungen. Beispiele (nach Kuypers)
 3 Vorlesung: Lagrange Mechank I 3.1 Zwangsbedngungen Im folgenden Kaptel werden wr uns mt Bewegungen beschäftgen, de geometrschen Zwangsbedngungen unterlegen, we etwa der Pendelbewegung, der Bewegung auf
3 Vorlesung: Lagrange Mechank I 3.1 Zwangsbedngungen Im folgenden Kaptel werden wr uns mt Bewegungen beschäftgen, de geometrschen Zwangsbedngungen unterlegen, we etwa der Pendelbewegung, der Bewegung auf
Klassische Theoretische Physik II (Theorie B) Sommersemester 2016
 Karlsruher Insttut für Technologe Insttut für Theore der Kondenserten Matere Klasssche Theoretsche Physk II Theore B Sommersemester 016 Prof. Dr. Alexander Mrln Musterlösung: Blatt 7. PD Dr. Igor Gorny,
Karlsruher Insttut für Technologe Insttut für Theore der Kondenserten Matere Klasssche Theoretsche Physk II Theore B Sommersemester 016 Prof. Dr. Alexander Mrln Musterlösung: Blatt 7. PD Dr. Igor Gorny,
Theoretische Physik: Mechanik
 Merln Mtschek, Verena Walbrecht Ferenkurs Theoretsche Physk: Mechank Sommer 2013 Vorlesung 3 Technsche Unverstät München 1 Fakultät für Physk Merln Mtschek, Verena Walbrecht Inhaltsverzechns 1 Symmetren
Merln Mtschek, Verena Walbrecht Ferenkurs Theoretsche Physk: Mechank Sommer 2013 Vorlesung 3 Technsche Unverstät München 1 Fakultät für Physk Merln Mtschek, Verena Walbrecht Inhaltsverzechns 1 Symmetren
29 zweite Ableitungen der thermodynamischen Potentiale spezifische Wärme (thermischer response) E = = = T V N V N V N = = κ T.
 hermodynamsche resonse -unktonen: 9 zwete Abletungen der thermodynamschen Potentale sezfsche Wärme (thermscher resonse) E C S be konstantem olumen (sochor):,,, be konstantem Druck (sobar): C S Komressbltät
hermodynamsche resonse -unktonen: 9 zwete Abletungen der thermodynamschen Potentale sezfsche Wärme (thermscher resonse) E C S be konstantem olumen (sochor):,,, be konstantem Druck (sobar): C S Komressbltät
I)1. Kinematik. EP WS 2009/10 Dünnweber/Faessler
 I)1. Knematk I) Mechank 1.Knematk (Bewegung) 2. Dynamk on Massenpunkten (Enfluss on Kräften) 3. Starre Körper 4.Deformerbare Meden 5. Schwngungen, Wellen, Akustk I)1. Knematk Bewegungslehre (Zel: Quanttate
I)1. Knematk I) Mechank 1.Knematk (Bewegung) 2. Dynamk on Massenpunkten (Enfluss on Kräften) 3. Starre Körper 4.Deformerbare Meden 5. Schwngungen, Wellen, Akustk I)1. Knematk Bewegungslehre (Zel: Quanttate
3.6 Molekulare Dynamik
 3.6 Molekulare Dynamk In den letzten 5 Jahrzehnten wurden drekte numersche Smulatonen zur statstschen Auswertung von Veltelchensystemen mmer wchtger. So lassen sch Phasenübergänge, aber auch makroskopsche
3.6 Molekulare Dynamk In den letzten 5 Jahrzehnten wurden drekte numersche Smulatonen zur statstschen Auswertung von Veltelchensystemen mmer wchtger. So lassen sch Phasenübergänge, aber auch makroskopsche
Theoretische Physik II: Analytische Mechanik und Spezielle Relativitätstheorie
 Theoretsche Physk II: Analytsche Mechank und Spezelle Relatvtätstheore Drk H. Rschke Sommersemester 2010 Inhaltsverzechns 1 Lagrange-Mechank 1 1.1 Zwangskräfte, Zwangsbedngungen und generalserte Koordnaten.....
Theoretsche Physk II: Analytsche Mechank und Spezelle Relatvtätstheore Drk H. Rschke Sommersemester 2010 Inhaltsverzechns 1 Lagrange-Mechank 1 1.1 Zwangskräfte, Zwangsbedngungen und generalserte Koordnaten.....
Kapitel 5. Symmetrien und Erhaltungsgrößen. 5.1 Symmetrietransformationen
 Kaptel 5 Symmetren un Erhaltungsgrößen 5.1 Symmetretransformatonen Betrachte en mechansches System mt en Koornaten q 1,... q f un er Lagrangefunkton L(q 1,... q f, q 1,... q f, t). Nun soll ene Transformaton
Kaptel 5 Symmetren un Erhaltungsgrößen 5.1 Symmetretransformatonen Betrachte en mechansches System mt en Koornaten q 1,... q f un er Lagrangefunkton L(q 1,... q f, q 1,... q f, t). Nun soll ene Transformaton
Kapitel 5 Systeme von Massenpunkten, Stöße
 Katel 5 ystee von Massenunkten, töße Drehoente und Drehuls enes Telchensystes O t : z r r r F x r F F F y F F t (acto = reacto) : F t äußeren Kräften F und F und nneren Kräften F = -F Drehoente : D D r
Katel 5 ystee von Massenunkten, töße Drehoente und Drehuls enes Telchensystes O t : z r r r F x r F F F y F F t (acto = reacto) : F t äußeren Kräften F und F und nneren Kräften F = -F Drehoente : D D r
Kreisel. koerperfestes KS. z y. raumfestes KS. Starrer Körper: System von Massepunkten m i, deren Abstände r i r j untereinander konstant sind.
 Kresel z y koerperfestes KS z y x raumfestes KS x Starrer Körper: System von Massepunkten m, deren Abstände r r j unterenander konstant snd. Der Zustand läßt sch beschreben durch: Poston des Schwerpunktes,
Kresel z y koerperfestes KS z y x raumfestes KS x Starrer Körper: System von Massepunkten m, deren Abstände r r j unterenander konstant snd. Der Zustand läßt sch beschreben durch: Poston des Schwerpunktes,
4. Lagrange-Formalismus
 y(t) ϑ 4. Lagrange-Formalsmus 4.0 Enführung Abbldung 4.1: Das sphärsche Pendel mt bewegtem Aufhängepunkt. R F mg Zel st es, enen enfachen Zugang zu komplzerten mechanschen Systemen zu entwckeln. Nach ener
y(t) ϑ 4. Lagrange-Formalsmus 4.0 Enführung Abbldung 4.1: Das sphärsche Pendel mt bewegtem Aufhängepunkt. R F mg Zel st es, enen enfachen Zugang zu komplzerten mechanschen Systemen zu entwckeln. Nach ener
Stochastische Prozesse
 INSTITUT FÜR STOCHASTIK SS 009 UNIVERSITÄT KARLSRUHE Blatt 4 Prv.-Doz. Dr. D. Kadelka Dpl.-Math. W. Lao Übungen zur Vorlesung Stochastsche Prozesse Musterlösungen Aufgabe 16: (Success Run, Fortsetzung)
INSTITUT FÜR STOCHASTIK SS 009 UNIVERSITÄT KARLSRUHE Blatt 4 Prv.-Doz. Dr. D. Kadelka Dpl.-Math. W. Lao Übungen zur Vorlesung Stochastsche Prozesse Musterlösungen Aufgabe 16: (Success Run, Fortsetzung)
1 Finanzmathematik. 1.1 Das Modell. Sei Xt
 1.1 Das Modell Se Xt der Pres enes Assets zur Zet t und X = X ) 1 d der Rd +-dmensonale Presprozess. Das Geld kann auch zu dem rskolosen Znssatz r be ener Bank angelegt werden. Der Wert deser Anlage wrd
1.1 Das Modell Se Xt der Pres enes Assets zur Zet t und X = X ) 1 d der Rd +-dmensonale Presprozess. Das Geld kann auch zu dem rskolosen Znssatz r be ener Bank angelegt werden. Der Wert deser Anlage wrd
Definition des linearen Korrelationskoeffizienten
 Defnton des lnearen Korrelatonskoeffzenten r xy x y y r x xy y 1 x x y y x Der Korrelatonskoeffzent st en Indkator dafür, we gut de Punkte (X,Y) zu ener Geraden passen. Sen Wert legt zwschen -1 und +1.
Defnton des lnearen Korrelatonskoeffzenten r xy x y y r x xy y 1 x x y y x Der Korrelatonskoeffzent st en Indkator dafür, we gut de Punkte (X,Y) zu ener Geraden passen. Sen Wert legt zwschen -1 und +1.
Lösungen der Aufgaben zu Kapitel 2
 Lösungen der Aufgaben zu Kaptel Abschntt 1 Aufgabe 1 Wr benutzen de Potenzrechenregeln, um ene Potenz von mt geradem Eponenten n oder mt ungeradem Eponenten n + 1 we folgt darzustellen: n n und n+1 n n
Lösungen der Aufgaben zu Kaptel Abschntt 1 Aufgabe 1 Wr benutzen de Potenzrechenregeln, um ene Potenz von mt geradem Eponenten n oder mt ungeradem Eponenten n + 1 we folgt darzustellen: n n und n+1 n n
I) Mechanik 1.Kinematik (Bewegung)
 I)1. Knematk I) Mechank 1.Knematk (Bewegung) 2. Dynamk on Massenpunkten (Enfluss on Kräften) 3. Starre Körper 4.Deformerbare Meden 5. Schwngungen, Wellen, Akustk I)1. Knematk Bewegungslehre (Zel: Quanttate
I)1. Knematk I) Mechank 1.Knematk (Bewegung) 2. Dynamk on Massenpunkten (Enfluss on Kräften) 3. Starre Körper 4.Deformerbare Meden 5. Schwngungen, Wellen, Akustk I)1. Knematk Bewegungslehre (Zel: Quanttate
An welche Stichwörter von der letzten Vorlesung können Sie sich noch erinnern?
 An welche Stchwörter von der letzten Vorlesung können Se sch noch ernnern? Gasgesetz ür deale Gase pv = nr Gelestete Arbet be sotherme Ausdehnung adabatsche Ausdehnung 2 n Reale Gase p + a 2 ( V nb) =
An welche Stchwörter von der letzten Vorlesung können Se sch noch ernnern? Gasgesetz ür deale Gase pv = nr Gelestete Arbet be sotherme Ausdehnung adabatsche Ausdehnung 2 n Reale Gase p + a 2 ( V nb) =
Übungsklausur zur Vorlesung Wahrscheinlichkeit und Regression Lösungen. Übungsklausur Wahrscheinlichkeit und Regression Die Lösungen
 Übungsklausur Wahrschenlchket und Regresson De Lösungen. Welche der folgenden Aussagen treffen auf en Zufallsexperment zu? a) En Zufallsexperment st en emprsches Phänomen, das n stochastschen Modellen
Übungsklausur Wahrschenlchket und Regresson De Lösungen. Welche der folgenden Aussagen treffen auf en Zufallsexperment zu? a) En Zufallsexperment st en emprsches Phänomen, das n stochastschen Modellen
Konkave und Konvexe Funktionen
 Konkave und Konvexe Funktonen Auch wenn es n der Wrtschaftstheore mest ncht möglch st, de Form enes funktonalen Zusammenhangs explzt anzugeben, so kann man doch n velen Stuatonen de Klasse der n Frage
Konkave und Konvexe Funktonen Auch wenn es n der Wrtschaftstheore mest ncht möglch st, de Form enes funktonalen Zusammenhangs explzt anzugeben, so kann man doch n velen Stuatonen de Klasse der n Frage
Einführung in die Robotertechnik. Dr.-Ing. Ralf Westphal,
 Enführung n de Robotertechnk Dr.-Ing. Ralf Westphal, 05.03.2012 Parallelknematken (SFB 562) Robotersteuerungsarchtekturen Montageplanung Moble Robotk Tefendatensensork Objekterkennung 3D Regstrerung Posenbestmmung
Enführung n de Robotertechnk Dr.-Ing. Ralf Westphal, 05.03.2012 Parallelknematken (SFB 562) Robotersteuerungsarchtekturen Montageplanung Moble Robotk Tefendatensensork Objekterkennung 3D Regstrerung Posenbestmmung
3. Lineare Algebra (Teil 2)
 Mathematk I und II für Ingeneure (FB 8) Verson /704004 Lneare Algebra (Tel ) Parameterdarstellung ener Geraden Im folgenden betrachten wr Geraden m eukldschen Raum n, wobe uns hauptsächlch de Fälle n bzw
Mathematk I und II für Ingeneure (FB 8) Verson /704004 Lneare Algebra (Tel ) Parameterdarstellung ener Geraden Im folgenden betrachten wr Geraden m eukldschen Raum n, wobe uns hauptsächlch de Fälle n bzw
Inhaltsverzeichnis. Vorbemerkungen 1
 Inhaltsverzechns Vorbemerkungen 1 1 Newtonsche Mechank 5 1.1 De Newtonschen Axome........................ 5 1.1.1 Wortlaut (übersetzt)...................... 5 1.1.2 Präzserung der knematschen Begrffe...........
Inhaltsverzechns Vorbemerkungen 1 1 Newtonsche Mechank 5 1.1 De Newtonschen Axome........................ 5 1.1.1 Wortlaut (übersetzt)...................... 5 1.1.2 Präzserung der knematschen Begrffe...........
nonparametrische Tests werden auch verteilungsfreie Tests genannt, da sie keine spezielle Verteilung der Daten in der Population voraussetzen
 arametrsche vs. nonparametrsche Testverfahren Verfahren zur Analyse nomnalskalerten Daten Thomas Schäfer SS 009 1 arametrsche vs. nonparametrsche Testverfahren nonparametrsche Tests werden auch vertelungsfree
arametrsche vs. nonparametrsche Testverfahren Verfahren zur Analyse nomnalskalerten Daten Thomas Schäfer SS 009 1 arametrsche vs. nonparametrsche Testverfahren nonparametrsche Tests werden auch vertelungsfree
Fachbereich Mathematik Prof. K. Grosse-Brauckmann D. Frisch WS 2007/08 10./ Gruppenübung
 Fachberech Mathematk Prof. K. Grosse-Brauckmann D. Frsch WS 27/8./.. 6. Übungsblatt zur Lnearen Algebra für Physker Gruppenübung Aufgabe G7 (Kern, Bld, Rang und Orthogonaltät) Gegeben se ene lneare Abbldung
Fachberech Mathematk Prof. K. Grosse-Brauckmann D. Frsch WS 27/8./.. 6. Übungsblatt zur Lnearen Algebra für Physker Gruppenübung Aufgabe G7 (Kern, Bld, Rang und Orthogonaltät) Gegeben se ene lneare Abbldung
Kapitel V. Parameter der Verteilungen
 Kaptel V Parameter der Vertelungen D. 5.. (Erwartungswert) Als Erwartungswert ener Zufallsvarablen X bezechnet man: E( X ) : Dabe se vorausgesetzt: = = + p falls X dskret f d falls X stetg und = + p
Kaptel V Parameter der Vertelungen D. 5.. (Erwartungswert) Als Erwartungswert ener Zufallsvarablen X bezechnet man: E( X ) : Dabe se vorausgesetzt: = = + p falls X dskret f d falls X stetg und = + p
Allgemeine Formulierung der Punktmechanik
 Kaptel 3 Allgemene Formulerung der Punktmechank Axom 2.2 besagt, daß der zetlche Bewegungsablauf enes Massenpunktes berechnet werden kann, wenn de Kräfte, welche auf den Massenpunkt wrken, vorgegeben snd.
Kaptel 3 Allgemene Formulerung der Punktmechank Axom 2.2 besagt, daß der zetlche Bewegungsablauf enes Massenpunktes berechnet werden kann, wenn de Kräfte, welche auf den Massenpunkt wrken, vorgegeben snd.
Dynamik starrer Körper
 Dynamk starrer Körper Bewegungen starrer Körper können n Translaton und Rotaton zerlegt werden. De Rotaton stellt enen nneren Frehetsgrad des Körpers dar, der be Punktmassen ncht exstert. Der Schwerpunkt
Dynamk starrer Körper Bewegungen starrer Körper können n Translaton und Rotaton zerlegt werden. De Rotaton stellt enen nneren Frehetsgrad des Körpers dar, der be Punktmassen ncht exstert. Der Schwerpunkt
2 Zufallsvariable und Verteilungen
 Zufallsvarable und Vertelungen 7 Zufallsvarable und Vertelungen Wr wollen uns jetzt mt Zufallsexpermenten beschäftgen, deren Ausgänge durch (reelle) Zahlen beschreben werden können, oder be denen man jedem
Zufallsvarable und Vertelungen 7 Zufallsvarable und Vertelungen Wr wollen uns jetzt mt Zufallsexpermenten beschäftgen, deren Ausgänge durch (reelle) Zahlen beschreben werden können, oder be denen man jedem
Informatik II. Minimalpolynome und Implikanten. Minimalpolynome. Minimalpolynome. Rainer Schrader. 27. Oktober Was bisher geschah: Definition
 Informatk II Raner Schrader und Implkanten Zentrum für Angewandte Informatk Köln 27. Oktober 2005 1 / 28 2 / 28 Was bsher geschah: jede Boolesche Funkton kann durch enfache Grundfunktonen dargestellt werden
Informatk II Raner Schrader und Implkanten Zentrum für Angewandte Informatk Köln 27. Oktober 2005 1 / 28 2 / 28 Was bsher geschah: jede Boolesche Funkton kann durch enfache Grundfunktonen dargestellt werden
Sei T( x ) die Tangente an den Graphen der Funktion f(x) im Punkt ( x 0, f(x 0 ) ) : T( x ) = f(x 0 ) + f (x 0 ) ( x - x 0 ).
 Taylorentwcklung (Approxmaton durch Polynome). Problemstellung Se T( x ) de Tangente an den Graphen der Funkton f(x) m Punkt ( x 0, f(x 0 ) ) : T( x ) = f(x 0 ) + f (x 0 ) ( x - x 0 ). Dann kann man de
Taylorentwcklung (Approxmaton durch Polynome). Problemstellung Se T( x ) de Tangente an den Graphen der Funkton f(x) m Punkt ( x 0, f(x 0 ) ) : T( x ) = f(x 0 ) + f (x 0 ) ( x - x 0 ). Dann kann man de
Lehrveranstaltung Stereostatik
 Lehrveranstaltung Stereostatk Thema 4: Vertelte Lasten Mechank 1 Vertelte Lasten 4.1 Problemstellung De Varablen n unseren Glechgewchtsbedngungen snd mmer Enzelkräfte (Bassenhet N) N bzw. Enzelmomente
Lehrveranstaltung Stereostatk Thema 4: Vertelte Lasten Mechank 1 Vertelte Lasten 4.1 Problemstellung De Varablen n unseren Glechgewchtsbedngungen snd mmer Enzelkräfte (Bassenhet N) N bzw. Enzelmomente
12 LK Ph / Gr Elektrische Leistung im Wechselstromkreis 1/5 31.01.2007. ω Additionstheorem: 2 sin 2 2
 1 K Ph / Gr Elektrsche estng m Wechselstromkres 1/5 3101007 estng m Wechselstromkres a) Ohmscher Wderstand = ˆ ( ω ) ( t) = sn ( ω t) t sn t ˆ ˆ P t = t t = sn ω t Momentane estng 1 cos ( t) ˆ ω = Addtonstheorem:
1 K Ph / Gr Elektrsche estng m Wechselstromkres 1/5 3101007 estng m Wechselstromkres a) Ohmscher Wderstand = ˆ ( ω ) ( t) = sn ( ω t) t sn t ˆ ˆ P t = t t = sn ω t Momentane estng 1 cos ( t) ˆ ω = Addtonstheorem:
Theoretische Physik 1 Mechanik
 Technsche Unverstät München Fakultät für Physk Ferenkurs Theoretsche Physk 1 Mechank Skrpt zu Vorlesung 4: Starrer Körper, Hamlton-Formalsmus gehalten von: Markus Krottenmüller & Markus Perner 30.08.01
Technsche Unverstät München Fakultät für Physk Ferenkurs Theoretsche Physk 1 Mechank Skrpt zu Vorlesung 4: Starrer Körper, Hamlton-Formalsmus gehalten von: Markus Krottenmüller & Markus Perner 30.08.01
Grundgedanke der Regressionsanalyse
 Grundgedanke der Regressonsanalse Bsher wurden durch Koeffzenten de Stärke von Zusammenhängen beschreben Mt der Regressonsrechnung können für ntervallskalerte Varablen darüber hnaus Modelle geschätzt werden
Grundgedanke der Regressonsanalse Bsher wurden durch Koeffzenten de Stärke von Zusammenhängen beschreben Mt der Regressonsrechnung können für ntervallskalerte Varablen darüber hnaus Modelle geschätzt werden
Rotation (2. Versuch)
 Rotaton 2. Versuch Bekannt snd berets Vektorfelder be denen das Lnenntegral über ene geschlossene Kurve Null wrd Stchworte: konservatve Kraft Potentalfelder Gradentenfeld. Es gbt auch Vektorfelder be denen
Rotaton 2. Versuch Bekannt snd berets Vektorfelder be denen das Lnenntegral über ene geschlossene Kurve Null wrd Stchworte: konservatve Kraft Potentalfelder Gradentenfeld. Es gbt auch Vektorfelder be denen
Bedingte Entropie. Bedingte Entropie. Bedingte Entropie. Kapitel 4: Bedingte Entropie I(X;Y) H(X Y) H(Y) H(X) H(XY)
 Bedngte Entrope Kaptel : Bedngte Entrope Das vorherge Theorem kann durch mehrfache Anwendung drekt verallgemenert werden H (... H ( = Ebenso kann de bedngt Entrope defnert werden Defnton: De bedngte Entrope
Bedngte Entrope Kaptel : Bedngte Entrope Das vorherge Theorem kann durch mehrfache Anwendung drekt verallgemenert werden H (... H ( = Ebenso kann de bedngt Entrope defnert werden Defnton: De bedngte Entrope
9 Komplexe Zahlen ( ) ( ) 9.1 Ziele. 9.2 Warum braucht man komplexe Zahlen? 9.3 Darstellung von komplexen Zahlen. r 2. j 2. j 1.
 Mathematk I / Komplexe Zahlen 9 Komplexe Zahlen 9. Zele Am Ende deses Kaptels hast Du ene Grundvorstellung was komplexe Zahlen snd. Du kannst se grafsch darstellen und enfache Berechnungen durchführen.
Mathematk I / Komplexe Zahlen 9 Komplexe Zahlen 9. Zele Am Ende deses Kaptels hast Du ene Grundvorstellung was komplexe Zahlen snd. Du kannst se grafsch darstellen und enfache Berechnungen durchführen.
9 Komplexe Zahlen ( ) ( ) 9.1 Ziele. 9.2 Warum braucht man komplexe Zahlen? 9.3 Darstellung von komplexen Zahlen. r 2. j 2. j 1.
 Mathematk I / Komplexe Zahlen 9 Komplexe Zahlen 9. Zele Am Ende deses Kaptels hast Du ene Grundvorstellung was komplexe Zahlen snd. Du kannst se grafsch darstellen und enfache Berechnungen durchführen.
Mathematk I / Komplexe Zahlen 9 Komplexe Zahlen 9. Zele Am Ende deses Kaptels hast Du ene Grundvorstellung was komplexe Zahlen snd. Du kannst se grafsch darstellen und enfache Berechnungen durchführen.
Vorlesung 3 Differentialgeometrie in der Physik 13
 Vorlesung 3 Dfferentalgeometre n der Physk 13 Bemerkung. Ist M Manngfaltgket, p M und φ : U R n Karte mt p U, so nennt man U auch Koordnatenumgebung und φ auch Koordnatensystem n p. Bespel 2.4 Seen R >
Vorlesung 3 Dfferentalgeometre n der Physk 13 Bemerkung. Ist M Manngfaltgket, p M und φ : U R n Karte mt p U, so nennt man U auch Koordnatenumgebung und φ auch Koordnatensystem n p. Bespel 2.4 Seen R >
d Alambert: Variationsprinzip in Differentialform (äquivalent zum Hamilton-Prinzip) = 0 (d Alambertsches Prinzip; δw = Z δr = 0 )
 Zusammenfassung Theoretsche Mechan d Alambert: Varatonsprnzp n Dfferentalform (äuvalent zum amlton-prnzp) δw ( F p ) * δr 0 (d Alambertsches Prnzp; δw Z δr 0 ) m allg.: p m * r m statschen Fall st: p 0
Zusammenfassung Theoretsche Mechan d Alambert: Varatonsprnzp n Dfferentalform (äuvalent zum amlton-prnzp) δw ( F p ) * δr 0 (d Alambertsches Prnzp; δw Z δr 0 ) m allg.: p m * r m statschen Fall st: p 0
Die mathematischen Grundlagen der Wellenmechanik
 De mathematschen Grundlagen der Wellenmechank Zustände und deren Darstellung En physkalsches System wrd durch enen Zustand u charaktersert, ndem es durch ene bestmmte expermentelle Präparaton gebracht
De mathematschen Grundlagen der Wellenmechank Zustände und deren Darstellung En physkalsches System wrd durch enen Zustand u charaktersert, ndem es durch ene bestmmte expermentelle Präparaton gebracht
Übungen zur Theoretischen Physik Fb SS 18
 Karlsruher Insttut für Technologe Insttut für Theore der Kondenserten Matere Übungen zur Theoretschen Physk Fb SS 8 Prof Dr A Shnrman Blatt PD Dr B Narozhny Lösungsvorschlag Thermodynamk von Phononen:
Karlsruher Insttut für Technologe Insttut für Theore der Kondenserten Matere Übungen zur Theoretschen Physk Fb SS 8 Prof Dr A Shnrman Blatt PD Dr B Narozhny Lösungsvorschlag Thermodynamk von Phononen:
Physik A VL11 ( )
 Physk A VL11 (0.11.01) Dynamk der Rotatonsbewegung I Kresbewegung und Kräfte Drehmoment und räghetsmoment Kresbewegung und Kräfte en Massepunkt (Schwerpunkt) führt nur ene ranslatonsbewegung aus ausgedehnte
Physk A VL11 (0.11.01) Dynamk der Rotatonsbewegung I Kresbewegung und Kräfte Drehmoment und räghetsmoment Kresbewegung und Kräfte en Massepunkt (Schwerpunkt) führt nur ene ranslatonsbewegung aus ausgedehnte
-70- Anhang: -Lineare Regression-
 -70- Anhang: -Lneare Regressn- Für ene Messgröße y f(x) gelte flgender mathematsche Zusammenhang: y a+ b x () In der Regel läßt sch durch enen Satz vn Messwerten (x, y ) aber kene Gerade zechnen, da de
-70- Anhang: -Lneare Regressn- Für ene Messgröße y f(x) gelte flgender mathematsche Zusammenhang: y a+ b x () In der Regel läßt sch durch enen Satz vn Messwerten (x, y ) aber kene Gerade zechnen, da de
Finite Differenzen. Tino Kluge. January 17,
 Enletung Explztes Fntes... Implzte Fnte... Startsete Ttelsete Fnte Dfferenzen Tno Kluge tno.kluge@hrz.tu-chemntz.de http://www.mathfnance.de/semnars/sdgl.html January 17, 2002 Sete 1 von 15 Vollbld Schleßen
Enletung Explztes Fntes... Implzte Fnte... Startsete Ttelsete Fnte Dfferenzen Tno Kluge tno.kluge@hrz.tu-chemntz.de http://www.mathfnance.de/semnars/sdgl.html January 17, 2002 Sete 1 von 15 Vollbld Schleßen
Polygonalisierung einer Kugel. Verfahren für die Polygonalisierung einer Kugel. Eldar Sultanow, Universität Potsdam, sultanow@gmail.com.
 Verfahren für de Polygonalserung ener Kugel Eldar Sultanow, Unverstät Potsdam, sultanow@gmal.com Abstract Ene Kugel kann durch mathematsche Funktonen beschreben werden. Man sprcht n desem Falle von ener
Verfahren für de Polygonalserung ener Kugel Eldar Sultanow, Unverstät Potsdam, sultanow@gmal.com Abstract Ene Kugel kann durch mathematsche Funktonen beschreben werden. Man sprcht n desem Falle von ener
Experimentalphysik 1. Vorlesung 1
 Technsche Unverstät München Fakultät für Physk Ferenkurs Expermentalphysk 1 WS 2016/17 Vorlesung 1 Ronja Berg (ronja.berg@tum.de) Katharna Sche (katharna.sche@tum.de) Inhaltsverzechns 1 Klasssche Mechank
Technsche Unverstät München Fakultät für Physk Ferenkurs Expermentalphysk 1 WS 2016/17 Vorlesung 1 Ronja Berg (ronja.berg@tum.de) Katharna Sche (katharna.sche@tum.de) Inhaltsverzechns 1 Klasssche Mechank
Experimentalphysik II (Kip SS 2007)
 permentalphsk II (Kp SS 007) Zusatvorlesungen: Z-1 n- und mehrdmensonale Integraton Z- Gradent, Dvergen und Rotaton Z-3 Gaußscher und Stokesscher Integralsat Z-4 Kontnutätsglechung Z-5 lektromagnetsche
permentalphsk II (Kp SS 007) Zusatvorlesungen: Z-1 n- und mehrdmensonale Integraton Z- Gradent, Dvergen und Rotaton Z-3 Gaußscher und Stokesscher Integralsat Z-4 Kontnutätsglechung Z-5 lektromagnetsche
22. Vorlesung Sommersemester
 22 Vorlesung Sommersemester 1 Bespel 2: Würfel mt festgehaltener Ecke In desem Fall wählt man den Koordnatenursprung n der Ecke und der Würfel st durch den Berech x = 0 a, y = 0 a und z = 0 a bestmmt De
22 Vorlesung Sommersemester 1 Bespel 2: Würfel mt festgehaltener Ecke In desem Fall wählt man den Koordnatenursprung n der Ecke und der Würfel st durch den Berech x = 0 a, y = 0 a und z = 0 a bestmmt De
Stochastische Prozesse
 INSTITUT FÜR STOCHASTIK SS 2009 UNIVERSITÄT KARLSRUHE Blatt 2 Prv.-Doz. Dr. D. Kadelka Dpl.-Math. W. Lao Übungen zur Vorlesung Stochastsche Prozesse Musterlösungen Aufgabe 7: (B. Fredmans Urnenmodell)
INSTITUT FÜR STOCHASTIK SS 2009 UNIVERSITÄT KARLSRUHE Blatt 2 Prv.-Doz. Dr. D. Kadelka Dpl.-Math. W. Lao Übungen zur Vorlesung Stochastsche Prozesse Musterlösungen Aufgabe 7: (B. Fredmans Urnenmodell)
Musterlösung zu Übung 4
 PCI Thermodynamk G. Jeschke FS 05 Musterlösung zu Übung erson vom 6. Februar 05) Aufgabe a) En Lter flüssges Wasser egt m H O, l ρ H O, l L 998 g L 998 g. ) De Stoffmenge n H O, l) von enem Lter flüssgen
PCI Thermodynamk G. Jeschke FS 05 Musterlösung zu Übung erson vom 6. Februar 05) Aufgabe a) En Lter flüssges Wasser egt m H O, l ρ H O, l L 998 g L 998 g. ) De Stoffmenge n H O, l) von enem Lter flüssgen
Elemente der Mathematik - Sommer 2016
 Elemente der Mathematk - Sommer 2016 Prof Dr Matthas Lesch, Regula Krapf Lösungen Übungsblatt 3 Aufgabe 9 (10 Punkte) Das Horner-Schema st ene Methode zum Auswerten enes Polynoms n a0 x an der Stelle s
Elemente der Mathematk - Sommer 2016 Prof Dr Matthas Lesch, Regula Krapf Lösungen Übungsblatt 3 Aufgabe 9 (10 Punkte) Das Horner-Schema st ene Methode zum Auswerten enes Polynoms n a0 x an der Stelle s
Beschreibung des Zusammenhangs zweier metrischer Merkmale. Streudiagramme Korrelationskoeffizienten Regression
 Beschrebung des Zusammenhangs zweer metrscher Merkmale Streudagramme Korrelatonskoeffzenten Regresson Alter und Gewcht be Kndern bs 36 Monaten Knd Monate Gewcht 9 9 5 8 3 4 7.5 4 3 6 5 3 6 4 3.5 7 35 5
Beschrebung des Zusammenhangs zweer metrscher Merkmale Streudagramme Korrelatonskoeffzenten Regresson Alter und Gewcht be Kndern bs 36 Monaten Knd Monate Gewcht 9 9 5 8 3 4 7.5 4 3 6 5 3 6 4 3.5 7 35 5
Eine kurze Einführung in die Dichtefunktionaltheorie (DFT)
 Ene kurze Enführung n de Dchtefunktonaltheore (DFT) Mchael Martns Lteratur: W. Koch, M.C. Holthausen A Chemst s Gude to Densty Functonal Theory Wley-VCH 2001 Dchtefunktonaltheore p.1 Enletung Im Falle
Ene kurze Enführung n de Dchtefunktonaltheore (DFT) Mchael Martns Lteratur: W. Koch, M.C. Holthausen A Chemst s Gude to Densty Functonal Theory Wley-VCH 2001 Dchtefunktonaltheore p.1 Enletung Im Falle
Tangentenvektoren und Tangentialraum
 angentenvektoren und angentalrau (kontravarante Vektoren oder enach Vektoren) Gegeben ene - densonale Manngaltgket M, denert an an ede Punkt den angentalrau M als den densonalen Vektorrau aller öglchen
angentenvektoren und angentalrau (kontravarante Vektoren oder enach Vektoren) Gegeben ene - densonale Manngaltgket M, denert an an ede Punkt den angentalrau M als den densonalen Vektorrau aller öglchen
Abbildung 3.1: Besetzungszahlen eines Fermigases im Grundzustand (a)) und für eine angeregte Konfiguration (b)).
 44 n n F F a) b) Abbldung 3.: Besetzungszahlen enes Fermgases m Grundzustand (a)) und für ene angeregte Konfguraton (b)). 3.3 Ferm Drac Statstk In desem Abschntt wollen wr de thermodynamschen Egenschaften
44 n n F F a) b) Abbldung 3.: Besetzungszahlen enes Fermgases m Grundzustand (a)) und für ene angeregte Konfguraton (b)). 3.3 Ferm Drac Statstk In desem Abschntt wollen wr de thermodynamschen Egenschaften
Klassische Theoretische Physik II: Mechanik
 Klasssche Theoretsche Physk II: Mechank Alexaner Shnrman Insttut für Theore er Konenserten Matere Karlsruher Insttut für Technologe 9. Jul 010 1 1 Lagrange-Glechungen 1. Art 1.1 Motverenes Bespel: en Penel
Klasssche Theoretsche Physk II: Mechank Alexaner Shnrman Insttut für Theore er Konenserten Matere Karlsruher Insttut für Technologe 9. Jul 010 1 1 Lagrange-Glechungen 1. Art 1.1 Motverenes Bespel: en Penel
Gauss sche Fehlerrrechnung
 Gauss sche Fehlerrrechnung T. Ihn 24. Oktober 206 Inhaltsverzechns Modell und Lkelhood 2 Alle Standardabwechungen σ snd bekannt, bzw. de Kovaranzmatrx der Daten st bekannt: Mnmeren der χ 2 -Funkton. 6
Gauss sche Fehlerrrechnung T. Ihn 24. Oktober 206 Inhaltsverzechns Modell und Lkelhood 2 Alle Standardabwechungen σ snd bekannt, bzw. de Kovaranzmatrx der Daten st bekannt: Mnmeren der χ 2 -Funkton. 6
Daten sind in Tabellenform gegeben durch die Eingabe von FORMELN können mit diesen Daten automatisierte Berechnungen durchgeführt werden.
 Ene kurze Enführung n EXCEL Daten snd n Tabellenform gegeben durch de Engabe von FORMELN können mt desen Daten automatserte Berechnungen durchgeführt werden. Menüleste Symbolleste Bearbetungszele aktve
Ene kurze Enführung n EXCEL Daten snd n Tabellenform gegeben durch de Engabe von FORMELN können mt desen Daten automatserte Berechnungen durchgeführt werden. Menüleste Symbolleste Bearbetungszele aktve
4. Energie, Arbeit, Leistung, Impuls
 34 35 4. Energe, Arbet, Lestung, Ipuls Zentrale Größen der Physk: Energe E, Enhet Joule ( [J] [N] [kg /s ] Es gbt zwe grundsätzlche Foren on Energe: knetsche Energe: entelle Energe: Arbet, Enhet Joule
34 35 4. Energe, Arbet, Lestung, Ipuls Zentrale Größen der Physk: Energe E, Enhet Joule ( [J] [N] [kg /s ] Es gbt zwe grundsätzlche Foren on Energe: knetsche Energe: entelle Energe: Arbet, Enhet Joule
Theoretische Physik B MECHANIK. Vorlesung SS 2003
 Theoretsche Physk B MECHANIK Vorlesung SS 2003 P. Wölfle Insttut für Theore der Kondenserten Matere Fakultät für Physk Unverstät Karlsruhe Homepage: http://www.tkm.un-karlsruhe.de/lehre/ Textverarbetung:
Theoretsche Physk B MECHANIK Vorlesung SS 2003 P. Wölfle Insttut für Theore der Kondenserten Matere Fakultät für Physk Unverstät Karlsruhe Homepage: http://www.tkm.un-karlsruhe.de/lehre/ Textverarbetung:
Einführung in die theoretische Physik 1
 Enführung n de theoretsche hysk 1 rof. Dr. L. Mathey Denstag 15:45 16:45 und Donnerstag 10:45 12:00 Begnn: 23.10.12 Jungus 9, Hörs 2 Mathey Enführung n de theor. hysk 1 1 Grundhypothese der Thermostatk
Enführung n de theoretsche hysk 1 rof. Dr. L. Mathey Denstag 15:45 16:45 und Donnerstag 10:45 12:00 Begnn: 23.10.12 Jungus 9, Hörs 2 Mathey Enführung n de theor. hysk 1 1 Grundhypothese der Thermostatk
Regressionsgerade. x x 1 x 2 x 3... x n y y 1 y 2 y 3... y n
 Regressonsgerade x x x x 3... x n y y y y 3... y n Bem Auswerten von Messrehen wrd häufg ene durch theoretsche Überlegungen nahegelegte lneare Bezehung zwschen den x- und y- Werten gesucht, d.h. ene Gerade
Regressonsgerade x x x x 3... x n y y y y 3... y n Bem Auswerten von Messrehen wrd häufg ene durch theoretsche Überlegungen nahegelegte lneare Bezehung zwschen den x- und y- Werten gesucht, d.h. ene Gerade
Klassische Mechanik. von Herbert Goldstein, Charles P Poole, Jr, John L Safko, Sr. 1. Auflage
 Klasssche Mechank von Herbert Goldsten, Charles P Poole, Jr, John L Safko, Sr 1. Auflage Klasssche Mechank Goldsten / Poole, Jr / Safko, Sr schnell und portofre erhältlch be beck-shop.de DIE FACHBUCHHANDLUNG
Klasssche Mechank von Herbert Goldsten, Charles P Poole, Jr, John L Safko, Sr 1. Auflage Klasssche Mechank Goldsten / Poole, Jr / Safko, Sr schnell und portofre erhältlch be beck-shop.de DIE FACHBUCHHANDLUNG
1 Definition und Grundbegriffe
 1 Defnton und Grundbegrffe Defnton: Ene Glechung n der ene unbekannte Funkton y y und deren Abletungen bs zur n-ten Ordnung auftreten heßt gewöhnlche Dfferentalglechung n-ter Ordnung Möglche Formen snd:
1 Defnton und Grundbegrffe Defnton: Ene Glechung n der ene unbekannte Funkton y y und deren Abletungen bs zur n-ten Ordnung auftreten heßt gewöhnlche Dfferentalglechung n-ter Ordnung Möglche Formen snd:
Statistik und Wahrscheinlichkeitsrechnung
 Statstk und Wahrschenlchketsrechnung Statstk und Wahrschenlchketsrechnung 5. Vorlesung Dr. Jochen Köhler.03.0 Statstk und Wahrschenlchketsrechnung Wchtg!!! Vorlesung Do 4.03.0 HCI G3 Übung 5 D 9.03.0 Fnk
Statstk und Wahrschenlchketsrechnung Statstk und Wahrschenlchketsrechnung 5. Vorlesung Dr. Jochen Köhler.03.0 Statstk und Wahrschenlchketsrechnung Wchtg!!! Vorlesung Do 4.03.0 HCI G3 Übung 5 D 9.03.0 Fnk
wird auch Spannweite bzw. Variationsbreite genannt ist definiert als die Differenz zwischen dem größten und kleinsten Messwert einer Verteilung:
 Streuungswerte: 1) Range (R) ab metrschem Messnveau ) Quartlabstand (QA) und mttlere Quartlabstand (MQA) ab metrschem Messnveau 3) Durchschnttlche Abwechung (AD) ab metrschem Messnveau 4) Varanz (s ) ab
Streuungswerte: 1) Range (R) ab metrschem Messnveau ) Quartlabstand (QA) und mttlere Quartlabstand (MQA) ab metrschem Messnveau 3) Durchschnttlche Abwechung (AD) ab metrschem Messnveau 4) Varanz (s ) ab
d da B A Die gesamte Erscheinung der magnetischen Feldlinien bezeichnet man als magnetischen Fluss. = 1 V s = 1 Wb
 S N De amte Erschenng der magnetschen Feldlnen bezechnet man als magnetschen Flss. = V s = Wb Kraftflssdchte oder magnetsche ndkton B. B d da B = Wb/m = T Für homogene Magnetfelder, we se m nneren von
S N De amte Erschenng der magnetschen Feldlnen bezechnet man als magnetschen Flss. = V s = Wb Kraftflssdchte oder magnetsche ndkton B. B d da B = Wb/m = T Für homogene Magnetfelder, we se m nneren von
Zur Erinnerung: System von Massenpunkten. dt i dt. 1 dt. Massenschwerpunkt
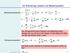 Massenschwerunkt r Zur rnnerung: yste on Massenunkten r dr dt r t M, M dr P dt M M M F dp d dt d M dt dt Ma chwerunktsyste Der chwerunkt enes ystes aus Massenunkten bewegt sch so, als ob er en Körer t
Massenschwerunkt r Zur rnnerung: yste on Massenunkten r dr dt r t M, M dr P dt M M M F dp d dt d M dt dt Ma chwerunktsyste Der chwerunkt enes ystes aus Massenunkten bewegt sch so, als ob er en Körer t
1.6 Energie 1.6.1 Arbeit und Leistung Wird ein Körper unter Wirkung der Kraft F längs eines Weges s verschoben, so wird dabei die Arbeit
 3.6 Energe.6. Arbe und Lesung Wrd en Körper uner Wrkung der Kraf F längs enes Weges s verschoben, so wrd dabe de Arbe W = F s Arbe = Kraf Weg verrche. In deser enfachen Form gülg, wenn folgende Voraussezungen
3.6 Energe.6. Arbe und Lesung Wrd en Körper uner Wrkung der Kraf F längs enes Weges s verschoben, so wrd dabe de Arbe W = F s Arbe = Kraf Weg verrche. In deser enfachen Form gülg, wenn folgende Voraussezungen
16. Vorlesung Sommersemester
 16. Vorlesung Sommersemester 1 Das Egenwertproblem In allgemener Form hat das Egenwertproblem de Form A x = λ x, (1) wobe A ene n n-matrx, x en n-dmensonaler Vektor und λ der Egenwert st (n Englsch: egenvector,
16. Vorlesung Sommersemester 1 Das Egenwertproblem In allgemener Form hat das Egenwertproblem de Form A x = λ x, (1) wobe A ene n n-matrx, x en n-dmensonaler Vektor und λ der Egenwert st (n Englsch: egenvector,
Fallstudie 1 Diskrete Verteilungen Abgabe: Aufgabentext und Lösungen schriftlich bis zum
 Abgabe: Aufgabentext und Lösungen schrftlch bs zum 15. 6. 2012 I. Thema: Zehen mt und ohne Zurücklegen Lesen Se sch zunächst folgenden Text durch! Wr haben bsher Stchprobenzehungen aus Grundgesamtheten
Abgabe: Aufgabentext und Lösungen schrftlch bs zum 15. 6. 2012 I. Thema: Zehen mt und ohne Zurücklegen Lesen Se sch zunächst folgenden Text durch! Wr haben bsher Stchprobenzehungen aus Grundgesamtheten
p : Impuls in Ns v : Geschwindigkeit in m/s
 -I.C9-4 Impuls 4. Impuls und Kraftstoß 4.. Impuls De Bewegung enes Körpers wrd bespelswese durch de Geschwndgket beschreben. Um de Bewegung enes Körpers zu ändern braucht man ene Kraft (Abb.). Dese führt
-I.C9-4 Impuls 4. Impuls und Kraftstoß 4.. Impuls De Bewegung enes Körpers wrd bespelswese durch de Geschwndgket beschreben. Um de Bewegung enes Körpers zu ändern braucht man ene Kraft (Abb.). Dese führt
Runge-Kutta-Theorie: Adjungierte Verfahren, A-Stabilität, Steife Systeme
 Runge-Kutta-Teore: Adjungerte Verfaren, A-Stabltät, Stefe Systeme Andre Neubert bat@un-paderborn.de Semnar Numerk für Informatker, SS2004: Runge-Kutta-Teore Sete Glederung : - Adjungerte Verfaren / Symmetrsce
Runge-Kutta-Teore: Adjungerte Verfaren, A-Stabltät, Stefe Systeme Andre Neubert bat@un-paderborn.de Semnar Numerk für Informatker, SS2004: Runge-Kutta-Teore Sete Glederung : - Adjungerte Verfaren / Symmetrsce
Der starre Körper. 1 Grundlagen. Dominik Fauser. 1.1 Denition. 1.2 Freiheitsgrade
 Der starre Körper Domnk Fauser 1 Grundlagen 1.1 Denton Als enen starren Körper bezechnet man en System von Massepunkten m, deren Abstände zuenander konstant snd: r j = r r j. Mest betrachtet man ene sehr
Der starre Körper Domnk Fauser 1 Grundlagen 1.1 Denton Als enen starren Körper bezechnet man en System von Massepunkten m, deren Abstände zuenander konstant snd: r j = r r j. Mest betrachtet man ene sehr
Resultate / "states of nature" / mögliche Zustände / möglicheentwicklungen
 Pay-off-Matrzen und Entschedung unter Rsko Es stehen verschedene Alternatven (Strategen) zur Wahl. Jede Stratege führt zu bestmmten Resultaten (outcomes). Man schätzt dese Resultate für jede Stratege und
Pay-off-Matrzen und Entschedung unter Rsko Es stehen verschedene Alternatven (Strategen) zur Wahl. Jede Stratege führt zu bestmmten Resultaten (outcomes). Man schätzt dese Resultate für jede Stratege und
Die kanonische Zustandssumme (System) und ihr Zusammenhang mit der molekularen Zustandssumme (Einzelmolekül) unterscheidbare Teilchen:
 De molekulare Zustandssumme βε = e mt β = De kanonsche Zustandssumme (System) und hr Zusammenhang mt der molekularen Zustandssumme (Enzelmolekül) unterschedbare elchen: Q = ununterschedbareelchen Q : =!
De molekulare Zustandssumme βε = e mt β = De kanonsche Zustandssumme (System) und hr Zusammenhang mt der molekularen Zustandssumme (Enzelmolekül) unterschedbare elchen: Q = ununterschedbareelchen Q : =!
7 Schrödingergleichung
 36 7 Schrödngerglechung 7 Schrödngerglechung De Schrödngerglechung spelt n der Quantenmechank ene zentrale Rolle. Mt hr wrd de Wellenfunkton des Systems berechnet. Der erste Bestandtel der Schrödngerglechung
36 7 Schrödngerglechung 7 Schrödngerglechung De Schrödngerglechung spelt n der Quantenmechank ene zentrale Rolle. Mt hr wrd de Wellenfunkton des Systems berechnet. Der erste Bestandtel der Schrödngerglechung
Neuronale Netze. M. Gruber (1) ausgeloste Reiz ist x (1) = (1) (s (1) ) mit (1) (s) = 1 sgn(s 1 ) sgn(s 2 ) T. .
 Neuronale Netze M. Gruber 7.11.015 Begnnen wr mt enem Bespel. Bespel 1 Wr konstrueren enen Klasskator auf der Menge X = [ 1; 1], dessen Wrkung man n Abb.1 rechts sehen kann. Auf der blauen Telmenge soll
Neuronale Netze M. Gruber 7.11.015 Begnnen wr mt enem Bespel. Bespel 1 Wr konstrueren enen Klasskator auf der Menge X = [ 1; 1], dessen Wrkung man n Abb.1 rechts sehen kann. Auf der blauen Telmenge soll
Lineare Regression (1) - Einführung I -
 Lneare Regresson (1) - Enführung I - Mttels Regressonsanalysen und kompleeren, auf Regressonsanalysen aserenden Verfahren können schenar verschedene, jedoch nenander üerführare Fragen untersucht werden:
Lneare Regresson (1) - Enführung I - Mttels Regressonsanalysen und kompleeren, auf Regressonsanalysen aserenden Verfahren können schenar verschedene, jedoch nenander üerführare Fragen untersucht werden:
8. Mathematische Begriffe der Thermodynamik. Basel, 2008
 8. Mathematsche Begre der Thermodnamk Basel, 2008 1. Enührung 8. Mathematsche Begre der Thermodnamk 2. Zustandsunktonen mehrerer Varabeln 3. Totales Derental 4. Homogene Funktonen 5. Mengen-Angaben 6.
8. Mathematsche Begre der Thermodnamk Basel, 2008 1. Enührung 8. Mathematsche Begre der Thermodnamk 2. Zustandsunktonen mehrerer Varabeln 3. Totales Derental 4. Homogene Funktonen 5. Mengen-Angaben 6.
18. Dynamisches Programmieren
 8. Dynamsches Programmeren Dynamsche Programmerung we gerge Algorthmen ene Algorthmenmethode, um Optmerungsprobleme zu lösen. We Dvde&Conquer berechnet Dynamsche Programmerung Lösung enes Problems aus
8. Dynamsches Programmeren Dynamsche Programmerung we gerge Algorthmen ene Algorthmenmethode, um Optmerungsprobleme zu lösen. We Dvde&Conquer berechnet Dynamsche Programmerung Lösung enes Problems aus
Bei Strecken höherer Ordnung wird auch hier die Strecke durch die Methode der Ersatzzeitkonstante
 Lösung Übung 9 Aufgabe: eglerauslegung mt blnearer Transformaton n s In der kontnuerlchen egelungstechnk wrd für gewöhnlch en PI-egler verwendet, um de größte Zetkonstante zu kompenseren bzw. be IT-Strecken
Lösung Übung 9 Aufgabe: eglerauslegung mt blnearer Transformaton n s In der kontnuerlchen egelungstechnk wrd für gewöhnlch en PI-egler verwendet, um de größte Zetkonstante zu kompenseren bzw. be IT-Strecken
Symbol Grösse Einheit. Gravitationskonstante Naturkonstante. Abstand zwischen den Massenmittelpunkten. Federverlängerung m.
 Kräfte Das ravtatonsgesetz m m r ewchtskraft m g Symbol rösse nhet ravtatonskraft ravtatonskonstante aturkonstante m, m Masse kg r Abstand zwschen den Massenmttelpunkten m kg m Zwschen zwe Körpern wrkt
Kräfte Das ravtatonsgesetz m m r ewchtskraft m g Symbol rösse nhet ravtatonskraft ravtatonskonstante aturkonstante m, m Masse kg r Abstand zwschen den Massenmttelpunkten m kg m Zwschen zwe Körpern wrkt
