Beschaffung. Prof. Dr. Martin Moog. Lehrstuhl für Forstliche Wirtschaftslehre
|
|
|
- Erich Geisler
- vor 8 Jahren
- Abrufe
Transkript
1 Beschaffung Begriffe des Beschaffungswesens Optimierung der Bestellmenge bei kontinuierlichem Verbrauch (Andler sche Formel) Optimierung der Bestellmenge bei diskontinuierlichem Verbrauch (WILO-Verfahren, Verfahren der wirtschaftlichsten Losgröße) Minimierung von Transportkosten (Lineare Programmierung) 1
2 Beschaffung Entscheidungsbereiche der Beschaffungspolitik Beschaffungsprogramm Beschaffungskonditionen Beschaffungsmethode Beschaffungskommunikation 2
3 Beschaffungskonditionen Beschaffungskonditionen Zahlungsbedingungen Sonstige Konditionen Zeitpunkt Art und Höhe Liefermenge Lieferzeitpunkt Lieferungsort Folgen bei Vertragsstörungen 3
4 Phasen des Beschaffungsprozesses Vorbereitung Zielklärung Bedarfsermittlung Marktforschung Einholung von Angeboten Vergleich der Angebote Entscheidung Durchführung Vertragsabschluß Abruf der Leistungen Prüfung der Güter Zahlungsfreigabe ggf. Lagerung Überwachung Terminkontrolle Kontrolle der Konditionen Kontrolle der Qualität 4
5 Bestellkosten bestellmengenabhängig und -unabhängig Bestellkosten bestellmengenabhängige Kosten bestellmengenunabhängige Kosten Zinsen für Kapitalbindung Lagerkosten i.e.s Kosten der Ausschreibung Kosten der Materialprüfung 5
6 Beschaffung Begriffe des Beschaffungswesens Optimierung der Bestellmenge bei kontinuierlichem Verbrauch (Andler sche Formel) Optimierung der Bestellmenge bei diskontinuierlichem Verbrauch (WILO-Verfahren, Verfahren der wirtschaftlichsten Losgröße) Minimierung von Transportkosten (Lineare Programmierung) 6
7 Lagerhaltung Lagerbestand Bestellzeitpunkt Bestellmenge Meldemenge eiserner Bestand Lieferzeitpunkt Zeit 7
8 Optimierung der Bestellmenge bei kontinuierlichem Verbrauch Kosten pro Periode Bestellmengenabhängige Kosten sind insbesondere die Zinskosten. Nimmt man an, daß im Mittel die halbe Bestellmenge gelagert werden muß, berechnen sich die Zinskosten als Produkt aus der halben Bestellmenge, multipliziert mit dem Preis des zu beschaffenden Produktes und dem Zinssatz in Hundertstel. Grafisch ergibt sich eine durch den Ursprung gehende Gerade. (m/2) x p x i/100 Bestellmenge 8
9 Optimierung der Bestellmenge bei kontinuierlichem Verbrauch Kosten pro Periode Die Kosten der Lagerung können z.t. als bestellmengenabhängige Kosten behandelt werden. Z.B. die Inanspruchnahme von Lagerraum, der auch alternativ verwendbar ist. Dann können die Lagerkosten wie die Zinskosten behandelt werden. Man addiert zum Zinssatz einfach einen Lagerkostensatz (l). Grafisch wird die durch den Ursprung gehende Gerade etwas steiler. (m/2) x p x ( i + l )/100 Bestellmenge 9
10 Optimierung der Bestellmenge bei kontinuierlichem Verbrauch Kosten pro Periode Bestellmengenunabhängige Kosten (K f ) sind z.b. Ausschreibungskosten. Die bestellmengenunabhängigen Kosten pro Periode berechnen sich einfach durch Multiplikation der fixen Kosten einer Bestellung mit der Anzahl der Bestellungen pro Periode. Letztere ergibt sich als Quotient der Bedarfsmenge pro Periode und der Bestellmenge. Grafisch ergibt sich eine fallende Kurve. Kf x B/m Bestellmenge 10
11 Optimierung der Bestellmenge bei kontinuierlichem Verbrauch Kosten pro Periode Es sei angenommen, es gäbe keine Mengenrabatte. Dann sind die für die zu beschaffenden Güter zu zahlenden Beträge in der Periode einfach das Produkt aus Periodenbedarf B und Preis P. Es besteht keine Abhängigkeit von der Bestellmenge. Grafisch ergibt sich eine der X-Achse parallele Gerade. B x P Bestellmenge 11
12 Daten für das Beispiel Jahresbedarf Preis Fixkosten der Bestellung Zins- und Lagerkostensatz Stück 1 GE GE 0,2 12
13 Optimierung der Bestellmenge bei kontinuierlichem Verbrauch Periodenkosten Periodenkosten Periodenbedarf x Preis Zins- und Lagerkosten Fixe Bestellkosten Bestellmenge 13
14 Optimierung der Bestellmenge bei kontinuierlichem Verbrauch Bestellmengen (m) Jahresbedarf x Preis Zins & Lagerkosten m/2*(i+l)/100 Kfix*b/m Summe (2-5) , , , , , , , , , ,
15 Die Andler sche Formel Kosten pro Periode Fixe Bestellkosten pro Periode K = B x P + K f x B/m + m x P i + l x Ausgabe pro Periode Lager- und Zinskosten pro Periode 15
16 Die Andler sche Formel Die Gleichung muß abgeleitet werden, um durch Nullsetzen das Minimum der Kurve zu finden K = B x P + K f x B/m + m x P i + l x dk = dm 0 => K f x B/m 2 + P i + l x = 0 Die 1. Ableitung kann man nach m auflösen, so daß sich eine Formel für die optimale Bestellmenge ergibt die sogen. ANDLER sche Formel. 16
17 Exkurs die Quotientenregel y = u / v u v u v y = v 2 0 x m K f xb x 1 (K f xb/m) = m 2 17
18 Die Andler sche Formel dk = dm 0 => K f x B/m 2 + P x ( i + l ) 2 = 0 P ( i + l ) = K f x B m 2 m 2 ist zu isolieren, indem erst mit m 2 multipliziert wird und dann durch K f xb geteilt wird. P ( i + l ) x m 2 2 K f x B x P ( i + l ) = = K f x B m 2 18
19 Die Andler sche Formel Kf * B m = opt P( i + *2 l) m opt optimale Bestellmenge Kf fixe Bestellkosten B Periodenbedarf (Jahresbedarf) P Preis für 1 Einheit des zu beschaffenden Gutes (i + l) zusammengefaßter Zins- und Lagerkostensatz in Hundertstel 19
20 Die Andler sche Formel m opt = 2.000*10.000*2 1(0,20) m opt optimale Bestellmenge Kf fixe Bestellkosten B Periodenbedarf (Jahresbedarf) P 1 Preis für 1 Einheit des zu beschaffenden Gutes (i + l) 0,20 zusammengafaßter Zins- und Lagerkostensatz in Hundertstel 20
21 Die Andler sche Formel 2.000* * 2 m opt = = 1(0,20 ) ,14 Kf fixe Bestellkosten B Periodenbedarf (Jahresbedarf) P 1 Preis für 1 Einheit des zu beschaffenden Gutes (i + l) 0,20 zusammengafaßter Zins- und Lagerkostensatz in Hundertstel 21
22 Optimierung der Bestellmenge bei kontinuierlichem Verbrauch - Modellerweiterungen Modellerweiterungen sind relativ einfach möglich, wenn nicht die Andler sche Formel benutzt werden soll, sondern die Berechnung unter Nutzung der elektronischen Datenverarbeitung durchgeführt werden kann. Tabellenkalkulationsprogramme sind hervorragend geeignet. Eine naheliegende Modellerweiterung ist die Berücksichtigung von Mengenrabatten. Ebenso ist die Berücksichtigung von Sprüngen in den Beschaffungskosten oder/und den Lagerkosten möglich. 22
23 Beschaffung Begriffe des Beschaffungswesens Optimierung der Bestellmenge bei kontinuierlichem Verbrauch (Andler sche Formel) Optimierung der Bestellmenge bei diskontinuierlichem Verbrauch (WILO( WILO-Verfahren,, Verfahren der wirtschaftlichsten Losgröße) Minimierung von Transportkosten (Lineare Programmierung) 23
24 Optimierung der Bestellmenge bei diskontinuierlichem Verbrauch 1. Periode 2. Periode 3. Periode 4. Periode Berechnung der durchschnittlichen Kosten für die 1. Periode Berechnung der durchschnittlichen Kosten für die 1. und 2. Periode Berechnung der durchschnittlichen Kosten für die 1., 2. und 3. Periode Beschaffung für die Anzahl von Perioden, für die die durchschnittlichen Kosten minimal sind. 24
25 Optimierung der Bestellmenge bei diskontinuierlichem Verbrauch Bedarfsplanung Planungs- Periode Bedarfsmenge M1 M2 M3 M4 M5 25
26 Lagerhaltung bei diskontinuierlichem Verbrauch 180 Lagerhaltung im Falle der Beschaffung für 3 Perioden Lagermenge Lagerhaltung im Falle der Beschaffung für 2 Perioden Perioden 26
27 Optimierung der Bestellmenge bei diskontinuierlichem Verbrauch Lagerbestand bei Beschaffung für die Perioden Periode M1 x 0,5 M2 M1 x 0,5 M3 M2 M1 x 0,5 M4 M3 M2 M1 x 0,5 2 M2 x 0,5 M3 M2 x 0,5 M4 M3 M2 x 0,5 3 M3 x 0,5 M4 M3 x 0,5 4 M4 x 05 27
28 Optimierung der Bestellmenge bei diskontinuierlichem Verbrauch Kosten Beschaffung für die Perioden Lagerkosten Fixe Bestellkosten Variable Bestellkosten Gesamtkosten 28
29 Optimierung der Bestellmenge bei diskontinuierlichem Verbrauch Vorgehensweise des WILO-Verfahrens zur Optimierung der Bestellmenge Schritt 1 Schritt 2a Schritt 2 b Schritt 2 c bis 2 n Schritt 3 Erstellung eines Verbrauchsplanes für n Perioden Berechnung der Durchschnittskosten pro verbrauchter Einheit bei Bestellung der für die erste Periode prognostizierten Menge Berechnung der Durchschnittskosten pro verbrauchter Einheit bei Bestellung der für die erste und zweite Periode prognostizierten Menge Wiederholung von Schritt 2 b unter Einbeziehung der jeweils nächsten Periode. Entscheidung für die Bestellmenge, bei der die geringsten Durchschnittskosten pro verbrauchter Einheit entstehen. 29
30 Optimierung der Bestellmenge bei diskontinuierlichem Verbrauch Beispiel 1. Periode 2. Periode 3. Periode 4. Periode Berechnung der durchschnittlichen Kosten für die 1. Periode Berechnung der durchschnittlichen Kosten für die 1. und 2. Periode Berechnung der durchschnittlichen Kosten für die 1., 2. und 3. Periode Beschaffung für die Anzahl von Perioden, für die die durchschnittlichen Kosten minimal sind. 30
31 Beschaffung Begriffe des Beschaffungswesens Optimierung der Bestellmenge bei kontinuierlichem Verbrauch (Andler sche Formel) Optimierung der Bestellmenge bei diskontinuierlichem Verbrauch (WILO-Verfahren, Verfahren der wirtschaftlichsten Losgröße) Minimierung von Transportkosten (Lineare Programmierung) 31
32 Optimierung von Transportkosten bei Beschaffungsvorgängen Bei Beschaffungsvorgängen in der Holzindustrie stellt sich relativ oft das Problem der Transportkostenminimierung. Beispielsweise ist für zwei oder mehr Spanplattenwerke, in denen Sägespäne eingesetzt sind, zu entscheiden, aus welchen Sägewerken, mit denen Lieferverträge bestehen, dieses Material antransportiert wird. Bekannt bzw. gegeben ist der Bedarf der Spanplattenwerke, Mindestund Höchstmengen der Lieferung aus den Sägewerken sowie Transportkosten. Ein so geartetes Problem läßt sich mit der sogen. Linearen Optimierung lösen. 32
33 Transportkostenminimierung - Beispiel Sägewerk I Sägewerk II Sägewerk III Bedarfsmenge Transport -kosten Plattenwerk 1 Plattenwerk Mindest- Menge Höchst- Menge
34 Transportkostenminimierung Zu lösen ist das folgende Gleichungssystem, dessen Gleichungen die Transportkosten zu den Plattenwerken angeben. Beschaffungsmenge vom Sägewerk 1 Transportkosten vom Sägewerk 1 Beschaffungsmeng e vom Sägewerk 3 Transportkosten vom Sägewerk 3 K P1 = M P1S1 x K P1S M P1S3 x K P1S3 K P2 = M P2S1 x K P2S M P2S3 x K P2S3 34
35 Transportkosten-Minimierungsaufgabe - Lösungstechnik Die Lösung kann mit dem Programm Excel erfolgen Es wird der sogenannte SOLVER benutzt, den man unter EXTRAS findet, das Programm löst lineare und teilweise auch nichtlineare Planungsaufgaben Einzugeben sind (a) die Zielfunktion und (b) die Restriktionen Die Restriktionen sind die Höchstmengen, ggf. auch die Mindestmengen und die sogen. Nichtnegativitätsbedingung (Liefermengen dürfen nicht negativ sein) 35
36 Transportkosten-Minimierungsaufgabe - Lösungstechnik 36
37 Lösung der Transportkosten-Minimierungsaufgabe Transportkosten Mengen Summen Restriktionen Lieferungen Säge 1 Säge 2 Säge 3 Säge 1 Säge 2 Säge 3 Mengen Transportkosten Bedarfsmengen Spalte *4+2*5+3* Plattenwerk Plattenwerk Summe Restriktionen Höchstmengen Das Werk 1 bezieht seine gesamte Menge vom Sägewerk 2, Werk 2 bekommt 250 Einheiten vom Sägewerk 1 und 600 Einheiten vom Sägewerk 3, die Bedarfsmengen sind gedeckt, die Höchstmengen nicht überschritten. Mindestmengen bei dieser Lösung unberücksichtigt. 37
Beschaffung. Prof. Dr. Martin Moog. Lehrstuhl für Forstliche Wirtschaftslehre
 Beschaffung Begriffe des Beschaffungswesens Optimierung der Bestellmenge bei kontinuierlichem Verbrauch (Andler sche Formel) Optimierung der Bestellmenge bei diskontinuierlichem Verbrauch (WILO-Verfahren
Beschaffung Begriffe des Beschaffungswesens Optimierung der Bestellmenge bei kontinuierlichem Verbrauch (Andler sche Formel) Optimierung der Bestellmenge bei diskontinuierlichem Verbrauch (WILO-Verfahren
Beschaffung. Entscheidungsbereiche. Beschaffungspolitik. Beschaffungsprogramm. Beschaffungskommunikation. Beschaffungsmethode. Beschaffungskonditionen
 Beschaffung Entscheidungsbereiche der Beschaffungspolitik Beschaffungsprogramm Beschaffungskonditionen Beschaffungsmethode Beschaffungskommunikation 1 Beschaffung Begriffe des Beschaffungswesens Optimierung
Beschaffung Entscheidungsbereiche der Beschaffungspolitik Beschaffungsprogramm Beschaffungskonditionen Beschaffungsmethode Beschaffungskommunikation 1 Beschaffung Begriffe des Beschaffungswesens Optimierung
2. Aufgabe Die Berechnung der optimalen Bestellmenge mittels der Andler'schen Formel basiert auf den vier Parametern
 1. Aufgabe (a) Welches Ziel verfolgt die Berechnung der optimalen Bestellmenge? (b) In welchen betrieblichen Situationen sollte von der optimalen Bestellmenge abgewichen werden? (c) Nennen und erläutern
1. Aufgabe (a) Welches Ziel verfolgt die Berechnung der optimalen Bestellmenge? (b) In welchen betrieblichen Situationen sollte von der optimalen Bestellmenge abgewichen werden? (c) Nennen und erläutern
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN
 HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR)
 Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Bestandsplanung und -steuerung: Die Berechnung der Bestellmengen
 Bestandsplanung und -steuerung: Die Berechnung der Bestellmengen Dortmund, Oktober 1998 Prof. Dr. Heinz-Michael Winkels, Fachbereich Wirtschaft FH Dortmund Emil-Figge-Str. 44, D44227-Dortmund, TEL.: (0231)755-4966,
Bestandsplanung und -steuerung: Die Berechnung der Bestellmengen Dortmund, Oktober 1998 Prof. Dr. Heinz-Michael Winkels, Fachbereich Wirtschaft FH Dortmund Emil-Figge-Str. 44, D44227-Dortmund, TEL.: (0231)755-4966,
Der monatliche Tarif für ein Handy wurde als lineare Funktion der Form f(x) = k x + d modelliert (siehe Grafik).
 1) Handytarif Der monatliche Tarif für ein Handy wurde als lineare Funktion der Form f(x) = k x + d modelliert (siehe Grafik). Euro Gesprächsminuten Tragen Sie in der folgenden Tabelle ein, welche Bedeutung
1) Handytarif Der monatliche Tarif für ein Handy wurde als lineare Funktion der Form f(x) = k x + d modelliert (siehe Grafik). Euro Gesprächsminuten Tragen Sie in der folgenden Tabelle ein, welche Bedeutung
BESCHAFFUNG. Betriebswirtschaftslehre
 BESCHAFFUNG Beschaffung und Lagerhaltung BESCHAFFUNG: Im weiteren Sinn: Bereitstellung von Input-Faktoren Arbeitskräften, finanziellen Mittel, Maschinen, Betriebsmittel,.. Im engeren Sinn: Beschaffung
BESCHAFFUNG Beschaffung und Lagerhaltung BESCHAFFUNG: Im weiteren Sinn: Bereitstellung von Input-Faktoren Arbeitskräften, finanziellen Mittel, Maschinen, Betriebsmittel,.. Im engeren Sinn: Beschaffung
2 Terme 2.1 Einführung
 2 Terme 2.1 Einführung In der Fahrschule lernt man zur Berechnung des Bremsweges (in m) folgende Faustregel: Dividiere die Geschwindigkeit (in km h ) durch 10 und multipliziere das Ergebnis mit sich selbst.
2 Terme 2.1 Einführung In der Fahrschule lernt man zur Berechnung des Bremsweges (in m) folgende Faustregel: Dividiere die Geschwindigkeit (in km h ) durch 10 und multipliziere das Ergebnis mit sich selbst.
Übungsaufgaben Tilgungsrechnung
 1 Zusatzmaterialien zu Finanz- und Wirtschaftsmathematik im Unterricht, Band 1 Übungsaufgaben Tilgungsrechnung Überarbeitungsstand: 1.März 2016 Die grundlegenden Ideen der folgenden Aufgaben beruhen auf
1 Zusatzmaterialien zu Finanz- und Wirtschaftsmathematik im Unterricht, Band 1 Übungsaufgaben Tilgungsrechnung Überarbeitungsstand: 1.März 2016 Die grundlegenden Ideen der folgenden Aufgaben beruhen auf
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
Logistik I. 4 Beschaffungslogistik (Teil c)
 Logistik I Quelle: Ehrmann Logistik I Lagermodell: Darstellung und Begriffe Bestand Max. Bestand Beschaffungsauslösebestand (Meldebest.) Bestellauslösebestand Durchschnittsbestand optimale Bestellmenge
Logistik I Quelle: Ehrmann Logistik I Lagermodell: Darstellung und Begriffe Bestand Max. Bestand Beschaffungsauslösebestand (Meldebest.) Bestellauslösebestand Durchschnittsbestand optimale Bestellmenge
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
1) Mit welcher Zahl muss 18 multipliziert werden, um 234 zu erhalten? Kontrolliere! 2) Finde die Zahl, mit der 171 multipliziert werden muss, um 4104
 1) Mit welcher Zahl muss 18 multipliziert werden, um 234 zu erhalten? Kontrolliere! 2) Finde die Zahl, mit der 171 multipliziert werden muss, um 4104 zu erhalten? Probe! 3) Von zwei Zahlen ist die eine
1) Mit welcher Zahl muss 18 multipliziert werden, um 234 zu erhalten? Kontrolliere! 2) Finde die Zahl, mit der 171 multipliziert werden muss, um 4104 zu erhalten? Probe! 3) Von zwei Zahlen ist die eine
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
 Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Wachstum 2. Michael Dröttboom 1 LernWerkstatt-Selm.de
 1. Herr Meier bekommt nach 3 Jahren Geldanlage 25.000. Er hatte 22.500 angelegt. Wie hoch war der Zinssatz? 2. Herr Meiers Vorfahren haben bei der Gründung Roms (753. V. Chr.) 1 Sesterze auf die Bank gebracht
1. Herr Meier bekommt nach 3 Jahren Geldanlage 25.000. Er hatte 22.500 angelegt. Wie hoch war der Zinssatz? 2. Herr Meiers Vorfahren haben bei der Gründung Roms (753. V. Chr.) 1 Sesterze auf die Bank gebracht
Übung zur Vorlesung Beschaffung und Produktion WT 2013. Übung 1
 Übung zur Vorlesung Beschaffung und Produktion WT 2013 Übung 1 Bitte bringen Sie zur Übung stets die Vorlesungsunterlagen, Ihre Mitschriften sowie Ihren Taschenrechner mit. In der Übung werden die Inhalte
Übung zur Vorlesung Beschaffung und Produktion WT 2013 Übung 1 Bitte bringen Sie zur Übung stets die Vorlesungsunterlagen, Ihre Mitschriften sowie Ihren Taschenrechner mit. In der Übung werden die Inhalte
Finanzmathematik. Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.
 Finanzmathematik Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de Das Tilgungsrechnen Für Kredite gibt es drei unterschiedliche
Finanzmathematik Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de Das Tilgungsrechnen Für Kredite gibt es drei unterschiedliche
XONTRO Newsletter. Makler. Nr. 16
 XONTRO Newsletter Makler Nr. 16 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische Staatsanleihen
XONTRO Newsletter Makler Nr. 16 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische Staatsanleihen
Simplex-Umformung für Dummies
 Simplex-Umformung für Dummies Enthält die Zielfunktion einen negativen Koeffizienten? NEIN Optimale Lösung bereits gefunden JA Finde die Optimale Lösung mit dem Simplex-Verfahren! Wähle die Spalte mit
Simplex-Umformung für Dummies Enthält die Zielfunktion einen negativen Koeffizienten? NEIN Optimale Lösung bereits gefunden JA Finde die Optimale Lösung mit dem Simplex-Verfahren! Wähle die Spalte mit
Aufgabe 5 Excel 2013 (Fortgeschrittene)
 - 1 - Aufgabe 5 Excel 2013 (Fortgeschrittene) 1. Starten Sie Excel und geben die Tabelle Hypothekenanalyse ein. Achten Sie bitte darauf, dass in den Zellen B10 und C11:G21 noch keine Angaben erfolgen.
- 1 - Aufgabe 5 Excel 2013 (Fortgeschrittene) 1. Starten Sie Excel und geben die Tabelle Hypothekenanalyse ein. Achten Sie bitte darauf, dass in den Zellen B10 und C11:G21 noch keine Angaben erfolgen.
1. Wie viel Zinsen bekommt man, wenn man 7000,00 1 Jahr lang mit 6 % anlegt?
 Zinsrechnung mit der Tabellenform: Berechnen der Jahreszinsen Ein Sparbuch mit 1600 wird mit 4% verzinst. Wie Zinsen erhält man im Jahr? Geg.: K = 1600 p% = 4% ges.: Z Das Kapital (Grundwert) entspricht
Zinsrechnung mit der Tabellenform: Berechnen der Jahreszinsen Ein Sparbuch mit 1600 wird mit 4% verzinst. Wie Zinsen erhält man im Jahr? Geg.: K = 1600 p% = 4% ges.: Z Das Kapital (Grundwert) entspricht
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Aufgabensammlung Bruchrechnen
 Aufgabensammlung Bruchrechnen Inhaltsverzeichnis Bruchrechnung. Kürzen und Erweitern.................................. 4. Addition von Brüchen................................... Multiplikation von Brüchen...............................
Aufgabensammlung Bruchrechnen Inhaltsverzeichnis Bruchrechnung. Kürzen und Erweitern.................................. 4. Addition von Brüchen................................... Multiplikation von Brüchen...............................
Mikroökonomik 9. Vorlesungswoche
 Mikroökonomik 9. Vorlesungswoche Tone Arnold Universität des Saarlandes 18. Dezember 2007 Tone Arnold (Universität des Saarlandes) 9. Vorlesungswoche 18. Dezember 2007 1 / 31 Volkswirtschaftliche Rente
Mikroökonomik 9. Vorlesungswoche Tone Arnold Universität des Saarlandes 18. Dezember 2007 Tone Arnold (Universität des Saarlandes) 9. Vorlesungswoche 18. Dezember 2007 1 / 31 Volkswirtschaftliche Rente
Grundlagen der Informatik
 Mag. Christian Gürtler Programmierung Grundlagen der Informatik 2011 Inhaltsverzeichnis I. Allgemeines 3 1. Zahlensysteme 4 1.1. ganze Zahlen...................................... 4 1.1.1. Umrechnungen.................................
Mag. Christian Gürtler Programmierung Grundlagen der Informatik 2011 Inhaltsverzeichnis I. Allgemeines 3 1. Zahlensysteme 4 1.1. ganze Zahlen...................................... 4 1.1.1. Umrechnungen.................................
Mathematik. UND/ODER Verknüpfung. Ungleichungen. Betrag. Intervall. Umgebung
 Mathematik UND/ODER Verknüpfung Ungleichungen Betrag Intervall Umgebung Stefan Gärtner 004 Gr Mathematik UND/ODER Seite UND Verknüpfung Kommentar Aussage Symbolform Die Aussagen Hans kann schwimmen p und
Mathematik UND/ODER Verknüpfung Ungleichungen Betrag Intervall Umgebung Stefan Gärtner 004 Gr Mathematik UND/ODER Seite UND Verknüpfung Kommentar Aussage Symbolform Die Aussagen Hans kann schwimmen p und
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 221 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird im Bereich der Rentenrechnung die zugehörige zu Beginn eines Jahres / einer Zeitperiode eingezahlt, so spricht
SS 2014 Torsten Schreiber 221 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird im Bereich der Rentenrechnung die zugehörige zu Beginn eines Jahres / einer Zeitperiode eingezahlt, so spricht
DOS-Sympas Scope Dateien in Excel einlesen
 Einleitung Daten, die mit dem DOS-Sympas Oszilloskop von intelligenten Modulen aufgezeichnet wurden, können einerseits als Bild im Bitmap-Format: oder andererseits als Textdatei gespeichert werden: Diese
Einleitung Daten, die mit dem DOS-Sympas Oszilloskop von intelligenten Modulen aufgezeichnet wurden, können einerseits als Bild im Bitmap-Format: oder andererseits als Textdatei gespeichert werden: Diese
Ohne Fehler geht es nicht Doch wie viele Fehler sind erlaubt?
 Ohne Fehler geht es nicht Doch wie viele Fehler sind erlaubt? Behandelte Fragestellungen Was besagt eine Fehlerquote? Welche Bezugsgröße ist geeignet? Welche Fehlerquote ist gerade noch zulässig? Wie stellt
Ohne Fehler geht es nicht Doch wie viele Fehler sind erlaubt? Behandelte Fragestellungen Was besagt eine Fehlerquote? Welche Bezugsgröße ist geeignet? Welche Fehlerquote ist gerade noch zulässig? Wie stellt
Lernmaterial für die Fernuni Hagen effizient und prüfungsnah
 Lernmaterial für die Fernuni Hagen effizient und prüfungsnah www.schema-f-hagen.de Sie erhalten hier einen Einblick in die Dokumente Aufgaben und Lösungen sowie Erläuterungen Beim Kauf erhalten Sie zudem
Lernmaterial für die Fernuni Hagen effizient und prüfungsnah www.schema-f-hagen.de Sie erhalten hier einen Einblick in die Dokumente Aufgaben und Lösungen sowie Erläuterungen Beim Kauf erhalten Sie zudem
2.2 Systeme des Bestandsmanagements
 . Systeme des Bestandsmanagements Was ist Bestandsmanagement? Grob gesagt, wird im Bestandsmanagement festgelegt, welche Mengen eines Produktes zu welchem Zeitpunkt zu bestellen sind Hierdurch wird der
. Systeme des Bestandsmanagements Was ist Bestandsmanagement? Grob gesagt, wird im Bestandsmanagement festgelegt, welche Mengen eines Produktes zu welchem Zeitpunkt zu bestellen sind Hierdurch wird der
Funktion Erläuterung Beispiel
 WESTFÄLISCHE WILHELMS-UNIVERSITÄT WIRTSCHAFTSWISSENSCHAFTLICHE FAKULTÄT BETRIEBLICHE DATENVERARBEITUNG Folgende Befehle werden typischerweise im Excel-Testat benötigt. Die Beispiele in diesem Dokument
WESTFÄLISCHE WILHELMS-UNIVERSITÄT WIRTSCHAFTSWISSENSCHAFTLICHE FAKULTÄT BETRIEBLICHE DATENVERARBEITUNG Folgende Befehle werden typischerweise im Excel-Testat benötigt. Die Beispiele in diesem Dokument
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
LU-Zerlegung. Zusätze zum Gelben Rechenbuch. Peter Furlan. Verlag Martina Furlan. Inhaltsverzeichnis. 1 Definitionen.
 Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
Jedes Jahr mehr Zinsen!
 Aufgabe 21 Zinsen erhält man für gewöhnlich nur für ein Jahr. Wenn man aber schon vorher an Erspartes möchte, muss man die Tageszinsen ermitteln. Erstelle eine Tabelle, die nach der Eingabe von Kapital,
Aufgabe 21 Zinsen erhält man für gewöhnlich nur für ein Jahr. Wenn man aber schon vorher an Erspartes möchte, muss man die Tageszinsen ermitteln. Erstelle eine Tabelle, die nach der Eingabe von Kapital,
Rationale Zahlen. Vergleichen und Ordnen rationaler Zahlen
 Rationale Zahlen Vergleichen und Ordnen rationaler Zahlen Von zwei rationalen Zahlen ist die die kleinere Zahl, die auf der Zahlengeraden weiter links liegt.. Setze das richtige Zeichen. a) -3 4 b) - -3
Rationale Zahlen Vergleichen und Ordnen rationaler Zahlen Von zwei rationalen Zahlen ist die die kleinere Zahl, die auf der Zahlengeraden weiter links liegt.. Setze das richtige Zeichen. a) -3 4 b) - -3
WinWerk. Prozess 4 Akonto. KMU Ratgeber AG. Inhaltsverzeichnis. Im Ifang 16 8307 Effretikon
 Prozess 4 Akonto WinWerk 8307 Effretikon Telefon: 052-740 11 11 Telefax: 052 740 11 71 E-Mail info@kmuratgeber.ch Internet: www.winwerk.ch Inhaltsverzeichnis 1 Akonto... 2 1.1 Allgemein... 2 2 Akontobeträge
Prozess 4 Akonto WinWerk 8307 Effretikon Telefon: 052-740 11 11 Telefax: 052 740 11 71 E-Mail info@kmuratgeber.ch Internet: www.winwerk.ch Inhaltsverzeichnis 1 Akonto... 2 1.1 Allgemein... 2 2 Akontobeträge
Vorab per E-Mail. Oberste Finanzbehörden der Länder
 Postanschrift Berlin: Bundesministeriu m der Finanzen, 11016 Berlin Christoph Weiser Unterabteilungsleiter IV C POSTANSCHRIFT Bundesministerium der Finanzen, 11016 Berlin Vorab per E-Mail Oberste Finanzbehörden
Postanschrift Berlin: Bundesministeriu m der Finanzen, 11016 Berlin Christoph Weiser Unterabteilungsleiter IV C POSTANSCHRIFT Bundesministerium der Finanzen, 11016 Berlin Vorab per E-Mail Oberste Finanzbehörden
Mathematik-Klausur vom 4.2.2004
 Mathematik-Klausur vom 4.2.2004 Aufgabe 1 Ein Klein-Sparer verfügt über 2 000, die er möglichst hoch verzinst anlegen möchte. a) Eine Anlage-Alternative besteht im Kauf von Bundesschatzbriefen vom Typ
Mathematik-Klausur vom 4.2.2004 Aufgabe 1 Ein Klein-Sparer verfügt über 2 000, die er möglichst hoch verzinst anlegen möchte. a) Eine Anlage-Alternative besteht im Kauf von Bundesschatzbriefen vom Typ
Sie haben das Recht, binnen vierzehn Tagen ohne Angabe von Gründen diesen Vertrag zu widerrufen.
 Widerrufsbelehrung Nutzt der Kunde die Leistungen als Verbraucher und hat seinen Auftrag unter Nutzung von sog. Fernkommunikationsmitteln (z. B. Telefon, Telefax, E-Mail, Online-Web-Formular) übermittelt,
Widerrufsbelehrung Nutzt der Kunde die Leistungen als Verbraucher und hat seinen Auftrag unter Nutzung von sog. Fernkommunikationsmitteln (z. B. Telefon, Telefax, E-Mail, Online-Web-Formular) übermittelt,
Tangentengleichung. Wie lautet die Geradengleichung für die Tangente, y T =? Antwort:
 Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Funktionaler Zusammenhang. Lehrplan Realschule
 Funktionaler Bildungsstandards Lehrplan Realschule Die Schülerinnen und Schüler nutzen Funktionen als Mittel zur Beschreibung quantitativer Zusammenhänge, erkennen und beschreiben funktionale Zusammenhänge
Funktionaler Bildungsstandards Lehrplan Realschule Die Schülerinnen und Schüler nutzen Funktionen als Mittel zur Beschreibung quantitativer Zusammenhänge, erkennen und beschreiben funktionale Zusammenhänge
3. LINEARE GLEICHUNGSSYSTEME
 176 3. LINEARE GLEICHUNGSSYSTEME 90 Vitamin-C-Gehalt verschiedener Säfte 18,0 mg 35,0 mg 12,5 mg 1. a) 100 ml + 50 ml + 50 ml = 41,75 mg 100 ml 100 ml 100 ml b) : Menge an Kirschsaft in ml y: Menge an
176 3. LINEARE GLEICHUNGSSYSTEME 90 Vitamin-C-Gehalt verschiedener Säfte 18,0 mg 35,0 mg 12,5 mg 1. a) 100 ml + 50 ml + 50 ml = 41,75 mg 100 ml 100 ml 100 ml b) : Menge an Kirschsaft in ml y: Menge an
Klassenarbeit zu linearen Gleichungssystemen
 Klassenarbeit zu linearen Gleichungssystemen Aufgabe : Bestimme die Lösungsmenge der Gleichungssysteme mit Hilfe des Additionsverfahrens: x + 4y = 8 5x y = x y = x y = Aufgabe : Bestimme die Lösungsmenge
Klassenarbeit zu linearen Gleichungssystemen Aufgabe : Bestimme die Lösungsmenge der Gleichungssysteme mit Hilfe des Additionsverfahrens: x + 4y = 8 5x y = x y = x y = Aufgabe : Bestimme die Lösungsmenge
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
Erfolg im Mathe-Abi. H. Gruber, R. Neumann. Prüfungsaufgaben Hessen
 H. Gruber, R. Neumann Erfolg im Mathe-Abi Prüfungsaufgaben Hessen Übungsbuch für den Grundkurs mit Tipps und Lösungen - plus Aufgaben für GTR und CAS Inhaltsverzeichnis Inhaltsverzeichnis 1 Ganzrationale
H. Gruber, R. Neumann Erfolg im Mathe-Abi Prüfungsaufgaben Hessen Übungsbuch für den Grundkurs mit Tipps und Lösungen - plus Aufgaben für GTR und CAS Inhaltsverzeichnis Inhaltsverzeichnis 1 Ganzrationale
Lineare Optimierung Ergänzungskurs
 Lineare Optimierung Ergänzungskurs Wintersemester 2015/16 Julia Lange, M.Sc. Literatur Werner, F.; Sotskov, Y.N. (2006): Mathematics of Economics and Business; Routledge; London Bemerkungen Diese Unterlagen
Lineare Optimierung Ergänzungskurs Wintersemester 2015/16 Julia Lange, M.Sc. Literatur Werner, F.; Sotskov, Y.N. (2006): Mathematics of Economics and Business; Routledge; London Bemerkungen Diese Unterlagen
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
Aufgabe 6 Excel 2013 (Fortgeschrittene) Musterlösung
 - 1 - Aufgabe 6 Excel 2013 (Fortgeschrittene) Musterlösung 1. Die Tabelle mit den Werten und Gewichten der Gegenstände, sowie die Spalte mit der Anzahl ist vorgegeben und braucht nur eingegeben zu werden
- 1 - Aufgabe 6 Excel 2013 (Fortgeschrittene) Musterlösung 1. Die Tabelle mit den Werten und Gewichten der Gegenstände, sowie die Spalte mit der Anzahl ist vorgegeben und braucht nur eingegeben zu werden
Planen mit mathematischen Modellen 00844: Computergestützte Optimierung. Autor: Dr. Heinz Peter Reidmacher
 Planen mit mathematischen Modellen 00844: Computergestützte Optimierung Leseprobe Autor: Dr. Heinz Peter Reidmacher 11 - Portefeuilleanalyse 61 11 Portefeuilleanalyse 11.1 Das Markowitz Modell Die Portefeuilleanalyse
Planen mit mathematischen Modellen 00844: Computergestützte Optimierung Leseprobe Autor: Dr. Heinz Peter Reidmacher 11 - Portefeuilleanalyse 61 11 Portefeuilleanalyse 11.1 Das Markowitz Modell Die Portefeuilleanalyse
Eine Logikschaltung zur Addition zweier Zahlen
 Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
Kosten-Leistungsrechnung Rechenweg Optimales Produktionsprogramm
 Um was geht es? Gegeben sei ein Produktionsprogramm mit beispielsweise 5 Aufträgen, die nacheinander auf vier unterschiedlichen Maschinen durchgeführt werden sollen: Auftrag 1 Auftrag 2 Auftrag 3 Auftrag
Um was geht es? Gegeben sei ein Produktionsprogramm mit beispielsweise 5 Aufträgen, die nacheinander auf vier unterschiedlichen Maschinen durchgeführt werden sollen: Auftrag 1 Auftrag 2 Auftrag 3 Auftrag
www.mathe-aufgaben.com
 Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit sin() f() =. Aufgabe : ( VP) Berechnen Sie das Integral ( )
Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit sin() f() =. Aufgabe : ( VP) Berechnen Sie das Integral ( )
Widerrufsbelehrung der Free-Linked GmbH. Stand: Juni 2014
 Widerrufsbelehrung der Stand: Juni 2014 www.free-linked.de www.buddy-watcher.de Inhaltsverzeichnis Widerrufsbelehrung Verträge für die Lieferung von Waren... 3 Muster-Widerrufsformular... 5 2 Widerrufsbelehrung
Widerrufsbelehrung der Stand: Juni 2014 www.free-linked.de www.buddy-watcher.de Inhaltsverzeichnis Widerrufsbelehrung Verträge für die Lieferung von Waren... 3 Muster-Widerrufsformular... 5 2 Widerrufsbelehrung
11.3 Komplexe Potenzreihen und weitere komplexe Funktionen
 .3 Komplexe Potenzreihen und weitere komplexe Funktionen Definition.) komplexe Folgen: z n = x n + j. y n mit zwei reellen Folgen x n und y n.) Konvergenz: Eine komplexe Folge z n = x n + j. y n heißt
.3 Komplexe Potenzreihen und weitere komplexe Funktionen Definition.) komplexe Folgen: z n = x n + j. y n mit zwei reellen Folgen x n und y n.) Konvergenz: Eine komplexe Folge z n = x n + j. y n heißt
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
Korrigenda Handbuch der Bewertung
 Korrigenda Handbuch der Bewertung Kapitel 3 Abschnitt 3.5 Seite(n) 104-109 Titel Der Terminvertrag: Ein Beispiel für den Einsatz von Future Values Änderungen In den Beispielen 21 und 22 ist der Halbjahressatz
Korrigenda Handbuch der Bewertung Kapitel 3 Abschnitt 3.5 Seite(n) 104-109 Titel Der Terminvertrag: Ein Beispiel für den Einsatz von Future Values Änderungen In den Beispielen 21 und 22 ist der Halbjahressatz
Repetitionsaufgaben: Lineare Funktionen
 Kantonale Fachschaft Mathematik Repetitionsaufgaben: Lineare Funktionen Zusammengestellt von Irina Bayer-Krakvina, KSR Lernziele: - Wissen, was ein Steigungsdreieck einer Geraden ist und wie die Steigungszahl
Kantonale Fachschaft Mathematik Repetitionsaufgaben: Lineare Funktionen Zusammengestellt von Irina Bayer-Krakvina, KSR Lernziele: - Wissen, was ein Steigungsdreieck einer Geraden ist und wie die Steigungszahl
EINFACHES HAUSHALT- KASSABUCH
 EINFACHES HAUSHALT- KASSABUCH Arbeiten mit Excel Wir erstellen ein einfaches Kassabuch zur Führung einer Haushalts- oder Portokasse Roland Liebing, im November 2012 Eine einfache Haushalt-Buchhaltung (Kassabuch)
EINFACHES HAUSHALT- KASSABUCH Arbeiten mit Excel Wir erstellen ein einfaches Kassabuch zur Führung einer Haushalts- oder Portokasse Roland Liebing, im November 2012 Eine einfache Haushalt-Buchhaltung (Kassabuch)
Planungsmethoden des SNP-Laufs
 Planungsmethoden des SNP-Laufs Heuristikbasierte Planung Optimierung in der SNP-Planung Seite 1 Ziel: (Durchführbarer) Plan zur Befriedigung einiger oder aller primär (und sekundär) Bedarfe auf einer,
Planungsmethoden des SNP-Laufs Heuristikbasierte Planung Optimierung in der SNP-Planung Seite 1 Ziel: (Durchführbarer) Plan zur Befriedigung einiger oder aller primär (und sekundär) Bedarfe auf einer,
Repetitionsaufgaben: Lineare Gleichungen
 Kantonale Fachschaft Mathematik Repetitionsaufgaben: Lineare Gleichungen Zusammengestellt von Hannes Ernst, KSR Lernziele: - Lineare Gleichungen von Hand auflösen können. - Lineare Gleichungen mit Parametern
Kantonale Fachschaft Mathematik Repetitionsaufgaben: Lineare Gleichungen Zusammengestellt von Hannes Ernst, KSR Lernziele: - Lineare Gleichungen von Hand auflösen können. - Lineare Gleichungen mit Parametern
ist die Vergütung für die leihweise Überlassung von Kapital ist die leihweise überlassenen Geldsumme
 Information In der Zinsrechnung sind 4 Größen wichtig: ZINSEN Z ist die Vergütung für die leihweise Überlassung von Kapital KAPITAL K ist die leihweise überlassenen Geldsumme ZINSSATZ p (Zinsfuß) gibt
Information In der Zinsrechnung sind 4 Größen wichtig: ZINSEN Z ist die Vergütung für die leihweise Überlassung von Kapital KAPITAL K ist die leihweise überlassenen Geldsumme ZINSSATZ p (Zinsfuß) gibt
n 0 1 2 3 4 5 6 7 8 9 10 11 12 S n 1250 1244, 085 1214, 075 1220, 136 1226, 167 Nach einem Jahr beträgt der Schuldenstand ca. 1177,09.
 Gymnasium Leichlingen 10a M Lö 2007/08.2 2/2 Aufgaben/Lösungen der Klassenarbeit Nr. 4 von Fr., 2008-04-25 2 45 Aufgabe 1: Die A-Bank bietet Kredite zu einem Zinssatz von 6% pro Jahr an. Ein privater Keditvermittler
Gymnasium Leichlingen 10a M Lö 2007/08.2 2/2 Aufgaben/Lösungen der Klassenarbeit Nr. 4 von Fr., 2008-04-25 2 45 Aufgabe 1: Die A-Bank bietet Kredite zu einem Zinssatz von 6% pro Jahr an. Ein privater Keditvermittler
Darlehen - als Möglichkeit der... -Finanzierung
 Darlehen - als Möglichkeit der.... -Finanzierung Situation: Bestattungsinstitut Thomas Bayer e. K. benötigt für ein Investitionsprojekt 0.000 Euro. Die Hausbank bietet dieses Darlehen mit folgenden Konditionen
Darlehen - als Möglichkeit der.... -Finanzierung Situation: Bestattungsinstitut Thomas Bayer e. K. benötigt für ein Investitionsprojekt 0.000 Euro. Die Hausbank bietet dieses Darlehen mit folgenden Konditionen
Inhaltsverzeichnis. - Beschreibung - Rendite - Kaufpreis - Stückzinsen - Verzinsung - Rendite - Berechnung. - Fazit. Beschreibung
 Inhaltsverzeichnis - Beschreibung - Rendite - Kaufpreis - Stückzinsen - Verzinsung - Rendite - Berechnung - Fazit Beschreibung Die US-Dollar Bundesanleihe ist eine Schuldverschreibung der Bundesrepublik
Inhaltsverzeichnis - Beschreibung - Rendite - Kaufpreis - Stückzinsen - Verzinsung - Rendite - Berechnung - Fazit Beschreibung Die US-Dollar Bundesanleihe ist eine Schuldverschreibung der Bundesrepublik
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen?
 Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Formelsammlung zur Kreisgleichung
 zur Kreisgleichung Julia Wolters 6. Oktober 2008 Inhaltsverzeichnis 1 Allgemeine Kreisgleichung 2 1.1 Berechnung des Mittelpunktes und Radius am Beispiel..... 3 2 Kreis und Gerade 4 2.1 Sekanten, Tangenten,
zur Kreisgleichung Julia Wolters 6. Oktober 2008 Inhaltsverzeichnis 1 Allgemeine Kreisgleichung 2 1.1 Berechnung des Mittelpunktes und Radius am Beispiel..... 3 2 Kreis und Gerade 4 2.1 Sekanten, Tangenten,
H. Gruber, R. Neumann. Erfolg im Mathe-Abi. Übungsbuch für den Wahlteil Baden-Württemberg mit Tipps und Lösungen
 H. Gruber, R. Neumann Erfolg im Mathe-Abi Übungsbuch für den Wahlteil Baden-Württemberg mit Tipps und Lösungen Inhaltsverzeichnis Analysis 1 Gebrochenrationale Funktion - Laptop... 7 2 Gebrochenrationale
H. Gruber, R. Neumann Erfolg im Mathe-Abi Übungsbuch für den Wahlteil Baden-Württemberg mit Tipps und Lösungen Inhaltsverzeichnis Analysis 1 Gebrochenrationale Funktion - Laptop... 7 2 Gebrochenrationale
WHB11 - Mathematik Klausur Nr. 3 AFS 3 Ökonomische Anwendungen linearer Funktionen
 Name: Note: Punkte: von 50 (in %: ) Unterschrift des Lehrers : Zugelassene Hilfsmittel: Taschenrechner, Geodreieck, Lineal Wichtig: Schreiben Sie Ihren Namen oben auf das Klausurblatt und geben Sie dieses
Name: Note: Punkte: von 50 (in %: ) Unterschrift des Lehrers : Zugelassene Hilfsmittel: Taschenrechner, Geodreieck, Lineal Wichtig: Schreiben Sie Ihren Namen oben auf das Klausurblatt und geben Sie dieses
Analysis I für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg WiSe 2015/16 Prof. Dr. M. Hinze Dr. P. Kiani Analysis I für Studierende der Ingenieurwissenschaften Lösungshinweise zu Blatt 2 Aufgabe 1: (12 Punkte) a) Beweisen
Fachbereich Mathematik der Universität Hamburg WiSe 2015/16 Prof. Dr. M. Hinze Dr. P. Kiani Analysis I für Studierende der Ingenieurwissenschaften Lösungshinweise zu Blatt 2 Aufgabe 1: (12 Punkte) a) Beweisen
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Senkung des technischen Zinssatzes und des Umwandlungssatzes
 Senkung des technischen Zinssatzes und des Umwandlungssatzes Was ist ein Umwandlungssatz? Die PKE führt für jede versicherte Person ein individuelles Konto. Diesem werden die Beiträge, allfällige Einlagen
Senkung des technischen Zinssatzes und des Umwandlungssatzes Was ist ein Umwandlungssatz? Die PKE führt für jede versicherte Person ein individuelles Konto. Diesem werden die Beiträge, allfällige Einlagen
Gewinn + Fremdkapitalzinsen 4000 + 800. Gesamtkapital 40000
 Klausur BWL Dauer 1h 30 min Nr. 1) Das Gesamtkapital einer Unternehmung soll 40 000, das Fremdkapital 10 000 betragen. Ein Gewinn ist in Höhe von 4000 erwirtschaftet. Auf das Fremdkapital sind 8% Zinsen
Klausur BWL Dauer 1h 30 min Nr. 1) Das Gesamtkapital einer Unternehmung soll 40 000, das Fremdkapital 10 000 betragen. Ein Gewinn ist in Höhe von 4000 erwirtschaftet. Auf das Fremdkapital sind 8% Zinsen
Quadratische Gleichungen
 Quadratische Gleichungen Aufgabe: Versuche eine Lösung zu den folgenden Zahlenrätseln zu finden:.) Verdoppelt man das Quadrat einer Zahl und addiert, so erhält man 00..) Addiert man zum Quadrat einer Zahl
Quadratische Gleichungen Aufgabe: Versuche eine Lösung zu den folgenden Zahlenrätseln zu finden:.) Verdoppelt man das Quadrat einer Zahl und addiert, so erhält man 00..) Addiert man zum Quadrat einer Zahl
Logistiklösungen. C-Teile-Management
 Logistiklösungen C-Teile-Management Kroning GmbH Industrie- und Landtechnik Stefan Warcaba Projektmanager Inhalt 1. Definition C-Teile 2. C-Teile DER Kostentreiber 3. Der konventionelle Beschaffungsprozess
Logistiklösungen C-Teile-Management Kroning GmbH Industrie- und Landtechnik Stefan Warcaba Projektmanager Inhalt 1. Definition C-Teile 2. C-Teile DER Kostentreiber 3. Der konventionelle Beschaffungsprozess
Aufgaben zur Finanzmathematik, Nr. 1
 Aufgaben zur Finanzmathematik, Nr. 1 1.) Ein Unternehmen soll einen Kredit in Höhe von 800.000 in fünf gleich großen Tilgungsraten zurückzahlen. Der Zinssatz beträgt 6,5 % p. a. Erstellen Sie einen Tilgungsplan!
Aufgaben zur Finanzmathematik, Nr. 1 1.) Ein Unternehmen soll einen Kredit in Höhe von 800.000 in fünf gleich großen Tilgungsraten zurückzahlen. Der Zinssatz beträgt 6,5 % p. a. Erstellen Sie einen Tilgungsplan!
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 193 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei einer Abschreibung werden eines Gutes während der Nutzungsdauer festgehalten. Diese Beträge stellen dar und dadurch
SS 2014 Torsten Schreiber 193 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei einer Abschreibung werden eines Gutes während der Nutzungsdauer festgehalten. Diese Beträge stellen dar und dadurch
Gewinnvergleichsrechnung
 Gewinnvergleichsrechnung Die Gewinnvergleichsrechnung stellt eine Erweiterung der Kostenvergleichsrechnung durch Einbeziehung der Erträge dar, die - im Gegensatz zu der Annahme bei der Kostenvergleichsrechnung
Gewinnvergleichsrechnung Die Gewinnvergleichsrechnung stellt eine Erweiterung der Kostenvergleichsrechnung durch Einbeziehung der Erträge dar, die - im Gegensatz zu der Annahme bei der Kostenvergleichsrechnung
Markovketten. Bsp. Page Ranking für Suchmaschinen. Wahlfach Entscheidung unter Risiko und stat. Datenanalyse 07.01.2015
 Markovketten Markovketten sind ein häufig verwendetes Modell zur Beschreibung von Systemen, deren Verhalten durch einen zufälligen Übergang von einem Systemzustand zu einem anderen Systemzustand gekennzeichnet
Markovketten Markovketten sind ein häufig verwendetes Modell zur Beschreibung von Systemen, deren Verhalten durch einen zufälligen Übergang von einem Systemzustand zu einem anderen Systemzustand gekennzeichnet
Theoretische Grundlagen der Informatik WS 09/10
 Theoretische Grundlagen der Informatik WS 09/10 - Tutorium 6 - Michael Kirsten und Kai Wallisch Sitzung 13 02.02.2010 Inhaltsverzeichnis 1 Formeln zur Berechnung Aufgabe 1 2 Hamming-Distanz Aufgabe 2 3
Theoretische Grundlagen der Informatik WS 09/10 - Tutorium 6 - Michael Kirsten und Kai Wallisch Sitzung 13 02.02.2010 Inhaltsverzeichnis 1 Formeln zur Berechnung Aufgabe 1 2 Hamming-Distanz Aufgabe 2 3
Anwendungsbeispiele Buchhaltung
 Rechnungen erstellen mit Webling Webling ist ein Produkt der Firma: Inhaltsverzeichnis 1 Rechnungen erstellen mit Webling 1.1 Rechnung erstellen und ausdrucken 1.2 Rechnung mit Einzahlungsschein erstellen
Rechnungen erstellen mit Webling Webling ist ein Produkt der Firma: Inhaltsverzeichnis 1 Rechnungen erstellen mit Webling 1.1 Rechnung erstellen und ausdrucken 1.2 Rechnung mit Einzahlungsschein erstellen
Geld wechseln kann als Visualisierung des Zehnerübergangs dienen. Die Zwischengrössen (CHF 2.-, 5.-, 20.-, 50.-) weglassen.
 E2 Rechnungen verstehen plus minus Verständnisaufbau Geld wechseln Geld wechseln kann als Visualisierung des Zehnerübergangs dienen. Die Zwischengrössen (CHF 2.-, 5.-, 20.-, 50.-) weglassen. Ich bezahle
E2 Rechnungen verstehen plus minus Verständnisaufbau Geld wechseln Geld wechseln kann als Visualisierung des Zehnerübergangs dienen. Die Zwischengrössen (CHF 2.-, 5.-, 20.-, 50.-) weglassen. Ich bezahle
1 C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R
 C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R L Ö S U N G E N Seite 7 n Wenn vier Menschen auf einem Quadratmeter stehen, dann hat jeder eine Fläche von 50 mal 50 Zentimeter
C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R L Ö S U N G E N Seite 7 n Wenn vier Menschen auf einem Quadratmeter stehen, dann hat jeder eine Fläche von 50 mal 50 Zentimeter
= = = = = = = = = = = = = = = = = =
 e~åçïéêâ Gewünschter Zielrechnungsbetrag kann nicht realisiert werden Hin und wieder wird die Frage an uns herangetragen, aus welchem Grunde es manchmal nicht möglich ist eine Wunschsumme innerhalb eines
e~åçïéêâ Gewünschter Zielrechnungsbetrag kann nicht realisiert werden Hin und wieder wird die Frage an uns herangetragen, aus welchem Grunde es manchmal nicht möglich ist eine Wunschsumme innerhalb eines
Wie Sie mit PO Convert eine Rechnung aus einer Bestellung erstellen können.
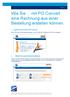 1 / 7 Wie Sie mit PO Convert eine Rechnung aus einer Bestellung erstellen können. 1. Loggen Sie sich in das OB10 Portal ein. Wenn Sie dabei Unterstützung benötigen, lesen Sie bitte die Anleitung Wie Sie
1 / 7 Wie Sie mit PO Convert eine Rechnung aus einer Bestellung erstellen können. 1. Loggen Sie sich in das OB10 Portal ein. Wenn Sie dabei Unterstützung benötigen, lesen Sie bitte die Anleitung Wie Sie
In diesem Tutorial lernen Sie, wie Sie einen Termin erfassen und verschiedene Einstellungen zu einem Termin vornehmen können.
 Tutorial: Wie erfasse ich einen Termin? In diesem Tutorial lernen Sie, wie Sie einen Termin erfassen und verschiedene Einstellungen zu einem Termin vornehmen können. Neben den allgemeinen Angaben zu einem
Tutorial: Wie erfasse ich einen Termin? In diesem Tutorial lernen Sie, wie Sie einen Termin erfassen und verschiedene Einstellungen zu einem Termin vornehmen können. Neben den allgemeinen Angaben zu einem
Erweiterung der Aufgabe. Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen:
 VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
Vorgehensweise bei Lastschriftverfahren
 Vorgehensweise bei Lastschriftverfahren Voraussetzung hierfür sind nötige Einstellungen im ControlCenter. Sie finden dort unter Punkt 29 die Möglichkeit bis zu drei Banken für das Lastschriftverfahren
Vorgehensweise bei Lastschriftverfahren Voraussetzung hierfür sind nötige Einstellungen im ControlCenter. Sie finden dort unter Punkt 29 die Möglichkeit bis zu drei Banken für das Lastschriftverfahren
Zwei einfache Kennzahlen für große Engagements
 Klecksen nicht klotzen Zwei einfache Risikokennzahlen für große Engagements Dominik Zeillinger, Hypo Tirol Bank Die meisten Banken besitzen Engagements, die wesentlich größer sind als der Durchschnitt
Klecksen nicht klotzen Zwei einfache Risikokennzahlen für große Engagements Dominik Zeillinger, Hypo Tirol Bank Die meisten Banken besitzen Engagements, die wesentlich größer sind als der Durchschnitt
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 3 1. Semester ARBEITSBLATT 3 RECHNEN MIT GANZEN ZAHLEN
 ARBEITSBLATT 3 RECHNEN MIT GANZEN ZAHLEN Wir wollen nun die Rechengesetze der natürlichen Zahlen auf die Zahlenmenge der ganzen Zahlen erweitern und zwar so, dass sie zu keinem Widerspruch mit bisher geltenden
ARBEITSBLATT 3 RECHNEN MIT GANZEN ZAHLEN Wir wollen nun die Rechengesetze der natürlichen Zahlen auf die Zahlenmenge der ganzen Zahlen erweitern und zwar so, dass sie zu keinem Widerspruch mit bisher geltenden
Mathematik-Klausur vom 16.4.2004
 Mathematik-Klausur vom 16..200 Aufgabe 1 Die Wucher-Kredit GmbH verleiht Kapital zu einem nominellen Jahreszinsfuß von 20%, wobei sie die anfallenden Kreditzinsen am Ende eines jeden Vierteljahres der
Mathematik-Klausur vom 16..200 Aufgabe 1 Die Wucher-Kredit GmbH verleiht Kapital zu einem nominellen Jahreszinsfuß von 20%, wobei sie die anfallenden Kreditzinsen am Ende eines jeden Vierteljahres der
Markus Mauritz 4BBW 97/98 BET - Referat. ABC Analyse (Kostenschwerpunktanalyse)
 ABC Analyse (Kostenschwerpunktanalyse) Allgemein: Die ABC Analyse (auch Kostenschwerpunktanalyse genannt) dient als wichtige Entscheidungsgrundlage auf allen Gebieten der Planung und Gestaltung in der
ABC Analyse (Kostenschwerpunktanalyse) Allgemein: Die ABC Analyse (auch Kostenschwerpunktanalyse genannt) dient als wichtige Entscheidungsgrundlage auf allen Gebieten der Planung und Gestaltung in der
Zur Wahrung der Widerrufsfrist reicht es aus, dass Sie die Mitteilung über die Ausübung des Widerrufsrechts vor Ablauf der Widerrufsfrist absenden.
 Widerrufsbelehrung der Firma Widerrufsbelehrung - Verträge für die Lieferung von Waren Ist der Kunde Unternehmer ( 14 BGB), so hat er kein Widerrufs- und Rückgaberecht gem. 312g BGB i. V. m. 355 BGB. Das
Widerrufsbelehrung der Firma Widerrufsbelehrung - Verträge für die Lieferung von Waren Ist der Kunde Unternehmer ( 14 BGB), so hat er kein Widerrufs- und Rückgaberecht gem. 312g BGB i. V. m. 355 BGB. Das
20 Modul Lager und Inventur
 20 Modul Lager und Inventur Alle Lagerbewegungen (Verkauf, Einkauf, Umbuchungen, Inventur) werden aufgezeichnet um die Lagerstände von Artikeln nachvollziehbar zu machen. Das Modul ist ab Version Standard
20 Modul Lager und Inventur Alle Lagerbewegungen (Verkauf, Einkauf, Umbuchungen, Inventur) werden aufgezeichnet um die Lagerstände von Artikeln nachvollziehbar zu machen. Das Modul ist ab Version Standard
Das große ElterngeldPlus 1x1. Alles über das ElterngeldPlus. Wer kann ElterngeldPlus beantragen? ElterngeldPlus verstehen ein paar einleitende Fakten
 Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Stellen Sie bitte den Cursor in die Spalte B2 und rufen die Funktion Sverweis auf. Es öffnet sich folgendes Dialogfenster
 Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
