Breite des ursprünglichen Blechs [cm]: b. Gleichung für den Rauminhalt der Kiste [cm 3 ]:
|
|
|
- Harry Grosse
- vor 5 Jahren
- Abrufe
Transkript
1 Die Pizza: Übung 4 12cm 12cm b 2b Breite des ursprünglichen Blechs [cm]: b Gleichung für den Rauminhalt der Kiste [cm 3 ]: (2b 24)(b 24)12 = 8736 Der Rechner liefert: b = 38-2 Gesuchte Breite: 38cm
2 Die Pizza: Übung 5 Zinssatz: p% Startkapital [CHF]: Kapital nach 1 J. [CHF]: ( 1 + p Kapital nach 2 J. [CHF]: ( 1 + p Gleichung für das Kapital nach 2 J. [CHF]: ) ) ( 1 + p ( 1 + p ) = : ( ) 1 + p = p 100 = ± p 100 = 1 ± p = 100 ± 101 ) Gesuchter Zinssatz: 1%
3 Die Pizza: Übung 6 Zinssatz: p% Startkapital [CHF]: Kapital nach einem Jahr [CHF]: ( 1 + p ) ( Kapital ( nach zwei ) Jahren ) [CHF]: ( p p 100 ) Gleichung ( ( für das ) Kapital ) ( nach 2 J. ) [CHF]: p p 100 = Der Rechner liefert: p = Gesuchter Zinssatz: 5%
4 Die Pizza: Übung 7 a) Anzahl Personen in der Reisegruppe: n Anzahl Belegungsmöglichkeiten der Frontplätze: Variationen ohne Wiederholungen der Länge 2 aus n Zeichen. n! (n 2)! = n(n 1) Gleichung für die Anzahl Belegungen: n(n 1) = 1892 b) Zahlen für n einsetzen, bis die Gleichung in eine wahre Aussage übergeht! Gesuchte Anzahl Personen: 44 c) L = { 43; 44}
5 Die Pizza: Übung 8 a) Anzahl SchülerInnen in der Klasse: n Anzahl Reinigungspaare: Kombinationen ohne Wiederholungen der Länge 2 aus n Zeichen. ( n 2 ) = n! 2!(n 2)! = n(n 1) 2 Gleichung für die Anzahl Reinigungspaare: n(n 1) 2 = 253 b) Zahlen für n einsetzen, bis die Gleichung in eine wahre Aussage übergeht! Gesuchte Anzahl SchülerInnen: 23 c) L = { 22; 23}
6 Die Pizza: Übung 9 Flugzeit Flugstrecke [s] [m] Stein t 4.90 t 2 Schall 4 t 344(4 t) Gleichung für die Flugstrecke : 4.90 t 2 = 344(4 t) Der Rechner liefert: t = Gesuchte Distanz: = m
7 Die Pizza: Übung 10a) y 12 A( 4 3) B( 1 4) 2 F(0 0) x 4 6 Nach dem Satz von Pythagoras gilt: AF = BF = = 25 = 5km = 17 = 4.123km
8 Die Pizza: Übung 10b) Nach dem Satz von Pythagoras gilt: AB = = 10 = 3.162km In 2 Minuten (= 30 1 h) fliegt der Vogelschwarm von A nach B. Für die konstante Fluggeschwindigkeit ergibt sich: = = km/h
9 Die Pizza: Übung 10c) Ansatz: y = mx + b m = ( 4) = 1 3 A( 4 3) einsetzen: 3 = 1 3 ( 4) + b 3 = b 13 3 = b Koordinatengleichung der Flugbahn: y = 1 3 x
10 Die Pizza: Übung 10d) 12 A( 4 3) 8 4 5km 2 F(0 0) 4 2 y x C y C C(x C y C ) x 4 6 Gesucht: C(x C y C ), wobei y C = 1 3 x C Nach dem Satz von Pythagoras gilt: x 2 + y2 C = 5 2 C x 2 C + ( 1 3 x C + 13 ) 2 3 = 25 Der Rechner liefert: x C = Es folgt: y C = = 4.8 Gesuchter Punkt: C( )
11 Die Pizza: Übung 10e) Vom Punkt A( 4 3) bis zum Punkt C( ) ist der Vogelschwarm im heiklen Gebiet. AC = (1.4 ( 4)) 2 + (4.8 3) 2 = = = = 5.692km Aus der Übung 10b) ist die Fluggeschwindigkeit bekannt. Für die gesuchte Zeit t ergibt sich mit der Formel t = s v : t = = 50 3 = 0.060h = 3.600min
12 Definition und Lösungsformel: Übung 21a) x 2 + 4x + µ = 0 Diskriminante D = µ = 16 4µ Genau zwei Lösungen, falls D > µ > 0 16 > 4µ 4 > µ Genau eine Lösung, falls D = 0. 4 = µ Keine Lösung, falls D < 0. 4 < µ Genau zwei Lösungen, falls µ < 4 Genau eine Lösung, falls µ = 4 Keine Lösung, falls µ > 4
13 Definition und Lösungsformel: Übung 21b) 3µx 2 2x 5 = 0 Diskriminante D = ( 2) 2 4 3µ ( 5) = µ Genau zwei Lösungen, falls D > µ > 0 60µ > 4 µ > 15 1 Genau eine Lösung, falls D = 0. µ = 15 1 Keine Lösung, falls D <. 0 µ < 15 1 Genau zwei Lösungen, falls µ > 1 15 Genau eine Lösung, falls µ = 1 15 Keine Lösung, falls µ < 1 15
14 Definition und Lösungsformel: Übung 21c) x 2 + µ = 2 3x 2 + 3x x 2 + 3x + µ 2 = 0 Diskriminante D = (µ 2) = 9 4µ + 8 = 17 4µ Genau zwei Lösungen, falls D > µ > 0 17 > 4µ 17 4 > µ Genau eine Lösung, falls D = = µ Keine Lösung, falls D < < µ Genau zwei Lösungen, falls µ < 17 4 Genau eine Lösung, falls µ = 17 4 Keine Lösung, falls µ > 17 4
15 Definition und Lösungsformel: Übung 22a1) x 2 4x y = 1 I 2x y = 6 II II: 2x y = 6 2x + 6 = y III in I: x 2 4x (2x + 6) = 1 x 2 4x 2x 6 = 1 x 2 6x 6 = 1 x 2 6x 7 = 0 (x + 1)(x 7) = 0 x 1 = 1 x 2 = 7 in III: y 1 = 4 y 2 = 20 L = {( 1 4); (7 20)}
16 Definition und Lösungsformel: Übung 22b1) (x 1) 2 + y 2 = 25 I x + 7y = 24 II II: x + 7y = 24 7y 24 = x III in I: (7y 24 1) 2 + y 2 = 25 (7y 25) 2 + y 2 = 25 49y 2 350y y 2 = 25 50y 2 350y = 0 y 2 7y + 12 = 0 (y 3)(y 4) = 0 y 1 = 3 y 2 = 4 in III: x 1 = 3 x 2 = 4 L = {( 3 3); (4 4)}
17 Definition und Lösungsformel: Übung 22c1) y = 2x 2 + x + 5 I y = x 2 8x + 11 II II I: 0 = 3x 2 9x = x 2 3x = (x 1)(x 2) x 1 = 1 x 2 = 2 in I: y 1 = 4 y 2 = 1 L = {(1 4); (2 1)}
18 Bruchgleichungen: Übung 23 Zeit pro Anteil Badewanne Badewanne [min] pro Minute Zufluss t 1 t Abfluss t t+2 In 12 Minuten ist 1 Badewanne voll: 12 1t 12 1 t+2 = 1 t(t + 2) 12(t + 2) 12t = t(t + 2) 12t t = t 2 + 2t 24 0 = t 2 + 2t 24 0 = (t 4)(t + 6) t 1/2 = 4-6 Gesuchte Zeit: 4min
19 Bruchgleichungen: Übung 24 Zeit pro Anteil Druckauftrag Druckauftrag [h] pro Stunde Neue Maschine t 1 t Alte Maschine t t+3 Wenn die neue Maschine während 10 Stunden und die alte Maschine während 6 Stunden drucken, wird 1 Druckauftrag erledigt: 10 1t t+3 = 1 t(t + 3) 10(t + 3) + 6t = t(t + 3) 10t t = t 2 + 3t 14t 30 0 = t 2 13t 30 0 = (t 15)(t + 2) t 1/2 = 15 2 Gesuchte Zeit: 15h
20 Bruchgleichungen: Übung 25a) 15 x 15cm x Streckenteilung im Goldenen Schnitt: 15 x x = x
21 Bruchgleichungen: Übung 25a) Streckenteilung im Goldenen Schnitt: 15 x x = x x(15 x) (15 x) 2 = 15x x + x 2 = 15x x 2 45x = 0 x 1/2 = 45± ( 45) = 45± Gesuchte Entfernung: 5.729cm
22 Bruchgleichungen: Übung 25b) x 10cm 10 x Streckenteilung im Goldenen Schnitt: 10 x x = x
23 Bruchgleichungen: Übung 25b) Streckenteilung im Goldenen Schnitt: 10 x x = x x(10 x) (10 x) 2 = 10x x + x 2 = 10x x 2 30x = 0 x 1/2 = 30± ( 30) = 30± Gesuchte Entfernung: 3.820cm
24 Bruchgleichungen: Übung 25c) Stehen die Breite und die Höhe der Photographie im Verhältnis des Goldenen Schnittes? ? = ? = Antwort: nein
25 Bruchgleichungen: Übung 27a1) 5 x = 11 2x 8x 40 + x = x = 4 L = {4}
26 Bruchgleichungen: Übung 27b1) 3 x = 5 x+2 x(x + 2) 3(x + 2) = 5x 3x + 6 = 5x 3x 6 = 2x : 2 3 = x L = {3}
27 Bruchgleichungen: Übung 27c1) 4 x 2 x+2 = 2 3 3x(x + 2) 12(x + 2) 6x = 2x(x + 2) 12x x = 2x 2 + 4x 6x + 24 = 2x 2 + 4x 6x 24 0 = 2x 2 2x 24 : 2 0 = x 2 x 12 0 = (x + 3)(x 4) x 1 = 3 x 2 = 4 L = { 3; 4}
28 Bruchgleichungen: Übung 27d1) x+2 x x 2 8x+12 x+2 x (x 2)(x 6) = 1 x 6 = 1 x 6 (x 2)(x 6) (x + 2)(x 6) + 4 = x 2 x 2 4x = x 2 x 2 4x 8 = x 2 x + 2 x 2 5x 6 = 0 (x + 1)(x 6) = 0 x 1 = 1 x 2 = 6 D L = { 1}
29 Bruchgleichungen: Übung 27e1) x x+4 x 3 2x = 5 2 2x(x + 4) 2x 2 (x 3)(x + 4) = 5x(x + 4) 2x 2 (x 2 + x 12) = 5x x x 2 x + 12 = 5x x 5x 2 20x 4x 2 21x + 12 = 0 x 1/2 = 21± ( 21) 2 4 ( 4) 12 8 = 21± L = { 5.770; 0.520}
30 Bruchgleichungen: Übung 27f1) x 2 x 32 x 2 3x 4 x+7 = x+8 x+1 x 4 x 2 x 32 (x+1)(x 4) x+7 = x+8 (x + 1)(x 4) x+1 x 4 x 2 x 32 (x + 7)(x 4) = (x + 8)(x + 1) x 2 x 32 (x 2 + 3x 28) = x 2 + 9x + 8 4x 4 = x 2 + 9x x = x x = (x + 12)(x + 1) x 1 = 12 x 2 = 1 D L = { 12}
31 Satz von Vieta: Übung 28 Falls x 1 und x 2 die Lösungen der Gleichung ax 2 +bx+c = 0 sind, so gilt nach der Lösungsformel: x 1 = b+ b 2 4ac 2a, x 2 = b b 2 4ac 2a Daraus folgt: x 1 +x 2 = b+ x 1 x 2 = b+ = 4ac 4a 2 = c a b 2 4ac 2a b 2 4ac 2a + b b 2 4ac 2a b b 2 4ac 2a = = b+ b 2 4ac b 2a b 2 4ac ( )( ) b+ b 2 4ac b b 2 4ac 4a 2 = 2b 2a = b a = b 2 (b 2 4ac) 4a 2 = 3. binomische Formel
32 Satz von Vieta: Übung 29a) a(x x 1 )(x x 2 ) = a(x 2 x x 1 x x 2 +x 1 x 2 ) = = a ( x 2 x(x 1 + x 2 ) + x 1 x 2 ) = = a ( x 2 x ( b a) + c a ) = ax 2 + bx + c Satz von Vieta
33 Satz von Vieta: Übung 29b) Der Term ax 2 + bx + c ist genau dann in ein Produkt aus Linearfaktoren zerlegbar, wenn die Gleichung ax 2 + bx + c = 0 Lösungen hat. Sind x 1 und x 2 die Lösungen von der Gleichung ax 2 +bx+c = 0, dann ist der Term ax 2 +bx+c in das Produkt a(x x 1 )(x x 2 ) zerlegbar.
34 Satz von Vieta: Übung 30a) Zu zerlegender Term: x x 1536 Dazugehörige quadratische Gleichung: x x 1536 = 0 x 1/2 =... = Es ergibt sich die Zerlegung: x x 1536 = (x 24)(x + 64)
35 Satz von Vieta: Übung 30b) Zu zerlegender Term: 2x 2 + 3x 135 Dazugehörige quadratische Gleichung: 2x 2 + 3x 135 = 0 x 1/2 =... = Es ergibt sich die Zerlegung: 2x 2 + 3x 135 = 2(x 15 2 )(x + 9)
36 Satz von Vieta: Übung 30c) Zu zerlegender Term: 6x 2 25x + 24 Dazugehörige quadratische Gleichung: 6x 2 25x + 24 = 0 x 1/2 =... = 8/3 3/2 Es ergibt sich die Zerlegung: 6x 2 25x + 24 = 6(x 8 3 )(x 3 2 )
37 Satz von Vieta: Übung 30d) Zu zerlegender Term: 3x 2 7x + 5 Dazugehörige quadratische Gleichung: 3x 2 7x + 5 = 0 x 1/2 =... keine Lösungen! Der Term 3x 2 7x + 5 ist nicht zerlegbar.
38 Satz von Vieta: Übung 30e) Zu zerlegender Term: 2x 2 9x + 5 Dazugehörige quadratische Gleichung: 2x 2 9x + 5 = 0 x 1/2 = 9± Es ergibt sich die Zerlegung: 2x 2 9x + 5 = 2(x )(x )
39 Satz von Vieta: Übung 30f) Zu zerlegender Term: 25x x Dazugehörige quadratische Gleichung: 25x x = 0 x 1/2 =... = 18 5 Es ergibt sich die Zerlegung: 25x x = 25(x )2
40 Quadratische Ungleichungen: Übung 32a1) (x + 2)(x 9) > 0 Es wird untersucht, für welche x die beiden Faktoren und schliesslich das Produkt welches Vorzeichen haben: (x + 2) (x 9) (x + 2)(x 9) R L =] ; 2[ ]9; [
41 Quadratische Ungleichungen: Übung 32b1) (x 5)(x 6) < 0 Es wird untersucht, für welche x die beiden Faktoren und schliesslich das Produkt welches Vorzeichen haben: (x 5) (x 6) (x 5)(x 6) R L =]5;6[
42 Quadratische Ungleichungen: Übung 34a1) x 2 3x 10 < 0 Linke Seite in ein Produkt zerlegen: (x + 2)(x 5) < 0 Es wird untersucht, für welche x die beiden Faktoren und schliesslich das Produkt welches Vorzeichen haben: (x + 2) (x 5) (x + 2)(x 5) R L =] 2;5[
43 Quadratische Ungleichungen: Übung 34b1) x 2 8x 15 x 2 8x Linke Seite in ein Produkt zerlegen: (x 3)(x 5) 0 Es wird untersucht, für welche x die beiden Faktoren und schliesslich das Produkt welches Vorzeichen haben: (x 3) (x 5) (x 3)(x 5) R L =] ;3] [5; [
44 Quadratische Ungleichungen: Übung 35a) 8x 2 + µx + 2 = 0 Diskriminante D = µ = µ 2 64 = (µ + 8)(µ 8) Es wird untersucht, für welche µ die Diskriminante welches Vorzeichen hat: (µ + 8) (µ 8) (µ + 8)(µ 8) R Genau zwei Lösungen, falls µ ] ; 8[ ]8; [ Genau eine Lösung, falls µ { 8; 8} Keine Lösung, falls µ ] 8; 8[
45 Quadratische Ungleichungen: Übung 35b) µx 2 4x + 2µ = 0 Diskriminante D = ( 4) 2 4 µ 2µ = 16 8µ 2 = = 8(µ + 2)(µ 2) Es wird untersucht, für welche µ die Diskriminante welches Vorzeichen hat: 8 (µ + 2) (µ 2) 8(µ + 2)(µ 2) R Genau zwei Lösungen, falls µ ] 2; 2[ Genau eine Lösung, falls µ { 2; 2} Keine Lösung, falls µ ] ; 2[ ] 2; [
46 Quadratische Ungleichungen: Übung 35c) 5x = µ 4 3µx 5x 2 + 3µx + 1 µ 4 = 0 Diskriminante D = (3µ) (1 µ 4 ) = 9µ2 + 5µ 20 = = 9(µ µ 1 )(µ µ 2 ) = 9(µ+1.794)(µ 1.239) Es wird untersucht, für welche µ die Diskriminante welches Vorzeichen hat: 9 (µ µ 1 ) (µ µ 2 ) 9(µ µ 1 )(µ µ 2 ) µ 1 µ R Zwei Lösungen, falls µ ] ; µ 1 [ ]µ 2 ; [ Eine Lösung, falls µ {µ 1 ; µ 2 } Keine Lösung, falls µ ]µ 1 ; µ 2 [
47 Quadratische Ungleichungen: Übung 36 Querschnittsdurchmesser [cm]: d d 8cm Die Bedingung für das Volumen führt zu zwei Ungleichungen: ( ) d 2 10 π πd π d2 10 π 5 10 π d π d 1.784
Lineare Gleichungen Exkurs: Binomische Formeln Quadratische Gleichungen Exkurs: Polynomdivision Polynomgleichungen
 Gleichungen Lineare Gleichungen Exkurs: Binomische Formeln Quadratische Gleichungen Exkurs: Polynomdivision Polynomgleichungen Lineare Gleichungen Lineare Gleichungen ax + b = 0 Lineare Gleichungen ax
Gleichungen Lineare Gleichungen Exkurs: Binomische Formeln Quadratische Gleichungen Exkurs: Polynomdivision Polynomgleichungen Lineare Gleichungen Lineare Gleichungen ax + b = 0 Lineare Gleichungen ax
Quadratische Gleichungen
 Quadratische Gleichungen 1/10 Quadratische Gleichungen Teil 1 Grundlagen Lehrstoff Gleichungen und Gleichungssysteme - Lösen von linearen und quadratischen Gleichungen in einer Variablen Inhalt Quadratische
Quadratische Gleichungen 1/10 Quadratische Gleichungen Teil 1 Grundlagen Lehrstoff Gleichungen und Gleichungssysteme - Lösen von linearen und quadratischen Gleichungen in einer Variablen Inhalt Quadratische
Klasse 9+ (Mittelstufe Plus) Hinweise und Lösungen
 Klasse 9+ (Mittelstufe Plus) Hinweise und Lösungen. a) (x + y) (x y) = x + xy + y [x xy + y ] = = x + xy + y x + xy y = 4xy b) z 3 z ) = z + z z z(z ) z (z ) (z 0; ) c) (8a 3 b) = ( 3²a3 b) = 3 4 a 6 b
Klasse 9+ (Mittelstufe Plus) Hinweise und Lösungen. a) (x + y) (x y) = x + xy + y [x xy + y ] = = x + xy + y x + xy y = 4xy b) z 3 z ) = z + z z z(z ) z (z ) (z 0; ) c) (8a 3 b) = ( 3²a3 b) = 3 4 a 6 b
Quadratische Gleichungen
 Quadratische Gleichungen 1/10 Quadratische Gleichungen Teil 2 Die Aufgaben in diesem beziehen sich auf Quadratische Gleichungen Teil I Grundlagen. Sie können nach Durcharbeiten dieses Skriptums beantwortet
Quadratische Gleichungen 1/10 Quadratische Gleichungen Teil 2 Die Aufgaben in diesem beziehen sich auf Quadratische Gleichungen Teil I Grundlagen. Sie können nach Durcharbeiten dieses Skriptums beantwortet
Brückenkurs Mathematik zum Sommersemester 2015
 HOCHSCHULE HANNOVER UNIVERSITY OF APPLIED SCIENCES AND ARTS Dipl.-Math. Xenia Bogomolec Brückenkurs Mathematik zum Sommersemester 2015 Übungsblatt 1 (Grundlagen) Aufgabe 1. Multiplizieren Sie folgende
HOCHSCHULE HANNOVER UNIVERSITY OF APPLIED SCIENCES AND ARTS Dipl.-Math. Xenia Bogomolec Brückenkurs Mathematik zum Sommersemester 2015 Übungsblatt 1 (Grundlagen) Aufgabe 1. Multiplizieren Sie folgende
Arbeitsblatt Gleichungen höheren Grades
 Mathematik-Service Dr. Fritsch www.math-service.de Tel. 061/776 Arbeitsblatt Gleichungen höheren Grades 1. Lösen Sie folgenden quadratischen Gleichungen mittels quadratischer Ergänzung! (a) x x + = 0 (b)
Mathematik-Service Dr. Fritsch www.math-service.de Tel. 061/776 Arbeitsblatt Gleichungen höheren Grades 1. Lösen Sie folgenden quadratischen Gleichungen mittels quadratischer Ergänzung! (a) x x + = 0 (b)
Lösungsmethoden von quadratischen Gleichungen
 Lösungsmethoden von quadratischen Gleichungen Lösen durch quadratische Ergänzung Eine quadratische Gleichung löst man folgendermaßen über das Verfahren der quadratischen Ergänzung: x 8x + 6 = 0 Dividiere
Lösungsmethoden von quadratischen Gleichungen Lösen durch quadratische Ergänzung Eine quadratische Gleichung löst man folgendermaßen über das Verfahren der quadratischen Ergänzung: x 8x + 6 = 0 Dividiere
Übungen: Bruchgleichungen 2
 Übungen: Bruchgleichungen 2 Im Teil 1 finden Sie die Aufgabenstellung, in Teil 2 die Ergebnisse und in Teil 3 die komplett durchgerechnete Lösung der Aufgabe. Teil 1: Aufgabenstellungen Bestimmen Sie die
Übungen: Bruchgleichungen 2 Im Teil 1 finden Sie die Aufgabenstellung, in Teil 2 die Ergebnisse und in Teil 3 die komplett durchgerechnete Lösung der Aufgabe. Teil 1: Aufgabenstellungen Bestimmen Sie die
QUADRATISCHE GLEICHUNGENN
 Schule Bundesgymnasium für Berufstätige Salzburg Thema Mathematik Arbeitsblatt A -.: Quadratische Gleichungen LehrerInnenteam m/ Mag Wolfgang Schmid Unterlagen QUADRATISCHE GLEICHUNGENN Definition: Eine
Schule Bundesgymnasium für Berufstätige Salzburg Thema Mathematik Arbeitsblatt A -.: Quadratische Gleichungen LehrerInnenteam m/ Mag Wolfgang Schmid Unterlagen QUADRATISCHE GLEICHUNGENN Definition: Eine
Gleichungen und Ungleichungen
 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme. Kapitel 3 Gleichungen und Ungleichungen linke Seite = rechte Seite Grundmenge: Menge aller Zahlen, die wir als Lösung der Gleichung
Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme. Kapitel 3 Gleichungen und Ungleichungen linke Seite = rechte Seite Grundmenge: Menge aller Zahlen, die wir als Lösung der Gleichung
Gleichungen und Ungleichungen
 Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
Gleichungen und Ungleichungen
 Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
Quadratische Funktion - Übungen
 Quadratische Funktion - Übungen 1a) "Verständnisfragen" zu "Scheitel und Allgemeine Form" - mit Tipps. Teilweise: Trotz der Tipps nicht immer einfach! Wir haben die Formeln: Allgemeine Form: y = a x 2
Quadratische Funktion - Übungen 1a) "Verständnisfragen" zu "Scheitel und Allgemeine Form" - mit Tipps. Teilweise: Trotz der Tipps nicht immer einfach! Wir haben die Formeln: Allgemeine Form: y = a x 2
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Einführung in die quadratischen Gleichungen
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Einführung in die quadratischen Gleichungen Das komplette Material finden Sie hier: School-Scout.de SCHOOL-SCOUT Quadratische Gleichungen
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Einführung in die quadratischen Gleichungen Das komplette Material finden Sie hier: School-Scout.de SCHOOL-SCOUT Quadratische Gleichungen
Gleichungsarten. Quadratische Gleichungen
 Gleichungsarten Quadratische Gleichungen Normalform: Dividiert man die allgemeine Form einer quadratischen Gleichung durch a, erhält man die Normalform der quadratischen Gleichung. x 2 +px+q=0 Lösungsformel:
Gleichungsarten Quadratische Gleichungen Normalform: Dividiert man die allgemeine Form einer quadratischen Gleichung durch a, erhält man die Normalform der quadratischen Gleichung. x 2 +px+q=0 Lösungsformel:
Mathematik-Übungssammlung für die Studienrichtung Facility Management
 Mathematik-Übungssammlung für die Studienrichtung Facility Management Auf den nachfolgenden Seiten finden Sie Übungen zum Stoff, welcher bei Studienbeginn vorausgesetzt wird. Der dazugehörige Stoff wird
Mathematik-Übungssammlung für die Studienrichtung Facility Management Auf den nachfolgenden Seiten finden Sie Übungen zum Stoff, welcher bei Studienbeginn vorausgesetzt wird. Der dazugehörige Stoff wird
1.3 Gleichungen und Ungleichungen
 1.3 Gleichungen und Ungleichungen Ein zentrales Thema der Algebra ist das Lösen von Gleichungen. Ganz einfach ist dies für sogenannte lineare Gleichungen a x = b Wenn hier a 0 ist, können wir beide Seiten
1.3 Gleichungen und Ungleichungen Ein zentrales Thema der Algebra ist das Lösen von Gleichungen. Ganz einfach ist dies für sogenannte lineare Gleichungen a x = b Wenn hier a 0 ist, können wir beide Seiten
Kapitel 1:»Rechnen« c 3 c 4 c) b 5 c 4. c 2 ) d) (2x + 3) 2 e) (2x + 0,01)(2x 0,01) f) (19,87) 2
 Kapitel :»Rechnen«Übung.: Multiplizieren Sie die Terme so weit wie möglich aus. a /5 a 5 Versuchen Sie, vorteilhaft zu rechnen. Übung.2: Berechnen Sie 9% von 2573. c 3 c 4 b 5 c 4 ( b 2 c 2 ) (2x + 3)
Kapitel :»Rechnen«Übung.: Multiplizieren Sie die Terme so weit wie möglich aus. a /5 a 5 Versuchen Sie, vorteilhaft zu rechnen. Übung.2: Berechnen Sie 9% von 2573. c 3 c 4 b 5 c 4 ( b 2 c 2 ) (2x + 3)
Übungen Mathematik I, M
 Übungen Mathematik I, M Übungsblatt, Lösungen (Stoff aus Mathematik 0).0.0. Berechnen Sie unter Verwendung des binomischen Lehrsatzes ( x + y) 7 Lösung: Nach dem binomischen Lehrsatz ist ( x + y) 7 = 7
Übungen Mathematik I, M Übungsblatt, Lösungen (Stoff aus Mathematik 0).0.0. Berechnen Sie unter Verwendung des binomischen Lehrsatzes ( x + y) 7 Lösung: Nach dem binomischen Lehrsatz ist ( x + y) 7 = 7
MATHEMATIK G9 LÖSEN VON GLEICHUNGEN
 MATHEMATIK G9 LÖSEN VON GLEICHUNGEN Viele mathematische (und naturwissenschaftliche) Probleme lassen sich dadurch lösen, dass man eine Gleichung (oder auch mehrere) aufstellt und diese dann löst. Wir werden
MATHEMATIK G9 LÖSEN VON GLEICHUNGEN Viele mathematische (und naturwissenschaftliche) Probleme lassen sich dadurch lösen, dass man eine Gleichung (oder auch mehrere) aufstellt und diese dann löst. Wir werden
( ) ( ). Dann heißt die Zahl
 Der Euklidische Abstand Seite 1 von 6 Der Euklidische Abstand Der Abstand zweier Punkte P und Q in der Modellebene ist eine Zahl, die von den Koordinaten der Punkte abhängt. Der Term, mit dem die Berechnung
Der Euklidische Abstand Seite 1 von 6 Der Euklidische Abstand Der Abstand zweier Punkte P und Q in der Modellebene ist eine Zahl, die von den Koordinaten der Punkte abhängt. Der Term, mit dem die Berechnung
Inhaltsverzeichnis. Mathematische Zeichen und Abkürzungen 9
 Inhaltsverzeichnis Mathematische Zeichen und Abkürzungen 9 1 Zahlenmengen und Anordnung der Zahlen auf der Zahlengeraden 11 1.1 Die Menge IN 0 der natürlichen Zahlen einschließlich der Null 11 1.2 Die
Inhaltsverzeichnis Mathematische Zeichen und Abkürzungen 9 1 Zahlenmengen und Anordnung der Zahlen auf der Zahlengeraden 11 1.1 Die Menge IN 0 der natürlichen Zahlen einschließlich der Null 11 1.2 Die
Zahlen und Funktionen
 Kapitel Zahlen und Funktionen. Mengen und etwas Logik Aufgabe. : Kreuzen Sie an, ob die Aussagen wahr oder falsch sind:. Alle ganzen Zahlen sind auch rationale Zahlen.. R beschreibt die Menge aller natürlichen
Kapitel Zahlen und Funktionen. Mengen und etwas Logik Aufgabe. : Kreuzen Sie an, ob die Aussagen wahr oder falsch sind:. Alle ganzen Zahlen sind auch rationale Zahlen.. R beschreibt die Menge aller natürlichen
Mathe Leuchtturm Übungsleuchtturm 5.Kl.
 1 by Mathe Leuchtturm Übungsleuchtturm 5.Kl. 014 Übungskapitel Erforderlicher Wissensstand (->Stoffübersicht im Detail siehe auch Wissensleuchtturm der 5.Klasse) Verschiedene Lösungsmethoden von quadratischen
1 by Mathe Leuchtturm Übungsleuchtturm 5.Kl. 014 Übungskapitel Erforderlicher Wissensstand (->Stoffübersicht im Detail siehe auch Wissensleuchtturm der 5.Klasse) Verschiedene Lösungsmethoden von quadratischen
Über das Rechteck weißt du, dass der Umfang 32 cm beträgt. Die Formel für den Umfang eines Rechtecks lautet 2 2.
 Aufgabe 1 Schritt 1: Skizze und Ansatz Über das Rechteck weißt du, dass der Umfang 32 cm beträgt. Die Formel für den Umfang eines Rechtecks lautet 2 2. Da du außerdem das Verhältnis der Seitenlängen kennst,
Aufgabe 1 Schritt 1: Skizze und Ansatz Über das Rechteck weißt du, dass der Umfang 32 cm beträgt. Die Formel für den Umfang eines Rechtecks lautet 2 2. Da du außerdem das Verhältnis der Seitenlängen kennst,
2015, MNZ. Jürgen Schmidt. 2.Tag. Vorkurs. Mathematik WS 2015/16
 Vorkurs Mathematik WS 2015/16 2.Tag Arten von Gleichungen Lineare Gleichungen (und Funktionen) 0 = ax + b (oft als Funktion: y = mx + n) a,b R Parameter m Anstieg, n Achsenabschnitt Quadratische Gleichungen
Vorkurs Mathematik WS 2015/16 2.Tag Arten von Gleichungen Lineare Gleichungen (und Funktionen) 0 = ax + b (oft als Funktion: y = mx + n) a,b R Parameter m Anstieg, n Achsenabschnitt Quadratische Gleichungen
Gleichungen Aufgaben und Lösungen
 Gleichungen Aufgaben und Lösungen http://www.fersch.de Klemens Fersch 6. Januar 3 Inhaltsverzeichnis Lineare Gleichung. a x + b = c....................................................... Aufgaben....................................................
Gleichungen Aufgaben und Lösungen http://www.fersch.de Klemens Fersch 6. Januar 3 Inhaltsverzeichnis Lineare Gleichung. a x + b = c....................................................... Aufgaben....................................................
1 Algebra Klass-Algebra. 1.2 Bruchterme und Bruchgleichungen
 1 Algebra 1.1 7.-Klass-Algebra 1. Vereinfachen Sie die folgenden Terme soweit wie möglich! (2x + 5y)(3x 4y) + (7x 10y)(6x 2y) (x + 4)(x 2 3x + 1) (x 2 + 6x 1)(x 2) x(2 3x) 2. Bestimmen Sie jeweils die
1 Algebra 1.1 7.-Klass-Algebra 1. Vereinfachen Sie die folgenden Terme soweit wie möglich! (2x + 5y)(3x 4y) + (7x 10y)(6x 2y) (x + 4)(x 2 3x + 1) (x 2 + 6x 1)(x 2) x(2 3x) 2. Bestimmen Sie jeweils die
Graphen quadratischer Funktionen und deren Nullstellen
 Binomische Formeln Mithilfe der drei binomischen Formeln kann man Funktionen bzw. Gleichungen vereinfachen. 1. Binomische Formel ( Plusformel ) a 2 + 2 a b+ b 2 = (a+ b) 2 Herleitung: (a+ b) 2 = (a+ b)
Binomische Formeln Mithilfe der drei binomischen Formeln kann man Funktionen bzw. Gleichungen vereinfachen. 1. Binomische Formel ( Plusformel ) a 2 + 2 a b+ b 2 = (a+ b) 2 Herleitung: (a+ b) 2 = (a+ b)
Eingangstest im Fach Mathematik Aufgaben zur Wiederholung und Vertiefung
 Eingangstest im Fach Mathematik Aufgaben zur Wiederholung und Vertiefung Hinweise: Liebe Schülerinnen und Schüler, der Eingangstest ist überstanden. Wenn Sie alle Aufgaben lösen konnten, so bringen Sie
Eingangstest im Fach Mathematik Aufgaben zur Wiederholung und Vertiefung Hinweise: Liebe Schülerinnen und Schüler, der Eingangstest ist überstanden. Wenn Sie alle Aufgaben lösen konnten, so bringen Sie
ALGEBRA Der Lösungsweg muss klar ersichtlich sein Schreiben Sie Ihre Lösungswege direkt auf diese Aufgabenblätter
 Berufsmaturitätsschule GIB Bern Aufnahmeprüfung 007 Mathematik Teil A Zeit: 45 Minuten Name / Vorname:... ALGEBRA Der Lösungsweg muss klar ersichtlich sein Schreiben Sie Ihre Lösungswege direkt auf diese
Berufsmaturitätsschule GIB Bern Aufnahmeprüfung 007 Mathematik Teil A Zeit: 45 Minuten Name / Vorname:... ALGEBRA Der Lösungsweg muss klar ersichtlich sein Schreiben Sie Ihre Lösungswege direkt auf diese
Lösung Semesterendprüfung
 MAE Mathematik: Analysis für Ingenieure Herbstsemester 07 Dr. Christoph Kirsch ZHAW Winterthur Aufgabe : Aufgabe : Lösung Semesterendprüfung a) Wir verwenden die Def. 4 der Vorlesung für die Implikation,
MAE Mathematik: Analysis für Ingenieure Herbstsemester 07 Dr. Christoph Kirsch ZHAW Winterthur Aufgabe : Aufgabe : Lösung Semesterendprüfung a) Wir verwenden die Def. 4 der Vorlesung für die Implikation,
ÅÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅÅÅÅ
 halbzeiten_rep_gesundheitlich-soziales_profil.nb Halbzeiten-Repetition gesundheitlich-soziales Profil Termumformungen:. Vereinfachen Sie: a) ( - a ) ( b b) Hx + 8 x + 6L H5 - xl ÅÅÅÅ Hx - 5 xl Hx - 6L
halbzeiten_rep_gesundheitlich-soziales_profil.nb Halbzeiten-Repetition gesundheitlich-soziales Profil Termumformungen:. Vereinfachen Sie: a) ( - a ) ( b b) Hx + 8 x + 6L H5 - xl ÅÅÅÅ Hx - 5 xl Hx - 6L
1. Ermitteln Sie zunächst sämtliche Nullstellen und deren Vielfachheit und geben Sie den Funktionsterm als Produkt an
 Aufgabenblock. Ermitteln Sie zunächst sämtliche Nullstellen und deren Vielfachheit und geben Sie den Funktionsterm als Produkt an a = + Nullstellen = + = / Um die Nullstellen zu ermitteln, muss der Funktionsterm
Aufgabenblock. Ermitteln Sie zunächst sämtliche Nullstellen und deren Vielfachheit und geben Sie den Funktionsterm als Produkt an a = + Nullstellen = + = / Um die Nullstellen zu ermitteln, muss der Funktionsterm
Wir gehen in dieser Vorlesung mit folgenden Zahlbereichen um: zweier ganzer Zahlen p und q schreiben kann.
 1 Grundlagen 1.1 Das Rechnen mit Zahlen Wir gehen in dieser Vorlesung mit folgenden Zahlbereichen um: N: natürliche Zahlen 1, 2, 3, 4, 5,... Z: ganze Zahlen..., 3, 2, 1, 0, 1, 2, 3,... Q: rationale Zahlen:
1 Grundlagen 1.1 Das Rechnen mit Zahlen Wir gehen in dieser Vorlesung mit folgenden Zahlbereichen um: N: natürliche Zahlen 1, 2, 3, 4, 5,... Z: ganze Zahlen..., 3, 2, 1, 0, 1, 2, 3,... Q: rationale Zahlen:
Quadratische Gleichungen. Kreise und Berührkreise. Binomische Formeln. Satz des Pythagoras. Goldener Schnitt
 Quadratische Gleichungen Kreise und Berührkreise Binomische Formeln Satz des Pythagoras Goldener Schnitt 9. Klasse Jens Möller Tel. 07551-6889 jmoellerowingen@aol.com Quadratische Gleichungen 1. Beispiel:
Quadratische Gleichungen Kreise und Berührkreise Binomische Formeln Satz des Pythagoras Goldener Schnitt 9. Klasse Jens Möller Tel. 07551-6889 jmoellerowingen@aol.com Quadratische Gleichungen 1. Beispiel:
Die Umkehrung des Potenzierens ist das Logarithmieren.
 Die Umkehrung des Potenzierens ist das Logarithmieren. Gilt a x = b, a,b > 0, a 1, so heißt x der Logarithmus von b zur Basis a. Bezeichnung: x = log a (b). Manchmal lassen wir die Angabe der Basis auch
Die Umkehrung des Potenzierens ist das Logarithmieren. Gilt a x = b, a,b > 0, a 1, so heißt x der Logarithmus von b zur Basis a. Bezeichnung: x = log a (b). Manchmal lassen wir die Angabe der Basis auch
Quadratische Funktion
 Quadratische Funktion 1. Übliche Formen 1) Allgemeine Form: y = f(x) = a x 2 + b x + c a, b, c Konstanten Grundlegender Fall a = 1, b = 0, c = 0, also y = x 2 : "Normalparabel" Vorteil: Keine Brüche für
Quadratische Funktion 1. Übliche Formen 1) Allgemeine Form: y = f(x) = a x 2 + b x + c a, b, c Konstanten Grundlegender Fall a = 1, b = 0, c = 0, also y = x 2 : "Normalparabel" Vorteil: Keine Brüche für
Wie schreibe ich einen Satz in ein Buch
 Grundlagen: Aussagen und Mengen 179 Grundlagen Grundlagen: Aussagen und Mengen 1. A = {1; ; ; ; ; 8; 1; } B = {17; 19; ; 9} C: Individuelle Lösungen A B 1 17 19 8 9 1. A = {0; 1; ; ; ; ; }; A = 7 B = {;
Grundlagen: Aussagen und Mengen 179 Grundlagen Grundlagen: Aussagen und Mengen 1. A = {1; ; ; ; ; 8; 1; } B = {17; 19; ; 9} C: Individuelle Lösungen A B 1 17 19 8 9 1. A = {0; 1; ; ; ; ; }; A = 7 B = {;
Fit für die Oberstufe Teil II - Gleichungen
 Gleichungen gibt es in verschiedenen Varianten: lineare und quadratische Gleichungen. Müssen zwei Gleichungen gleichzeitig erfüllt sein, ergibt sich daraus ein Gleichungssystem. Lineare Gleichungen (1
Gleichungen gibt es in verschiedenen Varianten: lineare und quadratische Gleichungen. Müssen zwei Gleichungen gleichzeitig erfüllt sein, ergibt sich daraus ein Gleichungssystem. Lineare Gleichungen (1
mathphys-online QUADRATISCHE FUNKTIONEN
 QUADRATICHE FUNKTIONEN Inhaltsverzeichnis Kapitel Inhalt eite Zuordnungsvorschriften, Funktionsgraph ymmetrie. ymmetrie zur. ymmetrie zu einer Parallelen zur Nullstellen Anzahl der Nullstellen 7 cheitel
QUADRATICHE FUNKTIONEN Inhaltsverzeichnis Kapitel Inhalt eite Zuordnungsvorschriften, Funktionsgraph ymmetrie. ymmetrie zur. ymmetrie zu einer Parallelen zur Nullstellen Anzahl der Nullstellen 7 cheitel
Aufgabenblatt: Binomische Formeln
 Aufgabenblatt: Binomische Formeln Aufgabe : a) (c + t) b) (x + ) c) ( + z) d) (g m) e) ( a ) f) (a b) g) (b a) h) (k m) i) (m k) Aufgabe : a) (p + q)(p q) b) (c + d)(c d) c) (x + )( x) d) (u + )( u ) e)
Aufgabenblatt: Binomische Formeln Aufgabe : a) (c + t) b) (x + ) c) ( + z) d) (g m) e) ( a ) f) (a b) g) (b a) h) (k m) i) (m k) Aufgabe : a) (p + q)(p q) b) (c + d)(c d) c) (x + )( x) d) (u + )( u ) e)
Damit kann die Kantenlänge s berechnet werden: s = s=17cm ; 3s = 51cm; 5s = 85 cm d) Volumen des Würfels: 2197cm 3
 1 a) b) c) d) 3 59.57 3.905493027 3.905 (mit TR lösen) 3 656.589 8.691562701 8.692 (mit TR lösen) 3 125.125 5.001666111 5.002 (mit TR lösen) 3 30.8994 3.137978874 3.138 (mit TR lösen) e) 3 30 1256 0.287989866
1 a) b) c) d) 3 59.57 3.905493027 3.905 (mit TR lösen) 3 656.589 8.691562701 8.692 (mit TR lösen) 3 125.125 5.001666111 5.002 (mit TR lösen) 3 30.8994 3.137978874 3.138 (mit TR lösen) e) 3 30 1256 0.287989866
Lösen von quadratischen Gleichungen mit der pq-formel. Aufgabe & Lösung Erläuterungen
 Thema Voraussetzungen Quadratwurzeln Lösen von quadratischen Gleichungen mit der pq-formel Aufgabe & Lösung Erläuterungen 1. Bestimme die Lösungen der Gleichung. Führe anschließend eine Probe durch. 1
Thema Voraussetzungen Quadratwurzeln Lösen von quadratischen Gleichungen mit der pq-formel Aufgabe & Lösung Erläuterungen 1. Bestimme die Lösungen der Gleichung. Führe anschließend eine Probe durch. 1
Berufliches Gymnasium Gelnhausen
 Berufliches Gymnasium Gelnhausen Fachbereich Mathematik Die inhaltlichen Anforderungen für das Fach Mathematik für Schülerinnen und Schüler, die in die Einführungsphase (E) des Beruflichen Gymnasiums eintreten
Berufliches Gymnasium Gelnhausen Fachbereich Mathematik Die inhaltlichen Anforderungen für das Fach Mathematik für Schülerinnen und Schüler, die in die Einführungsphase (E) des Beruflichen Gymnasiums eintreten
Quadratische Funktionen und Gleichungen Mathematik Jahrgangsstufe 9 (G8) Bergstadt-Gymnasium Lüdenscheid. Friedrich Hattendorf
 Mathematik Jahrgangsstufe 9 (G8) Lüdenscheid Friedrich Hattendorf 4. September 2014 Vorbemerkung Die Datei entsteht noch; noch nicht alles ist optimal Hinweis zum Ausdruck: (Fast) Alles sollte noch gut
Mathematik Jahrgangsstufe 9 (G8) Lüdenscheid Friedrich Hattendorf 4. September 2014 Vorbemerkung Die Datei entsteht noch; noch nicht alles ist optimal Hinweis zum Ausdruck: (Fast) Alles sollte noch gut
Übungen: Tangenten an ganzrationale Funktionen Lösungen und Lösungshinweise
 Übungen: Tangenten an ganzrationale Funktionen Lösungen und Lösungshinweise Aufgabe 1: Bestimme jeweils die 1. Ableitung der Funktionen. a) f(x) = (2 + x)(x² + 1) / Ausmultiplizieren = 2x² + 2 + x³ + x
Übungen: Tangenten an ganzrationale Funktionen Lösungen und Lösungshinweise Aufgabe 1: Bestimme jeweils die 1. Ableitung der Funktionen. a) f(x) = (2 + x)(x² + 1) / Ausmultiplizieren = 2x² + 2 + x³ + x
Gleichungen dritten und vierten Grades
 Karl-Franzens Universität Graz Institut für Mathematik und Wissenschaftliches Rechnen Heinrichstrasse 22/I 8010 Graz Gleichungen dritten und vierten Grades Sandra Fink und Benedikt Neuhold Mathematisches
Karl-Franzens Universität Graz Institut für Mathematik und Wissenschaftliches Rechnen Heinrichstrasse 22/I 8010 Graz Gleichungen dritten und vierten Grades Sandra Fink und Benedikt Neuhold Mathematisches
Aufgaben zu den ganzrationalen Funktionen
 Aufgaben zu den ganzrationalen Funktionen 1. Bestimmen Sie die Nullstellen folgender ganzrationaler Funktionen. a) y = x + x 6 b) y = x 3 3x + x c) y = (x + 4)(x + x ) d) y = x 4 5x + 4 e) y = x 3 + x
Aufgaben zu den ganzrationalen Funktionen 1. Bestimmen Sie die Nullstellen folgender ganzrationaler Funktionen. a) y = x + x 6 b) y = x 3 3x + x c) y = (x + 4)(x + x ) d) y = x 4 5x + 4 e) y = x 3 + x
Partialbruchzerlegung
 Partialbruchzerlegung W. Kippels 26. Oktober 2018 Inhaltsverzeichnis 1 Vorwort 2 2 Prinzip der Zerlegung 3 2.1 Nenner mit einfachen Nullstellen...................... 3 2.2 Nenner mit mehrfachen Nullstellen.....................
Partialbruchzerlegung W. Kippels 26. Oktober 2018 Inhaltsverzeichnis 1 Vorwort 2 2 Prinzip der Zerlegung 3 2.1 Nenner mit einfachen Nullstellen...................... 3 2.2 Nenner mit mehrfachen Nullstellen.....................
Jürgen Roth. Didaktik der Algebra. Modul 5. Jürgen Roth Didaktik der Algebra
 Jürgen Roth Didaktik der Algebra Modul 5 4.1 Inhalt Didaktik der Algebra 1 Ziele und Inhalte 2 Terme 3 Funktionen 4 Gleichungen 4.2 Didaktik der Algebra Kapitel 4: Gleichungen 4.3 Inhalt Kapitel 4: Gleichungen
Jürgen Roth Didaktik der Algebra Modul 5 4.1 Inhalt Didaktik der Algebra 1 Ziele und Inhalte 2 Terme 3 Funktionen 4 Gleichungen 4.2 Didaktik der Algebra Kapitel 4: Gleichungen 4.3 Inhalt Kapitel 4: Gleichungen
1 Zahlen. 1.1 Die Quadratwurzel. 1.2 Rechnen mit Quadratwurzeln. Grundwissen Mathematik 9
 Zahlen. Die Quadratwurzel Die Quadratwurzel a ist die nicht negative Lösung der Gleichung x a. a 0 0 0 a heißt Radikand Ein Teil der Quadratwurzeln sind rationale Zahlen (z.b. 9, 0,0 oder ), 9 andere dagegen
Zahlen. Die Quadratwurzel Die Quadratwurzel a ist die nicht negative Lösung der Gleichung x a. a 0 0 0 a heißt Radikand Ein Teil der Quadratwurzeln sind rationale Zahlen (z.b. 9, 0,0 oder ), 9 andere dagegen
Bruchterme 3. Sammlung der Aufgaben aus Bruchterme 1 und Bruchterme 2. Dort werden alle Methoden ausführlich an Beispielen besprochen
 ALGEBRA Bruchterme Sammlung der Aufgaben aus 0 Bruchterme und Bruchterme Dort werden alle Methoden ausführlich an Beispielen besprochen Zum Einsatz im Unterricht. Datei Nr. Stand. Juni 07 Friedrich W.
ALGEBRA Bruchterme Sammlung der Aufgaben aus 0 Bruchterme und Bruchterme Dort werden alle Methoden ausführlich an Beispielen besprochen Zum Einsatz im Unterricht. Datei Nr. Stand. Juni 07 Friedrich W.
Brüche, Polynome, Terme
 KAPITEL 1 Brüche, Polynome, Terme 1.1 Zahlen............................. 1 1. Lineare Gleichung....................... 3 1.3 Quadratische Gleichung................... 6 1.4 Polynomdivision........................
KAPITEL 1 Brüche, Polynome, Terme 1.1 Zahlen............................. 1 1. Lineare Gleichung....................... 3 1.3 Quadratische Gleichung................... 6 1.4 Polynomdivision........................
Einfache quadratische Funktionen und Gleichungen. x y Wertetabelle. y-achse
 Einfache quadratische Funktionen und Gleichungen Eine quadratische Funktion hat allgemein die Funktion: y = ax 2 + bx + c Dabei gilt: a, b und c R und a 0 Der Graph, der hierbei entsteht ist eine Parabel.
Einfache quadratische Funktionen und Gleichungen Eine quadratische Funktion hat allgemein die Funktion: y = ax 2 + bx + c Dabei gilt: a, b und c R und a 0 Der Graph, der hierbei entsteht ist eine Parabel.
Welche Nullstellen hat der Graph der Funktion a)
 Aufgabe 1 Welche Nullstellen hat der Graph der Funktion a) f (x)= (x 7)² (x+3)² Die Nullstellen sind 7 und -3. Beide Nullstellen sind doppelt, d.h. der Graph wechselt nicht die Seite der x-achse. b) Multipliziere
Aufgabe 1 Welche Nullstellen hat der Graph der Funktion a) f (x)= (x 7)² (x+3)² Die Nullstellen sind 7 und -3. Beide Nullstellen sind doppelt, d.h. der Graph wechselt nicht die Seite der x-achse. b) Multipliziere
ANGEWANDTE MATHEMATIK POLYNOMFUNKTIONEN. Autor: Wolfgang Kugler
 Autor: Wolfgang Kugler Inhaltsverzeichnis Definition Nullstellen und Linearfaktorzerlegung 5. Einfache reelle Nullstellen 5. Reelle Nullstellen mit höherer Vielfachheit 7.3 Komplee Nullstellen. Zusammenfassung
Autor: Wolfgang Kugler Inhaltsverzeichnis Definition Nullstellen und Linearfaktorzerlegung 5. Einfache reelle Nullstellen 5. Reelle Nullstellen mit höherer Vielfachheit 7.3 Komplee Nullstellen. Zusammenfassung
Klassenarbeit Mathematik Bearbeitungszeit 90 min. Mi SG26 D Gruppe A NAME: c) Überprüfen Sie das Ergebnis von a) mit dem Wurzelsatz von Vieta.
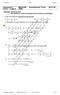 R. Brinkmann Seite 8..03 Klassenarbeit Mathematik Bearbeitungszeit 90 min. Mi 6..06 SG6 D Gruppe A NAME: Hilfsmittel: Taschenrechner. Alle Ergebnisse sind soweit möglich durch Rechnung zu begründen.. Lösen
R. Brinkmann Seite 8..03 Klassenarbeit Mathematik Bearbeitungszeit 90 min. Mi 6..06 SG6 D Gruppe A NAME: Hilfsmittel: Taschenrechner. Alle Ergebnisse sind soweit möglich durch Rechnung zu begründen.. Lösen
Übungen für die 1. Schularbeit 5. Klassen
 Übungen für die. Schularbeit 5. Klassen ) ) 4) 5) 6) 7) 8) Die folgende Grafik zeigt, wie sich im Schwimmbecken eines Hallenbades die Wassertiefe ( ) in den ersten 6 Stunden nach Öffnen des Abflusses verändert.
Übungen für die. Schularbeit 5. Klassen ) ) 4) 5) 6) 7) 8) Die folgende Grafik zeigt, wie sich im Schwimmbecken eines Hallenbades die Wassertiefe ( ) in den ersten 6 Stunden nach Öffnen des Abflusses verändert.
Quadratische Gleichungen
 Quadratische Gleichungen Alle aufgezeigten Lösungswege gelten für Gleichungen, die schon vereinfacht und zusammengefasst wurden. Es darf nur noch + vorhanden sein!!! (Also nicht + und auch nicht 3 ; bitte
Quadratische Gleichungen Alle aufgezeigten Lösungswege gelten für Gleichungen, die schon vereinfacht und zusammengefasst wurden. Es darf nur noch + vorhanden sein!!! (Also nicht + und auch nicht 3 ; bitte
Verschiedene Varianten von Aufgaben zu Parabeln
 Verschiedene Varianten von Aufgaben zu Parabeln 1) Gesucht werden die Nullstellen der Parabel mit der Gleichung: a) f(x) = 2x² 4x 16 b) f(x) = 5/3 (x 1) (x + 3) c) f(x) = - 1/2 (x + 4)² + 8 d) f(x) = 2x²
Verschiedene Varianten von Aufgaben zu Parabeln 1) Gesucht werden die Nullstellen der Parabel mit der Gleichung: a) f(x) = 2x² 4x 16 b) f(x) = 5/3 (x 1) (x + 3) c) f(x) = - 1/2 (x + 4)² + 8 d) f(x) = 2x²
Mathematik W7. Mag. Rainer Sickinger LMM, BR. v 1 Mag. Rainer Sickinger Mathematik W7 1 / 25
 Mathematik W7 Mag. Rainer Sickinger LMM, BR v 1 Mag. Rainer Sickinger Mathematik W7 1 / 25 Problem Angenommen wir haben eine quadratische Funktion ϕ : R R mit ϕ(x) = 1 3 x 2 2 3x 1 und wir wollen die Nullstellen
Mathematik W7 Mag. Rainer Sickinger LMM, BR v 1 Mag. Rainer Sickinger Mathematik W7 1 / 25 Problem Angenommen wir haben eine quadratische Funktion ϕ : R R mit ϕ(x) = 1 3 x 2 2 3x 1 und wir wollen die Nullstellen
Ich kenne den Nullproduktsatz und kann ihn anwenden, um Gleichungen in faktorisierter Form (wie (2x+5) (7 5x)=0 ) zu lösen.
 Klasse 9c Mathematik Vorbereitung zur Klassenarbeit Nr. am 1..018 Themen: Quadratische Funktionen und Gleichungen Checkliste Was ich alles können soll Ich kenne die allgemeine Form f(x) = ax²+bx+c und
Klasse 9c Mathematik Vorbereitung zur Klassenarbeit Nr. am 1..018 Themen: Quadratische Funktionen und Gleichungen Checkliste Was ich alles können soll Ich kenne die allgemeine Form f(x) = ax²+bx+c und
GMFH - Gesellschaft für Mathematik an Schweizer Fachhochschulen SMHES - Société pour les Mathématiques dans les Hautes Ecoles Spécialisées suisses
 GMFH - Gesellschaft für Mathematik an Schweizer Fachhochschulen SMHES - Société pour les Mathématiques dans les Hautes Ecoles Spécialisées suisses Mathematik-Referenzaufgaben zum Rahmenlehrplan für die
GMFH - Gesellschaft für Mathematik an Schweizer Fachhochschulen SMHES - Société pour les Mathématiques dans les Hautes Ecoles Spécialisées suisses Mathematik-Referenzaufgaben zum Rahmenlehrplan für die
math-circuit 10 Hefte kosten CHF Hefte kosten CHF 2.40 Wie viel kosten 2, 5 oder 6 Hefte? 5 Hefte kosten CHF 6. 6 Hefte kosten CHF 7.
 Im Bereich «Zuordnungen» 2 5 Proportionale, umgekehrt proportionale und andere Zuordnungen (ab LU ) Diese Übung kann man mit Kärtchen durchführen. Ist die Zuordnung proportional (p), umgekehrt proportional
Im Bereich «Zuordnungen» 2 5 Proportionale, umgekehrt proportionale und andere Zuordnungen (ab LU ) Diese Übung kann man mit Kärtchen durchführen. Ist die Zuordnung proportional (p), umgekehrt proportional
Schulmathematik: Lineare Algebra & Analytische Geometrie Kapitel 1: Gleichungen & Gleichungssysteme
 Schulmathematik: Lineare Algebra & Analytische Geometrie Kapitel 1: Gleichungen & Gleichungssysteme MAC.05043UB/MAC.05041PH, VU im SS 2017 http://imsc.uni-graz.at/pfeiffer/2017s/linalg.html Christoph GRUBER,
Schulmathematik: Lineare Algebra & Analytische Geometrie Kapitel 1: Gleichungen & Gleichungssysteme MAC.05043UB/MAC.05041PH, VU im SS 2017 http://imsc.uni-graz.at/pfeiffer/2017s/linalg.html Christoph GRUBER,
Ganzrationale Funktionen
 Eine Dokumentation von Sandro Antoniol Klasse 3f Mai 2003 Inhaltsverzeichnis: 1. Einleitung...3 2. Grundlagen...4 2.1. Symmetrieeigenschaften von Kurven...4 2.1.1. gerade Exponenten...4 2.1.2. ungerade
Eine Dokumentation von Sandro Antoniol Klasse 3f Mai 2003 Inhaltsverzeichnis: 1. Einleitung...3 2. Grundlagen...4 2.1. Symmetrieeigenschaften von Kurven...4 2.1.1. gerade Exponenten...4 2.1.2. ungerade
Inhalt. 1 Algebra-Wiederholung Funktionen Lineare Gleichungen, Ungleichungen und Gleichungssysteme... 23
 Inhalt Algebra-Wiederholung...................................... 5. Termumformungen: Rechengesetze... 6.2 Termumformungen: Ausmultiplizieren, binomische Formeln............ 8 Abschlusstest............................................
Inhalt Algebra-Wiederholung...................................... 5. Termumformungen: Rechengesetze... 6.2 Termumformungen: Ausmultiplizieren, binomische Formeln............ 8 Abschlusstest............................................
Kapitel 19 Partialbruchzerlegung
 Kapitel 19 Partialbruchzerlegung Mathematischer Vorkurs TU Dortmund Seite 1 / 15 Zur Erinnerung wiederholen wir Definition 4.5 [part] Es sei n N 0 und a 0, a 1,..., a n R mit a n 0. Dann heißt die Funktion
Kapitel 19 Partialbruchzerlegung Mathematischer Vorkurs TU Dortmund Seite 1 / 15 Zur Erinnerung wiederholen wir Definition 4.5 [part] Es sei n N 0 und a 0, a 1,..., a n R mit a n 0. Dann heißt die Funktion
Lösen einer Gleichung
 Zum Lösen von Gleichungen benötigen wir: mindestens einen Term eine Definition der in Frage kommenden Lösungen (Grundmenge) Die Grundmenge G enthält all jene Zahlen, die als Lösung für eine Gleichung in
Zum Lösen von Gleichungen benötigen wir: mindestens einen Term eine Definition der in Frage kommenden Lösungen (Grundmenge) Die Grundmenge G enthält all jene Zahlen, die als Lösung für eine Gleichung in
Diplom Mathematiker Wolfgang Kinzner. 17. Oktober Technische Universität München. Die abc-formel. W. Kinzner. Problemstellung.
 Diplom Mathematiker Wolfgang Kinzner Technische Universität München 17. Oktober 2013 1 / 9 Inhaltsverzeichnis 1 2 / 9 Inhaltsverzeichnis 1 2 2 / 9 Inhaltsverzeichnis 1 2 3 2 / 9 Inhaltsverzeichnis 1 2
Diplom Mathematiker Wolfgang Kinzner Technische Universität München 17. Oktober 2013 1 / 9 Inhaltsverzeichnis 1 2 / 9 Inhaltsverzeichnis 1 2 2 / 9 Inhaltsverzeichnis 1 2 3 2 / 9 Inhaltsverzeichnis 1 2
Die gleiche Lösung erhält man durch Äquivalenzumformung:
 R. Brinkmann http://brinkmann-du.de Seite 3..0 Quadratische Gleichungen Reinquadratische Gleichung Lösen Sie die Gleichung x = 5 Durch probieren erhält man die Lösung: x = 5 oder x = 5 Denn x = 5 = 5 oder
R. Brinkmann http://brinkmann-du.de Seite 3..0 Quadratische Gleichungen Reinquadratische Gleichung Lösen Sie die Gleichung x = 5 Durch probieren erhält man die Lösung: x = 5 oder x = 5 Denn x = 5 = 5 oder
1. Lineare Gleichungen
 1.2.0.2. Gleichungen und Ungleichungen 1. Lineare Gleichungen 1. 15xx [5 (12xx + 6) + 13xx] = 7xx + 15 2. Lösen Sie die folgende Gleichung und geben Sie die Lösungsmenge, in dem Sie nach den die Gleichung
1.2.0.2. Gleichungen und Ungleichungen 1. Lineare Gleichungen 1. 15xx [5 (12xx + 6) + 13xx] = 7xx + 15 2. Lösen Sie die folgende Gleichung und geben Sie die Lösungsmenge, in dem Sie nach den die Gleichung
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 2 3. Semester ARBEITSBLATT 2
 Mathematik: Mag. Schmid Wolfgang Areitslatt 3. Semester ARBEITSBLATT Natürlich treten quadratische Gleichungen nicht nur direkt auf, sondern entstehen nach verschiedenen Umformungen. Beispiel: Gi die Lösungsmenge
Mathematik: Mag. Schmid Wolfgang Areitslatt 3. Semester ARBEITSBLATT Natürlich treten quadratische Gleichungen nicht nur direkt auf, sondern entstehen nach verschiedenen Umformungen. Beispiel: Gi die Lösungsmenge
Wirtschaftsmathematik: Mathematische Grundlagen
 Wirtschaftsmathematik: Mathematische Grundlagen 1. Zahlen 2. Potenzen und Wurzeln 3. Rechenregeln und Vereinfachungen 4. Ungleichungen 5. Intervalle 6. Beträge 7. Lösen von Gleichungen 8. Logarithmen 9.
Wirtschaftsmathematik: Mathematische Grundlagen 1. Zahlen 2. Potenzen und Wurzeln 3. Rechenregeln und Vereinfachungen 4. Ungleichungen 5. Intervalle 6. Beträge 7. Lösen von Gleichungen 8. Logarithmen 9.
Übungsaufgaben zu quadratischen Gleichungen und Parabeln
 Übungsaufgaben zu quadratischen Gleichungen und Parabeln Binomische Formeln:. binomische Formel: ( a + b) = a + ab + b. binomische Formel:. binomische Formel: ( a b) = a ab + b ( a + b)(a b) = a b Lösungsformel
Übungsaufgaben zu quadratischen Gleichungen und Parabeln Binomische Formeln:. binomische Formel: ( a + b) = a + ab + b. binomische Formel:. binomische Formel: ( a b) = a ab + b ( a + b)(a b) = a b Lösungsformel
Bin ich in Mathe fit für die Oberstufe? Lösungen der Checkliste der Kompetenzen der Sekundarstufe I
 Gymnasium St. Wolfhelm Bin ich in Mathe fit für die Oberstufe? Lösungen der Checkliste der Kompetenzen der Sekundarstufe I Mit ihrer Hilfe kannst du selbstständig kontrollieren, ob du die abgefragten Kompetenzen
Gymnasium St. Wolfhelm Bin ich in Mathe fit für die Oberstufe? Lösungen der Checkliste der Kompetenzen der Sekundarstufe I Mit ihrer Hilfe kannst du selbstständig kontrollieren, ob du die abgefragten Kompetenzen
Mathematik-Vorbereitungskurs. ist ein. a b ist der und eine.
 Aufgaben. Vervollständigen Sie den Tet. a) Der Term (a + b) ist ein. a und b sind. b) Der Term + ist eine. und sind. ist eine. c) Der Term a b ist ein. a b ist der und eine.. Ergibt der Term (a (b c))
Aufgaben. Vervollständigen Sie den Tet. a) Der Term (a + b) ist ein. a und b sind. b) Der Term + ist eine. und sind. ist eine. c) Der Term a b ist ein. a b ist der und eine.. Ergibt der Term (a (b c))
Lineare Gleichungen: Übung 16a) Gesuchte Zahl: x. 7x + 65 = 12x 7x 65 = 5x : 5 13 = x. Gesuchte Zahl: 13
 Lineare Gleichungen: Übung 16a) Gesuchte Zahl: x 7x + 65 = 12x 7x 65 = 5x : 5 13 = x Gesuchte Zahl: 13 Lineare Gleichungen: Übung 16b) Kleinere natürliche Zahl: n Grössere natürliche Zahl: n + 3 (n + 3)
Lineare Gleichungen: Übung 16a) Gesuchte Zahl: x 7x + 65 = 12x 7x 65 = 5x : 5 13 = x Gesuchte Zahl: 13 Lineare Gleichungen: Übung 16b) Kleinere natürliche Zahl: n Grössere natürliche Zahl: n + 3 (n + 3)
2 Rechentechniken. 2.1 Potenzen und Wurzeln. Übersicht
 2 Rechentechniken Übersicht 2.1 Potenzen und Wurzeln.............................................. 7 2.2 Lösen linearer Gleichungssysteme..................................... 8 2.3 Polynome.........................................................
2 Rechentechniken Übersicht 2.1 Potenzen und Wurzeln.............................................. 7 2.2 Lösen linearer Gleichungssysteme..................................... 8 2.3 Polynome.........................................................
Als Untersuchungsbeispiel diene die Funktion: f(x) = x 6x + 5
 R. Brinkmann http://brinkmann-du.de Seite 07..009 Achsenschnittpunkte quadratischer Funktionen y P y ( 0 y ) s P ( 0) S y s f() P ( 0) s Bei der Betrachtung des Graphen in nebenstehender Abbildung fallen
R. Brinkmann http://brinkmann-du.de Seite 07..009 Achsenschnittpunkte quadratischer Funktionen y P y ( 0 y ) s P ( 0) S y s f() P ( 0) s Bei der Betrachtung des Graphen in nebenstehender Abbildung fallen
Sekundarschulabschluss für Erwachsene
 SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Arithmetik und Algebra A 2011 Totalzeit: 90 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl:
SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Arithmetik und Algebra A 2011 Totalzeit: 90 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl:
Mathematikaufgaben zur Vorbereitung auf das Studium
 Hochschule für Technik und Wirtschaft Dresden Fakultät Informatik / Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengänge Betriebswirtschaft International Business Dresden 05 . Mengen
Hochschule für Technik und Wirtschaft Dresden Fakultät Informatik / Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengänge Betriebswirtschaft International Business Dresden 05 . Mengen
Kapitel 7: Gleichungen
 1. Allgemeines Gleichungen Setzt man zwischen zwei Terme T 1 und T 2 ein Gleichheitszeichen (=), so entsteht eine Gleichung! Ungleichung Setzt man zwischen zwei Terme T 1 und T 2 ein Ungleichheitszeichen
1. Allgemeines Gleichungen Setzt man zwischen zwei Terme T 1 und T 2 ein Gleichheitszeichen (=), so entsteht eine Gleichung! Ungleichung Setzt man zwischen zwei Terme T 1 und T 2 ein Ungleichheitszeichen
Grundwissensaufgaben Klasse 10
 Grundwissensaufgaben Klasse 10 1.Grundwissensaufgaben zu Potenz- und Wurzelgesetzen: [Verwendung willkürlicher Zahlen und Buchstaben; eigene Aufgabenstellung] Fasse soweit wie möglich zusammen. a) ( 1,456)
Grundwissensaufgaben Klasse 10 1.Grundwissensaufgaben zu Potenz- und Wurzelgesetzen: [Verwendung willkürlicher Zahlen und Buchstaben; eigene Aufgabenstellung] Fasse soweit wie möglich zusammen. a) ( 1,456)
Partialbruchzerlegung für Biologen
 Partialbruchzerlegung für Biologen Rationale Funktionen sind Quotienten zweier Polynome, und sie tauchen auch in der Biologie auf. Die Partialbruchzerlegung bedeutet, einen einfacheren Ausdruck für eine
Partialbruchzerlegung für Biologen Rationale Funktionen sind Quotienten zweier Polynome, und sie tauchen auch in der Biologie auf. Die Partialbruchzerlegung bedeutet, einen einfacheren Ausdruck für eine
G8 Curriculum Mathematik Klasse 8
 G8 Curriculum Mathematik Klasse 8 1. Lerneinheit: Kongruenzabbildungen kongruente Figuren (20 Stunden) und Form - Eigenschaften ebener geometrischer Figuren erkennen und begründen - ebene Figuren mit vorgegebenen
G8 Curriculum Mathematik Klasse 8 1. Lerneinheit: Kongruenzabbildungen kongruente Figuren (20 Stunden) und Form - Eigenschaften ebener geometrischer Figuren erkennen und begründen - ebene Figuren mit vorgegebenen
Kapitel 4. Abbildungen = Funktionen. Oft hängt eine Größe von einer anderen ab. Beispiele: a) Höhe eines bestimmten Baumes von der Zeit
 Kapitel 4 Abbildungen = Funktionen 4.1 Abbildungen Oft hängt eine Größe von einer anderen ab. Beispiele: a) Höhe eines bestimmten Baumes von der Zeit b) Volumen eines Würfels von der Kantenlänge c) Alkoholgehalt
Kapitel 4 Abbildungen = Funktionen 4.1 Abbildungen Oft hängt eine Größe von einer anderen ab. Beispiele: a) Höhe eines bestimmten Baumes von der Zeit b) Volumen eines Würfels von der Kantenlänge c) Alkoholgehalt
Der Abstand zwischen den beiden Punkten ist gemäss dem Satz von Pythagoras gegeben durch
 4. 1 Ansatz m x + b = y m b 1 m3 b 4 m = 1, b = 1 4. m = 0.5 0.5 3 + b = b = 0.5 4. 3 6 = m 4 + 0.5 6 m 0. 5 1375. 4 4. 4 Parallel heisst, gleiche teigung. 4 = 0.5 3 + b 1 b 1 =.5 Die teigung der senkrechten
4. 1 Ansatz m x + b = y m b 1 m3 b 4 m = 1, b = 1 4. m = 0.5 0.5 3 + b = b = 0.5 4. 3 6 = m 4 + 0.5 6 m 0. 5 1375. 4 4. 4 Parallel heisst, gleiche teigung. 4 = 0.5 3 + b 1 b 1 =.5 Die teigung der senkrechten
Algebraische Gleichungen. Martin Brehm February 2, 2007
 Algebraische Gleichungen Martin Brehm February, 007 1. Der Begriff Algebra Algebraische Gleichungen Durch das herauskristalisieren von mehreren Teilgebieten der Algebra ist es schwer geworden eine einheitliche
Algebraische Gleichungen Martin Brehm February, 007 1. Der Begriff Algebra Algebraische Gleichungen Durch das herauskristalisieren von mehreren Teilgebieten der Algebra ist es schwer geworden eine einheitliche
Übungen zur Vorlesung Mathematik für Chemiker 1
 Prof. Dr. D. Egorova Prof. Dr. B. Hartke Lösungen Aufgabe Übungen zur Vorlesung Mathematik für Chemiker WiSe 204/5 Blatt 2 0.-2..204 f( x) = f(x) = gerade f( x) = f(x) = ungerade 8 6 4 2. f ( x) = ( x
Prof. Dr. D. Egorova Prof. Dr. B. Hartke Lösungen Aufgabe Übungen zur Vorlesung Mathematik für Chemiker WiSe 204/5 Blatt 2 0.-2..204 f( x) = f(x) = gerade f( x) = f(x) = ungerade 8 6 4 2. f ( x) = ( x
Algebra. Roger Burkhardt Fachhochschule Nordwestschweiz Hochschule für Technik Institut für Geistes- und Naturwissenschaft
 Algebra Roger Burkhardt roger.burkhardt@fhnw.ch Fachhochschule Nordwestschweiz Hochschule für Technik Institut für Geistes- und Naturwissenschaft FS 2010 Roger Burkhardt roger.burkhardt@fhnw.ch Algebra
Algebra Roger Burkhardt roger.burkhardt@fhnw.ch Fachhochschule Nordwestschweiz Hochschule für Technik Institut für Geistes- und Naturwissenschaft FS 2010 Roger Burkhardt roger.burkhardt@fhnw.ch Algebra
Informationen zur Prüfung der Fachschulreife an Berufsfachschulen
 Prüfungsvorbereitung Informationen zur Prüfung der Fachschulreife an Berufsfachschulen und Berufsaufbauschulen 1. Prüfungsdauer: 10 Minuten. Anzahl der dem Schüler vorgelegten Aufgaben: 3 3. Auswahl: Lehrer/-in
Prüfungsvorbereitung Informationen zur Prüfung der Fachschulreife an Berufsfachschulen und Berufsaufbauschulen 1. Prüfungsdauer: 10 Minuten. Anzahl der dem Schüler vorgelegten Aufgaben: 3 3. Auswahl: Lehrer/-in
Analysis: Ganzrationale Funktionen Analysis
 Analysis Ganzrationale Funktionen Nullstellen, Funktionen aufstellen, Extrempunkte, ymmetrie, Verhalten im Unendlichen Gymnasium Klasse 10 Alexander chwarz www.mathe-aufgaben.com Juni 014 1 Aufgabe 1:
Analysis Ganzrationale Funktionen Nullstellen, Funktionen aufstellen, Extrempunkte, ymmetrie, Verhalten im Unendlichen Gymnasium Klasse 10 Alexander chwarz www.mathe-aufgaben.com Juni 014 1 Aufgabe 1:
Vorbereitung auf die erste Klassenarbeit
 01 QUADRATISCHE FUNKTIONEN Wiederholungen Alles um Quadratische Funktionen Vorbereitung auf die erste Klassenarbeit Aufgabe 1: Schuljahr 2017/18 Seite 1/12 Aufgabe 2: Schuljahr 2017/18 Seite 2/12 Aufgabe
01 QUADRATISCHE FUNKTIONEN Wiederholungen Alles um Quadratische Funktionen Vorbereitung auf die erste Klassenarbeit Aufgabe 1: Schuljahr 2017/18 Seite 1/12 Aufgabe 2: Schuljahr 2017/18 Seite 2/12 Aufgabe
Vorkurs Mathematik Übungsaufgaben. Dozent Dr. Arne Johannssen
 Vorkurs Mathematik Übungsaufgaben 2 Dozent Dr. Arne Johannssen Lehrstuhl für Betriebswirtschaftslehre, insbesondere Mathematik und Statistik in den Wirtschaftswissenschaften Neues Logo: ie gesamte Universität
Vorkurs Mathematik Übungsaufgaben 2 Dozent Dr. Arne Johannssen Lehrstuhl für Betriebswirtschaftslehre, insbesondere Mathematik und Statistik in den Wirtschaftswissenschaften Neues Logo: ie gesamte Universität
Lösen von Bruchgleichungen
 Lösen von Bruchgleichungen Eine Bruchgleichung ist eine Gleichung wie diese hier: 3 3 6 1 2 4 = + 1 2 + 6 Ein Leitfaden zum Lösen von Gleichungen besagt: Eine Bruchgleichung löst man, indem man die Gleichung
Lösen von Bruchgleichungen Eine Bruchgleichung ist eine Gleichung wie diese hier: 3 3 6 1 2 4 = + 1 2 + 6 Ein Leitfaden zum Lösen von Gleichungen besagt: Eine Bruchgleichung löst man, indem man die Gleichung
