Probe zur Lösung der Berechnungsbeispiele BB_14.x: - Fortsetzung -
|
|
|
- Annegret Wolf
- vor 7 Jahren
- Abrufe
Transkript
1 Prof. Dr.-Ing. Rainer Ose Elektrotechnik für Ingenieure Grundlagen. Auflage, 2008 Fachhochschule Braunschweig/Wolfenbüttel -niversity of Applied Sciences- Probe zur Lösung der Berechnungsbeispiele BB_1.x: - Fortsetzung - Allgemeine Hinweise: Im Vordergrund der Aufgabenstellungen der Berechnungsbeispiele zum Kap. 1 steht die Konstruktion von Zeigerbildern. Da die manuelle Konstruktion maßstäblicher Zeigerbilder in der Regel relativ aufwändig und ungenau ist, wurden dem Bearbeiter im ersten Teil der Probe zu den BB 1.x Hinweise zur PC-gestützten Konstruktion gegeben werden (siehe Datei BB_1_A). BB 1.: Zeigerbild mit AB als Bezugszeiger Konstruieren Sie für die Schaltung des Berechnungsbeispiels 1. das maßstäbliche Zeigerbild aller Spannungen und Ströme für folgende Werte: Geg.: AB 10 V; f 1 khz; R 1 0 Ω; X 2 0 Ω; R 3 30 Ω; X 0 Ω Bild BB 1._1 zeigt die Simulationsschaltung zur Messung der Teilspannungen und des Gesamtstromes. Die Ströme I 1 und I 3 kann man über das OHMsche Gesetz aus den Spannungen 1 und 3 berechnen. Das erspart zwei zusätzliche Strommesser (Ameter) in der Simulationsschaltung. Bild BB 1._1: Simulationsschaltung zum BB 1. Tabelle BB 1. zeigt die mit dieser Simulation gewonnenen Messergebnisse.
2 Probe zur Lösung der BB_1.x Seite 2 Tabelle BB 1.: Simulationsergebnisse zum BB 1. Output File: Bedeutung: FREQ VM(D,B) VP(D,B) E E E+01 7,07 V ; FREQ VM(B,0) VP(B,0) E E+00.00E+01 7,07 V ; + FREQ VM(D,A) VP(D,A) E+03.11E E+01,1 V ; +9 FREQ VM(A,0) VP(A,0) 1.000E E E+01 8,8 V ; 31 FREQ IM(V_Ameter1) IP(V_Ameter1) I ges 1.000E E E ma ; +6 Für die Ströme I 1 und I 3 gilt dann: j I 1 1 / R 1 176,7 ma e und I 3 3 / R 3 171,33 ma e Probe: I ges I 1 + I 3 (12 12) ma + ( ) ma 216 ma + j 22 ma 217 ma e Mit diesen Werten kann das maßstäbliche Zeigerbild aller Spannungen (Bild BB 1._2; linke Seite) und aller Ströme (Bild BB 1._2; rechte Seite) konstruiert werden. Maßstab: 1 cm ˆ 1 V Maßstab: 1 cm ˆ 0 ma j 9 j 6 3 I 3 I 1 AB I ges 2 1 Bild BB 1._2: Zeigerbild der Spannungen (links) und der Ströme (rechts) zum BB 1.
3 Probe zur Lösung der BB_1.x Seite 3 BB 1.: Zeigerbild mit als Bezugszeiger Konstruieren Sie für die Schaltung des Berechnungsbeispiels 1. das maßstäbliche Zeigerbild aller Spannungen, wenn die Beträge aller Widerstände gleich sind. Bestimmen Sie aus dem Zeigerbild die j 0 Spannung AB für den Fall: 10 V e (Bezugszeiger im BB 1.) und führen Sie eine rechnerische Probe durch. Vereinfachung: X 1 R 2 X 3 X R R. Durch die gegebene Vereinfachung und der Kenntnis von kann man die Spannungen 2 und 3 durch folgende Überlegung bestimmen: 1) I hat die gleiche Phasenlage wie (ϕ I 0 ) 2) I eilt gegenüber um 90 voraus (ϕ I 90 ) 3) I 2 I + I eilt gegenüber um voraus (ϕ I2 ), weil I I (siehe Vereinfachung) ) 2 I 2 R 2 hat die gleiche Phasenlage wie I 2 (ϕ 2 ) ) 3 I 2 jx 3 steht senkrecht (vorauseilend) auf I 2 (ϕ 3 13 ) 6) Die Beträge von 2 und 3 sind gleich (siehe Vereinfachung) und es gilt: ) Maschensatz: AB Bild BB 1. zeigt das maßstäbliche (topografisch richtige) Zeigerbild. Maßstab: 1 cm ˆ 2 V AB 3 Grafische Lösung: Länge ( AB ) 11,2 cm AB 22, V Winkel ( AB ) 63 AB 22, V j63 2 Bild BB 1.: Zeigerbild der Spannungen im BB 1. Probe (z.b. mit der Spannungsteilerregel): AB AB R 2 + jx R + R // jx 3 // jx 1, + j0, 2,236 0, j0, R + jr + R //( jr) R + jr + 0,R j0,r R //( jr) 0,R j0,r j63, AB 22,36 V j63,
4 Probe zur Lösung der BB_1.x Seite BB 1.6: Maßstäbliches Zeigerbild einer Brückenschaltung (1) Berechnen Sie für das maßstäbliche Zeigerbild des Berechnungsbeispiels 1.6 die Zeigerlängen und die Winkel der Spannungen sowie 6 und 7. Der Bezugszeiger sei wieder 1. Für die Berechnung stehen lediglich die in der originalen Aufgabenstellung genannten Informationen zur Verfügung. Zur Präzisierung dieser erweiterten Aufgabenstellung werden zunächst noch einmal diejenigen Spannungszeiger gezeichnet, die proportional zu den in der originalen Aufgabenstellung angegebenen Widerstandswerten konstruiert werden können. Z 10Ω Es gilt: Länge{ } mit: Maßstab (oberer Zweig) Maßstab cm 2 3 x 2 A 7 E D 1 B Bild BB 1.6_1: Auszug aus dem Zeigerbild des BB 1.6 Nach dem Maschensatz (siehe blaue Zeiger im Bild BB 1.6_1) gilt: bzw.: } { } + j { } + { } + { } { } { j19,3 (3 + j 3, + + 3) cm (10 + j 3,) cm 10,9 cm Aus dem Spannungsdreieck B A E folgt (Bild BB 1.6_1): BE 7 x + j9, 7} j { x} + { } j { 2} + { } (j 3, + 3) cm,61 cm 7 { Der Zeiger 6 muss den gleichen Nullphasenwinkel aufweisen wie der Zeiger 7. Der Nullphasenwinkel des Zeigers ergibt sich dann gemäß Bild BB 1.6_2 aus: ϕ ϕ ,6. Die jeweiligen Zeigerlängen können aus Bild BB 1.6_2 bestimmt werden. Für das äußere rechtwinklige Dreieck gilt: { } sinα { } { } { } sinα,3 cm D B α E 7 mit: α ϕ 7 ϕ 30 Bild BB 1.6_2: Auszug aus dem Zeigerbild des BB 1.6
5 Probe zur Lösung der BB_1.x Seite Für das untere rechtwinklige Dreieck kann der Lehrsatz des PYTHAGORAS angewendet werden. 2 2 { DB } { } + { 6} DB bzw.: { } { } { } 7,3 cm,7cm Die Probe gelingt über den Maschensatz im unteren rechtwinkligen Dreieck: + DB j0,6 j9,2 6} (3 +,3 )cm,6cm { 6 (Probe stimmt!) Wie die berechneten Zeigerlängen zeigen, kommt es bei der grafischen Lösung (vgl. Lehrbuch BB 1.6) doch zu leichten Abweichungen. Mit den berechneten Zeigerlängen erhält man folgende Widerstandswerte: { 6},6cm R6,6,6 R 6 X 210Ω 180, 7Ω { },3cm X,3,3 { 7},61cm R7,61,61 R 7 X 210Ω 182, 7Ω { },3cm X,3,3 BB 1.7: Maßstäbliches Zeigerbild einer Brückenschaltung (2) Berechnen Sie für das maßstäbliche Zeigerbild des Berechnungsbeispiels 1.7 die Zeigerlängen und die Winkel der Spannungen und x sowie und 6. Der Bezugszeiger ist wieder 1. Für die Berechnung stehen lediglich die in der Aufgabenstellung genannten Informationen zur Verfügung. Die Berechnung wird nach Vorbild des BB 1.6 vorgenommen. Z 2R Es gilt: Länge{ } mit: Maßstab (oberer Zweig) Maßstab 3cm Die Summe der Spannungszeiger im oberen Zweig ergibt : ϕ bzw.: } { } j { } + { } j { } } { (3 j 1, + 1, j,) cm (, j 6) cm 7, cm { j j 3,1 e Der Schwerpunkt dieser erweiterten Aufgabenstellung besteht nun darin, den Betrag (hier: Zeigerlänge) und die Phasenlage von x zu bestimmen. Mit Kenntnis dieses Zeigers können dann die Daten des Zeigers über die linke obere Masche und des Zeigers 6 über die rechte obere Masche des Bildes 1.30 berechnet werden: Masche oben links: x Masche oben rechts: 6 x Für die Bestimmung von x gilt folgende Überlegung: Die Spannungszeiger und x sollen senkrecht aufeinander stehen. Gemäß Zählpfeil eilt x voraus. Der Nullphasenwinkel der Spannung x beträgt demzufolge: ϕ x ϕ ,9.
6 Probe zur Lösung der BB_1.x Seite 6 Die Herleitung einer Berechnungsvorschrift für die Zeigerlänge von x ist über das Zeigerbild möglich. Bild BB 1.7_1 zeigt auf der linken Seite das Zeigerbild mit 1 als Bezugszeiger. Durch eine Drehung um 3 nach links ( ϕ ) entsteht das auf der rechten Seite des Bildes BB 1.7_1 dargestellte Zeigerbild mit als Bezugszeiger x 3 2 x 6 6 Bild BB 1.7_1: Maßstäbliches Zeigerbild zum Berechnungsbeispiel 1.7 links: mit 1 als Bezugszeiger rechts: mit als Bezugszeiger Durch Zusammenfassung von sowie von entsteht die vereinfachte Darstellung des Bildes BB 1.7_2. Der Zeiger x teilt den Zeiger an der Stelle X in zwei Ersatzzeiger mit den Längen { 1 } 3 cm und { }, cm. Der oberhalb des Zeigers positionierte Anteil von x (Strecke XA) hat eine Länge von { 2 } 1, cm. Der Mittelpunkt des THALES-Kreises M teilt den Zeiger in zwei Teilzeiger mit je {0, } 3,7 cm. Diese Zeigerlänge entspricht dem Radius des Kreises. Setzt man nun diesen (hier grün dargestellten) Teilzeiger MS am Punkt M an und dreht seine Spitze auf den Punkt B, so erhält man Informationen über die Koordinaten dieses Punktes. XM 0,7cm Im vorliegenden Fall muss der Zeiger MS um den Winkel β arctan arctan 11, 3 {0, } 3,7cm nach rechts auf den Punkt B gedreht werden. Der Betrag seines Imaginärteils beschreibt jetzt die Länge der Strecke BX. Für den Zeiger MB gilt: MB MS jβ 0, j 90 j11,3 MB } (0,73cm + j3,677cm) { MB bzw.: MB { } {0, MB A 12 x { 1 } } j101,3 Der Zeiger x hat demzufolge die Länge: { x } Im { MB } + { 2 } (3, ,) cm,177 cm. X { BX } B { 2 } S M MS { } Bild BB 1.7_2: Auszug aus dem Zeigerbild des Bildes BB 1.7_1 3 6
7 Probe zur Lösung der BB_1.x Seite 7 Diese Länge stimmt mit der grafischen Lösung des BB 1.7 überein. Für den Zeiger x gilt dann in der originalen Darstellung des Zeigerbildes gemäß Bild BB 1.7_1 linke Seite: x j 36,9 { },177 cm (,1 + j3,11) cm x Nun können die Zeigerlängen von und 6 berechnet werden: Masche oben links: x bzw.: j10 } [3 j1, (,1 + j3,11)]cm (1,1 + j,61) cm,7cm { Masche oben rechts: 6 x bzw.: j1 6} [(,1 + j3,11) + 1, j,]cm (,6 j1,39) cm,81cm 6 { Probe: + 6 bzw.: { } (1,1+ j,61) cm + (,6 j1,39) cm (, (Probe stimmt!) j 6) cm j3,1 7,cm Eine Berechnung des in der originalen Aufgabenstellung gesuchten Wertes für den Widerstand R führt zu folgendem Ergebnis: 6 R { } ω L { } 6 6 R { R { } } 3 6,7cm,81cm,7 R 3R 2, 3R,81 Anmerkung: In der originalen Aufgabenstellung zum BB 1.7 wurde rechts neben dem Bild 1.30 versehentlich eine Zeigerlänge für ωl 6 von 3 cm angegeben, die nur für 1 / ωc Gültigkeit haben kann. Im unteren Zweig der Schaltung gilt doch ein anderer Maßstab! (Sorry) Zusätzliches Zahlenbeispiel: Berechnen Sie über die Aufbauelemente der Schaltung des BB 1.7 die Spannung x, wenn an die Schaltung eine Spannung 7, V e j 3 angelegt wird. Für die Masche oben links gilt: 1 x I1 ( R1 + ) I R I1 (2R jr) I 2, R jωc mit: I1( ) 1 1 R1 + + R3 + jωc jωc 2 2 und: I 2R jr + R j3r ( ) R + jωl 2,R + j3r 2R jr 2,R 10 + j 6 j7,3 x ( ) ( ) (0, + j0,2 0, + j0,9) 3R jr 2,R + j3r 2 1 x j0,69 7,V j 3 0,69 j 90,17V j 37 Auch diese Probe stimmt mit der Lösung der erweiterten Aufgabenstellung (siehe oben) überein!
8 Probe zur Lösung der BB_1.x Seite 8 BB 1.8: Maßstäbliches Zeigerbild einer Brückenschaltung (3) Berechnen Sie für das maßstäbliche Zeigerbild des Berechnungsbeispiels 1.8 die Spannungen und x sowie und 6. Der Bezugszeiger ist wieder 1. Für die Berechnung stehen lediglich die in der originalen Aufgabenstellung genannten Informationen zur Verfügung. Nach dem Maschensatz gilt im oberen Zweig der Schaltung des Berechnungsbeispiels 1.8: (10 j j0)v (0 j0)v 6V j 39 Der Zeiger x hat einen minimalen Betrag, wenn seine Verlängerung durch den Mittelpunkt des THALES-Kreises verläuft. Der Mittelpunkt des THALES-Kreises hat in der komplexen Ebene des Bildes BB 1.8 folgende Spannungskoordinaten: M TH 0, 2 V j 20 V Über die Spannungskoordinaten des Punkte A: A 10 V j 80 V kann man nun einen Ersatzzeiger berechnen, der vom Punkt A zum Mittelpunkt des THALES-Kreises gerichtet ist. Seine Phasenlage entspricht dem Nullphasenwinkel von x. Für diesen Ersatzzeiger gilt: AM TH M TH A 2 V j 20 V 10 V + j 80 V 1 V + j 60 V 61,8 V e j 76 Wenn man schließlich vom Betrag dieses Ersatzzeigers den halben Betrag der Gesamtspannung subtrahiert, erhält man den Betrag von x. Für x gilt dann: x 29,8 V e j 76 7,22 V + j 28,96 V. Mit Kenntnis von x können nun die Spannungen Maßstab: 1 cm ˆ 10 V und 6 berechnet werden. j Im {} Für die obere linke Masche im Bild 1.32 erhält man: x (10 j80 + 7,2 + j 71, (17,2 j1)v 3,8V j29)v Re {} Für die obere rechte Masche im Bild 1.32 erhält man: x (0 + j0 7,2 j29)v AM TH M TH j18, 6 (32,8 + j11)v 3,6V Probe: x + 6 (17,2 j1+ 32,8 + j11)v (0 j0)v 6V j 39 (0 j0)v 6V j 39 A (Probe stimmt!) Bild BB 1.8: Auszug aus dem Zeigerbild des BB 1.8
Prof. Dr.-Ing. Rainer Ose Elektrotechnik für Ingenieure Grundlagen 4. Auflage, Probe zur Lösung der Berechnungsbeispiele BB_14.
 Prof. Dr.-Ing. Rainer Ose Elektrotechnik für Ingenieure Grundlagen 4. Auflage, 2008 Fachhochschule Braunschweig/Wolfenbüttel -University of Applied Sciences- Probe zur Lösung der Berechnungsbeispiele BB_14.x:
Prof. Dr.-Ing. Rainer Ose Elektrotechnik für Ingenieure Grundlagen 4. Auflage, 2008 Fachhochschule Braunschweig/Wolfenbüttel -University of Applied Sciences- Probe zur Lösung der Berechnungsbeispiele BB_14.x:
Prof. Dr.-Ing. Rainer Ose Elektrotechnik für Ingenieure Grundlagen 4. Auflage, Probe zur Lösung der Berechnungsbeispiele BB_15.
 Pro. Dr.-ng. Rainer Ose Elektrotechnik ür ngenieure Grundlagen 4. Aulage, 28 Fachhochschule Braunschweig/Wolenbüttel -niversity o Applied Sciences- Probe zur Lösung der Berechnungsbeispiele BB_15.x: Allgemeine
Pro. Dr.-ng. Rainer Ose Elektrotechnik ür ngenieure Grundlagen 4. Aulage, 28 Fachhochschule Braunschweig/Wolenbüttel -niversity o Applied Sciences- Probe zur Lösung der Berechnungsbeispiele BB_15.x: Allgemeine
Prof. Dr.-Ing. Rainer Ose Elektrotechnik für Ingenieure Grundlagen 4. Auflage, Fortsetzung. Probe zur Lösung der Berechnungsbeispiele BB_5.
 Prof. Dr.-Ing. Rainer Ose Elektrotechnik für Ingenieure Grundlagen 4. Auflage, 2008 Fachhochschule Braunschweig/Wolfenbüttel -University of Applied Sciences- Probe zur Lösung der Berechnungsbeispiele BB_5.x:
Prof. Dr.-Ing. Rainer Ose Elektrotechnik für Ingenieure Grundlagen 4. Auflage, 2008 Fachhochschule Braunschweig/Wolfenbüttel -University of Applied Sciences- Probe zur Lösung der Berechnungsbeispiele BB_5.x:
Prof. Dr.-Ing. Rainer Ose Elektrotechnik für Ingenieure Grundlagen 4. Auflage, Probe zur Lösung der Berechnungsbeispiele BB_6.
 Prof. Dr.-Ing. Rainer Ose Elektrotechnik für Ingenieure Grundlagen 4. Auflage, 28 Fachhochschule Braunschweig/Wolfenbüttel -University of Applied Sciences- Probe zur Lösung der Berechnungsbeispiele BB_6.x:
Prof. Dr.-Ing. Rainer Ose Elektrotechnik für Ingenieure Grundlagen 4. Auflage, 28 Fachhochschule Braunschweig/Wolfenbüttel -University of Applied Sciences- Probe zur Lösung der Berechnungsbeispiele BB_6.x:
/U Wie groß ist den beiden unter 6. genannten Fällen der von der Spannungsquelle U 1 gelieferte Strom? als Formel. 1 + jωc = R 2.
 Aufgabe Ü6 Gegeben ist die angegebene Schaltung:. Berechnen Sie allgemein (als Formel) /. 2. Wie groß ist der Betrag von /? R 3. Um welchen Winkel ist gegenüber phasenverschoben? 4. Skizzieren Sie die
Aufgabe Ü6 Gegeben ist die angegebene Schaltung:. Berechnen Sie allgemein (als Formel) /. 2. Wie groß ist der Betrag von /? R 3. Um welchen Winkel ist gegenüber phasenverschoben? 4. Skizzieren Sie die
Gegeben ist die dargestellte Schaltung mit nebenstehenden Werten. Daten: U AB. der Induktivität L! und I 2. , wenn Z L. = j40 Ω ist? an!
 Grundlagen der Elektrotechnik I Aufgabe K4 Gegeben ist die dargestellte Schaltung mit nebenstehenden Werten. R 1 A R 2 Daten R 1 30 Ω R 3 L R 2 20 Ω B R 3 30 Ω L 40 mh 1500 V f 159,15 Hz 1. Berechnen Sie
Grundlagen der Elektrotechnik I Aufgabe K4 Gegeben ist die dargestellte Schaltung mit nebenstehenden Werten. R 1 A R 2 Daten R 1 30 Ω R 3 L R 2 20 Ω B R 3 30 Ω L 40 mh 1500 V f 159,15 Hz 1. Berechnen Sie
3 Ortskurven. 3.1 Einleitung. 3.2 Spannungs-/Widerstandsdiagramme in der Reihenschaltung
 C. FEPEL 3 Ortskurven 3. Einleitung Durch ein Zeigerbild wird ein bestimmter Betriebszustand eines Wechselstromnetzes bei konstanten Parametern (Amplitude und Frequenz der einspeisenden sinusförmigen Quellspannungen
C. FEPEL 3 Ortskurven 3. Einleitung Durch ein Zeigerbild wird ein bestimmter Betriebszustand eines Wechselstromnetzes bei konstanten Parametern (Amplitude und Frequenz der einspeisenden sinusförmigen Quellspannungen
5.5 Ortskurven höherer Ordnung
 2 5 Ortskurven 5.5 Ortskurven höherer Ordnung Ortskurve Parabel Die Ortskurvengleichung für die Parabel lautet P A + p B + p 2 C. (5.) Sie kann entweder aus der Geraden A + p B und dem Anteil p 2 C oder
2 5 Ortskurven 5.5 Ortskurven höherer Ordnung Ortskurve Parabel Die Ortskurvengleichung für die Parabel lautet P A + p B + p 2 C. (5.) Sie kann entweder aus der Geraden A + p B und dem Anteil p 2 C oder
Prüfung _1. Lösung. Seite-01. Aufgabe ET2 U Q2
 niversity of Applied Dipl.-Wirt. ng. (FH) Prüfung 6-_ Aufgabe ET Seite- Stand: 9..6; Bei dieser Aufgabe ist zu beachten, dass der Strom aus der Stromquelle negativ ist. Das bedeutet, dass man die Pfeilrichtung
niversity of Applied Dipl.-Wirt. ng. (FH) Prüfung 6-_ Aufgabe ET Seite- Stand: 9..6; Bei dieser Aufgabe ist zu beachten, dass der Strom aus der Stromquelle negativ ist. Das bedeutet, dass man die Pfeilrichtung
Grundlagen der Elektrotechnik 2 Seminaraufgaben
 ampus Duisburg Grundlagen der Elektrotechnik 2 Allgemeine und Theoretische Elektrotechnik Prof. Dr. sc. techn. Daniel Erni Version 2005.10 Trotz sorgfältiger Durchsicht können diese Unterlagen noch Fehler
ampus Duisburg Grundlagen der Elektrotechnik 2 Allgemeine und Theoretische Elektrotechnik Prof. Dr. sc. techn. Daniel Erni Version 2005.10 Trotz sorgfältiger Durchsicht können diese Unterlagen noch Fehler
Im dargestellten Drehstomnetz sind folgende Impedanzen angeschlossen:
 Aufgabe Ü3 Im dargestellten Drehstomnetz sind folgende Impedanzen angeschlossen: R = 1 Ω L1 W1 W4 I 1 R X C = 3 Ω X L = 2 3 Ω L2 W2 I 2 jx L -jx C = 13 V = 13 V e j120 L3 W3 W5 I 3 = 13 V e j120 N 1. Zeichnen
Aufgabe Ü3 Im dargestellten Drehstomnetz sind folgende Impedanzen angeschlossen: R = 1 Ω L1 W1 W4 I 1 R X C = 3 Ω X L = 2 3 Ω L2 W2 I 2 jx L -jx C = 13 V = 13 V e j120 L3 W3 W5 I 3 = 13 V e j120 N 1. Zeichnen
3 Lineare elektrische Gleichstromkreise
 3. Eigenschaften elektrischer Stromkreise 7 3 Lineare elektrische Gleichstromkreise 3. Eigenschaften elektrischer Stromkreise Lineare elektrische Stromkreise bestehen aus auelementen mit einer linearen
3. Eigenschaften elektrischer Stromkreise 7 3 Lineare elektrische Gleichstromkreise 3. Eigenschaften elektrischer Stromkreise Lineare elektrische Stromkreise bestehen aus auelementen mit einer linearen
Lehrfach: Grundlagen der Elektrotechnik. Versuch: Wechselstromnetzwerke
 WSNW P_10_05.docx Oc Lehrfach: Grundlagen der Elektrotechnik Versuch: Wechselstromnetzwerke Hochschule Zittau/Görlitz; Fakultät Elektrotechnik und Informatik Prof. Dr. techn. Stefan Kornhuber/Prof. Dr.-Ing.
WSNW P_10_05.docx Oc Lehrfach: Grundlagen der Elektrotechnik Versuch: Wechselstromnetzwerke Hochschule Zittau/Görlitz; Fakultät Elektrotechnik und Informatik Prof. Dr. techn. Stefan Kornhuber/Prof. Dr.-Ing.
P = U I cos ϕ. 3,52 kw 220 V 0,8 = 20 A. Der Phasenwinkel des Stroms wird aus dem Leistungsfaktor cos ϕ bestimmt: ϕ = arccos(0,8 ) = 36,87
 a) Strom nach Betrag und Phase: Der Betrag des Stroms wird aus der Wirkleistung bestimmt: P = U cos ϕ = P U cos ϕ = 3,52 kw 220 V 0,8 = 20 A Der Phasenwinkel des Stroms wird aus dem Leistungsfaktor cos
a) Strom nach Betrag und Phase: Der Betrag des Stroms wird aus der Wirkleistung bestimmt: P = U cos ϕ = P U cos ϕ = 3,52 kw 220 V 0,8 = 20 A Der Phasenwinkel des Stroms wird aus dem Leistungsfaktor cos
Lösungen Geometrie-Dossier Kreis 2 - Kreiskonstruktionen. Diese Aufgabe entspricht genau der Grundkonstruktion 2 (Genaueres kannst du dort nachlesen).
 Seiten 12-19 Aufgaben Kreiskonstruktionen (Achtung, Lösungen z.t. verkleinert gezeichnet) 1. 1. Mittelsenkrechte von PQ (Der Kreismittelpunkt muss auf der Mittelsenkrechten von zwei Kreispunkten liegen)
Seiten 12-19 Aufgaben Kreiskonstruktionen (Achtung, Lösungen z.t. verkleinert gezeichnet) 1. 1. Mittelsenkrechte von PQ (Der Kreismittelpunkt muss auf der Mittelsenkrechten von zwei Kreispunkten liegen)
Übung Grundlagen der Elektrotechnik B
 Übung Grundlagen der Elektrotechnik B Themengebiet E: Komplexe Zahlen Aufgabe 1: echnen mit komplexen Zahlen Stellen Sie die folgenden komplexen Zahlen in der arithmetischen Form (z = x + jy und der exponentiellen
Übung Grundlagen der Elektrotechnik B Themengebiet E: Komplexe Zahlen Aufgabe 1: echnen mit komplexen Zahlen Stellen Sie die folgenden komplexen Zahlen in der arithmetischen Form (z = x + jy und der exponentiellen
Prof. Dr.-Ing. Rainer Ose Elektrotechnik für Ingenieure Grundlagen 4. Auflage, Lösung der Übungsaufgabe ÜA_1_6.4.B:
 Prof. Dr.-ng. Rainer Ose Elektrotechnik für ngenieure Grundlagen 4. Auflage, 2008 Fachhochschule Braunschweig/Wolfenbüttel -niversity of Applied Sciences- Lösung der Übungsaufgabe ÜA_1_6.4.B: Für die Glühlampe
Prof. Dr.-ng. Rainer Ose Elektrotechnik für ngenieure Grundlagen 4. Auflage, 2008 Fachhochschule Braunschweig/Wolfenbüttel -niversity of Applied Sciences- Lösung der Übungsaufgabe ÜA_1_6.4.B: Für die Glühlampe
Schulübung zur Wiederholung. für die 4. Schulaufgabe
 Schulübung zur Wiederholung für die 4. Schulaufgabe Aufgabe 1 Bestimmung der Burggrabenweite Man beginnt mit der Seite ST. Vorgehensweise: Man beginnt mit der Seite ST. Aufgabe 1 Bestimmung der Burggrabenweite
Schulübung zur Wiederholung für die 4. Schulaufgabe Aufgabe 1 Bestimmung der Burggrabenweite Man beginnt mit der Seite ST. Vorgehensweise: Man beginnt mit der Seite ST. Aufgabe 1 Bestimmung der Burggrabenweite
Abitur 2011 G8 Abitur Mathematik Geometrie VI
 Seite http://www.abiturloesung.de/ Seite Abitur 0 G8 Abitur Mathematik Geometrie VI In einem kartesischen Koordinatensystem sind die Punkte A( 7 ), B(6 7 ) und C( ) gegeben. Teilaufgabe a (4 BE) Weisen
Seite http://www.abiturloesung.de/ Seite Abitur 0 G8 Abitur Mathematik Geometrie VI In einem kartesischen Koordinatensystem sind die Punkte A( 7 ), B(6 7 ) und C( ) gegeben. Teilaufgabe a (4 BE) Weisen
Gleichstromtechnik. Vorlesung 11: Strom- und Spannungsteilung. Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann
 Gleichstromtechnik Vorlesung 11: Strom- und Spannungsteilung Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Motivation Auf der Basis der Kirchhoffschen Gesetze wurden Methoden zur Zusammenfassung
Gleichstromtechnik Vorlesung 11: Strom- und Spannungsteilung Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Motivation Auf der Basis der Kirchhoffschen Gesetze wurden Methoden zur Zusammenfassung
E-Labor im WS / SS. Versuch Nr. 11 Netze an Sinusspannung konstanter Frequenz. Fakultät II Abteilung Maschinenbau. Gruppe:
 Abteilung Maschinenbau im WS / SS Gruppe: Name Vorname Matr.-Nr. Semester Verfasser(in) Teilnehmer(in) Teilnehmer(in) Professor(in) / Lehrbeauftragte(r): Datum der Durchführung: BITTE ANKREUZEN Messprotokoll
Abteilung Maschinenbau im WS / SS Gruppe: Name Vorname Matr.-Nr. Semester Verfasser(in) Teilnehmer(in) Teilnehmer(in) Professor(in) / Lehrbeauftragte(r): Datum der Durchführung: BITTE ANKREUZEN Messprotokoll
Themenbereich: Besondere Dreiecke Seite 1 von 6
 Themenbereich: Besondere Dreiecke Seite 1 von 6 Lernziele: - Kenntnis der Bezeichnungen für besondere Dreiecke - Kenntnis der Seiten- und Winkelbezeichnungen bei besonderen Dreiecken - Kenntnis der Eigenschaften
Themenbereich: Besondere Dreiecke Seite 1 von 6 Lernziele: - Kenntnis der Bezeichnungen für besondere Dreiecke - Kenntnis der Seiten- und Winkelbezeichnungen bei besonderen Dreiecken - Kenntnis der Eigenschaften
Elektrotechnik Protokoll - Wechselstromkreise. André Grüneberg Mario Apitz Versuch: 16. Mai 2001 Protokoll: 29. Mai 2001
 Elektrotechnik Protokoll - Wechselstromkreise André Grüneberg Mario Apitz Versuch: 6. Mai Protokoll: 9. Mai 3 Versuchsdurchführung 3. Vorbereitung außerhalb der Versuchszeit 3.. Allgemeine Berechnungen
Elektrotechnik Protokoll - Wechselstromkreise André Grüneberg Mario Apitz Versuch: 6. Mai Protokoll: 9. Mai 3 Versuchsdurchführung 3. Vorbereitung außerhalb der Versuchszeit 3.. Allgemeine Berechnungen
Umdruck zum Versuch. Basis 1 Eigenschaften einfacher Bauelemente und. Anwendung von Messgeräten
 Universität Stuttgart Fakultät Informatik, Elektrotechnik und Informationstechnik Umdruck zum Versuch Basis 1 Eigenschaften einfacher Bauelemente und Anwendung von Messgeräten Bitte bringen Sie zur Versuchsdurchführung
Universität Stuttgart Fakultät Informatik, Elektrotechnik und Informationstechnik Umdruck zum Versuch Basis 1 Eigenschaften einfacher Bauelemente und Anwendung von Messgeräten Bitte bringen Sie zur Versuchsdurchführung
Musterlösung zur. Klausur Grundlagen der Elektrotechnik I im SoSe 18. Aufgabe 1. Die Lösungen zu Aufgabe 1 folgen zum Ende des Dokuments.
 Musterlösung zur Klausur Grundlagen der Elektrotechnik I im SoSe 18 Aufgabe 1 Die Lösungen zu Aufgabe 1 folgen zum Ende des Dokuments. Aufgabe 2 1. R 1 = R a und R b = R 2 R L R 2 +R L 2. R 1 + R 2 = 1
Musterlösung zur Klausur Grundlagen der Elektrotechnik I im SoSe 18 Aufgabe 1 Die Lösungen zu Aufgabe 1 folgen zum Ende des Dokuments. Aufgabe 2 1. R 1 = R a und R b = R 2 R L R 2 +R L 2. R 1 + R 2 = 1
Schaltungen mit mehreren Widerständen
 Grundlagen der Elektrotechnik: WIDERSTANDSSCHALTUNGEN Seite 1 Schaltungen mit mehreren Widerständen 1) Parallelschaltung von Widerständen In der rechten Schaltung ist eine Spannungsquelle mit U=22V und
Grundlagen der Elektrotechnik: WIDERSTANDSSCHALTUNGEN Seite 1 Schaltungen mit mehreren Widerständen 1) Parallelschaltung von Widerständen In der rechten Schaltung ist eine Spannungsquelle mit U=22V und
BERUFSAKADEMIE S T U T T G A R T University of Cooperative Education. Höhere Mathematik II. Übungen. Komplexe Zahlen. i e π + 1=
 BERUFSAKADEMIE S T U T T G A R T University of Cooperative Education Höhere Mathematik II Übungen Komplexe Zahlen i e π + 0 8 R. Mohr FK Blatt Komplexe Zahlen I WS 004/ Aufgabe : Gegeben sind die komplexen
BERUFSAKADEMIE S T U T T G A R T University of Cooperative Education Höhere Mathematik II Übungen Komplexe Zahlen i e π + 0 8 R. Mohr FK Blatt Komplexe Zahlen I WS 004/ Aufgabe : Gegeben sind die komplexen
Ergänzung zu komplexe Zahlen
 Juli 2015 Übersicht 1 Ortskurven 2 Wechselstromkreis mit ohmschem und kapazitivem Widerstand (Parallelschaltung) i(t) u(t) R C Bei festen Werten für den ohmschen Widerstand R und die Kapazität C ergibt
Juli 2015 Übersicht 1 Ortskurven 2 Wechselstromkreis mit ohmschem und kapazitivem Widerstand (Parallelschaltung) i(t) u(t) R C Bei festen Werten für den ohmschen Widerstand R und die Kapazität C ergibt
Vorwort. Rainer Ose. Elektrotechnik für Ingenieure. Grundlagen. ISBN (Buch): ISBN (E-Book):
 Vorwort Rainer Ose Elektrotechnik für Ingenieure Grundlagen ISN (uch): 978-3-446-4344-4 ISN (E-ook): 978-3-446-43955-9 Weitere Informationen oder estellungen unter http://www.hanser-fachbuch.de/978-3-446-4344-4
Vorwort Rainer Ose Elektrotechnik für Ingenieure Grundlagen ISN (uch): 978-3-446-4344-4 ISN (E-ook): 978-3-446-43955-9 Weitere Informationen oder estellungen unter http://www.hanser-fachbuch.de/978-3-446-4344-4
Ü b u n g s a r b e i t z. Th. S c h a l t u n g e n
 Ü b u n g s a r b e i t z. Th. S c h a l t u n g e n Aufgabe 1 An der Stromquelle liegt die Spannung 100 V an. Die Einzelwiderstände haben die folgenden Größen: R 1 20 Ω, R 2 30 Ω, R 3 25 Ω, R 4 48 Ω,
Ü b u n g s a r b e i t z. Th. S c h a l t u n g e n Aufgabe 1 An der Stromquelle liegt die Spannung 100 V an. Die Einzelwiderstände haben die folgenden Größen: R 1 20 Ω, R 2 30 Ω, R 3 25 Ω, R 4 48 Ω,
Komplexe Zahlen und ihre Anwendung in der Elektrotechnik
 Praktikum für die Schüler der BOB Rosenheim im Rahmen des Workshops Komplexe Zahlen und ihre Anwendung in der Elektrotechnik SCHALTUNG 1 I ein Gegeben ist die Reihenschaltung eines Widerstandes R 10 k
Praktikum für die Schüler der BOB Rosenheim im Rahmen des Workshops Komplexe Zahlen und ihre Anwendung in der Elektrotechnik SCHALTUNG 1 I ein Gegeben ist die Reihenschaltung eines Widerstandes R 10 k
Musterlösung Grundlagen der Elektrotechnik B
 Prof. Dr.-Ing. Joachim Böcker Musterlösung Grundlagen der Elektrotechnik B 06.0.206 06.0.206 Musterlösung Grundlagen der Elektrotechnik B Seite von 3 Aufgabe : Gleichstrommaschine (20 Punkte) In dieser
Prof. Dr.-Ing. Joachim Böcker Musterlösung Grundlagen der Elektrotechnik B 06.0.206 06.0.206 Musterlösung Grundlagen der Elektrotechnik B Seite von 3 Aufgabe : Gleichstrommaschine (20 Punkte) In dieser
KOMPETENZHEFT ZUR TRIGONOMETRIE, II
 KOMPETENZHEFT ZUR TRIGONOMETRIE, II 1. Aufgabenstellungen Aufgabe 1.1. Bestimme alle Winkel in [0 ; 360 ], die Lösungen der gegebenen Gleichung sind, und zeichne sie am Einheitskreis ein. 1) sin(α) = 0,4
KOMPETENZHEFT ZUR TRIGONOMETRIE, II 1. Aufgabenstellungen Aufgabe 1.1. Bestimme alle Winkel in [0 ; 360 ], die Lösungen der gegebenen Gleichung sind, und zeichne sie am Einheitskreis ein. 1) sin(α) = 0,4
Technische Universität München Lehrstuhl für Technische Elektrophysik. Tutorübungen zu Elektromagnetische Feldtheorie. (Prof.
 Technische Universität München Lehrstuhl für Technische Elektrophysik Tutorübungen zu Elektromagnetische Feldtheorie Prof. Wachutka Wintersemester 08/09 Lösung Blatt 0 Allgemeines zum Thema komplexe Wechselstromrechnung
Technische Universität München Lehrstuhl für Technische Elektrophysik Tutorübungen zu Elektromagnetische Feldtheorie Prof. Wachutka Wintersemester 08/09 Lösung Blatt 0 Allgemeines zum Thema komplexe Wechselstromrechnung
FH Giessen-Friedberg StudiumPlus Dipl.-Ing. (FH) M. Beuler Grundlagen der Elektrotechnik Wechselstromtechnik
 4 4. Wechselgrößen Nimmt eine Wechselgröße in bestimmten aufeinander folgenden Zeitabständen wieder denselben Augenblickswert an, nennt man sie periodische Wechselgröße. Allgemeine Darstellung periodischer
4 4. Wechselgrößen Nimmt eine Wechselgröße in bestimmten aufeinander folgenden Zeitabständen wieder denselben Augenblickswert an, nennt man sie periodische Wechselgröße. Allgemeine Darstellung periodischer
Das Wechselstromparadoxon
 HTL Saalfelden Das Wechselstromparadoxon Seite von 6 Wilfried Rohm wrohm@aon.at Das Wechselstromparadoxon Mathematische / Fachliche Inhalte in Stichworten: Ortskurven, Komplexe Widerstände, Differentialrechnung
HTL Saalfelden Das Wechselstromparadoxon Seite von 6 Wilfried Rohm wrohm@aon.at Das Wechselstromparadoxon Mathematische / Fachliche Inhalte in Stichworten: Ortskurven, Komplexe Widerstände, Differentialrechnung
Komplexe Zahlen in der Elektrotechnik. ohne Ballast. von. Wolfgang Bengfort ET-Tutorials.de Elektrotechnik verstehen durch VIDEO-Tutorials
 Komplexe Zahlen in der Elektrotechnik ohne Ballast von Wolfgang Bengfort ET-Tutorials.de Elektrotechnik verstehen durch VIDEO-Tutorials Rechtlicher Hinweis: Alle Rechte vorbehalten. Dieses Buch darf ohne
Komplexe Zahlen in der Elektrotechnik ohne Ballast von Wolfgang Bengfort ET-Tutorials.de Elektrotechnik verstehen durch VIDEO-Tutorials Rechtlicher Hinweis: Alle Rechte vorbehalten. Dieses Buch darf ohne
2 Komplexe Rechnung in der Elektrotechnik
 Komplexe echnung in der Elektrotechnik. Einleitung Wechselstromnetwerke sind Netwerke, in denen sinusförmige Spannungen oder ströme gleicher Frequen auf ohmsche, induktive und kapaitive Widerstände wirken.
Komplexe echnung in der Elektrotechnik. Einleitung Wechselstromnetwerke sind Netwerke, in denen sinusförmige Spannungen oder ströme gleicher Frequen auf ohmsche, induktive und kapaitive Widerstände wirken.
Filter. Ortsverband Pulheim G40
 Filter Ortsverband Pulheim G40 Filter, Einführung 16.02.2018 Filter 2 Vierpol I e I a U e Vierpol U a Übertragungsverhalten bei I a = 0 ist A(jω) A jω = U a U e 16.02.2018 Filter 3 Streuparameter it wissen.de
Filter Ortsverband Pulheim G40 Filter, Einführung 16.02.2018 Filter 2 Vierpol I e I a U e Vierpol U a Übertragungsverhalten bei I a = 0 ist A(jω) A jω = U a U e 16.02.2018 Filter 3 Streuparameter it wissen.de
3. Übungen zum Kapitel Der Wechselstromkreis
 n n n n n n n n n n n n n n n n n n n n n n n Fachhochschule Köln University of Applied Sciences ologne ampus Gummersbach 18 Elektrotechnik Prof. Dr. Jürgen Weber Einführung in die Mechanik und Elektrote
n n n n n n n n n n n n n n n n n n n n n n n Fachhochschule Köln University of Applied Sciences ologne ampus Gummersbach 18 Elektrotechnik Prof. Dr. Jürgen Weber Einführung in die Mechanik und Elektrote
Geometrie-Dossier Kreis 2
 Geometrie-Dossier Kreis 2 Name: Inhalt: Konstruktion im Kreis (mit Tangenten, Sekanten, Passanten und Sehnen) Grundaufgaben Verwendung: Dieses Geometriedossier orientiert sich am Unterricht und liefert
Geometrie-Dossier Kreis 2 Name: Inhalt: Konstruktion im Kreis (mit Tangenten, Sekanten, Passanten und Sehnen) Grundaufgaben Verwendung: Dieses Geometriedossier orientiert sich am Unterricht und liefert
Anwendungen zu komplexen Zahlen
 HM an der HWS. Hj 08/9 Dr. Timo Essig, Dr. Marinela Wong timo.essig@kit.edu, wong@hw-schule.de Aufgabenblatt 7 Anwendungen zu komplexen Zahlen Achtung: Auf diesem Blatt schreiben wir die komplexe Einheit
HM an der HWS. Hj 08/9 Dr. Timo Essig, Dr. Marinela Wong timo.essig@kit.edu, wong@hw-schule.de Aufgabenblatt 7 Anwendungen zu komplexen Zahlen Achtung: Auf diesem Blatt schreiben wir die komplexe Einheit
Elektro- und Informationstechnik SS Mathematik I - Übungsblatt 05 Lösungsvorschläge
 - Übungsblatt 05 Lösungsvorschläge Aufgabe 1 Gegeben sind die beiden Spaltenvektoren im x-y-koordinatensystem a=[1, 2] T und b=[ 3, 1] T. a) Skizzieren Sie a und b im x-y-koordinatensystem. Dabei auf vollständige
- Übungsblatt 05 Lösungsvorschläge Aufgabe 1 Gegeben sind die beiden Spaltenvektoren im x-y-koordinatensystem a=[1, 2] T und b=[ 3, 1] T. a) Skizzieren Sie a und b im x-y-koordinatensystem. Dabei auf vollständige
Grundlagen der Elektrotechnik 1 Übungsaufgaben zur Wechselstromtechnik mit Lösung
 Grundlagen der Elektrotechnik Aufgabe Die gezeichnete Schaltung enthält folgende Schaltelemente:.0kΩ, ω.0kω, ω 0.75kΩ, /ωc.0k Ω, /ωc.3kω. Die gesamte Schaltung nimmt eine Wirkleistung P mw auf. C 3 C 3
Grundlagen der Elektrotechnik Aufgabe Die gezeichnete Schaltung enthält folgende Schaltelemente:.0kΩ, ω.0kω, ω 0.75kΩ, /ωc.0k Ω, /ωc.3kω. Die gesamte Schaltung nimmt eine Wirkleistung P mw auf. C 3 C 3
Gleichstromtechnik. Vorlesung 13: Superpositionsprinzip. Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann
 Gleichstromtechnik Vorlesung 13: Superpositionsprinzip Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Motivation Einige Schaltungen weisen mehr als eine Quelle auf, Beispiel Ersatzschaltbild
Gleichstromtechnik Vorlesung 13: Superpositionsprinzip Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Motivation Einige Schaltungen weisen mehr als eine Quelle auf, Beispiel Ersatzschaltbild
Aufgabe Summe Note Punkte
 Fachhochschule Südwestfalen - Meschede Prof. Dr. Henrik Schulze Klausur: Grundlagen der Elektrotechnik am 5. Juli 03 Name Matr.-Nr. Vorname Unterschrift Aufgabe 3 4 Summe Note Punkte Die Klausur umfasst
Fachhochschule Südwestfalen - Meschede Prof. Dr. Henrik Schulze Klausur: Grundlagen der Elektrotechnik am 5. Juli 03 Name Matr.-Nr. Vorname Unterschrift Aufgabe 3 4 Summe Note Punkte Die Klausur umfasst
= = cm. = = 4.66 cm. = cm. Anschliessend: A = r 2 π = π = π =
 Seiten 5 / 6 ufgaben Kreis 1 1 a) u Kreis r 15 30 cm ( 94.5 cm) Kreis r 15 5 cm ( 706.86 cm ) b) u Kreis r d 5.6 cm ( 17.59 cm) Kreis r.8 7.84 cm ( 4.63 cm ) c) u Kreis r 99 198 cm ( 6.04 cm) Kreis r 99
Seiten 5 / 6 ufgaben Kreis 1 1 a) u Kreis r 15 30 cm ( 94.5 cm) Kreis r 15 5 cm ( 706.86 cm ) b) u Kreis r d 5.6 cm ( 17.59 cm) Kreis r.8 7.84 cm ( 4.63 cm ) c) u Kreis r 99 198 cm ( 6.04 cm) Kreis r 99
WBK Bonn Abendrealschule Mathematik Vorklausur SoSe 2016
 Vorklausur SoSe 016 Aufgabe 1: Basiswissen (max. 15 Minuten) a) Eine Flasche Spülmittel enthält 10 mg eines Wirkstoffes. Für wie viele Flaschen reicht 1 kg dieses Wirkstoffes? 1 kg = 1000g 1 g = 1000 mg
Vorklausur SoSe 016 Aufgabe 1: Basiswissen (max. 15 Minuten) a) Eine Flasche Spülmittel enthält 10 mg eines Wirkstoffes. Für wie viele Flaschen reicht 1 kg dieses Wirkstoffes? 1 kg = 1000g 1 g = 1000 mg
Anwendungen komplexer Zahlen
 nwendungen komplexer Zahlen rbeitsblatt Dieser bschnitt eignet sich für fächerübergreifenden Unterricht mit Physik. In der Physik, speziell der Elektrotechnik, ist das chnen mit komplexen Zahlen ein wichtiges
nwendungen komplexer Zahlen rbeitsblatt Dieser bschnitt eignet sich für fächerübergreifenden Unterricht mit Physik. In der Physik, speziell der Elektrotechnik, ist das chnen mit komplexen Zahlen ein wichtiges
Symmetrische Komponenten - Einführung
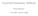 Symmetrische Komponenten - Einführung Hannes Zinnbauer. Juni 2005 - gesetzt in L A TEX Inhaltsverzeichnis Theoretische Betrachtung 2 2 Beispiel 6 Theoretische Betrachtung Es wird gezeigt, daß sich jedes
Symmetrische Komponenten - Einführung Hannes Zinnbauer. Juni 2005 - gesetzt in L A TEX Inhaltsverzeichnis Theoretische Betrachtung 2 2 Beispiel 6 Theoretische Betrachtung Es wird gezeigt, daß sich jedes
2.6. Aufgaben zu Kongruenzabbildungen
 Aufgabe.6. Aufgaben zu Kongruenzabbildungen Gegeben sind die Dreiecke ABC mit A(0 ), B( 0) und C(3 0) sowie A B C mit A ( ), B (3 ) und C ( ). Beschreibe die Abbildung, die das Dreieck ABC auf das Dreieck
Aufgabe.6. Aufgaben zu Kongruenzabbildungen Gegeben sind die Dreiecke ABC mit A(0 ), B( 0) und C(3 0) sowie A B C mit A ( ), B (3 ) und C ( ). Beschreibe die Abbildung, die das Dreieck ABC auf das Dreieck
Leitwerts- und Widerstandsdiagramm Graphische Lösung von Transformationsaufgaben
 Aus FUNKSCHAU Heft 14/1955, im Original -spaltig. Digitalisiert 10/016 von Eike Grund für http://www.radiomuseum.org mit freundlicher Genehmigung der FUNKSCHAU-Redaktion. Die aktuellen Ausgaben der FUNKSCHAU
Aus FUNKSCHAU Heft 14/1955, im Original -spaltig. Digitalisiert 10/016 von Eike Grund für http://www.radiomuseum.org mit freundlicher Genehmigung der FUNKSCHAU-Redaktion. Die aktuellen Ausgaben der FUNKSCHAU
Berechnen Sie den Umfang U des Grundstückes: a) mit Variablen (jeder Schritt muss ersichtlich sein). b) für a=5m.
 TG TECHNOLOGISCHE GRUNDLAGEN Seite 1 1 1.2.55 Berechnen Sie den Umfang U des Grundstückes: a) mit Variablen (jeder Schritt muss ersichtlich sein). b) für a5m. Kapitel 1 TG TECHNOLOGISCHE GRUNDLAGEN Seite
TG TECHNOLOGISCHE GRUNDLAGEN Seite 1 1 1.2.55 Berechnen Sie den Umfang U des Grundstückes: a) mit Variablen (jeder Schritt muss ersichtlich sein). b) für a5m. Kapitel 1 TG TECHNOLOGISCHE GRUNDLAGEN Seite
Lösungen zu Kapitel 2
 Elektrotechnik für Studium und Praxis: Lösungen Lösungen zu Kapitel Aufgabe.1 Aus der Maschengleichung ergibt sich: I 4 = U q1 + U q R 1 I 1 R I R I R 4 I 4 = 4 V + 1 V Ω 5 A Ω, A 5 Ω 4 A Ω I 4 = (4 +
Elektrotechnik für Studium und Praxis: Lösungen Lösungen zu Kapitel Aufgabe.1 Aus der Maschengleichung ergibt sich: I 4 = U q1 + U q R 1 I 1 R I R I R 4 I 4 = 4 V + 1 V Ω 5 A Ω, A 5 Ω 4 A Ω I 4 = (4 +
Koordinatengeometrie. Aufgabe 4 Untersuchen Sie die Funktion f(x) = x² 9.
 Koordinatengeometrie Aufgabe 1 Gegeben sind der Punkt P (-1; 9) sowie die Geraden g: 3x y + 6 = 0 und h: x + 4y 8 = 0. a) Die Geraden g und h schneiden einander im Punkt S. Berechnen Sie die exakten Koordinaten
Koordinatengeometrie Aufgabe 1 Gegeben sind der Punkt P (-1; 9) sowie die Geraden g: 3x y + 6 = 0 und h: x + 4y 8 = 0. a) Die Geraden g und h schneiden einander im Punkt S. Berechnen Sie die exakten Koordinaten
Übungsaufgaben zu Kapitel 1 und 2
 Hochschule für Technik und Wirtschaft Dresden Wintersemester 8/9 Fakultät Informatik/Mathematik Prof. Dr. B. Jung Übungsaufgaben zu Kapitel und Aufgabe : Vereinfachen Sie die folgenden komplexen Ausdrücke
Hochschule für Technik und Wirtschaft Dresden Wintersemester 8/9 Fakultät Informatik/Mathematik Prof. Dr. B. Jung Übungsaufgaben zu Kapitel und Aufgabe : Vereinfachen Sie die folgenden komplexen Ausdrücke
und der Kosinussatz cos(γ) = a2 + b 2 c 2 2 a b Sinussatz sin(β) = a b
 Blatt Nr 1906 Mathematik Online - Übungen Blatt 19 Dreieck Geometrie Nummer: 41 0 2009010074 Kl: 9X Aufgabe 1911: (Mit GTR) In einem allgemeinen Dreieck ABC sind a = 18782, c = 1511 und β = 33229 gegeben
Blatt Nr 1906 Mathematik Online - Übungen Blatt 19 Dreieck Geometrie Nummer: 41 0 2009010074 Kl: 9X Aufgabe 1911: (Mit GTR) In einem allgemeinen Dreieck ABC sind a = 18782, c = 1511 und β = 33229 gegeben
Wechselstrombrücken. Praktikum. Grundlagen der Elektrotechnik. Versuch: Versuchsanleitung. 0. Allgemeines
 Praktikum Grundlagen der Elektrotechnik Versuch: Wechselstrombrücken Versuchsanleitung 0. Allgemeines Eine sinnvolle Teilnahme am Praktikum ist nur durch eine gute Vorbereitung auf dem jeweiligen Stoffgebiet
Praktikum Grundlagen der Elektrotechnik Versuch: Wechselstrombrücken Versuchsanleitung 0. Allgemeines Eine sinnvolle Teilnahme am Praktikum ist nur durch eine gute Vorbereitung auf dem jeweiligen Stoffgebiet
Grundlagen der Elektrotechnik I
 Prof. Dr.-Ing. B. Schmülling Musterlösung zur Klausur Grundlagen der Elektrotechnik I im Wintersemester 27 / 28 Aufgabe : Die Lösungen zu Aufgabe folgen am Ende. Aufgabe 2:. U q = 3 V 2. R i = Ω 3. P =
Prof. Dr.-Ing. B. Schmülling Musterlösung zur Klausur Grundlagen der Elektrotechnik I im Wintersemester 27 / 28 Aufgabe : Die Lösungen zu Aufgabe folgen am Ende. Aufgabe 2:. U q = 3 V 2. R i = Ω 3. P =
Elektrotechnik Formelsammlung. Ersatzschaltbilder und Zeigerdiagramme des einphasigen Transformators. jx h. R Fe
 1) Vollständiges T-Ersatzschaltbild, Grundformeln jx σ R jx σ1 jx h Primärspannung Wicklungswiderstand primär Sekundärspannung R Wicklungswiderstand sekundär Quellenspannung X h Hauptinduktivität Eisenverlustwiderstand
1) Vollständiges T-Ersatzschaltbild, Grundformeln jx σ R jx σ1 jx h Primärspannung Wicklungswiderstand primär Sekundärspannung R Wicklungswiderstand sekundär Quellenspannung X h Hauptinduktivität Eisenverlustwiderstand
Musterlösung Grundlagen der Elektrotechnik B
 Prof. Dr.-Ing. Joachim Böcker Musterlösung Grundlagen der Elektrotechnik B 16.09.2014 16.09.2014 Musterlösung Grundlagen der Elektrotechnik B Seite 1 von 13 Aufgabe 1: Gleichstrommaschine (20 Punkte) LÖSUNG
Prof. Dr.-Ing. Joachim Böcker Musterlösung Grundlagen der Elektrotechnik B 16.09.2014 16.09.2014 Musterlösung Grundlagen der Elektrotechnik B Seite 1 von 13 Aufgabe 1: Gleichstrommaschine (20 Punkte) LÖSUNG
Grundlagen der Elektrotechnik I
 Prof. Dr.-Ing. B. Schmülling Musterlösung zur Klausur Grundlagen der Elektrotechnik I im Sommersemester 17 Aufgabe 1: Die Lösungen zu Aufgabe 1 folgen am Ende. Aufgabe : 1. I = 600 ma R a = 5,5 Ω R c =
Prof. Dr.-Ing. B. Schmülling Musterlösung zur Klausur Grundlagen der Elektrotechnik I im Sommersemester 17 Aufgabe 1: Die Lösungen zu Aufgabe 1 folgen am Ende. Aufgabe : 1. I = 600 ma R a = 5,5 Ω R c =
Verbundstudiengang Wirtschaftsingenieurwesen (Bachelor) Praktikum Grundlagen der Elektrotechnik und Elektronik
 erbundstudiengang Wirtschaftsingenieurwesen (Bachelor) Praktikum Grundlagen der Elektrotechnik und Elektronik ersuch 3 Grundschaltungen der Wechselstromtechnik Teilnehmer: Name orname Matr.-Nr. Datum der
erbundstudiengang Wirtschaftsingenieurwesen (Bachelor) Praktikum Grundlagen der Elektrotechnik und Elektronik ersuch 3 Grundschaltungen der Wechselstromtechnik Teilnehmer: Name orname Matr.-Nr. Datum der
Lösungen zum Thema Geometrie. Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt.
 Lösungen zum Thema Geometrie Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt. Höhe h c Winkelhalbierende w α Mittelsenkrechte ms c Seitenhalbierende s c b)
Lösungen zum Thema Geometrie Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt. Höhe h c Winkelhalbierende w α Mittelsenkrechte ms c Seitenhalbierende s c b)
E r g ä n z u n g. zur Trigonometrie
 E r g ä n z u n g zur Trigonometrie Klasse 10 b 2018 / 19 Deyke www.deyke.com Trigonometrie.pdf W I N K E L F U N K T I O N E N Die Strahlensätze und der Satz des Pythagoras sind bisher die einzigen Hilfsmittel
E r g ä n z u n g zur Trigonometrie Klasse 10 b 2018 / 19 Deyke www.deyke.com Trigonometrie.pdf W I N K E L F U N K T I O N E N Die Strahlensätze und der Satz des Pythagoras sind bisher die einzigen Hilfsmittel
Vorwiderstandsberechnung für LEDs
 B.Bulut (bx61) Inhaltsverzeichnis Thema Seite 1 Einleitung 1 2 Datenblatt vom LED 1 3 Vorwiderstand für eine LED 2 3.1 Bedeutung der Abkürzungen 3 3.2 Vorwiderstand für mehrere LEDs 3 4 Parallelschaltung
B.Bulut (bx61) Inhaltsverzeichnis Thema Seite 1 Einleitung 1 2 Datenblatt vom LED 1 3 Vorwiderstand für eine LED 2 3.1 Bedeutung der Abkürzungen 3 3.2 Vorwiderstand für mehrere LEDs 3 4 Parallelschaltung
Musterlösungen zu Grundlagen der Wechselstromtechnik
 Musterlösungen zu Grundlagen der Wechselstromtechnik W. Kippels 2. September 2016 Inhaltsverzeichnis 1 Grundgrößen der Wechselstromtechnik 2 1.1 Übungsfragen zu Grundgrößen der Wechselstromtechnik..........
Musterlösungen zu Grundlagen der Wechselstromtechnik W. Kippels 2. September 2016 Inhaltsverzeichnis 1 Grundgrößen der Wechselstromtechnik 2 1.1 Übungsfragen zu Grundgrößen der Wechselstromtechnik..........
Übungen Mathematik I, M
 Übungen Mathematik I, M Übungsblatt, Lösungen (Stoff aus Mathematik 0).0.0. Berechnen Sie unter Verwendung des binomischen Lehrsatzes ( x + y) 7 Lösung: Nach dem binomischen Lehrsatz ist ( x + y) 7 = 7
Übungen Mathematik I, M Übungsblatt, Lösungen (Stoff aus Mathematik 0).0.0. Berechnen Sie unter Verwendung des binomischen Lehrsatzes ( x + y) 7 Lösung: Nach dem binomischen Lehrsatz ist ( x + y) 7 = 7
Übungen zur Komplexen Rechnung in der Elektrotechnik
 Übungen zur Komplexen Rechnung in der Elektrotechnik Aufgabe 1 Gegeben ist nebenstehende Schaltung. Berechnen Sie den Komplexen Ersatzwiderstand Z der Schaltung sowie seinen Betrag Z und den Phasenverschiebungswinkel
Übungen zur Komplexen Rechnung in der Elektrotechnik Aufgabe 1 Gegeben ist nebenstehende Schaltung. Berechnen Sie den Komplexen Ersatzwiderstand Z der Schaltung sowie seinen Betrag Z und den Phasenverschiebungswinkel
Aufgabe 1 Transiente Vorgänge
 Aufgabe 1 Transiente Vorgänge S 2 i 1 i S 1 i 2 U 0 u C C L U 0 = 2 kv C = 500 pf Zum Zeitpunkt t 0 = 0 s wird der Schalter S 1 geschlossen, S 2 bleibt weiterhin in der eingezeichneten Position (Aufgabe
Aufgabe 1 Transiente Vorgänge S 2 i 1 i S 1 i 2 U 0 u C C L U 0 = 2 kv C = 500 pf Zum Zeitpunkt t 0 = 0 s wird der Schalter S 1 geschlossen, S 2 bleibt weiterhin in der eingezeichneten Position (Aufgabe
Der Satz des Pythagoras
 Der Satz des Pythagoras Das rechtwinklige Dreieck Jedes rechtwinklige Dreieck besitzt eine Hypotenuse (c), das ist die längste Seite des Dreiecks (bzw. diejenige gegenüber dem rechten Winkel). Die anderen
Der Satz des Pythagoras Das rechtwinklige Dreieck Jedes rechtwinklige Dreieck besitzt eine Hypotenuse (c), das ist die längste Seite des Dreiecks (bzw. diejenige gegenüber dem rechten Winkel). Die anderen
Mathematik I (MATHE1) Klausuren lineare Algebra & analytische Geometrie
 Mathematik I (MATHE1) Klausuren lineare Algebra & analytische Geometrie Prof. Dr. Thomas Risse www.weblearn.hs-bremen.de/risse/mai www.weblearn.hs-bremen.de/risse/mai/docs Fakultät Elektrotechnik & Informatik
Mathematik I (MATHE1) Klausuren lineare Algebra & analytische Geometrie Prof. Dr. Thomas Risse www.weblearn.hs-bremen.de/risse/mai www.weblearn.hs-bremen.de/risse/mai/docs Fakultät Elektrotechnik & Informatik
Grundlagen der Elektrotechnik 2 Übungsaufgaben
 ampus Duisburg Grundlagen der Elektrotechnik 2 Allgemeine und Theoretische Elektrotechnik Prof. Dr. sc. techn. Daniel Erni Version 2006.07 Trotz sorgfältiger Durchsicht können diese Unterlagen noch Fehler
ampus Duisburg Grundlagen der Elektrotechnik 2 Allgemeine und Theoretische Elektrotechnik Prof. Dr. sc. techn. Daniel Erni Version 2006.07 Trotz sorgfältiger Durchsicht können diese Unterlagen noch Fehler
i 2 (t) = 400 V 100 V = 4 f = 50 Hz A Fe 1. Wie groß müssen unter der Voraussetzung sinusförmiger Spannungen die ober- und unterspannungsseitigen
 Aufgabe Ü1 Aus einem vorhandenen Blechkern mit dem wirksamen Eisenquerschnitt A Fe 80 cm soll ein Wechselstromtransformator mit einer Nennleistung von S N 5 kva und dem Übersetzungsverhältnis ü U 1 /U
Aufgabe Ü1 Aus einem vorhandenen Blechkern mit dem wirksamen Eisenquerschnitt A Fe 80 cm soll ein Wechselstromtransformator mit einer Nennleistung von S N 5 kva und dem Übersetzungsverhältnis ü U 1 /U
Aufgabe Summe Note Mögliche Punkte Erreichte Punkte
 Universität Siegen Grundlagen der Elektrotechnik für Maschinenbauer Fachbereich 1 Prüfer : Dr.-Ing. Klaus Teichmann Datum : 7. April 005 Klausurdauer : Stunden Hilfsmittel : 5 Blätter Formelsammlung DIN
Universität Siegen Grundlagen der Elektrotechnik für Maschinenbauer Fachbereich 1 Prüfer : Dr.-Ing. Klaus Teichmann Datum : 7. April 005 Klausurdauer : Stunden Hilfsmittel : 5 Blätter Formelsammlung DIN
Aufgabe Summe Note Punkte
 Fachhochschule Südwestfalen - Meschede Prof. Dr. Henrik Schulze Lösungen zur Klausur: Grundlagen der Elektrotechnik am 3. Juli 06 Name Matr.-Nr. Vorname Unterschrift Aufgabe 3 4 Summe Note Punkte Die Klausur
Fachhochschule Südwestfalen - Meschede Prof. Dr. Henrik Schulze Lösungen zur Klausur: Grundlagen der Elektrotechnik am 3. Juli 06 Name Matr.-Nr. Vorname Unterschrift Aufgabe 3 4 Summe Note Punkte Die Klausur
4. Gemischte Schaltungen
 4. Einleitung Unter einer gemischten Schaltung, auch Gruppenschaltung genannt, versteht man eine Schaltung in der sowohl die eihen- als auch die Parallelschaltung vorkommt. 4.2 Die Maschen- und Knotenpunktregel
4. Einleitung Unter einer gemischten Schaltung, auch Gruppenschaltung genannt, versteht man eine Schaltung in der sowohl die eihen- als auch die Parallelschaltung vorkommt. 4.2 Die Maschen- und Knotenpunktregel
Grundlagen der Elektrotechnik I im Wintersemester 2017 / 2018
 +//6+ Prof. Dr.-Ing. B. Schmülling Klausur Grundlagen der Elektrotechnik I im Wintersemester 7 / 8 Bitte kreuzen Sie hier Ihre Matrikelnummer an (von links nach rechts). Vor- und Nachname: 3 4 3 4 3 4
+//6+ Prof. Dr.-Ing. B. Schmülling Klausur Grundlagen der Elektrotechnik I im Wintersemester 7 / 8 Bitte kreuzen Sie hier Ihre Matrikelnummer an (von links nach rechts). Vor- und Nachname: 3 4 3 4 3 4
Grundlagen der Elektrotechnik 3
 Grundlagen der Elektrotechnik 3 Kapitel 4 Ortskurven S. 1 4 Ortskurven Eine Ortskurve ist die Kurve, welche alle Endpunkte von eigern verbindet Eine Ortskurve kann Verlauf in Abhängigkeit von der Frequenz
Grundlagen der Elektrotechnik 3 Kapitel 4 Ortskurven S. 1 4 Ortskurven Eine Ortskurve ist die Kurve, welche alle Endpunkte von eigern verbindet Eine Ortskurve kann Verlauf in Abhängigkeit von der Frequenz
Grundlagen der Elektrotechnik Protokoll Schwingkreise. Christian Kötz, Jan Nabbefeld
 Grundlagen der Elektrotechnik Protokoll Schwingkreise Christian Kötz, Jan Nabbefeld 29. Mai 200 3. Versuchsdurchführung 3.. Versuchsvorbereitung 3..2. Herleitung Resonanzfrequenz und der 45 o Frequenz
Grundlagen der Elektrotechnik Protokoll Schwingkreise Christian Kötz, Jan Nabbefeld 29. Mai 200 3. Versuchsdurchführung 3.. Versuchsvorbereitung 3..2. Herleitung Resonanzfrequenz und der 45 o Frequenz
Parameter Das Buch Inhaltsverzeichnis Stichwortverzeichnis Aufgaben zum Selberrechnen Die Strukturierung
 Das Buch: Dieses Kapitel ist Teil eines Buches. Das vollständige Buch können Sie unter www.mathe-laden.de bestellen (falls Sie das möchten). Sie werden in diesem Buch ein paar Sachen finden, die nicht
Das Buch: Dieses Kapitel ist Teil eines Buches. Das vollständige Buch können Sie unter www.mathe-laden.de bestellen (falls Sie das möchten). Sie werden in diesem Buch ein paar Sachen finden, die nicht
Technische Universität Clausthal
 Technische Universität Clausthal Klausur im Sommersemester 2013 Grundlagen der Elektrotechnik I Datum: 09. September 2013 Prüfer: Prof. Dr.-Ing. Beck Institut für Elektrische Energietechnik Univ.-Prof.
Technische Universität Clausthal Klausur im Sommersemester 2013 Grundlagen der Elektrotechnik I Datum: 09. September 2013 Prüfer: Prof. Dr.-Ing. Beck Institut für Elektrische Energietechnik Univ.-Prof.
Lösung. Aufgabe 1: Gesucht: Formel: R Gesamt = R 1 + R 2 + R 3
 E-Technik 2g Lösung von "2F-Berechnen und Nachmessen (erste leichtere ersion)" Seite von 5 Lösung ufgabe : ) Skizziere eine Reihenschaltung mit folgenden Widerständen: R = k, R 2 =0 k, R 3 =330 k, Die
E-Technik 2g Lösung von "2F-Berechnen und Nachmessen (erste leichtere ersion)" Seite von 5 Lösung ufgabe : ) Skizziere eine Reihenschaltung mit folgenden Widerständen: R = k, R 2 =0 k, R 3 =330 k, Die
Übungsaufgaben Elektrotechnik/Elektronik für Medieninformatik
 HTW Dresden Fakultät Elektrotechnik Übungsaufgaben Elektrotechnik/Elektronik für Medieninformatik Gudrun Flach February 3, 2019 Grundlegende Begriffe Grundlegende Begriffe Aufgabe 1 Bestimmen Sie die Beziehungen
HTW Dresden Fakultät Elektrotechnik Übungsaufgaben Elektrotechnik/Elektronik für Medieninformatik Gudrun Flach February 3, 2019 Grundlegende Begriffe Grundlegende Begriffe Aufgabe 1 Bestimmen Sie die Beziehungen
Abituraufgaben Analytische Geometrie Wahlteil 2016 BW
 Abituraufgaben Analytische Geometrie Wahlteil 216 BW Aufgabe B1.1 In einem Koordinatensystem be-schreiben die Punkte 15, 15 2 und 2 6 Eckpunkte der rechteckigen Nutzfläche einer Tribüne (alle Koordinatenangaben
Abituraufgaben Analytische Geometrie Wahlteil 216 BW Aufgabe B1.1 In einem Koordinatensystem be-schreiben die Punkte 15, 15 2 und 2 6 Eckpunkte der rechteckigen Nutzfläche einer Tribüne (alle Koordinatenangaben
Ergebnisse des Praktikums Dreiphasensystem (Ströme) 1) Berechnung aller Ströme eines Dreiphasensystems (Verbraucher-Dreieckschaltung)
 HOCHSCHLE OSTFALA Fakultät Elektrotechnik Prof. Dr. Ose Version 1 16.11.09 Vorlesung Wechselstromtechnik Ergänzung zum SS 2009: Dreiphasensystem Ergebnisse des Praktikums Dreiphasensystem (Ströme) 1) Berechnung
HOCHSCHLE OSTFALA Fakultät Elektrotechnik Prof. Dr. Ose Version 1 16.11.09 Vorlesung Wechselstromtechnik Ergänzung zum SS 2009: Dreiphasensystem Ergebnisse des Praktikums Dreiphasensystem (Ströme) 1) Berechnung
G S. p = = 1 T. =5 K R,db K R
 TFH Berlin Regelungstechnik Seite von 0 Aufgabe 2: Gegeben: G R p =5 p 32ms p 32 ms G S p = p 250 ms p 8 ms. Gesucht ist das Bodediagramm von G S, G R und des offenen Regelkreises. 2. Bestimmen Sie Durchtrittsfrequenz
TFH Berlin Regelungstechnik Seite von 0 Aufgabe 2: Gegeben: G R p =5 p 32ms p 32 ms G S p = p 250 ms p 8 ms. Gesucht ist das Bodediagramm von G S, G R und des offenen Regelkreises. 2. Bestimmen Sie Durchtrittsfrequenz
Ersatzschaltbild und Zeigerdiagramm
 8. Betriebsverhalten des Einphasentransformators Seite Ersatzschaltbild und Zeigerdiagramm Jeder Transformator besteht grundsätzlich aus zwei magnetisch gekoppelten Stromkreisen. Bild 8.-: Aufbau und Flusslinien
8. Betriebsverhalten des Einphasentransformators Seite Ersatzschaltbild und Zeigerdiagramm Jeder Transformator besteht grundsätzlich aus zwei magnetisch gekoppelten Stromkreisen. Bild 8.-: Aufbau und Flusslinien
Vorbereitung zum Versuch
 Vorbereitung zum Versuch elektrische Messverfahren Armin Burgmeier (347488) Gruppe 5 2. Dezember 2007 Messungen an Widerständen. Innenwiderstand eines µa-multizets Die Schaltung wird nach Schaltbild (siehe
Vorbereitung zum Versuch elektrische Messverfahren Armin Burgmeier (347488) Gruppe 5 2. Dezember 2007 Messungen an Widerständen. Innenwiderstand eines µa-multizets Die Schaltung wird nach Schaltbild (siehe
Unterrichtsreihe zur Parabel
 Unterrichtsreihe zur Parabel Übersicht: 1. Einstieg: Satellitenschüssel. Konstruktion einer Parabel mit Leitgerade und Brennpunkt 3. Beschreibung dieser Punktmenge 4. Konstruktion von Tangenten 5. Beweis
Unterrichtsreihe zur Parabel Übersicht: 1. Einstieg: Satellitenschüssel. Konstruktion einer Parabel mit Leitgerade und Brennpunkt 3. Beschreibung dieser Punktmenge 4. Konstruktion von Tangenten 5. Beweis
Wechselstrom und Zeigerdiagramme ohne Ballast. von. Wolfgang Bengfort ET-Akademie.de / ET-Tutorials.de Elektrotechnik verstehen durch VIDEO-Tutorials
 Wechselstrom und Zeigerdiagramme ohne Ballast von Wolfgang Bengfort ET-Akademie.de / ET-Tutorials.de Elektrotechnik verstehen durch VIDEO-Tutorials Rechtlicher Hinweis: Alle Rechte vorbehalten. Dieses
Wechselstrom und Zeigerdiagramme ohne Ballast von Wolfgang Bengfort ET-Akademie.de / ET-Tutorials.de Elektrotechnik verstehen durch VIDEO-Tutorials Rechtlicher Hinweis: Alle Rechte vorbehalten. Dieses
Grundlagen der Elektrotechnik II Duale Hochschule Baden Württemberg Karlsruhe Dozent: Gerald Oberschmidt
 DHBW Karlsruhe Grundlagen der Elektrotechnik II Grundlagen der Elektrotechnik II Duale Hochschule Baden Württemberg Karlsruhe Dozent: Gerald Oberschmidt 5 Hoch und Tiefpässe 5. L--Hoch und Tiefpass Abbildung
DHBW Karlsruhe Grundlagen der Elektrotechnik II Grundlagen der Elektrotechnik II Duale Hochschule Baden Württemberg Karlsruhe Dozent: Gerald Oberschmidt 5 Hoch und Tiefpässe 5. L--Hoch und Tiefpass Abbildung
SCHRIFTLICHE ABSCHLUSSPRÜFUNG 2010 REALSCHULABSCHLUSS MATHEMATIK. Arbeitszeit: 180 Minuten
 Arbeitszeit: 180 Minuten Es sind die drei Pflichtaufgaben und zwei Wahlpflichtaufgaben zu bearbeiten. Seite 1 von 6 Pflichtaufgaben Pflichtaufgabe 1 (erreichbare BE: 10) a) Berechnen Sie den Wert des Terms
Arbeitszeit: 180 Minuten Es sind die drei Pflichtaufgaben und zwei Wahlpflichtaufgaben zu bearbeiten. Seite 1 von 6 Pflichtaufgaben Pflichtaufgabe 1 (erreichbare BE: 10) a) Berechnen Sie den Wert des Terms
Inhaltsverzeichnis. Inhaltsverzeichnis
 Inhaltsverzeichnis Inhaltsverzeichnis Einleitung 5 1 Zahlen 7 1.1 Zahlen und Zahlenmengen....................................... 7 1.2 Rechnen mit Zahlen und Termen....................................
Inhaltsverzeichnis Inhaltsverzeichnis Einleitung 5 1 Zahlen 7 1.1 Zahlen und Zahlenmengen....................................... 7 1.2 Rechnen mit Zahlen und Termen....................................
Trigonometrie. Mag. DI Rainer Sickinger HTL. v 1 Mag. DI Rainer Sickinger Trigonometrie 1 / 1
 Trigonometrie Mag. DI Rainer Sickinger HTL v 1 Mag. DI Rainer Sickinger Trigonometrie 1 / 1 Definition von Sinus, Cosinus und Tangens am Einheitskreis Im rechtwinkligen Dreieck ist der Winkel zwischen
Trigonometrie Mag. DI Rainer Sickinger HTL v 1 Mag. DI Rainer Sickinger Trigonometrie 1 / 1 Definition von Sinus, Cosinus und Tangens am Einheitskreis Im rechtwinkligen Dreieck ist der Winkel zwischen
Lo sung zu UÜ bung 1. I Schaltung Ersatzquellenberechnung. 1.1 Berechnung von R i
 Lo sung zu UÜ bung 1 I Schaltung 1 Schaltbild 1: 1.Schaltung mit Spannungsquelle 1. Ersatzquellenberechnung 1.1 Berechnung von R i Zunächst Ersatzschaltbild von den Klemmen aus betrachtet zeichnen: ESB
Lo sung zu UÜ bung 1 I Schaltung 1 Schaltbild 1: 1.Schaltung mit Spannungsquelle 1. Ersatzquellenberechnung 1.1 Berechnung von R i Zunächst Ersatzschaltbild von den Klemmen aus betrachtet zeichnen: ESB
Kreis, Zylinder, Kegel, Kugel
 Kreis, Zylinder, Kegel, Kugel Kreis Ziele: Kenntnis der Begriffe: Radius, Umfang, Durchmesser, Sehne, Sekante, Tangente, Berührungsradius einfache Berechnungen durchführen können, Formeln für Umfang und
Kreis, Zylinder, Kegel, Kugel Kreis Ziele: Kenntnis der Begriffe: Radius, Umfang, Durchmesser, Sehne, Sekante, Tangente, Berührungsradius einfache Berechnungen durchführen können, Formeln für Umfang und
Kreis - Tangente. 2. Vorbemerkung: Satz des Thales Eine Möglichkeit zur Bestimmung der Tangente benutzt den Satz des Thales.
 Kreis - Tangente 1. Allgemeines 2. Satz des Thales 3. Tangente an einem Punkt auf dem Kreis 4. Tangente über Analysis (an einem Punkt eines Ursprungkreises) 5. Tangente von einem Punkt (Pol) an den Kreis
Kreis - Tangente 1. Allgemeines 2. Satz des Thales 3. Tangente an einem Punkt auf dem Kreis 4. Tangente über Analysis (an einem Punkt eines Ursprungkreises) 5. Tangente von einem Punkt (Pol) an den Kreis
