Bifurkationen auf zweifarbigen Gittern
|
|
|
- Kristina Fromm
- vor 6 Jahren
- Abrufe
Transkript
1 Bifurkationen auf zweifarbigen Gittern In Anlehnung an den Vortrag gleichen Namens gehalten von Finn Kasulke am Nach der Arbeit Two-Color Patterns of Synchrony in Lattice Dynamical Systems von Yunjiao Wang und Martin Golubitsky (Houston, )
2 Vorwort Da diese Schrift nur Teile eines größeren Werkes wiedergibt, werden nicht alle verwendeten Begriffe hier definiert. Der Vortrag der eine Einführung in die Begrifflichkeiten gegeben hat, wurde am von Fabian Gnegel gehalten. Der Inhalt dieser Schrift setzt sich aus zwei Teilen zusammen. Im ersten Teil wird der zentrale Satz aus der ursprünglichen Arbeit betrachtet, der Aussagen über das Auftreten von Bifurkationen auf homogenen zweifarbigen Netzwerken macht, im zweiten Teil werden einige der auf hexagonalen Netzwerken auftretenden Muster untersucht. Die Auswahl der untersuchten Muster ist hierbei so getroffen worden, dass die Komplexität der Überlegungen, die zum Auffinden der Muster nötig sind, langsam ansteigt, während die Muster, die sich hauptsächlich durch eine Reihe von Fallunterscheidungen finden lassen, hier nicht aufgeführt sind. Inhalt Hauptsatz über Bifurkationen auf zweifarbigen Gittern Seite 3 Hexagonale Gitter: Klasse 66, 65,64 Seite 5 Klasse 63 Seite 5 Klasse 61 Seite 6 Klasse 41 Seite 7 Klasse 43 Seite 7 Unendliche Klassen Seite 9 Klasse 44 Seite 10 Nächst-naheste Kopplung Seite 12 2
3 Hauptsatz über Bifurkationen Satz: Für jede ausgeglichene Zweifärbung eines homogenen Systems, existiert eine Bifurkation mit Kodimension eins von einem homogenen Gleichgewicht aus, die zu einem Ast von Gleichgewichten entsprechend der gegebenen Zweifärbung führt. Beweis: Der Beweis wird nur für Netzwerke mit einem Typ von Kopplung vorgenommen. Sei also ein zweifarbiges homogenes Netzwerk gegeben. Dass wir eine Zweifärbung haben bedeutet, dass die Inputmengen von Zellen einer Farbe isomorph zueinander sind. Wir können das gesamte Netzwerk also auf ein System aus zwei Zellen reduzieren, nämlich das Quotientensystem des Netzwerks nach seinem durch die Färbung gegebenen Synchronieunterraum. Hierbei sind die Zellen 1 und 2 den verschiedenen Farben zugeordnet, bezeichne die Anzahl der Zellen von Typ i aus der Inputmenge von Zelle i, bezeichne die Anzahl der Zellen vom Typ j aus der Inputmenge von Zelle i mit. Beachte dass aufgrund der Homogenität des Netzwerkes gilt, dass Weil es sich um ein echtes gekoppeltes System handelt, gilt dass, also auch und. Das Quotientennetzwerk ist nun von der Form Hierbei tritt unter dem Balken der ersten Funktion genau mal, genau mal, unter dem Balken der zweiten Funktion genau mal und genau mal auf und die Funktion ist invariant unter Permutation der Einträge unter dem Balken. Gebe es nun einen Zweig trivialer Ruhelagen in, ohne Beschränkung der Allgemeinheit können wir diese in den Punkt verschieben. Sei weiterhin die Ableitung von nach der ersten Komponente, also die linearisierte Matrix der inneren Dynamik des Systems, die Ableitung von nach einer der Komponenten unter dem Balken, also die linearisierte Matrix der Kopplungsdynamik. Damit erhält man für das Zweizellensystem in Punkt die Jacobimatrix, die über abhängig von λ ist 3
4 Zur Untersuchung auftretender Bifurkationen, betrachtet man die Eigenwerte von. Sei hierzu zuerst ein Eigenwert von mit Eigenvektor. Dann gilt: Sei nun ein Eigenwert von mit Eigenvektor. Dann gilt: Damit sind die Eigenwerte von also die von und, wobei gilt, da wegen auch. Diese Matrizen sind von ausreichend allgemeiner Gestalt um keine Abhängigkeit der Eigenwerte voneinander aufzuweisen. Damit kann einen reellen Eigenwert haben, der die imaginäre Achse überquert, ohne dass es ein anderer Eigenwert von auch tut. Nach Crandall und Rabinowitz existiert damit ein nichttrivialer Lösungszweig von Gleichgewichten des Systems, der außerdem, da der Eigenvektor nicht im Synchronieunterraum liegt, die Synchronität des Systems bricht. Dieses neue Gleichgewicht mit des Quotientensystems erzeugt dann eine dem Muster entsprechende Färbung. 4
5 Hexagonale Gitter Sei ein Gitter gegeben, das von den Vektoren und aufgespannt wird. Ein Punkt in diesem Gitter hat 6 nächste Nachbarn, wir charakterisieren unser Muster also über das Tupel mit, wobei die Anzahl weißer Eingänge einer schwarzen Zelle und die Anzahl schwarzer Eingänge einer weißen Zelle ist. Wir müssen nur betrachten, da wir die anderen Fälle durch Tauschen der Farben bereits abgedeckt haben. Die 1 als untere Grenze ist damit begründet, dass eine 0 bedeuten würde, dass es keine Kopplung zwischen Zellen verschiedener Farbe gibt, unsere Zweifärbung wäre also eine Einfärbung. Im Folgenden schauen wir uns einige dieser Fälle an, die exemplarisch die nötigen Beweistechniken und Denkweisen zum Auffinden aller möglichen Muster demonstrieren. Klasse 66/65/64: Wir beginnen mit dem Betrachten einer schwarzen Zelle. Die vorne stehende sechs legt nahe, dass sie sechs weiße Nachbarn haben muss. Deswegen legt eine einzige schwarze Zelle an einem beliebigen Punkt im Gitter das lokale Muster fest, das im nebenstehenden Bild zu sehen ist. Die Existenz einer schwarzen Zelle ist gesichert, da wir nur echte Zweifärbungen betrachten wollen. Sofort kann man erkennen, dass die Klassen 66 und 65 keine Vertreter haben können, da jede weiße Zelle bereits zwei weiße Nachbarn hat, also unmöglich 6 bzw. 5 schwarze Nachbarn haben kann. Für den Fall 64 kann man eine beliebige der weißen Zellen im lokalen Muster betrachten, malt man ihre nötigen weiteren drei schwarzen Nachbarn ein, so sieht man, dass wir nun schwarze Zellen mit schwarzem Input haben, damit existiert also auch im Fall 64 kein zulässiges Muster. Klasse 63: Betrachten wir wieder das lokale Muster, die mit einem c markierte Zelle braucht nun noch zwei schwarze Nachbarn und einen weißen Nachbarn. Diese lassen sich auf drei verschiedene Weisen anordnen, bei der zweiten und dritten Variante liegen allerdings zwei schwarze Zellen nebeneinander, weswegen nur das erste Muster zulässig ist. Man kann erkennen, dass sich das markierte Dreieckt fortsetzt. Damit steht fest, dass ein Streifen entsteht, der sich unendlich weit fortsetzt, da das ursprüngliche Muster symmetrisch war, in beide Richtungen. 5
6 Ähnlich wird eine zweite Ausbreitungsrichtung determiniert, damit ist also das gesamte planare Muster festgelegt. Klasse 61: Wir beginnen wieder mit dem lokalen Muster, die weißen Zellen liegen alle bereits neben einer schwarzen, weswegen jede weitere Nachbarzelle weiß sein muss. Hier reicht es, wenn man die rechte Zelle und die Zelle unten rechts betrachtet. Die eingekreiste Zelle hat nun vier weiße Inputs, benötigt also noch einen weißen und einen schwarzen. Die beiden folgenden Bilder zeigen die möglichen Anordnungen, diese sind jedoch spiegelsymmetrisch entlang der mit einem L markierten Achse, weswegen es genügt, im weiteren Verlauf nur die Erste der beiden Möglichkeiten zu betrachten. Die markierte schwarze Zelle benötigt nun wieder nur weiße Inputs, dadurch erhalten wir erneut das lokale Muster, mit dem wir begonnen haben. Dies legt wegen der vorher getroffenen Symmetrieentscheidung jedoch noch keinen Streifen fest, aber das Auftreten des markierten Musters aus zwei Sechsecken ist gesichert, weswegen wir jetzt dieses genauer betrachten. Dort kann man nun einfach sehen, dass ein Streifen festgelegt wird. Genauso lässt sich durch einfache Fortsetzung erkennen, dass aus dem Streifen ein planares Muster folgt. 6
7 Klasse 41 In den Klassen 4j, sind die Muster rechts alle möglichen lokalen Muster um eine schwarze Zelle bis auf Symmetrie. Man kann sofort erkennen, dass es kein Muster im Fall 41 gibt, da immer eine weiße Zelle mit mindestens zwei schwarzen Nachbarn existiert. Klasse 43 Beginnend mit dem ersten lokalen Muster, kann man einfach das untere Muster folgern. Im letzten Bild kann man aufgrund der Symmetrie entlang der gestrichelten Linie annehmen, dass die erste Zelle schwarz ist und die zweite weiß. Wir erhalten dadurch wieder ein Muster aus zwei Sechsecken, das aber auch hier wegen der vorherigen Symmetrieüberlegung noch keinen Streifen festlegt. Betrachtet man nun die beiden Sechsecke, so geht aus ihnen direkt das planare Muster hervor. 7
8 Beginnt man hingegen mit dem zweiten lokalen Muster so gibt es drei Möglichkeiten das Muster von der markierten Zelle aus fortzusetzen. Die ersten beiden sind hierbei symmetrisch und enthalten das erste lokale Muster. Wir wissen bereits, welches planare Muster entsteht, wenn irgendwo das erste lokale Muster enthalten ist, also sind wir nur an dem dritten Fall interessiert. Dort stehen wir wieder vor dem gleichen Problem, wir erhalten also schon einen Streifen. Betrachtet man nun eine weiße Diagonale, so benötigt jede Zelle noch einen weißen und einen schwarzen Input, sobald eine Zelle festgelegt, ist auch die gesamte Diagonale festgelegt und wo die erste Zelle eingefärbt wird, ist wegen der Symmetrie egal. Dann folgt sofort die mit L2 markierte Diagonale, da jede schwarze Zelle auf L1 noch zwei schwarze Inputs benötigt, was jedoch für einen Widerspruch an den weißen Zellen sorgt. Damit erzeugt das zweite lokale Muster kein neues Muster. Betrachten wir nun das dritte lokale Muster. Eine einzelne Symmetrieüberlegung führt wieder direkt zu einem größeren lokalen Muster, dem gepunkteten unregelmäßigen Hexagon, das dann ohne weitere aufwändige Überlegungen ein planares Muster erzeugt, das von dem ersten gefundenen abweicht. Im Fall 43 existieren also zwei verschiedene ausgeglichene Muster. 8
9 Unendliche Klassen: In den Fällen 62, 53 und 44 lassen sich unendlich viele verschiedene ausgeglichene Muster finden, für die sich jedoch einfache Generierungsschemata angeben lassen. Exemplarisch werden wir die Klasse 44 untersuchen, vorher werden wir jedoch ein Lemma zeigen, das uns erst ermöglicht, die unendlich vielen Vertreter in einfacheren Schemata anzugeben. Außerdem geben wir zwei einfache Definitionen an. Definition: Eine Diagonale ist eine Gerade mit Steigung 0 oder eine Diagonale, entlang der sich weiße und schwarze Zellen abwechseln.. Eine alternierende Diagonale ist Lemma: Wenn die Anzahl schwarzer Inputs jeder weißen Zelle gleich der Anzahl weißer Inputs jeder schwarzen Zelle plus zwei ist, dann erhält man ein neues ausgeglichenes Muster, wenn man die Farben entlang einer alternierenden Diagonalen vertauscht. Beweis: Sei die Anzahl weißer Inputs jeder schwarzen Zelle,. Dann folgt aus der Vorraussetzung für die Inputmengen, dass jede schwarze Zelle schwarze Inputs hat, jede weiße Zelle schwarze Inputs und jede weiße Zelle weiße Inputs hat. Betrachtet man nun eine alternierende Diagonale, so ist sofort klar, dass jede an die alternierende Diagonale angrenzende Zelle von der alternierenden Diagonale einen weißen und einen schwarzen Input bekommt. Daran ändert sich nichts, wenn man die Farben vertauscht. Wir müssen also nur noch prüfen, ob die Inputmengen der Zellen auf der Diagonale selber erhalten bleiben. Dies geht jedoch sofort aus der folgenden Tabelle hervor, die sich leicht über die die am Anfang des Beweises aufgestellten Behauptungen über die Inputmengen ergibt. Damit ist alles gezeigt. Inputs Zelle auf L Von L Von L1 und L2 Weiß 2 Schwarze 0 Weiße m - 2 Schwarze 6 - m Weiße Schwarz 0 Schwarze 2 Weiße m - 2 Schwarze 6 - m Weiße 9
10 Klasse 44: Beginnen wir mit dem dritten lokalen Muster von Seite 7. Der unten gezeigte Prozess lässt sich beliebig weit fortführen, damit ist ein globales Muster festgelegt. Damit haben wir alle planaren Muster gefunden, die das dritte lokale Muster enthalten, wegen der Symmetrie der Klasse 44, gilt das ein ähnliches Muster aus drei derart nebeneinandern liegenden weißen Zellen hervorgeht, dass sich von dem gefundenen durch ein Vertauschen aller Farben ergibt. Für die weiteren Muster im Fall 44, benötigen wir folgende Hilfsaussage: Sind zwei nebeneinander liegende Diagonalen alternierend, so sind alle parallelen Diagonalen alternierend. Die Aussage erschließt sich leicht, wenn man das folgende Bild betrachtet. Jede Zelle braucht noch einen weißen und einen schwarzen Input, legt man nun eine Zelle fest, so ergibt sich direkt eine alternierende Diagonale. Iterativ erhält man dann das globale Muster. Das Muster aus alternierenden Diagonalen ist wie man sieht ein Vertreter der Klasse 44. Wie wir bereits wissen, können wir nun unendlich viele verschiedene Muster erzeugen, indem wir beginnen, alternierende Diagonalen zu vertauschen. Es ist noch zu zeigen, dass es keine weiteren Muster gibt, die wir nicht so erzeugen können. Beginnen wir hierzu mit dem lokalen Muster 1. Aus den folgenden Bildern und der Bemerkung über das Nichtauftreten des lokalen Musters 3, gehen die Muster aus alternierenden Diagonalen hervor. 10
11 Beginnen wir nun mit dem lokalen Muster Nummer zwei. Da wir schon wissen, welche planaren Muster aus dem Auftreten der lokalen Muster eins oder drei hervorgehen, können wir analog zum bereits betrachteten Fall 43, die erste und dritte Möglichkeit ausschließen, da sie das erste lokale Muster enthalten. Das Muster, dass sich aus dem oben festgelegten Streifen ergibt, enthält wie im unteren Bild zu sehen ist, parallele alternierende Diagonalen, die daraus zu erzeugenden planaren Muster sind also im vorherigen Fall schon abgedeckt worden. Damit haben wir erzeugende Muster für alle möglichen planaren Muster gefunden. Zum Schluss betrachten wir noch Muster mit nicht nur nahester sondern auch nächst-nahester Kopplung. In allen endlichen Klassen ist dies nun eine triviale Aufgabe, da wir nur die Zellen der erzeugenden Muster überprüfen müssen. Für die unendlichen Klassen ist dies nicht so einfach möglich. 11
12 Nächst-naheste Kopplung Betrachten wir nun die Muster mit nahester und nächstnahester Kopplung. Wie bereits erwähnt, genügt es bei den endlichen Klassen, die erzeugenden Muster zu betrachten. Das Muster aus Klasse 63 ist zum Beispiel auch nächst-nahest ausgeglichen, wie sich im nebenstehenden Bild leicht sehen lässt. Eine Charakterisierung des Musters lässt sich in Analogie zur Charakterisierung der nahesten Kopplung mit 6300 angeben. Analog kann man das aus dem dritten lokalen Muster hervorgegangene Muster aus Klasse 44 betrachten, um zu sehen, dass es unter nächst-nahester Kopplung nicht ausgeglichen ist. Betrachtet man die Inputmengen der schwarzen Zellen in den Mitten der Sechsecke, so sieht man sofort, dass sie nicht isomorph sind. Betrachtet man hingegen den rechts stehenden Vertreter von Klasse 44, so ist dieser offensichtlich ausgeglichen unter der Charakterisierung Würde man nun beginnen, alternierende Diagonalen zu vertauschen, so lässt sich leicht einsehen, dass die Charakterisierung nur aufrechterhalten werden kann, wenn man alle Zellen vertauscht. In dem Sinne gibt es nur einen einzigen Vertreter der Klasse Es lassen sich einfach noch jeweils ein Vertreter der Klassen 4433 und 4422 finden, indem man ein Gitter betrachtet, in dem von einer Zelle ausgehend nur die zweitnahesten Nachbarn jeder Zelle eingezeichnet sind. Dort reduziert sich das Problem wieder auf eines mit nahester Kopplung. Das Muster rechts ist das entsprechende Bild des Vertreters der Klasse
Seminararbeit für das SE Reine Mathematik- Graphentheorie
 Seminararbeit für das SE Reine Mathematik- Graphentheorie Der binäre Rang, der symplektische Graph, die Spektralzerlegung und rationale Funktionen Vortrag am 24.01.2012 Heike Farkas 0410052 Inhaltsverzeichnis
Seminararbeit für das SE Reine Mathematik- Graphentheorie Der binäre Rang, der symplektische Graph, die Spektralzerlegung und rationale Funktionen Vortrag am 24.01.2012 Heike Farkas 0410052 Inhaltsverzeichnis
x 2 2x + = 3 + Es gibt genau ein x R mit ax + b = 0, denn es gilt
 - 17 - Die Frage ist hier also: Für welche x R gilt x = x + 1? Das ist eine quadratische Gleichung für x. Es gilt x = x + 1 x x 3 = 0, und man kann quadratische Ergänzung machen:... ( ) ( ) x x + = 3 +
- 17 - Die Frage ist hier also: Für welche x R gilt x = x + 1? Das ist eine quadratische Gleichung für x. Es gilt x = x + 1 x x 3 = 0, und man kann quadratische Ergänzung machen:... ( ) ( ) x x + = 3 +
Eigenwerte und Eigenvektoren von Matrizen
 Eigenwerte und Eigenvektoren von Matrizen Das Eigenwertproblem Sei A eine quadratische Matrix vom Typ m,m. Die Aufgabe, eine Zahl λ und einen dazugehörigen Vektor x zu finden, damit Ax = λx ist, nennt
Eigenwerte und Eigenvektoren von Matrizen Das Eigenwertproblem Sei A eine quadratische Matrix vom Typ m,m. Die Aufgabe, eine Zahl λ und einen dazugehörigen Vektor x zu finden, damit Ax = λx ist, nennt
Lineare Algebra und Lösung linearer zeitinvarianter Differentialgleichungssysteme
 Übung Lineare Algebra und Lösung linearer zeitinvarianter Differentialgleichungssysteme Diese Übung beschäftigt sich mit Grundbegriffen der linearen Algebra. Im Speziellen werden lineare Abbildungen, sowie
Übung Lineare Algebra und Lösung linearer zeitinvarianter Differentialgleichungssysteme Diese Übung beschäftigt sich mit Grundbegriffen der linearen Algebra. Im Speziellen werden lineare Abbildungen, sowie
Guten Morgen und Willkommen zur Saalübung!
 Guten Morgen und Willkommen zur Saalübung! 1 Wie gewinnt man ein Spiel? Was ist ein Spiel? 2 Verschiedene Spiele Schach, Tic-Tac-Toe, Go Memory Backgammon Poker Nim, Käsekästchen... 3 Einschränkungen Zwei
Guten Morgen und Willkommen zur Saalübung! 1 Wie gewinnt man ein Spiel? Was ist ein Spiel? 2 Verschiedene Spiele Schach, Tic-Tac-Toe, Go Memory Backgammon Poker Nim, Käsekästchen... 3 Einschränkungen Zwei
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Optimalitätskriterien
 Kapitel 4 Optimalitätskriterien Als Optimalitätskriterien bezeichnet man notwendige oder hinreichende Bedingungen dafür, dass ein x 0 Ω R n Lösung eines Optimierungsproblems ist. Diese Kriterien besitzen
Kapitel 4 Optimalitätskriterien Als Optimalitätskriterien bezeichnet man notwendige oder hinreichende Bedingungen dafür, dass ein x 0 Ω R n Lösung eines Optimierungsproblems ist. Diese Kriterien besitzen
LU-Zerlegung. Zusätze zum Gelben Rechenbuch. Peter Furlan. Verlag Martina Furlan. Inhaltsverzeichnis. 1 Definitionen.
 Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
Diagramme aus Tabellen erstellen mit Calc (LibreOffice 4)
 Voraussetzungen Es muss eine Tabelle vorliegen, in der die Zahlen, die grafisch dargestellt werden sollen, zusammenhängend markiert werden können. Beispiel: Es ist sinnvoll, zunächst die Zellen zu markieren,
Voraussetzungen Es muss eine Tabelle vorliegen, in der die Zahlen, die grafisch dargestellt werden sollen, zusammenhängend markiert werden können. Beispiel: Es ist sinnvoll, zunächst die Zellen zu markieren,
Mathematik 1. Inhaltsverzeichnis. Prof. Dr. K. Melzer. karin.melzer@hs-esslingen.de http://www.hs-esslingen.de/de/mitarbeiter/karin-melzer.
 Mathematik 1 Prof Dr K Melzer karinmelzer@hs-esslingende http://wwwhs-esslingende/de/mitarbeiter/karin-melzerhtml Inhaltsverzeichnis 1 Matrizenrechnung 2 11 Matrixbegri 2 12 Spezielle Matrizen 3 13 Rechnen
Mathematik 1 Prof Dr K Melzer karinmelzer@hs-esslingende http://wwwhs-esslingende/de/mitarbeiter/karin-melzerhtml Inhaltsverzeichnis 1 Matrizenrechnung 2 11 Matrixbegri 2 12 Spezielle Matrizen 3 13 Rechnen
7 Die Determinante einer Matrix
 7 Die Determinante einer Matrix ( ) a11 a Die Determinante einer 2 2 Matrix A = 12 ist erklärt als a 21 a 22 det A := a 11 a 22 a 12 a 21 Es ist S 2 = { id, τ}, τ = (1, 2) und sign (id) = 1, sign (τ) =
7 Die Determinante einer Matrix ( ) a11 a Die Determinante einer 2 2 Matrix A = 12 ist erklärt als a 21 a 22 det A := a 11 a 22 a 12 a 21 Es ist S 2 = { id, τ}, τ = (1, 2) und sign (id) = 1, sign (τ) =
BONUS MALUS SYSTEME UND MARKOV KETTEN
 Fakultät Mathematik und Naturwissenschaften, Fachrichtung Mathematik, Institut für Mathematische Stochastik BONUS MALUS SYSTEME UND MARKOV KETTEN Klaus D. Schmidt Ringvorlesung TU Dresden Fakultät MN,
Fakultät Mathematik und Naturwissenschaften, Fachrichtung Mathematik, Institut für Mathematische Stochastik BONUS MALUS SYSTEME UND MARKOV KETTEN Klaus D. Schmidt Ringvorlesung TU Dresden Fakultät MN,
Minimale Darstellungen, Kommutator- und Fixräume, projektive Geometrie
 Notation Die in dieser Arbeit verwendete Notation ist im Wesentlichen Standard, so wie sie beispielsweise in [As] zu nden ist. Einige Abweichungen hiervon, Klarstellungen und zusätzliche Notationen (sofern
Notation Die in dieser Arbeit verwendete Notation ist im Wesentlichen Standard, so wie sie beispielsweise in [As] zu nden ist. Einige Abweichungen hiervon, Klarstellungen und zusätzliche Notationen (sofern
Austausch- bzw. Übergangsprozesse und Gleichgewichtsverteilungen
 Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Lösungen zum 3. Aufgabenblatt
 SS, Lineare Algebra Die Lösungen wurden erstellt von: Isabel Voigt, Vanessa Lamm und Matthias Rehder Hinweis: Eine Liste der zur Bearbeitung verwendeten Literatur ist unter www.mathematiwelt.com aufrufbar.
SS, Lineare Algebra Die Lösungen wurden erstellt von: Isabel Voigt, Vanessa Lamm und Matthias Rehder Hinweis: Eine Liste der zur Bearbeitung verwendeten Literatur ist unter www.mathematiwelt.com aufrufbar.
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Kapitel 15. Lösung linearer Gleichungssysteme
 Kapitel 15. Lösung linearer Gleichungssysteme Lineare Gleichungssysteme Wir befassen uns nun mit der Lösung im allgemeinen nichthomogener linearer Gleichungssysteme in zweifacher Hinsicht. Wir studieren
Kapitel 15. Lösung linearer Gleichungssysteme Lineare Gleichungssysteme Wir befassen uns nun mit der Lösung im allgemeinen nichthomogener linearer Gleichungssysteme in zweifacher Hinsicht. Wir studieren
Euklidischer Algorithmus, Restklassenring und seine Struktur, Chinesischer Restklassensatz
 Tobias Kraushaar Kaiserstr. 178 44143 Dortmund Matr.- Nr.: 122964 Euklidischer Algorithmus, Restklassenring und seine Struktur, Chinesischer Restklassensatz 1. EINLEITUNG... 2 2. HAUPTTEIL... 3 2.1. Der
Tobias Kraushaar Kaiserstr. 178 44143 Dortmund Matr.- Nr.: 122964 Euklidischer Algorithmus, Restklassenring und seine Struktur, Chinesischer Restklassensatz 1. EINLEITUNG... 2 2. HAUPTTEIL... 3 2.1. Der
Bestimmung einer ersten
 Kapitel 6 Bestimmung einer ersten zulässigen Basislösung Ein Problem, was man für die Durchführung der Simplexmethode lösen muss, ist die Bestimmung einer ersten zulässigen Basislösung. Wie gut das geht,
Kapitel 6 Bestimmung einer ersten zulässigen Basislösung Ein Problem, was man für die Durchführung der Simplexmethode lösen muss, ist die Bestimmung einer ersten zulässigen Basislösung. Wie gut das geht,
Vorwort. Günter M. Gramlich. Lineare Algebra. Eine Einführung ISBN: 978-3-446-43035-8. Weitere Informationen oder Bestellungen unter
 Vorwort Günter M. Gramlich Lineare Algebra Eine Einführung ISBN: 978-3-446-43035-8 Weitere Informationen oder Bestellungen unter http://www.hanser.de/978-3-446-43035-8 sowie im Buchhandel. Carl Hanser
Vorwort Günter M. Gramlich Lineare Algebra Eine Einführung ISBN: 978-3-446-43035-8 Weitere Informationen oder Bestellungen unter http://www.hanser.de/978-3-446-43035-8 sowie im Buchhandel. Carl Hanser
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Sei K ein Körper, a ij K für 1 i m, 1 j n. Weiters seien b 1,..., b m K. Dann heißt a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2... a m1
Lineare Gleichungssysteme Sei K ein Körper, a ij K für 1 i m, 1 j n. Weiters seien b 1,..., b m K. Dann heißt a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2... a m1
EINMALEINS BEZIEHUNGSREICH
 EINMALEINS BEZIEHUNGSREICH Thema: Übung des kleinen Einmaleins; operative Beziehungen erkunden Stufe: ab 2. Schuljahr Dauer: 2 bis 3 Lektionen Materialien: Kleine Einmaleinstafeln (ohne Farben), Punktefelder
EINMALEINS BEZIEHUNGSREICH Thema: Übung des kleinen Einmaleins; operative Beziehungen erkunden Stufe: ab 2. Schuljahr Dauer: 2 bis 3 Lektionen Materialien: Kleine Einmaleinstafeln (ohne Farben), Punktefelder
Gibt es verschiedene Arten unendlich? Dieter Wolke
 Gibt es verschiedene Arten unendlich? Dieter Wolke 1 Zuerst zum Gebrauch des Wortes unendlich Es wird in der Mathematik in zwei unterschiedlichen Bedeutungen benutzt Erstens im Zusammenhang mit Funktionen
Gibt es verschiedene Arten unendlich? Dieter Wolke 1 Zuerst zum Gebrauch des Wortes unendlich Es wird in der Mathematik in zwei unterschiedlichen Bedeutungen benutzt Erstens im Zusammenhang mit Funktionen
1 Das Lemma von Burnside und seine Anwendungen
 Das Lemma von Burnside und seine Anwendungen Mit dem Lemma von Burnside lassen sich Zählprobleme lösen, bei denen Symmetrien eine Rolle spielen. Betrachten wir als einführendes Beispiel die Anzahl der
Das Lemma von Burnside und seine Anwendungen Mit dem Lemma von Burnside lassen sich Zählprobleme lösen, bei denen Symmetrien eine Rolle spielen. Betrachten wir als einführendes Beispiel die Anzahl der
LINEARE ALGEBRA Ferienkurs. Hanna Schäfer Philipp Gadow
 LINEARE ALGERA Ferienkurs Hanna Schäfer Philipp Gadow INHALT Eigenwerte und Eigenvektoren. asiswechsel.2 Eigenwertgleichung 2.3 Diagonalisierbarkeit 5.4 Trigonalisierung 8.5 Zusatzmaterial 8 Aufgaben 9
LINEARE ALGERA Ferienkurs Hanna Schäfer Philipp Gadow INHALT Eigenwerte und Eigenvektoren. asiswechsel.2 Eigenwertgleichung 2.3 Diagonalisierbarkeit 5.4 Trigonalisierung 8.5 Zusatzmaterial 8 Aufgaben 9
Aufbau von Hichert-Graphik Schritt für Schritt
 Aufbau von Hichert-Graphik Schritt für Schritt Ausgangsdaten anlegen: o Sollte dann so aussehen: Umsatz Plan Ist Abweich. 60 40-20 o Details dazu: 4 Spaltenüberschriften eintragen: Plan, Ist, leer, Abweichung
Aufbau von Hichert-Graphik Schritt für Schritt Ausgangsdaten anlegen: o Sollte dann so aussehen: Umsatz Plan Ist Abweich. 60 40-20 o Details dazu: 4 Spaltenüberschriften eintragen: Plan, Ist, leer, Abweichung
Der Golay-Code und das Leech-Gitter
 Der Golay-Code und das Leech-Gitter Vortrag zum Seminar Gitter und Codes Nils Malte Pawelzik.5.5 Inhaltsverzeichnis Designs 3. Elementare Eigenschaften eines Designs und die Eindeutigkeit eines - (, 5,
Der Golay-Code und das Leech-Gitter Vortrag zum Seminar Gitter und Codes Nils Malte Pawelzik.5.5 Inhaltsverzeichnis Designs 3. Elementare Eigenschaften eines Designs und die Eindeutigkeit eines - (, 5,
Wie löst man Mathematikaufgaben?
 Wie löst man Mathematikaufgaben? Manfred Dobrowolski Universität Würzburg Wie löst man Mathematikaufgaben? 1 Das Schubfachprinzip 2 Das Invarianzprinzip 3 Das Extremalprinzip Das Schubfachprinzip Verteilt
Wie löst man Mathematikaufgaben? Manfred Dobrowolski Universität Würzburg Wie löst man Mathematikaufgaben? 1 Das Schubfachprinzip 2 Das Invarianzprinzip 3 Das Extremalprinzip Das Schubfachprinzip Verteilt
Algebra. Patrik Hubschmid. 8. Oktober 2013
 Algebra Patrik Hubschmid 8. Oktober 2013 Inhaltsverzeichnis 1 Fortführung der Gruppentheorie 7 1.1 Sylowsätze.................................... 7 3 Vorwort Dieses Skript zur Vorlesung Algebra im Wintersemester
Algebra Patrik Hubschmid 8. Oktober 2013 Inhaltsverzeichnis 1 Fortführung der Gruppentheorie 7 1.1 Sylowsätze.................................... 7 3 Vorwort Dieses Skript zur Vorlesung Algebra im Wintersemester
TEILWEISE ASYNCHRONE ALGORITHMEN
 TEILWEISE ASYNCHRONE ALGORITHMEN FRANK LANGBEIN Literatur: D. Berseas, J. Tsitsilis: Parallel and distributed computatoin, pp. 48 489 URI: http://www.langbein.org/research/parallel/ Modell teilweiser asynchroner
TEILWEISE ASYNCHRONE ALGORITHMEN FRANK LANGBEIN Literatur: D. Berseas, J. Tsitsilis: Parallel and distributed computatoin, pp. 48 489 URI: http://www.langbein.org/research/parallel/ Modell teilweiser asynchroner
Kapitel 8 Texte schreiben
 Kapitel 8 Texte schreiben Das Erstellen und Weiterverarbeiten von Text zählt zu den am häufigsten genutzten Aufgaben am Computer. Sie als Windows-10-Besitzer haben es leicht, denn Sie können gleich anfangen.
Kapitel 8 Texte schreiben Das Erstellen und Weiterverarbeiten von Text zählt zu den am häufigsten genutzten Aufgaben am Computer. Sie als Windows-10-Besitzer haben es leicht, denn Sie können gleich anfangen.
6 Symmetrische Matrizen und quadratische Formen
 Mathematik für Ingenieure II, SS 9 Freitag. $Id: quadrat.tex,v.5 9//5 ::59 hk Exp $ $Id: orthogonal.tex,v.4 9// ::54 hk Exp $ $Id: fourier.tex,v. 9// :: hk Exp $ Symmetrische Matrizen und quadratische
Mathematik für Ingenieure II, SS 9 Freitag. $Id: quadrat.tex,v.5 9//5 ::59 hk Exp $ $Id: orthogonal.tex,v.4 9// ::54 hk Exp $ $Id: fourier.tex,v. 9// :: hk Exp $ Symmetrische Matrizen und quadratische
Kochen mit Jordan. Vorbereitungen. Schnellzubereitung. JNF für Genießer wenn s noch etwas mehr sein darf
 Kochen mit Jordan Vorbereitungen Man nehme eine Matrix A R n n und bestimme ihr charakteristisches Polynom p(λ) = (λ c ) r (λ c j ) rj C[X] Dabei gilt: algebraische Vielfachheit r j ˆ= Länge des Jordanblocks
Kochen mit Jordan Vorbereitungen Man nehme eine Matrix A R n n und bestimme ihr charakteristisches Polynom p(λ) = (λ c ) r (λ c j ) rj C[X] Dabei gilt: algebraische Vielfachheit r j ˆ= Länge des Jordanblocks
Leitprogramm Bubblesort
 Leitprogramm Bubblesort Dr. Rainer Hauser Inhalt 1 Übersicht...1 2 Input-Block I: Der Sortieralgorithmus Bubblesort...2 3 Input-Block II: Die Effizienz von Bubblesort...6 4 Zusammenfassung...8 5 Lernkontrolle...9
Leitprogramm Bubblesort Dr. Rainer Hauser Inhalt 1 Übersicht...1 2 Input-Block I: Der Sortieralgorithmus Bubblesort...2 3 Input-Block II: Die Effizienz von Bubblesort...6 4 Zusammenfassung...8 5 Lernkontrolle...9
11. Primfaktorzerlegungen
 78 Andreas Gathmann 11 Primfaktorzerlegungen Euch ist sicher aus der Schule bekannt, dass sich jede positive ganze Zahl a als Produkt a = p 1 p n von Primzahlen schreiben lässt, und dass diese Darstellung
78 Andreas Gathmann 11 Primfaktorzerlegungen Euch ist sicher aus der Schule bekannt, dass sich jede positive ganze Zahl a als Produkt a = p 1 p n von Primzahlen schreiben lässt, und dass diese Darstellung
Kurzanleitung von Marina Ulmer 2004
 Kurzanleitung von Marina Ulmer 2004 Copyright 2004 Marina Ulmer www.freundschaftsbaender.de Es gibt zwei Kategorien an Freundschaftsbändern: Kategorie 1 (Bänder Nr. 01-60 und 101-140): Die Bänder werden
Kurzanleitung von Marina Ulmer 2004 Copyright 2004 Marina Ulmer www.freundschaftsbaender.de Es gibt zwei Kategorien an Freundschaftsbändern: Kategorie 1 (Bänder Nr. 01-60 und 101-140): Die Bänder werden
die Kunst, mit wenig Farbklexen bunte Bilder zu machen Halftoning, Dithering
 Farbreduktion die Kunst, mit wenig Farbklexen bunte Bilder zu machen Halftoning, Dithering zwei Schritte: geeignete Farben (Repäsentanten) finden Farbreduktion alle Bildfarben den Repräsentanten zuordnen
Farbreduktion die Kunst, mit wenig Farbklexen bunte Bilder zu machen Halftoning, Dithering zwei Schritte: geeignete Farben (Repäsentanten) finden Farbreduktion alle Bildfarben den Repräsentanten zuordnen
Excel Diagramme. Dateneingabe zur späteren Verarbeitung als Diagramm
 Excel Diagramme Dateneingabe zur späteren Verarbeitung als Diagramm Gib zunächst in Excel einige Zahlen ein, die du später in einem Diagramm darstellen möchtest. In diesem Beispiel verwende ich die Umsatzzahlen
Excel Diagramme Dateneingabe zur späteren Verarbeitung als Diagramm Gib zunächst in Excel einige Zahlen ein, die du später in einem Diagramm darstellen möchtest. In diesem Beispiel verwende ich die Umsatzzahlen
VOLTmonitor. VOLTmonitor. Schritt 1: Schaltung. file://localhost/users/rainer/xp-exchange/erzeugte%20websites/p... 1 of 10 07.07.
 VOLTmonitor VOLTmonitor LM3914 Voltanzeige Diese Voltanzeige wurde von www.pointofnoreturn.org vorgestellt. Meine Leistung besteht lediglich darin, die Anleitung ins Deutsche zu übersetzen. Schritt 1:
VOLTmonitor VOLTmonitor LM3914 Voltanzeige Diese Voltanzeige wurde von www.pointofnoreturn.org vorgestellt. Meine Leistung besteht lediglich darin, die Anleitung ins Deutsche zu übersetzen. Schritt 1:
9. Anwendungen der Fundamentalgruppe
 76 Andreas Gathmann 9. Anwendungen der Fundamentalgruppe Nachdem wir mit Hilfe von Überlagerungen nun in der Lage sind, Fundamentalgruppen zu berechnen, wollen wir in diesem abschließenden Kapitel noch
76 Andreas Gathmann 9. Anwendungen der Fundamentalgruppe Nachdem wir mit Hilfe von Überlagerungen nun in der Lage sind, Fundamentalgruppen zu berechnen, wollen wir in diesem abschließenden Kapitel noch
klar. Um die zweite Bedingung zu zeigen, betrachte u i U i mit u i = 0. Das mittlere -Zeichen liefert s
 Nachtrag zur allgemeinen Vektorraum-Theorie. 1.5.15. Direkte Summen. Sei V ein Vektorraum, seien U 1,..., U t Unterräume, wir schreiben V = U 1 U 2 U t = t i=1 U i falls die folgenden beiden Bedingungen
Nachtrag zur allgemeinen Vektorraum-Theorie. 1.5.15. Direkte Summen. Sei V ein Vektorraum, seien U 1,..., U t Unterräume, wir schreiben V = U 1 U 2 U t = t i=1 U i falls die folgenden beiden Bedingungen
Übungen zur Ingenieur-Mathematik III WS 2009/10 Blatt 10 21.12.2009
 Übungen zur Ingenieur-Mathematik III WS 2009/10 Blatt 10 21.12.2009 Aufgabe 35: Thema: Singulärwertzerlegung und assoziierte Unterräume Sei A eine m n Matrix mit Rang r und A = UDV T ihre Singulärwertzerlegung.
Übungen zur Ingenieur-Mathematik III WS 2009/10 Blatt 10 21.12.2009 Aufgabe 35: Thema: Singulärwertzerlegung und assoziierte Unterräume Sei A eine m n Matrix mit Rang r und A = UDV T ihre Singulärwertzerlegung.
Der Zwei-Quadrate-Satz von Fermat
 Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
(2) (x 2 1 + x 2 2 + + x 2 n)(y 2 1 + y 2 2 + + y 2 n) = z 2 1 + z 2 2 + + z 2 n
 Über die Komposition der quadratischen Formen von beliebig vielen Variablen 1. (Nachrichten von der k. Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-physikalische Klasse, 1898, S. 309 316.)
Über die Komposition der quadratischen Formen von beliebig vielen Variablen 1. (Nachrichten von der k. Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-physikalische Klasse, 1898, S. 309 316.)
TECHNISCHE UNIVERSITÄT MÜNCHEN. Abzählbarkeit, Injektivität, Sürjektivität und Bijektivität
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Friedrich Roesler Ralf Franken, PhD Max Lein Lineare Algebra 1 WS 26/7 en Blatt 4 13.11.26 Abzählbarkeit, Injektivität, Sürjektivität und Bijektivität
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Friedrich Roesler Ralf Franken, PhD Max Lein Lineare Algebra 1 WS 26/7 en Blatt 4 13.11.26 Abzählbarkeit, Injektivität, Sürjektivität und Bijektivität
Zwei Aufgaben, die auf windschiefe Regelflächen führen,
 Zwei Aufgaben, die auf windschiefe Regelflächen führen, von À. KIEFER (Zürich). (Als Manuskript eingegangen am 25. Januar 1926.) I. Gesucht im Raum der Ort des Punktes, von dem aus die Zentralprojektionen
Zwei Aufgaben, die auf windschiefe Regelflächen führen, von À. KIEFER (Zürich). (Als Manuskript eingegangen am 25. Januar 1926.) I. Gesucht im Raum der Ort des Punktes, von dem aus die Zentralprojektionen
(λ Ri I A+BR)v Ri = 0. Lässt sich umstellen zu
 Herleitung der oppenecker-formel (Wiederholung) Für ein System ẋ Ax + Bu (B habe Höchstrang) wird eine Zustandsregelung u x angesetzt. Der geschlossene egelkreis gehorcht der Zustands-Dgl. ẋ (A B)x. Die
Herleitung der oppenecker-formel (Wiederholung) Für ein System ẋ Ax + Bu (B habe Höchstrang) wird eine Zustandsregelung u x angesetzt. Der geschlossene egelkreis gehorcht der Zustands-Dgl. ẋ (A B)x. Die
Im Original veränderbare Word-Dateien
 Zeichnen mit Powerpoint Formen Mit PowerPoint kannst du einfache geometrische Formen wie Quadrate, Kreise, Sterne usw. zeichnen und diese mit zahlreichen optischen Effekten versehen. Diese Formen werden
Zeichnen mit Powerpoint Formen Mit PowerPoint kannst du einfache geometrische Formen wie Quadrate, Kreise, Sterne usw. zeichnen und diese mit zahlreichen optischen Effekten versehen. Diese Formen werden
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Bildverarbeitung Herbstsemester 2012. Kanten und Ecken
 Bildverarbeitung Herbstsemester 01 Kanten und Ecken 1 Inhalt Einführung Kantendetektierung Gradientenbasierende Verfahren Verfahren basierend auf der zweiten Ableitung Eckpunkterkennung Harris Corner Detector
Bildverarbeitung Herbstsemester 01 Kanten und Ecken 1 Inhalt Einführung Kantendetektierung Gradientenbasierende Verfahren Verfahren basierend auf der zweiten Ableitung Eckpunkterkennung Harris Corner Detector
Aufgabe 1. Sei A Mat(n n, R) mit Eigenwert 3. Dann gilt: Eig(A, 3) = Kern(A + 3E n ).
 Aufgabe Sei A Mat(n n, R) Eigenwert 3. Dann gilt: Eig(A, 3) = Kern(3A E n ). Sei A Mat(n n, R) Eigenwert 3. Dann gilt: Eig(A, 3) = Kern(A 3E n ). Sei A Mat(n n, R) Eigenwert 3. Dann gilt: Eig(A, 3) = Bild(A
Aufgabe Sei A Mat(n n, R) Eigenwert 3. Dann gilt: Eig(A, 3) = Kern(3A E n ). Sei A Mat(n n, R) Eigenwert 3. Dann gilt: Eig(A, 3) = Kern(A 3E n ). Sei A Mat(n n, R) Eigenwert 3. Dann gilt: Eig(A, 3) = Bild(A
Folienmodell zur Veranschaulichung der Bewegung von Erde und Mond um ihren gemeinsamen Schwerpunkt: (Verfasser: Werner B. Schneider, Stand 2/2010)
 Folienmodell zur Veranschaulichung der Bewegung von Erde und Mond um ihren gemeinsamen Schwerpunkt: (Verfasser: Werner B. Schneider, Stand 2/2010) Das mit dem Modell verfolgte Ziel besteht darin, die Bewegung
Folienmodell zur Veranschaulichung der Bewegung von Erde und Mond um ihren gemeinsamen Schwerpunkt: (Verfasser: Werner B. Schneider, Stand 2/2010) Das mit dem Modell verfolgte Ziel besteht darin, die Bewegung
Entscheidungsbäume. Definition Entscheidungsbaum. Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen?
 Entscheidungsbäume Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen? Definition Entscheidungsbaum Sei T ein Binärbaum und A = {a 1,..., a n } eine zu sortierenden Menge. T ist ein Entscheidungsbaum
Entscheidungsbäume Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen? Definition Entscheidungsbaum Sei T ein Binärbaum und A = {a 1,..., a n } eine zu sortierenden Menge. T ist ein Entscheidungsbaum
Computergraphik I. Scan Conversion: Lines & Co. Einordnung in die Pipeline. G. Zachmann Clausthal University, Germany zach@tu-clausthal.
 11/4/10 lausthal omputergraphik I Scan onversion of Lines. Zachmann lausthal University, ermany zach@tu-clausthal.de Einordnung in die Pipeline Rasterisierung der Objekte in Pixel Ecken-Werte interpolieren
11/4/10 lausthal omputergraphik I Scan onversion of Lines. Zachmann lausthal University, ermany zach@tu-clausthal.de Einordnung in die Pipeline Rasterisierung der Objekte in Pixel Ecken-Werte interpolieren
Computer Vision I. Nikos Canterakis. Lehrstuhl für Mustererkennung, Universität Freiburg,
 Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg, Literatur Richard Hartle and Andrew Zisserman. Multiple View Geometr in computer vision, Cambridge Universit Press, 2 nd Ed., 23. O.D.
Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg, Literatur Richard Hartle and Andrew Zisserman. Multiple View Geometr in computer vision, Cambridge Universit Press, 2 nd Ed., 23. O.D.
Basis und Dimension. Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren.
 Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Hinweise zum Online-Buchungssystem
 Hinweise zum Online-Buchungssystem An vielen Stellen innerhalb des Online-Buchungssystem finden Sie ein -Symbol, welches sich häufig in der oberen rechten Ecke befindet. Durch anklicken dieses Symbols
Hinweise zum Online-Buchungssystem An vielen Stellen innerhalb des Online-Buchungssystem finden Sie ein -Symbol, welches sich häufig in der oberen rechten Ecke befindet. Durch anklicken dieses Symbols
3 Quellencodierung. 3.1 Einleitung
 Source coding is what Alice uses to save money on her telephone bills. It is usually used for data compression, in other words, to make messages shorter. John Gordon 3 Quellencodierung 3. Einleitung Im
Source coding is what Alice uses to save money on her telephone bills. It is usually used for data compression, in other words, to make messages shorter. John Gordon 3 Quellencodierung 3. Einleitung Im
Fassade. Objektbasiertes Strukturmuster. C. Restorff & M. Rohlfing
 Fassade Objektbasiertes Strukturmuster C. Restorff & M. Rohlfing Übersicht Motivation Anwendbarkeit Struktur Teilnehmer Interaktion Konsequenz Implementierung Beispiel Bekannte Verwendung Verwandte Muster
Fassade Objektbasiertes Strukturmuster C. Restorff & M. Rohlfing Übersicht Motivation Anwendbarkeit Struktur Teilnehmer Interaktion Konsequenz Implementierung Beispiel Bekannte Verwendung Verwandte Muster
Jetzt wird auf die Zahl 2 geklickt und die Höhe der Zeile 2 eingestellt. Die Vorgehensweise ist wie
 Hergestellt nur für den privaten Gebrauch von Harry Wenzel. w Kopieren Vervielfältigen nur mit Genehmigung des Verfassers! apple Mit Excel einen Kalender für das Jahr 2013 erstellen. Vorab erst noch ein
Hergestellt nur für den privaten Gebrauch von Harry Wenzel. w Kopieren Vervielfältigen nur mit Genehmigung des Verfassers! apple Mit Excel einen Kalender für das Jahr 2013 erstellen. Vorab erst noch ein
Hans Walser, [20090509a] Wurzeln aus Matrizen
![Hans Walser, [20090509a] Wurzeln aus Matrizen Hans Walser, [20090509a] Wurzeln aus Matrizen](/thumbs/26/7816281.jpg) Hans Walser, [0090509a] Wurzeln aus Matrizen 1 Worum es geht Zu einer gegebenen,-matri A suchen wir,-matrizen B mit der Eigenschaft: BB = B = A. Wir suchen also Quadratwurzeln der Matri A. Quadrieren Wenn
Hans Walser, [0090509a] Wurzeln aus Matrizen 1 Worum es geht Zu einer gegebenen,-matri A suchen wir,-matrizen B mit der Eigenschaft: BB = B = A. Wir suchen also Quadratwurzeln der Matri A. Quadrieren Wenn
Lösungen zur Vorrundenprüfung 2006
 Lösungen zur Vorrundenprüfung 2006 Zuerst einige Bemerkungen zum Punkteschema. Eine vollständige und korrekte Lösung einer Aufgabe ist jeweils 7 Punkte wert. Für komplette Lösungen mit kleineren Fehlern
Lösungen zur Vorrundenprüfung 2006 Zuerst einige Bemerkungen zum Punkteschema. Eine vollständige und korrekte Lösung einer Aufgabe ist jeweils 7 Punkte wert. Für komplette Lösungen mit kleineren Fehlern
Webergänzung zu Kapitel 10
 Webergänzung zu Kapitel 10 10.1.4 Varianzanalyse (ANOVA: analysis of variance) Im Kapitel 10 haben wir uns hauptsächlich mit Forschungsbeispielen beschäftigt, die nur zwei Ergebnissätze hatten (entweder
Webergänzung zu Kapitel 10 10.1.4 Varianzanalyse (ANOVA: analysis of variance) Im Kapitel 10 haben wir uns hauptsächlich mit Forschungsbeispielen beschäftigt, die nur zwei Ergebnissätze hatten (entweder
Ein neuer Beweis, dass die Newton sche Entwicklung der Potenzen des Binoms auch für gebrochene Exponenten gilt
 Ein neuer Beweis, dass die Newton sche Entwicklung der Potenzen des Binoms auch für gebrochene Exponenten gilt Leonhard Euler 1 Wann immer in den Anfängen der Analysis die Potenzen des Binoms entwickelt
Ein neuer Beweis, dass die Newton sche Entwicklung der Potenzen des Binoms auch für gebrochene Exponenten gilt Leonhard Euler 1 Wann immer in den Anfängen der Analysis die Potenzen des Binoms entwickelt
Satz 25 A sei eine (n n)-matrix über K
 Satz 25 Satz 25 A sei eine (n n)-matrix über K Satz 25 A sei eine (n n)-matrix über K mit paarweise verschiedenen Eigenwerten λ 1,...,λ m. Satz 25 A sei eine (n n)-matrix über K mit paarweise verschiedenen
Satz 25 Satz 25 A sei eine (n n)-matrix über K Satz 25 A sei eine (n n)-matrix über K mit paarweise verschiedenen Eigenwerten λ 1,...,λ m. Satz 25 A sei eine (n n)-matrix über K mit paarweise verschiedenen
8 Diskrete Optimierung
 8 Diskrete Optimierung Definition 8.1. Ein Graph G ist ein Paar (V (G), E(G)) besteh aus einer lichen Menge V (G) von Knoten (oder Ecken) und einer Menge E(G) ( ) V (G) 2 von Kanten. Die Ordnung n(g) von
8 Diskrete Optimierung Definition 8.1. Ein Graph G ist ein Paar (V (G), E(G)) besteh aus einer lichen Menge V (G) von Knoten (oder Ecken) und einer Menge E(G) ( ) V (G) 2 von Kanten. Die Ordnung n(g) von
Optimierung für Wirtschaftsinformatiker: Analytische Optimierung ohne Nebenbedingungen
 Optimierung für Wirtschaftsinformatiker: Analytische Optimierung ohne Nebenbedingungen Dr. Nico Düvelmeyer Freitag, 1. Juli 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Einführung und Wiederholung Beispiel
Optimierung für Wirtschaftsinformatiker: Analytische Optimierung ohne Nebenbedingungen Dr. Nico Düvelmeyer Freitag, 1. Juli 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Einführung und Wiederholung Beispiel
!(0) + o 1("). Es ist damit möglich, dass mehrere Familien geschlossener Orbits gleichzeitig abzweigen.
 Bifurkationen an geschlossenen Orbits 5.4 167 der Schnittabbldung konstruiert. Die Periode T (") der zugehörigen periodischen Lösungen ergibt sich aus =! + o 1 (") beziehungsweise Es ist also t 0 = T (")
Bifurkationen an geschlossenen Orbits 5.4 167 der Schnittabbldung konstruiert. Die Periode T (") der zugehörigen periodischen Lösungen ergibt sich aus =! + o 1 (") beziehungsweise Es ist also t 0 = T (")
Das Werkzeug Verschieben/Kopieren wird über die Symbolleiste oder im Pull-Down-Menü Tools > Verschieben aktiviert.
 Verschieben/Kopieren-Werkzeug 95 Die Änderungswerkzeuge In den Kapiteln zuvor haben Sie gelernt, wie Sie mit den Zeichnen-Werkzeugen die in SketchUp vorhandenen Grundformen (Rechteck, Kreis, Bogen, Linie
Verschieben/Kopieren-Werkzeug 95 Die Änderungswerkzeuge In den Kapiteln zuvor haben Sie gelernt, wie Sie mit den Zeichnen-Werkzeugen die in SketchUp vorhandenen Grundformen (Rechteck, Kreis, Bogen, Linie
Programme deinstallieren,
 Programme deinstallieren, Programme mit Windows deinstallieren: Sie haben Programme auf Ihrem Rechner, die Sie gar nicht oder nicht mehr gebrauchen. Sie sollten solche Programme deinstallieren, denn die
Programme deinstallieren, Programme mit Windows deinstallieren: Sie haben Programme auf Ihrem Rechner, die Sie gar nicht oder nicht mehr gebrauchen. Sie sollten solche Programme deinstallieren, denn die
Kapitel 4. Euklidische Ringe und die Jordansche Normalform. 4.1 Euklidische Ringe
 Kapitel 4 Euklidische Ringe und die Jordansche Normalform 4.1 Euklidische Ringe Die Ringe der ganzen Zahlen, Z, sowie Polynomringe über Körpern, K[X], wobei K ein Körper ist, haben die folgenden Gemeinsamheiten:
Kapitel 4 Euklidische Ringe und die Jordansche Normalform 4.1 Euklidische Ringe Die Ringe der ganzen Zahlen, Z, sowie Polynomringe über Körpern, K[X], wobei K ein Körper ist, haben die folgenden Gemeinsamheiten:
Der gelbe Weg. Gestaltungstechnik: Malen und kleben. Zeitaufwand: 4 Doppelstunden. Jahrgang: 6-8. Material:
 Kurzbeschreibung: Entlang eines gelben Weges, der sich von einem zum nächsten Blatt fortsetzt, entwerfen die Schüler bunte Fantasiehäuser. Gestaltungstechnik: Malen und kleben Zeitaufwand: 4 Doppelstunden
Kurzbeschreibung: Entlang eines gelben Weges, der sich von einem zum nächsten Blatt fortsetzt, entwerfen die Schüler bunte Fantasiehäuser. Gestaltungstechnik: Malen und kleben Zeitaufwand: 4 Doppelstunden
Wahrnehmung und wahrnehmungsgerechte Gestaltung
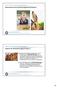 Wahrnehmung und wahrnehmungsgerechte Gestaltung 37 Gestalt in der Wahrnehmungspsychologie (1) Kants Idee des Vorwissens beeinflusste u.a. die Entwicklung der Gestaltpsychologie, der zufolge einige Aspekte
Wahrnehmung und wahrnehmungsgerechte Gestaltung 37 Gestalt in der Wahrnehmungspsychologie (1) Kants Idee des Vorwissens beeinflusste u.a. die Entwicklung der Gestaltpsychologie, der zufolge einige Aspekte
GF(2 2 ) Beispiel eines Erweiterungskörpers (1)
 GF(2 2 ) Beispiel eines Erweiterungskörpers (1) Im Kapitel 2.1 wurde bereits gezeigt, dass die endliche Zahlenmenge {0, 1, 2, 3} q = 4 nicht die Eigenschaften eines Galoisfeldes GF(4) erfüllt. Vielmehr
GF(2 2 ) Beispiel eines Erweiterungskörpers (1) Im Kapitel 2.1 wurde bereits gezeigt, dass die endliche Zahlenmenge {0, 1, 2, 3} q = 4 nicht die Eigenschaften eines Galoisfeldes GF(4) erfüllt. Vielmehr
1 Visual Basic for Application mit Excel (VBA)
 Informatikfreikurs WS 2008/2009 1 1 Visual Basic for Application mit Excel (VBA) 1.1 Mosaik Puzzle Das untenstehende Zahlenschema ist ein sogenanntes Mosaik Puzzle. Jede Zahl zeigt an, wie viele der (höchstens
Informatikfreikurs WS 2008/2009 1 1 Visual Basic for Application mit Excel (VBA) 1.1 Mosaik Puzzle Das untenstehende Zahlenschema ist ein sogenanntes Mosaik Puzzle. Jede Zahl zeigt an, wie viele der (höchstens
Einführung in die Java- Programmierung
 Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger horn@uni-koblenz.de WiSe 2012/13 1 Wichtig... Mittags Pommes... Praktikum A 230 C 207 (Madeleine) F 112 F 113 (Kevin) E
Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger horn@uni-koblenz.de WiSe 2012/13 1 Wichtig... Mittags Pommes... Praktikum A 230 C 207 (Madeleine) F 112 F 113 (Kevin) E
3.3 Eigenwerte und Eigenräume, Diagonalisierung
 3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
Erinnerung/Zusammenfassung zu Abbildungsmatrizen
 Erinnerung/Zusammenfassung zu Abbildungsmatrizen Thomas Coutandin (cthomas@student.ethz.ch) 7. November 2 Abbildungsmatrizen Im Folgenden betrachten wir stets endlich dimensionale K-Vektorräume (K irgend
Erinnerung/Zusammenfassung zu Abbildungsmatrizen Thomas Coutandin (cthomas@student.ethz.ch) 7. November 2 Abbildungsmatrizen Im Folgenden betrachten wir stets endlich dimensionale K-Vektorräume (K irgend
Einführung in die Vektor- und Matrizenrechnung. Matrizen
 Einführung in die Vektor- und Matrizenrechnung Matrizen Definition einer Matrix Unter einer (reellen) m x n Matrix A versteht man ein rechteckiges Schema aus reellen Zahlen, die wie folgt angeordnet sind:
Einführung in die Vektor- und Matrizenrechnung Matrizen Definition einer Matrix Unter einer (reellen) m x n Matrix A versteht man ein rechteckiges Schema aus reellen Zahlen, die wie folgt angeordnet sind:
Jinx! Konfiguration für LED-Player und LED-Controller-L
 Jinx! Ist eine sehr mächtige LED-Software zur Ansteuerung von LED-Controllern über verschiedene Protokolle und Schnittstellen. Die Konfiguration dieses Programmes für den Betrieb mit LED-Controller-L oder
Jinx! Ist eine sehr mächtige LED-Software zur Ansteuerung von LED-Controllern über verschiedene Protokolle und Schnittstellen. Die Konfiguration dieses Programmes für den Betrieb mit LED-Controller-L oder
6.4. Polarisation und Doppelbrechung. Exp. 51: Doppelbrechung am Kalkspat. Dieter Suter - 389 - Physik B2. 6.4.1. Polarisation
 Dieter Suter - 389 - Physik B2 6.4. Polarisation und Doppelbrechung 6.4.1. Polarisation Wie andere elektromagnetische Wellen ist Licht eine Transversalwelle. Es existieren deshalb zwei orthogonale Polarisationsrichtungen.
Dieter Suter - 389 - Physik B2 6.4. Polarisation und Doppelbrechung 6.4.1. Polarisation Wie andere elektromagnetische Wellen ist Licht eine Transversalwelle. Es existieren deshalb zwei orthogonale Polarisationsrichtungen.
1. Die Generierung eines Zweiphasensystems aus dem vorhandenen Dreiphasensystem
 Über die Möglichkeit, Eigenschaften elektrischer Antriebe, insbesondere Aufzugantriebe, mittels der Oszillografentechnik auf einfache Weise beurteilen zu können. Dipl.Ing. Wolfgang Rösch, ascentronic Gerätebau
Über die Möglichkeit, Eigenschaften elektrischer Antriebe, insbesondere Aufzugantriebe, mittels der Oszillografentechnik auf einfache Weise beurteilen zu können. Dipl.Ing. Wolfgang Rösch, ascentronic Gerätebau
Matrizennorm. Definition 1. Sei A M r,s (R). Dann heißt A := sup die Matrixnorm. Wir wissen zunächst nicht, ob A eine reelle Zahl ist.
 Matrizennorm Es seien r,s N Mit M r,s (R bezeichnen wir die Menge der reellen r s- Matrizen (also der linearen Abbildungen R s R r, und setze M s (R := M s,s (R (also die Menge der linearen Abbildungen
Matrizennorm Es seien r,s N Mit M r,s (R bezeichnen wir die Menge der reellen r s- Matrizen (also der linearen Abbildungen R s R r, und setze M s (R := M s,s (R (also die Menge der linearen Abbildungen
Invariantentheorie. Vorlesung 5. Invariantenringe zu Untergruppen
 Prof. Dr. H. Brenner Osnabrück WS 2012/2013 Invariantentheorie Vorlesung 5 Invariantenringe zu Untergruppen Proposition 5.1. Es sei R G R eine Operation einer Gruppe G auf einem kommutativen Ring durch
Prof. Dr. H. Brenner Osnabrück WS 2012/2013 Invariantentheorie Vorlesung 5 Invariantenringe zu Untergruppen Proposition 5.1. Es sei R G R eine Operation einer Gruppe G auf einem kommutativen Ring durch
Handbuch ECDL 2003 Professional Modul 3: Kommunikation Besprechungen anlegen und versenden
 Handbuch ECDL 2003 Professional Modul 3: Kommunikation Besprechungen anlegen und versenden Dateiname: ecdl_p3_02_02_documentation.doc Speicherdatum: 08.12.2004 ECDL 2003 Professional Modul 3 Kommunikation
Handbuch ECDL 2003 Professional Modul 3: Kommunikation Besprechungen anlegen und versenden Dateiname: ecdl_p3_02_02_documentation.doc Speicherdatum: 08.12.2004 ECDL 2003 Professional Modul 3 Kommunikation
Technical Support Knowledge Base
 Seite 1 von 6 Hello, Alois : Germany search Advanced Search Home» Support» Technical Support» Technical Support Knowledge Base Technical Support Knowledge Base Ist dies das von Ihnen gesuchte Dokument?
Seite 1 von 6 Hello, Alois : Germany search Advanced Search Home» Support» Technical Support» Technical Support Knowledge Base Technical Support Knowledge Base Ist dies das von Ihnen gesuchte Dokument?
Grundlagen des Software Engineering
 Grundlagen des Software Engineering Teil 1: SW-Management Fachrichtung Wirtschaftsinformatik FB Berufsakademie der FHW Berlin Prof. Dr. Gert Faustmann Einleitung Historie des Konfigurationsmanagements:
Grundlagen des Software Engineering Teil 1: SW-Management Fachrichtung Wirtschaftsinformatik FB Berufsakademie der FHW Berlin Prof. Dr. Gert Faustmann Einleitung Historie des Konfigurationsmanagements:
5.1 Drei wichtige Beweistechniken... 55 5.2 Erklärungen zu den Beweistechniken... 56
 5 Beweistechniken Übersicht 5.1 Drei wichtige Beweistechniken................................. 55 5. Erklärungen zu den Beweistechniken............................ 56 Dieses Kapitel ist den drei wichtigsten
5 Beweistechniken Übersicht 5.1 Drei wichtige Beweistechniken................................. 55 5. Erklärungen zu den Beweistechniken............................ 56 Dieses Kapitel ist den drei wichtigsten
Stufe. Schraube. Materialphysik II Prof. Dr. Guido Schmitz 05.07.2013. 12.4 Versetzungen
 12.4 Versetzungen Versetzungen sind linienhafte Störungen des Kristallgitters, die den abgeglittenen Teil eines Kristalls von dem noch nicht abgeglittenen Teil auf einer Gleitebene voneinander trennen.
12.4 Versetzungen Versetzungen sind linienhafte Störungen des Kristallgitters, die den abgeglittenen Teil eines Kristalls von dem noch nicht abgeglittenen Teil auf einer Gleitebene voneinander trennen.
Angewandte Strömungssimulation
 Angewandte Strömungssimulation 8. Vorlesung Stefan Hickel Visualisierung Prinzipien zur sinnvollen Ergebnisdarstellung! Achsen immer beschriften Einheiten angeben! Bei Höhenliniendarstellungen und Konturdarstellungen
Angewandte Strömungssimulation 8. Vorlesung Stefan Hickel Visualisierung Prinzipien zur sinnvollen Ergebnisdarstellung! Achsen immer beschriften Einheiten angeben! Bei Höhenliniendarstellungen und Konturdarstellungen
Visuelle Kryptographie
 Visuelle Kryptographie 14. April 2013 Visuelle Kryptographie 14. April 2013 1 / 21 1 Motivation 2 Grundlagen 3 Beispiele 4 Schlußbemerkungen 5 Lizenz Visuelle Kryptographie 14. April 2013 2 / 21 Einordnung
Visuelle Kryptographie 14. April 2013 Visuelle Kryptographie 14. April 2013 1 / 21 1 Motivation 2 Grundlagen 3 Beispiele 4 Schlußbemerkungen 5 Lizenz Visuelle Kryptographie 14. April 2013 2 / 21 Einordnung
Wassily Kandinsky: Structure joyeuse. Beschreibe die Figuren und zeichne sie aus freier Hand in dein Heft.
 6 Flächen Wie heißen die Figuren? a) Dreiecke Viereck d) Quadrat b) Kreis Quadrate e) Dreiecke Rechteck c) Rechtecke Viereck f) Kreis Wassily Kandinsky: Structure joyeuse Lege Vierecke. a) Nimm vier gleich
6 Flächen Wie heißen die Figuren? a) Dreiecke Viereck d) Quadrat b) Kreis Quadrate e) Dreiecke Rechteck c) Rechtecke Viereck f) Kreis Wassily Kandinsky: Structure joyeuse Lege Vierecke. a) Nimm vier gleich
Übung 2: Spezifikation von Auszügen eines Provisionssystems
 Übung 2: Spezifikation von Auszügen eines Provisionssystems Für die zweite Übung sollten Sie wieder auf einer einheitlichen Ausgangslage aufsetzen können. Dazu ist es nötig, zunächst einen groben Überblick
Übung 2: Spezifikation von Auszügen eines Provisionssystems Für die zweite Übung sollten Sie wieder auf einer einheitlichen Ausgangslage aufsetzen können. Dazu ist es nötig, zunächst einen groben Überblick
Leitfaden Lineare Algebra: Determinanten
 Leitfaden Lineare Algebra: Determinanten Die symmetrische Gruppe S n. Eine Permutation σ der Menge S ist eine bijektive Abbildung σ : S S. Ist S eine endliche Menge, so reicht es zu verlangen, dass σ injektiv
Leitfaden Lineare Algebra: Determinanten Die symmetrische Gruppe S n. Eine Permutation σ der Menge S ist eine bijektive Abbildung σ : S S. Ist S eine endliche Menge, so reicht es zu verlangen, dass σ injektiv
Dynamisch unterrichten mit Excel
 Reimund Albers Dynamisch unterrichten mit Excel Erstellen von Schiebereglern 1 Dynamisch unterrichten mit Excel oder: Wie erstelle ich einen Schieberegler in Excel? Beispiel: Demonstration der Abhängigkeit
Reimund Albers Dynamisch unterrichten mit Excel Erstellen von Schiebereglern 1 Dynamisch unterrichten mit Excel oder: Wie erstelle ich einen Schieberegler in Excel? Beispiel: Demonstration der Abhängigkeit
SO(2) und SO(3) Martin Schlederer. 06. Dezember 2012
 SO(2) und SO(3) Martin Schlederer 06. Dezember 2012 Inhaltsverzeichnis 1 Motivation 2 2 Wiederholung 2 2.1 Spezielle Orthogonale Gruppe SO(n)..................... 2 2.2 Erzeuger.....................................
SO(2) und SO(3) Martin Schlederer 06. Dezember 2012 Inhaltsverzeichnis 1 Motivation 2 2 Wiederholung 2 2.1 Spezielle Orthogonale Gruppe SO(n)..................... 2 2.2 Erzeuger.....................................
Tag 9: Datenstrukturen
 Tag 9: Datenstrukturen A) Datenstrukturen B) Cell Arrays C) Anwendungsbeispiel: Stimulation in einem psychophysikalischen Experiment A) Datenstrukturen Wenn man komplizierte Datenmengen verwalten möchte,
Tag 9: Datenstrukturen A) Datenstrukturen B) Cell Arrays C) Anwendungsbeispiel: Stimulation in einem psychophysikalischen Experiment A) Datenstrukturen Wenn man komplizierte Datenmengen verwalten möchte,
Elemente der Analysis II
 Elemente der Analysis II Kapitel 3: Lineare Abbildungen und Gleichungssysteme Informationen zur Vorlesung: http://www.mathematik.uni-trier.de/ wengenroth/ J. Wengenroth () 15. Mai 2009 1 / 35 3.1 Beispiel
Elemente der Analysis II Kapitel 3: Lineare Abbildungen und Gleichungssysteme Informationen zur Vorlesung: http://www.mathematik.uni-trier.de/ wengenroth/ J. Wengenroth () 15. Mai 2009 1 / 35 3.1 Beispiel
SUDOKU - Strategien zur Lösung
 SUDOKU Strategien v. /00 SUDOKU - Strategien zur Lösung. Naked Single (Eindeutiger Wert)? "Es gibt nur einen einzigen Wert, der hier stehen kann". Sind alle anderen Werte bis auf einen für eine Zelle unmöglich,
SUDOKU Strategien v. /00 SUDOKU - Strategien zur Lösung. Naked Single (Eindeutiger Wert)? "Es gibt nur einen einzigen Wert, der hier stehen kann". Sind alle anderen Werte bis auf einen für eine Zelle unmöglich,
6.2 Perfekte Sicherheit
 04 6.2 Perfekte Sicherheit Beweis. H(B AC) + H(A C) = H(ABC) H(AC) + H(AC) H(C) Wegen gilt Einsetzen in die Definition gibt = H(AB C). H(A BC) = H(AB C) H(B C). I(A; B C) = H(A C) H(AB C) + H(B C). Da
04 6.2 Perfekte Sicherheit Beweis. H(B AC) + H(A C) = H(ABC) H(AC) + H(AC) H(C) Wegen gilt Einsetzen in die Definition gibt = H(AB C). H(A BC) = H(AB C) H(B C). I(A; B C) = H(A C) H(AB C) + H(B C). Da
