Hermite-Polynome. Inhaltsverzeichnis
|
|
|
- Fritz Burgstaller
- vor 6 Jahren
- Abrufe
Transkript
1 Vortrag zum Seminar zur Analysis, Thomas Heinrichs Abel has left mathematicians enough to keep them busy for 500 years. Charles Hermite Dieser Vortrag behandelt vordergründig die sogenannten Hermite-Polynome nach Charles Hermite und einige ihrer Eigenschaften. Außerdem wird ein kurzer Blick auf Charles Hermite geworfen und einige Gebiete genannt, in denen die Hermite- Polynome Anwendung finden. Inhaltsverzeichnis 1 Charles Hermite Biographie Beitrag zur Mathematik Hermite-Polynome Definition Hermite-Polynome Erzeugende Funktion Rekursionsformeln Hermitesche Differentialgleichung 9 4 Orthogonalität Definition Orthogonalität Orthogonalität Hermite-Polynome Anwendung 13
2 1 Charles Hermite 1 Charles Hermite Charles Hermite ( 24. Dezember 1822 in Dieuze (Lothringen); 14. Januar 1901 in Paris) war ein französischer Mathematiker. Abbildung 1: Charles Hermite ca Biographie Hermite verließ als Student die École Polytechnique im Streit, nachdem ihm wegen unzureichender Leistungen strenge Bedingungen auferlegt wurden. In den folgenden Jahren entwickelte er sich aus eigener Kraft, im Austausch insbesondere mit Joseph Liouville, zu einem produktiven Mathematiker wurde er Lehrbeauftragter, 1869 Professor an der École Polytechnique; von 1876 bis 1897 unterrichtete er nur noch an der Sorbonne wurde er in die Académie des Sciences gewählt, 1883 in die römische Accademia dei Lincei. Hermite stand in engem Austausch mit Joseph Liouville, Charles-François Sturm und Augustin Louis Cauchy; zu seinen Schülern gehörten Gösta Mittag-Leffler, Jacques Hadamard und Henri Poincaré; er heiratete die Schwester von Joseph Bertrand und wurde Schwiegervater von Émile Picard. Beitrag zur Mathematik Hermite arbeitete in Zahlentheorie und Algebra, über orthogonale Polynome und elliptische Funktionen. Er erzielte wichtige Ergebnisse über doppelt periodische Funk- 2
3 2 Hermite-Polynome tionen und Invarianten quadratischer Formen löste er eine algebraische Gleichung fünften Grades mit Hilfe elliptischer Funktionen erzielte er sein wohl berühmtestes Resultat: Er bewies, dass die eulersche Zahl e transzendent ist; auf Hermites Methode aufbauend bewies Carl Louis Ferdinand von Lindemann 1882 die Transzendenz der Kreiszahl π (Unmöglichkeit der Quadratur des Kreises). Folgende mathematische Dinge werden heute nach Hermite benannt: Die hermitesche Differentialgleichung y 2xy + 2ny = 0, n N 0 ; die hermiteschen Polynome ; die hermitesche Interpolationsformel; die Bezeichnung zweier Matrizen, die adjungiert (also komplex konjugiert und transponiert) zueinander sind, auch als hermitesch konjugiert; die hermitesche Normalform für ganzzahlige Matrizen; die hermitesche Form; die hermitesche Funktion sowie der hermitesche Operator. 2 Hermite-Polynome In diesem Abschnitt werden die Hermite-Polynome, ihre erzeugende Funktion, sowie die Rekursionsformeln zur rekursiven Darstellung eingführt. Definition Hermite-Polynome (2.1) Definition (Hermite-Polynome) Die Hermite-Polynome, n N 0, in R[x] sind definiert durch dn = ( 1) n e x2 dx n e x2, n N 0. 3
4 2 Hermite-Polynome Durch diese Darstellung erhalten wir durch Differenzieren direkt die ersten Hermite- Polynome: H 0 (x) = ( 1) 0 e x2 e x2 = 1 H 1 (x) = ( 1) 1 e x2 e x2 ( 2x) = 2x H 2 (x) = ( 1) 2 e x2 e x2 (4x 2 2) = 4x 2 2 H 3 (x) = ( 1) 3 e x2 e x2 ( 8x x) = 8x 3 12x H 4 (x) = ( 1) 3 e x2 e x2 (16x 4 48x ) = 16x 4 48x Abbildung 2: Hermite-Polynome Hiermit leiten wir zum zweiten Unterabschnitt über. Erzeugende Funktion (2.2) Satz (erzeugende Funktion) Für x, t R gilt w(x, t) = e 2xt t2 = t n. Die Funktion w wird auch erzeugende Funktion der Hermite-Polynome genannt. 4
5 2 Hermite-Polynome Beweis Die Funktion w ist von t R abhängig und somit stetig differenzierbar. Daher kann sie für ein festes x um 0 in eine Taylorreihe entwickelt werden. Also hat man w(x, t) = e 2xt t2 = w (n) (x, 0) t n, für t R. Nun folgt [ w (n) n ] (x, 0) = w(x, t) tn t=0 [ n = t n e2xt t2 ] t=0 [ n ] = e x2 t n e (x t)2. t=0 Abschließend substituieren wir u = x t und erhalten [ d ( 1) n n ] e x2 du n e u2 = ( 1) n x2 dn e dx n e x2 =. u=x Daraus ergibt sich eine weitere Darstellung in folgendem (2.3) Korollar Sei n N 0. ist ein gerades bzw. ungerades Polynom vom Grad n, falls n gerade bzw. ungerade ist. Es gilt und inbesondere für x = 0 H n (0) = = n/2 k=0 ( 1) k k!(n 2k)! (2x)n 2k { 0, falls n ungerade, ( 1) n/2 (n/2)!, falls n gerade. Beweis Aus (2.2) und der Reihendarstellung der Exponentialfunktion erhält man = t n (2.2) = e 2xt e t2 = t 2l l! k=0 1 k! (2xt)k = k=0 1 k! (2xt)k t 2l l! l! t 2l 1 (2l)! (2xt)2l 5
6 2 Hermite-Polynome = = = = n n n/2 l! ( n/2 t 2l 1 (2n 2l)! (2xt)2n 2l l!(2n 2l)! (2x)2n 2l t 2n l!(n 2l)! (2x)n 2l t n l!(n 2l)! (2x)n 2l da man wegen der absoluten Konvergenz beliebig umordnen darf. Durch Kooeffizientenvergleich von t n folgt = = 0 l n/2 n/2 ) n/2 l!(n 2l)! (2x)n 2l = l!(n 2l)! (2x)n 2l t n, l!(n 2l)! (2x)n 2l und damit die Behauptung. Kommen wir nun zu einer rekursiven Darstellung der Hermite-Polynome im nächsten Unterabschnitt. (2.4) Satz (Rekursionsformeln) Für alle x R, n N gilt a) H n+1 (x) 2x + 2nH n 1 (x) = 0, Rekursionsformeln b) H n(x) = 2nH n 1 (x), c) H n (x) 2xH n(x) + 2n = 0. 6
7 2 Hermite-Polynome Beweis a) Aus (2.2) ergibt sich t w(x, t) = t e2xt t2 = (2x 2t)e 2xt t2 = (2x 2t)w(x, t) w(x, t) (2x 2t)w(x, t) = 0, t woraus man durch die Potenzreihendarstellung von w t t t n (2x 2t) t n 2x t n = 0 t n + 2t t n = 0 erhält. Da die Potenzreihe gliedweise differenzierbar ist, hat man (n 1)! tn 1 2x Nun folgt durch Indexverschiebung H n+1 (x) t n 2x H 1 (x) 2xH 0 (x) + }{{} =0 H n+1 (x) t n + 2 t n 2x t n + 2 H n 1 (x) (n 1)! tn = 0 Vergleicht man die Koeffizienten von t n, so folgt H n+1 (x) und damit die Behauptung. b) Analog zu (a) erhält man 2x H n(x) t n+1 = 0. t n H n 1(x) (n 1)! = 0 H n+1 (x) 2x + 2nH n 1 (x) = 0 w(x, t) = x x e2xt t2 = 2te 2xt t2 = 2tw(x, t) w(x, t) 2tw(x, t) = 0, x H n 1 (x) (n 1)! tn = 0 7
8 2 Hermite-Polynome also folgt durch die Potenzreihendarstellung x H n(x) H 0(x) + }{{} =0 t n 2 t n 2t H n(x) t n = 0 t n+1 = 0 t n 2 Daraus erhalten wir durch Indexverschiebung H n(x) t n 2 t n+1 = 0. H n 1 (x) (n 1)! tn = 0, und anschließend durch Koeffizientenvergleich von t n das gewünschte Resultat. c) Ergibt sich aus (a) und (b). Es gilt für alle n 2 woraus sofort H n(x) 2 H n 1(x) (n 1)! = 0 H n(x) 2nH n 1 (x) = 0 H n (x) = ( H n(x) ) (b) = 2nH n 1 (b) (x) = 4n(n 1)H n 2 (x), H n (x) 2xH n(x) + 2n = 4n(n 1)H n 2 (x) 4nxH n 1 (x) + 2n = 2n ( 2(n 1)H n 2 (x) 2xH n 1 (x) + ) }{{} =0,nach(a) = 0 folgt. Für n = 1 erhält man H 1 (x) 2xH 1 (x) + 2H 1(x) = (2x) 2x(2x) + 4x = 0 4x + 4x = 0. 8
9 3 Hermitesche Differentialgleichung 3 Hermitesche Differentialgleichung Kommen wir nun zu den Hermiteschen Differentialgleichungen in folgender Definition: (3.1) Definition (Hermitesche Differentialgleichung) Sei n N 0. Dann heißt y 2xy + 2ny = 0 die Hermitesche Differentialgleichung. (3.2) Korollar Die Hermite-Polynome genügen der Hermiteschen Differentialgleichung y 2xy + 2ny = 0. Beweis Folgt sofort aus (2.4)(c). Als Folgerung erhalten wir das (3.3) Korollar Die Funktion erfüllt die Differentialgleichung u n (x) = e x2 /2, n N 0, u n(x) + (2n + 1 x 2 )u n (x) = 0. Beweis Einsetzen der Funktion u n in die Differentialgleichung liefert ( e x 2 /2 ) + (2n + 1 x 2 )e x2 /2 = ( xe x2 /2 + e x2 /2 H n(x) ) + (2n + 1 x 2 )e x2 /2 = ( e x2 /2 ( x + H n(x)) ) + (2n + 1 x 2 )e x2 /2 = xe x2 /2 ( x + H n(x) ) + e x2 /2 ( x + H n(x) ) + (2n + 1 x 2 )e x2 /2 9
10 4 Orthogonalität = xe x2 /2 ( x + H n(x) ) + e x2 /2 ( xh n(x) + H n (x) ) + (2n + 1 x 2 )e x2 /2 = e x2 /2 H n (x) 2xe x2 /2 H n(x) + 2ne x2 /2 = e x2 /2 ( H n (x) 2xH n(x) + 2n ) }{{} =0,nach(2.4)(c) = 0. 4 Orthogonalität Nachfolgend wollen wir die Orthogonalität der Hermite-Polynome untersuchen. Zunächst zur Erinnerung folgende Definition Orthogonalität (4.1) Definition (Orthogonale Funktionen) Ein Funktionensystem g n, n N 0, nennt man orthogonal auf dem Intervall [a, b] mit dem Gewicht ϱ(x), wobei ϱ(x) > 0, für alle x [a, b], wenn b a ϱ(x)g n (x)g m (x)dx = 0, für alle n, m N 0 mit n = m gilt. Orthogonalität Hermite-Polynome (4.2) Satz Die Hermite-Polynome sind orthogonal mit dem Gewicht e x2. Daraus erhält man e x2 H m (x)dx = 0, für alle n, m N 0 mit n = m. 10
11 4 Orthogonalität Beweis Es gelten die Voraussetzungen und Bezeichnungen aus (3.3), dann erhält man ( u n(x) + (2n + 1 x 2 )u n (x) ) u m (x) ( u m(x) + (2m + 1 x 2 )u m (x) ) u n (x) = 0 u n(x)u m (x) + (2n + 1 x 2 )u n (x)u m (x) u m(x)u n (x) (2m + 1 x 2 )u m (x)u n (x) = 0 u n(x)u m (x) u n (x)u m(x) + (2n 2m)u n (x)u m (x) = 0 u n(x)u m (x) + u n(x)u m(x) u n(x)u m(x) u n (x)u m(x) +2(n m)u n (x)u m (x) = 0 d ( u dx n (x)u m (x) u n (x)u m(x) ) + 2(n m)u n (x)u m (x) = 0 Daraus folgt durch Integration über das Intervall (, ) [ ] k lim u n(x)u m (x) u n (x)u m(x) k k + lim k [ ( xe x 2 /2 + e x2 /2 H n(x) ) e x2 /2 H m (x) e x2 /2 ( xe x2 /2 H m (x) + e x2 /2 H m(x) )] k + 2(n m)u n (x)u m (x)dx = 0 2(n m)u n (x)u m (x)dx = 0 lim e x2 /2 ( H n(x)h m (x) H m(x) )] k + 2(n m) k }{{} =0 und somit Aus k [ 2(n m) u n (x)u m (x)dx = 0 n =m k u n (x)u m (x)dx = 0. u n (x)u m (x)dx = 0 u n (x) = e x2 /2 und u m (x) = e x2 /2 H m (x) (siehe (3.3)) ergibt sich schließlich das gewünschte Resultat e x2 H m (x)dx = 0, für alle n, m N 0 mit n = m. 11
12 4 Orthogonalität (4.3) Lemma Für n = m in (4.2) folgt e x2 H 2 n(x)dx = 2 n π, für alle n N. Beweis Zunächst betrachten wir die Fälle n = 0 und n = 1. Es gilt sowie = 4 e x2 H 2 0 (x)dx = e x2 H 2 1 (x)dx = } xe{{ x2 } x =u =v = 2 π = 2 1 1! π. 4e x2 x 2 dx e x2 dx = π = 2 0 0! π, }{{} dx partielle = [ 4 lim 1 Integration k 2 xe x2] k k }{{} =0 + 2 e x2 dx Sei also n 2. Nun benutzt man (2.4)(a), ersetzt n durch n 1, multipliziert mit und erhält H 2 n(x) 2xH n 1 (x) + 2(n 1)H n 2 (x) = 0. Des Weiteren ergibt sich aus (2.4)(a) durch Multiplizieren mit H n 1 (x) die Gleichung H n+1 (x)h n 1 (x) 2xH n 1 (x) + 2nHn 1 2 (x) = 0, die anschließend von der ersten Gleichung subtrahiert und mit e x2 wird. Es ergibt sich multipliziert H 2 n(x) 2nH 2 n 1 (x) + 2(n 1)H n 2(x) H n+1 (x)h n 1 (x) = 0 e x2 ( H 2 n (x) 2nH 2 n 1 (x) + 2(n 1)H n 2(x) H n+1 (x)h n 1 (x) ) = 0 e x2 H 2 n(x) 2ne x2 H 2 n 1 (x) + 2(n 1)e x2 H n 2 (x) e x2 H n+1 (x)h n 1 (x) = 0. 12
13 5 Anwendung Integriert man über das Intervall (, ) folgt e x2 H 2 n(x)dx 2n + 2(n 1) = 0 e x2 H 2 n 1 (x)dx e x2 H n 2 (x)dx } {{ } =0,nach (4.2) e x2 H n+1 (x)h n 1 (x)dx } {{ } =0,nach (4.2) e x2 Hn(x)dx 2 = 2n e x2 Hn 1 2 (x)dx. Diese Gleichung n 1 mal auf sich selber angewendet ergibt sich letztendlich e x2 H 2 n(x)dx = 2 n 1 e x2 H1 2 s.o. (x)dx = 2 n π. (4.4) Bemerkung Zusammengefasst ergibt sich aus (4.2) und (4.3) e x2 H m (x)dx = 2 n π δ nm, für alle n, m N 0. Kommen wir abschließend noch kurz zur Anwendung der Hermite-Polynome im letzten Abschnitt. 5 Anwendung Ihre Bedeutung erhalten die Hermite-Polynome durch ihre vielseitige Anwendbarkeit in der Physik. Zum Beispiel werden sie zur Konstruktion der orthonormierten Lösungsfunktionen des quantenmechanischen harmonischen Oszillators benötigt. 13
14 5 Anwendung Ein harmonischer Oszillator ist ein physikalisches System, bei dem die Zeitentwicklung eines der Systemparameter einer Sinusfunktion folgen, also harmonisch schwingen kann und damit der Differentialgleichung ẍ + ω 2 x = 0 genügt. Beispiele für harmonische Oszillatoren sind das Federpendel oder der Schwingkreis. Diese Lösungsfunktionen entsprechen den hermiteschen Funktionen h n, die man aus den Hermite-Polynomen H n durch Multiplikation mit der Gaußschen Normalverteilung erhält. (5.1) Definition (hermitsche Funktionen) Sei n N 0, dann nennt man h n (x) := 1 2 n π e x2 /2 die hermitschen Funktionen. 14
π und die Quadratur des Kreises
 π und die Quadratur des Kreises Schnupper-Uni für SchülerInnen 8. Februar 2006 Dr. Michael Welter http://www.math.uni-bonn.de/people/welter 1 Konstruktionen mit Zirkel und Lineal Gegeben sei eine Menge
π und die Quadratur des Kreises Schnupper-Uni für SchülerInnen 8. Februar 2006 Dr. Michael Welter http://www.math.uni-bonn.de/people/welter 1 Konstruktionen mit Zirkel und Lineal Gegeben sei eine Menge
5 Potenzreihenansatz und spezielle Funktionen
 5 Potenzreihenansatz und spezielle Funktionen In diesem Kapitel betrachten wir eine Methode zur Lösung linearer Differentialgleichungen höherer Ordnung, die sich anwenden läßt, wenn sich alle Koeffizienten
5 Potenzreihenansatz und spezielle Funktionen In diesem Kapitel betrachten wir eine Methode zur Lösung linearer Differentialgleichungen höherer Ordnung, die sich anwenden läßt, wenn sich alle Koeffizienten
cos(kx) sin(nx)dx =?
 3.5 Fourierreihen 3.5.1 Vorbemerkungen cos(kx) sin(nx)dx =? cos gerade Funktion x cos(kx) gerade Funktion sin ungerade Funktion x sin(nx) ungerade Funktion x cos(kx) sin(nx) ungerade Funktion Weil [, π]
3.5 Fourierreihen 3.5.1 Vorbemerkungen cos(kx) sin(nx)dx =? cos gerade Funktion x cos(kx) gerade Funktion sin ungerade Funktion x sin(nx) ungerade Funktion x cos(kx) sin(nx) ungerade Funktion Weil [, π]
Konvergenz im quadratischen Mittel - Hilberträume
 CONTENTS CONTENTS Konvergenz im quadratischen Mittel - Hilberträume Contents 1 Ziel 2 1.1 Satz........................................ 2 2 Endlich dimensionale Vektorräume 2 2.1 Defintion: Eigenschaften
CONTENTS CONTENTS Konvergenz im quadratischen Mittel - Hilberträume Contents 1 Ziel 2 1.1 Satz........................................ 2 2 Endlich dimensionale Vektorräume 2 2.1 Defintion: Eigenschaften
Die Quadratur des Kreises: Transzedenzbeweis von e
 Seminar Analysis III Universität Dortmund / Fachbereich Mathematik Die Quadratur des Kreises: Transzedenzbeweis von e Seminar vom 15.7.213 von Stephan Wolf (136425) Stephan Wolf: 1888s@web.de INHALTSVERZEICHNIS
Seminar Analysis III Universität Dortmund / Fachbereich Mathematik Die Quadratur des Kreises: Transzedenzbeweis von e Seminar vom 15.7.213 von Stephan Wolf (136425) Stephan Wolf: 1888s@web.de INHALTSVERZEICHNIS
Polynomiale Approximation. und. Taylor-Reihen
 Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
Mathematik für Anwender I
 Prof. Dr. H. Brenner Osnabrück WS 2011/2012 Mathematik für Anwender I Vorlesung 17 Potenzreihen Definition 17.1. Es sei (c n ) n N eine Folge von reellen Zahlen und x eine weitere reelle Zahl. Dann heißt
Prof. Dr. H. Brenner Osnabrück WS 2011/2012 Mathematik für Anwender I Vorlesung 17 Potenzreihen Definition 17.1. Es sei (c n ) n N eine Folge von reellen Zahlen und x eine weitere reelle Zahl. Dann heißt
Irrationalzahlen. Freiburger Mathematik Tage vom Dieter Wolke
 Irrationalzahlen Freiburger Mathematik Tage vom 30.09. 0.0.2005 Dieter Wolke. Die rationalen Zahlen, das heißt die gekürzten Brüche r a n mit n N {, 2, 3,...}, a Z {0, ±, ±,...} und a und n teilerfremd,
Irrationalzahlen Freiburger Mathematik Tage vom 30.09. 0.0.2005 Dieter Wolke. Die rationalen Zahlen, das heißt die gekürzten Brüche r a n mit n N {, 2, 3,...}, a Z {0, ±, ±,...} und a und n teilerfremd,
Lösungen der Aufgaben zu Kapitel 9
 Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Taylorentwicklung von Funktionen einer Veränderlichen
 Taylorentwicklung von Funktionen einer Veränderlichen 17. Januar 2013 KAPITEL 1. MATHEMATISCHE GRUNDLAGEN 1 Kapitel 1 Mathematische Grundlagen 1.1 Stetigkeit, Differenzierbarkeit und C n -Funktionen Der
Taylorentwicklung von Funktionen einer Veränderlichen 17. Januar 2013 KAPITEL 1. MATHEMATISCHE GRUNDLAGEN 1 Kapitel 1 Mathematische Grundlagen 1.1 Stetigkeit, Differenzierbarkeit und C n -Funktionen Der
Kleine Formelsammlung zu Mathematik für Ingenieure IIA
 Kleine Formelsammlung zu Mathematik für Ingenieure IIA Florian Franzmann 5. Oktober 004 Inhaltsverzeichnis Additionstheoreme Reihen und Folgen 3. Reihen...................................... 3. Potenzreihen..................................
Kleine Formelsammlung zu Mathematik für Ingenieure IIA Florian Franzmann 5. Oktober 004 Inhaltsverzeichnis Additionstheoreme Reihen und Folgen 3. Reihen...................................... 3. Potenzreihen..................................
April (Voll-) Klausur Analysis I für Ingenieure. Rechenteil
 April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
Analysis I Mathematik für InformatikerInnen II SoSe 12 Musterlösungen zur Prüfungsklausur vom 18. Juli 2012
 Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Faultät II Institut für Mathemati Unter den Linden 6, D-0099 Berlin Prof. Andreas Griewan Ph.D. Dr. Thomas M. Surowiec Dr. Fares Maalouf
Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Faultät II Institut für Mathemati Unter den Linden 6, D-0099 Berlin Prof. Andreas Griewan Ph.D. Dr. Thomas M. Surowiec Dr. Fares Maalouf
Partitionen II. 1 Geometrische Repräsentation von Partitionen
 Partitionen II Vortrag zum Seminar zur Höheren Funktionentheorie, 09.07.2008 Oliver Delpy In diesem Vortrag geht es um Partitionen, also um Aufteilung von natürlichen Zahlen in Summen. Er setzt den Vortrag
Partitionen II Vortrag zum Seminar zur Höheren Funktionentheorie, 09.07.2008 Oliver Delpy In diesem Vortrag geht es um Partitionen, also um Aufteilung von natürlichen Zahlen in Summen. Er setzt den Vortrag
Der Satz von Taylor. Kapitel 7
 Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Legendrepolynome. Sabine Ringkowski. Ausarbeitung zum Vortrag im Proseminar Analysis (Sommersemester 2009, Leitung Prof. Dr.
 Legendrepolynome Sabine Ringkowski Ausarbeitung zum Vortrag im Proseminar Analysis (Sommersemester 2009, Leitung Prof. Dr. Eberhard Freitag) Zusammenfassung: Die folgende Ausarbeitung beschäftigt sich
Legendrepolynome Sabine Ringkowski Ausarbeitung zum Vortrag im Proseminar Analysis (Sommersemester 2009, Leitung Prof. Dr. Eberhard Freitag) Zusammenfassung: Die folgende Ausarbeitung beschäftigt sich
Fourier-Reihen. Definition. Eine auf R definierte Funktion f heißt periodisch mit der Periode T 0, wenn f(x + T ) = f(x) x R.
 Fourier-Reihen Sehr häufig in der Natur begegnen uns periodische Vorgänge, zb beim Lauf der Gestirne am Nachthimmel In der Physik sind Phänomene wie Schwingungen und Wechselströme periodischer Natur Zumeist
Fourier-Reihen Sehr häufig in der Natur begegnen uns periodische Vorgänge, zb beim Lauf der Gestirne am Nachthimmel In der Physik sind Phänomene wie Schwingungen und Wechselströme periodischer Natur Zumeist
Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik II für biw/ciw/mach/mage/vt
 Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. F. Hettlich Dr. S. Schmitt Dipl.-Math. J. Kusch Karlsruhe, den 09.06.20 Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik
Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. F. Hettlich Dr. S. Schmitt Dipl.-Math. J. Kusch Karlsruhe, den 09.06.20 Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik
2.9 Die komplexen Zahlen
 LinAlg II Version 1 3. April 2006 c Rudolf Scharlau 121 2.9 Die komplexen Zahlen Die komplexen Zahlen sind unverzichtbar für nahezu jede Art von höherer Mathematik. Systematisch gehören sie zum einen in
LinAlg II Version 1 3. April 2006 c Rudolf Scharlau 121 2.9 Die komplexen Zahlen Die komplexen Zahlen sind unverzichtbar für nahezu jede Art von höherer Mathematik. Systematisch gehören sie zum einen in
Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13)
 1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
Kapitel 7. Funktionentheorie. 7.1 Holomorphe und harmonische Funktionen. 1. Definitionen
 Kapitel 7 Funktionentheorie In diesem Kapitel geht es meistens um Funktionen, die auf einem Gebiet G C definiert sind und komplexe Werte annehmen. Nach Lust, Laune und Bedarf wird C mit R identifiziert,
Kapitel 7 Funktionentheorie In diesem Kapitel geht es meistens um Funktionen, die auf einem Gebiet G C definiert sind und komplexe Werte annehmen. Nach Lust, Laune und Bedarf wird C mit R identifiziert,
3 Windungszahlen und Cauchysche Integralformeln
 3 3 Windungszahlen und Cauchysche Integralformeln 3. Definition: Sei geschlossener Integrationsweg oder Zyklus mit z 0 C \ Sp. Dann heißt n(, z 0 ) := dz z z 0 Windungszahl (oder: Index, Umlaufszahl) von
3 3 Windungszahlen und Cauchysche Integralformeln 3. Definition: Sei geschlossener Integrationsweg oder Zyklus mit z 0 C \ Sp. Dann heißt n(, z 0 ) := dz z z 0 Windungszahl (oder: Index, Umlaufszahl) von
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
18 Höhere Ableitungen und Taylorformel
 8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
Der harmonische Oszillator anhand eines Potentials
 Quantenmechanikvorlesung, Prof. Lang, SS04 Der harmonische Oszillator anhand eines Potentials Christine Krasser - Tanja Sinkovic - Sibylle Gratt - Stefan Schausberger - Klaus Passler Einleitung In der
Quantenmechanikvorlesung, Prof. Lang, SS04 Der harmonische Oszillator anhand eines Potentials Christine Krasser - Tanja Sinkovic - Sibylle Gratt - Stefan Schausberger - Klaus Passler Einleitung In der
Reihen/Partialsummenfolgen und vollständige Induktion. Robert Klinzmann
 Reihen/Partialsummenfolgen und vollständige Induktion Robert Klinzmann 3. Mai 00 Reihen / Partialsummen 1 Inhaltsverzeichnis 1 Vorwort Das Prinzip der vollständigen Induktion 3 3 Herleitung der Gauß schen
Reihen/Partialsummenfolgen und vollständige Induktion Robert Klinzmann 3. Mai 00 Reihen / Partialsummen 1 Inhaltsverzeichnis 1 Vorwort Das Prinzip der vollständigen Induktion 3 3 Herleitung der Gauß schen
Analysis I. 1. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
6 Der Harmonische Oszillator
 6 Der Harmonische Oszillator Ein Teilchen der Masse m bewege sich auf der x-achse unter dem Einfluß der Rückstellkraft Fx = mω x. 186 Die Kreisfrequenz ω bzw. die Federkonstante k := mω ist neben der Masse
6 Der Harmonische Oszillator Ein Teilchen der Masse m bewege sich auf der x-achse unter dem Einfluß der Rückstellkraft Fx = mω x. 186 Die Kreisfrequenz ω bzw. die Federkonstante k := mω ist neben der Masse
P n (1) P j (1) + ε 2, j=0. P(1) P j (1) + ε 2 < ε. log(1+x) =
 Zu ε > 0 gibt es ein N N mit P n (1) P j (1) < ε/2 für j,n > N, also gilt Es folgt (1 x) n 1 j=n+1 und schließlich mit n x j P n (1) P j (1) (1 x) ε 2 P n (1) P n (x) (1 x) P(1) P(x) (1 x) für x hinreichend
Zu ε > 0 gibt es ein N N mit P n (1) P j (1) < ε/2 für j,n > N, also gilt Es folgt (1 x) n 1 j=n+1 und schließlich mit n x j P n (1) P j (1) (1 x) ε 2 P n (1) P n (x) (1 x) P(1) P(x) (1 x) für x hinreichend
5 Lineare Algebra (Teil 3): Skalarprodukt
 5 Lineare Algebra (Teil 3): Skalarprodukt Der Begriff der linearen Abhängigkeit ermöglicht die Definition, wann zwei Vektoren parallel sind und wann drei Vektoren in einer Ebene liegen. Daß aber reale
5 Lineare Algebra (Teil 3): Skalarprodukt Der Begriff der linearen Abhängigkeit ermöglicht die Definition, wann zwei Vektoren parallel sind und wann drei Vektoren in einer Ebene liegen. Daß aber reale
Leitfaden a tx t
 Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Exponentialabbildung für Matrizen und Systeme von Differentialgleichungen
 Proseminar Lineare Algebra SS10 Exponentialabbildung für Matrizen und Systeme von Differentialgleichungen Simon Strahlegger Heinrich-Heine-Universität Betreuung: Prof. Dr. Oleg Bogopolski Inhaltsverzeichnis:
Proseminar Lineare Algebra SS10 Exponentialabbildung für Matrizen und Systeme von Differentialgleichungen Simon Strahlegger Heinrich-Heine-Universität Betreuung: Prof. Dr. Oleg Bogopolski Inhaltsverzeichnis:
8 Polynominterpolation
 8 Polynominterpolation Interpolations-Aufgabe: Von einer glatten Kurve seien nur lich viele Punktewerte gegeben. Wähle einen lichdimensionalen Funktionenraum. Konstruiere nun eine Kurve in diesem Funktionenraum
8 Polynominterpolation Interpolations-Aufgabe: Von einer glatten Kurve seien nur lich viele Punktewerte gegeben. Wähle einen lichdimensionalen Funktionenraum. Konstruiere nun eine Kurve in diesem Funktionenraum
INGENIEURMATHEMATIK. 8. Reihen. Sommersemester Prof. Dr. Gunar Matthies
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen
 20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
Grundkurs Mathematik II
 Prof. Dr. H. Brenner Osnabrück SS 2017 Grundkurs Mathematik II Vorlesung 53 Die rationalen Exponentialfunktionen Zu einer positiven Zahl b K aus einem angeordenten Körper K haben wir in der 27. Vorlesung
Prof. Dr. H. Brenner Osnabrück SS 2017 Grundkurs Mathematik II Vorlesung 53 Die rationalen Exponentialfunktionen Zu einer positiven Zahl b K aus einem angeordenten Körper K haben wir in der 27. Vorlesung
Die komplexe Exponentialfunktion und die Winkelfunktionen
 Die komplexe Exponentialfunktion und die Winkelfunktionen In dieser Zusammenfassung werden die für uns wichtigsten Eigenschaften der komplexen und reellen Exponentialfunktion sowie der Winkelfunktionen
Die komplexe Exponentialfunktion und die Winkelfunktionen In dieser Zusammenfassung werden die für uns wichtigsten Eigenschaften der komplexen und reellen Exponentialfunktion sowie der Winkelfunktionen
Die Fakultät. Thomas Peters Thomas Mathe-Seiten 13. September 2003
 Die Fakultät Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de 3. September 2003 Dieser Artikel gibt die Definition der klassischen Fakultät und führt von dort aus zunächst zu der Anwendung in Taylor-Reihen
Die Fakultät Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de 3. September 2003 Dieser Artikel gibt die Definition der klassischen Fakultät und führt von dort aus zunächst zu der Anwendung in Taylor-Reihen
Taylor-Entwicklung der Exponentialfunktion.
 Taylor-Entwicklung der Exponentialfunktion. Betrachte die Exponentialfunktion f(x) = exp(x). Zunächst gilt: f (x) = d dx exp(x) = exp(x). Mit dem Satz von Taylor gilt um den Entwicklungspunkt x 0 = 0 die
Taylor-Entwicklung der Exponentialfunktion. Betrachte die Exponentialfunktion f(x) = exp(x). Zunächst gilt: f (x) = d dx exp(x) = exp(x). Mit dem Satz von Taylor gilt um den Entwicklungspunkt x 0 = 0 die
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 22 Algebraische Körpererweiterung Satz 1. Sei K L eine Körpererweiterung und sei f L ein Element. Dann sind folgende Aussagen
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 22 Algebraische Körpererweiterung Satz 1. Sei K L eine Körpererweiterung und sei f L ein Element. Dann sind folgende Aussagen
Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik
 Karlsruher Institut für Technologie Institut für Analysis Dr. I. Anapolitanos Dipl.-Math. Sebastian Schwarz SS 7 4.5.7 Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik
Karlsruher Institut für Technologie Institut für Analysis Dr. I. Anapolitanos Dipl.-Math. Sebastian Schwarz SS 7 4.5.7 Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik
30 Die Gammafunktion und die Stirlingsche Formel
 3 Die Gammafunktion und die Stirlingsche Formel 35 Charakterisierung der Gammafunktion 36 Darstellung der Gammafunktion 38 Beziehung zwischen der Gammafunktion und der Zetafunktion 3 Stirlingsche Formel
3 Die Gammafunktion und die Stirlingsche Formel 35 Charakterisierung der Gammafunktion 36 Darstellung der Gammafunktion 38 Beziehung zwischen der Gammafunktion und der Zetafunktion 3 Stirlingsche Formel
Teil III. Fourieranalysis
 Teil III Fourieranalysis 3 / 3 Fourierreihen Ziel: Zerlegung einer gegebenen Funktion in Schwingungen Konkret: f : (, L) R gegebene Funktion Gesucht: Darstellung der Form ( f (x) = a + a n cos ( n L x)
Teil III Fourieranalysis 3 / 3 Fourierreihen Ziel: Zerlegung einer gegebenen Funktion in Schwingungen Konkret: f : (, L) R gegebene Funktion Gesucht: Darstellung der Form ( f (x) = a + a n cos ( n L x)
2.12 Potenzreihen. 1. Definitionen. 2. Berechnung 2.12. POTENZREIHEN 207. Der wichtigste Spezialfall von Funktionenreihen sind Potenzreihen.
 2.2. POTENZREIHEN 207 2.2 Potenzreihen. Definitionen Der wichtigste Spezialfall von Funktionenreihen sind Potenzreihen. Eine Potenzreihe mit Entwicklungspunkt x 0 ist eine Reihe a n x x 0 n. Es gilt: es
2.2. POTENZREIHEN 207 2.2 Potenzreihen. Definitionen Der wichtigste Spezialfall von Funktionenreihen sind Potenzreihen. Eine Potenzreihe mit Entwicklungspunkt x 0 ist eine Reihe a n x x 0 n. Es gilt: es
Ruprecht-Karls-Universität Heidelberg Mathematisches Institut. Ausarbeitung des Vortrags: Irrationale Zahlen
 Ruprecht-Karls-Universität Heidelberg Mathematisches Institut Ausarbeitung des Vortrags: Irrationale Zahlen Proseminar: Überraschungen und Gegenbeispiele in der reellen Analysis Dr. Gudrun Thäter von Jan
Ruprecht-Karls-Universität Heidelberg Mathematisches Institut Ausarbeitung des Vortrags: Irrationale Zahlen Proseminar: Überraschungen und Gegenbeispiele in der reellen Analysis Dr. Gudrun Thäter von Jan
Modellfall. Orthogonalität trigonometrischer Funktionen. Anwendungen: f : (0, L) R gegeben.
 Modellfall Anwendungen: Fragen: Digitalisierung / digitale Darstellung von Funktionen, insbesondere für Ton- und Bilddaten Digitale Frequenzfilter Datenkompression: Abspeichern der unteren Frequenzen Lösung
Modellfall Anwendungen: Fragen: Digitalisierung / digitale Darstellung von Funktionen, insbesondere für Ton- und Bilddaten Digitale Frequenzfilter Datenkompression: Abspeichern der unteren Frequenzen Lösung
f(x 0 ) = lim f(b k ) 0 0 ) = 0
 5.10 Zwischenwertsatz. Es sei [a, b] ein Intervall, a < b und f : [a, b] R stetig. Ist f(a) < 0 und f(b) > 0, so existiert ein x 0 ]a, b[ mit f(x 0 ) = 0. Wichtig: Intervall, reellwertig, stetig Beweis.
5.10 Zwischenwertsatz. Es sei [a, b] ein Intervall, a < b und f : [a, b] R stetig. Ist f(a) < 0 und f(b) > 0, so existiert ein x 0 ]a, b[ mit f(x 0 ) = 0. Wichtig: Intervall, reellwertig, stetig Beweis.
Übungen zur Theoretischen Physik 1 Lösungen zum Mathe-Test
 Prof. C. Greiner, Dr. H. van Hees Wintersemester 2012/2013 Übungen zur Theoretischen Physik 1 Lösungen zum Mathe-Test Aufgabe 1: Bruchrechnung Lösen Sie die folgenden Gleichungen nach x auf (a) x x 2 1
Prof. C. Greiner, Dr. H. van Hees Wintersemester 2012/2013 Übungen zur Theoretischen Physik 1 Lösungen zum Mathe-Test Aufgabe 1: Bruchrechnung Lösen Sie die folgenden Gleichungen nach x auf (a) x x 2 1
4 Anwendungen des Cauchyschen Integralsatzes
 4 Anwendungen des Cauchyschen Integralsatzes Satz 4. (Cauchysche Integralformel) Es sei f : U C komplex differenzierbar und a {z C; z z 0 r} U. Dann gilt f(a) = z z 0 =r z a dz. a z 0 9 Beweis. Aus dem
4 Anwendungen des Cauchyschen Integralsatzes Satz 4. (Cauchysche Integralformel) Es sei f : U C komplex differenzierbar und a {z C; z z 0 r} U. Dann gilt f(a) = z z 0 =r z a dz. a z 0 9 Beweis. Aus dem
Punktweise Konvergenz stückweise glatter Funktionen. 1 Vorbereitungen
 Vortrag zum Seminar zur Fourieranalysis, 3.10.007 Margarete Tenhaak Im letzten Vortrag wurde die Fourier-Reihe einer -periodischen Funktion definiert. Fourier behauptete, dass die Fourier-Reihe einer periodischen
Vortrag zum Seminar zur Fourieranalysis, 3.10.007 Margarete Tenhaak Im letzten Vortrag wurde die Fourier-Reihe einer -periodischen Funktion definiert. Fourier behauptete, dass die Fourier-Reihe einer periodischen
Das Additionstheorem für die Weierstrass sche -Funktion und elliptische Integrale. Peychyn Lai
 Das Additionstheorem für die Weierstrass sche -Funktion und elliptische Integrale Peychyn Lai 10. Oktober 2007 1 Einleitung Wir haben im letzten Vortrag die Weierstrass sche -Funktion kennengelernt, die
Das Additionstheorem für die Weierstrass sche -Funktion und elliptische Integrale Peychyn Lai 10. Oktober 2007 1 Einleitung Wir haben im letzten Vortrag die Weierstrass sche -Funktion kennengelernt, die
27 Taylor-Formel und Taylor-Entwicklungen
 136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
Analysis III. Teil I. Rückblick auf das letzte Semester. Themen aus dem SS Inhalt der letzten Vorlesung aus dem SS.
 Analysis III für Studierende der Ingenieurwissenschaften Technische Universität Hamburg-Harburg Reiner Lauterbach Teil I Rückblick auf das letzte Semester Fakultät für Mathematik, Informatik und Naturwissenschaften
Analysis III für Studierende der Ingenieurwissenschaften Technische Universität Hamburg-Harburg Reiner Lauterbach Teil I Rückblick auf das letzte Semester Fakultät für Mathematik, Informatik und Naturwissenschaften
x, y 2 f(x)g(x) dµ(x). Es ist leicht nachzuprüfen, dass die x 2 setzen. Dann liefert (5.1) n=1 x ny n bzw. f, g = Ω
 5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
Der Taylorsche Satz Herleitung und Anwendungen
 Der Taylorsche Satz Herleitung und Anwendungen Joachim Schneider Juni 2004 Zusammenfassung Es wird ein enfacher Beweis des Taylorsche Satz über die lokale Approximierbarkeit hinreichend glatter Funktionen
Der Taylorsche Satz Herleitung und Anwendungen Joachim Schneider Juni 2004 Zusammenfassung Es wird ein enfacher Beweis des Taylorsche Satz über die lokale Approximierbarkeit hinreichend glatter Funktionen
Beispiele: Harmonischer Oszillator und Kastenpotential
 Beispiele: Harmonischer Oszillator und Kastenpotential Ramona Wohlleb Mathematische Strukturen der Quantenmechanik Sommersemester 011 1 Der harmonische Oszillator In Analogie zum klassischen harmonischen
Beispiele: Harmonischer Oszillator und Kastenpotential Ramona Wohlleb Mathematische Strukturen der Quantenmechanik Sommersemester 011 1 Der harmonische Oszillator In Analogie zum klassischen harmonischen
Analysis I. Vorlesung 13. Gleichmäßige Stetigkeit
 Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Analysis I Vorlesung 13 Gleichmäßige Stetigkeit Die Funktion f: R + R +, x 1/x, ist stetig. In jedem Punkt x R + gibt es zu jedem ǫ > 0 ein δ > 0 mit f(u (x,δ))
Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Analysis I Vorlesung 13 Gleichmäßige Stetigkeit Die Funktion f: R + R +, x 1/x, ist stetig. In jedem Punkt x R + gibt es zu jedem ǫ > 0 ein δ > 0 mit f(u (x,δ))
Partielle Differentialgleichungen Kapitel 11
 Partielle Differentialgleichungen Kapitel Die Laplace- und Poisson- Gleichungen Die Struktur bei elliptischen Gleichungen zweiter Ordnung ist nicht wesentlich verschieden bei Operatoren mit konstanten
Partielle Differentialgleichungen Kapitel Die Laplace- und Poisson- Gleichungen Die Struktur bei elliptischen Gleichungen zweiter Ordnung ist nicht wesentlich verschieden bei Operatoren mit konstanten
Der Fundamentalsatz der Algebra. 1 Motivation
 Vortrag im Rahmen des Proseminars zur Analysis, 24. April 2006 Micha Bittner Motivation Den ersten des Fundamentalsatzes der Algebra erbrachte C.F. Gauss im Jahr 799 im Rahmen seiner Dissertation. Heute
Vortrag im Rahmen des Proseminars zur Analysis, 24. April 2006 Micha Bittner Motivation Den ersten des Fundamentalsatzes der Algebra erbrachte C.F. Gauss im Jahr 799 im Rahmen seiner Dissertation. Heute
Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung
 Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Dr. Gerhard Mülich Christian Maaß 6.Mai 8 Im letzten Vortrag haben wir gesehen, dass das
Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Dr. Gerhard Mülich Christian Maaß 6.Mai 8 Im letzten Vortrag haben wir gesehen, dass das
Anhang B: Quadratische Irrationalzahlen 1 Reel-quadratische Zahlkörper
 Anhang B: Quadratische Irrationalzahlen 1 Reel-quadratische Zahlkörper Eine reelle Zahl x Q heißt quadratische Irrationalzahl, wenn sie Lösung einer quadratischen Gleichung (1) ax bx c 0, a 0 mit rationalen
Anhang B: Quadratische Irrationalzahlen 1 Reel-quadratische Zahlkörper Eine reelle Zahl x Q heißt quadratische Irrationalzahl, wenn sie Lösung einer quadratischen Gleichung (1) ax bx c 0, a 0 mit rationalen
2 3 x3 17. x k dx = x k x k+1 k +1. Mit jeder weiteren partiellen Integration reduziert sich der Grad des Faktors x n, induktiv erhalten wir also
 Universität Konstanz Fachbereich Mathematik und Statistik Repetitorium Analysis 0 Dr DK Huynh Blatt 8 Aufgabe 6 Bestimmen Sie (a) (x + x 7x+)dx (c) (f) x n exp(x)dx (n N fest) sin (x)dx (g) (b) (d) ln(x)dx
Universität Konstanz Fachbereich Mathematik und Statistik Repetitorium Analysis 0 Dr DK Huynh Blatt 8 Aufgabe 6 Bestimmen Sie (a) (x + x 7x+)dx (c) (f) x n exp(x)dx (n N fest) sin (x)dx (g) (b) (d) ln(x)dx
Vorlesung Mathematik 2 für Ingenieure (Sommersemester 2016)
 1 Vorlesung Mathematik 2 für Ingenieure (Sommersemester 216) Kapitel 11: Potenzreihen und Fourier-Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
1 Vorlesung Mathematik 2 für Ingenieure (Sommersemester 216) Kapitel 11: Potenzreihen und Fourier-Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
Probestudium der Physik 2011/12
 Probestudium der Physik 2011/12 1 Schwingungen und Wellen: Einführung in die mathematischen Grundlagen 1.1 Die Sinus- und die Kosinusfunktion Die Sinusfunktion lässt sich genauso wie die Kosinusfunktion
Probestudium der Physik 2011/12 1 Schwingungen und Wellen: Einführung in die mathematischen Grundlagen 1.1 Die Sinus- und die Kosinusfunktion Die Sinusfunktion lässt sich genauso wie die Kosinusfunktion
REPETITORIUM DER HÖHEREN MATHEMATIK. Gerhard Merziger Thomas Wirth
 REPETITORIUM DER HÖHEREN MATHEMATIK Gerhard Merziger Thomas Wirth 6 INHALTSVERZEICHNIS Inhaltsverzeichnis Fl Formelsammlung F2 Formelsammlung Alphabete 11 Zeichenindex 12 1 Grundbegriffe 14 1.1 Logische
REPETITORIUM DER HÖHEREN MATHEMATIK Gerhard Merziger Thomas Wirth 6 INHALTSVERZEICHNIS Inhaltsverzeichnis Fl Formelsammlung F2 Formelsammlung Alphabete 11 Zeichenindex 12 1 Grundbegriffe 14 1.1 Logische
Klausur Analysis II
 WS 28/9 Prof. Dr. John M. Sullivan Kerstin Günther Technische Universität Berlin Fakultät II Institut für Mathematik Klausur Analysis II 6.2.28 Name: Vorname: Matr.-Nr.: Studiengang: Mit der Veröffentlichung
WS 28/9 Prof. Dr. John M. Sullivan Kerstin Günther Technische Universität Berlin Fakultät II Institut für Mathematik Klausur Analysis II 6.2.28 Name: Vorname: Matr.-Nr.: Studiengang: Mit der Veröffentlichung
13 Die trigonometrischen Funktionen
 13 Die trigonometrischen Funktionen Wir schreiben die Werte der komplexen Exponentialfunktion im Folgenden auch als e z = exp(z) (z C). Geometrisch definiert man üblicherweise die Werte der Winkelfunktion
13 Die trigonometrischen Funktionen Wir schreiben die Werte der komplexen Exponentialfunktion im Folgenden auch als e z = exp(z) (z C). Geometrisch definiert man üblicherweise die Werte der Winkelfunktion
und Unterdeterminante
 Zusammenfassung: Determinanten Definition: Entwicklungssätze: mit und Unterdeterminante (streiche Zeile i & Spalte j v. A, bilde dann die Determinante) Eigenschaften v. Determinanten: Multilinearität,
Zusammenfassung: Determinanten Definition: Entwicklungssätze: mit und Unterdeterminante (streiche Zeile i & Spalte j v. A, bilde dann die Determinante) Eigenschaften v. Determinanten: Multilinearität,
Meromorphe Funktionen
 Kapitel Meromorphe Funktionen Der Satz von Mittag-Leffler Zur Erinnerung: Die holomorphe Funktion f habe in z 0 C eine isolierte Singularität. Liegt eine Polstelle vor, so gibt es eine offene Umgebung
Kapitel Meromorphe Funktionen Der Satz von Mittag-Leffler Zur Erinnerung: Die holomorphe Funktion f habe in z 0 C eine isolierte Singularität. Liegt eine Polstelle vor, so gibt es eine offene Umgebung
Maclaurinsche Reihe 1-E1. Ma 2 Lubov Vassilevskaya
 Maclaurinsche Reihe 1-E1 Colin Maclaurin Colin Maclaurin (1698-1746), schottischer Mathematiker, der Erfinder der nach ihm benannten Maclaurinschen Reihe und Mitentwickler der Euler-Maclaurin-Formel. 1-E
Maclaurinsche Reihe 1-E1 Colin Maclaurin Colin Maclaurin (1698-1746), schottischer Mathematiker, der Erfinder der nach ihm benannten Maclaurinschen Reihe und Mitentwickler der Euler-Maclaurin-Formel. 1-E
Exponentialreihe von Matrizen
 Exponentialreihe von Matrizen Seminar zur Vorlesung "Geometrie für Lehramt" Sommersemester 20 Dozent: Prof. Dr. Lorenz Schwachhöfer Fakultät für Mathematik der Technischen Universität Dortmund Name: Kerstin
Exponentialreihe von Matrizen Seminar zur Vorlesung "Geometrie für Lehramt" Sommersemester 20 Dozent: Prof. Dr. Lorenz Schwachhöfer Fakultät für Mathematik der Technischen Universität Dortmund Name: Kerstin
Potenzreihenentwicklung im Reellen und Komplexen
 Potenzreihenentwicklung im Reellen und Komplexen Christoph Lassnig 26. Januar 20 Zusammenfassung Dieses Dokument bietet einen kleinen Überblick über Potenzreihen, sowie auf ihnen aufbauenden Sätzen und
Potenzreihenentwicklung im Reellen und Komplexen Christoph Lassnig 26. Januar 20 Zusammenfassung Dieses Dokument bietet einen kleinen Überblick über Potenzreihen, sowie auf ihnen aufbauenden Sätzen und
Kapitel 3: Die Sätze von Euler, Fermat und Wilson. 8 Der Satz von Euler
 Kapitel 3: Die Sätze von Euler, Fermat und Wilson In diesem Kapitel wollen wir nun die eulersche -Funktion verwenden, um einen berühmten Satz von Euler zu formulieren, aus dem wir dann mehrere interessante
Kapitel 3: Die Sätze von Euler, Fermat und Wilson In diesem Kapitel wollen wir nun die eulersche -Funktion verwenden, um einen berühmten Satz von Euler zu formulieren, aus dem wir dann mehrere interessante
Kapitel 1. Holomorphe Funktionen
 Kapitel 1 Holomorphe Funktionen Zur Erinnerung: I IR sei ein offenes Intervall, und sei z 0 I. Eine Funktion f : I IR heißt differenzierbar in z 0, falls der Limes fz fz 0 lim =: f z 0 z z 0 z z 0 existiert.
Kapitel 1 Holomorphe Funktionen Zur Erinnerung: I IR sei ein offenes Intervall, und sei z 0 I. Eine Funktion f : I IR heißt differenzierbar in z 0, falls der Limes fz fz 0 lim =: f z 0 z z 0 z z 0 existiert.
Aufgabe 1 Zeigen Sie mittels vollständiger Induktion, dass für alle n N. n(n + 1)(2n + 1) 6. j 2 = gilt.
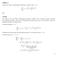 Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Konvergenz im quadratischen Mittel und Parsevalsche Gleichung
 Konvergenz im quadratischen Mittel und Parsevalsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Prof Dr Picard, gehalten von Helena Malinowski In vorhergehenden Vorträgen und dazugehörigen
Konvergenz im quadratischen Mittel und Parsevalsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Prof Dr Picard, gehalten von Helena Malinowski In vorhergehenden Vorträgen und dazugehörigen
3.1.3 Newtonsche Interpolationsformel / Dividierte Differenzen
 KAPITEL 3 INTERPOLATION UND APPROXIMATION 4 33 Newtonsche Interpolationsformel / Dividierte Differenzen Das Verfahren von Neville ist unpraktisch, wenn man das Polynom selbst sucht oder das Polynom an
KAPITEL 3 INTERPOLATION UND APPROXIMATION 4 33 Newtonsche Interpolationsformel / Dividierte Differenzen Das Verfahren von Neville ist unpraktisch, wenn man das Polynom selbst sucht oder das Polynom an
10 Potenz- und Fourierreihen
 10 Potenz- und Fourierreihen 10.1 Konvergenzbegriffe für Funktionenfolgen Im letzten Kapitel soll es noch einmal um eindimensionale Analysis gehen. Speziell werden wir uns mit Folgen und Reihen reeller
10 Potenz- und Fourierreihen 10.1 Konvergenzbegriffe für Funktionenfolgen Im letzten Kapitel soll es noch einmal um eindimensionale Analysis gehen. Speziell werden wir uns mit Folgen und Reihen reeller
Kapitel 5. Die trigonometrischen Funktionen Die komplexen Zahlen Folgen und Reihen in C
 Kapitel 5. Die trigonometrischen Funktionen 5.1. Die komplexen Zahlen 5.. Folgen und Reihen in C 5.10. Definition. Eine Folge (c n n N komplexer Zahlen heißt konvergent gegen c C, falls zu jedem ε > 0
Kapitel 5. Die trigonometrischen Funktionen 5.1. Die komplexen Zahlen 5.. Folgen und Reihen in C 5.10. Definition. Eine Folge (c n n N komplexer Zahlen heißt konvergent gegen c C, falls zu jedem ε > 0
Höhere Mathematik II für die Fachrichtung Physik. Lösungsvorschläge zum 11. Übungsblatt
 Institut für Analysis SS17 PD Dr. Peer Christian Kunstmann 7.7.17 Dipl.-Math. Leonid Chaichenets, Johanna Richter, M.Sc. Tobias Ried, M.Sc., Tobias Schmid, M.Sc. Höhere Mathematik II für die Fachrichtung
Institut für Analysis SS17 PD Dr. Peer Christian Kunstmann 7.7.17 Dipl.-Math. Leonid Chaichenets, Johanna Richter, M.Sc. Tobias Ried, M.Sc., Tobias Schmid, M.Sc. Höhere Mathematik II für die Fachrichtung
Implizite Funktionen. Ist für eine stetig differenzierbare Funktion f : R n R m R n. so lässt sich das Gleichungssystem
 Implizite Funktionen Ist für eine stetig differenzierbare Funktion f : R n R m R n f (x, y ) = (0,..., 0) t, det f x (x, y ) 0, so lässt sich das Gleichungssystem f k (x 1,..., x n, y 1,..., y m ) = 0,
Implizite Funktionen Ist für eine stetig differenzierbare Funktion f : R n R m R n f (x, y ) = (0,..., 0) t, det f x (x, y ) 0, so lässt sich das Gleichungssystem f k (x 1,..., x n, y 1,..., y m ) = 0,
1 Das Additionstheorem und Folgerungen
 Das Additionstheorem der -Funktion und elliptische Kurven Vortrag zum Seminar zur Funktionentheorie, 05.11.2007 Cornelia Wirtz Ziel dieses Vortrages ist es, das Additionstheorem der Weierstraß schen -Funktion
Das Additionstheorem der -Funktion und elliptische Kurven Vortrag zum Seminar zur Funktionentheorie, 05.11.2007 Cornelia Wirtz Ziel dieses Vortrages ist es, das Additionstheorem der Weierstraß schen -Funktion
3 Lineare Differentialgleichungen
 3 Lineare Differentialgleichungen In diesem Kapitel behandeln wir die allgemeine Theorie linearer Differentialgleichungen Sie werden zahlreiche Parallelen zur Theorie linearer Gleichungssysteme feststellen,
3 Lineare Differentialgleichungen In diesem Kapitel behandeln wir die allgemeine Theorie linearer Differentialgleichungen Sie werden zahlreiche Parallelen zur Theorie linearer Gleichungssysteme feststellen,
Algebraische und transzendente Zahlen -zum Beispiel und π ( Wurzel aus 2 und Pi )
 Algebraische und transzendente Zahlen -zum Beispiel und π ( Wurzel aus 2 und Pi ) π-tag Universität Bozen-Bolzano 13. März 2015 Franz Pauer Universität Innsbruck Institut für Fachdidaktik und Institut
Algebraische und transzendente Zahlen -zum Beispiel und π ( Wurzel aus 2 und Pi ) π-tag Universität Bozen-Bolzano 13. März 2015 Franz Pauer Universität Innsbruck Institut für Fachdidaktik und Institut
Über Potenzsummenpolynome
 Über Potenzsuenpolynoe Jörg Feldvoss I Sande 4b, D-21369 Nahrendorf Gerany Einleitung Für jede natürliche Zahl n bezeichnen wir it P n das n-te Potenzsuenpolyno, welches dadurch gegeben ist, dass es für
Über Potenzsuenpolynoe Jörg Feldvoss I Sande 4b, D-21369 Nahrendorf Gerany Einleitung Für jede natürliche Zahl n bezeichnen wir it P n das n-te Potenzsuenpolyno, welches dadurch gegeben ist, dass es für
11. Folgen und Reihen.
 - Funktionen Folgen und Reihen Folgen Eine Folge reeller Zahlen ist eine Abbildung a: N R Statt a(n) für n N schreibt man meist a n ; es handelt sich also bei einer Folge um die Angabe der Zahlen a, a
- Funktionen Folgen und Reihen Folgen Eine Folge reeller Zahlen ist eine Abbildung a: N R Statt a(n) für n N schreibt man meist a n ; es handelt sich also bei einer Folge um die Angabe der Zahlen a, a
Lösungsvorschläge zum 4. Übungsblatt, WS 2012/2013 Höhere Mathematik III für die Fachrichtung Physik
 Lösungsvorschläge zum 4. Übungsblatt, WS 202/203 Höhere Mathematik III für die Fachrichtung Physik Aufgabe 6 Bei allen Aufgabenteilen handelt es sich um (homogene bzw. inhomogene) lineare Differentialgleichungen
Lösungsvorschläge zum 4. Übungsblatt, WS 202/203 Höhere Mathematik III für die Fachrichtung Physik Aufgabe 6 Bei allen Aufgabenteilen handelt es sich um (homogene bzw. inhomogene) lineare Differentialgleichungen
1 Einführung, Terminologie und Einteilung
 Zusammenfassung Kapitel V: Differentialgleichungen 1 Einführung, Terminologie und Einteilung Eine gewöhnliche Differentialgleichungen ist eine Bestimmungsgleichung um eine Funktion u(t) einer unabhängigen
Zusammenfassung Kapitel V: Differentialgleichungen 1 Einführung, Terminologie und Einteilung Eine gewöhnliche Differentialgleichungen ist eine Bestimmungsgleichung um eine Funktion u(t) einer unabhängigen
2 Die komplexen Zahlen als reeller Vektorraum
 Erik Werner Algebraizität und Transzendenz 1 Humboldt-Universität zu Berlin Institut für Mathematik Berufsbezogenes Fachseminar - Zahlentheorie Dozent: Prof. Dr. Jürg Kramer WS 14/15, 8.12.14 Referent:
Erik Werner Algebraizität und Transzendenz 1 Humboldt-Universität zu Berlin Institut für Mathematik Berufsbezogenes Fachseminar - Zahlentheorie Dozent: Prof. Dr. Jürg Kramer WS 14/15, 8.12.14 Referent:
Die Gamma-Funktion, das Produkt von Wallis und die Stirling sche Formel. dt = lim. = lim = Weiters erhalten wir durch partielle Integration, dass
 Die Gamma-Funktion, das Produkt von Wallis und die Stirling sche Formel Zuerst wollen wir die Gamma-Funktion definieren, die eine Verallgemeinerung von n! ist. Dazu benötigen wir einige Resultate. Lemma.
Die Gamma-Funktion, das Produkt von Wallis und die Stirling sche Formel Zuerst wollen wir die Gamma-Funktion definieren, die eine Verallgemeinerung von n! ist. Dazu benötigen wir einige Resultate. Lemma.
10 Differenzierbare Funktionen
 10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
c < 1, (1) c k x k0 c k = x k0
 4.14 Satz (Quotientenkriterium). Es sei (x k ) Folge in K. Falls ein k 0 existiert, so dass für k k 0 gilt x k 0 und x k+1 x k c < 1, (1) so ist x k absolut konvergent. Beweis. Aus (1) folgt mit vollständiger
4.14 Satz (Quotientenkriterium). Es sei (x k ) Folge in K. Falls ein k 0 existiert, so dass für k k 0 gilt x k 0 und x k+1 x k c < 1, (1) so ist x k absolut konvergent. Beweis. Aus (1) folgt mit vollständiger
4.4 Hermitesche Formen
 44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
4.1 Grundlegende Konstruktionen Stetigkeit von Funktionen Eigenschaften stetiger Funktionen... 91
 Kapitel 4 Funktionen und Stetigkeit In diesem Kapitel beginnen wir Funktionen f : R R systematisch zu untersuchen. Dazu bauen wir auf den Begriff des metrischen Raumes auf und erhalten offene und abgeschlossene
Kapitel 4 Funktionen und Stetigkeit In diesem Kapitel beginnen wir Funktionen f : R R systematisch zu untersuchen. Dazu bauen wir auf den Begriff des metrischen Raumes auf und erhalten offene und abgeschlossene
Approximation von Funktionen
 von Funktionen Fakultät Grundlagen Februar 6 Fakultät Grundlagen von Funktionen Übersicht Problemstellung Taylorpolynom Taylorenreihe Zusammenhang von e-funktion und trigonometrischen Funktionen 3 Fakultät
von Funktionen Fakultät Grundlagen Februar 6 Fakultät Grundlagen von Funktionen Übersicht Problemstellung Taylorpolynom Taylorenreihe Zusammenhang von e-funktion und trigonometrischen Funktionen 3 Fakultät
Analysis I. 4. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 4. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine bijektive Abbildung f: M N. () Ein
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 4. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine bijektive Abbildung f: M N. () Ein
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Fourier-Reihen. Thomas Peters Thomas Mathe-Seiten 1. Dezember 2004
 Fourier-Reihen Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de. Dezember 4 Dieser Artikel gibt eine elementare Einführung in die Theorie der Fourier-Reihen. Er beginnt mit einer kurzen Analyse des
Fourier-Reihen Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de. Dezember 4 Dieser Artikel gibt eine elementare Einführung in die Theorie der Fourier-Reihen. Er beginnt mit einer kurzen Analyse des
Der quantenmechanische harmonische Oszillator
 88 Kapitel 0 Der quantenmechanische harmonische Oszillator In diesem Kapitel befassen wir uns mit den quantenmechanischen Eigenschaften eines der grundlegenden Modelle der Physik, dem harmonischen Oszillator.
88 Kapitel 0 Der quantenmechanische harmonische Oszillator In diesem Kapitel befassen wir uns mit den quantenmechanischen Eigenschaften eines der grundlegenden Modelle der Physik, dem harmonischen Oszillator.
Taylor-Entwicklungen und Taylor-Polynome.
 Taylor-Entwicklungen und Taylor-Polynome. Ausgangsfrage: Wie kann manf(x) in der Nähe vonx 0 approximieren? 0. Antwort:f(x) f(x 0 ) fürx x 0. 1. Antwort: Ist f differenzierbar, so gilt f(x) = f(x 0 )+f
Taylor-Entwicklungen und Taylor-Polynome. Ausgangsfrage: Wie kann manf(x) in der Nähe vonx 0 approximieren? 0. Antwort:f(x) f(x 0 ) fürx x 0. 1. Antwort: Ist f differenzierbar, so gilt f(x) = f(x 0 )+f
