Prof. Dr. Wolfgang Konen Mathematik 2, SS
|
|
|
- Edith Bachmeier
- vor 5 Jahren
- Abrufe
Transkript
1 Prof. Dr. Wolfgag Ko Mathmatk, SS Komplx Zahl Dr kürst Wg wsch w Wahrht m Rll führt übr das Komplx. [Jacus Hadamard, fra. Mathmatkr, ] Am Afag stad w so oft b wssschaftlch Etdckug d Nchtlösbarkt s Problms. D Nchtlösbarkt bstmmtr algbraschr Glchug hatt scho vorhr oft ur schrttws Erwtrug usrs Zahlbgrffs gführt: x + = 0 cht lösbar N, führt auf Z. x 5x = 0 cht lösbar Z, führt auf Q. x = /5 x = 0 cht lösbar Q, führt auf R. x x + = 0 cht lösbar R. x??? D komplx Zahl rlaub s, solch Glchug ud w wr sh wrd auch all algbrasch Glchug u lös... Dfto ud Darstllug komplxr Zahl Ausghd vo dr Glchug x 0 bw. x führ wr formal d Lösug x,. Df D -: magär Eht D magär Eht wrd durch dfrt. D Rchgst um Wurlh dürf NICHT allgm auf gatv Zahl übrtrag wrd: Bspl ur Warug:??? ( )( )???? RICHTIG: Mt als Symbol rch, für das glt, NICHT durch rst. Amrkug: I dr Elktrotchk wählt ma auch oft j als Bchr für d magär Eht, damt ma cht mt dm Symbol für d Strom (I, ) Koflkt kommt. Df D - Das Produkt b magär ud komplx Zahl b b r rll Zahl b mt dr magär Eht, hßt magär Zahl. ) D Summ r rll Zahl a ud r magär Zahl b st komplx Zahl: a b a hßt Raltl, b Imagärtl vo : ) D komplx Zahl R( ) a, Im() b. * a b hßt d u kojugrt-komplx Zahl. W. Ko ZD-MathSS-xt.docx St 79
2 Prof. Dr. Wolfgag Ko Mathmatk, SS ) D Mg C { a b;a, b R} hßt Mg dr komplx Zahl. Am.: D magär Zahl =b löst d Glchug = b, d (b)(b) = b = b. Bspl komplxr Zahl:, 5 7,, jd rll Zahl (s.u.). Df D - Rch mt komplx Zahl Für komplx Zahl =a +b ud =a +b glt d folgd Rchoprato: ) Glchht: a a b b ) Addto: a a (b b ) ) Multplkato: a a b b a b a b Bgrüdug Vorlsug! Für d komplx Addto ud Multplkato glt w für d rll Zahl das Kommutatvgst, das Assoatvgst ud das Dstrbutvgst (Bws durch Nachrch!) Mt komplx Zahl, dr Imagärtl 0 st, wrd w mt rll Zahl grcht: (a (a 0) (a 0) (a 0) (a 0) (a a a ) 0 ) 0 S lass sch dahr mt d rll Zahl dtfr; ma läßt 0 wg ud schrbt kur a statt a 0. I dsm S st R Tlmg vo C. Sat S - Btrag ) Das Produkt r komplx Zahl mt hrr kojugrt-komplx Zahl * st r rll: (a b)(a b) a b (ab ab) a b ) D Wurl aus dsm Produkt t ma d Btrag dr komplx Zahl: a b W. Ko ZD-MathSS-xt.docx St 80
3 Prof. Dr. Wolfgag Ko Mathmatk, SS Sat S - Subtrakto ud Dvso komplxr Zahl Für komplx Zahl =a +b ud =a +b glt: ) Es gbt C gau utrals Elmt dr Addto: 0 0, für das glt: C ) Zu jdr Zahl C gbt s gau vrss Elmt dr Addto = a b, für das glt: + ( ) =. Utr dr Subtrakto vrstht ma d Addto mt dm vrs Elmt: (a a ) (b b ) ) Es gbt C gau utrals Elmt dr Multplkato: E 0, für das glt: E C 4) Zu jdr Zahl C, 0+0, gbt s gau vrss Elmt dr Multplkato a b, für das glt: E. a Dvso: b a a a b b a b a b 0 b b a Bws Vorlsug! [odr Stgl, S. 09f] Sat S - Mrkrgl Subtrakto ud Dvso Für komplx Zahl =a +b ud =a +b glt: ) Zw komplx Zahl wrd subtrahrt, dm ma hr Ral- ud Imagärtl subtrahrt: (a a ) (b b ) ) Um durch komplx Zahl 0 u dvdr, muss ma d Bruch mt hrr kojugrt-komplx Zahl rwtr, damt dr Nr rll wrd (k mhr thält): * * Mrkrgl für Dvso wrd Vorlsug vorgrcht. Übug: Brch S ( )? 4? 4?.. Gaußsch Zahlb W. Ko ZD-MathSS-xt.docx St 8
4 Prof. Dr. Wolfgag Ko Mathmatk, SS Da komplx Zahl durch d Agab wr rllr Zahl dutg fstglgt wrd, lass sch d komplx Zahl d Pukt dr Eb, d.h. ds Vktorraums R uord: x yp() (x, y) D tsprchd graphsch Darstllug hßt Gaußsch Zahlb odr komplx Eb: Im() y r = x + y x R() I Aalog u d Polarkoordat ka d komplx Zahl Läg ds Pfls ud Wkl dargstllt wrd. Mt Hlf dr Trasformatosglchug: rgbt sch: x r cos,y r s x y r cos s x y auch durch d Mt Hlf dr Eulrsch Forml läßt sch ds Darstllug och bträchtlch vrfach: Sat S -4 Eulrsch Forml Für jd rll Zahl glt: cos s. Bws Vorlsug. Mt dsr Forml folgt d sogat Expotalform: r mt r x y ud ta = y x Df D -4: Darstllugsform komplxr Zahl. Algbrasch odr kartssch Form x y x R() y Im(). Trgoomtrsch Form W. Ko ZD-MathSS-xt.docx St 8
5 Prof. Dr. Wolfgag Ko Mathmatk, SS rcos s mt r R() Im(), ta Im() R(). Expotalform r r hßt Btrag, hßt Phas (odr Argumt odr Wkl) vo. Bd Form. ud. t ma auch Polarform. Amrkug:. Mt dm Wkl st auch k für jds gaahlg k Phas vo, d.h. d Phas st prodsch mt dr Prod. Isbsodr glt 0. Dr sog. Hauptwrt dr Phas lgt vor, w ], ].. Jd komplx Zahl hat R d Btrag (d Läg). 4. D Umrchug Polarform kartssch Form st fach: Eulrsch Forml but, Ral- ud Imagärtl ausrch. 5. B dr Umrchug kartssch Form Polarform muss ma b dr Ermttlug dr Phas aufpass. Ma rhält Abhäggkt vom Quadrat: y. odr 4. Quadrat: arcta x. odr. Quadrat: arcta I Vorlsug wrd d Forml für d. Quadrat (y>0, x<0) hrgltt [Papula, Bd., S. 00] y x I vl Programmbblothk (C, C++, Java, Matlab) st ds umfassdr Dfto ds Arcus Tags übr ata(y,x) ]-,] vrfügbar, d glch d obg Fallutrschdug macht: Bspl: ) x R(), y Im() Da dr Raltl gatv ud dr Imagärtl postv st, lgt d Zahl m. Quadrat. Für Btrag ud Phas folgt: o r 4 4, arcta 0 4 cos s o W. Ko ZD-MathSS-xt.docx St 8
6 Prof. Dr. Wolfgag Ko Mathmatk, SS ) 5 / 6 x R() cos(5 / 6).5, y Im() s(5 / 6).598 Übug: Rch S vo = x + y wdr urück auf r ud. Sat S -5 Für d Multplkato ud Dvso wr komplxr Zahl r, r dr Expotalform glt: r r Zw komplx Zahl wrd multplrt, dm ma d Bträg multplrt ud d Phas addrt. r r Zw komplx Zahl wrd dvdrt, dm ma d Bträg dvdrt ud d Phas subtrahrt. Bws durch Nachrch mt trgoomtrschr Form >> Hausaufgab. Amrkug:. Efach Mrkrgl: "Wd auf d üblch Potgst a!".. I dr trgoomtrsch Form rgb sch d aalog Rgl durch Awdug dr Eulrsch Forml.. Aus dr Expotalform dr Multplkato tmmt ma, daß d Multplkato mt r komplx Zahl gomtrsch r Strckug um d Btrag dr Zahl ud r Drhug um d Phaswkl tsprcht, ds t ma auch Drhstrckug. Java-Applt ur Drhstrckug: GUIComplxPla.htm.lk... Schwgug als komplx Zahl Drht ma d Zgr r komplx Zahl A A um d Ursprug, so lässt sch t ( t ) das durch (t) A A bschrb. Vo dr St btrachtt sh wr d Imagärtl y(t), dr susförmg Schwgug bschrbt. (Es glt (t)=x(t)+y(t).) Mt (t) lässt sch vlfach bssr rch als mt y(t). Z.B. ka ma (t) gfahrlos d Nr schrb, d s wrd Null (!), m Ggsat u y(t). E oft buttr Trck: Rll Fukto durch komplx Erwtrug rst, damt rch, um Schluss vom Ergbs ur d Raltl hm. Ist b vl Problm dr Elktrotchk ud dr Quatmchak fachr als r rll Rchug. (Wr rr a Hadamard: Dr kürst Wg wsch w Wahrht m Rll führt übr das Komplx.) Zw Zgr lass sch komplx addr, ud hlf so, komplrtr Schwgugsphäom darustll: W. Ko ZD-MathSS-xt.docx St 84
7 Prof. Dr. Wolfgag Ko Mathmatk, SS (t) A (t) A ω t ω 4A t A t 8ωt (t) (t) (t).. Pot komplxr Zahl bdutt " mal mal ". I dr Expotaldarstllug Aufgab ur Motvato: bdutt "mal", dass ma d Phas addr muss, d Bträg multplr. Btracht S also komplx Zahl vom Btrag. D Pot vo hab also auch d Btrag (klar?) Übrlg S graphsch m Zgrdagramm: Für wlch Phas glt, wa also addr sch glch Phas u Gsamtphas 0? Zch S d Zgr dr Gauss'sch Zahlb! W sht's aus für 4, für?... Pot mt rll Expot Zur Brchug vo Pot, Wurl ud Logarthm wrd d Expotalform mt k sämtlch Phas bötgt, d.h. r. Wd wr u d aus dr rll Rchug bkat Gst aalogr Ws a, kö Pot w folgt brcht wrd: c k c c ckc r r D Brückschtgug dr Prod st otwdg, da ma all Fäll d c k atürlch Zahl st, mhr als Lösug rhält. Gomtrsch hab all Pot d glch Btrag. D Spt dr ughörg Pfl lg all auf m Krs vom Radus c r. D Phas (bw. Wkl) utrschd sch um c. Spalfäll.) c st ga Zahl. Da st kc k wdr gaahlgs Vlfachs vo ud all Wkl fall usamm. I dsm Fall gbt s ur Lösug: r Bspl Vorlsug W. Ko ZD-MathSS-xt.docx St 85
8 Prof. Dr. Wolfgag Ko Mathmatk, SS Dr achfolgd Sat lfrt kompakt Zusammfassug vlr trgoomtrschr Addtosthorm: Sat S -6 (Sat vo Movr) cos s cos s Bw: folgt drkt aus d Potrchrgl ud dr Eulrsch Forml (Sat S -4). Übug: But S d Sat vo Movr, um d Addtosthorm für cos() ud s() hrult. Übug: Lt S d "ormal" Addtosthorm cos( ) coscos s s s( ) s cos coss aus dr Eulrsch Forml (Sat S -4) hr. Lösug d Übug..) c st dr Khrwrt r ga Zahl : c. Wr woll also d -t Wurl r k komplx Zahl bstmm: r. All Wurl lg auf m Krs mt dm Radus r. Ihr Wkl utrschd sch jwls um. Ma rhält für k 0,,,...( ) sgsamt vrschd Lösug, d für k = rgbt sch wdr d Lösug u k = 0. Bspl: Bstmmug dr drtt Wurl dr Zahl : 0,, 0 k k cos s cos4 s , k 0,, Übug: Zch S d komplx Zahl 0, ud dr komplx Zahlb. Wlch Wkl Grad schlß s mt dr x-achs? D Glchug f (a) a 0 bstt also komplx Lösug für a. W. Ko ZD-MathSS-xt.docx St 86
9 Prof. Dr. Wolfgag Ko Mathmatk, SS p.) c st ratoal Zahl. Wr kö ahm, dass c mt tlrfrmd Zahl p ud st. I dsm Fall rgät ma ach dm p-potr Faktor k ud s rgb sch vrschd Lösug: c r p p r p r pk p p k k c r c mt k 0,,..,( ) Bspl: k 5 k' 5 k' mt k 0,, 4.) c st rratoal Zahl. I dsm Fall st k gaahlgs Vlfachs vo c ga Zahl, dahr st für k gaahlgs k d Größ kc Vlfachs vo. Es gbt c dahr udlch vl Lösug, d all auf dm Krs mt dm Radus r lg.... Fudamtalsat dr Algbra W wr.) gsh hab, bstt d Glchug glt sogar wstlch mhr: a also komplx Lösug. Es Sat S -7 Fudamtalsat dr Algbra E algbrasch Glchug -t Grads (N) P () a a... a a0 0 W. Ko ZD-MathSS-xt.docx St 87
10 Prof. Dr. Wolfgag Ko Mathmatk, SS mt komplx Kofft a j bstt dr Mg C dr komplx Zahl gau "Lösug",,..., d.h. das Polyom P läßt sch w folgt Larfaktor rlg: P () a... Amrkug:. D,,... müss cht all vrschd s, dshalb "Lösug" Aführugsstrch.. Dsr Sat gt, dass mach Dg m Komplx fachr sd! Für rlls Polyom ka s k,, w,..., vl Lösug gb (d.h. vl lästg Fallutrschdug sd u bacht). Im Komplx gbt s mmr Larfaktor.. Folgrug: Jds Polyom P () mt hat mdsts C als Lösug. 4. Dr Sat st fach aufuschrb, abr xtrm schwr u bws. Bspl: Das Polyom P ( ) rfällt d rll Zahl offschtlch cht Larfaktor, da d Glchug 4 0 k rll Lösug hat. I d komplx Zahl läßt sch P w folgt rlg: 4 ( )( )( ) P () 4 4 Übug: Wlch, C lös d Glchug (4 ) Bstmm S d Lösug mt dr Mthod dr uadratsch Ergäug. Braucht ma ach N Z Q R C och größr Zahlkörpr als C? N, d d komplx Zahl C bld "algbrasch abgschloss" Körpr. D dr Fudamtalsat dr Algbra bsagt: "Jds Polyom mt komplx Kofft ud Grad größr 0 hat Nullstll C." Mt adr Wort: Währd s b d adr Zahlkörpr mmr och Polyomglchug übr dm Zahlkörpr gab, d cht lösbar war, gbt s jtt solch Glchug cht mhr: x + = 0 cht lösbar N, führt auf Z. x 5x = 0 cht lösbar Z, führt auf Q. x = /5 x = 0 cht lösbar Q, führt auf R. x x + = 0 cht lösbar R, führt auf C. x a x + a - x a 0 =0 lösbar C für all a C (!!) W. Ko ZD-MathSS-xt.docx St 88
11 Prof. Dr. Wolfgag Ko Mathmatk, SS Wso komplx Zahl "schö" sd: Awdugsfall Fraktal D Natur st komplx, d.h. vlgstaltg. Dr Msch vrsucht s durch möglchst fach Gst u bschrb. Mt dm vo Bot Madlbrot gführt Bgrff dr Fraktal hab d Mathmatkr twas twcklt, was aus fach Gst rstaulch komplx Mustr hrvorbrgt. E wchtg Roll spl dab d komplx Zahl. Btracht S d fach Rkurso 0 c mt,c C 0 Jtt stll wr ur d fach Frag: Für wlch c blbt d Folg bschräkt? 6 Ma mag rwart, dass rgd glatts Gbt dr komplx Eb d Atwort st. D Atwort st abr wstlch komplxr ud führt auf d Madlbrot-Mg, d auch utr dm Nam "Apflmäch" bkat st. Das Gbt st am Rad rfrast, mmr wdr tauch kovrgt Isl m dvrgt Mr auf ud vor allm: Das Mustr st slbstählch, d.h. s thält a vl Stll ählch vrklrtr Kop sr slbst. (Java-Applt vo oomfähg. Rot: für ds c blbt Folg bschräkt; adr Farb: für ds c sprgt d Folg mhr odr wgr schll jd Schrak) Slbstählch Struktur fd sch auch a vl Stll dr Natur: Far, Schflock, DNA-Faltug,... Nb dr ästhtsch Schöht dr fraktal Struktur hat hr mathmatsch Modllrug also vor allm Zwck: u vrsth, w ma komplx Systm aus fach Gst bschrb ka. (Das muss cht mmr mt komplx Zahl gschh, abr s vrfach oft das Lb ugm.) Iformatk-Awdugsfall Bldkomprsso: Bldr lass sch xtrm komprmr, w ma s aus fach "fraktal Bldugsgst" kostrur ka >> Itrrt Fuktosystm (IFS) 6 Das bdutt d mst Fäll: Wo kovrgrt d Folg? W. Ko ZD-MathSS-xt.docx St 89
12 Prof. Dr. Wolfgag Ko Mathmatk, SS Fat: Komplx Zahl Wou sd komplx Zahl gut?. Mt h lass sch vorhr ulösbar Glchug w = - lös. Währd ma vorhr ( d rll Zahl) b algbrasch Glchug umstädlch Fallutrschdug "hat k//mhrr Lösug" mach musst, glt jtt (m Körpr dr komplx Zahl) htlch dr Fudamtalsat dr Algbra (Sat S -7): E Glchug. Grads läßt sch gau Larfaktor rlg (hat gau Lösug).. D Gaußsch Zahlb gbt aschaulch Vorstllug vo komplx r Zahl als Vktor. D altratv Polar- odr Expotaldarstllug r komplx Zahl rlaubt fachs Multplr ud Potr.. D Eulrsch Forml cos s st dr wchtgst Forml dr mathmatsch Physk. Mt hr lass sch Schwgugsphäom (s- ud cos-fukto) kompakt schrb übr. Mt läßt sch vl fachr rch (Multplkato odr Potr durch Addto bw. Multplkato m Expot vl fachr als trgoomtrsch Addtosthorm!). Ma darf durch mmr dvdr, was b cos a d Nullstll cht rlaubt wär. a. Awdugsfall: Wchslstrombhug dr Elktrotchk gauso abr auch b adr Schwgugsphäom. 4. Wtrs Awdugsgbt (darauf komm wr spätr och) a. Fourrrh ud Fourrtrasformato; auch hr wrd d Brchug durch wstlch lchtr. D Fourrtrasformato splt dr für d tchsch Iformatk wchtg Sgalvrarbtug ud dr Bldvrarbtug groß Roll. b. Lös vo Dffrtalglchug (DGL): Mt dm Asat t, C, lass sch vrschd Typ vo DGLs gschloss lös..5.. Whr to go from hr Vrtfugsmöglchkt: W S mhr übr komplx Zahl lr woll ud wss woll, was ma och mt komplx Zahl mach ka: o o Lös komplrtr Itgral m Rll durch d "Umwg" übr d Gaußsch Zahlb Lös vo lar Dffrtalglchug übr Asat x(t) ( t) r(t). o Wchslstrombhug dr Elktrotchk [Stgl, S. 56-6] o Fraktal: schö Eführug [Schrodr94] ud schö Bldr [PtgR86] o IFS (Itrrt Fuktosystm) ur Bldkomprsso: [Barsly88] o Apflmäch Java programmr: W. Ko ZD-MathSS-xt.docx St 90
Prof. Dr. Wolfgang Konen Mathematik 2, SS2015 06.05.2015
 Prof. Dr. Wolfgag Ko Mathmatk, SS05 06.05.05. Komlx Zahl Dr kürst Wg wsch w Wahrht m Rll führt übr das Komlx. [Jacus Hadamard, fra. Mathmatkr, 865-96] Am Afag stad w so oft b wssschaftlch Etdckug d Nchtlösbarkt
Prof. Dr. Wolfgag Ko Mathmatk, SS05 06.05.05. Komlx Zahl Dr kürst Wg wsch w Wahrht m Rll führt übr das Komlx. [Jacus Hadamard, fra. Mathmatkr, 865-96] Am Afag stad w so oft b wssschaftlch Etdckug d Nchtlösbarkt
Prof. Dr. Wolfgang Konen Mathematik 2, SS
 Prof. Dr. Wolfgag Koe Mathematk, SS06 0.05.06. Komplexe Zahle Der küreste Weg wsche we Wahrhete m Reelle führt über das Komplexe. [Jacues Hadamard, fra. Mathematker, 865-96] Am Afag stad we so oft be wsseschaftlche
Prof. Dr. Wolfgag Koe Mathematk, SS06 0.05.06. Komplexe Zahle Der küreste Weg wsche we Wahrhete m Reelle führt über das Komplexe. [Jacues Hadamard, fra. Mathematker, 865-96] Am Afag stad we so oft be wsseschaftlche
Prof. Dr. Wolfgang Konen Mathematik 2, SS
 Prof. Dr. Wolfgag Koe Mathematk, SS07 4.05.07. Komplexe Zahle Der küreste Weg wsche we Wahrhete m Reelle führt über das Komplexe. [Jacues Hadamard, fra. Mathematker, 865-96] Am Afag stad we so oft be wsseschaftlche
Prof. Dr. Wolfgag Koe Mathematk, SS07 4.05.07. Komplexe Zahle Der küreste Weg wsche we Wahrhete m Reelle führt über das Komplexe. [Jacues Hadamard, fra. Mathematker, 865-96] Am Afag stad we so oft be wsseschaftlche
3. Spezielle diskrete Wahrscheinlichkeitsmodelle
 Lhrsuhl ür Emrsch Wrschasorschug ud Ökoomr Dr. Rolad Füss Sask II: Schlßd Sask SS 007 3. Szll dskr Wahrschlchksmodll 3. Glchvrlug Glchvrlug: B dr Glchvrlug ha jds Ergs d glch Erswahrschlchk: Wahrschlchksuko:
Lhrsuhl ür Emrsch Wrschasorschug ud Ökoomr Dr. Rolad Füss Sask II: Schlßd Sask SS 007 3. Szll dskr Wahrschlchksmodll 3. Glchvrlug Glchvrlug: B dr Glchvrlug ha jds Ergs d glch Erswahrschlchk: Wahrschlchksuko:
Eigenschaften trigonometrischer Reihen. Trigonometrische Reihen. Reihenentwicklung. Reihenentwicklung. Fourierreihenentwicklung
 roomrsch Rh Do: Rh dr Gsal a + a cos x + b s x + a cos x + L + a cos x + b s x +L hß roomrsch Rh. D Zahl a a, b,..., a, b,..., b: prodsch Fuko sd hr Koz. Escha roomrschr Rh a + a cos x + b s x + a cos
roomrsch Rh Do: Rh dr Gsal a + a cos x + b s x + a cos x + L + a cos x + b s x +L hß roomrsch Rh. D Zahl a a, b,..., a, b,..., b: prodsch Fuko sd hr Koz. Escha roomrschr Rh a + a cos x + b s x + a cos
Analyse metrischer Merkmale
 Aals mtrschr Mrkmal Bspl 0: Korrlatoskoffzt mooto Zusammhäg r 0.97 r 0. 8 Itrprtato? Adäquat Lösug? r 0.8 r 0. 99 Multvarat Dskrpto ud Eplorato vo Dat - Aals mtrschr Mrkmal 55 Aals mtrschr Mrkmal Mssug
Aals mtrschr Mrkmal Bspl 0: Korrlatoskoffzt mooto Zusammhäg r 0.97 r 0. 8 Itrprtato? Adäquat Lösug? r 0.8 r 0. 99 Multvarat Dskrpto ud Eplorato vo Dat - Aals mtrschr Mrkmal 55 Aals mtrschr Mrkmal Mssug
Technische Mechanik I
 Isttut für Tchsch ud Num. chk Prof. Dr.-Ig. Prof. E.h. P. Ebrhrd Tchsch chk I Prof. Dr.-Ig.. Hss WS 4/5. Tchsch chk I Prof. Dr.-Ig. Ptr Ebrhrd Prof. Dr.-Ig. chl Hss Vorlsug: D Vorlsug wrd für d Studrd
Isttut für Tchsch ud Num. chk Prof. Dr.-Ig. Prof. E.h. P. Ebrhrd Tchsch chk I Prof. Dr.-Ig.. Hss WS 4/5. Tchsch chk I Prof. Dr.-Ig. Ptr Ebrhrd Prof. Dr.-Ig. chl Hss Vorlsug: D Vorlsug wrd für d Studrd
MTBF Bericht. Mil-HDBK-217F Notice 2 + ANSI/VITA xxxxxxxxxxxxxxxxxxxxx
 Brcht xxxxxxxxxxxxx Ausgab. Jul 206 St vo Ihr Logo Ihr Frmam Brcht Ml-HDBK-27F Notc 2 + ANSI/VITA 5. xxxxxxxxxxxxxxxxxxxxx Ausgab. Jul 206 Ihr Frmam Ihr Adrss D-xxxxx Stuttgart Barbtt durch: Statstk, RAMS
Brcht xxxxxxxxxxxxx Ausgab. Jul 206 St vo Ihr Logo Ihr Frmam Brcht Ml-HDBK-27F Notc 2 + ANSI/VITA 5. xxxxxxxxxxxxxxxxxxxxx Ausgab. Jul 206 Ihr Frmam Ihr Adrss D-xxxxx Stuttgart Barbtt durch: Statstk, RAMS
Logarithmusfunktionen
 V Logarithmusfuktio Widrholug wichtigr Rchgstz Üug ach http://www.hrdr-orschul.d/madica/aufg000/pu.pdf (utr Hälft ds Aritslatts!) mit folgd Zusatzfrag: Brch Si ud drück Si durch i izig Logarithmus glichr
V Logarithmusfuktio Widrholug wichtigr Rchgstz Üug ach http://www.hrdr-orschul.d/madica/aufg000/pu.pdf (utr Hälft ds Aritslatts!) mit folgd Zusatzfrag: Brch Si ud drück Si durch i izig Logarithmus glichr
L Hospital - Lösungen der Aufgaben B1
 L Hospital - Lösug dr Aufgab B Gsucht: = Übrprüf ob di Rgl vo L'Hospital agwdt wrd darf Für ght dr Zählr gg L'Hospital darf agwdt wrd, Für ght dr Nr gg = da Zählr ud Nr gg gh Zählr ud Nr diffrzir: ' =
L Hospital - Lösug dr Aufgab B Gsucht: = Übrprüf ob di Rgl vo L'Hospital agwdt wrd darf Für ght dr Zählr gg L'Hospital darf agwdt wrd, Für ght dr Nr gg = da Zählr ud Nr gg gh Zählr ud Nr diffrzir: ' =
Das dine&shine KOnzept für Anlässe mit nachhaltiger Wirkung
 Das &sh KOzt für Aläss mt achhaltgr Wrkug Lass S us gmsam guts Tu. catrg solutos a r o v b y & s h a r o v b y & s h Usr acht Ltsätz Um usr Abscht kokrt lb u mss zu kö, hab wr acht Ltsätz frt. Ds Ltsätz
Das &sh KOzt für Aläss mt achhaltgr Wrkug Lass S us gmsam guts Tu. catrg solutos a r o v b y & s h a r o v b y & s h Usr acht Ltsätz Um usr Abscht kokrt lb u mss zu kö, hab wr acht Ltsätz frt. Ds Ltsätz
Grundlagen Kreditrisikomodelle
 Grudlag Krdtrsomodll Grudlag Krdtrsomodll (Fassug Aprl 6) /39 Marus Schch Emal: Marus.Schch@gmx.d Hompag: www.marus-schch.d Grudlag Krdtrsomodll Vorwort Dsr Artl stllt Eführug d Grudlag vo Krdtrsomodll
Grudlag Krdtrsomodll Grudlag Krdtrsomodll (Fassug Aprl 6) /39 Marus Schch Emal: Marus.Schch@gmx.d Hompag: www.marus-schch.d Grudlag Krdtrsomodll Vorwort Dsr Artl stllt Eführug d Grudlag vo Krdtrsomodll
Definitionen und Aussagen zu Potenzreihen
 Deftoe ud Aussage zu Potezrehe User bsherges Repertore a stetge Abblduge basert auf ratoale Fuktoe, also Ausdrücke, dee Addto, Subtrakto, Multplkato ud Dvso vorkomme. Auf dese Wese sd aber Epoetalfukto,
Deftoe ud Aussage zu Potezrehe User bsherges Repertore a stetge Abblduge basert auf ratoale Fuktoe, also Ausdrücke, dee Addto, Subtrakto, Multplkato ud Dvso vorkomme. Auf dese Wese sd aber Epoetalfukto,
Regressionsanalyse. Analyse der Residuen Feststellung der Größe Feststellung der Verlaufsform. Nichtlineare einfache Regression. Mehrfachregression
 Rgrssosaalys Aalys dr Rsdu Fststllug dr Größ Fststllug dr Vrlaufsform Nchtlar fach Rgrsso Mhrfachrgrsso Prof. Kück / Dr. Rcabal Dlgado Lhrstuhl Statstk Rgrsso II Bblograf: Prof. Dr. Kück Uvrstät Rostock
Rgrssosaalys Aalys dr Rsdu Fststllug dr Größ Fststllug dr Vrlaufsform Nchtlar fach Rgrsso Mhrfachrgrsso Prof. Kück / Dr. Rcabal Dlgado Lhrstuhl Statstk Rgrsso II Bblograf: Prof. Dr. Kück Uvrstät Rostock
Prof. Dr. Wolfgang Konen Mathematik 1, WS
 Prof Dr Wolfgg Ko Mthmtk, WS4 94 6 Lr Algr Du wolltst doch Algr, d hst du d Slt [Juls Vr, 88 95] E Algr cht hor dr Rchoprto stmmtr mthmtschr Ojkt D Ojkt dr lr Algr sd Vktor ud Mtr Huptl sd ( d rsformto
Prof Dr Wolfgg Ko Mthmtk, WS4 94 6 Lr Algr Du wolltst doch Algr, d hst du d Slt [Juls Vr, 88 95] E Algr cht hor dr Rchoprto stmmtr mthmtschr Ojkt D Ojkt dr lr Algr sd Vktor ud Mtr Huptl sd ( d rsformto
Prof. Dr. Wolfgang Konen Mathematik 1, WS
 Prof Dr Wolfgg Ko Mthmtk, WS6 6 6 Lr Algr Du wolltst doch Algr, d hst du d Slt [Juls Vr, 88 95] E Algr cht hor dr Rchoprto stmmtr mthmtschr Ojkt D Ojkt dr lr Algr sd Vktor ud Mtr Huptl sd ( d rsformto
Prof Dr Wolfgg Ko Mthmtk, WS6 6 6 Lr Algr Du wolltst doch Algr, d hst du d Slt [Juls Vr, 88 95] E Algr cht hor dr Rchoprto stmmtr mthmtschr Ojkt D Ojkt dr lr Algr sd Vktor ud Mtr Huptl sd ( d rsformto
Aktiv-Geflügelsortiment
 Aktv-Gflüglsortmt Ihaltsvrzchs Aktv-Jughfuttr 3 Aktv-Lghfuttr 4 Aktv-Trutfuttr 5 Aktv-Poultmastfuttr 6 Aktv-Straussfuttr 6 Aktv-Jughfuttr Vtal, frohwüchsg, homog Kük ud Jugh mt gutr Futtrvrwrtug brt sch
Aktv-Gflüglsortmt Ihaltsvrzchs Aktv-Jughfuttr 3 Aktv-Lghfuttr 4 Aktv-Trutfuttr 5 Aktv-Poultmastfuttr 6 Aktv-Straussfuttr 6 Aktv-Jughfuttr Vtal, frohwüchsg, homog Kük ud Jugh mt gutr Futtrvrwrtug brt sch
zu den 100 wichtigsten deutschen Wörtern
 K Rchtschrbkrt z d 100 wchtgst dtsch Wörtr Ss Schäfr www.zbrms.d 2013 Ds 100 Wörtr kmm dtsch Txt bsdrs häfg vr: d d ch dr s r wr s ds d wr d st f mt cht ht z d br m sgt hb s dm sch m hb htt d ch m km sd
K Rchtschrbkrt z d 100 wchtgst dtsch Wörtr Ss Schäfr www.zbrms.d 2013 Ds 100 Wörtr kmm dtsch Txt bsdrs häfg vr: d d ch dr s r wr s ds d wr d st f mt cht ht z d br m sgt hb s dm sch m hb htt d ch m km sd
dt ist stabil, wenn es für gegebene Werte ε > 0 und t 0 einen Wert η = η( ε,t 0 ) gibt, so daß jede
 . Sbl ud sbl soär Zusäd M urschd sbl ud sbl soär Zusäd, j chdm, ob ds Sysm ch Auslkug dr Näh dsr Zusäd vrblb odr ch. Khr ds Sysm ür d ursprüglch Zusd zurück, s s symposch sbl. Echs mchschs Alogo: sbl sbl
. Sbl ud sbl soär Zusäd M urschd sbl ud sbl soär Zusäd, j chdm, ob ds Sysm ch Auslkug dr Näh dsr Zusäd vrblb odr ch. Khr ds Sysm ür d ursprüglch Zusd zurück, s s symposch sbl. Echs mchschs Alogo: sbl sbl
3. Kräfte in einem Angriffspunkt
 3. Kräft m Agrffspukt 3. Zusammstz vo Kräft Btracht Abbldug 3... Zw Kräft, gat ud, grf m Pukt A s Körprs a. D Erfahrug zgt, dass ds Kräft durch zg Kraft, d sogat sultrd, rstzt wrd kö. Dslb rmttlt ma dadurch,
3. Kräft m Agrffspukt 3. Zusammstz vo Kräft Btracht Abbldug 3... Zw Kräft, gat ud, grf m Pukt A s Körprs a. D Erfahrug zgt, dass ds Kräft durch zg Kraft, d sogat sultrd, rstzt wrd kö. Dslb rmttlt ma dadurch,
Potenzsummen 1. Aus Übungsbeispielen zur vollständigen Induktion werden die folgenden Formeln geläufig sein:
 Kurzfassug Potzsumm Mhrr lmtar Möglcht zur Gwug!) vo Potzsummforml wrd rläutrt Dazu wrd Idutos ud Dffrzmthod vrwdt, cht abr aalytsch odr gomtrsch Eltug Potzsumm sd Ausdrüc dr Form ) ): Aus Übugsbspl zur
Kurzfassug Potzsumm Mhrr lmtar Möglcht zur Gwug!) vo Potzsummforml wrd rläutrt Dazu wrd Idutos ud Dffrzmthod vrwdt, cht abr aalytsch odr gomtrsch Eltug Potzsumm sd Ausdrüc dr Form ) ): Aus Übugsbspl zur
Handout zum Vortrag Josephsonkontakt
 Hadout zum Vortrag Josphsokotakt Thor ud Awdug ds Josphso - Effkts / Kotakts: Dr Josphso - Effkt st makroskopschr mssbarr kohärtr Tulffkt. Durch tuld Elktro bzw. Coopr-Paar wrd d bd Supraltr mtadr gkopplt.
Hadout zum Vortrag Josphsokotakt Thor ud Awdug ds Josphso - Effkts / Kotakts: Dr Josphso - Effkt st makroskopschr mssbarr kohärtr Tulffkt. Durch tuld Elktro bzw. Coopr-Paar wrd d bd Supraltr mtadr gkopplt.
Komplexitätsbetrachtungen. Komplexitätsbetrachtungen. Komplexitätsbetrachtungen. Komplexitätsbetrachtungen. Komplexitätsbetrachtungen Exponentiation
 Kompltätsbtrachtug Frag: W brcht ma! am ffztst?. Asatz:! O(). Asatz:! (-)! auch O(). Asatz: I:! sowso ur arstllbar für l (z.b.
Kompltätsbtrachtug Frag: W brcht ma! am ffztst?. Asatz:! O(). Asatz:! (-)! auch O(). Asatz: I:! sowso ur arstllbar für l (z.b.
y 2 Richtung!! x 1
 Austauschvrfahr : a a a a b a a a a b a a a a b a a a a b a a a a b a a a a b Pvot. Pvotlmt Pvot. D rstlch Pvotzl durch Pvot tl mt gatvm ( ) Vorzch.Pvotspalt wr durch Pvotlmt gtlt (oh Pvotlmt).rstlch Elmt
Austauschvrfahr : a a a a b a a a a b a a a a b a a a a b a a a a b a a a a b Pvot. Pvotlmt Pvot. D rstlch Pvotzl durch Pvot tl mt gatvm ( ) Vorzch.Pvotspalt wr durch Pvotlmt gtlt (oh Pvotlmt).rstlch Elmt
e = lim ( n n) und Folgerungen
 = lim + ud Folgrug Ergäzug zur Vorlsug Aalysis I, Dail Grisr, Dz. 2005 Satz: Si x = +, y = + +. Da gilt lim x = lim y = x ist strg mooto wachsd, y ist strg mooto falld. Isbsodr gilt für all x < < y. Bmrug:
= lim + ud Folgrug Ergäzug zur Vorlsug Aalysis I, Dail Grisr, Dz. 2005 Satz: Si x = +, y = + +. Da gilt lim x = lim y = x ist strg mooto wachsd, y ist strg mooto falld. Isbsodr gilt für all x < < y. Bmrug:
Wir betrachten hier nur den Fall m,n N, also m>0 und n>0. Die anderen Fälle, bei denen m=0 oder n=0 ist, können leicht selbst gelöst werden.
 Übugsaufgab Fourirrih Mahmaik III M Prof. Dr. B. Grabowski Bla 6 grabowski@hw-saarlad.d Lösug zu Übugs-Bla 6 Zu Aufgab Wir brach hir ur d Fall m, N, also m> ud >. Di adr Fäll, bi d m odr is, kö lich slbs
Übugsaufgab Fourirrih Mahmaik III M Prof. Dr. B. Grabowski Bla 6 grabowski@hw-saarlad.d Lösug zu Übugs-Bla 6 Zu Aufgab Wir brach hir ur d Fall m, N, also m> ud >. Di adr Fäll, bi d m odr is, kö lich slbs
Richtlinien für die Ausbildung zum Video School Trainer und zur Video School Trainerin
 Rchtl fü d Ausbldug zum Vdo School Ta ud zu Vdo School Ta Rchtl fü d Ausbldug zum Vdo School Ta ud zu Vdo School Ta Impssum Budsvostad SPIN Dutschlad. V. Budsbüo Rbcca Schö Kustma Staß 3 c 82327 Tutzg
Rchtl fü d Ausbldug zum Vdo School Ta ud zu Vdo School Ta Rchtl fü d Ausbldug zum Vdo School Ta ud zu Vdo School Ta Impssum Budsvostad SPIN Dutschlad. V. Budsbüo Rbcca Schö Kustma Staß 3 c 82327 Tutzg
Numerische Methoden in der Strömungstechnik
 Nmrsch Mthod dr Strömgstch WS 004/05 Dr.-Ig. Irs atl/dr.-ig. Fraco Magagato Fachgbt Strömgsmasch I. führg d Nmrsch Mthod CFD II. Grdglchg dr Strömgsmcha III. Dsrtsrg: Ft-Dffrz Mthod IV. Ft-Volm Mthod V.
Nmrsch Mthod dr Strömgstch WS 004/05 Dr.-Ig. Irs atl/dr.-ig. Fraco Magagato Fachgbt Strömgsmasch I. führg d Nmrsch Mthod CFD II. Grdglchg dr Strömgsmcha III. Dsrtsrg: Ft-Dffrz Mthod IV. Ft-Volm Mthod V.
SCHRITT 1. I - Allgemeine Informationen
 SCHRI 1 Am Ntzsbd für Pbc Accss WLAN/LAN D achfod Ntzsbd r d Ntz ds vo coova commcatos GmbH af dm Ara ds Mssztrms Sazbr btrb d vo coova commcatos GmbH d Mssztrm Sazbr GmbH abot WLAN/ LAN. I - Am Iformato
SCHRI 1 Am Ntzsbd für Pbc Accss WLAN/LAN D achfod Ntzsbd r d Ntz ds vo coova commcatos GmbH af dm Ara ds Mssztrms Sazbr btrb d vo coova commcatos GmbH d Mssztrm Sazbr GmbH abot WLAN/ LAN. I - Am Iformato
Einschub: Fourier-Transformation
 Ermlhys III TU Dormud WS/4 Shu Kh @ TU - Dormud. d Kl Eschub: Fourr-Trsormo Prodsch Vorgäg Nur ud Tch Erdroo, Hrzschlg, Schll, Lch, Schwgrs... movr d Zrlgug s Vorggs d blg Frquz. Bm Lch gschh ds m Prsm
Ermlhys III TU Dormud WS/4 Shu Kh @ TU - Dormud. d Kl Eschub: Fourr-Trsormo Prodsch Vorgäg Nur ud Tch Erdroo, Hrzschlg, Schll, Lch, Schwgrs... movr d Zrlgug s Vorggs d blg Frquz. Bm Lch gschh ds m Prsm
Die Anzahl der möglichen Mikrozustände, die zu einem bestimmten Makrozustand gehören nennt man die Permutabilität (Bezeichnung W ).
 6. Boltzma-Vrtlug Thrmodyam bhadlt Systm, d aus r groß Zahl vo Tlch (z.b. Atom, Molül) bsth. B dr marosopsch Bschrbug vrzchtt ma auf d gau Agab dr Zustäd allr Tlch (z.b. Posto, Gschwdgt) ud bschrbt das
6. Boltzma-Vrtlug Thrmodyam bhadlt Systm, d aus r groß Zahl vo Tlch (z.b. Atom, Molül) bsth. B dr marosopsch Bschrbug vrzchtt ma auf d gau Agab dr Zustäd allr Tlch (z.b. Posto, Gschwdgt) ud bschrbt das
Reihenentwicklung die Taylorentwicklung
 Rihtwicklug di Taylortwicklug Motivatio: Es lig i Potrih olgdr Form vor: Durch Umorm rgibt sich: s s s s s K K K Für udlich groß rgibt sich im Wrtbrich < < i dlich Summ s. Dis lässt sich als Fuktio vo
Rihtwicklug di Taylortwicklug Motivatio: Es lig i Potrih olgdr Form vor: Durch Umorm rgibt sich: s s s s s K K K Für udlich groß rgibt sich im Wrtbrich < < i dlich Summ s. Dis lässt sich als Fuktio vo
Regressionsanalyse. Bibliografie:
 Rgrssosaals Eführug Allgms Mthod dr klst Quadrat zur Bstmmug dr Paramtr dr lar Efachrgrsso Egschaft dr lar Klst- Quadrat-Efachrgrsso Lars Bstmmthtsmaß Prof. Kück / Dr. Rcaal Dlgado Lhrstuhl Statstk Rgrsso
Rgrssosaals Eführug Allgms Mthod dr klst Quadrat zur Bstmmug dr Paramtr dr lar Efachrgrsso Egschaft dr lar Klst- Quadrat-Efachrgrsso Lars Bstmmthtsmaß Prof. Kück / Dr. Rcaal Dlgado Lhrstuhl Statstk Rgrsso
Training 4: Sparen. Zinsen und Zinseszinsen
 Trag 4: Spar Z ud Zz r Wa bkommt du Z? C: W du Gld algt. B: D: r A: W du gut r kat. Trag 4/Erwtrug: Spar Z ud Zz/Prätato/St 2 W du dr Gld lht. W du Gld vo dr Bak brt. W Bak ud Sparka Gld vrd 2. Da gammlt
Trag 4: Spar Z ud Zz r Wa bkommt du Z? C: W du Gld algt. B: D: r A: W du gut r kat. Trag 4/Erwtrug: Spar Z ud Zz/Prätato/St 2 W du dr Gld lht. W du Gld vo dr Bak brt. W Bak ud Sparka Gld vrd 2. Da gammlt
R. Brinkmann Seite Achsenschnittpunkte von e- Funktionen und Exponentialgleichungen
 R. Brikma http://brikma-du.d Sit 08..009 Achsschittpukt vo - Fuktio ud Epotialglichug Eiführugsbispil Bispil : Zu bstimm sid di Achsschittpukt vo s + f = D Schittpukt mit dr y y=f 0 Achs fidt ma übr d
R. Brikma http://brikma-du.d Sit 08..009 Achsschittpukt vo - Fuktio ud Epotialglichug Eiführugsbispil Bispil : Zu bstimm sid di Achsschittpukt vo s + f = D Schittpukt mit dr y y=f 0 Achs fidt ma übr d
Leiterplatten und Modul Übersicht
 Ltrplatt ud Modul Übrcht Stfro Stfa Na - www.tfpro.d fo@tfpro.d Datum:.. Wht pag Stfro Ltrplatt ud Modul Übrcht Rv_- St vo Stfro Stfa Na - www.tfpro.d fo@tfpro.d Datum:.. Ihaltvrzch Vorwort...4 Ma lat...
Ltrplatt ud Modul Übrcht Stfro Stfa Na - www.tfpro.d fo@tfpro.d Datum:.. Wht pag Stfro Ltrplatt ud Modul Übrcht Rv_- St vo Stfro Stfa Na - www.tfpro.d fo@tfpro.d Datum:.. Ihaltvrzch Vorwort...4 Ma lat...
Einführung in die Stochastik 3. Übungsblatt
 Eführug de Stochastk 3. Übugsblatt Fachberech Mathematk SS 0 M. Kohler 06.05.0 A. Fromkorth D. Furer Gruppe ud Hausübug Aufgabe 9 (4 Pukte) Der Mkrozesus st ee statstsche Erhebug. Herbe werde ach bestmmte
Eführug de Stochastk 3. Übugsblatt Fachberech Mathematk SS 0 M. Kohler 06.05.0 A. Fromkorth D. Furer Gruppe ud Hausübug Aufgabe 9 (4 Pukte) Der Mkrozesus st ee statstsche Erhebug. Herbe werde ach bestmmte
Das Ziel ist das Ziel
 l tn-wc Tl 2 Das Zl st das Zl (c) 2013 Kathrn Pohnk/ tn-wcl - Slbst-Coachng & Mhr / Das Zl st das Zl / 1 l tn-wc Inhalt Tl 1 1. Enltung 2. Im Rückwärtsgang 3. Schrtt 1 Tl 2 1. Prsonal-Kanban - was st dnn
l tn-wc Tl 2 Das Zl st das Zl (c) 2013 Kathrn Pohnk/ tn-wcl - Slbst-Coachng & Mhr / Das Zl st das Zl / 1 l tn-wc Inhalt Tl 1 1. Enltung 2. Im Rückwärtsgang 3. Schrtt 1 Tl 2 1. Prsonal-Kanban - was st dnn
Das Max-Flow Min-Cut Theorem
 Das Max-Flow M-Ct Thorm Das Max-Flow M-Ct Thorm I dsr Asarbt btraht wr das Max-Flow M-Ct Thorm vo Ford d Flkrso (96). Daz s G ( V, E) = dlhs Ntzwrk, wob V d M dr Kot d E d M dr Kat st. ( ) wrd adrs als
Das Max-Flow M-Ct Thorm Das Max-Flow M-Ct Thorm I dsr Asarbt btraht wr das Max-Flow M-Ct Thorm vo Ford d Flkrso (96). Daz s G ( V, E) = dlhs Ntzwrk, wob V d M dr Kot d E d M dr Kat st. ( ) wrd adrs als
Höhere Mathematik 1 Kapitel 2 Lineare Algebra
 Höhr Mthmtk Kptl Lr lgr Prof. Dr.-Ig. Dtr Krus Höhr Mthmtk Kptl Ihltsvrzhs Lr lgr...-. Vktor m...-.. ddto vo Vktor...-.. Multplzr s Vktors mt m Sklr...-.. Btrg s Vktors...-6.. Vktor m Koordtsystm...-7..
Höhr Mthmtk Kptl Lr lgr Prof. Dr.-Ig. Dtr Krus Höhr Mthmtk Kptl Ihltsvrzhs Lr lgr...-. Vktor m...-.. ddto vo Vktor...-.. Multplzr s Vktors mt m Sklr...-.. Btrg s Vktors...-6.. Vktor m Koordtsystm...-7..
Quantenmechanik I. Musterlösung 4.
 Quatmchaik I. Mustrlösug 4. Hrbst 011 Prof. Rato Rr Übug 1. Rch mit Kommutator. Dr Kommutator [A, B] AB BA zwir Oprator ist liar i A, B ud atisymmtrisch: [A, B] [B, A]. a Zig di Produktrgl ud di Jacobi-Idtität,
Quatmchaik I. Mustrlösug 4. Hrbst 011 Prof. Rato Rr Übug 1. Rch mit Kommutator. Dr Kommutator [A, B] AB BA zwir Oprator ist liar i A, B ud atisymmtrisch: [A, B] [B, A]. a Zig di Produktrgl ud di Jacobi-Idtität,
Die Fourier-Transformation
 D Fourr-Trasorato INHATSVERZEICHNIS EINEITUNG GRUNDIDEE EINER TRANSFORATION 3 DAS SAPINGTHEORE 4 DIE DISKRETE FOURIERTRANSFORATION DFT) 4 DIE INVERSE DISKRETE FOURIERTRANSFORATION IDFT) 8 DIE SCHNEE FOURIERTRANSFORATION
D Fourr-Trasorato INHATSVERZEICHNIS EINEITUNG GRUNDIDEE EINER TRANSFORATION 3 DAS SAPINGTHEORE 4 DIE DISKRETE FOURIERTRANSFORATION DFT) 4 DIE INVERSE DISKRETE FOURIERTRANSFORATION IDFT) 8 DIE SCHNEE FOURIERTRANSFORATION
Die komplexen Zahlen Eine erste Einführung für Schüler und Schülerinnen
 De komplexe Zahle Ee erste Eführug für Schüler ud Schülere De Herkuft der Komplexe Zahle lässt sch we folgt beschrebe: De afäglche Probleme der Mathematk bestade dar, dass ma efache Recheoperatoe für mache
De komplexe Zahle Ee erste Eführug für Schüler ud Schülere De Herkuft der Komplexe Zahle lässt sch we folgt beschrebe: De afäglche Probleme der Mathematk bestade dar, dass ma efache Recheoperatoe für mache
 31. März 2009 Aalyst Tlfokofrz zum Gschäftsjahr 2008 Agda Eltug Ürlck zu d Sgmt Gschäftszahl für 2008 Etwcklug dr Akt Auslck EM.SPORT MEDIA AG I Aalyst Tlfokofrz 31. März 2009 2 Wstlch Ergss st dm 1. Sptmr
31. März 2009 Aalyst Tlfokofrz zum Gschäftsjahr 2008 Agda Eltug Ürlck zu d Sgmt Gschäftszahl für 2008 Etwcklug dr Akt Auslck EM.SPORT MEDIA AG I Aalyst Tlfokofrz 31. März 2009 2 Wstlch Ergss st dm 1. Sptmr
Wichtige Nummern. Ihre Meinung zählt! August 2012. Spitzenleistung Energieeffizienz im Opernhaus. Teilnehmen und gewinnen! Sparangebot.
 3 Füf r m Pr AbOopsr zu für d! gw StartKlar Lb Lsr ud Lsr, Eugè Iosco hat st fstgstllt: D Kust st uütz, abr dr Msch ka auf das Uütz b cht vrzcht. Vor allm hat Kust hr Prs. Hut sd Kulturbtrb gut brat, so
3 Füf r m Pr AbOopsr zu für d! gw StartKlar Lb Lsr ud Lsr, Eugè Iosco hat st fstgstllt: D Kust st uütz, abr dr Msch ka auf das Uütz b cht vrzcht. Vor allm hat Kust hr Prs. Hut sd Kulturbtrb gut brat, so
Der Satz von de Moivre / Laplace als Aussage über Binomialkoeffizienten
 Dr Satz vo d Movr / Laplac als ussa übr Boaloffzt JÖRG MEYER, HMEL Zusafassu: Batlch bt s Zusaha zwsch d stadardsrt Boalvrtlu rsts ud dr oralvrtlu, sbsodr t d Tr, x / adrrsts Hr wrd dutlch acht, dass sch
Dr Satz vo d Movr / Laplac als ussa übr Boaloffzt JÖRG MEYER, HMEL Zusafassu: Batlch bt s Zusaha zwsch d stadardsrt Boalvrtlu rsts ud dr oralvrtlu, sbsodr t d Tr, x / adrrsts Hr wrd dutlch acht, dass sch
StudiumPlus- SS 2017 Torsten Schreiber
 StudiumPlus- SS 07 Torst Schribr 44 Dis rg sollt Si uch oh Skript btwort kö: N Si di wichtigst Eigschft vo Mg! Wi kö Si i Itrvll dfiir? Wi fuktioirt di Modulo-Oprtio? Wofür brucht m ds d Morg Gstz? Ws
StudiumPlus- SS 07 Torst Schribr 44 Dis rg sollt Si uch oh Skript btwort kö: N Si di wichtigst Eigschft vo Mg! Wi kö Si i Itrvll dfiir? Wi fuktioirt di Modulo-Oprtio? Wofür brucht m ds d Morg Gstz? Ws
Der Approximationssatz von Weierstraß
 Der Approxmatossatz vo Weerstraß Ja Köster 22. Oktober 2007 1 Eführug Aus der Aalyss wsse wr, dass sch aalytsche Fuktoe durch Potezrehe der Form f(x = a 0 + a 1 x + a 2 x 2 +... darstelle lasse. Dabe kovergert
Der Approxmatossatz vo Weerstraß Ja Köster 22. Oktober 2007 1 Eführug Aus der Aalyss wsse wr, dass sch aalytsche Fuktoe durch Potezrehe der Form f(x = a 0 + a 1 x + a 2 x 2 +... darstelle lasse. Dabe kovergert
3.1 Definition, Einheitsvektoren, Komponenten, Rechenregeln, Vektorraum
 . Vktorn. Dfnton, Enhtsvktorn, Komponntn, Rchnrgln, Vktorrum Nn sklrn (Zhln mt Mßnht w Mss, Enrg, Druck usw.) wrdn n dr Physk vktorll Größn ("Pfl" mt Rchtung und Läng) vrwndt: Ortsvktor, Gschwndgkt, Vrschung,
. Vktorn. Dfnton, Enhtsvktorn, Komponntn, Rchnrgln, Vktorrum Nn sklrn (Zhln mt Mßnht w Mss, Enrg, Druck usw.) wrdn n dr Physk vktorll Größn ("Pfl" mt Rchtung und Läng) vrwndt: Ortsvktor, Gschwndgkt, Vrschung,
zur Freiwilligenarbeit im Alter
 12 0 2 r o A s r v r k G ü f hr d J s h ch zwsc s pä rä o r Eu d o S d u r A h k m S c F b F & r g D rw F r zu D & Fk zur Frwgrb m Ar V är ud Msch s wchg Bräg für d Gsschf. Ds rch vo dr Arb urschdchs Vr
12 0 2 r o A s r v r k G ü f hr d J s h ch zwsc s pä rä o r Eu d o S d u r A h k m S c F b F & r g D rw F r zu D & Fk zur Frwgrb m Ar V är ud Msch s wchg Bräg für d Gsschf. Ds rch vo dr Arb urschdchs Vr
Mathematik für Wirtschaftsinformatik. Ulrich Hoffmann. Technical Reports and Working Papers Leuphana Universität Lüneburg
 3 Jhrgg H Oor 3 ISSN 939-88 FIAL Mh ür Wrschsor Ulrch Ho Tchcl Rors d Worg Prs Luh Uvrsä Lüurg Hrsg dr Schrrh FINAL: Ulrch Ho Schrhorssrß D-335 Lüurg Mh ür Wrschsor Pro Dr rr Ulrch Ho Ürr Fssug Oor 3
3 Jhrgg H Oor 3 ISSN 939-88 FIAL Mh ür Wrschsor Ulrch Ho Tchcl Rors d Worg Prs Luh Uvrsä Lüurg Hrsg dr Schrrh FINAL: Ulrch Ho Schrhorssrß D-335 Lüurg Mh ür Wrschsor Pro Dr rr Ulrch Ho Ürr Fssug Oor 3
Eigenwerteinschließungen I
 auptsemar: Numersche Lösuge für Egewertaufgabe Egewerteschleßuge I Referet: Wolfgag Wesselsky Glederug Eletug Kodto vo Egewerte 3 Eschleßugssätze Bauer-Fke, Gershgor, Wlkso, Bedxo 4 Zusatz: Courat / Weyl
auptsemar: Numersche Lösuge für Egewertaufgabe Egewerteschleßuge I Referet: Wolfgag Wesselsky Glederug Eletug Kodto vo Egewerte 3 Eschleßugssätze Bauer-Fke, Gershgor, Wlkso, Bedxo 4 Zusatz: Courat / Weyl
2 Differentialrechnung und Anwendungen
 Diffrtialrchug ud Awdug 1 Diffrtialrchug ud Awdug Dr Bgriff ds Diffrtialquotit hat sich i zahlrich Awdug irhalb ud außrhalb dr Mathmatik als äußrst fruchtbar rwis. Bstimmug vo Etrmwrt, lokal Approimatio
Diffrtialrchug ud Awdug 1 Diffrtialrchug ud Awdug Dr Bgriff ds Diffrtialquotit hat sich i zahlrich Awdug irhalb ud außrhalb dr Mathmatik als äußrst fruchtbar rwis. Bstimmug vo Etrmwrt, lokal Approimatio
Klausur (Mathematik II) - Sommersemester 2013
 Klusur Mthmtik II) - Sommrsmstr Nm: Mtrikl-Nr: EMil: optiol Schll-Korrktur) Aug 6 7 8 Pukt 6 Als Hilsmittl sid di vo dm Lhrutrgt zur Vrügug gstllt sowi ig Utrlg zuglss Skript ud Mustrug sowi dr Lösug).
Klusur Mthmtik II) - Sommrsmstr Nm: Mtrikl-Nr: EMil: optiol Schll-Korrktur) Aug 6 7 8 Pukt 6 Als Hilsmittl sid di vo dm Lhrutrgt zur Vrügug gstllt sowi ig Utrlg zuglss Skript ud Mustrug sowi dr Lösug).
Kapitel XI. Funktionen mit mehreren Variablen
 Kaptel XI Fuktoe mt mehrere Varable D (Fuktoe vo uabhägge Varable Se R ud D( f R Ist jedem Vektor (Pukt (,,, D( f durch ee Vorschrft f ee reelle Zahl z = f (,,, zugeordet, so heßt f ee Fukto vo uabhägge
Kaptel XI Fuktoe mt mehrere Varable D (Fuktoe vo uabhägge Varable Se R ud D( f R Ist jedem Vektor (Pukt (,,, D( f durch ee Vorschrft f ee reelle Zahl z = f (,,, zugeordet, so heßt f ee Fukto vo uabhägge
Kommunikation. Begriffsdefinitionen aus dem Web
 Kommuikatio 28 I usrr Gsllschaft ist Kommuikatio shr wichtig. Oft vrstädig sich Msch problmlos mitiadr. Erst w s Schwirigkit gibt, mrk wir, dass Kommuikatiosprozss zimlich komplizirt si kö: Kommuikatio
Kommuikatio 28 I usrr Gsllschaft ist Kommuikatio shr wichtig. Oft vrstädig sich Msch problmlos mitiadr. Erst w s Schwirigkit gibt, mrk wir, dass Kommuikatiosprozss zimlich komplizirt si kö: Kommuikatio
INCIDENT MANAGEMENT SYSTEM
 INCIDENT MANAGEMENT SYSTEM Uivrslls Srvicud Vorgagsmaagmt WAS KANN i NORIS IMS TATSÄCHLICH FÜR IHR UNTERNEHMEN LEISTEN? Übrzug Si sich vo usrr vollitgrirt Awdug zur Erfassug, Barbitug, Dokumtatio ud Auswrtug
INCIDENT MANAGEMENT SYSTEM Uivrslls Srvicud Vorgagsmaagmt WAS KANN i NORIS IMS TATSÄCHLICH FÜR IHR UNTERNEHMEN LEISTEN? Übrzug Si sich vo usrr vollitgrirt Awdug zur Erfassug, Barbitug, Dokumtatio ud Auswrtug
Direkt-Vertrieb Hersteller vertreibt seine Ware direkt an den Kunden (B2C; B2B)
 (Eiführug) Optimirug Vrtribsprozss Sit: 1 Vrtribsart Dirkt-Vrtrib Hrstllr vrtribt si War dirkt a d Kud (B2C; B2B) Idirktr-Vrtrib War wrd übr Partr, Hädlr, Distributio, Ntzwrk agbot (B2C, B2B) Gmischtr
(Eiführug) Optimirug Vrtribsprozss Sit: 1 Vrtribsart Dirkt-Vrtrib Hrstllr vrtribt si War dirkt a d Kud (B2C; B2B) Idirktr-Vrtrib War wrd übr Partr, Hädlr, Distributio, Ntzwrk agbot (B2C, B2B) Gmischtr
Die Normalverteilung. Die Normal- oder Gauß-Verteilung ist die am häufigsten vorkommende Verteilung.
 D Normalvrtlung D Normal- odr Gauß-Vrtlung st d am häufgstn vorkommnd Vrtlung. S rd bschrbn durch folgndn funktonaln Zusammnhang G ( ) π S rd durch z Paramtr bschrbn: und Dr Zusammnhang zur nomal-vrtlung
D Normalvrtlung D Normal- odr Gauß-Vrtlung st d am häufgstn vorkommnd Vrtlung. S rd bschrbn durch folgndn funktonaln Zusammnhang G ( ) π S rd durch z Paramtr bschrbn: und Dr Zusammnhang zur nomal-vrtlung
(Markowitz-Portfoliotheorie)
 Thema : ortfolo-selekto ud m-s-rzp (Markowtz-ortfolotheore) Beurtelugskrtere be quadratscher Nutzefukto: Beroull-rzp + quadratsche Nutzefukto Thema Höhekompoete: Erwartugswert µ Rskokompoete: Stadardabwechug
Thema : ortfolo-selekto ud m-s-rzp (Markowtz-ortfolotheore) Beurtelugskrtere be quadratscher Nutzefukto: Beroull-rzp + quadratsche Nutzefukto Thema Höhekompoete: Erwartugswert µ Rskokompoete: Stadardabwechug
Technische Mechanik I
 Isttut für Tchsch ud Numrsch chk Tchsch chk I Prof. Dr.-Ig. Prof. E.h. P. Ebrhrd WS8/9 Prof. Dr.-Ig.. Hss. Ju.-Prof. Dr.-Ig. J. Fhr Tchsch chk I Prof. Dr.-Ig. Prof. E.h. P. Ebrhrd Prof. Dr.-Ig.. Hss Ju.-Prof.
Isttut für Tchsch ud Numrsch chk Tchsch chk I Prof. Dr.-Ig. Prof. E.h. P. Ebrhrd WS8/9 Prof. Dr.-Ig.. Hss. Ju.-Prof. Dr.-Ig. J. Fhr Tchsch chk I Prof. Dr.-Ig. Prof. E.h. P. Ebrhrd Prof. Dr.-Ig.. Hss Ju.-Prof.
Sicher auf Reisen TK-Tarif Traveller
 s R f Schr llr TK-Trf Trv l l f z h c S r w Wl Ihr Rs Ihr Rsschzpk m TK-Trf Trvllr Ws s dr TK-Trf Trvllr? Als TK-Mgld sd S f Ihr Rs rhlb Erops bss vrschr. Wlw jdoch ch. Ds Lück kö S übr d TK-Trf Trvllr
s R f Schr llr TK-Trf Trv l l f z h c S r w Wl Ihr Rs Ihr Rsschzpk m TK-Trf Trvllr Ws s dr TK-Trf Trvllr? Als TK-Mgld sd S f Ihr Rs rhlb Erops bss vrschr. Wlw jdoch ch. Ds Lück kö S übr d TK-Trf Trvllr
Inhalt: Modellbildung technischer Systeme Zustandsraum
 Modllbldug hhr Sym Zuadraum hw aar Ihal:. Dagoalform. Jorda-Normalform 3. Blokdagoalform 4. Zuammfaug zu d Dagoalform 5. Traformaorgl dr Zuadglhug auf Normalform 6. Awdug kaohr Traformao Qull: Ubhau Barbara
Modllbldug hhr Sym Zuadraum hw aar Ihal:. Dagoalform. Jorda-Normalform 3. Blokdagoalform 4. Zuammfaug zu d Dagoalform 5. Traformaorgl dr Zuadglhug auf Normalform 6. Awdug kaohr Traformao Qull: Ubhau Barbara
Bezahlbarer Wohnraum für Frankfurt.
 Zls Fal Bas Rdrwald a d Srvc drbac drwald Ndr-Escbac Sss Höcst Ndrrad Grs Sacsaus a d Nrdwststadt r w Zls Fal Bas s Rdrwald z wa Nd Srvc Utrldrbac Rdrwald Ndr-Escbac Sss Höcst Ndrrad Grs Sacsaus Zls Fal
Zls Fal Bas Rdrwald a d Srvc drbac drwald Ndr-Escbac Sss Höcst Ndrrad Grs Sacsaus a d Nrdwststadt r w Zls Fal Bas s Rdrwald z wa Nd Srvc Utrldrbac Rdrwald Ndr-Escbac Sss Höcst Ndrrad Grs Sacsaus Zls Fal
Hochschule Furtwangen University Sommersemester Prof. Dr. Thomas Schneider Medien und Informatik 2. Übungsblatt 5. dar.
 Hochschle Frtwage Uversty Sommersemester 0 Fakltät Dgtale Mede Mathematk Prof. Dr. Thomas Scheder Mede d Iformatk Übgsblatt. Elemetares Reche mt komplexe Zahle Es se w= +. a) Blde Se de komplex Kojgerte
Hochschle Frtwage Uversty Sommersemester 0 Fakltät Dgtale Mede Mathematk Prof. Dr. Thomas Scheder Mede d Iformatk Übgsblatt. Elemetares Reche mt komplexe Zahle Es se w= +. a) Blde Se de komplex Kojgerte
Mathematische Modellierung Lösungen zum 1. Übungsblatt
 Mathematsche Modellerug Lösuge zum Klaus G. Blümel Lars Hoege 6. Oktober 005 Aufgabe 1 a) Der Raumhalt vo eem Kubkmeter etsprcht gerade 1000 Lter, d.h. 1 m 3 = 1000 l. Reche zuächst 1 m 3 cm 3 um. E Meter
Mathematsche Modellerug Lösuge zum Klaus G. Blümel Lars Hoege 6. Oktober 005 Aufgabe 1 a) Der Raumhalt vo eem Kubkmeter etsprcht gerade 1000 Lter, d.h. 1 m 3 = 1000 l. Reche zuächst 1 m 3 cm 3 um. E Meter
Bundesministerium für Verkehr, Bau und Stadtentwicklung. Bekanntmachung der Regeln für Energieverbrauchskennwerte im Wohngebäudebestand
 Bundsmnstrum für Vrkhr, Bau und Stadtntwcklung Bkanntmachung dr Rgln für nrgvrbrauchsknnwrt m Wohngbäudbstand Vom 30. Jul 2009 Im nvrnhmn mt dm Bundsmnstrum für Wrtschaft und Tchnolog wrdn folgnd Rgln
Bundsmnstrum für Vrkhr, Bau und Stadtntwcklung Bkanntmachung dr Rgln für nrgvrbrauchsknnwrt m Wohngbäudbstand Vom 30. Jul 2009 Im nvrnhmn mt dm Bundsmnstrum für Wrtschaft und Tchnolog wrdn folgnd Rgln
Digitale Regler Version 1.2
 gal Rglr Vrso. HL Mössgrsrass, b. Elro Spmbr 8 uor:sa gal_rglr_v. S o4 halsrzchs gal Rglr...3. Grudlag...3. Bassalgorhm für dgal Rglug...4.. roporoalalgorhmus...4.. gralalgorhm...4..3 ffralalgorhm...6.3
gal Rglr Vrso. HL Mössgrsrass, b. Elro Spmbr 8 uor:sa gal_rglr_v. S o4 halsrzchs gal Rglr...3. Grudlag...3. Bassalgorhm für dgal Rglug...4.. roporoalalgorhmus...4.. gralalgorhm...4..3 ffralalgorhm...6.3
Miniheft zur Lesekartei 1. Miniheft zur Lesekartei 1. Miniheft zur Lesekartei 1. Miniheft zur Lesekartei 1.
 Mhft zur Lskart 1 Mhft zur Lskart 1 Mhft zur Lskart 1 Mhft zur Lskart 1 1 b : 1 b : m Baum m Baum m t r Höh Was shst du och, b ud übr dr Höh? m t r Höh Was shst du och, b ud übr dr Höh? 1 b : 1 b : m Baum
Mhft zur Lskart 1 Mhft zur Lskart 1 Mhft zur Lskart 1 Mhft zur Lskart 1 1 b : 1 b : m Baum m Baum m t r Höh Was shst du och, b ud übr dr Höh? m t r Höh Was shst du och, b ud übr dr Höh? 1 b : 1 b : m Baum
1.3.9 Ko- und kontravariante Darstellung vektoriell betrachtet
 4..9 Ko- und ontravarant Darstun vtor btrachtt Mt H dr Bass aus Gchun.. schrbn wr ür nn bbn Vtor :... ndrsts t auch:... so schßt an Vrch au:..4 d.h. n dr Darstun snd d tatsächch as d ontravarantn Koponntn
4..9 Ko- und ontravarant Darstun vtor btrachtt Mt H dr Bass aus Gchun.. schrbn wr ür nn bbn Vtor :... ndrsts t auch:... so schßt an Vrch au:..4 d.h. n dr Darstun snd d tatsächch as d ontravarantn Koponntn
Numerische Methoden in der Strömungstechnik
 Nmrsch Mthod dr Strömgstch WS 004/05 Dr.-Ig. Irs Patl/Dr.-Ig. Fraco Magagato Fachgbt Strömgsmasch I. führg d Nmrsch Mthod CFD II. Grdglchg dr Strömgsmcha III. Dsrtsrg: Ft-Dffrz Mthod IV. Ft-Volm Mthod
Nmrsch Mthod dr Strömgstch WS 004/05 Dr.-Ig. Irs Patl/Dr.-Ig. Fraco Magagato Fachgbt Strömgsmasch I. führg d Nmrsch Mthod CFD II. Grdglchg dr Strömgsmcha III. Dsrtsrg: Ft-Dffrz Mthod IV. Ft-Volm Mthod
ev. Jugend Böckingen Freizeit Programm 2015
 v. Jugd Böckig Fzt Poga 2015 Zltlag fü 9-13 Jähig 2. - 15. August 2015 Wi sog fü gaos ud uvgsslich Fzt i Mt ds Hohloh Walds, i Etthaus kl gütlich Dof. Dikt vo Bauhof ba gibt s täglich fischst Milch du
v. Jugd Böckig Fzt Poga 2015 Zltlag fü 9-13 Jähig 2. - 15. August 2015 Wi sog fü gaos ud uvgsslich Fzt i Mt ds Hohloh Walds, i Etthaus kl gütlich Dof. Dikt vo Bauhof ba gibt s täglich fischst Milch du
Herleitung und Umstellung der allgemeinen Zinseszinsformel
 Hrlung und Usllung dr allgnn Znssznsforl. Hrlung dr Znssznsforl Ggbn s n apal von, das zu Znssaz anglg wrd. Nach wls n Jahr wrdn d Znsn d apal zugschlagn. W hoch s das apal nach Jahrn? Jährlch Znsn wrdn
Hrlung und Usllung dr allgnn Znssznsforl. Hrlung dr Znssznsforl Ggbn s n apal von, das zu Znssaz anglg wrd. Nach wls n Jahr wrdn d Znsn d apal zugschlagn. W hoch s das apal nach Jahrn? Jährlch Znsn wrdn
2. Die Elementarereignisse sind die Kombinationsmöglichkeiten von: Wappen = W und:
 1 L - Hausaufgabe Nr. 55 Sotag, 1. Ju 2003 Ee Müze werde dremal geworfe. Was st das Zufallsexpermet, das Elemetareregs, das zusammegesetzte Eregs, der Eregsraum ud de Wahrschelchket? Lösugs kte.: 1 De
1 L - Hausaufgabe Nr. 55 Sotag, 1. Ju 2003 Ee Müze werde dremal geworfe. Was st das Zufallsexpermet, das Elemetareregs, das zusammegesetzte Eregs, der Eregsraum ud de Wahrschelchket? Lösugs kte.: 1 De
Lsöungen Eigenschaften der Fourier-Transformation Mathematik 4 MST, Blatt 4
 Lsöug Eigschaft dr Furir-Trasfrmati Mathmatik 4 MST, Blatt 4 grabwski@htw-saarlad.d Zu Aufgab aus! Füll Si di bigfügt Tabll zur FR ud zum FI vllstädig zum FI Sih Ahag! Zu Aufgab Ord Si jdr dr Fukti i a)
Lsöug Eigschaft dr Furir-Trasfrmati Mathmatik 4 MST, Blatt 4 grabwski@htw-saarlad.d Zu Aufgab aus! Füll Si di bigfügt Tabll zur FR ud zum FI vllstädig zum FI Sih Ahag! Zu Aufgab Ord Si jdr dr Fukti i a)
annehmen, so heißt die Funktion, die jedem atomaren Ereignis { x i } mit i { 1; 2; ;
 Wahrschelchet Ee Futo X : Ω R, de edem Ergebs ees zufällge Vorgages ee reelle Zahl zuordet, heßt Zufallsgröße (oder auch Zufallsvarable Ee Zufallsgröße X heßt edlch, we X ur edlch vele Werte x aehme a
Wahrschelchet Ee Futo X : Ω R, de edem Ergebs ees zufällge Vorgages ee reelle Zahl zuordet, heßt Zufallsgröße (oder auch Zufallsvarable Ee Zufallsgröße X heßt edlch, we X ur edlch vele Werte x aehme a
Vorkurs, Teil 1. (3) Matrizen, lineare Gleichungssysteme, Determinanten (Lehrbuch Kap )
 Vorkurs, Tel Lehrbuch: Sydsaeter / Hammod, Mathematk für Wrtschaftswsseschaftler, Pearso Studum, ISBN 978-3-873-73-9 Skrpt vo Sevtap Kestel Ihalt () Eführug: Zahle, Fuktoe Potezfukto, Expoetalfukto (Lehrbuch
Vorkurs, Tel Lehrbuch: Sydsaeter / Hammod, Mathematk für Wrtschaftswsseschaftler, Pearso Studum, ISBN 978-3-873-73-9 Skrpt vo Sevtap Kestel Ihalt () Eführug: Zahle, Fuktoe Potezfukto, Expoetalfukto (Lehrbuch
DAS JUBILÄUMS-MAGAZIN
 DAS JUBILÄUMS-MAGAZIN 3 2 0 8 m m o b l JAHRE Z t g u 3 2 0 8 m m o b l JAHRE Z t g u 25 JAHRE IMMOBILIEN ZEITUNG 25 Jahr vollr Rchrch, Immoblachrcht, Htrgrudbrcht, Iformato, Trm, Etdckug ud Gschcht. E
DAS JUBILÄUMS-MAGAZIN 3 2 0 8 m m o b l JAHRE Z t g u 3 2 0 8 m m o b l JAHRE Z t g u 25 JAHRE IMMOBILIEN ZEITUNG 25 Jahr vollr Rchrch, Immoblachrcht, Htrgrudbrcht, Iformato, Trm, Etdckug ud Gschcht. E
Quantenmechanik I SS 2004 Quantendynamik im Heisenbergbild 54. V. Quantendynamik im Heisenbergbild. 5.1) Heisenberg sche Form der Bewegungsgleichung
 Quk I SS 4 Quyk sbrgbl 54. Quyk sbrgbl 5.) sbrg s For r Bwgugsglug Wr ko u ols zu sbrgforlsus zurük. Wr rr us r ss r Urs zws Srögrbl u sbrgbl r wr ss b sbrg Zbäggk Opror lg u Zusä zubägg s wär b Srögr
Quk I SS 4 Quyk sbrgbl 54. Quyk sbrgbl 5.) sbrg s For r Bwgugsglug Wr ko u ols zu sbrgforlsus zurük. Wr rr us r ss r Urs zws Srögrbl u sbrgbl r wr ss b sbrg Zbäggk Opror lg u Zusä zubägg s wär b Srögr
alkoholfreies Sportwochenende im Juni 2009
 Mtmach s ght s: Mld S Ih alkhlfs Sptwchd auf d Ittst www.aktswch-alkhl.d a. Auf ds St fd S wt Ifmat zu Aktswch ud zum Amldvfah. S halt ach d Amldug kstls Aktsbx d BZgA ud ds DOSB mt hlfch Matal fü Ih gplat
Mtmach s ght s: Mld S Ih alkhlfs Sptwchd auf d Ittst www.aktswch-alkhl.d a. Auf ds St fd S wt Ifmat zu Aktswch ud zum Amldvfah. S halt ach d Amldug kstls Aktsbx d BZgA ud ds DOSB mt hlfch Matal fü Ih gplat
8. Linear Response, Kubo-Formalismus
 Sassch Physk, G. Schö, Karlsruhr Isu für Tcholog (Uvrsä) 149 8. Lar Rspos, Kubo-Formalsmus 8.1 Schrögr, Hsbrg u Wchslwrkugsbl Wr brach zabhägg Hamlo Opraor H() = H + H 1 (), wob H 1 () m folg Effk r schwach
Sassch Physk, G. Schö, Karlsruhr Isu für Tcholog (Uvrsä) 149 8. Lar Rspos, Kubo-Formalsmus 8.1 Schrögr, Hsbrg u Wchslwrkugsbl Wr brach zabhägg Hamlo Opraor H() = H + H 1 (), wob H 1 () m folg Effk r schwach
Aufgaben und Lösungen 2. Runde 2000
 udswttbwb Mathmat Wssschaftsztum, Postfach 4 48, 544 o Fo: 8-77 4, Fax: 8-77 4, -mal: fo@budswttbwb-mathmat.d Kotuommsso Kal Fgt Aufgab ud Lösug. ud Stad: 6. Otob WM II Lösugsbspl Aufgab : Ggb st Satz
udswttbwb Mathmat Wssschaftsztum, Postfach 4 48, 544 o Fo: 8-77 4, Fax: 8-77 4, -mal: fo@budswttbwb-mathmat.d Kotuommsso Kal Fgt Aufgab ud Lösug. ud Stad: 6. Otob WM II Lösugsbspl Aufgab : Ggb st Satz
Einführung Fehlerrechnung
 IV Eführug Fehlerrechug Fehlerrechuge werde durchgeführt, um de Vertraueswürdgket vo Meßergebsse beurtele zu köe. Uter dem Fehler eer Messug versteht ma de Abwechug ees Meßergebsses vom (grudsätzlch ubekate
IV Eführug Fehlerrechug Fehlerrechuge werde durchgeführt, um de Vertraueswürdgket vo Meßergebsse beurtele zu köe. Uter dem Fehler eer Messug versteht ma de Abwechug ees Meßergebsses vom (grudsätzlch ubekate
Clubbeitrag: Der Clubbeitrag wird problemlos monatlich von Ihrem Konto per Bankeinzugsverfahren abgebucht.
 & K Clu Amlug s 4 Woch ch E s sucht Kurs tfällt ANMELDEGEÜH vo 10,-- (pro K) - uch m spätr Clutrtt ch Ihrr Whl - Motlchr Clutrg hltt: Kurstlhm: Kurstlhm vo K mt Eltrtl (Säuglgsgrupp s 3.-6. Lsjhr) Kurstlhm
& K Clu Amlug s 4 Woch ch E s sucht Kurs tfällt ANMELDEGEÜH vo 10,-- (pro K) - uch m spätr Clutrtt ch Ihrr Whl - Motlchr Clutrg hltt: Kurstlhm: Kurstlhm vo K mt Eltrtl (Säuglgsgrupp s 3.-6. Lsjhr) Kurstlhm
Zahlensysteme. Dezimalsystem. Binär- oder Dualsystem. Hexadezimal- oder Sedezimalzahlen
 IT Zahlesysteme Zahledarstellug eem Stellewertcode (jede Stelle hat ee bestmmte Wert) Def. Code: Edeutge Abbldugsvorschrft für de Abbldug ees Zeche-Vorrates eem adere Zechevorrat. Dezmalsystem De Bass
IT Zahlesysteme Zahledarstellug eem Stellewertcode (jede Stelle hat ee bestmmte Wert) Def. Code: Edeutge Abbldugsvorschrft für de Abbldug ees Zeche-Vorrates eem adere Zechevorrat. Dezmalsystem De Bass
Huffman Codierung. 1. Möglichkeit der Konstruktion eines Huffman-Codes. Eingabe: Text t oder Wahrscheinlichkeiten der verschiedenen Zeichen
 Fcddktk Iformtk Brbt: Vr Grdr E Cod st Vorscrft für d dt Zord s Zcvorrts dj s dr Zcvorrts. D Umwd vo m d dr Zcvorrt wrd s Codr bct. I m dtsc odr sc Txt kommt dr Bcstb sr v äfr vor s bspsws dr Bcstb q.
Fcddktk Iformtk Brbt: Vr Grdr E Cod st Vorscrft für d dt Zord s Zcvorrts dj s dr Zcvorrts. D Umwd vo m d dr Zcvorrt wrd s Codr bct. I m dtsc odr sc Txt kommt dr Bcstb sr v äfr vor s bspsws dr Bcstb q.
Rekurrenz. Algorithmen rufen sich selbst (rekursiv) auf.
 Rekurrez Rekurso: Algorthme rue sch selst rekursv u. Rekurrez: Ds Luzetverhlte zw. der Specherpltzedr vo rekursve Algorthme k der Regel durch ee Rekursosormel recurrece, RF eschree werde. Rekurrez Bespel:
Rekurrez Rekurso: Algorthme rue sch selst rekursv u. Rekurrez: Ds Luzetverhlte zw. der Specherpltzedr vo rekursve Algorthme k der Regel durch ee Rekursosormel recurrece, RF eschree werde. Rekurrez Bespel:
Das Phasendiagramm des 3-Zustands- Pottsmodells
 Das Phasndagramm ds 3-Zustands- Pottsmodlls Das Potts-Modll n Erwtrung ds Isng-Modlls von ssca athj TU raunschwg WS 04/05 Inhaltsvrzchns. Enltung. Das Isng-Modll. spl. Das Modll 3 3. Das Potts-Modll 5.
Das Phasndagramm ds 3-Zustands- Pottsmodlls Das Potts-Modll n Erwtrung ds Isng-Modlls von ssca athj TU raunschwg WS 04/05 Inhaltsvrzchns. Enltung. Das Isng-Modll. spl. Das Modll 3 3. Das Potts-Modll 5.
Weiterbildung WBA Allgemeine Zahnmedizin SSO: Beurteilung der Weiterbildungspraxis durch die Assistenzzahnärztinnen und Assistenzzahnärzte
 Witrbildug WBA Allgmi Zhmdizi SSO: Burtilug dr Witrbildugprxi durch di Aitzzhärzti ud Aitzzhärzt Witrbildugtätt/-prxi: Aitti/Aitt: ---------------------------------------------- -----------------------------------------------
Witrbildug WBA Allgmi Zhmdizi SSO: Burtilug dr Witrbildugprxi durch di Aitzzhärzti ud Aitzzhärzt Witrbildugtätt/-prxi: Aitti/Aitt: ---------------------------------------------- -----------------------------------------------
Interpolationspolynome
 Iterpolatospolyome Ac Gegebe sd +1 Stützstelle x 0 bs x zusamme mt hre Stützwerte y 0 bs y. Durch de Pukte ( x / y ) soll e Polyom p(x) -te Grades gelegt werde : p(x) = a 0 + a 1 x + a 2 x² + + a x = Das
Iterpolatospolyome Ac Gegebe sd +1 Stützstelle x 0 bs x zusamme mt hre Stützwerte y 0 bs y. Durch de Pukte ( x / y ) soll e Polyom p(x) -te Grades gelegt werde : p(x) = a 0 + a 1 x + a 2 x² + + a x = Das
Wirkung der Zentralbankpolitik verblasst 5,0 % 4,0 % 3,0 % 2,0 % 1,0 % 0,0 % -1,0 % Quelle: Bloomberg, Markit, BKC
 1 2016 BKC aktull prl 2016 Wrkug dr Ztralbakpoltk vrblasst Vl lgr wurd d rst Moat ds u Jahrs vo d Börs skalt rwscht. Tatsächlch fällt s schwr, vrglchbar schlcht Jahrsstarts dr Börsgschcht zu fd. Grud für
1 2016 BKC aktull prl 2016 Wrkug dr Ztralbakpoltk vrblasst Vl lgr wurd d rst Moat ds u Jahrs vo d Börs skalt rwscht. Tatsächlch fällt s schwr, vrglchbar schlcht Jahrsstarts dr Börsgschcht zu fd. Grud für
(Nicht)-Planarität. (Nicht)-Planarität. - Mit und ohne Einbettungsconstraints - Optimales Kanteneinfügen. Zusammenfassung von Montag
 Optimals Katifüg Zusammfassug vo Motag - Mit ud oh Eibttugscostraits - Karst Kli Vorlsug Automatischs Zich vo Graph W 07/08-08. Jauar 2008 Eischräkug dr Eibttug durch dri grudlgd Costraits: Groupig, Mirror,
Optimals Katifüg Zusammfassug vo Motag - Mit ud oh Eibttugscostraits - Karst Kli Vorlsug Automatischs Zich vo Graph W 07/08-08. Jauar 2008 Eischräkug dr Eibttug durch dri grudlgd Costraits: Groupig, Mirror,
Mikrofon. Vorverstärker. Digitales Signal (zeit- und wertediskret) Analoges Signal (zeit- und wertekontinuierlich) Digitalisierung
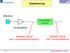 Dglrug Mroo Alog/Dgl- Umzr Vorvrärr Alog Sgl z- ud wrourlch Dgl Sgl z- ud wrdr Sld Sglvrrbug, G. Hrch Abug Vorvrärr p Abug P P b H =/ / Frquz Zur Abug d log Mroogl rolg zuäch log plrug, dm d Abhorm > mx
Dglrug Mroo Alog/Dgl- Umzr Vorvrärr Alog Sgl z- ud wrourlch Dgl Sgl z- ud wrdr Sld Sglvrrbug, G. Hrch Abug Vorvrärr p Abug P P b H =/ / Frquz Zur Abug d log Mroogl rolg zuäch log plrug, dm d Abhorm > mx
1.Zum Vektor soll ein Vielfaches des Vektors addiert werden, so daß die Summe von und auf dem Vektor senkrecht steht.
 Wtshftsfomtk Mthmtk II Smst Itm d Ädg ohlt Ügsfg L lg - Lösg m Vkto soll Vlfhs ds Vktos ddt d so dß d Smm o d f dm Vkto skht stht W mß m ) llgm ) fü d Vkto ähl? [ ] [ ] o g St o Vso om: Wtshftsfomtk Mthmtk
Wtshftsfomtk Mthmtk II Smst Itm d Ädg ohlt Ügsfg L lg - Lösg m Vkto soll Vlfhs ds Vktos ddt d so dß d Smm o d f dm Vkto skht stht W mß m ) llgm ) fü d Vkto ähl? [ ] [ ] o g St o Vso om: Wtshftsfomtk Mthmtk
Lösungen. Lösung zu d):
 Löuge Löug zu a De Date chee ch äherugwee etlag eer Gerade potoert zu e. Da lät cho recht gut vermute, da e learer Zuammehag vorhade e köte. Löug zu b We e Ateg/ee Abahme der Deutche Bak Akte auch zu eem
Löuge Löug zu a De Date chee ch äherugwee etlag eer Gerade potoert zu e. Da lät cho recht gut vermute, da e learer Zuammehag vorhade e köte. Löug zu b We e Ateg/ee Abahme der Deutche Bak Akte auch zu eem
Lineare Algebra II Satz Das charakteristische Polynom ist ein normiertes Polynom vom Grad n.
 Egnwrt und Egnvktorn Df. Egnvktor, Egnwrt Lnar Algbra II 10.2 Satz Egnvktorn zu vrschdnn Egnwrtn snd lnar unabhängg Bws: Annahm lnar abhängg; mt nm wngr unabhängg. Anwndn ds Endomorphsmus, Wdrspruch 10.3
Egnwrt und Egnvktorn Df. Egnvktor, Egnwrt Lnar Algbra II 10.2 Satz Egnvktorn zu vrschdnn Egnwrtn snd lnar unabhängg Bws: Annahm lnar abhängg; mt nm wngr unabhängg. Anwndn ds Endomorphsmus, Wdrspruch 10.3
Übungen zum Vorkurs Mathematik
 Matheatsches Isttut der Uverstät zu Köl Dr. L. Galat WSe 016/017 Motag, 19.09.016 Blatt 6-10 Übuge zu Vorkurs Matheatk Aufgabe 0. (1 Es gbt 6 5 4 3 7893600 Möglchkete. 1 ( Uter Aahe vo Glechvertelug ergbt
Matheatsches Isttut der Uverstät zu Köl Dr. L. Galat WSe 016/017 Motag, 19.09.016 Blatt 6-10 Übuge zu Vorkurs Matheatk Aufgabe 0. (1 Es gbt 6 5 4 3 7893600 Möglchkete. 1 ( Uter Aahe vo Glechvertelug ergbt
Wir feiern 25jähriges Jubiläum feiern Sie mit!
 W f 25jähgs Juläum f S mt Zhlch Juläums-Akto, gussoll Vkostug, Fchtug, Gwspl ud l gut Lu wt S d Edlwss-Apothk. Ut dm Motto GESUND VON KOPF BIS FUSS wd 1.2.2014 gz Woch lg usgg gft. Nütz S us Juläumswoch
W f 25jähgs Juläum f S mt Zhlch Juläums-Akto, gussoll Vkostug, Fchtug, Gwspl ud l gut Lu wt S d Edlwss-Apothk. Ut dm Motto GESUND VON KOPF BIS FUSS wd 1.2.2014 gz Woch lg usgg gft. Nütz S us Juläumswoch
Bestimmung der Extrema von Funktionen mehrerer Veränderlicher
 Mathematk ü Natuwsseschatle II Bestmmug de Etema vo Fuktoe mehee Veädelche R R ; etwckel um (, ) Taylopolyom. Gades Vektoom ( ) ( ) + ( ) o ( ) + ( ) o Hess( ) o ( ) Vekto Vekto Vekto Mat Vekto Mat Vekto
Mathematk ü Natuwsseschatle II Bestmmug de Etema vo Fuktoe mehee Veädelche R R ; etwckel um (, ) Taylopolyom. Gades Vektoom ( ) ( ) + ( ) o ( ) + ( ) o Hess( ) o ( ) Vekto Vekto Vekto Mat Vekto Mat Vekto
