4. Freie Energie/Enthalpie & Gibbs Gleichungen
|
|
|
- Jens Roth
- vor 7 Jahren
- Abrufe
Transkript
1 4. Freie Energie/Enthalie & Gibbs Gleichungen 4.3. Gibbs sche Gleichungen Fundamentalgleichungen der D weitere Fundamentalgleichungen basierend auf: einsetzen von (): d d d Ausdifferenzierung der Definition der Zustandsfunktionen für A, H und G einsetzen der ursrünglichen Fundamentalgleichung d = d - d freie Energie: A da da d d d ( d d) d d () da d d () Enthalie: H dh d d d einsetzen von (): dh ( d d) d d (3) dh d d freie Enthalie: G H einsetzen von (3): dh d d ( d d) d d (4) PC (0) Folien in Zusammenarbeit mit Julia Kunze in Anlehnung an Alexander Ogrodniks krit age: 03 d d
2 4. Freie Energie/Enthalie & Gibbs Gleichungen 4.3. Gibbs sche Gleichungen Fundamentalgleichungen der D d, dh, da, sind Zustandsfunktionen können durch vollständige Differentiale beschrieben werden innere Energie: d d d d d d alternativ: rein thermodynamische Definition der emeratur d d d für d=0 d d für d=0 d d PC (0) Folien in Zusammenarbeit mit Julia Kunze in Anlehnung an Alexander Ogrodniks krit age: 04
3 4. Freie Energie/Enthalie & Gibbs Gleichungen 4.3. Gibbs sche Gleichungen Fundamentalgleichungen der D d, dh, da, sind Zustandsfunktionen können durch vollständige Differentiale beschrieben werden freie Enthalie: d d G d G d G G alternativ: nützliche Beziehungen der - und -Abhängigkeit von G d d für d=0 d für d=0 PC (0) Folien in Zusammenarbeit mit Julia Kunze in Anlehnung an Alexander Ogrodniks krit age: 05 d G G
4 PC (0) age: 06 Folien in Zusammenarbeit mit Julia Kunze in Anlehnung an Alexander Ogrodniks krit Übersicht aller Gibbs schen Gleichungen mit ihren artiellen Ableitungen 4. Freie Energie/Enthalie & Gibbs Gleichungen 4.3. Gibbs sche Gleichungen Fundamentalgleichungen der D krit (Dr. Ogrodnik): Ka. 4. G G d d dh d d d d da d d d A H H A thermodynamische Definition der emeratur
5 4. Freie Energie/Enthalie & Gibbs Gleichungen 4.3. Gibbs sche Gleichungen Druckabhängigkeit von G G Druckabhängigkeit der freien Enthalie isotherm: da > 0, nimmt G mit dem Druck immer zu da molar von Gasen >> Flüssigkeiten, Feststoffe grössere Zunahme von G für Gase aus: P.W. Atkins, Physikalische Chemie (CH) isotherme Druckänderung: aus d G() G() d für Flüssigkeiten und Festkörer: konstant G () G( ) für ideale Gase: =nr G( ) G( ) d G( ) n R G( ) n R ln PC (0) Folien in Zusammenarbeit mit Julia Kunze in Anlehnung an Alexander Ogrodniks krit age: 07 afelanschrieb: Beisiel d
6 4. Freie Energie/Enthalie & Gibbs Gleichungen 4.3. Gibbs sche Gleichungen Druckabhängigkeit von G isotherme eränderung von G mit aus /-Diagramm gilt auch für reale Gase nicht verwechseln mit olumenarbeit! G d w d Isotherme Isotherme krit (Dr. Ogrodnik): Ka. 4. PC (0) Folien in Zusammenarbeit mit Julia Kunze in Anlehnung an Alexander Ogrodniks krit age: 08
7 4. Freie Energie/Enthalie & Gibbs Gleichungen 4.4. Gibbs-Helmholtz Gleichung emeraturabhängigkeit der freien Enthalie isobar: da die molar von Gasen >> Flüssigkeiten, Feststoffe (Grad der nordnung!) grössere -Abhängigkeit von G für Gase Gibbs-Helmholtz Gleichung: ausgehend von: G() H() () G H kombiniert mit artiellem Differential: G G H wir sehen säter, dass die Gleichgewichtskonstante einer Reaktion von G/ und nicht von G abhängt (G / ) suche Beziehung für:? afelanschrieb: Ableitung G PC (0) Folien in Zusammenarbeit mit Julia Kunze in Anlehnung an Alexander Ogrodniks krit age: 09 aus: P.W. Atkins, Physikalische Chemie (CH)
8 4. Freie Energie/Enthalie & Gibbs Gleichungen 4.4. Gibbs-Helmholtz Gleichung G / H Gibbs-Helmholtz Gleichung die -Abhängigkeit von G/ ist nur von der Enthalie H bestimmt und ist unabhängig von der Entroie! für chemische Reaktionen (isobar): RG / RH Fazit: bei bekanntem R H einer Reaktion is die -Abhängigkeit von G/ bekannt Anwendung: die Gleichgewichtskonstante K einer Reaktion ist eine Funtion in G/: Bestimmung der -Abhängigkeit von K nicht-kalorische Bestimmung von R H afelanschrieb: Erklärung RG R ln K PC (0) Folien in Zusammenarbeit mit Julia Kunze in Anlehnung an Alexander Ogrodniks krit age: 0
9 PC (0) age: Folien in Zusammenarbeit mit Julia Kunze in Anlehnung an Alexander Ogrodniks krit 4. Freie Energie/Enthalie & Gibbs Gleichungen 4.5. Maxwellgleichungen für jedes vollständige Differential (jede Zustandsfunktion): dy y F dx x F df x y hierfür gilt die chwarz sche Gleichung: (s. Aendix in Atkins oder krit Kaitel 4.4) y x x y x y F y x F d d d z.b. für die innere Energie: ergleich mit der Fundamentalgleichung: Maxwellgleichung:
10 PC (0) age: Folien in Zusammenarbeit mit Julia Kunze in Anlehnung an Alexander Ogrodniks krit 4. Freie Energie/Enthalie & Gibbs Gleichungen 4.5. Maxwellgleichungen Zusammenfassung der Maxwellgleichungen: d d d ) aus: d d dh ) aus: d d da 3) aus: d d 4) aus: mathematischer Zusammenhang thermodynamischer Grössen nützlich für weitere Ableitungen
11 PC (0) age: 3 Folien in Zusammenarbeit mit Julia Kunze in Anlehnung an Alexander Ogrodniks krit 4. Freie Energie/Enthalie & Gibbs Gleichungen 4.5. Maxwellgleichungen Anwendungsbeisiel - Binnendruck d d C d d d (s.. 06) zur Bestimmung von idealer und realer Gase (s.. 9) benötigen einen einfachen thermodynamischen Zusammenhang diesen liefert die Fundamentalgleichung: d d d Ableitung nach d bei d=0: kombiniert mit der Maxwellgleichuung: 0 ) ( Gas ideales m dw Gas a n a ) ( und (s.. 9)
12 4. Freie Energie/Enthalie & Gibbs Gleichungen 4.5. Maxwellgleichungen Anwendungsbeisiel - Joule-homson Koefficient J J H = Joule homson Koeffizient teigung der Isenthalen (s.. ) reales Gas J 0 d negativ Gas kühlt ab. reales Gas J 0 d ositiv Gas erwärmt sich. via Euler sche Kettenregel und Kehrwertregel (s.. 6): H Bestimmung von via Gibb sche Gleichung und Maxwellgleichung J C dh J C H d d afelanschrieb: Herleitung PC (0) Folien in Zusammenarbeit mit Julia Kunze in Anlehnung an Alexander Ogrodniks krit age: 4
13 4. Freie Energie/Enthalie & Gibbs Gleichungen 4.5. Maxwellgleichungen Anwendungsbeisiel - Joule-homson Koefficient J Korrelation mit dem erhalten eines idealen Gases ( J =0) J C ideal nr nr J C ideal = ideal < ideal > ideal J = 0 wie erwartet für ideales Gas J > 0, d.h. das Gas kühlt sich ab J < 0, d.h. das Gas wärmt sich auf weitere Details siehe krit (Dr. Ogrodnik): Ka. 4.5 PC (0) Folien in Zusammenarbeit mit Julia Kunze in Anlehnung an Alexander Ogrodniks krit age: 5
5. Die Thermodynamischen Potentiale
5. Die hermodynamischen Potentiale 5.1. Einführung der Potentiale Gibbs'sche Fundamentalgleichung. d = du + d, du + d δ Q d = = Ist die Entroie als Funktion von U und bekannt, = ( U, ) dann lassen sich
1. Thermodynamische Potentiale, Maxwellgleichungen
69 KAPIEL G hermodynamische Potentiale 1. hermodynamische Potentiale, Maxwellgleichungen hermodynamische Potentiale sind Funktionen von den Zustandsvariablen. Wir haben schon die innere Energie kennengelernt,
Der Zweite Hauptsatz der TD- Lernziele
Der Zweite Hautsatz der D- Lernziele o Einleitung o Entroie (Definition, Entroie als Zustandsfunktion, die Clausius sche Ungleichung) o Der Zweite Hautzatz der D o Die Entroieänderungen bei seziellen Prozessen
Der Zweite Hauptsatz der TD- Lernziele
Der Zweite Hautsatz der D- Lernziele o Einleitung o Entroie (Definition, Entroie als Zustandsfunktion, die Clausius sche Ungleichung) o Der Zweite Hautzatz der D o Die Entroieänderungen bei seziellen Prozessen
4. Freie Energie/Enthalpie & Gibbs Gleichungen
4. Freie Energie/Enthalpie & Gibbs Gleichungen 1. Eigenschaften der Materie in der Gasphase 2. Erster Hauptsatz: Arbeit und Wärme 3. Entropie und Zweiter Hauptsatz der hermodynamik 4. Freie Enthalpie G,
Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke)
Freie Universität Berlin W 006/007 Fachbereich Physik 8..006 tatistische Physik - heorie der Wärme (PD Dr. M. Falcke) Übungsblatt 9: hermodynamische Identitäten, hermische/kalorische Zustandsgleichung,
5 Thermodynamische Potentiale
3 Woche 5 hermodynamische Potentiale 51 Formale Einführung der Potentiale Es ist möglich, die extensiven Zustandsfunktionen (mit der Dimension der Energie) zu bilden, die die anderen ariablen als S,, N
1 I. Thermodynamik. 1.1 Ideales Gasgesetz. 1.2 Vereinfachte kinetische Gastheorie. 1.3 Erster Hauptsatz der Thermodynamik.
1 I. hermodynamik 1.1 Ideales Gasgesetz eilchenzahl N Stoffmenge: n [mol], N A = 6.022 10 23 mol 1 ; N = nn A molare Größen: X m = X/n ideales Gasgesetz: V = nr, R = 8.314JK 1 mol 1 Zustandsgrößen:, V,,
Physikalische Chemie Physikalsiche Chemie I SoSe 2009 Prof. Dr. Norbert Hampp 1/10 5. Zustandsfunktionen Idealer und Realer Gase. ZustandsÄnderungen
Prof. Dr. Norbert Ham 1/10 5. Zustandsfunktionen Idealer und Realer Gase ZustandsÄnderungen Die rennung zwischen unserem System und der ÅUmweltÇ wird durch eine Wand realisiert. WÄnde kånnen unterschiedliche
Der erste Hauptsatz der TD- Lernziele
Der erste Hautsatz der D- Lernziele o Einleitung o Zustandgrössen und funktionen o Wärme, Arbeit und Energie o Innere Energie o Der erste Hautsatz der hermodynamik o olumenarbeit o Wärmeübergänge o Die
T 1 T T Zustandsverhalten einfacher Systeme (Starthilfe S ) - Prozess und Zustandsänderung. Prozess (Q 12
. Zustandserhalten einfacher Systeme (Starthilfe S. 9-38) - Prozess und Zustandsänderung Zustandsänderung δq Prozess (Q ) - thermodynamisch einfache Systeme reiner Stoff feste flüssige damfförmige Phase
Temperaturabhängigkeit von Enthalpie H und Entropie S
Prof. Dr. Norbert Ham 1/5 8. emeraturabhängigkeit von Enthalie und Entroie emeraturabhängigkeit von Enthalie H und Entroie S In abellenwerken sind Enthalien und Entroien in der Regel bezogen auf Standardbedingungen,
Der Erste Hauptsatz der TD- Lernziele
hermodynamik (D) Fundamentale heorie der makroskoischen Eigenschaften der Materie: - Sontane Prozesse - Konzet der emeratur - Phasenübergänge - Energetik makroskoischer Phasen und chemischer Reaktionen
Musterlösung Klausur Physikalische Chemie I: Thermodynamik (Januar 2009)
Musterlösung Klausur Physikalische Chemie I: Thermodynamik (Januar 2009) Aufgabe 1: Reaktionsthermodynamik a) möglichst niedrige Temeratur (begünstigt exotherme Reaktionen) möglichst hoher Druck (begünstigt
I el U el. P el W V 23+W F23. Musterlösung SS Aufgabe (34 Punkte) a) Energiebilanz für die Kammer A im Zeitintervall t 12 :
Musterlösung SS. Aufgabe Punkte a Energiebilanz für die Kammer A im Zeitintervall t : W A, + W V A U A U A W A, P el t U el I el t W V A 0 U A U A m A c v A A 5 m A A V A R A 6 c v κ R 7 A A A A 8 A B
Die Eigenschaften einfacher
Die Eigenschaften einfacher ischungen Lernziele: Thermodynamische eschreibung von ischungen Partielle molare Grössen, TD von Ischhasen Chemisches Potenzial flüssiger Phasen Eigenschaften von Lösungen,
T p = T = RT. V b. ( ) 2 V p. V b. 2a(V b)2 V 3 RT. 2a(V b) V 3 (p+ a V 2 )
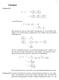3 Lösung zu 83. Lösungen ( C C = T ( = T ( ( ( 2 van-der-waals Gas: ( ( b + a 2 = T = T b a 2 Man beachte das dies nur eine andere Formulierung der van-der-waals Gleichung ist als auf dem letzten Aufgabenzettel.
PC-Übung Nr.3 vom
PC-Übung Nr.3 vom 31.10.08 Sebastian Meiss 25. November 2008 1. Die Säulen der Thermodynamik Beantworten Sie folgende Fragen a) Welche Größen legen den Zustand eines Gases eindeutig fest? b) Welche physikalischen
Thermodynamik. Kapitel 4. Nicolas Thomas
Thermodynamik Kapitel 4 Arbeit und Wärme Länge, x F Kolben Länge, x F Der Kolben wird sehr langsam um die Distanz -dx verschoben. dx Kolben Wieviel Arbeit mussten wir leisten, um den Kolben zu bewegen?
T4p: Thermodynamik und Statistische Physik Prof. Dr. H. Ruhl Übungsblatt 10 Lösungsvorschlag
4: hermodynamik und Statistische Physik Prof. Dr. H. Ruhl Übungsblatt 10 Lösungsvorschlag 1. Joule-homson-Effekt Ein Gasstrom wird von Bereich 1 (siehe Abbildung) mit einem Kolben durch eine oröse Wand
Der Erste Hauptsatz der TD- Lernziele
hermodynamik (D) Fundamentale heorie der makroskoischen Eigenschaften der Materie: - Sontane Prozesse - Konzet der emeratur - Phasenübergänge - Energetik makroskoischer Phasen und chemischer Reaktionen
Die innere Energie and die Entropie
Die innere Energie and die Entropie Aber fangen wir mit der Entropie an... Stellen Sie sich ein System vor, das durch die Entropie S, das Volumen V und die Stoffmenge n beschrieben wird. U ' U(S,V,n) Wir
Thermodynamik der Gase. Joule-Thomson-Prozeß (PHYWE)
hermodynamik der Gase Joule-homson-Prozeß (PHYWE) Ziel des Versuches ist es, den Joule-homson-Koeffizienten µ J für zwei verschiedene Gase zu bestimmen. Vorbereitung: - hermodynamik idealer/ realer Gase
Physikalische Chemie Physikalische Chemie I SoSe 2009 Prof. Dr. Norbert Hampp 1/8 15. Chemische Thermodynamik. ZustandsÄnderungen
Physikalische Chemie Physikalische Chemie I oe 2009 Prof. Dr. Norbert Ham 1/8 15. Chemische hermodynamik Zustandsnderungen Mit Hilfe des chemischen Potentials, knnen wir offene und kommunizierende ysteme
Die freie Energie wird also bei konstantem Volumen und konstanter Temperatur minimal
Die freie Energie wird also bei konstantem Volumen und konstanter Temperatur minimal 7.2 Die Enthalpie Die Enthalpie H ist definiert als H = U + pv, womit wir für die Änderung erhalten dh = pdv + TdS +
GPH2 Thermodynamik. 27. September Dieser Entwurf ist weder vollständig oder fehlerfrei noch ein offizielles Script zur Vorlesung.
GPH2 Thermodynamik Dieser Entwurf ist weder ollständig oder fehlerfrei noch ein offizielles Scrit zur Vorlesung. Für Anregungen und Kritik: mail@sibbar.de 27. Setember 2004 GPH2 Thermodynamik Seite 2 on
Einführung in die Physikalische Chemie Teil 2: Makroskopische Phänomene und Thermodynamik
Einführung in die Phsikalische Chemie Teil 2: Makroskopische Phänomene und Thermodnamik Kapitel 7: Boltzmann-Verteilung Kapitel 8: Statistische Beschreibung makroskopischer Grössen Kapitel 9: Thermodnamik:
0.1 Barometrische Höhenformel
0. Barometrische Höhenformel Da, wie aus den bisherigen Überlegungen hervorgegeangen ist, Gase komressibel sind, kann deren Dichte nicht als konstant angesehen werden. Dies hat Konsequenzen auf den Schweredruck
Inhalt der Vorlesung. 1. Eigenschaften der Gase. 0. Einführung
Inhalt der Vorlesung 0. Einführung 0.1 Themen der Physikal. Chemie 0.2 Grundbegriffe/ Zentrale Größe: Energie 0.3 Molekulare Deutung der inneren Energie U Molekülstruktur, Energieniveaus und elektromagn.
Inhalt 1 Grundlagen der Thermodynamik
Inhalt 1 Grundlagen der Thermodynamik..................... 1 1.1 Grundbegriffe.............................. 2 1.1.1 Das System........................... 2 1.1.2 Zustandsgrößen........................
Physikalisch-chemische Grundlagen der thermischen Verfahrenstechnik
Lüdecke Lüdecke Thermodynamik Physikalisch-chemische Grundlagen der thermischen Verfahrenstechnik Grundlagen der Thermodynamik Grundbegriffe Nullter und erster Hauptsatz der Thermodynamik Das ideale Gas
Differentiation nach einem Parameter Kettenregel
Differentiation nach einem Parameter Kettenregel 1-E Eine verkettete Funktion von zwei Variablen Abb. 1-1: Die Darstellung einer verketteten Funktion z = f (x, y) f x, y = x 2 2 y, x t = t 2, y t = t 2
Thermische Energie kann nicht mehr beliebig in andere Energieformen umgewandelt werden.
Wärmemenge: hermische Energie kann nicht mehr beliebig in andere Energieformen umgewandelt werden. Sie kann aber unter gewissen oraussetzungen von einem Körer auf einen nderen übertragen werden. Dabei
Musterlösung zu Übung 7
PCI hermodynamik G. Jeschke FS 05 Musterlösung zu Übung 7 08.04.05 a Der Goldbarren wird beim Einbringen in das Reservoir sprunghaft erwärmt. Der Wärmeaustausch erfolgt daher auf irreversiblem Weg. Um
PC-Übung Nr.1 vom
PC-Übung Nr.1 vom 17.10.08 Sebastian Meiss 25. November 2008 1. Allgemeine Vorbereitung a) Geben Sie die Standardbedingungen in verschiedenen Einheiten an: Druck p in Pa, bar, Torr, atm Temperatur T in
Die innere Energie eines geschlossenen Systems ist konstant
Rückblick auf vorherige Vorlesung Grundsätzlich sind alle möglichen Formen von Arbeit denkbar hier diskutiert: Mechanische Arbeit: Arbeit, die nötig ist um einen Massepunkt von A nach B zu bewegen Konservative
6 Thermodynamische Potentiale und Gleichgewichtsbedingungen
6 hermodynamische Potentiale und Gleichgewichtsbedingungen 6.1 Einführung Wir haben bereits folgende thermodynamische Potentiale untersucht: U(S,V ) S(U,V ) hermodynamische Potentiale sind Zustandsfunktionen
Besprechung der thermodynamischen Grundlagen von Wärmekraftmaschinen und Wärmepumpen
3.5 Zustandsänderung nderung von Gasen Ziel: Besrehung der thermodynamishen Grundlagen von Wärmekraftmashinen und Wärmeumen Zustand von Gasen wird durh Druk, olumen, und emeratur beshrieben thermodyn.
Institut für Physikalische Chemie Albert-Ludwigs-Universität Freiburg
Institut für Physikalische Chemie Albert-Ludigs-Universität Freiburg Lösungen zum 4. Übungsblatt zur orlesung Physikalische Chemie I SS 00 Prof. Dr. Bartsch 4. (6 Punkte) In einem Behälter mit der Grundfläche
Grundlagen der Physik II
Grundlagen der Physik II Othmar Marti 02. 07. 2007 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Wärmelehre Grundlagen der Physik II 02. 07. 2007 Inhaltsverzeichnis
9.4 Der 2. Hautsatz: spontane Prozesse und Entropie
9.4 Der 2. Hautsatz: spontane Prozesse und Entropie Beispiele für spontane Prozesse: Ein heisser Körper kühlt sich auf Umgebungstemperatur ab. Ein kalter Köper erwärmt sich auf Umgebungstemperatur. Die
Lehrbuch der Thermodynamik
Ulrich Nickel Lehrbuch der Thermodynamik Eine verständliche Einführung PhysChem Verlag Erlangen U. Nickel VII Inhaltsverzeichnis 1 GRUNDLAGEN DER THERMODYNAMIK 1 1.1 Einführung 1 1.2 Materie 2 1.3 Energie
Lehrbuch der Thermodynamik
Ulrich Nickel Lehrbuch der Thermodynamik Eine verständliche Einführung PhysChem Verlag Erlangen U.Nickel Vll Inhaltsverzeichnis 1 GRUNDLAGEN DER THERMODYNAMIK 1 1.1 Einführung l 1.2 Materie ' 2 1.3 Energie
wegen adiabater Kompression, d.h. kein Wärmeaustausch mit der Umgebung, gilt:
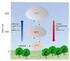Ü 7. Adiabate Komression on Luft Luft wird in einem adiabaten Zylinder on. bar, T 5 C solange erdichtet bis eine Endtemeratur on T 00 C erreicht wird. Gesucht sind die zur Verdichtung erforderliche Arbeit
Die Innere Energie U
Die Innere Energie U U ist die Summe aller einem System innewohnenden Energien. Es ist unmöglich, diese zu berechnen. U kann nicht absolut angegeben werden! Differenzen in U ( U) können gemessen werden.
Bernhard Härder. Einführung in die PHYSIKALISCHE CHEMIE ein Lehrbuch Chemische Thermodynamik W/ WESTAR.P WISSENSCHAFTEN. Skripte, Lehrbücher Band 2
Bernhard Härder Einführung in die PHYSIKALISCHE CHEMIE ein Lehrbuch Chemische Thermodynamik Skripte, Lehrbücher Band 2 W/ WESTAR.P WISSENSCHAFTEN Inhaltsverzeichnis Vorwort zur ersten Auflage Vorwort zur
Kompressor in CHEMCAD
Komressor in CHEMCAD Berechnungsmethoden Die im Menü des Komressors zu wählenden Berechnungsmethoden sollen hier näher besrochen werden: Die Auswahl besteht aus. Adiabatic,. Polytroic und 3. Polytroic
Physik I TU Dortmund WS2017/18 Gudrun Hiller Shaukat Khan Kapitel 6
Physik I U Dortmund WS07/8 Gudrun Hiller Shaukat Khan Kaitel 6 Seziische Wärme von Gasen Bei einatomigen Gasen (z.b. He): Bei zweiatomigen Gasen (z.b. N, O ): N k A Freiheitsgrade ür die kinetische Energie
Chemische Thermodynamik. Arbeitsbuch 4. 4., überarbeitete Auflage. Autoren. Mit 53 Bildern sowie zahlreichen Tabellen im Text und im Anhang
Arbeitsbuch 4 Chemische Thermodynamik Autoren Gert Wolf, Freiberg (federführender Autor) Wolfgang Schneider, Dresden 4., überarbeitete Auflage Mit 53 Bildern sowie zahlreichen Tabellen im Text und im Anhang
Grundlagen der Physik II
Grundlagen der Physik II Othmar Marti 05. 07. 2007 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Wärmelehre Grundlagen der Physik II 05. 07. 2007 Klausur Die Klausur
Verhalten reiner, realer Stoffe. Maxwellsche Beziehungen. Kapitel 7
Verhalten reiner, realer Stoffe Kaitel 7 Maxwellsche Beziehungen Verknüfen die energetischen Zustandsgrößen und die Entroie mit den thermischen Zustandsgrößen Zustandsgröße sezifische Innere Energie du
Einführung in die Physikalische Chemie Teil 1: Mikrostruktur der Materie
Einführung in die Physikalische Chemie Teil 1: Mikrostruktur der Materie Kapitel 1: Quantenmechanik Kapitel 2: Atome Kapitel 3: Moleküle Mathematische Grundlagen Schrödingergleichung Einfache Beispiele
Vorlesung Physikalische Chemie II WS 2017/18
Vorlesung Physikalische Chemie II WS 2017/18 Vorlesung für BA Life Science und Lehramt Chemie Prof. Dr. K. Hauser Fachbereich Chemie Karin.Hauser@uni-konstanz.de Termine Vorlesung (4 std.) Beginn 25.10.2017
Vorlesung PC I Thermodynamik Teil B: Thermodynamische Funktionen, Berechnungen und mathematische Methoden
Vorlesung PC I hermodynamik eil B: hermodynamische Funktionen, Berechnungen und mathematische Methoden Martin Quack, Jürgen Stohner Sommer 2006 2 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006
Diese Fragen sollten Sie auch ohne Skript beantworten können: Was beschreibt der Differenzenquotient? Wie kann man sich die Steigung im vorstellen? Wa
103 Diese Fragen sollten Sie auch ohne Skript beantworten können: Was beschreibt der Differenzenquotient? Wie kann man sich die Steigung im vorstellen? Was bedeutet das für die Ableitungen? Was ist eine
Aufgaben Kreisprozesse. 1. Ein ideales Gas durchläuft den im V(T)- Diagramm dargestellten Kreisprozess. Es ist bekannt:
Aufgaben Kreisrozesse. Ein ideales Gas durchläuft den im ()- Diagramm dargestellten Kreisrozess. Es ist bekannt: 8 cm 6 cm 00 K 8MPa MPa a) Geben Sie die fehlenden Zustandsgrößen, und für die Zustände
Probeklausur STATISTISCHE PHYSIK PLUS
DEPARTMENT FÜR PHYSIK, LMU Statistische Physik für Bachelor Plus WS 2011/12 Probeklausur STATISTISCHE PHYSIK PLUS NAME:... MATRIKEL NR.:... Bitte beachten: Schreiben Sie Ihren Namen auf jedes Blatt; Schreiben
3.2 Thermodynamische Gleichgewichte in Mehrkomponentensystemen
Inhalt Kapitel 3 3.0-1 3. Mehrkomponentensysteme 3.1 Partielle molare Zustandsgrößen 3.2 Thermodynamische Gleichgewichte in Mehrkomponentensystemen Das Chemische Potential reiner Stoffe und von Stoffen
Musterlösung zu Übung 7
PCI Thermodynamik G. eschke FS 011 Musterlösung zu Übung 7 (8. April 011) Aufgabe 1 (a) Die Shomate-Gleichung (Script (153)) lautet: C p (gas, T ) A + BT + CT + DT 3 + E T (1) Für das Kohlenstoffmonooxid
Musterlösung Übung 10
Musterlösung Übung 10 Aufgabe 1: Phasendiagramme Abbildung 1-1: Skizzen der Phasendiagramme von Wasser (links) und Ethanol (rechts). Die Steigung der Schmelzkurven sind zur besseren Anschaulichkeit überzogen
Das Chemische Gleichgewicht
Prof. Dr. Norbert Ham 1/6 14. Chemisches Gleichgewicht Das Chemische Gleichgewicht Chemische eaktionen, d.h. die Saltung und Neubildung von chemischen indungen, verlaufen immer so, dass sie sich einem
Zur Erinnerung. Wärmetransport durch: -Wärmekonvektion -Wärmestrahlung -Wärmeleitung. Planck sches Strahlungsgesetz. Stefan-Boltzman-Gesetz
Zur Erinnerung Stichworte aus der 9. orlesung: Wärmetransort durch: -Wärmekonvektion -Wärmestrahlung -Wärmeleitung Planck sches Strahlungsgesetz Stefan-Boltzman-Gesetz Wiensches erschiebungsgesetz Hautsätze
3.2 Thermodynamische Gleichgewichte in Mehrkomponentensystemen
Inhalt Kapitel 3 3.0-1 3. Mehrkomponentensysteme 3.1 Partielle molare Zustandsgrößen 3.2 Thermodynamische Gleichgewichte in Mehrkomponentensystemen Das Chemische Potential reiner Stoffe und von Stoffen
8. Mehrkomponentensysteme. 8.1 Partielle molare Größen. Experiment 1 unter Umgebungsdruck p:
8. Mehrkomponentensysteme 8.1 Partielle molare Größen Experiment 1 unter Umgebungsdruck p: Fügen wir einer Menge Wasser n mit Volumen V (molares Volumen v m =V/n) bei einer bestimmten Temperatur T eine
Zur Thermodynamik des idealen Gases (GK Physik 1)
Zur hermodynamik des idealen Gases (GK Physik 1 Zusammenfassung im Hinblick auf Prozesse. Reinhard Honegger, im Januar 2012. 1 Grundbegriffe 1.1 Zustandsgleichung = Ideale Gasgleichung Druck, olumen, emeratur
Physikalische Chemie I
M.Bredol / MP Physikalische Chemie I / 10.3.16 1 Physikalische Chemie I Nachname orname Matrikel Aufgabe Punkte erreicht Note 1 20 2 20 3 20 4 22 5 18 Summe: 100 1. Gegeben seien 20 g Kohlendioxid, die
Übungen zur VL Chemie für Biologen und Humanbiologen 05.12.2011 Lösung Übung 6
Übungen zur VL Chemie für Biologen und Humanbiologen 05.12.2011 Lösung Übung 6 Thermodynamik und Gleichgewichte 1. a) Was sagt die Enthalpie aus? Die Enthalpie H beschreibt den Energiegehalt von Materie
Wolfgang Heidemann. Technische Thermodynamik. Kompaktkurs für das Bachelorstudium. Wl LEY-VCH. Verlag GmbH & Co. KGaA
Wolfgang Heidemann Technische Thermodynamik Kompaktkurs für das Bachelorstudium Wl LEY-VCH Verlag GmbH & Co. KGaA Inhaltsverzeichnis Vorwort XI Nomenklatur XIII 1 Einleitung 1 1.1 Technische Thermodynamik
Thermodynamik I PVK - Tag 1. Nicolas Lanzetti
Thermodynamik I PVK - Tag 1 Nicolas Lanzetti Nicolas Lanzetti 04.01.2016 1 Hinweise zu dem PVK Name: Nicolas Lanzetti; 5. Semester Maschinenbau; Mail: lnicolas@student.ethz.ch; Raum: ML F34; Zeit: Montag-Mittwoch,
Musterlösung Übung 10
Musterlösung Übung 10 Aufgabe 1: Phasendiagramme Abbildung 1-1: Skizzen der Phasendiagramme von Wasser links) und Ethanol rechts). Die Steigung der Schmelzkurven sind zur besseren Anschaulichkeit überzogen
3 Diskussion und Beispiele
Woche 2 3 Diskussion und Beispiele 31 Abhängigkeit zwischen kalorischer und thermischer Zustandsgleichung Die kalorische und die thermische Zustandsgleichungen sind nicht unabhängig Aus den Integrabilitätsbedingungen
Lehrbuch der Thermodynamik
Ulrich Nickel Lehrbuch der Thermodynamik Eine verständliche Einführung Ж HANSER Carl Hanser Verlag München Wien VII Inhaltsverzeichnis 1 GRUNDBEGRIFFE DER THERMODYNAMIK 1 Einführung 1 Systeme 3 offene
Inhaltsverzeichnis Teil I Grundlagen der Thermodynamik Grundlagen Temperatur und Zustandsgleichungen
Inhaltsverzeichnis Teil I Grundlagen der Thermodynamik 1 Grundlagen... 3 1.1 Druck und mechanisches Gleichgewicht... 4 1.2 Thermodynamische Systeme... 5 1.3 Arbeit... 8 1.3.1 Arbeit in der Mechanik...
Das Ideale Gas Kinetische Gastheorie (auf atomarer Ebene)
Das Ideale Gas Kinetische Gastheorie (auf atomarer Ebene) Wir haben gesehen, dass ein sogenanntes 'ideales Gas' durch die Zustandsgleichung pv = νr T [1] beschrieben wird; wir wollen nun verstehen, welchen
Skizze zur Veranschaulichung der Legendretransformation
9 Die thermodynamischen Funktionen G und H Ehe das Schema des vorherigen Abschnittes zur Konstruktion weiterer thermodynamischer Potentiale zu Ende gebracht wird, kurz einige Erläuterungen zur Legendretransformation.
Thermodynamik. Thermodynamics. Markus Arndt. Quantenoptik, Quantennanophysik und Quanteninformation Universität Wien January 2008
Thermodynamik Thermodynamics Markus Arndt Quantenoptik, Quantennanophysik und Quanteninformation Universität Wien January 2008 Die Hauptsätze der Thermodynamik & Anwendungen in Wärmekraft und Kältemaschinen
Aufgaben zum Stirlingschen Kreisprozess Ein Stirling-Motor arbeite mit 50 g Luft ( M= 30g mol 1 )zwischen den Temperaturen = 350 C und T3
Aufgaben zum Stirlingschen Kreisrozess. Ein Stirling-Motor arbeite mit 50 g Luft ( M 0g mol )zwischen den emeraturen 50 C und 50 C sowie den olumina 000cm und 5000 cm. a) Skizzieren Sie das --Diagramm
Thermodynamik für Metallurgen und Werkstofftechniker
Von Prof. Dr.-lng. Martin G. Frohberg Mit 78 Bildern und 13 Tabellen Thermodynamik für Metallurgen und Werkstofftechniker EINE EINFÜHRUNG VEB DEUTSCHER VERLAG FÜR GRUNDSTOFFINDUSTRIE LEIPZIG 1 nhaltsverzeichnis
Die Bedeutung von Zustandsfunktionen:
Die Bedeutung von Zustandsfunktionen: Innere Energie und Enthalie 3.1 Die mathematischen Eigenschaften von Zustandsfunktionen... 54 3 3.2 Die Abhängigkeit von U von und... 57 3.3 Hängt die Innere Energie
Thermodynamik. Thermodynamik
Geschlossenes System: Energieaustausch, aber kein Materieaustausch mit der Umgebung. Innere Energie: Jeder Stoff hat in sich Energie in irgendeiner Form gespeichert: die innere Energie U. U 1 = innere
Karl Stephan Franz Mayinger. Thermodynamik. Grundlagen und technische Anwendungen. Zwölfte, neubearbeitete und erweiterte Auflage
Karl Stephan Franz Mayinger Thermodynamik Grundlagen und technische Anwendungen Zwölfte, neubearbeitete und erweiterte Auflage Band 2 Mehrstoffsysteme und chemische Reaktionen Mit 135 Abbildungen Springer-Verlag
D. Schuller. Thermodynamik
D. Schuller Thermodynamik uni-text Dieter Schuller Thermodynamik Methode zur Beschreibung stofflicher Systeme Lehrbuch tür Naturwissenschaftler Mit 25 Abbildungen Friedr. Vieweg + Sohn. Braunschweig Dr.
Allgemeine Speicherberechnung
doc 6. Seite von 5 Allgemeine Seicherberechnung echnische Daten Grundlage Die Berechnung eines Hydroseichers bezieht sich auf die Zustandsänderung des Gases im Hydroseicher. Die gleiche Veränderung erfolgt
Übung 4. SS 2013 Übung - Einführung in die Verbrennung - Methling, Özuylasi 1
Ziel: Grundlagen der chemischen Reaktionskinetik verstehen Verstehen qualitativer Reaktionsverläufe Aufstellung des Zeitgesetzes Umgang mit nicht reagierenden Stoßpartner (M) Berechnung Geschwindigkeitskoeffizient
Inhaltsverzeichnis Hinweise zur Benutzung Einführung in die Arbeits- und Denkweise Basis der Thermodynamik
Inhaltsverzeichnis 1 Hinweise zur Benutzung... 1 1.1 Ausrichtung...... 1 1.2 Lernhilfen und -kontrollen...... 4 2 Einführung in die Arbeits- und Denkweise... 9 2.1 Zielsetzung...... 9 2.2 Wichtige physikalische
7. Chemische Reaktionen
7. Chemische Reaktionen 7.1 Thermodynamik chemischer Reaktionen Welche Reaktion läuft spontan freiwillig ab? H 2 + I 2 2HI H 2 + I 2 2HI H 2 + I 2 2HI Wie ist der Energieumsatz einer Reaktion? Welche Wärme
Van der Waals-Theorie und Zustandsgleichung
Van der Waals-Theorie und Zustandsgleichung Eine verbesserte Zustandsgleichung für klassische Gase bei höheren Dichten liefert die Van der Waals-Gleichung. Diese Gleichung beschreibt auch den Phasenübergang
14 Massenwirkungsgesetz
14 Massenwirkungsgesetz Im vorherigen Abschnitt haben wir uns mit der Mischungsentroie beschäftigt, die aber nur einen Asekt der Mischung von idealen Gasen berücksichtigt, nämlich des Mischens und rennens
Physikalische Chemie 1 (Thermodyn. u. Elektrochemie) SS09 - Blatt 1 von 13. Klausur PC 1. Sommersemester :15 bis 11:45.
Physikalische Chemie 1 (Thermodyn. u. Elektrochemie) SS09 - Blatt 1 von 13 Klausur PC 1 Sommersemester 2009 03.08.2007 10:15 bis 11:45 Name: Vorname: geb. am: in: Matrikelnummer: Unterschrift: Für die
Höhere Experimentalphysik 1
Höhere Experimentalphysik 1 Institut für Angewandte Physik Goethe-Universität Frankfurt am Main 9. Vorlesung 20.01.2017 Was bisher geschah Thermodynamik Thermodynamische Systeme und Zustandsgrößen Gleichgewichtszustand
Werner Langbein. Thermodynamik. Gleichgewicht, Irreversible Prozesse, Schwankungen. Verlag Harri Deutsch
Werner Langbein Thermodynamik Gleichgewicht, Irreversible Prozesse, Schwankungen Verlag Harri Deutsch Einleitung 1 1 Gleichgewichtsthermodynaimiik 3 1 Thermodynamische Systeme 5 1.1 Geometrie und Inventar
Übung 1: Thermodynamik Berechnung von Aufschmelzkurven, Adiabat und Aufschmelzpfad
J K (thermische = MAGMATIMU und VULKANE ÜBUNG 1-2012 Übung 1: Thermodynamik Berechnung von Aufschmelzkurven, Adiabat und Aufschmelzfad U1.1 Rekaitulation der Theorie U1.1.1 Adiabtischer Gradient des festen
Physikalische Chemie I
Physikalische Chemie I 2017 Physikalische Chemie I Dozenten: Vorlesung Prof. Dr. Cornelia Palivan (Tel: 0612673839 Cornelia.Palivan@unibas.ch) Prof. Dr. Wolfgang Meier (Tel: 0612673802 Wolfgang.Meier@unibas.ch)
DAMPFDRUCK EINER REINEN FLÜSSIGKEIT. 1. Versuchsplatz. 2. Allgemeines zum Versuch
DAMPFDRUCK EINER REINEN FLÜSSIGKEI 1. ersuchslatz Komonenten: - hermostat - Woulffsche Flasche - Dreihalskolben mit ersuchssubstanz - hermometer - Druckmesser - Druckanzeige 2. Allgemeines zum ersuch Befindet
Das chemische Potential- eine Übersicht wichtiger Beziehungen
Das chemische Potential- eine Übersicht wichtiger Beziehungen Definition des chem. Potentials Das chemische Potential beschreibt die bhängigkeit der extensiven thermodynamischen Energiegrößen von der Stoffmenge.
Übungsblatt 2 ( )
Experimentalphysik für Naturwissenschaftler Universität Erlangen Nürnberg SS 01 Übungsblatt (11.05.01) 1) Geschwindigkeitsverteilung eines idealen Gases (a) Durch welche Verteilung lässt sich die Geschwindigkeitsverteilung