Übungsblatt 2 ( )
|
|
|
- Wilhelm Lorenz
- vor 7 Jahren
- Abrufe
Transkript
1 Experimentalphysik für Naturwissenschaftler Universität Erlangen Nürnberg SS 01 Übungsblatt ( ) 1) Geschwindigkeitsverteilung eines idealen Gases (a) Durch welche Verteilung lässt sich die Geschwindigkeitsverteilung eines idealen Gases beschreiben? (Formel) Maxwell-Boltzmann-Verteilung f(v) 4 m ( π k B T ) 3 v e mv (b) Skizzieren Sie diese Verteilung für zwei unterschiedliche Temperaturen. k B T (1) Figure 1: Maxwell-Boltzmann-Verteilung 1
2 Wie verhalten sich die Extrema bei unterschiedlichen Temperaturen? Welchen Wert hat das Integral über den gesamten Definitionsbereich? Wie berechnet man die Wahrscheinlichkeit, dass ein Teilchen eine Geschwindigkeit zwischen den Punkten v 1 und v besitzt? Die Kurve wird für größere Temperaturen breiter und flacher und weiterhin wandert das Extremum der Kurve hin zu größeren Geschwindigkeiten. Das Integral über den gesamten Definitionsbereich beträgt 1. Die Wahrscheinlichkeit ergibt sich zu: mit f(v) aus (1) W v v 1 f(v)dv () (c) Berechnen Sie die wahrscheinlichste Geschwindigkeit von Helium, unter Zuhilfenahme von oben genannter Verteilung, bei T 150 C. Die molare Masse von Helium beträgt 4 g mol. f(v) 4 m ( π k B T ) 3 v e mv k B T a v e bv (3) mit a 4 π ( m k B T ) 3 und b m k B T df(v) a v e bv + a v e bv ( b) v (4) dv Die wahrscheinlichste Geschwindigkeit entspricht dem Maximum der Verteilung. Weshalb die Ableitung nun Null gesetzt wird. a v e bv a b v 3 e b 0 (5) 1 b v 0 (6) 1 b kb T (7) m Aus R N A k B und M He m N A (da die molare Masse als Masse eines Teilchen Avogadro-Konstante definiert ist)folgt: RT (8) M He
3 Eingesetzt ergibt sich: 8, 314 J mol K 150 C 4 g mol 8, 314 J ( )K mol K kg mol 136 m s (9) (d) Berechnen Sie die mittlere Geschwindigkeit von Helium bei T 150 C. Aus der Vorlesung ist bekannt, dass für die mittlere Geschwindigkeit gilt: 8 kb T π m (10) Ersetzt man hierbei nun wieder wie oben k B R N A und M He m N A dann gilt: 8 R T π M He 1496 m s (11) Berechnen Sie außerdem die mittlere freie Weglänge und die mittlere Zeit zwischen zwei Stößen. Der Stoßquerschnitt von Helium beträgt cm und die Dichte des komprimierten Heliums ist 0, 3 kg m 3. mit v aus (11) folgt: x 1 ρ n σ 1 ρ N A M He σ 7, m (1) τ x 4, s (13) ) Wärmeaustausch Ein Topf voll Wasser (5l) soll von 0 auf 30 erhitzt werden (c W asser 4, 18 kj ). (a) Wie viel Energie muss dem Wasser hinzugegeben werden, um dieses aufzuheizen? Hinweis: Vernachlässigen Sie die Energie, die benötigt wird, um den Topf zu erhitzen. Um den Wärmeaustausch zu berechnen, benötigt man die Masse des Wassers. Diese ergibt sich daraus, dass 5l Wasser 5kg wiegen. Q m W asser c W asser T 5kg 4, 18 kj (30 0)K 09kJ (14) 3
4 (b) Welche Masse an heißem Eisen (T 90 C) würde das Wasser auf die gleiche Temperatur erhitzen? (c F e 0, 46 kj ) Die Energie, die dem Wasser zugeführt werden muss, um es auf 30 C zu erhitzen, muss also dem Eisen entzogen werden. Da das Eisen danach die gleiche Temperatur wie das erhitzte Wasser haben muss (thermodynamisches Gleichgewicht), gilt also für die Temperaturänderung des Eisens: T 90 C 30 C 60K. somit ergibt sich: Q 09kJ m F e c F e T (15) m F e Q c F e T 09kJ 7, 6kg (16) 0, 46 kj 60K (c) Wie viel Eisen aus Aufgabe (b) wird benötigt, wenn man berücksichtigt, dass der Topf auch auf 30 C erhitzt werden muss? (c T opf 0, 77 kj ; m T opf 1kg; T T opf 0 C) Q m T opf c T opf T 1kg 0, 77 kj m F e Q gesamt c F e T (30 0)K 7, 7kJ (17) 16, 7kJ 7, 85kg (18) 0, 46 kj 60K 3) Kreisprozess Wir betrachten einen Kreisprozess, der aus einer isochoren Abkühlung, einer isobaren Expansion und einer isothermen Kompression besteht. Die isochore Abkühlung startet bei 1 bar und 3 l (Punkt A). Danach beträgt die Temperatur 5 K (Punkt B). Während der isobaren Expansion dehnt sich das Volumen auf 1 l aus (Punkt C). (a) Berechnen Sie für jeden Eckpunkt (A, B, C) die Werte für V, p und T und zeichnen Sie ein P-V-Diagramm. Die gegebenen Werte sind: Punkt V P T A 3 l 1 bar B 5 K C 1 l Aus der isochoren Abkühlung folgt: V A V B 3l. Aus der isobaren Expansion folgt: p B p C : p, wobei der Zahlenwert unbekannt ist. Aus der isothermen Kompression gilt: T C T A : T, wobei auch hier der Zahlenwert unbekannt ist. 4
5 Somit sieht die Tabelle, wenn man das oben genannte berücksichtigt, folgendermaßen aus: Punkt V P T A 3 l 1 bar T B 3 l p 5 K C 1 l p T Es fehlen also nur noch zwei Werte, nämlich p und T, die man nun über die ideale Gasgleichung berechnen kann. Hierfür stellen wir erst einmal die ideale Gasgleichung für die drei Einzelschritte auf: Für den Schritt A B gilt: p A T p T B. Für den Schritt B C gilt: V B TB V C T. Hierbei sieht man sofort, dass in der zweiten Gleichung die einzige Unbekannte T ist. Daraus folgt, dass T 100K ist. Nun kann man entweder die dritte Gleichung C A aufstellen und daraus p berechnen:p V C p A V A. Oder man setzt das bereits ausgerechnete T in die erste Gleichung wieder ein und berechnet so p. Für p ergibt sich: p 3bar. Jetzt ist unsere Tabelle komplett und sieht folgendermaßen aus: Punkt V P T A 3 l 1 bar 100K B 3 l 3 bar 5K C 1 l 3 bar 100K Alle fett geschriebenen Werte sind angegeben, die kursiv geschriebenen lassen sich über die Beziehungen der Teilschritte erschließen und die übrigen Werte werden über die ideale Gasgleichung berechnet. Figure : P-V-Diagramm 5
6 (b) Berechnen Sie für diesen Kreisprozess den Wärmetransport, die verrichtete Arbeit sowie die Änderung der inneren Energie pro Teilschritt und für den gesamten Kreisprozess. Zuerst muss die Stoffmenge berechnet werden: n P V R T Somit gilt für die einzelnen Teilschritte: 1) isochore Abkühlung: 1bar 3l 8, 314 J n R T P V (19) 100K pa m3 4, 33mol (0) 8, 314 J 100K mol K mol K ) isobare Expansion W 1 0 (1) Q 1 U 1 n C V T n 3 R (5 100)K 4, 05kJ () 3) isotherme Kompression VE VE Q 3 W 3 pdv n R T V A V A Und für den gesamten Kreisprozess ergibt sich: W p V 3bar (1 3)l, 7kJ (3) U n C V T n 3 R (100 5)K 4, 05kJ (4) Q U W 4, 05kJ +, 7kJ 6, 75kJ (5) T 0 U 3 0 (6) dv V n R T ln(v A ) 4, 33mol R 100K ln( 1l ) 4, 99kJ V E 3l (7) Q kj U W Teilschritt kj kj 1-4,05-4,05 0 4,05 6,75 -, ,99 4,99 gesamt 0 -,9,9 U gesamt 0, da die innere Energie bei einem Kreisprozess erhalten bleibt. 6
7 (c) Berechnen Sie auch den Wirkungsgrad dieses Prozesses und vergleichen Sie diesen mit dem Carnot-Wirkungsgrad. Der Wirkungsgrad berechnet sich wie folgt: Für den Carnot-Wirkungsgrad gilt: η E nutz E in W ges Q, 9kJ 6, 75kJ 0, 34 (8) η Carnot T T 1 T 100K 5K 100K 0, 75 (9) Man sieht, dass η Carnot > η. Achtung! Dieser Kreisprozess macht vom physikalischen Standpunkt aus keinen Sinn. Dies liegt daran, dass im Endeffekt Arbeit gebraucht wird um Wärme vom Wärmebad ins Kältebad zu transportieren, was nicht sonderlich praktisch ist, da dieser Prozess auch ohne vorher eingespeiste Arbeit ablaufen würde. Im Detail heißt das dann, dass im Teilschritt 1 das angeschlossene Kältebad aufgeheizt wird (Wärme geht aus dem Kreisprozess hinaus). Im Teilschritt wird daraufhin das Wärmebad angeschlossen, welches Energie verliert und wodurch Nutzarbeit frei wird. Jetzt ist aber das Problem, dass diese gewonnene Nutzarbeit im Teilschritt 3 mehr als aufgebraucht wird und weiterhin ist es auch dort nur möglich dem Wärmebad einen Teil seiner ursprünglichen Energie zurückzuführen. Deshalb ist der Kreisprozess an sich sinnlos, um die Rechnungen zu üben aber vielleicht doch ganz hilfreich. Ein weiterer Punkt ist auch, da aufgrund der positiven Gesamtarbeit ein Wirkungsgrad keinen Sinn macht. Da somit das System nicht als Wärmekraftmaschine zu betrachten ist. Eine Betrachtung als Kühlmaschine ist ebenso nicht möglich, da eben das Kältebad aufgeheizt wird. Was man aber nun machen kann um den Kreisprozess noch zu retten ist, dass man ihn einfach in die andere Richtung laufen lässt. Somit kehren sich alle Vorzeichen der Energien um (da die T s und auch der Term ln( V A VE )) die Vorzeichen vertauschen). Also bekommt man vom System geleistete Arbeit (negatives Vorzeichen) indem man Wärme in das System hineinbringt. Um den Wirkungsgrad der umgekehrten Richtung zu berechnen muss man jetzt noch beachten, dass mal Wärme in den Kreisprozess hineingeführt wird. Und zwar einmal bei der isothermen Expansion und bei der isochoren Erwärmung. Somit ergibt sich dann die gesamte eingebrachte Energie als die Summe der einzelenen Wärmen. η E nutz E in W ges Q gesamt, 9kJ 4, 05kJ + 4, 99kJ 0, 5 (30) 7
Ferienkurs Experimentalphysik 2 - Donnerstag-Übungsblatt
 1 Aufgabe: Entropieänderung Ferienkurs Experimentalphysik 2 - Donnerstag-Übungsblatt 1 Aufgabe: Entropieänderung a) Ein Kilogramm Wasser bei = C wird in thermischen Kontakt mit einem Wärmereservoir bei
1 Aufgabe: Entropieänderung Ferienkurs Experimentalphysik 2 - Donnerstag-Übungsblatt 1 Aufgabe: Entropieänderung a) Ein Kilogramm Wasser bei = C wird in thermischen Kontakt mit einem Wärmereservoir bei
1 Thermodynamik allgemein
 Einführung in die Energietechnik Tutorium II: Thermodynamik Thermodynamik allgemein. offenes System: kann Materie und Energie mit der Umgebung austauschen. geschlossenes System: kann nur Energie mit der
Einführung in die Energietechnik Tutorium II: Thermodynamik Thermodynamik allgemein. offenes System: kann Materie und Energie mit der Umgebung austauschen. geschlossenes System: kann nur Energie mit der
1. Klausur zur Vorlesung Physikalische Chemie I
 1. Klausur zur Vorlesung Physikalische Chemie I Sommersemester 2006 8. Juni 2006 Angaben zur Person (BITTE LESERLICH UND IN DRUCKBUCHSTABEN) Name, Vorname... Geburtsdatum und -ort... Matrikelnummer...
1. Klausur zur Vorlesung Physikalische Chemie I Sommersemester 2006 8. Juni 2006 Angaben zur Person (BITTE LESERLICH UND IN DRUCKBUCHSTABEN) Name, Vorname... Geburtsdatum und -ort... Matrikelnummer...
Physik 2 (B.Sc. EIT) 2. Übungsblatt
 Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
T 300K,p 1,00 10 Pa, V 0, m,t 1200K, Kontrolle Physik Leistungskurs Klasse Hauptsatz, Kreisprozesse
 Kontrolle Physik Leistungskurs Klasse 2 7.3.207. Hauptsatz, Kreisprozesse. Als man früh aus dem Haus gegangen ist, hat man doch versehentlich die Kühlschranktür offen gelassen. Man merkt es erst, als man
Kontrolle Physik Leistungskurs Klasse 2 7.3.207. Hauptsatz, Kreisprozesse. Als man früh aus dem Haus gegangen ist, hat man doch versehentlich die Kühlschranktür offen gelassen. Man merkt es erst, als man
ST Der Stirling-Motor als Wärmekraftmaschine
 ST Der Stirling-Motor als Wärmekraftmaschine Blockpraktikum Herbst 2007 Gruppe 2b 24. Oktober 2007 Inhaltsverzeichnis 1 Grundlagen 2 1.1 Stirling-Kreisprozess............................. 2 1.2 Technische
ST Der Stirling-Motor als Wärmekraftmaschine Blockpraktikum Herbst 2007 Gruppe 2b 24. Oktober 2007 Inhaltsverzeichnis 1 Grundlagen 2 1.1 Stirling-Kreisprozess............................. 2 1.2 Technische
TU-München, Musterlösung. Experimentalphysik II - Ferienkurs Andreas Schindewolf
 TU-München, 18.08.2009 Musterlösung Experimentalphysik II - Ferienkurs Andreas Schindewolf 1 Random Kreisprozess a Wärme wird nur im isochoren Prozess ab zugeführt. Hier ist W = 0 und Q ab = nc V t b T
TU-München, 18.08.2009 Musterlösung Experimentalphysik II - Ferienkurs Andreas Schindewolf 1 Random Kreisprozess a Wärme wird nur im isochoren Prozess ab zugeführt. Hier ist W = 0 und Q ab = nc V t b T
Thermodynamische Hauptsätze, Kreisprozesse Übung
 Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 14.09.2010 Inhaltsverzeichnis Inhaltsverzeichnis 1 Thermodynamische Hauptsätze 3 1.1 Aufgabe 1:.................................... 3 1.2 Aufgabe
Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 14.09.2010 Inhaltsverzeichnis Inhaltsverzeichnis 1 Thermodynamische Hauptsätze 3 1.1 Aufgabe 1:.................................... 3 1.2 Aufgabe
Aufgaben Kreisprozesse. 1. Ein ideales Gas durchläuft den im V(T)- Diagramm dargestellten Kreisprozess. Es ist bekannt:
 Aufgaben Kreisrozesse. Ein ideales Gas durchläuft den im ()- Diagramm dargestellten Kreisrozess. Es ist bekannt: 8 cm 6 cm 00 K 8MPa MPa a) Geben Sie die fehlenden Zustandsgrößen, und für die Zustände
Aufgaben Kreisrozesse. Ein ideales Gas durchläuft den im ()- Diagramm dargestellten Kreisrozess. Es ist bekannt: 8 cm 6 cm 00 K 8MPa MPa a) Geben Sie die fehlenden Zustandsgrößen, und für die Zustände
Aufgaben zum Stirlingschen Kreisprozess Ein Stirling-Motor arbeite mit 50 g Luft ( M= 30g mol 1 )zwischen den Temperaturen = 350 C und T3
 Aufgaben zum Stirlingschen Kreisrozess. Ein Stirling-Motor arbeite mit 50 g Luft ( M 0g mol )zwischen den emeraturen 50 C und 50 C sowie den olumina 000cm und 5000 cm. a) Skizzieren Sie das --Diagramm
Aufgaben zum Stirlingschen Kreisrozess. Ein Stirling-Motor arbeite mit 50 g Luft ( M 0g mol )zwischen den emeraturen 50 C und 50 C sowie den olumina 000cm und 5000 cm. a) Skizzieren Sie das --Diagramm
Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 17
 Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik III (heorie F Statistische Mechanik) SS 17 Prof. Dr. Alexander Mirlin Blatt 2 PD Dr. Igor Gornyi,
Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik III (heorie F Statistische Mechanik) SS 17 Prof. Dr. Alexander Mirlin Blatt 2 PD Dr. Igor Gornyi,
U. Nickel Irreversible Volumenarbeit 91
 U. Nickel Irreversible Volumenarbeit 91 geben, wird die bei unterschiedlichem Innen- und Außendruck auftretende Arbeit als irreversible Volumenarbeit irr bezeichnet. Die nachfolgend angegebene Festlegung
U. Nickel Irreversible Volumenarbeit 91 geben, wird die bei unterschiedlichem Innen- und Außendruck auftretende Arbeit als irreversible Volumenarbeit irr bezeichnet. Die nachfolgend angegebene Festlegung
Allgemeine Gasgleichung und technische Anwendungen
 Allgemeine Gasgleichung und technische Anwendungen Ziele i.allgemeine Gasgleichung: Darstellung in Diagrammen: Begriffsdefinitionen : Iso bar chor them Adiabatische Zustandsänderung Kreisprozess prinzipiell:
Allgemeine Gasgleichung und technische Anwendungen Ziele i.allgemeine Gasgleichung: Darstellung in Diagrammen: Begriffsdefinitionen : Iso bar chor them Adiabatische Zustandsänderung Kreisprozess prinzipiell:
T4p: Thermodynamik und Statistische Physik Prof. Dr. H. Ruhl Übungsblatt 8 Lösungsvorschlag
 T4p: Thermodynamik und Statistische Physik Pro Dr H Ruhl Übungsblatt 8 Lösungsvorschlag 1 Adiabatengleichung Als adiabatische Zustandssänderung bezeichnet man einen thermodynamischen organg, bei dem ein
T4p: Thermodynamik und Statistische Physik Pro Dr H Ruhl Übungsblatt 8 Lösungsvorschlag 1 Adiabatengleichung Als adiabatische Zustandssänderung bezeichnet man einen thermodynamischen organg, bei dem ein
V 1. pdv mit p = = p 0 V 0 ln p 1. m = C H2 O T ln p 1. = P a 150m J 8K ln P a
 2 Lösungen Lösung zu 46. Nutze den 1. Hauptsatz du = Q + W = Q pdv. Bei einem isothermen Prozess ändert sich die innere Energie nicht: du = 0, was wir schon in mehreren Aufgaben zuvor benutzt haben. Also
2 Lösungen Lösung zu 46. Nutze den 1. Hauptsatz du = Q + W = Q pdv. Bei einem isothermen Prozess ändert sich die innere Energie nicht: du = 0, was wir schon in mehreren Aufgaben zuvor benutzt haben. Also
II. Wärmelehre. II.2. Die Hauptsätze der Wärmelehre. Physik für Mediziner 1
 II. Wärmelehre II.2. Die auptsätze der Wärmelehre Physik für Mediziner 1 1. auptsatz der Wärmelehre Formulierung des Energieerhaltungssatzes unter Einschluss der Wärmenergie: die Zunahme der Inneren Energie
II. Wärmelehre II.2. Die auptsätze der Wärmelehre Physik für Mediziner 1 1. auptsatz der Wärmelehre Formulierung des Energieerhaltungssatzes unter Einschluss der Wärmenergie: die Zunahme der Inneren Energie
Allgemeines Gasgesetz. PV = K o T
 Allgemeines Gasgesetz Die Kombination der beiden Gesetze von Gay-Lussac mit dem Gesetz von Boyle-Mariotte gibt den Zusammenhang der drei Zustandsgrößen Druck, Volumen, und Temperatur eines idealen Gases,
Allgemeines Gasgesetz Die Kombination der beiden Gesetze von Gay-Lussac mit dem Gesetz von Boyle-Mariotte gibt den Zusammenhang der drei Zustandsgrößen Druck, Volumen, und Temperatur eines idealen Gases,
a) Welche der folgenden Aussagen treffen nicht zu? (Dies bezieht sind nur auf Aufgabenteil a)
 Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
Versuch: Sieden durch Abkühlen
 ersuch: Sieden durch Abkühlen Ein Rundkolben wird zur Hälfte mit Wasser gefüllt und auf ein Dreibein mit Netz gestellt. Mit dem Bunsenbrenner bringt man das Wasser zum Sieden, nimmt dann die Flamme weg
ersuch: Sieden durch Abkühlen Ein Rundkolben wird zur Hälfte mit Wasser gefüllt und auf ein Dreibein mit Netz gestellt. Mit dem Bunsenbrenner bringt man das Wasser zum Sieden, nimmt dann die Flamme weg
O. Sternal, V. Hankele. 5. Thermodynamik
 5. Thermodynamik 5. Thermodynamik 5.1 Temperatur und Wärme Systeme aus vielen Teilchen Quelle: Wikimedia Commons Datei: Translational_motion.gif Versuch: Beschreibe 1 m 3 Luft mit Newton-Mechanik Beschreibe
5. Thermodynamik 5. Thermodynamik 5.1 Temperatur und Wärme Systeme aus vielen Teilchen Quelle: Wikimedia Commons Datei: Translational_motion.gif Versuch: Beschreibe 1 m 3 Luft mit Newton-Mechanik Beschreibe
! #!! % & ( )! ! +, +,# # !.. +, ) + + /) # %
 ! #! #!! % & ( )!! +, +,# #!.. +, ) + + /)!!.0. #+,)!## 2 +, ) + + 3 4 # )!#!! ), 5 # 6! # &!). ) # )!#! #, () # # ) #!# #. # ) 6 # ) )0 4 )) #, 7) 6!!. )0 +,!# +, 4 / 4, )!#!! ))# 0.(! & ( )!! 8 # ) #+,
! #! #!! % & ( )!! +, +,# #!.. +, ) + + /)!!.0. #+,)!## 2 +, ) + + 3 4 # )!#!! ), 5 # 6! # &!). ) # )!#! #, () # # ) #!# #. # ) 6 # ) )0 4 )) #, 7) 6!!. )0 +,!# +, 4 / 4, )!#!! ))# 0.(! & ( )!! 8 # ) #+,
Carnotscher Kreisprozess
 Carnotscher Kreisprozess (idealisierter Kreisprozess) 2 p 1, V 1, T 1 p(v) dv > 0 p 2, V 2, T 1 Expansionsarbeit wird geleistet dq fließt aus Wärmebad zu dq > 0 p 2, V 2, T 1 p(v) dv > 0 p 3, V 3, T 2
Carnotscher Kreisprozess (idealisierter Kreisprozess) 2 p 1, V 1, T 1 p(v) dv > 0 p 2, V 2, T 1 Expansionsarbeit wird geleistet dq fließt aus Wärmebad zu dq > 0 p 2, V 2, T 1 p(v) dv > 0 p 3, V 3, T 2
ÜBUNGEN ZUR VORLESUNG Physikalische Chemie I (PC I) (Prof. Meerholz, Hertel, Klemmer) Blatt 14,
 ÜBUNGEN ZUR VORLESUNG Physikalische Chemie I (PC I) (Prof. Meerholz, Hertel, Klemmer) Blatt 14, 12.02.2016 Aufgabe 1 Kreisprozesse Mit einem Mol eines idealen, monoatomaren Gases (cv = 3/2 R) wird, ausgehend
ÜBUNGEN ZUR VORLESUNG Physikalische Chemie I (PC I) (Prof. Meerholz, Hertel, Klemmer) Blatt 14, 12.02.2016 Aufgabe 1 Kreisprozesse Mit einem Mol eines idealen, monoatomaren Gases (cv = 3/2 R) wird, ausgehend
Der Zustand eines Systems ist durch Zustandsgrößen charakterisiert.
 Grundbegriffe der Thermodynamik Die Thermodynamik beschäftigt sich mit der Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur. Die Thermodynamik kann voraussagen,
Grundbegriffe der Thermodynamik Die Thermodynamik beschäftigt sich mit der Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur. Die Thermodynamik kann voraussagen,
Musterlösung Übungsklausur zur Vorlesung PC I Chemische Thermodynamik B.Sc.
 Musterlösung Übungsklausur zur Vorlesung PC I Chemische Thermodynamik B.Sc. Angaben zur Person: (bitte leserlich und in Druckbuchstaben) Name, Vorname: Geburtsdatum und ort: Matrikelnummer: Studienfach,
Musterlösung Übungsklausur zur Vorlesung PC I Chemische Thermodynamik B.Sc. Angaben zur Person: (bitte leserlich und in Druckbuchstaben) Name, Vorname: Geburtsdatum und ort: Matrikelnummer: Studienfach,
Physikalische Chemie: Kreisprozesse
 Physikalische Chemie: Kreisprozesse Version vom 29. Mai 2006 Inhaltsverzeichnis 1 Diesel Kreisprozess 2 1.1 Wärmemenge Q.................................. 2 1.2 Arbeit W.....................................
Physikalische Chemie: Kreisprozesse Version vom 29. Mai 2006 Inhaltsverzeichnis 1 Diesel Kreisprozess 2 1.1 Wärmemenge Q.................................. 2 1.2 Arbeit W.....................................
PC-Übung Nr.3 vom
 PC-Übung Nr.3 vom 31.10.08 Sebastian Meiss 25. November 2008 1. Die Säulen der Thermodynamik Beantworten Sie folgende Fragen a) Welche Größen legen den Zustand eines Gases eindeutig fest? b) Welche physikalischen
PC-Übung Nr.3 vom 31.10.08 Sebastian Meiss 25. November 2008 1. Die Säulen der Thermodynamik Beantworten Sie folgende Fragen a) Welche Größen legen den Zustand eines Gases eindeutig fest? b) Welche physikalischen
Thermodynamik Thermodynamische Systeme
 Thermodynamik Thermodynamische Systeme p... Druck V... Volumen T... Temperatur (in Kelvin) U... innere Energie Q... Wärme W... Arbeit Idealisierung; für die Betrachtung spielt die Temperatur eine entscheidende
Thermodynamik Thermodynamische Systeme p... Druck V... Volumen T... Temperatur (in Kelvin) U... innere Energie Q... Wärme W... Arbeit Idealisierung; für die Betrachtung spielt die Temperatur eine entscheidende
Übung 2. Ziel: Bedeutung/Umgang innere Energie U und Enthalpie H verstehen
 Ziel: Bedeutung/Umgang innere Energie U und Enthalpie H verstehen Wärmekapazitäten isochore/isobare Zustandsänderungen Standardbildungsenthalpien Heizwert/Brennwert adiabatische Flammentemperatur WS 2013/14
Ziel: Bedeutung/Umgang innere Energie U und Enthalpie H verstehen Wärmekapazitäten isochore/isobare Zustandsänderungen Standardbildungsenthalpien Heizwert/Brennwert adiabatische Flammentemperatur WS 2013/14
Thermodynamik I Klausur 1
 Aufgabenteil / 100 Minuten Name: Vorname: Matr.-Nr.: Das Aufgabenblatt muss unterschrieben und zusammen mit den (nummerierten und mit Namen versehenen) Lösungsblättern abgegeben werden. Nicht nachvollziehbare
Aufgabenteil / 100 Minuten Name: Vorname: Matr.-Nr.: Das Aufgabenblatt muss unterschrieben und zusammen mit den (nummerierten und mit Namen versehenen) Lösungsblättern abgegeben werden. Nicht nachvollziehbare
Kapitel IV Wärmelehre und Thermodynamik
 Kapitel IV Wärmelehre und Thermodynamik a) Definitionen b) Temperatur c) Wärme und Wärmekapazität d) Das ideale Gas - makroskopisch e) Das reale Gas / Phasenübergänge f) Das ideale Gas mikroskopisch g)
Kapitel IV Wärmelehre und Thermodynamik a) Definitionen b) Temperatur c) Wärme und Wärmekapazität d) Das ideale Gas - makroskopisch e) Das reale Gas / Phasenübergänge f) Das ideale Gas mikroskopisch g)
Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler
 TU München Reinhard Scholz Physik Department, T33 Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler http://www.wsi.tum.de/t33/teaching/teaching.htm Übung in Theoretischer Physik B (Thermodynamik)
TU München Reinhard Scholz Physik Department, T33 Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler http://www.wsi.tum.de/t33/teaching/teaching.htm Übung in Theoretischer Physik B (Thermodynamik)
Aufgabe 1 - Schiefe Ebene - (10 Punkte)
 - schriftlich Klasse: 4AW (Profil A) - (HuR) Prüfungsdauer: Erlaubte Hilfsmittel: Bemerkungen: 4h Taschenrechner TI-nspire CAS Der Rechner muss im Press-to-Test-Modus sein. Formelsammlung Beginnen Sie
- schriftlich Klasse: 4AW (Profil A) - (HuR) Prüfungsdauer: Erlaubte Hilfsmittel: Bemerkungen: 4h Taschenrechner TI-nspire CAS Der Rechner muss im Press-to-Test-Modus sein. Formelsammlung Beginnen Sie
10. Thermodynamik Der erste Hauptsatz Der zweite Hauptsatz Thermodynamischer Wirkungsgrad Der Carnotsche Kreisprozess
 Inhalt 10.10 Der zweite Hauptsatz 10.10.1 Thermodynamischer Wirkungsgrad 10.10.2 Der Carnotsche Kreisprozess Für kinetische Energie der ungeordneten Bewegung gilt: Frage: Frage: Wie kann man mit U Arbeit
Inhalt 10.10 Der zweite Hauptsatz 10.10.1 Thermodynamischer Wirkungsgrad 10.10.2 Der Carnotsche Kreisprozess Für kinetische Energie der ungeordneten Bewegung gilt: Frage: Frage: Wie kann man mit U Arbeit
Thermische Energie kann nicht mehr beliebig in andere Energieformen umgewandelt werden.
 Wärmemenge: hermische Energie kann nicht mehr beliebig in andere Energieformen umgewandelt werden. Sie kann aber unter gewissen oraussetzungen von einem Körer auf einen nderen übertragen werden. Dabei
Wärmemenge: hermische Energie kann nicht mehr beliebig in andere Energieformen umgewandelt werden. Sie kann aber unter gewissen oraussetzungen von einem Körer auf einen nderen übertragen werden. Dabei
Gesetz von Boyle. Empirisch wurde beobachtet, dass bei konstanter Temperatur gilt: p.v = Konstant bzw V 1 / p bzw p 1 / V.
 Gesetz von Boyle Empirisch wurde beobachtet, dass bei konstanter Temperatur gilt: p.v = Konstant bzw V 1 / p bzw p 1 / V Isothermen Gesetz von Gay-Lussac Jacques Charles und Joseph-Louis Gay-Lussac fanden
Gesetz von Boyle Empirisch wurde beobachtet, dass bei konstanter Temperatur gilt: p.v = Konstant bzw V 1 / p bzw p 1 / V Isothermen Gesetz von Gay-Lussac Jacques Charles und Joseph-Louis Gay-Lussac fanden
Physikalische Chemie 0 Klausur, 22. Oktober 2011
 Physikalische Chemie 0 Klausur, 22. Oktober 2011 Bitte beantworten Sie die Fragen direkt auf dem Blatt. Auf jedem Blatt bitte Name, Matrikelnummer und Platznummer angeben. Zu jeder der 25 Fragen werden
Physikalische Chemie 0 Klausur, 22. Oktober 2011 Bitte beantworten Sie die Fragen direkt auf dem Blatt. Auf jedem Blatt bitte Name, Matrikelnummer und Platznummer angeben. Zu jeder der 25 Fragen werden
Aufgaben zur Wärmelehre
 Aufgaben zur Wärmelehre 1. Ein falsch kalibriertes Quecksilberthermometer zeigt -5 C eingetaucht im schmelzenden Eis und 103 C im kochenden Wasser. Welche ist die richtige Temperatur, wenn das Thermometer
Aufgaben zur Wärmelehre 1. Ein falsch kalibriertes Quecksilberthermometer zeigt -5 C eingetaucht im schmelzenden Eis und 103 C im kochenden Wasser. Welche ist die richtige Temperatur, wenn das Thermometer
Die 4 Phasen des Carnot-Prozesses
 Die 4 Phasen des Carnot-Prozesses isotherme Expansion: A B V V T k N Q ln 1 1 isotherme Kompression: adiabatische Kompression: adiabatische Expansion: 0 Q Q 0 C D V V T k N Q ln 2 2 S Q 1 1 /T1 T 1 T 2
Die 4 Phasen des Carnot-Prozesses isotherme Expansion: A B V V T k N Q ln 1 1 isotherme Kompression: adiabatische Kompression: adiabatische Expansion: 0 Q Q 0 C D V V T k N Q ln 2 2 S Q 1 1 /T1 T 1 T 2
2.4 Kinetische Gastheorie - Druck und Temperatur im Teilchenmodell
 2.4 Kinetische Gastheorie - Druck und Temperatur im Teilchenmodell Mit den drei Zustandsgrößen Druck, Temperatur und Volumen konnte der Zustand von Gasen makroskopisch beschrieben werden. So kann zum Beispiel
2.4 Kinetische Gastheorie - Druck und Temperatur im Teilchenmodell Mit den drei Zustandsgrößen Druck, Temperatur und Volumen konnte der Zustand von Gasen makroskopisch beschrieben werden. So kann zum Beispiel
Maxwell-Boltzmann Verteilung. Mykola Zotko Frankfurt am Main
 Maxwell-Boltzmann Verteilung James Clerk Maxwell 1831-1879 Ludwig Boltzmann 1844-1906 Maxwell-Boltzmann Verteilung 1860 Geschwindigkeitsverteilung - eine Verteilungsfunktion, die angibt, mit welcher relativen
Maxwell-Boltzmann Verteilung James Clerk Maxwell 1831-1879 Ludwig Boltzmann 1844-1906 Maxwell-Boltzmann Verteilung 1860 Geschwindigkeitsverteilung - eine Verteilungsfunktion, die angibt, mit welcher relativen
1. Wärmelehre 1.1. Temperatur Wiederholung
 1. Wärmelehre 1.1. Temperatur Wiederholung a) Zur Messung der Temperatur verwendet man physikalische Effekte, die von der Temperatur abhängen. Beispiele: Volumen einer Flüssigkeit (Hg-Thermometer), aber
1. Wärmelehre 1.1. Temperatur Wiederholung a) Zur Messung der Temperatur verwendet man physikalische Effekte, die von der Temperatur abhängen. Beispiele: Volumen einer Flüssigkeit (Hg-Thermometer), aber
4 Hauptsätze der Thermodynamik
 I Wärmelehre -21-4 Hauptsätze der hermodynamik 4.1 Energieformen und Energieumwandlung Innere Energie U Die innere Energie U eines Körpers oder eines Systems ist die gesamte Energie die darin steckt. Es
I Wärmelehre -21-4 Hauptsätze der hermodynamik 4.1 Energieformen und Energieumwandlung Innere Energie U Die innere Energie U eines Körpers oder eines Systems ist die gesamte Energie die darin steckt. Es
Heissluftmotor ******
 luftmotor 8.3.302 luftmotor ****** 1 Motivation Ein luft- bzw. Stirlingmotor erzeugt mechanische Arbeit. Dies funktioniert sowohl mit einer Beheizung als auch mit einem Kältebad. Durch Umkehrung der Laufrichtung
luftmotor 8.3.302 luftmotor ****** 1 Motivation Ein luft- bzw. Stirlingmotor erzeugt mechanische Arbeit. Dies funktioniert sowohl mit einer Beheizung als auch mit einem Kältebad. Durch Umkehrung der Laufrichtung
Vorlesung Physik für Pharmazeuten PPh Wärmelehre
 Vorlesung Physik für Pharmazeuten PPh - 07 Wärmelehre Aggregatzustände der Materie im atomistischen Bild Beispiel Wasser Eis Wasser Wasserdampf Dynamik an der Wasser-Luft Grenzfläche im atomistischen Bild
Vorlesung Physik für Pharmazeuten PPh - 07 Wärmelehre Aggregatzustände der Materie im atomistischen Bild Beispiel Wasser Eis Wasser Wasserdampf Dynamik an der Wasser-Luft Grenzfläche im atomistischen Bild
2. so rasch ausströmen, dass keine Wärmeübertragung stattfinden kann.
 Aufgabe 33 Aus einer Druckluftflasche V 50 dm 3 ) mit einem Anfangsdruck p 0 60 bar strömt solange Luft in die Umgebung p U bar, T U 300 K), bis der Druck in der Flasche auf 0 bar gefallen ist. Dabei soll
Aufgabe 33 Aus einer Druckluftflasche V 50 dm 3 ) mit einem Anfangsdruck p 0 60 bar strömt solange Luft in die Umgebung p U bar, T U 300 K), bis der Druck in der Flasche auf 0 bar gefallen ist. Dabei soll
Musterlösung Klausur Physikalische Chemie I: Thermodynamik
 Musterlösung Klausur Physikalische Chemie I: hermodynamik Aufgabe : Dimerisierung von Stickstoffdioxid a Nach dem Prinzip des kleinsten Zwanges von LeChatelier sollte der Druck p möglichst klein und die
Musterlösung Klausur Physikalische Chemie I: hermodynamik Aufgabe : Dimerisierung von Stickstoffdioxid a Nach dem Prinzip des kleinsten Zwanges von LeChatelier sollte der Druck p möglichst klein und die
Hauptsatz der Thermodynamik
 0.7. Hauptsatz der Thermodynamik Die einem System von außen zugeführte Wärmemenge Q führt zu Erhöhung U der inneren Energie U und damit Erhöhung T der Temperatur T Expansion des olumens gegen den äußeren
0.7. Hauptsatz der Thermodynamik Die einem System von außen zugeführte Wärmemenge Q führt zu Erhöhung U der inneren Energie U und damit Erhöhung T der Temperatur T Expansion des olumens gegen den äußeren
Festkörper - System steht unter Atmosphärendruck gemessenen Wärmen erhalten Index p : - isoliert
 Kalorimetrie Mit Hilfe der Kalorimetrie können die spezifischen Wärmekapazitäten für Festkörper, Flüssigkeiten und Gase bestimmt werden. Kalorische Grundgleichung: ΔQ = c m ΔT Festkörper - System steht
Kalorimetrie Mit Hilfe der Kalorimetrie können die spezifischen Wärmekapazitäten für Festkörper, Flüssigkeiten und Gase bestimmt werden. Kalorische Grundgleichung: ΔQ = c m ΔT Festkörper - System steht
f) Ideales Gas - mikroskopisch
 f) Ideales Gas - mikroskopisch i) Annahmen Schon gehabt: Massenpunkte ohne Eigenvolumen Nur elastische Stöße, keine Wechselwirkungen Jetzt dazu: Wände vollkommen elastisch, perfekte Reflektoren Zeitliches
f) Ideales Gas - mikroskopisch i) Annahmen Schon gehabt: Massenpunkte ohne Eigenvolumen Nur elastische Stöße, keine Wechselwirkungen Jetzt dazu: Wände vollkommen elastisch, perfekte Reflektoren Zeitliches
Skript zur Vorlesung
 Skript zur Vorlesung 1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für
Skript zur Vorlesung 1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für
3 Der 1. Hauptsatz der Thermodynamik
 3 Der 1. Hauptsatz der Thermodynamik 3.1 Der Begriff der inneren Energie Wir betrachten zunächst ein isoliertes System, d. h. es können weder Teilchen noch Energie mit der Umgebung ausgetauscht werden.
3 Der 1. Hauptsatz der Thermodynamik 3.1 Der Begriff der inneren Energie Wir betrachten zunächst ein isoliertes System, d. h. es können weder Teilchen noch Energie mit der Umgebung ausgetauscht werden.
Statistische Zustandsgröße Entropie Energieentwertung bei Wärmeübertragungen II. Hauptsatz der Thermodynamik
 Statistische Zustandsgröße Entropie Energieentwertung bei Wärmeübertragungen II. Hauptsatz der hermodynamik Die nachfolgenden Ausführungen stellen den Versuch dar, die zugegeben etwas schwierige Problematik
Statistische Zustandsgröße Entropie Energieentwertung bei Wärmeübertragungen II. Hauptsatz der hermodynamik Die nachfolgenden Ausführungen stellen den Versuch dar, die zugegeben etwas schwierige Problematik
Grundlagen der Physik 2 Schwingungen und Wärmelehre
 Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik 21. 05. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 21. 05.
Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik 21. 05. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 21. 05.
1 I. Thermodynamik. 1.1 Ideales Gasgesetz. 1.2 Vereinfachte kinetische Gastheorie. 1.3 Erster Hauptsatz der Thermodynamik.
 1 I. hermodynamik 1.1 Ideales Gasgesetz eilchenzahl N Stoffmenge: n [mol], N A = 6.022 10 23 mol 1 ; N = nn A molare Größen: X m = X/n ideales Gasgesetz: V = nr, R = 8.314JK 1 mol 1 Zustandsgrößen:, V,,
1 I. hermodynamik 1.1 Ideales Gasgesetz eilchenzahl N Stoffmenge: n [mol], N A = 6.022 10 23 mol 1 ; N = nn A molare Größen: X m = X/n ideales Gasgesetz: V = nr, R = 8.314JK 1 mol 1 Zustandsgrößen:, V,,
Physik 2 ET, SoSe 2013 Aufgaben mit Lösung 2. Übung (KW 17/18)
 2. Übung (KW 17/18) Aufgabe 1 (T 3.1 Sauerstoffflasche ) Eine Sauerstoffflasche, die das Volumen hat, enthält ab Werk eine Füllung O 2, die bei Atmosphärendruck p 1 das Volumen V 1 einnähme. Die bis auf
2. Übung (KW 17/18) Aufgabe 1 (T 3.1 Sauerstoffflasche ) Eine Sauerstoffflasche, die das Volumen hat, enthält ab Werk eine Füllung O 2, die bei Atmosphärendruck p 1 das Volumen V 1 einnähme. Die bis auf
Experimentalphysik II: Thermodynamik
 Experimentalphysik II: Thermodynamik Ferienkurs Wintersemester 08/09 William Hefter 23/02/2009 Inhaltsverzeichnis 1 Thermodynamik 2 1.1 Temperatur, Wärme und Arbeit.................................. 2
Experimentalphysik II: Thermodynamik Ferienkurs Wintersemester 08/09 William Hefter 23/02/2009 Inhaltsverzeichnis 1 Thermodynamik 2 1.1 Temperatur, Wärme und Arbeit.................................. 2
1. EIN MOTOR LÄUFT MIT HEIßER LUFT
 Stirling-Motor 1. EIN MOTOR LÄUFT MIT HEIßER LUFT Stellt man den Kolben in Abb. 1 von dem kalten in das heiße Wasserbad, so dehnt sich die Luft im Kolben aus. Der Stempel kann eine Last hochheben Physiker
Stirling-Motor 1. EIN MOTOR LÄUFT MIT HEIßER LUFT Stellt man den Kolben in Abb. 1 von dem kalten in das heiße Wasserbad, so dehnt sich die Luft im Kolben aus. Der Stempel kann eine Last hochheben Physiker
Physikalisches Praktikum I
 Fachbereich Physik Physikalisches Praktikum I W21 Name: Verdampfungswärme von Wasser Matrikelnummer: Fachrichtung: Mitarbeiter/in: Assistent/in: Versuchsdatum: Gruppennummer: Endtestat: Folgende Fragen
Fachbereich Physik Physikalisches Praktikum I W21 Name: Verdampfungswärme von Wasser Matrikelnummer: Fachrichtung: Mitarbeiter/in: Assistent/in: Versuchsdatum: Gruppennummer: Endtestat: Folgende Fragen
Die innere Energie and die Entropie
 Die innere Energie and die Entropie Aber fangen wir mit der Entropie an... Stellen Sie sich ein System vor, das durch die Entropie S, das Volumen V und die Stoffmenge n beschrieben wird. U ' U(S,V,n) Wir
Die innere Energie and die Entropie Aber fangen wir mit der Entropie an... Stellen Sie sich ein System vor, das durch die Entropie S, das Volumen V und die Stoffmenge n beschrieben wird. U ' U(S,V,n) Wir
Wärmelehre Wärme als Energie-Form
 Wärmelehre Wärme als Energie-Form Joule's Vorrichtung zur Messung des mechanischen Wärme-Äquivalents alte Einheit: 1 cal = 4.184 J 1 kcal Wärme erwärmt 1 kg H 2 O um 1 K Wird einem Körper mit der Masse
Wärmelehre Wärme als Energie-Form Joule's Vorrichtung zur Messung des mechanischen Wärme-Äquivalents alte Einheit: 1 cal = 4.184 J 1 kcal Wärme erwärmt 1 kg H 2 O um 1 K Wird einem Körper mit der Masse
13.Wärmekapazität. EP Vorlesung 14. II) Wärmelehre
 13.Wärmekapazität EP Vorlesung 14 II) Wärmelehre 10. Temperatur und Stoffmenge 11. Ideale Gasgleichung 12. Gaskinetik 13. Wärmekapazität 14. Hauptsätze der Wärmelehre Versuche: Mechanisches Wärmeäquivalent
13.Wärmekapazität EP Vorlesung 14 II) Wärmelehre 10. Temperatur und Stoffmenge 11. Ideale Gasgleichung 12. Gaskinetik 13. Wärmekapazität 14. Hauptsätze der Wärmelehre Versuche: Mechanisches Wärmeäquivalent
Verbundstudium TBW Teil 1 Wärmelehre 1 3. Semester
 Verbundstudium TBW Teil 1 Wärmelehre 1 3. Semester 1. Temperaturmessung Definition der Temperaturskala durch ein reproduzierbares thermodynam. Phänomen, dem Thermometer Tripelpunkt: Eis Wasser - Dampf
Verbundstudium TBW Teil 1 Wärmelehre 1 3. Semester 1. Temperaturmessung Definition der Temperaturskala durch ein reproduzierbares thermodynam. Phänomen, dem Thermometer Tripelpunkt: Eis Wasser - Dampf
Stirling-Maschine (STI)
 TUM Anfängerpraktikum für Physiker II Wintersemester 26/27 Stirling-Maschine (STI) Inhaltsverzeichnis 5. Dezember 26 1. Einleitung...2 2. Thermodynamische Kreisprozesse...2 3. Versuchsdurchführung...3
TUM Anfängerpraktikum für Physiker II Wintersemester 26/27 Stirling-Maschine (STI) Inhaltsverzeichnis 5. Dezember 26 1. Einleitung...2 2. Thermodynamische Kreisprozesse...2 3. Versuchsdurchführung...3
11.2 Die absolute Temperatur und die Kelvin-Skala
 11. Die absolute Temperatur und die Kelvin-Skala p p 0 Druck p = p(t ) bei konstantem olumen 1,0 0,5 100 50 0-50 -100-150 -00-73 T/ C Tripelpunkt des Wassers: T 3 = 73,16 K = 0,01 C T = 73,16 K p 3 p Windchill-Faktor
11. Die absolute Temperatur und die Kelvin-Skala p p 0 Druck p = p(t ) bei konstantem olumen 1,0 0,5 100 50 0-50 -100-150 -00-73 T/ C Tripelpunkt des Wassers: T 3 = 73,16 K = 0,01 C T = 73,16 K p 3 p Windchill-Faktor
b ) den mittleren isobaren thermischen Volumenausdehnungskoeffizienten von Ethanol. Hinweis: Zustand 2 t 2 = 80 C = 23, kg m 3
 Aufgabe 26 Ein Pyknometer ist ein Behälter aus Glas mit eingeschliffenem Stopfen, durch den eine kapillarförmige Öffnung führt. Es hat ein sehr genau bestimmtes Volumen und wird zur Dichtebestimmung von
Aufgabe 26 Ein Pyknometer ist ein Behälter aus Glas mit eingeschliffenem Stopfen, durch den eine kapillarförmige Öffnung führt. Es hat ein sehr genau bestimmtes Volumen und wird zur Dichtebestimmung von
Mitschrift Thermodynamik
 Mitschrift hermodynamik Herleitung für den Gasdruck Berechnung des oberen Kreisradius d cosϕ dϕ dψ d N eilchen im Gesamtvolumen dn d N Aufschlagswahrscheinlichkeit eines eilchens Fläche df df sinϕ Gesamte
Mitschrift hermodynamik Herleitung für den Gasdruck Berechnung des oberen Kreisradius d cosϕ dϕ dψ d N eilchen im Gesamtvolumen dn d N Aufschlagswahrscheinlichkeit eines eilchens Fläche df df sinϕ Gesamte
PC-Übung Nr.1 vom
 PC-Übung Nr.1 vom 17.10.08 Sebastian Meiss 25. November 2008 1. Allgemeine Vorbereitung a) Geben Sie die Standardbedingungen in verschiedenen Einheiten an: Druck p in Pa, bar, Torr, atm Temperatur T in
PC-Übung Nr.1 vom 17.10.08 Sebastian Meiss 25. November 2008 1. Allgemeine Vorbereitung a) Geben Sie die Standardbedingungen in verschiedenen Einheiten an: Druck p in Pa, bar, Torr, atm Temperatur T in
Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Prof. Dr. U. Schollwöck Sommersemester 2013
 Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Klausur Prof. Dr. U. Schollwöck Sommersemester 2013 Matrikelnummer: Aufgabe 1 2 3 4 5 6 Summe Punkte Note: WICHTIG! Schreiben
Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Klausur Prof. Dr. U. Schollwöck Sommersemester 2013 Matrikelnummer: Aufgabe 1 2 3 4 5 6 Summe Punkte Note: WICHTIG! Schreiben
Thermodynamik. Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur
 Thermodynamik Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur kann voraussagen, ob eine chemische Reaktion abläuft oder nicht kann nichts über den zeitlichen
Thermodynamik Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur kann voraussagen, ob eine chemische Reaktion abläuft oder nicht kann nichts über den zeitlichen
Aufgabe 4 3. Hauptsatz* Beschreiben Sie in einem Satz die Aussage des dritten Hauptsatzes der Thermodynamik.
 E-Ep: Experimentalphysik Prof. J. Lipfert SS 018 Übungsblatt 5 Thermodynamik 5 Das 5. Übungsblatt wird in der Zentralübung am Dienstag den 15. Mai von 1-14 Uhr im großen Physikhörsaal besprochen. Aufgaben,
E-Ep: Experimentalphysik Prof. J. Lipfert SS 018 Übungsblatt 5 Thermodynamik 5 Das 5. Übungsblatt wird in der Zentralübung am Dienstag den 15. Mai von 1-14 Uhr im großen Physikhörsaal besprochen. Aufgaben,
Aufgabe 1 ( = 80)
 Aufgabe 1 (4 + 42 + 4 + 30 80) Ein rechtslaufender, reversibler, geschlossener Kreisprozess (KP) mit Luft ( 1.4, J 287 ) besteht aus folgenden Zustandsänderungen: K 1-2 Isentrope, wobei im Zustand 1 der
Aufgabe 1 (4 + 42 + 4 + 30 80) Ein rechtslaufender, reversibler, geschlossener Kreisprozess (KP) mit Luft ( 1.4, J 287 ) besteht aus folgenden Zustandsänderungen: K 1-2 Isentrope, wobei im Zustand 1 der
Perpetuum Mobile I. Ein Perpetuum mobile erster Art wird durch den ersten Hauptsatz der Thermodynamik ausgeschlossen.
 Perpetuum Mobile I Perpetuum mobile erster Art: Unter einem perpetuum mobile erster Art versteht man eine Vorrichtung, deren Teile, einmal angeregt, nicht nur dauernd in Bewegung bleiben, sondern dabei
Perpetuum Mobile I Perpetuum mobile erster Art: Unter einem perpetuum mobile erster Art versteht man eine Vorrichtung, deren Teile, einmal angeregt, nicht nur dauernd in Bewegung bleiben, sondern dabei
Q i + j. dτ = i. - keine pot. und kin. Energien: depot. - adiabate ZÄ: Q i = 0 - keine technische Arbeit: Ẇ t,j = 0
 Institut für hermodynamik hermodynamik - Formelsammlung. Hauptsätze der hermodynamik (a. Hauptsatz der hermodynamik i. Offenes System de = de pot + de kin + du = i Q i + j Ẇ t,j + ein ṁ ein h tot,ein aus
Institut für hermodynamik hermodynamik - Formelsammlung. Hauptsätze der hermodynamik (a. Hauptsatz der hermodynamik i. Offenes System de = de pot + de kin + du = i Q i + j Ẇ t,j + ein ṁ ein h tot,ein aus
Annahmen: Arbeitsmedium ist Luft, die spezifischen Wärmekapazitäten sind konstant
 Ü 11.1 Nachrechnung eines Otto-ergleichsprozesses (1) Annahmen: Arbeitsmedium ist Luft, die spezifischen Wärmekapazitäten sind konstant Anfangstemperatur T 1 288 K Anfangsdruck p 1 1.013 bar Maximaltemperatur
Ü 11.1 Nachrechnung eines Otto-ergleichsprozesses (1) Annahmen: Arbeitsmedium ist Luft, die spezifischen Wärmekapazitäten sind konstant Anfangstemperatur T 1 288 K Anfangsdruck p 1 1.013 bar Maximaltemperatur
Klausur zur Vorlesung Thermodynamik
 Institut für Thermodynamik 18. März 2011 Technische Universität Braunschweig Prof. Dr. Jürgen Köhler Klausur zur Vorlesung Thermodynamik Für alle Aufgaben gilt: Der Rechen- bzw. Gedankengang muss stets
Institut für Thermodynamik 18. März 2011 Technische Universität Braunschweig Prof. Dr. Jürgen Köhler Klausur zur Vorlesung Thermodynamik Für alle Aufgaben gilt: Der Rechen- bzw. Gedankengang muss stets
Zur Thermodynamik des idealen Gases (GK Physik 1)
 Zur hermodynamik des idealen Gases (GK Physik 1 Zusammenfassung im Hinblick auf Prozesse. Reinhard Honegger, im Januar 2012. 1 Grundbegriffe 1.1 Zustandsgleichung = Ideale Gasgleichung Druck, olumen, emeratur
Zur hermodynamik des idealen Gases (GK Physik 1 Zusammenfassung im Hinblick auf Prozesse. Reinhard Honegger, im Januar 2012. 1 Grundbegriffe 1.1 Zustandsgleichung = Ideale Gasgleichung Druck, olumen, emeratur
Thermodynamik 1 Klausur 08. September 2016
 Thermodynamik 1 Klausur 08. September 2016 Bearbeitungszeit: 150 Minuten Umfang der Aufgabenstellung: 7 nummerierte Seiten Alle Unterlagen zur Vorlesung und Übung sowie Lehrbücher und Taschenrechner sind
Thermodynamik 1 Klausur 08. September 2016 Bearbeitungszeit: 150 Minuten Umfang der Aufgabenstellung: 7 nummerierte Seiten Alle Unterlagen zur Vorlesung und Übung sowie Lehrbücher und Taschenrechner sind
Wärmelehre Zustandsänderungen ideales Gases
 Wärmelehre Zustandsänderungen ideales Gases p Gas-Gleichung 1.Hauptsatz p V = N k B T U Q W p 1 400 1 isobar 300 200 isochor isotherm 100 p 2 0 2 adiabatisch 0 1 2 3 4 5 V V 2 1 V Bemerkung: Mischung verschiedener
Wärmelehre Zustandsänderungen ideales Gases p Gas-Gleichung 1.Hauptsatz p V = N k B T U Q W p 1 400 1 isobar 300 200 isochor isotherm 100 p 2 0 2 adiabatisch 0 1 2 3 4 5 V V 2 1 V Bemerkung: Mischung verschiedener
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases. f=5 Translation + Rotation. f=7 Translation + Rotation +Vibration. Wiederholung
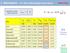 1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
Wärmelehre/Thermodynamik. Wintersemester 2007
 Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 007 ladimir Dyakonov #0 am 4.0.007 Folien im PDF Format unter: http://www.physik.uni-wuerzburg.de/ep6/teaching.html Raum E43, Tel. 888-5875,
Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 007 ladimir Dyakonov #0 am 4.0.007 Folien im PDF Format unter: http://www.physik.uni-wuerzburg.de/ep6/teaching.html Raum E43, Tel. 888-5875,
Ferienkurs Experimentalphysik 2 - Mittwoch-Übungsblatt. 1 Aufgabe: Adiabatengleichung fürs Ideale Gas
 Aufgabe: Gasrozess Ferienkurs Exerimentalhysik - Mittwoch-Übungsblatt 1 Aufgabe: Adiabatengleichung fürs Ideale Gas Aus dem 1. HS und den Wärmekaazitäten c und c olgt zusammen mit dem Adiabatenkoeffizienten
Aufgabe: Gasrozess Ferienkurs Exerimentalhysik - Mittwoch-Übungsblatt 1 Aufgabe: Adiabatengleichung fürs Ideale Gas Aus dem 1. HS und den Wärmekaazitäten c und c olgt zusammen mit dem Adiabatenkoeffizienten
Aufgabe 1 (10 Punkte, TTS & TTD1) Bitte alles LESBAR verfassen!!!
 Aufgabe 1 (10 Punkte, TTS & TTD1) Bitte alles LESBAR verfassen!!! 1.1. Wie erklärt man die dissipierte Energie in einem System? 1.. Kann man aus dieser noch etwas während der folgenden Prozesse in einer
Aufgabe 1 (10 Punkte, TTS & TTD1) Bitte alles LESBAR verfassen!!! 1.1. Wie erklärt man die dissipierte Energie in einem System? 1.. Kann man aus dieser noch etwas während der folgenden Prozesse in einer
Beispiel für ein thermodynamisches System: ideales Gas (Edelgas)
 10. Hauptsätze tze der Wärmelehre Thermodynamik: zunächst: Klassische Mechanik punktförmiger Teilchen, starrer und deformierbarer Körper aber: Bewegungsgleichungen für N=10 23 Teilchen mit 6N ariablen
10. Hauptsätze tze der Wärmelehre Thermodynamik: zunächst: Klassische Mechanik punktförmiger Teilchen, starrer und deformierbarer Körper aber: Bewegungsgleichungen für N=10 23 Teilchen mit 6N ariablen
2.1 Bestimmung einiger Isothermen von Schwefelhexafluorid SF 6
 Atom- und Kernphysi-Versuch 31 AKP-31-1 Zustandsgrößen realer Gase 1 Vorbereitung Koexistenz von Flüssigeiten und Dampf, Dampfdruc, Verdampfungswärme, Koexistenz von Festörper und Flüssigeit, Koexistenz
Atom- und Kernphysi-Versuch 31 AKP-31-1 Zustandsgrößen realer Gase 1 Vorbereitung Koexistenz von Flüssigeiten und Dampf, Dampfdruc, Verdampfungswärme, Koexistenz von Festörper und Flüssigeit, Koexistenz
Isotherme 3. 4 Adiabate 2 T 1. Adiabate Isotherme T 2. Arbeit nach außen = eingeschlossene Kurve
 Carnotscher Kreisprozess Carnot Maschine = idealisierte Maschine, experimentell nicht gut zu realisieren. Einfacher Kreisprozess aus zwei isothermen und zwei adiabatischen Zustandsänderungen. Arbeit nach
Carnotscher Kreisprozess Carnot Maschine = idealisierte Maschine, experimentell nicht gut zu realisieren. Einfacher Kreisprozess aus zwei isothermen und zwei adiabatischen Zustandsänderungen. Arbeit nach
Musterlösung zu Übung 7
 PCI hermodynamik G. Jeschke FS 05 Musterlösung zu Übung 7 08.04.05 a Der Goldbarren wird beim Einbringen in das Reservoir sprunghaft erwärmt. Der Wärmeaustausch erfolgt daher auf irreversiblem Weg. Um
PCI hermodynamik G. Jeschke FS 05 Musterlösung zu Übung 7 08.04.05 a Der Goldbarren wird beim Einbringen in das Reservoir sprunghaft erwärmt. Der Wärmeaustausch erfolgt daher auf irreversiblem Weg. Um
2 Grundbegriffe der Thermodynamik
 2 Grundbegriffe der Thermodynamik 2.1 Thermodynamische Systeme (TDS) Aufteilung zwischen System und Umgebung (= Rest der Welt) führt zu einer Klassifikation der Systeme nach Art der Aufteilung: Dazu: adiabatisch
2 Grundbegriffe der Thermodynamik 2.1 Thermodynamische Systeme (TDS) Aufteilung zwischen System und Umgebung (= Rest der Welt) führt zu einer Klassifikation der Systeme nach Art der Aufteilung: Dazu: adiabatisch
Hochschule Düsseldorf University of Applied Sciences. 13. April 2016 HSD. Energiespeicher. Thermodynamik
 13. April 2016 Energiespeicher Thermodynamik Prof. Dr. Alexander Braun // Energiespeicher // SS 2016 26. April 2017 Thermodynamik Grundbegriffe Prof. Dr. Alexander Braun // Energiespeicher // SS 2017 26.
13. April 2016 Energiespeicher Thermodynamik Prof. Dr. Alexander Braun // Energiespeicher // SS 2016 26. April 2017 Thermodynamik Grundbegriffe Prof. Dr. Alexander Braun // Energiespeicher // SS 2017 26.
Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti.
 (c) Ulm University p. 1/1 Grundlagen der Physik 2 Schwingungen und Wärmelehre 14. 05. 2007 Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik Universität Ulm (c) Ulm University p.
(c) Ulm University p. 1/1 Grundlagen der Physik 2 Schwingungen und Wärmelehre 14. 05. 2007 Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik Universität Ulm (c) Ulm University p.
Experimentalphysik für Naturwissenschaftler 2 Universität Erlangen Nürnberg SS 2009 Klausur ( )
 Nur vom Korrektor auszufüllen 1 2 3 4 5 6 7 8 9 10 Note Experimentalphysik für Naturwissenschaftler 2 Universität Erlangen Nürnberg SS 2009 Klausur (24.7.2009) Name: Studiengang: In die Wertung der Klausur
Nur vom Korrektor auszufüllen 1 2 3 4 5 6 7 8 9 10 Note Experimentalphysik für Naturwissenschaftler 2 Universität Erlangen Nürnberg SS 2009 Klausur (24.7.2009) Name: Studiengang: In die Wertung der Klausur
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik - Einführung in die Wärmelehre - Prof. Dr. Ulrich Hahn WS 2008/09 Entwicklung der Wärmelehre Sinnesempfindung: Objekte warm kalt Beschreibung der thermische Eigenschaften
Physik III im Studiengang Elektrotechnik - Einführung in die Wärmelehre - Prof. Dr. Ulrich Hahn WS 2008/09 Entwicklung der Wärmelehre Sinnesempfindung: Objekte warm kalt Beschreibung der thermische Eigenschaften
(VIII) Wärmlehre. Wärmelehre Karim Kouz WS 2014/ Semester Biophysik
 Quelle: http://www.pro-physik.de/details/news/1666619/neues_bauprinzip_fuer_ultrapraezise_nuklearuhr.html (VIII) Wärmlehre Karim Kouz WS 2014/2015 1. Semester Biophysik Wärmelehre Ein zentraler Begriff
Quelle: http://www.pro-physik.de/details/news/1666619/neues_bauprinzip_fuer_ultrapraezise_nuklearuhr.html (VIII) Wärmlehre Karim Kouz WS 2014/2015 1. Semester Biophysik Wärmelehre Ein zentraler Begriff
Experimentalphysik EP, WS 2011/12
 FAKULTÄT FÜR PHYSIK Ludwig-Maximilians-Universität München Prof. O. Biebel, PD. W. Assmann Experimentalphysik EP, WS 0/ Probeklausur (ohne Optik)-Nummer:. Februar 0 Hinweise zur Bearbeitung Alle benutzten
FAKULTÄT FÜR PHYSIK Ludwig-Maximilians-Universität München Prof. O. Biebel, PD. W. Assmann Experimentalphysik EP, WS 0/ Probeklausur (ohne Optik)-Nummer:. Februar 0 Hinweise zur Bearbeitung Alle benutzten
Physik 2 ET, SoSe 2013 Aufgaben mit Lösung 3. Übung (KW 19/20) Temperaturen ) Dampfmaschine )
 3. Übung (KW 19/20) Aufgabe 1 (T 4.1 Temperaturen ) Zwischen den beiden Wärmespeichern einer Carnot-Maschine (Wirkungsgrad η) besteht eine Temperaturdifferenz T. Welche Temperaturen und T t haben die beiden
3. Übung (KW 19/20) Aufgabe 1 (T 4.1 Temperaturen ) Zwischen den beiden Wärmespeichern einer Carnot-Maschine (Wirkungsgrad η) besteht eine Temperaturdifferenz T. Welche Temperaturen und T t haben die beiden
A 1.1 a Wie groß ist das Molvolumen von Helium, flüssigem Wasser, Kupfer, Stickstoff und Sauerstoff bei 1 bar und 25 C?
 A 1.1 a Wie groß ist das Molvolumen von Helium, flüssigem Wasser, Kupfer, Stickstoff und Sauerstoff bei 1 bar und 25 C? (-> Tabelle p) A 1.1 b Wie groß ist der Auftrieb eines Helium (Wasserstoff) gefüllten
A 1.1 a Wie groß ist das Molvolumen von Helium, flüssigem Wasser, Kupfer, Stickstoff und Sauerstoff bei 1 bar und 25 C? (-> Tabelle p) A 1.1 b Wie groß ist der Auftrieb eines Helium (Wasserstoff) gefüllten
4.6 Hauptsätze der Thermodynamik
 Thermodynamik.6 Hautsätze der Thermodynamik.6. Erster Hautsatz: Energieerhaltungssatz In einem abgeschlossenen System bleibt der gesamte Energievorrat, also die Summe aus Wärmeenergie, mechanischer Energie
Thermodynamik.6 Hautsätze der Thermodynamik.6. Erster Hautsatz: Energieerhaltungssatz In einem abgeschlossenen System bleibt der gesamte Energievorrat, also die Summe aus Wärmeenergie, mechanischer Energie
Zwei neue Basisgrössen in der Physik
 Nachtrag zur orlesung am vergangenen Montag Zwei neue Basisgrössen in der Physik 9. Wärmelehre, kinetische Gastheorie Temperatur T: Wärme ist verknüpft mit ungeordneter Bewegung der Atome oder Moleküle.
Nachtrag zur orlesung am vergangenen Montag Zwei neue Basisgrössen in der Physik 9. Wärmelehre, kinetische Gastheorie Temperatur T: Wärme ist verknüpft mit ungeordneter Bewegung der Atome oder Moleküle.
Thermodynamik Hauptsatz
 Thermodynamik. Hauptsatz Inhalt Wärmekraftmaschinen / Kälteprozesse. Hauptsatz der Thermodynamik Reversibilität Carnot Prozess Thermodynamische Temperatur Entropie Entropiebilanzen Anergie und Exergie
Thermodynamik. Hauptsatz Inhalt Wärmekraftmaschinen / Kälteprozesse. Hauptsatz der Thermodynamik Reversibilität Carnot Prozess Thermodynamische Temperatur Entropie Entropiebilanzen Anergie und Exergie
