Lagerreaktionen und Schnittgrößen eines verzweigten Gelenkrahmens
|
|
|
- Til Schneider
- vor 6 Jahren
- Abrufe
Transkript
1 . Aufgabe Lagerreaktionen und Schnittgrößen eines verzweigten Gelenkrahmens Geg.: Kräfte F, F = F, F Streckenlast q F a Moment M = Fa Maß a 5 F Ges.: a) Lagerreaktionen in B, C und Gelenkkräfte in G, b) Schnittgrößenverläufe analytisch, c) Schnittgrößenverläufe grafisch, d) Ort und Größe des betragsmäßig größten Biegemoments.
2 Lösung a) Lagerkräfte in B, C und Gelenkkräfte in G Freischnitte mit eingetragenen Lagerreaktionen und Gelenkkräften F F q F a 5 F F M Fa Gleichgewichtsgleichungen : F F qa F 0 () : F F 0 () Bv Gv Lager- und Gelenkkräfte : F F F 0 () : F F 0 (5) Bh Gh B : F a F a F a (6) : Gv F Gh F a q a 0 Gv () : F F F Cv Gv () : F F q a F 6 F F Bv Gv Cv Ch () C : F a M 0 (6) 5 () : FGh FGv F F qa F F 5 F F F F F () : Bh Gh (5) : F F F Ch M F a Gh Gv Gv Gh
3 b) Schnittgrößenverläufe analytisch Freischnitte mit eingetragenen Schnittreaktionen Schnitt 0 s a Gleichgewichtsgleichungen : FL F 0 : X: FQ qs F 0 s b 0 M q F s 5 FL F F F qs F Q s F a s Mb q F s s Fs a! FQ 0 sex a M s b ex 8 F a Fa Schnitt 0 s a : FL FCh 0 FL FCh F : FQ FCv 0 FQ FCv F X: M F s M b FCv s Fs b Cv 0 Schnitt 0 s a : FL FCh 0 FL FCh F : FQ FCv 0 FQ FCv F X: Mb FCv ( a s) Mb FCv ( a s ) M M 0 F a s Schnitt 0 s a : FL FBv 0 FL FBv F : FQ FBh 0 FQ FBh F X: M b FBhs 0 Mb FBhs Fs
4 c) Schnittgrößenverläufe grafisch Längskraftverlauf Querkraftverlauf Biegemomentenverlauf d) Ort und Größe des betragsmäßig größten Biegemomentes b max M M s a Fa b 6
5 . Aufgabe Ermittlung von Stabkräften und Längenänderungen der Stäbe Geg.: Längen a ; L,5 a, L a Streckenlast q 0 Dehnsteifigkeiten EA, EA EA, EA EA Temperaturdifferenz T > 0 Wärmeausdehnungskoeffizient Der Stab wird nicht erwärmt. Der Stab kann einer Temperaturdifferenz um T unterliegen. Vorausgesetzt wird, dass der Balken starr ist und die Beträge der Längenänderungen der Stäbe klein gegenüber der Stablängen sind ( L i << L i i =, ). Anmerkung: Die Lagerreaktionen in B sollen nicht berechnet werden. Ges.: a) Stabkräfte in den Stäben und mit Erwärmung des Stabes b) Längenänderung der Stäbe und mit Erwärmung des Stabes c) Stabkräfte in den Stäben und ohne Erwärmung des Stabes Lösung: Freischnitt: Gleichgewicht: B : FS a FS a q0a a 0 () System ist einfach statisch unbestimmt. FSil i Formänderungs-Beziehung: li i Tl i i (i =, ) EA i
6 Verformungsbetrachtung: a a Berechnung für a): Einsetzen in (): Stabkräfte: Berechnung für b): Längenänderung: Berechnung für c): mit l und l : l l FS l FS l Tl EA EA FS,5 a FS a Ta EA EA 8 8 FS FS T EA 8 8 FS a T EA a FS a q0a FS q0a T EA 9 6 FS q0a T EA FS q0a T EA 9 9 q0a 8 T EA 9 q0a 6 l a a Ta 9 EA 9 EA 9 EA 9 9 q0a 6 T EA 9 q0a l a a Ta Ta 8 EA 9 EA 8 EA 9 Stabkräfte: FS F 9 q a 8 q a 9 0 S 0 8
7 . Aufgabe Normalspannungsberechnung bei gerader Biegung mit Längskraft Geg.: Maß c, Länge L = 00c Streckenlast q 0, Kraft F = 00q 0 L Ges.: a) Maß e für die Lage des Flächenschwerpunktes des gegebenen Querschnittes b) Flächenmomente. Ordnung bezüglich der Achsen x und y des Schwerpunktes für gegebenen Querschnitt Lösung: Speziell für Einspannquerschnitt (z = L) d) Werte der Schnittgrößen e) Normalspannungsverteilung zz ( y) f) Ort und Größe der betragsmäßig größten Normalspannung a) Flächenschwerpunkt: xs 0 ysi Ai ys A y e,5c S,5c 9c
8 b) Flächenmomente. Ordnung i A y A i y Si Si i I xxi I yyi ysi A i Si x A i 5c 0,5c,5c c c c c,5c 7c 5 c 8 c c 5 c 5 c 0 c 8c 0 8 c 9 c 0 9c,5c 5 c 5 c 5 c 0 Flächenmomente für x y -Koordinatensystem: 5 5 Ixx Ixxi ysi Ai c c 5c 5 I 0,5 yy I yyi xsi Ai c c Transformation mit Satz von Steiner: xx xx S 5,5 9,75 yy yy S,5 I I y A c c c c I I x A c I 0 wegen Symmetrie xy d) Freischnitt und Gleichgewicht: M b F Q q 0 F L z 0 z L : FQ q0 z 0 FQ ( z L) q0l 00q0c : F F 0 L z B : Mb q0 z F ( z L) F 00q L 00 q c L 00 Mb( z L) q L q c
9 e) Normalspannungsverteilung FL Mbx zz y A I zz zz xx q0c q c y 9c,75c q0 q0., 8,98 y c c zz P P z y f) Betragsmäßig größte Spannung bei Punkt P q q zz y,5c., 8,98,5.69,6 c c oder P q0 q0 zz y,5c., 8,98,5 6,7 c c q0 zz.69,6 für y,5c max c 0 0 5
10 . Aufgabe Verformungsermittlung mittels der Differenzialgleichung der elastischen Linie für einen abgewinkelten Träger Geg.: Streckenlast q 0= konst. Maß b Biegesteifigkeit EI = konst. Ges.: a) Lagerreaktionen b) Verschiebung und Verdrehung der biegesteifen Ecke bei D Lösung: Freischneiden, Gleichgewicht: : F F 0 BH C F q b 0 : BV 0 9 B : M B q0b FC b 0 Einfach statisch unbestimmt, Statisch Unbestimmte : F C FBV q0b F F BH C 9 M B q0b FC b Schnittgrößen (Freischnitte): Momentenbilanzen: : M b FC z 0 : Mb q0z FC b 0 M b FC z Mb FC b q z 0
11 Gleichung der elastischen Linie: EIv '' Mb F z C ' EIv FC z C EIv FC z C z C 6 EIv '' Mb FC b q0z ' EIv F Cbz q0z C 6 z EIv FC b q z C z C 0 Rand- und Übergangsbedingungen: v z 0 0 () v z b () 0 ' ' 0 v z b v z () v z b 0 () ' v z b 0 (5) () C 0 () F b C b 0 6 C C F b 6 C () 5) FC b FC b C C 6 FC b q0 7b FC b 0 6 F b C 0 9 FC b q0b 7 9 FC q0b C q0b und C b 9 () q0b q08b q0b b C C 8 7 q 0 b C q0b 0 Lagerreaktionen: 7 FC q0b 0 7 FBH q0b 0 FBV q0b M B q0b q0b q0b q b 0 0
12 Verschiebung bei D: C q0b vdv v z 0,05 EI EI v v z b DH Verdrehung von D: 0 ' C q0b D v z 0 0,5 EI EI 7
13 5. Aufgabe Aus zwei Profilen und zusammengesetzter prismatischer Träger, einseitig eingespannt und durch Momente M T, M T und die Kraft F belastet. Geg.: Momente M T = 00 Nm, M T = 00 Nm Kraft F = 0 kn Längen l m, l 0,5 m 5 Elastizitätsmodul E,0 MPa Querkontraktionszahl 0, Querschnittsabmessungen d = 0 mm, d = 0 mm Ges.: a) Ort und Betrag der maximalen Torsionsschubspannung b) Relativverdrehung des Querschnittes D bezüglich des Querschnittes A c) Ort und Betrag der maximalen Normalspannung d) Ort und Betrag der maximalen Vergleichsspannung nach der Gestaltänderungsenergiehypothese Lösung: Freischnitte: Gleichgewicht: : Mt MT M T 0 : Mt M T 0 Mt MT M T 00Nm Mt M T 00 Nm : FL F 0 : FL F 0 FL F 0kN FL F 0kN
14 a) Maximale Torsionsschubspannung Mt max W t Mt mit Wt d 5.0,mm Wt 6 00Nm 56,6MPa 5.0,mm Mt mit Wt d.570,8mm Wt 6 00 Nm 6,7MPa.570,8 mm max 6,7MPa in Profil mit d am Außenrand b) Relativverdrehung Mtl AD AB BD mit ; GI M l M l AD AB BD GI GI AD t It t t t t d und E G 00 Nm 0,5m 0, 00 Nm m 0, 5 5,0 MPa 0 mm,0 MPa 0 mm AD 0,09 0,067 0,0869 AD,9 c) Maximale Normalspannung FL 0kN z 8,MPa A 0 mm FL 0kN z 6,7MPa A 0 mm 6,7 MPa in Profil mit d max d) Maximale Vergleichsspannung V z 0,0MPa V z 7,MPa 7,MPa in Profil mit d am Außenrand Vmax 0
Klausur Technische Mechanik
 Klausur Technische Mechanik 05/08/13 Matrikelnummer: Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise: Die Bearbeitungszeit der Klausur beträgt drei Stunden. Die Prüfung umfasst die
Klausur Technische Mechanik 05/08/13 Matrikelnummer: Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise: Die Bearbeitungszeit der Klausur beträgt drei Stunden. Die Prüfung umfasst die
4. Balken. Brücken Tragflügel KFZ-Karosserie: A-Säule, B-Säule Rahmen: Fahrrad, Motorrad. Prof. Dr. Wandinger 2. Festigkeitslehre TM 2.
 4. Balken Balken sind eindimensionale Idealisierungen für Bauteile, die Längskräfte, Querkräfte und Momente übertragen können. Die Querschnittsabmessungen sind klein gegenüber der Länge. Beispiele: Brücken
4. Balken Balken sind eindimensionale Idealisierungen für Bauteile, die Längskräfte, Querkräfte und Momente übertragen können. Die Querschnittsabmessungen sind klein gegenüber der Länge. Beispiele: Brücken
Herbst 2010 Seite 1/14. Gottfried Wilhelm Leibniz Universität Hannover Klausur Technische Mechanik II für Maschinenbau. Musterlösungen (ohne Gewähr)
 Seite 1/14 rage 1 ( 2 Punkte) Ein Stab mit kreisförmiger Querschnittsfläche wird mit der Druckspannung σ 0 belastet. Der Radius des Stabes ist veränderlich und wird durch r() beschrieben. 0 r () Draufsicht:
Seite 1/14 rage 1 ( 2 Punkte) Ein Stab mit kreisförmiger Querschnittsfläche wird mit der Druckspannung σ 0 belastet. Der Radius des Stabes ist veränderlich und wird durch r() beschrieben. 0 r () Draufsicht:
Klausur Technische Mechanik
 Institut für Mechanik und Fluiddynamik Prof. Dr.-Ing. Ams Matrikelnummer: Klausur Technische Mechanik 05/02/13 Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise: Die Bearbeitungszeit
Institut für Mechanik und Fluiddynamik Prof. Dr.-Ing. Ams Matrikelnummer: Klausur Technische Mechanik 05/02/13 Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise: Die Bearbeitungszeit
Übungsaufgaben Systemmodellierung WT 2015
 Übungsaufgaben Systemmodellierung WT 2015 Robert Friedrich Prof. Dr.-Ing. Rolf Lammering Institut für Mechanik Helmut-Schmidt-Universität / Universität der Bundeswehr Hamburg Holstenhofweg 85, 22043 Hamburg
Übungsaufgaben Systemmodellierung WT 2015 Robert Friedrich Prof. Dr.-Ing. Rolf Lammering Institut für Mechanik Helmut-Schmidt-Universität / Universität der Bundeswehr Hamburg Holstenhofweg 85, 22043 Hamburg
TU Dortmund. Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 3)
 Aufgabe 1 (Seite 1 von 3) Bei der Messung eines belasteten Blechs wurden drei Dehnungs-Messstreifen (DMS) verwendet und wie rechts dargestellt appliziert. Die Dehnungen der entsprechenden DMS wurden zu
Aufgabe 1 (Seite 1 von 3) Bei der Messung eines belasteten Blechs wurden drei Dehnungs-Messstreifen (DMS) verwendet und wie rechts dargestellt appliziert. Die Dehnungen der entsprechenden DMS wurden zu
Sommer Baustatik I+II Sessionsprüfung. Bemerkungen. ( und ) Montag, 08. August 2016, Uhr, HIL G 61 / HIL E 9
 Baustatik I+II Sessionsprüfung (101-0113-00 und 101-0114-00) Sommer 2016 Montag, 08. August 2016, 09.00 12.00 Uhr, HIL G 61 / HIL E 9 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in
Baustatik I+II Sessionsprüfung (101-0113-00 und 101-0114-00) Sommer 2016 Montag, 08. August 2016, 09.00 12.00 Uhr, HIL G 61 / HIL E 9 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in
Modulprüfung in Technischer Mechanik am 16. August Festigkeitslehre. Aufgaben
 Modulrüfung in Technischer Mechanik am 6. August 206 Aufgaben Name: Vorname: Matr.-Nr.: Fachrichtung: Hinweise: Bitte schreiben Sie deutlich lesbar. Zeichnungen müssen sauber und übersichtlich sein. Die
Modulrüfung in Technischer Mechanik am 6. August 206 Aufgaben Name: Vorname: Matr.-Nr.: Fachrichtung: Hinweise: Bitte schreiben Sie deutlich lesbar. Zeichnungen müssen sauber und übersichtlich sein. Die
1. Formänderungsenergie
 1. Formänderungsenergie 1.1 Grundlagen 1. Grundlastfälle 1.3 Beispiele.1-1 1.1 Grundlagen Zugstab: F L F x E, A F W u u An einem am linken Ende eingespannten linear elastischen Stab greift am rechten Ende
1. Formänderungsenergie 1.1 Grundlagen 1. Grundlastfälle 1.3 Beispiele.1-1 1.1 Grundlagen Zugstab: F L F x E, A F W u u An einem am linken Ende eingespannten linear elastischen Stab greift am rechten Ende
Klausur Technische Mechanik
 Institut für Mechanik und Fluiddynamik Institut für Mechanik und Fluiddynamik Klausur Technische Mechanik 10/02/10 Aufgabe S1 Gegeben ist ein durch eine Pendelstütze und ein Festlager A abgestütztes Fachwerk.
Institut für Mechanik und Fluiddynamik Institut für Mechanik und Fluiddynamik Klausur Technische Mechanik 10/02/10 Aufgabe S1 Gegeben ist ein durch eine Pendelstütze und ein Festlager A abgestütztes Fachwerk.
Dankert/Dankert: Technische Mechanik, 5. Auflage Lösungen zu den Aufgaben, Teil 4 (Kapitel 15-17)
 Dankert/Dankert: Technische Mechanik, 5. Auflage Lösungen zu den Aufgaben, Teil 4 (Kapitel 15-17) Lösung 15.1: Element-Steifigkeitsmatrix Jeweils drei 2*2-Untermatrizen einer Element- Steifigkeitsmatrix
Dankert/Dankert: Technische Mechanik, 5. Auflage Lösungen zu den Aufgaben, Teil 4 (Kapitel 15-17) Lösung 15.1: Element-Steifigkeitsmatrix Jeweils drei 2*2-Untermatrizen einer Element- Steifigkeitsmatrix
Klausur Technische Mechanik
 Klausur Technische Mechanik 07/02/12 Matrikelnummer: Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise: Die Bearbeitungszeit der Klausur beträgt drei Stunden. Die Prüfung umfasst die
Klausur Technische Mechanik 07/02/12 Matrikelnummer: Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise: Die Bearbeitungszeit der Klausur beträgt drei Stunden. Die Prüfung umfasst die
Dankert/Dankert: Technische Mechanik, 5. Auflage Lösungen zu den Aufgaben, Teil 5 (Kapitel 18)
 Dankert/Dankert: Technische Mechanik, 5. Auflage Lösungen zu den Aufgaben, Teil 5 (Kapitel 18) Lösung 18.1: Die Aufgabe wird nach der im Beispiel des Abschnitt 18.1.5 demonstrierten Strategie für die Lösung
Dankert/Dankert: Technische Mechanik, 5. Auflage Lösungen zu den Aufgaben, Teil 5 (Kapitel 18) Lösung 18.1: Die Aufgabe wird nach der im Beispiel des Abschnitt 18.1.5 demonstrierten Strategie für die Lösung
Übung zu Mechanik 2 Seite 16
 Übung zu Mechanik 2 Seite 16 Aufgabe 27 Ein Stab wird wie skizziert entlang der Stabachse durch eine konstante Streckenlast n beansprucht. Bestimmen Sie den Verlauf der Normalspannungen σ 11 (X 1 ) und
Übung zu Mechanik 2 Seite 16 Aufgabe 27 Ein Stab wird wie skizziert entlang der Stabachse durch eine konstante Streckenlast n beansprucht. Bestimmen Sie den Verlauf der Normalspannungen σ 11 (X 1 ) und
Biegung
 2. Biegung Wie die Normalkraft resultiert auch das Biegemoment aus einer Normalspannung. Das Koordinatensystem des Balkens wird so gewählt, dass die Flächenschwerpunkte der Querschnitte auf der x-achse
2. Biegung Wie die Normalkraft resultiert auch das Biegemoment aus einer Normalspannung. Das Koordinatensystem des Balkens wird so gewählt, dass die Flächenschwerpunkte der Querschnitte auf der x-achse
11 Balkenbiegung Technische Mechanik Balkenbiegung
 11 Balkenbiegung Balkenbiegung 2 Motivation / Einführung Ziele: Berechnung der Balkendurchbiegung (Deformation) Berechnung der Schnittgrößen für statisch unbestimmte Systeme Balken Definition Stabförmig;
11 Balkenbiegung Balkenbiegung 2 Motivation / Einführung Ziele: Berechnung der Balkendurchbiegung (Deformation) Berechnung der Schnittgrößen für statisch unbestimmte Systeme Balken Definition Stabförmig;
Rahmen. Rahmenwirkung Berechnung einfacher Systeme. Institut für Tragwerksentwurf. Tragwerkslehre 2
 Rahmen Rahmenwirkung Berechnung einfacher Systeme Rahmen Riegel vertikale Lasten horizontale Lasten Stiel biegesteife Ecke Vertikale und horizontale Lagerkräfte Vertikale und horizontale Lagerkräfte Rahmen
Rahmen Rahmenwirkung Berechnung einfacher Systeme Rahmen Riegel vertikale Lasten horizontale Lasten Stiel biegesteife Ecke Vertikale und horizontale Lagerkräfte Vertikale und horizontale Lagerkräfte Rahmen
2.4.2 Ebene Biegung. 140 Kap. 2.4 Biegung
 140 Kap. 2.4 Biegung Aufgabe 2 Ein exzentrischer Kreisring hat die Halbmesser R = 20 cm, r = 10 cm und die Exzentrizität e = 5 cm. Man suche die Hauptträgheitsmomente in Bezug auf seinen Schwerpunkt. 2.4.2
140 Kap. 2.4 Biegung Aufgabe 2 Ein exzentrischer Kreisring hat die Halbmesser R = 20 cm, r = 10 cm und die Exzentrizität e = 5 cm. Man suche die Hauptträgheitsmomente in Bezug auf seinen Schwerpunkt. 2.4.2
Biegelinie
 3. Biegelinie Die Biegemomente führen zu einer Verformung der Balkenachse, die als Biegelinie bezeichnet wird. Die Biegelinie wird beschrieben durch die Verschiebung v in y-richtung und die Verschiebung
3. Biegelinie Die Biegemomente führen zu einer Verformung der Balkenachse, die als Biegelinie bezeichnet wird. Die Biegelinie wird beschrieben durch die Verschiebung v in y-richtung und die Verschiebung
Leseprobe. Biegung. Kirbs TECHNISCHE MECHANIK. Studienbrief HDL HOCHSCHULVERBUND DISTANCE LEARNING. 3. Auflage 2008
 Leseprobe Kirbs Biegung TECHNISCHE MECHANIK Studienbrief -5-97 3. Auflage 8 HDL HOCHSCHULVERBUND DISTANCE LEARNING Verfasser: Prof. Dr.-Ing. Jörg Kirbs Professor für Technische Mechanik / Festigkeitslehre
Leseprobe Kirbs Biegung TECHNISCHE MECHANIK Studienbrief -5-97 3. Auflage 8 HDL HOCHSCHULVERBUND DISTANCE LEARNING Verfasser: Prof. Dr.-Ing. Jörg Kirbs Professor für Technische Mechanik / Festigkeitslehre
Biegelinie
 3. Biegelinie Die Biegemomente führen zu einer Verformung der Balkenachse, die als Biegelinie bezeichnet wird. Die Biegelinie wird beschrieben durch die Verschiebung v in y-richtung und die Verschiebung
3. Biegelinie Die Biegemomente führen zu einer Verformung der Balkenachse, die als Biegelinie bezeichnet wird. Die Biegelinie wird beschrieben durch die Verschiebung v in y-richtung und die Verschiebung
1. Zug und Druck in Stäben
 1. Zug und Druck in Stäben Stäbe sind Bauteile, deren Querschnittsabmessungen klein gegenüber ihrer änge sind: D Sie werden nur in ihrer ängsrichtung auf Zug oder Druck belastet. D Prof. Dr. Wandinger
1. Zug und Druck in Stäben Stäbe sind Bauteile, deren Querschnittsabmessungen klein gegenüber ihrer änge sind: D Sie werden nur in ihrer ängsrichtung auf Zug oder Druck belastet. D Prof. Dr. Wandinger
Klausur Technische Mechanik
 Klausur Technische Mechanik 10.09.2012 Matrikel: Folgende Angaben sind freiwillig: Name: Studiengang: Hinweise: Die Bearbeitungszeit der Klausur beträgt drei Stunden. Die Prüfung umfasst die drei Stoffgebiete
Klausur Technische Mechanik 10.09.2012 Matrikel: Folgende Angaben sind freiwillig: Name: Studiengang: Hinweise: Die Bearbeitungszeit der Klausur beträgt drei Stunden. Die Prüfung umfasst die drei Stoffgebiete
Untersuchen Sie das unten dargestellte System auf statische Unbestimmtheit. Bestimmen Sie die Biegelinie aus der Balkendifferentialgleichung und
 Biegelinien Statisch bestimmte Systeme Aufgabe 1 Untersuchen Sie das unten dargestellte System auf statische Unbestimmtheit. Bestimmen Sie die Biegelinie aus der Balkendifferentialgleichung und stellen
Biegelinien Statisch bestimmte Systeme Aufgabe 1 Untersuchen Sie das unten dargestellte System auf statische Unbestimmtheit. Bestimmen Sie die Biegelinie aus der Balkendifferentialgleichung und stellen
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 17. März 2012 Die Bearbeitungszeit für alle drei Aufgaben beträgt 90 Minuten.
 KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 7. März Die Bearbeitungszeit für alle drei Aufgaben beträgt 9 Minuten. AUFGABE (6 Punkte) Der Stab in Abb. mit l =,5 m ist in gelenkig gelagert und in abgestützt.
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 7. März Die Bearbeitungszeit für alle drei Aufgaben beträgt 9 Minuten. AUFGABE (6 Punkte) Der Stab in Abb. mit l =,5 m ist in gelenkig gelagert und in abgestützt.
Übung zu Mechanik 2 Seite 62
 Übung zu Mechanik 2 Seite 62 Aufgabe 104 Bestimmen Sie die gegenseitige Verdrehung der Stäbe V 2 und U 1 des skizzierten Fachwerksystems unter der gegebenen Belastung! l l F, l alle Stäbe: EA Übung zu
Übung zu Mechanik 2 Seite 62 Aufgabe 104 Bestimmen Sie die gegenseitige Verdrehung der Stäbe V 2 und U 1 des skizzierten Fachwerksystems unter der gegebenen Belastung! l l F, l alle Stäbe: EA Übung zu
Statik. Klausur am Name: Vorname: Matrikelnummer: (bitte deutlich schreiben)
 Lösung zur Diplomprüfung Frühjahr 2007 Prüfungsfach Statik Klausur am 26.02.2007 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 5 6 7 8 9 Summe mögliche Punkte 20 5
Lösung zur Diplomprüfung Frühjahr 2007 Prüfungsfach Statik Klausur am 26.02.2007 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 5 6 7 8 9 Summe mögliche Punkte 20 5
4. Das Verfahren von Galerkin
 4. Das Verfahren von Galerkin 4.1 Grundlagen 4.2 Methode der finiten Elemente 4.3 Beispiel: Stab mit Volumenkraft Prof. Dr. Wandinger 3. Prinzip der virtuellen Arbeit FEM 3.4-1 4.1 Grundlagen Das Verfahren
4. Das Verfahren von Galerkin 4.1 Grundlagen 4.2 Methode der finiten Elemente 4.3 Beispiel: Stab mit Volumenkraft Prof. Dr. Wandinger 3. Prinzip der virtuellen Arbeit FEM 3.4-1 4.1 Grundlagen Das Verfahren
Klausur Technische Mechanik
 Institut für Mechanik und Fluiddynamik Klausur Technische Mechanik 11/02/14 Matrikelnummer: Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise: Die Bearbeitungszeit der Klausur beträgt
Institut für Mechanik und Fluiddynamik Klausur Technische Mechanik 11/02/14 Matrikelnummer: Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise: Die Bearbeitungszeit der Klausur beträgt
MECHANIK & WERKSTOFFE
 MECHANIK & WERKSTOFFE Statik Lagerung von Körpern 1-wertig Pendelstütze Seil (keine Lasten dazwischen) (nur Zug) Loslager Anliegender Stab Kraft in Stabrichtung Kraft in Seilrichtung Kraft in Auflagefläche
MECHANIK & WERKSTOFFE Statik Lagerung von Körpern 1-wertig Pendelstütze Seil (keine Lasten dazwischen) (nur Zug) Loslager Anliegender Stab Kraft in Stabrichtung Kraft in Seilrichtung Kraft in Auflagefläche
Fakultät Maschinenwesen
 Fakultät Maschinenwesen TECHNISCHE UNIVERSITÄT DRESDEN Arbeitsgruppe Fernstudium TU Dresden. Fakultät Maschinenwesen/AG Fernstudium. 01062 Dresden Telefon: (0351) 463 33604 Telefax: (0351) 463 37717 Hinweise
Fakultät Maschinenwesen TECHNISCHE UNIVERSITÄT DRESDEN Arbeitsgruppe Fernstudium TU Dresden. Fakultät Maschinenwesen/AG Fernstudium. 01062 Dresden Telefon: (0351) 463 33604 Telefax: (0351) 463 37717 Hinweise
Klausur Technische Mechanik 2
 1.) (6+2+5 Punkte) Der aufkran ist im Gleichgewicht. Der obere dünnwandige waagrechte Balken hat die Breite, die öhe 1.5 und die Wandstärke s. Die dünnwandige aufradwelle hat den Radius /2 und die Wandstärke
1.) (6+2+5 Punkte) Der aufkran ist im Gleichgewicht. Der obere dünnwandige waagrechte Balken hat die Breite, die öhe 1.5 und die Wandstärke s. Die dünnwandige aufradwelle hat den Radius /2 und die Wandstärke
Aufgabe 1 - Lagerreaktionen
 KLAUSUR Technische Mechnik (. Semester 19.07.011 Prof. Volker Ulricht Duer: 10 min. Aufge 1 3 4 5 Σ Punkte 5 1 6 8 5 36 Aufge 1 - Lgerrektionen D F D Gegeen: Längen, =, Streckenlst, Krft F D, Moment Lgerrektionen
KLAUSUR Technische Mechnik (. Semester 19.07.011 Prof. Volker Ulricht Duer: 10 min. Aufge 1 3 4 5 Σ Punkte 5 1 6 8 5 36 Aufge 1 - Lgerrektionen D F D Gegeen: Längen, =, Streckenlst, Krft F D, Moment Lgerrektionen
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 19. März AUFGABE 1 (16 Punkte)
 KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 9. März 2 AUFGABE (6 Punkte) Der Stab 2 in Abb. mit l =,5 m ist in gelenkig gelagert und in 2 abgestützt. In wirkt die Kraft F = 5. N. a) Man bestimme die Reaktionen
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 9. März 2 AUFGABE (6 Punkte) Der Stab 2 in Abb. mit l =,5 m ist in gelenkig gelagert und in 2 abgestützt. In wirkt die Kraft F = 5. N. a) Man bestimme die Reaktionen
( und ) Winter Montag, 23. Januar 2017, Uhr, HCI G 7. Name, Vorname: Studenten-Nr.:
 Baustatik I+II Sessionsprüfung (101-0113-00 und 101-0114-00) Winter 2017 Montag, 23. Januar 2017, 09.00 12.00 Uhr, HCI G 7 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in beliebiger
Baustatik I+II Sessionsprüfung (101-0113-00 und 101-0114-00) Winter 2017 Montag, 23. Januar 2017, 09.00 12.00 Uhr, HCI G 7 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in beliebiger
Prüfung - Technische Mechanik II
 Prüfung - Technische Mechanik II SoSe 2013 2. August 2013 FB 13, Festkörpermechanik Prof. Dr.-Ing. F. Gruttmann Name: Matr.-Nr.: Studiengang: Platznummer Raumnummer Die Aufgaben sind nicht nach ihrem Schwierigkeitsgrad
Prüfung - Technische Mechanik II SoSe 2013 2. August 2013 FB 13, Festkörpermechanik Prof. Dr.-Ing. F. Gruttmann Name: Matr.-Nr.: Studiengang: Platznummer Raumnummer Die Aufgaben sind nicht nach ihrem Schwierigkeitsgrad
1.Kräfte, Fachwerk. 14,7 kn. Bestimmen Sie mit Hilfe des Sinussatzes die Stabkraft F1. 20 kn
 1.Kräfte, Fachwerk # Aufgaben Antw. P. Ein Wandkran wird durch eine Masse m mit F G über eine feste Rolle belastet. 1 Die beiden Stäbe sind Rohre mit einem Durchmesser-Verhältnis d/d = λ = 0,8. Die zulässige
1.Kräfte, Fachwerk # Aufgaben Antw. P. Ein Wandkran wird durch eine Masse m mit F G über eine feste Rolle belastet. 1 Die beiden Stäbe sind Rohre mit einem Durchmesser-Verhältnis d/d = λ = 0,8. Die zulässige
F DZ F AX F AZ. 11. Übungsblatt Flächenträgheitsmoment, Biegespannung WS 2009/2010. Tutoriumsaufgaben 1/13
 Univ. Prof. Dr. rer nat. olfgang H. Müller Materialtheorie - LKM, Sekr. MS Einsteinufer 5, 0587 Berlin. Übungsblatt Flächenträgheitsmoment, Biegespannung S 009/00 Tutoriumsaufgaben ) Das abgebildete Maschinenteil
Univ. Prof. Dr. rer nat. olfgang H. Müller Materialtheorie - LKM, Sekr. MS Einsteinufer 5, 0587 Berlin. Übungsblatt Flächenträgheitsmoment, Biegespannung S 009/00 Tutoriumsaufgaben ) Das abgebildete Maschinenteil
Technische Mechanik. Statik
 Hans Albert Richard Manuela Sander Technische Mechanik. Statik Lehrbuch mit Praxisbeispielen, Klausuraufgaben und Lösungen 4., überarbeitete und erweiterte Auflage Mit 263 Abbildungen ^ Springer Vieweg
Hans Albert Richard Manuela Sander Technische Mechanik. Statik Lehrbuch mit Praxisbeispielen, Klausuraufgaben und Lösungen 4., überarbeitete und erweiterte Auflage Mit 263 Abbildungen ^ Springer Vieweg
( ) Winter Montag, 19. Januar 2015, Uhr, HIL E 1. Name, Vorname: Studenten-Nr.:
 Baustatik I+II Sessionsprüfung (101-0113-00) Winter 2015 Montag, 19. Januar 2015, 09.00 12.00 Uhr, HIL E 1 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in beliebiger Reihenfolge bearbeitet
Baustatik I+II Sessionsprüfung (101-0113-00) Winter 2015 Montag, 19. Januar 2015, 09.00 12.00 Uhr, HIL E 1 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in beliebiger Reihenfolge bearbeitet
Statik. Klausur am Name: Vorname: Matrikelnummer: (bitte deutlich schreiben)
 Diplomprüfung Frühjahr 2009 Prüfungsfach Statik Klausur am 23.02.2009 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 5 5 25 25 30
Diplomprüfung Frühjahr 2009 Prüfungsfach Statik Klausur am 23.02.2009 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 5 5 25 25 30
6. Arbeitssatz, Prinzip der virtuellen Verschiebungen (PvV) und Prinzip der virtuellen Kräfte (PvK)
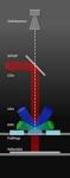 Technische Mechanik 2 (SS 2011) 6. Arbeitssatz, Prinzip der virtuellen Verschiebungen (PvV) und Prinzip der virtuellen Kräfte (PvK) Arbeit: 6.1 Grundbegriffe und Arbeitssatz 6.1 Grundbegriffe und Arbeitssatz
Technische Mechanik 2 (SS 2011) 6. Arbeitssatz, Prinzip der virtuellen Verschiebungen (PvV) und Prinzip der virtuellen Kräfte (PvK) Arbeit: 6.1 Grundbegriffe und Arbeitssatz 6.1 Grundbegriffe und Arbeitssatz
TECHNISCHE MECHANIK. Übungen zur Elastostatik. Prof. Dr.-Ing. Andreas Ettemeyer Prof. Dr.-Ing. Oskar Wallrapp Dr. Bernd Schäfer
 TECHNISCHE MECHANIK Übungen zur Elastostatik Prof. Dr.-Ing. Andreas Ettemeyer Prof. Dr.-Ing. Oskar Wallrapp Dr. Bernd Schäfer Fachhochschule München Fachbereich 06 - Feinwerk- und Mikrotechnik Technische
TECHNISCHE MECHANIK Übungen zur Elastostatik Prof. Dr.-Ing. Andreas Ettemeyer Prof. Dr.-Ing. Oskar Wallrapp Dr. Bernd Schäfer Fachhochschule München Fachbereich 06 - Feinwerk- und Mikrotechnik Technische
Technische Mechanik für Wirtschaftsingenieure
 Ulrich Gabbert/Ingo Raecke Technische Mechanik für Wirtschaftsingenieure 5., aktualisierte Auflage Mit 301 Abbildungen, 16 Tabellen, 83 Beispielen sowie einer CD-ROM Wi im Carl Hanser Verlag 1 Statik 11
Ulrich Gabbert/Ingo Raecke Technische Mechanik für Wirtschaftsingenieure 5., aktualisierte Auflage Mit 301 Abbildungen, 16 Tabellen, 83 Beispielen sowie einer CD-ROM Wi im Carl Hanser Verlag 1 Statik 11
Rheinische Fachhochschule Köln
 Rheinische Fachhochschule Köln Matrikel-Nr. Nachname Dozent Ianniello Musterlösung Semester Klausur BM, Ing.II K Datum 1.7.1 Genehmigte Hilfsmittel: Fach Urteil Statik +Festigkeit Ergebnis: Punkte Taschenrechner
Rheinische Fachhochschule Köln Matrikel-Nr. Nachname Dozent Ianniello Musterlösung Semester Klausur BM, Ing.II K Datum 1.7.1 Genehmigte Hilfsmittel: Fach Urteil Statik +Festigkeit Ergebnis: Punkte Taschenrechner
1.Fachwerke. F1 = 4,5 kn, F2 = 3,4 kn,
 1.Fachwerke # Frage Antw. P. F1 = 4,5 kn, F =,4 kn, 1 a Prüfen Sie das Fachwerk auf statische Bestimmtheit k=s+ ist hier 5 = 7 +, stimmt. Also ist das FW statisch bestimmt. 4 b Bestimmen Sie die Auflagerkraft
1.Fachwerke # Frage Antw. P. F1 = 4,5 kn, F =,4 kn, 1 a Prüfen Sie das Fachwerk auf statische Bestimmtheit k=s+ ist hier 5 = 7 +, stimmt. Also ist das FW statisch bestimmt. 4 b Bestimmen Sie die Auflagerkraft
1. Aufgabe: (ca. 16 % der Gesamtpunkte)
 Institut für Mechnik Prof. Dr.-Ing. hbil. P. Betsch Prof. Dr.-Ing. hbil. Th. Seelig Prüfung in Festigkeitslehre 0. März 05. Aufgbe: (c. 6 % der Gesmtpunkte) ) Wie viele unbhängige Spnnungskomponenten gibt
Institut für Mechnik Prof. Dr.-Ing. hbil. P. Betsch Prof. Dr.-Ing. hbil. Th. Seelig Prüfung in Festigkeitslehre 0. März 05. Aufgbe: (c. 6 % der Gesmtpunkte) ) Wie viele unbhängige Spnnungskomponenten gibt
Die den Träger belastende Streckenlast berechnet sich aus dem Querschnitt des Trägers und seiner Dichte zu: N 4
 Hochschule erseburg achbereich IW rof. Dr.-Ing. A. erklinger T II - estigkeitslehre - W Erlaubte Hilfsmittel: Alles, außer dem achbarn Seite 1/8 Datum:.0.015 ame: Aufgabe 1a: b: Die den Träger belastende
Hochschule erseburg achbereich IW rof. Dr.-Ing. A. erklinger T II - estigkeitslehre - W Erlaubte Hilfsmittel: Alles, außer dem achbarn Seite 1/8 Datum:.0.015 ame: Aufgabe 1a: b: Die den Träger belastende
1 Schubstarrer Balken
 Einsteinufer 5, 1587 Berlin PdvK Energiemethoden 7. Übungsblatt, WS 212/13, S. 1 1 Schubstarrer Balken Freischnitt und Schnittlasten für das reale System x läuft mit der Balkenachse, die strichlierte Linie
Einsteinufer 5, 1587 Berlin PdvK Energiemethoden 7. Übungsblatt, WS 212/13, S. 1 1 Schubstarrer Balken Freischnitt und Schnittlasten für das reale System x läuft mit der Balkenachse, die strichlierte Linie
2. Statisch bestimmte Systeme
 1 von 14 2. Statisch bestimmte Systeme 2.1 Definition Eine Lagerung nennt man statisch bestimmt, wenn die Lagerreaktionen (Kräfte und Momente) allein aus den Gleichgewichtsbedingungen bestimmbar sind.
1 von 14 2. Statisch bestimmte Systeme 2.1 Definition Eine Lagerung nennt man statisch bestimmt, wenn die Lagerreaktionen (Kräfte und Momente) allein aus den Gleichgewichtsbedingungen bestimmbar sind.
Aufgabe 1 (6 Punkte) Prüfungsklausur Technische Mechanik I. Techn. Mechanik & Fahrzeugdynamik
 Techn. Mechanik & Fahrzeugdynamik TM I Prof. Dr.-Ing. habil. Hon. Prof. (NUST) D. Bestle 8. September 018 Prüfungsklausur Technische Mechanik I Aufgabe 1 (6 Punkte) Zwei Gewichte (Massen m 1, m ) sind
Techn. Mechanik & Fahrzeugdynamik TM I Prof. Dr.-Ing. habil. Hon. Prof. (NUST) D. Bestle 8. September 018 Prüfungsklausur Technische Mechanik I Aufgabe 1 (6 Punkte) Zwei Gewichte (Massen m 1, m ) sind
Musterlösungen (ohne Gewähr)
 Herbst 010 Seite 1/0 rage 1 ( Punkte) Ein masseloser Balken der Länge l stützt sich wie skizziert über einen masselosen Stab auf dem Mittelpunkt P einer Rolle ab. Ein horizontal verlaufendes Seil verbindet
Herbst 010 Seite 1/0 rage 1 ( Punkte) Ein masseloser Balken der Länge l stützt sich wie skizziert über einen masselosen Stab auf dem Mittelpunkt P einer Rolle ab. Ein horizontal verlaufendes Seil verbindet
Hochschule Karlsruhe Technische Mechanik Statik. Aufgaben zur Statik
 S 1. Seilkräfte ufgaben zur Statik 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn m Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. S 2: Zentrales
S 1. Seilkräfte ufgaben zur Statik 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn m Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. S 2: Zentrales
Wiederholklausur Technische Mechanik WIM
 1.) (2+6+2 Punkte) Eine Spätzlepresse, an der nur senkrechte Kräfte wirken, soll untersucht werden. Der Zylinder in welchem sich der Teig befindet hat eine Grundfläche von A = ²/2. A B R a.) Welche Kraft
1.) (2+6+2 Punkte) Eine Spätzlepresse, an der nur senkrechte Kräfte wirken, soll untersucht werden. Der Zylinder in welchem sich der Teig befindet hat eine Grundfläche von A = ²/2. A B R a.) Welche Kraft
Kapitel 8. Verbundquerschnitte
 Kapitel 8 Verbundquerschnitte 8 8 Verbundquerschnitte 8.1 Einleitung... 279 8.2 Zug und Druck in Stäben... 279 8.3 Reine Biegung... 286 8.4 Biegung und Zug/Druck... 293 8.5 Zusammenfassung... 297 Lernziele:
Kapitel 8 Verbundquerschnitte 8 8 Verbundquerschnitte 8.1 Einleitung... 279 8.2 Zug und Druck in Stäben... 279 8.3 Reine Biegung... 286 8.4 Biegung und Zug/Druck... 293 8.5 Zusammenfassung... 297 Lernziele:
Aufgabe Max. Punkte Erreichte Punkte Gesamt 100
 Wintersemester 0/ Baumechanik II-Klausur ( tunden)-lösung. eptember 0 Name: Matrikelnummer: ufgabe Max. Punkte Erreichte Punkte 8 0 5 6 Gesamt 00 Bitte jede ufgabe auf einem neuen Blatt bearbeiten und
Wintersemester 0/ Baumechanik II-Klausur ( tunden)-lösung. eptember 0 Name: Matrikelnummer: ufgabe Max. Punkte Erreichte Punkte 8 0 5 6 Gesamt 00 Bitte jede ufgabe auf einem neuen Blatt bearbeiten und
Übung zu Mechanik 1 Seite 19
 Übung zu Mechanik 1 Seite 19 Aufgabe 33 Bestimmen Sie die Lage des Flächenschwerpunktes für den dargestellten Plattenbalkenquerschnitt! (Einheit: cm) Aufgabe 34 Betimmen Sie die Lage des Flächenschwerpunktes
Übung zu Mechanik 1 Seite 19 Aufgabe 33 Bestimmen Sie die Lage des Flächenschwerpunktes für den dargestellten Plattenbalkenquerschnitt! (Einheit: cm) Aufgabe 34 Betimmen Sie die Lage des Flächenschwerpunktes
Euler-Bernoulli-Balken
 Euler-Bernoulli-Balken 2 2.1 Einführende Bemerkungen Ein Balken ist als langer prismatischer Körper, der schematisch in Abb. 2.1 dargestellt ist, definiert. Die folgenden Ableitungen unterliegen hierbei
Euler-Bernoulli-Balken 2 2.1 Einführende Bemerkungen Ein Balken ist als langer prismatischer Körper, der schematisch in Abb. 2.1 dargestellt ist, definiert. Die folgenden Ableitungen unterliegen hierbei
Statik im Bauwesen. HUSS-MEDIEN GmbH Verlag Bauwesen Berlin. Fritz Bochmann/Werner Kirsch. Band 3: Statisch unbestimmte ebene Systeme
 Fritz Bochmann/Werner Kirsch Statik im Bauwesen Band 3: Statisch unbestimmte ebene Systeme 13. Auflage HUSS-MEDIEN GmbH Verlag Bauwesen 10400 Berlin Inhaltsverzeichnis Einführung 11.1. Allgemeine Grundlagen
Fritz Bochmann/Werner Kirsch Statik im Bauwesen Band 3: Statisch unbestimmte ebene Systeme 13. Auflage HUSS-MEDIEN GmbH Verlag Bauwesen 10400 Berlin Inhaltsverzeichnis Einführung 11.1. Allgemeine Grundlagen
5.1 Grundlagen zum Prinzip der virtuellen Kräfte
 5 Prinzip der virtuellen Kräfte 5. Grundlagen zum Prinzip der virtuellen Kräfte Das Prinzip der virtuellen Kräfte (PvK) stellt eine nwendung des Prinzips der virtuellen rbeit dar. Es dient zur Bestimmung
5 Prinzip der virtuellen Kräfte 5. Grundlagen zum Prinzip der virtuellen Kräfte Das Prinzip der virtuellen Kräfte (PvK) stellt eine nwendung des Prinzips der virtuellen rbeit dar. Es dient zur Bestimmung
20 Statik Die resultierende Kraft im ebenen Kräftesystem
 20 Statik Die resultierende Kraft im ebenen Kräftesstem 6.1.3 Beispiel zur Resultierenden im allgemeinen Kräftesstem An einem Brückenträger mit der Segmentlänge a=4m greifen die äußeren Kräfte F 1 =F 2
20 Statik Die resultierende Kraft im ebenen Kräftesstem 6.1.3 Beispiel zur Resultierenden im allgemeinen Kräftesstem An einem Brückenträger mit der Segmentlänge a=4m greifen die äußeren Kräfte F 1 =F 2
= = > > Aufgabe 1 (6 Punkte) Institut für Technische und Num. Mechanik Technische Mechanik IV Profs. P. Eberhard / M. Hanss WS 2014/15 K 2
 Institut für Technische und Num. Mechanik Technische Mechanik IV Profs. P. Eberhard / M. Hanss WS 014/15 K 1. Februar 015 Klausur in Technische Mechanik IV Nachname, Vorname E-Mail-Adresse (Angabe freiwillig)
Institut für Technische und Num. Mechanik Technische Mechanik IV Profs. P. Eberhard / M. Hanss WS 014/15 K 1. Februar 015 Klausur in Technische Mechanik IV Nachname, Vorname E-Mail-Adresse (Angabe freiwillig)
Technische Mechanik für Wirtschaftsingenieure
 Technische Mechanik für Wirtschaftsingenieure von Ulrich Gabbert, Ingo Raecke 2. Auflage Hanser München 2004 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 22807 8 Zu Leseprobe schnell und portofrei
Technische Mechanik für Wirtschaftsingenieure von Ulrich Gabbert, Ingo Raecke 2. Auflage Hanser München 2004 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 22807 8 Zu Leseprobe schnell und portofrei
Innere Beanspruchungen - Schnittgrößen
 Innere Beanspruchungen - Schnittgrößen Vorlesung und Übungen 1. Semester BA Architektur Q () M () M () Q () N () N () L - KIT Universität des Landes Baden-Württemberg und nationales orschungszentrum in
Innere Beanspruchungen - Schnittgrößen Vorlesung und Übungen 1. Semester BA Architektur Q () M () M () Q () N () N () L - KIT Universität des Landes Baden-Württemberg und nationales orschungszentrum in
WWT Frank Sandig Agricolastr. 16, 2310A Freiberg. 1. Belegaufgabe.
 Frank Sandig Agricolastr. 16, 310A 09599 Freiberg 4817 4.WWT sandigf@mailserver.tu-freiberg.de Maschinen- und Apparateelemente 1. Belegaufgabe Aufgabenstellung: Abgabezeitraum: 6.11. - 30.11.007 Übungsleiter:
Frank Sandig Agricolastr. 16, 310A 09599 Freiberg 4817 4.WWT sandigf@mailserver.tu-freiberg.de Maschinen- und Apparateelemente 1. Belegaufgabe Aufgabenstellung: Abgabezeitraum: 6.11. - 30.11.007 Übungsleiter:
Statik. Klausur am Name: Vorname: Matrikelnummer: (bitte deutlich schreiben)
 Diplomprüfung Herbst 2009 Prüfungsfach Statik Klausur am 05.10.2009 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 5 5 25 25 30
Diplomprüfung Herbst 2009 Prüfungsfach Statik Klausur am 05.10.2009 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 5 5 25 25 30
Musterlösung zur 10. Übung Mechanik II SS 08. Aufgabe 1: Schubspannungen infolge Querkraft: Bei dünnwandigen Querschnitten t 1, t 2
 Musterlösung ur 10. Übung Mechanik II SS 08 Aufgabe 1: Schubspannungen infolge Querkraft: Bei dünnwandigen Querschnitten t 1, t 2 b, h können die Schubspannungen in Richtung der bereichsweise einuführenden
Musterlösung ur 10. Übung Mechanik II SS 08 Aufgabe 1: Schubspannungen infolge Querkraft: Bei dünnwandigen Querschnitten t 1, t 2 b, h können die Schubspannungen in Richtung der bereichsweise einuführenden
Mechanik 2. Übungsaufgaben
 Mechanik 2 Übungsaufgaben Professor Dr.-Ing. habil. Jörg Schröder Universität Duisburg Essen, Standort Essen Fachbereich 10 - Bauwesen Institut für Mechanik Übung zu Mechanik 2 Seite 1 Aufgabe 1 Berechnen
Mechanik 2 Übungsaufgaben Professor Dr.-Ing. habil. Jörg Schröder Universität Duisburg Essen, Standort Essen Fachbereich 10 - Bauwesen Institut für Mechanik Übung zu Mechanik 2 Seite 1 Aufgabe 1 Berechnen
Prof. Dr.-Ing. P. Eberhard SoSe 2018 Ü1.1. Das abgebildete System aus zwei Körperpendeln soll untersucht werden.
 Prof. Dr.-Ing. P. Eberhard SoSe 2018 Ü1.1 Aufgabe 1**: Das abgebildete System aus zwei Körperpendeln soll untersucht werden. An Pendel 1 (Länge l 1, Schwerpunktsabstand d 1, Masse m 1 Trägheitsmoment bezüglich
Prof. Dr.-Ing. P. Eberhard SoSe 2018 Ü1.1 Aufgabe 1**: Das abgebildete System aus zwei Körperpendeln soll untersucht werden. An Pendel 1 (Länge l 1, Schwerpunktsabstand d 1, Masse m 1 Trägheitsmoment bezüglich
TECHNISCHE MECHANIK A (STATIK)
 Probeklausur im Fach TECHNISCHE MECHANIK A (STATIK) Nr. 6 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 2 3 4 5 6 Summe Punkte: 29,5 7 17 10 9,5 7 80 Davon erreicht Punkte: Gesamtergebnis
Probeklausur im Fach TECHNISCHE MECHANIK A (STATIK) Nr. 6 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 2 3 4 5 6 Summe Punkte: 29,5 7 17 10 9,5 7 80 Davon erreicht Punkte: Gesamtergebnis
= 13, cm 4. = 3, cm 4. 3, cm 4 y. cm 3 y
 Aufgabe : ) Biegespannungsverlauf: σ b, ) M M I I bh h b cm cm) cm cm), 8 cm, 56 cm σ b, ) N cm, 8 cm N cm, 56 cm 7, N cm 89, N cm ) Gleichung der neutralen Achse : σ b, ) : M M I 7, N cm 89, N cm P Die
Aufgabe : ) Biegespannungsverlauf: σ b, ) M M I I bh h b cm cm) cm cm), 8 cm, 56 cm σ b, ) N cm, 8 cm N cm, 56 cm 7, N cm 89, N cm ) Gleichung der neutralen Achse : σ b, ) : M M I 7, N cm 89, N cm P Die
Aufgabe 6. Lösungsvorschlag zu Aufgabe 6. Klausur Mechanik II vom 27. März 2007 Seite 1 von 12
 Klausur echanik II vom 7. ärz 7 Seite 1 von 1 ufge 6 a Der Querschnitt eines Trägers ist aus drei gleichen Rechtecken zusammengesetzt. a) estimmen Sie I yy und I zz! b) Wie groß ist I yz? y b S Gegeben:,
Klausur echanik II vom 7. ärz 7 Seite 1 von 1 ufge 6 a Der Querschnitt eines Trägers ist aus drei gleichen Rechtecken zusammengesetzt. a) estimmen Sie I yy und I zz! b) Wie groß ist I yz? y b S Gegeben:,
LÖSUNG a) + N + G U l * ] G K l F N a ^xz Q ^ Mi() = F N : l + G:l sin() G:l cos() =! F N = G[cos() sin()] = ; 549 G Fix = N G: cos() G: sin() =! N =
![LÖSUNG a) + N + G U l * ] G K l F N a ^xz Q ^ Mi() = F N : l + G:l sin() G:l cos() =! F N = G[cos() sin()] = ; 549 G Fix = N G: cos() G: sin() =! N = LÖSUNG a) + N + G U l * ] G K l F N a ^xz Q ^ Mi() = F N : l + G:l sin() G:l cos() =! F N = G[cos() sin()] = ; 549 G Fix = N G: cos() G: sin() =! N =](/thumbs/85/92476478.jpg) KLAUSUR ZUR TECNISCEN MECANIK I Termin:. Septemer AUFGABE ( Punkte) Für das in A. dargestellte System kennt man l =; 5 m, G =5 kn und =. Man estimme a) die Reaktionen in den Bindungen, ) die Schnittgrößen
KLAUSUR ZUR TECNISCEN MECANIK I Termin:. Septemer AUFGABE ( Punkte) Für das in A. dargestellte System kennt man l =; 5 m, G =5 kn und =. Man estimme a) die Reaktionen in den Bindungen, ) die Schnittgrößen
Einführung in die Statik und räumliche Kraftsysteme
 Leseprobe Kirbs Einführung in die Statik und räumliche Kraftsysteme TECHNISCHE MECHANIK Studienbrief 2-050-0904 3. Auflage 2008 HOCHSCHULVERBUND DISTANCE LEARNING Impressum Verfasser: Prof. Dr.-Ing. Jörg
Leseprobe Kirbs Einführung in die Statik und räumliche Kraftsysteme TECHNISCHE MECHANIK Studienbrief 2-050-0904 3. Auflage 2008 HOCHSCHULVERBUND DISTANCE LEARNING Impressum Verfasser: Prof. Dr.-Ing. Jörg
Sessionsprüfung Baustatik I+II. Sommer Freitag, 19. August 2011, Uhr, HIL G61
 Sessionsprüfung Baustatik I+II Sommer 011 Freitag, 19. August 011, 09.00 1.00 Uhr, HIL G61 Name, Vorname : Studenten-Nr. : Bemerkungen 1. Die Aufgaben dürfen in beliebiger Reihenfolge bearbeitet werden..
Sessionsprüfung Baustatik I+II Sommer 011 Freitag, 19. August 011, 09.00 1.00 Uhr, HIL G61 Name, Vorname : Studenten-Nr. : Bemerkungen 1. Die Aufgaben dürfen in beliebiger Reihenfolge bearbeitet werden..
1. Aufgabe: (ca. 12 % der Gesamtpunkte)
 . August 07. Aufgabe: (ca. % der Gesamtunkte) a) Skizzieren Sie an den dargestellten Stäben die Knickformen der vier Euler-Knickfälle inklusive Lagerung und geben Sie zum Eulerfall mit der höchsten Knicklast
. August 07. Aufgabe: (ca. % der Gesamtunkte) a) Skizzieren Sie an den dargestellten Stäben die Knickformen der vier Euler-Knickfälle inklusive Lagerung und geben Sie zum Eulerfall mit der höchsten Knicklast
TECHNISCHE MECHANIK A (STATIK)
 Probeklausur im Fach TECHNISCHE MECHANIK A (STATIK) Nr. 5 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 2 3 4 5 6 Summe Punkte: 31 7,5 17,5 9 10 5 80 Davon erreicht Punkte: Gesamtergebnis
Probeklausur im Fach TECHNISCHE MECHANIK A (STATIK) Nr. 5 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 2 3 4 5 6 Summe Punkte: 31 7,5 17,5 9 10 5 80 Davon erreicht Punkte: Gesamtergebnis
Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 1999 Matr.---Nr. :... Fachsemester:...
 Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 1999 Matr.---Nr. :... Fachsemester:... Baustatik 1/2 Semestrale am 28.07.1999 (Bearbeitungszeit 45 Minuten) max.
Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 1999 Matr.---Nr. :... Fachsemester:... Baustatik 1/2 Semestrale am 28.07.1999 (Bearbeitungszeit 45 Minuten) max.
Übersicht der ausführlich gelösten Beispiele und Aufgaben
 Inhalt / Übersicht der ausführlich gelösten Beispiele und Aufgaben XIII Übersicht der ausführlich gelösten Beispiele und Aufgaben Beispiele Dachbinder-Konstruktion aus Fachwerk und Vollwandträger; Auflagerkräfte
Inhalt / Übersicht der ausführlich gelösten Beispiele und Aufgaben XIII Übersicht der ausführlich gelösten Beispiele und Aufgaben Beispiele Dachbinder-Konstruktion aus Fachwerk und Vollwandträger; Auflagerkräfte
( und ) Sommer Samstag, 22. August 2015, Uhr, HIL G 15. Name, Vorname: Studenten-Nr.:
 Baustatik I+II Sessionsprüfung (101-0113-00 und 101-0114-00) Sommer 2015 Samstag, 22. August 2015, 09.00 12.00 Uhr, HIL G 15 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in beliebiger
Baustatik I+II Sessionsprüfung (101-0113-00 und 101-0114-00) Sommer 2015 Samstag, 22. August 2015, 09.00 12.00 Uhr, HIL G 15 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in beliebiger
Festigkeitslehre. Aufgaben
 Modurüfung in Technischer Mechanik am 8. März 06 Festigkeitsehre Aufgaben Name: Vorname: Matr.-Nr.: Fachrichtung: Hinweise: Bitte schreiben Sie deutich esbar. Zeichnungen müssen sauber und übersichtich
Modurüfung in Technischer Mechanik am 8. März 06 Festigkeitsehre Aufgaben Name: Vorname: Matr.-Nr.: Fachrichtung: Hinweise: Bitte schreiben Sie deutich esbar. Zeichnungen müssen sauber und übersichtich
TM 2 Übung, Aufgaben an der Tafel , Prof. Gerling, SS 2013
 TM Übung, Aufgaben an der Tafel 9.4.3, Prof. Gerling, SS 03 Dieser Text ist unter dieser Creative Commons Lizenz veröffentlicht. Wir erheben keinen Anspruch auf Vollständigkeit oder Richtigkeit. Falls
TM Übung, Aufgaben an der Tafel 9.4.3, Prof. Gerling, SS 03 Dieser Text ist unter dieser Creative Commons Lizenz veröffentlicht. Wir erheben keinen Anspruch auf Vollständigkeit oder Richtigkeit. Falls
Technische Mechanik II
 INSTITUT FÜR MECHANIK Technische Universität Darmstadt Prüfung Technische Mechanik II Prof. W. Becker Prof. D. Gross Prof. P. Hagedorn Jun. Prof. R. Müller am 5. Juli 005 (Name) (Vorname) (Matr.-Nr.) (Studiengang)
INSTITUT FÜR MECHANIK Technische Universität Darmstadt Prüfung Technische Mechanik II Prof. W. Becker Prof. D. Gross Prof. P. Hagedorn Jun. Prof. R. Müller am 5. Juli 005 (Name) (Vorname) (Matr.-Nr.) (Studiengang)
Aufgabe 6, Musterlösung
 usterlösungen Klausur echank II vm 6. ärz 008 Sete 1 vn 11 ufgabe 6 usterlösung uf de abgebldete Stahlschebe (Vrder- und Setenanscht) mt der Kantenlänge a und der Dcke t wrke unter enem Wnkel α de Kraft
usterlösungen Klausur echank II vm 6. ärz 008 Sete 1 vn 11 ufgabe 6 usterlösung uf de abgebldete Stahlschebe (Vrder- und Setenanscht) mt der Kantenlänge a und der Dcke t wrke unter enem Wnkel α de Kraft
2. Sätze von Castigliano und Menabrea
 2. Sätze von Castigliano und Menabrea us der Gleichheit von äußerer rbeit und Formänderungsenergie kann die Verschiebung am Lastangriffspunkt berechnet werden, wenn an der Struktur nur eine Last angreift.
2. Sätze von Castigliano und Menabrea us der Gleichheit von äußerer rbeit und Formänderungsenergie kann die Verschiebung am Lastangriffspunkt berechnet werden, wenn an der Struktur nur eine Last angreift.
Das Problem der inneren Kräfte in den Zugbändern der Tragkonstruktion des Schachtfördergefäßes
 IMW - Institutsmitteilung Nr. 8 (00) 117 Das Problem der inneren Kräfte in den Zugbändern der Tragkonstruktion des Schachtfördergefäßes Dzik, S.; Wolny, S.; Siemieniec, A. In dieser Abhandlung werden die
IMW - Institutsmitteilung Nr. 8 (00) 117 Das Problem der inneren Kräfte in den Zugbändern der Tragkonstruktion des Schachtfördergefäßes Dzik, S.; Wolny, S.; Siemieniec, A. In dieser Abhandlung werden die
Bestimmen Sie für den dargestellten Balken die Auflagerkräfte sowie die N-, Q- und M-Linie (ausgezeichnete Werte sind anzugeben).
 Technische Universität Darmstadt Technische Mechanik I B 13, G Kontinuumsmechanik Wintersemester 007/008 Prof. Dr.-Ing. Ch. Tsakmakis 9. Lösungsblatt Dr. rer. nat. P. Grammenoudis 07. Januar 008 Dipl.-Ing.
Technische Universität Darmstadt Technische Mechanik I B 13, G Kontinuumsmechanik Wintersemester 007/008 Prof. Dr.-Ing. Ch. Tsakmakis 9. Lösungsblatt Dr. rer. nat. P. Grammenoudis 07. Januar 008 Dipl.-Ing.
2. Definieren Sie die 2 Arten von Verzerrungen. Vorzeichenregeln.
 FESTIGKEITSLEHRE 1. Definieren Sie den Begriff "Widerstandsmoment". Erläutern Sie es für Rechteck und doppelt T Querschnitt. Antwort Die Widerstandsmomente sind geometrische Kennzeichen des Querschnittes.
FESTIGKEITSLEHRE 1. Definieren Sie den Begriff "Widerstandsmoment". Erläutern Sie es für Rechteck und doppelt T Querschnitt. Antwort Die Widerstandsmomente sind geometrische Kennzeichen des Querschnittes.
Baustatik I+II Sessionsprüfung. ( und ) Sommer Freitag, 11. August 2017, Uhr, HPH G 1/ HPH G 2.
 Baustatik I+II Sessionsprüfung (101-0113-00 und 101-0114-00) Sommer 2017 Freitag, 11. August 2017, 14.00 17.00 Uhr, HPH G 1/ HPH G 2 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in
Baustatik I+II Sessionsprüfung (101-0113-00 und 101-0114-00) Sommer 2017 Freitag, 11. August 2017, 14.00 17.00 Uhr, HPH G 1/ HPH G 2 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in
BAUSTATIK I KOLLOQUIUM 10, Lösung
 BAUSTATIK I KOLLOQUIUM 10, Lösung (101-011) Thema: Kraftmethode Aufgabe 1, Lösung Gegeben: Gesucht: Unterspanntes Fachwerk, EA = konstant für alle Stäbe Stabkräfte S i Grad der statischen Unbestimmtheit:
BAUSTATIK I KOLLOQUIUM 10, Lösung (101-011) Thema: Kraftmethode Aufgabe 1, Lösung Gegeben: Gesucht: Unterspanntes Fachwerk, EA = konstant für alle Stäbe Stabkräfte S i Grad der statischen Unbestimmtheit:
Fragen aus dem Repetitorium II
 Fragen aus dem Repetitorium II Folgend werden die Fragen des Repetitoriums II, welche ihr im Skript ab Seite 182 findet, behandelt. Die Seiten werden ständig aktualisiert und korrigiert, so daß es sich
Fragen aus dem Repetitorium II Folgend werden die Fragen des Repetitoriums II, welche ihr im Skript ab Seite 182 findet, behandelt. Die Seiten werden ständig aktualisiert und korrigiert, so daß es sich
Lösungen TM I Statik und Festigkeitslehre
 Technische Mechanik I L Lösungen TM I Statik und Festigkeitslehre Modellbildung in der Mechanik N Pa (Pascal). m.4536kg.38slug [a] m, [b] dimensionslos, [c] m, [d] m Dichte: kgm 3.94 3 slugft 3 Geschwindigkeit:
Technische Mechanik I L Lösungen TM I Statik und Festigkeitslehre Modellbildung in der Mechanik N Pa (Pascal). m.4536kg.38slug [a] m, [b] dimensionslos, [c] m, [d] m Dichte: kgm 3.94 3 slugft 3 Geschwindigkeit:
= 1kN F 1 F 2. = 2,5 kn. 2m 4m 2m. = 0,75 kn/m. Webinar: Statik Thema: Schnittgrößen
 Webinar Statik Thema Schnittgrößen Bestimme für die nachfolgenden beiden Aufgaben die Schnittgrößen und Schnittgrößenverläufe! F 1 = 1k = 2,5 k a) 30 = 0,75 k/m b) Lösung Teil a) Wir beginnen damit den
Webinar Statik Thema Schnittgrößen Bestimme für die nachfolgenden beiden Aufgaben die Schnittgrößen und Schnittgrößenverläufe! F 1 = 1k = 2,5 k a) 30 = 0,75 k/m b) Lösung Teil a) Wir beginnen damit den
Hochschule Karlsruhe Technische Mechanik Statik. Aufgaben zur Statik
 Aufgaben zur Statik S 1. Seilkräfte 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn Am Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. Addition
Aufgaben zur Statik S 1. Seilkräfte 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn Am Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. Addition
BAUMECHANIK I Prof. Dr.-Ing. Christian Barth
 BAUMECHANIK I Umfang V/Ü/P (ECTS) 2/2/0 (5) 2/2/0 2/2/0 2/2/0-2*/2*/0 - Diplom 5. 6. 7. 8. 9. 10. Definitionen und Klassifizierungen Kräfte und Kraftarten, Vektor, Vektorsysteme Darstellung vektorieller
BAUMECHANIK I Umfang V/Ü/P (ECTS) 2/2/0 (5) 2/2/0 2/2/0 2/2/0-2*/2*/0 - Diplom 5. 6. 7. 8. 9. 10. Definitionen und Klassifizierungen Kräfte und Kraftarten, Vektor, Vektorsysteme Darstellung vektorieller
TECHNISCHE MECHANIK A (STATIK)
 Probeklausur im Fach TECHNISCHE MECHANIK A (STATIK) Nr. 5 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 3 4 5 6 Summe Punkte: 31 7,5 17,5 9 10 5 80 Davon erreicht Punkte: Gesamtergebnis
Probeklausur im Fach TECHNISCHE MECHANIK A (STATIK) Nr. 5 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 3 4 5 6 Summe Punkte: 31 7,5 17,5 9 10 5 80 Davon erreicht Punkte: Gesamtergebnis
Einfeldträger mit Auskragung
 Vorlesung und Übungen 1. Semester B rchitektur IT Universität des andes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Schnittgrößen Beispiel 13.1.010 Dipl.-Ing.
Vorlesung und Übungen 1. Semester B rchitektur IT Universität des andes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Schnittgrößen Beispiel 13.1.010 Dipl.-Ing.
1. Aufgabe: (ca. 11% der Gesamtpunktzahl) Bitte beantworten Sie folgende Fragen: 1. Wie ist der Schubmittelpunkt definiert?
 . Aufgabe: (ca. % der Gesamtunktzah) Bitte beantworten Sie fogende Fragen:. Wie ist der Schubmitteunkt definiert?. Durch weche Einschränkungen des agemeinen dreidimensionaen Sannungszustandes ergibt sich
. Aufgabe: (ca. % der Gesamtunktzah) Bitte beantworten Sie fogende Fragen:. Wie ist der Schubmitteunkt definiert?. Durch weche Einschränkungen des agemeinen dreidimensionaen Sannungszustandes ergibt sich
