Physik PHB3/4 (Schwingungen, Wellen, Optik) 2.2 Gekoppelte Schwingungen
|
|
|
- Arthur Solberg
- vor 7 Jahren
- Abrufe
Transkript
1 9_GekoppeteShwingungen_BA_W.o - 5. Gekoppete Shwingungen.. Einführung Wenn zwei shwingungsfähige Systee in Verinung stehen, knn Energie usgetusht weren. er Energieustush hängt von er Stärke er Koppung. Beispie: Zwei Feerpene sin it einer Koppefeer er Feerkonstnte * iteinner verunen. Beohtungen: ie Einzessen führen i.a. keine hronishe Bewegung us. Wir Pene in Shwingungen versetzt, fängt uh Pene ngs n zu shwingen. Wenn Pene it xier Apitue shwingt, ist Pene vostänig zur Ruhe gekoen. ieser Vorgng wieerhot sih nun ugekehrt usw. 3 Wir ie Koppung verstärkt, ine ie Koppefeer stärker gespnnt wir, änern sih ie Shwingungszustäne rsher. * t t 4 ie Bewegungsfor geiht einer Shweung! eine Shweung ie Üergerung von zwei Shwingungen ist, stet sih ie Frge, wehe zwei Shwingungen üergert weren? Eigenshwingungen Für zwei esonere Anfngseingungen können wir iese zwei Shwingungen, ei enen sih ie Einzessen hronish ewegen, isoiert rsteen. iese usgezeihneten Bewegungsforen es Systes nennt n Eigenshwingungen, Norshwingungen oer Funentshwingungen. Eigenshwingungen für zwei gekoppete Fenpene. Eigenshwingung: ie Frequenz, it er ie Pene shwingen entspriht er eines einzenen (niht gekoppeten Penes. ie Shwingungen er eien Pene sin in Phse.
2 9_GekoppeteShwingungen_BA_W.o - /5. Eigenshwingung ie Frequenz hängt von er Koppung. ie Phsenge ist eenfs konstnt, er gegenphsig. ie geeine Shwingungsfor ist eine Üergerung ieser eien Eigenshwingungen. Anere Funentshwingungen können niht uftreten. Vergeeinerung: Ein Syste it f Shwingungsfreiheitsgren esitzt f Eigenshwingungen. Zu Beispie esitzt ein Moekü it N Atoen f = 3N 6 Shwingungsfreiheitsgre un it (3N 6 vershieene hronishe Shwingungsforen (Funentshwingungen. Jees Ato ewegt sih nn hronish un it er geihen Frequenz. hrkteristish für eine Eigenshwingung ist ie hronishe Bewegung er Mssenpunkte it er geihen Frequenz un fester Phsenge zueinner. Beispie. Trnsverse Eigenshwingungen einer Perenshnur Eine Perenshnur it N Mssenpunkten (it Feern gekoppet ht N Eigenshwingungen. ie Eigenshwingung it er höhsten Frequenz ist einen Zik-Zk-Bewegung. Üergng von eine konkreten Syste it N Freiheitsgren zu eine kontinuierihen Syste shwingene Site. Ausik uf s nähste Huptkpite: Wir in eine gekoppeten Shwingungssyste eine Msse (Shwingung ngestoßen, reitet sih iese Störung uf Grun er Koppung it en Nhrn us. ie Ausreitung ieser Störung heißt Wee. Von en 3N Freiheitsgren eines Systes von N Moeküen üssen 3 für ie Trnstion un 3 für ie Rottion gezogen weren, vereien insgest f = 3N - 6 Freiheitsgre für ie Shwingungen. Bei ineren Moeküen, wie O oer H sin nur zwei Rottionen ögih, so ss hier git: f = 3N 5.
3 .. Longituine Shwingungen gekoppeter Feerpene 9_GekoppeteShwingungen_BA_W.o - 3/5... Errten er Eigenshwingungen Geihgewiht (Ruhege: ie Feern soen zunähst niht vorgespnnt sein. (Wir weren jeoh später sehen, ss sih Ergenis nihts änert, wenn ie Feern uf Zug oer ruk vorgespnnt sin. Koppefeer ' Eigenshwingung : ie ittere Feer ist nie gespnnt! Beie Mssen ewegen sih it er geihen Frequenz un it konstnter Phsenge ' ( = synhrones Shwingen sin( t : Eigenshwingung : Beie Mssen ewegen sih gegenäufig it er geihen Frequenz un konstnter Phsenge. ( = synhrones Shwingen ' ges für eine Msse: ges = + ' ' sin( t :... Lösung er Bewegungsgeihungen (Norkoorintentrnsfortion ' Rüktreiene Kräfte F '( R F '( R it erhät n nh e Newtonshen Aktionsprinzip ie Bewegungsgeihungen '( '( ( ( s ist ein Syste von zwei gekoppeten ifferentigeihungen.
4 Entkoppung urh "geshikte Koorintentrnsfortion. (3 (4 Sue ( + ( ifferenz ( - ( 9_GekoppeteShwingungen_BA_W.o - 4/5 ( ( ( ( '( ( ' Entkoppete GL Lösungen: Eigenfrequenz ' Eigenfrequenz A t Eigenshwingung B t Eigenshwingung ie geeine Lösung ist nn eine Linerkointion er eien Eigenshwingungen. Wegen es Entkoppungsnstzes git für ie Shwingungen er Mssen un : A B os( t os( t A B os( t os( t...3 Beeutung er Eigenshwingungen - speziee Anregungseingungen Syste shwingt it Eigenshwingung Tere it üssen vershwinen. A os( t Shwerpunktsewegung: ( / / Anregungseingung: ( t ( t ( t ( t (z.b. eie Mssen shwingen hronish synhron it geiher Apitue un geiher Frequenz ittere Feer wir nie gespnnt - könnte entfernt weren Syste shwingt it Eigenshwingung Tere it üssen vershwinen. B os( t Retivewegung: Anregungseingung: ( t ( t ( t ( t (z.b. eie Mssen shwingen hronish it geiher Apitue un geiher Frequenz er synhron ittere Feer erfährt oppete ehnung
5 3 Anregungseingung (ie niht zu einer Eigenshwingung führt z.b.: ( t ( t ( t ( t ( t A os ( t B os A ( t A sin B ( t B sin 9_GekoppeteShwingungen_BA_W.o - 5/5 it erhät n s Lösungen ˆ os t (ost ost os t (ostos t eine trigonoetrishe Uforung iefert: os ( t os ( t sin ( t sin ( t zeitih ngs sih änerner Apituenfktor Shwingungsfor ist eine Shweung t t osoost sin tsint o o Entwikung für shwhe Koppung: ' << o ' o ' ' ' S o Energie in Energie in Shwinger Shwinger perioisher Energieustush eutung: ie Shwingung er Msse knn s erzwungene Shwingung i Resonnzf geeutet weren. Msse s Erreger shwingt it er Eigenfrequenz von Msse un äuft ieser (wie ei er erzwungenen Shwingung u / vorus. Befinet sih keine Energie ehr i Shwinger kehrt sih er Vorgng u - ei Nuurhgng er Shweung tritt nn ein Phsensprung ein.
6 ...4 Systetisher Lösungsnstz Beispie: zwei gekoppete Pene 9_GekoppeteShwingungen_BA_W.o - 6/5 x x Ruhege: Koppefeer entspnnt Bewegungsgeihungen (Keinwinkenäherung Rüktreiene Feerkräfte: (x = FR ( F ( R g( g ( ( ( A Errten er Eigenshwingungen Eigenshwingung ie ittere Feer ist nie gespnnt! Shwerpunktsewegung, synhrones Shwingen (Feer üerfüssig g os( t : Eigenshwingung Gegensinnige Bewegung synhrones Shwingen Feer oppet gespnnt (F = g os( t :
7 9_GekoppeteShwingungen_BA_W.o - 7/5 B Systetisher Lösungsnstz für gekoppete Shwingungen "Geshikte Koorinten", (sog. Norkoorinten zur Entkoppung er GL sin i geeinen shwierig zu finen. In er Mthetik git es zu ie Methoe er Eigenwertzw. Eigenvektorestiung. Ornen er GLn in ie For... j j j jn n Beispie n = für gekoppetes Feerpene g ( g ( ( g ( ( ( rsteung er GL it Vektoren un Mtrizen A Eigenfrequenzen estien Lösungsnstz für ie Eigenfrequenzen ( steht für zw. os( t os( t in e Lösungsnstz für ie Shwingungen un geihes un geihes hen, ist eine Eigenshwingung. Einsetzen in GL ( un ( ergit g ( g ( ( ('' ('' in Vektorfor: A Aes uf ie inke ringen g ( - ( - ( g + ( it erhät n ein hoogenes ineres Geihungssyste, s nur nn eine nihttrivie Lösung ht, wenn ie eterinnte er Koeffiziententrix. (Eigenwertgeihung et(
8 ie eterinnte ist nn eine Bestiungsgeihung n-ten Gres für. ie Geihung heißt "hrkteristishe Geihung". 9_GekoppeteShwingungen_BA_W.o - 8/5 g ( g ( ( g ( Lösung er qurtishen Geihung iefert ie Eigenfrequenzen un g. Lösung: g Eigenwert(frequenz g. Lösung: Eigenwert(frequenz Eigenshwingungsforen (Eigenvektoren estien (Koeffizienten un er weren urh Einsetzen von un in ('' oer ('' erittet. Eigenshwingung : g in ('' ergit: os( t os( t g Eigenshwingung : in ('' ergit: os( t os( t Ageeine Lösung ie geeine Lösung ergit sih urh Üergerung er Eigenshwingungsforen un. os( t os( t os( t os( t ie Koeffizienten un un ie Phsen un ergeen sih us en Anregungseingungen. Beispie: Syste shwingt it Eigenshwingung Tere it üssen vershwinen: = os( t os( t Syste shwingt it Eigenshwingung Tere it üssen vershwinen: = os( t os( t
9 ..4 Trnsverse Shwingungen gekoppeter Feerpene Gegenüersteung: ongituin / trnsvers ; n = ongituin trnsvers Ruhege: 9_GekoppeteShwingungen_BA_W.o - 9/5 = o o - Feern in Ruhege entspnnt - Feern strk vorgespnnt eff für eine Feer Eigenshwingung : - Feern shwh gespnnt un keine Ausenkungen eff ( - ittere Feer entspnnt - geihe Ausenkung - geihphsige Bewegung - Feern vorgespnnt - geihe Ausenkung - geihphsige Bewegung eff Eigenshwingung : - ittere Feer oppet gespnnt - geihe Ausenkung - gegenphsige Bewegung 3 - Feern vorgespnnt - geihe Ausenkung - gegenphsige Bewegung 3 eff eff eff
10 ongituin Bewegungsgeihungen ( ( 9_GekoppeteShwingungen_BA_W.o - /5 trnsvers Bewegungsgeihungen ( eff eff ( eff eff ie Feern soen nun für en ongituinen F eine Vorspnnung hen. o Bewegungsgeihungen für Vorspnnung ( - [ ( ] {[( ( ] } [ ( ] {[ ( ] oeres Vorzeihen: Stuhung unteres Vorzeihen. ehnung Nh e Ausutipizieren kürzt sih ( - herus un es ergeen sih ieseen Geihungen wie oen. ie Frequenz er ongituinen Shwingung ist it unhängig von er Feer-Vorspnnung. Kennzeihen von Eigenshwingungen: geihe Frequenz für e Mssenpunkte jee Msse führt eine hronishe Shwingung us konstnte Phsenge er Einzeshwingungen kein Energieustush Norshwingungen können s Resonnzfäe es gekoppeten Systes ufgefsst weren. Jee freie Shwingung eines gekoppeten Systes knn s Linerkointion seiner Eigenshwingungen eshrieen weren.
11 ..5 Weitere Beispiee gekoppeter Shwingungen 9_GekoppeteShwingungen_BA_W.o - /5 Beispie : s inere, reitoige Moekü Ein freies, ineres reitoiges Moekü weist 3N 5 = 4 Shwingungsfreiheitsgre uf un ht it 4 Norshwingungen (Beispie O : zwei Strekshwingungen (Änerung er Binungsängen zwei entrtete efortionsshwingungen (Änerung er Binungswinke Bewegungsgeihungen (für ongituine Strekshwingungen ( ( ( 3 ( Eine Lösung (trivi utet = = 3 = + t s ist er nur eine Shwerpunktsewegung un keine Shwingung, so ss sih noh zwei ongituine Strekshwingungen ergeen. Spezif: = = 3 ; = = Eigenshwingungen errten (trivi Shwerpunktsewegung synhrone Bewegung er äußeren Atoe (Shwerpunkt eit in Ruhe 3 synhrone Bewegung es itteren Atos (Shwerpunkt eit in Ruhe Lösung it systetishen Anstz ergit. t os( t 3 t t os( t os( t os( t os( t Norshwingungen von O syetrishe Strekshwingung s ( ~ = syetrishe Strekshwingung s ( ~ = (IR-ktiv entrtete efortionsshwingung ( ~ = 667 -
12 Beispie : Kpzitiv gekoppete L-Shwingkreise 9_GekoppeteShwingungen_BA_W.o - /5 s ehnishe Anogon zu gekoppeten L-Shwingkreisen sin ie eknnten gekoppeten Feerpene. Hier wir von er Shwingung es. Penes üer eine Koppeshnur eine perioishe Krft uf s. Pene usgeüt, ie ieses zu erzwungenen Shwingungen nregt. In er nähsten Phse ient nn s. Pene s Erreger. Bei iese Vorgng wir Energie perioish von eine Pene zu neren üertrgen. s perioishe An- un Ashween er Apitue ht s Aussehen einer Shweung, ie urh Üergerung zweier hronisher Shwingungen, en sog. Norshwingungen, zustne kot. Gnz ähnih sin ie Verhätnisse ei gekoppeten eektrishen Shwingungen. In er A. sin zwei kpzitiv gekoppete L-Shwingkreise gezeihnet. ie Koppung erfogt üer en Koppekonenstor k. Fießt z.b. vo inken Shwingkreis eine Lung Q uf k wirkt ie entstehene Spnnung U = Q/k wie eine treiene Spnnung für en rehten L-Kreis. ie Anwenung er Kirhhoffshen Sheifen- un Knotenrege iefert: L i i L u u u L k uk ul u i ik i U ik k Uk U Für ie Spnnungen üer un L git geein: Q u i un u L i L ifferenziert n ie eien Sheifengeihungen ergeen sih für en Spezif = = un L = L = L ie eien GL : i L i k k i L i i k k i Mit Hife er Knotenrege i k = i - i weren rus zwei gekoppete GL für ie Ströe i un i. i i i ( L L i i k i ( L L i i k Biet n ie Sue (+( un ie ifferenz (-( er eien Geihungen, wir s Geihungssyste it e Anstz i = i + i un i = i - i entkoppet. ( i i ( i i L ( i i ( ( i i L Lk ie Lösungen i un i sin ie eien Norshwingungen. Für ie eien Norfrequenzen un erhät n:
13 Norfrequenz L ie Norshwingung zu (i = = i - i entspriht e F, ss eie Ströe in iesee Rihtung fießen (i = i un k strofrei eit (i k =. er Koppekonenstor eit nn ier ungsfrei un könnte uh gnz weggessen weren. 9_GekoppeteShwingungen_BA_W.o - 3/5 Norfrequenz L Lk Bei (i = = i + i fießen ie eien Ströe in entgegengesetzter Rihtung (i = - i. er Koppekonenstor wir nn oppet so strk ufgeen (ik = i + i. ' ; L' L L ' ' L er geeine F stet eine Üergerung eier Shwingungsforen,.h. eine Shweung, r. Strke Koppung: er Grenzf k eeutet strke Koppung: ie eien Shwingkreise verhten sih wie ein einzener Shwingkreis it L = L + L un / = / + /. Shwhe Koppung: Shwhe Koppung iegt für k >> vor. ie treiene Spnnung Koppekonenstor U = Q/k wir retiv kein. Für k weren ie eien Shwingkreise sogr entkoppet, U geht, unhängig von wievie Lung e Konenstor zugeführt wir. er Koppekonenstor wirkt für A-Signe wie ein Kurzshußrht un zwingt ie Verinung er eien L-Kreise uf Erpotenti. Für shwhe Koppung ergit sih ie Shweungs- oer Austushfrequenz = - zu (Leiten Sie iese Beziehungen her: L k ie ittere Frequenz: / L k ergit sih zu:
14 Beispie 3: Inuktiv gekoppete L-Shwingkreise 9_GekoppeteShwingungen_BA_W.o - 4/5 In er A. sin zwei inuktiv gekoppete L-Shwingkreise gezeihnet. ie Koppung erfogt urh Annäherung er eien Spuen. s von Spue erzeugte Mgnetfe urhsetzt teiweise uh ie Spue un erzeugt in ihr eine zusätzihe Inuktionsspnnung u' in,l = -L i /, ie wie eine treiene Spnnung für en rehten L-Kreis wirkt un sih zur Inuktionsspnnung u in,l = -L i / iert. Ugekehrt git sinngeäß s geihe. ie Anwenung er Kirhhoffshen Sheifen- un Knotenrege uf ie Kreise un iefert: u u u' L L u u u' L L L L L U U Für ie Spnnungen üer un L git geein: Q u i un u L i L ul uin ifferenziert n ie eien Sheifengeihungen, ergeen sih für en Spezif = = un L = L = L ie eien gekoppeten GL : i i i L L ( i i i L L ( Biet n ie Sue (+( un ie ifferenz (-( er eien Geihungen, wir s Geihungssyste it e Anstz i = i + i un i = i - i entkoppet. ( i i ( i i ( L L ( L L ( i i ( i i (3 (4 ie Lösungen i un i sin ie eien Norshwingungen. Für ie eien Norfrequenzen un erhät n: (5 ( L L (6 ( L L I Norf stet ie freie Shwingung es gekoppeten Shwingkreises eine Üergerung er Norshwingungen it en Frequenzen un r.
15 Beispie 4: Wierstnsgekoppete L-Shwingkreise 9_GekoppeteShwingungen_BA_W.o - 5/5 In er A. sin zwei gekoppete L-Shwingkreise gezeihnet, ie it eine Wierstn gekoppet sin. ie Koppung uf en rehten Shwingkreis erfogt urh ie Spnnung, ie er Stro i i Wierstn R erzeugt. iese Spnnung wirk i rehten Shwingkreis wie eine erregene Spnnung. ie Anwenung er Kirhhoffshen Sheifen- un Knotenrege uf ie Kreise un iefert: u ul ur u R ul u i - i - i R = U L i i L i R R U Für en Spezif = = un L = L = L ergeen sih ie eien gekoppeten GL : Q i L ir R i Q irr L Wegen i - i - i R = (Q / - Q / - i R = git weiter: Q ( Q Q L Q Q ( Q Q R L R Q Q Q R Q ( L R L Q ( Q Q L Q Q L ( ( Biet n ie Sue (+( un ie ifferenz (-( er eien Geihungen, wir s Geihungssyste it e Anstz Q = Q + Q un Q = Q - Q entkoppet. Q Q Q L R Q L Q L L R L L ie Eigenshwingung it ist eine geäpfte Shwingung, währen ie Eigenshwingung it er Frequenz niht geäpft ist!
Baustatik. Berechnung statisch unbetsimmter Tragwerke: Band 1 Baustatik I, Berechnung statisch bestimmter Tragwerke. von Raimond Dallmann. 1.
 Busttik Berehnung sttish unetsimmter Trgwerke: Bn 1 Busttik I, Berehnung sttish estimmter Trgwerke von Rimon Dmnn 1. Aufge Busttik Dmnn shne un portofrei erhätih ei ek-shop.e DIE FACHBUCHHANDLUNG Hnser
Busttik Berehnung sttish unetsimmter Trgwerke: Bn 1 Busttik I, Berehnung sttish estimmter Trgwerke von Rimon Dmnn 1. Aufge Busttik Dmnn shne un portofrei erhätih ei ek-shop.e DIE FACHBUCHHANDLUNG Hnser
Mathematik PM Rationale Zahlen. Ist a kein Vielfaches von b, so entsteht eine neue Zahl, Bruch oder rationale Zahl genannt. Sie bilden die Menge Q.
 Mthetik PM Rtionle Zhlen Rtionle Zhlen. Einführung Die Gleihung = 9 ht ie Lösung. Z 9 9 Die Gleihung = ht ie Lösung. Z Definition Die Gleihung =, it, Z un 0, ht ie Ist kein Vielfhes von, so entsteht eine
Mthetik PM Rtionle Zhlen Rtionle Zhlen. Einführung Die Gleihung = 9 ht ie Lösung. Z 9 9 Die Gleihung = ht ie Lösung. Z Definition Die Gleihung =, it, Z un 0, ht ie Ist kein Vielfhes von, so entsteht eine
Ausarbeitung zum Satz von Brahmagupta. Thimo Wanders Dozent: Dr. Marco Sobiech Proseminar Lineare Algebra
 usreitung zum Stz von rhmgupt Thimo Wners ozent: r. Mro Soieh Proseminr Linere lger Sommersemester 2018 Inhltsverzeihnis 1 Einleitung 2 1.1 Nottion..................................... 2 2 Sehnenviereke
usreitung zum Stz von rhmgupt Thimo Wners ozent: r. Mro Soieh Proseminr Linere lger Sommersemester 2018 Inhltsverzeihnis 1 Einleitung 2 1.1 Nottion..................................... 2 2 Sehnenviereke
Maschinendynamik Formelsammlung Prof. Dr.- Ing. H. Bräutigam SS 2000 Seite 01. Coulombsche Reibungskraft : F R = µ * F N ( Rutschen ) c =
 Mshinendynik Foesung Pof. D.- Ing. H. Bäutig SS Seite Käftegeihungen : Couobshe Reibungskft : F R µ F N ( Rutshen ) Roen : Reibungskft R Gewihtskft : G g Seieibungskft : Fedekäfte : µ α F e F Gede Fede
Mshinendynik Foesung Pof. D.- Ing. H. Bäutig SS Seite Käftegeihungen : Couobshe Reibungskft : F R µ F N ( Rutshen ) Roen : Reibungskft R Gewihtskft : G g Seieibungskft : Fedekäfte : µ α F e F Gede Fede
a) Behauptung: Es gibt die folgenden drei stabilen Matchings:
 Musterlösung - ufgenltt 1 ufge 1 ) ehuptung: Es git ie folgenen rei stilen Mthings: ies knn mn ntürlih für ein so kleines eispiel urh etrhten ller möglihen 3! = 6 Mthings eweisen. Mn knn er uh strukturierter
Musterlösung - ufgenltt 1 ufge 1 ) ehuptung: Es git ie folgenen rei stilen Mthings: ies knn mn ntürlih für ein so kleines eispiel urh etrhten ller möglihen 3! = 6 Mthings eweisen. Mn knn er uh strukturierter
Dreiecke können einerseits nach den Eigenschaften ihrer Seiten und andererseits nach ihren Winkeln benannt werden. Einteilung nach den Seiten:
 gnz klr: Mthemtik 2 - s Ferienheft mit Erfolgsnzeiger 3 Rettungsring Eigenshften von reieken & Viereken Eigenshften von reieken Ein reiek ht immer 3 Ekpunkte, 3 Seiten un 3 Innenwinkel. ie eshriftung eines
gnz klr: Mthemtik 2 - s Ferienheft mit Erfolgsnzeiger 3 Rettungsring Eigenshften von reieken & Viereken Eigenshften von reieken Ein reiek ht immer 3 Ekpunkte, 3 Seiten un 3 Innenwinkel. ie eshriftung eines
1 Planarbeit Planarbeit
 Erreiten Sie sih shrittweise ie folgenen Themen. Notieren Sie gegeenenflls zu jeem Them Frgen. Lösen Sie jeweils ie zugehörige Kontrollufge. Kontrollieren Sie Ihre Lösung mit er Musterlösung. Lösen Sie
Erreiten Sie sih shrittweise ie folgenen Themen. Notieren Sie gegeenenflls zu jeem Them Frgen. Lösen Sie jeweils ie zugehörige Kontrollufge. Kontrollieren Sie Ihre Lösung mit er Musterlösung. Lösen Sie
Baustatik 1. Berechnung statisch bestimmter Tragwerke. Bearbeitet von Raimond Dallmann
 Busttik 1 Berehnung sttish estimmter Trgwerke Bereitet von Rimon Dmnn 4., ktuisierte Aufge 01. Buh. 08 S. Hrover ISBN 978 3 446 4331 4 Formt (B x L): 19,3 x 3, m Gewiht: 487 g Weitere Fhgeiete > Tehnik
Busttik 1 Berehnung sttish estimmter Trgwerke Bereitet von Rimon Dmnn 4., ktuisierte Aufge 01. Buh. 08 S. Hrover ISBN 978 3 446 4331 4 Formt (B x L): 19,3 x 3, m Gewiht: 487 g Weitere Fhgeiete > Tehnik
Automaten und formale Sprachen Notizen zu den Folien
 Automten un formle Sprhen Notizen zu en Folien 1 Grunlgen un formle Beweise Venn-Digrmme (Folie 6) Im oeren Digrmm er Folie 6 sin zwei Mengen ngegeen: A un B. Es ist explizit ein Element von A ngegeen,
Automten un formle Sprhen Notizen zu en Folien 1 Grunlgen un formle Beweise Venn-Digrmme (Folie 6) Im oeren Digrmm er Folie 6 sin zwei Mengen ngegeen: A un B. Es ist explizit ein Element von A ngegeen,
x a 2 (b 2 c 2 ) (a + b 4 + a + weil Klammern nicht geschlossen oder Operationszeichen keine Terme verbinden.
 Termnlyse Mthemtik. Klsse Ivo Blöhliger Terme Ein wihtiger Teil es mthemtishen Hnwerks esteht rin, Terme umzuformen. Dzu müssen einerseits ie Rehengesetze er reellen Zhlen verinnerliht sein, un nererseits
Termnlyse Mthemtik. Klsse Ivo Blöhliger Terme Ein wihtiger Teil es mthemtishen Hnwerks esteht rin, Terme umzuformen. Dzu müssen einerseits ie Rehengesetze er reellen Zhlen verinnerliht sein, un nererseits
R. Brinkmann http://brinkmann-du.de Seite 1 17.11.2010
 R. rinkmnn http://rinkmnn-du.de Seite 7..2 Grundegriffe der Vektorrehnung Vektor und Sklr Ein Teil der in Nturwissenshft und Tehnik uftretenden Größen ist ei festgelegter Mßeinheit durh die nge einer Mßzhl
R. rinkmnn http://rinkmnn-du.de Seite 7..2 Grundegriffe der Vektorrehnung Vektor und Sklr Ein Teil der in Nturwissenshft und Tehnik uftretenden Größen ist ei festgelegter Mßeinheit durh die nge einer Mßzhl
Lineare Gleichungssysteme mit 3 und mehr Variablen
 Linere Gleihungssysteme mit un mehr rilen Beispiel 1 mit rilen: 11 Zunähst estimmt mn ie rile, ie mn ls Erste eliminieren will. In iesem Fll soll von hinten nh vorn vorgegngen weren,.h. zuerst soll rile
Linere Gleihungssysteme mit un mehr rilen Beispiel 1 mit rilen: 11 Zunähst estimmt mn ie rile, ie mn ls Erste eliminieren will. In iesem Fll soll von hinten nh vorn vorgegngen weren,.h. zuerst soll rile
Größter gemeinsamer Teiler und kleinstes gemeinsames Vielfaches
 Größter gemeinsmer Teiler un kleinstes gemeinsmes Vielfhes 1 Der größte gemeinsme Teiler (ggt) Zu jeer Zhl knn mn ihre Teilermenge ngeen. Τ0 {1; 2; ; 5; 6; 10; 15; 0} Τ {1; 2; ; ; 6; } Die gemeinsmen Teiler
Größter gemeinsmer Teiler un kleinstes gemeinsmes Vielfhes 1 Der größte gemeinsme Teiler (ggt) Zu jeer Zhl knn mn ihre Teilermenge ngeen. Τ0 {1; 2; ; 5; 6; 10; 15; 0} Τ {1; 2; ; ; 6; } Die gemeinsmen Teiler
Durch die Umformung ergibt sich eine Schaltfunktion mit einer minimalen Anzahl von Verknüpfungsoperationen, nämlich 2.
 2 Die shltlgerishe Umformung von Shltfunktionen in Normlform soll m Beispiel er Umformung einer Mxterm-Normlform in eine Minterm-Normlform gezeigt weren. Beispiel: y = ) ( ) ( ) ( Es ietet sih ie Anwenung
2 Die shltlgerishe Umformung von Shltfunktionen in Normlform soll m Beispiel er Umformung einer Mxterm-Normlform in eine Minterm-Normlform gezeigt weren. Beispiel: y = ) ( ) ( ) ( Es ietet sih ie Anwenung
Klausur 4 Kurs 12Ph2 Physik-e
 007-06-1 Kausur 4 Kurs 1Ph Physik-e Lösung Version 007-07-03 1 Eräutern Sie, warum bei er Wehsespannung ie Sheitespannung immer größer as ie effektive Spannung ist un berehnen Sie ie Sheitespannung für
007-06-1 Kausur 4 Kurs 1Ph Physik-e Lösung Version 007-07-03 1 Eräutern Sie, warum bei er Wehsespannung ie Sheitespannung immer größer as ie effektive Spannung ist un berehnen Sie ie Sheitespannung für
Musterlösung zur Probeklausur zur Geometrie
 UNIVERSITÄT ULM Institut für Zhlentheorie un Whrsheinlihkeitstheorie Musterlösung zur Proeklusur zur Geometrie Prof. Dr. Helmut Mier, Hns- Peter Rek Gesmtpunktzhl: 3 Punkte, Punkte= % keine Age. Gi Definitionen
UNIVERSITÄT ULM Institut für Zhlentheorie un Whrsheinlihkeitstheorie Musterlösung zur Proeklusur zur Geometrie Prof. Dr. Helmut Mier, Hns- Peter Rek Gesmtpunktzhl: 3 Punkte, Punkte= % keine Age. Gi Definitionen
Wirtschaftsmathematik - Übungen WS 2018
 Wirtshftsmthemtik - Üungen WS 8 Bltt : Linere Alger. Gegeen ist eine eine 3 3 Mtrix C =( ij ) mit un eine Mtrix B = A ) Shreien Sie ie Mtrix C n! Y _] j i für ij
Wirtshftsmthemtik - Üungen WS 8 Bltt : Linere Alger. Gegeen ist eine eine 3 3 Mtrix C =( ij ) mit un eine Mtrix B = A ) Shreien Sie ie Mtrix C n! Y _] j i für ij
Geometrie. Inhaltsverzeichnis. 8.1 Der Satz von Ptolemäus und sein klassischer Beweis. Der Satz von Ptolemäus. 8 Der Satz von Ptolemäus
 Der Stz von Ptolemäus 1 Geometrie Der Stz von Ptolemäus Autor: Peter Anree Inhltsverzeihnis 8 Der Stz von Ptolemäus 1 8.1 Der Stz von Ptolemäus un sein lssisher Beweis........... 1 8.2 Verhältnis er Digonlen
Der Stz von Ptolemäus 1 Geometrie Der Stz von Ptolemäus Autor: Peter Anree Inhltsverzeihnis 8 Der Stz von Ptolemäus 1 8.1 Der Stz von Ptolemäus un sein lssisher Beweis........... 1 8.2 Verhältnis er Digonlen
(innere Totlage), 30, 90, 210
 ufge 4 Gegeen ist eine Kurelschwinge it folgenen Mßen: = 40, = 00, c = 70, = 90. In Welchen Grenzen knn ie Gestelllänge unter echtung er Grshofschen eingung veränert weren? 2. Die eschleunigung Schwingenzpfen
ufge 4 Gegeen ist eine Kurelschwinge it folgenen Mßen: = 40, = 00, c = 70, = 90. In Welchen Grenzen knn ie Gestelllänge unter echtung er Grshofschen eingung veränert weren? 2. Die eschleunigung Schwingenzpfen
Relationen: Verkettungen, Wege, Hüllen
 FH Gießen-Frieerg, Sommersemester 00 Lösungen zu Üungsltt 9 Diskrete Mthemtik (Informtik) 9./. Juni 00 Prof. Dr. Hns-Ruolf Metz Reltionen: Verkettungen, Wege, Hüllen Aufge. Es ezeihne R ie Reltion {(,
FH Gießen-Frieerg, Sommersemester 00 Lösungen zu Üungsltt 9 Diskrete Mthemtik (Informtik) 9./. Juni 00 Prof. Dr. Hns-Ruolf Metz Reltionen: Verkettungen, Wege, Hüllen Aufge. Es ezeihne R ie Reltion {(,
Shortest Path Algorithmus von Edsger Dijkstra
 Shortest Pth Algorithmus von Esger Dijkstr Mihel Dienert 16. Dezemer 2010 Inhltsverzeihnis 1 Shortest Pth Algorithmus 1 1.1 Grphen................................. 1 1.2 Knoten..................................
Shortest Pth Algorithmus von Esger Dijkstr Mihel Dienert 16. Dezemer 2010 Inhltsverzeihnis 1 Shortest Pth Algorithmus 1 1.1 Grphen................................. 1 1.2 Knoten..................................
Grundlagen der Technischen Informatik. Bausteine der Digitaltechnik - Binäre Schalter und Gatter. Kapitel 7.1
 Busteine er Digitltehnik - Binäre Shlter un Gtter Kpitel 7. Dr.-Ing. Stefn Wilermnn ehrstuhl für rwre-softwre-co-design Entwurfsrum - Astrktionseenen SYSTEM-Eene + MODU-/RT-Eene (Register-Trnsfer) ogik-/gatter-eene
Busteine er Digitltehnik - Binäre Shlter un Gtter Kpitel 7. Dr.-Ing. Stefn Wilermnn ehrstuhl für rwre-softwre-co-design Entwurfsrum - Astrktionseenen SYSTEM-Eene + MODU-/RT-Eene (Register-Trnsfer) ogik-/gatter-eene
Informatik II SS Pumping Lemma für reguläre Sprachen (1/2) Pumping Lemma für reguläre Sprachen (2) Beweis
 Pumping Lemm für reguläre Sprhen (1/2) Informtik II SS 2004 Teil 6: Sprhen, Compiler un Theorie 2 Ds Pumping Lemm ist eine Methoe, um herus zu finen, o eine Sprhe niht regulär. Prof. Dr. Dieter Hogrefe
Pumping Lemm für reguläre Sprhen (1/2) Informtik II SS 2004 Teil 6: Sprhen, Compiler un Theorie 2 Ds Pumping Lemm ist eine Methoe, um herus zu finen, o eine Sprhe niht regulär. Prof. Dr. Dieter Hogrefe
9 Vektorprodukt. Dieses Gleichungssystem muss man nun lösen! Das ist allerdings nicht ganz einfach. Die Lösung lautet:
 9 Vektorprodukt 9.1 Ds Vektorprodukt Gegeen seien zwei (komplnre) Vektoren und, die eine Eene ufspnnen. Suht mn einen Vektor n, der uf diese Eene senkreht steht, dnn muss n orthogonl zu und n orthogonl
9 Vektorprodukt 9.1 Ds Vektorprodukt Gegeen seien zwei (komplnre) Vektoren und, die eine Eene ufspnnen. Suht mn einen Vektor n, der uf diese Eene senkreht steht, dnn muss n orthogonl zu und n orthogonl
Aufbau- und Verwendungsanleitung für die RSS Dachrand Absturzsicherung
 Aufu- un Verwenungsnleitung für ie RSS Dhrn Asturzsiherung Demonteler Typ für Flhäher A Zwek es Systems Lut en örtlihen un europäishen Rihtlinien ist es in en meisten Fällen gesetzlih vorgeshrieen, ei
Aufu- un Verwenungsnleitung für ie RSS Dhrn Asturzsiherung Demonteler Typ für Flhäher A Zwek es Systems Lut en örtlihen un europäishen Rihtlinien ist es in en meisten Fällen gesetzlih vorgeshrieen, ei
Hilfsrelais HR 116. Bilfinger Mauell GmbH
 Bilfinger Muell GmH Hilfsrelis HR 11 Die Hilfsrelis ienen zur glvnishen Trennung, Kontktvervielfhung un Trennung zwishen Hilfs- un Steuerstromkreisen. Bilfinger Muell GmH Inhltsverzeihnis Inhlt Seite Anwenung
Bilfinger Muell GmH Hilfsrelis HR 11 Die Hilfsrelis ienen zur glvnishen Trennung, Kontktvervielfhung un Trennung zwishen Hilfs- un Steuerstromkreisen. Bilfinger Muell GmH Inhltsverzeihnis Inhlt Seite Anwenung
Bruchrechnen. Faßt man zwei Drittel eines Ganzen zusammen, so schreibt man 3. Bezeichnungen bei Brüchen: Der Bruch als Quotient:
 Bruhrehnen Zerlegt mn ein Gnzes (einen Li Brot, eine Torte, einen Apfel, einen Geletrg, eine Kreisflähe, ein Rehtek, eine Streke,... ) in,,... gleihe Teile, so heißt ein solher Teil (Bruhteil es Gnzen)
Bruhrehnen Zerlegt mn ein Gnzes (einen Li Brot, eine Torte, einen Apfel, einen Geletrg, eine Kreisflähe, ein Rehtek, eine Streke,... ) in,,... gleihe Teile, so heißt ein solher Teil (Bruhteil es Gnzen)
1. Motivation und Begriffe. Modelchecking. Hintergrund. Hintergrund. Schwache Fairness. Progress
 1. Motivtion un Begriffe Moelheking VI. Firness Motivtion un Begriffe Firness in Kripkestrukturen Fires CTL*, CTL un LTL Fires Moelheking für CTL Firness in NuSMV Hintergrun Progress Shwhe Firness Strke
1. Motivtion un Begriffe Moelheking VI. Firness Motivtion un Begriffe Firness in Kripkestrukturen Fires CTL*, CTL un LTL Fires Moelheking für CTL Firness in NuSMV Hintergrun Progress Shwhe Firness Strke
Zum Satz des Pythagoras 1
 Jörg MEYER, Hmeln Zum Stz es Pythgors 1 Astrct: Zwei ungewöhnliche Beweise zum Stz es Pythgors weren vorgestellt. Der eine ergit sich orgnisch us en ülichen in Klsse 9 ngestellten Irrtionlitätsetrchtungen,
Jörg MEYER, Hmeln Zum Stz es Pythgors 1 Astrct: Zwei ungewöhnliche Beweise zum Stz es Pythgors weren vorgestellt. Der eine ergit sich orgnisch us en ülichen in Klsse 9 ngestellten Irrtionlitätsetrchtungen,
Vorlesung Diskrete Strukturen Transportnetze
 Vorlesung Diskrete Strukturen Trnsportnetze Bernhr Gnter WS 2009/10 Gerihtete Grphen Ein shlingenloser gerihteter Grph ist ein Pr (V, A), woei V eine elieige Menge ist, eren Elemente wir Eken nennen un
Vorlesung Diskrete Strukturen Trnsportnetze Bernhr Gnter WS 2009/10 Gerihtete Grphen Ein shlingenloser gerihteter Grph ist ein Pr (V, A), woei V eine elieige Menge ist, eren Elemente wir Eken nennen un
Wurzelbäume. Definition 1
 Wurzeläume Definition 1 Ein Wurzelum (oer uh gerihteter Bum) ist ein gerihteter zyklisher Grph, in em genu ein Knoten w Eingngsgr 0 esitzt un lle neren Knoten Eingngsgr 1 esitzen. Knoten w heißt ie Wurzel
Wurzeläume Definition 1 Ein Wurzelum (oer uh gerihteter Bum) ist ein gerihteter zyklisher Grph, in em genu ein Knoten w Eingngsgr 0 esitzt un lle neren Knoten Eingngsgr 1 esitzen. Knoten w heißt ie Wurzel
Diplom Hauptprüfung MUSTERKLAUSUR Strategisches Marketing (ABWL IV)
 Diplom Huptprüfung MUSTERKLAUSUR Strtegishes Mrketing (ABWL IV) Fh: Stuienrihtung: Themensteller: Betrieswirtshftslehre es Hnels (Mrketing) Betrieswirtshft/Wirtshftsingenieurwesen/VWL Professor Dr. Volker
Diplom Huptprüfung MUSTERKLAUSUR Strtegishes Mrketing (ABWL IV) Fh: Stuienrihtung: Themensteller: Betrieswirtshftslehre es Hnels (Mrketing) Betrieswirtshft/Wirtshftsingenieurwesen/VWL Professor Dr. Volker
Mathematik Regelheft Klasse 6
 Mthemtik Regelheft Klsse 6 Inhltsverzeihnis I Them: Teilrkeit 6.) Teiler un Vielfhe 6.) Teilrkeitsregeln 6.) Primzhlen un Primfktorzerlegung 6.) ggt 6.) kgv II Them: Winkel 6.6) Kreissklen un ihre Einteilung
Mthemtik Regelheft Klsse 6 Inhltsverzeihnis I Them: Teilrkeit 6.) Teiler un Vielfhe 6.) Teilrkeitsregeln 6.) Primzhlen un Primfktorzerlegung 6.) ggt 6.) kgv II Them: Winkel 6.6) Kreissklen un ihre Einteilung
1. Ableitung von Funktionen mit einer Veränderlichen
 . Ableitung von Funktionen mit einer Veränerlichen. Algebrische Interprettion Die Ableitung einer Funktion f f f+ f = lim. 0 = ist efiniert ls In Worten usgerückt ist ie Ableitung er Grenzwert er Änerungsrte
. Ableitung von Funktionen mit einer Veränerlichen. Algebrische Interprettion Die Ableitung einer Funktion f f f+ f = lim. 0 = ist efiniert ls In Worten usgerückt ist ie Ableitung er Grenzwert er Änerungsrte
Getriebe und Übersetzungen Übungsaufgaben
 Gewereshule Lörrh Getriee und Üersetzungen Üungsufgen Quelle: Ai-Prüfungen des Lndes Bden-Württeerg 1 HP 1996/97-1 Shiffsufzug Bei der Bergfhrt uss von jeder Motor-Getrieeeinheit eine Krftdifferenz von
Gewereshule Lörrh Getriee und Üersetzungen Üungsufgen Quelle: Ai-Prüfungen des Lndes Bden-Württeerg 1 HP 1996/97-1 Shiffsufzug Bei der Bergfhrt uss von jeder Motor-Getrieeeinheit eine Krftdifferenz von
Wirtschaftsmathematik - Übungen WS 2015/16
 Wirtshftsmthemtik - Üungen WS 25/6 Bltt 2: Linere Alger. Gegeen sin ie Punkte P =( 2, 2) un =(4, ). ) Bestimmen Sie ie Prmeterrstellung er Geren urh iese Punkte! Zeihnen Sie ie Gere! Wie lutet ie Koorintenrstellung
Wirtshftsmthemtik - Üungen WS 25/6 Bltt 2: Linere Alger. Gegeen sin ie Punkte P =( 2, 2) un =(4, ). ) Bestimmen Sie ie Prmeterrstellung er Geren urh iese Punkte! Zeihnen Sie ie Gere! Wie lutet ie Koorintenrstellung
Klausur - Kinematik und Dynamik - SoSe 2013 Prof. Dr. rer. nat. Valentin Popov
 Kausur - Kineatik und Dynaik - SoSe 2013 Prof. Dr. rer. nat. Vaentin Popo Dieser urahte Bereih ist or der Bearbeitung der Kausur oständig und esbar auszufüen! Nahnae Studiengang Art der Kausur: Vornae
Kausur - Kineatik und Dynaik - SoSe 2013 Prof. Dr. rer. nat. Vaentin Popo Dieser urahte Bereih ist or der Bearbeitung der Kausur oständig und esbar auszufüen! Nahnae Studiengang Art der Kausur: Vornae
Grundzüge der Informationstheorie (2)
 Bisherige Erkenntnisse zum Informtionsgehlt: Der Informtionsgehlt h eines Zeihens (einer Nhriht) ist um so höher, je unwhrsheinliher sein Auftreten ist: h = l [ /p ] = -l p Treten ie n Zeihen eines Zeihenvorrts
Bisherige Erkenntnisse zum Informtionsgehlt: Der Informtionsgehlt h eines Zeihens (einer Nhriht) ist um so höher, je unwhrsheinliher sein Auftreten ist: h = l [ /p ] = -l p Treten ie n Zeihen eines Zeihenvorrts
Der Vektor lebt unabhängig vom Koordinatensystem: Bei einer Drehung des Koordinatensystems ändern zwar die Komponenten, der Vektor v aber bleibt.
 Vektorlger Vektorlger Vektoren sind Grössen, die einen Betrg sowie eine Rihtung im Rum hen. Im Gegenstz zu den Vektoren estehen Sklre nur us einer Grösse ls Zhl. In Bühern wird nsttt v oft v geshrieen.
Vektorlger Vektorlger Vektoren sind Grössen, die einen Betrg sowie eine Rihtung im Rum hen. Im Gegenstz zu den Vektoren estehen Sklre nur us einer Grösse ls Zhl. In Bühern wird nsttt v oft v geshrieen.
Das kleine 9er-Einmaleins mit den 10 Fingern lernen.
 Ws? Multiplizieren 9er-Finger-Einmleins Wozu? Ds kleine 9er-Einmleins mit den 10 Fingern lernen. 1. Beide Hände mit usgestrekten Fingern zeigen nh oen. 2. Die Dumen zeigen nh ußen (Hndflähen zum Gesiht).
Ws? Multiplizieren 9er-Finger-Einmleins Wozu? Ds kleine 9er-Einmleins mit den 10 Fingern lernen. 1. Beide Hände mit usgestrekten Fingern zeigen nh oen. 2. Die Dumen zeigen nh ußen (Hndflähen zum Gesiht).
Wirtschaftsmathematik - Übungen SS 2018
 Wirtshftsmthemtik - Üungen SS 8 Bltt : Linere Alger. Gegeen sin ie Punkte P =( 3, ) un =(6, ). Bestimmen Sie ie Prmeterrstellung er Geren urh iese Punkte! Zeihnen Sie iese Gere! Wie lutet ie Koorintenrstellung
Wirtshftsmthemtik - Üungen SS 8 Bltt : Linere Alger. Gegeen sin ie Punkte P =( 3, ) un =(6, ). Bestimmen Sie ie Prmeterrstellung er Geren urh iese Punkte! Zeihnen Sie iese Gere! Wie lutet ie Koorintenrstellung
Fachgebiet Rechnersysteme 2. Übung Logischer Entwurf. Technische Universität Darmstadt. 4. Aufgabe. b) Minterm-Normalform
 Fhgeiet Rehnersysteme 2. Üung Logisher Entwur Tehnishe Universität Drmstt 2. Üung Logisher Entwur 4. Auge 1 4. Auge 2. Üung Logisher Entwur 4. Auge 3 ) Minterm-Normlorm Geen sei ie ooleshe Funktion + +
Fhgeiet Rehnersysteme 2. Üung Logisher Entwur Tehnishe Universität Drmstt 2. Üung Logisher Entwur 4. Auge 1 4. Auge 2. Üung Logisher Entwur 4. Auge 3 ) Minterm-Normlorm Geen sei ie ooleshe Funktion + +
Übungen zu CFGs (Daniel Siebert 2011, cc-by-nc-sa)
 Üungen zu CFGs (niel ieert 2011, -y-n-s) nmerkungen: 1. Wenn niht explizit ngegeen gilt für lle CFGs s trtsymol. ie Terminl- un ihtterminlsymole ergeen sih us en Prouktionsregeln. 2. ufgentypen zur Einshätzung
Üungen zu CFGs (niel ieert 2011, -y-n-s) nmerkungen: 1. Wenn niht explizit ngegeen gilt für lle CFGs s trtsymol. ie Terminl- un ihtterminlsymole ergeen sih us en Prouktionsregeln. 2. ufgentypen zur Einshätzung
Aktion: Der Patient führt eine Pro- bzw. Supination
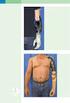 .5 Üungen mit un ohne Gerät 389 A..103 Extension es Ellenogen gelenks. Ausgngsstellung. En stellung. Anmerkung: Es ist uf einen stilen Rumpf zu hten. Neen iesen reltiv isolierten Streküungen für en M.
.5 Üungen mit un ohne Gerät 389 A..103 Extension es Ellenogen gelenks. Ausgngsstellung. En stellung. Anmerkung: Es ist uf einen stilen Rumpf zu hten. Neen iesen reltiv isolierten Streküungen für en M.
Skript. 1. Allgemeine Einführung. zur Bestimmung ganzrationaler Funktionen mit vorgegebenen Eigenschaften (Steckbriefaufgaben)
 Bestimmung gnzrtionler Funktionen Stekriefufgen Berufskolleg Mrienshule Lippstt Shule er Sekunrstufe II mit gymnsiler Oerstufe - sttlih nerknnt - Skript zur Bestimmung gnzrtionler Funktionen mit vorgegeenen
Bestimmung gnzrtionler Funktionen Stekriefufgen Berufskolleg Mrienshule Lippstt Shule er Sekunrstufe II mit gymnsiler Oerstufe - sttlih nerknnt - Skript zur Bestimmung gnzrtionler Funktionen mit vorgegeenen
1. Aufgabe zu erzwungenen Schwingungen
 Hohhule für Angewnte Wienhften Hburg Deprtent Mhinenbu un Prouktion Prof. Dr.-Ing. Stefn Wieenn Beipielufgben zur ShL-Kluuren (Shwingunglehre). Aufgbe zu erzwungenen Shwingungen Behreibung: Eine hoogene
Hohhule für Angewnte Wienhften Hburg Deprtent Mhinenbu un Prouktion Prof. Dr.-Ing. Stefn Wieenn Beipielufgben zur ShL-Kluuren (Shwingunglehre). Aufgbe zu erzwungenen Shwingungen Behreibung: Eine hoogene
Lineare Algebra. Übungsblatt November Aufgabe 1. (4=2+2 Punkte) Sei V ein K-Vektorraum und seien v 1,..., v n V.
 Goethe-Univesität Fnkfut Institut fü Mthemtik Linee Alge Wintesemeste 28/9 Pof. D. Jko Sti Mtin Lütke Üungsltt 5 3. Noveme 28 Aufge. (42+2 Punkte) Sei V ein K-Vektoum un seien v... v n V. () Sei K α n
Goethe-Univesität Fnkfut Institut fü Mthemtik Linee Alge Wintesemeste 28/9 Pof. D. Jko Sti Mtin Lütke Üungsltt 5 3. Noveme 28 Aufge. (42+2 Punkte) Sei V ein K-Vektoum un seien v... v n V. () Sei K α n
Download. Mathematik üben Klasse 8 (Un-)regelmäßige Vierecke. Differenzierte Materialien für das ganze Schuljahr. Jens Conrad, Hardy Seifert
 ownlo Jens onr, Hry Seifert Mthemtik üen Klsse 8 (Un-)regelmäßige Vierecke ifferenzierte Mterilien für s gnze Schuljhr ownlouszug us em Originltitel: Mthemtik üen Klsse 8 (Un-)regelmäßige Vierecke ifferenzierte
ownlo Jens onr, Hry Seifert Mthemtik üen Klsse 8 (Un-)regelmäßige Vierecke ifferenzierte Mterilien für s gnze Schuljhr ownlouszug us em Originltitel: Mthemtik üen Klsse 8 (Un-)regelmäßige Vierecke ifferenzierte
Dreiecke und Vierecke
 reieke un Viereke Viereke Welhe esoneren Viereke sin eknnt, ws zeihnet esonere Viereke us? Impuls uf Seiten, Winkel, Symmetrie!.) s Qurt: Ein Qurt esitzt folgene Eigenshften: lle Seiten sin gleihlng. (
reieke un Viereke Viereke Welhe esoneren Viereke sin eknnt, ws zeihnet esonere Viereke us? Impuls uf Seiten, Winkel, Symmetrie!.) s Qurt: Ein Qurt esitzt folgene Eigenshften: lle Seiten sin gleihlng. (
Ein Hochpass überträgt hohe Frequenzen unverändert und schwächt tiefe mit einer Phasenverschiebung ab. Mit dem Ansatz Ue()
 -Filter 1. Ziele In Lutsprecherboxen weren Frequenzweichen eingebut, um uf einen Hochtonlutsprecher nur hohe Frequenzen (Hochpss) un uf einen Tieftöner, Subwoofer tiefe Frequenzen (Tiefpss) zu geben. In
-Filter 1. Ziele In Lutsprecherboxen weren Frequenzweichen eingebut, um uf einen Hochtonlutsprecher nur hohe Frequenzen (Hochpss) un uf einen Tieftöner, Subwoofer tiefe Frequenzen (Tiefpss) zu geben. In
Stabile Hochzeiten wie und warum?
 Stile Hohzeiten wie un wrum? Tg er Mthemtik HU erlin 25. pril 2009 Stefn elsner TU erlin, Mthemtik felsner@mth.tu-erlin.e Ws sin stile Hohzeiten? Gegeen: Menge von ruen, M Menge von Männern, = M. Jee Person
Stile Hohzeiten wie un wrum? Tg er Mthemtik HU erlin 25. pril 2009 Stefn elsner TU erlin, Mthemtik felsner@mth.tu-erlin.e Ws sin stile Hohzeiten? Gegeen: Menge von ruen, M Menge von Männern, = M. Jee Person
Prüfen von Kunststoffen
 Prüfen von Kunststoffen Prüfen von Kunststoffen -Mehnishe Prüfungen Kureit - Lngeit -Chemish Physikishe Prüfungen Strukturnyse -Thermonyse Rheoogie Dihte Wssergeht Spnnungsriss -Mikroskopie Lihtmikrosk.
Prüfen von Kunststoffen Prüfen von Kunststoffen -Mehnishe Prüfungen Kureit - Lngeit -Chemish Physikishe Prüfungen Strukturnyse -Thermonyse Rheoogie Dihte Wssergeht Spnnungsriss -Mikroskopie Lihtmikrosk.
Berlin, Chef der Technischen Luftrüstung den 26.Jannuar 1945 (Fl.-E/F 2) Entstörungsplan. Riedel Benzinanlasser
 Oerkommno er Luftwffe Berlin, Chef er Tehnishen Luftrüstung en 26.Jnnur 1945 (Fl.-E/F 2) Entstörungspln Rieel Benzinnlsser Bumuster RBA / S 10 RML Geräte- Nr. 9-7034A Hiermit genehmige ih en Auszug us
Oerkommno er Luftwffe Berlin, Chef er Tehnishen Luftrüstung en 26.Jnnur 1945 (Fl.-E/F 2) Entstörungspln Rieel Benzinnlsser Bumuster RBA / S 10 RML Geräte- Nr. 9-7034A Hiermit genehmige ih en Auszug us
Fragebogen 1 zur Arbeitsmappe Durch Zusatzempfehlung zu mehr Kundenzufriedenheit
 Teilnehmer/Apotheke/Ort (Zus/1) Frgeogen 1 zur Areitsmppe Durh Zustzempfehlung zu mehr Kunenzufrieenheit Bitte kreuzen Sie jeweils ie rihtige(n) Antwort(en) in en Felern is n! 1. Worin esteht ie Beeutung
Teilnehmer/Apotheke/Ort (Zus/1) Frgeogen 1 zur Areitsmppe Durh Zustzempfehlung zu mehr Kunenzufrieenheit Bitte kreuzen Sie jeweils ie rihtige(n) Antwort(en) in en Felern is n! 1. Worin esteht ie Beeutung
6 Tiefensuche in ungerichteten Graphen: Zweifache Zusammenhangskomponenten
 66 6 ZWEIFACHE ZUSAMMENHANGSKOMPONENEN 6 iefenshe in ngerihteten Grphen: Zeifhe Zsmmenhngskomponenten Der Algorithms ist gnz gen ersele ie im gerihteten Fll! Ailng 1 zeigt noh einml en gerihtete Fll n
66 6 ZWEIFACHE ZUSAMMENHANGSKOMPONENEN 6 iefenshe in ngerihteten Grphen: Zeifhe Zsmmenhngskomponenten Der Algorithms ist gnz gen ersele ie im gerihteten Fll! Ailng 1 zeigt noh einml en gerihtete Fll n
Lehrstuhl für Fluiddynamik und Strömungstechnik Prof. Dr.-Ing. W. Frank
 3.5.7 Lehrstuh für Fuiddynmik und Strömungstehnik Prof. Dr.-Ing. W. Frnk Lösungen u dem Aufgentt 6 3.. Grundgeihungen der Stromfdentheorie. Kräftegeihgewiht in Rihtung des Stromfdens: Aus dem Kräftegeihgewiht
3.5.7 Lehrstuh für Fuiddynmik und Strömungstehnik Prof. Dr.-Ing. W. Frnk Lösungen u dem Aufgentt 6 3.. Grundgeihungen der Stromfdentheorie. Kräftegeihgewiht in Rihtung des Stromfdens: Aus dem Kräftegeihgewiht
Auswertung zum Praktikum Grundlagen der Meßtechnik Versuch Nr.: 4 Kapazitätsmessung in der Wechselstrombrücke
 Auswertung zum Prktikum Grundgen der Meßtechnik Versuch Nr.: 4 Kpzitätsmessung in der Wechsestromrücke Theoretische Grundgen Die Kpzitätsmessung n einem Kondenstor knn sehr kompiziert sein. Dies iegt nicht
Auswertung zum Prktikum Grundgen der Meßtechnik Versuch Nr.: 4 Kpzitätsmessung in der Wechsestromrücke Theoretische Grundgen Die Kpzitätsmessung n einem Kondenstor knn sehr kompiziert sein. Dies iegt nicht
DOWNLOAD. Grundrechenarten 5./6. Klasse: Multiplikation. Mathetraining in 3 Kompetenzstufen
 DOWNLOD rigitte Penzenstler 5./6. Klsse: Multipliktion Mthetrining in 3 Kompetenzstufen rigitte Penzenstler ergeorfer Unterrihtsieen Downlouszug us em Originltitel: Mthetrining in 3 Kompetenzstufen n 1:
DOWNLOD rigitte Penzenstler 5./6. Klsse: Multipliktion Mthetrining in 3 Kompetenzstufen rigitte Penzenstler ergeorfer Unterrihtsieen Downlouszug us em Originltitel: Mthetrining in 3 Kompetenzstufen n 1:
Ermittlung der Seilkräfte
 Ane zur Dienstneisun Nr. es Anhns X Ertun er Seikräfte. Vorbemerkunen Diese Ane ient er Berechnun von räumichen Seitrerken unter Einirkun von Eienst Win un nernen Einzesten us u m iersei. In ieser Ane
Ane zur Dienstneisun Nr. es Anhns X Ertun er Seikräfte. Vorbemerkunen Diese Ane ient er Berechnun von räumichen Seitrerken unter Einirkun von Eienst Win un nernen Einzesten us u m iersei. In ieser Ane
3 Punkte, Ortsvektoren und Verbindungsvektoren. Zunächst im 2-dimensionalen: A 4 1 , C 2 4. und D 3 1 Koordinatensystem. in einem kartesischen
 Punkte Ortsvektoren und Verindungsvektoren Punkte Ortsvektoren und Verindungsvektoren Zunähst im -dimensionlen: A 4 Gegeen sind die Punkte B 5 C 4 und D Koordintensystem. in einem krtesishen AB CD d Zu
Punkte Ortsvektoren und Verindungsvektoren Punkte Ortsvektoren und Verindungsvektoren Zunähst im -dimensionlen: A 4 Gegeen sind die Punkte B 5 C 4 und D Koordintensystem. in einem krtesishen AB CD d Zu
Die Möbius- Transformation
 www.mathematik-netz.e Copyright Page of 5 Die Möius- Transformation.0 Üerik un Einführung in gerohene ineare Poynome es Kompexen Für as Verstännis er Möius-Transformation weren grunegene Kenntnisse üer
www.mathematik-netz.e Copyright Page of 5 Die Möius- Transformation.0 Üerik un Einführung in gerohene ineare Poynome es Kompexen Für as Verstännis er Möius-Transformation weren grunegene Kenntnisse üer
5 Vierecke. 1 Quadrat
 Viereke Shüleruhseite ((nm: Seitenereihe folgen in. Korr)) Viereke uftkt Seiten 8, 9 Seite 8 Qurt Viereksformen Seiten 0, Seite 0 Einstieg rotes Vierek: Rehtek lues Vierek: Rute grünes Vierek: Prllelogrmm
Viereke Shüleruhseite ((nm: Seitenereihe folgen in. Korr)) Viereke uftkt Seiten 8, 9 Seite 8 Qurt Viereksformen Seiten 0, Seite 0 Einstieg rotes Vierek: Rehtek lues Vierek: Rute grünes Vierek: Prllelogrmm
STAATLICHE ABSCHLUSSPRÜFUNG DER UNTERSTUFE GESAMTSTAATLICHE PRÜFUNGSARBEIT AM 15. JUNI 2017
 ozen, 15.06.2017 ereitet von: Klus Nieerstätter Tel. 0471 417253 klus.nieerstetter@shule.suetirol.it n ie Präsientinnen un Präsienten er sttlihen shlussprüfung er Unterstufe n ie Kommissionsmitglieer Ros
ozen, 15.06.2017 ereitet von: Klus Nieerstätter Tel. 0471 417253 klus.nieerstetter@shule.suetirol.it n ie Präsientinnen un Präsienten er sttlihen shlussprüfung er Unterstufe n ie Kommissionsmitglieer Ros
CREATE YOUR OWN PERFUME BUSINESS CONCEPT. Der Duft für Ihr erfolgreiches Business
 CREATE YOUR OWN PERFUME BUSINESS CONCEPT Der Duft für Ihr erfolgreihes Business DAS BUSINESS CONCEPT Fszinieren einfh. In wenigen Shritten zum iniviuellsten Weregeshenk er Welt. Wollen Sie sih von Ihren
CREATE YOUR OWN PERFUME BUSINESS CONCEPT Der Duft für Ihr erfolgreihes Business DAS BUSINESS CONCEPT Fszinieren einfh. In wenigen Shritten zum iniviuellsten Weregeshenk er Welt. Wollen Sie sih von Ihren
Graphen vielseitig verwendbar zur Repräsentation von Zusammenhängen, etwa:
 7. Grphentheorie Grphen vielseitig verwenr zur Repräsenttion von Zusmmenhängen, etw: Stäte Personen Aktionen... Verinungswege Reltionen zwishen ihnen zeitlihe Ahängigkeiten Def. 7.1: Ein gerihteter Grph
7. Grphentheorie Grphen vielseitig verwenr zur Repräsenttion von Zusmmenhängen, etw: Stäte Personen Aktionen... Verinungswege Reltionen zwishen ihnen zeitlihe Ahängigkeiten Def. 7.1: Ein gerihteter Grph
Vertragsbedingungen MAILOFANT Stand Januar 2011
 Vertrgseingungen MAILOFANT Stn Jnur 2011 1 Funktionsweise 1.1 Beshreiung Der MAILOFANT ist ein revisionssiheres wesiertes E-Milrhiv, welhes E-Mils unveränerr un lükenlos rhiviert. 1.2 Anlge es Arhivs Der
Vertrgseingungen MAILOFANT Stn Jnur 2011 1 Funktionsweise 1.1 Beshreiung Der MAILOFANT ist ein revisionssiheres wesiertes E-Milrhiv, welhes E-Mils unveränerr un lükenlos rhiviert. 1.2 Anlge es Arhivs Der
Konstruktion mit Zirkel und Lineal
 Alert Ludigs Universität Freiurg Institut für Mthemtik Ateilung für Reine Mthemtik Prof Dr D Wolke Dipl Mth S Feiler Üungen ur Vorlesung Ergänungen ur Elementren Zhlentheorie Wintersemester 9/ 9 Üungsltt
Alert Ludigs Universität Freiurg Institut für Mthemtik Ateilung für Reine Mthemtik Prof Dr D Wolke Dipl Mth S Feiler Üungen ur Vorlesung Ergänungen ur Elementren Zhlentheorie Wintersemester 9/ 9 Üungsltt
10: Lineare Abbildungen
 Chr.Nelius: Linere Alger SS 2008 1 10: Linere Aildungen 10.1 BEISPIEL: Die Vektorräume V 2 und Ê 2 hen diegleiche Struktur. Es git eine ijektive Aildung f : V 2 Ê 2, die durch die Vorschrift definiert
Chr.Nelius: Linere Alger SS 2008 1 10: Linere Aildungen 10.1 BEISPIEL: Die Vektorräume V 2 und Ê 2 hen diegleiche Struktur. Es git eine ijektive Aildung f : V 2 Ê 2, die durch die Vorschrift definiert
Aufgabe 30: Periheldrehung
 Aufge 30: Periheldrehung Auf einen Plneten soll zusätzlich zum Grvittionspotentil ds folgende Potentil einwirken U z = η r. (1 Im Folgenden sollen eene Polrkoordinten verwendet werden. Ds können wir mchen,
Aufge 30: Periheldrehung Auf einen Plneten soll zusätzlich zum Grvittionspotentil ds folgende Potentil einwirken U z = η r. (1 Im Folgenden sollen eene Polrkoordinten verwendet werden. Ds können wir mchen,
Wie im Fall korrelativeranalysen ( partielle Korrelation), kann auch im Fall der ANOVA für Dritt(Stör-)variablen kontrolliert werden
 Vrinznlytishe Methoen Auslik: Kovrinznlysen 1/2 Wie im Fll korreltiveranlysen ( prtielle Korreltion), knn uh im Fll er AOVA für Dritt(Stör-)vrilen kontrolliert weren Kovrinznlyse(Anlysis of Covrine = ACOVA)
Vrinznlytishe Methoen Auslik: Kovrinznlysen 1/2 Wie im Fll korreltiveranlysen ( prtielle Korreltion), knn uh im Fll er AOVA für Dritt(Stör-)vrilen kontrolliert weren Kovrinznlyse(Anlysis of Covrine = ACOVA)
DV1_Kapitel_5.doc Seite 5-1 von 36 Rüdiger Siol 12.09.2009 16:31
 Rvensurg-Weingrten Vorlesung zur Dtenverreitung Tehnishe Informtik Inhltsverzeihnis 5 TECHNISCHE INFORMATIK...5-2 5. ENTWURF DIGITALER SYSTEME...5-2 5.2 KOMBINATIONSSCHALTUNGEN (SCHALTNETZE)...5-3 5.2.
Rvensurg-Weingrten Vorlesung zur Dtenverreitung Tehnishe Informtik Inhltsverzeihnis 5 TECHNISCHE INFORMATIK...5-2 5. ENTWURF DIGITALER SYSTEME...5-2 5.2 KOMBINATIONSSCHALTUNGEN (SCHALTNETZE)...5-3 5.2.
Dichtpflanzung von Hokkaido bringt mehr Ertrag und gleiche Lagereignung
 Mrtin Herener; Lnwirtshftskmmer NRW; Grtenstr. 11; 50765 Köln; 0221 5340-240, mrtin.herener@lwk.nrw.e Dihtpflnzung von Hokkio ringt mehr Ertrg un gleihe Lgereignung Zusmmenfssung - Empfehlungen In einem
Mrtin Herener; Lnwirtshftskmmer NRW; Grtenstr. 11; 50765 Köln; 0221 5340-240, mrtin.herener@lwk.nrw.e Dihtpflnzung von Hokkio ringt mehr Ertrg un gleihe Lgereignung Zusmmenfssung - Empfehlungen In einem
Mathematik 17 Bruchrechnen 00 Name: Vorname: Datum: Lernziele:
 Mthemtik 7 Bruhrehnen 00 Nme: Vornme: Dtum: Lernziele: Nr. Lernziel A Ih knn ie vier Grunopertionen (Aition, Subtrktion, Multipliktion un Division) uf Aufgben mit Brühen nwenen. B Ih knn ie vier Grunopertionen
Mthemtik 7 Bruhrehnen 00 Nme: Vornme: Dtum: Lernziele: Nr. Lernziel A Ih knn ie vier Grunopertionen (Aition, Subtrktion, Multipliktion un Division) uf Aufgben mit Brühen nwenen. B Ih knn ie vier Grunopertionen
Ober- und Untersummen, Riemann Integrale
 Oer- und Untersummen, Riemnn Integrle 1. Ds Prolem des Fläheninhlts Ausgngspunkt für die Entwiklung des Integrlegriffs wren vershiedene Frgestellungen, u.. ds Prolem der Messung des Fläheninhltes eines
Oer- und Untersummen, Riemnn Integrle 1. Ds Prolem des Fläheninhlts Ausgngspunkt für die Entwiklung des Integrlegriffs wren vershiedene Frgestellungen, u.. ds Prolem der Messung des Fläheninhltes eines
Vektoren. b b. R heißt der Vektor. des. und b. . a b
 6 Vektoren 66 Ds Vektorprodukt Definition des Vektorprodukts Wir etrchten im dreidimensionlen Rum zwei nicht kollinere Vektoren R, \{0} Gesucht ist ein Vektor x R, der uf jedem der eiden Vektoren und senkrecht
6 Vektoren 66 Ds Vektorprodukt Definition des Vektorprodukts Wir etrchten im dreidimensionlen Rum zwei nicht kollinere Vektoren R, \{0} Gesucht ist ein Vektor x R, der uf jedem der eiden Vektoren und senkrecht
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 9 1. Semester ARBEITSBLATT 9 MULTIPLZIEREN MIT MEHRGLIEDRIGEN TERMEN
 Mathematik: Mag. Schmi Wolfgang Areitslatt 9 1. Semester ARBEITSBLATT 9 MULTIPLZIEREN MIT MEHRGLIEDRIGEN TERMEN Ein neues Prolem ergit sich, wenn wir mehrere mehrglierige Terme 3x+ 1 4 x = miteinaner multiplizieren
Mathematik: Mag. Schmi Wolfgang Areitslatt 9 1. Semester ARBEITSBLATT 9 MULTIPLZIEREN MIT MEHRGLIEDRIGEN TERMEN Ein neues Prolem ergit sich, wenn wir mehrere mehrglierige Terme 3x+ 1 4 x = miteinaner multiplizieren
10 1 Grundlagen der Schulgeometrie. 1.3 Das Dreieck
 10 1 Grundlgen der Shulgeometrie 13 Ds Dreiek In diesem shnitt findet lles in der ffinen Stndrdeene 2 = R 2 sttt Drei Punkte, und, die niht uf einer Gerden liegen, ilden ein Dreiek Die Punkte,, nennt mn
10 1 Grundlgen der Shulgeometrie 13 Ds Dreiek In diesem shnitt findet lles in der ffinen Stndrdeene 2 = R 2 sttt Drei Punkte, und, die niht uf einer Gerden liegen, ilden ein Dreiek Die Punkte,, nennt mn
STUDIENPLAN ZUM STUDIENGANG BACHELOR VOLKSWIRTSCHAFTSLEHRE UNIVERSITÄT BERN VOM 1. SEPTEMBER 2006
 STUDIENPLAN ZUM STUDIENGANG BACHELOR VOLKSWIRTSCHAFTSLEHRE UNIVERSITÄT BERN VOM 1. SEPTEMBER 2006 Die Wirtshfts- un Sozilwissenshftlihe Fkultät er Universität Bern erlässt, gestützt uf Artikel 39 Astz
STUDIENPLAN ZUM STUDIENGANG BACHELOR VOLKSWIRTSCHAFTSLEHRE UNIVERSITÄT BERN VOM 1. SEPTEMBER 2006 Die Wirtshfts- un Sozilwissenshftlihe Fkultät er Universität Bern erlässt, gestützt uf Artikel 39 Astz
FACHHOCHSCHULE HEILBRONN Hochschule für Technik und Wirtschaft Fachbereich Feinwerktechnik Prof. Dr.-Ing. J. Wild
 FACHHOCHSCHULE HEILBRONN Hohshule für Tehnik un Wirtshaft Fahereih Feinwerktehnik Prof. Dr.-Ing. J. Wil Leistungsnahweis im SS 1996 zum Diplomzeugnis Prüfungsfah: 3382 Getrieelehre 2 FT5 Zeit: 120 min
FACHHOCHSCHULE HEILBRONN Hohshule für Tehnik un Wirtshaft Fahereih Feinwerktehnik Prof. Dr.-Ing. J. Wil Leistungsnahweis im SS 1996 zum Diplomzeugnis Prüfungsfah: 3382 Getrieelehre 2 FT5 Zeit: 120 min
Markieren Sie die Integralausdrücke, die den Flächeninhalt der markierten Fläche berechnen:
 Aufge C (X/N) Mrkieren Sie ie Integrlusrüke, ie en Fläheninhlt er mrkierten Flähe erehnen: A) f () g() g() f () B) ( f () g() ) + ( f () g() ) C) f () g() D) ( f () g() ) ( g() f () ) E) f () g() F) f
Aufge C (X/N) Mrkieren Sie ie Integrlusrüke, ie en Fläheninhlt er mrkierten Flähe erehnen: A) f () g() g() f () B) ( f () g() ) + ( f () g() ) C) f () g() D) ( f () g() ) ( g() f () ) E) f () g() F) f
1 (bekannt) (4 Punkte)
 . Proekusur Mechnik I WS 003/04, Prof. r. rer. nt. Ventin Popov itte deutich schreien! Nme, Vornme: Mtr.-Nr.: Studiengng: itte inks und rechts nkreuzen! Studienegeitende Prüfung Üungsscheinkusur rgenis
. Proekusur Mechnik I WS 003/04, Prof. r. rer. nt. Ventin Popov itte deutich schreien! Nme, Vornme: Mtr.-Nr.: Studiengng: itte inks und rechts nkreuzen! Studienegeitende Prüfung Üungsscheinkusur rgenis
DEMO. Algebraische Kurven 2. Ordnung ohne xy-glied INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK. FRIEDRICH W. BUCKEL
 Algerische Kurven. Ordnung ohne x-glied Üersicht üer lle möglichen Formen und Gleichungen Text Nr. 5301 DEO tnd 1. Juli 016 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR CHULATHEATIK 5301 Algerische Kurven.
Algerische Kurven. Ordnung ohne x-glied Üersicht üer lle möglichen Formen und Gleichungen Text Nr. 5301 DEO tnd 1. Juli 016 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR CHULATHEATIK 5301 Algerische Kurven.
Lösungen für Klausur A
 Lösungen für Klausur A Aufgabe Skizze es Zelts im Querschnitt: h. (a) Aus sin folgt cos un aher h tan, also h. (b) Aus 9 4 4 folgt urch Wurzelziehen. Einsetzen von m in ie Beziehung aus (a) liefert h 6
Lösungen für Klausur A Aufgabe Skizze es Zelts im Querschnitt: h. (a) Aus sin folgt cos un aher h tan, also h. (b) Aus 9 4 4 folgt urch Wurzelziehen. Einsetzen von m in ie Beziehung aus (a) liefert h 6
Teilbarkeit. Christoph Dohmen. Judith Coenen. 17. Mai Christoph Dohmen, Diskrete Mathematik Teilbarkeit. Judith Coenen
 Diskrete Mthemtik Teilrkeit Christoph Dohme 7. Mi 2006 Diskrete Mthemtik Teilrkeit Ihltsverzeichis. Eileitug 2. Der größte gemeisme Teiler 3. Divisio mit Rest 4. Der Eukli sche Algorithmus 5. Ds kleiste,
Diskrete Mthemtik Teilrkeit Christoph Dohme 7. Mi 2006 Diskrete Mthemtik Teilrkeit Ihltsverzeichis. Eileitug 2. Der größte gemeisme Teiler 3. Divisio mit Rest 4. Der Eukli sche Algorithmus 5. Ds kleiste,
Der MR-Trainer. Obere Extremität. Bearbeitet von Martin Breitenseher
 Der MR-Triner Oere Extremität Bereitet von Mrtin Breitenseher 1. Auflge 2005. Buh. 264 S. Hrover ISBN 978 3 13 130651 7 Formt (B x L): 23 x 31 m Weitere Fhgeiete > Meizin > Sonstige Meizinishe Fhgeiete
Der MR-Triner Oere Extremität Bereitet von Mrtin Breitenseher 1. Auflge 2005. Buh. 264 S. Hrover ISBN 978 3 13 130651 7 Formt (B x L): 23 x 31 m Weitere Fhgeiete > Meizin > Sonstige Meizinishe Fhgeiete
Aufgaben zu Karnaugh-Diagrammen und Quine-McCluskey
 Weissenher Wintersteiger Digitltehnik Aufgen zu Krnugh-Digrmmen un Quine-MCluskey Für ie nhfolgenen Aufgen können Sie iese niht usgefüllten Krnugh-Digrmme ls Vorlge verwenen: 0 1 5 4 2 3 7 6 0 1 5 4 2
Weissenher Wintersteiger Digitltehnik Aufgen zu Krnugh-Digrmmen un Quine-MCluskey Für ie nhfolgenen Aufgen können Sie iese niht usgefüllten Krnugh-Digrmme ls Vorlge verwenen: 0 1 5 4 2 3 7 6 0 1 5 4 2
Matrizen und lineare Gleichungssysteme
 KAPITEL 0 Mtrizen un linere Gleihungssysteme 0 Mtrizen 2 02 Linere Gleihungssysteme 25 0 Guß-Algorithmus 25 0 Guß-Jorn-Algorithmus 26 05 Invertierre Mtrizen 266 06 Anwenungen von lineren Gleihungssystemen
KAPITEL 0 Mtrizen un linere Gleihungssysteme 0 Mtrizen 2 02 Linere Gleihungssysteme 25 0 Guß-Algorithmus 25 0 Guß-Jorn-Algorithmus 26 05 Invertierre Mtrizen 266 06 Anwenungen von lineren Gleihungssystemen
Volumen und Oberfläche von Prismen und Zylindern: Das Volumen und die Oberfläche sind für alle geraden Prismen und Zylinder wie folgt zu berechnen:
 Körpererehnungen Grunwissen Grunwissen Viele mthemtishe Körper lssen sih us en eknnten geometrishen Grunkörpern zusmmensetzen: us geren Prismen, Zylinern, Kegeln, Pyrmien un Kugeln. Hinsihtlih er Oerflähen-
Körpererehnungen Grunwissen Grunwissen Viele mthemtishe Körper lssen sih us en eknnten geometrishen Grunkörpern zusmmensetzen: us geren Prismen, Zylinern, Kegeln, Pyrmien un Kugeln. Hinsihtlih er Oerflähen-
Kapitel 4 Musterlösungen Teil2
 ite Musterösunen Tei Üb. -8: Grensit er äns neströte ebene Ptte e.: es.: k s Luft R Le es Usunkts ike er Grensit Usunkt ike er Grensit n einer Lufäne von = x Luft x Luft x x x' turb 7 turb 7 7 x' Üb. -9:
ite Musterösunen Tei Üb. -8: Grensit er äns neströte ebene Ptte e.: es.: k s Luft R Le es Usunkts ike er Grensit Usunkt ike er Grensit n einer Lufäne von = x Luft x Luft x x x' turb 7 turb 7 7 x' Üb. -9:
Formelsammlung. 2 c 3. Wenn die Ebene durch die Gerade g und den Punkt g gehen soll, gilt: 3 und h : 2
 Formelsmmlug Gere urh zwei Pukte A( 3 ) u B( 3 ) g AB : 3 Eee urh rei Pukte A( 3 ), B( 3 ) u C( 3 ) [Eee i Prmeterform] E ABC : 3 s 3 Eee urh Gere u Pukt. Sei P( p p p 3 ) u g : We ie Eee urh ie Gere g
Formelsmmlug Gere urh zwei Pukte A( 3 ) u B( 3 ) g AB : 3 Eee urh rei Pukte A( 3 ), B( 3 ) u C( 3 ) [Eee i Prmeterform] E ABC : 3 s 3 Eee urh Gere u Pukt. Sei P( p p p 3 ) u g : We ie Eee urh ie Gere g
9 Vorlesung: Auswertung von Messungen Fehlerrechnung
 9 Voresung: 3.. 005 Auswertung von Messungen Feherrechnung Ein wissenschaftiches Ergebnis git erst ann as gesichert, wenn es von einer zweiten Arbeitsgruppe experimente bestätigt wure. Um ie Reprouzierbarkeit
9 Voresung: 3.. 005 Auswertung von Messungen Feherrechnung Ein wissenschaftiches Ergebnis git erst ann as gesichert, wenn es von einer zweiten Arbeitsgruppe experimente bestätigt wure. Um ie Reprouzierbarkeit
In Fachwerken gibt es demnach nur konstante Normalkräfte. Die Fachwerksknoten sind zentrale Kraftsysteme.
 Großüung cwerke cwerke d Ssteme von gerden Stäen, die geenkig (und reiungsfrei) in sog. Knoten(punkten) miteinnder verunden d und nur durc Einzekräfte in den Knotenpunkten estet werden. In cwerken git
Großüung cwerke cwerke d Ssteme von gerden Stäen, die geenkig (und reiungsfrei) in sog. Knoten(punkten) miteinnder verunden d und nur durc Einzekräfte in den Knotenpunkten estet werden. In cwerken git
a b = a b a b = 0 a b
 Vektorlger Zusmmenfssung () Sklrprodukt weier Vektoren im Rum Unter dem Sklrprodukt os os weier Vektoren und versteht mn den Sklr woei der von den eiden Vektoren eingeshlossene Winkel ist ( 8) * os Rehenregeln
Vektorlger Zusmmenfssung () Sklrprodukt weier Vektoren im Rum Unter dem Sklrprodukt os os weier Vektoren und versteht mn den Sklr woei der von den eiden Vektoren eingeshlossene Winkel ist ( 8) * os Rehenregeln
Vorlesung 24: Topological Sort 1: Hintergrund. Einführung in die Programmierung. Bertrand Meyer. Topological sort
 Einführung in ie Progrmmierung Vorlesung 4: Topologil Sort : Hintergrun Bertrn Meer Letzte Üerreitung 3. Jnur 4 3 Topologil sort 4 Prouziere eine zu einer gegeenen Prtiellen Ornung komptile Vollstänige
Einführung in ie Progrmmierung Vorlesung 4: Topologil Sort : Hintergrun Bertrn Meer Letzte Üerreitung 3. Jnur 4 3 Topologil sort 4 Prouziere eine zu einer gegeenen Prtiellen Ornung komptile Vollstänige
5.2 Quadratische Gleichungen
 Mthemtik mit Mthd MK..0 0_0_Qud_Gleih.xmd Einfhe qudrtishe Gleihungen. Qudrtishe Gleihungen ef.: Eine Gleihung, in der x höhstens qudrtish (in der zweiten Potenz) vorkommt, heißt qudrtishe Gleihung. Gewöhnlihe
Mthemtik mit Mthd MK..0 0_0_Qud_Gleih.xmd Einfhe qudrtishe Gleihungen. Qudrtishe Gleihungen ef.: Eine Gleihung, in der x höhstens qudrtish (in der zweiten Potenz) vorkommt, heißt qudrtishe Gleihung. Gewöhnlihe
Fragebogen E. Lothar Natter. Effizienzcoaching. Unternehmer und Führungskräfte. Firma: Straße: PLZ: Ort: Telefax: Telefon: www:
 Frgeogen E Lothr Ntter Effizienznlyse für Selstständige, Unternehmer und Führungskräfte Effizienzohing Firm: Strße: PLZ: Ort: Telefon: Telefx: E-Mil: www: Dtum: Shereiter: Untershrift: Pseudonym für die
Frgeogen E Lothr Ntter Effizienznlyse für Selstständige, Unternehmer und Führungskräfte Effizienzohing Firm: Strße: PLZ: Ort: Telefon: Telefx: E-Mil: www: Dtum: Shereiter: Untershrift: Pseudonym für die
KAPITEL 1 EINFÜHRUNG: STABILE MATCHINGS
 KPITEL 1 EINFÜHRUNG: STILE MTHINGS F. VLLENTIN,. GUNERT In iesem Kpitel weren wir ein erstes konkretes Prolem es Opertions Reserh kennenlernen. Es hnelt sih um s Prolem es stilen Mthings, ein wihtiges
KPITEL 1 EINFÜHRUNG: STILE MTHINGS F. VLLENTIN,. GUNERT In iesem Kpitel weren wir ein erstes konkretes Prolem es Opertions Reserh kennenlernen. Es hnelt sih um s Prolem es stilen Mthings, ein wihtiges
