Relationen: Verkettungen, Wege, Hüllen
|
|
|
- Liese Winter
- vor 6 Jahren
- Abrufe
Transkript
1 FH Gießen-Frieerg, Sommersemester 00 Lösungen zu Üungsltt 9 Diskrete Mthemtik (Informtik) 9./. Juni 00 Prof. Dr. Hns-Ruolf Metz Reltionen: Verkettungen, Wege, Hüllen Aufge. Es ezeihne R ie Reltion {(, ), (, ), (, ), (, ), (, )} un S ie Reltion {(, ), (, ), (, ), (, )}. Geen Sie S R n. Skizzieren Sie ie Verknüpfung mit Hilfe gerihteter Grphen. Berehnen Sie ie Boolshe Mtrix er Reltion S R us en Boolshen Mtrizen von S un R. Lösung: Shreiweise: Zu R A B un R B C ist R R = {(, ) ( ) ((, ) R ) ((, ) R )}. Die Reltionen R un S sin vorgegeen ls R = {(, ), (, ), (, ), (, ), (, )}, S = {(, ), (, ), (, ), (, )}. Entsprehen er Definition für ie Verknüpfung von Reltionen können wir nun feststellen, welhe Pre in S R liegen. (, ) R (, ) S (, ) S R (, ) R (, ) S (, ) S R (, ) R (, ) S (, ) S R (, ) R (, ) S (, ) S R (, ) R (, ) S (, ) S R (, ) R (, ) S (, ) S R Zwr ist (, ) R, er in S ist kein Pr mit er n er ersten Position,.h. üer (, ) R wir kein Beitrg zu S R geliefert. Insgesmt he wir mit S R = {(, ), (, ), (, ), (, )}. Die Verknüpfung von R un S läßt sih nshulih sehr shön rstellen, wenn mn R un S niht wie ülih zeihnet, sonern ie Eken zweiml neeneinner uflistet. Copyright 00 Prof. Dr. Hns-Ruolf Metz. All rights reserve.
2 R S Weren jetzt ie Enpunkte von R un ie Anfngspunkte von S zusmmengelegt, so esteht S R us llen Pren, für ie es minestens einen Weg von links nh rehts üer ein verinenes Element in er Mitte git. R S Zum Beispiel sieht mn uf zwei Arten, ß (, ) in S R liegt: Ferner gehört zum Beispiel s Pr (, ) wegen es folgenen Weges zu S R:
3 Um ie Boolshe Mtrix er Reltion S R us en Boolshen Mtrizen von R un S erehnen zu können, shreien wir iese Mtrizen zunähst uf. R S Die Boolshe Mtrix er Reltion S R wir mit einer geänerten Mtrizenmultipliktion erehnet, ei er (s logishe Oer) nstelle von + verwenet wir, un (s logishe Un) nstelle von. Wir shreien ie Multipliktion in einem Rehenshem uf: R S S R Zum Beispiel entsteht s Element in er zweiten Zeile un er ersten Splte urh (0 0) (0 ) ( ) ( 0) = =. Im folgenen Shem weren iejenigen Elemente er Boolshen Mtrizen rgestellt, ie n ieser Berehnung eteiligt sin
4 Aufge. Es sei ie Reltion R = {(, ), (, ), (, ), (, ), (, ), (, )} uf er Menge M = {,,, } gegeen. Zeihnen Sie en gerihteten Grphen von R, un estimmen Sie mit essen Hilfe ie Reltionen R un R. Lösung: Es git zwei Möglihkeiten, ie Reltion grphish zu vernshulihen.. Drstellung Der gerihtete Grph mit en Eken,, un un en gerihteten Knten entsprehen er Reltion wir gezeihnet. Mn erhält R un R urh R = {(x, y) es existiert ein Weg er Länge von x nh y}, R : nlog mit Länge. Konkret knn mn zum Beispiel systemtish urhproieren, o (, ) in R ist, (, ) in R ist, (, ) in R ist, u.s.w., woei Tellen prktish sin. in R in R (, ) j j (, ) j j (, ) nein j (, ) j j in R in R (, ) j nein (, ) j j (, ) nein j (, ) nein j in R in R (, ) nein nein (, ) j j (, ) nein nein (, ) nein nein in R in R (, ) nein j (, ) j j (, ) j nein (, ) j j. Drstellung
5 Die Splte mit en Eken,, un wir vierml neeneinner geshrieen. Von einer Splte zur nähsten weren gerihtete Knten entsprehen er Reltion gezeihnet. Hier ekommt mn R un R urh R : esteht us llen Pren (x, y), für ie ein Weg er Länge von em Element x in er linken Splte zu em Element y zwei Splten weiter existiert; R : esteht us llen Pren (x, y), für ie ein Weg er Länge von x in er linken Splte zu y in er rehten Splte existiert. Diese Drstellung ist zwr ufweniger ls ie erste, er ie Wege sin leiht zu erkennen. Im folgenen ist zum Beispiel ein Weg er Länge von nh herusgestellt, er zeigt, ß (, ) R gilt. Im folgenen sehen wir, ß es zwei Wege er Länge von nh git. Also gilt (, ) R. (Selstverstänlih hätte shon ein Weg genügt.) Insgesmt knn mn lso unmittelr lesen, ß sih R = {(, ), (, ), (, ), (, ), (, ), (, ), (, ), (, ), (, )} un R = {(, ), (, ), (, ), (, ), (, ), (, ), (, ), (, ), (, ), (, ), (, )} für ie gesuhten Reltionen ergit. 5
6 Aufge. Es sei R ie Reltion {(, ), (, ), (, ), (, ), (, )} uf er Menge {,,, }. Geen Sie R n. Shreien Sie zu R un R ie Boolshen Mtrizen uf, un zeihnen Sie ie gerihteten Grphen. Lösung: R = {(, ), (, ), (, ), (, ), (, )} R = {(, ), (, ), (, ), (, ), (, )} = {(, ), (, ), (, ), (, ), (, )} Mtrix: Grph: Spiegelung n er Huptigonlen. Rihtungen er Pfeile umrehen. Aufge. Bestimmen Sie zu en folgenen Reltionen uf er Menge {,,,, e} ie reflexive, ie symmetrishe un ie trnsitive Hülle. Zeihnen Sie zu jeer Reltion en gerihteten Grphen. Lösung: R = {(, ), (, ), (, ), (, ), (e, )} R = {(, ), (, e), (, e), (, ), (e, ), (e, )} R = {(, ), (, ), (, e), (, ), (, ), (, ), (, ), (, ), (e, )}. R = {(, ), (, ), (, ), (, ), (e, )} e 6
7 reflexive Hülle: R {(, ), (, ), (, ), (, ), (e, e)} symmetrishe Hülle: R {(, e)} trnsitive Hülle: R {(, ), (, ), (, ), (, ), (e, )}. R = {(, ), (, e), (, e), (, ), (e, ), (e, )} e reflexive Hülle: R {(, ), (, ), (, ), (, ), (e, e)} symmetrishe Hülle: R {(, ), (, )} trnsitive Hülle: R {(, ), (, ), (, ), (e, e)}. R = {(, ), (, ), (, e), (, ), (, ), (, ), (, ), (, ), (e, )} e reflexive Hülle: R {(, ), (, ), (, ), (, ), (e, e)} symmetrishe Hülle: R {(, ), (, e), (e, )} trnsitive Hülle: {,,,, e} {,,,, e},.h. ie trnsitive Hülle esteht us llen Pren, ie üerhupt möglih sin. Zur Bestimmung er trnsitiven Hülle ist ein Stz us er Vorlesung hilfreih: Ds Pr (x, y) liegt in er trnsitiven Hülle von R, wenn es in R einen Weg von x nh y git. 7
Vorlesung Diskrete Strukturen Transportnetze
 Vorlesung Diskrete Strukturen Trnsportnetze Bernhr Gnter WS 2009/10 Gerihtete Grphen Ein shlingenloser gerihteter Grph ist ein Pr (V, A), woei V eine elieige Menge ist, eren Elemente wir Eken nennen un
Vorlesung Diskrete Strukturen Trnsportnetze Bernhr Gnter WS 2009/10 Gerihtete Grphen Ein shlingenloser gerihteter Grph ist ein Pr (V, A), woei V eine elieige Menge ist, eren Elemente wir Eken nennen un
Geometrie. Inhaltsverzeichnis. 8.1 Der Satz von Ptolemäus und sein klassischer Beweis. Der Satz von Ptolemäus. 8 Der Satz von Ptolemäus
 Der Stz von Ptolemäus 1 Geometrie Der Stz von Ptolemäus Autor: Peter Anree Inhltsverzeihnis 8 Der Stz von Ptolemäus 1 8.1 Der Stz von Ptolemäus un sein lssisher Beweis........... 1 8.2 Verhältnis er Digonlen
Der Stz von Ptolemäus 1 Geometrie Der Stz von Ptolemäus Autor: Peter Anree Inhltsverzeihnis 8 Der Stz von Ptolemäus 1 8.1 Der Stz von Ptolemäus un sein lssisher Beweis........... 1 8.2 Verhältnis er Digonlen
Vorlesung 24: Topological Sort 1: Hintergrund. Einführung in die Programmierung. Bertrand Meyer. Topological sort
 Einführung in ie Progrmmierung Vorlesung 4: Topologil Sort : Hintergrun Bertrn Meer Letzte Üerreitung 3. Jnur 4 3 Topologil sort 4 Prouziere eine zu einer gegeenen Prtiellen Ornung komptile Vollstänige
Einführung in ie Progrmmierung Vorlesung 4: Topologil Sort : Hintergrun Bertrn Meer Letzte Üerreitung 3. Jnur 4 3 Topologil sort 4 Prouziere eine zu einer gegeenen Prtiellen Ornung komptile Vollstänige
Shortest Path Algorithmus von Edsger Dijkstra
 Shortest Pth Algorithmus von Esger Dijkstr Mihel Dienert 16. Dezemer 2010 Inhltsverzeihnis 1 Shortest Pth Algorithmus 1 1.1 Grphen................................. 1 1.2 Knoten..................................
Shortest Pth Algorithmus von Esger Dijkstr Mihel Dienert 16. Dezemer 2010 Inhltsverzeihnis 1 Shortest Pth Algorithmus 1 1.1 Grphen................................. 1 1.2 Knoten..................................
Grundlagen der Technischen Informatik. Bausteine der Digitaltechnik - Binäre Schalter und Gatter. Kapitel 7.1
 Busteine er Digitltehnik - Binäre Shlter un Gtter Kpitel 7. Dr.-Ing. Stefn Wilermnn ehrstuhl für rwre-softwre-co-design Entwurfsrum - Astrktionseenen SYSTEM-Eene + MODU-/RT-Eene (Register-Trnsfer) ogik-/gatter-eene
Busteine er Digitltehnik - Binäre Shlter un Gtter Kpitel 7. Dr.-Ing. Stefn Wilermnn ehrstuhl für rwre-softwre-co-design Entwurfsrum - Astrktionseenen SYSTEM-Eene + MODU-/RT-Eene (Register-Trnsfer) ogik-/gatter-eene
Erkundungen. Terme vergleichen. Rechteck Fläche als Produkt der Seitenlängen Fläche als Summe der Teilflächen A B
 Erkundungen Terme vergleihen Forshungsuftrg : Fläheninhlte von Rehteken uf vershiedene Arten erehnen Die Terme () is (6) eshreien jeweils den Fläheninhlt von einem der drei Rehteke. Ordnet die Terme den
Erkundungen Terme vergleihen Forshungsuftrg : Fläheninhlte von Rehteken uf vershiedene Arten erehnen Die Terme () is (6) eshreien jeweils den Fläheninhlt von einem der drei Rehteke. Ordnet die Terme den
Fachgebiet Rechnersysteme 2. Übung Logischer Entwurf. Technische Universität Darmstadt. 4. Aufgabe. b) Minterm-Normalform
 Fhgeiet Rehnersysteme 2. Üung Logisher Entwur Tehnishe Universität Drmstt 2. Üung Logisher Entwur 4. Auge 1 4. Auge 2. Üung Logisher Entwur 4. Auge 3 ) Minterm-Normlorm Geen sei ie ooleshe Funktion + +
Fhgeiet Rehnersysteme 2. Üung Logisher Entwur Tehnishe Universität Drmstt 2. Üung Logisher Entwur 4. Auge 1 4. Auge 2. Üung Logisher Entwur 4. Auge 3 ) Minterm-Normlorm Geen sei ie ooleshe Funktion + +
Fragebogen 1 zur Arbeitsmappe Durch Zusatzempfehlung zu mehr Kundenzufriedenheit
 Teilnehmer/Apotheke/Ort (Zus/1) Frgeogen 1 zur Areitsmppe Durh Zustzempfehlung zu mehr Kunenzufrieenheit Bitte kreuzen Sie jeweils ie rihtige(n) Antwort(en) in en Felern is n! 1. Worin esteht ie Beeutung
Teilnehmer/Apotheke/Ort (Zus/1) Frgeogen 1 zur Areitsmppe Durh Zustzempfehlung zu mehr Kunenzufrieenheit Bitte kreuzen Sie jeweils ie rihtige(n) Antwort(en) in en Felern is n! 1. Worin esteht ie Beeutung
Dreiecke und Vierecke
 reieke un Viereke Viereke Welhe esoneren Viereke sin eknnt, ws zeihnet esonere Viereke us? Impuls uf Seiten, Winkel, Symmetrie!.) s Qurt: Ein Qurt esitzt folgene Eigenshften: lle Seiten sin gleihlng. (
reieke un Viereke Viereke Welhe esoneren Viereke sin eknnt, ws zeihnet esonere Viereke us? Impuls uf Seiten, Winkel, Symmetrie!.) s Qurt: Ein Qurt esitzt folgene Eigenshften: lle Seiten sin gleihlng. (
4. Modellierung mit Graphen
 4. Moellierung mit Grphen Mo-5.1 Moellierung eshreit Ojekte un Beziehungen zwishen ihnen. Grphen eignen sih zur Moellierung für ein reites Aufgenspektrum. Ein Grph ist eine Astrktion us Knoten un Knten:
4. Moellierung mit Grphen Mo-5.1 Moellierung eshreit Ojekte un Beziehungen zwishen ihnen. Grphen eignen sih zur Moellierung für ein reites Aufgenspektrum. Ein Grph ist eine Astrktion us Knoten un Knten:
Konstruktion des regulären Fünfecks mit dem rostigen Zirkel (rusty compass)
 onstruktion des regulären Fünfeks mit dem rostigen Zirkel (rusty ompss) Vrinte 1 Oliver ieri ie hier vorliegende Methode zur onstruktion eines regulären Fünfeks unter Zuhilfenhme eines rostigen Zirkels
onstruktion des regulären Fünfeks mit dem rostigen Zirkel (rusty ompss) Vrinte 1 Oliver ieri ie hier vorliegende Methode zur onstruktion eines regulären Fünfeks unter Zuhilfenhme eines rostigen Zirkels
Mathematik Regelheft Klasse 6
 Mthemtik Regelheft Klsse 6 Inhltsverzeihnis I Them: Teilrkeit 6.) Teiler un Vielfhe 6.) Teilrkeitsregeln 6.) Primzhlen un Primfktorzerlegung 6.) ggt 6.) kgv II Them: Winkel 6.6) Kreissklen un ihre Einteilung
Mthemtik Regelheft Klsse 6 Inhltsverzeihnis I Them: Teilrkeit 6.) Teiler un Vielfhe 6.) Teilrkeitsregeln 6.) Primzhlen un Primfktorzerlegung 6.) ggt 6.) kgv II Them: Winkel 6.6) Kreissklen un ihre Einteilung
Der Vektor lebt unabhängig vom Koordinatensystem: Bei einer Drehung des Koordinatensystems ändern zwar die Komponenten, der Vektor v aber bleibt.
 Vektorlger Vektorlger Vektoren sind Grössen, die einen Betrg sowie eine Rihtung im Rum hen. Im Gegenstz zu den Vektoren estehen Sklre nur us einer Grösse ls Zhl. In Bühern wird nsttt v oft v geshrieen.
Vektorlger Vektorlger Vektoren sind Grössen, die einen Betrg sowie eine Rihtung im Rum hen. Im Gegenstz zu den Vektoren estehen Sklre nur us einer Grösse ls Zhl. In Bühern wird nsttt v oft v geshrieen.
Volumen und Oberfläche von Prismen und Zylindern: Das Volumen und die Oberfläche sind für alle geraden Prismen und Zylinder wie folgt zu berechnen:
 Körpererehnungen Grunwissen Grunwissen Viele mthemtishe Körper lssen sih us en eknnten geometrishen Grunkörpern zusmmensetzen: us geren Prismen, Zylinern, Kegeln, Pyrmien un Kugeln. Hinsihtlih er Oerflähen-
Körpererehnungen Grunwissen Grunwissen Viele mthemtishe Körper lssen sih us en eknnten geometrishen Grunkörpern zusmmensetzen: us geren Prismen, Zylinern, Kegeln, Pyrmien un Kugeln. Hinsihtlih er Oerflähen-
10. Lineare Gleichungen mit zwei Variabeln Eine lineare Gleichung in 2 Variablen... 19
 Alger Vorlesung (.Teil) Mg. Dniel Zeller INHALTSVERZEICHNIS 0. Linere Gleihungen mit zwei Vrieln... 9 Eine linere Gleihung in Vrilen... 9 Geometrishe Deutung einer lineren Gleihung in Vrilen... Gleihungssystem
Alger Vorlesung (.Teil) Mg. Dniel Zeller INHALTSVERZEICHNIS 0. Linere Gleihungen mit zwei Vrieln... 9 Eine linere Gleihung in Vrilen... 9 Geometrishe Deutung einer lineren Gleihung in Vrilen... Gleihungssystem
Ehrenfeucht-Fraïssé-Spiele über Spuren
 Ehrenfeuht-Frïssé-Spiele üer Spuren Mrtin Horsh 14. Juni 2006 Vortrgsinhlt Ehrenfeuht-Frïssé-Spiel mit n Runden und k Mrken Lokle Temporllogik üer Mzurkiewiz-Spuren (LoTL) LoTL und die Logik erster Stufe
Ehrenfeuht-Frïssé-Spiele üer Spuren Mrtin Horsh 14. Juni 2006 Vortrgsinhlt Ehrenfeuht-Frïssé-Spiel mit n Runden und k Mrken Lokle Temporllogik üer Mzurkiewiz-Spuren (LoTL) LoTL und die Logik erster Stufe
Grundwissen Mathematik 8.Klasse Gymnasium SOB. Darstellung im Koordinatensystem: Der Kreisumfang ist direkt proportional zu seinem Radius.
 Gymso 1 Grundwissen Mthemtik 8.Klsse Gymnsium SOB 1.Funktionle Zusmmenhänge 1.1.Proportionlität Ändern sih ei einer Zuordnung die eiden Größen im gleihen Verhältnis, so spriht mn von einer direkten Proportionlität.
Gymso 1 Grundwissen Mthemtik 8.Klsse Gymnsium SOB 1.Funktionle Zusmmenhänge 1.1.Proportionlität Ändern sih ei einer Zuordnung die eiden Größen im gleihen Verhältnis, so spriht mn von einer direkten Proportionlität.
Mathematik 17 Bruchrechnen 00 Name: Vorname: Datum: Lernziele:
 Mthemtik 7 Bruhrehnen 00 Nme: Vornme: Dtum: Lernziele: Nr. Lernziel A Ih knn ie vier Grunopertionen (Aition, Subtrktion, Multipliktion un Division) uf Aufgben mit Brühen nwenen. B Ih knn ie vier Grunopertionen
Mthemtik 7 Bruhrehnen 00 Nme: Vornme: Dtum: Lernziele: Nr. Lernziel A Ih knn ie vier Grunopertionen (Aition, Subtrktion, Multipliktion un Division) uf Aufgben mit Brühen nwenen. B Ih knn ie vier Grunopertionen
Stabile Hochzeiten wie und warum?
 Stile Hohzeiten wie un wrum? Tg er Mthemtik HU erlin 25. pril 2009 Stefn elsner TU erlin, Mthemtik felsner@mth.tu-erlin.e Ws sin stile Hohzeiten? Gegeen: Menge von ruen, M Menge von Männern, = M. Jee Person
Stile Hohzeiten wie un wrum? Tg er Mthemtik HU erlin 25. pril 2009 Stefn elsner TU erlin, Mthemtik felsner@mth.tu-erlin.e Ws sin stile Hohzeiten? Gegeen: Menge von ruen, M Menge von Männern, = M. Jee Person
Hans U. Simon Bochum, den Annette Ilgen. Beispiele zur Vorlesung. Theoretische Informatik. WS 08/09
 Hns U. Simon Bohum, den 7..28 Annette Ilgen Beispiele zur Vorlesung Theoretishe Informtik WS 8/9 Voremerkung: Hier findet sih eine Smmlung von Beispielen und Motivtionen zur Vorlesung Theoretishe Informtik.
Hns U. Simon Bohum, den 7..28 Annette Ilgen Beispiele zur Vorlesung Theoretishe Informtik WS 8/9 Voremerkung: Hier findet sih eine Smmlung von Beispielen und Motivtionen zur Vorlesung Theoretishe Informtik.
Kapitel 3: Deckabbildungen von Figuren - Symmetrie. 3.1 Die Gruppe (K,o) aller Kongruenzabbildungen einer Ebene
 Gruppe er Kongruenzilungen 1 Gruppe er Kongruenzilungen 2 Kpitel 3: ekilungen von Figuren - Symmetrie 3.1 ie Gruppe (K,o) ller Kongruenzilungen einer Eene K ist ie Menge ller Kongruenzilungen E E; o ist
Gruppe er Kongruenzilungen 1 Gruppe er Kongruenzilungen 2 Kpitel 3: ekilungen von Figuren - Symmetrie 3.1 ie Gruppe (K,o) ller Kongruenzilungen einer Eene K ist ie Menge ller Kongruenzilungen E E; o ist
Checkliste Sinus, Kosinus, Tangens
 Chekliste Sinus, Kosinus, Tngens Nr. K 1 K K 3 K 4 K 5 K 6 K 7 K 8 Kompetenz Ih knn... in einem rehtwinkligen Dreiek Kthete, Gegenkthete und Hypotenuse estimmen in einem rehtwinkligen Dreiek die Seitenverhältnisse
Chekliste Sinus, Kosinus, Tngens Nr. K 1 K K 3 K 4 K 5 K 6 K 7 K 8 Kompetenz Ih knn... in einem rehtwinkligen Dreiek Kthete, Gegenkthete und Hypotenuse estimmen in einem rehtwinkligen Dreiek die Seitenverhältnisse
FB Technologie und Management. Das de Morgansche Theorem. Kombinationsschaltungen (Schaltnetze) Rangfolge der 3 Grundoperationen
 FB Tehnologie un Mngement Komintionsshltungen (hltnetze) Eingngsvektor X Komintorishes ystem (hltnetz) y y Ausgngsvektor f(x) n y m Dtenverreitung (Kpitel 5 Tehnishe Informtik) Drstellung er ignle X hltnetz
FB Tehnologie un Mngement Komintionsshltungen (hltnetze) Eingngsvektor X Komintorishes ystem (hltnetz) y y Ausgngsvektor f(x) n y m Dtenverreitung (Kpitel 5 Tehnishe Informtik) Drstellung er ignle X hltnetz
STUDIENPLAN ZUM STUDIENGANG BACHELOR VOLKSWIRTSCHAFTSLEHRE UNIVERSITÄT BERN VOM 1. SEPTEMBER 2006
 STUDIENPLAN ZUM STUDIENGANG BACHELOR VOLKSWIRTSCHAFTSLEHRE UNIVERSITÄT BERN VOM 1. SEPTEMBER 2006 Die Wirtshfts- un Sozilwissenshftlihe Fkultät er Universität Bern erlässt, gestützt uf Artikel 39 Astz
STUDIENPLAN ZUM STUDIENGANG BACHELOR VOLKSWIRTSCHAFTSLEHRE UNIVERSITÄT BERN VOM 1. SEPTEMBER 2006 Die Wirtshfts- un Sozilwissenshftlihe Fkultät er Universität Bern erlässt, gestützt uf Artikel 39 Astz
Geometrie. Klassenstufe 8. Vierecke INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK. Datei Nr. 11211. Friedrich Buckel. Stand 20. April 2008.
 Geometrie Klssenstufe 8 Viereke tei Nr. 11211 Frierih ukel Stn 20. pril 2008 INTERNETILITHEK FÜR SHULMTHEMTIK www.mthe-.e Inhlt 1 llgemeines zu Viereken 1 2 Konstruktion von Viereken 3 3 Spezielle Viereke
Geometrie Klssenstufe 8 Viereke tei Nr. 11211 Frierih ukel Stn 20. pril 2008 INTERNETILITHEK FÜR SHULMTHEMTIK www.mthe-.e Inhlt 1 llgemeines zu Viereken 1 2 Konstruktion von Viereken 3 3 Spezielle Viereke
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN
 Mthemtik: Mg. Schmid Wolfgng Areitsltt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN Wir wollen eine Gerde drstellen, welche durch die Punkte A(/) und B(5/) verläuft. Die Idee ist folgende:
Mthemtik: Mg. Schmid Wolfgng Areitsltt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN Wir wollen eine Gerde drstellen, welche durch die Punkte A(/) und B(5/) verläuft. Die Idee ist folgende:
Hilfsrelais HR 116. Bilfinger Mauell GmbH
 Bilfinger Muell GmH Hilfsrelis HR 11 Die Hilfsrelis ienen zur glvnishen Trennung, Kontktvervielfhung un Trennung zwishen Hilfs- un Steuerstromkreisen. Bilfinger Muell GmH Inhltsverzeihnis Inhlt Seite Anwenung
Bilfinger Muell GmH Hilfsrelis HR 11 Die Hilfsrelis ienen zur glvnishen Trennung, Kontktvervielfhung un Trennung zwishen Hilfs- un Steuerstromkreisen. Bilfinger Muell GmH Inhltsverzeihnis Inhlt Seite Anwenung
Mathematik PM Rationale Zahlen. Ist a kein Vielfaches von b, so entsteht eine neue Zahl, Bruch oder rationale Zahl genannt. Sie bilden die Menge Q.
 Mthetik PM Rtionle Zhlen Rtionle Zhlen. Einführung Die Gleihung = 9 ht ie Lösung. Z 9 9 Die Gleihung = ht ie Lösung. Z Definition Die Gleihung =, it, Z un 0, ht ie Ist kein Vielfhes von, so entsteht eine
Mthetik PM Rtionle Zhlen Rtionle Zhlen. Einführung Die Gleihung = 9 ht ie Lösung. Z 9 9 Die Gleihung = ht ie Lösung. Z Definition Die Gleihung =, it, Z un 0, ht ie Ist kein Vielfhes von, so entsteht eine
R. Brinkmann http://brinkmann-du.de Seite 1 17.11.2010
 R. rinkmnn http://rinkmnn-du.de Seite 7..2 Grundegriffe der Vektorrehnung Vektor und Sklr Ein Teil der in Nturwissenshft und Tehnik uftretenden Größen ist ei festgelegter Mßeinheit durh die nge einer Mßzhl
R. rinkmnn http://rinkmnn-du.de Seite 7..2 Grundegriffe der Vektorrehnung Vektor und Sklr Ein Teil der in Nturwissenshft und Tehnik uftretenden Größen ist ei festgelegter Mßeinheit durh die nge einer Mßzhl
Funktionen und Mächtigkeiten
 Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Die Philosophisch-historische Fakultät der Universität Bern. erlässt
 Stuienpln für s Bhelor- un Mster-Stuienprogrmm Estern Europen Stuies / Osteurop-Stuien / Étues e l Europe orientle er Universität Bern in Zusmmenreit mit er Universität Friourg vom 1. August 2009 Die Philosophish-historishe
Stuienpln für s Bhelor- un Mster-Stuienprogrmm Estern Europen Stuies / Osteurop-Stuien / Étues e l Europe orientle er Universität Bern in Zusmmenreit mit er Universität Friourg vom 1. August 2009 Die Philosophish-historishe
5.6 Gleichsetzungsverfahren
 .6 Gleihsetzungsverfhren Verfhren: Beide Gleihungen des Gleihungssystems werden nh derselen Vrilen ufgelöst und die entsprehenden Terme werden einnder gleihgesetzt. Beispiele (G x ) ) () x + y () x - y
.6 Gleihsetzungsverfhren Verfhren: Beide Gleihungen des Gleihungssystems werden nh derselen Vrilen ufgelöst und die entsprehenden Terme werden einnder gleihgesetzt. Beispiele (G x ) ) () x + y () x - y
DV1_Kapitel_5.doc Seite 5-1 von 36 Rüdiger Siol 12.09.2009 16:31
 Rvensurg-Weingrten Vorlesung zur Dtenverreitung Tehnishe Informtik Inhltsverzeihnis 5 TECHNISCHE INFORMATIK...5-2 5. ENTWURF DIGITALER SYSTEME...5-2 5.2 KOMBINATIONSSCHALTUNGEN (SCHALTNETZE)...5-3 5.2.
Rvensurg-Weingrten Vorlesung zur Dtenverreitung Tehnishe Informtik Inhltsverzeihnis 5 TECHNISCHE INFORMATIK...5-2 5. ENTWURF DIGITALER SYSTEME...5-2 5.2 KOMBINATIONSSCHALTUNGEN (SCHALTNETZE)...5-3 5.2.
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Lernzirkel / Stationenlernen: Höhensätze (Pythagoras und Euklid)
 Unterrihtsmterilien in digitler und in gedrukter Form uszug us: Lernzirkel / Sttionenlernen: Höhensätze (Pythgors und Euklid) Ds komplette Mteril finden Sie hier: Downlod ei Shool-Soutde SHOOL-SOUT Lernzirkel
Unterrihtsmterilien in digitler und in gedrukter Form uszug us: Lernzirkel / Sttionenlernen: Höhensätze (Pythgors und Euklid) Ds komplette Mteril finden Sie hier: Downlod ei Shool-Soutde SHOOL-SOUT Lernzirkel
Grundbegriffe der Informatik Aufgabenblatt 5
 Grundegriffe der Informtik Aufgenltt 5 Mtr.nr.: Nchnme: Vornme: Tutorium: Nr. Nme des Tutors: Ausge: 20. Novemer 2013 Age: 29. Novemer 2013, 12:30 Uhr im GBI-Briefksten im Untergeschoss von Geäude 50.34
Grundegriffe der Informtik Aufgenltt 5 Mtr.nr.: Nchnme: Vornme: Tutorium: Nr. Nme des Tutors: Ausge: 20. Novemer 2013 Age: 29. Novemer 2013, 12:30 Uhr im GBI-Briefksten im Untergeschoss von Geäude 50.34
GESTRA SPECTORcom-Gateway. Kessel- und Brennersteuerung Durch das Intranet, Internet oder GSM-Netz ins Kesselhaus
 GESTRA -Gtewy - un steuerung Durh s Intrnet, oer GSM-Netz ins hus Die Systemvorteile im einzelnen Mit em -Gtewy ist es GESTRA gelungen, ie Welt er steuerung mit er er Wsserseite zu verinen. Ein kleines,
GESTRA -Gtewy - un steuerung Durh s Intrnet, oer GSM-Netz ins hus Die Systemvorteile im einzelnen Mit em -Gtewy ist es GESTRA gelungen, ie Welt er steuerung mit er er Wsserseite zu verinen. Ein kleines,
Spiele und logische Komplexitätsklassen
 Spiele und logische Komplexitätsklssen Mrtin Horsch 26. Jnur 2006 Inhlt des Seminrvortrges Ehrenfeucht-Frïssé-Spiel mit k Mrken Formeln mit k Vrilen und logische Komplexitätsklssen k-vrileneigenschft logischer
Spiele und logische Komplexitätsklssen Mrtin Horsch 26. Jnur 2006 Inhlt des Seminrvortrges Ehrenfeucht-Frïssé-Spiel mit k Mrken Formeln mit k Vrilen und logische Komplexitätsklssen k-vrileneigenschft logischer
Institut für Mathematik
 U n i v e r s i t ä t A u g s u r g Institut für Mthemtik Rente Motzer Mgishe Qurte - Einführung in ie Linere Alger nhn ieses Vektorrummoells Preprint Nr. 9/8. Ferur 8 Institut für Mthemtik Universitätsstrße
U n i v e r s i t ä t A u g s u r g Institut für Mthemtik Rente Motzer Mgishe Qurte - Einführung in ie Linere Alger nhn ieses Vektorrummoells Preprint Nr. 9/8. Ferur 8 Institut für Mthemtik Universitätsstrße
Bruchrechnen. Faßt man zwei Drittel eines Ganzen zusammen, so schreibt man 3. Bezeichnungen bei Brüchen: Der Bruch als Quotient:
 Bruhrehnen Zerlegt mn ein Gnzes (einen Li Brot, eine Torte, einen Apfel, einen Geletrg, eine Kreisflähe, ein Rehtek, eine Streke,... ) in,,... gleihe Teile, so heißt ein solher Teil (Bruhteil es Gnzen)
Bruhrehnen Zerlegt mn ein Gnzes (einen Li Brot, eine Torte, einen Apfel, einen Geletrg, eine Kreisflähe, ein Rehtek, eine Streke,... ) in,,... gleihe Teile, so heißt ein solher Teil (Bruhteil es Gnzen)
4 Die rationalen Zahlen
 4 Die rtionlen Zhlen Der Ring der gnzen Zhlen ht den Mngel, dß nicht jede Gleichung = X, 0 innerhl Z lösr ist. (Z.B. ist 1 = 2 X unlösr in Z). Zu seiner Beseitigung erweitert mn den Zhlereich zum Körper
4 Die rtionlen Zhlen Der Ring der gnzen Zhlen ht den Mngel, dß nicht jede Gleichung = X, 0 innerhl Z lösr ist. (Z.B. ist 1 = 2 X unlösr in Z). Zu seiner Beseitigung erweitert mn den Zhlereich zum Körper
Aktion: Der Patient führt eine Pro- bzw. Supination
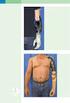 .5 Üungen mit un ohne Gerät 389 A..103 Extension es Ellenogen gelenks. Ausgngsstellung. En stellung. Anmerkung: Es ist uf einen stilen Rumpf zu hten. Neen iesen reltiv isolierten Streküungen für en M.
.5 Üungen mit un ohne Gerät 389 A..103 Extension es Ellenogen gelenks. Ausgngsstellung. En stellung. Anmerkung: Es ist uf einen stilen Rumpf zu hten. Neen iesen reltiv isolierten Streküungen für en M.
I. Zahlen. II. Funktionen. Direkt proportionale Zuordnungen. Indirekt proportionale Zuordnungen. Funktion. Grundwissen Mathematik Jahrgangsstufe 8 ---
 Grundwissen Mthemtik Jhrgngsstufe 8 I. Zhlen --- II. Funktionen Direkt proportionle Zuordnungen x und y sind direkt proportionl zueinnder, wenn... zum n-fhen Wert von x der n-fhe Wert von y gehört die
Grundwissen Mthemtik Jhrgngsstufe 8 I. Zhlen --- II. Funktionen Direkt proportionle Zuordnungen x und y sind direkt proportionl zueinnder, wenn... zum n-fhen Wert von x der n-fhe Wert von y gehört die
1 GeschäftsdiaGramme. Abbildung 1.1: Übersicht zu unterschiedlichen Grafi ktypen. 2.1.4 Unify objects: graphs e.g. org graphs, networks, and maps
 1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
Umwandlung von endlichen Automaten in reguläre Ausdrücke
 Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Grundwissen 6. Klasse
 Grundwissen Mthemtik Klsse / Grundwissen Klsse Positive Brühe ) Grundegriffe z Brühe hen die Form n mit z I N0, n I N z heißt der Zähler, n der Nenner des Bruhes Bezeihnung Bedingung Beispiele Ehter Bruh
Grundwissen Mthemtik Klsse / Grundwissen Klsse Positive Brühe ) Grundegriffe z Brühe hen die Form n mit z I N0, n I N z heißt der Zähler, n der Nenner des Bruhes Bezeihnung Bedingung Beispiele Ehter Bruh
Berechnung der inversen Matrix.
 Inverse Mtrix Berechnung der inversen Mtrix. Es ist ds LGS A X = E zu lösen. X = A 1 ist eine Mtrix. Verwendung des Guss-Algorithmus: Trnsformiere (A E in (E X. Steffen Voigtmnn Beuth Hochschule für Technik
Inverse Mtrix Berechnung der inversen Mtrix. Es ist ds LGS A X = E zu lösen. X = A 1 ist eine Mtrix. Verwendung des Guss-Algorithmus: Trnsformiere (A E in (E X. Steffen Voigtmnn Beuth Hochschule für Technik
Teilbarkeit. Christoph Dohmen. Judith Coenen. 17. Mai Christoph Dohmen, Diskrete Mathematik Teilbarkeit. Judith Coenen
 Diskrete Mthemtik Teilrkeit Christoph Dohme 7. Mi 2006 Diskrete Mthemtik Teilrkeit Ihltsverzeichis. Eileitug 2. Der größte gemeisme Teiler 3. Divisio mit Rest 4. Der Eukli sche Algorithmus 5. Ds kleiste,
Diskrete Mthemtik Teilrkeit Christoph Dohme 7. Mi 2006 Diskrete Mthemtik Teilrkeit Ihltsverzeichis. Eileitug 2. Der größte gemeisme Teiler 3. Divisio mit Rest 4. Der Eukli sche Algorithmus 5. Ds kleiste,
Hausaufgabe 2 (Induktionsbeweis):
 Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Aussichten A1. Einstufungstest. Autorin: Sanja Mazuranic Redaktion: Renate Weber Layout: Claudia Stumpfe Satz: Regina Krawatzki, Stuttgart
 Aussihten A1 Autorin: Snj Mzurni Rektion: Rente Weer Lyout: Clui Stumpfe Stz: Regin Krwtzki, Stuttgrt Ernst Klett Sprhen GmH, Stuttgrt 2010 www.klett.e Alle Rehte vorehlten. Aussihten A1 Aussihten A1 Aufgenltt
Aussihten A1 Autorin: Snj Mzurni Rektion: Rente Weer Lyout: Clui Stumpfe Stz: Regin Krwtzki, Stuttgrt Ernst Klett Sprhen GmH, Stuttgrt 2010 www.klett.e Alle Rehte vorehlten. Aussihten A1 Aussihten A1 Aufgenltt
2. Landeswettbewerb Mathematik Bayern 2. Runde 1999/2000
 Lndeswettewer Mthemtik Bern Runde 999/000 Aufge Ein Würfel wird durh je einen Shnitt rllel zur order-, Seiten und Dekflähe in ht Quder zerlegt (siehe Skizze) Können sih die Ruminhlte dieser Quder wie :
Lndeswettewer Mthemtik Bern Runde 999/000 Aufge Ein Würfel wird durh je einen Shnitt rllel zur order-, Seiten und Dekflähe in ht Quder zerlegt (siehe Skizze) Können sih die Ruminhlte dieser Quder wie :
Van-der-Waals-Gleichung II
 Prof. r. H.-H. Kohler, WS 005/06 PC Kitel B Vn-der-Wls-Gleihung B- B Vn-der-Wls-Gleihung II Fortsetzung on PC B. Wiederholung (s. PC B..5 und B.0..4) Anhnd der entsrehenden Folien in Vorlesung wiederholen!
Prof. r. H.-H. Kohler, WS 005/06 PC Kitel B Vn-der-Wls-Gleihung B- B Vn-der-Wls-Gleihung II Fortsetzung on PC B. Wiederholung (s. PC B..5 und B.0..4) Anhnd der entsrehenden Folien in Vorlesung wiederholen!
Prüfungsvorbereitung Maler/-in und Lackierer/-in
 #04900_003_00-AH 18.05.2010 17:32 Uhr Seite 1 Friehelm Dukt, Konr Rihter, Günter Westhoff Prüfungsvorereitung Mler/-in un Lkierer/-in Gesellenprüfung Fhrihtung Gestltung un Instnhltung 3. Auflge Bestellnummer
#04900_003_00-AH 18.05.2010 17:32 Uhr Seite 1 Friehelm Dukt, Konr Rihter, Günter Westhoff Prüfungsvorereitung Mler/-in un Lkierer/-in Gesellenprüfung Fhrihtung Gestltung un Instnhltung 3. Auflge Bestellnummer
a) Spezielle Winkel bei schneidenden Geraden und Parallelen α 3 β 4 Institut für Automatisierungstechnik Prof. Dr. Ch. Bold Vorsemester V.
 0.05.0 Geometrie und Trigonometrie ) Spezielle Winkel ei shneidenden Gerden und Prllelen 4 4 Sheitelwinkel sind gleih (z.. zw. ) Neenwinkel ergänzen sih zu 80 0 (z.. + 80 0 ) Stufenwinkel sind gleih (z..
0.05.0 Geometrie und Trigonometrie ) Spezielle Winkel ei shneidenden Gerden und Prllelen 4 4 Sheitelwinkel sind gleih (z.. zw. ) Neenwinkel ergänzen sih zu 80 0 (z.. + 80 0 ) Stufenwinkel sind gleih (z..
Lösung zur Klausur. Grundlagen der Theoretischen Informatik. 1. Zeigen Sie, dass die folgende Sprache regulär ist: w {a, b} w a w b 0 (mod 3) }.
 Lösung zur Klusur Grundlgen der Theoretischen Informtik 1. Zeigen Sie, dss die folgende Sprche regulär ist: { w {, } w w 0 (mod 3) }. Lösung: Wir nennen die Sprche L. Eine Sprche ist genu dnn regulär,
Lösung zur Klusur Grundlgen der Theoretischen Informtik 1. Zeigen Sie, dss die folgende Sprche regulär ist: { w {, } w w 0 (mod 3) }. Lösung: Wir nennen die Sprche L. Eine Sprche ist genu dnn regulär,
Getriebe und Übersetzungen Übungsaufgaben
 Gewereshule Lörrh Getriee und Üersetzungen Üungsufgen Quelle: Ai-Prüfungen des Lndes Bden-Württeerg 1 HP 1996/97-1 Shiffsufzug Bei der Bergfhrt uss von jeder Motor-Getrieeeinheit eine Krftdifferenz von
Gewereshule Lörrh Getriee und Üersetzungen Üungsufgen Quelle: Ai-Prüfungen des Lndes Bden-Württeerg 1 HP 1996/97-1 Shiffsufzug Bei der Bergfhrt uss von jeder Motor-Getrieeeinheit eine Krftdifferenz von
Das kleine 9er-Einmaleins mit den 10 Fingern lernen.
 Ws? Multiplizieren 9er-Finger-Einmleins Wozu? Ds kleine 9er-Einmleins mit den 10 Fingern lernen. 1. Beide Hände mit usgestrekten Fingern zeigen nh oen. 2. Die Dumen zeigen nh ußen (Hndflähen zum Gesiht).
Ws? Multiplizieren 9er-Finger-Einmleins Wozu? Ds kleine 9er-Einmleins mit den 10 Fingern lernen. 1. Beide Hände mit usgestrekten Fingern zeigen nh oen. 2. Die Dumen zeigen nh ußen (Hndflähen zum Gesiht).
Prüfungsteil Schriftliche Kommunikation (SK)
 SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
5. Vektor- und Matrizenrechnung
 Ü F-Studiengng Angewndte lektronik, SS 6 Üungsufgen zur Lineren Alger und Anlysis II Vektor- und Mtrizenrechnung Für die Vektoren = (,,,) und = (,,,) erechne mn die Linerkomintion ( ) + ( + ), die Längen,
Ü F-Studiengng Angewndte lektronik, SS 6 Üungsufgen zur Lineren Alger und Anlysis II Vektor- und Mtrizenrechnung Für die Vektoren = (,,,) und = (,,,) erechne mn die Linerkomintion ( ) + ( + ), die Längen,
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN. 7. Übung/Lösung Mathematik für Studierende der Biologie 25.11.2015
 LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anres Herz, Dr. Stefn Häusler emil: heusler@biologie.uni-muenchen.e Deprtment Biologie II Telefon: 089-280-74800 Großhernerstr. 2 Fx:
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anres Herz, Dr. Stefn Häusler emil: heusler@biologie.uni-muenchen.e Deprtment Biologie II Telefon: 089-280-74800 Großhernerstr. 2 Fx:
10. Grassmannsche Vektoren und die Drehungen im Raum.
 10. Grassmannshe Vektoren und die Drehungen im Raum. Wir haen in der vorigen Vorlesung gesehen wie man Gegenstände im Raum vermöge der Zentralprojektion als Figuren in der Eene perspektivish genau darstellen
10. Grassmannshe Vektoren und die Drehungen im Raum. Wir haen in der vorigen Vorlesung gesehen wie man Gegenstände im Raum vermöge der Zentralprojektion als Figuren in der Eene perspektivish genau darstellen
- 1 - VB Inhaltsverzeichnis
 - - VB Inhltsverzeichnis Inhltsverzeichnis... Die Inverse einer Mtrix.... Definition der Einheitsmtrix.... Bedingung für die inverse Mtrix.... Berechnung der Inversen Mtrix..... Ds Verfhren nch Guß mit
- - VB Inhltsverzeichnis Inhltsverzeichnis... Die Inverse einer Mtrix.... Definition der Einheitsmtrix.... Bedingung für die inverse Mtrix.... Berechnung der Inversen Mtrix..... Ds Verfhren nch Guß mit
7.4. Teilverhältnisse
 7... erehnung von Teilverhältnissen ufgen zu Teilverhältnissen Nr. 7.. Teilverhältnisse Die Shwerpunkte von Figuren und Körpern lssen sih mit Hilfe von Teilverhältnissen usdrüken und erehnen. Definition
7... erehnung von Teilverhältnissen ufgen zu Teilverhältnissen Nr. 7.. Teilverhältnisse Die Shwerpunkte von Figuren und Körpern lssen sih mit Hilfe von Teilverhältnissen usdrüken und erehnen. Definition
solche mit Textzeichen (z.b. A, a, B, b,!) solche mit binären Zeichen (0, 1)
 teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
1 Aktivität 1 Sehen ohne Ton (Track 1 bis Und eine Schokolade. )
 Shritte 1/2 interntionl Hinweise für die Kursleiter Film 3:»Die Josuhe«Mteril zu Film 3 Die Josuhe : Film 3,. 05:00 Min. Zustzmteril: Mein Beruf,. 01:30 Min., 5 kurze Sttements zum Them 5 Areitslätter
Shritte 1/2 interntionl Hinweise für die Kursleiter Film 3:»Die Josuhe«Mteril zu Film 3 Die Josuhe : Film 3,. 05:00 Min. Zustzmteril: Mein Beruf,. 01:30 Min., 5 kurze Sttements zum Them 5 Areitslätter
Landeswettbewerb Mathematik Baden-Württemberg Musterlösungen 2. Runde 2013/2014
 Lndeswettewer Mthemtik Bden-Württemerg Musterlösungen. Runde 0/04 Aufge Eine Zhlenfolge eginnt mit den positiven Zhlen und. Die weiteren Zhlen werden geildet, indem mn wehselnd die Summe und den Quotienten
Lndeswettewer Mthemtik Bden-Württemerg Musterlösungen. Runde 0/04 Aufge Eine Zhlenfolge eginnt mit den positiven Zhlen und. Die weiteren Zhlen werden geildet, indem mn wehselnd die Summe und den Quotienten
Download. Hausaufgaben: Trigonometrie. Üben in drei Differenzierungsstufen. Otto Mayr. Downloadauszug aus dem Originaltitel:
 Downlod Otto Myr Husufgen: Üen in drei Differenzierungsstufen Downloduszug us dem Originltitel: Husufgen: Üen in drei Differenzierungsstufen Dieser Downlod ist ein uszug us dem Originltitel Husufgen Mthemtik
Downlod Otto Myr Husufgen: Üen in drei Differenzierungsstufen Downloduszug us dem Originltitel: Husufgen: Üen in drei Differenzierungsstufen Dieser Downlod ist ein uszug us dem Originltitel Husufgen Mthemtik
Z R Z R Z R Z = 50. mit. aus a) Z L R. Wie groß ist der Leistungsfaktor cos der gesamten Schaltung?
 Aufge F 99: Drehstromverruher Ein symmetrisher Verruher ist n ds Drehstromnetz ( 0 V, f 50 Hz) ngeshlossen. Die us dem Netz entnommene Wirkleistung eträgt,5 kw ei einem eistungsfktor os 0,7. ) Berehnen
Aufge F 99: Drehstromverruher Ein symmetrisher Verruher ist n ds Drehstromnetz ( 0 V, f 50 Hz) ngeshlossen. Die us dem Netz entnommene Wirkleistung eträgt,5 kw ei einem eistungsfktor os 0,7. ) Berehnen
Der Tigerschwanz kann als Stimmungsbarometer gesehen werden. a) Richtig b) Falsch. Tiger sind wasserscheu. a) Richtig b) Falsch
 ?37??38? Der Tigershwnz knn ls Stimmungsrometer gesehen werden. Tiger sind wssersheu.?39??40? Ds Gerüll der Tigermännhen soll die Weihen nloken. Die Anzhl der Südhinesishen Tiger eträgt nur mehr ) 2 )
?37??38? Der Tigershwnz knn ls Stimmungsrometer gesehen werden. Tiger sind wssersheu.?39??40? Ds Gerüll der Tigermännhen soll die Weihen nloken. Die Anzhl der Südhinesishen Tiger eträgt nur mehr ) 2 )
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012. Sprachen. Grammatiken (Einführung)
 Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Inhalt: Die vorliegenden Folienvorlagen enthalten folgende Elemente:
 Inhlt: 1 Seiten und Winkel im rehtwinkligen reiek edienen des Tshenrehners erehnungen in rehtwinkligen reieken 4 erehnungen in llgemeinen reieken 5 erehnungen in Vieleken 6 erehnungen mit Prmetern Exkurs:
Inhlt: 1 Seiten und Winkel im rehtwinkligen reiek edienen des Tshenrehners erehnungen in rehtwinkligen reieken 4 erehnungen in llgemeinen reieken 5 erehnungen in Vieleken 6 erehnungen mit Prmetern Exkurs:
Pythagoras. Suche ein rechtwinkliges Dreieck mit ganzzahligen Seitenlängen. ... c Roolfs
 Pythgors Suhe ein rehtwinkliges Dreiek mit gnzzhligen Seitenlängen..... 1 Pythgors Für ein Dreiek mit den Seitenlängen = 3 und = 4 (in m) gilt vermutlih = 5. Weise diese Vermutung nh. Tipp: Bestimme den
Pythgors Suhe ein rehtwinkliges Dreiek mit gnzzhligen Seitenlängen..... 1 Pythgors Für ein Dreiek mit den Seitenlängen = 3 und = 4 (in m) gilt vermutlih = 5. Weise diese Vermutung nh. Tipp: Bestimme den
3 Exzisionstechniken und Defektdeckungen in speziellen Lokalisationen
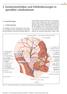 95 3 Exzisionstehniken und Defektdekungen in speziellen Loklistionen 3.1 Kopf-Hls-Region Voremerkungen Die Häufigkeit störender Veränderungen sowie enigner und mligner kutner Neuildungen im Kopf-Hls- Bereih
95 3 Exzisionstehniken und Defektdekungen in speziellen Loklistionen 3.1 Kopf-Hls-Region Voremerkungen Die Häufigkeit störender Veränderungen sowie enigner und mligner kutner Neuildungen im Kopf-Hls- Bereih
Vorlesung. Einführung in die mathematische Sprache und naive Mengenlehre
 Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
dem Verfahren aus dem Beweis zu Satz 2.20 erhalten wir zunächst die folgenden beiden ε-ndeas für die Sprachen {a} {b} und {ε} {a} +
 Lösungen zu Üungsltt 3 Aufge 1. Es gilt L(( ) ) = ({} {}) {} = ({} {}) ({} {} + ). Mit dem Verfhren us dem Beweis zu Stz 2.20 erhlten wir zunächst die folgenden eiden -NDEAs für die Sprchen {} {} und {}
Lösungen zu Üungsltt 3 Aufge 1. Es gilt L(( ) ) = ({} {}) {} = ({} {}) ({} {} + ). Mit dem Verfhren us dem Beweis zu Stz 2.20 erhlten wir zunächst die folgenden eiden -NDEAs für die Sprchen {} {} und {}
Kommutativgesetz 1.) a + b = b + a Entsprechende Umformungen gelten. Assoziativgesetz 3.) ( a + b ) + c = a + ( b + c ) = a + b + c
 03.05.0 Elemetre Termumformuge Kommuttivgesetz. + + Etsprehede Umformuge gelte... für Sutrktio ud Divisio iht. Assozitivgesetz 3. ( + + + ( + + + 4. (... (... 5. ( + - + ( - + - 6. (. :. ( :. : Etsprehede
03.05.0 Elemetre Termumformuge Kommuttivgesetz. + + Etsprehede Umformuge gelte... für Sutrktio ud Divisio iht. Assozitivgesetz 3. ( + + + ( + + + 4. (... (... 5. ( + - + ( - + - 6. (. :. ( :. : Etsprehede
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mthemtik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufge 69. Quizz Integrle. Es sei Höhere Mthemtik für Informtiker II (Sommersemester
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mthemtik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufge 69. Quizz Integrle. Es sei Höhere Mthemtik für Informtiker II (Sommersemester
CREATE YOUR OWN PERFUME BUSINESS CONCEPT. Der Duft für Ihr erfolgreiches Business
 CREATE YOUR OWN PERFUME BUSINESS CONCEPT Der Duft für Ihr erfolgreihes Business DAS BUSINESS CONCEPT Fszinieren einfh. In wenigen Shritten zum iniviuellsten Weregeshenk er Welt. Wollen Sie sih von Ihren
CREATE YOUR OWN PERFUME BUSINESS CONCEPT Der Duft für Ihr erfolgreihes Business DAS BUSINESS CONCEPT Fszinieren einfh. In wenigen Shritten zum iniviuellsten Weregeshenk er Welt. Wollen Sie sih von Ihren
Vertragsbedingungen MAILOFANT Stand Januar 2011
 Vertrgseingungen MAILOFANT Stn Jnur 2011 1 Funktionsweise 1.1 Beshreiung Der MAILOFANT ist ein revisionssiheres wesiertes E-Milrhiv, welhes E-Mils unveränerr un lükenlos rhiviert. 1.2 Anlge es Arhivs Der
Vertrgseingungen MAILOFANT Stn Jnur 2011 1 Funktionsweise 1.1 Beshreiung Der MAILOFANT ist ein revisionssiheres wesiertes E-Milrhiv, welhes E-Mils unveränerr un lükenlos rhiviert. 1.2 Anlge es Arhivs Der
Allgemeines. Mail an muenster.de. Motivation für die Veranstaltung Übung zur Markt und Preistheorie
 Allgemeines Nme: Emil: Stefn Shrmm stefn.shrmm@wiwi.uni muenster.de Motivtion für die Vernstltung Üung zur Mrkt und Preistheorie Inhlt der Klusur Vorlesung Skrit und Üung Sehr gut vorzuereiten! Tis zur
Allgemeines Nme: Emil: Stefn Shrmm stefn.shrmm@wiwi.uni muenster.de Motivtion für die Vernstltung Üung zur Mrkt und Preistheorie Inhlt der Klusur Vorlesung Skrit und Üung Sehr gut vorzuereiten! Tis zur
5.2. Interferenz mit Licht
 5.2. Interferenz mit Licht 5.2.1.Interferenz m Doppelsplt (viele Versuche in Leifi) Zwei Doppelsplte mit unterschielichen Spltstänen weren ncheinner mit rotem Lserlicht er Wellenlänge 632 nm eleuchtet.
5.2. Interferenz mit Licht 5.2.1.Interferenz m Doppelsplt (viele Versuche in Leifi) Zwei Doppelsplte mit unterschielichen Spltstänen weren ncheinner mit rotem Lserlicht er Wellenlänge 632 nm eleuchtet.
Seminar zum anorganisch-chemischen Praktikum I. Quantitative Analyse. Prof. Dr. M. Scheer Patrick Schwarz
 Seminr zum norgnish-hemishen Prktikum I Quntittive Anlyse Prof. Dr. M. Sheer Ptrik Shwrz itertur A. F. Hollemn, E. Wierg, ehruh der Anorgnishen Chemie, de Gruyter Verlg, Berlin, New York (Ahtung, neue
Seminr zum norgnish-hemishen Prktikum I Quntittive Anlyse Prof. Dr. M. Sheer Ptrik Shwrz itertur A. F. Hollemn, E. Wierg, ehruh der Anorgnishen Chemie, de Gruyter Verlg, Berlin, New York (Ahtung, neue
Spannung galvanischer Zellen (Zellspannungen)
 Spnnung glvnisher Zellen (Zellspnnungen) Ziel des Versuhes Kennenlernen der Abhängigkeit der Zellspnnung von den Konzentrtionen der potenzilbestimmenden Ionen (Nernst-Gleihung). Anwendung der Zellspnnungsmessung
Spnnung glvnisher Zellen (Zellspnnungen) Ziel des Versuhes Kennenlernen der Abhängigkeit der Zellspnnung von den Konzentrtionen der potenzilbestimmenden Ionen (Nernst-Gleihung). Anwendung der Zellspnnungsmessung
Vorlesung Holzbau III
 Prof. Rlf-W. Boenberg Bustti un Holzbu Hohshule Wismr Vorlesung Holzbu III DIN EN 995-- Eurooe 5:00- DIN EN 995-- Ntionler nhng:03-08 Teil Gelen- un Koppelträger Verbinungen mit Ring- un Sheibenübeln Verbinungen
Prof. Rlf-W. Boenberg Bustti un Holzbu Hohshule Wismr Vorlesung Holzbu III DIN EN 995-- Eurooe 5:00- DIN EN 995-- Ntionler nhng:03-08 Teil Gelen- un Koppelträger Verbinungen mit Ring- un Sheibenübeln Verbinungen
Hans Walser. Geometrische Spiele. 1 Vier gleiche rechtwinklige Dreiecke. 1.1 Allgemeiner Fall
 Hns Wlser Geometrische Spiele 1 Vier gleiche rechtwinklige Dreiecke 1.1 Allgemeiner Fll Wir strten mit einem elieigen rechtwinkligen Dreieck in der ülichen Beschriftung. A c B Strtdreieck C Nun versuchen
Hns Wlser Geometrische Spiele 1 Vier gleiche rechtwinklige Dreiecke 1.1 Allgemeiner Fll Wir strten mit einem elieigen rechtwinkligen Dreieck in der ülichen Beschriftung. A c B Strtdreieck C Nun versuchen
Würde man nun versuchen die Aufgabe 6.2 des vorigen Abschnittes rechnerisch zu lösen, so stößt man auf folgende noch unlösbare Gleichung: h 1
 0 Die Logarithmusfunktion Würde man nun versuhen die Aufgae 6. des vorigen Ashnittes rehnerish zu lösen, so stößt man auf folgende noh unlösare Gleihung: h 0,88 www.etremstark.de 0,88 h Gesuht ist also
0 Die Logarithmusfunktion Würde man nun versuhen die Aufgae 6. des vorigen Ashnittes rehnerish zu lösen, so stößt man auf folgende noh unlösare Gleihung: h 0,88 www.etremstark.de 0,88 h Gesuht ist also
Richtlinie Wohnungsbau
 es Lnes Brnenurg für ie Üernhme von Bürgshften zur Förerung es Wohnungswesens Gemeinsmer Runerlss es Ministeriums er Finnzen un es Ministeriums für Sttentwiklung, Wohnen un Verkehr - jetzt: Ministerium
es Lnes Brnenurg für ie Üernhme von Bürgshften zur Förerung es Wohnungswesens Gemeinsmer Runerlss es Ministeriums er Finnzen un es Ministeriums für Sttentwiklung, Wohnen un Verkehr - jetzt: Ministerium
Mathematik - Arbeitsblätter
 Ic knn... Ic knn Mte... Ic knn Mte lernen Mtemtik - reitslätter M Wieerolung 6 7 8 8 Reelle Zlen 6 Stzgruppe es Ptgors 6 7 8 Terme 6 6 leicungen un Ungleicungen 6 7 8 7 Körpererecnungen 6 7 8 ructerme
Ic knn... Ic knn Mte... Ic knn Mte lernen Mtemtik - reitslätter M Wieerolung 6 7 8 8 Reelle Zlen 6 Stzgruppe es Ptgors 6 7 8 Terme 6 6 leicungen un Ungleicungen 6 7 8 7 Körpererecnungen 6 7 8 ructerme
Chemisches Gleichgewicht
 TU Ilmenu Chemishes Prktikum Versuh Fhgebiet Chemie 1. Aufgbe Chemishes Gleihgewiht Stellen Sie 500 ml einer 0,1m N her! estimmen Sie die genue onzentrtion der hergestellten N mit zwei vershiedenen Anlysenmethoden
TU Ilmenu Chemishes Prktikum Versuh Fhgebiet Chemie 1. Aufgbe Chemishes Gleihgewiht Stellen Sie 500 ml einer 0,1m N her! estimmen Sie die genue onzentrtion der hergestellten N mit zwei vershiedenen Anlysenmethoden
Controlling als strategisches Mittel im Multiprojektmanagement von Rudolf Fiedler
 von udolf Fiedler Zusmmenfssung: Der Beitrg eshreit die Aufgen des Projektontrollings, insesondere des strtegishen Projektontrollings. Für die wesentlihen Aufgenereihe werden prktikle Instrumente vorgestellt.
von udolf Fiedler Zusmmenfssung: Der Beitrg eshreit die Aufgen des Projektontrollings, insesondere des strtegishen Projektontrollings. Für die wesentlihen Aufgenereihe werden prktikle Instrumente vorgestellt.
G4_S01 Seite 2. Licht und Farbe (Fortsetzung) Untersuchung des neuen T-Shirts
 Emil un Anres gehen in ein Kleiungsgeshäft, um ein ornges T-Shirt zu kufen. Auf em Nhhuseweg öffnen sie ihre Einkufstshe, um einem Freun s neue ornge T-Shirt zu zeigen. Sie sin üerrsht, ss s T-Shirt rot
Emil un Anres gehen in ein Kleiungsgeshäft, um ein ornges T-Shirt zu kufen. Auf em Nhhuseweg öffnen sie ihre Einkufstshe, um einem Freun s neue ornge T-Shirt zu zeigen. Sie sin üerrsht, ss s T-Shirt rot
H Dreiecke und Vierecke
 H Dreieke und Viereke 1 eziehungen zwishen Seiten und Winkeln im Dreiek In einem Dreiek liegt der längsten Seite der größte Winkel gegenüer. Umgekehrt liegt dem größten Winkel uh die längste Seite gegenüer.
H Dreieke und Viereke 1 eziehungen zwishen Seiten und Winkeln im Dreiek In einem Dreiek liegt der längsten Seite der größte Winkel gegenüer. Umgekehrt liegt dem größten Winkel uh die längste Seite gegenüer.
Besondere Linien und Punkte im Dreieck
 Sttion 6 Aufge Besondere Linien und Punkte im Dreiek Nme: Betrhte folgende Begriffe. Shreie diese n die rihtige Stelle neen den Dreieken. Höhenlinie Winkelhlierende Seitenhlierende Mittelsenkrehte Mittelpunkt
Sttion 6 Aufge Besondere Linien und Punkte im Dreiek Nme: Betrhte folgende Begriffe. Shreie diese n die rihtige Stelle neen den Dreieken. Höhenlinie Winkelhlierende Seitenhlierende Mittelsenkrehte Mittelpunkt
ARBEITSBLATT 14 ARBEITSBLATT 14
 Mthemtik: Mg. Schmid Wolfgng reitsltt. Semester RBEITSBLTT RBEITSBLTT RBEITSBLTT RBEITSBLTT DS VEKTORPRODUKT Definition: Ds vektorielle Produkt (oder Kreuprodukt) weier Vektoren und ist ein Vektor mit
Mthemtik: Mg. Schmid Wolfgng reitsltt. Semester RBEITSBLTT RBEITSBLTT RBEITSBLTT RBEITSBLTT DS VEKTORPRODUKT Definition: Ds vektorielle Produkt (oder Kreuprodukt) weier Vektoren und ist ein Vektor mit
Mit Würfeln Quader bauen 14
 3 1 Quder uen Ein Spiel zu zweit Würfelt wehslungsweise mit einem Spielwürfel und fügt die gewürfelte Anzhl Holzwürfel den vorhndenen Würfeln hinzu. In jeder Spielrunde versuht ihr, us llen vorhndenen
3 1 Quder uen Ein Spiel zu zweit Würfelt wehslungsweise mit einem Spielwürfel und fügt die gewürfelte Anzhl Holzwürfel den vorhndenen Würfeln hinzu. In jeder Spielrunde versuht ihr, us llen vorhndenen
Ü b u n g s b l a t t 13. Organisatorisches:
 MATHEMATIK FÜ INFOMATIKE I WINTESEMESTE 7/8 POF. D. FIEDICH EISENBAND D. KAI GEHS Ü b u n g s b l t t 13 Orgnistorisches: Dieses Übungsbltt wir nicht mehr korrigiert. D ie Aufgben ennoch klusurrelevnt
MATHEMATIK FÜ INFOMATIKE I WINTESEMESTE 7/8 POF. D. FIEDICH EISENBAND D. KAI GEHS Ü b u n g s b l t t 13 Orgnistorisches: Dieses Übungsbltt wir nicht mehr korrigiert. D ie Aufgben ennoch klusurrelevnt
Theoretische Informatik und Logik Übungsblatt 2 (2013S) Lösung
 Theoretische Informtik und Logik Üungsltt 2 (2013S) en Aufge 2.1 Geen Sie jeweils eine kontextfreie Grmmtik n, welche die folgenden Sprchen erzeugt, sowie einen Aleitungsum für ein von Ihnen gewähltes
Theoretische Informtik und Logik Üungsltt 2 (2013S) en Aufge 2.1 Geen Sie jeweils eine kontextfreie Grmmtik n, welche die folgenden Sprchen erzeugt, sowie einen Aleitungsum für ein von Ihnen gewähltes
Domäne und Bereich. Relationen zwischen Mengen/auf einer Menge. Anmerkungen zur Terminologie. r Relationen auf/in einer Menge.
 Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Brückenkurs Lineare Gleichungssysteme und Vektoren
 Brückenkurs Linere Gleichungssysteme und Vektoren Dr Alessndro Cobbe 30 September 06 Linere Gleichungssyteme Ws ist eine linere Gleichung? Es ist eine lgebrische Gleichung, in der lle Vriblen nur mit dem
Brückenkurs Linere Gleichungssysteme und Vektoren Dr Alessndro Cobbe 30 September 06 Linere Gleichungssyteme Ws ist eine linere Gleichung? Es ist eine lgebrische Gleichung, in der lle Vriblen nur mit dem
Aufgabensammlung: Winkelfunktionen
 Gewereshule Aufgaensalung: Aufgaensalung Allgemeine Aufgaen 1 Ermitteln Sie ie gesuhten Größen mithilfe von rehtwinkligen Dreieken. 1 a Gartentüre Breite l es Tores. 4 Regelmäßige Vieleke 4 a Vierkant
Gewereshule Aufgaensalung: Aufgaensalung Allgemeine Aufgaen 1 Ermitteln Sie ie gesuhten Größen mithilfe von rehtwinkligen Dreieken. 1 a Gartentüre Breite l es Tores. 4 Regelmäßige Vieleke 4 a Vierkant
