Die Schnittgrößen haben wir ja schon kennengelernt. Sie seien hier noch einmal zusammengefasst:
|
|
|
- Ludo Schmitz
- vor 6 Jahren
- Abrufe
Transkript
1 Der gerade Stab Die Schnittgrößen haben wir ja schon kennengelernt. Sie seien hier noch einmal zusammengefasst: N Normalkraft Q Querkraft M b Biegemoment M T Torsionsmoment Die Frage lautet nun, welche Spannungen und welche Verformungen durch diese Schnittgrößen hervorgerufen werden. Das soll in den folgenden Kapiteln erläutert werden.
2 Zusammenhang Schnittgrößen und Spannungen: uf einer Schnittfläche normal zur x-chse sieht man Spannungsvektoren der Form σ x = σ x e x + τ xy e y + τ xz e z Die resultierende Wirkung dieser Spannungsvektoren schlägt sich im resultierenden Schnittkraftvektor R(x) sowie im resultierenden Schnittmoment M(x) nieder. N(x) = Q y (x) = σ x (x, y, z)dydz τ xy (x, y, z)dydz R = σ x (x, y, z)d Q z (x) = τ xz (x, y, z)dydz M = r σ x (x, y, z) d M x (x) = yτ xz (x, y, z) zτ xy (x, y, z) dydz M y (x) = zσ x (x, y, z)dydz mit r = ye y + ze z M z (x) = yσ x (x, y, z)dydz
3 Beanspruchung durch Normalkraft Reine Zug-/Druckbelastung hat einen einachsigen Spannungszustand σ x zur Folge. Bei konstantem Querschnitt (x)=konst. kann man davon ausgehen, dass σ x im ganzen Querschnitt konstant ist: σ x = N, alle anderen Spannungen = 0. Nach dem Hookeschen Gesetz gilt (für T = 0): ε x = σ x E = N E, ε y = ε z = ν σ x E E Dehnsteifigkeit.
4 Gesucht ist nun die Verschiebungslinie u x für den nachfolgend skizzierten Stab: N x + dx = N + dn dx dx Darin ist p(x) eine in x-richtung verteilte Last von der Dimension [N/m]. Setzen wir ein differenziell kleines Stabelement der Länge dx ins Gleichgewicht, so ergibt sich: N + N + dn dx + p x dx = 0 p x dx = dn dx σ x x = N x = Eε x also dσ x dx = 1 dn dx = E dε x dx Den Zusammenhang zwischen Verzerrungen und Verschiebungen kennen wir bereits: ε x = du dx Somit folgt: 1 p x = E d2 u dx 2 d 2 u p x = dx2 E Differentialgleichung der Verschiebungslinie
5 Beispiel: Seil unter Eigengewicht, Dichte ρ, Länge l, konstante Querschnittsfläche geg.:ρ, l, E, ges.: u x, σ x p x = ρg x, σ max d 2 u dx 2 = ρg E du dx = ρg E x + C 1 u x = ρg E x C 1x + C 2 Die Integrationskonstanten folgen aus den Randbedingungen: u x = 0 = 0 C 2 = 0 u = du dx x = l u x = ρg E = 0 C 1 = ρgl E x2 lx 2 = ρg x 2l x 2E σ x x = Eε x x = ρg(l x) σ max = σ x x = 0 = ρgl Bei Vorgabe der Zugfestigkeit R m kann man eine nur vom Seilwerkstoff abhängende Reißlänge l R berechnen: l R = R m ρg
6 Beanspruchung auf Biegung Wir betrachten zunächst den Fall der reinen Biegung Voraussetzungen für reine Biegung: 1) Die Stabachse ist gerade (x-chse) 2) Der Stab hat konstanten Querschnitt 3) Die Querschnitte sind symmetrisch zur x-z Ebene 4) Die y-chse geht durch den geometrische Schwerpunkt der Querschnitte 5) Normalkraft N = 0 6) Torsionsmoment M x = 0 7) Biegemomentenkomponente M z = 0 8) Querkraftkomponente Q y = 0 9) Querkraftkomponente Q z = 0 10) Biegemomentenkomponente M y ist konstant. us den Voraussetzungen 3 und 4 folgt: x, y, z. Trägheitshauptachsen
7 Wenn obige Voraussetzungen erfüllt sind, dann lassen sich folgende ussagen treffen: I. Die Stabachse wird gebogen, aber nicht gedehnt. II. III. Beweis: lle Querschnitte bleiben eben und normal auf die Stabachse. Er treten nur Normalspannungen auf, aber keine Schubspannungen. Bei reiner Biegung ist jeder beliebige bschnitt des Stabes ein Spiegelbild seiner Nachbarn, somit müssen die Querschnittsebenen Symmetrieebenen sein und dies auch nach Deformation bleiben. Das ist nur möglich, wenn ussage II. gilt. Setzt man die einzelnen verformten bschnitte zusammen, so ergibt sich infolgedessen ein Kreisbogen mit Radius ρ.
8 Betrachten wir einen bschnitt der Länge dx im Detail: Gesucht wird nun ein Zusammenhang zwischen dem Krümmungsradius ρ und dem Biegemoment M y. usgehend von einer zunächst noch unbekannten Lage der ungedehnten Faser als Bezugsachse gilt: ds 0 = dx = ρdφ ds z = ρ + z dφ ε x z = ds(z) ds 0 ds 0 = ρ + z dφ ρdφ ρdφ = z ρ σ x = Eε x = E z ρ us Voraussetzung 5) ergibt sich N = σ x d = E ρ z d = 0 Definition des Flächen-SP! neutrale Faser (wird gebogen, aber nicht gedehnt) Das Integral verschwindet nur dann, wenn z vom geometrischen Schwerpunkt der Querschnitte ausgehend gezählt wird. Das definiert aber laut Voraussetzung 4) die Lage der x-chse. Damit ist die Stabachse die neutrale Faser und ussage I. bewiesen.
9 Es entstehen also Normalspannungen σ x in x-richtung, die über die Höhe z linear verteilt sind: Druck M y = 1 ρ = M y EJ y zσ x d = E ρ Zug z 2 d J y... FTRM bzgl. Schwerachse EJ y... Biegesteifigkeit [N/m²] Bei reiner Biegung sind, wie gesagt, alle Querschnitte Symmetrieebenen. Jede Spannungskomponente auf dem linken Schnittufer hat eine gespiegelte Entsprechung auf dem rechten Schnittufer. Beim Zusammenfügen der Schnittufer müssen diese nach außen hin verschwinden. Das ist aber nur dann möglich, wenn die Spannungsvektoren normal auf die Symmetrieebene stehen, also keine y- oder z-komponente haben. Daraus folgt, dass τ xy sowie τ xz null sein müssen. ussage III. Das ist auch im Einklang mit den Voraussetzungen 6), 8) und 9) Q y = τ xy d = 0 Mit σ x = Eε x = E z ρ σ x z = M y J y z wird daraus Q z = τ xz d = 0 M x = yτ xz zτ xy d = 0
10 Bei Vorliegen einer Querkraft Q z (x) und nicht konstantem Querschnitt sind die Voraussetzungen 2), 9), 10) nicht mehr erfüllt. Die Querkraft erzeugt Schubspannungen und eine Querschnittsverwölbung, die ussagen I., II. und III. gelten also nicht mehr exakt. Im Rahmen der Technischen Biegelehre geht man aber von der Bernoulli Hypothese aus: Solange die betrachteten Stäbe als schlank angesehen werden dürfen (d.h. Querschnittsabmessungen sind klein gegen die Länge), kann man näherungsweise davon ausgehen, dass die Querschnitte eben und normal zur Stabachse bleiben. Somit kann man schreiben: 1 ρ x = M y x EJ y x σ x x, z = M y x J y x z fundamental!!
11 Für die Trägerdimensionierung sind in erster Linie die Spannungen in den äußeren Fasern des Stabs interessant. Setzt man die Randfaserabstände e 1, e 2 in (*) ein, so erhält man die Extremwerte für die Biegespannungen σ 1, σ 2 : obere Randfaser σ 2 = M y J y e 2 untere Randfaser σ 1 = M y J y e 1 Definition: W y,1 = J y e 1, W y,2 = J y e 2. Widerstandsmoment [m³] also: σ 1 = M y W y,1, σ 2 = M y W y,2 wesentliche Formel zur Dimensionierung von Trägern!!
12 Beispiel: Dimensionierung eines Trägers der Länge l, Belastung P und q 0 zufolge Eigengewicht Geg.: P = 36kN σ zul = 140N/mm² l = 6m Ges.: IPE Träger lt. Norm, siehe beigefügtes Tabellenblatt = B = P 2 + q 0 l 2 M y,max = Pl 4 + q l W y,erf = M y,max σ zul = Pl 4σ zul + q 0l 2 8σ zul noch unbekannt Pl = = mm 3 = 386 cm 3 4σ zul chtung: I-Träger werden normalerweise stehend, d.h. mit Steg in Lastrichtung eingebaut. Steg Flansch Biegeachse
13 Warmgewalzte, mittelbreite I-Träger, IPE-Reihe nach DIN 1025 Blatt 5 (uszug) Maße für Kurzzeichen Querschnitwicht Ge- G Für die Biegeachse h b s t r I x W x i x I y W y i y x-x IPE mm mm mm mm mm cm 2 kg/m cm 4 cm 3 cm cm 4 cm 3 cm cm 3 cm ,8 5,2 5 7,64 6,0 80,1 20,0 3,24 8,49 3,69 1,05 11,6 6, ,1 5,7 7 10,3 8, ,2 4,07 15,9 5,79 1,24 19,7 8, ,4 6,3 7 13,2 10, ,0 4,90 27,7 8,65 1,45 30,4 10, ,7 6,9 7 16,4 12, ,3 5,74 144,9 12,3 1,65 44,2 12, ,0 7,4 9 20,1 15, ,58 68,3 16,7 1,84 61,9 14, ,3 8,0 9 23,9 18, , ,2 2,05 83,2 15, ,6 8, ,5 22, , ,5 2, , ,9 9, ,4 26, , ,3 2, , ,2 9, ,1 30, , ,3 2, , ,6 10, ,9 36, , ,2 3, , ,1 10, ,8 42, , ,5 3, , ,5 11, ,6 49, , ,5 3, , ,0 12, ,7 57, , , , ,6 13, ,5 66, , , , ,4 14, ,8 77, , , , ,2 16, , , , , ,1 17, , , , ,0 19, , , ,4 y-y S x s x I W i S x s x Flächenmoment 2. Grades Widerstandsmoment Trägheitsradius Flächenmoment 1. Grades des halben Querschnitts = I x /S x, bstand Druck- und Zugmittelpunkt
14 gewählt: IPE 270: W y,1 = W y,2 = W y = 429 cm 3 q 0 = 36.1kg/m g = 354 N/m = N/mm q 0 l 2 = = mm 3 = 11 cm 3 8σ zul W y,erf = = 397 cm 3 < 429 cm 3 Zum Vergleich, Einbau um 90 verdreht: Biegeachse W y = 62.2 cm 3, also nicht zulässig
15 Differentialgleichung der Biegelinie Mit Hilfe der Differentialgeometrie kann man zeigen: 1 ρ x = w 1 + w 2 ³ w w = dw dx, w = d2 w dx 2 zur Erinnerung: 1 ρ = M y EJ y w = d2 w dx 2 = M y x EJ y x Differentialgleichung der Biegelinie (2. Ordnung) Die Durchbiegung w x folgt dann durch 2-malige Integration. Die dabei auftretenden Integrationskonstanten können durch Rand- und Übergangsbedingungen bestimmt werden.
16 Biegelinie zufolge einer Temperaturverteilung Wir beschränken uns in weiterer Folge auf lineare Temperaturverteilungen über die Trägerhöhe. ds o = dx + α T o T ref dx ds u = dx + α T u T ref dx ds u dso = (r + h)dφ rdφ α T u T o dx = hdφ dφ dx = α T u T 0 = αθ h dφ dx = αθ = 1 ρ w ρdφ = dx w = αθ zufolge Temperaturmoment Definition: Θ = T u T 0 h Temperaturmoment [K/m]
17 durch Superposition ergibt sich d 2 w dx 2 = M y x EJ y x + αθ x Differentialgleichung der Biegelinie (inkl. Temperaturmoment) Bei statisch bestimmter Lagerung entstehen durch eine linear Temperaturverteilung über den Querschnitt keine zusätzlichen Spannungen. Bei allgemeiner Temperaturverteilung T x, y, z kann man Θ x wie folgt berechnen: Θ x = 1 J y x zt x, y, z d Im llgemeinen treten aber dann auch bei statisch bestimmter Lagerung Spannungen auf.
18 Beispiel: Biegelinie eines Trägers der Länge l, Belastung P und Streckenlast q 0, Biegesteifigkeit EJ y = B = P 2 + q 0 l 2 0 x l 2 : M x = x q 0 x 2 2 = P 2 + q 0 l 2 x q x w = M y x EJ y EJ y w = x + q 0 x 2 EJ y w = x2 2 + q x C 1 2 dx dx EJ y w = x3 6 + q x C 1x + C 2
19 Die Integrationskonstanten C 1 und C 2 folgen aus Randbedingungen: (1) w x = 0 = 0 C 2 = 0 (2) w x = l/2 = 0 = l2 + q l C 48 1 C 1 = l2 q 8 0 l 3 48 EJ y w = x3 6 + q x 4 l x q l 3 l2 0 x = x 48 8 x2 6 + q 0x x3 24 l3 48 w x = 1 48EJ y P + q 0 l x 3l 2 + 4x 2 + q 0 x 2x 3 l 3 w max = w x = l/2 = 1 P + q 48EJ 0 l l 3 3 y 8 q 0l 4 = Pl3 + 5 q 0 l 4 48EJ y 384 EJ y Nm 3 Nm ;2 m 4 = m uswertung für IPE 270, l =6m, P =36kN, E =210GPa: w max = = 13.8mm zufolge P zufolge q 0
20 Beispiel: unsymmetrisch belasteter Träger Geg.: P, a, b, EJ y Ges.: Biegelinie = P b a + b B = P a a + b Bereich I: 0 x a M I x = x = P b a + b x EJ y w I = P b a + b x EJ y w I = P b x 2 a + b 2 + C 1 EJ y w I = P b x 3 a + b 6 + C 1x + C 2 Bereich II: a x a + b M II x = x P x a = Pa P a a + b x EJ y w II = P a x Pa a + b EJ y w II = P a x 2 a + b 2 Pax + D 1 EJ y w II = P a x 3 x2 Pa a + b D 1x + D 2
21 Die Rand- und Übergangsbedingungen lauten: (1) w I x = 0 = 0 (2) w II x = a + b = 0 (3) w I x = a = w II x = a (4) w I x = a = w II x = a Randbedingungen Übergangsbedingungen (1) C 2 = 0 (2) 0 = Pa a:b 2 + D 1 (a + b) + D 2 3 a 3 b (3) P + C 6 a:b 1a + C 2 = P P 6 a:b 2 a3 + D 1 a + D 2 a 4 C 1, C 2, D 1, D 2 a 2 b a 3 (4) P + C 2 a:b 1 = P 2 a:b Pa2 + D 1
22 Beispiel: Statisch unbestimmt gelagerter Träger Geg.: q 0, l, EJ y Ges.: uflagereaktionen + B q 0 l = 0 B = q 0 l M x = x q 0 x 2 2 M E + l q 0 l 2 2 = 0 M l 2 E = l + q 0 2
23 EJ y w = x + q 0 x 2 EJ y w = x2 2 + q x C 1 EJ y w = x3 6 + q x C 1x + C 2 2 RB: w x = 0 = 0 0 = C 2 w x = l w x = l = 0 0 = l3 6 + q 0 = 0 0 = l2 2 + q 0 l C 1l l C 1 1 l 0 = 2 6 l q 0l 4 = 3 8 q 0l B = 5 8 q 0l M E = 1 8 q 0l 2
24 Beispiel: Beidseitig eingespannter Träger, nur durch ein Temperaturmoment belastet M x = M E = const.
25 EJ y w = M E EJ y αθ mit Θ = T u;t o h EJ y w = M E x EJ y αθx + C 1 EJ y w = M E x 2 2 EJ yαθ x2 2 + C 1x + C 2 RB: (1) w x = 0 = 0 C 2 = 0 (2) w x = 0 = 0 C 1 = 0 (3) w x = l = 0 M E + EJ y αθ l = 0 M E = EJ y αθ w x = 1 EJ y x 2 2 M E + EJ y αθ = 0 Stab bleibt gerade, aber nicht spannungsfrei. σ b = ± M E h J y 2 = ± EJ yαθh = ± 1 2J y 2 EαΘh nmerkung: ls RB (3) hätte man auch w x = l = 0 oder w x = l/2 = 0 anschreiben können. Man wäre auf dieselbe Lösung gekommen.
26 Erweiterungen usgehend von der Diff.-gl. der Biegelinie 2. Ordnung (ohne Berücksichtigung eines Temperaturmoments) und den bereits bekannten Beziehungen zwischen den Schnittgrößen des geraden Stabs und einer Streckenlast kann folgender Zusammenhang abgeleitet werden. EJ y (x)w = M y x d dx d dx EJ y(x) d²w dx² = dm(x) dx = Q x d dx d2 dx 2 EJ y(x) d2 w dx 2 = dq x dx = q x also für EJ y = konstant gilt dann: d 2 dx 2 EJ y(x) d2 w dx 2 = q x EJ y d 4 w dx 4 = EJ yw IV = q x Differentialgleichung der Biegelinie 4. Ordnung
27 Die DG 4. Ordnung eignet sich insbesondere für die Berechnung der Biegelinie eines Einfeldträgers mit verteilter Last: Man erhält dann w x durch 4-malige Integration. Die damit einhergehenden 4 Integrationskonstanten müssen wieder über Rand- und ggf. Übergangsbedingungen bestimmt werden. z.b. für den dargestellten Träger: (1) w x = 0 = 0 (2) w x = l = 0 (3) w x = 0 = 0 M x = 0 = 0 (4) w x = l = 0 M x = l = 0 wesentliche RB natürliche RB
28 Biegung mit Längskraft Die Lösungen für einen durch ein Normalkraft N x und ein Biegemoment M y können gemäß dem Superpositionsprinzip überlagert werden. x belasteten Stab σ x x, z = M y x J y x N x z + x Das führt zu einer Verschiebung der neutralen Faser. Neutrale Faser σ x = 0 Diese Verschiebung kann so groß sein, dass die neutrale Faser aus dem Querschnitt herausgeschoben wird. Dadurch treten im gesamten Querschnitt nur noch Zugoder nur noch Druckspannungen auf, es findet also kein Vorzeichenwechsel von σ x innerhalb des Querschnitts statt. Diesen Effekt macht man sich beispielsweise bei Spannbeton zu Nutze. Beton Stahlseil
29 Biegung von Stäben mit beliebigem Querschnitt Wir fordern nun nur noch, dass die Stabachse gerade ist und den geometrischen Schwerpunkt aller Querschnitte verbindet. Die y- sowie die z-chse gehen somit durch diesen Schwerpunkt, haben aber ansonsten eine allgemeine Lage, sind daher i.a. keine Trägheitshauptachsen. Ebenso erlauben wir eine allgemeine Belastung zufolge N x, M y x, M z x. Querkräfte und Torsionsmoment dürfen ebenfalls ungleich null sein, spielen aber in dieser Betrachtung keine Rolle. usgangspunkt: us geometrischen Gründen sind die Dehnungen linear über den Querschnitt verteilt, daher sind bei homogenen Trägern und bei Gültigkeit des Hookeschen Gesetzes auch die Spannungen linear verteilt. σ x x, y, z = C 0 x + C 1 x y + C 2 x z Zur Erinnerung: N x = σ x x, y, z d = C 0 x d + C 1 x yd + C 2 x zd M y x = zσ x x, y, z d = C 0 x zd + C 1 x zyd + C 2 x z²d M z x = yσ x x, y, z d = C 0 x yd C 1 x y 2 d C 2 x yzd (1) (2) (3)
30 Es treten wieder bereits vertraute Integrale auf: yd = zd = 0 weil der Koordinatenursprung voraussetzungsgemäß im Schwerpunkt liegt. y²d = J z z²d = J z zyd = yzd = J yz N x = C 0 x M y x = C 1 x J yz + C 2 x J y M z x = C 1 x J z C 2 x J yz (1) (2) (3) 3 Gleichungen für C 0 x, C 1 x, C 2 x Damit kann die Biegespannungsverteilung allgemein angeschrieben werden: N x σ x x, y, z = J yzm y x + J y M z x 2 y + J zm y x + J yz M z x J y J z J yz J y J z J yz 2 z uch bei reiner Belastung in der xz Ebene (also M z x = 0) tritt also ein Spannungsgradient in y- Richtung auf. Darüberhinaus kommt es i.a. zu einer Biegung aus der xz-ebene heraus. Man spricht daher von schiefer Biegung.
31 Für den Spezialfall, dass es sich bei y und z um Trägheitshauptachsen handelt, wird daraus die leichter zu merkende Formel: σ x x, y, z = N x M z x J z y + M y x J y z Die Trägerdurchbiegung hat dann ebenfalls eine zweite Komponente v(x) in y-richtung. Diese kann in völlig analoger Weise zur z-komponente w(x) aus einer Differentialgleichung berechnet werden. d²w dx 2 = M y x EJ y x + αθ y x d²v dx 2 = + M z x EJ z x + αθ z x Θ y Temperaturmoment um die y-chse: Θ z Temperaturmoment um die z-chse: Θ y x = 1 J y x Θ z x = 1 J z x zt x, y, z d yt x, y, z d
32 Wir betrachten nun den Fall eines durch eine Kraft in x-richtung belasteten Stabs. Fällt die Wirkungslinie dieser Kraft P nicht mit der Stabachse (also der x-chse) zusammen, so resultieren daraus neben der Normalkraft N i.a. auch noch die Biegemomente M y und M z. N = P M y = Pz P M z = Py P neutrale Faser σ x = 0 Die neutrale Faser ist durch folgende Geradengleichung definiert: σ x x, y, z = N M z y + M y z = 0 y = M yj z z + NJ z J z J y M z J y M z = z PJ z z J z y P J y y P
33 Insbesondere im Bauingenieurwesen ist es häufig gefordert, dass im gesamten Querschnitt die Normalspannungen σ x ein einheitliches Vorzeichen besitzen. Die Frage lautet nun, innerhalb welchen Bereichs der ngriffspunkt einer äußeren Längskraft liegen muss, damit diese Vorgabe erfüllt wird. Man nennt diesen Bereich dann die Kernfläche des Profils. Beispiel: Kernfläche eines Rechteckprofils Beispiel: Kernfläche eines Kreisprofils
Herbst 2010 Seite 1/14. Gottfried Wilhelm Leibniz Universität Hannover Klausur Technische Mechanik II für Maschinenbau. Musterlösungen (ohne Gewähr)
 Seite 1/14 rage 1 ( 2 Punkte) Ein Stab mit kreisförmiger Querschnittsfläche wird mit der Druckspannung σ 0 belastet. Der Radius des Stabes ist veränderlich und wird durch r() beschrieben. 0 r () Draufsicht:
Seite 1/14 rage 1 ( 2 Punkte) Ein Stab mit kreisförmiger Querschnittsfläche wird mit der Druckspannung σ 0 belastet. Der Radius des Stabes ist veränderlich und wird durch r() beschrieben. 0 r () Draufsicht:
Leseprobe. Biegung. Kirbs TECHNISCHE MECHANIK. Studienbrief HDL HOCHSCHULVERBUND DISTANCE LEARNING. 3. Auflage 2008
 Leseprobe Kirbs Biegung TECHNISCHE MECHANIK Studienbrief -5-97 3. Auflage 8 HDL HOCHSCHULVERBUND DISTANCE LEARNING Verfasser: Prof. Dr.-Ing. Jörg Kirbs Professor für Technische Mechanik / Festigkeitslehre
Leseprobe Kirbs Biegung TECHNISCHE MECHANIK Studienbrief -5-97 3. Auflage 8 HDL HOCHSCHULVERBUND DISTANCE LEARNING Verfasser: Prof. Dr.-Ing. Jörg Kirbs Professor für Technische Mechanik / Festigkeitslehre
Beispiele für gerade (einachsige) und schiefe (zweiachsige) Biegung: Betrachtung der Kräfte und Momente, die auf ein Balkenelement der Länge wirken:
 UNIVERITÄT IEGEN B 10 Lehrstuhl für Baustatik - chiefe Biegung - chiefe Biegung Kommt es bei einem Balken nicht nur u Durchbiegungen w in -Richtung, sondern auch u Durchbiegungen v in -Richtung, so spricht
UNIVERITÄT IEGEN B 10 Lehrstuhl für Baustatik - chiefe Biegung - chiefe Biegung Kommt es bei einem Balken nicht nur u Durchbiegungen w in -Richtung, sondern auch u Durchbiegungen v in -Richtung, so spricht
Lösungen TM I Statik und Festigkeitslehre
 Technische Mechanik I L Lösungen TM I Statik und Festigkeitslehre Modellbildung in der Mechanik N Pa (Pascal). m.4536kg.38slug [a] m, [b] dimensionslos, [c] m, [d] m Dichte: kgm 3.94 3 slugft 3 Geschwindigkeit:
Technische Mechanik I L Lösungen TM I Statik und Festigkeitslehre Modellbildung in der Mechanik N Pa (Pascal). m.4536kg.38slug [a] m, [b] dimensionslos, [c] m, [d] m Dichte: kgm 3.94 3 slugft 3 Geschwindigkeit:
Grundfachklausur Teil 2 / Statik II
 Technische Universität Darmstadt Institut für Werkstoffe und Mechanik im Bauwesen Fachgebiet Statik Prof. Dr.-Ing. Jens Schneider Grundfachklausur Teil 2 / Statik II im Sommersemester 204, am 08.09.204
Technische Universität Darmstadt Institut für Werkstoffe und Mechanik im Bauwesen Fachgebiet Statik Prof. Dr.-Ing. Jens Schneider Grundfachklausur Teil 2 / Statik II im Sommersemester 204, am 08.09.204
Spannungszustand
 1. Spannungszustand 1.1 Spannungsvektor und Spannungstensor 1.2 Hauptspannungen 1.3 Mohrsche Spannungskreise 1.4 Fließbedingung 1.5 Gleichgewichtsbedingungen 1.1-1 1.1 Spannungsvektor und Spannungstensor
1. Spannungszustand 1.1 Spannungsvektor und Spannungstensor 1.2 Hauptspannungen 1.3 Mohrsche Spannungskreise 1.4 Fließbedingung 1.5 Gleichgewichtsbedingungen 1.1-1 1.1 Spannungsvektor und Spannungstensor
Statik- und Festigkeitslehre I
 05.04.2012 Statik- und Festigkeitslehre I Prüfungsklausur 2 WS 2011/12 Hinweise: Dauer der Klausur: Anzahl erreichbarer Punkte: 120 Minuten 60 Punkte Beschriften Sie bitte alle Seiten mit und Matrikelnummer.
05.04.2012 Statik- und Festigkeitslehre I Prüfungsklausur 2 WS 2011/12 Hinweise: Dauer der Klausur: Anzahl erreichbarer Punkte: 120 Minuten 60 Punkte Beschriften Sie bitte alle Seiten mit und Matrikelnummer.
STATISCHE BERECHNUNG "Traverse Typ F32" Länge bis 10,00m Taiwan Georgia Corp.
 Ing. Büro für Baustatik 75053 Gondelsheim Tel. 0 72 52 / 9 56 23 Meierhof 7 STATISCHE BERECHNUNG "Traverse Typ F32" Länge bis 10,00m Taiwan Georgia Corp. Die statische Berechnung ist ausschließlich aufgestellt
Ing. Büro für Baustatik 75053 Gondelsheim Tel. 0 72 52 / 9 56 23 Meierhof 7 STATISCHE BERECHNUNG "Traverse Typ F32" Länge bis 10,00m Taiwan Georgia Corp. Die statische Berechnung ist ausschließlich aufgestellt
7.2 Dachverband Achse Pos A1
 7.2 Dachverband Achse 1 + 2 Pos A1 Dieser neukonstruierte Dachverband ersetzt den vorhandenen alten Verband. Um die Geschosshöhe der Etage über der Zwischendecke einhalten zu können, wird er auf dem Untergurt
7.2 Dachverband Achse 1 + 2 Pos A1 Dieser neukonstruierte Dachverband ersetzt den vorhandenen alten Verband. Um die Geschosshöhe der Etage über der Zwischendecke einhalten zu können, wird er auf dem Untergurt
STATISCHE BERECHNUNG "Traverse Typ Foldingtruss F52F" Länge bis 24,00m Elementlängen 0,60m - 0,80m - 1,60m - 2,40m Taiwan Georgia Corp.
 Ing. Büro für Baustatik 75053 Gondelsheim Tel. 0 72 52 / 9 56 23 Meierhof 7 STATISCHE BERECHNUNG "Traverse Typ Foldingtruss F52F" Länge bis 24,00m Elementlängen 0,60m - 0,80m - 1,60m - 2,40m Taiwan Georgia
Ing. Büro für Baustatik 75053 Gondelsheim Tel. 0 72 52 / 9 56 23 Meierhof 7 STATISCHE BERECHNUNG "Traverse Typ Foldingtruss F52F" Länge bis 24,00m Elementlängen 0,60m - 0,80m - 1,60m - 2,40m Taiwan Georgia
l p h (x) δw(x) dx für alle δw(x).
 1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
Berechnung von Trägerrosten mittels Kraftgrößenmethode
 Berechnung von Trägerrosten mittels Kraftgrößenmethode Bachelor Projekt eingereicht am Institut für Baustatik der Technischen Universität Graz im Oktober 2010 Verfasser: Betreuer: Novak Friedrich Dipl.-Ing.
Berechnung von Trägerrosten mittels Kraftgrößenmethode Bachelor Projekt eingereicht am Institut für Baustatik der Technischen Universität Graz im Oktober 2010 Verfasser: Betreuer: Novak Friedrich Dipl.-Ing.
2.1.8 Praktische Berechnung von statisch unbestimmten, homogenen
 Inhaltsverzeichnis 1 Einleitung... 1 1.1 Aufgaben der Elastostatik.... 1 1.2 Einige Meilensteine in der Geschichte der Elastostatik... 4 1.3 Methodisches Vorgehen zur Erarbeitung der vier Grundlastfälle...
Inhaltsverzeichnis 1 Einleitung... 1 1.1 Aufgaben der Elastostatik.... 1 1.2 Einige Meilensteine in der Geschichte der Elastostatik... 4 1.3 Methodisches Vorgehen zur Erarbeitung der vier Grundlastfälle...
Mathematische Methoden für Informatiker
 Prof. Dr. www.math.tu-dresden.de/ baumann 8.12.2016 20. Vorlesung Differentialgleichungen n-ter Ordnung Lösung einer Differentialgleichung Veranschaulichung der Lösungsmenge Anfangswertprobleme Differentialgleichungen
Prof. Dr. www.math.tu-dresden.de/ baumann 8.12.2016 20. Vorlesung Differentialgleichungen n-ter Ordnung Lösung einer Differentialgleichung Veranschaulichung der Lösungsmenge Anfangswertprobleme Differentialgleichungen
1 Technische Mechanik 2 Festigkeitslehre
 Russell C. Hibbeler 1 Technische Mechanik 2 Festigkeitslehre 5., überarbeitete und erweiterte Auflage Übersetzung aus dem Amerikanischen: Nicoleta Radu-Jürgens, Frank Jürgens Fachliche Betreuung und Erweiterungen:
Russell C. Hibbeler 1 Technische Mechanik 2 Festigkeitslehre 5., überarbeitete und erweiterte Auflage Übersetzung aus dem Amerikanischen: Nicoleta Radu-Jürgens, Frank Jürgens Fachliche Betreuung und Erweiterungen:
MEAU 3. Klasse - Mechanik Schritt für Schritt 2.05
 MEAU 3. Klasse - Mechanik Schritt für Schritt.05 1 Wiederholung... 5 1.1 Wiederholung Festigkeitslehre... 5 1.1.1 Beanspruchung auf Zug... 5 1.1.1.1 Die Verlängerung Δl und die Dehnung ε (Epsilon)... 5
MEAU 3. Klasse - Mechanik Schritt für Schritt.05 1 Wiederholung... 5 1.1 Wiederholung Festigkeitslehre... 5 1.1.1 Beanspruchung auf Zug... 5 1.1.1.1 Die Verlängerung Δl und die Dehnung ε (Epsilon)... 5
Einfache Spannungsnachweise
 luminium-zentrale Merkblatt K5 Einfache Spannungsnachweise Einfache Spannungsnachweise Inhalt 1. Einführung Seite 0 2. Rechenbeispiele Seite 04. Biegemomente und Durchbiegungen Tabelle 1 Seite 08 4. Tabellen
luminium-zentrale Merkblatt K5 Einfache Spannungsnachweise Einfache Spannungsnachweise Inhalt 1. Einführung Seite 0 2. Rechenbeispiele Seite 04. Biegemomente und Durchbiegungen Tabelle 1 Seite 08 4. Tabellen
Institut für Maschinenelemente und Konstruktionstechnik Klausur KT1 (alt KT2) SS 2011 Dr.-Ing. S. Umbach I
 Klausur KT1 (alt KT) SS 011 Dr.-Ing. S. Umbach I 30.08.011 Name, Vorname: Unterschrift: Matrikel- Nr.: Klausurbedingungen: Zugelassene Hilfsmittel sind dokumentenechtes Schreibzeug und Taschenrechner.
Klausur KT1 (alt KT) SS 011 Dr.-Ing. S. Umbach I 30.08.011 Name, Vorname: Unterschrift: Matrikel- Nr.: Klausurbedingungen: Zugelassene Hilfsmittel sind dokumentenechtes Schreibzeug und Taschenrechner.
4. Differentialgleichungen
 4. Differentialgleichungen Prof. Dr. Erich Walter Farkas 10.11.2011 Seite 1 Einleitung Viele in der Natur stattfindende Vorgänge können durch sogenannte Differentialgleichungen beschrieben werden. Unter
4. Differentialgleichungen Prof. Dr. Erich Walter Farkas 10.11.2011 Seite 1 Einleitung Viele in der Natur stattfindende Vorgänge können durch sogenannte Differentialgleichungen beschrieben werden. Unter
Hochschule Wismar University of Technology, Business and Design
 achgebiet austatik und Holzbau Prof. Ralf-W. oddenberg Hochschule Wismar University of Technology, usiness and esign Prüfung Technische Mechanik I vom 7.. 5 Name, Vorname : Matr.-Nr. : ufgabe Summe Punkte
achgebiet austatik und Holzbau Prof. Ralf-W. oddenberg Hochschule Wismar University of Technology, usiness and esign Prüfung Technische Mechanik I vom 7.. 5 Name, Vorname : Matr.-Nr. : ufgabe Summe Punkte
Technische Mechanik. Statik
 Hans Albert Richard Manuela Sander Technische Mechanik. Statik Lehrbuch mit Praxisbeispielen, Klausuraufgaben und Lösungen 4., überarbeitete und erweiterte Auflage Mit 263 Abbildungen ^ Springer Vieweg
Hans Albert Richard Manuela Sander Technische Mechanik. Statik Lehrbuch mit Praxisbeispielen, Klausuraufgaben und Lösungen 4., überarbeitete und erweiterte Auflage Mit 263 Abbildungen ^ Springer Vieweg
Institut für Technische und Num. Mechanik Technische Mechanik III Prof. Dr.-Ing. Prof. E. h. P. Eberhard WS 08/09 K 2. Aufgabe 1 (5 Punkte)
 Institut für Technische und Num. Mechanik Technische Mechanik III Prof. Dr.-Ing. Prof. E. h. P. Eberhard WS 8/9 K 6. Februar 9 Klausur in Technische Mechanik III Nachname Vorname Aufgabe (5 Punkte) Der
Institut für Technische und Num. Mechanik Technische Mechanik III Prof. Dr.-Ing. Prof. E. h. P. Eberhard WS 8/9 K 6. Februar 9 Klausur in Technische Mechanik III Nachname Vorname Aufgabe (5 Punkte) Der
www.statik-lernen.de Inhaltsverzeichnis Kräfte und Kraftarten Äußere und innere Kräfte Das zentrale Kräftesystem Momente Auflager Zustandslinien
 www.statik-lernen.de Grundlagen Inhaltsverzeichnis Kräfte und Kraftarten o Bestimmung von Kräften... Seite 1 o Graphische Darstellung... Seite 1 o Einheit der Kraft... Seite 1 o Kräftegleichgewicht...
www.statik-lernen.de Grundlagen Inhaltsverzeichnis Kräfte und Kraftarten o Bestimmung von Kräften... Seite 1 o Graphische Darstellung... Seite 1 o Einheit der Kraft... Seite 1 o Kräftegleichgewicht...
Bitte tragen Sie vor Abgabe Ihren Namen und Matrikel-Nr. ein, versehen Sie jedes Blatt mit einer Seitenzahl und geben Sie auch die Aufgabenblätter ab!
 Klausur TM1 für WI SS 99 Prüfer: Prof. Dr. M. Lindner NAME: MATRIKEL-NR.: Aufgabe Punkte erreicht 1 20 2 26 3 28 4 26 Summe 100 Bitte tragen Sie vor Abgabe Ihren Namen und Matrikel-Nr. ein, versehen Sie
Klausur TM1 für WI SS 99 Prüfer: Prof. Dr. M. Lindner NAME: MATRIKEL-NR.: Aufgabe Punkte erreicht 1 20 2 26 3 28 4 26 Summe 100 Bitte tragen Sie vor Abgabe Ihren Namen und Matrikel-Nr. ein, versehen Sie
1 Grundlagen: Abbildung mit Linsen
 C B C @ KOP/ Koppelprobleme KOP Dieses Kapitel beschäftigt sich mit Fragestellungen bezüglich der Verkopplung von Wellenleitern sowie Stecker oder Spleiÿe. Grundlagen: bbildung mit Linsen Zunächst werden
C B C @ KOP/ Koppelprobleme KOP Dieses Kapitel beschäftigt sich mit Fragestellungen bezüglich der Verkopplung von Wellenleitern sowie Stecker oder Spleiÿe. Grundlagen: bbildung mit Linsen Zunächst werden
Thema 10 Gewöhnliche Differentialgleichungen
 Thema 10 Gewöhnliche Differentialgleichungen Viele Naturgesetze stellen eine Beziehung zwischen einer physikalischen Größe und ihren Ableitungen (etwa als Funktion der Zeit dar: 1. ẍ = g (freier Fall;
Thema 10 Gewöhnliche Differentialgleichungen Viele Naturgesetze stellen eine Beziehung zwischen einer physikalischen Größe und ihren Ableitungen (etwa als Funktion der Zeit dar: 1. ẍ = g (freier Fall;
Beuth Hochschule für Technik Berlin
 Seite 1 sind ebene flächenförmige Konstruktionen, die in ihrer Ebene belastet werden und deren Bauhöhe im Verhältnis zur Stützweite groß ist. Es können ein- und mehrfeldrige Systeme ausgeführt werden;
Seite 1 sind ebene flächenförmige Konstruktionen, die in ihrer Ebene belastet werden und deren Bauhöhe im Verhältnis zur Stützweite groß ist. Es können ein- und mehrfeldrige Systeme ausgeführt werden;
Hydrostatik Mechanik von Fluiden im statischen Gleichgewicht. Fluide: Stoffe, die sich unter Einwirkung von Schubspannungen fortlaufend deformieren
 Hydrostatik Mechanik von Fluiden im statischen Gleichgewicht Fluide: Stoffe, die sich unter Einwirkung von Schubspannungen fortlaufend deformieren in ruhendem Fluid können keine tangentialen Spannungen
Hydrostatik Mechanik von Fluiden im statischen Gleichgewicht Fluide: Stoffe, die sich unter Einwirkung von Schubspannungen fortlaufend deformieren in ruhendem Fluid können keine tangentialen Spannungen
D. Bestle. Arbeitsunterlagen zur Vorlesung. Technische Mechanik I Statik und Festigkeitslehre
 D. Bestle Technische Mechanik I Statik und Festigkeitslehre Arbeitsunterlagen zur Vorlesung Lehrstuhl Technische Mechanik und Fahrzeugdynamik Prof. Dr. Ing. habil. Hon. Prof. (NUST) D. Bestle 1 Inhalt
D. Bestle Technische Mechanik I Statik und Festigkeitslehre Arbeitsunterlagen zur Vorlesung Lehrstuhl Technische Mechanik und Fahrzeugdynamik Prof. Dr. Ing. habil. Hon. Prof. (NUST) D. Bestle 1 Inhalt
Beispiel 1: Querschnittstragfähigkeit
 Titel: Querschnittstragfähigkeit Blatt: Seite 1 von 10 Beispiel 1: Querschnittstragfähigkeit Belastung: M y,ed = 190 knm N Ed = 700 kn V z,ed = 100 kn Material: S 235 Nachweis des Querschnitts nach DIN-EN
Titel: Querschnittstragfähigkeit Blatt: Seite 1 von 10 Beispiel 1: Querschnittstragfähigkeit Belastung: M y,ed = 190 knm N Ed = 700 kn V z,ed = 100 kn Material: S 235 Nachweis des Querschnitts nach DIN-EN
Statisch Unbestimmte Systeme
 3. Semester Seite 1/13 Statisch Unbestimmte Systeme 0. Inhalt 0. Inhalt 1 1. Allgemeines 1 2. Begriffe 2 3. Grundlagen 2 4. Freischneiden 2 4.1 Darstellung des Verfahrens am Zweifeldträger 2 4.2 Verallgemeinerte
3. Semester Seite 1/13 Statisch Unbestimmte Systeme 0. Inhalt 0. Inhalt 1 1. Allgemeines 1 2. Begriffe 2 3. Grundlagen 2 4. Freischneiden 2 4.1 Darstellung des Verfahrens am Zweifeldträger 2 4.2 Verallgemeinerte
Bestimmen Sie für den dargestellten Balken die Auflagerkräfte sowie die N-, Q- und M-Linie (ausgezeichnete Werte sind anzugeben).
 Technische Universität Darmstadt Technische Mechanik I B 13, G Kontinuumsmechanik Wintersemester 007/008 Prof. Dr.-Ing. Ch. Tsakmakis 9. Lösungsblatt Dr. rer. nat. P. Grammenoudis 07. Januar 008 Dipl.-Ing.
Technische Universität Darmstadt Technische Mechanik I B 13, G Kontinuumsmechanik Wintersemester 007/008 Prof. Dr.-Ing. Ch. Tsakmakis 9. Lösungsblatt Dr. rer. nat. P. Grammenoudis 07. Januar 008 Dipl.-Ing.
Statikbuch Charakteristische Werte Pitzl HVP Verbinder
 kompetent und leistungsstark Statikbuch Charakteristische Werte Pitzl HVP Verbinder einfach schnel l sichtbar oder ver deckt 1. Allgemeines Pitzl HVP Verbinder sind zweiteilige Verbinder für verdeckte
kompetent und leistungsstark Statikbuch Charakteristische Werte Pitzl HVP Verbinder einfach schnel l sichtbar oder ver deckt 1. Allgemeines Pitzl HVP Verbinder sind zweiteilige Verbinder für verdeckte
ELASTISCHE BETTUNG (ZUSAMMENFASSUNG) y z
 (ZUSENFSSUNG) rbeitsblätter. LLGEEINES. Sstem und Belastung Längsansicht: p( x) z, w x, u Biegesteifigkeit EI h Bettung c l Querschnittsdarstellung: p( x) p ( x) ( verschmiert) z h Bettung c b Bemerkung:
(ZUSENFSSUNG) rbeitsblätter. LLGEEINES. Sstem und Belastung Längsansicht: p( x) z, w x, u Biegesteifigkeit EI h Bettung c l Querschnittsdarstellung: p( x) p ( x) ( verschmiert) z h Bettung c b Bemerkung:
18 Höhere Ableitungen und Taylorformel
 8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
Praktikum Antriebssystemtechnik - Elektrisches Messen mechanischer Größen
 Praktikum Antriebssystemtechnik - Elektrisches Messen mechanischer Größen Name: Vorname: Mat.-Nr.: Studiengang: Datum: Note: Betreuer: Dipl.-Ing. Matthias vom Stein / fml Versuch 1: Drehzahl und Beschleunigung
Praktikum Antriebssystemtechnik - Elektrisches Messen mechanischer Größen Name: Vorname: Mat.-Nr.: Studiengang: Datum: Note: Betreuer: Dipl.-Ing. Matthias vom Stein / fml Versuch 1: Drehzahl und Beschleunigung
Gewöhnliche Dierentialgleichungen
 Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
Pflichtmodul Stahlbau - Bachelor
 Prof. Dr.-Ing. Dirk Werner 193 4.5.5 Die Interaktion von Moment, Normalkraft und Querkraft Bisher wurden Interaktionen für die gleichzeitige Wirkung zweier Schnittkraftkomponenten aufgeschrieben. In der
Prof. Dr.-Ing. Dirk Werner 193 4.5.5 Die Interaktion von Moment, Normalkraft und Querkraft Bisher wurden Interaktionen für die gleichzeitige Wirkung zweier Schnittkraftkomponenten aufgeschrieben. In der
Mathematik II Frühlingsemester 2015 Kap. 9: Funktionen von mehreren Variablen 9.2 Partielle Differentiation
 Mathematik II Frühlingsemester 2015 Kap. 9: Funktionen von mehreren Variablen 9.2 Partielle Differentiation www.math.ethz.ch/education/bachelor/lectures/fs2015/other/mathematik2 biol Prof. Dr. Erich Walter
Mathematik II Frühlingsemester 2015 Kap. 9: Funktionen von mehreren Variablen 9.2 Partielle Differentiation www.math.ethz.ch/education/bachelor/lectures/fs2015/other/mathematik2 biol Prof. Dr. Erich Walter
7. Ebene Balkenstatik
 7. Ebene Balkenstatik ls Balken oder Träger werden (prismatische) Bauteile beeichnet, die Lasten (Kräfte und omente) längs und quer u ihrer chse aufnehmen können. y q F Lastebene Die Längsachse eines horiontal
7. Ebene Balkenstatik ls Balken oder Träger werden (prismatische) Bauteile beeichnet, die Lasten (Kräfte und omente) längs und quer u ihrer chse aufnehmen können. y q F Lastebene Die Längsachse eines horiontal
(Man sagt dafür auch, dass die Teilmenge U bezüglich der Gruppenoperationen abgeschlossen sein muss.)
 3. Untergruppen 19 3. Untergruppen Nachdem wir nun einige grundlegende Gruppen kennengelernt haben, wollen wir in diesem Kapitel eine einfache Möglichkeit untersuchen, mit der man aus bereits bekannten
3. Untergruppen 19 3. Untergruppen Nachdem wir nun einige grundlegende Gruppen kennengelernt haben, wollen wir in diesem Kapitel eine einfache Möglichkeit untersuchen, mit der man aus bereits bekannten
Schweißnaht ST5. FRILO Software GmbH Stand:
 Schweißnaht ST5 FRILO Software GmbH www.frilo.de info@frilo.eu Stand: 01.07.2015 ST5 Schweißnaht ST5 Hinweis: Diese Dokumentation beschränkt sich auf die Eurocode-spezifische Beschreibung. Dokumentationen,
Schweißnaht ST5 FRILO Software GmbH www.frilo.de info@frilo.eu Stand: 01.07.2015 ST5 Schweißnaht ST5 Hinweis: Diese Dokumentation beschränkt sich auf die Eurocode-spezifische Beschreibung. Dokumentationen,
Formelzusammenstellung
 Übung zu Mechanik 4 - ormelsammlung Seite 4 ormelzusammenstellung. Grundbegriffe Harmonische Schwingung Sinusschwingung: (t) sin ( t + ϕ) Schwingungsamplitude: Kreisfrequenz: Phasenwinkel: requenz: f Schwingungsdauer,
Übung zu Mechanik 4 - ormelsammlung Seite 4 ormelzusammenstellung. Grundbegriffe Harmonische Schwingung Sinusschwingung: (t) sin ( t + ϕ) Schwingungsamplitude: Kreisfrequenz: Phasenwinkel: requenz: f Schwingungsdauer,
9.2 Invertierbare Matrizen
 34 9.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
34 9.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
6 Eigenlösungen der eindimensionalen Wellengleichung
 39 Kontinuierliche Systeme lassen sich als Schwinger mit unendlich vielen Freiheitsgraden interpretieren. Daher ist ein ähnliches ösungsverhalten wie bei linearen diskreten Systemen zu erwarten, d.h. die
39 Kontinuierliche Systeme lassen sich als Schwinger mit unendlich vielen Freiheitsgraden interpretieren. Daher ist ein ähnliches ösungsverhalten wie bei linearen diskreten Systemen zu erwarten, d.h. die
Buch Teil 1, Formelsammlung, Bemessungstabellen
 Fachhochschule Augsburg Stuiengang Bauingenieurwesen Name:... Holzbau SS 2007 Arbeitszeit: Hilfsmittel: 120 Minuten Buch Teil 1, Formelsammlung, Bemessungstabellen 1. Aufgabe (ca. 80 min) Gegeben: Statisches
Fachhochschule Augsburg Stuiengang Bauingenieurwesen Name:... Holzbau SS 2007 Arbeitszeit: Hilfsmittel: 120 Minuten Buch Teil 1, Formelsammlung, Bemessungstabellen 1. Aufgabe (ca. 80 min) Gegeben: Statisches
Nachweis Elastisch Elastisch eines I-Querschnittes mit zweiachsiger Biegung und Normalkraft
 Name : Nr. 4 03.00 60 1. Aufgabe Seite 1 Nachweis Elastisch Elastisch eines I-Querschnittes mit zweiachsiger Biegung und Normalkraft h 1 y b 1 t 3 4 s 5 6 7 8 9 z h Bezeichnungen der Abmessungen und Querschnittspunkte
Name : Nr. 4 03.00 60 1. Aufgabe Seite 1 Nachweis Elastisch Elastisch eines I-Querschnittes mit zweiachsiger Biegung und Normalkraft h 1 y b 1 t 3 4 s 5 6 7 8 9 z h Bezeichnungen der Abmessungen und Querschnittspunkte
Hochschule Karlsruhe Technische Mechanik Statik. Aufgaben zur Statik
 Aufgaben zur Statik S 1. Seilkräfte 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn Am Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. Addition
Aufgaben zur Statik S 1. Seilkräfte 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn Am Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. Addition
Lösung zur Übung 19 SS 2012
 Lösung zur Übung 19 SS 01 69) Beim radioaktiven Zerfall ist die Anzahl der pro Zeiteinheit zerfallenden Kerne dn/dt direkt proportional zur momentanen Anzahl der Kerne N(t). a) Formulieren Sie dazu die
Lösung zur Übung 19 SS 01 69) Beim radioaktiven Zerfall ist die Anzahl der pro Zeiteinheit zerfallenden Kerne dn/dt direkt proportional zur momentanen Anzahl der Kerne N(t). a) Formulieren Sie dazu die
Zugversuch. 1. Aufgabe. , A und Z! Bestimmen Sie ihre Größe mit Hilfe der vorliegenden Versuchsergebnisse! Werkstoffkennwerte E, R p0,2.
 1. Aufgabe An einem Proportionalstab aus dem Stahl X3CrNi2-32 mit rechteckigem Querschnitt im Messbereich (a 6,7 mm; b 3 mm; L 8mm) wurde in einem das dargestellte Feindehnungs- bzw. Grobdehnungsdiagramm
1. Aufgabe An einem Proportionalstab aus dem Stahl X3CrNi2-32 mit rechteckigem Querschnitt im Messbereich (a 6,7 mm; b 3 mm; L 8mm) wurde in einem das dargestellte Feindehnungs- bzw. Grobdehnungsdiagramm
Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder
 DGL Schwingung Physikalische Felder Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder Johannes Wiedersich 23. April 2008 http://www.e13.physik.tu-muenchen.de/wiedersich/
DGL Schwingung Physikalische Felder Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder Johannes Wiedersich 23. April 2008 http://www.e13.physik.tu-muenchen.de/wiedersich/
Biomechanik am PC. Was sind Geograbra-Modelle zur Biomechanik? Informationen zu den Modellen
 Biomechanik-Versuche im Computer geht das? Ja, mit den Geogebra-Modellen auf dieser Seite. Die dynamischen Modelle erlauben es biomechanische Zusammenhänge anschaulich darzustellen und eindrucksvoll zu
Biomechanik-Versuche im Computer geht das? Ja, mit den Geogebra-Modellen auf dieser Seite. Die dynamischen Modelle erlauben es biomechanische Zusammenhänge anschaulich darzustellen und eindrucksvoll zu
Baustatik & Festigkeitslehre Vorlesung & Übung
 Baustatik & Festigkeitslehre Vorlesung & Übung Vortragender: O.Univ.Prof. DI Dr. Dr. Konrad Bergmeister Kraftgrößenverfahren Wenn statisch unbestimmte Systeme berechnet werden sollen, müssen zusätzliche
Baustatik & Festigkeitslehre Vorlesung & Übung Vortragender: O.Univ.Prof. DI Dr. Dr. Konrad Bergmeister Kraftgrößenverfahren Wenn statisch unbestimmte Systeme berechnet werden sollen, müssen zusätzliche
Einfache Differentialgleichungen
 Differentialgleichungen (DGL) spielen in der Physik eine sehr wichtige Rolle. Im Folgenden behandeln wir die grundlegendsten Fälle 1, jeweils mit einer kurzen Herleitung der Lösung. Dann schliesst eine
Differentialgleichungen (DGL) spielen in der Physik eine sehr wichtige Rolle. Im Folgenden behandeln wir die grundlegendsten Fälle 1, jeweils mit einer kurzen Herleitung der Lösung. Dann schliesst eine
Formelsammlung. für die Klausur. Technische Mechanik I & II
 Formelsammlung für die Klausur Technische Mechanik I & II Vorwort Diese Formelsammlung ist dazu gedacht, das Suchen und Herumblättern in den Büchern während der Klausur zu vermeiden und somit Zeit zu sparen.
Formelsammlung für die Klausur Technische Mechanik I & II Vorwort Diese Formelsammlung ist dazu gedacht, das Suchen und Herumblättern in den Büchern während der Klausur zu vermeiden und somit Zeit zu sparen.
Übungsblatt 1 (13.05.2011)
 Experimentalphysik für Naturwissenschaftler Universität Erlangen Nürnberg SS 11 Übungsblatt 1 (13.5.11) 1) Wasserstrahl Der aus einem Wasserhahn senkrecht nach unten ausfließende Wasserstrahl verjüngt
Experimentalphysik für Naturwissenschaftler Universität Erlangen Nürnberg SS 11 Übungsblatt 1 (13.5.11) 1) Wasserstrahl Der aus einem Wasserhahn senkrecht nach unten ausfließende Wasserstrahl verjüngt
Festigkeit und Härte
 Festigkeit und Härte Wichtige Kenngrößen für die Verwendung metallischer Werkstoffe sind deren mechanische Eigenschaften unter statischer Beanspruchung bei Raumtemperatur (RT). Hierbei hervorzuheben sind
Festigkeit und Härte Wichtige Kenngrößen für die Verwendung metallischer Werkstoffe sind deren mechanische Eigenschaften unter statischer Beanspruchung bei Raumtemperatur (RT). Hierbei hervorzuheben sind
-BEMESSUNG EINFACHER BAUTEILE- Prof. Dr.-Ing. Jens Minnert Fachhochschule Gießen-Friedberg TEIL 7 BEMESSUNG IM STAHLBAU.
 STAHLBAU -BEMESSUNG EINFACHER BAUTEILE- Prof. Dr.-Ing. Jens Minnert Fachhochschule Gießen-Friedberg Nachweiskonzept Die Beanspruchung S d darf nicht größer sein als die Beanspruchbarkeit R d eines Bauteils
STAHLBAU -BEMESSUNG EINFACHER BAUTEILE- Prof. Dr.-Ing. Jens Minnert Fachhochschule Gießen-Friedberg Nachweiskonzept Die Beanspruchung S d darf nicht größer sein als die Beanspruchbarkeit R d eines Bauteils
Stahlbeton I+II Sessionsprüfung ( J) Sommer Samstag, 13. August 2016, Uhr, HIL F 61. Name, Vorname: Studenten-Nr.
 Stahlbeton I+II Sessionsprüfung (101-0126-01J) Sommer 2016 Samstag, 13. August 2016, 09.00 12.00 Uhr, HIL F 61 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Sofern nichts anderes angegeben ist, wird von
Stahlbeton I+II Sessionsprüfung (101-0126-01J) Sommer 2016 Samstag, 13. August 2016, 09.00 12.00 Uhr, HIL F 61 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Sofern nichts anderes angegeben ist, wird von
Buch/Skript Teil 1, Formelsammlung, Bemessungstabellen
 Fachhochschule Augsburg Studiengang Bauingenieurwesen... Name:... Holzbau SS 2009 Arbeitszeit: Hilfsmittel: 90 Minuten Buch/Sript Teil, Formelsammlung, Bemessungstabellen. Aufgabe (ca. 90 min) Gegeben:
Fachhochschule Augsburg Studiengang Bauingenieurwesen... Name:... Holzbau SS 2009 Arbeitszeit: Hilfsmittel: 90 Minuten Buch/Sript Teil, Formelsammlung, Bemessungstabellen. Aufgabe (ca. 90 min) Gegeben:
6) DIE EINFACHSTEN STATISCH BESTIMMTEN TRAEGER
 BAULEITER HOCHBAU S T A T I K / F E S T I G K E I T S L E H R E 6) DIE EINFACHSTEN STATISCH BESTIMMTEN TRAEGER 1) Definition für statisch bestimmte Systeme 2) Auflagerreaktionen beim einfachen Balken 3)
BAULEITER HOCHBAU S T A T I K / F E S T I G K E I T S L E H R E 6) DIE EINFACHSTEN STATISCH BESTIMMTEN TRAEGER 1) Definition für statisch bestimmte Systeme 2) Auflagerreaktionen beim einfachen Balken 3)
Testvorbereitung: Integrierender Faktor
 Testvorbereitung: Integrierender Faktor Markus Nemetz, markus.nemetz@tuwien.ac.at, TU Wien,.02.2007 Voraussetzung: Kenntnis der exakten Differentialgleichungen! Theoretische Grundlagen Eine nicht exakte
Testvorbereitung: Integrierender Faktor Markus Nemetz, markus.nemetz@tuwien.ac.at, TU Wien,.02.2007 Voraussetzung: Kenntnis der exakten Differentialgleichungen! Theoretische Grundlagen Eine nicht exakte
4. Allgemeines ebenes Kräftesystem
 4. llgemeines ebenes Kräftesystem Eine Gruppe von Kräften, die an einem starren Körper angreifen, bilden ein allgemeines Kräftesystem, wenn sich ihre Wirkungslinien nicht in einem gemeinsamen Punkt schneiden.
4. llgemeines ebenes Kräftesystem Eine Gruppe von Kräften, die an einem starren Körper angreifen, bilden ein allgemeines Kräftesystem, wenn sich ihre Wirkungslinien nicht in einem gemeinsamen Punkt schneiden.
R C 1s =0, C T 1
 Aufgaben zum Themengebiet Aufladen und Entladen eines Kondensators Theorie und nummerierte Formeln auf den Seiten 5 bis 8 Ein Kondensator mit der Kapazität = 00μF wurde mit der Spannung U = 60V aufgeladen
Aufgaben zum Themengebiet Aufladen und Entladen eines Kondensators Theorie und nummerierte Formeln auf den Seiten 5 bis 8 Ein Kondensator mit der Kapazität = 00μF wurde mit der Spannung U = 60V aufgeladen
Ingenieurholzbau I, WS 2005/06
 Fachhochschule Augsburg Studiengang Bauingenieurwesen Name:... Ingenieurholzbau I, WS 2005/06 Prüfungstag: 03.02.2006 Arbeitszeit: 90 Minuten Hilfsmittel: Formelsammlung, Bemessungstabellen Aufgabe 1 (ca.
Fachhochschule Augsburg Studiengang Bauingenieurwesen Name:... Ingenieurholzbau I, WS 2005/06 Prüfungstag: 03.02.2006 Arbeitszeit: 90 Minuten Hilfsmittel: Formelsammlung, Bemessungstabellen Aufgabe 1 (ca.
Kapitel VI. Euklidische Geometrie
 Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand
 Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand Vorüberlegung In einem seriellen Stromkreis addieren sich die Teilspannungen zur Gesamtspannung Bei einer Gesamtspannung U ges, der
Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand Vorüberlegung In einem seriellen Stromkreis addieren sich die Teilspannungen zur Gesamtspannung Bei einer Gesamtspannung U ges, der
Übungsaufgaben z. Th. Plattenkondensator
 Übungsaufgaben z. Th. Plattenkondensator Aufgabe 1 Die Platten eines Kondensators haben den Radius r 18 cm. Der Abstand zwischen den Platten beträgt d 1,5 cm. An den Kondensator wird die Spannung U 8,
Übungsaufgaben z. Th. Plattenkondensator Aufgabe 1 Die Platten eines Kondensators haben den Radius r 18 cm. Der Abstand zwischen den Platten beträgt d 1,5 cm. An den Kondensator wird die Spannung U 8,
27 Taylor-Formel und Taylor-Entwicklungen
 136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
Modulabschlussklausur Analysis II
 Modulabschlussklausur Analysis II. Juli 015 Bearbeitungszeit: 150 min Aufgabe 1 [5/10 Punkte] Es sei a R und f a : R 3 R mit f a (x, y, z) = x cos(y) + z 3 sin(y) + a 3 + (z + ay a y) cos(x) a) Bestimmen
Modulabschlussklausur Analysis II. Juli 015 Bearbeitungszeit: 150 min Aufgabe 1 [5/10 Punkte] Es sei a R und f a : R 3 R mit f a (x, y, z) = x cos(y) + z 3 sin(y) + a 3 + (z + ay a y) cos(x) a) Bestimmen
Kontrolle von Beispielen zum Kraftgrößenverfahren mit RuckZuck
 Kontrolle von Beispielen zum Kraftgrößenverfahren mit RuckZuck Bachelor Projekt eingereicht am Institut für Baustatik der Technischen Universität Graz im November 2009 Verfasser: Betreuer: Mario Jackisch
Kontrolle von Beispielen zum Kraftgrößenverfahren mit RuckZuck Bachelor Projekt eingereicht am Institut für Baustatik der Technischen Universität Graz im November 2009 Verfasser: Betreuer: Mario Jackisch
Mehmet Maraz. MechanikNachhilfe
 Mehmet Maraz MechanikNachhilfe 1. Auflage 015 Inhaltsverzeichnis 1 Statik 1 1.1 Lagerungen und Lagerreaktionen................. 1. Kräftegleichgewichte......................... 5 1..1 Drehmoment.........................
Mehmet Maraz MechanikNachhilfe 1. Auflage 015 Inhaltsverzeichnis 1 Statik 1 1.1 Lagerungen und Lagerreaktionen................. 1. Kräftegleichgewichte......................... 5 1..1 Drehmoment.........................
1.5 lineare Gleichungssysteme
 1.5 lineare Gleichungssysteme Inhaltsverzeichnis 1 Was ist ein lineares Gleichungssystem mit zwei Gleichungen und zwei Unbekannten? 2 2 Wie lösen wir ein lineares Gleichungssystem mit zwei Unbekannten?
1.5 lineare Gleichungssysteme Inhaltsverzeichnis 1 Was ist ein lineares Gleichungssystem mit zwei Gleichungen und zwei Unbekannten? 2 2 Wie lösen wir ein lineares Gleichungssystem mit zwei Unbekannten?
5.1 Determinanten der Ordnung 2 und 3. a 11 a 12 a 21 a 22. det(a) =a 11 a 22 a 12 a 21. a 11 a 21
 5. Determinanten 5.1 Determinanten der Ordnung 2 und 3 Als Determinante der zweireihigen Matrix A = a 11 a 12 bezeichnet man die Zahl =a 11 a 22 a 12 a 21. Man verwendet auch die Bezeichnung = A = a 11
5. Determinanten 5.1 Determinanten der Ordnung 2 und 3 Als Determinante der zweireihigen Matrix A = a 11 a 12 bezeichnet man die Zahl =a 11 a 22 a 12 a 21. Man verwendet auch die Bezeichnung = A = a 11
Berechnung statisch unbestimmter Systeme mit Hilfe des Kraftgrößenverfahrens
 Berechnung statisch unbestimmter Systeme mit Hilfe des Kraftgrößenverfahrens Bachelorprojekt eingereicht am Institut für Baustatik der Technischen Universität Graz im Wintersemester 2009/20 Verfasser:
Berechnung statisch unbestimmter Systeme mit Hilfe des Kraftgrößenverfahrens Bachelorprojekt eingereicht am Institut für Baustatik der Technischen Universität Graz im Wintersemester 2009/20 Verfasser:
3. Erhaltungsgrößen und die Newton schen Axiome
 Übungen zur T1: Theoretische Mechanik, SoSe13 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray James.Gray@physik.uni-muenchen.de 3. Erhaltungsgrößen und die Newton schen Axiome Übung 3.1:
Übungen zur T1: Theoretische Mechanik, SoSe13 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray James.Gray@physik.uni-muenchen.de 3. Erhaltungsgrößen und die Newton schen Axiome Übung 3.1:
Formelanhang Mathematik II
 Formelanhang Mathematik II Mechatronik 2. Sem. Prof. Dr. K. Blankenbach Wichtige Formeln: - Euler: e j = cos() + j sin() ; e -j = cos() - j sin() - Sinus mit Phase: Übersicht Differentialgleichungen (DGL)
Formelanhang Mathematik II Mechatronik 2. Sem. Prof. Dr. K. Blankenbach Wichtige Formeln: - Euler: e j = cos() + j sin() ; e -j = cos() - j sin() - Sinus mit Phase: Übersicht Differentialgleichungen (DGL)
CAE, Kap. 3.2, Preprocessing Randbedingungen
 Randbedingungen - In der FEA sind drei Arten von Randbedingungen u unterscheiden Smmetrie-Randbedingungen Belastungs-Randbedingungen - Aufgabe und Funktion von Randbedingungen: Abbildung und Berücksichtigung
Randbedingungen - In der FEA sind drei Arten von Randbedingungen u unterscheiden Smmetrie-Randbedingungen Belastungs-Randbedingungen - Aufgabe und Funktion von Randbedingungen: Abbildung und Berücksichtigung
Funktionen mehrerer Variabler
 Funktionen mehrerer Variabler Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Funktionen mehrerer Variabler Übersicht Funktionsbegriff 1 Funktionsbegriff Beispiele Darstellung Schnitte 2 Partielle Ableitungen
Funktionen mehrerer Variabler Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Funktionen mehrerer Variabler Übersicht Funktionsbegriff 1 Funktionsbegriff Beispiele Darstellung Schnitte 2 Partielle Ableitungen
Mathematik 3 für Informatik
 Gunter Ochs Wintersemester 5/6 Mathematik 3 für Informatik Lösungen zum Hausaufgabenblatt Lösungshinweise ohne Garnatie auf Fehlerfreiheit c 5. Berechnen Sie die folgenden unbestimmten Integrale: a x 4
Gunter Ochs Wintersemester 5/6 Mathematik 3 für Informatik Lösungen zum Hausaufgabenblatt Lösungshinweise ohne Garnatie auf Fehlerfreiheit c 5. Berechnen Sie die folgenden unbestimmten Integrale: a x 4
1. Einfache ebene Tragwerke
 Die Ermittlung der Lagerreaktionen einfacher Tragwerke erfolgt in drei Schritten: Freischneiden Aufstellen der Gleichgewichtsbedingungen Auflösen der Gleichungen Prof. Dr. Wandinger 3. Tragwerksanalyse
Die Ermittlung der Lagerreaktionen einfacher Tragwerke erfolgt in drei Schritten: Freischneiden Aufstellen der Gleichgewichtsbedingungen Auflösen der Gleichungen Prof. Dr. Wandinger 3. Tragwerksanalyse
Physik 1 MW, WS 2014/15 Aufgaben mit Lösung 6. Übung (KW 03/04) Aufzugskabine )
 6. Übung (KW 03/04) Aufgabe (M 9. Aufzugskabine ) In einem Aufzug hängt ein Wägestück der Masse m an einem Federkraftmesser. Dieser zeigt die Kraft F an. Auf welche Beschleunigung a z (z-koordinate nach
6. Übung (KW 03/04) Aufgabe (M 9. Aufzugskabine ) In einem Aufzug hängt ein Wägestück der Masse m an einem Federkraftmesser. Dieser zeigt die Kraft F an. Auf welche Beschleunigung a z (z-koordinate nach
6.3 Exakte Differentialgleichungen
 6.3. EXAKTE DIFFERENTIALGLEICHUNGEN 23 6.3 Exakte Differentialgleichungen Andere Bezeichnungen: Pfaffsche Dgl., Dgl. für Kurvenscharen, Nullinien Pfaffscher Formen. 1. Definitionen Pfaffsche Dgl, Dgl.
6.3. EXAKTE DIFFERENTIALGLEICHUNGEN 23 6.3 Exakte Differentialgleichungen Andere Bezeichnungen: Pfaffsche Dgl., Dgl. für Kurvenscharen, Nullinien Pfaffscher Formen. 1. Definitionen Pfaffsche Dgl, Dgl.
 POS: 001 Bezeichnung: Hallendach Thermodachelemente System M 1 : 75 1 2 3 45 9.10 BAUSTOFF : S 355 E-Modul E = 21000 kn/cm2 γm = 1.10 spez. Gewicht : 7.85 kg/dm3 QUERSCHNITTSWERTE Quersch. Profil I A Aq
POS: 001 Bezeichnung: Hallendach Thermodachelemente System M 1 : 75 1 2 3 45 9.10 BAUSTOFF : S 355 E-Modul E = 21000 kn/cm2 γm = 1.10 spez. Gewicht : 7.85 kg/dm3 QUERSCHNITTSWERTE Quersch. Profil I A Aq
Technische Mechanik 1
 Ergänzungsübungen mit Lösungen zur Vorlesung Aufgabe 1: Geben Sie die Koordinaten der Kraftvektoren im angegebenen Koordinatensystem an. Gegeben sind: F 1, F, F, F 4 und die Winkel in den Skizzen. Aufgabe
Ergänzungsübungen mit Lösungen zur Vorlesung Aufgabe 1: Geben Sie die Koordinaten der Kraftvektoren im angegebenen Koordinatensystem an. Gegeben sind: F 1, F, F, F 4 und die Winkel in den Skizzen. Aufgabe
5 Eigenwerte und die Jordansche Normalform
 Mathematik für Physiker II, SS Mittwoch 8.6 $Id: jordan.tex,v.6 /6/7 8:5:3 hk Exp hk $ 5 Eigenwerte und die Jordansche Normalform 5.4 Die Jordansche Normalform Wir hatten bereits erwähnt, dass eine n n
Mathematik für Physiker II, SS Mittwoch 8.6 $Id: jordan.tex,v.6 /6/7 8:5:3 hk Exp hk $ 5 Eigenwerte und die Jordansche Normalform 5.4 Die Jordansche Normalform Wir hatten bereits erwähnt, dass eine n n
Arbeitsunterlagen. Statik 2
 Arbeitsunterlagen Statik 2 WS 2014/15 Stand 07.10.2014 Inhalt 1. Vertiefung KGV 1.1 Eingeprägte Auflagerverformungen 1.2 Vorspannung 1.3 Systeme mit elastischer Lagerung 1.4 Ermittlung von Federsteifigkeiten
Arbeitsunterlagen Statik 2 WS 2014/15 Stand 07.10.2014 Inhalt 1. Vertiefung KGV 1.1 Eingeprägte Auflagerverformungen 1.2 Vorspannung 1.3 Systeme mit elastischer Lagerung 1.4 Ermittlung von Federsteifigkeiten
Wiederholungen aus. MMSM 1 (Statik)
 Wiederholungen aus MMSM 1 (Statik) Dr.-Ing. Ulrich Simon Ulmer Zentrum für Wissenschaftliches Rechnen (UZWR) www.uni-ulm.de/uzwr Inhalt Größen, Dimensionen, Einheiten Kraft, Moment, reikörperbild Statisches
Wiederholungen aus MMSM 1 (Statik) Dr.-Ing. Ulrich Simon Ulmer Zentrum für Wissenschaftliches Rechnen (UZWR) www.uni-ulm.de/uzwr Inhalt Größen, Dimensionen, Einheiten Kraft, Moment, reikörperbild Statisches
12 Gewöhnliche Differentialgleichungen
 12 Gewöhnliche Differentialgleichungen 121 Einführende Beispiele und Grundbegriffe Beispiel 1 ( senkrechter Wurf ) v 0 Ein Flugkörper werde zum Zeitpunkt t = 0 in der Höhe s = 0 t = 0 s = 0 mit der Startgeschwindigkeit
12 Gewöhnliche Differentialgleichungen 121 Einführende Beispiele und Grundbegriffe Beispiel 1 ( senkrechter Wurf ) v 0 Ein Flugkörper werde zum Zeitpunkt t = 0 in der Höhe s = 0 t = 0 s = 0 mit der Startgeschwindigkeit
Singularitäten in der FEM und deren Bewertung
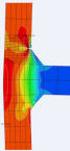 Singularitäten in der FEM und deren Bewertung Jeder FEM-Anwender wird früher oder später mit Spannungssingularitäten konfrontiert werden, sich dessen aber nicht unbedingt im Klaren sein. Dafür gibt es
Singularitäten in der FEM und deren Bewertung Jeder FEM-Anwender wird früher oder später mit Spannungssingularitäten konfrontiert werden, sich dessen aber nicht unbedingt im Klaren sein. Dafür gibt es
10.1 Ampère sches Gesetz und einfache Stromverteilungen
 1 Magnetostatik Solange keine Verwechslungen auftreten, werden wir in diesem und in den folgenden Kapiteln vom magnetischen Feld B an Stelle der magnetischen Induktion bzw. der magnetischen Flußdichte
1 Magnetostatik Solange keine Verwechslungen auftreten, werden wir in diesem und in den folgenden Kapiteln vom magnetischen Feld B an Stelle der magnetischen Induktion bzw. der magnetischen Flußdichte
& sind die Vektorkomponenten von und sind die Vektorkoordinaten von. A x. a) Der Betrag eines Vektors
 Einführu hnung Was ist ein Vektor? In Bereichen der Naturwissenschaften treten Größen auf, die nicht nur durch eine Zahlenangabe dargestellt werden können, wie Kraft oder Geschwindigkeit. Zur vollständigen
Einführu hnung Was ist ein Vektor? In Bereichen der Naturwissenschaften treten Größen auf, die nicht nur durch eine Zahlenangabe dargestellt werden können, wie Kraft oder Geschwindigkeit. Zur vollständigen
8 F Stahlbauprofile. Prof. Dr.-Ing. Christof Hausser, Prof. Dr.-Ing. Christoph Seeßelberg
 8.159 8 F Stahlbauprofile Prof. Dr.-Ing. Christof Hausser, Prof. Dr.-Ing. Christoph Seeßelberg Kurzzeichen für Walzmaterial (Beispiele) Kurzbezeichnung zeichnerisch IPE 240-4600 DIN 1025-5 HEB 400-8000
8.159 8 F Stahlbauprofile Prof. Dr.-Ing. Christof Hausser, Prof. Dr.-Ing. Christoph Seeßelberg Kurzzeichen für Walzmaterial (Beispiele) Kurzbezeichnung zeichnerisch IPE 240-4600 DIN 1025-5 HEB 400-8000
Die Exponentialfunktion. exp(x)
 Die Exponentialfunktion exp(x) Wir erinnern: Ist f : R R eine glatte Funktion, dann bezeichnet f (x) die Steigung von f im Punkt x. f (x) x x 0 x Wie sehen Funktionen aus mit 3 2 f f (x) = f(x) -3-2 -1
Die Exponentialfunktion exp(x) Wir erinnern: Ist f : R R eine glatte Funktion, dann bezeichnet f (x) die Steigung von f im Punkt x. f (x) x x 0 x Wie sehen Funktionen aus mit 3 2 f f (x) = f(x) -3-2 -1
Übungen zur Klassischen Theoretischen Physik III (Theorie C Elektrodynamik) WS Aufgabe 1: Ampère-Gesetz (2+2+2=6 Punkte)
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Klassischen Theoretischen Physik III (Theorie Elektrodynamik) WS 1-13 Prof. Dr. Alexander Mirlin Musterlösung:
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Klassischen Theoretischen Physik III (Theorie Elektrodynamik) WS 1-13 Prof. Dr. Alexander Mirlin Musterlösung:
Aufgabenblatt Z/ 01 (Physikalische Größen und Einheiten)
 Aufgabenblatt Z/ 01 (Physikalische Größen und Einheiten) Aufgabe Z-01/ 1 Welche zwei verschiedenen physikalische Bedeutungen kann eine Größe haben, wenn nur bekannt ist, dass sie in der Einheit Nm gemessen
Aufgabenblatt Z/ 01 (Physikalische Größen und Einheiten) Aufgabe Z-01/ 1 Welche zwei verschiedenen physikalische Bedeutungen kann eine Größe haben, wenn nur bekannt ist, dass sie in der Einheit Nm gemessen
Aufgabe Summe max. P Punkte
 Klausur Theoretische Elektrotechnik TET Probeklausur xx.xx.206 Name Matr.-Nr. Vorname Note Aufgabe 2 3 4 5 6 7 Summe max. P. 5 0 5 5 5 5 5 00 Punkte Allgemeine Hinweise: Erlaubte Hilfsmittel: Taschenrechner,
Klausur Theoretische Elektrotechnik TET Probeklausur xx.xx.206 Name Matr.-Nr. Vorname Note Aufgabe 2 3 4 5 6 7 Summe max. P. 5 0 5 5 5 5 5 00 Punkte Allgemeine Hinweise: Erlaubte Hilfsmittel: Taschenrechner,
Hubeinrichtung. FEM-Berechnung Hubbrücke
 Hubeinrichtung FEM-Berechnung Hubbrücke Material: S355J2G3 E = 210.000 N/mm 2 ; Rm = 490 N/mm 2 (1.0037) G = 83.000 N/mm 2 ; Re = 355 N/mm 2 ν = 0,3 ρ = 7,86 * 10-6 kg/mm 3 zul σ = Re / 1,1 = 355 / 1,1
Hubeinrichtung FEM-Berechnung Hubbrücke Material: S355J2G3 E = 210.000 N/mm 2 ; Rm = 490 N/mm 2 (1.0037) G = 83.000 N/mm 2 ; Re = 355 N/mm 2 ν = 0,3 ρ = 7,86 * 10-6 kg/mm 3 zul σ = Re / 1,1 = 355 / 1,1
