4. Übungsblatt zu Mathematik für Informatiker I, WS 2003/04
|
|
|
- Lilli Fiedler
- vor 8 Jahren
- Abrufe
Transkript
1 4. Übungsblatt zu Mathematik für Informatiker I, WS 2003/04 JOACHIM VON ZUR GATHEN, OLAF MÜLLER, MICHAEL NÜSKEN Abgabe bis Freitag, 14. November 2003, in den jeweils richtigen grünen oder roten Kasten auf dem D1-Flur. Einige Aufgaben werden von den Ziffern Deiner Matrikelnummer abhängen. Dazu bezeichne die Ziffern Deiner Matrikelnummer mit Ñ, Ñ, Ñ, Ñ, Ñ ¾, Ñ ½, Ñ ¼, sodass also È ¼ Ñ ½¼ Deine Matrikelnummer ist. Trage Deine Matrikelnummer hier ein, um ganz einfach Deine persönlichen Ziffern abzulesen. Ñ Ñ Ñ Ñ Ñ ¾ Ñ ½ Ñ ¼ Aufgabe 4.1 (Logik). (2 Punkte) Sei eine (unbekannte) reelle Zahl. Bestimme den Wahrheitswert: (i) Ü ¾ Ê e Ñ ½ Ü Ü Ñ µ ¾ ¼ µ Ý ¾ Ê e Ñ ½ Ý Ý Ñ µ ¾ ¼. (ii) Ü ¾ Ê e Ü Ñ ¾µ Ü Ñ µ ¾ ¼ µ Ý ¾ Ê e Ý Ñ ¾µ Ý Ñ µ ¾ ¼. (iii) Ü ¾ Ê e sin Ü Ñ ¼ Ü µ ¾ ¼ µ Ý ¾ Ê e sin Ý Ñ ¼ Ý µ ¾ ¼. (iv) Ü ¾ Ê e sin Ü Ñ ¼ Ü µ ¾ ¼ µ Ý ¾ Ê e sin Ü Ñ ¼ Ü µ ¾ ¼. Aufgabe 4.2 (Binäraddierer). (12 Punkte) Ziel dieser Aufgabe ist ein Algorithmus für die binäre Addition. Die binäre Addition läuft genauso ab, wie eine schriftliche Addition in der Schule nur eben zur Basis ¾ anstatt zur Basis ½¼. Man beginnt mit den beiden Bits ganz rechts und addiert diese. Das niederwertige Bit des Ergebnisses schreiben wir auf, das höherwertige nehmen wir als Übertrag mit in die nächste Spalte (zur Linken). Dort müssen dann drei Bits addiert werden. Wieder wird das niederwertige Bit der Summe als Ergebnis aufgeschrieben und das höherwertige als Übertrag...
2 (i) Für ½ erhalten wir einen Halbaddierer, der aus zwei einzelnen Bits ¼ und ¼ zwei Bits ½ und ¼ berechnet mit ½ ¾ ¼ ¼ ¼. Entwirf einen Algorithmus, der diese zwei Bits berechnet. Verwende dazu nur die Operationen,, und. (ii) Entwirf einen Algorithmus, der drei Bits ¼, ¼ und Ù addiert und zwei Bits ½ und ¼ berechnet mit ½ ¾ ¼ ¼ ¼ Ù. Verwende dazu nur die Operationen,, und und Halbaddierer. (Dies bzw. einen entsprechenden Schaltkreis nennt man dann einen Volladdierer.) (iii) Entwirf einen vollwertigen Algorithmus zur Addition zweier Binärzahlen: Algorithmus. Binäre Addition. Eingabe: Eine natürliche Zahl und Listen ½ ¼ µ, ½ ¼ µ mit ¾ ¼ ½. Ausgabe: Eine Liste ½ ¼ µ mit ¾ ¼ ½ und È ¼ ¾ È ¼ ½ ¾ ȼ ½ ¾ For ¼to ½ do Return ½ ¼ µ. Verwende dazu nur die Operationen,, und und Volladdierer. In einer Schleife soll ein Zwischenergebnis Ù¾ ½ ȼ ¾ berechnet werden, dass die Summe der unteren Bits von und darstellt; formuliere die genaue Bestimmungsgleichung. (iv) Zeige, dass Dein Algorithmus korrekt arbeitet. Verwende dabei die Bestimmungsgleichung als Schleifeninvariante. (v) Bestimme die Laufzeit Deines Algorithmus. [Es soll die Anzahl der eigentlichen logischen Operationen gezählt werden, die Schleifenkontrollen vernachlässigen wir.] (vi) Zeichne einen entsprechenden Schaltkreis für.
3 Aufgabe 4.3 (Quantoren). (2 Punkte) Sei ³ ܵ ein logischer Ausdruck, der von Ü abhängt. Drücke die Aussage Es gibt genau ein Ü mit der Eigenschaft ³ ܵ. durch den Allquantor und die logischen Operationen,,, µ sowie das Gleichheitszeichen aus. Aufgabe 4.4 (Logarithmen). (2 Punkte) (i) Stelle für ¼ die Lösung Ý der Gleichung ¾ Ý durch Logarithmen dar. (ii) Drücke den Logarithmus von Ü zur Basis durch Logarithmen zur Basis ¾ aus. Aufgabe 4.5 (Komplexe Zahlen). (3 Punkte) (i) Berechne Ñ ½ Ñ ½ µ Ñ Ñ ½ µ. (ii) Berechne Ñ ½ Ñ ½ µ Ñ Ñ ½ µ. (iii) Berechne den Betrag von Ñ ¾µ Ñ ½ ½µ. Aufgabe 4.6 (Stellenwertsysteme). (5 Punkte) Besonders in der Informatik sind Stellensysteme zu anderen Basen als ½¼ gebräuchlich und sehr wichtig. Für die Basis ½ verwenden wir die Buchstaben,..., für die hexadezimalen Ziffern(!) ½¼,...,½. Somit ist die hexadezimale Zahl µ ½ die Dezimalzahl ¾, nämlich ½ ½ ½. (i) Stelle Deine Matrikelnummer dezimal, hexadezimal, oktal, -adisch und binär dar. (ii) Berechne (schriftlich und ohne Taschenrechner) hexadezimal ¾ ¾µ ½ ½¼ µ ½. (iii) Berechne (schriftlich und ohne Taschenrechner) oktal ¾ ¼ µ ¾ µ. (iv) Wandle die Binärzahl ½¼¼½ ¼½½¼ ½¼¼½ ¼½½¼ ¼½½¼ ½¼¼½µ ¾ ins Dezimalsystem um. (v) Wandle die Binärzahl ½¼¼½ ¼½½¼ ½¼¼½ ¼½½¼ ¼½½¼ ½¼¼½µ ¾ ins Dezimalsystem um. (Achtung, da ist ein Komma drin!)
4
5 4. Übungsblatt zu Mathematik für Informatiker I, WS 2003/04, Mündlicher Teil JOACHIM VON ZUR GATHEN, OLAF MÜLLER, MICHAEL NÜSKEN Mündliche Aufgabe 4.7 (Quantoren). Drücke die Aussage Es gibt höchstens zwei Ü mit der Eigenschaft ³ ܵ. durch den Allquantor und die logischen Operationen,,, µ sowie das Gleichheitszeichen aus. Mündliche Aufgabe 4.8 (Komplexe Zahlen). (i) Berechne Ñ ¾ ½ Ñ µµ Ñ Ñ µ. (ii) Berechne Ñ ¾ ½ Ñ µµ Ñ Ñ µ. (iii) Berechne den Betrag von Ñ ¾ ¾ Ñ. Mündliche Aufgabe 4.9 (Stellenwertsysteme). Besonders in der Informatik sind Stellensysteme zu anderen Basen als ½¼ gebräuchlich und sehr wichtig. Für die Basis ½ verwenden wir die Buchstaben,..., für die hexadezimalen Ziffern(!) ½¼,...,½. Somit ist die hexadezimale Zahl µ ½ die Dezimalzahl ¾, nämlich ½ ½ ½. (i) Stelle Deine Matrikelnummer hexadezimal dar. (ii) Berechne (schriftlich und ohne Taschenrechner) hexadezimal ¾ ¾µ ½ ¼ ½ µ ½. (iii) Berechne (schriftlich und ohne Taschenrechner) oktal ¾ ¾µ ½¾¼ µ. (iv) Wandle die Binärzahl ½¼¼½ ½½½¼ ¼½¼½ ¼¼½¼ ¼¼¼½ ½½½½ ¼¼¼½µ ¾ ins Dezimalsystem um. (v) Wandle die Binärzahl ½¼¼½ ½½½¼ ¼½¼½ ¼¼½¼ ¼¼¼½ ½½½½ ¼¼¼½µ ¾ ins Dezimalsystem um. (Achtung, da ist ein Komma drin!)
6 Mündliche Aufgabe 4.10 (Algorithmus -adisch). Ziel dieser Aufgabe ist ein Algorithmus, der eine -adische Zahl in eine ganze (rechnerintern dargestellte) Zahl umwandelt. Die Eingabe sind also die Basis und eine Liste ½ ¼ µ von Ziffern ¾ ¼ ½ ½ und die Ausgabe soll die dadurch dargestellte Zahl Ü sein. Variante Aufwärts: Berechne in einer Schleife die durch die rechten Ziffern dargestellte Zahl. Variante Abwärts: Berechne in einer Schleife, die durch die linken Ziffern dargestellte Zahl. Für jede der beiden Varianten bearbeite die folgenden Schritte: (i) Entwickle den Algorithmus. (ii) Finde eine Schleifenvariante und beweise, dass sie gültig ist. (iii) Schliesse, dass der Algorithmus tatsächlich das gewünschte Ergebnis liefert. (iv) Bestimme die Laufzeit des Algorithmus. (v) Bestimme den Speicherbedarf des Algorithmus. Vergleiche die Laufzeiten und entscheide, welche Variante wohl günstiger ist.
Grundlagen der Informatik
 Mag. Christian Gürtler Programmierung Grundlagen der Informatik 2011 Inhaltsverzeichnis I. Allgemeines 3 1. Zahlensysteme 4 1.1. ganze Zahlen...................................... 4 1.1.1. Umrechnungen.................................
Mag. Christian Gürtler Programmierung Grundlagen der Informatik 2011 Inhaltsverzeichnis I. Allgemeines 3 1. Zahlensysteme 4 1.1. ganze Zahlen...................................... 4 1.1.1. Umrechnungen.................................
Daten verarbeiten. Binärzahlen
 Daten verarbeiten Binärzahlen In Digitalrechnern werden (fast) ausschließlich nur Binärzahlen eingesetzt. Das Binärzahlensystem ist das Stellenwertsystem mit der geringsten Anzahl von Ziffern. Es kennt
Daten verarbeiten Binärzahlen In Digitalrechnern werden (fast) ausschließlich nur Binärzahlen eingesetzt. Das Binärzahlensystem ist das Stellenwertsystem mit der geringsten Anzahl von Ziffern. Es kennt
Informationssysteme Gleitkommazahlen nach dem IEEE-Standard 754. Berechnung von Gleitkommazahlen aus Dezimalzahlen. HSLU T&A Informatik HS10
 Informationssysteme Gleitkommazahlen nach dem IEEE-Standard 754 Berechnung von Gleitkommazahlen aus Dezimalzahlen Die wissenschaftliche Darstellung einer Zahl ist wie folgt definiert: n = f * 10 e. f ist
Informationssysteme Gleitkommazahlen nach dem IEEE-Standard 754 Berechnung von Gleitkommazahlen aus Dezimalzahlen Die wissenschaftliche Darstellung einer Zahl ist wie folgt definiert: n = f * 10 e. f ist
Technische Informatik - Eine Einführung
 Martin-Luther-Universität Halle-Wittenberg Fachbereich Mathematik und Informatik Lehrstuhl für Technische Informatik Prof. P. Molitor Ausgabe: 2005-02-21 Abgabe: 2005-02-21 Technische Informatik - Eine
Martin-Luther-Universität Halle-Wittenberg Fachbereich Mathematik und Informatik Lehrstuhl für Technische Informatik Prof. P. Molitor Ausgabe: 2005-02-21 Abgabe: 2005-02-21 Technische Informatik - Eine
Theoretische Informatik SS 04 Übung 1
 Theoretische Informatik SS 04 Übung 1 Aufgabe 1 Es gibt verschiedene Möglichkeiten, eine natürliche Zahl n zu codieren. In der unären Codierung hat man nur ein Alphabet mit einem Zeichen - sagen wir die
Theoretische Informatik SS 04 Übung 1 Aufgabe 1 Es gibt verschiedene Möglichkeiten, eine natürliche Zahl n zu codieren. In der unären Codierung hat man nur ein Alphabet mit einem Zeichen - sagen wir die
Übungsaufgaben. - Vorgehensweise entsprechend dem Algorithmus der schriftlichen Multiplikation
 Übungsaufgaben Anmerkung Allen Beispielen soll noch hinzugefügt sein, dass wertvolle Hinweise, also die Tipps und Tricks die der schnellen maschinellen Multiplikation zu Grunde liegen, neben dem toff zur
Übungsaufgaben Anmerkung Allen Beispielen soll noch hinzugefügt sein, dass wertvolle Hinweise, also die Tipps und Tricks die der schnellen maschinellen Multiplikation zu Grunde liegen, neben dem toff zur
Musterlösung 2. Mikroprozessor & Eingebettete Systeme 1
 Musterlösung 2 Mikroprozessor & Eingebettete Systeme 1 WS2014/2015 Hinweis: Die folgenden Aufgaben erheben nicht den Anspruch, eine tiefergehende Kenntnis zu vermitteln; sie sollen lediglich den Einstieg
Musterlösung 2 Mikroprozessor & Eingebettete Systeme 1 WS2014/2015 Hinweis: Die folgenden Aufgaben erheben nicht den Anspruch, eine tiefergehende Kenntnis zu vermitteln; sie sollen lediglich den Einstieg
Eine Logikschaltung zur Addition zweier Zahlen
 Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
3 Zahlensysteme in der Digitaltechnik
 3 Zahlensysteme in der Digitaltechnik System Dezimal Hexadezimal Binär Oktal Basis, Radix 10 16 2 8 Zahlenwerte 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 A B C D E F 10 0 1 10 11 100
3 Zahlensysteme in der Digitaltechnik System Dezimal Hexadezimal Binär Oktal Basis, Radix 10 16 2 8 Zahlenwerte 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 A B C D E F 10 0 1 10 11 100
Lösungen: zu 1. a.) 0 0 1 1 b.) 1 1 1 1 c.) 0 1 1 0 + 1 1 0 0 + 0 0 1 1 + 0 1 1 1 1 1 1 1 1 0 0 1 0 1 1 0 1
 Lösungen: zu 1. a.) 0 0 1 1 b.) 1 1 1 1 c.) 0 1 1 0 + 1 1 0 0 + 0 0 1 1 + 0 1 1 1 1 1 1 1 1 0 0 1 0 1 1 0 1 vorzeichenlose Zahl: 15 vorzeichenlose Zahl: 18 vorzeichenlose Zahl: 13 Zweierkomplement: - 1
Lösungen: zu 1. a.) 0 0 1 1 b.) 1 1 1 1 c.) 0 1 1 0 + 1 1 0 0 + 0 0 1 1 + 0 1 1 1 1 1 1 1 1 0 0 1 0 1 1 0 1 vorzeichenlose Zahl: 15 vorzeichenlose Zahl: 18 vorzeichenlose Zahl: 13 Zweierkomplement: - 1
Einführung in die Programmierung
 Technische Universität Carolo Wilhelmina zu Brauschweig Institut für rechnergestützte Modellierung im Bauingenierwesen Prof. Dr.-Ing. habil. Manfred Krafczyk Pockelsstraße 3, 38106 Braunschweig http://www.irmb.tu-bs.de
Technische Universität Carolo Wilhelmina zu Brauschweig Institut für rechnergestützte Modellierung im Bauingenierwesen Prof. Dr.-Ing. habil. Manfred Krafczyk Pockelsstraße 3, 38106 Braunschweig http://www.irmb.tu-bs.de
Zahlensysteme Das 10er-System
 Zahlensysteme Übungsblatt für die entfallende Stunde am 22.10.2010. Das 10er-System... 1 Umrechnung in das 10er-System... 2 2er-System... 2 8er-System... 2 16er-System... 3 Umrechnung in andere Zahlensysteme...
Zahlensysteme Übungsblatt für die entfallende Stunde am 22.10.2010. Das 10er-System... 1 Umrechnung in das 10er-System... 2 2er-System... 2 8er-System... 2 16er-System... 3 Umrechnung in andere Zahlensysteme...
1. Das dekadische Ziffernsystem (Dezimalsystem) Eine ganze Zahl z kann man als Summe von Potenzen zur Basis 10 darstellen:
 Zahlensysteme. Das dekadische Ziffernsystem (Dezimalsystem) Eine ganze Zahl z kann man als Summe von Potenzen zur Basis darstellen: n n n n z a a... a a a Dabei sind die Koeffizienten a, a, a,... aus der
Zahlensysteme. Das dekadische Ziffernsystem (Dezimalsystem) Eine ganze Zahl z kann man als Summe von Potenzen zur Basis darstellen: n n n n z a a... a a a Dabei sind die Koeffizienten a, a, a,... aus der
Kapitel 4A: Einschub - Binärcodierung elementarer Datentypen. Einschub: Teile aus Kapitel 2 in Küchlin/Weber: Einführung in die Informatik
 Einschub: Binärcodierung elementarer Datentypen Teile aus Kapitel 2 in Küchlin/Weber: Einführung in die Informatik Unterscheide Zahl-Wert Zahl-Bezeichner Zu ein- und demselben Zahl-Wert kann es verschiedene
Einschub: Binärcodierung elementarer Datentypen Teile aus Kapitel 2 in Küchlin/Weber: Einführung in die Informatik Unterscheide Zahl-Wert Zahl-Bezeichner Zu ein- und demselben Zahl-Wert kann es verschiedene
Mathematische Grundlagen der Kryptographie. 1. Ganze Zahlen 2. Kongruenzen und Restklassenringe. Stefan Brandstädter Jennifer Karstens
 Mathematische Grundlagen der Kryptographie 1. Ganze Zahlen 2. Kongruenzen und Restklassenringe Stefan Brandstädter Jennifer Karstens 18. Januar 2005 Inhaltsverzeichnis 1 Ganze Zahlen 1 1.1 Grundlagen............................
Mathematische Grundlagen der Kryptographie 1. Ganze Zahlen 2. Kongruenzen und Restklassenringe Stefan Brandstädter Jennifer Karstens 18. Januar 2005 Inhaltsverzeichnis 1 Ganze Zahlen 1 1.1 Grundlagen............................
Jede Zahl muss dabei einzeln umgerechnet werden. Beginnen wir also ganz am Anfang mit der Zahl,192.
 Binäres und dezimales Zahlensystem Ziel In diesem ersten Schritt geht es darum, die grundlegende Umrechnung aus dem Dezimalsystem in das Binärsystem zu verstehen. Zusätzlich wird auch die andere Richtung,
Binäres und dezimales Zahlensystem Ziel In diesem ersten Schritt geht es darum, die grundlegende Umrechnung aus dem Dezimalsystem in das Binärsystem zu verstehen. Zusätzlich wird auch die andere Richtung,
Ein polyadisches Zahlensystem mit der Basis B ist ein Zahlensystem, in dem eine Zahl x nach Potenzen von B zerlegt wird.
 Zahlensysteme Definition: Ein polyadisches Zahlensystem mit der Basis B ist ein Zahlensystem, in dem eine Zahl x nach Potenzen von B zerlegt wird. In der Informatik spricht man auch von Stellenwertsystem,
Zahlensysteme Definition: Ein polyadisches Zahlensystem mit der Basis B ist ein Zahlensystem, in dem eine Zahl x nach Potenzen von B zerlegt wird. In der Informatik spricht man auch von Stellenwertsystem,
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
 Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Im Original veränderbare Word-Dateien
 Binärsystem Im Original veränderbare Word-Dateien Prinzipien der Datenverarbeitung Wie du weißt, führen wir normalerweise Berechnungen mit dem Dezimalsystem durch. Das Dezimalsystem verwendet die Grundzahl
Binärsystem Im Original veränderbare Word-Dateien Prinzipien der Datenverarbeitung Wie du weißt, führen wir normalerweise Berechnungen mit dem Dezimalsystem durch. Das Dezimalsystem verwendet die Grundzahl
Grundlagen der Informatik I Informationsdarstellung
 Grundlagen der Informatik I Informationsdarstellung Einführung in die Informatik, Gumm, H.-P./Sommer, M. Themen der heutigen Veranstaltung. ASCIi Code 2. Zeichenketten 3. Logische Operationen 4. Zahlendarstellung
Grundlagen der Informatik I Informationsdarstellung Einführung in die Informatik, Gumm, H.-P./Sommer, M. Themen der heutigen Veranstaltung. ASCIi Code 2. Zeichenketten 3. Logische Operationen 4. Zahlendarstellung
der Eingabe! Haben Sie das Ergebnis? Auf diesen schwarzen Punkt kommen wir noch zu sprechen.
 Medizintechnik MATHCAD Kapitel. Einfache Rechnungen mit MATHCAD ohne Variablendefinition In diesem kleinen Kapitel wollen wir die ersten Schritte mit MATHCAD tun und folgende Aufgaben lösen: 8 a: 5 =?
Medizintechnik MATHCAD Kapitel. Einfache Rechnungen mit MATHCAD ohne Variablendefinition In diesem kleinen Kapitel wollen wir die ersten Schritte mit MATHCAD tun und folgende Aufgaben lösen: 8 a: 5 =?
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR)
 Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
0, v 6 = 2 2. 1, v 4 = 1. 2. span(v 1, v 5, v 6 ) = span(v 1, v 2, v 3, v 4, v 5, v 6 ) 4. span(v 1, v 2, v 4 ) = span(v 2, v 3, v 5, v 6 )
 Aufgabe 65. Ganz schön span(n)end. Gegeben sei folgende Menge M von 6 Vektoren v, v,..., v 6 R 4 aus Aufgabe P 6: M = v =, v =, v =, v 4 =, v 5 =, v 6 = Welche der folgenden Aussagen sind wahr? span(v,
Aufgabe 65. Ganz schön span(n)end. Gegeben sei folgende Menge M von 6 Vektoren v, v,..., v 6 R 4 aus Aufgabe P 6: M = v =, v =, v =, v 4 =, v 5 =, v 6 = Welche der folgenden Aussagen sind wahr? span(v,
RSA-Verschlüsselung. Verfahren zur Erzeugung der beiden Schlüssel:
 RSA-Verschlüsselung Das RSA-Verfahren ist ein asymmetrisches Verschlüsselungsverfahren, das nach seinen Erfindern Ronald Linn Rivest, Adi Shamir und Leonard Adlemann benannt ist. RSA verwendet ein Schlüsselpaar
RSA-Verschlüsselung Das RSA-Verfahren ist ein asymmetrisches Verschlüsselungsverfahren, das nach seinen Erfindern Ronald Linn Rivest, Adi Shamir und Leonard Adlemann benannt ist. RSA verwendet ein Schlüsselpaar
Lineare Gleichungssysteme
 Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Gleichungen Lösen. Ein graphischer Blick auf Gleichungen
 Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Musterlösung 2. Mikroprozessor & Eingebettete Systeme 1
 Musterlösung 2 Mikroprozessor & Eingebettete Systeme 1 WS2013/2014 Hinweis: Die folgenden Aufgaben erheben nicht den Anspruch, eine tiefergehende Kenntnis zu vermitteln; sie sollen lediglich den Einstieg
Musterlösung 2 Mikroprozessor & Eingebettete Systeme 1 WS2013/2014 Hinweis: Die folgenden Aufgaben erheben nicht den Anspruch, eine tiefergehende Kenntnis zu vermitteln; sie sollen lediglich den Einstieg
Beispiel 48. 4.3.2 Zusammengesetzte Zufallsvariablen
 4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
0 Im folgenden sei die Wortlänge gleich 8 (d. h.: es wird mit Bytes gearbeitet).
 Aufgabe 0 Im folgenden sei die Wortlänge gleich 8 (d. h.: es wird mit Bytes gearbeitet). 1. i) Wie ist die Darstellung von 50 im Zweier =Komplement? ii) Wie ist die Darstellung von 62 im Einer =Komplement?
Aufgabe 0 Im folgenden sei die Wortlänge gleich 8 (d. h.: es wird mit Bytes gearbeitet). 1. i) Wie ist die Darstellung von 50 im Zweier =Komplement? ii) Wie ist die Darstellung von 62 im Einer =Komplement?
Diese Unterlage bezieht sich auf Excel 2010 (auf Deutsch). Die Benutzeroberfläche kann in anderen Versionen der Software erheblich anders aussehen.
 Vorbemerkung Diese Unterlage bezieht sich auf Excel 2010 (auf Deutsch). Die Benutzeroberfläche kann in anderen Versionen der Software erheblich anders aussehen. Einiges, das bei der Bearbeitung der Übung
Vorbemerkung Diese Unterlage bezieht sich auf Excel 2010 (auf Deutsch). Die Benutzeroberfläche kann in anderen Versionen der Software erheblich anders aussehen. Einiges, das bei der Bearbeitung der Übung
Protokoll zum Praktikum des Moduls Technische Informatik an der JLU Gießen
 Protokoll zum Praktikum des Moduls Technische Informatik an der JLU Gießen Technische Informatik Versuch 2 Julian Bergmann, Dennis Getzkow 8. Juni 203 Versuch 2 Einführung Im Versuch 2 sollte sich mit
Protokoll zum Praktikum des Moduls Technische Informatik an der JLU Gießen Technische Informatik Versuch 2 Julian Bergmann, Dennis Getzkow 8. Juni 203 Versuch 2 Einführung Im Versuch 2 sollte sich mit
Einführung in die Informatik I
 Einführung in die Informatik I Das Rechnen in Zahlensystemen zur Basis b=2, 8, 10 und 16 Prof. Dr. Nikolaus Wulff Zahlensysteme Neben dem üblichen dezimalen Zahlensystem zur Basis 10 sind in der Informatik
Einführung in die Informatik I Das Rechnen in Zahlensystemen zur Basis b=2, 8, 10 und 16 Prof. Dr. Nikolaus Wulff Zahlensysteme Neben dem üblichen dezimalen Zahlensystem zur Basis 10 sind in der Informatik
3. LINEARE GLEICHUNGSSYSTEME
 176 3. LINEARE GLEICHUNGSSYSTEME 90 Vitamin-C-Gehalt verschiedener Säfte 18,0 mg 35,0 mg 12,5 mg 1. a) 100 ml + 50 ml + 50 ml = 41,75 mg 100 ml 100 ml 100 ml b) : Menge an Kirschsaft in ml y: Menge an
176 3. LINEARE GLEICHUNGSSYSTEME 90 Vitamin-C-Gehalt verschiedener Säfte 18,0 mg 35,0 mg 12,5 mg 1. a) 100 ml + 50 ml + 50 ml = 41,75 mg 100 ml 100 ml 100 ml b) : Menge an Kirschsaft in ml y: Menge an
Übungen zu Informatik 1
 Communication Systems Group (CSG) Prof. Dr. Burkhard Stiller, Universität Zürich, Binzmühlestrasse 14, CH-8050 Zürich Telefon: +41 44 635 6710, Fax: +41 44 635 6809, stiller@ifi.uzh.ch Fabio Hecht, Telefon:
Communication Systems Group (CSG) Prof. Dr. Burkhard Stiller, Universität Zürich, Binzmühlestrasse 14, CH-8050 Zürich Telefon: +41 44 635 6710, Fax: +41 44 635 6809, stiller@ifi.uzh.ch Fabio Hecht, Telefon:
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHISCHE UIVERSITÄT MÜCHE Zentrum Mathematik PRF. R.R. JÜRGE RICHTER-GEBERT, VAESSA KRUMMECK, MICHAEL PRÄHFER Höhere Mathematik für Informatiker I (Wintersemester 003/004) Aufgabenblatt 1 (4. ktober 003)
TECHISCHE UIVERSITÄT MÜCHE Zentrum Mathematik PRF. R.R. JÜRGE RICHTER-GEBERT, VAESSA KRUMMECK, MICHAEL PRÄHFER Höhere Mathematik für Informatiker I (Wintersemester 003/004) Aufgabenblatt 1 (4. ktober 003)
FH Jena Prüfungsaufgaben Prof. Giesecke FB ET/IT Binäre Rechenoperationen WS 09/10
 FB ET/IT Binäre Rechenoperationen WS 9/ Name, Vorname: Matr.-Nr.: Zugelassene Hilfsmittel: beliebiger Taschenrechner eine selbst erstellte Formelsammlung Wichtige Hinweise: Ausführungen, Notizen und Lösungen
FB ET/IT Binäre Rechenoperationen WS 9/ Name, Vorname: Matr.-Nr.: Zugelassene Hilfsmittel: beliebiger Taschenrechner eine selbst erstellte Formelsammlung Wichtige Hinweise: Ausführungen, Notizen und Lösungen
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Binär- und Hexadezimal-Zahl Arithmetik.
 Binär- und Hexadezimal-Zahl Arithmetik. Prof. Dr. Dörte Haftendorn, MuPAD 4, http://haftendorn.uni-lueneburg.de Aug.06 Automatische Übersetzung aus MuPAD 3.11, 24.04.02 Version vom 12.10.05 Web: http://haftendorn.uni-lueneburg.de
Binär- und Hexadezimal-Zahl Arithmetik. Prof. Dr. Dörte Haftendorn, MuPAD 4, http://haftendorn.uni-lueneburg.de Aug.06 Automatische Übersetzung aus MuPAD 3.11, 24.04.02 Version vom 12.10.05 Web: http://haftendorn.uni-lueneburg.de
Theoretische Grundlagen der Informatik WS 09/10
 Theoretische Grundlagen der Informatik WS 09/10 - Tutorium 6 - Michael Kirsten und Kai Wallisch Sitzung 13 02.02.2010 Inhaltsverzeichnis 1 Formeln zur Berechnung Aufgabe 1 2 Hamming-Distanz Aufgabe 2 3
Theoretische Grundlagen der Informatik WS 09/10 - Tutorium 6 - Michael Kirsten und Kai Wallisch Sitzung 13 02.02.2010 Inhaltsverzeichnis 1 Formeln zur Berechnung Aufgabe 1 2 Hamming-Distanz Aufgabe 2 3
2 Darstellung von Zahlen und Zeichen
 2.1 Analoge und digitale Darstellung von Werten 79 2 Darstellung von Zahlen und Zeichen Computer- bzw. Prozessorsysteme führen Transformationen durch, die Eingaben X auf Ausgaben Y abbilden, d.h. Y = f
2.1 Analoge und digitale Darstellung von Werten 79 2 Darstellung von Zahlen und Zeichen Computer- bzw. Prozessorsysteme führen Transformationen durch, die Eingaben X auf Ausgaben Y abbilden, d.h. Y = f
Daten, Informationen, Kodierung. Binärkodierung
 Binärkodierung Besondere Bedeutung der Binärkodierung in der Informatik Abbildung auf Alphabet mit zwei Zeichen, in der Regel B = {0, 1} Entspricht den zwei möglichen Schaltzuständen in der Elektronik:
Binärkodierung Besondere Bedeutung der Binärkodierung in der Informatik Abbildung auf Alphabet mit zwei Zeichen, in der Regel B = {0, 1} Entspricht den zwei möglichen Schaltzuständen in der Elektronik:
Binäre Gleitkommazahlen
 Binäre Gleitkommazahlen Was ist die wissenschaftliche, normalisierte Darstellung der binären Gleitkommazahl zur dezimalen Gleitkommazahl 0,625? Grundlagen der Rechnerarchitektur Logik und Arithmetik 72
Binäre Gleitkommazahlen Was ist die wissenschaftliche, normalisierte Darstellung der binären Gleitkommazahl zur dezimalen Gleitkommazahl 0,625? Grundlagen der Rechnerarchitektur Logik und Arithmetik 72
11.3 Komplexe Potenzreihen und weitere komplexe Funktionen
 .3 Komplexe Potenzreihen und weitere komplexe Funktionen Definition.) komplexe Folgen: z n = x n + j. y n mit zwei reellen Folgen x n und y n.) Konvergenz: Eine komplexe Folge z n = x n + j. y n heißt
.3 Komplexe Potenzreihen und weitere komplexe Funktionen Definition.) komplexe Folgen: z n = x n + j. y n mit zwei reellen Folgen x n und y n.) Konvergenz: Eine komplexe Folge z n = x n + j. y n heißt
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
- Strukturentwurf elementarer Rechenwerke - Grund-Flipflop (RS-Flipflop) - Register, Schieberegister, Zähler
 3.Übung: Inhalte: - binäre Logik, boolsche Gleichungen - logische Grundschaltungen - trukturentwurf elementarer echenwerke - Grund-Flipflop (-Flipflop) - egister, chieberegister, Zähler Übung Informatik
3.Übung: Inhalte: - binäre Logik, boolsche Gleichungen - logische Grundschaltungen - trukturentwurf elementarer echenwerke - Grund-Flipflop (-Flipflop) - egister, chieberegister, Zähler Übung Informatik
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Vorkurs: Mathematik für Informatiker Steven Köhler, Anja Moldenhauer, Marcel Morisse
 Vorkurs: Mathematik für Informatiker Steven Köhler, Anja Moldenhauer, Marcel Morisse Wintersemester 2014/15 Aufgaben I-1. Es seien die folgenden Mengen A = {5,7,9}, B = {5,6,7} und C = {1,3,5,7,9} gegeben.
Vorkurs: Mathematik für Informatiker Steven Köhler, Anja Moldenhauer, Marcel Morisse Wintersemester 2014/15 Aufgaben I-1. Es seien die folgenden Mengen A = {5,7,9}, B = {5,6,7} und C = {1,3,5,7,9} gegeben.
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen
 Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Zahlensysteme. von Christian Bartl
 von Inhaltsverzeichnis Inhaltsverzeichnis... 2 1. Einleitung... 3 2. Umrechnungen... 3 2.1. Dezimalsystem Binärsystem... 3 2.2. Binärsystem Dezimalsystem... 3 2.3. Binärsystem Hexadezimalsystem... 3 2.4.
von Inhaltsverzeichnis Inhaltsverzeichnis... 2 1. Einleitung... 3 2. Umrechnungen... 3 2.1. Dezimalsystem Binärsystem... 3 2.2. Binärsystem Dezimalsystem... 3 2.3. Binärsystem Hexadezimalsystem... 3 2.4.
Zahlensysteme. Digitale Rechner speichern Daten im Dualsystem 435 dez = 1100110011 binär
 Zahlensysteme Menschen nutzen zur Angabe von Werten und zum Rechnen vorzugsweise das Dezimalsystem Beispiel 435 Fische aus dem Teich gefischt, d.h. 4 10 2 + 3 10 1 +5 10 0 Digitale Rechner speichern Daten
Zahlensysteme Menschen nutzen zur Angabe von Werten und zum Rechnen vorzugsweise das Dezimalsystem Beispiel 435 Fische aus dem Teich gefischt, d.h. 4 10 2 + 3 10 1 +5 10 0 Digitale Rechner speichern Daten
Kapiteltests zum Leitprogramm Binäre Suchbäume
 Kapiteltests zum Leitprogramm Binäre Suchbäume Björn Steffen Timur Erdag überarbeitet von Christina Class Binäre Suchbäume Kapiteltests für das ETH-Leitprogramm Adressaten und Institutionen Das Leitprogramm
Kapiteltests zum Leitprogramm Binäre Suchbäume Björn Steffen Timur Erdag überarbeitet von Christina Class Binäre Suchbäume Kapiteltests für das ETH-Leitprogramm Adressaten und Institutionen Das Leitprogramm
Übung zum Thema. Abmaße ablesen und Toleranzen berechnen
 Übung zum Thema Abmaße ablesen und Toleranzen berechnen Grundlage der Übung sind die Tabellen TB2-1 bis TB2-3 im Roloff/Matek Tabellenbuch Vorgehensweise: 1. Bestimmung der Grundtoleranz In TB2-1 stehen
Übung zum Thema Abmaße ablesen und Toleranzen berechnen Grundlage der Übung sind die Tabellen TB2-1 bis TB2-3 im Roloff/Matek Tabellenbuch Vorgehensweise: 1. Bestimmung der Grundtoleranz In TB2-1 stehen
Zahlensysteme: Oktal- und Hexadezimalsystem
 20 Brückenkurs Die gebräuchlichste Bitfolge umfasst 8 Bits, sie deckt also 2 8 =256 Möglichkeiten ab, und wird ein Byte genannt. Zwei Bytes, also 16 Bits, bilden ein Wort, und 4 Bytes, also 32 Bits, formen
20 Brückenkurs Die gebräuchlichste Bitfolge umfasst 8 Bits, sie deckt also 2 8 =256 Möglichkeiten ab, und wird ein Byte genannt. Zwei Bytes, also 16 Bits, bilden ein Wort, und 4 Bytes, also 32 Bits, formen
Black Box erklärt Zahlensysteme.
 Black Box erklärt Zahlensysteme. Jeder von uns benutzt aktiv mindestens zwei Zahlenssysteme, oftmals aber so selbstverständlich, dass viele aus dem Stegreif keines mit Namen nennen können. Im europäischen
Black Box erklärt Zahlensysteme. Jeder von uns benutzt aktiv mindestens zwei Zahlenssysteme, oftmals aber so selbstverständlich, dass viele aus dem Stegreif keines mit Namen nennen können. Im europäischen
Übungen für Woche 10
 Übungen für Woche 10 Martin Rubey 12. Januar 2011 Die folgenden Übungen sollen den Umgang mit Backtracking und kombinatorischen Spezies näherbringen. Genaue Hinweise gibt es erst auf Seite 5. Zur Erinnerung:
Übungen für Woche 10 Martin Rubey 12. Januar 2011 Die folgenden Übungen sollen den Umgang mit Backtracking und kombinatorischen Spezies näherbringen. Genaue Hinweise gibt es erst auf Seite 5. Zur Erinnerung:
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN
 HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
Zahlensysteme Seite -1- Zahlensysteme
 Zahlensysteme Seite -- Zahlensysteme Inhaltsverzeichnis Dezimalsystem... Binärsystem... Umrechnen Bin Dez...2 Umrechnung Dez Bin...2 Rechnen im Binärsystem Addition...3 Die negativen ganzen Zahlen im Binärsystem...4
Zahlensysteme Seite -- Zahlensysteme Inhaltsverzeichnis Dezimalsystem... Binärsystem... Umrechnen Bin Dez...2 Umrechnung Dez Bin...2 Rechnen im Binärsystem Addition...3 Die negativen ganzen Zahlen im Binärsystem...4
Grundlagen der Informatik (BSc) Übung Nr. 5
 Übung Nr. 5: Zahlensysteme und ihre Anwendung Bitte kreuzen Sie in der folgenden Auflistung alle Zahlensysteme an, zu welchen jeder Ausdruck als Zahl gehören kann! (Verwenden Sie 'x für Wahl, ' ' für Ausschluß
Übung Nr. 5: Zahlensysteme und ihre Anwendung Bitte kreuzen Sie in der folgenden Auflistung alle Zahlensysteme an, zu welchen jeder Ausdruck als Zahl gehören kann! (Verwenden Sie 'x für Wahl, ' ' für Ausschluß
Musterlösungen zur Linearen Algebra II Blatt 5
 Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Klausurteilnehmer. Wichtige Hinweise. Note: Klausur Informatik Programmierung, 17.09.2012 Seite 1 von 8 HS OWL, FB 7, Malte Wattenberg.
 Klausur Informatik Programmierung, 17.09.2012 Seite 1 von 8 Klausurteilnehmer Name: Matrikelnummer: Wichtige Hinweise Es sind keinerlei Hilfsmittel zugelassen auch keine Taschenrechner! Die Klausur dauert
Klausur Informatik Programmierung, 17.09.2012 Seite 1 von 8 Klausurteilnehmer Name: Matrikelnummer: Wichtige Hinweise Es sind keinerlei Hilfsmittel zugelassen auch keine Taschenrechner! Die Klausur dauert
http://www.olympiade-mathematik.de 2. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 7 Saison 1962/1963 Aufgaben und Lösungen
 2. Mathematik Olympiade Saison 1962/1963 Aufgaben und Lösungen 1 OJM 2. Mathematik-Olympiade Aufgaben Hinweis: Der Lösungsweg mit Begründungen und Nebenrechnungen soll deutlich erkennbar in logisch und
2. Mathematik Olympiade Saison 1962/1963 Aufgaben und Lösungen 1 OJM 2. Mathematik-Olympiade Aufgaben Hinweis: Der Lösungsweg mit Begründungen und Nebenrechnungen soll deutlich erkennbar in logisch und
Programmierkurs Java
 Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
a n + 2 1 auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert:
 Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
Aufgaben zu Stellenwertsystemen
 Aufgaben zu Stellenwertsystemen Aufgabe 1 a) Zähle im Dualsystem von 1 bis 16! b) Die Zahl 32 wird durch (100000) 2 dargestellt. Zähle im Dualsystem von 33 bis 48! Zähle schriftlich! Aufgabe 2 Wandle die
Aufgaben zu Stellenwertsystemen Aufgabe 1 a) Zähle im Dualsystem von 1 bis 16! b) Die Zahl 32 wird durch (100000) 2 dargestellt. Zähle im Dualsystem von 33 bis 48! Zähle schriftlich! Aufgabe 2 Wandle die
Sollsaldo und Habensaldo
 ollsaldo und abensaldo Man hört oft die Aussage "Ein ollsaldo steht im aben, und ein abensaldo steht im oll". Da fragt man sich aber, warum der ollsaldo dann ollsaldo heißt und nicht abensaldo, und warum
ollsaldo und abensaldo Man hört oft die Aussage "Ein ollsaldo steht im aben, und ein abensaldo steht im oll". Da fragt man sich aber, warum der ollsaldo dann ollsaldo heißt und nicht abensaldo, und warum
Definition und Begriffe
 Merkblatt: Das Dreieck Definition und Begriffe Das Dreieck ist ein Vieleck. In der Ebene ist es die einfachste Figur, die von geraden Linien begrenzt wird. Ecken: Jedes Dreieck hat drei Ecken, die meist
Merkblatt: Das Dreieck Definition und Begriffe Das Dreieck ist ein Vieleck. In der Ebene ist es die einfachste Figur, die von geraden Linien begrenzt wird. Ecken: Jedes Dreieck hat drei Ecken, die meist
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Skript und Aufgabensammlung Terme und Gleichungen Mathefritz Verlag Jörg Christmann Nur zum Privaten Gebrauch! Alle Rechte vorbehalten!
 Mathefritz 5 Terme und Gleichungen Meine Mathe-Seite im Internet kostenlose Matheaufgaben, Skripte, Mathebücher Lernspiele, Lerntipps, Quiz und noch viel mehr http:// www.mathefritz.de Seite 1 Copyright
Mathefritz 5 Terme und Gleichungen Meine Mathe-Seite im Internet kostenlose Matheaufgaben, Skripte, Mathebücher Lernspiele, Lerntipps, Quiz und noch viel mehr http:// www.mathefritz.de Seite 1 Copyright
Zahlenmauern. Dr. Maria Koth. Ausgehend von dieser einfachen Bauvorschrift ergibt sich eine Vielzahl an möglichen Aufgabenstellungen.
 Zahlenmauern Dr. Maria Koth Zahlenmauern sind nach einer einfachen Regel gebaut: In jedem Feld steht die Summe der beiden darunter stehenden Zahlen. Ausgehend von dieser einfachen Bauvorschrift ergibt
Zahlenmauern Dr. Maria Koth Zahlenmauern sind nach einer einfachen Regel gebaut: In jedem Feld steht die Summe der beiden darunter stehenden Zahlen. Ausgehend von dieser einfachen Bauvorschrift ergibt
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Binär Codierte Dezimalzahlen (BCD-Code)
 http://www.reiner-tolksdorf.de/tab/bcd_code.html Hier geht es zur Startseite der Homepage Binär Codierte Dezimalzahlen (BCD-) zum 8-4-2-1- zum Aiken- zum Exeß-3- zum Gray- zum 2-4-2-1- 57 zum 2-4-2-1-
http://www.reiner-tolksdorf.de/tab/bcd_code.html Hier geht es zur Startseite der Homepage Binär Codierte Dezimalzahlen (BCD-) zum 8-4-2-1- zum Aiken- zum Exeß-3- zum Gray- zum 2-4-2-1- 57 zum 2-4-2-1-
Binäre Bäume. 1. Allgemeines. 2. Funktionsweise. 2.1 Eintragen
 Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Information in einem Computer ist ein
 4 Arithmetik Die in den vorhergehenden Kapiteln vorgestellten Schaltungen haben ausschließlich einfache, Boole sche Signale verarbeitet. In diesem Kapitel wird nun erklärt, wie Prozessoren mit Zahlen umgehen.
4 Arithmetik Die in den vorhergehenden Kapiteln vorgestellten Schaltungen haben ausschließlich einfache, Boole sche Signale verarbeitet. In diesem Kapitel wird nun erklärt, wie Prozessoren mit Zahlen umgehen.
Sowohl die Malstreifen als auch die Neperschen Streifen können auch in anderen Stellenwertsystemen verwendet werden.
 Multiplikation Die schriftliche Multiplikation ist etwas schwieriger als die Addition. Zum einen setzt sie das kleine Einmaleins voraus, zum anderen sind die Überträge, die zu merken sind und häufig in
Multiplikation Die schriftliche Multiplikation ist etwas schwieriger als die Addition. Zum einen setzt sie das kleine Einmaleins voraus, zum anderen sind die Überträge, die zu merken sind und häufig in
Mikro-Controller-Pass 1
 Seite: 1 Zahlensysteme im Selbststudium Inhaltsverzeichnis Vorwort Seite 3 Aufbau des dezimalen Zahlensystems Seite 4 Aufbau des dualen Zahlensystems Seite 4 Aufbau des oktalen Zahlensystems Seite 5 Aufbau
Seite: 1 Zahlensysteme im Selbststudium Inhaltsverzeichnis Vorwort Seite 3 Aufbau des dezimalen Zahlensystems Seite 4 Aufbau des dualen Zahlensystems Seite 4 Aufbau des oktalen Zahlensystems Seite 5 Aufbau
2 Lineare Gleichungen mit zwei Variablen
 2 Lineare Gleichungen mit zwei Variablen Die Klasse 9 c möchte ihr Klassenzimmer mit Postern ausschmücken. Dafür nimmt sie 30, aus der Klassenkasse. In Klasse 7 wurden lineare Gleichungen mit einer Variablen
2 Lineare Gleichungen mit zwei Variablen Die Klasse 9 c möchte ihr Klassenzimmer mit Postern ausschmücken. Dafür nimmt sie 30, aus der Klassenkasse. In Klasse 7 wurden lineare Gleichungen mit einer Variablen
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
N Bit binäre Zahlen (signed)
 N Bit binäre Zahlen (signed) n Bit Darstellung ist ein Fenster auf die ersten n Stellen der Binär Zahl 0000000000000000000000000000000000000000000000000110 = 6 1111111111111111111111111111111111111111111111111101
N Bit binäre Zahlen (signed) n Bit Darstellung ist ein Fenster auf die ersten n Stellen der Binär Zahl 0000000000000000000000000000000000000000000000000110 = 6 1111111111111111111111111111111111111111111111111101
Zahlenwinkel: Forscherkarte 1. alleine. Zahlenwinkel: Forschertipp 1
 Zahlenwinkel: Forscherkarte 1 alleine Tipp 1 Lege die Ziffern von 1 bis 9 so in den Zahlenwinkel, dass jeder Arm des Zahlenwinkels zusammengezählt das gleiche Ergebnis ergibt! Finde möglichst viele verschiedene
Zahlenwinkel: Forscherkarte 1 alleine Tipp 1 Lege die Ziffern von 1 bis 9 so in den Zahlenwinkel, dass jeder Arm des Zahlenwinkels zusammengezählt das gleiche Ergebnis ergibt! Finde möglichst viele verschiedene
2. Negative Dualzahlen darstellen
 2.1 Subtraktion von Dualzahlen 2.1.1 Direkte Subtraktion (Tafelrechnung) siehe ARCOR T0IF Nachteil dieser Methode: Diese Form der Subtraktion kann nur sehr schwer von einer Elektronik (CPU) durchgeführt
2.1 Subtraktion von Dualzahlen 2.1.1 Direkte Subtraktion (Tafelrechnung) siehe ARCOR T0IF Nachteil dieser Methode: Diese Form der Subtraktion kann nur sehr schwer von einer Elektronik (CPU) durchgeführt
Übung RA, Kapitel 1.2
 Übung RA, Kapitel 1.2 Teil 1: Zahlen und Logik A) Aufgaben zu den ganzen Zahlen 1. Konvertieren Sie die folgenden Zahlen in die Binärform: 1984 Immer durch 2 teilen, der Rest ergibt das Bit. Jeweils mit
Übung RA, Kapitel 1.2 Teil 1: Zahlen und Logik A) Aufgaben zu den ganzen Zahlen 1. Konvertieren Sie die folgenden Zahlen in die Binärform: 1984 Immer durch 2 teilen, der Rest ergibt das Bit. Jeweils mit
Binärdarstellung von Fliesskommazahlen
 Binärdarstellung von Fliesskommazahlen 1. IEEE 754 Gleitkommazahl im Single-Format So sind in Gleitkommazahlen im IEEE 754-Standard aufgebaut: 31 30 24 23 0 S E E E E E E E E M M M M M M M M M M M M M
Binärdarstellung von Fliesskommazahlen 1. IEEE 754 Gleitkommazahl im Single-Format So sind in Gleitkommazahlen im IEEE 754-Standard aufgebaut: 31 30 24 23 0 S E E E E E E E E M M M M M M M M M M M M M
Codierungsverfahren SS 2011. Reed-Solomon-Codes zur Mehrblock-Bündelfehler-Korrektur
 Reed-Solomon-Codes zur Mehrblock-Bündelfehler-Korrektur Wie die zyklischen BCH-Codes zur Mehrbitfehler-Korrektur eignen sich auch die sehr verwandten Reed-Solomon-Codes (= RS-Codes) zur Mehrbitfehler-Korrektur.
Reed-Solomon-Codes zur Mehrblock-Bündelfehler-Korrektur Wie die zyklischen BCH-Codes zur Mehrbitfehler-Korrektur eignen sich auch die sehr verwandten Reed-Solomon-Codes (= RS-Codes) zur Mehrbitfehler-Korrektur.
1) Mit welcher Zahl muss 18 multipliziert werden, um 234 zu erhalten? Kontrolliere! 2) Finde die Zahl, mit der 171 multipliziert werden muss, um 4104
 1) Mit welcher Zahl muss 18 multipliziert werden, um 234 zu erhalten? Kontrolliere! 2) Finde die Zahl, mit der 171 multipliziert werden muss, um 4104 zu erhalten? Probe! 3) Von zwei Zahlen ist die eine
1) Mit welcher Zahl muss 18 multipliziert werden, um 234 zu erhalten? Kontrolliere! 2) Finde die Zahl, mit der 171 multipliziert werden muss, um 4104 zu erhalten? Probe! 3) Von zwei Zahlen ist die eine
Mikro-Controller-Pass 1
 MikroControllerPass Lernsysteme MC 805 Seite: (Selbststudium) Inhaltsverzeichnis Vorwort Seite 2 Addition Seite 3 Subtraktion Seite 4 Subtraktion durch Addition der Komplemente Dezimales Zahlensystem:Neunerkomplement
MikroControllerPass Lernsysteme MC 805 Seite: (Selbststudium) Inhaltsverzeichnis Vorwort Seite 2 Addition Seite 3 Subtraktion Seite 4 Subtraktion durch Addition der Komplemente Dezimales Zahlensystem:Neunerkomplement
Abschlussprüfung Realschule Bayern II / III: 2009 Haupttermin B 1.0 B 1.1
 B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
Klassenarbeit zu linearen Gleichungssystemen
 Klassenarbeit zu linearen Gleichungssystemen Aufgabe : Bestimme die Lösungsmenge der Gleichungssysteme mit Hilfe des Additionsverfahrens: x + 4y = 8 5x y = x y = x y = Aufgabe : Bestimme die Lösungsmenge
Klassenarbeit zu linearen Gleichungssystemen Aufgabe : Bestimme die Lösungsmenge der Gleichungssysteme mit Hilfe des Additionsverfahrens: x + 4y = 8 5x y = x y = x y = Aufgabe : Bestimme die Lösungsmenge
BITte ein BIT. Vom Bit zum Binärsystem. A Bit Of Magic. 1. Welche Werte kann ein Bit annehmen? 2. Wie viele Zustände können Sie mit 2 Bit darstellen?
 BITte ein BIT Vom Bit zum Binärsystem A Bit Of Magic 1. Welche Werte kann ein Bit annehmen? 2. Wie viele Zustände können Sie mit 2 Bit darstellen? 3. Gegeben ist der Bitstrom: 10010110 Was repräsentiert
BITte ein BIT Vom Bit zum Binärsystem A Bit Of Magic 1. Welche Werte kann ein Bit annehmen? 2. Wie viele Zustände können Sie mit 2 Bit darstellen? 3. Gegeben ist der Bitstrom: 10010110 Was repräsentiert
5. Übung: Binäres Rechnen und Fließkommazahlen Abteilung Verteilte Systeme, Universität Ulm
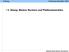 5. Übung: Binäres Rechnen und Fließkommazahlen Aufgabe 1: Binäres Rechnen a) Berechnen Sie: x = 01100101b*(0101101b-10110100b)+10101b. Alle Zahlen sind 8 Bit breit und in Zweierkomplement-Notation angegeben.
5. Übung: Binäres Rechnen und Fließkommazahlen Aufgabe 1: Binäres Rechnen a) Berechnen Sie: x = 01100101b*(0101101b-10110100b)+10101b. Alle Zahlen sind 8 Bit breit und in Zweierkomplement-Notation angegeben.
Prozentrechnung. Wir können nun eine Formel für die Berechnung des Prozentwertes aufstellen:
 Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Grundlagen der Informatik Übungen 1.Termin
 : : : : : : : : : : : : : : : : : : : : : : Grundlagen der Informatik Übungen 1.Termin Dipl.-Phys. Christoph Niethammer Grundlagen der Informatik 2012 1 : : : : : : : : : : : : : : : : : : : : : : Kontakt
: : : : : : : : : : : : : : : : : : : : : : Grundlagen der Informatik Übungen 1.Termin Dipl.-Phys. Christoph Niethammer Grundlagen der Informatik 2012 1 : : : : : : : : : : : : : : : : : : : : : : Kontakt
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen?
 Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Abamsoft Finos im Zusammenspiel mit shop to date von DATA BECKER
 Abamsoft Finos im Zusammenspiel mit shop to date von DATA BECKER Abamsoft Finos in Verbindung mit der Webshopanbindung wurde speziell auf die Shop-Software shop to date von DATA BECKER abgestimmt. Mit
Abamsoft Finos im Zusammenspiel mit shop to date von DATA BECKER Abamsoft Finos in Verbindung mit der Webshopanbindung wurde speziell auf die Shop-Software shop to date von DATA BECKER abgestimmt. Mit
Kurzanleitung MAN E-Learning (WBT)
 Kurzanleitung MAN E-Learning (WBT) Um Ihr gebuchtes E-Learning zu bearbeiten, starten Sie bitte das MAN Online- Buchungssystem (ICPM / Seminaris) unter dem Link www.man-academy.eu Klicken Sie dann auf
Kurzanleitung MAN E-Learning (WBT) Um Ihr gebuchtes E-Learning zu bearbeiten, starten Sie bitte das MAN Online- Buchungssystem (ICPM / Seminaris) unter dem Link www.man-academy.eu Klicken Sie dann auf
