3 Kritischer Bereich zum Niveau α = 0.10: K = (χ 2 k 1;1 α, + ) = (χ2 5;0.90, + ) = (9.236, + ) 4 Berechnung der realisierten Teststatistik:
|
|
|
- Sarah Blau
- vor 7 Jahren
- Abrufe
Transkript
1 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Auftragseigagsbeispiel, realisierte Teststatistik χ , p-wert: Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Beispiel: Chi-Quadrat-Apassugstest auf H : Y Geom(25) Geom(25)-Verteilug hat uedliche Träger {, 1, 2, } ud Wahrscheilichkeitsfuktio f χ 2 (4) (x) p 9832 p χ 4, 95 x χ p Geom(25) : N [, 1]; p Geom(25) (i) (1 25) i 25, Bedigug p i 5 ka also mit p i p Geom(25) (a i ) für a i : i 1 icht für alle i N erfüllt sei Klassierug hier also (trotz diskreter Verteilug) erforderlich Wege (für wachsedes i bzw a i ) abehmeder pi sivoll: Zusammefassug aller große i i der letzte Klasse K k so, dass Bedigug pi 5 für alle i {1,, k} erfüllt ist Wahrscheilichkeit (uter H ) pk für Klasse K k über Verteilugsfuktio oder als verbleibede Wahrscheilichkeit pk 1 k 1 i1 p i Je ach Verteilug F ud Stichprobeumfag köe aber auch komplexere Klassieruge ötig sei, um Bedigug pi 5 zu erfülle Schließede Statistik (WS 216/17) Folie 161 Schließede Statistik (WS 216/17) Folie Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Fortsetzug Beispiel Stichprobeiformatio: Häufigkeitsverteilug aus Klassierug eier eifache Stichprobe vom Umfag 1 zu Y liefert: a i i Gewüschtes Sigifikaziveau: α 1 Chi-Quadrat-Apassugstest: 1 Hypothese: H : F Y F Geom(25) H 1 : F Y F Geom(25) χ 2 ( i pi p ist uter H approximativ χ 2 (k 1)-verteilt, falls i1 i 5 für alle i gilt p i 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 3 Kritischer Bereich zum Niveau α 1: K (χ 2 k 1;1 α, + ) (χ2 5;9, + ) (9236, + ) 4 Berechug der realisierte Teststatistik: ( i p i p i K i i pi pi (, ] 32 (1 25) (, 1] 19 (1 25) (1, 2] 16 (1 25) (2, 3] 16 (1 25) (3, 4] 6 (1 25) (4, + ) i1 p i Σ χ Es gilt pi 5 für alle i {1,, 6} Näherug ok 5 Etscheidug: χ (9236, + ) K H wird abgeleht! (p-wert: 1 F χ 2 (5)(χ 2 ) 1 F χ 2 (5)(123366) ) Test kommt zum Ergebis, dass Y icht eier Geom(25)-Verteilug geügt Schließede Statistik (WS 216/17) Folie 163 Schließede Statistik (WS 216/17) Folie 164
2 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Beispiel: Chi-Quadrat-Apassugstest (F stetig) Klassierug bei stetige hypothetische Verteiluge ubedigt erforderlich Hier: Klassierug soll vorgegebe sei (evtl implizit durch bereits klassierte Stichprobeiformatio statt vollstädiger Urliste!) Bei eigeer Wahl der Klassierug: Vorsicht, da Klassierug Test beeiflusst! Beispiel: Utersuchug, ob Y N(, 1) Stichprobeiformatio (aus eifacher Stichprobe vom Umfag 2): K i (, 15] ( 15, 75] ( 75, ] (, 75] (75, 15] (15, ) i Gewüschtes Sigifikaziveau: α 5 Geeigeter Test: Chi-Quadrat-Apassugstest 1 Hypothese: H : F Y F N(,1) H 1 : F Y F N(,1) χ 2 ( i pi p ist uter H approximativ χ 2 (k 1)-verteilt, falls i1 i 5 für alle i gilt p i Schließede Statistik (WS 216/17) Folie Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 3 Kritischer Bereich zum Niveau α 5: K (χ 2 k 1;1 α, + ) (χ2 5;95, + ) (117, + ) 4 Berechug der realisierte Teststatistik: K i (a i 1, a i ] i pi F (a i ) F (a i 1 ) pi ( i p i pi (, 15] ( 15, 75] ( 75, ] (, 75] (75, 15] (15, + ) Σ Es gilt pi 5 für alle i {1,, 6} Näherug ok 5 Etscheidug: χ / (117, + ) K H wird icht abgeleht! (p-wert: 1 F χ 2 (5)(χ 2 ) 1 F χ 2 (5)(77828) ) Test ka Hypothese, dass Y stadardormalverteilt ist, icht verwerfe Schließede Statistik (WS 216/17) Folie Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Chi-Quadrat-Apassugstest auf parametrisches Verteilugsmodell Chi-Quadrat-Apassugstest ka auch durchgeführt werde, we statt (eizeler) hypothetischer Verteilug eie parametrische Klasse vo Verteiluge als hypothetische Verteilugsklasse fugiert Durchführug des Chi-Quadrat-Apassugstests da i zwei Schritte: 1 Schätzug der Verteilugsparameter ierhalb der hypothetische Verteilugsklasse mit der ML-Methode 2 Durchführug des (reguläre) Chi-Quadrat-Apassugstest mit der hypothetische Verteilug zu de geschätze Parameter Zu beachte: Verteilug der Testgröße χ2 ädert sich! Bei ML-Schätzug auf Basis der für die Durchführug des Chi-Quadrat-Apassugstest maßgebliche Klassierug der Stichprobe gilt uter H äherugsweise χ 2 χ 2 (k r 1), wobei r die Azahl der per ML-Methode geschätzte Parameter ist Werde die Verteilugsparameter icht aus de klassierte Date, soder aus de ursprügliche Date mit ML-Methode geschätzt, gilt diese Verteilugsaussage so icht mehr (Abweichug allerdigs moderat) Schließede Statistik (WS 216/17) Folie Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Zusammefassug: Chi-Quadrat-Apassugstest zur Apassug a parametrische Verteilugsfamilie Awedugsvoraussetzuge approx: Y beliebig verteilt, X 1,, X eif Stichprobe zu Y Familie vo Verteilugsfuktioe F θ für θ Θ vorgegebe k 1 Klassegreze a 1 < a 2 < < a k 1 vorgegebe Nullhypothese H : F Y F θ für ei θ Θ Gegehypothese H 1 : F Y F θ (für alle θ Θ) ( Teststatistik χ 2 ( i pi ) 2 i ) 2 ( p i 1 Verteilug (H ) i1 p i i1 p i 2 i p i1 i ) χ 2 ist uter H äherugsweise χ 2 (k r 1)-verteilt, we θ ML-Schätzer des r-dim Verteilugsparameters θ auf Basis klassierter Date ist (Verwedug vo θ siehe ute) (Näherug ur verüftig, falls pi 5 für i {1,, k}) Beötigte Größe p i F θ(a k ) F θ(a k 1 ) mit a :, a k :, i #{j {1,, } x j (a i 1, a i ]}, i {1,, k} Kritischer Bereich (χ 2 k r 1;1 α, ) zum Niveau α p-wert 1 F χ 2 (k r 1)(χ 2 ) Schließede Statistik (WS 216/17) Folie 168
3 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Beispiel: Chi-Quadrat-Apassugstest auf H : Y Geom(p) für p (, 1) Stichprobeiformatio: Häufigkeitsverteilug aus voragegageem Beispiel: a i i Erster Schritt: ML-Schätzug vo p mit Hilfe der klassierte Stichprobeiformatio: Ma ka zeige, dass der ML-Schätzer auf Basis der klassierte Stichprobe durch k p k + k i1 (i 1) i gegebe ist Hier erhält ma also die Realisatio p Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Zweiter Schritt: Durchführug des Chi-Quadrat-Apassugstest für H : F Y F 3333 (mit F p : F Geom(p) ) gege H 1 : F Y F 3333 uter Berücksichtigug der ML-Schätzug vo p durch geäderte Verteilug vo χ 2 uter H! Isgesamt: Chi-Quadrat-Apassugtest für Verteilugsfamilie: 1 Hypothese: H : F Y F p für ei p (, 1) (mit F p : F Geom(p) ) gege H 1 : F Y F p χ 2 ( i pi p ist uter H approximativ χ 2 (k 1 r)-verteilt, falls i1 i pi 5 für alle i gilt ud r-dimesioaler Verteilugsparameter per ML-Methode aus de klassierte Date geschätzt wurde 3 Kritischer Bereich zum Niveau α 1: K (χ 2 k 1 r;1 α, + ) (χ2 4;9, + ) (7779, + ) Schließede Statistik (WS 216/17) Folie 169 Schließede Statistik (WS 216/17) Folie 17 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 4 Berechug der realisierte Teststatistik: Eie ML-Schätzug aus de klassierte Date liefert de Schätzwert p 3333 für de ubekate Verteilugsparameter p ( i p i p i K i i pi pi (, ] 32 (1 3333) (, 1] 19 (1 3333) (1, 2] 16 (1 3333) (2, 3] 16 (1 3333) (3, 4] 6 (1 3333) (4, + ) i1 p i Σ χ Es gilt pi 5 für alle i {1,, 6} Näherug ok 5 Etscheidug: χ / (7779, + ) K H wird icht abgeleht! (p-wert: 1 F χ2 (4)(χ 2 ) 1 F χ2 (4)(48175) ) Test kommt zum Ergebis, dass Y Geom(p) icht verworfe werde ka (ML-Schätzug vo p: p 3333) 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Test auf geometrische Verteilug, realisierte Teststatistik χ , p-wert: 37 f χ 2 (4) (x) p 693 p 37 χ χ 4, 9 x Schließede Statistik (WS 216/17) Folie 171 Schließede Statistik (WS 216/17) Folie 172
4 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Uabhägigkeitstest 82 Chi-Quadrat-Uabhägigkeitstest (Kotigeztest) Bisher: Eifache Stichprobe X 1,, X zu eier Zufallsvariable Y Im Folgede: Betrachtug vo eifache Stichprobe zu mehrdimesioale Zufallsvariable bzw (später) mehrere (uabhägige) eifache Stichprobe zu mehrere Zufallsvariable Erste Problemstellug: Utersuchug vo zwei Zufallsvariable Y A, Y B auf stochastische Uabhägigkeit Erforderliche Stichprobeiformatio: Eifache Stichprobe (X A 1, X B 1 ), (X A 2, X B 2 ),, (X A, X B ) vom Umfag zu zweidimesioaler Zufallsvariable (Y A, Y B ) Testidee: de bei Uabhägigkeit vo Y A, Y B bestehede Zusammehag zwische Radverteiluge vo Y A ud Y B sowie gemeisamer Verteilug vo (Y A, Y B ) ausutze: Gemeisame Wahrscheilichkeite stimme bei Uabhägigkeit mit Produkt der Radwahrscheilichkeite überei (falls (Y A, Y B ) diskret) Daher spreche gerige Abweichuge zwische gemeisame (relative) Häufigkeite ud Produkt der (relative) Radhäufigkeite für Uabhägigkeit, große Abweichuge dagege Schließede Statistik (WS 216/17) Folie Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Uabhägigkeitstest 82 Betrachtete Awedugssituatioe: 1 Sowohl Y A als auch Y B sid diskret mit weige Auspräguge, i der Stichprobe trete die Auspräguge a 1,, a k vo Y A bzw b 1,, b l vo Y B auf 2 Y A ud Y B sid diskret mit viele Auspräguge oder stetig, die Stichprobeiformatio wird da mit Hilfe vo Klassieruge A 1 (, a 1], A 2 (a 1, a 2],, A k (a k 1, ) vo Y A bzw B 1 (, b 1], B 2 (b 1, b 2],, B l (b l 1, ) vo Y B zusammegefasst 3 Mischforme vo 1 ud 2 Der Vergleich zwische (i der Stichprobe) beobachtete gemeisame absolute Häufigkeite ij ud bei Uabhägigkeit (auf Basis der Radhäufigkeite) zu erwartede gemeisame absolute Häufigkeite erfolgt durch die Größe χ 2 l i1 j1 ( ij ) 2, wobei ij die beobachtete gemeisame Häufigkeite für (a i, b j ) bzw (A i, B j ) aus der Stichproberealisatio ud i j i j die erwartete gemeisame Häufigkeite aus de Radhäufigkeite i vo a i bzw A i ud j vo b j bzw B j sid (i {1,, k}, j {1,, l}) Schließede Statistik (WS 216/17) Folie Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Uabhägigkeitstest 82 Für wachsede Stichprobeumfag kovergiert die Verteilug der Testgröße χ 2 bei Gültigkeit vo H : Y A, Y B sid stochastisch uabhägig gege die χ 2 ((k 1) (l 1))-Verteilug Die Näherug der Verteilug vo χ 2 uter H ist für edliche Stichprobeumfag verüftig, falls gilt: 5 für alle i {1,, k}, j {1,, l} Wie beim Chi-Quadrat-Apassugstest spreche große Werte der Teststatistik χ 2 gege die Nullhypothese Y A ud Y B sid stochastisch uabhägig, währed kleie Werte für H spreche Als kritischer Bereich zum Sigifikaziveau α ergibt sich also etspreched: K (χ 2 (k 1) (l 1);1 α, ) Die Testgröße χ 2 ist eg verwadt mit der bei der Berechug des korrigierte Pearsosche Kotigezkoeffiziete beötigte Größe χ 2 Aalog zum Chi-Quadrat-Apassugstest ka der Chi-Quadrat-Uabhägigkeitstest ebefalls auf Merkmale Y A bzw Y B agewedet werde, dere Auspräguge a 1,, a k bzw b 1,, b l och icht Zufallsvariable-koform als reelle Zahle kodiert wurde Schließede Statistik (WS 216/17) Folie Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Uabhägigkeitstest 82 Darstellug der Stichprobeiformatio üblicherweise i Kotigeztabelle der Form Y A \ Y B b 1 b 2 b l a l a l bzw Y A \ Y B B 1 B 2 B l A l A l a k k1 k2 kl A k k1 k2 kl Beötigte Größe i j köe da ach Ergäzug der Kotigeztabelle um ihre Radhäufigkeite i l j1 ij ud j k i1 ij i weiterer Tabelle mit aalogem Aufbau Y A \ Y B B 1 B 2 B l i A 1 ñ ñ ñ 1l 1 l 1 A 2 ñ ñ ñ 2l 2 l 2 A k ñ k1 k 1 ñ k2 k 2 ñ kl k l k j 1 2 l (hier für 2 Variate) oder (falls geüged Raum vorhade) direkt i der Kotigeztabelle berechet werde Schließede Statistik (WS 216/17) Folie 176
5 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Uabhägigkeitstest 82 Zusammefassug: Chi-Quadrat-Uabhägigkeitstest Awedugs- approximativ: (Y A, Y B ) beliebig verteilt voraussetzuge (X1 A, X1 B ),, (X A, X B ) eifache Stichprobe zu (Y A, Y B ) Auspräguge {a 1,, a k } vo Y A, {b 1,, b l } vo Y B oder Klassegreze a 1 < < a k 1 zu Y A, b 1 < < b l 1 zu Y B Nullhypothese H : Y A,Y B stochastisch uabhägig Gegehypothese H 1 : Y A,Y B icht stochastisch uabhägig Teststatistik l χ 2 ( ij ) 2 l ij 2 Verteilug (H ) Beötigte Größe i1 j1 i1 j1 χ 2 ist äherugsweise χ 2 ((k 1) (l 1))-verteilt, falls H gilt (Näherug ur verüftig, falls 5 für alle i, j) ij #{m {1,, } (x m, y m) A i B j } für alle i, j mit A i {a i }, B j {b j } bzw Klasse A i, B j ach vorg Greze, i j mit i l j1 ij, j k i1 ij, Kritischer Bereich (χ 2 (k 1) (l 1);1 α, ) zum Niveau α p-wert 1 F χ 2 ((k 1) (l 1))(χ 2 ) Schließede Statistik (WS 216/17) Folie Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Uabhägigkeitstest 82 Beispiel: Zusammehag Geschlecht/tägl Fahrzeit (PKW) Utersuchugsgegestad: Sid die beide Zufallsvariable Geschlecht (Y A ) ud täglich mit PKW zurückgelegte Strecke (Y B ) stochastisch uabhägig? Stichprobeiformatio: (Kotigez-)Tabelle mit gemeisame (i der Stichprobe vom Umfag 2 beobachtete) Häufigkeite, wobei für Y B eie Klassierug i die Klasse kurz, mittel ud lag durchgeführt wurde: Fahrzeit (Y B ) Geschlecht (Y A ) kurz mittel lag Mälich Weiblich Gewüschtes Sigifikaziveau: α 5 Geeigeter Test: Chi-Quadrat-Uabhägigkeitstest 1 Hypothese: H : Y A, Y B stochastisch uabhägig gege H 1 : Y A, Y B stoch abhägig l χ 2 ( ij ) 2 ist uter H approximativ i1 j1 χ 2 ((k 1) (l 1))-verteilt, falls 5 für alle 1 i k ud 1 j l Schließede Statistik (WS 216/17) Folie Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Uabhägigkeitstest 82 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Uabhägigkeitstest 82 3 Kritischer Bereich zum Niveau α 5: K (χ 2 (k 1) (l 1);1 α, + ) (χ2 2;95, + ) (5991, + ) 4 Berechug der realisierte Teststatistik: Um Radhäufigkeite i ud j ergäzte Tabelle der gemeisame Häufigkeite: Tabelle der i j : Y A \ Y B kurz mittel lag i Mälich Weiblich j Y A \ Y B kurz mittel lag i Mälich Weiblich j Es gilt 5 für alle 1 i 2 ud 1 j 3 Näherug ok 4 (Fortsetzug: Berechug der realisierte Teststatistik) χ 2 5 Etscheidug: 2 i1 j1 3 ( ij ) 2 ( ( ( ( ( ( χ (5991, + ) K H wird abgeleht! (p-wert: 1 F χ2 (2)(χ 2 ) 1 F χ2 (2)(122547) ) Der Test kommt also zum Ergebis, dass die beide Zufallsvariable Geschlecht ud tägliche Fahrzeit (PKW) stochastisch abhägig sid Schließede Statistik (WS 216/17) Folie 179 Schließede Statistik (WS 216/17) Folie 18
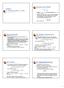
Beispiel: p-wert bei Chi-Quadrat-Anpassungstest (Grafik) Auftragseingangsbeispiel, realisierte Teststatistik χ 2 = , p-wert: 0.
 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Auftragseigagsbeispiel, realisierte Teststatistik χ 2 = 12075, p-wert: 00168 f χ 2 (4)
8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Auftragseigagsbeispiel, realisierte Teststatistik χ 2 = 12075, p-wert: 00168 f χ 2 (4)
Beispiel: p-wert bei Chi-Quadrat-Anpassungstest (Grafik) Auftragseingangsbeispiel, realisierte Teststatistik χ 2 = , p-wert: 0.
 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 8.1 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Auftragseigagsbeispiel, realisierte Teststatistik χ 2 = 12.075, p-wert: 0.0168 f χ
8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 8.1 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Auftragseigagsbeispiel, realisierte Teststatistik χ 2 = 12.075, p-wert: 0.0168 f χ
Gütefunktion und Fehlerwahrscheinlichkeiten Rechtsseitiger Test (µ 0 = 500) zum Signifikanzniveau α = Interpretation von Testergebnissen I
 6 Hypothesetests Gauß-Test für de Mittelwert bei bekater Variaz 6.3 Gütefuktio ud Fehlerwahrscheilichkeite Rechtsseitiger Test (µ 0 = 500) zum Sigifikaziveau α = 0.30 6 Hypothesetests Gauß-Test für de
6 Hypothesetests Gauß-Test für de Mittelwert bei bekater Variaz 6.3 Gütefuktio ud Fehlerwahrscheilichkeite Rechtsseitiger Test (µ 0 = 500) zum Sigifikaziveau α = 0.30 6 Hypothesetests Gauß-Test für de
4 Schwankungsintervalle Schwankungsintervalle 4.2
 4 Schwakugsitervalle Schwakugsitervalle 4. Bemerkuge Die bekate Symmetrieeigeschaft Φ(x) = 1 Φ( x) bzw. Φ( x) = 1 Φ(x) für alle x R überträgt sich auf die Quatile N p der Stadardormalverteilug i der Form
4 Schwakugsitervalle Schwakugsitervalle 4. Bemerkuge Die bekate Symmetrieeigeschaft Φ(x) = 1 Φ( x) bzw. Φ( x) = 1 Φ(x) für alle x R überträgt sich auf die Quatile N p der Stadardormalverteilug i der Form
2. Repetition relevanter Teilbereiche der Statistik
 . Repetitio Statistik Ökoometrie I - Peter Stalder. Repetitio relevater Teilbereiche der Statistik (Maddala Kapitel ) Zufallsvariable ud Wahrscheilichkeitsverteiluge Zufallsvariable X (stochastische Variable)
. Repetitio Statistik Ökoometrie I - Peter Stalder. Repetitio relevater Teilbereiche der Statistik (Maddala Kapitel ) Zufallsvariable ud Wahrscheilichkeitsverteiluge Zufallsvariable X (stochastische Variable)
Kapitel 5: Schließende Statistik
 Kapitel 5: Schließede Statistik Statistik, Prof. Dr. Kari Melzer 5. Schließede Statistik: Typische Fragestellug ahad vo Beispiele Beispiel Aus 5 Messwerte ergebe sich für die Reißfestigkeit eier Garsorte
Kapitel 5: Schließede Statistik Statistik, Prof. Dr. Kari Melzer 5. Schließede Statistik: Typische Fragestellug ahad vo Beispiele Beispiel Aus 5 Messwerte ergebe sich für die Reißfestigkeit eier Garsorte
h a 2 b 1 h a1 b 2 h a1 b 1 h a1. h a 2. h.b1 h ij h 11 h 12 h 21 a b h. j h 1. h 2. h.1 a b h i. =h i1 h i2... h i m h. j =h 1j h 2j... h k j h.
 Kotigeztabelle / Kreuztabelle für 2 diskrete /omialskalierte Variable ethält: 1. absolute gemeisame Häufigkeite h 11 h 12 h 21 für Kombiatioe vo zwei Merkmale / Variable a b steht also für mit jeweils
Kotigeztabelle / Kreuztabelle für 2 diskrete /omialskalierte Variable ethält: 1. absolute gemeisame Häufigkeite h 11 h 12 h 21 für Kombiatioe vo zwei Merkmale / Variable a b steht also für mit jeweils
Forschungsstatistik I
 Prof. Dr. G. Meihardt 6. Stock, Taubertsberg R. 06-06 (Persike) R. 06-31 (Meihardt) Sprechstude jederzeit ach Vereibarug Forschugsstatistik I Dr. Malte Persike persike@ui-maiz.de http://psymet03.sowi.ui-maiz.de/
Prof. Dr. G. Meihardt 6. Stock, Taubertsberg R. 06-06 (Persike) R. 06-31 (Meihardt) Sprechstude jederzeit ach Vereibarug Forschugsstatistik I Dr. Malte Persike persike@ui-maiz.de http://psymet03.sowi.ui-maiz.de/
Wirksamkeit, Effizienz
 3 Parameterpuktschätzer Eigeschafte vo Schätzfuktioe 3.3 Wirksamkeit, Effiziez Defiitio 3.5 (Wirksamkeit, Effiziez Sei W eie parametrische Verteilugsaahme mit Parameterraum Θ. 1 Seie θ ud θ erwartugstreue
3 Parameterpuktschätzer Eigeschafte vo Schätzfuktioe 3.3 Wirksamkeit, Effiziez Defiitio 3.5 (Wirksamkeit, Effiziez Sei W eie parametrische Verteilugsaahme mit Parameterraum Θ. 1 Seie θ ud θ erwartugstreue
Statistik. 5. Schließende Statistik: Typische Fragestellung anhand von Beispielen. Kapitel 5: Schließende Statistik
 Statistik Kapitel 5: Schließede Statistik 5. Schließede Statistik: Typische Fragestellug ahad vo Beispiele Beispiel 1» Aus 5 Messwerte ergebe sich für die Reißfestigkeit eier Garsorte der arithmetische
Statistik Kapitel 5: Schließede Statistik 5. Schließede Statistik: Typische Fragestellug ahad vo Beispiele Beispiel 1» Aus 5 Messwerte ergebe sich für die Reißfestigkeit eier Garsorte der arithmetische
Wirksamkeit, Effizienz. Beispiel: Effizienz. Mittlerer quadratischer Fehler (MSE) Konsistenz im quadratischen Mittel
 3 arameterpuktschätzer Eigeschafte vo Schätzfuktioe 3.3 Wirksamkeit, Effiziez 3 arameterpuktschätzer Eigeschafte vo Schätzfuktioe 3.3 Beispiel: Effiziez Defiitio 3.5 (Wirksamkeit, Effiziez Sei W eie parametrische
3 arameterpuktschätzer Eigeschafte vo Schätzfuktioe 3.3 Wirksamkeit, Effiziez 3 arameterpuktschätzer Eigeschafte vo Schätzfuktioe 3.3 Beispiel: Effiziez Defiitio 3.5 (Wirksamkeit, Effiziez Sei W eie parametrische
Tests statistischer Hypothesen
 KAPITEL 0 Tests statistischer Hypothese I der Statistik muss ma oft Hypothese teste, z.b. muss ma ahad eier Stichprobe etscheide, ob ei ubekater Parameter eie vorgegebee Wert aimmt. Zuerst betrachte wir
KAPITEL 0 Tests statistischer Hypothese I der Statistik muss ma oft Hypothese teste, z.b. muss ma ahad eier Stichprobe etscheide, ob ei ubekater Parameter eie vorgegebee Wert aimmt. Zuerst betrachte wir
10. Testen von Hypothesen Seite 1 von 6
 10. Teste vo Hypothese Seite 1 vo 6 10.1 Eiführug i das Teste vo Hypothese Eie Hypothese ist eie Vermutug bzw. Behauptug über die Wahrscheilichkeit eies Ereigisses. Mit Hilfe eies geeigete Tests (=Testverfahre)
10. Teste vo Hypothese Seite 1 vo 6 10.1 Eiführug i das Teste vo Hypothese Eie Hypothese ist eie Vermutug bzw. Behauptug über die Wahrscheilichkeit eies Ereigisses. Mit Hilfe eies geeigete Tests (=Testverfahre)
Wirksamkeit, Effizienz
 3 Parameterpuktschätzer Eigeschafte vo Schätzfuktioe 3.3 Wirksamkeit, Effiziez Defiitio 3.5 (Wirksamkeit, Effiziez Sei W eie parametrische Verteilugsaahme mit Parameterraum Θ. 1 Seie θ ud θ erwartugstreue
3 Parameterpuktschätzer Eigeschafte vo Schätzfuktioe 3.3 Wirksamkeit, Effiziez Defiitio 3.5 (Wirksamkeit, Effiziez Sei W eie parametrische Verteilugsaahme mit Parameterraum Θ. 1 Seie θ ud θ erwartugstreue
14 Statistische Beziehungen zwischen nomi nalen Merkmalen
 14 Statistische Beziehuge zwische omi ale Merkmale 14.1 Der Chi Quadrat Test auf Uabhägigkeit für Vier Feldertafel 14.2 Der Chi Quadrat Test auf Uabhägigkeit für r s Kotigeztafel 14.3 Zusammmehagsmaße
14 Statistische Beziehuge zwische omi ale Merkmale 14.1 Der Chi Quadrat Test auf Uabhägigkeit für Vier Feldertafel 14.2 Der Chi Quadrat Test auf Uabhägigkeit für r s Kotigeztafel 14.3 Zusammmehagsmaße
5.4.2 Die empirische Verteilungsfunktion als Ausgangspunkt
 Tests 9 5.4 Der Kolmogorov Smirov Test Grudlage für de Kolmogorov Smirov Apassugs Test ist ei Satz vo Kolmogorov, die asymptotische Verteilug eier Statistik Δ betreffed. Aus Δ ergibt sich durch Modifikatio
Tests 9 5.4 Der Kolmogorov Smirov Test Grudlage für de Kolmogorov Smirov Apassugs Test ist ei Satz vo Kolmogorov, die asymptotische Verteilug eier Statistik Δ betreffed. Aus Δ ergibt sich durch Modifikatio
Evaluierung einer Schulungsmaßnahme: Punktezahl vor der Schulung Punktezahl nach der Schulung. Autoritarismusscore vor/nach Projekt
 2.4.5 Gauss-Test ud t-test für verbudee Stichprobe 2.4.5.8 Zum Begriff der verbudee Stichprobe Verbudee Stichprobe: Vergleich zweier Merkmale X ud Y, die jetzt a deselbe Persoe erhobe werde. Vorsicht:
2.4.5 Gauss-Test ud t-test für verbudee Stichprobe 2.4.5.8 Zum Begriff der verbudee Stichprobe Verbudee Stichprobe: Vergleich zweier Merkmale X ud Y, die jetzt a deselbe Persoe erhobe werde. Vorsicht:
6 Vergleich mehrerer unverbundener Stichproben
 6 Vergleich mehrerer uverbudeer Stichprobe 6.1 Die eifaktorielle Variazaalyse Die eifaktorielle Variazaalyse diet der Utersuchug des Eiflusses eier kategorieller (bzw. ichtmetrischer) Variable, die die
6 Vergleich mehrerer uverbudeer Stichprobe 6.1 Die eifaktorielle Variazaalyse Die eifaktorielle Variazaalyse diet der Utersuchug des Eiflusses eier kategorieller (bzw. ichtmetrischer) Variable, die die
Die notwendigen Verteilungstabellen finden Sie z.b. hier:
 Fakultät für Mathematik Istitute IAG ud IMO Prof. Dr. G. Kyureghya/Dr. M. Hödig Schätz- ud Prüfverfahre Die otwedige Verteilugstabelle fide Sie z.b. hier: http://www.ivwl.ui-kassel.de/kosfeld/lehre/zeitreihe/verteilugstabelle.pdf
Fakultät für Mathematik Istitute IAG ud IMO Prof. Dr. G. Kyureghya/Dr. M. Hödig Schätz- ud Prüfverfahre Die otwedige Verteilugstabelle fide Sie z.b. hier: http://www.ivwl.ui-kassel.de/kosfeld/lehre/zeitreihe/verteilugstabelle.pdf
2.3 Kontingenztafeln und Chi-Quadrat-Test
 2.3 Kotigeztafel ud Chi-Quadrat-Test Die Voraussetzuge a die Date i diesem Kapitel sid dieselbe, wie im voragegagee Kapitel, ur dass die Stichprobe hier aus Realisieruge vo kategorielle Zufallsvariable
2.3 Kotigeztafel ud Chi-Quadrat-Test Die Voraussetzuge a die Date i diesem Kapitel sid dieselbe, wie im voragegagee Kapitel, ur dass die Stichprobe hier aus Realisieruge vo kategorielle Zufallsvariable
Lehrstuhl für Empirische Wirtschaftsforschung und Ökonometrie Dr. Roland Füss Statistik II: Schließende Statistik SS 2007
 Lehrstuhl für Empirische Wirtschaftsforschug ud Ökoometrie Dr. Rolad Füss Statistik II: Schließede Statistik SS 2007 6. Grezwertsätze Der wichtigste Grud für die Häufigkeit des Auftretes der Normalverteilug
Lehrstuhl für Empirische Wirtschaftsforschug ud Ökoometrie Dr. Rolad Füss Statistik II: Schließede Statistik SS 2007 6. Grezwertsätze Der wichtigste Grud für die Häufigkeit des Auftretes der Normalverteilug
Tests für beliebige Zufallsvariable
 Kapitel 10 Tests für beliebige Zufallsvariable 10.1 Der Chi-Quadrat-Apassugstest Sei x eie gaz beliebige Zufallsvariable, dere Dichtefuktio icht oder icht geau bekat ist. Beispiel: Es seie z.b. mittels
Kapitel 10 Tests für beliebige Zufallsvariable 10.1 Der Chi-Quadrat-Apassugstest Sei x eie gaz beliebige Zufallsvariable, dere Dichtefuktio icht oder icht geau bekat ist. Beispiel: Es seie z.b. mittels
,,, xn. 3. Intervallschätzungen Zufallsstichproben und Stichprobenfunktionen Zufallsstichproben. Zufallsvariablen mit
 3. Itervallschätzuge 3.1. Zufallsstichprobe ud Stichprobefuktioe 3.1.1 Zufallsstichprobe 1 Sei eie Zufallsvariable ud seie gemeisamer Verteilug,,,, Zufallsvariable mit - da heiße 1,,, Zufallsstichprobe
3. Itervallschätzuge 3.1. Zufallsstichprobe ud Stichprobefuktioe 3.1.1 Zufallsstichprobe 1 Sei eie Zufallsvariable ud seie gemeisamer Verteilug,,,, Zufallsvariable mit - da heiße 1,,, Zufallsstichprobe
Übungen mit dem Applet erwartungstreu
 Übuge mit dem Applet erwartugstreu Visualisierug vo erwartugstreu Begriffe ud statischer Hitergrud. Visualisieruge mit dem Applet..3. Zufallsstreuug der Eizelwerte...3. Mittelwerte 3.3 Variaz. 4.4 Variaz
Übuge mit dem Applet erwartugstreu Visualisierug vo erwartugstreu Begriffe ud statischer Hitergrud. Visualisieruge mit dem Applet..3. Zufallsstreuug der Eizelwerte...3. Mittelwerte 3.3 Variaz. 4.4 Variaz
3.2 Wilcoxon Rangsummentest
 3. Wilcoxo Ragsummetest Wir gehe davo aus, dass zwei Teilstichprobe x 1, x,..., x 1 ud y1, y,..., y vorliege, wobei die erste Teilstichprobe aus Realisieruge vo uabhägig ud idetisch stetig verteilte Zufallsvariable
3. Wilcoxo Ragsummetest Wir gehe davo aus, dass zwei Teilstichprobe x 1, x,..., x 1 ud y1, y,..., y vorliege, wobei die erste Teilstichprobe aus Realisieruge vo uabhägig ud idetisch stetig verteilte Zufallsvariable
3 Vergleich zweier unverbundener Stichproben
 3 Vergleich zweier uverbudeer Stichprobe 3. Der Zweistichprobe t-test Es wird vorausgesetzt, dass die beide Teilstichprobe x, x,..., x ud y, y,..., y jeweils aus (voeiader uabhägige) ormalverteilte Grudgesamtheite
3 Vergleich zweier uverbudeer Stichprobe 3. Der Zweistichprobe t-test Es wird vorausgesetzt, dass die beide Teilstichprobe x, x,..., x ud y, y,..., y jeweils aus (voeiader uabhägige) ormalverteilte Grudgesamtheite
Mathematik 2 für Naturwissenschaften
 Has Walser Mathematik 2 für Naturwisseschafte 2 3 3 4 6 4 5 0 0 5 6 5 20 5 6 Modul 209 Tabelle Has Walser: Modul 209, Tabelle ii Ihalt Fakultäte... 2 Biomialkoeffiziete... 2 3 Biomische Verteilug... 3
Has Walser Mathematik 2 für Naturwisseschafte 2 3 3 4 6 4 5 0 0 5 6 5 20 5 6 Modul 209 Tabelle Has Walser: Modul 209, Tabelle ii Ihalt Fakultäte... 2 Biomialkoeffiziete... 2 3 Biomische Verteilug... 3
Vl Statistische Prozess- und Qualitätskontrolle und Versuchsplanung Übung 5
 Vl Statistische Prozess- ud Qualitätskotrolle ud Versuchsplaug Übug 5 Aufgabe ) Sei p = P(A) die Wahrscheilichkeit für ei Ereigis A, dh., es gilt 0 p. Bereche Sie das Maximum der Fuktio f(p) = p(-p). Aufgabe
Vl Statistische Prozess- ud Qualitätskotrolle ud Versuchsplaug Übug 5 Aufgabe ) Sei p = P(A) die Wahrscheilichkeit für ei Ereigis A, dh., es gilt 0 p. Bereche Sie das Maximum der Fuktio f(p) = p(-p). Aufgabe
Testen statistischer Hypothesen
 Kapitel 9 Teste statistischer Hypothese 9.1 Eiführug, Sigifiaztests Sigifiaztest für µ bei der ormalverteilug bei beatem σ = : X i seie uabhägig ud µ, ) verteilt, µ sei ubeat. Stelle eie Hypothese über
Kapitel 9 Teste statistischer Hypothese 9.1 Eiführug, Sigifiaztests Sigifiaztest für µ bei der ormalverteilug bei beatem σ = : X i seie uabhägig ud µ, ) verteilt, µ sei ubeat. Stelle eie Hypothese über
Kontingenztabellen. Chi-Quadrat-Test. Korrelationsanalyse zwischen kategorischen Merkmalen. 1. Unabhängigkeitstest
 Kotigeztabelle. Chi-Quadrat-Test KAD 1.11. 1. Uabhägigkeitstest. Apassugstest. Homogeitätstest Beispiel 1 ohe Frau 8 75 1 Ma 48 49 97 76 14? Korrelatiosaalyse zwische kategorische Merkmale Häufigkeitstabelle
Kotigeztabelle. Chi-Quadrat-Test KAD 1.11. 1. Uabhägigkeitstest. Apassugstest. Homogeitätstest Beispiel 1 ohe Frau 8 75 1 Ma 48 49 97 76 14? Korrelatiosaalyse zwische kategorische Merkmale Häufigkeitstabelle
Vl Statistische Prozess und Qualitätskontrolle und Versuchsplanung Übung 3
 Vl Statistische Prozess ud Qualitätskotrolle ud Versuchsplaug Übug 3 Aufgabe ) Die Schichtdicke X bei eier galvaische Beschichtug vo Autoteile sei ormalverteilt N(μ,σ ). 4 Teile werde galvaisch beschichtet.
Vl Statistische Prozess ud Qualitätskotrolle ud Versuchsplaug Übug 3 Aufgabe ) Die Schichtdicke X bei eier galvaische Beschichtug vo Autoteile sei ormalverteilt N(μ,σ ). 4 Teile werde galvaisch beschichtet.
Statistische Modelle und Parameterschätzung
 Kapitel 2 Statistische Modelle ud Parameterschätzug 2. Statistisches Modell Die bisher betrachtete Modellierug eies Zufallsexperimetes erforderte isbesodere die Festlegug eier W-Verteilug. Oft besteht
Kapitel 2 Statistische Modelle ud Parameterschätzug 2. Statistisches Modell Die bisher betrachtete Modellierug eies Zufallsexperimetes erforderte isbesodere die Festlegug eier W-Verteilug. Oft besteht
6. Grenzwertsätze. 6.1 Tschebyscheffsche Ungleichung
 6. Grezwertsätze 6.1 Tschebyscheffsche Ugleichug Sofer für eie Zufallsvariable X die Verteilug bekat ist, lässt sich die Wahrscheilichkeit dafür bestimme, dass X i eiem bestimmte Itervall liegt. Wie ist
6. Grezwertsätze 6.1 Tschebyscheffsche Ugleichug Sofer für eie Zufallsvariable X die Verteilug bekat ist, lässt sich die Wahrscheilichkeit dafür bestimme, dass X i eiem bestimmte Itervall liegt. Wie ist
Korrelationsanalyse zwischen kategorischen Merkmalen. Kontingenztabellen. Chi-Quadrat-Test
 Kotigeztabelle. Chi-Quadrat-Test Korrelatiosaalyse zwische kategorische Merkmale Beispiel 1 ohe Frau 8 75 1 Ma 48 49 97 76 14? Häufigkeitstabelle (Kotigeztabelle): eie tabellarische Darstellug der gemeisame
Kotigeztabelle. Chi-Quadrat-Test Korrelatiosaalyse zwische kategorische Merkmale Beispiel 1 ohe Frau 8 75 1 Ma 48 49 97 76 14? Häufigkeitstabelle (Kotigeztabelle): eie tabellarische Darstellug der gemeisame
(a) Richtig, die Varianz ist eine Summe quadratischer Größen.
 Aufgabe 1 (10 Pukte) Welche der folgede Aussage sid richtig? (a) Richtig, die Variaz ist eie Summe quadratischer Größe. (b) Falsch, die Abweichug ordialer Merkmale vom Media ist icht defiiert - also auch
Aufgabe 1 (10 Pukte) Welche der folgede Aussage sid richtig? (a) Richtig, die Variaz ist eie Summe quadratischer Größe. (b) Falsch, die Abweichug ordialer Merkmale vom Media ist icht defiiert - also auch
Wahrscheinlichkeitstheorie und Statistik vom
 INSTITUT FÜR MATHEMATISCHE STOCHASTIK WS 005/06 UNIVERSITÄT KARLSRUHE Priv.-Doz. Dr. D. Kadelka Klausur Wahrscheilichkeitstheorie ud Statistik vom 9..006 Musterlösuge Aufgabe A: Gegebe sei eie Urliste
INSTITUT FÜR MATHEMATISCHE STOCHASTIK WS 005/06 UNIVERSITÄT KARLSRUHE Priv.-Doz. Dr. D. Kadelka Klausur Wahrscheilichkeitstheorie ud Statistik vom 9..006 Musterlösuge Aufgabe A: Gegebe sei eie Urliste
Auszüge der nichtparametrischen Statisik
 Empirische Wirtschaftsforschug - 1 - Auszüge der ichtparametrische Statisik Kapitel 1: Räge ud lieare Ragstatistike Aahme, Defiitioe ud Eigeschafte (1.1) Aahme: (a) (b) Die Date x 1,, x sid midestes ordial.
Empirische Wirtschaftsforschug - 1 - Auszüge der ichtparametrische Statisik Kapitel 1: Räge ud lieare Ragstatistike Aahme, Defiitioe ud Eigeschafte (1.1) Aahme: (a) (b) Die Date x 1,, x sid midestes ordial.
Harmonisches Mittel. Streuungsmaße. Die mittlere Abweichung. Die Standardabweichung. Die Varianz. Statistik 3. Vorlesung, März 11, ,...
 Statistik. Vorlesug, März, 9 Harmoisches Mittel xh = w wk +... + x x k Wobei w, w,... w k sid die gewichte (w + w + w +...+ w k = Beispiel: wir habe km mit eier Geschwidigkeit vo km/h, ud eie adere km
Statistik. Vorlesug, März, 9 Harmoisches Mittel xh = w wk +... + x x k Wobei w, w,... w k sid die gewichte (w + w + w +...+ w k = Beispiel: wir habe km mit eier Geschwidigkeit vo km/h, ud eie adere km
Diskrete Zufallsvariablen
 Erste Beispiele diskreter Verteiluge Diskrete Zufallsvariable Beroulli-Verteilug Eie diskrete Zufallsvariable heißt beroulliverteilt mit arameter p, falls sie die Wahrscheilichkeitsfuktio p,, f ( ) ( )
Erste Beispiele diskreter Verteiluge Diskrete Zufallsvariable Beroulli-Verteilug Eie diskrete Zufallsvariable heißt beroulliverteilt mit arameter p, falls sie die Wahrscheilichkeitsfuktio p,, f ( ) ( )
11 Likelihoodquotiententests
 11 Likelihoodquotietetests I de Paragraphe 7-10 wurde beste Tests UMP-Tests oder UMPU-Tests i spezielle Verteilugssituatioe hergeleitet Hier soll u ei allgemeies Kostruktiosprizip für Tests vo zusammegesetzte
11 Likelihoodquotietetests I de Paragraphe 7-10 wurde beste Tests UMP-Tests oder UMPU-Tests i spezielle Verteilugssituatioe hergeleitet Hier soll u ei allgemeies Kostruktiosprizip für Tests vo zusammegesetzte
Kapitel 6 : Punkt und Intervallschätzer
 7 Kapitel 6 : Pukt ud Itervallschätzer Puktschätzuge. I der Statistik wolle wir Rückschlüsse auf das Wahrscheilichkeitsgesetz ziehe, ach dem ei vo us beobachtetes Zufallsexperimet abläuft. Hierzu beobachte
7 Kapitel 6 : Pukt ud Itervallschätzer Puktschätzuge. I der Statistik wolle wir Rückschlüsse auf das Wahrscheilichkeitsgesetz ziehe, ach dem ei vo us beobachtetes Zufallsexperimet abläuft. Hierzu beobachte
Eingangsprüfung Stochastik,
 Eigagsprüfug Stochastik, 5.5. Wir gehe stets vo eiem Wahrscheilichkeitsraum (Ω, A, P aus. Die Borel σ-algebra auf wird mit B bezeichet, das Lebesgue Maß auf wird mit λ bezeichet. Aufgabe ( Pukte Sei x
Eigagsprüfug Stochastik, 5.5. Wir gehe stets vo eiem Wahrscheilichkeitsraum (Ω, A, P aus. Die Borel σ-algebra auf wird mit B bezeichet, das Lebesgue Maß auf wird mit λ bezeichet. Aufgabe ( Pukte Sei x
Parameterschätzung. Kapitel Schätzfunktionen
 Kapitel 8 Parameterschätzug 8.1 Schätzfuktioe Def. 8.1.1: Es seie X 1,X,...,X uabhägige ZV, die alle die gleiche Verteilug besitze. θ sei ei ubekater Parameter dieser Verteilug. X 1,X,...,X ist als eie
Kapitel 8 Parameterschätzug 8.1 Schätzfuktioe Def. 8.1.1: Es seie X 1,X,...,X uabhägige ZV, die alle die gleiche Verteilug besitze. θ sei ei ubekater Parameter dieser Verteilug. X 1,X,...,X ist als eie
Mathematik 2 für Naturwissenschaften
 Has Walser Mathematik für Naturwisseschafte 00 180 160 Fraue 140 10 100 80 80 100 10 140 160 180 00 Mäer Modul 08 Teste vo Hypothese Has Walser: Modul 08, Teste vo Hypothese ii Ihalt 1 Ma-Whitey-U-Test
Has Walser Mathematik für Naturwisseschafte 00 180 160 Fraue 140 10 100 80 80 100 10 140 160 180 00 Mäer Modul 08 Teste vo Hypothese Has Walser: Modul 08, Teste vo Hypothese ii Ihalt 1 Ma-Whitey-U-Test
Kapitel 3: Bedingte Wahrscheinlichkeiten und Unabhängigkeit
 - 18 - (Kapitel 3 : Bedigte Wahrscheilichkeite ud Uabhägigkeit) Kapitel 3: Bedigte Wahrscheilichkeite ud Uabhägigkeit Wird bei der Durchführug eies stochastische Experimets bekat, daß ei Ereigis A eigetrete
- 18 - (Kapitel 3 : Bedigte Wahrscheilichkeite ud Uabhägigkeit) Kapitel 3: Bedigte Wahrscheilichkeite ud Uabhägigkeit Wird bei der Durchführug eies stochastische Experimets bekat, daß ei Ereigis A eigetrete
Musterlösung für die Klausur zur Vorlesung Stochastik I im WiSe 2014/2015
 Musterlösug für die Klausur zur Vorlesug Stochastik I im WiSe 204/205 Teil I wahr falsch Aussage Gilt E[XY ] = E[X]E[Y ] für zwei Zufallsvariable X ud Y mit edlicher Variaz, so sid X ud Y uabhägig. Für
Musterlösug für die Klausur zur Vorlesug Stochastik I im WiSe 204/205 Teil I wahr falsch Aussage Gilt E[XY ] = E[X]E[Y ] für zwei Zufallsvariable X ud Y mit edlicher Variaz, so sid X ud Y uabhägig. Für
Kapitel VI. Einige spezielle diskrete Verteilungen
 Kapitel VI Eiige spezielle diskrete Verteiluge D 6 (Hypergeometrische Verteilug) Eie Zufallsvariable X heißt hypergeometrisch verteilt, we sie folgede Wahrscheilichkeitsfuktio besitzt: M N M P ( X ) p
Kapitel VI Eiige spezielle diskrete Verteiluge D 6 (Hypergeometrische Verteilug) Eie Zufallsvariable X heißt hypergeometrisch verteilt, we sie folgede Wahrscheilichkeitsfuktio besitzt: M N M P ( X ) p
Statistik und Wahrscheinlichkeitsrechnung
 Statistik ud Wahrscheilichkeitsrechug Statistik ud Wahrscheilichkeitsrechug Übug 6 3.03.20 Ihalt der heutige Übug Aufgabe D.7: Reche mit Zufallsvariable Erwartugswert- ud Variazoperator Statistik ud Wahrscheilichkeitsrechug
Statistik ud Wahrscheilichkeitsrechug Statistik ud Wahrscheilichkeitsrechug Übug 6 3.03.20 Ihalt der heutige Übug Aufgabe D.7: Reche mit Zufallsvariable Erwartugswert- ud Variazoperator Statistik ud Wahrscheilichkeitsrechug
Konfidenzintervalle. Praktische Übung Stochastik SS 2017 Lektion 10 1
 Kofidezitervalle Praktische Übug Stochastik SS 017 Lektio 10 1 Kofidezitervalle Geerelle Aahme: Parametrisches Modell (P ϑ ) ϑ Θ Beobachtuge X 1,..., X u.i.v. ach P ϑ mit ubekatem ϑ Θ Grudidee: Schätzer
Kofidezitervalle Praktische Übug Stochastik SS 017 Lektio 10 1 Kofidezitervalle Geerelle Aahme: Parametrisches Modell (P ϑ ) ϑ Θ Beobachtuge X 1,..., X u.i.v. ach P ϑ mit ubekatem ϑ Θ Grudidee: Schätzer
Das kollektive Risikomodell. 12. Mai 2009
 Kirill Rudik Das kollektive Risikomodell 12. Mai 2009 4.1 Eileitug Wir betrachte i diesem Kapitel die Gesamtforderuge im Laufe eies Jahres. Beim Abschluss eies Versicherugsvertrages weiß der Versicherer
Kirill Rudik Das kollektive Risikomodell 12. Mai 2009 4.1 Eileitug Wir betrachte i diesem Kapitel die Gesamtforderuge im Laufe eies Jahres. Beim Abschluss eies Versicherugsvertrages weiß der Versicherer
Übungen Abgabetermin: Freitag, , 10 Uhr THEMEN: Testtheorie
 Uiversität Müster Istitut für Mathematische Statistik Stochastik WS 203/204, Blatt Löwe/Heusel Aufgabe (4 Pukte) Übuge Abgabetermi: Freitag, 24.0.204, 0 Uhr THEMEN: Testtheorie Die Sollstärke der Rohrwäde
Uiversität Müster Istitut für Mathematische Statistik Stochastik WS 203/204, Blatt Löwe/Heusel Aufgabe (4 Pukte) Übuge Abgabetermi: Freitag, 24.0.204, 0 Uhr THEMEN: Testtheorie Die Sollstärke der Rohrwäde
Empirische Verteilungsfunktion
 KAPITEL 3 Empirische Verteilugsfuktio 3.1. Empirische Verteilugsfuktio Seie X 1,..., X uabhägige ud idetisch verteilte Zufallsvariable mit theoretischer Verteilugsfuktio F (t) = P[X i t]. Es sei (x 1,...,
KAPITEL 3 Empirische Verteilugsfuktio 3.1. Empirische Verteilugsfuktio Seie X 1,..., X uabhägige ud idetisch verteilte Zufallsvariable mit theoretischer Verteilugsfuktio F (t) = P[X i t]. Es sei (x 1,...,
Parameter von Häufigkeitsverteilungen
 Kapitel 3 Parameter vo Häufigkeitsverteiluge 3. Mittelwerte Mo Der Modus (:= häufigster Wert, Abk.: Mo) ist der Merkmalswert mit der größte Häufigkeit, falls es eie solche gibt. Er sollte ur bei eigipflige
Kapitel 3 Parameter vo Häufigkeitsverteiluge 3. Mittelwerte Mo Der Modus (:= häufigster Wert, Abk.: Mo) ist der Merkmalswert mit der größte Häufigkeit, falls es eie solche gibt. Er sollte ur bei eigipflige
Statistik und Wahrscheinlichkeitsrechnung
 Statistik ud Wahrscheilichkeitsrechug Dr. Joche Köhler 9.04.008 Äderug Übugsstude Statistik ud Wahrscheilichkeitsrechug Die Gruppe vo Markus trifft sich am Doerstag statt im HCI D zusamme mit der Gruppe
Statistik ud Wahrscheilichkeitsrechug Dr. Joche Köhler 9.04.008 Äderug Übugsstude Statistik ud Wahrscheilichkeitsrechug Die Gruppe vo Markus trifft sich am Doerstag statt im HCI D zusamme mit der Gruppe
Kleine Formelsammlung Beschreibende Statistik
 Kleie Formelsammlug Beschreibede Statistik Prof. Dr. Philipp Sibbertse Wirtschaftswisseschaftliche Fakultät Leibiz Uiversität Haover Ihaltsverzeichis 1 Lage- ud Streuugsmaße 2 1.1 Der Media...................................
Kleie Formelsammlug Beschreibede Statistik Prof. Dr. Philipp Sibbertse Wirtschaftswisseschaftliche Fakultät Leibiz Uiversität Haover Ihaltsverzeichis 1 Lage- ud Streuugsmaße 2 1.1 Der Media...................................
1 Randomisierte Bestimmung des Medians
 Praktikum Diskrete Optimierug (Teil 0) 0.07.006 Radomisierte Bestimmug des Medias. Problemstellug ud Ziel I diesem Abschitt stelle wir eie radomisierte Algorithmus zur Bestimmug des Medias vor, der besser
Praktikum Diskrete Optimierug (Teil 0) 0.07.006 Radomisierte Bestimmug des Medias. Problemstellug ud Ziel I diesem Abschitt stelle wir eie radomisierte Algorithmus zur Bestimmug des Medias vor, der besser
Dr. Jürgen Senger INDUKTIVE STATISTIK. Wahrscheinlichkeitstheorie, Schätz- und Testverfahren
 Dr. Jürge Seger INDUKTIVE STATISTIK Wahrscheilichkeitstheorie, Schätz- ud Testverfahre ÜBUNG. - LÖSUNGEN. ypothesetest für die Dicke vo Plättche Die Dicke X vo Plättche, die auf eier bestimmte Maschie
Dr. Jürge Seger INDUKTIVE STATISTIK Wahrscheilichkeitstheorie, Schätz- ud Testverfahre ÜBUNG. - LÖSUNGEN. ypothesetest für die Dicke vo Plättche Die Dicke X vo Plättche, die auf eier bestimmte Maschie
Erläuterung Beispiel III
 3 Parameterpuktschätzer Maximum-Likelihood-Methode 3.2 Maximum-Likelihood-Methode ML-Methode Weitere geläufige Schätzmethode: Maximum-Likelihood-Methode Vor Erläuterug der Methode: eileitedes Beispiel
3 Parameterpuktschätzer Maximum-Likelihood-Methode 3.2 Maximum-Likelihood-Methode ML-Methode Weitere geläufige Schätzmethode: Maximum-Likelihood-Methode Vor Erläuterug der Methode: eileitedes Beispiel
3. Grundbegrie der Schätztheorie
 Statistik, Abschitt 3. 3. Grudbegrie der Schätztheorie I der kormatorische Statistik will ma uter aderem auf Grud eier Stichprobe vom Umfag Iformatioe über ubekate Parameter θ der Verteilug F der zugrudeliegede
Statistik, Abschitt 3. 3. Grudbegrie der Schätztheorie I der kormatorische Statistik will ma uter aderem auf Grud eier Stichprobe vom Umfag Iformatioe über ubekate Parameter θ der Verteilug F der zugrudeliegede
Formelsammlung Statistik 29. Januar 2019
 Formelsammlug Statistik Seite 1 Formelsammlug Statistik 9. Jauar 019 Witersemester 018/19 Adreas Löpker, HTW Dresde 1. Deskriptive Statistik (F1) Stichprobe x vom Umfag, Stichprobe y vom Umfag m x = (x
Formelsammlug Statistik Seite 1 Formelsammlug Statistik 9. Jauar 019 Witersemester 018/19 Adreas Löpker, HTW Dresde 1. Deskriptive Statistik (F1) Stichprobe x vom Umfag, Stichprobe y vom Umfag m x = (x
2.2.1 Lagemaße. Exkurs: Quantile. und n. p n
 Ekurs: Quatile Ausgagspukt : Geordete Urliste Jeder Wert p, mit 0 < p
Ekurs: Quatile Ausgagspukt : Geordete Urliste Jeder Wert p, mit 0 < p
Evaluation & Forschungsstrategien
 Evaluatio & Forschugsstrategie WS2/2 Prof. Dr. G. Meihardt Johaes Guteberg Uiversität Maiz Prizipie des statistische Schliesses Samplig - Modellvorstellug Populatio Samplig Stichprobe Kewerte x Theoretische
Evaluatio & Forschugsstrategie WS2/2 Prof. Dr. G. Meihardt Johaes Guteberg Uiversität Maiz Prizipie des statistische Schliesses Samplig - Modellvorstellug Populatio Samplig Stichprobe Kewerte x Theoretische
(4) = 37,7 % mit 37,7 % Wahrscheinlichkeit sind es höchstens 4 Fahrräder, das ist recht hoch; man kann also die Behauptung nicht wirklich ablehnen.
 Schülerbuchseite 98 1 Lösuge vorläufig IV Beurteilede Statistik S. 98 p S. 1 p w a t Tabelle Tabelle dowloadbar im Iteretauftritt 1 Teste vo Hypothese 1 a) Erwartugswert μ = 5 ud Stadardabweichug σ = 1,6;
Schülerbuchseite 98 1 Lösuge vorläufig IV Beurteilede Statistik S. 98 p S. 1 p w a t Tabelle Tabelle dowloadbar im Iteretauftritt 1 Teste vo Hypothese 1 a) Erwartugswert μ = 5 ud Stadardabweichug σ = 1,6;
Einführung in die Wahrscheinlichkeitstheorie Lösungen zum Wiederholungsblatt
 TUM, Zetrum Mathematik Lehrstuhl für Mathematische Physik WS 23/4 Prof. Dr. Silke Rolles Thomas Höfelsauer Felizitas Weider Eiführug i die Wahrscheilichkeitstheorie Lösuge zum Wiederholugsblatt Aufgabe
TUM, Zetrum Mathematik Lehrstuhl für Mathematische Physik WS 23/4 Prof. Dr. Silke Rolles Thomas Höfelsauer Felizitas Weider Eiführug i die Wahrscheilichkeitstheorie Lösuge zum Wiederholugsblatt Aufgabe
Reader Teil 1: Beschreibende Statistik
 Dr. Katharia Best Sommersemester 2011 14. April 2011 Reader Teil 1: Beschreibede Statistik WiMa-Praktikum Um Date darzustelle ud eie Übersicht über die Struktur der Date zu erstelle, stellt die beschreibede
Dr. Katharia Best Sommersemester 2011 14. April 2011 Reader Teil 1: Beschreibede Statistik WiMa-Praktikum Um Date darzustelle ud eie Übersicht über die Struktur der Date zu erstelle, stellt die beschreibede
Maximum-Likelihood-Methode (ML-Methode)
 3 Parameterpuktschätzer Maximum-Likelihood-Methode 3.2 Maximum-Likelihood-Methode (ML-Methode Weitere geläufige Schätzmethode: Maximum-Likelihood-Methode Vor Erläuterug der Methode: eileitedes Beispiel
3 Parameterpuktschätzer Maximum-Likelihood-Methode 3.2 Maximum-Likelihood-Methode (ML-Methode Weitere geläufige Schätzmethode: Maximum-Likelihood-Methode Vor Erläuterug der Methode: eileitedes Beispiel
Maximum-Likelihood-Methode (ML-Methode)
 3 Parameterpuktschätzer Maximum-Likelihood-Methode 3.2 Maximum-Likelihood-Methode (ML-Methode) Weitere geläufige Schätzmethode: Maximum-Likelihood-Methode Vor Erläuterug der Methode: eileitedes Beispiel
3 Parameterpuktschätzer Maximum-Likelihood-Methode 3.2 Maximum-Likelihood-Methode (ML-Methode) Weitere geläufige Schätzmethode: Maximum-Likelihood-Methode Vor Erläuterug der Methode: eileitedes Beispiel
1) Wahrscheinlichkeitsbegriff und Rechnen mit Wahrscheinlichkeiten. P A = lim r N LI: ={ 1 LII: LIII: P A =1 P A
 FORMELSAMMLUNG V03 Alle Formel ohe Gewähr auf Korrektheit Grudlage der Wahrscheilichkeitstheorie 1) Wahrscheilichkeitsbegriff ud Reche mit Wahrscheilichkeite Relative Häufigkeit r N A = h N A N = Abs.
FORMELSAMMLUNG V03 Alle Formel ohe Gewähr auf Korrektheit Grudlage der Wahrscheilichkeitstheorie 1) Wahrscheilichkeitsbegriff ud Reche mit Wahrscheilichkeite Relative Häufigkeit r N A = h N A N = Abs.
Schätzen von Populationswerten
 Schätze vo Populatioswerte SS00 7.Sitzug vom.06.00 Schätze vo Populatioswerte Ziel: Ermöglichug vo Aussage über die Grudgesamtheit ahad vo Stichprobedate Logische Methode: Iduktiosschluß Grudlage des Iduktiosschlusses:
Schätze vo Populatioswerte SS00 7.Sitzug vom.06.00 Schätze vo Populatioswerte Ziel: Ermöglichug vo Aussage über die Grudgesamtheit ahad vo Stichprobedate Logische Methode: Iduktiosschluß Grudlage des Iduktiosschlusses:
Übung zur Vorlesung Statistik I WS Übungsblatt 8
 Übug zur Vorlesug Statistik I WS 2013-2014 Übugsblatt 8 9. Dezember 2013 Aufgabe 25 (4 Pukte): Sei X B(, p) eie biomial verteilte Zufallsvariable. Schreibe Sie i R eie Fuktio PWert, die für jedes Ergebis
Übug zur Vorlesug Statistik I WS 2013-2014 Übugsblatt 8 9. Dezember 2013 Aufgabe 25 (4 Pukte): Sei X B(, p) eie biomial verteilte Zufallsvariable. Schreibe Sie i R eie Fuktio PWert, die für jedes Ergebis
V. Tests bez. zweier Verteilungsfunktionen
 7 V. Tests bez. zweier Verteilugsfuktioe Seie X ud Y zwei uabhägige oralverteilte Zufallsvariable, für die zwei kokrete Stichprobe x, x,..., x bzw. y, y,..., y it de Ufäge bzw vorliege. a) X ud Y seie
7 V. Tests bez. zweier Verteilugsfuktioe Seie X ud Y zwei uabhägige oralverteilte Zufallsvariable, für die zwei kokrete Stichprobe x, x,..., x bzw. y, y,..., y it de Ufäge bzw vorliege. a) X ud Y seie
Schätzung der Kovarianzmatrix
 Schätzug der Kovariazmatri Aus eiem Esemble vo Beobachtuge { i } ka die Kovariazmatri (Zetralmomete) geschätzt werde: C E{( )( ) } R ˆ 1 k ˆ k ˆ k 1 Schätzwert (edliche Summe): C ( )( ) ud dem Schätzwert:
Schätzug der Kovariazmatri Aus eiem Esemble vo Beobachtuge { i } ka die Kovariazmatri (Zetralmomete) geschätzt werde: C E{( )( ) } R ˆ 1 k ˆ k ˆ k 1 Schätzwert (edliche Summe): C ( )( ) ud dem Schätzwert:
Ökonometrie Formeln und Tabellen
 Ökoometrie Formel ud Tabelle Formelsammlug 1 Lieares Modell ud KQ-Schätzug 11 Eifachregressio Lieares Modell: Y i = β 0 + β 1 x i + U i, i = 1,2,, Aahme des lieare Modells: A1: E[U i ] = 0 für alle i =
Ökoometrie Formel ud Tabelle Formelsammlug 1 Lieares Modell ud KQ-Schätzug 11 Eifachregressio Lieares Modell: Y i = β 0 + β 1 x i + U i, i = 1,2,, Aahme des lieare Modells: A1: E[U i ] = 0 für alle i =
Kreuztabellenanalyse und Assoziationsmaße
 FB 1 W. Ludwig-Mayerhofer Statistik 1 Herzlich willkomme zur Vorlesug Statistik Zusammehäge zwische omiale (ud/oder ordiale) Merkmale: aalyse ud FB 1 W. Ludwig-Mayerhofer Statistik 2 eige sich zur Darstellug
FB 1 W. Ludwig-Mayerhofer Statistik 1 Herzlich willkomme zur Vorlesug Statistik Zusammehäge zwische omiale (ud/oder ordiale) Merkmale: aalyse ud FB 1 W. Ludwig-Mayerhofer Statistik 2 eige sich zur Darstellug
Schätzung der Kovarianzmatrix
 Schätzug der Kovariazmatrix Aus eiem Esemble vo Beobachtuge {x i } ka die Kovariazmatrix (Zetralmomete) geschätzt werde: C = E{( x µ )( x µ ) } = R µ µ xx x x xx x x ˆ 1 C ˆ ˆ xx = xk µ x xk µ x k = 1
Schätzug der Kovariazmatrix Aus eiem Esemble vo Beobachtuge {x i } ka die Kovariazmatrix (Zetralmomete) geschätzt werde: C = E{( x µ )( x µ ) } = R µ µ xx x x xx x x ˆ 1 C ˆ ˆ xx = xk µ x xk µ x k = 1
Diplomvorprüfung Stochastik
 Uiversität Karlsruhe TH Istitut für Stochastik Prof. Dr. N. Bäuerle Name: Vorame: Matr.-Nr.: Diplomvorprüfug Stochastik 10. Oktober 2006 Diese Klausur hat bestade, wer midestes 16 Pukte erreicht. Als Hilfsmittel
Uiversität Karlsruhe TH Istitut für Stochastik Prof. Dr. N. Bäuerle Name: Vorame: Matr.-Nr.: Diplomvorprüfug Stochastik 10. Oktober 2006 Diese Klausur hat bestade, wer midestes 16 Pukte erreicht. Als Hilfsmittel
Statistische Tests zu ausgewählten Problemen
 Eiführug i die statistische Testtheorie Statistische Tests zu ausgewählte Probleme Teil : Tests für Erwartugswerte Statistische Testtheorie I Eiführug Beschräkug auf parametrische Testverfahre Beschräkug
Eiführug i die statistische Testtheorie Statistische Tests zu ausgewählte Probleme Teil : Tests für Erwartugswerte Statistische Testtheorie I Eiführug Beschräkug auf parametrische Testverfahre Beschräkug
Statistik, Abschnitt (1) Gegeben sei der Stichprobenvektor (X 1,..., X n ). Die Stichprobenfunktion. ˆµ k := 1 n. Xi k (1) i=1.
 Statistik, Abschitt.. Schätzmethode.. Mometemethode Für Parameter, die sich i bekater Weise aus de Momete zusammesetze, erhält ma Schätzuge, idem ma die theoretische Momete durch die sogeate empirische
Statistik, Abschitt.. Schätzmethode.. Mometemethode Für Parameter, die sich i bekater Weise aus de Momete zusammesetze, erhält ma Schätzuge, idem ma die theoretische Momete durch die sogeate empirische
Klausur zu Methoden der Statistik II (mit Kurzlösung) Wintersemester 2015/2016. Aufgabe 1
 Lehrstuhl für Statistik ud Ökoometrie der Otto-Friedrich-Uiversität Bamberg Prof. Dr. Susae Rässler Klausur zu Methode der Statistik II (mit Kurzlösug) Witersemester 2015/2016 Aufgabe 1 Die leideschaftliche
Lehrstuhl für Statistik ud Ökoometrie der Otto-Friedrich-Uiversität Bamberg Prof. Dr. Susae Rässler Klausur zu Methode der Statistik II (mit Kurzlösug) Witersemester 2015/2016 Aufgabe 1 Die leideschaftliche
Prof. Dr. Roland Füss Statistik II SS 2008
 1. Grezwertsätze Der wichtigste Grud für die Häufigkeit des Auftretes der Normalverteilug ergibt sich aus de Grezwertsätze. Grezwertsätze sid Aussage über eie Zufallsvariable für de Fall, dass die Azahl
1. Grezwertsätze Der wichtigste Grud für die Häufigkeit des Auftretes der Normalverteilug ergibt sich aus de Grezwertsätze. Grezwertsätze sid Aussage über eie Zufallsvariable für de Fall, dass die Azahl
Schätzen von Populationswerten
 Schätze vo Populatioswerte 7.Sitzug 35 Seite, SoSe 003 Schätze vo Populatioswerte Ziel: Ermöglichug vo Aussage über die Grudgesamtheit ahad vo Stichprobedate Logische Methode: Iduktiosschluss Grudlage
Schätze vo Populatioswerte 7.Sitzug 35 Seite, SoSe 003 Schätze vo Populatioswerte Ziel: Ermöglichug vo Aussage über die Grudgesamtheit ahad vo Stichprobedate Logische Methode: Iduktiosschluss Grudlage
2. Schätzverfahren 2.1 Punktschätzung wirtschaftlicher Kennzahlen. Allgemein: Punktschätzung eines Parameters:
 . Schätzverfahre. Puktschätzug wirtschaftlicher Kezahle Allgemei: Puktschätzug eies Parameters: Ermittlug eies Schätzwertes für eie ubekate Parameter eier Zufallsvariable i der Grudgesamtheit mit Hilfe
. Schätzverfahre. Puktschätzug wirtschaftlicher Kezahle Allgemei: Puktschätzug eies Parameters: Ermittlug eies Schätzwertes für eie ubekate Parameter eier Zufallsvariable i der Grudgesamtheit mit Hilfe
Wahrscheinlichkeitsrechnung & Statistik - Ergänzung zum Skript
 Wahrscheilichkeitsrechug & Statistik - Ergäzug zum Skript Prof. Schweizer 9. Oktober 008 Mitschrift: Adreas Steiger Warug: Wir sid sicher dass diese Notize eie Mege Fehler ethalte. Betrete der Baustelle
Wahrscheilichkeitsrechug & Statistik - Ergäzug zum Skript Prof. Schweizer 9. Oktober 008 Mitschrift: Adreas Steiger Warug: Wir sid sicher dass diese Notize eie Mege Fehler ethalte. Betrete der Baustelle
Konfidenzintervall_fuer_pi.doc Seite 1 von 6. Konfidenzintervall für den Anteilswert π am Beispiel einer Meinungsumfrage
 Kofidezitervall_fuer_pi.doc Seite 1 vo 6 Kofidezitervall für de Ateilswert π am Beispiel eier Meiugsumfrage Nach eier Meiugsumfrage der Wochezeitug Bezirksblatt vom März 005, ei halbes Jahr vor de Ladtagswahle
Kofidezitervall_fuer_pi.doc Seite 1 vo 6 Kofidezitervall für de Ateilswert π am Beispiel eier Meiugsumfrage Nach eier Meiugsumfrage der Wochezeitug Bezirksblatt vom März 005, ei halbes Jahr vor de Ladtagswahle
X X Schätzen von Vertrauensintervallen Schwankungsintervall
 .. Schätze vo Vertrauesitervalle..1. Schwakugsitervall Beispiel: X = Betrag vo Geldüberweisuge, ormalverteilt, µ = 5000, = 1000 Zufallsstichprobe mit = 100, Schätzer für µ: X X Gesucht: Itervall, i dem
.. Schätze vo Vertrauesitervalle..1. Schwakugsitervall Beispiel: X = Betrag vo Geldüberweisuge, ormalverteilt, µ = 5000, = 1000 Zufallsstichprobe mit = 100, Schätzer für µ: X X Gesucht: Itervall, i dem
8. Regressionsanalyse
 8. Regressiosaalyse Beschreibug der Abhägigkeit zweier Merkmale Gegebe eie Stichprobe (X ; Y ) : : : (X ; Y ) zur Grudgesamtheit (X; Y ), = corr(x; Y ) Korrelatioskoe ziet, R empirischer Korrelatioskoe
8. Regressiosaalyse Beschreibug der Abhägigkeit zweier Merkmale Gegebe eie Stichprobe (X ; Y ) : : : (X ; Y ) zur Grudgesamtheit (X; Y ), = corr(x; Y ) Korrelatioskoe ziet, R empirischer Korrelatioskoe
Maximum Likelihood Version 1.6
 Maximum Likelihood Versio 1.6 Uwe Ziegehage 15. November 2005 Logarithmegesetze log a (b) + log a (c) = log a (b c) (1) log a (b) log a (c) = log a (b/c) (2) log a (b c ) = c log a (b) (3) Ableitugsregel
Maximum Likelihood Versio 1.6 Uwe Ziegehage 15. November 2005 Logarithmegesetze log a (b) + log a (c) = log a (b c) (1) log a (b) log a (c) = log a (b/c) (2) log a (b c ) = c log a (b) (3) Ableitugsregel
Praktikum Vorbereitung Fertigungsmesstechnik Statistische Qualitätskontrolle
 Praktikum Vorbereitug Fertigugsmesstechik Statistische Qualitätskotrolle Bei viele Erzeugisse ist es icht möglich jedes Werkstück zu prüfe, z.b.: bei Massefertigug. Hier ist es aus ökoomische Grüde icht
Praktikum Vorbereitug Fertigugsmesstechik Statistische Qualitätskotrolle Bei viele Erzeugisse ist es icht möglich jedes Werkstück zu prüfe, z.b.: bei Massefertigug. Hier ist es aus ökoomische Grüde icht
Übungen mit dem Applet Taylor-Entwickung von Funktionen
 Taylor-Etwickug vo Fuktioe Übuge mit dem Applet Taylor-Etwickug vo Fuktioe Ziele des Applets... Mathematischer Hitergrud... 3 Vorschläge für Übuge... 3 3. Siusfuktio si(...3 3. Cosiusfuktio cos(...4 3.3
Taylor-Etwickug vo Fuktioe Übuge mit dem Applet Taylor-Etwickug vo Fuktioe Ziele des Applets... Mathematischer Hitergrud... 3 Vorschläge für Übuge... 3 3. Siusfuktio si(...3 3. Cosiusfuktio cos(...4 3.3
Normalverteilung. Voraussetzung und verwandte Themen. Einführung. Ziel und Nutzen. Grundlagen
 h Normalverteilug Voraussetzug ud verwadte Theme Für diese Beschreibuge sid Grudlage der Statistik ud isbesodere der statistische Verteiluge vorteilhaft. Weiterführede Theme sid: www.versuchsmethode.de/verteilugstests.pdf
h Normalverteilug Voraussetzug ud verwadte Theme Für diese Beschreibuge sid Grudlage der Statistik ud isbesodere der statistische Verteiluge vorteilhaft. Weiterführede Theme sid: www.versuchsmethode.de/verteilugstests.pdf
Aufgabe 1. d) Berechnen Sie die Wahrscheinlichkeit dafür, dass Axel 1,5 Stunden warten muss.
 Lehrstuhl für Statistik ud Ökoometrie Otto-Friedrich-Uiversität Bamberg Prof. Dr. Susae Rässler Aufgabe 1 Aufgrud eier Sommergrippe muss Studet Axel seie Hausarzt aufsuche. Um die Wartezeit besser abschätze
Lehrstuhl für Statistik ud Ökoometrie Otto-Friedrich-Uiversität Bamberg Prof. Dr. Susae Rässler Aufgabe 1 Aufgrud eier Sommergrippe muss Studet Axel seie Hausarzt aufsuche. Um die Wartezeit besser abschätze
D-ITET Wahrscheinlichkeitstheorie und Statistik FS 2017 Prof. P. Nolin. Musterlösung 11 = Φ( 6/5) = 1 Φ(6/5) = = 0.
 D-ITET Wahrscheilichkeitstheorie ud Statistik FS 17 Prof. P. Noli Musterlösug 11 1. Sei Φ die Verteilugsfuktio der Stadardormalverteilug. a Da T B N 6, 4, ist T B + 6/4 stadardormalverteilt. Folglich ist
D-ITET Wahrscheilichkeitstheorie ud Statistik FS 17 Prof. P. Noli Musterlösug 11 1. Sei Φ die Verteilugsfuktio der Stadardormalverteilug. a Da T B N 6, 4, ist T B + 6/4 stadardormalverteilt. Folglich ist
Diskrete Wahrscheinlichkeitstheorie Wiederholungsklausur
 Techische Uiversität Müche Sommersemester 007 Istitut für Iformatik Prof. Dr. Javier Esparza Diskrete Wahrscheilichkeitstheorie Wiederholugsklausur LÖSUNG Hiweis: Bei alle Aufgabe wird ebe dem gefragte
Techische Uiversität Müche Sommersemester 007 Istitut für Iformatik Prof. Dr. Javier Esparza Diskrete Wahrscheilichkeitstheorie Wiederholugsklausur LÖSUNG Hiweis: Bei alle Aufgabe wird ebe dem gefragte
Grundsätzlich sollen Varianz bzw. Standardabweichung Maße dafür sein, wie stark eine Verteilung um ihren Erwartungswert streut.
 Eie Iterpretatiosfrage habe ich zu eiem Beispiel das i der der letzte Vorlesug behadelt wurde: Auf Folie.7 zur Variaz. Dort wird ei Beispiel eier stetige Zufallsvariable geat (Warte a eier S-Bah-Haltestelle).
Eie Iterpretatiosfrage habe ich zu eiem Beispiel das i der der letzte Vorlesug behadelt wurde: Auf Folie.7 zur Variaz. Dort wird ei Beispiel eier stetige Zufallsvariable geat (Warte a eier S-Bah-Haltestelle).
Lösungen ausgewählter Übungsaufgaben zum Buch. Elementare Stochastik (Springer Spektrum, 2012) Teil 4: Aufgaben zu den Kapiteln 7 und 8
 1 Lösuge ausgewählter Übugsaufgabe zum Buch Elemetare Stochastik (Spriger Spektrum, 2012) Teil 4: Aufgabe zu de Kapitel 7 ud 8 Aufgabe zu Kapitel 7 Zu Abschitt 7.1 Ü7.1.1 Ω sei höchstes abzählbar, ud X,
1 Lösuge ausgewählter Übugsaufgabe zum Buch Elemetare Stochastik (Spriger Spektrum, 2012) Teil 4: Aufgabe zu de Kapitel 7 ud 8 Aufgabe zu Kapitel 7 Zu Abschitt 7.1 Ü7.1.1 Ω sei höchstes abzählbar, ud X,
Statistik und Biometrie. Deskriptive Statistik I
 Statistik ud Biometrie Deskriptive Statistik I Spruch des Tages Traue keier Statistik, die du icht selbst gefaelscht hast Wiederholug Merkmale Beobachtugseiheite sid Träger vo Merkmale Wiederholug Die
Statistik ud Biometrie Deskriptive Statistik I Spruch des Tages Traue keier Statistik, die du icht selbst gefaelscht hast Wiederholug Merkmale Beobachtugseiheite sid Träger vo Merkmale Wiederholug Die
Empirische Ökonomie 1 Sommersemester Formelsammlung. Statistische Grundlagen. Erwartungswert und Varianz einer Zufallsvariable.
 Empirische Ökoomie 1 Sommersemester 2013 Formelsammlug Hiweis: Alle Variable, Parameter ud Symbole sid wie i de Vorlesugsuterlage defiiert. Statistische Grudlage Erwartugswert Erwartugswert ud Variaz eier
Empirische Ökoomie 1 Sommersemester 2013 Formelsammlug Hiweis: Alle Variable, Parameter ud Symbole sid wie i de Vorlesugsuterlage defiiert. Statistische Grudlage Erwartugswert Erwartugswert ud Variaz eier
