Mathematische und statistische Methoden I
|
|
|
- Gerhardt Gärtner
- vor 6 Jahren
- Abrufe
Transkript
1 Prof. Dr. G. Meinhardt 6. Stock, Wallstr. 3 (Raum 06-06) Sprechstunde jederzeit nach Vereinbarung und nach der Vorlesung. Mathematische und statistische Methoden I Dr. Malte Persike persike@uni-mainz.de WS 00/0 Fachbereich Sozialwissenschaften Psychologisches Institut Johannes Gutenberg Universität Mainz Folie
2 Grundlagen Gleichung Minimierung Normalgleichungen Grundlagen Oft werden in psychologischen Untersuchungen nicht nur ein sondern mehrere UVn betrachtet, die eine AV beeinflussen. Beispiele: Abhängigkeit der Lebenszufriedenheit von sozialem, ökonomischem und Gesundheitsstatus; Beeinflussung sportlicher Leistung durch Trainingszustand und Anwesenheit von Zuschauern. Solche Fragestellungen werden auch als multifaktoriell bezeichnet Problem: Die Berechnung vieler paarweiser Korrelationen im multifaktoriellen Fall vernachlässigt mögliche Zusammenhänge zwischen den Prädiktoren Folie
3 Grundlagen Gleichung Minimierung Normalgleichungen Grundgleichung Die vorherzusagende Variable (AV, y-wert) wird als Kriterium bezeichnet, die vorhersagenden Variablen (UVn, x-werte) als Prädiktoren. Die Vorhersagegleichung der multiplen Regression mit k Prädiktoren wird geschrieben als ˆ = k k y b b x b x b x Bei standardisierten Daten verwendet man das Symbol β für die k Regressionsparameter (bzw. -gewichte ) ˆ = β + β + + βk k y z z z Folie 3
4 Grundlagen Gleichung Minimierung Normalgleichungen Folie 4 Regression Methode der kleinsten Quadrate (KQ-Kriterium) Zur Minimierung des Vorhersagefehlers wird oft das Kleinste-Quadrate Kriterium verwendet (KQ; oder Ordinary Least Squares, OLS) Parameter der multiplen Regressionsgleichung werden so gewählt, dass das Quadrat der Abweichungen von gemessenem und geschätztem Wert minimiert wird Für eine Versuchsperson i aus allen n gelte: y = yˆ + e e = y yˆ i i i i i i beobachteter Kriteriumswert = vorhergesagter Wert + Messfehler Dann soll für alle n Datenwerte erreicht werden, dass n ( y yˆ ) e = i i i i= i= n min Minimierung der Quadratsumme des Vorhersagefehlers
5 Grundlagen Gleichung Minimierung Regression Methode der kleinsten Quadrate (KQ-Kriterium) Mithilfe der Allgemeinen Gleichung der einfachen linearen Regression lässt sich für die Streuung des Vorhersagefehlers QS e also schreiben: n n ( ˆ e i i) ( i 0 i i k ik) i= i= QS = y y = y b b x b x b x min Normalgleichungen bzw. in der standardisierten Form n n ( ˆ ) ( β β β ) QS = z z = z z z z e y y y x x k x i= i= i i i i i ik min Folie 5 Die Minimierung der Regressionsparameter erfolgt über partielle Differenzierung nach jedem einzelnen der b- bzw. β-gewichte
6 Grundlagen Gleichung Minimierung Normalgleichungen Folie 6 Regression Normalgleichungen der multiplen Regression Die partielle Differenzierung der nichtstandardisierten Gleichung mit k Prädiktoren führt immer auf ein System von k+ Normalgleichungen, das wie folgt aufgebaut ist: n n n n n y = b + b x + b x + + b x 0 k k i= i= i= i= i= n n n n n yx = b0 x+ b x + b xx + + bk xx k i= i= i= i= i= n n n n n yx = b0 x + b x x + b x + + bk xxk i= i= i= i= i= n n n n yx = b x + b x x + b x x + + bk x k 0 k k k i= i= i= i= n i= k
7 Grundlagen Gleichung Minimierung Normalgleichungen Regression Normalgleichungen der multiplen Regression In der standardisierten Form ergibt sich ein System von k Normalgleichungen: n n n n zx z y = β zx + β zx z x + + β k zx z xk i= i= i= i= n n n n zx z y = β zx z x + β zx + + β k zx z x i= i= i= i= n n n n zx zy = β zx zx + β zx zx + + βk zx i= i= i= i= k k k k k Folie 7
8 Grundlagen Gleichung Minimierung Normalgleichungen Regression - Zusammenfassung Die partielle Differenzierung einer multiplen Regressionsgleichung mit k Prädiktoren führt immer auf ein System von k+ (bzw. k) Normalgleichungen Prinzip: Die summierte Ausgangsgleichung wird nacheinander mit Prädiktor x 0 x k (bzw. z z k ) multipliziert Die Normalgleichungen liefern dann für k+ (bzw. k) unbekannte Regressionsparameter genau so viele Gleichungen. Dieses Gleichungssystem kann nun durch Substitution oder Diagonalisierung für die Parameter gelöst werden Folie 8
9 Interpretation der b und β Matrixalgebraische Berechnung Zusammenfassung Folie 9 Matrixalgebraische Berechnung der multiplen Regression Wir haben gesehen, dass die Normalgleichungen der multiplen Regression für standardisierte Daten lauteten: n n n n zx z y = β zx + β zx z x + + β k zx z xk i= i= i= i= n n n n zx z y = β zx z x + β zx + + β k zx z x i= i= i= i= n n n n zx zy = β zx zx + β zx zx + + βk zx i= i= i= i= k k k k Weiterhin ist die Korrelation zweier Variablen x p und x q : n r = z z x x i, x i, x n i = p q p q k
10 Matrixalgebraische Berechnung der multiplen Regression Damit reduziert sich das Normalgleichungssystem zu: Interpretation der b und β Matrixalgebraische Berechnung Zusammenfassung r = β + β r + β r + + β r x y x x 3 x x k x x 3 r = β r + β + β r + + β r x y x x 3 x x k x x 3 r = β r + β r + β + + β r x y x x x x 3 k x x r = β r + β r + β r + + β x y x x x x 3 x x k k k k 3 k k k k In Matrixnotation ist dies: R xx β = r mit T xy Rxx = Z Z n Folie 0
11 Interpretation der b und β Matrixalgebraische Berechnung der multiplen Regression In Matrixnotation ist dies: wobei: R xx β = Rxx = k k r xy mit Rxx T = Z Z n Matrix der Prädiktorinterkorrelationen Matrixalgebraische Berechnung Zusammenfassung Folie
12 Interpretation der b und β Matrixalgebraische Berechnung Zusammenfassung Folie Exkurs: Die Korrelationsmatrix R Aufbau und Bedeutung Die Korrelationsmatrix R stellt die Korrelationen zwischen k Variablen in Matrixschreibweise dar. Sie ist quadratisch und enthält k k Korrelationen x x x k x x x r r r r rk rk k k k Die Hauptdiagonale enthält die Korrelationen der Variablen mit sich selbst (r xx = ) Die untere und obere Dreiecksmatrix sind symmetrisch
13 Interpretation der b und β Matrixalgebraische Berechnung Zusammenfassung Matrixalgebraische Berechnung der multiplen Regression In Matrixnotation ist dies: wobei: R xx β = r xy mit Rxx T = Z Z n Rxx = k k Matrix der Prädiktorinterkorrelationen rxy = k Vektor der Kriteriumskorrelationen β = k Vektor der Regressionsgewichte Z = n k Vektor der z-standardisierten Daten Lösung: Inverse Interkorrelationsmatrix vormultiplizieren R R β = R r xx xx xx xy β = R r xx xy Folie 3
14 Interpretation der b und β Matrixalgebraische Berechnung Zusammenfassung Matrixalgebraische Berechnung Rückrechnung der unstandardisierten Parameter Wurden die β-parameter für die z-standardisierten Daten matrixalgebraisch bestimmt, kann die Berechnung der unstandardisierten b-parameter vorgenommen werden über SDy bi = βi mit i =,,..., k SD x i Die Konstante b 0 wird dann berechnet als b0 = y bx bx... bkxk Folie 4
15 Interpretation der b und β Matrixalgebraische Berechnung Zusammenfassung Interpretation der Lösung b- und β-gewichte Die Größe eines b-gewichtes gibt an, um wieviele Einheiten sich der Wert des unstandardisierten Kriteriums verändert, wenn der Betrag des unstandardisierten Prädiktors um steigt. Die Größe des β-gewichtes gibt dasselbe für die standardisierten Variablen an Das b-gewicht beantwortet die Frage: Ich möchte einen der Prädiktoren um erhöhen. Welchen sollte ich wählen, damit das Kriterium maximal steigt? Das β-gewicht beantwortet die Frage: Mit welchem Prädiktor erhöhe ich das Kriterium am effizientesten? Folie 5 Das b-gewicht liefert also eine absolute, das β-gewicht eine relative Information.
16 Interpretation der b und β Matrixalgebraische Berechnung Zusammenfassung Regression Vereinfachung bei nur einem Prädiktor Bei nur einem Prädiktor vereinfacht sich die Berechnung der Regressionsgewichte erheblich. b s = rxy s. Steigung: oder y x b ŷ = b0 + b x = cov( xy, ) s x. y-achsenabschnitt: b0 = y b x Folie 6
17 Regression Zusammenfassung Interpretation der b und β Matrixalgebraische Berechnung Zusammenfassung Oft ist in der Psychologie die Vorhersage des Wertes einer bestimmten Variablen unter Kenntnis der Ausprägung anderer Variablen gefordert. Die bekannten Variablen wird dabei als Prädiktoren, Unabhängige Variablen (UVn) oder Erklärende Variablen bezeichnet Die vorherzusagende Variable wird als Kriterium, Abhängige Variable (AVn) oder Response bezeichnet Folie 7
18 Regression Zusammenfassung Interpretation der b und β Matrixalgebraische Berechnung Zusammenfassung Drei Hauptfragestellungen der Regressionsrechnung:. Gibt es eine statistische Beziehung zwischen zwei Variablen, die die Vorhersage der AV aus der UV erlaubt?. Kann eine möglichst einfache mathematische Regel formuliert werden, die diesen Zusammenhang beschreibt? ˆ = k k y b b x b x b x 3. Wie gut ist diese Regel im Hinblick auf die Vorhersage? Folie 8
19 Regression Zusammenfassung Interpretation der b und β Matrixalgebraische Berechnung Zusammenfassung Gründe für die Annahme einer linearen Gleichung: Lineare Zusammenhänge sind einfach zu verstehen Lineare Zusammenhänge sind mathematisch und statistisch einfach zu behandeln Lineare Gleichungen haben sich vielfach als gute Approximationen für komplexe Beziehungen erwiesen Achtung: Auch wenn die Beziehung zwischen zwei ZVn linear aussieht, muss es sich nicht zwangsläufig um einen linearen Zusammenhang handeln. Folie 9
20 Interpretation der b und β Matrixalgebraische Berechnung Zusammenfassung Regression Zusammenfassung Vorsicht bei der Interpretation der Regressionsgleichung Bei der Korrelationsrechnung bedeutet ein Zusammenhang niemals Kausalität, lediglich Assoziation Bei der Regressionsrechnung gilt zunächst dasselbe Die Kausalitätsvermutung wird (wenn überhaupt) schon bei der Aufstellung der Regressionsgleichung getroffen, nicht erst bei der Interpretation der Ergebnisse. Um tatsächlich Kausalität festzustellen, müssen weitere Randbedingungen vorliegen (z.b. zeitliche Antezedenz von Ursache vor Wirkung). Folie 0
21 Relevante Excel Funktionen MMULT() MTRANS() MINV() Folie
22 Kennwerte Test der Gewichte gegen Null Kennwerte der multiplen Regression. Der multiple Korrelationskoeffizient R Definition: Der multiple Korrelationskoeffizient R repräsentiert die Korrelation zwischen dem Kriterium y und allen Prädiktoren x x k Dabei berücksichtigt R etwaige Interkorrelationen zwischen den Prädiktoren (und entfernt sie) Der multiple Korrelationskoeffizient R ist definiert als R yxx xk j xjy j= k = β r Folie Er ist mathematisch äquivalent zur Korrelation zwischen den gemessenen y-werten und den vorhergesagten y dach -Werten, also R yxx x = ryy k ˆ
23 Kennwerte Test der Gewichte gegen Null Kennwerte der multiplen Regression. Der multiple Determinationskoeffizient R² Definition: Der multiple Determinationskoeffizient R² repräsentiert die Varianzaufklärung, die alle Prädiktoren x x k am Kriterium y leisten Der multiple Determinationskoeffizient R² ist definiert als Erklärte Streuung Fehlerstreuung R = = Gesamt-Streuung Gesamt-Streuung Folie 3 Rechnerisch: R Var( yˆ ) Var( e) n = = = Var( y) Var( y) n i= n n i= ( y yˆ ) ( y y)
24 Kennwerte Test der Gewichte gegen Null Kennwerte der multiplen Regression 3. Abhängigkeit a) Sind die Prädiktoren unabhängig, so sind die ß-Gewichte gleich den Kriteriumskorrelationen und die aufgeklärte Varianz ist die Summe der Quadrate der ß-Gewichte Folie 4 Erklärung: Bei perfekt unabhängigen Prädiktoren ist die Prädiktorinterkorrelationsmatrix R xx gleich der Identitätsmatrix I. Damit gilt für den multiplen Korrelationskoeffizienten R Und R² ist einfach die Summe der quadrierten Kriteriumskorrelationen β = I r β = r R R xy k yxx x = r k xjy j= k yxx x = r k xjy j= xy
25 Kennwerte Test der Gewichte gegen Null Kennwerte der multiplen Regression 3. Abhängigkeit a) Sind die Prädiktoren unabhängig, so sind die ß-Gewichte gleich den Kriteriumskorrelationen und die aufgeklärte Varianz ist die Summe der Quadrate der ß-Gewichte b) Sind die Prädiktoren abhängig (interkorreliert), so sind 3 Fälle zu unterscheiden:. Der Prädiktor klärt zumindest Teile der Varianz am Kriterium auf, die andere Prädiktoren nicht aufklären: er ist nützlich.. Der Prädiktor enthält Information, die bereits andere Prädiktoren enthalten: er ist redundant. Der Prädiktor unterdrückt irrelevante Varianz in anderen Prädiktoren: er ist ein Suppressor Folie 5
26 Kennwerte Test der Gewichte gegen Null Kennwerte der multiplen Regression 3a. Nützlichkeit Nützlichkeit = Der Beitrag, den eine Variable zur Varianzaufklärung des Kriteriums leistet, der von den anderen Variablen nicht geleistet wird Die Nützlichkeit einer Variablen x j berechnet sich als U = R R j y, x y, x,,..., k, j,,..., k U j ist also der Betrag, um den R² wächst, wenn die Variable x j in die multiple Regressionsgleichung aufgenommen wird. Folie 6
27 Kennwerte Test der Gewichte gegen Null Kennwerte der multiplen Regression 3b. Redundanz Redundanz = die vielen Variablen messen Aspekte gemeinsam, so dass man prinzipiell weniger Prädiktoren benötigte unerwünschter Aspekt Die Variable x j ist redundant zur Vorhersage von Variable y wenn gilt β r < r x x y x y j j j Prädiktoren enthalten empirisch nahezu immer gemeinsame Varianzanteile und sind somit teilweise redundant. Echte Redundanz liegt aber erst gemäß obiger Definition vor. Folie 7 Multikollinearität: Die Kovarianz eines Prädiktors mit dem Kriterium ist in den anderen Prädiktoren (fast) vollständig enthalten extremer Fall von Redundanz.
28 Kennwerte Test der Gewichte gegen Null Kennwerte der multiplen Regression 3c. Suppression r x y r x x r x y =0 x x y x bindet irrelevante Prädiktorinformation x hängt nicht mit y zusammen, trotzdem erhöht sie R² Folie 8
29 Kennwerte Test der Gewichte gegen Null Kennwerte der multiplen Regression 3c. Suppression Defintion: Eine Variable x j ist ein Suppressor, wenn gilt: U x j > r x y j Die Zunahme der erklärten Varianz durch Aufnahme der Variable ist also größer als die einzelne Varianzaufklärung. Vereinfachung: Bei nur zwei Prädiktoren x und x ist x ein Supressor, wenn gilt: r -r xx xzx. > r xz -rx z Folie 9
30 Kennwerte Test der Gewichte gegen Null Statistischer Test der Gewichte Fragestellung Neben der Aussage über die Nützlichkeit eines Prädiktors ist man oft daran interessiert, ob er überhaupt mit dem Kriterium zusammenhängt Grundgedanke: Ein Prädiktor, der in keiner Verbindung zum Kriterium steht, sollte den Wert β j = 0 haben. Ein Prädiktor, der an der Veränderung des Kriteriums beteiligt ist, sollte einen Wert β j 0 haben. Problem: Allein aufgrund der zufälligen Auswahl der Merkmalsträger für die Stichprobe wird ein β-gewicht niemals perfekt Null sein ( Stichprobenfehler ). Folie 0
31 Kennwerte Test der Gewichte gegen Null Statistischer Test der Gewichte Fragestellung Frage: Wie unterschiedlich zu Null muss ein β-gewicht sein, damit wir begründet annehmen können, dass diese Abweichung nicht zufällig ist? Es existieren einfache statistische Verfahren zur (probabilistischen) Beantwortung dieser Fragestellung Ebenso kann geprüft werden, ob der multiple Korrelationskoeffizient zufällig zustande gekommen ist oder auf tatsächlichen systematischen Zusammenhängen zwischen Kriterium und Prädiktoren beruht Folie
32 Grundlagen Linearisierbare Formen Polynome Nichtlineare Regression Grundlagen Bei einer Reihe psychologischer Fragestellungen ergeben sich nichtlineare Zusammenhänge zwischen UV & AV. Beispiele: Reaktionszeit, Blutalkohol und psychomotorische Leistungen, Fehlerraten in Leistungstests bei verschiedenen Aufgabenschwierigkeiten Solche nichtlinearen Zusammenhänge lassen sich in zwei Klassen einteilen:. Zusammenhänge, die sich durch eine einfache (nichtlineare) Transformationen in lineare Zusammenhänge überführen lassen Folie. Zusammenhänge, für die eine nichtlineare Regressionsgleichung gelöst werden muss.
33 Grundlagen Linearisierbare Formen Polynome Nichtlineare Regression Linearisierbare und polynomische Formen Fall : Linearisierende Transformation, z.b. ˆ ( ) ln ˆ ln ln ln 0 0 y = b xb y = b + b x ( ) ( ) ( ) (hier nicht behandelt) Fall : Nicht (einfach) linearisierbar ŷ = b + b x+ b x 0 Folie 3
34 Grundlagen Nichtlineare Regression Beispiel: Logistische Regression 0.8 Linearisierbare Formen Polynome Folie 4 Gemessene Daten verlaufen ogivenförmig und variieren zwischen 0 und Umformung der y-werte durch Logarithmieren bewirkt eine Linearisierung der Daten Mithilfe dieser neuen y-werte kann eine lineare Regression bestimmt werden, um die Parameter b 0 und b zu errechnen
35 Grundlagen Linearisierbare Formen Polynome Grundlagen und Durchführung Häufig können Merkmalszusammenhänge durch Polynome. oder 3. Ordnung gut beschrieben werden, d.h. oder ŷ = b + b x+ b x 0 ŷ = b + b x+ b x + b x Dies ist formal eine lineare multiple Regression, allerdings nicht mit mehreren Prädiktoren, sondern mit einem Prädiktor sowie Transformationen seiner selbst. Folie 5
36 Grundlagen Linearisierbare Formen Polynome Grundlagen und Durchführung Eine solche polynomische Regression wird berechnet, indem die transformierten Prädiktorterme bestimmt werden Dann wird eine übliche lineare multiple Regression durchgeführt Die Einträge der Korrelationsmatrix sind dabei dann die Korrelationen des Prädiktors mit sich selbst in den transformierten Formen Es können alle Kennwerte und Gütemaße der multiplen Regression bestimmt werden. Folie 6 Die polyn. Regression ist auch über die KQ-Methode (inkl. Normalgleichungen) herzuleiten. Dies führt auf dasselbe Ergebnis wie der hier verfolgte Ansatz.
37 Voraussetzungen Voraussetzungen der Regression Mathematische und statistische Betrachtung Residualplot Mathematisch ist eine multiple Regression praktisch immer zu rechnen, da nur in Ausnahmefällen die Invertierung der Prädiktorinterkorrelationsmatrix fehlschlägt Statistisch aber sollen eine Reihe von Voraussetzungen erfüllt sein, damit Kennwerte und inferenzstatistische Verfahren (z.b. der statistische Test der β Gewichte) anwendbar sind die Regressionsgleichung empirische Aussagekraft besitzt Folie
38 Voraussetzungen Residualplot Voraussetzungen der Regression. Skalenniveaus Die Prädiktoren können entweder intervallskaliert oder dichotom sein Das Kriterium muss intervallskaliert sein und die Skala soll unbeschränkt sein (keine untere und obere Schranke Ungebundenheit) Für andere Skalenniveaus des Kriteriums existieren verschiedene Regressionsvarianten: Logistische Regression für dichotome Kriteriumsvariablen Multinomiale Regression für nominalskalierte Kriterien Ordinale Regression für ordinalskalierte Kriterien Folie 3
39 Voraussetzungen Residualplot Voraussetzungen der Regression. Eigenschaften der Prädiktoren Keine zu hohen Interkorrelationen zwischen den Prädiktoren, i.e. Vermeidung von Multikollinearität Es sollen alle wesentlichen Einflussvariablen des Kriteriums erfasst werden, d.h. hinreichend hohes R² Der Zusammenhang zwischen den Prädiktoren und dem Kriteriums soll dem Modell der Regressionsgleichung entsprechen (linear, polynomisch etc.) Es soll eine hinreichend hohe Stichprobengröße vorliegen, Daumenregeln empfehlen hier zwischen 5 und 5 Personen pro Prädiktor Folie 4
40 Voraussetzungen Residualplot Voraussetzungen der Regression 3. Eigenschaften der Fehler bzw. Residuen Hinweis: Der Vorhersagefehler in der Regression wird auch als Residuum bezeichnet Die Residuen dürfen nicht untereinander korreliert sein, d.h. die Höhe des Vorhersagefehlers für Merkmalsträger darf nicht den Fehler für Merkmalsträger beeinflussen Die Residuen sollen normalverteilt sein Für die Residuen soll der erwartete Mittelwert 0 sein Folie 5 Die Residuen sollen dem Gebot der Homoskedastizität genügen, d.h. ihre Varianz soll unabhängig vom Kriteriumswert sein.
41 Voraussetzungen Residualplot Der Residualplot Eigenschaften der Fehler bzw. Residuen Für die meisten der Fehlereigenschaften gibt es statistische Tests zur Voraussetzungsprüfung z.b. Variance Inflation Factor (VIF) für Multikollinearität, Durbin-Watson Test für Unkorreliertheit, Levene-Test für Homoskedastizität, Kolmogoroff-Smirnov Test für Normalverteilung Der Residualplot ist ein optisches Verfahren zur Prüfung der Voraussetzungen Er stellt die beobachteten Kriteriumswerte (x-achse) und die Residuen (y-achse) gegenüber An ihm kann man Homoskedastizität, Modellpassung (und auch Normalverteiltheit) optisch gut überprüfen Folie 6
42 Voraussetzungen Der Residualplot Eigenschaften der Fehler bzw. Residuen Residualplot Folie 7 Hinweis: Für die Residuen werden zumeist die z-standardisierten Residuen gewählt
43 Voraussetzungen Der Residualplot Eigenschaften der Fehler bzw. Residuen Residualplot Folie 8
Multiple Regression. Ziel: Vorhersage der Werte einer Variable (Kriterium) bei Kenntnis der Werte von zwei oder mehr anderen Variablen (Prädiktoren)
 Multiple Regression 1 Was ist multiple lineare Regression? Ziel: Vorhersage der Werte einer Variable (Kriterium) bei Kenntnis der Werte von zwei oder mehr anderen Variablen (Prädiktoren) Annahme: Der Zusammenhang
Multiple Regression 1 Was ist multiple lineare Regression? Ziel: Vorhersage der Werte einer Variable (Kriterium) bei Kenntnis der Werte von zwei oder mehr anderen Variablen (Prädiktoren) Annahme: Der Zusammenhang
Quantitative Methoden der Bildungsforschung
 Glieung Wieholung Korrelationen Grundlagen lineare Regression Lineare Regression in SPSS Übung Wieholung Korrelationen Standardisiertes Zusammenhangsmaß (unstandardisiert: Kovarianz) linearer Zusammenhang
Glieung Wieholung Korrelationen Grundlagen lineare Regression Lineare Regression in SPSS Übung Wieholung Korrelationen Standardisiertes Zusammenhangsmaß (unstandardisiert: Kovarianz) linearer Zusammenhang
Regressionsanalysen. Zusammenhänge von Variablen. Ziel der Regression. ( Idealfall )
 Zusammenhänge von Variablen Regressionsanalysen linearer Zusammenhang ( Idealfall ) kein Zusammenhang nichtlinearer monotoner Zusammenhang (i.d.regel berechenbar über Variablentransformationen mittels
Zusammenhänge von Variablen Regressionsanalysen linearer Zusammenhang ( Idealfall ) kein Zusammenhang nichtlinearer monotoner Zusammenhang (i.d.regel berechenbar über Variablentransformationen mittels
Modul G.1 WS 07/08: Statistik 17.01.2008 1. Die Korrelation ist ein standardisiertes Maß für den linearen Zusammenhangzwischen zwei Variablen.
 Modul G.1 WS 07/08: Statistik 17.01.2008 1 Wiederholung Kovarianz und Korrelation Kovarianz = Maß für den linearen Zusammenhang zwischen zwei Variablen x und y Korrelation Die Korrelation ist ein standardisiertes
Modul G.1 WS 07/08: Statistik 17.01.2008 1 Wiederholung Kovarianz und Korrelation Kovarianz = Maß für den linearen Zusammenhang zwischen zwei Variablen x und y Korrelation Die Korrelation ist ein standardisiertes
Das Dialogfeld für die Regressionsanalyse ("Lineare Regression") findet sich im Statistik- Menu unter "Regression"-"Linear":
 Lineare Regression Das Dialogfeld für die Regressionsanalyse ("Lineare Regression") findet sich im Statistik- Menu unter "Regression"-"Linear": Im einfachsten Fall werden mehrere Prädiktoren (oder nur
Lineare Regression Das Dialogfeld für die Regressionsanalyse ("Lineare Regression") findet sich im Statistik- Menu unter "Regression"-"Linear": Im einfachsten Fall werden mehrere Prädiktoren (oder nur
Korrelation - Regression. Berghold, IMI
 Korrelation - Regression Zusammenhang zwischen Variablen Bivariate Datenanalyse - Zusammenhang zwischen 2 stetigen Variablen Korrelation Einfaches lineares Regressionsmodell 1. Schritt: Erstellung eines
Korrelation - Regression Zusammenhang zwischen Variablen Bivariate Datenanalyse - Zusammenhang zwischen 2 stetigen Variablen Korrelation Einfaches lineares Regressionsmodell 1. Schritt: Erstellung eines
Forschungsstatistik I
 Prof. Dr. G. Meinhardt. Stock, Nordflügel R. 0-49 (Persike) R. 0- (Meinhardt) Sprechstunde jederzeit nach Vereinbarung Forschungsstatistik I Dr. Malte Persike persike@uni-mainz.de WS 008/009 Fachbereich
Prof. Dr. G. Meinhardt. Stock, Nordflügel R. 0-49 (Persike) R. 0- (Meinhardt) Sprechstunde jederzeit nach Vereinbarung Forschungsstatistik I Dr. Malte Persike persike@uni-mainz.de WS 008/009 Fachbereich
Weitere Fragestellungen im Zusammenhang mit einer linearen Einfachregression
 Weitere Fragestellungen im Zusammenhang mit einer linearen Einfachregression Speziell im Zusammenhang mit der Ablehnung der Globalhypothese werden bei einer linearen Einfachregression weitere Fragestellungen
Weitere Fragestellungen im Zusammenhang mit einer linearen Einfachregression Speziell im Zusammenhang mit der Ablehnung der Globalhypothese werden bei einer linearen Einfachregression weitere Fragestellungen
Mathematische und statistische Methoden II
 Methodenlehre e e Prof. Dr. G. Meinhardt 6. Stock, Wallstr. 3 (Raum 06-206) Sprechstunde jederzeit nach Vereinbarung und nach der Vorlesung. Mathematische und statistische Methoden II Dr. Malte Persike
Methodenlehre e e Prof. Dr. G. Meinhardt 6. Stock, Wallstr. 3 (Raum 06-206) Sprechstunde jederzeit nach Vereinbarung und nach der Vorlesung. Mathematische und statistische Methoden II Dr. Malte Persike
2. Korrelation, lineare Regression und multiple Regression
 multiple 2.2 Lineare 2.2 Lineare 1 / 130 2.2 Lineare 2 / 130 2.1 Beispiel: Arbeitsmotivation Untersuchung zur Motivation am Arbeitsplatz in einem Chemie-Konzern 25 Personen werden durch Arbeitsplatz zufällig
multiple 2.2 Lineare 2.2 Lineare 1 / 130 2.2 Lineare 2 / 130 2.1 Beispiel: Arbeitsmotivation Untersuchung zur Motivation am Arbeitsplatz in einem Chemie-Konzern 25 Personen werden durch Arbeitsplatz zufällig
Fragen und Antworten zu Kapitel 18
 Fragen und Antworten zu Kapitel 18 (1) Nennen Sie verschiedene Zielsetzungen, die man mit der Anwendung der multiplen Regressionsanalyse verfolgt. Die multiple Regressionsanalyse dient der Kontrolle von
Fragen und Antworten zu Kapitel 18 (1) Nennen Sie verschiedene Zielsetzungen, die man mit der Anwendung der multiplen Regressionsanalyse verfolgt. Die multiple Regressionsanalyse dient der Kontrolle von
a) Zeichnen Sie in das nebenstehende Streudiagramm mit Lineal eine Regressionsgerade ein, die Sie für passend halten.
 Statistik für Kommunikationswissenschaftler Wintersemester 2009/200 Vorlesung Prof. Dr. Helmut Küchenhoff Übung Cornelia Oberhauser, Monia Mahling, Juliane Manitz Thema 4 Homepage zur Veranstaltung: http://www.statistik.lmu.de/~helmut/kw09.html
Statistik für Kommunikationswissenschaftler Wintersemester 2009/200 Vorlesung Prof. Dr. Helmut Küchenhoff Übung Cornelia Oberhauser, Monia Mahling, Juliane Manitz Thema 4 Homepage zur Veranstaltung: http://www.statistik.lmu.de/~helmut/kw09.html
Lösungen zu Janssen/Laatz, Statistische Datenanalyse mit SPSS 1
 LÖSUNG 9B a) Lösungen zu Janssen/Laatz, Statistische Datenanalyse mit SPSS 1 Man kann erwarten, dass der Absatz mit steigendem Preis abnimmt, mit höherer Anzahl der Außendienstmitarbeiter sowie mit erhöhten
LÖSUNG 9B a) Lösungen zu Janssen/Laatz, Statistische Datenanalyse mit SPSS 1 Man kann erwarten, dass der Absatz mit steigendem Preis abnimmt, mit höherer Anzahl der Außendienstmitarbeiter sowie mit erhöhten
Kommentierter SPSS-Output für die multiple Regressionsanalyse (SPSS-Version 17)
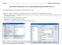 R.Niketta Multiple Regressionsanalyse Kommentierter SPSS-Output für die multiple Regressionsanalyse (SPSS-Version 17) Daten: Selbstdarstellung und Kontaktsuche in studi.vz (POK VIII, AG 3) Fragestellung:
R.Niketta Multiple Regressionsanalyse Kommentierter SPSS-Output für die multiple Regressionsanalyse (SPSS-Version 17) Daten: Selbstdarstellung und Kontaktsuche in studi.vz (POK VIII, AG 3) Fragestellung:
Inhaltsverzeichnis. Regressionsanalyse. http://mesosworld.ch - Stand vom: 20.1.2010 1
 Inhaltsverzeichnis Regressionsanalyse... 2 Lernhinweise... 2 Einführung... 2 Theorie (1-8)... 2 1. Allgemeine Beziehungen... 3 2. 'Best Fit'... 3 3. 'Ordinary Least Squares'... 4 4. Formel der Regressionskoeffizienten...
Inhaltsverzeichnis Regressionsanalyse... 2 Lernhinweise... 2 Einführung... 2 Theorie (1-8)... 2 1. Allgemeine Beziehungen... 3 2. 'Best Fit'... 3 3. 'Ordinary Least Squares'... 4 4. Formel der Regressionskoeffizienten...
Einleitung 19. Teil I Datenanalyse und Modellbildung Grundlagen 25
 Inhaltsverzeichnis Einleitung 19 Zu diesem Buch 19 Konventionen in diesem Buch 20 Was Sie nicht lesen müssen 21 Falsche Voraussetzungen 21 Wie dieses Buch aufgebaut ist 21 Teil I: Datenanalyse und Grundlagen
Inhaltsverzeichnis Einleitung 19 Zu diesem Buch 19 Konventionen in diesem Buch 20 Was Sie nicht lesen müssen 21 Falsche Voraussetzungen 21 Wie dieses Buch aufgebaut ist 21 Teil I: Datenanalyse und Grundlagen
Kapitel 23 Lineare Regression
 Kapitel 23 Lineare Regression Sowohl einfache als auch multiple Regressionsanalysen können Sie mit dem Befehl STATISTIK REGRESSION LINEAR... durchführen. Dabei lassen sich mit Hilfe diverser Optionen zahlreiche
Kapitel 23 Lineare Regression Sowohl einfache als auch multiple Regressionsanalysen können Sie mit dem Befehl STATISTIK REGRESSION LINEAR... durchführen. Dabei lassen sich mit Hilfe diverser Optionen zahlreiche
3 Zusammenhangsmaße Zusammenhangshypothesen
 3 Zusammenhangsmaße Zusammenhangshypothesen Zusammenhänge (zwischen 2 Variablen) misst man mittels Korrelationen. Die Wahl der Korrelation hängt ab von: a) Skalenniveau der beiden Variablen: 1) intervallskaliert
3 Zusammenhangsmaße Zusammenhangshypothesen Zusammenhänge (zwischen 2 Variablen) misst man mittels Korrelationen. Die Wahl der Korrelation hängt ab von: a) Skalenniveau der beiden Variablen: 1) intervallskaliert
Multivariate Analysemethoden
 Multivariate Analysemethoden 30.04.2014 Günter Meinhardt Johannes Gutenberg Universität Mainz Einführung Was sind multivariate Analysemethoden? Vorlesung Übung/Tut Prüfung Verfahrensdarstellung in Überblick
Multivariate Analysemethoden 30.04.2014 Günter Meinhardt Johannes Gutenberg Universität Mainz Einführung Was sind multivariate Analysemethoden? Vorlesung Übung/Tut Prüfung Verfahrensdarstellung in Überblick
Kontingenzkoeffizient (nach Pearson)
 Assoziationsmaß für zwei nominale Merkmale misst die Unabhängigkeit zweier Merkmale gibt keine Richtung eines Zusammenhanges an 46 o jl beobachtete Häufigkeiten der Kombination von Merkmalsausprägungen
Assoziationsmaß für zwei nominale Merkmale misst die Unabhängigkeit zweier Merkmale gibt keine Richtung eines Zusammenhanges an 46 o jl beobachtete Häufigkeiten der Kombination von Merkmalsausprägungen
Allgemeine Regressionsanalyse. Kovariablen / Prädiktoren / unabhängige Variablen X j R d, evtl. deterministisch
 Prof. Dr. J. Franke Statistik II für Wirtschaftswissenschaftler 9.1 Allgemeine Regressionsanalyse Daten (X j, Y j ), j = 1,..., N unabhängig Kovariablen / Prädiktoren / unabhängige Variablen X j R d, evtl.
Prof. Dr. J. Franke Statistik II für Wirtschaftswissenschaftler 9.1 Allgemeine Regressionsanalyse Daten (X j, Y j ), j = 1,..., N unabhängig Kovariablen / Prädiktoren / unabhängige Variablen X j R d, evtl.
6.2 Regressionsanalyse
 c-kennzahlensystem (ROCI) 6. Regressionsanalyse Die Regressionsanalyse zählt zu den wichtigsten Analysemethoden des Kommunikationscontrollings und hat ihre tiefen Wurzeln in der Statistik. Im Rahmen des
c-kennzahlensystem (ROCI) 6. Regressionsanalyse Die Regressionsanalyse zählt zu den wichtigsten Analysemethoden des Kommunikationscontrollings und hat ihre tiefen Wurzeln in der Statistik. Im Rahmen des
EINFACHE LINEARE REGRESSION MODUL 13 PROSEMINAR DESKRIPTIVE STATISTIK ANALYSE UND DARSTELLUNG VON DATEN I GÜNTER HAIDER WS 1999/2000
 INSTITUT FÜR ERZIEHUNGSWISSENSCHAFT - UNIVERSITÄT SALZBURG PROSEMINAR DESKRIPTIVE STATISTIK ANALYSE UND DARSTELLUNG VON DATEN I GÜNTER HAIDER WS 1999/2 MODUL 13 EINFACHE LINEARE REGRESSION Erziehungswissenschaft/Haider
INSTITUT FÜR ERZIEHUNGSWISSENSCHAFT - UNIVERSITÄT SALZBURG PROSEMINAR DESKRIPTIVE STATISTIK ANALYSE UND DARSTELLUNG VON DATEN I GÜNTER HAIDER WS 1999/2 MODUL 13 EINFACHE LINEARE REGRESSION Erziehungswissenschaft/Haider
Korrelation (II) Korrelation und Kausalität
 Korrelation (II) Korrelation und Kausalität Situation: Seien X, Y zwei metrisch skalierte Merkmale mit Ausprägungen (x 1, x 2,..., x n ) bzw. (y 1, y 2,..., y n ). D.h. für jede i = 1, 2,..., n bezeichnen
Korrelation (II) Korrelation und Kausalität Situation: Seien X, Y zwei metrisch skalierte Merkmale mit Ausprägungen (x 1, x 2,..., x n ) bzw. (y 1, y 2,..., y n ). D.h. für jede i = 1, 2,..., n bezeichnen
Herzlich Willkommen zur Vorlesung Statistik
 Herzlich Willkommen zur Vorlesung Statistik Thema dieser Vorlesung: Kovarianz und Korrelation Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften
Herzlich Willkommen zur Vorlesung Statistik Thema dieser Vorlesung: Kovarianz und Korrelation Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften
Assoziation & Korrelation
 Statistik 1 für SoziologInnen Assoziation & Korrelation Univ.Prof. Dr. Marcus Hudec Einleitung Bei Beobachtung von 2 Merkmalen für jeden Merkmalsträger stellt sich die Frage, ob es systematische Zusammenhänge
Statistik 1 für SoziologInnen Assoziation & Korrelation Univ.Prof. Dr. Marcus Hudec Einleitung Bei Beobachtung von 2 Merkmalen für jeden Merkmalsträger stellt sich die Frage, ob es systematische Zusammenhänge
Angewandte Ökonometrie, WS 2012/13, 1. Teilprüfung am 6.12.2012 - Lösungen. Das folgende Modell ist ein GARCH(1,1)-Modell:
 Angewandte Ökonometrie, WS 2012/13, 1. Teilprüfung am 6.12.2012 - Lösungen LV-Leiterin: Univ.Prof.Dr. Sylvia Frühwirth-Schnatter 1 Wahr oder falsch? 1. Das folgende Modell ist ein GARCH(1,1)-Modell: Y
Angewandte Ökonometrie, WS 2012/13, 1. Teilprüfung am 6.12.2012 - Lösungen LV-Leiterin: Univ.Prof.Dr. Sylvia Frühwirth-Schnatter 1 Wahr oder falsch? 1. Das folgende Modell ist ein GARCH(1,1)-Modell: Y
Einseitig gerichtete Relation: Mit zunehmender Höhe über dem Meeresspiegel sinkt im allgemeinen die Lufttemperatur.
 Statistik Grundlagen Charakterisierung von Verteilungen Einführung Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsverteilungen Schätzen und Testen Korrelation Regression Einführung Die Analyse und modellhafte
Statistik Grundlagen Charakterisierung von Verteilungen Einführung Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsverteilungen Schätzen und Testen Korrelation Regression Einführung Die Analyse und modellhafte
Willkommen zur Vorlesung Statistik
 Willkommen zur Vorlesung Statistik Thema dieser Vorlesung: Varianzanalyse Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften Prof. Dr. Wolfgang
Willkommen zur Vorlesung Statistik Thema dieser Vorlesung: Varianzanalyse Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften Prof. Dr. Wolfgang
Grundlagen quantitativer Sozialforschung Interferenzstatistische Datenanalyse in MS Excel
 Grundlagen quantitativer Sozialforschung Interferenzstatistische Datenanalyse in MS Excel 16.11.01 MP1 - Grundlagen quantitativer Sozialforschung - (4) Datenanalyse 1 Gliederung Datenanalyse (inferenzstatistisch)
Grundlagen quantitativer Sozialforschung Interferenzstatistische Datenanalyse in MS Excel 16.11.01 MP1 - Grundlagen quantitativer Sozialforschung - (4) Datenanalyse 1 Gliederung Datenanalyse (inferenzstatistisch)
Datenanalyse mit Excel. Wintersemester 2013/14
 Datenanalyse mit Excel 1 KORRELATIONRECHNUNG 2 Korrelationsrechnung Ziel der Korrelationsrechnung besteht im bivariaten Fall darin, die Stärke des Zusammenhangs zwischen zwei interessierenden statistischen
Datenanalyse mit Excel 1 KORRELATIONRECHNUNG 2 Korrelationsrechnung Ziel der Korrelationsrechnung besteht im bivariaten Fall darin, die Stärke des Zusammenhangs zwischen zwei interessierenden statistischen
2. Deskriptive Statistik 2.1. Häufigkeitstabellen, Histogramme, empirische Verteilungsfunktionen
 4. Datenanalyse und Modellbildung Deskriptive Statistik 2-1 2. Deskriptive Statistik 2.1. Häufigkeitstabellen, Histogramme, empirische Verteilungsfunktionen Für die Auswertung einer Messreihe, die in Form
4. Datenanalyse und Modellbildung Deskriptive Statistik 2-1 2. Deskriptive Statistik 2.1. Häufigkeitstabellen, Histogramme, empirische Verteilungsfunktionen Für die Auswertung einer Messreihe, die in Form
Kommentierter SPSS-Ausdruck zur logistischen Regression
 Daten: POK V AG 3 (POKV_AG3_V07.SAV) Kommentierter SPSS-Ausdruck zur logistischen Regression Fragestellung: Welchen Einfluss hat die Fachnähe und das Geschlecht auf die interpersonale Attraktion einer
Daten: POK V AG 3 (POKV_AG3_V07.SAV) Kommentierter SPSS-Ausdruck zur logistischen Regression Fragestellung: Welchen Einfluss hat die Fachnähe und das Geschlecht auf die interpersonale Attraktion einer
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
 Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Profil A 49,3 48,2 50,7 50,9 49,8 48,7 49,6 50,1 Profil B 51,8 49,6 53,2 51,1 51,1 53,4 50,7 50 51,5 51,7 48,8
 1. Aufgabe: Eine Reifenfirma hat für Winterreifen unterschiedliche Profile entwickelt. Bei jeweils gleicher Geschwindigkeit und auch sonst gleichen Bedingungen wurden die Bremswirkungen gemessen. Die gemessenen
1. Aufgabe: Eine Reifenfirma hat für Winterreifen unterschiedliche Profile entwickelt. Bei jeweils gleicher Geschwindigkeit und auch sonst gleichen Bedingungen wurden die Bremswirkungen gemessen. Die gemessenen
Multinomiale logistische Regression
 Multinomiale logistische Regression Die multinomiale logistische Regression dient zur Schätzung von Gruppenzugehörigkeiten bzw. einer entsprechenden Wahrscheinlichkeit hierfür, wobei als abhänginge Variable
Multinomiale logistische Regression Die multinomiale logistische Regression dient zur Schätzung von Gruppenzugehörigkeiten bzw. einer entsprechenden Wahrscheinlichkeit hierfür, wobei als abhänginge Variable
6Korrelationsanalyse:Zusammenhangsanalysestetiger Merkmale
 6Korrelationsanalyse:Zusammenhangsanalysestetiger Merkmale 6.1 Korrelationsanalyse 6.1 Korrelationsanalyse Jetzt betrachten wir bivariate Merkmale (X, Y ), wobei sowohl X als auch Y stetig bzw. quasi-stetig
6Korrelationsanalyse:Zusammenhangsanalysestetiger Merkmale 6.1 Korrelationsanalyse 6.1 Korrelationsanalyse Jetzt betrachten wir bivariate Merkmale (X, Y ), wobei sowohl X als auch Y stetig bzw. quasi-stetig
Fortgeschrittene Statistik Logistische Regression
 Fortgeschrittene Statistik Logistische Regression O D D S, O D D S - R A T I O, L O G I T T R A N S F O R M A T I O N, I N T E R P R E T A T I O N V O N K O E F F I Z I E N T E N, L O G I S T I S C H E
Fortgeschrittene Statistik Logistische Regression O D D S, O D D S - R A T I O, L O G I T T R A N S F O R M A T I O N, I N T E R P R E T A T I O N V O N K O E F F I Z I E N T E N, L O G I S T I S C H E
Kapitel 4: Binäre Regression
 Kapitel 4: Binäre Regression Steffen Unkel (basierend auf Folien von Nora Fenske) Statistik III für Nebenfachstudierende WS 2013/2014 4.1 Motivation Ausgangssituation Gegeben sind Daten (y i, x i1,...,
Kapitel 4: Binäre Regression Steffen Unkel (basierend auf Folien von Nora Fenske) Statistik III für Nebenfachstudierende WS 2013/2014 4.1 Motivation Ausgangssituation Gegeben sind Daten (y i, x i1,...,
Standardab er des. Testwert = 145.5 95% Konfidenzintervall. T df Sig. (2-seitig) Differenz Untere Obere -2.011 698.045-5.82-11.50 -.14.
 Aufgabe : einfacher T-Test Statistik bei einer Stichprobe Standardfehl Standardab er des Mittelwert weichung Mittelwertes 699 39.68 76.59 2.894 Test bei einer Sichprobe Testwert = 45.5 95% Konfidenzintervall
Aufgabe : einfacher T-Test Statistik bei einer Stichprobe Standardfehl Standardab er des Mittelwert weichung Mittelwertes 699 39.68 76.59 2.894 Test bei einer Sichprobe Testwert = 45.5 95% Konfidenzintervall
Institut für Soziologie Benjamin Gedon. Methoden 2. Regressionsanalyse IV: Transformation und Interaktion
 Institut für Soziologie Methoden 2 Regressionsanalyse IV: Transformation und Interaktion Inhalt 1. Zusammenfassung letzte Sitzung 2. Weitere Annahmen und Diagnostik 3. Transformationen zur besseren Interpretierbarkeit
Institut für Soziologie Methoden 2 Regressionsanalyse IV: Transformation und Interaktion Inhalt 1. Zusammenfassung letzte Sitzung 2. Weitere Annahmen und Diagnostik 3. Transformationen zur besseren Interpretierbarkeit
6.1 Grundbegriffe und historischer Hintergrund
 Kapitel 6 Regression 61 Grundbegriffe und historischer Hintergrund Bedeutung der Regression: Eines der am häufigsten verwendeten statistischen Verfahren Vielfache Anwendung in den Sozialwissenschaften
Kapitel 6 Regression 61 Grundbegriffe und historischer Hintergrund Bedeutung der Regression: Eines der am häufigsten verwendeten statistischen Verfahren Vielfache Anwendung in den Sozialwissenschaften
Multiple Regression II: Signifikanztests, Gewichtung, Multikollinearität und Kohortenanalyse
 Multiple Regression II: Signifikanztests,, Multikollinearität und Kohortenanalyse Statistik II Übersicht Literatur Kausalität und Regression Inferenz und standardisierte Koeffizienten Statistik II Multiple
Multiple Regression II: Signifikanztests,, Multikollinearität und Kohortenanalyse Statistik II Übersicht Literatur Kausalität und Regression Inferenz und standardisierte Koeffizienten Statistik II Multiple
Klausur zur Vorlesung Multivariate Verfahren, SS 2006 6 Kreditpunkte, 90 min
 Klausur, Multivariate Verfahren, SS 2006, 6 Kreditpunkte, 90 min 1 Prof. Dr. Fred Böker 08.08.2006 Klausur zur Vorlesung Multivariate Verfahren, SS 2006 6 Kreditpunkte, 90 min Gesamtpunkte: 39 Aufgabe
Klausur, Multivariate Verfahren, SS 2006, 6 Kreditpunkte, 90 min 1 Prof. Dr. Fred Böker 08.08.2006 Klausur zur Vorlesung Multivariate Verfahren, SS 2006 6 Kreditpunkte, 90 min Gesamtpunkte: 39 Aufgabe
Statistik Einführung // Lineare Regression 9 p.2/72
 Statistik Einführung Lineare Regression Kapitel 9 Statistik WU Wien Gerhard Derflinger Michael Hauser Jörg Lenneis Josef Ledold Günter Tirler Rosmarie Wakolbinger Statistik Einführung // Lineare Regression
Statistik Einführung Lineare Regression Kapitel 9 Statistik WU Wien Gerhard Derflinger Michael Hauser Jörg Lenneis Josef Ledold Günter Tirler Rosmarie Wakolbinger Statistik Einführung // Lineare Regression
Planen mit mathematischen Modellen 00844: Computergestützte Optimierung. Autor: Dr. Heinz Peter Reidmacher
 Planen mit mathematischen Modellen 00844: Computergestützte Optimierung Leseprobe Autor: Dr. Heinz Peter Reidmacher 11 - Portefeuilleanalyse 61 11 Portefeuilleanalyse 11.1 Das Markowitz Modell Die Portefeuilleanalyse
Planen mit mathematischen Modellen 00844: Computergestützte Optimierung Leseprobe Autor: Dr. Heinz Peter Reidmacher 11 - Portefeuilleanalyse 61 11 Portefeuilleanalyse 11.1 Das Markowitz Modell Die Portefeuilleanalyse
Multivariate Statistik
 Hermann Singer Multivariate Statistik 1 Auflage 15 Oktober 2012 Seite: 12 KAPITEL 1 FALLSTUDIEN Abbildung 12: Logistische Regression: Geschätzte Wahrscheinlichkeit für schlechte und gute Kredite (rot/blau)
Hermann Singer Multivariate Statistik 1 Auflage 15 Oktober 2012 Seite: 12 KAPITEL 1 FALLSTUDIEN Abbildung 12: Logistische Regression: Geschätzte Wahrscheinlichkeit für schlechte und gute Kredite (rot/blau)
Zusammenhänge zwischen metrischen Merkmalen
 Zusammenhänge zwischen metrischen Merkmalen Darstellung des Zusammenhangs, Korrelation und Regression Daten liegen zu zwei metrischen Merkmalen vor: Datenpaare (x i, y i ), i = 1,..., n Beispiel: x: Anzahl
Zusammenhänge zwischen metrischen Merkmalen Darstellung des Zusammenhangs, Korrelation und Regression Daten liegen zu zwei metrischen Merkmalen vor: Datenpaare (x i, y i ), i = 1,..., n Beispiel: x: Anzahl
Christian FG Schendera. Regressionsanalyse. mit SPSS. 2. korrigierte und aktualisierte Auflage DE GRUYTER OLDENBOURG
 Christian FG Schendera Regressionsanalyse mit SPSS 2. korrigierte und aktualisierte Auflage DE GRUYTER OLDENBOURG Inhalt Vorworte V 1 Korrelation 1 1.1 Einführung 1 1.2 Erste Voraussetzung: Das Skalenniveau
Christian FG Schendera Regressionsanalyse mit SPSS 2. korrigierte und aktualisierte Auflage DE GRUYTER OLDENBOURG Inhalt Vorworte V 1 Korrelation 1 1.1 Einführung 1 1.2 Erste Voraussetzung: Das Skalenniveau
Microsoft Excel 2010 Matrix-Funktionen
 Hochschulrechenzentrum Justus-Liebig-Universität Gießen Microsoft Excel 2010 Matrix-Funktionen Matrix-Funktionen in Excel 2010 Seite 1 von 7 Inhaltsverzeichnis Einleitung... 2 Integrierte Matrixfunktionen...
Hochschulrechenzentrum Justus-Liebig-Universität Gießen Microsoft Excel 2010 Matrix-Funktionen Matrix-Funktionen in Excel 2010 Seite 1 von 7 Inhaltsverzeichnis Einleitung... 2 Integrierte Matrixfunktionen...
Überblick über die Verfahren für Ordinaldaten
 Verfahren zur Analyse ordinalskalierten Daten 1 Überblick über die Verfahren für Ordinaldaten Unterschiede bei unabhängigen Stichproben Test U Test nach Mann & Whitney H Test nach Kruskal & Wallis parametrische
Verfahren zur Analyse ordinalskalierten Daten 1 Überblick über die Verfahren für Ordinaldaten Unterschiede bei unabhängigen Stichproben Test U Test nach Mann & Whitney H Test nach Kruskal & Wallis parametrische
Regression. Multiple Regression und Generalisierte Lineare Modelle. U. Mortensen
 Regression Multiple Regression und Generalisierte Lineare Modelle U. Mortensen Multivariate Methoden Psychologisches Institut der Universität Mainz WS 2011/12 11. 11. 2011 korrigiert: 08. 05. 2015 1 Inhaltsverzeichnis
Regression Multiple Regression und Generalisierte Lineare Modelle U. Mortensen Multivariate Methoden Psychologisches Institut der Universität Mainz WS 2011/12 11. 11. 2011 korrigiert: 08. 05. 2015 1 Inhaltsverzeichnis
1 Statistische Grundlagen
 Konzepte in Empirische Ökonomie 1 (Winter) Hier findest Du ein paar Tipps zu den Konzepten in Empirische 1. Wenn Du aber noch etwas Unterstützung kurz vor der Klausur brauchst, schreib uns eine kurze Email.
Konzepte in Empirische Ökonomie 1 (Winter) Hier findest Du ein paar Tipps zu den Konzepten in Empirische 1. Wenn Du aber noch etwas Unterstützung kurz vor der Klausur brauchst, schreib uns eine kurze Email.
Kategoriale abhängige Variablen: Logit- und Probit -Modelle. Statistik II
 Kategoriale abhängige Variablen: Logit- und Probit -Modelle Statistik II Wiederholung Literatur Annahmen und Annahmeverletzungen Funktionen Exponenten, Wurzeln usw. Das Problem Das binäre Logit-Modell
Kategoriale abhängige Variablen: Logit- und Probit -Modelle Statistik II Wiederholung Literatur Annahmen und Annahmeverletzungen Funktionen Exponenten, Wurzeln usw. Das Problem Das binäre Logit-Modell
6. Auswertung mehrdimensionaler Daten
 6. Auswertung mehrdimensionaler Daten Bisher: Auswertungsmethoden für Daten eines einzelnen Merkmals, z.b. Diskrete Klassierung Grafische Darstellungen (Verteilungsfunktion) Lagemaße Streungsmaße Schiefemaße
6. Auswertung mehrdimensionaler Daten Bisher: Auswertungsmethoden für Daten eines einzelnen Merkmals, z.b. Diskrete Klassierung Grafische Darstellungen (Verteilungsfunktion) Lagemaße Streungsmaße Schiefemaße
Auswertung von kritischen Daten Vorgehensweise anhand eines Beispiels Visual-XSel 10.0
 Auswertung von kritischen Daten Vorgehensweise anhand eines Beispiels Visual-XSel 10.0??? Curt Ronniger 2007 Bei Neueinstieg in das Programm, sollte zunächst die Dokumentation XSelDoE10.pdf gelesen werden.
Auswertung von kritischen Daten Vorgehensweise anhand eines Beispiels Visual-XSel 10.0??? Curt Ronniger 2007 Bei Neueinstieg in das Programm, sollte zunächst die Dokumentation XSelDoE10.pdf gelesen werden.
Mathematik für Informatiker II. Beispiellösungen zur Probeklausur. Aufgabe 1. Aufgabe 2 (5+5 Punkte) Christoph Eisinger Sommersemester 2011
 Mathematik für Informatiker II Christoph Eisinger Sommersemester 211 Beispiellösungen zur Probeklausur Aufgabe 1 Gegeben sind die Polynome f, g, h K[x]. Zu zeigen: Es gibt genau dann Polynome h 1 und h
Mathematik für Informatiker II Christoph Eisinger Sommersemester 211 Beispiellösungen zur Probeklausur Aufgabe 1 Gegeben sind die Polynome f, g, h K[x]. Zu zeigen: Es gibt genau dann Polynome h 1 und h
ε heteroskedastisch BINARY CHOICE MODELS Beispiele: Wahlentscheidung Kauf langlebiger Konsumgüter Arbeitslosigkeit Schätzung mit OLS?
 BINARY CHOICE MODELS 1 mit Pr( Y = 1) = P Y = 0 mit Pr( Y = 0) = 1 P Beispiele: Wahlentscheidung Kauf langlebiger Konsumgüter Arbeitslosigkeit Schätzung mit OLS? Y i = X i β + ε i Probleme: Nonsense Predictions
BINARY CHOICE MODELS 1 mit Pr( Y = 1) = P Y = 0 mit Pr( Y = 0) = 1 P Beispiele: Wahlentscheidung Kauf langlebiger Konsumgüter Arbeitslosigkeit Schätzung mit OLS? Y i = X i β + ε i Probleme: Nonsense Predictions
Motivation. Jede Messung ist mit einem sogenannten Fehler behaftet, d.h. einer Messungenauigkeit
 Fehlerrechnung Inhalt: 1. Motivation 2. Was sind Messfehler, statistische und systematische 3. Verteilung statistischer Fehler 4. Fehlerfortpflanzung 5. Graphische Auswertung und lineare Regression 6.
Fehlerrechnung Inhalt: 1. Motivation 2. Was sind Messfehler, statistische und systematische 3. Verteilung statistischer Fehler 4. Fehlerfortpflanzung 5. Graphische Auswertung und lineare Regression 6.
Aufgabenstellung Aufgabe 1: Betrachten Sie das folgende ökonometrische Modell: y t = α + βx t + u t (1)
 Klausur: Einführung in die Ökonometrie Prüfer: Prof. Dr. Karl-Heinz Paqué Dr.Ludwigv.Auer Semester: WS 1999/00 Als Hilfsmittel sind zugelassen: nicht-programmierbarer Taschenrechner Diese Klausur besteht
Klausur: Einführung in die Ökonometrie Prüfer: Prof. Dr. Karl-Heinz Paqué Dr.Ludwigv.Auer Semester: WS 1999/00 Als Hilfsmittel sind zugelassen: nicht-programmierbarer Taschenrechner Diese Klausur besteht
Weiterbildungskurs Stochastik
 Hansruedi Künsch Seminar für Statistik Departement Mathematik, ETH Zürich 24. Juni 2009 Inhalt STATISTIK DER BINOMIALVERTEILUNG 1 STATISTIK DER BINOMIALVERTEILUNG 2 Fragestellungen Typische Fragestellungen
Hansruedi Künsch Seminar für Statistik Departement Mathematik, ETH Zürich 24. Juni 2009 Inhalt STATISTIK DER BINOMIALVERTEILUNG 1 STATISTIK DER BINOMIALVERTEILUNG 2 Fragestellungen Typische Fragestellungen
Lineare Strukturgleichungsmodelle (LISREL) Konfirmatorische Faktorenanalyse (CFA)
 Interdisziplinäres Seminar Lineare Strukturgleichungsmodelle (LISREL) Konfirmatorische Faktorenanalyse (CFA) WS 2008/09 19.11.2008 Julia Schiele und Lucie Wink Dozenten: Prof. Dr. Bühner, Prof. Dr. Küchenhoff
Interdisziplinäres Seminar Lineare Strukturgleichungsmodelle (LISREL) Konfirmatorische Faktorenanalyse (CFA) WS 2008/09 19.11.2008 Julia Schiele und Lucie Wink Dozenten: Prof. Dr. Bühner, Prof. Dr. Küchenhoff
Teil II: Einführung in die Statistik
 Teil II: Einführung in die Statistik (50 Punkte) Bitte beantworten Sie ALLE Fragen. Es handelt sich um multiple choice Fragen. Sie müssen die exakte Antwortmöglichkeit angeben, um die volle Punktzahl zu
Teil II: Einführung in die Statistik (50 Punkte) Bitte beantworten Sie ALLE Fragen. Es handelt sich um multiple choice Fragen. Sie müssen die exakte Antwortmöglichkeit angeben, um die volle Punktzahl zu
Binäre abhängige Variablen
 Binäre abhängige Variablen Thushyanthan Baskaran thushyanthan.baskaran@awi.uni-heidelberg.de Alfred Weber Institut Ruprecht Karls Universität Heidelberg Einführung Oft wollen wir qualitative Variablen
Binäre abhängige Variablen Thushyanthan Baskaran thushyanthan.baskaran@awi.uni-heidelberg.de Alfred Weber Institut Ruprecht Karls Universität Heidelberg Einführung Oft wollen wir qualitative Variablen
Bestimmung einer ersten
 Kapitel 6 Bestimmung einer ersten zulässigen Basislösung Ein Problem, was man für die Durchführung der Simplexmethode lösen muss, ist die Bestimmung einer ersten zulässigen Basislösung. Wie gut das geht,
Kapitel 6 Bestimmung einer ersten zulässigen Basislösung Ein Problem, was man für die Durchführung der Simplexmethode lösen muss, ist die Bestimmung einer ersten zulässigen Basislösung. Wie gut das geht,
Rekursionen. Georg Anegg 25. November 2009. Methoden und Techniken an Beispielen erklärt
 Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
Lineare Gleichungssysteme
 Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
SFB 833 Bedeutungskonstitution. Kompaktkurs. Datenanalyse. Projekt Z2 Tübingen, Mittwoch, 18. und 20. März 2015
 SFB 833 Bedeutungskonstitution Kompaktkurs Datenanalyse Projekt Z2 Tübingen, Mittwoch, 18. und 20. März 2015 Messen und Skalen Relativ (Relationensystem): Menge A von Objekten und eine oder mehrere Relationen
SFB 833 Bedeutungskonstitution Kompaktkurs Datenanalyse Projekt Z2 Tübingen, Mittwoch, 18. und 20. März 2015 Messen und Skalen Relativ (Relationensystem): Menge A von Objekten und eine oder mehrere Relationen
Vorkurs Mathematik Übungen zu Differentialgleichungen
 Vorkurs Mathematik Übungen zu Differentialgleichungen Als bekannt setzen wir die folgenden Umformungen voraus: e ln(f(x)) = f(x) e f(x)+c = e f(x) e c e ln(f(x)) +c = f(x) e c = f(x) c f ( g(x) ) g (x)
Vorkurs Mathematik Übungen zu Differentialgleichungen Als bekannt setzen wir die folgenden Umformungen voraus: e ln(f(x)) = f(x) e f(x)+c = e f(x) e c e ln(f(x)) +c = f(x) e c = f(x) c f ( g(x) ) g (x)
Kategoriale abhängige Variablen:
 Kategoriale abhängige Variablen: Logit- und Probit -Modelle Statistik II Literatur Annahmen und Annahmeverletzungen Funktionen Exponenten, Wurzeln usw. Das Problem Das binäre Logit-Modell Statistik II
Kategoriale abhängige Variablen: Logit- und Probit -Modelle Statistik II Literatur Annahmen und Annahmeverletzungen Funktionen Exponenten, Wurzeln usw. Das Problem Das binäre Logit-Modell Statistik II
Business Value Launch 2006
 Quantitative Methoden Inferenzstatistik alea iacta est 11.04.2008 Prof. Dr. Walter Hussy und David Tobinski UDE.EDUcation College im Rahmen des dokforums Universität Duisburg-Essen Inferenzstatistik Erläuterung
Quantitative Methoden Inferenzstatistik alea iacta est 11.04.2008 Prof. Dr. Walter Hussy und David Tobinski UDE.EDUcation College im Rahmen des dokforums Universität Duisburg-Essen Inferenzstatistik Erläuterung
Klausur zu Methoden der Statistik I (mit Kurzlösung) Wintersemester 2007/2008. Aufgabe 1
 Lehrstuhl für Statistik und Ökonometrie der Otto-Friedrich-Universität Bamberg Prof. Dr. Susanne Rässler Klausur zu Methoden der Statistik I (mit Kurzlösung) Wintersemester 2007/2008 Aufgabe 1 Ihnen liegt
Lehrstuhl für Statistik und Ökonometrie der Otto-Friedrich-Universität Bamberg Prof. Dr. Susanne Rässler Klausur zu Methoden der Statistik I (mit Kurzlösung) Wintersemester 2007/2008 Aufgabe 1 Ihnen liegt
Diskriminanzanalyse Beispiel
 Diskriminanzanalyse Ziel bei der Diskriminanzanalyse ist die Analyse von Gruppenunterschieden, d. h. der Untersuchung von zwei oder mehr Gruppen hinsichtlich einer Vielzahl von Variablen. Diese Methode
Diskriminanzanalyse Ziel bei der Diskriminanzanalyse ist die Analyse von Gruppenunterschieden, d. h. der Untersuchung von zwei oder mehr Gruppen hinsichtlich einer Vielzahl von Variablen. Diese Methode
Bachelorabschlussseminar Dipl.-Kfm. Daniel Cracau
 1 Einführung in die statistische Datenanalyse Bachelorabschlussseminar Dipl.-Kfm. Daniel Cracau 2 Gliederung 1.Grundlagen 2.Nicht-parametrische Tests a. Mann-Whitney-Wilcoxon-U Test b. Wilcoxon-Signed-Rank
1 Einführung in die statistische Datenanalyse Bachelorabschlussseminar Dipl.-Kfm. Daniel Cracau 2 Gliederung 1.Grundlagen 2.Nicht-parametrische Tests a. Mann-Whitney-Wilcoxon-U Test b. Wilcoxon-Signed-Rank
Kurzanleitung. Auswertung, Fehlerrechnung und Ergebnisdarstellung. Praktikum Physikalisch-Chemische Experimente
 Kurzanleitung zur Auswertung, Fehlerrechnung und Ergebnisdarstellung im Praktikum Physikalisch-Chemische Experimente Dr. Markus Braun Institut für Physikalische und Theoretische Chemie Goethe-Universität
Kurzanleitung zur Auswertung, Fehlerrechnung und Ergebnisdarstellung im Praktikum Physikalisch-Chemische Experimente Dr. Markus Braun Institut für Physikalische und Theoretische Chemie Goethe-Universität
Elemente der Analysis II
 Elemente der Analysis II Kapitel 3: Lineare Abbildungen und Gleichungssysteme Informationen zur Vorlesung: http://www.mathematik.uni-trier.de/ wengenroth/ J. Wengenroth () 15. Mai 2009 1 / 35 3.1 Beispiel
Elemente der Analysis II Kapitel 3: Lineare Abbildungen und Gleichungssysteme Informationen zur Vorlesung: http://www.mathematik.uni-trier.de/ wengenroth/ J. Wengenroth () 15. Mai 2009 1 / 35 3.1 Beispiel
Einführung in die Tensorrechnung
 1. Definition eines Tensors Tensoren sind Grössen, mit deren Hilfe man Skalare, Vektoren und weitere Grössen analoger Struktur in ein einheitliches Schema zur Beschreibung mathematischer und physikalischer
1. Definition eines Tensors Tensoren sind Grössen, mit deren Hilfe man Skalare, Vektoren und weitere Grössen analoger Struktur in ein einheitliches Schema zur Beschreibung mathematischer und physikalischer
Kapitel 15: Differentialgleichungen
 FernUNI Hagen WS 00/03 Kapitel 15: Differentialgleichungen Differentialgleichungen = Gleichungen die Beziehungen zwischen einer Funktion und mindestens einer ihrer Ableitungen herstellen. Kommen bei vielen
FernUNI Hagen WS 00/03 Kapitel 15: Differentialgleichungen Differentialgleichungen = Gleichungen die Beziehungen zwischen einer Funktion und mindestens einer ihrer Ableitungen herstellen. Kommen bei vielen
Charakteristikenmethode im Beispiel
 Charakteristikenmethode im Wir betrachten die PDE in drei Variablen xu x + yu y + (x + y )u z = 0. Das charakteristische System lautet dann ẋ = x ẏ = y ż = x + y und besitzt die allgemeine Lösung x(t)
Charakteristikenmethode im Wir betrachten die PDE in drei Variablen xu x + yu y + (x + y )u z = 0. Das charakteristische System lautet dann ẋ = x ẏ = y ż = x + y und besitzt die allgemeine Lösung x(t)
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler Wintersemester 3/4 (.3.4). (a) Für z = + i und z = 3 4i berechne man z z und z z. Die Ergebnisse sind in kartesischer Form anzugeben.
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler Wintersemester 3/4 (.3.4). (a) Für z = + i und z = 3 4i berechne man z z und z z. Die Ergebnisse sind in kartesischer Form anzugeben.
Auswertung und Darstellung wissenschaftlicher Daten (1)
 Auswertung und Darstellung wissenschaftlicher Daten () Mag. Dr. Andrea Payrhuber Zwei Schritte der Auswertung. Deskriptive Darstellung aller Daten 2. analytische Darstellung (Gruppenvergleiche) SPSS-Andrea
Auswertung und Darstellung wissenschaftlicher Daten () Mag. Dr. Andrea Payrhuber Zwei Schritte der Auswertung. Deskriptive Darstellung aller Daten 2. analytische Darstellung (Gruppenvergleiche) SPSS-Andrea
Übung 3: Einfache Graphiken und Näherungen durch Regression
 Übung 3: Einfache Graphiken und Näherungen durch Regression M. Schlup, 9. August 010 Aufgabe 1 Einfache Graphik Für die abgegebene Leistung P = UI eines linearen, aktiven Zweipols mit Leerlaufspannung
Übung 3: Einfache Graphiken und Näherungen durch Regression M. Schlup, 9. August 010 Aufgabe 1 Einfache Graphik Für die abgegebene Leistung P = UI eines linearen, aktiven Zweipols mit Leerlaufspannung
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Computer Vision: Optische Flüsse
 Computer Vision: Optische Flüsse D. Schlesinger TUD/INF/KI/IS Bewegungsanalyse Optischer Fluss Lokale Verfahren (Lukas-Kanade) Globale Verfahren (Horn-Schunck) (+ kontinuierliche Ansätze: mathematische
Computer Vision: Optische Flüsse D. Schlesinger TUD/INF/KI/IS Bewegungsanalyse Optischer Fluss Lokale Verfahren (Lukas-Kanade) Globale Verfahren (Horn-Schunck) (+ kontinuierliche Ansätze: mathematische
Ausgewählte Kapitel der Statistik: Regressions- u. varianzanalytische Modelle Lösung von Grundaufgaben mit SPSS Statistics 20.0
 1 Ausgewählte Kapitel der Statistik: Regressions- u. varianzanalytische Modelle Lösung von Grundaufgaben mit SPSS Statistics 20.0 Text: grund1_spss20.doc Daten: grund1_?.sav Lehrbuch: W. Timischl, Biostatistik.
1 Ausgewählte Kapitel der Statistik: Regressions- u. varianzanalytische Modelle Lösung von Grundaufgaben mit SPSS Statistics 20.0 Text: grund1_spss20.doc Daten: grund1_?.sav Lehrbuch: W. Timischl, Biostatistik.
3.3 Eigenwerte und Eigenräume, Diagonalisierung
 3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
12. Bivariate Datenanalyse. In den Kapiteln 4-11 wurden univariate Daten betrachtet:
 12. Bivariate Datenanalyse Während einer nur Zahlen im Kopf hat, kann er nicht auf den Kausalzusammenhang kommen Anonymus In den Kapiteln 4-11 wurden univariate Daten betrachtet: Von univariaten Daten
12. Bivariate Datenanalyse Während einer nur Zahlen im Kopf hat, kann er nicht auf den Kausalzusammenhang kommen Anonymus In den Kapiteln 4-11 wurden univariate Daten betrachtet: Von univariaten Daten
Name: Klasse: Datum: Klassenarbeit Wachstumsvorgänge Kl10-Gruppe B
 Name: Klasse: Datum: Teil B Klassenarbeit Wachstumsvorgänge Kl0-Gruppe B. Gegeben ist die Exponentialfunktion y=f x =0.8 2 x ; x R. (9P) a) Geben Sie die folgenden Eigenschaften dieser Funktion an! Wertebereich,
Name: Klasse: Datum: Teil B Klassenarbeit Wachstumsvorgänge Kl0-Gruppe B. Gegeben ist die Exponentialfunktion y=f x =0.8 2 x ; x R. (9P) a) Geben Sie die folgenden Eigenschaften dieser Funktion an! Wertebereich,
(2) Mittels welcher Methode ist es im ALM möglich kategoriale Variablen als Prädiktoren in eine Regressionsgleichung zu überführen?
 Beispielaufgaben LÖSUNG (1) Grenzen Sie eine einfache lineare Regression von einem Random Intercept Modell mit nur einem Level1-Prädiktor ab! a. Worin unterscheiden sich die Voraussetzungen? - MLM braucht
Beispielaufgaben LÖSUNG (1) Grenzen Sie eine einfache lineare Regression von einem Random Intercept Modell mit nur einem Level1-Prädiktor ab! a. Worin unterscheiden sich die Voraussetzungen? - MLM braucht
DOE am Beispiel Laserpointer
 DOE am Beispiel Laserpointer Swen Günther Ein wesentliches Ziel im Rahmen der Neuproduktentwicklung ist die aus Kundesicht bestmögliche, d.h. nutzenmaximale Konzeption des Produktes zu bestimmen (vgl.
DOE am Beispiel Laserpointer Swen Günther Ein wesentliches Ziel im Rahmen der Neuproduktentwicklung ist die aus Kundesicht bestmögliche, d.h. nutzenmaximale Konzeption des Produktes zu bestimmen (vgl.
Klausur zu Methoden der Statistik I (mit Kurzlösung) Sommersemester 2008. Aufgabe 1
 Lehrstuhl für Statistik und Ökonometrie der Otto-Friedrich-Universität Bamberg Prof. Dr. Susanne Rässler Klausur zu Methoden der Statistik I (mit Kurzlösung) Sommersemester 2008 Aufgabe 1 I) Einige Mitarbeiter
Lehrstuhl für Statistik und Ökonometrie der Otto-Friedrich-Universität Bamberg Prof. Dr. Susanne Rässler Klausur zu Methoden der Statistik I (mit Kurzlösung) Sommersemester 2008 Aufgabe 1 I) Einige Mitarbeiter
Name: Klasse: Datum: Klassenarbeit Wachstumsvorgänge Kl10-Gruppe A
 Name: Klasse: Datum: Teil B Klassenarbeit Wachstumsvorgänge Kl10-Gruppe A 1. Gegeben ist die Exponentialfunktion y=f x = 0,5 x ; x R. (9P) a) Geben Sie die folgenden Eigenschaften dieser Funktion an! Wertebereich,
Name: Klasse: Datum: Teil B Klassenarbeit Wachstumsvorgänge Kl10-Gruppe A 1. Gegeben ist die Exponentialfunktion y=f x = 0,5 x ; x R. (9P) a) Geben Sie die folgenden Eigenschaften dieser Funktion an! Wertebereich,
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Allgemeines Lineares Modell: Univariate Varianzanalyse und Kovarianzanalyse
 Allgemeines Lineares Modell: Univariate Varianzanalyse und Kovarianzanalyse Univariate Varianz- und Kovarianzanlyse, Multivariate Varianzanalyse und Varianzanalyse mit Messwiederholung finden sich unter
Allgemeines Lineares Modell: Univariate Varianzanalyse und Kovarianzanalyse Univariate Varianz- und Kovarianzanlyse, Multivariate Varianzanalyse und Varianzanalyse mit Messwiederholung finden sich unter
Dokumentation. estat Version 2.0
 Dokumentation estat Version 2.0 Installation Die Datei estat.xla in beliebiges Verzeichnis speichern. Im Menü Extras AddIns... Durchsuchen die Datei estat.xla auswählen. Danach das Auswahlhäkchen beim
Dokumentation estat Version 2.0 Installation Die Datei estat.xla in beliebiges Verzeichnis speichern. Im Menü Extras AddIns... Durchsuchen die Datei estat.xla auswählen. Danach das Auswahlhäkchen beim
Mathematik 1. Inhaltsverzeichnis. Prof. Dr. K. Melzer. karin.melzer@hs-esslingen.de http://www.hs-esslingen.de/de/mitarbeiter/karin-melzer.
 Mathematik 1 Prof Dr K Melzer karinmelzer@hs-esslingende http://wwwhs-esslingende/de/mitarbeiter/karin-melzerhtml Inhaltsverzeichnis 1 Matrizenrechnung 2 11 Matrixbegri 2 12 Spezielle Matrizen 3 13 Rechnen
Mathematik 1 Prof Dr K Melzer karinmelzer@hs-esslingende http://wwwhs-esslingende/de/mitarbeiter/karin-melzerhtml Inhaltsverzeichnis 1 Matrizenrechnung 2 11 Matrixbegri 2 12 Spezielle Matrizen 3 13 Rechnen
