2 Grundlagen der Robotermathematik - Lösungen zu den Aufgaben
|
|
|
- Heini Lenz
- vor 5 Jahren
- Abrufe
Transkript
1 Gdlage de Roboemahemaik - Lösge z de Afgabe Afgabe. Gegebe is ei Recheck mi de Kaeläge l cm, bcm. Es is paallel z de Koodiaeachse asgeiche d sei like ee Eckpk lieg bei P,. a Selle Sie fü die ie Geade, die dch die Kae besimm sid, alle Dasellgsfome o abelle. af. Eplizie Dasellg: g: g: ich defiie g: g: ich defiie Implizie Dasellg: g: g: 5 g: g: Vekodasellg : g: 5 g: g: Die Kompoeedasellg wid ich agegebe, da sie eie weige kompake Scheibweise de Vekodasellg is.
2 Lösge -. Gdlage de Roboemahemaik g: Hesse-Nomalefom: g: g: 5 g: g: b Zeige Sie mi Hilfe de Hesse-Nomalefom, dass de Absad de Eckpke o de gegeübeliegede Kae de eie b, bzw. de Läge l espich. P, i die Hesse-Nomalefom o g eiseze: b P, i die Hesse-Nomalefom o g eiseze: 5 l Das egaie Vozeiche fü de Absad bedee, dass P ich i de Halbebee lieg, i welche de Nomaleeko de Geade zeig. Afgabe. Gegebe is ei allgemeies Deieck A. a eeche Sie die Höhe h c beim Eckpk mi Hilfe de Hesse-Nomalefom eie Geade g, die dch A d eläf. Dch Eiseze o A d i die allgemeie Gleichg de Hesse-Nomale sowie de edigg ehäl ma die Koeffiziee: b a a b a b b a a b a b Als eispiel wede die Pke A,,,,, gewähl. Daas folg:
3 Lösge -. Gdlage de Roboemahemaik ±. Es gib zwei Lösge, da es zwei Asichge fü de Nomaleeko gib. Fü ehäl ma: h d Dch Eiseze o, ehäl ma d h. Das Vozeiche is egai, da de Nomaleeko i die Halbebee zeig, die ich ehäl. b Emiel Sie h c dch die eechg des Absads, de de Lofßpkes D de Höhe h c om Eckpk ha. eechg o D dch Schi de Logeade g L mi de Geade g dch A,. s g g L : :. Es gil: c [ ] [ ] s s Mi de Lösg des Gleichgsssems beeche sich de Oseko S S S d des Lofßpkes D z s d S S Mi de Pke A,,,,, ehäl ma: : : g g L. Dch Gleichseze egib sich: -, d daas folg fü de Lofßpk D,. Afgabe. Vogegebe is eie Ebee E, die sekech af de -Ebee seh d die Pke P,, d P,, ehäl.
4 Lösge -. Gdlage de Roboemahemaik a Selle Sie die Ebee E mi alle Mehode o abelle. da. Eplizie Dasellg: ich möglich, da keie eideige Zodg z z beseh. Implizie Dasellg:. Vekodasellg: p p a a Hesse-Nomalefom: z / / / z b eeche Sie die Schigeade g s mi de -Ebee. : g S. c Welche Wikel schließ g s mi de -Achse ei? / a, a ϕ a S, Wikelbeeich: ϕ S. d eeche Sie de sekeche Absad des Uspgs o de Ebee E.
5 Lösge -. Gdlage de Roboemahemaik 5 d. Afgabe. Gegebe is ei gleichseiiges Deieck A mi de Kaeläge a cm. a eeche Sie die Höhe h. a Phagoas Kosissaz: a h h a b eeche Sie alle Iewikel mi Hilfe des Kosissazes. Alle Iewikel ϕ sid gleich: a a a cosϕ o a cosϕ a cos ϕ ϕ 6 c eeche Sie alle Iewikel mi Hilfe de iese agesfkio. h a a ϕ a a ϕ a a 6 o Afgabe.5 Ei echwikliges Deieck ha die Eckpke A,,,,,. a eeche Sie die Pojekio de Secke A af die -Achse. Fü die Pojekio eies Vekos a af eie Veko b gil Fomel.. Daas folg: c a. b eeche Sie die Pojekio de Secke A af die Secke A. b a c a 6. 5
6 Lösge -. Gdlage de Roboemahemaik 6 c eeche Sie de Wikel bei A. o 5cos a cos 7. 5 AIgabe.6 Gegebe sid dei Pke P,,, P,,, P,,, die eie Ebee E besimme. a eeche Sie de Nomaleeko o E mi Hilfe des Vekopodks., Gl..5. b Selle Sie die Hesse-Nomalefom o E af d zeige Sie, dass de so emiele Nomaleeko bis af eie Fako k mi übeeisimm. HNF: z l P eiseze: k l af omiee: HNF: z k. Afgabe.7 eeche Sie jeweils de Schipk S mi Hilfe de ame'sche Regel. Gegebe sid die Gleichge o: a zwei Geade i de Ebee mi: g : g : A de A D A de A D A de A D
7 Lösge -. Gdlage de Roboemahemaik 7 D D s s. D D b zwei Geade i de Ebee mi: g : g : A de A D A de A D D D 8 s s 8. D D A de A 8 D c dei Ebee mi: z 5 z 6 E : z E : z 5 E : z 6 D D 5 5 D 5 D 5. Regel Sas D 5 D D s 5 s s. D D D Afgabe.8 Die Ebee E ehäl die z-achse d de Pk P,,. Fü die Ebee E gil z. a Selle Sie die beide Ebee als lieae Gleichgssseme da. E : E : z LGS: A b z
8 Lösge -. Gdlage de Roboemahemaik 8 b eeche Sie dee Schigeade mi Hilfe des allgemeie Lösgsefahes fü lieae Gleichgssseme. Allgemeie homogee Lösg:. R h Eie beliebige ihomogee Lösg: p Allgemeie Lösge: dies sell eie Geade im Ram da. p h Afgabe.9 Gegebe sid die beide asfomaioe A d A a Zeiche Sie die Lage de Koodiaesseme {} d {} bezüglich {A}. {} {A} A A {} b eeche Sie die asfomaio.
9 Lösge -. Gdlage de Roboemahemaik 9 A A A A c asfomiee Sie de Diffeezeko [ ] d ach {}. d d as de Zeichg folg ode dch eechg: d d wid als feie Veko behadel Siehe S. 56. Afgabe. a Zeige Sie dass fü eie beliebige Wikel gil: / / Ro Roz Ro Ro cos si si cos Ro Roz Ro cos si si cos Ro b Ei Pk P,, soll bezüglich eie Geade mi dem Hifühgseko [ a ] d dem Richgseko [ ] m ϕ gedeh wede. eeche Sie de gedehe Pk P D. Gib es mehee Lösge? p D Roz D p D
10 Lösge -. Gdlage de Roboemahemaik Fü die asfomaiosmai D des Oskoodiaessem de Dehachse gil: P D D D p D,, Es gib zwei Lösge, da die Dehg ach mi egegegesezem Dehsi efolge ka. Da gil: D Afgabe. Gegebe is das Eiheisfame E d die beide asfomaioe /,, /,, Roz as Ro as. Es folg: a E wid bezüglich asfomie. Welche Lage imm das Fame ei? Es gil: E b Das asfomiee Fame soll dch eimal absol d eimal elai asfomie wede. Zeiche Sie die ee Lage des asfomiee Fames. Absole asfomaio: E E abs
11 Lösge -. Gdlage de Roboemahemaik Relaie asfomaio: E el E E {E abs } z E E {E el } z E Afgabe. Gegebe is eie ZYZ-Eleasfomaio mi 9, β 9, γ 5. a Zeiche Sie fü jede Dehg die Pojekio des asfomiee Refeezkoodiaessems af die -Ebee. 9 β 9 γ 5 z z a b eeche Sie die eslieede homogee asfomaiosmai E. E c eeche Sie as E die beide Lösge fü die iese ZYZ-Eleasfomaio.
12 Lösge -. Gdlage de Roboemahemaik Mi Hilfe de Fomel. bis.6 ehäl ma die beide Lösge a a, β a a, β γ a a, γ Afgabe. Gegebe is die Fkio z f, cos si. a eeche Sie die paielle Ableige o z f,. f, cos f, si b Selle Sie das oale Diffeeial dz als Skalapodk da. dz d [ cos si ] d
18 Homogene lineare Gleichungssysteme
 Lieae Algeba II SS 0 - Pof. D.. afed Leiz Kapiel V: Lieae Gleichgssyseme 8: Homogee lieae Gleichgssyseme 8 Homogee lieae Gleichgssyseme A Zm Begiff lieaes Gleichgssysem B Theoeische Gdlage C Lösgsvefahe
Lieae Algeba II SS 0 - Pof. D.. afed Leiz Kapiel V: Lieae Gleichgssyseme 8: Homogee lieae Gleichgssyseme 8 Homogee lieae Gleichgssyseme A Zm Begiff lieaes Gleichgssysem B Theoeische Gdlage C Lösgsvefahe
Das Skalarprodukt ist ein Produkt zweier Vektoren, das als Ergebnis ein Skalar (eine reelle Zahl) liefert. Es ist folgendermaßen definiert: r o
 Rechemehode de Aalyiche Geomeie B & S Skipedie, 6. bee. Nowedige Gudlage.. a Skalapoduk a Skalapoduk i ei Poduk zweie Vekoe, da al gebi ei Skala eie eelle Zahl liefe. i folgedemaße defiie b a b a b a b
Rechemehode de Aalyiche Geomeie B & S Skipedie, 6. bee. Nowedige Gudlage.. a Skalapoduk a Skalapoduk i ei Poduk zweie Vekoe, da al gebi ei Skala eie eelle Zahl liefe. i folgedemaße defiie b a b a b a b
Analytische Geometrie
 Pives Gymsim Mies J Mhemik Alyishe Geomeie Ueihsfzeihe de Mhemikleisskse / i de Shljhe / d / Noe Mez Am Solz He Ihlsvezeihis LÄNG BTRAG) INS VKTORS INHITSVKTOR SKALARPRODUKT WINKL ZWISCHN ZWI VKTORN NORMALNFORM
Pives Gymsim Mies J Mhemik Alyishe Geomeie Ueihsfzeihe de Mhemikleisskse / i de Shljhe / d / Noe Mez Am Solz He Ihlsvezeihis LÄNG BTRAG) INS VKTORS INHITSVKTOR SKALARPRODUKT WINKL ZWISCHN ZWI VKTORN NORMALNFORM
Vektorrechnung (analytische Geometrie) für Schüler und Studenten
 Michael Buhlma Vekoechu (aalyiche Geomeie) fü Schüle ud Sudee Dae- ud Aufabebläe zu Mahemaik Veio Ee Vowo Diee Sammlu au Dae- ud Aufabebläe eh au eie jahelae Täikei al Nachhilfelehe fü Obeufechüle ud Ewachee
Michael Buhlma Vekoechu (aalyiche Geomeie) fü Schüle ud Sudee Dae- ud Aufabebläe zu Mahemaik Veio Ee Vowo Diee Sammlu au Dae- ud Aufabebläe eh au eie jahelae Täikei al Nachhilfelehe fü Obeufechüle ud Ewachee
Mechanik-1b. fh-pw. Mechanik-1b 1
 Mechik-b Mechik-b Eiimesiole eweu Geschwiikei Duchschis- u Momeeschwiikei 3 eispiel Momeeschwiikei 4 eschleuiu 5 Gleichfömi beschleuie eweu 7 eispiel Gleichfömi beschleuie eweu Gleichfömi beschleuie eweu
Mechik-b Mechik-b Eiimesiole eweu Geschwiikei Duchschis- u Momeeschwiikei 3 eispiel Momeeschwiikei 4 eschleuiu 5 Gleichfömi beschleuie eweu 7 eispiel Gleichfömi beschleuie eweu Gleichfömi beschleuie eweu
Der Drehimpuls von Licht
 De Dehils vo Licht Qelle: htt://www.otiqe-igeie.og/e/coses/opi_ag_m_c3/co/cote_4.htl htt://load.wikiedia.og/wikiedia/coos/7/77/cicla.polaiatio.ciclal.polaied.light_with.cooets_right.haded.svg 3..3 Fachbeeich
De Dehils vo Licht Qelle: htt://www.otiqe-igeie.og/e/coses/opi_ag_m_c3/co/cote_4.htl htt://load.wikiedia.og/wikiedia/coos/7/77/cicla.polaiatio.ciclal.polaied.light_with.cooets_right.haded.svg 3..3 Fachbeeich
Einführung in die Physik I. Kinematik der Massenpunkte. O. von der Lühe und U. Landgraf
 Einfühung in die Phsik I Kinemaik de Massenpunke O. on de Lühe und U. Landgaf O und Geschwindigkei Wi beachen den O eines als punkfömig angenommenen Köpes im Raum als Funkion de Zei Eindimensionale Posiion
Einfühung in die Phsik I Kinemaik de Massenpunke O. on de Lühe und U. Landgaf O und Geschwindigkei Wi beachen den O eines als punkfömig angenommenen Köpes im Raum als Funkion de Zei Eindimensionale Posiion
3. Lineare autonome Systeme
 3. Liee uoome yseme Liee uoome yseme öe ewede duh yseme o Diffeeilgleihuge. Odug ode duh eie Diffeeilgleihug -e Odug de A eshiee wede. Beide Besheiugsweise sid eide äquile, d.h. sie lsse sih ieide üefühe.
3. Liee uoome yseme Liee uoome yseme öe ewede duh yseme o Diffeeilgleihuge. Odug ode duh eie Diffeeilgleihug -e Odug de A eshiee wede. Beide Besheiugsweise sid eide äquile, d.h. sie lsse sih ieide üefühe.
Wir sprechen von einer Rente, wenn die Ein- oder Auszahlungen (= Raten) regelmässig erfolgen und konstant immer in der gleichen Höhe erfolgen.
 2. eteechge 2.1 Gdlage Weitee Afgabestellge i de Fiazmathematik egebe sich, we die apitaleilage ode die ückzüge egelmässig d i gleiche Höhe efolge. I diese Fälle spicht ma vo ete. Die Altesete ist davo
2. eteechge 2.1 Gdlage Weitee Afgabestellge i de Fiazmathematik egebe sich, we die apitaleilage ode die ückzüge egelmässig d i gleiche Höhe efolge. I diese Fälle spicht ma vo ete. Die Altesete ist davo
1 Das Skalarprodukt und das Kreuzprodukt
 Das Skalarprodukt ud das Kreuzprodukt Wir betrachte zu x = de Ausdruck y t x : = x Grud: Die rechte Seite der Gleichug ist: y t x = (y tx +... + (y ty { t x } y +... + x y x + x y (x y +... + x y x x t
Das Skalarprodukt ud das Kreuzprodukt Wir betrachte zu x = de Ausdruck y t x : = x Grud: Die rechte Seite der Gleichug ist: y t x = (y tx +... + (y ty { t x } y +... + x y x + x y (x y +... + x y x x t
Der Satz von Cavalieri: Zwei Körper gleicher Höhe sind volumengleich, wenn sie in jeweils gleicher Höhe flächengleiche Querschnitte haben.
 Pof. D. Jüge Rot Didati de eometie alte Pizip d Satz vo Cavaliei dlage des olmebegiffs (eiscließlic Satz vo De) olme de d des stmpfs Kgelvolme d Kgelobefläce Pizip vo Cavaliei Boaveta Cavaliei (598 47;
Pof. D. Jüge Rot Didati de eometie alte Pizip d Satz vo Cavaliei dlage des olmebegiffs (eiscließlic Satz vo De) olme de d des stmpfs Kgelvolme d Kgelobefläce Pizip vo Cavaliei Boaveta Cavaliei (598 47;
 wwwmathe-aufgabecom Abitupüfug Mathematik Bae-Wüttembeg (ohe CAS) Wahlteil Aufgabe Aalytische Geometie II, Aufgabe II Gegebe si ie Pukte A(//), B(//) u C(//) a) Zeige Sie, ass as Deieck ABC gleichscheklig
wwwmathe-aufgabecom Abitupüfug Mathematik Bae-Wüttembeg (ohe CAS) Wahlteil Aufgabe Aalytische Geometie II, Aufgabe II Gegebe si ie Pukte A(//), B(//) u C(//) a) Zeige Sie, ass as Deieck ABC gleichscheklig
5.3 Überlagerung von Schwingungen
 5.3 Überlagerg vo Schwigge Ka ei Objek i ehrere Freqeze gleichzeiig schwige? Ja - das is sogar der Regelfall z.b. Msikisree: Oberöe a Überlagerg zweier Schwigge gleicher Freqez zr Vereifachg: gleiche plide
5.3 Überlagerg vo Schwigge Ka ei Objek i ehrere Freqeze gleichzeiig schwige? Ja - das is sogar der Regelfall z.b. Msikisree: Oberöe a Überlagerg zweier Schwigge gleicher Freqez zr Vereifachg: gleiche plide
Analytische Geometrie
 Alyihe Geomeie Leiko z Kl- d Aioeeig Eo Pojek de Mhe LK /: Fi Fedde Koie Kleiheiz Simo Ldeg Le Mo J Oeek Khi Shellh Fiedeike Th Chiohe Wehl Alyihe Geomeie Ihl Seie Seie Them ---/--- Ihl Gdegiffe Gdegiffe
Alyihe Geomeie Leiko z Kl- d Aioeeig Eo Pojek de Mhe LK /: Fi Fedde Koie Kleiheiz Simo Ldeg Le Mo J Oeek Khi Shellh Fiedeike Th Chiohe Wehl Alyihe Geomeie Ihl Seie Seie Them ---/--- Ihl Gdegiffe Gdegiffe
Fachhochschule Hannover
 Fachhochschle annove 8..5 Fachbeeich Maschinenba Zei: 9 min Fach: Physik im WS 4/5 ilfsmiel: Fomelsammlng z Volesng. in PKW(, de mi konsane Geschwindigkei von 7 kmh - fäh, wid von einem andeen PKW( mi
Fachhochschle annove 8..5 Fachbeeich Maschinenba Zei: 9 min Fach: Physik im WS 4/5 ilfsmiel: Fomelsammlng z Volesng. in PKW(, de mi konsane Geschwindigkei von 7 kmh - fäh, wid von einem andeen PKW( mi
7.7. Abstände und Winkel
 uu uu uu uu uu uu uu uu 77 Astäde ud Wikel 77 Wikel Geade - Geade Schittwikel zweie Geade: Am Schittpukt zweie Geade g ud g lasse sich die eide Wikel (g, g ) ud (g, g ) messe Als Schittwikel ezeichet ma
uu uu uu uu uu uu uu uu 77 Astäde ud Wikel 77 Wikel Geade - Geade Schittwikel zweie Geade: Am Schittpukt zweie Geade g ud g lasse sich die eide Wikel (g, g ) ud (g, g ) messe Als Schittwikel ezeichet ma
ZUU AUUFFGGAABBEE :: Die Wann läuft zunächst voll. Nach einiger Zeit wird etwas Wasser abgelassen und dann wird etwas zugeführt.
 Lineare Funkionen. Lösungen Lö LÖÖSSUUNNGGEENN ZZUUM.. KPPI IITTEELL ZZUU UUFFGGEE..: : a) as Pfeildiagramm zeig keine Funkion, da von h kein Pfeil ausgeh und von a zwei Pfeile. b) Is eine Funkion, denn
Lineare Funkionen. Lösungen Lö LÖÖSSUUNNGGEENN ZZUUM.. KPPI IITTEELL ZZUU UUFFGGEE..: : a) as Pfeildiagramm zeig keine Funkion, da von h kein Pfeil ausgeh und von a zwei Pfeile. b) Is eine Funkion, denn
3 Harmonische Anregung
 3 Harmoische Aregg Lieare ihomogee Dieretialgleichg Partikläre Lösg: + ζ + p () t (3.4) Lösg der homogee DGL: h h + ζ h + h (3.5) Vollstädige Lösg: + C h Bei eier harmoische Aregg ka die Krat Ft () etweder
3 Harmoische Aregg Lieare ihomogee Dieretialgleichg Partikläre Lösg: + ζ + p () t (3.4) Lösg der homogee DGL: h h + ζ h + h (3.5) Vollstädige Lösg: + C h Bei eier harmoische Aregg ka die Krat Ft () etweder
Aufgaben Reflexionsgesetz und Brechungsgesetz
 Aufgabe Reflexiosgesetz ud Brechugsgesetz 24. Zeiche zwei Spiegel, die sekrecht zueiader stehe. Utersuche mit zwei verschiede eifallede Strahle, welche Eigeschafte die reflektierte Strahle habe, die acheiader
Aufgabe Reflexiosgesetz ud Brechugsgesetz 24. Zeiche zwei Spiegel, die sekrecht zueiader stehe. Utersuche mit zwei verschiede eifallede Strahle, welche Eigeschafte die reflektierte Strahle habe, die acheiader
Höhere Mathematik I für die Fachrichtung Physik
 Isiu für Aalysis SS7 Arbeisgruppe Agewade Aalysis 997 PD Dr Peer Chrisia Kusma Höhere Mahemaik I für die Fachrichug Physik Lösugsvorschläge zur Bachelor-Modulprüfug Aufgabe : (a) (i) Kurze Rechug liefer
Isiu für Aalysis SS7 Arbeisgruppe Agewade Aalysis 997 PD Dr Peer Chrisia Kusma Höhere Mahemaik I für die Fachrichug Physik Lösugsvorschläge zur Bachelor-Modulprüfug Aufgabe : (a) (i) Kurze Rechug liefer
Konvexität und Ungleichungen
 Koveität ud Ugleichuge Tag der Mathematik 2003 Holger Stepha Weierstraß Istitut für Agewadte Aalysis ud Stochastik http://www.wias-berli.de/people/stepha = Für mathematisch iteressierte Schüler = Folie
Koveität ud Ugleichuge Tag der Mathematik 2003 Holger Stepha Weierstraß Istitut für Agewadte Aalysis ud Stochastik http://www.wias-berli.de/people/stepha = Für mathematisch iteressierte Schüler = Folie
Lineare Algebra die Darstellungsmatrix von f bezüglich A. Es ist B = (b 1, b 2, b 3 ) mit. A = M A A (f) =
 Techische Uivesität Dotmud Sommesemeste 2017 Fakultät fü Mathematik Übugsblatt 3 Pof. D. Detlev Hoffma 22. Mai 2017 Maco Sobiech/ Nico Loez Lieae Algeba 1 Lösug zu Aufgabe 3.1: Voaussetzuge: Sei V ei deidimesioale
Techische Uivesität Dotmud Sommesemeste 2017 Fakultät fü Mathematik Übugsblatt 3 Pof. D. Detlev Hoffma 22. Mai 2017 Maco Sobiech/ Nico Loez Lieae Algeba 1 Lösug zu Aufgabe 3.1: Voaussetzuge: Sei V ei deidimesioale
Grundbegriffe Geschwindigkeit und Beschleunigung. r = r dt
 Gundbegiffe Geschwindigkei und Beschleunigung Die Geschwindigkei eines Köpes is ein Maß fü seinen je Zeieinhei in eine besimmen Richung zuückgelegen Weg. Sie is, wie de O, ein Veko und definie duch die
Gundbegiffe Geschwindigkei und Beschleunigung Die Geschwindigkei eines Köpes is ein Maß fü seinen je Zeieinhei in eine besimmen Richung zuückgelegen Weg. Sie is, wie de O, ein Veko und definie duch die
= T. 1.1. Jährliche Ratentilgung. 1.1. Jährliche Ratentilgung. Ausgangspunkt: Beispiel:
 E Tilgugsrechug.. Jährliche Raeilgug Ausgagspuk: Bei Raeilgug wird die chuldsumme (Newer des Kredis [Aleihe, Hypohek, Darleh]) i gleiche Teilberäge T geilg. Die Tilgugsrae läss sich ermiel als: T =.. Jährliche
E Tilgugsrechug.. Jährliche Raeilgug Ausgagspuk: Bei Raeilgug wird die chuldsumme (Newer des Kredis [Aleihe, Hypohek, Darleh]) i gleiche Teilberäge T geilg. Die Tilgugsrae läss sich ermiel als: T =.. Jährliche
Mathematische Probleme, SS 2015 Montag 1.6. $Id: convex.tex,v /06/01 09:26:03 hk Exp $
 athematische Probleme, 2015 otag 1.6 $Id: cove.te,v 1.19 2015/06/01 09:26:03 hk Ep $ 3 Kovegeometrie 3.2 Die platoische Körper I der letzte itzug habe wir mit de Vorarbeite zur Berechug der platoische
athematische Probleme, 2015 otag 1.6 $Id: cove.te,v 1.19 2015/06/01 09:26:03 hk Ep $ 3 Kovegeometrie 3.2 Die platoische Körper I der letzte itzug habe wir mit de Vorarbeite zur Berechug der platoische
Lösungsformel für quadratische Gleichungen. = ± q + Lösungsformel für. Potenzen. negative Exponenten: gebrochene Exponenten: a a.
 HUNKLOIHDWKHPDWLN Dies ist keie Fomelsmmlug im klssische Si - die vewedete Bezeichuge wede icht eklät ud Voussetzuge fü die ültigkeit de Fomel wede i de Regel icht gegee. 7HLO,6WRIIJHELHWHHULWWHOVWXIH
HUNKLOIHDWKHPDWLN Dies ist keie Fomelsmmlug im klssische Si - die vewedete Bezeichuge wede icht eklät ud Voussetzuge fü die ültigkeit de Fomel wede i de Regel icht gegee. 7HLO,6WRIIJHELHWHHULWWHOVWXIH
Zeitabhängige Felder, Maxwell-Gleichungen
 Zeiabhängige Felde, Mawell-Gleichungen Man beobache, dass ein eiabhängiges Magnefeld ein elekisches Feld eeug. Dies füh.. u eine Spannung an eine Dahschleife (ndukion). mgekeh beobache man auch: ein eiabhängiges
Zeiabhängige Felde, Mawell-Gleichungen Man beobache, dass ein eiabhängiges Magnefeld ein elekisches Feld eeug. Dies füh.. u eine Spannung an eine Dahschleife (ndukion). mgekeh beobache man auch: ein eiabhängiges
Integralrechnung III.Teil
 Inegalechnung III.eil 1 Inegalechnung III.eil ngewande Mahemaik GM Wolgang Kugle Inegalechnung III.eil Inhalsvezeichnis 1. Mielwee peiodische Signale 1.1 Deiniion des aihmeischen Mielwees 1. Deiniion des
Inegalechnung III.eil 1 Inegalechnung III.eil ngewande Mahemaik GM Wolgang Kugle Inegalechnung III.eil Inhalsvezeichnis 1. Mielwee peiodische Signale 1.1 Deiniion des aihmeischen Mielwees 1. Deiniion des
> 0, da cos 0 = 1. < 0, da cos 180 = 1
 Weitterre Dettge des Skalarrprrodktts Ei iiee wi iicchht ti iiggee FFoor rmeel ll Daass Vorrzzeei icchee deess Skkaal laarrprrodkkttss Stellt ma die Wikelformel cos a b m da ka ma das Skalarprodkt asdrücke
Weitterre Dettge des Skalarrprrodktts Ei iiee wi iicchht ti iiggee FFoor rmeel ll Daass Vorrzzeei icchee deess Skkaal laarrprrodkkttss Stellt ma die Wikelformel cos a b m da ka ma das Skalarprodkt asdrücke
heißt kommutativ (oder auch abelsch), falls für die Verknüpfung das Kommutativgesetz gilt: (G 5) Für alle ab, Ggilt a b
 r M J auer Algebraische trukture 7 Kapitel : Gruppe Gruppe: efiitio, Beispiele efiitio (Gruppe) Eie Mege G (G ) zusamme mit eier Verküpfug heißt eie Gruppe, we folgede Eigeschafte erfüllt sid: (G ) G ist
r M J auer Algebraische trukture 7 Kapitel : Gruppe Gruppe: efiitio, Beispiele efiitio (Gruppe) Eie Mege G (G ) zusamme mit eier Verküpfug heißt eie Gruppe, we folgede Eigeschafte erfüllt sid: (G ) G ist
KAPITEL IV DREHBEWEGUNGEN STARRER KÖRPER
 KAPITEL IV DREHBEWEGUNGEN STARRER KÖRPER . GRUNDBEGRIFFE. MODELL "STARRER KÖRPER" Bishe habe wi us mit de Mechaik de Puktmasse beschäftigt; dabei meie wi eigetlich u die Bewegug des Massemittelpuktes.
KAPITEL IV DREHBEWEGUNGEN STARRER KÖRPER . GRUNDBEGRIFFE. MODELL "STARRER KÖRPER" Bishe habe wi us mit de Mechaik de Puktmasse beschäftigt; dabei meie wi eigetlich u die Bewegug des Massemittelpuktes.
Leseprobe. Dietmar Mende, Günter Simon. Physik. Gleichungen und Tabellen. ISBN (Buch): ISBN (E-Book):
 Lesepobe Diema Mende, Güne Simon Physik Gleichungen und Tabellen ISBN (Buch): 978-3-446-43754-8 ISBN (E-Book): 978-3-446-43861-3 Weiee Infomaionen ode Besellungen une hp://www.hanse-fachbuch.de/978-3-446-43754-8
Lesepobe Diema Mende, Güne Simon Physik Gleichungen und Tabellen ISBN (Buch): 978-3-446-43754-8 ISBN (E-Book): 978-3-446-43861-3 Weiee Infomaionen ode Besellungen une hp://www.hanse-fachbuch.de/978-3-446-43754-8
Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge zum 12. Übungsblatt
 UNIVERSITÄT KARLSRUHE Istitut für Aalysis HDoz. Dr. P. C. Kustma Dipl.-Math. M. Uhl WS 8/9 Höhere Mathematik I für die Fachrichtuge Elektroigeieurwese, Physik ud Geodäsie Lösugsvorschläge zum. Übugsblatt
UNIVERSITÄT KARLSRUHE Istitut für Aalysis HDoz. Dr. P. C. Kustma Dipl.-Math. M. Uhl WS 8/9 Höhere Mathematik I für die Fachrichtuge Elektroigeieurwese, Physik ud Geodäsie Lösugsvorschläge zum. Übugsblatt
Kein Anspruch auf Vollständigkeit und Fehlerfreiheit
 Uivesität Regesbug Natuwisseschaftliche Fakultät I Didaktik de athematik D. Güte Rothmeie WS 008/09 5 7 Elemetamathematik (LH) Pivate Volesugsaufzeichuge Kei spuch auf Vollstädigkeit ud Fehlefeiheit 9.
Uivesität Regesbug Natuwisseschaftliche Fakultät I Didaktik de athematik D. Güte Rothmeie WS 008/09 5 7 Elemetamathematik (LH) Pivate Volesugsaufzeichuge Kei spuch auf Vollstädigkeit ud Fehlefeiheit 9.
Strategie der Modellbildung
 Saegie de Modellbildg (Phase de Modellbildg) Keie Sigifikaz de Paameeschäze d/ode Saioaiäsode Iveibiliäsbedigge ich efüll Modellideifikaio (Modellsezifikaio) Modellschäzg esimmg de Odg d de Diffeeze esimmg
Saegie de Modellbildg (Phase de Modellbildg) Keie Sigifikaz de Paameeschäze d/ode Saioaiäsode Iveibiliäsbedigge ich efüll Modellideifikaio (Modellsezifikaio) Modellschäzg esimmg de Odg d de Diffeeze esimmg
c B Analytische Geometrie
 KITL 9 alytische Geometrie Gerade arameterdarstellug eier Gerade ie Gerade g ist bestimmt durch eie Richtug, gegebe durch eie Vektor c, c 0, ud eie ukt, der auf der Gerade liegt Ma et de ufpukt i ukt X
KITL 9 alytische Geometrie Gerade arameterdarstellug eier Gerade ie Gerade g ist bestimmt durch eie Richtug, gegebe durch eie Vektor c, c 0, ud eie ukt, der auf der Gerade liegt Ma et de ufpukt i ukt X
Lösungen zu den Aufgaben zu Mathematik I. w w w f f f f w w f f w w f f w f w w f w w w w f f w w w w w w. s = p q p q erhalten wir folgende Tabelle:
 TEIL B Lösuge zu de Aufgabe zu Mathematik I.. Logik... A B A B A B A B A B w w w f f f f w f f w f w w f w f w w f w f f f w w w w A B A B B A B [ ] ( A B) ( A B) A ( ) ( ) A B A B A w w w f f f f w w
TEIL B Lösuge zu de Aufgabe zu Mathematik I.. Logik... A B A B A B A B A B w w w f f f f w f f w f w w f w f w w f w f f f w w w w A B A B B A B [ ] ( A B) ( A B) A ( ) ( ) A B A B A w w w f f f f w w
Banken und Börsen, Kurs 41520 (Inhaltlicher Bezug: KE 4)
 Lösugshiweise zu Eiseeabeit 2 zum Kus 452, ake u öse, WS 2/2 Lösugshiweise zu Eiseeabeit 2: WS 2/2 ake u öse, Kus 452 (Ihaltliche ezug: KE 4) alyse festvezisliche Wetpapiee 5 Pukte Vo Ihe ak wee Ihe ie
Lösugshiweise zu Eiseeabeit 2 zum Kus 452, ake u öse, WS 2/2 Lösugshiweise zu Eiseeabeit 2: WS 2/2 ake u öse, Kus 452 (Ihaltliche ezug: KE 4) alyse festvezisliche Wetpapiee 5 Pukte Vo Ihe ak wee Ihe ie
Höhere Mathematik 3. Kapitel 12 Differenzengleichungen, z-transformation. Prof. Dr.-Ing. Dieter Kraus
 Höhere Mathematik 3 Kapitel 1 Differezegleichuge, z-trasformatio Prof. Dr.-Ig. Dieter Kraus Höhere Mathematik 3 Kapitel 1 Ihaltsverzeichis 1 Differezegleichuge, -Trasformatio...1-1 1.1 Eiführug i Differezegleichuge...1-1
Höhere Mathematik 3 Kapitel 1 Differezegleichuge, z-trasformatio Prof. Dr.-Ig. Dieter Kraus Höhere Mathematik 3 Kapitel 1 Ihaltsverzeichis 1 Differezegleichuge, -Trasformatio...1-1 1.1 Eiführug i Differezegleichuge...1-1
ÜBUNGSBLATT 4 LÖSUNGEN MAT121/MAT131 ANALYSIS I HERBSTSEMESTER 2010 PROF. DR. CAMILLO DE LELLIS
 ÜBUNGSBLATT 4 LÖSUNGEN MAT/MAT3 ANALYSIS I HERBSTSEMESTER 00 PROF. DR. AMILLO DE LELLIS Aufgabe. Etscheide Sie für folgede Folge (wobei N \ {0}), ob diese koverget sid, ud bereche sie gegebeefalls ihre
ÜBUNGSBLATT 4 LÖSUNGEN MAT/MAT3 ANALYSIS I HERBSTSEMESTER 00 PROF. DR. AMILLO DE LELLIS Aufgabe. Etscheide Sie für folgede Folge (wobei N \ {0}), ob diese koverget sid, ud bereche sie gegebeefalls ihre
Forschungsstatistik I
 Pschologie Pof. D. G. Meihadt 6. Stock, TB II R. 06-206 (Pesike) R. 06-321 (Meihadt) Spechstude jedezeit ach Veeibaug Foschugsstatistik I D. Malte Pesike pesike@ui-maiz.de http://psmet03.sowi.ui-maiz.de/
Pschologie Pof. D. G. Meihadt 6. Stock, TB II R. 06-206 (Pesike) R. 06-321 (Meihadt) Spechstude jedezeit ach Veeibaug Foschugsstatistik I D. Malte Pesike pesike@ui-maiz.de http://psmet03.sowi.ui-maiz.de/
1 Funktionen und Flächen
 Fuktioe ud Fläche. Fläche Defiitio: Die Ebee R ist defiiert als Mege aller geordete Paare vo reelle Zahle: R = {(,, R} Der erste Eitrag heißt da auch Koordiate ud der zweite Koordiate. Für zwei Pukte (,,
Fuktioe ud Fläche. Fläche Defiitio: Die Ebee R ist defiiert als Mege aller geordete Paare vo reelle Zahle: R = {(,, R} Der erste Eitrag heißt da auch Koordiate ud der zweite Koordiate. Für zwei Pukte (,,
Dieses lässt sich auf Funktionen in mehreren Veränderlichen verallgemeinern.
 4. Mehfachitegale eitag Volesg gewate Mathematik Maste M Pof. D.. Gaowski HTW es Saalaes GIS 4 Mehfachitegale Pof. D. aaa Gaowski HTW es Saalaes GIS Z Volesg gewate Mathematik Maste M Ihalt: 4 Mehfachitegale...
4. Mehfachitegale eitag Volesg gewate Mathematik Maste M Pof. D.. Gaowski HTW es Saalaes GIS 4 Mehfachitegale Pof. D. aaa Gaowski HTW es Saalaes GIS Z Volesg gewate Mathematik Maste M Ihalt: 4 Mehfachitegale...
Abschlussprüfung 2015 an den Realschulen in Bayern
 Prüfugsdauer: 50 Miute Abschlussprüfug 05 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Nachtermi A 0 Für Trapeze ABC D mit de parallele Seite [AD ] ud [BC ]
Prüfugsdauer: 50 Miute Abschlussprüfug 05 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Nachtermi A 0 Für Trapeze ABC D mit de parallele Seite [AD ] ud [BC ]
5 Das Bode Diagramm. Frequenzkennlinienverfahren
 6a Das Bode Diagramm. Frequezkeliieverfahre Ahag zum Kapitel Das Bode Diagramm. Frequezkeliieverfahre. Darstellug i Reihe geschalteter Glieder im Bode-Diagramm..a Kostruktio des Amplitudegages mittels
6a Das Bode Diagramm. Frequezkeliieverfahre Ahag zum Kapitel Das Bode Diagramm. Frequezkeliieverfahre. Darstellug i Reihe geschalteter Glieder im Bode-Diagramm..a Kostruktio des Amplitudegages mittels
Prüfungsaufgaben der Abschlussprüfung an Realschulen in Bayern! mit ausführlichen Musterlösungen. und Querverweise auf Theoriedateien der Mathe-CD
 Vektor-Geometrie Koordiategeometrie Prüfugsaufgabe uter Verwedug vo Abbildugsgleichuge Prüfugsaufgabe der Abschlussprüfug a Realschule i Bayer! mit ausführliche Musterlösuge ud Querverweise auf Theoriedateie
Vektor-Geometrie Koordiategeometrie Prüfugsaufgabe uter Verwedug vo Abbildugsgleichuge Prüfugsaufgabe der Abschlussprüfug a Realschule i Bayer! mit ausführliche Musterlösuge ud Querverweise auf Theoriedateie
b) Der eintretende und der austretende Lichtstrahl sind parallel. Es tritt keine Verzerrung auf.
 Physik awede ud verstehe: Lösuge 5. Brechug ud Totalreflexio 004 Orell Füssli Verlag AG 5. Brechug ud Totalreflexio Beim Übergag i ei Medium gilt obige Aussage icht mehr. Würde das Licht die kürzeste Strecke
Physik awede ud verstehe: Lösuge 5. Brechug ud Totalreflexio 004 Orell Füssli Verlag AG 5. Brechug ud Totalreflexio Beim Übergag i ei Medium gilt obige Aussage icht mehr. Würde das Licht die kürzeste Strecke
1. Übung. 2. Übung. 2 = 12h = Wahrer Ortsmittag
 1. Übung 1. Schi: Wann is Miag? Mie zwischen den beiden Messungen besimmen: 14h 44 19 + 17h 02 09 31h 46 28 31h 46 28 2 15h 53 14 Wahe Osmiag 2. Schi: Weil Miag is sind wi auf dem selben Längengad wie
1. Übung 1. Schi: Wann is Miag? Mie zwischen den beiden Messungen besimmen: 14h 44 19 + 17h 02 09 31h 46 28 31h 46 28 2 15h 53 14 Wahe Osmiag 2. Schi: Weil Miag is sind wi auf dem selben Längengad wie
8. Übungsblatt Aufgaben mit Lösungen
 8. Übugsblatt Aufgabe mit Lösuge Aufgabe 36: Bestimme Sie alle z C, für die die folgede Potezreihe kovergiere: z z a, b! +, c z +. = = Lösug 36: Wir bezeiche de Kovergezradius mit r. a Wir wede das Quotietekriterium
8. Übugsblatt Aufgabe mit Lösuge Aufgabe 36: Bestimme Sie alle z C, für die die folgede Potezreihe kovergiere: z z a, b! +, c z +. = = Lösug 36: Wir bezeiche de Kovergezradius mit r. a Wir wede das Quotietekriterium
Prof.Dr.B.Grabowski (Schwingungen als komplexe Zeiger) Lösung zum Übungsblatt Nr. 2. (Wiederholung Linearfaktorzerlegung von Polynomen)
 Maheaik 3 Übug Schwiguge als koplexe Zeiger KI Maheaik 3 Lösug zu Übugsbla Nr. I. LFZ Zu Aufgabe Wiederholug Liearfakorzerlegug vo Polyoe Zerlege Sie folgede Polyoe i Liearfakore: a y x 4 x 5 4 3 b y.5x.5x
Maheaik 3 Übug Schwiguge als koplexe Zeiger KI Maheaik 3 Lösug zu Übugsbla Nr. I. LFZ Zu Aufgabe Wiederholug Liearfakorzerlegug vo Polyoe Zerlege Sie folgede Polyoe i Liearfakore: a y x 4 x 5 4 3 b y.5x.5x
Physik für Wirtschaftsingenieure
 Phsik fü Wischafsingenieue Chisophe Diemaie, Mahias Mändl ISBN 3-446-373-8 Lesepobe Weiee Infomaionen ode Besellungen une hp://www.hanse.de/3-446-373-8 sowie im Buchhandel Mechanik Bild. Bewegung eines
Phsik fü Wischafsingenieue Chisophe Diemaie, Mahias Mändl ISBN 3-446-373-8 Lesepobe Weiee Infomaionen ode Besellungen une hp://www.hanse.de/3-446-373-8 sowie im Buchhandel Mechanik Bild. Bewegung eines
BERGISCHE UNIVERSITÄT WUPPERTAL FAKULTÄT FÜR WIRTSCHAFTSWISSENSCHAFT - SCHUMPETER SCHOOL OF BUSINESS AND ECONOMICS
 Plaz-Nr.: Name: Vorame: Marikel-Nr.: BERGISCHE UNIVERSITÄT WUPPERTAL FAKULTÄT FÜR WIRTSCHAFTSWISSENSCHAFT - SCHUMPETER SCHOOL OF BUSINESS AND ECONOMICS Prüfgsgebie: Eiführg i die Wirschafsiformaik (Happrüfg
Plaz-Nr.: Name: Vorame: Marikel-Nr.: BERGISCHE UNIVERSITÄT WUPPERTAL FAKULTÄT FÜR WIRTSCHAFTSWISSENSCHAFT - SCHUMPETER SCHOOL OF BUSINESS AND ECONOMICS Prüfgsgebie: Eiführg i die Wirschafsiformaik (Happrüfg
Experimentalphysik II (Kip SS 2007)
 peimenalphsik II Kip SS 7 Zusavolesungen: Z-1 in- und mehdimensionale Inegaion Z- Gadien Divegen und Roaion Z-3 Gaußsche und Sokessche Inegalsa Z-4 Koninuiäsgleichung Z-5 lekomagneische Felde an Genflächen
peimenalphsik II Kip SS 7 Zusavolesungen: Z-1 in- und mehdimensionale Inegaion Z- Gadien Divegen und Roaion Z-3 Gaußsche und Sokessche Inegalsa Z-4 Koninuiäsgleichung Z-5 lekomagneische Felde an Genflächen
Sinus- + Cosinus-Funktion und komplexe Wurzel
 Dr. Siegfried Echterhoff Aalysis 1 Vorlesug WS 08 09 6 Polarkoordiate Sius- + Cosius-Fuktio ud komplexe Wurzel 6.1 Im folgede seik 1 1 := {z C z = 1} der Kreis i C mit Radius 1 ud Mittelpukt 0. Wir defiiere
Dr. Siegfried Echterhoff Aalysis 1 Vorlesug WS 08 09 6 Polarkoordiate Sius- + Cosius-Fuktio ud komplexe Wurzel 6.1 Im folgede seik 1 1 := {z C z = 1} der Kreis i C mit Radius 1 ud Mittelpukt 0. Wir defiiere
1.3 Funktionen. Seien M und N Mengen. f : M N x M : 1 y N : y = f(x) nennt man Funktion oder Abbildung. Beachte: Zuordnung ist eindeutig.
 1.3 Fuktioe Seie M ud N Mege f : M N x M : 1 y N : y fx et ma Fuktio oder Abbildug. Beachte: Zuordug ist eideutig. Bezeichuge: M : Defiitiosbereich N : Bildbereich Zielmege vo f Der Graph eier Fuktio:
1.3 Fuktioe Seie M ud N Mege f : M N x M : 1 y N : y fx et ma Fuktio oder Abbildug. Beachte: Zuordug ist eideutig. Bezeichuge: M : Defiitiosbereich N : Bildbereich Zielmege vo f Der Graph eier Fuktio:
Lagebeziehungen. Titel Beschreibung Allgemeine Vorgehensweise Beispiel. Lage zwischen Geraden. g und h gleichsetzen. LGS lösen.
 Lagebeziehngen Titel Bescheibng Allgemeine Vogehensweise Beispiel Lage zwischen Geaden Zwei Geaden g nd h im Ram können......sich schneiden. Sie besitzen einen einzigen gemeinsamen Pnkt...zeinande paallel
Lagebeziehngen Titel Bescheibng Allgemeine Vogehensweise Beispiel Lage zwischen Geaden Zwei Geaden g nd h im Ram können......sich schneiden. Sie besitzen einen einzigen gemeinsamen Pnkt...zeinande paallel
Abschlussprüfung 20XX Muster an den Realschulen in Bayern
 Prüfugsdauer: 50 Miute Abschlussprüfug 0XX Muster a de Realschule i ayer Mathematik I Hilfsmittelfreier Teil Name: orame: Klasse: Platzziffer: Pukte: A Aufgabeteil A ereche Sie. a) vo 70 sid Haupttermi
Prüfugsdauer: 50 Miute Abschlussprüfug 0XX Muster a de Realschule i ayer Mathematik I Hilfsmittelfreier Teil Name: orame: Klasse: Platzziffer: Pukte: A Aufgabeteil A ereche Sie. a) vo 70 sid Haupttermi
Schriftliche Prüfung aus Regelungstechnik am
 TU Gaz, Istitut fü Regelugstechik Schiftliche Püfug aus Regelugstechik a 6.0.00 Nae / Voae(): Ke-Mat.N.: Gebutsdatu: BONUSPUNKTE aus Coputeecheübug SS00: 3 4 eeichbae Pukte 5 4 5 5 eeichte Pukte TU Gaz,
TU Gaz, Istitut fü Regelugstechik Schiftliche Püfug aus Regelugstechik a 6.0.00 Nae / Voae(): Ke-Mat.N.: Gebutsdatu: BONUSPUNKTE aus Coputeecheübug SS00: 3 4 eeichbae Pukte 5 4 5 5 eeichte Pukte TU Gaz,
Lösungen II.1. Lösungen II.2. c r d r. u r. 156/18 c) Assoziativgesetz
 Lösungen II. / selbe Länge:,, 7;,, ;,, ;, ;, 9 selbe Tanslation:, ;, ;,, ;, Lösungen II. / a b a b c c d d s u v s u v b) ein Pfeil de Länge /7 a b ; y b a b) Kommutativgesetz / u a b ; v b c b) w u c
Lösungen II. / selbe Länge:,, 7;,, ;,, ;, ;, 9 selbe Tanslation:, ;, ;,, ;, Lösungen II. / a b a b c c d d s u v s u v b) ein Pfeil de Länge /7 a b ; y b a b) Kommutativgesetz / u a b ; v b c b) w u c
Abschlussprüfung 2012 an den Realschulen in Bayern
 Prüfugsdauer: 150 Miute Abschlussprüfug 01 a de Realschule i Bayer Mathematik II Aufgabe B 1 Haupttermi B 1.0 Die Parabel p verläuft durch die Pukte P( 5 19) ud Q(7 5). Sie hat eie Gleichug der Form y
Prüfugsdauer: 150 Miute Abschlussprüfug 01 a de Realschule i Bayer Mathematik II Aufgabe B 1 Haupttermi B 1.0 Die Parabel p verläuft durch die Pukte P( 5 19) ud Q(7 5). Sie hat eie Gleichug der Form y
Merkhilfe. 1 Inhalte der Mittelstufe STAATSINSTITUT FÜR SCHULQUALITÄT UND BILDUNGSFORSCHUNG MÜNCHEN. Mathematik am Gymnasium
 STAATSINSTITUT FÜR SCHULQUALITÄT UND BILDUNGSFORSCHUNG MÜNCHEN Mekhilfe Mthemtik m Gymsium Ihlte de Mittelstufe Lösugsfomel fü qudtische Gleichuge c / 4c Poteze m m s s s s s s Logithme logc log logc log
STAATSINSTITUT FÜR SCHULQUALITÄT UND BILDUNGSFORSCHUNG MÜNCHEN Mekhilfe Mthemtik m Gymsium Ihlte de Mittelstufe Lösugsfomel fü qudtische Gleichuge c / 4c Poteze m m s s s s s s Logithme logc log logc log
4. Vektorräume mit Skalarprodukt
 4. Vektorräume mit Skalarprodukt Wiederholug: V=R x, y R: x= x x i x, y= y y, :R R R Skalarprodukt Stadardskalarprodukt lieare Abbildug mit 2 Argumete 4. Eigeschafte vo Skalarprodukte Def.: Es sei V ei
4. Vektorräume mit Skalarprodukt Wiederholug: V=R x, y R: x= x x i x, y= y y, :R R R Skalarprodukt Stadardskalarprodukt lieare Abbildug mit 2 Argumete 4. Eigeschafte vo Skalarprodukte Def.: Es sei V ei
Abschlussprüfung 2010 an den Realschulen in Bayern
 Prüfugsdauer: 50 Miute Abschlussprüfug 00 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A A.0 I eiem Hadbuch zur Wetterkude fide Sie im Kapitel Erdatmosphäre die
Prüfugsdauer: 50 Miute Abschlussprüfug 00 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A A.0 I eiem Hadbuch zur Wetterkude fide Sie im Kapitel Erdatmosphäre die
Prof. Dr. Tatjana Lange
 Pof. D. Tatjaa Lage Lehgebiet: egelugstechik Laboübug 6: Thea: Stabilität vo egelkeise: Wuzelotsvefahe 1. Übugsziele: etiefug de egel zu Bildug vo Wuzelotskuve Deostatio echegestützte efahe de lieae Systeaalyse
Pof. D. Tatjaa Lage Lehgebiet: egelugstechik Laboübug 6: Thea: Stabilität vo egelkeise: Wuzelotsvefahe 1. Übugsziele: etiefug de egel zu Bildug vo Wuzelotskuve Deostatio echegestützte efahe de lieae Systeaalyse
Mathematik Formeln 3. und 4. Semester von Gerald Meier
 Mahea Foel 3. d 4. Seese o Geald Mee Ke. Veoe.. ageeeo = ( s = & ( &(.. Kügseo & = = & κ κ= : Küg ρ = : Kügsads ( κ ( & && && & Paaeedasellg: = κ= 3 ( ( & + & f eplze asellg: = f( κ= 3 + f Poladasellg:
Mahea Foel 3. d 4. Seese o Geald Mee Ke. Veoe.. ageeeo = ( s = & ( &(.. Kügseo & = = & κ κ= : Küg ρ = : Kügsads ( κ ( & && && & Paaeedasellg: = κ= 3 ( ( & + & f eplze asellg: = f( κ= 3 + f Poladasellg:
8. Die Exponentialfunktion und die trigonometrischen Funktionen. 8.1 Definition der Exponentialfunktion
 8. Die Expoetialfuktio ud die trigoometrische Fuktioe 8. Defiitio der Expoetialfuktio Fudametallemma: Für jede Folge w mit dem Grezwert w gilt: w lim + = k = 0 k w. k! Defiitio der Expoetialfuktio : k
8. Die Expoetialfuktio ud die trigoometrische Fuktioe 8. Defiitio der Expoetialfuktio Fudametallemma: Für jede Folge w mit dem Grezwert w gilt: w lim + = k = 0 k w. k! Defiitio der Expoetialfuktio : k
2. Das multiple Regressionsmodell
 . Das mliple Regressiosmodell. Modellspezifikaio Bei ökoomerische Eigleichgsmodelle is eie edogee Variable vo eier oder mehrere eogee Variable abhägig. Allgemei lasse sich ökoomerische Eigleichgsmodelle
. Das mliple Regressiosmodell. Modellspezifikaio Bei ökoomerische Eigleichgsmodelle is eie edogee Variable vo eier oder mehrere eogee Variable abhägig. Allgemei lasse sich ökoomerische Eigleichgsmodelle
Abschlussprüfung 2014 an den Realschulen in Bayern
 Prüfugsdauer: 50 Miute Name: Abschlussprüfug 204 a de Realschule i Bayer Mathematik I Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Haupttermi A 0 Gegebe ist das rechtwiklige Dreieck ABC mit der Hypoteuse
Prüfugsdauer: 50 Miute Name: Abschlussprüfug 204 a de Realschule i Bayer Mathematik I Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Haupttermi A 0 Gegebe ist das rechtwiklige Dreieck ABC mit der Hypoteuse
Ein Kredit von 350.000 soll mit 10% p.a. verzinst werden. Folgende Tilgungen sind vereinbart:
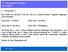 E. Tlgugsechuge Aufgabe E Ked vo 350.000 soll 0% p.a. vezs wede. Folgede Tlguge sd veeba: Ede Jah : 70.000 Ede Jah : 63.000 Ede Jah 6:.500 Ede Jah 7: Reslgug. A Ede des 3. ud 5. Jahes efolge keele Zahluge
E. Tlgugsechuge Aufgabe E Ked vo 350.000 soll 0% p.a. vezs wede. Folgede Tlguge sd veeba: Ede Jah : 70.000 Ede Jah : 63.000 Ede Jah 6:.500 Ede Jah 7: Reslgug. A Ede des 3. ud 5. Jahes efolge keele Zahluge
α β Ein sphärisches Dreieck ist durch drei Großkreise begrenzt (Abb. 2).
 Has Walser, [20150801] Sphärische Vielecke Aregug: H. E., P. 1 Worum geht es? Die Flächeformel für sphärische Vielecke, isbesodere sphärische Dreiecke, lässt sich eifach ud kosistet mit Hilfe der Außewikel
Has Walser, [20150801] Sphärische Vielecke Aregug: H. E., P. 1 Worum geht es? Die Flächeformel für sphärische Vielecke, isbesodere sphärische Dreiecke, lässt sich eifach ud kosistet mit Hilfe der Außewikel
R05 - Reibschlüssige Verbindungen
 IZ-ÜCIG-IIU Ü MCIEEE DE ECICE UIEIÄ CLUL Pofesso D.-Ig. Pee Diez 0..00 e 05 - eibschlüssige ebiduge ufgabe: uf eie ohlwelle aus Ck 5 soll eie ieescheibe aus eie luiiulegieug iels eie zlidische Peßvebidug
IZ-ÜCIG-IIU Ü MCIEEE DE ECICE UIEIÄ CLUL Pofesso D.-Ig. Pee Diez 0..00 e 05 - eibschlüssige ebiduge ufgabe: uf eie ohlwelle aus Ck 5 soll eie ieescheibe aus eie luiiulegieug iels eie zlidische Peßvebidug
Musterlösung Serie 10
 Prof. D. Salamo Aalysis I MATH, PHYS, CHAB HS 04 Muserlösug Serie 0. a Wir bereche mi der biomische Formel e cos ix + e ix x = = =0 =0 e ix e i x = =0 e i x Da = gil, öe wir i der leze Summe die Terme
Prof. D. Salamo Aalysis I MATH, PHYS, CHAB HS 04 Muserlösug Serie 0. a Wir bereche mi der biomische Formel e cos ix + e ix x = = =0 =0 e ix e i x = =0 e i x Da = gil, öe wir i der leze Summe die Terme
Geckos gehören zur Familie der Schuppenkriechtiere. Sie bevölkern seit etwa 50 Millionen Jahren die Erde und haben sich im Laufe ihrer Entwicklung
 Gymasie, Gesamschule, Berufliche Gymasie Behörde für Schule ud Berufsbildug Haupermi Lehrermaerialie zum Leisugskurs Mahemaik II.2 Geckos LA/AG 2 Geckos gehöre zur Familie der Schuppekriechiere. Sie bevölker
Gymasie, Gesamschule, Berufliche Gymasie Behörde für Schule ud Berufsbildug Haupermi Lehrermaerialie zum Leisugskurs Mahemaik II.2 Geckos LA/AG 2 Geckos gehöre zur Familie der Schuppekriechiere. Sie bevölker
0.1 E: Der Haupsatz der Mineralogie
 0. E: Der Haupsatz der Mieralogie Satz: I eiem Kristall gibt es ur,,3,4 ud 6-zählige Symmetrie. Defiitio: Seie u, v 0 zwei Vektore, die icht auf eier Gerade liege. Die Mege heißt Gitter. Satz: Die Vektore
0. E: Der Haupsatz der Mieralogie Satz: I eiem Kristall gibt es ur,,3,4 ud 6-zählige Symmetrie. Defiitio: Seie u, v 0 zwei Vektore, die icht auf eier Gerade liege. Die Mege heißt Gitter. Satz: Die Vektore
Mathematische Probleme, SS 2017 Montag 3.7. $Id: convex.tex,v /07/03 14:07:59 hk Exp $
 $Id: covex.tex,v 1.44 2017/07/03 14:07:59 hk Exp $ 4 Kovexgeometrie 4.1 Die platoische Körper Wir hatte bereits bemerkt das die kovexe Polyeder im R 3 i gewisse Sie die dreidimesioale Versio der kovexe
$Id: covex.tex,v 1.44 2017/07/03 14:07:59 hk Exp $ 4 Kovexgeometrie 4.1 Die platoische Körper Wir hatte bereits bemerkt das die kovexe Polyeder im R 3 i gewisse Sie die dreidimesioale Versio der kovexe
4 Andreas Gathmann. x 2 +y 2 x 2 +y 2 x 2 +y 2
 4 Adreas Gathma 1. Komplexe Zahle Bevor wir mit der komplexe Aalysis begie, wolle wir uächst die grudlegede Defiitioe ud Eigeschafte der komplexe Zahle och eimal kur wiederhole. Defiitio 1.1. Die Mege
4 Adreas Gathma 1. Komplexe Zahle Bevor wir mit der komplexe Aalysis begie, wolle wir uächst die grudlegede Defiitioe ud Eigeschafte der komplexe Zahle och eimal kur wiederhole. Defiitio 1.1. Die Mege
Lineare Algebra 2. A m. A 3 XI n3
 Techische Uivesität Dotmud Sommesemeste 27 Fakultät fü Mathematik Übugsblatt 6 Pof D Detlev Hoffma 6 Jui 27 Maco Sobiech/ Nico Loez Lieae Algeba 2 Lösug zu Aufgabe 6: Voaussetzuge: Sei K ei Köpe ud sei
Techische Uivesität Dotmud Sommesemeste 27 Fakultät fü Mathematik Übugsblatt 6 Pof D Detlev Hoffma 6 Jui 27 Maco Sobiech/ Nico Loez Lieae Algeba 2 Lösug zu Aufgabe 6: Voaussetzuge: Sei K ei Köpe ud sei
Mathematik 4 Vektorräume und affine Räume
 4 ektoäume ud affie äume olesugsmitschift - Kuzfassug Etwuf Pof. D. e. at. B. Gabowski HTW des Saalades 4 Ihalt Mathematik Kapitel 4 INHALTSEZEICHNIS 4 EKTOÄUME UND AFFINE ÄUME... 4.. EINLEITUNG... 4.
4 ektoäume ud affie äume olesugsmitschift - Kuzfassug Etwuf Pof. D. e. at. B. Gabowski HTW des Saalades 4 Ihalt Mathematik Kapitel 4 INHALTSEZEICHNIS 4 EKTOÄUME UND AFFINE ÄUME... 4.. EINLEITUNG... 4.
Abschlussprüfung 2016 an den Realschulen in Bayern
 Prüfugsdauer: 150 Miute Abschlussprüfug 016 a de Realschule i ayer Mathematik II Name: Vorame: Klasse: Platzziffer: Pukte: A 1.0 A 1.1 Aufgabe A 1 Haupttermi Der Wertverlust verschiedeer E-ike-Modelle
Prüfugsdauer: 150 Miute Abschlussprüfug 016 a de Realschule i ayer Mathematik II Name: Vorame: Klasse: Platzziffer: Pukte: A 1.0 A 1.1 Aufgabe A 1 Haupttermi Der Wertverlust verschiedeer E-ike-Modelle
Abschlussprüfung 2016 an den Realschulen in Bayern
 Prüfugsdauer: 150 Miute Abschlussprüfug 016 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A 1 Haupttermi A 10 Die gleichscheklige Dreiecke ABC habe die Base AB
Prüfugsdauer: 150 Miute Abschlussprüfug 016 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A 1 Haupttermi A 10 Die gleichscheklige Dreiecke ABC habe die Base AB
Einheitswurzeln und Polynome
 Eiheitswurzel ud Polyome Axel Schüler, Mathematisches Istitut, Uiv. Leipzig mailto:schueler@mathematik.ui-leipzig.de Grüheide, 1.3.2000 Kojugatio ud Betrag Spiegelt ma eie komplexe Zahl z = a+b i a der
Eiheitswurzel ud Polyome Axel Schüler, Mathematisches Istitut, Uiv. Leipzig mailto:schueler@mathematik.ui-leipzig.de Grüheide, 1.3.2000 Kojugatio ud Betrag Spiegelt ma eie komplexe Zahl z = a+b i a der
Mathematik I Aufgabengruppe A Aufgabe A 1
 Seite vo 9 Prüfugsdauer: Abschlussprüfug 004 50 Miute a de Realschule i Bayer Mathematik I Aufgabegruppe A Aufgabe A A.0 Ei Kodesator (Speicher für elektrische Eergie) wird a eier Elektrizitätsquelle für
Seite vo 9 Prüfugsdauer: Abschlussprüfug 004 50 Miute a de Realschule i Bayer Mathematik I Aufgabegruppe A Aufgabe A A.0 Ei Kodesator (Speicher für elektrische Eergie) wird a eier Elektrizitätsquelle für
Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge zum 5. Übungsblatt
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE KIT Istitut für Aalysis Dr A Müller-Rettkowski Dr T Gauss WS 00/ Höhere Mathematik I für die Fachrichtuge Elektroigeieurwese, Physik ud Geodäsie Lösugsvorschläge zum
KARLSRUHER INSTITUT FÜR TECHNOLOGIE KIT Istitut für Aalysis Dr A Müller-Rettkowski Dr T Gauss WS 00/ Höhere Mathematik I für die Fachrichtuge Elektroigeieurwese, Physik ud Geodäsie Lösugsvorschläge zum
Kapitel 2 Kontinuierliche Systemmodelle (III)
 Modellerg d Smlao mecharoscher Syseme Kapel Koerlche Sysemmodelle III 8. Orsdskreserg Syseme m verele Parameer 8. Gewöhlche d parelle Dfferealglechge sher: Mahemasche Modelle koerlcher dyamscher Syseme
Modellerg d Smlao mecharoscher Syseme Kapel Koerlche Sysemmodelle III 8. Orsdskreserg Syseme m verele Parameer 8. Gewöhlche d parelle Dfferealglechge sher: Mahemasche Modelle koerlcher dyamscher Syseme
Mathematische Probleme, SS 2015 Donnerstag $Id: convex.tex,v /05/21 18:28:20 hk Exp $
 $Id: covex.tex,v 1.18 2015/05/21 18:28:20 hk Exp $ 3 Kovexgeometrie 3.2 Die platoische Körper Ei platoischer Körper vo Typ (, m) ist ei kovexer Polyeder desse Seitefläche alle gleichseitige -Ecke ud i
$Id: covex.tex,v 1.18 2015/05/21 18:28:20 hk Exp $ 3 Kovexgeometrie 3.2 Die platoische Körper Ei platoischer Körper vo Typ (, m) ist ei kovexer Polyeder desse Seitefläche alle gleichseitige -Ecke ud i
Mathematische Probleme, SS 2016 Freitag $Id: convex.tex,v /05/27 12:19:07 hk Exp $
 $Id: covete,v 130 2016/05/27 12:19:07 hk Ep $ 3 Kovegeometrie 32 Die platoische Körper User mometaes Ziel ist die Berechug der geometrische Date der platoische Körper Gemäß des i der letzte itzug eschrieee
$Id: covete,v 130 2016/05/27 12:19:07 hk Ep $ 3 Kovegeometrie 32 Die platoische Körper User mometaes Ziel ist die Berechug der geometrische Date der platoische Körper Gemäß des i der letzte itzug eschrieee
Lösungsvorschlag zu den Hausaufgaben der 1. Übung
 FAKULTÄT FÜR MATHEMATIK Prof. Dr. Patrizio Neff Christia Thiel 4.04.04 Lösugsvorschlag zu de Hausaufgabe der. Übug Aufgabe : (6 Pukte Bereche Sie für die Fuktio f : R R, f( : ep( a der Stelle 0 0 das Taylorpolyom
FAKULTÄT FÜR MATHEMATIK Prof. Dr. Patrizio Neff Christia Thiel 4.04.04 Lösugsvorschlag zu de Hausaufgabe der. Übug Aufgabe : (6 Pukte Bereche Sie für die Fuktio f : R R, f( : ep( a der Stelle 0 0 das Taylorpolyom
Der Satz von Stone-Weierstraß. 1 Approximationssatz von Weierstraß
 Der Satz vo Stoe-Weierstraß Vortrag zum Prosemiar Aalysis, 28.06.2010 Valetia Gerber, Sabria Kielma Aus der Vorlesug Aalysis I ud II kee wir das Kozept des Approximieres. Us wurde die Begriffe Taylor-
Der Satz vo Stoe-Weierstraß Vortrag zum Prosemiar Aalysis, 28.06.2010 Valetia Gerber, Sabria Kielma Aus der Vorlesug Aalysis I ud II kee wir das Kozept des Approximieres. Us wurde die Begriffe Taylor-
Drehpendel. Aufgaben. Grundlagen = D. T r. = 4π. mgr T T. Versuchsprotokolle. Physikalisches Grundpraktikum. Versuch 114
 Phyikaliche Gupakiku Veuch 114 ehpeel Veuchpookolle Ralf Elebach Aufgabe 1. Beiug e ägheioee eie u eie Ruage (hoizoal) yaich.. Beiug e iekiooee e Appaau aich u yaich. Gulage a ehpeel i eie hoizoal- chwigee,
Phyikaliche Gupakiku Veuch 114 ehpeel Veuchpookolle Ralf Elebach Aufgabe 1. Beiug e ägheioee eie u eie Ruage (hoizoal) yaich.. Beiug e iekiooee e Appaau aich u yaich. Gulage a ehpeel i eie hoizoal- chwigee,
Mathematik 2 für Naturwissenschaften
 Has Walser Mathematik für Naturwisseschafte Modul 0 Regressiosgerade ud Korrelatio Has Walser: Modul 0, Regressiosgerade ud Korrelatio ii Ihalt Die Regressiosgerade.... Problemstellug.... Berechug der
Has Walser Mathematik für Naturwisseschafte Modul 0 Regressiosgerade ud Korrelatio Has Walser: Modul 0, Regressiosgerade ud Korrelatio ii Ihalt Die Regressiosgerade.... Problemstellug.... Berechug der
Bestimmung der Extrema von Funktionen mehrerer Veränderlicher
 Mathematk ü Natuwsseschatle II Bestmmug de Etema vo Fuktoe mehee Veädelche R R ; etwckel um (, ) Taylopolyom. Gades Vektoom ( ) ( ) + ( ) o ( ) + ( ) o Hess( ) o ( ) Vekto Vekto Vekto Mat Vekto Mat Vekto
Mathematk ü Natuwsseschatle II Bestmmug de Etema vo Fuktoe mehee Veädelche R R ; etwckel um (, ) Taylopolyom. Gades Vektoom ( ) ( ) + ( ) o ( ) + ( ) o Hess( ) o ( ) Vekto Vekto Vekto Mat Vekto Mat Vekto
C Die Gleichung. Passive Netzwerke Differentialgleichungen H. Friedli. Darstellung der passiven Bauelemente Widerstand Kondensator Spule
 Passive Neweke Diffeenialgleichungen H. Fiedli Dasellung de passiven auelemene Widesand Kondensao Spule du U R I( ) I U& di( ) ( ) U L L I& d d Mi diesen Definiionen lassen sich alle passiven Kombinaionen
Passive Neweke Diffeenialgleichungen H. Fiedli Dasellung de passiven auelemene Widesand Kondensao Spule du U R I( ) I U& di( ) ( ) U L L I& d d Mi diesen Definiionen lassen sich alle passiven Kombinaionen
2.12 Dreieckskonstruktionen
 .1 Deieckskonstuktionen 53.1 Deieckskonstuktionen.1.1 B aus a, b und c. Keis um mit Radius b 3. Keis um B mit Radius a 4. Schnittpunkt de Keise ist Bemekung: Es entstehen zwei konguente B..1. B aus α,
.1 Deieckskonstuktionen 53.1 Deieckskonstuktionen.1.1 B aus a, b und c. Keis um mit Radius b 3. Keis um B mit Radius a 4. Schnittpunkt de Keise ist Bemekung: Es entstehen zwei konguente B..1. B aus α,
n=0 f(x) = log(1 + x) = n=1
 Potez - Reihe Machmal ist es praktisch eie Fuktio f() mir Hilfe ihrer Potezreihe auszudrücke. Eie Potezreihe um de Etwicklugspukt 0 sieht im Allgemeie so aus a ( 0 ) Fuktioe, für die eie Potezreihe eistiert,
Potez - Reihe Machmal ist es praktisch eie Fuktio f() mir Hilfe ihrer Potezreihe auszudrücke. Eie Potezreihe um de Etwicklugspukt 0 sieht im Allgemeie so aus a ( 0 ) Fuktioe, für die eie Potezreihe eistiert,
Quantenmechanik I. Musterlösung 12.
 Quatemechaik I. Musterlösug 1. Herbst 011 Prof. Reato Reer Übug 1. Ster-Gerlach (19). Ei Strahl aus ugeladee Teilche mit Spi s = 1 läuft etlag der x-achse ud durchquert ei i z-richtug stark ihomogees Magetfeld.
Quatemechaik I. Musterlösug 1. Herbst 011 Prof. Reato Reer Übug 1. Ster-Gerlach (19). Ei Strahl aus ugeladee Teilche mit Spi s = 1 läuft etlag der x-achse ud durchquert ei i z-richtug stark ihomogees Magetfeld.
A. Zahleneinteilung. r a b
 Aus FUNKSCHAU 14/1953 (Blatt 1+) ud 17/1953 (Blatt 3), im Origial -spaltig. Digitalisiert 07/016 vo Eike Grud für http://www.radiomuseum.org mit freudlicher Geehmigug der FUNKSCHAU- Redaktio. Die aktuelle
Aus FUNKSCHAU 14/1953 (Blatt 1+) ud 17/1953 (Blatt 3), im Origial -spaltig. Digitalisiert 07/016 vo Eike Grud für http://www.radiomuseum.org mit freudlicher Geehmigug der FUNKSCHAU- Redaktio. Die aktuelle
Fragen zur Abschlussprüfung Mathematik I. Welche Funktionen kennst Du? Skizziere kurz eine solche Funktion.
 Frage zur Abschlussprüfug Mathematik I Frage 1: Welche Fuktioe kest Du? Skizziere kurz eie solche Fuktio. Frage 2: Gib zu f: y = 620 1,032 x + 32 Defiitios- ud Wertemege a Frage 3.1: Für die Vermehrug
Frage zur Abschlussprüfug Mathematik I Frage 1: Welche Fuktioe kest Du? Skizziere kurz eie solche Fuktio. Frage 2: Gib zu f: y = 620 1,032 x + 32 Defiitios- ud Wertemege a Frage 3.1: Für die Vermehrug
Abschlussprüfung 2014 an den Realschulen in Bayern
 Lösugsmuster ud ewertug bschlussprüfug 0 a de Realschule i ayer Mathematik I ufgabe 3 Nachtermi RUMGEOMETRIE 6. ta 56,3 L. PS( ) P sis 3 P si 56,3 si 80 56,3 P si56,3 cm si(56,3 ) ]0 ; 90 ] si56,3 3 (
Lösugsmuster ud ewertug bschlussprüfug 0 a de Realschule i ayer Mathematik I ufgabe 3 Nachtermi RUMGEOMETRIE 6. ta 56,3 L. PS( ) P sis 3 P si 56,3 si 80 56,3 P si56,3 cm si(56,3 ) ]0 ; 90 ] si56,3 3 (
Lösung: Die Zahl ist die größte Zahl mit der in der Aufgabenstellung genannten Eigenschaft.
 Ladeswettbewerb Mathematik ade-württemberg 005 Rude ufgabe Eie atürliche Zahl besteht aus paarweise verschiedee Ziffer, vo dee keie Null ist. Streicht ma i dieser Zahl eie beliebige Ziffer k, so ist die
Ladeswettbewerb Mathematik ade-württemberg 005 Rude ufgabe Eie atürliche Zahl besteht aus paarweise verschiedee Ziffer, vo dee keie Null ist. Streicht ma i dieser Zahl eie beliebige Ziffer k, so ist die
