Lösungen zum Crashkurs: Statik Teil 1 Thema: Gleichgewichtsbedingungen, Schnittgrö ßen und Fla chenschwerpunkte
|
|
|
- Maya Paulina Frei
- vor 5 Jahren
- Abrufe
Transkript
1 1 Lösungen zum Crashkurs: Statik Tei 1 Thema: Geichgewichtsbedingungen, Schnittgrö ßen und Fa chenschwerpunkte Aufgabe zum Fächenschwerpunkt y Gebe die Schwerpunktkoordinaten für das oben dargestete Profi bzg. des eingezeichneten Koordinatensystems an! In dieser Aufgabe zeige ich zwei Mögichkeiten zur Berechnung des Schwerpunktes auf. Einma verwende ich die baue Fäche, indem ich diese in Teifächen zeregen. Zum anderen betrachten wir ein gesamtes Quadrat der Länge 8*4 und ziehen die Aussparungen (ebenfas in Teifächen zeregt) von diesem Quadrat ab. Die zweite Berechnung so aufzeigen, wie mit Aussparungen gerechnet wird. Verwendete Formen: s = i A i A i y s = y i A i A i
2 2 Aufgabe zur Streckenast (Resutierende und Angriffspunkt) Bestimme fu r jeden beasteten Trager die Resutierende R der Streckenast sowie ihren Angriffspunkt R. Diese Aufgabe so euch aufzeigen, wie ihr mit Streckenasten umgehen müsst, wenn ihr z.b. Aufagerkräfte berechnen sot. In diesem Fa muss die Streckenast zu einer Resutierenden zusammengefasst werden, die dann in die Geichgewichtsbedingungen eingeht. Für die Momentengeichgewichtsbedingung muss zusätzich die Lage der Resutierenden bekannt sein, um den Hebearm bestimmen zu können. Ich zeige euch außerdem, wie ihr die Resutierende und die Lage der Resutierenden mittes Integration von q() ermittet. Hinweis: Parabefö rmige Streckenast in der Mitschrift - PDF
3 3 Aufgabe zur Kräftezeregung, Aufagerkräften und Schnittgrößen F A B 40 C 2a a a a Das skizzierte System ist durch eine konstante Streckenast q() und eine Einzekraft F beastet. Gegeben: a,, F = a a) Berechne die Aufagerkra fte! - Bide die Resutierende der Streckenast sowie den Angriffspunkt! - Fu hre die Kra ftezeregung durch! - Berechne die Aufagerkra fte aus den Geichgewichtsbedingungen! b) Bestimme die Schnittgrö ßenvera ufe fu r das gesamte System. Das System wird nun durch eine ineare Streckenast beastet. q() F A B 40 C a) Berechne die Aufagerkra fte! 2a a a a b) Bestimme die Schnittgrö ßenvera ufe fu r das gesamte System. Diese Aufgabe so euch zeigen, wie ihr die Streckenasten zur Berechnung von Aufagerkräften berücksichtigt, wie ihr Schnittgrößen mit und ohne Streckenasten berechnet sowie die Kräftezeregung durchführt.
4 4 Lösung Aufgabe 1) y In Teifa chen mit bekannter Schwerpunktage zeregen: y Wir haben das Dreieck in zwei rechtwinkige Dreiecke zeregt, fu r weche die Schwerpunktage bekannt ist. Vom rechten Winke ausgehend iegt der Schwerpunkt eines Dreiecks bei 1/3 der Lange und bei 1/3 der Hö he.
5 5 y /3 8/3 2 8 As nachstes kö nnen wir mit der Berechnung beginnen. Die Forme zur Berechnung eines Schwerpunktes fu r zusammengesetzte Fa che ist: Verwendete Formen: s = i A i A i y s = y i A i A i Wir beginnen mit dem Schwerpunkt in -Richtung: Fäche 1: Rechtwinkiges Dreieck 1 = Abstand vom Koordinatenursprung hin zum Schwerpunkt der 1. Fache in -Richtung 1 =2 2 3 = 4 3 A 1 = Facheninhat der 1. Facheninhat A 1 = =6 Fäche 2: Rechtwinkiges Dreieck 2 = Abstand vom Koordinatenursprung hin zum Schwerpunkt der 2. Fache in -Richtung 2 = =14 3
6 6 A 2 = Facheninhat der 2. Facheninhat A 2 = =24 Anwendung der Forme: s = i A i A i = 1 A A 2 A 1 +A 2 = = As nachsten betrachten wir den Abstand des Schwerpunktes der Gesamtfache vom Koordinatenursprung in y-richtung. y 1 = Abstand vom Koordinatenursprung hin zum Schwerpunkt der 1. Fache in y-richtung y 1 =2 y 2 = Abstand vom Koordinatenursprung hin zum Schwerpunkt der 2. Fache in y-richtung y 2 =2 Anwendung der Forme: y i A i y s = = y 1A 1 +y 2 A 2 = =2 A i A 1 +A
7 7 Aternative Berechnung über Aussparung: 2 2 Aussparung 1 8/3 Aussparung y 6 2/3 2 8 Berechnung der Gesamtfa che (Quadrat) und Subtraktion der Aussparungen. Fa che 1 Gesamtfäche Quadrat 1 = Abstand vom Koordinatenursprung zum Schwerpunkt der Gesamtfache in -Richtung Der Schwerpunkt eines Rechtecks iegt in der Mitte: 1 =5 A 1 =10 6=60 Fache 2 Dreieckige Fache 2 = Abstand vom Koordinatenursprung zum Schwerpunkt der 2.Fache in -Richtung 2 = 2 3 A 2 = =6 Fache 3 Dreieckige Fache
8 8 3 = Abstand vom Koordinatenursprung zum Schwerpunkt der 3.Fache in -Richtung 3 = =22 3 A 3 = =24 Anwenden der Forme: s = i A i A i = 1 A 1 2 A 2 3 A 3 A 1 A 2 A 3 = = Fu r die Schwerpunktage in y-richtung git: y 1 =3 y 2 =y 3 =4 y i A i y s = = y 1A 1 y 2 A 2 y 3 A 3 = =2 A i A 1 A 2 A
9 9 Lösung Aufgabe 2 Die Resutierende kann uber zwei Wege ermittet werden: Facheninhat der gegebenen Streckenast (sofern bekannt) oder Integration von q(). Der Angriffspunkt der Resutierenden der Streckenast iegt im Schwerpunkt der Fache. Der Schwerpunkt ist entweder bekannt oder kann u ber die Integration bestimmt werden.
10 10 Variante 1 - Fächeninhat und bekannter Schwerpunkt Fu r bekannte Fachen (rechteckige Streckenast, dreieckige Streckenast) kann die Resutierende einfach ermittet werden, indem der Fa cheninhat berechnet wird. Rechteckige Streckenast = rechteckige Fache Fäche Rechteck = Höhe ma Breite R= Fäche Dreieck = Höhe ma Breite durch zwei R= 2 Die Resutierende einer Streckenast greift immer im Schwerpunkt der Fache an. Fur Rechteck und Dreieck sote die Schwerpunktage bekannt sein. Schwerpunkt Rechteck = mittig R = ½
11 11 Schwerpunkt Dreieck = vom rechten Winke ausgehend bei 1/3 der Länge R = ½ 2/3 1/3 Variante 2 Resutierende und Schwerpunkt über Integration Diese Variante ist einma angewendet reativ einfach und unkompiziert und kann auch auch Streckenasten mit Fa chen angewendet werden, die nicht bekannt sind. Zunachst benö tigen wir hier die Funktion q(). Diese kö nnen wir erhaten, wenn wir ein Koordinatensystem hinzuziehen: q() q() Der Bakenanfang ist dabei der Koordinatenursprung: q() q()
12 12 As nächstes kann für ineare Funktionen die Geradengeichung herangezogen werden: q ()=m+b m = Steigung b = Beginn der Funktion auf der y-achse Fu r die inke Funktion git: b= m Und damit: q ()= Fu r die rechte Funktion git: b m= -Schritte in -Richtung (Nenner), -Schritte in y-richtung (Zaher). Beide positiv, wei Schritte in positive Achsenrichtungen. Und damit: q ()= Resutierende mittes Integration bestimmen Nachdem die Funktionen q() ermittet sind, kö nnen wir die Resutierende bestimmen, indem wir diese nach d integrieren: R= q()d Das Integra spieget nichts anderes as den Facheninhat wieder. Die Streckenast wirkt von = 0 bis =, dies sind auch die Grenzen: R= 0 q()d
13 13 Integration fu r die rechteckige Streckenast durchfu hren: R= 0 d=[ ] 0 = 0= Die rechteckige Streckenast mit konstantem hat aso eine Resutierende von: R= Integration fu r die dreieckige Streckenast durchfu hren: q R= 0 0 d= d= 0 [ = ]0 [ ]= 1 2 Der Schwerpunkt der Streckenasten ist der Angriffspunkt der Resutierenden und kann ebenfas mittes Integration bestimmt werden: q() d 0 R = q()d 0 Der Nenner ist hierbei die Resutierende, die wir bereits oben berechnet haben Wir berechnen aso noch den Za her: 0 1 q() d= 0 d=[ 2 2 = 1 ]0 2 2 Rechteckige Streckenast 0 q q() d= d= [ = 1 ]0 3 2 Dreieckige Streckenast Anwendung der Forme: R = = R = = q 3 0 Schwerpunkt der rechteckigen Streckenast Schwerpunkt der dreieckigen Streckenast
14 14 Lösung Aufgabe 3 Aufgabe zur Kräftezeregung, Aufagerkräften und Schnittgrößen F A B 40 C 2a a a a Das skizzierte System ist durch eine konstante Streckenast q() und eine Einzekraft F beastet. a) Berechne die Aufagerkra fte! - Bide die Resutierende der Streckenast sowie den Angriffspunkt! R=2a =2F Facheninhat rechteckige Fache R =a Schwerpunkt iegt in der Mitte, von -ausgehend bei =a R = 2a = 2F F A a B 40 C 2a a a a
15 15 - Fu hre die Kra ftezeregung durch! Die Kraft F iegt im 3. Quadranten. Damit zeigt die -Komponente in Richtung der negativen - Achse und die y-komponente in Richtung der negativen y-achse. y F 40 Kraftkomponente in -Richtung iegt am Winke, ist aso die Ankathete und damit wird der Kosinus verwendet: Fcos(40 ) Betrag der Kraftkomponente in -Richtung Kraftkomponente in y-richtung iegt nicht am Winke, ist aso die Gegenkathete und damit wird der Sinus verwendet: Fsin(40 ) Betrag der Kraftkomponente in y-richtung Zur Veranschauichung von Ankathete und Gegenkathete kann die grafische Vektoraddition der beiden Komponenten durchgefu hrt werden, die Resutierende ist dann die Kraft F: Ankathete Gegenkathete 40 Hypotenuse R = 2a = 2F F sin(40 ) A a B F cos(40 ) C 2a a a a
16 16 - Berechne die Aufagerkra fte aus den Geichgewichtsbedingungen! Zuna chst benö tigen wir den Freischnitt: R = 2a = 2F F sin(40 ) F cos(40 ) a A B v C 2a a a a As na chstes kö nnen wir die Aufagerkra fte aus den Geichgewichtsbedingungen berechnen: : Fcos(40 ) =F cos(40 ) :A v +B+C R F sin(40 ) Zu viee Unbekannte Auch bei de Momentengeichgewichtsbedingung werden mindestens zwei Unbekannte anfaen. Wir haben aso 4 Unbekannte und drei Geichgewichtsbedingungen fu r das Gesamtsystem gegeben. Da aber ein Geenk vorhanden ist, kö nnen wir das System in zwei Teisysteme zeregen und fu r jedes Teisystem die drei Geichgewichtsbedingungen anwenden. R = 2a F sin(40 ) G v G h G h F cos(40 ) a A G v B v C 2a a a a
17 17 Linkes Teisystem: Horizontae Geichgewichtsbedingung: : +G h G h = = F cos(40 ) Vertikae Geichgewichtsbedingung: :A v G v R Momentengeichgewichtsbedingung um A oder G (hier A): R a G v 2 a G v = R = F mit R = 2F 2 Anwendung der vertikaen Geichgewichtsbedingung fu hrt uns auf A v : A v =G v +R= F+2F=F Rechtes Teisystem: Vertikae Geichgewichtsbedingung: :G v +B+C F sin(40 ) Momentengeichgewichtsbedingung um B oder C (hier C): G v 3a B 2 a+fsin(40 ) a B2 a= G v 3 a+f sin(40 ) a nach B aufösen durch 2a teien B= 3 2 G v F sin(40 ) Einsetzen von G v = -F B= 3 2 F+ 1 2 F sin(40 )
18 18 B=F( sin(40 ))=1,82 F 2 Aus der vertikaen Geichgewichtsbedingung kö nnen wir C berechnen: C= G v B+Fsin(40 ) C=F 1,82 F+F sin(40 )=F(1 1,82+sin(40 ))= 0,18 F Es ergeben sich die fogenden Lagerkräfte: =F cos(40 ) A v =F B=1,82F C= 0,18F b) Schnittgrößen Danach kö nnen die Schnittgrö ßen berechnet werden. Hierzu betrachten wir zunachst das inke und rechte Schnittufer: Linkes (positives Schnittufer) Rechtes (negatives Schnittufer) M N Q y z Am inken (positiven) Schnittufer zeigen die Schnittgrö ßen in positive Achsenrichtung in Bezug auf das obige,y,z-koordinatensystem. Das Moment ist am inken Schnittufer ein inksdrehendes Moment, weches in der Physik as positives Moment definiert ist. Am rechten (negativen)
19 19 Schnittufer zeigen die Schnittgrö ßen in negative Achsenrichtung. Das Moment ist hierbei ein rechtsdrehendes Moment. Es werden Schnitte durchgefu hrt bei: Statische Unstetigkeiten Einzeasten, Knicke in Streckenasten. Geometrische Unstetigkeiten Knicke der Bakenachse, (z.b. Rahmen) Schnitte: F sin(40 ) F cos(40 ) a A B v C 2a a a a 1.Schnitt: M 1 N 1 A v Q 1
20 20 Anwendung der Geichgewichtsbedingungen zur Berechnung der Schnittgrö ßen. Normakraft : +N 1 N 1 = = Fcos(40 ) Normakraftverauf fu r den 1. Bereich (0 <= <= 2a) Querkraft Mit Integra: Fu r die Querkraft wird das Integra q()d Richtung der Streckenast anzugeben. verwendet. Das Vorzeichen ist entsprechend der Für eine rechteckige Streckenast git q() =. :A v Q 1 0 q0 d Resutierende der Streckenast as Integra Q 1 0 q0 d Integra aufö sen Ohne Integra: Ohne Integra biden wir die Resutierende der Teistreckenast mit der Lange und der Hö he. Der Angriffspunkt ist im Schwerpunkt der Teistreckenast, bei der Ha fte der La nge (die La nge ist hier ). Der Angriffspunkt wird aber erst fu r die Momentengeichgewichtsbedingung reevant. R() = * M 1 :A v Q 1 R() N 1 Q 1 A v /2 /2 Q 1 Einsetzen von A v = F: Q 1 =F Querkraftverauf fu r den 1. Bereich (0 <= <= 2a)
21 21 Moment Mit Integra Fu r das Schnittmoment wird das Integra q() d d verwendet. Das Vorzeichen ist entsprechend der Drehrichtung der Streckenast auf den Schnitt zu wa hen. Für eine rechteckige Streckenast git q() =. : A v + 0 d d+m 1 Resutierende der Streckenast as Integra M 1 0 [ d ] d 0 [q0 ] d 1. Integra (inneres) aufö sen M 1 0 q0 d Integra aufö sen und Grenzen einsetzen Ohne Integra R() = * M 1 N 1 A v /2 /2 Q 1 Ohne Integra biden wir das Moment auf den Schnitt, indem wir die Teiresutierende R() mit ihrem Hebearm mutipizieren. Dieser betra gt /2: : A v +R () 2 +M 1 R() =
22 22 A v + 2 +M 1 M A v = F M 1 =F Momentenverauf fu r den 1. Bereich (0 <= <= 2a) Die Schnittgrö ßen fu r den 1. Schnitt sind bestimmt. Wir betrachten as nachstes den zweiten Schnitt (inkes Schnittufer). R = 2a = 2F M 2 A v a Q 2 N 2 2a Normakraft : +N 2 N 2 = = Fcos(40 ) Normakraftverauf fu r den 2. Bereich (2a <= <= 3a) Querkraft :A v R Q 2 Q 2 R=F 2 F= F Querkraftverauf fu r den 2. Bereich (2a <= <= 3a)
23 23 Moment A v +R ( a)+m 2 M 2 R ( a) M 2 =F 2F ( a) M 2 =F 2F +2 F a M 2 = F +2F a Momentenverauf fu r den 2. Bereich (2a <= <= 3a) As nachstes betrachten wir den 3. Schnitt und wahen das inke Schnittufer aus. R = 2F M 3 A v a B Q 3 N 3 2a a Normakraft : +N 3 N 3 = = Fcos(40 ) Normakraftverauf fu r den 3. Bereich (3a <= <= 4a) Querkraft :A v R+B Q 3 Q 3 R+B=F 2F+1,82 F,82F Querkraftverauf fu r den 3. Bereich (3a <= <= 4a)
24 24 Moment A v +R ( a) B ( 3 a)+m 3 M 3 R ( a)+b ( 3a) A v = F, R = 2F, B = 1,82 F M 3 =F 2F( a)+1,82 F ( 3a) M 3 =F 2F +2F a+1,82f 1,82F 3 a M 3,82 F 3,46 Fa Momentenverauf fu r den 3. Bereich (3a <= <= 4a) Wir betrachten as na chstes den 4. Schnitt und das rechte Schnittufer. M 4 Q 4 N 4 C 2a a a a Normakraft : N 4 N 4 Normakraftverauf fu r den 4. Bereich (4a <= <= 5a) Querkraft :C+Q 4 Q 4 = C,18 F Querkraftverauf fu r den 4. Bereich (4a <= <= 5a) Moment M 4 +C (5 a ) M 4 = 0,18F (5a )= 0,9F a+0,18f M 4,18F 0,9F a Momentenverauf fu r den 4. Bereich (4a <= <= 5a)
25 25 Lösung zur Aufgabe 3 Tei 2 2a a a a q() F A B 40 C Bide die Resutierende der Streckenast sowie den Angriffspunkt! R= a q =q a=f 0 0 Facheninhat dreieckige Fache R = a= 4 a Schwerpunkt Rechteck von Bakenanfang ausgehend (Beginn -Achse) 3 A 4/3 a R = ½ 2a = F B F sin(40 ) F cos(40 ) C 2a a a a - Berechne die Aufagerkra fte aus den Geichgewichtsbedingungen!
26 26 Zuna chst benö tigen wir den Freischnitt: R = ½ 2a = F F sin(40 ) F cos(40 ) 4/3 a A B v C 2a a a a As na chstes kö nnen wir die Aufagerkra fte aus den Geichgewichtsbedingungen berechnen: : Fcos(40 ) =F cos(40 ) :A v +B+C R F sin(40 ) Zu viee Unbekannte Betrachtung der Teisysteme: R = F F sin(40 ) G h G h G v F cos(40 ) 2/3 a A G v B v C 2a a a a
27 27 Linkes Teisystem: Horizontae Geichgewichtsbedingung: : +G h G h = = F cos(40 ) Vertikae Geichgewichtsbedingung: :A v G v R Momentengeichgewichtsbedingung um A oder G (hier A): R 4 3 a G v 2a G v = 2 3 F mit R = F Anwendung der vertikaen Geichgewichtsbedingung fu hrt uns auf A v : A v =G v +R= 2 3 F+F=1 3 F Rechtes Teisystem: Vertikae Geichgewichtsbedingung: :G v +B+C F sin(40 ) Momentengeichgewichtsbedingung um B oder C (hier C): G v 3a B 2 a+fsin(40 ) a B2 a= G v 3 a+f sin(40 ) a nach B aufösen durch 2a teien B= 3 2 G v F sin(40 ) Einsetzen von G v = -2/3 F
28 28 B= F+ 1 2 F sin(40 ) B=1,32F Aus der vertikaen Geichgewichtsbedingung kö nnen wir C berechnen: C= G v B+Fsin(40 ) C= 2 3 F 1,32F+F sin(40 )=F(2 3 1,32+sin(40 ))= 0,01 F Es ergeben sich die fogenden Lagerkräfte (auf 2 Nachkommasteen gerundet): =F cos(40 ) A v = 2 3 F B=1,32F C= 0,01F Schnittgrößen: Schnitte: F sin(40 ) F cos(40 ) A v B C 2a a a a
29 29 1.Schnitt: M 1 N 1 A v Q 1 Anwendung der Geichgewichtsbedingungen zur Berechnung der Schnittgrö ßen. Normakraft : +N 1 N 1 = = Fcos(40 ) Normakraftverauf fu r den 1. Bereich (0 <= <= 2a) Querkraft Mit Integra: Fu r die Querkraft wird das Integra q()d Richtung der Streckenast anzugeben. verwendet. Das Vorzeichen ist entsprechend der Für eine rechteckige Streckenast git q() = /. Hier ist = 2a. :A v Q 1 q0 0 2 a d Q a d 4 a 2 Resutierende der Streckenast as Integra Integra aufö sen
30 30 Ohne Integra: Wir mu ssen in diesem Fa den Strahensatz anwenden, denn hier ist die Hö he des Kraftpfeis nicht bekannt. Strahensatz: Es verhaten sich die Abschnitte auf den Paraeen wie die ihnen entsprechenden, vom Scheite S aus gemessenen Strecken auf jeweis derseben Geraden. A q C AB =q (gesucht) SB = Teistreckenast S B D CD = SD =2a Ausgangsstreckenast Strahensatz: AB SB = CD SD q = 2 a q = 2 a Wir haben mit q die Hö he der Teistreckenast bestimmt. Es kann dann der Facheninhat (=Resutierende) der dreieckigen Streckenast wie fogt berechnet werden (Hö he ma Lange durch 2). R= 1 2 q = 1 2 2a 2 R ( )= a 2 M 1 :A v Q 1 R() N 1 Q a 2 4a 2 A v 2/3 1/3 Q 1
31 31 Einsetzen von A v = 2/3 F: Q 1 = 2 3 F 4 a 2 Querkraftverauf fu r den 1. Bereich (0 <= <= 2a) Moment Mit Integra Fu r das Schnittmoment wird das Integra q() d d verwendet. Das Vorzeichen ist entsprechend der Drehrichtung der Streckenast auf den Schnitt zu wa hen. Für eine rechteckige Streckenast git q() = /. Hier ist = 2a. : A v a d d+m 1 Resutierende der Streckenast as Integra M 1 0 [ 2a d] d =A q v 0 [ 0 4 a 2 ] d 1. Integra (inneres) aufö sen M a 2 d = A v 12a 3 2. Integra aufö sen und Grenzen einsetzen Ohne Integra R ( )= a 2 M 1 N 1 A v 2/3 1/3 Q 1 Ohne Integra biden wir das Moment auf den Schnitt, indem wir die Teiresutierende R() mit ihrem Hebearm mutipizieren. Dieser betra gt 1/3 :
32 32 : A v +R () 3 +M 1 R ()= a 2 A v + 4 a M 1 M 1 12a 3 A v = 2/3 F M 1 = 2 3 F 12 a 3 Momentenverauf fu r den 1. Bereich (0 <= <= 2a) Die Schnittgrö ßen fu r den 1. Schnitt sind bestimmt. Wir betrachten as nachstes den zweiten Schnitt (inkes Schnittufer). R = ½ 2a = F M 2 N 2 A v 4/3 a 2/3 a Q 2 2a Normakraft : +N 2 N 2 = = Fcos(40 ) Normakraftverauf fu r den 2. Bereich (2a <= <= 3a) Querkraft :A v R Q 2 A v = 2/3 F, R = F
33 33 Q 2 R= 2 3 F F= 1 3 F Querkraftverauf fu r den 2. Bereich (2a <= <= 3a) Moment A v +R ( 4 3 a)+m 2 M 2 R ( 4 3 a) M 2 = 2 3 F F ( 4 3 a) M 2 = 2 3 F F +F 4 3 a M 2 = 1 3 F F a Momentenverauf fu r den 2. Bereich (2a <= <= 3a) As nachstes betrachten wir den 3. Schnitt und wahen das inke Schnittufer aus. R = F M 3 A v 4/3 a 2/3 a B Q 3 N 3 2a a Normakraft : +N 3 N 3 = = Fcos(40 ) Normakraftverauf fu r den 3. Bereich (3a <= <= 4a)
34 34 Querkraft :A v R+B Q 3 Q 3 R+B = 2 3 F F+1,32F,99 F mit A v = 2/3 F, R = F, B = 1,32 F Querkraftverauf fu r den 3. Bereich (3a <= <= 4a) Moment A v +R ( 4 3 a) B ( 3 a)+m 3 M 3 R ( 4 3 a)+b ( 3a) A v = 2/3 F, R = F, B = 1,32 F M 3 = 2 3 F F( 4 a)+1,32f ( 3 a) 3 M 3 = 2 3 F F + 4 F a + 1,32F 3,96F a 3 M 3 = 0,99F 2,63Fa Momentenverauf fu r den 3. Bereich (3a <= <= 4a) Wir betrachten as na chstes den 4. Schnitt und das rechte Schnittufer. M 4 Q 4 N 4 C 2a a a a
35 35 Normakraft : N 4 N 4 Normakraftverauf fu r den 4. Bereich (4a <= <= 5a) Querkraft :C+Q 4 Q 4 = C,01 F Querkraftverauf fu r den 4. Bereich (4a <= <= 5a) Moment M 4 +C (5 a ) M 4 = 0,01F (5a )= 0,05F a+0,01f M 4 = 0,01F 0,05 Fa Momentenverauf fu r den 4. Bereich (4a <= <= 5a)
Intensivkurs Statik Teil 1
 Intensivkurs Statik Tei 1 Themen: Aufagekräfte und Zwischenreaktionen berechnen Kräftezeregung Geichgewichtsbedingungen Statische Bestimmtheit Notwendige Bedingungen: Abzähkriterium Hinreichende Bedingung:
Intensivkurs Statik Tei 1 Themen: Aufagekräfte und Zwischenreaktionen berechnen Kräftezeregung Geichgewichtsbedingungen Statische Bestimmtheit Notwendige Bedingungen: Abzähkriterium Hinreichende Bedingung:
= 1kN F 1 F 2. = 2,5 kn. 2m 4m 2m. = 0,75 kn/m. Webinar: Statik Thema: Schnittgrößen
 Webinar Statik Thema Schnittgrößen Bestimme für die nachfolgenden beiden Aufgaben die Schnittgrößen und Schnittgrößenverläufe! F 1 = 1k = 2,5 k a) 30 = 0,75 k/m b) Lösung Teil a) Wir beginnen damit den
Webinar Statik Thema Schnittgrößen Bestimme für die nachfolgenden beiden Aufgaben die Schnittgrößen und Schnittgrößenverläufe! F 1 = 1k = 2,5 k a) 30 = 0,75 k/m b) Lösung Teil a) Wir beginnen damit den
Institut für Allgemeine Mechanik der RWTH Aachen
 Institut für Agemeine Mechanik der RWTH Aachen Prof. Dr.-Ing. D. Weichert 9.Übung Mechanik II SS 27 18.6.6 Abgabetermin 9.Übung: 25.7.6 14: Uhr 1. Aufgabe Der skizzierte, statisch unbestimmte aken wird
Institut für Agemeine Mechanik der RWTH Aachen Prof. Dr.-Ing. D. Weichert 9.Übung Mechanik II SS 27 18.6.6 Abgabetermin 9.Übung: 25.7.6 14: Uhr 1. Aufgabe Der skizzierte, statisch unbestimmte aken wird
q = 3 kn/m Abb. 1: Eingespannter, abgeknickter Träger unter Gleichstrecken-und Punktlast.
 ateriatheorie - LK, Sekr. S Einsteinufer 5, 1587 Berin 6. Übungsbatt Schnittgrößen am biegesteifen Träger WS 11/1 1. ür den in bb. 1 dargesteten, mit einer Einzekraft und einer Geichstreckenast beasteten
ateriatheorie - LK, Sekr. S Einsteinufer 5, 1587 Berin 6. Übungsbatt Schnittgrößen am biegesteifen Träger WS 11/1 1. ür den in bb. 1 dargesteten, mit einer Einzekraft und einer Geichstreckenast beasteten
Aufgabe 1 (Seite 1 von 2) Das dargestellte Fachwerk ist in den Punkten A und B gelagert und wird durch die Einzelkräfte F 1,F 2 und F 3 belastet.
 Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Aufgabe 1 (Seite 1 von 2) Das dargestete Fachwerk ist in den Punkten A und B geagert und wird durch die Einzekräfte F 1,F 2 und F 3
Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Aufgabe 1 (Seite 1 von 2) Das dargestete Fachwerk ist in den Punkten A und B geagert und wird durch die Einzekräfte F 1,F 2 und F 3
Baustatik 2. Berechnung statisch unbestimmter Tragwerke. von Raimond Dallmann. 1. Auflage
 Baustatik Berechnung statisch unbestimmter Tragwerke von Raimond Damann 1. Aufage Baustatik Damann schne und portofrei erhätich bei beck-shop.de DIE FACHBUCHHANDLUNG Hanser München 006 Verag C.H. Beck
Baustatik Berechnung statisch unbestimmter Tragwerke von Raimond Damann 1. Aufage Baustatik Damann schne und portofrei erhätich bei beck-shop.de DIE FACHBUCHHANDLUNG Hanser München 006 Verag C.H. Beck
1. Aufgabe: (ca. 11% der Gesamtpunktzahl) Bitte beantworten Sie folgende Fragen: 1. Wie ist der Schubmittelpunkt definiert?
 . Aufgabe: (ca. % der Gesamtunktzah) Bitte beantworten Sie fogende Fragen:. Wie ist der Schubmitteunkt definiert?. Durch weche Einschränkungen des agemeinen dreidimensionaen Sannungszustandes ergibt sich
. Aufgabe: (ca. % der Gesamtunktzah) Bitte beantworten Sie fogende Fragen:. Wie ist der Schubmitteunkt definiert?. Durch weche Einschränkungen des agemeinen dreidimensionaen Sannungszustandes ergibt sich
3.7 Sonderprobleme Ausnutzung der Symmetrie und Antimetrie. Größe. Belastung
 VORLESUGSAUSKRIPT BAUSTATIK I II (UVERTIEFT).7 Sonderrobeme.7. Ausnutzung der Symmetrie und Antimetrie Durch die Ausnutzung der Symmetrie und Antimetrie kann der Grad der statischen Unbestimmtheit (u.
VORLESUGSAUSKRIPT BAUSTATIK I II (UVERTIEFT).7 Sonderrobeme.7. Ausnutzung der Symmetrie und Antimetrie Durch die Ausnutzung der Symmetrie und Antimetrie kann der Grad der statischen Unbestimmtheit (u.
a) Zeigen Sie, dass sich für eine lange Spule die magn. Flussdichte in der Mitte mit der Näherungsformel berechnen lässt.
 Aufgaben Magnetfed einer Spue 83. In einer Spue(N = 3, =,5m), die in Ost-West-Richtung iegt, wird eine Magnetnade gegen die Nord-Süd-Richtung um 11 ausgeenkt. Berechnen Sie die Stärke des Stromes in 5
Aufgaben Magnetfed einer Spue 83. In einer Spue(N = 3, =,5m), die in Ost-West-Richtung iegt, wird eine Magnetnade gegen die Nord-Süd-Richtung um 11 ausgeenkt. Berechnen Sie die Stärke des Stromes in 5
Das Trägheitsmoment und der Satz von Steiner
 Übungen zu Theoretische Physik I - echanik im Sommersemester 3 Batt 9 vom 4.6.3 Abgabe:.7. Aufgabe 38 Punkte Das Trägheitsmoment und der Satz von Steiner Berechnen Sie das Trägheitsmoment eines Zyinders
Übungen zu Theoretische Physik I - echanik im Sommersemester 3 Batt 9 vom 4.6.3 Abgabe:.7. Aufgabe 38 Punkte Das Trägheitsmoment und der Satz von Steiner Berechnen Sie das Trägheitsmoment eines Zyinders
Aus Kapitel 6. Technische Mechanik. Aufgaben. 6.1 Berechnen Sie mithilfe des Arbeitssatzes die Lagerreaktionen des abgebildeten Trägers.
 6 ufgaben Kap 6 us Kapite 6 ufgaben 6 erechnen Sie mithife des rbeitssatzes die Lagerreaktionen des abgebideten Trägers 6 erechnen Sie mithife des rbeitssatzes die Veräufe von Querkraft und iegemoment
6 ufgaben Kap 6 us Kapite 6 ufgaben 6 erechnen Sie mithife des rbeitssatzes die Lagerreaktionen des abgebideten Trägers 6 erechnen Sie mithife des rbeitssatzes die Veräufe von Querkraft und iegemoment
1. Klausur Mechanik I SS 05, Prof. Dr. V. Popov
 . Kausur Mechanik I SS 05, Prof. Dr. V. Popov itte deutich schreiben! Name, Vorname: Matr.-Nr.: Studiengang: itte inks und rechts ankreuen! Studienbegeitende Prüfung Ergebnis ins WWW Übungsscheinkausur
. Kausur Mechanik I SS 05, Prof. Dr. V. Popov itte deutich schreiben! Name, Vorname: Matr.-Nr.: Studiengang: itte inks und rechts ankreuen! Studienbegeitende Prüfung Ergebnis ins WWW Übungsscheinkausur
Festigkeitslehre. Aufgaben
 Modurüfung in Technischer Mechanik am 8. März 06 Festigkeitsehre Aufgaben Name: Vorname: Matr.-Nr.: Fachrichtung: Hinweise: Bitte schreiben Sie deutich esbar. Zeichnungen müssen sauber und übersichtich
Modurüfung in Technischer Mechanik am 8. März 06 Festigkeitsehre Aufgaben Name: Vorname: Matr.-Nr.: Fachrichtung: Hinweise: Bitte schreiben Sie deutich esbar. Zeichnungen müssen sauber und übersichtich
Kurs: Statik Thema: Allgemeine Kräftegruppe Bestimmung der Resultierenden F 5
 Kurs: Statik Thema: Allgemeine Kräftegruppe Bestimmung der esultierenden Aufgabe: Belasteter Balken F 5 F 1 F 2 F 3 F 4 F 5 55 110 a a a a a Gegeben: F1 = 20 N F2 = 15 N F3 = 30 N F4 = 10 N F5 = 45 N a
Kurs: Statik Thema: Allgemeine Kräftegruppe Bestimmung der esultierenden Aufgabe: Belasteter Balken F 5 F 1 F 2 F 3 F 4 F 5 55 110 a a a a a Gegeben: F1 = 20 N F2 = 15 N F3 = 30 N F4 = 10 N F5 = 45 N a
C Mathematische Grundlagen
 C Mathematische Grundagen C.1 Summen Mit dem Summenzeichen werden Rechenanweisungen zum Addieren kompakt geschrieben. Sie assen sich oft mit Hife der Summenregen vereinfachen. C.1 Gibt es insgesamt n Werte
C Mathematische Grundagen C.1 Summen Mit dem Summenzeichen werden Rechenanweisungen zum Addieren kompakt geschrieben. Sie assen sich oft mit Hife der Summenregen vereinfachen. C.1 Gibt es insgesamt n Werte
TU Dortmund. Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 3)
 Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 3) a) Ein as masseos anzusehender Baken, bestehend aus einem dünnwandigen U-Profi (t a), ist an der inken Seite eingespannt und wird an seinem rechten
Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 3) a) Ein as masseos anzusehender Baken, bestehend aus einem dünnwandigen U-Profi (t a), ist an der inken Seite eingespannt und wird an seinem rechten
Technische Mechanik III (Dynamik)
 Institut für Mechanische Verfahrenstechnik und Mechanik Bereich Angewandte Mechanik Vorprüfung Technische Mechanik III (Dynamik) Montag, 31.08.009, 9:00 11:00 Uhr Bearbeitungszeit: h Aufgabe 1 (6 Punkte)
Institut für Mechanische Verfahrenstechnik und Mechanik Bereich Angewandte Mechanik Vorprüfung Technische Mechanik III (Dynamik) Montag, 31.08.009, 9:00 11:00 Uhr Bearbeitungszeit: h Aufgabe 1 (6 Punkte)
5.1.5 Pendel = Sinusbewegung ******
 V55 5..5 ****** Motivation Dieser sehr schöne Versuch zeigt, dass die Projektion einer Kreisbewegung eine Sinusbewegung ergibt. Damit deckt sie sich mit einer simutanen Pendebewegung derseben Frequenz.
V55 5..5 ****** Motivation Dieser sehr schöne Versuch zeigt, dass die Projektion einer Kreisbewegung eine Sinusbewegung ergibt. Damit deckt sie sich mit einer simutanen Pendebewegung derseben Frequenz.
Bestimmen Sie für den dargestellten Balken die Auflagerkräfte sowie die N-, Q- und M-Linie (ausgezeichnete Werte sind anzugeben).
 Technische Universität Darmstadt Technische Mechanik I B 13, G Kontinuumsmechanik Wintersemester 007/008 Prof. Dr.-Ing. Ch. Tsakmakis 9. Lösungsblatt Dr. rer. nat. P. Grammenoudis 07. Januar 008 Dipl.-Ing.
Technische Universität Darmstadt Technische Mechanik I B 13, G Kontinuumsmechanik Wintersemester 007/008 Prof. Dr.-Ing. Ch. Tsakmakis 9. Lösungsblatt Dr. rer. nat. P. Grammenoudis 07. Januar 008 Dipl.-Ing.
 Abiturprüfung Mathematik 006 Baden-Württemberg (ohne CAS) Haupttermin Pfichttei - Aufgaben Aufgabe : ( VP) Biden Sie die Abeitung der Funktion f mit f(x) = sin(4x ). 8 Aufgabe : ( VP) Geben Sie eine Stammfunktion
Abiturprüfung Mathematik 006 Baden-Württemberg (ohne CAS) Haupttermin Pfichttei - Aufgaben Aufgabe : ( VP) Biden Sie die Abeitung der Funktion f mit f(x) = sin(4x ). 8 Aufgabe : ( VP) Geben Sie eine Stammfunktion
Mathematische Probleme, SS 2013 Donnerstag $Id: convex.tex,v /10/22 15:58:28 hk Exp $
 $Id: convex.tex,v.2 203/0/22 5:58:28 hk Exp $ 3 Konvexgeometrie 3.2 Die patonischen Körper Ein patonischer Körper von Typ (n, m) ist ein konvexer Poyeder dessen Seitenfäche ae geichseitige n-ecke und in
$Id: convex.tex,v.2 203/0/22 5:58:28 hk Exp $ 3 Konvexgeometrie 3.2 Die patonischen Körper Ein patonischer Körper von Typ (n, m) ist ein konvexer Poyeder dessen Seitenfäche ae geichseitige n-ecke und in
Projektion. Kapitel Bildebene P 2. Sehstrahlen P 1. Projektionszentrum (Augenpunkt) Objekt. Bildebene
 Kapite 14 Projektion 14.1 Bidebene Für die Aneige am weidimensionaen Ausgabegerät muß eine Abbidung (Projektion) der räumichen, dreidimensionaen Sene auf eine weidimensionae Projektionsebene erfogen. Gegeben
Kapite 14 Projektion 14.1 Bidebene Für die Aneige am weidimensionaen Ausgabegerät muß eine Abbidung (Projektion) der räumichen, dreidimensionaen Sene auf eine weidimensionae Projektionsebene erfogen. Gegeben
TU Dortmund. Fakultät Maschinenbau Institut für Mechanik Prof. Dr.-Ing. A. Menzel Prof. Dr.-Ing. J. Mosler. Herbst 2014
 Herbst 2014 Herbst 2014 Aufgabe 1 (Seite 1 von 3) a) Der dargestete, in A und C geagerte Baken wird durch eine Streckenast q 0 sowie eine Einzekraft F beastet. Im Punkt B befindet sich ein Vogeenk. q 0
Herbst 2014 Herbst 2014 Aufgabe 1 (Seite 1 von 3) a) Der dargestete, in A und C geagerte Baken wird durch eine Streckenast q 0 sowie eine Einzekraft F beastet. Im Punkt B befindet sich ein Vogeenk. q 0
0,6 m. 0,4m. Gegeben seien die obigen drei auf den Balken wirkenden Kräfte mit:
 Kurs: Statik Thema: Resultierende bestimmen Aufgabe 1) Wo liegt bei der Berechnung der Resultierenden der Unterschied zwischen Kräften mit einem gemeinsamen Angriffspunkt und Kräften mit unterschiedlichen
Kurs: Statik Thema: Resultierende bestimmen Aufgabe 1) Wo liegt bei der Berechnung der Resultierenden der Unterschied zwischen Kräften mit einem gemeinsamen Angriffspunkt und Kräften mit unterschiedlichen
Theoretische Physik I: Mechanik
 Lösung der Ergänzungsvoresung zu Theoretische Physik I: Mechanik Sommersemester Wofram Weise, Thomas He. Mai Technische Universität München E-Mai (Thomas He) the@h.tum.de Überbick In dieser Zentraübung
Lösung der Ergänzungsvoresung zu Theoretische Physik I: Mechanik Sommersemester Wofram Weise, Thomas He. Mai Technische Universität München E-Mai (Thomas He) the@h.tum.de Überbick In dieser Zentraübung
Interferenz an einer CD
 Interferenz an einer CD Oaf Merkert (Manue Sitter) 18. Dezember 2005 1 Versuchsaufbau Abbidung 1: Versuchsanordnung mit Laser und CD [1] Ein auf einem Tisch aufgesteter Laser mit der Weenänge λ wird im
Interferenz an einer CD Oaf Merkert (Manue Sitter) 18. Dezember 2005 1 Versuchsaufbau Abbidung 1: Versuchsanordnung mit Laser und CD [1] Ein auf einem Tisch aufgesteter Laser mit der Weenänge λ wird im
TU Dortmund. Fakultät Maschinenbau Institut für Mechanik Prof. Dr.-Ing. A. Menzel Prof. Dr.-Ing. J. Mosler. Frühjahr 2016
 Frühjahr 2016 Frühjahr 2016 Aufgabe 1 (Seite 1 von 3) a) Das rechts dargestete System wird durch eine inear veraufende Streckenast (Maximawert q 0 ) beastet. Der Baken weist die Biegesteifigkeit EI und
Frühjahr 2016 Frühjahr 2016 Aufgabe 1 (Seite 1 von 3) a) Das rechts dargestete System wird durch eine inear veraufende Streckenast (Maximawert q 0 ) beastet. Der Baken weist die Biegesteifigkeit EI und
Statik und Tragwerkslehre B
 Bacheor - Studiengang Bauingenieurwesen Prüfungsfach Statik und Tragwerksehre B Kausur am 27.02.2012 Name: Vorname: Matr.-Nr.: (bitte deutich schreiben) (9-steig) Aufgabe 1 2 3 4 Summe mögiche Punkte 15
Bacheor - Studiengang Bauingenieurwesen Prüfungsfach Statik und Tragwerksehre B Kausur am 27.02.2012 Name: Vorname: Matr.-Nr.: (bitte deutich schreiben) (9-steig) Aufgabe 1 2 3 4 Summe mögiche Punkte 15
Berechnung von Wurzeln
 Sieginde Fürst Berechnung von Wurzen Rekursive Fogen Zinseszinsforme; Heronverfahren Inhate Berechnung eines mit Zinsesezins verzinsten Kapitas auf zwei Arten Heronforme Einschranken von Wurzen Ziee Erernen
Sieginde Fürst Berechnung von Wurzen Rekursive Fogen Zinseszinsforme; Heronverfahren Inhate Berechnung eines mit Zinsesezins verzinsten Kapitas auf zwei Arten Heronforme Einschranken von Wurzen Ziee Erernen
Trigonometrie. Mag. DI Rainer Sickinger HTL. v 1 Mag. DI Rainer Sickinger Trigonometrie 1 / 1
 Trigonometrie Mag. DI Rainer Sickinger HTL v 1 Mag. DI Rainer Sickinger Trigonometrie 1 / 1 Definition von Sinus, Cosinus und Tangens am Einheitskreis Im rechtwinkligen Dreieck ist der Winkel zwischen
Trigonometrie Mag. DI Rainer Sickinger HTL v 1 Mag. DI Rainer Sickinger Trigonometrie 1 / 1 Definition von Sinus, Cosinus und Tangens am Einheitskreis Im rechtwinkligen Dreieck ist der Winkel zwischen
Technische Universität Berlin. Abt. I Studierenden Service Studienkolleg / Preparatory Course
 Technische Universität Berin Abt. I Studierenden Service Studienkoeg / Preparatory Course Schriftiche Prüfung zur Feststeung der Eignung ausändischer Studienbewerber zum Hochschustudium im Lande Berin
Technische Universität Berin Abt. I Studierenden Service Studienkoeg / Preparatory Course Schriftiche Prüfung zur Feststeung der Eignung ausändischer Studienbewerber zum Hochschustudium im Lande Berin
Technische Universität Berlin. Abt. I Studierenden Service Studienkolleg / Preparatory Course
 Technische Universität Berin Abt. I Studierenden Service Studienkoeg / Preparatory Course Schriftiche Prüfung zur Feststeung der Eignung ausändischer Studienbewerber zum Hochschustudium im Lande Berin
Technische Universität Berin Abt. I Studierenden Service Studienkoeg / Preparatory Course Schriftiche Prüfung zur Feststeung der Eignung ausändischer Studienbewerber zum Hochschustudium im Lande Berin
Frage 1: ( 2 Punkte) Frage 2: ( 1 Punkte) Frage 3: ( 1 Punkte) Herbst 2009 Seite 1/9
 Gottfried Wihem Leibniz Universität Hnnover Kusur Technische echnik für schinenbu Seite /9 rge : ( Punkte) Geben Sie den voständigen Stz der Geichgewichtsbedingungen für ds D und 3D nichtzentre Kräftesystem
Gottfried Wihem Leibniz Universität Hnnover Kusur Technische echnik für schinenbu Seite /9 rge : ( Punkte) Geben Sie den voständigen Stz der Geichgewichtsbedingungen für ds D und 3D nichtzentre Kräftesystem
a) Wie hoch ist die Leiter? b) Wie weit stehen die beiden Fußpunkte auseinander? Abbildung 1: Eine Stehleiter
 1. Berechnen Sie die jeweils fehlenden Größen (Winkel α, β und γ, Seiten a, b und c) in den folgenden Dreiecken: a) a = 5 cm, b = 9 cm, γ = 90 b) c = 9 cm, a = 6 cm, γ = 56, 3 (Überlegen Sie zuerst, wo
1. Berechnen Sie die jeweils fehlenden Größen (Winkel α, β und γ, Seiten a, b und c) in den folgenden Dreiecken: a) a = 5 cm, b = 9 cm, γ = 90 b) c = 9 cm, a = 6 cm, γ = 56, 3 (Überlegen Sie zuerst, wo
HLW Graz. 2. Schularbeit 1HL[ Gc 2 ] 6. April Angewandte Mathematik
![HLW Graz. 2. Schularbeit 1HL[ Gc 2 ] 6. April Angewandte Mathematik HLW Graz. 2. Schularbeit 1HL[ Gc 2 ] 6. April Angewandte Mathematik](/thumbs/63/48987233.jpg) Sa 2 2. Schularbeit 1HL[ Gc 2 ] 6. April 2011 Md 2 A 1. Forme die Gleichung p V = R s T nach T um (Gesetz von Gay-Lussac, mit p = Druck, V = Volumen, R s ist die Gaskonstante und T die Temperatur in Kelvin)!
Sa 2 2. Schularbeit 1HL[ Gc 2 ] 6. April 2011 Md 2 A 1. Forme die Gleichung p V = R s T nach T um (Gesetz von Gay-Lussac, mit p = Druck, V = Volumen, R s ist die Gaskonstante und T die Temperatur in Kelvin)!
Biegelinie: PSfrag replacements. I : w I (x) = q 1l 4 [( x. II : w II (x) = (q 2 q 1 )l 4 [ ( x. ges (x) = w I (x) + w II (x) (19) l 24 + q x 3 )
 Mechanik I Prof. Popov SS 05, 9. Woche Lösungshinweise Seite Biegeinienberechnung statisch bestimmter und unbestimmter Systeme Version. Juni 005 aus schanken Baken Aufgabe 9 a PSfrag repacements qx = q
Mechanik I Prof. Popov SS 05, 9. Woche Lösungshinweise Seite Biegeinienberechnung statisch bestimmter und unbestimmter Systeme Version. Juni 005 aus schanken Baken Aufgabe 9 a PSfrag repacements qx = q
Der Satz des Pythagoras
 Der Satz des Pythagoras Das rechtwinklige Dreieck Jedes rechtwinklige Dreieck besitzt eine Hypotenuse (c), das ist die längste Seite des Dreiecks (bzw. diejenige gegenüber dem rechten Winkel). Die anderen
Der Satz des Pythagoras Das rechtwinklige Dreieck Jedes rechtwinklige Dreieck besitzt eine Hypotenuse (c), das ist die längste Seite des Dreiecks (bzw. diejenige gegenüber dem rechten Winkel). Die anderen
1. Ebene gerade Balken
 1. Ebene gerade Balken Betrachtet werden gerade Balken, die nur in der -Ebene belastet werden. Prof. Dr. Wandinger 4. Schnittlasten bei Balken TM 1 4.1-1 1. Ebene gerade Balken 1.1 Schnittlasten 1.2 Balken
1. Ebene gerade Balken Betrachtet werden gerade Balken, die nur in der -Ebene belastet werden. Prof. Dr. Wandinger 4. Schnittlasten bei Balken TM 1 4.1-1 1. Ebene gerade Balken 1.1 Schnittlasten 1.2 Balken
a) Das dargestellte Fachwerk ist in den Punkten A und B gelagert und wird, wie dargestellt, durch drei Einzelkräfte belastet. L 1
 Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 2) a) Das dargestete Fachwerk ist in den Punkten A und B geagert und wird, wie
Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 2) a) Das dargestete Fachwerk ist in den Punkten A und B geagert und wird, wie
Musterlösungen (ohne Gewähr)
 Seite 1/14 Frage 1 ( Punkte) Geben Sie die Fächenträgheitsmomente beügich der y- und der -Achse an! a a a Gegeben: a. y a I yy = I = Fächenträgheitsmoment beügich der y-achse: ( ) I yy = aa a(a) 1 + =
Seite 1/14 Frage 1 ( Punkte) Geben Sie die Fächenträgheitsmomente beügich der y- und der -Achse an! a a a Gegeben: a. y a I yy = I = Fächenträgheitsmoment beügich der y-achse: ( ) I yy = aa a(a) 1 + =
Prüfung in Methode der finiten Elemente. Matrikelnummer: Studiengang: Wiederholer
 Universität Stuttgart INSTITUT MECH NIK FUR Prüfung in Methode der finiten Eemente Name, Vorname: Matrikenummer: Studiengang: Wiederhoer Emai: Unterschrift: Hauptfach: Bitte beachten Sie Fogendes: 1. Es
Universität Stuttgart INSTITUT MECH NIK FUR Prüfung in Methode der finiten Eemente Name, Vorname: Matrikenummer: Studiengang: Wiederhoer Emai: Unterschrift: Hauptfach: Bitte beachten Sie Fogendes: 1. Es
Aufgaben mit Lösungen zum Themengebiet: Geometrie bei rechtwinkligen Dreiecken
 Übungsaufgaben zur Satzgruppe des Pythagoras: 1) Seiten eines rechtwinkligen Dreiecks Sind folgende Aussagen richtig oder falsch? Verbessere, wenn notwendig! Die Katheten grenzen an den rechten Winkel.
Übungsaufgaben zur Satzgruppe des Pythagoras: 1) Seiten eines rechtwinkligen Dreiecks Sind folgende Aussagen richtig oder falsch? Verbessere, wenn notwendig! Die Katheten grenzen an den rechten Winkel.
Sessionsprüfung Baustatik I+II. Winter 2008/09. Montag, 26. Januar 2009, Uhr, HIL E7
 Sessionsprüfung austatik I+II Winter 2008/09 Montag, 26. Januar 2009, 09.00 12.00 Uhr, HIL E7 Name, Vorname : Studenten-Nr. : emerkungen 1. e ufgaben haben das geiche Gewicht. 2. Die ufgaben dürfen in
Sessionsprüfung austatik I+II Winter 2008/09 Montag, 26. Januar 2009, 09.00 12.00 Uhr, HIL E7 Name, Vorname : Studenten-Nr. : emerkungen 1. e ufgaben haben das geiche Gewicht. 2. Die ufgaben dürfen in
TU Dortmund. Vorname: Nachname: Matr.-Nr.:
 Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Aufgabe 1 (Seite 1 von 3) a) Die nebenstehend skizzierte, inks eingespannte Konsoe wird wie dargestet durch Traktionen (eingeprägte
Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Aufgabe 1 (Seite 1 von 3) a) Die nebenstehend skizzierte, inks eingespannte Konsoe wird wie dargestet durch Traktionen (eingeprägte
3.6 Einführung in die Vektorrechnung
 3.6 Einführung in die Vektorrechnung Inhaltsverzeichnis Definition des Vektors 2 2 Skalare Multiplikation und Kehrvektor 4 3 Addition und Subtraktion von Vektoren 5 3. Addition von zwei Vektoren..................................
3.6 Einführung in die Vektorrechnung Inhaltsverzeichnis Definition des Vektors 2 2 Skalare Multiplikation und Kehrvektor 4 3 Addition und Subtraktion von Vektoren 5 3. Addition von zwei Vektoren..................................
Selbsteinschätzungstest Auswertung und Lösung
 Selbsteinschätzungstest Auswertung und Lösung Abgaben: 46 / 587 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: Durchschnitt: 7 Frage (Diese Frage haben ca. 0% nicht beantwortet.) Welcher Vektor
Selbsteinschätzungstest Auswertung und Lösung Abgaben: 46 / 587 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: Durchschnitt: 7 Frage (Diese Frage haben ca. 0% nicht beantwortet.) Welcher Vektor
Statik und Tragwerkslehre B
 Bacheor - Studiengang Bauingenieurwesen Prüfungsfach Statik und Tragwerksehre B Kausur am 29.08.2011 Name: Vorname: Matr.-Nr.: (bitte deutich schreiben) (9-steig) Aufgabe 1 2 3 4 Summe mögiche Punkte 15
Bacheor - Studiengang Bauingenieurwesen Prüfungsfach Statik und Tragwerksehre B Kausur am 29.08.2011 Name: Vorname: Matr.-Nr.: (bitte deutich schreiben) (9-steig) Aufgabe 1 2 3 4 Summe mögiche Punkte 15
TU Dortmund. Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 3)
 akutät Maschinenbau Prof. Dr.-Ing.. Menze Prof. Dr.-Ing. J. Moser ufgabe 1 (Seite 1 von 3) Das dargestete achwerk ist in den Punkten und geagert und wird durch vier unterschiediche Einzekräfte, 1, 2, 3
akutät Maschinenbau Prof. Dr.-Ing.. Menze Prof. Dr.-Ing. J. Moser ufgabe 1 (Seite 1 von 3) Das dargestete achwerk ist in den Punkten und geagert und wird durch vier unterschiediche Einzekräfte, 1, 2, 3
Finite-Elemente-Methode
 11. Übung Prof. Dr.-Ing. W. Fischer Fachhochschue Dortmund Knicken und Beuen 1. Bestimmen Sie sowoh anaytisch wie auch mit Hife des FEM-Systems HyperWorks 14 für einen Stah-Kragträger der Länge = 1 m (quadratischer
11. Übung Prof. Dr.-Ing. W. Fischer Fachhochschue Dortmund Knicken und Beuen 1. Bestimmen Sie sowoh anaytisch wie auch mit Hife des FEM-Systems HyperWorks 14 für einen Stah-Kragträger der Länge = 1 m (quadratischer
Lösungen zu den. Übungsaufgaben. Höhere Festigkeitslehre
 akutät 3 zu den Übungsaufgaben Wintersemester 4/5 Dr. C. Katzenschwanz festigkeit.userweb.mwn.de Die mit( ) gekennzeichneten Aufgaben sind ehemaige Prüfungsaufgaben. Version.5 Wintersemester 4/5 8. Oktober
akutät 3 zu den Übungsaufgaben Wintersemester 4/5 Dr. C. Katzenschwanz festigkeit.userweb.mwn.de Die mit( ) gekennzeichneten Aufgaben sind ehemaige Prüfungsaufgaben. Version.5 Wintersemester 4/5 8. Oktober
Vortest zur Ingenieurmathematik
 Vortest zur Ingenieurmathematik Liebe Studienanfängerinnen und Studienanfänger! Sie haben sich für einen ingenieurwissenschaftlichen Studiengang entschieden. Ein wichtiges Rüstzeug für ein erfolgreiches
Vortest zur Ingenieurmathematik Liebe Studienanfängerinnen und Studienanfänger! Sie haben sich für einen ingenieurwissenschaftlichen Studiengang entschieden. Ein wichtiges Rüstzeug für ein erfolgreiches
Schnittgrößen und Vorzeichenkonvention
 Schnittgrößen und Vorzeichenkonvention Die äußeren Kräfte (Belastungen) auf einem Tragwerk verursachen innere Kräfte in einem Tragwerk. Da diese inneren Kräfte nur durch ein Freischneiden veranschaulicht
Schnittgrößen und Vorzeichenkonvention Die äußeren Kräfte (Belastungen) auf einem Tragwerk verursachen innere Kräfte in einem Tragwerk. Da diese inneren Kräfte nur durch ein Freischneiden veranschaulicht
4. Das (symmetrische) - im Querschnitt dreieckige - Dach eines Hauses ist 3,50 Meter
 1. Eine 7 Meter lange Leiter lehnt an einer Hauswand. Sie schließt mit dem Boden eine Winkel von 70 ein. a) In welcher Höhe lehnt die Leiter an der Wand? b) Wie weit ist der Fußpunkt der Leiter von der
1. Eine 7 Meter lange Leiter lehnt an einer Hauswand. Sie schließt mit dem Boden eine Winkel von 70 ein. a) In welcher Höhe lehnt die Leiter an der Wand? b) Wie weit ist der Fußpunkt der Leiter von der
1.12 Einführung in die Vektorrechung
 . Einführung in die Vektorrechung Inhaltsverzeichnis Definition des Vektors Skalare Multiplikation und Kehrvektor 3 3 Addition und Subtraktion von Vektoren 3 3. Addition von zwei Vektoren..................................
. Einführung in die Vektorrechung Inhaltsverzeichnis Definition des Vektors Skalare Multiplikation und Kehrvektor 3 3 Addition und Subtraktion von Vektoren 3 3. Addition von zwei Vektoren..................................
2. Statisch bestimmte Systeme
 1 von 14 2. Statisch bestimmte Systeme 2.1 Definition Eine Lagerung nennt man statisch bestimmt, wenn die Lagerreaktionen (Kräfte und Momente) allein aus den Gleichgewichtsbedingungen bestimmbar sind.
1 von 14 2. Statisch bestimmte Systeme 2.1 Definition Eine Lagerung nennt man statisch bestimmt, wenn die Lagerreaktionen (Kräfte und Momente) allein aus den Gleichgewichtsbedingungen bestimmbar sind.
2. Schularbeit 1HL 13. April 2012
 2. Schularbeit 1HL 13. April 2012 1. a) Kreuzen Sie an, ob die Abbildung den Graphen einer Funktion x y zeigt und begru nden Sie Ihre Entscheidung! ist Graph einer Funktion ist nicht Graph einer Funktion
2. Schularbeit 1HL 13. April 2012 1. a) Kreuzen Sie an, ob die Abbildung den Graphen einer Funktion x y zeigt und begru nden Sie Ihre Entscheidung! ist Graph einer Funktion ist nicht Graph einer Funktion
1 PdvV für ein System aus starren Körpern
 Materiatheorie - LKM, Sekr. MS PdvV und PdvK Energiemethoden 06. Übungsbatt, WS 01/13, S. 1 1 PdvV für ein System aus starren Körpern Zur Bestimmung der fünf gesuchten Lagerreaktionen muss das System auf
Materiatheorie - LKM, Sekr. MS PdvV und PdvK Energiemethoden 06. Übungsbatt, WS 01/13, S. 1 1 PdvV für ein System aus starren Körpern Zur Bestimmung der fünf gesuchten Lagerreaktionen muss das System auf
Ermitteln Sie die Koordinaten des Schnittpunktes dieser beiden Geraden und erklären Sie Ihre Vorgehensweise!
 Aufgabe 2 Lagebeziehungen von Geraden im Raum Gegeben sind zwei Geraden g und h in 3. =( 3 Die Gerade g ist durch eine Parameterdarstellung X 4 2 Die Gerade h verläuft durch die Punkte A = (0 8 0 und B
Aufgabe 2 Lagebeziehungen von Geraden im Raum Gegeben sind zwei Geraden g und h in 3. =( 3 Die Gerade g ist durch eine Parameterdarstellung X 4 2 Die Gerade h verläuft durch die Punkte A = (0 8 0 und B
FH Gießen-Friedberg, FB 06 (MNI) Lösungen zu Übungsblatt 8 Einführung in die höhere Mathematik 6. Dezember 2006 Prof. Dr. H.-R.
 FH Gießen-Friedberg, FB 06 (MNI) Lösungen zu Übungsblatt 8 Einführung in die höhere Mathematik 6. Dezember 006 Prof. Dr. H.-R. Metz Aufgabe 1 Skizzieren Sie die Funktionen e x, ln(x) = log e (x) und e
FH Gießen-Friedberg, FB 06 (MNI) Lösungen zu Übungsblatt 8 Einführung in die höhere Mathematik 6. Dezember 006 Prof. Dr. H.-R. Metz Aufgabe 1 Skizzieren Sie die Funktionen e x, ln(x) = log e (x) und e
1. Temperaturabhängige Widerstände
 V e r s u c h. Temperaturabhängige Widerstände. Einführung Im Technikbereich finden oft Prozesse statt, bei denen die Messung, Steuerung und egeung von Temperaturen eine wichtige oe spieen. Temperaturabhängige
V e r s u c h. Temperaturabhängige Widerstände. Einführung Im Technikbereich finden oft Prozesse statt, bei denen die Messung, Steuerung und egeung von Temperaturen eine wichtige oe spieen. Temperaturabhängige
KIT SS Klassische Theoretische Physik II. V: Prof. Dr. M. Mühlleitner, Ü: Dr. M. Rauch. Klausur 2 Lösung. 11. Oktober 2012, Uhr
 KIT SS 1 Kassische Theoretische Physik II : Prof. Dr. M. Müheitner, Ü: Dr. M. Rauch Kausur Lösung 11. Oktober 1, 8-1 Uhr Aufgabe 1: Kurzfragen 4+4+=1 Punkte a Die Transformationen und zugehörigen Erhatungsgrößen
KIT SS 1 Kassische Theoretische Physik II : Prof. Dr. M. Müheitner, Ü: Dr. M. Rauch Kausur Lösung 11. Oktober 1, 8-1 Uhr Aufgabe 1: Kurzfragen 4+4+=1 Punkte a Die Transformationen und zugehörigen Erhatungsgrößen
Fourierreihenentwicklung Prof. K. Weinberg Universität Siegen Lehrstuhl für Festkörpermechanik
 Fourierreihenentwickung Prof. K. Weinberg Universität Siegen Lehrstuh für Festkörpermechanik Mathematische Grundagen für Einfachreihenentwickungen Für viee mathematische, physikaische und technische Probeme
Fourierreihenentwickung Prof. K. Weinberg Universität Siegen Lehrstuh für Festkörpermechanik Mathematische Grundagen für Einfachreihenentwickungen Für viee mathematische, physikaische und technische Probeme
Lineare Funktionen. Das rechtwinklige (kartesische) Koordinatensystem. Funktionen
 Das rechtwinklige (kartesische) Koordinatensystem Funktionen Funktion: Eine Funktion ist eine eindeutige Zuordnung. Jedem x D wird genau eine reelle Zahl zugeordnet. Schreibweise: Funktion: f: x f (x)
Das rechtwinklige (kartesische) Koordinatensystem Funktionen Funktion: Eine Funktion ist eine eindeutige Zuordnung. Jedem x D wird genau eine reelle Zahl zugeordnet. Schreibweise: Funktion: f: x f (x)
b) Von welchen Parametern hängen die Eigenschwingungsfrequenzen ab?
 Techn. Mechanik & Fahrzeugdynamik TM III Prof. Dr.-Ing. habi. Hon. Prof. (NUST) D. Beste 4. März 17 Prüfungskausur Technische Mechanik III Famiienname, Vorname Matrike-Nummer Fachrichtung Aufgabe 1 (9
Techn. Mechanik & Fahrzeugdynamik TM III Prof. Dr.-Ing. habi. Hon. Prof. (NUST) D. Beste 4. März 17 Prüfungskausur Technische Mechanik III Famiienname, Vorname Matrike-Nummer Fachrichtung Aufgabe 1 (9
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck
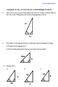 Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Aufgabe 1: Gegeben ist das dargestellte statische System, das aus einer starren Stange und zwei Fachwerkstäben (Dehnsteifigkeit EA ) besteht.
 ufgabe : Gegeben ist das dargestete statische System, das aus einer starren Stange und zwei achwerkstäben (Dehnsteifigkeit E ) besteht. starr B Bestimmen Sie die kritische Knickast krit für das dargestete
ufgabe : Gegeben ist das dargestete statische System, das aus einer starren Stange und zwei achwerkstäben (Dehnsteifigkeit E ) besteht. starr B Bestimmen Sie die kritische Knickast krit für das dargestete
Mathematik I Pflichtteil - Nachtermin Aufgabe P 1. Klasse: Platzziffer: Punkte:
 Prüfungsdauer: Abschlussprüfung 2006 150 Minuten an den Realschulen in Bayern R4/R6 Mathematik I Pflichtteil - Nachtermin Aufgabe P 1 Name: Vorname: Klasse: Platzziffer: Punkte: P 1.0 Gegeben sind der
Prüfungsdauer: Abschlussprüfung 2006 150 Minuten an den Realschulen in Bayern R4/R6 Mathematik I Pflichtteil - Nachtermin Aufgabe P 1 Name: Vorname: Klasse: Platzziffer: Punkte: P 1.0 Gegeben sind der
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Abschluss Realschule Bayern Lösungen
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Abschluss 2018 - Realschule Bayern Lösungen Das komplette Material finden Sie hier: School-Scout.de Inhaltsverzeichnis Mathematik
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Abschluss 2018 - Realschule Bayern Lösungen Das komplette Material finden Sie hier: School-Scout.de Inhaltsverzeichnis Mathematik
Aufgabe 1 (7 Punkte) Prüfungsklausur Technische Mechanik II. v A im Punkt A die Geschwindigkei-
 Techn. Mechanik & Fahrzeugdynamik TM II Prof. Dr.-Ing. habi. Hon. Prof. (NUST) D. Beste. März 7 Prüfungskausur Technische Mechanik II Famiienname, Vorname Aufgabe (7 Punkte) Eine Grubenpumpe aus dem Bergbaumuseum
Techn. Mechanik & Fahrzeugdynamik TM II Prof. Dr.-Ing. habi. Hon. Prof. (NUST) D. Beste. März 7 Prüfungskausur Technische Mechanik II Famiienname, Vorname Aufgabe (7 Punkte) Eine Grubenpumpe aus dem Bergbaumuseum
Trigonometrie. In der Abbildung: der Winkel 120 (Gradenmaß) ist 2π = 2π (Bogenmaß).
 Trigonometrie. Winkel: Gradmaß oder Bogenmaß In der Schule lernt man, dass Winkel im Gradmass, also als Zahlen zwischen 0 und 60 Grad angegeben werden. In der Mathematik arbeitet man lieber mit dem Bogenmaß,
Trigonometrie. Winkel: Gradmaß oder Bogenmaß In der Schule lernt man, dass Winkel im Gradmass, also als Zahlen zwischen 0 und 60 Grad angegeben werden. In der Mathematik arbeitet man lieber mit dem Bogenmaß,
BAUSTATIK II KOLLOQUIUM 2, Lösung
 BAUSTATIK II KOLLOQUIU, Lösung (11-114) Thema: Verformungsmethode Aufgabe 1, Lösung Gegeben: System (, EI konstant, c f ), Einwirkungen EI Gesucht: Schnittkraftinien q q und T 6EI n 1 Verformungen quaitativ:
BAUSTATIK II KOLLOQUIU, Lösung (11-114) Thema: Verformungsmethode Aufgabe 1, Lösung Gegeben: System (, EI konstant, c f ), Einwirkungen EI Gesucht: Schnittkraftinien q q und T 6EI n 1 Verformungen quaitativ:
Bewegung geladener Teilchen in elektrischen Feldern; homogenes Feld, Zentralfeld
 1111 Bewegung geadener Teichen in eektrischen Federn; homogenes Fed, Zentrafed Bewegung in homogenen Federn Geadene Teichen erfahren in eektrischen Federn Kräfte; diese bewirken nach dem 2 Newton-Gesetz
1111 Bewegung geadener Teichen in eektrischen Federn; homogenes Fed, Zentrafed Bewegung in homogenen Federn Geadene Teichen erfahren in eektrischen Federn Kräfte; diese bewirken nach dem 2 Newton-Gesetz
Herzlich willkommen zur Demo der mathepower.de Aufgabensammlung
 Herzlich willkommen zur der Um sich schnell innerhalb der ca. 350.000 Mathematikaufgaben zu orientieren, benutzen Sie unbedingt das Lesezeichen Ihres Acrobat Readers: Das Icon finden Sie in der links stehenden
Herzlich willkommen zur der Um sich schnell innerhalb der ca. 350.000 Mathematikaufgaben zu orientieren, benutzen Sie unbedingt das Lesezeichen Ihres Acrobat Readers: Das Icon finden Sie in der links stehenden
1 GRUNDLAGEN 1.4 Massvorsätze und Zehnerpotenzen
 GRUNDLAGEN.4 Massvorsätze und Zehnerpotenzen.4. Zehnerpotenzen Kommt in einem Produkt immer derselbe Faktor vor, so schreibt man das Produkt in der Potenzschreibweise. Zahlen in der Form 0 5 heissen Zehnerpotenzen.
GRUNDLAGEN.4 Massvorsätze und Zehnerpotenzen.4. Zehnerpotenzen Kommt in einem Produkt immer derselbe Faktor vor, so schreibt man das Produkt in der Potenzschreibweise. Zahlen in der Form 0 5 heissen Zehnerpotenzen.
TECHNISCHE MECHANIK A (STATIK)
 Probeklausur im Fach TECHNISCHE MECHANIK A (STATIK) Nr. 5 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 3 4 5 6 Summe Punkte: 31 7,5 17,5 9 10 5 80 Davon erreicht Punkte: Gesamtergebnis
Probeklausur im Fach TECHNISCHE MECHANIK A (STATIK) Nr. 5 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 3 4 5 6 Summe Punkte: 31 7,5 17,5 9 10 5 80 Davon erreicht Punkte: Gesamtergebnis
(von Punkt A nach Punkt B) gemessen und auch die entsprechenden Zenitwinkel z B
 Aufgabe a.1 Verwendet dieses elementare geometrische Verhältnis der Strecken, um die Höhe eines Turmes oder eines sonstigen hohen Gebäudes in eurer Nähe zu bestimmen. Dokumentiert euer Experiment. Wiederholt
Aufgabe a.1 Verwendet dieses elementare geometrische Verhältnis der Strecken, um die Höhe eines Turmes oder eines sonstigen hohen Gebäudes in eurer Nähe zu bestimmen. Dokumentiert euer Experiment. Wiederholt
bzw. m 2 sowie zwei Federn und einem viskosen Dämpfer. die Eigenfrequenz des Systems für die Drehschwingung um den Punkt A und starr 3, 0 m
 MODULPRÜFUNG BAUDYNAMIK 09.0.015 Aufgabe 1 Der nachfogend dargestete Einmassenschwinger so untersucht werden. Das System besteht aus einem starren Baken mit den bereichsweise konstanten Massen m 1 bzw.
MODULPRÜFUNG BAUDYNAMIK 09.0.015 Aufgabe 1 Der nachfogend dargestete Einmassenschwinger so untersucht werden. Das System besteht aus einem starren Baken mit den bereichsweise konstanten Massen m 1 bzw.
1 Einleitung. 2 Sinus. Trigonometrie
 1 Einleitung Die Trigonometrie (trigonon - griechisch für Dreieck) und die trigonometrischen Funktionen sind wichtige mathematische Werkzeuge zur Beschreibung der Natur. In der Physik werden trigonometrische
1 Einleitung Die Trigonometrie (trigonon - griechisch für Dreieck) und die trigonometrischen Funktionen sind wichtige mathematische Werkzeuge zur Beschreibung der Natur. In der Physik werden trigonometrische
Die Oberfläche der Verpackung besteht aus sechs Teilen: 2 Trapeze (vorne und hinten), und 4 Rechtecke.
 Aufgabe 1a) Schritt 1: Oberflächenformel aufstellen Gesucht ist die Oberfläche des Prismas. Das heißt, 2, mit G als Grundfläche und M als Mantel. Die Oberfläche der Verpackung besteht aus sechs Teilen:
Aufgabe 1a) Schritt 1: Oberflächenformel aufstellen Gesucht ist die Oberfläche des Prismas. Das heißt, 2, mit G als Grundfläche und M als Mantel. Die Oberfläche der Verpackung besteht aus sechs Teilen:
27. Vorlesung Wintersemester
 27. Voresung Wintersemester 1 Nichtineare Dynamik: Agemeines Eine wichtige neue Erkenntnis zur kassischen Mechanik, die erst durch die Verwendung von Computern mögich war, ist die verbüffende Kompexität
27. Voresung Wintersemester 1 Nichtineare Dynamik: Agemeines Eine wichtige neue Erkenntnis zur kassischen Mechanik, die erst durch die Verwendung von Computern mögich war, ist die verbüffende Kompexität
F = m g sin. = sin dt l l = Pendellänge ( vom Aufhängepunkt bis zum Mittelpunkt der Kugel)
 S1 Mathematisches und physikaisches Pende Stoffgebiet: Versuchszie: Literatur: Schwingungen agemein, mathematisches Pende, physikaisches Pende, Steinerscher Satz Mathematische Behandung von Schwingungsvorgängen
S1 Mathematisches und physikaisches Pende Stoffgebiet: Versuchszie: Literatur: Schwingungen agemein, mathematisches Pende, physikaisches Pende, Steinerscher Satz Mathematische Behandung von Schwingungsvorgängen
Vorwort. Raimond Dallmann. Baustatik 2. Berechnung statisch unbestimmter Tragwerke ISBN:
 Vorwort Raimond Damann Baustatik Berechnung statisch unbestimmter Tragwerke ISBN: 97--446-4199- Weitere Informationen oder Besteungen unter http://www.hanser.de/97--446-4199- sowie im Buchhande. Car Hanser
Vorwort Raimond Damann Baustatik Berechnung statisch unbestimmter Tragwerke ISBN: 97--446-4199- Weitere Informationen oder Besteungen unter http://www.hanser.de/97--446-4199- sowie im Buchhande. Car Hanser
Lage zweier Ebenen. Suche alle Punkte von E 1 die in E 2 enthalten sind. Setze also die Parameterform von E 1 in die Koordinatenform von E 2.
 LAGE Lage zweier Ebenen Suche alle Punkte von E die in E 2 enthalten sind. Setze also die Parameterform von E in die Koordinatenform von E 2. B = E : X E 2 : x + x 2 + x 3 = Parameterform (PF) in Koordinatenform
LAGE Lage zweier Ebenen Suche alle Punkte von E die in E 2 enthalten sind. Setze also die Parameterform von E in die Koordinatenform von E 2. B = E : X E 2 : x + x 2 + x 3 = Parameterform (PF) in Koordinatenform
Lösungsvorschlag Serie 1
 D-HEST Dr. A. Caspar Prof. N. Hungerbüher Mathematik III HS 2016 Lösungsvorschag Serie 1 1. Dicker Pui - bad kommt der Winter Um eine Körpertemperatur von T M = 37 C auch bei küherem Wetter haten zu können,
D-HEST Dr. A. Caspar Prof. N. Hungerbüher Mathematik III HS 2016 Lösungsvorschag Serie 1 1. Dicker Pui - bad kommt der Winter Um eine Körpertemperatur von T M = 37 C auch bei küherem Wetter haten zu können,
A] 40 % + 25 % + 12,5 % B] 30 % + 50 % + 16,6 %
![A] 40 % + 25 % + 12,5 % B] 30 % + 50 % + 16,6 % A] 40 % + 25 % + 12,5 % B] 30 % + 50 % + 16,6 %](/thumbs/55/35914069.jpg) 5 Prozentrechnen Übung 50 Der ganze Streifen entspricht 100 % = 1 000 = 1. Welche Prozent- und Promillesätze stellen die unterschiedlich getönten Flächen dar? Abb. 27 1. 2. 3. Übung 51 Der volle Winkel
5 Prozentrechnen Übung 50 Der ganze Streifen entspricht 100 % = 1 000 = 1. Welche Prozent- und Promillesätze stellen die unterschiedlich getönten Flächen dar? Abb. 27 1. 2. 3. Übung 51 Der volle Winkel
2. Schularbeit 2HLMd 8. Mai 2013
 10 12 Punkte: Befriedigend 15 16 Punkte: Sehr gut HLW Graz Angewandte Mathematik 2. Schularbeit 2HLMd 8. Mai 201 1. In einem Haus soll ein Treppenlift errichtet werden. a) Stufenho he und Stufenbreite
10 12 Punkte: Befriedigend 15 16 Punkte: Sehr gut HLW Graz Angewandte Mathematik 2. Schularbeit 2HLMd 8. Mai 201 1. In einem Haus soll ein Treppenlift errichtet werden. a) Stufenho he und Stufenbreite
2 Schwerpunktslehre. Flächenschwerpunkt mm. 8,65 mm. 125,25 mm 1906 mm. 15,22 mm ,36 cm. y0 = = = = cm.
 Schwerpuktsehre Fächeschwerpukt 01. [cm ] y [cm] y [cm ] 1 9 0,9 8,1 7, 05 4,15 9, 6 16, 05 Σ y 7,6 y0 1 y1 + y Σ y Σ y 7,6 cm y0,8 cm,8 mm 16,05 cm 0. [cm ] y [cm] y [cm ] 1 50 1 50 67,8 0, 5 051 60 59,
Schwerpuktsehre Fächeschwerpukt 01. [cm ] y [cm] y [cm ] 1 9 0,9 8,1 7, 05 4,15 9, 6 16, 05 Σ y 7,6 y0 1 y1 + y Σ y Σ y 7,6 cm y0,8 cm,8 mm 16,05 cm 0. [cm ] y [cm] y [cm ] 1 50 1 50 67,8 0, 5 051 60 59,
2. Stabilitätsprobleme und Theorie II. Ordnung
 Baustatik WS 212/213 2. Stabiitätsprobeme und Theorie II. Ordnung 2.6 Berücksichtigung der geometrischen Imperfektionen Imperfektionen Bisher: Annahme der perfekten Tragwerke und des perfekten Bauprozesses!
Baustatik WS 212/213 2. Stabiitätsprobeme und Theorie II. Ordnung 2.6 Berücksichtigung der geometrischen Imperfektionen Imperfektionen Bisher: Annahme der perfekten Tragwerke und des perfekten Bauprozesses!
Darstellende Geometrie Übungen. Tutorial zu Übungsblatt: Schatten in Axonometrie
 Tutoria zu Übungsbatt: Schatten in Axonometrie BEISIEL Schatten des otrechten Stabes durch auf der waagrechten Grundebene:. Um diesen Schatten zu finden wird der Lichtstrah L durch den unkt und der Grundrissichtstrah
Tutoria zu Übungsbatt: Schatten in Axonometrie BEISIEL Schatten des otrechten Stabes durch auf der waagrechten Grundebene:. Um diesen Schatten zu finden wird der Lichtstrah L durch den unkt und der Grundrissichtstrah
Statik und Tragwerkslehre B
 UMWELTINGENIEURWISSENSCHATEN, STATIK UND DYNAMIK Bacheor - Studiengang Bauingenieurwesen Prüfungsfach Statik und Tragwerksehre B Kausur am 21.02.2011 Name: Vorname: Matr.-Nr.: (bitte deutich schreiben)
UMWELTINGENIEURWISSENSCHATEN, STATIK UND DYNAMIK Bacheor - Studiengang Bauingenieurwesen Prüfungsfach Statik und Tragwerksehre B Kausur am 21.02.2011 Name: Vorname: Matr.-Nr.: (bitte deutich schreiben)
Algebra Für welche reellen Zahlen m hat das folgende Gleichungssystem nur die triviale
 Algebra 1 www.schulmathe.npage.de Aufgaben 1. Für welche reellen Zahlen m hat das folgende Gleichungssystem nur die triviale Lösung? x + y + mz = 0 mx y + z = 0 x + y + z = 0. Welche Punkte P z der z-achse
Algebra 1 www.schulmathe.npage.de Aufgaben 1. Für welche reellen Zahlen m hat das folgende Gleichungssystem nur die triviale Lösung? x + y + mz = 0 mx y + z = 0 x + y + z = 0. Welche Punkte P z der z-achse
Rechnen mit Vektoren. 1. Vektoren im Koordinatensystem Freie Vektoren in der Ebene
 Rechnen mit 1. im Koordinatensystem 1.1. Freie in der Ebene 1) Definition Ein Vektor... Zwei sind gleich, wenn... 2) Das ebene Koordinatensystem Wir legen den Koordinatenursprung fest, ferner zwei zueinander
Rechnen mit 1. im Koordinatensystem 1.1. Freie in der Ebene 1) Definition Ein Vektor... Zwei sind gleich, wenn... 2) Das ebene Koordinatensystem Wir legen den Koordinatenursprung fest, ferner zwei zueinander
Realschule Abschlussprüfung
 Realschule Abschlussprüfung Annegret Sonntag 4. Januar 2010 Inhaltsverzeichnis 1 Strategie zur Berechnung von ebenen Figuren (Trigonometrie) 3 1.1 Skizze.................................................
Realschule Abschlussprüfung Annegret Sonntag 4. Januar 2010 Inhaltsverzeichnis 1 Strategie zur Berechnung von ebenen Figuren (Trigonometrie) 3 1.1 Skizze.................................................
Mathematik Name: Nr.4 K1 Punkte: /32 Note: Schnitt:
 Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden dürfen.) Aufgabe 1:[P] Bestimmen
Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden dürfen.) Aufgabe 1:[P] Bestimmen
Rechtwinklige Dreiecke konstruieren
 1 Vertiefen 1 Rechtwinklige Dreiecke konstruieren zu Aufgabe Schulbuch, Seite 106 Dreiecke konstruieren a) Konstruiere die Dreiecke mit den Angaben aus der Tabelle. Miss dann die übrigen Maße und vervollständige
1 Vertiefen 1 Rechtwinklige Dreiecke konstruieren zu Aufgabe Schulbuch, Seite 106 Dreiecke konstruieren a) Konstruiere die Dreiecke mit den Angaben aus der Tabelle. Miss dann die übrigen Maße und vervollständige
