Hesse-Normalform einer Ebene

Transkript

1 Hesse-Normalform einer Ebene Der Ortsvektor x eines Punktes X auf einer Ebene durch P orthogonal zu einem Normalenvektor n erfüllt x n = d, d = p n. Ò Ò ½ Ò È Ç Hesse-Normalform einer Ebene 1-1

2 Bei der Normalform wird dabei n = 1 und d 0 angenommen. In diesem Fall ist d der Abstand der Ebene zum Ursprung. Der Normalenvektor zeigt vom Ursprung in Richtung der Ebene. Hesse-Normalform einer Ebene 1-2

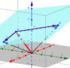
3 Ebene E durch P = (1, 2, 3) mit Normalenvektor n = (2, 2, 1) t /3 Hesse-Normalform einer Ebene 2-1

4 Ebene E durch P = (1, 2, 3) mit Normalenvektor n = (2, 2, 1) t /3 Normierung: n = σ n/ n = σ(2, 2, 1) t /3 Hesse-Normalform einer Ebene 2-2

5 Ebene E durch P = (1, 2, 3) mit Normalenvektor n = (2, 2, 1) t /3 Normierung: n = σ n/ n = σ(2, 2, 1) t /3 Wahl des Vorzeichens σ so, dass 1 0 d = p n = 2 σ = σ d.h. σ = 1 und d = 3 Hesse-Normalform einer Ebene 2-3

6 Ebene E durch P = (1, 2, 3) mit Normalenvektor n = (2, 2, 1) t /3 Normierung: n = σ n/ n = σ(2, 2, 1) t /3 Wahl des Vorzeichens σ so, dass 1 0 d = p n = 2 σ = σ d.h. σ = 1 und d = 3 Hesse-Normalform E : x n = d, d.h. E : 2 3 x x x 3 = 3 Hesse-Normalform einer Ebene 2-4

7 Ebene E durch P = (1, 2, 3) mit Normalenvektor n = (2, 2, 1) t /3 Normierung: n = σ n/ n = σ(2, 2, 1) t /3 Wahl des Vorzeichens σ so, dass 1 0 d = p n = 2 σ = σ d.h. σ = 1 und d = 3 Hesse-Normalform E : x n = d, d.h. E : 2 3 x x x 3 = 3 X = (4, 0, 1) E, denn x n = 1 3 ( ) = d Hesse-Normalform einer Ebene 2-5

8 Ebene E durch P = (1, 2, 3) mit Normalenvektor n = (2, 2, 1) t /3 Normierung: n = σ n/ n = σ(2, 2, 1) t /3 Wahl des Vorzeichens σ so, dass 1 0 d = p n = 2 σ = σ d.h. σ = 1 und d = 3 Hesse-Normalform E : x n = d, d.h. E : 2 3 x x x 3 = 3 X = (4, 0, 1) E, denn x n = 1 3 ( ) = d X = (0, 0, 0) / E, denn x n = 0 d Hesse-Normalform einer Ebene 2-6

9 Umrechnen von Ebenendarstellungen: Hesse-Normalform einer Ebene 3-1

10 Umrechnen von Ebenendarstellungen: (i) Ebene durch den Punkt P, aufgespannt durch zwei nicht parallele Vektoren u, v: Hesse-Normalform einer Ebene 3-2

11 Umrechnen von Ebenendarstellungen: (i) Ebene durch den Punkt P, aufgespannt durch zwei nicht parallele Vektoren u, v: Parameterdarstellung E : x = p + s u + t v, s, t R Hesse-Normalform einer Ebene 3-3

12 Umrechnen von Ebenendarstellungen: (i) Ebene durch den Punkt P, aufgespannt durch zwei nicht parallele Vektoren u, v: Parameterdarstellung E : x = p + s u + t v, s, t R weitere Punkte Q, R E: q = p + u, r = p + v Drei-Punkte-Form E : [ x p, q p, r p] = 0 Hesse-Normalform einer Ebene 3-4

13 Umrechnen von Ebenendarstellungen: (i) Ebene durch den Punkt P, aufgespannt durch zwei nicht parallele Vektoren u, v: Parameterdarstellung E : x = p + s u + t v, s, t R weitere Punkte Q, R E: q = p + u, r = p + v Drei-Punkte-Form E : [ x p, q p, r p] = 0 normierter Normalenvektor n u v = σ u v mit σ { 1, 1} so gewählt, dass d = p n 0 Hesse-Normalform E : x n = d Hesse-Normalform einer Ebene 3-5

14 (ii) Ebene durch drei Punkte P, Q und R, die ein echtes Dreieck bilden: Hesse-Normalform einer Ebene 3-6

15 (ii) Ebene durch drei Punkte P, Q und R, die ein echtes Dreieck bilden: Drei-Punkte-Form E : [ x p, q p, r p ] = 0 Hesse-Normalform einer Ebene 3-7

16 (ii) Ebene durch drei Punkte P, Q und R, die ein echtes Dreieck bilden: Drei-Punkte-Form E : [ x p, q p, r p ] = 0 Vektoren, die E aufspannen u = PQ, v = PR Hesse-Normalform einer Ebene 3-8

17 (ii) Ebene durch drei Punkte P, Q und R, die ein echtes Dreieck bilden: Drei-Punkte-Form E : [ x p, q p, r p ] = 0 Vektoren, die E aufspannen u = PQ, v = PR Konstruktion der Hesse-Normalform wie in (i) Hesse-Normalform einer Ebene 3-9

18 (iii) Ebene durch einen Punkt P und einen Normalvektor n: Hesse-Normalform einer Ebene 3-10

19 (iii) Ebene durch einen Punkt P und einen Normalvektor n: Hesse-Normalform mit n 0 = σ n/ n und σ { 1, 1} E : x n 0 = d, d = p n 0 0 Hesse-Normalform einer Ebene 3-11

20 (iii) Ebene durch einen Punkt P und einen Normalvektor n: Hesse-Normalform mit n 0 = σ n/ n und σ { 1, 1} Vektoren, die E aufspannen E : x n 0 = d, d = p n 0 0 u = n x, v = n u mit x λ n Hesse-Normalform einer Ebene 3-12

21 (iii) Ebene durch einen Punkt P und einen Normalvektor n: Hesse-Normalform mit n 0 = σ n/ n und σ { 1, 1} Vektoren, die E aufspannen E : x n 0 = d, d = p n 0 0 u = n x, v = n u mit x λ n Konstruktion der Drei-Punkte-Form wie in (i) Hesse-Normalform einer Ebene 3-13

22 Ebene durch die Punkte P = (7, 2, 0), Q = (1, 6, 2), R = ( 1, 8, 3) Hesse-Normalform einer Ebene 4-1

23 Ebene durch die Punkte P = (7, 2, 0), Q = (1, 6, 2), R = ( 1, 8, 3) Drei-Punkte-Form E : x 2, 6 2, 8 2 = Hesse-Normalform einer Ebene 4-2

24 Ebene durch die Punkte P = (7, 2, 0), Q = (1, 6, 2), R = ( 1, 8, 3) Drei-Punkte-Form E : x 2, 6 2, 8 2 = Differenzen der Ortsvektoren Richtungen, die die Ebene aufspannen u = 6 PQ = 8, v = 8 PR = Hesse-Normalform einer Ebene 4-3

25 Ebene durch die Punkte P = (7, 2, 0), Q = (1, 6, 2), R = ( 1, 8, 3) Drei-Punkte-Form E : x 2, 6 2, 8 2 = Differenzen der Ortsvektoren Richtungen, die die Ebene aufspannen u = 6 PQ = 8, v = 8 PR = Parameterdarstellung der Ebene E : x = 2 + s 8 + t 10, s, t R Hesse-Normalform einer Ebene 4-4

26 Normalenvektor n = u v = = Hesse-Normalform einer Ebene 4-5

27 Normalenvektor Normierung: n = u v = = n 0 = σ mit σ { 1, 1} so gewählt, dass 7 2/3 0 d = p n 0 = 2 σ 1/3 = σ( 4) 0 2/3 d.h. σ = 1 und d = 4 Hesse-Normalform einer Ebene 4-6

28 Normalenvektor Normierung: n = u v = = n 0 = σ mit σ { 1, 1} so gewählt, dass 7 2/3 0 d = p n 0 = 2 σ 1/3 = σ( 4) 0 2/3 d.h. σ = 1 und d = 4 Hesse-Normalform E : 2 3 x x x 3 = 4 Hesse-Normalform einer Ebene 4-7