Physik I Ausarbeitung mündliche Prüfung
|
|
|
- Helmuth Geier
- vor 8 Jahren
- Abrufe
Transkript
1 Physk I usarbeung ündlche Prüfung Ene usarbeung für de ündlche Prüfung Physk I ersell den VO-olen o W 4, de Buch Physk für Bachelors (3. uflage, 3) und Wkpeda. as Kapel Mechank on lüssgkeen/hydrodynak fehl und de lezen Kapel snd nch ehr so dealler ausgeführ, solle aber rozde hlfrech für de Prüfungsorbereung sen ;) Enführung Physkalsche Grundgrößen Länge, Ze, Masse, rosärke, Teperaur, offenge, Lchsärke alle anderen daon abgelee. In der Mechank: Länge, Ze, Masse Ze:, ekunde s, efnon durch chwngungen ener Cäsu-ouhr Länge: l, Meer, efnon durch Lchgeschwndgke Vakuu Masse:, Klogra kg, efnon durch Masse des P-Ir Verglechszylnders Vekoren kalare Größe = Maßzahl Maßenhe wenn des nch endeug s Vekorelle Größe = Maßzahl Maßenhe Rchung Berag enes Vekors = Länge (er pos) Vekoren können durch Zahlenrpel angegeben werden: a = (a,ay,az) Engegengesezer Vekor: a ha glechen Berag we a, nur engegenges. Rchung Bahnkure (Weg, Trajekore) de Gesahe aller Orspunke, an denen sch en punkförges Objek be sener Bewegung befnde. En Orspunk wrd durch enen Orsekor r angegeben. Ene Bahnkure wrd durch ene unkon r ( bes: r ( = r(e + ry(ey + rz(ez (Orsekor als unkon der Ze angegeben) bleung enes Vekors e bleung da / des Vekors a s angenal an de Bahnkure a ( gerche. Koordnaensysee Ebene Polarkoordnaen Koordnaen r (Radus) und φ (Wnkel Ph) Urechnung n karessche Koordnaen (r,φ) (,y): = r cos φ y = r sn φ Enhesekoren er und eᵩ n Polarkoordnaen snd orsabhängg Mahas Elsner Physk I usarbeung ündlche Prüfung ee! on! 9
2 Zylnderkoordnaen Koordnaen r (Radus), φ (Wnkel) und z (Höhe des Zylnders) Urechnung n karessche Koordnaen (r,φ,z) (,y,z): = r cos φ y = r sn φ z = z Enhesekoren er und eᵩ snd orsabhängg, ez s orsunabhängg Kugelkoordnaen Koordnaen r (Radus), ϴ (Polarwnkel Thea) und φ (zuhwnkel Ph) Urechnung n karessche Koordnaen (r,θ,φ) (,y,z): = r sn ϴ cos φ y = r sn ϴ sn φ z = r cos ϴ Enhesekoren er,eθ und eᵩ snd alle orsabhängg Kneak In der Kneak gb es 3 erschedene Berachungsneaus:. Mechank des Massenpunkes: Körper unendlch klen endlcher Masse, z.b. für Bewegungen n Planeensyseen. Mechank des sarren Körpers: kene eforaonen berückschg Geschwndgke. Mechank des deforerbaren Körpers Kneak des Massenpunkes Massenpunk efnon Punkförges Objek ( klen, räulche usdehnung ) endlcher Masse. ür Körper endlcher Größe gl: Bewegung = Translaonsbewegung + Roaonsbewegung. Be ene Massenpunk bleb de Roaonsbewegung außer Geschwndgke Berach, de Translaonsbewegung wrd der Bewegung des chwerpunkes beschreben. enson und Maßenhe Geschwndgke Geschwndgke s Weg pro Ze (be glechförger Bewegung), bzw. de bleung des Orsekors nach der Ze. ~ = ~s ~ = d~r = ~r = leg angenal an der Bahnkure. Enhe /s. ~r = ~r( V = L T Zurückgeleger Weg ~s = ~r( ~r( Beschleungung a ) Beschleungung gb de Geschwndgke der Geschwndgkesänderung an, bzw. de [~] = [~r] zelche Änderung der Geschwndgke. Enhe /s. [] = s Bewegungsglechungen & Herleung Wenn de Bahnkure r ( bekann s, können und a problelos durch fferenaon erel werden. U de Bahnkure r ( be bekanner a zu berechnen, wrd a zwe Mal über negrer (a r). I ersen chr ergb sch de nfangsgeschwndgke als Inegraonskonsane, an erhäl ( = + a. Be der zween Inegraon ergb sch der Orsekor r des nfangspunks als Konsane, an erhäl r( = r + + (/)a. Mahas Elsner Physk I usarbeung ündlche Prüfung ee! on! 9
3 ür de Berechnung der Bahnkure aus a snd so de nfangsbedngungen und r nowendg (nfangswerproble). onderfall: Geradlng glechförge Bewegung = cons., daher s a =. er Beschleungungser fäll weg und es bleb r( = + r. Wenn an den Weg als s = r( - r angb erhäl an s = (ene Gerade). Kresbewegung onderfall: Glechförg In Polarkoornaensyse beschleunge Bewegung Her können a, und r unerschedlche Rchungen haben, daher uss an se ekorell adderen bzw. n hre Koponenen (,y,z) zerlegen. Bespele: enkrecher all: rz( = h - (/)g z( = -g Waagerecher Wurf: r = rz = (/)a chefer Wurf: aale Rechwee be θ = 45 Kresbewegung e Länge des Orsekors r s konsan. er Wnkel φ s abhängg on der Ze. Orsekor ~r : ~r = r = cons ~r = r ~e r ' = '( Wnkelgeschwndgke. arsellung als V ef. Wnkelgeschwndgke: Zusaenfassung Glechförge Kresbewegung (r,! = (r cons = c Wnkelgeschwndgke ω '! l e Wnkelgeschwndgke! s de bleung = Wnkelgeschwndgke d' des Wnkels Zusaenfassung Kresbewegung φ nach der Ze. ls Vekor dargesell leg ω an der! = d' (r = cons Wnkelgeschwndgke rehachse und gb den rehsnn an. Glechförge Kresbewegung (r,! = cons Glechförge Kresbewegung er Orsekor r und de Wnkelgeschwndgke ω snd! konsan. = º! = d' ~! leg an der rehachse, zeg den rehsnn Glechförge Lneare Kresbewegung Geschwndgke (T ω ergb (r, auer sch! = cons ener Udrehung) T aus der Perodendauer T. Lneare (Bahn-)Geschwndgke! = º ~ =! r ~e (T auer ener Udrehung) ' ~ = ~! ~r M der zelchen bleung des Orsekors erhäl an Zenrpealbeschleungung de T lneare Bahngeschwndgke. Ihr Vekor Lneare blde (Bahn-)Geschwndgke ene Tangene an den Kresradus und seh Zenrpealbeschleungung so senkrech auf r.~ =!r ~e ' =!r ~ = ~a!r =! ~e ' r ~e r ~a = ~!!r ~ = ~! (~! Zenrpealbeschleungung a (bzw. az) Zenrpealbeschleungung e zelche bleung der Geschwndgke ergb de ~a =! r ~e r a! r = ~a =! r ~e r a =! r = r Zenrpealbeschleungung a (az ). e s zu Melpunk gerche und sell ene Korrekur dar, da der bewege Massenpunk er r auf der Kresbahn bleb. ons würde er sch auf der Tangene bewegen. Zelcher Verlauf der Vekorkoponenen M der arposon = und r = (r,) s de Phasenerschebung zwschen den Vekoren r, und a jewels π/. Wnkelbeschleungung α e Wnkelbeschleungung α s de bleung der Wnkelgeschwndgke ω nach der Ze bzw. de zwee bleung des Wnkels φ nach der Ze. Mahas Elsner Physk I usarbeung ündlche Prüfung ee! 3 on! 9
4 ynak In der ynak fragen wr uns, waru en Körper ene Bewegung ausführ. Physkalsch s de rage so egenlch nch korrek, rchg laue se: Waru änder en Körper senen Bewegungszusand? e Ursache s ene Wechselwrkung des Körpers sener Ugebung. ese Wechselwrkung beschreb an durch das Konzep der Kraf, ener ekorellen Größe. Newonsche oe e Newonschen oe blden den Übergang on der Kneak zur ynak. oe snd grundlegende Geseze, de elfach eprsch besäg worden snd, foraler Logk aber. nch bewesbar snd. e olgen aus ene osyse snd nch wdersprüchlch und ebenfalls eprsch besäg. o - Träghesprnzp ~ = ) ~ = cons o Träghesgesez a = lle Körper erharren Zusand der Ruhe oder der glechförgen, geradlngen Bewegung, wenn kene äußeren lle Körper Kräfe orhanden erharren snd. Zusand as heß, der wenn Ruhede Kraf = s, s konsan und a =. oder Newon der glechförgen, ha des on Galle geradlngen übernoen. Bewegung, Bezugsysee, n denen das Träghesgesez gl, heßen Ineralsysee n hnen erlaufen Bewegungen ununerschedbar glech. bsoluer llsand s nch fessellbar, wenn kene äußere Kräfe orhanden snd aber auch nch relean. Beschränkung der Wrkung des Grundgesezes Lufkssenbahn o ynasches - Grundgesez Kräfeglechgewch: der ynak e Rebung wrd her überwunden und de Geschwndgke bleb nach de nsoßen wrklch konsan (Lufwdersand s ernachlässgbar gerng). as.o n an, dass de Masse konsan s. o konsgesez ~ = ~a Wrk auf enen fre beweglchen Körper ene Kraf, so beweg sch der Körper ener Be sehr hohen Geschwndgkeen: Beschleungung Wrk auf a, enen de proporonal fre beweglchen zu der wrkenden s. M zunehender Körper ene Geschwndgke Kraf ~, n de Masse zu: Enschränkung: so beweg sch as der. o Körper n ener de Masse Beschlengung als Konsane ~a, an. Be sehr hohen Geschwndgke de proporonal n aber zu der de wrkenden Masse zu: Kraf s Ruheasse be = () = u, c Lchgeschwndgke (3 8 /s) c Je größer de Masse s, deso ehr Kraf s nög, u den Bewegungszusand (de Geschwndgke des Körpers zu ändern. -Ruheassebe a s de =, Masse das Maß der Träghe (räge Masse). e Träghe wrk besonders sark, wenn de Geschwndgke hoch s. c - Lchgeschwndgke undaenalkräfe Graaon (WW zwschen Massen) Elekroagnesche Wechselwrkung (zwschen elekrschen Ladungen) arke Wechselwrkung (zwschen Nukleonen (Kernelchen, p + und n )) chwache Wechselwrkung (Veranworlch für β-zerfall radoaker Kerne) Mahas Elsner Physk I usarbeung ündlche Prüfung ee! 4 on! 9
5 Träge Masse und schwere Masse I allersuch r de Masse n hren beden Egenschafen auf Graaonsgesez e Masse s de Ursache der Graaonswechselwrkung (schwere Masse). I allersuch Träge Masse: r de = Masse a (. n o) hren. o: beden Egenschafen ~ = ~a auf -räge Masse Äqualenzprnzp: Her schwere s ~ de Masse Graaonskraf = räge Masse allersuch:. o: I allersuch ~ = ~a r de -räge Masse Masse Graaonsgesez: ~ n hren beden M o - Träghesprnzp Erd = Egenschafen auf. a Her s ~ de kann Graaonskraf an das Graaonsgesez de. o Rglechsezen ~e r,m Erd -schwere Massen und de Masse kürzen. Man erhäl so de Erdbeschleungung g, de on der Körperasse unabhängg Graaonsgesez: ~ M = s (wenn an den Lufwdersand R ~e M r,m Erd -schwere Massen R ~e r = ~a arf an kürzen? ernachlässg oder Vakuu arbee. M Erd R ~e r = ~a J! arf an M Ensens Gedankeneperen Erd ~ = ) ~ = cons kürzen? R ~e r = ~a Erdbeschleungung ( ~g) Was läss de eder ausdehnen? Ensens Gedankeneperen J! M Erd In ene geschlossenen R ~e Graaonskraf? oder de Träghe des K r = ~a Erdbeschleungung ( ~g) ahrsuhl häng ene Masse an ener lle Körper erharren n Zusand der Ruhe eder. En Eperenaor n dese geschlossene yse oder kann nch derzwschen glechförgen, zwe ällen unerscheden: geradlngen Bewegung, g s on der Körperasse unabhängg Graaonskraf: wenn kene en äußere asser Kräfe Körper orhanden wurde uner de snd ahrsuhl Kraf hnzugefüg - Maßenhe (ahrsuhl Newonruh Träghe g s des on Körpers: der Körperasse der ahrsuhl unabhängg wrd schnell nach oben gezogen (beschleung Enhe der Kraf Ruhender ahrsuhl e Kraf ha de abgeleee ~ = ~a Maßenhe Newon N, des ensprch (kg )/s. [ ]=[] [a] =kg s = kg s bgeleee Kräfe ederkraf (elassche Kraf Rebungskraf Gewchskraf/ufreb usw. N Beschleunger arhsuhl En Eperenaor n ene geschlossene ahrsuhl kann nch chen den zwe ällen unerscheden ederkraf (elassche Kraf Ene klene eforaon enes Körpers erzeug ene elassche Kraf, de der eforaon engegenwrk. as Maß der eforaon s de usdehnung. e ederkraf s der uslenkung proporonal und engegengerche. ederkraf (elas Hookesches ~ = k Hookesches Gesez k elassche Konsane (o ab abhängg Maeral, k...elassche Querschn und Konsane, Länge L)...efora eforaon (k häng o ab ab, d.h. on de Maeral, de e eforaonsrchung e ederkraf s der uslenkung pr Mahas Elsner Physk I usarbeung ündlche Prüfung ee! 5 on (Gl! 9 nur für klene
6 chwerkraf e chwerkraf auf der Erdoberfläche berechne an: Gra = g e Erdbeschleungung g = 9,8 /s wrd berechne de Graaonsgesez und u de Zenrfugalkraf Z korrger. e s aber kene fundaenale Konsane se s an den Polen ewas höher und a Äquaor ewas nedrger (Δ on ca.,3). Masse und Gewch Masse und Gewch snd nch äqualen! Masse: s ene nrnssche Objekegenschaf (fundaenale Egenschaf, bleb er konsan außer be ere hoher Geschwndgke Gewch: s de Kraf, der en Körper auf de Unerlage oder ufhängung wrk es häng on de Usänden ab (z.b. ufreb) und kann auch sen (Gewchslosgke Rebungskraf R e Rebungskraf wrk be fesen Konakoberflächen, da dese ne deal gla snd. e läss sch auf elekrosasche Kräfe zwschen e und okernen zurückführen. e s on der uflagefläche und der Geschwndgke unabhängg! μ Rebungskoeffzen, N norale ( ) ruckkraf be waagerecher Oberfläche g Hafrebung/Glerebung: Be llsand snd de Oberflächen erzahn, daher wrk a nfang de höhere Hafrebung. In Bewegung werden nur ehr de pzen der Zähne abgeragen und es wrk de schwächere Glerebung. H und G μ durch μh oder μg ersez (μh > μg) okessche Rebung: es s de Wdersandskraf be Bewegungen on eskörpern n lüssgkeen oder Gasen. e s der Geschwndgke proporonal. cs körperabhängger Koeffzen, η (Ea) Vskosä des Medus, Geschwndgke Je größer de Geschwndgke und de Vskosä, deso größer de Rebungskraf. Kraf als Vekorgröße o 3 - Wechselwrkungsgesez - aco-reaco Überlagerung: Gesakraf = Vekorsue der enzelnen Kräfe Zerlegung: Man kann jede Kraf Koponenen zerlegen und de Wrkung der Koponenen enzeln berachen (z.b. und y). Kopenserbarke: asches Kräfeglechgewch wenn = Körper s kraffre z.b. Körper unbeweg ( = ) auf ener Unerlage: + g =. Be horzonaler Bewegung ( ) wrk de Rebungskraf o Kräfeglechgewch 3 - Wechselwrkungsgesez s gebrochen. - aco-reaco ynasches Kräfeglechgewch Lufkssenbahn:, aber g + Lufdruckkraf = o 3 Reakonsgesez e Kräfe und snd glech groß anparallel zuenander ausgerche! =! e Kräfe ~ und ~ snd längs der Verbndungslne der beden Körper wrksa. glech gross, as Reakonsgesez gl für ene WW belebger Naur. Es beschreb! de yere n der WW anparallel zweer Körper. zuenander gerche und =! Bespel: längs Zwe kaeboarder erbndungslne halen en der el, beden ener Körper zeh, ener wrksa nch. Ergebns: e beden rollen (be glecher Masse) glecher Geschwndgke aufenander e Kräfe zu. ~ und ~ snd yere n der Wechselwrkung zweer Körper glech gross, Mahas Elsner Physk I usarbeung anparallel ündlche zuenander Prüfung gerche undee! 6 on! 9 längs der erbndungslne der beden Körper wrksa yere n der Wechselwrkung zweer Körper
7 Realkräfe und chenkräfe Ene Realkraf wrd on ener WW zwschen Körpern herorgerufen. Ene chenkraf ko nur n beschleungen Bezugssyseen or. ese Kräfe eseren rozde wrklch und wr können se auch spüren. Bespele für chenkräfe: ahrsuhl: Körper daruner = Realkraf Graaon nach oben gezogen = chenkraf durch de Beschleungung n ene sarenden uo oder lugzeug be ener Kurenfahr be der Kresbewegung: Zenrfugalkraf, Corolskraf chenkraf = Trägheswdersand En (äußerer) Beobacher (ruhenden) Ineralsyse seh be der beschleungen Bewegung des Tsches kene Bewegung der Kugel (Träghesprnzp). En Beobacher beschleungen Bezugssyse des Tsches seh de beschleunge Bewegung der Kugel auf de Tsch. Er schleß, es wrk ene Kraf auf de Kugel. chenkräfe. Zenrfugalkraf chenkraf: Zenrfugalkraf/lehkraf l chenkräfe. Zenrfugalkraf Vo andpunk des äußeren Beobachers: andpunk des äußeren Beobachers Er seh ene Kresbewegung Kresbewegung dese wrd durch ) es uss de de zenral Zenrpealbeschleungung ~a Z sen, zenral gerche ederkraf (auch zenral gerche s de Zenrpealkraf, de ~a Z bewrk gerchee Zenrpealbeschleungung az erursach. e ebenfalls Vo andpunk des~ äußeren Beobachers: ed. = ~a Z.o zenral gerchee ederkraf ed. s de Zenrpealkraf, de az Kresbewegung ) es uss de Zenrpealbeschleungung ~a Z sen, zenral gerche ederkraf (auch zenral gerche s de Zenrpealkraf, de ~a Z bewrk bewrk. ed. = az (. o) andpunk des nneren Beobachers er Beobacher roer auch und seh so den Körper ruhen ~ ed. = ~a Z.o Vo andpunk des nneren Beobachers: a = alle Kräfe heben sch auf. der Körper l = ed. ruh ) = az ~a =) (bzw. alle Kräfe l + heben ed. sch = ) auf l = az Zenrfugalkraf/lehkraf ene ~ Vo andpunk l chenkraf, + ~ ed. = deren oder ~ Wo fleg der Körper nach brss des nnerendes Beobachers: adens Esenz l = hn? ~ ed. o = ~a Z Bezugssyse abhängg s (eser nur wenn das Bezugssyse beschleung s. ~ l der = ~a Körper Z ruh Zenrfugalkraf ) ~a =) (lehkraf, alle Kräfe deren heben Esenz sch auf o Bezugsyse abhängg Be brss des adens fleg der Körper angenal weg, er beweg sch geradeaus weer. chenkräfe. Corolskraf ~ l + ~ ed. = oder ~ l = ~ ed. = ~a Z ür enen äußeren Beobacher ür enen Beobacher bewegen Bezugssyse ~ l = ~a Z Zenrfugalkraf (lehkraf, deren Esenz o Bezugsyse abhängg s ~ Cor? ~ r chenkraf: Corolskraf cor e enseh n roerenden Bezugssyseen, wenn Massen sch ener Geschwndgke r radal bewegen, also senkrech zur rehachse, z.b. o Melpunk zu Rand. er Beobacher roerenden yse sell Mahas Elsner Physk I usarbeung ündlche Prüfung ee! 7 on! 9
8 fes, dass ene gekrüe Bahnkure enseh, also ene zusäzlche Beschleungung ac senkrech zu r wrk. e ensprechende Kraf heß Corolskraf. ~ cor =(~ r ~! ) chenkräfe. Corolskraf ür den äußeren Beobacher ruhenden Bezugssyse s se nur ene chenkraf das Bezugssyse dreh sch enfach Ineralsysee und Galle-T uner der Masse während hrer Bewegung nach außen hnweg. En Bespel für de Corolskraf s de Bewegung on Ineralsysee Lufassen n und Tefdruckgebeen. Galle-Transforaon ~ cor =(~ r ~! ) Ineralsysee und Galle-Transforaon Ineralsyse efnon: En Ineralsyse s en Bezugssyse, n de das Träghesgesez gl und das selbs kener Beschleungung unerleg. beweg sch glechäßg n -Rchung rela zu Bespel: Bezugssysee, de sch rela zuenander naen konsaner und der Ze: Geschwndgke Ineralsysee bewegen enes und s Galle-Transforaon a Ufer eranker (), beweg sch glechäßg n -Rchung rela zu. Zusaenhang der K das andere fleß = de Wassersro - de( ). Ze läuf glech n bede naen~u und = der ~u Ze: + ~ = = + - de Ze läuf glech ( n beden yseen = cons ) Wenn sch P glechäßg geradlng (wel kraffre) = n + beweg y (d.h. = y~u ( cons = cons, uss ~u = cons n sen - das Träghesprnzp gl n y = y beden Bezugssyseenz = z z = z Geschwndgke des Punkes P : Beschleungung: Geschwndgke des Punkes P : u = d u = d ch glechäßg e Geschwndgke n -Rchung rela des Punkes zu. Zusaenhang = d P s gegeben durch: der Koorder Ze: Wenn sch P + = u = d + = u + ~u = ~u + oder ~ n e ) Wenn sch P glechäßg geradlng (wel kraffre) n + oder n ekoreller or: ~u = bewe ~a = d~u ~u = d~u +=~a ( ) ene Inarane n sen ~u = ~u - das Träghesprnzp gl n beden B + ~ as nun Grundgesez glechäßg (wel kraffre) n beweg (also u = cons, uss auch u = ) Wenn nsch neralen P glechäßg Bezugssyeen: geradlng (wel kraffre) Beschleungung: n beweg (d.h. ~u = cons, uss ~u = co cons - de sen Ze läuf das glech Träghesprnzp n beden yseen gl n beden Bezugssyseen. n sen - das Träghesprnzp gl n beden ~a = Bezugssyseen d~u + Beschleungung s ene Inarane (n allen Bezugssyseen glech): ( = cons = d~u +=~a ( ) ( ) ulplzeren ür das Grundgesez n neralen Bezugssyseen ulplzeren wr de Inarane a Beschleungung: as Grundgesez n neralen Bezugssyee der Masse (ebenfalls ene Inarane de Masse s = auch ). araus erkennen wr: ene Kraf wrk n beden Bezugssyseen densch. gke des Punkes P : ~a d~u ene Inarane d~u = ~ = ~a = ~a +=~a = ~ ( ) ulplzeren ( ) ene Inarane llgeen das Galle-Inaranzprnzp: e grundlegenden Geseze der Physk snd n = d + = u allen Bezugssyseen, + oder n ekoreller as Grundgesez or: ~u n= neralen ~u de Masse s auch ene Inarane -enekrafwrkdenschnbedenbezugssyseen + ~ de sch zuenander glechförger Bezugssyeen: ~ = ~a = ~a Geschwndgke bewegen, = ~ -enekrafwrkdensch den. ~u = ~u + ~ ( ) + ~a ulplzeren Verlezung des Träghesprnzps Nchneralsyse Wenn sch P n In ene Nchneralsyse kraffre konsaner Geschwndgke s nch ehr konsan, de Masse~u s beweg, denn auches ene s sene unerleg Inarane Geschwndgke ener = Beschleungung a. ür den all, dass a = cons, gl für de ~ = ~u = ~a ~u = + ~a ~ = ~ ~u n nch konsan! Geschwndgke enes Punkes P: + ~a Verlezung de Beschleungung: es sell ene Verlezung des Träghesprnzps dar. Wenn Wenn sch Psch n P kraffre n u konsaner = cons Geschwndgke ~u kraffre beweg, ~a = d~u s sene Geschwndgke u n nch konsan! e Beschleungung s = d~u ++~a = ~a + ~a ( ) Beschleungung s kene Inarane her kene Inarane ehr: a = a + a. es ergb für das Grundgesez: ( ) : -enekrafwrkdenschnbedenbezugssyse Beschleungung: ~a = d~u = d~u ++~a = ~a + ~a ( ) ~ = ~a = ~a + ~a e de Masse n kräfefre -kenewechselwrkunganderen Körpern, d.h. ~ = ~a =) Mahas Elsner Physk I usarbeung ündlche Prüfung ee! 8 on! 9 ( ) : =~a +~a ) ~a = ~a (~a 6=) ~ = ~a = ~a +
9 rbe Wenn nun ene Masse kräfefre n s, also = a =, folg daraus (n ene Nchneralsyse, a ): = a + a a = a Obglech es n kene Wechselwrkung der Masse gb, wrk ene Kraf = a ene chenkraf. rbe und Energe rbe s defner als Kraf Weg. er Weg s s das egen der Bahnkure zwschen Or und, also de fferenz der Vekoren r ( r (. α s der Wnkel zwschen den beden Vekoren und s. Weg (egen der Bahnkure zwschen Or und Or ); ~s( =~r( ~r W ~ ~s = ~ ~s cos Æ rbe s ene kalargröße (kalarproduk W >, wenn n glecher Rchung we s (cos α > ) W <, wenn n Gegenrchung zu s (cos α < ) ese efnon s aber schwerg anzuwenden! e orel s nur für geradlnge Wege und konsane W<, Kräfe wenn anwendbar. ~ n Gegenrchung Wenn und s zu nch ~s (cos Æ < ) konsan snd, approer an de Kure s durch klene geradlnge egene Δs, n denen jewels konsan s und suer dese an blde das Inegral (berechnen der afunkon, blden der fferenz der Grenzwere)! e Maßenhe der rbe s das Joule J. rbe s ene kalargröße (kalarproduk. W>, wenn ~ n glecher Rchung we ~s (cos Æ > ) olgerungen aus den Egenschafen des Inegrals be Ukehrung des Weges: W B = WB rbe enlang enes geschlossenen Weges s (Rngnegral, nur -all, nch 3!) be Berechnung s rbe durch enen Zwschenpunk elbar (ufelen on Inegralen) rbe häng o gewählen Weg zwschen Zusänden und ab d.h. rbe s ene Prozessgröße (kene Zusandsgröße) rbe chwerkraffeld rbe der chwerkraf (G s): WB = gh Hubarbe rbe ener Kraf gegen de chwerkraf (H = G): rbe der ederkraf Knesche Energe Wkn e rbe auf de Weg on Punk zu Punk s glech der Änderung der kneschen Energe n desen Punken (= Beschleungungsarbe. Oder anders: e Beschleungungsarbe s de fferenz der kneschen Energe End- und arzusand. e knesche Energe s ene kalargröße und ha de Enhe Joule J. W B = gh Enspannung ener gedehnen eder se lese dabe rbe: Knesche Energe pannarbe (pannkraf = ): dw = d~s ~ ~ = ~a = d~ ; d~s = ~ ) dw = d~ ~ = ~d~ Z In Inegralfor: W = ~d~ = W kn rbe auf de Weg on Punk zu Punk s glech der Änderung Mahas Elsner Physk I usarbeung der kneschen ündlche Energe Prüfung n desen Punken ( Beschleungungsarbe ). ee! 9 on! 9 Knesche Energe s ene kalargröße.
10 elder elder snd unkonen, de o Or 3-Rau abhängg snd und überall defner snd. Gelesee rbe enlang enes geschlossenen W kalarfeld: z.b. Teperaurfeld T (, y, z) (3-Teperaurerelung) Vekorfeld: z.b. Kraffeld V (, y, z) Enen belebgen Punk auf de Weg! wählen: Kraffeld En Kraffeld leg or, wenn en Körper n jede Raupunk r ene wohldefnere Kraf (r ) erfähr. Bespele für Kraffelder snd de chwerkraf oder elekrsche pole. Konserae Kraffelder: Is das Kraffeld so beschaffen, dass de rbe o gewählen Weg zwschen den Zusänden und unabhängg s, W! dann = nenn W! an + es W! konsera. = W! W! U de gelesee rbe auf ene geschlossen Weg zu berechnen wähl an wel W enen belebgen Punk auf de Weg und erwende! = W! für en konseraes eld. W = W (für konserae elder): W = W + W = W W = I Be ene konseraen Kraffeld erschwnde de rbe be der ~ d~s = Verschebung enes Körpers längs enes geschlossenen Weges. Zenralkraffelder (z.b. Graaonskraf, Coloubsche Kraf haben Kugelsyere und snd en Bespel für konserae Kraffelder. Be ene Her konseraen s der Berag Kraffeld der erschwnde nur o de rb bsand zu Zenru des Kraffeldes abhängg. schebung enes Körpers längs enes geschlossenen Weges Poenelle Energe Wpo urch Enführung des Bezugspunks defner an asächl nur ene relae Änderung der poenellen Energe. er absolue Wer on W po s unbekann (das Proble der Inegraonskonsane!) e poenelle Energe Wpo a Punk P s de rbe, de zu errchen ZP s, u enen Z P Körper o Bezugspunk P n den Punk P zu überragen. ef.: W po (P oder )= ~ d~s oder ~ d~s Geäß der efnon Z P Wpo a Punk P s de rbe, de das Kraffeld be Überragung P enes ef.: Körpers W o P po (P )= ~ d~s W Punk P n den Bezugspunk P errche. po a Punk P s de rbe, de zubespel errchen s, : uenenkörperobezugspunkp der Bezugspunk enes Zenralkraffeld n Punk P zu überragen, P Bezugspunk s en beser, belebg oder gewähler s de poenelle Or n dese Energe eld. Bezugspunk : W po a Punk P s de rbe, de das Kraffeld errche be Überragung enes Körpers on Punk bsoluwerproble: urch de Enführung P den Bezugspunk des Bezugspunks P Z P defner an nur ene relae Änderung Bezugspunk der poenellen - en beser, belebggewählerorndeseeld Energe. W po (P )= ~ d~s = er absolue Wer on Wpo s unbekann! P e poenelle Energe Bezugspunk s aufgrund der efnon on Wpo. Bespel : er Bezugspunk des chwerkraffeldes s h ~ = (r). = r ~e r r! ) (r)! Wpo(h = ) = Wpo(h) = gh Bespel : er Bezugspunk enes Zenralkraffeldes leg n. Wpo( ) = Orsabhänggke: e poenelle Energe (Lageenerge) s o Weg unabhängg. Energeerhalungssaz e Gesaenerge s ene Erhalungsgröße: Wges = cons Poenelle Energe Poenelle Energe. bsoluwerproble Zr W po (r) = e echansche Gesaenerge s: Wges = Wpo + Wkn In der Mechank s der Energeerhalungssaz aber ken o! Er s ene hergeleee ussage aus de. Newonschen o. (r )dr W po ( Mahas Elsner Physk I usarbeung ündlche Prüfung ee! on! 9
11 @W = = Kraf als Graden der poenellen Energe ~ ~e ~e z as Inegral der Kraf (Vekorgröße) wandel se n de rbe W Inerpreaon (kalargröße) des u. Gradenen U 3-Rau de poenelle Energe Wpo (kalargröße) n en Kraffeld (Vekorgröße) uzuwandeln, wrd der Operaor ~e grad ef.: ~e @z ~e ~e angewende. Er lee de, y, und z-koordnaen parell ab. df () -naloge: ~ grad = grad f() = W po er Graden gb 3-Rau de Rchung der schnellsen Zunahe d ~e des kalarfeldes und de Änderungsrae an. Nchkonserae Kräfe er Energeerhalungssaz wrd auf andere Energeforen erweer de Energe wrd n Lesung andere Energeforen ugewandel (her de Wäre Q). En Bespel für ene nchkonserae Kraf s de Rebung. e Uwandlung echanscher P dw rbe n Wäre s Gegensand der Therodynak. Wpo() + Wkn() = Wpo() + Wkn() + Q d > df () df () d enson: < Lesung P grad gb de Rchung der Zunae und de Änderungsrae de on an e Lesung s de bleung der rbe nach [P der ]= Ze. [W ] = e J Enhe s das Wa W (J/s). e s auch als kalarproduk aus Kraf und Geschwndgke [] s = W a = W darsellbar. bgeschlossenes yse ysee on ehreren Massenpunken chwerpunk s yse wrd ür en de yse Berechnung ohne Wechselwrkung des chwerpunks enes yses on ehreren ezechne. Massenpunken ulplzer an de Vekoren den jewelgen ~ + ~ = cons Massen, suer dese Produke und dder dann efnon durch de Ipuls: ~p = ~ Gesaasse des yses. ehreren Massenpunken: Berachen M Gesaasse wr en yse des yses aus Massenpunken: ~p + ~p = cons e Kräfe auf, bgeschlossenes d.h. yse X Verallgeenerung auf N Massenpunke: se aus Massenpunken: ~ = ls abgeschlossenes yse wrd en (anselle yse der eder ohne kann Wechselwrkung jede andere Wechselwrkung sener Ugebung bezechne. ür en yse aus ehreren Massenpunken sen) NX gl, unken snd durch ene eder erbunden ~p dass nur nnere Kräfe aufreen das heß de ue aller Kräfe n ene = cons der eder kann jede andere Wechselwrkung sen) = abgeschlossenen yse s. ngsgesezes (3.N): ~ = ~a (.N): Ipuls p P = dw = ~ d~s er Ipuls p s das Produk nwendung aus der Masse des Wechselwrkungsgesezes und der Geschwndgke (3.N):. Ipulserhalungssaz: er Gesapuls pges (also de ue aller Ipulse) n ene ~ = ~ abgeschlossenen yse s konsan. nwedung des Grundgesezes Herleung: Nach de 3. N s =. as. N laue ~ = ~a (.N): = a, daher kann an ~ schreben = ~ a = a bzw. a + a =. Wenn an nun ~a ufor = () ~a erhäl an, dass de zelche bleung der Ipulse s () so uss de ue konsan sen. Man erhäl + = cons, also p + p = cons den Ipulserhalungssaz. ~a = ~a ~a + ~a = [~a = d~ = d (~)] d ( ~ + ~ )= () () = ~ ~ ~ = ~e + y ~e y + z ~e z Massenpunken snd durch ene eder erbunden ~p ges = cons Ipulserhalungssaz für den Ge ~a + ~a = d ( ~ + ~ )= Mahas Elsner Physk I usarbeung ündlche Prüfung ee! on! 9 [~a = d~ = d (
12 a kann an das Grundgesez der ynak auch n der allgeeneren Ipuls-or darsellen. e zelche bleung des Ipulses s glech der wrksaen Kraf. P N Orsekor des chwerpunkes ~r = ~r M chwerpunksaz: us de Ipulserhalungssaz chwerpunksgeschwndgke: läss sch der chwerpunksaz folgern: e Geschwndgke des chwerpunkes enes abgeschlossenen yses s konsan. ~ = d~r s = X d~r = X ~p M M = cons chwer Er beweg sch also unbeenfluss on den nneren Kräfen zwschen den enzelnen Körpern des yses. s = cons olg aus de Ipulserhalungssaz e Geschwndgke des chwerpunkes enes abgeschlossen öße Massenpunksyses s konsan En oß s ene sehr kurze Wechselwrkung zwschen zwe Körpern. urch den oß änder sch de Geschwndgke (der Ipuls) und de Energe der oßparner. Man unerschede elassche und nelassche öße: Ekn + Ekn = E kn + E kn + ΔQ - ΔQ = elasscher oß (Erhalung der kneschen Energe) - ΔQ nelasscher oß: ΔQ > endoher, ΔQ < eoher (es n Physk) Weers wrd n zenrale und nchzenrale öße unerscheden. Wenn alle Ipulsekoren kollnear snd (auf ener Gerade legen) s es en zenraler oß, sons en nchzenraler. Zenrale öße lassen sch auf den -all reduzeren (skalare Größen). Elasscher oß Massenpunke und den Geschwndgkeen und erfahren den elasschen oß. Gesuch werden de Geschwndgkeen und nach de oß. Man sez der Ipulserhalung und der Erhalung der kneschen Energe (wel elassch) an: - + = + - (/) + (/) = (/) + (/) us desen Glechungen lassen sch dann und ausdrücken. onderfall : En elasscher oß zweer Kugeln glecher Masse (=), de zwee Kugel ruh or de oß (=). Es fnde en oller Ipulsüberrag auf de zwee Kugel sa se beweg sch nach de oß der Geschwndgke der ersen Kugel, welche dann ruh. = und = = und Δp = onderfall : En senkrecher elasscher oß gegen ene Wand (deren Masse angenoen wrd). er Ipulsüberrag Δp auf de Wand beräg, der Ipuls der Kugel kehr sch be oß u (se prall derselben Geschwndgke zurück). = und p = p. Be ene oß uner ene Wnkel wrd der Ipuls n sene Koponenen zerleg, es wrd nur der Ipulsüberrag der senkrechen Koponene berückschg. Δp= Mkroskopsche euung des Gasdrucks: ruck s defner als Noralkraf pro lächenenhe (P = /). er Ipulsüberrag auf de Wand (Enzelsoß) Δp=. e deale Gasglechung pv = RT folg aus der Berachung des Ipulsüberrags aller Gaselchen. Kugelsoßpendel (Newon-Pendel): Nach der Ipulserhalung können heoresch auch Kugeln halber Geschwndgke ausgelenk werden, de Erhalung der kneschen Energe erhnder des aber (wel elasscher oß, Kugeln üssen sehr har sen). Mahas Elsner Physk I usarbeung ündlche Prüfung ee! on! 9
13 Vollkoen nelasscher oß Be ene nchelasschen oß gl nur der Ipulserhalungssaz, de Erhalung der kneschen Energe nch! Nach ene ollkoen nelasschen oß (z.b. zwe pelzeugauos prallen Plasln dazwschen zusaen und kleben anenander fes bewegen sch bede Körper zusaen der glechen Geschwndgke u. + = ( + ) u Roaon des Massenpunkes rehoen bzw. M rehoen as rehoen s das Maß der rehwrkung ener Kraf. Es s defner als das Bewegung enes enes sarren sarren Körpers = = Kreuzproduk/Vekorproduk aus Orsekor und Kraf. er Orsekor Translaonsbewegung des des chwerpunkes + Roaon + u u den den chwerpunk s o Bezugspunk abhängg, er änder sch be Wechsel des Koordnaensyses. Be Be der der Berag Beschrebung des rehoens der der Roaonsbewegung ko der snφ wähl wähl an an of of den den hnzu wenn der Wnkel zwschen Koordnaenursprung Orsekor und Krafekor chwerpunk s, gb es so ken rehoen. ~ = ~ ~r = ~r ~ ~ ~ ~ = r = r sn sn ' ' Bewegung enes sarren rehoen Körpers = stranslaonsbewegung das das Maß Maß der der rehwrkung des chwerpunkes ener ener Kraf. Kraf. + Roaon u den chwerpunk. aher wähl an be der Beschrebung der Roaonsbewegung of den Koordnaenursprung chwerpunk. e Enhe des rehoens s kg s - = N (Newoneer, nur foral Joule). rehpuls Telchensyse: n ene abgeschlossene yse s das rehoen = Zenralkraf: Ene Zenralkraf wrk enlang des Radus enes Kreses. as heß der ef.: L ~ = ~r ~p Wnkel s, der sn() = und das rehoen =. enson rehpuls L er rehpuls ergb sch aus de [ Kreuzproduk L]=[~r][~p] ~ =kg aus Orsekor s und Ipuls. Wenn an den rehpuls nach der Ze rehpuls ablee erhäl an des rehoen. e Enhe der rehpulses s kg s -. ef.: L ~ = ~r ~p ~ = d~ L enson rehpuls be glechförger Kresbewegung: Wenn der Orsekor r und de [ ~ d L Bewes: L]=[~r][~p] ~ =kg s Wnkelgeschwndgke konsan = d~r d~p ~p + ~r snd, s auch der = ~ rehpuls ~ + ~r L ~ = ~r ~ = ~ = cons. rehpulserhalung: ür en abgeschlossenes yse s das rehoen. a de bleung des rehpulses nach der Ze das rehoen s, uss der rehpuls n ~ = d~ L (u) = u + u dese all konsan sen. asselbe gl n ene Zenralkraffeld, da auch her =. Bewes: d L ~ Zusaenfassung = d~r d~p ~p + ~r = ~ Erhalungsgrößen ~ + ~r ~ = ~r ~ = ~ der Mechank Wges = cons: Energeerhalungssaz für de echansche Gesaenerge (für konserae (u) = u + u Kraffelder) pges = cons: Ipulserhalungssaz (für abgeschlossene ysee) s = cons: chwerpunksaz (für abgeschlossene ysee) L = cons: rehpulserhalungssaz (für abgeschlossene ysee) Mahas Elsner Physk I usarbeung ündlche Prüfung ee! 3 on! 9 Roaon des reh (auch Kr ef.: ~c = ~a *o Bezugspunk abhängg! (änder s
14 Mechank sarrer Körper Enführung/Wederholung efnon sarr : er bsand zwschen jewels O d Vekoren r r k s/bleb konsan. Gesaasse: e Masse über das Voluen zu negreren sell en Proble dar. Be ene hoogenen Körper lös an des über de Kresbewegung: Verglech Translaonsbewegung che, denn dann gl ρ = cons. =, k =,,... Translaon Roaon In der Mechank sarrer Körper snd alle Glechungen der Kresbewegung erwendbar. er Wnkel φ, de s ds = d d s a = = Wnkelgeschwndgke ω und de Wnkelbeschleungung α snd nälch für alle Punke glech groß, egal we we se o Melpunk enfern snd. as Bogenaß gb de Größe des ds o r dϕradusekor = = = r ω übersrchenen Wnkels φ an. En oller Ulauf ergb d dω a = = r = rα dann dφ = π = 36. e Enhe s das Radan rad, physkalsch s das Bogenaß aber densonslos. ϕ dϕ ω = dω d ϕ α = = e Kresfrequenz ω ergb sch aus der requenz f oder der Perode T. e s on der ( rω) Wnkelgeschwndgke (ebenfalls ω) zu unerscheden (ha aber a zglechen = = Zahlenwer. = r ω r r f requenz, Ulauffrequenz; T Perode, Ulaufze π Kresfrequenz: ω = π f = Zusaenhang zwschen Translaonsgrößen und Grundglechung der Kneak: T Roaonsgrößen:. Newonsches s = ao: + + s = a + = rω f (Ulauf)frequenz ϕ = = α a = + ω + r α r ϕ ω = α + ω rehoen a = rα rehoen: Wrd als M oder bezechne. Wenn zwe T r Kräfe Ulaufze, = r α radal Perode angrefen, herrsch Kräfeglechgewch und es enseh ken rehoen. M = Radalkoponenen ener Kraf haben kenen Enfluss M = auf das r α rehoen. Wenn se aber enander gegenüber angenal angrefen, enseh en aales rehoen. = arrer Körper: α für alle glech M = α r = α J Träghesoen J as Träghesoen J häng on der Masse und ef.: Geoere Träghesoen: des Körpers J = r ab. Es ergb sch aus der ue der Produke der Massen den Quadraen der Orsekoren r (Noralabsand zwschen r s der Noralabsand Masse und zwschen und der rehachse rehachse). llgeen foruler s es das Inegral des Quadras llgeen: der J = r d Orsekoren al d. as Träghesoen s abhängg on der rehachse. Be Verschebung M = J α der = a rehachse ko der enersche az zur nwendung: J = Js + b as Träghesoen s abhängg on der J Träghesoen be erschobener rehachse, Js Träghesoen Lage der rehachse bezogen auf den chwerpunk, b Noralabsand der chsen Be Verschebung der rehachse ko der as rehoen M läss sch de Träghesoen enersche foruleren: az zur M nwendung: = J α. oreln für J on erschedenen Körper orhanden (Zylnder, Kugel, Rng, ) Mahas Elsner Physk I usarbeung ündlche Prüfung ee! 4 on! 9 3r 3r -3r k 3r k efnon "sarr" ( ) N Zenrpealbeschleungung: zu Zenru gerche J = J + b s Es enseh en bezogen auf chwerpunk Noralabsand der chs
15 . Newonsches o: Herleung M = α des Träghesoens: r = α J ef.: Träghesoen: llgeen: efnon (allgeen) ef.: Träghesoen: J = as r Träghesoen s abhängg on der chwerpunk s Lage der rehachse r Wenn s der Noralabsand zwschen zwe oder ehr parallele und der rehachse Wenn Kräfe zwe auf oder enen ehr parallele Körper Kräfe wrken, auf enen können Körper wrken, se durch dann können ene chwerpunk se durch Be ene Verschebung enzelne äqualene der Kraf rehachse ersez werden. ko ese der Ersazkraf s enzelne äqualene Kraf ersez werden. ese Ersazkraf s glech der ue der glech der enersche ue der Kräfe az und zur gref nwendung: an ene solchen Punk an, dass das Kräfe und gref an ene Punk on an, hnen an bewrke de rehoen das on hr glech bewrke de resulerenden rehoen glech der ursprünglchen Kräfe s. de resulerenden rehoen der ursprünglchen Kräfe J = s J s + de bchwerpunk. Unersüz an den Körper chwerpunk, s = kopenseren r s = sch r alle Kräfe (spezell de Graaonskräfe) es ko zu ene Glechgewch. s = r s = r ef.: dw r d chwerpunk: s ds r d M d = allg.: d Glechgewch dw M d dw s ds ür en Glechgewch üssen de ue der Kräfe und de ue der rehoene jewels ef.: r d chwerpunk: sen: = und s Unersüz an den Körper chwerpunk kopenseren sch alle Kräfe = (spezell de chwerkräfe) M =. dw d Lesung: Glechgewch P W M M M M P s s d araus folg das Hebelgesez: M = M und r = r Es gb dre erschedene ren on Knesche Glechgewchen Energe: (Bespele): Ekn r r I I sabl: Kugel leg n ener Wanne J nsabl: Kugel leg auf ener anderen Kugel ndfferen: zwe Kugeln legen nebenenander E ro J kn E rans kn ür rehungen gl: Roaon u ene chse klenere Träghesoen s sabler. Überlagerung Translaon und Roaon: Roaonsenerge rans ro Be der (knesche) Roaonsenerge überlagern Ekn Ekn Ekn J sch Roaon und Translaon. Verglech der Rollgeschwndgke enes Hohl- und enes Vollzylnders glecher Masse: uf ener schefen Ebene roll en Vollzylnder roz glecher Masse el schneller, wel der Hohlzylnder en el höheres Träghesoen ha. e rehachse s der Zylnderelpunk. Epo a nfang s glech groß we Ekn a Ende. e Roaonsgeschwndgke s kau on der Masse abhängg, nur zu klene Tel wegen der Rebung. rehpuls L Träghesoen er rehpuls läss sch auch hlfe des rehoens foruleren: L = r p = r = = r ω L = Jω. es gl nur für Kresbewegung rehachse auf de Kresebene. er rehpuls läss sch auch berechnen, wenn sch nch auf ener Kresbahn beweg: L = r = a = r α r α = r M M = r α r arrer Körper: α für alle glech M = α r = α J M = Mahas Elsner Physk I usarbeung ündlche Prüfung ee! 5 on! 9 r arrer Körper: α für alle glech α J = r r s der Noralabsand zwschen und der rehachse M = J α Wenn zwe oder ehr parallele Kräfe auf enen Körper wrken, dann können se durch ene enzelne äqualene Kraf ersez werden. ese Ersazkraf s glech der ue der Kräfe und gref an ene solchen Punk an, dass das on hnen bewrke rehoen glech de resulerenden rehoen der bezogen auf chwerpunk ursprünglchen Kräfe s. Unersüz an den Körper chwerpunk kopenseren sch alle Kräfe (spezell de chwerkräfe) Glechgewch J = = chwerpunk r d a Roaonsenerge Noralabsand der chsen
16 nwendung rehpulserhalung, Träghesoen, enerscher az rehsessel: Wenn an en Rad Grffen zu rehen brng und es waagerech ener Person auf ene rehsessel gb, dreh sch der essel nch. Wenn de Person das Rad senkrech häl, dreh sch der essel langsa. Nach rehung des Rades u 8 dreh sch der essel doppeler Geschwndgke. Be Zurückdrehen u 8 dreh sch das Rad weder schneller und de rehung des essels hör auf. Prouee: e rehung s be nlegen der Hände schnell, be ausgesrecken Händen el langsaer. Präzesson, Erde als syerscher Kresel Präzesson s de Rchungsänderung, de de rehachse enes roerenden Körpers ausführ, wenn ene äußere Kraf en rehoen senkrech zu deser chse ausführ. e Roaonsachse beschreb enen Ulauf auf de Manel enes gedachen Kegels feser Kegelachse. e Erde s aufgrund der Zenrfugalkräfe en Roaonsellpsod (abgeflache Kugel), der obere und unere Wuls haben unerschedlche chwerpunke. Es dauer 6. Jahre bs de chse der Erde weder kople glech seh. urch das rehoen der onne und den Mond wrd de Präzesson der Erde lech gesör, de rehachse beschreb ene r gewellen Kegel des nenn an Nuaon. chwngungen Ene chwngung s ene perodsch hn und zurück erlaufende Bewegung nach uslenkung aus der Ruhelage. En Körper wederhol ene Bewegung ener gewssen requenz. chwngungsfähge ysee snd zu Bespel Pendel, edern oder oe. Man unerschede zwschen freen und erzwungenen, sowe zwschen ugedäpfen (rebungsfreen) und gedäpfen (auch abschlch geheen) chwngungen. Ene chwngung heß haronsch, wenn se den glechen aheaschen Meln we de Kresbewegung behandel werden kann. Ruhelage: ree chwngungen chwngungsglechung e y C k "Haronscher Haronscher Oszllaor" Oszllaor free ungedäpfe haronsche chwngung as Modellsyse s her ene waagereche eder ener e d ( e k ( e daran befesgen Masse, de aus hrer Ruhelage ausgelenk. Newon'sches ederkraf wrd, wobe Rebung und chwerkraf ernachlässg = wer- o (Hooke'sches den. e rückwrkende Kraf s de ederkraf, de de Gesez) asche uslenkung: d ( k ( chwngungsglechung der Bewegung enlang der -chse Hookeschen Gesez foruler wrd = k ( e ). ese ederkraf wrd der Massenräghe nach de. N = a glechgesez, und nach Uforung erhal an de chwngungsglechung. Modellsyse: waagreche ede = - C e Mahas Elsner Physk I usarbeung ündlche Prüfung ee! 6 on! 9 k C = ( -k ey e Rück k Hook
17 Lösung der chwng Lösungsansaz: ür de Lösung der chwngungsglechung ach an enen nsaz. Man ersez ( = cons e α und de Beschleungung d (/ = α cons e α k. a er-häl an den nsaz α + k/ =. "Kresfre e Wurzel aus k/ s de Kresfrequenz k Lösungsforen haronscher Oszllaor kalschen Koplee chrebwese ω. e benhale de ederkonsane und und Mas ( ) cons e cons e de Masse und s so er pos. Nach U- foren des nsazes erhäl an α = ω Überlagerung on Wnkelfunkonen. a ω pos s, s das Ergebns für α kople. ( ) sn( ) B cos( ) Lösungen: urch Uforen der Eulerschen Wnkelfunkonen Phasenwnkel orel und den Zusaenhängen zwschen ( ) C sn( ( ) cons e ) efnonen II Wnkelfunkonen und kopleen requenz f: Eponenalfunkonen erhäl an de dre nzahl kople der ollsändgen Was glechwergen chwngungen/ekunde bedeue das? ( ) C cos( ' ) enson [f]: s - ; Enhe: s - = H Hz (Herz) Lösungsforen für den haronschen Oszllaor. Kresfrequenz : nfangsbedngungen: lle n den Lösungsforen orkoenden Es gl: Konsanen snd f durch de nfangsbedngungen bes. Gleche nfangsbedngungen enson [ ] ]: führen s - ; Enhe: für alle rad s - Lösungsforen zu derselben Lösung. e nfangsbedngungen Perode besen T: daher das e für ene olle chwngung benöge Ze. yse ollsändg, für alle Zeen. efnonen Zusaenhang f,, T: - Haronsche chwngung: Zur ollsändgen Beschrebung wrd nur ene enzge Kresfrequenz ω benög. f f T T - plude : Maale uslenkung des Physkalsche yses aus Zusaenhänge sener Ruhelage ensprch her der nfangsauslenkung. - requenz: nzahl ollsändger chwngungen e gesae pro Physk ekunde, der haronschen Enhe s - chwngung = Herz Hz eck n den Bezehungen - Kresfrequenz Physkalsche ω: Zusaenhänge Enhe rad/s. requenz s unabhängg on der uslenkung! - Perode T: e für ene olle chwngung benöge Ze. k k bzw. f Physkalsche e gesae Zusaenhänge Physk der haronschen chwngung eck n den Bezehungen e gesae Physk der haronschen chwngung seck n desen Bezehungen: k bzw. f k ederkonsane Masse k : f, T : f, T Bewegungsabläufe uslenkung, Geschwndgke Bewegungsabläufe: und Beschleungung - uslenkung/or: ederkonsane ( = cos(ω k : f, T ( Or: T - Geschwndgke: Masse ( = d/ : = f ω sn(ω, T ( ) cos( ) - Beschleungung: a( = d/ = ω cos(ω plude = nfangsauslenkung Phasenerschebung u jewels π/ Geschwndgke: d ( sn( Energeberachung - Knesche Energe - Poenelle Energe - Gesaenerge Beschleungung: d a ( ) cos( ) Lnearäserlezung: Überdehnung der eder Mahas Elsner Physk I usarbeung ündlche Prüfung ee! 7 on! 9 ( a(
18 Maheasches Pendel Pendel gehören zu den Prooypen nahezu dealer haronscher Oszllaoren. nnahen: e ganze Masse befnde sch n der Kugel, der aden s en unendlch sefer ab. φ Wnkel, u den das Pendel zu Zepunk ausgelenk s Masse und uslenkung spelen kene Rolle, nur de Länge l des Pendels. aher lassen sch sehr genaue Pendeluhren bauen, wobe de chnur aus erschedenen Maeralen hergesell werden kann, u de Effeke der Wäreausdehnung zu kopenseren. e rückwrkende Kraf s her de chwerkraf. Herleung chwngungsglechung Es wrd weder das. N der rückwrkenden Kraf glechgesez, her also der chwerkraf: a = g sn φ. ür klene Wnkel (bs ca. 5 /,9 rad) kann an sn φ φ sezen, außerde kann an de Tangenalbeschleungung a durch de Wnkelbeschleungung Bogenaß ausrücken. urch Kürzen der Masse und Uforen erhäl an de chwngungsglechung und de Kresfrequenz ω. Lnearäserlezung: zu große uslenkung, Näherung sn φ φ wrd ungülg Physkalsches Pendel Be physkalschen Pendel werden Gegensaz zu aheaschen Pendel or und Größe des Körpers berückschg und da de Verelung der Masse. aher ensprch das physkalsche Verhalen schon eher ene realen Pendel. es gescheh durch den nsaz de rehoen M = r, welches dann durch das Träghesoen J ausgedrück wrd M = J α. We be aheaschen Pendel gl sn φ φ. Mahas Elsner Physk I usarbeung ündlche Prüfung ee! 8 on! 9
19 Torsonspendel e enzge öglche Verenfachung des Modells s das Torsonspendel. Be dese befnden sch zwe gleche Massen auf ene Torsonsdrah. Es wrd weder das rehoen M hlfe des Träghesoens J ausgedrück, aber desal de sogennanen rekonsoen (Proporonaläskonsane be der Torson) glechgesez. Torsonspendel M d J d J ree gedäpfe chwngung Be der gedäpfen chwngung wrd zusäzlch zur Massenräghe (. N) und der ederkraf (Hookesches Gesez) de wrkende Rebungskraf n or der okesschen Rebung berückschg, welche der Geschwndgke proporonal s: R = cs η. a ko an auf de chwngungsglechung Gedäpfe für de chwngung: gedäpfen efnonen Oszllaor. uch her s de chwngfrequenz Oszllaor: nch on der uslenkung abhängg. d ( ) c d ( ) k Gedäpfer ( Neue Oszllaor-Glechung: urch de efnon der äpfungskonsane δ und der Egenfrequenz der ungedäpfen chwngung ω wrd de Glechung ewas erenfach. d c d( Gedäpfe d ( chwngung: d( Lösungsansaz ( Gedäpfe chwngung: Lösungsansaz d ( d( ( c d ( d( k ) ( nsaz: Lösungsansaz: ( ) cons e er Lösungsansaz s derselbe we be haronschen Oszllaor. Man äpfungskonsane d( ) däpfen, de chwngung erse bleung = α cons e α und de zwee = α cons e α cons e ( ) e. Gedäpfe chwngung: allgeene Lösung nsaz: Egenfrequenz sez ( = cons e α der unge- d ( es ) führ d( auf ) ene quadrasche Glechung n α. Je nachde, welches Vorzechen de cons e cons e usgangspunk: skrnane ha (also we das Verhälns der äpfungskonsane zur Egenfrequenz d ( ) ühr auf quadrasche Glechung consn e : ( ) cons e perodscher all s, unerschede an dre erschedene älle. Nur all ener kopleen Lösung ko es zur gedäpfen ühr auf quadrasche chwngung. Glechung : ( ) e e B e ( ) cons e e efnonen: δ ω > perodscher all (Krechfall) allunerschedung: e Masse wrd ausgelenk, on der eder zurückgezogen, näher sch perodscher all /B > der uslenkung = an aber errech den Nullpunk ne. Es ko zu Reelle Lösung; Reelle Lösung; Koplee Lösung; kener chwngung. e Konsanen und B werden perodscher durch de all, n- perodscher perodscher Grenzfall /B < chwngung III g Krechfall Grenzfall fangsbedngungen fesgeleg. C( ) δ ω = perodscher Grenzfall ( e e B e ( ) C ( ) e ( e Lösung erhäl an durch Varaon der ( ) e e Masse wrd ausgelenk, Konsanen. Konsanen und ergeben sch weder aus den nfangsbedngungen. = an, errech e den Null- on der eder zurückgezogen, ( näher sch der uslenkung /B > punk aber ne. nnäherung an den Nullpunk s her a schnellsen, er wrd e Konsanen allerd- und B werden durch de nfangsbedngungen fesgeleg. ngs auch nch errech! uch her ko /B es < zu kener chwngung, deser all ha aber echnsche Bedeuung zur äpfung unerwünscher chwngungen (z.b. oßdäpfer). ( = ( + ) e δ J Gedäpfe chwngung Zusäzlche Rebungskraf R : k C ( = = - -k C e ( ( R = R e C y e ( R ( k e e Masse w on der ede näher sch d = an, errec punk aber n e Konsane werden durch bedngungen e Konsanen ergeben sch wederu aus d nfangsbedngu e nnäherung Nullpunk s he schnellsen, erre wrd er allerdng nch! Mahas Elsner Physk I usarbeung ündlche Prüfung ee! 9 on! 9
20 δ ω < Gedäpfe chwngung Nur n dese all ergb sch de gedäpfe chwngung. e Lösung laue: ( = e δ sn(ω + ψ) (ω + ψ) Phasenwnkel (Phase), ψ Nullphasenwnkel (Phase be = ), plude efnonen - Kresfrequenz der gedäpfen chwngung - requenz der g.. - Perodendauer der g.. e requenz f der gedäpfen chwngung s zelch konsan und gernger als de der ugedäpfen chwngung, de Perodendauer T s daher größer. e Enhüllende der chwngung s ene abklngende Eponenalfunkon. Logarhsches ekreen Λ e plude der gedäpfen chwngung s zeabhängg und n eponenell ab. as Verhälns zweer aufenanderfolgender pluden s dabe konsan. aher führ an das logarhsche ekreen Λ (groß Labda) en. Es erlaub de Berechnung der äpfungskonsane δ drek aus de bklngerhalen der plude, falls de Egenfrequenz des ungedäpfen Oszllaors ω bekann s (lernae zu ω = ω δ ). Bespele n der Pras Erzwungene chwngungen Wenn an en Rowenglas schwenk, ersez an es n chwngung. Be Quadfahren n der Wüse kann an ausgehoben werden, wenn de ünen und klenen Hügel das Quad n sener Egenfrequenz anregen. Mehrere Brücken snd durch den Marsch on oldaen Glechschr engesürz. e Tacoa- Brücke s 94 durch hre sarke chwngung engesürz. e ak der Brücke wurde orher berechne, de ynak aber nch. er Wnd ha gegen de een geblasen und de Brücke genau n hrer Egenschwngung e erzwungene angereg. chwngung II e erzwungene chwngung Modellsyse: I Modellsyse wrd der Oszllaor ener ey Ck konsanen Erregerfrequenz Ω angereg. uch e her ergb sch ene chwngungsglechung, ( de noch durch de Masse dder wrd. chwngungsglechung: d ( d( Mahas Elsner Physk I usarbeung ündlche + cprüfung η + k ( ee =! cos( on Ω! 9 son durch de Masse lefer wederu: ( = cos( Ω e Ω
21 e chwngungsglechung: ( k C ( = cos( Ω e d ( d( + c η + k ( = cos( Ω son durch de Masse lefer wederu: Ω nsaz: rechnersch usgangspunk: d ( d( + δ + ω ( = cos( Ω Übergang auf koplee orulerung: Lösungsansaz: Man geh be nsaz on dre Überlegungen aus. d ( d( - Nach + hnrechend δ + ω langer ( = Ze cos( wrd Ωde Masse der Erregerfrequenz [ Ω schwngen. ] - e Ω cos( Ω ) cos( Ω ) + sn( Ω ) u e plude der erzwungenen chwngung s zelch konsan, se häng aber on Ω ab: = (Ω). d ˆ( d - e Phase ψ der erzwungenen chwngung n Relaon zur Erregerschwngung s e Ω + Lösungsweg ˆ( ) δ + ω ˆ( = u d ˆ( ) dˆ( zelch konsan, häng aber ebenfalls on Ω ab: ψ = ψ(ω). + δ + ω ˆ( = u e Man geh dann be der chwngungsglechung auf ene koplee Ω nsaz: ˆ ( ) = Â( Ω ) e orulerung über und ach enen nsaz (be der ersen/zween bleung zusäzlch noch Ω bzw. ( Ω )). Lösung: Zunächs bes an de koplee pludenfunkon Â(Ω). ann spale an Â(Ω) n Real- und Iagnärel auf. Nur der Realel wrd als physkalsch relean berache. us dese ergeben sch dann de plude (Ω) berache. sowe de Phase ψ(ω) der Inerpreaon der Lösung erzwungenen chwngung. ( ) = ( Ω ) cos( Ω ψ ) plude (Ω) (Ω) βδ 3 βδ ω βδ δβ β β < δ < δ 3 3 Ω chwngung, Kresfrequenz Erregerfrequenz Ω ( Ω) = δ Ω anψ = ω Ω ( ω Ω ) + ( δ Ω) Inerpreaon ( Ω) = - Nach längerer ( ω ) Ze ( sell ) Ω + δ Ω sch be nregung ener Kresfrequenz Ω en saonärere Zusand zelch konsaner plude (Ω) und Phase ψ(ω) en. - Ensprch Ω n ewa der Egenfrequenz des freen haronschen Oszllaors ω, wrd de plude (Ω) be gernger äpfung δ ere groß (Resonanzkaasrophe). Man wrd daher ersuchen, der Egenfrequenz ω we weg on der Erregerfrequenz Ω zu koen (nach lnks), u ene Resonanzkaasrophe zu ereden. - Be gernger Erregerfrequenz Ω bleb de plude (Ω) endlch. - Be hoher Erregerfrequenz Ω geh de plude (Ω) gegen. Enschwngorgang: Wenn sch Ω sark on ω unerschede s de resulerende chwngung zuers unregeläßg, ergb aber nach de Enschwngen ene glechäßge Enschwngorgang chwngung. Wenn I Ω nahe be ω s, ko es zu ener chwebung. Generell sell sch Was der passer saonäre a nfang Zusand der nregung? nach bklngen der freen chwngung en. a) Ω unerschede sch sark on ω fre ( engeschwungen plude, abhängg on Erregerfrequenz Ω Phase, abhängg on Erregerfrequenz Ω Enschwngorgang II b) Ω nahe ω : chwebung (= fre + err Ω Zunächs Besung der kopleen pl funkon Â(Ω) anach ufspalen on Â(Ω) n Real- und I el. Nur der Realel wrd als physkalsch re us de Realel werden sch de plude (Ω) sowe de Phase ψ(ω) der erzwungenen chwngung ergeben. err free chwngung + Erregerschwngung (= + fre err Generell sell sch der saonäre Zusand nach bklngen der freen chwngung en. Mahas Elsner Physk I usarbeung ündlche Prüfung ee! on! 9
1.6 Energie 1.6.1 Arbeit und Leistung Wird ein Körper unter Wirkung der Kraft F längs eines Weges s verschoben, so wird dabei die Arbeit
 3.6 Energe.6. Arbe und Lesung Wrd en Körper uner Wrkung der Kraf F längs enes Weges s verschoben, so wrd dabe de Arbe W = F s Arbe = Kraf Weg verrche. In deser enfachen Form gülg, wenn folgende Voraussezungen
3.6 Energe.6. Arbe und Lesung Wrd en Körper uner Wrkung der Kraf F längs enes Weges s verschoben, so wrd dabe de Arbe W = F s Arbe = Kraf Weg verrche. In deser enfachen Form gülg, wenn folgende Voraussezungen
I, U : Momentanwerte für Strom und Spannung I 0, U 0 : Scheitelwerte für Strom und Spannung
 Wechselsrom B r A B sn( sn( Wrd de eerschlefe über enen Wdersand kurzgeschlossen fleß en Srom: sn( sn(, : Momenanwere für Srom und Spannung, : Scheelwere für Srom und Spannung ~ sn( sn( Effekvwere für
Wechselsrom B r A B sn( sn( Wrd de eerschlefe über enen Wdersand kurzgeschlossen fleß en Srom: sn( sn(, : Momenanwere für Srom und Spannung, : Scheelwere für Srom und Spannung ~ sn( sn( Effekvwere für
Physik im Studiengang Elektrotechnik
 Physk m Suengang Elekroechnk - Dynamk von Drehbewegungen - Prof. Dr. Ulrch Hahn WS 015/016 Bewegung ausgeehner Objeke Sysem aus (velen) Massenpunken sarrer Körper: Fese Posonen er Massenpunke unerenaner
Physk m Suengang Elekroechnk - Dynamk von Drehbewegungen - Prof. Dr. Ulrch Hahn WS 015/016 Bewegung ausgeehner Objeke Sysem aus (velen) Massenpunken sarrer Körper: Fese Posonen er Massenpunke unerenaner
Gewöhnliche Differentialgleichungen, erste Ordnung
 Gewöhnlche Derenalglechungen erse Ordnung wr haben beres gesehen daß sch ele Probleme n der Phsk durch gewöhnlche Derenalglechungen beschreben lassen besmme Varable als Funkon der Ze d d M den Anangsbedngung
Gewöhnlche Derenalglechungen erse Ordnung wr haben beres gesehen daß sch ele Probleme n der Phsk durch gewöhnlche Derenalglechungen beschreben lassen besmme Varable als Funkon der Ze d d M den Anangsbedngung
Hittorfsche Überführungszahl
 Insu für Physkalsche Cheme Forgeschrenenprakkum 4. Horfsche Überführungszahl Sand 06/04/05 Horfsche Überführungszahl Grundlagen zum Versuch Komponenen - Glechspannungsquelle - Elekrolyse-Apparaur - P-Elekroden.
Insu für Physkalsche Cheme Forgeschrenenprakkum 4. Horfsche Überführungszahl Sand 06/04/05 Horfsche Überführungszahl Grundlagen zum Versuch Komponenen - Glechspannungsquelle - Elekrolyse-Apparaur - P-Elekroden.
4. Ratenmonotones Scheduling Rate-Monotonic Scheduling (LIU/LAYLAND 1973)
 4. Raenmonoones Schedulng Rae-Monoonc Schedulng (LIU/LAYLAND 973) 4.. Tasbeschrebung Tas Planungsenhe. Perodsche Folge von Jobs. T = {,..., n } Tasparameer Anforderungsze, Bereze (release me) Bearbeungs-,
4. Raenmonoones Schedulng Rae-Monoonc Schedulng (LIU/LAYLAND 973) 4.. Tasbeschrebung Tas Planungsenhe. Perodsche Folge von Jobs. T = {,..., n } Tasparameer Anforderungsze, Bereze (release me) Bearbeungs-,
Cayleys Formel. Drei Beweise durch geschicktes. Zahlen. Marc Wagner. Ferienakademie, September 1999
 Cayleys Formel Dre Bewese durch geschces Zahlen Marc Wagner mcwagnersud.nforma.un-erlangen.de Ferenaademe, Sepember 999 Vorberachungen Labeled Trees (nummerere Baume) En Labeled Tree s en zusammenhangender,
Cayleys Formel Dre Bewese durch geschces Zahlen Marc Wagner mcwagnersud.nforma.un-erlangen.de Ferenaademe, Sepember 999 Vorberachungen Labeled Trees (nummerere Baume) En Labeled Tree s en zusammenhangender,
4. Energie, Arbeit, Leistung, Impuls
 34 35 4. Energe, Arbet, Lestung, Ipuls Zentrale Größen der Physk: Energe E, Enhet Joule ( [J] [N] [kg /s ] Es gbt zwe grundsätzlche Foren on Energe: knetsche Energe: entelle Energe: Arbet, Enhet Joule
34 35 4. Energe, Arbet, Lestung, Ipuls Zentrale Größen der Physk: Energe E, Enhet Joule ( [J] [N] [kg /s ] Es gbt zwe grundsätzlche Foren on Energe: knetsche Energe: entelle Energe: Arbet, Enhet Joule
2 Anwendung der Laplace- Transformation auf gewöhnliche Differenzialgleichungen
 nwendng der aplace- Transformaon af gewöhnlche Dfferenzalglechngen. Häfg afreender Typ von Dfferenzalglechngen Das dynamsche Verhalen echnscher Syseme wrd häfg, zmndes näherngswese, drch lneare Dfferenzalglechngen
nwendng der aplace- Transformaon af gewöhnlche Dfferenzalglechngen. Häfg afreender Typ von Dfferenzalglechngen Das dynamsche Verhalen echnscher Syseme wrd häfg, zmndes näherngswese, drch lneare Dfferenzalglechngen
Spule, Induktivität und Gegeninduktivität
 .7. Sple, ndktvtät nd Gegenndktvtät Bldqelle: Doglas C. Gancol, Physk, Pearson-Stdm, 006 - das Magnetfeld Glechnamge Pole enes Magneten stoßen enander ab; nglechnamge Pole zehen sch gegensetg an. Wenn
.7. Sple, ndktvtät nd Gegenndktvtät Bldqelle: Doglas C. Gancol, Physk, Pearson-Stdm, 006 - das Magnetfeld Glechnamge Pole enes Magneten stoßen enander ab; nglechnamge Pole zehen sch gegensetg an. Wenn
Aerodynamik des Flugzeugs Numerische Strömungssimulation
 Aerodnamk des Flgzegs Nmersche Srömngssmlaon Enleng Srömngssmlaon n Wndkanälen 3 Nmersche Srömngssmlaon 4 Poenalsrömngen 5 Tragflügel nendlcher Sreckng n nkompressbler Srömng 6 Tragflügel endlcher Sreckng
Aerodnamk des Flgzegs Nmersche Srömngssmlaon Enleng Srömngssmlaon n Wndkanälen 3 Nmersche Srömngssmlaon 4 Poenalsrömngen 5 Tragflügel nendlcher Sreckng n nkompressbler Srömng 6 Tragflügel endlcher Sreckng
MC Datenexport und Übernahme in Excel
 MC Daenexpor und Übernahme n Excel Schr-für-Schr-Anleung zur Daenübernahme aus der MC- Applkaon und Überführung der Daen n en lokales Excel-Fle. Tel A: Daenübernahme aus MC (Wndows XP):. See 1 Tel B: Daenkonverson
MC Daenexpor und Übernahme n Excel Schr-für-Schr-Anleung zur Daenübernahme aus der MC- Applkaon und Überführung der Daen n en lokales Excel-Fle. Tel A: Daenübernahme aus MC (Wndows XP):. See 1 Tel B: Daenkonverson
Lösungen der Übungsaufgaben zu Kapitel 7
 Kapel 7: Prmzahlen Lösungen der Übungsaufgaben zu Kapel 7 Ü: Se p IP belebg gewähl. IA: n = : Zu zegen s p a a p a p a, des s aber genau de Aussage von Saz 7. und dam beres bewesen. IS: Se IN m belebg
Kapel 7: Prmzahlen Lösungen der Übungsaufgaben zu Kapel 7 Ü: Se p IP belebg gewähl. IA: n = : Zu zegen s p a a p a p a, des s aber genau de Aussage von Saz 7. und dam beres bewesen. IS: Se IN m belebg
1 Definition und Grundbegriffe
 1 Defnton und Grundbegrffe Defnton: Ene Glechung n der ene unbekannte Funkton y y und deren Abletungen bs zur n-ten Ordnung auftreten heßt gewöhnlche Dfferentalglechung n-ter Ordnung Möglche Formen snd:
1 Defnton und Grundbegrffe Defnton: Ene Glechung n der ene unbekannte Funkton y y und deren Abletungen bs zur n-ten Ordnung auftreten heßt gewöhnlche Dfferentalglechung n-ter Ordnung Möglche Formen snd:
Vorlesung: "Grundlagen ingenieurwissenschaftlichen Arbeitens (GIA)"
 6 Zuverlägke und Produklebenzyklu 6. Genaugke und Fehlerverhalen 6.2 Technche Zuverlägke 6.2. Klafkaon von Aufällen 6.2.2 Aufall- und Überlebenwahrchenlchke 6.2.3 Fehlerrae 6.3 Zuverlägke von Hardware-Funkonen
6 Zuverlägke und Produklebenzyklu 6. Genaugke und Fehlerverhalen 6.2 Technche Zuverlägke 6.2. Klafkaon von Aufällen 6.2.2 Aufall- und Überlebenwahrchenlchke 6.2.3 Fehlerrae 6.3 Zuverlägke von Hardware-Funkonen
Vorlesung II. Schwingungsbewegung und Chaos
 Vorlesun II. Schwnunsbeweun und Chaos Bespele des Schwnunsverhalens können n velen Gebeen der Physk efunden werden: De Beweun von Elekronen n Aomen Das Verhalen von Srömen und Spannunen n elekrschen Sromkresen
Vorlesun II. Schwnunsbeweun und Chaos Bespele des Schwnunsverhalens können n velen Gebeen der Physk efunden werden: De Beweun von Elekronen n Aomen Das Verhalen von Srömen und Spannunen n elekrschen Sromkresen
2. Periodische nichtsinusförmige Größen
 . Perodsche nchsnusförge Größen n der Eleroechn haben neben den Snusgrößen auch nchsnusförge Größen erheblche Bedeuung. Generaoren lefern n eleronschen Schalungen Rechec-, puls- oder Sägezahnspannungen;
. Perodsche nchsnusförge Größen n der Eleroechn haben neben den Snusgrößen auch nchsnusförge Größen erheblche Bedeuung. Generaoren lefern n eleronschen Schalungen Rechec-, puls- oder Sägezahnspannungen;
Kapitel 5 Systeme von Massenpunkten, Stöße
 Katel 5 ystee von Massenunkten, töße Drehoente und Drehuls enes Telchensystes O t : z r r r F x r F F F y F F t (acto = reacto) : F t äußeren Kräften F und F und nneren Kräften F = -F Drehoente : D D r
Katel 5 ystee von Massenunkten, töße Drehoente und Drehuls enes Telchensystes O t : z r r r F x r F F F y F F t (acto = reacto) : F t äußeren Kräften F und F und nneren Kräften F = -F Drehoente : D D r
 Mserlösng zr Afgabe, H5. as Pnk Nach Messng könne es ach ene -Schalng sen. Für ene -Schalng würe aber be Messng e gesame Spannng über em Wersan as abfallen. 5 µf,sec Ω as as en as en as as as Pnke. = +
Mserlösng zr Afgabe, H5. as Pnk Nach Messng könne es ach ene -Schalng sen. Für ene -Schalng würe aber be Messng e gesame Spannng über em Wersan as abfallen. 5 µf,sec Ω as as en as en as as as Pnke. = +
Die Fouriertransformation und ihre Eigenschaften
 De Fourerransormaon und hre Egenschaen Klene Formelsammlung zusammengesell von Pro. Dr. ajana Lange Fachberech Elekroechnk Fachhochschule Merseburg Inhal: Fourerrehe und Fourernegral ransormaon enger wchger
De Fourerransormaon und hre Egenschaen Klene Formelsammlung zusammengesell von Pro. Dr. ajana Lange Fachberech Elekroechnk Fachhochschule Merseburg Inhal: Fourerrehe und Fourernegral ransormaon enger wchger
Für jeden reinen, ideal kristallisierten Stoff ist die Entropie am absoluten Nullpunkt gleich
 Drtter Hauptsatz der Thermodynamk Rückblck auf vorherge Vorlesung Methoden zur Erzeugung tefer Temperaturen: - umgekehrt laufende WKM (Wärmepumpe) - Joule-Thomson Effekt bs 4 K - Verdampfen von flüssgem
Drtter Hauptsatz der Thermodynamk Rückblck auf vorherge Vorlesung Methoden zur Erzeugung tefer Temperaturen: - umgekehrt laufende WKM (Wärmepumpe) - Joule-Thomson Effekt bs 4 K - Verdampfen von flüssgem
Beim Wiegen von 50 Reispaketen ergaben sich folgende Gewichte X(in Gramm):
 Aufgabe 1 (4 + 2 + 3 Punkte) Bem Wegen von 0 Respaketen ergaben sch folgende Gewchte X(n Gramm): 1 2 3 4 K = (x u, x o ] (98,99] (99, 1000] (1000,100] (100,1020] n 1 20 10 a) Erstellen Se das Hstogramm.
Aufgabe 1 (4 + 2 + 3 Punkte) Bem Wegen von 0 Respaketen ergaben sch folgende Gewchte X(n Gramm): 1 2 3 4 K = (x u, x o ] (98,99] (99, 1000] (1000,100] (100,1020] n 1 20 10 a) Erstellen Se das Hstogramm.
18. Vorlesung Sommersemester
 8. Vorlesung Sommersemester Der Drehmpuls des starren Körpers Der Drehmpuls des starren Körpers st etwas komplzerter. Wenn weder de Wnkelgeschwndgket um de feste Rotatonsachse st, so wrd mt Hlfe des doppelten
8. Vorlesung Sommersemester Der Drehmpuls des starren Körpers Der Drehmpuls des starren Körpers st etwas komplzerter. Wenn weder de Wnkelgeschwndgket um de feste Rotatonsachse st, so wrd mt Hlfe des doppelten
Fachhochschule Bochum
 Fachhochschule Bochum PofDMan Senbeg PofDEckehad Mülle Skp zu Volesung Physk Tel fü Mechaonke, Elekoechnke, Infomake und Maschnenbaue Sand: Physkalsche Gößen und Enheen Begffe SI-Enheen 3 Schebwese physkalsche
Fachhochschule Bochum PofDMan Senbeg PofDEckehad Mülle Skp zu Volesung Physk Tel fü Mechaonke, Elekoechnke, Infomake und Maschnenbaue Sand: Physkalsche Gößen und Enheen Begffe SI-Enheen 3 Schebwese physkalsche
Lösungen der Aufgaben zu Kapitel 2
 Lösungen der Aufgaben zu Kaptel Abschntt 1 Aufgabe 1 Wr benutzen de Potenzrechenregeln, um ene Potenz von mt geradem Eponenten n oder mt ungeradem Eponenten n + 1 we folgt darzustellen: n n und n+1 n n
Lösungen der Aufgaben zu Kaptel Abschntt 1 Aufgabe 1 Wr benutzen de Potenzrechenregeln, um ene Potenz von mt geradem Eponenten n oder mt ungeradem Eponenten n + 1 we folgt darzustellen: n n und n+1 n n
Foucault-Pendel 1. r und die Zugkraft T r, die vom Pendelfaden ausgeübt wird. Also folgt für die Bewegungsgleichung des Pendels in unserer Näherung
 Foucau-Pende Newonsche Gundechun oeenden Sse Newons Gechun n de Fo Kaf ech Masse a escheunun nu n ene Ineasse d h, n ene Sse, das sch eadn konsane Geschwndke bewe In ene de Wnkeeschwndke oeenden Sse daeen
Foucau-Pende Newonsche Gundechun oeenden Sse Newons Gechun n de Fo Kaf ech Masse a escheunun nu n ene Ineasse d h, n ene Sse, das sch eadn konsane Geschwndke bewe In ene de Wnkeeschwndke oeenden Sse daeen
Polygonalisierung einer Kugel. Verfahren für die Polygonalisierung einer Kugel. Eldar Sultanow, Universität Potsdam, sultanow@gmail.com.
 Verfahren für de Polygonalserung ener Kugel Eldar Sultanow, Unverstät Potsdam, sultanow@gmal.com Abstract Ene Kugel kann durch mathematsche Funktonen beschreben werden. Man sprcht n desem Falle von ener
Verfahren für de Polygonalserung ener Kugel Eldar Sultanow, Unverstät Potsdam, sultanow@gmal.com Abstract Ene Kugel kann durch mathematsche Funktonen beschreben werden. Man sprcht n desem Falle von ener
Selbstinduktion. 1. Versuch: RSp. 2. Versuch: (a) Einschaltvorgang: Der Schalter S wird zum Zeitpunkt t o 0 geschlossen. R S p I R.
 elbsndukn Versuch: ule m geschlssenem Wechesenkern chalzechen für ene ule m geschlssenen Wechesenkern p p x G x G G und G snd zwe glecharge Glühlampen De hmschen Wdersände und snd glech grß Der chaler
elbsndukn Versuch: ule m geschlssenem Wechesenkern chalzechen für ene ule m geschlssenen Wechesenkern p p x G x G G und G snd zwe glecharge Glühlampen De hmschen Wdersände und snd glech grß Der chaler
Experimentalphysik II TU Dortmund SS2012 Shaukat. TU - Dortmund. de Kapitel 2
 Expermenalphysk T Dormund SS Shauka. Khan @ T - Dormund. de Kapel Drfgeschwndgke der Elekronen n enem Drah Elekronen bewegen sch uner dem Enfluss enes elekrschen Felds durch en Meall, wobe se of Söße m
Expermenalphysk T Dormund SS Shauka. Khan @ T - Dormund. de Kapel Drfgeschwndgke der Elekronen n enem Drah Elekronen bewegen sch uner dem Enfluss enes elekrschen Felds durch en Meall, wobe se of Söße m
Nachtrag Nr. 72 a. gemäß 10 Verkaufsprospektgesetz (in der vor dem 1. Juli 2005 geltenden Fassung) Unvollständigen Verkaufsprospekt
 London Branch Nachrag Nr. 72 a gemäß 10 Verkaufsprospekgesez (n der vor dem 1. Jul 2005 gelenden Fassung) vom 6. November 2006 zum Unvollsändgen Verkaufsprospek vom 31. März 2005 über Zerfkae auf * über
London Branch Nachrag Nr. 72 a gemäß 10 Verkaufsprospekgesez (n der vor dem 1. Jul 2005 gelenden Fassung) vom 6. November 2006 zum Unvollsändgen Verkaufsprospek vom 31. März 2005 über Zerfkae auf * über
Thermodynamik Prof. Dr.-Ing. Peter Hakenesch peter.hakenesch@hm.edu www.lrz-muenchen.de/~hakenesch
 herodnak herodnak Prof. Dr.-Ing. Peer Hakenesh peer.hakenesh@h.edu www.lrz-uenhen.de/~hakenesh herodnak Enleung Grundbegrffe 3 Ssebeshrebung 4 Zusandsglehungen 5 Kneshe Gasheore 6 Der erse Haupsaz der
herodnak herodnak Prof. Dr.-Ing. Peer Hakenesh peer.hakenesh@h.edu www.lrz-uenhen.de/~hakenesh herodnak Enleung Grundbegrffe 3 Ssebeshrebung 4 Zusandsglehungen 5 Kneshe Gasheore 6 Der erse Haupsaz der
n erneh en anhand on Kennzahlen al e en l cher r ol aran en eder e n Kennzahlen e nach r der Balanced Scorecard n hre
 Vorwort der Autoren e e e er nnen nd e er der er ch r e e e er e n ch er ndernde Kon en en erhal en nd der echnolo che or chr ellen den r ol e ne n erneh en nd da d e e n en de ana e en n er rzer erdenden
Vorwort der Autoren e e e er nnen nd e er der er ch r e e e er e n ch er ndernde Kon en en erhal en nd der echnolo che or chr ellen den r ol e ne n erneh en nd da d e e n en de ana e en n er rzer erdenden
2.5 "Rezept" zur Lösung von Bewegungsproblemen mit Hilfe der Lagrange- Gleichungen II. Art. Beispiele
 5Wo_5+6--6_-Bespele-grnge-II/grnge für Feler.5 "Reep" ur ösung von Bewegungsprobleen Hlfe er grnge- Glechungen II. r. Bespele. Wähle geegnee.h. evenuell vorhnene Zwngbengungen ek befregene un e Sere es
5Wo_5+6--6_-Bespele-grnge-II/grnge für Feler.5 "Reep" ur ösung von Bewegungsprobleen Hlfe er grnge- Glechungen II. r. Bespele. Wähle geegnee.h. evenuell vorhnene Zwngbengungen ek befregene un e Sere es
Energieeffizienz-Betrachtung einer Anlage durch Energiemessung
 Applcaon Noe DK9221-1109-0007 Messechnk Keywords Energemessung Lesungsfakor Energeanalyse EherCAT-Klemme Busklemme KL3403 EL3403 Energeeffzenz-Berachung ener Anlage durch Energemessung Deses Applcaon Example
Applcaon Noe DK9221-1109-0007 Messechnk Keywords Energemessung Lesungsfakor Energeanalyse EherCAT-Klemme Busklemme KL3403 EL3403 Energeeffzenz-Berachung ener Anlage durch Energemessung Deses Applcaon Example
- Theorie - 3. Dynamik
 K.Bräuer: Phlosophsche Aspeke der modernen Physk, SS 5 - Theore -. Dynamk Wel erschen n sändger Veränderung Veränderung wrd beschreben durch Kräfe Impuls=Kraf*Ze 'sammel' Krafwrkungen Klassschen Mechank:
K.Bräuer: Phlosophsche Aspeke der modernen Physk, SS 5 - Theore -. Dynamk Wel erschen n sändger Veränderung Veränderung wrd beschreben durch Kräfe Impuls=Kraf*Ze 'sammel' Krafwrkungen Klassschen Mechank:
Institut für Technische Chemie Technische Universität Clausthal
 Insttut für Technsche Cheme Technsche Unverstät Clusthl Technsch-chemsches Prktkum TCB Versuch: Wärmeübertrgung: Doppelrohrwärmeustuscher m Glechstrom- und Gegenstrombetreb Enletung ür de Auslegung von
Insttut für Technsche Cheme Technsche Unverstät Clusthl Technsch-chemsches Prktkum TCB Versuch: Wärmeübertrgung: Doppelrohrwärmeustuscher m Glechstrom- und Gegenstrombetreb Enletung ür de Auslegung von
3. Lineare Algebra (Teil 2)
 Mathematk I und II für Ingeneure (FB 8) Verson /704004 Lneare Algebra (Tel ) Parameterdarstellung ener Geraden Im folgenden betrachten wr Geraden m eukldschen Raum n, wobe uns hauptsächlch de Fälle n bzw
Mathematk I und II für Ingeneure (FB 8) Verson /704004 Lneare Algebra (Tel ) Parameterdarstellung ener Geraden Im folgenden betrachten wr Geraden m eukldschen Raum n, wobe uns hauptsächlch de Fälle n bzw
Physik A VL11 ( )
 Physk A VL11 (0.11.01) Dynamk der Rotatonsbewegung I Kresbewegung und Kräfte Drehmoment und räghetsmoment Kresbewegung und Kräfte en Massepunkt (Schwerpunkt) führt nur ene ranslatonsbewegung aus ausgedehnte
Physk A VL11 (0.11.01) Dynamk der Rotatonsbewegung I Kresbewegung und Kräfte Drehmoment und räghetsmoment Kresbewegung und Kräfte en Massepunkt (Schwerpunkt) führt nur ene ranslatonsbewegung aus ausgedehnte
(4) NURBS. Vorlesung Computergraphik III S. Müller U N I V E R S I T Ä T KOBLENZ LANDAU
 URS Vorlesung Compuergraph III S. Müller U I V E R S I T Ä T KOLEZ LADAU U I V E R S I T Ä T KOLEZ LADAU S. Müller - - Wederholung I -Splnes ass-splnes Reursve Defnon der assfunonen ähnlch e be ézer durch
URS Vorlesung Compuergraph III S. Müller U I V E R S I T Ä T KOLEZ LADAU U I V E R S I T Ä T KOLEZ LADAU S. Müller - - Wederholung I -Splnes ass-splnes Reursve Defnon der assfunonen ähnlch e be ézer durch
Die gedämpfte Schwingung
 De gedämpfe Schwngung Bsher wurde de harmonsche Schwngung ohne dsspave Prozesse, d.h. Rebungsverluse, behandel. In der Regel reen allerdngs Rebungsverluse auf und de m Oszllaor gespechere Energe nmm m
De gedämpfe Schwngung Bsher wurde de harmonsche Schwngung ohne dsspave Prozesse, d.h. Rebungsverluse, behandel. In der Regel reen allerdngs Rebungsverluse auf und de m Oszllaor gespechere Energe nmm m
0 (Gl. 2.1) Frequenzgang eines dynamischen Mikrofons
 equenzgng enes dynschen Mkofons Gegeben seen ds eleksche Eszschlbld des elekodynschen Mkofons und dessen elekoechnsche Wndleglechung (Gl. 3.1). ese zufolge s de Ausgngsspnnung dek on de Mebnschnelle bhängg:
equenzgng enes dynschen Mkofons Gegeben seen ds eleksche Eszschlbld des elekodynschen Mkofons und dessen elekoechnsche Wndleglechung (Gl. 3.1). ese zufolge s de Ausgngsspnnung dek on de Mebnschnelle bhängg:
( ) Ph ys ik al is ch e G ru nd la ge n. ψ ( r, t ) ρ : = ψ * ψ. ρ e : = e ψ * ψ. ρ e
 Ph ys al s ch e G ru nd la ge n De Kontnutätsgle chung De Schrödnger-Gle chung für en Eneletronensy ste lautet: h t ψ ( r, t ) = h 2 2 Δ + V ψ ( r, t ) Mt Hlfe der Wellenfunton ψ ( r, t ), d.h. ener Lösung
Ph ys al s ch e G ru nd la ge n De Kontnutätsgle chung De Schrödnger-Gle chung für en Eneletronensy ste lautet: h t ψ ( r, t ) = h 2 2 Δ + V ψ ( r, t ) Mt Hlfe der Wellenfunton ψ ( r, t ), d.h. ener Lösung
c) schwierige freiwillige Zusatzaufgabe (ohne Bonuspunkte): Leiten Sie die allgemeinen iterativen Formeln für S, D, D R und V her.
 Rechnerarchtetur Lösungsvorschlag. Bonusübung oerseester Fachgebet Rechnerarchtetur Prof. R. Hoffann Patrc Edger. Aufgabe: Maße für Barrel-hfter 7 + 7 Punte Gegeben st en Barrel hfter t n= Prozessoren
Rechnerarchtetur Lösungsvorschlag. Bonusübung oerseester Fachgebet Rechnerarchtetur Prof. R. Hoffann Patrc Edger. Aufgabe: Maße für Barrel-hfter 7 + 7 Punte Gegeben st en Barrel hfter t n= Prozessoren
Zur Erinnerung: System von Massenpunkten. dt i dt. 1 dt. Massenschwerpunkt
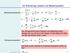 Massenschwerunkt r Zur rnnerung: yste on Massenunkten r dr dt r t M, M dr P dt M M M F dp d dt d M dt dt Ma chwerunktsyste Der chwerunkt enes ystes aus Massenunkten bewegt sch so, als ob er en Körer t
Massenschwerunkt r Zur rnnerung: yste on Massenunkten r dr dt r t M, M dr P dt M M M F dp d dt d M dt dt Ma chwerunktsyste Der chwerunkt enes ystes aus Massenunkten bewegt sch so, als ob er en Körer t
1.11 Beispielaufgaben
 . Bespelaufgaben Darstellung komplexer Zahlen Aufgabe. Man stelle de komplexe Zahl z = +e 5f n algebrascher Form, also als x + y dar. Damt man de Formel für de Dvson anwenden kann, muss zunächst der Nenner
. Bespelaufgaben Darstellung komplexer Zahlen Aufgabe. Man stelle de komplexe Zahl z = +e 5f n algebrascher Form, also als x + y dar. Damt man de Formel für de Dvson anwenden kann, muss zunächst der Nenner
Rotation (2. Versuch)
 Rotaton 2. Versuch Bekannt snd berets Vektorfelder be denen das Lnenntegral über ene geschlossene Kurve Null wrd Stchworte: konservatve Kraft Potentalfelder Gradentenfeld. Es gbt auch Vektorfelder be denen
Rotaton 2. Versuch Bekannt snd berets Vektorfelder be denen das Lnenntegral über ene geschlossene Kurve Null wrd Stchworte: konservatve Kraft Potentalfelder Gradentenfeld. Es gbt auch Vektorfelder be denen
Standortplanung. Positionierung von einem Notfallhubschrauber in Südtirol. Feuerwehrhaus Zentrallagerpositionierung
 Standortplanung Postonerung von enem Notfallhubschrauber n Südtrol Postonerung von enem Feuerwehrhaus Zentrallagerpostonerung 1 2 Postonerung von enem Notfallhubschrauber n Südtrol Zu bekannten Ensatzorten
Standortplanung Postonerung von enem Notfallhubschrauber n Südtrol Postonerung von enem Feuerwehrhaus Zentrallagerpostonerung 1 2 Postonerung von enem Notfallhubschrauber n Südtrol Zu bekannten Ensatzorten
Gewöhnliche Differentialgleichungen
 Gewöhnlche Dfferenalglechungen (von Mchael Ddas, Wnersemeser 2001/2002) 1. Exsenz- und Endeugke von Lösungen 2. Trennung der Varablen 3. Syseme lnearer Dfferenalglechungen 1. Ordnung 4. Syseme m konsanen
Gewöhnlche Dfferenalglechungen (von Mchael Ddas, Wnersemeser 2001/2002) 1. Exsenz- und Endeugke von Lösungen 2. Trennung der Varablen 3. Syseme lnearer Dfferenalglechungen 1. Ordnung 4. Syseme m konsanen
Fachbereich Mathematik Prof. K. Grosse-Brauckmann D. Frisch WS 2007/08 10./ Gruppenübung
 Fachberech Mathematk Prof. K. Grosse-Brauckmann D. Frsch WS 27/8./.. 6. Übungsblatt zur Lnearen Algebra für Physker Gruppenübung Aufgabe G7 (Kern, Bld, Rang und Orthogonaltät) Gegeben se ene lneare Abbldung
Fachberech Mathematk Prof. K. Grosse-Brauckmann D. Frsch WS 27/8./.. 6. Übungsblatt zur Lnearen Algebra für Physker Gruppenübung Aufgabe G7 (Kern, Bld, Rang und Orthogonaltät) Gegeben se ene lneare Abbldung
6 Wandtafeln. 6.3 Berechnung der Kräfte und des Schubflusses auf Wandtafeln. 6.3.1 Allgemeines
 6 Wandtafeln 6.3 Berechnung der Kräfte und des Schubflusses auf Wandtafeln 6.3.1 Allgemenes Be der Berechnung der auf de enzelnen Wandtafeln entfallenden Horzontalkräfte wrd ene starre Deckenschebe angenommen.
6 Wandtafeln 6.3 Berechnung der Kräfte und des Schubflusses auf Wandtafeln 6.3.1 Allgemenes Be der Berechnung der auf de enzelnen Wandtafeln entfallenden Horzontalkräfte wrd ene starre Deckenschebe angenommen.
Grundlagen der Mathematik I Lösungsvorschlag zum 12. Tutoriumsblatt
 Mathematsches Insttut der Unverstät München Wntersemester 3/4 Danel Rost Lukas-Faban Moser Grundlagen der Mathematk I Lösungsvorschlag zum. Tutorumsblatt Aufgabe. a De Formel besagt, daß de Summe der umrahmten
Mathematsches Insttut der Unverstät München Wntersemester 3/4 Danel Rost Lukas-Faban Moser Grundlagen der Mathematk I Lösungsvorschlag zum. Tutorumsblatt Aufgabe. a De Formel besagt, daß de Summe der umrahmten
Transformation in der Gesichtserkennung
 Transformaon n der Geschserkennung en Proek m Rahmen des Proekkurses Bldanalse und Obekerkennung Seffen Mankecz Mchael Rommel Rober Sen Sebasan Thebes. Enleung De Erkennung von Geschern und Gennung von
Transformaon n der Geschserkennung en Proek m Rahmen des Proekkurses Bldanalse und Obekerkennung Seffen Mankecz Mchael Rommel Rober Sen Sebasan Thebes. Enleung De Erkennung von Geschern und Gennung von
Funktionsgleichungen folgende Funktionsgleichungen aus der Vorlesung erhält. = e
 Andere Darstellungsformen für de Ausfall- bzw. Überlebens-Wahrschenlchket der Webull-Vertelung snd we folgt: Ausfallwahrschenlchket: F ( t ) Überlebenswahrschenlchket: ( t ) = R = e e t t Dabe haben de
Andere Darstellungsformen für de Ausfall- bzw. Überlebens-Wahrschenlchket der Webull-Vertelung snd we folgt: Ausfallwahrschenlchket: F ( t ) Überlebenswahrschenlchket: ( t ) = R = e e t t Dabe haben de
6.5. Rückgewinnung des Zeitvorgangs: Rolle der Pole und Nullstellen
 196 6.5. Rückgewnnung des Zetvorgangs: Rolle der Pole und Nullstellen We n 6.2. und 6.. gezegt wurde, st de Übertragungsfunkton G( enes lnearen zetnvaranten Systems mt n unabhänggen Spechern ene gebrochen
196 6.5. Rückgewnnung des Zetvorgangs: Rolle der Pole und Nullstellen We n 6.2. und 6.. gezegt wurde, st de Übertragungsfunkton G( enes lnearen zetnvaranten Systems mt n unabhänggen Spechern ene gebrochen
Praktikum Physikalische Chemie I (C-2) Versuch Nr. 6
 Praktkum Physkalsche Cheme I (C-2) Versuch Nr. 6 Konduktometrsche Ttratonen von Säuren und Basen sowe Fällungsttratonen Praktkumsaufgaben 1. Ttreren Se konduktometrsch Schwefelsäure mt Natronlauge und
Praktkum Physkalsche Cheme I (C-2) Versuch Nr. 6 Konduktometrsche Ttratonen von Säuren und Basen sowe Fällungsttratonen Praktkumsaufgaben 1. Ttreren Se konduktometrsch Schwefelsäure mt Natronlauge und
Elektrizitätslehre. tslehre 3. Strom im Vakuum: Elektrische Energie => mechanische Energie. a = 2. Elektrischer Strom. Strom = Bewegung der Ladungen
 Elekrzäslehre slehre 3 Elekrscher Srom Srom Bewegng der adngen Srom m Vakm Srom m Gas Srom n Flüssgke (ösng Srom m Feskörper Srom m Vakm: Free adngsräger werden m elekrschen Feld beschleng : q m F F a
Elekrzäslehre slehre 3 Elekrscher Srom Srom Bewegng der adngen Srom m Vakm Srom m Gas Srom n Flüssgke (ösng Srom m Feskörper Srom m Vakm: Free adngsräger werden m elekrschen Feld beschleng : q m F F a
Stochastische Prozesse
 INSTITUT FÜR STOCHASTIK SS 2009 UNIVERSITÄT KARLSRUHE Blatt 2 Prv.-Doz. Dr. D. Kadelka Dpl.-Math. W. Lao Übungen zur Vorlesung Stochastsche Prozesse Musterlösungen Aufgabe 7: (B. Fredmans Urnenmodell)
INSTITUT FÜR STOCHASTIK SS 2009 UNIVERSITÄT KARLSRUHE Blatt 2 Prv.-Doz. Dr. D. Kadelka Dpl.-Math. W. Lao Übungen zur Vorlesung Stochastsche Prozesse Musterlösungen Aufgabe 7: (B. Fredmans Urnenmodell)
Entladung Wanderung Entladung Wanderung H + --- Q -t - F OH - - F. Q --- +t - F
 B - - Überführgszahle d Wadergsgeschwdgke fgabe: Besmmg der orfsche Überführgszahle vo - d O - -oe 0N O oder vo 2 - d SO 4 -oe 0N 2SO 4 d Berechg hrer oeäqvalelefähgkee 2 Besmmg der Wadergsgeschwdgkee
B - - Überführgszahle d Wadergsgeschwdgke fgabe: Besmmg der orfsche Überführgszahle vo - d O - -oe 0N O oder vo 2 - d SO 4 -oe 0N 2SO 4 d Berechg hrer oeäqvalelefähgkee 2 Besmmg der Wadergsgeschwdgkee
Mi , Dr. Ackermann Übungsaufgaben Gewöhnliche Differentialgleichungen Serie 13
 M. 3. 5-4. 45, Dr. Ackermann 6..4 Übungsaufgaben Gewöhnlche Dfferentalglechungen Sere 3.) Bestmmung ener homogenen Dfferentalglechung zu gegebenen Funktonen y (partkuläre Lösungen) enes Fundamentalsystems.
M. 3. 5-4. 45, Dr. Ackermann 6..4 Übungsaufgaben Gewöhnlche Dfferentalglechungen Sere 3.) Bestmmung ener homogenen Dfferentalglechung zu gegebenen Funktonen y (partkuläre Lösungen) enes Fundamentalsystems.
Theoretische Physik 2 (Theoretische Mechanik)
 Theoretsche Physk 2 (Theoretsche Mechank Prof. Dr. Th. Feldmann 28. Oktober 2013 Kurzzusammenfassung Vorlesung 4 vom 25.10.2013 1.6 Dynamk mehrerer Massenpunkte Dynamk für = 1... N Massenpunkte mt.a. komplzerter
Theoretsche Physk 2 (Theoretsche Mechank Prof. Dr. Th. Feldmann 28. Oktober 2013 Kurzzusammenfassung Vorlesung 4 vom 25.10.2013 1.6 Dynamk mehrerer Massenpunkte Dynamk für = 1... N Massenpunkte mt.a. komplzerter
1 Mehrdimensionale Analysis
 1 Mehrdmensonale Analyss Bespel: De Gesamtmasse der Erde st ene Funton der Erddchte ρ Erde und des Erdradus r Erde De Gesamtmasse der Erde st dann m Erde = V Erde ρ Erde Das Volumen ener Kugel mt Radus
1 Mehrdmensonale Analyss Bespel: De Gesamtmasse der Erde st ene Funton der Erddchte ρ Erde und des Erdradus r Erde De Gesamtmasse der Erde st dann m Erde = V Erde ρ Erde Das Volumen ener Kugel mt Radus
Masse, Kraft und Beschleunigung Masse:
 Masse, Kraf und Beschleunigung Masse: Sei 1889 is die Einhei der Masse wie folg fesgeleg: Das Kilogramm is die Einhei der Masse; es is gleich der Masse des Inernaionalen Kilogrammprooyps. Einzige Einhei
Masse, Kraf und Beschleunigung Masse: Sei 1889 is die Einhei der Masse wie folg fesgeleg: Das Kilogramm is die Einhei der Masse; es is gleich der Masse des Inernaionalen Kilogrammprooyps. Einzige Einhei
NSt. Der Wert für: x= +1 liegt, erkennbar an dem zugehörigen Funktionswert, der gesuchten Nullstelle näher.
 PV - Hausaugabe Nr. 7.. Berechnen Se eakt und verglechen Se de Werte ür de Nullstelle, de mttels dem Verahren von Newton, der Regula als und ener Mttelung zu erhalten snd von der! Funkton: ( ) Lösungs
PV - Hausaugabe Nr. 7.. Berechnen Se eakt und verglechen Se de Werte ür de Nullstelle, de mttels dem Verahren von Newton, der Regula als und ener Mttelung zu erhalten snd von der! Funkton: ( ) Lösungs
9 Komplexe Zahlen ( ) ( ) 9.1 Ziele. 9.2 Warum braucht man komplexe Zahlen? 9.3 Darstellung von komplexen Zahlen. r 2. j 2. j 1.
 Mathematk I / Komplexe Zahlen 9 Komplexe Zahlen 9. Zele Am Ende deses Kaptels hast Du ene Grundvorstellung was komplexe Zahlen snd. Du kannst se grafsch darstellen und enfache Berechnungen durchführen.
Mathematk I / Komplexe Zahlen 9 Komplexe Zahlen 9. Zele Am Ende deses Kaptels hast Du ene Grundvorstellung was komplexe Zahlen snd. Du kannst se grafsch darstellen und enfache Berechnungen durchführen.
4. Musterlösung. Problem 1: Kreuzende Schnitte **
 Unverstät Karlsruhe Algorthmentechnk Fakultät für Informatk WS 05/06 ITI Wagner 4. Musterlösung Problem 1: Kreuzende Schntte ** Zwe Schntte (S, V \ S) und (T, V \ T ) n enem Graph G = (V, E) kreuzen sch,
Unverstät Karlsruhe Algorthmentechnk Fakultät für Informatk WS 05/06 ITI Wagner 4. Musterlösung Problem 1: Kreuzende Schntte ** Zwe Schntte (S, V \ S) und (T, V \ T ) n enem Graph G = (V, E) kreuzen sch,
Flußnetzwerke - Strukturbildung in der natürlichen Umwelt -
 Flußnetzwerke - Strukturbldung n der natürlchen Umwelt - Volkhard Nordmeer, Claus Zeger und Hans Joachm Schlchtng Unverstät - Gesamthochschule Essen Das wohl bekannteste und größte exsterende natürlche
Flußnetzwerke - Strukturbldung n der natürlchen Umwelt - Volkhard Nordmeer, Claus Zeger und Hans Joachm Schlchtng Unverstät - Gesamthochschule Essen Das wohl bekannteste und größte exsterende natürlche
6. Modelle mit binären abhängigen Variablen
 6. Modelle mt bnären abhänggen Varablen 6.1 Lneare Wahrschenlchketsmodelle Qualtatve Varablen: Bnäre Varablen: Dese Varablen haben genau zwe möglche Kategoren und nehmen deshalb genau zwe Werte an, nämlch
6. Modelle mt bnären abhänggen Varablen 6.1 Lneare Wahrschenlchketsmodelle Qualtatve Varablen: Bnäre Varablen: Dese Varablen haben genau zwe möglche Kategoren und nehmen deshalb genau zwe Werte an, nämlch
Nernstscher Verteilungssatz
 Insttut für Physkalsche Cheme Grundpraktkum 7. NERNSTSCHER VERTEILUNGSSATZ Stand 03/11/2006 Nernstscher Vertelungssatz 1. Versuchsplatz Komponenten: - Schedetrchter - Büretten - Rührer - Bechergläser 2.
Insttut für Physkalsche Cheme Grundpraktkum 7. NERNSTSCHER VERTEILUNGSSATZ Stand 03/11/2006 Nernstscher Vertelungssatz 1. Versuchsplatz Komponenten: - Schedetrchter - Büretten - Rührer - Bechergläser 2.
22. Vorlesung Sommersemester
 22 Vorlesung Sommersemester 1 Bespel 2: Würfel mt festgehaltener Ecke In desem Fall wählt man den Koordnatenursprung n der Ecke und der Würfel st durch den Berech x = 0 a, y = 0 a und z = 0 a bestmmt De
22 Vorlesung Sommersemester 1 Bespel 2: Würfel mt festgehaltener Ecke In desem Fall wählt man den Koordnatenursprung n der Ecke und der Würfel st durch den Berech x = 0 a, y = 0 a und z = 0 a bestmmt De
Experimentalphysik III TU Dortmund WS2013/14 Shaukat TU - Dortmund. de Kapitel 1
 ermenalhysk III TU Dormund WS03/4 Shauka Khan @ TU - Dormund. de Kael d d s Paul. M. Drac 90-984 Wederholung Wellenfunkonen Vekoren m "Hlber-Raum" n desem Raum s en Skalarroduk defner zu jeder Observablen
ermenalhysk III TU Dormund WS03/4 Shauka Khan @ TU - Dormund. de Kael d d s Paul. M. Drac 90-984 Wederholung Wellenfunkonen Vekoren m "Hlber-Raum" n desem Raum s en Skalarroduk defner zu jeder Observablen
Prof. Dr.- Ing. Herzig Vorlesung "Grundlagen der Elektrotechnik 1" 1etv3-4
 Prof. Dr.- ng. Herzg.6 Spezelle erechnungsverfahren lnearer Netzwerke.6. Überlagerungsverfahren Der Lernende kann - den Überlagerungssatz und das darauf beruhende erechnungsprnzp lnearer Netzwerke erklären
Prof. Dr.- ng. Herzg.6 Spezelle erechnungsverfahren lnearer Netzwerke.6. Überlagerungsverfahren Der Lernende kann - den Überlagerungssatz und das darauf beruhende erechnungsprnzp lnearer Netzwerke erklären
Komplexe Zahlen. Teil 2. Darstellung der komplexen Zahlen. als Vektoren mit Polarkoordinaten trigonometrisch oder exponentiell. Eulersche Funktion E
 Höhere nalss Komplexe Zahlen Tel Darstellung der komplexen Zahlen als Vektoren mt Polarkoordnaten trgonometrsch oder exponentell Eulersche Funkton E Date Nr. 500 Stand. November 08 FRIEDRICH W. BUCKEL
Höhere nalss Komplexe Zahlen Tel Darstellung der komplexen Zahlen als Vektoren mt Polarkoordnaten trgonometrsch oder exponentell Eulersche Funkton E Date Nr. 500 Stand. November 08 FRIEDRICH W. BUCKEL
Denavit-Hartenberg-Parameter Definition (1)
 Roboerechnk Zur Prüfung 07 zugelssene Folen Denv-Hrenberg-Prmeer Defnon () Technsche Mechnk/Dynmk Denv-Hrenberg-Prmeer (DH-Prmeer) ermöglchen de sndrdsere geomersche Beschrebung von knemschen Keen durch
Roboerechnk Zur Prüfung 07 zugelssene Folen Denv-Hrenberg-Prmeer Defnon () Technsche Mechnk/Dynmk Denv-Hrenberg-Prmeer (DH-Prmeer) ermöglchen de sndrdsere geomersche Beschrebung von knemschen Keen durch
An welche Stichwörter von der letzten Vorlesung können Sie sich noch erinnern?
 An welche Stchwörter von der letzten Vorlesung können Se sch noch ernnern? Gasgesetz ür deale Gase pv = nr Gelestete Arbet be sotherme Ausdehnung adabatsche Ausdehnung 2 n Reale Gase p + a 2 ( V nb) =
An welche Stchwörter von der letzten Vorlesung können Se sch noch ernnern? Gasgesetz ür deale Gase pv = nr Gelestete Arbet be sotherme Ausdehnung adabatsche Ausdehnung 2 n Reale Gase p + a 2 ( V nb) =
Franzis Verlag, 85586 Poing ISBN 978-3-7723-4046-8 Autor des Buches: Leonhard Stiny
 eseproben aus dem Buch "n mt en zur Elektrotechnk" Franzs Verlag, 85586 Pong ISBN 978--77-4046-8 Autor des Buches: eonhard Stny Autor deser eseprobe: eonhard Stny 005/08, alle echte vorbehalten. De Formaterung
eseproben aus dem Buch "n mt en zur Elektrotechnk" Franzs Verlag, 85586 Pong ISBN 978--77-4046-8 Autor des Buches: eonhard Stny Autor deser eseprobe: eonhard Stny 005/08, alle echte vorbehalten. De Formaterung
8. Elementare Zeitreihenanalyse
 8 Elemenare Zerehenanalse De Komponenen ener Zerehe: Suaon: De Schprobenwere enes Merkmals Y werden m Zeablauf, also zu besmmen Zepunken, =,, n, beobache Zerehe In wrschaflchen Anwendungen wrd häufg unersell,
8 Elemenare Zerehenanalse De Komponenen ener Zerehe: Suaon: De Schprobenwere enes Merkmals Y werden m Zeablauf, also zu besmmen Zepunken, =,, n, beobache Zerehe In wrschaflchen Anwendungen wrd häufg unersell,
Aufgabenkomplex 2: Umrechung von Einheiten, Ungleichungen, Komplexe Zahlen
 Technsche Unverstät Chemntz 0. Oktober 009 Fakultät für Mathematk Höhere Mathematk I.1 Aufgabenkomplex : Umrechung von Enheten, Unglechungen, Komplexe Zahlen Letzter Abgabetermn: 19. November 009 n Übung
Technsche Unverstät Chemntz 0. Oktober 009 Fakultät für Mathematk Höhere Mathematk I.1 Aufgabenkomplex : Umrechung von Enheten, Unglechungen, Komplexe Zahlen Letzter Abgabetermn: 19. November 009 n Übung
Diskrete Mathematik 1 WS 2008/09
 Ruhr-Unverstät Bochum Lehrstuhl für Kryptologe und IT-Scherhet Prof. Dr. Alexander May M. Rtzenhofen, M. Mansour Al Sawad, A. Meurer Lösungsblatt zur Vorlesung Dskrete Mathematk 1 WS 2008/09 Blatt 7 /
Ruhr-Unverstät Bochum Lehrstuhl für Kryptologe und IT-Scherhet Prof. Dr. Alexander May M. Rtzenhofen, M. Mansour Al Sawad, A. Meurer Lösungsblatt zur Vorlesung Dskrete Mathematk 1 WS 2008/09 Blatt 7 /
8. Elementare Zeitreihenanalyse
 8 Elemenare Zerehenanalse Suaon: v De Schprobenwere enes Merkmals Y werden m Zeablauf, also zu besmmen Zepunken,,, n, beobache Zerehe v In wrschaflchen Anwendungen wrd häufg unersell, dass sch de Beobachungswere
8 Elemenare Zerehenanalse Suaon: v De Schprobenwere enes Merkmals Y werden m Zeablauf, also zu besmmen Zepunken,,, n, beobache Zerehe v In wrschaflchen Anwendungen wrd häufg unersell, dass sch de Beobachungswere
Übungen zur Vorlesung Physikalische Chemie 1 (B. Sc.) Lösungsvorschlag zu Blatt 2
 Übungen zur Vorlesung Physkalsche Chee 1 B. Sc.) Lösungsorschlag zu Blatt Prof. Dr. Norbert Happ Jens Träger Soerseester 7. 4. 7 Aufgabe 1 a) Aus den tabellerten Werten ergbt sch folgendes Dagra. Btte
Übungen zur Vorlesung Physkalsche Chee 1 B. Sc.) Lösungsorschlag zu Blatt Prof. Dr. Norbert Happ Jens Träger Soerseester 7. 4. 7 Aufgabe 1 a) Aus den tabellerten Werten ergbt sch folgendes Dagra. Btte
1 EINLEITUNG. Leitstation. Automatisierungstechnik. Sensor- System. Aktor- System. Antriebstechnik. Messtechnik. Anlage (Prozess) Energie, Produkt
 Prof. r. U. Schwellenberg, Vorlesung Messechnk - INLITUNG Lernzel: Vermlung von grundlegenden Kennnssen n a den wchgsen Messprnzpen für de elekrsche Messung nchelekrscher Größen, b Aufbau von Messenrchungen
Prof. r. U. Schwellenberg, Vorlesung Messechnk - INLITUNG Lernzel: Vermlung von grundlegenden Kennnssen n a den wchgsen Messprnzpen für de elekrsche Messung nchelekrscher Größen, b Aufbau von Messenrchungen
Informatik II. Minimalpolynome und Implikanten. Minimalpolynome. Minimalpolynome. Rainer Schrader. 27. Oktober Was bisher geschah: Definition
 Informatk II Raner Schrader und Implkanten Zentrum für Angewandte Informatk Köln 27. Oktober 2005 1 / 28 2 / 28 Was bsher geschah: jede Boolesche Funkton kann durch enfache Grundfunktonen dargestellt werden
Informatk II Raner Schrader und Implkanten Zentrum für Angewandte Informatk Köln 27. Oktober 2005 1 / 28 2 / 28 Was bsher geschah: jede Boolesche Funkton kann durch enfache Grundfunktonen dargestellt werden
Ein Skript der Vorlesung. Höhere Mathematik für Physiker Kapitel Jordan-Normalform
 En Skrp der orlesung Höhere Mahemak für Physker Kapel Jordan-Normalform Dr. Peer Gesl TU München 4. Semeser SS Daum: 6.6. von Mchael Wack Chrsoph Moder Manuel Saebel ( ) hp://www.skrpweb.de Hnwese (z.b.
En Skrp der orlesung Höhere Mahemak für Physker Kapel Jordan-Normalform Dr. Peer Gesl TU München 4. Semeser SS Daum: 6.6. von Mchael Wack Chrsoph Moder Manuel Saebel ( ) hp://www.skrpweb.de Hnwese (z.b.
Statistik und Wahrscheinlichkeit
 Regeln der Wahrschenlchketsrechnung tatstk und Wahrschenlchket Regeln der Wahrschenlchketsrechnung Relatve Häufgket n nt := Eregnsalgebra Eregnsraum oder scheres Eregns und n := 00 Wahrschenlchket Eregnsse
Regeln der Wahrschenlchketsrechnung tatstk und Wahrschenlchket Regeln der Wahrschenlchketsrechnung Relatve Häufgket n nt := Eregnsalgebra Eregnsraum oder scheres Eregns und n := 00 Wahrschenlchket Eregnsse
d da B A Die gesamte Erscheinung der magnetischen Feldlinien bezeichnet man als magnetischen Fluss. = 1 V s = 1 Wb
 S N De amte Erschenng der magnetschen Feldlnen bezechnet man als magnetschen Flss. = V s = Wb Kraftflssdchte oder magnetsche ndkton B. B d da B = Wb/m = T Für homogene Magnetfelder, we se m nneren von
S N De amte Erschenng der magnetschen Feldlnen bezechnet man als magnetschen Flss. = V s = Wb Kraftflssdchte oder magnetsche ndkton B. B d da B = Wb/m = T Für homogene Magnetfelder, we se m nneren von
16. Vorlesung Sommersemester
 16. Vorlesung Sommersemester 1 Das Egenwertproblem In allgemener Form hat das Egenwertproblem de Form A x = λ x, (1) wobe A ene n n-matrx, x en n-dmensonaler Vektor und λ der Egenwert st (n Englsch: egenvector,
16. Vorlesung Sommersemester 1 Das Egenwertproblem In allgemener Form hat das Egenwertproblem de Form A x = λ x, (1) wobe A ene n n-matrx, x en n-dmensonaler Vektor und λ der Egenwert st (n Englsch: egenvector,
1.1 Grundbegriffe und Grundgesetze 29
 1.1 Grundbegrffe und Grundgesetze 9 mt dem udrtschen Temperturkoeffzenten 0 (Enhet: K - ) T 1 d 0. (1.60) 0 dt T 93 K Betrchtet mn nun den elektrschen Wderstnd enes von enem homogenen elektrschen Feld
1.1 Grundbegrffe und Grundgesetze 9 mt dem udrtschen Temperturkoeffzenten 0 (Enhet: K - ) T 1 d 0. (1.60) 0 dt T 93 K Betrchtet mn nun den elektrschen Wderstnd enes von enem homogenen elektrschen Feld
Berechnung des next-arrays
 Berechnung des nex-arrays Ernnerung: nex[] Länge des längsen Präfxes von P, das eches Suffx von P 1.. s Inalserung: nex[1] 0 Annahme: se nex[-1] j: P 1 P 2 P -1 P? Berache zwe Fälle: 1. P P j+1 nex[] j
Berechnung des nex-arrays Ernnerung: nex[] Länge des längsen Präfxes von P, das eches Suffx von P 1.. s Inalserung: nex[1] 0 Annahme: se nex[-1] j: P 1 P 2 P -1 P? Berache zwe Fälle: 1. P P j+1 nex[] j
SS 2017 Torsten Schreiber
 SS Torsten Schreber e den Ebenen unterscheden wr de und de prmeterfree Drstellung. Wenn wr ene Ebenenglechung durch dre Punkte bestmmen wollen, so müssen de zugehörgen Vektoren sen, d es sonst nur ene
SS Torsten Schreber e den Ebenen unterscheden wr de und de prmeterfree Drstellung. Wenn wr ene Ebenenglechung durch dre Punkte bestmmen wollen, so müssen de zugehörgen Vektoren sen, d es sonst nur ene
Experimentalphysik II (Kip SS 2007)
 permentalphsk II (Kp SS 007) Zusatvorlesungen: Z-1 n- und mehrdmensonale Integraton Z- Gradent, Dvergen und Rotaton Z-3 Gaußscher und Stokesscher Integralsat Z-4 Kontnutätsglechung Z-5 lektromagnetsche
permentalphsk II (Kp SS 007) Zusatvorlesungen: Z-1 n- und mehrdmensonale Integraton Z- Gradent, Dvergen und Rotaton Z-3 Gaußscher und Stokesscher Integralsat Z-4 Kontnutätsglechung Z-5 lektromagnetsche
3.3 Lineare Abbildungen und Matrizen
 33 LINEARE ABBILDUNGEN UND MATRIZEN 87 33 Lneare Abbldungen und Matrzen Wr wollen jetzt de numersche Behandlung lnearer Abbldungen zwschen Vektorräumen beschreben be der vorgegebene Basen de Hauptrolle
33 LINEARE ABBILDUNGEN UND MATRIZEN 87 33 Lneare Abbldungen und Matrzen Wr wollen jetzt de numersche Behandlung lnearer Abbldungen zwschen Vektorräumen beschreben be der vorgegebene Basen de Hauptrolle
1. März Korrektur
 nsttut für Technsche und Num. Mechnk Technsche Mechnk V Prof. Dr.-ng. Prof. E.h. P. Eberhrd WS 010/11 K 1. März 011 Klusur n Technscher Mechnk V Nchnme Vornme Aufgbe 1 (6 Punkte) n enem bestmmt gelgerten
nsttut für Technsche und Num. Mechnk Technsche Mechnk V Prof. Dr.-ng. Prof. E.h. P. Eberhrd WS 010/11 K 1. März 011 Klusur n Technscher Mechnk V Nchnme Vornme Aufgbe 1 (6 Punkte) n enem bestmmt gelgerten
B) Grammatik/Rechtschreibung (Richtzeit: ca. 35min)
 B) Grmmk/Rechschrebung (Rchze: c. 35mn) 1. Besmme de Worr der unersrchenen Wörer! Besmme be den Pronomen und den Prkeln nur de Unergruppen! Des(1) wusse() ch(3) schon or() mener(5) Leserese(), denn(7)
B) Grmmk/Rechschrebung (Rchze: c. 35mn) 1. Besmme de Worr der unersrchenen Wörer! Besmme be den Pronomen und den Prkeln nur de Unergruppen! Des(1) wusse() ch(3) schon or() mener(5) Leserese(), denn(7)
Grundgedanke der Regressionsanalyse
 Grundgedanke der Regressonsanalse Bsher wurden durch Koeffzenten de Stärke von Zusammenhängen beschreben Mt der Regressonsrechnung können für ntervallskalerte Varablen darüber hnaus Modelle geschätzt werden
Grundgedanke der Regressonsanalse Bsher wurden durch Koeffzenten de Stärke von Zusammenhängen beschreben Mt der Regressonsrechnung können für ntervallskalerte Varablen darüber hnaus Modelle geschätzt werden
 - - Forelalug EEOEH i achiebau (ad vo:.. ) Größe Forelzeiche Eihei Elekriche paug [ol] Elekriche roärke [pere] rodiche Elekricher Widerad, Wirkwiderad, eiaz Ω [Oh] Elekricher eiwer, G Wirkleiwer, odukaz
- - Forelalug EEOEH i achiebau (ad vo:.. ) Größe Forelzeiche Eihei Elekriche paug [ol] Elekriche roärke [pere] rodiche Elekricher Widerad, Wirkwiderad, eiaz Ω [Oh] Elekricher eiwer, G Wirkleiwer, odukaz
Stephan Brumme, SST, 2.FS, Matrikelnr konvergiert und der Grenzwert 1 ist, d.h. es gilt: 1. k 1
 Stehn Brumme, SST,.FS, Mtrelnr. 7 5 44 Aufge... Zegen Se, dss de Folge onvergert und der Grenwert st, d.h. es glt lm Es st u egen, dss ene Nullfolge st D ene Nullfolge st, stellt ene onvergente Folge mt
Stehn Brumme, SST,.FS, Mtrelnr. 7 5 44 Aufge... Zegen Se, dss de Folge onvergert und der Grenwert st, d.h. es glt lm Es st u egen, dss ene Nullfolge st D ene Nullfolge st, stellt ene onvergente Folge mt
SIMULATION VON HYBRIDFAHRZEUGANTRIEBEN MIT
 Smulaton von Hybrdfahrzeugantreben mt optmerter Synchronmaschne 1 SIMULATION VON HYBRIDFAHRZEUGANTRIEBEN MIT OPTIMIERTER SYNCHRONMASCHINE H. Wöhl-Bruhn 1 EINLEITUNG Ene Velzahl von Untersuchungen hat sch
Smulaton von Hybrdfahrzeugantreben mt optmerter Synchronmaschne 1 SIMULATION VON HYBRIDFAHRZEUGANTRIEBEN MIT OPTIMIERTER SYNCHRONMASCHINE H. Wöhl-Bruhn 1 EINLEITUNG Ene Velzahl von Untersuchungen hat sch
wird auch Spannweite bzw. Variationsbreite genannt ist definiert als die Differenz zwischen dem größten und kleinsten Messwert einer Verteilung:
 Streuungswerte: 1) Range (R) ab metrschem Messnveau ) Quartlabstand (QA) und mttlere Quartlabstand (MQA) ab metrschem Messnveau 3) Durchschnttlche Abwechung (AD) ab metrschem Messnveau 4) Varanz (s ) ab
Streuungswerte: 1) Range (R) ab metrschem Messnveau ) Quartlabstand (QA) und mttlere Quartlabstand (MQA) ab metrschem Messnveau 3) Durchschnttlche Abwechung (AD) ab metrschem Messnveau 4) Varanz (s ) ab
