Target Volatility & Risk Control Indizes. Ulrich Stoof (Bloomberg LP) & Christian Menn (RIVACON & FH Mainz)
|
|
|
- Claus Feld
- vor 8 Jahren
- Abrufe
Transkript
1 Target Volatility & Risk Control Indizes Ulrich Stoof (Bloomberg LP) & Christian Menn (RIVACON & FH Mainz)
2 Agenda Einleitung/Motivation Der Risk Control Mechanismus Exkurs: Varianz- und Volatilitätsschätzer Konkrete Beispiele: DAX, SPX, SX5E Bewertung von Optionen auf Risk Control Indizes Eine Approximationsformel zur Optionsbewertung May 16, 2013 Target Volatility & Risk Control Indizes 2
3 Agenda Einleitung/Motivation Der Risk Control Mechanismus Exkurs: Varianz- und Volatilitätsschätzer Konkrete Beispiele: DAX, SPX, SX5E Bewertung von Optionen auf Risk Control Indizes Eine Approximationsformel zur Optionsbewertung May 16, 2013 Target Volatility & Risk Control Indizes 3
4 Einleitung / Motivation Klassische Garantiestruktur: Zero-Bond + α Option Einflussfaktoren: Zinsen Forwards Volatilitäten May 16, 2013 Target Volatility & Risk Control Indizes 4
5 Einleitung / Motivation Aktuelle Niedrigzinsphase lässt klassische Garantieprodukte unattraktiv aussehen. Mögliche Auswege: Niedrige Partizipationsraten Exotische Optionen mit hoher Knock-Out- Wahrscheinlichkeit auf klassische Underlyings (Barriers, Cliquets etc.) Klassische Optionen auf exotische Underlyings Risk- Control-Indizes / Portfolios May 16, 2013 Target Volatility & Risk Control Indizes 5
6 Agenda Einleitung/Motivation Der Risk Control Mechanismus Exkurs: Varianz- und Volatilitätsschätzer Konkrete Beispiele: DAX, SPX, SX5E Bewertung von Optionen auf Risk Control Indizes Eine Approximationsformel zur Optionsbewertung May 16, 2013 Target Volatility & Risk Control Indizes 6
7 Der Risk-Control-Mechanismus: Ziele Konstruiere einen Index mit der Möglichkeit a) Die Volatilität zu steuern / vorzugeben b) Den Forward zu steuern / vorzugeben Dynamisches Portfolio als Excess- bzw. Total-Return- Index May 16, 2013 Target Volatility & Risk Control Indizes 7
8 Der Risk-Control-Mechanismus: Das Prinzip Wähle ein volatiles Asset A (z.b. Aktie, Index, Fond), und ein schwankungsarmes Asset B (z.b. Geldmarktkonto) Typische Annahme: die Volatilität des Assets B ist vernachlässigbar gering. Bilde ein Portfolio: P t = ω t A t + 1 ω t B t May 16, 2013 Target Volatility & Risk Control Indizes 8
9 Der Risk-Control-Mechanismus: Die Formel I RC t = I RC t π RC t 1 r t 1 τ Indexstand des RC Index Tagesrendite des RC-Index Optionaler Excess Return Faktor π t RC = ω t 1 π t A + 1 ω t 1 π t B Dynamisches Portfoliogewicht Renditen der Assets A und B May 16, 2013 Target Volatility & Risk Control Indizes 9
10 Bestimmung des Portfoliogewichts ω Aus der Formel für die Varianz einer Summe von Zufallsvariablen ergibt sich: Vπ RC 2 t = ω t 1 Vπ A t + 2ω t 1 (1 ω t 1 ) Cov π A B t, π t =0 + 1 ω t 1 2 Vπ t B =0 Vπ RC 2 A t = ω t 1 Vπ t bzw. σ RC πt = ω t 1 σ πt A ω t 1 = σ TARGET σ πt A May 16, 2013 Target Volatility & Risk Control Indizes 10
11 Agenda Einleitung/Motivation Der Risk Control Mechanismus Exkurs: Varianz- und Volatilitätsschätzer Konkrete Beispiele: DAX, SPX, SX5E Bewertung von Optionen auf Risk Control Indizes Eine Approximationsformel zur Optionsbewertung May 16, 2013 Target Volatility & Risk Control Indizes 11
12 Exkurs: Varianz- und Volatilitätsschätzung Aus historischen Daten: Klassischer Varianzschätzer Exponentially Weighted Moving Average Aus impliziten Volatilitäten: Z.B. VIX/VSTOXX (faire Varianzswap-Raten) May 16, 2013 Target Volatility & Risk Control Indizes 12
13 Exkurs: Varianz- und Volatilitätsschätzung Klassischer Varianzschätzer: σ 2 t,n = 252 N 1 N i=1 log S t i S t i 1 2 Exponentially Weighted Moving Average σ 2 2 t,ρ = ρ σ t 1,ρ + 1 ρ 252 log S 2 t S t 1 May 16, 2013 Target Volatility & Risk Control Indizes 13
14 Performance Beispiel I Indexzeitreihe: 100, 90, 100, 102: INDEX RC10-INDEX May 16, 2013 Target Volatility & Risk Control Indizes 14
15 Performance Beispiel II Indexzeitreihe: +0.5% pro Tag INDEX RC-INDEX May 16, 2013 Target Volatility & Risk Control Indizes 15
16 Indexzeitreihe -2% pro Tag Performance Beispiel III INDEX RC-INDEX May 16, 2013 Target Volatility & Risk Control Indizes 16
17 Agenda Einleitung/Motivation Der Risk Control Mechanismus Exkurs: Varianz- und Volatilitätsschätzer Konkrete Beispiele: DAX, SPX, SX5E Bewertung von Optionen auf Risk Control Indizes Eine Approximationsformel zur Optionsbewertung May 16, 2013 Target Volatility & Risk Control Indizes 17
18 Beispiele für Risk-Control-Indizes DAX RC10 Excess/Total Return Variante Volschätzung aus 20-/60-Tages historische Volatilität Leverage Cap 150% SPX Excess/Total Return Volatilitätsschätzung mittels EWMA SX5E Excess und Total Return Variante Volschätzung aus impliziten Volatilitäten (VSTOXX) Leverage Cap 150% May 16, 2013 Target Volatility & Risk Control Indizes 18
19 Agenda Einleitung/Motivation Der Risk Control Mechanismus Exkurs: Varianz- und Volatilitätsschätzer Konkrete Beispiele: DAX, SPX, SX5E Bewertung von Optionen auf Risk Control Indizes Eine Approximationsformel zur Optionsbewertung May 16, 2013 Target Volatility & Risk Control Indizes 19
20 Optionen auf RC-Indizes Durch den Risk-Control-Mechanismus können neue Underlyings erzeugt werden, mit vorgegebenen Eigenschaften bezüglich Forward (Total-Return/Excess- Return) und Volatilität. Nutze diese Underlyings als Basis für Optionsstrategien (z.b. zur Konstruktion von Garantiestrukturen) May 16, 2013 Target Volatility & Risk Control Indizes 20
21 Exkurs: Bewertung von Optionen Um eine Option auf ein Underlying bewerten zu können, benötigt man die risikoneutrale Dynamik des Underlyings, d.h. man benötigt den Forward (Drift), sowie die Volatilität. Allgemeine Bewertungsformel: p = DF E Payoff May 16, 2013 Target Volatility & Risk Control Indizes 21
22 Exkurs: Bewertung von Optionen Bekanntestes Beispiel: Geometrische Brownsche Bewegung / Black-Scholes-Formel C = DF F N d 1 K N d 2 Allgemeiner: Local Volatility mit PDE-Lösung (falls möglich) oder MC-Verfahren Noch allgemeiner: Mehrfaktormodelle, z.b. Stochastic Volatility May 16, 2013 Target Volatility & Risk Control Indizes 22
23 MC-Bewertung einer Option auf einen RC-Index Bestimme/kalibriere Dynamik des Basisunderlyings (aus Plain-Vanilla-Optionen) Simuliere Basis-Underlying (Monte-Carlo) Bestimme Pfade des RC-Underlyings mit Hilfe der Formel für das Portfoliogewichts Auswertung des Optionspayoffs auf den Pfaden Diskontierung Aufwändige Implementierung May 16, 2013 Target Volatility & Risk Control Indizes 23
24 Optionspreise für verschiedene Target Vols 30 Underlying: S=100, Zins=0%, Volatilität=30% Laufzeit 5 Jahre ATM-Call ATM-Call RC ATM-Asian Call (quarterly fixing) ATM-Asian Call RC (quarterly fixing) 0 30% 20% 10% 5% 1% Target Volatility May 16, 2013 Target Volatility & Risk Control Indizes 24
25 Optionspreise Excess vs Total Return RC Underlying: S=100, Volatilität=30% Laufzeit 5 Jahre, Quarterly Asianing Total Return, Zins=1% Excess Return, Zins=1% Total Return, Zins=2.5% Excess Return, Zins=2.5% Total Return, Zins=5% Excess Return, Zins=5% % 20% 10% 5% 1% Target Volatility May 16, 2013 Target Volatility & Risk Control Indizes 25
26 Agenda Einleitung/Motivation Der Risk Control Mechanismus Exkurs: Varianz- und Volatilitätsschätzer Konkrete Beispiele: DAX, SPX, SX5E Bewertung von Optionen auf Risk Control Indizes Eine Approximationsformel zur Optionsbewertung May 16, 2013 Target Volatility & Risk Control Indizes 26
27 Dynamik eines RC-Index (Approximation) Am Beispiel des DAX RC10 Excess Return ergibt sich: Drift (lokal): μ t RC = ω t 1 μ t DAX μ t EONIA Volatilität (lokal): σ t RC = ω t 1 σ t DAX 10% Verwendung dieser Größen in der klassischen Bewertungsformel (Black-Scholes) führt zu guten Approximationen Einziges Problem: Was ist ein guter Schätzer für ω = E(ω t 1 ) May 16, 2013 Target Volatility & Risk Control Indizes 27
28 Herleitung der Drift Formel für den DAX RC10 ER I RC t = I RC t π RC t 1 r t 1 τ =1+μ t RC 1+π t RC r t 1 τ μ t RC = ω t 1 π t DAX + 1 ω t 1 π t EONIA r t 1 τ μ t RC = ω t 1 π t DAX + 1 ω t 1 r t 1 τ r t 1 τ μ t RC = ω t 1 (π t DAX π t EONIA ) May 16, 2013 Target Volatility & Risk Control Indizes 28
29 Ergebnisse (echte Vol, 5y ATM Call) Call DAX Excess Return 6 Approximation, vol=target vol 4 Approximation, vol=95% target vol % 12.5% 10.0% 7.5% 5.0% May 16, 2013 Target Volatility & Risk Control Indizes 29
30 Ergebnisse (echte Vol, 5y Asian Call) Asian Call DAX Excess Return Approximation, vol=target vol Approximation, vol=95% target vol % 12.5% 10.0% 7.5% 5.0% May 16, 2013 Target Volatility & Risk Control Indizes 30
31 Zusammenfassung Generisches Verfahren zur Bestimmung von RC Indizes kann auf alternative Underlyings (z.b. Fonds) angewendet werden Das Verfahren kann auch auf zwei risky Assets angewendet werden, z.b. Aktien- und Bond-Index (s. S&P RC 2.0) Bewertung von Derivaten allgemein nur mit aufwendiger MC-Implementierung möglich Mithilfe der Approximationsformel kann eine Bewertung näherungsweise ohne großen Aufwand durchgeführt werden May 16, 2013 Target Volatility & Risk Control Indizes 31
32 Anhang / Verweise DAX Familie Index-Guide: Bloomberg: Definition of Historical Volatility Estimates STOXX Strategy Index Guide: S&P Index Guide: risk-control-indices/en/us/?indexId=sp-500-risk-control-indices May 16, 2013 Target Volatility & Risk Control Indizes 32
33 Kontakt Christian Menn Web: May 16, 2013 Target Volatility & Risk Control Indizes 33
Derivate und Bewertung
 . Dr. Daniel Sommer Marie-Curie-Str. 0 6049 Frankfurt am Main Klausur Derivate und Bewertung.......... Wintersemester 006/07 Klausur Derivate und Bewertung Wintersemester 006/07 Aufgabe 1: Statische Optionsstrategien
. Dr. Daniel Sommer Marie-Curie-Str. 0 6049 Frankfurt am Main Klausur Derivate und Bewertung.......... Wintersemester 006/07 Klausur Derivate und Bewertung Wintersemester 006/07 Aufgabe 1: Statische Optionsstrategien
Finanzwirtschaft. Teil II: Bewertung. Zinssätze und Renten
 Zinssätze und Renten 1 Finanzwirtschaft Teil II: Bewertung Zinssätze und Renten Agenda Zinssätze und Renten 2 Effektivzinsen Spot-Zinsen Forward-Zinsen Bewertung Kennziffern Zusammenfassung Zinssätze und
Zinssätze und Renten 1 Finanzwirtschaft Teil II: Bewertung Zinssätze und Renten Agenda Zinssätze und Renten 2 Effektivzinsen Spot-Zinsen Forward-Zinsen Bewertung Kennziffern Zusammenfassung Zinssätze und
Aktienanleihe. Konstruktion, Kursverhalten und Produktvarianten. 18.02.2015 Christopher Pawlik
 Aktienanleihe Konstruktion, Kursverhalten und Produktvarianten 18.02.2015 Christopher Pawlik 2 Agenda 1. Strukturierung der Aktienanleihe 04 2. Ausstattungsmerkmale der Aktienanleihen 08 3. Verhalten im
Aktienanleihe Konstruktion, Kursverhalten und Produktvarianten 18.02.2015 Christopher Pawlik 2 Agenda 1. Strukturierung der Aktienanleihe 04 2. Ausstattungsmerkmale der Aktienanleihen 08 3. Verhalten im
Anlegerinformationen zu den Garantiefonds der Union Investment Luxembourg S.A.
 Anlegerinformationen zu den Garantiefonds der Union Investment Luxembourg S.A. Union Investment Luxembourg S.A. stellt Anlegern, die in die unten aufgeführten Garantiefonds investiert haben, ergänzende
Anlegerinformationen zu den Garantiefonds der Union Investment Luxembourg S.A. Union Investment Luxembourg S.A. stellt Anlegern, die in die unten aufgeführten Garantiefonds investiert haben, ergänzende
Internationale Finanzierung 7. Optionen
 Übersicht Kapitel 7: 7.1. Einführung 7.2. Der Wert einer Option 7.3. Regeln für Optionspreise auf einem arbitragefreien Markt 7.3.1. Regeln für Calls 7.3.2. Regeln für Puts 7.3.3. Die Put Call Parität
Übersicht Kapitel 7: 7.1. Einführung 7.2. Der Wert einer Option 7.3. Regeln für Optionspreise auf einem arbitragefreien Markt 7.3.1. Regeln für Calls 7.3.2. Regeln für Puts 7.3.3. Die Put Call Parität
Finanzmanagement 5. Optionen
 Übersicht Kapitel 5: 5.1. Einführung 5.2. Der Wert einer Option 5.3. Regeln für Optionspreise auf einem arbitragefreien Markt 5.3.1. Regeln für Calls 5.3.2. Regeln für Puts 5.3.3. Die Put Call Parität
Übersicht Kapitel 5: 5.1. Einführung 5.2. Der Wert einer Option 5.3. Regeln für Optionspreise auf einem arbitragefreien Markt 5.3.1. Regeln für Calls 5.3.2. Regeln für Puts 5.3.3. Die Put Call Parität
Einleitung. Das Ein-Perioden-Modell ist das einfachste. von derivaten Finanzinstrumenten (hier: Optionen) zu erklären.
 Einleitung Das Ein-Perioden-Modell ist das einfachste Modell, um die Idee der Preisgebung von derivaten Finanzinstrumenten (hier: Optionen) zu erklären. naive Idee der Optionspreisbestimmung: Erwartungswertprinzip
Einleitung Das Ein-Perioden-Modell ist das einfachste Modell, um die Idee der Preisgebung von derivaten Finanzinstrumenten (hier: Optionen) zu erklären. naive Idee der Optionspreisbestimmung: Erwartungswertprinzip
Vertical-Spreads Iron Condor Erfolgsaussichten
 www.mumorex.ch 08.03.2015 1 Eigenschaften Erwartung Preis Long Calls Long Puts Kombination mit Aktien Vertical-Spreads Iron Condor Erfolgsaussichten www.mumorex.ch 08.03.2015 2 www.mumorex.ch 08.03.2015
www.mumorex.ch 08.03.2015 1 Eigenschaften Erwartung Preis Long Calls Long Puts Kombination mit Aktien Vertical-Spreads Iron Condor Erfolgsaussichten www.mumorex.ch 08.03.2015 2 www.mumorex.ch 08.03.2015
Das Black-Scholes Marktmodell
 Das Black-Scholes Marktmodell Andreas Eichler Institut für Finanzmathematik Johannes Kepler Universität Linz 8. April 2011 1 / 14 Gliederung 1 Einleitung Fortgeschrittene Finanzmathematik einfach erklärt
Das Black-Scholes Marktmodell Andreas Eichler Institut für Finanzmathematik Johannes Kepler Universität Linz 8. April 2011 1 / 14 Gliederung 1 Einleitung Fortgeschrittene Finanzmathematik einfach erklärt
Turbozertifikate So schlagen Sie den Markt
 So schlagen Sie den Markt Indexstand: 3.500 Punkte Basispreis: 3.000 Punkte Kursschwelle: 3.000 Punkte Laufzeit: 1 Jahr Index (100:1) Basispreis 35,00 Euro 30,00 Euro Zins + 1,50 Euro (BP 3.000 Punkte*5%)
So schlagen Sie den Markt Indexstand: 3.500 Punkte Basispreis: 3.000 Punkte Kursschwelle: 3.000 Punkte Laufzeit: 1 Jahr Index (100:1) Basispreis 35,00 Euro 30,00 Euro Zins + 1,50 Euro (BP 3.000 Punkte*5%)
Aufgaben Brealey/Myers [2003], Kapitel 21
![Aufgaben Brealey/Myers [2003], Kapitel 21 Aufgaben Brealey/Myers [2003], Kapitel 21](/thumbs/25/5752225.jpg) Quiz: 1, 2, 4, 6, 7, 10 Practice Questions: 1, 3, 5, 6, 7, 10, 12, 13 Folie 0 Lösung Quiz 7: a. Das Optionsdelta ergibt sich wie folgt: Spanne der möglichen Optionspreise Spanne der möglichen Aktienkurs
Quiz: 1, 2, 4, 6, 7, 10 Practice Questions: 1, 3, 5, 6, 7, 10, 12, 13 Folie 0 Lösung Quiz 7: a. Das Optionsdelta ergibt sich wie folgt: Spanne der möglichen Optionspreise Spanne der möglichen Aktienkurs
Musterlösung Übung 3
 Musterlösung Übung 3 http://www.hoadley.net/options/ http://www.eeh.ee.ethz.ch/en/power/power-systems-laboratory/services 1. Optionsbewertung nach Black / Scholes a) Bewerten Sie eine Call-Option mit den
Musterlösung Übung 3 http://www.hoadley.net/options/ http://www.eeh.ee.ethz.ch/en/power/power-systems-laboratory/services 1. Optionsbewertung nach Black / Scholes a) Bewerten Sie eine Call-Option mit den
Übung zu Forwards, Futures & Optionen
 Übung zu Forwards, Futures & Optionen Vertiefungsstudium Finanzwirtschaft Dr. Eric Nowak SS 2001 Finanzwirtschaft Wahrenburg 15.05.01 1 Aufgabe 1: Forward auf Zerobond Wesentliche Eckpunkte des Forwardgeschäfts:
Übung zu Forwards, Futures & Optionen Vertiefungsstudium Finanzwirtschaft Dr. Eric Nowak SS 2001 Finanzwirtschaft Wahrenburg 15.05.01 1 Aufgabe 1: Forward auf Zerobond Wesentliche Eckpunkte des Forwardgeschäfts:
Nicht-rekombinierbare Binomialbäume und ihre Anwendung in der Finanzmathematik Betreuer: Lars Grüne
 Nicht-rekombinierbare Binomialbäume und ihre Anwendung in der Finanzmathematik Betreuer: Lars Grüne Michaela Baumann Universität Bayreuth Dornbirn, 12. März 2015 Motivation Ein Kunde möchte bei einer Bank
Nicht-rekombinierbare Binomialbäume und ihre Anwendung in der Finanzmathematik Betreuer: Lars Grüne Michaela Baumann Universität Bayreuth Dornbirn, 12. März 2015 Motivation Ein Kunde möchte bei einer Bank
Musterlösung Übung 2
 Musterlösung Übung 2 http://www.hoadley.net/options/ http://www.eeh.ee.ethz.ch/en/power/power-systems-laboratory/services 1. Optionsbewertung nach Black / Scholes a) Bewerten Sie eine Call-Option mit den
Musterlösung Übung 2 http://www.hoadley.net/options/ http://www.eeh.ee.ethz.ch/en/power/power-systems-laboratory/services 1. Optionsbewertung nach Black / Scholes a) Bewerten Sie eine Call-Option mit den
Seminar Finanzmathematik
 Seminar Finanzmathematik Simulationen zur Black-Scholes Formel von Christian Schmitz Übersicht Zufallszahlen am Computer Optionspreis als Erwartungswert Aktienkurse simulieren Black-Scholes Formel Theorie
Seminar Finanzmathematik Simulationen zur Black-Scholes Formel von Christian Schmitz Übersicht Zufallszahlen am Computer Optionspreis als Erwartungswert Aktienkurse simulieren Black-Scholes Formel Theorie
Seminar Finanzmathematik
 Seminar Finanzmathematik Simulationen zur Black-Scholes Formel Seite 1 von 24 Zufallszahlen am Computer 3 Gleichverteilte Zufallszahlen 3 Weitere Verteilungen 3 Quadratische Verteilung 4 Normalverteilung
Seminar Finanzmathematik Simulationen zur Black-Scholes Formel Seite 1 von 24 Zufallszahlen am Computer 3 Gleichverteilte Zufallszahlen 3 Weitere Verteilungen 3 Quadratische Verteilung 4 Normalverteilung
Bewertung von Optionen auf CO2- Zertifikate mittels des Verfahrens von Black-Scholes
 www.markedskraft.com Bewertung von Optionen auf CO2- Zertifikate mittels des Verfahrens von Black-Scholes Diplomarbeit von Florian Frank Arendal Postboks 62 NO-4801 Arendal Norway Tel +47 37 00 97 00 Fax
www.markedskraft.com Bewertung von Optionen auf CO2- Zertifikate mittels des Verfahrens von Black-Scholes Diplomarbeit von Florian Frank Arendal Postboks 62 NO-4801 Arendal Norway Tel +47 37 00 97 00 Fax
VALUATION Übung 5 Terminverträge und Optionen. Adrian Michel Universität Bern
 VALUATION Übung 5 Terminverträge und Optionen Adrian Michel Universität Bern Aufgabe Tom & Jerry Aufgabe > Terminpreis Tom F Tom ( + R) = 955'000 ( + 0.06) = 99'87. 84 T = S CHF > Monatliche Miete Jerry
VALUATION Übung 5 Terminverträge und Optionen Adrian Michel Universität Bern Aufgabe Tom & Jerry Aufgabe > Terminpreis Tom F Tom ( + R) = 955'000 ( + 0.06) = 99'87. 84 T = S CHF > Monatliche Miete Jerry
Materialien zur Vorlesung. Rendite und Risiko
 Materialien zur Vorlesung Rendite und Risiko Burkhard Erke Quellen: Brealey/Myers, Kap. 7 Mai 2006 Lernziele Langfristige Rendite von Finanzanlagen: Empirie Aktienindizes Messung von Durchschnittsrenditen
Materialien zur Vorlesung Rendite und Risiko Burkhard Erke Quellen: Brealey/Myers, Kap. 7 Mai 2006 Lernziele Langfristige Rendite von Finanzanlagen: Empirie Aktienindizes Messung von Durchschnittsrenditen
Anlageempfehlung. Anlageempfehlung
 GVA Vermögensaufbau Volkmar Heinz, Richard-Strauss-Straße 71, 81679 München Anlageempfehlung Ihr Berater: GVA Vermögensaufbau Volkmar Heinz Richard-Strauss-Straße 71 81679 München Telefon +49 89 5205640
GVA Vermögensaufbau Volkmar Heinz, Richard-Strauss-Straße 71, 81679 München Anlageempfehlung Ihr Berater: GVA Vermögensaufbau Volkmar Heinz Richard-Strauss-Straße 71 81679 München Telefon +49 89 5205640
Indikatoren nicht Alles oder alles Nichts?
 Indikatoren nicht Alles oder alles Nichts? Technische Analyse mit einem neuen Indikator! Trendfolgeindikatoren Gleitende Durchschnitte MACD Trendbestimmungs -indikatoren Momentum Oszillatoren Bollinger
Indikatoren nicht Alles oder alles Nichts? Technische Analyse mit einem neuen Indikator! Trendfolgeindikatoren Gleitende Durchschnitte MACD Trendbestimmungs -indikatoren Momentum Oszillatoren Bollinger
Derivate und Bewertung
 . Dr. Daniel Sommer Marie-Curie-Str. 30 60439 Franfurt am Main Klausur Derivate und Bewertung.......... Wintersemester 2008/09 Klausur Derivate und Bewertung Wintersemester 2008/09 Aufgabe 1: Zinsurven,
. Dr. Daniel Sommer Marie-Curie-Str. 30 60439 Franfurt am Main Klausur Derivate und Bewertung.......... Wintersemester 2008/09 Klausur Derivate und Bewertung Wintersemester 2008/09 Aufgabe 1: Zinsurven,
DIE WELT DER STRUKTURIERTEN PRODUKTE DAS BUCH ZUR SVSP SWISS DERIVATIVE MAP
 DIE WELT DER STRUKTURIERTEN PRODUKTE DAS BUCH ZUR SVSP SWISS DERIVATIVE MAP Martin F. Meier Paolo Vanini Philippe Béguelin Daniel Manser Eric Wasescha HERAUSGEBER PARTNER Teil 1 1 Einleitung 8 1.1 Die
DIE WELT DER STRUKTURIERTEN PRODUKTE DAS BUCH ZUR SVSP SWISS DERIVATIVE MAP Martin F. Meier Paolo Vanini Philippe Béguelin Daniel Manser Eric Wasescha HERAUSGEBER PARTNER Teil 1 1 Einleitung 8 1.1 Die
Geometrische Brownsche Bewegung und Brownsche Brücke
 Geometrische Brownsche Bewegung und Brownsche Brücke Korinna Griesing Dozentin: Prof. Dr. Christine Müller 17. April 2012 Korinna Griesing 1 (26) Inhalt Motivation Statistische Methoden Geometrische Brownsche
Geometrische Brownsche Bewegung und Brownsche Brücke Korinna Griesing Dozentin: Prof. Dr. Christine Müller 17. April 2012 Korinna Griesing 1 (26) Inhalt Motivation Statistische Methoden Geometrische Brownsche
Monte-Carlo-Simulationen mit Copulas. Kevin Schellkes und Christian Hendricks 29.08.2011
 Kevin Schellkes und Christian Hendricks 29.08.2011 Inhalt Der herkömmliche Ansatz zur Simulation logarithmischer Renditen Ansatz zur Simulation mit Copulas Test und Vergleich der beiden Verfahren Fazit
Kevin Schellkes und Christian Hendricks 29.08.2011 Inhalt Der herkömmliche Ansatz zur Simulation logarithmischer Renditen Ansatz zur Simulation mit Copulas Test und Vergleich der beiden Verfahren Fazit
Inhalt. Danksagungen... 11 Zur Motivation, mit Optionen zu handeln... 13 Einleitung... 17
 FBV Danksagungen... 11 Zur Motivation, mit Optionen zu handeln... 13 Einleitung... 17 Teil I: Optionsgrundlagen... 25 Kapitel 1: Was sind Optionen?... 26 Warum Optionen handeln?... 27 Bestandteile einer
FBV Danksagungen... 11 Zur Motivation, mit Optionen zu handeln... 13 Einleitung... 17 Teil I: Optionsgrundlagen... 25 Kapitel 1: Was sind Optionen?... 26 Warum Optionen handeln?... 27 Bestandteile einer
Deutsche Asset & Wealth Management. Marktbericht. Johannes Müller Frankfurt, 17. Februar 2014. Bei diesen Informationen handelt es sich um Werbung
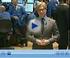 Marktbericht Johannes Müller Frankfurt, 17. Februar 2014 Bei diesen Informationen handelt es sich um Werbung Aktien Die Langfristperspektive Unternehmensgewinne Unternehmensgewinne USA $ Mrd, log* 00 0
Marktbericht Johannes Müller Frankfurt, 17. Februar 2014 Bei diesen Informationen handelt es sich um Werbung Aktien Die Langfristperspektive Unternehmensgewinne Unternehmensgewinne USA $ Mrd, log* 00 0
Renditequellen der Anlagemärkte
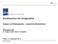 Renditequellen der Anlagemärkte Analyse von Risikoprämien empirische Erkenntnisse PPCmetrics AG Dr. Diego Liechti, Senior Consultant Zürich, 13. Dezember 2013 Inhalt Einführung Aktienrisikoprämie Weitere
Renditequellen der Anlagemärkte Analyse von Risikoprämien empirische Erkenntnisse PPCmetrics AG Dr. Diego Liechti, Senior Consultant Zürich, 13. Dezember 2013 Inhalt Einführung Aktienrisikoprämie Weitere
Andrei Anissimov DAS GROSSE HANDBUCH DER OPTIONS STRATEGIEN. Die Schritt-fiir-Schritt-Anleitung für ein. stabiles Einkommen an der Börse FBV
 Andrei Anissimov DAS GROSSE HANDBUCH DER OPTIONS STRATEGIEN Die Schritt-fiir-Schritt-Anleitung für ein stabiles Einkommen an der Börse FBV INHALT Danksagungen 11 Zur Motivation, mit Optionen zu handeln
Andrei Anissimov DAS GROSSE HANDBUCH DER OPTIONS STRATEGIEN Die Schritt-fiir-Schritt-Anleitung für ein stabiles Einkommen an der Börse FBV INHALT Danksagungen 11 Zur Motivation, mit Optionen zu handeln
Aktien, Optionen (und Credit Default Swaps)
 Aktien, Optionen (und s) Andreas Eichler Institut für Finanzmathematik Johannes Kepler Universität Linz 8. Februar 2009 1 / 7 Gliederung 1 Was ist Finanzmathematik Denkweise im Umgang mit Finanzprodukten
Aktien, Optionen (und s) Andreas Eichler Institut für Finanzmathematik Johannes Kepler Universität Linz 8. Februar 2009 1 / 7 Gliederung 1 Was ist Finanzmathematik Denkweise im Umgang mit Finanzprodukten
Risikoeinstellungen empirisch
 Risikoeinstellungen empirisch Risk attitude and Investment Decisions across European Countries Are women more conservative investors than men? Oleg Badunenko, Nataliya Barasinska, Dorothea Schäfer http://www.diw.de/deutsch/soep/uebersicht_ueber_das_soep/27180.html#79569
Risikoeinstellungen empirisch Risk attitude and Investment Decisions across European Countries Are women more conservative investors than men? Oleg Badunenko, Nataliya Barasinska, Dorothea Schäfer http://www.diw.de/deutsch/soep/uebersicht_ueber_das_soep/27180.html#79569
6. Aktien. Aktien sind Wertpapiere, in denen das Anteilsrecht an einer Aktiengesellschaft verbrieft ist. Rechtsgrundlage: Aktiengesetz
 6. Aktien Aktien sind Wertpapiere, in denen das Anteilsrecht an einer Aktiengesellschaft verbrieft ist. Rechtsgrundlage: Aktiengesetz Kennziffern für Aktien Kennzahlen für Aktien Ertragskennzahlen Risikokennzahlen
6. Aktien Aktien sind Wertpapiere, in denen das Anteilsrecht an einer Aktiengesellschaft verbrieft ist. Rechtsgrundlage: Aktiengesetz Kennziffern für Aktien Kennzahlen für Aktien Ertragskennzahlen Risikokennzahlen
Sensitivitätsfaktoren
 Sensitivitätsfaktoren Überblick Sensitivitätsfaktoren zeigen die Änderungen des Optionspreises, wenn sich eine Einflussgröße ändert Sensitivitätsfaktoren werden mit einem Optionspreismodell errechnet Einflussgrößen:
Sensitivitätsfaktoren Überblick Sensitivitätsfaktoren zeigen die Änderungen des Optionspreises, wenn sich eine Einflussgröße ändert Sensitivitätsfaktoren werden mit einem Optionspreismodell errechnet Einflussgrößen:
Die Black-Scholes-Gleichung
 Die Black-Scholes-Gleichung Franziska Merk 22.06.2012 Outline Optionen 1 Optionen 2 3 Optionen Eine Kaufoption ist ein Recht, eine Aktie zu einem heute (t=0) festgelegten Preis E an einem zukünftigen Zeitpunkt
Die Black-Scholes-Gleichung Franziska Merk 22.06.2012 Outline Optionen 1 Optionen 2 3 Optionen Eine Kaufoption ist ein Recht, eine Aktie zu einem heute (t=0) festgelegten Preis E an einem zukünftigen Zeitpunkt
Inflationsbereinigte Chance-Risiko-Profile von Lebensversicherungsprodukten Stefan Graf, Alexander Kling, Jochen Ruß
 Stefan Graf WiMa 2011 Ulm November 2011 Inflationsbereinigte Chance-Risiko-Profile von Lebensversicherungsprodukten Stefan Graf, Alexander Kling, Jochen Ruß Seite 2 Agenda Chance-Risiko-Profile Nominale
Stefan Graf WiMa 2011 Ulm November 2011 Inflationsbereinigte Chance-Risiko-Profile von Lebensversicherungsprodukten Stefan Graf, Alexander Kling, Jochen Ruß Seite 2 Agenda Chance-Risiko-Profile Nominale
Optionsbewertung. Christof Heuer und Fabian Lenz. 2. Februar 2009
 nach Black-Scholes mit sprüngen 2. Februar 2009 nach Black-Scholes mit sprüngen Inhaltsverzeichnis 1 Einleitung Optionsarten Modellannahmen 2 Aktienmodell Beispiele für e ohne Sprung 3 nach Black-Scholes
nach Black-Scholes mit sprüngen 2. Februar 2009 nach Black-Scholes mit sprüngen Inhaltsverzeichnis 1 Einleitung Optionsarten Modellannahmen 2 Aktienmodell Beispiele für e ohne Sprung 3 nach Black-Scholes
Verhindert, dass eine Methode überschrieben wird. public final int holekontostand() {...} public final class Girokonto extends Konto {...
 PIWIN I Kap. 8 Objektorientierte Programmierung - Vererbung 31 Schlüsselwort: final Verhindert, dass eine Methode überschrieben wird public final int holekontostand() {... Erben von einer Klasse verbieten:
PIWIN I Kap. 8 Objektorientierte Programmierung - Vererbung 31 Schlüsselwort: final Verhindert, dass eine Methode überschrieben wird public final int holekontostand() {... Erben von einer Klasse verbieten:
Aufgaben zur Vorlesung Finanzmanagement
 Aufgaben zur Vorlesung Finanzmanagement B. rke FH Gelsenkirchen, Abteilung Bocholt February 4, 006 Aufgabenblatt: "Bewertung von Optionen" 1 Lösungshinweise 1 uropean Put Option Zeichnen Sie den einer
Aufgaben zur Vorlesung Finanzmanagement B. rke FH Gelsenkirchen, Abteilung Bocholt February 4, 006 Aufgabenblatt: "Bewertung von Optionen" 1 Lösungshinweise 1 uropean Put Option Zeichnen Sie den einer
Kapitalerhöhung - Verbuchung
 Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Zertifikate in volatilen Märkten
 Zertifikate in volatilen Märkten Wien, 19. Februar 2008 Folie 1 Übersicht Indexentwicklung ATX ATX tägliche Schlusskurse 5.500,00 4.500,00 3.500,00 2.500,00 1.500,00 500,00 19.1.1998 19.1.2000 19.1.2002
Zertifikate in volatilen Märkten Wien, 19. Februar 2008 Folie 1 Übersicht Indexentwicklung ATX ATX tägliche Schlusskurse 5.500,00 4.500,00 3.500,00 2.500,00 1.500,00 500,00 19.1.1998 19.1.2000 19.1.2002
NRW EONIA-Anleihe. Schatzanweisung des Landes Nordrhein-Westfalen
 NRW EONIA-Anleihe Schatzanweisung des Landes Nordrhein-Westfalen EONIA Beschreibung EONIA = Euro OverNight Index Average Stellt den offiziellen Durchschnittstageszinssatz dar, der von Finanzinstituten
NRW EONIA-Anleihe Schatzanweisung des Landes Nordrhein-Westfalen EONIA Beschreibung EONIA = Euro OverNight Index Average Stellt den offiziellen Durchschnittstageszinssatz dar, der von Finanzinstituten
Inhaltsverzeichnis XVII. Abkürzungsverzeichnis... XXIII. Symbolverzeichnis...XXVII. Abbildungsverzeichnis...XXXI. Tabellenverzeichnis...
 XVII Abkürzungsverzeichnis... XXIII Symbolverzeichnis...XXVII Abbildungsverzeichnis...XXXI Tabellenverzeichnis... XXXV 1 Einführung...1 1.1 Entwicklung und Bedeutung der Optionsbewertung...1 1.2 Problemstellung...4
XVII Abkürzungsverzeichnis... XXIII Symbolverzeichnis...XXVII Abbildungsverzeichnis...XXXI Tabellenverzeichnis... XXXV 1 Einführung...1 1.1 Entwicklung und Bedeutung der Optionsbewertung...1 1.2 Problemstellung...4
Dynamik von Optionen
 Dynamik von Optionen Plan Der Optionspreis und seine Einflussfaktoren Wert des Calls / Puts bei unterschiedlichen Marktbedingungen Änderung des Optionspreises bei Änderung eines oder mehrerer Einflussfaktoren
Dynamik von Optionen Plan Der Optionspreis und seine Einflussfaktoren Wert des Calls / Puts bei unterschiedlichen Marktbedingungen Änderung des Optionspreises bei Änderung eines oder mehrerer Einflussfaktoren
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Erfolgreich handeln mit Optionen
 Erfolgreich handeln mit Optionen INHALT 01 GRUNDLAGEN VON 05 OPTIONEN 02 GRIECHEN 13 Delta 14 Gamma 18 Vega 21 Theta 24 03 VOLATILITÄT 27 Historische Volatilität 29 Implizite Volatilität 31 Volatility
Erfolgreich handeln mit Optionen INHALT 01 GRUNDLAGEN VON 05 OPTIONEN 02 GRIECHEN 13 Delta 14 Gamma 18 Vega 21 Theta 24 03 VOLATILITÄT 27 Historische Volatilität 29 Implizite Volatilität 31 Volatility
Hedging. Andreas Eichler, Christian Irrgeher. 13. Februar 2011. Institut für Finanzmathematik Johannes Kepler Universität Linz
 Was bedeutet? Andreas Eichler, Christian Irrgeher Institut für Finanzmathematik Johannes Kepler Universität Linz 13. Februar 2011 1 / 7 Was bedeutet? Gliederung 1 Was bedeutet? 2 3 Marktmodell von Black
Was bedeutet? Andreas Eichler, Christian Irrgeher Institut für Finanzmathematik Johannes Kepler Universität Linz 13. Februar 2011 1 / 7 Was bedeutet? Gliederung 1 Was bedeutet? 2 3 Marktmodell von Black
Volatilitätsstrategie mit Optionen
 MT AG MANAGING TECHNOLOGY IMPROVING BUSINESS PERFORMANCE Volatilitätsstrategie mit Optionen Referent: Guido Neander, Senior-Berater, MT AG, Ratingen Agenda Begriffsdefinitionen Optionen Volatilität Preisbestimmungsfaktoren
MT AG MANAGING TECHNOLOGY IMPROVING BUSINESS PERFORMANCE Volatilitätsstrategie mit Optionen Referent: Guido Neander, Senior-Berater, MT AG, Ratingen Agenda Begriffsdefinitionen Optionen Volatilität Preisbestimmungsfaktoren
Transparentes Reporting von strukturierten Produkten. Zürich, 2. Oktober 2008 Rolf Burgermeister
 Transparentes Reporting von strukturierten Produkten Zürich, 2. Oktober 2008 Rolf Burgermeister Agenda 1. Einführung 2. Konzept: effektives Exposure 3. Umsetzung bei Wegelin & Co. 4. Zusammenfassung und
Transparentes Reporting von strukturierten Produkten Zürich, 2. Oktober 2008 Rolf Burgermeister Agenda 1. Einführung 2. Konzept: effektives Exposure 3. Umsetzung bei Wegelin & Co. 4. Zusammenfassung und
Anlageempfehlung. Anlageempfehlung
 GVA Vermögensaufbau Volkmar Heinz, Richard-Strauss-Straße 71, 81679 München Anlageempfehlung Ihr Berater: GVA Vermögensaufbau Volkmar Heinz Richard-Strauss-Straße 71 81679 München Telefon +49 89 5205640
GVA Vermögensaufbau Volkmar Heinz, Richard-Strauss-Straße 71, 81679 München Anlageempfehlung Ihr Berater: GVA Vermögensaufbau Volkmar Heinz Richard-Strauss-Straße 71 81679 München Telefon +49 89 5205640
Convertible Bonds as an Instrument of Employee Participation: Initial- versus Final Taxation of the Monetary Profit
 Convertible Bonds as an Instrument of Employee Participation: Initial- versus Final Taxation of the Monetary Profit 3. Jahreskonferenz Risk Governance Siegen, 15.10.2015 Lehrstuhl für Betriebswirtschaftliche
Convertible Bonds as an Instrument of Employee Participation: Initial- versus Final Taxation of the Monetary Profit 3. Jahreskonferenz Risk Governance Siegen, 15.10.2015 Lehrstuhl für Betriebswirtschaftliche
Value at Risk Einführung
 Value at Risk Einführung Veranstaltung Risk Management & Computational Finance Dipl.-Ök. Hans-Jörg von Mettenheim mettenheim@iwi.uni-hannover.de Institut für Wirtschaftsinformatik Leibniz Universität Hannover
Value at Risk Einführung Veranstaltung Risk Management & Computational Finance Dipl.-Ök. Hans-Jörg von Mettenheim mettenheim@iwi.uni-hannover.de Institut für Wirtschaftsinformatik Leibniz Universität Hannover
Finanzwirtschaft. Teil II: Bewertung
 Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
Inhaltsverzeichnis Kapitel 0 - Einführung und Grundlagen 11 Kapitel 1 - Renditen auf Finanzmärkten 37 Kapitel 2 - Risiko auf Finanzmärkten 61
 Inhaltsverzeichnis Kapitel 0 - Einführung und Grundlagen 11 0.1 Gegenstandsbereich der Finance als wissenschaftliche Disziplin 0.2 Kernthemen der Finance 0.3 Entwicklungsmerkmale der Finanzmärkte - 0.4
Inhaltsverzeichnis Kapitel 0 - Einführung und Grundlagen 11 0.1 Gegenstandsbereich der Finance als wissenschaftliche Disziplin 0.2 Kernthemen der Finance 0.3 Entwicklungsmerkmale der Finanzmärkte - 0.4
Der Informationsgehalt von Optionspreisen
 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Martin Wallmeier Der Informationsgehalt von Optionspreisen Mit 62
2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Martin Wallmeier Der Informationsgehalt von Optionspreisen Mit 62
Finanzierungsvarianten für Immobilien im Ausland und Golf Immobilien
 Finanzierungsvarianten für Immobilien im Ausland und Golf Immobilien Grundsätzliches Schweizer Banken gewähren in der Regel Hypotheken nur auf Immobilien im Inland, allenfalls noch im grenznahen Ausland.
Finanzierungsvarianten für Immobilien im Ausland und Golf Immobilien Grundsätzliches Schweizer Banken gewähren in der Regel Hypotheken nur auf Immobilien im Inland, allenfalls noch im grenznahen Ausland.
Die passende Struktur? Darauf kommt es an.
 Professionelles Vermögensmanagement Die passende Struktur? Darauf kommt es an. Besser anlegen. Die Komplexität von Vermögensanlagen erfordert Zeit und gute Marktkenntnisse. Vertrauen Sie dabei auf jemanden,
Professionelles Vermögensmanagement Die passende Struktur? Darauf kommt es an. Besser anlegen. Die Komplexität von Vermögensanlagen erfordert Zeit und gute Marktkenntnisse. Vertrauen Sie dabei auf jemanden,
Das theoretische Konzept eines Volatilitätsderivates und seine Anwendung auf die DAX-Optionen
 Randolf Roth Das theoretische Konzept eines Volatilitätsderivates und seine Anwendung auf die DAX-Optionen Technische Universität Darmstadt Fachbereich 1 Betriebswirtschaftliche Bibliothek Inventar-Nr.
Randolf Roth Das theoretische Konzept eines Volatilitätsderivates und seine Anwendung auf die DAX-Optionen Technische Universität Darmstadt Fachbereich 1 Betriebswirtschaftliche Bibliothek Inventar-Nr.
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
DAXplus Covered Call Der Covered Call-Strategieindex
 DAXplus Covered Call Der Covered Call-Strategieindex Investment mit Puffer In Zeiten, in denen Gewinne aus reinen Aktienportfolios unsicher sind, bevorzugen Anleger Produkte mit einer höheren Rendite bei
DAXplus Covered Call Der Covered Call-Strategieindex Investment mit Puffer In Zeiten, in denen Gewinne aus reinen Aktienportfolios unsicher sind, bevorzugen Anleger Produkte mit einer höheren Rendite bei
DIPLOM. Abschlussklausur der Vorlesung Bank I, II:
 Seite 1 von 9 Name: Matrikelnummer: DIPLOM Abschlussklausur der Vorlesung Bank I, II: Bankmanagement und Theory of Banking Seite 2 von 9 DIPLOM Abschlussklausur der Vorlesung Bank I, II: Bankmanagement
Seite 1 von 9 Name: Matrikelnummer: DIPLOM Abschlussklausur der Vorlesung Bank I, II: Bankmanagement und Theory of Banking Seite 2 von 9 DIPLOM Abschlussklausur der Vorlesung Bank I, II: Bankmanagement
zu Aufgabe 3b) Binomialmodell: C 0 = S 0 B(a n;p ) E r -n B(a n;p*) Hier: C 0 = S 0 0,909 165,28 = 16,53
 zu Aufgabe 3b) Binomialmodell: C 0 S 0 B(a n;p ) E r -n B(a n;p*) Hier: C 0 S 0 0,909 65,8 6,53 Frage: Wie setzt sich das Duplikationsportfolio des Calls (anteiliger Aktienkauf teilweise kreditfinanziert)
zu Aufgabe 3b) Binomialmodell: C 0 S 0 B(a n;p ) E r -n B(a n;p*) Hier: C 0 S 0 0,909 65,8 6,53 Frage: Wie setzt sich das Duplikationsportfolio des Calls (anteiliger Aktienkauf teilweise kreditfinanziert)
Anhand des bereits hergeleiteten Models erstellen wir nun mit der Formel
 Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
Derivatebewertung im Binomialmodell
 Derivatebewertung im Binomialmodell Roland Stamm 27. Juni 2013 Roland Stamm 1 / 24 Agenda 1 Einleitung 2 Binomialmodell mit einer Periode 3 Binomialmodell mit mehreren Perioden 4 Kritische Würdigung und
Derivatebewertung im Binomialmodell Roland Stamm 27. Juni 2013 Roland Stamm 1 / 24 Agenda 1 Einleitung 2 Binomialmodell mit einer Periode 3 Binomialmodell mit mehreren Perioden 4 Kritische Würdigung und
Pädagogische Hochschule Thurgau. Lehre Weiterbildung Forschung
 Variante 1 Swisscom-Router direkt ans Netzwerk angeschlossen fixe IP-Adressen (kein DHCP) 1. Aufrufen des «Netz- und Freigabecenters». 2. Doppelklick auf «LAN-Verbindung» 3. Klick auf «Eigenschaften» 4.
Variante 1 Swisscom-Router direkt ans Netzwerk angeschlossen fixe IP-Adressen (kein DHCP) 1. Aufrufen des «Netz- und Freigabecenters». 2. Doppelklick auf «LAN-Verbindung» 3. Klick auf «Eigenschaften» 4.
Die Methode des Robusten Trends und der CAC40 (Frankreich)
 Die Methode des Robusten Trends und der CAC40 (Frankreich) von Dr. Hans Uhlig Zusammenfassung Auch für den CAC40 lässt sich ein robuster Trend bestimmen, wie es für den DAX bereits gezeigt werden konnte
Die Methode des Robusten Trends und der CAC40 (Frankreich) von Dr. Hans Uhlig Zusammenfassung Auch für den CAC40 lässt sich ein robuster Trend bestimmen, wie es für den DAX bereits gezeigt werden konnte
Eckpfeiler der neuen Regelung:
 Zertifikate-Emittenten weisen im Produktinformationsblatt (PIB) bereits seit einigen Jahren Performance-Szenarien aus. Während die konkrete Bestimmung dieser Szenarien bislang den Emittenten überlassen
Zertifikate-Emittenten weisen im Produktinformationsblatt (PIB) bereits seit einigen Jahren Performance-Szenarien aus. Während die konkrete Bestimmung dieser Szenarien bislang den Emittenten überlassen
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Hedging von Zinsrisiken. Vertiefungsstudium Finanzwirtschaft Prof. Dr. Mark Wahrenburg. Bond Yields und Preise von Zerobonds
 Hedging von Zinsrisiken Vertiefungsstudium Finanzwirtschaft Prof. Dr. Mark Wahrenburg Bond Yields und Preise von Zerobonds 3 Zerobonds mit Nominalwert F=100 yield to maturity r=10% (horizontale Zinskurve),
Hedging von Zinsrisiken Vertiefungsstudium Finanzwirtschaft Prof. Dr. Mark Wahrenburg Bond Yields und Preise von Zerobonds 3 Zerobonds mit Nominalwert F=100 yield to maturity r=10% (horizontale Zinskurve),
Kauf Kurs. letzter Kurs. Gewinn in % / Verlust in 112 ISHARES FTSE MIB ACC 5.599,80 26,79% Italien EUR 49,91 EUR 63,28 26,79%
 ei der ausgewiesenen Performance handelt es sich um eine Performance ohne Gebühren und Steuern. Die tatsächliche Performance kann durch abweichende 03.02.14 Referenz-Portfolio Fonds, ETFs und Zertifikate
ei der ausgewiesenen Performance handelt es sich um eine Performance ohne Gebühren und Steuern. Die tatsächliche Performance kann durch abweichende 03.02.14 Referenz-Portfolio Fonds, ETFs und Zertifikate
Positionstrading. am 27.2.2012. Webinarbeginn um 19:00 Uhr. email des PTT: positiontrading@nextleveltrader.de 27.2.2012 1
 am 27.2.2012 Webinarbeginn um 19:00 Uhr email des PTT: positiontrading@nextleveltrader.de 27.2.2012 1 Agenda für das Webinar am 27.2.2012: Depotcheck: Besprechung der laufenden Positionen (Auswahl) Ordercheck:
am 27.2.2012 Webinarbeginn um 19:00 Uhr email des PTT: positiontrading@nextleveltrader.de 27.2.2012 1 Agenda für das Webinar am 27.2.2012: Depotcheck: Besprechung der laufenden Positionen (Auswahl) Ordercheck:
Down & Out Put auf DJ EuroStoxx 50 Preiswerte Absicherung & Mittel zur Replikation bekannter strukturierter Produkte
 Down & Out Put auf DJ EuroStoxx 50 Preiswerte Absicherung & Mittel zur Replikation bekannter strukturierter Produkte Gute Gründe für die Nutzung eines Down & Out Put Die Aktienmärkte haben im Zuge der
Down & Out Put auf DJ EuroStoxx 50 Preiswerte Absicherung & Mittel zur Replikation bekannter strukturierter Produkte Gute Gründe für die Nutzung eines Down & Out Put Die Aktienmärkte haben im Zuge der
Thema 21: Risk Management mit Optionen, Futures, Forwards und Swaps
 Thema 21: Risk Management mit Optionen, Futures, Forwards und Swaps Derivate Der Begriff Derivate kommt aus dem Lateinischen und heißt soviel wie abgeleitet. Derivate ist der Sammelbegriff für Optionen,
Thema 21: Risk Management mit Optionen, Futures, Forwards und Swaps Derivate Der Begriff Derivate kommt aus dem Lateinischen und heißt soviel wie abgeleitet. Derivate ist der Sammelbegriff für Optionen,
CAPM Die Wertpapierlinie
 CAPM Die Wertpapierlinie Systematisches und unsystematisches Risiko Frank von Oppenkowski 6. Semester Betriebswirtschaftslehre SP Finanzwirtschaft 1 Die Wertpapierlinie (= CAPM) Gliederung 2 Wie man Erträge
CAPM Die Wertpapierlinie Systematisches und unsystematisches Risiko Frank von Oppenkowski 6. Semester Betriebswirtschaftslehre SP Finanzwirtschaft 1 Die Wertpapierlinie (= CAPM) Gliederung 2 Wie man Erträge
ALM in der betrieblichen Altersversorgung
 ALM in der betrieblichen Altersversorgung Projekte AP2 KP 2. staatlicher schwedischer Rentenfond Rentenversicherung für genossenschaftliche Betriebe 1 Ziel des ALM Finde (statische) Handelsstrategie, um
ALM in der betrieblichen Altersversorgung Projekte AP2 KP 2. staatlicher schwedischer Rentenfond Rentenversicherung für genossenschaftliche Betriebe 1 Ziel des ALM Finde (statische) Handelsstrategie, um
Inhalt. Vorwort... 9. 1.2 Das zinslose Risiko... 17. 1.5 Zusammenfassung... 28. 3.5 Zusammenfassung... 101. Risiko?... 110
 Inhalt Vorwort..................................... 9 1 Einführung: Was dieses Buch erreichen soll......... 11 1.1 Welche Anlageformen gibt es?................ 13 1.2 Das zinslose Risiko........................
Inhalt Vorwort..................................... 9 1 Einführung: Was dieses Buch erreichen soll......... 11 1.1 Welche Anlageformen gibt es?................ 13 1.2 Das zinslose Risiko........................
Admiral Academy WEBINAR TRADING VON ANFANG AN! TAG 2: Aktienhandel, Fonds, Optionsscheine, Devisen und CFDs. Wann trade ich was, Vorund Nachteile.
 Admiral Academy TRADING VON ANFANG AN! TAG 2: Aktienhandel, Fonds, Optionsscheine, Devisen und CFDs. Wann trade ich was, Vorund Nachteile. Aktienhandel: Aktien sind die Basis für (fast) alle Wertpapiere:
Admiral Academy TRADING VON ANFANG AN! TAG 2: Aktienhandel, Fonds, Optionsscheine, Devisen und CFDs. Wann trade ich was, Vorund Nachteile. Aktienhandel: Aktien sind die Basis für (fast) alle Wertpapiere:
Güte von Tests. die Wahrscheinlichkeit für den Fehler 2. Art bei der Testentscheidung, nämlich. falsch ist. Darauf haben wir bereits im Kapitel über
 Güte von s Grundlegendes zum Konzept der Güte Ableitung der Gütefunktion des Gauss im Einstichprobenproblem Grafische Darstellung der Gütefunktionen des Gauss im Einstichprobenproblem Ableitung der Gütefunktion
Güte von s Grundlegendes zum Konzept der Güte Ableitung der Gütefunktion des Gauss im Einstichprobenproblem Grafische Darstellung der Gütefunktionen des Gauss im Einstichprobenproblem Ableitung der Gütefunktion
Faktor-Zertifikate Ist aktuell der ideale Moment zum Einstieg? Faktor-Zertifikate, eine Klasse für sich
 Faktor-Zertifikate Ist aktuell der ideale Moment zum Einstieg? Faktor-Zertifikate, eine Klasse für sich Börsentag Stuttgart 12.09.2015 Faktor-Zertifikate DAX 30 Kursverlauf 1 Jahr 13000 12500 12000 11500
Faktor-Zertifikate Ist aktuell der ideale Moment zum Einstieg? Faktor-Zertifikate, eine Klasse für sich Börsentag Stuttgart 12.09.2015 Faktor-Zertifikate DAX 30 Kursverlauf 1 Jahr 13000 12500 12000 11500
Financial Engineering....eine Einführung
 Financial Engineering...eine Einführung Aufgabe 1: Lösung Überlegen Sie sich, wie man eine Floating Rate Note, die EURIBOR + 37 bp zahlt in einen Bond und einen Standard-Swap (der EURIBOR zahlt) zerlegen
Financial Engineering...eine Einführung Aufgabe 1: Lösung Überlegen Sie sich, wie man eine Floating Rate Note, die EURIBOR + 37 bp zahlt in einen Bond und einen Standard-Swap (der EURIBOR zahlt) zerlegen
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Kurzbeschreibung. Eingaben zur Berechnung. Das Optionspreismodell. Mit dem Eurex-OptionMaster können Sie
 Kurzbeschreibung Mit dem Eurex-OptionMaster können Sie - theoretische Optionspreise - Optionskennzahlen ( Griechen ) und - implizite Volatilitäten von Optionen berechnen und die errechneten Preise bei
Kurzbeschreibung Mit dem Eurex-OptionMaster können Sie - theoretische Optionspreise - Optionskennzahlen ( Griechen ) und - implizite Volatilitäten von Optionen berechnen und die errechneten Preise bei
Contracts for Difference (CFDs) Kennzahlen Q2 2009
 RESEARCH CENTER FOR FINANCIAL SERVICES Contracts for Difference (CFDs) Kennzahlen Q2 29 Statistik im Auftrag des Contracts for Difference Verband e. V. München, im Juli 29 Steinbeis Research Center for
RESEARCH CENTER FOR FINANCIAL SERVICES Contracts for Difference (CFDs) Kennzahlen Q2 29 Statistik im Auftrag des Contracts for Difference Verband e. V. München, im Juli 29 Steinbeis Research Center for
Contracts for Difference (CFDs) Kennzahlen Q2 2009
 RESEARCH CENTER FOR FINANCIAL SERVICES Contracts for Difference (CFDs) Kennzahlen Q2 29 Statistik im Auftrag des Contracts for Difference Verband e. V. München, im Juli 29 Steinbeis Research Center for
RESEARCH CENTER FOR FINANCIAL SERVICES Contracts for Difference (CFDs) Kennzahlen Q2 29 Statistik im Auftrag des Contracts for Difference Verband e. V. München, im Juli 29 Steinbeis Research Center for
 Definition Gegenwartswert (Barwert) Der Wert des Geldes ist, über den man in der Gegenwart verfügen kann, ist grösser als der Wert des Geldes, den man in der Zukunft erhalten/zahlen wird. Diskontierung
Definition Gegenwartswert (Barwert) Der Wert des Geldes ist, über den man in der Gegenwart verfügen kann, ist grösser als der Wert des Geldes, den man in der Zukunft erhalten/zahlen wird. Diskontierung
Bewertung von Barriere Optionen im CRR-Modell
 Bewertung von Barriere Optionen im CRR-Modell Seminararbeit von Susanna Wankmueller. April 00 Barriere Optionen sind eine Sonderform von Optionen und gehören zu den exotischen Optionen. Sie dienen dazu,
Bewertung von Barriere Optionen im CRR-Modell Seminararbeit von Susanna Wankmueller. April 00 Barriere Optionen sind eine Sonderform von Optionen und gehören zu den exotischen Optionen. Sie dienen dazu,
einfache Rendite 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110
 Übungsbeispiele 1/6 1) Vervollständigen Sie folgende Tabelle: Nr. Aktie A Aktie B Schlusskurs in Schlusskurs in 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110 Arithmetisches Mittel Standardabweichung
Übungsbeispiele 1/6 1) Vervollständigen Sie folgende Tabelle: Nr. Aktie A Aktie B Schlusskurs in Schlusskurs in 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110 Arithmetisches Mittel Standardabweichung
Das Bayes-Theorem. Christian Neukirchen Gleichwertige Leistungsfeststellung, Juni 2005
 Das Bayes-Theorem Christian Neukirchen Gleichwertige Leistungsfeststellung, Juni 2005 Ein lahmer Witz Heute im Angebot: Ein praktisches Beispiel zur Einleitung Kurze Wiederholung der Überblick über Reverend
Das Bayes-Theorem Christian Neukirchen Gleichwertige Leistungsfeststellung, Juni 2005 Ein lahmer Witz Heute im Angebot: Ein praktisches Beispiel zur Einleitung Kurze Wiederholung der Überblick über Reverend
Anlageempfehlung. Anlageempfehlung. Musterdepot-Risikominimiert. Herr DDI Mag. Christian Czurda Hauptstraße 155 - Haus 14 2391 Kaltenleutgeben
 Czurda Christian DDI Mag., Hauptstraße 1 - Haus 14, 2391 Kaltenleutgeben Herr DDI Mag. Christian Czurda Hauptstraße 1 - Haus 14 2391 Kaltenleutgeben Anlageempfehlung Musterdepot-Risikominimiert Czurda
Czurda Christian DDI Mag., Hauptstraße 1 - Haus 14, 2391 Kaltenleutgeben Herr DDI Mag. Christian Czurda Hauptstraße 1 - Haus 14 2391 Kaltenleutgeben Anlageempfehlung Musterdepot-Risikominimiert Czurda
Anleitung zur Portfolio Simulation auf www.qa-partners.com
 QAP Analytic Solutions Anleitung zur Portfolio Simulation auf www.qa-partners.com April 2015 1 VORSTELLUNG Das Portfolio-Simulations-Tool auf www.qa-partners.com wurde intern entwickelt, um eigene Investment-Strategien
QAP Analytic Solutions Anleitung zur Portfolio Simulation auf www.qa-partners.com April 2015 1 VORSTELLUNG Das Portfolio-Simulations-Tool auf www.qa-partners.com wurde intern entwickelt, um eigene Investment-Strategien
Over 45 Years ofreliable Investing TM
 Over 45 Years ofreliable Investing TM Wenngleich frustrierend, sind Zeiträume mit enttäuschenden Resultaten des Marktes nicht ohne Präzedenzfall. Die Vergangenheit zeigt jedoch, dass auf diese schwierigen
Over 45 Years ofreliable Investing TM Wenngleich frustrierend, sind Zeiträume mit enttäuschenden Resultaten des Marktes nicht ohne Präzedenzfall. Die Vergangenheit zeigt jedoch, dass auf diese schwierigen
Wertpapiere in den Augen der Vorarlberger. Eine Studie von IMAS International im Auftrag von Erste Bank & Sparkassen
 Wertpapiere in den Augen der Vorarlberger Eine Studie von IMAS International im Auftrag von Erste Bank & Sparkassen Studiendesign Auftraggeber: Erste Bank der oesterreichischen Sparkassen Durchführungszeitraum:
Wertpapiere in den Augen der Vorarlberger Eine Studie von IMAS International im Auftrag von Erste Bank & Sparkassen Studiendesign Auftraggeber: Erste Bank der oesterreichischen Sparkassen Durchführungszeitraum:
Bauchgefühl oder kühle Berechnung Wer wird Fußball-Weltmeister 2014?
 Bauchgefühl oder kühle Berechnung Wer wird Fußball-Weltmeister 2014? Prof. Dr. Michael Feindt Karlsruher Institut für Technologie (KIT) Founder and Chief Scientific Advisor, Blue Yonder Wer wird Weltmeister?
Bauchgefühl oder kühle Berechnung Wer wird Fußball-Weltmeister 2014? Prof. Dr. Michael Feindt Karlsruher Institut für Technologie (KIT) Founder and Chief Scientific Advisor, Blue Yonder Wer wird Weltmeister?
Garantieverzinsung als Funktion der Gesamtverzinsung in der Lebensversicherung. 16. Mai 2014 Philip van Hövell
 Garantieverzinsung als Funktion der Gesamtverzinsung in der Lebensversicherung 16. Mai 2014 Philip van Hövell Agenda Einführung Garantiezins & Überschuss Maximaler Garantiezins Gesamtverzinsung & Anlagerendite
Garantieverzinsung als Funktion der Gesamtverzinsung in der Lebensversicherung 16. Mai 2014 Philip van Hövell Agenda Einführung Garantiezins & Überschuss Maximaler Garantiezins Gesamtverzinsung & Anlagerendite
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 221 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird im Bereich der Rentenrechnung die zugehörige zu Beginn eines Jahres / einer Zeitperiode eingezahlt, so spricht
SS 2014 Torsten Schreiber 221 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird im Bereich der Rentenrechnung die zugehörige zu Beginn eines Jahres / einer Zeitperiode eingezahlt, so spricht
Produktanalyse C-QUADRAT ARTS Fonds. Jänner 2008 Marketingmitteilung nur zur internen Verwendung
 Produktanalyse Fonds Jänner 2008 Marketingmitteilung nur zur internen Verwendung C-QUADRAT Produktanalyse Fonds Folie 2 Total Return Balanced >> Wertentwicklung seit Auflage 24.11.2003 Total Return Balanced
Produktanalyse Fonds Jänner 2008 Marketingmitteilung nur zur internen Verwendung C-QUADRAT Produktanalyse Fonds Folie 2 Total Return Balanced >> Wertentwicklung seit Auflage 24.11.2003 Total Return Balanced
2. Mai 2011. Geldtheorie und -politik. Die Risiko- und Terminstruktur von Zinsen (Mishkin, Kapitel 6)
 Geldtheorie und -politik Die Risiko- und Terminstruktur von Zinsen (Mishkin, Kapitel 6) 2. Mai 2011 Überblick Bestimmung des Zinssatzes im Markt für Anleihen Erklärung der Dynamik von Zinssätzen Überblick
Geldtheorie und -politik Die Risiko- und Terminstruktur von Zinsen (Mishkin, Kapitel 6) 2. Mai 2011 Überblick Bestimmung des Zinssatzes im Markt für Anleihen Erklärung der Dynamik von Zinssätzen Überblick
Die Welt der Strukturierten Produkte
 Die Welt der Strukturierten Produkte Das Buch zur SVSP Swiss Derivative Map Martin F. Meier, Daniel Sandmeier Teil 1 1 Einleitung 8 4 2 Der Markt für Strukturierte Produkte 12 2.1 Einführung 12 2.1.1 Entwicklung
Die Welt der Strukturierten Produkte Das Buch zur SVSP Swiss Derivative Map Martin F. Meier, Daniel Sandmeier Teil 1 1 Einleitung 8 4 2 Der Markt für Strukturierte Produkte 12 2.1 Einführung 12 2.1.1 Entwicklung
Step by Step Webserver unter Windows Server 2003. von Christian Bartl
 Step by Step Webserver unter Windows Server 2003 von Webserver unter Windows Server 2003 Um den WWW-Server-Dienst IIS (Internet Information Service) zu nutzen muss dieser zunächst installiert werden (wird
Step by Step Webserver unter Windows Server 2003 von Webserver unter Windows Server 2003 Um den WWW-Server-Dienst IIS (Internet Information Service) zu nutzen muss dieser zunächst installiert werden (wird
