PC II Kinetik und Struktur. Kapitel 5. Symmetrie
|
|
|
- Bertold Brodbeck
- vor 6 Jahren
- Abrufe
Transkript
1 PC II Kinetik und Struktur Kapitel 5 Symmetrie Symmetrie Wozu? Symmetrieoperationen, Punktgruppen, Charakterentafeln Symmetrie von Molekülen, Orbitalen, Schwingungen 1
2 Was ist Symmetrie? 2
3 Symmetrie - Anwendung & Nutzen! Integrale - Wann sind bestimmte Integrale = 0? Schwingungen von Molekülen IR, UV/VIS-Spektroskopie - Auswahlregeln (Bandenzahl) NMR-Spektroskopie - Anzahl Resonanzen MO-Theorie der chemischen Bindung Liganden Kristallographie Strukturanalyse (zusätzliche Symmetrieoperation: Translation..) Literatur verstehen - Gebrauch von Symmetriesymbolen ist in der chemischen Literatur etabliert. 3
4 Symmetrie und Erhaltungssätze Homogenität der Zeit Erhaltung der Energie (t t o +t beeinflusst nicht die Bewegungsgleichungen) Homogenität des Raums Erhaltung des Impulses Isotropie des Raums Erhaltung des Drehimpulses 4
5 Was ist Symmetrie und was sind Symmetrieoperationen? Eine Aktion, die das Objekt genauso aussehen läßt wie vor dieser Transformation, wird Symmetrieoperation genannt. Typische Symmetrieoperationen sind Spiegelung, Rotation, und Inversion. 5
6 Symmetriesymbol gibt Strukturinformation Ein Symbol wie etwa D 4 h kann eine präzisere und eindeutigere Strukturinformation vermitteln, als dies mit vielen Worten möglich wäre. So erlaubt die Aussage, dass das [Ni (CN) 4 ] 2- -Ion D 4 h -Symmetrie besitzt, die Schlussfolgerungen, dass es a) planar gebaut ist, b) alle Ni-CN-Gruppen linear sind, c) die C-Ni-C-Winkel alle 90 betragen und d) die vier CN-Gruppen sowie die vier Ni-C-Bindungen streng äquivalent sind. 6
7 Symmetrie und Eigenschaften Die Symmetrie bestimmt die Eigenschaften der Materie. Beispiel: Elektrisches Dipolmoment eines homonuklearen zweiatomigen Moleküls: Annahme: das Molekül A-A hat ein Dipolmoment μ parallel zur positiven z-achse: Symmetrieschlussfolgerung: A-A muss das gleiche Dipolmoment μ in entgegengesetzter Richtung (-z) haben : Fazit: Das Molekül hat kein Dipolmoment, d.h. μ z = 0! 7
8 Symmetrie und Spektroskopie Schlussfolgerung: Das Molekül A 2 besitzt kein Dipolmoment, d.h. μ z = 0! Vibration oder Rotation von homonuklearen zweiatomigen Molekülen können nicht mit Licht angeregt werden! Die Atmosphäre ist durchsichtig und wir wissen warum! 8
9 Symmetrie und Spektroskopie Fullerene C 60 Nur 4 Schwingungsfrequenzen werden beobachtet, obwohl 3N-6 = = 174 Freiheitsgrade vorliegen! - Warum? 9
10 Symmetrie und Integrale Wenn wir die Symmetrie einer Funktion kennen, dann können wir sagen, ob das Integral Null oder ungleich Null ist (und uns damit viel Rechenarbeit sparen) a +a sin x dx = 0 0 +π cos x dx = Allgemein ist die (symmetrische) Integration über einer Funktion f(x), die ungerade bezüglich eines Symmetriezentrums ist, gleich Null, z.b. gilt für f(x) = -f(-x) immer -a +a f(x) dx = 0 Dies gilt auch für das Produkt von Funktionen (gerade*gerade = gerade; gerade*ungerade = ungerade; ungerade*gerade = ungerade; ungerade*ungerade = gerade) -a +a (x²) (sin x) (cos x) dx = 0, aber a +a (sinh x)² (sin x) (tan x) dx 0 10
11 Symmetrie und Atomorbitale Diese Atomorbitale haben unterschiedliche Symmetrie (bezgl. der z- Achse) und können NICHT untereinander wechselwirken. s + p x p z + p x 11
12 Symmetrie und Atomorbitale Symmetrie zweier p-orbitale bei Spiegelung an einer Ebene 12
13 Symmetrie - empirisch Körper zeigen unterschiedliche Symmetrieeigenschaften (Hauptdiagonale) Kugel Würfel 90 Jede Rotation um Achse bringt Kugel wieder auf Deckung mit sich selbst Ausgewählte Symmetrieelemente des Würfels (Rotationsachsen) geringere Symmetrie als Kugel Systematische Behandlung: Gruppentheorie 13
14 Symmetrie Symmetrieoperationen: Zu jeder Symmetrieoperation gibt es ein zugehöriges Symmetrieelement zusätzlich noch weitere Symmetrieoperationen 14
15 Symmetrie Zu jeder Symmetrieoperationen gibt es ein entsprechendes Symmetrieelement: eine Ebene, eine Linie oder einen Punkt. So erfolgt beispielsweise eine Rotation um eine Achse, eine Spiegelung an einer Ebene und eine Inversion an einem Punkt. Einige Objekte sind symmetrischer als andere: Eine Kugel ist symmetrischer als ein Würfel, da sie gleich aussieht nach Rotation um irgendeinen Winkel, während ein Würfel nur dann unverändert aussieht, wenn er um bestimmte Winkel (90, 180 und 270 ) um genau festgelegte Achsen (zentrale Achse zwischen gegenüberliegenden Flächen, Hauptachsendiagonale und Mittenhalbierende gegenüberliegender Seiten) gedreht wird. Auch Moleküle bleiben bei bestimmten Symmetrieoperationen unverändert. NH 3, H 2 O, C 6 H 6, CBrClF. Wir klassifizieren die Moleküle nach ihrem gemeinsamen Satz von Symmetrieelementen. So können wir die oben beschriebenen molekularen und spektroskopischen Eigenschaften bestimmen. 15
16 I. Symmetrieoperationen und Symmetrieelemente: Identität, E C 3 H 6 O 3 DNA CHClBrF Die Symmetrieoperation der Identität, Symbol E, besteht darin nichts zu tun (Rotation um 0 ): Jedes Objekt (Molekül) besitzt diese Symmetrieoperation. - notwendig für vollständige Beschreibung innerhalb der Gruppentheorie E = neutrales Element 16
17 II. Symmetrieoperation: n-zählige Rotationsachse, C n Die n-zählige Rotation um eine n-fache Symmetrieachse, C n entspricht einer Rotation um 360 o /n. Die Operation C 1 ist eine Rotation um 360 o, was der Identity E entspricht. C 6 H 6 Molekül hat eine sechszählige Achse C 6 und 6 zweizählige C 2 -Achsen. Falls ein Molekül mehrere Rotations-Symmetrieachsen hat, dann wird die mit dem größten n Hauptachse genannt. 17
18 II. Symmetrieoperation: n-zählige Rotationsachse, C n H 2 O hat eine zweizählige Achse C 2 -Achse 360 /2 = 180 Atome kommen bei Drehung um 180 wieder zur Deckung NH 3 hat eine dreizählige Achse C 3 -Achse 360 /3 = 120 Atome kommen bei Drehung um 120 (C 3 ) und 240 (C 32 ) wieder zur Deckung ebenso: C 4, C 5, C 6.. C n -Achsen Hauptachse: Achse höchster Zähligkeit: z-achse 18
19 II. Symmetrieoperation: 2-fache Rotationsachse, C 2 C 2 19
20 II. Symmetrieoperation: 3-zählige Rotationsachse, C 3 C 3 Ammoniak NH
21 Symmetrieoperation Rotation C 4 1 C 4 C C 4 = C C C C Bezeichnung: allgemein: m C n Drehung um: m 360 /n z.b /4=180 = 21 C 2 2 C 4
22 II. Symmetrieoperationen: n-fache Rotationsachse, C 6 C 6 Benzol: eine C 6 -Achse (senkrecht auf Molekülebene) und sechs (dazu senkrechte) C 2 -Achsen. 22
23 Bezeichnung der Drehachsen z C 4 OC OC Pt CO CO 2+ C 2 C 2 C 2 C 2 Hauptdrehachse: C 4 z-achse 23
24 Koordinatensystem z - Ursprung Zentralatom z.b. CH 4 C-Atom y - Drehachse höchster Zähligkeit ist z-achse tetraedrische Moleküle x,y,z Achsen colinear mit C 2 -Achsen x - planare Moleküle a) wenn z-achse auf Molekülebene (XeF 4, NH 3 ) x-achse beinhaltet größte Atomzahl (parallel einer Bindung) b) wenn z-achse in Ebene, dann x auf Molekülebene (H 2 O) y z y x x - rechtshändiges Koordinatensystem: z y x x H O z H y Bei der positiven Drehrichtung wird die positive x-achse auf kürzestem Wege auf die positive y-achse überführt (und diese bei einem räumlichen Koordinatensystem anschließend wiederum auf kürzestem Weg in die Richtung 17:06 der positiven z-achse). PC II-Kap.y 24
25 II. Symmetrieoperation: -zählige Rotation, C HCN HC 7 N Bei allen linearen Moleküle (also auch zweiatomige) ist die Molekülachse eine C -Achse, da jegliche Rotation um irgendeinen (d.h. unendlich viele) Winkel das Molekül unverändert lässt. 25
26 III. Symmetrieoperation: Spiegelung, σ Die Spiegelung an einer Symmetrieebene wird durch σ beschrieben. Wasser 2 Spiegelebenen stehen senkrecht aufeinander σ v and σ v Hauptdrehachse (hier C 2 -Achse) liegt in Spiegelebenen Symmetrieelement: Ebene Symmetrieoperation: Spiegelung 26
27 Unterscheidung von Spiegelungen Spiegelung parallel zur Hauptdrehachse (vertikal): σ v Spiegelung senkrecht zur Hauptdrehachse (horizontal): σ h Besonderheit: Spiegelung in Diederebene, also in der Winkelhalbierenden zweier C 2 -Achsen: σ d C 2 C 3 C 2 C 2 σ h σ v σ d 27
28 III. Symmetrieoperation: Spiegelung, σ Die Spiegelung an einer Symmetrieebene wird durch σ beschrieben. Die Lage der Spiegelebene relativ zur molekularen Hauptachse C n wird durch einen Index gekennzeichnet. σ h bezeichnet eine Ebene, die senkrecht zur Hauptachse liegt, also horizontal. σ v ist das Symbol für eine vertikale Spiegelebene, die die Hauptachse enthält. Wenn diese Spiegelebene den Winkel zwischen einem Paar von C 2 -Achsen halbiert, dann spricht man von einer diagonalen Spiegelebene σ d. 28
29 Dieder-Spiegelebenen C 6 - Hauptachse c 2 -Achse σ d c 2 -Achse c 2 -Achse c 6 (z-achse) σ d σ d diedrische Spiegelebenen σ d schneiden C 2 -Achsen senkrecht zur Hauptachse 29
30 Horizontale Spiegelebene σ h Cl Cl Pt Cl Cl 2- σ h σ h Cl Cl Pt Cl Cl 2- d z 2-Orbital symmetrisch π-orbital antisymmetrisch 30
31 Definition von Spiegelebenen: σ h, σ d, σ v C 6 31
32 IV. Symmetrieoperationen: Inversion, i??? SF 6 SF 4 PF 5 Die Inversion transformiert alle Koordinaten eines Objekts gemäß: (x,y,z) (-x,-y,-z) Symmetrieelement ist der Punkt (das Inversionszentrum). 32
33 V. Symmetrieoperation: n-zählige Drehspiegelung, S n Methan CH 4 Ethan C 2 H 6 Die n-zählige Drehspiegelung setzt sich aus zwei Transformationen zusammen: Die erste Transformation ist eine Rotation um 360 o /n und die zweite Transformation ist eine Spiegelung an einer Ebene, die senkrecht zur Rotationsachse liegt. Dabei ist zu beachten, dass keine der Einzeloperationen für sich eine Symmetrieoperation sein muss. Z.B. hat das CH 4 -Molekül drei S 4 Achsen. 33
34 Symmetrieoperation: Drehspiegelachse Kombination aus Drehachse und Spiegelung an Ebene auf Drehachse hier S 4 -Drehspiegelachse: Kombination aus C 4 -Achse und Spiegelebene σ z.b. Methan hat eine Drehspiegelachse (S 4 ): C 4 90 σ C 2, S 4 Tetraeder 3 S 4 -Achsen X M X C 2, S 4 C 2, S 4 X 34 X
35 S 6 -Drehspiegelachse H H H H H H 60 Ethan Newman Projektion H H σ H 35 H H H
36 Beispiel Drehspiegelung, S 2 Spiegelung Drehung trans-dichlorethylen Spiegelung mit anschließender Drehung - oder umgekehrt, Operationen sind vertauschbar! 36
37 Zusammenfassung Symmetrieoperationen Symmetrieoperationen: Identität E n-zählige Rotation C n Spiegelung σ ( σ v, σ d, σ h ) Inversion i Drehspiegelung S n Mit Hilfe der 5 Symmetrieoperationen werden alle Moleküle klassifiziert. 37
38 Klassifizierung von Molekülen Nomenklatur nach Schönfliess (Standard für Punktgruppen von Molekülen) Herman-Mauguin (Standard für Festkörper; Nomenklatur ineinander überführbar) Punktgruppenliste: C 1 ; C i ; C s ; C n ; C nv ; C nh ; D n ; D nh ; D d ; S n ; T und O Arthur Moritz Schönflies *17. April 1853 in Landsberg an der Warthe, Deutschland (jetzt Gorzów, Polen) Mai 1928 in Frankfurt am Main 38
39 Die molekularen Symmetrie-Punktgruppen C 1, C i, C s C 1 : Ein Molekül gehört zur C 1 -Punktgruppe, wenn es nur das (Symmetrie-)Element der Identität E enthält. Beispiel: DNA. C i : Ein Molekül gehört zur C i -Punktgruppe, wenn es (nur) die beiden Operationen Identität E und Inversion i hat. Beispiel: Beispiel: C 2 H 2 Br 2 Cl 2 (PDB,VRLM). C s : Ein Molekül gehört zur C s -Punktgruppe, wenn es (nur) aus den beiden Elementen Identität E und Spiegelebene σ besteht. Beispiel: HDO oder ClNO 39
40 Die molekularen Symmetrie-Punktgruppen: C n Ein Molekül gehört zur C n -Punktgruppe, wenn es eine n-zählige Rotationsachse besitzt. Beispiel: Gruppe C 2 H 2 O 2 gehört zur C n - Punktgruppe, da es die (Symmetrie-)Elemente E und C 2 hat. 40
41 Die molekularen Symmetrie-Punktgruppen: C nv Ein Molekül gehört zur C nv -Punktgruppe, wenn es neben der Identität E und einer C n -Achse, n vertikale Spiegelebenen σ v hat. H 2 O NH 3 Beispiele: H 2 O gehört zur C 2v -Gruppe, da es die Elemente E, C 2 und zwei vertikale Spiegelebenen (σ v und σ v ) hat. NH 3 gehört zur C 3v -Gruppe, da es die Elemente E, C 3 und drei vertikale Spiegelebenen σ v hat. Alle zweiatomigen heteronuklearen Moleküle gehören zur C v -Gruppe, da alle Rotationen um die internukleare Achse und alle Spiegelungen quer zu dieser Achse Symmetrieoperationen sind. 41
42 Die molekularen Symmetrie-Punktgruppen: C nh Ein Molekül gehört zur C nh -Punktgruppe, wenn es neben der Identität E und einer C n -Achse zusätzlich eine horizontale Spiegelebene σ h besitzt. Butadien C 4 H 6 Beispiele: Butadien C 4 H 6 gehört zur C 2h -Gruppe, B(OH) 3 zur C 3h Gruppe. 42
43 Beziehung zwischen C 2, σ h und Inversion i C 2 σ h = i Wenn eine C 2 und σ h Symmetrie besteht, dann gibt es auch eine Inversion. Daher besteht die C 2h -Gruppe aus einer C 2 -Achse, einer horizontalen Spiegelebene σ h und der Inversion i. 43
44 Die molekularen Symmetrie-Punktgruppen: D n Ein Molekül gehört zur D n -Punktgruppe, wenn es eine n-zählige Hauptachse C n und n zweizählige Achsen senkrecht zu C n aufweist. D 6 - Punktgruppe 44
45 Die molekularen Symmetrie-Punktgruppen: D nh Ein Molekül gehört zur D nh -Punktgruppe, wenn es neben einer C n -Operation noch eine horizontale Spiegelebene σ h gibt. Als Konsequenz haben diese Moleküle n senkrechte Symmetrieebenen σ v im Winkel von 360 o /2n zueinander. Benzol C 6 H 6 Beispiele: BF 3 hat die Symmetrieelemente E, C 3, 3 C 2, und σ h und gehört daher zur D 3h Gruppe. C 6 H 6 hat die Elemente E, C 6, 3 C 2, 3 C 2 ' und σ h und gehört daher zur D 6h -Gruppe. Alle zweiatomigen homonuklearen Moleküle, wie O 2, N 2 und andere, gehören zur D h -Gruppe. Andere Beispiele sind CO 2 (D h ), C 2 H 2 (D h ). 45
46 Die molekularen Symmetrie-Punktgruppen: D nd Ein Molekül gehört zur D nd -Punktgruppe, wenn es neben einer C n -Operation noch eine Dieder-Spiegelebene σ d gibt. Examples: the twisted, 90 o allene belongs to D 2d group, while the staggered confirmation of ethane belongs to D 3d group. 46
47 Die molekularen Symmetrie-Punktgruppen: S n Ein Molekül gehört zur S n -Punktgruppe, wenn es eine S n -Achse gibt. Beispiel: Tetraphenylmethan gehört zur Symmetriegruppe S 4. Die Gruppe S 2 entspricht C i, und solche Moleküle werden unter C i geführt. 47
48 Die kubischen Gruppen: T d und O h Es gibt viele wichtige Moleküle mit mehr als einer Hauptachse, wie beispielsweise CH 4 oder SF 6. Die meisten gehören zur kubischen Gruppe, insbesondere zu den Tetraeder Gruppen T, T d und T h, oder zu den Oktaeder Gruppen O und O h. Tetraedrische Moleküle Oktaedrische Moleküle CH 4 : T d -Gruppe SF 6 : O h -Gruppe 48
49 Die kubischen Gruppen: T und O 49
50 Zusammenfassung der Klassifizierungen von Molekülen Gruppen Symmetrieelemente Operationen (O) Ordnung Nichtrotatorische Gruppe C 1 kein Symmetrieelement: nichtaxiale Gruppe E 1 C i Spezialfall der nichtaxialen Gruppe (n = 1): C i E, i 2 C s Spezialfall nichtaxiale Gruppe C nh = C 2 : nur eine Spiegelebene E, σ h 2 zyklische Gruppe C n n-zählige Rotationsachse E, C n1,.. C n-1 n n S 2n 2n-zählige Drehspiegelachse fällt mit C n zusammen E, S 2n, S 2 2n (= C 2n2 σ n = C n ),...S 2n-1 2n 2n C nv C n und n Spiegelebenen, deren Schnittgerade die E, C n1 C n-1 n, σ (1) v σ (n) v 2n Referenzachse ist C nh C n und σ h zur Referenzachse E, C 1 n... C n-1 n, σ h C 1 n = S 1 n... S n-1 n 2n Diedergruppe D n n-zählige Referenzachse C n und n 2-zählige Drehachsen dazu: C (1), 2.. C (n) 2 E, C n1 C n-1 n, nc 2 ( C n ) 2n D nh Symmetrieelemente von D n sowie eine Spiegelebene zu C n Alle O. D n und σ h, nσ v 4n D nd Symmetrieelemente von D n sowie n Spiegelebenen, die C n enthalten und die Winkel zwischen den n C (n) 2 halbieren Alle O. D n und S 2n,, S 2n-1 2n, nσ d 4n Teraedergruppe T d Oktaedergruppe O h Ikosaedergruppe I h 4 C 3 durch die Ecken, 3 C 2 durch die Mittelpunkte jeweils gegenüberliegende Kanten, 6 σ durch jeweils eine Kante und den Mittelpunkt, 3 S 4 kolinear mit C 2 3 C 4 durch die Ecken, 4 C 3 durch die Mitten jeweils gegenüberliegender Flächen, 6 C 2 durch die Mitten gegenüberliegender Kanten, 3 σ h zu C 4, 3 S 4 kolinear zu C 4, 4 S 6 kolinear zu C 3, 6 σ d und i. Insgesamt 24 Operationen: 24 E, 4C 3, 4C 32, 3C 2, 3S 4, 3S 43, 6σ d Insgesamt 48 Operationen: E, 4C 3, 4C 32, 6C 2, 3C 4, 3C 43, 3C 2, i, 3S 4, 3S 43, 4S 6, 4S 65, 3σ h, 6σ d Alle Symmetrieelemente eines Ikosaeders E, 6C 5, 6C 52, 6C 53, 6C 54, 10C 3, 10C 32, 15C 2, i, 6S 10, 6S 103, 6S 107, 6S 109, 10S 6, 10S 65, 15σ
51 Kurze Zusammenfassung der Klassifizierungen von Molekülen Symbol Ordnung Operation (english) (Nonrotational Groups) C 1 1 E asymmetrisch C s 2 E, σ h C i 2 E, i zyklische Gruppe (Single-Axis groups (n = 2, 3,., )) C n n E, C n,.., C n n-1 dissymmetrisch C nv 2n E, C n,.., C n n-1, nσ v ( n / 2 σ v und n / 2 σ d für gerades n) C nh 2n E, C n,.., C n n-1, σ h S 2n 2n E, S 2n,.., S 2n 2n-1 C v E, C, σ v (noncentrosymmetric linear) Diedergruppe (Dihedral Groups (n = 2, 3,.., )) D n 2n E, C n,.., C n n-1, nc 2 ( C n ) dissymetrisch D nd 4n E, C n,.., C n n-1, S 2n,.., S 2n 2n-1, nc 2 ( C n ), nσ d D nh 4n E, C n,.., C n n-1, nc 2 ( C n ), σ h, nσ v D h E, C, S, C 2 ( C ), σ h, σ v, i (centrosymmetric linear) kubische Gruppen (Cubic Groups) T d 24 E, 4C 3, 4C 32, 3C 2, 3S 4, 3S 43, 6σ d (tetrahedron) O h 48 E, 4C 3, 4C 32, 6C 2, 3C 4, 3C 43, 3C 2 (= C 42 ), i, 3S 4, 3S 43, 4S 6, 4S 65, 3σ h, 6σ d (octahedron) I h 120 E, 6C 5, 6C 52, 6C 53, 6C 54, 10C 3, 10C 32, 15C 2, i, 6S 10, 6S 103, 6S 107, 6S 109, 10S 6, 10S 65, 15σ (icosahedron, dodecahedron) Ordnung: Gesamtzahl der Symmetrieoperationen z.b. C 2v : n = 2 Ordnung = 2*2=4 51
52 Symmetrieoperationen: Identität E n-zählige Rotation C n Spiegelung σ ( σ v, σ d, σ h ) Inversion i Drehspiegelung S n Punktgruppen: C 1, C i,c s C n, C nv, C nh, S n, D n, D nh, D nd, T, O, I 52
53 Beispiele für Punktgruppen O F Br Cl Cl N S Ph B H Me Cl Br H H C 1 C S Cl C i Br C 2 Cl C 3v F F F H N O F F F I H B B O O F N C 4v C F 2h C 3h D H 3h Fe Fe Co D 5h D 5d D 3 chiral! 53 F F F Co F O h F F C 60 I h
54 Bestimmung der Punktgruppe eines Moleküls Beispiel: Punktgruppe von Ferrocen (D 5h ) 1) Fe C 5 C 5 2) C 2 Fe = C 2 3) Fe σ h D 5h :06 54
55 Einige Konsequenzen der Molekülsymmetrie Nach Bestimmung der Punktgruppe eines Moleküls können bereits einige Eigenschaften benannt werden: Polarität Polare Moleküle besitzen ein permanentes elektrisches Dipolmoment, wie z.b. NaCl, O 3, NH 3, etc.. Reine Rotationsübergänge können nur in polaren Molekülen stattfinden. Falls das Molekül zur C n Gruppe (n>1), gehört, dann kann es KEINE KOMPONENTE des Dipolmoments senkrecht zur Symmetrieachse haben, sondern nur parallel zur Symmetrieachse. Das gleiche gilt für C nv -Moleküle. Moleküle, die zu irgend einer anderen Gruppe, außer C s gehören, haben überhaupt kein Dipolmoment, da bei ihnen Symmetrieoperationen immer ein Ende des Moleküls ins andere transformieren. Nur C n -, C nv - oder C s -Moleküle haben ein permanentes Dipolmoment. Chiralität Ein chirales Molekül darf nicht durch eine Spiegeltransformation in sich selbst überführt werden. Ein achirales Molekül wird durch eine Spiegeltransformation in sich selbst überführt. Ein chirales Molekül darf keine Drehspiegelachse S n haben. Moleküle mit Inversion i gehören zur S 2 -Gruppe und können daher nicht chiral sein. (Wg. S 1 = σ, sind Moleküle mit einer Spiegelebene achiral). 55
56 Konsequenzen der Symmetrie Ψ = φ 1 φ 2 dτ = 0 falls φ 1 φ 2 nicht symmetrisch ist. 56
57 Symmetrie & Chiralität Br I) asymmetrisch = chiral - nur Identität E F I Cl II) dissymmetrisch = chiral - nur C n -Achsen Me Me C 2 I) & II) identische skalare aber unterschiedliche vektorielle Eigenschaften z.b. Siedepunkt (skalar) Wechselwirkung mit polarisiertem Licht (vektoriell) III) symmetrisch = achiral i, S n, σ identische skalare und vektorielle Eigenschaften M e M e σ 57
58 NMR-Spektroskopie homotope Protonen (Kerne) C n -Achsen Me Me gleiche chemische Verschiebung unabhängig vom Lösungsmittel C 2 enantiotope Protonen (Kerne) σ CH 3 CH 3 σ gleiche chemische Verschiebung in achiralem Lösungsmittel kann in chiralem Lösungsmittel unterschiedlich sein diastereotope Protonen (Kerne) keine Symmetrie Me CH 3 CH 3 chemische Verschiebung kann in a/chiralem Lösungsmittel unterschiedlich sein (kann zufällig gleich sein) 58
59 NMR-Spektroskopie wichtig hierbei: Zunächst auf Homotopie überprüfen! CH 3 CH 3 C 2 σ homotop! C 2 CH 3 CH 3 H H H H H H H H C 2 H H C 2 H H homotop! 1 Resonanz! koppeln nicht! CH 3 H H CH 3 H H CH 3 CH 3 1 H-NMR-Spektrum 4 H 6 H δ ppm
60 Symmetrie-Klassifizierung der Moleküle Definition einer Gruppe Wir haben die Moleküle nach ihrer Symmetrie klassifiziert und einer Gruppe zugeordnet. Nach der Gruppentheorie bilden die Symmetrieoperationen eine Gruppe, wenn sie den folgenden Axiomen genügen: Wenn die Operationen A und B zur selben Gruppe gehören, dann gilt für A B = C, dass C ebenfalls eine Operation (ein Element) der selben Gruppe ist. Dabei kann A B B A sein (dies ist dann eine nichtabelsche Gruppe). Eine der Operationen in der Gruppe ist die Identitätsoperation E ( die Eins ). A E = E A = A. Die Inverse (reziproke) jeder Operation ist auch eine Operation der Gruppe: wenn A zur Gruppe gehört, dann ist A -1 ebenfalls eine Operation der Gruppe. Es gilt: A A -1 = A -1 A = E. Die Multiplikation der Operationen ist assoziativ: A B C = (A B) C= A (B C). 60
61 Gruppen-Multiplikationstabelle - Beispiel NH 3 Dies sind alle Symmetrieoperationen des NH 3 -Moleküls: E, C 3+, C 3-, σ v, σ v, σ v Wir wollen zeigen, dass sie eine Gruppe bilden (σ v = σ c, σ v = σ a, σ v,= σ b ): C 3 - C 3 + = E a c b c a b σ va C 3 = σ vc C 3 σ va = σ vb b c a a b c 61
62 Multiplikation Tabelle: C 3v Gruppe C 3v E C 3 + C 3 - σ v σ v σ v E E C 3 + C 3 - σ v σ v σ v C + 3 C + 3 C - 3 E σ v σ v σ v C - 3 C - 3 E C + 3 σ v σ v σ v σ v σ v σ v σ v E C - 3 C + 3 σ v σ v σ v σ v C + 3 E C - 3 σ v σ v σ v σ v C - 3 C + 3 E Die Gesamtzahl der Operationen in einer Gruppe wird Gruppenordnung genannt. Die Ordnung von C 3v ist 6. Jede Punktgruppe ist charakterisiert durch ihre eigene Multiplikationstabelle. 62
63 Symmetrieoperationen - Gruppentheorie Br b C 2 C Br a [E] Br Br Cl Cl a b a b = Br Br Cl Cl a b a b [σ v ] Br Br Cl Cl a b a b = Br Br Cl Cl b a a b σ v Cl a Cl b σ v ' [C 2 ] Br Br Cl Cl a b a b = Br Br Cl Cl b a b a [σ v ] Br Br Cl Cl a b a b = Br Br Cl Cl a b b a [E], [C 2 ], [σ v ], [σ v. ] Matrizen 63
64 Matrixdarstellung der Symmetrieoperationen Es gibt beliebig viele Darstellungen 64
65 Klasse von Symmetrieoperationen: C 3v σ v σ v Punktgruppe C 3v : 6 Symmetrieoperationen σ v 3 Klassen E C 31 =C 3+, C 32 =C 3-, σ v, σ v, σ v 65
66 Charaktertafel - Beispiel Punktgruppe C 2v Schönflies Symbol Symmetrieoperation R (jede ist eine Klasse) g: Anzahl Operationen in einer Klasse (hier jeweils 1) Gesamtzahl der Operationen C 2v E C 2 σ v (xz) σ' v (yz) h = 4 MULLIKEN Symbole Γ i A 1 A z R z z 2, x 2, y 2 xy B x, R y xz B y, R x yz z Der Charakter χ i (R) eines Elements ist die Spur der Matrix für dieses Element. Transformation der karthesischen Koordinaten x,y,z und Rotationen R i und lineare Fkt. dieser Koordinaten (rechts entspr. quadr. Fkt.). x y 66
67 Bestimmung der Punktgruppe eines Moleküls Beispiel: Punktgruppe von Ferrocen (D 5h ) 1) Fe C 5 C 5 2) C 2 Fe = C 2 3) Fe σ h D 5h :06 67
68 Charaktertafel - Beispiel Punktgruppe C 3v Schönflies Symbol Symmetrieoperation R (jede ist eine Klasse) g: Anzahl Operationen in einer Klasse Gesamtzahl der Operationen (quadr. C 3v E 2 C 3 3 σ v h = 6 (lineare Fkt.) Fkt.) MULLIKEN Symbole Γ i A z z 2, x 2 +y 2 A R z E (x,y), (R x,r y ) Der Charakter χ i (R) eines Elements ist die Spur der Matrix für dieses Element. xy, (x 2 -y 2 ), (xz,yz) Transformation der karthesischen Koordinaten x,y,z und Rotationen R i und lineare Funktionen dieser Koordinaten (rechts entspr. quadr. Fkt.). 68
69 Robert Sanderson Mulliken * 7. Juni 1896 in Newburyport, MA (USA) Oktober 1986 in Arlington, VA (USA) Nobelpreis für Chemie
70 MULLIKEN Symbole 1. Die Dimension der Charaktere ist durch einen der Buchstaben gekennzeichnet: In der Vibrationsspektroskopie ersetzt F das T. Die häufigsten Gruppen C nv, D nh und D nd haben nur Charaktere der Dimension 1 und Die eindimensionalen Charaktere sind A oder B, abhängig vom Wert von χ(c n ), wobei C n die Hauptrotationsachse ist. A und B geben also an, ob sich das Vorzeichen ändert (B) oder gleich bleibt (A). Dimension Mulliken-Symbol 1 A oder B 2 E 3 T 4 G 5 H χ(c n ) Symbol +1 A 1 B 70
71 MULLIKEN Symbole (Indices) Die Indices spiegeln eine weitere Symmetrieklassifizierung wider: 3. Falls das Molekül eine C 2 Achse oder eine Spiegelebene σ oder σ d senkrecht zur Hauptachse C n hat, dann ändert sich das Vorzeichen einer Funktion bzw. bleibt erhalten und wird als antisymmetrisch bzw. symmetrisch bezeichnet. Analoge Indices gibt es für E und T, aber die Regeln sind komplizierter. 4. Abhängig von der Operation der Inversion i, erhält das Mulliken-Symbol den Index g für gerade und u für ungerade. 5. Abhängig vom Verhalten einer Funktion bei Spiegelung an einer horizontalen Ebene erhält das Mulliken-Symbol einen oder zwei Striche. 6. zusätzliche Unterscheidungen bzgl. Drehungen und Spiegelungen (Indeces 1,2,3, ): Funktion Index Vorzeichen bleibt 1 Vorzeichenänderung 2 χ(i) Index +1 g 1 u χ(σ h ) Kennzeichnung +1 ' 1 "
72 Charaktertabelle der Punktgruppen C 2 und C 2v Falls das Molekül eine C 2 Achse oder eine Spiegelebene σ oder σ d senkrecht zur Hauptachse C n hat, dann ändert sich das Vorzeichen einer Funktion bzw. bleibt erhalten C 2 E C 2 h = 2; lineare Fkt. quadratische Fkt. A 1 1 T z ; R z x 2 ; y 2 ; z 2 ; xy B 1-1 T x ; T y ; R x ; R y xz ; yz C 2v E C 2 σ v (xz) σ' v (yz) h = 4 lineare Fkt. quadratische Fkt. Funktion Index A z z 2, x 2, y 2 Vorzeichen bleibt 1 Vorzeichenänderung 2 A R z xy B x, R y xz B y, R x yz 72
73 Regeln (Beispiel C 3v ) R g h = Σ i χ i (E)² = 1²+1²+2² C 3v E 2 C 3 3 σ v Σ R g R.χ i (R)² = h = 1. 1²+2. 1²+3. (-1)² = 1. 2²+2. (-1)²+3. 0² Γ i A A E Σ R g R.χ i (R). χ k (R) = h δ ik Beispiele A 2. E = = 0 A 1. A 2 = = 0 Genau so verhalten sich orthogonale Vektoren! Daher ist jeder Vektor so darstellbar: reduzible Darstellung irreduzible Darstellung χ(r) = Σ i a i.χ i (R) a i = 1 / h Σ R g R.χ i (R). χ(r) 73
74 reduzible Darstellung: Ausreduzieren χ(r) = Σ i a i.χ i (R) irreduzible Darstellung Koeffizienten für irreduzible Darstellung: a i = 1 / h Σ R g R.χ i (R). χ(r) irreduzible Darstellung reduzible Darstellung 74
75 Ende Kapitel 5 Und nun zu den Anwendungen in Kapitel 6 75
ACF-Vorkurs: Symmetrie in der Anorganischen Chemie
 ACF-Vorkurs: Symmetrie in der Anorganischen Chemie Stichworte: - Symmetrielemente - Punktgruppen - Charaktertafeln - Anwendung in der MO-Theorie I.1 Zur qualitativen Beschreibung genügt es oft, die Form
ACF-Vorkurs: Symmetrie in der Anorganischen Chemie Stichworte: - Symmetrielemente - Punktgruppen - Charaktertafeln - Anwendung in der MO-Theorie I.1 Zur qualitativen Beschreibung genügt es oft, die Form
Seminar zum Praktikum Anorganische Chemie III III
 Seminar zum Praktikum Anorganische Chemie III III Metallorganische Chemie Dr. J. Wachter IR-Teil3 www.chemie.uni-regensburg.de/anorganische_chemie/scheer/lehre.html www.chemie.uniregensburg.de/anorganische_chemie/wachter/lehre.html
Seminar zum Praktikum Anorganische Chemie III III Metallorganische Chemie Dr. J. Wachter IR-Teil3 www.chemie.uni-regensburg.de/anorganische_chemie/scheer/lehre.html www.chemie.uniregensburg.de/anorganische_chemie/wachter/lehre.html
Absorptionsspektrum von PTCDA und DiMe-PTCDI
 3. Gruppentheorie Absorption coefficient *10 5 6 4 2 0 Absorptionsspektrum von PTCDA und DiMe-PTCDI PTCDA Wavelength / nm 800 700 600 500 400 HOMO-LUMO Übergang S 0 -S 1 transition S 0 -S 2 transition
3. Gruppentheorie Absorption coefficient *10 5 6 4 2 0 Absorptionsspektrum von PTCDA und DiMe-PTCDI PTCDA Wavelength / nm 800 700 600 500 400 HOMO-LUMO Übergang S 0 -S 1 transition S 0 -S 2 transition
O ist gegenüber C 2. invariant. Allgemein bezeichnet man mit C n. ist symmetrisch gegenüber, das JCl Ion gegenüber C 4
 107 KAPITEL J Symmetrien 1. Einleitung a) Warum Symmetriebetrachtungen? Je komplizierter die Probleme, desto mehr spielen Symmetriebetrachtungen eine Rolle. Die Symmetriebetrachtungen in der Molekülphysik
107 KAPITEL J Symmetrien 1. Einleitung a) Warum Symmetriebetrachtungen? Je komplizierter die Probleme, desto mehr spielen Symmetriebetrachtungen eine Rolle. Die Symmetriebetrachtungen in der Molekülphysik
Symmetrieelemente C 3 C 2 C 3 O H H N H H H
 Symmetrieelemente Ein Symmetrielement liegt vor, wenn ein Objekt (hier: Molekül) durch eine Symmetrieoperation mit sich selbst zur Deckung gebracht werden kann. neue und alter Orientierung nicht unterscheidbar
Symmetrieelemente Ein Symmetrielement liegt vor, wenn ein Objekt (hier: Molekül) durch eine Symmetrieoperation mit sich selbst zur Deckung gebracht werden kann. neue und alter Orientierung nicht unterscheidbar
2. Exkurs: Spaziergang durch die Gruppentheorie!"#$
 2. Exkurs: Spaziergang durch die Gruppentheorie $ Gruppentheorie ein durchaus kompliziertes Teilgebiet der Mathematik!" Gegenstand: systematische Behandlung von Symmetrie!" Bei Verzicht auf mathematische
2. Exkurs: Spaziergang durch die Gruppentheorie $ Gruppentheorie ein durchaus kompliziertes Teilgebiet der Mathematik!" Gegenstand: systematische Behandlung von Symmetrie!" Bei Verzicht auf mathematische
Anorganische Chemie III
 Seminar zur Vorlesung Anorganische Chemie III Wintersemester 2015/16 Christoph Wölper Institut für Anorganische Chemie der Universität Duisburg-Essen Wiederholung Was bisher geschah # Darstellungen für
Seminar zur Vorlesung Anorganische Chemie III Wintersemester 2015/16 Christoph Wölper Institut für Anorganische Chemie der Universität Duisburg-Essen Wiederholung Was bisher geschah # Darstellungen für
Symmetrie und Anwendungen
 PC II Kinetik und Struktur Kapitel 6 Symmetrie und Anwendungen Symmetrie von Schwingungen und Orbitalen, Klassifizierung von Molekülschwingungen Auswahlregeln: erlaubte verbotene Übergänge IR-, Raman-,
PC II Kinetik und Struktur Kapitel 6 Symmetrie und Anwendungen Symmetrie von Schwingungen und Orbitalen, Klassifizierung von Molekülschwingungen Auswahlregeln: erlaubte verbotene Übergänge IR-, Raman-,
Outline. 1 Vektoren im Raum. 2 Komponenten und Koordinaten. 3 Skalarprodukt. 4 Vektorprodukt. 5 Analytische Geometrie. 6 Lineare Räume, Gruppentheorie
 Outline 1 Vektoren im Raum 2 Komponenten und Koordinaten 3 Skalarprodukt 4 Vektorprodukt 5 Analytische Geometrie 6 Lineare Räume, Gruppentheorie Roman Wienands (Universität zu Köln) Mathematik II für Studierende
Outline 1 Vektoren im Raum 2 Komponenten und Koordinaten 3 Skalarprodukt 4 Vektorprodukt 5 Analytische Geometrie 6 Lineare Räume, Gruppentheorie Roman Wienands (Universität zu Köln) Mathematik II für Studierende
Verknüpfung zweier C 2 Drehachsen
 Phsikalische und Theoretische Methoden der Anorganischen Chemie, WS 2009/10 Verknüpfung zweier Drehachsen 2 C (360 /2) = C 360 /2 D (360 /2) Phsikalische und Theoretische Methoden der Anorganischen Chemie,
Phsikalische und Theoretische Methoden der Anorganischen Chemie, WS 2009/10 Verknüpfung zweier Drehachsen 2 C (360 /2) = C 360 /2 D (360 /2) Phsikalische und Theoretische Methoden der Anorganischen Chemie,
Anorganische Chemie 3 (3.1) Teil 1 - Symmetrie. Was ist Symmetrie?
 Anorganische Chemie 3 (3.1) Teil 1 - Symmetrie Was ist Symmetrie? AC3 WS 2011/12 1 Symmetrie (griechisch = Ebenmaß, Gleichmaß) bedeutet die gesetzmäßige Wiederholung eines Motivs und damit die Übereinstimmung
Anorganische Chemie 3 (3.1) Teil 1 - Symmetrie Was ist Symmetrie? AC3 WS 2011/12 1 Symmetrie (griechisch = Ebenmaß, Gleichmaß) bedeutet die gesetzmäßige Wiederholung eines Motivs und damit die Übereinstimmung
Metallorganische Chemie und Katalyse der Übergangsmetalle
 etallorganische Chemie und Katalyse der Übergangsmetalle Nadia C. ösch-zanetti Institut für Anorganische Chemie der Universität Göttingen Inhalt indestens eine etall-kohlenstoffbindung n CR 3 n CR 2 n
etallorganische Chemie und Katalyse der Übergangsmetalle Nadia C. ösch-zanetti Institut für Anorganische Chemie der Universität Göttingen Inhalt indestens eine etall-kohlenstoffbindung n CR 3 n CR 2 n
2 Symmetrieoperationen und -elemente. 1.8 Klassen 2 SYMMETRIEOPERATIONEN UND -ELEMENTE 7
 SYMMETRIEOPERATIONEN UND -ELEMENTE 7.8 Klassen Zweck: Zusammenfassen zueinander ähnlicher (konjugierter) Elemente einer Gruppe. Durch Bestimmung aller Klassen ergibt sich eine eindeutige Zerlegung on G:
SYMMETRIEOPERATIONEN UND -ELEMENTE 7.8 Klassen Zweck: Zusammenfassen zueinander ähnlicher (konjugierter) Elemente einer Gruppe. Durch Bestimmung aller Klassen ergibt sich eine eindeutige Zerlegung on G:
Gruppentheorie und Symmetrie in der Chemie
 Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-7569 Stuttgart Stuttgart, 8. Mai M. Schütz, Vorlesung Gruppentheorie
Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-7569 Stuttgart Stuttgart, 8. Mai M. Schütz, Vorlesung Gruppentheorie
Gruppentheorie und Symmetrie in der Chemie
 Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-70569 Stuttgart Stuttgart, 3. Mai 00 Stabilizers von Atomen Ein Operator
Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-70569 Stuttgart Stuttgart, 3. Mai 00 Stabilizers von Atomen Ein Operator
Schrödinger-Gleichung
 Schrödinger-Gleichung abgeleitet aus Teilchen-Welle-Dualismus (de Broglie) Ψ = Ε Ψ Der amiltonian enthält kinetische und potentielle Energie aller Teilchen wirkt auf die Wellenfunktion Ψ. Ψ 2 beschreibt
Schrödinger-Gleichung abgeleitet aus Teilchen-Welle-Dualismus (de Broglie) Ψ = Ε Ψ Der amiltonian enthält kinetische und potentielle Energie aller Teilchen wirkt auf die Wellenfunktion Ψ. Ψ 2 beschreibt
Gruppentheorie ERNST MORITZ ARNDT UNIVERSITÄT GREIFSWALD. Mathematisch-Naturwissenschaftliche Fakultät INSTITUT FÜR BIOCHEMIE
 ERNST MORITZ ARNDT UNIVERSITÄT GREIFSWALD Mathematisch-Naturwissenschaftliche Fakultät INSTITUT FÜR BIOCHEMIE Arbeitskreis Physikalische Chemie Prof. Dr. Walter Langel Gruppentheorie Molekülschwingungen
ERNST MORITZ ARNDT UNIVERSITÄT GREIFSWALD Mathematisch-Naturwissenschaftliche Fakultät INSTITUT FÜR BIOCHEMIE Arbeitskreis Physikalische Chemie Prof. Dr. Walter Langel Gruppentheorie Molekülschwingungen
Molekülsymmetrie. A.1 Symmetriepunktgruppen. Symmetrieelemente und Symmetrieoperationen
 A Molekülsymmetrie Jedes Molekül hat gewisse Symmetrieeigenschaften, es läßt sich einer bestimmten Symmetriepunktgruppe zuordnen. Damit können die Methoden der Gruppentheorie angewandt werden. Dies gestattet
A Molekülsymmetrie Jedes Molekül hat gewisse Symmetrieeigenschaften, es läßt sich einer bestimmten Symmetriepunktgruppe zuordnen. Damit können die Methoden der Gruppentheorie angewandt werden. Dies gestattet
Hexagonal dichtest gepackte Struktur
 Hexagonal dichtest gepackte Struktur Auch diese Struktur ist sehr wichtig, da sie von sehr vielen Systemen angenommen wird (kein Bravaisgitter). Das einfach hexagonale Bravais-Gitter (in 3-dim): zwei-dim:
Hexagonal dichtest gepackte Struktur Auch diese Struktur ist sehr wichtig, da sie von sehr vielen Systemen angenommen wird (kein Bravaisgitter). Das einfach hexagonale Bravais-Gitter (in 3-dim): zwei-dim:
z y n ; C n n-m Cn = E
 9. Molekülsymmetrie (Punktgruppen) 9. Symmetrieelemente und -operationen (SE und SO) Koordinatenzuweisung erfolgt nach der Finger-Regel der rechten Hand: y z D Zf Mf z y = z y Identität E = C Drehung um
9. Molekülsymmetrie (Punktgruppen) 9. Symmetrieelemente und -operationen (SE und SO) Koordinatenzuweisung erfolgt nach der Finger-Regel der rechten Hand: y z D Zf Mf z y = z y Identität E = C Drehung um
Das Schwingungsspektrum von Wasser
 Das Schwingungsspektrum von Wasser Vortrag im Rahmen des Seminars zum anorganisch-chemischen Fortgeschrittenenpraktikum Institut für Anorganische Chemie Universität Karlsruhe Matthias Ernst Freitag, 29.6.2006
Das Schwingungsspektrum von Wasser Vortrag im Rahmen des Seminars zum anorganisch-chemischen Fortgeschrittenenpraktikum Institut für Anorganische Chemie Universität Karlsruhe Matthias Ernst Freitag, 29.6.2006
Ausarbeitung zum Vortrag Symmetrie in der Molekülphysik
 WWU Münster Institut für Theoretische Physik Seminar zur Theorie der Atome, Kerne und kondensierten Materie Ausarbeitung zum Vortrag Symmetrie in der Molekülphysik Marcel Hahn, m hahn07@uni-muenster.de
WWU Münster Institut für Theoretische Physik Seminar zur Theorie der Atome, Kerne und kondensierten Materie Ausarbeitung zum Vortrag Symmetrie in der Molekülphysik Marcel Hahn, m hahn07@uni-muenster.de
Stereochemie organischer Verbindungen
 Stereochemie organischer Verbindungen Stereochemische Prinzipien 1.1 Symmetrie, Symmetrieoperationen, Punktgruppen Der Begriff Stereochemie (griech: stereos = Feststoff) bezieht sich auf die Betrachtung
Stereochemie organischer Verbindungen Stereochemische Prinzipien 1.1 Symmetrie, Symmetrieoperationen, Punktgruppen Der Begriff Stereochemie (griech: stereos = Feststoff) bezieht sich auf die Betrachtung
Theoretische Chemie II. (Gruppentheorie)
 Theoretische Chemie II (Gruppentheorie) Modul BCh 4.4 Sommersemester 2016 i Vorwort Dieses Skript enthält die wesentlichen Inhalte, mathematischen Formeln und Abbildungen der Vorlesung Theoretische Chemie
Theoretische Chemie II (Gruppentheorie) Modul BCh 4.4 Sommersemester 2016 i Vorwort Dieses Skript enthält die wesentlichen Inhalte, mathematischen Formeln und Abbildungen der Vorlesung Theoretische Chemie
Auswirkungen der Symmetrien auf physikalische Effekte
 Auswirkungen der Symmetrien auf physikalische Effekte Teil 1 Elektrische Polarisation 1. Elektrische Polarisation In einem elektrisch nicht leitenden Körper also in einem Dielektrikum verschieben sich
Auswirkungen der Symmetrien auf physikalische Effekte Teil 1 Elektrische Polarisation 1. Elektrische Polarisation In einem elektrisch nicht leitenden Körper also in einem Dielektrikum verschieben sich
Einführung in den Symmetriebegriff und gruppentheoretische Grundlagen
 Einführung in den Symmetriebegriff und gruppentheoretische Grundlagen Stephanie Artmeier WS 0/ Inhaltsverzeichnis Einführung... Gruppen.... Beispiel gleichseitiges Dreieck... 3. Darstellung von Gruppen...
Einführung in den Symmetriebegriff und gruppentheoretische Grundlagen Stephanie Artmeier WS 0/ Inhaltsverzeichnis Einführung... Gruppen.... Beispiel gleichseitiges Dreieck... 3. Darstellung von Gruppen...
5. Raum-Zeit-Symmetrien: Erhaltungssätze
 5. Raum-Zeit-Symmetrien: Erhaltungssätze Unter Symmetrie versteht man die Invarianz unter einer bestimmten Operation. Ein Objekt wird als symmetrisch bezeichnet, wenn es gegenüber Symmetrieoperationen
5. Raum-Zeit-Symmetrien: Erhaltungssätze Unter Symmetrie versteht man die Invarianz unter einer bestimmten Operation. Ein Objekt wird als symmetrisch bezeichnet, wenn es gegenüber Symmetrieoperationen
2. Punktgruppen/Kristallklassen
 2. Punktgruppen/Kristallklassen Symmetrie mit konstantem Punkt M+K-Basiskurs Kristallographie und Beugung, WS 2016/2017, C. Röhr 2.1. Einleitung Definitionen, Nomenklatur, Klassifizierung I: Rotationen
2. Punktgruppen/Kristallklassen Symmetrie mit konstantem Punkt M+K-Basiskurs Kristallographie und Beugung, WS 2016/2017, C. Röhr 2.1. Einleitung Definitionen, Nomenklatur, Klassifizierung I: Rotationen
Symmetrie und Struktur
 Symmetrie und Struktur Eine Einführung in die Gruppentheorie Von Prof. Sidney RA. Kettle University of East Anglia, Norwich Aus dem Englischen übersetzt von Dr. Elke Buchholz, Aachen Mit 167 Bildern und
Symmetrie und Struktur Eine Einführung in die Gruppentheorie Von Prof. Sidney RA. Kettle University of East Anglia, Norwich Aus dem Englischen übersetzt von Dr. Elke Buchholz, Aachen Mit 167 Bildern und
7. Wie lautet die Inverse der Verkettung zweier linearer Abbildungen? 9. Wie kann die Matrixdarstellung einer linearen Abbildung aufgestellt werden?
 Kapitel Lineare Abbildungen Verständnisfragen Sachfragen Was ist eine lineare Abbildung? Erläutern Sie den Zusammenhang zwischen Unterräumen, linearer Unabhängigkeit und linearen Abbildungen! 3 Was ist
Kapitel Lineare Abbildungen Verständnisfragen Sachfragen Was ist eine lineare Abbildung? Erläutern Sie den Zusammenhang zwischen Unterräumen, linearer Unabhängigkeit und linearen Abbildungen! 3 Was ist
20. und 21. Vorlesung Sommersemester
 2. und 21. Vorlesung Sommersemester 1 Der Spezialfall fester Drehachse Aus dem Trägheitstensor sollte der früher behandelte Spezialfall fester Drehachse wieder hervorgehen. Wenn man ω = ω n mit einem Einheitsvektor
2. und 21. Vorlesung Sommersemester 1 Der Spezialfall fester Drehachse Aus dem Trägheitstensor sollte der früher behandelte Spezialfall fester Drehachse wieder hervorgehen. Wenn man ω = ω n mit einem Einheitsvektor
g g 1 = g 1 g = e. (79)
 B Anhang B B.1 Kristallographische Symmetriegruppen B.1.1 Definition Eine Menge G = {g 1, g 2,...,g k,... } von Elementen g k nennt man eine Gruppe, wenn die Verknüpfung (Operator: ) der Elemente g k die
B Anhang B B.1 Kristallographische Symmetriegruppen B.1.1 Definition Eine Menge G = {g 1, g 2,...,g k,... } von Elementen g k nennt man eine Gruppe, wenn die Verknüpfung (Operator: ) der Elemente g k die
1. Vektoralgebra 1.0 Einführung Vektoren Ein Vektor ist eine Größe, welche sowohl einen Zahlenwert (Betrag) als auch eine Richtung hat.
 1. Vektoralgebra 1.0 Einführung Vektoren Ein Vektor ist eine Größe, welche sowohl einen Zahlenwert (Betrag) als auch eine Richtung hat. übliche Beispiele: Ort r = r( x; y; z; t ) Kraft F Geschwindigkeit
1. Vektoralgebra 1.0 Einführung Vektoren Ein Vektor ist eine Größe, welche sowohl einen Zahlenwert (Betrag) als auch eine Richtung hat. übliche Beispiele: Ort r = r( x; y; z; t ) Kraft F Geschwindigkeit
Kapitel 2: Mathematische Grundlagen
 [ Computeranimation ] Kapitel 2: Mathematische Grundlagen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 2. Mathematische Grundlagen
[ Computeranimation ] Kapitel 2: Mathematische Grundlagen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 2. Mathematische Grundlagen
Gruppentheorie und Symmetrie in der Chemie
 Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring, D-709 Stuttgart Stuttgart, 8. Juli 00 M. Schütz, Vorlesung Gruppentheorie
Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring, D-709 Stuttgart Stuttgart, 8. Juli 00 M. Schütz, Vorlesung Gruppentheorie
Wiederholung der letzten Vorlesungsstunde:
 Wiederholung der letzten Vorlesungsstunde: Chemische Bindungen, starke, schwache Bindungen, Elektronenpaarbindung, bindende und freie Elektronenpaare, Oktettregel, Edelgaskonfiguration, Lewis-Formeln,
Wiederholung der letzten Vorlesungsstunde: Chemische Bindungen, starke, schwache Bindungen, Elektronenpaarbindung, bindende und freie Elektronenpaare, Oktettregel, Edelgaskonfiguration, Lewis-Formeln,
Vektoren, Vektorräume
 Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
Auswahlregeln UV/VIS-Spektroskopie
 Auswahlregeln UV/VIS-Spektroskopie H H H H Ethen: π-π*übergang erlaubt? π LUMO π HOMO hν zunächst Punktgruppe bestimmen Symmetrieoperationen σ xz σ yz C 2 (x) C 2 (z) σ xy i C 2 (y) 3 Spiegelebenen i,
Auswahlregeln UV/VIS-Spektroskopie H H H H Ethen: π-π*übergang erlaubt? π LUMO π HOMO hν zunächst Punktgruppe bestimmen Symmetrieoperationen σ xz σ yz C 2 (x) C 2 (z) σ xy i C 2 (y) 3 Spiegelebenen i,
Gruppentheorie und Symmetrie in der Chemie
 Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-70569 Stuttgart Stuttgart, 26. April 2002 Mathematische Definition
Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-70569 Stuttgart Stuttgart, 26. April 2002 Mathematische Definition
LCAO-Ansatz und Punktsymmetrie
 LCAO-Ansatz und Punktsymmetrie Quantenchemische Rechenmethoden: Grundlagen und Anwendungen M+K-Kurs, 3.2015 Nutzen von Symmetrie bei quantenchemischen Rechnungen (LCAO-Ansatz) Wiederholung Punktgruppen
LCAO-Ansatz und Punktsymmetrie Quantenchemische Rechenmethoden: Grundlagen und Anwendungen M+K-Kurs, 3.2015 Nutzen von Symmetrie bei quantenchemischen Rechnungen (LCAO-Ansatz) Wiederholung Punktgruppen
Bindungen: Kräfte, die Atome zusammenhalten, Bindungsenergie,
 Wiederholung der letzten Vorlesungsstunde: Thema: Chemische h Bindungen Bindungen: Kräfte, die Atome zusammenhalten, Bindungsenergie, unterschiedliche Arten chemischer Bindungen, Atombindung, kovalente
Wiederholung der letzten Vorlesungsstunde: Thema: Chemische h Bindungen Bindungen: Kräfte, die Atome zusammenhalten, Bindungsenergie, unterschiedliche Arten chemischer Bindungen, Atombindung, kovalente
3 Geometrische Klassifikation der Bewegungen im R 2 und R 3
 3 Geometrische Klassifikation der Bewegungen im R 2 und R 3 Sei f : R n R n eine Bewegung Sie kann beschrieben werden in der Form Dabei ist T (f)(x) = A x f(x) = Ax + b mit A O(n) und b R n Definition:
3 Geometrische Klassifikation der Bewegungen im R 2 und R 3 Sei f : R n R n eine Bewegung Sie kann beschrieben werden in der Form Dabei ist T (f)(x) = A x f(x) = Ax + b mit A O(n) und b R n Definition:
3.3. Drehungen und Spiegelungen
 3.3. Drehungen und Spiegelungen Drehungen und Spiegelungen in der Ebene Die Multiplikation einer komplexen Zahl z = x + i y (aufgefaßt als Punkt oder Ortsvektor der Ebene) mit der Zahl w = e ( ) = i φ
3.3. Drehungen und Spiegelungen Drehungen und Spiegelungen in der Ebene Die Multiplikation einer komplexen Zahl z = x + i y (aufgefaßt als Punkt oder Ortsvektor der Ebene) mit der Zahl w = e ( ) = i φ
Aus dem Beispiel lässt sich ablesen (und auch beweisen, siehe Mathematikvorlesung): Die Einheitsvektoren des Koordinatensystems K sind die Spalten der
 7 Aus dem Beispiel lässt sich ablesen (und auch beweisen, siehe Mathematikvorlesung): Folgerung: Drehmatrizen haben die Determinante. Folgerung: Drehmatrizen sind orthogonale Matrizen, das heißt D = D
7 Aus dem Beispiel lässt sich ablesen (und auch beweisen, siehe Mathematikvorlesung): Folgerung: Drehmatrizen haben die Determinante. Folgerung: Drehmatrizen sind orthogonale Matrizen, das heißt D = D
Modul: Allgemeine Chemie
 Modul: Allgemeine Chemie 5. Grundlagen der chemischen Bindung Ionenbindung Eigenschaften, Ionengitter, Kugelpackung Strukturtypen, Kreisprozesse Kovalente Bindung Lewis Formeln, Oktettregel, Formalladungen
Modul: Allgemeine Chemie 5. Grundlagen der chemischen Bindung Ionenbindung Eigenschaften, Ionengitter, Kugelpackung Strukturtypen, Kreisprozesse Kovalente Bindung Lewis Formeln, Oktettregel, Formalladungen
2. Struktur von Festkörpern
 . Struktur von Festkörpern Energie-Minimum wird erreicht, wenn jedes Atom möglichst dieselbe Umgebung hat Periodische Anordnung von Atomen. Periodische Anordnung erleichtert theoretische Beschreibung erheblich.
. Struktur von Festkörpern Energie-Minimum wird erreicht, wenn jedes Atom möglichst dieselbe Umgebung hat Periodische Anordnung von Atomen. Periodische Anordnung erleichtert theoretische Beschreibung erheblich.
Stereochemische Einflüsse Topizität
 Stereochemische Einflüsse Topizität Lage und Form von NMR-Signalen werden nicht nur durch die unmittelbare chemische Umgebung der betreffenden Kerne, also durch die Konstitution, beeinflusst, sondern auch
Stereochemische Einflüsse Topizität Lage und Form von NMR-Signalen werden nicht nur durch die unmittelbare chemische Umgebung der betreffenden Kerne, also durch die Konstitution, beeinflusst, sondern auch
2.3.4 Drehungen in drei Dimensionen
 2.3.4 Drehungen in drei Dimensionen Wir verallgemeinern die bisherigen Betrachtungen nun auf den dreidimensionalen Fall. Für Drehungen des Koordinatensystems um die Koordinatenachsen ergibt sich 1 x 1
2.3.4 Drehungen in drei Dimensionen Wir verallgemeinern die bisherigen Betrachtungen nun auf den dreidimensionalen Fall. Für Drehungen des Koordinatensystems um die Koordinatenachsen ergibt sich 1 x 1
Kurs Röntgenstrukturanalyse, Teil 1: Der kristalline Zustand
 Kurs Röntgenstrukturanalyse, Teil 1: Der kristalline Zustand Beispiel 1: Difluoramin M. F. Klapdor, H. Willner, W. Poll, D. Mootz, Angew. Chem. 1996, 108, 336. Gitterpunkt, Gitter, Elementarzelle, Gitterkonstanten,
Kurs Röntgenstrukturanalyse, Teil 1: Der kristalline Zustand Beispiel 1: Difluoramin M. F. Klapdor, H. Willner, W. Poll, D. Mootz, Angew. Chem. 1996, 108, 336. Gitterpunkt, Gitter, Elementarzelle, Gitterkonstanten,
1 Trägheitstensor (Fortsetzung)
 1 Trägheitstensor (Fortsetzung) Wir verallgemeinern den in der letzten Stunde gefundenen Trägheitstensor auf den Fall einer kontinuierlichen Massenverteilung durch die Einführung der Integration über das
1 Trägheitstensor (Fortsetzung) Wir verallgemeinern den in der letzten Stunde gefundenen Trägheitstensor auf den Fall einer kontinuierlichen Massenverteilung durch die Einführung der Integration über das
Festk0203_ /11/2002. Neben Translationen gibt es noch weitere Deckoperationen die eine Struktur in sich überführen können:
 Festk234 37 11/11/22 2.9. Drehungen und Drehinversionen Bereits kennen gelernt: Translationssymmetrie. Neben Translationen gibt es noch weitere Deckoperationen die eine Struktur in sich überführen können:
Festk234 37 11/11/22 2.9. Drehungen und Drehinversionen Bereits kennen gelernt: Translationssymmetrie. Neben Translationen gibt es noch weitere Deckoperationen die eine Struktur in sich überführen können:
Symmetrien. Transformationen. Affine und euklidische Räume
 Symmetrien Transformationen Der Gruppenbegriff entwickelte sich aus dem Begriff der Transformationsgruppe. In dieser Form tauchen auch die meisten Gruppen in der Mathematik, Physik, Chemie, Kristallographie,
Symmetrien Transformationen Der Gruppenbegriff entwickelte sich aus dem Begriff der Transformationsgruppe. In dieser Form tauchen auch die meisten Gruppen in der Mathematik, Physik, Chemie, Kristallographie,
Gruppentheorie und Symmetrie in der Chemie
 Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-70569 Stuttgart Stuttgart, 0. April 00 M. Schütz, Vorlesung Gruppentheorie
Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-70569 Stuttgart Stuttgart, 0. April 00 M. Schütz, Vorlesung Gruppentheorie
Invariantentheorie. Bewegungen
 Prof. Dr. H. Brenner Osnabrück WS 2012/2013 Invariantentheorie Vorlesung 21 In den folgenden Vorlesungen werden wir die endlichen Untergruppen G SL 2 (C) und ihre Invariantenringe klassifizieren. Dieses
Prof. Dr. H. Brenner Osnabrück WS 2012/2013 Invariantentheorie Vorlesung 21 In den folgenden Vorlesungen werden wir die endlichen Untergruppen G SL 2 (C) und ihre Invariantenringe klassifizieren. Dieses
Lineare Algebra. Mathematik II für Chemiker. Daniel Gerth
 Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Theoretische Physik 1, Mechanik
 Theoretische Physik 1, Mechanik Harald Friedrich, Technische Universität München Sommersemester 2009 Mathematische Ergänzungen Vektoren und Tensoren Partielle Ableitungen, Nabla-Operator Physikalische
Theoretische Physik 1, Mechanik Harald Friedrich, Technische Universität München Sommersemester 2009 Mathematische Ergänzungen Vektoren und Tensoren Partielle Ableitungen, Nabla-Operator Physikalische
P 2 - Piezoelektrizität
 56 P2 Piezoelektrizität P 2 - Piezoelektrizität Ein Kristall, dessen Punktgruppe (Kristallklasse) kein Symmetriezentrum (Z) aufweist, kann prinzipiell piezoelektrisch sein Das heißt, der auf den Kristall
56 P2 Piezoelektrizität P 2 - Piezoelektrizität Ein Kristall, dessen Punktgruppe (Kristallklasse) kein Symmetriezentrum (Z) aufweist, kann prinzipiell piezoelektrisch sein Das heißt, der auf den Kristall
Das Schwingungsspektrum von H 2 O
 zum Vortrag Das Schwingungsspektrum von 2 O im ahmen des Seminars zum OC-F-Praktikums Allein aus der Kenntnis der Symmetrie eines Moleküls können ückschlüsse auf und Voraussagen über das Verhalten des
zum Vortrag Das Schwingungsspektrum von 2 O im ahmen des Seminars zum OC-F-Praktikums Allein aus der Kenntnis der Symmetrie eines Moleküls können ückschlüsse auf und Voraussagen über das Verhalten des
LCAO-Ansatz und Punktsymmetrie
 LCAO-Ansatz und Punktsymmetrie Quantenchemische Rechenmethoden: Grundlagen und Anwendungen M+K-Kurs, 3.2017 Nutzen von Symmetrie bei quantenchemischen Rechnungen (LCAO-Ansatz) Wiederholung Punktgruppen
LCAO-Ansatz und Punktsymmetrie Quantenchemische Rechenmethoden: Grundlagen und Anwendungen M+K-Kurs, 3.2017 Nutzen von Symmetrie bei quantenchemischen Rechnungen (LCAO-Ansatz) Wiederholung Punktgruppen
5 Lineare Algebra (Teil 3): Skalarprodukt
 5 Lineare Algebra (Teil 3): Skalarprodukt Der Begriff der linearen Abhängigkeit ermöglicht die Definition, wann zwei Vektoren parallel sind und wann drei Vektoren in einer Ebene liegen. Daß aber reale
5 Lineare Algebra (Teil 3): Skalarprodukt Der Begriff der linearen Abhängigkeit ermöglicht die Definition, wann zwei Vektoren parallel sind und wann drei Vektoren in einer Ebene liegen. Daß aber reale
9 WOODWARD-HOFFMANN-REGELN 92
 9 WOODWARD-HOFFMANN-REGELN 92 Die SMOs des Reaktanden und der Produkte (die nach Idealisierung nicht mehr unterschieden werden) müssen konstruiert und nach ihrer Knotenstruktur energetisch klassifiziert
9 WOODWARD-HOFFMANN-REGELN 92 Die SMOs des Reaktanden und der Produkte (die nach Idealisierung nicht mehr unterschieden werden) müssen konstruiert und nach ihrer Knotenstruktur energetisch klassifiziert
Endliche Gruppen orthogonaler Transformationen in dreidimensionalen reellen Vektorräumen
 Endliche Gruppen orthogonaler Transformationen in dreidimensionalen reellen Vektorräumen Proseminar: Geometrie und Darstellungstheorie Fakultät für Mathematik Basierend auf Finite Reflection Groups von
Endliche Gruppen orthogonaler Transformationen in dreidimensionalen reellen Vektorräumen Proseminar: Geometrie und Darstellungstheorie Fakultät für Mathematik Basierend auf Finite Reflection Groups von
Anorganische Chemie III - Festkörperchemie
 Mathematisch-Naturwissenschaftliche Fakultät Institut für Chemie Abteilung Anorganische Chemie/Festkörperchemie Prof. Dr. Martin Köckerling Vorlesung Anorganische Chemie III - Festkörperchemie 1 Wiederholung
Mathematisch-Naturwissenschaftliche Fakultät Institut für Chemie Abteilung Anorganische Chemie/Festkörperchemie Prof. Dr. Martin Köckerling Vorlesung Anorganische Chemie III - Festkörperchemie 1 Wiederholung
2. Kristallstrukturen 2.1 Bindungsarten
 2. Kristallstrukturen 2.1 Bindungsarten Bindungskräfte zwischen den Atomen ermöglichen systematische und geordnete Anlagerung der Atome Entstehung von Kristallstrukturen Metall-Ion (+) Metallische Bindung
2. Kristallstrukturen 2.1 Bindungsarten Bindungskräfte zwischen den Atomen ermöglichen systematische und geordnete Anlagerung der Atome Entstehung von Kristallstrukturen Metall-Ion (+) Metallische Bindung
: Quantenmechanische Lösung H + 2. Molekülion und. Aufstellen der Schrödingergleichung für das H + 2
 H + 2 Die molekulare Bindung : Quantenmechanische Lösung Aufstellen der Schrödingergleichung für das H + 2 Molekülion und Lösung Wichtige Einschränkung: Die Kerne sind festgehalten H Ψ(r) = E Ψ(r) (11)
H + 2 Die molekulare Bindung : Quantenmechanische Lösung Aufstellen der Schrödingergleichung für das H + 2 Molekülion und Lösung Wichtige Einschränkung: Die Kerne sind festgehalten H Ψ(r) = E Ψ(r) (11)
Hans Delfs. Übungen zu Mathematik III für Medieninformatik
 Hans Delfs Übungen zu Mathematik III für Medieninformatik 1 RÄUMLICHE DARSTELLUNGEN VON OBJEKTEN 1 1 Räumliche Darstellungen von Objekten Der Einheitswürfel ist der achsenparallele Würfel in A 3, der von
Hans Delfs Übungen zu Mathematik III für Medieninformatik 1 RÄUMLICHE DARSTELLUNGEN VON OBJEKTEN 1 1 Räumliche Darstellungen von Objekten Der Einheitswürfel ist der achsenparallele Würfel in A 3, der von
4 Lineare Abbildungen
 17. November 2008 34 4 Lineare Abbildungen 4.1 Lineare Abbildung: Eine Funktion f : R n R m heißt lineare Abbildung von R n nach R m, wenn für alle x 1, x 2 und alle α R gilt f(αx 1 ) = αf(x 1 ) f(x 1
17. November 2008 34 4 Lineare Abbildungen 4.1 Lineare Abbildung: Eine Funktion f : R n R m heißt lineare Abbildung von R n nach R m, wenn für alle x 1, x 2 und alle α R gilt f(αx 1 ) = αf(x 1 ) f(x 1
Spektroskopie-Seminar SS NMR-Spektroskopie. H-NMR-Spektroskopie. nuclear magnetic resonance spectroscopy- Kernmagnetresonanzspektroskopie
 1 H-NMR-Spektroskopie nuclear magnetic resonance spectroscopy- Kernmagnetresonanzspektroskopie 4 NMR-Spektroskopie 5.1 1 H-NMR-Spektroskopie Wasserstoffatome ( 1 H, natürliche Häufigkeit 99,985 %) mit
1 H-NMR-Spektroskopie nuclear magnetic resonance spectroscopy- Kernmagnetresonanzspektroskopie 4 NMR-Spektroskopie 5.1 1 H-NMR-Spektroskopie Wasserstoffatome ( 1 H, natürliche Häufigkeit 99,985 %) mit
09. Lineare Abbildungen und Koordinatentransformationen
 09. Lineare Abbildungen und Koordinatentransformationen Definition. Seien V und W Vektorräume. Unter einer linearen Abbildung versteht man eine Abbildung F : V W, v F v w mit folgender Eigenschaft: F λ
09. Lineare Abbildungen und Koordinatentransformationen Definition. Seien V und W Vektorräume. Unter einer linearen Abbildung versteht man eine Abbildung F : V W, v F v w mit folgender Eigenschaft: F λ
OC 3 - Stereochemie. Allgemeine Hintergründe
 OC 3 - Stereochemie Allgemeine Hintergründe Einführung Folie Nr. 2 3-dimensionale Anordnung (relativ/absolut) in der realen Welt sind extrem wichtig Bild rechts: http://de.wikipedia.org/wiki/pfefferminz,
OC 3 - Stereochemie Allgemeine Hintergründe Einführung Folie Nr. 2 3-dimensionale Anordnung (relativ/absolut) in der realen Welt sind extrem wichtig Bild rechts: http://de.wikipedia.org/wiki/pfefferminz,
Computer Vision I. Nikos Canterakis. Lehrstuhl für Mustererkennung, Universität Freiburg
 Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 5 Quadriken Polarität Transformationen Klassifikation von Quadriken Geraden in Regelquadriken Die kubische Wendelinie (twisted
Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 5 Quadriken Polarität Transformationen Klassifikation von Quadriken Geraden in Regelquadriken Die kubische Wendelinie (twisted
gegeben: G sei endliche Gruppe, jede Untergruppe von G sei ein Normalteiler zu zeigen: je zwei Elemente teilerfremder Ordnung kommutieren
 Stefan K. 4.Übungsblatt Algebra I Aufgabe 1 gegeben: G sei endliche Gruppe, jede Untergruppe von G sei ein Normalteiler von G zu zeigen: je zwei Elemente teilerfremder Ordnung kommutieren Beweis: Seien
Stefan K. 4.Übungsblatt Algebra I Aufgabe 1 gegeben: G sei endliche Gruppe, jede Untergruppe von G sei ein Normalteiler von G zu zeigen: je zwei Elemente teilerfremder Ordnung kommutieren Beweis: Seien
3. Elastizitätsgesetz
 3. Elastizitätsgesetz 3.1 Grundlagen 3.2 Isotropes Material 3.3 Orthotropes Material 3.4 Temperaturdehnungen 1.3-1 3.1 Grundlagen Elastisches Material: Bei einem elastischen Material besteht ein eindeutig
3. Elastizitätsgesetz 3.1 Grundlagen 3.2 Isotropes Material 3.3 Orthotropes Material 3.4 Temperaturdehnungen 1.3-1 3.1 Grundlagen Elastisches Material: Bei einem elastischen Material besteht ein eindeutig
44 Orthogonale Matrizen
 44 Orthogonale Matrizen 44.1 Motivation Im euklidischen Raum IR n haben wir gesehen, dass Orthonormalbasen zu besonders einfachen und schönen Beschreibungen führen. Wir wollen das Konzept der Orthonormalität
44 Orthogonale Matrizen 44.1 Motivation Im euklidischen Raum IR n haben wir gesehen, dass Orthonormalbasen zu besonders einfachen und schönen Beschreibungen führen. Wir wollen das Konzept der Orthonormalität
Symmetrie von Naturgesetzen - Galilei-Transformationen und die Invarianz der Newton schen Gesetze
 Symmetrie von Naturgesetzen - Galilei-Transformationen und die Invarianz der Newton schen Gesetze Symmetrie (Physik) (aus Wikipedia, der freien Enzyklopädie) Symmetrie ist ein grundlegendes Konzept der
Symmetrie von Naturgesetzen - Galilei-Transformationen und die Invarianz der Newton schen Gesetze Symmetrie (Physik) (aus Wikipedia, der freien Enzyklopädie) Symmetrie ist ein grundlegendes Konzept der
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 10 Bewegungen Wir haben schon mehrfach die Würfelgruppe betrachtet, also die Gruppe der eigentlichen Symmetrien an einem Würfel.
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 10 Bewegungen Wir haben schon mehrfach die Würfelgruppe betrachtet, also die Gruppe der eigentlichen Symmetrien an einem Würfel.
4.1. Vektorräume und lineare Abbildungen
 4.1. Vektorräume und lineare Abbildungen Mengen von Abbildungen Für beliebige Mengen X und Y bezeichnet Y X die Menge aller Abbildungen von X nach Y (Reihenfolge beachten!) Die Bezeichnungsweise erklärt
4.1. Vektorräume und lineare Abbildungen Mengen von Abbildungen Für beliebige Mengen X und Y bezeichnet Y X die Menge aller Abbildungen von X nach Y (Reihenfolge beachten!) Die Bezeichnungsweise erklärt
Musterlösung Serie 3. ITET Diskrete Mathematik WS 02/03 R. Suter. d) Für beliebige a, b G gilt
 ITET Diskrete Mathematik WS 2/3 R. Suter. a) r s = r + )s + ). Assoziativität: Ist erfüllt, denn Musterlösung Serie 3 r s) t = r + )s + ) + ) t + ) = r + )s + )t + ) = r + ) s + )t + ) + ) = r s t) Neutrales
ITET Diskrete Mathematik WS 2/3 R. Suter. a) r s = r + )s + ). Assoziativität: Ist erfüllt, denn Musterlösung Serie 3 r s) t = r + )s + ) + ) t + ) = r + )s + )t + ) = r + ) s + )t + ) + ) = r s t) Neutrales
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 1 Beispiele zu Symmetrien Wir beginnen diese Vorlesung, indem wir am Beispiel der Symmetrien an einem Würfel den Gruppenbegriff
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 1 Beispiele zu Symmetrien Wir beginnen diese Vorlesung, indem wir am Beispiel der Symmetrien an einem Würfel den Gruppenbegriff
4. Stereochemie. Das wichtigste Kriterium für Chiralität ist, dass sich Objekt und Spiegelbild nicht zur Deckung bringen lassen.
 4. Stereochemie Auch die cis-trans-isomerie zählt zur Stereoisomerie: 4.1 Chirale Moleküle Chirale Moleküle besitzen ein asymmetrisches C- Atom = Chiralitätszentrum. Das wichtigste Kriterium für Chiralität
4. Stereochemie Auch die cis-trans-isomerie zählt zur Stereoisomerie: 4.1 Chirale Moleküle Chirale Moleküle besitzen ein asymmetrisches C- Atom = Chiralitätszentrum. Das wichtigste Kriterium für Chiralität
Lineare Algebra. 1 Lineare Abbildungen
 Lineare Algebra Die lineare Algebra ist ein Teilgebiet der Mathematik, welches u. A. zur Beschreibung geometrischer Abbildungen und diverser Prozesse und zum Lösen linearer Gleichungssysteme mit Hilfe
Lineare Algebra Die lineare Algebra ist ein Teilgebiet der Mathematik, welches u. A. zur Beschreibung geometrischer Abbildungen und diverser Prozesse und zum Lösen linearer Gleichungssysteme mit Hilfe
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
-dimensionale Darstellungen
 1.9 2 1 2 -dimensionale Darstellungen Auf einer Fläche F (2 dimensional) wird eine Operation ausgeführt Zum Beispiel wir eine Verschiebung um den Vektor t durchgeführt. Gemeint ist der Körper, der überstrichen
1.9 2 1 2 -dimensionale Darstellungen Auf einer Fläche F (2 dimensional) wird eine Operation ausgeführt Zum Beispiel wir eine Verschiebung um den Vektor t durchgeführt. Gemeint ist der Körper, der überstrichen
Kapitel 3 Lineare Algebra
 Kapitel 3 Lineare Algebra Inhaltsverzeichnis VEKTOREN... 3 VEKTORRÄUME... 3 LINEARE UNABHÄNGIGKEIT UND BASEN... 4 MATRIZEN... 6 RECHNEN MIT MATRIZEN... 6 INVERTIERBARE MATRIZEN... 6 RANG EINER MATRIX UND
Kapitel 3 Lineare Algebra Inhaltsverzeichnis VEKTOREN... 3 VEKTORRÄUME... 3 LINEARE UNABHÄNGIGKEIT UND BASEN... 4 MATRIZEN... 6 RECHNEN MIT MATRIZEN... 6 INVERTIERBARE MATRIZEN... 6 RANG EINER MATRIX UND
TC1 Grundlagen der Theoretischen Chemie
 TC1 Grundlagen der Theoretischen Chemie Irene Burghardt (burghardt@chemie.uni-frankfurt.de) Praktikumsbetreuung: Sarah Römer (roemer@em.uni-frankfurt.de) Simona Scheit (simona.scheit@googlemail.com) Juanma
TC1 Grundlagen der Theoretischen Chemie Irene Burghardt (burghardt@chemie.uni-frankfurt.de) Praktikumsbetreuung: Sarah Römer (roemer@em.uni-frankfurt.de) Simona Scheit (simona.scheit@googlemail.com) Juanma
4. Isomerie von Komplexverbindungen
 4. Isomerie von Komplexverbindungen 4. Isomerie bei Koordinationsverbindungen Grundsätzlich unterscheidet man Konstitutionsisomerie Strukturisomerie) und Stereoisomerie (Konfigutationsisomerie). Konstitutionsisomerie:
4. Isomerie von Komplexverbindungen 4. Isomerie bei Koordinationsverbindungen Grundsätzlich unterscheidet man Konstitutionsisomerie Strukturisomerie) und Stereoisomerie (Konfigutationsisomerie). Konstitutionsisomerie:
Mathematik für Chemische Technologie 2
 Mathematik für Chemische Technologie 2 Themenüberblick: Funktionen mehrerer unabhängigen Veränderlichen Vektoralgebra Lineare Gleichungssysteme und Determinanten Fehlerrechnung Schwerpunkt des Sommersemesters
Mathematik für Chemische Technologie 2 Themenüberblick: Funktionen mehrerer unabhängigen Veränderlichen Vektoralgebra Lineare Gleichungssysteme und Determinanten Fehlerrechnung Schwerpunkt des Sommersemesters
Mathematische Grundlagen
 Mathematische Grundlagen Oliver Deussen Mathematische Grundlagen 1 Affine Räume um Zeichenebene bzw. Raum zu beschreiben, muß vorher ein Koordinatensystem festgelegt werden durch geometrische Fragestellungen
Mathematische Grundlagen Oliver Deussen Mathematische Grundlagen 1 Affine Räume um Zeichenebene bzw. Raum zu beschreiben, muß vorher ein Koordinatensystem festgelegt werden durch geometrische Fragestellungen
4.4. Rang und Inversion einer Matrix
 44 Rang und Inversion einer Matrix Der Rang einer Matrix ist die Dimension ihres Zeilenraumes also die Maximalzahl linear unabhängiger Zeilen Daß der Rang sich bei elementaren Zeilenumformungen nicht ändert
44 Rang und Inversion einer Matrix Der Rang einer Matrix ist die Dimension ihres Zeilenraumes also die Maximalzahl linear unabhängiger Zeilen Daß der Rang sich bei elementaren Zeilenumformungen nicht ändert
Vorbereitung für die Prüfung Mathematik II für Informatiker
 Technische Universität Ilmenau SS 2010 Institut für Mathematik Inf Prof. Dr. Michael Stiebitz Vorbereitung für die Prüfung Mathematik II für Informatiker 1 Lineare Algebra Aufgabe 1 Schauen Sie sich die
Technische Universität Ilmenau SS 2010 Institut für Mathematik Inf Prof. Dr. Michael Stiebitz Vorbereitung für die Prüfung Mathematik II für Informatiker 1 Lineare Algebra Aufgabe 1 Schauen Sie sich die
Musterlösungen Blatt Mathematischer Vorkurs. Sommersemester Dr. O. Zobay. Matrizen
 Musterlösungen Blatt 8 34007 Mathematischer Vorkurs Sommersemester 007 Dr O Zobay Matrizen Welche Matrixprodukte können mit den folgenden Matrizen gebildet werden? ( 4 5 A, B ( 0 9 7, C 8 0 5 4 Wir können
Musterlösungen Blatt 8 34007 Mathematischer Vorkurs Sommersemester 007 Dr O Zobay Matrizen Welche Matrixprodukte können mit den folgenden Matrizen gebildet werden? ( 4 5 A, B ( 0 9 7, C 8 0 5 4 Wir können
Grundwissen Abitur Geometrie 15. Juli 2012
 Grundwissen Abitur Geometrie 5. Juli 202. Erkläre die Begriffe (a) parallelgleiche Pfeile (b) Vektor (c) Repräsentant eines Vektors (d) Gegenvektor eines Vektors (e) Welcher geometrische Zusammenhang besteht
Grundwissen Abitur Geometrie 5. Juli 202. Erkläre die Begriffe (a) parallelgleiche Pfeile (b) Vektor (c) Repräsentant eines Vektors (d) Gegenvektor eines Vektors (e) Welcher geometrische Zusammenhang besteht
Wiederholung der letzten Vorlesungsstunde: Thema: Chemische Bindungen II
 Wiederholung der letzten Vorlesungsstunde: Thema: Chemische Bindungen II Elektronenpaarbindung, Elektronegativität, polare Atombindung, Dipolmoment, Hybridisierung von Atomorbitalen, sp 3 -, sp 2 -, sp-hybridorbitale,
Wiederholung der letzten Vorlesungsstunde: Thema: Chemische Bindungen II Elektronenpaarbindung, Elektronegativität, polare Atombindung, Dipolmoment, Hybridisierung von Atomorbitalen, sp 3 -, sp 2 -, sp-hybridorbitale,
Lineare Algebra und analytische Geometrie II
 Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 51 Numerische Bedingungen für endliche Symmetriegruppen im Raum Lemma 51.1. Es sei G SO 3 (R) eine endliche
Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 51 Numerische Bedingungen für endliche Symmetriegruppen im Raum Lemma 51.1. Es sei G SO 3 (R) eine endliche
Lösbarkeit linearer Gleichungssysteme
 Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
2. Linear Combination of Atomic Orbitals
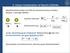 . Linear Combination of Atomi Orbitals Molekülorbitale werden mit ilfe des Variationsansatzes erhalten. Beispiel: -atomiges Molekül Atom, ϕ Atom, ϕ amilton-operator: Orthonormierung: ˆ ϕ El. Atom ϕ = =
. Linear Combination of Atomi Orbitals Molekülorbitale werden mit ilfe des Variationsansatzes erhalten. Beispiel: -atomiges Molekül Atom, ϕ Atom, ϕ amilton-operator: Orthonormierung: ˆ ϕ El. Atom ϕ = =
Dynamik von Molekülen. Rotationen und Schwingungen von Molekülen
 Rotationen und Schwingungen von Molekülen Schwingungen und Rotationen Bis jetzt haben wir immer den Fall betrachtet, daß die Kerne fest sind Was geschieht nun, wenn sich die Kerne bewegen können? Zwei
Rotationen und Schwingungen von Molekülen Schwingungen und Rotationen Bis jetzt haben wir immer den Fall betrachtet, daß die Kerne fest sind Was geschieht nun, wenn sich die Kerne bewegen können? Zwei
Übungsblatt
 Übungsblatt 3 3.5.27 ) Die folgenden vier Matrizen bilden eine Darstellung der Gruppe C 4 : E =, A =, B =, C = Zeigen Sie einige Gruppeneigenschaften: a) Abgeschlossenheit: Berechnen Sie alle möglichen
Übungsblatt 3 3.5.27 ) Die folgenden vier Matrizen bilden eine Darstellung der Gruppe C 4 : E =, A =, B =, C = Zeigen Sie einige Gruppeneigenschaften: a) Abgeschlossenheit: Berechnen Sie alle möglichen
5.2 Drehimpuls, Drehmoment und Trägheitstensor
 186 KAPITEL 5. STARRE KÖRPER 5. Drehimpuls, Drehmoment und Trägheitstensor Wie wir im vorhergehenden Abschnitt gesehen haben, besitzt ein starrer Körper 3 Freiheitsgrade zur Beschreibung seiner Position
186 KAPITEL 5. STARRE KÖRPER 5. Drehimpuls, Drehmoment und Trägheitstensor Wie wir im vorhergehenden Abschnitt gesehen haben, besitzt ein starrer Körper 3 Freiheitsgrade zur Beschreibung seiner Position
Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 3 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick
 Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 3 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick gsheldr@shelx.uni-ac.gwdg.de Das Gitter Kristalle bestehen
Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 3 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick gsheldr@shelx.uni-ac.gwdg.de Das Gitter Kristalle bestehen
