2. Übungsblatt zu Algorithmen II im WS 2011/2012

Transkript

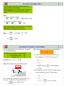
1 Karlruher Iniu für Technologie Iniu für Theoreiche Informaik Prof. Dr. Peer Sander Moriz Kobizch, Denni Schieferdecker. Übungbla zu Algorihmen II im WS 0/0 hp://algo.ii.ki.edu/algorihmenii.php Aufgabe (Kleinaufgaben: A Suche) Muerlöungen a) Sei po( ) eine gülige Poenialfunkion für die Suche nach Knoen in Graph G(V, E). Überprüfen Sie, ob po c = po + c, c = con. ebenfall eine gülige Poenialfunkion darell. b) Kann e vorkommen, da eine A Suche mehr Knoen abuch al eine Suche mi Dijkra Algorihmu für die gleiche Anfrage? Begründen Sie warum nich oder geben Sie ein Beipiel an. a) E i zu überprüfen, ob gil. c(u, v) + po c (v) po c (u) 0 () po c (u) µ(u, ) () Bedingung () i immer erfüll. Nach Einezen ergib ich c(u, v) + po(v) po(u) 0. Da nach Vorauezung po( ) eine gülige Poenialfunkion i, i die erfüll. Bedingung () i hingegen nur erfüll, wenn c µ(u, ) po(u) f.a. u V. Dami i po c ( ) nur für geeignee Wahl von c eine gülige Poenialfunkion. (Bemerkung: Fall po() = 0 f.a. Poeniale geforder i (ana nur po() 0), gil c = 0!) b) Im bidirekionalen Fall kann die durchau einfach vorkommen. Im unidirekionalen Fall häng e von der Reihenfolge der beracheen Knoen gleicher Dianz ab. Nehmen wir eine FIFO Ordnung der Knoen gleichen Gewiche an (z.b. in einer Bucke Queue), o i folgender Graph ein Beipiel. Die Dijkra Suche cann die Knoen in der Reihenfolge:, a, b,, während A die Knoen in der Reihenfolge, b, a, c, cann. (0) a () [] [] [0] b () c [0] (0) () [0] Legende: Were in eckigen Klammern geben Knoenpoeniale an, Were in runden Klammern reduziere Kanengewiche.

2 Aufgabe (Rechnen: Monoone ganzzahlige Prioriy Queue ) Bei einer Auführung von Dijkra Algorihmu wird folgender Auchni an Prioriy Queue Operaionen prookollier: iner(a, 06 [000] ) ( Parameer: Knoenbezeichnung, Dianz [Dianz binär] ) iner(b, 0 [000] ) iner(c, 07 [00] ) deleemin() deleemin() iner(d, [000] ) deleemin() iner(e, 6 [0000] ) Zuäzlich wien Sie, da da maximale Kanengewich im Graphen C = 6 beräg und da vor der eren prookollieren Operaion da leze enhalene Elemen au der Prioriy Queue enfern wurde. Diee hae den Wer min =. a) Führen Sie die Operaionen auf einer Bucke Queue au. Geben Sie den Zuand der Daenrukur nach jeder Operaion an. b) Wieviele Bucke werden für eine Auführung auf einem Radix Heap benöig? Führen Sie die Operaionen auf einem Radix Heap au. Geben Sie den Zuand der Daenrukur und den Werebereich der Bucke nach jeder Operaion an.

3 a) Bucke Queue: iner(a, 06 [000] ): min = (a, 6) iner(b, 0 [000] ): min = (b, 0) (a, 6) iner(c, 07 [0000] ): (für monoone Prioriy Queue nur wichig, da Elemene au [min, min + C] ammen!) (c, 7) (b, 0) (a, 6) min = deleemin(): (c, 7) (b, 0) min = 6 deleemin(): min = 7 (b, 0) iner(d, [000] ): min = 7 (b, 0) (d, ) deleemin(): min = 0 (d, ) iner(e, 6 [0000] ): min = 0 (e, 6) (d, )

4 b) Radix Heap: (E werden K + Bucke benöig: B[ ], B[0],..., B[K]; mi K = + log C = ergeben ich Bucke.) iner(a, 06 [000] ): - 0 (a, 06 [000]) min = [000] iner(b, 0 [000] ): - 0 (a, 06 [000]) (b, 0 [000]) min = [000] iner(c, 07 [00] ): - 0 (a, 06 [000]) (b, 0, [000]) (c, 07 [00]) min = [000] deleemin(): (B[] i der ere gefülle Bucke; min wird auf da kleine enhalene Elemen (6) geez; die Elemene in B[] werden neu vereil und anchließend da Elemen in B[ ] enfern) - 0 (c, 07 [00]) (b, 0 [000]) min = 6 [000] deleemin(): - 0 (b, 0 [000]) 7 8 min = 7 [00] iner(d, [000] ): - 0 (b, 0 [000]) (d, [000]) 7 8 min = 7 [00] deleemin(): - 0 (d, [000]) 0 6 min = 0 [000] iner(e, 6 [0000] ): - 0 (d, [000]) (e, 6 [0000]) 0 6 min = 0 [000] 4

5 Aufgabe (Analye: Laufzei von Dijkra Algorihmu) Gegeben ei ein gericheer Graph G = (V, E) mi V = n und E = m, owie eine Kanengewichungfunkion c : E R + 0. a) Beweien Sie die Behaupung au der Vorleung, da für m = Ω(n log n log log n) Dijkra Algorihmu mi einem binary heap eine durchchniliche Laufzei von O(m) beiz. b) Eine pezielle Prioriy Queue habe folgende Laufzeieigenchafen: iner: O(log n) decreaekey: O() deleemin: O( m) (ob eine Daenrukur mi dieen Eigenchafen exiier und Dijkra Algorihmu mi ihr korrek arbeie, i eine andere Frage, aber wir nehmen für diee Aufgabe an e ginge :-) ) Geben ie eine kleine obere Schranke für die Laufzei von Dijkra Algorihmu uner Verwendung dieer Prioriy Queue an. Uner welcher Bedingung an da Verhälni der Anzahl Knoen n zu Kanen m wird die Laufzei linear in der Eingabegröße? c) Geben Sie eine Klae von Graphen an, für die die Anzahl an deleemin Operaionen von einem beliebigen Knoen zu allen erreichbaren Knoen linear von der Pfadlänge µ(, ) abhäng, gegeben da m = Ω(n).

6 a) Für die durchchniliche Laufzei von Dijkra Algorihmu mi einem binary heap gil: O(m + n log m n log n) Zu zeigen i, ob diee Laufzei in O(m) lieg für die gegebene Wahl von m = Ω(n log n log log n). Wähle den kleinmöglichen Wer für m. Fall die Auage dieen Wer gil, gil ie icher auch für alle größeren m. Eingeez und umgeform ergib ich: n log n log log n O(n log n log log n + n log log n) n kürzen = O(n log n log log n + n log(log n log log n) log n) log ab=log a+log b = O(n log n log log n + n log log n + n log log log n log n) log log log n=o(log log n) = O(n log n log log n) = O(m) Dami lieg die Laufzei in O(m). Für eine geringere Abhängigkei, z.b. m = O(n) würde der zweie Term den eren im O-Kalkül dominieren und die Umformung würde nich zu O(m) führen. b) Allgemein gil für die Laufzei von Dijkra Algorihmu: O(m + m T decreaekey (n) + n (T deleemin (n) + T iner (n))) Mi den angegebenen Laufzeien eingeez ergib ich: O(m + n m + n log n) Uner den Forderungen n m = O(m) und n log n = O(m) i die Laufzei linear in m. Die lä ich umformen zu Ω(n) = m und Ω(n log n) = m. Dami ergib ich m = Ω(n ). c) Eine Klae von Graphen, die diee Anforderungen erfüll, lä ich wie folg konruieren: Man bilde eine gerichee Kee von n Knoen, verbunden durch Kanen mi Gewich. Außerdem füge man von jedem Knoen i zu log n Nachfolgern j eine Kane mi Gewich größer oder gleich der Dianz zwichen i und j auf der Kee ein. Beipiel mi Knoen 6

7 Aufgabe 4 (Enwurf: All Pair Shore Pah ) Sie ind von der Finanzaufichbehörde beaufrag worden, einen Algorihmu zu enwickeln, der Irregulariäen im Devienhandel möglich zeinah aufdecken kann. Zu dieem Zweck erhalen Sie die akuellen direken Wechelkure w i,j von Währung i nach Währung j für alle gehandelen Währungen. Dabei bedeue z.b. w i,j = 4, da man für Einhei au Währung i genau 4 Einheien au Währung j erhäl. Eine Unregelmäßigkei ri dann auf, wenn eine Möglichkei exiier, eine Währung i in eine Währung j über mehrere Zwichenwechel zu auchen, o da der Errag der Wechel weniger al die Hälfe de direken Wechel von Währung i nach j erziel. Auf Rückfrage vericher Ihnen Ihr Aufraggeber außerdem, da eine geldgenerierende Schleife (leider) nich aufreen kann. a) Formulieren Sie da Problem al graphenheoreiche Problem. D.h. bilden Sie die gegebenen Informaionen auf Knoen und Kanen eine Graphen ab und inerpreieren Sie die geelle Aufgabe al Problem auf dem von Ihnen definieren Graphen. b) Bechreiben Sie einen Algorihmu, der da Problem lö. c) Erweiern Sie Ihren Algorihmu, o da er auch die Folge an Wecheln augeben kann, die eine Unregelmäßigkei verurach. d) Ihr Algorihmu mu k Währungen überwachen. Geben Sie eine Laufzei für Ihren Algorihmu an, die nur von k abhäng. Hinwei: log ab = log a + log b. a) Modellierung de Problem al Graph: Knoen enprechen Währungen, Kanen erlauben Geldwecheln. Kanengewiche geben den Logarihmu de Wechelkure an. E ergib ich ein volländiger Graph mi k Knoen. Der Graph kann negaive Kanengewiche aber lau Vorgabe keine negaiven Zyklen enhalen. Geuch ind kürzee Verbindungen von jedem Knoen zu jedem anderen. b) Führe eine All-To-All Suche durch und prüfe für je zwei Währungen i, j, ob der berechnee kürzee Aband kleiner al log 0.w i,j i. Triff die zu, melde eine Unregelmäßigkei. c) E müen zuäzlich paren Zeiger gepeicher werden. Über diee kann man rückwär von der Zielwährung die Folge an Wecheln rekonruieren. d) Der Graph ha n = k Knoen und m = k(k )/ Kanen (volländiger Graph). Der verwendee Algorihmu brauch allgemein O(nm + n log n) Laufzei. Eingeez ergib ich eine Laufzei von O(k ). 7

8 Aufgabe (Rechnen: A Suche) Gegeben ei der unen abgebildee Graph. An den Kanen ind Koen für die Nuzung der Verbindung eingeragen und die Knoen ragen Orkoordinaen. a) Ergänzen Sie den gegebenen Graphen um Knoenpoeniale für eine A Suche von nach. Verwenden Sie die Manhaen-Dianz ( ˆ= Einnorm ) al Abchäzung für die Enfernung zum Ziel. Hinwei: : (x, y ), (x, y ) = y y + x x. b) Tragen Sie die reduzieren Kanengewiche in den Graphen ein. c) Wieviele deleemin Operaionen führ die A Suche auf dem Graphen au? Wieviele eine normale Suche mi Dijkra Algorihmu? [4, 4] [, ] [, ] 0 [4, 0] [, 0] [, 0] [, 0] [0, 0] 8

9 a) Knoenpoeniale po( ) in Knoen eingeragen; Kanengewiche c( ) durch reduziere Gewiche c( ) : c(u, v) = c(u, v) + po(v) po(u) erez: [4, 4] [8] 0 [6] [, ] 0 6 [4] [, ] 6 [4] [] [] [] [0] [4, 0] [, 0] [, 0] [, 0] [0, 0] b) Siehe vorherige Teilaufgabe. c) Die A Suche benöig deleemin Operaionen, die normale Suche hingegen 8. Die enprechenden Suchräume ind in den folgenden Abbildungen eingezeichne. Die Knoennummerierung gib die Reihenfolge der deleemin Operaionen an. A : Dijkra: [4, 4] 0 [4, 4] [, ] 0 4 [, ] 6 [, ] 6 6 [, ] [4, 0] [, 0] [, 0] [, 0] [0, 0] 7 8 [4, 0] [, 0] [, 0] [, 0] [0, 0] 9

10 Aufgabe 6 (Einführung+Analye: Bidirekionaler Dijkra) In Vorleung und Saalübung wurde eine bidirekionale Variane von Dijkra Algorihmu angeprochen, die in dieer Aufgabe näher uneruch werden oll. Zur Wiederholung: Gegeben ei wie üblich ein gericheer Graph G = (V, E) mi V = n und E = m, owie eine Kanengewichungfunkion c : E R + 0. Geuch i der kürzee Pfad p =,..., zwichen zwei Punken, V. Eine bidirekionale Suche lö diee Problem wie folg: E werden zwei unidirekionale Suchen mi Dijkra Algorihmu geare. Die Vorwäruche beginn bei Knoen und operier auf dem normalen Graphen G, auch Vorwärgraph genann. Die Rückwäruche beginn bei Knoen und operier auf dem Rückwärgraph G r = (V, E r ) mi Kanengewichungfunkion c r. Dieer Graph eneh au G durch Umkehrung aller Kanen. Der Algorihmu cann abwechelnd einen Knoen in der Vorwäruche und in der Rückwäruche, beginnend mi der Vorwäruche. Wird während de Scan von Knoen u Kane (u, v) relaxier, o wird überprüf, ob die Dianz d forward [v] + d backward [v] kleiner i al die momenan minimale gefundene Dianz von nach und diee gegebenenfall angepa (d forward [v] gib die biher kürzee gefundene Dianz von nach v in der Vorwäruche und d backward [v] die biher kürzee gefundene Dianz von v nach in der Rückwäruche an). Sobald ein Knoen in einer Richung gecann werden oll, der berei in der anderen Richung gecann worden i, kann die Suche beende werden (Abbruchbedingung). Die akuelle minimale gefundene Dianz i dann die aächliche minimale Dianz zwichen und. a) Zeichnen Sie den Rückwärgraph G r zum angegebenen Graphen. Geben Sie die Kanengewiche c(a, d), c r (a, d) owie c(b, e), c r (b, e) an. a b e c (Kane (b, e) i eine bidirekionale [bzw. ungerichee] Kane) b) Geben Sie an, in welcher Reihenfolge der unen angegebene Graph durchlaufen wird. d c) Zeigen Sie, da die Abbruchbedingung korrek i. d) Wann kann e paieren, da die Suche nach dem Scan von Knoen u beende wird, dieer aber nich Teil de kürzeen Wege i. Geben Sie ein Beipiel an. 0

11 a) Rückwärgraph G r : a b e Kanengewiche: c(a, d) =, c r (a, d) = c(b, e) =, c r (b, e) = Allgemein gil c(u, v) = c r (v, u). c E ind einfach alle Pfeile umgedreh worden. b) Vorwäruche: Rückwäruche: d 4 Die Zahlen in den Knoen geben die Reihenfolge an, in der ie gecann worden ind. Sobald die Vorwäruche den Knoen mi Nummer cann, i die Suche beende, da er chon in Rückwärrichung gecann wurde. c) Nehmen wir an, e exiiere ein Knoen u, der in beiden Queue gelöch wurde, aber d(, ) < d(, u)+d(u, ) ei noch nich bekann. Da die Knoen in reng monooner Reihenfolge gecann werden, ind in der Vorwäruche berei alle Knoen v mi d(, v) < d(, u) gecann worden. Gleiche gil für Knoen v mi d(v, ) < d(u, ) in der Rückwäruche. Berachen wir den kürzeen Pfad p = { = n,..., n k = }. Weierhin berachen wir den Knoen mi maximalem i, o da d(, n i ) < d(, u) owie den Knoen mi minimalem j, o da d(n j, ) < d(u, ). Da d(, ) noch nich bekann i, mu gelen: i < j (on wäre die Dianz bekann). Folglich exiier aber ein Knoen n x in p mi d(, n x ) d(, u) owie d(n x, ) d(u, ). Dami wäre aber auch d(, ) d(, u) + d(u, ) > d(, ), wa ein Widerpruch i. d) Der abgebildee Graph i ein mögliche Beipiel. C E A D 4 4 B Die Vorwäruche bearbeie die Knoen in der Reihenfolge A,C,B,E,D. Die Rückwäruche bearbeie die Knoen in der Reihenfolge D,E,B,C,A. Nach drei abwechelnden Schrien wurde B folglich in beiden Suchräumen gecann. Der kürzee Weg folg aber der Roue A,C,E,D.

12 Aufgabe 7 (Analye: Bidirekionaler Dijkra) a) Gegeben ei ein Giergraph G mi allen Kanengewichen gleich. Wieviele Knoen wird eine bidirekionale Suche beuchen in Abhängigkei von Aband d zwichen Sar und Ziel? Wieviele die unidirekionale Suche? Beipiel eine Giergraphen b) Geben Sie ein Beipiel an, in dem die bidirekionale Suche von nach exponeniell weniger Knoen beuch al die unidirekionale Suche. c) Geben Sie ein Beipiel, in dem die bidirekionale Suche von nach mehr Knoen beuch al die unidirekionale Suche. d) Zeigen Sie, da die bidirekionale Suche nie mehr al doppel o viele Knoen beuch al die unidirekionale Suche.

13 a) Dijkra Algorihmu cann Knoen kreiförmig um den Sarknoen. Für den Kreiumfang gemeen in Knoen gil im Gridgraph: u(r) = (r + ) + (r ) = 4r (Einnorm). Im Falle der unidirekionalen Suche werden Kreie mi Radiu bi d volländig und der Krei mi Radiu d eilweie abgeuch. Dami werden d r=0 u(r) + = + 4(d )(d )/ + bi d r=0 u(r) = + 4(d )(d )/ + 4d Knoen gecann. Die zuäzliche + enprich dem Scannen de Sarknoen. Im Falle der bidirekionalen Suche werden für jede Richung Kreie mi Radiu bi d/ volländig und der Krei mi Radiu d/ + eilweie abgeuch. Dami werden zwichen d r=0 u(r) + = + 4( d/ )( d/ )/ + und d r=0 u(r) = + 4( d/ )( d/ )/ + 4( d/ + ) Knoen in jeder Richung gecann. Vergleich man beide Ergebnie, o ell man fe, da die bidirekionale Suche nur ungefähr halb o viele Knoen cann wie die unidirekionale Suche. b) Von wird ein Baum mi allen Kanengewichen gleich aufgepann, deen Bläer über jeweil eine Kane mi Gewich n mi verbunden ind bi auf ein Bla, da über eine Kane mi Gewich mi verbunden i. Die unidirekionale Suche beuch alle n Knoen. Die bidirekionale Suche beuch nur O(log n) Knoen. n- n- n- n- c) Der abgebildee Graph i ein mögliche Beipiel. Unidirekionale Suche cann Knoen, bidirekionale Suche 9. d) Sei k die Anzahl Knoen, die von der unidirekionalen Suche beuch werden. Die bidirekionale Suche führ zwei unabhängige unidirekionale Suchen au. Dabei enprich die Vorwäruche der unidirekionalen Suche. Beide Suchrichungen wecheln ich ab und e wird mi der Vorwärrichung begonnen. Ha die bidirekionale Suche k Schrie durchgeführ, enfallen davon k auf die Vorwärrichung. Die Vorwäruche ha dami die gleichen k Knoen abgeuch wie die unidirekionale Suche, einchließlich de Zielknoen. Da er in der Gegenrichung auch chon abgeuch wurde (al erer Knoen), kann die Suche beende werden.