Bewertungsmethoden in der Versicherungsmathematik
|
|
|
- Sophia Baum
- vor 7 Jahren
- Abrufe
Transkript
1 Bewerungmehoden in der Vericherungmahemaik Techniche Reerven und Markwere II Johanne Pacheag Mahemaiche Iniu der Univeriä zu Köln Sommeremeer 2010 Bereuung: Prof. Schmidli, Dr. Eienberg
2 1 Inhalverzeichni 1 Leiungpflich und Zahlungröme Die markwirchafliche Leiungpflich Die Rückkauf-Opion Ineniäbaiere Bewerung von Rückkauf-Opionen Inervenion-baiere Bewerung von Rückkauf-Opionen Markwirchafliche Verbindlichkeien Prämienfreie Vericherungopionen Eine einfache prämienfreie Policenbewerung Inervenionbaiere Bewerung der prämienfreien Verragopion
3 1 1 Leiungpflich und Zahlungröme In dieem Kapiel führen wir die Idee der Zahlungvorgänge ein und uneruchen, wie der markwirchafliche Aufbau durch garaniere Zahlungen und nich-garaniere, alo zufällige Zahlungen, beeinflu wird. Die Zahlungvorgänge ind die Elemene der Geamzahlungröme in einem Vericherungverrag. In unerem Beipiel alo folgende: b ad dn(), b a ()I(n), πi()d und (b a (n) b a ())I(n). Die ere Aufgabe in Verbindung mi einer präzien Bechreibung der Zahlungröme i, die ochaichen Phänomene, wovon die Schadenanforderung abhäng, zu idenifizieren. Für beimme elemenare Vericherungen piel der Todezeipunk eine wichige Rolle. E erwei ich al nüzlich, einen ochaichen Proze Z einzuführen, der auf dem ochaichen Todezeipunk baier. Der Todezeipunk wird durch die Wahrcheinlichkeivereilung eine Zählprozee N modellier, beipielweie über die Einführung einer deerminiichen Ineniä µ. Um Schadenforderungen zu formaliieren führen wir einen Zahlungproze B ein, oda B() die kumulieren Zahlungen de Vericherer an den Vericheren in der Zeipanne [0, ] widerpiegel. D.h. da Zahlungen vom Vericheren an da Unernehmen al negaive Zahlungen aufreen. Wir geben die Zahlungen in eiger Zei an, obwohl ie prakich geehen dikre ind, z.b. jeweil zu Beginn eine Mona. Wir ezen n al Zeihorizon de Vericherungverrag fe und können dann die Schadenforderungen durch den Zahlungproze audrücken: B() = 0 db() (1) wobei db() = b ad dn() + b a ()I()dɛ(, n) πi() d. (2) Hier i ɛ(, n) ein Indikaorproze für n. Durch die Inegraion in der eren Gleichung werden die infinieimalen Änderungen db aufummier, wobei anchließend die Elemene dieer Änderungen aufgelie ind. Der Proze Z dien dazu, eine Anzahl elemenarer Schadenforderungen in der Leben- und Penionvericherung genau zu bechreiben. Allerding gib
4 2 e viele Fälle die durch olch einen Proze nich bechrieben werden können. Ein Beipiel i die Prämienbefreiung. Diee und andere Formen von Berufunfähigkeivericherungen können bechrieben werden durch die Erweierung de Zuandraum von Z mi einem drien Zuand, nämlich unfähig. Nach dem Zuammenfaen der Schadenforderungen in einen Zahlungproze uchen wir nach dem akuellen Wer und dem Markwer de Zahlungprozee. Durch da No-Arbirage-Prinzip erhalen wir, da der akuelle Wer die Summe der akuellen Were der Einzelelemene i. Der akuelle Wer eine Zahlungprozee B() zur Zei über da Zeiinervall (, n] i alo n r db(). Bezieh man nun noch da Prinzip der Riikoreuung (=Diverifikaion, iehe Seie 24) mi ein, o erhalen wir folgende Ergebni für den Markwer zur Zei eine Zahlungprozee: E n e R ] r db(). 1.1 Die markwirchafliche Leiungpflich In dieem Abchni berachen wir den Zahlungproze in einer markwirchaflichen Zuammenezung der Verbindlichkeien. Wir bezeichnen mi B(, ) den zur Zei garanieren Zahlungrom. Für erhalen wir db(, ) = πi() d + b ad dn() + b a ()I() dɛ(, n), (3) V g n () = E e R ] r db(, ). (4) Demenprechend bezeichne B b (, ) den nich garanieren Zahlungrom zur Zei und e gil db b (, ) = (b a () b a ())I() dɛ(, n), (5) V b n () = E e R ] r db b (, ). (6) Die Differenz V () V g () ha ihre Urache in den kumulieren Sicherheimargen in den garanieren Zahlungen, bezeichne mi C(, ), o da für
5 3 gil dc(, ) = I()c(, ) d, (7) V () V g n () = E e R ] r dc(, ). (8) Wir erinnern daran, da dadurch da individuelle Prämienpoenial erzeug wird, ofern U() V () V (). Wir beenden diee Kapiel, indem wir un nochmal die vorgechlagene Definiion de individuellen Bonupoenial angucken (für U() V ()). Naürlich gelen folgende Ungleichungen: [ V ib () = (E n e R ]) + r dc(, ) E [( n E n e R ) + ] r dc(, ) e R ] r dc + (, ) Hierbei können die lezen beiden Gleichungen al alernaive Definiionen der eren angeehen werden. Die Definiionen immen überein, ofern c(, ) für alle enweder poiiv oder negaiv i. Die Definiionen de individuellen Bonupoenial können durch genauere Bechreibung der Verwendung der Sicherheimargen präziier werden. 2 Die Rückkauf-Opion 2.1 Ineniäbaiere Bewerung von Rückkauf-Opionen Wir benuzen erneu ein Markov-Modell mi drei Zuänden (d.h. der Proze i durch die Übergangwahrcheinlichkeien von einem Zuand i in einen anderen Zuand j gekennzeichne). Der Zuand Rückkauf wird zur Zei erreich mi der Rückkauf-Ineniä ν und führ zur Zahlung einer Rückkaufprämie G(). Die führ zur folgenden Differenialgleichung, wobei V ur die geamen Rückellungen beinhale: d d V ur () = r()v ur () + π µ()(b ad V ur ()) ν()(g() V ur ()) V ur (n) = b a (n)
6 4 Wir fordern einen explizien Audruck für die Rückkauf-Opion, z.b. V ur V. Dann kann gezeig werden, da die zuäzliche Reerve gechrieben werden kann al V ur () V () = n r+µ+ν ν()(g() V ()) d (9) Die Berechnung beinhale die zukünfigen Were von G und V nach Rechnunggrundlagen zweier Ordnung. Wir berachen den Fall, da der Rückkaufwer der echnichen Reerve gleich. Sei zunäch V () < V (), d.h. X() < 0. Dann können wir zeigen, da gil, wobei V ur () V () (V () V ())p() (10) p() = n ν ν() d. (11) Fall jedoch V () V (), d.h. X() 0 o gil V ur () V () 0 (12) Zuammengenommen erhalen wir alo folgende Ungleichung: V ur () V () = n r+µ+ν ν()(v () V ()) d 0. Darau folgern wir mi den Rechnunggrundlagen 2. Ordnung { } V ur () V () max p()(g() V ()), Inervenion-baiere Bewerung von Rückkauf-Opionen Wir berückichigen nun, da der Verichere von einer Rückkauf-Opion Gebrauch mach, ofern e ich für ihn lohn. Ein Problem bei dieer Sichweie i, da e hiorich nur ehr elen opimal war, eine Vericherung zurück zu kaufen. Andererei lieg die auch gar nich im Ineree der Vericherungunernehmen, wehalb ich diee vor yemaichem Rückkauf chüzen. Der Verichere oll nun ofor zurückkaufen, obald er darau einen Voreil ziehen kann.
7 5 Berache einen allgemeinen Zahlungproze B. Mi Rückkauf-Opion liefer un da No-Arbirage-Prinzip den Markwer al V ur τ () = max E r db() + e R ] τ r I(τ)G(τ), (13) τ n wobei wir G(n) = 0 ezen. Hier i τ der Zeipunk de Rückkauf. Offenichlich mu der Verichere den Rückkauf zur Zei encheiden aufgrund der bi dahin verfügbaren Informaionen. Man könne ich die Informaion zur Zei al σ -Algebra A denken. Demnach gil alo A A. Der Informaionflu wird alo durch eine Filraion bechrieben. Man prich bei τ dehalb auch von einer Soppzei. Wir definieren den Proze Y ur (, u) durch Y ur (, u) = u r db() + e R u r I(u)G(u). (14) Alo i Y ur (, u) der akuelle Wer der Zahlungen an den Vericheren inkluive Rückkaufprämie gegeben dem Rückkauf zum Zeipunk u. Korollar Sofern V () G() für alle i e opimal, nich zurückzukaufen und e gil V ur () = V (). 2. Fall Y ur (, u) ein Submaringal i, i e nie opimal zurückzukaufen. E gil V ur () = V (). 3. Fall Y ur (, u) ein Supermaringal i, i e opimal ofor zurückzukaufen und wir haben V ur () = G(). Die Aufgabe i nun, gegeben einen Wer de Geamzahlungprozee, diee geamen Rückellungen in Rückellungen für garaniere Zahlungen V g,ur und für nich-garaniere Zahlungen V b,ur zu unereilen. Eine Möglichkei i folgende: V g,ur τ () = max E r db(, ) + e R ] τ r I(τ)G(, τ). τ n Hierbei wird dann V b,ur al Differenz V ur V g,ur berache. G(, τ) i der Rückkaufwer zur Zei τ gegeben da keine Dividenden in (, τ] augechüe werden. Wir führen den Proze Y g,ur (, u) wie folg ein:
8 6 Y g,ur (, u) = τ r db(, ) + e R τ r I(τ)G(, τ) (15) Dami i Y g,ur (, u) genau der akuelle Wer der garanieren Zahlungen gegeben da der Verrag zum Zeipunk u zurückgekauf wird. Lemma 2.2 Nehme an, da G(, u) = V (, u). Dann kann Y g,ur (, u) folgendermaßen umgechrieben werden: Y g,ur (, u) = V () u wobei M ur (, ) ein Maringal i. r I()c(, ) d + M ur (, u), (16) Korollar Für c(, ) 0 gil V g,ur () = V (). 2. Fall c(, ) 0, o folg Y g,ur (, u) = V g (). Bewei. Im eren Fall büß der Verichere die zukünfigen poiiven Sicherheimargen ein, wenn er den Verrag beibehäl. Die wird durch oforigen Rückkauf verhinder, oda die garanieren Zahlungen den Rückkaufwer annehmen. Im zweien Fall mach der Vericherungnehmer maximalen Gewinn, wenn er die Police bi zum Schlu behäl, alo nehmen die garanieren Zahlungen denelben Wer an wie ohne Rückkaufopion. 2.3 Markwirchafliche Verbindlichkeien E gelen folgende Beziehungen für da individuelle Bonupoenial: V ib = max(v, V g ) V g V g,ur V g, (17) mi G(, u) = V (, u). Nach Korollar 2.3 haben wir Gleichhei mi der alen Definiion, ofern c(, ) enweder poiiv oder negaiv für alle i. In der lezen Ungleichung wird eine alernaive Definiion vorgechlagen, die nich von der Dividendenvereilung abhäng.
9 7 3 Prämienfreie Vericherungopionen 3.1 Eine einfache prämienfreie Policenbewerung Augangpunk zur Bewerung von beiragfreien Verragopionen i wieder ein Modell mi drei Zuänden, und zwar lebend mi Prämienzahlung, beiragfreie Police und der Zuand o. Wir führen jedoch keine Ineniä zur beiragfreien Police ein wie im vorangegangen Kapiel zur Rückkaufopion. Dor gal V () V g () = n r+µ c(, ) d. (18) Ein Teil der Sicherheimargen in den garanieren Zahlungen wird gedeck durch zukünfige Prämien. Jedoch ollen wir dann bei der beiragfreien Police auch eine Reerve anlegen für die auf dieen Prämien baierende Dividende. Die Leiungpflich bzgl. Dividenden au den zukünfigen Prämien i gegeben durch da Bonupoenial eine Verrag mi Prämien π und Anzahlung Null zur Zei. Wir berechnen nun diee Bonupoenial, indem wir die Leiungen de augegebenen Verrag uneruchen. Wir halen un an folgende Noaion: V + () = b ad A 1 x+n + ba () n E x+ (19) V g+ () = b ad A 1 x+n + ba () n E x+. (20) Der obere Index + kennzeichne, da hier nur Leiungen einbezogen wurden. Dami können wir die Lebenrenen a x+n umchreiben: und a x+n wie folg a x+n = V + () V () π (21) a x+n = V g+ () V g (). (22) π Die Anzahl Einheien von garanieren Leiungen, β(), die zur Zei au den zukünfigen Prämien erbrach werden können, werden durch da Äquivalenzprinzip fegeleg:
10 8 β() ( b ad A 1 x+n + ba () n Ex+ ) = πa x+n, (23) wodurch ich für β() ergib β() = V + () V () V +. (24) () Zuvor haen wir chon geehen, da da Bonupoenial eine Vericherungverrag zur Zei der Emiion dem negaiven Markwer der garanieren Leiungen gleich, die im Verrag vereinbar wurden. Da Bonupoenial der neuen Vericherung i gegeben durch β() ( b ad A 1 x+n + ba () n E x+ ) + πax+n, da wir umchreiben können zu V () V g+ () V + () V g (). (25) Die oll nun uner Wer für eine prämienfreie Opion werden. Dieer Wer mu zum Markwer der garanieren Leiungen addier werden, um chließlich den Wer der garanieren Zahlungen inkluive Opion zur prämienfreien Police zu erhalen. Dami haben wir erreich: ( V () V g+ () V + () ) V g () + V g () = V () V g+ () V + =: V f (). (26) () Wir wollen da individuelle Bonupoenial zerlegen in ein Poenial V bp baierend auf den Prämien und V bf der prämienfreien Police. Wir berachen die Siuaion V V V f V g. Dann kann V ib = V V g zerleg werden in V ib = V bf + V bp = ( V V f) + ( V f V g).
11 9 Der Markwer von garanieren Zahlungen eine Verrag, augeell zur Zei, kann auch augedrück werden durch die Markwere der Sicherheimargen. Allerding kann eine Siuaion enehen, wo diee negaiv ind. Da diee dann nich al Dividenden vereil werden können, wird da Bonupoenial auf Null geez. Dami gil alo: V bp = max(v f, V g ) V g. (27) Wir können zu jeder Zei uner Berückichigung aller möglichen Beziehungen zwichen V, V, V f und V g die Bonupoeniale folgendermaßen audrücken: V bf = (V V g ( V f V g) + ) + (V V g ( V V g) + ) + ( V bp = V V g V V g ( V f V g) ) Inervenionbaiere Bewerung der prämienfreien Verragopion Wir behandeln nun die prämienfreie Verragopion genau o wie zuvor chon die Rückkaufopion im vorangegangenen Kapiel. Der Verichere wechel auch hier in die prämienfreie Police, wenn e ich für ihn lohn. Uner Anaz i nich frei von Kriik. So gib e keinerlei hioriche Beweie für eine Siuaion, wo die Umwandlung in eine prämienfreie Police opimal war. Und auch hier würde da Vericherungunernehmen durch z.b. zuäzliche Koen die yemaiche Umwandlung unarakiv machen (können). Wir nehmen an, da der Verichere ofor umwandel, obald e für ihn einen Voreil darell. Wir berachen einen allgemeinen Zahlungproze B. Bei der Einführung der prämienfreien Verragopion liefer ein Arbirageargumen den Markwer inkluive unerer Opion: V free τ () = max E r db() + e R ] τ r I(τ)(V f (τ) + X f (τ)). τ n Hier enprich V free genau unerem V ur wenn man die Rückkaufprämie G() durch die Reerve V f (τ)+x f (τ) erez. τ i der Zeipunk der Umwandlung
12 10 bzw. da Verragende, je nachdem wa zuer aufri. Der Verichere mu offenichlich über eine Umwandlung mi der ihm bi dahin zur Verfügung ehenden Informaion encheiden. Dami i τ Soppzei. Der Wer X f (τ) i die unvereile Reerve bei Umwandlung. Wir wollen V free () genauer uneruchen und führen dehalb den Proze ein, wobei Y free (, u) = u r db() + e R u r I(u)(V f (u) + X f (u)) (28) V f () = V () V g+ () V +. (29) () Hier i Y free (, u) eine Funkion von u, nämlich der Wer aller Zahlungen an den Vericheren, inkluive Leiungpflich und nich garaniere Leiungen ab Umwandlung gegeben da die Umwandlung zum Zeipunk u paier. Korollar Fall V () V f () + X f () für alle, o i e opimal nie umzuwandeln und e gil V free () = V (). 2. Fall Y free (, u) ein Submaringal i, o i e niemal opimal umzuwandeln und e gil ebenfall V free () = V (). 3. Fall Y free (, u) ein Supermaringal i, o i e opimal, ofor umzuwandeln und e gil V free () = V f () + X f (). Gegeben einen Wer de geamen Zahlungprozee wollen wir dieen nun unereilen in eine Reerve für die garanieren Zahlungen, V g,free, und eine Reerve für die nich garanieren, V b,free. Wir machen folgende Definiion: wobei V g,free τ () = max E r db(, ) + e R ] τ r I(τ)V f (, τ), τ n V f (, τ) = V (, τ) V g+ (, τ) V +. (, τ) Dann können wir V b,free al Differenz V free V g,free anezen. Bei der prämienfreien Police haben wir außerdem ganz analog zur Rückkauf- Opion folgende Reula:
13 11 Korollar Sofern V () V f () + X f () für alle i e opimal, niemal umzuwandeln und e gil V free () = V (). 2. Fall Y free (, u) ein Submaringal i, i e nie opimal umzuwandeln. E gil V free () = V (). 3. Fall Y free (, u) ein Supermaringal i, i e opimal ofor umzuwandeln und wir haben V free () = V f () + X f (). Für nähere Informaionen ei u.a. auf da Buch On Valuaion and Conrol in Life and Penion Inurance von Mogen Seffenen, 2002, verwieen.
Stochastische Differentialgleichungen
 INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik Lösungsvorschläge zum 6. Übungsblatt
 Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Seminar Bewertungsmethoden in der Personenversicherungsmathematik
 Seminar Bewerungsmehoden in der Personenversicherungsmahemaik Akuarielle und finanzmahmaische Bewerung I Xiaoying Xu Mahemaisches Insiu der Universiä zu Köln Sommersemeser 2010 Bereuung: Prof Schmidli,
Seminar Bewerungsmehoden in der Personenversicherungsmahemaik Akuarielle und finanzmahmaische Bewerung I Xiaoying Xu Mahemaisches Insiu der Universiä zu Köln Sommersemeser 2010 Bereuung: Prof Schmidli,
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 7 5. Semester ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE
 Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Abbildungsmaßstab und Winkelvergrößerung
 Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
KAPITEL 2 KÜRZESTE WEGE
 KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
Restkapazität. = O( V ) mal kritisch. Also gibt es insgesamt höchstens O( V E ) Augmentierungen.
 Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Fakultät Grundlagen. s = t. gleichförm ig
 Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Messung der Ladung. Wie kann man Ladungen messen? /Kapitel Formeln auf S.134: Elektrische Ladung
 --- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
--- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
Geometric Algebra Computing Transformationen in LA und CGA Dr. Dietmar Hildenbrand
 Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
Mathematik 1 für Maschinenbau, M. Schuchmann (SoSe 2013) Aufgabenblatt 5 (Ebenen)
 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
6 Stochastische Differentialgleichungen
 6 Sochaiche Differenialgleichungen Viele deerminiiche Modelle der Naur- und der Wirchafwienchafen laen ich mi Hilfe von Differenialgleichungen audrücken. Mi dem Io-Inegral und der Io-Formel haben wir die
6 Sochaiche Differenialgleichungen Viele deerminiiche Modelle der Naur- und der Wirchafwienchafen laen ich mi Hilfe von Differenialgleichungen audrücken. Mi dem Io-Inegral und der Io-Formel haben wir die
Westfälische Hochschule - Fachbereich Informatik & Kommunikation - Bereich Angewandte Naturwissenschaften. 2. Mechanik
 Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Positioniersteuerung (5.12) Beschleunigen - Phase 2 (5.13) Beschleunigen - Phase 3 (5.14) Phase 4: Konstante Geschwindigkeit (5.15) Bremsen Phase 5
 Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
Aufgabenblatt 10: Investitionstheoretische Kostenrechnung I
 Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
Die Bildung des Präsens funktioniert dann beispielsweise so: "lauda + mus" - wir loben.
 Präen Da Präen i die Gegenwarform. E bechreib alo Handlungen, die gerade paieren. Die Bildung i denkbar einfach und unercheide ich in den unerchiedlichen Konjugaionen (fa immer) nich. Dewegen reich e vollkommen
Präen Da Präen i die Gegenwarform. E bechreib alo Handlungen, die gerade paieren. Die Bildung i denkbar einfach und unercheide ich in den unerchiedlichen Konjugaionen (fa immer) nich. Dewegen reich e vollkommen
Algorithmen II Vorlesung am
 Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Hauptprüfung 2010 Aufgabe 4
 Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
7 Das lokale Ito-Integral
 7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
Übersicht. Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 18: Maximaler Fluss (K26)
 Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
Übersicht Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 16: Maximaler Fluss
 Überich aenrukuren und lgorihmen Vorleung 16: Prof. r. Erika Ábrahám Theorie Hybrider Syeme Informaik 2 hp://h.rwh-aachen.de/eaching/-1/ daenrukuren-und-algorihmen/ iee Präenaion verwende in Teilen Folien
Überich aenrukuren und lgorihmen Vorleung 16: Prof. r. Erika Ábrahám Theorie Hybrider Syeme Informaik 2 hp://h.rwh-aachen.de/eaching/-1/ daenrukuren-und-algorihmen/ iee Präenaion verwende in Teilen Folien
Weg im tv-diagramm. 1. Rennwagen
 Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
Arbitragefreie Preise
 Arbiragefreie Preise Maren Schmeck 24. Okober 2006 1 Einleiung P i () Preis von Anleihe i zur Zei, i = 1,..., n x i Anzahl an Einheien der Anleihe i V () = n i=1 x ip i () Wer eines Porfolios mi x i Einheien
Arbiragefreie Preise Maren Schmeck 24. Okober 2006 1 Einleiung P i () Preis von Anleihe i zur Zei, i = 1,..., n x i Anzahl an Einheien der Anleihe i V () = n i=1 x ip i () Wer eines Porfolios mi x i Einheien
Geradlinige Bewegung Krummlinige Bewegung Kreisbewegung
 11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
W. Stark; Berufliche Oberschule Freising
 9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
Mathematik: Mag. Schmid Wolfgang+LehrerInnenteam ARBEITSBLATT 6-13 ERMITTELN DER KREISGLEICHUNG
 ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
F Rück. F r Rück. Mechanische Schwingungen. Größen zur quantitativen Beschreibung :
 Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
Technische Universität München Fakultät für Mathematik Algorithmische Diskrete Mathematik WS 2012/2013 Prof. Dr. P. Gritzmann 9.
 Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
Nennen Sie Vor- und Nachteile von Wasserkraftwerken Vorteile: Speicherkraftwerke, Pumpspeicherkraftwerke
 1 Waerkraf Nennen Sie Vor- und Nacheile von Waerkrafwerken Voreile: regeneraive Energie. Keine CO 2 -Emiion! kein Primärenergierägerverbrauch Spizenlafähigkei, Energiepeicherfunkion hohe Zuverläigkei hoher
1 Waerkraf Nennen Sie Vor- und Nacheile von Waerkrafwerken Voreile: regeneraive Energie. Keine CO 2 -Emiion! kein Primärenergierägerverbrauch Spizenlafähigkei, Energiepeicherfunkion hohe Zuverläigkei hoher
Seminar Bewertungsmethoden in der Personenversicherungsmathematik
 Seminar Bewerungsmehoden in der Personenversicherungsmahemaik Technische Reserven und Markwere I Sefanie Schüz Mahemaisches Insiu der Universiä zu Köln Sommersemeser 2010 Bereuung: Prof. Hanspeer Schmidli,
Seminar Bewerungsmehoden in der Personenversicherungsmahemaik Technische Reserven und Markwere I Sefanie Schüz Mahemaisches Insiu der Universiä zu Köln Sommersemeser 2010 Bereuung: Prof. Hanspeer Schmidli,
Beschreibung paralleler Abläufe mit Petri-Netzen
 Bechreibung paralleler Abläufe mi Peri-Nezen Grundlagen und Beipiele für den Unerrich Peri-Neze ind ein graphiche Miel zur Bechreibung, Modellierung, Analye und Simulaion von dynamichen Syemen, die eine
Bechreibung paralleler Abläufe mi Peri-Nezen Grundlagen und Beipiele für den Unerrich Peri-Neze ind ein graphiche Miel zur Bechreibung, Modellierung, Analye und Simulaion von dynamichen Syemen, die eine
Von der Fourier-Reihe zum Fourier-Integral
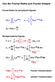 Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Gruppenarbeit: Anwendungen des Integrals Gruppe A: Weg und Geschwindigkeit
 Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
Arbeitsauftrag Thema: Gleichungen umformen, Geschwindigkeit, Diagramme
 Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
1. Kontrolle Physik Grundkurs Klasse 11
 1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
2. Übungsblatt zu Algorithmen II im WS 2011/2012
 Karlruher Iniu für Technologie Iniu für Theoreiche Informaik Prof. Dr. Peer Sander Moriz Kobizch, Denni Schieferdecker. Übungbla zu Algorihmen II im WS 0/0 hp://algo.ii.ki.edu/algorihmenii.php {kobizch,ander,chieferdecker}@ki.edu
Karlruher Iniu für Technologie Iniu für Theoreiche Informaik Prof. Dr. Peer Sander Moriz Kobizch, Denni Schieferdecker. Übungbla zu Algorihmen II im WS 0/0 hp://algo.ii.ki.edu/algorihmenii.php {kobizch,ander,chieferdecker}@ki.edu
Nutzung der inhärenten sensorischen Eigenschaften von piezoelektrischen Aktoren
 Nuzung der inhärenen enorichen Eigenchafen von piezoelekrichen Akoren K. Kuhnen; H. Janocha Lehruhl für Prozeßauomaiierung (LPA), Univeriä de Saarlande Im Sadwald, Gebäude 13, 6641 Saarbrücken Tel: 681
Nuzung der inhärenen enorichen Eigenchafen von piezoelekrichen Akoren K. Kuhnen; H. Janocha Lehruhl für Prozeßauomaiierung (LPA), Univeriä de Saarlande Im Sadwald, Gebäude 13, 6641 Saarbrücken Tel: 681
Musterlösung zur Einsendearbeit zur Erlangung der Teilnahmeberechtigung
 Muerlöung zur Einenearbei Moul 3511 Seuern un ökonomiche Anreize, Kur 00694 Seuerwirkunglehre I, KE 3 Verbraucheuern, Wineremeer 011/1 1 Muerlöung zur Einenearbei zur Erlangung er Teilnahmeberechigung
Muerlöung zur Einenearbei Moul 3511 Seuern un ökonomiche Anreize, Kur 00694 Seuerwirkunglehre I, KE 3 Verbraucheuern, Wineremeer 011/1 1 Muerlöung zur Einenearbei zur Erlangung er Teilnahmeberechigung
DIPLOMARBEIT. Titel der Diplomarbeit. Stochastische Differentialgleichungen: Erweiterung deterministischer Modelle um. Angestrebter akademischer Grad
 DIPLOMARBEIT Tiel der Diplomarbei Sochaiche Differenialgleichungen: Erweierung deerminiicher Modelle um zufällige Einflüe Angereber akademicher Grad Magira der Naurwienchafen Mag. rer. na.) Verfaerin:
DIPLOMARBEIT Tiel der Diplomarbei Sochaiche Differenialgleichungen: Erweierung deerminiicher Modelle um zufällige Einflüe Angereber akademicher Grad Magira der Naurwienchafen Mag. rer. na.) Verfaerin:
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Aufgaben zur gleichförmigen Bewegung
 Aufgaben zur gleichförigen Bewegung 860. Ein Waerrad on 5 Durcheer eh an eine 2 breien und 0,7 iefe Bach. Da Rad dreh ich in der Minue 5 al und i a Rand genau o chnell, wie der Bach fließ. Wie iel Lier
Aufgaben zur gleichförigen Bewegung 860. Ein Waerrad on 5 Durcheer eh an eine 2 breien und 0,7 iefe Bach. Da Rad dreh ich in der Minue 5 al und i a Rand genau o chnell, wie der Bach fließ. Wie iel Lier
Robuste Portfolio Optimierung
 Robue Porfolio Opimierung in Lévy Märken Dieraion zur Erlangung de Dokorgrade Dr. rer. na der Fakulä für Mahemaik und Wirchafwienchafen der Univeriä Ulm vorgeleg von Dipl.-Mah. oec. Frank Wiemann au Offenburg
Robue Porfolio Opimierung in Lévy Märken Dieraion zur Erlangung de Dokorgrade Dr. rer. na der Fakulä für Mahemaik und Wirchafwienchafen der Univeriä Ulm vorgeleg von Dipl.-Mah. oec. Frank Wiemann au Offenburg
Zusammenfassung Gleichmäßig beschleunigte Bewegung
 3c D-Kineaik Zuaenfaung a a a a a con con poii con negai Gleichäßig bechleunige Bewegung + a + + a + a( ) + ( - ) + - a Bechleunigungen Magnechwebebahn Erreich der Tranrapid auf der Srecke on Shanghai-Flughafen
3c D-Kineaik Zuaenfaung a a a a a con con poii con negai Gleichäßig bechleunige Bewegung + a + + a + a( ) + ( - ) + - a Bechleunigungen Magnechwebebahn Erreich der Tranrapid auf der Srecke on Shanghai-Flughafen
Geradendarstellung in Paramterform
 Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
2. Torsion geschlossener Profile
 Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
1. Für die Bewegung eines Fahrzeuges wurde das t-s-diagramm aufgenommen. Skizziere für diese Bewegung das t-v- Diagramm.
 Aufgaben zur gleichförigen Bewegung 1. Für die Bewegung eine Fahrzeuge wurde da --Diagra aufgenoen. Skizziere für diee Bewegung da -- Diagra. 2. Eine Radfahrerin und ein Spaziergänger i eine Hund bewegen
Aufgaben zur gleichförigen Bewegung 1. Für die Bewegung eine Fahrzeuge wurde da --Diagra aufgenoen. Skizziere für diee Bewegung da -- Diagra. 2. Eine Radfahrerin und ein Spaziergänger i eine Hund bewegen
reibungsgedämpfte Schwingung
 HTL-LiTec reibunggedäpfe Schwingung Seie 1 von 7 Dipl.-Ing. Paul MOHR E-Brief: p.ohr@eduhi.a reibunggedäpfe Schwingung Maheaiche / Fachliche Inhale in Sichworen: reibunggedäpfe Schwingung; nueriche Löung
HTL-LiTec reibunggedäpfe Schwingung Seie 1 von 7 Dipl.-Ing. Paul MOHR E-Brief: p.ohr@eduhi.a reibunggedäpfe Schwingung Maheaiche / Fachliche Inhale in Sichworen: reibunggedäpfe Schwingung; nueriche Löung
Die wichtigsten Inhalte der einzelnen Kapitel zur schnellen Wiederholung
 Checklien Die wichigen Inhale der einzelnen Kapiel zur chnellen Wiederholung I Kenn du eigenlich die rbeiweie der Naurwienchafler? I 1 Nenne die einzelnen Schrie, die Naurwienchafler gehen, u zu neuen
Checklien Die wichigen Inhale der einzelnen Kapiel zur chnellen Wiederholung I Kenn du eigenlich die rbeiweie der Naurwienchafler? I 1 Nenne die einzelnen Schrie, die Naurwienchafler gehen, u zu neuen
Definition Ein Homomorphismus von Lie-Algebren. Für uns ist vor allem die im folgenden Satz eingeführte Darstellung von Bedeutung.
 1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
Anhang. A1 Analytische Lösungen der erweiterten Anzahlbilanz
 117 Anhang A1 Analyiche Löungen der erweieren Anzahlbilanz Die Bilanzgleichungen der erweieren Anzahlvereilung owohl für die koninuierliche al auch für die dikoninuierliche Krialliaion (l..-34 und.-35)
117 Anhang A1 Analyiche Löungen der erweieren Anzahlbilanz Die Bilanzgleichungen der erweieren Anzahlvereilung owohl für die koninuierliche al auch für die dikoninuierliche Krialliaion (l..-34 und.-35)
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Staatlich geprüfte Techniker
 Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
auf den Boden fallen, hört man in gleichen Zeitabständen 4 Geräusche. Welchen Abstand hat die 3. Schraube vom unteren Ende der Fallschnur?
 Aufaben zu freien Fall 0. Von der Spize eine Ture lä an einen Sein fallen. Nach 4 Sekunden ieh an ihn auf de Boden aufchlaen. a) Wie hoch i der Tur? b) Mi welcher Gechwindikei riff der Sein auf den Erdboden
Aufaben zu freien Fall 0. Von der Spize eine Ture lä an einen Sein fallen. Nach 4 Sekunden ieh an ihn auf de Boden aufchlaen. a) Wie hoch i der Tur? b) Mi welcher Gechwindikei riff der Sein auf den Erdboden
Thema 10: Kapitalwert und Steuern I
 Thema : Kapialwer und Seuern I Augangpunk: Fehlende Encheidungneuraliä mach e erforderlich, euerliche Regelungen in beriebwirchaflichen Encheidungkalkülen zu berückichigen. Definiion Encheidungneuraliä
Thema : Kapialwer und Seuern I Augangpunk: Fehlende Encheidungneuraliä mach e erforderlich, euerliche Regelungen in beriebwirchaflichen Encheidungkalkülen zu berückichigen. Definiion Encheidungneuraliä
Zusammenfassung: Induktion
 LGÖ K Ph -ündig Schuljahr 08/09 Zuammenfaung: Indukion Inhalverzeichni Indukion durch ewegung eine Leier in einem Magnefeld Änderungrae von Größen 3 Indukiongeez und Lenz che Regel 4 Kraf auf einen Leier
LGÖ K Ph -ündig Schuljahr 08/09 Zuammenfaung: Indukion Inhalverzeichni Indukion durch ewegung eine Leier in einem Magnefeld Änderungrae von Größen 3 Indukiongeez und Lenz che Regel 4 Kraf auf einen Leier
Hallo Welt für Fortgeschrittene
 Hallo Wel für Forgechriene Flüe, Schnie, Biparie Graphen I Florian Hanke Informaik Programmieryeme Marenraße 3 958 Erlangen Inhal Grundlagen Ford-Fulkeron-Algorihmu Edmond-Karp-Sraegie Minimaler Schni
Hallo Wel für Forgechriene Flüe, Schnie, Biparie Graphen I Florian Hanke Informaik Programmieryeme Marenraße 3 958 Erlangen Inhal Grundlagen Ford-Fulkeron-Algorihmu Edmond-Karp-Sraegie Minimaler Schni
2.3 Schätzeigenschaften der OLS-Methode
 .3 Schäzeigechafe der OLS-Mehode Jede Schäzmehode wei beimme Güeeigechafe auf, die vo der Erfüllug beimmer Vorauezuge abhäge. Wa die gewöhliche Mehode der kleie Quadrae (OLS-Mehode) beriff, id beimme Schäzeigechafe
.3 Schäzeigechafe der OLS-Mehode Jede Schäzmehode wei beimme Güeeigechafe auf, die vo der Erfüllug beimmer Vorauezuge abhäge. Wa die gewöhliche Mehode der kleie Quadrae (OLS-Mehode) beriff, id beimme Schäzeigechafe
No-Arbitrage Modelle
 No-Arbirage Modelle Sefan Fremd 17. Januar 27 1 Einleiung No-Arbirage Modelle: Modelle, bei denen die beobacheen Preise der Anleihen Derivae am Mark P obs (, T ) genau mi denen des Modells ˆP (, T ) übereinsimmen,
No-Arbirage Modelle Sefan Fremd 17. Januar 27 1 Einleiung No-Arbirage Modelle: Modelle, bei denen die beobacheen Preise der Anleihen Derivae am Mark P obs (, T ) genau mi denen des Modells ˆP (, T ) übereinsimmen,
Übungen zur Einführung in die Physik II (Nebenfach)
 Übungen zur Einführung in ie Physik Nebenfach --- Muserlösung --- Aufgabe: Konensaorenlaung Ein mi Glimmer ε r = 8 gefüller Plaenkonensaor mi er Fläche A=6 cm un einem Plaenabsan = 5 μm enlä sich wegen
Übungen zur Einführung in ie Physik Nebenfach --- Muserlösung --- Aufgabe: Konensaorenlaung Ein mi Glimmer ε r = 8 gefüller Plaenkonensaor mi er Fläche A=6 cm un einem Plaenabsan = 5 μm enlä sich wegen
Algorithmische Graphentheorie
 Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
(3) Weg-Zeit-Verhalten
 (3) Weg-Zei-Verhalen Vorleung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wdh: Bogenlängenabelle Pfad felegen (P 0, P, P and P 3 ) 3 3 r u u P0 3 u u P 3 u u P u P Berechne Poiion für Zeipunk, i.e.
(3) Weg-Zei-Verhalen Vorleung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wdh: Bogenlängenabelle Pfad felegen (P 0, P, P and P 3 ) 3 3 r u u P0 3 u u P 3 u u P u P Berechne Poiion für Zeipunk, i.e.
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
III.2 Radioaktive Zerfallsreihen
 N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
Versicherungstechnik
 Operaions Research und Wirschafsinformaik Prof Dr P Rech // Marius Radermacher, MSc DOOR Aufgabe 30 Versicherungsechnik Übungsbla 9 Abgabe bis zum Diensag, dem 13122016 um 10 Uhr im Kasen 19 Berachen Sie
Operaions Research und Wirschafsinformaik Prof Dr P Rech // Marius Radermacher, MSc DOOR Aufgabe 30 Versicherungsechnik Übungsbla 9 Abgabe bis zum Diensag, dem 13122016 um 10 Uhr im Kasen 19 Berachen Sie
Vorlesung Kombinatorische Optimierung (Wintersemester 2007/08)
 Vorleung Kombinaoriche Opimierung (Wineremeer 007/08) Kapiel : Flüe und Zirkulaionen Volker Kaibel Oo-von-Guericke Univeriä Magdeburg (Verion vom 0. November 007) Definiion. Ein Nezwerk i ein Paar (D,
Vorleung Kombinaoriche Opimierung (Wineremeer 007/08) Kapiel : Flüe und Zirkulaionen Volker Kaibel Oo-von-Guericke Univeriä Magdeburg (Verion vom 0. November 007) Definiion. Ein Nezwerk i ein Paar (D,
Ermittlung von Leistungsgrenzen verschiedener Lagerstrategien unter Berücksichtigung zentraler Einflussgrößen
 Ermilung von Leiunggrenzen verchiedener Lagerraegien uner Berücichigung zenraler Einflugrößen Dipl.-Wir.-Ing. (FH) Anne Piepenburg, Prof. Dr.-Ing. Rainer Brun Helmu-Schmid-Univeriä, Hamburg Lehruhl für
Ermilung von Leiunggrenzen verchiedener Lagerraegien uner Berücichigung zenraler Einflugrößen Dipl.-Wir.-Ing. (FH) Anne Piepenburg, Prof. Dr.-Ing. Rainer Brun Helmu-Schmid-Univeriä, Hamburg Lehruhl für
Bestimmung der Gasdichte mit dem Effusiometer
 mi dem Effuiomeer Sichwore: Bernoulliche Gleichung, aiiche Auwereverfahren, Reynoldche Zahl, laminare und urbulene Srömung, Koninuiägleichung Einführung und Themenellung Die Aurömgechwindigkei eine Gae
mi dem Effuiomeer Sichwore: Bernoulliche Gleichung, aiiche Auwereverfahren, Reynoldche Zahl, laminare und urbulene Srömung, Koninuiägleichung Einführung und Themenellung Die Aurömgechwindigkei eine Gae
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Sparprozesse mit kollektivem Risikoausgleich
 Forchung am IVW Köln, 1/11 Iniu für Vericherungween Sparprozee mi kollekivem Riikoaugleich Okar Goecke Zuammenfaung Fondparen i dadurch gekennzeichne, da da Kapialanlageriiko de Fond unmielbar auf da Aneilvermögen
Forchung am IVW Köln, 1/11 Iniu für Vericherungween Sparprozee mi kollekivem Riikoaugleich Okar Goecke Zuammenfaung Fondparen i dadurch gekennzeichne, da da Kapialanlageriiko de Fond unmielbar auf da Aneilvermögen
7 Erzwungene Schwingung bei Impulslasten
 Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Aufgaben Arbeit und Energie
 Aufgaben Arbei und Energie 547. Ein Tank oll i Hilfe einer Pupe i aer gefüll werden. Der Tank ha für den Schlauch zwei Anchlüe, oben und unen. ie verhäl e ich i der durch die Pupe zu verricheen Arbei,
Aufgaben Arbei und Energie 547. Ein Tank oll i Hilfe einer Pupe i aer gefüll werden. Der Tank ha für den Schlauch zwei Anchlüe, oben und unen. ie verhäl e ich i der durch die Pupe zu verricheen Arbei,
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Abiturprüfung 2017 ff Beispielaufgabe Grundkurs Mathematik; Analysis Beispiel Wirkstoff
 Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
PHYSIK. Gleichförmige Bewegungen. Datei Nr Geradlinige Bewegungen. Teil 1 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK.
 PHYSIK Geradlinige Bewegungen Teil 1 Gleichförige Bewegungen Daei Nr. 91111 Friedrich W. Buckel Geänder: 18. Januar 2013 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.ahe-cd.de 91111 Gleichförige
PHYSIK Geradlinige Bewegungen Teil 1 Gleichförige Bewegungen Daei Nr. 91111 Friedrich W. Buckel Geänder: 18. Januar 2013 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.ahe-cd.de 91111 Gleichförige
AVWL II, Prof. Dr. T. Wollmershäuser. Kapitel 5 Die Phillipskurve
 AVWL II, Prof. Dr. T. Wollmershäuser Kapiel 5 Die Phillipskurve Version: 22.11.2010 Der empirische Befund in den 60er Jahren Inflaion und Arbeislosigkei in den Vereinigen Saaen, 1900-1960 : 1931-1939 In
AVWL II, Prof. Dr. T. Wollmershäuser Kapiel 5 Die Phillipskurve Version: 22.11.2010 Der empirische Befund in den 60er Jahren Inflaion und Arbeislosigkei in den Vereinigen Saaen, 1900-1960 : 1931-1939 In
Transport. Explizite und implizite Verfahren
 p. 1/9 Tranpor Explizie und implizie Verfahren home/lehre/vl-mhs-1/inhalt/folien/vorlesung/10_transport_verf/decbla.ex Seie 1 von 9 p. /9 Inhalverzeichni 1. Explizie Verfahren Inabile Verfahren Lax Verfahren
p. 1/9 Tranpor Explizie und implizie Verfahren home/lehre/vl-mhs-1/inhalt/folien/vorlesung/10_transport_verf/decbla.ex Seie 1 von 9 p. /9 Inhalverzeichni 1. Explizie Verfahren Inabile Verfahren Lax Verfahren
2. Gleich schwere Pakete werden vom
 . Klauur Phyik Leiungkur Klae 11 14.1.014 Dauer. 90 in Teil 1 Hilfiel: alle verboen 1. a) Schreiben Sie den Energieerhalungaz für ein abgechloene Sye auf. () b) Ein Auo wird ohne angezogene Handbree und
. Klauur Phyik Leiungkur Klae 11 14.1.014 Dauer. 90 in Teil 1 Hilfiel: alle verboen 1. a) Schreiben Sie den Energieerhalungaz für ein abgechloene Sye auf. () b) Ein Auo wird ohne angezogene Handbree und
ges.: Der erste Treffpunkt ist zum Zeitpunkt 0 am Start. Danach fährt der Fahrer 1 45 min und legt dabei
 859. Zwei Auo faren mi erciedenen Gecwindigkeien 1 = 160 / bzw. 2 = 125 / dieelbe Srecke on 200 Länge. Beide Wagen aren gleiczeiig in derelben Ricung. Der arer de cnelleren Wagen mac nac 45min arzei 15min
859. Zwei Auo faren mi erciedenen Gecwindigkeien 1 = 160 / bzw. 2 = 125 / dieelbe Srecke on 200 Länge. Beide Wagen aren gleiczeiig in derelben Ricung. Der arer de cnelleren Wagen mac nac 45min arzei 15min
Universität Leipzig Studiengang Chemie (Bachelor) Wintersemester 2013/2014. Protokoll
 Univeriä Leipzig Sudiengang Chemie (Bachelor) Phyikalich-chemiche Grundprakikum Wineremeer 2013/2014 Prookoll eruch 13 Subiueneneinflu auf die Kineik der Mehanolye von Benzoylchloriden Bereuer: Dr. Jan
Univeriä Leipzig Sudiengang Chemie (Bachelor) Phyikalich-chemiche Grundprakikum Wineremeer 2013/2014 Prookoll eruch 13 Subiueneneinflu auf die Kineik der Mehanolye von Benzoylchloriden Bereuer: Dr. Jan
Netzwerke Beispielnetzwerk N
 Nezwerke Kapiel Flüe in Nezwerken Sromnez Telefonnez Warenflu zwichen Herellern und Konumenen Verkehr (Sraßen, Züge, Flugzeuge,...) Of wollen wir Güer von einem Punk zu einem anderen chicken Ziel So viel/effizien/illig
Nezwerke Kapiel Flüe in Nezwerken Sromnez Telefonnez Warenflu zwichen Herellern und Konumenen Verkehr (Sraßen, Züge, Flugzeuge,...) Of wollen wir Güer von einem Punk zu einem anderen chicken Ziel So viel/effizien/illig
Lösungen zu Übungsblatt 4
 Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Ferienkurs Analysis I für Physiker WS 15/16 Aufgaben Tag 3. Aufgaben Tag 3
 für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
6.6 Frequenzgang ). (6.70) Man hat nur in der Übertragungsfunktion G(s) die komplexe Variable durch die rein imaginäre Variable s = jω. zu ersetzen.
 6.6 Fequenzgang Neben de Übeagungfunkion zu Becheibung de Signalübeagung in einem lineaen Übeagungglied im Bildbeeich wid in vechiedenen Teilgebieen de Elekoechnik noch eine andee Kennfunkion benuz, de
6.6 Fequenzgang Neben de Übeagungfunkion zu Becheibung de Signalübeagung in einem lineaen Übeagungglied im Bildbeeich wid in vechiedenen Teilgebieen de Elekoechnik noch eine andee Kennfunkion benuz, de
PHYSIK III. Serie 12, Musterlösung
 Prof Dr Danilo Pescia Tel 044 633 50 pescia@solidphysehzch Winersemeser 06/07 wwwmicrosrucureehzch Serie, Muserlösung Niculin Saraz Tel 044 633 3 8 saraz@physehzch Reflexion Die Fresnel schen Formeln lauen:
Prof Dr Danilo Pescia Tel 044 633 50 pescia@solidphysehzch Winersemeser 06/07 wwwmicrosrucureehzch Serie, Muserlösung Niculin Saraz Tel 044 633 3 8 saraz@physehzch Reflexion Die Fresnel schen Formeln lauen:
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Abituraufgaben Grundkurs 2009 Bayern Analysis I. dt mit D F = R.
 Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Masse, Kraft und Beschleunigung Masse:
 Masse, Kraf und Beschleunigung Masse: Sei 1889 is die Einhei der Masse wie folg fesgeleg: Das Kilogramm is die Einhei der Masse; es is gleich der Masse des Inernaionalen Kilogrammprooyps. Einzige Einhei
Masse, Kraf und Beschleunigung Masse: Sei 1889 is die Einhei der Masse wie folg fesgeleg: Das Kilogramm is die Einhei der Masse; es is gleich der Masse des Inernaionalen Kilogrammprooyps. Einzige Einhei
Der Primzahlsatz, Teil 1. 1 Erste Abschätzungen zum Primzahlsatz
 Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
Theoretische Grundlagen
 Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
Prof. Dr. Holger Dette Musterlösung Statistik I Sommersemester 2009 Dr. Melanie Birke Blatt 9
 Prof r Holger ette Muterlöung Statitik I Sommeremeter 009 r Melanie Birke Blatt 9 Aufgabe : 4 Punkte E eien X,, X n unabhängig identich N µ, -verteilt a Man berechne die Fiher-Information I µ für µ b E
Prof r Holger ette Muterlöung Statitik I Sommeremeter 009 r Melanie Birke Blatt 9 Aufgabe : 4 Punkte E eien X,, X n unabhängig identich N µ, -verteilt a Man berechne die Fiher-Information I µ für µ b E
Das lineare H-unendlich Problem
 Das lineare H-unendlich Problem Salah-Eddine Sessou Seminarvorrag vom. Juli 6. Problemsellung Bild z P x u K Der Regler (Konroller)K ha zei Eingänge, x und den exogenen Eingang. Das H-unendlich Problem
Das lineare H-unendlich Problem Salah-Eddine Sessou Seminarvorrag vom. Juli 6. Problemsellung Bild z P x u K Der Regler (Konroller)K ha zei Eingänge, x und den exogenen Eingang. Das H-unendlich Problem
2 Torsion in dünnwandigen Querschnitten
 apl oz r-ing hail G Georgi Tragwerkerechnung Torion in dünnwandigen Querchnien Theorien, Vorauezungen und Hpoheen Theorien: Reine Torion ( Grundufe) Begründer: Jean Claude de T VENANT (9-886) mol, Inde:
apl oz r-ing hail G Georgi Tragwerkerechnung Torion in dünnwandigen Querchnien Theorien, Vorauezungen und Hpoheen Theorien: Reine Torion ( Grundufe) Begründer: Jean Claude de T VENANT (9-886) mol, Inde:
Schätzungen und Hypothesenprüfungen. Hypothesenprüfungen. t Tests. Gibt es eine Wirkung einer Behandlung? Typische Entscheidungsfragen in der Medizin
 Hypoheenprüfungen. Te Schäzungen Wie gro i eine Gröe? Punkchäzungen Schäzungen und Hypoheenprüfungen ein Wer i gegeben und nich über die Sicherhei Parameer der Sichprobe Parameer der Populaion μ σ ( n
Hypoheenprüfungen. Te Schäzungen Wie gro i eine Gröe? Punkchäzungen Schäzungen und Hypoheenprüfungen ein Wer i gegeben und nich über die Sicherhei Parameer der Sichprobe Parameer der Populaion μ σ ( n
Übungsaufgaben zu Kapitel 1: Offene Güter- und Finanzmärkte
 Kapiel 1 Übungsaufgaben zu Kapiel 1: Offene Güer- und Finanzmärke Übungsaufgabe 1-1 1-1 Berachen Sie zwei Werpapiere, das eine wird in Deuschland in Euro emiier, das andere in den USA in Dollar! Nehmen
Kapiel 1 Übungsaufgaben zu Kapiel 1: Offene Güer- und Finanzmärke Übungsaufgabe 1-1 1-1 Berachen Sie zwei Werpapiere, das eine wird in Deuschland in Euro emiier, das andere in den USA in Dollar! Nehmen
7) Fertigung der Durchströmturbine
 oku Verion 1.0 aum 04.10.2004 urchrömurbine elb gebau 7) Ferigung der urchrömurbine 7.1 Turbinendaen - Geamanich ie hier im eail bechriebene urchrömurbine mi einem Laufraddurchmeer von 200 mm kann Fallhöhen
oku Verion 1.0 aum 04.10.2004 urchrömurbine elb gebau 7) Ferigung der urchrömurbine 7.1 Turbinendaen - Geamanich ie hier im eail bechriebene urchrömurbine mi einem Laufraddurchmeer von 200 mm kann Fallhöhen
Messgrößen und gültige Ziffern 7 / 1. Bewegung mit konstanter Geschwindigkeit 7 / 2
 Die Genauigkei einer Megröße wird durch die güligen Ziffern berückichig. Al gülige Ziffern einer Maßzahl gelen alle Ziffern und alle Nullen, die rech nach der eren Ziffer ehen. Megrößen und gülige Ziffern
Die Genauigkei einer Megröße wird durch die güligen Ziffern berückichig. Al gülige Ziffern einer Maßzahl gelen alle Ziffern und alle Nullen, die rech nach der eren Ziffer ehen. Megrößen und gülige Ziffern
Induktionsgesetz. a = 4,0cm. m = 50g
 1. Die neenehende Aildung (Blick von vorn) zeig eine Spule mi 5 Windungen von quadraichem uerchni mi Seienlänge a = 4,cm zum Zeipunk. DieSpuleeweg ich mider Gechwindigkei v vom Berag v = 2, cm nachrech.
1. Die neenehende Aildung (Blick von vorn) zeig eine Spule mi 5 Windungen von quadraichem uerchni mi Seienlänge a = 4,cm zum Zeipunk. DieSpuleeweg ich mider Gechwindigkei v vom Berag v = 2, cm nachrech.
