6 Stochastische Differentialgleichungen
|
|
|
- Frauke Maurer
- vor 6 Jahren
- Abrufe
Transkript
1 6 Sochaiche Differenialgleichungen Viele deerminiiche Modelle der Naur- und der Wirchafwienchafen laen ich mi Hilfe von Differenialgleichungen audrücken. Mi dem Io-Inegral und der Io-Formel haben wir die Grundlagen für ochaiche Differenialgleichungen geleg, mi denen ich nun auch viele ochaiche Modelle mahemaich formulieren laen. Gegeben einen Wahrcheinlichkeiraum mi Browncher Bewegung und Browncher Sandardfilraion owie zwei eige Funkionen µ : R R R und σ : R R R nennen wir die Gleichung dx = µ(, X )d + σ(, X )db, X = x ochaiche Differenialgleichung. Für dieen Begriff verwenden durchweg die engliche Abkürzung SDE (ochaic differenial equaion). In Inegralform gechrieben laue die Gleichung X = x + µ(, X )d + σ(, X )db und ein eiger adapierer ochaicher Proze X der diee Gleichung erfüll heiß Löung der SDE. E i einfach zu ehen, da jede Löung auomaich ein Io-Proze im Sinne de lezen Kapiel i. Wir nennen µ(, X ) Drifkoeffizien und σ(, X ) Diffuionkoeffizien der Gleichung. E ei nochmal an die unerchiedliche Rolle der zwei Terme bei der Bechreibung de lokalen Trend und der lokalen Variabiliä von X erinner, wie ie am Beginn von Kapiel 5 dikuier wurde. 6.1 Beipiele Sochaicher Differenialgleichungen Geomeriche Brownche Bewegung Wir berachen die ochaiche Differenialgleichung dx = µx d + σx db, X = x (6.1) mi µ R, σ > und x. Diee SDE bechreib einen ochaichen Proze deen lokale Wachum ich genauo wie eine lokale Variabiliä proporional zum augenblicklichen Wer verhäl. Ander geag ind die relaiven Änderungen de Prozee von konaner Größenordnung. Diee Hypohee i ewa in finanzmahemaichen Modellen, z.b. bei der Bechreibung eine Akienkure zureffend, wo Kurgewinne bzw. -verlue immer relaiv zum Baiwer zu inerpreieren ind. Al einfacher Anaz zum Auffinden einer Löung biee ich X = f(, B ) mi f 6
2 aureichend differenzierbar an. Nach der Io-Formel gil 7 dx = ( f (, X ) + 1 ) 2 f xx(, X ) d + f x (, X )db, und ein Koeffizienenvergleich mi (6.1) liefer σf(, x) = f x (, x), µf(, x) = f (, x) f xx(, x). Die Löung der eren Gleichung i von der Geal f(, x) = exp(σx + g()); einezen in die zweie Gleichung liefer g () = µ σ2 2. Wir erhalen alo al Löung der ochaichen Differenialgleichung (6.1) den Proze ( X = x exp σb + ) ) (µ σ2, 2 auch geomeriche Brownche Bewegung genann und Bai für da Finanzmarkmodell von Black & Schole. E ei bemerk, da wir an dieer Selle noch nich auchließen können, da auch noch andere Löungen der SDE (6.1) exiieren; wir werden aber im nächen Abchni zeigen, da die nich der Fall i. Der Ornein-Uhlenbeck-Proze Al näche wenden wir un der ochaichen Differenialgleichung dx = λx d + σdb, X = x (6.2) mi λ, σ > und x R zu. Wir ellen fe, da bei dieer SDE der Diffuionkoeffizien im Gegenaz zu (6.1) nich proporional zum augenblicklichen Wer, ondern immer von konaner Größenordnung σ i. Der Driferm λx i negaiv, wenn X poiiv i und poiiv wenn X negaiv i, mi aboluer Größe proporional zu X. Wir können alo davon augehen, da der Proze X langfriig geehen roz ochaicher Flukuaionen dazu endier in die Nähe der Null zurückzukehren. Diee Phänomen wird auch al mean-reverion (Rückkehr zum Mielwer) bechrieben. Da ochaiche Modell (6.4) wurde von den Phyikern Ornein und Uhlenbeck zur Modellierung der Gechwindigkei einzelner Gamoleküle verwende. Zugrundeliegende Annahme i dabei da die Gechwindigkei eine einzelnen Molekül zwar zufällig flukuier, aber lezendlich nich zu ark von der Durchchnigechwindigkei der Geamhei aller Moleküle abweichen darf, und daher eine Tendenz der Rückkehr zum 7 Zur Vereinfachung der Noaion chreiben wir ab nun die pariellen Ableiungen miel iefgeellen Indice, d.h. f := f, fxx := 2 f x 2, ec. 61
3 Abbildung 1: Vier Pfade einer geomerichen Brownchen Bewegung mi Parameern µ =.1, σ = 1. 62
4 Mielwer (mean-reverion) aufweien mu. Eine weiere wichige Anwendung finde die SDE (6.5) in der Finanzmahemaik, wo ie al Vaicek-Modell für Zinraen bekann i. Der einfache Anaz X = f(, B ) führ bei dieer SDE nich mehr zum Ziel. Man könne jedoch vermuen, da e ich aufgrund der einfachen Srukur de Diffuionerm bei X um einen Gaußchen Proze handel. Wir wien au Kapiel 4, da Io-Inegrale von deerminiichen Inegranden, d.h. von der Geal b()db Beipiele für Gaußche Prozee ind. Um eine ewa allgemeinere Klae von Gaußchen Prozeen abzudecken wählen wir den Anaz { X = a() x + b()db }. (6.3) Beache da X da Produk der zwei Io-Prozee Y = a() und Z = x + b()db i. Weier gil [Y, Z] = und wir erhalen nach Anwendung der Produkformel au Korrolar 5.9 { } dx = a () x + b()db d + a()b()db. Mi der Annahme a() > lä ich die umchreiben al Koeffizienenvergleich mi (6.4) liefer dx = a () a() d + a()b()db. a () a() = λ, a()b() = σ. Die Löungen dieer Gleichungen ind a() = e λ und b() = σe λ. Au dem Anaz (6.3) erhalen wir alo X = e λ {x + σ e λ db } = e λ x + σ e λ( ) db al Löung der Ornein-Uhlenbeck SDE (6.4). Au dieer Darellung folg mi den Eigenchafen de Io-Inegral E [X ] = e λ x und Var(X ) = σ 2 e 2λ( ) d = σ2 2λ (1 e 2λ ). Für gil alo E [X ] und Var(X ) σ2 2λ. Da X ein Gaußcher Proze i, chließen wir darau da die Vereilung von X für gegen eine Normalvereilung 63
5 mi Mielwer und Varianz σ2 2λ konvergier. Die Exienz olch einer Grenzvereilung für unercheide den Ornein-Uhlenbeck weenlich von anderen ochaichen Prozeen wie der (gewöhnlichen)brownchen Bewegung oder der geomerichen Brownchen Bewegung. Abbildung 2: Vier Pfade eine Ornein-Uhlenbeck-Prozee mi Parameern λ = 2, σ = 1. Die Brownche Brücke Wir berachen die Differenialgleichung dx = 1 1 X d + σdb, X = x, [, 1). (6.4) Der Einfachhei halber laen wir X bei aren, d.h. wir ezen x =. Wie chon beim Ornein-Uhlenbeck-Proze i da Vorzeichen de Driferm dem Vorzeichen von X genau engegengeez, der Proze zeig alo eine Tendenz zur Null zurückzukehren. Hier wäch aber der Driferm umo ärker je näher ich der Ein 64
6 annäher, und i für = 1 ogar ingulär. Au dieem Grund berachen wir die SDE auch nur auf dem Inerval [, 1). Wegen der ähnlichen Geal können wir auch hier probieren den Anaz (6.3) anzuwenden und erhalen die Gleichungen Die Löungen dieer Gleichungen ind und omi gil a () a() = 1, a()b() = σ. 1 a() = 1 und b() = σ 1 1 X = σ(1 ) 1 db. Wieder laen ich Erwarungwer und Auokovarianz diee Gaußchen Prozee leich berechnen und wir erhalen mi < 1 E [X ] = und Cov(X, X ) = σ 2 1 (1 )(1 ) (1 u) 2 du = σ2 (1 ). Inbeondere gil E [ ] X 2 = σ 2 (1 ) und omi lim 1 E [ ] X 2 =. Wir können ogar zeigen, da der Proze X für 1 fa icher gegen konvergier. Angenommen e gäbe eine Folge n 1, oda mi poiiver Wahrcheinlichkei lim n X 2 n > gil. Dann erhalen wir mi dem Lemma von Faou [ ] < E lim n X2 n lim inf E [ X 2 ] n n = und omi einen Widerpruch. Wir können alo X zu einem eigen ochaichen Proze auf dem abgechloenen Inerval [, 1] forezen, indem wir den Wer X 1 = hinzufügen. Die o definiere Brownche Brücke i ein Gaußcher Proze der bei X = are und auch fa icher wieder bei X 1 = ende. 6.2 Exienz und Eindeuigkei von Löungen Häufig laen ich die Löungen von ochaichen Differenialgleichungen nich in gechloener Form angeben. Dennoch können wir hinreichende Bedingungen für die Exienz und Eindeuigkei einer Löung formulieren. Theorem 6.1. Wenn die Koeffizienen der ochaichen Differenialgleichung dx = µ(, X )d + σ(, X )db, X = x, [, T ] (6.5) 65
7 Abbildung 3: Vier Pfade einer Brownchen Brücke mi Parameer σ = 1. 66
8 die Lipchiz-Bedingung und die Wachumbedingung µ(, x) µ(, y) 2 + σ(, x) σ(, y) 2 K x y 2 (6.6) µ(, x) 2 + σ(, x) 2 K(1 + x 2 ) (6.7) für alle (, x) [, T ] R erfüllen, dann exiier ein eiger adapierer Proze der (6.5) erfüll und welcher gleichmäßig in L 2 (dp ) bechränk i: up E [ X 2 ] <. [,T ] Sei Y eine weiere eige und gleichmäßig in L 2 (dp ) bechränke Löung von (6.5), dann ind X und Y ununercheidbar. Bewei von Theorem 6.1: Eindeuigkei. Der einfachere Teil de Beweie i die Eindeuigkei. Wir nehmen an da zwei eige gleichmäßig in L 2 (dp ) bechränke Löungen X und Y der SDE (6.5) auf [, T ] exiieren und berachen deren Differenz X Y = (µ(, X ) µ(, Y )) d + Mihilfe der Ungleichung (a + b) 2 2a 2 + 2b 2 erhalen wir (σ(, X ) σ(, Y )) db. E [ [ ( (X Y ) 2] ) 2 ] [ ( ) 2 ] 2E µ(, X ) µ(, Y )d +2E σ(, X ) σ(, Y )d. (6.8) Aufgrund der Lipchiz-Bedinung an σ(, x) gil (σ(, X ) σ(, Y )) 2 K(X Y ) 2, worau gemeinam mi der gleichmäßigen L 2 (dp )-Bechränkhei von X und Y folg da σ(, X ) σ(, Y ) H 2 [, T ]. Wir können alo auf da zweie Inegral in (6.8) die Io-Iomerie anwenden. Da ere Inegral chäzen wir mi der Cauchy-Schwarzchen Ungleichung ab und erhalen uner erneuer Verwendung der Lipchiz-Bedingung E [ [ ( (X Y ) 2] 2 ] [ ( 2 ] 2E µ(, X ) µ(, Y )) d + 2E σ(, X ) σ(, Y )) d C E [ (X Y ) 2] d <,, [, T ] 67
9 mi C = 2K max(1, T ). Wir ehen alo da g() = E [ (X Y ) 2] die Inegralungleichung 8 g() C g()d erfüll. Seze nun M = up [,T ] g(). Au der Ungleichung folg g() MC. Erneue Anwenden liefer g() MC und nach n Ieraionen erhalen wir g() MCn n /n!. Da n! ärker wäch al n folg mi n, da g() = für alle [, T ]. Dami gil X = Y fa icher für alle [, T ]. Da X und Y eige Prozee ind, folg mi Lemma 1.1 die Ununercheidbarkei von X und Y. Für den Exienzbewei können wir eine Idee au der Theorie der gewöhnlichen Differenialgleichungen übernehmen die Picard-Ieraion. Wir ezen X () x und definieren eine Folge (X (n) ) n N von ochaichen Prozeen miel X (n+1) = x + µ(, X (n) )d + σ(, X (n) )db. (6.9) Zuer i zu zeigen, da die Prozee X (n) aächlich wohldefinier ind. Lemma 6.2. Wenn X (n) auf [, T ] in L 2 (dp ) bechränk i, dann gil σ(, X (n) ) H 2 [, T ] und µ(, X (n) ) L 2 (d dp ). auf [, T ] in L 2 (dp ) be- Weier i auch der durch (6.9) definiere Proze X (n+1) chränk. Bewei. Aufgrund [ der L 2 -Bechränkhei von X (n) exiier ein C >, oda ( ) ] 2 up [,T ] E X (n) = C <. Au der Wachumbedingung (6.7) folg E [ T ] ( ) 2 σ(, X (n) ) d T K(1 + C) und dami σ(, X (n) ) H 2 [, T ]. Au der Io-Iomerie erhalen wir alo ( T E σ(, X (n) ) 2 )db = E [ T ] ( ) 2 σ(, X (n) ) d T K(1 + C). Ebeno folg au der Wachumbedingung (6.7) µ(, x) 2 K(1 + x 2 ) und dami nach 8 Diee Inegralungleichung i eine beonder einfache Form der Gronwall-Ungleichung die auch in der Theorie der gewöhnlichen DGLen eine Rolle piel. 68
10 Anwendung der Cauchy-Schwarzchen Ungleichung ( T E µ(, X (n) )d ) 2 T K(1 + C). Da Zuammenfügen der Abchäzungen für Drif- und Diffuionerm zeig nun die L 2 -Bechränkhei von X (n+1). Der näche Schri beeh darin zu zeigen, da die Folge der Picard-Ieraionen aächlich gegen einen eigen Proze X konvergier. Ähnlich wie in der Konrukion de Io-Inegral al eigen Proze in Theorem 3.8 benöigen wir dafür pfadweie Konvergenz in der Supremumnorm auf dem Raum C[, T ] der eigen Funkionen. Schlüel dazu i folgende Abchäzung: Lemma 6.3. Wenn die Koeffizienen µ und σ in (6.9) die Lipchiz-Bedinung (6.6) erfüllen, dann exiier ein C > oda für die Prozee X (n) der Picard-Ieraion (6.9) die Ungleichung gil. [ ( E up X (n+1) Bewei. Wir zerlegen X (n+1) D = ) ] 2 X (n) C X (n) und den Beirag der Diffuionerme M = ( ( [ E (X (n) X (n 1) ) 2] d (6.1) in den Beirag der Driferme µ(, X (n) σ(, X (n) ) ) µ(, X (n 1) ) d ) ) σ(, X (n 1) ) db. Wir haben berei gezeig, da σ(, X (n) ) in H 2 [, T ] lieg und folgern darau, da M ein Maringal i. Weier gil ( up X (n+1) ) 2 X (n) 2 up D up M 2. Wir chäzen zuer den Driferm mi der Cauchy-Schwarzchen Ungleichung ab, und erhalen ( 2 up D 2 µ(, X (n) ) µ(, X )) (n 1) d. (6.11) 69
11 Auf den Maringalerm wenden wir die Doobche Ungleichung und die Io-Iomerie an und erhalen [ ] E up M 2 4E [ [ M 2 ] ( ) ] 2 = 4E σ(, X (n) ) σ(, X (n 1) ) d. (6.12) Die Schranken (6.11) und (6.12) gemeinam mi der Lipchiz-Bedingung (6.6) und der Wahl der Konanen C := 8K max(1, T ) liefern die Behaupung. E bleib nur noch die Konvergenz der Picard-Ieraion gegen eine Löung der ochaichen Differenialgleichung zu zeigen. Bewei von Theorem 6.1: Exienz. Wir definieren [ g n () = E up X (n+1) X (n) 2]. (6.13) Mi der Abchäzung au Lemma 6.3 gil g n () C g n 1 ()d n 1. (6.14) Au den Bedingungen an µ und σ folg zunäch, da eine Konane M exiier, oda g () M für [, T ]. Mi der Ungleichung (6.14) folg g 1 () MC und nach n-maliger Anwendung chließlich g n () MC n n /n!. Die Markowche Ungleichung liefer darau [ P up X (n+1) X (n) ] 2 2 n g n ()2 n M (2CT )n. n! Die reche Seie i über n N ummierbar und au dem Lemma von Borel-Canelli folg die Exienz einer Menge A F mi P [A] = 1, oda die Folge der Funkionen X (n) (ω) für jede ω A eine Cauchy-Folge in C[, T ] bezüglich der Supremumnorm bilde. Wir chließen da eine eige Funkion X (ω) exiier mi X up [,T ] X (n) fa icher. E bleib zu zeigen, da der konruiere Proze X in L 2 (dp ) bechränk und aächlich eine Löung der SDE 6.5 i. Au (6.13) erhalen wir X (n+1) X (n) 2 T g n (T ), [, T ]. L 2 (dp ) 7
12 Au (6.14) folg ogar, da n= g n(t ) < und dami, da die X (n) auch in L 2 (dp ) eine Cauchy-Folge bilden. Wir haben alo gezeig da lim n X (n) = X auch in L 2 (dp ) für alle [, T ] gil. Au der Lipchizbedinung (6.6) erhalen wir [ T ( E σ(, X (n) ] ) 2 T [ ) σ(, X (n 1) ) d K E (X (n) Da g n () eine eigende Funkion i, folg darau σ(, X (n) ) σ(, X (n 1) 2 KT g n 1 (T ). L 2 (dp d) ) Analog folg für den Driferm die Abchäzung µ(, X (n) ) µ(, X (n 1) 2 KT g n 1 (T ). L 2 (dp d) ) X (n 1) ) 2] d T K g n 1 ()d. Au der eren Abchäzung chließen wir uner Verwendung der Io-Iomerie die Konvergenz σ(, X (n) )db und au der zweien Abchäzung die Konvergenz µ(, X (n) )db σ(, X )db, in L 2 (dp ) (6.15) µ(, X )db, in L 2 (dp ). (6.16) Wir berachen nun die Picard-Ieraion (6.9) für ein fixe [, T ]. Auf der linken Seie gil X (n) X fa icher. Die gezeige L 2 -Konvergenz in (6.15) und (6.16) lä ich durch Auwahl einer Teilfolge (n k ) k N zu fa icherer Konvergen verärken. Mi n k erhalen wir alo X = x + µ(, X )d + σ(, X )db, fa icher. Da beide Seien der Gleichung eig in ind erhalen wir mi Lemma 1.1 ogar Gleichhei bi auf Ununercheidbarkei und haben gezeig, da der konruiere Proze X aächlich die SDE (6.5) lö. 71
13 6.3 Numeriche Löungmehoden Euler-Schema Bei der numerichen Löung von ochaichen Differenialgleichungen uch man auf einem dikreen Gier = < 1 < < N = T nach einer möglich guen Näherung ˆX( i ) für die aächliche Löung X( i ) der SDE. Auch hier können wir Anleihen bei den Mehoden für gewöhnliche Differenialgleichungen nehmen. Für die einfache Mehode, da Euler-Schema erezen wir in der SDE einfach die infinieimalen Terme d und db durch die finien Differenzen i+1 i bzw. B i+1 B i. Zuäzlich können wir die Skalierungeigenchaf und die Unabhängigkei der Inkremene der Brownchen Bewegung aunuzen und erhalen folgende Rekurion ˆX( i+1 ) = ˆX( i ) + a ( i, ˆX( i ) ) [ i+1 i ] + b ( i, ˆX( i ) ) i+1 i Z i, (6.17) mi Sarwer ˆX() = x, wobei (Z i ) i N unabhängige andardnormalvereile Zufallgrößen ind. Da prakich jede Numerikofware die Erzeugung von normalvereilen Zufallzahlen ermöglich, i da Euler-Schema (6.17) ehr leich zu implemenieren. Wähl man die Gierweie h = i+1 i konan, o lä ich da Euler-Schema noch kompaker al ˆX((i + 1)h) = ˆX(ih) + a ( ih, ˆX(ih) ) h + b ( ih, ˆX(ih) ) hz i, chreiben. Milein-Schema Wie bei den Mehoden für gewöhnliche Differenialgleichungen kann man veruchen da numeriche Näherungverfahren durch Hinzufügen von Termen höherer Ordnung zu verbeern. Bei genauerer Berachung de Euler-Schema fäll auf da die Approximaion de Driferm von Größenordnung O(h) i, die Approximaion de Diffuionerm hingegen von Größenordnung O( h) (in Wahrcheinlichkei). E lieg alo Nahe, ich bei der Verbeerung de Verfahren zunäch einmal auf die Approximaion de Diffuionerm zu konzenieren. In Inegralchreibweie gechrieben verwende da Euler-Schema für dieen Term die Näherung +h b(, X )db b(, X ) [B +h B ]. (6.18) Zur Vereinfachung berachen wir nun den Fall, da a(, X ) und b(, X ) nich explizi vom Zeiparameer abhängen und von der Form a(x ) und b(x ) ind. Wenn wir 72
14 auf b(x ) die Io-Formel anwenden erhalen wir b(x ) = b(x ) + ( b (X u ) + 1 ) 2 b (X u )b 2 (X u ) du + b (X u )b(x u )db u. Wegen einer höheren Größenordnung vernachläßigen wir den d-erm und erhalen die Approximaion b(x ) b(x ) + b (X )b(x ) (B B ). Eingeez in die linke Seie von (6.18) ergib ich +h Wir berechnen +h b(x )db b(x ) (B +h B ) + b (X )b(x ) (B B )db = +h B db B (B +h B ) = +h (B B )db. = 1 2 (B2 +h ( + h)) 1 2 (B2 ) B (B +h B ) = = 1 2 (B +h B ) 2 h 2, und wir erhalen chließlich da Milein-Schema ˆX((i + 1)h) = ˆX(ih) + a ( ˆX(ih) ) h + b ( ˆX(ih) ) hzi b ( ˆX(ih) ) b ( ˆX(ih) ) h(z 2 i 1) wobei (Z i ) i N wie zuvor unabhängige andardnormalvereile Zufallgrößen ind. Man beache, da die beiden ochaichen Terme im Milein-Schema unkorrelier ind, denn E [ Z i (Z 2 i 1)] =. Fehlerordnung Naürlich i bei den vorgeellen Verfahren die Konvergenz zur aächlichen Löung X für h zu zeigen und auch die Größe de Dikreiierungfehler i von Ineree. Man nenn ein Dikreiierungverfahren von arker Fehlerordnung δ >, wenn 73
15 eine Konane C exiier, oda 9 [ ] X(T E ) ˆX(Nh) Ch δ für alle aureichend kleinen h. Für eine fegelege Funkionenklae G meien die Klae der eig differenzierbaren Funkionen mi polynomiell bechränken Ableiungen heiß ein Dikreiierungverfahren von chwacher Fehlerordnung δ >, wenn für jede f G eine Konane C f exiier, oda [ ˆX(Nh))] E [f(x(t ))] E f( Cf h δ, für alle aureichend kleinen h gil. Wenn die Klae G nur Lipchizeige Funkionen enhäl gil [ ˆX(Nh))] [ ] X(T E [f(x(t ))] E f( Kf E ) ˆX(Nh) für paende K f und die chwache Fehlerordnung i e größer al die arke Fehlerordnung. Die Moivaion den Begriff der chwachen Fehlerordnung einzuführen i, da in vielen Anwendungen, ewa in der Finanzmahemaik, die Auwerung von Erwarungweren der Form E [f(x(t ))] da lezendliche Ziel der numerichen Berechnung i. Bei manchen Verfahren i uner beimmen Vorauezungen die chwache Fehlerordnung höher al die arke und ie ind daher numerich guariger al die arke Fehlerordnung uggerier. E gil folgende Reula: Theorem 6.4. Gegeben ei eine ochaiche Differenialgleichung dx = a(x )d + b(x )db, X = x deren Koeffizienen die Vorauezungen von Theorem 6.1 erfüllen. Dann i da Euler- Schema von arker Konvergenzordnung 1 2. Wenn zuäzlich a C1 (R) und b C 2 (R) gil, o i da Milein-Schema von arker Konvergenzordnung 1. Ein Bewei finde ich in Kloeden and Plaen [1995, Theorem 1.2.2, Theorem 1.6.3]. Für zeiabhängige Koeffizienen a(, X ) und b(, X ) gil da Reula uner milden zuäzlichen Vorauezungen ebenfall. Wie oben bemerk, i die chwache Konvergenzordnung der bechriebenen Verfahren uner Umänden höher. Fall beipielweie a und b viermal eig differenzierbar mi polynomiell bechränken Ableiungen ind, o i die chwache Konvergenzordnung de Euler-Verfahren 1 (iehe Glaerman [24, Kap ]). 9 In der Fachlieraur werden auch leich abweichende Formen der Fehlerordnung verwende. Wir orienieren un an der Terminolgie von Kloeden and Plaen [1995]. 74
Stochastische Differentialgleichungen
 INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik Lösungsvorschläge zum 6. Übungsblatt
 Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 7 5. Semester ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE
 Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
DIPLOMARBEIT. Titel der Diplomarbeit. Stochastische Differentialgleichungen: Erweiterung deterministischer Modelle um. Angestrebter akademischer Grad
 DIPLOMARBEIT Tiel der Diplomarbei Sochaiche Differenialgleichungen: Erweierung deerminiicher Modelle um zufällige Einflüe Angereber akademicher Grad Magira der Naurwienchafen Mag. rer. na.) Verfaerin:
DIPLOMARBEIT Tiel der Diplomarbei Sochaiche Differenialgleichungen: Erweierung deerminiicher Modelle um zufällige Einflüe Angereber akademicher Grad Magira der Naurwienchafen Mag. rer. na.) Verfaerin:
KAPITEL 2 KÜRZESTE WEGE
 KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
Mathematik 1 für Maschinenbau, M. Schuchmann (SoSe 2013) Aufgabenblatt 5 (Ebenen)
 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Algorithmen II Vorlesung am
 Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Abbildungsmaßstab und Winkelvergrößerung
 Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Mathematik: Mag. Schmid Wolfgang+LehrerInnenteam ARBEITSBLATT 6-13 ERMITTELN DER KREISGLEICHUNG
 ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
7 Das lokale Ito-Integral
 7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
Restkapazität. = O( V ) mal kritisch. Also gibt es insgesamt höchstens O( V E ) Augmentierungen.
 Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Anhang. A1 Analytische Lösungen der erweiterten Anzahlbilanz
 117 Anhang A1 Analyiche Löungen der erweieren Anzahlbilanz Die Bilanzgleichungen der erweieren Anzahlvereilung owohl für die koninuierliche al auch für die dikoninuierliche Krialliaion (l..-34 und.-35)
117 Anhang A1 Analyiche Löungen der erweieren Anzahlbilanz Die Bilanzgleichungen der erweieren Anzahlvereilung owohl für die koninuierliche al auch für die dikoninuierliche Krialliaion (l..-34 und.-35)
Bewertungsmethoden in der Versicherungsmathematik
 Bewerungmehoden in der Vericherungmahemaik Techniche Reerven und Markwere II Johanne Pacheag Mahemaiche Iniu der Univeriä zu Köln Sommeremeer 2010 Bereuung: Prof. Schmidli, Dr. Eienberg 1 Inhalverzeichni
Bewerungmehoden in der Vericherungmahemaik Techniche Reerven und Markwere II Johanne Pacheag Mahemaiche Iniu der Univeriä zu Köln Sommeremeer 2010 Bereuung: Prof. Schmidli, Dr. Eienberg 1 Inhalverzeichni
Arbeitsauftrag Thema: Gleichungen umformen, Geschwindigkeit, Diagramme
 Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Die Bildung des Präsens funktioniert dann beispielsweise so: "lauda + mus" - wir loben.
 Präen Da Präen i die Gegenwarform. E bechreib alo Handlungen, die gerade paieren. Die Bildung i denkbar einfach und unercheide ich in den unerchiedlichen Konjugaionen (fa immer) nich. Dewegen reich e vollkommen
Präen Da Präen i die Gegenwarform. E bechreib alo Handlungen, die gerade paieren. Die Bildung i denkbar einfach und unercheide ich in den unerchiedlichen Konjugaionen (fa immer) nich. Dewegen reich e vollkommen
Fakultät Grundlagen. s = t. gleichförm ig
 Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Weg im tv-diagramm. 1. Rennwagen
 Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
Technische Universität München Fakultät für Mathematik Algorithmische Diskrete Mathematik WS 2012/2013 Prof. Dr. P. Gritzmann 9.
 Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
Aufgabenblatt 10: Investitionstheoretische Kostenrechnung I
 Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
25. Flüsse in Netzen. Motivation. Fluss. Flussnetzwerk
 Moivaion 25. Flüe in Nezen Flunezwerk, Maximaler Flu, Schni, Renezwerk, Max-flow Min-cu, Ford-Fulkeron Mehode, Edmond-Karp Algorihmu, Maximale Biparie Maching [Oman/Widmayer, Kap. 9.7, 9.8.1], [Cormen
Moivaion 25. Flüe in Nezen Flunezwerk, Maximaler Flu, Schni, Renezwerk, Max-flow Min-cu, Ford-Fulkeron Mehode, Edmond-Karp Algorihmu, Maximale Biparie Maching [Oman/Widmayer, Kap. 9.7, 9.8.1], [Cormen
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Übersicht Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 16: Maximaler Fluss
 Überich aenrukuren und lgorihmen Vorleung 16: Prof. r. Erika Ábrahám Theorie Hybrider Syeme Informaik 2 hp://h.rwh-aachen.de/eaching/-1/ daenrukuren-und-algorihmen/ iee Präenaion verwende in Teilen Folien
Überich aenrukuren und lgorihmen Vorleung 16: Prof. r. Erika Ábrahám Theorie Hybrider Syeme Informaik 2 hp://h.rwh-aachen.de/eaching/-1/ daenrukuren-und-algorihmen/ iee Präenaion verwende in Teilen Folien
MATLAB: Kapitel 4 Gewöhnliche Differentialgleichungen
 4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
Übersicht. Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 18: Maximaler Fluss (K26)
 Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
Messung der Ladung. Wie kann man Ladungen messen? /Kapitel Formeln auf S.134: Elektrische Ladung
 --- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
--- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
Anfangswertprobleme gewöhnlicher Differentialgleichungen
 13. Großübung Anfangswerprobleme gewöhnlicher Differenialgleichungen gesuch: mi T und y () = f(, ), y( ) = y (1) y( j+1 ) = y( j ) + j+1 j f(s, y(s)) ds () Idee: Erseze Inegral durch Quadraurformel Näherungen
13. Großübung Anfangswerprobleme gewöhnlicher Differenialgleichungen gesuch: mi T und y () = f(, ), y( ) = y (1) y( j+1 ) = y( j ) + j+1 j f(s, y(s)) ds () Idee: Erseze Inegral durch Quadraurformel Näherungen
Hauptprüfung 2010 Aufgabe 4
 Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
2 Torsion in dünnwandigen Querschnitten
 apl oz r-ing hail G Georgi Tragwerkerechnung Torion in dünnwandigen Querchnien Theorien, Vorauezungen und Hpoheen Theorien: Reine Torion ( Grundufe) Begründer: Jean Claude de T VENANT (9-886) mol, Inde:
apl oz r-ing hail G Georgi Tragwerkerechnung Torion in dünnwandigen Querchnien Theorien, Vorauezungen und Hpoheen Theorien: Reine Torion ( Grundufe) Begründer: Jean Claude de T VENANT (9-886) mol, Inde:
Definition Ein Homomorphismus von Lie-Algebren. Für uns ist vor allem die im folgenden Satz eingeführte Darstellung von Bedeutung.
 1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
F Rück. F r Rück. Mechanische Schwingungen. Größen zur quantitativen Beschreibung :
 Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
2. Torsion geschlossener Profile
 Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
1. Kontrolle Physik Grundkurs Klasse 11
 1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
Nutzung der inhärenten sensorischen Eigenschaften von piezoelektrischen Aktoren
 Nuzung der inhärenen enorichen Eigenchafen von piezoelekrichen Akoren K. Kuhnen; H. Janocha Lehruhl für Prozeßauomaiierung (LPA), Univeriä de Saarlande Im Sadwald, Gebäude 13, 6641 Saarbrücken Tel: 681
Nuzung der inhärenen enorichen Eigenchafen von piezoelekrichen Akoren K. Kuhnen; H. Janocha Lehruhl für Prozeßauomaiierung (LPA), Univeriä de Saarlande Im Sadwald, Gebäude 13, 6641 Saarbrücken Tel: 681
Geometric Algebra Computing Transformationen in LA und CGA Dr. Dietmar Hildenbrand
 Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
Algorithmische Graphentheorie
 Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
(3) Weg-Zeit-Verhalten
 (3) Weg-Zei-Verhalen Vorleung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wdh: Bogenlängenabelle Pfad felegen (P 0, P, P and P 3 ) 3 3 r u u P0 3 u u P 3 u u P u P Berechne Poiion für Zeipunk, i.e.
(3) Weg-Zei-Verhalen Vorleung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wdh: Bogenlängenabelle Pfad felegen (P 0, P, P and P 3 ) 3 3 r u u P0 3 u u P 3 u u P u P Berechne Poiion für Zeipunk, i.e.
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
W. Stark; Berufliche Oberschule Freising
 9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
Gruppenarbeit: Anwendungen des Integrals Gruppe A: Weg und Geschwindigkeit
 Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
Robuste Portfolio Optimierung
 Robue Porfolio Opimierung in Lévy Märken Dieraion zur Erlangung de Dokorgrade Dr. rer. na der Fakulä für Mahemaik und Wirchafwienchafen der Univeriä Ulm vorgeleg von Dipl.-Mah. oec. Frank Wiemann au Offenburg
Robue Porfolio Opimierung in Lévy Märken Dieraion zur Erlangung de Dokorgrade Dr. rer. na der Fakulä für Mahemaik und Wirchafwienchafen der Univeriä Ulm vorgeleg von Dipl.-Mah. oec. Frank Wiemann au Offenburg
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Einführung in gewöhnliche Differentialgleichungen
 Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Ausgleichsrechnung - Lineare Regression
 ugleichrechnung - Lineare Regreion Die biher berachee Fehlerrechnung i gu verwendbar wenn ich die beracheen Größen dire een laen. Of ind phialiche Größen für eine diree Meung aber nur chwer zugänglich;
ugleichrechnung - Lineare Regreion Die biher berachee Fehlerrechnung i gu verwendbar wenn ich die beracheen Größen dire een laen. Of ind phialiche Größen für eine diree Meung aber nur chwer zugänglich;
8 Der Reiterationssatz
 53 8 Der Reieraionaz Definiion 8. Seien {A,A } ein Inerpolaionpaar,E ein Banachraum mi A A E A +A, und θ. i E gehör zur Klae Kθ;A,A, fall ein c > exiier, o da für alle a E und alle, <
53 8 Der Reieraionaz Definiion 8. Seien {A,A } ein Inerpolaionpaar,E ein Banachraum mi A A E A +A, und θ. i E gehör zur Klae Kθ;A,A, fall ein c > exiier, o da für alle a E und alle, <
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
No-Arbitrage Modelle
 No-Arbirage Modelle Sefan Fremd 17. Januar 27 1 Einleiung No-Arbirage Modelle: Modelle, bei denen die beobacheen Preise der Anleihen Derivae am Mark P obs (, T ) genau mi denen des Modells ˆP (, T ) übereinsimmen,
No-Arbirage Modelle Sefan Fremd 17. Januar 27 1 Einleiung No-Arbirage Modelle: Modelle, bei denen die beobacheen Preise der Anleihen Derivae am Mark P obs (, T ) genau mi denen des Modells ˆP (, T ) übereinsimmen,
Laplace Transformation
 Prof. Dr. Michael Eiermann Höhere Mahemaik 3 (verief) Kapiel L Laplace Tranformaion Die Laplace Tranformaion verwandel Anfangwerprobleme für lineare Differenialgleichungen mi konanen Koeffizienen in algebraiche
Prof. Dr. Michael Eiermann Höhere Mahemaik 3 (verief) Kapiel L Laplace Tranformaion Die Laplace Tranformaion verwandel Anfangwerprobleme für lineare Differenialgleichungen mi konanen Koeffizienen in algebraiche
12.6 Aufgaben zur Laplace-Transformation
 292 12. Aufgaben zu linearen Gleichungen 12.6 Aufgaben zur Laplace-Tranformation A B C D Man löe die folgenden Anfangwertprobleme durch Laplace-Tranformation: 1) ẍ ẋ x = ; x() = ẋ() = 1 2) x (3) 6ẍ + 12ẋ
292 12. Aufgaben zu linearen Gleichungen 12.6 Aufgaben zur Laplace-Tranformation A B C D Man löe die folgenden Anfangwertprobleme durch Laplace-Tranformation: 1) ẍ ẋ x = ; x() = ẋ() = 1 2) x (3) 6ẍ + 12ẋ
Kapitel : Exponentiell-beschränktes Wachstum
 Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Positioniersteuerung (5.12) Beschleunigen - Phase 2 (5.13) Beschleunigen - Phase 3 (5.14) Phase 4: Konstante Geschwindigkeit (5.15) Bremsen Phase 5
 Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
Transport. Explizite und implizite Verfahren
 p. 1/9 Tranpor Explizie und implizie Verfahren home/lehre/vl-mhs-1/inhalt/folien/vorlesung/10_transport_verf/decbla.ex Seie 1 von 9 p. /9 Inhalverzeichni 1. Explizie Verfahren Inabile Verfahren Lax Verfahren
p. 1/9 Tranpor Explizie und implizie Verfahren home/lehre/vl-mhs-1/inhalt/folien/vorlesung/10_transport_verf/decbla.ex Seie 1 von 9 p. /9 Inhalverzeichni 1. Explizie Verfahren Inabile Verfahren Lax Verfahren
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
3.4 Systeme linearer Differentialgleichungen
 58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
Ferienkurs Analysis I für Physiker WS 15/16 Aufgaben Tag 3. Aufgaben Tag 3
 für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
7) Fertigung der Durchströmturbine
 oku Verion 1.0 aum 04.10.2004 urchrömurbine elb gebau 7) Ferigung der urchrömurbine 7.1 Turbinendaen - Geamanich ie hier im eail bechriebene urchrömurbine mi einem Laufraddurchmeer von 200 mm kann Fallhöhen
oku Verion 1.0 aum 04.10.2004 urchrömurbine elb gebau 7) Ferigung der urchrömurbine 7.1 Turbinendaen - Geamanich ie hier im eail bechriebene urchrömurbine mi einem Laufraddurchmeer von 200 mm kann Fallhöhen
Inhaltsübersicht. Funktionenraum Fouriertransformation Laplacetransformation Partialbruchzerlegung Faltung
 Inhalüberich Kapiel : Reihenenwicklungen und Tranformaionen: au x mach u und wieder zurück Funkionenraum Fourierranformaion Laplaceranformaion Parialbruchzerlegung Falung Noizen zur Vorleung Mahemaik für
Inhalüberich Kapiel : Reihenenwicklungen und Tranformaionen: au x mach u und wieder zurück Funkionenraum Fourierranformaion Laplaceranformaion Parialbruchzerlegung Falung Noizen zur Vorleung Mahemaik für
Diese 3 Signale haben als Anregungssignale am Eingang eines Systems besondere Bedeutung für die lineare Systemtheorie erlangt.
 16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
Zusammenfassung Gleichmäßig beschleunigte Bewegung
 3c D-Kineaik Zuaenfaung a a a a a con con poii con negai Gleichäßig bechleunige Bewegung + a + + a + a( ) + ( - ) + - a Bechleunigungen Magnechwebebahn Erreich der Tranrapid auf der Srecke on Shanghai-Flughafen
3c D-Kineaik Zuaenfaung a a a a a con con poii con negai Gleichäßig bechleunige Bewegung + a + + a + a( ) + ( - ) + - a Bechleunigungen Magnechwebebahn Erreich der Tranrapid auf der Srecke on Shanghai-Flughafen
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Bitte beginnen Sie jede neue Aufgabe auf einem neuen Blatt!
 Soereeer 010 Bla 1 (on 7) Sudiengang: BT(B) / CI(B) Seeer Prüfungfach: Phyik Fachnuer: 04, 071, 07 Hilfiel: Manukrip, Lieraur, Tachenrechner Zei:10 Minuen Ingea ind 10 Punke erreichbar. Bie beginnen Sie
Soereeer 010 Bla 1 (on 7) Sudiengang: BT(B) / CI(B) Seeer Prüfungfach: Phyik Fachnuer: 04, 071, 07 Hilfiel: Manukrip, Lieraur, Tachenrechner Zei:10 Minuen Ingea ind 10 Punke erreichbar. Bie beginnen Sie
Ermittlung von Leistungsgrenzen verschiedener Lagerstrategien unter Berücksichtigung zentraler Einflussgrößen
 Ermilung von Leiunggrenzen verchiedener Lagerraegien uner Berücichigung zenraler Einflugrößen Dipl.-Wir.-Ing. (FH) Anne Piepenburg, Prof. Dr.-Ing. Rainer Brun Helmu-Schmid-Univeriä, Hamburg Lehruhl für
Ermilung von Leiunggrenzen verchiedener Lagerraegien uner Berücichigung zenraler Einflugrößen Dipl.-Wir.-Ing. (FH) Anne Piepenburg, Prof. Dr.-Ing. Rainer Brun Helmu-Schmid-Univeriä, Hamburg Lehruhl für
Abiturprüfung Baden-Württemberg 1986
 c 001 by Rainer Müller - www.emah.de 1 Lösng Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR a Asympoen Senkreche Asympoen Es
c 001 by Rainer Müller - www.emah.de 1 Lösng Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR a Asympoen Senkreche Asympoen Es
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
u(t) sin(kωt)dt, k > 0
 Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Aufgaben zur gleichförmigen Bewegung
 Aufgaben zur gleichförigen Bewegung 860. Ein Waerrad on 5 Durcheer eh an eine 2 breien und 0,7 iefe Bach. Da Rad dreh ich in der Minue 5 al und i a Rand genau o chnell, wie der Bach fließ. Wie iel Lier
Aufgaben zur gleichförigen Bewegung 860. Ein Waerrad on 5 Durcheer eh an eine 2 breien und 0,7 iefe Bach. Da Rad dreh ich in der Minue 5 al und i a Rand genau o chnell, wie der Bach fließ. Wie iel Lier
Grenzwertsätze für Zeitreihen
 KAPIEL 6 Grenzwersäze für Zeireihen In diesem Kapiel sellen wir wichige Grenzwersäze für saionäre Zeireihen {X n } in diskreer Zei zusammen. Sei µ = E(X ) und ρ(k) = E(X 1 µ)(x 1+k µ) = Cov (X 1, X 1+k
KAPIEL 6 Grenzwersäze für Zeireihen In diesem Kapiel sellen wir wichige Grenzwersäze für saionäre Zeireihen {X n } in diskreer Zei zusammen. Sei µ = E(X ) und ρ(k) = E(X 1 µ)(x 1+k µ) = Cov (X 1, X 1+k
Von der Fourier-Reihe zum Fourier-Integral
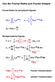 Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Geradendarstellung in Paramterform
 Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
8 Martingaldarstellung und Doob-Meyer Zerlegung
 8 Martingaldartellung und Doob-Meyer Zerlegung 8.1 Der Martingaldartellungatz In Kapitel 3 haben wir gezeigt, da da Ito-Integral eine H -Integranden ein tetige Martingal it. Der Martingaldartellungatz
8 Martingaldartellung und Doob-Meyer Zerlegung 8.1 Der Martingaldartellungatz In Kapitel 3 haben wir gezeigt, da da Ito-Integral eine H -Integranden ein tetige Martingal it. Der Martingaldartellungatz
4 Die K-Methode. Sei {A 0,A 1 } Interpolationspaar. Das Peetre sche K-Funktional ist definiert als. ( a 0 A 0 +t a 1 A 1 ), a A 0 +A 1, t > 0
 25 4 Die K-Mehode Sei {A,A } Inerpolaionpaar. Da Peere che K-Funkional i definier al K,a;A,A K,a : a a + a a i A i,i, a A + a A, a A +A, > Bemerkung : wenn {A,A } fixier K,a anelle von K,a;A,A K,a a A
25 4 Die K-Mehode Sei {A,A } Inerpolaionpaar. Da Peere che K-Funkional i definier al K,a;A,A K,a : a a + a a i A i,i, a A + a A, a A +A, > Bemerkung : wenn {A,A } fixier K,a anelle von K,a;A,A K,a a A
reibungsgedämpfte Schwingung
 HTL-LiTec reibunggedäpfe Schwingung Seie 1 von 7 Dipl.-Ing. Paul MOHR E-Brief: p.ohr@eduhi.a reibunggedäpfe Schwingung Maheaiche / Fachliche Inhale in Sichworen: reibunggedäpfe Schwingung; nueriche Löung
HTL-LiTec reibunggedäpfe Schwingung Seie 1 von 7 Dipl.-Ing. Paul MOHR E-Brief: p.ohr@eduhi.a reibunggedäpfe Schwingung Maheaiche / Fachliche Inhale in Sichworen: reibunggedäpfe Schwingung; nueriche Löung
3.2 Autoregressive Prozesse (AR-Modelle) AR(p)-Prozesse
 3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
Laplacetransformation in der Technik
 Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
2.1 STURMSCHES ANFANGSWERTPROBLEM UND DGL 2. ORDNUNG
 . STURMSCHES ANANGSWERTPROBLEM UND DGL. ORDNUNG S o genanne Anfangwerprobleme reen ehr häufig bei naurwienchaflichen un echnichen Problemellungen auf. Hierbei hanel e ich in er Regel um DGL. Ornung oer.
. STURMSCHES ANANGSWERTPROBLEM UND DGL. ORDNUNG S o genanne Anfangwerprobleme reen ehr häufig bei naurwienchaflichen un echnichen Problemellungen auf. Hierbei hanel e ich in er Regel um DGL. Ornung oer.
Mathematik III DGL der Technik
 Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Abiturprüfung Baden-Württemberg 1986
 001 - hp://www.emah.de 1 Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR Ihr Schabild sei K. a Unersche K af Asympoen, Schnipnke
001 - hp://www.emah.de 1 Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR Ihr Schabild sei K. a Unersche K af Asympoen, Schnipnke
1. Für die Bewegung eines Fahrzeuges wurde das t-s-diagramm aufgenommen. Skizziere für diese Bewegung das t-v- Diagramm.
 Aufgaben zur gleichförigen Bewegung 1. Für die Bewegung eine Fahrzeuge wurde da --Diagra aufgenoen. Skizziere für diee Bewegung da -- Diagra. 2. Eine Radfahrerin und ein Spaziergänger i eine Hund bewegen
Aufgaben zur gleichförigen Bewegung 1. Für die Bewegung eine Fahrzeuge wurde da --Diagra aufgenoen. Skizziere für diee Bewegung da -- Diagra. 2. Eine Radfahrerin und ein Spaziergänger i eine Hund bewegen
7. Vorlesung Wintersemester
 7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Fokker-Planck-Gleichung
 Fokker-Planck-Gleichung Beschreibung sochasischer Prozesse David Kleinhans kleinhan@uni-muenser.de WWU Münser David Kleinhans, WWU Münser Fokker-Planck-Gleichung Beschreibung elemenarer sochasischer Prozesse
Fokker-Planck-Gleichung Beschreibung sochasischer Prozesse David Kleinhans kleinhan@uni-muenser.de WWU Münser David Kleinhans, WWU Münser Fokker-Planck-Gleichung Beschreibung elemenarer sochasischer Prozesse
Theoretische Grundlagen
 Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
III.2 Radioaktive Zerfallsreihen
 N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
Staatlich geprüfte Techniker
 Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Geradlinige Bewegung Krummlinige Bewegung Kreisbewegung
 11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
Lösungen zu Übungsblatt 4
 Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Motivation der Dierenzial- und Integralrechnung
 Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
Zeitreihenökonometrie
 Zeireihenökonomerie Kapiel 4 Schäzung univariaer Zeireihenmodelle Y = c+ α Y + + α Y + ε + βε + + β ε p p q q Problem: Direke Schäzung der Parameer α,, αp und β,, βq über OLS nich möglich, da die Residuen
Zeireihenökonomerie Kapiel 4 Schäzung univariaer Zeireihenmodelle Y = c+ α Y + + α Y + ε + βε + + β ε p p q q Problem: Direke Schäzung der Parameer α,, αp und β,, βq über OLS nich möglich, da die Residuen
Prof. Dr. Holger Dette Musterlösung Statistik I Sommersemester 2009 Dr. Melanie Birke Blatt 9
 Prof r Holger ette Muterlöung Statitik I Sommeremeter 009 r Melanie Birke Blatt 9 Aufgabe : 4 Punkte E eien X,, X n unabhängig identich N µ, -verteilt a Man berechne die Fiher-Information I µ für µ b E
Prof r Holger ette Muterlöung Statitik I Sommeremeter 009 r Melanie Birke Blatt 9 Aufgabe : 4 Punkte E eien X,, X n unabhängig identich N µ, -verteilt a Man berechne die Fiher-Information I µ für µ b E
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 13 Wintersemester 2011/2012
 Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
2.2 Rechnen mit Fourierreihen
 2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
Integralrechnung. Grundidee der Integralrechnung. Einführung des Riemann- Integrals
 1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
Hallo Welt für Fortgeschrittene
 Hallo Wel für Forgechriene Flüe, Schnie, Biparie Graphen I Florian Hanke Informaik Programmieryeme Marenraße 3 958 Erlangen Inhal Grundlagen Ford-Fulkeron-Algorihmu Edmond-Karp-Sraegie Minimaler Schni
Hallo Wel für Forgechriene Flüe, Schnie, Biparie Graphen I Florian Hanke Informaik Programmieryeme Marenraße 3 958 Erlangen Inhal Grundlagen Ford-Fulkeron-Algorihmu Edmond-Karp-Sraegie Minimaler Schni
 Ergänzung Kpiel 5. Whl der Führunggröße Whl der Führunggröße für Lgeregelungen Biher wurde mei on einem prungförmigen Verluf der Führunggröße w( ugegngen. Viele regelungechniche Anwendungen weien uch ein
Ergänzung Kpiel 5. Whl der Führunggröße Whl der Führunggröße für Lgeregelungen Biher wurde mei on einem prungförmigen Verluf der Führunggröße w( ugegngen. Viele regelungechniche Anwendungen weien uch ein
3. Partielle Differentialgleichungen
 3.. Grundlagen und Klassifikaion Welche Ordnung haben diese Gleichungen?? 3.4.1 Lineare parielle Differenialgleichungen. Ordnung Analogie: Klassifikaion Kegelschnie 1 3.4.3 Korrek geselle Probleme Anfangs-
3.. Grundlagen und Klassifikaion Welche Ordnung haben diese Gleichungen?? 3.4.1 Lineare parielle Differenialgleichungen. Ordnung Analogie: Klassifikaion Kegelschnie 1 3.4.3 Korrek geselle Probleme Anfangs-
