Integralrechnung. Grundidee der Integralrechnung. Einführung des Riemann- Integrals
|
|
|
- Bernhard Huber
- vor 7 Jahren
- Abrufe
Transkript
1 1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden. Zur Hisorie siehe auch: hp://de.wikipedia.org/wiki/inegralrechnung Das Inegral is ein Oberbegriff für das unbesimme und das besimme Inegral. Die Berechnung von Inegralen heiß Inegraion, Inegraion und Differeniaion sind zueinander inverse Operaionen. Der Begriff Inegral geh auf Johann Bernoulli zurück; heue sprich man vom Riemann`schen Inegral, wenn es um das Problem der Flächenberechnung uner einer Kurve geh. Das Inegralzeichen repräsenier lezlich eine Summaion ensprechender infiniesimaler Beiräge. Einführung des Riemann- Inegrals f f f f mi Sammfunkion ( ) ( c ) f MERKE: Die Sammfunkion is bis auf eine Konsane besimm. Geomerische Inerpreaion: f =lim f = (a) l che uner er urve f -Berechnung des Flächeninhales uner einer beliebigen Kurve f(x) im Inervall [a,b] Schreibweise: f lim f Differenial f Inegran a, Inegraionsgrenzen Seie: 1/8
2 2/8 besimmes Inegral wird genuz, um Flächeninhale zwischen dem Funkionsgraphen und der x-achse zu berechnen z.b.: dx= I = 2 4 [ ] unbesimmes Inegral ordne einer Funkion die Menge der Sammfunkionen zu f = F(x) + c0 z.b.: c0, c0 = cons. Definiion. (Sammfunkion) Sei I ein Inervall un f: I ine unkion : I heiß Sammfunkion von f, falls F differenzierbar auf I is und F'(x) = f(x) für alle x I gil. Haupsaz der Differenial- und Inegralrechnung (HDI) Der HDI beinhale zwei grundlegende Aussagen. Die erse Aussage beriff die Exisenz von Sammfunkionen und den Zusammenhang von Ableiung und Inegral. Sei f: [a, ] mi eine reell erige seige unkion auf em a geschlossenen Inervall [a, ], so is für alle [a, ] die Inegralfunkion : [a, ] mi f() ifferenzier ar un eine ammfunkion zu f, h, es gil für alle [a, ] Zu beachen is, dass die Funkion F aufgrund der Exisenz des Riemann-Inegrals für seige Funkionen an allen Sellen in [a, b] definier is. Der zweie Teil des Sazes erklär, wie Inegrale berechne werden können. ei f: [a, ] eine seige unkion mi er ammfunkion : [a, ], ann gil ie e on ei niz ormel: (a) Eigenschafen des Inegrals = c = c = - ( Minus beachen bei Verauschen der Grenzen )
3 3/8 = 0; = 0 Einfache Beispiele unbesimme Inegrale ( c = cons ) = cos c ; = sin x+c ; e = e x c ; e e c ; dx= ln x + c0; besimme Inegrale = [x³] = 4³ = 64 [FE] - = [ + x³ + 4x] - = 2³ - (- 2³) (-8) = 32 [FE] Inegraionsmehoden Poenzregel c ; c cons (n ; n ) Subsiuionsregel Siehe Keenregel! Beispiel 1 Berechnung des Inegrals sin für eine beliebige reele Zahl a > 0: Durch die Subsiuion erhäl man und:
4 4/8 sin sin() sin() [ cos()] ( cos( a) cos) ( cos( a)) Beispiel 2 Berechnung des Inegrals cos Durch die Subsiuion erhäl man bzw. und dami cos cos() (sin sin) Es wird also durch ersez und durch. Die unere Grenze des Inegrals Umgewandel und die obere Grenze wird dabei in in Beispiel 3 Berechnung des Inegrals Man subsiuiere () sin() arcsin. Daraus ergib sich cos() Mi sin () cos () erhäl man sin () cos() cos () Das Ergebnis kann mi parieller Inegraion oder mi der rigonomerischen Formel cos () cos und einer weieren Subsiuion berechne werden.
5 5/8 Spezialfälle der Subsiuion o Logarihmische Inegraion Inegrale mi der speziellen Form Zähler des Inegranden is Ableiung des Nenners können sehr einfach mi Hilfe der logarihmischen Inegraion gelös werden, was einen Spezialfall der Subsiuionsmehode darsell: f f ln f (f ) o Eulersche Subsiuion Nach einem Saz von Bernoulli lassen sich alle Inegrale des Typs a c und elemenar inegrieren. Beispiel: Durch die Subsiuion also,, und ergib sich: ln ln ( ) o Lineare Subsiuion Inegrale mi linearen Verkeungen können wie folg berechne werden: f(m n) m (m n) ( m ) Für das besimme Inegral gil ensprechend: f(m n) [ (m n)] ( m ) m Berechnung von Inegralen durch parielle Inegraion Zu Berechnung des Inegrals von Produken: u v uv = uv- u v dx (parielle Inegraion = Umkehrung der Produkregel aus der Differenialrechnung) Gu an en ar, enn ie ammfunkion zu u ekann o er leich zu esimmen is Herleiung: [u v] u v u v
6 6/8 Links kompensieren sich Ableiung und Inegral und es verbleib die Sammfunkion der Ableiung u v [u v] a - u v b Es gil die Fausregel: ln wird abgeleie e inegrier Beispiele: a) e u v dx 1) u ; v e 2) u ; v e Einsezen in: u v u v u v 1 0 [x e ] - ( e ) = -1e e e e e b) ln u v u ; u(x)= v ln ; v e Einsezen in die Formel: [ ln ] - = [ ] = = 10,3 c) e u ; u v e ; v(x)= e 1 e 1 Nebenrechnung: e u siuion: a a z u e u e Rücksu siuion: e e e e e = e e Nebenrechnung: e u u v e v e e e e e e e e
7 7/8 e e e e ( e e ) e e e c0 Bei der Inegraion sind ofmals Kombinaionen von mehreren Inegraionsmehoden nöig. Berechnung von Inegralen mi Hilfe der Keenregel Allgemein gil: f(g) f g f (g) g d(f(g(x))) = f(g) Beseh as Inegral aus ußerer mal innerer A leiung: f (g) g f(g) Bsp: Spezialfälle: A) f (g) = ln g c0 Bsp: dx = ln c0 B) f (g) g g g g c0 Berechnung von Inegralen mi Hilfe der Parialbruchzerlegung Anwendung: Zur Berechnung des Inegrals Form f(x)= bei gebrochen raionalen Funkionen der Idee: Umwandlung der Funkion in eine Summe von Teilbrüchen. Teilbrüche können über verschiedene andere Inegraionsmehoden gelös werden. Durchführung am Beispiel: 1. Schri: In eine Summe von Teilbrüche verwandeln - Besimmung der Nullsellen des Nennerpolynoms: x²+3x+ 1= -2; x2= -1 - Zuordnung eines Parialbruches: = und = f(x)=
8 8/8 - Besimmung der Variablen A und B: F(x) = A B Für x=-1: f(x) =3=A(-1+1)+B(- ) B B Für x=-2: f(x) = 3=A(-2+1)+B(-2+2)=-A A Schri: Berechnung des Inegrals -3 Subsiuieren: u= x+2; v=x+1-3 = -3ln u ln v c = -3ln +3ln + c =3ln + c Also: ln c Es gil die allgemeine Formel: a= ; b= ln c Skrip ersell von P. Lehmann und S. Gujahr
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
2.2 Rechnen mit Fourierreihen
 2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
Analysis 3.
 Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Ferienkurs Analysis I für Physiker WS 15/16 Aufgaben Tag 3. Aufgaben Tag 3
 für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
Elementare Lösungsmethoden für gewöhnliche Differentialgleichungen
 454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
1 Lokale Änderungsrate und Gesamtänderung
 Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Gewöhnliche Differentialgleichungen
 Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
Diese 3 Signale haben als Anregungssignale am Eingang eines Systems besondere Bedeutung für die lineare Systemtheorie erlangt.
 16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Kurven in der Ebene und im Raum
 Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
7.3. Partielle Ableitungen und Richtungsableitungen
 7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Einführung in gewöhnliche Differentialgleichungen
 Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Mathematikaufgaben > Analysis > Funktionenscharen
 Michael Buhlmann Mahemaikaugaben > Analysis > Funkionenscharen Augabe: Unersuche die ganz raionale Funkionenschar + 8 mi Parameer > 0 au: Nullsellen, Hoch- und Tiepunke, Monoonie, Wendepunke, Krümmung,
Michael Buhlmann Mahemaikaugaben > Analysis > Funkionenscharen Augabe: Unersuche die ganz raionale Funkionenschar + 8 mi Parameer > 0 au: Nullsellen, Hoch- und Tiepunke, Monoonie, Wendepunke, Krümmung,
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann
 Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann Aufgabe Im abgelaufenen Jahr haen einige große deusche Firmen hohe prozenuale Gewinnzuwächse. Gleichzeiig wurden eilweise massiv
Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann Aufgabe Im abgelaufenen Jahr haen einige große deusche Firmen hohe prozenuale Gewinnzuwächse. Gleichzeiig wurden eilweise massiv
Motivation: Sampling. (14) Sampling. Motivation: Sampling. Beispiele. Beispiel Kreisscheibe. Beispiel: Kreisscheibe
 Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
7. Funktionalgleichung der Zeta-Funktion
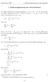 Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Zwischenwerteigenschaft
 Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
7 Das lokale Ito-Integral
 7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Analysis: Exponentialfunktionen Analysis
 www.mahe-aufgaben.com Analysis: Eponenialfunkionen Analysis Übungsaufgaben u Eponenialfunkionen Pflich- und Wahleil gesames Soffgebie (insbesondere Funkionsscharen) ohne Wachsum Gymnasium ab J Aleander
www.mahe-aufgaben.com Analysis: Eponenialfunkionen Analysis Übungsaufgaben u Eponenialfunkionen Pflich- und Wahleil gesames Soffgebie (insbesondere Funkionsscharen) ohne Wachsum Gymnasium ab J Aleander
Technische Universität München. Lösung Montag SS 2012
 Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Abituraufgaben Grundkurs 2009 Bayern Analysis I. dt mit D F = R.
 Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Mathematik III DGL der Technik
 Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Herleitung: Effektivwerte
 Herleing: Effekivwere elekre.gihb.io December 16, 1 1 Definiion Der Effekivwer is die Spannng einer Wechselgröße im zeilichen Miel, drch die mi einer Gleichqelle die selbe Leisng an einem Verbracher abfallen
Herleing: Effekivwere elekre.gihb.io December 16, 1 1 Definiion Der Effekivwer is die Spannng einer Wechselgröße im zeilichen Miel, drch die mi einer Gleichqelle die selbe Leisng an einem Verbracher abfallen
MATLAB: Kapitel 4 Gewöhnliche Differentialgleichungen
 4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
4. Erhaltungssätze für Masse und Impuls
 4. Erhalngssäze für Masse n Impls Wie ie klassische Mechanik basier ie Srömngsmechanik af er Erhalng von Masse Impls Energie Die Erhalngsgeseze gelen für as infiniesimal kleine Flielemen n für reiimensionale
4. Erhalngssäze für Masse n Impls Wie ie klassische Mechanik basier ie Srömngsmechanik af er Erhalng von Masse Impls Energie Die Erhalngsgeseze gelen für as infiniesimal kleine Flielemen n für reiimensionale
Stammgruppe trifft sich zum Museumsrundgang Experte erklärt jeweils sein Plakat
 Fachag Mahemaik: Kurvenscharen Ablauf: 1. Sunde Gemeinsame Einsiegsaufgabe. Sunde Sammgruppenaufgaben Sammgruppen (a bis 6 Schüler) Jedes Gruppenmiglied erhäl eine unerschiedliche Aufgabe A, B, C, D in
Fachag Mahemaik: Kurvenscharen Ablauf: 1. Sunde Gemeinsame Einsiegsaufgabe. Sunde Sammgruppenaufgaben Sammgruppen (a bis 6 Schüler) Jedes Gruppenmiglied erhäl eine unerschiedliche Aufgabe A, B, C, D in
Abiturprüfung Mathematik 2012 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1
 Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Differenzieren von Funktionen zwischen Banachräumen
 Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
Kontinuierliche Fourier Transformation
 Koninuierliche Fourier ransformaion f () is eine nichperiodische Funkion. Um die Frequenzen in einem beliebigen Zeisignal zu besimmen, inerpreieren wir die Funkion f () als periodische Funkion mi Periode.
Koninuierliche Fourier ransformaion f () is eine nichperiodische Funkion. Um die Frequenzen in einem beliebigen Zeisignal zu besimmen, inerpreieren wir die Funkion f () als periodische Funkion mi Periode.
Motivation der Dierenzial- und Integralrechnung
 Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
Lösungsvorschläge zu ausgewählten Übungsaufgaben aus Storch/Wiebe: Lehrbuch der Mathematik Band 1, 3.Aufl. (Version 2010), Kapitel 6
 Lösungsvorschläge zu ausgewählen Übungsaufgaben aus Sorch/Wiebe: Lehrbuch der Mahemaik Band, 3.Aufl. Version, Kapiel 6 6 Sammfunkionen und Inegrale Abschni 6.A, Variane zu Aufg. 5, p. 44.4. : Man gebe
Lösungsvorschläge zu ausgewählen Übungsaufgaben aus Sorch/Wiebe: Lehrbuch der Mahemaik Band, 3.Aufl. Version, Kapiel 6 6 Sammfunkionen und Inegrale Abschni 6.A, Variane zu Aufg. 5, p. 44.4. : Man gebe
mathphys-online Abschlussprüfung Berufliche Oberschule 2009 Mathematik 12 Technik - A I - Lösung Teilaufgabe 1.0 Gegeben ist die reelle Funktion f( x)
 Abschlussprüfung Berufliche Oberschule 9 Mahemaik Technik - A I - Lösung Teilaufgabe. Gegeben is die reelle Funkion f( x) in der Definiionsmenge ID f = IR. Teilaufgabe. (4 BE) Unersuchen Sie das Verhalen
Abschlussprüfung Berufliche Oberschule 9 Mahemaik Technik - A I - Lösung Teilaufgabe. Gegeben is die reelle Funkion f( x) in der Definiionsmenge ID f = IR. Teilaufgabe. (4 BE) Unersuchen Sie das Verhalen
1 Integrale von Funktionen in mehreren Variablen
 $Id: inegral.ex,v 1.12 2015/10/26 13:46:09 hk Exp $ 1 Inegrale von Funkionen in mehreren Variablen 1.1 Das Rieman Inegral im R n Im lezen Semeser wurde die Differenialrechnung auf Funkionen f(x 1,...,
$Id: inegral.ex,v 1.12 2015/10/26 13:46:09 hk Exp $ 1 Inegrale von Funkionen in mehreren Variablen 1.1 Das Rieman Inegral im R n Im lezen Semeser wurde die Differenialrechnung auf Funkionen f(x 1,...,
f ( x) = x + x + 1 (quadratische Funktion) f '( x) = x + (Ableitungsfunktion)
 R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
Analysis II Musterlösung 12. für t [ 0, 2π). y
 .. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
.. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
7. Vorlesung Wintersemester
 7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
Lösung zur Hausaufgabe in Topologie und Differentialrechnung mehrerer Variablen SS x 1. x 2. x 1+x 2+x 3
 Bl Nr. 11 Simon Reisser Lösung zur Husufgbe in Topologie und Differenilrechnung mehrerer Vriblen SS 17 Aufgbe () Sei f(x 1, x, x 3 ) = (y 1, y, y 3 ) = (e x1x x3, e x1x+x3, e xx3 ) und dg(y 1, y, y 3 )
Bl Nr. 11 Simon Reisser Lösung zur Husufgbe in Topologie und Differenilrechnung mehrerer Vriblen SS 17 Aufgbe () Sei f(x 1, x, x 3 ) = (y 1, y, y 3 ) = (e x1x x3, e x1x+x3, e xx3 ) und dg(y 1, y, y 3 )
Fourier- und Laplace- Transformation
 Skrium zur Vorlesung Mahemaik für Ingenieure Fourier- und Lalace- Transformaion Teil 3: Lalace-Transformaion Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) Fachhochschule
Skrium zur Vorlesung Mahemaik für Ingenieure Fourier- und Lalace- Transformaion Teil 3: Lalace-Transformaion Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) Fachhochschule
Zentrale schriftliche Abiturprüfungen im Fach Mathematik
 Zenrale schrifliche Abiurprüfungen im Fach Mahemaik Aufgabe 9: Radioakiver Zerfall Beim radioakiven Zerfall einer Subsanz S 1 beschreib m 1 () die Masse der noch nich zerfallenen Subsanz zum Zeipunk mi
Zenrale schrifliche Abiurprüfungen im Fach Mahemaik Aufgabe 9: Radioakiver Zerfall Beim radioakiven Zerfall einer Subsanz S 1 beschreib m 1 () die Masse der noch nich zerfallenen Subsanz zum Zeipunk mi
Lösungen zu Übungsblatt 4
 Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Eigenwerte und Eigenvektoren
 Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Serpentine DEMO. Text Nr Stand FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK.
 Serpenine Te Nr. 560 Snd 6.3.6 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 560 Serpenine Vorwor Die Serpenine is eine lgebrische Kurve 3. Grdes, die mn uf einer geomerischen Eigenschf definieren
Serpenine Te Nr. 560 Snd 6.3.6 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 560 Serpenine Vorwor Die Serpenine is eine lgebrische Kurve 3. Grdes, die mn uf einer geomerischen Eigenschf definieren
Diskrete Integratoren und Ihre Eigenschaften
 Diskree Inegraoren und Ihre Eigenschafen Whie Paper von Dipl.-Ing. Ingo Völlmecke Indusrielle eglersrukuren werden im Allgemeinen mi Hilfe von Inegraoren aufgebau. Aufgrund des analogen Schalungsaufbaus
Diskree Inegraoren und Ihre Eigenschafen Whie Paper von Dipl.-Ing. Ingo Völlmecke Indusrielle eglersrukuren werden im Allgemeinen mi Hilfe von Inegraoren aufgebau. Aufgrund des analogen Schalungsaufbaus
Grundlagen der Elektrotechnik 3
 Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
Ganzrationale Funktionenscharen. 4. Grades. Umfangreiche Aufgaben. Lösungen ohne CAS und GTR. Alle Methoden ganz ausführlich. Datei Nr.
 Ganzraionale Funkionenscharen. Grades Umfangreiche Aufgaben Lösungen ohne CAS und GTR Alle Mehoden ganz ausführlich Daei Nr. 7 Sand 3. Sepember 06 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
Ganzraionale Funkionenscharen. Grades Umfangreiche Aufgaben Lösungen ohne CAS und GTR Alle Mehoden ganz ausführlich Daei Nr. 7 Sand 3. Sepember 06 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
Abschlussprüfung an Fachoberschulen in Bayern Mathematik mit CAS 2015 Analysis A2 Ausbildungsrichtung Technik
 MK.7.05 B5_T_A MK_Loes.xmc Abschlussprüfung an Fachoberschulen in Bayern Mahemaik mi 05 Analysis A Ausbilungsrichung Technik.0 Gegeben sin ie reellen Funkionen f a : x --> x x x Definiionsmenge D fa R
MK.7.05 B5_T_A MK_Loes.xmc Abschlussprüfung an Fachoberschulen in Bayern Mahemaik mi 05 Analysis A Ausbilungsrichung Technik.0 Gegeben sin ie reellen Funkionen f a : x --> x x x Definiionsmenge D fa R
um (x + X) 4 auszurechnen verwenden wir den Binomischen Lehrsatz (a+b) n = a n + ( n 1 )a n-1* b 1 + + b n ( n k ) = in Gleichung einsetzen
 Mahemaik I Übungsaufgaben 8 Lösungsorschläge on T. Meyer Era-Mahemaik-Übung: 005--06 Aufgabe Berechnen Sie die Ableiung der Funkion f an einer beliebigen Selle 0 ohne Verwendung irgendwelcher Vorkennnisse
Mahemaik I Übungsaufgaben 8 Lösungsorschläge on T. Meyer Era-Mahemaik-Übung: 005--06 Aufgabe Berechnen Sie die Ableiung der Funkion f an einer beliebigen Selle 0 ohne Verwendung irgendwelcher Vorkennnisse
Übungen zur Klausur 11M1 21/05/2008 Seite 1 von 5
 Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Demo-Text für Funktionen und Kurven. Differentialgeometrie INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK. Friedrich Buckel.
 Funkionen und Kurven Differenialgeomerie Tex Nummer: 5 Sand: 9. März 6 Demo-Tex für www.mahe-cd.de INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mahe-cd.de 5 Differenialgeomerie Vorwor Das Thema Kurven is
Funkionen und Kurven Differenialgeomerie Tex Nummer: 5 Sand: 9. März 6 Demo-Tex für www.mahe-cd.de INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mahe-cd.de 5 Differenialgeomerie Vorwor Das Thema Kurven is
Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik Lösungsvorschläge zum 6. Übungsblatt
 Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Analysis: Ganzrationale Funktionen Analysis Ganzrationale Funktionen Differenzialrechnung, Extrem- und Wendepunkte
 www.mahe-aufgaben.com Analysis: Ganzraionale Funkionen Analysis Ganzraionale Funkionen Differenzialrechnung, Exrem- und Wendepunke Gymnasium Klasse 0 Alexander Schwarz www.mahe-aufgaben.com Juni 0 www.mahe-aufgaben.com
www.mahe-aufgaben.com Analysis: Ganzraionale Funkionen Analysis Ganzraionale Funkionen Differenzialrechnung, Exrem- und Wendepunke Gymnasium Klasse 0 Alexander Schwarz www.mahe-aufgaben.com Juni 0 www.mahe-aufgaben.com
mittlere bremsende Kraft auf das Teilchen um diesen Mittelwert fluktuierende stochastische Kraft f(t) stochastischer Prozess
 Brownsche Bewegung schweres Teilchen mi Masse m und Geschwindigkei v beweg sich in Flüssigkei von leichen Teilchen. Dieses Brownsche Teilchen wird von den Molekülen der Flüssigkei gesoßen. Söße bewirken:
Brownsche Bewegung schweres Teilchen mi Masse m und Geschwindigkei v beweg sich in Flüssigkei von leichen Teilchen. Dieses Brownsche Teilchen wird von den Molekülen der Flüssigkei gesoßen. Söße bewirken:
Traktrix DEMO. Text Nr Stand 11. Mai 2016 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK.
 Trkri Te Nr. 540 Snd. Mi 06 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mhe-cd.de 540 Trkri Vorwor Die Trkri is eine Kurve für gehobenemhemische Ansprüche. Ineressn is schon ihre mechnische
Trkri Te Nr. 540 Snd. Mi 06 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mhe-cd.de 540 Trkri Vorwor Die Trkri is eine Kurve für gehobenemhemische Ansprüche. Ineressn is schon ihre mechnische
22 Stetigkeit von Funktionen
 Abschni 22 Seigkei von Funkionen R Plao 47 22 Seigkei von Funkionen 221 Einührung Deiniion 221 Sei W D!Reine Funkion mi Deiniionsbereich D R a) an nenn die Funkion im Punk o 2 D seig, alls lim / D o /!
Abschni 22 Seigkei von Funkionen R Plao 47 22 Seigkei von Funkionen 221 Einührung Deiniion 221 Sei W D!Reine Funkion mi Deiniionsbereich D R a) an nenn die Funkion im Punk o 2 D seig, alls lim / D o /!
Berechnungen am Wankelmotor
 HTL Saalfelen Wankelmoor Seie von 7 Schmihuber Heinrich heinrich_schmihuber@homail.com Berechnungen am Wankelmoor Link zur Beispielsübersich Mahemaische / Fachliche Inhale in Sichworen: Linieninegral,
HTL Saalfelen Wankelmoor Seie von 7 Schmihuber Heinrich heinrich_schmihuber@homail.com Berechnungen am Wankelmoor Link zur Beispielsübersich Mahemaische / Fachliche Inhale in Sichworen: Linieninegral,
Fit für die Q-Phase? Mathematiktraining für die Schüler und Schülerinnen des Beruflichen Gymnasiums Gelnhausen
 Fi für die Q-Phase? Mahemaikraining für die Schüler und Schülerinnen des. Gleichungen (mi und ohne Parameer) Löse folgende Gleichungen:. 4 7.6 e ( e )..7 4 4 k k. 6.8 6 0.4 4 4 4 49.9 cos..0 4.6. e e.7
Fi für die Q-Phase? Mahemaikraining für die Schüler und Schülerinnen des. Gleichungen (mi und ohne Parameer) Löse folgende Gleichungen:. 4 7.6 e ( e )..7 4 4 k k. 6.8 6 0.4 4 4 4 49.9 cos..0 4.6. e e.7
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkeit Seminararbeit aus Numerik von Differentialgleichungen
 Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Zu jedem Typ gibt es eine Menge von möglichen Denotationen der Ausdrücke dieses Typs. Diese Menge wird Domäne des betreffenden Typs genannt.
 2 Theorie der semanischen Typen 2.2.2 Semanik von TL Menge der omänen Zu jedem Typ gib es eine Menge von möglichen enoaionen der Ausdrücke dieses Typs. iese Menge wird omäne des bereffenden Typs genann.
2 Theorie der semanischen Typen 2.2.2 Semanik von TL Menge der omänen Zu jedem Typ gib es eine Menge von möglichen enoaionen der Ausdrücke dieses Typs. iese Menge wird omäne des bereffenden Typs genann.
Übungen zur Ingenieur-Mathematik III WS 2009/10 Blatt = r cos t. mit 0 t 2π und interpretieren Sie das Ergebnis geometrisch.
 Übungen zur Ingenieur-Mahemaik III WS 9/ Bla 3 7.. Aufgabe 59: Berechnen Sie die Bogenlänge der Schraubenlinie r γ() := r h mi π und inerpreieren Sie das Ergebnis geomerisch. Lösung: Der Tangenialvekor
Übungen zur Ingenieur-Mahemaik III WS 9/ Bla 3 7.. Aufgabe 59: Berechnen Sie die Bogenlänge der Schraubenlinie r γ() := r h mi π und inerpreieren Sie das Ergebnis geomerisch. Lösung: Der Tangenialvekor
Merkmale flexibler Fertigung
 FFS.41 PROF.DR.-ING. K.RALL TUHH 2-295 - 1 FFS.42 Die Aufgabe des Bedieners wurde anspruchsvoller (wenige psychische und physische Belasung, dafür mehr Warung, Überwachung, Sörungsbeseiigung). Die Ferigung
FFS.41 PROF.DR.-ING. K.RALL TUHH 2-295 - 1 FFS.42 Die Aufgabe des Bedieners wurde anspruchsvoller (wenige psychische und physische Belasung, dafür mehr Warung, Überwachung, Sörungsbeseiigung). Die Ferigung
Fourier-Transformation Linearität, Symmetrie, Verschiebung, Skalierung, Faltung, Modulation
 Übung 3 Fourier-Transformaion Lineariä, Symmerie, Verschiebung, Skalierung, Falung, Modulaion Lernziele - wissen und versehen, dass der Berag der Fourier-Transformieren einer reellen Funkion gerade is.
Übung 3 Fourier-Transformaion Lineariä, Symmerie, Verschiebung, Skalierung, Falung, Modulaion Lernziele - wissen und versehen, dass der Berag der Fourier-Transformieren einer reellen Funkion gerade is.
Motivation der Dierenzial- und Integralrechnung
 Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen Hochschule Esslingen SS 2010 4 3 2 1 0 5 10 15 20 25 30 Fakulä Grundlagen (Hochschule Esslingen) SS 2010 1 / 9 Übersich 1 Vorberachungen Ableiungsbegri
Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen Hochschule Esslingen SS 2010 4 3 2 1 0 5 10 15 20 25 30 Fakulä Grundlagen (Hochschule Esslingen) SS 2010 1 / 9 Übersich 1 Vorberachungen Ableiungsbegri
5.5. Abstrakte Abituraufgaben zu Exponentialfunktionen
 5.5. Absrake Abiuraufgaben zu Eponenialfunkionen Aufgabe : Kurvenunersuchung, Inegraion, Opimierungsaufgabe Gegeben is die Funkion f() ( ) e,5. a) Unersuchen Sie das Schaubild von f auf Achsenschnipunke,
5.5. Absrake Abiuraufgaben zu Eponenialfunkionen Aufgabe : Kurvenunersuchung, Inegraion, Opimierungsaufgabe Gegeben is die Funkion f() ( ) e,5. a) Unersuchen Sie das Schaubild von f auf Achsenschnipunke,
Ganzrationale Funktionen (Polynomfunktionen) - Berechnung von Nullstellen, Gleichungen höheren Grades -
 GS - 3.0.05 - gara_0_berechnenns.mcd Ganzraionale Funkionen (Polynomfunkionen) - Berechnung von, Gleichungen höheren Grades -. Gleichungen höheren Grades Gegeben is der Funkionserm f( ) a n n + a n n +...
GS - 3.0.05 - gara_0_berechnenns.mcd Ganzraionale Funkionen (Polynomfunkionen) - Berechnung von, Gleichungen höheren Grades -. Gleichungen höheren Grades Gegeben is der Funkionserm f( ) a n n + a n n +...
SERVICE NEWSLETTER. Einführung in die Mechanik Teil 2: Kinematik (2)
 Einührung in ie Mechanik Teil : Kinemaik Ausgabe: 9 / 4 In iesem Teil er Reihe wollen wir anhan eines Zahlenbeispiels en Deomaionsgraienen als zenrale Größe zur Beschreibung er Deormaion in er Kinemaik
Einührung in ie Mechanik Teil : Kinemaik Ausgabe: 9 / 4 In iesem Teil er Reihe wollen wir anhan eines Zahlenbeispiels en Deomaionsgraienen als zenrale Größe zur Beschreibung er Deormaion in er Kinemaik
4.7. Exponential- und Logarithmusfunktionen
 ... Eonenialfunkionen Definiion:.. Eonenial- und Logarihmusfunkionen Die Funkion f() = c a mi D = R, c und a R + \{}heiß Eonenialfunkion zur Basis a. Die Eonenialfunkion zur Basis a = e mi der Eulerschen
... Eonenialfunkionen Definiion:.. Eonenial- und Logarihmusfunkionen Die Funkion f() = c a mi D = R, c und a R + \{}heiß Eonenialfunkion zur Basis a. Die Eonenialfunkion zur Basis a = e mi der Eulerschen
ABITURPRÜFUNG 2002 LEISTUNGSFACH MATHEMATIK (HAUPTTERMIN)
 ABITURPRÜFUNG 00 LEISTUNGSFACH MATHEMATIK (HAUPTTERMIN) Arbeiszei: Hilfsmiel: 70 Minuen Taschenrechner (nich programmierbar, nich grafikfähig) Tafelwerk Der Prüfungseilnehmer wähl von den Aufgaben A1 und
ABITURPRÜFUNG 00 LEISTUNGSFACH MATHEMATIK (HAUPTTERMIN) Arbeiszei: Hilfsmiel: 70 Minuen Taschenrechner (nich programmierbar, nich grafikfähig) Tafelwerk Der Prüfungseilnehmer wähl von den Aufgaben A1 und
Masse, Kraft und Beschleunigung Masse:
 Masse, Kraf und Beschleunigung Masse: Sei 1889 is die Einhei der Masse wie folg fesgeleg: Das Kilogramm is die Einhei der Masse; es is gleich der Masse des Inernaionalen Kilogrammprooyps. Einzige Einhei
Masse, Kraf und Beschleunigung Masse: Sei 1889 is die Einhei der Masse wie folg fesgeleg: Das Kilogramm is die Einhei der Masse; es is gleich der Masse des Inernaionalen Kilogrammprooyps. Einzige Einhei
3.2 Autoregressive Prozesse (AR-Modelle) AR(p)-Prozesse
 3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
(2) Kinematik. Vorlesung Animation und Simulation S. Müller U N I V E R S I T Ä T KOBLENZ LANDAU
 () Kinemaik Vorlesung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wiederholung I roblem (ersmal): Kamerainerpolaion Augpunk und Blickrichung Gue Wahl: Hermie-Splines Definiion von Keyframes Knoenpunk
() Kinemaik Vorlesung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wiederholung I roblem (ersmal): Kamerainerpolaion Augpunk und Blickrichung Gue Wahl: Hermie-Splines Definiion von Keyframes Knoenpunk
Theoretische Physik I/II
 Theoreische Physik I/II Prof. Dr. M. Bleicher Insiu für Theoreische Physik J.. Goehe-Universiä Frankfur Aufgabenzeel IV 9. Mai hp://h.physik.uni-frankfur.de/ baeuchle/u Lösungen Die Vorlesung wird durch
Theoreische Physik I/II Prof. Dr. M. Bleicher Insiu für Theoreische Physik J.. Goehe-Universiä Frankfur Aufgabenzeel IV 9. Mai hp://h.physik.uni-frankfur.de/ baeuchle/u Lösungen Die Vorlesung wird durch
Abiturprüfung 2017 ff Beispielaufgabe Grundkurs Mathematik; Analysis Beispiel Wirkstoff
 Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Flugzeugaerodynamik I Lösungsblatt 2
 Flugzeugaerodynamik I Lösungsbla 2 Lösung Aufgabe Bei der vorliegenden Aufgabe handel es sich um die Nachrechenaufgabe der Skele Theorie. a) Der Koeffizien A 1 is durch die Wölbung des gegebenen Skeles
Flugzeugaerodynamik I Lösungsbla 2 Lösung Aufgabe Bei der vorliegenden Aufgabe handel es sich um die Nachrechenaufgabe der Skele Theorie. a) Der Koeffizien A 1 is durch die Wölbung des gegebenen Skeles
Laplacetransformation in der Technik
 Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Zeit (in h) Ausflussrate (in l/h)
 Aufgabe 6 (Enwicklung einer Populaion): (Anforderungen: Inerpreaion von Schaubildern; Inegralfunkion in der Praxis) Von einer Populaion wird - jeweils in Abhängigkei von der Zei - die Geburenrae (in Individuen
Aufgabe 6 (Enwicklung einer Populaion): (Anforderungen: Inerpreaion von Schaubildern; Inegralfunkion in der Praxis) Von einer Populaion wird - jeweils in Abhängigkei von der Zei - die Geburenrae (in Individuen
Mathematik für Physiker I
 Mahemaik für Physiker I Themenübersich Michael Junk Raum G 47 Beispiel Bewegung 4 Verfolger Esefania Jeder beweg sich mi feser Geschwindigkei immer in Richung zum Vorgänger Dieer B. Paparaz Verona Auf
Mahemaik für Physiker I Themenübersich Michael Junk Raum G 47 Beispiel Bewegung 4 Verfolger Esefania Jeder beweg sich mi feser Geschwindigkei immer in Richung zum Vorgänger Dieer B. Paparaz Verona Auf
3. Partielle Differentialgleichungen
 3.. Grundlagen und Klassifikaion Welche Ordnung haben diese Gleichungen?? 3.4.1 Lineare parielle Differenialgleichungen. Ordnung Analogie: Klassifikaion Kegelschnie 1 3.4.3 Korrek geselle Probleme Anfangs-
3.. Grundlagen und Klassifikaion Welche Ordnung haben diese Gleichungen?? 3.4.1 Lineare parielle Differenialgleichungen. Ordnung Analogie: Klassifikaion Kegelschnie 1 3.4.3 Korrek geselle Probleme Anfangs-
u(t) sin(kωt)dt, k > 0
 Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Hauptachsentransformation
 Haupachsenransformaion Erinnerung: A M n is genau ann nich inverierbar, wenn es ein x R n, x gib, mi A x. Definiion. Sei A M n eine Marix. Ein Vekor v R n, v heiß Eigenvekor von A zum Eigenwer λ R, wenn
Haupachsenransformaion Erinnerung: A M n is genau ann nich inverierbar, wenn es ein x R n, x gib, mi A x. Definiion. Sei A M n eine Marix. Ein Vekor v R n, v heiß Eigenvekor von A zum Eigenwer λ R, wenn
Übungen zur Experimentalphysik II Aufgabenblatt 3 - Lösung
 KW /15 Prof. Dr. R. Reifarh, Dr. J. Glorius Übungen zur Experimenalphysik II Aufgabenbla 3 - Lösung Aufgabe 1: a) Die Laung q im Volumen V beräg: q = ρ(r) V = ρ(r)4πr r = 4πAr 3 r Für ie Laung Q erhalen
KW /15 Prof. Dr. R. Reifarh, Dr. J. Glorius Übungen zur Experimenalphysik II Aufgabenbla 3 - Lösung Aufgabe 1: a) Die Laung q im Volumen V beräg: q = ρ(r) V = ρ(r)4πr r = 4πAr 3 r Für ie Laung Q erhalen
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 6 5. Semester ARBEITSBLATT 6 PARAMETERDARSTELLUNG EINER GERADEN
 ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
Näherung einer Wechselspannung
 HL Seyr Wechselsromparabel Seie 1 von 1 Nieros Bernhard bernhard.nieros@hl-seyr.ac.a Näherung einer Wechselspannung Mahemaische / Fachliche Inhale in Sichworen: Polynomfunkion, allgemeine Sinusschwingung,
HL Seyr Wechselsromparabel Seie 1 von 1 Nieros Bernhard bernhard.nieros@hl-seyr.ac.a Näherung einer Wechselspannung Mahemaische / Fachliche Inhale in Sichworen: Polynomfunkion, allgemeine Sinusschwingung,
Analysis I. 14. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Anlysis I 4. Übungssunde Seven Biln sevenb@suden.ehz.ch biln.uk/eching June 6, 07 Erinnerung Sz. (Prielle Inegrion) f (x) g(x)dx = [ ] b f(x)g(x) f(x) g (x)dx. Sz 6..5 (Subsiuion) Sei f : [, b] R seig,
Anlysis I 4. Übungssunde Seven Biln sevenb@suden.ehz.ch biln.uk/eching June 6, 07 Erinnerung Sz. (Prielle Inegrion) f (x) g(x)dx = [ ] b f(x)g(x) f(x) g (x)dx. Sz 6..5 (Subsiuion) Sei f : [, b] R seig,
Durch Modellierung beschreibt man Vorgänge aus der Natur sowie industrielle Prozesse
 Kapiel Modellierung Durch Modellierung beschreib man Vorgänge aus der Naur sowie indusrielle Prozesse mi mahemaischen Werkzeugen, zum Beispiel Gleichungen oder Ungleichungen. Modellierung geschieh durch
Kapiel Modellierung Durch Modellierung beschreib man Vorgänge aus der Naur sowie indusrielle Prozesse mi mahemaischen Werkzeugen, zum Beispiel Gleichungen oder Ungleichungen. Modellierung geschieh durch
Lösung Abiturprüfung 1994 Leistungskurs (Baden-Württemberg)
 Lösung Abiurprüfung 1994 Leisungskurs (Baden-Würemberg) Analysis I.1. a) D f = IR / { 1 } f x= = K besiz keine Nullsellen 1x f ' x= 8 1x = 8 K besiz keine Exremsellen senkreche Asymoe : x= 1 waagereche
Lösung Abiurprüfung 1994 Leisungskurs (Baden-Würemberg) Analysis I.1. a) D f = IR / { 1 } f x= = K besiz keine Nullsellen 1x f ' x= 8 1x = 8 K besiz keine Exremsellen senkreche Asymoe : x= 1 waagereche
1.) Integralrechnung a) Ermitteln Sie das Marktgleichgewicht zwischen Angebot und Nachfrage:
 Übungen: Mahemaik zur Klausurvorbereiung (erweier) Jürgen Meisel Mahemaik.) Inegralrechnung a) Ermieln Sie das Markgleichgewich zwischen Angebo und Nachfrage: pa x x = + ( ) = + und p ( x) x b) Ermieln
Übungen: Mahemaik zur Klausurvorbereiung (erweier) Jürgen Meisel Mahemaik.) Inegralrechnung a) Ermieln Sie das Markgleichgewich zwischen Angebo und Nachfrage: pa x x = + ( ) = + und p ( x) x b) Ermieln
Multiple Regression: Übung 1
 4. Muliple Regression Ökonomerie I - Peer Salder 1 Muliple Regression: Übung 1 Schäzung einer erweieren Konsumfunkion für die Schweiz Wir unersuchen die Abhängigkei der Konsumausgaben der Schweizer Haushale
4. Muliple Regression Ökonomerie I - Peer Salder 1 Muliple Regression: Übung 1 Schäzung einer erweieren Konsumfunkion für die Schweiz Wir unersuchen die Abhängigkei der Konsumausgaben der Schweizer Haushale
