Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik Lösungsvorschläge zum 6. Übungsblatt
|
|
|
- Silvia Knopp
- vor 5 Jahren
- Abrufe
Transkript
1 Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla Aufgabe Wir wiederholen ein paar Deail der Charakeriikberechnung: In der Vorleung haben wir Gleichungen de Typ a, u u = b, u, D, in D R n berache Hier ind a : D J R n und b : D J R gegeben, wobei J ein Inervall in R i Uner dieen Typ fäll auch die Gleichung der Aufgabe 32: Schreib man nämlich u die Koordinaen au zu =, dann können wir D = R,, a, u = und b, u = wählen Die Charakeriiken, die wir k = noier haben, bedeuen dann da folgende: Die Grundcharakeriik k = i ein pezieller Weg im Or-Zei-Raum R, i ein reeller Parameer, von dem man hoff, auf ihm die Löung u der Gleichung zu kennen: Nämlich oll der Wer u k gegeben ein durch den zweien Teil der Charakeriik, alo durch u k = Die Beimmung der Charakeriiken erfolg durch Löen de og charakeriichen Syem k = a k, w = b k, 2 vgl Vorleung, wa wir nun konkre mi der vorgegebenen Gleichung un wollen: Da Differenialgleichungyem 2 laue hier k = w = Die zweie Zeile löen wir ofor zu = con, alo ewa = w Die ere Zeile löen wir dann konequenerweie zu w k = + k Nun können wir noch den Sarpunk k der Charakeriik wählen: Wir un die der Einfachhei halber durch ξ ξ k = mi einem reellen Parameer ξ, weil auf Γ = { : ξ R} die Anfangwere vorgegeben ind Die Anfangbedingung ergib uξ, = w = fξ, alo fξ ξ k = +
2 Für den Löungkandidaen u erhäl man alo die Informaion u, = fξ, fall = fξ + ξ k = für ein R gil, ander geag, fall = fξ+ξ die zweie Zeile ergib =, wa man in die ere Zeile einez a Wie eben erwähn, i u, = fξ für = fξ + ξ 3 Die Bedingung 3 i für jede fe gewähle und jede fe gewähle R eindeuig nach ξ auflöbar, wa wir jez nachweien Kommenar: Die nachfolgende Rechnung ha eine einfache geomeriche Inerpreaion: Verchiedene Grundcharakeriiken chneiden ich nich! Fall: Sei ξ R Wir nehmen an, da 3 erfüll i Wegen fξ gil fξ für jede Dami folg ξ = fξ, o da fξ = i Inbeondere laue 3 dann = ξ Alo i ξ eindeuig fegeleg Andererei lö die Wahl ξ = naürlich die Gleichung 3 2 Fall: > Fall ξ die Gleichung 3 lö, mu ξ > gelen, denn on wäre ξ und = + ξ Berachen wir 3 al Funkion g : [, [,, ξ = fξ + ξ Dann i g umkehrbar, denn g i wegen g ξ = e ξ + > für alle ξ, ξ2 auf [, reng monoon wachend und e gil g = Dehalb eiier genau ein ξ > o, da 3 gil Kommenar: Die obige Rechnung ha gezeig, da da obige u wohldefinier i Da u aächlich da urprüngliche Problem lö, folg dann au Abchni 44 der Vorleung oder lä ich alernaiv direk nachprüfen: E gil u, = f g, wobei g die Umkehrfunkion vom obigen g i Wende nun den Saz über die Ableiung der Umkehrfunkion au HM II an Man berechne außerdem u, = fξ ξ, indem man hξ = ξ fξ nach ξ differenzier und dann darau die Ableiung der Umkehrfunkion von h, alo die Ableiung von ξ, beimm k b Nehmen wir an, u i eine Löung der Gleichung und i eine Löung von 2 Dann gil nach der Keenregel u k = u k k = u k a k, = 4 Alo i hier u auf Grundcharakeriiken konan Nun nehmen wir zuäzlich an, da f eig differenzierbar i und nich monoon wachend In dieem Fall eiieren alo < mi f > f Die dazugehörigen Grundcharakeriiken k = f + und k = 2 f +
3 chneiden ich dann, denn die Schnigleichung k = k f + = f + f f = ha eine Löung > Dami kann eine Löung u von höchen bi zu dem Zeipunk = = f f eiieren, da on ein Widerpruch zur Konanz von u auf Grundcharakeriiken vgl 4 eneh u k = u k = f f = u k = u k Aufgabe 2 Wir bringen die Gleichung in die Form a,, u u = b,, u da i mi = co,, alo gil hier a,, u = und b,, u = Wir beimmen die Charakeriiken k, wobei k k = Da charakeriiche Syem 2 laue hier k 2 k = k k 2 w = cok2 = Wir erhalen k 2 = + c 2 und dami k = co + c 2, worau k = in + c 2 + c folg Außerdem erhalen wir wieder = con =: w in + Für jede Wahl von c, c 2 R 2 c2 + c erhalen wir alo eine Grundcharakeriik ; + c 2 wir bezeichnen diee mi k c,c 2 k Fazi: Für jede Wahl von c, c 2 R 2 c,c 2 und w erhalen wir eine Charakeriik w Wir ellen fe, da k c,c 2 in + c c 2 = = k c, gil, dh k c,c 2 und k c, ind nur Umparameriierungen der gleichen Kurve und e genüg eine davon zu uneruchen Wir wählen daher im folgenden e c 2 = und a k c, chreiben wir k c Wir uneruchen nun Randpunke r =, R und unercheiden dabei drei Fälle: Fall: r =, mi feem, 2π unerer Rand Wir überlegen un, welche Grundcharakeriik durch den Punk, verläuf: Au k c =! folg in + c =, =, alo c = Dh die Grundcharakeriik k verläuf bei = durch Für h > gil inh + k h = h k c h Q, mi anderen Woren: die Grundcharakeriik läuf nach Q hinein 2 Fall: r =, mi feem [, linker Rand Für genügend kleine h > i inh +, 2π, alo Wir überlegen un wieder, welche Grundcharakeriik durch den Punk, verläuf: Au k c =! folg in+c =, =, alo c = in Dh die Grundcharakeriik k in verläuf bei = durch Für h > gil in + h in k in + h = + h Nach dem Mielweraz gib e ξ, + h mi in + h in = h coξ Mi genügend kleinem h > lieg ξ nahe bei e gil aber e ξ > E gil dann alo 3
4 in + h in > fall P := [, π 2 [ 3 2 π, 5 2 π [ 7 2 π, 9 2π und in + h in < fall N := [ π 2, 3 2 π [ 5 2 π, 7 2 π [ 9 2 π, 2 π Für P und genügend kleinem h > gil alo k in + h Q, mi anderen Woren: die Grundcharakeriik läuf in dieem Fall nach Q hinein Für N und genügend kleinem h > gil analog k in + h / Q, mi anderen Woren: die Grundcharakeriik läuf in dieem Fall au Q herau E gil [, = P N, dh wir haben alle möglichen Fälle uneruch 3 Fall: r = 2π, mi feem [, recher Rand Wir überlegen un wieder, welche Grundcharakeriik durch den Punk 2π, verläuf: Au k c =! 2π folg in + c = 2π, =, alo c = 2π in Dh die Grundcharakeriik 2π k 2π in verläuf bei = durch Für h > gil 2π + in + h in k 2π in + h = + h Wir verwenden die Vorzeichenüberlegungen zu in + h in von oben und erhalen: Für N und genügend kleinem h > gil k in + h Q, mi anderen Woren: die Grundcharakeriik läuf in dieem Fall nach Q hinein Für P und genügend kleinem h > gil k in + h / Q, mi anderen Woren: die Grundcharakeriik läuf in dieem Fall au Q herau Da waren wieder alle möglichen Fälle Zuammenfaung: Für r R rein :=, 2π {} {} P {2π} N läuf die Grundcharakeriik nach Q hinein, für r R \ R rein läuf ie au Q herau Aufgabe 3 Wir bringen die Gleichung in die Form a,, u u = b,, u, alo gil hier u a,, u =, b,, u = u Anfangwere ind vorgegeben auf Γ := {ξ, : ξ R} und e gil dor uξ, = ξ =: fξ Da charakeriiche Syem laue: k = a k2 k, = ak, k 2, = w = b k, = bk, k 2, = Für jede fee ξ ξ = Γ löen wir da charakeriiche Syem mi folgenden Anfangweren k ξ vgl Abchni 44, Skripum: = w fξ, Alo k = ξ, k 2 =, w = fξ, = ξ Somi folg k 2 = und = ξe, wa auf k = k 2 = ξe, alo k = ξ e wegen k = ξ führ Für jede fee ξ ξ = Γ erhalen wie o eine Charakeriik Diee bezeichnen wir mi k, ξ w, ξ E gil alo k, ξ ξ e = und w, ξ = ξe für alle R Zur Veranchaulichung zeichnen wir einige Grundcharakeriiken nämlich für ξ =, ξ = /2, 4
5 ξ =, ξ = /2 und ξ = in den Argumenraum: Da i naürlich jeweil der an der eren Winkelhalbierenden gepiegele Funkiongraph der Funkion ξ e Wir beobachen dabei und rechnen leich nach, da gil: Jede Grundcharakeriik geh durch Nämlich jeweil bei = : k, ξ = Durch mi verläuf keine Grundcharakeriik Durch alle übrigen Punke, alo alle Punke mi geh genau eine Grundcharakeriik Da zeigen wir o: Sei, mi gegeben Wir uchen ξ ξ = o, da e ein gib mi k, ξ = Da i gleichbedeuend mi { k, ξ = ξ e { = = k 2, ξ bzw = = ξ = e Da bedeue: Die Grundcharakeriik k, e den Punk, und zwar bei = und nur diee verläuf durch Einen Kandidaen für den Wer der Löung an der Selle, mi erhalen wir jez durch Auweren von w, e bei = : u, = u k, e = w, e = e e = Durch Einezen prüf man leich nach, da u, = aächlich die parielle Differenialgleichung am Anfangbedingung bi zum Zeipunk = lö genauer: auf R, Über den Zeipunk = hinau lä ich die Löung nich forezen Aufgabe 4 Für =, 2, 3 R 3 \ { } eze u = = /2 Offenbar i u auf R 3 \ { } zweimal eig differenzierbar Für jede =, 2, 3 R 3 \ { } gil /2 2 u = /2 2 2 = / = 2 3 3/
6 Anwenden der eindimenionalen Produk- und Keenregel ergib omi u = u = 3 = = 3 3 k 3 4 k= Fazi: u i harmonich k= k k 3 = 3 + k 3 4 k k= k = k= 2 k 5 = k= 2 k }{{} = 2 Alernaiv: Au der HM II wien wir, wie der Laplaceoperaor auf eine radialymmeriche Funkion wirk I f :, R durch f := definier, o lä ich = u = = f für alle R3 \ { } chreiben Inbeondere i f auf, zweimal eig differenzierbar mi f = 2 und f = 2 3 Mi dem Reula 6 au Kapiel 292 HM II folg u = f + 3 f = = für alle R3 \ { } Aufgabe 5 a E ei u eine harmoniche Funkion Wir uchen eine holomorphe Funkion f mi Re f = u Dabei ezen wir v = Im f, o da f = u + iv gil Lau Saz in 3 KAI i f holomorph genau dann, wenn u und v C -Funkionen ind und die Cauchy-Riemannchen Differenialgleichungen gelen, alo u = y v, y u = v Die harmoniche Funkion u i per definiionem eine C 2 -Funkion Sei, y Ω fe gewähl Wegen der Bedingung y v = u ezen wir v, y := y y u, ỹ dỹ + c, wobei die reche Seie eine Sammfunkion in y bei fegehalenem ein oll So eine Sammfunkion eiier immer, zuminde lokal! Au dem Haupaz der Differenial- und Inegralrechnung folg, da v eine C -Funkion i Wir prüfen nun, da auch die zweie Cauchy-Riemannche Differenialgleichung v = y u erfüll i Nach einem Saz in 4 gil y y v, y = u, 2 ỹ dỹ + c = yu, 2 ỹ dỹ + c = [ y u, ỹ ] ỹ=y ỹ=y + c y y = y u, y + y u, y + c = y u, y, wobei die zweie Gleichung au der Taache folg, da u harmonich i Dabei haben wir c := y u, y d gewähl, dami c = y u, y gil Nach beagem Reula au 3 KAI i f = u + iv eine holomorphe Funkion b Für, y, haben wir u y, y = 2y und dami v 2 +y 2 2, y = u y, y = 2y nach den Cauchy-Riemannchen Differenialgleichungen E folg 2y y v, y = 2 + y 2 d = y 2 + cy mi einer gewien Funkion c Au der Bedingung v y = u chließen wir v y, y = 2 + y 2 + 2y y c y! = u, y = y y 2 2 c y = 2 +y 2 2
7 Wir wählen cy = jede andere Konane häe e auch gean und erhalen für, y f + iy = u, y + iv, y = 2 + y 2 + i y 2 + y 2 = iy 2 + y 2 = iy iy + iy = + iy Inbeondere i u al Realeil der holomorphen Funkion f nach Beipiel 2 in 5 harmonich c Annahme: E gib eine auf C \ {} holomorphe Funkion f o, da u = Re f gil Dann folg au den Cauchy-Riemannchen Differenialgleichungen für z = + iy mi, y R f z = u, y + iv, y = u, y iu y, y Für u, y = ln 2 + y 2,, y,, erhäl man und analog Einezen in ergib u, y = 2 + y y 2 = y 2 u y, y = y 2 + y 2 f z = f + iy = iy 2 + y 2 = + iy = z Die i unmöglich, weil z /z auf C\{} keine Sammfunkion beiz Dehalb i die anfängliche Annahme falch und e eiier keine auf C \ {} holomorphe Funkion f mi u = Re f [Wäre f auf C \ {} holomorph mi f z = /z für alle z, dann würde für die durch γ = e i gegebene Kurve γ : [, 2π] C gelen = f f = γ f z dz = γ z dz = 2πi Widerpruch!] wwwmahkiedu/iana/lehre/hm3eec25w/
Mathematik 1 für Maschinenbau, M. Schuchmann (SoSe 2013) Aufgabenblatt 5 (Ebenen)
 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 7 5. Semester ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE
 Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Mathematik: Mag. Schmid Wolfgang+LehrerInnenteam ARBEITSBLATT 6-13 ERMITTELN DER KREISGLEICHUNG
 ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
Stochastische Differentialgleichungen
 INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
Elementare Lösungsmethoden für gewöhnliche Differentialgleichungen
 454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Geradendarstellung in Paramterform
 Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Hauptprüfung 2010 Aufgabe 4
 Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
2.2 Rechnen mit Fourierreihen
 2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
1. Kontrolle Physik Grundkurs Klasse 11
 1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
Algorithmen II Vorlesung am
 Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
2. Torsion geschlossener Profile
 Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Fakultät Grundlagen. s = t. gleichförm ig
 Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
KAPITEL 2 KÜRZESTE WEGE
 KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge zum 15. Übungsblatt
 Karlruher Intitut für Technologie (KIT) Intitut für Analyi Dr. A. Müller-Rettkowki Dipl.-Math. M. Uhl WS 9/ Höhere Mathematik I für die Fachrichtungen Elektroingenieurween, Phyik und Geodäie Löungvorchläge
Karlruher Intitut für Technologie (KIT) Intitut für Analyi Dr. A. Müller-Rettkowki Dipl.-Math. M. Uhl WS 9/ Höhere Mathematik I für die Fachrichtungen Elektroingenieurween, Phyik und Geodäie Löungvorchläge
Restkapazität. = O( V ) mal kritisch. Also gibt es insgesamt höchstens O( V E ) Augmentierungen.
 Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Messung der Ladung. Wie kann man Ladungen messen? /Kapitel Formeln auf S.134: Elektrische Ladung
 --- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
--- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
Lösungen zu Übungsblatt 4
 Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
W. Stark; Berufliche Oberschule Freising
 9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
Demo-Text für Funktionen und Kurven. Differentialgeometrie INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK. Friedrich Buckel.
 Funkionen und Kurven Differenialgeomerie Tex Nummer: 5 Sand: 9. März 6 Demo-Tex für www.mahe-cd.de INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mahe-cd.de 5 Differenialgeomerie Vorwor Das Thema Kurven is
Funkionen und Kurven Differenialgeomerie Tex Nummer: 5 Sand: 9. März 6 Demo-Tex für www.mahe-cd.de INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mahe-cd.de 5 Differenialgeomerie Vorwor Das Thema Kurven is
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Abituraufgaben Grundkurs 2009 Bayern Analysis I. dt mit D F = R.
 Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Integralrechnung. Grundidee der Integralrechnung. Einführung des Riemann- Integrals
 1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
6 Stochastische Differentialgleichungen
 6 Sochaiche Differenialgleichungen Viele deerminiiche Modelle der Naur- und der Wirchafwienchafen laen ich mi Hilfe von Differenialgleichungen audrücken. Mi dem Io-Inegral und der Io-Formel haben wir die
6 Sochaiche Differenialgleichungen Viele deerminiiche Modelle der Naur- und der Wirchafwienchafen laen ich mi Hilfe von Differenialgleichungen audrücken. Mi dem Io-Inegral und der Io-Formel haben wir die
Abbildungsmaßstab und Winkelvergrößerung
 Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Zwischenwerteigenschaft
 Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
3.4 Systeme linearer Differentialgleichungen
 58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
Anhang. A1 Analytische Lösungen der erweiterten Anzahlbilanz
 117 Anhang A1 Analyiche Löungen der erweieren Anzahlbilanz Die Bilanzgleichungen der erweieren Anzahlvereilung owohl für die koninuierliche al auch für die dikoninuierliche Krialliaion (l..-34 und.-35)
117 Anhang A1 Analyiche Löungen der erweieren Anzahlbilanz Die Bilanzgleichungen der erweieren Anzahlvereilung owohl für die koninuierliche al auch für die dikoninuierliche Krialliaion (l..-34 und.-35)
7.3. Partielle Ableitungen und Richtungsableitungen
 7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
Abiturprüfung Mathematik 2012 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1
 Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Technische Universität München. Lösung Montag SS 2012
 Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Weg im tv-diagramm. 1. Rennwagen
 Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
MATLAB: Kapitel 4 Gewöhnliche Differentialgleichungen
 4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
f ( x) = x + x + 1 (quadratische Funktion) f '( x) = x + (Ableitungsfunktion)
 R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 11 LAGEBEZIEHUNG DREIER EBENEN
 Mahemaik Mag. Schmid Wolfgang Arbeisbla. Semeser ARBEITSBLATT LAGEBEZIEHUNG DREIER EBENEN Nachdem wir die Lage weier Ebenen unersuch haben, wollen wir uns nun mi der Lage von drei Ebenen beschäfigen. Anders
Mahemaik Mag. Schmid Wolfgang Arbeisbla. Semeser ARBEITSBLATT LAGEBEZIEHUNG DREIER EBENEN Nachdem wir die Lage weier Ebenen unersuch haben, wollen wir uns nun mi der Lage von drei Ebenen beschäfigen. Anders
Technische Universität München Fakultät für Mathematik Algorithmische Diskrete Mathematik WS 2012/2013 Prof. Dr. P. Gritzmann 9.
 Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
Arbeitsauftrag Thema: Gleichungen umformen, Geschwindigkeit, Diagramme
 Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkeit Seminararbeit aus Numerik von Differentialgleichungen
 Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Lösung - Serie 8. D-MAVT/D-MATL Analysis I HS 2018 Dr. Andreas Steiger. MC-Aufgaben (Online-Abgabe) 1. Was für eine Kurve stellt die Parametrisierung
 D-MAVT/D-MATL Analysis I HS 018 Dr. Andreas Seiger Lösung - Serie 8 MC-Aufgaben Online-Abgabe 1. Was für eine Kurve sell die Paramerisierung sin1 r = cos1, R dar? a Ein Kreis. Es gil x + y = sin 1 + cos
D-MAVT/D-MATL Analysis I HS 018 Dr. Andreas Seiger Lösung - Serie 8 MC-Aufgaben Online-Abgabe 1. Was für eine Kurve sell die Paramerisierung sin1 r = cos1, R dar? a Ein Kreis. Es gil x + y = sin 1 + cos
Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann
 Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann Aufgabe Im abgelaufenen Jahr haen einige große deusche Firmen hohe prozenuale Gewinnzuwächse. Gleichzeiig wurden eilweise massiv
Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann Aufgabe Im abgelaufenen Jahr haen einige große deusche Firmen hohe prozenuale Gewinnzuwächse. Gleichzeiig wurden eilweise massiv
1. Für die Bewegung eines Fahrzeuges wurde das t-s-diagramm aufgenommen. Skizziere für diese Bewegung das t-v- Diagramm.
 Aufgaben zur gleichförigen Bewegung 1. Für die Bewegung eine Fahrzeuge wurde da --Diagra aufgenoen. Skizziere für diee Bewegung da -- Diagra. 2. Eine Radfahrerin und ein Spaziergänger i eine Hund bewegen
Aufgaben zur gleichförigen Bewegung 1. Für die Bewegung eine Fahrzeuge wurde da --Diagra aufgenoen. Skizziere für diee Bewegung da -- Diagra. 2. Eine Radfahrerin und ein Spaziergänger i eine Hund bewegen
Geradlinige Bewegung Krummlinige Bewegung Kreisbewegung
 11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
Aufgaben zur gleichförmigen Bewegung
 Aufgaben zur gleichförigen Bewegung 860. Ein Waerrad on 5 Durcheer eh an eine 2 breien und 0,7 iefe Bach. Da Rad dreh ich in der Minue 5 al und i a Rand genau o chnell, wie der Bach fließ. Wie iel Lier
Aufgaben zur gleichförigen Bewegung 860. Ein Waerrad on 5 Durcheer eh an eine 2 breien und 0,7 iefe Bach. Da Rad dreh ich in der Minue 5 al und i a Rand genau o chnell, wie der Bach fließ. Wie iel Lier
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
2 Torsion in dünnwandigen Querschnitten
 apl oz r-ing hail G Georgi Tragwerkerechnung Torion in dünnwandigen Querchnien Theorien, Vorauezungen und Hpoheen Theorien: Reine Torion ( Grundufe) Begründer: Jean Claude de T VENANT (9-886) mol, Inde:
apl oz r-ing hail G Georgi Tragwerkerechnung Torion in dünnwandigen Querchnien Theorien, Vorauezungen und Hpoheen Theorien: Reine Torion ( Grundufe) Begründer: Jean Claude de T VENANT (9-886) mol, Inde:
Übungsblatt 2 Physik für Ingenieure 1
 Übunbla Phyik für Inenieure 1 Ohmar Mari, (ohmar.mari@phyik.uni-ulm.de) 3. 1. 1 1 Aufaben für die Übununden Kinemaik 1 1. Ein Maepunk bewe ich nach der Gleichun () = in(ω). Konruieren ie und berechnen
Übunbla Phyik für Inenieure 1 Ohmar Mari, (ohmar.mari@phyik.uni-ulm.de) 3. 1. 1 1 Aufaben für die Übununden Kinemaik 1 1. Ein Maepunk bewe ich nach der Gleichun () = in(ω). Konruieren ie und berechnen
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Kapitel : Exponentiell-beschränktes Wachstum
 Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Übungen zur Klausur 11M1 21/05/2008 Seite 1 von 5
 Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Casrigiano Dr. M. Prähofer Zenralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zenrum Mahemaik Mahemaik 3 für Physik (Analysis ) hp://www-hm.ma.um.de/ss/ph/ 49. Eine reguläre Kurve ha keinen Knick
Prof. Dr. D. Casrigiano Dr. M. Prähofer Zenralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zenrum Mahemaik Mahemaik 3 für Physik (Analysis ) hp://www-hm.ma.um.de/ss/ph/ 49. Eine reguläre Kurve ha keinen Knick
Kurven in der Ebene und im Raum
 Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Westfälische Hochschule - Fachbereich Informatik & Kommunikation - Bereich Angewandte Naturwissenschaften. 2. Mechanik
 Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
7 Das lokale Ito-Integral
 7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
Aufgabenblatt 10: Investitionstheoretische Kostenrechnung I
 Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
7. Vorlesung Wintersemester
 7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
Gewöhnliche Differentialgleichungen
 Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Ferienkurs Analysis I für Physiker WS 15/16 Aufgaben Tag 3. Aufgaben Tag 3
 für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
1 Lokale Änderungsrate und Gesamtänderung
 Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
ZUU AUUFFGGAABBEE :: Die Wann läuft zunächst voll. Nach einiger Zeit wird etwas Wasser abgelassen und dann wird etwas zugeführt.
 Lineare Funkionen. Lösungen Lö LÖÖSSUUNNGGEENN ZZUUM.. KPPI IITTEELL ZZUU UUFFGGEE..: : a) as Pfeildiagramm zeig keine Funkion, da von h kein Pfeil ausgeh und von a zwei Pfeile. b) Is eine Funkion, denn
Lineare Funkionen. Lösungen Lö LÖÖSSUUNNGGEENN ZZUUM.. KPPI IITTEELL ZZUU UUFFGGEE..: : a) as Pfeildiagramm zeig keine Funkion, da von h kein Pfeil ausgeh und von a zwei Pfeile. b) Is eine Funkion, denn
MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 13 Wintersemester 2011/2012
 Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
Differenzieren von Funktionen zwischen Banachräumen
 Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
PHYSIK. Gleichförmige Bewegungen. Datei Nr Geradlinige Bewegungen. Teil 1 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK.
 PHYSIK Geradlinige Bewegungen Teil 1 Gleichförige Bewegungen Daei Nr. 91111 Friedrich W. Buckel Geänder: 18. Januar 2013 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.ahe-cd.de 91111 Gleichförige
PHYSIK Geradlinige Bewegungen Teil 1 Gleichförige Bewegungen Daei Nr. 91111 Friedrich W. Buckel Geänder: 18. Januar 2013 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.ahe-cd.de 91111 Gleichförige
Übungen zur Ingenieur-Mathematik III WS 2009/10 Blatt = r cos t. mit 0 t 2π und interpretieren Sie das Ergebnis geometrisch.
 Übungen zur Ingenieur-Mahemaik III WS 9/ Bla 3 7.. Aufgabe 59: Berechnen Sie die Bogenlänge der Schraubenlinie r γ() := r h mi π und inerpreieren Sie das Ergebnis geomerisch. Lösung: Der Tangenialvekor
Übungen zur Ingenieur-Mahemaik III WS 9/ Bla 3 7.. Aufgabe 59: Berechnen Sie die Bogenlänge der Schraubenlinie r γ() := r h mi π und inerpreieren Sie das Ergebnis geomerisch. Lösung: Der Tangenialvekor
Positioniersteuerung (5.12) Beschleunigen - Phase 2 (5.13) Beschleunigen - Phase 3 (5.14) Phase 4: Konstante Geschwindigkeit (5.15) Bremsen Phase 5
 Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
Bewertungsmethoden in der Versicherungsmathematik
 Bewerungmehoden in der Vericherungmahemaik Techniche Reerven und Markwere II Johanne Pacheag Mahemaiche Iniu der Univeriä zu Köln Sommeremeer 2010 Bereuung: Prof. Schmidli, Dr. Eienberg 1 Inhalverzeichni
Bewerungmehoden in der Vericherungmahemaik Techniche Reerven und Markwere II Johanne Pacheag Mahemaiche Iniu der Univeriä zu Köln Sommeremeer 2010 Bereuung: Prof. Schmidli, Dr. Eienberg 1 Inhalverzeichni
Berechnen Sie die Extrem- und Wendepunkte des Graphen von f 1. Berechnen Sie die Gleichung der Tangente an den Graphen von f 1 an der Stelle 2.
 Miniserium für Schule und Berufsbildung 05 Bei der Bearbeiung der Aufgabe dürfen alle Funkionen des Taschenrechners genuz werden. Aufgabe : Analysis Gegeben is eine Funkionenschar durch f () = e mi R;
Miniserium für Schule und Berufsbildung 05 Bei der Bearbeiung der Aufgabe dürfen alle Funkionen des Taschenrechners genuz werden. Aufgabe : Analysis Gegeben is eine Funkionenschar durch f () = e mi R;
F Rück. F r Rück. Mechanische Schwingungen. Größen zur quantitativen Beschreibung :
 Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
Die Bildung des Präsens funktioniert dann beispielsweise so: "lauda + mus" - wir loben.
 Präen Da Präen i die Gegenwarform. E bechreib alo Handlungen, die gerade paieren. Die Bildung i denkbar einfach und unercheide ich in den unerchiedlichen Konjugaionen (fa immer) nich. Dewegen reich e vollkommen
Präen Da Präen i die Gegenwarform. E bechreib alo Handlungen, die gerade paieren. Die Bildung i denkbar einfach und unercheide ich in den unerchiedlichen Konjugaionen (fa immer) nich. Dewegen reich e vollkommen
Analysis II Musterlösung 12. für t [ 0, 2π). y
 .. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
.. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
Abiturprüfung 2017 ff Beispielaufgabe Grundkurs Mathematik; Analysis Beispiel Wirkstoff
 Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Bewegungsgleichung einer gleichförmig beschleunigten Rakete (2)
 Auor: Wler Bilin von 8 wler.bilin.h/blog/.5.3 :4 Bewegunggleihung einer gleihförmig behleunigen Rkee () Dieng, 6. April 3 - :57 Auor: wbi hemen: Wien, Phyik, Komologie D Löen der reliviihen Bewegunggleihung
Auor: Wler Bilin von 8 wler.bilin.h/blog/.5.3 :4 Bewegunggleihung einer gleihförmig behleunigen Rkee () Dieng, 6. April 3 - :57 Auor: wbi hemen: Wien, Phyik, Komologie D Löen der reliviihen Bewegunggleihung
Geometric Algebra Computing Transformationen in LA und CGA Dr. Dietmar Hildenbrand
 Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
Laplace Transformation
 Prof. Dr. Michael Eiermann Höhere Mahemaik 3 (verief) Kapiel L Laplace Tranformaion Die Laplace Tranformaion verwandel Anfangwerprobleme für lineare Differenialgleichungen mi konanen Koeffizienen in algebraiche
Prof. Dr. Michael Eiermann Höhere Mahemaik 3 (verief) Kapiel L Laplace Tranformaion Die Laplace Tranformaion verwandel Anfangwerprobleme für lineare Differenialgleichungen mi konanen Koeffizienen in algebraiche
22 Stetigkeit von Funktionen
 Abschni 22 Seigkei von Funkionen R Plao 47 22 Seigkei von Funkionen 221 Einührung Deiniion 221 Sei W D!Reine Funkion mi Deiniionsbereich D R a) an nenn die Funkion im Punk o 2 D seig, alls lim / D o /!
Abschni 22 Seigkei von Funkionen R Plao 47 22 Seigkei von Funkionen 221 Einührung Deiniion 221 Sei W D!Reine Funkion mi Deiniionsbereich D R a) an nenn die Funkion im Punk o 2 D seig, alls lim / D o /!
Übungen zur Einführung in die Physik II (Nebenfach)
 Übungen zur Einführung in ie Physik Nebenfach --- Muserlösung --- Aufgabe: Konensaorenlaung Ein mi Glimmer ε r = 8 gefüller Plaenkonensaor mi er Fläche A=6 cm un einem Plaenabsan = 5 μm enlä sich wegen
Übungen zur Einführung in ie Physik Nebenfach --- Muserlösung --- Aufgabe: Konensaorenlaung Ein mi Glimmer ε r = 8 gefüller Plaenkonensaor mi er Fläche A=6 cm un einem Plaenabsan = 5 μm enlä sich wegen
Lösung zur Hausaufgabe in Topologie und Differentialrechnung mehrerer Variablen SS x 1. x 2. x 1+x 2+x 3
 Bl Nr. 11 Simon Reisser Lösung zur Husufgbe in Topologie und Differenilrechnung mehrerer Vriblen SS 17 Aufgbe () Sei f(x 1, x, x 3 ) = (y 1, y, y 3 ) = (e x1x x3, e x1x+x3, e xx3 ) und dg(y 1, y, y 3 )
Bl Nr. 11 Simon Reisser Lösung zur Husufgbe in Topologie und Differenilrechnung mehrerer Vriblen SS 17 Aufgbe () Sei f(x 1, x, x 3 ) = (y 1, y, y 3 ) = (e x1x x3, e x1x+x3, e xx3 ) und dg(y 1, y, y 3 )
Übungen zur Ingenieur-Mathematik III WS 2017/2018 Blatt
 Übungen zur Ingenieur-Mahemaik III WS 7/8 Bla 7..7 Aufgabe 9: Berechnen Sie ie Länge zweier Kurven auf er Eroberfläche (im Kugelmoell, ie S. Peersburg ( N, O mi Anchorage in Alaska ( N, 5 W verbinen. Lösung:
Übungen zur Ingenieur-Mahemaik III WS 7/8 Bla 7..7 Aufgabe 9: Berechnen Sie ie Länge zweier Kurven auf er Eroberfläche (im Kugelmoell, ie S. Peersburg ( N, O mi Anchorage in Alaska ( N, 5 W verbinen. Lösung:
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Aufgabe 1: a) (i) und (ii) und (iv) 1 Punkt b) (i) 1 Punkt c) (i) 1 Punkt d) (iv) 1 Punkt e) (B) 1 Punkt f) (iv) 1 Punkt g) (i) und (ii) 2 Punkte h
 Aufgabe : a) i) un ii) un i) Punk b) i) Punk c) i) Punk ) i) Punk e) B) Punk f) i) Punk g) i) un ii) Punke i) un iii) un i) un ).5 lu.5 Punk Aufgabe : Venuri Ror Punke) a. Volumenrom Für ieen Aufgabeneil
Aufgabe : a) i) un ii) un i) Punk b) i) Punk c) i) Punk ) i) Punk e) B) Punk f) i) Punk g) i) un ii) Punke i) un iii) un i) un ).5 lu.5 Punk Aufgabe : Venuri Ror Punke) a. Volumenrom Für ieen Aufgabeneil
Von der Fourier-Reihe zum Fourier-Integral
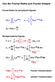 Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Versicherungstechnik
 Operaions Research und Wirschafsinformaik Prof Dr P Rech // Marius Radermacher, MSc DOOR Aufgabe 30 Versicherungsechnik Übungsbla 9 Abgabe bis zum Diensag, dem 13122016 um 10 Uhr im Kasen 19 Berachen Sie
Operaions Research und Wirschafsinformaik Prof Dr P Rech // Marius Radermacher, MSc DOOR Aufgabe 30 Versicherungsechnik Übungsbla 9 Abgabe bis zum Diensag, dem 13122016 um 10 Uhr im Kasen 19 Berachen Sie
Name: Punkte: Note: Ø:
 Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
auf den Boden fallen, hört man in gleichen Zeitabständen 4 Geräusche. Welchen Abstand hat die 3. Schraube vom unteren Ende der Fallschnur?
 Aufaben zu freien Fall 0. Von der Spize eine Ture lä an einen Sein fallen. Nach 4 Sekunden ieh an ihn auf de Boden aufchlaen. a) Wie hoch i der Tur? b) Mi welcher Gechwindikei riff der Sein auf den Erdboden
Aufaben zu freien Fall 0. Von der Spize eine Ture lä an einen Sein fallen. Nach 4 Sekunden ieh an ihn auf de Boden aufchlaen. a) Wie hoch i der Tur? b) Mi welcher Gechwindikei riff der Sein auf den Erdboden
Analysis: Exponentialfunktionen Analysis
 www.mahe-aufgaben.com Analysis: Eponenialfunkionen Analysis Übungsaufgaben u Eponenialfunkionen Pflich- und Wahleil gesames Soffgebie (insbesondere Funkionsscharen) ohne Wachsum Gymnasium ab J Aleander
www.mahe-aufgaben.com Analysis: Eponenialfunkionen Analysis Übungsaufgaben u Eponenialfunkionen Pflich- und Wahleil gesames Soffgebie (insbesondere Funkionsscharen) ohne Wachsum Gymnasium ab J Aleander
Definition Ein Homomorphismus von Lie-Algebren. Für uns ist vor allem die im folgenden Satz eingeführte Darstellung von Bedeutung.
 1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
Mathematikaufgaben > Analysis > Funktionenscharen
 Michael Buhlmann Mahemaikaugaben > Analysis > Funkionenscharen Augabe: Unersuche die ganz raionale Funkionenschar + 8 mi Parameer > 0 au: Nullsellen, Hoch- und Tiepunke, Monoonie, Wendepunke, Krümmung,
Michael Buhlmann Mahemaikaugaben > Analysis > Funkionenscharen Augabe: Unersuche die ganz raionale Funkionenschar + 8 mi Parameer > 0 au: Nullsellen, Hoch- und Tiepunke, Monoonie, Wendepunke, Krümmung,
Analysis 3.
 Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Transport. Explizite und implizite Verfahren
 p. 1/9 Tranpor Explizie und implizie Verfahren home/lehre/vl-mhs-1/inhalt/folien/vorlesung/10_transport_verf/decbla.ex Seie 1 von 9 p. /9 Inhalverzeichni 1. Explizie Verfahren Inabile Verfahren Lax Verfahren
p. 1/9 Tranpor Explizie und implizie Verfahren home/lehre/vl-mhs-1/inhalt/folien/vorlesung/10_transport_verf/decbla.ex Seie 1 von 9 p. /9 Inhalverzeichni 1. Explizie Verfahren Inabile Verfahren Lax Verfahren
