Grundlegende Algorithmen Kapitel 6: Flussprobleme
|
|
|
- Dorothea Kästner
- vor 6 Jahren
- Abrufe
Transkript
1 Grundlegende Algorihmen Kapiel 6: Fluprobleme Chriian Scheideler WS Kapiel 6 1
2 Grundlagen Definiion 6.1: Ein Flunezwerk (G,,,c) beeh au einem gericheen Graph G=(V,E), einer Quelle V, einer Senke V und einer Kapaziäfunkion c:v V R 0, o da c(u,v) = 0 fall (u,v) E. Wir werden im folgenden annehmen, da ֆ G u ֆ G für alle u V i. Definiion 6.2: Sei (G,,,c) ein Flunezwerk. a) Ein Flu in G i eine Funkion f:v V R, o da f(u, v) c(u, v) für alle u, v V (Kapaziäbedingungen) f(u, v) = - f(v, u) für alle u, v V (Aniymmerie) Σ v V f(u, v) = 0 für alle u V \ {, } (Fluerhalungbedingungen) b) Der Wer f einer Flufunkion f i definier al f =Σ v V f (, v) Kapiel 6 2
3 Grundlagen Bemerkung 6.3: E ei f ein Flu oder ein Flunezwerk (G,,,c). Dann a) f (v, v) = 0 für alle v V (wegen Aniymmerie). b) Σ u V f (u, v) = 0 für alle v V \ {, } (Fluerhalung & Aniymm.). c) Für alle u, v V mi (u, v), (v, u) E gil f (u, v) = f (v, u) = 0. d) Für alle v V \ {, } gil Σ f (u, v) = -Σ f (u,v) u V u V f (u, v) > 0 f (u, v) < 0 e) f mi f (u, v) = 0 für alle u, v V i ein Flu Kapiel 8 3
4 Grundlagen Beipiel für güligen Flu: u x f (u, v) c(u, v), f = v 11 1 y f(v,u)=1, alo f(u,v)=-1 nach Aniymmerie. Da implizier, da für da Paar {u,v} nich gleichzeiig in beide Richungen Flu fließen kann. Warum i da nich nowendig? Kapiel 8
5 Grundlagen Bemerkung 6.: Der in aufließende Flu i gleich dem in einfließenden Flu, wa nich chwer zu ehen i. Zunäch ellen wir fe wegen der Aniymmerie fe: Σ v V Σ w V f(v,w) = Σ {v,w} (f(v,w)+f(w,v)) + Σ v V f(v,v) = 0 Weierhin gil wegen der Fluerhalung: Σ v V Σ w V f(v,w) = Σ w V f(,w) + Σ w V f(,w) = f + Σ w V f(,w) Alo gil wegen der Aniymmerie: f = Σ w V f(w,) Kapiel 8 5
6 Grundlagen Alernaive Definiion von Flüen: Definiion 6.5: Sei (G,,,c) ein Flunezwerk. Ein Flu in G i eine Funkion f : E R 0 o da 0 f (u, v) c (u, v) für alle (u, v) E (Kapaziäbedingungen) Σ v V f (u, v) -Σ v V f (v, u) = 0 für alle u V \ {, } (Fluerhalungbedingungen) Definiion 6.5 i inuiiver, wobei Definiion 6.2 rerikiver i und manchmal leichere Beweie erlaub. Wir benuzen die alernaive Definiion 6.5 in päeren Teilen diee Kapiel Kapiel 6 6
7 Problem MAXFLOW: Eingabe: Ein Flunezwerk (G,,,c). Augabe: Ein Flu f in G mi maximalem Wer f. Bemerkung 6.6: Ein maximale Fluproblem (G, 1,, p, 1, q, c) mi mehreren Quellen 1,, p und mehreren Senken 1, q mi dem Ziel, o viele Güer wie möglich von den Quellen zu den Senken zu ranporieren, kann einfach auf da original MAXFLOW-Problem reduzier werden: Konruiere Gɑ = (Vɑ, Eɑ) und cˈ wie folg: Vɑ = V {, } Eɑ = E {(, i ) 1 i p} {( i, ) 1 i q} cɑ (u, v) = c (u, v) u, v V u = oder v = Dann exiier ein Flu f von 1,, p mi 1,, q Wer ϕ in (G, 1,, p, 1, q, c) genau dann, wenn ein Flu fɑ von nach in (Gɑ,,, cɑ) mi Wer ϕ exiier Kapiel p G G 1 q 8 8
8 Definiion 6.7: E ei (G,,,c) ein Flunezwerk. Für X, Y V bezeichnen wir f (X, Y) = Σ Σ f (x, y), c(x, Y) = Σ x X y Y Σ c (x, y) und X v = X \ {v} x X y Y X Y Lemma 6.8: E ei (G,,,c) ein Flunezwerk und e ei f ein Flu in G. Dann gil für alle X, Y, Z V. a) f (X, X) = 0 b) f (X, Y) = -f (Y, X) c) Wenn X Y = dann f (X Y, Z) = f (X, Z) + f (Y, Z) und f (Z, X Y) = f (Z, X) + f (Z, Y) Bewei: Übung Kapiel 6 8
9 Die Ford-Fulkeron Mehode Definiion 6.9: E ei (G,,,c) ein Flunezwerk und f ein Flu in G. a) Für u, v V i die Rekapaziä c f (u,v) definier al c f (u,v) = c (u,v) f (u,v). b) Da Reidualnezwerk G f = (V,E f ) i definier al E f = { (u,v) V V c f (u,v) > 0} c) Ein einfacher Pfad P von zu in G f wird augmenierender Pfad genann. Die Rekapaziä c f (P) von P i definier al c f (P) = min {c f (u,v) (u,v) P} Kapiel 6 9
10 Die Ford-Fulkeron Mehode Beipiel: augmenierender Pfad und Fluaugmenierung Flunezwerk: G u x v 11 1 y Kapiel 6 10
11 Beipiel: augmenierender Pfad und Fluaugmenierung Flunezwerk: G Reidualnezwerk: G f u v x y u v x y Kapiel 6 11
12 Beipiel: augmenierender Pfad und Fluaugmenierung Flunezwerk: G Reidualnezwerk mi augmenierendem Pfad: G f u v x y u v x y Kapiel 6 12
13 Beipiel: augmenierender Pfad und Fluaugmenierung Flunezwerk: G u 10 v x Reidualnezwerk mi augmenierendem Pfad: G f 8 3 y v y u x Augmeniere Flunezwerk: G u x v y Kapiel 6 13
14 Beipiel: augmenierender Pfad und Fluaugmenierung Flunezwerk: Reidualnezwerk mi augmenierendem Pfad: G u v x G f 12 u 8 3 y v x 7 y 5 15 Augmeniere Flunezwerk: Neue Reidualnezwerk: G u x G f 5 u 12 x v y v y Kapiel 6 1
15 Der Ford-Fulkeron Algorihmu FORDFULKERSON (Flunezwerk G = (V, E),,, c)) { für jede Kane (u, v) E { f [u, v] := 0; f [v, u] := 0; } // iniialiiere leeren Flu G f = Reidualnezwerk von G bezüglich f; olange (Ů ein Pfad P von zu in G f ) // P i der augmenierende Pfad { // berechne maximal hinzufügbaren Flu via P c f (P) := min {c f (u, v) (u, v) P)}; // c f (u, v) = c (u, v) f (u, v) } für jede Kane (u, v) P { f [u, v] := f [u, v] + c f (P); f [v, u] := - f [u, v]; } G f := Reidualnezwerk von G bezüglich f; } gib f au // akualiiere den Flu von P Kapiel 6 15
16 Lemma 6.10: E ei (G,,, c) ein Flunezwerk und f ein Flu in G. E ei G f ein Reidualnezwerk von G induzier durch f und e ei fɑ ein Flu in G f. Dann i (f + fˈ)(u, v) = f (u, v) + fˈ (u, v) ein güliger Flu in G mi Wer f + fˈ = f + fˈ. Lemma 6.11: E ei (G,,, c) ein Flunezwerk und f ein Flu in G. E ei G f da Reidualnezwerk von G induzier durch f und e ei P ein augmenierender Pfad in G f. Dann i f P : V V R mi f P (u,v) = c f (P) wenn (u,v) auf P -c f (P) wenn (v,u) auf P 0 on ein güliger Flu in G f mi Wer f P = c f (P) > 0. Korollar 6.12: E ei (G,,, c) ein Flunezwerk und f ein Flu in G. E ei G f da Reidualnezwerk von G induzier durch f und e ei P ein augmenierender Pfad in G f. E ei f P definier wie in Lemma Dann i fˈ = f + f P ein güliger Flu in G mi Wer f ˈ = f + f P = f + f P > f Kapiel 6 16
17 Beipiel: Ford-Fulkeron Algorihmu Flunezwerk: G 16 u 12 x v 1 y Kapiel 6 17
18 Beipiel: Ford-Fulkeron Algorihmu Flunezwerk: G Reidualnezwerk mi augmenierendem Pfad: G f 16 u 12 x u 12 x v 1 y 13 v 1 y Kapiel 6 18
19 Beipiel: Ford-Fulkeron Algorihmu Flunezwerk: Reidualnezwerk mi augmenierendem Pfad: G 16 u 12 x 20 G f 16 u 12 x v 1 y 13 v 1 y Augmeniere Flunezwerk: G 12 u 16 x v 1 y Kapiel 6 19
20 Beipiel: Ford-Fulkeron Algorihmu Flunezwerk: Reidualnezwerk mi augmenierendem Pfad: G 16 u 12 x 20 G f 16 u 12 x v 1 y 13 v 1 y Augmeniere Flunezwerk: Neue Reidualnezwerk mi augmenierendem Pfad: G u v x y 7 20 G f u v x y Kapiel 6 20
21 Beipiel: Ford-Fulkeron Algorihmu Flunezwerk: Reidualnezwerk mi augmenierendem Pfad: G u 12 9 x 7 20 G f u 8 5 x v 1 y 13 v 10 y Kapiel 6 21
22 Beipiel: Ford-Fulkeron Algorihmu Flunezwerk: Reidualnezwerk mi augmenierendem Pfad: G u 12 9 x 7 20 G f u 8 5 x v 1 y 13 v 10 y Augmeniere Flunezwerk: G 12 u x v 11 1 y Kapiel 6 22
23 Beipiel: Ford-Fulkeron Algorihmu Flunezwerk: Reidualnezwerk mi augmenierendem Pfad: G u 12 9 x 7 20 G f u 8 5 x v 1 y 13 v 10 y Augmeniere Flunezwerk: G 12 u x Neue Reidualnezwerk mi augmenierendem Pfad: G f u x v 11 1 y 13 v 11 3 y Kapiel 6 23
24 Beipiel: Ford-Fulkeron Algorihmu Flunezwerk: Reidualnezwerk mi augmenierendem Pfad: G u 12 9 x G f u x v y v y Kapiel 6 2
25 Beipiel: Ford-Fulkeron Algorihmu Flunezwerk: Reidualnezwerk mi augmenierendem Pfad: G u 12 9 x G f u x v 11 1 y 13 v 11 3 y Augmeniere Flunezwerk: G u x v 11 1 y Kapiel 6 25
26 Beipiel: Ford-Fulkeron Algorihmu Flunezwerk: Reidualnezwerk mi augmenierendem Pfad: G u 12 9 x G f u x v 11 1 y 13 v 11 3 y Augmeniere Flunezwerk: G u x Neue Reidualnezwerk mi augmenierendem Pfad: G f u x v 11 1 y 13 v 3 11 y Kapiel 8 26
27 Beipiel: Ford-Fulkeron Algorihmu Flunezwerk: Reidualnezwerk mi augmenierendem Pfad: G u x G f u x v 11 1 y 5 v 11 3 y Kapiel 8 27
28 Beipiel: Ford-Fulkeron Algorihmu Flunezwerk: Reidualnezwerk mi augmenierendem Pfad: G u x G f u x v 11 1 y 5 v 11 3 y Augmeniere Flunezwerk: G u x v 11 1 y Kapiel 8 28
29 Beipiel: Ford-Fulkeron Algorihmu Flunezwerk: Reidualnezwerk mi augmenierendem Pfad: G u x G f u x v 11 1 y 5 v 11 3 y Augmeniere Flunezwerk: Neue Reidualnezwerk mi augmenierendem Pfad: G u x G u x v 11 1 y 1 v 11 3 y Kapiel 6 29
30 Beipiel: Ford-Fulkeron Algorihmu u x v y Flunezwerk: G 10 u x v y G f Kapiel 6 30 u x v y Augmeniere Flunezwerk: G 10 u x v y G
31 Schnie von Flunezwerken Definiion 6.13: E ei (G,,, c) ein Flunezwerk und f ein Flu in G. a) Ein Schni (S, T) von G i eine Aufeilung von V in S und T = V \ S o da S und T. b) Der Flu über einen Schni (S, T) i f(s, T). c) Die Kapaziä eine Schnie (S, T) i c(s, T). Bemerkung 6.1: a) Die Definiion eine Flue i konien mi den Flüen, die in den Beipielen berechne wurden: Flüe von T zu S werden abgezogen: f (S, T) = Σ Σ f (x, y) (wobei f (x, y) < 0 fall f (y,x) > 0). x S y T b) Die Definiion einer Kapaziä eine Schnie i konien mi den Kapaziäen, die am Ende de vorigen Beipiel berechne wurden: Kanen von T zu S fügen der Kapaziä de Schnie nich hinzu: c (S, T) = Σ Σ c (x, y) wobei c (x, y) 0. x S y T Kapiel 6 31
32 Lemma 6.15: E ei (G,,, c) ein Flunezwerk und f ein Flu in G. E ei (S, T) ein Schni von G. Dann gil Und inbeondere auch f (S, T) = f. f = f (, V ) = f (V, ). Korollar 6.16: E ei (G,,, c) ein Flunezwerk. Dann i der Wer von jedem Flu f in G nach oben bechränk durch die Kapaziä eine beliebigen Schni in G. G u x G f u x v 11 1 y v 11 1 y Kapiel 8 32
33 Theorem 6.17: (Max-Flow Min-Cu Theorem) E ei (G,,,c) ein Flunezwerk und f ein Flu in G. Dann ind folgende Auagen äquivalen. a) f i ein maximaler Flu in G. b) Da Reidualnezwerk G f von G bezüglich f enhäl keinen augmenierenden Pfad. c) f = c(s, T) für einen Schni (S, T) von G. Bewei: a) b): b) a) gil wegen Korollar 6.12 und dami auch a) b). b) c): Sei S die Menge der Knoen, die von in G f erreichbar ind. Dann i (S,T) mi T=V\S ein Schni und f(s,t)=c(s,t) nach Definiion von G f. Alo i nach Lemma 6.15 f =c(s,t). c) a): Folg au Korollar Korollar 6.18: Sei (G,,, c) ein Flunezwerk mi ganzzahlige Kapaziäen c(u, v). Dann berechne der Ford-Fulkeron Algorihmu einen maximalen Flu f in Zei O ( E f ) Kapiel 8 33
34 Bemerkung 6.19: a) Die Schranke an die Laufzei von FORDFULKERSON i charf: G=G f u G f u G f u v v v b) Wenn die Kapaziäen raionale Zahlen ind, dann kann man ie auf ganze Zahlen kalieren und die Funkion FORDFULKERSON auf da kaliere Nezwerk anwenden. c) Wenn die Kapaziäen nich ganzzahlig ind, dann erminier FORDFULKERSON uner Umänden nich, und der Flu f, den FORDFULKERSON akualiier, konverier uner Umänden nich gegen den maximalen Flu Kapiel 8 3
35 Probleme mi irraionalen Kapaziäen Zu c): Sei φ=( 5 1)/2 0,61803 o gewähl, da 1-φ=φ 2. Um zu zeigen, da der Ford-Fulkeron Algorihmu hängen bleib, berachen wir den folgenden Graphen: X X X 1 1 φ X X X Wir aren mi dem leeren Flu. Nach Anwendung de roen Pfade ind die reidualen Kapaziäen der horizonalen Kanen 1, 0 und φ Kapiel 8 35
36 Probleme mi irraionalen Kapaziäen A B C Angenommen, die horizonalen reidualen Kapaziäen ind φ k-1, 0 und φ k für ein ungerade k N. 1. Augmeniere enlang B, wa φ k zum Flu hinzufüg. Die reidualen Kapaziäen ind nun φ k+1, φ k und Augmeniere enlang C, wa φ k zum Flu hinzufüg. Die reidualen Kapaziäen ind nun φ k+1, 0 und φ k. 3. Augmeniere enlang B, wa φ k+1 zum Flu hinzufüg. Die reidualen Kapaziäen ind nun 0, φ k+1 und φ k+2.. Augmeniere enlang A, wa φ k+1 zum Flu hinzufüg. Die reidualen Kapaziäen ind nun φ k+1, 0 und φ k Kapiel 8 36
37 Probleme mi irraionalen Kapaziäen D.h. Nach n+1 Augmenierungen ind die reidualen Kapaziäen φ 2n-2, 0 und φ 2n-1. Wenn die Anzahl der Augmenierungen gegen reb, konvergier der Wer de Flue gegen 1+2Σ i 0 φ i = 1+2/(1-φ) = + 5 < 7 obwohl der maximale Fluwer 2X+1 i. X X X 1 1 φ X X X Kapiel 8 37
38 Edmond-Karp Algorihmen Fazi: Ford-Fulkeron Algorihmu lä zuviele Freiräume in der Wahl de augemenierenden Pfade ellen Edmond und Karp zwei Heuriiken vor, um effizien maximale Flüe zu beimmen. Heuriik 1: Wähle den augmenierenden Pfad mi dem größen Wer. Heuriik 2: Wähle den kürzeen augmenierenden Pfad Kapiel 8 38
39 Edmond-Karp Algorihmen Theorem 6.20: Sei (G,,, c) ein Flunezwerk mi ganzzahlige Kapaziäen c(u, v). Dann berechne Heuriik 1 einen maximalen Flu f in Zei O( E 2 log E log f ). Bewei: Sei f* ein maximaler Flu in G. Sei f ein beliebiger Flu in G und f ein maximaler Flu im reidualen Graph G f. (Anfang i f leer und dami f =f*.) Sei e die Engpakane im gewählen augmenierenden Pfad. S V: Knoen, die von au mi Kanen der Kapaziä >c(e) erreichbar ind. T=V\S: nich leer wegen Wahl von e. E gil: c(s,t) c(e) E und c(s,t) f. Alo i c(e) f / E. Wer von f eig alo mindeen um Fakor (1+1/ E ) an Kapiel 8 39
40 Edmond-Karp Algorihmen Theorem 6.20: Sei (G,,, c) ein Flunezwerk mi ganzzahlige Kapaziäen c(u, v). Dann berechne Heuriik 1 einen maximalen Flu f in Zei O( E 2 log E log f ). Bewei (Forezung): Wer von f eig alo mindeen um Fakor (1+1/ E ) an. (1+1/ E ) k f* genau dann, wenn k E ln f*. E reichen alo E ln f* augmenierende Pfade, um zum maximalen Flu zu gelangen. Zei für Berechnung eine augmenierenden Pfade mi größem Wer: O( E log E ). (Da i eine Übung.) Alo Geamzei O( E 2 log E log f ) Kapiel 8 0
41 Edmond-Karp Algorihmen Analye von Heuriik 2: G i : reiduale Nezwerk nach i. Augmenierungchrien, d.h. G 0 =G. Für Knoen v ei di i (v) die Dianz (d.h. die Anzahl Kanen de kürzeen gericheen Pfade) von zu v in G i. Kein Weg von nach v: di i (v)=. Lemma 6.21: Für jeden Knoen v mi di i (v)= gil auch di i+1 (v)= Kapiel 8 1
42 Edmond-Karp Algorihmen Lemma 6.21: Für jeden Knoen v mi di i (v)= gil auch di i+1 (v)=. Bewei: Berache beliebigen Knoen v V mi di i (v)=. U: Menge aller Knoen, die Weg zu v haben. Dann gil auch für alle u U, da di i (u)=. Angenommen, di i+1 (v). Dann mu in Runde i ein augmenierende Pfad augewähl worden ein, der durch einen Knoen in U führ. (Warum?) In dieem Fall mu e aber einen Weg von zu einem Knoen in U gegeben haben, ein Widerpruch! Kapiel 8 2
43 Edmond-Karp Algorihmen Lemma 6.22: Für jeden Knoen v V gil di i+1 (v) di i (v). Bewei: v=: rivial, da immer di i ()=0. v : Indukion über Dianz zu. p=(,,u,v): kürzeer Weg von nach v in G i+1. (Kein Weg, dann ind wir nach Lemma 6.21 ferig.) Da dieer ein kürzeer Weg i, gil di i+1 (u)=di i+1 (v)-1. Nach Indukionvorauezung i di i+1 (u) di i (u). Fall 1: (u,v) war Kane in G i. Dann i di i (v) di i (u)+1. Alo i di i+1 (v)=di i+1 (u)+1 di i (v). Fall 2: (u,v) war keine Kane in G i. Dann war (v,u) eine Kane im i-en augmenierenden Pfad. In dem Fall i (v,u) auf einem kürzeen Weg von in G i und dami auch di i (v) di i (u) Kapiel 8 3
44 Edmond-Karp Algorihmen Lemma 6.23: Während der Abarbeiung von Heuriik 2 kann jede Kane (u,v) höchen V /2-mal vom reidualen Graphen verchwinden. Bewei: Angenommen, (u,v) i in den reidualen Graphen G i und G j+1 aber nich in den reidualen Graphen G i+1,,g j. Dann mu (u,v) im i-en augmenierenden Pfad liegen, alo di i (v)=di i (u)+1 ein. Weierhin mu (v,u) im j-en augmenierenden Pfad liegen, alo di j (u)=di j (v)+1 ein. Zuammen mi Lemma 6.22 folg di j (u) = di j (v)+1 di i (v)+1 = di i (u)+2 Da jede endliche Dianz höchen V -1 ein kann, kann (u,v) höchen V /2-mal verchwinden Kapiel 8
45 Edmond-Karp Algorihmen Jez ind wir owei, eine Laufzeichranke für Heuriik 2 zu berechnen. Da jede Kane höchen V /2-mal verchwinden kann, gib e höchen E V /2 Ereignie, in denen eine Kane verchwinde. Aber mindeen eine Kane verchwinde in jeder Ieraion, o da der Algorihmu nach höchen E V /2 Ieraionen halen mu. Da ein kürzeer augmenierender Pfad in O( E ) Zei gefunden werden kann, gil: Theorem 6.2: Sei (G,,, c) ein Flunezwerk mi ganzzahlige Kapaziäen c(u, v). Dann berechne Heuriik 2 einen maximalen Flu in Zei O( E 2 V ) Kapiel 8 5
46 Dinic Algorihmu Die Laufzei von Heuriik 2 häng nich länger von dem Wer de maximalen Flue ab, aber ie i noch zu groß. Wir präenieren jez einen Algorihmu von Dinic, der lediglich O( V 2 E ) Zei benöig. Definiion 6.25: Ein Flu f in einem Flunezwerk (G,,, c) heiß blockierend, wenn e auf jedem Weg von nach mindeen eine auriere Kane gib. Eine Kane e heiß aurier, fall f(e)=c(e) i. Bemerkung: Nich jeder blockierende Flu i maximal, aber jeder maximale Flu i blockierend Kapiel 8 6
47 Dinic Algorihmu Definiion 6.26: Der Level eine Knoen v i definier durch level(v)=δ f (,v) (die Anzahl der Kanen enlang eine kürzeen Wege in G f von nach v). Der Levelgraph L f i ein Teilgraph in G f, der alle Kanen (u,v) enhäl mi (u,v) G f und level(u)=level(v)-1. Lemma 6.27: L f enhäl alle kürzeen augmenierenden Wege und i in O(m) Zei (z.b. über BFS) konruierbar Kapiel 8 7
48 Dinic Algorihmu Dinic Algorihmu: beginne mi leerem Flu f wiederhole finde einen blockierenden Flu f in L f eze f:=f+f bi Senke nich mehr erreichbar in L f Lemma 6.28: Dinic Algorihmu häl nach höchen n-1 Ieraionen der Schleife Kapiel 8 8
49 Dinic Algorihmu Lemma 6.28: Dinic Algorihmu häl nach höchen n-1 Ieraionen der Schleife. Bewei: Berache eine fee Ieraion und ei vorher: Flu f und Funkion level nachher: Flu f und Funkion level Eine Kane (v,w) in L f i enweder eine Kane in G f (wenn die Kane nich aurier wurde) oder eine umgekehre Kane in L f. Für jede Kane (v,w) G f gil daher level(w) level(v)+1. Darau folg, da level () level() i. Berache dazu Pfad in L f : v w E gil ogar level ()>level(), wie wir ehen werden Kapiel 8 9
50 Dinic Algorihmu Lemma 6.28: Dinic Algorihmu häl nach höchen n-1 Ieraionen der Schleife. Bewei (Forezung): Angenommen, level ()=level(). Dann mu e einen kürzeen Weg p von nach in G f geben, der auch kürzeer Weg in G f war (da level(w)=level(v)+1 für alle Kanen (v,w) in p). Jede Kane von p i dann in L f, und keine von dieen i aurier worden. Da i aber ein Widerpruch zu der Annahme, da wir einen blockierenden Flu in L f gewähl haben. In jedem Schleifendurchlauf erhöh ich alo der Aband von zu in G f um mindeen 1. Da der kürzee Weg von nach nich länger al n-1 ein kann (fall einer exiier), folg da Lemma Kapiel 8 50
51 Dinic Algorihmu Auf Einheinezen benöig man ogar noch weniger Ieraionen. Definiion 6.29: Ein Einheinez i ein Flunezwerk (G,,,c) mi ganzzahligen Kapaziäen, in dem jeder Knoen v V\{,} genau eine hineingehende Kane mi Kapaziä 1 oder genau eine hinauführende Kane mi Kapaziä 1 ha. Bemerkung: Wenn ein Knoen genau eine hineingehende Kane mi Kapaziä 1 ha, o kann er mehrere herauführende Kanen beizen (und anderherum) Kapiel 8 51
52 Dinic Algorihmu Beipiel für Einheinez: : Kapaziä 1 : beliebige Kapaziä Kapiel 8 52
53 Dinic Algorihmu Lemma 6.30: Für ein Einheinez häl Dinic Algorihmu nach höchen 2 n-2 Ieraionen. Bewei: Wir berachen eine fee Ieraion. Sei f der momenane Flu und f* der maximale Flu, beide ganzzahlig. Dann i f*-f ein Flu in G f. Da G ein Einheinez i, i f*(e)-f(e) auf jeder Kane e in {-1,0,1}. Wir eilen die Kanen, auf denen f*(e)-f(e)=1 i, in eine Sammlung von Wegen von nach auf. Da gib e exak f* - f Wege von nach. (Bewei: Übung) Diee Wege ind knoendijunk (bi auf und ). Dehalb gib e einen augmenierenden Weg mi höchen (n-2)/( f* - f )+1 Knoen. Nach n-2 Ieraionen gil, da der kürzee augmenierende Weg mindeen n-2 +1 Knoen beiz (nach Lemma 6.28 enfern ich zunehmend von ). E gil n (n-2)/( f* - f )+1 f* - f n-2. Nach höchen n-2 weieren Ieraionen ha man alo den max. Flu Kapiel 8 53
54 Dinic Algorihmu Wie finde man einen blockierenden Flu? Verwende wiederhol Tiefenuche: wiederhole finde einen Weg p von nach in L f über Tiefenuche und chicke den Fluwer c f (p) über p bi kein augmenierender Weg in L f mehr übrig Lemma 6.31: Die Laufzei zur Ermilung eine blockierenden Flue i O(n m). Theorem 6.32: Die Laufzei von Dinic Algorihmu i O(n 2 m) Kapiel 8 5
55 Dinic Algorihmu Theorem 6.33: Die Laufzei von Dinic Algorihmu auf Einheinezen i O( n m). Bewei: Bei der Suche nach einem blockierenden Flu mu jeder Knoen im Einheinez nur einmal beuch werden, da er auf höchen einem augmenierenden Pfad liegen kann. Ein blockierender Flu kann alo in Zei O(m) gefunden werden. Mi Lemma 6.30 folg dann die Laufzei Kapiel 8 55
56 Dinic Algorihmu Anwendung von Dinic Algorihmu: Maching maximaler Kardinaliä in biparien Graphen. Theorem 6.3: Dinic Algorihmu auf dem biparien Graphen G=(V,E) erweier um und berechne einen maximalen Flu f in Zei O( n m), für den f die Größe de Maching maximaler Kardinaliä in G i Kapiel 8 56
57 Dinic Algorihmu Bewei: f M : Sei M ein Maching maximaler Kardinaliä in G. Dann i der Flu f, der M und alle Kanen von und zu M verwende, ein legaler Flu mi Wer f = M und dami f M Kapiel 8 57
58 Dinic Algorihmu Bewei: M f : Sei f ein maximaler Flu in G erweier um und. Dann i die Menge M,der Kanen, die f in G verwende, ein Maching mi M = f und dami M f Kapiel 8 58
59 Goldberg Algorihmu Inuiion: Ein Flunezwerk i ein Flüigkeinezwerk: Kanen enprechen Rohren und Knoen enprechen Rohrverknüpfungen. Jeder Knoen ha ein Reervoir, da eine beliebige Menge Flüigkei ammeln kann. Jeder Knoen, ein Reervoir und alle eine Rohrverknüpfungen ind auf einer Plaform, deen Höhe eig, wenn der Algorihmu abläuf Kapiel 6 59
60 Inuiion: Knoenhöhen beimmen, wie der Flu durch da Nezwerk geleie wird: der Flu fließ immer bergab. Iniial pump die Quelle oviel Flu wie möglich in da Nezwerk (= c(, V )). Wenn der Flu einen Zwichenknoen erreich, ammel er ich in deen Reervoir. Von dor wird er päer bergab geleie. Wenn alle nichaurieren Rohre, die einen Knoen u verlaen, zu Knoen v führen, die oberhalb von u liegen, o wird die Höhe von u erhöh, d. h. der Knoen u wird gelife. Wenn der geame Flu, der zur Senke fließen kann, dor angekommen i, wird der überchüige Flu in den Reervoiren zur Quelle zurückgechick, indem Zwichenknoen über die Höhe der Quelle hinau gelife werden Kapiel 6 60
61 Goldberg Algorihmu Definiion 6.35: Sei (G,,,c) ein Flunezwerk. Ein Präflu i eine Funkion f:v V R, o da f (u, v) c (u, v) für alle u, v V (Kapaziäbedingungen) f (u, v) = - f (v, u) für alle u, v V (Aniymmerie) f (V, u) 0 für alle u V \ {} (Präflubedingung) Der Überchu eine Knoen v i definier al e f (v)=f(v,v). Ein Knoen v heiß akiv, fall e f (v)>0. Goldberg Algorihmu wei jedem Knoen v eine Höhe h(v) N 0 zu. Die Höhenfunkion i legal, fall h()= V, h()=0 und für alle Kanen (v,w) in G f gil, da h(v) h(w)+1. (D.h. für alle (v,w) E mi h(v)>h(w)+1 mu gelen, da (v,w) E f.) Eine Kane (v,w) in G f heiß zuläig, fall h(v)>h(w). (Zuammen mi der vorigen Bedingung folg darau, da h(v)=h(w)+1.) Kapiel 8 61
62 Goldberg Algorihmu Grundlegende Operaionen: Puh(u,v): chieb oviel Flu wie möglich von u nach v Lif(u): heb u owei an wie möglich, ohne die Legaliä der Höhenfunkion zu verlezen. Formal: Puh(u,v): δ:=min{e f (u),c f (u,v)} f(u,v):=f(u,v)+δ c f (u,v):=c f (u,v)-δ c f (v,u):=c f (v,u)+δ e f (u):=e f (u)-δ e f (v):=e f (v)+δ Lif(u): h(u):=min{ h(v)+1 (u,v) E f } Kapiel 8 62
63 Goldberg Algorihmu Goldberg Algorihmu arbeie wie folg: Preflow-Puh Algorihmu: for each u V\{} do h(u):=0; e f (u):=0 for each (u,v) E do f(u,v):=0; f(v,u):=0 h():= V for each (,u) E do f(,u):=c(,u); f(u,):=-f(,u); e f (u):=c(,u) while (e gib akiven Knoen u) do if (e gib zuläige Kane (u,v) ) hen Puh(u,v) ele Lif(u) Kapiel 8 63
64 Beipiel: Kapaziäen ind ro markier Kapiel 6 6
65 Beipiel: Nach der Iniialiierungphae: Nach der Iniialiierungphae: wurde auf Höhe 7 gelife. Alle anderen Knoen ehen auf Höhe 0. Jede Kane au wurde aurier. Alle anderen Kanen haben Flu 0. Nun i keine PUSH-Operaion anwendbar. Anwendbare Operaionen ind LIFT(u), LIFT(v) oder LIFT(w) Kapiel 6 65
66 Beipiel: Nach LIFT(v): Nach der Iniialiierungphae: Die Höhe von h(v) wurde auf 1 + min {h [u] (v, u) E f } = = 1 geez. Anwendbare Operaionen ind nun LIFT(u), LIFT(w) oder PUSH(v, u), PUSH(v, w), PUSH(v, x), PUSH(v, y), PUSH(v, ) Kapiel 6 66
67 Beipiel: Nach PUSH(v, y): Nach der Iniialiierungphae: Anwendbare Operaionen ind nun LIFT(u), LIFT(w), LIFT(y) oder PUSH(v, u), PUSH(v, w), PUSH(v, x), PUSH(v, ) Kapiel 6 67
68 Beipiel: Nach der Iniialiierungphae: Nach LIFT(y): Die Höhe h(y) wurde auf 1 + min{h[u] (y, u) E f } = = 1 geez. Anwendbare Operaionen ind nun LIFT(u), LIFT(w) oder PUSH(v, u), PUSH(v, w), PUSH(v, x), PUSH(v, ), PUSH(y, ) Kapiel 6 68
69 Beipiel: Nach der Iniialiierungphae: Nach PUSH(y, ): Anwendbare Operaionen ind nun LIFT(u), LIFT(w) oder PUSH(v, u), PUSH(v, w), PUSH(v, x), PUSH(v, ). Der Algorihmu wird forgeführ, bi weder PUSH noch LIFT Operaionen anwendbar ind Kapiel 8 69
70 Goldberg Algorihmu Lemma 6.36: Zu jedem Zeipunk de Algorihmu gil e f () 0 und für alle Knoen v V\{}, da e f (v) 0. Bewei: Wir führen eine volländige Indukion über die Anzahl der augeführen Puh und Lif Operaionen durch. Anfang i da Lemma offenichlich wahr. Wir nehmen alo an, e i zu einem Zeipunk wahr. Dann erhäl jede Fluveränderung in der Puh Operaion aufgrund der Wahl von δ die Eigenchaf, da e f (v) 0 für alle v V\{}. (Lif änder nich an e f (v).) E gil alo Σ u V\{} f(v,u) 0. Deweieren gil für jede aniymmeriche Funkion f: Σ u V f(v,u) = 0. Darau folg, da e f ()=f(v,) 0 ein mu Kapiel 8 70
71 Goldberg Algorihmu Lemma 6.37: Jeder Lif(u) Aufruf erhäl die Legaliä der Höhenfunkion und erhöh h(u) um mindeen 1. Bewei: Eine Lif Operaion wird nur dann für einen Knoen u durchgeführ, wenn e keine zuläige Kane (u,v) gib und dami h(u) h(v) für alle (u,v) E f i. Da die neue Höhe h (u)=min{h(v)+1 (u,v) E f } i, folg, da h (u)>h(u) und h (u) h(v)+1 für alle (u,v) E f i Kapiel 8 71
72 Goldberg Algorihmu Lemma 6.38 (Superopimaliä): Für einen legalen Präflu f und eine legale Höhenfunkion h gib e keinen augmenierenden Pfad in G f. Bewei: Angenommen, e gäbe einen augmenierenden Pfad (=v 1,v 2,,v l=) in G f. Da die Höhen der Knoen mi der Zei nur anwachen können (iehe Lemma 6.37), gil h() n, und da niemal akiv ein kann, gil h()=0. Darau folg, da n h() h(v 2 )+1 h(v 3 )+2 h()+l-1 = l-1 n-1 da der augmenierende Pfad einfach i und omi höchen n Knoen enhalen kann. Wir haben alo einen Widerpruch Kapiel 8 72
73 Goldberg Algorihmu Lemma 6.39 (Opimaliä): Wenn e keinen akiven Knoen in G f gib, dann i der Präflu ein maximaler Flu. Bewei: Wenn e keinen Knoen u V\{,} gib mi e f (u)>0, dann gil für alle Knoen u V\{,} nach Lemma 6.36, da e f (u)=0. Der Präflu i alo ein legaler Flu. Die Maximaliä de Flue folg au Lemma 6.38 und dem Maxflow-Mincu Theorem. Wir müen nur noch zeigen, da der Algorihmu erminier Kapiel 8 73
74 Goldberg Algorihmu Lemma 6.0: Für jeden akiven Knoen u gib e einen Pfad in G f von u nach. Bewei: Sei U die Menge der Knoen, die in G f von u erreichbar ind. Fall U i, dann haben alle Knoen in U wegen Lemma 6.36 einen nichnegaiven Überchu. Der Flu in U hinein mu 0 ein, denn gäbe e eine Kane (v,w) E mi v U und w U und f(v,w)>0, dann wäre auch c f (w,v) f(v,w)>0. Alo gil 0 = Σ v V\U f(v,u) Σ v V\U f(v,u) - Σ v U f(v,v\u) = Σ v V\U f(v,u) - Σ v U f(v,v\u) + Σ v U f(v,u) - Σ v U f(v,u) = Σ v U ( f(v,v) f(v,v) ) = Σ v U\{u} ( f(v,v) f(v,v) ) + 2e f (u) > 0 Wir haben alo einen Widerpruch, und omi mu in U ein Kapiel 8 7
75 Goldberg Algorihmu Lemma 6.1: Für jeden akiven Knoen v V gil h(v) 2n-1. Bewei: Da aufgrund Lemma 6.36 und per Definiion nie akiv ein können, gil zu jeder Zei h()=n und h()=0. Berache einen beliebigen akiven Knoen u V\{,}. Nach Lemma 6.0 i von u erreichbar in G f. Sei p=(u=v 1,v 2,,v l =) ein einfacher Pfad von u nach. Wir wien, da h()=n i. Weierhin gil h(v i ) h(v i+1 )+1 für alle i {1,...,l-1}. Darau folg, da h(u) n+l 2n-1 i, da der Weg nich enhalen kann und omi l n-1 i. Jez ind wir owei, den Aufwand für die Lif und Puh Operaionen zu berechnen Kapiel 8 75
76 Goldberg Algorihmu Lemma 6.2: Die Geamzahl der Lif Operaionen i O(n 2 ) und deren Zeikomplexiä i O(n m). Bewei: Aufgrund von Lemma 6.37 und 6.1 können höchen 2n-1 Lif Operaionen auf jeden Knoen angewand werden. Ingeam wird die Lif Operaion alo höchen O(n 2 )-mal augeführ. Die Koen einer Lif(v) Operaion ind gleich dem augehenden Grad von v in G f, da wir für jede v alle eine adjazenen Knoen überprüfen müen. Die Geamkoen der Lif Operaion ind alo nach oben hin bechränk durch Σ v V (2n-1) deg(v) = O(n m) wobei deg(v) der (augehende) Grad von Knoen v i Kapiel 8 76
77 Goldberg Algorihmu Eine Puh Operaion i äigend, fall δ=c f (u,v) i, und on nichäigend. Lemma 6.3: Die Geamzahl aller äigenden Puh Operaionen i O(n m). Bewei: Nach einem äigenden Puh auf (u,v) können wir nich nochmal Flu von u nach v chieben, ofern v nich vorher eine Puh Operaion auf (v,u) durchgeführ ha. Da h(u)=h(v)+1 bei Puh(u,v) und h(v)=h(u)+1 bei Puh(v,u) gelen mu und die Höhen der Knoen monoon eigen, mu ich alo die Höhe von u für einen nochmaligen äigenden Puh enlang (u,v) um mindeen 2 erhöh haben. Über (u,v) kann e omi höchen (2n-1)/2 äigende Puh Operaionen geben, worau eine Geamzahl von O(n m) äigenden Puh Operaionen folg Kapiel 8 77
78 Goldberg Algorihmu Lemma 6.: Die Geamzahl der nichäigenden Puh Operaionen i O(n 2 m). Bewei: Wir verwenden die Poenialfunkion Φ=Σ akive v V h(v). Am Anfang i Φ=0, da alle Höhen akiver Knoen gleich 0 ind. Wir unercheiden zwichen drei Typen von Operaionen, die Φ verändern: Nichäigender Puh enlang Kane (v,w): Dann wird Knoen v deakivier und omi Φ um h(v) verminder. Auf der anderen Seie kann w nun akiv werden, wa Φ um h(w) erhöhen kann. Da aber h(v)=h(w)+1 gil, wird Φ immer um mindeen 1 erniedrig. Säigender Puh enlang Kane (v,w): Da kann Φ um höchen 2n-1 erhöhen, da im wor cae v akiv bleib und w akiv wird und h(w) 2n-1 i. Lif Operaion: Die Lif Operaionen erhöhen Φ zuammen um höchen (2n-1)n. Da e nur O(n m) äigende Puh Operaionen gib, kann ich Φ durch diee um höchen O(n 2 m) erhöhen. Φ kann ich durch die Lif Operaionen um höchen O(n 2 ) erhöhen. Ingeam kann Φ alo um höchen O(n 2 m) erhöh werden. Da immer Φ 0 gil, i die Anzahl der nichäigenden Puh Operaionen maximal O(n 2 m) Kapiel 8 78
79 Goldberg Algorihmu Da eine Puh Operaion nur konane Zei benöig, ergib ich au den Lemma eine Geamlaufzei von O(n 2 m) für Goldberg Algorihmu. Durch eine verbeere Auwahl der Puh und Lif Operaionen kann man diee Laufzei noch verbeern. Regeln für die Wahl der akiven Knoen: FIFO: Die akiven Knoen werden in einer FIFO Queue verwale, d.h. neue akive Knoen werden hinen in die Queue eingefüg und vorne raugenommen. Dami i eine Laufzei von O(n 3 ) erreichbar. Highe-Label-Fir: Nimm immer den akiven Knoen mi der höchen Höhe. Dami i ogar eine Laufzei von O( m n 2 ) erreichbar Kapiel 8 79
80 Weiere Varianen Goldberg, 1985: FIFO PPA: O( V 3 ). Goldberg, Tarjan, 1986: Verbeerer FIFO PPA: O( V E log ( V 2 E )). Goldberg, Tarjan, 1986, Cheriyan, Mahehwari 1989: Highe Label PPA: O( V 2 E ). Ahuja, Orlin 1989: Exce Scaling PPA: O( V E log( V 2 f max )). Ahuja, Orlin, Tarjan, 1989: Improved Exce Scaling PPA: O( V E log( V log f max / E + 2)). Randomiiere Varianen Kapiel 8 80
81 Gechiche de maximalen Flualgorihmu G = (V, E) mi V = n, E = m, U Wer de maximalen Flue Kapiel 6 81
82 Varianen de maximalen Fluproblem Knoenkapaziäen u c wird lokal erez durch u 1 u 2 c Ungerichee Graphen wird lokal c c u 1 u u 2 2 u 2 u c erez durch 2 c c c Kapiel 6 82
83 Minimaler Schni mi minimaler Anzahl an Kanen Problem MINCUTMINEDGES: Eingabe: Ein Flunezwerk (G,,, c) Augabe: Ein minimaler Schni von (G,,, c) mi minimaler Anzahl von Kanen (zwichen allen minimalen Schnien) Tranformiere (G,,, c) in ein Flunezwerk (G,,, c ) mi c (u, v) = M c(u, v) + 1, bei dem M E + 1 eine Konane i. Eine Löung de MAXFLOW Problem in (G,,, c ) ergib einen minimalen Schni (S, T) mi c (S, T) = M c(s, T) + {e E e S T} minimaler Schni in G Anzahl der Kanen über Schni Kapiel 6 83
84 Zirkulaionen Definiion 6.5: a) Ein Zirkulaionnezwerk i ein Tripel (G, b, c), wobei G = (V, E) ein direker Graph i und b, c : E R mi b(e) c (e) für alle e E. b) Eine Zirkulaion f i ein Flu ohne eine Quelle oder Senke. Formal: f : E R mi 1. b(e) f (e) c (e) für alle e E (Kapaziäbedingungen) 2. Σ (u, v) E f(u, v) = Σ (v, w) E f(v, w) für alle v V (Fluerhalungbedingungen) Problem CIRCULATE: Eingabe: ein Zirkulaionnezwerk (G, b, c) Augabe: eine Zirkulaion f für (G, b, c) Redefiniere da Reidualnezwerk G f = (V, E f ) mi E f = {(u, v) V V c f (u, v) > 0)} und c(u, v) f(u, v) fall f(u, v) < b(u, v) c f (u,v) = c(u, v) - f(u, v) + max{f(v, u) b(v, u), 0} fall f(u, v) b(u, v) Reidualkapaziä wie zuvor maximaler Flu, der gerichen werden kann Kapiel 6 8
85 Zirkulaionen Zirkulaion CIRCULATE (Zirkulaionnezwerk (G, b, c)) { f(e) = 0 für alle e E; /* iniialiiere rivialen nich zuläigen Flu*/ while ( e E : f(e) < b(e)) { wähle (u, v) E mi f(u, v) < b(u, v); /* Flu auf Kane (u, v) i zu klein*/ if ( ein Pfad P von v nach u in G f ) { /* beache die Redefiniion von G f! */ C = (P, (u, v)) i ein Krei mi (u, v) C; chicke δ = min e C c f (e) Flu enlang de Kreie C; /* augmenierender Flu auf (u, v) */ } ele reurn(null); /* e exiier keine Zirkulaion */ } /* while */ reurn(f); } /* CIRCULATE */ Der Algorihmu CIRCULATE erminier. Fall er eine Funkion f zurückliefer, dann i f eine zuläige Zirkulaion für (G, b, c). Wenn der Algorihmu NULL zurückliefer, exiier keine zuläige Zirkulaion (G, b, c). Lemma 6.6: (G, b, c) mi G = (V, E) ha eine zuläige Zirkulaion für jede Menge U V Σ b(u, v) Σ c(v, u) (u, v) (U, Ū) (v, u) (Ū, U) Kapiel 6 85
86 Zirkulaionen Lemma 6.6: (G, b, c) mi G = (V, E) ha eine zuläige Zirkulaion für jede Menge U V Bewei: Σ b(u, v) Σ c(v, u) (u, v) (U,Ū) (u, v) (Ū,U) : : Sei f eine Zirkulaion für (G,b,c). Dann gil für alle v V Σ (u,v) E f(u,v) = Σ (v,w) E f(v,w) Alo gil für jede Menge U V: Σ (u,v) (U,Ū) b(u,v) Σ (u,v) (U,Ū) f(u,v) = Σ (v,w) (Ū,U) f(v,w) Σ (v,w) (Ū,U) c(v,w) Kapiel 6 86
87 Zirkulaionen Bewei (Forezung): : Angenommen, e gib keine Zirkulaion f für (G,b,c). Dann gib der Algorihm CIRCULATE NULL au. D.h. e gib eine Kane e=(u,v) E mi f(e)<b(e), für die e keinen Pfad in G f von v nach u gib. Definiere U={w V v w in G f }. Dann i v U und u Ū und für alle (x,y) (U,Ū): c f (x,y)=0. Alo i f(e)=c(e) für alle e (U,Ū) und f(e) b(e) für alle e (Ū,U). Alo i Σ (u,v) (Ū,U) b(u,v) > Σ (u,v) (Ū,U) f(u,v) = Σ (v,w) (U,Ū) f(v,w) = Σ (v,w) (U,Ū) c(v,w) Kapiel 8 87
88 Unere Schranken für Kanenflüe Definiion 6.7: a) Ein bechränke Flunezwerk i ein Tupel (G,,, b, c), wobei (G,,, c) ein Flunezwerk i und b : E R eine Funkion, die zuläige Flüe nach unen bechränk, wobei b (e) c (e) für alle e E. b) Ein bechränker Flu f für (G,,, b, c) i ein Flu für (G,,, c) mi b (e) f (e) für alle e E. Problem LOWERBOUNDEDFLOW: Eingabe: ein bechränke Flunezwerk (G,,, b, c) Augabe: ein bechränker Flu f für (G,,, b, c) mi maximalem Wer f Kapiel 6 88
89 Unere Schranken für Kanenflüe BOUNDEDFLOW (bechränke Flunezwerk (G,,, b, c)){ konruiere ein Zirkulaionnezwerk (G, b, c ) mi G = G + (, ); b (e) = b(e); c (e) = c(e) für alle e E; b (, ) = 0; c (, ) = ; f = CIRCULATE(G, b, c ); if (f = NULL) reurn (NULL); f = zuläiger Flu für (G,,, b, c) erhalen au f durch Löchen der Kane (, ) und deren Flu; löe da MAXFLOW Problem für (G,,, c) mi f al iniialem Flu und Reidualkapaziäen c (u, v) = c(u, v) f(u, v) + max{f(v, u) b(v, u), 0} für (u, v) E f wie zuvor max. zu löchender Flu e ei g der maximale Flu berechne für (G,,, c); reurn(g); } /* BOUNDEDFLOW */ Wenn der Algorihmu BOUNDEDFLOW NULL zurückliefer, dann exiier kein bechränker Flu für (G,,, b, c). Andernfall liefer der Algorihmu BOUNDEDFLOW eine Löung f für da Problem LOWERBOUNDEDFLOW zurück Kapiel 6 89
90 Minimale Fluproblem Problem MINFLOW: Eingabe: ein bechränke Flunezwerk (G,,, b, c) Augabe: ein bechränker Flu für (G,,, b, c) mi minimalem Wer f MINIMUMFLOW (bechränke Flunezwerk (G,,, b, c)) { h = BOUNDEDFLOW(G,,, b, c); if (h = NULL) reurn(null); konruiere Flunezwerk (G R, R, R, c R ) mi G R = (V, E R ), E R = {(v, u) (u, v) E}; R = ; R = ; c R (u, v) = c f (u, v) für alle (u, v) E R, wobei c f () die redefinieren Reidualkapaziäen ind; löe da MAXFLOW Problem für (G R, R, R, c R ) und e ei g der maximale Flu für (G R, R, R, c R ); f = h g; reurn(f); } /* MINIMUMFLOW */ Wenn der Algorihmu MINIMUMFLOW NULL zurückliefer, exiier kein zuläiger bechränker Flu für (G,,, b, c). Andernfall liefer der Algorihmu MINIMUMFLOW eine Löung f für Problem MINFLOW zurück Kapiel 6 90
91 Flüe mi minimalen Koen a)ein Flunezwerk mi Kanenkoen i ein Tupel (G,,, c, γ), wobei G = (V, E) ein gericheer Graph i, c : E N 0 Kanenkapaziäen bechreib, und γ : E N 0 Kanenkoen bechreib, d.h. γ(e) ind die Koen, um eine Einhei Flu über e zu enden. b) Die Koen eine Flue f von nach in G ind γ(f) := Σ e E γ(e) f(e). e E Problem MINCOSTMAXFLOW: Eingabe: Ein Flunezwerk (G,,, c, γ) Augabe: Ein maximaler Flu f mi minimalen Koen γ(f). O.B.d.A. nehmen wir an, da G=(V,E) nur einfach gerichee Kanen ha, d.h. e gib keine Knoen u,v V mi (u,v),(v,u) E Kapiel 8 91
92 Flüe mi minimalen Koen Sei f ein Flu. Koen eine augmenierenden Pfade p zu f: γ(p) = Σ (u,v) p:(u,v) E c f (p) γ(u,v) Σ (u,v) p:(v,u) E c f (p) γ(v,u) Ein augmenierender Krei bzgl. f i ein augmenierender Pfad, deen erer und lezer Knoen idenich i. Lemma 6.9: Zu jedem augmenierenden Krei p bezüglich eine Flue f gib e einen Flu f mi f = f und γ(f )=γ(f) + γ(p). Bewei: Sei f =f+p. Dann i f nach wie vor ein legaler Flu. Ferner gil für die Koen von f : γ(f ) = γ(f) + Σ (u,v) p:(u,v) E c f (p) γ(u,v) Σ (u,v) p:(v,u) E c f (p) γ(v,u) = γ(f) + γ(p) Kapiel 8 92
93 Flüe mi minimalen Koen Saz 6.50: Ein Flu f ha minimale Koen uner allen Flüen mi Fluwer f genau dann, wenn e keinen augmenierenden Krei mi negaiven Koen gib. Bewei: : Folg au Lemma 6.9. : : Sei f ein Flu, der keine minimalen Koen beiz. Sei g ein Flu mi minimalen Koen und g = f. Berache da reiduale Nezwerk G g-f = (V,E g-f ) mi E g-f = E + g-f E - g-f, wobei E + g-f = {(u,v) g(u,v) > f(u,v) } und E - g-f = {(v,u) g(u,v) < f(u,v) } Seien die Kanenkapaziäen definier al c g-f = g(e)-f(e). Dann gil für alle Knoen v V, da Σ u V c g-f (u,v) Σ w V c g-f (v,w) = 0 (Deail an der Tafel) Kapiel 8 93
94 Flüe mi minimalen Koen Bewei (Forezung): Sei nun c min = min{c g-f (u,v) (u,v) E g-f }. Wenn wir bei einem beliebigen Knoen v V mi Kanen in G g-f aren, gib e immer eine Kane (v,w) mi c g-f (v,w) c min, und jeder noch nich vorher beuche Knoen mu aufgrund der Kapaziäerhalung auch wieder verlaen werden können. Da die Anzahl der Knoen durch V bechränk i, i daher ein augmenierender Krei in G g-f konruierbar. Enfern man dieen, i die Kapaziäerhalung nach wie vor erfüll. G g-f kann alo in eine Menge augmenierender Kreie zerleg werden. Wende man diee Kreie auf f an, erhäl man g. Da γ(g) < γ(f) i, mu alo mindeen einer dieer Kreie negaive Koen haben Kapiel 8 9
95 Flüe mi minimalen Koen Fall die Kanenkapaziäen und Kanenkoen ganzzahlig und durch eine Konane C bechränk ind, können wir den folgenden Polynomialzeialgorihmu zur Berechnung eine maximalen Flue mi minimalen Koen durchführen: Verwende Ford-Fulkeron zur Berechnung eine maximalen Flue. Laufzei: O(C n m). Suche nach augmenierenden Kreien mi negaiven Koen in G f bi keine olche Kreie mehr zu finden ind. Ein negaiver augmenierender Krei kann miel Bellman-Ford in O(n m) Zei gefunden werden (warum?). Jeder olche Krei ha eine ganzzahlige Kapaziä >0 und ganzzahlige Koen <0. D.h. die Koen de maximalen Flue verringern ich um mindeen 1 für jeden olchen augmenierenden Krei. Die Geamlaufzei für dieen Teil i alo O(C n 2 m). Forgechrienere Techniken können einen maximalen Flu mi minimalen Koen auch für beliebige Kapaziäen und Koen berechnen (iehe z.b. da Buch von Ahuja, Magnani und Orlin: Nework Flow) Kapiel 8 95
96 Flüe mi minimalen Koen Definiion 6.8: a) Ein Flunezwerk mi Kanenkoen i ein Tupel (G, c, γ, δ), wobei G = (V, E) ein gericheer Graph i, c : E N 0 Kanenkapaziäen bechreib, δ : V N 0 Knoenbedarfe bechreib, Σ v V δ(v) = 0 i und γ : E N 0 Kanenkoen bechreib, d.h. γ(e) ind die Koen, um eine Einhei Flu über e zu enden. Beache: δ(v) > 0 eh für Knoen, die Flu konumieren, während δ(v) < 0 Knoen bezeichne, die Flu produzieren. b) Ein Flu f mi minimalen Koen für (G, c, γ, δ) i eine Funkion f : E N 0 mi 1. f(e) c(e) für alle e E (Kapaziäbedingungen) 2. Σ (u,v) E f(u, v) - Σ (v,w) E f(v, w) = δ(v) für alle v V, (Fluerhalung) der die Koen γ(f) := Σ e E γ(e) f(e) minimier. Problem MINCOSTFLOW: Eingabe: Ein Flunezwerk mi Kanenkoen (G, c, γ, δ) Augabe: Ein Flu f mi minimalen Koen für (G, c, γ, δ) Löung möglich durch Kombinaion de LOWERBOUNDEDFLOW Problem mi dem MINCOSTMAXFLOW Problem Kapiel 6 96
97 Anwendungen de maximalen Fluproblem Scheduling auf uniformen parallelen Machinen Die Aufgabe i e, eine Menge J von Job auf m uniformen parallelen Machinen auzuführen. Jeder Job j J ha Bearbeiungzei p j (z. B. Anzahl der Machinenage) Sarermin r j : Der ere Tag, an dem Job j verfügbar i Fälligkeidaum d j : Der Tag, an dem Job j erledig ein mu. Weierhin reffen wir folgende Annahmen: r j + p j d j Eine Machine kann jeweil nur an einem Job arbeien. Jeder Job kann jeweil nur an einer Machine laufen. Unerbrechung i erlaub, d. h. ein Job kann unerbrochen werden und läuf an verchiedenen Tagen auf verchiedenen Machinen Kapiel 6 97
98 Beipiel: Job, m = 3 Machinen j p j r j d j Sorierung von {r j, d j j J} reulier in einer Folge (1, 3,, 5, 7, 9), die fünf Inervalle [1, 3], [3, ], [, 5], [5, 7] und [7, 9] pezifizier. E ei T k,l da Inervall, da an Tag k are und am Tag l + 1 ende: T 1,2, T 3,3, T,, T 5,6 und T 7,8. Tranformiere da Problem in ein Flunezwerk (G,,, c) wie rech angegeben. Dann gil: Da Schedulingproblem ha eine zuläige Löung genau dann, wenn der maximale Flu in G den Wer Σ j J p j = 8.5 ha. Die obige Konrukion kann verallgemeiner werden (Übung) Kapiel 6 98
99 Vereile Rechnen auf einer Zweiprozeor Machine Ein Compueryem ha zwei (nich nowendigerweie ideniche) Prozeoren. Wir wollen ein ehr große Programm auführen, da au einer Menge J von Modulen beeh, welche mieinander ineragieren. Die folgenden Koen ind gegeben: α i : Koen der Berechnung von Modul i auf Prozeor 1. β i : Koen der Berechnung von Modul i auf Prozeor 2. γ i,j : Koen der Inerprozekommunikaion wenn i und j verchiedenen Prozeoren zugeeil ind. Wenn i und j dem gleichen Prozeor zugeeil ind, beragen die Kommunikaionkoen 0. Ziel: Finde eine Zuweiung der Module auf die Prozeoren, o da die Geamkoen beehend au Rechenkoen und Kommunikaionkoen minimier werden Kapiel 6 99
100 Gegeben ei eine Menge J von Modulen und Koen α j, β j, γ i,j. Konruiere ein Flunezwerk (G,,, c), G = (V, E) wie folg: V = {, } J E = {(, j) j J} {(j, ) j J} {(i, j) i, j J, γ i,j >0} β j c (i, j) = α i γ i,j wenn i = wenn j = wenn i, j Lemma 6.52: In der obigen Konrukion gil: die Geamkoen einer opimalen Zuweiung von Modulen auf Prozeoren i gleich der Kapaziä eine minimalen Schnie (S, T) von G Kapiel 6 100
101 Beipiel: j α j β j γ i,j Kapiel 6 101
102 Beipiel: j α j β j γ i,j Kapiel 6 102
103 Tanker Scheduling Eine Schifffahrgeellchaf ha vereinbar, Waren rechzeiig zwichen mehreren verchiedenen Quell-Ziel-Paaren auzuliefern. Für ihre ju-in-ime Waren haben die Kunden präzie Aulieferungermine fegeleg, an denen die Waren ihren Beimmungor erreichen müen. Die Schifffahrgeellchaf mu felegen, wie hoch die minimale Anzahl von Schiffen ein mu, dami die Aulieferungermine der Waren eingehalen werden können. Beipiel: Termine der Waren Waren Quelle Ziel Termin 1 A C 3 2 A C 8 3 B D 3 B C 6 Fahrzei (voll) C D A 3 2 B 2 3 Fahrzei (leer) A B C 2 1 D 1 2 Nezwerk N = (V N, E N ) der zuläigen Folgen von aufeinanderfolgenden Schiffouren (i, j) E N wenn ein Schiff den Job i auführen kann und dann Job j Kapiel 6 103
104 Da Nezwerk von zuläigen Sequenzen von zwei aufeinanderfolgenden Schiffouren wird in ein Flumodell (G,,, b, c) ranformier: Knoen für die Schiffouren ind verdoppel: i i. neue Knoen und werden hinzugefüg. Kanen werden von zu i, von i zu und von i zu i gezogen für alle Schiffouren i. Außerdem werden Kanen von i zu j gezogen, genau dann wenn (i, j) E N. Alle Kanen haben Kapaziä 1, und die Kanen (u, i ) haben eine unere Schranke b(i,j) = 1. Lemma 6.53: Jede Löung de minimalen Fluproblem für (G,,, b, c) korrepondier zu einer Löung für da Tanker Scheduling Problem und umgekehr Kapiel 6 10
105 Da Baeball Eliminierungproblem Siehe auch: T. Bernhol, A. Gülich, T. Hofmeier, N. Schmid, I. Wegener: Komplexiäheorie, effiziene Algorihmen und die Bundeliga. Informaik Spekrum, 25:(6), 2002, pp Beipiel: In der Deuchen Fußballliga, Saion 6/65, zwei Runden vor dem Ende der Saion ah die Tabelle au wie rech angegeben. Für Sieg/Unenchieden/Niederlage erhiel ein Team damal 2/1/0 Punke. I 1860 München noch ein Kandida, der den Tiel gewinnen kann? 1860 München ha noch zwei Spiele zu pielen, o da da Team noch Punke gewinnen und omi auf 37 Punke kommen kann. Auf den eren Blick i die Anwor Ja. Sand vor den lezen zwei Runden: Team Punke 1 Werder Bremen FC Köln 36 3 Boruia Dormund München 33 Aber die Dinge ind nich o einfach Kapiel 6 105
106 Die Dinge ind aber nich o einfach. Hier ind die relichen Spiele der eren vier Mannchafen: Sand vor den lezen zwei Runden: Team Punke 1 Werder Bremen FC Köln 36 3 Boruia Dormund München 33 Reliche Spiele der eren vier: Werder Bremen - Boruia Dormund 1. FC Köln - 1. FC Nürnberg 1860 München - MSV Duiburg 1. FC Nürnberg - Werder Bremen Boruia Dormund - 1. FC Köln Hamburger SV München Darau folg, da 1860 München die Meierchaf nich mehr gewinnen kann. Warum? Kapiel 6 106
107 Die Dinge ind aber nich o einfach. Hier ind die relichen Spiele der eren vier Mannchafen: Sand vor den lezen zwei Runden: Team Punke 1 Werder Bremen FC Köln 36 3 Boruia Dormund München 33 Reliche Spiele der eren vier: Werder Bremen - Boruia Dormund 1. FC Köln - 1. FC Nürnberg 1860 München - MSV Duiburg 1. FC Nürnberg - Werder Bremen Boruia Dormund - 1. FC Köln Hamburger SV München Darau folg, da 1860 München die Meierchaf nich mehr gewinnen kann. Werder Bremen, der 1. FC Köln und Boruia Dormund haben noch zwei Spiele unereinander zu pielen, daher erhalen ie mindeen zuäzliche Punke. Zuammen haben ie dann mindeen = 112 Punke, alo mu einer von ihnen mindeen 112/3 = 38 Punke haben. Eine andere Argumenaion i die folgende: Wir nehmen an, da 1860 München mi 37 Punken Tabellenerer wird. Aber dann mu Werder Bremen die relichen zwei Spiele verlieren. Boruia Dormund ha, nachdem ie gegen Werder Bremen gewonnen haben, 37 Punke und müen gegen den 1. FC Köln verlieren. Aber dann ha der 1. FC Köln 38 Punke (ein Widerpruch) Kapiel 6 107
108 Formale Modell n Mannchafen 1,2,..., n pielen mehrere Runden gegeneinander um die Meierchaf. Wir befinden un in der Mie der Saion und wollen wien, ob uner Lieblingeam n noch Meier werden kann. E gele, da Mannchaf i genau w(i) der biher gepielen Spiele gewonnen ha, 1 i n. Weier ei g(i, j) die Anzahl der Spiele, die Mannchaf i noch gegen Mannchaf j pielen mu, 1 i j n. Wir bezeichnen Mannchaf i al eliminier, wenn ie nich mehr Meier werden kann. Da Problem i e, zu encheiden, ob Mannchaf n eliminier werden kann. Beipiel: i w(i) g(i,j) Die Mannchafen erhalen 1 Punk für einen Sieg, 0 Punke für eine Niederlage. Unenchieden ind nich möglich. Mannchaf ha bi zum jezigen Zeipunk 0 Siege, mu jedoch noch je einmal gegen Mannchaf 1 und 2 anreen und noch 3mal gegen Mannchaf 3. I Mannchaf eliminier? Kapiel 6 108
109 Da bemögliche Szenario für Mannchaf n ri ein, wenn ie alle verbleibenden Spiele gewinn und omi ingeam W = w(n) + g(j, n) viele Punke erreich. Mannchaf n kann nich eliminier werden, wenn die relichen Spiele zwichen den anderen Team o augehen können, da alle anderen Team am Ende der Saion höchen W Siege haben. E bezeichne x(i, j) die Anzahl der g(i, j) verbleibenden Spiele, die Mannchaf i gegen Mannchaf j gewinn. Dann gil n-1 Σ j=1 n Σ x(i, j) + x(j, i) = g(i, j) = g(j, i), 1 i, j n E ei W(i) = w(i) + j=1 x(i, j) die Anzahl der Siege von Mannchaf i am Ende der Saion 1 i n. Mannchaf n kann Meier werden, wenn e eine Möglichkei gib, die Saion o zu Ende zu pielen, da gil W W (i), 1 i < n Kapiel 6 109
110 Mannchaf n kann nich eliminier werden, wenn e ganze Zahlen x(i, j) 0, 1 i, j n gib, o da x(i, j) + x(j, i) = g(i, j) = g(j, i), 1 i, j n und n-1 n Σ Σ j=1 j=1 W = w(n) + g(j, n) w(i) + x(i, j) = W (i), 1 i < n i w(i) 0 0 g(i, j) Σ W = w() + g(j, ) = = 5 Nach den drei verbleibenden j=1 Spielen zwichen Mannchaf 1 und 2 gil enweder x(1, 2) 2 oder x(2, 1) 2 und daher oder W(1) = w(1) + x(1, j) + 2 = 6 n n Σ Σ j=1 W(2) = w(2) + x(2, j) + 2 = 6 j= Kapiel 6 110
111 Wir formulieren da Baeball Eliminaionproblem al ein maximale Fluproblem, in dem der Flu, der von der Quelle zur Senke gechick wird, die verbleibenden Spiele zwichen den Mannchafen i und j repräenier, 1 i, j < n. Formal konruiere (G,,, c), G = (V, E) wie folg: E ei F = n-2 n-1 Σ Σ i=1 j=i+1 g(i, j). V = {, } {(i, j) 1 i < j < n} {1,..., n 1} E = {(, (i, j)) 1 i j < n} {((i, j), i), ((i, j), j) 1 i j < n} {(i, ) 1 i < n} c(, (i, j)) = g(i, j) c((i, j), i) = F c((i, j), j) = F c(i, ) = W w(i) Kapiel 6 111
112 Beipiel (forgeez): i w(i) 0 0 g(i, j) Der maximale Flu i < 5 = F, d.h. kein güliger Augang möglich. Lemma 6.5: Mannchaf n i nich eliminier, genau dann wenn der maximale Flu in G gleich F i Kapiel 6 112
25. Flüsse in Netzen. Motivation. Fluss. Flussnetzwerk
 Moivaion 25. Flüe in Nezen Flunezwerk, Maximaler Flu, Schni, Renezwerk, Max-flow Min-cu, Ford-Fulkeron Mehode, Edmond-Karp Algorihmu, Maximale Biparie Maching [Oman/Widmayer, Kap. 9.7, 9.8.1], [Cormen
Moivaion 25. Flüe in Nezen Flunezwerk, Maximaler Flu, Schni, Renezwerk, Max-flow Min-cu, Ford-Fulkeron Mehode, Edmond-Karp Algorihmu, Maximale Biparie Maching [Oman/Widmayer, Kap. 9.7, 9.8.1], [Cormen
Algorithmen II Vorlesung am
 Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Übersicht. Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 18: Maximaler Fluss (K26)
 Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
Algorithmische Graphentheorie
 Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Netzwerke Beispielnetzwerk N
 Nezwerke Kapiel Flüe in Nezwerken Sromnez Telefonnez Warenflu zwichen Herellern und Konumenen Verkehr (Sraßen, Züge, Flugzeuge,...) Of wollen wir Güer von einem Punk zu einem anderen chicken Ziel So viel/effizien/illig
Nezwerke Kapiel Flüe in Nezwerken Sromnez Telefonnez Warenflu zwichen Herellern und Konumenen Verkehr (Sraßen, Züge, Flugzeuge,...) Of wollen wir Güer von einem Punk zu einem anderen chicken Ziel So viel/effizien/illig
KAPITEL 2 KÜRZESTE WEGE
 KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
Vorlesung Kombinatorische Optimierung (Wintersemester 2007/08)
 Vorleung Kombinaoriche Opimierung (Wineremeer 007/08) Kapiel : Flüe und Zirkulaionen Volker Kaibel Oo-von-Guericke Univeriä Magdeburg (Verion vom 0. November 007) Definiion. Ein Nezwerk i ein Paar (D,
Vorleung Kombinaoriche Opimierung (Wineremeer 007/08) Kapiel : Flüe und Zirkulaionen Volker Kaibel Oo-von-Guericke Univeriä Magdeburg (Verion vom 0. November 007) Definiion. Ein Nezwerk i ein Paar (D,
Stochastische Differentialgleichungen
 INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
Übungsblatt 4 Lösungsvorschläge
 Insiu für Theoreische Informaik Lehrsuhl Prof. Dr. D. Wagner Übungsbla 4 Lösungsvorschläge Vorlesung Algorihmenechnik im WS 09/10 Problem 1: Flüsse [vgl. Kapiel 4.1 im Skrip] ** Gegeben sei ein Nezwerk
Insiu für Theoreische Informaik Lehrsuhl Prof. Dr. D. Wagner Übungsbla 4 Lösungsvorschläge Vorlesung Algorihmenechnik im WS 09/10 Problem 1: Flüsse [vgl. Kapiel 4.1 im Skrip] ** Gegeben sei ein Nezwerk
Wiederholung. Algorithmen und Datenstrukturen Kapitel 10. Motivation. Begriffe und Definitionen
 Algorihmen nd Daenrkren Kapiel Frank Heimann heimann@informaik.ni-hambrg.de 6. Janar 2016 Frank Heimann heimann@informaik.ni-hambrg.de 1/ Graphen Grndlagen Definiion nd Darellng Tiefen- nd Breienche Topologiche
Algorihmen nd Daenrkren Kapiel Frank Heimann heimann@informaik.ni-hambrg.de 6. Janar 2016 Frank Heimann heimann@informaik.ni-hambrg.de 1/ Graphen Grndlagen Definiion nd Darellng Tiefen- nd Breienche Topologiche
2.6.1 Definition und Darstellung Ausspähen von Graphen Minimal spannende Bäume Kürzeste Pfade 2.6.
 .6 Graphen.6. Definition und Dartellung.6. Aupähen von Graphen.6.3 Minimal pannende Bäume.6.4 Kürzete Pfade.6.5 Maximaler Flu .6.5 Maximaler Flu.6.5. Flunetzwerke.6.5. Ford-Fulkeron-Methode.6.5.3 Algorithmu
.6 Graphen.6. Definition und Dartellung.6. Aupähen von Graphen.6.3 Minimal pannende Bäume.6.4 Kürzete Pfade.6.5 Maximaler Flu .6.5 Maximaler Flu.6.5. Flunetzwerke.6.5. Ford-Fulkeron-Methode.6.5.3 Algorithmu
Fluß. Flußnetzwerk. Definition 6.2. Es sei N = (G, c, s, t) ein Flußnetzwerk. Für einen Knoten
 6. Flüe un Zuornungen Fluß In ieem Kapiel weren Bewerungen von Kanen al maximale Kapaziäen inerpreier, ie üer iee Kane pro Zeieinhei ranporier weren können. Wir können un einen Graphen al Verorgungnezwerk
6. Flüe un Zuornungen Fluß In ieem Kapiel weren Bewerungen von Kanen al maximale Kapaziäen inerpreier, ie üer iee Kane pro Zeieinhei ranporier weren können. Wir können un einen Graphen al Verorgungnezwerk
b) Das Restnetzwerk zu f sieht folgendermaßen aus:
 Techniche Univeriä München Zenrum Mhemik Dikree Opimierung: Grundlgen (MA 0) Prof Dr R Hemmecke, Dr R Brndenerg, MSc-Mh B Wilhelm Üungl 7 Aufge 7 Die folgende Aildung zeig ein Nezwerk N mi einen Flukpziäen
Techniche Univeriä München Zenrum Mhemik Dikree Opimierung: Grundlgen (MA 0) Prof Dr R Hemmecke, Dr R Brndenerg, MSc-Mh B Wilhelm Üungl 7 Aufge 7 Die folgende Aildung zeig ein Nezwerk N mi einen Flukpziäen
Geradlinige Bewegung Krummlinige Bewegung Kreisbewegung
 11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
Mathematik: Mag. Schmid Wolfgang+LehrerInnenteam ARBEITSBLATT 6-13 ERMITTELN DER KREISGLEICHUNG
 ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
Kapitel 7: Flüsse in Netzwerken und Anwendungen Gliederung der Vorlesung
 Gliederung der Vorleung. Falltudie Bipartite Graphen. Grundbegriffe 3. Elementare Graphalgorithmen und Anwendungen 4. Minimal pannende Bäume 5. Kürzete Pfade 6. Traveling Saleman Problem 7. Flüe in Netzwerken
Gliederung der Vorleung. Falltudie Bipartite Graphen. Grundbegriffe 3. Elementare Graphalgorithmen und Anwendungen 4. Minimal pannende Bäume 5. Kürzete Pfade 6. Traveling Saleman Problem 7. Flüe in Netzwerken
Hauptprüfung 2010 Aufgabe 4
 Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Arbeitsauftrag Thema: Gleichungen umformen, Geschwindigkeit, Diagramme
 Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Weg im tv-diagramm. 1. Rennwagen
 Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
6. Primal-duale Algorithmen
 6. Einführung... 6. Der primal-duale Algorihmu... 6 6. Bemerkungen zum primal-dualen Algorihmu... 7 6. Ein primal-dualer Algorihmu für da Kürzee-Wege-Problem... 8... 9 6.6 Ein primal-dualer Algorihmu für
6. Einführung... 6. Der primal-duale Algorihmu... 6 6. Bemerkungen zum primal-dualen Algorihmu... 7 6. Ein primal-dualer Algorihmu für da Kürzee-Wege-Problem... 8... 9 6.6 Ein primal-dualer Algorihmu für
1 Fluss in Graphen. 1.1 Das Residuennetzwerk 10/20 10/30 10/30 10/15 20/20 20/40 20/30. Praktikum Algorithmen-Entwurf (Teil 4)
 Prkikum Algorihmen-Enwurf (Teil 4) 1.11.211 1 1 Flu in Grphen E ei ein gericheer Grph G = (V,E) gegeen. Jeder Kne e de Grphen ei eine Kpziä c(e) N zugeordne. Weier eien zwei Knoen de Grphen ugezeichne:
Prkikum Algorihmen-Enwurf (Teil 4) 1.11.211 1 1 Flu in Grphen E ei ein gericheer Grph G = (V,E) gegeen. Jeder Kne e de Grphen ei eine Kpziä c(e) N zugeordne. Weier eien zwei Knoen de Grphen ugezeichne:
Westfälische Hochschule - Fachbereich Informatik & Kommunikation - Bereich Angewandte Naturwissenschaften. 2. Mechanik
 Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
Abbildungsmaßstab und Winkelvergrößerung
 Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Effiziente Algorithmen und Datenstrukturen II
 Effiziente Algorithmen und Datenstrukturen II Prof. Dr. Christian Scheideler Technische Universität München, 25. April 2006 1 Algorithmen für maximale Flüsse 1.1 Flüsse Ein Flussnetzwerk G = (V, E) ist
Effiziente Algorithmen und Datenstrukturen II Prof. Dr. Christian Scheideler Technische Universität München, 25. April 2006 1 Algorithmen für maximale Flüsse 1.1 Flüsse Ein Flussnetzwerk G = (V, E) ist
Fakultät Grundlagen. s = t. gleichförm ig
 Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Beschreibung paralleler Abläufe mit Petri-Netzen
 Bechreibung paralleler Abläufe mi Peri-Nezen Grundlagen und Beipiele für den Unerrich Peri-Neze ind ein graphiche Miel zur Bechreibung, Modellierung, Analye und Simulaion von dynamichen Syemen, die eine
Bechreibung paralleler Abläufe mi Peri-Nezen Grundlagen und Beipiele für den Unerrich Peri-Neze ind ein graphiche Miel zur Bechreibung, Modellierung, Analye und Simulaion von dynamichen Syemen, die eine
Die Lösungen der Übungsaufgaben werden durch folgendes Lemma etwas vereinfacht:
 Prof. Dr. D. Kuske, M.Sc. M. Huschenbe Fachgebie Theoreische Informaik, TU Ilmenau Muserlösung zum 2. Übungsbla Auomaenheorie Die Lösungen der Übungsaufgaben werden durch folgendes Lemma ewas vereinfach:
Prof. Dr. D. Kuske, M.Sc. M. Huschenbe Fachgebie Theoreische Informaik, TU Ilmenau Muserlösung zum 2. Übungsbla Auomaenheorie Die Lösungen der Übungsaufgaben werden durch folgendes Lemma ewas vereinfach:
Kürzeste Wege. 1 Einleitung. Wie kommt man am schnellsten von München nach Stuttgart?
 Kürzee Wege Wie komm man am chnellen von München nach Sugar? Melanie Herzog Wolfgang Ferdinand Riedl Lehruhl M für Angewande Geomerie und Dikree Mahemaik Techniche Univeriä München Vorauezungen: Grundlagen:
Kürzee Wege Wie komm man am chnellen von München nach Sugar? Melanie Herzog Wolfgang Ferdinand Riedl Lehruhl M für Angewande Geomerie und Dikree Mahemaik Techniche Univeriä München Vorauezungen: Grundlagen:
Grundlagen: Algorithmen und Datenstrukturen
 Grundlagen: Algorithmen und Datentrukturen Prof. Dr. Hanjo Täubig Lehrtuhl für Effiziente Algorithmen (Prof. Dr. Ernt W. Mayr) Intitut für Informatik Techniche Univerität München Sommeremeter H. Täubig
Grundlagen: Algorithmen und Datentrukturen Prof. Dr. Hanjo Täubig Lehrtuhl für Effiziente Algorithmen (Prof. Dr. Ernt W. Mayr) Intitut für Informatik Techniche Univerität München Sommeremeter H. Täubig
1. Für die Bewegung eines Fahrzeuges wurde das t-s-diagramm aufgenommen. Skizziere für diese Bewegung das t-v- Diagramm.
 Aufgaben zur gleichförigen Bewegung 1. Für die Bewegung eine Fahrzeuge wurde da --Diagra aufgenoen. Skizziere für diee Bewegung da -- Diagra. 2. Eine Radfahrerin und ein Spaziergänger i eine Hund bewegen
Aufgaben zur gleichförigen Bewegung 1. Für die Bewegung eine Fahrzeuge wurde da --Diagra aufgenoen. Skizziere für diee Bewegung da -- Diagra. 2. Eine Radfahrerin und ein Spaziergänger i eine Hund bewegen
Messung der Ladung. Wie kann man Ladungen messen? /Kapitel Formeln auf S.134: Elektrische Ladung
 --- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
--- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
2. Torsion geschlossener Profile
 Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Institut für Informatik. Aufgaben zur Klausur Grundlagen der Technische Informatik 1 und 2
 NIVESITÄT LEIPZIG Iniu für Informaik Prüfungaufgaben Klauur zur Vorleung WS 2/2 und SS 2 b. Techniche Informaik Prof. Dr. do Kebchull Dr. Paul Herrmann Dr. Han-Joachim Lieke Daum:. Juli 2 hrzei: 8-3 Or:
NIVESITÄT LEIPZIG Iniu für Informaik Prüfungaufgaben Klauur zur Vorleung WS 2/2 und SS 2 b. Techniche Informaik Prof. Dr. do Kebchull Dr. Paul Herrmann Dr. Han-Joachim Lieke Daum:. Juli 2 hrzei: 8-3 Or:
Induktionsgesetz. a = 4,0cm. m = 50g
 1. Die neenehende Aildung (Blick von vorn) zeig eine Spule mi 5 Windungen von quadraichem uerchni mi Seienlänge a = 4,cm zum Zeipunk. DieSpuleeweg ich mider Gechwindigkei v vom Berag v = 2, cm nachrech.
1. Die neenehende Aildung (Blick von vorn) zeig eine Spule mi 5 Windungen von quadraichem uerchni mi Seienlänge a = 4,cm zum Zeipunk. DieSpuleeweg ich mider Gechwindigkei v vom Berag v = 2, cm nachrech.
F Rück. F r Rück. Mechanische Schwingungen. Größen zur quantitativen Beschreibung :
 Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
23. Kürzeste Wege. Flussüberquerung (Missionare und Kannibalen) Das ganze Problem als Graph. Formulierung als Graph
 Fluüberquerung (Miionare und Kannibalen). Kürzete Wege Problem: Drei Kannibalen und drei Miionare tehen an einem Ufer eine Flue. Ein dort bereittehende Boot fat maimal zwei Peronen. Zu keiner Zeit dürfen
Fluüberquerung (Miionare und Kannibalen). Kürzete Wege Problem: Drei Kannibalen und drei Miionare tehen an einem Ufer eine Flue. Ein dort bereittehende Boot fat maimal zwei Peronen. Zu keiner Zeit dürfen
4.7 Der Algorithmus von Dinic für maximalen Fluss
 4.7 Der Algorithmus von Dinic für maximalen Fluss Wir kennen bereits den Algorithmus von Ford Fulkerson zur Suche nach einem maximalen Fluss in einem Graphen. Wir lernen nun einen Algorithmus für maximalen
4.7 Der Algorithmus von Dinic für maximalen Fluss Wir kennen bereits den Algorithmus von Ford Fulkerson zur Suche nach einem maximalen Fluss in einem Graphen. Wir lernen nun einen Algorithmus für maximalen
4 Die K-Methode. Sei {A 0,A 1 } Interpolationspaar. Das Peetre sche K-Funktional ist definiert als. ( a 0 A 0 +t a 1 A 1 ), a A 0 +A 1, t > 0
 25 4 Die K-Mehode Sei {A,A } Inerpolaionpaar. Da Peere che K-Funkional i definier al K,a;A,A K,a : a a + a a i A i,i, a A + a A, a A +A, > Bemerkung : wenn {A,A } fixier K,a anelle von K,a;A,A K,a a A
25 4 Die K-Mehode Sei {A,A } Inerpolaionpaar. Da Peere che K-Funkional i definier al K,a;A,A K,a : a a + a a i A i,i, a A + a A, a A +A, > Bemerkung : wenn {A,A } fixier K,a anelle von K,a;A,A K,a a A
Lösungen zu Übungsblatt 4
 Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Staatlich geprüfte Techniker
 Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Zwischenwerteigenschaft
 Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
8 Kürzeste Wege KÜRZESTE WEGE. Hier sind alle Graphen gerichtet und gewichtet, d.h. wir haben eine Kostenfunktion K : E R dabei.
 04 8 KÜRZESTE WEGE 8 Kürzee Wege Hier ind alle Graphen geriche nd geiche, d.h. ir haben eine Koenfnkion K : E R dabei. Alo ea: 5 7 0 4 K(, ) = 5,K(, ) =,K(, ) = 7,K(, 4) = 0 I W = ( 0,,..., k ) irgendein
04 8 KÜRZESTE WEGE 8 Kürzee Wege Hier ind alle Graphen geriche nd geiche, d.h. ir haben eine Koenfnkion K : E R dabei. Alo ea: 5 7 0 4 K(, ) = 5,K(, ) =,K(, ) = 7,K(, 4) = 0 I W = ( 0,,..., k ) irgendein
1. Kontrolle Physik Grundkurs Klasse 11
 1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
6. Flüsse und Zuordnungen
 6. Flüsse und Zuordnungen Flußnetzwerke 6. Flüsse und Zuordnungen In diesem Kapitel werden Bewertungen von Kanten als maximale Kapazitäten interpretiert, die über diese Kante pro Zeiteinheit transportiert
6. Flüsse und Zuordnungen Flußnetzwerke 6. Flüsse und Zuordnungen In diesem Kapitel werden Bewertungen von Kanten als maximale Kapazitäten interpretiert, die über diese Kante pro Zeiteinheit transportiert
W. Stark; Berufliche Oberschule Freising
 9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
Von der Fourier-Reihe zum Fourier-Integral
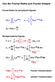 Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Messgrößen und gültige Ziffern 7 / 1. Bewegung mit konstanter Geschwindigkeit 7 / 2
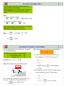 Die Genauigkei einer Megröße wird durch die güligen Ziffern berückichig. Al gülige Ziffern einer Maßzahl gelen alle Ziffern und alle Nullen, die rech nach der eren Ziffer ehen. Megrößen und gülige Ziffern
Die Genauigkei einer Megröße wird durch die güligen Ziffern berückichig. Al gülige Ziffern einer Maßzahl gelen alle Ziffern und alle Nullen, die rech nach der eren Ziffer ehen. Megrößen und gülige Ziffern
reibungsgedämpfte Schwingung
 HTL-LiTec reibunggedäpfe Schwingung Seie 1 von 7 Dipl.-Ing. Paul MOHR E-Brief: p.ohr@eduhi.a reibunggedäpfe Schwingung Maheaiche / Fachliche Inhale in Sichworen: reibunggedäpfe Schwingung; nueriche Löung
HTL-LiTec reibunggedäpfe Schwingung Seie 1 von 7 Dipl.-Ing. Paul MOHR E-Brief: p.ohr@eduhi.a reibunggedäpfe Schwingung Maheaiche / Fachliche Inhale in Sichworen: reibunggedäpfe Schwingung; nueriche Löung
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Abiturprüfung 2017 ff Beispielaufgabe Grundkurs Mathematik; Analysis Beispiel Wirkstoff
 Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Inhalt. 1. Flußprobleme. 2. Matching. 3. Lineares Programmieren. 4. Ganzzahliges Programmieren. 5. NP-Vollständigkeit. 6. Approximationsalgorithmen
 Effiziente Algorithmen Einführung 1 Inhalt 1. Flußprobleme 2. Matching. Lineares Programmieren 4. Ganzzahliges Programmieren 5. NP-Vollständigkeit 6. Approximationsalgorithmen 7. Backtracking und Branch-and-Bound
Effiziente Algorithmen Einführung 1 Inhalt 1. Flußprobleme 2. Matching. Lineares Programmieren 4. Ganzzahliges Programmieren 5. NP-Vollständigkeit 6. Approximationsalgorithmen 7. Backtracking und Branch-and-Bound
Minimal spannende Bäume
 Minimal pannende Bäume Geuch: : ein minimal pannender Baum u G,, d.h. eine minimale Teilmenge E min E der Kanen, o da G min = (V,E( min,d) uammenhängend ngend und die Summe der Kanengewiche minimal i.
Minimal pannende Bäume Geuch: : ein minimal pannender Baum u G,, d.h. eine minimale Teilmenge E min E der Kanen, o da G min = (V,E( min,d) uammenhängend ngend und die Summe der Kanengewiche minimal i.
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
Flüsse, Schnitte, bipartite Graphen
 Flüe, Schnie, iprie Grphen Michel Eicher 06. Juni 0 Michel Eicher Flüe, Schnie, iprie Grphen 06. Juni 0 / 48 Deniionen Nezwerk Flu Üerich Mximler Flu Ford-Fulkeron Minimler Schni Edmond-Krp 3 Redukionen
Flüe, Schnie, iprie Grphen Michel Eicher 06. Juni 0 Michel Eicher Flüe, Schnie, iprie Grphen 06. Juni 0 / 48 Deniionen Nezwerk Flu Üerich Mximler Flu Ford-Fulkeron Minimler Schni Edmond-Krp 3 Redukionen
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Abiturprüfung Mathematik 2012 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1
 Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
ges.: Der erste Treffpunkt ist zum Zeitpunkt 0 am Start. Danach fährt der Fahrer 1 45 min und legt dabei
 859. Zwei Auo faren mi erciedenen Gecwindigkeien 1 = 160 / bzw. 2 = 125 / dieelbe Srecke on 200 Länge. Beide Wagen aren gleiczeiig in derelben Ricung. Der arer de cnelleren Wagen mac nac 45min arzei 15min
859. Zwei Auo faren mi erciedenen Gecwindigkeien 1 = 160 / bzw. 2 = 125 / dieelbe Srecke on 200 Länge. Beide Wagen aren gleiczeiig in derelben Ricung. Der arer de cnelleren Wagen mac nac 45min arzei 15min
Datenstrukturen & Algorithmen
 Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Graphenalgorithmen Maximaler Fluss Einleitung Flussnetzwerke Ford-Fulkerson Fulkerson Methode Maximales bipartites Matching
Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Graphenalgorithmen Maximaler Fluss Einleitung Flussnetzwerke Ford-Fulkerson Fulkerson Methode Maximales bipartites Matching
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4: Flüsse
 Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4: Flüsse Dipl-Math. Wolfgang Kinzner 3.4.2012 Kapitel 4: Flüsse Flüsse Netzwerk, Fluss, s,t-schnitt, Kapazität MaxFlow-MinCut-Theorem Restnetzwerk
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4: Flüsse Dipl-Math. Wolfgang Kinzner 3.4.2012 Kapitel 4: Flüsse Flüsse Netzwerk, Fluss, s,t-schnitt, Kapazität MaxFlow-MinCut-Theorem Restnetzwerk
Aufgaben Arbeit und Energie
 Aufgaben Arbei und Energie 547. Ein Tank oll i Hilfe einer Pupe i aer gefüll werden. Der Tank ha für den Schlauch zwei Anchlüe, oben und unen. ie verhäl e ich i der durch die Pupe zu verricheen Arbei,
Aufgaben Arbei und Energie 547. Ein Tank oll i Hilfe einer Pupe i aer gefüll werden. Der Tank ha für den Schlauch zwei Anchlüe, oben und unen. ie verhäl e ich i der durch die Pupe zu verricheen Arbei,
Positioniersteuerung (5.12) Beschleunigen - Phase 2 (5.13) Beschleunigen - Phase 3 (5.14) Phase 4: Konstante Geschwindigkeit (5.15) Bremsen Phase 5
 Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
(3) Weg-Zeit-Verhalten
 (3) Weg-Zei-Verhalen Vorleung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wdh: Bogenlängenabelle Pfad felegen (P 0, P, P and P 3 ) 3 3 r u u P0 3 u u P 3 u u P u P Berechne Poiion für Zeipunk, i.e.
(3) Weg-Zei-Verhalen Vorleung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wdh: Bogenlängenabelle Pfad felegen (P 0, P, P and P 3 ) 3 3 r u u P0 3 u u P 3 u u P u P Berechne Poiion für Zeipunk, i.e.
VU Algorithmen auf Graphen Übungsblatt 2 - Aufgabe 2 Transformation einer MaxFlow- in eine MinCost Circulation Instanz
 VU Algorithmen auf Graphen Übungsblatt 2 - Aufgabe 2 Transformation einer MaxFlow- in eine MinCost Circulation Instanz Gruppe A: Bernhard Stader, Georg Ziegler, Andreas Zugaj 10. November 2004 Inhaltsverzeichnis
VU Algorithmen auf Graphen Übungsblatt 2 - Aufgabe 2 Transformation einer MaxFlow- in eine MinCost Circulation Instanz Gruppe A: Bernhard Stader, Georg Ziegler, Andreas Zugaj 10. November 2004 Inhaltsverzeichnis
Versuchsprotokoll. Datum:
 Laborveruch Elekroechnik I eruch 2: Ozillokop und Funkiong. Hochchule Bremerhaven Prof. Dr. Oliver Zielinki / Han Sro eruchprookoll Teilnehmer: Name: 1. 2. 3. 4. Tea Daum: Marikelnummer: 2. Ozillokop und
Laborveruch Elekroechnik I eruch 2: Ozillokop und Funkiong. Hochchule Bremerhaven Prof. Dr. Oliver Zielinki / Han Sro eruchprookoll Teilnehmer: Name: 1. 2. 3. 4. Tea Daum: Marikelnummer: 2. Ozillokop und
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Laufzeit. Finden eines Matchings maximaler Kardinalität dauert nur O( E min{ V 1, V 2 }) mit der Ford Fulkerson Methode.
 Effiziente Algorithmen Flußprobleme 81 Laufzeit Finden eines Matchings maximaler Kardinalität dauert nur O( E min{ V 1, V 2 }) mit der Ford Fulkerson Methode. Der Fluß ist höchstens f = min{ V 1, V 2 }.
Effiziente Algorithmen Flußprobleme 81 Laufzeit Finden eines Matchings maximaler Kardinalität dauert nur O( E min{ V 1, V 2 }) mit der Ford Fulkerson Methode. Der Fluß ist höchstens f = min{ V 1, V 2 }.
Dijkstras Algorithmus: Pseudocode
 Dijktra Algorithmu: Peudocode initialize d, parent all node are non-canned while 9 non-canned node u with d[u] < u := non-canned node v with minimal d[v] relax all edge (u,v) out of u u i canned now Behauptung:
Dijktra Algorithmu: Peudocode initialize d, parent all node are non-canned while 9 non-canned node u with d[u] < u := non-canned node v with minimal d[v] relax all edge (u,v) out of u u i canned now Behauptung:
1 Lokale Änderungsrate und Gesamtänderung
 Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Musterlösung zur Einsendearbeit zur Erlangung der Teilnahmeberechtigung
 Muerlöung zur Einenearbei Moul 3511 Seuern un ökonomiche Anreize, Kur 00694 Seuerwirkunglehre I, KE 3 Verbraucheuern, Wineremeer 011/1 1 Muerlöung zur Einenearbei zur Erlangung er Teilnahmeberechigung
Muerlöung zur Einenearbei Moul 3511 Seuern un ökonomiche Anreize, Kur 00694 Seuerwirkunglehre I, KE 3 Verbraucheuern, Wineremeer 011/1 1 Muerlöung zur Einenearbei zur Erlangung er Teilnahmeberechigung
6 Flüsse und Matchings
 6. Flüsse in Netzwerken Flußnetzwerke 6 Flüsse und Matchings In diesem Kapitel werden Bewertungen von Kanten als maximale Kapazitäten interpretiert, die über diese Kante pro Zeiteinheit transportiert werden
6. Flüsse in Netzwerken Flußnetzwerke 6 Flüsse und Matchings In diesem Kapitel werden Bewertungen von Kanten als maximale Kapazitäten interpretiert, die über diese Kante pro Zeiteinheit transportiert werden
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Casrigiano Dr. M. Prähofer Zenralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zenrum Mahemaik Mahemaik 3 für Physik (Analysis ) hp://www-hm.ma.um.de/ss/ph/ 49. Eine reguläre Kurve ha keinen Knick
Prof. Dr. D. Casrigiano Dr. M. Prähofer Zenralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zenrum Mahemaik Mahemaik 3 für Physik (Analysis ) hp://www-hm.ma.um.de/ss/ph/ 49. Eine reguläre Kurve ha keinen Knick
Nutzung der inhärenten sensorischen Eigenschaften von piezoelektrischen Aktoren
 Nuzung der inhärenen enorichen Eigenchafen von piezoelekrichen Akoren K. Kuhnen; H. Janocha Lehruhl für Prozeßauomaiierung (LPA), Univeriä de Saarlande Im Sadwald, Gebäude 13, 6641 Saarbrücken Tel: 681
Nuzung der inhärenen enorichen Eigenchafen von piezoelekrichen Akoren K. Kuhnen; H. Janocha Lehruhl für Prozeßauomaiierung (LPA), Univeriä de Saarlande Im Sadwald, Gebäude 13, 6641 Saarbrücken Tel: 681
Gruppenarbeit: Anwendungen des Integrals Gruppe A: Weg und Geschwindigkeit
 Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
Arbitragefreie Preise
 Arbiragefreie Preise Maren Schmeck 24. Okober 2006 1 Einleiung P i () Preis von Anleihe i zur Zei, i = 1,..., n x i Anzahl an Einheien der Anleihe i V () = n i=1 x ip i () Wer eines Porfolios mi x i Einheien
Arbiragefreie Preise Maren Schmeck 24. Okober 2006 1 Einleiung P i () Preis von Anleihe i zur Zei, i = 1,..., n x i Anzahl an Einheien der Anleihe i V () = n i=1 x ip i () Wer eines Porfolios mi x i Einheien
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Flüsse in Netzwerken
 Proseminar Theoretische Informatik, Prof. Wolfgang Mulzer, SS 17 Flüsse in Netzwerken Zusammenfassung Gesa Behrends 24.06.2017 1 Einleitung Unterschiedliche technische Phänomene wie der Flüssigkeitsdurchfluss
Proseminar Theoretische Informatik, Prof. Wolfgang Mulzer, SS 17 Flüsse in Netzwerken Zusammenfassung Gesa Behrends 24.06.2017 1 Einleitung Unterschiedliche technische Phänomene wie der Flüssigkeitsdurchfluss
Theoretische Grundlagen
 Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
11. GRAPHEN 3 FLÜSSE UND SPANNBÄUME
 Algorithmen und Datenstrukturen 11. GRAPHEN 3 FLÜSSE UND SPANNBÄUME Algorithmen und Datenstrukturen - Ma5hias Thimm (thimm@uni-koblenz.de) 1 Algorithmen und Datenstrukturen 11.1. BERECHNUNG MAXIMALER FLÜSSE
Algorithmen und Datenstrukturen 11. GRAPHEN 3 FLÜSSE UND SPANNBÄUME Algorithmen und Datenstrukturen - Ma5hias Thimm (thimm@uni-koblenz.de) 1 Algorithmen und Datenstrukturen 11.1. BERECHNUNG MAXIMALER FLÜSSE
Abituraufgaben Grundkurs 2009 Bayern Analysis I. dt mit D F = R.
 Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Übungen zur Einführung in die Physik II (Nebenfach)
 Übungen zur Einführung in ie Physik Nebenfach --- Muserlösung --- Aufgabe: Konensaorenlaung Ein mi Glimmer ε r = 8 gefüller Plaenkonensaor mi er Fläche A=6 cm un einem Plaenabsan = 5 μm enlä sich wegen
Übungen zur Einführung in ie Physik Nebenfach --- Muserlösung --- Aufgabe: Konensaorenlaung Ein mi Glimmer ε r = 8 gefüller Plaenkonensaor mi er Fläche A=6 cm un einem Plaenabsan = 5 μm enlä sich wegen
Bestimmung der Erdbeschleunigung g
 Beiun der Erdbechleuniun Mai G 68 uorin: Cornelia Sin eilneher: Daniel Guyo Diana Bednarczyk Fabian Fleicher Heinrich Südeyer Inkje Dörin Rain orabi René Könnecke Galileo Galilei G 68: rookoll zur Beiun
Beiun der Erdbechleuniun Mai G 68 uorin: Cornelia Sin eilneher: Daniel Guyo Diana Bednarczyk Fabian Fleicher Heinrich Südeyer Inkje Dörin Rain orabi René Könnecke Galileo Galilei G 68: rookoll zur Beiun
Motivation. Finanzmathematik in diskreter Zeit
 Moivaion Finanzmahemaik in diskreer Zei Eine Hinführung zu akuellen Forschungsergebnissen Alber-Ludwigs-Universiä Freiburg Prof. Dr. Thorsen Schmid Abeilung für Mahemaische Sochasik Freiburg, 22. April
Moivaion Finanzmahemaik in diskreer Zei Eine Hinführung zu akuellen Forschungsergebnissen Alber-Ludwigs-Universiä Freiburg Prof. Dr. Thorsen Schmid Abeilung für Mahemaische Sochasik Freiburg, 22. April
Algorithmentheorie. 13 - Maximale Flüsse
 Algorithmentheorie 3 - Maximale Flüsse Prof. Dr. S. Albers Prof. Dr. Th. Ottmann . Maximale Flüsse in Netzwerken 5 3 4 7 s 0 5 9 5 9 4 3 4 5 0 3 5 5 t 8 8 Netzwerke und Flüsse N = (V,E,c) gerichtetes Netzwerk
Algorithmentheorie 3 - Maximale Flüsse Prof. Dr. S. Albers Prof. Dr. Th. Ottmann . Maximale Flüsse in Netzwerken 5 3 4 7 s 0 5 9 5 9 4 3 4 5 0 3 5 5 t 8 8 Netzwerke und Flüsse N = (V,E,c) gerichtetes Netzwerk
Name: Punkte: Note: Ø:
 Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Gleichförmige Bewegung
 Gleichförmige Bewegung 1. Grundwien (a) Ein PKW fähr mi der konanen Gechwindigkei v = 16 km auf der Auobahn. Wie lange brauch da Auo für eine 00m lange h Srecke? (b) Wird ein geeiche 50 g-sück an eine
Gleichförmige Bewegung 1. Grundwien (a) Ein PKW fähr mi der konanen Gechwindigkei v = 16 km auf der Auobahn. Wie lange brauch da Auo für eine 00m lange h Srecke? (b) Wird ein geeiche 50 g-sück an eine
Kürzere reguläre Ausdrücke aus deterministischen endlichen Automaten
 Kürzere reguläre Audrücke au deerminiichen endlichen Auomaen by Hermann Gruber Iniu für Informaik, Juu-Liebig-Univeriä Gieen, Arndrae 2, D-35392 Gieen. Februar 2009 gemeinam mi Marku Holzer (JLU Gieen).
Kürzere reguläre Audrücke au deerminiichen endlichen Auomaen by Hermann Gruber Iniu für Informaik, Juu-Liebig-Univeriä Gieen, Arndrae 2, D-35392 Gieen. Februar 2009 gemeinam mi Marku Holzer (JLU Gieen).
Kapitel 11 Produktion, Sparen und der Aufbau von Kapital
 apiel 11 Produkion, Sparen und der Aufbau von apial Vorbereie durch: Florian Barholomae / Sebasian Jauch / Angelika Sachs Die Wechselwirkung zwischen Produkion und apial Gesamwirschafliche Produkionsfunkion:
apiel 11 Produkion, Sparen und der Aufbau von apial Vorbereie durch: Florian Barholomae / Sebasian Jauch / Angelika Sachs Die Wechselwirkung zwischen Produkion und apial Gesamwirschafliche Produkionsfunkion:
2.3 Schätzeigenschaften der OLS-Methode
 .3 Schäzeigechafe der OLS-Mehode Jede Schäzmehode wei beimme Güeeigechafe auf, die vo der Erfüllug beimmer Vorauezuge abhäge. Wa die gewöhliche Mehode der kleie Quadrae (OLS-Mehode) beriff, id beimme Schäzeigechafe
.3 Schäzeigechafe der OLS-Mehode Jede Schäzmehode wei beimme Güeeigechafe auf, die vo der Erfüllug beimmer Vorauezuge abhäge. Wa die gewöhliche Mehode der kleie Quadrae (OLS-Mehode) beriff, id beimme Schäzeigechafe
Transport. Explizite und implizite Verfahren
 p. 1/9 Tranpor Explizie und implizie Verfahren home/lehre/vl-mhs-1/inhalt/folien/vorlesung/10_transport_verf/decbla.ex Seie 1 von 9 p. /9 Inhalverzeichni 1. Explizie Verfahren Inabile Verfahren Lax Verfahren
p. 1/9 Tranpor Explizie und implizie Verfahren home/lehre/vl-mhs-1/inhalt/folien/vorlesung/10_transport_verf/decbla.ex Seie 1 von 9 p. /9 Inhalverzeichni 1. Explizie Verfahren Inabile Verfahren Lax Verfahren
Musterlösungen zur Klausur Informatik III WS 02/03 Seite 1
 Muserlösungen zur Klausur Infrmaik III WS 02/03 Seie Aufgabe. ( Punke) Es seien zwei Schlangen S, S 2 und ein Keller K gegeben. In S befinden sich die Zahlen, 2,..., n(n > 2) (in dieser Reihenflge). Sie
Muserlösungen zur Klausur Infrmaik III WS 02/03 Seie Aufgabe. ( Punke) Es seien zwei Schlangen S, S 2 und ein Keller K gegeben. In S befinden sich die Zahlen, 2,..., n(n > 2) (in dieser Reihenflge). Sie
Bericht zur Prüfung im Oktober 2007 über Finanzmathematik und Investmentmanagement
 Berich zur Prüfung im Okober 7 über Finanzmahemaik und Invesmenmanagemen (Grundwissen) Peer Albrech (Mannheim) Am 5 Okober 7 wurde zum zweien Mal eine Prüfung im Fach Finanzmahemaik und Invesmenmanagemen
Berich zur Prüfung im Okober 7 über Finanzmahemaik und Invesmenmanagemen (Grundwissen) Peer Albrech (Mannheim) Am 5 Okober 7 wurde zum zweien Mal eine Prüfung im Fach Finanzmahemaik und Invesmenmanagemen
SR MVP die Sharpe Ratio des varianzminimalen
 Prüfung inanzmahemaik und Invesmenmanagemen 4 Aufgabe : (4 Minuen) a) Gegeben seien zwei Akien mi zugehörigen Einperiodenrendien R und R. Es gele < ρ(r,r )
Prüfung inanzmahemaik und Invesmenmanagemen 4 Aufgabe : (4 Minuen) a) Gegeben seien zwei Akien mi zugehörigen Einperiodenrendien R und R. Es gele < ρ(r,r )
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Nennen Sie Vor- und Nachteile von Wasserkraftwerken Vorteile: Speicherkraftwerke, Pumpspeicherkraftwerke
 1 Waerkraf Nennen Sie Vor- und Nacheile von Waerkrafwerken Voreile: regeneraive Energie. Keine CO 2 -Emiion! kein Primärenergierägerverbrauch Spizenlafähigkei, Energiepeicherfunkion hohe Zuverläigkei hoher
1 Waerkraf Nennen Sie Vor- und Nacheile von Waerkrafwerken Voreile: regeneraive Energie. Keine CO 2 -Emiion! kein Primärenergierägerverbrauch Spizenlafähigkei, Energiepeicherfunkion hohe Zuverläigkei hoher
auf den Boden fallen, hört man in gleichen Zeitabständen 4 Geräusche. Welchen Abstand hat die 3. Schraube vom unteren Ende der Fallschnur?
 Aufaben zu freien Fall 0. Von der Spize eine Ture lä an einen Sein fallen. Nach 4 Sekunden ieh an ihn auf de Boden aufchlaen. a) Wie hoch i der Tur? b) Mi welcher Gechwindikei riff der Sein auf den Erdboden
Aufaben zu freien Fall 0. Von der Spize eine Ture lä an einen Sein fallen. Nach 4 Sekunden ieh an ihn auf de Boden aufchlaen. a) Wie hoch i der Tur? b) Mi welcher Gechwindikei riff der Sein auf den Erdboden
7.3. Partielle Ableitungen und Richtungsableitungen
 7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
Kapitel 1: Flussalgorithmen
 Netzwerke und Flüsse Ein Flussnetzwerk ist ein gerichteter Graph G = (V, E, c) mit zwei ausgewählten Knoten q, s V und einer Kapazitätsfunktion c : E N 0. Die Quelle q hat Eingangsgrad 0 und die Senke
Netzwerke und Flüsse Ein Flussnetzwerk ist ein gerichteter Graph G = (V, E, c) mit zwei ausgewählten Knoten q, s V und einer Kapazitätsfunktion c : E N 0. Die Quelle q hat Eingangsgrad 0 und die Senke
15. Elementare Graphalgorithmen
 Graphen sind eine der wichtigste Modellierungskonzepte der Informatik Graphalgorithmen bilden die Grundlage vieler Algorithmen in der Praxis Zunächst kurze Wiederholung von Graphen. Dann Darstellungen
Graphen sind eine der wichtigste Modellierungskonzepte der Informatik Graphalgorithmen bilden die Grundlage vieler Algorithmen in der Praxis Zunächst kurze Wiederholung von Graphen. Dann Darstellungen
