TU Dortmund. Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 3)
|
|
|
- Wilhelmine Geisler
- vor 6 Jahren
- Abrufe
Transkript
1 Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 3) Eine Kugel (Masse m 1 ) bewegt sich in Punkt A mit der initialen Geschwindigkeit v A unter dem Winkel γ zur Horizontalen. Nach dem Auftreffen auf die zunächst glatte Bahn in Punkt B, stößt die Kugel vollkommen elastisch auf den Körper der Masse m 2 in Punkt C. Anschließend bewegt sich dieser Körper über die Bahn zu Punkt F, wobei im Abschnitt von Punkt D bis E Reibung auftritt. Die genauen Abmessungen, sowie das zu verwendende Koordinatensystem sind der Abbildung zu entnehmen. µ=0 g µ y 1 F v A µ=0 E ϕ r B α m h 1 γ h 1 m 3 h 2 x 2 D A C b l a) Geben Sie für den Flug der Kugel von A nach B den Ortsvektor s(t)=x(t)e x + y(t)e y als Funktion der Zeit t in kartesischen Koordinaten an. (1,5 Punkte) s(t) = e x + e y Berechnen Sie die Geschwindigkeit v A in Abhängigkeit der in der Abbildung gegebenen Größen, sodass die Kugel in Punkt B von oben auf die Bahn trifft. (1,0 Punkte) v A =
2 Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 2 von 3) b) Berechnen Sie die Geschwindigkeit v C der Kugel unmittelbar vor dem Stoß mit dem Körper der Masse m 2. Der Höhenunterschied zwischen den Punkten B und C ist h 2. (1,0 Punkte) Hinweis: Die Geschwindigkeit v B in B ist für diesen Aufgabenteil gegeben. v C = c) Berechnen Sie die Geschwindigkeit v C des Körpers (Masse m 2 ) kurz nach dem vollkommen elastischen Stoß und bestimmen Sie das Masseverhältnis von m 1 und m 2, sodass die Kugel nach dem Stoß in Ruhe bleibt. (1,0 Punkte) Hinweis: Die Geschwindigkeit v C der Kugel kurz vor dem Stoß ist gegeben. v C = m 1 m 2 = d) Berechnen Sie den maximalen Reibungskoeffizienten µ 1 auf dem Bahnabschnitt von Punkt D nach E, sodass der Körper (Masse m 2 ) in Punkt F zum Stillstand kommt. (1,5 Punkte) Hinweis: Die Geschwindigkeit v C des Körpers (m 2 ) kurz nach dem Stoß mit der Kugel kann als gegeben betrachtet werden und muss nicht ersetzt werden. µ 1 =
3 Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 3 von 3) e) Berechnen Sie die Winkelgeschwindigkeit ϕ in dem Abschnitt von E bis F. (2,0 Punkte) Hinweis: Die Geschwindigkeit v C ist erneut gegeben. ϕ = Berechnen Sie die maximale Geschwindigkeit v E des Masseklotz in Punkt E, sodass der Körper (Masse m 2 ) die Bahn im folgenden Streckenabschnitt nicht verlässt. (2,0 Punkte) Hinweis: Die Geschwindigkeit v C ist erneut gegeben. v E <
4 Vorname: Nachname: Matr.-Nr.: Aufgabe 2 (Seite 1 von 3) Das nebenstehende System befindet sich im Schwerefeld. Es besteht aus einer drehbar gelagerten Stange (Masse M, Länge L) an deren Ende ein Hohlrad (Masse m, Radius r) mit sechs Speichen (jeweils Masse m/6) gelenkig angebracht ist. Das Hohlrad rollt schlupffrei auf einer Kreisbahn (Radius R) ab. Das Stangenende ist über ein Seil mit einer ungespannten Feder (Federkonstante k, ungespannte Länge x 0 ) und einem Dämpfer (Dämpferkonstante d) verbunden. m,r m 6,r ψ g ϕ NN M,L l 0 R x k d a) Geben Sie die Koordinaten x und ψ in Abhängigkeit der Koordinate ϕ an.(1,0 Punkte) x(ϕ) = ψ(ϕ) = b) Geben Sie die kinetische EnergieE kin des Systems inklusive aller Massenträgheitsmomente in Abhängigkeit der Koordinaten ϕ, ψ und x an. (3,0 Punkte) Hinweis: Ihre Ergebnisse aus Aufgabenteil a) sollen nicht eingesetzt werden. Das auf seinen Schwerpunkt bezogene Massenträgheitsmoment eines Hohlrades der Masse M mit dem Radius R ist gegeben durch Θ Hohlrad = M R 2. E kin =
5 Vorname: Nachname: Matr.-Nr.: Aufgabe 2 (Seite 2 von 3) c) Geben Sie die potentielle Energie E pot des Systems in Abhängigkeit der Koordinaten ϕ, ψ und x bezogen auf das vorgegebene Nullniveau NN an. (2,0 Punkte) Hinweis: Ihre Ergebnisse aus Aufgabenteil a) sollen nicht eingesetzt werden. E pot = d) Geben Sie die virtuelle Arbeit δw der nichtkonservativen Kräfte in Abhängigkeit der Koordinaten ϕ, ψ und x an. (1,0 Punkte) Hinweis: Ihre Ergebnisse aus Aufgabenteil a) sollen nicht eingesetzt werden. δw = Aufgabenteil e) befindet sich auf der nächsten Seite!
6 Vorname: Nachname: Matr.-Nr.: Aufgabe 2 (Seite 3 von 3) e) Für ein anderes konservatives System sind die kinetische und potentielle Energie in Abhängigkeit der Koordinate ϕ durch E kin = 17 6 ma2 ϕ 2, E pot = 3mgacosϕ+2ca 2 (sinϕ) ca2 (sinϕ) 2, vorgegeben. Bestimmen Sie die Bewegungsgleichung für kleine Auslenkungen um die Lage ϕ=0. (2,0 Punkte) Geben Sie die Eigenkreisfrequenz ω 0 für kleine Auslenkungen um die Lage ϕ=0 an. (1,0 Punkte) ω 0 =
7 Vorname: Nachname: Matr.-Nr.: Aufgabe 3 (Seite 1 von 3) Bei dem dargestellten Motor wird die Kurbelwelle AB durch eine Pleuelstange BC sowie einen um den Winkel α geneigten Kolben in Punkt C angetrieben. Im dargestellten Zeitpunkt ist die Geschwindigkeit des Kolbensv C bekannt. Die Bezeichnungen und Abmessungen können Sie der nebenstehenden Skizze entnehmen. α 2l C v C β B e y ω l A e x a) Bestimmen Sie die Lage r M = r y M e y des Momentanpols M der Pleuelstange BC und zeichen Sie diesen in obige Skizze ein. (2,0 Punkte) r y M = Bestimmen Sie die Winkelgeschwindigkeit ω gemäß des eingezeichneten Drehsinns für die dargestellte Lage des Systems. (2,0 Punkte) ω =
8 Vorname: Nachname: Matr.-Nr.: Aufgabe 3 (Seite 2 von 3) Der Motor ist nun zu einem anderen Zeitpunkt dargestellt. Die weiteren Bezeichnungen und Abmessungen können Sie der nebenstehenden Skizze entnehmen. α C v C 2l e y γ B A e x ω 1, ω 1 l b) Berechnen Sie die Geschwindigkeit v B sowie die Beschleunigung a B in Punkt B für die dargestellte Lage des Systems. Geben Sie die Vektorkomponenten im {e x,e y }-Koordinatensystem an und nehmen Sie an, dass ω 1 und ω 1 bekannt sind. (3,0 Punkte) Hinweis: Beachten Sie den eingezeichneten Drehsinn der gegebenen Größen. v B = e x + e y a B = e x + e y
9 Vorname: Nachname: Matr.-Nr.: Aufgabe 3 (Seite 3 von 3) Der Motor ist nun erneut zu einem anderen Zeitpunkt dargestellt. Die Bezeichnungen und Abmessungen können Sie der nebenstehenden Skizze entnehmen. 45 C 2l v C, a C ω 2, ω 2 e y 45 A e x B l c) Bestimmen Sie die Winkelgeschwindigkeit ω 2 und den Betrag der Geschwindigkeit v C in Punkt C für die dargestellte Lage des Systems. Beachten Sie die eingezeichneten Richtungen/Drehsinne. Nehmen Sie dabei an, dass die Geschwindigkeit in Punkt B als v B = vb x e x +v y B e y gegeben ist. (3,0 Punkte) ω 2 = v C = v C =
10 Frühjahr 2016
11 Frühjahr 2016 Aufgabe 1 (Seite 1 von 3) Eine Punktmasse (Masse m) befindet sich auf einer reibungsfreien schiefen Ebene (Neigungswinkel α) im Schwerefeld der Erde. Im Punkt A ist die Geschwindigkeit v A der Punktmasse bekannt. h y v A m x A α B g C α µ D a) Berechnen Sie die Geschwindigkeit v B der Punktmasse in Punkt B. b (1,0 Punkte) v B = Wie groß muss die Geschwindigkeit v A mindestens sein, damit Punkt B erreicht wird? (1,0 Punkte) v A b) Die Punktmasse verlässt die schiefe Ebene in Punkt B mit der nun vorgegebenen Geschwindigkeit v B > 0 und überfliegt anschließend einen Spalt der Breite b. Geben sie zunächst den Ortsvektor s(t) = x(t)e x + y(t)e y als Funktion der Zeit t in kartesischen Koordinaten an. (1,5 Punkte) Hinweis: Verwenden Sie hier NICHT ihr Ergebnis für v B aus Aufgabenteil a)! s(t) = e x + e y
12 Frühjahr 2016 Aufgabe 1 (Seite 2 von 3) Geben Sie den Winkel α an, für den die Punktmasse bei vorgegebener Geschwindigkeit v B exakt Punkt C erreicht. (1,5 Punkte) Hinweis: sin(2α)=2 sin(α) cos(α) α = Wie groß ist die maximale Höhe y max der Punktmasse beim Überfliegen des Spaltes? Hinweis: Das obige Ergebnis für α soll hier NICHT eingesetzt werden! (1,0 Punkte) y max = c) Es soll nun davon ausgegangen werden, dass die Punktmasse exakt in Punkt C landet und dort die vorgegebene Geschwindigkeit v C entlang der reibungsbehafteten schiefen Ebene (Neigungswinkel α) aufweist. Geben Sie den Gleitreibungskoeffizienten µ an, für den die Masse genau in Punkt D zum Stillstand kommt. (1,0 Punkte) Hinweis: v C soll NICHT eingesetzt werden! µ =
13 Frühjahr 2016 Aufgabe 1 (Seite 3 von 3) d) Zwei Massen m 1 und m 2 =2m 1 bewegen sich auf einer reibungsfreien Bahn mit den Geschwindigkeiten v 1 und v 2 =v 1 /2 in horizontaler Richtung. m 1 m 2 v 1 v 2 2c l 1 l 2 > l 1 Bestimmen Sie die kinetische Energie nach einem vollplastischen Stoß beider Punktmassen. (1,0 Punkte) E kin = Bestimmen Sie die bei diesem Stoß dissipierte Energie. (1,0 Punkte) E kin = Die beiden Punktmassen treffen anschließend auf eine ungespannte Feder mit der Federsteifigkeit 2 c. Bestimmen Sie die Geschwindigkeit v der Punktmassen als Funktion der Federstauchung l. (1,0 Punkte) v( l) =
14 Frühjahr 2016 Aufgabe 2 (Seite 1 von 3) Das dargestellte, im Schwerefeld der Erde befindliche System besteht aus einer abgesetzten Rolle, einer masselosen Umlenkrolle sowie einem Masseklotz, welche alle eine homogene Dichteverteilung aufweisen. Die Teilelemente sind über ein dehnstarres Seil in der gezeigten Weise miteinander verbunden. Des Weiteren besteht das System aus einer Feder (Federsteifigkeit c) sowie aus einem Dämpfer (Dämpferkonstante d). Alle weiteren Informationen bezüglich des Systems und der jeweiligen Bestandteile sind der Zeichnung zu entnehmen. Die Feder ist in der dargestellten Lage ungespannt. ϕ g r 2 x l r 1 R 1 m y c h d α M,Θ ψ N.N. a) Geben Sie die Schwerpunkts- und Winkelgeschwindigkeit, ẋ und ψ, der abgesetzten Rolle sowie die Geschwindigkeit ẏ des Masseklotzes in Abhängigkeit der Winkelgeschwindigkeit ϕ der masselosen Umlenkrolle an. (1,5 Punkte) ẋ( ϕ) = ψ( ϕ) = ẏ( ϕ) =
15 Frühjahr 2016 Aufgabe 2 (Seite 2 von 3) b) Hinweis: Für die Lösung der Teilaufgabe b) sollen NICHT die Ergebnisse aus Aufgabenteil a) verwendet werden! Bestimmen Sie die kinetische Energie des Systems E kin in Abhängigkeit der vorgegebenen Koordinaten. (1,5 Punkte) E kin = Bestimmen Sie diepotentielle Energie des Systems E pot inabhängigkeit der vorgegebenen Koordinaten bezogen auf das dargestellte Nullniveau N.N. (1,5 Punkte) E pot = Bestimmen Sie die virtuelle Arbeit δw der nichtkonservativen Kräfte in Abhängigkeit der vorgegebenen Koordinaten. (0,5 Punkte) δw = c) Im Folgenden sind die potentielle und kinetische Energie sowie die virtuelle Arbeit der nicht-konservativen Kräfte eines schwingfähigen Systems gegeben. Bei den einzelnen Größen handelt es sich um eine Masse m, ein Trägheitsmoment Θ, eine Länge l, die Erdbeschleunigung g sowie Federsteifigkeiten c und k. Der Winkel ϕ beschreibt den Freiheitsgrad des Systems, welches einem eingeprägten Moment M 0 cos(ωt) ausgesetzt ist. E kin = 2Θ ϕ 2 E pot = 5cl 2 [1 cos(ϕ)]+kϕ 3 +7mgl δw = 2M 0 cos(ϕ) cos(ωt)δϕ
16 Frühjahr 2016 Aufgabe 2 (Seite 3 von 3) Stellen Sie die Bewegungsgleichung bezüglich des Freiheitsgrades ϕ für beliebig große Auslenkungen auf. (2,0 Punkte) Geben Sie die linearisierte Form der Bewegungsgleichung für kleine Auslenkungen um die Ausgangslage (ϕ = 0) an. (1,5 Punkte) Bestimmen Sie anhand der zuvor aufgestellten linearisierten Bewegungsgleichung die Eigenkreisfrequenz ω und die Amplitude A der erregten Schwingung im eingeschwungenen Zustand. (1,5 Punkte) ω = A =
17 Frühjahr 2016 Aufgabe 3 (Seite 1 von 2) Dargestellt ist die Momentaufnahme eines kinematischen Systems zu einem bestimmten Zeitpunkt, in dem die Winkelbeschleunigung ω 3 bekannt sei. Die Teilkörper des Systems weisen eine homogene Masseverteilung sowie einen konstanten Querschnitt auf. l O l e y 1 e x ω 1 A C ω 2 S 2 ω 3 3 5l B l a) Bestimmen Sie die Geschwindigkeiten v A (ω 1 ) = v Ax e x + v Ay e y und v B (ω 3 ) = v Bx e x + v By e y,diewinkelgeschwindigkeiten ω 1 (ω 3 )undω 2 (ω 3 )sowiediegeschwindigkeitv S (ω 3 ) = v Sx e x +v Sy e y des Schwerpunktes S des Stabes 2. (6,0 Punkte) Hinweis: Die unbekannten Winkelgeschwindigkeiten sind gemäß des durch das gegebene Koordinatensystem definierten Drehsinns positiv anzunehmen. v A (ω 1 ) = e x + e y v B (ω 3 ) = e x + e y ω 1 (ω 3 ) = ω 2 (ω 3 ) = v S (ω 3 ) = e x + e y
18 Frühjahr 2016 Aufgabe 3 (Seite 2 von 2) b) Für das nun gegebene System sind die Winkelgeschwindigkeiten ω 1, ω 2 und ω 3 sowie die Winkelbeschleunigung ω 3 in der dargestellten Konfigurationbekannt. Der Drehsinn dieser Größen richtet sich nach dem vorgegebenen Koordinatensystem. e y ω 1 A C O e x 1 ω ω 3, ω 3 l l l B BerechnenSiedieWinkelbeschleunigungen ω 1 und ω 2 derstäbe1und2fürdieabgebildete Konfiguration des Systems in Abhängigkeit der gegebenen Größen. (3,0 Punkte) Hinweis: Die unbekannten Winkelbeschleunigungen sind gemäß des durch das gegebene Koordinatensystem definierten Drehsinns positiv anzunehmen. ω 1 = ω 2 = Geben Sie die Position r M = r Mx e x + r My e y des Momentanpols M für Körper 2 in der gezeigten Konfiguration an. (1,0 Punkt) r M = e x + e y
19 Herbst 2015
20 Herbst 2015 Aufgabe 1 (Seite 1 von 3) Das dargestellte System besteht aus einem starren Dreiecksträger sowie zwei starren Kreisscheiben A und B. Der Dreiecksträger setzt sich dabei aus drei homogenen, starren Stäben zusammen und ist im Punkt O frei drehbar gelagert. Beide Kreisscheiben bewegen sich auf einer Kreisbahn und rollen in den dargestellten Berührpunkten C und D schlupffrei ab. Die jeweiligen Abmessungen und Massen der Körper sind der nebenstehenden Zeichnung zu entnehmen. β B D m 5,r m 3 m 2 ϕ e ϕ O m 1 e r l A α C m 4,r a) Bestimmen Sie dieortsvektoren der Stabschwerpunkte im (e r,e ϕ )-System. (1,5 Punkte) r S1 = r S2 = r S3 = Bestimmen Sie das Gesamtträgheitsmoment Θ,O des aus den Stäben mit den Massen m 1, m 2, m 3 bestehenden Dreiecksträgers bezüglich des Punktes O. (1,5 Punkte) Θ,O =
21 Herbst 2015 Aufgabe 1 (Seite 2 von 3) b) Geben Sie die kinetische Energie E kin ( ϕ, α, β) des Systems an. Verwenden Sie in diesem Aufgabenteil den allgemeinen Ausdruck Θ O für das Trägheitsmoment des Dreiecksträgers. Die Winkelgeschwindigkeiten α und β sollen zunächst als unabhängig angesehen werden. (2,5 Punkte) E kin ( ϕ, α, β) = c) Spezifizieren Sie die Winkelgeschwindigkeiten α und β als Funktion von ϕ. (2,0 Punkte) α( ϕ) = β( ϕ) = d) Die kinetische Energie des Gesamtsystems lässt sich in der Form E kin = 1 2 Θ sys ϕ 2 mit einem hier als bekannt vorausgesetzten Systemträgheitsmoment Θ sys darstellen. Zusätzlich greife ein konstantes Moment M 0 in positiver Drehrichtung um das Drehzentrum O an, welches das System antreibt. Geben Sie auf Basis dieser Größen die Bewegungsgleichung des Systems bezüglich ϕ an. (1,0 Punkte)
22 Herbst 2015 Aufgabe 1 (Seite 3 von 3) Geben Sie die Lösung der Bewegungsgleichung für die Anfangsbedingungen ϕ(t = 0) = 0, ϕ(t = 0) = ϕ 0 an. (1,5 Punkte) ϕ(t) =
23 Herbst 2015 Aufgabe 2 (Seite 1 von 3) Eine starre Stange (Masse M, Länge l) wird aus der dargestellten Ruhelage (ω S = 0) im Schwerefeld g losgelassen und stößt im Punkt A vollkommen elastisch auf eine zylindrische Scheibe (Masse m, Radius r), welche zunächst auf der glatten Ebene zwischen A und B reibungsfrei gleitet. Zwischen den Punkten B und D ist die Bahn rauh (Reibkoeffizient µ), sodass die starre Scheibe dort ideal abrollt (Rollreibung ist zu vernachlässigen). Im Punkt D trifft die Scheibe vollkommen elastisch auf eine ideal glatte Platte, die von einer Feder (Federkonstante c) gehalten wird. l M y A ω S m,r µ = 0 x µ 0 µ 0 g h N.N. A B C c a) Geben Sie die Winkelgeschwindigkeit ω S sowie die Geschwindigkeit des Berührpunktes A der Stange unmittelbar vor dem Stoß mit der Scheibe an. (1,0 Punkte) D ω S = v A = Berechnen Sie die Geschwindigkeit v A der Scheibe unmittelbar nachdem Stoß.In welchem Verhältnis müssen die Massen m und M stehen, sodass die Stange nach dem Stoß in Ruhe verweilt? (2,0 Punkte) v A = m M =
24 Herbst 2015 Aufgabe 2 (Seite 2 von 3) b) Gehen Sie nun davon aus, dass die Geschwindigkeit der Scheibe unmittelbar nach dem Stoß durch v A = v 0 gegeben ist. Berechnen Sie die Geschwindigkeit sowie die Winkelgeschwindigkeit der Scheibe in Punkt C. (1,0 Punkte) v C = ω C = c) Gehen Sie nun davon aus, dass die Geschwindigkeit der Scheibe in Punkt C durch v C gegeben ist. Berechnen Sie die maximale Stauchung l der Feder während des Kontaktes mit der Scheibe in Punkt D. (2,0 Punkte) l = d) Ein Gleitkörper (Masse m) weist in der dargestellten Lage die Geschwindigkeit v 0 auf und bewegt sich eine reibungsfreie Ebene hinauf. In Punkt A (vertikaler Abstand h 0 ) geht die Ebene in eine kreisförmige Bahn (Radius R) über. R ϕ 30 A g Welchen Wert v0 min muss die Geschwindigkeit des Körpers in der dargestellten Lage mindestens haben, damit dieser den Punkt A erreicht? (1,0 Punkte) y x v 0 h 0 m v min 0
25 Herbst 2015 Aufgabe 2 (Seite 3 von 3) Berechnen Sie den maximalen Wert v0 max des Körpers in der dargestellten Lage, sodass dieser an keinem Punkt der kreisförmigen Bahn diese verlässt. Tragen Sie auch wesentlich Zwischenschritte in das folgende Kästchen ein. (3,0 Punkte)
26 Herbst 2015 Aufgabe 3 (Seite 1 von 3) a) Für ein schwingfähiges System bestehend aus Massen m, einer Feder c und einem Dämpfer d sind die kinetische Energie, die potentielle Energie und die generalisierte Kraft Q gegeben. Die Größen l und r sind systemspezifische Abmessungen und α ein Winkel. E kin (u) = m u 2, E pot (u) = mg[(2u+l) sinα+2r cosα]+ c 2 u2, Q(u) = d u. Stellen Sie die Bewegungsgleichung des Systems bezüglich u auf. (2,0 Punkte) Bestimmen Sie basierend auf obiger Bewegungsgleichung den Abklingkoeffizienten δ, die Eigenfrequenz der ungedämpften Schwingung ω, und die Eigenfrequenz der gedämpften Schwingung ω d. (1,5 Punkte) δ = ω = ω d =
27 Herbst 2015 Aufgabe 3 (Seite 2 von 3) b) Das dargestellte System besteht aus einer Masse m 2, zwei schlupffrei abrollenden Stufenrollen, einer reibungsfrei geführten starren Stange sowie einem Feder-Dämpfer-Element, welches starr im Punkt A an das System angeschlossen ist. Ein auf der linken Stufenrolle aufgewickeltes Seil ist über eine als masselos anzunehmende Umlenkrolle mit der Masse m 2 verbunden. Die linke, massebehaftete Stufenrolle setzt sich aus zwei Vollzylindern (kleinestufung:radiusr 1, Masse 1/5M;großeStufung:RadiusR 1, Masse 4/5M)zusammen. Die dargestellte Feder ist für den nicht näher spezifizierten Wert x=x 0 entspannt. Beachten Sie, dass x = 0 nicht die statische Ruhelage beschreibt! ϕ l x r 2 R 2 g M d r 1 R 1 c A m 1 m 2 y h α N.N. Geben Sie die Geschwindigkeiten ẋ und ẏ als Funktion von ϕ an. (1,0 Punkte) ẋ( ϕ) = ẏ( ϕ) =
28 Herbst 2015 Aufgabe 3 (Seite 3 von 3) Bestimmen Sie die potentielle Energie E pot des Systems in Abhängigkeit von x, y sowie den gegebenen Größen bezogen auf das dargestellte Nullniveau N.N. (3,0 Punkte) E pot = Bestimmen Sie die kinetische Energie E kin des Systems in Abhängigkeit von ẋ, ẏ, ϕ und den gegebenen Größen. Beachten Sie, dass die Massenträgheitsmomente nicht als gegeben angesehen werden können und demnach konkret bestimmt werden sollen. (2,5 Punkte) E kin =
29 Frühjahr 2015
30 Frühjahr 2015 Aufgabe 1 (Seite 1 von 2) Die dargestellte Punktmasse (Punkt C, Masse m) gleitet reibungsfrei in einer kreisförmigen Führung (Radius r). Die Punktmasse ist über zwei gelenkig in Punkt B miteinander gekoppelten, masselosen Stäben 1 und 2 mit dem Lager in Punkt A verbunden. Stab 1 weist eine zeitlich konstante Winkelgeschwindigkeit ω 1 auf. Für den gezeigten Zustand des Systems gilt ϕ 3 = π/4. Das System steht nicht unter dem Einfluss des Erd-Schwerefelds. C ω 2, ω 2 2 B e t m r e r ϕ 3 ω 3, ω 3 1 ω 1 = const. e y 2a A e x b a Hinweis: Sämtliche Lösungen zu dieser Aufgabe sind bezüglich der in obiger Skizze vorgegebenen Koordinaten-Basisvektoren e x, e y oder e r, e t anzugeben. a) Berechnen Sie in Abhängigkeit von ω 1 die Winkelgeschwindigkeiten ω 2 des Stabs 2 und ω 3 der Punktmasse um den Mittelpunkt der Kreisbahnführung sowie die Komponenten der Geschwindigkeit v C = v Cr e r +v Ct e t in Punkt C bezüglich des e r, e t -Koordinatensystems oder v C = v Cx e x + v Cy e y bezüglich des e x, e y -Koordinatensystems für die dargestellte Lage. (4,0 Punkte) Lösung in Kästchen auf der nächsten Seite eintragen!
31 Frühjahr 2015 Aufgabe 1 (Seite 2 von 2) ω 2 (ω 1 ) = ω 3 (ω 1 ) = v Cr = v Ct = oder v Cx = v Cy = b) Berechnen Sie die Winkelbeschleunigungen ω 2 des Stabs 2 und ω 3 der Punktmasse um den Mittelpunkt der Kreisbahnführung. ω 2 und ω 3 sind nun in allgemeiner Form vorgegeben. Verwenden Sie NICHT die in Aufgabenteil a) berechneten Werte. (3,0 Punkte) ω 2 (ω 1,ω 2,ω 3 ) = ω 3 (ω 1,ω 2,ω 3 ) = c) Für andere geometrische Abmessungen des Systems gilt ω 3 = 4 2ω 1 und ω 3 = 4[8+ 2]ω1 2. Berechnen Sie basierend auf diesen Vorgaben den Betrag der Auflagerreaktion in Punkt C sowie die Stabkraft S 2 in Stab 2 für den dargestellten Zustand des Systems. (3,0 Punkte) C = S 2 =
32 Frühjahr 2015 Aufgabe 2 (Seite 1 von 3) Der Boden und die Wände des dargestellten Flipperautomaten sind als reibungsfrei anzunehmen. Der Boden ist um den Winkel α geneigt. Eine dünne Zylinderscheibe der Masse m, welche als Punktmasse angenommen werden soll, soll mit Hilfe einer Feder (Federsteifigkeit c) aus dem dargestellten Schacht bewegt werden. Zwischen den Punkten A und B weist die Außenwand eine Kreisform auf (Radius r). B D r ϕ A Schnitt D-D y a a g y x z m α C x D b a) Berechnen Sie die Bedingung für die initiale, gesamte Federstauchung l, sodass die Punktmasse den Punkt A erreicht und damit den Schacht verlässt. Es gilt dabei die Annahme l a. (2,0 Punkte) l
33 Frühjahr 2015 Aufgabe 2 (Seite 2 von 3) b) DieGeschwindigkeit der Punktmasse in Punkt Aist nun durch v A > 0 vorgegeben. Stellen Sie zunächst die Kräftesätze(Impulssätze) für die Punktmasse in radialer und tangentialer Richtung für beliebige Winkel ϕ unter der Annahme auf, dass die Punktmasse stets Kontakt zur Wand hat. Spezifizieren Sie die auftretenden Beschleunigungen in Abhängigkeit der Winkelgeschwindigkeit ω = ϕ der Punktmasse um den Mittelpunkt der Kreisbahn sowie deren Winkelbeschleunigung ω. (2,0 Punkte) Geben Sie die konkreten Zusammenhänge der Winkelgeschwindigkeit ω und der Winkelbeschleunigung ω der Punktmasse entlang der Kreisbahn in Abhängigkeit der gegebenen Größen g, r, α, v A sowie des Winkels ϕ an. (3,0 Punkte) ω = ω =
34 Frühjahr 2015 Aufgabe 2 (Seite 3 von 3) c) Die als Punktmasse anzusehende Scheibe (Masse m) trifft nun mit der Geschwindigkeit v = v x e x +v y e y im Abstand d auf den linken Flipper (Massenträgheitsmoment Θ bezogen auf den Drehpunkt E) auf, dessen Winkelgeschwindigkeit in diesem Moment ω beträgt und dessen Oberkante exakt parallel zur x-achse verläuft. Der nachfolgende Stoß ist als vollkommen elastisch und die Oberfläche des Flippers als perfekt glatt anzusehen. f E ω d Θ y m x Berechnen Sie die Komponenten der Geschwindigkeit der Punktmasse v = v x e x + v y e y unmittelbar nach dem Stoßvorgang unter der Voraussetzung, dass die Abmessung f vernachlässigt und somit der Flipper als horizontaler Stab angenähert werden kann. (3,0 Punkte) v x = v y =
35 Frühjahr 2015 Aufgabe 3 (Seite 1 von 2) Das dargestellte System besteht aus einer starren Kreisscheibe (Masse M, Radius R) welche über zwei starre Stangen (Masse m, Länge l) mit einem Festlager verbunden ist und schlupffrei auf dem Untergrund abrollt. Die wie dargestellt angebundene Feder (Federsteifigkeit c) ist bei einer nicht näher spezifizierten Länge l 0 entspannt. A y x ψ m,l c B m,l g M C ξ ϕ NN R a) Geben Sie die Geschwindigkeiten ξ sowie ϕ als Funktion der Geschwindigkeit ψ sowie den gegebenen Größen an. (1,0 Punkte) ξ( ψ) = ϕ( ψ) = b) Berechnen Sie die Funktion der kinetischen Energie E kin in Abhängigkeit der Koordinaten ψ, ϕ und ξ sowie den gegebenen Größen. Verwenden Sie hier NICHT die in Aufgabenteil a) berechneten kinematischen Zusammenhänge. (3,0 Punkte) E kin ( ψ, ϕ, ξ) =
36 Frühjahr 2015 Aufgabe 3 (Seite 2 von 2) c) Bestimmen Sie die Funktion der potentiellen Energie E pot in Abhängigkeit von ψ und ξ sowie den gegebenen Größen bezogen auf das dargestellte Nullniveau NN.(1,0 Punkte) E pot (ψ,ξ) = d) Für ein anderes konservatives System mit einem Freiheitsgrad ϕ sind die Masse m, ein Radius r sowie die potentielle und kinetische Energie zu E pot (ϕ) = 2 π mgr[1 cos(ϕ)] sowie E kin(ϕ) = mr 2 ϕ 2 [ 1 2 π cos(ϕ) ] gegeben. Stellen Sie basierend auf diesen Energien die Bewegungsgleichung des Systems bezüglich ϕ für große Auslenkungen auf. (3,0 Punkte) Geben Sie die linearisierte Form der obigen Bewegungsgleichung für kleine Auslenkungen um ϕ = 0 an. (1,0 Punkte) Bestimmen Sie die Periodendauer T der Eigenschwingung des Systems basierend auf der linearisierten Bewegungsgleichung. (1,0 Punkte) T =
37 Herbst 2014
38 Herbst 2014 Aufgabe 1 (Seite 1 von 3) Das dargestellte System besteht aus homogenen, starren Körpern, welche durch dehnstarre Seile miteinander verbunden sind. Die jeweiligen Massen und Abmessungen sind der Zeichnung zu entnehmen, wobei das Massenträgheitsmoment der gesamten abgesetzten Rolle 4 bezüglich des zugehörigen Schwerpunktes D durch θ 4 gegeben ist und die Rolle 2 als masselos angesehen werden soll. Der Kreisring 1 rollt dabei zu jedem Zeitpunkt schlupffrei ab und die Seile sind stets gespannt. g 2 ϕ 3 m 3 C r 3 3 β m 4, θ 4 ϕ 4 D r 4 4 M 0 B R 4 ϕ 2 1 2r 2 ϕ 1 x 1 A m 1 r 1 α y x µ 0 Erweitern Sie die folgenden Skizzen der Teilkörper 1, 3 und 4 zu vollständigen Freikörperbildern (inklusive etwaiger Auflagerreaktionen). (2,0 Punkte)
39 Herbst 2014 Aufgabe 1 (Seite 2 von 3) a) Geben Sie die Impulsbilanz (Kräftesatz) des Kreisrings 1 bezüglich der x 1 -Koordinate an. (1,0 Punkte) b) Geben Sie die Drehimpulsbilanz (Drallsatz) des Kreisrings 1 bezüglich des Schwerpunkts und der ϕ 1 -Koordinate an. Spezifizieren Sie das zu verwendende Massenträgheitsmoment mittels der gegebenen Größen. (1,0 Punkte) c) Geben Sie die Impulsbilanz (Kräftesatz) der Rolle 3 bezüglich der y-koordinate an. (1,0 Punkte) d) Geben Sie die Drehimpulsbilanz (Drallsatz) der Rolle 4 bezüglich des Schwerpunkts und der ϕ 4 -Koordinate an. (1,0 Punkte)
40 Herbst 2014 Aufgabe 1 (Seite 3 von 3) f) Geben Sie die folgenden kinematischen Bindungen zwischen den Geschwindigkeiten der einzelnen Koordinaten und der Geschwindigkeit des Freiheitsgrades x 1 an. (2,0 Punkte) ϕ 1 (ẋ 1 ) = ϕ 2 (ẋ 1 ) = ϕ 3 (ẋ 1 ) = ϕ 4 (ẋ 1 ) = Berechnen Sie die von dem Moment M 0 vom Zeitpunkt t = 0 bis zum Zeitpunkt t = t 1 verrichtete Arbeit W M0. Das System befindet sich anfänglich in Ruhe (x 1 (t = 0) = 0, ẋ 1 (t = 0) = 0) und es gilt x 1 (t 1 ) = a. (2,0 Punkte) W M0 =
41 Herbst 2014 Aufgabe 2 (Seite 1 von 3) Die unten gezeigte Bahn besteht aus zwei reibungsbehafteten Ebenen (Gleitreibungskoeffizient µ, Länge l) sowie zwei als reibungsfrei anzunehmenden Kreisbögen (Öffnungswinkel α). Im Punkt D befindet sich das Ende einer elastischen Feder (Federsteifigkeit c), welche in der dargestellten Lage entspannt ist. Bis zu einem Zeitpunkt t t 0 wird ein als Punktmasse anzusehender Körper (Masse m) im Punkt O in Ruhe gehalten. Dann wird dieser los gelassen, wobei vorausgesetzt werden soll, dass sich der Körper anschließend tatsächlich in Bewegung setzt (Hangabtriebskraft größer als Haftreibungskraft). O m l y µ A α B r µ NN l g r C ϕ D c x a) Geben Sie die potenzielle Energie (Lageenergie) Epot O des angegebenen Nullniveaus NN an. (1,0 Punkte) α des Körpers im Punkt O bezüglich E O pot = Geben Sie die verrichtete Reibarbeit WR OA A an. (1,0 Punkte) auf der Strecke zwischen den Punkten O und W OA R =
42 Herbst 2014 Aufgabe 2 (Seite 2 von 3) Berechnen Sie die Geschwindigkeit v B der Masse im Punkt B. (1,5 Punkte) v B = b) DieGeschwindigkeit des Körpersim Punkt B ist nun durch v B > 0 vorgegeben. Berechnen Sie die Geschwindigkeit im Punkt C. Verwenden Sie nicht den oben berechneten Wert für v B. (1,0 Punkte) v C = c) Die Geschwindigkeit des Körpers im Punkt C ist nun durch v C > 0 vorgegeben. Geben Sie zunächst die Funktion der Geschwindigkeit v(ϕ) des Körpers in Abhängigkeit des Winkels ϕ an. Verwenden Sie nicht den oben berechneten Wert für v C. (1,5 Punkte) v(ϕ) =
43 Herbst 2014 Aufgabe 2 (Seite 3 von 3) Geben Sie des Weiteren die Funktion der Normalkraft N(ϕ) zwischen Körper und Bahn in Abhängigkeit des Winkels ϕ an. (1,5 Punkte) N(ϕ) = Geben Sie die Bedingung für den Öffnungswinkel α an, so dass der Körper an keiner Stelle der kreisförmigen Bahn zwischen den Punkten C und D den Kontakt zu dieser verliert. (1,0 Punkte) α d) Die Geschwindigkeit des Körpers im Punkt D ist nun durch v D > 0 vorgegeben. Geben Sie die Gleichung zur Bestimmung der Stauchung l der Feder an. Ein Auflösen dieser Gleichung nach l ist nicht erforderlich. (1,5 Punkte)
44 Herbst 2014 Aufgabe 3 (Seite 1 von 2) Das dargestellte System besteht aus zwei starren Kreisscheiben (Masse M 1 bzw. M 2, Radius jeweils R), welche über eine starre Stange (Masse m, Länge l) verbunden sind und schlupffrei auf dem Untergrund abrollen. Die Bewegung findet auf einer schiefen Ebene (Neigungswinkel α) und unter Einfluss der Erdbeschleunigung g statt. Die wie dargestellt angeknüpfte Feder ist für den nicht näher spezifizierten Wert ξ = ξ 0 entspannt. Beachten Sie, dass ξ = 0 nicht die statische Ruhelage beschreibt. ξ x g M 1,R m,l α M 2,R c NN a) GebenSiedenZusammenhangzwischen dengeschwindigkeiten ξ undẋan.(1,0 Punkte) ξ(ẋ) = b) Bestimmen Sie die potentielle Energie E pot in Abhängigkeit der Koordinate ξ und den gegebenen Größen bezogen auf das dargestellte Nullniveau NN. (3,0 Punkte) E pot (ξ) =
45 Herbst 2014 Aufgabe 3 (Seite 2 von 2) c) Bestimmen Sie die kinetische Energie E kin in Abhängigkeit der Koordinate ξ und den gegebenen Größen. Beachten Sie, dass insbesondere die Massenträgheitsmomente nicht als gegeben angesehen werden können. (2,0 Punkte) E kin ( ξ) = d) Für einen nicht näher spezifizierten Sonderfall und unter Verwendung einer abweichenden Koordinate η ergeben sich im Folgenden die Energien des Systems zu E pot (η) = 3mgη sin(α)+1/2cη 2, E kin (η) = 2m η 2. Stellen Sie basierend auf diesen Energien die Bewegungsgleichung dieses Sonderfalls bezüglich η auf. (2,0 Punkte) Bestimmen Sie, basierend auf obiger Bewegungsgleichung, die Eigenkreisfrequenz ω 0 sowie die Periodendauer T der Eigenschwingung des Systems. (2,0 Punkte) ω 0 = T =
46 Frühjahr 2014
47 Frühjahr 2014 Aufgabe 1 (Seite 1 von 3) Das dargestellte System besteht aus homogenen, starren Körpern, die durch dehnstarre Seile miteinander verbunden sind und sich im Schwerefeld der Erde (Erdbeschleunigung g) befinden. Die jeweiligen Massen, Massenträgheitsmomente und Abmessungen sind der Zeichnung zu entnehmen. Rolle 2 wird von dem konstanten Drehmoment M 0 angetrieben. Der Haftreibungskoeffizient zwischen der Rolle 1 welche zu allen Zeitpunkten schlupffrei abrollt und der schiefen Ebene (Neigungswinkel α) beträgt µ 0. Das Massenträgheitsmoment der gesamten abgesetzen Rolle 3 ist durch θ 3 gegeben. x 1 ϕ 2 g 1 m 1 ϕ 1 r 2 m 2 2 α r 1 µ 0 M 0 r 3 m 3, θ 3 3 ϕ 3 R 3 x 3 4 m 4 x 4 a) Tragen Sie im nachfolgenden Bild sämtliche fehlenden Kräfte bzw. Momente ein. Die Auflagersymbole sollen in der Zeichnung beibehalten und nicht freigeschnitten werden. (1,5 Punkte)
48 Frühjahr 2014 Aufgabe 1 (Seite 2 von 3) b) Geben Sie die Impulsbilanz (Kräftesatz) der Rolle 1 bezüglich der der x 1 -Koordinate an. (1,0 Punkte) c) Geben Sie die Drehimpulsbilanz (Drallsatz) der Rolle 1 bezüglich des zugehörigen Momentanpols und der ϕ 1 -Koordinate an. Spezifizieren Sie θ 1 mittels der gegebenen Größen. (1,0 Punkte) d) Geben Sie die Drehimpulsbilanz(Drallsatz) der Rolle 2 bezüglich ihres Schwerpunktes und der ϕ 2 -Koordinate an. Spezifizieren Sie θ 2 mittels der gegebenen Größen. (1,0 Punkte) e) Geben Sie die Impulsbilanz (Kräftesatz) der Rolle 3 bezüglich der x 3 -Koordinate an. (1,0 Punkte) f) Geben Sie die Drehimpulsbilanz (Drallsatz) der Rolle 3 bezüglich ihres Schwerpunktes und der ϕ 3 -Koordinate an. (1,0 Punkte)
49 Frühjahr 2014 Aufgabe 1 (Seite 3 von 3) g) GebenSie die Impulsbilanz (Kräftesatz) der Masse 4 bezüglich der x 4 -Koordinatean. (1,0 Punkte) h) Geben Sie die (Winkel-)Geschwindigkeiten ẋ 1, ϕ 1, ẋ 3, ϕ 3, ẋ 4 in Abhängigkeit von ϕ 2 an. (2,5 Punkte) ẋ 1 = ϕ 1 = ẋ 3 = ϕ 3 = ẋ 4 =
50 Frühjahr 2014 Aufgabe 2 (Seite 1 von 2) Eine Punktmasse m befindet sich auf der dargestellten Bahn und wird aus der Ruhe durch eine vorgespannte Feder (Federsteifigkeit c) auf reibungsfreiem Untergrund bis zum Punkt A beschleunigt. An dieser Stelle (Punkt A) löst sich die Masse von der Feder. Die geraden Abschnitte der Bahn sind reibungsbehaftet (Reibkoeffizienten µ 1 bzw. µ 2 ) während die kreisförmigen Abschnitte (Radien R 1 bzw. R 2 ) reibungsfrei sind. µ = 0 E y g α µ 2 D R 2 x c x m µ 1 ϕ R 1 C l 2 N.N. µ = 0 A l 1 B µ = 0 a) Berechnen Sie die Geschwindigkeit der Punktmasse im Punkt A in Abhängigkeit der aufgebrachten Federstauchung x. (1,0 Punkte) v A = Geben Sie weiterhin die Geschwindigkeit der Punktmasse im Punkt B in Abhängigkeit von x an, nachdem diese über den rauhen (Reibkoeffizient µ 1 ) Bahnabschnitt AB der Länge l 1 geglitten ist. (1,0 Punkte) v B =
51 Frühjahr 2014 Aufgabe 2 (Seite 2 von 2) b) Berechnen Sie den Betrag der Bahngeschwindigkeit v(ϕ) der Punktmasse im Verlauf des ersten reibungsfreien Kreisbogens BC in Abhängigkeit des Winkels ϕ und einer als bekannt anzunehmenden Geschwindigkeit v B im Punkt B. (2,0 Punkte) Setzen Sie nicht die Geschwindigkeit v B aus dem vorigen Aufgabenteil ein! v(ϕ) = Geben Sie weiterhin die Geschwindigkeit der Punktmasse im Punkt D in Abhängigkeit von v B an, nachdem diese über den rauhen (Reibkoeffizient µ 1 ) Bahnabschnitt CD der Länge l 2 geglitten ist. (2,0 Punkte) v B = c) Die beiden Bahnabschnitte AB und CD sind nun als reibungsfrei (µ 1 = µ 2 = 0) anzunehmen, die Punktmasse wird erneut durch Stauchung der Feder am Anfang der Bahn beschleunigt. Berechnen Sie die maximale Vorspannkraft der Feder F 0 so, dass die Punktmasse im oberen Kreisbogen DE (Radius R 2 ) nicht von der Bahn abhebt. Tragen Sie dazu in dem folgenden Kästchen auch das Zwischenergebnis für die Geschwindigkeit v D im Punkt D ein. (4,0 Punkte) v D = F 0 =
52 Frühjahr 2014 Aufgabe 3 (Seite 1 von 3) Im dargestellten System wird ein Körper der Masse m reibungsfrei in einer Nut geführt und ist durch eine Feder (Federsteifigkeit c) und einen Dämpfer (Dämpfungskonstante d) innerhalb der Nut gestützt. Über eine starre, masselose Stange der Länge l ist der Körper mit einer drehbaren Scheibe (Radius R, Masse M) exzentrisch (Exzentrizität e) verbunden. Die Feder ist in der Lage ϕ = 0 ungespannt. Die Erdbeschleunigung ist zu vernachlässigen. c ϕ m x l d e R M a) Bestimmen Sie mittels der gegebenen Größen die kinetische und potentielle Energie des Gesamtsystems. Verwenden Sie dazu die Koordinaten ϕ und x. (2,0 Punkte) E kin = E pot =
53 Frühjahr 2014 Aufgabe 3 (Seite 2 von 3) b) Bestimmen Sie die virtuelle Arbeit δw der nichtkonservativen Lasten in Abhängigkeit der Koordinate x. (1,0 Punkte) δw = c) Geben Sie die kinematische Beziehung der Koordinate x als Funktion von ϕ für große Auslenkungen an. (2,5 Punkte) x(ϕ) = d) In dem unten dargestellten System rollt eine Scheibe (Masse M, Radius R) schlupffrei auf dem Untergrund ab. Eine Feder (Federsteifigkeit c) ist exzentrisch (Exzentrizität e) an der Scheibe angebracht. An ihrem äußeren Rand ist die Scheibe des Weiteren mit einem Dämpfer (Dämpfungskonstante d) verbunden. In der dargestellten Ruhelage der Scheibe ( ϕ = 0) ist die Feder ungespannt. Die Erdbeschleunigung ist zu vernachlässigen. ϕ d e y x R M c
54 Frühjahr 2014 Aufgabe 3 (Seite 3 von 3) Bestimmen Sie die Bewegungsdifferentialgleichung des Systems bezüglich der Koordinate ϕ unter der Annahme kleiner Auslenkungen. Geben Sie unbedingt wesentliche Zwischenschritte an, welche zur Lösung der Aufgabe notwendig sind. (3,5 Punkte) Wie lauten die Eigenkreisfrequenz ω 0 und der Abklingkoeffizient δ des Systems? (1,0 Punkte) ω 0 =
55 Herbst 2013
56 Herbst 2013 Aufgabe 1 (Seite 1 von 3) Das dargestellte System besteht aus homogenen, starren Körpern, die durch dehnstarre, schlupffrei abrollende Seile miteinander verbunden sind und sich im Schwerefeld der Erde (Erdbeschleunigung g) befinden. Die jeweiligen Massen und Abmessungen der Körper sind der Zeichnung zu entnehmen. Es wird davon ausgegangen, dass die Massen 1 und 6 auf rauhen schiefen Ebenen gleiten. ϕ 2 r 2 R 2 g x 1 m 1 m 2 r 5 ϕ 5 x 6 m 5 m 6 β α x 3 R 3 C m 3 ϕ 3 x 4 m 4
57 Herbst 2013 Aufgabe 1 (Seite 2 von 3) a) Zeichnen Sie ein vollständiges Freikörperbild (2 Punkte) b) Geben Sie die Impulsbilanz (Kräftesatz) der Masse 1 bezüglich der x 1 -Koordinate an. (1 Punkt) c) Geben Sie die Drehimpulsbilanz(Drallsatz) der Rolle 2 bezüglich ihres Schwerpunktes und derϕ 2 -Koordinatean.DasMassenträgheitsmoment derrolle2istdabeialsθ 2 vorgegeben. (1 Punkt) d) Geben Sie die Impulsbilanz (Kräftesatz) der Rolle 3 bezüglich der x 3 -Koordinate an. (1 Punkt)
58 Herbst 2013 Aufgabe 1 (Seite 3 von 3) e) Geben Sie die Drehimpulsbilanz (Drallsatz) der Rolle 3 bezüglich des Punktes C und der ϕ 3 -Koordinate an. Spezifizieren Sie θ 3 mittels der gegebenen Größen. (1 Punkt) f) Geben Sie die Impulsbilanz (Kräftesatz) der Masse 6 bezüglich der x 6 -Koordinate an. (1 Punkt) g) Es sei nun das folgende modifizierte System gegeben. Geben Sie ϕ 2, ϕ 3 und x 3 in Abhängigkeit von x 1 für das modifizierte System an. (3 Punkte) ϕ 2 ϕ 2 = r 2 R 2 g x 3 = x 1 m 1 m 2 ϕ 3 = β R 3 x 3 m 3 ϕ 3 x 4 m 4
59 Herbst 2013 Aufgabe 2 (Seite 1 von 2) Ein punktförmiger Körper der Masse m gleitet von einer Kraft F angetrieben auf einer reibungsbehafteten schiefen Ebene vom Punkt O zum Punkt A. Auf dem reibungsbehafteten Abschnitt beträgt der Gleitreibungskoeffizient µ. Die Kraft F wirkt ausschließlich im Abschnitt O A auf das System ein. Sämtliche Kreisbögen weisen den Radius r auf. g µ B C l ϕ 0 A r r D ϕ 0 c α N.N. m O l 1 α F a) Berechnen Sie die Größe der richtungstreuen, zeitlich konstanten Kraft F, derart dass der Massenpunkt im Punkt A die Geschwindigkeit v A erreicht. Der Massenpunkt befindet sich im Punkt O in Ruhe. F= 3,0 P. b) Wie groß muss der Betrag der Geschwindigkeit v A mindestens sein, damit der Massenpunkt den Punkt B erreicht? Hinweis: Es soll hier davon ausgegangen werden, dass die Kraft F nicht mehr auf die Masse einwirkt und diese ständigen Kontakt zur Bahn haben soll. v A 1,0 P.
60 Herbst 2013 Aufgabe 2 (Seite 2 von 2) c) Wie groß darf die Geschwindigkeit v A des Massenpunkts maximal sein, damit der Massenpunkt die Bahn auf seinem Weg vom Punkt A zum Punkt B nicht verlässt? v A 3,0 P. d) Der Betrag der Geschwindigkeit der Punktmasse im Punkt A ist nun durch v A so vorgegeben, dass beide Kriterien aus den vorherigen Teilaufgaben erfüllt sind. Geben Sie die Geschwindigkeit des Massenpunktes in Abhängigkeit der Geschwindigkeit v A im Punkt D an. v D = 1,0 P. e) Im Punkt D stößt der Massenpunkt gegen eine starre Kontaktplatte, die mit einer Feder der Steifigkeit c verbunden ist. Legen Sie die Steifigkeit der Feder c so aus, dass sich eine maximale Stauchung der Feder von l einstellt. Der Betrag der Geschwindigkeit der Punktmasse im Punkt D ist durch v D gegeben. c= 2,0 P.
61 Herbst 2013 Aufgabe 3 (Seite 1 von 2) Ein System aus starren, homogenen Stäben (Länge 2l und Länge l) und einer starren, homogenen Kreisscheibe (Radius l/2) ist im Punkt A drehbar gelagert. Die Komponenten sind starr aneinander befestigt und das System ist darüber hinaus mit den dargestellten Federn und Dämpfern (Materialkonstanten sind der Zeichnung zu entnehmen) verbunden. Im Punkt B wird das System durch eine zeitabhängige Kraft F(t) belastet, wobei in der gezeichneten Ausgangslage F(t = 0) = 0 gilt und die Federn ungespannt sind. Der Einfluss der Schwerkraft ist zu vernachlässigen. l l d D C c F(t) B l/2 2m 8m l y m l x ϕ c T A a) Berechnen Sie das Massenträgheitsmoment θ (A) des Systems bezüglich des Punktes A. (1 Punkt) θ (A) = b) Geben Sie die horizontale Verschiebung x B des Punkte B sowie die horizontale Geschwindigkeit ẋ D des Punktes D in Abhängigkeit von ϕ und ϕ für große Auslenkungen des Systems an. (2 Punkte) x B = ẋ D =
62 Herbst 2013 Aufgabe 3 (Seite 2 von 2) c) Geben Sie die potentielle Energie E pot bezüglich des Drehwinkels ϕ für große Auslenkungen des Systems an. (1 Punkt) E pot = Das Massenträgheitsmoment des Systems ist nun als θ gegeben. Geben Sie die Bewegungs- Differentialgleichung bezüglich des Drehwinkels ϕ für große Auslenkungen des Systems an. (3 Punkte) d) Es ist nun folgende Bewegungs-Differentialgleichung für große Auslenkungen in φ gegeben: 4θ φ+3dl 2 cos(φ) φ +cl 2 [ 7 sin(φ) cos(φ)+sin(φ)+2 sin(φ) 2] = l cos(φ)f(t) Geben Sie die linearisierte Form der gegebenen Bewegungs-Differentialgleichung für kleine Auslenkungen (φ 1) an. (1 Punkt) Geben Sie für F(t) = F 0 cos(ωt) die Weg-Zeit-Funktion φ(t) für den eingeschwungenen Zustand an. Spezifizieren Sie dazu die Konstanten der allgemeinen Lösung: φ(t) = C cos(ωt φ 0 ) (2 Punkte)
63 Frühjahr 2013
64 Frühjahr 2013 Aufgabe 1 (Seite 1 von 3) Das dargestellte System besteht aus homogenen, starren Körpern, die durch dehnstarre, schlupffrei abrollende Seile miteinander verbunden sind und sich im Schwerefeld der Erde (Erdbeschleunigung g) befinden. Die beiden den Freiheitsgraden ϑ 1 und ϑ 2 zugeordneten Planetenrollen (je Radius r 3, Masse m 3 ) sind an einen ortsfest drehbar gelagerten Planetenträger (Gesamtmasse M 2 ) angeknüpft und rollen in einem rauhen Hohlzylinder schlupffrei ab. Das Seil wird über eine in Punkt A gelagerte Stufenrolle (Masse M 1 ) gelenkt und von einem Masseklotz (Masse M 0 ) gezogen. R 1 ϑ 2 l s α r 1 A ψ µ r 3,m 3 r 2 eϕ R 2 er ϕ M 2 r 3,m 3 g M 0 x 0 ϑ 1 µ a) Zeichnen Sie ein vollständiges Freikörperbild, wobei Trägheitsterme vernachlässigt werden können. g
65 Frühjahr 2013 Aufgabe 1 (Seite 2 von 3) b) Geben Sie die Impulsbilanz (Kräftesatz) des Klotzes (Masse M 0 ) bzgl. der x 0 -Koordinate an. Geben Sie die Drehimpulsbilanz (Drallsatz) der in Punkt A gelagerten Stufenrolle bezüglich ihres Schwerpunktes und der ψ-koordinate an. Die schwerpunktsbezogene Massenträgheit sei als θ 1 gegeben und soll hier nicht spezifiziert werden. Geben Sie die Drehimpulsbilanz (Drallsatz) des ortsfest drehbar gelagerten Planetenträgers (Gesamtmasse M 2 ) bezüglich seines Schwerpunktes und der ϕ-koordinate an. Die schwerpunktsbezogene Massenträgheit sei als θ 2 gegeben und soll hier nicht spezifiziert werden. c) Spezifizieren Sie nun das schwerpunktbezogene Massenträgheitsmoment θ 2 des Planetenträgers.DerPlanetenträgerbestehtauseinerStufenrolle(kleineStufung:Radiusr 2,Masse 1/3M 2, große Stufung: Radius R 2, Masse 2/3M 2 ) und zwei angeschweißten Stäben (je Länge l s, Masse m s ). θ 2 =
66 Frühjahr 2013 Aufgabe 1 (Seite 3 von 3) d) Geben Sie die Winkelgeschwindigkeit ϑ 1 in Abhängigkeit von ϕ an. ϑ 1 ( ϕ) = e) Geben Sie nun die Winkelgeschwindigkeiten ψ, ϕ, ϑ1 und ϑ 2 in Abhängigkeit von ẋ 0 an. ψ(ẋ 0 ) = ϕ(ẋ 0 ) = ϑ 1 (ẋ 0 ) = ϑ 2 (ẋ 0 ) =
67 Frühjahr 2013 Aufgabe 2 (Seite 1 von 2) Ein punktförmiger Körper der Masse m beginnt im Punkt O aus der Ruhelage heraus eine glatte, schiefe Ebene (Länge L, µ = 0) herunterzugleiten. Im Punkt 1 geht die schiefe Ebene tangential in eine rauhe Kreisbahn über (Gleitreibungskoeffizient µ, Radius r, Winkel θ). Die Geschwindigkeit zwischen Punkt 1 und 2 ist mittels eines äußeren Antriebs konstant gehalten, so dass in diesem Bereich v = const. und insbesondere v 1 = v 2 = v gilt. Die rauhe Kreisbahn mündet im Punkt 2 tangential in eine rauhe, schiefe Ebene (Neigungswinkel β, Länge L, µ=0). Im Punkt 3 befindet sich ein punktförmiger Körper der Masse 2m, welcher dort in Ruhe gehalten wird. Im Punkt 3 geht die glatte, schiefe Ebene tangential in eine glatte Kreisbahn über (µ=0). Im Punkt 4 befindet sich das Ende einer elastischen Feder (Steifigkeit/Federkonstante c). Das System befindet sich im Schwerfeld der Erde (Erdbeschleunigung g). m L g H O r 1 θ µ ψ α 2 β L 2m ϕ L/4 r C β 3 4 x N.N. a) GebenSiediepotentielleEnergieE O pot impunktobezüglichdesvorgegebenennullniveaus N.N. in Abhängigkeit der Größen m, g, H, r und ϕ an. E O pot =
68 Frühjahr 2013 Aufgabe 2 (Seite 2 von 2) b) Geben Sie die Reibkraft R(ψ) als Funktion von ψ unter Berücksichtigung der Vorgabe v 1 = v bzgl. des Punktes 1 an. Hinweis: Nicht mit dem Ergebnis der vorherigen Teilaufgabe weiterrechnen! R(ψ) = Berechnen Sie die auf der Strecke von Punkt 1 zu Punkt 2 verrichtete Reibarbeit W R. W R = c) Nehmen Sie an, dass nun v 3 = v am Punkt 3 vorgegeben ist. Geben Sie den Betrag der Geschwindigkeit beider Massen v 1 (für Masse m) und v 2 (für Masse 2m) unmittelbar nach dem vollplastischen Stoß an. Hinweis: Mit Ausnahme des Kraftstoßes sind alle etwaigen Kräfte während des Stoßvorgangs zu vernachlässigen! v 1 = v 2 = d) Bestimmen Sie die Federsteifigkeit/Federkonstante c derart, dass die maximale Stauchung der Feder l/5 betragen soll. Nehmen Sie hier an, dass nur ein Körper der Masse 3m Kontakt mit der Feder hat. Die Geschwindigkeit dieser Masse ist im Punkt 4 zu v 4 = v 4 = 6v vorgegeben. c =
69 Frühjahr 2013 Aufgabe 3 (Seite 1 von 2) Das dargestellte System befindet sich im Schwerefeld der Erde (Erdbeschleunigung g). Das masselose Seil rollt schlupffrei über zwei homogene Kreisscheiben (Massen M, m und Radien R, r). Dessen Ende ist mit einer Parallelschaltung einer Feder (Federsteifigkeit c) und eines Dämpfers (Dämpfungskonstante d) verbunden. Das Seil soll als stets gespannt angenommen werden. Die Feder ist in der Ausgangslage ungespannt. c d M,R g h y N.N. m,r Geg.: m, M, r, R, c, d, g. a) Geben Sie die gesamte kinetische Energie E kin sowie die gesamte potenzielle Energie E pot des Systems in Abhängigkeit des Freiheitsgrades y an. E kin = E pot =
70 Frühjahr 2013 Aufgabe 3 (Seite 2 von 2) b) Geben Sie die zugehörige Bewegungs-Differentialgleichung an. c) Bei vernachlässigter Schwerkraft und Federsteifigkeit (g = c = 0) sowie einem bestimmten, nicht näher aufgeführten Verhältnis zwischen den Massen hat die Bewegungsdifferentialgleichung die Form 5 m ÿ +d ẏ = 0. Geben Sie y(t) für die Anfangsbedingungen y(t = 0) = 0, ẏ(t = 0) = d m an. y(t) =
71 Herbst 2012
72 Herbst 2012 Aufgabe 1 (Seite 1 von 2) Ein System aus starren, homogenen Stäben ist im Punkt A drehbar gelagert und des Weiteren mit den dargestellten Federn und Dämpfern(Materialkonstanten sind der Zeichnung zu entnehmen) verbunden. Im Punkt D ist zusätzlich eine Punktmasse (Masse m) angebracht. Im Punkt E wird das System durch eine zeitabhängige Kraft F(t) belastet, wobei in der gezeichneten Ausgangslage F(t = 0) = 0 gilt und die Federn ungespannt sind. Der Einfluss der Schwerkraft ist zu vernachlässigen. y D d l F(t) ϕ m m E c B c T A 4m d C x l l 2l a) Berechnen Sie das Massenträgheitsmoment θ (A) des Systems bezüglich des Punktes A. θ (A) = b) Geben Sie die vertikale Verschiebung y B des Punktes B sowie die Geschwindigkeitskoordinate ẋ D des Punktes D in Abhängigkeit von ϕ und ϕ für große Auslenkungen des Systems an. y B = ẋ D =
73 Herbst 2012 Aufgabe 1 (Seite 2 von 2) c) Das Massenträgheitsmoment des Systems sei nun als θ gegeben. Geben Sie für die Annahme kleiner Auslenkungen (ϕ 1) die Bewegungs-Differentialgleichung bezüglich des Drehwinkels ϕ an. Nennen Sie die Bedingung für die Federkonstante c, so dass sich für das gegebene System eine schwach gedämpfte Schwingung ergeben würde. Spezifizieren Sie für F(t) = F 0 cos(ωt) die Konstanten C und ϕ 0 der allgemeinen Lösung für den eingeschwungenen Zustand. ϕ(t) = C cos(ωt ϕ 0 ) C = ϕ 0 =
74 Herbst 2012 Aufgabe 2 (Seite 1 von 3) Das dargestellte System besteht aus homogenen, starren Körpern, die durch dehnstarre, schlupffrei abrollende Seile miteinander verbunden sind und sich im Schwerefeld der Erde (Erdbeschleunigung g) befinden. Die jeweiligen Massen und Abmessungen sind der Zeichnung zu entnehmen. Es wird davon ausgegangen, dass die Rollen 1 und 3 auf rauhen Ebenen schlupffrei abrollen. Dabei wird Rolle 1 von dem konstanten Drehmoment M 0 die schiefe Ebene hinauf angetrieben. Die Umlenkrolle in Punkt A ist als masselos anzusehen. 1 2 ϕ 1 ϕ 2 g R 1 M 0 3 r x m 1 3 x 1 m r α r 3 ϕ 3 m 3 A x 4 4 m 4 a) Zeichnen Sie ein vollständiges Freikörperbild
75 Herbst 2012 Aufgabe 2 (Seite 2 von 3) b) Geben Sie die Impulsbilanz (Kräftesatz) der Rolle 1 bezüglich der x 1 -Koordinate an. c) Geben Sie die Drehimpulsbilanz(Drallsatz) der Rolle 1 bezüglich ihres Schwerpunktes und der ϕ 1 -Koordinate an. Das Massenträgheitsmoment dieser Rolle bezüglich ihres Schwerpunktes (identisch mit Mittelpunkt) ist als θ 1 vorgegeben. d) Geben Sie die Drehimpulsbilanz(Drallsatz) der Rolle 2 bezüglich ihres Schwerpunktes und der ϕ 2 -Koordinate an. Spezifizieren Sie das benötigte Massenträgheitsmoment mittels der gegebenen Größen. e) Geben Sie die Impulsbilanz (Kräftesatz) der Rolle 3 bezüglich der x 3 -Koordinate an. f) Geben Sie die Drehimpulsbilanz(Drallsatz) der Rolle 3 bezüglich ihres Schwerpunktes und der ϕ 3 -Koordinate an. Spezifizieren Sie das benötigte Massenträgheitsmoment mittels der gegebenen Größen. g) Geben Sie die Impulsbilanz (Kräftesatz) der Masse 4 bezüglich der x 4 -Koordinate an.
76 Herbst 2012 Aufgabe 2 (Seite 3 von 3) h) Geben Sie die (Winkel-)Geschwindigkeiten ẋ 1, ϕ 2, ẋ 3, ϕ 3 und ẋ 4 in Abhängigkeit von ϕ 1 an. ẋ 1 ( ϕ 1 ) = ϕ 2 ( ϕ 1 ) = ẋ 3 ( ϕ 1 ) = ϕ 3 ( ϕ 1 ) = ẋ 4 ( ϕ 1 ) =
77 Herbst 2012 Aufgabe 3 (Seite 1 von 2) Eine punktförmiger Körper der Masse m rutscht aus seiner Ruhelage (Höhe h bezüglich N.N.) im Punkt O eine reibungslose Ebene hinab. Auf seinem Weg über die Punkte A bis H passiert er 2 reibungsbehaftete Teilabschnitte mit den Gleitreibungskoeffizienten µ 1 und µ 2. Sämtliche Kreisbögen weisen den Radius r auf. y O m g x I D l 2 E h µ 1 C α r r α F µ 2 N.N. α r θ A B l 1 l 3 α γ γ r G φ H a) Berechnen Sie den Betrag der Geschwindigkeit der Punktmasse zwischen den Punkten A und B als Funktion des Winkels θ. v(θ) A B = b) Berechnen Sie den Betrag der Geschwindigkeit der Punktmasse im Punkt C. v C =
78 Herbst 2012 Aufgabe 3 (Seite 2 von 2) c) DerBetragderGeschwindigkeit derpunktmasse impunktc istnundurchv C vorgegeben, wobei diese als groß genug vorausgesetzt ist, um Punkt D zu erreichen. Geben Sie die Geschwindigkeit der Punktmasse in Abhängigkeit der Größe v C in den Punkten F und G an. v F = v G = d) Im Punkt G stößt die Punktmasse mit dem gegebenen Geschwindigkeitsbetrag v G gegen einen masselosen Stab, welcher mit einer Drehfeder (Federkonstante c T ) verbunden ist. Berechnen Sie die Winkelgeschwindigkeit der Punktmasse zwischen den Punkten G und H. φ=
79 Frühjahr 2012
80 Frühjahr 2012 Aufgabe 1 (Seite 1 von 2) Ein starrer Stab (Länge 2l, Masse m) ist wie dargestellt gelagert. Die im Punkt A befindliche Drehfeder weist die Federsteifigkeit (Federkonstante) c T, der im Punkt B angeschlossene viskose Dämpfer die Dämpferkonstante d auf. Im Punkt C ist ein System aus parallel und seriell geschalteten Federn (Federsteifigkeiten bzw. /-konstanten c 1 bis c 4 ) angebracht. Zudem wird das unter dem Einfluss des Schwerefelds (Erdbeschleunigung g) stehende System im Punkt C durch eine zeitabhängige Kraft F(t) belastet. Für den Zeitpunkt t = t 0 = 0 gelte F(t 0 ) = 0 sowie, dass sämtliche Federn ungespannt sind. l F(t) g C B m c 2 c 1 d c 3 c 4 l ϕ y c T x A a) Geben Sie die effektive Steifigkeit (Federkonstante) c eff des Federsystems in Abhängigkeit der Werte c 1, c 2, c 3 und c 4 an. c eff = b) Berechnen Sie das Massenträgheitsmoment θ (A) des Stabes bezüglich des Punktes A. θ (A) =
ERGEBNISSE TECHNISCHE MECHANIK III-IV
 ERGEBNISSE TECHNISCHE MECHANIK III-IV Lehrstuhl für Technische Mechanik, TU Kaiserslautern SS 213, 23.7.213 1. Aufgabe: (TMIII) y C z x A ω B D b r a Im skizzierten System dreht sich die KurbelAB (Länger)
ERGEBNISSE TECHNISCHE MECHANIK III-IV Lehrstuhl für Technische Mechanik, TU Kaiserslautern SS 213, 23.7.213 1. Aufgabe: (TMIII) y C z x A ω B D b r a Im skizzierten System dreht sich die KurbelAB (Länger)
9. Übungsblatt zur VL Einführung in die Klassische Mechanik und Wärmelehre Modul P1a, 1. FS BPh 8. Dezember 2009
 9. Übungsblatt zur VL Einführung in die Klassische Mechanik und Wärmelehre Modul P1a, 1. FS BPh 8. Dezember 009 Aufgabe 9.1: Doppelfeder Eine Kugel wird im Schwerefeld der Erde zwischen zwei Federn mit
9. Übungsblatt zur VL Einführung in die Klassische Mechanik und Wärmelehre Modul P1a, 1. FS BPh 8. Dezember 009 Aufgabe 9.1: Doppelfeder Eine Kugel wird im Schwerefeld der Erde zwischen zwei Federn mit
Institut für Technische und Num. Mechanik Technische Mechanik III Prof. Dr.-Ing. Prof. E. h. P. Eberhard WS 08/09 K 2. Aufgabe 1 (5 Punkte)
 Institut für Technische und Num. Mechanik Technische Mechanik III Prof. Dr.-Ing. Prof. E. h. P. Eberhard WS 8/9 K 6. Februar 9 Klausur in Technische Mechanik III Nachname Vorname Aufgabe (5 Punkte) Der
Institut für Technische und Num. Mechanik Technische Mechanik III Prof. Dr.-Ing. Prof. E. h. P. Eberhard WS 8/9 K 6. Februar 9 Klausur in Technische Mechanik III Nachname Vorname Aufgabe (5 Punkte) Der
2. Lagrange-Gleichungen
 2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
Mehmet Maraz. MechanikNachhilfe
 Mehmet Maraz MechanikNachhilfe 1. Auflage 015 Inhaltsverzeichnis 1 Statik 1 1.1 Lagerungen und Lagerreaktionen................. 1. Kräftegleichgewichte......................... 5 1..1 Drehmoment.........................
Mehmet Maraz MechanikNachhilfe 1. Auflage 015 Inhaltsverzeichnis 1 Statik 1 1.1 Lagerungen und Lagerreaktionen................. 1. Kräftegleichgewichte......................... 5 1..1 Drehmoment.........................
3. Erhaltungsgrößen und die Newton schen Axiome
 Übungen zur T1: Theoretische Mechanik, SoSe13 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray James.Gray@physik.uni-muenchen.de 3. Erhaltungsgrößen und die Newton schen Axiome Übung 3.1:
Übungen zur T1: Theoretische Mechanik, SoSe13 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray James.Gray@physik.uni-muenchen.de 3. Erhaltungsgrößen und die Newton schen Axiome Übung 3.1:
Hochschule Karlsruhe Technische Mechanik Statik. Aufgaben zur Statik
 Aufgaben zur Statik S 1. Seilkräfte 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn Am Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. Addition
Aufgaben zur Statik S 1. Seilkräfte 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn Am Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. Addition
Blatt 03.1: Scheinkräfte
 Fakultät für Physik T1: Klassische Mechanik, SoSe 2016 Dozent: Jan von Delft Übungen: Benedikt Bruognolo, Sebastian Huber, Katharina Stadler, Lukas Weidinger http://www.physik.uni-muenchen.de/lehre/vorlesungen/sose_16/t1_theor_mechanik/
Fakultät für Physik T1: Klassische Mechanik, SoSe 2016 Dozent: Jan von Delft Übungen: Benedikt Bruognolo, Sebastian Huber, Katharina Stadler, Lukas Weidinger http://www.physik.uni-muenchen.de/lehre/vorlesungen/sose_16/t1_theor_mechanik/
Aufgabe 11.1 (Fragen zu Kreisbewegungen und Drehungen)
 Physik VNT Aufgabenblätter und 2 7. Übung 4. KW) Aufgabe. Fragen zu Kreisbewegungen und Drehungen) a) Beurteilen Sie, welche der folgenden Aussagen jeweils wahr oder falsch ist: Wenn sich ein Körper gleichförmig
Physik VNT Aufgabenblätter und 2 7. Übung 4. KW) Aufgabe. Fragen zu Kreisbewegungen und Drehungen) a) Beurteilen Sie, welche der folgenden Aussagen jeweils wahr oder falsch ist: Wenn sich ein Körper gleichförmig
Kinetik. Schwerpunktsatz (Impulssatz) F 2. F i (1) F 3 S F 4 F 1. r S. F ix. F ir. F iy. F iz. m z S = i. Technische Mechanik III FS 1
 und Eperimentelle Mechanik FS 1 Kinetik Bisher wurde nur die Kinematik von Bewegungen untersucht (d.h. Weg, Geschwindigkeit und Beschleunigung). Es sollen nun Kräfte (später auch Momente) mit diesen kinematischen
und Eperimentelle Mechanik FS 1 Kinetik Bisher wurde nur die Kinematik von Bewegungen untersucht (d.h. Weg, Geschwindigkeit und Beschleunigung). Es sollen nun Kräfte (später auch Momente) mit diesen kinematischen
Theoretische Physik I: Lösungen Blatt Michael Czopnik
 Theoretische Physik I: Lösungen Blatt 2 15.10.2012 Michael Czopnik Aufgabe 1: Scheinkräfte Nutze Zylinderkoordinaten: x = r cos ϕ y = r sin ϕ z = z Zweimaliges differenzieren ergibt: ẍ = r cos ϕ 2ṙ ϕ sin
Theoretische Physik I: Lösungen Blatt 2 15.10.2012 Michael Czopnik Aufgabe 1: Scheinkräfte Nutze Zylinderkoordinaten: x = r cos ϕ y = r sin ϕ z = z Zweimaliges differenzieren ergibt: ẍ = r cos ϕ 2ṙ ϕ sin
Lösungsblatt Rolle und Gewichte (2P) Mechanik (Physik, Wirtschaftsphysik, Physik Lehramt) (WS07/08)
 sblatt Mechanik Physik, Wirtschaftsphysik, Physik Lehramt WS07/08 Wolfgang v. Soden wolfgang.soden@uni-ulm.de. 0. 008 74 Rolle und Gewichte P Zwei Gewichte mit Massen m = kg bzw. m = 3kg sind durch einen
sblatt Mechanik Physik, Wirtschaftsphysik, Physik Lehramt WS07/08 Wolfgang v. Soden wolfgang.soden@uni-ulm.de. 0. 008 74 Rolle und Gewichte P Zwei Gewichte mit Massen m = kg bzw. m = 3kg sind durch einen
Formelsammlung. Lagrange-Gleichungen: q k. Zur Koordinate q k konjugierter Impuls: p k = L. Hamilton-Funktion: p k. Hamiltonsche Gleichungen: q k = H
 Formelsammlung Lagrange-Gleichungen: ( ) d L dt q k L q k = 0 mit k = 1,..., n. (1) Zur Koordinate q k konjugierter Impuls: p k = L q k. (2) Hamilton-Funktion: n H(q 1,..., q n, p 1,..., p n, t) = p k
Formelsammlung Lagrange-Gleichungen: ( ) d L dt q k L q k = 0 mit k = 1,..., n. (1) Zur Koordinate q k konjugierter Impuls: p k = L q k. (2) Hamilton-Funktion: n H(q 1,..., q n, p 1,..., p n, t) = p k
Die Entwicklung des Erde-Mond-Systems
 THEORETISCHE AUFGABE Nr. 1 Die Entwicklung des Erde-Mond-Systems Wissenschaftler können den Abstand Erde-Mond mit großer Genauigkeit bestimmen. Sie erreichen dies, indem sie einen Laserstrahl an einem
THEORETISCHE AUFGABE Nr. 1 Die Entwicklung des Erde-Mond-Systems Wissenschaftler können den Abstand Erde-Mond mit großer Genauigkeit bestimmen. Sie erreichen dies, indem sie einen Laserstrahl an einem
PN 1 Klausur Physik für Chemiker
 PN 1 Klausur Physik für Chemiker Prof. T. Liedl Ihr Name in leserlichen Druckbuchstaben München 2011 Martrikelnr.: Semester: Klausur zur Vorlesung PN I Einführung in die Physik für Chemiker Prof. Dr. T.
PN 1 Klausur Physik für Chemiker Prof. T. Liedl Ihr Name in leserlichen Druckbuchstaben München 2011 Martrikelnr.: Semester: Klausur zur Vorlesung PN I Einführung in die Physik für Chemiker Prof. Dr. T.
Kinematik des starren Körpers
 Technische Mechanik II Kinematik des starren Körpers Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/2010 Übersicht 1. Kinematik des Massenpunktes
Technische Mechanik II Kinematik des starren Körpers Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/2010 Übersicht 1. Kinematik des Massenpunktes
8.1 Gleichförmige Kreisbewegung 8.2 Drehung ausgedehnter Körper 8.3 Beziehung: Translation - Drehung 8.4 Vektornatur des Drehwinkels
 8. Drehbewegungen 8.1 Gleichförmige Kreisbewegung 8.2 Drehung ausgedehnter Körper 8.3 Beziehung: Translation - Drehung 8.4 Vektornatur des Drehwinkels 85 8.5 Kinetische Energie der Rotation ti 8.6 Berechnung
8. Drehbewegungen 8.1 Gleichförmige Kreisbewegung 8.2 Drehung ausgedehnter Körper 8.3 Beziehung: Translation - Drehung 8.4 Vektornatur des Drehwinkels 85 8.5 Kinetische Energie der Rotation ti 8.6 Berechnung
Experimentalphysik für Naturwissenschaftler 1 Universität Erlangen Nürnberg WS 2008/09 Klausur ( )
 Nur vom Korrektor auszufüllen 1 2 3 4 5 6 7 8 9 1 Note Experimentalphysik für Naturwissenschaftler 1 Universität Erlangen Nürnberg WS 28/9 Klausur (6.2.29 Name: Studiengang: In die Wertung der Klausur
Nur vom Korrektor auszufüllen 1 2 3 4 5 6 7 8 9 1 Note Experimentalphysik für Naturwissenschaftler 1 Universität Erlangen Nürnberg WS 28/9 Klausur (6.2.29 Name: Studiengang: In die Wertung der Klausur
Rotation. Versuch: Inhaltsverzeichnis. Fachrichtung Physik. Erstellt: U. Escher A. Schwab Aktualisiert: am 29. 03. 2010. Physikalisches Grundpraktikum
 Fachrichtung Physik Physikalisches Grundpraktikum Versuch: RO Erstellt: U. Escher A. Schwab Aktualisiert: am 29. 03. 2010 Rotation Inhaltsverzeichnis 1 Aufgabenstellung 2 2 Allgemeine Grundlagen 2 2.1
Fachrichtung Physik Physikalisches Grundpraktikum Versuch: RO Erstellt: U. Escher A. Schwab Aktualisiert: am 29. 03. 2010 Rotation Inhaltsverzeichnis 1 Aufgabenstellung 2 2 Allgemeine Grundlagen 2 2.1
Versuch P1-20 Pendel Vorbereitung
 Versuch P1-0 Pendel Vorbereitung Gruppe Mo-19 Yannick Augenstein Versuchsdurchführung: 9. Januar 01 Inhaltsverzeichnis Aufgabe 1 1.1 Reduzierte Pendellänge............................. 1. Fallbeschleunigung
Versuch P1-0 Pendel Vorbereitung Gruppe Mo-19 Yannick Augenstein Versuchsdurchführung: 9. Januar 01 Inhaltsverzeichnis Aufgabe 1 1.1 Reduzierte Pendellänge............................. 1. Fallbeschleunigung
Ferienkurs Experimentalphysik 1
 1 Fakultät für Physik Technische Universität München Bernd Kohler & Daniel Singh Probeklausur WS 2014/2015 27.03.2015 Bearbeitungszeit: 90 Minuten Aufgabe 1: Romeo und Julia (ca. 15 min) Julia befindet
1 Fakultät für Physik Technische Universität München Bernd Kohler & Daniel Singh Probeklausur WS 2014/2015 27.03.2015 Bearbeitungszeit: 90 Minuten Aufgabe 1: Romeo und Julia (ca. 15 min) Julia befindet
2. Momentanpol. Für die Geschwindigkeit eines beliebigen Punktes P eines starren Körpers gilt: y A ), v Py. =v Ay
 ufgabenstellung: Für die Geschwindigkeit eines beliebigen Punktes P eines starren Körpers gilt: Gesucht ist der Punkt П, dessen momentane Geschwindigkeit null ist. Lösung: v Px =x ( y P y ), v Py =y +
ufgabenstellung: Für die Geschwindigkeit eines beliebigen Punktes P eines starren Körpers gilt: Gesucht ist der Punkt П, dessen momentane Geschwindigkeit null ist. Lösung: v Px =x ( y P y ), v Py =y +
Experimentalphysik für Naturwissenschaftler 1 Universität Erlangen Nürnberg WS 2009/10 Klausur ( )
 Nur vom Korrektor auszufüllen 1 2 3 4 5 6 7 8 9 10 Note Experimentalphysik für Naturwissenschaftler 1 Universität Erlangen Nürnberg WS 2009/10 Klausur (12.2.2010) Name: Studiengang: In die Wertung der
Nur vom Korrektor auszufüllen 1 2 3 4 5 6 7 8 9 10 Note Experimentalphysik für Naturwissenschaftler 1 Universität Erlangen Nürnberg WS 2009/10 Klausur (12.2.2010) Name: Studiengang: In die Wertung der
Prüfung in Technischer Mechanik 1
 Prüfung in Technischer Mechanik 1 Sommersemester 015 4. August 015, 08:00-10:00 Uhr MUSTERLÖSUNG MUSTERLÖSUNG MUSTERLÖSUNG MUSTERLÖSUNG MUSTERLÖSUNG Bitte beachten Sie die folgenden Punkte: Die Prüfung
Prüfung in Technischer Mechanik 1 Sommersemester 015 4. August 015, 08:00-10:00 Uhr MUSTERLÖSUNG MUSTERLÖSUNG MUSTERLÖSUNG MUSTERLÖSUNG MUSTERLÖSUNG Bitte beachten Sie die folgenden Punkte: Die Prüfung
Theoretische Mechanik
 Theoretische Mechanik Übungen R. Kirschner, ITP, Univ. Leipzig 1-1 1. Betrachten Sie ein System aus 4 Massenpunkten, ( r i,m i ),i = 1,2,3,4, das sich in trivialer geradlinig-gleichförmiger Bewegung befindet.
Theoretische Mechanik Übungen R. Kirschner, ITP, Univ. Leipzig 1-1 1. Betrachten Sie ein System aus 4 Massenpunkten, ( r i,m i ),i = 1,2,3,4, das sich in trivialer geradlinig-gleichförmiger Bewegung befindet.
1. Einfache ebene Tragwerke
 Die Ermittlung der Lagerreaktionen einfacher Tragwerke erfolgt in drei Schritten: Freischneiden Aufstellen der Gleichgewichtsbedingungen Auflösen der Gleichungen Prof. Dr. Wandinger 3. Tragwerksanalyse
Die Ermittlung der Lagerreaktionen einfacher Tragwerke erfolgt in drei Schritten: Freischneiden Aufstellen der Gleichgewichtsbedingungen Auflösen der Gleichungen Prof. Dr. Wandinger 3. Tragwerksanalyse
Vordiplomsklausur Physik
 Institut für Physik und Physikalische Technologien der TU-Clausthal; Prof. Dr. W. Schade Vordiplomsklausur Physik 14.Februar 2006, 9:00-11:00 Uhr für den Studiengang: Maschinenbau intensiv (bitte deutlich
Institut für Physik und Physikalische Technologien der TU-Clausthal; Prof. Dr. W. Schade Vordiplomsklausur Physik 14.Februar 2006, 9:00-11:00 Uhr für den Studiengang: Maschinenbau intensiv (bitte deutlich
Klausur zur Vorlesung E1 Mechanik (6 ECTS)
 Ludwig Maximilians Universität München Fakultät für Physik Klausur zur Vorlesung E1 Mechanik WS 2013/2014 17. Feb. 2014 für Studierende im Lehramt und Nebenfach Physik (6 ECTS) Prof. J. Rädler, Prof. H.
Ludwig Maximilians Universität München Fakultät für Physik Klausur zur Vorlesung E1 Mechanik WS 2013/2014 17. Feb. 2014 für Studierende im Lehramt und Nebenfach Physik (6 ECTS) Prof. J. Rädler, Prof. H.
Klausur Physik 1 (GPH1) am Fachbereich Elektrotechnik und Informatik, Fachbereich Mechatronik und Maschinenbau
 Name, Matrikelnummer: Klausur Physik 1 (GPH1) am 16.5.08 Fachbereich Elektrotechnik und Informatik, Fachbereich Mechatronik und Maschinenbau Zugelassene Hilfsmittel: Beiblätter zur Vorlesung Physik 1 ab
Name, Matrikelnummer: Klausur Physik 1 (GPH1) am 16.5.08 Fachbereich Elektrotechnik und Informatik, Fachbereich Mechatronik und Maschinenbau Zugelassene Hilfsmittel: Beiblätter zur Vorlesung Physik 1 ab
Aufgabe 1: Klausur Physik für Maschinenbauer (SS 2009) Lösungen 1. (10 Punkte)
 Klausur Physik für Maschinenbauer (SS 2009) Lösungen 1 Aufgabe 1: Schiefe Ebene Auf einer reibungsfreien, schiefen Ebene mit dem Winkel 30 befindet sich eine Kiste der Masse m = 100 kg zunächst in Ruhe.
Klausur Physik für Maschinenbauer (SS 2009) Lösungen 1 Aufgabe 1: Schiefe Ebene Auf einer reibungsfreien, schiefen Ebene mit dem Winkel 30 befindet sich eine Kiste der Masse m = 100 kg zunächst in Ruhe.
B.2. Lösungsskizzen der Übungsaufgaben zum Kapitel 2
 B. sskizzen B.. sskizzen der Übungsaufgaben zum Kapitel Aufgabe 13 (Karusell) Ein Mann steht neben einem Karussell. Beschreiben sie seine Bewegung in einem im Karussell verankerten Bezugssystem, das sich
B. sskizzen B.. sskizzen der Übungsaufgaben zum Kapitel Aufgabe 13 (Karusell) Ein Mann steht neben einem Karussell. Beschreiben sie seine Bewegung in einem im Karussell verankerten Bezugssystem, das sich
Klausur Physik 1 (GPH1) am 8.7.02
 Name, Matrikelnummer: Klausur Physik 1 (GPH1) am 8.7.02 Fachbereich Elektrotechnik und Informatik, Fachbereich Mechatronik und Maschinenbau Zugelassene Hilfsmittel: Beiblätter zur Vorlesung Physik 1 im
Name, Matrikelnummer: Klausur Physik 1 (GPH1) am 8.7.02 Fachbereich Elektrotechnik und Informatik, Fachbereich Mechatronik und Maschinenbau Zugelassene Hilfsmittel: Beiblätter zur Vorlesung Physik 1 im
Pendel. Versuch: P Vorbereitung - Inhaltsverzeichnis. Physikalisches Anfängerpraktikum 1 Wintersemester 2005/06 Julian Merkert ( )
 Physikalisches Anfängerpraktikum 1 Gruppe Mo-16 Wintersemester 005/06 Julian Merkert (1999) Versuch: P1-0 Pendel - Vorbereitung - Vorbemerkung Das einfachste Modell, um einen Pendelversuch zu beschreiben,
Physikalisches Anfängerpraktikum 1 Gruppe Mo-16 Wintersemester 005/06 Julian Merkert (1999) Versuch: P1-0 Pendel - Vorbereitung - Vorbemerkung Das einfachste Modell, um einen Pendelversuch zu beschreiben,
Klausur Physik 1 (GPH1) am
 Name, Matrikelnummer: Klausur Physik 1 (GPH1) am 18.9.09 Fachbereich Elektrotechnik und Informatik, Fachbereich Mechatronik und Maschinenbau Zugelassene Hilfsmittel: Beiblätter zur Vorlesung Physik 1 ab
Name, Matrikelnummer: Klausur Physik 1 (GPH1) am 18.9.09 Fachbereich Elektrotechnik und Informatik, Fachbereich Mechatronik und Maschinenbau Zugelassene Hilfsmittel: Beiblätter zur Vorlesung Physik 1 ab
5 Kreisbewegung und Rotation (rotación, la)
 5 Kreisbewegung und Rotation Hofer 1 5 Kreisbewegung und Rotation (rotación, la) A1: Nenne Beispiele für kreisförmige Bewegungen und Drehungen aus dem Alltag! A2: Nenne die grundlegenden Bewegungsformen
5 Kreisbewegung und Rotation Hofer 1 5 Kreisbewegung und Rotation (rotación, la) A1: Nenne Beispiele für kreisförmige Bewegungen und Drehungen aus dem Alltag! A2: Nenne die grundlegenden Bewegungsformen
Physik 1 Hydrologen/VNT, WS 2014/15 Lösungen Aufgabenblatt 8. Feder )
 Aufgabenblatt 8 Aufgabe 1 (M 4. Feder ) Ein Körper der Masse m wird in der Höhe z 1 losgelassen und trifft bei z = 0 auf das Ende einer senkrecht stehenden Feder mit der Federkonstanten k, die den Fall
Aufgabenblatt 8 Aufgabe 1 (M 4. Feder ) Ein Körper der Masse m wird in der Höhe z 1 losgelassen und trifft bei z = 0 auf das Ende einer senkrecht stehenden Feder mit der Federkonstanten k, die den Fall
Bitte tragen Sie vor Abgabe Ihren Namen und Matrikel-Nr. ein, versehen Sie jedes Blatt mit einer Seitenzahl und geben Sie auch die Aufgabenblätter ab!
 Klausur TM1 für WI SS 99 Prüfer: Prof. Dr. M. Lindner NAME: MATRIKEL-NR.: Aufgabe Punkte erreicht 1 20 2 26 3 28 4 26 Summe 100 Bitte tragen Sie vor Abgabe Ihren Namen und Matrikel-Nr. ein, versehen Sie
Klausur TM1 für WI SS 99 Prüfer: Prof. Dr. M. Lindner NAME: MATRIKEL-NR.: Aufgabe Punkte erreicht 1 20 2 26 3 28 4 26 Summe 100 Bitte tragen Sie vor Abgabe Ihren Namen und Matrikel-Nr. ein, versehen Sie
Anleitung zum Physikpraktikum für Oberstufenlehrpersonen Resonanz (R) Herbstsemester Physik-Institut der Universität Zürich
 Anleitung zum Physikpraktikum für Oberstufenlehrpersonen Resonanz (R) Herbstsemester 2016 Physik-Institut der Universität Zürich Inhaltsverzeichnis 4 Resonanz (R) 4.1 4.1 Einleitung........................................
Anleitung zum Physikpraktikum für Oberstufenlehrpersonen Resonanz (R) Herbstsemester 2016 Physik-Institut der Universität Zürich Inhaltsverzeichnis 4 Resonanz (R) 4.1 4.1 Einleitung........................................
4.3 Systeme von starren Körpern. Aufgaben
 Technische Mechanik 3 4.3-1 Prof. Dr. Wandiner ufabe 1: 4.3 Ssteme von starren Körpern ufaben h S L h D L L L D h H L H SH Ein PKW der Masse m mit Vorderradantrieb zieht einen Seelfluzeuanhäner der Masse
Technische Mechanik 3 4.3-1 Prof. Dr. Wandiner ufabe 1: 4.3 Ssteme von starren Körpern ufaben h S L h D L L L D h H L H SH Ein PKW der Masse m mit Vorderradantrieb zieht einen Seelfluzeuanhäner der Masse
I.6.3 Potentielle Energie eines Teilchensystems. m i. N z i. i=1. = gmz M. i=1. I.6.4 Kinetische Energie eines Teilchensystems
 I.6.3 Potentielle Energie eines Teilchensystems Beispiel: Einzelmassen im Schwerefeld U i = m i gz i jetzt viele Massen im Schwerefeld: Gesamtenergie U = m i gz i m i z i = gm m i = gmz M Man muss also
I.6.3 Potentielle Energie eines Teilchensystems Beispiel: Einzelmassen im Schwerefeld U i = m i gz i jetzt viele Massen im Schwerefeld: Gesamtenergie U = m i gz i m i z i = gm m i = gmz M Man muss also
14. Mechanische Schwingungen und Wellen
 14. Mechanische Schwingungen und Wellen Schwingungen treten in der Technik in vielen Vorgängen auf mit positiven und negativen Effekten (z. B. Haarrisse, Achsbrüche etc.). Deshalb ist es eine wichtige
14. Mechanische Schwingungen und Wellen Schwingungen treten in der Technik in vielen Vorgängen auf mit positiven und negativen Effekten (z. B. Haarrisse, Achsbrüche etc.). Deshalb ist es eine wichtige
Übungen zu Physik 1 für Maschinenwesen
 Physikdepartment E13 WS 011/1 Übungen zu Physik 1 für Maschinenwesen Prof. Dr. Peter Müller-Buschbaum, Dr. Eva M. Herzig, Dr. Volker Körstgens, David Magerl, Markus Schindler, Moritz v. Sivers Vorlesung
Physikdepartment E13 WS 011/1 Übungen zu Physik 1 für Maschinenwesen Prof. Dr. Peter Müller-Buschbaum, Dr. Eva M. Herzig, Dr. Volker Körstgens, David Magerl, Markus Schindler, Moritz v. Sivers Vorlesung
Physik I Übung 10 - Lösungshinweise
 Physik I Übung - Lösungshinweise Stefan Reutter WS / Moritz Kütt Stand: 7. Februar Franz Fujara Aufgabe War die Weihnachtspause vielleicht doch zu lang? Bei der Translation eines Massenpunktes und der
Physik I Übung - Lösungshinweise Stefan Reutter WS / Moritz Kütt Stand: 7. Februar Franz Fujara Aufgabe War die Weihnachtspause vielleicht doch zu lang? Bei der Translation eines Massenpunktes und der
Klausur Experimentalphysik (1. Termin)
 Helmut-Schmidt-Universität Universität der Bundeswehr Hamburg Fachbereich Elektrotechnik Univ.-Prof. Dr. D. Kip Experimentalphysik und Materialwissenschaften Telefon: 6541 2457 Klausur Experimentalphysik
Helmut-Schmidt-Universität Universität der Bundeswehr Hamburg Fachbereich Elektrotechnik Univ.-Prof. Dr. D. Kip Experimentalphysik und Materialwissenschaften Telefon: 6541 2457 Klausur Experimentalphysik
Erzwungene Schwingungen
 Fachrichtung Physik Physikalisches Grundpraktikum Versuch: ES Erstellt: M. Kauer B. Scholz Aktualisiert: am 28. 06. 2016 Erzwungene Schwingungen Inhaltsverzeichnis 1 Aufgabenstellung 2 2 Theoretische Grundlagen
Fachrichtung Physik Physikalisches Grundpraktikum Versuch: ES Erstellt: M. Kauer B. Scholz Aktualisiert: am 28. 06. 2016 Erzwungene Schwingungen Inhaltsverzeichnis 1 Aufgabenstellung 2 2 Theoretische Grundlagen
Formelsammlung. Physik. [F] = kg m s 2 = N (Newton) v = ṡ = ds dt. [v] = m/s. a = v = s = d2 s dt 2 [s] = m/s 2. v = a t.
![Formelsammlung. Physik. [F] = kg m s 2 = N (Newton) v = ṡ = ds dt. [v] = m/s. a = v = s = d2 s dt 2 [s] = m/s 2. v = a t. Formelsammlung. Physik. [F] = kg m s 2 = N (Newton) v = ṡ = ds dt. [v] = m/s. a = v = s = d2 s dt 2 [s] = m/s 2. v = a t.](/thumbs/48/24282507.jpg) Formelsammlung Physik Mechanik. Kinematik und Kräfte Kinematik Erstes Newtonsches Axiom (Axio/Reaxio) F axio = F reaxio Zweites Newtonsches Axiom Translationsbewegungen Konstante Beschleunigung F = m a
Formelsammlung Physik Mechanik. Kinematik und Kräfte Kinematik Erstes Newtonsches Axiom (Axio/Reaxio) F axio = F reaxio Zweites Newtonsches Axiom Translationsbewegungen Konstante Beschleunigung F = m a
Themengebiet: Mechanik. Tabelle 1: Gegenüberstellung der sich entsprechenden Größen bei Translation und Rotation
 Seite 1 1 Literatur Themengebiet: Mechanik W. Kranzer, So interessant ist Physik, Köln, 1982, S. 63-65, 331-335 R. L. Page, The Physics of Human Movement, Exeter, 1978, S. 45-56 2 Grundlagen 2.1, Drehmoment,
Seite 1 1 Literatur Themengebiet: Mechanik W. Kranzer, So interessant ist Physik, Köln, 1982, S. 63-65, 331-335 R. L. Page, The Physics of Human Movement, Exeter, 1978, S. 45-56 2 Grundlagen 2.1, Drehmoment,
Physik 1 für Ingenieure
 Physik 1 für Ingenieure Othmar Marti Experimentelle Physik Universität Ulm Othmar.Marti@Physik.Uni-Ulm.de Skript: http://wwwex.physik.uni-ulm.de/lehre/physing1 Übungsblätter und Lösungen: http://wwwex.physik.uni-ulm.de/lehre/physing1/ueb/ue#
Physik 1 für Ingenieure Othmar Marti Experimentelle Physik Universität Ulm Othmar.Marti@Physik.Uni-Ulm.de Skript: http://wwwex.physik.uni-ulm.de/lehre/physing1 Übungsblätter und Lösungen: http://wwwex.physik.uni-ulm.de/lehre/physing1/ueb/ue#
gp : Gekoppelte Pendel
 U N I V E R S I T Ä T R E G E N S B U R G Naturwissenschaftliche Fakultät II - Physik Anleitung zum Physikpraktikum für Chemiker Versuch gp : Gekoppelte Pendel Dr. Stephan Giglberger Dr. Tobias Korn Manuel
U N I V E R S I T Ä T R E G E N S B U R G Naturwissenschaftliche Fakultät II - Physik Anleitung zum Physikpraktikum für Chemiker Versuch gp : Gekoppelte Pendel Dr. Stephan Giglberger Dr. Tobias Korn Manuel
2.4 Fall, Wurf und Federkräfte
 2.4. FALL, WURF UND FEDERKRÄFTE 47 2.4 Fall, Wurf und Federkräfte Sie haben jetzt die Begriffe Arbeit, potentielle und kinetische Energie, sowie die Energieerhaltung kennengelernt. Wir wollen nun einige
2.4. FALL, WURF UND FEDERKRÄFTE 47 2.4 Fall, Wurf und Federkräfte Sie haben jetzt die Begriffe Arbeit, potentielle und kinetische Energie, sowie die Energieerhaltung kennengelernt. Wir wollen nun einige
10. Versuch: Schiefe Ebene
 Physikpraktikum für Pharmazeuten Universität Regensburg Fakultät Physik 10. Versuch: Schiefe Ebene In diesem Versuch untersuchen Sie Mechanik der schiefen Ebene, indem Sie mithilfe dem statischen und dynamischen
Physikpraktikum für Pharmazeuten Universität Regensburg Fakultät Physik 10. Versuch: Schiefe Ebene In diesem Versuch untersuchen Sie Mechanik der schiefen Ebene, indem Sie mithilfe dem statischen und dynamischen
Aufgaben zu Kapitel 14
 Aufgaben zu Kapitel 14 1 Aufgaben zu Kapitel 14 Verständnisfragen Aufgabe 14.1 Haben (reelle) lineare Gleichungssysteme mit zwei verschiedenen Lösungen stets unendlich viele Lösungen? Aufgabe 14.2 Gibt
Aufgaben zu Kapitel 14 1 Aufgaben zu Kapitel 14 Verständnisfragen Aufgabe 14.1 Haben (reelle) lineare Gleichungssysteme mit zwei verschiedenen Lösungen stets unendlich viele Lösungen? Aufgabe 14.2 Gibt
3. Mathematikschulaufgabe
 Arbeitszeit 40min 1.0 Gegeben sind die Punkte A (-I1) und B (6I-1), sowie die Gerade g mit der Gleichung y = 0,5x + 3. Führe die folgenden Berechnungen jeweils auf zwei Stellen gerundet aus. 1.1 Berechne
Arbeitszeit 40min 1.0 Gegeben sind die Punkte A (-I1) und B (6I-1), sowie die Gerade g mit der Gleichung y = 0,5x + 3. Führe die folgenden Berechnungen jeweils auf zwei Stellen gerundet aus. 1.1 Berechne
Physikpraktikum für Pharmazeuten Universität Regensburg Fakultät Physik. 4. Versuch: Atwoodsche Fallmaschine
 Physikpraktikum für Pharmazeuten Universität Regensburg Fakultät Physik 4. Versuch: Atwoodsche Fallmaschine 1 Einführung Wir setzen die Untersuchung der beschleunigten Bewegung in diesem Versuch fort.
Physikpraktikum für Pharmazeuten Universität Regensburg Fakultät Physik 4. Versuch: Atwoodsche Fallmaschine 1 Einführung Wir setzen die Untersuchung der beschleunigten Bewegung in diesem Versuch fort.
Inhaltsverzeichnis Einleitung Die Kinematik des Punktes Kinetik des Massenpunktes
 Inhaltsverzeichnis 1 Einleitung... 1 1.1 Aufgabenstellungen der Dynamik.... 1 1.2 Einige Meilensteine in der Geschichte der Dynamik... 3 1.3 EinteilungundInhaltedesBuches... 5 1.4 ZieledesBuches... 6 2
Inhaltsverzeichnis 1 Einleitung... 1 1.1 Aufgabenstellungen der Dynamik.... 1 1.2 Einige Meilensteine in der Geschichte der Dynamik... 3 1.3 EinteilungundInhaltedesBuches... 5 1.4 ZieledesBuches... 6 2
Mathematische Methoden in den Ingenieurwissenschaften 1. Übungsblatt
 Prof Dr M Gerdts Dr A Dreves J Michael Wintertrimester 216 Mathematische Methoden in den Ingenieurwissenschaften 1 Übungsblatt Aufgabe 1 : (Schwimmer Ein Schwimmer möchte einen Fluss der Breite b > überqueren,
Prof Dr M Gerdts Dr A Dreves J Michael Wintertrimester 216 Mathematische Methoden in den Ingenieurwissenschaften 1 Übungsblatt Aufgabe 1 : (Schwimmer Ein Schwimmer möchte einen Fluss der Breite b > überqueren,
Geometrie. 1 Vektorielle analytische Geometrie der Ebene, Kegelschnitte
 Geometrie Geometrie W. Kuhlisch Brückenkurs 206. Vektorrechnung und analytische Geometrie der Ebene, Kegelschnitte 2. Vektorrechnung und analytische Geometrie des Raumes, Anwendungen in der Geometrie,
Geometrie Geometrie W. Kuhlisch Brückenkurs 206. Vektorrechnung und analytische Geometrie der Ebene, Kegelschnitte 2. Vektorrechnung und analytische Geometrie des Raumes, Anwendungen in der Geometrie,
Kapitel VI. Euklidische Geometrie
 Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Dynamischer Entwurf von Achterbahnfiguren
 Dynamischer Entwurf von Achterbahnfiguren Prof. Dr.-Ing.. Rill 1 Einleitung Bei der Entwicklung von Achterbahnfiguren wird in der Regel die Bahngeometrie vorgegeben. Mit Hilfe von Simulationsprogrammen
Dynamischer Entwurf von Achterbahnfiguren Prof. Dr.-Ing.. Rill 1 Einleitung Bei der Entwicklung von Achterbahnfiguren wird in der Regel die Bahngeometrie vorgegeben. Mit Hilfe von Simulationsprogrammen
Grundlagen der Kinematik und Dynamik
 INSTITUT FÜR UNFALLCHIRURGISCHE FORSCHUNG UND BIOMECHANIK Grundlagen der Biomechanik des Bewegungsapparates Grundlagen der Kinematik und Dynamik Dr.-Ing. Ulrich Simon Ulmer Zentrum für Wissenschaftliches
INSTITUT FÜR UNFALLCHIRURGISCHE FORSCHUNG UND BIOMECHANIK Grundlagen der Biomechanik des Bewegungsapparates Grundlagen der Kinematik und Dynamik Dr.-Ing. Ulrich Simon Ulmer Zentrum für Wissenschaftliches
Herbst 2010 Seite 1/14. Gottfried Wilhelm Leibniz Universität Hannover Klausur Technische Mechanik II für Maschinenbau. Musterlösungen (ohne Gewähr)
 Seite 1/14 rage 1 ( 2 Punkte) Ein Stab mit kreisförmiger Querschnittsfläche wird mit der Druckspannung σ 0 belastet. Der Radius des Stabes ist veränderlich und wird durch r() beschrieben. 0 r () Draufsicht:
Seite 1/14 rage 1 ( 2 Punkte) Ein Stab mit kreisförmiger Querschnittsfläche wird mit der Druckspannung σ 0 belastet. Der Radius des Stabes ist veränderlich und wird durch r() beschrieben. 0 r () Draufsicht:
Zentrifugalkraft beim Karussell
 Seil, Länge L m Also: Zentrifugalkraft beim Karussell tan( α) y = α r F Z r G ω r = x r r ' KS : mitrotierendes Koordinatensystem m G r α 2 m ω g r ' F r Z F r gesamt 2 ω sin( α) L = g Fragestellung: Um
Seil, Länge L m Also: Zentrifugalkraft beim Karussell tan( α) y = α r F Z r G ω r = x r r ' KS : mitrotierendes Koordinatensystem m G r α 2 m ω g r ' F r Z F r gesamt 2 ω sin( α) L = g Fragestellung: Um
Energie und Energieerhaltung
 Arbeit und Energie Energie und Energieerhaltung Es gibt keine Evidenz irgendwelcher Art dafür, dass Energieerhaltung in irgendeinem System nicht erfüllt ist. Energie im Austausch In mechanischen und biologischen
Arbeit und Energie Energie und Energieerhaltung Es gibt keine Evidenz irgendwelcher Art dafür, dass Energieerhaltung in irgendeinem System nicht erfüllt ist. Energie im Austausch In mechanischen und biologischen
Aufgaben. zu Inhalten der 5. Klasse
 Aufgaben zu Inhalten der 5. Klasse Universität Klagenfurt, Institut für Didaktik der Mathematik (AECC-M) September 2010 Zahlbereiche Es gibt Gleichungen, die (1) in Z, nicht aber in N, (2) in Q, nicht
Aufgaben zu Inhalten der 5. Klasse Universität Klagenfurt, Institut für Didaktik der Mathematik (AECC-M) September 2010 Zahlbereiche Es gibt Gleichungen, die (1) in Z, nicht aber in N, (2) in Q, nicht
Physik für Mediziner und Zahmediziner
 Physik für Mediziner und Zahmediziner Vorlesung 03 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 1 Arbeit: vorläufige Definition Definition der Arbeit (vorläufig): Wird auf
Physik für Mediziner und Zahmediziner Vorlesung 03 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 1 Arbeit: vorläufige Definition Definition der Arbeit (vorläufig): Wird auf
Rechenübungen zur Physik 1 im WS 2011/2012
 Rechenübungen zur Physik 1 im WS 011/01. Klausur Fr. März 01 9.00-1.00 Uhr N/N6 Name, Vorname: Geburtstag: Ihre Identifizierungs-Nr. ID= 99 Hinweise: Studentenausweis: Hilfsmittel: Lösungen: Zusatzblätter:
Rechenübungen zur Physik 1 im WS 011/01. Klausur Fr. März 01 9.00-1.00 Uhr N/N6 Name, Vorname: Geburtstag: Ihre Identifizierungs-Nr. ID= 99 Hinweise: Studentenausweis: Hilfsmittel: Lösungen: Zusatzblätter:
Versuch M1: Feder- und Torsionsschwingungen
 Versuch M1: Feder- und Torsionsschwingungen Aufgaben: Federschwingungen: 1 Bestimmen Sie durch Messung der Dehnung in Abhängigkeit von der Belastung die Richtgröße D (Federkonstante k) von zwei Schraubenfedern
Versuch M1: Feder- und Torsionsschwingungen Aufgaben: Federschwingungen: 1 Bestimmen Sie durch Messung der Dehnung in Abhängigkeit von der Belastung die Richtgröße D (Federkonstante k) von zwei Schraubenfedern
Kontaktzeitmessungen beim Venustransit und die Ableitung der Sonnenentfernung
 Kontaktzeitmessungen beim Venustransit und die Ableitung der Sonnenentfernung Udo Backhaus 14. Dezember 2004 1 Prinzip Die Messung der Astronomischen Einheit durch Kontaktzeitmessungen beim Venustransit
Kontaktzeitmessungen beim Venustransit und die Ableitung der Sonnenentfernung Udo Backhaus 14. Dezember 2004 1 Prinzip Die Messung der Astronomischen Einheit durch Kontaktzeitmessungen beim Venustransit
Physik 1 VNT Aufgabenblatt 8 5. Übung (50. KW)
 Physik 1 VNT Aufgabenblatt 8 5. Übung (5. KW) 5. Übung (5. KW) Aufgabe 1 (Achterbahn) Start v h 1 25 m h 2 2 m Ziel v 2? v 1 Welche Geschwindigkeit erreicht die Achterbahn in der Abbildung, wenn deren
Physik 1 VNT Aufgabenblatt 8 5. Übung (5. KW) 5. Übung (5. KW) Aufgabe 1 (Achterbahn) Start v h 1 25 m h 2 2 m Ziel v 2? v 1 Welche Geschwindigkeit erreicht die Achterbahn in der Abbildung, wenn deren
Lösung Übungsserie 7 (Bewegungen auf Bahnkurven in SIMULINK modellieren)
 Name: Seite: 1 Fachhochschule Nordwestschweiz (FHNW) Hochschule für Technik Lösung Übungsserie 7 (Bewegungen auf Bahnkurven in SIMULINK modellieren) Dozent: R. Burkhardt (roger.burkhardt@fhnw.ch) Büro:
Name: Seite: 1 Fachhochschule Nordwestschweiz (FHNW) Hochschule für Technik Lösung Übungsserie 7 (Bewegungen auf Bahnkurven in SIMULINK modellieren) Dozent: R. Burkhardt (roger.burkhardt@fhnw.ch) Büro:
3. Zentrales ebenes Kräftesystem
 3. Zentrales ebenes Kräftesystem Eine ruppe von Kräften, die an einem starren Körper angreifen, bilden ein zentrales Kräftesystem, wenn sich die Wirkungslinien aller Kräfte in einem Punkt schneiden. f
3. Zentrales ebenes Kräftesystem Eine ruppe von Kräften, die an einem starren Körper angreifen, bilden ein zentrales Kräftesystem, wenn sich die Wirkungslinien aller Kräfte in einem Punkt schneiden. f
Grundwissen. Physik. Jahrgangsstufe 8
 Grundwissen Physik Jahrgangsstufe 8 Grundwissen Physik Jahrgangsstufe 8 Seite 1 1. Energie; E [E] = 1Nm = 1J (Joule) 1.1 Energieerhaltungssatz Formulierung I: Energie kann nicht erzeugt oder vernichtet
Grundwissen Physik Jahrgangsstufe 8 Grundwissen Physik Jahrgangsstufe 8 Seite 1 1. Energie; E [E] = 1Nm = 1J (Joule) 1.1 Energieerhaltungssatz Formulierung I: Energie kann nicht erzeugt oder vernichtet
Fadenpendel. Phase Inhalt Sozialform Medien Standards Hinführung Fadenpendel am Beispiel einer Schiffschaukel Plenum Arbeitsblätter E1
 .1 Stundenverlaufsplan Phase Inhalt Sozialform Medien Standards Hinführung Fadenpendel am Beispiel einer Schiffschaukel Plenum Arbeitsblätter E1 Hypothesenbildung Von welchen Größen hängt die Periode eines
.1 Stundenverlaufsplan Phase Inhalt Sozialform Medien Standards Hinführung Fadenpendel am Beispiel einer Schiffschaukel Plenum Arbeitsblätter E1 Hypothesenbildung Von welchen Größen hängt die Periode eines
In der Physik definiert man Arbeit durch das Produkt aus Kraft und Weg:
 Werkstatt: Arbeit = Kraft Weg Viel Kraft für nichts? In der Physik definiert man Arbeit durch das Produkt aus Kraft und Weg: W = * = F * s FII bezeichnet dabei die Kraftkomponente in Wegrichtung s. Die
Werkstatt: Arbeit = Kraft Weg Viel Kraft für nichts? In der Physik definiert man Arbeit durch das Produkt aus Kraft und Weg: W = * = F * s FII bezeichnet dabei die Kraftkomponente in Wegrichtung s. Die
5. Arbeit und Energie
 Inhalt 5.1 Arbeit 5.2 Konservative Kräfte 5.3 Potentielle Energie 5.4 Kinetische Energie 5.1 Arbeit 5.1 Arbeit Konzept der Arbeit führt zur Energieerhaltung. 5.1 Arbeit Wird Masse m mit einer Kraft F von
Inhalt 5.1 Arbeit 5.2 Konservative Kräfte 5.3 Potentielle Energie 5.4 Kinetische Energie 5.1 Arbeit 5.1 Arbeit Konzept der Arbeit führt zur Energieerhaltung. 5.1 Arbeit Wird Masse m mit einer Kraft F von
Technische Mechanik 1
 Ergänzungsübungen mit Lösungen zur Vorlesung Aufgabe 1: Geben Sie die Koordinaten der Kraftvektoren im angegebenen Koordinatensystem an. Gegeben sind: F 1, F, F, F 4 und die Winkel in den Skizzen. Aufgabe
Ergänzungsübungen mit Lösungen zur Vorlesung Aufgabe 1: Geben Sie die Koordinaten der Kraftvektoren im angegebenen Koordinatensystem an. Gegeben sind: F 1, F, F, F 4 und die Winkel in den Skizzen. Aufgabe
Orientierungshilfen für die Zugangsprüfung Physik
 Orientierungshilfen für die Zugangsprüfung Physik Anliegen der Prüfung Die Zugangsprüfung dient dem Herausstellen der Fähigkeiten des Prüflings, physikalische Zusammenhänge zu erkennen. Das physikalische
Orientierungshilfen für die Zugangsprüfung Physik Anliegen der Prüfung Die Zugangsprüfung dient dem Herausstellen der Fähigkeiten des Prüflings, physikalische Zusammenhänge zu erkennen. Das physikalische
Es ergibt sich eine Kraft F von 343N. Diese ist aber zu gering um die Schale zu zerbrechen.
 1) Eine Möwe findet eine Muschel, die sie allerdings mit dem Schnabel nicht öffnen kann. Deshalb fliegt sie auf und lässt die Muschel auf felsigen Boden fallen, sodass die Schale zerbricht. a) Welche Kraft
1) Eine Möwe findet eine Muschel, die sie allerdings mit dem Schnabel nicht öffnen kann. Deshalb fliegt sie auf und lässt die Muschel auf felsigen Boden fallen, sodass die Schale zerbricht. a) Welche Kraft
Technische Mechanik III (Dynamik)
 Institut für Mechanische Verfahrenstechnik und Mechanik Bereich Angewandte Mechanik Vorprüfung Technische Mechanik III (Dynamik) Montag, 31.08.009, 9:00 11:00 Uhr Bearbeitungszeit: h Aufgabe 1 (6 Punkte)
Institut für Mechanische Verfahrenstechnik und Mechanik Bereich Angewandte Mechanik Vorprüfung Technische Mechanik III (Dynamik) Montag, 31.08.009, 9:00 11:00 Uhr Bearbeitungszeit: h Aufgabe 1 (6 Punkte)
Arbeit und Energie. Brückenkurs, 4. Tag
 Arbeit und Energie Brückenkurs, 4. Tag Worum geht s? Tricks für einfachere Problemlösung Arbeit Skalarprodukt von Vektoren Leistung Kinetische Energie Potentielle Energie 24.09.2014 Brückenkurs Physik:
Arbeit und Energie Brückenkurs, 4. Tag Worum geht s? Tricks für einfachere Problemlösung Arbeit Skalarprodukt von Vektoren Leistung Kinetische Energie Potentielle Energie 24.09.2014 Brückenkurs Physik:
Oberstufe (11, 12, 13)
 Department Mathematik Tag der Mathematik 1. Oktober 009 Oberstufe (11, 1, 1) Aufgabe 1 (8+7 Punkte). (a) Die dänische Flagge besteht aus einem weißen Kreuz auf rotem Untergrund, vgl. die (nicht maßstabsgerechte)
Department Mathematik Tag der Mathematik 1. Oktober 009 Oberstufe (11, 1, 1) Aufgabe 1 (8+7 Punkte). (a) Die dänische Flagge besteht aus einem weißen Kreuz auf rotem Untergrund, vgl. die (nicht maßstabsgerechte)
3.3 Klassifikation quadratischer Formen auf R n
 3.3. Klassifikation quadratischer Formen auf R n 61 3.3 Klassifikation quadratischer Formen auf R n Wir können den Hauptsatz über symmetrische Matrizen verwenden, um uns einen Überblick über die Lösungsmengen
3.3. Klassifikation quadratischer Formen auf R n 61 3.3 Klassifikation quadratischer Formen auf R n Wir können den Hauptsatz über symmetrische Matrizen verwenden, um uns einen Überblick über die Lösungsmengen
Abschlussprüfung an Fachoberschulen im Schuljahr 2004/2005
 Abschlussprüfung an Fachoberschulen im Schuljahr 200/200 Haupttermin: Nach- bzw Wiederholtermin: 0909200 Fachrichtung: Technik Fach: Physik Prüfungsdauer: 210 Minuten Hilfsmittel: - Formelsammlung/Tafelwerk
Abschlussprüfung an Fachoberschulen im Schuljahr 200/200 Haupttermin: Nach- bzw Wiederholtermin: 0909200 Fachrichtung: Technik Fach: Physik Prüfungsdauer: 210 Minuten Hilfsmittel: - Formelsammlung/Tafelwerk
9 Periodische Bewegungen
 Schwingungen Schwingung Zustand y wiederholt sich in bestimmten Zeitabständen Mit Schwingungsdauer (Periode, Periodendauer) T Welle Schwingung breitet sich im Raum aus Zustand y wiederholt sich in Raum
Schwingungen Schwingung Zustand y wiederholt sich in bestimmten Zeitabständen Mit Schwingungsdauer (Periode, Periodendauer) T Welle Schwingung breitet sich im Raum aus Zustand y wiederholt sich in Raum
Übung zur Vorlesung Grundlagen der Fahrzeugtechnik I. Übung
 Institut für Fahrzeugsystemtechnik Lehrstuhl für Fahrzeugtechnik Leiter: Prof. Dr. rer. nat. Frank Gauterin Rintheimer Querallee 2 76131 Karlsruhe Übung zur Vorlesung Grundlagen der Fahrzeugtechnik I Übung
Institut für Fahrzeugsystemtechnik Lehrstuhl für Fahrzeugtechnik Leiter: Prof. Dr. rer. nat. Frank Gauterin Rintheimer Querallee 2 76131 Karlsruhe Übung zur Vorlesung Grundlagen der Fahrzeugtechnik I Übung
Versuch M7 für Nebenfächler Rotations- und Translationsbewegung
 Versuch M7 für Nebenfächler Rotations- und Translationsbewegung I. Physikalisches Institut, Raum HS126 Stand: 21. Oktober 2015 generelle Bemerkungen bitte Versuchsaufbau (Nummer) angeben bitte Versuchspartner
Versuch M7 für Nebenfächler Rotations- und Translationsbewegung I. Physikalisches Institut, Raum HS126 Stand: 21. Oktober 2015 generelle Bemerkungen bitte Versuchsaufbau (Nummer) angeben bitte Versuchspartner
Trigonometrie. bekannte Zusammenhänge. 4-Streckensatz: groß/klein = groß/klein. Zusammenhänge im allgemeinen Dreieck:
 Trigonometrie bekannte Zusammenhänge 4-Streckensatz: groß/klein = groß/klein Zusammenhänge im allgemeinen Dreieck: Summe zweier Seiten größer als dritte Seitenlänge: a + b > c Innenwinkelsumme: Summe der
Trigonometrie bekannte Zusammenhänge 4-Streckensatz: groß/klein = groß/klein Zusammenhänge im allgemeinen Dreieck: Summe zweier Seiten größer als dritte Seitenlänge: a + b > c Innenwinkelsumme: Summe der
Physik für Elektroingenieure - Formeln und Konstanten
 Physik für Elektroingenieure - Formeln und Konstanten Martin Zellner 18. Juli 2011 Einleitende Worte Diese Formelsammlung enthält alle Formeln und Konstanten die im Verlaufe des Semesters in den Übungsblättern
Physik für Elektroingenieure - Formeln und Konstanten Martin Zellner 18. Juli 2011 Einleitende Worte Diese Formelsammlung enthält alle Formeln und Konstanten die im Verlaufe des Semesters in den Übungsblättern
Fadenpendel (M1) Ziel des Versuches. Theoretischer Hintergrund
 Fadenpendel M) Ziel des Versuches Der Aufbau dieses Versuches ist denkbar einfach: eine Kugel hängt an einem Faden. Der Zusammenhang zwischen der Fadenlänge und der Schwingungsdauer ist nicht schwer zu
Fadenpendel M) Ziel des Versuches Der Aufbau dieses Versuches ist denkbar einfach: eine Kugel hängt an einem Faden. Der Zusammenhang zwischen der Fadenlänge und der Schwingungsdauer ist nicht schwer zu
Arbeitsblatt Arbeit und Energie
 Arbeitsblatt Arbeit und Energie Arbeit: Wird unter der Wirkung einer Kraft ein Körper verschoben, so leistet die Kraft die Arbeit verrichtete Arbeit Kraft Komponente der Kraft in Wegrichtung; tangentiale
Arbeitsblatt Arbeit und Energie Arbeit: Wird unter der Wirkung einer Kraft ein Körper verschoben, so leistet die Kraft die Arbeit verrichtete Arbeit Kraft Komponente der Kraft in Wegrichtung; tangentiale
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck
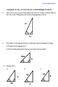 Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
In der oben gezeichneten Anordnung soll am Anfang der Looping-Bahn (1) eine Stahlkugel reibungsfrei durch die Bahn geschickt werden.
 Skizze In der oben gezeichneten Anordnung soll am Anfang der Looping-Bahn (1) eine Stahlkugel reibungsfrei durch die Bahn geschickt werden. Warum muß der Höhenunterschied h1 größer als Null sein, wenn
Skizze In der oben gezeichneten Anordnung soll am Anfang der Looping-Bahn (1) eine Stahlkugel reibungsfrei durch die Bahn geschickt werden. Warum muß der Höhenunterschied h1 größer als Null sein, wenn
