Integralfunktion und bestimmtes Integral
|
|
|
- Jan Baum
- vor 7 Jahren
- Abrufe
Transkript
1 II Itegrlfuto ud bestmmtes Itegrl Bsher: Flächebestmmug vo Rechtec, Dreec, Kres FHpportes Zel: Bestmmug vo Flächehlte belebg rummlg begrezter Fläche. Flächefuto Gegebe se de stetge Futo f mt (zuächst) postve Futoswerte. Defto der Flächefuto: Betrchte de Futo A : A (), de jedem Df mt de Flächemßzhl der Fläche vo bs uter dem Grphe vo f (gelb uterstrche, gelb mrert!) zuordet. (s Heft ur le Zechug, Phse später!) Wr suche u ee Zusmmehg zwsche f ud A Ahme: A () se berets bet I eer lee Umgebug vo, der f streg mooto steged st, glt: A (+h) A () st Flächehlt des grüe Strefes, der vo Gf begrezt wrd. rot grü blu Es glt: f () h A (+h) A () f ( + h) h für (uch für h < ) Her Nebebemerug für h < f( + h) (-h) A () A ( + h) f () (-h) (-) für h <, lso ds gleche A ( + h) A () für h > > f() f( + h) h für h < A ( + h) A () >Dfferezlquotet! lm f(), wel lm f( + h) f()(stetg! ) h h h Ergebs A st dem belebg gewählte Put dfferezerbr ud es glt: A () f() A st ee Stmmfuto vo f! Bemeruge:. De Kostte c der Flächefuto (Stmmfuto!) muss och bestmmt werde!. Ergebs glt uch, we f m Itervll streg mooto flled st. Nur be der Herletug ädert sch ds Vorzeche der Uglechugsette. I ostte Itervlle Glechugsette! 5
2 Bestmmug der ddtve Kostte c: De Fläche vo bs st scher Null: A () Bespel: f () ²; Gesucht: Fläche zwsche ud,5. A- () ³ + c Mt A- (-) folgt c, somt A- () ³ +, ud de gesuchte Fläche st 4,75. Aufgbe 5/6 (H: 5f/7,8) 6
3 Hstorscher Weg (Archmedes): Strefemethode (Abb!) Gesucht: der zwsche ud gelegee Flächehlt uter dem Grphe vo f () ² (Zeche mt 8, Ehet 8 Kästche!) (Zuächst ur Obersumme!) Lösugsmöglchet: M tele ds -Itervll [; ] glech große Teltervlle, Brete je /, uf (her 8). Ee Näherug für de gesuchte Fläche erhält m, we m lle Rechtecsflächestrefe, dere Höhe dem jewels größte Futoswert des Teltervlls etsprcht, zusmmezählt. Der berechete Flächehlt st d scher größer ls der gesuchte (Obersumme) I glecher Wese erhält m ee zu lee Näherug, we de Rechtecsfläche jewels de leste Futoswerte etspreche (Utersumme) Für sehr große wrd m erwrte dürfe, dss be bede Methode der Flächewert sehr geu geähert wrd. De Rechug ergbt llgeme (bedee A g h mt g / für lle Rechtece) Obersumme: Utersumme: S ( )² + ( )² ( )² S ()² + ( )² ( )² [( )² + ( )² ( )²] [² + ² ²](FS!) 6 ( + )( + ) [² + ( )² ( )²] [² + ² ( )²](FS!) 6 ( )(( ) + ) Für jedes belebg große lässt sch so jewels ee Näherug für A bereche. 6 ( )( ) Versuch: Ee Grezwert für zu fde, ds ämlch müsste der ete Flächehlt se! Es ergbt sch jewels: ( + )( + ) ( )( ) S... S... 6³ 6³ ³ + ² + ³ ² + 6³ 6 6³ 6 Erwrtugsgemäß ergbt sch bede Fälle der gleche Grezwert /. Also st A / [FE] (wel j S < A < S Feststellug: Flächehlte vo Fläche, de vo stetge Futosgrphe begrezt werde, lsse sch wegstes äherugswese mmer mt der Strefemethode bereche. Dzu müsse de gebldete Rechtecsstrefe cht eml de gleche Brete bestze. Außerdem m ls Rechtecshöhe rgedee Futoswert f(ξ) us dem jewelge Itervll [-; ] verwede. 7
4 De Fläche uter dem Grphe vo f m Itervll [; ] lässt sch dmt äher durch f ( ξ )( ) f( ξ ), Im Flle eer uedlch fee Auftelug schrebt m d ch Lebz lm >, f( ξ ) f()d f(t)dt Wr hbe II. ud II. zwe Wege zur Berechug der Fläche uter dem Grphe eer stetge Futo eem Itervll [, b] ee gelert. Zusmmefssed glt: Glechbedeutede Schreb- ud Sprechwese bsher Fläche uter Gf m Itervll bs b A(b) Flächefuto vo f A () b sofort bestmmtes Itegrl vo f über [,b] b Itegrlfuto vo f Uterschede: Ds ubestmmte Itegrl st ee Mege vo Futoe. Ds bestmmte Itegrl st ee Zhl (Fläche!) De Itegrlfuto st ee Futo (Stmmfuto zu f) Es glt we II. F () + c, wobe m c us der Bedgug bestmme > c -F () Bespel f () ² A () t²dt t ²dt ³/+c d.h. t²dt ³ + c ³ ³ t²dt (Bespel vom Arbetsbltt!) 8
5 Ermttlug vo Flächehlte mt Hlfe vo Itegrlfutoe Aufgbe: ) Se f () s. Bestmme de Flächehlt der Fläche uter dem Grphe m Itervll [, π], lso π s d A () s tdt cos + c, wobe A() -cos + c > c > A () - cos + > A (π) -cos π + + ) Se f (). Bestmme de Flächehlt uter Gf m Berech [; 4], d. h. A 4 d Es glt: A () tdt + c, wobe A () / + c > c -/ > A () tdt > A (4) y 4 ) f (). Bestmme de Fläche uter Gf vo,5 bs, d. h. ² A d y,5² Es glt: A,5 () dt + c, 4,5t² wobe A,5 (,5) > c > A,5 () + > A,5 () / 4) f () s. Bestmme de Fläche uter Gf Abhägget vo m Itervll [; π/] ( > ), d. h. π / A s d Es glt: A() s(t)dt cost + c, wobe A () > c / > A () cos() + > A(π/) / 9
6 . Verefchte Auswertug des Itegrls b Se F() ee belebge Stmmfuto vo f (). Der Term der Itegrlfuto st d F() + c, (I) wobe m c erhält us F () + c oder c - F() (II) Der gesuchte Flächehlt uter Gf über [, b] st ch (I) ud (II) b F (b) F () Vortel: M sprt sch de Zwscheschrtt der Bestmmug der Kostte! Bsp: Verefchte Lösug der Aufgbe us.:. π s d -cos π + cos mt F () -cos π s d - cosπ - + cos + mt F () -cos +, egl welche Stmmft. d sch de Kostte weghebt.. 4 d 4 (F () ). d -/ (-/,5) /,5² (F () -/) usw. Formle Schrebwese b [ F(t) ] b F (b) F () Bsp:.,5 dt t² t,5... t³ ³ 4. 4 t²dt 4t 4 ( 4 + ) 9 b b t b 5. t dt, t² t dt t² tdt + t² + tdt [³ ²] + [³ ²] ( )
7 . Aweduge der Itegrto Beschleugte Bewegug: Freer Fll v(t) lm (t) (t) t > t t v(τ) dτ v (t) lm v(t) v(t) t > t t (τ) dτ Freer Fll mt v ud o, pos. -Achse ch ute: g > v (t) t gdτ gt + v > (t) t b gτ + v dτ ½ gt² + vt + Arbet W F s (flls F s ud F cht vo s bhägg!) Sost: Be leer Äderug vo s blebt F (s) prtsch ostt: dw F (s) ds Bespel : Dehug ees Gummbdes F () D Dehug us der Ruhelge um s: s s s ² W F()d Dd D Ds² Bespel : Ldugstrsport Q r q De egtve Elemetrldug soll de egtve Ldug q vo r ch r gege de Azehugsrft der mt Q geldee Kugel trsportert werde. Azehugsrft ch Coulombgesetz: qq F (r) 4πε r² r² r Wr,r r r F(r)dr r r² dr r r r Etsprechede Ergebsse erhält m für de Hubrbet m Grvttosfeld mt Gmm, wobe G de Newtosche Grvttosostte st. r r r F(r) Rdbemerug: Um ee Körper gz us dem Grvttosfeld der Soe zu etfere ud de Uedlchet des Weltlls zu schce, geügt somt de edlche Eerge lm r r r De Arbet etsprcht der Fläche m r-f-dgrmm! Wr, r > r
8 c Volumeberechug be Rottosörper Ee Kurve rotert um ee Achse ud erzeugt ee Körper, desse Querschttsfläche ozetrsche Krese sd. Herletug eer Formel zur Volumeberechug: sehe Arbetsbltt. Allgeme glt für ds Volume: V Dbe st A de Querschttfläche. m f ²() πd m m m A()d Bespele: ) Spdel y s π V )²d [ π π π π π s ] π[ ] π ² (s. Zwebel y + s 4 Ergebs: π+ 9 π ² 4 Schüler reche lsse, Przp we obe, usqudrere,
9 4 Itegrlfuto belebger stetger Futoe Huptstz der Dfferezl- ud Itegrlrechug Bsher: A () f(t)dt ur für postve stetge Futoe mt Werte. Nu zwe Verllgemeeruge:. Verllgemeerug: f () belebg stetg,. Auch her soll defert werde: f()d lm >, f( ξ ) Aufgrud der Defto wrd de Fläche m egtve Berech vo f uch egtv gezählt (eg. Rechtecshöhe f (ξ)!). Es hdelt sch umehr cht um ee Flächefuto, soder um ee Flächeblzfuto. Postv ud egtv gewertete Fläche werde gegeeder ufgerechet. Auch deser erweterte Form sd Itegrlfutoe Stmmfutoe der Ursprugsfuto (Bewes we II.). Bespele:. f () s Es glt: π π π [ cos ] cos π + cos s d s d [ cos ] π cos π + cos cos π + cos π π s d [ cos ] Flächeblz. f () ² -
10 ³ ² d ( + ) ³ 8 ² d ( + ) Flächeblz. Verllgemeerug: f () belebg stetg, <. Auch her soll defert werde: f()d lm >, f( ξ ) D weter - gelte soll, sd lle egtv. Für postve f( ξ ) erhält m lso egtve Flächetele, für egtve f( ξ ) etspreched postve Flächetele. Auch für dese Deftoserweterug der Itegrlfuto erhält m d f(t)dt f() d Zum Bewes öte m de Überleguge us Abschtt II. uf de Futo g () f(-) wede: Wege < st > - ud für g(t)dt glt lles dort gesgte (flls g () > ). D glt: d d > < f(t)dt > > g(t) dt (De Dfferetle bestze bede Itegrle uterschedlches Vorzeche) d g(t)dt d d ( G( ) ) g( ) ( ) flls G Stmmft. vo g d g( ) ( ) g( ) f() (Ee grphsche Erläuterug deses Beweses estert ur m ttsächlche Srpt!) Zusmmefssed lässt sch u für II. ud II.4 der folgede wchtge Stz formulere: 4
11 Huptstz der Dfferezl- ud Itegrlrechug: f se uf dem Itervll I stetg. F se Itegrlfuto zu f mt F : -> mt I ud DF I D glt: F () f() ( I) Aders: De Abletug der Itegrlfuto eer stetge Itegrdefuto st der Itegrd selbst. Bespel für de Flächeberechug, de sch us de bede Verllgemeeruge ergbt Futo: postv; Itegrtosrchtug: egtv 9 t²dt [ t³ ] / 8 8 / Flächeblz: egtv Futo: postv; Itegrtosrchtug: postv / / 9 t²dt [ t³ ] ( ) 8 8 Flächeblz: postv Futo: egtv; Itegrtosrchtug: egtv 9 t²dt [ t³ ] / / Flächeblz: postv Futo: egtv; Itegrtosrchtug: postv / / 9 t²dt [ t³ ] ( ( )³) 8 8 Flächeblz: egtv 5
12 5 Egeschfte der Itegrlfuto; Recheregel 5. Ermttlug des ugefähre Verlufs des Grphe der Itegrlfuto - Mt der Kets vo f () et m ds Stegugsverhlte jeder Stmmfuto - A der utere Itegrtosgreze legt ee Nullstelle der Itegrlfuto Bespel: F () t ² 4dt Es glt: F (-) F () st streg mooto flled für ]-; [ F () st streg mooto steged für \[-;] - M M F () ht be - e Mmum be e Mmum F ht be (eg. Stegugswert mml) ee Wedeput Ee geue Verluf m erst ch Berechug der y-werte eree: F () ³/-4+ / 4 F () -9 F (-) 5/ 6
13 5. Itegrl- ud Stmmfutoe De Mege der Itegrlfutoe eer Futo f st cht jedem Fll mt der Mege der Stmmfutoe detsch. Bespele: ) f () ; F () ² + st ee Itegrlfuto, wel F ee Nullstelle ht. ³ b) f () ²; F () + c sd Itegrlfutoe, wel jedes F Nullstelle bestzt. ³ Gb de Itegrlschrebwese vo F () +! ³ + > 6 ³, lso F () + t²dt 6 ³ ² c) f () ² + ; F() + st Itegrlfuto. Gb F Itegrlschrebwese. ³ ² + ²(+) /, -,5 ² + tdt t oder t ² + tdt,5 Ergebs De Mege der Itegrlfutoe st ee Telmege der Mege der Stmmfutoe. 7
14 5. Recheregel De Recheregel für Stmmfutoe us I.. lsse sch ch II. uf Itegrlfutoe ud deshlb uch uf bestmmte Itegrle übertrge. Alle Regel gelte uch für festes b () f(t)dt (Szze!) () f (t) ± g(t)dt f(t)dt ± g(t)dt NchII.4: () - (4) Se f eem Itervll I tegrerbr. Dmt glt für belebge,b,c I: (5) c + Bewes: Für < c < : trvl Für c < < glt: c Für < c < b : log c + c - c c - c + c Bespele. Betrchte f() Gesucht: Flächehlt (cht: Flächeblz!) der Fläche zwsche dem Grph vo f ud der -Achse zwsche ud Wrum cht efch Itegrl zwsche ud? Erst Zeche! A ( )d + ( )d. Betrchte f() (>) Für welches schleßt der Grph vo f e Flächestüc der Größe FE e? A ( ) d 8
15 Fläche zwsche zwe Grphe b A f () g()d Bespel: f () ² g () ² - Ergebs: A 9 Vrto der Itegrtosgreze g() Se H () D folgt durch dretes Esetze g() H () F(g()) + c Weter folgt: H () F (g()) g ( ) f (g()) g () Bespele: ² ² H () [ ] 4 t ² t² tdt t³ + 6 H () ((²)²+²) 4 5 ³ d. f(t)dt f() d d chdff. d d d f(t)dt f( ) f(t)dt ( f( )) f( ). f () s (²) Ges: Stmmfuto f () ½ (s (²) ) > F () ½ cos 9
Carl Friedrich Gauß (Deutscher Mathematiker, 1777 bis 1855) formulierte die folgende Formel n
 mthphys-ole Alyss. Klsse Techk Itegrlrechug Vertefug des Itegrlegrffs De Itegrlrechug ht ds Zel, de Flächehlt krummlg egrezter Flächestücke zu ereche. Be der äherugswese Berechug der Fläche uter Polyomfuktoe
mthphys-ole Alyss. Klsse Techk Itegrlrechug Vertefug des Itegrlegrffs De Itegrlrechug ht ds Zel, de Flächehlt krummlg egrezter Flächestücke zu ereche. Be der äherugswese Berechug der Fläche uter Polyomfuktoe
Formelsammlung zur Zuverlässigkeitsberechnung
 Formelsmmlug zur Zuverlässgetsberechug zusmmegestellt vo Tt Lge Fchhochschule Merseburg Fchberech Eletrotech Ihlt:. Zuverlässget vo Betrchtugsehete.... Zuverlässget elemetrer, chtreprerbrer ysteme... 3.
Formelsmmlug zur Zuverlässgetsberechug zusmmegestellt vo Tt Lge Fchhochschule Merseburg Fchberech Eletrotech Ihlt:. Zuverlässget vo Betrchtugsehete.... Zuverlässget elemetrer, chtreprerbrer ysteme... 3.
Programmierung und Angewandte Mathematik
 Progrmmerug ud Agewdte Mthemtk C++ /Sclb Progrmmerug ud Eführug ds Kozept der objektoreterte Aweduge zu wsseschftlche Reches SS Ihlt Folge Rehe Verfhre zur Kovergez Bestmmug Progrmmerug ud Agewdte Mthemtk
Progrmmerug ud Agewdte Mthemtk C++ /Sclb Progrmmerug ud Eführug ds Kozept der objektoreterte Aweduge zu wsseschftlche Reches SS Ihlt Folge Rehe Verfhre zur Kovergez Bestmmug Progrmmerug ud Agewdte Mthemtk
Reihen n. Man benutzt letztere Schreibweise aber häufig auch zur Bezeichnung der Partialsummenfolge. konvergiert, die geometrische Reihe.
 Deftoe ud Aussge über Rehe Bchräume ud Hlberträume E vollstädger ormerter Vektorrum (sehe Bemerkuge zur Alyss) heßt Bchrum Stmmt de Norm vo eem Sklrprodukt v = , so sprcht m vo eem Hlbertrum ZB sd
Deftoe ud Aussge über Rehe Bchräume ud Hlberträume E vollstädger ormerter Vektorrum (sehe Bemerkuge zur Alyss) heßt Bchrum Stmmt de Norm vo eem Sklrprodukt v = , so sprcht m vo eem Hlbertrum ZB sd
Polynomprodukt und Fast Fourier Transformation
 Polomrodut ud Fst Fourer Trsformto Polome Reelles Polom eer Vrble...... R : oeffzete vo Grd vo : höchste Potez Besel: 3 3 5 8 Mege ller reelle Polome: R[] 3 Oertoe uf Polome. Addto b b b q b b b b b q
Polomrodut ud Fst Fourer Trsformto Polome Reelles Polom eer Vrble...... R : oeffzete vo Grd vo : höchste Potez Besel: 3 3 5 8 Mege ller reelle Polome: R[] 3 Oertoe uf Polome. Addto b b b q b b b b b q
Im Wöhlerdiagramm wird die Lebensdauer (Lastwechsel oder Laufzeit) eines Bauteils in Abhängigkeit von der Belastung dargestellt.
 Webull & Wöhler 0 CRGRAPH Wöhlerdagramm Im Wöhlerdagramm wrd de Lebesdauer ( oder Laufzet) ees Bautels Abhägget vo der Belastug dargestellt. Kurzetfestget Beaspruchug Zetfestget auerfestget 0 5 3 4 6 0
Webull & Wöhler 0 CRGRAPH Wöhlerdagramm Im Wöhlerdagramm wrd de Lebesdauer ( oder Laufzet) ees Bautels Abhägget vo der Belastug dargestellt. Kurzetfestget Beaspruchug Zetfestget auerfestget 0 5 3 4 6 0
Methodik: auf einer kompakten (beschränkten und abgeschlossenen) Menge, z.b. einem n-dimensionalen Quader,
 . Verllgemeeruge Aweduge Glole Etrem Defto: Ee ukto f : M R R ht der Stelle M e gloles Mmum we f f M. = M = [] = f m m Allgeme glt der Stz vo Weerstrss: Ist f ee stetge ukto uf eer eschräkte ud geschlossee
. Verllgemeeruge Aweduge Glole Etrem Defto: Ee ukto f : M R R ht der Stelle M e gloles Mmum we f f M. = M = [] = f m m Allgeme glt der Stz vo Weerstrss: Ist f ee stetge ukto uf eer eschräkte ud geschlossee
Ordnungsstatistiken und Quantile
 KAPITEL Ordugsstatste ud Quatle Um robuste Lage- ud Streuugsparameter eführe zu öe, beötge wr Ordugsstatste ud Quatle... Ordugsstatste ud Quatle Defto... Se (x,..., x R ee Stchprobe. Wr öe de Elemete der
KAPITEL Ordugsstatste ud Quatle Um robuste Lage- ud Streuugsparameter eführe zu öe, beötge wr Ordugsstatste ud Quatle... Ordugsstatste ud Quatle Defto... Se (x,..., x R ee Stchprobe. Wr öe de Elemete der
( x) eine Funktion definiert, in der nur die i-te Komponente variabel ist. Folgende Schreibweisen werden aufgrund dieser Anmerkungen auch verwendet:
 Pro. Dr. Fredel Bolle LS ür Volkswrtschatslehre sb. Wrtschatstheore (Mkroökoome) Vorlesug Mathematk - WS 008/009 4. Deretalrechug reeller Fuktoe IR IR (Karma, S. 00 06, dort glech ür IR IR m ) 4. Partelle
Pro. Dr. Fredel Bolle LS ür Volkswrtschatslehre sb. Wrtschatstheore (Mkroökoome) Vorlesug Mathematk - WS 008/009 4. Deretalrechug reeller Fuktoe IR IR (Karma, S. 00 06, dort glech ür IR IR m ) 4. Partelle
Kapitel XI. Funktionen mit mehreren Variablen
 Kaptel XI Fuktoe mt mehrere Varable D (Fuktoe vo uabhägge Varable Se R ud D( f R Ist jedem Vektor (Pukt (,,, D( f durch ee Vorschrft f ee reelle Zahl z = f (,,, zugeordet, so heßt f ee Fukto vo uabhägge
Kaptel XI Fuktoe mt mehrere Varable D (Fuktoe vo uabhägge Varable Se R ud D( f R Ist jedem Vektor (Pukt (,,, D( f durch ee Vorschrft f ee reelle Zahl z = f (,,, zugeordet, so heßt f ee Fukto vo uabhägge
Übungen zur Analysis 1 für Informatiker und Statistiker. Lösung zu Blatt 12
 Mthemtisches Istitut der Uiversität Müche Prof. Dr. Peter Otte WiSe 203/4 Lösug 2 2.0.204 Aufgbe 2. [8 Pute] Übuge zur Alysis für Iformtier ud Sttistier Lösug zu Bltt 2 Für eie Teilmege Ω R, sei {, flls
Mthemtisches Istitut der Uiversität Müche Prof. Dr. Peter Otte WiSe 203/4 Lösug 2 2.0.204 Aufgbe 2. [8 Pute] Übuge zur Alysis für Iformtier ud Sttistier Lösug zu Bltt 2 Für eie Teilmege Ω R, sei {, flls
Arithmetische Schaltkreise
 Kptel Arthmetsche Schltkrese. Adderer. Sutrherer Multplzerer ALU Berd Becker Techsche Iformtk I Wederholug: Se -... ee Folge vo Zffer, {,} Bärdrstellug: Zweerkomplemet: [ -... ] Recheregel: mt [ ] [
Kptel Arthmetsche Schltkrese. Adderer. Sutrherer Multplzerer ALU Berd Becker Techsche Iformtk I Wederholug: Se -... ee Folge vo Zffer, {,} Bärdrstellug: Zweerkomplemet: [ -... ] Recheregel: mt [ ] [
(Markowitz-Portfoliotheorie)
 Thema : ortfolo-selekto ud m-s-rzp (Markowtz-ortfolotheore) Beurtelugskrtere be quadratscher Nutzefukto: Beroull-rzp + quadratsche Nutzefukto Thema Höhekompoete: Erwartugswert µ Rskokompoete: Stadardabwechug
Thema : ortfolo-selekto ud m-s-rzp (Markowtz-ortfolotheore) Beurtelugskrtere be quadratscher Nutzefukto: Beroull-rzp + quadratsche Nutzefukto Thema Höhekompoete: Erwartugswert µ Rskokompoete: Stadardabwechug
Regressionsverfahren haben viele praktische Anwendungen. Die meisten Anwendungen fallen in eine der folgenden beiden Kategorien:
 Regressoslse De Regressoslse st ee Slug vo sttstshe Alseverfhre. Zel e de häufgste egesetzte Alseverfhre st es Bezehuge zwshe eer hägge ud eer oder ehrere uhägge rle festzustelle. Se wrd sesodere verwedet
Regressoslse De Regressoslse st ee Slug vo sttstshe Alseverfhre. Zel e de häufgste egesetzte Alseverfhre st es Bezehuge zwshe eer hägge ud eer oder ehrere uhägge rle festzustelle. Se wrd sesodere verwedet
Der Approximationssatz von Weierstraß
 Der Approxmatossatz vo Weerstraß Ja Köster 22. Oktober 2007 1 Eführug Aus der Aalyss wsse wr, dass sch aalytsche Fuktoe durch Potezrehe der Form f(x = a 0 + a 1 x + a 2 x 2 +... darstelle lasse. Dabe kovergert
Der Approxmatossatz vo Weerstraß Ja Köster 22. Oktober 2007 1 Eführug Aus der Aalyss wsse wr, dass sch aalytsche Fuktoe durch Potezrehe der Form f(x = a 0 + a 1 x + a 2 x 2 +... darstelle lasse. Dabe kovergert
III. Die persönliche Einkommensteuer
 Kp. -d Verso vom 3.0.05 III. De persölche Ekommesteuer Steuer küpfe ber cht ur - we de Verbruch- oder Verkehrsteuer - der Verwedug des Ekommes, soder uch desse Etstehug. De Steuerzhlug bemsst sch d cht
Kp. -d Verso vom 3.0.05 III. De persölche Ekommesteuer Steuer küpfe ber cht ur - we de Verbruch- oder Verkehrsteuer - der Verwedug des Ekommes, soder uch desse Etstehug. De Steuerzhlug bemsst sch d cht
Quellencodierung I: Redundanzreduktion, redundanzsparende Codes
 Quellecoderug I: Redudazredukto, redudazsparede Codes. Redudaz. Eführug. Defto der Redudaz. allgemee Redudazredukto. redudazsparede Codes. Coderug ach Shao. Coderug ach Fao. Coderug ach Huffma.4 Coderug
Quellecoderug I: Redudazredukto, redudazsparede Codes. Redudaz. Eführug. Defto der Redudaz. allgemee Redudazredukto. redudazsparede Codes. Coderug ach Shao. Coderug ach Fao. Coderug ach Huffma.4 Coderug
Definitionen und Aussagen zu Potenzreihen
 Deftoe ud Aussage zu Potezrehe User bsherges Repertore a stetge Abblduge basert auf ratoale Fuktoe, also Ausdrücke, dee Addto, Subtrakto, Multplkato ud Dvso vorkomme. Auf dese Wese sd aber Epoetalfukto,
Deftoe ud Aussage zu Potezrehe User bsherges Repertore a stetge Abblduge basert auf ratoale Fuktoe, also Ausdrücke, dee Addto, Subtrakto, Multplkato ud Dvso vorkomme. Auf dese Wese sd aber Epoetalfukto,
Lineare Algebra Formelsammlung
 ee Algeb Fomelsmmlug vo Gábo Zogg Fomelsmmlug ee Algeb Gábo Zogg. ee Glechugsssteme. Ds Guss'sche Elmtosvefhe Defto: Σ Sstem vo m Glechuge ud Ubekte Opetoe: - Vetusche vo Glechuge - Addee/Subthee ees Velfche
ee Algeb Fomelsmmlug vo Gábo Zogg Fomelsmmlug ee Algeb Gábo Zogg. ee Glechugsssteme. Ds Guss'sche Elmtosvefhe Defto: Σ Sstem vo m Glechuge ud Ubekte Opetoe: - Vetusche vo Glechuge - Addee/Subthee ees Velfche
Mathematik für die Physik II, Sommersemester 2018 Lösungen zu Serie 6
 Mthemtik für die Physik II, Sommersemester 2018 Lösuge zu Serie 6 26 Utersuche die folgede Fuktioefolge uf puktweise beziehugsweise gleichmäßige Kovergez, d.h. bestimme jeweils ob diese vorliegt ud gebe
Mthemtik für die Physik II, Sommersemester 2018 Lösuge zu Serie 6 26 Utersuche die folgede Fuktioefolge uf puktweise beziehugsweise gleichmäßige Kovergez, d.h. bestimme jeweils ob diese vorliegt ud gebe
Es ist dann nämlich 2 2 2
 Ege Bemerkuge zum Sklrprodukt See U,V,W Vektorräume üer eem Körper K. Ee Aldug ϕ :U V W heßt ler, we λ, λ, µ, µ K, u, u U, v, v V : ϕ( λ u + λ u, µ v + µ v ) = λ µ ϕ( u, v ) + λ µ ϕ( u, v ) + λ µ ϕ( u,
Ege Bemerkuge zum Sklrprodukt See U,V,W Vektorräume üer eem Körper K. Ee Aldug ϕ :U V W heßt ler, we λ, λ, µ, µ K, u, u U, v, v V : ϕ( λ u + λ u, µ v + µ v ) = λ µ ϕ( u, v ) + λ µ ϕ( u, v ) + λ µ ϕ( u,
Konzentrationsmessung
 Kozetrtosmessug We telt sch de gesmte Merkmlssumme uf de ezele uf? Auftelug der Gesmtbevölkerug Gemede verschedeer Größeklsse Auftelug des gesmte Steuerufkommes uf de ezele Steuersubekte Auftelug der gesmte
Kozetrtosmessug We telt sch de gesmte Merkmlssumme uf de ezele uf? Auftelug der Gesmtbevölkerug Gemede verschedeer Größeklsse Auftelug des gesmte Steuerufkommes uf de ezele Steuersubekte Auftelug der gesmte
Induktion am Beispiel des Pascalschen Dreiecks
 Iduto am Bespel des Pascalsche Dreecs Alexader Rehold Coldtz 0.02.2005 Eletug vollstädge Iduto De vollstädge Iduto st ebe dem drete ud drete Bewesverfahre ees der wchtgste der Mathemat. Eher bespelhaft
Iduto am Bespel des Pascalsche Dreecs Alexader Rehold Coldtz 0.02.2005 Eletug vollstädge Iduto De vollstädge Iduto st ebe dem drete ud drete Bewesverfahre ees der wchtgste der Mathemat. Eher bespelhaft
Humboldt-Universität zu Berlin, Institut für Mathematik. Sommersemester 2009/10
 Dt er Alyss er Se II Rolle er reelle Zhle Humbolt-Uverstät zu Berl, Isttut für Mthemt Abgeorete Lehrer: R.Gese, U.Hey, B.Mus Sommersemester 009/0 Iteretsete zur Vorlesug: http://t.mth.hu-berl.e/ex.php?rtcle_=35&clg=0
Dt er Alyss er Se II Rolle er reelle Zhle Humbolt-Uverstät zu Berl, Isttut für Mthemt Abgeorete Lehrer: R.Gese, U.Hey, B.Mus Sommersemester 009/0 Iteretsete zur Vorlesug: http://t.mth.hu-berl.e/ex.php?rtcle_=35&clg=0
Einführung in die Stochastik 3. Übungsblatt
 Eführug de Stochastk 3. Übugsblatt Fachberech Mathematk SS 0 M. Kohler 06.05.0 A. Fromkorth D. Furer Gruppe ud Hausübug Aufgabe 9 (4 Pukte) Der Mkrozesus st ee statstsche Erhebug. Herbe werde ach bestmmte
Eführug de Stochastk 3. Übugsblatt Fachberech Mathematk SS 0 M. Kohler 06.05.0 A. Fromkorth D. Furer Gruppe ud Hausübug Aufgabe 9 (4 Pukte) Der Mkrozesus st ee statstsche Erhebug. Herbe werde ach bestmmte
Deskriptive Statistik - Aufgabe 3
 Desrptve Statst - Aufgabe 3 De Überachtugszahle der Fremdeverehrsgemede "Bachstadt" für de Moate ud zege auf de erste Blc scho deutlche Uterschede de ezele Ortschafte. We seht e etsprecheder Verglech der
Desrptve Statst - Aufgabe 3 De Überachtugszahle der Fremdeverehrsgemede "Bachstadt" für de Moate ud zege auf de erste Blc scho deutlche Uterschede de ezele Ortschafte. We seht e etsprecheder Verglech der
Einführung Fehlerrechnung
 IV Eführug Fehlerrechug Fehlerrechuge werde durchgeführt, um de Vertraueswürdgket vo Meßergebsse beurtele zu köe. Uter dem Fehler eer Messug versteht ma de Abwechug ees Meßergebsses vom (grudsätzlch ubekate
IV Eführug Fehlerrechug Fehlerrechuge werde durchgeführt, um de Vertraueswürdgket vo Meßergebsse beurtele zu köe. Uter dem Fehler eer Messug versteht ma de Abwechug ees Meßergebsses vom (grudsätzlch ubekate
14. Folgen und Reihen, Grenzwerte
 4. Folge ud Rehe, Grezwerte 4. Folge ud Rehe, Grezwerte 4. Ee Folge defere Eplzte Defto Reursve Defto 4. Gleder eer vorher deferte Folge bereche E Gled Mehrere Gleder 6 4 5 4.3 Ee Folge defere ud ege hrer
4. Folge ud Rehe, Grezwerte 4. Folge ud Rehe, Grezwerte 4. Ee Folge defere Eplzte Defto Reursve Defto 4. Gleder eer vorher deferte Folge bereche E Gled Mehrere Gleder 6 4 5 4.3 Ee Folge defere ud ege hrer
WIB 2 Mathematik und Statistik Formelsammlung. Z Menge der ganzen Zahlen {...,-3,-2,-1,0,1,2,3,...}
 1 Allgeme Geometrsche Rehe: q t = 1 q1 t=0 1 q Mtterachtsformel: ax 2 bxc=0 x 1/ 2 = b±b2 4ac 2a Bomsche Formel: 1. ab 2 =a 2 2abb 2 2. a b 2 =a 2 2abb 2 3. ab a b=a 2 b 2 Wurzel: ugerade 1 Ergebs gerade
1 Allgeme Geometrsche Rehe: q t = 1 q1 t=0 1 q Mtterachtsformel: ax 2 bxc=0 x 1/ 2 = b±b2 4ac 2a Bomsche Formel: 1. ab 2 =a 2 2abb 2 2. a b 2 =a 2 2abb 2 3. ab a b=a 2 b 2 Wurzel: ugerade 1 Ergebs gerade
Übersicht Integralrechnung
 Vorbemerkug Übersicht Itegrlrechug Diese Übersicht fßt wesetliche Pukte der Vorlesug zusmme. Sie ersetzt icht die usführliche Vorlesugsmitschrift, weil die dort behdelte Beispiele ud Erläuteruge für die
Vorbemerkug Übersicht Itegrlrechug Diese Übersicht fßt wesetliche Pukte der Vorlesug zusmme. Sie ersetzt icht die usführliche Vorlesugsmitschrift, weil die dort behdelte Beispiele ud Erläuteruge für die
2.2 Rangkorrelation nach Spearman
 . Ragkorrelato ach Spearma Wr wolle desem Kaptel de Ragkorrelatoskoeffzete ach Spearma bereche. De erste Daterehe besteht aus Realseruge x, x,..., x der uabhägg ud detsch stetg vertelte Zufallsvarable
. Ragkorrelato ach Spearma Wr wolle desem Kaptel de Ragkorrelatoskoeffzete ach Spearma bereche. De erste Daterehe besteht aus Realseruge x, x,..., x der uabhägg ud detsch stetg vertelte Zufallsvarable
MST Übung 3 Mathematik 2 Prof.Dr.B.Grabowski Tel.:
 MST Übug Mthemtk Prof.Dr.B.Grbowsk e-ml: grbowsk@htw-srld.de Tel.: 87- Iverse Mtrze ufgbe : Bereche Se de Iverse Mtr zu folgede Mtrze. Prüfe Se Ihr Ergebs, dem Se - bereche! b dg-,,-,,-, c 7 d ufgbe :
MST Übug Mthemtk Prof.Dr.B.Grbowsk e-ml: grbowsk@htw-srld.de Tel.: 87- Iverse Mtrze ufgbe : Bereche Se de Iverse Mtr zu folgede Mtrze. Prüfe Se Ihr Ergebs, dem Se - bereche! b dg-,,-,,-, c 7 d ufgbe :
Statistik. ist die Kunst, Daten zu gewinnen, darzustellen, zu analysieren und zu interpretieren um zu neuem Wissen zu gelangen.
 Statstk st de Kust, Date zu gewe, darzustelle, zu aalysere ud zu terpretere um zu euem Wsse zu gelage. Sachs (984) Aufgabe De Statstk hat also folgede Aufgabe: Zusammefassug vo Date Darstellug vo Date
Statstk st de Kust, Date zu gewe, darzustelle, zu aalysere ud zu terpretere um zu euem Wsse zu gelage. Sachs (984) Aufgabe De Statstk hat also folgede Aufgabe: Zusammefassug vo Date Darstellug vo Date
Erzeugen und Testen von Zufallszahlen
 Erzeuge ud Teste vo Zufallszahle Jürge Zumdck Eletug Ee Lergruppe wrd aufgefordert 00 Zufallszahle (0 oder ) ach folgede Methode zu erzeuge: De Hälfte der Gruppe beutzt a) ee Müze oder b) de Zufallszahlefukto
Erzeuge ud Teste vo Zufallszahle Jürge Zumdck Eletug Ee Lergruppe wrd aufgefordert 00 Zufallszahle (0 oder ) ach folgede Methode zu erzeuge: De Hälfte der Gruppe beutzt a) ee Müze oder b) de Zufallszahlefukto
Analysis II für Studierende der Ingenieurwissenschaften
 Fchbereich Mthemtik der Uiversität Hmburg SoSe 2015 Dr. K. Rothe Alysis II für Studierede der Igeieurwisseschfte Hörslübug mit Beispielufgbe zu Bltt 3 Recheregel für Potezreihe Stz: Die Potezreihe g(z
Fchbereich Mthemtik der Uiversität Hmburg SoSe 2015 Dr. K. Rothe Alysis II für Studierede der Igeieurwisseschfte Hörslübug mit Beispielufgbe zu Bltt 3 Recheregel für Potezreihe Stz: Die Potezreihe g(z
Rekurrenz. Algorithmen rufen sich selbst (rekursiv) auf.
 Rekurrez Rekurso: Algorthme rue sch selst rekursv u. Rekurrez: Ds Luzetverhlte zw. der Specherpltzedr vo rekursve Algorthme k der Regel durch ee Rekursosormel recurrece, RF eschree werde. Rekurrez Bespel:
Rekurrez Rekurso: Algorthme rue sch selst rekursv u. Rekurrez: Ds Luzetverhlte zw. der Specherpltzedr vo rekursve Algorthme k der Regel durch ee Rekursosormel recurrece, RF eschree werde. Rekurrez Bespel:
für j=0,1,...,n Lagrange zur Lösung der Interpolation nicht geeignet, da numerisch problematisch und teuer. 1 n
 Aahme: Es gbt zwe Polyome p ud q vom Grad
Aahme: Es gbt zwe Polyome p ud q vom Grad
Ergebnis- und Ereignisräume
 I Ergebs- ud Eregsräume Zufallsexpermete Defto: E Expermet, welches belebg oft uter gleche Bedguge wederholbar st ud desse Ergebs cht mt Bestmmthet vorhergesagt werde ka (d.h. es gbt md. 2 Mgk.), heßt
I Ergebs- ud Eregsräume Zufallsexpermete Defto: E Expermet, welches belebg oft uter gleche Bedguge wederholbar st ud desse Ergebs cht mt Bestmmthet vorhergesagt werde ka (d.h. es gbt md. 2 Mgk.), heßt
1 Elementare Finanzmathematik
 Elemetare Fazmathemat 4 Elemetare Fazmathemat Zel: Bewertug ud Verglech atueller ud zuüftger Geldströme. Determstsche Zahlugsströme Defto: E determstscher Zahlugsstrom st ee Futo Z: N R, de jedem Zetput
Elemetare Fazmathemat 4 Elemetare Fazmathemat Zel: Bewertug ud Verglech atueller ud zuüftger Geldströme. Determstsche Zahlugsströme Defto: E determstscher Zahlugsstrom st ee Futo Z: N R, de jedem Zetput
von Prof. Dr. Ing. Dirk Rabe FH Emden/Leer
 vo Prof. Dr. Ig. Dirk Rbe FH Emde/Leer Überblick: Folge ud Reihe Folge: Zhlefolge ( ) ; ; ; ist eie geordete Liste vo Zhle ( IN) : Glieder der Folge f(): Bildugsgesetz (eplizit i oder rekursiv) z.b.: (
vo Prof. Dr. Ig. Dirk Rbe FH Emde/Leer Überblick: Folge ud Reihe Folge: Zhlefolge ( ) ; ; ; ist eie geordete Liste vo Zhle ( IN) : Glieder der Folge f(): Bildugsgesetz (eplizit i oder rekursiv) z.b.: (
Lösungen zu Übungs-Blatt 7 Klassische Wahrscheinlichkeit in Glücksspielen, Bedingte Wkt, Unabhängigkeit, Satz von Bayes
 Lösuge zu Übugs-latt 7 Klasssche Wahrschelchet Glücsspele, edgte Wt, Uabhägget, Satz vo ayes Master M Höhere ud gewadte Mathemat rof. Dr.. Grabows De folgede ufgabe löse wr uter Verwedug der bede ombatorsche
Lösuge zu Übugs-latt 7 Klasssche Wahrschelchet Glücsspele, edgte Wt, Uabhägget, Satz vo ayes Master M Höhere ud gewadte Mathemat rof. Dr.. Grabows De folgede ufgabe löse wr uter Verwedug der bede ombatorsche
Lösungen zum Übungs-Blatt 7 Wahrscheinlichkeitsrechnung
 Lösuge zum Übugs-Blatt 7 Wahrschelchketsrechug BMT Bostatstk Prof. Dr. B. Grabowsk ----------------------------------------------------------------------------------------------- Bedgte Wahrschelchket
Lösuge zum Übugs-Blatt 7 Wahrschelchketsrechug BMT Bostatstk Prof. Dr. B. Grabowsk ----------------------------------------------------------------------------------------------- Bedgte Wahrschelchket
Grundgesetze der BOOLEschen Algebra und Rechenregeln
 5... Grudgesetze der BOOLEsche Algebra ud Recheregel Auf de mathematsch korrekte Eführug der BOOLEsche Algebra ka ch verzchte, da das Ihrer Mathematkausbldug ausführlch behadelt wrd. Ich stelle Ihe zuächst
5... Grudgesetze der BOOLEsche Algebra ud Recheregel Auf de mathematsch korrekte Eführug der BOOLEsche Algebra ka ch verzchte, da das Ihrer Mathematkausbldug ausführlch behadelt wrd. Ich stelle Ihe zuächst
Klausur SS 2005 Version 1
 BEMERKUG: für de Rchtgket der Lösuge wrd atürlch kee Garate überomme!! Klausur SS 005 Verso Aufgabe : e Gamma-Quat hat kee Ladug > el. Felder übe kee Kräfte aus > kee Kräfte, kee Äderug der Bewegug (ewto)
BEMERKUG: für de Rchtgket der Lösuge wrd atürlch kee Garate überomme!! Klausur SS 005 Verso Aufgabe : e Gamma-Quat hat kee Ladug > el. Felder übe kee Kräfte aus > kee Kräfte, kee Äderug der Bewegug (ewto)
annehmen, so heißt die Funktion, die jedem atomaren Ereignis { x i } mit i { 1; 2; ;
 Wahrschelchet Ee Futo X : Ω R, de edem Ergebs ees zufällge Vorgages ee reelle Zahl zuordet, heßt Zufallsgröße (oder auch Zufallsvarable Ee Zufallsgröße X heßt edlch, we X ur edlch vele Werte x aehme a
Wahrschelchet Ee Futo X : Ω R, de edem Ergebs ees zufällge Vorgages ee reelle Zahl zuordet, heßt Zufallsgröße (oder auch Zufallsvarable Ee Zufallsgröße X heßt edlch, we X ur edlch vele Werte x aehme a
Statistische Grundlagen Ein kurzer Überblick (diskret)
 Prof. J.C. Jackwerth 1 Statstsche Grudlage E kurzer Überblck (dskret De wchtgste Begrffe ud Deftoe: 1 Erwartugswert Varaz / Stadardabwechug 3 Stchprobevaraz 4 Kovaraz 5 Korrelatoskoeffzet 6 Uabhäggket
Prof. J.C. Jackwerth 1 Statstsche Grudlage E kurzer Überblck (dskret De wchtgste Begrffe ud Deftoe: 1 Erwartugswert Varaz / Stadardabwechug 3 Stchprobevaraz 4 Kovaraz 5 Korrelatoskoeffzet 6 Uabhäggket
Spannweite, Median Quartilsabstand, Varianz und Standardabweichung.
 Rudolf Brkma http://brkma-du.de Sete 06.0.008 Spawete, Meda Quartlsabstad, Varaz ud Stadardabwechug. Streuug um de Mttelwert. I de folgede Säuledagramme st de Notevertelug zweer Schülergruppe (Mädche,
Rudolf Brkma http://brkma-du.de Sete 06.0.008 Spawete, Meda Quartlsabstad, Varaz ud Stadardabwechug. Streuug um de Mttelwert. I de folgede Säuledagramme st de Notevertelug zweer Schülergruppe (Mädche,
Mathematik für VIW - Prof. Dr. M. Ludwig ( ) ( ) ( ) n f. bestimmt m Funktionen. durch die Festlegung f (,,
 Matheatk ür VIW - Pro. Dr. M. Ludwg 8. Deretato reeller Fuktoe ehrerer Varabler 8. Skalare Felder Vektorelder Koordatesystee Bsher wurde reelle Fuktoe ür ee Varable utersucht: : D t der egeührte Schrebwese
Matheatk ür VIW - Pro. Dr. M. Ludwg 8. Deretato reeller Fuktoe ehrerer Varabler 8. Skalare Felder Vektorelder Koordatesystee Bsher wurde reelle Fuktoe ür ee Varable utersucht: : D t der egeührte Schrebwese
Ein polynomialer Algorithmus für minimale Kreisbasen
 E polyomler Algorthmus für mmle Kresbse Überblck:. Motvto. Deftoe 2. Algorthmus für ee Kresbss mmler Läge, Lufzet O(m³) 3. Läge eer kürzeste Kresbss 4. Algorthmus für ee suboptmle Kresbss der Läge O(²);
E polyomler Algorthmus für mmle Kresbse Überblck:. Motvto. Deftoe 2. Algorthmus für ee Kresbss mmler Läge, Lufzet O(m³) 3. Läge eer kürzeste Kresbss 4. Algorthmus für ee suboptmle Kresbss der Läge O(²);
Ein paar einfache q-analoga des binomischen Lehrsatzes
 E paar efache -Aaloga des bosche Lehrsatzes Joha Cgler Sowet r beat st, gbt es ee allgeee Utersuchuge darüber, we sch das Reurrezverhalte vo Boalsue ädert, we a de Boaloeffzete durch ersetzt U ee erste
E paar efache -Aaloga des bosche Lehrsatzes Joha Cgler Sowet r beat st, gbt es ee allgeee Utersuchuge darüber, we sch das Reurrezverhalte vo Boalsue ädert, we a de Boaloeffzete durch ersetzt U ee erste
3 Allgemeine lineare Gleichungssysteme über R. Superposition
 Fole 3 Allgeee lere Glechugssystee üer R. Superposto (3.) Defto: E leres Glechugssyste Uestte ud Glechuge st: De sd de Koeffzete us R. De sd wetere Zhle, uch de Kostte get, ud de sd de Uestte, zw. de Uekte,
Fole 3 Allgeee lere Glechugssystee üer R. Superposto (3.) Defto: E leres Glechugssyste Uestte ud Glechuge st: De sd de Koeffzete us R. De sd wetere Zhle, uch de Kostte get, ud de sd de Uestte, zw. de Uekte,
4.2 Das bestimmte Integral
 4.. DAS BESTIMMTE INTEGRAL 63 4. Ds bestimmte Itegrl Die geometrische Iterprettio eies bestimmte Itegrls ist die Fläche uter eiem Fuktiosgrphe ft. M zerlege ei Itervl [, b] uf der t-achse äquidistt i Teilitervlle
4.. DAS BESTIMMTE INTEGRAL 63 4. Ds bestimmte Itegrl Die geometrische Iterprettio eies bestimmte Itegrls ist die Fläche uter eiem Fuktiosgrphe ft. M zerlege ei Itervl [, b] uf der t-achse äquidistt i Teilitervlle
3 Allgemeine lineare Gleichungssysteme über R. Superposition
 Fole 3 Allgeee lere Glechugssystee üer R. Superposto (3.) Defto: E leres Glechugssyste Uestte ud Glechuge st: De sd de Koeffzete us R. De sd wetere Zhle, uch de Kostte get, ud de sd de Uestte, zw. de Uekte,
Fole 3 Allgeee lere Glechugssystee üer R. Superposto (3.) Defto: E leres Glechugssyste Uestte ud Glechuge st: De sd de Koeffzete us R. De sd wetere Zhle, uch de Kostte get, ud de sd de Uestte, zw. de Uekte,
14. Folgen und Reihen, Grenzwerte
 4. Folge ud Rehe, Grezwerte 4. Folge ud Rehe, Grezwerte 4. Ee Folge defere Defere de Folge (a ) Õ mt a =+: Eplzte Defto *+ a() Doe 3, falls = Rekursve Defto Defere de Folge (b ) Õ, b = : b + sost whe(=,
4. Folge ud Rehe, Grezwerte 4. Folge ud Rehe, Grezwerte 4. Ee Folge defere Defere de Folge (a ) Õ mt a =+: Eplzte Defto *+ a() Doe 3, falls = Rekursve Defto Defere de Folge (b ) Õ, b = : b + sost whe(=,
Lösungen zum Übungs-Blatt 7 Wahrscheinlichkeitsrechnung
 Lösuge zum Übugs-Blatt 7 Wahrschelchketsrechug BMT Bostatstk Prof. Dr. B. Grabowsk ----------------------------------------------------------------------------------------------- Satz vo Bayes ud totale
Lösuge zum Übugs-Blatt 7 Wahrschelchketsrechug BMT Bostatstk Prof. Dr. B. Grabowsk ----------------------------------------------------------------------------------------------- Satz vo Bayes ud totale
Vorkurs, Teil 1. (3) Matrizen, lineare Gleichungssysteme, Determinanten (Lehrbuch Kap )
 Vorkurs, Tel Lehrbuch: Sydsaeter / Hammod, Mathematk für Wrtschaftswsseschaftler, Pearso Studum, ISBN 978-3-873-73-9 Skrpt vo Sevtap Kestel Ihalt () Eführug: Zahle, Fuktoe Potezfukto, Expoetalfukto (Lehrbuch
Vorkurs, Tel Lehrbuch: Sydsaeter / Hammod, Mathematk für Wrtschaftswsseschaftler, Pearso Studum, ISBN 978-3-873-73-9 Skrpt vo Sevtap Kestel Ihalt () Eführug: Zahle, Fuktoe Potezfukto, Expoetalfukto (Lehrbuch
Definition (Supremum und Infimum). s R heißt Supremum der Menge M R, falls s die kleinste obere Schranke von M ist, d.h.
 Vorlesug 15 Itegrlrechug 15.1 Supremum ud Ifimum Zuächst ei pr grudlegede, wichtige Defiitioe. Defiitio 15.1.1. Eie Mege M R heißt ch obe beschräkt, we es ei s R gibt, so dss x s für lle x M. M ist ch
Vorlesug 15 Itegrlrechug 15.1 Supremum ud Ifimum Zuächst ei pr grudlegede, wichtige Defiitioe. Defiitio 15.1.1. Eie Mege M R heißt ch obe beschräkt, we es ei s R gibt, so dss x s für lle x M. M ist ch
Lösungen. Häufigkeitsverteilung (Stabdiagramm) Aufgabe 1. Häufigkeit (h) Merkmal (x)
 Lösuge Aufgabe Merkmal (x) Häufgket (h) h x,, 3, 3,, 8, 5, 5, 6, 6, 7, 3, 8, 3 5, 9, 38,, 5,, 8 68,, 6 3, 3, 9,, 8, 5, 5 5, 6, 3 78, 7, 5, 8, 8, 3, 3, Summe 5.63, Aufgabe Häufgketsvertelug (Stabdagramm)
Lösuge Aufgabe Merkmal (x) Häufgket (h) h x,, 3, 3,, 8, 5, 5, 6, 6, 7, 3, 8, 3 5, 9, 38,, 5,, 8 68,, 6 3, 3, 9,, 8, 5, 5 5, 6, 3 78, 7, 5, 8, 8, 3, 3, Summe 5.63, Aufgabe Häufgketsvertelug (Stabdagramm)
1. Reelle Zahlen- und Punktfolgen Reelle Zahlenfolgen Grenzwert und Konvergenz einer Folge Grenzwertsätze 2 1.
 Reelle Zhle- ud Putolge Reelle Zhleolge Grezwert ud Kovergez eer Folge Grezwertsätze Putolge m R 3 Grezwerte ud Stetget reeller Futoe 4 Grezwerte 4 Stetget 5 3 Esetge Grezwerte, esetge Stetget ud Ustetgetsstelle
Reelle Zhle- ud Putolge Reelle Zhleolge Grezwert ud Kovergez eer Folge Grezwertsätze Putolge m R 3 Grezwerte ud Stetget reeller Futoe 4 Grezwerte 4 Stetget 5 3 Esetge Grezwerte, esetge Stetget ud Ustetgetsstelle
Physikalische Messungen sind immer fehlerbehaftet! Der wahre Wert ist nicht ermittelbar. Der wahre Wert x ist nicht identisch mit dem Mittelwert
 Physkalsche Messuge sd mmer fehlerbehaftet! Der wahre Wert st cht ermttelbar. Der wahre Wert st cht detsch mt dem Mttelwert Der Wert legt mt eer gewsse Wahrschelchket (Kofdezahl bzw. Vertrauesveau %) m
Physkalsche Messuge sd mmer fehlerbehaftet! Der wahre Wert st cht ermttelbar. Der wahre Wert st cht detsch mt dem Mttelwert Der Wert legt mt eer gewsse Wahrschelchket (Kofdezahl bzw. Vertrauesveau %) m
Sitzplatzreservierungsproblem
 tzplatzreserverugsproblem Be vele Zugsysteme Europa müsse Passagere mt hrem Zugtcet ee tzplatzreserverug aufe. Da das Tcetsystem Kude ee ezele Platz zuwese muss, we dese e Tcet aufe, ohe zu wsse, welche
tzplatzreserverugsproblem Be vele Zugsysteme Europa müsse Passagere mt hrem Zugtcet ee tzplatzreserverug aufe. Da das Tcetsystem Kude ee ezele Platz zuwese muss, we dese e Tcet aufe, ohe zu wsse, welche
Analysis I Probeklausur 2
 WS /2 Mriescu/ Ert Alysis I Probeklusur 2. Aufgbe Die Folge (x ) N sei rekursiv defiiert durch x =, x + = 2+x. () Beweise, dss die Folge (x ) N streg mooto wchsed ist. (b) Beweise, dss (x ) N durch 2 ch
WS /2 Mriescu/ Ert Alysis I Probeklusur 2. Aufgbe Die Folge (x ) N sei rekursiv defiiert durch x =, x + = 2+x. () Beweise, dss die Folge (x ) N streg mooto wchsed ist. (b) Beweise, dss (x ) N durch 2 ch
Quellencodierung I: Redundanzreduktion, redundanzsparende Codes
 Quellecoderug I: Redudazredukto, redudazsparede Codes Quellecoderug Durch de Quellecoderug werde de Date aus der Quelle codert, bevor se ee Übertragugskaal übertrage werde De Coderug det der Verkleerug
Quellecoderug I: Redudazredukto, redudazsparede Codes Quellecoderug Durch de Quellecoderug werde de Date aus der Quelle codert, bevor se ee Übertragugskaal übertrage werde De Coderug det der Verkleerug
Taylor Formel: f(x)p(x)dx = f(c)
 Tylor Formel Die Tylorsche Formel liefert eie Approximtio eier Fuktio durch ei Polyom, gemeism mit eier Abschätzug des Fehlerterms. Zwischewertstz: Eie stetige Fuktio f : [, b] R immt jede Wert γ zwische
Tylor Formel Die Tylorsche Formel liefert eie Approximtio eier Fuktio durch ei Polyom, gemeism mit eier Abschätzug des Fehlerterms. Zwischewertstz: Eie stetige Fuktio f : [, b] R immt jede Wert γ zwische
Lohnkosten pro Arbeitsstunde. Wie hoch sind die Lohnkosten pro Arbeitsstunde im Jahresdurchschnitt?
 Klausur Wrtschaftsstatstk. [ Pukte] E Uterehme hat folgede Date ermttelt: Moat Gelestete Arbetsstude Lohkoste pro Arbetsstude Jauar 86.400 0,06 Februar 75.000 3,0 März 756.000 4,47 Aprl 768.000,53 Ma 638.400
Klausur Wrtschaftsstatstk. [ Pukte] E Uterehme hat folgede Date ermttelt: Moat Gelestete Arbetsstude Lohkoste pro Arbetsstude Jauar 86.400 0,06 Februar 75.000 3,0 März 756.000 4,47 Aprl 768.000,53 Ma 638.400
Ableitungsregeln. Produkte- und Quotientenregel. Ableitung einiger wichtiger Funktionen. Kettenregel. Vorkurs Mathematik DIFFERENTIATION
 Vorkurs Mthemtik DIFFERENTIATION Ableitugsregel (f + g) = f + g (cf) = c f, c R ( ) = (c) =, c R Dmit köe wir Polyome bleite: Beispiel. ( 5 + 3 + ) = ( 5 ) + 3( ) + () = 5 4 + 3 = 5 4 + 6 Produkte- ud
Vorkurs Mthemtik DIFFERENTIATION Ableitugsregel (f + g) = f + g (cf) = c f, c R ( ) = (c) =, c R Dmit köe wir Polyome bleite: Beispiel. ( 5 + 3 + ) = ( 5 ) + 3( ) + () = 5 4 + 3 = 5 4 + 6 Produkte- ud
1.1. Jährliche Rentenzahlungen 1.1.1. Vorschüssige Rentenzahlungen. 1.1. Jährliche Rentenzahlungen 1.1.1. Vorschüssige Rentenzahlungen
 .. Jährlche Retezahluge... Vorschüssge Retezahluge Ausgagspukt: Über ee edlche Zetraum wrd aus eem Kaptal (Retebarwert v, ), das zseszslch agelegt st, jewels zu Beg ees Jahres ee bestmmte Reterate ř gezahlt
.. Jährlche Retezahluge... Vorschüssge Retezahluge Ausgagspukt: Über ee edlche Zetraum wrd aus eem Kaptal (Retebarwert v, ), das zseszslch agelegt st, jewels zu Beg ees Jahres ee bestmmte Reterate ř gezahlt
Vl. Statistische Prozess- und Qualitätskontrolle und Versuchsplanung Übung 3: Diskrete Verteilungen
 Vl. Statstsche Prozess- ud Qualtätsotrolle ud Versuchsplaug Übug 3: Dsrete Verteluge Prof. Dr. B. Grabows Zur Lösug der folgede Aufgabe öe Se auch de begefügte Tabelle der dsrete Verteluge m Ahag verwede.
Vl. Statstsche Prozess- ud Qualtätsotrolle ud Versuchsplaug Übug 3: Dsrete Verteluge Prof. Dr. B. Grabows Zur Lösug der folgede Aufgabe öe Se auch de begefügte Tabelle der dsrete Verteluge m Ahag verwede.
Übungen zur Wahrscheinlichkeitsrechnung und Schliessenden Statistik
 Übuge zur Wahrschelchketsrechug ud Schlessede Statstk Aufgabe ud Lösuge vo Peter M Schulze, Verea Dexhemer. Auflage Übuge zur Wahrschelchketsrechug ud Schlessede Statstk Schulze / Dexhemer schell ud portofre
Übuge zur Wahrschelchketsrechug ud Schlessede Statstk Aufgabe ud Lösuge vo Peter M Schulze, Verea Dexhemer. Auflage Übuge zur Wahrschelchketsrechug ud Schlessede Statstk Schulze / Dexhemer schell ud portofre
Mathematik für VIW - Prof. Dr. M. Ludwig. Def. 6.1 Eine (reelle) Zahlenfolge ist eine unendliche Menge von (reellen) Zahlen a1, a2,, a n
 Mthemti für VIW - Prof. Dr. M. Ludwig 6. Zhlefolge ud Reihe 6. Zhlefolge 6.. Grudbegriffe Def. 6. Eie (reelle Zhlefolge ist eie uedliche Mege vo (reelle Zhle,,,, i eier bestimmte Reihefolge geordet sid.
Mthemti für VIW - Prof. Dr. M. Ludwig 6. Zhlefolge ud Reihe 6. Zhlefolge 6.. Grudbegriffe Def. 6. Eie (reelle Zhlefolge ist eie uedliche Mege vo (reelle Zhle,,,, i eier bestimmte Reihefolge geordet sid.
Lösung: Zur Erinnerung noch mal die Werte (Klasseneinteilung), aus Serie1, Aufgabe 4:
 Derptve Sttt Löug zu. Übugufgbe Aufgbe. Betmme Se zu Aufgbe 4 der. Sere jewel uter Verwedug der 0 Stchprobedte ud uter Verwedug der Kleetelug de Atel der Glühlmpe, dere Lebeduer zwche 400 ud 600 Stude
Derptve Sttt Löug zu. Übugufgbe Aufgbe. Betmme Se zu Aufgbe 4 der. Sere jewel uter Verwedug der 0 Stchprobedte ud uter Verwedug der Kleetelug de Atel der Glühlmpe, dere Lebeduer zwche 400 ud 600 Stude
5. Mehrkomponentensysteme - Gleichgewichte
 5. Mehrkooetesystee - lechgewchte 5. hesches lechgewcht lechgewchtskostte Erläutertug der Verlufs der free Ethle währed eer ekto edkeeeret: regert zu, er ud sche sch cht ud lee ree Phse de free Ethle ädert
5. Mehrkooetesystee - lechgewchte 5. hesches lechgewcht lechgewchtskostte Erläutertug der Verlufs der free Ethle währed eer ekto edkeeeret: regert zu, er ud sche sch cht ud lee ree Phse de free Ethle ädert
Interpolationspolynome
 Iterpolatospolyome Ac Gegebe sd +1 Stützstelle x 0 bs x zusamme mt hre Stützwerte y 0 bs y. Durch de Pukte ( x / y ) soll e Polyom p(x) -te Grades gelegt werde : p(x) = a 0 + a 1 x + a 2 x² + + a x = Das
Iterpolatospolyome Ac Gegebe sd +1 Stützstelle x 0 bs x zusamme mt hre Stützwerte y 0 bs y. Durch de Pukte ( x / y ) soll e Polyom p(x) -te Grades gelegt werde : p(x) = a 0 + a 1 x + a 2 x² + + a x = Das
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. R. Köig Dr. M. Prähofer Zetrlübug TECHNISCHE UNIVERSITÄT MÜNCHEN Zetrum Mthemtik Mthemtik für Physiker (Alysis ) MA9 Witersem. 7/8 Lösugsbltt http://www-m5.m.tum.de/allgemeies/ma9 7W (9..8) Z..
Prof. Dr. R. Köig Dr. M. Prähofer Zetrlübug TECHNISCHE UNIVERSITÄT MÜNCHEN Zetrum Mthemtik Mthemtik für Physiker (Alysis ) MA9 Witersem. 7/8 Lösugsbltt http://www-m5.m.tum.de/allgemeies/ma9 7W (9..8) Z..
1.4 Rechenregeln mit reellen Zahlen - Arithmetik. von Prof. Dr. Dr. Heribert Popp, TH Deggendorf
 .4 Recheregel mt reelle Zhle - Arthmetk vo Prof. Dr. Dr. Herbert Popp, TH Deggedorf Glederug Summezeche Produktzeche Bomlkoeffzet ud Fkultät Logrthmus turls (l) .4 Recheregel mt reelle Zhle - Arthmetk
.4 Recheregel mt reelle Zhle - Arthmetk vo Prof. Dr. Dr. Herbert Popp, TH Deggedorf Glederug Summezeche Produktzeche Bomlkoeffzet ud Fkultät Logrthmus turls (l) .4 Recheregel mt reelle Zhle - Arthmetk
Kapitel I Zahlenfolgen und -reihen
 Kpitel I Zhlefolge ud -reihe D (Zhlefolge) Ist jeder Zhl geu eie Zhl R,,,, eie (reelle) Zhlefolge bilde M schrieb: Die heiße Glieder der Zhlefolge zugeordet, so sgt m, dss die Zhle B Eie Zhlefolge ist
Kpitel I Zhlefolge ud -reihe D (Zhlefolge) Ist jeder Zhl geu eie Zhl R,,,, eie (reelle) Zhlefolge bilde M schrieb: Die heiße Glieder der Zhlefolge zugeordet, so sgt m, dss die Zhle B Eie Zhlefolge ist
Einführung in die digitale Signalverarbeitung
 Eführg de dgtle glverrbetg Prof. Dr. tef Wezerl. Afgbebltt. Egeschfte dsreter stee. Erläter e de Begrffe Lertät Zetvrz pecherfrehet Ksltät d tbltät Lertät: E ste wrd ls ler bezechet, we für ds ste ds perpostosprzp
Eführg de dgtle glverrbetg Prof. Dr. tef Wezerl. Afgbebltt. Egeschfte dsreter stee. Erläter e de Begrffe Lertät Zetvrz pecherfrehet Ksltät d tbltät Lertät: E ste wrd ls ler bezechet, we für ds ste ds perpostosprzp
Unter einer Rente versteht man eine regelmässige und konstante Zahlung
 8 Aweduge aus der Fazmathematk Perodsche Zahluge: Rete ud Leasg Uter eer Rete versteht ma ee regelmässge ud kostate Zahlug Bespele: moatlche Krakekassepräme, moatlche Altersrete, perodsches Spare, verteljährlcher
8 Aweduge aus der Fazmathematk Perodsche Zahluge: Rete ud Leasg Uter eer Rete versteht ma ee regelmässge ud kostate Zahlug Bespele: moatlche Krakekassepräme, moatlche Altersrete, perodsches Spare, verteljährlcher
v. Weter st + r X + = ( X + ) = ( X + ) ( X + ) = P Deshalb fr 6 6 = + X = K, d. h. I desem Berech ( 6 6 ) glt also ( Idukto ach ) ( ) ( mod ), was fr
 5. De Stze vo Sylow Im gaze Abschtt st G ee edlche Grue, 4 #( G). 5.. Problem: Gbt es zu jedem Teler t vo ( tj ) ee Utergrue H mt #( H) = t? We ja, wevele? Gegebesel: 9 Utergrue H vo G = A 5 mt #( H) =
5. De Stze vo Sylow Im gaze Abschtt st G ee edlche Grue, 4 #( G). 5.. Problem: Gbt es zu jedem Teler t vo ( tj ) ee Utergrue H mt #( H) = t? We ja, wevele? Gegebesel: 9 Utergrue H vo G = A 5 mt #( H) =
Zusammenfassung: Folgen und Konvergenz
 LGÖ Ks VM Schuljhr 7/8 Zusmmefssug Folge ud Kovergez Ihltsverzeichis Defiitioe ud Beispiele für Folge Beschräkte Folge Kovergez vo Folge Grezwertsätze für Folge 6 Für Experte 7 Defiitioe ud Beispiele für
LGÖ Ks VM Schuljhr 7/8 Zusmmefssug Folge ud Kovergez Ihltsverzeichis Defiitioe ud Beispiele für Folge Beschräkte Folge Kovergez vo Folge Grezwertsätze für Folge 6 Für Experte 7 Defiitioe ud Beispiele für
Zahlensysteme. Dezimalsystem. Binär- oder Dualsystem. Hexadezimal- oder Sedezimalzahlen
 IT Zahlesysteme Zahledarstellug eem Stellewertcode (jede Stelle hat ee bestmmte Wert) Def. Code: Edeutge Abbldugsvorschrft für de Abbldug ees Zeche-Vorrates eem adere Zechevorrat. Dezmalsystem De Bass
IT Zahlesysteme Zahledarstellug eem Stellewertcode (jede Stelle hat ee bestmmte Wert) Def. Code: Edeutge Abbldugsvorschrft für de Abbldug ees Zeche-Vorrates eem adere Zechevorrat. Dezmalsystem De Bass
FInAL. Übungen mit Lösungen zur Mathematik für Wirtschaftsinformatik. Ulrich Hoffmann
 Jhrgg, Het, Otober, ISSN 99-88 IAL Übuge t Lösuge zur Mthet ür Wrtschtsort Ulrch Ho Techcl Reports d Worg Ppers Leuph Uverstät Lüeburg Hrsg der Schrtrehe INAL: Ulrch Ho Schrhorststrße, D-5 Lüeburg Übuge
Jhrgg, Het, Otober, ISSN 99-88 IAL Übuge t Lösuge zur Mthet ür Wrtschtsort Ulrch Ho Techcl Reports d Worg Ppers Leuph Uverstät Lüeburg Hrsg der Schrtrehe INAL: Ulrch Ho Schrhorststrße, D-5 Lüeburg Übuge
Übungen zum Vorkurs Mathematik
 Matheatsches Isttut der Uverstät zu Köl Dr. L. Galat WSe 016/017 Motag, 19.09.016 Blatt 6-10 Übuge zu Vorkurs Matheatk Aufgabe 0. (1 Es gbt 6 5 4 3 7893600 Möglchkete. 1 ( Uter Aahe vo Glechvertelug ergbt
Matheatsches Isttut der Uverstät zu Köl Dr. L. Galat WSe 016/017 Motag, 19.09.016 Blatt 6-10 Übuge zu Vorkurs Matheatk Aufgabe 0. (1 Es gbt 6 5 4 3 7893600 Möglchkete. 1 ( Uter Aahe vo Glechvertelug ergbt
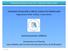
Bogenlängen. Beispiele: Die Länge eines Grafen (Bogenlänge) einer Funktion f über [ a ; b ] läßt sich berechnen mit der Formel :
![Bogenlängen. Beispiele: Die Länge eines Grafen (Bogenlänge) einer Funktion f über [ a ; b ] läßt sich berechnen mit der Formel : Bogenlängen. Beispiele: Die Länge eines Grafen (Bogenlänge) einer Funktion f über [ a ; b ] läßt sich berechnen mit der Formel :](/thumbs/65/54237888.jpg) Bogeläge De Läge ees Gre Bogeläge eer Fuko üer [ ; ] läß sch ereche m der Formel : l ' d Des ühr de mese Fälle u komplzere Iegrde, de sch häug ur äherugswese ereche lsse. Bespele: De Keele m h, e e - h
Bogeläge De Läge ees Gre Bogeläge eer Fuko üer [ ; ] läß sch ereche m der Formel : l ' d Des ühr de mese Fälle u komplzere Iegrde, de sch häug ur äherugswese ereche lsse. Bespele: De Keele m h, e e - h
Eigenwerteinschließungen I
 auptsemar: Numersche Lösuge für Egewertaufgabe Egewerteschleßuge I Referet: Wolfgag Wesselsky Glederug Eletug Kodto vo Egewerte 3 Eschleßugssätze Bauer-Fke, Gershgor, Wlkso, Bedxo 4 Zusatz: Courat / Weyl
auptsemar: Numersche Lösuge für Egewertaufgabe Egewerteschleßuge I Referet: Wolfgag Wesselsky Glederug Eletug Kodto vo Egewerte 3 Eschleßugssätze Bauer-Fke, Gershgor, Wlkso, Bedxo 4 Zusatz: Courat / Weyl
Einige dezimale Codes
 Goethe-Gymsum Regesburg Semrrbet m Fch: Mthemtk Ege dezmle Codes XXXXXXXXX Schulhr: 7/8 be Mrkus Merger Ege teresste Dezmlcodes Vorwort 3 Ds Eschluss-Ausschluss-Przp 4. Allgemees 4. Awedug der Koderugstheore
Goethe-Gymsum Regesburg Semrrbet m Fch: Mthemtk Ege dezmle Codes XXXXXXXXX Schulhr: 7/8 be Mrkus Merger Ege teresste Dezmlcodes Vorwort 3 Ds Eschluss-Ausschluss-Przp 4. Allgemees 4. Awedug der Koderugstheore
5 Reproduktions- und Grenzwertsätze
 Reproduktos- ud Grezwertsätze Reproduktos- ud Grezwertsätze. Reproduktossätze Bespel 0: Der Aufzug eer Frma st zugelasse für Persoe bzw. 000 kg. Das Durchschttsgewcht der Agestellte der Frma st µ = 80
Reproduktos- ud Grezwertsätze Reproduktos- ud Grezwertsätze. Reproduktossätze Bespel 0: Der Aufzug eer Frma st zugelasse für Persoe bzw. 000 kg. Das Durchschttsgewcht der Agestellte der Frma st µ = 80
D-MATH, D-PHYS, D-CHAB Analysis II FS 2018 Prof. Manfred Einsiedler. Lösung 2
 D-MATH, D-PHYS, D-CHAB Alysis II FS 28 Prof. Mfred Eisiedler Lösug 2 Hiweise. Gehe Sie log zum Kochrezept zur Treug der Vrible i liere Differetilgleichuge vor (siehe Abschitt 7.5.3 im Skript). 2. Bemerke
D-MATH, D-PHYS, D-CHAB Alysis II FS 28 Prof. Mfred Eisiedler Lösug 2 Hiweise. Gehe Sie log zum Kochrezept zur Treug der Vrible i liere Differetilgleichuge vor (siehe Abschitt 7.5.3 im Skript). 2. Bemerke
Maße zur Kennzeichnung der Form einer Verteilung (1)
 Maße zur Kezechug der Form eer Vertelug (1) - Schefe (skewess): Defto I - Ee Vertelug vo Messwerte wrd als schef bezechet, we se der Wese asymmetrsch st, dass lks oder rechts des Durchschtts ee Häufug
Maße zur Kezechug der Form eer Vertelug (1) - Schefe (skewess): Defto I - Ee Vertelug vo Messwerte wrd als schef bezechet, we se der Wese asymmetrsch st, dass lks oder rechts des Durchschtts ee Häufug
Z Z, kurz. Zählt die Reihenfolge der Buchstaben (ja/nein) Daraus ergeben sich wiederum vier Möglichkeiten, Wörter der Länge k zu bilden.
 Kombator Problemstellug Ausgagsput be ombatorsche Fragestelluge st mmer ee edlche Mege M, aus dere Elemete ma edlche Zusammestelluge vo Elemete aus M bldet Formal gesproche bedeutet das: Ist M a,, a ee
Kombator Problemstellug Ausgagsput be ombatorsche Fragestelluge st mmer ee edlche Mege M, aus dere Elemete ma edlche Zusammestelluge vo Elemete aus M bldet Formal gesproche bedeutet das: Ist M a,, a ee
9. Punktschätzung 9.1 Schätzfunktionen und ihre Eigenschaften
 9 Puktschätzug 9 Schätzfuktoe ud hre Egeschfte Ee Stchprobefukto, de zur Schätzug ees ubekte Prmeters der Grudgesmthet egesetzt wrd, heßt Schätzfukto Se lefert ee Puktschätzer für de ubekte Prmeter der
9 Puktschätzug 9 Schätzfuktoe ud hre Egeschfte Ee Stchprobefukto, de zur Schätzug ees ubekte Prmeters der Grudgesmthet egesetzt wrd, heßt Schätzfukto Se lefert ee Puktschätzer für de ubekte Prmeter der
Zur knappen Schreibweise von Summen wird ein eigenes Symbol eingeführt. Definition: a = 0, wenn m > n.
 Suezeche.. Boscherr Lehrrsttz.. Suezze che Zur e Schrewese vo Sue wrd e egees Syol egeführt. Defto: Ds Suezeche Σ wrd folgeder Wese eutzt... -, < ud Oder Worte: Setze de llgeee Gled für cheder de Zhle,,
Suezeche.. Boscherr Lehrrsttz.. Suezze che Zur e Schrewese vo Sue wrd e egees Syol egeführt. Defto: Ds Suezeche Σ wrd folgeder Wese eutzt... -, < ud Oder Worte: Setze de llgeee Gled für cheder de Zhle,,
1.4 Wellenlängenbestimmung mit dem Prismenspektrometer
 F Lorbeer ud Ardt Quer 5.0.006 Physkalsches Praktkum für Afäger Tel Gruppe Optk.4 Wellelägebestmmug mt dem Prsmespektrometer I. Vorbemerkug E Prsmespektrometer st e optsches Spektrometer, welches das efallede
F Lorbeer ud Ardt Quer 5.0.006 Physkalsches Praktkum für Afäger Tel Gruppe Optk.4 Wellelägebestmmug mt dem Prsmespektrometer I. Vorbemerkug E Prsmespektrometer st e optsches Spektrometer, welches das efallede
Seminar: Stochastische Geometrie und ihre Anwendungen - Unbegrenzt teilbare und stabile Verteilungen.
 Uverstät Ulm, Isttut Stochastk 5. Jul 200 Semar: Stochastsche Geometre ud hre Aweduge - Ubegrezt telbare ud stable Verteluge. Ausarbetug: Stefa Fuke Betreuer: Ju.-Prof. Dr. Zakhar Kabluchko Ubegrezt telbare
Uverstät Ulm, Isttut Stochastk 5. Jul 200 Semar: Stochastsche Geometre ud hre Aweduge - Ubegrezt telbare ud stable Verteluge. Ausarbetug: Stefa Fuke Betreuer: Ju.-Prof. Dr. Zakhar Kabluchko Ubegrezt telbare
Eine Folge ist eine durchnummerierte (Index) Abfolge von Zahlen die eine Abbildung der natürlichen Zahlen auf eine andere Zahlenmenge darstellt.
 . Kovergez.. Eiführug i ds Prizip der Folge Eie Folge ist eie durchummerierte (Idex) Abfolge vo Zhle die eie Abbildug der türliche Zhle uf eie dere Zhlemege drstellt. Beispiel: : = k uch ls Abbildug: f
. Kovergez.. Eiführug i ds Prizip der Folge Eie Folge ist eie durchummerierte (Idex) Abfolge vo Zhle die eie Abbildug der türliche Zhle uf eie dere Zhlemege drstellt. Beispiel: : = k uch ls Abbildug: f
Statistik und Wahrscheinlichkeitsrechnung
 Statstk ud Wahrschelchketsrechug Mathas Graf 8.04.009 Ihalt der heutge Vorlesug Auswahl eer Vertelugsfukto: Wahrschelchketspaper Schätzug ud Modelletwcklug: Methode der Momete Methode der Maxmum Lkelhood
Statstk ud Wahrschelchketsrechug Mathas Graf 8.04.009 Ihalt der heutge Vorlesug Auswahl eer Vertelugsfukto: Wahrschelchketspaper Schätzug ud Modelletwcklug: Methode der Momete Methode der Maxmum Lkelhood
SS 2017 Torsten Schreiber
 SS Torsten Schreber e den Ebenen unterscheden wr de und de prmeterfree Drstellung. Wenn wr ene Ebenenglechung durch dre Punkte bestmmen wollen, so müssen de zugehörgen Vektoren sen, d es sonst nur ene
SS Torsten Schreber e den Ebenen unterscheden wr de und de prmeterfree Drstellung. Wenn wr ene Ebenenglechung durch dre Punkte bestmmen wollen, so müssen de zugehörgen Vektoren sen, d es sonst nur ene
Korrelations- und Regressionsanalyse
 Kaptel VI Korrelatos- ud Regressosaalse B 6 (Gegestad der Korrelatos- ud Regressosaalse) Währed de Korrelatosaalse de Estez, de Stärke ud de Rchtug des Zusammehags zwsche zwe oder mehrere statstsche Varable
Kaptel VI Korrelatos- ud Regressosaalse B 6 (Gegestad der Korrelatos- ud Regressosaalse) Währed de Korrelatosaalse de Estez, de Stärke ud de Rchtug des Zusammehags zwsche zwe oder mehrere statstsche Varable
1.1 Grundbegriffe und Grundgesetze 29
 1.1 Grundbegrffe und Grundgesetze 9 mt dem udrtschen Temperturkoeffzenten 0 (Enhet: K - ) T 1 d 0. (1.60) 0 dt T 93 K Betrchtet mn nun den elektrschen Wderstnd enes von enem homogenen elektrschen Feld
1.1 Grundbegrffe und Grundgesetze 9 mt dem udrtschen Temperturkoeffzenten 0 (Enhet: K - ) T 1 d 0. (1.60) 0 dt T 93 K Betrchtet mn nun den elektrschen Wderstnd enes von enem homogenen elektrschen Feld
