Frustration ist ein alltägliches Phänomen, und
|
|
|
- Irmela Thomas
- vor 8 Jahren
- Abrufe
Transkript
1 FESTKÖRPERPHYSIK Topologische Spinflüssigkeiten Frustrtion mgnetischer Momente durch widerstreitende Kopplungen knn zu Spinflüssigkeiten mit topologischer Ordnung führen. Ki Phillip Schmidt und Simon Trest Frustrtion knn phsiklisch gesehen durchus positiv wirken und komplee, reichhltige Phänomene hervorrufen. Dzu gehört eispielsweise die topologische Ordnung in Quntenmgneten, die nicht nur us der Sicht der Festkörperphsik, sondern uch der Qunteninformtion oder Mthemtik esonders interessnt ist. Inzwischen ist uch die eperimentelle Relisierung solcher topologisch geordneter Ssteme in Reichweite gerückt. A. 1 Die geometrische Frustrtion tritt z. B. in einem Gitter us Dreiecken mit gemeinsmen Ecken uf, wenn direkt enchrte Spins (lue Kugeln) ntiferromgnetisch wechselwirken (). Konkret sind lle mit Frgezeichen mrkierten Spins frustriert. Die Austusch Frustrtion in () ist für den zentrlen mit einem Frgezeichen versehenen Frustrtion ist ein lltägliches Phänomen, und sie ist ntürlich uch Phsikern nicht fremd. Sie wissen er Frustrtion durchus zu schätzen, etw wenn sich diese ei einem Sstem einstellt, uf ds gleichzeitig widerstreende Kräfte wirken und es nicht llen gleichermßen folgen knn. Denn ds knn interessnte Konsequenzen hen. Ein Beispiel us dem Bereich der Festkörperphsik sind frustrierte Qunten mgnete, in denen die elementren mgnetischen Momente meist Spins gennnt miteinnder üer verschiedene Austuschwechselwirkungen koppeln, die jedoch nicht lle gleichzeitig minimiert werden können. Die geometrische Frustrtion tritt immer dnn uf, wenn die von einem Antiferromgneten fvorisierte ntiprllele Anordnung enchrter Spins (Néel-Ordnung) nicht kommensurel ist mit den elementren Busteinen eines Gitters. Besonders klr wird dies ei Spins uf einem isolierten Dreieck: D es nie möglich ist, lle drei Spins ntiferromgnetisch nzuordnen, leit ein Spin immer frustriert. Geometrisch frustrierte Gitter sind deswegen häufig us Dreiecken ufgeut, woei sich enchrte Dreiecke eine Ecke teilen (A. 1). Wichtige Beispiele sind ds dreidimensionle Prochlor-Gitter oder ds zweidimensionle Kgomé-Gitter. Besonders usgeklügelte Formen der Austuschwechselwirkung, deren gleichzeitige Minimierung für einen gegeenen Spin niemls erfüllr sein können, erluen es eenflls, einen Quntenmgneten zu frustrieren. Dies ist eispielsweise der Fll für einen Quntenspin, der mit ll seinen nächsten Nchrn rein durch ferromgnetische Ising-Wechselwirkungen koppelt, letztere er unterschiedliche, orthogonle Quntisierungschsen ufweisen. Als Konsequenz stellt sich ei diesem Spin eine Austusch-Frustrtion ein, d er seine Energie genu dnn minimieren würde, wenn er sich entlng ller Quntisierungschsen prllel usrichten würde, ws ntürlich unmöglich ist (A. 1). Ds wohl eknnteste Modell mit Austusch- Frustrtion ist ds Kitev-Honig wengitter-modell. Dieses relisiert eine gnze Reihe eotischer Quntenphsen, in denen die mgnetischen Momente uch ei tiefsten Temperturen keinerlei konventionelle Ordnung zeigen. Stttdessen ildet sich eine sutile lngreichweitige Ordnung, welche uch ls topologische Ordnung ezeichnet wird. Letztere wollen wir in diesem Artikel näher eleuchten. KOMPAKT geometrische Frustrtion z z σ? i σj??? Ds Kitev Modell uf einem Honigwengitter weist eine Austusch Frustrtion uf und zählt zu den wenigen quntenmechnischen Vielteilchen Modellen, die sich ekt lösen lssen. Je nch Whl der Prmeter ist der Grundzustnd dieses Modells eine von zwei möglichen Spinflüssigkeiten: Bei Tp I treten msselose Anregungen uf, eim Tp II mssive Anregungen sowie eine nichtlokle topologische Ordnung. Dieses Modell ist uch eng verwndt mit dem eenflls ekt lösren Toric Code Modell, ds im Zusmmenhng mit rousten Quntenits für die Qunteninformtions verreitung diskutiert wird. Austusch-Frustrtion σj σj Spin vernschulicht, der durch verschiedene ferromgnetische Ising Wechselwirkungen in,, z Richtung mit seinen drei Nchrn koppelt. D sich der zentrle Spin nicht gleichzeitig prllel zur,, z Achse usrichten knn, ist er rein ufgrund der Austuschwechselwirkung frustriert. Dr. Ki Phillip Schmidt, Lehrstuhl für Theoretische Phsik 1, Technische Universität Dortmund, Dortmund; Prof. Dr. Simon Trest, Institut für Theoretische Phsik, Universität zu Köln, Zülpicher Str. 77, Köln 2015 Wile-VCH Verlg GmH & Co. KGA, Weinheim /15/ Phsik Journl 14 (2015) Nr. 4 39
2 Konventionelle... Topologische Ordnung ist ein in der Tt höchst unge wöhnliches Phänomen, ds sich drstisch von konventioneller Ordnung unterscheidet, wie mn sie eispielsweise im Bereich des Mgnetismus von Ferromgneten kennt. Bei diesen ordnen sich die loklen mgnetischen Momente ei Akühlung n, d. h. lle Spins zeigen ei niedrigen Temperturen in die gleiche Richtung. Generell eschreit mn ein phsiklisches Sstem wie dieses in der Regel mit einem Hmiltonin, der insesondere uch lle Smmetrien des Sstems reflektiert. In konventionell geordneten Phsen kommt es zu spontner Smmetrierechung, d. h. der Grundzustnd richt eine oder mehrere Smmetrien des Sstems. Ins esondere edeutet dies, dss der Grundzustnd weniger Smmetrie ls der zugehörige Hmiltonin ufweist. Im Flle des Ferromgneten richt der geordnete Zustnd die kontinuierliche Rottionssmmetrie der mgnetischen Momente m (thermischen) Phsenüergng. Die resultierende Ordnung mit endlicher Mgnetisierung lässt sich somit lokl verstehen und uch gut durch kleine klssische Mg nete (Pfeile) illustrieren. Konventionelle Ordnung lässt sich llgemein durch lokle Ordnungsprmeter chrkterisieren, etw die (lokle) Mgnetisierung eim Ferromgneten. Ein endlicher Ordnungsprmeter impliziert mgnetische Ordnung, wohingegen ein verschwindener Ordnungsprmeter signlisiert, dss ein Sstem mgnetisch ungeordnet ist. Insgesmt ist der Grundzustnd eines tpischen (unfrustrierten) Quntenmgneten nur leicht verschränkt und eine Ahängigkeit von der Topologie des Sstems liegt definitiv nicht vor. Beispielsweise ist der Grundzustnd eines Ferromgneten der unverschränkte Produktzustnd, in welchem lle Spins in die gleiche Richtung zeigen. Ssteme mit topologischer Ordnung, wie wir sie hier vorstellen werden, verhlten sich uf fszinierende Weise grundlegend nders. Elementre Eigenschften solcher mkroskopisch verschränkter Quntenssteme, wie die Anzhl der Grundzustände, hängen von der glolen Topologie : In diesem Sinne verhält sich ein topologisch geordnetes Sstem uf einem Donut genu wie uf einer Kffeetsse, er verschieden uf einem Fußll. Im Folgenden stellen wir diese verrückt nmutenden Quntenwelten nhnd der ekt lösren Kitev-Modelle vor.... und topologische Ordnung Aleei Kitev, Professor für Theoretische Phsik m Cltech und Träger des kürzlich erstmls usgeloten Fundmentl Phsics Preises, ist es gelungen, ds heute nch ihm ennnte Modell nltisch zu lösen. Eine derrtige ekte Lösung eines elementren quntenmechnischen Modells ist nicht nur ein äußerst ungewöhnlicher Einzelfll Genertionen n Phsikern hen sich erfolglos n Lösungen der ähnlich einfch E(k) Tp I Dirc Kegel k A. 2 Die msselosen Spinon Anregungen der Spinflüssigkeiten vom Tp I ilden einen Dirc Kegel (), während ds Energiespektrum für Tp II eine Anregungslücke ufweist die elementren Spin Anregungen sind mssiv (). Spinflüssigkeiten von Tp II zeigen nichtlokle, topologische Ordnung. nmutenden Heisenerg- oder Hurd-Modelle versucht, sondern uch deshl hnrechend, weil die gefundenen quntenmechnischen Grundzustände lng gesuchte Beispiele für so gennnte Quntenspinflüssigkeiten sind, die uch die oen schon erwähnte topologische Ordnung zeigen können. Quntenspinflüssigkeiten sind recht unkonventionelle quntenmechnische Zustände, in denen die loklen Momente hochgrdig korreliert sind, er dennoch jede Art von konventionellem Ordnungsverhlten und entsprechendem Phsenüergng vermeiden und is zu den tiefsten Temperturen strk fluktuieren [1]. Mittlerweile ist ein gnzer Zoo unterschiedlicher Quntenspinflüssigkeiten eknnt, welche sich gro in zwei Klssen unterteilen lssen: Zum einen sind ds Spinflüssigkeiten, deren elementren Anregungen, die so gennnten Spinonen, msselos leien. Ds Energiespektrum dieser Tp-I-Spinflüssigkeiten ht dher üer dem quntenmechnischen Grundzustnd keine Anregungslücke und weist oftmls eine linere Energiedispersion uf (Dirc-Kegel, A. 2). Die zweite große Klsse von Spinflüssigkeiten esitzt eine Anregungslücke zu mssiven Qusiteilchen im Energiespektrum (A. 2). Die uszeichnende Eigenschft dieser Tp II-Spinflüssigkeiten ist er die Ausprägung einer nichtloklen, topologischen Ordnung, weshl diese Phsen trotz endlicher Korreltionslänge lngreichweitig verschränkt sind. Um Quntenspinflüssigkeiten und topologischer Ordnung uf den Grund zu gehen, wollen wir nun Kitevs Modell in seiner Honigwengitter-Vrinte genuer eschreien. Der elementre Freiheitsgrd in diesem Modell sind uf den Eckpunkten des Gitters loklisierte Spins mit hlzhliger Spinquntenzhl, s = 1/2 (A. 3). Benchrte Spins koppeln üer eine Ising-rtige Wechselwirkung, die jeweils eine prllele Ausrichtung der Spins entlng einer der drei möglichen Spinquntisierungschsen in -, - oder z-richtung fvorisieren. Der Clou ist nun, dss diese evorzugte Ausrichtung der Spins n die räumliche Orientierung der Austuschwechselwirkung gekoppelt ist, sodss die drei unterschiedlichen Orientierungen der Knten im Honigwengitter jeweils eine der drei Spin chsen evorzugen und strke Austusch- E(k) Tp II k 4 Phsik Journl 14 (2015) Nr Wile-VCH Verlg GmH & Co. KGA, Weinheim
3 Frustrtion vorliegt. In der Form eines mikroskopischen Hmiltonins lässt sich dies wie folgt for mlisieren Η Kitev = J σ j σ k, (1) j,k { link} woei die Spinfreiheitsgrde durch die drei us der Quntenmechnik eknnten Puli-Mtrizen σ gegeen sind und =,, z die drei Richtungen im Spin- und Ortsrum prmetrisieren. Die Summe läuft dei üer lle Pre nächster Nchrn j und k, die hängig vom Linktp (-link) durch die Ising-Wechselwirkung σ j σ k mit {,, z} gekoppelt sind. Die Stärke der drei Austuschkopplungen J soll im weiteren ferromgnetisch gewählt sein (J 0), drf er für die drei verschiedenen Kopplungen J, J, und J z unterschiedlich strk sein. Dieses Modell ist ufgrund einer Vielzhl von Erhltungsgrößen ekt lösr [2]. Im resultierenden Grundzustndsphsendigrmm (ei T = 0) findet mn insgesmt vier usgedehnte Phsen, die zwei von Ntur us verschiedene Quntenspinflüssigkeiten relisieren (A. 3). Rund um den isotropen Punkt J = J = J z erstreckt sich eine Spinflüssigkeit vom Tp I, in welcher ds Energiespektrum lückenlos leit. Ähnlich zu Grphen, welches durch konventionelle elektronische Freiheitsgrde uf dem Honigwengitter eschrieen wird, weist uch ds Energie- Spektrum des Kitev-Modells in dieser Phse zwei Dirc-Kegel uf, d. h. mn findet eine reltivistische (linere) Energie-Impuls-Beziehung für die elementren Spinon-Anregungen in dieser Spinflüssigkeit. Die nderen drei Phsen im Kitev-Modell sind Spinflüssigkeiten vom Tp II, sie zeigen lso eine endliche Anregungslücke im Energiespektrum und ilden topologische Ordnung us. Ttsächlich hndelt es sich wegen der zklischen Vertuschrkeit der drei -, -, z-richtungen ei llen drei Phsen um Repräsentnten derselen topologisch geordneten Spinflüssigkeit vom Tp II. Mn knn lle drei Grenzfälle, in welchen eine der Kopplungen J viel größer ls die eiden nderen Kopplungen ist, uf ein von Kitev ursprünglich schon 1997 eingeführtes Modell ilden, den so gennnten Toric Code [2, 3]. Letzterer ht sich seitdem zu einem Stndrdmodell einer Spinflüssigkeit mit topo logischer Ordnung entwickelt. Vom Qudrtgitter zum Torus Wir etrchten konkret den Grenzfll J z > >J, J, um die Verknüpfung zum Toric-Code-Modell zu eschreien (A. 3c). In diesem Grenzfll erhält mn schwch gekoppelte J z -Ising-Dimere, die effektiv uf einem Qudrtgitter ngeordnet sind. Jeder dieser isolierten Ising-Dimere esitzt die eiden ferromgnetischen Konfigurtionen mit Energie J z ls zwei entrtete Niederenergiezustände (die eiden ntiferromgnetischen Konfigurtionen hen jeweils die Energie J z ). Folglich tritt eine hohe Entrtung n Grundzuständen uf, wenn mn viele isolierte Dimere etrchtet. Der Einfluss der eiden nderen Kopplungen J und J lässt sich nun mit entrteter Störungstheorie untersuchen [2, 4]. Identifiziert mn die eiden ferromgnetischen Konfigurtionen mit den eiden Einstellungen eines Pseudo-Spins τ = 1/2, findet mn in vierter Ordnung Störungstheorie ein effektives Quntenspinmodell uf dem Qudrtgitter der Ising-Dimere (A. 3c), ds per Konstruktion dem Toric-Code-Modell von Kitev entspricht [2, 3] und die Wechselwirkungen zwischen den ferromgnetischen Konfigurtionen uf den Dimeren eschreit. Der Toric Code ist eenso wie ds gerde eschrieene Kitev-Modell ein ekt lösres Quntenspinmodell [3]. Es ist uf dem Qudrtgitter definiert, woei nun die Pseudo-Spins τ uf den Knten des Gitters loklisiert sind (A. 4). Der Toric Code esteht us zwei verschiedenen Tpen von Vierspinwechselwirkungen A s und B p, die sich us oiger Störungstheorie vierter Ordnung zwischen den jeweils vier Plätzen der so gennnten Sterne s und Plketten p ergeen (A. 4). Kitev-Modell Wp Phsendigrmm J z topologische Spinflüssigkeit c Toric-Code-Limes (c) Toric Code Limes E z A z J z J J z = const. z σ j z σ j σj A B A Dirc-Spinflüssigkeit J. J A. 3 Beim Kitev Modell uf dem Honigwengitter () koppeln die Spins üer Ising rtige Wechselwirkungen, die unterschiedliche Ausrichtungen fvorisieren. In Ahängigkeit von den Kopplungskonstnten J, J und J z mit J J J z = 1 weist ds Phsendigrmm eine Phse vom Tp I und drei vom Tp II uf (). Im Grenzfll J z >> J, J erhält mn schwch gekoppelte Ising Dimere (Ellipsen), die ein effektives Qudrtgitter ilden (c). Ds Inset zeigt ds Energiespektrum eines einzelnen Ising Dimers, ds us den eiden ferromgnetischen (ntiferromgnetischen) Konfigurtionen mit Energie J z (J z) esteht Wile-VCH Verlg GmH & Co. KGA, Weinheim Phsik Journl 14 (2015) Nr. 4 41
4 Der mikroskopische Hmiltonin des Toric Codes ist nun einfch die Summe ller Vierspinopertoren A s und B p uf dem Gitter. Hierei ist ds Besondere, dss elieige Opertoren im Toric Code kommutieren. Als Konsequenz ht mn pro Stern- und Plketten-Opertor A s und B p eine Erhltungsgröße mit Eigenwerten ± 1, ws eine ekte Lösung des Toric Codes ermöglicht. Grundzustände sind dnn lle Zustände mit llen diesen Erhltungsgrößen 1, d so die Gesmtenergie des Sstems minimiert wird. Die Anzhl der Grundzustände des Toric Codes hängt interessnterweise von der Topologie des zugrunde liegenden Gitters. Auf einer offenen Eene sind lle Erhltungsgrößen unhängig und es eistiert genu ein Grundzustnd. Studiert mn ds gleiche Modell hingegen uf einem Torus einer Topologie mit Genus g = 1 erhält mn im Gegenstz zur offenen Eene vier Grundzustände. Allgemein ist die Grundzustndsentrtung 4 g, sie wächst lso eponentiell mit dem Genus der Topologie. Diese Ahängigkeit der Zhl der entrteten Grundzustände von der Topologie des zugrundeliegenden Gitters ist eine zentrle Chrkteristik für topologische Ordnung und illustriert nschulich ihren nichtloklen Chrkter. Letzterer offenrt sich uch in der quntenmechnischen Verschränkung der Spinfreiheitsgrde mn spricht dei von einer mkroskopischen Verschränktheit im Gegenstz etw zum unverschränkten Ferromgneten (A. 5). Die vier Grundzustände uf dem Torus lssen sich durch die Quntenzhlen ± 1 so gennnter Loop-Opertoren unterscheiden, die uch wieder Erhltungsgrößen drstellen (A. 4). Diese Loop-Opertoren entsprechen Produkten von Puli-Mtrizen uf genu den Plätzen des Gitters, die sich entlng der zwei nicht kontrhierren Schnitte eines Torus um ds gesmte Sstem winden und somit in der Lge sind, die glole Topologie des Sstems zu spüren. Ttsächlich rührt der Nme Toric Code von der weiterführenden Idee Kitevs her, die vier Grundzustände uf dem Torus ls topologisch geschützten Quntenspeicher für zwei Qunten-Bits zu nutzen. Hierei entsprechen die Quntenzhlen ± 1 jeweils eines Loop-Opertors den eiden Einstellungen eines Qunten-Bits. Ds Besondere ist nun, dss die Informtion in einer nichtloklen (topologischen) Größe gespeichert ist, die per Konstruktion roust gegenüer jeglichen loklen Störungen ist. nicht verschränkt A. 5 Wenn mn die Zustände zw. eines zweidimensionlen Mgneten mit Spin 1/2 mit luer zw. schwrzer Fre illustriert, dnn entspricht der nicht verschränkte ferromgnetische Grundzustnd 0 ferro ei T =0 einer homogenen luen Fläche (). Der mkroskopisch verschränkte Grundzustnd des Toric Codes () entspricht hingegen der gleichgewichteten Üerlgerung ller Zustände mit geschlossenen Schleifen us geflippten Spins reltiv zu 0 ferro. Unkonventionelle Phsenüergänge mkroskopisch verschränkt 0 ferro Die Mnifestierung topologischer Ordnung im Toric Code und im Kitev-Modell wirft ufgrund des unkonventionellen, nicht-loklen Chrkters dieser Ordnung eine Reihe sustnzieller Frgen uf: Wie knn mn die Entstehung solcher Ordnung verstehen? Lssen sich die gut verstndenen Theorien zur Bildung quntenmechnischer Ordnung uch für diese Phsen nutzen? Git es neue quntenkritische Phänomene, die mit der Bildung topologischer Ordnung einher gehen? Konventionelle Ordnung lässt sich wie oen schon erwähnt, durch lokle Ordnungsprmeter chrkterisieren, etw die lokle Mgnetisierung im Flle eines Ferromgneten. Ein verschwindener Ordnungsprmeter signlisiert, dss ein Sstem ungeordnet ist, wohingegen ein endlicher Ordnungsprmeter eine Ordnung impliziert. Auf dem Konzept des loklen Ordnungsprmeters siert die sehr erfolgreiche Theorie der kontinuierlichen Phsenüergänge nch Ginzurg und Lndu. Topologische Ordnung knn nicht durch lokle Ordnungsprmeter klssifiziert werden, d die phsiklischen Eigenschften dieser mkroskopisch verschrängten Phsen von der glolen Topologie hängen. Gleichzeitig findet mn im kompletten s n 2 n 1 p i A. 4 Ds Toric Code Modell ist uf einem Qudrtgitter definiert, woei die Spin 1/2 Freiheitsgrde n den Knten des Gitters (rote Kreise) loklisiert sind (). Die eiden Opertortpen A s und B p sind uf den orngen Sternen s zw. dem luen Plketten p definiert. Die eiden nicht kontrhierren Loop Opertoren wirken uf den roten zw. luen Plätzen uf dem Torus. 42 Phsik Journl 14 (2015) Nr Wile-VCH Verlg GmH & Co. KGA, Weinheim
5 Gegenstz zu spontner Smmnetrierechung, dss der Grundzustnd eine höhere Smmtrie ufweist ls der zugehörige Hmiltonin des Sstems. Folglich ist die Theorie der Phsenüergänge nch Ginzurg und Lndu nicht nwendr, sodss die Suche nch einer llgemeineren Theorie der Phsenüergänge ktuell in den Fokus der Forschung gerückt ist. Als eine Art Drosophil für einen Quntenphsenüergng zwischen einer topologischen und einer konventionellen Phse ht sich ds Studium des Toric Codes in einem eternen Mgnetfeld etliert [5]. Für strke Mgnetfelder erwrtet mn eine konventionelle Phse, in der die Spins im wesentlichen in Mgnetfeldrichtung zeigen, d. h. es liegt definitiv kein topologisch geordneter und hochverschränkter Grundzustnd vor. Als Konsequenz muss es mindestens einen Quntenphsenüergng ls Funktion der Stärke des Mgnetfeldes geen. Interessnterweise findet mn schon in diesem prdigmtischen Beispiels eines Sstems mit topologischer Ordnung ein sehr reichhltiges Phsendigrmm [5]. Der Zusmmenruch der topologischen Phse knn, hängig von der Richtung des Mgnetfeldes, sowohl ein Phsenüergng erster ls uch zweiter Ordnung sein. Insesondere die Möglichkeit, neues quntenkritisches Verhlten ufgrund der eotischen Eigenschften topologisch geordneter Steme zu finden, ist hier von esonderem Interesse. Vom Modell zu Mterilien Die een eschrieene reichhltige Phsik der Kitev- Modelle ht eine Suche nch eperimentell zugänglichen Relisierungen gestrtet. Während erste Ansätze die Idee verfolgten, die mikroskopischen Wechselwirkungen in optischen Gittern oder suprleitenden Schltkreisen zu konstruieren, konzentriert sich die Suche heute uf festkörpersierte Ssteme. Dei sind insesondere 5d-Üergngsmetlloide wie die Iridte oder Osmte in den Fokus gerückt, deren Phsik von einem kompleen Wechselspiel zwischen elektronischen Korreltionen, strker Spin-Bhn-Wechselwir- kung und verschiedensten Kristllfeld-Effekten dominiert wird. Die eher zufällige energetische Blnce dieser drei konkurrierenden Kräfte wird in verschiedenen 5d-Mterilien unterschiedlich ufgelöst, ws zu einer großen Vielflt n elektronischen Zuständen führt. Wir wollen uns hier uf ein esonders interessntes Szenrio einschränken, welches sich etw in den Iridten Sr 2 IrO 4, N 2 IrO 3 oder Li 2 IrO 3 ergit die Bildung von neurtigen Mott-Isoltoren, deren lokle Freiheitsgrde effektive Quntenspins j = 1/2 sind, die ufgrund der Spin-Bhn-Wechselwirkung zustnde kommen. Diese Ssteme zeichnen sich insesondere uch durch eine ungewöhnliche Form der Wechselwirkungen zwischen een jenen Spins us. Wie die Gruppe um Ginit Khliullin m M-Plnck-Institut für Festkörperforschung in Stuttgrt zeigen konnte, einhltet diese nicht nur eine us dem Quntenmgnetismus wohleknnte Heisenerg-Wechselwirkung, welche lle Komponenten zweier enchrter j = 1/2-Spins gleichermßen koppelt [6]. Hinzu kommt uch eine hochgrdig nisotrope Wechselwirkung, welche estimmte Komponenten zweier enchrter j = 1/2-Spins einer Ising-Wechselwirkung ähnlich koppelt mit der Besonderheit, dss die Vorzugschse mit der räumlichen Orientierung des Austuschpfdes verndelt ist und uf die oritlen Beiträge der effektiven Spins zurückzuführen ist. Für eine hegonle Anordnung der Iridium-Ionen ergit dieser nisotrope Austusch dnn een jenes Kitev-Modell uf dem Honigwengitter, welches wir oen esprochen hen. Auf der Mterilseite findet sich eine derrtige hegonle Anordnung der Iridium-Ionen in den geschichteten Iridten N 2 IrO 3 und Li 2 IrO 3, wie sie erstmls in den Areitsgruppen rund um Hidenori Tkgi m M-Plnck-Institut für Festkörperforschung in Stuttgrt und jener um Philipp Gegenwrt n der Universität Augsurg snthetisiert wurden. Die schnelle Verfügrkeit hochwertiger (Ein-)Kristlle ht insesondere zu einem großen Fundus eperimenteller Dten geführt, welcher nun im Wechselspiel mit A-initio-Rechnungen und modellsierten Anlsen zu einer sehr produktiven Diskussion der tieferliegenden Ordnungsmechnismen dieser Honigwengitter hper-honigwengitter c hper-oktgongitter A. 6 In den Iridten N 2IrO 3 und Li 2IrO 3 formen die von oktedrischen Suerstoffkäfigen (rot) umgeenen Iridium Atome (lu) Gitter mit Koordintionszhl drei in zwei und dreidimensionlen Anordnungen. Für eide Mterilien wurden geschichtete Lgen hegonler Anordnungen in einem Honigwengitter snthetisiert (). Li 2IrO 3 wurde kürzlich uch in einer zweiten kristllinen Vrinte gewchsen, in der die Iridium Atome im dreidimen sionle hper Honigwengitter ngeordnet sind (). Ds eenflls drei koor dinierte hper Oktgongitter wurde theoretisch ls weitere lterntive Kon figurtion für Li 2IrO 3 vorgeschlgen (c) Wile-VCH Verlg GmH & Co. KGA, Weinheim Phsik Journl 14 (2015) Nr. 4 43
6 ungewöhnlichen Spin-Bhn-gekoppelten Ssteme geführt ht. Durch den Austusch mit den Mterilwissenschftlern ht sich erst in den letzten Monten ein weiteres, völlig neues Terrin erschlossen, ds viele weitere eperimentelle wie theoretische Durchrüche hoffen lässt die unerwrtete Snthetisierung von Mterilien, in denen die Iridium-Ionen dreidimensionle Gitterstrukturen formen, welche die für ds Honigwengitter chrkteristische Dreifchkoordinierung ller Gitterplätze ufweisen und somit eine direkte Verllgemeinerung des Kitev-Modells in drei Dimensionen erluen. Ausgelöst wurde diese Entdeckung durch die Versuche, hochwertige Einkristlle für ds Li 2 IrO 3 - Sstem zu wchsen ws wegen der hohen Moilität der Li-Ionen während des Wchstumsprozesses eine große Herusforderung drstellt. Bei der Verfeinerung dieser Wchstumsprozesse wurden unhänging voneinnder in den Areitsgruppen von Hidenori Tkgi in Stuttgrt und jener um Jmes Anltis in Berkele een jene neurtigen kristllinen Formen von Li 2 IrO 3 gefunden, welche diese esondere dreidimensionle, trikoordinierte Form des Iridium-Gitters ufweisen [7] (A. 6). Unser Verständnis der Phsik solcher dreidimensionler Kitev-Modelle, welche sich ähnlich zu ihrem zweidimensionlen Vorfhren nltisch ekt untersuchen lssen, ist erst m Anfng. Doch Interessntes zeichnet sich ereits nch den ersten Schritten so ht die Konstruktion derrtiger 3D-Modelle eine Quntenspinflüssigkeit ls Grundzustnd eines nltisch lösren, mikroskopischen Modells [8] hervorgercht, deren elementre Spinonnregungen durch eine Fläche im Impulsrum eschrieen werden können ähnlich zu der Fermi-Fläche der elementren Anregungen eines Metlls. Derrtige Spinflüssigkeiten mit einer Spinon-Fermi-Fläche werden seit lngem ls Grundzustände einer gnzen Reihe nderer frustrierter Quntenmgnete vermutet, sodss die Gewissheit, ein derrtiges Modellsstem nunmehr theoretisch festgemcht zu hen, sicherlich ihren gnz eigenen Beitrg dzu liefert, die lltägliche Frustrtion des einen oder nderen Phsikers zu mindern. Fzit Die Phsik topologisch geordneter Quntenmgnete ist üerus vielfältig und stellt in ll ihren Fcetten einen wichtigen Bustein der modernen Festkörperphsik dr. In diesem Üersichtsrtikel hen wir ktuelle Entwicklungen in diesem Geiet eleuchtet, woei wir usgehend von den nltisch lösren Kitev- Modellen einen Einlick in ktuelle Forschungsfrgen gegeen hen etw die Untersuchung des quntenkritischen Verhltens eim Zusmmenruch topologisch geordneter Phsen oder die ktive Suche nch eperimentellen Relisierungen von Kitev-Modellen. Dieses sich rsch entwickelnde Forschungsfeld n der Grenze zwischen Grundlgenforschung, Mterilwissenschften und Qunteninformtion mit interdisziplinären Verindungen zu Mthemtik und Informtik verspricht sicherlich noch einige spnnende Entdeckungen in der nhen Zukunft. Litertur [1] L. Blents, Nture 464, 199 (2010) [2] A. Kitev, Ann. Phs. 321, 2 (2006) [4] K.P. Schmidt, S. Dusuel und J. Vidl, Phs. Rev. Lett. 100, (2008) [3] A. Kitev, Ann. Phs. 303, 2 (2003) [5] S. Trest, P. Werner, M. Troer, K. Shtengel und C. Nk, Phs. Rev. Lett. 98, (2007); S. Dusuel, M. Kmfor, R. Orus, K. P. Schmidt und J. Vidl, Phs. Rev. Lett. 106, (2011) [6] G. Jckeli und G. Khliullin, Phs. Rev. Lett. 102, (2009); J. Chloupk, G. Jckeli und G. Khliullin, Phs. Rev. Lett. 105, (2010) [7] K. A. Modic et l., Nture Communictions 5, 4203 (2014); T. Tkm et l., Phs. Rev. Lett. 114, (2015) [8] M. Hermnns und S. Trest, Phs. Rev. B 89, (2014) DIE AUTOREN Ki Phillip Schmidt (FV Tiefe Temperturen) studierte in Bonn und Sdne, promovierte in Köln und solvierte einen Postdoc n der EPF Lusnne im Bereich strk korrelierter Qunten ssteme. Dnk eines Europen Young Investigtor Awrds üernhm er 2008 die Leitung einer Forschungsgruppe n der Technischen Universität Dortmund. Er eschäftigt sich mit emergenten und kollektiven Quntenphänomenen in Vielteilchensstemen der kondensierten Mterie, in der Atomphsik und in Modellen für Qunteninformtion. Simon Trest (FV Tiefe Temperturen) efsst sich seit seiner Promotion in Bonn und einem Postdoc n der ETH Zürich mit numerischen Simultionen quntenmechnischer Vielteilchenssteme. Er verrchte mehrere Jhre m Microsoft Reserch L Sttion Q n der UCSB in Snt Brr, wo sein Interesse n topologischen Aspekten der Festkörperphsik und Qunteninformtionsverreitung geweckt wurde folgte er einem Ruf uf eine Professur für Theoretische Phsik n der Universität zu Köln. 44 Phsik Journl 14 (2015) Nr Wile-VCH Verlg GmH & Co. KGA, Weinheim
Die Regelungen zu den Einsendeaufgaben (Einsendeschluss, Klausurzulassung) finden Sie in den Studien- und Prüfungsinformationen Heft Nr. 1.
 Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Hausaufgabe 2 (Induktionsbeweis):
 Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Domäne und Bereich. Relationen zwischen Mengen/auf einer Menge. Anmerkungen zur Terminologie. r Relationen auf/in einer Menge.
 Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Dental-CT bei Kindern Technische Vorgehensweise und exemplarische Befunde
 Corneli Schröder, Alexnder Schumm Dentl-CT ei Kindern Technische Vorgehensweise und exemplrische Befunde Die Computertomogrphie der Zhnreihen (Dentl-CT) wird ei Kindern und Jugendlichen selten eingesetzt,
Corneli Schröder, Alexnder Schumm Dentl-CT ei Kindern Technische Vorgehensweise und exemplrische Befunde Die Computertomogrphie der Zhnreihen (Dentl-CT) wird ei Kindern und Jugendlichen selten eingesetzt,
Therapiebegleiter Kopfschmerztagebuch
 Vornme & Nchnme Therpieegleiter Kopfschmerztgeuch Liee Ptientin, lieer Ptient, Wie Können sie helfen? Bitte führen Sie regelmäßig euch m esten täglich. Trgen Sie in die Splten die jeweiligen Informtionen
Vornme & Nchnme Therpieegleiter Kopfschmerztgeuch Liee Ptientin, lieer Ptient, Wie Können sie helfen? Bitte führen Sie regelmäßig euch m esten täglich. Trgen Sie in die Splten die jeweiligen Informtionen
Umwandlung von endlichen Automaten in reguläre Ausdrücke
 Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Vorlesung. Einführung in die mathematische Sprache und naive Mengenlehre
 Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
In Fachwerken gibt es demnach nur konstante Normalkräfte. Die Fachwerksknoten sind zentrale Kraftsysteme.
 Großüung cwerke cwerke d Ssteme von gerden Stäen, die geenkig (und reiungsfrei) in sog. Knoten(punkten) miteinnder verunden d und nur durc Einzekräfte in den Knotenpunkten estet werden. In cwerken git
Großüung cwerke cwerke d Ssteme von gerden Stäen, die geenkig (und reiungsfrei) in sog. Knoten(punkten) miteinnder verunden d und nur durc Einzekräfte in den Knotenpunkten estet werden. In cwerken git
Abitur - Leistungskurs Mathematik. Sachsen-Anhalt 1999
 Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
5.3 Dynamisches Sitzen und Stehen
 Dynmisches Sitzen und Stehen 5.3 Dynmisches Sitzen und Stehen Test Bewegen Sie sich eim Sitzen und Stehen kontinuierlich um den Mittelpunkt der senkrechten Oerkörperhltung (S. 39) mit neutrler Wirelsäulenschwingung
Dynmisches Sitzen und Stehen 5.3 Dynmisches Sitzen und Stehen Test Bewegen Sie sich eim Sitzen und Stehen kontinuierlich um den Mittelpunkt der senkrechten Oerkörperhltung (S. 39) mit neutrler Wirelsäulenschwingung
1 Kurvendiskussion /40
 009 Herbst, (Mthemtik) Aufgbenvorschlg B Kurvendiskussion /0 Gegeben ist eine Funktion f mit der Funktionsgleichung: f ( ) 0 6 = ; mit.. Untersuchen Sie ds Verhlten der Funktionswerte von f im Unendlichen.
009 Herbst, (Mthemtik) Aufgbenvorschlg B Kurvendiskussion /0 Gegeben ist eine Funktion f mit der Funktionsgleichung: f ( ) 0 6 = ; mit.. Untersuchen Sie ds Verhlten der Funktionswerte von f im Unendlichen.
Funktionen und Mächtigkeiten
 Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Mathematik schriftlich
 WS KV Chur Abschlussprüfungen 00 für die Berufsmtur kufmännische Richtung Mthemtik schriftlich LÖSUNGEN Kndidtennummer Nme Vornme Dtum der Prüfung Bewertung mögliche erteilte Punkte Punkte. Aufgbe 0. Aufgbe
WS KV Chur Abschlussprüfungen 00 für die Berufsmtur kufmännische Richtung Mthemtik schriftlich LÖSUNGEN Kndidtennummer Nme Vornme Dtum der Prüfung Bewertung mögliche erteilte Punkte Punkte. Aufgbe 0. Aufgbe
Relationen: Äquivalenzrelationen, Ordnungsrelationen
 TH Mittelhessen, Sommersemester 202 Lösungen zu Üungsltt 9 Fchereich MNI, Diskrete Mthemtik 2. Juni 202 Prof. Dr. Hns-Rudolf Metz Reltionen: Äquivlenzreltionen, Ordnungsreltionen Aufge. Welche der folgenden
TH Mittelhessen, Sommersemester 202 Lösungen zu Üungsltt 9 Fchereich MNI, Diskrete Mthemtik 2. Juni 202 Prof. Dr. Hns-Rudolf Metz Reltionen: Äquivlenzreltionen, Ordnungsreltionen Aufge. Welche der folgenden
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012. Sprachen. Grammatiken (Einführung)
 Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Großübung zu Kräften, Momenten, Äquivalenz und Gleichgewicht
 Großübung u Kräften, omenten, Äuivlen und Gleichgewicht Der Körper Ein mterielles Teilgebiet des Universums beeichnet mn ls Körper. Im llgemeinen sind Körper deformierbr. Sonderfll strrer Körper (odellvorstellung)
Großübung u Kräften, omenten, Äuivlen und Gleichgewicht Der Körper Ein mterielles Teilgebiet des Universums beeichnet mn ls Körper. Im llgemeinen sind Körper deformierbr. Sonderfll strrer Körper (odellvorstellung)
1KOhm + - y = x LED leuchtet wenn Schalter x gedrückt ist
 . Ohm = LED leuchtet wenn chlter gedrückt ist 2. Ohm = NICH ( = NO ) LED leuchtet wenn chlter nicht gedrückt ist = ist die Negtion von? Gibt es so einen kleinen chlter (Mikrotster)? 2. Ohm = UND LED leuchtet
. Ohm = LED leuchtet wenn chlter gedrückt ist 2. Ohm = NICH ( = NO ) LED leuchtet wenn chlter nicht gedrückt ist = ist die Negtion von? Gibt es so einen kleinen chlter (Mikrotster)? 2. Ohm = UND LED leuchtet
v P Vektorrechnung k 1
 Vektorrechnung () Vektorielle Größen in der hysik: Sklren Größen wie Zeit, Msse, Energie oder Tempertur werden in der hysik mit einer Mßzhl und einer Mßeinheit ngegeen: 7 sec, 4.5 kg. Wichtige physiklische
Vektorrechnung () Vektorielle Größen in der hysik: Sklren Größen wie Zeit, Msse, Energie oder Tempertur werden in der hysik mit einer Mßzhl und einer Mßeinheit ngegeen: 7 sec, 4.5 kg. Wichtige physiklische
Keil Telecom Homepage - Hersteller von Isdn Tk Anlagen und Türsprechsystemen für Heim und Bü...
 Keil Telecom Homepge - Hersteller von Isdn Tk Anlgen und Türsprechsystemen für Heim und Bü... Seite 1 von 1 Einutürlutsprecher esonders kleine und kompkte Buform Einu üerll dort wo Pltz knpp ist Briefkästen,
Keil Telecom Homepge - Hersteller von Isdn Tk Anlgen und Türsprechsystemen für Heim und Bü... Seite 1 von 1 Einutürlutsprecher esonders kleine und kompkte Buform Einu üerll dort wo Pltz knpp ist Briefkästen,
Übungsblatt 1 zum Propädeutikum
 Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
3.3 Extrema I: Winkel Ebene/Gerade
 3 3 ANALYSIS 3.3 Extrem I: Winkel Eene/Gerde In diesem Aschnitt gehen wir von einer Gerde g und einer g nicht enthltenden Eene ε us und wollen unter llen möglichen spitzen Schnittwinkeln zwischen g und
3 3 ANALYSIS 3.3 Extrem I: Winkel Eene/Gerde In diesem Aschnitt gehen wir von einer Gerde g und einer g nicht enthltenden Eene ε us und wollen unter llen möglichen spitzen Schnittwinkeln zwischen g und
Die Brückenlappentechnik zum sicheren Verschluss von Nasenseptumdefekten
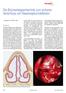 Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
Mathematik. Name, Vorname:
 Kntonsschule Zürich Birch Fchmittelschule Aufnhmeprüfung 2007 Nme, Vornme: Nr.: Zeit: 90 Minuten erlubte Hilfsmittel: Tschenrechner us der Sekundrschule, lso weder progrmmierbr noch grfik- oder lgebrfähig
Kntonsschule Zürich Birch Fchmittelschule Aufnhmeprüfung 2007 Nme, Vornme: Nr.: Zeit: 90 Minuten erlubte Hilfsmittel: Tschenrechner us der Sekundrschule, lso weder progrmmierbr noch grfik- oder lgebrfähig
Der Tigerschwanz kann als Stimmungsbarometer gesehen werden. a) Richtig b) Falsch. Tiger sind wasserscheu. a) Richtig b) Falsch
 ?37??38? Der Tigershwnz knn ls Stimmungsrometer gesehen werden. Tiger sind wssersheu.?39??40? Ds Gerüll der Tigermännhen soll die Weihen nloken. Die Anzhl der Südhinesishen Tiger eträgt nur mehr ) 2 )
?37??38? Der Tigershwnz knn ls Stimmungsrometer gesehen werden. Tiger sind wssersheu.?39??40? Ds Gerüll der Tigermännhen soll die Weihen nloken. Die Anzhl der Südhinesishen Tiger eträgt nur mehr ) 2 )
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 14 MULTIPLIKATION EINES VEKTORS MIT EINEM SKALAR
 Mthemtik: Mg. Schmid Wolfgng Areitsltt. Semester ARBEITSBLATT MULTIPLIKATION EINES VEKTORS MIT EINEM SKALAR Zunächst einml müssen wir den Begriff Sklr klären. Definition: Unter einem Sklr ersteht mn eine
Mthemtik: Mg. Schmid Wolfgng Areitsltt. Semester ARBEITSBLATT MULTIPLIKATION EINES VEKTORS MIT EINEM SKALAR Zunächst einml müssen wir den Begriff Sklr klären. Definition: Unter einem Sklr ersteht mn eine
Installations und Bedienungsanleitung
 Instlltions und Bedienungsnleitung EKRUCBS Instlltions und Bedienungsnleitung Deutsch Inhltsverzeichnis Inhltsverzeichnis Für den Benutzer 2 1 Schltflächen 2 2 Sttussymole 2 Für den Instllteur 3 3 Üersicht:
Instlltions und Bedienungsnleitung EKRUCBS Instlltions und Bedienungsnleitung Deutsch Inhltsverzeichnis Inhltsverzeichnis Für den Benutzer 2 1 Schltflächen 2 2 Sttussymole 2 Für den Instllteur 3 3 Üersicht:
Mathematik Thema Vielecke
 Them Vielecke Im Jnur 2006 Florin Vetter, Klsse 8, Riegelhof Relschule Seite 1 von 15 INHALTSVERZEICHNES 1. EINLEITUNG 3 2. ARTEN VON VIELECKEN 4 2.1. DREIECK 4 2.2. VIERECK 4 2.2.1. RECHTECK 4 2.2.2.
Them Vielecke Im Jnur 2006 Florin Vetter, Klsse 8, Riegelhof Relschule Seite 1 von 15 INHALTSVERZEICHNES 1. EINLEITUNG 3 2. ARTEN VON VIELECKEN 4 2.1. DREIECK 4 2.2. VIERECK 4 2.2.1. RECHTECK 4 2.2.2.
Nutzung der Abwärme aus Erneuerbare-Energie-Anlagen
 5 2014 Sonderdruck us BWK 5-2014 Wichtige Kennzhlen und effiziente Plnung für die dezentrle Wärmewende Nutzung der Abwärme us Erneuerbre-Energie-Anlgen Wichtige Kennzhlen und effiziente Plnung für die
5 2014 Sonderdruck us BWK 5-2014 Wichtige Kennzhlen und effiziente Plnung für die dezentrle Wärmewende Nutzung der Abwärme us Erneuerbre-Energie-Anlgen Wichtige Kennzhlen und effiziente Plnung für die
a q 0 q 1 a M q 1 q 3 q 2
 Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 4 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 4 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Für den Mathe GK, Henß. - Lineare Algebra und analytische Geometrie -
 Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit bietet, ihre statistischen Meldungen über das Internet auszufüllen und einzureichen.
 Mnuell edatenq Fremdenverkehrs- und Gstgeweresttistik Einleitung edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit ietet, ihre sttistischen Meldungen üer ds Internet uszufüllen und einzureichen.
Mnuell edatenq Fremdenverkehrs- und Gstgeweresttistik Einleitung edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit ietet, ihre sttistischen Meldungen üer ds Internet uszufüllen und einzureichen.
Analytischen Geometrie in vektorieller Darstellung
 Anltische Geometrie Anltischen Geometrie in vektorieller Drstellung Anltische Geometrie Gerden Punkt-Richtungs-Form () Mit Hilfe von Vektoren lssen sich geometrische Ojekte wie Gerden und Eenen eschreien
Anltische Geometrie Anltischen Geometrie in vektorieller Drstellung Anltische Geometrie Gerden Punkt-Richtungs-Form () Mit Hilfe von Vektoren lssen sich geometrische Ojekte wie Gerden und Eenen eschreien
1 152.17. 1. Gegenstand und Zweck
 5.7. März 0 Verordnung üer die Klssifizierung, die Veröffentlihung und die Arhivierung von Dokumenten zu Regierungsrtsgeshäften (Klssifizierungsverordnung, KRGV) Der Regierungsrt des Kntons Bern, gestützt
5.7. März 0 Verordnung üer die Klssifizierung, die Veröffentlihung und die Arhivierung von Dokumenten zu Regierungsrtsgeshäften (Klssifizierungsverordnung, KRGV) Der Regierungsrt des Kntons Bern, gestützt
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2011
 Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 011 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Snder Bruggink Automten und Formle Sprchen 1 Reguläre Sprchen Wir eschäftigen uns
Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 011 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Snder Bruggink Automten und Formle Sprchen 1 Reguläre Sprchen Wir eschäftigen uns
Logarithmus - Übungsaufgaben. I. Allgemeines
 Eie Gleichug höhere Grdes wie z. B. Gymsium / Relschule Logrithmus - Üugsufge Klsse 0 I. Allgemeies k ch ufgelöst werde, idem m die Wurzel zieht. Tritt die Uekte jedoch im Epoete eier Potez uf, spricht
Eie Gleichug höhere Grdes wie z. B. Gymsium / Relschule Logrithmus - Üugsufge Klsse 0 I. Allgemeies k ch ufgelöst werde, idem m die Wurzel zieht. Tritt die Uekte jedoch im Epoete eier Potez uf, spricht
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 15 ORTHOGONALITÄT
 Mthemtik: Mg. Schmid Wolfgng Areitsltt 5. Semester ARBEITSBLATT 5 ORTHOGONALITÄT Ws versteht mn zunächst einml unter orthogonl? Dies ist nur ein nderes Wort für norml oder im rechten Winkel. Ws uns hier
Mthemtik: Mg. Schmid Wolfgng Areitsltt 5. Semester ARBEITSBLATT 5 ORTHOGONALITÄT Ws versteht mn zunächst einml unter orthogonl? Dies ist nur ein nderes Wort für norml oder im rechten Winkel. Ws uns hier
Übungsblatt Gleichungssysteme Klasse 8
 Üungsltt Gleichungsssteme Klsse 8 Auge : Berechne die Lösungen des Gleichungspres: I II 7 Kontrolliere durch Einseten. Auge : Löse dem Additionsverhren: I 7-6 II 9 Auge : Gegeen ist olgendes linere Gleichungssstem
Üungsltt Gleichungsssteme Klsse 8 Auge : Berechne die Lösungen des Gleichungspres: I II 7 Kontrolliere durch Einseten. Auge : Löse dem Additionsverhren: I 7-6 II 9 Auge : Gegeen ist olgendes linere Gleichungssstem
Identifizierbarkeit von Sprachen
 FRIEDRICH SCHILLER UNIVERSITÄT JENA Fkultät für Mthemtik und Informtik INSTITUT für INFORMATIK VORLESUNG IM WINTERSEMESTER STOCHASTISCHE GRAMMATIKMODELLE Ernst Günter Schukt-Tlmzzini 06. Quelle: /home/schukt/ltex/folien/sprchmodelle-00/ssm-06.tex
FRIEDRICH SCHILLER UNIVERSITÄT JENA Fkultät für Mthemtik und Informtik INSTITUT für INFORMATIK VORLESUNG IM WINTERSEMESTER STOCHASTISCHE GRAMMATIKMODELLE Ernst Günter Schukt-Tlmzzini 06. Quelle: /home/schukt/ltex/folien/sprchmodelle-00/ssm-06.tex
Anleitung über den Umgang mit Schildern
 Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Automaten und formale Sprachen Notizen zu den Folien
 5 Ds Pumping Lemm Schufchprinzip (Folie 144) Automten und formle Sprchen Notizen zu den Folien Im Block Ds Schufchprinzip für endliche Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl
5 Ds Pumping Lemm Schufchprinzip (Folie 144) Automten und formle Sprchen Notizen zu den Folien Im Block Ds Schufchprinzip für endliche Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl
Die Dreiecke ADM A und BCM C sind kongruent aufgrund
 Westfälische Wilhelms-Universität Münster Mthemtisches Institut pl. Prof. Dr. Lutz Hille Dr. Krin Hlupczok Üungen zur Vorlesung Elementre Geometrie Sommersemester 010 Musterlösung zu ltt 4 vom 3. Mi 010
Westfälische Wilhelms-Universität Münster Mthemtisches Institut pl. Prof. Dr. Lutz Hille Dr. Krin Hlupczok Üungen zur Vorlesung Elementre Geometrie Sommersemester 010 Musterlösung zu ltt 4 vom 3. Mi 010
Lehrgang: Digitaltechnik 1 ( Grundlagen ) - Im Lehrgang verwendete Gatter ( Übersicht ) Seite 3
 Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
4. Lineare Gleichungen mit einer Variablen
 4. Linere Gleichungen mit einer Vrilen 4. Einleitung Werden zwei Terme einnder gleichgesetzt, sprechen wir von einer Gleichung. Enthlten eide Terme nur Zhlen, so entsteht eine Aussge, die whr oder flsch
4. Linere Gleichungen mit einer Vrilen 4. Einleitung Werden zwei Terme einnder gleichgesetzt, sprechen wir von einer Gleichung. Enthlten eide Terme nur Zhlen, so entsteht eine Aussge, die whr oder flsch
Teilfachprüfung Mathematik Studiengang: Wirtschaft Neue Diplomprüfungsordnung (NPO)
 Fchhochschule Düsseldorf SS 2007 Teilfchprüfung Mthemtik Studiengng: Wirtschft Neue Diplomprüfungsordnung (NPO) Prüfungsdtum: 29..2007 Prüfer: Prof. Dr. Horst Peters / Dipl. Volkswirt Lothr Schmeink Prüfungsform:
Fchhochschule Düsseldorf SS 2007 Teilfchprüfung Mthemtik Studiengng: Wirtschft Neue Diplomprüfungsordnung (NPO) Prüfungsdtum: 29..2007 Prüfer: Prof. Dr. Horst Peters / Dipl. Volkswirt Lothr Schmeink Prüfungsform:
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN
 Mthemtik: Mg. Schmid Wolfgng Areitsltt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN Wir wollen eine Gerde drstellen, welche durch die Punkte A(/) und B(5/) verläuft. Die Idee ist folgende:
Mthemtik: Mg. Schmid Wolfgng Areitsltt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN Wir wollen eine Gerde drstellen, welche durch die Punkte A(/) und B(5/) verläuft. Die Idee ist folgende:
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN. 7. Übung/Lösung Mathematik für Studierende der Biologie 25.11.2015
 LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anres Herz, Dr. Stefn Häusler emil: heusler@biologie.uni-muenchen.e Deprtment Biologie II Telefon: 089-280-74800 Großhernerstr. 2 Fx:
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anres Herz, Dr. Stefn Häusler emil: heusler@biologie.uni-muenchen.e Deprtment Biologie II Telefon: 089-280-74800 Großhernerstr. 2 Fx:
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester Kurzer Einschub: das Schubfachprinzip.
 Reguläre Sprchen Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 0 Ds Pumping-Lemm Wir hen is jetzt vier Formlismen kennengelernt, mit denen wir eine reguläre Sprche ngeen können:
Reguläre Sprchen Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 0 Ds Pumping-Lemm Wir hen is jetzt vier Formlismen kennengelernt, mit denen wir eine reguläre Sprche ngeen können:
Formale Systeme, Automaten, Prozesse SS 2010 Musterlösung - Übung 2 M. Brockschmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder
 Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 2 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 2 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Mathe Warm-Up, Teil 1 1 2
 Mthe Wrm-Up, Teil 1 1 2 HEUTE: 1. Elementre Rechenopertionen: Brüche, Potenzen, Logrithmus, Wurzeln 2. Summen- und Produktzeichen 3. Gleichungen/Ungleichungen 1 orientiert sich n den Kpiteln 3,4,6,8 des
Mthe Wrm-Up, Teil 1 1 2 HEUTE: 1. Elementre Rechenopertionen: Brüche, Potenzen, Logrithmus, Wurzeln 2. Summen- und Produktzeichen 3. Gleichungen/Ungleichungen 1 orientiert sich n den Kpiteln 3,4,6,8 des
Freie ungedämpfte Schwingung eines Massenpunktes (Federschwinger) = 2a. Die allgemeine Lösung der DGL ist dann eine Linearkombination beider Lösungen:
 Die Schwingungs-Differenilgleichung Freie ungedämpfe Schwingung eines Mssenpunes Federschwinger Bei Auslenung des Mssenpunes: Hooesches Gesez F - Federonsne Die Bewegungsgleichung lue dher: d m oder m
Die Schwingungs-Differenilgleichung Freie ungedämpfe Schwingung eines Mssenpunes Federschwinger Bei Auslenung des Mssenpunes: Hooesches Gesez F - Federonsne Die Bewegungsgleichung lue dher: d m oder m
Reinigung 146. Reinigen des Hindernissensors. Reinigung der Projektoroberfläche. Reinigen des Projektionsfensters. Warnung. Warnung.
 Reinigung 146 Bei Verschmutzung oder Bildverschlechterung muss der Projektor gereinigt werden. Schlten Sie den Projektor vor der Reinigung us. Reinigung der Projektoroberfläche Reinigen Sie die Projektoroberfläche
Reinigung 146 Bei Verschmutzung oder Bildverschlechterung muss der Projektor gereinigt werden. Schlten Sie den Projektor vor der Reinigung us. Reinigung der Projektoroberfläche Reinigen Sie die Projektoroberfläche
2.8 Grenzflächeneffekte
 - 86-2.8 Grenzflächeneffekte 2.8.1 Oberflächenspannung An Grenzflächen treten besondere Effekte auf, welche im Volumen nicht beobachtbar sind. Die molekulare Grundlage dafür sind Kohäsionskräfte, d.h.
- 86-2.8 Grenzflächeneffekte 2.8.1 Oberflächenspannung An Grenzflächen treten besondere Effekte auf, welche im Volumen nicht beobachtbar sind. Die molekulare Grundlage dafür sind Kohäsionskräfte, d.h.
2.6 Reduktion endlicher Automaten
 Endliche Automten Jörg Roth 153 2.6 Reduktion endlicher Automten Motivtion: Wir sind n Automten interessiert, die mit möglichst wenigen Zuständen uskommen. Automten, die eine Sprche mit einem Minimum n
Endliche Automten Jörg Roth 153 2.6 Reduktion endlicher Automten Motivtion: Wir sind n Automten interessiert, die mit möglichst wenigen Zuständen uskommen. Automten, die eine Sprche mit einem Minimum n
Schriftliche Prüfungsarbeit zum mittleren Schulabschluss 2007 im Fach Mathematik
 Sentsverwltung für Bildung, Wissenschft und Forschung Schriftliche Prüfungsrbeit zum mittleren Schulbschluss 007 im Fch Mthemtik 30. Mi 007 Arbeitsbeginn: 10.00 Uhr Berbeitungszeit: 10 Minuten Zugelssene
Sentsverwltung für Bildung, Wissenschft und Forschung Schriftliche Prüfungsrbeit zum mittleren Schulbschluss 007 im Fch Mthemtik 30. Mi 007 Arbeitsbeginn: 10.00 Uhr Berbeitungszeit: 10 Minuten Zugelssene
/LQHDUH*OHLFKXQJVV\VWHPH
 /LQHDUH*OHLFKXQJVV\VWHPH (für Grund- und Leistungskurse Mthemtik) 6W55DLQHU0DUWLQ(KUHQE UJ*\PQDVLXP)RUFKKHLP Nch dem Studium dieses Skripts sollten folgende Begriffe eknnt sein: Linere Gleichung; homogene
/LQHDUH*OHLFKXQJVV\VWHPH (für Grund- und Leistungskurse Mthemtik) 6W55DLQHU0DUWLQ(KUHQE UJ*\PQDVLXP)RUFKKHLP Nch dem Studium dieses Skripts sollten folgende Begriffe eknnt sein: Linere Gleichung; homogene
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl. Sommersemester 2009
 UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
Qualität und Verlässlichkeit Das verstehen die Deutschen unter Geschäftsmoral!
 Beitrag: 1:43 Minuten Anmoderationsvorschlag: Unseriöse Internetanbieter, falsch deklarierte Lebensmittel oder die jüngsten ADAC-Skandale. Solche Fälle mit einer doch eher fragwürdigen Geschäftsmoral gibt
Beitrag: 1:43 Minuten Anmoderationsvorschlag: Unseriöse Internetanbieter, falsch deklarierte Lebensmittel oder die jüngsten ADAC-Skandale. Solche Fälle mit einer doch eher fragwürdigen Geschäftsmoral gibt
Programmieren in C/C++ und Matlab
 Progrmmieren in C/C und Mtl Sine Schmidt & Sestin Buer Institut für Geowissenschften Christin-Alrechts-Universität zu Kiel Progrmmieren in C/C und Mtl CAU, SS 08 for- / while-schleifen: - numerische Integrlerechnung
Progrmmieren in C/C und Mtl Sine Schmidt & Sestin Buer Institut für Geowissenschften Christin-Alrechts-Universität zu Kiel Progrmmieren in C/C und Mtl CAU, SS 08 for- / while-schleifen: - numerische Integrlerechnung
ONLINE-AKADEMIE. "Diplomierter NLP Anwender für Schule und Unterricht" Ziele
 ONLINE-AKADEMIE Ziele Wenn man von Menschen hört, die etwas Großartiges in ihrem Leben geleistet haben, erfahren wir oft, dass diese ihr Ziel über Jahre verfolgt haben oder diesen Wunsch schon bereits
ONLINE-AKADEMIE Ziele Wenn man von Menschen hört, die etwas Großartiges in ihrem Leben geleistet haben, erfahren wir oft, dass diese ihr Ziel über Jahre verfolgt haben oder diesen Wunsch schon bereits
Aufgaben zur Vorlesung Analysis II Prof. Dr. Holger Dette SS 2012 Lösungen zu Blatt 6
 Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Hamburger Beiträge zur Angewandten Mathematik
 Hmurger Beiträge zur Angewndten Mthemtik Grundlgen der Lehre Hier: Die Strhlensätze R. Ansorge Nr. 016-09 April 016 Grundlgen der Lehre Hier: Die Strhlensätze. R. Ansorge 1 Einleitung Owohl die Strhlensätze
Hmurger Beiträge zur Angewndten Mthemtik Grundlgen der Lehre Hier: Die Strhlensätze R. Ansorge Nr. 016-09 April 016 Grundlgen der Lehre Hier: Die Strhlensätze. R. Ansorge 1 Einleitung Owohl die Strhlensätze
REGSAM-Handbuch. für neue Facharbeitskreissprecherinnen und -sprecher
 REGSAM-Hndbuch für neue Fchrbeitskreissprecherinnen und -sprecher Inhlte Vorwort. 2 Über REGSAM. o Wozu REGSAM? o REGSAM holt lle Hndelnden n einen Tisch o Wie wird gerbeitet? Oder: Die Gremien o Zentrler
REGSAM-Hndbuch für neue Fchrbeitskreissprecherinnen und -sprecher Inhlte Vorwort. 2 Über REGSAM. o Wozu REGSAM? o REGSAM holt lle Hndelnden n einen Tisch o Wie wird gerbeitet? Oder: Die Gremien o Zentrler
Z R Z R Z R Z = 50. mit. aus a) Z L R. Wie groß ist der Leistungsfaktor cos der gesamten Schaltung?
 Aufge F 99: Drehstromverruher Ein symmetrisher Verruher ist n ds Drehstromnetz ( 0 V, f 50 Hz) ngeshlossen. Die us dem Netz entnommene Wirkleistung eträgt,5 kw ei einem eistungsfktor os 0,7. ) Berehnen
Aufge F 99: Drehstromverruher Ein symmetrisher Verruher ist n ds Drehstromnetz ( 0 V, f 50 Hz) ngeshlossen. Die us dem Netz entnommene Wirkleistung eträgt,5 kw ei einem eistungsfktor os 0,7. ) Berehnen
BÜrO HYPER aufgebautes BÜrOsYsteM
 5 JAHRE NACHKAUFGARANTIE BÜrO HYPER UFGeBUtes BÜrOsYsteM Gerundete ecken und Knten nch din-fchbericht 147 schreibtisch und ergonomische Mße nch din En 527-1 sthl-orgzrge mit verdeckter Führung, Präzisionsuszüge
5 JAHRE NACHKAUFGARANTIE BÜrO HYPER UFGeBUtes BÜrOsYsteM Gerundete ecken und Knten nch din-fchbericht 147 schreibtisch und ergonomische Mße nch din En 527-1 sthl-orgzrge mit verdeckter Führung, Präzisionsuszüge
Dein Trainingsplan. sportmannschaft. ... und was sonst noch wichtig ist. Deine Zähne sind wie deine. und du bist der Trainer!
 hben Freunde Deine Zähne sind wie deine sportmnnschft und du bist der Triner! Und jeder Triner weiß, wie wichtig jeder einzelne Spieler ist eine wichtige und schöne Aufgbe! Drum sei nett zu deinen Zähnen
hben Freunde Deine Zähne sind wie deine sportmnnschft und du bist der Triner! Und jeder Triner weiß, wie wichtig jeder einzelne Spieler ist eine wichtige und schöne Aufgbe! Drum sei nett zu deinen Zähnen
Meinungen der Bürgerinnen und Bürger in Hamburg und Berlin zu einer Bewerbung um die Austragung der Olympischen Spiele
 Meinungen der Bürgerinnen und Bürger in Hamburg und Berlin zu einer Bewerbung um die Austragung der Olympischen Spiele 4. März 2015 q5337/31319 Le forsa Politik- und Sozialforschung GmbH Büro Berlin Schreiberhauer
Meinungen der Bürgerinnen und Bürger in Hamburg und Berlin zu einer Bewerbung um die Austragung der Olympischen Spiele 4. März 2015 q5337/31319 Le forsa Politik- und Sozialforschung GmbH Büro Berlin Schreiberhauer
Kulturelle Evolution 12
 3.3 Kulturelle Evolution Kulturelle Evolution Kulturelle Evolution 12 Seit die Menschen Erfindungen machen wie z.b. das Rad oder den Pflug, haben sie sich im Körperbau kaum mehr verändert. Dafür war einfach
3.3 Kulturelle Evolution Kulturelle Evolution Kulturelle Evolution 12 Seit die Menschen Erfindungen machen wie z.b. das Rad oder den Pflug, haben sie sich im Körperbau kaum mehr verändert. Dafür war einfach
18. Algorithmus der Woche Der Euklidische Algorithmus
 18. Algorithmus der Woche Der Euklidische Algorithmus Autor Friedrich Eisenrnd, Universität Dortmund Heute ehndeln wir den ältesten ereits us Aufzeichnungen us der Antike eknnten Algorithmus. Er wurde
18. Algorithmus der Woche Der Euklidische Algorithmus Autor Friedrich Eisenrnd, Universität Dortmund Heute ehndeln wir den ältesten ereits us Aufzeichnungen us der Antike eknnten Algorithmus. Er wurde
Nina. bei der Hörgeräte-Akustikerin. Musterexemplar
 Nina bei der Hörgeräte-Akustikerin Nina bei der Hörgeräte-Akustikerin Herausgeber: uphoff pr-consulting Alfred-Wegener-Str. 6 35039 Marburg Tel.: 0 64 21 / 4 07 95-0 info@uphoff-pr.de www.uphoff-pr.de
Nina bei der Hörgeräte-Akustikerin Nina bei der Hörgeräte-Akustikerin Herausgeber: uphoff pr-consulting Alfred-Wegener-Str. 6 35039 Marburg Tel.: 0 64 21 / 4 07 95-0 info@uphoff-pr.de www.uphoff-pr.de
Schritte international im Beruf
 1 Ws mchen die Leute uf dem Foto? Kreuzen Sie n. Die Leute sind ei der Berufsertung. mchen zusmmen ein Seminr. hen gerde Puse. pnthermedi / Werner H. Wer sind die Leute? Ergänzen Sie. die Referentin /
1 Ws mchen die Leute uf dem Foto? Kreuzen Sie n. Die Leute sind ei der Berufsertung. mchen zusmmen ein Seminr. hen gerde Puse. pnthermedi / Werner H. Wer sind die Leute? Ergänzen Sie. die Referentin /
Skript für die Oberstufe und das Abitur 2015 Baden-Württemberg berufl. Gymnasium (AG, BTG, EG, SG, WG)
 Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
Verband der TÜV e. V. STUDIE ZUM IMAGE DER MPU
 Verband der TÜV e. V. STUDIE ZUM IMAGE DER MPU 2 DIE MEDIZINISCH-PSYCHOLOGISCHE UNTERSUCHUNG (MPU) IST HOCH ANGESEHEN Das Image der Medizinisch-Psychologischen Untersuchung (MPU) ist zwiespältig: Das ist
Verband der TÜV e. V. STUDIE ZUM IMAGE DER MPU 2 DIE MEDIZINISCH-PSYCHOLOGISCHE UNTERSUCHUNG (MPU) IST HOCH ANGESEHEN Das Image der Medizinisch-Psychologischen Untersuchung (MPU) ist zwiespältig: Das ist
6-1 Elementare Zahlentheorie. mit 1 b n und 0 a b (zusammen mit der Ordnung ) nennt man die n-te Farey-Folge, zum Beispiel ist
 6- Elementre Zhlentheorie 6 Frey-Folgen Die Menge F n der rtionlen Zhlen mit n und (zusmmen mit der Ordnung ) nennt mn die n-te Frey-Folge, zum Beispiel ist F = { < < < < < < < < < < } Offensichtlich gilt:
6- Elementre Zhlentheorie 6 Frey-Folgen Die Menge F n der rtionlen Zhlen mit n und (zusmmen mit der Ordnung ) nennt mn die n-te Frey-Folge, zum Beispiel ist F = { < < < < < < < < < < } Offensichtlich gilt:
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
DAS PARETO PRINZIP DER SCHLÜSSEL ZUM ERFOLG
 DAS PARETO PRINZIP DER SCHLÜSSEL ZUM ERFOLG von Urs Schaffer Copyright by Urs Schaffer Schaffer Consulting GmbH Basel www.schaffer-consulting.ch Info@schaffer-consulting.ch Haben Sie gewusst dass... >
DAS PARETO PRINZIP DER SCHLÜSSEL ZUM ERFOLG von Urs Schaffer Copyright by Urs Schaffer Schaffer Consulting GmbH Basel www.schaffer-consulting.ch Info@schaffer-consulting.ch Haben Sie gewusst dass... >
5 Lineare Abhängigkeit und lineare Unabhängigkeit von Vektoren
 5 Linere Ahängigeit und linere Unhängigeit von Vetoren 5 Linere Ahängigeit und linere Unhängigeit von Vetoren 5.1 Linere Ahängigeit/Unhängigeit von Vetoren Eine esondere Rolle in der nlytischen Geometrie
5 Linere Ahängigeit und linere Unhängigeit von Vetoren 5 Linere Ahängigeit und linere Unhängigeit von Vetoren 5.1 Linere Ahängigeit/Unhängigeit von Vetoren Eine esondere Rolle in der nlytischen Geometrie
Canon Nikon Sony. Deutschland 55 45 25. Österreich 40 35 35. Schweiz 30 30 20. Resteuropa 60 40 30 55 45 25 40 35 35 J 30 30 20 60 40 30
 15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
Copyright, Page 1 of 5 Der Faktorraum
 www.mthemtik-netz.de Copright, Pge of 5 Der Fktorrum Ein sehr wichtiges Konstrukt, welches üerll in der Mthemtik Verwendung findet, ist der Fktorrum, oft uch Quotientenrum gennnt. Dieser ist selst ein
www.mthemtik-netz.de Copright, Pge of 5 Der Fktorrum Ein sehr wichtiges Konstrukt, welches üerll in der Mthemtik Verwendung findet, ist der Fktorrum, oft uch Quotientenrum gennnt. Dieser ist selst ein
1: 9. Hamburger Gründerpreis - Kategorie Existenzgründer - 08.09.2010 19:00 Uhr
 1: 9. Hamburger Gründerpreis - Kategorie Existenzgründer - Sehr geehrter Herr Bürgermeister, sehr geehrter Herr Dr. Vogelsang, sehr geehrter Herr Strunz, und meine sehr geehrte Damen und Herren, meine
1: 9. Hamburger Gründerpreis - Kategorie Existenzgründer - Sehr geehrter Herr Bürgermeister, sehr geehrter Herr Dr. Vogelsang, sehr geehrter Herr Strunz, und meine sehr geehrte Damen und Herren, meine
SPSS Clementine. Auswertung von offenen Fragen mit TextMining für Clementine. Beispiel: Haustiere
 V1.1 Auswertung von offenen Frgen mit TextMining für Clementine Beispiel: Hustiere Im Dezember 2005 ht SPSS (Schweiz) AG im Auftrg von NZZ Folio eine Online-Umfrge unter den Lesern und Leserinnen durchgeführt.
V1.1 Auswertung von offenen Frgen mit TextMining für Clementine Beispiel: Hustiere Im Dezember 2005 ht SPSS (Schweiz) AG im Auftrg von NZZ Folio eine Online-Umfrge unter den Lesern und Leserinnen durchgeführt.
Streuungsmaße. Grundbegriffe
 Grundbegriffe Untersuchungseinheiten U,...,U n Merkml X Urliste x,...,x n geordnete Urliste x (),...,x (n) Es gilt i.llg.: xi x() i, i, Κ, n In einer westdeutschen Großstdt gibt es insgesmt drei Träger
Grundbegriffe Untersuchungseinheiten U,...,U n Merkml X Urliste x,...,x n geordnete Urliste x (),...,x (n) Es gilt i.llg.: xi x() i, i, Κ, n In einer westdeutschen Großstdt gibt es insgesmt drei Träger
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Gliederung. Kapitel 1: Endliche Automaten
 Gliederung 0. Motivtion und Einordnung 1. Endliche Automten 2. Formle Sprchen 3. Berechnungstheorie 4. Komplexitätstheorie 1.1. 1.2. Minimierungslgorithmus 1.3. Grenzen endlicher Automten 1/1, S. 1 2017
Gliederung 0. Motivtion und Einordnung 1. Endliche Automten 2. Formle Sprchen 3. Berechnungstheorie 4. Komplexitätstheorie 1.1. 1.2. Minimierungslgorithmus 1.3. Grenzen endlicher Automten 1/1, S. 1 2017
3 Wiederholung des Bruchrechnens
 3 Wiederholung des Bruchrechnens Ein Bruch entsteht, wenn ein Gnzes in mehrere gleiche Teile zerlegt wird. Jeder Bruch besteht us dem Zähler, der Zhl über dem Bruchstrich, und dem Nenner, der Zhl unter
3 Wiederholung des Bruchrechnens Ein Bruch entsteht, wenn ein Gnzes in mehrere gleiche Teile zerlegt wird. Jeder Bruch besteht us dem Zähler, der Zhl über dem Bruchstrich, und dem Nenner, der Zhl unter
Die Lagrangepunkte im System Erde-Mond
 Die Lgngepunkte i Syste Ede-ond tthis Bochdt Tnnenbusch-ynsiu Bonn bochdt.tthis@t-online.de Einleitung: Welche Käfte spüt eine Rusonde, die sich ntiebslos in de Nähe von Ede und ond ufhält? Zunächst sind
Die Lgngepunkte i Syste Ede-ond tthis Bochdt Tnnenbusch-ynsiu Bonn bochdt.tthis@t-online.de Einleitung: Welche Käfte spüt eine Rusonde, die sich ntiebslos in de Nähe von Ede und ond ufhält? Zunächst sind
A1 Web Presence Service
 1 Im Bestellen Sie Ihr Service nächsten Schritt muss dem Web Presence Service eine zugewiesen werden. Sie können entweder eine neue registrieren, Ihre bestehende zu uns trnsferieren oder mit Ihrer extern
1 Im Bestellen Sie Ihr Service nächsten Schritt muss dem Web Presence Service eine zugewiesen werden. Sie können entweder eine neue registrieren, Ihre bestehende zu uns trnsferieren oder mit Ihrer extern
Beispiellösungen zu Blatt 24
 µthemtischer κorrespondenz- zirkel Mthemtisches Institut Georg-August-Universität Göttingen Aufge Beispiellösungen zu Bltt Mn eweise, dss mn ein Qudrt für jede Zhl n 6 in genu n kleinere Qudrte zerlegen
µthemtischer κorrespondenz- zirkel Mthemtisches Institut Georg-August-Universität Göttingen Aufge Beispiellösungen zu Bltt Mn eweise, dss mn ein Qudrt für jede Zhl n 6 in genu n kleinere Qudrte zerlegen
4. Chemische Bindung
 4. Chemische Bindung 4... Vlenzindungs-Modell: Oktettegel Die Bildung enegetisch egünstigte Elektonenkonfigutionen (die esondes stil sind) wid ngestet Eine esondes stile Konfigution ist die Edelgskonfigution
4. Chemische Bindung 4... Vlenzindungs-Modell: Oktettegel Die Bildung enegetisch egünstigte Elektonenkonfigutionen (die esondes stil sind) wid ngestet Eine esondes stile Konfigution ist die Edelgskonfigution
R. Brinkmann http://brinkmann-du.de Seite 1 17.11.2010
 R. rinkmnn http://rinkmnn-du.de Seite 7..2 Grundegriffe der Vektorrehnung Vektor und Sklr Ein Teil der in Nturwissenshft und Tehnik uftretenden Größen ist ei festgelegter Mßeinheit durh die nge einer Mßzhl
R. rinkmnn http://rinkmnn-du.de Seite 7..2 Grundegriffe der Vektorrehnung Vektor und Sklr Ein Teil der in Nturwissenshft und Tehnik uftretenden Größen ist ei festgelegter Mßeinheit durh die nge einer Mßzhl
3 Module in C. 4 Gültigkeit von Namen. 5 Globale Variablen (2) Gültig im gesamten Programm
 3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
Test 2: Universitäts- oder Fachhochschulstudium? 24 Auswertung: Universitäts- oder Fachhochschulstudium? 27
 Inhalt Einleitung 7 Erläuterungen zu den Tests 9 Test 1: Berufliche Ausbildung oder Studium? 10 Ausbildungsmöglichkeiten nach dem Abitur oder der Fachhochschulreife 10 Auswertung: Berufliche Ausbildung
Inhalt Einleitung 7 Erläuterungen zu den Tests 9 Test 1: Berufliche Ausbildung oder Studium? 10 Ausbildungsmöglichkeiten nach dem Abitur oder der Fachhochschulreife 10 Auswertung: Berufliche Ausbildung
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Kegelschnitte. Geschichte der Kegelschnitte
 Kegelschnitte Kegelschnitte ds sind geometrische Figuren, die sich ergeen, wenn mn einen Kegel und eine Eene einnder schneiden lässt. Wir unterscheiden 3 Tpen von Kegelschnitten: Prel, Ellipse und Hperel.
Kegelschnitte Kegelschnitte ds sind geometrische Figuren, die sich ergeen, wenn mn einen Kegel und eine Eene einnder schneiden lässt. Wir unterscheiden 3 Tpen von Kegelschnitten: Prel, Ellipse und Hperel.
Übungsblatt 1. Vorlesung Theoretische Grundlagen der Informatik im WS 17/18
 Institut für Theoretische Informtik Lehrstuhl Prof. Dr. D. Wgner Üungsltt Vorlesung Theoretische Grundlgen der Informtik im WS 78 Ausge 9. Oktoer 27 Age 7. Novemer 27, : Uhr (im Ksten im UG von Geäude
Institut für Theoretische Informtik Lehrstuhl Prof. Dr. D. Wgner Üungsltt Vorlesung Theoretische Grundlgen der Informtik im WS 78 Ausge 9. Oktoer 27 Age 7. Novemer 27, : Uhr (im Ksten im UG von Geäude
Grundwissen am Ende der Jahrgangsstufe 9. Wahlpflichtfächergruppe II / III
 Grundwissen m Ende der Jhrgngsstufe 9 Whlpflichtfächergruppe II / III Funktionsbegriff Gerdengleichungen ufstellen und zu gegebenen Gleichungen die Grphen der Gerden zeichnen Ssteme linerer Gleichungen
Grundwissen m Ende der Jhrgngsstufe 9 Whlpflichtfächergruppe II / III Funktionsbegriff Gerdengleichungen ufstellen und zu gegebenen Gleichungen die Grphen der Gerden zeichnen Ssteme linerer Gleichungen
offene Netzwerke. In diesem Sinn wird auch interkulturelle Kompetenz eher als Prozess denn als Lernziel verstanden.
 correct zu verstehen. Ohne Definitionen von interkultureller Kompetenz vorwegnehmen zu wollen: Vor allem gehört dazu, einen selbstbewussten Standpunkt in Bezug auf kulturelle Vielfalt und interkulturelles
correct zu verstehen. Ohne Definitionen von interkultureller Kompetenz vorwegnehmen zu wollen: Vor allem gehört dazu, einen selbstbewussten Standpunkt in Bezug auf kulturelle Vielfalt und interkulturelles
ARBEITSBLATT 5L-6 FLÄCHENBERECHNUNG MITTELS INTEGRALRECHNUNG
 Mthemtik: Mg. Schmid WolfgngLehrerInnentem RBEITSBLTT 5L-6 FLÄHENBEREHNUNG MITTELS INTEGRLREHNUNG Geschichtlich entwickelte sich die Integrlrechnug us folgender Frgestellung: Wie knn mn den Flächeninhlt
Mthemtik: Mg. Schmid WolfgngLehrerInnentem RBEITSBLTT 5L-6 FLÄHENBEREHNUNG MITTELS INTEGRLREHNUNG Geschichtlich entwickelte sich die Integrlrechnug us folgender Frgestellung: Wie knn mn den Flächeninhlt
Frohe Weihnachten und ein gutes neues Jahr!
 Frohe Weihnachten und ein gutes neues Jahr! Die mit dem Stern * gekennzeichneten Übungen sind nicht verpflichtend, aber sie liefern zusätzliche Punkte. Unten wird immer mit I das reelle Intervall [0, 1]
Frohe Weihnachten und ein gutes neues Jahr! Die mit dem Stern * gekennzeichneten Übungen sind nicht verpflichtend, aber sie liefern zusätzliche Punkte. Unten wird immer mit I das reelle Intervall [0, 1]
5) Laplace-Wahrscheinlichkeit eines Zufallsexperiments
 von Jule Menzel, 12Q4 5) Lplce-Whrscheinlichkeit eines ufllsexperiments Ergenis ω 1 ω 2 ω 3 ω 4 ω 1 Ω ω 2 ω 3 ω 4 Ergenismenge ist ein Ereignis ist Teilmenge von Ω kurz: c Ω Ws ist ein Ereignis? Beispiel:
von Jule Menzel, 12Q4 5) Lplce-Whrscheinlichkeit eines ufllsexperiments Ergenis ω 1 ω 2 ω 3 ω 4 ω 1 Ω ω 2 ω 3 ω 4 Ergenismenge ist ein Ereignis ist Teilmenge von Ω kurz: c Ω Ws ist ein Ereignis? Beispiel:
