(1) +q für i = 3. P(c,c,0) für i = 3. Abbildung 1: System mit drei Punktladungen

Transkript

1 Felder und Wellen /8 Klusur H6 Aufgbe 6 Punkte) Gegeben sei die in Abbildung drgestellte Anordnung dreier Punktldungen q i, die sih n festen Positionen P i in derxy Ebene befinden. Es gelte überll im um κ = und ε = ε r ε sowie: +q für i = P,,) für i = q i = q für i = 2 P i x i,y i,z i ) = P,,) für i = 2 ) +q für i = 3 P,,) für i = 3 Abbildung : System mit drei Punktldungen ) Zeihnen Sie in Abbildung die Vektoren der uf die Ldungq 3 wirkenden Kräfte F 3 und F 23 sowie der drus resultierenden Krft F 3 qulittiv unter Berüksihtigung der ihtung ein. b) Berehnen Sie den Betrg der Krft F 3 sowie ihren Winkelφbezüglih der positivenx Ahse. Die Ldungen q, q 2 und q 3 werden nun durh eine im Koordintenursprung zentrierte Kugel mit dius r ersetzt. Es gelten nhfolgende Verteilungen für Ldung und reltive Dielektrizitätszhl: i = für r<r ε r,i = für r<r r) = ε r r) = 2) = k/r 7 für r r ε r, = α für r r ) Berehnen Sie die elektrishe Feldstärke E im gnzen um. d) Berehnen Sie unter Vernhlässigung von eibungskräften die notwendige Energie W, um eine Punktldung q 4 vom PunktP 4,3b,) nhp 5 b,,) zu vershieben b r ). r 2 Hinweis: Für die dem System zugeführte potentielle Energie gilt W pot = Fd s. r e) Nun seien E = E r e r e r undε = ε r ε fürr r. Berehnen Sie die EnergieW ges im um für r r, ). Hinweis: Die Aufgbenteile ) & b), ) & d) sowie e) sind jeweils unbhängig voneinnder lösbr.

2 Felder und Wellen 2/8 Klusur H6 Lösung 6 Punkte) ) Lösung siehe Abbildung : Abbildung 2: System mit drei Punktldungen b) N Punktldungen Krftgleihung: F ij = 4πε qiq j r 2 ij e rij Die resultierende Krft uf die Ldungq 3 ergibt sih nh dem Superpositionsprinzip somit zu F 3 = F 3 + F 23 = 4πε q q 3 e r3 2 r3 + q ) 2q 3 e r23 2 r23 = q2 4πε 2) 2 e r 3 2 e r 23 Die ihtungsvektoren e rij zeigen von q i nh q j. In krtesishen Koordinten lssen sie sih unter Berüksihtigung der Geometrie in Abbildung d.h. θ = 45 ) shreiben ls e r3 = osθ) e x +sinθ) e y = e x + e y )/ 2 ) e r23 = e x Betrg und ihtung der Krft ergeben sih dnn us ihren Komponenten F x undf y. F 3 = F 2 2 3,x +F 3,y = q2 4πε ) ) φ = tn F3,y +π F 3,x ) = tn 2 +π ) 2 q2.74 4πε r ε 2

3 Felder und Wellen 3/8 Klusur H6 ) E-Feld Kugelsymmetrie: Mterilgleihung: E = Er r) e r d s = e r dr D = ε E = εr ε E D = ε r ε E Ds E-Feld wird mit Dd f = dv Stz von Guss) berehnet: 2π π r 2π π εe r r 2 sinϑ)dϑdϕ = r ) r 2 sinϑ)dϑdϕdr r < r : 4πε i r 2 E r,i = 4π E r,i = r r ) }{{} i= r 2 dr r r : 4πε r 2 E r, = 4π ε r, ε r 2 E r, = + αε r 2 E r, = E r, = d) Energie, Kräfte und Momente [ k 4 r r r r 4 k 4αε r 2 r ir ) r 2 dr + r ) r 2 dr r k r 5 dr ] r r ) r 4 r 4 r 4 r 4 Krftgesetz: F = Q E r 2 Gemäß dem Hinweis W = Fd s ergibt sih die gesuhte Energie dmit zu r W e = q 4 b 3b = q 4k 4αε = q 4k 4αε W e = q 4k 4αε E d s b 3b [ rr 4 2 3br 4 r 2 r 4 r dr 6 ] b 5r 5 3b 5b b) 5 )

4 Felder und Wellen 4/8 Klusur H6 e) Elektrishe Energie Die Feldenergiedihte für linere, isotrope Medien berehnet sih zu w e = 2 ε E 2 und für die elektrishe Energie gilt llgemein W e = w e dv Im Bereihr r folgt drus W e, = = r 2π π r r 2π π r = 2πε E 2 ε E 2 r, r 2 sinϑ)dϑdϕdr 2 ε r r e 2r E ) 2 r e r r 2 sinϑ)dϑdϕdr dr [ = 2πε r ε E ] r 2 e 2r r W e, = πε r ε E e 2r e 2r) Die Gesmtenergie für r r ergibt sih dnn zuw ges, = lim r W e, r). W ges = πε r ε E e 2r

5 Felder und Wellen 5/8 Klusur H6 Aufgbe 2 6 Punkte) Gegeben ist ein Zylinderkondenstor. L κ Φ = I S ε r = Φ i i U Die innere Elektrode des Kondenstors mit dem PotentilΦ i = U befinde sih bei i, die äußere Elektrode mit dem PotentilΦ = bei. Beide Elektroden besitzen eine unendlih hohe Leitfähigkeit. Der Zwishenrum ist mit einem Dielektrikum mit der Dielektrizitätε = ε gefüllt. Der Kondenstor ht die LängeL. ndeffekte seien vernhlässigbr. Zunähst sei der Kondenstor mit einem nihtleitenden Mteril κ = ) gefüllt und der Shlter S geöffnet I = ). ) Berehnen Sie mit der Lplegleihung ds elektrishe Potentil Φ und bestimmen Sie dbei lle freien Prmeter nhnd der gegebenen ndbedingungen. b) Berehnen Sie ds elektrishe Feld E zwishen beiden Zylindern ls Funktion der Spnnung U. ) Bestimmen die Ldung uf der inneren Elektrode Q i und der äußeren Elektrode Q. Die folgenden Teilufgben sind unbhängig von ) bis ). Von nun n sei die Leitfähigkeit des Dielektrikums im Zwishenrum winkelbhängig: ϕ κϕ) = κ sin 2) Der Shlter S sei nun geshlossen und die Stromquelle liefert einen konstnten Strom I = 2Qκ πε, der durh den Kondenstor fließt. d) Berehnen Sie nhnd des gegebenen Stroms I ds elektrishe Feld E in Abhängigkeit von der LdungQ. e) Bestimmen Sie die Stromdihte J,ϕ) und die Verlustleistungsdihte dw j dt in Abhängigkeit von der LdungQ.

6 Felder und Wellen 6/8 Klusur H6 Lösung 2 6 Punkte) ) Wegen der Symmetrie und Vernhlässigung von ndeffekten giltφ = Φr) unde = Er) e r. Φ = Φ ) = Φ = C Φ) = C ln)+c 2 Es gelten folgende ndbedingungen: Φ i ) = U undφ ) = = C ln )+C 2 U = C ln i )+C 2 U = C ln i ) ln )) U C = ) ln i C 2 = U ) ln ) ln i Φ) = U U ) ln) ) ln ) ln i ln i b) E = grdφ = Φ e = U ln ) i e ) Zur Bestimmung der Ldungen uf den Elektroden werden zunähst die entsprehenden Flähenldungsdihten mit σ = D n2 D n berehnet. σ i = D i ) = ln σ = D ) = ln ε U i ) i ε U i ) Die Ldung ergibt sih wegen Q i = σ i dϕdz us der Multipliktion der Ldungsdihte mit der Flähe der inneren bzw. äußeren Elektrode

7 Felder und Wellen 7/8 Klusur H6 Q i = A i σ i = 2π i L ln Q = A σ = 2π L ln ε U ) i = ε 2πL )U i ln i ε U ) = ε 2πL )U i ln i d) Wegen der Symmetrie und Vernhlässigung von ndeffekten giltφ = Φr) unde = Er) e r. Es gilt: I = J,ϕ)d f = κϕ) Ed f 2Qκ πε = L 2π 2Qκ πε = E ) κ L ϕ κ sin E ) dϕ dz 2) 2π ϕ sin 2) dϕ 2Qκ = E ) 4κ L πε Q E ) = 2πε L E = E ) e e) J,ϕ) = κϕ) E ϕ Q J,ϕ) = κ sin 2) 2πε L e Die Verlustleistungsdihte ist gegeben durh: dw j dt = J E = κϕ) E 2 ϕ = κ sin 2 ) ) 2 Q 2πε L

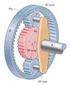
8 Felder und Wellen 8/8 Klusur H6 Aufgbe 3 6 Punkte) Gegeben sei eine ringförmige Toroidspule mit N Windungen, innerem dius und der Kntenlänge des qudrtishen Spulenquershnitts. Durh den Drht der Spule fließt der StromI. Es giltµ = µ. ndeffekte können vernhlässigt werden. I z φ Abbildung 3: Toroidspule mit qudrtishem Quershnitt. Ansih von shräg oben. ) Berehnen Sie die mgnetishe Flussdihte B innerhlb der Spule, d.h. für lle,+). Skizzieren Sie B in Abbildung 4. I φ Abbildung 4: Toroidspule: Ansiht von oben b) Berehnen Sie die FeldenergieW m des mgnetishen Feldes im Inneren der Spule. Bestimmen Sie mit Hilfe der berehneten Feldenergie den Selbstinduktionskoeffizienten L.

9 Felder und Wellen 9/8 Klusur H6 Nun wird eine rehtekige Leitershleife in die Toroidspule eingebrht. Diese wird, beginnend m inneren nd, mit der Geshwindigkeit v in rdiler ihtung zum äußeren nd bewegt siehe Abbildung 5). Die Leitershleife ht den Widerstnd L, eine Breite von und eine 3 Höhe von und verlässt während der gesmten Zeit die Toroidspule niht. 2 Gehen Sie im Folgenden dvon us, dss der in der Leitershleife induzierte Strom den Stromkreis und ds Mgnetfeld der Toroidspule niht beeinflusst. I /2 L i L v /3 Abbildung 5: Leitershleife in Toroidspule ) Berehnen Sie den mgnetishen Flussφ m t) durh die Leitershleife. Wie in Abbildung 5 drgestellt, befindet sih die Leitershleife zum Zeitpunkt t = m inneren nd der Toroidspule. d) Berehnen Sie den in der Leitershleife induzierten Strom i L t). e) Nun werde ds Feld ußerhlb der Toroidspule betrhtet. Skizzieren Sie den Verluf der mgnetishen Feldlinien in Abbildung 6 und bestimmen Sie ds Integrl Hd s entlng einer der Feldlinien. I z φ Abbildung 6: Toroidspule, Ansiht von shräg oben.

10 Felder und Wellen /8 Klusur H6 Lösung 3 6 Punkte) ) Mit dem Durhflutungsgesetz Hd s = Jd f ergibt sih H 2π e ϕ = NI Somit ergibt sih für die mgnetishe Flussdihte für,+) B = µ NI 2π e ϕ B I φ b) Die Feldenergie ergibt sih zu W m = = = w m dv H 2 Bdv 2π + 2 µ = 2 µ N 2 I 2 2π = µ 4π N2 I 2 ln + ) 2 NI ddϕdz 2π d ) + Der Selbstinduktionskoeffizient L ergibt sih durh Koeffizientenvergleih mit

11 Felder und Wellen /8 Klusur H6 zu W m = 2 LI2 L = µ 2π N2 ln ) + ) Der mgnetishe Fluss durh die Leitershleife für t, 2 ) ist gegeben durh 3v Φ m t) = Bd f = vt +vt = µ NI 4π ln µ NI 2π e ϕ e ϕ ddz + 3 +vt +vt d) Der in der Leitershleife induzierte Strom ergibt sih gemäß dem Ohmshen Gesetz zu ) i L t) = U L,indt) L. Der Grund für ds Vorzeihen ist die in der Skizze eingezeihnete Stromrihtung. Die in der Leitershleife induzierte Spnnung ist gegeben durh U L,ind t) = dφ mt). dt Somit ergibt sih NI d + i L t) = µ 4π L dt ln +vt ) 3 +vt NI +vt = µ 4π L + +vt v +vt) v + +vt) 3 +vt) 3 2 = µ NI 4π L v + 3 +vt 3 +vt) 2 NI v = µ 2π L +vt)+ +vt) 3 für t, 2 3v ).

12 Felder und Wellen 2/8 Klusur H6 e) Ds äußere Feld entspriht etw dem Feld einer einzelnen Windungszhl N = ) runden Leitershleife, d in der Toroidspule der Strom I kreisförmig in ϕ-ihtung fließt. Somit folgt mit dem Durhflutungsgesetz Hd s = I. B I z φ

13 Felder und Wellen 3/8 Klusur H6 Aufgbe 4 6 Punkte) Gegeben ist ein Wellenleiter, der us zwei prllelen, leitenden Pltten besteht. Die Pltten sind in y- und z-ihtung unendlih usgedehnt und hben den Abstnd d. Im um zwishen den Pltten befindet sih Vkuum. x z d y In z-ihtung breitet sih zwishen den Pltten eine TM-Welle us. Ds E-Feld der Welle ist gegeben durh: E z = sink x x)e jωt kzz), E x = j k z k x osk x x)e jωt kzz). Lösen Sie folgende Aufgben: ) Leiten Sie us den MAXWELL-Gleihungen die Berehnungsvorshrift für ds B-Feld der TM- Welle her. Berehnen Sie nshließend mit Ihrer hergeleiteten ehenvorshrift ds B-Feld der TM-Welle. b) Welhe Bedingung müssen fürk x gelten? Erläutern Sie deren physiklishe Bedeutung. Stellen Sie lle gültigen Lösungen mthemtish dr! ) Berehnen Sie k z ls Funktion von ω und k x und setzen Sie Ihr Ergebnis für k x us Aufgbe b) ein. Für die Berehnung gilt die Wellengleihung E µε d2 E dt 2 = beziehungsweise H µε d2 H dt 2 =. d) Bestimmen Sie die CutOff-Frequenz der ersten Mode, wenn der Abstnd d zwishen den beiden Pltten d = 5 m beträgt. Nehmen Sie dzu die Lihtgeshwindigkeit im Vkuum mit = µ ε 3 8 m n. s

14 Felder und Wellen 4/8 Klusur H6 Lösung 4 6 Punkte) ) Bestimmung des B-Feldes Ds B-Feld wird us dem E-Feld berehnet. Die einzelnen Komponenten des E-Feldes sind in der Aufgbenstellung gegeben: E z = sink x x)e jωt kzz), E x = j k z k x osk x x)e jωt kzz). Aus der ottion des E-Feldes lässt sih die negtive zeitlihe Ableitung des B-Feldes bestimmen: rot E = d B dt. Für die die ottion des E-Feldes ergibt sih: rote Ez = e x y E ) y Ex + e y z z E ) z x Es gilt für die einzelnen Terme des ersten und letzten Summnden: E z y =, E y z =, E y x =, E x y =. Somit ergibt sih für die ottion des E-Feldes: rote Ex = e y z = e y j 2k2 z osk x x) e jωt kzz) k x ) k 2 = e z y +k x k x osk x x)e jωt kzz). Ey + e z x E ) x. y E ) z x ) k x osk x x) e jωt kzz) Durh Integrtion über die Zeit t und nshließende Multipliktion mit ergibt sih ds B-Feld zu ) B = e y jω k x + k2 z osk x x)e jωt kzz) = e y j ω k x k x + k2 z k x ) osk x x)e jωt kzz). b) Bedingung fürk x Ds E-Feld muss uf den leitenden Pltten vershwinden, lso zu Null gesetzt werden: E z x = )! = Bedingung ist erfüllt, d sin) =, E z x = d)! = Bedingung ist erfüllt für sink x d) = k x = nπ d für lle n Z.

15 Felder und Wellen 5/8 Klusur H6 ) Berehnung vonk z Zur Berehnung der Wellenzhl k z in Abhängigkeit von ω und k x wird die z-komponente der Wellengleihung E µε d2 E dt 2 verwendet: E z = 2 E z x + 2 E z 2 y 2 }{{} = + 2 E z z 2. Die vereinfhte Wellengleihung ergibt sih dmit zu E z µε d2 E z dt 2 = 2 E z x E z z 2 µε 2 E z t 2. Auflösen führt zu = 2 E z + 2 E z µε 2 E z x 2 z 2 t 2 = kxsink 2 x x)e jωt kzz) kz 2 sink x x)e jωt kzz) +µεω 2 sink x x)e jωt kzz) = k 2 x k 2 z +µεω 2. Fürk z ergibt sih dmit k z = nπ µεω 2 kx 2 = µεω 2 d ) 2 für lle n Z. d) Bestimmung der CutOff-Frequenz Einsetzen von k z = in die Lösung us Aufgbenteil ) liefert: nπ ) 2 = µεω 2 d nπ ) 2 µεω 2 = d ω = d µε nπ = nπ d. Mit ω = 2πf ergibt sih f = n 2d. Ds Einsetzen von n =, = 3 8 m s und d = 5m liefert eine Frequenz von f = 3 8m s m = s = Hz = GHz.

16 Felder und Wellen 6/8 Klusur H6 Aufgbe 5 6 Punkte) Eine elektromgnetishe Welle mit dem E-Feld der Form E e = E e e jωt k z) e x j e y ) breitet sih in positive z-ihtung im Vkuum z < ) us und trifft bei z = uf einen Bereih mit dünnem Plsm z > ). Im Plsm gelte ε r = ω2. ω ω 2 sei die Plsmkreisfrequenz. Im gnzen um gelte µ = µ. ) Wie ist die Welle im Vkuum polrisiert? Geben Sie eine kurze Begründung n. b) Berehnen Sie ds H-Feld der hinlufenden Welle mittels der llgemeinen MAXWELL-Gleihung. Stellen Sie die Beziehung zwishen dem E- und H-Feld mittels des Wellenwiderstndes Γ = µ ε her. Hinweis: Mhen Sie für die weiteren Aufgbenteile ) bis e) den Anstz für ds E-Feld der trnsmittierten im dünnen Plsm: E t = E t e jωt k z) e x j e y ) ) Geben Sie die Grenzbedingungen n der Grenzflähe bei z = n. Berehnen Sie drus die H-Felder, der n der Grenzflähe reflektierten und trnsmittierte Welle in Abhängigkeit vone e. d) Berehnen Sie k im Plsm mit der llgemeinen Wellengleihung. Geben Sie k für die Fälle ω > ω und ω < ω n. e) Berehnen Sie fürω > ω den komplexen Poynting-Vektor S = 2 E H in Abhängigkeit von E t im dünnen Plsm.

17 Felder und Wellen 7/8 Klusur H6 Lösung 5 6 Punkte) ) Die Welle ist zirkulr polrisiert. Die e x und die e y Komponente sind um j = e jπ/2, d.h. um 9 phsenvershoben und die Beträge der Amplituden E x und E y sind identish. b) rote = B ) e x E ) ) y Ex + e y = jωµ H 2) z z jk ) [ e x jee e jωt k z) ) + e y Ee e jωt k z) )] = jωµ He 3) k ωµ E e e jωt k z) j e x + e y ) = H e 4) ω µ ε ωµ E e e jωt k z) j e x + e y ) = H e 5) ε E e e jωt kz) j e x + e y ) = H µ e 6) }{{} H e 7) ) Die Tgentilkomponenten der Summe ller E- und H-Felder n der Grenzflähez = müssen identish sein: E e +E r = E t H e +H r = H t 8) 9) µ Γ = ε µ Γ = ) ε ω2 ω 2 ) ) H e +H r = H t 2) Γ H e Γ H r = Γ H t 3) Elimintion von H t : Γ H e Γ H r = Γ H e +Γ H r 4) H e Γ Γ ) H r Γ +Γ ) = 5) 6)

18 Felder und Wellen 8/8 Klusur H6 Aufgelöst nhh r : H r = H e Γ Γ Γ +Γ H r = Γ Γ Γ +Γ Γ E e e jωt+k z) j e x + e y ) 8) und drus Bestimmung von H t : H t = 2Γ Γ +Γ H e H t = 2Γ Γ +Γ Γ E e e jωt k z) j e x + e y ) 2) d) k knn durh Einsetzen von E x in die Wellengleihung berehnet werden. mit 7) 9) E x +ω 2 ε ε r µe x = 2) jk ) 2 E x +ω 2 ε ε r µe x = 22) k 2 +ω 2 ε ε r µ = 23) k 2 = ω 2 ε ε r µ 24) ε r = ω2 ω 2 25) k 2 = ε µω 2 ω 2 ) 26) ω > ω : k = ± ε µω 2 ω) 2 27) Im Fll einer Ausbreitung in positive z-ahse, wie in Aufgbe gegeben: k = + ε µω 2 ω) 2 28) ω < ω : k = ±j ε µω 2 ω 2 ) 29) Im Flle einer Ausbreitung in positive z-ahse reine Dämpfung) k = j ε µω 2 ω 2 ) := jk I 3) e) S = 2 E H S = 2 E te jωt k z) e x j e y ) [ H t e jωt k z) j e x + e y ) ] 3) 32) mit H t = Et Γ folgt: S = 2 E2 t Γ e x j e y ) j e x + e y ) 33) S = E2 t 2Γ +) e z S = E2 t Γ e z 34) 35)