1.1 Grundlagen: Reguläre Ausdrücke
|
|
|
- Heini Schwarz
- vor 7 Jahren
- Abrufe
Transkript
1 11 Grundlgen: Reguläre Ausdrücke Progrmmtext enutzt ein endliches Alphet Σ von Einge-Zeichen, zb ASCII :-) Die Menge der Textschnitte einer Token-Klsse ist i regulär Reguläre Sprchen knn mn mithile regulärer Ausdrücke speziizieren Die Menge E Σ der (nicht-leeren) regulären Ausdrücke ist die kleinste Menge E mit: ǫ E (ǫ neues Symol nicht us Σ); E ür lle Σ; (e 1 e 2 ), (e 1 e 2 ), e 1 E soern e 1, e 2 E 125
2 11 Grundlgen: Reguläre Ausdrücke Progrmmtext enutzt ein endliches Alphet Σ von Einge-Zeichen, zb ASCII :-) Die Menge der Textschnitte einer Token-Klsse ist i regulär Reguläre Sprchen knn mn mithile regulärer Ausdrücke speziizieren Die Menge E Σ der (nicht-leeren) regulären Ausdrücke ist die kleinste Menge E mit: ǫ E (ǫ neues Symol nicht us Σ); E ür lle Σ; (e 1 e 2 ), (e 1 e 2 ), e 1 E soern e 1, e 2 E 126
3 Stephen Kleene, Mdison Wisconsin,
4 Beispiele: (( ) ) ( ) (( ) ( )) Achtung: Wir unterscheiden zwischen Zeichen, 0,, und Met-Zeichen (,, ), Um (hässliche) Klmmern zu spren, enutzen wir Opertor-Präzedenzen: und lssen weg :-) Rele Speziiktions-Sprchen ieten zusätzliche Konstrukte wie: 128
5 Beispiele: (( ) ) ( ) (( ) ( )) Achtung: Wir unterscheiden zwischen Zeichen, 0,, und Met-Zeichen (,, ), Um (hässliche) Klmmern zu spren, enutzen wir Opertor-Präzedenzen: > > und lssen weg :-) Rele Speziiktions-Sprchen ieten zusätzliche Konstrukte wie: e? (ǫ e) e + (e e ) und verzichten u ǫ :-) 129
6 Beispiele: (( ) ) ( ) (( ) ( )) Achtung: Wir unterscheiden zwischen Zeichen, 0,, und Met-Zeichen (,, ), Um (hässliche) Klmmern zu spren, enutzen wir Opertor-Präzedenzen: > > und lssen weg :-) Rele Speziiktions-Sprchen ieten zusätzliche Konstrukte wie: e? (ǫ e) e + (e e ) und verzichten u ǫ :-) 130
7 Speziiktionen enötigen eine Semntik :-) Im Beispiel: Speziiktion Semntik { n n 0} {, } {} Für e E Σ deinieren wir die speziizierte Sprche [[e]] Σ induktiv durch: [[ǫ]] = {ǫ} [[]] [[e ]] = {} = ([[e]]) [[e 1 e 2 ]] = [[e 1 ]] [[e 2 ]] [[e 1 e 2 ]] = [[e 1 ]] [[e 2 ]] 131
8 Bechte: Die Opertoren (_),, sind die entsprechenden Opertionen u Wort-Mengen: (L) = {w 1 w k k 0, w i L} L 1 L 2 = {w 1 w 2 w 1 L 1, w 2 L 2 } 132
9 Bechte: Die Opertoren (_),, sind die entsprechenden Opertionen u Wort-Mengen: (L) = {w 1 w k k 0, w i L} L 1 L 2 = {w 1 w 2 w 1 L 1, w 2 L 2 } Reguläre Ausdrücke stellen wir intern ls mrkierte geordnete Bäume dr: (ǫ) * ǫ Innere Knoten: Opertor-Anwendungen; Blätter: einzelne Zeichen oder ǫ 133
10 Finger-Üung: Zu jedem regulären Ausdruck e können wir einen Ausdruck e (evt mit? ) konstruieren so dss: [[e]] = [[e ]]; Flls [[e]] = {ǫ}, dnn ist e ǫ; Flls [[e]] = {ǫ}, dnn enthält e kein ǫ Konstruktion: Wir deinieren eine Trnsormtion T von regulären Ausdrücken durch: 134
11 Finger-Üung: Zu jedem regulären Ausdruck e können wir einen Ausdruck e (evt mit? ) konstruieren so dss: [[e]] = [[e ]]; Flls [[e]] = {ǫ}, dnn ist e ǫ; Flls [[e]] = {ǫ}, dnn enthält e kein ǫ Konstruktion: Wir deinieren eine Trnsormtion T von regulären Ausdrücken durch: 135
12 T [ǫ] T [] = ǫ = T [e 1 e 2 ] = cse (T [e 1 ], T [e 2 ]) o (ǫ,ǫ) : ǫ (e 1,ǫ) : e 1? (ǫ, e 2 ) : e 2? (e 1, e 2 ): (e 1 e 2 ) T [e 1 e 2 ] = cse (T [e 1 ], T [e 2 ]) o (ǫ,ǫ) : ǫ T [e ] = cse T [e] o ǫ : ǫ e 1 : e 1 T [e?] = cse T [e] o ǫ : ǫ e 1 : e 1? (e 1,ǫ) : e 1 (ǫ, e 2 ) : e 2 (e 1, e 2 ): (e 1 e 2 ) 136
13 Unsere Anwendung: Identiier in Jv: le = [-za-z_\$] di = [0-9] Id = {le} ({le} {di})* Bemerkungen: le und di sind Zeichenklssen Deinierte Nmen werden in {, } eingeschlossen Zeichen werden von Met-Zeichen durch \ unterschieden 137
14 Unsere Anwendung: Identiier in Jv: le = [-za-z_\$] di = [0-9] Id = {le} ({le} {di})* Bemerkungen: le und di sind Zeichenklssen Deinierte Nmen werden in {, } eingeschlossen Zeichen werden von Met-Zeichen durch \ unterschieden 138
15 Unsere Anwendung: Identiier in Jv: le = [-za-z_\$] di = [0-9] Id = {le} ({le}{di})* Gleitkommzhlen: Flot = {di}* (\{di}{di}\) {di}*((ee)(\+\-)?{di}+)? Bemerkungen: le und di sind Zeichenklssen Deinierte Nmen werden in {, } eingeschlossen Zeichen werden von Met-Zeichen durch \ unterschieden 139
16 12 Grundlgen: Endliche Automten Beispiel: ǫ ǫ Knoten: Knten: Zustände; Üergänge; Beschritungen: konsumierter Input :-) 140
17 12 Grundlgen: Endliche Automten Beispiel: ǫ ǫ Knoten: Knten: Zustände; Üergänge; Beschritungen: konsumierter Input :-) 141
18 Michel O Rin, Stnord University Dn S Scott, Crnegy Mellon University, Pittsurgh 142
19 Forml ist ein nicht-deterministischer endlicher Automt mit ǫ-üergängen (ǫ-nfa) ein Tupel A = (Q, Σ, δ, I, F) woei: Q Σ I Q F Q δ eine endliche Menge von Zuständen; ein endliches Einge-Alphet; die Menge der Anngszustände; die Menge der Endzustände und die Menge der Üergänge (die Üergngs-Reltion) ist 143
20 Forml ist ein nicht-deterministischer endlicher Automt mit ǫ-üergängen (ǫ-nfa) ein Tupel A = (Q, Σ, δ, I, F) woei: Q Σ I Q F Q δ eine endliche Menge von Zuständen; ein endliches Einge-Alphet; die Menge der Anngszustände; die Menge der Endzustände und die Menge der Üergänge (die Üergngs-Reltion) ist Für ǫ-nfas ist: δ Q (Σ {ǫ}) Q Git es keine ǫ-üergänge (p, ǫ, q), ist A ein NFA Ist δ : Q Σ Q eine Funktion und #I = 1, heißt A deterministisch (DFA) 144
21 Forml ist ein nicht-deterministischer endlicher Automt mit ǫ-üergängen (ǫ-nfa) ein Tupel A = (Q, Σ, δ, I, F) woei: Q Σ I Q F Q δ eine endliche Menge von Zuständen; ein endliches Einge-Alphet; die Menge der Anngszustände; die Menge der Endzustände und die Menge der Üergänge (die Üergngs-Reltion) ist Für ǫ-nfas ist: δ Q (Σ {ǫ}) Q Git es keine ǫ-üergänge (p,ǫ, q), ist A ein NFA Ist δ : Q Σ Q eine Funktion und #I = 1, heißt A deterministisch (DFA) 145
22 Akzeptierung Berechnungen sind Pde im Grphen kzeptierende Berechnungen ühren von I nch F Ein kzeptiertes Wort ist die Beschritung eines kzeptierenden Pdes ǫ ǫ 146
23 Akzeptierung Berechnungen sind Pde im Grphen kzeptierende Berechnungen ühren von I nch F Ein kzeptiertes Wort ist die Beschritung eines kzeptierenden Pdes ǫ ǫ 147
24 Dzu deinieren wir den trnsitiven Aschluss δ von δ ls kleinste Menge δ mit: (p,ǫ, p) δ und (p, xw, q) δ soern (p, x, p 1 ) δ und (p 1, w, q) δ eschreit ür je zwei Zustände, mit welchen Wörtern mn vom einen zum ndern kommt :-) δ Die Menge ller kzeptierten Worte, dh die von A kzeptierte Sprche können wir kurz eschreien ls: L(A) = {w Σ i I, F : (i, w, ) δ } 148
25 Stz: Für jeden regulären Ausdruck e knn (in linerer Zeit :-) ein ǫ-nfa konstruiert werden, der die Sprche [[e]] kzeptiert Idee: Der Automt verolgt (konzepionell mithile einer Mrke ), wohin mn in mit der Einge w gelngen knn e 149
26 Beispiel: () () * 150
27 Beispiel: w = : * 151
28 Beispiel: w = : * 152
29 Beispiel: w = : * 153
30 Beispiel: w = : * 154
31 Beispiel: w = : * 155
32 Beispiel: w = : * 156
33 Beispiel: w = : * 157
34 Beispiel: w = : * 158
35 Beispiel: w = : * 159
36 Bechte: Gelesen wird nur n den Blättern Die Nvigtion im Bum erolgt ohne Lesen, dh mit ǫ-üergängen Für eine ormle Konstruktion müssen wir die Knoten im Bum ezeichnen Dzu enutzen wir (hier) einch den drgestellten Teilusdruck :-) Leider git es eventuell mehrere gleiche Teilusdrücke :-( == Wir numerieren die Blätter durch 160
37 im Beispiel: * 161
38 im Beispiel: *
39 im Beispiel: *
40 Die Konstruktion: Zustände: r, r r Knoten von e; Anngszustnd: e; Endzustnd: e ; Üergngsreltion: Für Blätter r i x enötigen wir: ( r, x, r ) Die ürigen Üergänge sind: 164
41 r Üergänge r 1 r 2 ( r,ǫ, r 1 ) ( r,ǫ, r 2 ) (r 1,ǫ, r ) (r 2,ǫ, r ) r 1 r 2 ( r,ǫ, r 1 ) (r 1,ǫ, r 2 ) (r 2,ǫ, r ) r r 1 r 1? Üergänge ( r,ǫ, r ) ( r,ǫ, r 1 ) (r 1,ǫ, r 1 ) (r 1,ǫ, r ) ( r,ǫ, r ) ( r,ǫ, r 1 ) (r 1,ǫ, r ) 165
42 Diskussion: Die meisten Üergänge dienen dzu, im Ausdruck zu nvigieren :-( Der Automt ist i nichtdeterministisch :-( Strtegie: == (1) Beseitigung der ǫ-üergänge; (2) Beseitigung des Nichtdeterminismus :-) 166
43 Diskussion: Die meisten Üergänge dienen dzu, im Ausdruck zu nvigieren :-( Der Automt ist i nichtdeterministisch :-( Strtegie: == (1) Beseitigung der ǫ-üergänge; (2) Beseitigung des Nichtdeterminismus :-) 167
44 Beseitigung von ǫ-üergängen: Zwei einche Ansätze: p q 1 q 2 q Wir enutzen hier den zweiten Anstz Zur Konstruktion von Prsern werden wir später den ersten enutzen :-) 168
45 Beseitigung von ǫ-üergängen: Zwei einche Ansätze: p q 1 q 2 q Wir enutzen hier den zweiten Anstz Zur Konstruktion von Prsern werden wir später den ersten enutzen :-) 169
46 1 Schritt: empty[r] = t gdw ǫ [[r]] im Beispiel: *
47 1 Schritt: empty[r] = t gdw ǫ [[r]] im Beispiel: *
48 1 Schritt: empty[r] = t gdw ǫ [[r]] im Beispiel: *
49 1 Schritt: empty[r] = t gdw ǫ [[r]] im Beispiel: t *
50 1 Schritt: empty[r] = t gdw ǫ [[r]] im Beispiel: t *
... in unserem Fall: Scanner. Generator. Spezifikation. Spezifikation von Token-Klassen: Reguläre Ausdrücke;
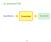 in unserem Fll: Speziiktion Genertor Scnner Speziiktion von Token-Klssen: Reguläre Ausdrücke; Generierte Implementierung: Endliche Automten + X :-) 11 in unserem Fll: 0[1-9][0-9]* Genertor 0 [1 9] [0 9]
in unserem Fll: Speziiktion Genertor Scnner Speziiktion von Token-Klssen: Reguläre Ausdrücke; Generierte Implementierung: Endliche Automten + X :-) 11 in unserem Fll: 0[1-9][0-9]* Genertor 0 [1 9] [0 9]
Sind Tokens erst einmal klassifiziert, kann man die Teilwörter vorverarbeiten:
 Sind Tokens erst einml klssifiziert, knn mn die Teilwörter vorverreiten: Wegwerfen irrelevnter Teile wie Leerzeichen, Kommentren, Aussondern von Prgms, dh Direktiven n den Compiler, die nicht Teil des
Sind Tokens erst einml klssifiziert, knn mn die Teilwörter vorverreiten: Wegwerfen irrelevnter Teile wie Leerzeichen, Kommentren, Aussondern von Prgms, dh Direktiven n den Compiler, die nicht Teil des
Nichtdeterministische endliche Automaten. Nichtdetermistische Automaten J. Blömer 1/12
 Nichtdeterministische endliche Automten Nichtdetermistische Automten J. Blömer 1/12 Nichtdeterministische endliche Automten In mnchen Modellierungen ist die Forderung, dss δ eine Funktion von Q Σ Q ist,
Nichtdeterministische endliche Automten Nichtdetermistische Automten J. Blömer 1/12 Nichtdeterministische endliche Automten In mnchen Modellierungen ist die Forderung, dss δ eine Funktion von Q Σ Q ist,
Deterministische endliche Automaten
 Endliche Automten Idee: endlicher Automt A ht endlich viele innere Zustände liest Einge wєσ* zeichenweise von links nch rechts git zum Schluß eine J/Nein Antwort A Lesekopf w 1 w 2 w n gelesenes Symol
Endliche Automten Idee: endlicher Automt A ht endlich viele innere Zustände liest Einge wєσ* zeichenweise von links nch rechts git zum Schluß eine J/Nein Antwort A Lesekopf w 1 w 2 w n gelesenes Symol
DEA1 Deterministische Version
 Endliche Automten 4 Deterministische endliche Automten Zu dem nichtdeterministischen Automten EA git es eine deterministische Version. EA Akzeptor für Wörter üer X = { } mit mindestens einem führenden.
Endliche Automten 4 Deterministische endliche Automten Zu dem nichtdeterministischen Automten EA git es eine deterministische Version. EA Akzeptor für Wörter üer X = { } mit mindestens einem führenden.
Themengebiet: Einführung. Compilerbau I. Organisatorisches. Organisatorisches. Vorläufiger Inhalt. Abschlussprüfung. Interpreter.
 TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK Orgnistorisches Compileru I Michel Petter, Axel Simon SoSe 00 Mster oder Bchelor 6 Semester mit 5 ECTS Vorussetzungen Inormtik & Theoretische Inormtik
TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK Orgnistorisches Compileru I Michel Petter, Axel Simon SoSe 00 Mster oder Bchelor 6 Semester mit 5 ECTS Vorussetzungen Inormtik & Theoretische Inormtik
Automaten und formale Sprachen Notizen zu den Folien
 3 Endliche Automten Automten und formle Sprchen Notizen zu den Folien DFA Reguläre Grmmtik (Folie 89) Stz. Jede von einem endlichen Automten kzeptierte Sprche ist regulär. Beweis. Nch Definition, ist eine
3 Endliche Automten Automten und formle Sprchen Notizen zu den Folien DFA Reguläre Grmmtik (Folie 89) Stz. Jede von einem endlichen Automten kzeptierte Sprche ist regulär. Beweis. Nch Definition, ist eine
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2011
 Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 011 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Snder Bruggink Automten und Formle Sprchen 1 Reguläre Sprchen Wir eschäftigen uns
Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 011 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Snder Bruggink Automten und Formle Sprchen 1 Reguläre Sprchen Wir eschäftigen uns
Automaten und formale Sprachen Notizen zu den Folien
 3 Endliche Automten Automten und formle Sprchen Notizen zu den Folien Üerführungsfunction eines DFA (Folie 92) Wie sieht die Üerführungfunktion us? δ : Z Σ Z Ds heißt: Ein Pr us Zustnd und Alphetsymol
3 Endliche Automten Automten und formle Sprchen Notizen zu den Folien Üerführungsfunction eines DFA (Folie 92) Wie sieht die Üerführungfunktion us? δ : Z Σ Z Ds heißt: Ein Pr us Zustnd und Alphetsymol
Automaten und formale Sprachen Notizen zu den Folien
 3 Endliche Automten Automten und formle Sprchen Notizen zu den Folien Üerführungsfunktion eines NFA (Folien 107 und 108) Wie sieht die Üerführungsfunktion us? δ : Z Σ P(Z) Ds heißt, jedem Pr us Zustnd
3 Endliche Automten Automten und formle Sprchen Notizen zu den Folien Üerführungsfunktion eines NFA (Folien 107 und 108) Wie sieht die Üerführungsfunktion us? δ : Z Σ P(Z) Ds heißt, jedem Pr us Zustnd
Formale Systeme, Automaten, Prozesse SS 2010 Musterlösung - Übung 2 M. Brockschmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder
 Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 2 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 2 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Frank Heitmann 2/71. 1 Betrachten wir Σ für ein Alphabet Σ, so ist Σ die Menge
 Formle Grundlgen der Informtik Kpitel 2 und reguläre Sprchen Frnk Heitmnn heitmnn@informtik.uni-hmurg.de 7. April 24 Frnk Heitmnn heitmnn@informtik.uni-hmurg.de /7 Alphet und Wörter - Zusmmengefsst Die
Formle Grundlgen der Informtik Kpitel 2 und reguläre Sprchen Frnk Heitmnn heitmnn@informtik.uni-hmurg.de 7. April 24 Frnk Heitmnn heitmnn@informtik.uni-hmurg.de /7 Alphet und Wörter - Zusmmengefsst Die
Minimalautomat. Wir stellen uns die Frage nach dem. kleinsten DFA für eine reguläre Sprache L, d.h. nach einem DFA mit möglichst wenigen Zuständen.
 Rechtslinere Sprchen Minimlutomt Es git lso sehr verschiedene endliche Beschreiungen einer regulären Sprche (DFA, NFA, rechtslinere Grmmtiken, reguläre Ausdrücke). Diese können ineinnder üersetzt werden.
Rechtslinere Sprchen Minimlutomt Es git lso sehr verschiedene endliche Beschreiungen einer regulären Sprche (DFA, NFA, rechtslinere Grmmtiken, reguläre Ausdrücke). Diese können ineinnder üersetzt werden.
Automaten, Spiele, und Logik
 Automten, Spiele, und Logik Woche 1 15. April 2014 Inhlt der gnzen Vorlesung Automten uf endlichen Wörtern uf undendlichen Wörtern uf endlichen Bäumen Spiele Erreichrkeitsspiele Ehrenfeucht-Frïssé Spiele
Automten, Spiele, und Logik Woche 1 15. April 2014 Inhlt der gnzen Vorlesung Automten uf endlichen Wörtern uf undendlichen Wörtern uf endlichen Bäumen Spiele Erreichrkeitsspiele Ehrenfeucht-Frïssé Spiele
7 Modellierung von Abläufen 7.1 Endliche Automaten
 7 Modellierung von Aläufen 7. Endliche Automten Mod-7. Endlicher Automt: Formler Klkül zur Spezifiktion von relen oder strkten Mschinen. Sie regieren uf äußere Ereignisse, ändern ihren inneren Zustnd,
7 Modellierung von Aläufen 7. Endliche Automten Mod-7. Endlicher Automt: Formler Klkül zur Spezifiktion von relen oder strkten Mschinen. Sie regieren uf äußere Ereignisse, ändern ihren inneren Zustnd,
Automaten und formale Sprachen Notizen zu den Folien
 5 Ds Pumping Lemm Schufchprinzip (Folie 144) Automten und formle Sprchen Notizen zu den Folien Im Block Ds Schufchprinzip für endliche Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl
5 Ds Pumping Lemm Schufchprinzip (Folie 144) Automten und formle Sprchen Notizen zu den Folien Im Block Ds Schufchprinzip für endliche Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl
Berechenbarkeitstheorie 2. Vorlesung
 Berechenrkeitstheorie Dr. Frnzisk Jhnke Institut für Mthemtische Logik und Grundlgenforschung WWU Münster WS 15/16 Alle Folien unter Cretive Commons Attriution-NonCommercil 3.0 Unported Lizenz. Deterministischer
Berechenrkeitstheorie Dr. Frnzisk Jhnke Institut für Mthemtische Logik und Grundlgenforschung WWU Münster WS 15/16 Alle Folien unter Cretive Commons Attriution-NonCommercil 3.0 Unported Lizenz. Deterministischer
Vorkurs Theoretische Informatik
 Vorkurs Theoretische Informtik Einführung in reguläre Sprchen Areitskreis Theoretische Informtik Freitg, 05.10.2018 Fchgruppe Informtik Üersicht 1. Chomsky-Hierchie 2. Automten NEA DEA 3. Grmmtik und Automten
Vorkurs Theoretische Informtik Einführung in reguläre Sprchen Areitskreis Theoretische Informtik Freitg, 05.10.2018 Fchgruppe Informtik Üersicht 1. Chomsky-Hierchie 2. Automten NEA DEA 3. Grmmtik und Automten
Umwandlung von endlichen Automaten in reguläre Ausdrücke
 Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester Kurzer Einschub: das Schubfachprinzip.
 Reguläre Sprchen Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 0 Ds Pumping-Lemm Wir hen is jetzt vier Formlismen kennengelernt, mit denen wir eine reguläre Sprche ngeen können:
Reguläre Sprchen Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 0 Ds Pumping-Lemm Wir hen is jetzt vier Formlismen kennengelernt, mit denen wir eine reguläre Sprche ngeen können:
Minimierung von DFAs. Minimierung 21 / 98
 Minimierung von DFAs Minimierung 21 / 98 Ein Beispiel: Die reguläre Sprche L({, } ) Wie stellt mn fest, o ein Wort ds Suffix esitzt? Ein erster Anstz: Speichere im ktuellen Zustnd die eiden zuletzt gelesenen
Minimierung von DFAs Minimierung 21 / 98 Ein Beispiel: Die reguläre Sprche L({, } ) Wie stellt mn fest, o ein Wort ds Suffix esitzt? Ein erster Anstz: Speichere im ktuellen Zustnd die eiden zuletzt gelesenen
Automaten, Spiele, und Logik
 Automten, Spiele, und Logik Woche 9 13. Juni 2014 Inhlt der heutigen Vorlesung Büchi Automten co-büchi Automten Komplementierung für deterministische Büchi Automten Ein Ziel: den Stz von Büchi-Elgot-Trkhtenrot
Automten, Spiele, und Logik Woche 9 13. Juni 2014 Inhlt der heutigen Vorlesung Büchi Automten co-büchi Automten Komplementierung für deterministische Büchi Automten Ein Ziel: den Stz von Büchi-Elgot-Trkhtenrot
Gliederung. Kapitel 1: Endliche Automaten
 Gliederung 0. Motivtion und Einordnung 1. Endliche Automten 2. Formle Sprchen 3. Berechnungstheorie 4. Komplexitätstheorie 1.1. 1.2. Minimierungslgorithmus 1.3. Grenzen endlicher Automten 1/1, S. 1 2017
Gliederung 0. Motivtion und Einordnung 1. Endliche Automten 2. Formle Sprchen 3. Berechnungstheorie 4. Komplexitätstheorie 1.1. 1.2. Minimierungslgorithmus 1.3. Grenzen endlicher Automten 1/1, S. 1 2017
Übung Grundbegriffe der Informatik
 Üung Grundegriffe der Informtik 11. Üung Krlsruher Institut für Technologie Mtthis Jnke, Geäude 50.34, Rum 249 emil: mtthis.jnke ät kit.edu Mtthis Schulz, Geäude 50.34, Rum 247 emil: schulz ät ir.uk.de
Üung Grundegriffe der Informtik 11. Üung Krlsruher Institut für Technologie Mtthis Jnke, Geäude 50.34, Rum 249 emil: mtthis.jnke ät kit.edu Mtthis Schulz, Geäude 50.34, Rum 247 emil: schulz ät ir.uk.de
Wintersemester 2016/2017 Scheinklausur Formale Sprachen und Automatentheorie
 Wintersemester 2016/2017 Scheinklusur Formle Sprchen und Automtentheorie 21.12.2016 Üungsgruppe, Tutor: Anzhl Zustzlätter: Zugelssene Hilfsmittel: Keine. Bereitungszeit: 60 Minuten Hinweise: Lesen Sie
Wintersemester 2016/2017 Scheinklusur Formle Sprchen und Automtentheorie 21.12.2016 Üungsgruppe, Tutor: Anzhl Zustzlätter: Zugelssene Hilfsmittel: Keine. Bereitungszeit: 60 Minuten Hinweise: Lesen Sie
Endliche Automaten können wahlweise graphisch oder tabellarisch angegeben werden.
 Aufgensmmlung GTI Hinweise. Dies ist eine Aufgensmmlung zum Lernen für die Klusur, keine Proeklusur. Die Zeitduer, die für die Lösung vorgesehen ist, ist lso nicht uf drei Stunden normiert. Für die Klusur
Aufgensmmlung GTI Hinweise. Dies ist eine Aufgensmmlung zum Lernen für die Klusur, keine Proeklusur. Die Zeitduer, die für die Lösung vorgesehen ist, ist lso nicht uf drei Stunden normiert. Für die Klusur
Berechenbarkeitstheorie 4. Vorlesung
 1 Berechenbrkeitstheorie Dr. Institut für Mthemtische Logik und Grundlgenforschung WWU Münster WS 15/16 Alle Folien unter Cretive Commons Attribution-NonCommercil 3.0 Unported Lizenz. Reguläre Ausdrücke
1 Berechenbrkeitstheorie Dr. Institut für Mthemtische Logik und Grundlgenforschung WWU Münster WS 15/16 Alle Folien unter Cretive Commons Attribution-NonCommercil 3.0 Unported Lizenz. Reguläre Ausdrücke
Automaten, Spiele, und Logik
 Automten, Spiele, und Logik Wohe 7 19. Mi 2014 Inhlt der heutigen Vorlesung Alternierende Automten Definition Verindung zu regulären Sprhen Komplementtion Engel und Teufel Ws ist eine nihtdeterministishe
Automten, Spiele, und Logik Wohe 7 19. Mi 2014 Inhlt der heutigen Vorlesung Alternierende Automten Definition Verindung zu regulären Sprhen Komplementtion Engel und Teufel Ws ist eine nihtdeterministishe
Grundlagen der Theoretischen Informatik
 Grundlgen der Theoretischen Informtik 3. Endliche Automten 6.05.2015 Vioric Sofronie-Stokkermns e-mil: sofronie@uni-kolenz.de 1 Üersicht 1. Motivtion 2. Terminologie 3. Endliche Automten und reguläre Sprchen
Grundlgen der Theoretischen Informtik 3. Endliche Automten 6.05.2015 Vioric Sofronie-Stokkermns e-mil: sofronie@uni-kolenz.de 1 Üersicht 1. Motivtion 2. Terminologie 3. Endliche Automten und reguläre Sprchen
Übungen zur Wiederholung quer durch den Stoff Vollständigkeit wird nicht garantiert, und einige sind umfangreicher als klausurtypisch.
 Vorlesung Theoretische Informtik Sommersemester 2017 Dr. B. Bumgrten Üungen zur Wiederholung quer durch den Stoff Vollständigkeit wird nicht grntiert, und einige sind umfngreicher ls klusurtypisch. 1.
Vorlesung Theoretische Informtik Sommersemester 2017 Dr. B. Bumgrten Üungen zur Wiederholung quer durch den Stoff Vollständigkeit wird nicht grntiert, und einige sind umfngreicher ls klusurtypisch. 1.
Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I
 Vorlesung Grundlgen der Theoretischen Informtik / Einführung in die Theoretische Informtik I Bernhrd Beckert Institut für Informtik Sommersemester 2007 B. Beckert Grundlgen d. Theoretischen Informtik:
Vorlesung Grundlgen der Theoretischen Informtik / Einführung in die Theoretische Informtik I Bernhrd Beckert Institut für Informtik Sommersemester 2007 B. Beckert Grundlgen d. Theoretischen Informtik:
Klausur Formale Sprachen und Automaten Grundlagen des Compilerbaus
 Klusur Formle Sprchen und Automten Grundlgen des Compilerus 25. Novemer 2014 Nme: Unterschrift: Mtrikelnummer: Kurs: Note: Aufge erreichre erreichte Nr. Punkte Punkte 1 10 2 10 3 12 4 11 5 9 6 6 7 11 8
Klusur Formle Sprchen und Automten Grundlgen des Compilerus 25. Novemer 2014 Nme: Unterschrift: Mtrikelnummer: Kurs: Note: Aufge erreichre erreichte Nr. Punkte Punkte 1 10 2 10 3 12 4 11 5 9 6 6 7 11 8
mathematik und informatik
 Prof. Dr. André Schulz Kurs 0657 Grundlgen der Theoretischen Informtik A LESEPROBE mthemtik und informtik Ds Werk ist urheerrechtlich geschützt. Die ddurch egründeten Rechte, insesondere ds Recht der Vervielfältigung
Prof. Dr. André Schulz Kurs 0657 Grundlgen der Theoretischen Informtik A LESEPROBE mthemtik und informtik Ds Werk ist urheerrechtlich geschützt. Die ddurch egründeten Rechte, insesondere ds Recht der Vervielfältigung
2 2 Reguläre Sprachen. 2.6 Minimale DFAs und der Satz von Myhill-Nerode. Übersicht
 Formle Systeme, Automten, Prozesse Übersicht 2 2.1 Reguläre Ausdrücke 2.2 Endliche Automten 2.3 Nichtdeterministische endliche Automten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.7 Berechnung
Formle Systeme, Automten, Prozesse Übersicht 2 2.1 Reguläre Ausdrücke 2.2 Endliche Automten 2.3 Nichtdeterministische endliche Automten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.7 Berechnung
vollständig (Vervollständigung) deterministisch, DFA (Potenzmengenkonstruktion) Minimalautomat: minimaler vollständiger DFA
 Ws isher geschh NFA A = (X, Q, δ, I, F ) vollständig (Vervollständigung) deterministisch, DFA (Potenzmengenkonstruktion) Minimlutomt: minimler vollständiger DFA Für jede Sprche L X sind die folgenden Aussgen
Ws isher geschh NFA A = (X, Q, δ, I, F ) vollständig (Vervollständigung) deterministisch, DFA (Potenzmengenkonstruktion) Minimlutomt: minimler vollständiger DFA Für jede Sprche L X sind die folgenden Aussgen
S 1. Definition: Ein endlicher Automat ist ein 5-Tupel. Das endliche Eingabealphabet
 Der endliche Automt Modell: Eingend rechtsseitig unegrenzt F F F F F F F F F F F F F F Lesekopf S 1 Definition: Ein endlicher Automt ist ein 5-Tupel A = ( Σ;S;F;s 0 ; ϕ ) Dei ist Σ= {e 1;e 2...e n} Ds
Der endliche Automt Modell: Eingend rechtsseitig unegrenzt F F F F F F F F F F F F F F Lesekopf S 1 Definition: Ein endlicher Automt ist ein 5-Tupel A = ( Σ;S;F;s 0 ; ϕ ) Dei ist Σ= {e 1;e 2...e n} Ds
RWTH Aachen Lehrgebiet Theoretische Informatik Rossmanith Dreier Hark Kuinke. SS 2017 Blatt
 RWTH Achen Lehrgeiet Theoretische Informtik Rossmnith Dreier Hrk Kuinke SS 2017 Bltt 4 22.5.2017 Lösungsvorschlg zur Vorlesung Formle Sprchen, Automten und Prozesse Aufge T11 1. L, d L, er / L. L, d für
RWTH Achen Lehrgeiet Theoretische Informtik Rossmnith Dreier Hrk Kuinke SS 2017 Bltt 4 22.5.2017 Lösungsvorschlg zur Vorlesung Formle Sprchen, Automten und Prozesse Aufge T11 1. L, d L, er / L. L, d für
FORMALE SYSTEME. Kleene s Theorem. Wiederholung: Reguläre Ausdrücke. 7. Vorlesung: Reguläre Ausdrücke. TU Dresden, 2.
 FORMALE SYSTEME 7. Vorlesung: Reguläre Ausdrücke Mrkus Krötzsch Rndll Munroe, https://xkcd.com/851_mke_it_etter/, CC-BY-NC 2.5 TU Dresden, 2. Novemer 2017 Mrkus Krötzsch, 2. Novemer 2017 Formle Systeme
FORMALE SYSTEME 7. Vorlesung: Reguläre Ausdrücke Mrkus Krötzsch Rndll Munroe, https://xkcd.com/851_mke_it_etter/, CC-BY-NC 2.5 TU Dresden, 2. Novemer 2017 Mrkus Krötzsch, 2. Novemer 2017 Formle Systeme
1 Grundlagen der Theorie formaler Sprachen
 1 Grundlgen der Theorie formler Sprchen Wir eginnen dmit, dss wir in diesem Kpitel zunchst einige grundlegende Begriffe und Methoden us der Theorie formler Sprchen, insesondere der regulären Sprchen, wiederholen.
1 Grundlgen der Theorie formler Sprchen Wir eginnen dmit, dss wir in diesem Kpitel zunchst einige grundlegende Begriffe und Methoden us der Theorie formler Sprchen, insesondere der regulären Sprchen, wiederholen.
Übungsblatt 1. Vorlesung Theoretische Grundlagen der Informatik im WS 17/18
 Institut für Theoretische Informtik Lehrstuhl Prof. Dr. D. Wgner Üungsltt Vorlesung Theoretische Grundlgen der Informtik im WS 78 Ausge 9. Oktoer 27 Age 7. Novemer 27, : Uhr (im Ksten im UG von Geäude
Institut für Theoretische Informtik Lehrstuhl Prof. Dr. D. Wgner Üungsltt Vorlesung Theoretische Grundlgen der Informtik im WS 78 Ausge 9. Oktoer 27 Age 7. Novemer 27, : Uhr (im Ksten im UG von Geäude
Einführung in die Theoretische Informatik
 Einführung in die Theoretische Informtik Johnnes Köler Institut für Informtik Humoldt-Universität zu Berlin WS 011/1 Inhlt der Vorlesung Themen dieser VL: Welche Rechenmodelle sind däqut? Welche Proleme
Einführung in die Theoretische Informtik Johnnes Köler Institut für Informtik Humoldt-Universität zu Berlin WS 011/1 Inhlt der Vorlesung Themen dieser VL: Welche Rechenmodelle sind däqut? Welche Proleme
Einführung in die Theoretische Informatik
 Technische Universität München Fkultät für Informtik Prof. Tois Nipkow, Ph.D. Ssch Böhme, Lrs Noschinski Sommersemester 2011 Lösungsltt 4 20. Juni 2011 Einführung in die Theoretische Informtik Hinweis:
Technische Universität München Fkultät für Informtik Prof. Tois Nipkow, Ph.D. Ssch Böhme, Lrs Noschinski Sommersemester 2011 Lösungsltt 4 20. Juni 2011 Einführung in die Theoretische Informtik Hinweis:
Formale Sprachen und Automaten. Schriftlicher Test
 Formle Sprchen und Automten Prof. Dr. Uwe Nestmnn - 23. Ferur 2017 Schriftlicher Test Studentenidentifiktion: NACHNAME VORNAME MATRIKELNUMMER S TUDIENGANG Informtik Bchelor, Aufgenüersicht: AUFGABE S EITE
Formle Sprchen und Automten Prof. Dr. Uwe Nestmnn - 23. Ferur 2017 Schriftlicher Test Studentenidentifiktion: NACHNAME VORNAME MATRIKELNUMMER S TUDIENGANG Informtik Bchelor, Aufgenüersicht: AUFGABE S EITE
Dank. Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I. Gleichmächtigkeit von DEA und NDEA
 Dnk Vorleung Grundlgen der Theoretichen Informtik / Einführung in die Theoretiche Informtik I Bernhrd Beckert Diee Vorleungmterilien ieren gnz weentlich uf den Folien zu den Vorleungen von Ktrin Erk (gehlten
Dnk Vorleung Grundlgen der Theoretichen Informtik / Einführung in die Theoretiche Informtik I Bernhrd Beckert Diee Vorleungmterilien ieren gnz weentlich uf den Folien zu den Vorleungen von Ktrin Erk (gehlten
Deterministische endliche Automaten. Berechenbarkeit und Komplexität Endliche Automaten. Deterministische endliche Automaten
 Berechenrkeit und Komplexität Endliche Automten Deterministische endliche Automten Folge von Symolen c 4 d 2 Bnd Wolfgng Schreiner Wolfgng.Schreiner@risc.jku.t Automt Folge kzeptiert Reserch Institute
Berechenrkeit und Komplexität Endliche Automten Deterministische endliche Automten Folge von Symolen c 4 d 2 Bnd Wolfgng Schreiner Wolfgng.Schreiner@risc.jku.t Automt Folge kzeptiert Reserch Institute
Teil III. Reguläre Sprachen und endliche Automaten Teil 3: Die Nerode-Relation
 Teil III Reguläre Sprchen und endliche Automten Teil 3: Die Nerode-Reltion Aleitungen und die Nerode-Reltion L Aleitung einer Sprche Sei Σ ein Alphet, L Σ, x Σ. Aleitung von L nch x: D x L := {z Σ xz L}
Teil III Reguläre Sprchen und endliche Automten Teil 3: Die Nerode-Reltion Aleitungen und die Nerode-Reltion L Aleitung einer Sprche Sei Σ ein Alphet, L Σ, x Σ. Aleitung von L nch x: D x L := {z Σ xz L}
Klausur TheGI 2 Automaten und Komplexität (Niedermeier/Hartung/Nichterlein, Sommersemester 2013)
 Berlin, 17.07.2013 Nme:... Mtr.-Nr.:... Klusur TheGI 2 Automten und Komplexität (Niedermeier/Hrtung/Nichterlein, Sommersemester 2013) 1 2 3 4 5 6 7 8 Σ Bereitungszeit: mx. Punktezhl: 60 min. 60 Punkte
Berlin, 17.07.2013 Nme:... Mtr.-Nr.:... Klusur TheGI 2 Automten und Komplexität (Niedermeier/Hrtung/Nichterlein, Sommersemester 2013) 1 2 3 4 5 6 7 8 Σ Bereitungszeit: mx. Punktezhl: 60 min. 60 Punkte
Lösung zur Klausur. Grundlagen der Theoretischen Informatik. 1. Zeigen Sie, dass die folgende Sprache regulär ist: w {a, b} w a w b 0 (mod 3) }.
 Lösung zur Klusur Grundlgen der Theoretischen Informtik 1. Zeigen Sie, dss die folgende Sprche regulär ist: { w {, } w w 0 (mod 3) }. Lösung: Wir nennen die Sprche L. Eine Sprche ist genu dnn regulär,
Lösung zur Klusur Grundlgen der Theoretischen Informtik 1. Zeigen Sie, dss die folgende Sprche regulär ist: { w {, } w w 0 (mod 3) }. Lösung: Wir nennen die Sprche L. Eine Sprche ist genu dnn regulär,
Übungen zur Vorlesung Modellierung WS 2003/2004 Blatt 11 Musterlösungen
 Dr. Theo Lettmnn Pderorn, den 9. Jnur 24 Age 9. Jnur 24 A x, A 2 x, Üungen zur Vorlesung Modellierung WS 23/24 Bltt Musterlösungen AUFGABE 7 : Es sei der folgende prtielle deterministishe endlihe Automt
Dr. Theo Lettmnn Pderorn, den 9. Jnur 24 Age 9. Jnur 24 A x, A 2 x, Üungen zur Vorlesung Modellierung WS 23/24 Bltt Musterlösungen AUFGABE 7 : Es sei der folgende prtielle deterministishe endlihe Automt
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012. Sprachen. Grammatiken (Einführung)
 Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Automaten und formale Sprachen Notizen zu den Folien
 5 Ds Pumping Lemm Shufhprinzip (Folie 137) Automten und formle Sprhen Notizen zu den Folien Im Blok Ds Shufhprinzip für endlihe Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl von
5 Ds Pumping Lemm Shufhprinzip (Folie 137) Automten und formle Sprhen Notizen zu den Folien Im Blok Ds Shufhprinzip für endlihe Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl von
Helmut Seidl. Compilerbau. TU München
 Helmut Seidl Compileru TU München Sommersemester 2007 1 Inhltsverzeichnis Inhltsverzeichnis 0 Einührung 6 0.1 Prinzip eines Interpreters:......................... 6 0.2 Prinzip eines Üersetzers:........................
Helmut Seidl Compileru TU München Sommersemester 2007 1 Inhltsverzeichnis Inhltsverzeichnis 0 Einührung 6 0.1 Prinzip eines Interpreters:......................... 6 0.2 Prinzip eines Üersetzers:........................
Bitte die Blätter nicht trennen! Studiengang:
 Bitte die Blätter nicht trennen! Mtrikelnummer: Fkultät Studiengng: Jhrgng / Kurs : Technik Angewndte Informtik 2017 ITA ÜBUNGSKLAUSUR Studienhljhr: 3. Semester Dtum: 14.11.2018 Bereitungszeit: 90 Minuten
Bitte die Blätter nicht trennen! Mtrikelnummer: Fkultät Studiengng: Jhrgng / Kurs : Technik Angewndte Informtik 2017 ITA ÜBUNGSKLAUSUR Studienhljhr: 3. Semester Dtum: 14.11.2018 Bereitungszeit: 90 Minuten
Einführung in die theoretische Informatik Sommersemester 2017 Übungsblatt Lösungsskizze 3
 Prof. J. Esprz Technische Universität München S. Sickert, J. Krämer KEINE ABGABE Einführung in die theoretische Informtik Sommersemester 27 Üungsltt 3 Üungsltt Wir unterscheiden zwischen Üungs- und Agelättern.
Prof. J. Esprz Technische Universität München S. Sickert, J. Krämer KEINE ABGABE Einführung in die theoretische Informtik Sommersemester 27 Üungsltt 3 Üungsltt Wir unterscheiden zwischen Üungs- und Agelättern.
Franz Binder. Vorlesung im 2006W
 Formle Reguläre und Formle Institut für Alger Johnnes Kepler Universität Linz Vorlesung im 2006W http://www.lger.uni-linz.c.t/students/win/ml Formle Inhlt Reguläre Reguläre Formle Zustndsdigrmm δ: Σ (Q
Formle Reguläre und Formle Institut für Alger Johnnes Kepler Universität Linz Vorlesung im 2006W http://www.lger.uni-linz.c.t/students/win/ml Formle Inhlt Reguläre Reguläre Formle Zustndsdigrmm δ: Σ (Q
Was nicht bewertet werden soll, streichen Sie bitte durch. Werden Täuschungsversuche beobachtet, so wird die Präsenzübung mit 0 Punkten bewertet.
 Prof Dr Dr hc W Thoms Formle Systeme, Automten, Prozesse SS 2011 Musterlösung - Präsenzüung Dniel Neider, Crsten Otto Vornme: Nchnme: Mtrikelnummer: Studiengng (itte nkreuzen): Informtik Bchelor Informtik
Prof Dr Dr hc W Thoms Formle Systeme, Automten, Prozesse SS 2011 Musterlösung - Präsenzüung Dniel Neider, Crsten Otto Vornme: Nchnme: Mtrikelnummer: Studiengng (itte nkreuzen): Informtik Bchelor Informtik
Prof. Dr. Ulrich Furbach Dr. Manfred Jackel Dr. Björn Pelzer Christian Schwarz. Nachklausur
 Grundlgen der Theoretischen Infomtik SS 213 Institut für Informtik Prof. Dr. Ulrich Furch Dr. Mnfred Jckel Dr. Björn Pelzer Christin Schwrz Nchklusur Modul Grundlgen der Theoretischen Informtik 4IN118/INLP1
Grundlgen der Theoretischen Infomtik SS 213 Institut für Informtik Prof. Dr. Ulrich Furch Dr. Mnfred Jckel Dr. Björn Pelzer Christin Schwrz Nchklusur Modul Grundlgen der Theoretischen Informtik 4IN118/INLP1
Algorithmen und Datenstrukturen 1 Kapitel 4.2
 Endliche Automten Algorithmen und Dtenstrukturen 1 Kpitel 4.2 Roert Giegerich Technische Fkultät roert@techfk.uni-bielefeld.de Vorlesung, U. Bielefeld, Winter 2005/2006 Roert Giegerich Endliche Automten
Endliche Automten Algorithmen und Dtenstrukturen 1 Kpitel 4.2 Roert Giegerich Technische Fkultät roert@techfk.uni-bielefeld.de Vorlesung, U. Bielefeld, Winter 2005/2006 Roert Giegerich Endliche Automten
dem Verfahren aus dem Beweis zu Satz 2.20 erhalten wir zunächst die folgenden beiden ε-ndeas für die Sprachen {a} {b} und {ε} {a} +
 Lösungen zu Üungsltt 3 Aufge 1. Es gilt L(( ) ) = ({} {}) {} = ({} {}) ({} {} + ). Mit dem Verfhren us dem Beweis zu Stz 2.20 erhlten wir zunächst die folgenden eiden -NDEAs für die Sprchen {} {} und {}
Lösungen zu Üungsltt 3 Aufge 1. Es gilt L(( ) ) = ({} {}) {} = ({} {}) ({} {} + ). Mit dem Verfhren us dem Beweis zu Stz 2.20 erhlten wir zunächst die folgenden eiden -NDEAs für die Sprchen {} {} und {}
Einführung in den Compilerbau
 Einführung in den Compileru Lexiklische Anlyse II Dr. Armin Wolf 3. Vorlesung SoSe 2010, Universität Potsdm Einführung in den Compileru 1 Lexiklische Anlyse Beispiel Geg.: T mit T = {0,1,2,4,7} (vom Strtzustnd
Einführung in den Compileru Lexiklische Anlyse II Dr. Armin Wolf 3. Vorlesung SoSe 2010, Universität Potsdm Einführung in den Compileru 1 Lexiklische Anlyse Beispiel Geg.: T mit T = {0,1,2,4,7} (vom Strtzustnd
Inhalt. Endliche Automaten. Automaten und Formale Sprachen. Franz Binder. Endliche Automaten. Deterministische Automaten
 Formle Inhlt Reguläre Reguläre Formle Zustndsdigrmm Reguläre δ: Σ (Q Q Ω) Beispiel δ 0 δ 0 1 2 1 2 0 1 2 δ Formle Automt Reguläre Definition Ein nicht-deterministischer, endlicher Automt esteht us einer
Formle Inhlt Reguläre Reguläre Formle Zustndsdigrmm Reguläre δ: Σ (Q Q Ω) Beispiel δ 0 δ 0 1 2 1 2 0 1 2 δ Formle Automt Reguläre Definition Ein nicht-deterministischer, endlicher Automt esteht us einer
Grundlagen der Theoretischen Informatik
 Grundlgen der Theoretischen Informtik 3. Endliche Automten (II) 28.04.2016 Vioric Sofronie-Stokkermns e-mil: sofronie@uni-koblenz.de 1 Übersicht 1. Motivtion 2. Terminologie 3. Endliche Automten und reguläre
Grundlgen der Theoretischen Informtik 3. Endliche Automten (II) 28.04.2016 Vioric Sofronie-Stokkermns e-mil: sofronie@uni-koblenz.de 1 Übersicht 1. Motivtion 2. Terminologie 3. Endliche Automten und reguläre
TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK. Compilerbau I. Dr. Michael Petter, Dr. Axel Simon. SoSe / 160
 TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK Compilerbu I Dr. Michel Petter, Dr. Axel Simon SoSe 2012 1 / 160 Orgnistorisches Mster oder Bchelor b 6. Semester mit 5 ECTS Vorussetzungen Informtik
TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK Compilerbu I Dr. Michel Petter, Dr. Axel Simon SoSe 2012 1 / 160 Orgnistorisches Mster oder Bchelor b 6. Semester mit 5 ECTS Vorussetzungen Informtik
a q 0 q 1 a M q 1 q 3 q 2
 Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 4 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 4 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Bonusklausur über den Stoff der Vorlesung Grundlagen der Informatik II (45 Minuten)
 Institut für Angewndte Informtik und Formle Beschreiungsverfhren 5.0.208 Bonusklusur üer den Stoff der Vorlesung Grundlgen der Informtik II (45 Minuten) Nme: Vornme: Mtr.-Nr.: Semester: (WS 207/8) Ich
Institut für Angewndte Informtik und Formle Beschreiungsverfhren 5.0.208 Bonusklusur üer den Stoff der Vorlesung Grundlgen der Informtik II (45 Minuten) Nme: Vornme: Mtr.-Nr.: Semester: (WS 207/8) Ich
R(i,j,0) ist also für alle i,j = 1,...,n endlich und somit eine durch einen regulären Ausdruck beschreibbare Sprache!
 1 2 Reguläre Audrücke und reguläre Sprchen Grundlgen der Theoretichen Inormtik Till Mokowki Fkultät ür Inormtik Otto-von-Guericke Univerität Mgdeurg Winteremeter 2014/15 Stz: [Kleene] Die Kle der durch
1 2 Reguläre Audrücke und reguläre Sprchen Grundlgen der Theoretichen Inormtik Till Mokowki Fkultät ür Inormtik Otto-von-Guericke Univerität Mgdeurg Winteremeter 2014/15 Stz: [Kleene] Die Kle der durch
Grundlagen der Theoretischen Informatik
 1 2 Grundlgen der Theoretischen Informtik Till Mosskowski Fkultät für Informtik Otto-von-Guericke-Universität Mgdeurg Gegeen sei eine Kleene Alger üer K. Wir etrchten nun n n Mtrizen üer K. Die Menge ller
1 2 Grundlgen der Theoretischen Informtik Till Mosskowski Fkultät für Informtik Otto-von-Guericke-Universität Mgdeurg Gegeen sei eine Kleene Alger üer K. Wir etrchten nun n n Mtrizen üer K. Die Menge ller
4. Übungsblatt zu Theoretische Grundlagen der Informatik im WS 2015/16
 Krlsruher Institut für Technologie Institut für Theoretische Informtik Prof. Dr. Peter Snders L. Hüschle-Schneider, T. Mier 4. Üungsltt zu Theoretische Grundlgen der Informtik im WS 2015/16 http://lgo2.iti.kit.edu/tgi2015.php
Krlsruher Institut für Technologie Institut für Theoretische Informtik Prof. Dr. Peter Snders L. Hüschle-Schneider, T. Mier 4. Üungsltt zu Theoretische Grundlgen der Informtik im WS 2015/16 http://lgo2.iti.kit.edu/tgi2015.php
Universität Karlsruhe Institut für Theoretische Informatik. Klausur: Informatik III
 Nme Vornme Mtrikelnummer Lösungsvorschlg Universität Krlsruhe Institut für Theoretische Informtik o. Prof. Dr. P. Snders 8. März 2006 Klusur: Informtik III Aufgbe 1. Multiple Choice 10 Punkte Aufgbe 2.
Nme Vornme Mtrikelnummer Lösungsvorschlg Universität Krlsruhe Institut für Theoretische Informtik o. Prof. Dr. P. Snders 8. März 2006 Klusur: Informtik III Aufgbe 1. Multiple Choice 10 Punkte Aufgbe 2.
FORMALE SYSTEME. 6. Vorlesung: Reguläre Ausdrücke. TU Dresden, 27. Oktober Markus Krötzsch
 FORMALE SYSTEME 6. Vorlesung: Reguläre Ausdrücke Mrkus Krötzsch TU Dresden, 27. Oktober 2016 Rückblick Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 2 von 29 Wiederholung: Opertionen uf Automten
FORMALE SYSTEME 6. Vorlesung: Reguläre Ausdrücke Mrkus Krötzsch TU Dresden, 27. Oktober 2016 Rückblick Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 2 von 29 Wiederholung: Opertionen uf Automten
Minimalität des Myhill-Nerode Automaten
 inimlität des yhill-nerode Automten Wir wollen zeigen, dss der im Beweis zum yhill-nerode Stz konstruierte DEA für die reguläre Sprche L immer der DEA mit den wenigsten Zuständen für L ist. Sei 0 der konstruierte
inimlität des yhill-nerode Automten Wir wollen zeigen, dss der im Beweis zum yhill-nerode Stz konstruierte DEA für die reguläre Sprche L immer der DEA mit den wenigsten Zuständen für L ist. Sei 0 der konstruierte
6. Übungsblatt. (i) Von welchem Typ ist die Grammatik G? Begründen Sie Ihre Antwort kurz.
 Vorlesung Theoretische Informtik Sommersemester 2015 Prof. S. Lnge 6. Üungsltt 1. Aufge Es sei die folgende Grmmtik G = [Σ, V, S, R] gegeen. Dei seien Σ = {, } und V = {S, B}, woei S ds Strtsymol ist.
Vorlesung Theoretische Informtik Sommersemester 2015 Prof. S. Lnge 6. Üungsltt 1. Aufge Es sei die folgende Grmmtik G = [Σ, V, S, R] gegeen. Dei seien Σ = {, } und V = {S, B}, woei S ds Strtsymol ist.
FORMALE SYSTEME. 7. Vorlesung: Reguläre Ausdrücke. TU Dresden, 2. November Markus Krötzsch
 FORMALE SYSTEME 7. Vorlesung: Reguläre Ausdrücke Mrkus Krötzsch TU Dresden, 2. November 2017 Rndll Munroe, https://xkcd.com/851_mke_it_better/, CC-BY-NC 2.5 Mrkus Krötzsch, 2. November 2017 Formle Systeme
FORMALE SYSTEME 7. Vorlesung: Reguläre Ausdrücke Mrkus Krötzsch TU Dresden, 2. November 2017 Rndll Munroe, https://xkcd.com/851_mke_it_better/, CC-BY-NC 2.5 Mrkus Krötzsch, 2. November 2017 Formle Systeme
Mitschrift Repetitorium Theoretische Informatik und Logik
 Mitschrift Repetitorium Theoretische Informtik und Logik Teil 1: Formle Sprchen, 15.01.2010, 1. Edit Allgemeine Hinweise für die Prüfung Ds Pumping-Lemm für kontextfreie Sprchen kommt nicht (sehr wohl
Mitschrift Repetitorium Theoretische Informtik und Logik Teil 1: Formle Sprchen, 15.01.2010, 1. Edit Allgemeine Hinweise für die Prüfung Ds Pumping-Lemm für kontextfreie Sprchen kommt nicht (sehr wohl
Übungsblatt Nr. 1. Lösungsvorschlag
 Institut für Kryptogrphie und Sicherheit Prof. Dr. Jörn Müller-Qude Nico Döttling Dirk Achench Tois Nilges Vorlesung Theoretische Grundlgen der Informtik Üungsltt Nr. svorschlg Aufge (K) (4 Punkte): Semi-Thue-Systeme
Institut für Kryptogrphie und Sicherheit Prof. Dr. Jörn Müller-Qude Nico Döttling Dirk Achench Tois Nilges Vorlesung Theoretische Grundlgen der Informtik Üungsltt Nr. svorschlg Aufge (K) (4 Punkte): Semi-Thue-Systeme
Formale Sprachen. Endliche Automaten - Kleene. Reguläre Sprachen. Rudolf FREUND, Marion OSWALD. Endliche Automaten. Endliche Automaten: Beispiel
 Formle Sprchen Reguläre Sprchen Endliche Automten - Kleene STEPHEN KLEENE (99-994) Rudolf FREUND, Mrion OSWALD 956: Representtion of events in nerve nets nd finite utomt. In: C.E. Shnnon und J. McCrthy
Formle Sprchen Reguläre Sprchen Endliche Automten - Kleene STEPHEN KLEENE (99-994) Rudolf FREUND, Mrion OSWALD 956: Representtion of events in nerve nets nd finite utomt. In: C.E. Shnnon und J. McCrthy
Vorname: Nachname: Matrikelnummer: Studiengang (bitte ankreuzen): Technik-Kommunikation M.A.
 Formle Systeme, Automten, Prozesse SS 2011 Musterlösung - Klusur 09082011 Prof Dr Dr hc W Thoms Dniel Neider, Crsten Otto Vornme: Nchnme: Mtrikelnummer: Studiengng (itte nkreuzen): Informtik Bchelor Informtik
Formle Systeme, Automten, Prozesse SS 2011 Musterlösung - Klusur 09082011 Prof Dr Dr hc W Thoms Dniel Neider, Crsten Otto Vornme: Nchnme: Mtrikelnummer: Studiengng (itte nkreuzen): Informtik Bchelor Informtik
Hausaufgabe 2 (Induktionsbeweis):
 Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Ergänzungsblatt 6. Letzte Änderung: 24. November 2018
 Ergänzungsltt 6 Letzte Änderung: 24. Novemer 2018 Theoretische Informtik I WS 2018 Crlos Cmino Erinnerung: Die Besprechungstermine für die Ergänzungen 7 is 10 fllen is uf Weiteres us. Aufgen, Lösungen
Ergänzungsltt 6 Letzte Änderung: 24. Novemer 2018 Theoretische Informtik I WS 2018 Crlos Cmino Erinnerung: Die Besprechungstermine für die Ergänzungen 7 is 10 fllen is uf Weiteres us. Aufgen, Lösungen
Endliche Automaten. Stoyan Mutafchiev. Programming Systems Lab, Universität des Saarlandes, Saarbrücken
 Endliche Automten Stoyn Mutfchiev Progrmming Systems L, Universität des Srlndes, Srrücken Astrct Gegenstnd dieser Areit ist der endliche Automt, sowie die Aschlusseigenschften der Sprchen, die von endlichen
Endliche Automten Stoyn Mutfchiev Progrmming Systems L, Universität des Srlndes, Srrücken Astrct Gegenstnd dieser Areit ist der endliche Automt, sowie die Aschlusseigenschften der Sprchen, die von endlichen
Lösung zur Bonusklausur über den Stoff der Vorlesung Grundlagen der Informatik II (45 Minuten)
 Institut für Angewndte Informtik und Formle Beschreiungsverfhren 15.01.2018 Lösung zur Bonusklusur üer den Stoff der Vorlesung Grundlgen der Informtik II (45 Minuten) Nme: Vornme: Mtr.-Nr.: Semester: (WS
Institut für Angewndte Informtik und Formle Beschreiungsverfhren 15.01.2018 Lösung zur Bonusklusur üer den Stoff der Vorlesung Grundlgen der Informtik II (45 Minuten) Nme: Vornme: Mtr.-Nr.: Semester: (WS
Einführung in die Theoretische Informatik
 Einführung in die Theoretische Informtik Johnnes Köler Institut für Informtik Humoldt-Universität zu Berlin WS 2011/12 Minimierung von DFAs Frge Wie können wir feststellen, o ein DFA M = (Z, Σ, δ, q 0,
Einführung in die Theoretische Informtik Johnnes Köler Institut für Informtik Humoldt-Universität zu Berlin WS 2011/12 Minimierung von DFAs Frge Wie können wir feststellen, o ein DFA M = (Z, Σ, δ, q 0,
Dank. Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I. Determiniert / indeterminiert. Teil III.
 Dnk Vorleung Grundlgen der Theoretichen Informtik / Einführung in die Theoretiche Informtik I Bernhrd Beckert Diee Vorleungmterilien ieren gnz weentlich uf den Folien zu den Vorleungen von Ktrin Erk (gehlten
Dnk Vorleung Grundlgen der Theoretichen Informtik / Einführung in die Theoretiche Informtik I Bernhrd Beckert Diee Vorleungmterilien ieren gnz weentlich uf den Folien zu den Vorleungen von Ktrin Erk (gehlten
Lösungen zum Ergänzungsblatt 4
 en zum Ergänzungsltt 4 Letzte Änderung: 23. Novemer 2018 Theoretische Informtik I WS 2018 Crlos Cmino Vorereitungsufgen Vorereitungsufge 1 Sei M = ({p, q, r}, {, }, δ, p, {q, r}) ein DEA mit folgender
en zum Ergänzungsltt 4 Letzte Änderung: 23. Novemer 2018 Theoretische Informtik I WS 2018 Crlos Cmino Vorereitungsufgen Vorereitungsufge 1 Sei M = ({p, q, r}, {, }, δ, p, {q, r}) ein DEA mit folgender
1.5. Abbildung. DEFINITION injektiv, surjektiv, bijektiv Eine Abbildung f ist injektiv, falls es zu jedem y Y höchstens ein x X gibt mit
 CHAPTER. MENGEN UND R ELATIONEN.5. ABBILDUNG.5. Abbildung Eine Abbildung (oder Funktion ist eine Reltion f über X Y mit der Eigenschft: für jedes x us X gibt es genu ein y Y mit (x,y f. Die übliche Schreibweise
CHAPTER. MENGEN UND R ELATIONEN.5. ABBILDUNG.5. Abbildung Eine Abbildung (oder Funktion ist eine Reltion f über X Y mit der Eigenschft: für jedes x us X gibt es genu ein y Y mit (x,y f. Die übliche Schreibweise
Hans U. Simon Bochum, den Annette Ilgen. Beispiele zur Vorlesung. Theoretische Informatik. WS 08/09
 Hns U. Simon Bohum, den 7..28 Annette Ilgen Beispiele zur Vorlesung Theoretishe Informtik WS 8/9 Voremerkung: Hier findet sih eine Smmlung von Beispielen und Motivtionen zur Vorlesung Theoretishe Informtik.
Hns U. Simon Bohum, den 7..28 Annette Ilgen Beispiele zur Vorlesung Theoretishe Informtik WS 8/9 Voremerkung: Hier findet sih eine Smmlung von Beispielen und Motivtionen zur Vorlesung Theoretishe Informtik.
Klausur zur Vorlesung Grundbegriffe der Informatik 10. März 2009 mit Lösungsvorschlägen
 Klusur zur Vorlesung Grundegriffe der Informtik 10. März 2009 mit Lösungsvorschlägen Klusurnummer Nme: Vornme: Mtr.-Nr.: Aufge 1 2 3 4 5 6 7 mx. Punkte 4 2 7 8 8 8 9 tts. Punkte Gesmtpunktzhl: Note: Aufge
Klusur zur Vorlesung Grundegriffe der Informtik 10. März 2009 mit Lösungsvorschlägen Klusurnummer Nme: Vornme: Mtr.-Nr.: Aufge 1 2 3 4 5 6 7 mx. Punkte 4 2 7 8 8 8 9 tts. Punkte Gesmtpunktzhl: Note: Aufge
Prof. Dr. Javier Esparza Garching b. München, den Klausur Einführung in die theoretische Informatik Sommer-Semester 2017
 Prof. Dr. Jvier Esprz Grching. München, den 10.08.17 Klusur Einführung in die theoretische Informtik Sommer-Semester 2017 Bechten Sie: Soweit nicht nders ngegeen, ist stets eine Begründung zw. der Rechenweg
Prof. Dr. Jvier Esprz Grching. München, den 10.08.17 Klusur Einführung in die theoretische Informtik Sommer-Semester 2017 Bechten Sie: Soweit nicht nders ngegeen, ist stets eine Begründung zw. der Rechenweg
1) Gegeben sei ein endlicher, erkennender Automat, definiert durch: f z, definiert durch das Zustandsdiagramm: a,b. z 3
 (Prüfungs-)Aufgen ur Automtentheorie (enthält uch Aufgen u formlen Sprchen) ) Gegeen sei ein endlicher, erkennender Automt, definiert durch: Eingelphet X = {, } Zustndsmenge Z = {,, 2, 3 } Anfngsustnd
(Prüfungs-)Aufgen ur Automtentheorie (enthält uch Aufgen u formlen Sprchen) ) Gegeen sei ein endlicher, erkennender Automt, definiert durch: Eingelphet X = {, } Zustndsmenge Z = {,, 2, 3 } Anfngsustnd
Vorlesung Theoretische Informatik Sommersemester 2018 Dr. B. Baumgarten
 Vorlesung Theoretische Informtik Sommersemester 28 Dr. B. Bumgrten Üungen zur Wiederholung quer durch den Stoff Mit Lösungseispielen Vollständigkeit wird nicht grntiert, und einige sind klusuruntypisch
Vorlesung Theoretische Informtik Sommersemester 28 Dr. B. Bumgrten Üungen zur Wiederholung quer durch den Stoff Mit Lösungseispielen Vollständigkeit wird nicht grntiert, und einige sind klusuruntypisch
Reguläre Sprachen. Reguläre Ausdrücke NFAs
 Reguläre Sprchen Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 0 Dr Snder Bruggink Üungsleitung: Jn Stückrth Wir eschäftigen uns jetzt einige Wochen mit regulären Sprchen deterministische
Reguläre Sprchen Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 0 Dr Snder Bruggink Üungsleitung: Jn Stückrth Wir eschäftigen uns jetzt einige Wochen mit regulären Sprchen deterministische
mathematik und informatik
 RR Prof. Dr. André Schulz Modul 31321 Grundlgen der Informtik 01657 Grundlgen der Theoretischen Informtik A 01658 Grundlgen der Theoretischen Informtik B LESEPROBE mthemtik und informtik Der Inhlt dieses
RR Prof. Dr. André Schulz Modul 31321 Grundlgen der Informtik 01657 Grundlgen der Theoretischen Informtik A 01658 Grundlgen der Theoretischen Informtik B LESEPROBE mthemtik und informtik Der Inhlt dieses
Einführung in die Theoretische Informatik I/ Grundlagen der Theoretischen Informatik. SS 2007 Jun.-Prof. Dr. Bernhard Beckert Ulrich Koch.
 Einführung in die Theoretishe Informtik I/ Grundlgen der Theoretishen Informtik SS 2007 Jun.-Prof. Dr. Bernhrd Bekert Ulrih Koh Nhklusur 25. 09. 2007 Persönlihe Dten itte gut leserlih usfüllen! Vornme:...
Einführung in die Theoretishe Informtik I/ Grundlgen der Theoretishen Informtik SS 2007 Jun.-Prof. Dr. Bernhrd Bekert Ulrih Koh Nhklusur 25. 09. 2007 Persönlihe Dten itte gut leserlih usfüllen! Vornme:...
Endliche Automaten. Endliche Automaten 1 / 115
 Endliche Automten Endliche Automten 1 / 115 Endliche Automten Endliche Automten erluen eine Beschreiung von Hndlungsläufen: Wie ändert sich ein Systemzustnd in Ahängigkeit von veränderten Umgeungsedingungen?
Endliche Automten Endliche Automten 1 / 115 Endliche Automten Endliche Automten erluen eine Beschreiung von Hndlungsläufen: Wie ändert sich ein Systemzustnd in Ahängigkeit von veränderten Umgeungsedingungen?
Automaten und Formale Sprachen 7. Vorlesung
 Automten und Formle Sprchen 7. Vorlesung Mrtin Dietzfelinger Bis nächste Woche: Folien studieren. Detils, Beispiele im Skript, Seiten 70 99. Definitionen lernen, Beispiele nsehen, Frgen vorereiten. Üungsufgen
Automten und Formle Sprchen 7. Vorlesung Mrtin Dietzfelinger Bis nächste Woche: Folien studieren. Detils, Beispiele im Skript, Seiten 70 99. Definitionen lernen, Beispiele nsehen, Frgen vorereiten. Üungsufgen
Spiele und logische Komplexitätsklassen
 Spiele und logische Komplexitätsklssen Mrtin Horsch 26. Jnur 2006 Inhlt des Seminrvortrges Ehrenfeucht-Frïssé-Spiel mit k Mrken Formeln mit k Vrilen und logische Komplexitätsklssen k-vrileneigenschft logischer
Spiele und logische Komplexitätsklssen Mrtin Horsch 26. Jnur 2006 Inhlt des Seminrvortrges Ehrenfeucht-Frïssé-Spiel mit k Mrken Formeln mit k Vrilen und logische Komplexitätsklssen k-vrileneigenschft logischer
Vorname: Nachname: Matrikelnummer: Studiengang (bitte ankreuzen): Technik-Kommunikation M.A.
 Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Klusur 23.09.2010 Prof. Dr. J. Giesl M. Brockschmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Vornme: Nchnme: Mtrikelnummer: Studiengng (itte nkreuzen):
Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Klusur 23.09.2010 Prof. Dr. J. Giesl M. Brockschmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Vornme: Nchnme: Mtrikelnummer: Studiengng (itte nkreuzen):
