Mathematik im Berufskolleg
|
|
|
- Alma Fischer
- vor 6 Jahren
- Abrufe
Transkript
1 Bohner Ott Deusch Mathematik im Berufskolleg Gesamtband Merkur M Verlag Rinteln
2 Wirtschaftswissenschaftliche Bücherei für Schule und Prais Begründet von Handelsschul-Direktor Dipl.-Hdl. Friedrich Hutkap Die Verfasser: Roland Ott Studium der Mathematik an der Universität Tübingen urt Bohner Lehrauftrag Mathematik an der SW Wangen Studium der Mathematik und Phsik an der Universität onstanz Ronald Deusch Lehrauftrag Mathematik am BSZ Bietigheim-Bissingen Studium der Mathematik an der Universität Tübingen Fast alle in diesem Buch erwähnten Hard- und Softwarebezeichnungen sind eingetragene Warenzeichen. Das Werk und seine Teile sind urheberrechtlich geschützt. Jede Nutzung in anderen als den gesetzlich zugelassenen Fällen bedarf der vorherigen schriftlichen Einwilligung des Verlages. Hinweis zu 5a UrhG: Weder das Werk noch seine Teile dürfen ohne eine solche Einwilligung eingescannt und in ein Netzwerk eingestellt werden. Dies gilt auch für Intranets von Schulen und sonstigen Bildungseinrichtungen. Umschlag: Adrian Schulz Foto: Mall of Berlin Bild reis links: Christian Schwier fotolia.com Bild reis rechts: irill edrinski fotolia.com * * * * * * * * * *. Auflage b MERUR VERLAG RINTELN Gesamtherstellung: MERUR VERLAG RINTELN Hutkap GmbH & Co. G, 75 Rinteln info@merkur-verlag.de; lehrer-service@merkur-verlag.de Internet: ISBN
3 Polnomfunktionen (Ganzrationale Funktionen) 5.. Die Steigung einer Geraden Die Straße steigt auf 00 m horizontaler Strecke 0 m an. 00 m 0 m 0% Man sagt, die Straße hat eine Steigung von m = 0 00 m ist das Längenverhältnis von vertikaler Strecke zu horizontaler Strecke. Die Abbildung stellt den Verlauf einer Straße im oordinatensstem dar. a) Welche Steigung hat die Straße? Was würde auf dem Verkehrsschild stehen? b) Bestimmen Sie die Geradengleichung.? a) Aus dem Schaubild lässt sich ablesen: Steigungsdreieck Das Verhältnis von -oordinate zur -oordinate eines Geradenpunktes ist konstant. Dieses Verhältnis heißt Steigung der Geraden m. m = = = konstant b) Aus = folgt =, die Gerade hat die Gleichung =. Das Schaubild der linearen Funktion f mit f () = ;, verläuft durch den Ursprung O. ist eine Ursprungsgerade. Zeichnen Sie das Schaubild der Funktion f mit f () = 0, mithilfe der Steigung. Steigung m = 0, = 5 bedeutet: Man geht vom Ursprung 5 Einheiten nach rechts und anschließend Einheiten nach unten. 5 6
4 6 I Funktionen Ursprungsgerade und Steigung. Winkelhalbierende: =. Winkelhalbierende: = Ursprungsgerade: = m = 0,5 = 0,5 = 0 = = = = Für m > 0 ist eine Gerade steigend, für m < 0 ist eine Gerade fallend. Für m = 0 liegt die Gerade auf der -Achse. ist das Schaubild der linearen Funktion f. Bestimmen Sie eine Gleichung der Geraden G. G Durch Ablesen: f () = 0,5 Die Ursprungsgerade wird um nach unten verschoben. Die Steigung bleibt erhalten. Die Geradengleichung lautet also = 0,5. Hinweis: G schneidet die -Achse in S (0 ). b = heißt -Achsenabschnitt. S Steigungsdreieck G Beachten Sie: Die allgemeine Geradengleichung in Hauptform lautet: = m + b Steigung -Achsenabschnitt b Steigungsdreieck
5 Polnomfunktionen (Ganzrationale Funktionen) 7 Aufgaben Zeichnen Sie eine Gerade durch den Punkt A mit der Steigung m. a) A (0 0), m = b) A (0 ), m =,5 c) A ( ), m = d) A ( 0), m = 0,5 Zeichnen Sie die Geraden g und h in ein geeignetes oordinatensstem ein. a) g: = ; h: = + b) g: = 5 ; h: = Zeichnen Sie die Geraden g: = 95 und h: = für 0 0. Wählen Sie auf der -Achse die Einteilung LE 00. ist das Schaubild der linearen Funktion f mit f () = 5 ;. a) Zeichnen Sie. Verschieben Sie um nach oben. Geben Sie den Funktionsterm an. b) Spiegeln Sie an der -Achse. Geben Sie die Geradengleichung an. 5 Abbildung zeigt drei Geraden. Bestimmen Sie jeweils die zugehörige Geradengleichung. g 8 6 Abb. h Steigungswinkel einer Geraden k f ist das Schaubild der linearen Funktion f mit f () = Unter welchem Winkel schneidet f die -Achse? ;. Aus m = = tan ( ) folgt für den Steigungswinkel tan ( ) = = 6,57 Hinweis: = 5 entspricht der Steigung m =. Beachten Sie: f Unter dem Steigungswinkel einer Geraden g versteht man den Winkel zwischen 0 und 80, den sie mit der -Achse bildet. = (-Achse; g) Aufgaben Gegeben ist die Gerade g durch ihre Gleichung. Geben Sie den Steigungswinkel der Geraden g an. a) g: = + b) g: = 5 c) g: = +
6 8 I Funktionen Steigung aus zwei gegebenen Punkten Eine Gerade g verläuft durch die Punkte S (0 ) und A ( ). Zeichnen Sie die Gerade g. Bestimmen Sie die Steigung von g aus den oordinaten der zwei Geradenpunkte. Wir lesen die Steigung m aus dem Steigungsdreieck ab: m = 0 = Verallgemeinerung Berechnung der Steigung m: Differenz der -Werte: = Differenz der -Werte: 0 = Steigung m: m = = 0 = Steigung der Geraden: m = S (0 ) S ( ) S (0 ) A ( ) 0 A ( ) A ( ) = 0 = Beachten Sie: Für die Steigung m einer Geraden gilt: Differenz der -Werte m = Differenz der -Werte = =. Dabei sind und bzw. und die oordinaten von Geradenpunkten, die frei gewählt werden dürfen. P ( ) P ( ) = = Aufgaben Die Gerade g verläuft durch die Punkte A und B. Berechnen Sie die Steigung von g. a) A ( ), B (5 6) b) A ( ), B ( 7) c) A (0 5), B ( 8 7 ) Für eine lineare Funktion f gilt: f () = und f ( ) = 5. Bestimmen Sie die Steigung der zugehörigen Geraden.
7 9 Funktionen Seite 57 durch Ausklammern und Anwendung des Satzes vom Nullprodukt e ) = 0 Ausklammern von : = ( ) = 0 Satz vom Nullprodukt: = 0 = 0 en: = 0; = ) = 0 Ausklammern von : ( 9 + 0) = 0 Satz vom Nullprodukt: = = 0 von = 0 ergibt: = 5; = en: = 0; = 5; = Hinweis: = 0 ist doppelte ; = 5 und = sind zwei einfache en. ) 9 ( + ) = 0 Satz vom Nullprodukt anwenden: 9 = 0 ( + ) = 0 en: = 0; = ) = 0 Ausklammern von : ( ) = 0 Satz vom Nullprodukt: = 0 = 0. Wurzel ziehen: = 0 = Eakte en: = 0; = Beachten Sie: Gleichungen der Form a + b + c = 0; a 0 a + b + c = 0; a 0 löst man durch Ausklammern der höchsten gemeinsamen Potenz von und Anwendung des Satzes vom Nullprodukt. Aufgaben Lösen Sie die Gleichung. a) 6 = 0 b) 7 = 0 c) 0 = 0 Lösen Sie. a) 0,5 + = 0 b) = 0 c) = d) + = 0 e) 5 = 0 f),5 + = 0 g) ( 8) = 0 h) ( ) = 0 i) ( 5) ( ) = 0 Eva behauptet: Die der Gleichung + 5 = 0 führt auf ( )( ) = 0. Hat Eva Recht? Bestimmen Sie ggf. die en.
8 Polnomfunktionen (Ganzrationale Funktionen) 95 durch Substitution e ) = 0 Substitution = z ( = z ) z 9 z + 0 = 0 der quadratischen Gleichung in z: z = ; z = 5 Rücksubstitution: z = = = ± z = = 5 = ± 5 en: = ± ; = ± 5 ) = 0 Substitution = z ( = z ) z z = 0 der quadratischen Gleichung in z: z = ; z = Rücksubstitution: z = = = ± z = = Diese Gleichung = hat keine wegen 0. en: = ± Beachten Sie: Gleichungen der Form a + b + c = 0; a, b, c 0 löst man durch Substitution. Die Substitution = z ergibt eine quadratische Gleichung in z. Die Rücksubstitution liefert die gesuchten en in. Aufgaben Lösen Sie die Gleichung. a) = 0 b) + = 0 c) = 0 Lösen Sie. a) = b) + = c) d) 8 = 7 e) 9 ( ) ( + ) = 0 f) g) = 0 h) = 8 i) = 0 9 ( ) ( + ) = 9 ( ) = 0 Geben Sie eine Gleichung mit den drei en = ± und = an. Zeigen Sie: Die Gleichung + = hat keine. 5 Für welchen Wert von a 0 hat die Gleichung 6 ( 6 + a) = 0 die =? Berechnen Sie für diesen Fall die weiteren en. 6 Bestimmen Sie die Anzahl der en von + t = 0 in Abhängigkeit von t.
9 96 Funktionen von Polnomgleichungen Gleichungstp sverfahren mit en lineare Gleichung (a 0) a + b = 0 = 0 = 8 quadratische Gleichung (a 0) a + c = 0 = = 8 = ± 8 a + b = 0 Nullprodukt 8 = 0 ( 8) = 0 = 0; = 8 a + b + c = 0 = b ± b a c a 8 + = 0 = 8 ± 56 Gleichung. Grades (a 0) a + d = 0 = 0 8 = 0 = 8 = 8 a + b + c = 0 von ausklammern 8 = 0 ( ) = 0 = 0 = 0 = 0; = Gleichung. Grades (a 0) a + d = 0 = 0 = = 8 = ± 8 a + b + c = 0 same Potenz von ausklammern Nullprodukt 8 + = 0 ( 8 + ) = 0 = = 0 = 0; = 8 ± 56 a + c + e = 0 = z ( = z ) = 0 z 8 z + 7 = 0 z = 7; z = = ± 7 ; = ±
10 Polnomfunktionen (Ganzrationale Funktionen) 97 Aufgaben Lösen Sie. a) = 0 b) 9 = 0 c) = 0 Bestimmen Sie alle en. a) + = 0 b) = c) 6 ( )( + ) = 0 Lösen Sie die Gleichungen. a) + 5 = b) 5 ( 0 ) = 9 5 c) 8 ( 0 ) = 0 d) = e) ( ) ( + ) = 0 f) 9 8 ( ) = 0 g) 0,5 = 0 h) + = 0 i) j) = 0 k) 0, = 0,8 l) ( 8 ) = 0 = Für welchen Wert von a hat die Gleichung a = 0 die =? 5 Geben Sie eine mögliche Gleichung an. a) = 0, = und = sind die en einer Gleichung dritten Grades. b) = 0 und = sind die einzigen en einer Gleichung dritten Grades. 6 Geben Sie für die Gleichung ( + 6) = 0 drei verschiedene äquivalente Gleichungen an. 7 Schreiben Sie die Gleichung = in der Form ( )( )( ) = 0 mit geeigneten Zahlen,,. 8 Eine Gleichung. Grades hat die en 0 und ±. Bestimmen Sie zwei mögliche Gleichungen. 9 Ma und Anja führen folgende Umformungen durch. Finden Sie die Fehler und lösen Sie die Gleichung. Ma Anja
11 urvenuntersuchung 9. Etrempunkte Die Funktion f mit f () = beschreibt näherungsweise die wöch entlichen Verkaufszahlen von Rasenmähern. Dabei ist die Zeit in Wochen nach Wiedereröffnung der Geschäftsräume. Untersuchen Sie die Entwicklung der Verkaufszahlen. Das Schaubild von f wird gezeichnet. Die Verkaufszahlen nehmen zu bis zur Woche mit Stück, danach nehmen sie ab bis zur Woche 0 mit verkauften Rasenmähern, um danach wieder zuzunehmen. Erläuterungen Man liest ab: f ist monoton für Im Übergang von wachsend zu fallend liegt ein Hochpunkt, von fallend zu wachsend liegt ein Tiefpunkt H wachsend fallend wachsend < < < 0 > 0 f () > 0 f () < 0 f () > 0 f () = 0 H T f (0) = 0 T Beachten Sie: Ein urvenpunkt P ( f ( ) ) heißt 5 Hochpunkt Tiefpunkt 6, wenn f ( ) der 5 größte kleinste6 Funktionswert für alle aus einer Umgebung von ist. Dieser 5 größte kleinste6 Funktionswert f ( ) heißt relatives (lokales) 5 Maimum Minimum 6. Notwendige Bedingung für (lokale) Etremstellen: f ( ) = 0. Dabei liegt im Innern des Definitionsbereichs. Hochpunkte bzw. Tiefpunkte nennt man Etrempunkte des Schaubildes von f. Der -Wert des Etrempunktes heißt Etremstelle. Nachweis für Etrempunkte (. Möglichkeit): Nachweis mit Vorzeichenwechsel ( VZW von f ()): VZW von f () an der Stelle Hinweis: f () = f () =,75 > 0; f () = 0; f (5) =,5 < 0 = = 0 von von + nach nach + führt auf einen Hochpunkt Tiefpunkt mit f () = und f (0) = H ( ) T (0 )
12 50 III Differenzialrechnung Nachweis mithilfe der zweiten Ableitung von f (. Möglichkeit): 5 H Graph von f 0 Schaubild von f 5 0 T 5 Schaubild von f Graph von f f () ist die Steigung des Schaubildes von f an der Stelle Die Steigung des Graphen von f an der Stelle = = 0 ist negativ ist positiv. Das bedeutet: f () < 0 f (0) > 0 Das Schaubild von f hat dort einen Hochpunkt Tiefpunkt Hinweis: = ist Maimalstelle, = 0 ist Minimalstelle. Berechnung von f () und f (0) Zweite Ableitung von f: f () = 7 Einsetzen der -Werte in f (): f () = < 0 f (0) = > 0 Bestimmung von Etrempunkten Notwendige Bedingung: f () = 0 liefert die Stellen,,... mit waagrechter Tangente. Nachweis für Hochpunkt bzw. Tiefpunkt. Möglichkeit durch Vorzeichen-Untersuchung von f () Hat f () an der Stelle einen Vorzeichenwechsel von + nach 5, so hat der Graph von f einen von nach +6 5 Hochpunkt H ( f ( )) Tiefpunkt T ( f ( )) 6.. Möglichkeit durch Einsetzen von in f () Ist 5 f ( ) < 0 f ( ) > 06, so hat der Graph von f einen 5 Hochpunkt H ( f ( )) Tiefpunkt T ( f ( )) 6.
13 urvenuntersuchung 5 Gegeben ist die Funktion f mit f () = + ; mit Graph. Berechnen Sie die oordinaten der Hoch- und Tiefpunkte. Ableitungen: f () = + ; f () = + Notwendige Bedingung für Etremstellen: f () = 0 + = 0 Stellen mit waagrechter Tangente: = ; = Nachweis durch Einsetzen der -Werte in f () f () = > 0: f hat in = ein (relatives) Minimum, hat einen Tiefpunkt an der Stelle =. f () = < 0: f hat in = ein (relatives) Maimum, hat einen Hochpunkt an der Stelle =. Mit f () = und f () = 0 erhält man: Tiefpunkt T ( ); Hochpunkt H ( 0) Schaubild : H 5 T Berechnen Sie die Etremstellen von f mit f () = 0,5 + cos () für ]0; [. Welche ist die Minimalstelle? Ableitungen: f () = 0,5 sin (); f () = cos () Notwendige Bedingung für Etremstellen: f () = 0 0,5 sin () = 0 sin () = 0,5 z. B. mithilfe der Tabelle: = 6 ; = 5 6 Nachweis durch Einsetzen der -Werte in f () f ( 6 ) = 0,866 < 0 f hat in = 6 ein (relatives) Maimum. f ( 5 Schaubild von f 6 ) = 0,866 > 0 f hat in = 5 6 ein (relatives) Minimum. = 5 6 ist die Minimalstelle. Maimum Minimum Hinweis: f ( ) ist der absolut kleinste -Wert, f ( ) ist das absolute Minimum auf ]0; [. Das relative Maimum ist auch das absolute Maimum auf ]0; [.
14 Flächeninhaltsberechnung mithilfe der Integralrechnung 9 ist der Graph von f mit f () = e, G ist der Graph von g mit g () = e + ;. und G schließen für eine Fläche ein. Berechnen Sie deren Inhalt. Schnittstellen von und G: f () = g () für = 0 Schnittstelle mit VZW: = 0,5 0,5 0,5 ( f () g ()) d = ( f () g ()) d = 0,5 0,5 ( ) d = [ ] 0,5 =,5 ( ) d = 0,5 Inhalt der Fläche: A =,5 + 0,5 =,5 G 5 Der Graph von f mit f () = sin ( );, begrenzt mit der Parallelen zur -Achse durch S (0 ) auf [0; ] eine Fläche mit Inhalt A. Wie groß ist diese Fläche? Die Gerade mit = verläuft durch die Hochpunkte von, sie berührt auf dem Intervall [0; nur in =. Integration von 0 bis : 0 ( sin ( )) d = [ + cos ( ) ] 0 = A = = ist der Graph von f mit f () = sin ( ) ;. Die Abbildung zeigt zwei Flächenstücke. Berechnen Sie den Flächeninhalt eines der beiden Flächenstücke g Schnittstellen durch Ablesen: = ; = ; = Wegen der Smmetrie von und g zu W ( ) sind die Flächen gleich groß. Fläche zwischen und -Achse: ( sin ( ) ) d = [ 6 cos ( ) ] = 6 < 0 Flächeninhalt: A = 6 Trapezinhalt: A T = + = 5 oder A + A = + = 5 Gesuchte Fläche: A = 5 ( 6 ) = 6 Alternative mit ( f () g ()) d Geradengleichung von g aufstellen ( = + ) A = ( f () g ()) d = 6 A T g
15 0 IV Integralrechnung Beachten Sie : Inhalt der Fläche, die von den urven von f und G von g auf dem Intervall [a; b] umschlossen wird. a) Berechnung der Schnittstellen Bed.: f () = g () f () g () = 0 liefert die Schnittstellen,, b) Integration der Differenzfunktion mit f () g () a ( f () g ()) d b ( f () g ()) d c) Addition der Beträge der Integral werte ergibt den Inhalt der Gesamtfläche. A ges = A + A A A G Hinweis: Nicht über eine Schnittstelle mit Vorzeichenwechsel hinweg integrieren. = a = b Vergleichen Sie die Vorgehensweise: Fläche zwischen der urve von f und der -Achse auf dem Intervall [a; b] a) Berechnung der Nullstellen: Bed.: f () = 0 liefert die Nullstellen,, b) Integration über f ()d A f () d a b f () d c) Addition der Beträge der Integralwerte ergibt den Inhalt der Gesamtfläche. A ges = A + A Hinweis: Nicht über eine Nullstelle mit Vorzeichenwechsel hinweg integrieren. = a A = b Aufgaben Berechnen Sie den Inhalt der markierten Fläche. 5 = = = cos() +
16 Flächeninhaltsberechnung mithilfe der Integralrechnung ist der Graph der Funktion f mit f () = + ;. a) Geben Sie eine Stammfunktion von f an und berechnen Sie den Inhalt der Fläche, die von und der -Achse im. Feld eingeschlossen wird. b) schließt mit der Parabel P von g mit g () = ;, zwei Flächenstücke ein. Wie groß ist die Fläche, die den Punkt D ( 0) enthält? Die Funktionen f und g sind durch f () = sin () und g() = cos () gegeben. Jan behauptet: f ( ) ) = g ( ). Stimmt das? Wie groß ist die markierte Fläche? Graph von f Graph von g und G sind die Schaubilder der Funktionen f mit f () = e + und g mit g () =. Berechnen Sie den Inhalt der markierten Fläche. G 5 ist das Schaubild der Funktion f mit f () = ( ) ( ) ;. a) Skizzieren Sie. b) Die Tangente an im Ursprung begrenzt mit eine Fläche. Berechnen Sie den Inhalt. Markieren Sie die Fläche in Ihrer Skizze. 6 Für sind zwei Funktionen f und g gegeben mit f () = ( + ) und g () =. Die zugehörigen Graphen begrenzen eine Fläche. Berechnen Sie den Inhalt A dieser Fläche. 7 und G sind die Graphen der Funktionen f und g mit f () = + + ; und g () = ;. a) Zeigen Sie: G berührt in = und schneidet in =. b) und G begrenzen im. Quadranten eine Fläche. Berechnen Sie den Inhalt dieser Fläche. 0
17 IV Integralrechnung 8 ist das Schaubild der Funktion f mit f () = ( );. Die Gerade g schneidet die urve in = und =., g und die -Achse schließen im. Feld eine Fläche ein. Berechnen Sie deren Inhalt. 9 Gegeben ist f mit f () = e + 0,5 + ; mit Graph. Wie lässt sich der Inhalt A der markierten Fläche bestimmen? Geben Sie A an. Welche Bedeutung hat die Gerade g? Gegen welchen Wert strebt der Flächeninhalt, wenn die rechte Grenze gegen strebt? 8 6 A g 0 ist das Schaubild von f mit f () = sin ( ),. begrenzt mit der -Achse eine Fläche auf dem Intervall [ 0; ] mit Inhalt A. Die Funktion f soll nun auf [ 0; ] durch eine ganzrationale Funktion p zweiten Grades angenähert werden. und die Parabel G von p berühren sich in den gemeinsamen Punkten von mit der -Achse. G begrenzt mit der -Achse eine Fläche mit Inhalt B. Gegeben ist die Funktion f durch f () = + ; und der Graph von g in der Abbildung. Die Graphen von f und g begrenzen für einen See. Der Graph von f bildet modellhaft die nördliche und die zu g gehörende Parabel die südliche Uferbegrenzungslinie. Die -Achse verläuft in West-Ost-Richtung ( LE km). Berechnen Sie die Größe der Seefläche. 0 0 Graph von g Gegeben sind die Schaubilder g und f zweier Funktionen g und f (siehe Abbildung) g g und f begrenzen eine Fläche mit dem Inhalt A. A ist der Flächenanteil von A, der im ersten Quadranten liegt. Geben Sie ein geeignetes Vorgehen zur Bestimmung des Flächeninhaltes von A an. f A
Mathematik im Berufskolleg I
 1 Bohner Ott Deusch Mathematik im Berufskolleg I Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 2016 ISBN 978-3-8120-0234-9 Das Werk und seine Teile sind urheberrechtlich geschützt.
1 Bohner Ott Deusch Mathematik im Berufskolleg I Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 2016 ISBN 978-3-8120-0234-9 Das Werk und seine Teile sind urheberrechtlich geschützt.
Ausführliche Lösungen
 Bohner Ihlenburg Ott Deusch Mathematik für berufliche Gmnasien Jahrgangsstufen und Analsis und Stochastik Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 5. Auflage 05 ISBN 978--80-8- Das
Bohner Ihlenburg Ott Deusch Mathematik für berufliche Gmnasien Jahrgangsstufen und Analsis und Stochastik Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 5. Auflage 05 ISBN 978--80-8- Das
Mathematik im Berufskolleg
 Ausführliche Lösungen zu Mathematik im Berufskolleg Gesamtband Bohner Ott Deusch Mathematik im Berufskolleg Gesamtband Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab. Auflage 06 ISBN 978--80-059-7
Ausführliche Lösungen zu Mathematik im Berufskolleg Gesamtband Bohner Ott Deusch Mathematik im Berufskolleg Gesamtband Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab. Auflage 06 ISBN 978--80-059-7
Trigonometrische Funktionen
 Trigonometrische Funktionen. Gegeben ist die Funktion f() = (sin( π )) Ihr Graph sei K. a) Skizzieren Sie K im Intervall [0,]. Geben Sie die Periode von f an. Geben Sie alle Hoch- und Tiefpunkte von K
Trigonometrische Funktionen. Gegeben ist die Funktion f() = (sin( π )) Ihr Graph sei K. a) Skizzieren Sie K im Intervall [0,]. Geben Sie die Periode von f an. Geben Sie alle Hoch- und Tiefpunkte von K
Mathematik für das kaufmännische Berufskolleg I (BK I)
 Mathematik für das kaufmännische Berufskolleg I (BK I) Bearbeitet von Kurt Bohner, Peter Ihlenburg, Roland Ott 6. Auflage 2016. Taschenbuch. 188 S. Softcover ISBN 978 3 8120 0234 9 Gewicht: 340 g Wirtschaft
Mathematik für das kaufmännische Berufskolleg I (BK I) Bearbeitet von Kurt Bohner, Peter Ihlenburg, Roland Ott 6. Auflage 2016. Taschenbuch. 188 S. Softcover ISBN 978 3 8120 0234 9 Gewicht: 340 g Wirtschaft
Gebrochen rationale Funktion f(x) = x2 +1
 Gebrochen rationale Funktion f() = +. Der Graph der Funktion f ist punktsmmetrisch, es gilt: f( ) = ( ) + f() = f( ) = + = + = f(). An der Stelle = 0 ist f nicht definiert, an dieser Stelle liegt ein Pol
Gebrochen rationale Funktion f() = +. Der Graph der Funktion f ist punktsmmetrisch, es gilt: f( ) = ( ) + f() = f( ) = + = + = f(). An der Stelle = 0 ist f nicht definiert, an dieser Stelle liegt ein Pol
Korrekturblatt zu 3206 / 6. Auflage 2014
 Korrekturblatt zu 306 / 6. Auflage 014 Lehrbuch Seite 56 3. c) g() = f() + 4 G K 1 1 3 4 Lehrbuch Seite 109 9. Eine Gleichung 3. Grades lasst sich grafisch durch den Graph einer Polnomfunktion 3. Grades
Korrekturblatt zu 306 / 6. Auflage 014 Lehrbuch Seite 56 3. c) g() = f() + 4 G K 1 1 3 4 Lehrbuch Seite 109 9. Eine Gleichung 3. Grades lasst sich grafisch durch den Graph einer Polnomfunktion 3. Grades
Matur-/Abituraufgaben Analysis
 Matur-/Abituraufgaben Analysis 1. Tropfen Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1 ) im Intervall 1. Die Kurve k bildet zusammen mit ihrem Spiegelbild k eine zur -Achse symmetrische
Matur-/Abituraufgaben Analysis 1. Tropfen Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1 ) im Intervall 1. Die Kurve k bildet zusammen mit ihrem Spiegelbild k eine zur -Achse symmetrische
Mathemathik-Prüfungen
 M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
9 Funktionen und ihre Graphen
 57 9 Funktionen und ihre Graphen Funktionsbegriff Eine Funktion ordnet jedem Element aus einer Menge D f genau ein Element aus einer Menge W f zu. mit = f(), D f Die Menge aller Funktionswerte nennt man
57 9 Funktionen und ihre Graphen Funktionsbegriff Eine Funktion ordnet jedem Element aus einer Menge D f genau ein Element aus einer Menge W f zu. mit = f(), D f Die Menge aller Funktionswerte nennt man
Mathematisches Thema Quadratische Funktionen 1. Art Anwenden. Klasse 10. Schwierigkeit x. Klasse 10. Mathematisches Thema
 Quadratische Funktionen 1 1.) Zeige, dass die Funktion in der Form f() = a 2 + b +c geschrieben werden kann und gebe a, b und c an. a) f() = ( -5) ( +7) b) f() = ( -1) ( +1) c) f() = 3 ( - 4) 2.) Wie heißen
Quadratische Funktionen 1 1.) Zeige, dass die Funktion in der Form f() = a 2 + b +c geschrieben werden kann und gebe a, b und c an. a) f() = ( -5) ( +7) b) f() = ( -1) ( +1) c) f() = 3 ( - 4) 2.) Wie heißen
FH- Kurs Mathematik Übungsaufgaben für 2. Klausur
 Aufgabe 1: Gegeben ist die Funktion f mit 1 f x = x x x + x R 8 3 2 ( ) = ( 3 9 + 27);. a) Untersuchen sie das Schaubild K von f auf Schnittpunkte mit den Koordinatenachsen, Hoch- und Tiefpunkte. Zeichnen
Aufgabe 1: Gegeben ist die Funktion f mit 1 f x = x x x + x R 8 3 2 ( ) = ( 3 9 + 27);. a) Untersuchen sie das Schaubild K von f auf Schnittpunkte mit den Koordinatenachsen, Hoch- und Tiefpunkte. Zeichnen
Abiturprüfung Mathematik 2008 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe Für jedes t f t () + t R ist die Funktion f t gegeben durch = mit R. Das Schaubild von f t heißt K t.. (6 Punkte)
Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe Für jedes t f t () + t R ist die Funktion f t gegeben durch = mit R. Das Schaubild von f t heißt K t.. (6 Punkte)
Pflichtteil... 2. Wahlteil Analysis 1... 6. Wahlteil Analysis 2... 9. Wahlteil Analysis 3... 13. Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analsis 1... 6 Wahlteil Analsis... 9 Wahlteil Analsis 3... 13 Wahlteil Analtische Geometrie 1... 16 Wahlteil Analtische Geometrie... 3 Lösungen: 006 Pflichtteil Lösungen zur Prüfung
Pflichtteil... Wahlteil Analsis 1... 6 Wahlteil Analsis... 9 Wahlteil Analsis 3... 13 Wahlteil Analtische Geometrie 1... 16 Wahlteil Analtische Geometrie... 3 Lösungen: 006 Pflichtteil Lösungen zur Prüfung
Arbeitsblätter zur Vergleichsklausur EF. Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf.
 Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
5.5. Abituraufgaben zu ganzrationalen Funktionen
 .. Abituraufgaben zu ganzrationalen Funktionen Aufgabe : Kurvendiskussion, Fläche zwischen zwei Schaubildern () Untersuchen Sie f(x) x x und g(x) x auf Symmetrie, Achsenschnittpunkte, Extrempunkts sowie
.. Abituraufgaben zu ganzrationalen Funktionen Aufgabe : Kurvendiskussion, Fläche zwischen zwei Schaubildern () Untersuchen Sie f(x) x x und g(x) x auf Symmetrie, Achsenschnittpunkte, Extrempunkts sowie
Abschlussprüfung an der Fachoberschule im Schuljahr 2008 / 2009
 Senatsverwaltung für Bildung, Wissenschaft und Forschung Abschlussprüfung an der Fachoberschule im Schuljahr 008 / 009 Fach Mathematik (B) Name, Vorname Klasse Prüfungstag 7. Mai 009 Prüfungszeit Zugelassene
Senatsverwaltung für Bildung, Wissenschaft und Forschung Abschlussprüfung an der Fachoberschule im Schuljahr 008 / 009 Fach Mathematik (B) Name, Vorname Klasse Prüfungstag 7. Mai 009 Prüfungszeit Zugelassene
Linearisierung einer Funktion Tangente, Normale
 Linearisierung einer Funktion Tangente, Normale 1 E Linearisierung einer Funktion Abb. 1 1: Die Gerade T ist die Tangente der Funktion y = f (x) im Punkt P Eine im Punkt x = a differenzierbare Funktion
Linearisierung einer Funktion Tangente, Normale 1 E Linearisierung einer Funktion Abb. 1 1: Die Gerade T ist die Tangente der Funktion y = f (x) im Punkt P Eine im Punkt x = a differenzierbare Funktion
Mathematik im Berufskolleg I
 Bohner Ott Deusch Mathematik im Berufskolleg I Merkur M Verlag Rinteln Wirtschaftswissenschaftliche Bücherei für Schule und Prais Begründet von Handelsschul-Direktor Dipl.-Hdl. Friedrich Hutkap Die Verfasser:
Bohner Ott Deusch Mathematik im Berufskolleg I Merkur M Verlag Rinteln Wirtschaftswissenschaftliche Bücherei für Schule und Prais Begründet von Handelsschul-Direktor Dipl.-Hdl. Friedrich Hutkap Die Verfasser:
Demo: Mathe-CD. Prüfungsaufgaben Mündliches Abitur. Analysis. Teilbereich 1: Ganzrationale Funktionen 1. März 2002
 Prüfungsaufgaben Mündliches Abitur Analysis Teilbereich : Ganzrationale Funktionen Hier nur Aufgaben als Demo Datei Nr. 9 März 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Vorwort Die in dieser Reihe von
Prüfungsaufgaben Mündliches Abitur Analysis Teilbereich : Ganzrationale Funktionen Hier nur Aufgaben als Demo Datei Nr. 9 März 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Vorwort Die in dieser Reihe von
Musteraufgaben Fachoberschule 2017 Mathematik
 Musteraufgaben Fachoberschule 07 Funktionsuntersuchung /8 Gegeben ist die Funktion f mit der Funktionsgleichung f(x) = 0,05x 0,75x +,x +,8 und dem Definitionsbereich x [0;0]. Der Graph G f der Funktion
Musteraufgaben Fachoberschule 07 Funktionsuntersuchung /8 Gegeben ist die Funktion f mit der Funktionsgleichung f(x) = 0,05x 0,75x +,x +,8 und dem Definitionsbereich x [0;0]. Der Graph G f der Funktion
Analysis. A1 Funktionen/Funktionsklassen. 1 Grundbegriffe. 2 Grundfunktionen
 A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
Mathematik-Vorbereitungskurs. ist ein. a b ist der und eine.
 Aufgaben. Vervollständigen Sie den Tet. a) Der Term (a + b) ist ein. a und b sind. b) Der Term + ist eine. und sind. ist eine. c) Der Term a b ist ein. a b ist der und eine.. Ergibt der Term (a (b c))
Aufgaben. Vervollständigen Sie den Tet. a) Der Term (a + b) ist ein. a und b sind. b) Der Term + ist eine. und sind. ist eine. c) Der Term a b ist ein. a b ist der und eine.. Ergibt der Term (a (b c))
Abiturprüfung 2000 LK Mathematik Baden-Württemberg
 Abiturprüfung 000 LK Mathematik Baden-Württemberg Aufgabe I 1 Analysis ( )² Gegeben ist die Funktion f durch f ( ) = ; D f. Ihr Schaubild sei K. ( 4) a) Geben Sie die maimale Definitionsmenge D f an. Untersuchen
Abiturprüfung 000 LK Mathematik Baden-Württemberg Aufgabe I 1 Analysis ( )² Gegeben ist die Funktion f durch f ( ) = ; D f. Ihr Schaubild sei K. ( 4) a) Geben Sie die maimale Definitionsmenge D f an. Untersuchen
Analysis: Klausur Analysis
 Analysis Klausur zur Integralrechnung Stammfunktionsberechnung, Flächenberechnung, Rotationsvolumen, Funktionen zu Änderungsraten (Bearbeitungszeit: 9 Minuten) Gymnasium J1 Aleander Schwarz www.mathe-aufgaben.com
Analysis Klausur zur Integralrechnung Stammfunktionsberechnung, Flächenberechnung, Rotationsvolumen, Funktionen zu Änderungsraten (Bearbeitungszeit: 9 Minuten) Gymnasium J1 Aleander Schwarz www.mathe-aufgaben.com
Bohner Ihlenburg Ott. Mathematik für Berufsfachschulen. Merkur. Verlag Rinteln
 Bohner Ihlenburg Ott Mathematik für Berufsfachschulen Merkur M Verlag Rinteln 3 Wirtschaftswissenschaftliche Bücherei für Schule und Praxis Begründet von Handelsschul-Direktor Dipl.-Hdl. Friedrich Hutkap
Bohner Ihlenburg Ott Mathematik für Berufsfachschulen Merkur M Verlag Rinteln 3 Wirtschaftswissenschaftliche Bücherei für Schule und Praxis Begründet von Handelsschul-Direktor Dipl.-Hdl. Friedrich Hutkap
Abitur - Grundkurs Mathematik. Sachsen-Anhalt 2002. Gebiet G1 - Analysis
 Abitur - Grundkurs Mathematik Sachsen-Anhalt Gebiet G - Analsis Aufgabe.. Der Graph einer ganzrationalen Funktion f dritten Grades mit einer Funktionsgleichung der Form f a b c d a,b,c,d, R schneidet die
Abitur - Grundkurs Mathematik Sachsen-Anhalt Gebiet G - Analsis Aufgabe.. Der Graph einer ganzrationalen Funktion f dritten Grades mit einer Funktionsgleichung der Form f a b c d a,b,c,d, R schneidet die
11 Üben X Affine Funktionen 1.01
 Üben X Aine Funktionen.0 Zeichne die Graphen zu olgenden Funktionsgleichungen! + + d c b a Augabenkarte von MUED Lösung X Aine Funktionen.0 + + d c b a Üben X Aine Funktionen.0 Bestimme die Funktionsgleichung
Üben X Aine Funktionen.0 Zeichne die Graphen zu olgenden Funktionsgleichungen! + + d c b a Augabenkarte von MUED Lösung X Aine Funktionen.0 + + d c b a Üben X Aine Funktionen.0 Bestimme die Funktionsgleichung
 Abiturprüfung Mathematik 0 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f() = ( sin() + 7) 5. Aufgabe : ( VP) Berechnen Sie eine Stammfunktion
Abiturprüfung Mathematik 0 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f() = ( sin() + 7) 5. Aufgabe : ( VP) Berechnen Sie eine Stammfunktion
Übungsaufgaben II zur Klausur 1
 Übungsaufgaben II zur Klausur. Ableitungen 0. Führen Sie für g mit f ( +,9 8 eine vollständige Kurvendiskussion (siehe S. 9f durch. Markieren Sie alle von Ihnen bestimmten Punkte in der abschließenden
Übungsaufgaben II zur Klausur. Ableitungen 0. Führen Sie für g mit f ( +,9 8 eine vollständige Kurvendiskussion (siehe S. 9f durch. Markieren Sie alle von Ihnen bestimmten Punkte in der abschließenden
Aufgaben für Klausuren und Abschlussprüfungen
 Grundlagenwissen: Ableitungen, Flächen unter Kurven, Nullstellen, Etremwerte, Wendepunkte.. Bestimmen Sie die Stammfunktion F() der folgenden Funktionen. Die Konstante C darf weggelassen werden. a) f()
Grundlagenwissen: Ableitungen, Flächen unter Kurven, Nullstellen, Etremwerte, Wendepunkte.. Bestimmen Sie die Stammfunktion F() der folgenden Funktionen. Die Konstante C darf weggelassen werden. a) f()
Graphen zuordnen und Funktionsterme ermitteln
 Aufgaben Analsis Flächenberechnung Ganzrationale Funktion Tangenten ohne Einsatz des GTR Integralfunktion Graphen zuordnen und Funktionsterme ermitteln Wahr oder falsch? Integralfunktion Wahr oder falsch?
Aufgaben Analsis Flächenberechnung Ganzrationale Funktion Tangenten ohne Einsatz des GTR Integralfunktion Graphen zuordnen und Funktionsterme ermitteln Wahr oder falsch? Integralfunktion Wahr oder falsch?
Lineare Funktionen y = m x + n Sekundarstufe I u. II Funktion ist monoton fallend, verläuft vom II. in den IV.
 LINEARE FUNKTIONEN heißt Anstieg oder Steigung heißt y-achsenabschnitt Graphen linearer Funktionen sind stets Geraden Konstante Funktionen Spezialfall Graphen sind waagerechte Geraden (parallel zur x-achse)
LINEARE FUNKTIONEN heißt Anstieg oder Steigung heißt y-achsenabschnitt Graphen linearer Funktionen sind stets Geraden Konstante Funktionen Spezialfall Graphen sind waagerechte Geraden (parallel zur x-achse)
Unterlagen für die Lehrkraft Zentrale Klausur am Ende der Einführungsphase 2011 Mathematik
 ZK M A1 (mit CAS) Seite 1 von 5 Unterlagen für die Lehrkraft Zentrale Klausur am Ende der Einführungsphase 011 Mathematik 1. Aufgabenart Analysis. Aufgabenstellung siehe Prüfungsaufgabe. Materialgrundlage
ZK M A1 (mit CAS) Seite 1 von 5 Unterlagen für die Lehrkraft Zentrale Klausur am Ende der Einführungsphase 011 Mathematik 1. Aufgabenart Analysis. Aufgabenstellung siehe Prüfungsaufgabe. Materialgrundlage
Wirtschaftswissenschaftliche Bücherei für Schule und Praxis Begründet von Handelsschul-Direktor Dipl.-Hdl. Friedrich Hutkap
 Wirtschaftswissenschaftliche Bücherei für Schule und Praxis Begründet von Handelsschul-Direktor Dipl.-Hdl. Friedrich Hutkap Die Verfasser: Roland Ott Lehrauftrag Mathematik an der KSW Wangen Studium der
Wirtschaftswissenschaftliche Bücherei für Schule und Praxis Begründet von Handelsschul-Direktor Dipl.-Hdl. Friedrich Hutkap Die Verfasser: Roland Ott Lehrauftrag Mathematik an der KSW Wangen Studium der
c) Das Schaubild von verläuft im Schnittpunkt mit der y-achse steiler als die erste Winkelhalbierende.
 VP b) Das Schaubild von hat für 36 genau zwei Wendepunkte. c) Das Schaubild von verläuft im Schnittpunkt mit der y-achse steiler als die erste Winkelhalbierende. 3. Gegeben ist die Funktionenschar mit
VP b) Das Schaubild von hat für 36 genau zwei Wendepunkte. c) Das Schaubild von verläuft im Schnittpunkt mit der y-achse steiler als die erste Winkelhalbierende. 3. Gegeben ist die Funktionenschar mit
Abschlussaufgabe Nichttechnik - Analysis II
 Analysis NT GS - 0.06.06 - m06_ntalsg_gs.mcd Abschlussaufgabe 006 - Nichttechnik - Analysis II.0 Gegeben sind die reellen Funktionen fx ( ) mit ID f = ID g = IR. ( ) = x und gx ( ) = fx ( ) +. Zeigen Sie,
Analysis NT GS - 0.06.06 - m06_ntalsg_gs.mcd Abschlussaufgabe 006 - Nichttechnik - Analysis II.0 Gegeben sind die reellen Funktionen fx ( ) mit ID f = ID g = IR. ( ) = x und gx ( ) = fx ( ) +. Zeigen Sie,
Arbeitsblatt 4: Kurvendiskussion - Von Skizzen zu Extremstellen-Bedingungen
 Arbeitsblatt 4: Kurvendiskussion - Von Skizzen zu Etremstellen-Bedingungen Häufig sind Ableitungsfunktionsterme leichter zu handhaben als die Terme der Ausgangsfunktonen, weil sie niedrigere Eponenten
Arbeitsblatt 4: Kurvendiskussion - Von Skizzen zu Etremstellen-Bedingungen Häufig sind Ableitungsfunktionsterme leichter zu handhaben als die Terme der Ausgangsfunktonen, weil sie niedrigere Eponenten
Mathematik LK13 Kursarbeit Musterlösung Aufgabe I:
 Mathematik LK13 Kursarbeit 1 6.11.14 Musterlösung Aufgabe I: Analysis I 1. Spaß mit natürlichen Eponentialfunktionen Gegeben sind die Funktionen f ()=e ( + ) und g ( )=5 e Untersuchen Sie beide Funktionen
Mathematik LK13 Kursarbeit 1 6.11.14 Musterlösung Aufgabe I: Analysis I 1. Spaß mit natürlichen Eponentialfunktionen Gegeben sind die Funktionen f ()=e ( + ) und g ( )=5 e Untersuchen Sie beide Funktionen
Die Steigung m ist ein Quotient zweier Differenzen und heißt daher Differenzenquotient.
 Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
1 Die natürliche Exponentialfunktion und ihre Ableitung
 Schülerbuchseite 5 5 Lösungen vorläuig VI Natürliche Eponential- und Logarithmusunktion Die natürliche Eponentialunktion und ihre Ableitung S. 5 Durch Ausprobieren erkennt man, dass < a
Schülerbuchseite 5 5 Lösungen vorläuig VI Natürliche Eponential- und Logarithmusunktion Die natürliche Eponentialunktion und ihre Ableitung S. 5 Durch Ausprobieren erkennt man, dass < a
x 2 x 1.Untersuchen Sie die Schaubilder der Funktion auf ihre Symmetrieeigenschaften. (Achsensymmetrie/ Punktsymmetrie)
 I. Grenzverhalten von Funktionen. Verhalten einer Funktion für bzw.. Bestimmen Sie den Grenzwert a) b) ) ( + ( ) c) ( + ) ( ) II. Symmetrie.Untersuchen Sie die Schaubilder der Funktion auf ihre Symmetrieeigenschaften.
I. Grenzverhalten von Funktionen. Verhalten einer Funktion für bzw.. Bestimmen Sie den Grenzwert a) b) ) ( + ( ) c) ( + ) ( ) II. Symmetrie.Untersuchen Sie die Schaubilder der Funktion auf ihre Symmetrieeigenschaften.
1 Die zweite Ableitung
 Schülerbuchseite 5 Lösungen vorläuig und deren Graphen Die zweite Ableitung S. Um den Graphen der Ableitung zu skizzieren, sucht man zuerst die Punkte mit waagrechten Tangenten. so erhält man die Nullstellen
Schülerbuchseite 5 Lösungen vorläuig und deren Graphen Die zweite Ableitung S. Um den Graphen der Ableitung zu skizzieren, sucht man zuerst die Punkte mit waagrechten Tangenten. so erhält man die Nullstellen
Mathematik Abitur Zusammenfassung Marius Buila
 Mathematik Abitur Zusammenfassung Marius Buila 1.Analysis 1.1 Grundlagen: Ableitung f (u) ist Steigung in Punkt P (u/f(u)) auf K f(x) = a * x r f (x) = a * r * x r-1 Tangentengleichung: y= f (u) * (x-u)
Mathematik Abitur Zusammenfassung Marius Buila 1.Analysis 1.1 Grundlagen: Ableitung f (u) ist Steigung in Punkt P (u/f(u)) auf K f(x) = a * x r f (x) = a * r * x r-1 Tangentengleichung: y= f (u) * (x-u)
www.mathe-aufgaben.com
 Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit sin() f() =. Aufgabe : ( VP) Berechnen Sie das Integral ( )
Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit sin() f() =. Aufgabe : ( VP) Berechnen Sie das Integral ( )
)e2 (3 x2 ) a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen Sie das Verhalten von f für x.
 Analysis Aufgabe aus Abiturprüfung Bayern GK (abgeändert). Gegeben ist die Funktion f(x) = ( x )e ( x ). a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen
Analysis Aufgabe aus Abiturprüfung Bayern GK (abgeändert). Gegeben ist die Funktion f(x) = ( x )e ( x ). a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen
Pflichtteil - Exponentialfunktion
 Pflichtteil - Eponentialfunktion Aufgabe (Ableiten) Bestimme die. und. Ableitung der folgenden Funktionen: a) f() = ln() + b) g() = e Aufgabe (Integrieren) Berechnen Sie die Integrale: a) e d b) c) h()
Pflichtteil - Eponentialfunktion Aufgabe (Ableiten) Bestimme die. und. Ableitung der folgenden Funktionen: a) f() = ln() + b) g() = e Aufgabe (Integrieren) Berechnen Sie die Integrale: a) e d b) c) h()
 Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit x f(x) = (x + 5) e. Aufgabe : ( VP) Gegeben ist die Funktion
Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit x f(x) = (x + 5) e. Aufgabe : ( VP) Gegeben ist die Funktion
Übungen zu Kurvenscharen
 Übungen zu Kurvenscharen. Gegeben ist die Geradenschar g t : = (t ) ( t) + 9 (t 9) mit D(g t ) = R, t R. a) Zeichnen Sie die Graphen der Funktionen g und g in ein Koordinatensstem. b) Geben Sie die Schnittpunkte
Übungen zu Kurvenscharen. Gegeben ist die Geradenschar g t : = (t ) ( t) + 9 (t 9) mit D(g t ) = R, t R. a) Zeichnen Sie die Graphen der Funktionen g und g in ein Koordinatensstem. b) Geben Sie die Schnittpunkte
Aufgaben zum Grundwissen Mathematik 11. Jahrgangstufe Teil 1
 Aufgaben zum Grundwissen Mathematik 11. Jahrgangstufe Teil 1 Lehrplan: M 11.1.1 Graphen gebrochen-rationaler Funktionen M 11.1.2 Lokales Differenzieren Passende Kapitel im Schulbuch Fokus Mathematik 11:
Aufgaben zum Grundwissen Mathematik 11. Jahrgangstufe Teil 1 Lehrplan: M 11.1.1 Graphen gebrochen-rationaler Funktionen M 11.1.2 Lokales Differenzieren Passende Kapitel im Schulbuch Fokus Mathematik 11:
1 x x2 3 mit D f = IR. Teilaufgabe 1.1 (5 BE) Berechnen Sie die Nullstellen der Funktion f und geben Sie das Symmetrieverhalten von G f.
 Abschlussprüfung Berufliche Oberschule 0 Mathematik Nichttechnik - A II - Lösung Teilaufgabe.0 Gegeben ist die reelle Funktion f( x) x x mit D f = IR. Teilaufgabe. (5 BE) Berechnen Sie die Nullstellen
Abschlussprüfung Berufliche Oberschule 0 Mathematik Nichttechnik - A II - Lösung Teilaufgabe.0 Gegeben ist die reelle Funktion f( x) x x mit D f = IR. Teilaufgabe. (5 BE) Berechnen Sie die Nullstellen
Lineare Funktionen. Klasse 8 Aufgabenblatt für Lineare Funktionen Datum: Donnerstag,
 Lineare Funktionen Aufgabe 1: Welche der folgenden Abbildungen stellen eine Funktion dar? Welche Abbildungen stellen eine lineare Funktion dar? Ermittle für die linearen Funktionen eine Funktionsgleichung.
Lineare Funktionen Aufgabe 1: Welche der folgenden Abbildungen stellen eine Funktion dar? Welche Abbildungen stellen eine lineare Funktion dar? Ermittle für die linearen Funktionen eine Funktionsgleichung.
5.3. Aufgaben zur Kurvenuntersuchung ganzrationaler Funktionen
 .. Aufgaben zur Kurvenuntersuchung ganzrationaler Funktionen Aufgabe : Kurvendiskussion Untersuche die folgenden Funktionen auf Symmetrie, Achsenschnittpunkte, Etrem- und Wendepunkte und zeichne ein Schaubild
.. Aufgaben zur Kurvenuntersuchung ganzrationaler Funktionen Aufgabe : Kurvendiskussion Untersuche die folgenden Funktionen auf Symmetrie, Achsenschnittpunkte, Etrem- und Wendepunkte und zeichne ein Schaubild
Analysis: Trigonometr. Funktionen Analysis Trigonometrische Funktionen Pflicht- und Wahlteilaufgaben
 Analysis Trigonometrische Funktionen Pflicht- und Wahlteilaufgaben Gymnasium Oberstufe J oder J Alexander Schwarz www.mathe-aufgaben.com Dezember 0 Pflichtteilaufgaben (ohne GTR): Aufgabe : Leite die folgenden
Analysis Trigonometrische Funktionen Pflicht- und Wahlteilaufgaben Gymnasium Oberstufe J oder J Alexander Schwarz www.mathe-aufgaben.com Dezember 0 Pflichtteilaufgaben (ohne GTR): Aufgabe : Leite die folgenden
Kurvendiskussion Ganzrationale Funktion Aufgaben und Lösungen
 Kurvendiskussion Ganzrationale Funktion Aufgaben und http://www.fersch.de Klemens Fersch 9. August 0 Inhaltsverzeichnis Ganzrationale Funktion Quadratische Funktionen f x) = ax + bx + c 8. Aufgaben...................................................
Kurvendiskussion Ganzrationale Funktion Aufgaben und http://www.fersch.de Klemens Fersch 9. August 0 Inhaltsverzeichnis Ganzrationale Funktion Quadratische Funktionen f x) = ax + bx + c 8. Aufgaben...................................................
TK II Mathematik 2. Feststellungsprüfung Nachprüfung Arbeitszeit: 120 Minuten
 . Feststellungsprüfung Nachprüfung 19.0.005 1. Untersuchen Sie die Funktion p ( ) = + 16 auf Monotonie und geben Sie auf Grund dieses Ergebnisses die Lage des Scheitels an. (10. Der Graph einer ganz rationalen
. Feststellungsprüfung Nachprüfung 19.0.005 1. Untersuchen Sie die Funktion p ( ) = + 16 auf Monotonie und geben Sie auf Grund dieses Ergebnisses die Lage des Scheitels an. (10. Der Graph einer ganz rationalen
Urs Wyder, 4057 Basel Funktionen. f x x x x 2
 Urs Wyder, 4057 Basel Urs.Wyder@edubs.ch Funktionen f 3 ( ) = + f ( ) = sin(4 ) Inhaltsverzeichnis DEFINITION DES FUNKTIONSBEGRIFFS...3. NOTATION...3. STETIGKEIT...3.3 ABSCHNITTSWEISE DEFINIERTE FUNKTIONEN...4
Urs Wyder, 4057 Basel Urs.Wyder@edubs.ch Funktionen f 3 ( ) = + f ( ) = sin(4 ) Inhaltsverzeichnis DEFINITION DES FUNKTIONSBEGRIFFS...3. NOTATION...3. STETIGKEIT...3.3 ABSCHNITTSWEISE DEFINIERTE FUNKTIONEN...4
R. Brinkmann Seite
 R. Brinkmann http://brinkmann-du.de Seite 9..8 Linearen Funktion Aus der Sekundarstufe I sind Ihnen die Graphen linearer Funktionen als Geraden bekannt und deren Funktionsgleichungen als Geradengleichungen.
R. Brinkmann http://brinkmann-du.de Seite 9..8 Linearen Funktion Aus der Sekundarstufe I sind Ihnen die Graphen linearer Funktionen als Geraden bekannt und deren Funktionsgleichungen als Geradengleichungen.
6 Bestimmung linearer Funktionen
 1 Bestimmung linearer Funktionen Um die Funktionsvorschrift einer linearen Funktion zu bestimmen, muss man ihre Steigung ermitteln. Dazu sind entweder Punkte gegeben oder man wählt zwei Punkte P 1 ( 1
1 Bestimmung linearer Funktionen Um die Funktionsvorschrift einer linearen Funktion zu bestimmen, muss man ihre Steigung ermitteln. Dazu sind entweder Punkte gegeben oder man wählt zwei Punkte P 1 ( 1
Lösungen Kapitel A: Funktionen
 Lösungen Kapitel A: Funktionen Arbeitsblatt 01: Abhängigkeiten entstehen a) Zu Beginn des Tages befinden sich 10 Besucher am Strand. Bis um 4 Uhr nachts haben alle den Strand verlassen. Um 6 Uhr sind bereits
Lösungen Kapitel A: Funktionen Arbeitsblatt 01: Abhängigkeiten entstehen a) Zu Beginn des Tages befinden sich 10 Besucher am Strand. Bis um 4 Uhr nachts haben alle den Strand verlassen. Um 6 Uhr sind bereits
Einstieg. Bogenmaß. Allgemeine Formeln
 2 Einstieg Differenzialrechnung * Integralrechnung * Geometrie Stochastik * Zusatzthemen * Prüfungsaufgaben Wiederholung einiger Formeln Aufgaben aus dem Pflichtteil Schaubilder und Funktionsterme Streckung
2 Einstieg Differenzialrechnung * Integralrechnung * Geometrie Stochastik * Zusatzthemen * Prüfungsaufgaben Wiederholung einiger Formeln Aufgaben aus dem Pflichtteil Schaubilder und Funktionsterme Streckung
Bayern FOS BOS 12 Fachabiturprüfung 2015 Mathematik (Nichttechnische Ausbildungsrichtungen) Analysis A I
 Bayern FOS BOS Fachabiturprüfung 05 Mathematik (Nichttechnische Ausbildungsrichtungen) Analysis A I.0 Nebenstehende Abbildung zeigt den Graphen G f ' der ersten Ableitungsfunktion einer in ganz 0 definierten
Bayern FOS BOS Fachabiturprüfung 05 Mathematik (Nichttechnische Ausbildungsrichtungen) Analysis A I.0 Nebenstehende Abbildung zeigt den Graphen G f ' der ersten Ableitungsfunktion einer in ganz 0 definierten
Diese Funktion ist mein Typ!
 Diese Funktion ist mein Typ! Überblick über die wichtigsten Funktionstypen der 10.Jgst.: Lineare Funktionen Quadratische Funktionen Ganzrationale Funktionen Gebrochen-rationale Funktionen Trigonometrische
Diese Funktion ist mein Typ! Überblick über die wichtigsten Funktionstypen der 10.Jgst.: Lineare Funktionen Quadratische Funktionen Ganzrationale Funktionen Gebrochen-rationale Funktionen Trigonometrische
eine Musteraufgabe Wir betrachten die Funktion f mit f(x) = x3 + 3x 2-6x + 2.
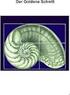 Wir betrachten die Funktion f mit f(x) = - 1 3 x3 + 3x 2-6x + 2. a) Zeigen Sie, dass das Schaubild von f symmetrisch zum Punkt Z(3 2) ist. b) Bestimmen Sie die Koordinaten der Achsenschnittpunkte des Schaubilds
Wir betrachten die Funktion f mit f(x) = - 1 3 x3 + 3x 2-6x + 2. a) Zeigen Sie, dass das Schaubild von f symmetrisch zum Punkt Z(3 2) ist. b) Bestimmen Sie die Koordinaten der Achsenschnittpunkte des Schaubilds
Mathematik. Merkur. Haarmann Wolpers. zur Erlangung der allgemeinen Hochschulreife Technische Fachrichtungen Band 1.
 Haarmann Wolpers Mathematik zur Erlangung der allgemeinen Hochschulreife Technische Fachrichtungen Band 1 Merkur Verlag Rinteln Wirtschaftswissenschaftliche Bücherei für Schule und Praxis Begründet von
Haarmann Wolpers Mathematik zur Erlangung der allgemeinen Hochschulreife Technische Fachrichtungen Band 1 Merkur Verlag Rinteln Wirtschaftswissenschaftliche Bücherei für Schule und Praxis Begründet von
Wurzelfunktionen Aufgaben
 Wurzelfunktionen Aufgaben. Für jedes k (k > 0) ist die Funktion f k (x) = 8 (x k ) kx, 0 x gegeben. a) Untersuchen Sie die Funktion f k auf Nullstellen und Extrema. Ermitteln Sie lim f k(x) sowie für 0
Wurzelfunktionen Aufgaben. Für jedes k (k > 0) ist die Funktion f k (x) = 8 (x k ) kx, 0 x gegeben. a) Untersuchen Sie die Funktion f k auf Nullstellen und Extrema. Ermitteln Sie lim f k(x) sowie für 0
Über die Bedeutung der zwei Zahlen m und x 1 für das Aussehen des Graphen wird an anderer Stelle informiert.
 Lineare Funktionen - Term - Grundwissen Woran erkennt man, ob ein Funktionsterm zu einer Linearen Funktion gehört? oder Wie kann der Funktionsterm einer Linearen Funktion aussehen? Der Funktionsterm einer
Lineare Funktionen - Term - Grundwissen Woran erkennt man, ob ein Funktionsterm zu einer Linearen Funktion gehört? oder Wie kann der Funktionsterm einer Linearen Funktion aussehen? Der Funktionsterm einer
Die Summen- bzw. Differenzregel
 Die Summen- bzw Differenzregel Seite Kapitel mit Aufgaben Seite WIKI Regeln und Formeln Level Grundlagen Aufgabenblatt ( Aufgaben) Lösungen zum Aufgabenblatt Aufgabenblatt (7 Aufgaben) Lösungen zum Aufgabenblatt
Die Summen- bzw Differenzregel Seite Kapitel mit Aufgaben Seite WIKI Regeln und Formeln Level Grundlagen Aufgabenblatt ( Aufgaben) Lösungen zum Aufgabenblatt Aufgabenblatt (7 Aufgaben) Lösungen zum Aufgabenblatt
Erfolg im Mathe-Abi 2014
 Gruber I Neumann Erfolg im Mathe-Abi 2014 Schleswig-Holstein Übungsbuch Prüfungsaufgaben mit Tipps und Lösungen Inhaltsverzeichnis 1. Aufgabensatz... 7 2. Aufgabensatz... 12 3. Aufgabensatz... 17 4. Aufgabensatz...
Gruber I Neumann Erfolg im Mathe-Abi 2014 Schleswig-Holstein Übungsbuch Prüfungsaufgaben mit Tipps und Lösungen Inhaltsverzeichnis 1. Aufgabensatz... 7 2. Aufgabensatz... 12 3. Aufgabensatz... 17 4. Aufgabensatz...
1 Ableiten der Sinus- und Kosinusfunktion
 Schülerbuchseite 6 8 Lösungen vorläufig Ableiten der Sinus- und Kosinusfunktion S. 6 Vermutung: Da das Zeit-Weg-Diagramm eine Sinuskurve und das zugehörige Zeit-Geschwindigkeits-Diagramm 8 eine Kosinuskurve
Schülerbuchseite 6 8 Lösungen vorläufig Ableiten der Sinus- und Kosinusfunktion S. 6 Vermutung: Da das Zeit-Weg-Diagramm eine Sinuskurve und das zugehörige Zeit-Geschwindigkeits-Diagramm 8 eine Kosinuskurve
Mathematik-Lexikon. Abszisse Die x-koordinate eines Punktes -> Ordinate
 Mathematik-Lexikon HM00 Abszisse Die x-koordinate eines Punktes -> Ordinate Aufstellen von Funktionstermen Gesucht: Ganzrationale Funktion n-ten Grades: ƒ(x) = a n x n + a n-1 x n-1 + a n- x n- +... +
Mathematik-Lexikon HM00 Abszisse Die x-koordinate eines Punktes -> Ordinate Aufstellen von Funktionstermen Gesucht: Ganzrationale Funktion n-ten Grades: ƒ(x) = a n x n + a n-1 x n-1 + a n- x n- +... +
Mathematik - Oberstufe
 Mathematik - Oberstufe Pflicht- /Wahlteilaufgaben und Musterlösungen ur Integralrechnung Zielgruppe: Oberstufe Gymnasium Schwerpunkt: Stammfunktion, Flächenberechnung, Rotationsvolumen Aleander Schwar
Mathematik - Oberstufe Pflicht- /Wahlteilaufgaben und Musterlösungen ur Integralrechnung Zielgruppe: Oberstufe Gymnasium Schwerpunkt: Stammfunktion, Flächenberechnung, Rotationsvolumen Aleander Schwar
= / 40. Abschlussprüfung Fachoberschule 2012 (Mathematik) Aufgabenvorschlag B. Gegeben ist die Funktion f mit der Funktionsgleichung
 Abschlussprüfung Fachoberschule () Aufgabenvorschlag B / 4 Gegeben ist die Funktion f mit der Funktionsgleichung 4 f ( x) x x x = + +. Dazu ist ein Rechteck gegeben, dessen Seiten parallel zu den Koordinatenachsen
Abschlussprüfung Fachoberschule () Aufgabenvorschlag B / 4 Gegeben ist die Funktion f mit der Funktionsgleichung 4 f ( x) x x x = + +. Dazu ist ein Rechteck gegeben, dessen Seiten parallel zu den Koordinatenachsen
Untersuchen Sie die Funktion f auf Monotonie und auf die Existenz von lokalen Extrema.
 Gegeben sind die Funktionen f und g durch y y f() g(), ln, D f R, und! 0. Ihre Graphen werden mit F bzw. G bezeichnet. a) Ermitteln Sie den größtmöglichen Definitionsbereich D f der Funktion f. Untersuchen
Gegeben sind die Funktionen f und g durch y y f() g(), ln, D f R, und! 0. Ihre Graphen werden mit F bzw. G bezeichnet. a) Ermitteln Sie den größtmöglichen Definitionsbereich D f der Funktion f. Untersuchen
1 /41. Abschlussprüfung Fachoberschule 2010, (Mathematik) Aufgabenvorschlag B
 , (Mathematik) / Gegeben ist eine Funktion f mit der Funktionsgleichung f ( x) = x x + x 6x+ ; x. Untersuchen Sie das Symmetrieverhalten des Graphen von f und begründen Sie Ihre Aussage. /. Untersuchen
, (Mathematik) / Gegeben ist eine Funktion f mit der Funktionsgleichung f ( x) = x x + x 6x+ ; x. Untersuchen Sie das Symmetrieverhalten des Graphen von f und begründen Sie Ihre Aussage. /. Untersuchen
(Tipp: Formelbuch!) x3 dx?
 Integralrechnung. bestimmte und unbestimmte Integrale (a) x ( + x ) dx =? (b) e x + e x dx =? (c) x 3 x + x x 6x + 9 dx =? (d) x cos x dx =?. Bestimmtes Integral x3 3x + 9 x dx =? 4 3. Bestimmtes Integral
Integralrechnung. bestimmte und unbestimmte Integrale (a) x ( + x ) dx =? (b) e x + e x dx =? (c) x 3 x + x x 6x + 9 dx =? (d) x cos x dx =?. Bestimmtes Integral x3 3x + 9 x dx =? 4 3. Bestimmtes Integral
Exemplar für Prüfer/innen
 Exemplar für Prüfer/innen Kompensationsprüfung zur standardisierten kompetenzorientierten schriftlichen Reifeprüfung AHS Juni 2016 Mathematik Kompensationsprüfung 3 Angabe für Prüfer/innen Hinweise zur
Exemplar für Prüfer/innen Kompensationsprüfung zur standardisierten kompetenzorientierten schriftlichen Reifeprüfung AHS Juni 2016 Mathematik Kompensationsprüfung 3 Angabe für Prüfer/innen Hinweise zur
Lineare Funktion. Wolfgang Kippels 3. November Inhaltsverzeichnis
 Lineare Funktion Wolfgang Kippels. November 0 Inhaltsverzeichnis Grundlegende Zusammenhänge. Aufbau der Linearen Funktion......................... Nullstellenbestimmung............................. Schnittpunktbestimmung............................
Lineare Funktion Wolfgang Kippels. November 0 Inhaltsverzeichnis Grundlegende Zusammenhänge. Aufbau der Linearen Funktion......................... Nullstellenbestimmung............................. Schnittpunktbestimmung............................
Zuammenfassung: Reelle Funktionen
 Zuammenfassung: Reelle Funktionen 1 Grundlegendes a) Zahlenmengen IN = {1; 2; 3; 4;...} Natürliche Zahlen IN 0 = IN {0} Natürliche Zahlen mit 0 ZZ = {... ; 2; 1; 0; 1; 2;...} Ganze Zahlen Q = { z z ZZ,
Zuammenfassung: Reelle Funktionen 1 Grundlegendes a) Zahlenmengen IN = {1; 2; 3; 4;...} Natürliche Zahlen IN 0 = IN {0} Natürliche Zahlen mit 0 ZZ = {... ; 2; 1; 0; 1; 2;...} Ganze Zahlen Q = { z z ZZ,
1. Vereinfache wie im Beispiel: 3. Vereinfache wie im Beispiel: 4. Schreibe ohne Wurzel wie im Beispiel:
 1. Zahlenmengen Wissensgrundlage Aufgabenbeispiele Gib die jeweils kleinstmögliche Zahlenmenge an, welche die Zahl enthält? R Q Q oder All diejenigen Zahlen, die sich nicht mehr durch Brüche darstellen
1. Zahlenmengen Wissensgrundlage Aufgabenbeispiele Gib die jeweils kleinstmögliche Zahlenmenge an, welche die Zahl enthält? R Q Q oder All diejenigen Zahlen, die sich nicht mehr durch Brüche darstellen
e-funktionen f(x) = e x2
 e-funktionen f(x) = e x. Smmetrie: Der Graph ist achsensmmetrisch, da f( x) = f(x).. Nullstellen: Bed.: f(x) = 0 Es sind keine Nullstellen vorhanden, da e x stets positiv ist. 3. Extrema: notw. Bed.: f
e-funktionen f(x) = e x. Smmetrie: Der Graph ist achsensmmetrisch, da f( x) = f(x).. Nullstellen: Bed.: f(x) = 0 Es sind keine Nullstellen vorhanden, da e x stets positiv ist. 3. Extrema: notw. Bed.: f
Zusammenfassung und Wiederholung zu Geraden im IR ²
 Seite 1 von 5 Definition einer Geraden Wir zeichnen mithilfe einer Wertetabelle den Graphen der linearen Funktion f mit f 0,5 1. Fülle hierzu die Wertetabelle fertig aus: 4 3 1 0 1 3 4 f f4 0,54 1 3...,5...
Seite 1 von 5 Definition einer Geraden Wir zeichnen mithilfe einer Wertetabelle den Graphen der linearen Funktion f mit f 0,5 1. Fülle hierzu die Wertetabelle fertig aus: 4 3 1 0 1 3 4 f f4 0,54 1 3...,5...
1 Grundlagen 8 Funktionen 8 Differenzenquotient und Änderungsrate 9 Ableitung 11
 Inhalt A Differenzialrechnung 8 Grundlagen 8 Funktionen 8 Differenzenquotient und Änderungsrate 9 Ableitung 2 Ableitungsregeln 2 Potenzregel 2 Konstantenregel 3 Summenregel 4 Produktregel 4 Quotientenregel
Inhalt A Differenzialrechnung 8 Grundlagen 8 Funktionen 8 Differenzenquotient und Änderungsrate 9 Ableitung 2 Ableitungsregeln 2 Potenzregel 2 Konstantenregel 3 Summenregel 4 Produktregel 4 Quotientenregel
Wirtschaftswissenschaftliche Bücherei für Schule und Praxis Begründet von Handelsschul-Direktor Dipl.-Hdl. Friedrich Hutkap
 Wirtschaftswissenschaftliche Bücherei für Schule und Praxis Begründet von Handelsschul-Direktor Dipl.-Hdl. Friedrich Hutkap Die Verfasser: Kurt Bohner Studium der Mathematik und Physik an der Universität
Wirtschaftswissenschaftliche Bücherei für Schule und Praxis Begründet von Handelsschul-Direktor Dipl.-Hdl. Friedrich Hutkap Die Verfasser: Kurt Bohner Studium der Mathematik und Physik an der Universität
Vorbereitungskurs Mathematik
 BBS Gerolstein Vorbereitungskurs Mathematik Vorbereitungskurs Mathematik für die Berufsoberschule II www.bbs-gerolstein.de/cms/download/mathematik/vorkurs-mathe-bos-.pdf bzw. www.p-merkelbach.de/bos/mathe/vorkurs-mathe-bos-.pdf
BBS Gerolstein Vorbereitungskurs Mathematik Vorbereitungskurs Mathematik für die Berufsoberschule II www.bbs-gerolstein.de/cms/download/mathematik/vorkurs-mathe-bos-.pdf bzw. www.p-merkelbach.de/bos/mathe/vorkurs-mathe-bos-.pdf
Wahrscheinlichkeitsrechnung. Trigonometrie Sinus und Kosinus
 Gymnasium Neutraubling Grundwissen Mathematik 10. Jahrgangsstufe Wissen und Können Aufgaben, Beispiele und Erläuterungen 1. Bedingte Wahrscheinlichkeit Bezeichnungen: P(A): Wahrscheinlichkeit des Ereignisses
Gymnasium Neutraubling Grundwissen Mathematik 10. Jahrgangsstufe Wissen und Können Aufgaben, Beispiele und Erläuterungen 1. Bedingte Wahrscheinlichkeit Bezeichnungen: P(A): Wahrscheinlichkeit des Ereignisses
Kapitel 8 Einführung der Integralrechnung über Flächenmaße
 8. Flächenmaße 8.1 Flächenmaßfunktionen zu nicht negativen Randfunktionen Wir wenden uns einem auf den ersten Blick neuen Thema zu, der Ermittlung des Flächenmaßes A von Flächen A, die vom nicht unterhalb
8. Flächenmaße 8.1 Flächenmaßfunktionen zu nicht negativen Randfunktionen Wir wenden uns einem auf den ersten Blick neuen Thema zu, der Ermittlung des Flächenmaßes A von Flächen A, die vom nicht unterhalb
Matura2016-Lösung. Problemstellung 1
 Matura-Lösung Problemstellung. Die Funktion f( = + 9k + müsste bei = den Wert annehmen, also gilt + 9k + = k =. Wir betrachten den Bereich mit positiven Werten. Dann gilt: f ( = 8 + 8 = = ; = Bei liegt
Matura-Lösung Problemstellung. Die Funktion f( = + 9k + müsste bei = den Wert annehmen, also gilt + 9k + = k =. Wir betrachten den Bereich mit positiven Werten. Dann gilt: f ( = 8 + 8 = = ; = Bei liegt
Ergänzungsheft Erfolg im Mathe-Abi
 Ergänzungsheft Erfolg im Mathe-Abi Hessen Prüfungsaufgaben Grundkurs 2012 Grafikfähiger Taschenrechner (GTR), Computeralgebrasystem (CAS) Dieses Heft enthält Übungsaufgaben für GTR und CAS sowie die GTR-
Ergänzungsheft Erfolg im Mathe-Abi Hessen Prüfungsaufgaben Grundkurs 2012 Grafikfähiger Taschenrechner (GTR), Computeralgebrasystem (CAS) Dieses Heft enthält Übungsaufgaben für GTR und CAS sowie die GTR-
Kreissektoren und Bogenmaß
 M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius gilt für einen Kreissektor mit Mittelpunktswinkel : Länge des Kreisbogens Fläche des Kreissektors = = 360 360 Das Bogenmaß eines Winkels ist
M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius gilt für einen Kreissektor mit Mittelpunktswinkel : Länge des Kreisbogens Fläche des Kreissektors = = 360 360 Das Bogenmaß eines Winkels ist
Kreissektoren und Bogenmaß
 M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius gilt für einen Kreissektor mit Mittelpunktswinkel : Länge des Kreisbogens Fläche des Kreissektors = 2 = 360 360 Das Bogenmaß eines Winkels ist
M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius gilt für einen Kreissektor mit Mittelpunktswinkel : Länge des Kreisbogens Fläche des Kreissektors = 2 = 360 360 Das Bogenmaß eines Winkels ist
Ergänzungsprüfung. zum Erwerb der Fachhochschulreife Mathematik (nichttechnische Ausbildungsrichtung)
 Ergänzungsprüfung zum Erwerb der Fachhochschulreife 2006 Prüfungsfach: Mathematik (nichttechnische Ausbildungsrichtung) Prüfungstag: Donnerstag, 22. Juni 2006 Prüfungsdauer: 09:00 12:00 Uhr Hilfsmittel:
Ergänzungsprüfung zum Erwerb der Fachhochschulreife 2006 Prüfungsfach: Mathematik (nichttechnische Ausbildungsrichtung) Prüfungstag: Donnerstag, 22. Juni 2006 Prüfungsdauer: 09:00 12:00 Uhr Hilfsmittel:
Abiturprüfung Mathematik 2014 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen
 Abiturprüfung Mathematik Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil Aufgabe : Bilden Sie die Ableitung der Funktion f
Abiturprüfung Mathematik Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil Aufgabe : Bilden Sie die Ableitung der Funktion f
Mathematik Name: Nr.4 K1 Punkte: /30 Note: Schnitt:
 K Punkte: / Note: Schnitt: 9.5.6 Pflichtteil (etwa 4 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden
K Punkte: / Note: Schnitt: 9.5.6 Pflichtteil (etwa 4 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden
Kurvendiskussion einer ganzrationalen Funktion
 Kurvendiskussion einer ganzrationalen Funktion Lernzuflucht 24. November 20 L A TEX M. Neumann Folgende Funktion soll in einer Kurvendiskussion bearbeitet werden: f(x) = x 4 2x 2 ; D = R () Diese Funktion
Kurvendiskussion einer ganzrationalen Funktion Lernzuflucht 24. November 20 L A TEX M. Neumann Folgende Funktion soll in einer Kurvendiskussion bearbeitet werden: f(x) = x 4 2x 2 ; D = R () Diese Funktion
1 /40. dargestellt werden.
 Abschlussprüfung Fachoberschule 0 () Aufgabenvorschlag B /40 Auf der Berliner Stadtautobahn A00 / Autobahndreieck Charlottenburg wurde über einen bestimmten Zeitraum die Staulänge l in Abhängigkeit von
Abschlussprüfung Fachoberschule 0 () Aufgabenvorschlag B /40 Auf der Berliner Stadtautobahn A00 / Autobahndreieck Charlottenburg wurde über einen bestimmten Zeitraum die Staulänge l in Abhängigkeit von
Polynome. Michael Spielmann. 1 ganzrationale Funktionen, Polynome 1. 2 Kurvenverlauf 1. 3 Symmetrie 2. 4 Nullstellen und Linearfaktoren 3
 Polnome Michael Spielmann Inhaltsverzeichnis ganzrationale Funktionen, Polnome Kurvenverlauf Smmetrie Nullstellen und Linearfaktoren 5 Polnomdivision 6 Kurvenverlauf an Nullstellen 5 7 Nullstellen und
Polnome Michael Spielmann Inhaltsverzeichnis ganzrationale Funktionen, Polnome Kurvenverlauf Smmetrie Nullstellen und Linearfaktoren 5 Polnomdivision 6 Kurvenverlauf an Nullstellen 5 7 Nullstellen und
12 M-Gk1/5 Led Übungen zur 1. Klausur 3. September Kurvendiskussion. Im Folgenden sei die Funktion f(x) = 1 6 x3 1 2 x 1 3 gegeben!
 12 M-Gk1/5 Led Übungen zur 1. Klausur 3. September 2008 1. Kurvendiskussion. Im Folgenden sei die Funktion f(x) = 1 6 x3 1 2 x 1 3 gegeben! a) Untersuche den Graphen von f(x) auf Standardsymmetrien (Punktsymmetrie
12 M-Gk1/5 Led Übungen zur 1. Klausur 3. September 2008 1. Kurvendiskussion. Im Folgenden sei die Funktion f(x) = 1 6 x3 1 2 x 1 3 gegeben! a) Untersuche den Graphen von f(x) auf Standardsymmetrien (Punktsymmetrie
Weitere Aufgaben Mathematik (BLF, Abitur) Hinweise und Beispiele zu hilfsmittelfreien Aufgaben
 Weitere Aufgaben Mathematik (BLF, Abitur) Hinweise und Beispiele zu hilfsmittelfreien Aufgaben Aufgabe C Gegeben ist eine Funktion f durch f ( ) = + 3. Gesucht sind lineare Funktionen, deren Graphen zum
Weitere Aufgaben Mathematik (BLF, Abitur) Hinweise und Beispiele zu hilfsmittelfreien Aufgaben Aufgabe C Gegeben ist eine Funktion f durch f ( ) = + 3. Gesucht sind lineare Funktionen, deren Graphen zum
Mathematik Einführungsphase. Plenum Lineare Funktionen. Lineare Funktionen. Eine kurze Wiederholung
 Lineare Funktionen Eine kurze Wiederholung Mathematik Einführungsphase Eine lineare Funktion ist zunächst einmal eine Funktion, d.h. eine eindeutige Zuordnung, bei der jedem x-wert aus einem Definitionsbereich
Lineare Funktionen Eine kurze Wiederholung Mathematik Einführungsphase Eine lineare Funktion ist zunächst einmal eine Funktion, d.h. eine eindeutige Zuordnung, bei der jedem x-wert aus einem Definitionsbereich
