Wenn mindestens eine Bedingung verletzt ist, dann liegt Biegezustand vor (s. u.)
|
|
|
- Harry Hoch
- vor 6 Jahren
- Abrufe
Transkript
1 Tgwksbcnung l. Doz. D.-Ing. bil. G. Gogi. (Rottions-)Scln Scl gkümmts Fläcntgwk mit blibig Blstung Rottionsscl Midinkuv (Ezugnd) ist von Dwinkl um fst Acs unbängig Vousstzungn: sinngmäß di glicn wi bi Scibn und Plttn. Mmbnzustnd Annm: Nomlsnnungn glicmäßig üb Wndstäk vtilt, d unbängig von z-oodint (nlog zu Scib) in Scubsnnungn (bn Hutsnnungszustnd) Vousstzungn fü Mmbnzustnd: Mittlfläc vläuft sttig gkümmt Sclndick nict sungft vändlic sttig Vtilung d Fläcnlstn Rndkäft tngntil zu Mittlfläc ngifnd Rndbdingungn binflussn Fomändungn nu in tngntil Rictung Wnn mindstns in Bdingung vltzt ist, dnn ligt Bigzustnd vo (s. u.) Hi: Blstung nu duc Innnduck (Bälttoi) nu szill Gomtin (kin Hlitung d llgminn Toi).. uglscl ϑ ϕ : π + π ϑϑ (.9) Rdil Aufwitung u us: π + u π u ν ε ( ν ϑϑ ) π E E ν u E (.) 68 5 /..7
2 l. Doz. D.-Ing. bil. G. Gogi Tgwksbcnung.. Zylindscl Anwndung: Flugzugumf in goß Hö Rdil Aufwitung u ϕ us: l : l+ l : π π (.) u ν ε ( ν ) E E u ν E (.).. glscl ξ Gomti: cot ϑ sin ϑ ξ ϑ : π sinϑ + π ϑϑ ϑϑ Ø ϑϑ ϑϑ sinϑ (.) ϑϑdϕ ξ dϕ d d dξ ϑ ϑdϕ+( d ϑϑdϕ) : dξdϕsinϑ+ dϕdξ cot ϑ sin ϑ sin ϑ 5 /..7 69
3 Tgwksbcnung l. Doz. D.-Ing. bil. G. Gogi. Bigzustnd d iszylindscl Di Bigtoi ist u.. bi dm so gnnntn Rndstöoblm nzuwndn. Diss titt z. B. bi d ombintion vscidn Fläcntgwk (Scl/ Scl, Scl/Pltt, Scl/Scib) uf, z. B.: uglscl Zylindscl Unsttigkitn n dn Scnittn: Aufttn von Momnt und Qukft isltt Hlitung in Dgl. fü di dil Aufwitung w d Zylindscl Gomti: u u zw, ε u u zw, ε,, ε zz, u, z,w w u w, w, + w+ z π + z π w + z π + z + + w w z z z... Rinntwicklung fü z HOOEscs Gstz: E E w z z ( ε +νε ) u, z w, +ν +... ν ν E E w z z ε +νε + +ν ν ν u z ( )... ( u, zw, ). 7 5 /..7 w, u zw, il Vscibung d Mittlfläc vgl. Pltt
4 l. Doz. D.-Ing. bil. G. Gogi Tgwksbcnung Scnittgößn ( s. (.), S. ): z m z + dz, E w z w z u +ν z+ w, +ν z +... dz ν Tm mit z und z lifn kinn Bitg, Tm b z wdn vnclässigt: E u,, w w u, m + w w, ν ν ν mit: E Bigstifigkit (s. Pltt) (.) ν z E w z w z n + dz u w, z dz +ν + +ν +, ν Tm mit z und z lifn kinn Bitg, Tm b E w w n u +ν D u +ν n ν z,, konst. (s. u.). wdn vnclässigt: E mit: D D Dnstifigkit (.5) ν n : u, ν D w E w w nϕ dz +ν u D +νu ν,,. folgt üb di Glicgwictsbdingungn (s. u.) zu: u m w,,, 5 /..7 7
5 Tgwksbcnung l. Doz. D.-Ing. bil. G. Gogi Glicgwictsbdingungn: ϕ dϕ dϕ m n z, w d n ϕ nd ϕ ϕ n ϕ n ϕ m ϕ d m+dm n+dn m ϕ dϕd +d n ϕ Blstung nu duc Innnduck (Bält) : dn dϕ : d dϕ n ddϕ+ dϕ d ϕ : dm dϕ dϕ d. ϕ Folgungn: n n konst. nϕ, + m, nϕ m, +. Einstzn d Scnittgößn in di obig Glicgwictsbdingung lift n w D w n w ν w +ν ν + D D, Mit 7 n w und : wid dus IV w n w w D ν + Dν + IV n w D ( ν ) w ν + 5 /..7
6 l. Doz. D.-Ing. bil. G. Gogi Tgwksbcnung ν n w k w IV + vgl. Blkn: Biglini Dgl.. Odnung (.6) mit: ( ν ) E ( ν ) ( ν ) D k E k ν k k Abklingfkto (.7) Rndbdingungn: Im Allgminn gilt, dss n jdm d Ränd (ins Bics) Rndbdingungn zu Bstimmung d Intgtionskonstntn nggbn wdn könnn. ingsnnt Rnd glnkig glgt Rnd fi Rnd : w w : w m : m Lösung d Dgl.: Allgmin Lösung: w w +w Anstz fü omogn Lösung ( nlog [/] ): w A λ i i Cktistisc Glicung und dn Lösungn: λ + k i... λ ± ± i k. 5 /..7 7
7 Tgwksbcnung l. Doz. D.-Ing. bil. G. Gogi Homogn Lösung: ( + ) ( ) ( + ) ( ) w A + A + A + A ik ik ik ik A + A + A + A k ik k ik k ik k ik ( ) ( ) A + A + A + A k ik ik k ik ik ( cos sin ) ( cos sin ) ( cos sin ) + A ( cos k isin k) k A k + i k + A k i k k A k i k k ( cos sin ) ( cos sin ) k C k C k C k C k Stz von MOIVRE [/6] ( cos sin ) ( cos sin ) w C k C k C k C k kl k l Sclnläng (.8) Abklingvltn d Rndstöungn: ( cos sin ) ( cos sin ) kl w k C k + C k + C k + C k Abklingnmit wcsndml Abklingnmit wcsndm -k -k(l-) l l: ussclißlic Vwndung dstms l: ussclißlic Vwndung dstms k k( l ) Wnn ist in Scl lng? kl π: l π π k,... ( zum Vglic : ) π ( ν ) l,5 fü ν, (.9) Bisil: mm l mm mm 7 5 /..7
8 l. Doz. D.-Ing. bil. G. Gogi Tgwksbcnung Szill Ptikulälösungn: offn Bält (kin Innnduck) unt Längskft (Ringkft) F n F : n π F π n IV w A w ν F k A A w ν F ν F k E F ν F E gsclossn Bält (Innnduck ) unt Längskft (Ringkft) F n F : n π π + F π n + F IV w A w ν k A + F ν ν A F + + F k k E E ν w ν F E Anmkung: Di dil Aufwitung w in Zylindscl unt Innnduck ( F ) nc d Mmbntoi btägt ( s. (.), S. 68 ): w ν E. Di Ptikulälösung nc d Bigtoi stimmt lso mit d Lösung nc d Mmbntoi übin. 5 /..7 75
9 Tgwksbcnung l. Doz. D.-Ing. bil. G. Gogi Bisil: iszylindscl unt Rndlstn l m m Gg.: m,, l m, 9 mm, ν, Gs.: Abklingvltn d Gößn w, w, m, D l mm mm mm mm,5,5 9,5 75 l mm > 75 mm, knn di Scl ls lng btctt wdn. D wd Innnduck noc zusätzlic Ailkäft wikn, buct nu di omogn Lösung d lngn Scl bücksictigt zu wdn: k w C cos k+ C sin k. Üb di bidn Rndbdingungn: m () m w () k C () w () k ( C + C ) wdn di Intgtionskonstntn bstimmt zu: C C m + k k m. k Dmit lutn di Egbniss: k w k m ( cos k sin k) + cos k k w k k m cosk ( cosk sink) k + + w k k m ( cos k+ sin k) + sin k m k k w k m sin k+ ( sin k+ cos k) /..7
10 l. Doz. D.-Ing. bil. G. Gogi Tgwksbcnung Szill m fin Rnd (bi ) gilt dnn: w() + k ( k m ) w () + k w () m w (). ( k m ) Di llgmin Lösung wid in di zwi duc di Blstung bdingtn Antil ufgsltt: ; m : m ; : k k w cos k w m ( cos k sin k ) k k k k w ( cosk+ sink) w m cosk k k k k w sin k w m ( cos k + sin k) k k k k w ( sin k + cos k) w m sin k. Dis Bziungn wdn nomit: k k w w cos k k k w w cosk+ sin k k w w sin k ( k) k w w sin k+ cos k k k w w k k k w w cosk ( cos sin k) k w w cos k+ sin k k w w sin k. k Fü di gfisc Dstllung wdn bcnt: ( ν ),9 k, 8 m mm m 75 mm: k,. 5 /..7 77
11 Tgwksbcnung l. Doz. D.-Ing. bil. G. Gogi Blstung duc :.5 w( k) w( k) w( k) w( k) Blstung duc m :.5 wm( k) wm( k) wm( k) wm( k) k Wi us bidn Digmmn sictlic, klingn di duc di Rndstöungn vo gufnn Scnittgößn in Fom gdämft Scwingungn vom Rnd sc b. Bi 75 mm btgn si nu noc c. % /..7
Lösungsmethoden für Differentialgleichungen 2. Ordnung
 Lösungsmthodn fü Diffntialglichungn. Odnung Bhandlung in Rih von Tn d Dgl.. Odnung, fü di infach Lösungsmöglichkitn istin bzw. di sich auf Dgl. st Odnung zuückfühn lassn.. T =f(,) ( kommt nicht vo) wid
Lösungsmthodn fü Diffntialglichungn. Odnung Bhandlung in Rih von Tn d Dgl.. Odnung, fü di infach Lösungsmöglichkitn istin bzw. di sich auf Dgl. st Odnung zuückfühn lassn.. T =f(,) ( kommt nicht vo) wid
Lösungsmethoden für Differentialgleichungen 2. Ordnung
 Lösungsmthodn fü Diffntialglichungn. Odnung Bhandlung in Rih von Tn d Dgl.. Odnung, fü di infach Lösungsmöglichkitn istin bzw. di sich auf Dgl. st Odnung zuückfühn lassn.. T f(,) ( kommt nicht vo) wid
Lösungsmthodn fü Diffntialglichungn. Odnung Bhandlung in Rih von Tn d Dgl.. Odnung, fü di infach Lösungsmöglichkitn istin bzw. di sich auf Dgl. st Odnung zuückfühn lassn.. T f(,) ( kommt nicht vo) wid
Präsenz-Aufgaben = i. (a) i 15 = i 14 i = (i 2 ) 7 i = ( 1) 7 i = i i 15 = 0 + ( 1)i, i (i i) = i 1 = i i 15 = 0 + 1i,
 Präsenz-Aufgben 1. 1. Schreiben Sie z in der Form z α + βi mit α,β R. Aus der Vorlesung ist beknnt: i i i 1, i 1 1 i i i i i 1 i. () i 15 i 1 i (i ) 7 i ( 1) 7 i i i 15 + ( 1)i, (b) i 15 1 i 15 () 1 i
Präsenz-Aufgben 1. 1. Schreiben Sie z in der Form z α + βi mit α,β R. Aus der Vorlesung ist beknnt: i i i 1, i 1 1 i i i i i 1 i. () i 15 i 1 i (i ) 7 i ( 1) 7 i i i 15 + ( 1)i, (b) i 15 1 i 15 () 1 i
Die Addition von Vektoren gilt das Kommutativgesetz und das Distributivgesetz: a 0 a und 0 0
 Vktohnung Vkton, sind Gößn, u dn vollständig Chktisiung sowohl in Mßhl, d Btg, ls uh in Rihtung im Rum fodlih sind. Bispil: Kft, Gshwindigkit, Bshlunigung, Winklgshwindigkit, Winklshlunigung sowi lktish
Vktohnung Vkton, sind Gößn, u dn vollständig Chktisiung sowohl in Mßhl, d Btg, ls uh in Rihtung im Rum fodlih sind. Bispil: Kft, Gshwindigkit, Bshlunigung, Winklgshwindigkit, Winklshlunigung sowi lktish
Wie in der letzten Vorlesung besprochen, ergibt die Differenz zwischen den Standardbildungsenthalpien
 Vorlsung 0 Spnnungsnrgi dr Cyclolkn Wi in dr ltztn Vorlsung bsprochn, rgibt di Diffrnz zwischn dn Stndrdbildungsnthlpin dr Cyclolkn C n n und dm n-fchn Bitrg für di C - Gruppn [n (-0.) kj mol - ] di Ringspnnung.
Vorlsung 0 Spnnungsnrgi dr Cyclolkn Wi in dr ltztn Vorlsung bsprochn, rgibt di Diffrnz zwischn dn Stndrdbildungsnthlpin dr Cyclolkn C n n und dm n-fchn Bitrg für di C - Gruppn [n (-0.) kj mol - ] di Ringspnnung.
f : G R ϕ n 1 (x 1,...,x n 1 ) Das ist zwar die allgemeine Form, aber es ist nützlich sie sich für den R 2 und R 3 explizit anzuschauen.
 Trnsformtionsstz von Sebstin üller Integrtion über Normlgebiete Allgemein knn mn im R n ein Normlgebiet wie folgt definieren: G : { R n 1 b, ϕ 1 ( 1 ) ψ 1 ( 1 ), ϕ ( 1, ) 3 ψ ( 1, ),... ϕ n 1 ( 1,...,
Trnsformtionsstz von Sebstin üller Integrtion über Normlgebiete Allgemein knn mn im R n ein Normlgebiet wie folgt definieren: G : { R n 1 b, ϕ 1 ( 1 ) ψ 1 ( 1 ), ϕ ( 1, ) 3 ψ ( 1, ),... ϕ n 1 ( 1,...,
Zeitverhalten eines Hochpass-Messgliedes
 n zur Znrlübung dr Vorlsung Grundlgn dr Msshnik von Prof. Dollingr, niv. dr Bundswhr Münhn, L2 - OHNE GEWÄH - Zivrhln ins Hohpss-Mssglids Ggbn is di Shlung us Abb. mi ) Ermiln Si di Diffrnilglihung für
n zur Znrlübung dr Vorlsung Grundlgn dr Msshnik von Prof. Dollingr, niv. dr Bundswhr Münhn, L2 - OHNE GEWÄH - Zivrhln ins Hohpss-Mssglids Ggbn is di Shlung us Abb. mi ) Ermiln Si di Diffrnilglihung für
Übungen zur Atomphysik II
 U AP 3 f-pw Übug zu Atompysik II Boscs Atommodll, Piodsystm Das Bosc Atommodll Wassstoffatom 5 lktoadi ds H-Atoms Bispil: H-Atom, Aziugskaft 7 Bispil: H-Atom, Ioisiugsgi 9 Quatzal lktoscal Piodsystm 3
U AP 3 f-pw Übug zu Atompysik II Boscs Atommodll, Piodsystm Das Bosc Atommodll Wassstoffatom 5 lktoadi ds H-Atoms Bispil: H-Atom, Aziugskaft 7 Bispil: H-Atom, Ioisiugsgi 9 Quatzal lktoscal Piodsystm 3
Satellitengeodäsie. Bahnenergie. Torsten Mayer-Gürr
 508.535 Sllingodäsi Bhnngi Tosn My-Gü Tosn My-Gü Zusmmnfssung Kpl Tosn My-Gü 7.03.05 Bwgungsglichung ds Kplpoblms Bwgungsglichung ds Kplpoblms: Diffnilglichung. Odnung 3 Bsimm bis uf 6 Ingionskonsnn =>
508.535 Sllingodäsi Bhnngi Tosn My-Gü Tosn My-Gü Zusmmnfssung Kpl Tosn My-Gü 7.03.05 Bwgungsglichung ds Kplpoblms Bwgungsglichung ds Kplpoblms: Diffnilglichung. Odnung 3 Bsimm bis uf 6 Ingionskonsnn =>
Lineare DGL zweiter Ordnung
 Universität Duisburg-Essen Essen, 03.06.01 Fkultät für Mthemtik S. Buer C. Hubcsek C. Thiel Linere DGL zweiter Ordnung Betrchten wir ds AWP { x + x + bx = 0 mit, b, t 0, x 0, v 0 R. Der Anstz xt 0 = x
Universität Duisburg-Essen Essen, 03.06.01 Fkultät für Mthemtik S. Buer C. Hubcsek C. Thiel Linere DGL zweiter Ordnung Betrchten wir ds AWP { x + x + bx = 0 mit, b, t 0, x 0, v 0 R. Der Anstz xt 0 = x
Lösen einer Gleichung 3. Grades
 Lösen eine Gleichung Gdes We sich uf dieses Abenteue einlssen will, bucht einige Kenntnisse übe komlee Zhlen Es eicht be, wenn mn folgende Schvehlte kennt und kochezettig (mn nehme) nwenden knn: Es gibt
Lösen eine Gleichung Gdes We sich uf dieses Abenteue einlssen will, bucht einige Kenntnisse übe komlee Zhlen Es eicht be, wenn mn folgende Schvehlte kennt und kochezettig (mn nehme) nwenden knn: Es gibt
Pflichtteilaufgaben zu Stammfunktion, Integral. Baden-Württemberg
 Pflichttilaufgabn zu Stammfunktion, Intgral Badn-Württmbrg Hilfsmittl: kin allgminbildnd Gymnasin Alandr Schwarz www.math-aufgabn.com August 5 Übungsaufgabn: Ü: Gbn Si in Stammfunktion f mit 5 f() = +
Pflichttilaufgabn zu Stammfunktion, Intgral Badn-Württmbrg Hilfsmittl: kin allgminbildnd Gymnasin Alandr Schwarz www.math-aufgabn.com August 5 Übungsaufgabn: Ü: Gbn Si in Stammfunktion f mit 5 f() = +
Pflichtteilaufgaben zu Stammfunktion, Integral. Baden-Württemberg
 Pflichttilaufgabn zu Stammfunktion, Intgral Badn-Württmbrg Hilfsmittl: kin allgminbildnd Gymnasin Alandr Schwarz www.math-aufgabn.com Sptmbr 6 Übungsaufgabn: Ü: Gbn Si in Stammfunktion f mit 5 f() = +
Pflichttilaufgabn zu Stammfunktion, Intgral Badn-Württmbrg Hilfsmittl: kin allgminbildnd Gymnasin Alandr Schwarz www.math-aufgabn.com Sptmbr 6 Übungsaufgabn: Ü: Gbn Si in Stammfunktion f mit 5 f() = +
1. Bestimmen Sie Radius und Mittelpunkt des Krümmungskreises an die Parabel y = x 2 in ihrem Scheitelpunkt.
 Mathmatik I Übungsaufgabn Lösungsvoschläg von T. My Eta-Mathmatik-Übung: 5--. Bstimmn Si Radius und Mittlpunkt ds Kümmungskiss an di Paabl y in ihm Schitlpunkt. Allgmin Glichung d Schitlpunktfom in Paabl
Mathmatik I Übungsaufgabn Lösungsvoschläg von T. My Eta-Mathmatik-Übung: 5--. Bstimmn Si Radius und Mittlpunkt ds Kümmungskiss an di Paabl y in ihm Schitlpunkt. Allgmin Glichung d Schitlpunktfom in Paabl
Übung zur Vorlesung PC II Quantenchemische Modellsysteme, Atom und Molekülspektroskopie B.Sc. Blatt 7
 Pof.. Nobt pp Wintsst 9/ 7. Novb 9 nil Khlöß Übung zu Volsung PC II Quntnchisch Mollsyst, Ato un Molkülspktoskopi B.Sc. Bltt 7. i uphys Si ist in Si i Spktu s ton Wssstoffs. Si bginnt bi 6 n un nt bi,
Pof.. Nobt pp Wintsst 9/ 7. Novb 9 nil Khlöß Übung zu Volsung PC II Quntnchisch Mollsyst, Ato un Molkülspktoskopi B.Sc. Bltt 7. i uphys Si ist in Si i Spktu s ton Wssstoffs. Si bginnt bi 6 n un nt bi,
5.4. Aufgaben zur Kurvenuntersuchung zusammengesetzter Funktionen
 5.. Aufgbn zu Kuvnunsuchung zusmmngsz Funkionn Aufgb : Kuvndiskussion von Eponnilfunkionn Unsuch ds Schubild d Funkion f uf Symmi, Achsnschnipunk, Vhln fü ±, Em- und Wndpunk. Skizzi ds Schubild im wsnlichn
5.. Aufgbn zu Kuvnunsuchung zusmmngsz Funkionn Aufgb : Kuvndiskussion von Eponnilfunkionn Unsuch ds Schubild d Funkion f uf Symmi, Achsnschnipunk, Vhln fü ±, Em- und Wndpunk. Skizzi ds Schubild im wsnlichn
9. Bewegungen geladener Teilchen im homogenen Magnetfeld
 9. wgungn gladn ilchn i hoognn Magntfld Elkton F = (allgin: = Q ) F F F F ist Zntiptalkaft, das Elkton (allgin: ilchn) bwgt sich i auf in Kisbahn! ( blibt i glich) Magntfld wgn sich Ladungn snkcht zu Magntfld,
9. wgungn gladn ilchn i hoognn Magntfld Elkton F = (allgin: = Q ) F F F F ist Zntiptalkaft, das Elkton (allgin: ilchn) bwgt sich i auf in Kisbahn! ( blibt i glich) Magntfld wgn sich Ladungn snkcht zu Magntfld,
Kryptologie am Voyage 200
 Mag. Michal Schnidr, Krypologi am Voyag200 Khvnhüllrgymn. Linz Krypologi am Voyag 200 Sinn dr Vrschlüsslung is s, inn Tx (Klarx) so zu vrändrn, dass nur in auorisirr Empfängr in dr Lag is, dn Klarx zu
Mag. Michal Schnidr, Krypologi am Voyag200 Khvnhüllrgymn. Linz Krypologi am Voyag 200 Sinn dr Vrschlüsslung is s, inn Tx (Klarx) so zu vrändrn, dass nur in auorisirr Empfängr in dr Lag is, dn Klarx zu
Basiswissen > Geometrie im Raum > Trigonometrie in Körpern > Streckenzug
 www.shullv.d Bsiswissn > Gomtri im Rum > Trigonomtri in Körprn > Strknzug Strknzug Spikzttl Augn 1. Läng ds Strknzugs rhnn In disr Aug sollst du dn Strknzug ds gzihntn Hus vom Nikolus rhnn. Am inhstn ist
www.shullv.d Bsiswissn > Gomtri im Rum > Trigonomtri in Körprn > Strknzug Strknzug Spikzttl Augn 1. Läng ds Strknzugs rhnn In disr Aug sollst du dn Strknzug ds gzihntn Hus vom Nikolus rhnn. Am inhstn ist
Gegeben sei eine elektromagnetische Welle mit Ausbreitung in z-richtung und einer Amplitude in x-richtung:
 38. Polaisation 38.1. Einfühung Ggbn si in lktomagntisch Wll mit Ausbitung in z-richtung und in Amplitud in x-richtung: E = E 0 i 0 i... Einhitsvkto in x-richtung Di vollständig mathmatisch Bschibung unt
38. Polaisation 38.1. Einfühung Ggbn si in lktomagntisch Wll mit Ausbitung in z-richtung und in Amplitud in x-richtung: E = E 0 i 0 i... Einhitsvkto in x-richtung Di vollständig mathmatisch Bschibung unt
Aufgabe 1. Magnetische Kraft (2+4)
 Übungn zu Physik II Elktoynaik SS 5 Lösungn zu Übungsblatt 65 Bspchung a Mi 965 ufgab Magntisch Kaft a Mssung s agntischn Fls Ein chtckig Litschlif hängt vtikal i Zntu ins goßn Magntn, so ass as agntisch
Übungn zu Physik II Elktoynaik SS 5 Lösungn zu Übungsblatt 65 Bspchung a Mi 965 ufgab Magntisch Kaft a Mssung s agntischn Fls Ein chtckig Litschlif hängt vtikal i Zntu ins goßn Magntn, so ass as agntisch
Ausgewählte Beispiele zu BIST
 usgwält ispil zu IST Vkszin Ds nnstnd Vkszin dutt, dss in Stß i 100 m wgt Entfnung um 12 m nstigt. Pt uptt: Ein Stigung von 100% wüd dutn, dss di Stß snkt wi in Flswnd nstigt! Wl zwi d folgndn gündungn
usgwält ispil zu IST Vkszin Ds nnstnd Vkszin dutt, dss in Stß i 100 m wgt Entfnung um 12 m nstigt. Pt uptt: Ein Stigung von 100% wüd dutn, dss di Stß snkt wi in Flswnd nstigt! Wl zwi d folgndn gündungn
} Gaußsches Gesetz (eine der Maxwell-Gleichungen)
 imntalhsik II TU Dotmun SS Shaukat Khan @ TU - Dotmun. Kaitl Wiholung q F q F q F ga s P P ga,, iv ot,, Coulombschs Gst, lktischs Fl Kaft / Laung lktischs Potnial bit / Laung Gaint, Divgn, otation Gaußsch
imntalhsik II TU Dotmun SS Shaukat Khan @ TU - Dotmun. Kaitl Wiholung q F q F q F ga s P P ga,, iv ot,, Coulombschs Gst, lktischs Fl Kaft / Laung lktischs Potnial bit / Laung Gaint, Divgn, otation Gaußsch
Gabelstapler III. Modul: Arbeits- bzw. Personenkörbe
 A Mod: Ai- w. Ponnkö Thm: Ai- w. Ponnkö Knwinn mi ARAMS Si wdn f 12 Sin mi fondn nhn (. ch) m Thm infomi! Wi n vo, wm d Thm wichi i nd w Si chn hn! NHALT: Sichhihinwi Af d Aiko Ein nd Vwndnwck Ein d Aiko
A Mod: Ai- w. Ponnkö Thm: Ai- w. Ponnkö Knwinn mi ARAMS Si wdn f 12 Sin mi fondn nhn (. ch) m Thm infomi! Wi n vo, wm d Thm wichi i nd w Si chn hn! NHALT: Sichhihinwi Af d Aiko Ein nd Vwndnwck Ein d Aiko
Optimale Absicherung. für gesetzlich Versicherte. Betriebliche Krankenversicherung. f ü r M it. Je tz t ex
 Optimal Absichung fü gstzlich Vsicht Btiblich Kanknvsichung o t il g ba V U n s c h l a a b it!! f ü M it s ic h n k lu s iv J tz t x io K o n d it n n Btiblich Kanknvsichung Kanknzusatzvsichungn fü gstzlich
Optimal Absichung fü gstzlich Vsicht Btiblich Kanknvsichung o t il g ba V U n s c h l a a b it!! f ü M it s ic h n k lu s iv J tz t x io K o n d it n n Btiblich Kanknvsichung Kanknzusatzvsichungn fü gstzlich
Ein herzliches Grüß Gott in Memmelsdorf! www.drei-kronen.de
 Ein hzlichs Güß Gott in Mmmlsdof! www.di-konn.d Güß Gott! In Fankn stht das bst Witshaus imm ggnüb d Kich. So wi auch uns Bauigasthof: Di Di Konn bfindn sich sit mh als 555 Jahn ggnüb dm Mmmlsdof Gottshaus.
Ein hzlichs Güß Gott in Mmmlsdof! www.di-konn.d Güß Gott! In Fankn stht das bst Witshaus imm ggnüb d Kich. So wi auch uns Bauigasthof: Di Di Konn bfindn sich sit mh als 555 Jahn ggnüb dm Mmmlsdof Gottshaus.
h ergibt schließlich:
 Löungn: 007 Pflictbric r Winkl ε knn im mrkirtn rick brcnt wrdn rin gilt: in ε = rcnung dr Hö : i Hö knn im mrkirtn rick mit dm Stz d Pytgor brcnt wrdn gilt: ε = (0,5) = (0,5) Und mit = 4, cm: = 4,41 0,5
Löungn: 007 Pflictbric r Winkl ε knn im mrkirtn rick brcnt wrdn rin gilt: in ε = rcnung dr Hö : i Hö knn im mrkirtn rick mit dm Stz d Pytgor brcnt wrdn gilt: ε = (0,5) = (0,5) Und mit = 4, cm: = 4,41 0,5
Notizen zur Vorlesung Analysis 3
 Notizen zur Vorlesung Anlysis 3 Henrik chumcher TUHH, 26. Jnur 207 2 Integrtion über Oberflächen 2. Oberflächenintegrl einer Funktion Definition 2.37 (Metrische Fundmentlform) ei R 2 ein reguläres Gebiet
Notizen zur Vorlesung Anlysis 3 Henrik chumcher TUHH, 26. Jnur 207 2 Integrtion über Oberflächen 2. Oberflächenintegrl einer Funktion Definition 2.37 (Metrische Fundmentlform) ei R 2 ein reguläres Gebiet
5.5. Aufgaben zur Integralrechnung
 .. Aufgn ur Ingrlrchnung Aufg : Smmfunkionn Bsimmn Si jwils ll Smmfunkionn für di folgndn Funkionn: ) f() f) f() k) f() n mi n R\{} p) f() 6 + 7 + ) f() g) f() l) f() + 6 q) f() f() h) f() m) f() + + r)
.. Aufgn ur Ingrlrchnung Aufg : Smmfunkionn Bsimmn Si jwils ll Smmfunkionn für di folgndn Funkionn: ) f() f) f() k) f() n mi n R\{} p) f() 6 + 7 + ) f() g) f() l) f() + 6 q) f() f() h) f() m) f() + + r)
266. Die Abbildung stellt eine. Aufgaben zur Lorentzkraft
 Aufgabn zu Lontzkaft 46. in lktonntahl titt it in Gchwindigkit von v 0 1,96 * 10 6-1 nkcht zu dn Fldlinin in in hoogn Magntfld it d agntichn Fludicht B 1,6 * 10 - in. a) klän Si, wau ich d lktonntahl auf
Aufgabn zu Lontzkaft 46. in lktonntahl titt it in Gchwindigkit von v 0 1,96 * 10 6-1 nkcht zu dn Fldlinin in in hoogn Magntfld it d agntichn Fludicht B 1,6 * 10 - in. a) klän Si, wau ich d lktonntahl auf
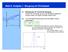
Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m.
![Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m. Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m.](/thumbs/74/70413961.jpg) Stz 6.5 (Mittelwertstz der Integrlrechnung) Sei f : [, b] R stetig. Dnn gibt es ein ξ [, b], so dss 9:08.06.2015 gilt. f dx = (b )f(ξ) Lemm 6.6 Sei f : [, b] R stetig und m f(x) M für lle x [, b]. Dnn
Stz 6.5 (Mittelwertstz der Integrlrechnung) Sei f : [, b] R stetig. Dnn gibt es ein ξ [, b], so dss 9:08.06.2015 gilt. f dx = (b )f(ξ) Lemm 6.6 Sei f : [, b] R stetig und m f(x) M für lle x [, b]. Dnn
Digitaltechnik. TI-Tutorium. 17. Januar 2012. Tutorium von K. Renner für die Vorlesung Digitaltechnik und Entwurfsverfahren am KIT
 Digitltchnik I-utorium 17. Jnur 2012 utorium von K. Rnnr für di Vorlsung Digitltchnik und Entwurfsvrfhrn m KI hmn Orgnistorischs Anmrkungn zum Übungsbltt 9 Korrktur inr Foli von ltztr Woch Schltwrk Divrs
Digitltchnik I-utorium 17. Jnur 2012 utorium von K. Rnnr für di Vorlsung Digitltchnik und Entwurfsvrfhrn m KI hmn Orgnistorischs Anmrkungn zum Übungsbltt 9 Korrktur inr Foli von ltztr Woch Schltwrk Divrs
Kapitel 9 Integralrechnung für Funktionen einer Veränderlichen 9.6 Volumen von Rotationskörpern
 Wolte/Dhn: Anlsis Individuell c Spinge 75 Kpitel 9 Integlechnung fü Funktionen eine Veändelichen 9.6 Volumen von Rottionsköpen Wi wenden uns jetzt de Bestimmung des Volumens eines sogennnten Rottionsköpes
Wolte/Dhn: Anlsis Individuell c Spinge 75 Kpitel 9 Integlechnung fü Funktionen eine Veändelichen 9.6 Volumen von Rottionsköpen Wi wenden uns jetzt de Bestimmung des Volumens eines sogennnten Rottionsköpes
Aufgaben zur Analytischen Mechanik SS 2013 Blatt 10 - Lösungen. Aufgabe 1 Wiederholung Eigenwerte und Eigenvektoren (15 Punkte)
 Aufgben zur Anlytischen Mechnik SS 013 Bltt 10 - en Aufgbe 1 Wiederholung Eigenwerte und Eigenvektoren (15 Punkte Bestimmen Sie Eigenwerte λ 1 und λ sowie die Eigenvektoren v 1 und v der folgenden Mtrix:
Aufgben zur Anlytischen Mechnik SS 013 Bltt 10 - en Aufgbe 1 Wiederholung Eigenwerte und Eigenvektoren (15 Punkte Bestimmen Sie Eigenwerte λ 1 und λ sowie die Eigenvektoren v 1 und v der folgenden Mtrix:
Pflichtteilaufgaben zu Gleichungen. Baden-Württemberg
 Badn-Württmbrg: Training Glichungn www.math-aufgabn.com Pflichttilaufgabn zu Glichungn Badn-Württmbrg Hilfsmittl: kin allgminbildnd Gymnasin Alandr Schwarz www.math-aufgabn.com Sptmbr 6 Badn-Württmbrg:
Badn-Württmbrg: Training Glichungn www.math-aufgabn.com Pflichttilaufgabn zu Glichungn Badn-Württmbrg Hilfsmittl: kin allgminbildnd Gymnasin Alandr Schwarz www.math-aufgabn.com Sptmbr 6 Badn-Württmbrg:
Pflichtteilaufgaben zu Gleichungen. Baden-Württemberg
 Badn-Württmbrg: Training Glichungn www.math-aufgabn.com Pflichttilaufgabn zu Glichungn Badn-Württmbrg Hilfsmittl: kin allgminbildnd Gymnasin Alandr Schwarz www.math-aufgabn.com Sptmbr 7 Badn-Württmbrg:
Badn-Württmbrg: Training Glichungn www.math-aufgabn.com Pflichttilaufgabn zu Glichungn Badn-Württmbrg Hilfsmittl: kin allgminbildnd Gymnasin Alandr Schwarz www.math-aufgabn.com Sptmbr 7 Badn-Württmbrg:
2. Dynamische Lichtstreuung (DLS)
 . Dynamisch Lichsuun DLS Phoonnkolaionsspkoskopi Di molkula Bwun in d Pob füh zu zilichn Flukuaionn in d nnsiä ds Sulichs. J klin das Suvolumn, dso auspä di Flukuaionn Di Foml fü dn diffnilln Suuschni
. Dynamisch Lichsuun DLS Phoonnkolaionsspkoskopi Di molkula Bwun in d Pob füh zu zilichn Flukuaionn in d nnsiä ds Sulichs. J klin das Suvolumn, dso auspä di Flukuaionn Di Foml fü dn diffnilln Suuschni
κ Κα π Κ α α Κ Α
 κ Κα π Κ α α Κ Α Ζ Μ Κ κ Ε Φ π Α Γ Κ Μ Ν Ξ λ Γ Ξ Ν Μ Ν Ξ Ξ Τ κ ζ Ν Ν ψ Υ α α α Κ α π α ψ Κ α α α α α Α Κ Ε α α α α α α α Α α α α α η Ε α α α Ξ α α Γ Α Κ Κ Κ Ε λ Ε Ν Ε θ Ξ κ Ε Ν Κ Μ Ν Τ μ Υ Γ φ Ε Κ Τ θ
κ Κα π Κ α α Κ Α Ζ Μ Κ κ Ε Φ π Α Γ Κ Μ Ν Ξ λ Γ Ξ Ν Μ Ν Ξ Ξ Τ κ ζ Ν Ν ψ Υ α α α Κ α π α ψ Κ α α α α α Α Κ Ε α α α α α α α Α α α α α η Ε α α α Ξ α α Γ Α Κ Κ Κ Ε λ Ε Ν Ε θ Ξ κ Ε Ν Κ Μ Ν Τ μ Υ Γ φ Ε Κ Τ θ
Für Wachstumsprozesse, die nach dem logistischen Wachstumsmodell ablaufen, gilt: (1)
 Dr Arnlf Schönli, Logistischs Wchstm in dr Prxis Logistischs Wchstm in dr Prxis Für Wchstmsrozss, di nch dm logistischn Wchstmsmodll lfn, gilt: ( ( t ( Drin sind (t zw di Polionn z dn Zitnktn t zw t, nd
Dr Arnlf Schönli, Logistischs Wchstm in dr Prxis Logistischs Wchstm in dr Prxis Für Wchstmsrozss, di nch dm logistischn Wchstmsmodll lfn, gilt: ( ( t ( Drin sind (t zw di Polionn z dn Zitnktn t zw t, nd
r [0, ), φ [0, 2π), ϑ [0, π]
![r [0, ), φ [0, 2π), ϑ [0, π] r [0, ), φ [0, 2π), ϑ [0, π]](/thumbs/66/55480332.jpg) ET2 Koodinatenssteme 1 Koodinatenssteme Zlindekoodinaten Kugelkoodinaten P(,,) P(,,) P(,,) P(,,ϑ) cos ϑ sin ϑ sin ϑ sin cos sin ϑ cos sin ϑ = cos = sin = [, ), [, 2π), (-, ) = sin ϑ cos = sin ϑ sin = cos
ET2 Koodinatenssteme 1 Koodinatenssteme Zlindekoodinaten Kugelkoodinaten P(,,) P(,,) P(,,) P(,,ϑ) cos ϑ sin ϑ sin ϑ sin cos sin ϑ cos sin ϑ = cos = sin = [, ), [, 2π), (-, ) = sin ϑ cos = sin ϑ sin = cos
SS 2017 Torsten Schreiber
 SS 7 ostn Schib 7 D Eukliisch Vktoaum wi uch i i gbilt. Dis sthn fü i i Achsn s Raums un biln in, a si um Einn aufinan sthn un um Ann i Läng ist. Wnn in Ga uch wi Punkt finit wi so hält man im Bich Vkton
SS 7 ostn Schib 7 D Eukliisch Vktoaum wi uch i i gbilt. Dis sthn fü i i Achsn s Raums un biln in, a si um Einn aufinan sthn un um Ann i Läng ist. Wnn in Ga uch wi Punkt finit wi so hält man im Bich Vkton
Vernetztes Laden eine Herausforderung
 Vntzts Ldn in Husfodun NTT DATA Mobilitätskonfnz 2. Oktob 2014, Win Jün Hiß, Lit Pilotiun & Klinsin EnBW Options Ws ist ds Zilbild in d E-Mobilität? Vntzts Ldn in Husfodun 2 E-Mobilität ist Til ds vntztn
Vntzts Ldn in Husfodun NTT DATA Mobilitätskonfnz 2. Oktob 2014, Win Jün Hiß, Lit Pilotiun & Klinsin EnBW Options Ws ist ds Zilbild in d E-Mobilität? Vntzts Ldn in Husfodun 2 E-Mobilität ist Til ds vntztn
Grundlagen der Energietechnik. Netze und Betriebsmittel. Netzformen
 Pof. D. n. Post tz und Btibsitt Gundn d Enitchnik tz und Btibsitt tzfon EEG. Sp. 7 unächst so noch in duf hinwisn wdn, dß Vsounsntz Dhstontz (Ausnh HGÜ) sind. Di Ausnhn sind in. Aus nitchnisch Sicht intssit
Pof. D. n. Post tz und Btibsitt Gundn d Enitchnik tz und Btibsitt tzfon EEG. Sp. 7 unächst so noch in duf hinwisn wdn, dß Vsounsntz Dhstontz (Ausnh HGÜ) sind. Di Ausnhn sind in. Aus nitchnisch Sicht intssit
Experimentalphysik II (Kip SS 2007)
 Epeimentalphysik II (Kip SS 7) Zusatzvolesungen: Z- Ein- und mehdimensionale Integation Z- Gadient, Divegenz und Rotation Z-3 Gaußsche und Stokessche Integalsatz Z-4 Kontinuitätsgleichung Z-5 Elektomagnetische
Epeimentalphysik II (Kip SS 7) Zusatzvolesungen: Z- Ein- und mehdimensionale Integation Z- Gadient, Divegenz und Rotation Z-3 Gaußsche und Stokessche Integalsatz Z-4 Kontinuitätsgleichung Z-5 Elektomagnetische
Volumen von Rotationskörpern, Bogenlänge und Mantelfläche
 Modul Integle 3 Volumen von Rottionsköpen, Bogenlänge und Mntelfläche In diesem Modul geht es um einige spezielle Anwendungen de Integlechnung, und Volumin, Längen und Flächen zu estimmen. Fngen wi mit
Modul Integle 3 Volumen von Rottionsköpen, Bogenlänge und Mntelfläche In diesem Modul geht es um einige spezielle Anwendungen de Integlechnung, und Volumin, Längen und Flächen zu estimmen. Fngen wi mit
HÖHERE ANALYSIS. 51 Untermannigfaltigkeiten des R n
 - 49 - HÖHERE NLYSIS 51 Untermnnigfltigkeiten des R n 51.1 Die verschiedenen Beschreibungen von Untermnnigfltigkeiten (51.1.13 Krten: Spezilfälle : Der nschuung wegen sollte mn stets die Spezilfälle für
- 49 - HÖHERE NLYSIS 51 Untermnnigfltigkeiten des R n 51.1 Die verschiedenen Beschreibungen von Untermnnigfltigkeiten (51.1.13 Krten: Spezilfälle : Der nschuung wegen sollte mn stets die Spezilfälle für
Für den Flächeninhalt des Dreiecks A BEG gilt: A BEG =
 008 Pflichtrich Für dn Flächninhalt ds ricks EG gilt: EG = E G i Strckn E und G kann man rchnn, wnn man im rchtwinklign rick EG dn Winkl ε und di Strck EG knnt rchnung ds Winkls ε: n Winkl ε stimmt man
008 Pflichtrich Für dn Flächninhalt ds ricks EG gilt: EG = E G i Strckn E und G kann man rchnn, wnn man im rchtwinklign rick EG dn Winkl ε und di Strck EG knnt rchnung ds Winkls ε: n Winkl ε stimmt man
Elektromagnetische Felder eines bewegten geladenen Drahtes
 lktomagntisch Wlln Kapitl 16 lktomagntisch Wlln Figu 1. Das adial lktisch Fld, das on inm unndlich langn, gadn, positi gladnn Daht zugt wid. 16.1 Fld ins bwgtn gladnn Dahts Wi habn in Kap. 15.5.1 das lktisch
lktomagntisch Wlln Kapitl 16 lktomagntisch Wlln Figu 1. Das adial lktisch Fld, das on inm unndlich langn, gadn, positi gladnn Daht zugt wid. 16.1 Fld ins bwgtn gladnn Dahts Wi habn in Kap. 15.5.1 das lktisch
Aufgabenblatt 1 6 Prüfungsaufgaben Klassenstufe 10. Alle Lösungen auf CD. Datei Nr Ausdruck nur von der CD aus möglich.
 Püfungsufgben Köpebeecnungen Aufgbenbltt 6 Püfungsufgben Klssenstufe 0 Alle Lösungen uf CD Dtei N. 6 Ausduck nu von de CD us möglic Fiedic Buckel Juni 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 6 Köpebeecnungen
Püfungsufgben Köpebeecnungen Aufgbenbltt 6 Püfungsufgben Klssenstufe 0 Alle Lösungen uf CD Dtei N. 6 Ausduck nu von de CD us möglic Fiedic Buckel Juni 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 6 Köpebeecnungen
Beispiele. elektrisch: RC-Glied. hydraulisch: Stoßdämpfer
 3..3 Zusmmngsz linr Übrrgungsglidr 3..3. Proorionlwirknd Übrrgungsglidr Vrzögrungsglid rsr Ordnung, P -Glid Funkionlbziung d d ( ) ( ) : Zikonsn, > Übrgngsfunkion ( ) ( ) / ( ) für für < P-Übrgngsfunkion
3..3 Zusmmngsz linr Übrrgungsglidr 3..3. Proorionlwirknd Übrrgungsglidr Vrzögrungsglid rsr Ordnung, P -Glid Funkionlbziung d d ( ) ( ) : Zikonsn, > Übrgngsfunkion ( ) ( ) / ( ) für für < P-Übrgngsfunkion
Aufgabe 1. Aufgabe 2. Übungsblatt 2. Woche. Ein zweiter Punkt erfährt die Beschleunigung. Zum Zeitpunkt 0 hat. Gesucht ist:
 Aufgab 1 Ein unkt 1 fäht in Bschlunigung ω. Zum Zitpunkt hat di Gschwindigkit 2 und bfindt sich am Ot. Ein zwit unkt fäht di Bschlunigung. Zum Zitpunkt hat di Gschwindigkit und bfindt sich am Ot. Gsucht
Aufgab 1 Ein unkt 1 fäht in Bschlunigung ω. Zum Zitpunkt hat di Gschwindigkit 2 und bfindt sich am Ot. Ein zwit unkt fäht di Bschlunigung. Zum Zitpunkt hat di Gschwindigkit und bfindt sich am Ot. Gsucht
Rollender Zylinder in Zylinder
 Übungen zu Theoretische Physik I - echnik im Sommersemester 013 Bltt 10 vom 1.07.13 Abgbe: 08.07. Aufgbe 43 Rollender Zylinder in Zylinder Ein homogener Zylinder (Gesmtmsse, Rdius, Trägheitsmoment bzgl.
Übungen zu Theoretische Physik I - echnik im Sommersemester 013 Bltt 10 vom 1.07.13 Abgbe: 08.07. Aufgbe 43 Rollender Zylinder in Zylinder Ein homogener Zylinder (Gesmtmsse, Rdius, Trägheitsmoment bzgl.
Kondensator an Gleichspannung
 Musrlösung Übungsbla Elkrochnisch Grundlagn, WS / Musrlösung Übungsbla 2 Prof. aiingr / ammr sprchung: 6..2 ufgab Spul an Glichspannung Ggbn is di Schalung nach bb. -. Di Spannung bräg V. Di Spul ha di
Musrlösung Übungsbla Elkrochnisch Grundlagn, WS / Musrlösung Übungsbla 2 Prof. aiingr / ammr sprchung: 6..2 ufgab Spul an Glichspannung Ggbn is di Schalung nach bb. -. Di Spannung bräg V. Di Spul ha di
Handout zu Übung 1. Vorbemerkung: Hinweise auf Fehler sind willkommen. Keine Gewähr für die vollständige Richtigkeit der Ausführungen.
 Übung zu Mikro III (SS 05) Tri Vi Dang Handout zu Übung Vorbmrkung: Hinwis auf Fhlr sind willkommn. Kin Gwähr für di vollständig Richtigkit dr usführungn. Thma : Thori ds llgminn Glichgwichts Das Framwork
Übung zu Mikro III (SS 05) Tri Vi Dang Handout zu Übung Vorbmrkung: Hinwis auf Fhlr sind willkommn. Kin Gwähr für di vollständig Richtigkit dr usführungn. Thma : Thori ds llgminn Glichgwichts Das Framwork
Blatt 6, Aufgabe 1: Beugung am Einzelspalt
 Aua a, Blatt 6, Aua : Buun am Einzlspalt a Bdinunn ü Faunho-Buun: Sowohl di Lichtqull als auch d Boachtunsschim müssn lativ zum Spalt unndlich ntnt sin. s Di Intnsitätsvtilun wid duch di c-funtion schin:
Aua a, Blatt 6, Aua : Buun am Einzlspalt a Bdinunn ü Faunho-Buun: Sowohl di Lichtqull als auch d Boachtunsschim müssn lativ zum Spalt unndlich ntnt sin. s Di Intnsitätsvtilun wid duch di c-funtion schin:
5 Ellipsen, Parabeln und Hyperbeln
 5 Ellipsen, Prbeln und Hperbeln Ellipsen: Seien b > reelle Zhlen und E = E,b := { + b = } Eine Qudrik Q R heißt Ellipse, wenn es reelle Zhlen b > gibt, so dss q E,b. Die Kurven E,b heißen Ellipsen in metrischer
5 Ellipsen, Prbeln und Hperbeln Ellipsen: Seien b > reelle Zhlen und E = E,b := { + b = } Eine Qudrik Q R heißt Ellipse, wenn es reelle Zhlen b > gibt, so dss q E,b. Die Kurven E,b heißen Ellipsen in metrischer
Kapitel 2. Schwerpunkt
 Kpitel Schwepunkt Schwepunkt Volumenschwepunkt Fü einen Köpe mit dem Volumen V emittelt mn die Koodinten des Schwepunktes S (Volumenmittelpunkt) us S dv dv z S S z S dv dv z dv dv z S S S Flächenschwepunkt
Kpitel Schwepunkt Schwepunkt Volumenschwepunkt Fü einen Köpe mit dem Volumen V emittelt mn die Koodinten des Schwepunktes S (Volumenmittelpunkt) us S dv dv z S S z S dv dv z dv dv z S S S Flächenschwepunkt
Schleswig-Holstein 2009 Leistungskurs Mathematik Thema: Analysis. ( x) . (14 P) g mit ( ) Berechnen Sie die Schnittpunkte der Graphen von f a und
 Ministrium für Bildung und Frun Schlsig-Holstin 9 Listungskurs Mthmtik Thm: Anlysis Aufg Ggn ist di Funktionnschr f mit f ( ) = (, IR ) ) Untrsuchn Si di Funktionnschr f uf Nullstlln, ds Vrhltn im Unndlichn,
Ministrium für Bildung und Frun Schlsig-Holstin 9 Listungskurs Mthmtik Thm: Anlysis Aufg Ggn ist di Funktionnschr f mit f ( ) = (, IR ) ) Untrsuchn Si di Funktionnschr f uf Nullstlln, ds Vrhltn im Unndlichn,
2.5 Messbare Mengen und Funktionen
 1 2.5 Messbre Mengen und Funktionen Definition Eine beschränkte Menge M R n heißt messbr, flls die chrkteristische Funktion χ M integrierbr ist. Die Zhl vol n (M) := χ M dµ n nennt mn ds Volumen von M.
1 2.5 Messbre Mengen und Funktionen Definition Eine beschränkte Menge M R n heißt messbr, flls die chrkteristische Funktion χ M integrierbr ist. Die Zhl vol n (M) := χ M dµ n nennt mn ds Volumen von M.
2. Grundgleichungen der linearen FEM
 . Grundgleichungen der lineren FEM Fchbereich Prof. Dr.-Ing. Mschinenbu Abteilung Mschinenbu. Ekurs Mtrizenrechnung Zum weiteren Verständnis der FEM sind einige Grundkenntnisse in der Mtrizenlgebr erforderlich!
. Grundgleichungen der lineren FEM Fchbereich Prof. Dr.-Ing. Mschinenbu Abteilung Mschinenbu. Ekurs Mtrizenrechnung Zum weiteren Verständnis der FEM sind einige Grundkenntnisse in der Mtrizenlgebr erforderlich!
Musterlösung der 1. Klausur zur Vorlesung
 Prof. Dr. M. Röger Dipl.-Mth. C. Zwilling Fkultät für Mthemtik TU Dortmund Musterlösung der. Klusur zur Vorlesung Anlysis I (24.02.206) Wintersemester 205/6 Aufgbe. Sei R mit sin() 0. Der Beweis erfolgt
Prof. Dr. M. Röger Dipl.-Mth. C. Zwilling Fkultät für Mthemtik TU Dortmund Musterlösung der. Klusur zur Vorlesung Anlysis I (24.02.206) Wintersemester 205/6 Aufgbe. Sei R mit sin() 0. Der Beweis erfolgt
Theoretische Physik IV - Blatt 3
 Theoretische Physi IV - Bltt 3 Christopher Bronner, Frn Essenberger FU Berlin 4.November 006 Aufgbe 5 Energieeigenfuntionen Uns ist folgendes Potentil gegeben, wobei V 0 > 0 sei: V (x) V 0 bei x [, ] V
Theoretische Physi IV - Bltt 3 Christopher Bronner, Frn Essenberger FU Berlin 4.November 006 Aufgbe 5 Energieeigenfuntionen Uns ist folgendes Potentil gegeben, wobei V 0 > 0 sei: V (x) V 0 bei x [, ] V
Kapitel IV Euklidische Vektorräume. γ b
 Kpitel IV Euklidische Vektorräume 1 Elementrgeometrie in der Eene Sei E die Zeicheneene In der Schule lernt mn: (11) Stz des Pythgors: Sei E ein Dreieck mit den Seiten, und c, und sei γ der c gegenüerliegende
Kpitel IV Euklidische Vektorräume 1 Elementrgeometrie in der Eene Sei E die Zeicheneene In der Schule lernt mn: (11) Stz des Pythgors: Sei E ein Dreieck mit den Seiten, und c, und sei γ der c gegenüerliegende
Lösungen zu den Übungsaufgaben
 Lösungen zu den Übungsufgben Aufgbe A.2. Ist k L () mit k(x)dx = und ist f : beschränkt, Lebesgue-messbr und stetig in x, dnn gilt lim r r k(x y r )f(y)dy = f(x). Lösung A.2. Zunächst ist mit der Substitutionsregel
Lösungen zu den Übungsufgben Aufgbe A.2. Ist k L () mit k(x)dx = und ist f : beschränkt, Lebesgue-messbr und stetig in x, dnn gilt lim r r k(x y r )f(y)dy = f(x). Lösung A.2. Zunächst ist mit der Substitutionsregel
Versiera der Agnesi INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK. FRIEDRICH W. BUCKEL. Text Nr Stand
 Vesie de Agnesi Tet N. 5455 Stnd 5.. FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mthe-cd.de 5455 Vesie de Agnesi Vowot Die Vesie de Agnesi ist eine lgebische Kuve. Gdes, die mn uf eine
Vesie de Agnesi Tet N. 5455 Stnd 5.. FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mthe-cd.de 5455 Vesie de Agnesi Vowot Die Vesie de Agnesi ist eine lgebische Kuve. Gdes, die mn uf eine
5.5.Abituraufgaben zu Logarithmusfunktionen
 5.5.Aiturufgn zu Logrithmusfunktionn Aufg : urvnuntrsuchung mit Prmtr, Intgrtion ohn GTR () Für jds rll t und > 0 sind di Funktionn f t und g ggn durch f t () (ln + t) und g() Ds Schuild von f t hißt t
5.5.Aiturufgn zu Logrithmusfunktionn Aufg : urvnuntrsuchung mit Prmtr, Intgrtion ohn GTR () Für jds rll t und > 0 sind di Funktionn f t und g ggn durch f t () (ln + t) und g() Ds Schuild von f t hißt t
Analysis II (lehramtsbezogen): Rechnen mit Integralen
 Anlysis II (lehrmtsbezogen): Rechnen mit Integrlen A. Ppke. November Substitution Wir wiederholen kurz die grundlegende Methode der Substitution und wenden sie im Beispiel n. Stz. (Integrtion durch Substitution).
Anlysis II (lehrmtsbezogen): Rechnen mit Integrlen A. Ppke. November Substitution Wir wiederholen kurz die grundlegende Methode der Substitution und wenden sie im Beispiel n. Stz. (Integrtion durch Substitution).
BÜROZENTRUM FALKENBRUNNEN. Chemnitzer-Str. 48, 48a, 48b, 50 / Würzburger Str. 35 01187 Dresden
 BÜROZENTRUM FALKENBRUNNEN Chmnitz-. 48, 48a, 48b, 50 / Wüzbug. 35 01187 Dsdn OBJEKT OBJEKT INDIVIDUELLES UND GROSSZÜGIGES BÜRO- UND EINZELHANDELS-ENSEMBLE Das Büozntum Falknbunnn bitt modn und funk- nn
BÜROZENTRUM FALKENBRUNNEN Chmnitz-. 48, 48a, 48b, 50 / Wüzbug. 35 01187 Dsdn OBJEKT OBJEKT INDIVIDUELLES UND GROSSZÜGIGES BÜRO- UND EINZELHANDELS-ENSEMBLE Das Büozntum Falknbunnn bitt modn und funk- nn
Auswertung P2-60 Transistor- und Operationsverstärker
 Auswrtung P2-60 Trnsistor- und Oprtionsrstärkr Michl Prim & Tobis Volknndt 26. Juni 2006 Aufgb 1.1 Einstufigr Trnsistorrstärkr Wir butn di Schltung gmäß Bild 1 uf, wobi wir dn 4,7µ F Kondnstor, sttt ds
Auswrtung P2-60 Trnsistor- und Oprtionsrstärkr Michl Prim & Tobis Volknndt 26. Juni 2006 Aufgb 1.1 Einstufigr Trnsistorrstärkr Wir butn di Schltung gmäß Bild 1 uf, wobi wir dn 4,7µ F Kondnstor, sttt ds
Felder und Wellen. Musterlösung zur 13. Übung. 30. Aufgabe WS 2016/2017. Hinlaufende Welle: E d = E d e j(ωt k d r) e y
 Felder und Wellen WS 6/7 Musterlösung zur 3. Übung 3. Aufgbe Hinlufende Welle: E e = E e e jωt k e r) e y ke = k cosφ e e z +sinφ e e x ) Reflektierte Welle: E r = E r e jωt k r r) e y kr = k cosφ r e
Felder und Wellen WS 6/7 Musterlösung zur 3. Übung 3. Aufgbe Hinlufende Welle: E e = E e e jωt k e r) e y ke = k cosφ e e z +sinφ e e x ) Reflektierte Welle: E r = E r e jωt k r r) e y kr = k cosφ r e
Uneigentliche Riemann-Integrale
 Uneigentliche iemnn-integrle Zweck dieses Abschnitts ist es, die Vorussetzungen zu lockern, die wir n die Funktion f : [, b] bei der Einführung des iemnn-integrls gestellt hben. Diese Vorussetzungen wren:
Uneigentliche iemnn-integrle Zweck dieses Abschnitts ist es, die Vorussetzungen zu lockern, die wir n die Funktion f : [, b] bei der Einführung des iemnn-integrls gestellt hben. Diese Vorussetzungen wren:
AnKa Hyp. , tan α= Weil die Ankathete des einen Winkels der Gegenkathete des anderen entspricht, gilt auch: sin α = cos β und sinβ = cosα.
 Trigonometrie Wenn mn die Trigonometrischen Funktionen Sinus, Kosinus und Tngens berechnen will, ist es wichtig, uf welchen Winkel sie sich beziehen. Die Kthete, die direkt m Winkel nliegt, heißt Ankthete
Trigonometrie Wenn mn die Trigonometrischen Funktionen Sinus, Kosinus und Tngens berechnen will, ist es wichtig, uf welchen Winkel sie sich beziehen. Die Kthete, die direkt m Winkel nliegt, heißt Ankthete
b f(x)p(x) dx = f(ξ) 2e 2 , Hess f (2, 0) =
 Es seien U R n offen und ψ : U R n stetig differenzierbr. Weiter sei f : U R zweiml stetig differenzierbr. Kennzeichnen Sie whre Aussgen mit W und flsche Aussgen mit F. F Flls dψ(x) ein Isomorphismus für
Es seien U R n offen und ψ : U R n stetig differenzierbr. Weiter sei f : U R zweiml stetig differenzierbr. Kennzeichnen Sie whre Aussgen mit W und flsche Aussgen mit F. F Flls dψ(x) ein Isomorphismus für
6.4 Uneigentliche Integrale
 6.4 Uneigentliche Integrle 3 Beispiele : d + + d ( + ) t + d t t d t ( t + t + t ) + t + t t ln ( + t) + c + ln ( + + ) + c + t rctn + c 6.4 Uneigentliche Integrle bisher : beschränkte Funktionen uf endlichen
6.4 Uneigentliche Integrle 3 Beispiele : d + + d ( + ) t + d t t d t ( t + t + t ) + t + t t ln ( + t) + c + ln ( + + ) + c + t rctn + c 6.4 Uneigentliche Integrle bisher : beschränkte Funktionen uf endlichen
Unabhängige Beratung zu Ihrer Heizungsanlage. Die Heizungsvisite ist ein geförderter Kurz-Check für Bremer Haushalte
 Unbhängig Btung zu Ih Hizungsnlg Di Hizungsvisit ist in gfödt Kuz-Chck fü Bm Hushlt 80 Poznt d Hizungn in Dutschlnd bitn Optimiungspotnzil. Lssn Si dh Ih Hizung jtzt bi in Hizungsvisit übpüfn od sich zu
Unbhängig Btung zu Ih Hizungsnlg Di Hizungsvisit ist in gfödt Kuz-Chck fü Bm Hushlt 80 Poznt d Hizungn in Dutschlnd bitn Optimiungspotnzil. Lssn Si dh Ih Hizung jtzt bi in Hizungsvisit übpüfn od sich zu
Prof. Dr. Siegfried Echterhoff.. 1 HAUPTSATZ DER INTEGRAL UND DIFFERENTIALRECHNUNG
 Vorlesung SS 29 Anlysis 2 HAUPTSATZ DER INTEGRAL UND DIFFERENTIALRECHNUNG Teil : Fortsetzung des Studiums von Funktionen in einer reellen Vriblen (Integrtion und Tylorreihen). Huptstz der Integrl und Differentilrechnung
Vorlesung SS 29 Anlysis 2 HAUPTSATZ DER INTEGRAL UND DIFFERENTIALRECHNUNG Teil : Fortsetzung des Studiums von Funktionen in einer reellen Vriblen (Integrtion und Tylorreihen). Huptstz der Integrl und Differentilrechnung
12. Multipolstrahlung
 Langwlln - Nähung Zu witn Bhandlung von Gl. (.3 machn wi di Langwlln - Nähung. Multipolstahlung Wi btachtn jtzt in Ladungs- und Stomvtilung im Gbit x < d. Wi habn in Kap..5 bzw. 5.4 fstgstllt, dass di
Langwlln - Nähung Zu witn Bhandlung von Gl. (.3 machn wi di Langwlln - Nähung. Multipolstahlung Wi btachtn jtzt in Ladungs- und Stomvtilung im Gbit x < d. Wi habn in Kap..5 bzw. 5.4 fstgstllt, dass di
Aufgaben zu Kapitel 7
 7.1 G W A B zu 7.1 zu 7.2 7.2 Ajznzmtrix: 000111 000111 000111 111000 111000 111000 G : W : : A : B : : A, B, A, B, A, B, G, W, G, W, G, W, s ist niht möglih, n Grphn ürshniungsfri zihnn. 7.3 Di Isomorphiilung
7.1 G W A B zu 7.1 zu 7.2 7.2 Ajznzmtrix: 000111 000111 000111 111000 111000 111000 G : W : : A : B : : A, B, A, B, A, B, G, W, G, W, G, W, s ist niht möglih, n Grphn ürshniungsfri zihnn. 7.3 Di Isomorphiilung
Lösungsvorschläge zum 9. Übungsblatt.
 Übung zur Anlysis II SS 1 Lösungsvorschläge zum 9. Übungsbltt. Aufgbe 33 () A : {(x, y) R : x [ 1, 1] und y oder x und y [ 1, 1]}. (b) A : {(x, y) R : x < y < 1 + x }. (c) A : {(x, y) R : x < y < 1 + x
Übung zur Anlysis II SS 1 Lösungsvorschläge zum 9. Übungsbltt. Aufgbe 33 () A : {(x, y) R : x [ 1, 1] und y oder x und y [ 1, 1]}. (b) A : {(x, y) R : x < y < 1 + x }. (c) A : {(x, y) R : x < y < 1 + x
MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 2 Wintersemester 2011/2012
 Prof. Dr. O. Junge, A. Bittrcher Zentrum Mthemtik - M3 Technische Universität München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT Wintersemester / Tutorübungsufgben (3..-4..) Aufgbe T Seien R und α positiv. Die
Prof. Dr. O. Junge, A. Bittrcher Zentrum Mthemtik - M3 Technische Universität München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT Wintersemester / Tutorübungsufgben (3..-4..) Aufgbe T Seien R und α positiv. Die
Staatlich geprüfter Techniker
 uszug aus dm Lnmatial Fotbildungslhgang Staatlich gpüft Tchnik uszug aus dm Lnmatial sstchnik (uszüg) D-Tchnikum ssn /.daa-tchnikum.d, Infolin: 0201 83 16 510 Gundlagn zu ustung u. Intptation von sstn
uszug aus dm Lnmatial Fotbildungslhgang Staatlich gpüft Tchnik uszug aus dm Lnmatial sstchnik (uszüg) D-Tchnikum ssn /.daa-tchnikum.d, Infolin: 0201 83 16 510 Gundlagn zu ustung u. Intptation von sstn
C t S f. E r F g. H u C s. U p H q. L b A j. S x T n. j c g s. n v R H. r f T a. e a I o. y g W i o o L e c a B i o n e n. v I u m b M x H c x z
 y g W i o o L c a B i o n n a I o E a f i E s l t f n v R H v I u m b M x H c x z S x T n T w Z E h V n u i C t S f p F o E R K o y a l H u C s t A V U K g K U p H q h D x G f U s q f y g L b A j w E u
y g W i o o L c a B i o n n a I o E a f i E s l t f n v R H v I u m b M x H c x z S x T n T w Z E h V n u i C t S f p F o E R K o y a l H u C s t A V U K g K U p H q h D x G f U s q f y g L b A j w E u
e n e a Chancenzuschaf
 s p a n, um n uch Sp a n, u m n u Chancnzuschaf f n m i al b Li ag Landt Konsol i di ungsst at gi dfdplandt agsf akt i on 2013bi s2017 f dpf akt i onn w. d 2013 2014 2015 2016 2017 in Mio. Euo 1. Mhinnahmn
s p a n, um n uch Sp a n, u m n u Chancnzuschaf f n m i al b Li ag Landt Konsol i di ungsst at gi dfdplandt agsf akt i on 2013bi s2017 f dpf akt i onn w. d 2013 2014 2015 2016 2017 in Mio. Euo 1. Mhinnahmn
Mathematik 1 für Bauwesen 14. Übungsblatt
 Mthemtik für Buwesen Übungsbltt Fchbereich Mthemtik Wintersemester 0/0 Dr Ivn Izmestiev 8/900 Dr Vince Bárány, M Sc Juli Plehnert Gruppenübung Aufgbe G () Berechnen Sie ds Volumen des Rottionskörpers,
Mthemtik für Buwesen Übungsbltt Fchbereich Mthemtik Wintersemester 0/0 Dr Ivn Izmestiev 8/900 Dr Vince Bárány, M Sc Juli Plehnert Gruppenübung Aufgbe G () Berechnen Sie ds Volumen des Rottionskörpers,
Maschinendynamik Formelsammlung Prof. Dr.- Ing. H. Bräutigam SS 2000 Seite 01. Coulombsche Reibungskraft : F R = µ * F N ( Rutschen ) c =
 Mshinendynik Foesung Pof. D.- Ing. H. Bäutig SS Seite Käftegeihungen : Couobshe Reibungskft : F R µ F N ( Rutshen ) Roen : Reibungskft R Gewihtskft : G g Seieibungskft : Fedekäfte : µ α F e F Gede Fede
Mshinendynik Foesung Pof. D.- Ing. H. Bäutig SS Seite Käftegeihungen : Couobshe Reibungskft : F R µ F N ( Rutshen ) Roen : Reibungskft R Gewihtskft : G g Seieibungskft : Fedekäfte : µ α F e F Gede Fede
Heizlastberechnung Seite 1 von 5. Erläuterung der Tabellenspalten in den Heizlast-Tabellen nach DIN EN 12831
 Hizlastbrchnung Sit 1 von 5 Erläutrung dr Tabllnspaltn in dn Hizlast-Tablln nach DIN EN 12831 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 3x4x5 6-7 12 + 13 8 x 11 x 14 15 x Θ Orintirung Bautil Anzahl Brit Läng
Hizlastbrchnung Sit 1 von 5 Erläutrung dr Tabllnspaltn in dn Hizlast-Tablln nach DIN EN 12831 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 3x4x5 6-7 12 + 13 8 x 11 x 14 15 x Θ Orintirung Bautil Anzahl Brit Läng
Bis zu 20 % Ra. b b. a h
 btt! Bis zu 20 % R www.gvb.ch h? ic s b b d d u W s s d ich t lück lo s s u H Ih h ic s W i v Mit us kö Si Ih Hus udum vsich Mit us Zustzvsichug ist Ih Vsichugsschutz i ud Sch W glichzitig i Lück i d Gbäudvsichug
btt! Bis zu 20 % R www.gvb.ch h? ic s b b d d u W s s d ich t lück lo s s u H Ih h ic s W i v Mit us kö Si Ih Hus udum vsich Mit us Zustzvsichug ist Ih Vsichugsschutz i ud Sch W glichzitig i Lück i d Gbäudvsichug
Höhere Mathematik II für die Fachrichtung Informatik. Lösungsvorschläge zum 8. Übungsblatt
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmnn SS Höhere Mthemtik II für die Fchrichtung Informtik Lösungsvorschläge zum 8. Übungsbltt Aufgbe 9 erechnen
KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmnn SS Höhere Mthemtik II für die Fchrichtung Informtik Lösungsvorschläge zum 8. Übungsbltt Aufgbe 9 erechnen
c a+ bzw. f(x) dx. c a bzw. 1 =
 3. Uneigentliche Integrle Die Funktion f sei uf dem rechts oenen Intervll x < b erklrt und uf jedem bgeschlossenen Teilintervll [, c], c < b, stuckweise stetig, b R { }. Dnn der Integrlbegri erweitert
3. Uneigentliche Integrle Die Funktion f sei uf dem rechts oenen Intervll x < b erklrt und uf jedem bgeschlossenen Teilintervll [, c], c < b, stuckweise stetig, b R { }. Dnn der Integrlbegri erweitert
3. Grad Ist die höchste vorkommende Potenz : y`, (y`)², (y`)³ y`: 1. Grad (linear), (y`)² : 2. Grad (quadrat) dx dt
 IV. Diffrnialglichngn: z.b. y d Klassifiaion von Diffrnialglichngn 1. Gwöhnlich / Parill Dgl. y f, 1 nabhängig Variabl gwöhnlich Dgl mhr Variabln : parill Dgl. Ordnng Is di höchs vorommnd bling y, y...
IV. Diffrnialglichngn: z.b. y d Klassifiaion von Diffrnialglichngn 1. Gwöhnlich / Parill Dgl. y f, 1 nabhängig Variabl gwöhnlich Dgl mhr Variabln : parill Dgl. Ordnng Is di höchs vorommnd bling y, y...
Übung zur Vorlesung Einführung in die Algebra Prof. Dr. J. H. Bruinier Stephan Ehlen
 Übung zur Vorlesung Einführung in die Algebr Prof. Dr. J. H. Bruinier Stephn Ehlen Soerseester 2009 Lösungshinweise zu Übungsbltt 5 Aufgbe G5. Ordnungen berechnen () () Gegeben k gilt k k 0 in /n genu
Übung zur Vorlesung Einführung in die Algebr Prof. Dr. J. H. Bruinier Stephn Ehlen Soerseester 2009 Lösungshinweise zu Übungsbltt 5 Aufgbe G5. Ordnungen berechnen () () Gegeben k gilt k k 0 in /n genu
Komplexe Integration
 Komplexe Integrtion Michel Hrtwig 23. April 2004 Der Unterschied zwischen reeller und komplexer Integrtion Vorbemerkung: Aus Gründen der Anschulichkeit, hbe ich weitgehend uf eine exkte mthemtische Drstellung
Komplexe Integrtion Michel Hrtwig 23. April 2004 Der Unterschied zwischen reeller und komplexer Integrtion Vorbemerkung: Aus Gründen der Anschulichkeit, hbe ich weitgehend uf eine exkte mthemtische Drstellung
Das Röthenbacher Saure-Zipfel-Flatrate-Turnier
 Ds Röthnbch Su-Zipfl-Fltt-Tuni Lngwil im Jnu? Nicht mit uns! D s R ö t h Bi uns ght s dn Sun Zipfln n dn Kgn! Di Bognschützn d SSG Röthnbch ldn hzlich in zum 4. Röthnbch Su-Zipfl-Fltt-Tuni m Smstg, dn
Ds Röthnbch Su-Zipfl-Fltt-Tuni Lngwil im Jnu? Nicht mit uns! D s R ö t h Bi uns ght s dn Sun Zipfln n dn Kgn! Di Bognschützn d SSG Röthnbch ldn hzlich in zum 4. Röthnbch Su-Zipfl-Fltt-Tuni m Smstg, dn
MC-Serie 12 - Integrationstechniken
 Anlysis D-BAUG Dr. Meike Akveld HS 15 MC-Serie 1 - Integrtionstechniken 1. Die Formel f(x) dx = xf(x) xf (x) dx i) ist im Allgemeinen flsch. ii) folgt us der Sustitutionsregel. iii) folgt us dem Huptstz
Anlysis D-BAUG Dr. Meike Akveld HS 15 MC-Serie 1 - Integrtionstechniken 1. Die Formel f(x) dx = xf(x) xf (x) dx i) ist im Allgemeinen flsch. ii) folgt us der Sustitutionsregel. iii) folgt us dem Huptstz
Serie 13 Lösungsvorschläge
 D-Mth Mss und Integrl FS 204 Prof. Dr. D. A. Slmon Serie 3 Lösungsvorschläge. Sei I := [, b] R ein kompktes Intervll und sei B 2 I die Borel-σ-Algebr. Def. Eine Funktion f : I R heisst von beschränkter
D-Mth Mss und Integrl FS 204 Prof. Dr. D. A. Slmon Serie 3 Lösungsvorschläge. Sei I := [, b] R ein kompktes Intervll und sei B 2 I die Borel-σ-Algebr. Def. Eine Funktion f : I R heisst von beschränkter
Crash-Course Physik Vorlesung 1
 Crsh-Cours Physik Vorlsung 1 Trigonomtri: Lösungn 21. Sptmbr 2016 1. Notir für di folgndn vir rhtwinklign Drik di An- und Ggnktht ds jwils ingtrgnn Winkls: b α d f β Anktht von α ist b, Ggnktht ist. Anktht
Crsh-Cours Physik Vorlsung 1 Trigonomtri: Lösungn 21. Sptmbr 2016 1. Notir für di folgndn vir rhtwinklign Drik di An- und Ggnktht ds jwils ingtrgnn Winkls: b α d f β Anktht von α ist b, Ggnktht ist. Anktht
Analysen und Ergebnisse der Qualifizierungsberater im III. Quartal 2010
 Analysn d Egbniss d Qualifizigsbat im III. Quatal 2 III. Quatal 2 Batgn d Analysn d Qualifizigsbat Im 3. Quatal ds Jahs 2 wudn 83 Btib bzw. Untnhmn batn. In 38 Untnhmn wud in Qualifizigsbdaf fü.3 Mitabit
Analysn d Egbniss d Qualifizigsbat im III. Quatal 2 III. Quatal 2 Batgn d Analysn d Qualifizigsbat Im 3. Quatal ds Jahs 2 wudn 83 Btib bzw. Untnhmn batn. In 38 Untnhmn wud in Qualifizigsbdaf fü.3 Mitabit
Drehung. Die orthogonale n n-matrix 1 0. c s. Zeile j. s c
 Drehung Die orthogonale n n-matrix Q i,j... Zeile i c s... Zeile j s c... mit c = cos ϕ und s = sin ϕ beschreibt eine Drehung um den Winkel ϕ in der x i x j -Ebene des R n. Drehung - Drehung Die orthogonale
Drehung Die orthogonale n n-matrix Q i,j... Zeile i c s... Zeile j s c... mit c = cos ϕ und s = sin ϕ beschreibt eine Drehung um den Winkel ϕ in der x i x j -Ebene des R n. Drehung - Drehung Die orthogonale
Erfolg im Mathe-Abi. H. Gruber, R. Neumann. Prüfungsaufgaben Hessen
 H. Grubr, R. Numann Erfolg im Math-Abi Prüfungsaufgabn Hssn Übungsbuch für dn Listungskurs mit Tipps und Lösungn - plus Aufgabn für GTR und CAS Inhaltsvrzichnis Inhaltsvrzichnis Analysis 1 Ganzrational
H. Grubr, R. Numann Erfolg im Math-Abi Prüfungsaufgabn Hssn Übungsbuch für dn Listungskurs mit Tipps und Lösungn - plus Aufgabn für GTR und CAS Inhaltsvrzichnis Inhaltsvrzichnis Analysis 1 Ganzrational
