Physik III Übung 10 - Lösungshinweise

Transkript

1 Physik III Übung - Lösungshinweise Stefn Reutter WiSe Moritz Kütt Stnd:..3 Frnz Fujr Die folgenden Aufgben behndeln Stoff der letzten Vorlesungswoche vor dem Jhreswechsel und llgemeine Wiederholungsufgben. Sie sind nicht Bonus-relevnt (müssen nicht vorgerechnet oder bgegeben werden). Eine gewisse Relevnz für die Klusur ist ber nicht uszuschließen. Wer möchte, knn Ergebnisse m Montg, den 4..3 bgeben. Diese werden dnn korrigiert. Dies ist ber freiwillig. Stofflicher Einschub: Ds Auge ht ein begrenztes Auflösungsvermögen. Es knn zwei Objekte getrennt uflösen, wenn ds zentrle Beugungsmxim des einen gerde im ersten Beugungsminim des nderen liegt. Mn knn dzu ds Ryleigh sche Kriterium der Auflösung definieren: α k =. λ p Dbei ist p der Durchmesser der Pupille. Zwei Objekte müssen mindestens unter dem Winkel α k erscheinen, um getrennt ufgelöst zu werden. Aufgbe Wer sieht die Löcher im Käse? Vor dir liegt ein gigntisch großer Käse. Es ist ein Schweizer Emmentler, erkennbr n seinen Löchern im Abstnd von d = 6 mm. ) Der Käse wird mit Licht der Wellenlänge λ = 5 nm beleuchtet. Ws ist die mximle Entfernung, bei der du ihn zweifelsfrei ls Schweizer Emmentler identifizieren knnst? (Zum identifizieren musst du die Löcher einzeln erkennen). Nimm einen Pupillendurchmesser von p = 5 mm n. b) Knnst du den Käse bei rotem oder bei violettem Licht us größerer Entfernung eindeutig identifizieren? Wrum?

2 Lösungshinweise: ) Abstnd zum Käse: l. Die Strhlen von zwei benchbrten Löchern schließen den Winkel α ein, dbei ist dnn (mit Kleinwinkelnäherung): sin α = x l α Aus dem Einschub nehmen wir ds Ryleigh sche Kriterium α k =. λ p = α x l =.λ p l = x p.λ = 49.m b) Bei violettem Licht ist die mögliche Entfernung größer. Violettes Licht ht eine kürzere Wellenlänge und l ist umgekehrt proportionl zur Wellenlänge. Aufgbe Beugungsmuster m Doppelsplt Licht mit einer Wellenlänge von 55 nm trifft uf zwei Splte mit Breite.3 mm und Abstnd.5 mm. ) Wieviele Mxim des Strukturfktors liegen in der gesmten Breite des nullten Mximums des Formfktors? (Der Formfktor ist ds Beugungsbild des Einzelspltes, der Strukturfktor ds überlgerte Bild des Doppelsplts.) b) Wie verhält sich die Intensität des dritten Strukturfktor-Mximums uf einer Seite von der Mitte zur Intensität des zentrlen (nullten) Mximums? Lösungshinweise: Für den Winkel θ, unter dem ds erste Minimum des Formfktors bei einer Spltbreite b zu sehen ist, gilt: sin θ = λ b Für den Winkel θ m, unter dem ds m-te Mximum des Strukturfktors bei einem Spltbstnd zu sehen ist, gilt: θ m = mλ

3 Wenn ds m-te Mximum ds erste ist, ds nicht mehr zu sehen ist, gilt θ = θ m, bzw: mλ = λ b m = b Ds m-te Mximum ist ds erste, ds nicht mehr zu sehen ist. Im Mximum des Formfktors liegen dher zwei ml (m ) Mxim plus noch ds zentrle, lso N =(m ) + = 9 =m = b b) Bei einem Einzelsplt hängt die Intensität I über folgende Formel mit der Phsendifferenz φ und der Intensität in der Mitte I zusmmen: I = I sin φ φ Wir müssen nun die Phsendifferenz m Ort des dritten Strukturfktor-Mximums berechnen: φ = π λ b sin θ 3 = π λ b 3λ =6π b = 6 5 π I 3 =I sin φ φ I 3 I = sin 6 π 5 = π 3

4 Aufgbe 3 Hinter Gittern Die Winkeldifferenz von zwei Linien mit den Wellenlängen λ und λ + λ hinter einem Gitter mit n Linien pro Längeneinheit wird näherungsweise durch λ θ = λ n m gegeben. Zeige, dsss dies stimmt. m ist dbei die Ordnung der Linien. Lösungshinweise: Nicht gnz einfcher Weg: Bei n Linien pro Längeneinheit hben die Linien den Abstnd g =. Ds m-te Interferenzmximum liegt dnn n bei g sin θ = mλ Ds leiten wir nun nch λ b und ersetzen g. m =g dθ dλ cos θ nm = dθ dλ cos θ n = m Wir mchen us den Differentilen Differenzen: n = m dθ dλ cos θ θ λ cos θ θ = nm λ cos θ = nm λ sin θ sin θ können wir mithilfe der ersten Gleichung ersetzen: nm λ θ = n m λ = nm nm = λ λ n m λ n m λ 4

5 Aufgbe 4 Fourier und Beugung Korrektur: In der Aufgbenstellung wren zwei Vorzeichenfehler, und zwr in der Definition der Fouriertrnsformtion und der Pttersonfunktion. Wie Prof. Fujr in der Vorlesung drgestellt ht, knn mn mit Fouriertrnsformtionen tolle Beugungsbilder berechnen. Wir wollen ds hier exemplrisch für den Formfktor eines Einzelsplts mit Breite b tun. Wir schuen von oben uf die Anordnung, in der ds Licht sich prllel zur x-achse bewegt. Der Splt ht die Dichtefunktion : b ρ(x, y) = < y < b, x = : sonst ) Berechne die eindimensionle Fouriertrnsformtion in Richtung des Spltes k α k k ρ(x, k y ) = ρ(x, y)e ik y y dy Dbei ist k = k k der sog. Streuvektor, die Differenz zwischen dem usfllenden Wellenvektor und dem einfllenden Wellenvektor und zeigt in Richtung des Streuwinkels, unter dem mn ds Gnze betrchtet. Für ds Beugungsbild ist nur die y-komponente von k relevnt, d nur sie in Spltrichtung geht. b) Beweise, dss ds Betrgsqudrt der Fouriertrnsformierten ρ(x, k y ) proportionl zum in der Vorlesung hergeleiteten Beugungsmuster des Einzelspltes ist, indem du k y durch sin α usdrückst. Wichtig hierbei ist, dss k = k gilt, die Streuung lso elstisch ist. c) (Ht nichts mit ) und b) zu tun:) Zeige mthemtisch, dss ds Betrgsqudrt der Fouriertrnsformierten gleich der Fouriertrnsformierten der Pttersonfunktion p(y) = f (y )f (y + y )dy ist. 5

6 Lösungshinweise: ) Die stückweise definierte Spltfunktion knn mn durch die Integrtionsgrenzen berücksichtigen ρ(x, k y ) = b e ik y y dy b = e ik y b e ik y b ik y k y b sin = k y b) Ds Beugungsmuster us der Vorlesung ist sin πb sin α λ I = I πb sin α λ Ds sieht schon so ähnlich us wie die Fouriertrnsformierte von oben, wir müssen nur noch den Wellenvektor richtig ersetzen. Die y-komponente des usfllenden Wellenvektors muss (siehe Skizze) k y = sin α k = sin α k = sin α π λ k α k y sein, wobei die zweite Gleichheit in der Aufgbe gegeben ist. Setzt mn ds in ds Ergebnis für die Fouriertrnsformierte ein, erhält mn ρ(x, k y ) = sin πb sin α λ πb sin α λ Bildet mn nun noch ds Betrgsqudrt, kommt bis uf den Vorfktor I ds gleiche Ergebnis herus wie in der Vorlesung gennnt. c) Ds Betrgsqudrt der Fouriertrnsformierten F der Funktion f ergibt sich zu ( bezeichnet die komplexe Konjugtion) F(k) = F(k)F (k) = f (x)e ikx dx f (x )e ikx dx k = f (x)f (x )e ik (x x ) dxdx = f (x + ξ)f (x )e ikξ dx dξ 6

7 Wobei in der letzten Zeile ξ = x x substituiert wurde. Zieht mn den nun von x unbhängigen Exponentilfktor us dem inneren Integrl herus (und verwendet, dss f eine reellwertige Funktion ist), erhält mn F(k) = f (x + ξ)f (x )dx e ikξ dξ = p(ξ)dξ Aufgbe 5 Die Frbenlehre Folgende Szene spielt im Himmel oder wohin Leute wie Newton, Goethe und Huygens kommen. Goethe: Also, bester Sir Isc, ich bleibe dbei: Die Frben sind nicht von vornherein im weißen Licht, sondern sie werden erst durch die frbigen Dinge drus erzeugt. Newton: Jetzt lssen Sie mich erst fertig ufbuen. Ds ist nicht meine ursprüngliche Anordnung, weil ich hier kein Prism uftreiben konnte. Aber hier hbe ich eine Schwungfeder vom Erzengel Gbriel, die tut s uch. So. Ist ds weißes Licht, ds d vorn druffällt? Gut. Jetzt hlten Sie ml Ihr Auge dorthin, Herr Geheimrt. Ws sehen Sie? Goethe: Ein prächtiges Grün. Newton: N, lso. Goethe: Jetzt sgen Sie mir bitte, ws ist denn ds eigentlich, grünes Licht? Huygens: Räuspert sich vernehmlich. Newton: Schon gut, Herr Kollege. Ich hbe j inzwischen uch dzugelernt. Also, ds Grün, ds Sie gesehen hben, ist eine hrmonische Welle mit der Wellenlänge.5 µm. Goethe: Und Sie versichern, dss Sie die.5 µm nicht irgendwie hineingeschmuggelt hben in Ihre Apprtur? Newton: Allerdings, ds versichere ich. Goethe: H, mein Bester! Jetzt betrchten Sie den Renommiertvismus von Seiner Heiligkeit genuer. D sind doch periodische feine Seitenstrhlen, viel feiner ls bei irdischen Flügelbesitzern, oder nicht? Newton: Ntürlich. Aber nicht, wie Sie vielleicht denken, in.5 µm Abstnd. Goethe: Zugegeben. Aber von d, wo Sie mich hingestellt hben, liegt jeder Seitenstrhl um genu.5 µm weiter entfernt ls der benchbrte. Sie hben lso eine Periodizität von.5 µm in Ihrer Apprtur. Kein Wunder, dss entsprechendes Licht heruskommt. 7

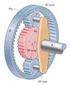
8 Wer ht recht? Wie wäre die Lge, wenn Newton ein Prism gehbt hätte? Lösungshinweise: Die Aufgbe hben wir us dem Gerthsen übernommen. Hier ist seine Antwort dzu: Offensichtlich ist Goethe in keiner schlechten Position. In Wirklichkeit ht er übrigens von der Munition, die Young und Fresnel ihm lieferten, wenig Notiz genommen und sie jedenflls in seiner Frbenlehre nicht usgenutzt. Feine Beugungsgitter konnte mn dmls noch nicht herstellen. Es ist oft nicht leicht zu entscheiden, ob wir etws, z. B. die Frben, mchen oder nur finden. Sind die hrmonischen Teilwellen wirklich in einem zusmmengesetzten Wellenvorgng drin, oder konstruiert sie die Fourier-Methode erst drus? Dss wir diese Teilwellen direkt hören, ist ein Argument für Newton, ber ds Ohr ist j selbst ein Fourier-Anlystor. Ds Auge rbeitet nders und knn z. B. nicht entscheiden, ob ein Weiß us llen Frben oder nur us zwei engen, komplementären Spektrlberei- chen zusmmengesetzt ist. Dss ein Gitter ein Fourier-Anlystor ist, sieht mn leicht ein, beim Prism weniger leicht. Aber uch Absorption und Dispersion beruhen uf dem Mitschwingen tomrer Oszilltoren. Ws ist ds Primäre, Rele: Der zusmmengesetzte Wellenzug oder die Teil- wellen, die Spektrllinien? Ws heißt überhupt Relität oder Existenz? Existierte ds Them us dem Andnte des Klvierkonzerts d-moll schon, bevor es Mozrt einfiel? Als Michelngelo einen riesigen Block Crrr- Mrmor erblickte, rief er: D ist der Dvid drin. Jemnd wndte ein, im Mrmor steckten bestenflls Ammoniten, ber keine nckten Jünglinge. Michelngelo führte den experimentellen Beweis: Er stoppte seinen Meißel hrschrf dort, wo die Hut des Dvid begnn. Mchte er ihn oder fnd er ihn? Aufgbe 6 Mgnetfeld des L I P Durch die Leiterschleife in der Abbildung ( = 4.7 cm) fließt ein Strom I = 3 A. ) Wie groß ist der Betrg des Mgnetfeldes m Punkt P. b) In welche Richtung geht ds Mgnetfeld n diesem Punkt? Hinweis: 4.7 cm sind nicht lng! 8

9 Lösungshinweise: P r α I x α Ds Mgnetfeld eines kurzen Leiters wie oben in der Abbildung htten wir schon ml hergeleitet (zwr nicht für Winkel, ist ber ähnlich). Es berechnet sich mit den Winkeln wie in der Abbildung zu (Mgnetfeld in positive z-richtung, us dem Bltt herus): B = µ I cos α cos α 4π r Ds Problem der Aufgbe knn mn in sechs solche Leiterstücke zerlegen - zwei dvon geben gr keinen Beitrg. Alle nderen, sowie die Winkel sind in der folgenden Abbildung mrkiert (Winkel immer gegen Uhrzeigersinn, Winkelnummerierung nch Stromflussrichtung). 9

10 α P P I I α α 3 α 4 P α 8 P I I α 6 α 5 α 7 Nun noch usrechnen: B = µ I 4π = µ I 4π = µ I 4π = µ I 4π cos α cos α + cos α 3 cos α 4 + cos α5 cos α 6 + cos α 7 cos α

11 Aufgbe 7 Spce Tlk Du beobchtest ein geldenes Teilchen. Es ruht, denn es ist kein elektrisches Feld vorhnden. Dfür existiert ber ein großräumiges Mgnetfeld. Ein Rumfhrer fliegt vorbei und beobchtet ds gleiche Teilchen. Er funkt: D fliegt ein geldenes Teilchen mit <kkrrkkzz>. Es herrscht ein Mgnetfeld von <kkrrkkzz>. Trotz der <kkrrkkzz> fliegt ds Teilchen genu <kkrrkkzz>. Also muss ein <kkrrkkzz> herrschen, ds die <kkrrkkzz> kompensiert, und zwr vom Betrg <kkrrkkzz> in der Richtung <kkrrkkzz>. ) Ws ht der Rumfhrer gesgt? b) In seiner Rkete ist uch eine geldenes Teilchen. Wie verhält es sich für den Rumfhrer? Wrum? c) Wie verhält sich ds Teilchen in der Rkete für uns? Lösungshinweise: Wir lssen ds Rumschiff mit Geschwindigkeit v in irgendeine Richtung fliegen. ) D fliegt ein geldenes Teilchen mit Geschwindigkeit v uf mich zu. Es herrscht ein Mgnetfeld von B. Trotz der Lorentzkrft q v B fliegt ds Teilchen genu gerdlinig. Also muss ein elektrisches Feld herrschen, ds die Lorentzkrft gerde kompensiert, und zwr vom Betrg qv B sin θ in Richtung senkrecht zum Mgnetfeld und zur Geschwindigkeit. b) Es wird entsprechend des elektrischen Feldes, ds der Rumfhrer sieht, beschleunigt. c) Wir führen die Bewegung uf die Lorentz-Krft zurück, die uf bewegte Ldungen durch ds Mgnetfeld wirkt. Mn merke lso: ob elektrische oder mgnetische Felder vorliegen, hängt vom Bewegungszustnd des Betrchters b (Reltivität). Bei hohen Geschwindigkeiten wird ds Gnze noch ein wenig komplizierter, d die Komponenten der Felder in Bewegungsrichtung sich dnn unter Lorentztrnsformtion nders verhlten ls die Felder senkrecht dzu. Aufgbe 8 Holzzylinder Ein Holzzylinder der Msse m = 5 g und Länge L = cm liegt uf einer schiefen Ebenen. Um den Zylinder ist in longitudinler Richtung eine Spule mit Windungen gewickelt, so dss die Achse des Zylinders in der Ebene der Spule liegt. Der Zylinder wird so losgelssen, dss die Spulenebene prllel zur schiefen Ebene ist. Im gnzen Rum herrscht noch ein nch oben gerichtetes vertikles Mgnetfeld mit dem Betrg B =.5 T. Wie groß muss der Strom durch die Spule mindestens sein, dmit der Zylinder nicht die Ebene hinbrollt? Lösungshinweise: Wir nehmen n: die Achse des Zylinders ist prllel zur x-achse.

12 Durch die Schwerkrft wirkt uf den Zylinder ein Drehmoment. Die Schwerkrft greift im Schwerpunkt (Mittelpunkt des Zylinders) n, er rotiert um den Auflgepunkt uf der schiefen Ebene. Den Verbindungsvektor Auflgepunkt-Mittelpunkt bezeichnen wir ls r, und bestimmen ihn (α ist der Winkel der schiefen Ebene). Die Schwerkrft geht in negtive z-richtung. Ds Drehmoment ist nun: r = r sin α cos α F = mg M g = r F = rmg sin α e x Fließt der Strom durch die Spule von oben betrchtet gegen den Uhrzeigersinn, so ht sie ein ds folgende mgnetische Moment: µ = nia sin α = nir L sin α cos α cos α Ds Drehmoment, welches durch den Strom verurscht wird ist nun ( B = B e z ): M B = µ B = BnI r L sin α e x Dmit sich der Zylinder nicht bewegt, müssen sich die Drehmomente ufheben: Aufgbe 9 Lnge Drähte M g + M b! = rmg sin α e x + BnI r L sin α e x = I = mg BnL =.45 A Zwei lnge, gerde Drähte (Abstnd zueinnder d = 4 cm) sind von einem homogenen Isoltor mit der reltiven Permebilität µ r = umgeben. Durch die Drähte fließen Ströme von je 4 A in entgegengesetzen Richtungen. ) Wie strk ist ds Mgnetfeld in der Mitte der Fläche zwischen beiden Drähten? b) Welche Krft wirkt pro Längeneinheit uf die Drähte? Lösungshinweise: ) Ds Mgnetfeld ddiert sich in der Mitte. Für unendlich lnge gerde Leiter ergibt sich B = µ µ r H = µ µ r I πr =. T b) Die Drähte müssen sich nziehen. Die Krft uf ein Leiterelement ist F = IB = µ µ r I = 3.8 N/m πr

13 Aufgbe Rottion im Mgnetfeld Ein Metllstb (Länge l) rotiert mit konstnter Winkelgeschwindigkeit um ein Ende. Ein homogenes Mgnetfeld vom Betrg B steht senkrecht zur Rottionsebene. ) Zeichne ds Problem. b) Ein Körper mit Ldung q befinde sich im Abstnd r von der Drehchse. Zeige, dss uf ihn die mgnetische Krft F m = qbrω wirkt. c) Zeige, dss zwischen den Enden des Stbes die Potentildifferenz U = Bωl herrscht. d) Zeichne eine rdile gerichtete Linie ein. Wir definieren θ ls den Winkel zwischen der Linie und dem Metllstb. Zeige, dss die Fläche des Kreisusschnittes, der von dieser Linie und dem Stb begrenzt wird, A = l θ ist. e) Berechne den mgnetischen Fluss durch die in d) beschriebene Fläche. Zeige, dss du durch Anwendung des Frdy schen Induktionsgesetzes die Beziehung U ind = Bωl erhälst. Lösungshinweise: ) Ds bekommst du selber hin. b) Es wirkt ntürlich die Lorentz-Krft F m = q v B = q ( ω r) B = qbrω Wobei wir usgenutzt hben, dss ω in Mgnetfeldrichtung zeigt, sodss v senkrecht zu B steht. c) Im Gleichgewicht muss die Lorentzkrft (die nch ußen bzw. innen zeigt, je nch Drehrichtung) gerde durch eine elektrische Krft kompensiert werden. Diese muss mn nur noch hochintegrieren l l l U = Edr = F m q dr = Brωdr = Bωl d) Der Gesmtkreis ht eine Fläche von πl. Der Kreisusschnitt, der von den beiden Linien begrenzt wird, ht einen Anteil von θ n dieser Fläche. Dnn muss die Fläche des Kreisusschnitts π gleich A = θ π πl = l θ sein. 3

14 Mn knn uch die Eins in Polrkoordinten hochintegrieren A = θ l rdrdφ = l θ e) φ m = B da = BA = l θ B A Die induzierte Spnnung ist gleich der mgnetischen Flussänderung U ind = dφ m dt = BȦ = l θ B = l ωb Aufgbe Wechselstromkreis S R ~ U C L R L R Ω 3 Ω L 5 mh C 8 µf V ν Hz R L U mx ) Berechne mit Hilfe von Zeigerdigrmmen die Impednz des Stromkreises, wenn der Schlter S geschlossen ist. b) Wie groß ist die Impednz bei geöffnetem Schlter? c) Welche Spnnung fällt m Widerstnd R L b, wenn der Schlter offen/geschlossen ist? d) Welche Ergebnisse erhälst du für Aufgbe ) bis c) bei einer Wechselspnnungsfrequenz von Hz. e) Wir wollen die Anordnung ls Tiefpssfilter verwenden. Muss dzu der Schlter geöffnet oder geschlossen sein? 4

15 Lösungshinweise: Allemein betrchtet knn mn die Gesmtimpednz der Schltung wie folgt herleiten: Die Spule und R L sind in Reihe geschltet, die Impednz der beiden ist lso Z = R L + ix L. Z wiederum befindet sich in einer Prllelschltung mit dem Kondenstor. Die Impednz der drei Elemente nennen wir Z. = + Z ix C Z = + ix C R L + ix L = R L + i(x L X C ) X C X L ix C R L Z = X C X L ix C R L R L + i(x L X C ) Für später ist es geschickt, Relteil und Imginärteil in getrennte Summnden zu verbnnen. Ds mcht mn m besten durch Erweiterung mit dem komplex Konjugierten des Nenners (R L i(x L X C )). Z = R L X C R L + (X L X C ) i X C R L + X L(X L X C ) R L + (X L X C ) Diese Impednz befindet sich in Reihe mit dem Widerstnd R, dmit ist die Gesmtimpednz Z = R + Z = R L X C R L + (X L X C ) i X C R L + X L(X L X C ) R L + (X L X C ) ) Mit Zeigerdigrmmen ist ds sehr ufwändig, mn muss uf jeden Fll immer Beträge usrechnen. Ds wr etws blöd in der Aufgbenstellung. Für Zeigerdigrmme siehe Übung 4, Aufgbe 4. Wir rechnen nur... Wenn der Schlter geschlossen ist, ist die Spule überbrückt. Dmit ist X L =. X C = =.99 kω πνc Z = 3 Ω i(.45 Ω) Z = 4 Ω i(.45 Ω) Z = Ω = 4 Ω 5

16 Die Phse der Impednz knn mn wie folgt berechnen ϕ = rctn I(Z) R(Z) =.45 = b) Die Spule ist nun im Stromkreis, der Blindwiderstnd der Induktivität ist dnn Dmit ergibt sich weiter X L = πν L = 9.4 Ω Z =4.3 Ω + i(9. Ω) Z =4.3 Ω ϕ =.6 c) geschlossener Schlter: Kirchhoffsche Mschenregel für Spnnungsquelle + Widerstnd R + Lstwiderstnd R L : U RI U RL = U RL =U RI U RL =U UR Z =( R Z )U mx cos(ωt δ) ( R Z )U mx =75 V ω =π s δ = rctn.45 4 offener Schlter: Zusätzlich noch Induktivität in der Msche U RI X L I U RL = U RL =U RI X L I U RL =U U(R + X L) Z ( R + X L )U mx =53 V Z ω =π s =.647 =( R + X L )U mx cos(ωt δ) Z δ = rctn X L = rctn 9.4 R + R L 4 = 3.3 6

17 d-) X C = πνc = 9.9 Ω X L = Z =9.7 Ω i(3.8 Ω) Z =9.7 Ω i(3.8 Ω) Z =3.6 Ω ϕ = rctn I(Z) R(Z) = = 35.7 d-b) X C = πνc = 9.9 Ω X L =πν L = 94 Ω Z =.4 Ω i(.3 Ω) Z =. Ω i(.3 Ω) Z =.6 Ω ϕ = rctn I(Z) R(Z) =.3. = 63.8 d-c) geschlossener Schlter ( R Z )U mx =55.8 V ω =π s δ = rctn = 35.7 offener Schlter ( R + X L )U mx = Z ω =π s δ = rctn X L = rctn 94 R + R L 4 = 87.6 e) Bei hohen Frequenzen und offenem Schlter gibt es einen größerern Spnnungsbfll m Lstwiderstnd, bei niedrigen Frequenzen fst gr keinen. Dher eignet sich diese Schltung mit offenem Schlter gut ls Tiefpssfiler. 7

18 Aufgbe Verschiebungsstrom E 5 NC Links ist der Feldverluf eines gleichförmigen elektrischen Feldes gezeigt. Berechne den Verschiebungsstrom durch eine.6 m große Fläche senkrecht zum Feld für die verschiedenen Zeitintervlle (ignoriere dbei die Knicke). Lösungshinweise: Der Verschiebungsstrom ist I v = A ɛ de dt (t )dt In den verschiedenen Bereichen knn mn die Steigung der Kurve, lso die Ableitung des elektrischen Feldes, blesen I = ɛ E A = ɛ 5 V/m.6 m =.7 A 4 6 s I = I 3 =.8 A 8