Numerische Programmierung Konkrete Mathematik
|
|
|
- Ewald Messner
- vor 6 Jahren
- Abrufe
Transkript
1 Numerische Progrmmierung Konkrete Mthemtik Litertur o Numerik für Informtiker (Huckle/Schneider) = Numerische Methoden o Folien voriger Semester o Herzerger: Wissenschftliches Rechnen o Opfer: Numerik für Anfänger o Üerhuer: Computer-Numerik o Khner/Moler/Nsh: Numericl Methods nd Softwre o Dhmen/Reusken: Numerik für Ingenieure und Nturwiss. 1
2 I. Wrum Numerik? 1. Zu Computer Science gehört uch die Numerik, genuso wie Dtennken, Softwre Engineering. Ursprung der Informtik ist die Numerik! Alles ws mit Computer zu tun ht, gehört zu CS! z.b. - Rechner-Arithmetik, Prllelrechner, usw. - Computergrphik (Flächen, Kurven) - Bildverreitung (Komprimierung, Filtern, Anlyse) : JPEG - Soundverreitung: MP3 - Informtion Retrievl, Prozessverwltung
3 . Wissenschftliches Rechnen Verund von Nturwissenschft, Mthemtik, Numerik, Informtik zur Lösung wiss. Proleme: z.b. Wettervorhersge, Rketensteuerung, Strömungs-Simultion (NASA, BMW, Siemens, ) 3. Numerik zur Lösung von Informtik-Prolemen z.b. - Wrteschlngen, Betriesmittelzuteilung, und Stochstische Automten, - Neuronle Netze und Fuzzy-Logik, - Räuer-Beute-Modelle zur Ressourcenverteilung 3
4 Vorussetzungen us der Informtik: - Zhldrstellung - Progrmmiersprche (JAVA) - (Komplexitätstheorie) Zur Mthemtik: Numerik ls Fortführung der Reinen Mthemtik mit nderen Mitteln: t z.b. estimme - e dt, - Gleichungssysteme, Nullstellen - Grenzwerte, Eigenwerte (Resonnzen) - Interpoltion kontinuierlich versus diskret! 4
5 Vorussetzungen us der Mthemtik: Tylor-Entwicklung und Mittelwertstz, Aleitungen, Summen und Reihen, trigonometrische Funktionen, Linere Gleichungssysteme, Vektoren und Mtrizen, Normen, Komplexe Zhlen. Flls Frgen zu mthemtischen Grundlgen uftuchen: Bitte mich sofort druf ufmerksm mchen und nchfrgen! 5
6 II. Rechnerrithmetik und Rundungsfehler Motto: Die ntürlichen Zhlen ht der liee Gott gemcht, lles ndere ist Menschenwerk. L. Kronecker Noody is perfect Osgood zu Dphne (Jerry) in Some like it hot Beispiel: Digitlisierung von Audio Audcity, JPEG 6
7 Prolem: Endlichkeit! Die Menge IR der reellen Zhlen esteht us unendlich vielen Zhlen mit unendlich vielen Stellen! Jeder Computer ist endlich!.1. Definition: Die endliche Menge M der in einem Rechner drstellren Zhlen heißt Mschinenzhlen Wir unterscheiden gnzzhlige Mschinenzhlen und Mschinenzhlen für reelle Zhlen (=Gleitpunktzhlen). 7
8 1.Prolem: Aildung R M liefert Fehler.Prolem: Arithmetische Opertionen + - * / : M x M M gilt nicht! Zum ersten Prolem:. Definition: Eine Aildung rd: R M ezeichnen wir ls Rundung, wenn gilt: x rd( x) min x m mm Dies ist keine eindeutige Definition von rd! Andere Möglichkeiten sttt rd: ceil, floor, to zero Minimlforderung: rd( m) m für mm Rundungsfehler (soluter): f rd ( x) : x rd( x) 8
9 Zum zweiten Prolem (rithmetische Opertionen) : M x : M M M M y : rd( x y) Genuso definieren wir für -, *, / die Näherungsopertoren Beispiele von Mschinenzhlen: M, * M, / M Quntisierung von Musik- oder Bildwerten: 8 Bit, 16 Bit Geldeträge, Wechsel/Aktienkurse: DAX 3577,7 Alterntiven zu Mschinenzhlen und -rithmetik? - Rechnen mit elieig vielen Stellen (symolisches Rechnen, MATHEMATICA, MAPLE) - Rechnen mit Intervllen (Intervll-Arithmetik) 9
10 Folien-Beispiel: Modell: Jede Zhl repräsentiert durch drei Dezimlstellen und Position des Dezimlpunkts: und Dher = Also Resultt: 0.11 Exktes Ergenis ei voller Stellenzhl: = Volle Stellenzhl führt zu ufwendigen Rechnungen, Zhlen würden zu lng! Speicherpltz! Rechenzeit! 10
11 Intervllrithmetik uf 3 Stellen (Folien-Beispiel): Repräsentiere Zhlen durch Einschließungsintervlle: Untere Intervllgrenze der Lösung: Oere Grenze: Resultt: Lösung von liegt im Intervll [ 0.11, ] Vorteil: Exkte Informtion üer Lge und Qulität der Lösung Nchteil: Rechenzeit! Ev. Ergenisintervll sehr groß! 11
12 .3. Definition: Festkommzhlen ls Mschinenzhlen n 1 n nk, m 1 m j mit 0,1,,9, k j IN n1, n,, nk, m1,, mj, Beispiele: - Geldeträge wie Euro.Cent, j= - Wechselkursngen, wie ($ zu ), j=4, k=1 - Börsenindizes: DAX , j=, k=4. - Alte Tschenrechner verwendeten Festpunktzhlen. 1
13 Für prktisches Rechnen ungenügend! Zu wenige gnze, zw. reelle Zhlen drstellr! Sehr große Zhlen? Sehr kleine Zhlen? Zhlen mit vielen Nchkommstellen? Zusätzlich große Rundungsfehler. Börsenindex Vncouver Strt des Indexes mit Wert Bei jedem Verkufereignis (c pro Tg) wurde der Index neu erechnet uf drei Stellen nch dem Komm: Rechne mit vier Stellen nch dem Komm und dnn Aschneiden der vierten Stelle. (Qusi rechnen wie mit gnzen Zhlen in C) Nch Monten wurde ngegeen. Der whre Wert: Systemtischer Fehler, der sehr oft uftritt! 13
14 Lndtgswhl 199 in Schleswig-Holstein: Grüne erhielten 4.97%. Zur Drstellung der Ergenisse Festkomm mit einer Stelle nch dem Komm, ( j=1 ); lso Anzeige des Ergenisses ls 5.0%. Fehler wurde erst entdeckt, nchdem offizielle Ergenisse ereits veröffentlicht wren. Rechnen(?) mit Exel!!! Diese Zhlendrstellungen werden wir i.f. nicht verwenden 14
15 .4. Integer(Mschinen)zhlen Endlicher Ausschnitt us den gnzen Zhlen Z symmetrisch um Null ngeordnet. Mn verschiet den Ausschnitt so, dss lle Zhlen positiv werden: Menge der Integer-Mschinenzhlen M z t1 i0 i m i t1, m i 0,1, i 0,, t 1 t IN git die Stellenzhl n, zw. Bits. 15
16 Stufenzhlen: i mit 0 i t-1 Also M = < - t-1, t-1-1 > Bei 3 Bits (=4 Bytes) ergit sich der Zhlenereich der gnzzhligen Mschinenzhlen dher zwischen - 31 = und 31-1= Folien-Beispiel: Drstellung der Dezimlzhl 11 mit t = 5 11 = 7 16 (d 11+16=7) = ( ) 16 = 16 + (8+3) 4 = (+1) 4 = 1* 4 +1* 3 +0* +1* 1 +1* 0-4 (11011), nicht 11=(01011) oder -11 = 5 16 (00101) 16
17 Zu Bechten: - Fehler ei Bereichsüerschreitung (Overflow) ev. Wrp-round-Effekt. - Integer-Division in Progrmmiersprchen: 1 / 3 = 0 Division ohne Rest oder Rundung zur Null (Aschneiden). - Division durch 0 (Beispiel: USS Yorktown) Vorteil: Null ht nur eine Drstellung! Sonst treten ei Integerzhlen keine Rundungsfehler uf! 17
18 Stelle x IR.5. Gleitpunktzhlen durch Vorzeichen, Mntisse m und Exponenten e dr, zgl. Bsis >1: x ( 1) m e Wir etrchten nur = (=8,10,16 kommen kum vor) Beispiel: Drstellungen der Zhl 16: mit v=0, m = -i und e = i+4. 18
19 Normierung ist notwendig, dmit Drstellung eindeutig: Der Exponent ist stets so zu wählen, dss die Mntisse m genu eine von Null verschiedene Stelle vor dem Komm ht. Also in unserem Beispiel 16 = Vorsicht: ndere Bücher normieren so, dss erste Stelle hinter dem Komm von Null verschieden! (lso 16 = = + (0.1) 5 ) 19
20 .6. Definition: Normierte Gleitpunktzhlen Die Menge M der (reellen) Mschinenzhlen esteht us Zhlen der Form Vorzeichen: Mntisse: t 1 i e x ( 1) x i i0 0,1, Exponent: Integerzhl e. 0,1, x 0 1, x i sonst Also ht die Mntisse eigentlich t Stellen; er die erste Stelle muss nicht gespeichert werden, d sie wegen der Normierung 1 ist. Dher werden für die Mntisse nur (t-1)-bits gerucht! 0
21 Bei Zhlen nhe 0 knn die Normierung ufgehoen werden (sog. sunormle Gleitpunktzhlen)! Ausnhmeregeln, flls Exponent miniml oder mximl ist! Exponent wird gespeichert ls gnzzhlige Integer- Mschinenzhl wie vorher eschrieen! 1
22 Folien-Beispiel: 13.6 = = 8 + (4+1.6) = (1+0.6) = (1/ + 0.1) = / + ( ) = /+1/16 + ( ) Also im Zweiersystem 13.6 = ( ) Als normierte Gleitpunktzhl: ( 1) ( ) 3 mit e=3.
23 Die Zhl 13.6 in verschiedenen Genuigkeiten: t Drstellung Rundung Fehler (1.1) (1.11) (1.110) (1.1011) ( ) * ( ) 3 * 3 * 3 * 3 * 3 * 3 uf uf uf (1.6) (0.4) (0.4) (0.1) (0.1) (0.05) 10 3
24 Anzhl der für Mntisse und Exponent enutzten Bit und drus sich ergeende Rechengenuigkeit und Exponentenereich ei IEEE-Dtentyp flot und doule: Typ flot doule Mntisse 3( 5 1 ( 1 ) ) t Exponent 8 11 [ e min, e mx ] 16, *10 10, *10 4
25 IEEE-Stndrd (single precision, 3 Bit): Exponent e mit 8 Bit, gespeichert in der positiven Form p = e + 17 p=( ) ist dnn kleinstmöglicher Exponent. Ist uch noch in der Mntisse (is uf Normierung) lles 0, so wird diese Zhl ls Null interpretiert. Entsprechend p=( ) = 55 ls unendlich (NN oder Not numer) -16 <= e <= 17 entspricht 1 <= p <= 54 Für die Mntisse leien 3 Bit (4 unter Berücksichtigung der Normierung). 1 Bit für Vorzeichen Insgesmt 1+3+8=3 Bit. 5
26 Beispiel Arine endete die erste Arine 5 durch Selstzerstörung 40 sec nch Strt. Ursche: 36.7 sec nch Strt versuchte der Bordcomputer den Wert der horizontlen Geschwindigkeit von 64 Bit Gleitpunkt in 16 Bit signed Integer umzurechnen. Der sich ergeende Wert wr zu groß 6
27 Overflow Asturz des Computers, Üerge n Bck-up-Rechner, der er us demselen Grund ereits gestürzt wr Kein Lenksystem mehr instiler Flug Selstzerstörung. Benutzte Softwre stmmte von Arine 4. Arine 5 wr schneller! Umwndlung wr nicht gesichert! Bereits Konrd Zuse verwendete in seinen Z1-Z4 Gleitpunktzhlen. 7
28 Rundung e.7. Def.: Für x ( 1) 1. x1x... xt 1xt... definieren wir v e 1 1. x x x für x 0 rd( x) t 1 1 t v e t1 rd( x) 1 1. x1x xt 1 für xt 1 und xt xt 1xt v e rd( x) 1 1. x1x xt 1 für xt 1 und xt 1xt xt v e t1 rd( x) 1 1. x1x xt 1 für xt 1 und xt 1xt xt Fll: Aschneiden, flls x t = 0;. Fll: Letztes Bit wird um eins erhöht, flls x t =1 und 3. Fll: (x t =1) oder x t x t1xt 1000 rd( 1. x1x xt 01) 1. x1x xt 0 rd(1. x x x 11) 1. x x 1 t1 1 t 1 x t Rundung so, dss letztes Bit 0 wird. 8
29 Es knn ev. Overflow uftreten (zu großer Exponent). Dieser Fll wird er im Folgenden ignoriert (Fehlermeldung?) Es knn Underflow uftreten. In der Regel wird dnn einfch die kleine Zhl zu 0 gesetzt. Die Rundungsfehlernlyse in den folgenden Aschnitten wird nur für Normlfll durchgeführt (ohne Over/Underflow) Dei ist nur die Mntisse wichtig! Der Exponent spielt keine Rolle, weil dei keine Fehler uftreten. 9
30 .8. Asoluter Rundungsfehler: f rd ( x) f rd ( x) x rd( x) t 1 e et x rd( x) Prolem: Ein soluter Fehler von der Größe 0.1 ist - ei der Zhl.1 recht groß, er - ei der Zhl sehr klein. 1 Beispiel: 1 Million + 1 Jhr lter Dinosurierknochen Dher sinnvollere Definition durch 30
31 f rel ( x) :.9. Reltiver Rundungsfehler: frd( x) x x rd( x) x : für x 0 Dnn gilt: x f rel x ( x) x et et e x d wegen Normierung die Mntisse in [1,] liegt: Mntisse stets (1...) < lso m >= 1, d.h. x >= e t Außerdem gilt durch Umformung von.9:.10.: rd( x) mit x x x 1 x x t Gerundete Zhl=Ausgngszhl, is uf Fktor (1±ε) x 31
32 Def.: Die oere Schrnke für den reltiven Fehler, der ei der Rundung mit t-stelliger Mntisse uftreten knn, heißt Mschinengenuigkeit, und ergit sich ls t Andere Möglichkeit, die Mschinengenugkeit zu definieren: Größte positive Zhl y= -k, so dss 1.0 y 1.0 Beispiel t=, = ¼ = (0.01) ; (1.0 1) (1.0) Mntissenlänge (Bits) Genuigkeit 3
33 Gleitpunktrithmetik.1. Def. (Relisierung einer Mschinenopertion): - Berechne für Mschinenzhlen ds Ergenis der Opertion mit höherer Genuigkeit (qusi exkt) - Runde dieses Resultt wieder uf Mschinenzhl. Ddurch ist der uftretende Fehler usschließlich gegeen durch den Rundungsfehler, der im letzten Schritt uftritt! 33
34 Beispiel Addition + M : Ausgngspunkt: Normierte Gleitpunktdrstellung eider Zhlen - Verschiee ei einer Zhl den Exponenten, so dss eide Zhlen den gleichen Exponenten hen. - Addiere nun die Mntissen. - Normlisiere ds Ergenis (verschiee ds Komm). - Runde ds Ergenis. 34
35 Folien-Beispiel: x=7/4 und y=3/8 x+y=17/8 Mntisse mit t=3 (1.11) 0 + M (1.10) = = (111) + (1.10) = ( ) = ( ) 1 = (1.00) 1. Also x + y = 17 / 8, er x+ M y =. Asoluter Fehler : 17/8 = 1/8 Reltiver Fehler: 1/8 17 / % Zum Vergleich: Bei t=3 ist die Mschinengenuigkeit 3 1.5% Der uftretende Fehler + der Gleitpunktddition entsteht lso durch die schließenden Rundung! 35
36 Nch.10 und.11 gilt dher.13. x M y rd( x y) ( x y)(1 ) mit Mschinengenuigkeit In der Prxis ersetzt mn die exkte Addition der Mntissen (Schritt ) durch eine Addition mit höherer Genuigkeit, meist mit doppelter Genuigkeit. Dnch Rundung uf Mschinenzhl. Ähnliches Modell ei Multipliktion / Division und uch ei nderen Funktionsuswertungen. Beispiel: Relisierung der Gleitpunkt-Division in INTEL- Prozessor und INTEL-Pentium-Bug
37 Fehlerfortpflnzung und Rundungsfehlernlyse Prolem: Rundungsfehler in der Einge und ei jeder durchgeführten Gleitpunktopertion können sich so uswirken, dss m Ende einer Berechnung ein vollkommen flsches Resultt heruskommt. Beispiel: Mit Tschenrechner strte mit Zhl und wiederhole k-ml die Wurzelopertion. Dnch strte mit diesem Endresultt und wiederhole k-ml ds Qudrieren. Endresultt sollte stets wieder sein. Für k genügend groß erhält mn er 1. (MATLAB) AUFGABE: Finde essere Art der Berechnung! 37
38 1 1 1 ) ( ) ( ) ( ) )(1 ) )(1 (( ) )(1 ) (( ) )(1 ( c c c c c e c e f M M 1, Einführendes Folien-Beispiel zur Epsilontik: Addition dreier Mschinenzhlen y=++c Zerlege Gesmtrechnung in zwei Grundopertionen: 1. e=+ M und. f=e+ M c mit Mschinengenuigkeit Vernchlässigung der Terme höherer Ordnung (in, 3,...): 38
39 Dmit ergit sich für den reltiven Fehler in erster Näherung: und die Aschätzung 1 ) ( ) ( c c f 1 1 ) ) ( ) ( ( ) ( c c c c c y f y y f rel c c y f rel 1 ) ( 1 39
40 Wnn wird der reltive Fehler groß? Wenn + >> ++c, oder ++c 0 Andere Reihenfolge der Berechnung liefert Fktoren (+c)/(++c) oder (+c)/(++c) ; Es wird jeweils der Fehler, der ei der ersten Addition uftritt, verstärkt. 40
Computer Vision Group Prof. Daniel Cremers. Fließkomma-Arithmetik und Fehlerfortpflanzung
 Computer Vision Group Prof. Dniel Cremers Fließkomm-Arithmetik und Fehlerfortpflnzung Fließkomm-Arithmetik Definition einer Mschinenopertion: 1. Berechne für Mschinenzhlen ds Ergenis der Opertion mit höherer
Computer Vision Group Prof. Dniel Cremers Fließkomm-Arithmetik und Fehlerfortpflnzung Fließkomm-Arithmetik Definition einer Mschinenopertion: 1. Berechne für Mschinenzhlen ds Ergenis der Opertion mit höherer
Wann wird der relative Fehler groß?
 Wnn wird der reltive Fehler groß? Wenn >> c, oder c 0 Andere Reihenfolge der Berechnung liefert Fktoren (c)/(c) oder (c)/(c) ; Es wird jeweils der Fehler, der ei der ersten Addition uftritt, verstärkt.
Wnn wird der reltive Fehler groß? Wenn >> c, oder c 0 Andere Reihenfolge der Berechnung liefert Fktoren (c)/(c) oder (c)/(c) ; Es wird jeweils der Fehler, der ei der ersten Addition uftritt, verstärkt.
Numerische Programmierung
 - 1 - Numerische Programmierung Konkrete Mathematik Literatur Numerik für Informatiker (Huckle/Schneider) = Numerische Methoden Folien voriger Semester Herzberger: Wissenschaftliches Rechnen Opfer: Numerik
- 1 - Numerische Programmierung Konkrete Mathematik Literatur Numerik für Informatiker (Huckle/Schneider) = Numerische Methoden Folien voriger Semester Herzberger: Wissenschaftliches Rechnen Opfer: Numerik
Umwandlung von endlichen Automaten in reguläre Ausdrücke
 Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Grundkurs Mathematik. Einführung in die Integralrechnung. Lösungen und Ergebnisse zu den Aufgaben
 Seite Einführung in die Integrlrechnung Lösungen und Ergenisse Gr Stefn Gärtner Grundkurs Mthemtik Einführung in die Integrlrechnung Lösungen und Ergenisse zu den Aufgen Von llen Wissenschftlern können
Seite Einführung in die Integrlrechnung Lösungen und Ergenisse Gr Stefn Gärtner Grundkurs Mthemtik Einführung in die Integrlrechnung Lösungen und Ergenisse zu den Aufgen Von llen Wissenschftlern können
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN
 Mthemtik: Mg. Schmid Wolfgng Areitsltt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN Wir wollen eine Gerde drstellen, welche durch die Punkte A(/) und B(5/) verläuft. Die Idee ist folgende:
Mthemtik: Mg. Schmid Wolfgng Areitsltt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN Wir wollen eine Gerde drstellen, welche durch die Punkte A(/) und B(5/) verläuft. Die Idee ist folgende:
2. Klausur in K2 am
 Nme: Punkte: Note: Ø: Profilfch Physik Azüge für Drstellung: Rundung:. Klusur in K m.. 04 Achte uf die Drstellung und vergiss nicht Geg., Ges., Formeln, Einheiten, Rundung...! Aufge ) (8 Punkte) In drei
Nme: Punkte: Note: Ø: Profilfch Physik Azüge für Drstellung: Rundung:. Klusur in K m.. 04 Achte uf die Drstellung und vergiss nicht Geg., Ges., Formeln, Einheiten, Rundung...! Aufge ) (8 Punkte) In drei
Ungleichungen. Jan Pöschko. 28. Mai Einführung
 Ungleichungen Jn Pöschko 8. Mi 009 Inhltsverzeichnis Einführung. Ws sind Ungleichungen?................................. Äquivlenzumformungen..................................3 Rechnen mit Ungleichungen...............................
Ungleichungen Jn Pöschko 8. Mi 009 Inhltsverzeichnis Einführung. Ws sind Ungleichungen?................................. Äquivlenzumformungen..................................3 Rechnen mit Ungleichungen...............................
4 Die rationalen Zahlen
 4 Die rtionlen Zhlen Der Ring der gnzen Zhlen ht den Mngel, dß nicht jede Gleichung = X, 0 innerhl Z lösr ist. (Z.B. ist 1 = 2 X unlösr in Z). Zu seiner Beseitigung erweitert mn den Zhlereich zum Körper
4 Die rtionlen Zhlen Der Ring der gnzen Zhlen ht den Mngel, dß nicht jede Gleichung = X, 0 innerhl Z lösr ist. (Z.B. ist 1 = 2 X unlösr in Z). Zu seiner Beseitigung erweitert mn den Zhlereich zum Körper
Monte-Carlo-Integration
 Monte-Crlo-Integrtion von Dietmr Herrmnn, Anzing Kurzfssung: An Hnd eines einfchen Beispiels wird gezeigt, dß jedes Integrl ls Erwrtungswert einer reellen Zufllsgröße ufgefßt werden knn. een einer symptotischen
Monte-Crlo-Integrtion von Dietmr Herrmnn, Anzing Kurzfssung: An Hnd eines einfchen Beispiels wird gezeigt, dß jedes Integrl ls Erwrtungswert einer reellen Zufllsgröße ufgefßt werden knn. een einer symptotischen
Berechnung von Flächen unter Kurven
 Berechnung von Flächen unter Kurven Es soll die Fläche unter einer elieigen (stetigen) Kurve erechnet werden. Dzu etrchten wir die (sog.) Flächenfunktion, mit der die zu erechnende Fläche qusi ngenähert
Berechnung von Flächen unter Kurven Es soll die Fläche unter einer elieigen (stetigen) Kurve erechnet werden. Dzu etrchten wir die (sog.) Flächenfunktion, mit der die zu erechnende Fläche qusi ngenähert
ARBEITSBLATT 5L-6 FLÄCHENBERECHNUNG MITTELS INTEGRALRECHNUNG
 Mthemtik: Mg. Schmid WolfgngLehrerInnentem RBEITSBLTT 5L-6 FLÄHENBEREHNUNG MITTELS INTEGRLREHNUNG Geschichtlich entwickelte sich die Integrlrechnug us folgender Frgestellung: Wie knn mn den Flächeninhlt
Mthemtik: Mg. Schmid WolfgngLehrerInnentem RBEITSBLTT 5L-6 FLÄHENBEREHNUNG MITTELS INTEGRLREHNUNG Geschichtlich entwickelte sich die Integrlrechnug us folgender Frgestellung: Wie knn mn den Flächeninhlt
wertyuiopasdfghjklzxcvbnmqwertyui
 qwertyuiopsdfghjklzxcvnmqwerty uiopsdfghjklzxcvnmqwertyuiopsd fghjklzxcvnmqwertyuiopsdfghjklzx Aufgen M-Beispielen cvnmqwertyuiopsdfghjklzxcvnmq Vorereitung uf die. Schulreit wertyuiopsdfghjklzxcvnmqwertyui
qwertyuiopsdfghjklzxcvnmqwerty uiopsdfghjklzxcvnmqwertyuiopsd fghjklzxcvnmqwertyuiopsdfghjklzx Aufgen M-Beispielen cvnmqwertyuiopsdfghjklzxcvnmq Vorereitung uf die. Schulreit wertyuiopsdfghjklzxcvnmqwertyui
Vorkurs Mathematik Fachhochschule Frankfurt, Fachbereich 2. Fachhochschule Frankfurt am Main Fachbereich Informatik und Ingenieurwissenschaften
 Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
1 Folgen von Funktionen
 Folgen von Funktionen Wir etrchten Folgen von reell-wertigen Funktionen f n U R mit Definitionsereicht U R und interessieren uns für ntürliche Konvergenzegriffe. Genuer setzen wir uns mit folgenden Frgen
Folgen von Funktionen Wir etrchten Folgen von reell-wertigen Funktionen f n U R mit Definitionsereicht U R und interessieren uns für ntürliche Konvergenzegriffe. Genuer setzen wir uns mit folgenden Frgen
1.7 Inneres Produkt (Skalarprodukt)
 Inneres Produkt (Sklrprodukt) 17 1.7 Inneres Produkt (Sklrprodukt) Montg, 27. Okt. 2003 7.1 Wir erinnern zunächst n die Winkelfunktionen sin und cos, deren Wirkung wir m Einheitskreis vernschulichen: ϕ
Inneres Produkt (Sklrprodukt) 17 1.7 Inneres Produkt (Sklrprodukt) Montg, 27. Okt. 2003 7.1 Wir erinnern zunächst n die Winkelfunktionen sin und cos, deren Wirkung wir m Einheitskreis vernschulichen: ϕ
Das Rechnen mit Logarithmen
 Ds Rechnen mit Logrithmen Etw in der 0. Klssenstufe kommt mn in Kontkt mit Logrithmen. Für die, die noch nicht so weit sind oder die, die schon zu weit dvon entfernt sind, hier noch einml ein kleiner Einblick:
Ds Rechnen mit Logrithmen Etw in der 0. Klssenstufe kommt mn in Kontkt mit Logrithmen. Für die, die noch nicht so weit sind oder die, die schon zu weit dvon entfernt sind, hier noch einml ein kleiner Einblick:
- 1 - VB Inhaltsverzeichnis
 - - VB Inhltsverzeichnis Inhltsverzeichnis... Die Inverse einer Mtrix.... Definition der Einheitsmtrix.... Bedingung für die inverse Mtrix.... Berechnung der Inversen Mtrix..... Ds Verfhren nch Guß mit
- - VB Inhltsverzeichnis Inhltsverzeichnis... Die Inverse einer Mtrix.... Definition der Einheitsmtrix.... Bedingung für die inverse Mtrix.... Berechnung der Inversen Mtrix..... Ds Verfhren nch Guß mit
Skript für die Oberstufe und das Abitur 2015 Baden-Württemberg berufl. Gymnasium (AG, BTG, EG, SG, WG)
 Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
10 Anwendungen der Integralrechnung
 9 nwendungen der Integrlrechnung Der Inhlt von 9 wren die verschiedenen Verfhren zur Berechnung eines Integrls Der Inhlt von sind die verschiedenen Bedeutungen, die ein Integrl hen knn Die Integrlrechnung
9 nwendungen der Integrlrechnung Der Inhlt von 9 wren die verschiedenen Verfhren zur Berechnung eines Integrls Der Inhlt von sind die verschiedenen Bedeutungen, die ein Integrl hen knn Die Integrlrechnung
Bestimmtes (Riemannsches) Integral / Integral als Grenzwert einer Summe : Bedeutung: Fläche unter einer Funktion innerhalb bestimmter Grenzen
 III. Integrlrechnung : Bestimmtes (Riemnnsches Integrl / Integrl ls Grenzwert einer Summe : Bedeutung: Fläche unter einer Funktion innerhl estimmter Grenzen yf( y n y n ( Δ Berechnung der Fläche A unter
III. Integrlrechnung : Bestimmtes (Riemnnsches Integrl / Integrl ls Grenzwert einer Summe : Bedeutung: Fläche unter einer Funktion innerhl estimmter Grenzen yf( y n y n ( Δ Berechnung der Fläche A unter
Die Keplersche Fassregel
 Die Keplersche Fssregel K. Gerer Bei vielen Aufgen, z.b. ei der Lösung von Differentilgleichungen, tucht die Schwierigkeit uf, dss Integrtionen nicht durchgeführt werden können. So können z.b. die folgenden
Die Keplersche Fssregel K. Gerer Bei vielen Aufgen, z.b. ei der Lösung von Differentilgleichungen, tucht die Schwierigkeit uf, dss Integrtionen nicht durchgeführt werden können. So können z.b. die folgenden
5.5. Integralrechnung
 .. Integrlrechnung... Berechnung von Integrlen mit der Streifenmethode Definition: Gegeen seien, R mit < und eine uf [; ] stetige Funktion f. Der orientierte Inhlt der Fläche, die durch die -Achse, ds
.. Integrlrechnung... Berechnung von Integrlen mit der Streifenmethode Definition: Gegeen seien, R mit < und eine uf [; ] stetige Funktion f. Der orientierte Inhlt der Fläche, die durch die -Achse, ds
Mathematik Bruchrechnung Grundwissen und Übungen
 Mthemtik Bruchrechnung Grundwissen und Übungen von Stefn Gärtner (Gr) Stefn Gärtner -00 Gr Mthemtik Bruchrechnung Seite Inhlt Inhltsverzeichnis Seite Grundwissen Ws ist ein Bruch? Rtionle Zhlen Q Erweitern
Mthemtik Bruchrechnung Grundwissen und Übungen von Stefn Gärtner (Gr) Stefn Gärtner -00 Gr Mthemtik Bruchrechnung Seite Inhlt Inhltsverzeichnis Seite Grundwissen Ws ist ein Bruch? Rtionle Zhlen Q Erweitern
1. Kapitel: Arithmetik. Ergebnisse mit und ohne Lösungsweg
 Arithmetik Lösungen Lö. Kpitel: Arithmetik. Ergenisse mit und ohne Lösungsweg Zu Aufge.: ) 7 ist eine rtionle Zhl, d sie sich ls Bruch us zwei gnzen Zhlen (Nenner 0) drstellen lässt: 7 7. 6 ) Eenso, denn
Arithmetik Lösungen Lö. Kpitel: Arithmetik. Ergenisse mit und ohne Lösungsweg Zu Aufge.: ) 7 ist eine rtionle Zhl, d sie sich ls Bruch us zwei gnzen Zhlen (Nenner 0) drstellen lässt: 7 7. 6 ) Eenso, denn
5. Vektor- und Matrizenrechnung
 Ü F-Studiengng Angewndte lektronik, SS 6 Üungsufgen zur Lineren Alger und Anlysis II Vektor- und Mtrizenrechnung Für die Vektoren = (,,,) und = (,,,) erechne mn die Linerkomintion ( ) + ( + ), die Längen,
Ü F-Studiengng Angewndte lektronik, SS 6 Üungsufgen zur Lineren Alger und Anlysis II Vektor- und Mtrizenrechnung Für die Vektoren = (,,,) und = (,,,) erechne mn die Linerkomintion ( ) + ( + ), die Längen,
Vorlesung. Einführung in die mathematische Sprache und naive Mengenlehre
 Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Begriffe: Addition Subtraktion Multiplikation Division. Summe Differenz Produkt Quotient a + b a b a b a : b
 Grundlgen 0.0. Zhlbereiche ntürliche Zhlen: N = {0; ; 2;...} (nch DIN 547) N = N \ {0} gnze Zhlen: Z = {... 2; ; 0; ; 2;...} rtionle Zhlen: Q = { p p, q Z, q 0} q Q besteht us llen Bruchzhlen. reelle Zhlen:
Grundlgen 0.0. Zhlbereiche ntürliche Zhlen: N = {0; ; 2;...} (nch DIN 547) N = N \ {0} gnze Zhlen: Z = {... 2; ; 0; ; 2;...} rtionle Zhlen: Q = { p p, q Z, q 0} q Q besteht us llen Bruchzhlen. reelle Zhlen:
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mthemtik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufge 69. Quizz Integrle. Es sei Höhere Mthemtik für Informtiker II (Sommersemester
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mthemtik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufge 69. Quizz Integrle. Es sei Höhere Mthemtik für Informtiker II (Sommersemester
Nullstellen quadratischer Gleichungen
 Nullstellen qudrtischer Gleichungen Rolnd Heynkes 5.11.005, Achen Nch y ufgelöst hen qudrtische Gleichungen die Form y = x +x+c. Zeichnet mn für jedes x uf der rechten Seite und ds drus resultierende y
Nullstellen qudrtischer Gleichungen Rolnd Heynkes 5.11.005, Achen Nch y ufgelöst hen qudrtische Gleichungen die Form y = x +x+c. Zeichnet mn für jedes x uf der rechten Seite und ds drus resultierende y
Wurzeln. bestimmen. Dann braucht man Wurzeln. Treffender müsste man von Quadratwurzeln sprechen. 1. Bei Quadraten, deren Fläche eine Quadratzahl ist,
 Seitenlängen von Qudrten lssen sich mnchml sehr leicht und mnchml etws schwerer Wurzeln bestimmen. Dnn brucht mn Wurzeln. Treffender müsste mn von Qudrtwurzeln sprechen. Sie stehen in enger Beziehung zu
Seitenlängen von Qudrten lssen sich mnchml sehr leicht und mnchml etws schwerer Wurzeln bestimmen. Dnn brucht mn Wurzeln. Treffender müsste mn von Qudrtwurzeln sprechen. Sie stehen in enger Beziehung zu
Die Regelungen zu den Einsendeaufgaben (Einsendeschluss, Klausurzulassung) finden Sie in den Studien- und Prüfungsinformationen Heft Nr. 1.
 Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
ARBEITSBLATT 14 ARBEITSBLATT 14
 Mthemtik: Mg. Schmid Wolfgng reitsltt. Semester RBEITSBLTT RBEITSBLTT RBEITSBLTT RBEITSBLTT DS VEKTORPRODUKT Definition: Ds vektorielle Produkt (oder Kreuprodukt) weier Vektoren und ist ein Vektor mit
Mthemtik: Mg. Schmid Wolfgng reitsltt. Semester RBEITSBLTT RBEITSBLTT RBEITSBLTT RBEITSBLTT DS VEKTORPRODUKT Definition: Ds vektorielle Produkt (oder Kreuprodukt) weier Vektoren und ist ein Vektor mit
Mitschrift Repetitorium Theoretische Informatik und Logik
 Mitschrift Repetitorium Theoretische Informtik und Logik Teil 1: Formle Sprchen, 15.01.2010, 1. Edit Allgemeine Hinweise für die Prüfung Ds Pumping-Lemm für kontextfreie Sprchen kommt nicht (sehr wohl
Mitschrift Repetitorium Theoretische Informtik und Logik Teil 1: Formle Sprchen, 15.01.2010, 1. Edit Allgemeine Hinweise für die Prüfung Ds Pumping-Lemm für kontextfreie Sprchen kommt nicht (sehr wohl
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mthemtik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mthemtik für Informtiker I (Wintersemester 00/00) Aufgbenbltt (. Oktober 00)
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mthemtik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mthemtik für Informtiker I (Wintersemester 00/00) Aufgbenbltt (. Oktober 00)
2.8. Absoluter Rundungsfehler:
 .8. Asoluter Rundungsehler: rd rd rd t e et rd Prolem: Ein soluter Fehler von der Größe 0. ist - ei der Zhl. reht groß, er - ei der Zhl 3456.7 sehr klein. Beispiel: Million + Jhr lter Dinosurierknohen
.8. Asoluter Rundungsehler: rd rd rd t e et rd Prolem: Ein soluter Fehler von der Größe 0. ist - ei der Zhl. reht groß, er - ei der Zhl 3456.7 sehr klein. Beispiel: Million + Jhr lter Dinosurierknohen
Multiplikative Inverse
 Multipliktive Inverse Ein Streifzug durch ds Bruchrechnen in Restklssen von Yimin Ge, Jänner 2006 Viele Leute hben Probleme dbei, Brüche und Restklssen unter einen Hut zu bringen. Dieser kurze Aufstz soll
Multipliktive Inverse Ein Streifzug durch ds Bruchrechnen in Restklssen von Yimin Ge, Jänner 2006 Viele Leute hben Probleme dbei, Brüche und Restklssen unter einen Hut zu bringen. Dieser kurze Aufstz soll
Lösung zur Klausur. Grundlagen der Theoretischen Informatik. 1. Zeigen Sie, dass die folgende Sprache regulär ist: w {a, b} w a w b 0 (mod 3) }.
 Lösung zur Klusur Grundlgen der Theoretischen Informtik 1. Zeigen Sie, dss die folgende Sprche regulär ist: { w {, } w w 0 (mod 3) }. Lösung: Wir nennen die Sprche L. Eine Sprche ist genu dnn regulär,
Lösung zur Klusur Grundlgen der Theoretischen Informtik 1. Zeigen Sie, dss die folgende Sprche regulär ist: { w {, } w w 0 (mod 3) }. Lösung: Wir nennen die Sprche L. Eine Sprche ist genu dnn regulär,
v P Vektorrechnung k 1
 Vektorrechnung () Vektorielle Größen in der hysik: Sklren Größen wie Zeit, Msse, Energie oder Tempertur werden in der hysik mit einer Mßzhl und einer Mßeinheit ngegeen: 7 sec, 4.5 kg. Wichtige physiklische
Vektorrechnung () Vektorielle Größen in der hysik: Sklren Größen wie Zeit, Msse, Energie oder Tempertur werden in der hysik mit einer Mßzhl und einer Mßeinheit ngegeen: 7 sec, 4.5 kg. Wichtige physiklische
11. DER HAUPTSATZ DER DIFFERENTIAL- UND INTEGRALRECHNUNG
 91 Dieses Skript ist ein Auszug mit Lücken us Einführung in die mthemtische Behndlung der Nturwissenschften I von Hns Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie ds Buch uch kufen und
91 Dieses Skript ist ein Auszug mit Lücken us Einführung in die mthemtische Behndlung der Nturwissenschften I von Hns Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie ds Buch uch kufen und
vollständig (Vervollständigung) deterministisch, DFA (Potenzmengenkonstruktion) Minimalautomat: minimaler vollständiger DFA
 Ws isher geschh NFA A = (X, Q, δ, I, F ) vollständig (Vervollständigung) deterministisch, DFA (Potenzmengenkonstruktion) Minimlutomt: minimler vollständiger DFA Für jede Sprche L X sind die folgenden Aussgen
Ws isher geschh NFA A = (X, Q, δ, I, F ) vollständig (Vervollständigung) deterministisch, DFA (Potenzmengenkonstruktion) Minimlutomt: minimler vollständiger DFA Für jede Sprche L X sind die folgenden Aussgen
Orientierungstest Mathematische Grundlagen
 Orientierungstest Mthemtische Grundlgen Lösungen:. Welche Zhlenmengen git es? Beispiele? Menge der ntürlichen Zhlen N {,,, } Menge der gnzen Zhlen Z {,, 0,,, } Menge der rtionlen Zhlen Q Menge ller ls
Orientierungstest Mthemtische Grundlgen Lösungen:. Welche Zhlenmengen git es? Beispiele? Menge der ntürlichen Zhlen N {,,, } Menge der gnzen Zhlen Z {,, 0,,, } Menge der rtionlen Zhlen Q Menge ller ls
Für den Mathe GK, Henß. - Lineare Algebra und analytische Geometrie -
 Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
RESULTATE UND LÖSUNGEN
 TG TECHNOLOGISCHE GRUNDLAGEN Kpitel 3 Mthemtik Kpitel 3.2 Alger Grundrechenrten RESULTATE UND LÖSUNGEN Verfsser: Hns-Rudolf Niedererger Elektroingenieur FH/HTL Vordergut 1, 8772 Nidfurn 055-654 12 87 Ausge:
TG TECHNOLOGISCHE GRUNDLAGEN Kpitel 3 Mthemtik Kpitel 3.2 Alger Grundrechenrten RESULTATE UND LÖSUNGEN Verfsser: Hns-Rudolf Niedererger Elektroingenieur FH/HTL Vordergut 1, 8772 Nidfurn 055-654 12 87 Ausge:
Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* aller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt:
 8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012. Sprachen. Grammatiken (Einführung)
 Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
2. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004
 Universität Krlsruhe Theoretische Informtik Fkultät für Informtik WS 2003/04 ILKD Prof. Dr. D. Wgner 14. April 2004 2. Klusur zur Vorlesung Informtik III Wintersemester 2003/2004 Lösung! Bechten Sie: Bringen
Universität Krlsruhe Theoretische Informtik Fkultät für Informtik WS 2003/04 ILKD Prof. Dr. D. Wgner 14. April 2004 2. Klusur zur Vorlesung Informtik III Wintersemester 2003/2004 Lösung! Bechten Sie: Bringen
Grenzwerte von Funktionen
 Grenzwert und Stetigkeit von Funktionen Methodische Bemerkungen H Hinweise und didktisch-methodische Anmerkungen zum Einstz der Areitslätter und Folien für den Themenkreis Grenzwert und Stetigkeit von
Grenzwert und Stetigkeit von Funktionen Methodische Bemerkungen H Hinweise und didktisch-methodische Anmerkungen zum Einstz der Areitslätter und Folien für den Themenkreis Grenzwert und Stetigkeit von
2. Das Rechnen mit ganzen Zahlen (Rechnen in )
 . Ds Rechnen mit gnzen Zhlen (Rechnen in ).1 Addition und Subtrktion 5 + = 7 Summnd Summnd Summe 5 - = 3 Minuend Subtrhend Differenz In Aussgen mit Vriblen lssen sich nur gleiche Vriblen ddieren bzw. subtrhieren.
. Ds Rechnen mit gnzen Zhlen (Rechnen in ).1 Addition und Subtrktion 5 + = 7 Summnd Summnd Summe 5 - = 3 Minuend Subtrhend Differenz In Aussgen mit Vriblen lssen sich nur gleiche Vriblen ddieren bzw. subtrhieren.
Bruchterme. Franz Embacher
 mthe online Skripten http://www.mthe-online.t/skripten/ Bruchterme Frnz Emcher Fkultät für Mthemtik der Universität Wien E-mil: frnz.emcher@univie.c.t WWW: http://homepge.univie.c.t/frnz.emcher/ In diesem
mthe online Skripten http://www.mthe-online.t/skripten/ Bruchterme Frnz Emcher Fkultät für Mthemtik der Universität Wien E-mil: frnz.emcher@univie.c.t WWW: http://homepge.univie.c.t/frnz.emcher/ In diesem
13 Rekonfigurierende binäre Suchbäume
 13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
Mathe Warm-Up, Teil 1 1 2
 Mthe Wrm-Up, Teil 1 1 2 HEUTE: 1. Elementre Rechenopertionen: Brüche, Potenzen, Logrithmus, Wurzeln 2. Summen- und Produktzeichen 3. Gleichungen/Ungleichungen 1 orientiert sich n den Kpiteln 3,4,6,8 des
Mthe Wrm-Up, Teil 1 1 2 HEUTE: 1. Elementre Rechenopertionen: Brüche, Potenzen, Logrithmus, Wurzeln 2. Summen- und Produktzeichen 3. Gleichungen/Ungleichungen 1 orientiert sich n den Kpiteln 3,4,6,8 des
Übungsblatt 1 zum Propädeutikum
 Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
Kapitel 13. Taylorentwicklung Motivation
 Kpitel 13 Tylorentwicklung 13.1 Motivtion Sei D R offen. Sie erinnern sich: Eine in D stetig differenzierbre Funktion f : D R wird durch die linere Funktion g(x) = f() + f ()(x ) in einer Umgebung von
Kpitel 13 Tylorentwicklung 13.1 Motivtion Sei D R offen. Sie erinnern sich: Eine in D stetig differenzierbre Funktion f : D R wird durch die linere Funktion g(x) = f() + f ()(x ) in einer Umgebung von
Differenzial- und Integralrechnung III
 Differenzil- und Integrlrechnung III Riner Huser April 2012 1 Einleitung 1.1 Polynome und Potenzfunktionen Die Polynome oder Polynomfunktionen lssen sich durch die endliche Anzhl von n+1 Prmetern i R in
Differenzil- und Integrlrechnung III Riner Huser April 2012 1 Einleitung 1.1 Polynome und Potenzfunktionen Die Polynome oder Polynomfunktionen lssen sich durch die endliche Anzhl von n+1 Prmetern i R in
Berechnung der inversen Matrix.
 Inverse Mtrix Berechnung der inversen Mtrix. Es ist ds LGS A X = E zu lösen. X = A 1 ist eine Mtrix. Verwendung des Guss-Algorithmus: Trnsformiere (A E in (E X. Steffen Voigtmnn Beuth Hochschule für Technik
Inverse Mtrix Berechnung der inversen Mtrix. Es ist ds LGS A X = E zu lösen. X = A 1 ist eine Mtrix. Verwendung des Guss-Algorithmus: Trnsformiere (A E in (E X. Steffen Voigtmnn Beuth Hochschule für Technik
Grundbegriffe der Informatik Aufgabenblatt 5
 Grundegriffe der Informtik Aufgenltt 5 Mtr.nr.: Nchnme: Vornme: Tutorium: Nr. Nme des Tutors: Ausge: 20. Novemer 2013 Age: 29. Novemer 2013, 12:30 Uhr im GBI-Briefksten im Untergeschoss von Geäude 50.34
Grundegriffe der Informtik Aufgenltt 5 Mtr.nr.: Nchnme: Vornme: Tutorium: Nr. Nme des Tutors: Ausge: 20. Novemer 2013 Age: 29. Novemer 2013, 12:30 Uhr im GBI-Briefksten im Untergeschoss von Geäude 50.34
Spiele und logische Komplexitätsklassen
 Spiele und logische Komplexitätsklssen Mrtin Horsch 26. Jnur 2006 Inhlt des Seminrvortrges Ehrenfeucht-Frïssé-Spiel mit k Mrken Formeln mit k Vrilen und logische Komplexitätsklssen k-vrileneigenschft logischer
Spiele und logische Komplexitätsklssen Mrtin Horsch 26. Jnur 2006 Inhlt des Seminrvortrges Ehrenfeucht-Frïssé-Spiel mit k Mrken Formeln mit k Vrilen und logische Komplexitätsklssen k-vrileneigenschft logischer
Hans Walser. Geometrische Spiele. 1 Vier gleiche rechtwinklige Dreiecke. 1.1 Allgemeiner Fall
 Hns Wlser Geometrische Spiele 1 Vier gleiche rechtwinklige Dreiecke 1.1 Allgemeiner Fll Wir strten mit einem elieigen rechtwinkligen Dreieck in der ülichen Beschriftung. A c B Strtdreieck C Nun versuchen
Hns Wlser Geometrische Spiele 1 Vier gleiche rechtwinklige Dreiecke 1.1 Allgemeiner Fll Wir strten mit einem elieigen rechtwinkligen Dreieck in der ülichen Beschriftung. A c B Strtdreieck C Nun versuchen
Repetitionsaufgaben Logarithmusgleichungen
 Kntonle Fchschft Mthemtik Repetitionsufgben Logrithmusgleichungen Inhltsverzeichnis A) Vorbemerkungen B) Lernziele C) Repetition Logrithmen D) Logrithmusgleichungen 4 E) Aufgben mit Musterlösungen 5 A)
Kntonle Fchschft Mthemtik Repetitionsufgben Logrithmusgleichungen Inhltsverzeichnis A) Vorbemerkungen B) Lernziele C) Repetition Logrithmen D) Logrithmusgleichungen 4 E) Aufgben mit Musterlösungen 5 A)
BRÜCKENKURS MATHEMATIK
 Brückenkurs Linere Gleichungssysteme - Prof. r. M. Ludwig BRÜCKENKURS MATHEMATIK LINEARE GLEICHUNGSSYSTEME Schwerpunkte: Modellbildung Lösungsmethoden Geometrische Interprettion Prof. r. hbil. M. Ludwig
Brückenkurs Linere Gleichungssysteme - Prof. r. M. Ludwig BRÜCKENKURS MATHEMATIK LINEARE GLEICHUNGSSYSTEME Schwerpunkte: Modellbildung Lösungsmethoden Geometrische Interprettion Prof. r. hbil. M. Ludwig
dem Verfahren aus dem Beweis zu Satz 2.20 erhalten wir zunächst die folgenden beiden ε-ndeas für die Sprachen {a} {b} und {ε} {a} +
 Lösungen zu Üungsltt 3 Aufge 1. Es gilt L(( ) ) = ({} {}) {} = ({} {}) ({} {} + ). Mit dem Verfhren us dem Beweis zu Stz 2.20 erhlten wir zunächst die folgenden eiden -NDEAs für die Sprchen {} {} und {}
Lösungen zu Üungsltt 3 Aufge 1. Es gilt L(( ) ) = ({} {}) {} = ({} {}) ({} {} + ). Mit dem Verfhren us dem Beweis zu Stz 2.20 erhlten wir zunächst die folgenden eiden -NDEAs für die Sprchen {} {} und {}
Kurvenintegrale. 17. Juli 2006 (Korrigierte 2. Version) 1 Kurvenintegrale 1. Art (d.h. f ist Zahl, kein Vektor)
 Kurvenintegrle Christin Mosch, Theoretische Chemie, Universität Ulm, christin.mosch@uni-ulm.de 7. Juli 26 (Korrigierte 2. Version Kurvenintegrle. Art (d.h. f ist Zhl, kein Vektor Bei Kurvenintegrlen. Art
Kurvenintegrle Christin Mosch, Theoretische Chemie, Universität Ulm, christin.mosch@uni-ulm.de 7. Juli 26 (Korrigierte 2. Version Kurvenintegrle. Art (d.h. f ist Zhl, kein Vektor Bei Kurvenintegrlen. Art
Brückenkurs Lineare Gleichungssysteme und Vektoren
 Brückenkurs Linere Gleichungssysteme und Vektoren Dr Alessndro Cobbe 30 September 06 Linere Gleichungssyteme Ws ist eine linere Gleichung? Es ist eine lgebrische Gleichung, in der lle Vriblen nur mit dem
Brückenkurs Linere Gleichungssysteme und Vektoren Dr Alessndro Cobbe 30 September 06 Linere Gleichungssyteme Ws ist eine linere Gleichung? Es ist eine lgebrische Gleichung, in der lle Vriblen nur mit dem
MC-Serie 12 - Integrationstechniken
 Anlysis D-BAUG Dr. Meike Akveld HS 15 MC-Serie 1 - Integrtionstechniken 1. Die Formel f(x) dx = xf(x) xf (x) dx i) ist im Allgemeinen flsch. ii) folgt us der Sustitutionsregel. iii) folgt us dem Huptstz
Anlysis D-BAUG Dr. Meike Akveld HS 15 MC-Serie 1 - Integrtionstechniken 1. Die Formel f(x) dx = xf(x) xf (x) dx i) ist im Allgemeinen flsch. ii) folgt us der Sustitutionsregel. iii) folgt us dem Huptstz
Lehrgang: Digitaltechnik 1 ( Grundlagen ) - Im Lehrgang verwendete Gatter ( Übersicht ) Seite 3
 Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
Kapitel 1. Anschauliche Vektorrechnung
 Kpitel 1 nschuliche Vektorrechnung 1 2 Kpitel I: nschuliche Vektorrechnung Montg, 13. Oktoer 03 Einordnung Dieses erste Kpitel ht motivierenden Chrkter. Es führt n die geometrische nschuung nknüpfend die
Kpitel 1 nschuliche Vektorrechnung 1 2 Kpitel I: nschuliche Vektorrechnung Montg, 13. Oktoer 03 Einordnung Dieses erste Kpitel ht motivierenden Chrkter. Es führt n die geometrische nschuung nknüpfend die
Grundwissen Mathematik 8.Klasse Gymnasium SOB. Darstellung im Koordinatensystem: Der Kreisumfang ist direkt proportional zu seinem Radius.
 Gymso 1 Grundwissen Mthemtik 8.Klsse Gymnsium SOB 1.Funktionle Zusmmenhänge 1.1.Proportionlität Ändern sih ei einer Zuordnung die eiden Größen im gleihen Verhältnis, so spriht mn von einer direkten Proportionlität.
Gymso 1 Grundwissen Mthemtik 8.Klsse Gymnsium SOB 1.Funktionle Zusmmenhänge 1.1.Proportionlität Ändern sih ei einer Zuordnung die eiden Größen im gleihen Verhältnis, so spriht mn von einer direkten Proportionlität.
Integralrechnung. www.mathe-total.de. Aufgabe 1
 Integrlrechnung Aufgbe Bestimme die Fläche zwischen der Kurve der Funktion f() = und -Achse über dem Intervll I = [; 3] näherungsweise. Bestimme die Obersumme und Teile ds Intervll I in drei gleich große
Integrlrechnung Aufgbe Bestimme die Fläche zwischen der Kurve der Funktion f() = und -Achse über dem Intervll I = [; 3] näherungsweise. Bestimme die Obersumme und Teile ds Intervll I in drei gleich große
Dr. Günter Rothmeier Kein Anspruch auf Vollständigkeit Elementarmathematik (LH) und Fehlerfreiheit
 WS 008/09 7 Elementrmthemtik (LH) und Fehlerfreiheit. Zhlenbereiche... Die rtionlen Zhlen... Definition Die Definition der rtionlen Zhlen erfolgt hier innermthemtisch ebenflls wie diejenige der gnzen Zhlen
WS 008/09 7 Elementrmthemtik (LH) und Fehlerfreiheit. Zhlenbereiche... Die rtionlen Zhlen... Definition Die Definition der rtionlen Zhlen erfolgt hier innermthemtisch ebenflls wie diejenige der gnzen Zhlen
Dr. Günter Rothmeier Kein Anspruch auf Vollständigkeit Elementarmathematik (LH) und Fehlerfreiheit
 Nturwissenschftliche Fkultät I Didktik der Mthemtik Privte Vorlesungsufzeichnungen Kein Anspruch uf Vollständigkeit 5 7 Elementrmthemtik (LH) und Fehlerfreiheit. Zhlenereiche.4 Die Reellen Zhlen.4.. Definition
Nturwissenschftliche Fkultät I Didktik der Mthemtik Privte Vorlesungsufzeichnungen Kein Anspruch uf Vollständigkeit 5 7 Elementrmthemtik (LH) und Fehlerfreiheit. Zhlenereiche.4 Die Reellen Zhlen.4.. Definition
Die Brückenlappentechnik zum sicheren Verschluss von Nasenseptumdefekten
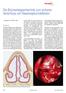 Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
a) Potenzieren ausgesprochen als Beispiel a b = c a = Basis a hoch b = c 4 3 = 64 b = Exponent c = Potenzwert
 8. Potenzen 8. Einführung in Potenzen / Wurzeln / Logrithmen Neen den klssischen Grundrechenopertionen git es weitere Opertionen, welche Beziehungen zwischen Zhlen schffen: Potenzieren Rdizieren Wurzelziehen)
8. Potenzen 8. Einführung in Potenzen / Wurzeln / Logrithmen Neen den klssischen Grundrechenopertionen git es weitere Opertionen, welche Beziehungen zwischen Zhlen schffen: Potenzieren Rdizieren Wurzelziehen)
Teilbarkeitsregeln. 6.1 Grundwissen Mathematik Algebra Klasse 6. Teilbarkeit durch 2: Eine Zahl ist durch 2 teilbar, wenn die Endziffer gerade ist.
 6.1 Grundwissen Mthemtik Algebr Klsse 6 Teilbrkeitsregeln Definition und Regeln Teilbrkeit durch 2: Eine Zhl ist durch 2 teilbr, wenn die Endziffer gerde ist. Teilbrkeit durch 3: Eine Zhl ist durch 3 teilbr,
6.1 Grundwissen Mthemtik Algebr Klsse 6 Teilbrkeitsregeln Definition und Regeln Teilbrkeit durch 2: Eine Zhl ist durch 2 teilbr, wenn die Endziffer gerde ist. Teilbrkeit durch 3: Eine Zhl ist durch 3 teilbr,
1. Rechensteine und der Pythagoräische Lehrsatz.
 1. Rechensteine und der Pythgoräische Lehrstz. Der Beginn der wissenschftlichen Mthemtik fällt mit dem Beginn der Philosophie zusmmen. Er knn uf die Pythgoräer zurückdtiert werden. Die Pythgoräer wren
1. Rechensteine und der Pythgoräische Lehrstz. Der Beginn der wissenschftlichen Mthemtik fällt mit dem Beginn der Philosophie zusmmen. Er knn uf die Pythgoräer zurückdtiert werden. Die Pythgoräer wren
8 Integralrechnung. 8.1 Das Riemann-Integral
 8 Integrlrechnung Der Integrlbegriff ist wie der Ableitungsbegriff motiviert durch die physiklische Beschreibung von Bewegungsbläufen (Geschwindigkeit, Beschleunigung). Er ist u.. uch von Bedeutung bei
8 Integrlrechnung Der Integrlbegriff ist wie der Ableitungsbegriff motiviert durch die physiklische Beschreibung von Bewegungsbläufen (Geschwindigkeit, Beschleunigung). Er ist u.. uch von Bedeutung bei
Wirtschaftsmathematik 00053: Mathematik für Wirtschaftswissenschaftler I Kurseinheit 2: Lineare Algebra II. Autor: Univ.-Prof. Dr.
 Wirtschftsmthemtik 0005: Mthemtik für Wirtschftswissenschftler I Kurseinheit : Linere Alger II Leseproe Autor: Univ.-Prof. Dr. Wilhelm Rödder 5. Linere Gleichungssysteme und Mtrixgleichungen So verwundert
Wirtschftsmthemtik 0005: Mthemtik für Wirtschftswissenschftler I Kurseinheit : Linere Alger II Leseproe Autor: Univ.-Prof. Dr. Wilhelm Rödder 5. Linere Gleichungssysteme und Mtrixgleichungen So verwundert
Lösung: a) 1093 1100 b) 1093 1090
 OvTG Guting, Grundwissen Mthemtik 5. Klsse 1. Ntürliche Zhlen Dezimlsystem Mn nennt die Zhlen, die mn zum Zählen verwendet, 10963 = 1 10000+ 0 1000+ 9 100+ 6 10 + 3 1 ntürliche Zhlen. Der Stellenwert der
OvTG Guting, Grundwissen Mthemtik 5. Klsse 1. Ntürliche Zhlen Dezimlsystem Mn nennt die Zhlen, die mn zum Zählen verwendet, 10963 = 1 10000+ 0 1000+ 9 100+ 6 10 + 3 1 ntürliche Zhlen. Der Stellenwert der
1. Übungsblatt zur Analysis II
 Fchereich Mthemtik Prof Dr Steffe Roch Nd Sissouo WS 9/ 69 Üugsltt zur Alysis II Gruppeüug Aufge G Bestimme Sie für jede der folgede Fuktioe f : [, ] R ds utere ud oere Itegrl ud etscheide Sie, o die Fuktio
Fchereich Mthemtik Prof Dr Steffe Roch Nd Sissouo WS 9/ 69 Üugsltt zur Alysis II Gruppeüug Aufge G Bestimme Sie für jede der folgede Fuktioe f : [, ] R ds utere ud oere Itegrl ud etscheide Sie, o die Fuktio
$Id: integral.tex,v /05/15 13:14:04 hk Exp $ $Id: uneigentlich.tex,v /05/15 13:21:33 hk Exp $
 Mthemtik für Ingenieure II, SS 9 Freitg 15.5 $Id: integrl.te,v 1.1 9/5/15 13:14:4 hk Ep $ $Id: uneigentlich.te,v 1. 9/5/15 13:1:33 hk Ep $ Integrlrechnung.5 Sonstige Integrtionstechniken Wir kommen nun
Mthemtik für Ingenieure II, SS 9 Freitg 15.5 $Id: integrl.te,v 1.1 9/5/15 13:14:4 hk Ep $ $Id: uneigentlich.te,v 1. 9/5/15 13:1:33 hk Ep $ Integrlrechnung.5 Sonstige Integrtionstechniken Wir kommen nun
Canon Nikon Sony. Deutschland 55 45 25. Österreich 40 35 35. Schweiz 30 30 20. Resteuropa 60 40 30 55 45 25 40 35 35 J 30 30 20 60 40 30
 15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
Übungen zu Wurzeln III
 A.Nenner rtionl mchen: Nenner ist Qudrtwurzel: 5 bc 1.).).).) 5.) 1 15 9 bc.).) 8.) 9.) 10.) 5 5 B.Nenner rtionl mchen: Nenner ist höhere Wurzel: 1 1 9 5 1 1.).).).) 5.).) 5 C.Nenner rtionl mchen: Nenner
A.Nenner rtionl mchen: Nenner ist Qudrtwurzel: 5 bc 1.).).).) 5.) 1 15 9 bc.).) 8.) 9.) 10.) 5 5 B.Nenner rtionl mchen: Nenner ist höhere Wurzel: 1 1 9 5 1 1.).).).) 5.).) 5 C.Nenner rtionl mchen: Nenner
Gebrochenrationale Funktionen (Einführung)
 Gebrochenrtionle Funktionen (Einführung) Ac Eine gebrochenrtionle Funktion R ist von der Form R(x) P(x) und Q(x) gnzrtionle Funktionen n-ten Grdes sind. P(x) Q(x), wobei Im Allgemeinen ht eine gebrochenrtionle
Gebrochenrtionle Funktionen (Einführung) Ac Eine gebrochenrtionle Funktion R ist von der Form R(x) P(x) und Q(x) gnzrtionle Funktionen n-ten Grdes sind. P(x) Q(x), wobei Im Allgemeinen ht eine gebrochenrtionle
Einführung in die Lineare Algebra
 Einführung in die Linere Alger Linere Gleichungssysteme Dieses Kpitels dient zur Motivtion und Vorereitung der systemtischen Drstellung. Wir hen dfür ds wichtigste Prolem der elementren lineren Alger gewählt,
Einführung in die Linere Alger Linere Gleichungssysteme Dieses Kpitels dient zur Motivtion und Vorereitung der systemtischen Drstellung. Wir hen dfür ds wichtigste Prolem der elementren lineren Alger gewählt,
Präfixcodes und der Huffman Algorithmus
 Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
Numerische Integration durch Extrapolation
 Numerische Integrtion durch Extrpoltion Pblo Thiel Romberg-Verfhren Idee: Im Gegenstz zur numerischen Integrtion mit Hilfe der einfchen bzw. zusmmengesetzten Trpez-, Simpson-, 3/8- oder zum Beispiel der
Numerische Integrtion durch Extrpoltion Pblo Thiel Romberg-Verfhren Idee: Im Gegenstz zur numerischen Integrtion mit Hilfe der einfchen bzw. zusmmengesetzten Trpez-, Simpson-, 3/8- oder zum Beispiel der
(Analog nennt man a die und b die des Winkels β.)
 Mthemtik Einführung Ws edeutet ds Wort und mit ws eschäftigt sich die? Eine kleine Wortkunde: tri edeutet 'drei' Beispiel: Trithlon,... gon edeutet 'Winkel'/'Eck' Beispiel: Pentgon ds Fünfeck mit 5 Winkeln
Mthemtik Einführung Ws edeutet ds Wort und mit ws eschäftigt sich die? Eine kleine Wortkunde: tri edeutet 'drei' Beispiel: Trithlon,... gon edeutet 'Winkel'/'Eck' Beispiel: Pentgon ds Fünfeck mit 5 Winkeln
1KOhm + - y = x LED leuchtet wenn Schalter x gedrückt ist
 . Ohm = LED leuchtet wenn chlter gedrückt ist 2. Ohm = NICH ( = NO ) LED leuchtet wenn chlter nicht gedrückt ist = ist die Negtion von? Gibt es so einen kleinen chlter (Mikrotster)? 2. Ohm = UND LED leuchtet
. Ohm = LED leuchtet wenn chlter gedrückt ist 2. Ohm = NICH ( = NO ) LED leuchtet wenn chlter nicht gedrückt ist = ist die Negtion von? Gibt es so einen kleinen chlter (Mikrotster)? 2. Ohm = UND LED leuchtet
Mathematik PM Rechenarten
 Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
3 Module in C. 4 Gültigkeit von Namen. 5 Globale Variablen (2) Gültig im gesamten Programm
 3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
Kapitel IV Euklidische Vektorräume. γ b
 Kpitel IV Euklidische Vektorräume 1 Elementrgeometrie in der Eene Sei E die Zeicheneene In der Schule lernt mn: (11) Stz des Pythgors: Sei E ein Dreieck mit den Seiten, und c, und sei γ der c gegenüerliegende
Kpitel IV Euklidische Vektorräume 1 Elementrgeometrie in der Eene Sei E die Zeicheneene In der Schule lernt mn: (11) Stz des Pythgors: Sei E ein Dreieck mit den Seiten, und c, und sei γ der c gegenüerliegende
Bruchterme I. Definitionsmenge eines Bruchterms
 Bruchterme I Definitionsmenge eines Bruchterms Alle zulässigen Einsetzungen in einen Bruchterm ilden die Definitionsmenge D. Einsetzungen, für die der Nenner Null wird, gehören nicht zur Definitionsmenge.
Bruchterme I Definitionsmenge eines Bruchterms Alle zulässigen Einsetzungen in einen Bruchterm ilden die Definitionsmenge D. Einsetzungen, für die der Nenner Null wird, gehören nicht zur Definitionsmenge.
Falls die Werte von X als Ergebnisse eines Zufallsvorgangs resultieren, wird X zu einer stetigen Zufallsvariable.
 Sttistik I für Sttistiker, Mthemtiker und Informtiker Lösungen zu Bltt 11 Gerhrd Tutz, Jn Ulbricht, Jn Gertheiss WS 7/8 Theorie: Stetige Zufllsvriblen Begriff Stetigkeit: Eine Vrible oder ein Merkml X
Sttistik I für Sttistiker, Mthemtiker und Informtiker Lösungen zu Bltt 11 Gerhrd Tutz, Jn Ulbricht, Jn Gertheiss WS 7/8 Theorie: Stetige Zufllsvriblen Begriff Stetigkeit: Eine Vrible oder ein Merkml X
Programmieren in C/C++ und Matlab
 Progrmmieren in C/C und Mtl Sine Schmidt & Sestin Buer Institut für Geowissenschften Christin-Alrechts-Universität zu Kiel Progrmmieren in C/C und Mtl CAU, SS 08 for- / while-schleifen: - numerische Integrlerechnung
Progrmmieren in C/C und Mtl Sine Schmidt & Sestin Buer Institut für Geowissenschften Christin-Alrechts-Universität zu Kiel Progrmmieren in C/C und Mtl CAU, SS 08 for- / while-schleifen: - numerische Integrlerechnung
5 Gleichungen (1. Grades)
 Mthemtik PM Gleichungen (. Grdes) Gleichungen (. Grdes). Einführung Betrchtet mn und (, Q) und vergleicht sie miteinnder, so git es Möglichkeiten:. > ist grösser ls. = ist gleich gross wie. < ist kleiner
Mthemtik PM Gleichungen (. Grdes) Gleichungen (. Grdes). Einführung Betrchtet mn und (, Q) und vergleicht sie miteinnder, so git es Möglichkeiten:. > ist grösser ls. = ist gleich gross wie. < ist kleiner
Mathematik Brückenkurs
 Rumpfskript zur Vorlesung Mthemtik-Brückenkurs /86 Mthemtik Brückenkurs im Fchbereich Informtik & Elektrotechnik Rumpfskript V7 Rumpfskript zur Vorlesung Mthemtik-Brückenkurs /86 Inhltsverzeichnis Mengen...
Rumpfskript zur Vorlesung Mthemtik-Brückenkurs /86 Mthemtik Brückenkurs im Fchbereich Informtik & Elektrotechnik Rumpfskript V7 Rumpfskript zur Vorlesung Mthemtik-Brückenkurs /86 Inhltsverzeichnis Mengen...
Klausur TheGI 2 Automaten und Komplexität (Niedermeier/Hartung/Nichterlein, Sommersemester 2013)
 Berlin, 17.07.2013 Nme:... Mtr.-Nr.:... Klusur TheGI 2 Automten und Komplexität (Niedermeier/Hrtung/Nichterlein, Sommersemester 2013) 1 2 3 4 5 6 7 8 Σ Bereitungszeit: mx. Punktezhl: 60 min. 60 Punkte
Berlin, 17.07.2013 Nme:... Mtr.-Nr.:... Klusur TheGI 2 Automten und Komplexität (Niedermeier/Hrtung/Nichterlein, Sommersemester 2013) 1 2 3 4 5 6 7 8 Σ Bereitungszeit: mx. Punktezhl: 60 min. 60 Punkte
Mathematik schriftlich
 WS KV Chur Abschlussprüfungen 00 für die Berufsmtur kufmännische Richtung Mthemtik schriftlich LÖSUNGEN Kndidtennummer Nme Vornme Dtum der Prüfung Bewertung mögliche erteilte Punkte Punkte. Aufgbe 0. Aufgbe
WS KV Chur Abschlussprüfungen 00 für die Berufsmtur kufmännische Richtung Mthemtik schriftlich LÖSUNGEN Kndidtennummer Nme Vornme Dtum der Prüfung Bewertung mögliche erteilte Punkte Punkte. Aufgbe 0. Aufgbe
Theoretische Informatik und Logik Übungsblatt 2 (2013S) Lösung
 Theoretische Informtik und Logik Üungsltt 2 (2013S) en Aufge 2.1 Geen Sie jeweils eine kontextfreie Grmmtik n, welche die folgenden Sprchen erzeugt, sowie einen Aleitungsum für ein von Ihnen gewähltes
Theoretische Informtik und Logik Üungsltt 2 (2013S) en Aufge 2.1 Geen Sie jeweils eine kontextfreie Grmmtik n, welche die folgenden Sprchen erzeugt, sowie einen Aleitungsum für ein von Ihnen gewähltes
Franz Binder. Vorlesung im 2006W
 Formle Reguläre und Formle Institut für Alger Johnnes Kepler Universität Linz Vorlesung im 2006W http://www.lger.uni-linz.c.t/students/win/ml Formle Inhlt Reguläre Reguläre Formle Zustndsdigrmm δ: Σ (Q
Formle Reguläre und Formle Institut für Alger Johnnes Kepler Universität Linz Vorlesung im 2006W http://www.lger.uni-linz.c.t/students/win/ml Formle Inhlt Reguläre Reguläre Formle Zustndsdigrmm δ: Σ (Q
