i=1 j=1 Die Zeitentwicklung dieses generalisierten Impulses wird durch die Euler Lagrange-Gleichung dl i dt = I ij ϕ j = L
|
|
|
- Heinz Meyer
- vor 6 Jahren
- Abrufe
Transkript
1 86 Lgrnge-Formlismus: Anwendungen IV.. b Bewegungsgleichungen Entsprechend den 6 Freiheitsgrden eines strren Körpers wählt mn ls verllgemeinerte Koordinten für die Beschreibung seiner Bewegung einerseits die 3 krtesischen Koordinten X i des Ortsvektors X eines bestimmten Punkts des Körpers und ndererseits drei Winkel ϕ i ; die letzteren beschreiben Drehungen des strren Körpers um drei zueinnder senkrechte x i -Achsen, die reltiv zum Körper fest bleiben. Die zugehörigen verllgemeinerten Geschwindigkeiten sind Ẋi und ϕ i : die drei ϕ i sind die krtesischen Komponenten der Winkelgeschwindigkeit ω = ϕ des Körpers. Die Stndrd-Lgrnge-Funktion des strren Körpers lutet dnn L ( {X i }, {ϕ i }, {Ẋi }, { ϕ i } ) = M 3 (Ẋi ) ϕ i I ij ϕ j V ( {X i }, {ϕ i } ), (IV.4) i=1 mit einem Potentil V. Dbei sind die I ij die Komponenten des Trägheitstensors bezüglich der körperfesten Drehchsen, die den drei Winkeln ϕ i entsprechen. Ausgehend von dieser Lgrnge- Funktion liefern die Euler Lgrnge-Gleichungen (III.1) die Bewegungsgleichungen des strren Körpers. Trnsltionsbewegung des strren Körpers Betrchten wir zuerst die Bewegungsgleichung für die Koordinten X i. Lut der Definition (III.13) ist der zu X i knonisch konjugierte Impuls durch i,j=1 p i L = MẊi (IV.5) Ẋi gegeben. Dies ist offensichtlich die i-te krtesische Komponente des Gesmtimpulses p = M X des strren Körpers. Dnn lutet die dmit ssoziierte Euler Lgrnge-Gleichung dp i dt = MẌi = L X i = V X i. (IV.5b) Auf der rechten Seite ist V/ X i die i-te Komponente der Gesmtkrft uf den strren Körper. Flls X(t) die Position im Inertilsystem B I des Schwerpunkts des Körpers ist, entspricht Gl. (IV.5b) dem üblichen Schwerpunktstz (II.1) für ein Mehrteilchensystem. Rottionsbewegung des strren Körpers Benutzt mn die uf Gl. (IV.) offensichtlich Symmetrie I ij = I ji für jedes mögliches Pr (i, j), so findet mn für den zu ϕ i knonisch konjugierten verllgemeinerten Impuls L i = L 3 ϕ i = I ij ϕ j. (IV.6) Dies ist die i-te krtesische Komponente des Eigendrehimpulses des strren Körpers um den Nullpunkt von B. Die Zeitentwicklung dieses generlisierten Impulses wird durch die Euler Lgrnge-Gleichung dl i dt = 3 j=1 j=1 I ij ϕ j = L ϕ i = V ϕ i (IV.6b) gegeben, wobei die verllgemeinerte Krft uf der rechten Seite der Gleichung ds Drehmoment ist. Beispiel: Homogener dünner Stb ls physiklisches Pendel Sei ein homogener unendlich dünner Stb mit Länge l und linerer Mssendichte (d.h. Msse pro Längeneinheit) µ. Dementsprechend ist seine Gesmtmsse M = µl. Ein Endpunkt des Stbs ist m Nullpunkt des Koordintensystems eines rumfesten Inertilsystems ufgehängt. Der Stb knn sich in der (Y, Z)-Ebene, d.h. um die X-Achse, unter dem
2 IV. Strre Körper 87 Einfluss des Schwerefeldes g e Z drehen. Somit bildet der Stb ein ebenes Pendel. (37) Als körperfestes Koordintensystem wird ein System mit dem Nullpunkt O im Aufhängepunkt, mit der x-achse prllel zur X-Achse des Z rumfesten Systems und der y-achse entlng des Stbs. Somit streckt O sich der Stb von y = bis y = l. Für dieses eindimensionle System z knn mn dnn für eine beliebige Funktion f der Position θ l y l ρ( r)f( r) d 3 r = µ(y)f(x=, y, z =) dy V schreiben; mit f 1 ergibt sich z.b. die Gesmtmsse M = µl. Y Abbildung IV. Wer nicht mit einer lineren Mssendichte µ(y), sondern mit der üblichen Mssendichte (pro Volumeneinheit) ρ( r) rbeiten möchte, knn einfch ρ( r) = µ(y) δ(x)δ(z) betrchten: mit dieser Mssendichte ergibt sich genu die obige Gleichung. Sei θ der Ablenkwinkel des Stbs us der Lotrichtung. D θ einer Drehung um die x-achse entspricht, gilt in der Sprche der Gl. (IV.4) (IV.6) (d.h. mit x = x 1 ) θ = ϕ 1. Dnn ist ϕ 1 = θ: um eine Bewegungsgleichung für θ zu erhlten, sollte mn Gl. (IV.6b) mit i = 1 benutzen. D wir nur eine Rottionsbewegung um die x-achse betrchten wollen, ist die Winkelgeschwindigkeit ω = θ e X, d.h. mit nur einer ϕ 1 -Komponente: ϕ = ϕ 3 =. Dementsprechend ist nur die Komponente I 11 des Trägheitstensors um den Punkt O nötig, um Gl. (IV.6b) für i = 1 zu schreiben: Aus Gl. (IV.b) folgt dnn I 11 = dl 1 dt l = 3 I 1j ϕ j = I 11 θ. j=1 µ(y)y dy = µl3 3 = Ml 3, wobei wir benutzt hben, dss r δ 11 (x) für x = z = einfch gleich y ist. Betrchten wir jetzt ds Potentil des Stbs im Schwerefeld. Für ein Mssenelement µ dy im Abstnd y vom Aufhängepunkt, entsprechend einer Höhe Z = y cos θ (vgl. Abb. IV.) ist es V = (µ dy)gz = µg cos θ y dy. Die potentielle Energie des gnzen Stbs ist dnn V = l ( µg cos θ)y dy = µg l l cos θ cos θ = Mg. Dbei erkennt mn, dss l cos θ/ die Höhe des Schwerpunkts des Stbs ist: lles pssiert, ls ob die gnze Msse in diesem Schwerpunkt konzentriert wäre. Schließlich ist die Bewegungsgleichung (IV.6b) für θ I 11 θ = Ml 3 = V θ = Mg l sin θ 3g θ = sin θ. l Diese Gleichung ist mthemtisch ähnlich der Gl. (III.5) für ds mthemtische Pendel und wird ähnlich gelöst IV.. c Trägheitstensor Um zu zeigen, dss die I ij die (krtesischen) Komponenten eines Tensors bilden, soll mn ihr Verhlten unter Drehungen untersuchen. (38) Sei R eine Drehmtrix. Unter ihrer Wirkung trnsformieren sich die Komponenten eines Ortsvektors bezüglich B gemäß x i x i = R i ix i. (37) Im Gegenstz zum mthemtischen Pendel des III..4 mit msselosem Stb und Punktmsse m Ende wird dieses System mit mssebehftetem Stb physiklisches Pendel gennnt. (38) Einige Definitionen und Ergebnisse über Tensoren werden im Anhng A drgestellt.
3 88 Lgrnge-Formlismus: Anwendungen Dementsprechend trnsformiert sich ds Produkt x i x j in x i x j = R j j Ri i xi x j. Andererseits gilt R i i R j j δij = R i i δ ij (R T ) j j = R i i (R T ) j i = δ i j, wobei R T die zu R trnsponierte Mtrix bezeichnet, die gleichzeitig die inverse Drehmtrix R 1 ist, wie in der letzten Gleichung benutzt wurde. Somit trnsformieren sich beide Terme mit Indizes in der Definition (IV.) der I ij gleich unter Drehungen, und zwr derrt, dss I ij sich insgesmt gemäß I ij I i j = R i i R j j Iij = R i i(r T ) j j Iij (IV.7) trnsformiert, d.h. wie die Komponenten eines Tensors zweiter Stufe. In tensorieller Form lutet der Trägheitstensor I = [ m ( x ) g 1 ] x x flls der strrer Körper us diskreten Mssenpunkten besteht, oder I = ρ( r) [ r g 1 r r ] (IV.8) (IV.8b) für einen kontinuierlichen Körper. In diesen Formeln bezeichnet ds Tensorprodukt (vgl. A.1.3 b A.1.3 c), während g 1 der inverse metrische Tensor (vgl. A.1.4) ist, dessen Komponenten in einer krtesischen Bsis g ij = δ ij sind. Identifiziert mn den Tensor I mit einer 3 3-Mtrix mit Elementen I ij, die ebenflls mit I bezeichnet wird, so knn die letzte Gleichung noch in Mtrixform ls I I = R I R T (IV.9) geschrieben werden. Gleichermßen gilt für die Rottionsenergie in Gl. (IV.3) T Rot. = 1 ωi (t)i ij ω j (t) = 1 ω(t)t I ω(t) (IV.3) mit dem zu ω(t) trnsponierten Zeilenvektor ω(t) T. Für den Eigendrehimpuls (IV.6) gilt L = I ω. (IV.31) Entsprechend der tensoriellen Ntur von I können Rottionsenergie und Drehimpuls noch in geometrischer Form geschrieben werden: T Rot. = 1 ω(t) I ω(t), L = I ω wobei die Kontrktion zweier Tensoren bezeichnet. Trägheitsmoment Sei e der Einheitsvektor entlng einer beliebigen Richtung in R 3. Ds Trägheitsmoment des strren Körpers bezüglich der (Dreh)Achse prllel zu dieser Richtung, die durch den Ursprungspunkt des körperfesten Bezugssystem geht, wird durch I = e i I ij e j = e T I e = e I e (IV.3) definiert, wobei {e i } i=1,,3 die Koordinten von e bezeichnen. Beispielsweise ist ds relevnte Trägheitsmoment für eine Rottionsbewegung um eine Achse in Richtung des Bsisvektors e 3 einfch die Komponente I 33 = e T 3 I e 3. Dbei gilt I 33 = [ ( x ) ] δ m 33 x 3 x 3 = [ (x ) 1 ( ) ] m + x
4 IV. Strre Körper 89 d.h. unter Einführung der Projektion x, von x uf der (x 1, x )-Ebene orthogonl zur Drehchse I 33 = m ( x, ). (IV.33) Dbei ist ( x, ) ds Qudrt des Abstnds des Mssenpunkts von der Drehchse. Im Kontinuumlimes wird dieses Trägheitsmoment zu I 33 = ρ( r) r d3 r. (IV.33b) Für eine Rottionsbewegung mit Winkelgeschwindigkeit ω = ω e 3 um diese Richtung ist die Rottionsenergie T Rot. = 1 I33 ω. D I 33 utomtisch positiv ist, gilt ds uch für diese kinetische Energie. Beispiel: homogener Zylinder Sei ein homogener Vollzylinder mit Mssendichte ρ, Rdius R und x 3 Höhe h. Dementsprechend ist seine Gesmtmsse M = πr hρ. Der Zylinder dreht sich um seine eigene Achse, welche die Richtung x 3 definiert. h In Zylinderkoordinten (r, θ, z x 3 ) ist der Abstnd eines Punkts von der Drehchse genu gleich der Rdilkoordinte r. Somit lutet R ds durch Gl. (IV.33b) gegebene Trägheitsmoment des Zylinders um Abbildung IV.3 diese Achse h [ π ( R ) ] I 33 = ρ r r dr dθ dz = ρ πr4 h = MR. (IV.34) Ds letztere Ergebnis ist unbhängig von der Höhe h (genuer ist diese versteckt in der Gesmtmsse), so dss es uch im Grenzfll einer unendlich dünnen Scheibe h gilt. Eigenschften des Trägheitstensors Wie schon erwähnt wurde ist der Trägheitstensor ein symmetrischer Tensor, d.h. I ij = I ji für lle i, j = 1,, 3. Dies bedeutet zuerst, dss nur 6 seiner Komponenten unbhängig voneinnder sind. Ähnlich einer symmetrischen reellen Mtrix besitzt ein symmetrischer reeller Tensor zweiter Stufe nur reelle Eigenwerte und ist orthogonl digonlisierbr. Ds heißt, mn knn eine Orthonormlbsis { e 1, e, e 3} finden, in welcher der Tensor, oder genuer seine Mtrixdrstellung, die Digonlform I 1 I = I (IV.35) I 3 nnimmt, mit den reellen Eigenwerten I 1, I, I 3 der Mtrix, die wie oben schon bemerkt lle positiv sind. Diese Eigenwerte werden Huptträgheitsmomente des strren Körpers gennnt, während die zugehörigen Eigenvektoren { eī}ī= 1,, 3 Einheitsvektoren entlng der Huptträgheitschsen sind. Im Huptchsensystem d.h. im Koordintensystem, dessen Achsen die Huptträgheitschsen des strren Körpers sind nimmt die Rottionsenergie des Körpers die einfche Form T Rot. = 1 ( [I ) ( ) ( ) ] 1 ω 1 + I ω + I3 ω 3 n. Bemerkung: Genu wie der Trägheitstensor selber hängen seine Huptträgheitselemente von der Whl des Bezugspunkts O b. Die folgende Eigenschft bezieht sich uf den Fll, wo der Bezugspunkt im Schwerpunkt des strren Körpers ist.
5 9 Lgrnge-Formlismus: Anwendungen Besitzt ein strrer Körper Symmetrien, wie z.b. Invrinz unter der Spiegelung bezüglich einer Ebene oder Rottionssymmetrie, so sind die entsprechenden Symmetrieelemente, insbesondere Symmetriechsen, einfch mit den Huptträgheitschsen reltiv zum Körperschwerpunkt verknüpft. Um dieses Ergebnis zu illustrieren, betrchten wir die nichtdigonle Elemente des Trägheitstensors, z.b. I 1. Die Definition (IV.b) gibt I 1 = ρ( r) ( r δ 1 x 1 x ) d 3 r = ρ(x 1, x, x 3 )( x 1 x ) dx 1 dx dx 3 = 1 ρ(x 1, x, x 3 )( x 1 x x 1 x ) dx 1 dx dx 3. Wie unter Gl. (IV.b) schon diskutiert wurde, knn der Integrtionsbereich mit einer geeigneten Definition von ρ uf R 3 erweitert werden, ws wir hier nnehmen. Führt mn die Substitution x 1 u x 1 für den zweiten Summnden in den Klmmern, so ergibt sich I 1 = 1 [ ] [ρ(x 1, x, x 3 )x 1 x dx 1 dx dx 3 ρ( u, x, x 3 )( u)x du dx dx 3 = 1 [ ρ(x 1, x, x 3 ) + ρ( x 1, x, x 3 ) ] x 1 x dx 1 dx dx 3, wobei in der zweiten Zeile die Integrtionsvrible u des zweiten Terms in x 1 umbennnt wurde. Flls der strre Körper symmetrisch unter Spiegelungen bezüglich der Ebene x 1 = ist, so dss ρ( x 1, x, x 3 ) = ρ(x 1, x, x 3 ) für lle Werte von x, x 3, dnn ist I 1 =. Allgemeiner findet mn, dss die Symmetriechsen des strren Körpers, flls einige vorhnden sind, uch seine Huptträgheitschsen sind. Klssifiktion von Trägheitstensoren Je nch den Werten der Huptträgheitsmomente lssen sich drei verschiedene Fälle unterscheiden: Für I 1 I I 3 I 1 sind die Eigenvektoren { e 1, e, e 3} und somit die Huptträgheitschsen eindeutig (39) definiert. Dnn spricht mn von einem unsymmetrischen Kreisel. Ein einfches Beispiel dvon ist ein homogener Quder, dessen Knten unterschiedliche Längen b c hben: die Symmetriechsen des Quders sind seine Huptträgheitschsen (reltiv zum Schwerpunkt), die zugehörigen Trägheitsmomente sind unterschiedlich. Für I 1 = I I 3 ist der Eigenvektor e 3 bzw. die entsprechende Huptchse eindeutig definiert. Dgegen gibt es Entrtung in der (x 1, x )-Ebene, in welcher jedes Pr von orthogonlen Achsen ls Huptträgheitschsen betrchtet werden knn. Dies entspricht dem Modell des symmetrischen Kreisels. Beispiele sind ein eindimensionler Stb prllel zur x 3 -Achse: x 1 = x = geben sofort I 33 = und I 11 = I ; oder ein homogener Zylinder (im llgemeinen Fll), insbesondere eine zweidimensionle Scheibe in der Ebene x 3 =, für die mn einfch I 11 = I = 1 I33 nchprüft. Für I 1 = I = I 3 sind die Achsen jedes Koordintensystems Huptträgheitschsen, entsprechend einem Kugelkreisel. Dies ist z.b. der trivile Fll des Trägheitstensors einer homogenen Kugel um drei Achsen, die durch ihren Schwerpunkt verläuft. Flls der Rdius der Kugel verschwindet, d.h. die Kugel wird zu einem Punkt, ist I = : somit verschwinden der Eigendrehimpuls und die Rottionsenergie eines Mssenpunkts, wie bisher stillschweigend ngenommen wurde! (39)... bis uf ein Minus Zeichen für die Einheitseigenvektoren.
6 IV. Strre Körper 91 Offensichtlich sind die drei (Hupt)Trägheitsmomente eines homogenen Würfels um seine drei Symmetriechsen lle gleich, d.h. der Mtrixdrstellung des Trägheitstensors I ist in der zugehörigen Bsis proportionl zur Einheitsmtrix. Dnn gilt dies noch in jeder beliebigen Bsis, so dss die Momente um jedes Triplett von Achsen, die durch seinen Schwerpunkt gehen, sind lle gleich. Während die Unbhängigkeit des Trägheitsmoments von der Richtung einer durch den Schwerpunkt durchlufenden Drehchse intuitiv im Fll der Kugel ist, wirkt sie bei dem Würfel überrschend. Dbei ist unsere (4) Intuition flsch, denn wir stellen uns die gnzen Mssenverteilungen ρ( r) vor die offensichtlich unterschiedlich für eine Kugel und einen Würfel sind, während ds Trägheitsmoment bzw. der Trägheitstensor nur einem sehr geringen Anteil der in dieser Mssenverteilungen enthltenen Informtion entspricht. Für die Rottionsbewegung der Körper reicht ber diese Informtion us. Steinerscher Stz Trägheitsmomente um die Symmetriechsen eines strren Körpers d.h. entsprechend dem Fll, wo der Ursprungspunkt des Koordintensystems in der Definition (IV.) im Schwerpunkt des Körpers liegt sind oft unter Betrchtung der betreffenden Symmetrie einfcher zu berechnen. Oft dreht sich der strre Körper ber um eine Achse, die nicht durch seinen Schwerpunkt durchläuft. Ansttt ds Trägheitsmoment um die verschobene Drehchse explizit us Definition (IV.) zu berechnen, ist es dnn schneller, ds folgende Resultt zu benutzen. Theorem (Stz von Steiner (o) ): Ds Trägheitsmoment eines strren Körpers mit Msse M um eine beliebige Achse im Abstnd L von seinem Schwerpunkt ist gegeben durch die Summe us ML und dem Trägheitsmoment des Körpers um die prllele Drehchse, die durch den Schwerpunkt geht. (IV.36) Bezeichnet mn mit I bzw. I ds Drehmoment um eine durch den Schwerpunkt durchlufende Drehchse bzw. um eine dzu prllele Achse im Abstnd L vom Schwerpunkt, so lutet der Steiner sche Stz I = I + ML. (IV.36b) Zum Beweis dieses Stzes betrchte mn neben dem körperfesten Bezugssystem B mit Ursprung im Schwerpunkt des strren Körpers ein zweites körperfestes Bezugssystem B, dessen Nullpunkt um b reltiv zu B verschoben ist, während die Koordintenchsen von B prllel zu denen von B bleiben. Dnn gilt für die Position jedes (Mssen)Punkts (41) des strren Körpers reltiv zu beiden Bezugssystemen x = x b. Dies gibt für den Trägheitstensor reltiv zu B I ij = [ ( x ) ] δ m ij x i x j = [ ( x m b ) ] δ ij (x i b i )(x j b j ) = I ij δ ij b m x + b i m x j + b j m x i + ( m b δ ij b i b j). Dbei verschwinden der zweite, der dritte und der vierte Beiträge der zweiten Zeile, während die Summe der Mssen im fünften Term durch die Gesmtmsse ersetzt werden knn. Somit ergibt sich die tensorielle Form des Steinerschen Stzes: I ij = I ij + M ( b δ ij b i b j). (IV.36c) (4)... oder zumindest die des Autors! (41) Hier wird der Beweis für ein System us diskreten Mssenpunkten drgelegt. Die Leserin knn prüfen, dss sich der Beweis ohne Schwierigkeit uf den Fll eines kontinuierlichen Systems übersetzen lässt. (o) J. Steiner,
7 9 Lgrnge-Formlismus: Anwendungen Um ds Drehmoment um eine gegebene Achse zu erhlten, multipliziert mn diese Gleichung mit den Komponenten des Einheitsvektors in Richtung der Achse, vgl. Gl. (IV.3), worus sich Gl. (IV.36b) ergibt. Beispiel: homogener Zylinder () Wir betrchten nochmls den homogenen Vollzylinder (Msse M, Rdius R) der Abb. (IV.3), der sich jetzt um eine Achse drehen soll, die prllel zu seiner Symmetriechse ist, um den Abstnd L ber verschoben ist. Dnn ist gemäß dem Steinerschen Stz (IV.36) ds Trägheitsmoment des Zylinders um diese Achse I 33 = I 33 + ML = MR + ML, h x 3 L x 3 R Abbildung IV.4 wobei der Ausdruck (IV.34) des Trägheitsmoments um die Symmetriechse benutzt wurde.
Rollender Zylinder in Zylinder
 Übungen zu Theoretische Physik I - echnik im Sommersemester 013 Bltt 10 vom 1.07.13 Abgbe: 08.07. Aufgbe 43 Rollender Zylinder in Zylinder Ein homogener Zylinder (Gesmtmsse, Rdius, Trägheitsmoment bzgl.
Übungen zu Theoretische Physik I - echnik im Sommersemester 013 Bltt 10 vom 1.07.13 Abgbe: 08.07. Aufgbe 43 Rollender Zylinder in Zylinder Ein homogener Zylinder (Gesmtmsse, Rdius, Trägheitsmoment bzgl.
Blatt 9. Bewegung starrer Körper- Lösungsvorschlag
 Fkultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhnov Übungen zu Klssischer Mechnik (T) im SoSe 0 Bltt 9. Bewegung strrer Körper- Lösungsvorschlg Aufgbe 9.. Trägheitstensor
Fkultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhnov Übungen zu Klssischer Mechnik (T) im SoSe 0 Bltt 9. Bewegung strrer Körper- Lösungsvorschlg Aufgbe 9.. Trägheitstensor
Brückenkurs Lineare Gleichungssysteme und Vektoren
 Brückenkurs Linere Gleichungssysteme und Vektoren Dr Alessndro Cobbe 30 September 06 Linere Gleichungssyteme Ws ist eine linere Gleichung? Es ist eine lgebrische Gleichung, in der lle Vriblen nur mit dem
Brückenkurs Linere Gleichungssysteme und Vektoren Dr Alessndro Cobbe 30 September 06 Linere Gleichungssyteme Ws ist eine linere Gleichung? Es ist eine lgebrische Gleichung, in der lle Vriblen nur mit dem
Vektoren. Definition. Der Betrag eines Vektors. Spezielle Vektoren
 Vektoren In nderen Bereichen der Nturwissenschften treten Größen uf, die nicht nur durch eine Zhlenngbe drgestellt werden können, wie Krft, die Geschwindigkeit. Zur vollständigen Beschreibung z.b. der
Vektoren In nderen Bereichen der Nturwissenschften treten Größen uf, die nicht nur durch eine Zhlenngbe drgestellt werden können, wie Krft, die Geschwindigkeit. Zur vollständigen Beschreibung z.b. der
8 Längenberechnungen Winkelberechnungen - Skalarprodukt
 8 Längenberechnungen Winkelberechnungen - Sklrprodukt 8 Längenberechnungen Winkelberechnungen - Sklrprodukt Wir wissen, wie mn zwei Vektoren und b ddiert b b. Mn knn zwei Vektoren ber uch miteinnder multiplizieren!
8 Längenberechnungen Winkelberechnungen - Sklrprodukt 8 Längenberechnungen Winkelberechnungen - Sklrprodukt Wir wissen, wie mn zwei Vektoren und b ddiert b b. Mn knn zwei Vektoren ber uch miteinnder multiplizieren!
10.3 Statische Momente, Schwerpunkte und Trägheitsmomente
 1.3 Sttische Momente, Schwerpunkte und Trägheitsmomente Sttisches Moment M g eines Mssenpunktes P (der Msse m) bezüglich einer Gerden g: M g := ml Msse Hebelrm l Abstnd von P zu g g 9 P l Bei n Mssenpunkten
1.3 Sttische Momente, Schwerpunkte und Trägheitsmomente Sttisches Moment M g eines Mssenpunktes P (der Msse m) bezüglich einer Gerden g: M g := ml Msse Hebelrm l Abstnd von P zu g g 9 P l Bei n Mssenpunkten
f : G R ϕ n 1 (x 1,...,x n 1 ) Das ist zwar die allgemeine Form, aber es ist nützlich sie sich für den R 2 und R 3 explizit anzuschauen.
 Trnsformtionsstz von Sebstin üller Integrtion über Normlgebiete Allgemein knn mn im R n ein Normlgebiet wie folgt definieren: G : { R n 1 b, ϕ 1 ( 1 ) ψ 1 ( 1 ), ϕ ( 1, ) 3 ψ ( 1, ),... ϕ n 1 ( 1,...,
Trnsformtionsstz von Sebstin üller Integrtion über Normlgebiete Allgemein knn mn im R n ein Normlgebiet wie folgt definieren: G : { R n 1 b, ϕ 1 ( 1 ) ψ 1 ( 1 ), ϕ ( 1, ) 3 ψ ( 1, ),... ϕ n 1 ( 1,...,
Algebra - Lineare Abbildungen
 Algebr - Linere Abbildungen oger Burkhrdt (roger.burkhrdt@fhnw.ch) 8 Hochschule für Technik . Der Vektorrum Hochschule für Technik Hochschule für Technik 4 Vektorrum Definition: Ein Vektorrum über einen
Algebr - Linere Abbildungen oger Burkhrdt (roger.burkhrdt@fhnw.ch) 8 Hochschule für Technik . Der Vektorrum Hochschule für Technik Hochschule für Technik 4 Vektorrum Definition: Ein Vektorrum über einen
Ungleichungen. Jan Pöschko. 28. Mai Einführung
 Ungleichungen Jn Pöschko 8. Mi 009 Inhltsverzeichnis Einführung. Ws sind Ungleichungen?................................. Äquivlenzumformungen..................................3 Rechnen mit Ungleichungen...............................
Ungleichungen Jn Pöschko 8. Mi 009 Inhltsverzeichnis Einführung. Ws sind Ungleichungen?................................. Äquivlenzumformungen..................................3 Rechnen mit Ungleichungen...............................
Theoretische Mechanik - Übungen 10 WS 2016/17
 Prof. Dr. A. Ms Institut für Physik N A W I G R A Z Theoretische Mechnik - Übungen 1 WS 16/17 Aufgbe P: Poissonklmmern Präsenzufgben 15. Dezember 16 ) Betrchten Sie zwei Erhltungsgrößen A und B, d. h.
Prof. Dr. A. Ms Institut für Physik N A W I G R A Z Theoretische Mechnik - Übungen 1 WS 16/17 Aufgbe P: Poissonklmmern Präsenzufgben 15. Dezember 16 ) Betrchten Sie zwei Erhltungsgrößen A und B, d. h.
G2 Grundlagen der Vektorrechnung
 G Grundlgen der Vektorrechnung G Grundlgen der Vektorrechnung G. Die Vektorräume R und R Vektoren Beispiel: Physiklische Größen wie Krft und Geschwindigkeit werden nicht nur durch ihre Mßzhl und ihre Einheit,
G Grundlgen der Vektorrechnung G Grundlgen der Vektorrechnung G. Die Vektorräume R und R Vektoren Beispiel: Physiklische Größen wie Krft und Geschwindigkeit werden nicht nur durch ihre Mßzhl und ihre Einheit,
Kapitel IV Euklidische Vektorräume. γ b
 Kpitel IV Euklidische Vektorräume 1 Elementrgeometrie in der Eene Sei E die Zeicheneene In der Schule lernt mn: (11) Stz des Pythgors: Sei E ein Dreieck mit den Seiten, und c, und sei γ der c gegenüerliegende
Kpitel IV Euklidische Vektorräume 1 Elementrgeometrie in der Eene Sei E die Zeicheneene In der Schule lernt mn: (11) Stz des Pythgors: Sei E ein Dreieck mit den Seiten, und c, und sei γ der c gegenüerliegende
11. DER HAUPTSATZ DER DIFFERENTIAL- UND INTEGRALRECHNUNG
 91 Dieses Skript ist ein Auszug mit Lücken us Einführung in die mthemtische Behndlung der Nturwissenschften I von Hns Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie ds Buch uch kufen und
91 Dieses Skript ist ein Auszug mit Lücken us Einführung in die mthemtische Behndlung der Nturwissenschften I von Hns Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie ds Buch uch kufen und
1.2. Orthogonale Basen und Schmistsche Orthogonalisierungsverfahren.
 .. Orthogonle Bsen und Schmistsche Orthogonlisierungsverfhren. Definition.. Eine Bsis B = { b, b,..., b n } heit orthogonl, wenn die Vektoren b i, i =,,..., n, prweise orthogonl sind, d.h. bi b j = fur
.. Orthogonle Bsen und Schmistsche Orthogonlisierungsverfhren. Definition.. Eine Bsis B = { b, b,..., b n } heit orthogonl, wenn die Vektoren b i, i =,,..., n, prweise orthogonl sind, d.h. bi b j = fur
Klassische Theoretische Physik II (Theorie B) Sommersemester 2016
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Klassische Theoretische Physik II (Theorie B) Sommersemester 2016 Prof. Dr. Alexander Mirlin Musterlösung: Blatt 12. PD
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Klassische Theoretische Physik II (Theorie B) Sommersemester 2016 Prof. Dr. Alexander Mirlin Musterlösung: Blatt 12. PD
Notizen zur Vorlesung Analysis 3
 Notizen zur Vorlesung Anlysis 3 Henrik chumcher TUHH, 26. Jnur 207 2 Integrtion über Oberflächen 2. Oberflächenintegrl einer Funktion Definition 2.37 (Metrische Fundmentlform) ei R 2 ein reguläres Gebiet
Notizen zur Vorlesung Anlysis 3 Henrik chumcher TUHH, 26. Jnur 207 2 Integrtion über Oberflächen 2. Oberflächenintegrl einer Funktion Definition 2.37 (Metrische Fundmentlform) ei R 2 ein reguläres Gebiet
10. Riemannsche Geometrie I: Riemannsche Metrik. Variable Bilinearformen.
 10. Riemnnsche Geometrie I: Riemnnsche Metrik Wir können in der hyperbolischen Geometrie noch nicht wirklich messen. Hierfür bruchen wir ein Riemnnsches Längen- und Winkelmß, d.h. eine Riemnnsche Geometrie.
10. Riemnnsche Geometrie I: Riemnnsche Metrik Wir können in der hyperbolischen Geometrie noch nicht wirklich messen. Hierfür bruchen wir ein Riemnnsches Längen- und Winkelmß, d.h. eine Riemnnsche Geometrie.
Beispiele: cos(x) dx = sin(x) + c (1) e t dt = e t + c (2)
 . Stmmfunktion Definition Stmmfunktion: Gegeen sei eine Funktion f(). Gesucht ist eine Funktion F (), so dss d = f(). Die Funktion F() heisst Stmmfunktion. Schreiweise: F () = f()d. Mn spricht uch vom
. Stmmfunktion Definition Stmmfunktion: Gegeen sei eine Funktion f(). Gesucht ist eine Funktion F (), so dss d = f(). Die Funktion F() heisst Stmmfunktion. Schreiweise: F () = f()d. Mn spricht uch vom
π 2 r 2 r 2 sin 2 (t)r cos(t) dt π 2 cos2 (t) cos(t) dt = r 2 π dt = cos(x) sin(x) u v = cos(x) sin(x) + = cos(x) sin(x) + x
 Wir substituieren x x(t) r sin(t), t [ π, π ]. Dnn ist x (t) r cos(t), lso r x dx π π r π r r sin (t)r cos(t) dt π cos (t) cos(t) dt r π π cos (t) dt Wir integrieren cos mittels prtieller Integrtion: Sei
Wir substituieren x x(t) r sin(t), t [ π, π ]. Dnn ist x (t) r cos(t), lso r x dx π π r π r r sin (t)r cos(t) dt π cos (t) cos(t) dt r π π cos (t) dt Wir integrieren cos mittels prtieller Integrtion: Sei
14. INTEGRATION VON VEKTORFUNKTIONEN
 120 Dieses Skript ist ein Auszug mit Lücken us Einführung in die mthemtische Behndlung der Nturwissenschften I von Hns Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie ds Buch uch kufen und
120 Dieses Skript ist ein Auszug mit Lücken us Einführung in die mthemtische Behndlung der Nturwissenschften I von Hns Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie ds Buch uch kufen und
Proseminar über Multimediale Lineare Algebra und Analytische Geometrie
 Studiengng Diplom-Berufspädgogik Unterrichtsfch Mthemtik Proseminr über Multimedile Linere Algebr und Anlytische Geometrie Ausrbeitung einer Sttsexmensufgbe us der Lineren Algebr Aufgbe 5 usgerbeitet von:
Studiengng Diplom-Berufspädgogik Unterrichtsfch Mthemtik Proseminr über Multimedile Linere Algebr und Anlytische Geometrie Ausrbeitung einer Sttsexmensufgbe us der Lineren Algebr Aufgbe 5 usgerbeitet von:
F A = 2F, F B = F, F C = 2F. Dabei verläuft F A entlang der vorderen Flächendiagonalen, F B und F C verlaufen entlang der Kanten.
 Wintersemester / ZÜ. Aufgbe. z C Die Eckpunkte A, B, C eines Würfels (Kntenlänge ) sind die Anfngspunkte der Vektoren F A, F B, F C mit folgenden Beträgen: F C F A F, F B F, F C F. A x F A O B F B y Dbei
Wintersemester / ZÜ. Aufgbe. z C Die Eckpunkte A, B, C eines Würfels (Kntenlänge ) sind die Anfngspunkte der Vektoren F A, F B, F C mit folgenden Beträgen: F C F A F, F B F, F C F. A x F A O B F B y Dbei
- 1 - VB Inhaltsverzeichnis
 - - VB Inhltsverzeichnis Inhltsverzeichnis... Die Inverse einer Mtrix.... Definition der Einheitsmtrix.... Bedingung für die inverse Mtrix.... Berechnung der Inversen Mtrix..... Ds Verfhren nch Guß mit
- - VB Inhltsverzeichnis Inhltsverzeichnis... Die Inverse einer Mtrix.... Definition der Einheitsmtrix.... Bedingung für die inverse Mtrix.... Berechnung der Inversen Mtrix..... Ds Verfhren nch Guß mit
Höhere Mathematik II für die Fachrichtung Informatik. Lösungsvorschläge zum 8. Übungsblatt
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmnn SS Höhere Mthemtik II für die Fchrichtung Informtik Lösungsvorschläge zum 8. Übungsbltt Aufgbe 9 erechnen
KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmnn SS Höhere Mthemtik II für die Fchrichtung Informtik Lösungsvorschläge zum 8. Übungsbltt Aufgbe 9 erechnen
BINOMISCHE FORMELN FRANZ LEMMERMEYER
 BINOMISCHE FORMELN FRANZ LEMMERMEYER Ds Distributivgesetz. Die binomischen Formeln sind im wesentlichen Vrinten des Distributivgesetzes. Dieses kennen wir schon; es besgt, dss () (b + = b + c und ( + b)c
BINOMISCHE FORMELN FRANZ LEMMERMEYER Ds Distributivgesetz. Die binomischen Formeln sind im wesentlichen Vrinten des Distributivgesetzes. Dieses kennen wir schon; es besgt, dss () (b + = b + c und ( + b)c
Thema 7 Konvergenzkriterien (uneigentliche Integrale)
 Them 7 Konvergenzkriterien (uneigentliche Integrle) In diesem Kpitel betrchten wir unendliche Reihen n= n, wobei ( n ) eine Folge von reellen Zhlen ist. Die Reihe konvergiert gegen s (oder s ist die Summe
Them 7 Konvergenzkriterien (uneigentliche Integrle) In diesem Kpitel betrchten wir unendliche Reihen n= n, wobei ( n ) eine Folge von reellen Zhlen ist. Die Reihe konvergiert gegen s (oder s ist die Summe
Einführung in die Vektorrechnung (GK)
 Einführung in die Vektorrechnung (GK) Michel Spielmnn Inhltsverzeichnis Grundlegende Definitionen Geometrische Vernschulichung. Punkte..................................... Pfeile.....................................
Einführung in die Vektorrechnung (GK) Michel Spielmnn Inhltsverzeichnis Grundlegende Definitionen Geometrische Vernschulichung. Punkte..................................... Pfeile.....................................
9.2.3 Durchbiegen eines Balkens ******
 9.2.3 ****** 1 Motivtion Ein einseitig eingespnnter Blken wird m offenen Ende belstet. Die Durchbiegung hängt von der Orientierung und dmit vom Flächenträgheitsmoment des Blkens b. 2 Experiment b b s 1
9.2.3 ****** 1 Motivtion Ein einseitig eingespnnter Blken wird m offenen Ende belstet. Die Durchbiegung hängt von der Orientierung und dmit vom Flächenträgheitsmoment des Blkens b. 2 Experiment b b s 1
Abiturprüfung Mathematik 2013 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1
 www.mthe-ufgben.com Abiturprüfung Mthemtik 013 (Bden-Württemberg) Berufliche Gymnsien Anlysis, Aufgbe 1 1.1 Die Funktion f ist gegeben durch π f( x) = + sin x ; x. Ds Schubild von f ist K. 1.1.1 (8 Punkte)
www.mthe-ufgben.com Abiturprüfung Mthemtik 013 (Bden-Württemberg) Berufliche Gymnsien Anlysis, Aufgbe 1 1.1 Die Funktion f ist gegeben durch π f( x) = + sin x ; x. Ds Schubild von f ist K. 1.1.1 (8 Punkte)
t 1 t cos(t) sin(t) haben als Spur jeweils den Einheitshalbkreis in der oberen Halbebene.
 Kpitel Kurvenintegrle Kurven Sei I = [, b] R ein Intervll Eine Weg ist eine Abbildung dieses Intervlls in den R d, d, : I R d Dbei nennt mn () den Anfngspunkt, (b) den Endpunkt und ds Bild ([, b]) die
Kpitel Kurvenintegrle Kurven Sei I = [, b] R ein Intervll Eine Weg ist eine Abbildung dieses Intervlls in den R d, d, : I R d Dbei nennt mn () den Anfngspunkt, (b) den Endpunkt und ds Bild ([, b]) die
Beispiel 1:Der Runge-Lenz Vektor [2 Punkte]
![Beispiel 1:Der Runge-Lenz Vektor [2 Punkte] Beispiel 1:Der Runge-Lenz Vektor [2 Punkte]](/thumbs/59/43248755.jpg) Übungen Theoretische Physik I (Mechanik) Blatt 9 (Austeilung am: 1.9.11, Abgabe am 8.9.11) Hinweis: Kommentare zu den Aufgaben sollen die Lösungen illustrieren und ein besseres Verständnis ermöglichen.
Übungen Theoretische Physik I (Mechanik) Blatt 9 (Austeilung am: 1.9.11, Abgabe am 8.9.11) Hinweis: Kommentare zu den Aufgaben sollen die Lösungen illustrieren und ein besseres Verständnis ermöglichen.
2.5 Messbare Mengen und Funktionen
 1 2.5 Messbre Mengen und Funktionen Definition Eine beschränkte Menge M R n heißt messbr, flls die chrkteristische Funktion χ M integrierbr ist. Die Zhl vol n (M) := χ M dµ n nennt mn ds Volumen von M.
1 2.5 Messbre Mengen und Funktionen Definition Eine beschränkte Menge M R n heißt messbr, flls die chrkteristische Funktion χ M integrierbr ist. Die Zhl vol n (M) := χ M dµ n nennt mn ds Volumen von M.
1 Koordinatentransformationen
 Technische Universität München Andres Wörfel Ferienkurs Anlysis für Physiker Vorlesung Mittwoch SS 0 Them des heutigen Tges sind zuerst Koordintentrnsformtionen, dnn implizite Funktionen. Diese zwei Kpitel
Technische Universität München Andres Wörfel Ferienkurs Anlysis für Physiker Vorlesung Mittwoch SS 0 Them des heutigen Tges sind zuerst Koordintentrnsformtionen, dnn implizite Funktionen. Diese zwei Kpitel
4.6 Integralrechnung III. Inhaltsverzeichnis
 4.6 Integrlrechnung III Inhltsverzeichnis 1 Integrlrechnung 10.03.2010 Theorie und Übungen 2 1 Exponentilfunktionen Aus der Differentilrechnung wissen wir, dss gilt: f(x)=e x f (x)=e x Stz 1 Für die ntürliche
4.6 Integrlrechnung III Inhltsverzeichnis 1 Integrlrechnung 10.03.2010 Theorie und Übungen 2 1 Exponentilfunktionen Aus der Differentilrechnung wissen wir, dss gilt: f(x)=e x f (x)=e x Stz 1 Für die ntürliche
Lineare DGL zweiter Ordnung
 Universität Duisburg-Essen Essen, 03.06.01 Fkultät für Mthemtik S. Buer C. Hubcsek C. Thiel Linere DGL zweiter Ordnung Betrchten wir ds AWP { x + x + bx = 0 mit, b, t 0, x 0, v 0 R. Der Anstz xt 0 = x
Universität Duisburg-Essen Essen, 03.06.01 Fkultät für Mthemtik S. Buer C. Hubcsek C. Thiel Linere DGL zweiter Ordnung Betrchten wir ds AWP { x + x + bx = 0 mit, b, t 0, x 0, v 0 R. Der Anstz xt 0 = x
Multiplikative Inverse
 Multipliktive Inverse Ein Streifzug durch ds Bruchrechnen in Restklssen von Yimin Ge, Jänner 2006 Viele Leute hben Probleme dbei, Brüche und Restklssen unter einen Hut zu bringen. Dieser kurze Aufstz soll
Multipliktive Inverse Ein Streifzug durch ds Bruchrechnen in Restklssen von Yimin Ge, Jänner 2006 Viele Leute hben Probleme dbei, Brüche und Restklssen unter einen Hut zu bringen. Dieser kurze Aufstz soll
7 Bewegung von Punkten
 81 7 Bewegung von Punkten 7.1 Übersicht Bewegung von Punkten Differenzierbrkeit. Wo liegt die Ableitung Tylorreihe, Vektordreieck Physiklische Bezeichnungen Abstnd zu einer Kurve Geschwindigkeit Bogenlänge
81 7 Bewegung von Punkten 7.1 Übersicht Bewegung von Punkten Differenzierbrkeit. Wo liegt die Ableitung Tylorreihe, Vektordreieck Physiklische Bezeichnungen Abstnd zu einer Kurve Geschwindigkeit Bogenlänge
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl. Sommersemester 2009
 UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
Der Vektor lebt unabhängig vom Koordinatensystem: Bei einer Drehung des Koordinatensystems ändern zwar die Komponenten, der Vektor v aber bleibt.
 Vektorlger Vektorlger Vektoren sind Grössen, die einen Betrg sowie eine Rihtung im Rum hen. Im Gegenstz zu den Vektoren estehen Sklre nur us einer Grösse ls Zhl. In Bühern wird nsttt v oft v geshrieen.
Vektorlger Vektorlger Vektoren sind Grössen, die einen Betrg sowie eine Rihtung im Rum hen. Im Gegenstz zu den Vektoren estehen Sklre nur us einer Grösse ls Zhl. In Bühern wird nsttt v oft v geshrieen.
Matrizen und Determinanten
 Mtrizen und Determinnten Im bschnitt Vektorlgebr Rechenregeln für Vektoren Multipliktion - Sklrprodukt, Vektorprodukt, Mehrfchprodukte wurde in einem Vorgriff bereits eine interessnte mthemtische Konstruktion
Mtrizen und Determinnten Im bschnitt Vektorlgebr Rechenregeln für Vektoren Multipliktion - Sklrprodukt, Vektorprodukt, Mehrfchprodukte wurde in einem Vorgriff bereits eine interessnte mthemtische Konstruktion
8 Integralrechnung. 8.1 Das Riemann-Integral
 8 Integrlrechnung Der Integrlbegriff ist wie der Ableitungsbegriff motiviert durch die physiklische Beschreibung von Bewegungsbläufen (Geschwindigkeit, Beschleunigung). Er ist u.. uch von Bedeutung bei
8 Integrlrechnung Der Integrlbegriff ist wie der Ableitungsbegriff motiviert durch die physiklische Beschreibung von Bewegungsbläufen (Geschwindigkeit, Beschleunigung). Er ist u.. uch von Bedeutung bei
1. Stegreifaufgabe aus der Physik Lösungshinweise
 . Stegreifufgbe us der Physik Lösungshinweise Gruppe A Aufgbe Ds.Newtonsche Gesetz lässt sich zum Beispiel so formulieren: Wirkt uf einen Körper keine Krft (oder ist die Summe ller Kräfte null) so bleibt
. Stegreifufgbe us der Physik Lösungshinweise Gruppe A Aufgbe Ds.Newtonsche Gesetz lässt sich zum Beispiel so formulieren: Wirkt uf einen Körper keine Krft (oder ist die Summe ller Kräfte null) so bleibt
Es soll der Betrag eines Vektors berechnet werden, wenn dieser in Komponenten oder Koordinatenschreibweise gegeben ist. a 3. x 2
 R. Brinkmnn http://brinkmnn-du.de Seite 8.. Vektoren im krtesischen Koordintensystem Betrg eines Vektors Es soll der Betrg eines Vektors berechnet werden, wenn dieser in Komponenten oder Koordintenschreibweise
R. Brinkmnn http://brinkmnn-du.de Seite 8.. Vektoren im krtesischen Koordintensystem Betrg eines Vektors Es soll der Betrg eines Vektors berechnet werden, wenn dieser in Komponenten oder Koordintenschreibweise
Wie muss x gewählt werden, so dass K 1 anschließend einen geraden Stoß mit K 3 ausführt?
 ZÜ 2.1 Aufgbe 2.1 Drei Kugeln K 1, K 2 und K 3 Mssen, m 2 und m 3 befinden sich in einer Rille und berühren sich nicht. Die erste Kugel gleitet mit der Geschwindigkeit v1 und stößt vollkommen elstisch
ZÜ 2.1 Aufgbe 2.1 Drei Kugeln K 1, K 2 und K 3 Mssen, m 2 und m 3 befinden sich in einer Rille und berühren sich nicht. Die erste Kugel gleitet mit der Geschwindigkeit v1 und stößt vollkommen elstisch
Fachhochschule Jena Fachbereich GW. Serie Nr.: 2 Semester: 1
 Fchhochschule Jen Fchbereich GW Tutorium Mthemtik I Studiengng: BT/MT - Bchelor Serie Nr.: 2 Semester: Them: Vektorrechnung und Geometrie Auf die Lehrmterilien im Internet ( Zum selbständigen Üben ) empfehle
Fchhochschule Jen Fchbereich GW Tutorium Mthemtik I Studiengng: BT/MT - Bchelor Serie Nr.: 2 Semester: Them: Vektorrechnung und Geometrie Auf die Lehrmterilien im Internet ( Zum selbständigen Üben ) empfehle
Einführung in die Festkörperphysik I Prof. Peter Böni, E21
 Einführung in die Festkörperphsik I Prof. Peter Böni, E21 Lösung zum 2. Übungsbltt (Besprechung: 0. - 1. Oktober 2006) P. Niklowitz, E21 Aufgbe 2.1: Zweidimensionle Wigner-Seitz-Zellen Vernschulichen Sie,
Einführung in die Festkörperphsik I Prof. Peter Böni, E21 Lösung zum 2. Übungsbltt (Besprechung: 0. - 1. Oktober 2006) P. Niklowitz, E21 Aufgbe 2.1: Zweidimensionle Wigner-Seitz-Zellen Vernschulichen Sie,
1.7 Inneres Produkt (Skalarprodukt)
 Inneres Produkt (Sklrprodukt) 17 1.7 Inneres Produkt (Sklrprodukt) Montg, 27. Okt. 2003 7.1 Wir erinnern zunächst n die Winkelfunktionen sin und cos, deren Wirkung wir m Einheitskreis vernschulichen: ϕ
Inneres Produkt (Sklrprodukt) 17 1.7 Inneres Produkt (Sklrprodukt) Montg, 27. Okt. 2003 7.1 Wir erinnern zunächst n die Winkelfunktionen sin und cos, deren Wirkung wir m Einheitskreis vernschulichen: ϕ
1 Mechanik starrer Körper
 1 Mechanik starrer Körper 1.1 Einführung Bisher war die Mechanik auf Massepunkte beschränkt. Nun gehen wir den Schritt zu starren Körpern. Ein starrer Körper ist ein System aus Massepunkten, welche nicht
1 Mechanik starrer Körper 1.1 Einführung Bisher war die Mechanik auf Massepunkte beschränkt. Nun gehen wir den Schritt zu starren Körpern. Ein starrer Körper ist ein System aus Massepunkten, welche nicht
Präsenz-Aufgaben = i. (a) i 15 = i 14 i = (i 2 ) 7 i = ( 1) 7 i = i i 15 = 0 + ( 1)i, i (i i) = i 1 = i i 15 = 0 + 1i,
 Präsenz-Aufgben 1. 1. Schreiben Sie z in der Form z α + βi mit α,β R. Aus der Vorlesung ist beknnt: i i i 1, i 1 1 i i i i i 1 i. () i 15 i 1 i (i ) 7 i ( 1) 7 i i i 15 + ( 1)i, (b) i 15 1 i 15 () 1 i
Präsenz-Aufgben 1. 1. Schreiben Sie z in der Form z α + βi mit α,β R. Aus der Vorlesung ist beknnt: i i i 1, i 1 1 i i i i i 1 i. () i 15 i 1 i (i ) 7 i ( 1) 7 i i i 15 + ( 1)i, (b) i 15 1 i 15 () 1 i
Strahl Eine gerade Linie, die auf einer Seite von einem Punkt begrenzt wird, (Anfangspunkt) heißt Strahl.
 1. 1. 2. Strecke B B Gerde Eine gerde, von zwei Punkten begrenzte Linie heißt Strecke. Eine gerde Linie, die nicht begrenzt ist, heißt Gerde. D.h. eine Gerde ht keine Endpunkte! 2. 3. 3. g Strhl Eine gerde
1. 1. 2. Strecke B B Gerde Eine gerde, von zwei Punkten begrenzte Linie heißt Strecke. Eine gerde Linie, die nicht begrenzt ist, heißt Gerde. D.h. eine Gerde ht keine Endpunkte! 2. 3. 3. g Strhl Eine gerde
10.2 Kurven und Bogenlänge
 10.2 Kurven und Bogenlänge Definition: Sei c = (c 1,..., c n ) : [, b] R n eine stetige Funktion. Dnn wird c ls Kurve im R n bezeichnet; c() heißt Anfngspunkt, c(b) heißt Endpunkt von c. c heißt geschlossene
10.2 Kurven und Bogenlänge Definition: Sei c = (c 1,..., c n ) : [, b] R n eine stetige Funktion. Dnn wird c ls Kurve im R n bezeichnet; c() heißt Anfngspunkt, c(b) heißt Endpunkt von c. c heißt geschlossene
3. Mathematik-Schularbeit für die 5. Klasse Autor: Gottfried Gurtner
 3. Mthemtik-Schulrbeit für die 5. Klsse Autor: Gottfried Gurtner Arbeitszeit: 75 Minuten Lernstoff: Mthemtische Grundkompetenzen: AG.1 Einfche Terme und Formeln ufstellen, umformen und im Kontext deuten
3. Mthemtik-Schulrbeit für die 5. Klsse Autor: Gottfried Gurtner Arbeitszeit: 75 Minuten Lernstoff: Mthemtische Grundkompetenzen: AG.1 Einfche Terme und Formeln ufstellen, umformen und im Kontext deuten
Vorkurs Mathematik DIFFERENTIATION
 Vorkurs Mthemtik 6 DIFFERENTIATION Beispiel (Ableitung von sin( )). Es seien f() = sin g() = h() =f(g()) = sin. (f () =cos) (g () =) Also ist die Ableitung von h: h () =f (g())g () =cos = cos. Mn nennt
Vorkurs Mthemtik 6 DIFFERENTIATION Beispiel (Ableitung von sin( )). Es seien f() = sin g() = h() =f(g()) = sin. (f () =cos) (g () =) Also ist die Ableitung von h: h () =f (g())g () =cos = cos. Mn nennt
Starrer Körper: Drehimpuls und Drehmoment
 Starrer Körper: Drehimpuls und Drehmoment Weitere Schreibweise für Rotationsenergie: wobei "Dyade" "Dyadisches Produkt" Def.: "Dyadisches Produkt", liefert bei Skalarmultiplikation mit einem Vektor : und
Starrer Körper: Drehimpuls und Drehmoment Weitere Schreibweise für Rotationsenergie: wobei "Dyade" "Dyadisches Produkt" Def.: "Dyadisches Produkt", liefert bei Skalarmultiplikation mit einem Vektor : und
Hier wurde die Jacobi-Determinante der ZylinderKoordinaten verwendet (det J = ρ). Wir führen zunächst die ρ-integration durch: (R 2 H sin 2 φ )
 b) Für einen Zylinder bieten sich Zylinderkoordinaten an. Legt man den Ursprung in den Schwerpunkt und die z- bzw. x 3 - Achse entlang der Zylinderachse, verschwinden alle Deviationsmomente. Dies liegt
b) Für einen Zylinder bieten sich Zylinderkoordinaten an. Legt man den Ursprung in den Schwerpunkt und die z- bzw. x 3 - Achse entlang der Zylinderachse, verschwinden alle Deviationsmomente. Dies liegt
5.1 Charakterisierung relativ kompakter und kompakter
 Kpitel 5 Kompkte Mengen 5.1 Chrkterisierung reltiv kompkter und kompkter Mengen X sei im weiteren ein Bnchrum. Definition 5.1. Eine Menge K X heißt kompkt, wenn us jeder offenen Überdeckung von K eine
Kpitel 5 Kompkte Mengen 5.1 Chrkterisierung reltiv kompkter und kompkter Mengen X sei im weiteren ein Bnchrum. Definition 5.1. Eine Menge K X heißt kompkt, wenn us jeder offenen Überdeckung von K eine
b f(x)p(x) dx = f(ξ) 2e 2 , Hess f (2, 0) =
 Es seien U R n offen und ψ : U R n stetig differenzierbr. Weiter sei f : U R zweiml stetig differenzierbr. Kennzeichnen Sie whre Aussgen mit W und flsche Aussgen mit F. F Flls dψ(x) ein Isomorphismus für
Es seien U R n offen und ψ : U R n stetig differenzierbr. Weiter sei f : U R zweiml stetig differenzierbr. Kennzeichnen Sie whre Aussgen mit W und flsche Aussgen mit F. F Flls dψ(x) ein Isomorphismus für
Gebrochenrationale Funktionen (Einführung)
 Gebrochenrtionle Funktionen (Einführung) Ac Eine gebrochenrtionle Funktion R ist von der Form R(x) P(x) und Q(x) gnzrtionle Funktionen n-ten Grdes sind. P(x) Q(x), wobei Im Allgemeinen ht eine gebrochenrtionle
Gebrochenrtionle Funktionen (Einführung) Ac Eine gebrochenrtionle Funktion R ist von der Form R(x) P(x) und Q(x) gnzrtionle Funktionen n-ten Grdes sind. P(x) Q(x), wobei Im Allgemeinen ht eine gebrochenrtionle
2 Trigonometrische Formeln
 Mthemtische Probleme, SS 013 Donnerstg.5 $Id: trig.tex,v 1.3 013/05/03 10:50:31 hk Exp hk $ Trigonometrische Formeln.1 Die Additionstheoreme In der letzten Sitzung htten wir geometrische Herleitungen der
Mthemtische Probleme, SS 013 Donnerstg.5 $Id: trig.tex,v 1.3 013/05/03 10:50:31 hk Exp hk $ Trigonometrische Formeln.1 Die Additionstheoreme In der letzten Sitzung htten wir geometrische Herleitungen der
1.2 Der goldene Schnitt
 Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
3. Ganzrationale Funktionen
 3. Gnzrtionle Funktionen ) Definitionen und Beispiele Definition: Eine gnzrtionle Funktion n-ten Grdes ht ls Definitionsterm ein Polynom n-ten Grdes, d.h. y = f() = n n n-1 n-1 1 0. n 0, i ( i = 1, n)
3. Gnzrtionle Funktionen ) Definitionen und Beispiele Definition: Eine gnzrtionle Funktion n-ten Grdes ht ls Definitionsterm ein Polynom n-ten Grdes, d.h. y = f() = n n n-1 n-1 1 0. n 0, i ( i = 1, n)
10 Das Riemannsche Integral
 10 Ds Riemnnsche Integrl 50 10 Ds Riemnnsche Integrl Ziel dieses Prgrphen ist es, den Inhlt einer Fläche, die vom Grphen einer Funktion berndet wird, exkt zu definieren. f(b) f() = t 0 t1 t2 t3 t4 t5 t
10 Ds Riemnnsche Integrl 50 10 Ds Riemnnsche Integrl Ziel dieses Prgrphen ist es, den Inhlt einer Fläche, die vom Grphen einer Funktion berndet wird, exkt zu definieren. f(b) f() = t 0 t1 t2 t3 t4 t5 t
a S 1 S 2 S G e z a/2 e y e x a/2 Abbildung 1: Werbetafel.
 VU Modellbildun Beispiele zu Kpitel : Mechnische Systeme 1.) Geeben ist die in Abbildun 1 drestellte Werbetfel mit der Msse m. Die Werbetfel ist mittels zwei Seilen S 1 und S n einer Wnd befestit. Außerdem
VU Modellbildun Beispiele zu Kpitel : Mechnische Systeme 1.) Geeben ist die in Abbildun 1 drestellte Werbetfel mit der Msse m. Die Werbetfel ist mittels zwei Seilen S 1 und S n einer Wnd befestit. Außerdem
Differenzial- und Integralrechnung III
 Differenzil- und Integrlrechnung III Riner Huser April 2012 1 Einleitung 1.1 Polynome und Potenzfunktionen Die Polynome oder Polynomfunktionen lssen sich durch die endliche Anzhl von n+1 Prmetern i R in
Differenzil- und Integrlrechnung III Riner Huser April 2012 1 Einleitung 1.1 Polynome und Potenzfunktionen Die Polynome oder Polynomfunktionen lssen sich durch die endliche Anzhl von n+1 Prmetern i R in
Mathematik 1 für Bauwesen 14. Übungsblatt
 Mthemtik für Buwesen Übungsbltt Fchbereich Mthemtik Wintersemester 0/0 Dr Ivn Izmestiev 8/900 Dr Vince Bárány, M Sc Juli Plehnert Gruppenübung Aufgbe G () Berechnen Sie ds Volumen des Rottionskörpers,
Mthemtik für Buwesen Übungsbltt Fchbereich Mthemtik Wintersemester 0/0 Dr Ivn Izmestiev 8/900 Dr Vince Bárány, M Sc Juli Plehnert Gruppenübung Aufgbe G () Berechnen Sie ds Volumen des Rottionskörpers,
MATHEMATIK GRUNDWISSEN KLASSE 5
 MATHEMATIK GRUNDWISSEN KLASSE 5 Them NATÜRLICHE ZAHLEN Zählen und Ordnen Ntürliche Zhlen werden zum Zählen und Ordnen verwendet Stefn ist beim 100m-Luf ls 2. ins Ziel gekommen. Große Zhlen und Zehnerpotenzen
MATHEMATIK GRUNDWISSEN KLASSE 5 Them NATÜRLICHE ZAHLEN Zählen und Ordnen Ntürliche Zhlen werden zum Zählen und Ordnen verwendet Stefn ist beim 100m-Luf ls 2. ins Ziel gekommen. Große Zhlen und Zehnerpotenzen
Quadratische Funktionen
 Qudrtische Funktionen Die Scheitelpunktform ist eine spezielle Drstellungsform von qudrtischen Funktionen, nhnd der viele geometrische Eigenschften des Funktionsgrphen bgelesen werden können. Abbildung
Qudrtische Funktionen Die Scheitelpunktform ist eine spezielle Drstellungsform von qudrtischen Funktionen, nhnd der viele geometrische Eigenschften des Funktionsgrphen bgelesen werden können. Abbildung
VII. Folgen und Reihen von Funktionen (Vertauschung von Grenzprozessen)
 VII. Folgen und Reihen von Funktionen (Vertuschung von Grenzprozessen) Definition. Sei {f n } eine Folge von Funktionen, die uf einer Menge E definiert sind. Die Folgen der Funktionswerte {f n (x)} seien
VII. Folgen und Reihen von Funktionen (Vertuschung von Grenzprozessen) Definition. Sei {f n } eine Folge von Funktionen, die uf einer Menge E definiert sind. Die Folgen der Funktionswerte {f n (x)} seien
Mathematik-Tutorium: Handwerkszeug und Kochrezepte für Maschinenbauer
 Vektorrechnung Differentilrechnung Integrlrechnung Mthemtik-Tutorium: Hndwerkszeug und Kochrezepte für Mschinenbuer Johnnes Wiedersich 7. Dezember 007 http://www.e13.physik.tu-muenchen.de/wiedersich/ Vektorrechnung
Vektorrechnung Differentilrechnung Integrlrechnung Mthemtik-Tutorium: Hndwerkszeug und Kochrezepte für Mschinenbuer Johnnes Wiedersich 7. Dezember 007 http://www.e13.physik.tu-muenchen.de/wiedersich/ Vektorrechnung
2 Vektoren in der Mechanik
 11 2 Vektoren in der Mechnik Viele Größen der Mechnik, in der Sttik insbesondere Krft und Moment, hben die Eigenschft von Vektoren im dreidimensionlen Rum. Die Mechnik nutt dher die Methoden und Rechenregeln
11 2 Vektoren in der Mechnik Viele Größen der Mechnik, in der Sttik insbesondere Krft und Moment, hben die Eigenschft von Vektoren im dreidimensionlen Rum. Die Mechnik nutt dher die Methoden und Rechenregeln
8.1 Gleichförmige Kreisbewegung 8.2 Drehung ausgedehnter Körper 8.3 Beziehung: Translation - Drehung 8.4 Vektornatur des Drehwinkels
 8. Drehbewegungen 8.1 Gleichförmige Kreisbewegung 8.2 Drehung ausgedehnter Körper 8.3 Beziehung: Translation - Drehung 8.4 Vektornatur des Drehwinkels 85 8.5 Kinetische Energie der Rotation ti 8.6 Berechnung
8. Drehbewegungen 8.1 Gleichförmige Kreisbewegung 8.2 Drehung ausgedehnter Körper 8.3 Beziehung: Translation - Drehung 8.4 Vektornatur des Drehwinkels 85 8.5 Kinetische Energie der Rotation ti 8.6 Berechnung
Prüfung - Technische Mechanik III
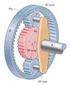 Prüfung - Technische Mechnik III WS 11/12 16. Februr 2012 FB 13, Festkörpermechnik Prof. Dr.-Ing. F. Gruttmnn Nme: Mtr.-Nr.: Studiengng: Pltznummer Einverständniserklärung: Ich stimme hiermit zu, dss meine
Prüfung - Technische Mechnik III WS 11/12 16. Februr 2012 FB 13, Festkörpermechnik Prof. Dr.-Ing. F. Gruttmnn Nme: Mtr.-Nr.: Studiengng: Pltznummer Einverständniserklärung: Ich stimme hiermit zu, dss meine
Trägheitsmomente starrer Körper
 Trägheitsmomente starrer Körper Mit Hilfe von Drehschwingungen sollen für einen Würfel und einen Quader die Trägheitsmomente für verschiedene Drehachsen durch den Schwerpunkt gemessen werden. Das zugehörige
Trägheitsmomente starrer Körper Mit Hilfe von Drehschwingungen sollen für einen Würfel und einen Quader die Trägheitsmomente für verschiedene Drehachsen durch den Schwerpunkt gemessen werden. Das zugehörige
Lineare Algebra und analytische Geometrie I
 Prof Dr H Brenner Osnbrück WS 2015/2016 Linere Algebr und nlytische Geometrie I Vorlesung 4 In der lineren Algebr wird stets ein Körper K zugrunde gelegt, wobei mn dbei grundsätzlich n die reellen Zhlen
Prof Dr H Brenner Osnbrück WS 2015/2016 Linere Algebr und nlytische Geometrie I Vorlesung 4 In der lineren Algebr wird stets ein Körper K zugrunde gelegt, wobei mn dbei grundsätzlich n die reellen Zhlen
Spezialfall m 1 = m 2 und v 2 = 0
 Spezialfall m 1 = m 2 und v 2 = 0 Impulserhaltung: Quadrieren ergibt Energieerhaltung: Deshalb muss gelten m v 1 = m( u 1 + u 2 ) m 2 v 1 2 = m 2 ( u 2 1 + 2 u 1 u 2 + u 2 ) 2 m 2 v2 1 = m 2 ( u 2 1 +
Spezialfall m 1 = m 2 und v 2 = 0 Impulserhaltung: Quadrieren ergibt Energieerhaltung: Deshalb muss gelten m v 1 = m( u 1 + u 2 ) m 2 v 1 2 = m 2 ( u 2 1 + 2 u 1 u 2 + u 2 ) 2 m 2 v2 1 = m 2 ( u 2 1 +
Anhang D: Stabilität t linearer Systeme
 Anhng D: Stbilität t linerer Systeme (- / ) Im{G o (jω) Re{G o (jω) ω FHD Prof. Dr.-Ing. Gernot Freitg Seite Regelungstechnik - Stbilitätskriterien tskriterien Aufgbe: Entwurf stbiler Regelkreise Problem:
Anhng D: Stbilität t linerer Systeme (- / ) Im{G o (jω) Re{G o (jω) ω FHD Prof. Dr.-Ing. Gernot Freitg Seite Regelungstechnik - Stbilitätskriterien tskriterien Aufgbe: Entwurf stbiler Regelkreise Problem:
Vektoren. Karin Haenelt
 Vektoren Grundbegriffe für ds Informtion Retrievl Krin Henelt 13.10.2013 Anltische Geometrie und Linere Algebr Geometrie: Konstruktionsverfhren mit Zirkel und Linel Anltische Geometrie: Umsetzung geometrischer
Vektoren Grundbegriffe für ds Informtion Retrievl Krin Henelt 13.10.2013 Anltische Geometrie und Linere Algebr Geometrie: Konstruktionsverfhren mit Zirkel und Linel Anltische Geometrie: Umsetzung geometrischer
kann man das Riemannsche Unter- bzw. Oberintegral auch wie folgt definieren: xk+1 x k
 Integrlrechnung Definition 1 (Treppenfunktion, Zerlegung eines Intervlls): Sei [, b] R ein Intervll. Eine Funktion g : [, b] R heißt Treppenfunktion, flls es eine Zerlegung := { =: 0 < 1
Integrlrechnung Definition 1 (Treppenfunktion, Zerlegung eines Intervlls): Sei [, b] R ein Intervll. Eine Funktion g : [, b] R heißt Treppenfunktion, flls es eine Zerlegung := { =: 0 < 1
Eine Relation R in einer Menge M ist transitiv, wenn für alle x, y, z M gilt: (x R y y R z) x R z
 Reltionen, 11 Reltionen Reltion ist einfch gesgt eine Beziehung zwischen Elementen von Mengen. In der Geometrie sind z.b. die Reltionen "ist gleich", "ist senkrecht zu", "ist prllel zu" eknnt. Die letzten
Reltionen, 11 Reltionen Reltion ist einfch gesgt eine Beziehung zwischen Elementen von Mengen. In der Geometrie sind z.b. die Reltionen "ist gleich", "ist senkrecht zu", "ist prllel zu" eknnt. Die letzten
2 Lineare Operatoren. T(αx + βy) = αtx + βty x,y X, α, β K. (b) Ist T linear, so heißt
 2 Linere Opertoren Im Folgenden seien X,Y, Z stets normierte Räumen über dem selben Körper K = C oder K = R. 2.1. Definition. () Eine Abbildung T : X Y heißt liner, flls T(αx + βy) = αtx + βty x,y X, α,
2 Linere Opertoren Im Folgenden seien X,Y, Z stets normierte Räumen über dem selben Körper K = C oder K = R. 2.1. Definition. () Eine Abbildung T : X Y heißt liner, flls T(αx + βy) = αtx + βty x,y X, α,
Uneigentliche Riemann-Integrale
 Uneigentliche iemnn-integrle Zweck dieses Abschnitts ist es, die Vorussetzungen zu lockern, die wir n die Funktion f : [, b] bei der Einführung des iemnn-integrls gestellt hben. Diese Vorussetzungen wren:
Uneigentliche iemnn-integrle Zweck dieses Abschnitts ist es, die Vorussetzungen zu lockern, die wir n die Funktion f : [, b] bei der Einführung des iemnn-integrls gestellt hben. Diese Vorussetzungen wren:
{ } Menge der natürlichen Zahlen { } Menge der natürlichen Zahlen mit Null { } Menge der ganzen Zahlen
 Themen Ntürliche und gnze gerde Eigenschften Besonderheiten - Beispiele { } Menge der ntürlichen { } Menge der ntürlichen mit Null { } Menge der gnzen IN = 1;2;3;4;... IN 0 = 0;1;2;3;4;... Z =...; 3; 2;
Themen Ntürliche und gnze gerde Eigenschften Besonderheiten - Beispiele { } Menge der ntürlichen { } Menge der ntürlichen mit Null { } Menge der gnzen IN = 1;2;3;4;... IN 0 = 0;1;2;3;4;... Z =...; 3; 2;
Thema 11 Vektorwertige Funktionen, Kurven
 Them 11 Vektorwertige Funktionen, Kurven Definition 1 Eine Kurve in R n ist eine stetige Abbildung uf einem Intervll I mit Werten in R n. Wir verwenden den Buchstben c für Kurven und schreiben c = (c 1,...,c
Them 11 Vektorwertige Funktionen, Kurven Definition 1 Eine Kurve in R n ist eine stetige Abbildung uf einem Intervll I mit Werten in R n. Wir verwenden den Buchstben c für Kurven und schreiben c = (c 1,...,c
Theoretische Physik: Mechanik
 Ferienkurs Theoretische Physik: Mechanik Blatt 4 - Lösung Technische Universität München 1 Fakultät für Physik 1 Zwei Kugeln und der Satz von Steiner Nehmen Sie zwei Kugeln mit identischem Radius R und
Ferienkurs Theoretische Physik: Mechanik Blatt 4 - Lösung Technische Universität München 1 Fakultät für Physik 1 Zwei Kugeln und der Satz von Steiner Nehmen Sie zwei Kugeln mit identischem Radius R und
KLASSISCHE KINEMATIK UND GRAVITATION
 KLASSISCHE KINEMATIK UND GRAVITATION KLAUS KRÖNCKE Die klssische Kinemtik wurde im wesentlichen von Isc Newton (643-727) egründet und fußt uf folgenden Annhmen: Der solute Rum leit vermöge seiner Ntur
KLASSISCHE KINEMATIK UND GRAVITATION KLAUS KRÖNCKE Die klssische Kinemtik wurde im wesentlichen von Isc Newton (643-727) egründet und fußt uf folgenden Annhmen: Der solute Rum leit vermöge seiner Ntur
Anforderungsniveau Prüfungsteil Sachgebiet digitales Hilfsmittel erhöht B Analysis CAS
 Gemeinsme Abiturufgbenpools der Länder Aufgbensmmlung Aufgbe für ds Fch Mthemtik Kurzbeschreibung Anforderungsniveu Prüfungsteil Schgebiet digitles Hilfsmittel erhöht B Anlysis CAS 1 Aufgbe 1 Gegeben ist
Gemeinsme Abiturufgbenpools der Länder Aufgbensmmlung Aufgbe für ds Fch Mthemtik Kurzbeschreibung Anforderungsniveu Prüfungsteil Schgebiet digitles Hilfsmittel erhöht B Anlysis CAS 1 Aufgbe 1 Gegeben ist
Thema 13 Integrale, die von einem Parameter abhängen, Integrale von Funktionen auf Teilmengen von R n
 Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
Grundwissen Mathematik 8. Klasse. Eigenschaften Besonderheiten - Beispiele
 Themen Direkte Proportionlität Eigenschften Besonderheiten - Beispiele Zwei Größen und y heißen direkt proportionl, wenn gilt: Zum k-fchen Wert von gehört der k-fche Wert von y; Der Quotient q = y ht für
Themen Direkte Proportionlität Eigenschften Besonderheiten - Beispiele Zwei Größen und y heißen direkt proportionl, wenn gilt: Zum k-fchen Wert von gehört der k-fche Wert von y; Der Quotient q = y ht für
9 Teilchensysteme. 9.1 Schwerpunkt
 der Impuls unter ganz allgemeinen Bedingungen erhalten bleibt. Obwohl der Impulserhaltungssatz, wie wir gesehen haben, aus dem zweiten Newton schen Axiom folgt, ist er tatsächlich allgemeiner als die Newton
der Impuls unter ganz allgemeinen Bedingungen erhalten bleibt. Obwohl der Impulserhaltungssatz, wie wir gesehen haben, aus dem zweiten Newton schen Axiom folgt, ist er tatsächlich allgemeiner als die Newton
Das Rechnen mit Logarithmen
 Ds Rechnen mit Logrithmen Etw in der 0. Klssenstufe kommt mn in Kontkt mit Logrithmen. Für die, die noch nicht so weit sind oder die, die schon zu weit dvon entfernt sind, hier noch einml ein kleiner Einblick:
Ds Rechnen mit Logrithmen Etw in der 0. Klssenstufe kommt mn in Kontkt mit Logrithmen. Für die, die noch nicht so weit sind oder die, die schon zu weit dvon entfernt sind, hier noch einml ein kleiner Einblick:
10: Lineare Abbildungen
 Chr.Nelius: Linere Alger SS 2008 1 10: Linere Aildungen 10.1 BEISPIEL: Die Vektorräume V 2 und Ê 2 hen diegleiche Struktur. Es git eine ijektive Aildung f : V 2 Ê 2, die durch die Vorschrift definiert
Chr.Nelius: Linere Alger SS 2008 1 10: Linere Aildungen 10.1 BEISPIEL: Die Vektorräume V 2 und Ê 2 hen diegleiche Struktur. Es git eine ijektive Aildung f : V 2 Ê 2, die durch die Vorschrift definiert
Resultat: Hauptsatz der Differential- und Integralrechnung
 17 Der Huptstz der Differentil- und Integrlrechnung Lernziele: Konzept: Stmmfunktion Resultt: Huptstz der Differentil- und Integrlrechnung Methoden: prtielle Integrtion, Substitutionsregel Kompetenzen:
17 Der Huptstz der Differentil- und Integrlrechnung Lernziele: Konzept: Stmmfunktion Resultt: Huptstz der Differentil- und Integrlrechnung Methoden: prtielle Integrtion, Substitutionsregel Kompetenzen:
Grundlagen der Integralrechnung
 Grundlgen der Integrlrechnung W. Kippels 0. April 2014 Inhltsverzeichnis 1 Ds unbestimmte Integrl 2 2 Ds bestimmte Integrl 4 Beispielufgben 7.1 Beispielufgbe 1............................... 7.2 Beispielufgbe
Grundlgen der Integrlrechnung W. Kippels 0. April 2014 Inhltsverzeichnis 1 Ds unbestimmte Integrl 2 2 Ds bestimmte Integrl 4 Beispielufgben 7.1 Beispielufgbe 1............................... 7.2 Beispielufgbe
Einführung in die Integralrechnung
 Einführung in die Integrlrechnung Vorbereitung für ds Probestudium n der LMU München 3. bis 7. September von W. Frks und O. Forster Integrle ls Flächeninhlte. Motivtion Flächeninhlte von Rechtecken sind
Einführung in die Integrlrechnung Vorbereitung für ds Probestudium n der LMU München 3. bis 7. September von W. Frks und O. Forster Integrle ls Flächeninhlte. Motivtion Flächeninhlte von Rechtecken sind
Grundwissen Mathematik 8
 Grundwissen Mthemtik 8 Proportionle Zuordnung Gehört bei einer Zuordnung zweier Größen zu einem Vielfchen der einen Größe ds gleiche Vielfche der nderen Größe, so heißt sie proportionle Zuordnung. Die
Grundwissen Mthemtik 8 Proportionle Zuordnung Gehört bei einer Zuordnung zweier Größen zu einem Vielfchen der einen Größe ds gleiche Vielfche der nderen Größe, so heißt sie proportionle Zuordnung. Die
Tag der Mathematik 2016
 Gruppenwettbewerb Einzelwettbewerb Mthemtische Hürden Aufgben mit en Aufgbe G mit Der römische Brunnen Aufsteigt der Strhl und fllend gießt Er voll der Mrmorschle Rund, Die, sich verschleiernd, überfließt
Gruppenwettbewerb Einzelwettbewerb Mthemtische Hürden Aufgben mit en Aufgbe G mit Der römische Brunnen Aufsteigt der Strhl und fllend gießt Er voll der Mrmorschle Rund, Die, sich verschleiernd, überfließt
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN
 Mthemtik: Mg. Schmid Wolfgng Areitsltt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN Wir wollen eine Gerde drstellen, welche durch die Punkte A(/) und B(5/) verläuft. Die Idee ist folgende:
Mthemtik: Mg. Schmid Wolfgng Areitsltt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN Wir wollen eine Gerde drstellen, welche durch die Punkte A(/) und B(5/) verläuft. Die Idee ist folgende:
7.9A. Nullstellensuche nach Newton
 7.9A. Nullstellensuche nch Newton Wir hben früher bemerkt, dß zur Auffindung von Nullstellen einer gegebenen Funktion oft nur Näherungsverfhren helfen. Eine lte, ber wirkungsvolle Methode ist ds Newton-Verfhren
7.9A. Nullstellensuche nch Newton Wir hben früher bemerkt, dß zur Auffindung von Nullstellen einer gegebenen Funktion oft nur Näherungsverfhren helfen. Eine lte, ber wirkungsvolle Methode ist ds Newton-Verfhren
Integrationsmethoden
 Universität Perborn Dezember 8 Institut für Mthemtik C. Kiser Integrtionsmethoen Prtielle Integrtion (Prouktintegrtion) Unbestimmte Integrtion er Prouktregel (u v) () = u ()v() + u()v () liefert (u v)()
Universität Perborn Dezember 8 Institut für Mthemtik C. Kiser Integrtionsmethoen Prtielle Integrtion (Prouktintegrtion) Unbestimmte Integrtion er Prouktregel (u v) () = u ()v() + u()v () liefert (u v)()
Versuch dp : Drehpendel
 U N I V E R S I T Ä T R E G E N S B U R G Naturwissenschaftliche Fakultät II - Physik Anleitung zum Physikpraktikum für Chemiker Versuch dp : Drehpendel Inhaltsverzeichnis Inhaltsverzeichnis 1 Einführung
U N I V E R S I T Ä T R E G E N S B U R G Naturwissenschaftliche Fakultät II - Physik Anleitung zum Physikpraktikum für Chemiker Versuch dp : Drehpendel Inhaltsverzeichnis Inhaltsverzeichnis 1 Einführung
