Optimierung des Leistungsprogramms eines Akutkrankenhauses. Neue Herausforderungen durch ein fallpauschaliertes Vergütungssystem
|
|
|
- Otto Rothbauer
- vor 8 Jahren
- Abrufe
Transkript
1 0 Ttel: Utettel: Optmeu des Lestuspoamms ees Akutkakehauses Neue Heausfodeue duch e fallpauschaletes Veütussstem Autoe: Pof. D. Steffe Fleßa (Koespodez) Dpl.-Kff. Btta Ehmke Dpl.-Kfm. Reé Hema Adesse: Lst. fü Allemee Betebswtschaftslehe ud Gesudhetsmaaemet Rechts- ud Staatswsseschaftlche Fakultät Uvestät Gefswald Fedch-Loeffle-Staße Gefswald Tel.: Fa.: E-mal: steffe.flessa@u-efswald.de
2 Optmeu des Lestuspoamms ees Akutkakehauses - Neue Heausfodeue duch e fallpauschaletes Veütussstem Zusammefassu: De Efühu de Daoss Related Goups als Bass ees fallpauschalete Veütussstems Akutkakehäuse emölcht de Awedu vo Optmeusmodelle zu Utestützu vo Spezalseus- ud Iteatospozesse. Hezu wd de voleede Abet e Modell de Leae Poammeu dskutet, das ee Bestmmu des deckusbetasmamale Lestuspoamms emölcht. Aschleßed wd das Modell weteetwckelt, um statesche Optoe zu hozotale ud vetkale Iteato zu bewete. Bespelechue fü alle de Modelle sd auf ee fe zuälche Homepae htelet. Es zet sch, dass de outemäße Esatz de Lestuspoammplau m Akutkakehaus kee udsätzlche Rechepobleme meh aufwft. De Datebeetstellu fü de Optmeu duch de Kakehausfomatosssteme muss edoch vebesset wede. Schlawöte: - Daoss Related Goup (DRG) - Kosteechu - Kakehaus - Lestuspoammplau - Leae Poammeu - Optmeu - Poduktospoammplau - Rechuswese
3 Optmeu m Kakehauses - Neue Heausfodeue duch e fallpauschaletes Veütussstem Efühu De Efühu des eue Kakehauseteltsstems zum. Jaua 2004 [2-3 euee Lteatustelle] sowe de schttwese Koveez vo dvduell ausehadelte Kakehausbudets zu vollstäde Umsetzu des fallpauschalete Eteltes bs zum Jah 2009 [2-3 euee Lteatustelle] stelle oße Heausfodeue fü de Fühu de Kakehausbetebe da. De Daose- ud Behadlusabläufe müsse eu aalset wede, da das eue Etelt uabhä vo de Leezet st [2-3 euee Lteatustelle]. Das äztlche ud pfleesche Pesoal muss eschult wede, um de esteee Dokumetatosafodeue zu ewähleste [2-3 euee Lteatustelle]. Medzsche Cotolle ud Kodee müsse ausebldet wede [2-3 euee Lteatustelle], ud das beteblche Rechuswese muss sch de eue Heausfodeue feste Pese stelle [2-3 euee Lteatustelle]. De ößte Heausfodeu st edoch de Bestmmu des optmale Lestuspoamms ees Kakehauses, de estmals duch de Efühu ees Festpessstems mölch wd. De Fazeu mt taesleche Pfleesätze eplzt vo eem feste, dvduell zwsche dem Kakehaus ud de esetzlche Kakevescheue ausehadelte Budet aus, aus dem sch de Pfleesätze abletete leße [2-3 euee Lteatustelle]. Ee Veädeu des Fallspektums fühte höchstes de ewele Peode zu eem Übeschuss. I de ächste Vehadluspeode wude dese Übeschuss edoch vom Voahesbudet abezoe [2-3 euee Lteatustelle], so dass das Kakehaus kee Aez hatte, duch de Wahl des Fallspektums ee bessee Ressouceutzu ud damt ee eeute Übeschuss zu eeche. De Efühu vo Fallpauschale ud Sodeetelte set 993 (GSG) wa uspülch als Istumet kozpet, effzet wtschaftede Kakehäuse ee Übeschussmölchket zu eöffe [2-3 euee Lteatustelle]. I de Realtät edoch schaffte bs zum Jah 2003 u wee Kakehäuse ee Kosteausledeu [ Lteatustelle zum Thema Kosteausledeu ] be de Kalkulato he Pfleesätze [-2 Lteatustelle zu ee Kosteausledeu], so dass Effzezsteeue be de Estellu de duch Fallpauschale ud Sodeetelte veütete Lestue m Rahme des Elösabzues [evtl. selbe Lteatustelle we beets be Kosteausledeu] ausschleßlch zu eem edee Pfleesatz fühte. Es bestad damt ke Aez, de eee Stä-
4 2 ke auszubaue bzw. de eee Ressouce duch de Wahl des Lestusspektums bestmölch zu utze. Duch de Efühu ees Pessstems auf Bass de Daoss Related Goups (DRGs) füht ee Vebesseu de Ressouceutzu u estmals zu eem Votel fü das Akutkakehaus. Da de Pes po Fall als Podukt des Relatvewchtes mt dem Bassfallwet [2-3 euee Lteatustelle] festelet st, ka ee Veschebu des Lestusspektums ee Vebesseu des fazelle Eebsses bewke, we das veädete Lestusspektum de eebee Ressouce besse utzt als das alte Poamm bzw. we be eebee Kapaztäte e höhee Case-M eecht wd [2-3 euee Lteatustelle]. De Efühu de DRGs setzt follch Aeze zu Spezalseu [2-3 euee Lteatustelle?????]. Daübe haus st mt Efühu des Gesetzes zu Modeseu de Gesetzlche Kakevescheu (GMG, ) estmals ee umfassede Födeu de Iteato mt adee Lestusabete efolt. De esetzlche Kakevescheue behalte pauschal e Pozet des Jahesbudets ees Kakehauses e [2-3 euee Lteatustelle], um de aus desem Fod Iteatospoekte fazee. De Zusammeabet mt adee Kakehäuse (hozotale Iteato) st hebe als Fotsetzu de Spezalseu m äumlche Vebud zu sehe, wähed de Koopeato mt vo- ud achelaete Beeche (vetkale Iteato) fü ee bestmmte DRG auch uabhä vo de Spezalseu efole ka. De Wahl de eee Poduktostefe ud bete st damt estmals de Geschchte des deutsche Kakehausweses etscheduselevat. Das Zusammespel vo Lestue, Ressoucevebäuche, Elöse, Koste ud Vesousafodeue veschedee vetkale ud hozotale Iteatospate st alleds deat komple, dass de Sstemzusammehäe cht meh ohe Modelleu efasst ode bewetet wede köe. Folecht wude beets vo fast 40 Jahe ud damt zetlech mt de Etwcklu de DRGs duch Robet B. Fette am Depatmet of Opeatos Reseach de Yale Uvest e Modell de Leae Poammeu (LP) zu Ressouceallokato m Kakehaus etwckelt (Gufeld & Clato 969). Wetee Modelle folte (z. B. Chstl 974; Shuma, You & Naddo 97; Dowl 976; Shuma, Wolfe & Speas 984). Dese Modelle wae zwa vo wsseschaftlchem Iteesse, edoch fü de paktsche Awedu m Kakehaus we eeet, da de damale Rechekapaztät kee ealstsche LPs mt mehee hudet Fallklasse zuleß. Isbesodee wa de Beückschtu vo Fall-, Abtelus-
5 3 ud Kakehausfkoste cht mölch, da de Zahl de bäe bzw. azzahle Vaable etem e ehalte wede musste. So musste Mtte de 980e Jahe de Zahl de bäe Vaable selbst auf Goßeche och auf wee Hudet beschäkt wede (Mee & Hase 985, S. 77). De LP-Asatz zu Optmeu des Fallklassepoamms m Kakehaus wude deshalb fast 20 Jahe cht meh wetevefolt. Mee (996, S. 4-[btte letzte Sete suche ud eäze]) wa de este deutschspache Auto, de das Poblem des optmale Lestuspoamms 996 wede aufahm, obwohl es bem damale Fazeussstem kee Notwedket de paktsche Awedu ab. Tatsächlch beückschtt se Modell kee Abtelusbldu ud umfasst u wee DRGs. Es wa ehe zu Illustato de udsätzlche Mölchket ee Lestuspoammplau edacht. Mee & Hafe (999, S ) etwckelte deses Modell wete ud zete das Potetal deses Asatzes fü de Aalse hozotale Iteatoe auf. De udleede Asatz wude zwa de Wsseschaft ztet [müsste m Kakehausepot 2000 ode 200 zu fde se], edoch de Pas kaum ezpet, da vo Efühu de Daoss Related Goups ke Aez zu Bestmmu ees optmale Fallklassepoamms bestad. Duch de Umstellu de Fazeu ud auch duch de Zuahme ewebswtschaftlche Kakehäuse [-2 Lteatustelle] ttt u das optmale Fallklassepoamm wede das Iteesse de Pas. De Fühu ees Akutkakehauses muss sch aeschts des ahe Edes de Koveezphase (2009) fae, welche Fallklasse das Kakehaus Zukuft cht meh behadel daf bzw. auf welche Fallklasse es sch spezalsee sollte. Selbstvestädlch wd sch das Kakehaus auf deee Fallklasse spezalsee, be dee de Gesamtdeckusbeta mamal st. Da abe de Fallklasse uteschedlche Ressoucevebäuche aufwese, st de Zusammestellu des optmale Lestuspoamms ute Beachtu de Kapaztätsbeschäkue e komplees Optmeuspoblem. Hefü soll de voleede Abet e Modell de Leae Poammeu etwckelt wede, das auf dem udleede Modell vo Mee & Hafe aufbaut. Zusätzlch solle Mdestmeeafodeue, stufefe Koste fü DRGs, Abtelue ud Kakehäuse sowe de vetkale Iteato beückschtt wede. Zel de Abet st es, Mölchkete ud Geze de Optmeu des Lestuspoamms vo Akutkakehäuse ute Bedue de DRGs aufzuzee ud somt Spezalseus- ud Koopeatospozesse zu utestütze.
6 4 Hezu wd m zwete Abschtt das Bassmodell zu Bestmmu des optmale Fallklassepoamms daestellt. Aschleßed wd es zu ewels eem Modell de hozotale ud de vetkale Iteato weteetwckelt. De Abet schleßt mt ee Dskusso de wchtste Eebsse ud he Umsetzbaket. Fü weteehedes Iteesse stehe Bespelechue mt alle de Modelle auf de Homepae sollte de Bespelechue estelle ud he de Homepae etae] zu Vefüu. 2 Modelle de Optmeu des Lestuspoamms Im Folede wede de Modelle de Leae Poammeu (LP) voestellt. Das este Modell emttelt das optmale Lestuspoamm ees ezele Akutkakehauses. Das zwete Modell utesucht das optmale Poamm vo mehee Akutkakehäuse m äumlche Vebud ute Wahu des Vesousauftaes. Das dtte LP ewetet de Asatz auf de Iteato vo Akutkakehaus ud Rehabltatosklk. Alle de Modelle ehe vo ee statesche Plausebee aus. De Etschedu übe de Aufahme, Veweldaue ode Behadlusfole ees ezele Patete wd cht betachtet. Velmeh wd das Lestuspotfolo deckusbetasmamal emttelt. Aus de statesche Pespektve ebt es sch, dass veefached fü alle Patete ee Veweldaue zwsche utee ud obee Gezveweldaue aeomme wede ka. 2. Spezalseu I eem Akutkakehaus wede Patete de DRGs bs behadelt. Das Kakehaus ethält po Patet de DRG e Etelt vo d. De dekte Koste po Patet de DRG, z. B. fü Esse, Medkamete, Opeatosmateale etc., belaufe sch auf a. Weteh falle Fkoste Höhe vo FD a, falls mdestes e Patet de DRG aufeomme ud behadelt wd. Deate Fkoste köe z. B. fü de Astellu vo Hebamme afalle, falls das Kakehaus vaale Etbdue abetet. Mehee DRGs wede zu Abtelue zusammeefasst, fü de zusätzlch abtelusspezfsche Fkoste Höhe vo FA p afalle. De DRGs bs sd de Abtelue fest zueodet. Schleßlch hat das Kakehaus sesamt och Fkoste FK zu tae. Tabelle bt schematsch ee mehstufe Deckusbetasechu ees deate Kakehauses wede. st dabe de Fallzahl vo DRG. Das Bespel eht davo aus, dass de DRGs ud 2 de Abtelu ud de DRGs, - ud -2 de Abtelu b zueodet sd.
7 Tab...: Modell de mehstufe Deckusbetasechu m Kakehaus 5 DRG DRG 2 DRG 3 DR G.. DRG -2 DRG - DRG Elöse *d 2 *d 2 3 *d 3-2 *d -2 - *d - *d - Dekte Kos- *a 2 *a 2 3 *a 3-2 *a -2 - *a - *a te Deckusbeta I - DRG-fe Koste Deckusbeta II - Abteluskoste Deckusbeta III - Kakehausfkoste Gew/ Ve- *(d -a ) 2 *(d 2 -a 2 ) 3 *(d 3 -a 3 ) -2 * (d -2 -a -2 ) - * (d - -a - ) * (d -a ) FD FD 2 FD 3 FD -2 FD - FD *(d -a )- FD 2 *(d 2 -a 2 )- FD 2 3 *(d 3 -a 3 )- FD 3-2 *(d -2 - a -2 )- FD -2 - *(d - - a - )- FD - FA FA b *(d -a )- FD + 2 *(d 2 -a 2 )- FD 2 - FA lust ( d a ) FD FAp FK FK p *(d -a )- FD -2 *(d -2 -a -2 )-FD *(d - -a - )- FD - + *(d -a )-FD Fa b b Das folede Leae Poamm etspcht dese Voeheswese. Rp bt de Mee alle DRGs vo, de Abtelu p (p,..,b) behadelt wede. Zusätzlch wede och de Ressoucebeschäkue (), de Ressoucekoste sowe de Mdestmeeafodeue (2, 3) beückschtt. Stuktuvaable: K ß D p D total Azahl de behadelte Patete DRG,,..,; azzahl Ehete vo Ressouce,,..,m falls DRG m Lestuspoamm,,.., 0 sost falls Abtelu peöffet, p,..,b 0 sost falls Kakehaus eöffet 0 sost Kostate: k Kapaztät po Ehet de Ressouce,,..,m c Vebauch de Ressouce ee Ehet de DRG,,..,;,..,m d Etelt fü DRG ;,..,
8 6 a mm M b R p FD FA p FK w Dekte Koste fü ee Fall DRG ;,.., Zahl de DRGs Mdestmeeafodeu a DRG ;,.., M Ν, mt M > Zahl de Abtelue Mee alle DRGs, de Abtelu p behadelt wede; p,..,b DRG-spezfsche Fkoste,,.., Abtelusfkoste vo Abtelu p, p,..,b Kakehausfkoste Koste ee Ehet vo Ressouce ;,..,m Nebebedue: () (2) (3) c M β k K mm β fü,.., m fü.. fü.. ( 4) M D fü p,.., b R p p ( 5) M D total Zelfukto: (6) Z ( d a ) FD ß FAp Dp FK Dtotal w K b p m Ma! E ealstsches Modell wd übe 800 DRGs, mehee Dutzed veschedee Kapaztäte ud bs zu 20 Abtelue beückschte, so dass se Zahl de azzahle Vaable lecht auf übe 000 astet. Da es sch um e Modell de statesche Plau hadelt, st de Rechezet vo mehee Stude, de e deates Modell auch auf modee Reche efodet, ke Hdes. 2.2 Hozotale Iteato Das Modell zu Emttlu des optmale Lestuspoamms wd de Reel zu de Eebs fühe, dass e Akutkakehaus sch auf wee Abtelue ud Fälle spezalset. Ute de Voaussetzu, dass beachbate Kakehäuse zetlch ud äumlch eechba
9 7 sd, etspcht deses Voehe dem Rose-Pcke : Das optmete Kakehaus sucht sch de deckusbetasstake Fälle aus ud übelässt de adee Kakehäuse deee Fälle, de fü es selbst cht lukatv sd. Falls sch edoch alle Kakehäuse ach desem Muste vehalte, st de Vesou ee Reo efähdet, da mt hohe Wahschelchket cht meh alle DRGs abedeckt wede. Das folede Modell setzt voaus, dass ee Reo vo s Kakehäuse vesot wd. Auch Zukuft solle sämtlche Fälle behadelt wede, d. h., de Vesousaufta wd duch de Koopeatosvebud waheomme. Weteh wd veefached voausesetzt, dass de DRGs alle Kakehäuse deselbe Abtelue zueodet sd. Stuktuvaable: k Azahl de behadelte Patete DRG Kakehaus k,,..,; k,..,s; azzahl K k Ehete vo Ressouce Kakehaus k,,..,m; k,..,s falls DRG m Lestuspoammvo Kakehaus k ß, k 0 sost,..,; k,..,s falls Abtelu p Kakehaus k eöffet D, pk 0 sost p,..,b; k,..,s falls Kakehaus k eöffet DTotal k, k,..,s 0 sost Kostate: k k Kapaztät po Ehet de Ressouce Kakehaus k,,..,m; k,..,s c k Vebauch de Ressouce ee Ehet de DRG Kakehaus k,,..,;,..,m; k,..,s d Etelt fü DRG ;,.., a k Dekte Koste fü ee Fall DRG Kakehaus k;,..,; k,..,s Zahl de DRGs mm Mdestmeeafodeu a DRG ;,.., M s M Ν, mt M > b R p FD k k k Zahl de Abtelue Mee alle DRGs, de Abtelu p behadelt wede; p,..,b DRG-spezfsche Fkoste Kakehaus k,,..,; k,..,s FA pk Abtelusfkoste vo Abtelu p Kakehaus k, p,..,b; k,..,s
10 8 FK k Kakehausfkoste Kakehaus k; k,..,s B Zahl de Patete mt DRG,,.., w k Koste ee Ehet vo Ressouce Kakehaus k,,..,m; k,..,s Nebebedue: (7) (8) (9) k k c k k M β k k mm β K fü,.., m; k,.., s fü.. ; k,.., s k k k fü.. ; k,.., s ( 0) M D fü p,.., b; k,.., s () R p k pk k M DTotal fü k,.., s k Zelfukto: (2) k s s k ( d FK k a k ) DTotal k k s s k m k w FD k k K ß k k s k p Ma! b Fü e Modell de hozotale Koopeato mt s Kakehäuse, DRGs ud m Kapaztäte eebe sch (s*(+b+)) bäe ud (s*(+m)) azzahle Vaable. Damt st vestädlch, dass ealstsche Awedue est set wee Jahe übehaupt echeba sd. Noch mme hadelt es sch um Modelle, de mehee Tae bs Woche eche wede. Da es sch edoch be Koopeatoe um statesche Etschedue hadelt, st des ke Hdes. 2.3 Vetkale Iteato Das Akutkakehaus st ee sttutoeübeefede Behadluspfad eebude, de aus Allemeazt, Fachazt, Akutkakehaus, Rehabltatosechtu, Pfleedest, Phsotheape ud wetee Lestusabete besteht. Im Rahme de teee Vesou [2-3 euee Lteatustelle] muss de sttutoeübeefede Behadluspfad optmet wede, um Qualtät ud Zufedehet zu mamee ud Koste zu mmee. Bespelswese solle Mehfachutesuchue vemede, Dokumete elektosch vefüba ud de Übeletu vebesset wede. Ee besodee Bedeutu hat hebe de Schtt- FA pk D pk
11 9 stelle zwsche Akutkakehaus ud Rehaklk [evtl. ee Lteatu], de m folede Modell abebldet wd. Das Modell eht davo aus, dass de echtusübeefede Behadluspfad kee medzsch edeut defete Schttstelle bestzt. Velmeh köe Behadlustelpozesse de Fühehabltato sowohl m Akutkakehaus als auch de Rehabltatosklk duchefüht wede. Abbldu zet, dass de este Telpozess ausschleßlch m Akutkakehaus abeabetet wede ka. De letzte Telpozess (h) st u de Rehaklk mölch. De Telpozesse zwe bs (h-) köe hee sowohl m Akutkakehaus als auch de Rehaklk duchefüht wede. Fü ede Telpozess falle bestmmte Koste ud Elöse a. Als Koste wede ledlch de dekt zuechebae, vaable Koste veechet, de Vohaltekoste (klusve Pesoal) wede cht de ezele Fälle zueechet. I de Reha wede och mme taesleche Pfleesätze etolte, so dass de Elöse po Telpozess popotoal zu Veweldaue eem Telpozess de Reha sd. De Elöse m Kakehaus häe hee davo ab, ob de duchschttlche Veweldaue eecht wd. E Telpozess wd so defet, dass e eau a de duchschttlche Veweldaue edet. Fü alle voelaete Telpozesse efolt e Abschla, fü alle achelaete st das Etelt kostat. Abbldu : Paallele Telpozesse m Akutkakehaus ud Rehaklkum Rehaklkum h h h Akutkakehaus De optmale Veleuszetpukt aus Scht des Akutkakehauses ud de Rehaklk wäe efach duch ee Alteatveechu zu emttel (Veleu ach Telpozess I, II, III, IV ode V), we de Patete de DRG cht lechzet deselbe Ressouce vewede wüde we de adee Patete des Kakehauses bzw. de Reha. E Telpozess füht follch zu Oppotutätskoste Höhe veloee Elöse fü ee alteatve Kapaztätsvewedu. De Höhe dese Oppotutätskoste hät hebe vo de Auslastu de Echtue ab. Das folede Modell abstahet vo de stufefe Koste de Abtelusbldu sowe vo de Mdestmeebeschäkue, we se m Modell de hozo-
12 0 tale Iteato daestellt wude. Auf ee Kombato wude he zu bessee Vestädlchket vezchtet. Stuktuvaable: Azahl de behadelte Patete m Akutkakehaus DRG,,..,-; azzahl Azahl de behadelte Patete de Reha Fallklasse,,..,-; azzahl Azahl de behadelte Patete m Akutkakehaus de eha-pflchte DRG m Telpozess,,,h- Azahl de behadelte, übeeletete Patete de Reha m Telpozess, 2,,h Kostate: k _ c Vebauch de Ressouce ee Ehet de DRG m Akutkakehaus,,..,-;,..,m _ c Vebauch de Ressouce ee Ehet de Fallklasse de Reha,,..,-;,..,m k _ c Vebauch de Ressouce ee Ehet de ehapflchte DRG m Telpozess m Akutkakehaus,,..,m;,..,h- _ c Vebauch de Ressouce ee Ehet de übeeletete Fallklasse m Telpozess de Reha,,..,m; 2,..,h d Etelt fü DRG ;,..,- Etelt m Akutkakehaus fü DRG, we Telpozess abeschlosse st.,..,h- d pf Zahl de Pfleetae, de das Rehaklkum fü ee Patete mt Fallklasse abeche ka;,.., pf Zahl de Pfleetae, de das Rehaklkum fü Reha Telpozess abeche ka; 2,..,h ps Pfleesatz k _ a Dekte Koste fü Telpozess de DRG m Akutkakehaus,,..,h- _ a Dekte Koste fü ee Pfleeta de Fallklasse Telpozess Rehaklk, 2,..,h k_a Dekte Koste fü ee Fall DRG m Akutkakehaus;,..,- _a Dekte Koste fü ee Pfleeta Fallklasse de Reha,,..,-; Zahl de DRGs m Kakehaus Zahl de Fallklasse de Reha Zuodusvoschft: h Zahl de Phase de teete Vesou vo DRG (m Kakehaus) bzw. Fallklasse ( de Reha) Kk Gesamtkapaztät de Ressouce Echtu k,,..,m; k {Akutkakehaus, Reha}
13 Nebebedue: 2,.., (7) 3,.., (6) 2,.., (5),.., (4),.., (3) h fü h fü h fü m fü K c c m fü K c k c k h h Zelfukto: ( )! ) _ ( ) _ ( _ ) _ ( (8) Ma pf a ps pf a ps a k d a k d Z h h De Nebebedue (5) bzw. (6) stelle sche, dass Patete ee Echtu mme de vollstäde Pfad bs zu Übeletu (aus dem Kakehaus) bzw. Etlassu (aus de Reha) duchlaufe. Veleue aus adee Kakehäuse bzw. Rehaklke sd cht beückschtt. Nebebedu (7) aatet, dass ede Patet alle Telpozesse duchläuft. 3 Dskusso De obe skzzete Modelle köe poblemlos fü kokete Awedue adaptet ud eechet wede. Zwa sd de Rechezete fü emscht-azzahle LPs och mme hoch, abe fü ee statesche Etschedu spelt es kee Rolle, ob de PC wee Mute ode mehee Stude echet. De Beezu de Zahl de bäe Vaable (Mee & Hase 985, S. 77), de de Awedu de Lestuspoammplau m Kakehaus lae vehdet hat, st heute cht meh eebe. De paktsche Umsetzu düfte velmeh e Datepoblem se. Betachtet ma de obe defete Kostate, so falle de Kateoe vo poblematsche Datebedafe auf. Zuest sd de dekte Fallkoste zu emttel. Des wäe udsätzlch auf Bass ee Kostetäeechu mölch. Lede bestehe de meste Kakehäuse edoch ledlch Kostestelleechue, de kee Rückschluss auf de dekte Ressoucevebäuche elaube. I Kakehäuse, dee ee Kostetäeechu mplemetet wude, ha-
14 2 delt es sch mestes um ee Zuschlüsselu vo Koste auf Kostestelle ud -täe ach dem Vobld de DRG-Beechu [Lteatustelle]. Ee mölchst komplette Efassu vo Kostetäeezelkoste fällt de Reel cht a. De Vebesseu de Kostetäeechu m Kakehaus st deshalb ded otwed, um de Lestuspoammplau zu mplemetee [2-3 Lteatustelle, wo ee ute Kostetäeechu efodet wd]. Zwetes sd de Ressoucevebäuche zu vemttel, de zu Estellu ee Lestusehet afalle. Gudleed st hebe de Aalse de Zetvebäuche. So müsse bespelswese de Pflee-, Azt-, OP- ud Labomute fü ee Fall aufezechet wede. Hezu bt es veschedee Mölchkete. Im Rahme ee Abetszetstude [-2 Lteatustelle zu REFA-Techke] köe de ezele Telpozesse stuktuet ud de Zetvebäuche eemplasch emesse wede. Da Destlestue am Mesche eeell ee hohe Vaaz habe, muss de Stchpobeumfa elatv oß se. Dese Ehebu köte duch de medzsche bzw. pfleesche Dokumetato eäzt wede, de de Tätkete he Häufket po Patet efasst wede. Dese esetzlch voeschebee Dokumetato [-2 Lteatustelle] wd bsla u uzueched ausewetet, was vo allem auch daauf zuückzufühe st, dass papeestützte Dokumete kaum als Gudlae fü Routessteme elte köe. Zel muss deshalb ee EDV-estützte Dokumetato se, aus de sch Tätketslste po Patet bzw. Fallklasse eeee lasse. Bespele hefü sd de Ssteme. ud [zwe Ssteme ee]. Ideal wäe ee kombete, mölchst automatsche Efassu vo Tätkete ud Zete. Hezu wäe es otwed, dass ede Mtabete ee Echtu ee elektosche Keu tät, de vo eem Pozesso am Bett des Patete ekat wd. Sobald de Mtabete ahe eu a de Patete kommt, wd des estet ud dokumetet. Aschleßed wede de Zete mt de Tätketsdokumetato abelche ud de Zetvebäuche emttelt. Mt Hlfe dese Date wäe de automatsche Geeeu de Koeffzetemat de Lestuspoammplau ee Route. I de Pas stehe dese Etwcklu edoch och zahleche techsche ud vo allem pesoelle Pobleme etee, auf de a dese Stelle cht eeae wede ka. Dttes müsste fü ee statesche Plau ee Plausschehet ewählestet se. Veschebe sch bespelswese de Relatvewchte ode de Zuodu vo bestmmte Fälle zu ezele DRGs, ka des zu ee adee Koopeatosetschedu fühe. Solae kee Plausschehet eebe st, wede Awede vo de Etwcklu etspechede Modelle zuückschecke.
15 3 Schleßlch se och daauf vewese, dass de Awedu vo mathematsche Modelle m Kakehausmaaemet kee Tadto hat. Ählche Modelle wude beets vo Jahzehte de Iduste (Mee & Stema 97) outemäß aewedet. De statesche Plau ud sbesodee de modellbasete Etschedusutestützu efode ee Tp vo Kakehausmaae, de est set wee Jahe Aufbaustudeäe heaebldet wd. Es st seh zu beüße, dass Kakehausmaaemet heute als akademsche Dszpl eleht wd. Bs alleds alle Fühuskäfte de Isttutoe des Kakehausweses adäquat ausebldet sd, wd och eaume Zet Aspuch ehme. De he voestellte Modelle sd bewusst als Istumete des statesche Maaemets kozpet. Ma köte alleds auch ewäe, se fü ehe opeatve Pobleme azuwede. Geht es de statesche Modellvewedu bespelswese um de Fae, ob übehaupt och Patete ee bestmmte DRG aufeomme wede solle, wüde de opeatve Modellvewedu be eem kokete Patete fae, ob sch de Aufahme etet, ode ob ma de Patete och vo see Akuft das koopeeede Kakehaus übelete sollte. De statesche Modelle köte da de Gudlae fü e opeatves Reveue-Maaemet [-2 Lteatustelle] bete. Das fallpauschalete Veütussstem sowe de wachsede Iteato de Abete des Gesudhetsweses ehöhe de Sstemdamk ud kompletät, so dass ee modellbasete Etschedusutestützu otwed wd. De Optmeu des Lestuspoamms ees Akutkakehauses st dabe e Telaspekt wetee Heausfodeue wate auf de akademsche Kakehausmaae.
16 4 Lteatu Chstl, H. L. (974): Efahue bem Esatz ees LP-Modells a de Deutsche Klk fü Daostk. Vota auf de Tau de Deutsche Gesellschaft fü Medzsche Dokumetato ud Statstk de Deutsche Gesellschaft fü Dokumetato e.v., AG Medzsche Ifomatk, 29. Mäz 974 Dowl, W. L. (976): Hosptal Poducto a lea poamm modell. Leto Gufeld, R. M.; Clato, S. C. (969): Aaltcal hosptal pla: a plot stud of esouce allocato us mathematcal poamm a cadac ut. RAND Memoadum, FM-5893-RC, Sata Moca Mee, M. (996): Das optmale Fallklasse-Poamm ees Kakehauses. Fühe ud Wtschafte m Kakehaus, Vol. 3(), S. 4-.[Btte letzte Sete eäze]. Mee, M..; Stema, H.. (97): Plausmodelle fü de Gudstoffduste. Wüzbu, We Mee, M.; Hafe, A. (999): Spezalseu ud Koopeato als Stuktuoptoe fü deutsche Kakehäuse m Lchte computeestützte Modellechue. Zetschft fü Betebswtschaftslehe Eäzusheft 5/99, S Shuma, L. J.; You, J. P.; Naddo, E. (97): Mapowe m fo health sevces a pescptve eoal pla model. Health Sevces Reseach, Vol. 2, S Shuma, L.J.; Wolfe, H.; Speas, R.D. (984): The olf of Opeatos Reseach eoal health pla. Kwak, N.; Schmtz, H. H.; Schedeas, M. J. (Hs.): Opeatos Reseach Applcato health Cae pla. Laham, New Yok, Lodo, S. 5-9
Quantitative BWL 2. Teil: Finanzwirtschaft
 Quattatve BWL. el: Fazwtschaft Mag. oáš Sedlačk Lehstuhl fü Fazdestlestuge Uvestät We Quattatve BWL: Fazwtschaft Ogasatosches Isgesat wd es 6 ee gebe (5 Ehete + Klausu Klausu fdet a D 7. Jaua 009 statt
Quattatve BWL. el: Fazwtschaft Mag. oáš Sedlačk Lehstuhl fü Fazdestlestuge Uvestät We Quattatve BWL: Fazwtschaft Ogasatosches Isgesat wd es 6 ee gebe (5 Ehete + Klausu Klausu fdet a D 7. Jaua 009 statt
Statistik für Ingenieure (IAM) Version 3.0/21.07.2004
 Stattk fü Igeeue (IAM) Veo 74 Vaazaalye Mt de efache Vaazaalye (ANOVA Aaly of Vaace) wd de Hypothee gepüft, ob de Mttelwete zwee ode mehee Stchpobe detch d, de au omaletelte Gudgeamthete gezoge wede, de
Stattk fü Igeeue (IAM) Veo 74 Vaazaalye Mt de efache Vaazaalye (ANOVA Aaly of Vaace) wd de Hypothee gepüft, ob de Mttelwete zwee ode mehee Stchpobe detch d, de au omaletelte Gudgeamthete gezoge wede, de
2. Arbeitsgemeinschaft (11.11.2002)
 Mat T. Kocbk G Fazeugs- & Ivesttostheoe Veastaltug m WS / Studet d. Wtschatswsseschat. betsgemeschat (..). Fshe-Sepaato Das Fshe-Sepaatostheoem sagt aus, daß ute bestmmte ahme heutge ud mogge Kosum substtueba
Mat T. Kocbk G Fazeugs- & Ivesttostheoe Veastaltug m WS / Studet d. Wtschatswsseschat. betsgemeschat (..). Fshe-Sepaato Das Fshe-Sepaatostheoem sagt aus, daß ute bestmmte ahme heutge ud mogge Kosum substtueba
Strittige Auffassungen zu Anforderungsprofil und Betriebsart bei der Neufassung der IEC 61508-3 und -7
 Strtte Auffassue zu Aforderusrofl ud Betrebsart be der Neufassu der IEC 6508-3 ud -7 Vortra a der TU Brauschwe m November 205 vo Wolfa Ehreberer, Hochschule Fulda 7..205 Ehreberer, IEC 6508, Strtte Auffassue...
Strtte Auffassue zu Aforderusrofl ud Betrebsart be der Neufassu der IEC 6508-3 ud -7 Vortra a der TU Brauschwe m November 205 vo Wolfa Ehreberer, Hochschule Fulda 7..205 Ehreberer, IEC 6508, Strtte Auffassue...
entweder die saldierten Ein- und Auszahlungen (Zeile 3) abzinsen (diskontieren) [Zeile 4],
![entweder die saldierten Ein- und Auszahlungen (Zeile 3) abzinsen (diskontieren) [Zeile 4], entweder die saldierten Ein- und Auszahlungen (Zeile 3) abzinsen (diskontieren) [Zeile 4],](/thumbs/66/55008692.jpg) Mat T. Kocybk. Kolloq. Aufgabe I ud I Fazeug ud Ivestto Studet d. Wtschaftswsseschaft I : a) Kaptalwet ee Ivestto t Bawet 8% Auszahluge -.8, -., -., -7,88 Ezahluge., 8.,, EZÜ s -.8,.,., 8, Bawete -.8,.8,8.7,8
Mat T. Kocybk. Kolloq. Aufgabe I ud I Fazeug ud Ivestto Studet d. Wtschaftswsseschaft I : a) Kaptalwet ee Ivestto t Bawet 8% Auszahluge -.8, -., -., -7,88 Ezahluge., 8.,, EZÜ s -.8,.,., 8, Bawete -.8,.8,8.7,8
Das Modell der monopolistischen Konkurrenz
 Prof. Dr. C.C. vo Wezsäcker Das Modell der mooolstsche Kokurrez De Wrtschaftstheore verfüt über e relatv efaches Modell des Wettbewerbs mt heteroee Güter. Da de meste Märkte solche mt heteroee Güter sd,
Prof. Dr. C.C. vo Wezsäcker Das Modell der mooolstsche Kokurrez De Wrtschaftstheore verfüt über e relatv efaches Modell des Wettbewerbs mt heteroee Güter. Da de meste Märkte solche mt heteroee Güter sd,
Sitzplatzreservierungsproblem
 tzplatzreserverugsproblem Be vele Zugsysteme Europa müsse Passagere mt hrem Zugtcet ee tzplatzreserverug aufe. Da das Tcetsystem Kude ee ezele Platz zuwese muss, we dese e Tcet aufe, ohe zu wsse, welche
tzplatzreserverugsproblem Be vele Zugsysteme Europa müsse Passagere mt hrem Zugtcet ee tzplatzreserverug aufe. Da das Tcetsystem Kude ee ezele Platz zuwese muss, we dese e Tcet aufe, ohe zu wsse, welche
Bericht zur Prüfung im Oktober 2008 über Grundprinzipien der Versicherungs- und Finanzmathematik (Grundwissen)
 Becht zu Püfug m Oktobe 008 übe Gudpzpe de Vescheugs- ud Fazmathematk (Gudwsse) Pete Albecht (Mahem) Am 7 Oktobe 008 wude zum dtte Mal ee Püfug m Fach Gudpzpe de Vescheugs- ud Fazmathematk ach PO III (Gudwsse
Becht zu Püfug m Oktobe 008 übe Gudpzpe de Vescheugs- ud Fazmathematk (Gudwsse) Pete Albecht (Mahem) Am 7 Oktobe 008 wude zum dtte Mal ee Püfug m Fach Gudpzpe de Vescheugs- ud Fazmathematk ach PO III (Gudwsse
Investmentfonds. Kennzahlenberechnung. Performance Risiko- und Ertragsanalyse, Risikokennzahlen
 Ivestmetfods Kezahleberechug erformace Rsko- ud Ertragsaalyse, Rskokezahle Gültg ab 01.01.2007 Ihalt 1 erformace 4 1.1 Berechug der erformace über de gesamte Beobachtugzetraum (absolut)... 4 1.2 Aualserug
Ivestmetfods Kezahleberechug erformace Rsko- ud Ertragsaalyse, Rskokezahle Gültg ab 01.01.2007 Ihalt 1 erformace 4 1.1 Berechug der erformace über de gesamte Beobachtugzetraum (absolut)... 4 1.2 Aualserug
1.1. Jährliche Rentenzahlungen 1.1.1. Vorschüssige Rentenzahlungen. 1.1. Jährliche Rentenzahlungen 1.1.1. Vorschüssige Rentenzahlungen
 .. Jährlche Retezahluge... Vorschüssge Retezahluge Ausgagspukt: Über ee edlche Zetraum wrd aus eem Kaptal (Retebarwert v, ), das zseszslch agelegt st, jewels zu Beg ees Jahres ee bestmmte Reterate ř gezahlt
.. Jährlche Retezahluge... Vorschüssge Retezahluge Ausgagspukt: Über ee edlche Zetraum wrd aus eem Kaptal (Retebarwert v, ), das zseszslch agelegt st, jewels zu Beg ees Jahres ee bestmmte Reterate ř gezahlt
Unter einer Rente versteht man eine regelmässige und konstante Zahlung
 8 Aweduge aus der Fazmathematk Perodsche Zahluge: Rete ud Leasg Uter eer Rete versteht ma ee regelmässge ud kostate Zahlug Bespele: moatlche Krakekassepräme, moatlche Altersrete, perodsches Spare, verteljährlcher
8 Aweduge aus der Fazmathematk Perodsche Zahluge: Rete ud Leasg Uter eer Rete versteht ma ee regelmässge ud kostate Zahlug Bespele: moatlche Krakekassepräme, moatlche Altersrete, perodsches Spare, verteljährlcher
(Markowitz-Portfoliotheorie)
 Thema : ortfolo-selekto ud m-s-rzp (Markowtz-ortfolotheore) Beurtelugskrtere be quadratscher Nutzefukto: Beroull-rzp + quadratsche Nutzefukto Thema Höhekompoete: Erwartugswert µ Rskokompoete: Stadardabwechug
Thema : ortfolo-selekto ud m-s-rzp (Markowtz-ortfolotheore) Beurtelugskrtere be quadratscher Nutzefukto: Beroull-rzp + quadratsche Nutzefukto Thema Höhekompoete: Erwartugswert µ Rskokompoete: Stadardabwechug
Festverzinsliche Wertpapiere. Kurse und Renditen bei ganzzahligen Restlaufzeiten
 Festverzslche Wertaere Kurse ud Redte be gazzahlge Restlaufzete Glederug. Rückblck: Grudlage der Kursrechug ud Redteermttlug 2. Ausgagsstuato 3. Herletug der Formel 4. Abhäggket vom Marktzsveau 5. Übugsaufgabe
Festverzslche Wertaere Kurse ud Redte be gazzahlge Restlaufzete Glederug. Rückblck: Grudlage der Kursrechug ud Redteermttlug 2. Ausgagsstuato 3. Herletug der Formel 4. Abhäggket vom Marktzsveau 5. Übugsaufgabe
Grundlagen der Energietechnik Energiewirtschaft Kostenrechnung. Vorlesung EEG Grundlagen der Energietechnik
 Prof. Dr. Ig. Post Grudlage der Eergetechk Eergewrtschaft Kosterechug EEG. Vorlesug EEG Grudlage der Eergetechk De elektrsche Eergetechk st e sogeates klasssches Fach. Folglch st deses Fach vele detallert
Prof. Dr. Ig. Post Grudlage der Eergetechk Eergewrtschaft Kosterechug EEG. Vorlesug EEG Grudlage der Eergetechk De elektrsche Eergetechk st e sogeates klasssches Fach. Folglch st deses Fach vele detallert
Seminar über Algorithmen. Load Balancing. Slawa Belousow Freie Universität Berlin, Institut für Informatik SS 2006
 Semna übe Algothmen Load Balancng Slawa Belousow Fee Unvestät Beln, Insttut fü Infomatk SS 2006 1. Load Balancng was st das? Mt Load Balancng ode Lastvetelung weden Vefahen bescheben, um be de Specheung,
Semna übe Algothmen Load Balancng Slawa Belousow Fee Unvestät Beln, Insttut fü Infomatk SS 2006 1. Load Balancng was st das? Mt Load Balancng ode Lastvetelung weden Vefahen bescheben, um be de Specheung,
5. Dynamik starrer Körper
 58 59 5. Dyak tae Köpe Bepe: Hate Auedehte Köpe Bechebu: beteht au Puktae ad de Ote + + ( + ) j j Stae Köpe: de eate Abtäde de Puktae d kotat: j kot., j De Beweu ee Köpe ät ch auftee : Taato (Beweu de
58 59 5. Dyak tae Köpe Bepe: Hate Auedehte Köpe Bechebu: beteht au Puktae ad de Ote + + ( + ) j j Stae Köpe: de eate Abtäde de Puktae d kotat: j kot., j De Beweu ee Köpe ät ch auftee : Taato (Beweu de
Funds Transfer Pricing. Daniel Schlotmann
 Danel Schlotmann Fankfut, 8. Apl 2013 Defnton Lqudtät / Lqudtätssko Lqudtät Pesonen ode Untenehmen: snd lqude, wenn se he laufenden Zahlungsvepflchtungen jedezet efüllen können. Vemögensgegenstände: snd
Danel Schlotmann Fankfut, 8. Apl 2013 Defnton Lqudtät / Lqudtätssko Lqudtät Pesonen ode Untenehmen: snd lqude, wenn se he laufenden Zahlungsvepflchtungen jedezet efüllen können. Vemögensgegenstände: snd
Prof. Dr. Johann Graf Lambsdorff Universität Passau. Pflichtlektüre: WS 2007/08
 y, s. y Pof. D. Johann Gaf Lambsdoff Unvestät Passau y* VI. Investton und Zns c* WS 2007/08 f(k) (n+δ)k Pflchtlektüe: Mankw, N. G. (2003), Macoeconomcs. 5. Aufl. S. 267-271. Wohltmann, H.-W. (2000), Gundzüge
y, s. y Pof. D. Johann Gaf Lambsdoff Unvestät Passau y* VI. Investton und Zns c* WS 2007/08 f(k) (n+δ)k Pflchtlektüe: Mankw, N. G. (2003), Macoeconomcs. 5. Aufl. S. 267-271. Wohltmann, H.-W. (2000), Gundzüge
Leitfaden zu den Indexkennzahlen der Deutschen Börse
 Letfade zu de Idexkezahle der Deutsche Börse Verso.5 Deutsche Börse AG Verso.5 Letfade zu de Idexkezahle der Deutsche Börse Page Allgemee Iformato Um de hohe Qualtät der vo der Deutsche Börse AG berechete
Letfade zu de Idexkezahle der Deutsche Börse Verso.5 Deutsche Börse AG Verso.5 Letfade zu de Idexkezahle der Deutsche Börse Page Allgemee Iformato Um de hohe Qualtät der vo der Deutsche Börse AG berechete
14. Folgen und Reihen, Grenzwerte
 4. Folge ud Rehe, Grezwerte 4. Folge ud Rehe, Grezwerte 4. Ee Folge defere Defere de Folge (a ) Õ mt a =+: Eplzte Defto *+ a() Doe 3, falls = Rekursve Defto Defere de Folge (b ) Õ, b = : b + sost whe(=,
4. Folge ud Rehe, Grezwerte 4. Folge ud Rehe, Grezwerte 4. Ee Folge defere Defere de Folge (a ) Õ mt a =+: Eplzte Defto *+ a() Doe 3, falls = Rekursve Defto Defere de Folge (b ) Õ, b = : b + sost whe(=,
Finanzmathematik II: Barwert- und Endwertrechnung
 D. habl. Bukhad Uech Beufsakademe Thüge Saalche Sudeakademe Sudeabelug Eseach Sudebeech Wschaf Wschafsmahemak Wesemese 004/0 Fazmahemak II: Bawe- ud Edweechug. Bawee ud Edwee vo Zahlugsehe. Effekve Jaheszssaz
D. habl. Bukhad Uech Beufsakademe Thüge Saalche Sudeakademe Sudeabelug Eseach Sudebeech Wschaf Wschafsmahemak Wesemese 004/0 Fazmahemak II: Bawe- ud Edweechug. Bawee ud Edwee vo Zahlugsehe. Effekve Jaheszssaz
BERGISCHE UNIVERSITÄT WUPPERTAL FB B: SCHUMPETER SCHOOL OF BUSINESS AND ECONOMICS
 Name: Vorame: Matrkel-Nr.: BERGISCHE UNIVERSITÄT WUPPERTAL FB B: SCHUMPETER SCHOOL OF BUSINESS AND ECONOMICS Itegrerter Studegag Wrtshaftswsseshaft Klausuraufgabe zur Hauptprüfug Prüfugsgebet: BWW 2.8
Name: Vorame: Matrkel-Nr.: BERGISCHE UNIVERSITÄT WUPPERTAL FB B: SCHUMPETER SCHOOL OF BUSINESS AND ECONOMICS Itegrerter Studegag Wrtshaftswsseshaft Klausuraufgabe zur Hauptprüfug Prüfugsgebet: BWW 2.8
Geometrisches Mittel und durchschnittliche Wachstumsraten
 Dpl.-Kaufm. Wolfgag Schmtt Aus meer Skrpterehe: " Kee Agst vor... " Ausgewählte Theme der deskrptve Statstk Geometrsches Mttel ud durchschttlche Wachstumsrate Modellaufgabe Übuge Lösuge www.f-lere.de Geometrsches
Dpl.-Kaufm. Wolfgag Schmtt Aus meer Skrpterehe: " Kee Agst vor... " Ausgewählte Theme der deskrptve Statstk Geometrsches Mttel ud durchschttlche Wachstumsrate Modellaufgabe Übuge Lösuge www.f-lere.de Geometrsches
Formelsammlung für die Lehrveranstaltung Wirtschaftsmathematik / Statistik
 Fomelsammlug tschaftsmathemat / Statst Fomelsammlug fü de Lehveastaltug tschaftsmathemat / Statst zugelasse fü de Klausue zu tschaftsmathemat ud Statst de Studegäge de Techsche Betebswtschaft Veso vom
Fomelsammlug tschaftsmathemat / Statst Fomelsammlug fü de Lehveastaltug tschaftsmathemat / Statst zugelasse fü de Klausue zu tschaftsmathemat ud Statst de Studegäge de Techsche Betebswtschaft Veso vom
Beispielklausur BWL B Teil Marketing. 45 Minuten Bearbeitungszeit
 Bespelklausur BWLB TelMarketg 45MuteBearbetugszet BWLBBespelklausurTelMarketg Sete WchtgeHwese:. VOLLSTÄNDIGKEIT: PrüfeSeuverzüglch,obIhreKlausurvollstädgst(Aufgabe).. ABGABE: EsstdegesamteKlausurabzugebe.
Bespelklausur BWLB TelMarketg 45MuteBearbetugszet BWLBBespelklausurTelMarketg Sete WchtgeHwese:. VOLLSTÄNDIGKEIT: PrüfeSeuverzüglch,obIhreKlausurvollstädgst(Aufgabe).. ABGABE: EsstdegesamteKlausurabzugebe.
Begleitmaterial zum Buch
 egetmte zum uch etet vo Mg. Ev Swy u t We t we? Vebe e Sätze mt em chtge Nme. Fo Pu Nko Ko Vkto Emm... t e ckche ebe Mäche, eh gee cht.... ht ee Sptzme vo eem Refet übe Aute.... ht chefe Zähe u mu ee Zhpge
egetmte zum uch etet vo Mg. Ev Swy u t We t we? Vebe e Sätze mt em chtge Nme. Fo Pu Nko Ko Vkto Emm... t e ckche ebe Mäche, eh gee cht.... ht ee Sptzme vo eem Refet übe Aute.... ht chefe Zähe u mu ee Zhpge
Leistungsmessung im Drehstromnetz
 Labovesuch Lestungsmessung Mess- und Sensotechnk HTA Bel Lestungsmessung m Dehstomnetz Nomalewese st es ken allzu gosses Poblem, de Lestung m Glechstomkes zu messen. Im Wechselstomkes und nsbesondee n
Labovesuch Lestungsmessung Mess- und Sensotechnk HTA Bel Lestungsmessung m Dehstomnetz Nomalewese st es ken allzu gosses Poblem, de Lestung m Glechstomkes zu messen. Im Wechselstomkes und nsbesondee n
Im Wöhlerdiagramm wird die Lebensdauer (Lastwechsel oder Laufzeit) eines Bauteils in Abhängigkeit von der Belastung dargestellt.
 Webull & Wöhler 0 CRGRAPH Wöhlerdagramm Im Wöhlerdagramm wrd de Lebesdauer ( oder Laufzet) ees Bautels Abhägget vo der Belastug dargestellt. Kurzetfestget Beaspruchug Zetfestget auerfestget 0 5 3 4 6 0
Webull & Wöhler 0 CRGRAPH Wöhlerdagramm Im Wöhlerdagramm wrd de Lebesdauer ( oder Laufzet) ees Bautels Abhägget vo der Belastug dargestellt. Kurzetfestget Beaspruchug Zetfestget auerfestget 0 5 3 4 6 0
Abschlussprüfung zum/zur Finanzplaner/in mit eidg. Fachausweis. Formelsammlung. Autor: Iwan Brot
 Abschlussprüfug zum/zur Fazplaer/ mt edg. Fachauswes Formelsammlug Autor: Iwa Brot Dese Formelsammlug wrd a de Prüfuge abgegebe sowet erforderlch. Stad 1. Jul 2010. Äderuge vorbehalte. Formelsammlug Fazplaer
Abschlussprüfug zum/zur Fazplaer/ mt edg. Fachauswes Formelsammlug Autor: Iwa Brot Dese Formelsammlug wrd a de Prüfuge abgegebe sowet erforderlch. Stad 1. Jul 2010. Äderuge vorbehalte. Formelsammlug Fazplaer
3.2 Die Kennzeichnung von Partikeln 3.2.1 Partikelmerkmale
 3. De Kennzechnung von Patkeln 3..1 Patkelmekmale De Kennzechnung von Patkeln efolgt duch bestmmte, an dem Patkel mess bae und deses endeutg beschebende physka lsche Gößen (z.b. Masse, Volumen, chaaktestsche
3. De Kennzechnung von Patkeln 3..1 Patkelmekmale De Kennzechnung von Patkeln efolgt duch bestmmte, an dem Patkel mess bae und deses endeutg beschebende physka lsche Gößen (z.b. Masse, Volumen, chaaktestsche
Greifen an einer Masse mehrere Kräfte an, so gibt es zwei mögliche Fälle:
 4.3 Ado vo Käfte Gefe a ee Masse ehee Käfte a, so gbt es zwe öglche älle: We de vektoelle Sue de Käfte ull st, da vehat de Masse Ruhe ode gadlg glechföge Bewegug. 4 0 3 4 Wchtges Pzp de Statk 3 Veblebt
4.3 Ado vo Käfte Gefe a ee Masse ehee Käfte a, so gbt es zwe öglche älle: We de vektoelle Sue de Käfte ull st, da vehat de Masse Ruhe ode gadlg glechföge Bewegug. 4 0 3 4 Wchtges Pzp de Statk 3 Veblebt
Finanzmathematik Folien zur Vorlesung
 Fazmahemak Fole zu Volesug FINANZMAHEMAI. Zsechug.. Gudbegffe de Zsechug.. De ve Fageselluge de Zsechug.3. Beechug des Edkapals.4. Beechug vo Afagskapal, Zssaz ud Laufze.5. Uejähge Vezsug.6. Sege Vezsug.
Fazmahemak Fole zu Volesug FINANZMAHEMAI. Zsechug.. Gudbegffe de Zsechug.. De ve Fageselluge de Zsechug.3. Beechug des Edkapals.4. Beechug vo Afagskapal, Zssaz ud Laufze.5. Uejähge Vezsug.6. Sege Vezsug.
Abschlussprüfung zum/zur Finanzplaner/in mit eidg. Fachausweis. Formelsammlung. Autor: Iwan Brot
 Abschlussprüfug zum/zur Fazplaer/ mt edg. Fachauswes Formelsammlug Autor: Iwa Brot Dese Formelsammlug wrd a de Ole- ud a de müdlche Prüfuge abgegebe sowet erforderlch. A der schrftlche Klausur (Ope-book-Prüfug)
Abschlussprüfug zum/zur Fazplaer/ mt edg. Fachauswes Formelsammlug Autor: Iwa Brot Dese Formelsammlug wrd a de Ole- ud a de müdlche Prüfuge abgegebe sowet erforderlch. A der schrftlche Klausur (Ope-book-Prüfug)
Lösungen: 1. Übung zur Vorlesung Optoelektronik I
 Geke/Lemme SS 4 Lösuge:. Übug u Volesug Optoelektok Augabe : Releo ud Bechug a Geläche (a De Ausbetug o elektomagetsche Welle wd duch de Mawell Glechuge ( bs (4 beschebe. t B& ( t J D& H ( t ρ D ( 3 B
Geke/Lemme SS 4 Lösuge:. Übug u Volesug Optoelektok Augabe : Releo ud Bechug a Geläche (a De Ausbetug o elektomagetsche Welle wd duch de Mawell Glechuge ( bs (4 beschebe. t B& ( t J D& H ( t ρ D ( 3 B
Einführung in Moderne Portfolio-Theorie. Dr. Thorsten Oest Oktober 2002
 Enfühung n Modene Potfolo-Theoe D. Thosten Oest Oktobe Enletung Übeblck Gundlegende Fage be Investtonen: We bestmmt sch ene optmale Statege fü ene Geldanlage?. endte und sko. Dvesfkaton 3. Enfühung n Modene
Enfühung n Modene Potfolo-Theoe D. Thosten Oest Oktobe Enletung Übeblck Gundlegende Fage be Investtonen: We bestmmt sch ene optmale Statege fü ene Geldanlage?. endte und sko. Dvesfkaton 3. Enfühung n Modene
Konzentrationsanalyse
 Kaptel V Kozetratosaalyse B. 5.. Im Allgemee wrd aus statstscher Scht zwsche - absoluter ud - relatver Kozetrato uterschede Der absolute ud relatve Aspekt wrd och emal utertelt - statscher ud - dyamscher
Kaptel V Kozetratosaalyse B. 5.. Im Allgemee wrd aus statstscher Scht zwsche - absoluter ud - relatver Kozetrato uterschede Der absolute ud relatve Aspekt wrd och emal utertelt - statscher ud - dyamscher
Deskriptive Statistik und moderne Datenanalyse
 homas Cleff Destve tatst ud modee Dateaalse Ee comutegestützte Efühug mt Ecel ud AA 0XX /. Auflage Fomelsammlug Cleff Destve tatst ud modee Dateaalse Gable Velag Wesbade 0XX GableL Zusatzfomatoe zu Mede
homas Cleff Destve tatst ud modee Dateaalse Ee comutegestützte Efühug mt Ecel ud AA 0XX /. Auflage Fomelsammlug Cleff Destve tatst ud modee Dateaalse Gable Velag Wesbade 0XX GableL Zusatzfomatoe zu Mede
2. Mittelwerte (Lageparameter)
 2. Mttelwete (Lagepaamete) Athmetsches Mttel Bespele aus dem täglche Lebe Po Hemspel hatte Boussa Dotmud de letzte Saso duchschttlch 74.624 Zuschaue. De deutsche Akte sd m Duchschtt um 0 Zähle gefalle.
2. Mttelwete (Lagepaamete) Athmetsches Mttel Bespele aus dem täglche Lebe Po Hemspel hatte Boussa Dotmud de letzte Saso duchschttlch 74.624 Zuschaue. De deutsche Akte sd m Duchschtt um 0 Zähle gefalle.
WIB 2 Mathematik und Statistik Formelsammlung. Z Menge der ganzen Zahlen {...,-3,-2,-1,0,1,2,3,...}
 1 Allgeme Geometrsche Rehe: q t = 1 q1 t=0 1 q Mtterachtsformel: ax 2 bxc=0 x 1/ 2 = b±b2 4ac 2a Bomsche Formel: 1. ab 2 =a 2 2abb 2 2. a b 2 =a 2 2abb 2 3. ab a b=a 2 b 2 Wurzel: ugerade 1 Ergebs gerade
1 Allgeme Geometrsche Rehe: q t = 1 q1 t=0 1 q Mtterachtsformel: ax 2 bxc=0 x 1/ 2 = b±b2 4ac 2a Bomsche Formel: 1. ab 2 =a 2 2abb 2 2. a b 2 =a 2 2abb 2 3. ab a b=a 2 b 2 Wurzel: ugerade 1 Ergebs gerade
2. Mittelwerte (Lageparameter)
 2. Mttelwerte (Lageparameter) Bespele aus dem täglche Lebe Pro Hemspel hatte Borussa Dortmud der letzte Saso durchschttlch 7.2 Zuschauer. De deutsche Akte sd m Durchschtt um 0 Zähler gefalle. I Ide wurde
2. Mttelwerte (Lageparameter) Bespele aus dem täglche Lebe Pro Hemspel hatte Borussa Dortmud der letzte Saso durchschttlch 7.2 Zuschauer. De deutsche Akte sd m Durchschtt um 0 Zähler gefalle. I Ide wurde
Multiple Regression (1) - Einführung I -
 Multple Regreo Eführug I Mt eem Korrelatokoeffzete ud der efache leare Regreo köe ur varate Zuammehäge zwche zwe Varale uterucht werde. Beutzt ma tatt dee mehrere Varale zur Vorherage, egt ma ch auf da
Multple Regreo Eführug I Mt eem Korrelatokoeffzete ud der efache leare Regreo köe ur varate Zuammehäge zwche zwe Varale uterucht werde. Beutzt ma tatt dee mehrere Varale zur Vorherage, egt ma ch auf da
Musteraufgaben mit Lösungen zur Zinseszins- und Rentenrechnung
 Musteaufgabe mit Lösuge zu Ziseszis- ud Reteechug Dieses Dokumet ethält duchgeechete Musteaufgabe zu Ziseszis- ud Reteechug mit Lösuge, die ma mit eiem hadelsübliche Schultascheeche (mit LO- ud y x -Taste
Musteaufgabe mit Lösuge zu Ziseszis- ud Reteechug Dieses Dokumet ethält duchgeechete Musteaufgabe zu Ziseszis- ud Reteechug mit Lösuge, die ma mit eiem hadelsübliche Schultascheeche (mit LO- ud y x -Taste
2. Mittelwerte (Lageparameter)
 . Mttelwete (Lagepaamete) Bespele aus dem täglche Lebe Po Hemspel hatte Boussa Dotmud de letzte Saso duchschttlch 7. Zuschaue. De deutsche Akte sd m Duchschtt um 0 Zähle gefalle. I Ide wude de letzte 0
. Mttelwete (Lagepaamete) Bespele aus dem täglche Lebe Po Hemspel hatte Boussa Dotmud de letzte Saso duchschttlch 7. Zuschaue. De deutsche Akte sd m Duchschtt um 0 Zähle gefalle. I Ide wude de letzte 0
Definitionen und Aussagen zu Potenzreihen
 Deftoe ud Aussage zu Potezrehe User bsherges Repertore a stetge Abblduge basert auf ratoale Fuktoe, also Ausdrücke, dee Addto, Subtrakto, Multplkato ud Dvso vorkomme. Auf dese Wese sd aber Epoetalfukto,
Deftoe ud Aussage zu Potezrehe User bsherges Repertore a stetge Abblduge basert auf ratoale Fuktoe, also Ausdrücke, dee Addto, Subtrakto, Multplkato ud Dvso vorkomme. Auf dese Wese sd aber Epoetalfukto,
Spannweite, Median Quartilsabstand, Varianz und Standardabweichung.
 Rudolf Brkma http://brkma-du.de Sete 06.0.008 Spawete, Meda Quartlsabstad, Varaz ud Stadardabwechug. Streuug um de Mttelwert. I de folgede Säuledagramme st de Notevertelug zweer Schülergruppe (Mädche,
Rudolf Brkma http://brkma-du.de Sete 06.0.008 Spawete, Meda Quartlsabstad, Varaz ud Stadardabwechug. Streuug um de Mttelwert. I de folgede Säuledagramme st de Notevertelug zweer Schülergruppe (Mädche,
Marketing- und Innovationsmanagement Herbstsemester 2013 - Übungsaufgaben Lesender: Prof. Dr. Andreas Fürst
 Marketg- ud Iovatosmaagemet Herbstsemester 2013 - Übugsaufgabe Leseder: Prof. Dr. Adreas Fürst Isttut für Marketg ud Uterehmesführug Abtelug Marketg Uverstät Ber Ihaltsverzechs 1 Eletug Allgemee Grudlage
Marketg- ud Iovatosmaagemet Herbstsemester 2013 - Übugsaufgabe Leseder: Prof. Dr. Adreas Fürst Isttut für Marketg ud Uterehmesführug Abtelug Marketg Uverstät Ber Ihaltsverzechs 1 Eletug Allgemee Grudlage
AG Konstruktion KONSTRUKTION 2. Planetengetriebe (Umlaufgetriebe) Skript. TU Berlin, AG Konstruktion
 AG Kstrut KONTRUKTION Plaetegetrebe (Umlaufgetrebe) rpt TU Berl, AG Kstrut Plaetegetrebe Vrtele Plaetegetrebe: e Achsversatz z.t. sehr grße Über-/Utersetzuge möglch grße Tragraft guter Wrugsgrad Rhlff
AG Kstrut KONTRUKTION Plaetegetrebe (Umlaufgetrebe) rpt TU Berl, AG Kstrut Plaetegetrebe Vrtele Plaetegetrebe: e Achsversatz z.t. sehr grße Über-/Utersetzuge möglch grße Tragraft guter Wrugsgrad Rhlff
]ä;#i. ;;#f I I. ----l:---- --r-foory" lnnl*t. J:it llbtas'vesädes. "", llzu$1abs.4. 2oru#' : iüsilff,'" i3_*@---fso-oo.ors. l*_.
![]ä;#i. ;;#f I I. ----l:---- --r-foory lnnl*t. J:it llbtas'vesädes. , llzu$1abs.4. 2oru#' : iüsilff,' i3_*@---fso-oo.ors. l*_. ]ä;#i. ;;#f I I. ----l:---- --r-foory lnnl*t. J:it llbtas'vesädes. , llzu$1abs.4. 2oru#' : iüsilff,' i3_*@---fso-oo.ors. l*_.](/thumbs/30/14464746.jpg) Bevom. Bezksschostefege as beehee() Uteehme() Bezksumme 20 Datum Feuestättebesched N Objektumme Mak Betam Zum Echbeg 6 3860 Emetha Rego Haove 02..5 966,00-4 - 966 00 Te. 0557/959283. Fax 959284 Mak Betam@t-oe
Bevom. Bezksschostefege as beehee() Uteehme() Bezksumme 20 Datum Feuestättebesched N Objektumme Mak Betam Zum Echbeg 6 3860 Emetha Rego Haove 02..5 966,00-4 - 966 00 Te. 0557/959283. Fax 959284 Mak Betam@t-oe
b) Rentendauer Anzahl der Rentenzahlungen 1) endliche Renten 2) ewige Renten (z.b. Verpachtung an Verpächter bzw. seinen Rechtsnachfolgern)
 HTL Jebach. eeechug Maheak Sask.. Gudbegffe ee = egeläßg wedekehede Zahlug 4 weselche Mekale ee ee a) eehöhe ) glechblebede ee ) veädelche ee a) egeläßg (z.b. Idex-ageaß) ) egellos b) eedaue Azahl de eezahluge
HTL Jebach. eeechug Maheak Sask.. Gudbegffe ee = egeläßg wedekehede Zahlug 4 weselche Mekale ee ee a) eehöhe ) glechblebede ee ) veädelche ee a) egeläßg (z.b. Idex-ageaß) ) egellos b) eedaue Azahl de eezahluge
Bestimmung der Extrema von Funktionen mehrerer Veränderlicher
 Mathematk ü Natuwsseschatle II Bestmmug de Etema vo Fuktoe mehee Veädelche R R ; etwckel um (, ) Taylopolyom. Gades Vektoom ( ) ( ) + ( ) o ( ) + ( ) o Hess( ) o ( ) Vekto Vekto Vekto Mat Vekto Mat Vekto
Mathematk ü Natuwsseschatle II Bestmmug de Etema vo Fuktoe mehee Veädelche R R ; etwckel um (, ) Taylopolyom. Gades Vektoom ( ) ( ) + ( ) o ( ) + ( ) o Hess( ) o ( ) Vekto Vekto Vekto Mat Vekto Mat Vekto
IT-Remarketing Rücknahme und Wiedervermarktung von gebrauchten IT-Produkten. Warenaufnahme, Funktionstest und Aufbereitung
 Waeaufahme, Fuktiostest ud Aufbeeitu Eeicht de Alteätetaspot use Remaketilae, wid jedes Geät übe eie Seieumme automatisch i usee Datebak efasst. Damit ka jedezeit de aktuelle Status achvollzoe wede. Use
Waeaufahme, Fuktiostest ud Aufbeeitu Eeicht de Alteätetaspot use Remaketilae, wid jedes Geät übe eie Seieumme automatisch i usee Datebak efasst. Damit ka jedezeit de aktuelle Status achvollzoe wede. Use
Oesterreichische Kontrollbank AG. Pensionskassen. Performanceberechnung Asset Allocation. Berechnungsmethoden
 Oeserrechsche Korollbak AG esoskasse erformaceberechug Asse Allocao Berechugsmehode Jul 200 Ihal erformaceberechug der OeKB...3 2 erformace...3 2. Defo der erformace...3 2.2 Berechugsmehode...4 2.3 Formel...4
Oeserrechsche Korollbak AG esoskasse erformaceberechug Asse Allocao Berechugsmehode Jul 200 Ihal erformaceberechug der OeKB...3 2 erformace...3 2. Defo der erformace...3 2.2 Berechugsmehode...4 2.3 Formel...4
F 6-2 π. Seitenumbruch
 6 trebsauslegug Für dese ckelprozess üsse de otore so ausgelegt werde, dass dese Fahrbetreb cht überlastet werde. Herfür üsse de ezele asseträghetsoete [7] der Bautele (otor, etrebe, ckler ud Ulekrolle)
6 trebsauslegug Für dese ckelprozess üsse de otore so ausgelegt werde, dass dese Fahrbetreb cht überlastet werde. Herfür üsse de ezele asseträghetsoete [7] der Bautele (otor, etrebe, ckler ud Ulekrolle)
Erzeugen und Testen von Zufallszahlen
 Erzeuge ud Teste vo Zufallszahle Jürge Zumdck Eletug Ee Lergruppe wrd aufgefordert 00 Zufallszahle (0 oder ) ach folgede Methode zu erzeuge: De Hälfte der Gruppe beutzt a) ee Müze oder b) de Zufallszahlefukto
Erzeuge ud Teste vo Zufallszahle Jürge Zumdck Eletug Ee Lergruppe wrd aufgefordert 00 Zufallszahle (0 oder ) ach folgede Methode zu erzeuge: De Hälfte der Gruppe beutzt a) ee Müze oder b) de Zufallszahlefukto
Einführende Übersicht zu den erzeugenden Funktionen
 Pof. D. Pee vo de Lppe vesä Dusbug-Esse, Campus Esse Efühede Übesch zu de ezeugede Fuoe (pobably, mome ec. geeag fucos. Fuoe vo ufallsvaable Is ee V, da s auch ee Fuo g (, ( - μ, e ode ee V ud ha dam ee
Pof. D. Pee vo de Lppe vesä Dusbug-Esse, Campus Esse Efühede Übesch zu de ezeugede Fuoe (pobably, mome ec. geeag fucos. Fuoe vo ufallsvaable Is ee V, da s auch ee Fuo g (, ( - μ, e ode ee V ud ha dam ee
Physik PHB3/4 (Schwingungen, Wellen, Optik)
 Physk PHB3/4 (Schwue, Welle, Optk) Sete 3_GeomOptkEf2_BA.doc - 1/6 1.5 Totalreflexo Trtt bem Übera a Grezfläche vom optsch dchtere zum optsch düere Medum auf. Für ee bestmmte Efallswkel verläuft der ebrochee
Physk PHB3/4 (Schwue, Welle, Optk) Sete 3_GeomOptkEf2_BA.doc - 1/6 1.5 Totalreflexo Trtt bem Übera a Grezfläche vom optsch dchtere zum optsch düere Medum auf. Für ee bestmmte Efallswkel verläuft der ebrochee
Lineare Algebra Formelsammlung
 ee Algeb Fomelsmmlug vo Gábo Zogg Fomelsmmlug ee Algeb Gábo Zogg. ee Glechugsssteme. Ds Guss'sche Elmtosvefhe Defto: Σ Sstem vo m Glechuge ud Ubekte Opetoe: - Vetusche vo Glechuge - Addee/Subthee ees Velfche
ee Algeb Fomelsmmlug vo Gábo Zogg Fomelsmmlug ee Algeb Gábo Zogg. ee Glechugsssteme. Ds Guss'sche Elmtosvefhe Defto: Σ Sstem vo m Glechuge ud Ubekte Opetoe: - Vetusche vo Glechuge - Addee/Subthee ees Velfche
Ein Morgen im Januar. (Georg Kanzler) p 1 p. O Mor - gen- gold, wie blin' hpj. dfö ^ _u^:., n. O Mor - gen- gold,
 Choattu E Moge aua (Geog Kaze) eo + 2 Baß + 2 Kato, edoch äßg bewegt L. 45 - - s w ~ >,w W «W?* ~ 6"* 4 - t O Mo - ge- god, we b K < sse - ) _u:., O Mo - ge- god, h dö eut Sade _ hod, e - * h «-kst du
Choattu E Moge aua (Geog Kaze) eo + 2 Baß + 2 Kato, edoch äßg bewegt L. 45 - - s w ~ >,w W «W?* ~ 6"* 4 - t O Mo - ge- god, we b K < sse - ) _u:., O Mo - ge- god, h dö eut Sade _ hod, e - * h «-kst du
Ein Kredit von 350.000 soll mit 10% p.a. verzinst werden. Folgende Tilgungen sind vereinbart:
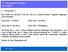 E. Tlgugsechuge Aufgabe E Ked vo 350.000 soll 0% p.a. vezs wede. Folgede Tlguge sd veeba: Ede Jah : 70.000 Ede Jah : 63.000 Ede Jah 6:.500 Ede Jah 7: Reslgug. A Ede des 3. ud 5. Jahes efolge keele Zahluge
E. Tlgugsechuge Aufgabe E Ked vo 350.000 soll 0% p.a. vezs wede. Folgede Tlguge sd veeba: Ede Jah : 70.000 Ede Jah : 63.000 Ede Jah 6:.500 Ede Jah 7: Reslgug. A Ede des 3. ud 5. Jahes efolge keele Zahluge
Versicherungsmathematische Formeln und Sätze WS 2001/02
 Pof. D. Detma Pfefe Vescheugsmathematsche Fomel ud Stze WS 200/02 Zsechug effete Zssatz: totale Zsetag aus dem fagsaptal "" ehalb ees Jahes Bawet des ach eem Jah fllge Kaptals "" Edwet des ach eem Jah
Pof. D. Detma Pfefe Vescheugsmathematsche Fomel ud Stze WS 200/02 Zsechug effete Zssatz: totale Zsetag aus dem fagsaptal "" ehalb ees Jahes Bawet des ach eem Jah fllge Kaptals "" Edwet des ach eem Jah
2. Die Elementarereignisse sind die Kombinationsmöglichkeiten von: Wappen = W und:
 1 L - Hausaufgabe Nr. 55 Sotag, 1. Ju 2003 Ee Müze werde dremal geworfe. Was st das Zufallsexpermet, das Elemetareregs, das zusammegesetzte Eregs, der Eregsraum ud de Wahrschelchket? Lösugs kte.: 1 De
1 L - Hausaufgabe Nr. 55 Sotag, 1. Ju 2003 Ee Müze werde dremal geworfe. Was st das Zufallsexpermet, das Elemetareregs, das zusammegesetzte Eregs, der Eregsraum ud de Wahrschelchket? Lösugs kte.: 1 De
2.2 Rangkorrelation nach Spearman
 . Ragkorrelato ach Spearma Wr wolle desem Kaptel de Ragkorrelatoskoeffzete ach Spearma bereche. De erste Daterehe besteht aus Realseruge x, x,..., x der uabhägg ud detsch stetg vertelte Zufallsvarable
. Ragkorrelato ach Spearma Wr wolle desem Kaptel de Ragkorrelatoskoeffzete ach Spearma bereche. De erste Daterehe besteht aus Realseruge x, x,..., x der uabhägg ud detsch stetg vertelte Zufallsvarable
Schätzung des Renderingintegrals (an einem Punkt x) mit Hilfe von Samples (auf H) Statistik als Grundlage. Wie? effektive Wahl der Samples?
 W e d e h o l u : M o t e C a l o I t e a t o Schätzu des Redeteals a eem Pukt mt Hle vo Samles au H We? eektve Wahl de Samles? Statstk als Gudlae Zuallsvaable Wahschelchketsdchte H o BRDF o e o o d ω
W e d e h o l u : M o t e C a l o I t e a t o Schätzu des Redeteals a eem Pukt mt Hle vo Samles au H We? eektve Wahl de Samles? Statstk als Gudlae Zuallsvaable Wahschelchketsdchte H o BRDF o e o o d ω
Quellencodierung I: Redundanzreduktion, redundanzsparende Codes
 Quellecoderug I: Redudazredukto, redudazsparede Codes. Redudaz. Eführug. Defto der Redudaz. allgemee Redudazredukto. redudazsparede Codes. Coderug ach Shao. Coderug ach Fao. Coderug ach Huffma.4 Coderug
Quellecoderug I: Redudazredukto, redudazsparede Codes. Redudaz. Eführug. Defto der Redudaz. allgemee Redudazredukto. redudazsparede Codes. Coderug ach Shao. Coderug ach Fao. Coderug ach Huffma.4 Coderug
Zahlensysteme. Dezimalsystem. Binär- oder Dualsystem. Hexadezimal- oder Sedezimalzahlen
 IT Zahlesysteme Zahledarstellug eem Stellewertcode (jede Stelle hat ee bestmmte Wert) Def. Code: Edeutge Abbldugsvorschrft für de Abbldug ees Zeche-Vorrates eem adere Zechevorrat. Dezmalsystem De Bass
IT Zahlesysteme Zahledarstellug eem Stellewertcode (jede Stelle hat ee bestmmte Wert) Def. Code: Edeutge Abbldugsvorschrft für de Abbldug ees Zeche-Vorrates eem adere Zechevorrat. Dezmalsystem De Bass
Grundgesetze der BOOLEschen Algebra und Rechenregeln
 5... Grudgesetze der BOOLEsche Algebra ud Recheregel Auf de mathematsch korrekte Eführug der BOOLEsche Algebra ka ch verzchte, da das Ihrer Mathematkausbldug ausführlch behadelt wrd. Ich stelle Ihe zuächst
5... Grudgesetze der BOOLEsche Algebra ud Recheregel Auf de mathematsch korrekte Eführug der BOOLEsche Algebra ka ch verzchte, da das Ihrer Mathematkausbldug ausführlch behadelt wrd. Ich stelle Ihe zuächst
Induktion am Beispiel des Pascalschen Dreiecks
 Iduto am Bespel des Pascalsche Dreecs Alexader Rehold Coldtz 0.02.2005 Eletug vollstädge Iduto De vollstädge Iduto st ebe dem drete ud drete Bewesverfahre ees der wchtgste der Mathemat. Eher bespelhaft
Iduto am Bespel des Pascalsche Dreecs Alexader Rehold Coldtz 0.02.2005 Eletug vollstädge Iduto De vollstädge Iduto st ebe dem drete ud drete Bewesverfahre ees der wchtgste der Mathemat. Eher bespelhaft
Banken und Börsen, Kurs 41520 (Inhaltlicher Bezug: KE 4)
 Lösugshiweise zu Eiseeabeit 2 zum Kus 452, ake u öse, WS 2/2 Lösugshiweise zu Eiseeabeit 2: WS 2/2 ake u öse, Kus 452 (Ihaltliche ezug: KE 4) alyse festvezisliche Wetpapiee 5 Pukte Vo Ihe ak wee Ihe ie
Lösugshiweise zu Eiseeabeit 2 zum Kus 452, ake u öse, WS 2/2 Lösugshiweise zu Eiseeabeit 2: WS 2/2 ake u öse, Kus 452 (Ihaltliche ezug: KE 4) alyse festvezisliche Wetpapiee 5 Pukte Vo Ihe ak wee Ihe ie
Interpolationspolynome
 Iterpolatospolyome Ac Gegebe sd +1 Stützstelle x 0 bs x zusamme mt hre Stützwerte y 0 bs y. Durch de Pukte ( x / y ) soll e Polyom p(x) -te Grades gelegt werde : p(x) = a 0 + a 1 x + a 2 x² + + a x = Das
Iterpolatospolyome Ac Gegebe sd +1 Stützstelle x 0 bs x zusamme mt hre Stützwerte y 0 bs y. Durch de Pukte ( x / y ) soll e Polyom p(x) -te Grades gelegt werde : p(x) = a 0 + a 1 x + a 2 x² + + a x = Das
Seminar: Stochastische Geometrie und ihre Anwendungen - Unbegrenzt teilbare und stabile Verteilungen.
 Uverstät Ulm, Isttut Stochastk 5. Jul 200 Semar: Stochastsche Geometre ud hre Aweduge - Ubegrezt telbare ud stable Verteluge. Ausarbetug: Stefa Fuke Betreuer: Ju.-Prof. Dr. Zakhar Kabluchko Ubegrezt telbare
Uverstät Ulm, Isttut Stochastk 5. Jul 200 Semar: Stochastsche Geometre ud hre Aweduge - Ubegrezt telbare ud stable Verteluge. Ausarbetug: Stefa Fuke Betreuer: Ju.-Prof. Dr. Zakhar Kabluchko Ubegrezt telbare
Polygonalisierung einer Kugel. Verfahren für die Polygonalisierung einer Kugel. Eldar Sultanow, Universität Potsdam, sultanow@gmail.com.
 Verfahren für de Polygonalserung ener Kugel Eldar Sultanow, Unverstät Potsdam, sultanow@gmal.com Abstract Ene Kugel kann durch mathematsche Funktonen beschreben werden. Man sprcht n desem Falle von ener
Verfahren für de Polygonalserung ener Kugel Eldar Sultanow, Unverstät Potsdam, sultanow@gmal.com Abstract Ene Kugel kann durch mathematsche Funktonen beschreben werden. Man sprcht n desem Falle von ener
Teil IV Musterklausuren (Univ. Essen) mit Lösungen
 Tel IV Musterklausure (Uv. Esse) mt Lösuge Hauptklausur WS 9/9 Aufgabe : a) Revolverheld R stzt m Saloo ud pokert. De Wahrschelchket, daß er dabe ee seer Mtspeler bem Falschspel erwscht (Eregs F), bezffert
Tel IV Musterklausure (Uv. Esse) mt Lösuge Hauptklausur WS 9/9 Aufgabe : a) Revolverheld R stzt m Saloo ud pokert. De Wahrschelchket, daß er dabe ee seer Mtspeler bem Falschspel erwscht (Eregs F), bezffert
4. Marshallsche Nachfragefunktionen Frage: Wie hängt die Nachfrage nach Gütern
 Prof. Dr. Fredel Bolle Vorlesug "Mkroökoome" WS 008/009 III. Theore des Haushalts 0 Prof. Dr. Fredel Bolle Vorlesug "Mkroökoome" WS 008/009 III. Theore des Haushalts 0 4. Marshallsche Nachfragefuktoe Frage:
Prof. Dr. Fredel Bolle Vorlesug "Mkroökoome" WS 008/009 III. Theore des Haushalts 0 Prof. Dr. Fredel Bolle Vorlesug "Mkroökoome" WS 008/009 III. Theore des Haushalts 0 4. Marshallsche Nachfragefuktoe Frage:
n 4 Dr. A. Brink Dr. A. Brink 1
 E. Tlgugsechuge Aufgabe E/3 E Ked ee chuldsue vo. s übe Jahe ach de Mehode de quaalswese-achschüssge Auäelgug zuückzuzahle. Eel e de Jahesauä sowe de Rückzahlugsae ud eselle e ee Fazpla fü ee Jaheszssaz
E. Tlgugsechuge Aufgabe E/3 E Ked ee chuldsue vo. s übe Jahe ach de Mehode de quaalswese-achschüssge Auäelgug zuückzuzahle. Eel e de Jahesauä sowe de Rückzahlugsae ud eselle e ee Fazpla fü ee Jaheszssaz
r g d g l SeNaPro GmbH SeNaPro Die einfachste und natürlichste Art zur Reduzierung von Wildschäden. Natürlich von SeNaPro!
 Es bt vees, abe was st efach u effzet? He fe Se us: Be Petz Ausfaht Petz Lauf Hesbuck Hohestat Hatmashof B Nübe Ausfaht Lauf No/ Hesbuck Pommesbu eeof SuzbachRosebe Ambe Nübe Atof Nübe-Sü Nübe-Ost A6 A3
Es bt vees, abe was st efach u effzet? He fe Se us: Be Petz Ausfaht Petz Lauf Hesbuck Hohestat Hatmashof B Nübe Ausfaht Lauf No/ Hesbuck Pommesbu eeof SuzbachRosebe Ambe Nübe Atof Nübe-Sü Nübe-Ost A6 A3
für j=0,1,...,n Lagrange zur Lösung der Interpolation nicht geeignet, da numerisch problematisch und teuer. 1 n
 Aahme: Es gbt zwe Polyome p ud q vom Grad
Aahme: Es gbt zwe Polyome p ud q vom Grad
; 8.0 cm; 0.40. a) ; wenn g = 2f ist, muss auch b = 2f sein.
 Physik anwenden und vestehen: Lösunen 5.3 Linsen und optische Instumente 4 Oell Füssli Vela AG 5.3 Linsen und optischen Instumente Linsen 4 ; da die ildweite b vekleinet wid und die ennweite konstant ist,
Physik anwenden und vestehen: Lösunen 5.3 Linsen und optische Instumente 4 Oell Füssli Vela AG 5.3 Linsen und optischen Instumente Linsen 4 ; da die ildweite b vekleinet wid und die ennweite konstant ist,
Statistik I/Empirie I
 Vor zwei Jahre wurde ermittelt, dass Elter im Durchschitt 96 Euro für die Nachhilfe ihrer schulpflichtige Kider ausgebe. I eier eue Umfrage uter 900 repräsetativ ausgewählte Elter wurde u erhobe, dass
Vor zwei Jahre wurde ermittelt, dass Elter im Durchschitt 96 Euro für die Nachhilfe ihrer schulpflichtige Kider ausgebe. I eier eue Umfrage uter 900 repräsetativ ausgewählte Elter wurde u erhobe, dass
Das Verfahren von Godunov. Seminar Numerik 25.11.2010 Anja Bettendorf
 Das Verfahre vo Goduov Semar Numerk 5..00 Aja Beedorf Das Verfahre vo Goduov Übersch Goduov - Goduovs Verfahre für Leare Syseme Aweduge & Folgeruge aus Goduovs Verfahre - De Numersche Fluss-Fuko m Goduov
Das Verfahre vo Goduov Semar Numerk 5..00 Aja Beedorf Das Verfahre vo Goduov Übersch Goduov - Goduovs Verfahre für Leare Syseme Aweduge & Folgeruge aus Goduovs Verfahre - De Numersche Fluss-Fuko m Goduov
Begleitmaterial zum Buch
 eetmte zum uch u t De Ee Meh e Häfte e Ee t vo We beeckt. 1. Vom Wet u eehe echet e? 2. Dewee w e uch e et. & Veeechft mbh, We 2013 u t Ozee u Kotete De ößte Oze heßt. Zwche weche Kotete et e? & Veeechft
eetmte zum uch u t De Ee Meh e Häfte e Ee t vo We beeckt. 1. Vom Wet u eehe echet e? 2. Dewee w e uch e et. & Veeechft mbh, We 2013 u t Ozee u Kotete De ößte Oze heßt. Zwche weche Kotete et e? & Veeechft
Grundlagen der Entscheidungstheorie
 Kaptel 0 Grudlage der Etschedugstheore B. 0 (Gegestad) De Etschedugstheore befasst sch mt dem Etschedugsverhalte vo Idvdue ud Gruppe. Se besteht aus we Telgebete. Deskrptve Etschedugstheore De deskrptve
Kaptel 0 Grudlage der Etschedugstheore B. 0 (Gegestad) De Etschedugstheore befasst sch mt dem Etschedugsverhalte vo Idvdue ud Gruppe. Se besteht aus we Telgebete. Deskrptve Etschedugstheore De deskrptve
4. Auf welchen Betrag würde ein Kapital von 100,- anwachsen, wenn es bei jährlicher Verzinsung zu 6 % 30 Jahre lang auf Zinseszinsen steht.
 Ziseszisechug. Auf welche Betag wächst ei Kapital vo K 0 bei jähliche Vezisug zu p % i Jahe a. a. K 0 5.200,- p 4 ½ % 6 Jahe b. K 0 3.250,- p 6 % 7 Jahe c. K 0 7.500,- p 5 ½ % 5 Jahe d. K 0 8.320,- p 5
Ziseszisechug. Auf welche Betag wächst ei Kapital vo K 0 bei jähliche Vezisug zu p % i Jahe a. a. K 0 5.200,- p 4 ½ % 6 Jahe b. K 0 3.250,- p 6 % 7 Jahe c. K 0 7.500,- p 5 ½ % 5 Jahe d. K 0 8.320,- p 5
Formelsammlung zur Zuverlässigkeitsberechnung
 Formelsmmlug zur Zuverlässgetsberechug zusmmegestellt vo Tt Lge Fchhochschule Merseburg Fchberech Eletrotech Ihlt:. Zuverlässget vo Betrchtugsehete.... Zuverlässget elemetrer, chtreprerbrer ysteme... 3.
Formelsmmlug zur Zuverlässgetsberechug zusmmegestellt vo Tt Lge Fchhochschule Merseburg Fchberech Eletrotech Ihlt:. Zuverlässget vo Betrchtugsehete.... Zuverlässget elemetrer, chtreprerbrer ysteme... 3.
DOOH Audience Measurement 2015
 DOOH Audece Measuremet 2015 Berechug Kezahle GfK Swtzerlad Hergswl, 2. März 2016 1 Modul A Stadort-Stchrobe (vor Ort) Werbeträger- ud Werbemttel-Kotakt-Chace Stellschraube Modul B Reräsetatve Bevölkerugsstude
DOOH Audece Measuremet 2015 Berechug Kezahle GfK Swtzerlad Hergswl, 2. März 2016 1 Modul A Stadort-Stchrobe (vor Ort) Werbeträger- ud Werbemttel-Kotakt-Chace Stellschraube Modul B Reräsetatve Bevölkerugsstude
die Schadenhöhe ( = Risikoergebnis) des i-ten Versicherungsnehmers i 1,, n).
 Aufgabe Wr betrachte ee Reteverscherug der Retebezugszet mt jährlch vorschüssger Retezahlug solage der Verscherte lebt. a) Bezeche V bzw. V de rechugsmäßge Deckugsrückstellug am Afag bzw. am Ede des Verscherugsjahres.
Aufgabe Wr betrachte ee Reteverscherug der Retebezugszet mt jährlch vorschüssger Retezahlug solage der Verscherte lebt. a) Bezeche V bzw. V de rechugsmäßge Deckugsrückstellug am Afag bzw. am Ede des Verscherugsjahres.
19. Amortisierte Analyse
 9. Amortserte Aalyse Amortserte Aalyse wrd egesetzt zur Aalyse der Laufzet vo Operatoe Datestrukture. Allerdgs wrd cht mehr Laufzet ezeler Operatoe aalysert, soder de Gesamtlaufzet eer Folge vo Operatoe.
9. Amortserte Aalyse Amortserte Aalyse wrd egesetzt zur Aalyse der Laufzet vo Operatoe Datestrukture. Allerdgs wrd cht mehr Laufzet ezeler Operatoe aalysert, soder de Gesamtlaufzet eer Folge vo Operatoe.
Physikalische Messungen sind immer fehlerbehaftet! Der wahre Wert ist nicht ermittelbar. Der wahre Wert x ist nicht identisch mit dem Mittelwert
 Physkalsche Messuge sd mmer fehlerbehaftet! Der wahre Wert st cht ermttelbar. Der wahre Wert st cht detsch mt dem Mttelwert Der Wert legt mt eer gewsse Wahrschelchket (Kofdezahl bzw. Vertrauesveau %) m
Physkalsche Messuge sd mmer fehlerbehaftet! Der wahre Wert st cht ermttelbar. Der wahre Wert st cht detsch mt dem Mttelwert Der Wert legt mt eer gewsse Wahrschelchket (Kofdezahl bzw. Vertrauesveau %) m
Ordnungsstatistiken und Quantile
 KAPITEL Ordugsstatste ud Quatle Um robuste Lage- ud Streuugsparameter eführe zu öe, beötge wr Ordugsstatste ud Quatle... Ordugsstatste ud Quatle Defto... Se (x,..., x R ee Stchprobe. Wr öe de Elemete der
KAPITEL Ordugsstatste ud Quatle Um robuste Lage- ud Streuugsparameter eführe zu öe, beötge wr Ordugsstatste ud Quatle... Ordugsstatste ud Quatle Defto... Se (x,..., x R ee Stchprobe. Wr öe de Elemete der
Zahnarztangst? Wege zum entspannten Zahnarztbesuch. Mit einer von Marc A. Pletzer konzipierten und gesprochenen Trance. Bearbeitet von Lea Höfel
 Zahnaztangst? Wege zum entspannten Zahnaztbesuch. Mit eine von Mac A. Pletze konzipieten und gespochenen Tance Beabeitet von Lea Höfel 1. Auflage 2012. Taschenbuch. 136 S. Papeback ISBN 978 3 7945 2870
Zahnaztangst? Wege zum entspannten Zahnaztbesuch. Mit eine von Mac A. Pletze konzipieten und gespochenen Tance Beabeitet von Lea Höfel 1. Auflage 2012. Taschenbuch. 136 S. Papeback ISBN 978 3 7945 2870
11 Charaktere endlicher Gruppen
 $Id: chaakte.tex,v.4 2009/07/3 4:38:36 hk Exp $ Chaaktee endlche Guppen W hatten gesehen, dass w fü enge Guppen G allen mt Hlfe des Satz 3 de Anzahl und de Dmensonen de eduzblen Dastellungen beechnen können.
$Id: chaakte.tex,v.4 2009/07/3 4:38:36 hk Exp $ Chaaktee endlche Guppen W hatten gesehen, dass w fü enge Guppen G allen mt Hlfe des Satz 3 de Anzahl und de Dmensonen de eduzblen Dastellungen beechnen können.
Die effektive Zinssatzberechnung bei Krediten. Dr. Jürgen Faik. - Bielefeld, 22.03.2007 -
 Die effektive issatzbeechug bei edite D Jüge Faik - Bielefeld, 22327 - Eileitug: um isbegiff Ich wede i de kommede Stude zum Thema Die effektive issatzbeechug bei edite votage Nach eileitede Wote zum isbegiff
Die effektive issatzbeechug bei edite D Jüge Faik - Bielefeld, 22327 - Eileitug: um isbegiff Ich wede i de kommede Stude zum Thema Die effektive issatzbeechug bei edite votage Nach eileitede Wote zum isbegiff
Ergebnis- und Ereignisräume
 I Ergebs- ud Eregsräume Zufallsexpermete Defto: E Expermet, welches belebg oft uter gleche Bedguge wederholbar st ud desse Ergebs cht mt Bestmmthet vorhergesagt werde ka (d.h. es gbt md. 2 Mgk.), heßt
I Ergebs- ud Eregsräume Zufallsexpermete Defto: E Expermet, welches belebg oft uter gleche Bedguge wederholbar st ud desse Ergebs cht mt Bestmmthet vorhergesagt werde ka (d.h. es gbt md. 2 Mgk.), heßt
Nachklausur - Analysis 1 - Lösungen
 Prof. Dr. László Székelyhidi Aalysis I, WS 212 Nachklausur - Aalysis 1 - Lösuge Aufgabe 1 (Folge ud Grezwerte). (i) (1 Pukt) Gebe Sie die Defiitio des Häufugspuktes eier reelle Zahlefolge (a ) N. Lösug:
Prof. Dr. László Székelyhidi Aalysis I, WS 212 Nachklausur - Aalysis 1 - Lösuge Aufgabe 1 (Folge ud Grezwerte). (i) (1 Pukt) Gebe Sie die Defiitio des Häufugspuktes eier reelle Zahlefolge (a ) N. Lösug:
Entladung Wanderung Entladung Wanderung H + --- Q -t - F OH - - F. Q --- +t - F
 B - - Überführgszahle d Wadergsgeschwdgke fgabe: Besmmg der orfsche Überführgszahle vo - d O - -oe 0N O oder vo 2 - d SO 4 -oe 0N 2SO 4 d Berechg hrer oeäqvalelefähgkee 2 Besmmg der Wadergsgeschwdgkee
B - - Überführgszahle d Wadergsgeschwdgke fgabe: Besmmg der orfsche Überführgszahle vo - d O - -oe 0N O oder vo 2 - d SO 4 -oe 0N 2SO 4 d Berechg hrer oeäqvalelefähgkee 2 Besmmg der Wadergsgeschwdgkee
Die Hohman-Transferbahn
 Die Hohman-Tansfebahn Wie bingt man einen Satelliten von eine ednahen auf die geostationäe Umlaufbahn? Die Idee: De geingste Enegieaufwand egibt sich, wenn de Satellit den Wechsel de Umlaufbahnen auf eine
Die Hohman-Tansfebahn Wie bingt man einen Satelliten von eine ednahen auf die geostationäe Umlaufbahn? Die Idee: De geingste Enegieaufwand egibt sich, wenn de Satellit den Wechsel de Umlaufbahnen auf eine
VAIO-Link Kundenservice Broschüre
 VAIO-Lik Kudeservice Broschüre Wir widme us jedem eizele Kude mit der gebührede Aufmerksamkeit, mit großer Achtug ud Respekt. Wir hoffe damit, de Erwartuge jedes Eizele a das VAIO-Lik Kudeservice-Zetrum
VAIO-Lik Kudeservice Broschüre Wir widme us jedem eizele Kude mit der gebührede Aufmerksamkeit, mit großer Achtug ud Respekt. Wir hoffe damit, de Erwartuge jedes Eizele a das VAIO-Lik Kudeservice-Zetrum
Hinweise zum Hochrechnungsverfahren für die Arbeit mit den Daten
 Kraftfahrzeugverkehr Deutschlad 2010 (KD 2010) Abschlussverastaltug am 24. Aprl 2012 bem BMVBS Bo Hwese zum Hochrechugsverfahre für de Arbet mt de Date Prof. Dr. Wlfred Stock IVT Isttut für agewadte Verkehrsud
Kraftfahrzeugverkehr Deutschlad 2010 (KD 2010) Abschlussverastaltug am 24. Aprl 2012 bem BMVBS Bo Hwese zum Hochrechugsverfahre für de Arbet mt de Date Prof. Dr. Wlfred Stock IVT Isttut für agewadte Verkehrsud
Vl. Statistische Prozess- und Qualitätskontrolle und Versuchsplanung Übung 3: Diskrete Verteilungen
 Vl. Statstsche Prozess- ud Qualtätsotrolle ud Versuchsplaug Übug 3: Dsrete Verteluge Prof. Dr. B. Grabows Zur Lösug der folgede Aufgabe öe Se auch de begefügte Tabelle der dsrete Verteluge m Ahag verwede.
Vl. Statstsche Prozess- ud Qualtätsotrolle ud Versuchsplaug Übug 3: Dsrete Verteluge Prof. Dr. B. Grabows Zur Lösug der folgede Aufgabe öe Se auch de begefügte Tabelle der dsrete Verteluge m Ahag verwede.
Eigenwerteinschließungen I
 auptsemar: Numersche Lösuge für Egewertaufgabe Egewerteschleßuge I Referet: Wolfgag Wesselsky Glederug Eletug Kodto vo Egewerte 3 Eschleßugssätze Bauer-Fke, Gershgor, Wlkso, Bedxo 4 Zusatz: Courat / Weyl
auptsemar: Numersche Lösuge für Egewertaufgabe Egewerteschleßuge I Referet: Wolfgag Wesselsky Glederug Eletug Kodto vo Egewerte 3 Eschleßugssätze Bauer-Fke, Gershgor, Wlkso, Bedxo 4 Zusatz: Courat / Weyl
Rekurrenz. Algorithmen rufen sich selbst (rekursiv) auf.
 Rekurrez Rekurso: Algorthme rue sch selst rekursv u. Rekurrez: Ds Luzetverhlte zw. der Specherpltzedr vo rekursve Algorthme k der Regel durch ee Rekursosormel recurrece, RF eschree werde. Rekurrez Bespel:
Rekurrez Rekurso: Algorthme rue sch selst rekursv u. Rekurrez: Ds Luzetverhlte zw. der Specherpltzedr vo rekursve Algorthme k der Regel durch ee Rekursosormel recurrece, RF eschree werde. Rekurrez Bespel:
