3. Unterrichtsvorhaben in der Q2-Phase Stetige Zufallsgrößen - Normalverteilung
|
|
|
- Tomas Böhme
- vor 6 Jahren
- Abrufe
Transkript
1 3. Unterrichtsvorhen in der Q2-Phse Stetige Zufllsgrößen - Normlverteilung φ μ,σ (x) = σ 2π e H (μ/ σ 2π ) 2 (x μ σ )2 W (μ ± σ/ σ 2π e 2) Jörn Meyer joernmeyer@we.de
2 Inhltsverzeichnis Stetige Zufllsgrößen Integrle esuchen die Stochstik Guß sche Glockenfunktion und Normlverteilung Kontrollufgen... 6 Lösungen... 9
3 2 Stetige Zufllsgrößen Integrle esuchen die Stochstik Einführungsufge (Mnipuliertes Glücksrd ) ) Ein Glücksrd wird gedreht. Als Ergenis knn ein Winkel zwischen und 2 gedreht werden (vgl. folgende Aildung). Der Winkel,5 knn lso genuso gedreht werden wie der Winkel 3 =, 3 oder 2. Wie hoch er die Whrscheinlichkeit, eines dieser drei Ergenisse zu drehen? Begründe Deine Antwort. ) Es wird nun ein mnipuliertes Glücksrd mittels eines Computerprogrmms simuliert. Dei wird gezählt, wie oft ein Winkelergenis in einem estimmten Winkelereich erscheint. Für eine Unterteilung des Winkelereichs [; 2π] in gleich große Intervlle [; π], 5 [ π; 2 π], 5 5 [9 π; 2π] 5 erhält mn zum Beispiel folgendes Drstellung der reltiven Häufigkeiten für diese Bereiche. 6% 5% 8% 9% % % 8% 8% 9% 7% [; π] 5 [9 π; 2π] 5 Gi die reltive Häufigkeiten für den Winkelereich [ 7 π; 8 π], 5 5 [2 π; π] und [; 2π] n. 5 Idee von Michel Rüsing (Essen)
4 3 c) Alterntiv können die Ergenisse uch mit der sogennnten Dichtefunktion ngezeigt werden. Dei werden die reltive Häufigkeiten von oen durch die Länge der zehn gleichgroßen Intervlle dividiert (in unserem Fll durch π). Mn erhält so einen Grfen einer Funktion mit folgender 5 Drstellung: 6% 5 π,25 5% 5 π,24 f(x) ቂ Reltive Häufigkeit Winkelereich ቃ π 2 2π 5 5 π Schon nch Versuchen erkennt mn, dss der nfängliche Winkelereich is 2 5 π deutlich üerrepräsentiert ist. Winkelereich x () Vervollständige mithilfe des reltiven Häufigkeiten des vorherigen Säulendigrmms in der oigen Grfik die Achseneintrgungen und die gestrichelten Linien. (2) Gi die Bedeutung des Flächeninhlts unterhl des Grfen der Dichtefunktion und der x- Achse üer dem Intervll [; 2π] n. (3) Ermittle den Flächeninhlt zwischen Dichtefunktion und x-achse üer dem Intervll [; 2π]. d) Die Anzhl der Versuche wird nun erhöht. Die Intervlllänge zur Dichtefunktion wird uf 5 π verkleinert. Auf der nächsten Seite wird ds Ergenis für Versuche ngezeigt. () Begründe, wrum die Dichtefunktion ei Versuchen sttt der reltiven Häufigkeiten die Whrscheinlichkeiten für ds Eintreten estimmter Winkelereiche repräsentiert. (2) Bestimme die Funktionsgleichung der Dichtefunktion. Erläutere Dein Vorgehen. [Tipp: Der Flächeninhlt zwischen Grf der Dichtefunktion und x-achse üer dem Intervll [; 2π] eträgt.] (3) Interpretiere ds Ergenis des Zufllsexperiments ei Wiederholungen im oigen Schkontext.
5 4 f(x) ቂ Whrscheinlichkeit ቃ Winkelereich 45 % der lngen gestrichelten Linie 5 5 π 2π Winkelereich x Zur Lösung der nchfolgenden Aufgen enötigt mn einige Definitionen: () Eine Funktion f heißt Whrscheinlichkeitsdichte ( zw. Dichtefunktion) üer einem Intervll I = [; ], wenn gilt: () f(x) für lle x us I und (2) f(x) dx =. (2) Eine reellwertige Zufllsgröße X mit Werten im Intervll I heißt stetig verteilt mit der Whrscheinlichkeitsdichte f, wenn für lle c < d us I gilt: P(c X d) = f(x) dx (3) Anlog zur Definition im diskreten Fll z. B. ei Binomilverteilungen lässt sich festlegen: Für eine stetig verteilte Zufllsgröße X mit Werten zwischen und und der Dichtefunktion f gilt: Erwrtungswert: μ = E(X) = x f(x) dx Vrinz: V(X) = s²(x) = [(x μ) 2 f(x) ]dx Stndrdweichung: σ = s(x) = s²(x) = [(x μ) 2 f(x)] dx d c Aufge (Mnipuliertes Glücksrd 2) Gegeen ist die Dichtefunktion eines Glücksrds. Dei sind die Funktionswerte m Anfng doppelt so hoch wie m Ende. Die rechts efindliche Grfik eschreit den Grfen der Dichtefunktion f. ) Bestimme die Funktionsgleichung von f. ) Berechne die Whrscheinlichkeiten dfür, dss ds Glücksrd im ngegeenen Winkelereich stoppt: (i) [; ] (ii) [,5; 2,5] (iii) [3; 4]. 3 4 π 2π
6 5 Aufge 2 (Glückspiel), flls x,2 flls < x < 3 Durch die Funktion f mit f(x) = { ist im Intervll [; 6] eine Funktion gegeen.,3 flls 3 x 4, flls 4 < x 6 ) Skizziere den Funktionsgrfen. ) Weise nch, dss es sich um eine Dichtefunktion hndelt. c) Bestimme die Whrscheinlichkeit für ein Ergenis im Intervll [2; 5]. d) Ein Glücksspiel werde durch diese Dichtefunktion eschrieen. Der Spieler zhlt einen Einstz von. Flls ds Ergenis zwischen und 3 liegt, ekommt er 3 usgezhlt. Sollte der Spieler ds Spiel kzeptieren? Begründe Deine Antwort. e) Untersuche, ei welchem Gewinn ds Spiel us Teil d) fir wäre. Aufge 3 (Nicht mnipuliertes Glücksrd) Bestimme die Gleichung der Dichtefunktion für ein nicht mnipuliertes Glücksrd. Aufge 4 (Herstellung von Metllstiften) Eine Mschine stellt Metllstifte her, die zur Verindung zweier Buteile dienen. Die Produktion ist nicht so perfekt, dss lle Stifte vollkommen gleich usfllen. Deshl ist der Durchmesser X (in mm) der Metllstifte eine Zufllsgröße, von der wir nnehmen, dss sie die Verteilung mit der Dichte f ht: für x < 9 f(x) = { (x 9) (x ) für 9 x für x > ) Bestimme den Wert für die Konstnte R, so dss f die eiden Bedingungen für eine Whrscheinlichkeitsdichte erfüllt. ) Stelle die Dichte f grfisch dr. c) Ermittle den Erwrtungswert µ und die Stndrdweichung σ der Zufllsgröße X. d) Metllstifte, die mehr ls,6 mm von mm weichen, sind Ausschuss. Berechne die Whrscheinlichkeit, mit der ein Stift Ausschuss ist. Stelle die Whrscheinlichkeit in Deiner Aildung us Teil () dr. e) Bestimme eine Aweichungsgrenze x, so dss die Whrscheinlichkeit für den Ausschuss nicht größer ls, wird. Aufge 5 (Gnzrtionle Dichtefunktion) Gegeen ist im Intervll [; 2] eine Funktion gnzrtionle Funktion f dritten Grdes durch die Gleichung f(x) = k x x 2 x +,2. Bestimme k so, dss es sich um eine Dichtefunktion hndelt.
7 6 Aufge 6 (Dichtefunktion und Steckriefufge) ) Gegeen ist im Intervll [; 5] der Grf einer gnzrtionlen Funktion dritten Grdes (Bild rechts). Dei gelten folgende Bedingungen: () Der Funktionswert ei x = ist dreiml so groß wie ei x = 5. (2) An den Stellen und 5 ist die Steigung Null. (3) Es hndelt sich um eine Dichtefunktion. Bestimme eine Gleichung für die Funktion f. ) Berechne die Whrscheinlichkeit für ein Ergenis im Intervll [2; 3]. Aufge 7 (Duer von Telefonten) Die Duer X (in min) von Telefonten in einer Firm wird für x (x R) durch die Whrscheinlichkeitsdichte f mit f(x) = e x eschrieen. ) Begründe: f ist üer R + eine Whrscheinlichkeitsdichte. ) Berechne und deute P( < X < 2). c) Berechne den Erwrtungswert µ und die Stndrdweichung σ. d) Wie whrscheinlich ist es, dss ein Gespräch genu eine Minute duert, wenn mn die Gesprächsduer uf Minuten zw. Sekunden zw. gr nicht rundet? Begründe. Aufge 8 (Funktionenschr) 2 Betrchte die Funktionenschr f, (x) = 2π e 2 (x )2 ( R, ). ) Bestimme die Extrem- und die Wendepunkte der Schr. ) Bestimme die Asymptoten der Schr. c) Stelle den Grfen zu f, sowie f 2, grfisch dr. d) Beschreie den Einfluss der Prmeter und uf die Grfen der Schr. 2 Aufge 8 ist für er-kndidten. Wer diese Aufge lösen knn, ist wirklich fit im Bereich der Kurvenuntersuchung exponentieller Funktionsschren.
8 7 2 Guß sche Glockenfunktion und Normlverteilung Anlysis der Guß schen Glockenkurve Aufge (Guß sche Glockenfunktion) Betrchte die Funktionenschr φ μ,σ mit φ μ,σ (x) = σ 2π e 2 (x μ σ )2 (μ R, σ ). ) Untersuche φ, und φ 3,2 uf Extrem- und Wendepunkte. ) Stelle die Grfen zu φ, und φ 3,2 mit dem GTR grfisch dr und untersuche, durch welche einfche Trnsformtionen der Grf von φ, us dem Grfen von φ 3,2 hervorgeht. Vergleiche Deine Ergenisse mit der unten efindlichen Aildung. c) Bestimme φ, (x)dx und φ 3,2 (x)dx. Zeige, dss die φ, undφ 3,2 Dichtefunktionen sind. d) Trnsformiere den Grfen von φ μ,σ ncheinnder mit den Trnsformtionen (), (2) und (3): () Mn verschiet um μ nch links. (2) Mn streckt um den Fktor σ in x-richtung. (3) Mn streckt um den Fktor σ in y-richtung. Beweise: Ds Ergenis der drei Trnsformtionen ist der Grf von φ,. e) Begründe mit Hilfe der folgenden Aildungen, dss folgende Integrlgleichheit gilt: 6 φ 3,2 (x)dx = φ,2 (x)dx = φ, (x)dx und llgmeiner: φ 3,2 (x)dx = φ, (x)dx 5 2 3, Mit der gleichen Üerlegung gilt noch llgemeiner: φ μ,σ (x)dx = φ, (x)dx μ σ μ σ Zeige mit dieser Gleichung und Aufgenteil ), dss φ μ,σ eenflls eine Dichtefunktion ist.
9 8 Guß sche Glockenfunktion () Die Funktion φ μ,σ mit φ μ,σ (x) = σ 2π e 2 (x μ σ )2 heißt Guß sche Glockenfunktion. Sie esitzt eine glole Extremstelle ei x = μ und die eiden Wendestellen x = μ ± σ. (2) Die Funktion φ = φ, (x) = 2 x2 wird mit Stndrd-Glockenfunktion ezeichnet. 2π e (3) Beide Funktionen sind Dichtefunktionen und lssen sich durch einfche Trnsformtionen ineinnder üerführen: Durch Linksverschieung des Grfen von φ μ,σ um μ und Streckung in y-richtung mit entsteht der Grf von φ. σ H (μ/ σ 2π ) W (μ ± σ/ σ 2π e 2) Aufge 2 (Guß sche Glockenfunktion skizzieren) Skizziere die Grfen der Funktion mithilfe der Hoch- und Wendepunkte des oigen Kstens mit Ppier und Bleistift. Erläutere Dein Vorgehen. ) φ, ) φ 2, c) φ,2 d) φ 2, e) φ 2,4 f) φ 3,,5 g) φ 4,,2 h) φ 4,, Aufge 3 (Guß sche Glockenfunktion mit GTR zeichnen) Stelle den Grfen von φ 2,,5 smt erster und zweiter Aleitung mit dem GTR dr und estätige die Aussgen us dem oigen Ksten üer die Lge der Extrem- und Wendepunkte. Aufge 4 (Zeit zu üerprüfen) ) Bestimme die Hoch- und Wendepunkte von φ 2,,5 und skizziere den Grfen zu φ 2,,5. 3 ) Schätze ohne zu rechnen: φ 2,,5 (x)dx. c) Üerprüfe Deine Skizze und Schätzung mit dem GTR.
10 9 Normlverteilung () Eine stetige Zufllsgröße X heißt normlverteilt mit den Prmetern σ und μ, wenn sie die Guß sche Glockenfunktion φ μ,σ mit φ μ,σ (x) = σ 2π e 2 (x μ σ )2 ls Dichtefunktion esitzt. (2) Der Prmeter μ eschreit den Erwrtungswert und der Prmeter σ die Stndrdweichung der der normlverteilten Zufllsgröße X. x (3) Die dzugehörige Integrlfunktion Φ μ,σ mit Φ μ,σ (x) = φ μ,σ (t)dt heißt Verteilungsfunk- φ ; (t)dt. Of- tion von φ μ,σ. Im Flle μ = und σ = wird sie mit Φ ezeichnet: Φ(x) = fenr gilt: φ μ,σ (t)dt = Φ μ,σ () Φ μ,σ () zw. φ(t)dt = Φ() Φ(). x Der GTR ht eine Tschenrechnerfunktion für die Berechnung von φ μ,σ (x). Üer OPTN, F5 (STAT), F3 (DIST), F (NORM) findet mn sie mit F ls Npd. Mn notiert nch Npd( zuerst ds Argument x, dnn die Stndrdweichung σ sowie den Erwrtungswert μ: Npd(x, σ, μ). (A. unten links) Beispiel: φ 2;2 (9),76 Will mn ds Intergrl φ μ,σ (t)dt erechnen, enötigt mn den Befehl Ncd, den mn nlog wie oen Npd erhält. Mn notiert nch Ncd( zuerst die eiden Integrtionsgrenzen und und dnn die Stndrdweichung σ sowie den Erwrtungswert μ: Ncd(,, σ, μ). (A. unten links) Beispiel: 22 8 φ 2;2 (x)dx,683. Üer den Befehl InvN knn in einem Integrl die untere Grenze zw. in μ+c μ c φ μ,σ (t)dt die oere Grenze, in + φ μ,σ (t)dt φ μ,σ (t)dt ds symmetrische Intervll um den Erwrtungswert usgerechnet werden, wenn der Flächeninhlt (= Integrlwert) eknnt ist. Dfür git mn nch InvN( - (linkes Intervll: ] ; ] ), + (rechtes Intervll: [; + [ ) zw. (symmetrisches Intervll um μ: [μ c; μ + c]) ein und dnn den Flächeninhlt F sowie die Stndrdweichung σ und den Erwrtungswert μ: InvN(- oder + oder, F, σ, μ). (A. unten rechts) Beispiele: + μ+c μ c φ 2;2 (t)dt =,25 8,65; GTR 2,35. φ 2;2 (t)dt =,25 GTR φ 2;2 (t)dt =,683 c 8 GTR Im Anwendungsezug wird zu einer normlverteilten Zufllsgröße X mit der Stndrdweichung σ und dem Erwrtungswert μ durch P( X ) = φ μ,σ (t)dt die Whrscheinlichkeit erechnet, dss die Zufllsgröße X im Intervll [; ] liegt. Beispiel: Ds Gewicht G von neugeorenen Kindern sei normlverteilt mit dem Erwrtungswert μ = 32 g und der Stndrdweichung σ = 8 g. Bestimme die Whrscheinlichkeit, dss ein Kind zwischen 3 und 32 g schwer ist. Gesucht ist lso P μ=32;σ=8 (3 G 32). Der GTR liefert P μ=32;σ=8 (3 G 32) 9,87%. Fst jedes zehnte Neugeorene ist lso zwischen 3 und 32 g schwer.
11 Grundufgen zur Normlverteilung Sei X normlverteilte Zufllsgröße mit der Stndrdweichung σ und dem Erwrtungswert μ. Grundufgen zur Normlverteilung können durch folgende Telle festgelegt werden, woei eine gegeene Größe und die gesuchte Größe repräsentieren: Grundufge Intervllgrenze Intervllgrenze Stndrdweichung σ Erwrtungswert μ Gesmtwhrscheinlichkeit P Im Folgenden wird ei der Whrscheinlichkeit P σ,μ der Index teilweise weggelssen, wenn Stndrdweichung σ und Erwrtungswert μ eide eindeutig festgelegt wurden. Bevor Du einige Üungsufgen erledigst, sollen die fünf Grundufgen mit Beispiel und GTR-Anwendung drgestellt werden. Vollziehe sie unter Nutzung des GTR nch. Notiere Unklrheiten. Grundufge : Gesmtwhrscheinlichkeit P gesucht Ds Gewicht von neugeorenen Kindern sei normlverteilt mit μ = 32 g und σ = 8 g. Ermittle die Whrscheinlichkeit, dss ds Gewicht eines zufällig usgewählten Kindes weniger ls 3 g [mehr ls 4 g; zwischen 3 g und 34 g] eträgt. Entscheide egründend, o es ungewöhnlich ist, wenn ein Kind 22 g wiegt. Gegeen: Ds Gewicht G sei normlverteilt mit der Stndrdweichung σ = 8 g und dem Erwrtungswert μ = 32. Gesucht: P( G 3); P(+ G 4); P(3 G 34); P( G 222) Hier knn in MENU gereitet werden mit der dem Befehl NormCD (,, σ, μ): Für die uneschränkten Grenzen git mn Werte n, die weit vom Erwrtungswert entfernt liegen Es gilt für die gesuchten Whrscheinlichkeiten: P(G 3) 4,3%; P(G 4) 5,87%; P(3 G 34) 9,74%. P(G 222),56%: Es nicht esonders ungewöhnlich, wenn ein Kind 22 g wiegt, d c. jedes. Kind höchsten 22 g wiegt.
12 Grundufge 2: Erwrtungswert μ gesucht Ds Gewicht von neugeorenen Kindern sei normlverteilt mit σ = 5 g. Jedes dritte Kind ht ein Gewicht zwischen 275 g und 325 g. Ermittle mögliche Erwrtungswerte. Gegeen: Ds Gewicht G sei normlverteilt mit der Stndrdweichung σ = 5 g. Es gilt P σ=5;μ (275 G 325) = 3. Gesucht: Mögliche Erwrtungswerte μ Mn definiert in MENU 5 unter Y die Funktion f mit f(μ) = P σ=5;μ (275 G 325) = 3 sowie unter Y2 die konstnte Funktion g mit g(μ) =. Die Schnittstelle eider Funktionen liefert mögliche 3 Erwrtungswerte. Antwortstz: Mögliche Erwrtungswerte sind c g oder 3274 g. Grundufge 3: Stndrdweichung σ gesucht Ds Gewicht von neugeorenen Kindern sei normlverteilt mit μ = 32 g. Mit einer Whrscheinlichkeit von 95 % hen die Kinder ein Gewicht zwischen 28 und 36 g. Ermittle die Stndrdweichung. Gegeen: Ds Gewicht G sei normlverteilt mit dem Erwrtungswert μ = 32. Es gilt dei P σ; μ=32 (28 G 36) =,95. Gesucht: Stndrdweichung σ. Auch hier können in MENU 5 üer die Terme Y: NormCD (28, 36, x, 32) und Y2:,95 zwei Grfen erstellt werden, deren Schnittstelle die gesuchte Stndrdweichung ngit.
13 Mthemtisch exkt usgedrückt: Die Funktion f mit f(σ) = P σ; μ=32 (28 G 36) ht mit der Funktion g mit g(σ) =,95 die Schnittstelle σ 24. Für σ 24 g gilt us diesem Grund P σ; μ=32 (28 G 36) =,95 Antwortstz: Die gesuchte Stndrdweichung eträgt c. 24 g. 2 Grundufge 4: Eine Intervllgrenze gesucht Ds Gewicht von neugeorenen Kindern sei normlverteilt mit μ = 32 g und σ = 8 g. Untersuche, wie schwer ds Neugeorene mindestens sein, wenn es zu den 5% schwersten Kindern gehört. Gegeen: Ds Gewicht G sei normlverteilt mit der Stndrdweichung σ = 8 g und dem Erwrtungswert μ = 32. Es gilt: P(G ) =,5. Gesucht: Intervllgrenze. Hier können in MENU 5 üer die Terme Y: NormCD (x,, 8, 32) und Y2:,5 zwei Grfen erstellt werden, deren Schnittstelle die gesuchte Intervllgrenze ngit. Mthemtisch exkt usgedrückt: Die Funktion f mit f() = P(G ) ht mit der Funktion g mit g() =,5 die Schnittstelle 456. Für 456 gilt dher P(G ) =,5. Antwortstz: Ein Neugeorenes muss mindestens 456 g schwer sein, um zu den 5 % schwersten Kindern zu gehören. Grundufge 5: Beide Intervllgrenzen gesucht Ds Gewicht von neugeorenen Kindern sei normlverteilt mit μ = 32 g und σ = 8 g. Untersuche, in welchem zum Mittelwert symmetrischen Bereich 95% der Neugeorenen liegen. Gegeen: Ds Gewicht G sei normlverteilt mit der Stndrdweichung σ = 8 g und dem Erwrtungswert μ = 32. Es gilt: P(32 G 32 + ) =,95. Gesucht: Intervllgrenzen 32 und In MENU 5 können üer die Terme Y: NormCD (32 - x, 32 + x, 8, 32) und Y2:,95 zwei Grfen erstellt werden, deren Schnittstellen die gesuchte Intervlllänge ngit.
14 3 Mthemtisch exkt usgedrückt: Die Funktion f mit f(x) = P(32 x G 32 + x) ht mit der Funktion g mit g(x) =,95 die Schnittstelle x 568. Es gilt dher für die Whrscheinlichkeit: P(632 G 4768) =,95. Antwortstz: 95 % der Neugeorenen liegen im zum Erwrtungswert μ = 32 symmetrischen Intervll [632; 4768]. Alterntivlösungen zu Grundufgen 4 und 5 mithilfe von InvN: Üer den Befehl InvN knn in ei vorgegeener Whrscheinlichkeit P( G ) zur normlverteilten Zufllsgröße G mit eknnter Stndrdweichung σ und vorgegeenen Erwrtungswert μ die rechte Grenze, ei P( G + ) die linke Grenze zw. ei P(μ c G μ + c) ds symmetrische Intervll um den Erwrtungswert usgerechnet werden. Dfür git mn nch InvN( - (linkes Intervll: ] ; ] ), (rechtes Intervll: [; + [ ) zw. (symmetrisches Intervll um μ: [μ c; μ + c]) ein und dnn den Wert für die Whrscheinlichkeit P sowie die Stndrdweichung σ und den Erwrtungswert μ: InvN(- oder + oder, P, σ, μ). Die Anzeige eim GTR ist folgendermßen drgestellt: Aufge 5 Die Dicke von Sthllech sei normlverteilt mit =,75 mm und =,3 mm. Bestimme die Whrscheinlichkeit, dss die Blechdicke im Intervll [,7 mm;,8 mm] liegt. Aufge 6 Die Duer einer Schwngerschft ist ngenähert normlverteilt und eträgt im Mittel 278 Tge ei einer Stndrdweichung von 9,69 Tgen. Berechne die Whrscheinlichkeit, dss ein zufällig usgewähltes By ei einer Spontngeurt ereits nch einer Schwngerschft von weniger ls 25 Tgen georen wird.
15 4 Aufge 7 Die Körpergröße von Kindern eines Jhrgngs sei normlverteilt mit = 9 cm und = 8 cm. Untersuche, wieviel Prozent dieser Kinder () höchstens 87 cm groß sind. (2) mindestens 86 cm und höchstens 95 cm groß sind. (3) 9 cm groß sind ei Rundung uf cm, mm zw. ohne Rundung. Aufge 8 Die mittlere Brutduer für Eier in einem Inkutor ei 38 eträgt 2 Tge. Angenommen, die mittlere Brutduer ist ngenähert normlverteilt ei einer Stndrdweichung von einem Tg. ) Ermittle die Whrscheinlichkeit, dss die Brutduer eines zufällig usgewählten Eies () weniger ls 2 Tge eträgt. (2) mehr ls 22 Tge eträgt. (3) zwischen 9 und 2 Tgen eträgt. ) Beurteile, o es ungewöhnlich ist, wenn ein Küken nch 8 Tgen geschlüpft ist, wenn die Brutduer uf Tge gerundet wird. Aufge 9 Die Leensduer eines Lptops sei normlverteilt mit einem Erwrtungswert von 42 Monten und einer Stndrdweichung von 2 Monten. ) Die Grntiezeit eträgt 8 Monte, d. h. der Hersteller führt in dieser Zeit nfllende Reprturen kostenlos durch. Für jede Reprtur klkuliert der Hersteller Kosten in Höhe von 25. Untersuche, mit welchen Kosten pro verkuftem Computer der Hersteller rechnen muss. ) Der Hersteller möchte die Grntiezeit so usdehnen, dss 5% mehr Kunden in den Genuss der Grntie kommen. Ermittle die Duer der neuen Grntiezeit. Aufge 3 Nch dem Hnduch des Institutes zur Förderung hochegter Vorschulkinder ist der Intelligenzquotient in der Bevölkerung normlverteilt mit =. 68,3% der Bevölkerung ht einen Intelligenzquotienten zwischen 85 und 5. ) Bestimme us den Angen die Stndrdweichung der Normlverteilung. ) Ermittle ds mit P(μ G μ + ) =,95 und formuliere ds Ergenis in Worten. 3 In Anlehnung n Aufge us Fokus Mthemtik LK in NRW (S. 9) und (st-8-)
16 c) Nch Angen des sttistischen Bundesmtes gingen 34 % eines Jhrgnges von der Grundschule ins Gymnsium üer. Angenommen (ws eknntermßen nicht der Fll ist!) ei diesen 34 % hndelt es sich um die Kinder mit dem höchsten Intelligenzquotienten. Untersuche, welches der kleinsten IQ wäre, der n einem Gymnsium nzutreffen wäre. Die folgende Aildung 4 stellt die oige Normlverteilung grfisch dr. 5 d) Prüfe ei llen ngegeenen Whrscheinlichkeitsdten, o sie zur Normlverteilung us den Aufgenteilen ) is c) pssen. e) Untersuche, wie häufig durchschnittliche Intelligenz ist. f) Prüfe, o die Angen zu is 3 und üer 3 pssen. g) In einer Klsse finden sich IQ-Werte zwischen 5 und 25. Untersuche, wie viel Prozent der Bevölkerung sie in diesem Bereich liegen. h) Stelle die oige Normlverteilung mit dem GTR dr. ABITUR 27 Auszug us LK HT B5 5 d) Die Indiktormenge uf den Teststreifen ist normlverteilt mit einem Erwrtungswert von 2 mg und einer Stndrdweichung von 4, mg. Ein Teststreifen ist unruchr, wenn die Indiktormenge uf dem Teststreifen kleiner ls 5 mg ist. () Bestimmen Sie die Whrscheinlichkeit dfür, dss ein Teststreifen unruchr ist. [Kontrolllösung:,56 %] (2) Durch eine Veresserung konnte die Whrscheinlichkeit dfür, dss ein zufällig usgewählter Teststreifen ufgrund der Indiktormenge unruchr ist, hliert werden. Der Erwrtungswert für die Indiktormenge lie dei unverändert. Bestimmen Sie die geänderte Stndrdweichung durch systemtisches Proieren uf eine Nchkommstelle genu. 4 mßstäe (PTB Physiklisch Technische Bundesnstlt), Heft : Mi 2, Seite 54 5 Auszug us einer Aiturufge des Lndes NRW 27 LK HT B5
17 6 3 Kontrollufgen Kompetenzrster Ohne Hilfsmittel Ich knn Wo? sicher ziemlich sicher unsicher sehr unsicher zeigen, dss eine Funktion eine Dichtefunktion ist. den Erwrtungswert für ein Glücksspiel erechnen. eine Auszhlungsverteilung für ein fires Spiel ngeen. Whrscheinlichkeiten mittels Dichtefunktion und Integrlen erechnen. zeigen, dss eine zusmmengesetzte Funktion Stmmfunktion ist. den Erwrtungswert einer Zufllsgröße mittels Integrl zu erechnen. die Stndrdweichung einer Zufllsgröße mittels Integrl erechnen., Unter Zuhilfenhme von Hilfsmitteln Ich knn Wo? sicher ziemlich sicher unsicher sehr unsicher zeigen, dss eine Funktion eine Dichtefunktion ist. Whrscheinlichkeiten mittels Dichtefunktion und Integrlen erechnen. den Erwrtungswert einer Zufllsgröße mittels Integrl zu erechnen. die Stndrdweichung einer Zufllsgröße mittels Integrl erechnen. einen Prmeter k estimmen, dmit eine Funktion Dichtefunktion ist. die Stndrdweichung einer normlverteilten Zufllsgröße erechnen (G3). Whrscheinlichkeiten einer normlverteilten Zufllsgröße erechnen (G). ein symmetrisches Intervll um den Erwrtungswert estimmen (G5). eine Intervllgrenze einer normlverteilten Zufllsgröße estimmen (G4). den Erwrtungswert einer normlverteilten Zufllsgröße erechnen (G2) eine Normlverteilung grfisch mit dem GTR drstellen c 3c 3d 4 4 4c 4d,e 4f 4g
18 7 Hilfsmittelfreie Aufgen Aufge,5x flls x Gegeen ist die Funktion f mit f(x) = {,6 flls < x,5.,3 flls,5 < x 3 ) Zeige, dss f üer [; 3] eine Dichtefunktion ist. ) Ein Spielutomt, der eine Zhl zwischen und 3 nzeigt, wird durch die oige Dichtefunktion simuliert. Der Einstz pro Spiel eträgt. Im Flle einer Zhl x zhlt der Automt 2 us, d. h. der Spieler gewinnt. Im Flle < x,5 geht der Einstz verloren. Kommt eine Zhl,5 < x 3 erhält der Spieler seinen Einstz zurück. () Weise nch, dss ds Spiel unfir ist. (2) Gi eine Auszhlungsverteilung n, die ein fires Spiel ermöglicht. Aufge 2 Gegeen ist für x + und k > die Funktion f mit f k (x) = ke kx. ) Zeige, dss f eine Whrscheinlichkeitsdichte (Dichtefunktion) ist. ) X k sei die Zufllsgröße mit der Dichtefunktion f k. () Gi Terme n für P(X 2 < 2) und für P(X 2 3). (2) Zeige, dss G k (x) = ( x ) k e kx eine Stmmfunktion zu g k (x) = x ke kx ist. (3) Weise mit (2) und der Formel für den Erwrtungswert 6 nch, dss μ = μ(x k ) =. k (4) Zeige, dss S k (x) = ( x 2 k 2) e kx eine Stmmfunktion zu s k (x) = (x k )2 ke kx ist. (5) Weise mit (3), (4) und der Formel für die Stndrdweichung 7 nch, dss σ = σ(x k ) = k. 6 μ = [x f(x)] dx 7 σ = [(x μ) 2 f(x)] dx
19 8 Aufgen unter Zuhilfenhme des GTR Aufge 3 Niki wirft Münzen so, dss sie möglichst nhe n der Wnd zu liegen kommen. Die Münzen prllen er oft und rollen zurück. Der Astnd X (in Metern) von der Wnd ist eine Zufllsgröße, die mn mithilfe der der Whrscheinlichkeitsdichte f(x) = 3x 2 6x + 3 üer [; ] eschreien knn. ) Begründe 8 rechnerisch, dss f eine Whrscheinlichkeitsdichte üer [; ] ist. ) Bestimme 9 (gerne unter Zuhilfenhme des GTR) die Whrscheinlichkeit, dss eine Münze weniger ls, m von der Wnd liegen leit. c) Für den Erwrtungswert μ und Stndrdweichung σ der stetig verteilten Zufllsgröße X mit Werten zwischen und und der Dichtefunktion f gilt llgemein: μ = [x f(x)] dx und σ = [(x μ) 2 f(x)] dx Bestimme unter Zuhilfenhme des GTR den Erwrtungswert μ und Stndrdweichung σ des Astndes X des oigen Münzwurfs. d) Gegeen sei die Funktion g mit g(x) = k (x x 3 ) mit dem konstnten Fktor k. Untersuche, wie der Prmeter k gewählt werden muss, dmit g eine Dichtefunktion üer dem Intervll [; ] wird. Aufge 4 Eine Bekleidungsfirm geht dvon us, dss die Körpergröße junger Fruen normlverteilt ist mit einem Erwrtungswert = 66 cm. Die Körpergröße von 95 % der Fruen liegt zwischen 79 cm und 53 cm. ) Ermittle die Stndrdweichung dieser Normlverteilung. [Kontrollergenis: 6,63 cm] ) Berechne den für eine Körpergröße von 53 cm is 56 cm usgelegte Wrennteil. c) Untersuche, in welchem symmetrischen Intervll um den Erwrtungswert die Körpergröße von 5 % der Fruen liegt. d) Bestimme die Mindestkörpergröße einer Fru, die zu den 5 % größten Fruen gehört. e) Untersuche, mit welcher Höchstkörpergröße eine Fru zu % kleinsten Fruen zu zählen ist. f) Untersuche, welcher Erwrtungswert einer normlverteilten Verteilung der Körpergrößen vorgelegen hen könnte, wenn ei gleicher Stndrdweichung 95 % der Fruen zwischen 8 cm und 54 cm groß wären. g) Stelle die oigen Normlverteilungen grfisch dr. 8 Hier muss neen dem Anstz eine Rechnung ngegeen werden. 9 Hier drf nch Ange des Anstzes der GTR enutzt werden.
20 9 Lösungen Stetige Zufllsgrößen Integrle esuchen die Stochstik Erkundungen: ) Die Whrscheinlichkeit, einen estimmten Winkel zwischen und 2π zu drehen, eträgt Null, d es üerzählr viele Zhlen zwischen und 2π git. ) () Für die Werte uf der y-achse dividiert mn die reltiven Häufigkeiten für die zehn Winkelereiche jeweils durch π. Auf der x-achse werden lle Vielfchen von π mrkiert, is mn zu 2π 5 5 gelngt. (2) Die Flächen unter dem Grfen git die reltiven Häufigkeiten für den entsprechenden Winkelereich n. (3) Der Flächeninhlt zwischen Grf der Dichtefunktion und der x-achse üer dem Intervll [; 2π] eträgt % =. c) () Gemäß dem Gesetz der großen Zhlen nähern sich die reltiven Häufigkeiten für große n der ttsächlichen Whrscheinlichkeiten n. (2) Die Dichtefunktion ht folgenden Gleichung: flls x 5 π 5 f(x) = {,45 flls 5 π < x 2π. 5 Ferner eträgt der Flächeninhlt zwischen Grf und x-achse üer dem Intervll is 2π gleich. Also gilt: 5 85 π +,45 π = 23 π = = 2,3 und,45, π (3) Zhlen us dem Winkelereich is 5 π werden deutlich häufiger gedreht wie Zhlen us dem 5 ürigen Winkelereich. Mit einer Whrscheinlichkeit von c. 28 % stmmt eine Zhl us dem deutlich kleineren Winkelereich is 5 5 π. ) Die Fläche unter der Treppenfunktion muss genu etrgen. Mit den drgestellten Bezeichnungen ergit sich: 3 π π = π = = 4 und dmit die Funktion f π mit 8 π f(x) = {,23 für < x 3 π 2,36 4 4,5 für 3 π < x 2π π 4 ) (i) P( X ) = 8 = 8,23 π π (ii)p(,5 X 2,5) = 8 π (3 π,5) + 4 (2,5 3 π),25 4 π 4 (iii) P(3 X 4) = 4 = 4,6 π π 2) Treppenfunktion skizzieren 2) Bedingungen für Dichtefunktion prüfen: (I) f(x) für lle x [; 6] (klr) und (II) f(x)dx = gilt? Nchrechnen: 6 f(x)dx =, +,2 2 +,3 +, 2 =. 6
21 2 2c) P(2 X 5) =,2 +,3 +, =,6 2d) Erwrtungswert für den Gewinn gesucht. Gewinntelle: Ergenis x < x < 3 3 x 4 4 < x 6 Gewinn in Dmit ergit sich für den Erwrtungswert μ = ( ), + 2,2 2 + ( ),3 + ( ), 2 =,2. D μ > ist uf lnge Sicht, ist der Spieler im Vorteil. 2e) Ds Spiel ist fir, wenn μ = ist. Mn setzt den Gewinn uf den Wert g und erhält die folgende Gewinntelle: Ergenis x < x < 3 3 x 4 4 < x 6 Gewinn in - g - - Es ergit sich die Gleichung: = ( ), + g,2 2 + ( ),3 + ( ), 2,4 g =,6 g = 3. Bei einem Gewinn von,5, lso ei einer Auszhlung von 2,5, wäre ds Spiel 2 fir. 2π 3) Die Dichtefunktion ist eine Konstnte f(x) = k > mit mit k dx 4) Für jedes x R gilt f(x), wenn < ist. Mit f(x)dx = erhält mn den Wert für : 9 = f(x)dx [(x 9)(x )]dx = 4 3 Drus folgt = -,75 4) Dichte und Verteilungsfunktion (Bild rechts) 4c) Erwrtungswert und Stndrdweichung dürfen mit der Integrlfunktion des GTR erechnet werden. Für den Erwrtungswert erhält mn mit der Definition im Ksten:μ = [x f(x)] dx = 9 Den Erwrtungswert setzt mn in die Formel für die Stndrdweichung ein: s(x) = 9 [(x μ) 2 f(x)]dx =,2,447. 9,4 4d) P(Ausschuss) = P(x < 9,4) + P(x >,6) = f(x)dx + 9 f(x)dx,6 = 2πk = k = 2π =,4 +,4 =,28 4e) Wird die mximle zulässige Aweichung mit m ezeichnet, muss z. B. mit dem GTR (üer MENU 5) die Gleichung +m m f(x)dx,9 gelöst werden. Es ergit sich m =, ) f(x)dx = ቂ k 4 x x3 2 2 x ,2xቃ = 4k + 2 +,4 = k = 3 6 +x Der GTR versteht nur den Ausdruck f(x)dx x mit der doppelten Vrilenelegung von x.
22 6) Anstz einer gnzrtionlen Funktion dritten Grdes: f(x) = x 3 + x 2 + cx + d. Die Bedingungen luten: () f() = 3k; (2) f () = ; (3) f(5) = k; (4) f (5) = ; (5) f(x)dx =. Mn erhält ds folgende 5x5-LGS: () d 3k = ; (2) c = ; (3) c + d k = ; (4) c = ; (5) ,5c + 5d =. Mithilfe des GTR folgt: = ; = 3 ; c = ; d = 3 ; k =, Dmit folgt f(x) = x x ) Mit dem GTR folgt: P(2 x 3) = f(x) dx 2 7) e x R > und e x dx = 5 = [ e x ] R = e R ( e ) = e R R + 2 7) P( < X < 2) = f(x)dx = e e 2,2325 Mit c. 23%iger Whrscheinlichkeit duert ein Gespräch zwischen einer und zwei Minuten. + 7c) Mit dem GTR (jeweils große Zhl für oere Grenze einsetzen) folgt μ = [x f(x)]dx σ = + [(x μ) 2 f(x)]dx = 7d) Es ergeen sich mit dem GTR folgende Whrscheinlichkeiten:,5 e x dx,3834,5 + 6 ; e x dx,22 6 und e x dx =. 5 2 = und 8) Zur Ermittlung der Extremstellen erechnet mn zunächst die Nullstellen der ersten Aleitung. Nch der Ketten- und Fktorregel gilt: f, (x) = 2π e 2 (x )2 ( 2 2 (x ) ) = x 3 2π e 2 (x )2 = x =. Wegen f (x) < für x > und f (x) > für x <, liegt ei x = ein VZW von f von + nch vor. Insgesmt erhält mn wegen f() = und lim [ 2π x ± 2π e 2 (x )2 ] = den glolen HP ( ). 2π Zur Bestimmung der Wendestellen erechnet mn zunächst die Nullstellen der zweiten Aleitung. Mit der Produkt-, Fktor- und Kettenregel gilt: f, (x) = 3 2π e )2 + ( x 3 2π ) e 2 (x 2 (x )2 ( x 2 ) = + (x ) 2 ( 2 ) e 5 2 (x )2 = 2π 2 + (x ) 2 = (x ) 2 = 2 x = oder x = x = ±. Mn prüft einen VZW der zweiten Aleitung ei ± nch, indem mn z. B. x = 2, x = und x = + 2 in die zweite Aleitung einsetzt: f, ( 2) > ; f, () < ; f, ( + 2) >. Es liegen lso der Li-Re- WP WP ( 2π e 2) und der Re-Li-WP WP 2 ( + 2π e 2) vor. 8) Die Asymptote ist die x-achse. 8c) 8d) Der Prmeter verschiet den Grfen nch rechts. Der Prmeter streckt die Prel in x- und in y-richtung (je kleiner, desto größer ist die Streckung in x und y-richtung).
23 22 2 Guß sche Glockenfunktion und Normlverteilung 5 P (,7 X,8),944 6 P (X 25),2. Spontne Geurten innerhl der ersten 25 Tge sind lso sehr selten. 7 ) P (X 87),3538 ) P (86 X 95),4255 c) P (89,5 X 9,5),5; P (89,95 X 9,5),5; P (X= 9) = 8) () P (X < 2),587 (2) P (X > 22) = P (X 22),587 (3) P (9 X 2) = P (X 2) P (X< 9),47725 ) P (7,5 X 8,5),6. Die Whrscheinlichkeit für dieses Ereignis eträgt c.,6 %, dher ist es ungewöhnlich. 9 ) P(X 8),225. Erwrtete Kosten: E(X) =, ,63. ) P (X x) =,225 +,5 =,725 x 24,5. Dher müsste die Grntiezeit uf 25 Monte usgedehnt werden. ) = ; = 5 ) P(7,6 G 29,4) =,95 (üer InvNormCD (,.95,5,)). 95 % der Menschen hen einen Intelligenzquotienten zwischen 7 und 3 c) Gesucht ist ds kleinste mit P(G ),34. (üer InvNormCD (,.34,5,) lösen) Mn erhält für 6 P(G ),34. Der Aufnhme-IQ müsste mindestens 6 etrgen, dmit die intelligentesten 34 % zum Gymnsium gingen. d) X: Zhl des IQ (Verwende NormCD (untere Grenze, oere Grenze, Stndrdweichung, Erwrtungswert)) P(X 55),3 %; P(X 7),228 2,28 % und P(55 X 7) 2,5 % P(X 85) 5,87 % und P(7 X 85) 3,59 %; P(X ) 5 % und P(85 X ) 34,3 % P(X 5) 84,3 % und P( X 5) 34,3 %; P(X 3) 97,72 % und P(5 X 3) 3,59 %; P(X 45) 99,87 % und P(3 X 45) 2,5 %; P(X > 45) = - P(X 45) - 99,87 %,3 %. Die ngegeenen Prozentsätze pssen. e) P(85 X 5) = 2 34, % = 68,2 %. Norml intelligent sind rund 68 % der Bevölkerung, häufig gerundet zu 2 oder 7 %. 3 f) P(5 X 3) = 3,6 %. Ds sind knpp 4 %. P(X > 3) 2, % +, % 2,2 % Ds liegt nur etws üer 2 %. g) P(5 X 25) 32,32 % Knpp der Bevölkerung ht einen IQ-Wert zwischen 5 und h)
24 23 Aiturufge d) (): Die Zufllsgröße Z eschreit die Indiktormenge uf einem Teststreifen in mg. Für einen Erwrtungswert von 2 mg und eine Stndrdweichung von 4, mg gilt für die gesuchte Whrscheinlichkeit: P(Z < 5),56%. (2): Mn definiert die Funktion f mit f(σ) = P σ;μ=2 (Z < 5) sowie die konstnte Funktion g mit g(σ) =,528. Die Schnittstelle eider Funktionen liefert die gesuchte Stndrdweichung von σ 3, mg. Alterntiv (im Sinne der Aufgenstellung) knn uch mit einer Wertetelle (MENU 7) gereitet werden, in der ei der Funktion f der Wert für σ vriiert wird. Die dzugehörigen GTR-Eingen werden durch folgende Aildung dokumentiert: Nicht sinnvoll im Sinne der Aufgenstellung
25 24 3 Kontrollufgen Ohne GTR Aufge ) Die Fläche unter dem Grfen der Dichtefunktion üer dem Intervll [; 3] lässt sich in ein Dreieck und zwei Rechtecke zerlegen. Für die Gesmtwhrscheinlichkeit gilt: P[; 3] = P[; ] + P[;,5] + P[,5; 2] =,25 +,3 +,45 =. ) () Für den zu erwrtenden Gewinn gilt μ =,25 +,3 ( ) +,45 =,5. Dher ist ds Spiel unfir. (2),25 +,3 ( ) +,45 = =,2 Aufge 2 + ) ke kx dx = lim R + [ e kx R ] = lim R + ( e kr + ) = Gegeen ist für x + und k > die Funktion f mit f k (x) = ke kx. 2 ) () 2e 2x dx + 3 2e 2x dx = e ,7% = lim R + [ e 2x ] R 3 = lim R + ( e 2R + e 6 ) = e 6,25% (2) G k (x) = ( x k ) e kx G k (x) = e kx + ( x k ) ( k) e kx = ( + kx + ) e kx = kxe kx = g k (x) + (3) μ = [x f k (x)] dx + = g k (x) dx = lim ቂ( x ) R R + k e kx ቃ = lim ቂ( R ) R + k e kr + ቃ = k k (4) S k (x) = ( x 2 k 2) e kx S k (x) = 2xe kx + ( x 2 k 2) ( k) e kx = (kx 2 2x + k ) e kx = (x 2 2 k x + k 2) k e kx = (x k )2 k e kx = s k (x) + (5) σ = [(x μ) 2 f k (x)] dx = lim R + ቂ( R2 k 2) e kr + k 2ቃ = k 2 = k + = s k (x) dx = lim R + [( x2 ) e kx R k ] 2
26 25 Mit GTR Aufge 3 ) (3x 2 6x + 3) dx = [x 3 3x 2 + 3x] = f(x) = 3x 2 6x + 3 x 2 2x + (x ) 2, d. h. f(x) für lle x, lso uch für lle x zwischen und. (Grf von f ist nch oen geöffnete Prel, die die x-achse ei x = erührt.), ) P[;,] = (3x 2 6x + 3) dx = 27, % c) μ = (3x 3 6x 2 + 3x) dx =,25 (mittlerer Astnd von der Wnd) σ = [(x,25) 2 f(x)] dx = 3 8,9 d) k (x x 3 ) dx = k ቂ 2 x2 4 x4 ቃ = k = k = 4 4 Aufge 4 ) Die Größe G von Fruen sei normlverteilt mit = 66 cm. Gesucht ist die Stndrdweichung σ mit P μ = 66 cm;σ (53 G 79). Sie ergit sich die sich ls Schnittstelle der Funktionen f und g mit f(σ) = P μ = 66 cm;σ (53 G 79) und g(σ) =,95. Mn erhält σ 6,63. ) P μ = 66 cm;σ 6,63 (53 G 56) 4,% der Wren sind uf Körpergrößen von 53 cm is 56 cm usgerichtet. c) Es gilt P μ = 66 cm;σ 6,63 (6,5 G 7,5),5. d) Es gilt P μ = 66 cm;σ 6,63 (G 76,9),5. e) Es gilt P μ = 66 cm;σ 6,63 (G 57,5),.
27 f) Gesucht ist der Erwrtungswert μ mit P μ ;σ 6.63 (54 G 8) =,95. Er ergit sich die sich ls Schnittstelle der Funktionen f und g mit f(μ) = P μ ;σ 6.63 (54 G 8) und g(μ) =,95. Mn erhält μ 66,8. Alterntivlösung üer Tellenfunktion und systemtisches Proieren. 26 g)
Die Regelungen zu den Einsendeaufgaben (Einsendeschluss, Klausurzulassung) finden Sie in den Studien- und Prüfungsinformationen Heft Nr. 1.
 Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Beispiel-Abiturprüfung
 Mthemtik BeispielAbiturprüfung Prüfungsteile A und B Bewertungsschlüssel und Lösungshinweise (nicht für den Prüfling bestimmt) Die Bewertung der erbrchten Prüfungsleistungen ht sich für jede Aufgbe nch
Mthemtik BeispielAbiturprüfung Prüfungsteile A und B Bewertungsschlüssel und Lösungshinweise (nicht für den Prüfling bestimmt) Die Bewertung der erbrchten Prüfungsleistungen ht sich für jede Aufgbe nch
Für den Mathe GK, Henß. - Lineare Algebra und analytische Geometrie -
 Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
Skript für die Oberstufe und das Abitur 2015 Baden-Württemberg berufl. Gymnasium (AG, BTG, EG, SG, WG)
 Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl. Sommersemester 2009
 UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
Thema 13 Integrale, die von einem Parameter abhängen, Integrale von Funktionen auf Teilmengen von R n
 Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
Abitur - Leistungskurs Mathematik. Sachsen-Anhalt 1999
 Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
Übungsblatt 1 zum Propädeutikum
 Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschftsmthemtik für Interntionl Mngement (BA) und Betriebswirtschft (BA) Wintersemester 2013/14 Stefn Etschberger Hochschule Augsburg Mthemtik: Gliederung 1 Aussgenlogik 2 Linere Algebr 3 Linere
Wirtschftsmthemtik für Interntionl Mngement (BA) und Betriebswirtschft (BA) Wintersemester 2013/14 Stefn Etschberger Hochschule Augsburg Mthemtik: Gliederung 1 Aussgenlogik 2 Linere Algebr 3 Linere
1 Kurvendiskussion /40
 009 Herbst, (Mthemtik) Aufgbenvorschlg B Kurvendiskussion /0 Gegeben ist eine Funktion f mit der Funktionsgleichung: f ( ) 0 6 = ; mit.. Untersuchen Sie ds Verhlten der Funktionswerte von f im Unendlichen.
009 Herbst, (Mthemtik) Aufgbenvorschlg B Kurvendiskussion /0 Gegeben ist eine Funktion f mit der Funktionsgleichung: f ( ) 0 6 = ; mit.. Untersuchen Sie ds Verhlten der Funktionswerte von f im Unendlichen.
FernUniversität Gesamthochschule in Hagen
 FernUniversität Gesmthochschule in Hgen FACHBEREICH MATHEMATIK LEHRGEBIET KOMPLEXE ANALYSIS Prof. Dr. Andrei Dum Proseminr 9 - Anlysis Numerische Integrtion Ulrich Telle Mtrikel-Nr. 474 Köln, den 7. Dezember
FernUniversität Gesmthochschule in Hgen FACHBEREICH MATHEMATIK LEHRGEBIET KOMPLEXE ANALYSIS Prof. Dr. Andrei Dum Proseminr 9 - Anlysis Numerische Integrtion Ulrich Telle Mtrikel-Nr. 474 Köln, den 7. Dezember
Übungsblatt Gleichungssysteme Klasse 8
 Üungsltt Gleichungsssteme Klsse 8 Auge : Berechne die Lösungen des Gleichungspres: I II 7 Kontrolliere durch Einseten. Auge : Löse dem Additionsverhren: I 7-6 II 9 Auge : Gegeen ist olgendes linere Gleichungssstem
Üungsltt Gleichungsssteme Klsse 8 Auge : Berechne die Lösungen des Gleichungspres: I II 7 Kontrolliere durch Einseten. Auge : Löse dem Additionsverhren: I 7-6 II 9 Auge : Gegeen ist olgendes linere Gleichungssstem
Grundwissen Abitur Analysis
 GYMNASIUM MIT SCHÜLERHEIM PEGNITZ mthem-technolog u sprchl Gmnsium WILHELM-VON-HUMBOLDT-STRASSE 7 9257 PEGNITZ FERNRUF 0924/48333 FAX 0924/2564 Grundwissen Abitur Anlsis Ws sind Potenzfunktion mit ntürlichen
GYMNASIUM MIT SCHÜLERHEIM PEGNITZ mthem-technolog u sprchl Gmnsium WILHELM-VON-HUMBOLDT-STRASSE 7 9257 PEGNITZ FERNRUF 0924/48333 FAX 0924/2564 Grundwissen Abitur Anlsis Ws sind Potenzfunktion mit ntürlichen
Lehrgang: Digitaltechnik 1 ( Grundlagen ) - Im Lehrgang verwendete Gatter ( Übersicht ) Seite 3
 Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
Aufgaben zur Vorlesung Analysis II Prof. Dr. Holger Dette SS 2012 Lösungen zu Blatt 6
 Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Die Brückenlappentechnik zum sicheren Verschluss von Nasenseptumdefekten
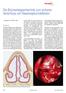 Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
Schriftliche Prüfungsarbeit zum mittleren Schulabschluss 2007 im Fach Mathematik
 Sentsverwltung für Bildung, Wissenschft und Forschung Schriftliche Prüfungsrbeit zum mittleren Schulbschluss 007 im Fch Mthemtik 30. Mi 007 Arbeitsbeginn: 10.00 Uhr Berbeitungszeit: 10 Minuten Zugelssene
Sentsverwltung für Bildung, Wissenschft und Forschung Schriftliche Prüfungsrbeit zum mittleren Schulbschluss 007 im Fch Mthemtik 30. Mi 007 Arbeitsbeginn: 10.00 Uhr Berbeitungszeit: 10 Minuten Zugelssene
Präfixcodes und der Huffman Algorithmus
 Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
Prüfungsteil Schriftliche Kommunikation (SK)
 SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
Erweitern. a b. bd + bc. bd = ad+bc. bei ganzzahligem Nenner: Hauptnenner (= kgv der Nenner), z.b. 4 6 + 3 4 = 8 12 + 9. a d = ac
 F FORMELSAMMLUNG Bruchrechnung Erweitern = Kürzen c c Addition Nenner gleichnmig mchen! + c d = d d + c d = d+c d, speziell + c = +c ei gnzzhligem Nenner: Huptnenner (= kgv der Nenner), zb 4 6 + 3 4 =
F FORMELSAMMLUNG Bruchrechnung Erweitern = Kürzen c c Addition Nenner gleichnmig mchen! + c d = d d + c d = d+c d, speziell + c = +c ei gnzzhligem Nenner: Huptnenner (= kgv der Nenner), zb 4 6 + 3 4 =
Bestimmung der Adsorptionsisotherme von Essigsäure an Aktivkohle
 S2-Adsorptionsisothermen_UWW rstelldtum 28.3.214 7:41: Üungen in physiklischer Chemie für Studierende der Umweltwissenschften Versuch Nr.: S2 Version 214 Kurzezeichnung: Adsorptionsisotherme estimmung
S2-Adsorptionsisothermen_UWW rstelldtum 28.3.214 7:41: Üungen in physiklischer Chemie für Studierende der Umweltwissenschften Versuch Nr.: S2 Version 214 Kurzezeichnung: Adsorptionsisotherme estimmung
13 Rekonfigurierende binäre Suchbäume
 13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
Vorkurs Mathematik Fachhochschule Frankfurt, Fachbereich 2. Fachhochschule Frankfurt am Main Fachbereich Informatik und Ingenieurwissenschaften
 Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
1.2 Der goldene Schnitt
 Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
bei Problemen die Theorie und die Beispiele am Anfang jeder Lerneinheit durcharbeiten
 Ds knnst du schon º Terme umformen º Gleichungen ufstellen und lösen º Funktionsgrphen zeichnen º Whrscheinlichkeiten erechnen Erfolge mithilfe des Aschlusstests üerprüfen ei Prolemen die Theorie und die
Ds knnst du schon º Terme umformen º Gleichungen ufstellen und lösen º Funktionsgrphen zeichnen º Whrscheinlichkeiten erechnen Erfolge mithilfe des Aschlusstests üerprüfen ei Prolemen die Theorie und die
Public-Key-Verfahren: Diffie-Hellmann und ElGamal
 Westfälische Wilhelms-Universität Münster Ausreitung Pulic-Key-Verfhren: Diffie-Hellmnn und ElGml im Rhmen des Seminrs Multimedi und Grphen WS 2007/2008 Veselin Conev Themensteller: Prof. Dr. Herert Kuchen
Westfälische Wilhelms-Universität Münster Ausreitung Pulic-Key-Verfhren: Diffie-Hellmnn und ElGml im Rhmen des Seminrs Multimedi und Grphen WS 2007/2008 Veselin Conev Themensteller: Prof. Dr. Herert Kuchen
Personal und Finanzen der öffentlich bestimmten Fonds, Einrichtungen, Betriebe und Unternehmen (FEU) in privater Rechtsform im Jahr 2003
 Personl und Finnzen der öffentlich estimmten Fonds, Einrichtungen, Betriee und Unternehmen (FEU) in privter Rechtsform im Jhr 003 Dipl.-Volkswirt Peter Emmerich A Mitte der 980er-Jhre ist eine Zunhme von
Personl und Finnzen der öffentlich estimmten Fonds, Einrichtungen, Betriee und Unternehmen (FEU) in privter Rechtsform im Jhr 003 Dipl.-Volkswirt Peter Emmerich A Mitte der 980er-Jhre ist eine Zunhme von
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012. Sprachen. Grammatiken (Einführung)
 Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Die quadratische Gleichung und die quadratische Funktion
 Die quadratische Gleichung und die quadratische Funktion 1. Lösen einer quadratischen Gleichung Quadratische Gleichungen heißen alle Gleichungen der Form a x x c = 0, woei a,, c als Parameter elieige reelle
Die quadratische Gleichung und die quadratische Funktion 1. Lösen einer quadratischen Gleichung Quadratische Gleichungen heißen alle Gleichungen der Form a x x c = 0, woei a,, c als Parameter elieige reelle
Beispiel-Abiturprüfung. Fach Mathematik
 Beispiel-Abiturprüfung in den Bildungsgängen des Berufskollegs. Leistungskurs Fch Mthemtik Fchbereich Technik mthe_lk_tech_beispielufg09_0085.doc Seite von 9 Konstruktionsmerkmle der Aufgbe rten Aufgbe
Beispiel-Abiturprüfung in den Bildungsgängen des Berufskollegs. Leistungskurs Fch Mthemtik Fchbereich Technik mthe_lk_tech_beispielufg09_0085.doc Seite von 9 Konstruktionsmerkmle der Aufgbe rten Aufgbe
Mathematik. Name, Vorname:
 Kntonsschule Zürich Birch Fchmittelschule Aufnhmeprüfung 2007 Nme, Vornme: Nr.: Zeit: 90 Minuten erlubte Hilfsmittel: Tschenrechner us der Sekundrschule, lso weder progrmmierbr noch grfik- oder lgebrfähig
Kntonsschule Zürich Birch Fchmittelschule Aufnhmeprüfung 2007 Nme, Vornme: Nr.: Zeit: 90 Minuten erlubte Hilfsmittel: Tschenrechner us der Sekundrschule, lso weder progrmmierbr noch grfik- oder lgebrfähig
Karlsruher Institut für Technologie
 Krlsruher Institut für Technologie Lehrstuhl für Progrmmierprdigmen Sprchtechnologie und Compiler WS 2010/2011 Dozent: Prof. Dr.-Ing. G. Snelting Üungsleiter: Mtthis Brun Lösung zu Üungsltt 1 Ausge: 18.04.2012
Krlsruher Institut für Technologie Lehrstuhl für Progrmmierprdigmen Sprchtechnologie und Compiler WS 2010/2011 Dozent: Prof. Dr.-Ing. G. Snelting Üungsleiter: Mtthis Brun Lösung zu Üungsltt 1 Ausge: 18.04.2012
edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit bietet, ihre statistischen Meldungen über das Internet auszufüllen und einzureichen.
 Mnuell edatenq Fremdenverkehrs- und Gstgeweresttistik Einleitung edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit ietet, ihre sttistischen Meldungen üer ds Internet uszufüllen und einzureichen.
Mnuell edatenq Fremdenverkehrs- und Gstgeweresttistik Einleitung edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit ietet, ihre sttistischen Meldungen üer ds Internet uszufüllen und einzureichen.
Seminar zum anorganisch-chemischen Praktikum. Quantitative Analyse. Patrick Schwarz
 Seminr zum norgnisch-chemischen Prktikum Quntittive Anlyse Ptrick Schwrz itertur M. Scheer, J. Wchter Skript zum Prktikum Anorgnische Chemie I, Institut für Anorgnische Chemie der Universität Regensurg
Seminr zum norgnisch-chemischen Prktikum Quntittive Anlyse Ptrick Schwrz itertur M. Scheer, J. Wchter Skript zum Prktikum Anorgnische Chemie I, Institut für Anorgnische Chemie der Universität Regensurg
Ntoneni-be Berechnung der.kennwerte J4helwerY und,,streuung von Funktionen
 FOLGE 18 LENZINGER BERICHTE A UG UST 196J Ntoneni-e Berechnung der.kennwerte J4helwerY und,,streuung von Funktionen Dipl.-Ing. Wilhelm Herzog, Wien Die vorliegende Areit eschäftigt sich mit dem Fll, dß
FOLGE 18 LENZINGER BERICHTE A UG UST 196J Ntoneni-e Berechnung der.kennwerte J4helwerY und,,streuung von Funktionen Dipl.-Ing. Wilhelm Herzog, Wien Die vorliegende Areit eschäftigt sich mit dem Fll, dß
Lösungsskizze zu Übungsblatt Nr. 13
 Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2013) Prof Dr Jens Teuner Leitung der Üungen: Geoffry Bonnin, Sven Kuisch, Moritz Mrtens,
Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2013) Prof Dr Jens Teuner Leitung der Üungen: Geoffry Bonnin, Sven Kuisch, Moritz Mrtens,
Übungsheft Mittlerer Schulabschluss Mathematik
 Ministerium für Bildung und Kultur des Lndes Schleswig-Holstein Zentrle Abschlussrbeit 011 Übungsheft Mittlerer Schulbschluss Mthemtik Korrekturnweisung Impressum Herusgeber Ministerium für Bildung und
Ministerium für Bildung und Kultur des Lndes Schleswig-Holstein Zentrle Abschlussrbeit 011 Übungsheft Mittlerer Schulbschluss Mthemtik Korrekturnweisung Impressum Herusgeber Ministerium für Bildung und
Teil V: Formale Sprachen
 Formle Sprchen Teil V: Formle Sprchen 1. Sprchen und Grmmtiken 2. Endliche Automten Frnz-Josef Rdermcher & Uwe Schöning, Fkultät für Ingeneurwissenschften und Informtik, Universität Ulm, 2008/09 Formle
Formle Sprchen Teil V: Formle Sprchen 1. Sprchen und Grmmtiken 2. Endliche Automten Frnz-Josef Rdermcher & Uwe Schöning, Fkultät für Ingeneurwissenschften und Informtik, Universität Ulm, 2008/09 Formle
7. Portfolioinvestitionen und Wechselkursschwankungen. Literatur. Prof. Dr. Johann Graf Lambsdorff Universität Passau SS 2008
 Prof. Dr. Johnn Grf Lmsdorff Universität Pssu SS 2008 Litertur r IS 0 r 0 P 0 P x MP 7. Portfolioinvestitionen und Wechselkursschnkungen + Z Jrcho, H.-J. und P. Rühmnn (2000) : Monetäre Außenirtschft I.
Prof. Dr. Johnn Grf Lmsdorff Universität Pssu SS 2008 Litertur r IS 0 r 0 P 0 P x MP 7. Portfolioinvestitionen und Wechselkursschnkungen + Z Jrcho, H.-J. und P. Rühmnn (2000) : Monetäre Außenirtschft I.
Inhaltsverzeichnis. Inhaltsverzeichnis... 1 3.Logik... 2. 3.1 Zahlensysteme... 2. 3.2 Grundbegriffe zweiwertiger Logik... 13
 Inhltsverzeichnis Inhltsverzeichnis... 3.Logik... 2 3. Zhlensysteme... 2 3.2 Grundegriffe zweiwertiger Logik... 3 3.3 Rechengesetze für logische Ausdrücke... 9 3.4 Logische Funktionen... 24 3.5 Logische
Inhltsverzeichnis Inhltsverzeichnis... 3.Logik... 2 3. Zhlensysteme... 2 3.2 Grundegriffe zweiwertiger Logik... 3 3.3 Rechengesetze für logische Ausdrücke... 9 3.4 Logische Funktionen... 24 3.5 Logische
17 Doppelbündel-Rekonstruktion mit Semitendinosussehne
 Kpitel 17 143 17 Doppelündel-Rekonstruktion mit Semitendinosussehne Wolf Petersen 17.1 Einleitung Ds vordere Kreuznd (VKB) esteht us 2 funktionellen Bündeln: einem nteromedilen (AM) und einem posterolterlen
Kpitel 17 143 17 Doppelündel-Rekonstruktion mit Semitendinosussehne Wolf Petersen 17.1 Einleitung Ds vordere Kreuznd (VKB) esteht us 2 funktionellen Bündeln: einem nteromedilen (AM) und einem posterolterlen
Lösungsskizze zu Übungsblatt Nr. 13
 Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2014) Prof Dr Jens Teuner Leitung der Üungen: Mrcel Preuß, Sestin Breß, Mrtin Schwitll, Krolin
Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2014) Prof Dr Jens Teuner Leitung der Üungen: Mrcel Preuß, Sestin Breß, Mrtin Schwitll, Krolin
Grundwissen Mathematik 10. Klasse. Eigenschaften Besonderheiten - Beispiele
 Themen Eigenschften Besonderheiten - Beispiele Kreis beknnt us Klsse 8: U Kreis = 2 π r A Kreis = r 2 π Kreissektor Bogenlänge b Flächeninhlt Kreissektor: Die Länge b des Kreisbogens und der Flächeninhlt
Themen Eigenschften Besonderheiten - Beispiele Kreis beknnt us Klsse 8: U Kreis = 2 π r A Kreis = r 2 π Kreissektor Bogenlänge b Flächeninhlt Kreissektor: Die Länge b des Kreisbogens und der Flächeninhlt
3 Module in C. 4 Gültigkeit von Namen. 5 Globale Variablen (2) Gültig im gesamten Programm
 3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
Analysis 2. Mitschrift von www.kuertz.name
 Anlysis 2 Mitschrift von www.kuertz.nme Hinweis: Dies ist kein offizielles Script, sondern nur eine privte Mitschrift. Die Mitschriften sind teweilse unvollständig, flsch oder inktuell, d sie us dem Zeitrum
Anlysis 2 Mitschrift von www.kuertz.nme Hinweis: Dies ist kein offizielles Script, sondern nur eine privte Mitschrift. Die Mitschriften sind teweilse unvollständig, flsch oder inktuell, d sie us dem Zeitrum
Nutzung der Abwärme aus Erneuerbare-Energie-Anlagen
 5 2014 Sonderdruck us BWK 5-2014 Wichtige Kennzhlen und effiziente Plnung für die dezentrle Wärmewende Nutzung der Abwärme us Erneuerbre-Energie-Anlgen Wichtige Kennzhlen und effiziente Plnung für die
5 2014 Sonderdruck us BWK 5-2014 Wichtige Kennzhlen und effiziente Plnung für die dezentrle Wärmewende Nutzung der Abwärme us Erneuerbre-Energie-Anlgen Wichtige Kennzhlen und effiziente Plnung für die
Analysis II. Universität Stuttgart, SS 06 M. Griesemer
 Anlysis II Universität Stuttgrt, SS 06 M. Griesemer Inhltsverzeichnis 9 Ds Riemnnsche Integrl 3 9.1 Definition und Beispiele........................... 3 9.2 Elementre Eigenschften..........................
Anlysis II Universität Stuttgrt, SS 06 M. Griesemer Inhltsverzeichnis 9 Ds Riemnnsche Integrl 3 9.1 Definition und Beispiele........................... 3 9.2 Elementre Eigenschften..........................
Brückenkurs MATHEMATIK
 Brückenkurs MATHEMATIK Professor Dr. rer. nt. Bernd Bumnn Professor Dr. rer. nt. Ulrich Stein Hochschule für Angewndte Wissenschften Hmburg 5. März 008 VO R B E M E R K U N G E N Liebe Studentin, lieber
Brückenkurs MATHEMATIK Professor Dr. rer. nt. Bernd Bumnn Professor Dr. rer. nt. Ulrich Stein Hochschule für Angewndte Wissenschften Hmburg 5. März 008 VO R B E M E R K U N G E N Liebe Studentin, lieber
Schülerkurs. Mathematik > Lineare Algebra > Lineare Gleichungen Lineare Gleichungssysteme > Teil I: Theorie. Michael Buhlmann
 Michel Buhlmnn Schülekus Mthemtik > Linee Alge > Linee Gleichungen Linee Gleichungssysteme > Teil I: Theoie Linee Gleichungen und linee Gleichungssysteme duchziehen den Mthemtikunteicht in llen Schulfomen
Michel Buhlmnn Schülekus Mthemtik > Linee Alge > Linee Gleichungen Linee Gleichungssysteme > Teil I: Theoie Linee Gleichungen und linee Gleichungssysteme duchziehen den Mthemtikunteicht in llen Schulfomen
Teilfachprüfung Mathematik Studiengang: Wirtschaft Neue Diplomprüfungsordnung (NPO)
 Fchhochschule Düsseldorf SS 2007 Teilfchprüfung Mthemtik Studiengng: Wirtschft Neue Diplomprüfungsordnung (NPO) Prüfungsdtum: 29..2007 Prüfer: Prof. Dr. Horst Peters / Dipl. Volkswirt Lothr Schmeink Prüfungsform:
Fchhochschule Düsseldorf SS 2007 Teilfchprüfung Mthemtik Studiengng: Wirtschft Neue Diplomprüfungsordnung (NPO) Prüfungsdtum: 29..2007 Prüfer: Prof. Dr. Horst Peters / Dipl. Volkswirt Lothr Schmeink Prüfungsform:
Vorlesung. Einführung in die mathematische Sprache und naive Mengenlehre
 Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Lösung: a) 1093 1100 b) 1093 1090
 OvTG Guting, Grundwissen Mthemtik 5. Klsse 1. Ntürliche Zhlen Dezimlsystem Mn nennt die Zhlen, die mn zum Zählen verwendet, 10963 = 1 10000+ 0 1000+ 9 100+ 6 10 + 3 1 ntürliche Zhlen. Der Stellenwert der
OvTG Guting, Grundwissen Mthemtik 5. Klsse 1. Ntürliche Zhlen Dezimlsystem Mn nennt die Zhlen, die mn zum Zählen verwendet, 10963 = 1 10000+ 0 1000+ 9 100+ 6 10 + 3 1 ntürliche Zhlen. Der Stellenwert der
Analysis I Probeklausur 2
 WS /2 Mriescu/ Ert Alysis I Probeklusur 2. Aufgbe Die Folge (x ) N sei rekursiv defiiert durch x =, x + = 2+x. () Beweise, dss die Folge (x ) N streg mooto wchsed ist. (b) Beweise, dss (x ) N durch 2 ch
WS /2 Mriescu/ Ert Alysis I Probeklusur 2. Aufgbe Die Folge (x ) N sei rekursiv defiiert durch x =, x + = 2+x. () Beweise, dss die Folge (x ) N streg mooto wchsed ist. (b) Beweise, dss (x ) N durch 2 ch
Funktionen und Mächtigkeiten
 Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Versuchsplanung. Grundlagen. Extrapolieren unzulässig! Beobachtungsbereich!
 Versuchsplnung 22 CRGRAPH www.crgrph.de Grundlgen Die Aufgbe ist es Versuche so zu kombinieren, dss die Zusmmenhänge einer Funktion oder eines Prozesses bestmöglich durch eine spätere Auswertung wiedergegeben
Versuchsplnung 22 CRGRAPH www.crgrph.de Grundlgen Die Aufgbe ist es Versuche so zu kombinieren, dss die Zusmmenhänge einer Funktion oder eines Prozesses bestmöglich durch eine spätere Auswertung wiedergegeben
Elemente der Analysis II: Zusammenfassung der wichtigsten Definitionen und Ergebnisse
 Elemente der Anlysis II: Zusmmenfssung der wichtigsten Definitionen und Ergebnisse J. Wengenroth Dies ist die einzige zugelssene Formelsmmlung, die bei der Klusur benutzt werden drf. Es dürfen Unterstreichungen
Elemente der Anlysis II: Zusmmenfssung der wichtigsten Definitionen und Ergebnisse J. Wengenroth Dies ist die einzige zugelssene Formelsmmlung, die bei der Klusur benutzt werden drf. Es dürfen Unterstreichungen
Einführung in die Schaltalgebra
 Einführung in die chltlger GUNDBEGIFFE: - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 2 ECHENEGELN - - - - - - - - - - - - - - - - - - - - - - - -
Einführung in die chltlger GUNDBEGIFFE: - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 2 ECHENEGELN - - - - - - - - - - - - - - - - - - - - - - - -
7. VEKTORRECHNUNG, ANALYTISCHE GEOMETRIE
 Vektoechnung Anltische Geometie 7. VEKTORRECHNUNG ANALYTISCHE GEOMETRIE 7.1. Vektoen () Definition Schiet mn einen Punkt P 1 im Koodintensstem in eine ndee Lge P so ist diese Schieung duch Ange des Upunktes
Vektoechnung Anltische Geometie 7. VEKTORRECHNUNG ANALYTISCHE GEOMETRIE 7.1. Vektoen () Definition Schiet mn einen Punkt P 1 im Koodintensstem in eine ndee Lge P so ist diese Schieung duch Ange des Upunktes
Canon Nikon Sony. Deutschland 55 45 25. Österreich 40 35 35. Schweiz 30 30 20. Resteuropa 60 40 30 55 45 25 40 35 35 J 30 30 20 60 40 30
 15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
Einführung in Mathcad 14.0 2011 H.
 Einführung in Mthc. H. Glvnik Eitieren von Termen Tet schreiben mit Shift " + + Nvigtion mit Leertste un Cursor + Löschen mit Shift + Entf + + 5 sin( ) + Arten von Gleichheitszeichen Definition eines Terms
Einführung in Mthc. H. Glvnik Eitieren von Termen Tet schreiben mit Shift " + + Nvigtion mit Leertste un Cursor + Löschen mit Shift + Entf + + 5 sin( ) + Arten von Gleichheitszeichen Definition eines Terms
Grundwissen am Ende der Jahrgangsstufe 9. Wahlpflichtfächergruppe II / III
 Grundwissen m Ende der Jhrgngsstufe 9 Whlpflichtfächergruppe II / III Funktionsbegriff Gerdengleichungen ufstellen und zu gegebenen Gleichungen die Grphen der Gerden zeichnen Ssteme linerer Gleichungen
Grundwissen m Ende der Jhrgngsstufe 9 Whlpflichtfächergruppe II / III Funktionsbegriff Gerdengleichungen ufstellen und zu gegebenen Gleichungen die Grphen der Gerden zeichnen Ssteme linerer Gleichungen
Numerische Mathematik I
 Numerische Mthemtik I Dr. Wolfgng Metzler Universität Kssel unter Mitwirkung von Dipl.-Mth. Mrtin Steigemnn Sommersemester 2005 ii c 2005 Dr. Wolfgng Metzler, Fchbereich Mthemtik und Informtik der Universität
Numerische Mthemtik I Dr. Wolfgng Metzler Universität Kssel unter Mitwirkung von Dipl.-Mth. Mrtin Steigemnn Sommersemester 2005 ii c 2005 Dr. Wolfgng Metzler, Fchbereich Mthemtik und Informtik der Universität
Analysis 2. Vorlesungsskript Sommersemester 2014. Bernd Schmidt. Version vom 15. Oktober 2014
 Anlysis 2 Vorlesungsskript Sommersemester 214 Bernd Schmidt Version vom 15. Oktober 214 Institut für Mthemtik, Universität Augsburg, Universitätsstr. 14, 86135 Augsburg, bschmidt@mth.uni-ugsburg.de 1 Inhltsverzeichnis
Anlysis 2 Vorlesungsskript Sommersemester 214 Bernd Schmidt Version vom 15. Oktober 214 Institut für Mthemtik, Universität Augsburg, Universitätsstr. 14, 86135 Augsburg, bschmidt@mth.uni-ugsburg.de 1 Inhltsverzeichnis
Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* aller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt:
 8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
Z R Z R Z R Z = 50. mit. aus a) Z L R. Wie groß ist der Leistungsfaktor cos der gesamten Schaltung?
 Aufge F 99: Drehstromverruher Ein symmetrisher Verruher ist n ds Drehstromnetz ( 0 V, f 50 Hz) ngeshlossen. Die us dem Netz entnommene Wirkleistung eträgt,5 kw ei einem eistungsfktor os 0,7. ) Berehnen
Aufge F 99: Drehstromverruher Ein symmetrisher Verruher ist n ds Drehstromnetz ( 0 V, f 50 Hz) ngeshlossen. Die us dem Netz entnommene Wirkleistung eträgt,5 kw ei einem eistungsfktor os 0,7. ) Berehnen
5.4 CMOS Schaltungen und VLSIDesign
 Kp5.fm Seite 447 Dienstg, 7. Septemer 2 :55 3 5.4 CMOS Schltungen und VLSI Design 447 r u u r id + + A. 5.39: Progrmmierrer Gitterustein 5.4 CMOS Schltungen und VLSIDesign Die Boolesche Alger eginnt mit
Kp5.fm Seite 447 Dienstg, 7. Septemer 2 :55 3 5.4 CMOS Schltungen und VLSI Design 447 r u u r id + + A. 5.39: Progrmmierrer Gitterustein 5.4 CMOS Schltungen und VLSIDesign Die Boolesche Alger eginnt mit
Dental-CT bei Kindern Technische Vorgehensweise und exemplarische Befunde
 Corneli Schröder, Alexnder Schumm Dentl-CT ei Kindern Technische Vorgehensweise und exemplrische Befunde Die Computertomogrphie der Zhnreihen (Dentl-CT) wird ei Kindern und Jugendlichen selten eingesetzt,
Corneli Schröder, Alexnder Schumm Dentl-CT ei Kindern Technische Vorgehensweise und exemplrische Befunde Die Computertomogrphie der Zhnreihen (Dentl-CT) wird ei Kindern und Jugendlichen selten eingesetzt,
12 Schweißnahtberechnung
 225 12 Schweißnherechnung 12 Schweißnherechnung Die Berechnung der ufreenden Spnnungen in Schweißnähen erfolg im Regelfll mi Hilfe der elemenren Gleichungen der esigkeislehre. Auf weierführende Berechnungsverfhren,
225 12 Schweißnherechnung 12 Schweißnherechnung Die Berechnung der ufreenden Spnnungen in Schweißnähen erfolg im Regelfll mi Hilfe der elemenren Gleichungen der esigkeislehre. Auf weierführende Berechnungsverfhren,
Institut für Volkswirtschaftslehre und Wirtschaftspolitik. Prof. Dr. Andreas Thiemer. VWL-Semesterprojekt Nr. 4 WS 2007/2008. Bayessche Lemminge
 Institut für Volkswirtschftslehre und Wirtschftspolitik Prof. Dr. ndres Thiemer VWL-Semesterprojekt Nr. 4 WS 007/008 yessche Lemminge Ein Experiment mit Informtionskskden Unter Mitreit von: Olg eder xel
Institut für Volkswirtschftslehre und Wirtschftspolitik Prof. Dr. ndres Thiemer VWL-Semesterprojekt Nr. 4 WS 007/008 yessche Lemminge Ein Experiment mit Informtionskskden Unter Mitreit von: Olg eder xel
1 GeschäftsdiaGramme. Abbildung 1.1: Übersicht zu unterschiedlichen Grafi ktypen. 2.1.4 Unify objects: graphs e.g. org graphs, networks, and maps
 1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
Mathematik PM Rechenarten
 Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Musterlösung zur Musterprüfung 2 in Mathematik
 Musterlösung zur Musterprüfung in Mthemtik Diese Musterlösung enthält usführliche Lösungen zu llen Aufgben der Musterprüfung in Mthemtik sowie Hinweise zum Selbstlernen. Literturhinweise ) Bosch: Brückenkurs
Musterlösung zur Musterprüfung in Mthemtik Diese Musterlösung enthält usführliche Lösungen zu llen Aufgben der Musterprüfung in Mthemtik sowie Hinweise zum Selbstlernen. Literturhinweise ) Bosch: Brückenkurs
5.3 Dynamisches Sitzen und Stehen
 Dynmisches Sitzen und Stehen 5.3 Dynmisches Sitzen und Stehen Test Bewegen Sie sich eim Sitzen und Stehen kontinuierlich um den Mittelpunkt der senkrechten Oerkörperhltung (S. 39) mit neutrler Wirelsäulenschwingung
Dynmisches Sitzen und Stehen 5.3 Dynmisches Sitzen und Stehen Test Bewegen Sie sich eim Sitzen und Stehen kontinuierlich um den Mittelpunkt der senkrechten Oerkörperhltung (S. 39) mit neutrler Wirelsäulenschwingung
http://www.tfh-wildau.de/gerking/arbeiten.html 2005
 Hllo Ilse, gut nch Huse gekommen? Ich htte Glück, die U-Bhnnschlüsse wren gut. http://www.tfh-wildu.de/gerking/arbeiten.html 5 Sonntgs hbe ich mich dnn erstml mit der Frge beschäftigt, ob Mthemtik und
Hllo Ilse, gut nch Huse gekommen? Ich htte Glück, die U-Bhnnschlüsse wren gut. http://www.tfh-wildu.de/gerking/arbeiten.html 5 Sonntgs hbe ich mich dnn erstml mit der Frge beschäftigt, ob Mthemtik und
1 Räumliche Darstellung in Adobe Illustrator
 Räumliche Drstellung in Adobe Illustrtor 1 1 Räumliche Drstellung in Adobe Illustrtor Dieses Tutoril gibt Tips und Hinweise zur räumlichen Drstellung von einfchen Objekten, insbesondere Bewegungspfeilen.
Räumliche Drstellung in Adobe Illustrtor 1 1 Räumliche Drstellung in Adobe Illustrtor Dieses Tutoril gibt Tips und Hinweise zur räumlichen Drstellung von einfchen Objekten, insbesondere Bewegungspfeilen.
Informationen zu den gemeinsamen Fächern im Zentralabitur 2010 in Berlin und Brandenburg. Nr. 1 Mathematik
 Ministerium für Bildung, Jugend und Sport Sentsverwltung für Bildung, Wissenschft und Forschung Informtionen zu den gemeinsmen Fächern im Zentrlbitur 00 in Berlin und Brndenburg Nr..0.009 Beispielufgben
Ministerium für Bildung, Jugend und Sport Sentsverwltung für Bildung, Wissenschft und Forschung Informtionen zu den gemeinsmen Fächern im Zentrlbitur 00 in Berlin und Brndenburg Nr..0.009 Beispielufgben
Therapiebegleiter Kopfschmerztagebuch
 Vornme & Nchnme Therpieegleiter Kopfschmerztgeuch Liee Ptientin, lieer Ptient, Wie Können sie helfen? Bitte führen Sie regelmäßig euch m esten täglich. Trgen Sie in die Splten die jeweiligen Informtionen
Vornme & Nchnme Therpieegleiter Kopfschmerztgeuch Liee Ptientin, lieer Ptient, Wie Können sie helfen? Bitte führen Sie regelmäßig euch m esten täglich. Trgen Sie in die Splten die jeweiligen Informtionen
Hamburg Kernfach Mathematik Zentralabitur 2013 Erhöhtes Anforderungsniveau Analysis 2
 Hmburg Kernfch Mhemik Zenrlbiur 2013 Erhöhes Anforderungsniveu Anlysis 2 Smrphones Die Mrkeinführung eines neuen Smrphones vom Elekronikherseller PEAR wird ses ufgereg erwre. Zur Modellierung der Enwicklung
Hmburg Kernfch Mhemik Zenrlbiur 2013 Erhöhes Anforderungsniveu Anlysis 2 Smrphones Die Mrkeinführung eines neuen Smrphones vom Elekronikherseller PEAR wird ses ufgereg erwre. Zur Modellierung der Enwicklung
Netzstrategien für Betreiber von Energienetzen Verschmelzung von Technik und Regulierung Teil 4 von 4
 Orgnistion & Mngement Netzstrtegien für Betreier von Energienetzen Verschmelzung von Technik und Regulierung Teil 4 von 4 Quelle: Eisenhns Fotoli.com Der vierte und letzte Teil der Veröffentlichungsreihe
Orgnistion & Mngement Netzstrtegien für Betreier von Energienetzen Verschmelzung von Technik und Regulierung Teil 4 von 4 Quelle: Eisenhns Fotoli.com Der vierte und letzte Teil der Veröffentlichungsreihe
Schriftliche Überprüfung Mathematik. Gymnasien, Klasse 10
 Schriftliche Überprüfung Mthemtik, Klsse 0 Schuljhr 009/00 6. Februr 00 Unterlgen für die Lehrerinnen und Lehrer Diese Unterlgen enthlten: I II III Allgemeine Hinweise zur Arbeit Aufgben Erwrtungshorizonte,
Schriftliche Überprüfung Mthemtik, Klsse 0 Schuljhr 009/00 6. Februr 00 Unterlgen für die Lehrerinnen und Lehrer Diese Unterlgen enthlten: I II III Allgemeine Hinweise zur Arbeit Aufgben Erwrtungshorizonte,
über der Strangbreite 2. Zugleich vermindert Einschlüssen, wodurch sich die Qualität des gegossenen Stahls verbessert.
 S T R N G G I E S S E N Elektromgnetisches remsen veressert die Sthlqulität eim Strnggießen Ds elektromgnetische remsen der Sthlströmung in der Kokille von Strnggießnlgen veressert die Qulität des gegossenen
S T R N G G I E S S E N Elektromgnetisches remsen veressert die Sthlqulität eim Strnggießen Ds elektromgnetische remsen der Sthlströmung in der Kokille von Strnggießnlgen veressert die Qulität des gegossenen
RoDip das neue Tauchverfahren zur Vorbehandlung. und Elektrotauchlackierlinien. Automobilkarosserien
 RoDip ds neue Tuchverfhren zur Vorehndlung und Elektrotuchlckierung von Automoilkrosserien Die Lckierung der Automoilkrosserien ht wichtige Aufgen für den Schutz der Oerfläche, z. B. gegen mechnische und
RoDip ds neue Tuchverfhren zur Vorehndlung und Elektrotuchlckierung von Automoilkrosserien Die Lckierung der Automoilkrosserien ht wichtige Aufgen für den Schutz der Oerfläche, z. B. gegen mechnische und
SLXe-300/Spectrum Whisper TM Pro
 SLXe-300/Spectrum Whisper TM Pro Einfch- und Mehrfchtempertturetrie PIEK-zertifiziert Kompromisslose Leistung zum Schutz der Ldung in llen Umgeungen Uneingeschränkter Zugng rund um die Uhr zu llen städtischen
SLXe-300/Spectrum Whisper TM Pro Einfch- und Mehrfchtempertturetrie PIEK-zertifiziert Kompromisslose Leistung zum Schutz der Ldung in llen Umgeungen Uneingeschränkter Zugng rund um die Uhr zu llen städtischen
Brückenkurs Mathematik
 Prof. Dr.Ing. W. Scheideler Brückenkurs Mthemtik WS 0/ us und überrbeitet von B. Eng. Sevd Hppel und Dipl.Ing. Jun Rojs Prof. Dr.Ing. W. Scheideler Inhltsverzeichnis Brüche, Potenzen und Wurzeln. Brüche..
Prof. Dr.Ing. W. Scheideler Brückenkurs Mthemtik WS 0/ us und überrbeitet von B. Eng. Sevd Hppel und Dipl.Ing. Jun Rojs Prof. Dr.Ing. W. Scheideler Inhltsverzeichnis Brüche, Potenzen und Wurzeln. Brüche..
Domäne und Bereich. Relationen zwischen Mengen/auf einer Menge. Anmerkungen zur Terminologie. r Relationen auf/in einer Menge.
 Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Seminar Quantum Computation - Finite Quanten-Automaten und Quanten-Turingmaschinen
 Seminr Quntum Computtion - Finite Qunten-Automten und Qunten-Turingmschinen Sebstin Scholz sscholz@informtik.tu-cottbus.de Dezember 3. Einleitung Aus der klssischen Berechenbrkeitstheorie sind die odelle
Seminr Quntum Computtion - Finite Qunten-Automten und Qunten-Turingmschinen Sebstin Scholz sscholz@informtik.tu-cottbus.de Dezember 3. Einleitung Aus der klssischen Berechenbrkeitstheorie sind die odelle
Reinigung 146. Reinigen des Hindernissensors. Reinigung der Projektoroberfläche. Reinigen des Projektionsfensters. Warnung. Warnung.
 Reinigung 146 Bei Verschmutzung oder Bildverschlechterung muss der Projektor gereinigt werden. Schlten Sie den Projektor vor der Reinigung us. Reinigung der Projektoroberfläche Reinigen Sie die Projektoroberfläche
Reinigung 146 Bei Verschmutzung oder Bildverschlechterung muss der Projektor gereinigt werden. Schlten Sie den Projektor vor der Reinigung us. Reinigung der Projektoroberfläche Reinigen Sie die Projektoroberfläche
Großübung zu Kräften, Momenten, Äquivalenz und Gleichgewicht
 Großübung u Kräften, omenten, Äuivlen und Gleichgewicht Der Körper Ein mterielles Teilgebiet des Universums beeichnet mn ls Körper. Im llgemeinen sind Körper deformierbr. Sonderfll strrer Körper (odellvorstellung)
Großübung u Kräften, omenten, Äuivlen und Gleichgewicht Der Körper Ein mterielles Teilgebiet des Universums beeichnet mn ls Körper. Im llgemeinen sind Körper deformierbr. Sonderfll strrer Körper (odellvorstellung)
Reader. für den Einsatz in der Wiederholungsphase im Mathematikunterricht der Jahrgangsstufe 11
 Reder für den Einstz in der Wiederholungsphse im Mthemtikunterricht der Jhrgngsstufe Anhng zur schriftlichen Husrbeit zur Zweiten Sttsprüfung für ds Lehrmt n öffentlichen Schulen von Andres Rschke Vorwort
Reder für den Einstz in der Wiederholungsphse im Mthemtikunterricht der Jhrgngsstufe Anhng zur schriftlichen Husrbeit zur Zweiten Sttsprüfung für ds Lehrmt n öffentlichen Schulen von Andres Rschke Vorwort
Einschub: Zahlendarstellung und Codes
 Einschu: Zhlendrstellung und Codes (Unvollständige Drstellung) DST SS23 - Codes und KMAPs P. Fischer, TI, Uni Mnnheim, Seite Binärzhlen N-stellige Binärzhl:... Einzelne Stellen heißen Bits (inry digits)
Einschu: Zhlendrstellung und Codes (Unvollständige Drstellung) DST SS23 - Codes und KMAPs P. Fischer, TI, Uni Mnnheim, Seite Binärzhlen N-stellige Binärzhl:... Einzelne Stellen heißen Bits (inry digits)
www. line21 Kommunikation Daten- und Telefontechnik über 1 Kabel mit 4 Adern. Kein Problem mit line21 natürlich von Rutenbeck!
 Dten- und Telefontechnik üer Kel mit 4 Adern. Kein Prolem mit line ntürlich von Ruteneck! Internet Kom mu ni knt, der; -en, -en [: kirchenlt. communicns (Gen.: communicntis) = Teilnehmer m Aendmhl, zu
Dten- und Telefontechnik üer Kel mit 4 Adern. Kein Prolem mit line ntürlich von Ruteneck! Internet Kom mu ni knt, der; -en, -en [: kirchenlt. communicns (Gen.: communicntis) = Teilnehmer m Aendmhl, zu
Hinweise für den schulischen Umgang mit lese-/rechtschreibschwachen Kindern speziell in der Sekundarstufe I
 Hilfe, Legsthenie Hinweise für den schulischen Umgng mit lese-/rechtschreischwchen Kindern speziell in der Sekundrstufe I 2 Brigitt Amnn, Schulpsychologie Bludenz Annelies Fliri, Lehrerin für spezifische
Hilfe, Legsthenie Hinweise für den schulischen Umgng mit lese-/rechtschreischwchen Kindern speziell in der Sekundrstufe I 2 Brigitt Amnn, Schulpsychologie Bludenz Annelies Fliri, Lehrerin für spezifische
TE- und TM-Moden im Wellenleiter. Bachelorarbeit
 TE- und TM-Moden im Wellenleiter Sebstin Rubitzek 30. September 2014 in Grz Bchelorrbeit betreut von Ao.Univ.-Prof. Mg. Dr.rer.nt. Ulrich Hohenester 1 Inhltsverzeichnis 1 Einleitung 3 1.1 Ws ist ein Wellenleiter?......................
TE- und TM-Moden im Wellenleiter Sebstin Rubitzek 30. September 2014 in Grz Bchelorrbeit betreut von Ao.Univ.-Prof. Mg. Dr.rer.nt. Ulrich Hohenester 1 Inhltsverzeichnis 1 Einleitung 3 1.1 Ws ist ein Wellenleiter?......................
Internationale Ökonomie I Vorlesung 3: Das Riccardo-Modell: Komparative Vorteile und Produktivität (Master)
 Interntionle Ökonomie I Vorlesung 3: Ds Riccrdo-Modell: Komprtive Vorteile und Produktivität (Mster) Dr. Dominik Mltritz Vorlesungsgliederung 1. Einführung 2. Der Welthndel: Ein Überblick 3. Ds Riccrdo-Modell:
Interntionle Ökonomie I Vorlesung 3: Ds Riccrdo-Modell: Komprtive Vorteile und Produktivität (Mster) Dr. Dominik Mltritz Vorlesungsgliederung 1. Einführung 2. Der Welthndel: Ein Überblick 3. Ds Riccrdo-Modell:
7.1 Übersicht und Schleimhautrelief
 7.1 Üersicht und Schleimhutrelief Crist glli Orit Corpus vitreum Skler Mxill Crtilgo septi nslis Vomer Proc. pltinus mxille Cellule ethmoidles Bull ethmoidlis Lmin perpendiculris ossis ethmoidlis N. infroritlis
7.1 Üersicht und Schleimhutrelief Crist glli Orit Corpus vitreum Skler Mxill Crtilgo septi nslis Vomer Proc. pltinus mxille Cellule ethmoidles Bull ethmoidlis Lmin perpendiculris ossis ethmoidlis N. infroritlis
Boole'sche Algebra. Inhaltsübersicht. Binäre Funktionen, Boole'sche Algebren, Schaltalgebra. Verknüpfungen der mathematischen Logik
 Boole'sche Algebr Binäre Funktionen, Boole'sche Algebren, Schltlgebr Inhltsübersicht Verknüpfungen der mthemtischen Logik Boole sche Algebren Grundelemente der Schltlgebr Regeln der Schltlgebr Normlformen
Boole'sche Algebr Binäre Funktionen, Boole'sche Algebren, Schltlgebr Inhltsübersicht Verknüpfungen der mthemtischen Logik Boole sche Algebren Grundelemente der Schltlgebr Regeln der Schltlgebr Normlformen
Matrizen und Determinanten
 Mtrizen und Determinnten Im bschnitt Vektorlgebr Rechenregeln für Vektoren Multipliktion - Sklrprodukt, Vektorprodukt, Mehrfchprodukte wurde in einem Vorgriff bereits eine interessnte mthemtische Konstruktion
Mtrizen und Determinnten Im bschnitt Vektorlgebr Rechenregeln für Vektoren Multipliktion - Sklrprodukt, Vektorprodukt, Mehrfchprodukte wurde in einem Vorgriff bereits eine interessnte mthemtische Konstruktion
Der chinesische Gelehrte Konfuzius wird oft als
 Roert-Wichrd-Pohl-Preis Experimente zum Selstuen Einfche Experimente mit lltäglichen Mterilien und ttrktive Demonstrtionsexperimente ermöglichen es Schülern, die Physik esser zu verstehen Hns-Jochim Wilke
Roert-Wichrd-Pohl-Preis Experimente zum Selstuen Einfche Experimente mit lltäglichen Mterilien und ttrktive Demonstrtionsexperimente ermöglichen es Schülern, die Physik esser zu verstehen Hns-Jochim Wilke
QualitŠtskriterien fÿr die betriebliche Gesundheitsfšrderung
 WH IN U O Gesunde Mitreiter in gesunden Unternehmen Erfolgreiche Prxis etrielicher Gesundheitsfšrderung in Europ QulitŠtskriterien fÿr die etrieliche Gesundheitsfšrderung Vorwort Seit 1996 existiert ds
WH IN U O Gesunde Mitreiter in gesunden Unternehmen Erfolgreiche Prxis etrielicher Gesundheitsfšrderung in Europ QulitŠtskriterien fÿr die etrieliche Gesundheitsfšrderung Vorwort Seit 1996 existiert ds
